高考阶段滚动检测3
2022年高考生物一轮单元双测卷第三单元光合作用和细胞呼吸综合(A卷新题练)通用考试版.docx

2022年高考生物一轮复习单元滚动双测卷(通用版)第三单元光合作用和细胞呼吸综合A卷新题基础练一、选择题:本题共20小题,每小题2分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(2021-陕西宝鸡市模拟)溶酶体内pH与细胞质基质中的pH不同,溶酶体内pH<5,这与溶酶体膜上的质子泵(见下图)有关。
下列相关叙述正确的是()a侧A.a侧为细胞质基质,其pH大于4. 6B.细胞中合成的水解酶通过主动运输进入溶酶体C.溶酶体膜上仅有质子泵载体蛋白而无其他载体蛋白D.当细胞程序性死亡时,溶酶体可合成多种水解酶2.(2021-四川南充市•阊中中学模拟)下列有关实验的叙述,正确的是()A.“观察洋葱表皮细胞的质壁分离”活动中,能观察到水分子的双向运动B.“观察叶绿体”活动中,为便于观察到细胞质的流动将叶绿体作为标志C.“检测生物组织中的蛋白质”时先加入2 mL双缩腿试剂A,再加入等量的双缩腿试剂BD.“观察线粒体”活动中,配置健那绿染液时,可将0.5g健那绿溶解于50mL蒸馅水中,加温到30-40笆, 使其充分溶解3.(2021-昆明市•云南师大附中模拟)缴氨霉素是原核生物产生的一种由12个氨基酸组成的环状多肽,其作用于动物细胞后可提高K+顺浓度梯度运输的速率,还会抑制线粒体中ATP的合成,下列说法不正确的是()A.缴氨霉素中含有12个肽键B.缀氨霉素可抑制K+的主动运输C.缴氨霉素可促进K+的协助扩散D.控制缴氨霉素合成的基因位于染色体上4.(2021-浙江模拟)洋葱是常用的生物学实验材料。
下列有关实验中不能达到预期目的的是()A. 洋葱表皮细胞质壁分离过程中,吸水能力逐渐增强B. 用紫色洋葱鳞片叶外表皮观察植物细胞的质壁分离不需染色C. 用高倍镜观察叶绿体形态,需保持洋葱内表皮细胞的活性D. 用蚕作为实验材料,观察组织中的油脂分布情况5. (2021•天津北辰区•高三一模)很多实验必需先制作装片,然后在显微镜下观察。
高考化学一轮大题冲关滚动练【3】电化学原理综合应用题ppt课件

解析 + 2e
-
其反应原理为阳极:Fe-2e-===Fe2+、阴极:2H+
+ 2- 2+ 3+ 3+ ===H2↑, Cr2O7 + 6Fe + 14H ===2Cr + 6Fe
+ 7H2O , Cr3 + + 3OH - ===Cr(OH)3↓ , Fe3 + + 3OH - ===Fe(OH)3↓。 16.8 g 1 (1) -1·=0.05 mol。 56 g· mol 6 (2)图 1 中,Cr 作负极,Cu 作正极,Cr 比铜活泼。图 2
- 3+ 3+ Cr2O 2 发生反应,生成的 Fe 和 Cr 在阴极区与 7
OH-结合生成 Fe(OH)3 和 Cr(OH)3 沉淀除去。 (1) 若阳极铁质量减少 16.8 g ,则理论上被还原的
2- Cr2O7 的物质的量为________mol。
大题冲关滚动练之三——电化学原理综合应用题
1 2 3 4 5 6Fra bibliotek(2)在下图装置中,观察到图 1 装置铜电极上产生大量的 无色气泡,而在图 2 装置中当开关 K 断开时,铬电极无 现象,K 闭合时,铬电极上产生大量无色气体,并变成 红棕色气体。根据上述现象试推测金属铬的两个重要化 学性质_________________、__________________。
大题冲关滚动练之三——电化学原理综合应用题
大题冲关滚动练之三——电化学原理综合应用题
1 2 3 4 5 6
(2)芒硝化学式为 Na2SO4· 10H2O,无色晶体,易溶于水, 是一种分布很广泛的硫酸盐矿物。该小组同学设想,如 果模拟工业上离子交换膜法制烧碱的方法,用上图 2 所 示装置电解硫酸钠溶液来制取氢气、氧气、硫酸和氢氧 化钠,无论从节省能源还是从提高原料的利用率而言都 更加符合绿色化学理念。 ①该电解槽的阳极反应式为__________________。此时 通过阴离子交换膜的离子数 __________( 填“大于”、 “小于”或“等于”)通过阳离子交换膜的离子数。
单元滚动检测卷 高考数学(理)

高三单元滚动检测卷·数学考生注意:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共4页。
2.答卷前,考生务必用蓝、黑色字迹的钢笔或圆珠笔将自己的姓名、班级、学号填写在相应位置上。
3.本次考试时间120分钟,满分150分。
单元检测一集合与常用逻辑用语第Ⅰ卷一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.(2015·重庆)已知集合A={1,2,3},B={2,3},则()A.A=B B.A∩B=∅C.A B D.B A2.已知集合A={x|x2-2x-3≥0},B={x|-2≤x<2},则A∩B等于()A.[-2,-1]B.[-1,1]C.[-1,2) D.[1,2)3.(2015·长春外国语学校高三期中)已知集合A={-1,0,1,2},B={x|1≤2x<4},则A∩B等于()A.{-1,0,1} B.{0,1,2}C.{0,1} D.{1,2}4.(2015·宜昌调研)下列说法中,正确的是()A.命题“若am2<bm2,则a<b”的逆命题是真命题B.命题“存在x0∈R,x20-x0>0”的否定是“对任意的x∈R,x2-x≤0”C.命题“p或q”为真命题,则命题p和命题q均为真命题D.已知x∈R,则“x>1”是“x>2”的充分不必要条件5.(2015·吉林三模)已知p:x>1或x<-3,q:x>a,若q是p的充分不必要条件,则a的取值范围是()A.[1,+∞) B.(-∞,1]C.[-3,+∞) D.(-∞,-3]6.已知命题p:存在x0∈(-∞,0),2x0<3x0,命题q:任意x∈(0,1),log2x<0,则下列命题为真命题的是()A .p 且qB .p 或(綈q )C .(綈p )且qD .p 且(綈q )7.(2015·赣州市十二县市期中)已知p :x ≥k ,q :3x +1<1,如果p 是q 的充分不必要条件,则实数k 的取值范围是( )A .[2,+∞)B .(2,+∞)C .[1,+∞)D .(-∞,-1]8.已知两个集合A ={x |y =ln(-x 2+x +2)},B ={x |2x +1e -x≤0},则A ∩B 等于( ) A .[12,2) B .(-1,-12] C .(-1,e) D .(2,e)9.(2015·大连二模)已知集合A ={(x ,y )|x (x -1)+y (y -1)≤r },集合B ={(x ,y )|x 2+y 2≤r 2},若A ⊆B ,则实数r 可以取的一个值是( ) A.2+1 B. 3 C .2 D .1+2210.(2016·黄冈中学月考)下列四种说法中,①命题“存在x ∈R ,x 2-x >0”的否定是“对于任意x ∈R ,x 2-x <0”;②命题“p 且q 为真”是“p 或q 为真”的必要不充分条件;③已知幂函数f (x )=x α的图像经过点(2,22),则f (4)的值等于12; ④已知向量a =(3,-4),b =(2,1),则向量a 在向量b 方向上的射影是25. 说法正确的个数是( )A .1B .2C .3D .411.(2015·宜春模拟)设P ,Q 为两个非空实数集合,定义集合P *Q ={z |z =a ÷b ,a ∈P ,b ∈Q },若P ={-1,0,1},Q ={-2,2},则集合P *Q 中元素的个数是( )A .2B .3C .4D .512.若p :a ∈R ,|a |<1,q :关于x 的二次方程x 2+(a +1)x +a -2=0的一个根大于零,另一个根小于零,则p 是q 的( )A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件第Ⅱ卷二、填空题(本大题共4小题,每小题5分,共20分.把答案填在题中横线上)13.设集合A ={5,log 2(a +3)},B ={a ,b },若A ∩B ={2},则A ∪B =________________.14.给定两个命题,命题p :对任意实数x 都有ax 2>-ax -1恒成立,命题q :关于x 的方程x 2-x +a =0有实数根.若“p 或q ”为真命题,“p 且q ”为假命题,则实数a 的取值范围是________________.15.(2015·石家庄二模)已知命题p :x 2-3x -4≤0;命题q :x 2-6x +9-m 2≤0,若綈q 是綈 p 的充分不必要条件,则实数m 的取值范围是__________________.16.(2015·河南顶级名校入学定位考试)已知有限集A ={a 1,a 2,a 3,…,a n }(n ≥2,n ∈N ).如果A 中元素a i (i =1,2,3,…,n )满足a 1a 2…a n =a 1+a 2+…+a n ,就称A 为“复活集”,给出下列结论:①集合⎩⎨⎧⎭⎬⎫-1+52,-1-52是“复活集”;②若a 1,a 2∈R ,且{a 1,a 2}是“复活集”,则a 1a 2>4;③若a 1,a 2∈N +,则{a 1,a 2}不可能是“复活集”;④若a i ∈N ,则“复活集”A 有且只有一个,且n =3.其中正确的结论有________.(填上你认为正确的所有结论的序号)三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)17.(10分)已知集合A ={x |x 2-5x +6=0},B ={x |mx +1=0},且A ∪B =A ,求实数m 的值组成的集合.18.(12分)已知集合A ={y |y =x 2-32x +1,x ∈[34,2]},B ={x |x +m 2≥1}.若A ⊆B ,求实数m 的取值范围.19.(12分)(2015·宿迁剑桥国际学校上学期期中)已知集合A ={x |y =1-2x +1x +1},B ={x |[x -(a +1)][x -(a +4)]<0}.(1)若A ∩B =A ,求a 的取值范围;(2)若A ∩B ≠∅,求a 的取值范围.20.(12分)设函数f (x )=lg(x 2-x -2)的定义域为集合A ,函数g (x )=3-|x |的定义域为集合B .(1)求A ∩B ;(2)若C ={x |m -1<x <2m +1},C ⊆B ,求实数m 的取值范围.21.(12分)(2015·潍坊高三质检)已知集合A ={x |x 2-3x +2≤0},集合B ={y |y =x 2-2x +a },集合C ={x |x 2-ax -4≤0}.命题p :A ∩B ≠∅,命题q :A ⊆C .(1)若命题p 为假命题,求实数a 的取值范围;(2)若命题p 且q 为真命题,求实数a 的取值范围.22.(12分)(2015·湖北省教学合作联考)已知集合U =R ,集合A ={x |(x -2)(x -3)<0},函数y=lg x -(a 2+2)a -x的定义域为集合B . (1)若a =12,求集合A ∩(∁U B ); (2)命题p :x ∈A ,命题q :x ∈B ,若q 是p 的必要条件,求实数a 的取值范围.答案解析1.D [由于2∈A,2∈B,3∈A,3∈B,1∈A,1∉B ,故A ,B ,C 均错,D 是正确的,选D.]2.A [A ={x |x ≤-1或x ≥3},故A ∩B =[-2,-1],选A.]3.C [B ={x |1≤2x <4}={x |0≤x <2},则A ∩B ={0,1},故选C.]4.B [对于A ,当m =0时,逆命题不正确;对于B ,由特称命题与全称命题的关系知显然正确;命题“p 或q ”为真命题,则命题p 和命题q 中至少有一个是真命题,不一定全为真命题,故C 不正确;“x >1”是“x >2”的必要不充分条件,D 不正确.选B.]5.A [设P ={x |x >1或x <-3},Q ={x |x >a },因为q 是p 的充分不必要条件,所以Q P ,因此a ≥1,故选A.]6.C [命题p :存在x 0∈(-∞,0),2x 0<3x 0为假命题,命题q :任意x ∈(0,1),log 2x <0为真命题,所以(綈p )且q 为真命题.]7.B [∵3x +1<1,∴3x +1-1=2-x x +1<0, 即(x -2)(x +1)>0,∴x >2或x <-1,∵p 是q 的充分不必要条件,∴k >2,故选B.]8.B [由A 中的函数y =ln(-x 2+x +2),得到-x 2+x +2>0,即x 2-x -2<0, 整理得:(x -2)(x +1)<0,即-1<x <2,∴A =(-1,2),由B 中的不等式变形得:(2x +1)(e -x )≤0,且e -x ≠0,即(2x +1)(x -e)≥0,且x ≠e ,解得:x ≤-12或x >e , 即B =(-∞,-12]∪(e ,+∞), 则A ∩B =(-1,-12].故选B.] 9.A [A ={(x ,y )|(x -12)2+(y -12)2≤r +12},B ={(x ,y )|x 2+y 2≤r 2},由于A ,B 都表示圆上及圆内的点的坐标,要满足A ⊆B ,则两圆内切或内含.故圆心距满足22≤|r |-r +12,将四个选项中的数分别代入,可知只有A 选项满足,故选A.]10.A [①命题“存在x ∈R ,x 2-x >0”的否定是“对于任意x ∈R ,x 2-x ≤0”,故①不正确;②命题“p 且q 为真”,则命题p 、q 均为真,所以“p 或q 为真”.反之“p 或q 为真”,则p 、q 不见得都真,所以不一定有“p 且q 为真”,所以命题“p 且q 为真”是“p 或q 为真”的充分不必要条件,故命题②不正确;③由幂函数f (x )=x α的图像经过点(2,22),所以2α=22,所以α=-12,所以幂函数为f (x )=x -12, 所以f (4)=4-12=12,所以命题③正确; ④向量a 在向量b 方向上的射影是|a |cos θ=a ·b |b |=25=255,θ是a 和b 的夹角,故④错误.故选A.]11.B [当a =0时,无论b 取何值,z =a ÷b =0;当a =-1,b =-2时,z =(-1)÷(-2)=12; 当a =-1,b =2时,z =(-1)÷2=-12; 当a =1,b =-2时,z =1÷(-2)=-12; 当a =1,b =2时,z =1÷2=12. 故P *Q ={0,-12,12},该集合中共有3个元素.] 12.A [p :a ∈R ,|a |<1⇔-1<a <1⇒a -2<0,可知满足q 的方程有两根,且两根异号,条件充分;条件不必要,如a =1时,方程的一个根大于零,另一个根小于零.也可以把命题q 中所有满足条件的a 的范围求出来,再进行分析判断,实际上一元二次方程两根异号的充要条件是两根之积小于0,对于本题就是a -2<0,即a <2.]13.{1,2,5}解析 由A ∩B ={2}可得:log 2(a +3)=2,∴a =1,∴b =2,∴A ∪B ={1,2,5}.14.(-∞,0)∪(14,4) 解析 若p 为真命题,则a =0或⎩⎪⎨⎪⎧a >0,a 2-4a <0,即0≤a <4;若q 为真命题,则(-1)2-4a ≥0,即a ≤14. 因为“p 或q ”为真命题,“p 且q ”为假命题,所以p ,q 中有且仅有一个为真命题.若p 真q 假,则14<a <4;若p 假q 真,则a <0. 综上,实数a 的取值范围为(-∞,0)∪(14,4). 15.(-∞,-4]∪[4,+∞)解析 綈q 是綈p 的充分不必要条件,等价于p 是q 的充分不必要条件.由题意可得p : -1≤x ≤4,q :(x -3+m )(x -3-m )≤0.当m =0时,显然不符合题意;当m >0时,有⎩⎪⎨⎪⎧ 3-m <-1,3+m ≥4或⎩⎪⎨⎪⎧ 3-m ≤-1,3+m >4⇒m ≥4; 当m <0时,有⎩⎪⎨⎪⎧ 3+m <-1,3-m ≥4或⎩⎪⎨⎪⎧3+m ≤-1,3-m >4 ⇒m ≤-4.综上,m 的取值范围是(-∞,-4]∪[4,+∞).16.①③④解析 ∵-1+52×-1-52=-1+52+-1-52=-1,故①是正确的.②不妨设a 1+a 2=a 1a 2=t ,则由一元二次方程根与系数的关系,知a 1,a 2是一元二次方程x 2-tx +t =0的两个根,由Δ>0,可得t <0或t >4,故②错.③不妨设A 中a 1<a 2<a 3<…<a n ,由a 1a 2…a n =a 1+a 2+…+a n <na n ,得a 1a 2…a n -1<n ,当n =2时,即有a 1<2,∴a 1=1,于是1+a 2=a 2,无解,即不存在满足条件的“复活集”A ,故③正确.当n =3时,a 1a 2<3,故只能a 1=1,a 2=2,解得a 3=3,于是“复活集”A 只有一个,为{1,2,3}.当n ≥4时,由a 1a 2…a n -1≥1×2×3×…×(n -1),得n >1×2×3×…×(n -1),也就是说“复活集”A 存在的必要条件是n >1×2×3×…×(n -1),事实上,1×2×3×…×(n -1)≥(n -1)(n -2)=n 2-3n +2=(n -2)2-2+n >n ,矛盾,∴当n ≥4时不存在“复活集”A ,故④正确.17.解 A ={x |x 2-5x +6=0}={2,3},∵A ∪B =A ,∴B ⊆A .①当m =0时,B =∅,B ⊆A ,故m =0;②当m ≠0时,由mx +1=0,得x =-1m. ∵B ⊆A ,∴-1m =2或-1m =3,得m =-12或m =-13. ∴实数m 的值组成的集合为{0,-12,-13}. 18.解 因为y =(x -34)2+716,x ∈[34,2],所以y ∈[716,2].又因为A ⊆B ,所以1-m 2≤716.解得m ≥34或m ≤-34. 19.解 若x ∈A ,则1-2x +1x +1≥0,即-x x +1≥0,所以⎩⎪⎨⎪⎧x (x +1)≤0,x +1≠0,解得-1<x ≤0,所以A ={x |-1<x ≤0};若x ∈B ,则[x -(a +1)]·[x -(a +4)]<0,解得a +1<x <a +4,所以B ={x |a +1<x <a +4}.(1)若A ∩B =A ,则A ⊆B ,所以⎩⎪⎨⎪⎧a +1≤-1,a +4>0,解得-4<a ≤-2. (2)若A ∩B =∅,则a +4≤-1或a +1≥0,即a ≤-5或a ≥-1,所以若A ∩B ≠∅,则a 的取值范围是(-5,-1).20.解 (1)要使函数f (x )有意义,则x 2-x -2>0,解得x >2或x <-1,即A ={x |x >2或x <-1}.要使g (x )有意义,则3-|x |≥0,解得-3≤x ≤3,即B ={x |-3≤x ≤3},∴A ∩B ={x |x >2或x <-1}∩{x |-3≤x ≤3}={x |-3≤x <-1或2<x ≤3}.(2)若C =∅,则m ≤-2,C ⊆B 恒成立;若m >-2,要使C ⊆B 成立,则⎩⎪⎨⎪⎧ m >-2,m -1≥-3,2m +1≤3,解得-2<m ≤1. 综上,m ≤1.即实数m 的取值范围是(-∞,1].21.解 ∵A ={x |x 2-3x +2≤0}={x |1≤x ≤2},y =x 2-2x +a =(x -1)2+a -1≥a -1,∴B ={y |y ≥a -1},C ={x |x 2-ax -4≤0},(1)由命题p 为假命题可得A ∩B =∅,∴a -1>2,∴a >3.(2)∵命题p 且q 为真命题,∴p ,q 都为真命题,即A ∩B ≠∅且A ⊆C .∴⎩⎪⎨⎪⎧ a -1≤2,1-a -4≤0,4-2a -4≤0,解得0≤a ≤3.22.解 (1)因为集合A ={x |2<x <3},又a =12, 所以函数y =lg x -(a 2+2)a -x =lg x -9412-x , 由x -9412-x >0,可得集合B ={x |12<x <94}, ∁U B ={x |x ≤12或x ≥94}, 故A ∩(∁U B )={x |94≤x <3}. (2)因为q 是p 的必要条件等价于p 是q 的充分条件,即A ⊆B , 由A ={x |2<x <3},而集合B 应满足x -(a 2+2)a -x>0, 因为a 2+2-a =(a -12)2+74>0, 故B ={x |a <x <a 2+2},依题意就有⎩⎪⎨⎪⎧a ≤2,a 2+2≥3,即a ≤-1或1≤a ≤2, 所以实数a 的取值范围是(-∞,-1]∪[1,2].。
重庆市2024届高三第三次联合诊断检测数学试卷(解析版)

2024年重庆市高考数学三诊试卷一、单选题:本题共8小题,每小题5分,共40分.在每小题给出的选项中,只有一项是符合题目要求的.1.已知集合2{|10}A x x =-=,集合{}1,1,3B a a =+-,若A B ⊆,则=a ()A.1-B.0C.1D.2【答案】B 【解析】【分析】利用子集的概念求解.【详解】集合{}2{|10}1,1A x x =-==-,集合{}1,1,3B a a =+-,若A B ⊆,又11a a +>-,所以1111a a +=⎧⎨-=-⎩,解得0.a =故选:B2.设复数z 满足2i 1z z -=,则z 的虚部为()A.13B.13-C.3D.3-【答案】A 【解析】【分析】设复数i(,R)z a b a b =+∈,根据题意,列出方程,结合复数相等,求得b 的值,即可求解.【详解】设复数i(,R)z a b a b =+∈,因为复数z 满足2i 1z z -=,可得()22i i i 1a b a b +--=,即()22i 1a b b a -+-=,则21a b -=,20b a -=,解得13b =,所以复数z 的虚部为13.故选:A.3.已知一种服装的销售量(y 单位:百件)与第x 周的一组相关数据统计如表所示,若两变量x ,y 的经验回归方程为ˆ 1.37.9yx =-+,则=a ()x 12345y66a31A.2B.3C.4D.5【答案】C 【解析】【分析】根据统计图表中的数据,求得样本中心,代入回归直线方程,即可求解.【详解】解:由统计图表中的数据,可得()11234535x =⨯++++=,()116663155a y a +=⨯++++=,即样本中心为16(3,5a +,因为两变量,x y 的经验回归方程为ˆ 1.37.9yx =-+,则161.337.95a+-⨯+=,解得 4.a =故选:C.4.若圆锥的母线长为2,且母线与底面所成角为π4,则该圆锥的侧面积为()A.B.2πC. D.4π【答案】C 【解析】【分析】根据题意,求得圆锥底面圆的半径,结合圆锥的侧面积公式,即可求解.【详解】圆锥的母线长为2,母线与底面所成角为π4,所以底面圆的半径为2sin π4r ==,所以该圆锥的侧面积为π2S ==侧.故选:C5.重庆某高校去年招收学生来自成渝地区2400人,除成渝外的西部地区2000人,中部地区1400人,东部地区1800人,港澳台地区400人.学校为了解学生的饮食习惯,拟选取40人作样本调研,为保证调研结果的代表性,则从该校去年招收的成渝地区学生中不同的抽样结果种数为()A.402400C B.242400C C.122400C D.102400C 【答案】C 【解析】【分析】根据分层抽样的性质计算即可。
滚动检测(三)

滚动检测(三)(时间:120分钟满分:150分)【选题明细表】一、选择题(每小题5分,共60分)1.(2012年高考辽宁卷)已知全集U={0,1,2,3,4,5,6,7,8,9},集合A={0,1,3,5,8},集合B={2,4,5,6,8},则(∁U A)∩(∁U B)等于( B ) (A){5,8} (B){7,9}(C){0,1,3} (D){2,4,6}解析:∁U A={2,4,6,7,9},∁U B={0,1,3,7,9},则(∁U A)∩(∁U B)={7,9}.故选B.2.(2013徐州模拟)命题“若f(x)是奇函数,则f(-x)是奇函数”的否命题是( B )(A)若f(x)是偶函数,则f(-x)是偶函数(B)若f(x)不是奇函数,则f(-x)不是奇函数(C)若f(-x)是奇函数,则f(x)是奇函数(D)若f(-x)不是奇函数,则f(x)不是奇函数解析:否命题既否定题设又否定结论.故选B.3.若已知函数f(x)=则f(f(1))+f log3的值是( A )(A)7 (B)2 (C)5 (D)3解析:∵f(1)=log21=0,∴f(f(1))=f(0)=90+1=2.又log3<0,∴f log3=+1=5,∴f(f(1))+f log3=2+5=7.故选A.4.(2013皖南八校模拟)“m=”是“直线(m+2)x+3my+1=0与直线(m-2)x+(m+2)y-3=0相互垂直”的( B )(A)充分必要条件(B)充分而不必要条件(C)必要而不充分条件(D)既不充分也不必要条件解析:由两直线垂直的充要条件知(m+2)²(m-2)+3m(m+2)=0,解得m=-2或,∴m=时,两直线垂直,反之不成立.故选B.5.下列函数中,最小正周期为π,且图象关于直线x=对称的函数是( B )(A)y=2sin 2x+ (B)y=2sin 2x-(C)y=2sin + (D)y=2sin 2x-解析:∵函数最小正周期为π, ∴ω=2.又图象关于x=对称,∴f =±2,代入验证知选B.6.已知平面向量a,b 满足|a|=3,|b|=2,a 与b 的夹角为120°,若(a+mb)⊥a,则实数m 的值为( D ) (A)1 (B) (C)2 (D)3 解析:∵(a+mb)⊥a, ∴(a+mb)²a=0,∴|a|2+m ²|a|²|b|cos 120°=0,即9+m ²3³2³-=0, ∴m=3.故选D.7.(2013山东实验中学诊断)设S n 为等差数列{a n }的前n 项和,已知a 1+a 3+a 11=6,那么S 9等于( C ) (A)2 (B)8 (C)18 (D)36解析:设等差数列的公差为d,则由a1+a3+a11=6,可得3a1+12d=6,∴a1+4d=2=a5.∴S9==9a5=9³2=18.故选C.8.(2013年高考天津卷)设变量x,y满足约束条件则目标函数z=y-2x的最小值为( A )(A)-7 (B)-4 (C)1 (D)2解析:如图阴影部分为不等式组表示的区域,平移直线y-2x=0,当直线过B(5,3)时即x=5,y=3时,z=y-2x最小,z min=3-2³5=-7.故选A.9.(2013山东省烟台市高三期末测试)已知第一象限的点(a,b)在直线2x+3y-1=0上,则+的最小值为( B )(A)24 (B)25 (C)26 (D)27解析:因为第一象限的点(a,b)在直线2x+3y-1=0上,所以有2a+3b-1=0,a>0,b>0,即2a+3b=1,所以+=+(2a+3b)=4+9++≥13+2=25,当且仅当=,即a=b=取等号,所以+的最小值为25.故选B.10.(2013豫北六校联考)已知△ABC中角A,B,C的对边分别为a,b,c,面积为,b=,B=,则△ABC的周长等于( A )(A)3+(B)3(C)2+(D)解析:由余弦定理得b2=a2+c2-2accos B,即a2+c2-ac=3.又△ABC的面积为ac²sin =,即ac=2,所以a2+c2+2ac=9,所以a+c=3,即a+c+b=3+.故选A.11.已知{a n}是首项为1的等比数列,若S n是{a n}的前n项和,且28S3=S6,则数列的前4项和为( C )(A)或4 (B)或4(C)(D)解析:设数列{a n}的公比为q.当q=1时,由a1=1,得28S3=28³3=84.而S6=6,两者不相等,因此不合题意.当q≠1时,由28S3=S6及首项为1,得=.解得q=3.所以数列{a n}的通项公式为a n=3n-1.所以数列的前4项和为1+++=.故选C.12.(2012年高考湖南卷)设定义在R上的函数f(x)是最小正周期为2π的偶函数,f′(x)是f(x)的导函数,当x∈[0,π]时,0<f(x)<1;当x∈(0,π)且x≠时,x-f′(x)>0.则函数y=f(x)-sin x在[-2π,2π]上的零点个数为( B )(A)2 (B)4 (C)5 (D)8解析:由题意当<x<π时,f′(x)>0,∴f(x)在,π上是增函数.当0<x<时,f′(x)<0,∴f(x)在0,上是减函数.设π≤x≤2π,则0≤2π-x≤π.由f(x)是以2π为最小正周期的偶函数知f(2π-x)=f(x).故π≤x≤2π时,0<f(x)<1.依题意作出草图(略)可知,y1=f(x)与y2=sin x在[-2π,2π]上有四个交点.故选B.二、填空题(每小题5分,共20分)13.(2013温州适应性测试)在平行四边形ABCD中,已知AB=2,AD=1,∠BAD=60°,E为CD的中点,则²= .解析:²=+²(+)=+²(-)=-²-=1-³1³2cos 60°-³4=-.答案:-14.已知等比数列{a n}中,a1=3,a4=81,若数列{b n}满足b n=log3a n,则数列的前n项和S n= .解析:设等比数列{a n}的公比为q,则=q3=27,解得q=3.所以a n=a1q n-1=3³3n-1=3n,故b n=log3a n=n,所以==-.则S n=1-+-+…+-=1-=.答案:15.(2013山东省烟台市莱州一中高三质检)若实数x,y满足如果目标函数z=x-y的最小值为-2,则实数m= .解析:先做出表示的平面区域,由z=x-y得y=x-z可知,直线的截距最大时,z取得最小值,此时直线方程为y=x-(-2)=x+2,作出直线y=x+2,交y=2x-1于A点,如图所示,由图可知,目标函数在该点取得最小值,所以直线x+y=m也过A点,由得代入x+y=m得,m=3+5=8.答案:816.(2013山东省青岛市高三期中测试)已知x>0,y>0,lg 2x+lg 8y=lg2,则+的最小值是.解析:由x>0,y>0,lg 2x+lg 8y=lg 2,得lg (2x8y)=lg 2,即2x+3y=2,所以x+3y=1,所以+=+(x+3y)=2++≥2+2=4,当且仅当=,即x2=9y2时取等号,所以最小值为4.答案:4三、解答题(共70分)17.(本小题满分10分)(2013山东省实验中学高三第三次诊断)记f(x)=ax2-bx+c,若不等式f(x)>0的解集为(1,3),试解关于t的不等式f(|t|+8)<f(2+t2). 解:由题意知f(x)=a(x-1)(x-3),且a<0,故二次函数在区间[2,+∞)上是减函数.又因为8+|t|≥8,2+t2≥2,故由二次函数的单调性知不等式f(|t|+8)<f(2+t2),等价于8+|t|>2+t2即|t|2-|t|-6<0,故|t|<3即不等式的解为:-3<t<3.18.(本小题满分12分)已知向量a=(1,sin x),b=cos2x+,sin x,函数f(x)=a²b-cos 2x.(1)求函数f(x)的解析式及其单调递增区间;(2)当x∈0,时,求函数f(x)的值域.解:(1)f(x)=a²b-cos 2x=cos2x++sin2x-cos 2x=cos 2xcos -sin2xsin +-cos 2x=-sin2x+.令2kπ+≤2x+≤2kπ+(k∈Z)得:kπ+≤x≤kπ+(k∈Z),∴单调递增区间为kπ+,kπ+,k∈Z.(2)当x∈0,时,则2x+∈,,sin2x+∈,1,故f(x)的值域是-,0.19.(本小题满分12分)(2013福州模拟)等比数列{a n}中,a1=2,a4=16.(1)求数列{a n}的通项公式;(2)若a3,a5分别为等差数列{b n}的第4项和第16项,求数列{b n}的前n项和S n.解:(1)设数列{a n}的公比为q,由已知得16=2q3,解得q=2.所以a n=a1q n-1=2³2n-1=2n.(2)由(1)得a3=8,a5=32,则b4=8,b16=32.设{b n}的公差为d,则有解得则数列{b n}的前n项和S n=nb1+d=2n+³2=n2+n.20.(本小题满分12分)某厂生产某种产品的年固定成本为250万元,每生产x千件,需另投入成本为C(x).当年产量不足80千件时,C(x)=x2+10x(万元);当年产量不小于80千件时,C(x)=51x+-1450(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.(1)写出年利润L(万元)关于年产量x(千件)的函数解析式;(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大? 解:(1)当0<x<80时,L(x)=0.05³1000x-x2-10x-250=-x2+40x-250;当x≥80时,L(x)=0.05³1000x-51x-+1450-250=1200-x+.∴L(x)=(2)当0<x<80时,L(x)=-(x-60)2+950,此时,当x=60时,L(x)取得最大值L(60)=950(万元);当x≥80时,L(x)=1200-x+≤1200-2=1200-200=1000.此时,当x=,即x=100时,L(x)取得最大值1000万元.所以,当年产量为100千件时,该厂在这一商品的生产中所获利润最大,最大利润为1000万元.21.(本小题满分12分)已知递增的等比数列{a n}满足:a2+a3+a4=28,且a3+2是a2,a4的等差中项.(1)求数列{a n}的通项公式;lo a n,S n=b1+b2+…+b n,求S n.(2)若b解:(1)设等比数列{a n}的首项为a1,公比为q.依题意,有2(a3+2)=a2+a4,代入a2+a3+a4=28,得a3=8.∴a2+a4=20.∴解得或又{a n}为递增数列,∴∴a n=2n.(2)∵b n=2n²lo2n=-n²2n,∴-S n=1³2+2³22+3³23+…+n³2n.①∴-2S n=1³22+2³23+3³24+…+(n-1)³2n+n³2n+1.②①-②得S n=2+22+23+…+2n-n²2n+1=-n²2n+1=2n+1-n²2n+1-2.∴S n=2n+1-n²2n+1-2.22.(本小题满分12分)(2013武汉月考)已知函数f(x)=e x(x2+ax-a),其中a是常数.(1)当a=1时,求曲线y=f(x)在点(1,f(1))处的切线方程;(2)若存在实数k,使得关于x的方程f(x)=k在[0,+∞)上有两个不相等的实数根,求k的取值范围.解:(1)由f(x)=e x(x2+ax-a)可得f′(x)=e x[x2+(a+2)x].当a=1时,f(1)=e,f′(1)=4e.所以曲线y=f(x)在点(1,f(1))处的切线方程为y-e=4e(x-1),即y=4ex-3e.(2)令f′(x)=e x[x2+(a+2)x]=0,解得x=-(a+2)或x=0.当-(a+2)≤0,即a≥-2时,在区间[0,+∞)上,f′(x)≥0,所以f(x)是[0,+∞)上的增函数,所以方程f(x)=k在[0,+∞)上不可能有两个不相等的实数根.当-(a+2)>0,即a<-2时,f′(x),f(x)随x的变化情况如下表:由上表可知函数f(x)在[0,+∞)上的最小值为f(-(a+2))=.因为函数f(x)是(0,-(a+2))上的减函数,是(-(a+2),+∞)上的增函数,且当x≥-a时,有f(x)≥e-a²(-a)>-a,又f(0)=-a.所以要使方程f(x)=k在[0,+∞)上有两个不相等的实数根,k的取值范围是,-a.。
2024届高考语文(新高考全国Ⅰ卷)学情检测模拟试题(三)含解析

2024届高考语文(新高考全国Ⅰ卷)学情检测模拟试题(三)一、现代文阅读(本大题共9小题,共60分)阅读下面的文字,完成下面小题。
材料一:传统的扎染艺术,色彩风格大致分为两个类别。
一类是以大理白族为代表的靛蓝为主的蓝白色调风格,另一类是以四川自贡为代表的红白、绿白等鲜艳浓烈的色调风格。
不论是怎么样的色彩风格,植物染料都是民间印染技艺的主要原料。
除了植物染料,扎染在染色时也会使用矿物质染料,用色相对被划分为红、黄、蓝色系。
扎染的艺术魅力也体现在了色彩的表现形式上。
单色扎染的晕染效果具有中国写意画般的意境,与之不同的是,多色套染则呈现不同色彩的视觉碰撞,有强烈的视觉刺激,让人产生新的梦幻般的视觉享受。
除了这两种染色技法,常见的还有涂染着色法、罩染着色法、局部防染法,艺术效果各异,但都具有独特的魅力。
相较云南大理白族地区凝重、素雅的蓝白扎染而言,以四川自贡地区为主的蜀缬色彩浓烈、绚丽多彩,可以说是久负盛名。
早在唐代,民间献入宫廷的织物里面就有四川蜀缬。
四川蜀缬的工艺技法可以说是极为丰富,针法灵活,会运用绞、缝、扎、捆、叠、缚、夹等多种结扎技法,图形纹样也会设计使用多种吉祥寓意的纹样,例如我们熟知的牡丹、荷花、凤凰等等,在结扎时每个结的大小、松紧、稀密又各不相同,与此同时,其在染色时也格外注意色彩的层次变化,所以四川蜀缬扎染到最后的艺术成品就各有不同,绚丽多姿。
它常常用深色染料作为背景,突出多次套色而形成的多种色彩融合,艺术风格鲜艳而又浓烈。
扎染图案纹样多种多样,主要是以点、线、面为主的几何纹样和具有特殊意义的民间图腾这两种最为经典。
民间图腾大多数为写实图案,通常反应自然界中的动物、风景,或者日常生活中的人物、生活场景,以艺术的手法(寓意、象征、虚构等)将其展现在织物上,例如传统的五福捧寿、松鹤延年、莲生贵子等图样。
与之相比,几何纹样大多数为抽象图案。
它以设计最为基本的点、线、面去描述对象,具有高度的装饰性和艺术表达力,常常给予人们想象的空间,例如鹿胎缬、鱼子缬、玛瑙缬、青碧缬、三套缬等图样。
福建省南平市2024届高三下学期第三次质量检测数学试题(解析版)

南平市2024届高三第三次质量检测数学试题(考试时间:120分钟满分:150分)注意事项:1.答卷前,考生务必在试题卷、答题卡规定的地方填写自己的准考证号、姓名.考生要认真核对答题卡上粘贴的条形码的“准考证号、姓名”与考生本人准考证号、姓名是否一致.2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其它答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若复数z 满足()i 2i i z z +=-,则z =()A.1B.C.D.2【答案】A 【解析】【分析】根据复数代数形式的运算法则化简复数,再根据复数模的计算公式计算即可.【详解】由题意可知,复数z 满足i 2i(i)z z +=-,则可转化为2i (2i)(12i)43i 12i (12i)(12i)55z --+===+--+,所以||1z ==.故选:A.2.已知,a b ∈R ,那么22log log a b >是1122a b⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【答案】A 【解析】【分析】根据对数函数和指数函数的单调性可得.【详解】因为0,0a b >>,且2log y x =在()0,∞+上单调递增,所以22log log 0a b a b >⇒>>,又12xy ⎛⎫= ⎪⎝⎭在R 上单调递减,所以11,,22aba b a b ⎛⎫⎛⎫⇔∈ ⎪⎪⎝⎭⎝⎭R ,所以2211log log 33aba b a b ⎛⎫⎛⎫>⇒>>< ⎪ ⎪⎝⎭⎝⎭,1133ab⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭成立,0b a <<时,不能得出22log log a b >成立.故选:A .3.已知向量a ,b 满足4a = ,2b = ,,150a b =︒ ,则a 在b上的投影向量为()A.bB.C.b-D.【答案】D 【解析】【分析】利用||cos ,||b a a b b,计算可得a 在b上的投影向量.【详解】a 在b上的投影向量为:1||cos ,4cos1502||b a a b b b =︒=.故选:D.4.对任意非零实数α,当x 充分小时,()11x x αα+≈+⋅.如:1121 2.2524⎛⎫==≈⨯+⨯= ⎪⎝⎭的近似值为()A.1.906B.1.908C.1.917D.1.919【答案】C 【解析】化为131218⎡⎤⎛⎫⋅+-⎪⎢⎥⎝⎭⎣⎦,根据新定义,直接计算取近似值即可.【详解】1312218⎛⎫==⋅⋅- ⎝⎭131112121 1.917838⎡⎤⎡⎤⎛⎫⎛⎫=⋅+-≈+⨯-≈ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦.故选:C .5.已知π1tan 62α⎛⎫+= ⎪⎝⎭,则2πcos 23α⎛⎫-= ⎪⎝⎭()A.35-B.34C.45-D.45【答案】A 【解析】【分析】由同角三角函数的基本关系求出2π1sin 65α⎛⎫+= ⎪⎝⎭,再由二倍角的余弦公式和诱导公式化简代入即可得出答案.【详解】因为π1tan 62α⎛⎫+= ⎪⎝⎭,所以22πsin 16π2cos 6ππsin cos 166αααα⎧⎛⎫+ ⎪⎪⎝⎭⎪=⎛⎫⎪+ ⎪⎨⎝⎭⎪⎪⎛⎫⎛⎫+++=⎪ ⎪ ⎪⎝⎭⎝⎭⎩,解得:2π1sin 65α⎛⎫+= ⎪⎝⎭,22ππππcos 2cos 2πcos 212sin 3666αααα⎡⎤⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫-=+-=-+=--+ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦⎣⎦131255⎡⎤=--⨯=-⎢⎥⎣⎦.故选:A .6.关于t 的实系数二次不等式()210t b t a +-+<的解集为()2,1--,若1x y a b -=,(),x y ∈R ,则2x y-的最小值为()A.12B.C.2D.【答案】C 【解析】【分析】由已知可得21--,是一元二次方程()210t b t a +-+=的根,进而可得24a b =⎧⎨=⎩,可得1412222y x yyy y-+==+,可求2x y -的最小值.【详解】因为关于t 的实系数二次不等式()210t b t a +-+<的解集为()2,1--,所以21--,是一元二次方程()210t b t a +-+=的根,所以21(1)2(1)b a --=--⎧⎨-⨯-=⎩,解得24a b =⎧⎨=⎩,所以241x y -=,所以241x y =+,所以141222,22y x yy y y -+==+≥=当且仅当0,1y x ==时取等号.所以2x y -的最小值为2.故选:C.7.在正四面体ABCD 中,P 为棱AD 的中点,过点A 的平面α与平面PBC 平行,平面α 平面ABD m =,平面α 平面ACD n =,则m ,n 所成角的余弦值为()A.3B.13C.23D.33【答案】B 【解析】【分析】由面面平行的性质定理可得//m BP ,//n PC ,所以m ,n 所成角即为BPC ∠,在BPC △中,由余弦定理求解即可.【详解】因为平面//α平面PBC ,α 平面ABD m =,平面PBC ⋂面ABD BP =,所以//m BP ,因为平面//α平面PBC ,α 平面ACD n =,平面PBC ⋂面ACD PC =,所以//n PC ,所以m ,n 所成角即为,BP PC 所成角,而,BP PC 所成角为BPC ∠,设正四面体ABCD 的棱长为2,所以2AB AC AD BD BC =====,所以BP CP ===所以1cos 3BPC ∠==.故选:B .8.已知椭圆C 的焦点为()11,0F -,()21,0F ,点A 在C 上,点B 在y 轴上,11F A F B ⊥ ,2223F A F B =-,则C 的方程为()A.2212x y += B.22132x y +=C.22143x y += D.22154x y +=【答案】D 【解析】【分析】由题意设椭圆C 的方程为:222211x y a a +=-,由,11F A F B ⊥ ,2223F A F B =- 可求出54,33A ⎛⎫ ⎪⎝⎭或54,33A ⎛⎫- ⎪⎝⎭,代入椭圆方程化简即可得求出25a =,即可得出答案.【详解】因为椭圆C 的焦点为()11,0F -,()21,0F ,所以设椭圆C 的方程为:222211x y a a +=-,设()00,B y ,(),A m n ,()21,0F ,则()()2201,,1,F A m n F B y =-=- ,因为2223F A F B =-,所以()0211323m n y⎧-=-⨯-⎪⎪⎨⎪=-⎪⎩,所以052,33m n y ==-,所以052,33A y ⎛⎫- ⎪⎝⎭,又因为11F A F B ⊥ ,所以()101082,,1,33F A y F B y ⎛⎫=-= ⎪⎝⎭,所以2082033y -=,所以02y =±,所以54,33A ⎛⎫ ⎪⎝⎭或54,33A ⎛⎫- ⎪⎝⎭,因为A 在C 上,所以2225169911a a +=-,即42950250a a -+=,解得:25a =或259a =,因为椭圆C 的焦点在x 轴上,所以25a =.故C 的方程为22154x y +=.故选:D.二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9.六位评委给某选手的评分分别为:16,18,20,20,22,24.去掉最高分和最低分,所得新数据与原数据相比不变的是()A.极差B.众数C.平均数D.第25百分位数【答案】BC 【解析】【分析】根据题意,由数据的中位数、平均数、方差、众数的定义,分析可得答案.【详解】从6个原始评分中去掉1个最高分、1个最低分,得到4个新数据为:18,20,20,22,极差为:22184-=,众数为:20,平均数为:18202022204+++=,因为0.2541⨯=,所以第25百分位数为1820192+=,而原数据:16,18,20,20,22,24,极差为:24168-=,众数为:20,平均数为:161820202224206+++++=,因为0.256 1.5⨯=,所以第25百分位数为18,所以所得新数据与原数据相比不变的是:众数和平均数.故选:BC.10.已知圆C :()()221225x y -+-=,直线l :()()()211740m x m y m m +++--=∈R ,则()A.直线l 过定点()3,1B.圆C 被x轴截得的弦长为C.当2m =-时,圆C 上恰有2个点到直线l 距离等于4D.直线l 被圆C 截得的弦长最短时,l 的方程为250x y --=【答案】ACD 【解析】【分析】直线l 的方程变形为:()2740x y m x y +-++-=,令m 的系数等于零,即可判断A ;()1,2C 到x 轴的距离为2,求出圆C 被x 轴截得的弦长可判断B ;计算出当2m =-时,圆心到直线的距离即可判断C ;当PC l ⊥时,弦长最短,即可判断D.【详解】对于A ,直线l 的方程变形为:()2740x y m x y +-++-=,令27040x y x y +-=⎧⎨+-=⎩,解得31x y =⎧⎨=⎩,所以直线l 恒过定点()3,1P ,故A 正确;对于B ,圆C 的圆心()1,2C ,半径=5r ,()1,2C到x 轴的距离为2,所以圆C 被x 轴截得的弦长为=,故B 错误;对于C ,当2m =-时,直线l :3100x y +-=,此时圆心()1,2C 到直线l 的距离102d ==,而542r d -=-<,所以当2m =-时,圆C 上恰有2个点到直线l 的距离等于4,故C 正确.对于D ,当PC l ⊥时,弦长最短,此时1121231l CPk k =-=-=--,因为直线l 过定点()3,1P ,所以l 的方程为:()123y x -=-,化简为:250x y --=,故D 正确.故选:ACD.11.已知函数()f x 及其导函数()f x '的定义域均为R ,记()()g x f x '=.()f x 满足()()213244f x f x x ---=-,()1g x -的图象关于直线1x =对称,则()A.()()202f f -=B.()11g =C.()1y f x x =+-为奇函数D.()1001100k g k ==∑【答案】ABD 【解析】【分析】对于A ,将恒等式代换变形得到()()112f x f x x +--=,再代入特殊值即可验证A ;对于B ,在()()112f x f x x +--=两边求导得到()()112g x g x ++-=,再代入特殊值即可验证B ;对于C ,举出()πsin2x f x x =+,()ππ1cos 22xg x =+作为反例即可说明C 错误;对于D ,证明()()112g x g x -++=,再对求和式变形即可验证D.【详解】对于A ,由()()213244f x f x x ---=-可知222213244222x x x f f +++⎛⎫⎛⎫⋅---⋅=⋅- ⎪ ⎪⎝⎭⎝⎭,即()()112f x f x x +--=.从而()()111121f f +--=⋅,即()()202f f -=,故A 正确;对于B ,在()()112f x f x x +--=两边同时求导,可得()()112f x f x ''++-=,即()()112g x g x ++-=.代入0x =即得()11g =,故B 正确;对于C ,考虑()πsin2x f x x =+,()ππ1cos 22x g x =+,则()()g x f x =',且()()()()()()π21π32213221sin32sin44cos πcos π4422x x f x f x x x x x x x -----=-+---=--+=-,()()()()()ππππ11111cos 1cos 02222x x g x g x g x g x ⎛⎫-⎛⎫+----=--=+-+= ⎪ ⎪⎝⎭⎝⎭,故此时()(),f x g x 满足全部条件,但()()π1π11sin 1cos22x xf x x x x ++-=++-=+并不是奇函数(因为显然不过原点),故C 错误;之前已证()()112g x g x ++-=,再由()1g x -的图象关于直线1x =对称,知()()1111g x g x +-=--,即()()g x g x =-.故()()()()()()()()11111211212g x g x g x g x g x g x g x g x -++=-++=-+--=-+--=.所以()()()()100505011143412502100k k k g k g k g k ====-+-==⨯=∑∑∑,故D 正确.故选:ABD.【点睛】关键点点睛:本题的关键点在于对恒等式的换元及变形,需要选取恰当的换元方式方可简化等式.三、填空题:本题共3小题,每小题5分,共15分.12.已知集合(){}2,4A x y yx ==,(){},B x y y x ==,则A B ⋂的子集个数为______.【答案】4【解析】【分析】先求交集中的元素,根据元素个数可得子集个数.【详解】由24y x y x ⎧=⎨=⎩解得00x y =⎧⎨=⎩或1414x y ⎧=⎪⎪⎨⎪=⎪⎩,所以11(0,0),(,)44A B ⎧⎫⋂=⎨⎬⎩⎭,有两个元素,所以A B ⋂的子集个数为224=.故答案为:4.13.函数()()sin 0f x x ωω=>在区间ππ,63⎡⎤-⎢⎥⎣⎦上单调递增,且在区间()0,2π上恰有两个极值点,则ω的取值范围是______.【答案】3544ω<≤【解析】【分析】利用正弦型函数的单调性可得302ω<≤,利用正弦型函数的极值点可得3544ω<≤.【详解】由()()sin 0f x x ωω=>在区间3π,6π⎡⎤-⎢⎥⎣⎦上单调递增,可得ππ2π62k ω-≥-+,ππ2π32k ω≤+,k ∈Z ,即312k ω≤-,362k ω≤+,k ∈Z ,即302ω<≤,又()()sin 0f x x ωω=>在区间()0,2π上恰有两个极值点,可得3π5π2π22ω<≤,即3544ω<≤.综上,3544ω<≤.故答案为:3544ω<≤.14.在正四棱台1111ABCD A B C D -中,2AB =,111A B =,且该正四棱台的每个顶点均在表面积为8π的球O 上,则平面11BCC B 截球O 所得截面的面积为______.【答案】8π7##8π7【解析】【分析】先求出外接球的半径与球心位置;再做辅助线证明出2O F ⊥平面11B BCC ,在21EO E 中,设2,EF x O F d ==,结合图象列出关于,x d 的方程组,最后解出截面圆的半径即可.【详解】由球O 的表面积为8π,所以24π8πS R ==,可知球O ,设上下底面的中心分别为12,O O ,因为2AB =,从而可知球O 的球心与下底面ABCD 的中心2O 重合;分别取11B C 和BC 的中点1E E 、,连接112111212,,,,,C O EO E E E O EO O O ,则在直角梯形112C O O C 中得1262O O =,则在直角梯形112E O O E 中得12E E =,过点2O 作1E E 的垂线,垂足为F ,由于BC ⊥平面112E O O E ,2O F ⊂平面112E O O E ,所以2BC O F ⊥,由21OF EE ⊥,1EE BC E = ,1,EE BC ⊂平面11B BCC ,从而2O F ⊥平面11B BCC ,在21EO E 中,设2,EF x O F d ==,则172E F x =-,则221x d +=,和22222x d ⎛⎫⎛-+= ⎪ ⎪ ⎪⎝⎭⎝⎭,联立解得:276,77x d ==,又因为平面11B BCC 截球所得平面图形为圆面,所以圆面的半径287r =,所以圆面面积为28ππ7r =.【点睛】方法点睛:构建方程组利用勾股定理解截面圆半径是解决立体几何的一种重要方法.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.已知函数()31ln 222f x ax x x x=--+,且()f x 图象在1x =处的切线斜率为0.(1)求a 的值;(2)令()()g x f x '=,求()g x 的最小值.【答案】(1)1(2)0【解析】【分析】(1)对()f x 求导,可得()10f '=,解方程即可得出答案;(2)由(1)知函数()31ln 222f x x x x x =--+,对()f x 求导,令()211ln (0)22g x x x x =+->,对()g x 求导,判断()g x '与0的大小得出()g x 的单调性,即可求出()g x 的最小值.【小问1详解】因为()31ln 222f x ax x x x =--+,所以()()2311ln 22f x a x x -+'=+,因为()f x 图象在1x =处的切线斜率为0,所以()10f '=,即31022a -+=,所以1a =.【小问2详解】由(1)知函数()31ln 222f x x x x x=--+,()f x 的定义域为()0,∞+,()211ln 22f x x x =+-',则()211ln (0)22g x x x x =+->,求导得()233111x g x x x x='-=-,当01x <<时,()0g x '<,当1x >时,()0g x '>,则函数()g x 在()0,1上递减,在()1,∞+上递增,()()min 10g x g ==.16.建盏为宋代名瓷之一,是中国古代黑瓷的巅峰之作,其采用福建建阳特有的高铁黏土和天然釉矿为原料烧制而成,工艺难度大,成功率低.假设建盏烧制开窑后经检验分为成品和废品两类,现有建盏10个,其中5个由工匠甲烧制,3个由工匠乙烧制,2个由工匠丙烧制,甲、乙、丙三人烧制建盏的成品率依次为0.2,0.1,0.3.(1)从这10个建盏中任取1个,求取出的建盏是成品的概率;(2)每件建盏成品的收入为1000元,每件废品的收入为0元.乙烧制的这3件建盏的总收入为X 元,求X 的分布列及数学期望.【答案】(1)0.19(2)分布列见解析,数学期望为300元【解析】【分析】(1)设事件B 为“取得的建盏是成品”,事件1A ,2A ,3A 分别表示“取得的建盏是由甲、乙、丙烧制的”,求得每个事件的概率,进而利用()()()()()()()112233P B P A P BA P A PB A P A P B A =++∣∣∣可求取出的建盏是成品的概率;(2)这3件中成品的件数为Y .由题可知13,10Y B ⎛⎫~ ⎪⎝⎭,利用二项分布的概率公式可求X 分布列及数学期望.【小问1详解】设事件B 为“取得的建盏是成品”,事件1A ,2A ,3A 分别表示“取得的建盏是由甲、乙、丙烧制的”.则()151102P A ==,()230.310P A ==,()321105P A ==.又()10.2P BA =∣,()20.2PB A =∣,()30.3P B A =∣,所以()()()()()()()112233P B P A P BA P A PB A P A P B A =++∣∣∣0.50.20.30.10.20.30.19=⨯+⨯+⨯=【小问2详解】设这3件中成品的件数为Y .由题可知13,10Y B ⎛⎫~ ⎪⎝⎭.因为1000X Y =,X 的可能取值为0,1000,2000,3000所以()()03031972900C 10101000P X P Y ⎛⎫⎛⎫===== ⎪ ⎪⎝⎭⎝⎭,()()12131924310001C 10101000P X P Y ⎛⎫⎛⎫=====⎪ ⎪⎝⎭⎝⎭,()()2123192720002C 10101000P X P Y ⎛⎫⎛⎫===== ⎪ ⎪⎝⎭⎝⎭,()()33319130003C 10101000P X P Y ⎛⎫⎛⎫=====⎪ ⎪⎝⎭⎝⎭,所以X 的分布列为X100020003000P7291000243100027100011000所以()72924327101000200030003001000100010001000E X =⨯+⨯+⨯+⨯=元.17.如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,AB CD ∥,AB BC AD CD ==<,2π3ABC ∠=.M ,N 分别为棱CD ,PD 上的动点(与端点不重合),且CM DN CD DP=.(1)求证:AD ⊥平面APC ;(2)若3AP =,设平面AMN 与平面APC 所成的角为α,求cos α的最大值.【答案】(1)证明见解析(2)155【解析】【分析】(1)解法一:由AB BC AD ==,AB CD ∥,2π3ABC ∠=,推出AD AC ⊥,又PA ⊥平面ABCD ,由线面垂直判定定理可得AD ⊥平面PAC ;解法二:同解法一:(2)解法一:设1AD =,建立空间直角坐标系A xyz -,令CM DNCD DPλ==,设()111,,M x y z ,()222,,N x y z ,设平面AMN 的法向量为(),,n x y z =,由cos n AD n ADα⋅=⋅ ,利用基本不等式求解最值;解法二:不妨设1AD =,由AC ,AD ,AP 两两垂直,故建立如图所示的空间直角坐标系A xyz -,求解平面AMN 的法向量为(),,n x y z =,由cos n AD n ADα⋅=⋅ ,利用基本不等式求解最值.【小问1详解】解法一:因为AB BC AD ==,AB CD ∥,2π3ABC ∠=,所以π6CAB ∠=,2πππ362CAD ∠=-=,即AD AC ⊥又PA ⊥平面ABCD ,所以PA AD ⊥因为AC PA A ⋂=,,AC PA ⊂平面PAC ,所以AD ⊥平面PAC ;解法二:同解法一.【小问2详解】解法一:设1AD =,如图所示,建立空间直角坐标系A xyz -.令CM DNCD DPλ==,()0,1λ∈,设()111,,M x y z ,()222,,N x y z 则有CM CD λ=,DN DPλ=即()()111,x y z λ-=,解得))1,,0M λλ-同理可得()0,1N λ-设平面AMN 的法向量为(),,n x y z =,由)()10,10,n AM x y n AN y z λλλ⎧⋅=-+=⎪⎨⋅=-=⎪⎩ 令1x =,则)1y λλ-=,()221z λλ-=.得平面AMN的一个法向量为)()22111,,n λλλλ⎛⎫-- = ⎪⎝⎭又由(1)可知()0,1,0AD =是平面APC 的一个法向量,则有cos n ADn ADα⋅==⋅5==当且仅当211λλ-⎛⎫=⎪⎝⎭,即12λ=时取“=”又π0,2α⎛⎫∈ ⎪⎝⎭,所以cosα的最大值15cos5α=解法二:不妨设1AD=,由AC,AD,AP两两垂直,故建立如图所示的空间直角坐标系A xyz-,则根据题意可得:())1,1,0AM AC ADλλλ=+-=-()()10,,AN AD APλλλ=+-=,()0,1λ∈,设平面AMN的一个法向量为(),,n x y z=,())1010n AM x yn AN y zλλλ⎧⋅=+-=⎪⎨⋅=+-=⎪⎩取1x=,1yλ=-,()221zλλ=-于是()2231,,11nλλλ⎛⎫⎪=⎪--⎝⎭,cos5α=当且仅当211λλ-⎛⎫=⎪⎝⎭,即12λ=时取“=”又π0,2α⎛⎫∈ ⎪⎝⎭,所以cos α的最大值15cos 5α=.18.已知()11,0A -,()21,0A ,直线1A P ,2A P 相交于点P ,且它们的斜率之积是4,记点P 的轨迹为曲线C(1)求C 的方程;(2)不过1A ,2A 的直线l 与C 交于M ,N 两点,直线1MA 与2NA 交于点S ,点S 在直线12x =上,证明:直线l 过定点.【答案】(1)()22114y x x -=≠±(2)证明见解析【解析】【分析】(1)由斜率公式结合题意即可列式,化简即可得解.(2)设直线l 的方程为:()1x my n n =+≠±,将其与椭圆方程联立,从而122841mny y m -+=-,21224441n y y m -⋅=-,思路一:由斜率公式、(1)中结论以及点S 在直线12x =上,可得1143A N A Mk k =-,从而结合韦达定理可得n 为定值2,由此即可得证;思路二:联立直线1MA 与直线2NA 的方程,可得()()12121111y yx x x x +=-+-,在里面代入12x =,结合韦达定理即可得出n 为定值,由此即可得证.【小问1详解】设(),P x y ,则()111PA y k x x =≠-+,()211PA y k x x =≠-,由已知,有()4111y yx x x ⋅=≠±+-,故C 的方程为()22114y x x -=≠±.【小问2详解】解法一:设()11,M x y ,()22,N x y ,若直线l 的斜率为0,则直线1MA 与2NA 的交点在y 轴上,与已知矛盾,故设直线l 的方程为:()1x my n n =+≠±,由2244x my n x y =+⎧⎨-=⎩,得()222418440m y mny n -++-=,()22Δ16410m n =+->,则122841mn y y m -+=-,21224441n y y m -⋅=-,由点S 在直线12x =上,设1,2S t ⎛⎫⎪⎝⎭,则121312A M t k t ==+,22112N A tk t==--,所以213A M NA k k =-,又124A N A N k k ⋅=,则()1134A N A M k k ⋅-=,即1143A N A M k k =-,21214113y y x x ⋅=-++,()()12213411y y my n my n -=++++,()()()()221212434410my y mn m y y n ++++++=,()()()222224484344104141n mn m mn m n m m --+++++=--,220n n --=,所以1n =-(舍去),或2n =,所以l 的方程为2x my =+,过定点()2,0解法二:设()11,M x y ,()22,N x y ,若直线l 的斜率为0,则直线1MA 与2NA 的交点在y 轴上,与已知矛盾,故设直线l 的方程为:()1x my n n =+≠±,由2244x my n x y =+⎧⎨-=⎩得,()222418440m y mny n -++-=,()22Δ16410m n =+->,则122841mn y y m -+=-,21224441n y y m -⋅=-,所以()()2121212n y y mny y-+=-⋅,即()()2121212n y y my y n-+=-,又直线1MA 的方程为()1111y y x x =++,直线2NA 的方程为()2211y y x x =--,联立直线1MA 与直线2NA 的方程,可得()()12121111y y x x x x +=-+-,又点S 在直线12x =上,故()()2112131y x y x +=--,所以()()()()()()21211121212121111111y x y my n my y n y y x y my n my y n y +++++==-+-+-()()()()()()()()()()21212222121211111122111122n y y n y y n y y n nnn y y n n y y y n y nn-+-+-++-+==⋅++--+--+-()()()()2121111131111n y n y n n n n y n y n +--++=⋅==---++--,故2n =,直线l 的方程为2x my =+,过定点()2,0.19.若数列{}n c 共有()*,3m m m ∈≥N 项,对任意()*,i i i m ∈≤N 都有1i m i c c S +-=(S 为常数,且0S >),则称数列{}n c 是S 关于m 的一个积对称数列.已知数列{}n a 是S 关于m 的一个积对称数列.(1)若3m =,11a =,22a =,求3a 的值;(2)已知数列{}n b 是公差为()0d d ≠的等差数列,111b =-,若10m =,2n n nb a b +=,求d 和S 的值;(3)若数列{}n a 是各项均为正整数的单调递增数列,求证:12112153m m m m a a a a Sa a a a --++⋅⋅⋅++<.【答案】(1)4(2)1,2S d ==(3)证明见解析【解析】【分析】(1)依题意可得22S a a =,从而求出3a ;(2)依题意11i ia a S -=,即可得到21311i ii ib b S b b +--⨯=,再结合等差数列通项公式得到()2222222222111111121311109d i d i d b b d S d i d i d b b d -++++=-+-++,再根据对应系数相等得到方程组,解得即可;(3)依题意可得()1222111,31211m i i i a S S S S i m m a a i i i i -+⎛⎫=≤<=-<≤≥ ⎪--+⎝⎭,再利用裂项相消法计算可得.【小问1详解】依题意224S a a ==,又13a a S =,所以314Sa a ==.【小问2详解】法一:由10m =知对任意i ()*,10i i ∈≤N 都有11i i a a S -=,即()()()()112131*********i i i i b i d b i db b S b b b i d b i d+--+++-⨯=⨯=+-+-,所以()()222112221112111310119b i i d b d S bi i db d++-+=+-+-+,所以()2222222222111111121311109d i d i d b b d S d i d i d b b d -++++=-+-++,所以()22222222111111111213109d d S d d S d b b d S d b b d ⎧-=-⎪⎪=⎨⎪++=-++⎪⎩,因为0d ≠,111b =-,所以2112240S d b d =⎧⎨+=⎩,即12S d =⎧⎨=⎩.法二:当1,2i =时由11029S a a a a ==得31241111029b b b b S b b b b =⨯=⨯,所以1111111121131098b d b d b d b d b b d b d b d++++⨯=⨯+++,即()()()()22222221111111110161211122710b b d db b d d b b d d b b d ++⨯++=++⨯+,令21110p b b d =+,22111211q b b d d =++,则()()221616p d q q d p +=+,因为0d ≠,111b =-,所以p q =,2221111101211b b d b b d d +=++,即2d =,1S =,当110i ≤≤时都有()()()()2131111112111212112111210i i i i i i i i b b a a b b i i +----++-+-=⨯=⨯-+--+-92132113292i i S i i-+-=⨯==-+-,所以2d =,1S =成立.【小问3详解】由已知1m a a S =,21m a a S -=,…,1i m i a a S +-=,所以()1222111,31211m i i i a S S S S i m m a a i i i i -+⎛⎫=≤<=-<≤≥ ⎪--+⎝⎭,所以112222*********m m m a a a S a a a m -⎛⎫++⋅⋅⋅+≤+++⋅⋅⋅+ ⎪⎝⎭1111111111114224354611S m m ⎡⎤⎛⎫<++-+-+⋅⋅⋅+- ⎪⎢⎥-+⎝⎭⎣⎦1111111111115142231142233S S S m m ⎡⎤⎡⎤⎛⎫⎛⎫<+++--<+++= ⎪ ⎪⎢⎥⎢⎥+⎝⎭⎝⎭⎣⎦⎣⎦,即12112153m m m m a a a a S a a a a --++⋅⋅⋅++<.【点睛】关键点点睛:对于新定义型问题,关键是理解定义,第三问关键是利用放缩法得到()1222111,31211m i i i a S S S S i m m a a i i i i -+⎛⎫=≤<=-<≤≥ ⎪--+⎝⎭,再由裂项相消法求和.。
高三数学 阶段滚动检测(三)-人教版高三全册数学试题

阶段滚动检测(三)一、选择题1.(2016·某某“四地六校”联考)已知集合A ={x |x 2-2x -3≤0},B ={x |log 2(x 2-x )>1},则A ∩B 等于() A .(2,3] B .(2,3) C .(-3,-2)D .[-3,-2)2.(2016·)设a ,b 是向量,则“|a |=|b |”是“|a +b |=|a -b |”的() A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件D .既不充分也不必要条件3.(2016·某某质检)已知命题p :“∃x ∈R ,e x-x -1≤0”,则綈p 为() A .∃x 1,x 2∈R ,(f (x 2)-f (x 1))(x 2-x 1)≤0 B .∀x 1,x 2∈R ,(f (x 2)-f (x 1))(x 2-x 1)≤0 C .∃x 1,x 2∈R ,(f (x 2)-f (x 1))(x 2-x 1)<0 D .∀x 1,x 2∈R ,(f (x 2)-f (x 1))(x 2-x 1)<04.(2016·某某)已知函数f (x )的定义域为R .当x <0时,f (x )=x 3-1;当-1≤x ≤1时,f (-x )=-f (x );当x >12时,f ⎝⎛⎭⎪⎫x +12=f ⎝⎛⎭⎪⎫x -12,则f (6)等于()A .-2B .-1C .0D .25.设a ≠0,函数f (x )=⎩⎪⎨⎪⎧4log 2(-x ),x <0,|x 2+ax |,x ≥0.若f [f (-2)]=4,则f (a )等于()A .8B .4C .2D .16.已知a >0,且a ≠1,函数y =log a x ,y =a x,y =x +a 在同一坐标系中的图象可能是()7.(2017·某某质检)已知函数f (x )=32,2,(1),2,x x x x ⎧≥⎪⎨⎪-<⎩若关于x 的方程f (x )=k 有两个不同的实根,则实数k 的取值X 围是() A .(-1,1) B .(0,1) C .(0,1]D .(-1,0)8.如图,将45°直角三角板和30°直角三角板拼在一起,其中45°直角三角板的斜边与30°直角三角板的30°角所对的直角边重合.若DB →=x ·DC →+y ·DA →,x >0,y >0,则x ,y 的值分别为()A.3,1 B .1+3, 3 C .2, 3D.3,1+ 39.已知sin(x -2 017π)=13,x ∈⎝ ⎛⎭⎪⎫π,3π2,则tan 2x 等于() A.24B .-24C.427D .4 210.已知△ABC 三边a ,b ,c 上的高分别为12,22,1,则cos A 等于()A.32 B .-22 C .-24D .-3411.(2015·课标全国Ⅰ)设函数f (x )=e x(2x -1)-ax +a ,其中a <1,若存在唯一的整数x 0使得f (x 0)<0,则a 的取值X 围是()A.⎣⎢⎡⎭⎪⎫-32e ,1 B.⎣⎢⎡⎭⎪⎫-32e ,34 C.⎣⎢⎡⎭⎪⎫32e ,34D.⎣⎢⎡⎭⎪⎫32e ,1 12.已知O 是锐角△ABC 的外心,tan A =22,若cos B sin C AB →+cos C sin BAC →=2mAO →,则m 等于() A.33B.32 C .3 D.53二、填空题13.若f (x )=x +2⎠⎛01f (t )d t ,则f (1)=________.14.若tan α=3,则sin 2α+3cos 2αsin 2α+2sin αcos α-5=________.15.如图,梯形ABCD 中,AB ∥CD ,AB =6,AD =DC =2,若AC →·BD →=-14,则AD →·BC →=________.16.关于函数f (x )=cos 2x -23sin x cos x ,有下列命题: ①对任意x 1,x 2∈R ,当x 1-x 2=π时,f (x 1)=f (x 2)成立;②f (x )在区间⎣⎢⎡⎦⎥⎤-π6,π3上单调递增;③函数f (x )的图象关于点(π12,0)对称;④将函数f (x )的图象向左平移5π12个单位长度后所得到的图象与函数y =2sin 2x 的图象重合.其中正确的命题是________.(注:把你认为正确的序号都填上) 三、解答题17.已知函数f (x )=⎩⎪⎨⎪⎧-x -1,x <-2,x +3,-2≤x ≤12,5x +1,x >12.(1)求函数f (x )的最小值;(2)已知m ∈R ,p :关于x 的不等式f (x )≥m 2+2m -2对任意x ∈R 恒成立,q :函数y =(m2-1)x是增函数,若p 正确,q 错误,某某数m 的取值X 围.18.已知|a |=4,|b |=3,(2a -3b )·(2a +b )=61. (1)求a 与b 的夹角θ;(2)若c =t a +(1-t )b ,且b·c =0,求t 及|c |.19.设向量a =(3sin x ,cos x ),b =(cos x ,cos x ),记f (x )=a·b . (1)求函数f (x )的最小正周期;(2)试用“五点法”画出函数f (x )在区间⎣⎢⎡⎦⎥⎤-π12,11π12上的简图,并指出该函数的图象可由y =sin x (x ∈R )的图象经过怎样的平移和伸缩变换得到;(3)若函数g (x )=f (x )+m ,x ∈⎣⎢⎡⎦⎥⎤-π6,π3的最小值为2,试求出函数g (x )的最大值.20.已知函数f (x )=x 2x -a,a ∈R .(1)求函数f (x )的单调区间;(2)若f (x )在(1,2)上是单调函数,求a 的取值X 围.21.在△ABC 中,AB →=(-3sin x ,sin x ),AC →=(sin x ,cos x ). (1)设f (x )=AB →·AC →,若f (A )=0,求角A 的值;(2)若对任意的实数t ,恒有|AB →-tAC →|≥|BC →|,求△ABC 面积的最大值.22.某地棚户区改造建筑用地平面示意图如图所示,经规划调研确定,棚改规划建筑用地区域近似为圆面,该圆面的内接四边形ABCD 是原棚户区建筑用地,测量可知边界AB =AD =4万米,BC =6万米,CD =2万米.(1)请计算原棚户区建筑用地ABCD 的面积及AC 的长;(2)因地理条件的限制,边界AD ,DC 不能变更,而边界AB ,BC 可以调整,为了提高棚户区建筑用地的利用率,请在ABC 上设计一点P ,使得棚户区改造后的新建筑用地APCD 的面积最大,并求出最大值. 答案精析1.A[因为A ={x |x 2-2x -3≤0}={x |(x -3)(x +1)≤0}={x |-1≤x ≤3}=[-1,3],B ={x |log 2(x 2-x )>1}={x |x 2-x >2}={x |x <-1或x >2}=(-∞,-1)∪(2,+∞),所以A ∩B =(2,3]. 故选A.]2.D[若|a |=|b |成立,则以a ,b 为邻边构成的四边形为菱形,a +b ,a -b 表示该菱形的对角线,而菱形的两条对角线长度不一定相等,所以|a +b |=|a -b |不一定成立;反之,若|a +b |=|a -b |成立,则以a ,b 为邻边构成的四边形为矩形,而矩形的邻边长度不一定相等,所以|a |=|b |不一定成立.所以“|a |=|b |”是“|a +b |=|a -b |”的既不充分也不必要条件.]3.C[已知全称命题p :∀x ∈M ,p (x ),则否定为綈p :∃x 0∈M ,綈p (x 0),故选C.] 4.D[∵当x >12时,f ⎝ ⎛⎭⎪⎫x +12=f ⎝ ⎛⎭⎪⎫x -12,即f (x )=f (x +1),∴T =1,∴f (6)=f (1).当x <0时,f (x )=x 3-1且-1≤x ≤1时,f (-x )=-f (x ),∴f (6)=f (1)=-f (-1)=2,故选D.] 5.A[由f (-2)=4log 22=2,f (2)=|4+2a |=4,解得a =-4,所以f (a )=f (-4)=4log 24=8,故选A.]6.C[∵函数y =a x与y =log a x 互为反函数,∴它们的图象关于直线y =x 对称,∴选项B 的图象不正确;当0<a <1时,y =log a x 与y =a x都随x 的增大而减小,y =x +a 的图象与y 轴的交点在y =1的下方,只有选项C 的图象正确;当a >1时,y =log a x 与y =ax都随x 的增大而增大,y =x +a 的图象与y 轴的交点在y =1的上方,没有选项符合要求.] 7.B[根据题意作出函数f (x )=⎩⎪⎨⎪⎧2x,x ≥2,?x -1?3,x <2的图象,如图.关于x 的方程f (x )=k 有两个不同的实根等价于函数f (x )=⎩⎪⎨⎪⎧2x,x ≥2,?x -1?3,x <2的图象与直线y =k 有两个不同的公共点,则由图象可知当k ∈(0,1)时,满足题意.故选B.] 8.B[设AD =DC =1,则AC =2,AB =22,BC = 6.在△BCD 中,由余弦定理,得DB 2=DC2+CB 2-2DC ·CB ·cos(45°+90°)=7+2 3.以D 为原点,DA 为x 轴,DC 为y 轴建立平面直角坐标系(图略),则D (0,0),A (1,0),C (0,1),由DB →=x ·DC →+y ·DA →,得B (y ,x ),∴CB →=(y ,x -1),DB →=(y ,x ),∴6=(x -1)2+y 2,x 2+y 2=7+23,∴x =1+3,y = 3.] 9.C[因为sin(x -2 017π)=13,所以sin x =-13,又x ∈⎝ ⎛⎭⎪⎫π,3π2,所以cos x =-223,所以tan x =24, 所以tan 2x =2×241-⎝ ⎛⎭⎪⎫242=427.]10.C[设△ABC 面积为S ⇒a =4S ,b =22S ,c =2S ⇒cos A =(22)2+22-422×22×2=-24,故选C.]11.D[由已知函数关系式,先找到满足f (x 0)<0的整数x 0,由x 0的唯一性列不等式组求解. ∵f (0)=-1+a <0,∴x 0=0.又∵x 0=0是唯一的使f (x )<0的整数,∴⎩⎪⎨⎪⎧f (-1)≥0,f (1)≥0,即⎩⎪⎨⎪⎧e -1[2×(-1)-1]+a +a ≥0,e(2×1-1)-a +a ≥0,解得a ≥32e.又∵a <1,∴32e≤a <1,经检验a =34,符合题意,故选D.]12.A[取AB 的中点D ,连接OD , 则OD ⊥AB , ∴OD →·AB →=0, ∵AO →=AD →+DO →,∴cos B sin C AB →+cos C sin B AC →=2mAO → =2m (AD →+DO →),∴cos B sin C AB →2+cos C sin B AC →·AB → =2mAD →·AB →+2mDO →·AB →,∴cos B sin C |AB →|2+cos C sin B |AC →||AB →|cos A =2m ·12|AB →|2=m |AB →|2, 由正弦定理可得cos B sin C sin 2C +cos C sin B sin B sin C cos A =m sin 2C ,即cos B +cos C cos A =m sin C ,又cos B =-cos(A +C )=-cos A cos C +sin A sin C , ∴sin A sin C =m sin C ,∴m =sin A , 又tan A =22,∴m =sin A =33.] 13.0解析 记a =⎠⎛01f (t )d t ,则f (x )=x +2a ,故⎠⎛01f (x )d x =⎠⎛01(x +2a )d x =12+2a ,所以a =12+2a ,a =-12,故f (x )=x -1,f (1)=0.14.-1235解析 由题意知cos α≠0, ∵sin 2α+3cos 2αsin 2α+2sin αcos α-5=sin 2α+3cos 2α-4sin 2α+2sin αcos α-5cos 2α =tan 2α+3-4tan 2α+2tan α-5, ∴tan 2α+3-4tan 2α+2tan α-5=9+3-36+6-5=-1235, 即sin 2α+3cos 2αsin 2α+2sin αcos α-5=-1235. 15.-2解析 ∵AC →·BD →=(AD →+DC →)·(BC →+CD →)=AD →·BC →+(AD →-BC →-CD →)·CD →=AD →·BC →+(AD →+DC →+CB →)·CD →=AD →·BC →+AB →·CD →, ∴AD →·BC →-6×2=-14⇒AD →·BC →=-2. 16.①③解析 f (x )=cos 2x -23sin x cos x =cos 2x -3sin 2x =2cos ⎝⎛⎭⎪⎫2x +π3. 因为f (x 1)=2cos ⎝ ⎛⎭⎪⎫2x 1+π3=2cos ⎣⎢⎡⎦⎥⎤2(x 2+π)+π3=2cos ⎝⎛⎭⎪⎫2x 2+π3=f (x 2),故①正确;当x ∈⎣⎢⎡⎦⎥⎤-π6,π3时,2x +π3∈[0,π],所以函数f (x )在区间⎣⎢⎡⎦⎥⎤-π6,π3上单调递减,故②错误;f ⎝ ⎛⎭⎪⎫π12=2cos ⎝⎛⎭⎪⎫2×π12+π3=2cos π2=0,故③正确;函数f (x )的图象向左平移5π12个单位长度后得到的图象所对应的函数解析式为y =2cos ⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫x +5π12+π3=-2cos ⎝ ⎛⎭⎪⎫2x +π6,易知该图象与函数y =2sin 2x 的图象不重合,故④错误.17.解 (1)作出函数f (x )的图象,如图所示.可知函数f (x )在x =-2处取得最小值1.(2)若p 正确,则由(1)得m 2+2m -2≤1,即m 2+2m -3≤0, 所以-3≤m ≤1.若q 正确,则函数y =(m 2-1)x是增函数, 则m 2-1>1,解得m <-2或m > 2.又p 正确q 错误,则⎩⎨⎧-3≤m ≤1,-2≤m ≤2,解得-2≤m ≤1.即实数m 的取值X 围是[-2,1].18.解 (1)由(2a -3b )·(2a +b )=61,得a·b =-6, ∴cos θ=a·b |a||b|=-64×3=-12.又0≤θ≤π,∴θ=2π3.(2)∵b·c =b ·[t a +(1-t )b ]=t a·b +(1-t )b 2=-15t +9=0,∴t =35,∴|c |2=⎝ ⎛⎭⎪⎫35a +25b 2=10825,∴|c |=635.19.解 (1)f (x )=a·b =3sin x cos x +cos 2x =32sin 2x +1+cos 2x 2=sin(2x +π6)+12,∴函数f (x )的最小正周期T =2π2=π.(2)列表如下:x-π12 2π12 5π12 8π12 11π12 2x +π6π2 π3π2 2πsin(2x +π6)0 1 0 -1 0 y123212-1212描点,连线得函数f (x )在区间⎣⎢⎡⎦⎥⎤-π12,11π12上的简图如图所示:y =sin x 的图象向左平移π6个单位长度后得到y =sin(x +π6)的图象,再保持纵坐标不变,横坐标缩短为原来的12后得到y =sin(2x +π6)的图象,最后将y =sin(2x +π6)的图象向上平移12个单位长度后得到y =sin(2x +π6)+12的图象. (3)g (x )=f (x )+m =sin(2x +π6)+12+m . ∵x ∈⎣⎢⎡⎦⎥⎤-π6,π3, ∴2x +π6∈⎣⎢⎡⎦⎥⎤-π6,5π6,∴sin(2x +π6)∈⎣⎢⎡⎦⎥⎤-12,1, ∴g (x )的值域为⎣⎢⎡⎦⎥⎤m ,32+m . 又函数g (x )的最小值为2,∴m =2,∴g (x )max =32+m =72. 20.解 (1)f (x )的定义域为{x |x ≠a }.f ′(x )=x (x -2a )(x -a )2. ①当a =0时,f ′(x )=1,则f (x )的单调递增区间为(-∞,0),(0,+∞).②当a >0时,由f ′(x )>0,得x >2a 或x <0,此时0<a <2a ;由f ′(x )<0,得0<x <a 或a <x <2a ,则f (x )的单调递增区间为(2a ,+∞),(-∞,0),单调递减区间为(0,a ),(a,2a ).③当a <0时,由f ′(x )>0,得x >0或x <2a ,此时2a <a <0;由f ′(x )<0,得2a <x <a 或a <x <0, 则函数f (x )的单调递增区间为(-∞,2a ),(0,+∞),单调递减区间为(2a ,a ),(a,0).(2)①当a ≤0时,由(1)可知,f (x )在(1,2)上单调递增,满足题意;②当0<2a ≤1,即0<a ≤12时,由(1)可知,f (x )在(2a ,+∞)上单调递增,即在(1,2)上单调递增,满足题意;③当1<2a <2,即12<a <1时,由(1)可得,f (x )在(1,2)上不具有单调性,不满足题意; ④当2a =2,即a =1时,由(1)可知,f (x )在(a,2a )上单调递减,即在(1,2)上单调递减,满足题意;⑤当1<a <2时,因为f (x )的定义域为{x |x ≠a },显然f (x )在(1,2)上不具有单调性,不满足题意;⑥当a ≥2时,由(1)可知,f (x )在(0,a )上单调递减,即在(1,2)上单调递减,满足题意.综上所述,a ≤12或a =1或a ≥2. 21.解 (1)f (x )=AB →·AC →=-3sin 2x +sin x cos x =-3×1-cos 2x 2+sin 2x 2=sin ⎝⎛⎭⎪⎫2x +π3-32. ∵f (A )=0,∴sin ⎝⎛⎭⎪⎫2A +π3=32, 又2A +π3∈⎝ ⎛⎭⎪⎫π3,2π+π3, ∴2A +π3=2π3,∴A =π6. (2)由|AB →-tAC →|≥|BC →|,得|CB →+(1-t )AC →|≥|BC →|,则|CB →|2+2(1-t )CB →·AC →+(1-t )2|AC →|2≥|BC →|2,故对任意的实数t ,恒有2(1-t )CB →·AC →+(1-t )2|AC →|2≥0,故CB →·AC →=0,即BC ⊥AC .∵|AB →|=4sin 2x ≤2,|AC →|=1,∴BC =AB 2-AC 2≤3,∴△ABC 的面积S =12BC ·AC ≤32, ∴△ABC 面积的最大值为32. 22.解 (1)根据题意知,四边形ABCD 内接于圆,∴∠ABC +∠ADC =180°.在△ABC 中,由余弦定理,得AC 2=AB 2+BC 2-2AB ·BC ·cos∠ABC ,即AC 2=42+62-2×4×6×cos∠ABC .在△ADC 中,由余弦定理,得 AC 2=AD 2+DC 2-2AD ·DC ·cos∠ADC ,即AC 2=42+22-2×4×2×cos∠ADC .又cos ∠ABC =-cos ∠ADC ,∴cos ∠ABC =12,AC 2=28, 即AC =27万米,又∠ABC ∈(0,π),∴∠ABC =π3. ∴S 四边形ABCD =S △ABC +S △ADC =12×4×6×sin π3+12×2×4×sin 2π3=83(平方万米). (2)由题意知,S 四边形APCD =S △ADC +S △APC ,且S △ADC =12AD ·CD ·sin 2π3=23(平方万米). 设AP =x ,CP =y ,则 S △APC =12xy sin π3=34xy . 在△APC 中,由余弦定理,得AC 2=x 2+y 2-2xy ·cosπ3=x 2+y 2-xy =28, 又x 2+y 2-xy ≥2xy -xy =xy ,当且仅当x =y 时取等号,∴xy ≤28.∴S 四边形APCD =23+34xy ≤23+34×28=93(平方万米), 故所求面积的最大值为93平方万米,此时点P 为ABC 的中点.。
《创新设计》2021版高考数学(浙江版文理通用)一轮复习练习:阶段滚动检测(三) Word版含答案

阶段滚动检测(三)(建议用时:90分钟) 一、选择题1.设全集U 为整数集,集合A ={x ∈N |y =7x -x 2-6},B ={x ∈Z |-1<x ≤3},则右图中阴影部分表示的集合的真子集的个数为( ) A.3B.4C.7D.8解析 由于A ={x ∈N |y =7x -x 2-6}={x ∈N |7x -x 2-6≥0}={x ∈N |1≤x ≤6},由题意知,图中阴影部分表示的集合为A ∩B ={1,2,3},所以其真子集有∅,{1},{2},{3},{1,2},{1,3},{2,3},共7个. 答案 C2.曲线y =x 2+ln x 在点(1,1)处的切线方程为( ) A.3x -y -2=0 B.x -3y +2=0 C.3x +y -4=0D.x +3y -4=0解析 y ′=2x +1x ,故y ′|x =1=3,故在点(1,1)处的切线方程为y -1=3(x -1),化简整理得3x -y -2=0. 答案 A3.若函数f (x )=x 2+ax +1在x =1处取极值,则a =( )A.1B.2C.3D.4解析 f ′(x )=⎝ ⎛⎭⎪⎪⎫x 2+a x +1′=(x 2+a )′(x +1)-(x 2+a )(x +1)′(x +1)2=x 2+2x -a(x +1)2, ∵x =1为函数的极值点, ∴f ′(1)=0,即3-a =0,∴a =3. 答案 C4.(2022·金华重点中学联考)设x ,y ∈R ,则“x 2+y 2≥9”是“x >3且y ≥3”的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件D.既不充分也不必要条件解析 当x =-4时满足x 2+y 2≥9,但不满足x >3,所以充分性不成立;反之,当x >3且y ≥3时,肯定有x 2+y 2≥9,所以必要性成立,即“x 2+y 2≥9”是“x >3且y ≥3”的必要不充分条件,故选B. 答案 B5.(2022·杭州质量检测)如图,在平面直角坐标系中,AC 平行于x 轴,四边形ABCD 是边长为1的正方形,记四边形位于直线x =t (t >0)左侧图形的面积为f (t ),则f (t )的大致图象是( )解析 由题意得,f (t )=⎩⎪⎨⎪⎧t 2⎝⎛⎭⎪⎫0<t ≤22,-(t -2)2+1⎝ ⎛⎭⎪⎫22<t <2,1(t ≥2),故其图象为C. 答案 C6.已知a ≤1-x x +ln x 对任意x ∈⎣⎢⎡⎦⎥⎤12,2恒成立,则a 的最大值为( )A.0B.1C.2D.3解析 令f (x )=1-x x +ln x ,则f ′(x )=x -1x 2,当x ∈⎣⎢⎡⎭⎪⎫12,1时,f ′(x )<0,当x ∈(1,2]时,f ′(x )>0,∴f (x )在⎣⎢⎡⎭⎪⎫12,1上单调递减,在(1,2]上单调递增,∴f (x )min =f (1)=0,∴a ≤0. 答案 A7.设函数f (x )在定义域内可导,y =f (x )的图象如图所示,则函数y =f ′(x )的图象可能是( )解析 如图所示,当x ∈(-∞,x 0)时,函数f (x )为增函数,当x ∈(x 0,0)和x ∈(0,+∞)时,函数f (x )为减函数,∴x =x 0是函数f (x )的极大值点,可得f ′(x 0)=0,且当x ∈(-∞,x 0)时,f ′(x )>0,当x ∈(x 0,0)和x ∈(0,+∞)时,f ′(x )<0.由此对比各个选项,可得函数y =f ′(x )的图象只有A 项符合.答案 A8.对任意实数a ,b 定义运算“⊗”:a ⊗b =⎩⎨⎧b ,a -b ≥1,a ,a -b <1.设f (x )=(x 2-1)⊗(4+x ),若函数y =f (x )+k 的图象与x 轴恰有三个不同交点,则k 的取值范围是( ) A.(-2,1) B.[0,1] C.[-2,0)D.[-2,1)解析 当x 2-1≥4+x +1,即x ≤-2或x ≥3时,f (x )=4+x ,当x 2-1<4+x +1,即-2<x <3时,f (x )=x 2-1,如图所示,作出f (x )的图象,由图象可知,要使-k =f (x )有三个根,需满足-1<-k ≤2,即-2≤k < 1.答案 D9.函数f (x )的定义域是R ,f (0)=2,对任意x ∈R ,f (x )+f ′(x )>1,则不等式e x ·f (x )>e x +1的解集为( ) A.{x |x >0} B.{x |x <0}C.{x |x <-1或x >1}D.{x |x <-1或0<x <1}解析 构造函数g (x )=e x ·f (x )-e x .由于g ′(x )=e x ·f (x )+e x ·f ′(x )-e x =e x [f (x )+f ′(x )]-e x >e x -e x =0,所以g (x )=e x ·f (x )-e x 为R 上的增函数.由于g (0)=e 0·f (0)-e 0=1,故原不等式化为g (x )>g (0),解得x >0.答案 A10.已知函数f (x )=x (ln x -ax )有两个极值点,则实数a 的取值范围是( ) A.(-∞,0) B.⎝ ⎛⎭⎪⎫0,12 C.(0,1)D.(0,+∞)解析 由题知,x >0,f ′(x )=ln x +1-2ax ,由于函数f (x )有两个极值点,则f ′(x )=0有两个不等的正根,故y =ln x +1与y =2ax 的图象有两个不同的交点(x >0),则a >0.设函数y =ln x +1上任一点(x 0,1+ln x 0)处的切线为l ,则k l =y ′=1x 0,当直线l 过坐标原点时,1x 0=1+ln x 0x 0,则x 0=1,从而令2a =1,∴a =12.结合函数图象知0<a <12. 答案 B 二、填空题11.已知函数f (x )=f ′⎝ ⎛⎭⎪⎫π4cos x +sin x ,则f ⎝ ⎛⎭⎪⎫π4的值为________.解析 ∵f ′(x )=-f ′⎝ ⎛⎭⎪⎫π4sin x +cos x ,∴f ′⎝ ⎛⎭⎪⎫π4=-f ′⎝ ⎛⎭⎪⎫π4sin π4+cos π4, ∴f ′⎝ ⎛⎭⎪⎫π4=2-1,∴f ⎝ ⎛⎭⎪⎫π4=(2-1)cos π4+sin π4=1. 答案 112.(2022·杭州高三模拟)给出下列命题:①“数列{a n }为等比数列”是“数列{a n a n +1}为等比数列”的充分不必要条件; ②“a =2”是“函数f (x )=|x -a |在区间[2,+∞)上为增函数”的充要条件;③“m =3”是“直线(m +3)x +my -2=0与直线mx -6y +5=0相互垂直”的充要条件; ④设a ,b ,c 分别是△ABC 三个内角A ,B ,C 所对的边,若a =1,b =3,则A =30°是B =60°的必要不充分条件. 其中真命题的序号是________.解析 对于①,当数列{a n }为等比数列时,易知数列{a n a n +1}是等比数列,但当数列{a n a n +1}为等比数列时,数列{a n }未必是等比数列,如数列1,3,2,6,4,12,8明显不是等比数列,而相应的数列3,6,12,24,48,96是等比数列,因此①正确;对于②,当a ≤2时,函数f (x )=|x -a |在区间[2,+∞)上是增函数,因此②不正确;对于③,当m =3时,相应两条直线垂直,反之,这两条直线垂直时,不肯定有m =3,也可能m =0.因此③不正确;对于④,由题意得b a =sin B sin A =3,若B =60°,则sin A =12,留意到b >a ,故A =30°,反之,当A =30°时,有sin B =32,由于b >a ,所以B =60°或B =120°,因此④正确.综上所述,真命题的序号是①④. 答案 ①④13.(2022·杭州重点中学联考)对于任意x ∈R ,满足(a -2)x 2+2(a -2)x -4<0恒成立的全部实数a构成集合A ,使不等式|x -4|+|x -3|<a 的解集为空集的全部实数a 构成集合B ,则A ∩(∁R B )=________.解析 对于任意x ∈R ,不等式(a -2)x 2+2(a -2)x -4<0恒成立,则a =2或⎩⎪⎨⎪⎧a <2,Δ=4(a -2)2+16(a -2)<0,解得-2<a ≤2,所以集合A =(-2,2].当不等式|x -4|+|x -3|<a 有解时,a >(|x -4|+|x -3|)min =1,所以解集为空集的全部实数a 构成集合B =(-∞,1], 则∁R B =(1,+∞),所以A ∩(∁R B )=(-2,2]∩(1,+∞)=(1,2]. 答案 (1,2]14.若不等式2x ln x ≥-x 2+ax -3对x ∈(0,+∞)恒成立,则实数a 的取值范围是________. 解析 2x ln x ≥-x 2+ax -3,则a ≤2ln x +x +3x ,设h (x )=2ln x +x +3x (x >0),则h ′(x )=(x +3)(x -1)x 2.当x ∈(0,1)时,h ′(x )<0,函数h (x )单调递减;当x ∈(1,+∞)时,h ′(x )>0,函数h (x )单调递增,所以h (x )min =h (1)=4,则a ≤h (x )min =4,故实数a 的取值范围是(-∞,4]. 答案 (-∞,4] 三、解答题15.已知函数f (x )=e x (ax +b )-x 2-4x ,曲线y =f (x )在点(0,f (0))处的切线方程为y =4x +4. (1)求a ,b 的值;(2)争辩f (x )的单调性,并求f (x )的极大值. 解 (1)f ′(x )=e x (ax +a +b )-2x -4.由已知得f (0)=4,f ′(0)=4,故b =4,a +b =8.从而a =4,b =4. (2)由(1)知,f (x )=4e x (x +1)-x 2-4x , f ′(x )=4e x(x +2)-2x -4=4(x +2)⎝ ⎛⎭⎪⎫e x -12.令f ′(x )=0,得x =-ln 2或x =-2.从而当x ∈(-∞,-2)∪(-ln 2,+∞)时,f ′(x )>0; 当x ∈(-2,-ln 2)时,f ′(x )<0.故f (x )在(-∞,-2),(-ln 2,+∞)上单调递增,在(-2,-ln 2)上单调递减. 当x =-2时,函数f (x )取得极大值,极大值为f (-2)=4(1-e -2.) 16.(2022·南山中学月考)已知函数f (x )=sin x (x ≥0),g (x )=ax (x ≥0). (1)若f (x )≤g (x )恒成立,求实数a 的取值范围; (2)当a 取(1)中的最小值时,求证:g (x )-f (x )≤16x 3. (1)解 令h (x )=sin x -ax (x ≥0), 则h ′(x )=cos x -a .①若a ≥1,h ′(x )=cos x -a ≤0,h (x )=sin x -ax (x ≥0)单调递减,h (x )≤h (0)=0, 则sin x ≤ax (x ≥0)成立.②若0<a <1,存在x 0∈⎝⎛⎭⎪⎫0,π2,使得cos x 0=a ,当x ∈(0,x 0),h ′(x )=cos x -a >0,h (x )=sin x -ax (x ∈(0,x 0))单调递增,h (x )>h (0)=0,不合题意.③当a ≤0,结合f (x )与g (x )的图象可知明显不合题意. 综上可知,a ≥1.即实数a 的取值范围是[1,+∞). (2)证明 当a 取(1)中的最小值为1时, g (x )-f (x )=x -sin x .设H (x )=x -sin x -16x 3(x ≥0),则H ′(x )=1-cos x -12x 2.令G (x )=1-cos x -12x 2, 则G ′(x )=sin x -x ≤0(x ≥0),所以G (x )=1-cos x -12x 2在[0,+∞)上单调递减,此时G (x )=1-cos x -12x 2≤G (0)=0, 即H ′(x )=1-cos x -12x 2≤0,所以H (x )=x -sin x -16x 3在x ∈[0,+∞)上单调递减.所以H (x )=x -sin x -16x 3≤H (0)=0, 则x -sin x ≤16x 3(x ≥0).所以,当a 取(1)中的最小值时,g (x )-f (x )≤16x 3. 17.已知函数f (x )=a ln x x +1+bx,曲线y =f (x )在点(1,f (1))处的切线方程为x +2y -3=0. (1)求a ,b 的值;(2)假如当x >0,且x ≠1时,f (x )>ln x x -1+kx,求k 的取值范围. 解 (1)f ′(x )=a ⎝ ⎛⎭⎪⎫x +1x -ln x(x +1)2-bx 2.由于直线x +2y -3=0的斜率为-12,且过点(1,1),故⎩⎪⎨⎪⎧f (1)=1,f ′(1)=-12,即⎩⎪⎨⎪⎧b =1,a 2-b =-12.解得a =1,b =1. (2)由(1)知f (x )=ln x x +1+1x,所以 f (x )-⎝ ⎛⎭⎪⎫ln x x -1+k x =11-x 2⎣⎢⎡⎦⎥⎤2ln x +(k -1)(x 2-1)x . 考虑函数h (x )=2ln x +(k -1)(x 2-1)x (x >0),则h ′(x )=(k -1)(x 2+1)+2xx 2.(ⅰ)设k ≤0,由h ′(x )=k (x 2+1)-(x -1)2x 2知,当x ≠1时,h ′(x )<0,而h (1)=0,故当x ∈(0,1)时,h (x )>0.可得11-x 2h (x )>0; 当x ∈(1,+∞)时,h (x )<0,可得11-x 2h (x )>0. 从而当x >0,且x ≠1时,f (x )-⎝ ⎛⎭⎪⎫ln x x -1+k x >0,即f (x )>ln x x -1+kx.(ⅱ)设0<k <1,由于当x ∈⎝ ⎛⎭⎪⎫1,11-k 时,(k -1)(x 2+1)+2x >0.故h ′(x )>0,而h (1)=0,故当x ∈⎝ ⎛⎭⎪⎫1,11-k 时,h (x )>0,可得11-x 2h (x )<0.与题设冲突.(ⅲ)设k ≥1,此时h ′(x )>0,而h (1)=0,故当x ∈(1,+∞)时,h (x )>0,可得11-x 2h (x )<0,与题设冲突.综合得k 的取值范围为(-∞,0]. 18.(2022·陕西检测)设函数f (x )=e x -ax -1.(1)若函数f (x )在R 上单调递增,求a 的取值范围; (2)当a >0时,设函数f (x )的最小值为g (a ),求证: g (a )≤0;(3)求证:对任意的正整数n ,都有1n +1+2n +1+3n +1+…+n n +1<(n +1)n +1.(1)解 由题意知f ′(x )=e x -a ≥0对x ∈R 均成立,又e x >0(x ∈R ),故a 的取值范围为(-∞,0].(2)证明 由a >0,及f ′(x )=e x -a 可得,函数f (x )在(-∞,ln a )上单调递减,在(ln a ,+∞)上单调递增,故函数f (x )的最小值为g (a )=f (ln a )=e ln a -a ln a -1=a -a ln a -1,则g ′(a )=-ln a , 故当a ∈(0,1)时,g ′(a )>0,当a ∈(1,+∞)时,g ′(a )<0,从而可知g (a )在(0,1)上单调递增,在(1,+∞)上单调递减,又g (1)=0,故g (a )≤0. (3)证明 当a =1时,f (x )=e x -x -1,由(2)可知,e x -x -1≥0,当且仅当x =0时等号成立. ∴当x ≠0时,总有e x >x +1.于是,可得当x ≠0时,(x +1)n +1<(e x )n +1=e (n +1)x (n ∈N *). 令x +1=1n +1,即x =-n n +1,可得⎝ ⎛⎭⎪⎫1n +1n +1<e -n;令x +1=2n +1,即x =-n -1n +1,可得⎝ ⎛⎭⎪⎫2n +1n +1<e -(n -1);令x +1=3n +1,即x =-n -2n +1,可得⎝ ⎛⎭⎪⎫3n +1n +1<e -(n -2);……令x +1=n n +1,即x =-1n +1,可得⎝ ⎛⎭⎪⎫n n +1n +1<e -1.对以上各式求和可得:⎝ ⎛⎭⎪⎫1n +1n +1+⎝ ⎛⎭⎪⎫2n +1n +1+⎝ ⎛⎭⎪⎫3n +1n +1+…+⎝ ⎛⎭⎪⎫n n +1n +1<e -n +e -(n -1)+e -(n -2)+…+e -1=e -n (1-e n )1-e =e -n -11-e =1-e -n e -1<1e-1<1.故对任意的正整数n ,都有1n +1+2n +1+3n +1+…+n n+1<(n +1)n +1.阶段。
2021高考数学新高考版一轮习题:专题3 阶段滚动检测(二) (含解析)

一、单项选择题1.已知集合A ={x |-2≤x ≤3},B ={x |x 2-3x ≤0},则A ∪B 等于( ) A .[-2,3] B .[-2,0] C .[0,3]D .[-3,3]2.已知条件p :|x +1|>2,条件q :x >a ,且綈p 是綈q 的充分不必要条件,则实数a 的取值范围是( )A .a ≤1B .a ≥1C .a ≥-1D .a ≤-33.(2020·重庆模拟)命题p :∃x 0>0,x 0+1x 0=2,则綈p 为( )A .∀x >0,x +1x =2B .∀x >0,x +1x ≠2C .∀x ≤0,x +1x=2D .∀x ≤0,x +1x≠24.已知函数f (x )=⎩⎪⎨⎪⎧log 3(x +m )-1,x ≥0,12 019,x <0的图象经过点(3,0),则f (f (2))等于( )A .2 019 B.12 019C .2D .15.若函数f (x )=13x 3-f ′(-1)x 2+x +5,则f ′(1)的值为( )A .2B .-2C .6D .-66.三个数a =0.312,b =log 20.31,c =20.31之间的大小关系为( ) A .a <c <b B .a <b <c C .b <a <cD .b <c <a7.(2019·湖南师大附中博才实验中学月考)函数f (x )=e x +1x (1-e x )(其中e 为自然对数的底数)的图象大致为( )8.函数f (x )=2e x -a (x -1)2有且只有一个零点,则实数a 的取值范围是( ) A.⎝⎛⎭⎫e 4,1 B .(1,2e] C.⎝⎛⎭⎫0,e 32 D.⎝⎛⎭⎫-∞,e 32 二、多项选择题9.已知a >b >0,c >1,则下列各式不成立的是( ) A .sin a >sin b B .c a >c b C .a c <b cD.c -1b <c -1a10.下列命题为假命题的是( ) A .“A ∩B =A ”的充要条件是“A ⊆B ”B .若a ,b ,c ∈R ,则“ac 2>bc 2”是“a >b ”的充分不必要条件C .若椭圆x 216+y 225=1的两个焦点为F 1,F 2,且弦AB 过点F 1,则△ABF 2的周长为16D .“a =1”是“函数f (x )=a -e x1+a e x 在定义域上是奇函数”的充要条件11.在下列函数中,其中最小值为2的函数的是( ) A .y =⎪⎪⎪⎪x +1x B .y =x 2+2x 2+1C .y =log 2x +log x 2(x >0且x ≠1)D .y =tan x +1tan x ,0<x <π212.下列函数中,满足“对任意的x 1,x 2∈(0,+∞),使得f (x 1)-f (x 2)x 1-x 2<0”成立的是( )A .f (x )=-x 2-2x +1B .f (x )=x -1xC .f (x )=x +1D .f (x )=12log (2)x +1三、填空题13.已知函数f (x )=x 2+2(a -1)x +2在区间(-∞,5]上为减函数,则实数a 的取值范围为________;当a =2时,函数f (x )在[-3,2]上的值域为________.14.在曲线f (x )=sin x -cos x ,x ∈⎝⎛⎭⎫-π2,π2的所有切线中,斜率为1的切线方程为________. 15.设函数f (x )=e x -1e x -2x ,若f (a -3)+f (2a 2)≤0,则实数a 的取值范围为________.16.对一定义域为D 的函数y =f (x )和常数c ,若对任意正实数ξ,∃x ∈D 使得0<|f (x )-c |<ξ成立,则称函数y =f (x )为“敛c 函数”,现给出如下函数:①f (x )=x (x ∈Z );②f (x )=⎝⎛⎭⎫12x+1(x ∈Z );③f (x )=log 2x ;④f (x )=x -1x .其中为“敛1函数”的有________.(填序号)四、解答题17.设函数f (x )=6+x +ln(2-x )的定义域为A ,集合B ={x |2x >1}. (1)求A ∪B ;(2)若集合{x |a <x <a +1}是A ∩B 的子集,求实数a 的取值范围.18.计算:(1)(3-1)0+(3-π)2+1318-⎛⎫⎪⎝⎭;(2)2lg 5+lg 25+2log32.19.(2019·天津调研)设函数f (x)=lgax+1(a∈R),且f (1)=0.(1)求a的值;(2)求f (x)的定义域;(3)判断f (x)在区间(0,+∞)上的单调性,并用单调性定义证明.20.为了落实国务院“提速降费”的要求,某市移动公司欲下调移动用户消费资费.已知该公司共有移动用户10万人,人均月消费50元.经测算,若人均月消费下降x %,则用户人数会增加x8万人.(1)若要保证该公司月总收入不减少,试求x 的取值范围;(2)为了布局“5G 网络”,该公司拟定投入资金进行5G 网络基站建设,投入资金方式为每位用户月消费中固定划出2元进入基站建设资金,若使该公司总盈利最大,试求x 的值.(总盈利资金=总收入资金-总投入资金)21.已知函数f (x )=13x 3+ax +b (a ,b ∈R )在x =2处取得极小值-43.(1)求函数f (x )的单调递增区间;(2)若13x 3+ax +b ≤m 2+m +103对x ∈[-4,3]恒成立,求实数m 的取值范围.22.(2019·北京四中期中)已知函数f (x )=ln x +1x .(1)求函数f (x )的单调区间;(2)设函数g (x )=(x +1)ln x -x +1,证明:当x >0且x ≠1时,x -1与g (x )同号.答案精析1.A 2.B 3.B 4.B 5.C 6.C 7.A 8.C 9.ACD 10.CD11.ABD [对于A ,y =⎪⎪⎪⎪x +1x =|x |+1|x |≥2|x |·1|x |=2,当且仅当x =±1时取等号,正确; 对于B ,y =x 2+2x 2+1=x 2+1+1x 2+1≥2,当且仅当x =0时取等号,正确;对于C ,当x ∈(0,1)时,log x 2<0,log 2x <0,得y =log 2x +log x 2(x >0且x ≠1)的最小值不可能为2,错误;对于D ,x ∈⎝⎛⎭⎫0,π2,所以tan x ∈(0,+∞),令tan x =t ,所以t ∈(0,+∞),所以y =t +1t ≥2,当且仅当t =1时取等号,正确.]12.AD [根据题意,“对任意的x 1,x 2∈(0,+∞),使得f (x 1)-f (x 2)x 1-x 2<0”,则函数f (x )在(0,+∞)上为减函数,据此依次分析选项:对于选项A ,f (x )=-x 2-2x +1为二次函数,其对称轴为x =-1,在(0,+∞)上单调递减,符合题意;对于选项B ,f (x )=x -1x ,其导数f ′(x )=1+1x 2>0,所以f (x )在(0,+∞)上单调递增,不符合题意;对于选项C ,f (x )=x +1为一次函数,所以f (x )在(0,+∞)上单调递增,不符合题意;对于选项D ,f (x )=12log (2)x +1,在(0,+∞)上单调递减,符合题意.] 13.(-∞,-4] [1,10] 14.x -y -1=0 15.⎣⎡⎦⎤-32,1 解析 根据题意,函数f (x )=e x -1e x -2x ,其导数f ′(x )=e x +1e x -2,f ′(x )=e x +1e x -2≥0恒成立,则函数f (x )在R 上为增函数,又因为f (-x )=e -x -e x +2x =-f (x ),所以f (x )为奇函数,原式等价于f (a -3)≤-f (2a 2), f (a -3)≤f (-2a 2),a -3≤-2a 2,2a 2+a -3≤0, (2a +3)(a -1)≤0,-32≤a ≤1.16.②③④解析 由新定义知,对任意正实数ξ,∃x ∈D 使得0<|f (x )-c |<ξ成立, 即0<|f (x )-c |<ξ有解.对于函数①解得,1-ξ<x <1+ξ,且x ≠1,x ∈Z ,因为ξ为任意正实数,所以无解,故函数①不是“敛1函数”;对于函数②解得,x >-log 2ξ且x ∈Z ,故函数②是“敛1函数”;对于函数③解得,21-ξ<x <21+ξ,且x ≠2,故函数③是“敛1函数”;对于函数④解得,|x |>1ξ,故函数④是“敛1函数”.因此正确答案为②③④.17.解 (1)由⎩⎪⎨⎪⎧6+x ≥0,2-x >0得,-6≤x <2,由2x >1得,x >0,∴A =[-6,2), B =(0,+∞), ∴A ∪B =[-6,+∞). (2)A ∩B =(0,2),∵集合{x |a <x <a +1}是A ∩B 的子集,∴⎩⎪⎨⎪⎧a ≥0,a +1≤2,解得0≤a ≤1,∴a 的取值范围是[0,1].18.解 (1)原式=1+|3-π|+2=1+π-3+2=π. (2)原式=lg 25+lg 25+3=lg ⎝⎛⎭⎫25×25+3=4.19.解 (1)根据题意,函数f (x )=lgax +1(a ∈R ),且f (1)=0, 则f (1)=lg a 2=0,则a2=1,解得a =2.(2)根据题意,f (x )=lg2x +1, 必有2x +1>0,解得x >-1,即函数f (x )的定义域为(-1,+∞). (3)根据题意,f (x )=lg 2x +1在(0,+∞)上的单调递减, 证明:设0<x 1<x 2, f (x 1)-f (x 2)=lg2x 1+1-lg 2x 2+1=lgx 2+1x 1+1=lg(x 2+1)-lg(x 1+1), 又由0<x 1<x 2,则lg(x 2+1)>lg(x 1+1),即f (x 1)-f (x 2)>0,即函数f (x )在(0,+∞)上单调递减. 20.解 (1)根据题意,设该公司的总收入为W 万元, 则W =50⎝⎛⎭⎫10+x 8⎝⎛⎭⎫1-x100,0<x <100, 若该公司月总收入不减少, 则有50⎝⎛⎭⎫10+x 8⎝⎛⎭⎫1-x100≥10×50, 解得0<x ≤20.(2)设该公司盈利为y 万元,则y =50⎝⎛⎭⎫10+x 8⎝⎛⎭⎫1-x 100-2⎝⎛⎭⎫10+x 8=-x216+x +480,0<x <100, 结合二次函数的性质分析可得,当x =8时,该公司的总盈利最大. 21.解 (1)f ′(x )=x 2+a , 由f ′(2)=0得a =-4,由f (2)=-43得b =4,则f (x )=13x 3-4x +4,令f ′(x )=x 2-4>0得x >2或x <-2,∴f (x )的单调递增区间为(-∞,-2),(2,+∞). (2)由f (-4)=-43,f (-2)=283,f (2)=-43,f (3)=1,所以f (x )在[-4,3]上的最大值为283,要使13x 3+ax +b ≤m 2+m +103对x ∈[-4,3]恒成立,只要f (x )max ≤m 2+m +103就可以了,即283≤m 2+m +103, 解得m ≥2或m ≤-3,所以实数m 的取值范围是(-∞,-3]∪[2,+∞). 22.(1)解 函数f (x )的定义域是(0,+∞), 又f ′(x )=1x -1x 2=x -1x 2,令f ′(x )=0,得x =1,当x 变化时,f ′(x )与f (x )的变化情况如下表,所以f (x )的单调递增区间是(1,+∞),单调递减区间是(0,1). (2)证明 函数g (x )的定义域是(0,+∞), 又g ′(x )=ln x +x +1x -1=ln x +1x =f (x ),由(1)可知,f (x )min =f (1)=1, 所以当x >0时,g ′(x )>0,所以g(x)在区间(0,+∞)上单调递增.因为g(1)=0,所以当x>1时,g(x)>g(1)=0且x-1>0;当0<x<1时,g(x)<g(1)=0且x-1<0,所以当x>0且x≠1时,x-1与g(x)同号.。
2011年高考地理38分钟阶段性同步滚动检测 产业转移

2011年高考地理38分钟阶段性同步滚动检测(32)(2010-08-19 07:33:51)转载标签:经济产业转移高考地理内部交易劳动力日本启迪慧想校园分类:教改鸡精(地理教育教学研究)2011年高考地理38分钟阶段性同步滚动检测(32)国际产业转移(附答案解析)注意事项:1.本试卷分第1卷(选择题)和第Ⅱ卷(非选择题)两部分。
满分72分。
考试时间38分钟。
2.考查范围:国际产业转移第1卷(选择题共60分)一.选择题(共60分)(一)单项选择题:本大题共18小题,每小题2分,共36分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.发展中国家为了吸引发达国家来投资,首先要改善投资环境以减少企业生产的内部交易成本,下列举措中哪个不是由发展中国家提供的?()A.劳动力B.基础设施C.技术、设备D.服务2.一些发达国家将部分家电生产企业迁往中国、东南亚等地,主要是考虑利用当地()A.洁净的环境B.先进的科技C.廉价劳动力和土地D.便捷的交通3.近年来,台湾电子企业为降低生产成本,提高国际竞争力,生产工厂大量西移至广东东莞等地,其考虑的主要因素是()A.管理成本B.劳动成本C.市场成本D.原料成本4.与北京、上海等地相比,呼和浩特建乳品加工厂的优越条件是()A.交通运输便捷B.原料供应充足C.市场庞大D.技术领先5.影响国际产业转移的三大主要因素中,不包括()A.市场B.劳动力C.环境污染D.内部交易成本6.在青岛市黄岛经济开发区建有许多跨国公司的出口加工区,这些出口加工企业的兴建主要是什么因素的影响?()A.劳动力因素B.内部交易成本因素C.国际经济形势变化D.市场因素7.20世纪下半叶,东亚的劳动密集型产业转移比较典型,20世纪80年代产业转移的主要对象地区是()A.我国中西部地区B.我国东部沿海地区C.台湾、香港地区D.韩国下图表示20世纪下半叶东亚劳动密集型产业转移主要对象国(或地区)的变化。
2024届重庆市普通高中高三第三次教学质量检测试题考试数学试题

2024届重庆市普通高中高三第三次教学质量检测试题考试数学试题注意事项:1. 答题前,考生先将自己的姓名、准考证号填写清楚,将条形码准确粘贴在考生信息条形码粘贴区。
2.选择题必须使用2B 铅笔填涂;非选择题必须使用0.5毫米黑色字迹的签字笔书写,字体工整、笔迹清楚。
3.请按照题号顺序在各题目的答题区域内作答,超出答题区域书写的答案无效;在草稿纸、试题卷上答题无效。
4.保持卡面清洁,不要折叠,不要弄破、弄皱,不准使用涂改液、修正带、刮纸刀。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.定义在R 上函数()f x 满足()()f x f x -=,且对任意的不相等的实数[)12,0,x x ∈+∞有()()12120f x f x x x -<-成立,若关于x 的不等式()()()2ln 3232ln 3f mx x f f mx x --≥--++在[]1,3x ∈上恒成立,则实数m 的取值范围是( ) A .1ln6,126e ⎡⎤+⎢⎥⎣⎦B .1ln3,126e ⎡⎤+⎢⎥⎣⎦C .1ln3,23e ⎡⎤+⎢⎥⎣⎦D .1ln6,23e ⎡⎤+⎢⎥⎣⎦2.执行如下的程序框图,则输出的S 是( )A .36B .45C .36-D .45- 3.用数学归纳法证明,则当时,左端应在的基础上加上( )A .B .C .D .4.在关于x 的不等式2210ax x ++>中,“1a >”是“2210ax x ++>恒成立”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件5.已知复数z 满足()11z i i +=-(i 为虚数单位),则z 的虚部为( )A .i -B .iC .1D .1-6.己知函数()()1,0,ln ,0,kx x f x x x ->⎧=⎨--<⎩若函数()f x 的图象上关于原点对称的点有2对,则实数k 的取值范围是( )A .(),0-∞B .()0,1C .()0,∞+D .10,2⎛⎫ ⎪⎝⎭7.用一个平面去截正方体,则截面不可能是( ) A .正三角形B .正方形C .正五边形D .正六边形8.已知集合2{|1}A x x =<,{|ln 1}B x x =<,则 A .{|0e}A B x x =<< B .{|e}A B x x =< C .{|0e}A B x x =<<D .{|1e}AB x x =-<<9.已知集合{}1,0,1,2A =-,{}|lg(1)B x y x ==-,则A B =( )A .{2}B .{1,0}-C .{}1-D .{1,0,1}-10.已知i 为虚数单位,实数,x y 满足(2)x i i y i +=-,则||x yi -= ( ) A .1B .2C .3D .511.如图,点E 是正方体ABCD -A 1B 1C 1D 1的棱DD 1的中点,点F ,M 分别在线段AC ,BD 1(不包含端点)上运动,则( )A .在点F 的运动过程中,存在EF //BC 1B .在点M 的运动过程中,不存在B 1M ⊥AEC .四面体EMAC 的体积为定值D .四面体FA 1C 1B 的体积不为定值 12.51(1)x x-+展开项中的常数项为 A .1B .11C .-19D .51二、填空题:本题共4小题,每小题5分,共20分。
2024-2025学年云南省昆明市高三第三次联考数学检测试卷

2024-2025学年云南省昆明市高三第三次联考数学检测试卷本试卷共19题.全卷满分150分.考试用时120分钟.注意事项:1.答题前,先将自己的姓名、准考证号填写在试卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置.2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.写在试卷、草稿纸和答题卡的非答题区域均无效.3.非选择题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内.写在试卷、草稿纸和答题卡上的非答题区域均无效.4.考试结束后,请将本试卷和答题卡一并上交.一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 下列说法错误的是( )A. 若随机变量,则当较小时,对应的正态曲线“瘦高”,随机变量X 的分()2,X N μσ~σ布比较集中B. 在做回归分析时,可以用决定系数刻画模型的回归效果,若越大,则说明模型拟合2R 2R 的效果越好C. 在一元线性回归模型中,如果相关系数,表明两个变量的相关程度很强0.98r =D. 对于一组数据,,…,,若所有数据均变成原来的2倍,则变为原来的2倍1x 2x n x 2s 2. 若的展开式中第2项与第8项的系数相等,则展开式中系数最大的项为( 1nx x ⎛⎫+ ⎪⎝⎭)A. 第3项B. 第4项C. 第5项D. 第6项3. 函数的部分图象大致为()()()e1cos e 1xx x f x +=-A.B.C.D.4. 已知长方体的体积为,且,则长方体外1111ABCD A B C D -1612AA =1111ABCD A B C D -接球体积的最小值为()A.D. 25π6π125π5. 在平面内,设是直线的法向量(直线的法向量:直线的方向向量为,若向量,n l l a n a ⊥则向量叫做直线l 的法向量),是平面内的两个定点,,,若动点P 满n,M N M l ∈N l ∉足.则动点P 的轨迹为()PM n PN n⋅=A. 圆B. 椭圆C. 双曲线D. 抛物线6. 已知,,,是方程的两个根,则(α()0,πβ∈tan αtan β240x -+=αβ+=)A. B. C. D. 或π32π34π3π32π37. 已知曲线的方程为,若经过点Γ()()222222220xy x y x y x y ++++--=的直线l 与曲线有四个交点,则直线l 的斜率的取值范围是()()4,2A --ΓA. B. 711,,12322⎛⎫⎛⎫ ⎪ ⎪⎝⎭⎝⎭177,,172323⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭ C. D. 7,123⎛⎫ ⎪⎝⎭1,17⎛⎫- ⎪⎝⎭8. 将1,2,3,4,5,6,7这七个数随机地排成一个数列、记第i 项为,若()1,2,,7i a i =⋅⋅⋅,,,则这样的数列共有( )123a a a <<345a a a >>567a a a <<A. 70个B. 71个C. 80个D. 81个二、多项选择题:本题共3小题,每小题6分,共18分.在每小题给出的四个选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.9. 已知复数z 不为0,其共轭复数为,下列说法正确的是( )z A.22z z=B. 复平面内,z 与所对应的点关于实轴对称z C. ,与都是实数z z +z z -z z ⋅D. 若,则z 在复平面内所对应的点的轨迹为圆1zz =10. 已知的内角A ,B ,C 的对边分别为a ,b ,c ,,.若三角形有两解,ABC V 8b =45C =︒则边c 的取值可以是( )A. 5B. 6C. 7D. 811. 已知双曲线,过原点的直线AC ,BD 分别交双曲线于A ,C 和B ,D 四点2213y x -=(A ,B ,C ,D 四点逆时针排列),且两直线斜率之积为,则的可能值为(13-tan AOB ∠)A.D.三、填空题:本题共3小题,每小题5分,共15分.12. 已知数列是公差不为0的等差数列,现从中随机删除两项,得到{}()16,n a n n *≤≤∈N 一个新的数列.这两组数据的极差相同的概率为______.13. 若函数在处有极小值,则______.()()2f x x x a =+1x =-a =14. 已知函数,为的零点,为()()sin f x x ωϕ=+0ω>π2ϕ≤π8x =-()f x π8x =图象的对称轴,且在上不单调,则的最小值为______.()f x ()f x ππ,186⎛⎫⎪⎝⎭ω四、解答题:本题共5小题,其中第15题13分,第16、17题15分,第18、19题17分,共77分.解答应写出文字说明、证明过程或演算步骤.15. 体育运动是强身健体的重要途径,随着“中国儿童青少年体育健康促进行动方案(2020-2030)”的发布,体育运动受到各地中小学的高度重视,众多青少年的体质健康得到很大的改善.我们把每周体育锻炼时间超过8小时的学生称为“运动达人”,为了了解“运动达人”与性别是否有关系,我们对随机抽取的80名学生的性别进行了统计,其中女生与男生的人数之比为,男生中“运动达人”占,女生中“运动达人”占.1:31234(1)根据所给数据完成下面的列联表,并判断能否有90%的把握认为“运动达人”与性22⨯别有关?女生男生合计运动达人非运动达人合计(2)现从抽取的“运动达人”中,按性别采用分层抽样抽取3人参加体育知识闯关比赛,已知其中男、女生独立闯关成功的概率分别为与,在恰有两人闯关成功的条件下,求有女生3423闯关成功的概率.附:,.()()()()()22n ad bc K a b c d a c b d -=++++n a b c d =+++()2P K k≥0.1000.0500.0250.010k2.7063.8415.0246.63516. 已知数列满足,,数列满足.{}n a 12a =()()12n n n a n a a n +⎧⎪=⎨+⎪⎩为奇数为偶数{}n b 21n n b a -=(1)求,的值;2b 3b (2)证明:数列是等差数列;{}n b (3)求数列的前项和.{}n a 2n 2n S 17. 如图,在四棱锥中,平面平面,是等边三角形,四P ABCD -PAD ⊥ABCD PAD △边形是梯形,且,,,点是ABCD //AB CD 2AD BD ==12DC AB ==G 的重心,与交于点.PAD △AC BDM (1)证明:平面;//GM PCD (2)求平面与平面的夹角的余弦值.PBC PAD 18. 已知F 为抛物线的焦点,点M 在抛物线C 上,O 为坐标原点,()2:20C x py p =>的外接圆与抛物线C 的准线相切,且该圆面积为.OFM △9π4(1)求抛物线C 的方程;(2)设,B 是抛物线C 上异于A 的一点,直线AB 与直线交于点P ,过点()2,1A 2y x =-P 作x 轴的垂线交抛物线C 于点N ,求点F 到直线的距离的取值范围.BN d 19. 已知函数,.()23ln f x x x a x=-+a ∈R (1)当时,求函数在区间上的最小值;1a =()f x []1,2x ∈(2)若函数在区间上单调递减,求a 的取值范围;()f x []1,2(3)若函数的图象上存在两点,,且,使得()g x ()11,A x y ()22,B x y 12x x <,则称为“拉格朗日中值函数”,并称线段的中()()1212122g x g x x x g x x -+⎛⎫'=⎪-⎝⎭()y g x =AB 点为函数的一个“拉格朗日平均值点”.试判断函数是否为“拉格朗日中值函数”,若是,()f x 判断函数的“拉格朗日平均值点”的个数;若不是,说明理由.()f x。
2022高考生物(全国卷 地区专用)总复习_阶段滚动练3(六~七单元) Word版含解析

阶段滚动练3(六~七单元)一、选择题1.(2021江苏扬州中学开学测试,18)下图甲是将加热杀死的S型细菌与R型活菌混合注射到小鼠体内后两种细菌的含量变化,图乙是利用同位素标记技术完成噬菌体侵染细菌试验的部分操作步骤。
下列相关叙述不正确的是( )A.图甲中AB对应的时间段内,小鼠体内还没形成大量的抗R型细菌的抗体B.图甲中,后期消灭的大量S型细菌是由R型细菌转化并增殖而来的C.图乙沉淀物中新形成的子代噬菌体完全没有放射性D.图乙中若用32P标记亲代噬菌体,裂解后子代噬菌体中大部分具有放射性2.R型肺炎双球菌无荚膜,菌落粗糙,对青霉素敏感。
S型肺炎双球菌有荚膜,菌落光滑,对青霉素敏感。
在多代培育的S型菌中分别出一种抗青霉素的S型(记为PenrS型)突变菌株。
现用S型菌、PenrS型菌与R 型菌进行一系列试验,其中对试验结果的猜测,不正确的是( )项目甲组乙组丙组丁组培育基含青霉素的培育基一般培育基含青霉素的培育基一般培育基试验处理S型菌的DNA和活的R型菌PenrS型菌的DNA和活的R型菌PenrS型菌的DNA和活的R型菌PenrS型菌的DNA、DNA酶和活R型菌结果猜测同时消灭光滑型和粗糙型两种菌落同时消灭光滑型和粗糙型两种菌落两种菌落都不行能消灭仅消灭粗糙型菌落A.甲组 B.乙组 C.丙组 D.丁组3.(2021安徽马鞍山二中期中,10)如图表示一个DNA分子的片段,下列有关表述正确的是( )A .④代表的物质中储存着遗传信息B.不同生物的DNA分子中④的种类无特异性C.转录时该片段的两条链都可作为模板链D.DNA分子中A与T碱基对含量越高,其结构越稳定4.(2021湖南长沙长郡中学月考,4)DNA分子中的碱基C被氧化后会转变为碱基U,细胞中的一种糖苷酶能够识别出碱基U,将其切除,之后核酸内切酶能识别和切除残留下的脱氧核糖和磷酸基团,最终由其他酶将缺口修复。
下列相关叙述正确的是( )A.细胞中糖苷酶被水解得到的单体可能是葡萄糖和氨基酸B.糖苷酶能识别和切割DNA分子中的磷酸二酯键C.DNA缺口修复需DNA聚合酶和DNA连接酶发挥作用D.若基因损伤未被准时修复肯定导致其100%的子代DNA具有突变基因5.下图表示DNA复制的过程,结合图示推断,下列有关叙述不正确的是( )A.DNA复制过程中首先需要解旋酶破坏DNA双链之间的氢键,解开双链B.DNA分子的复制具有双向复制的特点,生成的两条子链的方向相反C.从图示可知,DNA分子具有多起点复制的特点,缩短了复制所需的时间D.DNA分子的复制需要DNA聚合酶将单个脱氧核苷酸连接成为DNA片段6.Qβ噬菌体的遗传物质(QβRNA)是一条单链RNA,当噬菌体侵染大肠杆菌后,QβRNA马上作为模板翻译出成熟蛋白、外壳蛋白和RNA复制酶。
数学高三滚动测试卷

一、选择题(每题5分,共50分)1. 已知函数f(x) = 2x - 3,则f(-1)的值为()A. -5B. -2C. 1D. 42. 下列不等式中,正确的是()A. 3x > 2x + 1B. 3x ≤ 2x + 1C. 3x ≥ 2x + 1D. 3x < 2x + 13. 已知等差数列{an}的公差为d,若a1 = 2,a3 = 8,则d的值为()A. 2B. 3C. 4D. 54. 已知等比数列{bn}的公比为q,若b1 = 3,b3 = 27,则q的值为()A. 3B. 6C. 9D. 125. 若复数z满足|z - 2| = 3,则z的取值范围是()A. z = 5B. z = 1C. z = 0D. z = -16. 已知函数f(x) = x^2 - 4x + 4,则f(x)的对称轴为()A. x = 1B. x = 2C. x = 3D. x = 47. 若等差数列{an}的前n项和为Sn,且a1 = 2,S5 = 50,则公差d为()A. 4B. 5C. 6D. 78. 已知函数f(x) = |x - 2|,则f(x)在x = 2处的导数为()A. 0B. 1C. -1D. 不存在9. 若复数z满足|z - 1| = 2,则z的取值范围是()A. z = 3B. z = 1C. z = 0D. z = -110. 已知函数f(x) = (x - 1)^2,则f(x)在x = 1处的切线斜率为()A. 0B. 1C. -1D. 不存在二、填空题(每题5分,共50分)11. 已知等差数列{an}的公差为d,若a1 = 3,a4 = 11,则d的值为______。
12. 已知等比数列{bn}的公比为q,若b1 = 4,b3 = 64,则q的值为______。
13. 已知函数f(x) = 2x - 1,则f(-3)的值为______。
14. 已知复数z满足|z - 1| = 2,则z的取值范围是______。
2024-2025学年高三一轮复习联考(三)_全国卷文数(含答案)

2024届高三一轮复习联考(三)全国卷文科数学试题注意事项:1.答卷前,考生务必将自己的姓名、考场号、座位号、准考证号填写在答题卡上.2.回答选择题时,选出每小题答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号,回答非选择题时,将答案写在答题卡上,写在本试卷上无效.3.考试结束后,将本试卷和答题卡一并交回,考试时间为120分钟,满分150分一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}{}212,1A xx B x x =<<=∣∣,则A B ⋃=()A.[)1,2-B.(),2∞-C.[)1,3- D.[]1,2-2.命题2:,220p x R x x ∀∈+-<的否定p ⌝为()A.2000,220x R x x ∃∈+->B.2,220x R x x ∀∈+-C.2,220x R x x ∀∈+->D.2000,220x R x x ∃∈+-3.3.已知复数2(1i)z =+(i 为虚数单位),则复数z 的虚部为()A.2B.2- C.2iD.2i-4.若函数()222,0,log ,0,x x x f x x x ⎧-=⎨>⎩则()2f f ⎡⎤-=⎣⎦()A.2- B.2 C.3- D.35.已知1sin 62πα⎛⎫-= ⎪⎝⎭,则2cos 23πα⎛⎫+= ⎪⎝⎭()A.14-B.14C.12-D.126.函数()21x xe ef x x --=+在[]3,3-上的大致图象为()A.B.C. D.7.函数2sin cos21y x x=-+的最小值是()A.3-B.1-C.32- D.12-8.已知数列{}n a的前n项和22nS n n m=-++,且对任意*1,0n nn N a a+∈-<,则实数m 的取值范为是()A.()2,∞-+ B.(),2∞--C.()2,∞+ D.(),2∞-9.已知等比数列()*a满足4221,m nq a a a≠=,(其中,*m n N∈),则91m n+的最小值为()A.6 B.16 C.32 D.210.已知函数()cos3f x xπ⎛⎫=+⎪⎝⎭,若()f x在[]0,a上的值域为11,2⎡⎤-⎢⎥⎣⎦,则实数a的取值范为()A.40,3π⎛⎤⎥⎝⎦B.24,33ππ⎡⎤⎢⎥⎣⎦C.2,3π∞⎡⎫+⎪⎢⎣⎭ D.25,33ππ⎡⎤⎢⎥⎣⎦11.设4sin1,3sin2,2sin3a b c===,则()A.a b c<< B.c b a<<C.c a b<< D.a c b<<12.已矨,,A B C均在球O的球面上运动,且满足3AOBπ∠=,若三棱锥O ABC-体积的最大值为6,则球O的体积为()A.12πB.48πC.D.二、填空题:本题共4小题,每小题5分,共20分.13.已知()(1,,a k b==,若a b⊥,则k=__________.14.已知{}n a是各项不全为零的等差数列,前n项和是n S,且2024S S=,若()2626nS S m=≠,则正整数m=__________.15.设,m n为不重合的直线,,,αβγ为不重合的平面,下列是αβ∥成立的充分条件的有()(只填序号).①,m a m β⊂∥②,,m n n m αβ⊂⊥⊥③,αγβγ⊥⊥④,m m αβ⊥⊥16.已知函数()14sin ,01,2,1,x x x f x x x π-<⎧=⎨+>⎩若关于x 的方程()()()2[]210f x m f x m --+-=恰有5个不同的实数解,则实数m 的取值集合为__________.三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:60分.17.(12分)已知数列{}n a 满足12122,log log 1n n a a a +==+,(1)求数列{}n a 的通项公式;(2)求(){}32nn a -的前n 项和nS.18.(12分)已知ABC 中,三个内角,,A B C 的对边分别为,,,,cos cos 2cos 4a b c C a A c C b B π=+=.(1)求tan A ;(2)若c =,求ABC 的面积.19.(12分)如图,在四棱锥P ABCD -中,底面ABCD 是矩形,O 是BC 的中点,PB PC ==,22PD BC AB ===.(1)求证:平而PBC ⊥平面ABCD ;(2)求点A 到平面PCD 的距离.20.(12分)已知数列()n a 满足()21112122222326n n n n n a a a a n -+-++++=-⋅+ .(1)求{}n a 的通项公式;(2)若2n an n b a =+,求数列n b 的前n 项和T .21.(12分)已知函数()ln x af x ex x -=-+.(1)当1a =时,求曲线()f x 在点()()1,1f 处的切线方程,(2)当0a 时,证明,()2f x x >+.(二)选考题:共10分.请考生在第22,23题中任选一题作答.如果多做,则按所做的第一题计分.22.[选修4-4:坐标系与参数方程](10分)在平面直角坐标系,xOy 中,直线l的参数方程为2,21,2x a y t ⎧=+⎪⎪⎨⎪=⎪⎩(t 为参数),以O 为极点,x 轴的非负半轴为极轴建立极坐标系,曲线C 的极坐标方程为22413sin ρθ=+.(1)求直线l 和曲线C 的直角坐标方程;(2)若曲线C 经过伸缩变换,2,x x y y ⎧=⎪⎨⎪='⎩'得到曲线C ',若直线l 与曲线C '有公共点,试求a 的取值范围.23.[选修4-5:不等式选讲](10分)已知函数()22(0)f x x x t t =++->,若函数()f x 的最小值为5.(1)求t 的值;(2)若,,a b c 均为正实数,且2a b c t ++=,求1412a b c++的最小值.2024届高三一轮复习联考(三)全国卷文科数学参考答案及评分意见1.A【解析】由21x ,即()()110x x -+,解得11x -,所以{}11B xx =-∣,所以{12}A B xx ⋃=-<∣.故选A .2.D 【解析】2,220x x x ∀∈+-<R 的否定为:2000,220x x x ∃∈+-R ,故选D.3.A 【解析】2(1i)2i z =+=,即复数z 的虚部为2,故选A .4.D【解析】()()()222(2)228,8log 83f f -=--⨯-===,故选D.5.C 【解析】因为1sin 62πα⎛⎫-= ⎪⎝⎭,所以2211cos 2cos 2cos 22sin 11366622ππππααπαα⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫+=-+=--=--=-=- ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦.故选C.6.A 【解析】()()2e e 1x xf x f x x ---==-+,所以函数()y f x =是奇函数,排除B 选项,又()22e e 215f --=>,排除C ,D 选项,故选A.7.D 【解析】由题意,函数22sin cos212sin 2sin y x x x x =-+=+,令[]sin 1,1t x =∈-,可得221122222y t t t ⎛⎫=+=+- ⎪⎝⎭,当12t =-,即1sin 2x =-时,函数取得最小值,最小值为12-.故选D.8.A【解析】因为10n n a a +-<,所以数列{}n a 为递减数列,当2n 时,()2212(1)2123n n n a S S n n m n n m n -⎡⎤=-=-++---+-+=-+⎣⎦,故可知当2n 时,{}n a 单调递减,故{}n a 为递减数列,只需满足21a a <,即112m m-+⇒-.故选A .9.D【解析】由等比数列的性质,可得()911911918,10102888m n m n m n m n m n n m ⎛⎛⎫⎛⎫+=+=++=+++= ⎪ ⎪ ⎝⎭⎝⎭⎝,当且仅当6,2m n ==时,等号成立,因此,91m n +的最小值为2.故选D.10.B 【解析】()cos 3f x x π⎛⎫=+⎪⎝⎭,结合图象,()f x 的值域是11,,0,2333x a x a πππ⎡⎤-++⎢⎣⎦,于是533a πππ+,解得2433aππ,所以实数a 的取值范围为24,33ππ⎡⎤⎢⎥⎣⎦.故选B.11.B 【解析】设()()2sin cos sin ,x x x xf x f x x x -==',令()()cos sin ,sing x x x x g x x x =-'=-,当()0,x π∈时,()0g x '<,故()g x 在()0,π上递减,()()()00,0g x g f x <=∴<',故()sin xf x x=在()0,π上递减,023π<<< .()()sin3sin232,,2sin33sin232f f ∴<<<,故c b <,()()()sin 2012,sin1,sin22sin1,3sin232sin14sin12ππππππ-<<-<<<-<-<-,故b a <,故c b a <<,故选B.12.C 【解析】如图所示,当点C 位于垂直于面AOB 的直径端点时,三棱锥O ABC -的体积最大,设球O 的半径为R ,此时231133632212O ABC C AOB V V R R --==⨯⨯⨯==,故3R =O 的体积为343R V π==,故选C.13.3-【解析】0a b a b ⊥⇔⋅=,所以()(1,10,3k k ⋅=+==-.14.18【解析】设等差数列{}n a 的首项和公差分别为1,a d ,则2122n d d S n a n ⎛⎫=+- ⎪⎝⎭,所以n S 可看成关于n 的二次函数,由二次函数的对称性及202426,m S S S S ==,可得20242622m++=,解得18m =.15.④【解析】根据线面的位置关系易知,①②③中面α和面β可能相交也可能平行,④:若m α⊥且m β⊥,根据面面平行的判定可知垂直于同一直线的两平面互相平行,故④正确.16.()3,1--【解析】作出函数()f x 的大致图象,如图所示,令()t f x =,则()()()2[]210f x m f x m --+-=可化为()()()221110t m t m t m t --+-=-+-=,则11t =或21t m =-,则关于x 的方程()()()2[]210f x m f x m --+-=恰有5个不同的实数解等价于()t f x =的图象与直线12,t t t t ==的交点个数之和为5个,由图可得函数()t f x =的图象与直线1t t =的交点个数为2,所以()t f x =的图象与直线2t t =的交点个数为3个,即此时214m <-<,解得31m -<<-.17.【解析】(1)在数列{}n a 中,已知12122log log log 1n n n na a a a ++-==,所以12n na a +=,.即{}n a 是首项为12a =,公比为2的等比数列,所以()1*222n n n a n -=⨯=∈N .(2)由()()32322nn n a n -=-⨯,故()()231124272352322n n n S n n -=⨯+⨯+⨯++-⨯+-⨯ ,所以()()23412124272352322nn n S n n +=⨯+⨯+⨯++-⨯+-⨯ ,则()23123222322n n n S n +⎡⎤-=+⨯+++--⨯⎣⎦,()()()11212433221053212n n n n n ++-=-+⨯--⨯=-+-⋅-,故()110352n n S n +=+-⋅.18.【解析】(1)解法一:由题,cos cos 2cos a A c C b B +=,由正弦定理得,sin2sin cos sin cos B A A C C =+,.3,,sin2sin 2sin 2cos2422C A B C B A A A ππππ⎛⎫⎛⎫=++==-=-=- ⎪ ⎪⎝⎭⎝⎭,所以1cos2sin cos 2A A A -=+,221sin cos sin cos 2A A A A --=22tan 1tan 1tan 12A A A --=+,化简得2tan 2tan 30A A --=,解得tan 3A =或tan 1A =-(舍去).解法二:由题,cos cos 2cos a A c C b B +=,由正弦定理得,2sin2sin2sin2B A C =+,即()()()()2sin2sin sin B A C A C A C A C ⎡⎤⎡⎤=++-++--⎣⎦⎣⎦,即()()sin2sin cos B A C A C =+-,又A B C π++=,故()sin sin A C B +=,所以()2sin cos sin cos B B B A C =-,又0B π<<,故sin 0B ≠,所以()2cos cos B A C =-,又A B C π++=,故()cos cos B A C =-+,化简得sin sin 3cos cos A C A C =,因此tan tan 3A C =且tan 1C =,所以tan 3A =.(2)由(1)知tan 3A =,因此()tan tan tan tan 21tan tan A CB AC A C+=-+=-=-,.所以sin 10A =,sin 5B =2sin 2C =,因为,6sin sin a c a A C==,.所以1125sin 612225ABC S ac B ==⨯⨯= .19.【解析】(1)因为,PB PC O =是BC 的中点,所以PO BC ⊥,在直角POC 中,1PC OC ==,所以PO =,在矩形ABCD 中,1,2AB BC ==,所以DO =,又因为2PD =,所以在POD 中,222PD PO OD =+,即PO OD ⊥.而,,BC OD O BC OD ⋂=⊂平面ABCD ,所以PO ⊥平面ABCD ,而PO ⊂平面PBC ,所以平面PBC ⊥平面ABCD .'(2)由(1)平面PBC ⊥平面ABCD ,且DC BC ⊥,所以DC ⊥平面PBC ,所以DC PC ⊥,即PCD 是直角三角形,因为1PC CD ==,所以13122PDC S =⨯=,又知11212ACD S =⨯⨯= ,PO ⊥平面ABCD ,设点A 到平面PCD 的距离为d ,则A PCD P ACD V V --=,即1133PCD ACD S d S PO ⨯⨯=⨯⨯ ,即1311323d ⨯⨯=⨯⨯所以263d =,所以点A 到平面PCD 的距离为3..20.【解析】(1)由题当1n =时,()111223262a +=-⋅+=,即11a =.()21112122222326n n n n n a a a a n -+-++++=-⋅+ ①当2n 时,()211212222526n n n a a a n --+++=-⋅+ ②.①-②得()()()1223262526212nn n n n a n n n +=-⋅+--⋅-=-⋅,所以21n a n =-..(2)由(1)知,212221n an n n b a n -=+=+-,则()()()()3521212325221n n T n -=++++++++- ()()3521222213521n n -=+++++++++-⋅()()212214121232..1423nn n n n +⨯-+-+-=+=-21.【解析】(1)当1a =时,()()111e ln ,e 1x xf x x x f x x--=-+=-+',所以()()12,11f f '==,.则切线方程为()211y x -=⨯-,.即10x y -+=曲线()f x 在点()()1,1f 处的切线方程为10x y -+=.(2)证明:要证()2f x x >+,即证e ln 2x a x -->,设()eln ,0x aF x x x -=->,即证()2F x >,当0a 时,()()1e 1e ln ,ex a x ax ax F x x F x x x----=-=-='在()0,∞+上为增函数,且()e1x ah x x -=-中,()()0100e 110,1e 1e 10a a h h --=⨯-=-=-->.故()0F x '=在()0,∞+上有唯一实数根0x ,且()00,1x ∈..当()00,x x ∈时,()0F x '<,当()0,x x ∞∈+时,()0F x '>,从而当0x x =时,()F x 取得最小值.由()00F x '=,得001ex ax -=,故()()000001eln 2x aF x F x x x a a x -=-=+->.综上,当0a 时,()2F x >即()2f x x >+.22.【解析】(1)由题2,21,2x a t y t ⎧=+⎪⎪⎨⎪=⎪⎩(t 为参数),消去参数t得直线:20l x a -=,.22413sin ρθ=+,即2224cos 4sin ρθθ=+,即曲线C 的直角坐标方程为2214x y +=.(2)由,2,x x y y ⎧=⎪⎨⎪='⎩'得2,,x x y y =⎧⎨=''⎩又2214x y +=,所以()()22214x y +'=',即'2'21x y +=,所以曲线C '的方程是221x y +=,.由1d =得11a -.所以a 的取值范围是[]1,1-.23.【解析】(1)()222f x x x t x x t x t =++-=++-+-,()2222y x x tx x t t t =++-+--=+=+,当2x t -时等号成立,.⋅又知当x t =时,x t -取得最小值,所以当x t =时,()f x 有最小值,此时()min ()25f x f t t ==+=,所以3t =..(2)由(1)知,23a b c ++=,()22141114111162(121)232333a b c a b c a b c ⎛⎫++=++++=++= ⎪⎝⎭,当且仅当333,,824a b c ===时取等号,所以1412a b c ++的最小值为163.。
高考数学滚动过关检测三 集合、常用逻辑用语、不等式、函数与导数、三角函数与解三角形
滚动过关检测三 集合、常用逻辑用语、不等式、函数与导数、三角函数与解三角形一、单项选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.[2022·河北保定模拟]已知P ={1,2,3},Q ={y |y =2cos θ,θ∈R },则P ∩Q =( )A .{1}B .{1,2}C .{2,3}D .{1,2,3}2.[2022·广东清远一中月考]“cos α=32”是“cos 2α=12”的( ) A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件3.已知a =log 35,b =log 23,c =2-0.3,则a ,b ,c 的大小关系为( )A .c <b <aB .b <c <aC .c <a <bD .a <b <c4.已知函数f (x )=A sin(ωx +φ)A >0,ω>0,|φ|<π2的部分图象如图所示,则( )A .f (x )=2sin ⎝⎛⎭⎫2x +π6 B .f (x )=2sin ⎝⎛⎭⎫2x +π3 C .f (x )=2sin ⎝⎛⎭⎫x +π3 D .f (x )=2sin ⎝⎛⎭⎫x -π6 5.[2022·山东淄博模拟]函数f (x )=(e x +e -x )tan x 的部分图象大致为( )6.[2022·河北衡水中学模拟]已知cos θ-sin θ=43,则θ的终边在( ) A .第一象限 B .第二象限C .第三象限D .第四象限7.[2022·湖南株洲模拟]在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c ,若23a cos C -3b cos C =3c cos B ,则角C 的大小为( )A.π6B.π4C.π3D.2π38.[2022·皖南八校联考]已知函数f (x )=(3a )x -x 3a (a >1),当x ≥2e 时,f (x )≥0恒成立,则实数a 的取值范围为 A.⎝⎛⎭⎫e 3,+∞ B.⎣⎡⎭⎫2e 3,+∞ C .(1,e) D.⎝⎛⎦⎤1,2e 3 二、多项选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分.9.下列说法正确的有( )A .终边在y 轴上的角的集合为θ⎪⎪ θ=π2+2k π,k ∈Z B .已知3a =4b =12,则1a +1b=1 C .已知x ,y ∈R +,且1x +4y=1,则x +y 的最小值为8 D .已知幂函数f (x )=kx a 的图象过点(2,4),则k +a =310.[2022·辽宁丹东模拟]已知a ,b ∈R ,且3a <3b <1,则( )A .a 2<b 2B .ln|a |>ln|b |C.b a +a b>2 D .a +b +2ab >0 11.[2022·河北石家庄一中月考]对于△ABC ,有如下判断,其中正确的判断是( )A .若cos A =cosB ,则△ABC 为等腰三角形B .若△ABC 为锐角三角形,有A +B >π2,则sin A >cos B C .若a =8,c =10,B =60°,则符合条件的△ABC 有两个D .若sin 2A +sin 2B <sin 2C ,则△ABC 是钝角三角形12.[2022·辽宁沈阳模拟]函数f (x )为定义在R 上的偶函数,且在[0,+∞)上单调递增,函数g (x )=x [f (x )-f (2)],则( )A .函数h (x )=f (x )cos x 为奇函数B .f (x )的解析式可能是f (x )=e x +e -x -x 2C .函数g (x )有且只有3个零点D .不等式g (x )≤0的解集为[-2,2]三、填空题:本大题共4小题,每小题5分,共20分.把答案填在题中的横线上.13.设函数f (x )=⎩⎪⎨⎪⎧2x ,x ≤0log 2x ,x >0,则f ⎝⎛⎭⎫f ⎝⎛⎭⎫12=________. 14.[2022·湖北石首一中月考]在△ABC 中,已知sin A sin B sin C =357,则此三角形最大内角度数为________.15.已知cos ⎝⎛⎭⎫π6-x =13,则cos ⎝⎛⎭⎫5π6+x -sin 2⎝⎛⎭⎫x -π6=________. 16.[2022·浙江杭州模拟]函数f (x )=2x -x 2的零点个数为________,若函数f (x )=a x -x 2(a >1)恰有两个零点,则a =________.四、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.17.(10分)[2022·北京海淀模拟]设△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,且a sin B =3b cos A .(1)求角A 的大小;(2)再从以下三组条件中选择一组条件作为已知条件,使三角形存在且唯一确定,并求△ABC 的面积. 第①组条件:a =19,c =5;第②组条件:cos C =13,c =42; 第③组条件:AB 边上的高h =3,a =3.18.(12分)[2022·山东日照模拟]已知函数f (x )=cos(πx +φ)⎝⎛⎭⎫0<φ<π2的部分图象如图所示.(1)求φ及图中x 0的值;(2)设g (x )=f (x )+f ⎝⎛⎭⎫x +13,求函数g (x )在区间⎣⎡⎦⎤-12,13上的最大值和最小值.19.(12分)[2021·新高考Ⅰ卷]记△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知b 2=ac ,点D 在边AC 上,BD sin ∠ABC =a sin C .(1)证明:BD = b ;(2)若AD =2DC ,求cos ∠ABC .20.(12分)已知:f (x )=3sin(π+x )sin ⎝⎛⎭⎫x -π2+cos 2⎝⎛⎭⎫π2+x -12. (1)求函数f (x )的单调递增区间;(2)在△ABC 中,A ,B ,C 的对边分别为a ,b ,c ,若f (A )=1,a =2,求△ABC 面积的最大值.21.(12分)[2022·湖北九师联盟]已知函数f (x )=ln x ,g (x )=x 2-x +1.(1)求函数h (x )=f (x )-g (x )的极值;(2)证明:有且只有两条直线与函数f (x ),g (x )的图象都相切.22.(12分)[2022·广东茂名五校联考]已知函数f (x )=ln x +x 2-ax .(1)当a =3时,求曲线y =f (x )在点P (1,f (1))处的切线方程;(2)若x 1,x 2(x 1<x 2)是函数f (x )的两个极值点,证明:f (x 1)-f (x 2)>ln a 28+64-a 416a 2.。
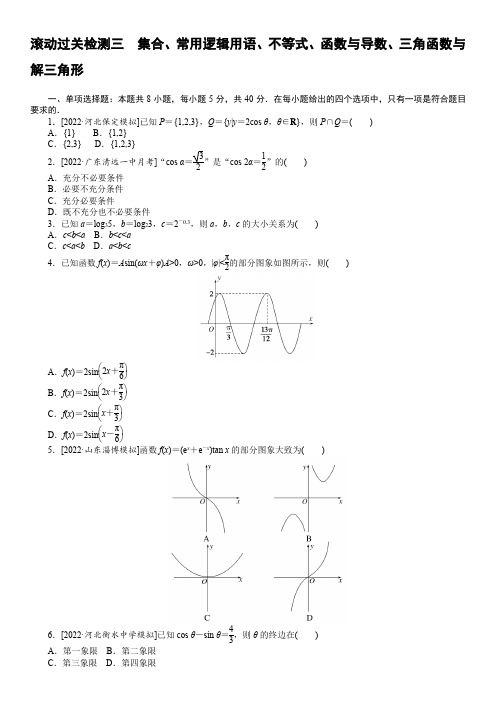
2015高考数学(人教A版,理科)大一轮总复习滚动检测 6套

解析:由已知得 g(x)=ax2+ax-2a=a(x+2)(x-1), ∴g(x)的图象与 x 轴的交点坐标为(-2,0),(1,0),且-2 和 1 是函数 f(x)的极值点.故 选 D. 答案:D
x,x≤0, 10. (2014 山东省青岛市高三模拟)已知函数 f(x)= 2 若函数 g(x)=f(x)-m 有 x -x,x>0,
)
1-ln x,x>1, 解析:依题意得 f(x)=sgn(ln x)-ln x=0,x=1, -1-ln x,0<x<1. 1 令 f(x)=0 得 x=e,1, ,所以函数有 3 个零点. e 故选 C. 答案:C 5.设集合 A={x||x-a|<1,x∈R},B={x||x-b|>2,x∈R}.若 A⊆B,则实数 a,b 必满足( ) B.|a+b|≥3 D.|a-b|≥3
A.|a+b|≤3 C.|a-b|≤3
解析:由题意可得 A={x|a-1<x<a+1},对集合 B 有 x<b-2 或 x>b+2,因为 A⊆ B,所以有 b-2≥a+1 或 b+2≤a-1,解得 a-b≥3 或 a-b≤-3,即|a-b|≥3.故选 D. 答案:D 6.(2014 安徽省蚌埠市高三质检)对于原命题“单调函数不是周期函数”,下列说法正 确的是( )
A.逆命题为“周期函数不是单调函数” B.否命题“单调函数是周期函数” C.逆否命题“周期函数是单调函数” D.以上三者都不正确 解析: 原命题可改写为“若一个函数是单调函数, 则它不是周期函数”根据四种命题的 构成可得,选项 A、B、C 均不正确.故选 D. 答案:D 7.牛奶保鲜时间因储藏温度的不同而不同,假定保鲜时间 y 与储藏温度 x 的关系为指 数型函数 y=kax,若牛奶在 0 ℃的冰箱中,保鲜时间约为 100 h,在 5 ℃的冰箱中,保鲜时 间约是 80 h,那么在 10 ℃时的保鲜时间是( A.49 h C.64 h
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、选择题1.集合A ={(x ,y )|y =lg(x +1)-1},B ={(x ,y )|x =m },若A ∩B =∅,则实数m 的取值范围是( ) A .(-∞,1) B .(-∞,1] C .(-∞,-1)D .(-∞,-1]2.(2015·厦门质检)若一系列函数的解析式相同,值域相同,但定义域不同,则称这些函数为“同族函数”,则函数解析式为y =x 2+1,值域为{1,3}的同族函数有( ) A .1个B .2个C .3个D .4个3.将函数f (x )=sin ⎝ ⎛⎭⎪⎫2x +π3的图象向左平移φ个单位,得到偶函数g (x )的图象,则φ的最小正值为( ) A.π12B.5π12C.π3D.π64.在平面直角坐标系中,若不等式组⎩⎪⎨⎪⎧x +y -1≥0,x -1≤0,ax -y +1≥0(a 为常数)所表示的平面区域的面积等于4,则a 的值为( ) A .-5B .3C .5D .75.(2015·杭州二检)设平行于y 轴的直线分别与函数y 1=log 2x 及y 2=log 2x+2的图象交于B ,C 两点,点A (m ,n )位于函数y 2=log 2x +2的图象上,若△ABC 为正三角形,则m ·2n等于( ) A .8 3 B .12 C .12 3D .156.已知一次函数f (x )=kx +b 的图象经过点P (1,2)和Q (-2,-4),令a n =f (n )f (n +1),n ∈N *,记数列⎩⎨⎧⎭⎬⎫1a n 的前n 项和为S n ,当S n =625时,n 的值等于( )A .24B .25C .23D .267.若正数x ,y 满足x +3y =5xy ,则3x +4y 的最小值是( ) A.245B.285C .5D .6 8.已知关于x 的方程⎝ ⎛⎭⎪⎫12x =1+lg a 1-lg a有正根,则实数a 的取值范围是( )A .(0,1) B.⎝ ⎛⎭⎪⎫110,10 C.⎝⎛⎭⎪⎫110,1D .(10,+∞)二、填空题9.(2015·贵阳二检)如图,在△ABC 中,∠B =45°,D 是BC 边上一点,AD =5,AC =7,DC =3,则AB 的长为________.10.对于一切实数x ,令[x ]为不大于x 的最大整数,则函数f (x )=[x ]称为“高斯函数”或“取整函数”.若a n =f ⎝ ⎛⎭⎪⎫n 3,n ∈N *,S n 为数列{a n }的前n 项和,则S 3n =________. 11.若关于x 的方程22x-2xa +a +1=0有两个不同的正实根,则实数a 的取值范围为________.12.(2015·苏锡常镇一调)已知实数x ,y 满足x >y >0,且x +y ≤2,则2x +3y +1x -y的最小值为________.13.已知关于x 的方程2sin(x +π4)=k 在[0,π]上有两解,则实数k 的取值范围是________.14.定义f (1,1)=1,f (m ,n )∈N *(m ,n ∈N *),且对任意的m ,n ∈N *,都有f (m +1,1)=2f (m,1),f (m ,n +1)=f (m ,n )+2.给出以下三个结论:(1)f (1,5)=9;(2)f (5,1)=16;(3)f (5,6)=26. 其中正确结论的个数为________.15.若不等式组⎩⎪⎨⎪⎧|x |+|y |≤2,y +2≤k (x +1)表示的平面区域为三角形,则实数k 的取值范围是________________. 三、解答题16.(2015·杭州一检)在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知cos2A +32=2cos A .(1)求角A 的大小;(2)若a =1,求△ABC 的周长l 的取值范围.17.已知函数f (x )=a ln x -x +a -1x. (1)若a =4,求f (x )的极值;(2)若f (x )在定义域内无极值,求实数a 的取值范围.18.(2015·长春三模)已知数列{a n }中,a 1=1,其前n 项的和为S n ,且满足a n =2S 2n2S n -1(n ≥2).(1)求证:数列⎩⎨⎧⎭⎬⎫1S n 是等差数列;(2)证明:当n≥2时,S1+12S2+13S3+…+1nS n<32.19.(2015·湖州期末)已知二次函数f(x)=x2+bx+c(b,c∈R).(1)若f(-1)=f(2),且不等式x≤f(x)≤2|x-1|+1对x∈[0,2]恒成立,求函数f(x)的解析式;(2)若c<0,且函数f(x)在[-1,1]上有两个零点,求2b+c的取值范围.20.(2015·河南高考适应性测试)已知数列{a n}的各项均为正数,且a1=2,a n=a2n+1+4a n+1+2.(1)令b n=log2(a n+2),证明:数列{b n}是等比数列;(2)设c n=nb n,求数列{c n}的前n项和S n.答案解析1.D [由A ∩B =∅,知⎩⎪⎨⎪⎧y =lg(x +1)-1,x =m ,无解,即y +1=lg(m +1)无解,则m +1≤0,得m ≤-1,故选D.]2.C [由x 2+1=1得x =0,由x 2+1=3得x =±2,所以函数的定义域可以是{0,2},{0,-2},{0,2,-2},故值域为{1,3}的同族函数共有3个.]3.A [由题意得:g (x )=sin[2(x +φ)+π3]=sin ⎝⎛⎭⎪⎫2x +2φ+π3,则2φ+π3=k π+π2,k ∈Z ,可得φ的最小正值为π12,故选A.]4.D [直线ax -y +1=0过点(0,1),作出可行域如图,知可行域由点A (1,0),B (1,a +1),C (0,1)组成的三角形的内部(包括边界),且a >-1,则其面积等于12×(a +1)×1=4,解得a=7.]5.B [由题意知,n =log 2m +2,所以m =2n -2.又根据函数解析式可知BC =2,所以可知B (m+3,n -1)在y 1=log 2x 的图象上,所以n -1=log 2(m +3),即m =2n -1-3,所以2n=43,所以m =3,所以m ·2n=3×43=12.故选B.]6.A [把P ,Q 的坐标代入一次函数的解析式得k =2,b =0,故f (x )=2x .a n =2n ·2(n +1), 1a n =14⎝ ⎛⎭⎪⎫1n -1n +1, 所以S n =14⎝ ⎛⎭⎪⎫1-12+12-13+…+1n -1n +1=14⎝ ⎛⎭⎪⎫1-1n +1=n 4(n +1),令S n =625,解得n =24.] 7.C [x +3y =5xy ,即x +3y 5xy =1,即15⎝ ⎛⎭⎪⎫3x +1y =1, 故3x +4y =(3x +4y )×15⎝ ⎛⎭⎪⎫3x +1y=15⎝ ⎛⎭⎪⎫13+12y x +3x y ≥15(13+236)=5,当且仅当12y x =3xy,即x =2y 时等号成立.]8.C [方程⎝ ⎛⎭⎪⎫12x =1+lg a 1-lg a有正根,等价于0<1+lg a 1-lg a <1,解1+lg a 1-lg a >0,得-1<lg a <1;解1+lg a 1-lg a <1,得2lg a 1-lg a <0,得lg a <0或lg a >1.所以0<1+lg a1-lg a<1等价于-1<lg a <0,即实数a的取值范围是⎝ ⎛⎭⎪⎫110,1.] 9.562解析 在△ACD 中,cos ∠ADC =52+32-722×5×3=-12,又因为∠ADC ∈(0°,180°),所以∠ADC =120°, 所以∠ADB =60°.在△ABD 中,由正弦定理得AB sin 60°=ADsin 45°, 所以AB =562.10.32n 2-12n 解析 当n =3k ,n =3k +1,n =3k +2时,均有a n =f ⎝ ⎛⎭⎪⎫n 3=⎣⎢⎡⎦⎥⎤n 3,所以S 3n =0+0+1+1+13个+2+2+23个+…+(n -1)+(n -1)+(n -1,3个)+n =3×1+n -12×(n -1)+n =32n 2-12n . 11.(2+22,+∞)解析 从方程中分离a ,得a =22x+12x -1,设t =2x,则a =t 2+1t -1=t -1+2t -1+2.因为原方程有两个不同的正实根,所以t =2x >20=1,即t -1>0. 所以t -1+2t -1≥2(t -1)·2t -1=22,当且仅当t -1=2,即t =1+2时取等号,但此时t 只有一个解,不满足题意,所以不能取等号.所以a =t -1+2t -1+2>22+2.故填(2+22,+∞). 12.3+224解析 由题意可得x -y >0,14(2x +2y )≤1,所以2x +3y +1x -y ≥⎝ ⎛⎭⎪⎫2x +3y +1x -y ×14[(x +3y )+(x -y )]=14⎣⎢⎡⎦⎥⎤3+2(x -y )x +3y +x +3y x -y ≥14⎣⎢⎡⎦⎥⎤3+2 2(x -y )x +3y ·x +3y x -y =3+224,当且仅当⎩⎪⎨⎪⎧x +y =2,2(x -y )x +3y=x +3yx -y ,即⎩⎨⎧x =22-1y =3-22时取等号,所以2x +3y +1x -y的最小值为3+224. 13.1≤k < 2解析 令f (x )=2sin(x +π4)(0≤x ≤π),作出函数f (x )的图象如图中实线部分.则当1≤k <2时,直线y =k 与函数f (x )=2sin(x +π4)(0≤x ≤π)的图象有两个公共点,即当1≤k <2时,原方程有两解. 14.3 解析 由f (m +1,1)f (m ,1)=2,得f (m,1)=f (1,1)·2m -1=2m -1,由f (m ,n +1)-f (m ,n )=2,得f (m ,n )=f (m,1)+2(n -1),∴f (m ,n )=2m -1+2(n -1).∴f (1,5)=21-1+2×(5-1)=9,f (5,1)=25-1+2×(1-1)=16, f (5,6)=25-1+2×(6-1)=26.故正确结论的个数为3.15.(-∞,-2)∪⎝ ⎛⎦⎥⎤0,23 解析 如图,只有直线y +2=k (x +1)从直线m 到直线n 移动,或者从直线a 到直线b 移动时,不等式组⎩⎪⎨⎪⎧|x |+|y |≤2,y +2≤k (x +1)表示的平面区域才是三角形.故实数k 的取值范围是0<k ≤23或者k <-2.16.解 (1)根据二倍角公式:cos2x =2cos 2x -1, 得2cos 2A +12=2cos A ,即4cos 2A -4cos A +1=0,所以(2cos A -1)2=0,所以cos A =12.因为0<A <π,所以A =π3.(2)根据正弦定理:a sin A =b sin B =csin C ,又a =1,得b =23sin B ,c =23sin C , 所以l =1+b +c =1+23(sin B +sin C ).因为A =π3,所以B +C =2π3,所以l =1+23[sin B +sin ⎝⎛⎭⎪⎫2π3-B ]=1+2sin ⎝⎛⎭⎪⎫B +π6.因为0<B <2π3,所以l ∈(2,3].17.解 (1)当a =4时,f (x )=4ln x -x +3x(x >0),f ′(x )=4x -1-3x 2=-x 2+4x -3x2, 令f ′(x )=0,解得x =1或x =3. 当0<x <1或x >3时,f ′(x )<0, 当1<x <3时,f ′(x )>0,f (1)=2,f (3)=4ln3-2,所以f (x )的极小值为2,极大值为4ln3-2.(2)f (x )=a ln x -x +a -1x(x >0), f ′(x )=a x -1-a -1x 2=-x2+ax -(a -1)x 2,f (x )在定义域内无极值,即f ′(x )≥0或f ′(x )≤0在定义域上恒成立.即方程f ′(x )=0在(0,+∞)上无变号零点. 设g (x )=-x 2+ax -(a -1),则Δ≤0或⎩⎪⎨⎪⎧Δ≥0,a2≤0,g (0)≤0,解得a =2,所以实数a 的取值范围为{2}.18.证明 (1)当n ≥2时,S n -S n -1=2S 2n 2S n -1,S n -1-S n =2S n S n -1,1S n -1S n -1=2,从而⎩⎨⎧⎭⎬⎫1S n 是以1为首项,2为公差的等差数列.(2)由(1)可知,1S n =1S 1+(n -1)×2=2n -1,∴S n =12n -1, ∴当n ≥2时,1nS n =1n (2n -1)<1n (2n -2)=12·1n (n -1)=12⎝ ⎛⎭⎪⎫1n -1-1n ,从而S 1+12S 2+13S 3+…+1n S n <1+12(1-12+12-13+…+1n -1-1n )=32-12n <32.19.解 (1)因为f (-1)=f (2),所以b =-1,因为当x ∈[0,2]时,都有x ≤f (x )≤2|x -1|+1,所以有f (1)=1,即c =1,所以f (x )=x 2-x +1.(2)因为f (x )在[-1,1]上有两个零点,且c <0,-------------------------------------------------------------------奋斗没有终点任何时候都是一个起点-----------------------------------------------------信达 所以有⎩⎪⎨⎪⎧f (-1)≥0,f (1)≥0,c <0⇒⎩⎪⎨⎪⎧ -b +c +1≥0,b +c +1≥0,c <0, 通过线性规划知识可得-2<2b +c <2. 20.(1)证明 由a n =a 2n +1+4a n +1+2得a n +2=a 2n +1+4a n +1+4=(a n +1+2)2.因为a n >0,所以a n +2=a n +1+2.因为b n +1b n =log 2(a n +1+2)log 2(a n +2)=log 2a n +2log 2(a n +2)=12, 又b 1=log 2(a 1+2)=2,所以数列{b n }是首项为2,公比为12的等比数列. (2)解 由(1)知,b n =2×⎝ ⎛⎭⎪⎫12n -1,则c n =2n ⎝ ⎛⎭⎪⎫12n -1. S n =2×⎝ ⎛⎭⎪⎫120+4×⎝ ⎛⎭⎪⎫121+…+2(n -1)⎝ ⎛⎭⎪⎫12n -2+2n ⎝ ⎛⎭⎪⎫12n -1,① 12S n =2×⎝ ⎛⎭⎪⎫121+4×⎝ ⎛⎭⎪⎫122+…+2(n -1)⎝ ⎛⎭⎪⎫12n -1+2n ⎝ ⎛⎭⎪⎫12n .② ①-②得 12S n =2×⎝ ⎛⎭⎪⎫120+2×⎝ ⎛⎭⎪⎫121+2×⎝ ⎛⎭⎪⎫122+…+2×⎝ ⎛⎭⎪⎫12n -1-2n ×⎝ ⎛⎭⎪⎫12n =2⎣⎢⎡⎦⎥⎤1-⎝ ⎛⎭⎪⎫12n 1-12-2n ×⎝ ⎛⎭⎪⎫12n =4-(4+2n )⎝ ⎛⎭⎪⎫12n . 所以S n =8-(n +2)⎝ ⎛⎭⎪⎫12n -2.。
