中考数学第一轮复习专题训练一
2023年中考数学一轮复习专题训练:一次函数的定义(含答案)

2023年中考数学专题训练:一次函数的定义一、单选题1.下列函数中,属于一次函数的是( )A .1y x =B .12x y +=C .21y x =+D .y kx b =+(k 、b 是常数)2.对于一次函数y kx b =+(k ,b 为常数),下表中给出5组自变量及其对应的函数值,其中恰好有1个函数值计算有误,则这个错误的函数值是( )A .14-B .12-C .8-D .5- 3.已知正比例函数12y x =-的图象经过点()6,m ,则m 的值为( ) A .1- B .2- C .3- D .-12 4.下列各点在直线112y x =-+上的是( ) A .(0,1)- B .(2,0)- C .11(,)24 D .(4,)1- 5.若点()2A a -,在函数3y x =-+的图象上,则a 的值为( )A .1B .1-C .5D .5- 6.关于函数21y x =+,下列结论正确的是( )A .函数必经过点()21-,B .y 随x 的值增大而增大C .当12x <时,0y < D .图象经过第一、三、四象限 7.已知()124m y m x-=-+是一次函数,则m 的值为( ) A .1 B .2C .2-D .2± 8.汽车由北京驶往相距120千米的天津,它的平均速度是30千米/时,则汽车距天津的路程S (千米)与行驶时间t (时)的函数关系及自变量的取值范围是( ) A .()1203004S t t =-≤≤B .()3004S t t =≤≤C .()120300S t t =->D .()304S t t ==二、填空题9.将点(2,3)P --向右平移3个长度单位,再向上平移a 个长度单位得到点Q ,点Q 恰好在直线23y x =-上,则a 的值为_____.10.如果点()2,A a -在函数114y x =-+的图象上,那么a 的值等于______. 11.当一次函数()2533y m x m =-+-的图像与y 轴的交点在x 轴的上方时,m 满足的条件是___________.12.若点()P a b ,在一次函数34y x =+的图像上,则代数式162a b -+=___________.13.若点3(2)A -,,(43)B ,,(1,)C a -在同一条直线上,则a 的值__________. 14.若点()2,a 在一次函数31y x 的图像上,则a 的值为______. 15.函数()212n y m xm n +-=-+,当m =__,n = __时为正比例函数;当m __,n = __时为一次函数. 16.若一次函数126y k x k =()()的图象经过第一,三,四象限,则k 的取值范围是________.三、解答题17.已知:y 与2x +成正比例,且1x =时,y =-6.(1)求y 与x 之间的函数关系式.(2)判断点()34M -,是否在这个函数的图象上.18.已知2y -与x 成正比例,且当2x =-时,4y =-.(1)写出y 与x 之间的函数关系式;(2)当4x =时,求y 的值;(3)求函数图像与x 轴的交点坐标.19.为提高学生的身体素质,某中学计划购买篮球和排球共50个,已知篮球每个80元,排球每个60元,设购买篮球x 个,购买篮球和排球的总费用为y 元.(1)求y 与x 之间的表达式;(2)如果购买篮球的个数是排球个数的32倍,则购买篮球和排球的总费用是多少?20.小明从阳山往广州邮寄一件包裹,邮资收费标准为每千克0.9元,并每件另加收手续费3.5元.(1)求总邮资y(元)与包裹重量x(千克)之间的函数关系式;(2)若小明所付总邮资为12.5元,则小明的包裹重量为多少?参考答案:1.B2.B3.C4.D5.C6.B7.C8.A9.210.3211.1m >且52m ≠ 12.913.12-14.715. 0 0 2≠ 0 16.13k << 17.(1)y x =--24 (2)()34M -,不在这个函数的图象上18.(1)32y x =+(2)14 (3)203⎛⎫- ⎪⎝⎭,19.(1)203000y x =+(2)3600元20.(1)0935y .x .=+(2)10千克。
2021年九年级中考数学 一轮专题训练:三角形的面积(一)

如果别人思考数学的真理像我一样深入持久,他也会找到我的发现。
——高斯2021年中考数学一轮专题训练:三角形的面积(一)1.如图所示,在△ABC中,已知点D,E,F分别为边BC,AD,CE的中点,且S△ABC =4cm2,则S△DEF等于()A.2cm2B.1cm2C.2D.22.如图,AD是△ABC中BC边上的中线,E、F分别是AD、BE的中点,若△BFD的面积为1,则△ABC的面积为()A.3 B.8 C.4 D.63.如图,在△ABC中,AD、AE分别是边BC上的中线与高,AE=4,△ABC的面积为12,则CD的长为()A.2 B.3 C.4 D.54.能把一个任意三角形分成面积相等的两部分是()A.角平分线B.中线C.高D.A、B、C都可以5.如图为一张方格纸,纸上有一灰色三角形,其顶点均位于某两网格线的交点上,若每一小正方形的边长均为1,则灰色三角形的面积为()A.7 B.7.5 C.8 D.8.56.如图,将三角形ABC沿直线AB向右平移后得到三角形BDE,连接CD,CE,若三角形ACD的面积为10,则三角形BCE的面积为()A.4 B.5 C.6 D.107.如图,在△ABC中,点D、E分别为BC、AD的中点,EF=2FC,若△ABC的面积为12cm2,则△BEF的面积为()A.2cm2B.3cm2C.4cm2D.5cm28.如图,△ABC中,AD是BC边上的中线,CE是△ACD中AD边上的中线,如果△ABC的面积是20,那么△ACE的面积是()A.10 B.6 C.5 D.49.如图,△ABC中,点D,E分别是边BC,BA的中点,△ABC的面积为32,则△DEB 的面积为()A.条件不足,无法确定B.4C.8 D.1610.已知AD是△ABC的中线,BE是△ABD的中线,若△ACD的面积为20,则△ABE 的面积为()A.5 B.10 C.15 D.1811.如图,D、E分别是△ABC的边AB、BC上的点,AD═2BD,BE=CE,设△ADF 的面积为S1,△CEF的面积为S2,若S△ABC=12,则S1﹣S2=()A.1.5 B.2 C.3 D.0.512.如图,△ABC的中线AD、BE相交于点P,四边形与△ABP的面积分别记为S1、S2,则S1与S2的大小关系为()A.S1>S2B.S1=S2C.S1<S2D.以上都有可能13.如图,△ABC的面积为10,点D为线段BC的中点,将△ABD沿着射线BC的方向平移使得点B与点D重合,得到△EDC,则△EDC的面积为()A.2.5 B.4 C.5 D.1014.如图在8×5的正方形网格中,AB、AC是经过格点的线段,如果能找到这样的格点M,使得S=S△ABM,这样的点M的个数是()△ACMA.1 B.2 C.3 D.415.如图,在四边形ABCD中,AD∥BC,AB=AD,BC=6,△BCD的面积为9,则点D到AB的距离为()A.3 B.4.5 C.6 D.916.如图所示,在△ABC中,点D、E分别在AB、AC边上,且AD:BD=3:4,AE:CE=2:1.连接DE,那么S:S四边形BCED=()△ADEA.B.C.D.17.如图,△ABC的面积是1,AD是△ABC的中线,AF=FD,CE=EF,则△DEF 的面积为()A.B.C.D.18.如图,在△ABC中,E是BC上一点,BC=3BE,点F是AC的中点,若S△ABC=a,则S△ADF﹣S△BDE=()A.a B.a C.a D.a19.如图,A、B、C的坐标分别为:A(﹣4,0)、B(2,0),C(0,6),在线段AB 或线段BC上找一点P,使△ACP面积为整数且S△ACP≤S△ABC,则满足条件的点P 的个数是()A.4 B.6 C.8 D.1020.已知点A(1,0),B(0,2),点P在x轴上,且△PAB的面积为5,则点P的坐标是()A.(﹣4,0)B.(3,5)C.(3,﹣5)D.(﹣4,0)或(6,0)参考答案1.解:∵点D是BC的中点,∴S△ADC=S△ABC,∵点E是AD的中点,∴S△DCE=S△ADC=S△ABC,∵点F是CE的中点,∴S△DEF=S△DCE=S△ABC=×4=(cm2),故选:C.2.解:∵F是BE的中点,∴BF=EF,∴S△EFD=S△BFD,又∵S△BDE=S△EFD+S△BFD,∴S△BDE=2S△BFD=2×1=2.同理,S△ABC=2S△ABD=2×2S△BDE=4×2=8.故选:B.3.解:∵△ABC的面积为12,∴×AE×BC=12,∴BC==6,∵AD是边BC上的中线,∴CD=BC=3.故选:B.4.解:三角形的中线把三角形分成等底等高的两个三角形,面积相等,所以,能把一个任意三角形分成面积相等的两部分是中线.故选:B.5.解:灰色三角形的面积为:4×4﹣﹣﹣=7,故选:A.6.解:∵△ABC沿直线AB向右平移后到达△BDE的位置,∴AB=BD,BC∥DE,∴S△ABC=S△BCD=S△ACD=×10=5,∵DE∥BC,∴S△BCE=S△BCD=5.故选:B.7.解:∵D是BC的中点,∴S△ABD=S△ADC(等底等高的三角形面积相等),∵E是AD的中点,∴S△ABE=S△BDE,S△ACE=S△CDE(等底等高的三角形面积相等),∴S△ABE=S△DBE=S△DCE=S△AEC,∴S△BEC=S△ABC=6cm2.∵EF=2FC,∴S△BEF=S△BCE,∴S△BEF=S△BEC=4cm2.故选:C.8.解:∵AD是BC上的中线,△ABC的面积是20,∴S△ACD=S△ABD=S△ABC=10,∵CE是△ACD中AD边上的中线,∴S△ACE=S△CED=S△ACD=5.故选:C.9.解:∵D、E分别是BC,AB的中点,∴S△DEB=S△ABD,S△ABD=S△ABC,∴S△DEB=S△ABC=×32=8.故选:C.10.解:∵AD是△ABC的中线,△ACD的面积为20,∴S△ABD=S△ACD,=20,∵BE是△ABD的中线,∴S△ABE=S△DBE,而S△ABE=20÷2=10.故选:B.11.解:∵BE=CE,∴BE=BC,∵S△ABC=12,∴S△ABE=S△ABC=×12=6.∵AD=2BD,S△ABC=12,∴S△BCD=S△ABC=4,∵S△ABE﹣S△BCD=(S△ADF+S四边形BEFD)﹣(S△CEF+S四边形BEFD)=S△ADF﹣S△CEF,即S△ADF﹣S△CEF=S△ABE﹣S△BCD=6﹣4=2.故选:B.12.解:连接DE,∵△ABC的中线AD、BE相交于点P,∴DE∥AB,∴S△ABD=S△ABE,∴S△PBD=S△PAE,∵S△ABE=S2+S△PAE=S△BCE=S△PBD+S1,∴S1=S2,∴S1与S2的大小关系为相等,故选:B.13.解:∵△ABC的面积为10,点D为线段BC的中点,∴△ABD的面积=△ABC的面积=5,∵将△ABD沿着射线BC的方向平移使得点B与点D重合,得到△EDC,∴△EDC的面积=△ABD的面积=5,故选:C.14.解:如图所示:故使得S△ACM=S△ABM的格点M的个数是3个.故选:C.15.解:作DH⊥BC于H,DE⊥BA交BA的延长线于E.∵AB=AD,∴∠ABD=∠ADB,∵AD∥BC,∴∠ADB=∠DBC,∴∠ABD=∠DBC,∵DE⊥BE,DH⊥BC,∴DE=DH,∵S△DBC=•BC•DH=6,∴×6×DH=9,∴DH=3,∴DE=3,故选:A.16.解:连接BE,设△ABC的面积为S,∵AE:CE=2:1.∴S△ABE=S,∵AD:BD=3:4,∴S△ADE=S△ABE=×S=S,∴S△ADE:S四边形BCED=2:5,故选:B.17.解:∵△ABC的面积是1,AD是△ABC的中线,∴S△ACD=S△ABC=,∵AF=FD,∴DF=AD,∴S△CDF=S△ACD=×=,∵CE=EF,∴S△DEF=S△CDF=×=,故选:D.18.解:∵BC=3BE,∴S△AEC=S△ABC=a,∵点F是AC的中点,∴S△BCF=S△ABC=,∴S△AEC﹣S△BCF=a,即S△ADF+S四边形CEDF﹣(S△BDE+S四边形CEDF)=a,∴S△ADF﹣S△BDE=a,故选:C.19.解:∵A(﹣4,0)、B(2,0),C(0,6),∴AB=6,OC=6,∴,∵S△ACP≤S△ABC,∴S△ACP≤,当P点在AB边上时,设P(x,0),则AP=x+4,∴,∴x≤﹣,∵△ACP面积为整数,∴为整数,又∵x+4≤∴x+4=或或1或,即x=﹣或﹣或﹣3或﹣,故在AB上存在4个点,使得△ACP面积为整数且S△ACP≤S△ABC,过点4个点作AC的平行线与BC有四个交点,所得四个交点为P点,也满足△ACP面积为整数且S△ACP≤S△ABC,∴满足条件的点P的个数有8个,故选:C.20.解:如图,设P(m,0).由题意:•|1﹣m|•2=5,解得m=﹣4或6,∴P(﹣4,0)或(6,0).故选:D.一天,毕达哥拉斯应邀到朋友家做客。
中考数学一轮复习专题突破训练—相似三角形

中考数学一轮复习专题突破训练—相似三角形一、单选题1.(2022·北京市第十三中学九年级期中)如图,点D,E分别在△ABC的AB,AC边上,且DE△BC,如果AD:AB=2:3,那么DE:BC等于()A.3:2B.2:5C.2:3D.3:5【答案】C【分析】根据相似三角形的判定与性质即可得出结果.【详解】解:△DE∥BC,△△ADE△△ABC,△DE:BC=AD:AB=2:3;故选:C.2.(2022·辽宁鞍山市·九年级期末)如图,在平行四边形ABCD中,点E是AB 的中点,CE和BD交于点O,若S△EOB=1,则四边形AEOD的面积为()A.4B.5C.6D.7【答案】B根据平行四边形的性质和相似的判定和性质,可以得到△BOC和△COD的面积,从而可以得到△BCD的面积,再根据△ABD和△BCD的面积一样,即可得到四边形AEOD的面积.【详解】解:△在平行四边形ABCD中,点E是AB的中点,△CD△AB,CD=AB=2BE△△DOC△△BOE,△OC CDOE BE=2,△S△EOB=1,△S△BOC=2,S△DOC=4,△S△BCD=6,△S△DAB=6,△四边形AEOD的面积为:S△DAB-S△EOB=6-1=5,故选:B.3.(2022·全国九年级专题练习)如图,已知AB△CD△EF,AD:AF=3:5,BE=12,那么CE的长等于()A.2B.4C.245D.365【分析】根据平行线分线段成比例得到3125BC =,然后利用比例性质计算出BC ,从而求出CE 即可. 【详解】解:△AB △CD △EF , △BC AD BE AF =,即3125BC =, △BC =365, △CE =BE -BC =12-365=245, 故选C .4.(2022·全国九年级专题练习)下列四条线段中,不能成比例的是( ) A.a =2,b =4,c =3,d =6 B .a ,b c =1,d C .a=6,b =4,c =10,d =5 D .a b =c d =2【答案】C 【分析】根据比例线段的概念,让最小的和最大的相乘,另外两条相乘,看它们的积是否相等即可得出答案. 【详解】解:A 、2×6=3×4,能成比例; B1 C 、4×10≠5×6,不能成比例;D 、523152⨯=⨯,能成比例. 故选:C .5.(2022·四川省成都市石室联合中学)如图,在ABC 中,点E 和点F 分别在边AB ,AC 上,且//EF BC ,若3AE =,6EB =,9BC =,则EF 的长为( )A .1B .92C .12D .3【答案】D 【分析】证明△AEF △△ABC ,根据相似三角形的性质列出比例式,代入计算得到答案. 【详解】 △//EF BC , △AEF ABC ∽, △EF AEBCAB, △3AE =,6EB =, 9BC =, △399EF =, △3EF =. 故选D .6.(2022·全国九年级课时练习)将三角形纸片(ABC )按如图所示的方式折叠,使点C 落在AB 边上的点D ,折痕为EF .已知3,4AB AC BC ===,若以点B 、D 、F 为顶点的三角形与ABC 相似,那么CF 的长度是( )A .2B .127或2 C .127D .125或2 【答案】B 【分析】分两种情况:若BFD C ∠=∠或若BFD A ∠=∠,再根据相似三角形的性质解题 【详解】△ABC 沿EF 折叠后点C 和点D 重合, △FD CF =,设CF x =,则,4FD CF x BF x ===-,以点B 、D 、F 为顶点的三角形与ABC 相似,分两种情况: △若BFD C ∠=∠,则BF FDBC AC =,即443x x -=,解得127x =; △若BFD A ∠=∠,则BF FD AB AC =,即433x x -=,解得2x =. 综上,CF 的长为127或2, 故选:B .7.(2022·全国九年级课时练习)已知线段a 、b 、c 、d 满足ab cd =,把它改写成比例式,错误的是( ) A .::a d c b = B .::a b c d =C .::d a b c =D .::a c d b =【答案】B【分析】根据比例的基本性质:外项之积等于内项之积,对选项一一分析,选出正确答案即可.【详解】解:A、a:d=c:b△ab=cd,故正确;B、a:b=c:d△ad=bc,故错误;C、d:a=b:c△dc=ab,故正确;D、a:c=d:b△ab=cd,故正确.故选:B.8.(2022·全国九年级课时练习)下列结论不正确的是()A.所有的矩形都相似B.所有的正三角形都相似C.所有的等腰直角三角形都相似D.所有的正八边形都相似【答案】A【分析】根据相似图形的判定判断即可;【详解】所有的矩形不一定都相似,故A错误,符合题意;因为正三角形的每个角都等于60︒,满足两个角对应相等,所有的正三角形都相似,故B正确;︒︒︒,满足两个角对应相等,因为等腰直角三角形的三个角分别为,45,45,90所有的等腰直角三角形都相似,故C正确;因为正八边形的每个角都相等,每条边都相等,所有的正八边形都相似,故D 正确; 故选A .9.(2022·全国)如果23a b =,那么2a bb-的结果是( ) A .12- B .43-C .43D .12【答案】B 【分析】根据比例的性质即可得到结论. 【详解】 △a b=23,△可设a =2k ,b =3k , △2a bb -=2k-6k 3k =-43. 故选B .10.(2022·沙坪坝·重庆一中)下列命题正确的是( ) A .位似图形一定是相似图形 B .任意两个菱形一定相似CD .23、24、25能作为直角三角形的三边长 【答案】A 【分析】根据位似图形,相似图形的定义可判断A 、B ,根据平方根的定义和勾股定理的逆定理,可判断C 、D . 【详解】解:A. 位似图形一定是相似图形,故原命题正确,符合题意; B. 任意两个菱形不一定相似,故原命题错误,不符合题意;C.±D. 23、24、25不能作为直角三角形的三边长,故原命题错误,不符合题意, 故选A . 二、填空题11.(2022·山东省青岛第二十六中学九年级期中)如果2x =3y ,那么x yy +=___. 【答案】52【分析】直接利用已知得出x =32y ,进而代入得出答案. 【详解】 解:△2x =3y , △x =32y ,△3522y yx y y y ++==.故答案为:52.12.(2022·全国九年级专题练习)ABC 中,D 、E 分别在AB 、AC 上,DE △BC ,ADE 是ABC 缩小后的图形,若DE 把ABC 的面积分成相等的两部分,则AD :AB =_____【分析】如图根据BC △DE ,可以得到△ADE △△ABC ,则21=2AED ABC S AD S AB ⎛⎫= ⎪⎝⎭△△ ,由此即可求解. 【详解】 解:△BC △DE , △△ADE △△ABC ,△DE 把△ABC 的面积分成相等的两部分,△21()2AED ABCS AD SAB ∆∆==, △22AD AB =, 故答案为:22.13.(2022·全国)如图,AC 与BD 相交于点O ,在△AOB 和△DOC 中,已知OA OBOD OC=,又因为________,可证明△AOB △△DOC .【答案】△AOB=△DOC【分析】根据相似三角形的判定,两边对应成比例,夹角相等,两三角形相似解答.【详解】解:△OA OBOD OC=,△AOB=△DOC,△△AOB△△DOC(两边对应成比例,夹角相等,两三角形相似).故答案为:△AOB=△DOC.14.(2022·全国九年级专题练习)如图:梯形ADFE相似于梯形EFCB,若AD=3,BC=4,则AEBE=__.3【分析】根据相似的性质,列出比例式,根据已知条件即可求得.【详解】因为梯形ADFE相似于梯形EFCB,所以AD EFEF BC=,即EF=23所以323AE ADBE EF===315.(2022·合肥市第四十五中学九年级)如图,正方形ABCD中,点E是BC的中点,点F是CD上一点,分别以AE、AF为对称轴,折叠△ABE、△ADF,使得AB和AD与AG重合,连接BG交AE于点H,连接CG.(1)HE:AH=______;(2)S△AFE:S正方形ABCD=______.【答案】1:4 5:12【分析】(1)根据翻折的性质得到△GHE=△BHE=90°,再根据△HEB=△BEA,从而证明△HEB△△BEA,得出HE BEBE AE=,设正方形边长为2x,则BE=x,AB=2x,由勾股定理求出AE,从而求出HE和AH,得出结论;(2)由S△AFE=12(S正方形ABCD﹣S△FCE),正方形ABCD的边长为2x,FG=DF=m,则EF =x + m,CF=2 x﹣m,,由勾股定理求出m即可.【详解】解:(1)△AE为对称轴,△△AEG△△AEB,BG△AE,△△GHE=△BHE=90°,又△△HEB=△BEA,△△HEB△△BEA,△HE BEBE AE=,在正方形ABCD 中,设边长为2x ,△点E 是BC 的中点,则BE =x ,AB =2x ,△AE=,△HE =225BE x AE ==,△AH =AE ﹣HE=,△HE :AH x =1:4. 故答案为:1:4;(2)设正方形ABCD 的边长为2x ,则S 正方形ABCD =4x 2,△S △AFE =12(S 正方形ABCD ﹣S △FCE ),CE =BE =GE =x ,设FG =DF =m ,则EF =x + m ,CF =2 x ﹣m ,在△EFC 中,△EF 2=CE 2+CF 2,△(m +x )2=(2 x ﹣m )2+ x 2,解得:m =23x ,△CE =2 x ﹣m =43x ,△S △CFE =12×CE ×CF =12×24233x x x ⨯=, △S △AFE =12×(4 x 2﹣223x )=253x , △S △AFE :S 正方形ABCD =225:43x x =5:12.故答案为:5:12.三、解答题16.(2022·辽宁鞍山市·九年级期末)如图,将△ABC绕点A旋转得到△ADE,连接BD,CE.求证:△ADB△△AEC.【答案】见解析.【分析】由题知,将△ABC绕点A旋转得到△ADE,可得到AC=AE,AB=AD,△CAE=△BAD,即可证明.【详解】△将△ABC绕点A旋转得到△ADE,△AC=AE,AB=AD,△CAE=△BAD,△AE AC,AD AB△△ADB△△AEC.17.(2022·广西贺州市·九年级期中)如图,已知在△ABC中,DE△BC,EF△AB,AE=2CE,AB=6,BC=9.求:(1)求BD的长度;(2)求DE的长度.【答案】(1)2;(2)6【分析】(1)由平行线分线段成比例得出比例式,即可得出结果;(2)由平行线分线段成比例得出比例式,即可得出结果.【详解】解:(1)△AE =2CE , △12CE AE =, △DE △BC , △13BD CE AB AC ==, △AB =6,△BD =2;(2)△EF △AB , △23AE BF AC BC ==, △BC =9,△BF =6,又△DE △BC ,△四边形BDEF 是平行四边形,△DE =BF =6.18.(2022·全国九年级专题练习)已知:如图,△ABC =△CDB =90°,AC =a ,BC =b ,当BD 与a 、b 之间满足怎样的关系时,这两个三角形相似?【答案】2b BD a =或22b a b BD -=【分析】由AB △BC ,BD △CD 得到△ABC =△BDC =90°,再利用勾股定理计算出22AB a b -根据直角三角形相似的判定方法,当AB BD AC BC =,Rt △ABC △Rt △BDC ;当=BC AC BD BC时然后分别利用比例性质可表示出BD 与a 和b 的关系. 【详解】解:△AC =a ,BC =b ,△ABC =△CDB =90°,△AB 22a b -△当BD BC AB AC=时, 即22b a b BD -=Rt △ABC △Rt △BDC ; △当BD BC CB AC=时, 即2b BD a=时,Rt △ABC △Rt △CDB ,. 19.(2020·北京市第六十六中学九年级期中)如图,在Rt△ABC 中,△C =90°,D 是AB 上一点,E 是BC 上一点,AC =6,BC =8,BD =4,BE =5.求证:DE △AB .【答案】见解析【分析】利用勾股定理可求得AB =10,则有12BE AB =,12BD BC =,结合△B =△B ,可证得△BDE △△BCA ,从而有△BDE =△C =90°,即可得证.【详解】证明:△△C =90°,AC =6,BC =8,△AB 2210AC BC +=,△BD =4,BE =5, △12BE AB =,12BD BC =, △△B =△B ,△△BDE △△BCA ,△△BDE =△C =90°,即DE △AB .20.(2022·全国九年级专题练习)如图:小明欲测量一座古塔的高度,他站在该塔的影子上前后移动,直到他本身影子的顶端正好与塔的影子的顶端重叠,此时他距离该塔18 m ,已知小明的身高是1.6 m ,他的影长是2 m .(1)图中△ABC 与△ADE 是否相似?为什么?(2)求古塔的高度.【答案】(1)相似,见解析;(2)16m【分析】(1)根据在同一时刻物高和影长成正比,即在同一时刻的两个物体,影子,经过物体顶部的太阳光线三者构成的两个直角三角形相似;(2)利用相似三角形的性质求得相应线段的长即可.【详解】解:(1)△ABC△△ADE.△BC△AE,DE△AE,△△ACB=△AED=90°.△△A=△A,△△ABC△△ADE;(2)由(1)得△ABC△△ADE,△AC BC=AE DE△AC=2m,AE=2+18=20m,BC=1.6m,△2 1.6=,20DE△DE=16m,即古塔的高度为16m.21.(2022·全国九年级专题练习)在锐角△ABC中,AD,CE分别为BC,AB边上的高,△ABC 和△BDE 的面积分别等于18和2,DE =2,求AC 边上的高.【答案】6【分析】由已知条件得到△CEB =△ADB =90°,推出△ADB △△CEB ,根据相似三角形的性质得到BD :AB =BE :BC ,证得△BDE △△BAC ,得到S △BDE :S △ABC =(DE :AC )2,于是求得AC =6,然后根据三角形的面积公式即可得到结果.【详解】过点B 做BF △AC ,垂足为点F ,△AD ,CE 分别为BC ,AB 边上的高,△△ADB =△CEB =90°,又△△B =△B ,△Rt △ADB △Rt △CEB , △BD AB BE CB =,即BD BE AB CB=, 且△B =△B ,△△EBD △△CBA , △221189BED BCA S DE S AC ⎛⎫=== ⎪⎝⎭, △13DE AC =, 又△DE =2,△AC =6,△1182ABCS AC BF =⋅=, 6BF ∴=.22.(2022·湖南师大附中博才实验中学)如图,在正方形ABCD 中,点G 是对角线上一点,CG 的延长线交AB 于点E ,交DA 的延长线于点F ,连接AG .(1)求证:AG CG =;(2)若9GE GF ⋅=,求CG 的长.【答案】(1)见解析;(2)CG =3【分析】(1)根据正方形的性质得到△ADB =△CDB =45°,AD =CD ,从而利用全等三角形的判定定理推出△ADG △△CDG (SAS ),进而利用全等三角形的性质进行证明即可;(2)根据正方形的性质得到AD △CB ,推出△FCB =△F ,由(1)可知△ADG △△CDG ,利用全等三角形的性质得到△DAG =△DCG ,结合图形根据角之间的和差关系△DAB -△DAG =△DCB -△DCG ,推出△BCF =△BAG ,从而结合图形可利用相似三角形的判定定理得到△AEG △△F AG ,进而根据相似三角形的性质进行求解即可.【详解】解:(1)证明:△BD 是正方形ABCD 的对角线,△△ADB =△CDB =45°,又AD =CD ,在△ADG 和△CDG 中,AD CD ADG CDG DG DG =⎧⎪∠=∠⎨⎪=⎩, △△ADG △△CDG (SAS ),△AG =CG ;(2)解:△四边形ABCD 是正方形,△AD △CB ,△△FCB =△F ,由(1)可知△ADG △△CDG ,△△DAG =△DCG ,△△DAB -△DAG =△DCB -△DCG ,即△BCF =△BAG ,△△EAG =△F ,又△EGA =△AGF ,△△AEG △△F AG ,△GE GA GA GF =,即GA 2=GE •GF ,△GA =3或GA =-3(舍去),根据(1)中的结论AG =CG ,△CG =3.23.(2022·浙江杭州·翠苑中学九年级)如图,在矩形ABCD 中,E 是CD 上一点,AE AB =,作BF AE ⊥.(1)求证:ADE BFA ≅△△;(2)连结BE ,若BCE 与ADE 相似,求AD AB . 【答案】(1)见解析;(23【分析】(1)根据矩形的性质得出90D DAB ∠=∠=︒,求出90DAE FAB ∠+∠=︒,90FBA FAB ∠+∠=︒,求出D AFB ∠=∠,DAE FBA ∠=∠,再根据全等三角形的判定推出即可;(2)根据矩形的性质得出90C D ∠=∠=︒,//DC AB ,根据平行线的性质得出CEB ABE ∠=∠,设CEB ABE x ∠=∠=︒,根据等腰三角形的性质求出AEB EBA x ∠=∠=︒,根据相似三角形的性质得出两种情况:△DEA CEB x ∠=∠=︒,根据180DEA AEB CEB ∠+∠+∠=︒得出180x x x ++=,求出x ,再解直角三角形求出AE 和AD ,再求出答案即可;△DEA EBC ∠=∠,设DEA EBC y ∠=∠=︒,求出(2)180DEA AEB CEB y x ∠+∠+∠=+︒=︒,()90EBC CEB y x ∠+∠=+︒=︒,求出x ,再得出答案即可.【详解】解:(1)证明:四边形ABCD 是矩形,90D DAB ∴∠=∠=︒,90DAE FAB ∴∠+∠=︒,BF AE ⊥,90AFB ∴∠=︒,D AFB ∴∠=∠,90FBA FAB ∠+∠=︒,DAE FBA ∴∠=∠,在ADE ∆和BFA ∆中DAE FBA D AFB AE AB ∠=∠⎧⎪∠=∠⎨⎪=⎩, ()ADE BFA AAS ∴∆≅∆;(2)四边形ABCD 是矩形,90C D ∴∠=∠=︒,//DC AB ,CEB ABE ∴∠=∠,设CEB ABE x ∠=∠=︒,AE AB =,AEB EBA x ∴∠=∠=︒,当BCE ∆与ADE ∆相似时,有两种情况:△DEA CEB x ∠=∠=︒,180DEA AEB CEB ∠+∠+∠=︒,180x x x ∴++=,解得:60x =,即60DEA ∠=︒,906030DAE ∴∠=︒-︒=︒,2AE DE ∴=,由勾股定理得:AD , AE AB =,∴AD AD AB AE = △DEA EBC ∠=∠,设DEA EBC y ∠=∠=︒,CEB EBA AEB x ∠=∠=∠=︒,则(2)180DEA AEB CEB y x x y x ∠+∠+∠=︒+︒+︒=+︒=︒, 在Rt BCE ∆中,()90EBC CEB y x y x ∠+∠=︒+︒=+︒=︒, 即218090y x y x +=⎧⎨+=⎩, 解得:90x =︒,即90CEB ∠=︒,此时点E 和点C 重合,BEC ∆不存在,舍去;△AD AB =。
2021年 中考一轮复习数学专题突破训练:《圆综合性压轴题》(一)

2021年中考一轮复习数学专题突破训练:《圆综合性压轴题》(一)1.如图1,△ABC内接于⊙O,∠ACB=60°,D,E分别是,的中点,连结DE分别交AC,BC于点F,G.(1)求证:△DFC∽△CGE;(2)若DF=3,tan∠GCE=,求FG的长;(3)如图2,连结AD,BE,若=x,=y,求y关于x的函数表达式.2.如图,已知△ABC,以BC为直径的⊙O交AB于点D,点E为的中点,连结CE交AB 于点F,且AF=AC.(1)判断直线AC与⊙O的位置关系,并说明理由;(2)若⊙O的半径为2,sin A=,求CE的长.3.如图,在Rt△ABC中,∠C=90°,点O在斜边AB上,以O为圆心,OB为半径作⊙O,分别与BC、AB相交于点D、E,连接AD,已知∠CAD=∠B.(1)求证:AD是⊙O的切线;(2)若∠B=30°,AO=,求的长;(3)若AC=2,BD=3,求AE的长.4.如图1,CD是⊙O的直径,弦AB⊥CD,垂足为点E,连结CA.(1)若∠ACD=30°,求劣弧AB的度数;(2)如图2,连结BO并延长交⊙O于点G,BG交AC于点F,连结AG.①若tan∠CAE=2,AE=1,求AG的长;②设tan∠CAE=x,=y,求y关于x的函数关系式.5.如图,⊙O的半径为5,弦BC=6,A为BC所对优弧上一动点,△ABC的外角平分线AP 交⊙O于点P,直线AP与直线BC交于点E.(1)如图1.①求证:点P为的中点;②求sin∠BAC的值;(2)如图2,若点A为的中点,求CE的长;(3)若△ABC为非锐角三角形,求PA•AE的最大值.6.已知AB为⊙O的直径,C为⊙O上一动点,连接AC,BC,在BA的延长线上取一点D,连接CD,使CD=CB.(1)如图1,若AC=AD,求证:CD是⊙O的切线;(2)如图2,延长DC交⊙O于点E,连接AE.i)若⊙O的直径为,sin B=,求AD的长;ii)若CD=2CE,求cos B的值.7.已知△ABC内接于⊙O,AB=AC,∠ABC的平分线与⊙O交于点D,与AC交于点E,连接CD并延长与⊙O过点A的切线交于点F,记∠BAC=α.(1)如图1,若α=60°;①直接写出的值为;②当⊙O的半径为4时,直接写出图中阴影部分的面积为;(2)如图2.若α<60°,,DE=6,求DC的长.8.定义:有一个内角等于与其相邻的两个内角之差的四边形称为幸福四边形.(1)已知∠A=120°,∠B=50°,∠C=α,请直接写出一个α的值,使四边形ABCD为幸福四边形;(2)如图1,△ABC中,D、E分别是边AB,AC上的点,AE=DE.求证:四边形DBCE为幸福四边形;(3)在(2)的条件下,如图2,过D,E,C三点作⊙O,与边AB交于另一点F,与边BC 交于点G,且BF=FC.①求证:EG是⊙O的直径;②连结FG,若AE=1,BG=7,∠BGF﹣∠B=45°,求EG的长和幸福四边形DBCE的周长.9.如图,AB和CD为⊙O的直径,AB⊥CD,点E为CD上一点,CE=CA,延长AE交⊙O于点F,连接CF交AB于点G.(1)求证:CE2=AE•AF;(2)求证:∠ACF=3∠BAF;(3)若FG=2,求AE的长.10.如图,AB为⊙O的直径,点C为⊙O上一点,点D为AB延长线上一点,连接CD,作CE ⊥AB于点E,∠OCE=∠D.(1)求证:CD是⊙O的切线;(2)点F为CD上一点,连接OF交CE于点G,G为OF中点,求证:OC2=CD•CF;(3)在(2)的条件下,CF=DF,若OC=2,求CG.参考答案1.解:(1)∵点D是的中点,∴,∴∠ACD=∠CED,∵点E是的中点,∴,∴∠CDE=∠BCG,∴△DFC∽△CGE;(2)由(1)知,∠ACD=∠CED,∠CDE=∠BCG,∴∠ACD+∠CDE=∠CED+∠BCG,∴∠CFG=∠CGF,∵CF=CG,∵∠ACB=60°,∴△CFG是等边三角形,如图1,过点C作CH⊥FG于H,∴∠DHC=90°,设FH=a,∴∠FCH=30°,∴FG=CF=2a,CH=a,∵DF=3,∴DH=DF+FH=3+a,∵∠GCE=∠CDE,tan∠GCE=,∴tan∠CDE=,在Rt△CHD中,tan∠CDE==,∴=,∴a=1,∴FG=2a=2;(3)如图2,连接AE,则∠AEB=∠ACB=60°,∠DAE=∠CAD+∠CAE=∠ACD+∠CDF=∠CFG=60°,∴∠AEB=∠DAE,∴BE∥AD,设BE与AD的距离为h,∴=,∴S△ABE =•S△ADE,∵D ,E 分别是,的中点,∴CD =AD ,BE =CE ,∴S △ABE =•S △ADE ,过点D 作DM ⊥AC 于M ,∵,∴AD =CD ,∴AC =2CM ,由(2)知,△CFG 是等边三角形,∴∠CFG =60°,∴∠DFM =60°,∴∠MDF =30°,设MF =m ,则DM =m ,DF =2m ,∵=x , ∴CF =x •DF =2mx ,∴CG =CF =2mx ,由(1)知,△DFC ∽△CGE ,∴, ∴=, ∴S △ABE =•S △ADE =S △ADE ,∴S 四边形ABED =S △ADE +S △ABE =S △ADE , ∵MF =m ,CF =x •DF =2mx ,∴CM =MF +CF =m +2mx =(2x +1)m ,∴AC =2CM =2(2x +1)m ,∴AF=AC﹣CF=2(2x+1)m﹣2mx=2(x+1)m,过点A作AN⊥DF于N,=AF•DM=DF•AN,∴S△ADF∴AN===(x+1)m,过点C作CP⊥FG,由(2)知,PF=CF=mx,CP=mx,∴y===•=•=•=•=.2.(1)AC与⊙O相切,证明:连接BE,∵BC是⊙O的直径,∴∠E=90°,∴∠EBD+∠BFE=90°,∵AF=AC,∴∠ACE=∠AFC,∵E为弧BD中点,∴∠EBD=∠BCE,∴∠ACE+∠BCE=90°,∴AC⊥BC,∵BC为直径,∴AC是⊙O的切线.(2)解:∵⊙O的半为2∴BC=4,在Rt△ABC中,sin A==,∴AB=5,∴AC==3,∵AF=AC,∴AF=3,BF=5﹣3=2,∵∠EBD=∠BCE,∠E=∠E,∴△BEF∽△CEB,∴==,∴EC=2EB,设EB=x,EC=2x,由勾股定理得:x2+4x2=16,∴x=(负数舍去),即CE=.3.解:(1)如图1,连接OD,∵∠ACB=90°,∴∠CAD+∠ADC=90°,∵OB=OD,∴∠B=∠ODB,∵∠CAD=∠B,∴∠CAD=∠ODB,∴∠ODB+∠ADC=90°,∴∠ADO=90°,又∵OD是半径,∴AD是⊙O的切线;(2)∵∠B=30°,∠ACB=90°,∴∠CAD=30°,∠CAB=60°,∴∠DAB=30°,∴OD=AO,∴OD=,∵OD=OB,∠B=30°,∴∠B=∠ODB=30°,∴∠DOB=120°,∴劣弧BD的长==π;(3)如图2,连接DE,∵BE是直径,∴∠BDE=90°,∴∠ACB=∠EDB=90°,∴AC∥DE,∵∠B=∠CAD,∠ACD=∠EDB,∴△ACD∽△BDE,∴,∴设CD=2x,DE=3x,∵AC∥DE,∴,∴,∴x=,∴CD=1,BC=BD+CD=4,∴AB===2,∵DE∥AC,∴,∴AE=×2=.4.解:(1)如图1,连接OA,OB,∵CD是⊙O的直径,弦AB⊥CD,∴=,∴∠AOD=∠BOD,∵∠ACD=30°,∴∠AOD=60°,∴∠AOB=120°,∴劣弧AB的度数是120°;(2)①∵CD⊥AB,∴AE=BE=1,∠AEC=90°,在Rt△AEC中,tan∠CAE==2,∴CE=2,设OE=x,则OC=2﹣x=OB,在Rt△OEB中,由勾股定理得:OB2=OE2+BE2,即(2﹣x)2=x2+1,解得:x=,∴OE=,∵OG=OB,AE=BE,∴OE是△AGB的中位线,∴AG=2OE=;②∵BG是⊙O的直径,∴∠BAG=90°,∵∠BAG=∠BEO=90°,∴OC∥AG,∴∠C=∠GAC,∵∠GFA=∠OFC,∴△GAF∽△OCF,∴,∵,且GF+BF=2OG,∴OG=•GF,∵OF=OG﹣GF,∴OF=,∴=,如图3,连接OA,∵OA=OC,AG=2OE,∴==,∵tan∠CAE==x,∴CE=x•AE=OA+OE,∴AE=,Rt△AOE中,OA2=OE2+AE2,∴OA2=OE2+()2,即OA2=OE2+(OA2+2OA•OE+OE2),两边同时除以OA2,得:1=()2+(+1)2,设=a,则原方程变形为:a2+(a2+2a+1)﹣1=0,(1+)a2++﹣1=0,(a+1)[(1+)a+(﹣1)]=0,∴a1=﹣1(舍),a2=,∴=,∴=,∴y=﹣.5.(1)①证明:如图1,连接PC,∵A、P、B、C四点内接于⊙O,∴∠PAF=∠PBC,∵AP平分∠BAF,∴∠PAF=∠BAP,∵∠BAP=∠PCB,∴∠PCB=∠PBC,∴PB=PC,∴=,∴点P为的中点;②解:如图2,过P作PG⊥BC于G,交BC于G,交⊙O于H,连接OB,∴,∴PH是直径,∵∠BPC=∠BAC,∠BOG=∠BPG=∠BPC,∵OG⊥BC,∴BG=BC=3,Rt△BOG中,∵OB=5,∴sin∠BAC=sin∠BOG==;(2)解:如图3,过P作PG⊥BC于G,连接OC,由(1)知:PG过圆心O,且CG=3,OC=OP=5,∴OG=4,∴PG=4+5=9,∴PC===3,设∠APC=x,∵A是的中点,∴=,∴∠ABC=∠ABP=x,∵PB=PC,∴∠PCB=∠PBC=2x,△PCE中,∠PCB=∠CPE+∠E,∴∠E=2x﹣x=x=∠CPE,∴CE=PC=3;(3)解:如图4,过点C作CQ⊥AB于Q,∵∠ACE=∠P,∠CAE=∠PAF=∠PAB,∴△ACE∽△APB,∴,∴PA•AE=AC•AB,∵sin∠BAC=,∴CQ=AC•sin∠BAC=AC,=AB•CQ=,∴S△ABC,∴PA•AE=S△ABC∵△ABC为非锐角三角形,∴点A运动到使△ABC为直角三角形时,如图5,△ABC的面积最大,Rt△ABC中,AB=10,BC=6,∴AC=8,此时PA•AE=×=80.6.(1)证明:连接OC,∵CD=BC,∴∠B=∠D,∵AC=AD,∴∠D=∠ACD,∴∠B=∠ACD,∵OA=OC,∴∠BAC=∠OCA,∵AB为⊙O的直径,∴∠ACB=90°,∴∠B+∠BAC=90°,∴∠ACD+∠OCA=90°,∴∠DCO=90°,∴OC⊥CD,∴CD是⊙O的切线;解:(2)i)连接OC,∵∠ACB=90°,AB=,sin B=,在Rt△ACB中,AC=AB•sin B,∴AC==1,在Rt△ACB中,BC===3,∵OB=CO,∴∠OCB=∠B,∵∠B=∠D,∴∠OCB=∠D,∵∠CBO=∠DBC,∴△COB∽△DCB,∴,∴CB2=OB•BD,∵AB=,∴OA=OB=,∴BD=32×=,∴AD=BD﹣AB=;ii)连接CO,∵CD=2CE,设CE=k,∴CD=BC=2k,∴DE=3k,∵∠E=∠B,∠OCB=∠B=∠D,∴△DAE∽△COB,∴,设⊙O的半径为r,∴AD=r,∴BD=AD+AB=r+2r=r,∵△COB∽△DCB,∴,∴BC2=OB•BD,∴(2k)2=r×r,∴k=r,∴BC=2k=r,∴cos B=.7.解:(1)如图1,连接OA,AD,∵AF是⊙O的切线,∴∠OAF=90°,∵AB=AC,∠BAC=60°,∴△ABC是等边三角形,∴∠ABC=∠ACB=∠BAC=60°,∵BD平分∠ABC,∴∠ABD=∠CBD=30°,∵∠ADB=∠ACB=60°,∴∠BAD=90°,∴BD是⊙O的直径,∵OA=OB=OD,∴∠ABO=∠OAB=30°,∠OAD=∠ADO=60°,∵∠BDC=∠BAC=60°,∴∠ADF=180°﹣60°﹣60°=60°=∠OAD,∴OA∥DF,∴∠F=180°﹣∠OAF=90°,∵∠DAF=30°,∴tan30°==,故答案为:;②∵⊙O的半径为4,∴AD=OA=4,DF=AD=2,∵∠AOD=60°,∴阴影部分的面积为:S梯形AODF ﹣S扇形OAD=•AF•(DF+OA)﹣=×(2+4)﹣π=6﹣π;故答案为:6﹣π;(2)如图2,连接AD,连接AO并延长交⊙O于点H,连接DH,则∠ADH=90°,∴∠DAH+∠DHA=90°,∵AF与⊙O相切,∴∠DAH+∠DAF=∠FAO=90°,∴∠DAF=∠DHA,∵BD平分∠ABC,∴∠ABD=∠CBD,∵=,∴∠CAD=∠DHA=∠DAF,∵AB=AC,∴∠ABC=∠ACB,∵四边形ABCD内接于⊙O,∴∠ABC+∠ADC=180°,∵∠ADF+∠ADC=180°,∴∠ADF=∠ABC,∵∠ADB=∠ACB=∠ABC,∴∠ADF=∠ADB,在△ADF和△ADE中,∴△ADF≌△ADE(ASA),∴DF=DE=6,∵=,∴DC=9.8.(1)解:∵∠A=120°,∠B=50°,∠C=α,∴∠D=360°﹣120°﹣50°﹣α=190°﹣α,若∠A=∠B﹣∠D,则120°=50°﹣(190°﹣α),解得:α=260°(舍),若∠A=∠D﹣∠B,则120°=(190°﹣α)﹣50°,解得:a=20°,若∠B=∠A﹣∠C,则50°=120°﹣α,解得:α=70°,若∠B=∠C﹣∠A,则50°=α﹣120°,解得:α=170°,若∠C=∠B﹣∠D,则α=50°﹣(190°﹣α),无解,若∠C=∠D﹣∠B,则α=(190°﹣α)﹣50°,解得:α=70°,若∠D=∠A﹣∠C,则190°﹣α=120°﹣α,无解,若∠D=∠C﹣∠A,则190°﹣α=α﹣120°,解得:α=155°,综上,α的值是20°或70°或170°或155°(写一个即可),故答案为:20°或70°或170°或155°(写一个即可);(2)证明:如图1,设∠A=x,∠C=y,则∠B=180°﹣x﹣y,∵AE=DE,∴∠ADE=∠A=x,∴∠BDE=180°﹣x,在四边形DBCE中,∠B=180°﹣x﹣y=∠BDE﹣∠C,∴四边形DBCE为幸福四边形;(3)①证明:如图2,∵D、F、G、E四点都在⊙O上,∴∠ADE=∠FGE,∵∠ADE=∠A,∴∠FGE=∠A,∵∠FGE=∠ACF,∴∠A=∠ACF,∵BF=CF,∴∠B=∠BCF,∵∠A+∠B+∠BCA=180°,∴∠ACF+∠BCF=90°,即∠ACB=90°,∴EG是⊙O的直径;②如图3,过E作EH⊥AB于H,连接DG,∵BF=CF,∴∠B=∠BCF=∠BDG,∴BG=DG=7,∵EG是⊙O的直径,∴∠GDE=90°,∵DE=AE=1,∴EG==5,∵∠BGF﹣∠B=45°,∠BGF﹣∠BCF=∠CFG,∴∠CFG=∠CEG=45°,∴△ECG是等腰直角三角形,∴CE=CG=5,∴BC=7+5=12,AC=5+1=6,∴AB===6,∵∠AHE=∠ACB=90°,∠A=∠A,∴△AHE∽△ACB,∴,即,∴AH=,∵AE=DE,EH⊥AD,∴AD=2AH=,∴幸福四边形DBCE的周长=BD+ED+CE+BC=6﹣+1+5+12=18+.9.解:(1)∵AB和CD为⊙O的直径,AB⊥CD,∴,∴∠ACE=∠AFC,∵∠CAE=∠FAC,∴△ACE∽△AFC,∴,∴AC2=AE•AF,∵AC=CE,∴CE2=AE•AF;(2)∵AB⊥CD,∴∠AOC=90°,∵OA=OC,∴∠ACE=∠OAC=45°,∴∠AFC=∠AOC=45°,∵AC=CE,∴∠CAE=∠AEC=(180°﹣∠ACO)=67.5°,∴∠BAF=∠CAF﹣∠OAC=22.5°,∵∠AEC=∠AFC+∠DAF=45°+∠DCF=67.5°,∴∠DCF=22.5°,∴∠ACF=∠OCA+∠DAF=67.5°=3×22.5°=3∠BAF;(3)如图,过点G作GH⊥CF交AF于H,∴∠FGH=90°,∵∠AFC=45°,∴∠FHG=45°,∴HG=FG=2,∴FH=2,∵∠BAF=22.5°,∠FHG=45°,∴∠AGH=∠FHG﹣∠BAF=22.5°=∠BAF,∴AH=HG=2,∴AF=AH+FH=2+2,由(2)知,∠OAE=∠OCG,∵∠AOE=∠COG=90°,OA=OC,∴△AOE≌△COG(SAS),∴OE=OG,∠AEO=∠CGO,∴∠OEF=∠OGF,连接EG,∵OE=OG,∴∠OEG=∠OGE=45°,∴∠FEG=∠FGE,∴EF=FG=2,∴AE=AF﹣EF=2+2﹣2=2.10.证明:(1)∵CE⊥AB,∴∠D+∠DCE=90°,∵∠OCE=∠D,∴∠OCE+∠DCE=90°,∴∠OCD=90°,又∵OC是半径,∴CD是⊙O的切线;(2)∵∠OCF=90°,G为OF中点,∴CG=GF=OF,∴∠GCF=∠GFC,∵∠D+∠COD=90°=∠D+∠DCE,∴∠DCE=∠COE=∠CFG,又∵∠OCF=∠OCD=90°,∴△OCF∽△DCO,∴,∴OC2=CF•CD;(3)∵CF=DF,∴CD=2CF,∵OC2=CF•CD,∴4=CF×2CF,∴CF=,∴OF===,∴CG=.。
中考数学一轮复习 专题01 有理数(基础训练)(原卷版)

专题01 有理数【基础训练】一、单选题1.(2021·西宁市教育科学研究院中考真题)中国人最先使用负数,魏晋时期的数学家刘徽在其著作《九章算术注》中,用不同颜色的算筹(小棍形状的记数工具)分别表示正数和负数(红色为正,黑色为负).如图1表示的是(+2)+(-2),根据这种表示法,可推算出图2所表示的算式是( )A .()()36+++B .()()36++-C .()()36-++D .()(36)-+-2.(2021·山东滨州市·中考真题)在数轴上,点A 表示-2.若从点A 出发,沿数轴的正方向移动4个单位长度到达点B ,则点B 表示的数是( )A .-6B .-4C .2D .4 3.(2021·广西百色市·中考真题)﹣2022的相反数是( )A .﹣2022B .2022C .±2022D .2021 4.(2021·广西桂林市·中考真题)有理数3,1,﹣2,4中,小于0的数是( ) A .3 B .1 C .﹣2 D .4 5.(2021·湖北荆门市·中考真题)2021的相反数的倒数是( ).A .2021-B .2021C .12021-D .12021 6.(2021·内蒙古呼和浩特市·中考真题)几种气体的液化温度(标准大气压)如表:A .氦气B .氮气C .氢气D .氧气 7.(2021·湖北襄阳市·中考真题)下列各数中最大的是( )A .3-B .2-C .0D .18.(2021·山东济宁市·中考真题)若盈余2万元记作2+万元,则2-万元表示( ) A .盈余2万元 B .亏损2万元 C .亏损2-万元 D .不盈余也不亏损 9.(2021·广东深圳市·中考真题)计算|1tan 60|-︒的值为( )A .1B .0C 1D .1 10.(2021·湖北鄂州市·中考真题)实数6的相反数等于( )A .6-B .6C .6±D .1611.(2021·湖北恩施土家族苗族自治州·中考真题)-6的相反数是( )A .-6B .6C .6±D .1612.(2021·黑龙江齐齐哈尔市·中考真题)五张不透明的卡片,正面分别写有实数1-,115 5.06006000600006……(相邻两个6之间0的个数依次加1).这五张卡片除正面的数不同外其余都相同,将它们背面朝上混合均匀后任取一张卡片,取到的卡片正面的数是无理数的概率是( )A .15B .25C .35D .4513.(2021·广东广州市·中考真题)如图,在数轴上,点A 、B 分别表示a 、b ,且0a b +=,若6AB =,则点A 表示的数为( )A .3-B .0C .3D .6-14.(2021·广东广州市·中考真题)下列运算正确的是( )A .()22--=-B .3=C .()22346a b a b =D .(a -2)2=a 2-415.(2021·贵州安顺市·中考真题)如图,已知数轴上,A B 两点表示的数分别是,a b ,则计算b a -正确的是( )A .b a -B .-a bC .a b +D .a b --16.(2021·内蒙古中考真题)下列运算结果中,绝对值最大的是( )A .1(4)+-B .4(1)-C .1(5)-- D17.(2021·黑龙江大庆市·中考真题)下列说法正确的是( )A .||x x <B .若|1|2x -+取最小值,则0x =C .若11x y >>>-,则||||x y <D .若|1|0x +≤,则1x =-18.(2021·河北中考真题)如图,将数轴上-6与6两点间的线段六等分,这五个等分点所对应数依次为1a ,2a ,3a ,4a ,5a ,则下列正确的是( )A .30a >B .14a a =C .123450a a a a a ++++=D .250a a +<19.(2021·湖南邵阳市·中考真题)如图,若数轴上两点M ,N 所对应的实数分别为m ,n ,则m n +的值可能是( )A .2B .1C .1-D .2-20.(2021·河北中考真题)能与3645⎛⎫-- ⎪⎝⎭相加得0的是( ) A .3645-- B .6354+ C .6354-+ D .3645-+ 21.(2021·四川达州市·中考真题)﹣23的相反数是( ) A .﹣32 B .﹣23 C .23 D .3222.(2021·浙江宁波市·中考真题)在﹣3,﹣1,0,2这四个数中,最小的数是( ) A .﹣3 B .﹣1 C .0 D .223.(2021·安徽中考真题)9-的绝对值是( )A .9B .9-C .19D .19- 24.(2021·四川南充市·中考真题)数轴上表示数m 和2m +的点到原点的距离相等,则m 为( )A .2-B .2C .1D .1-25.(2021·山东枣庄市·中考真题)如图,数轴上有三个点A﹣B﹣C ,若点A﹣B 表示的数互为相反数,则图中点C 对应的数是( )A .﹣2B .0C .1D .4二、填空题 26.(2021·辽宁盘锦市·2________27.(2021·江苏常州市·中考真题)数轴上的点A 、B 分别表示3-、2,则点__________离原点的距离较近(填“A ”或“B ”).28.(2021·湖北随州市·()012021π+-=______.29.(2021·湖北鄂州市·中考真题)已知实数a 、b30b +=,若关于x 的一元二次方程20x ax b -+=的两个实数根分别为1x 、2x ,则1211x x +=_____________. 30.(2021·甘肃兰州市·中考真题)《九章算术》中注有“今两算得失相反,要令正负以名之”大意为:今有两数若其意义相反,则分别叫做正数与负数.若水位上升1m 记作1m +,则下降2m 记作______m .三、解答题31.(2021·广西桂林市·中考真题)计算:|﹣3|+(﹣2)2.32.(2021·河北中考真题)某书店新进了一批图书,甲、乙两种书的进价分别为4元/本、10元/本.现购进m 本甲种书和n 本乙种书,共付款Q 元.(1)用含m ,n 的代数式表示Q ;(2)若共购进4510⨯本甲种书及3310⨯本乙种书,用科学记数法表示Q 的值.33.(2021·西宁市教育科学研究院中考真题)计算: 121(2)|3|2-⎛⎫-+-- ⎪⎝⎭. 34.(2021·山西中考真题)(1)计算:()()24311822⎛⎫-⨯-+-⨯ ⎪⎝⎭. (2)下面是小明同学解不等式的过程,请认真阅读并完成相应任务.2132132x x -->- 解:()()2213326x x ->--第一步42966x x ->--第二步49662x x ->--+第三步510x ->-第四步2x >第五步任务一:填空:﹣以上解题过程中,第二步是依据______________(运算律)进行变形的;﹣第__________步开始出现错误,这一步错误的原因是________________;任务二:请直接写出该不等式的正确解集.35.(2021·浙江台州市·中考真题)小华输液前发现瓶中药液共250毫升,输液器包装袋上标有“15滴/毫升”.输液开始时,药液流速为75滴/分钟.小华感觉身体不适,输液10分钟时调整了药液流速,输液20分钟时,瓶中的药液余量为160毫升.(1)求输液10分钟时瓶中的药液余量;(2)求小华从输液开始到结束所需的时间.。
2024成都中考数学第一轮专题复习 圆的有关概念及性质 知识精练(含答案)

2024成都中考数学第一轮专题复习圆的有关概念及性质知识精练基础题1. (2023江西)如图,点A,B,C,D均在直线l上,点P在直线l外,则经过其中任意三个点,最多可画出圆的个数为()A. 3B. 4C. 5D. 6第1题图2. (2023广东省卷)如图,AB是⊙O的直径,∠BAC=50°,则∠D=()第2题图A. 20°B. 40°C. 50°D. 80°3. (2023广元)如图,AB是⊙O的直径,点C,D在⊙O上,连接CD,OD,A C.若∠BOD=124°,则∠ACD的度数是()A. 56°B. 33°C. 28°D. 23°第3题图4. (2023山西)如图,四边形ABCD内接于⊙O,AC,BD为对角线,BD经过圆心O.若∠BAC =40°,则∠DBC的度数为()第4题图A. 40°B. 50°C. 60°D. 70°5. (2023安徽)如图,正五边形ABCDE内接于⊙O,连接OC,OD,则∠BAE-∠COD=()A. 60°B. 54°C. 48°D. 36°第5题图6. (2023赤峰)如图,圆内接四边形ABCD中,∠BCD=105°,连接OB,OC,OD,BD,∠BOC =2∠COD,则∠CBD的度数是()第6题图A. 25°B. 30°C. 35°D. 40°7. [新考法—数学文化](2023岳阳)我国古代数学名著《九章算术》中有这样一道题:“今有圆材,径二尺五寸.欲为方版,令厚七寸,问广几何?”结合下图,其大意是:今有圆形材质,直径BD为25寸,要做成方形板材,使其厚度CD达到7寸,则BC的长是() A. 674寸 B. 25寸C. 24寸D. 7寸第7题图8. (2023杭州)如图,在⊙O中,半径OA,OB互相垂直,点C在劣弧AB上.若∠ABC=19°,则∠BAC=()第8题图A. 23°B. 24°C. 25°D. 26°9. (2023广西)赵州桥是当今世界上建造最早,保存最完整的中国古代单孔敞肩石拱桥.如图,主桥拱呈圆弧形,跨度约为37 m,拱高约为7 m,则赵州桥主桥拱半径R约为()第9题图A. 20 mB. 28 mC. 35 mD. 40 m10. (2023凉山州)如图,在⊙O中,OA⊥BC,∠ADB=30°,BC=23,则OC=()A. 1B. 2C. 2 3D. 4第10题图11. 如图,点A,B,D在⊙O上,CD垂直平分AB于点C.现测得AB=CD=16,则圆形宣传图标的半径为()第11题图A. 12B. 10C. 8D. 612. 如图,在平面直角坐标系中,⊙O的半径为4,弦AB的长为3,过O作OC⊥AB于点C,则OC的长度是________;⊙O内一点D的坐标为(-2,1),当弦AB绕O点顺时针旋转时,点D到AB的距离的最小值是________.第12题图13. (2023武汉)如图,OA,OB,OC都是⊙O的半径,∠ACB=2∠BA C.(1)求证:∠AOB=2∠BOC;(2)若AB=4,BC=5,求⊙O的半径.第13题图拔高题14. (2023吉林省卷)如图,AB,AC是⊙O的弦,OB,OC是⊙O的半径,点P为OB上任意一点(点P不与点B重合),连接CP.若∠BAC=70°,则∠BPC的度数可能是()A. 70°B. 105°C. 125°D. 155°第14题图15. 如图,正方形ABCD 内接于⊙O ,点E 为弧AB 的中点,连接DE 与AB 交于点F .若AB=1,记△ADF 的面积为S 1,△AEF 的面积为S 2,则S 1S 2的值为________.第15题图16. 如图,以原点O 为圆心的圆交x 轴于A ,B 两点,交y 轴的正半轴于点C ,且点A 的坐标为(-2,0),D 为第一象限内⊙O 上的一点,若∠OCD =75°,则AD 的长为________.第16题图参考答案与解析1. D 【解析】本题考查了确定圆的条件及圆的有关定义及性质.∵过不在同一直线上的三个点一定能作一个圆,∴要经过题中所给的3个点画圆,除选定直线l 外的点P 外,再在直线l 上的A ,B ,C ,D 四个点中任选其中2个即可画圆.∵从A ,B ,C ,D 四个点中任选其中2个点的方法可以是AB ,AC ,AD ,BC ,BD ,CD ,共6种,∴最多可以画出圆的个数为6.2. B 【解析】∵AB 是⊙O 的直径,∠BAC =50°,∴∠ACB =90°,∠B =180°-50°-90°=40°.∵AC =AC ,∴∠D =∠B =40°.3. C 【解析】∵∠BOD =124°,∴∠AOD =180°-124°=56°,∴∠ACD =12∠AOD =28°. 4. B 【解析】∵BD 经过圆心O ,∴∠BCD =90°.∵∠BDC =∠BAC =40°,∴∠DBC =90°-∠BDC =50°.5. D 【解析】∵五边形ABCDE 是正五边形,∴∠BAE =(5-2)×180°5=108°,∠COD =360°5=72°,∴∠BAE -∠COD =108°-72°=36°. 6. A 【解析】∵∠BCD =105°,∴∠BAD =180°-105°=75°,∴∠BOD =150°.∵∠BOC=2∠COD ,∴∠COD =13 ∠BOD =50°,∴∠CBD =12∠COD =25°. 7. C 【解析】∵BD 是圆的直径,∴∠BCD =90°.∵BD =25,CD =7,∴在Rt △BCD 中,由勾股定理得,BC =252-72 =24(寸).8. D 【解析】如解图,连接OC ,∵∠ABC =19°,∴∠AOC =2∠ABC =38°.∵半径OA ,OB 互相垂直,∴∠AOB =90°,∴∠BOC =90°-38°=52°,∴∠BAC =12∠BOC =26°.第8题解图9. B 【解析】如解图,在Rt △OAB 中,由勾股定理,得AO 2+AB 2=OB 2,即(R -7)2+(372)2=R 2,解得R ≈28(m).第9题解图10. B 【解析】如解图,连接OB ,设OA 交BC 于点E ,∵∠ADB =30°,∴∠AOB =60°.∵OA ⊥BC ,BC =23 ,∴BE =12 BC =3 .在Rt △BOE 中,sin ∠AOB =BE OB,∴sin 60°=3OB =32,∴OB =2,∴OC =2.第10题解图11. B 【解析】如解图,连接OA ,设圆形宣传图标的半径为R ,∵CD 垂直平分AB ,AB=CD =16,∴CD 过点O ,AC =BC =12 AB =12×16=8,∠DCA =90°.∵AO =OD =R ,∴在Rt △AOC 中,由勾股定理,得OC 2+AC 2=OA 2,即(16-R )2+82=R 2,解得R =10,即圆形宣传图标的半径为10.第11题解图 12. 552 ;552 -5 【解析】如解图,连接OB ,∵OC ⊥AB ,∴BC =12 AB =32.由勾股定理,得OC =OB 2-BC 2 =552.当OD ⊥AB 时,点D 到AB 的距离最小,由勾股定理,得OD =22+12 =5 ,∴点D 到AB 的距离的最小值为552 -5 .第12题解图13. (1)证明:由圆周角定理,得∠ACB =12 ∠AOB ,∠BAC =12∠BOC . ∵∠ACB =2∠BAC ,∴∠AOB =2∠BOC ;(2)解:如解图,过点O 作半径OD ⊥AB 于点E ,连接BD .则∠DOB =12∠AOB ,AE =BE . ∵∠AOB =2∠BOC ,∴∠DOB =∠BOC .∴BD =BC .∵AB =4,BC =5 ,∴BE =2,DB =5 .在Rt △BDE 中,∵∠DEB =90°,∴DE =BD 2-BE 2 =1.在Rt △BOE 中,∵∠OEB =90°,∴OB 2=(OB -1)2+22,∴OB =52, 即⊙O 的半径是 52.第13题解图14. D 【解析】如解图,连接BC ,∵∠BAC =70°,∴∠BOC =2∠BAC =140°.∵OB =OC ,∴∠OBC =∠OCB =180°-140°2=20°.∵点P 为OB 上任意一点(点P 不与点B 重合),∴0°<∠OCP <20°.∵∠BPC =∠BOC +∠OCP =140°+∠OCP ,∴140°<∠BPC <160°,故选D.第14题解图15. 2(2 +1) 【解析】如解图,连接OE 交AB 于点G ,连接AC .根据垂径定理的推论,得OE ⊥AB ,AG =BG .由题意可得,AC 为⊙O 的直径,AC =2 ,则圆的半径是22.根据正方形的性质,得∠OAF =45°,∴OG =12 ,EG =2-12.∵OE ∥AD ,∴△ADF ∽△GEF ,∴FE FD =EG DA =2-12 .∵△ADF 与△AEF 等高,∴S 1S 2 =S △ADF S △AEF=DF EF =2(2 +1).第15题解图16. 23 【解析】如解图,连接OD ,BD .∵A (-2,0),∴OA =OB =2,∴AB =4.∵OC =OD ,∴∠OCD =∠ODC =75°,∴∠DOC =180°-2×75°=30°,∴∠DOB =90°-30°=60°,∴∠DAB =12∠DOB =30°.∵AB 是⊙O 的直径,∴∠ADB =90°,∴AD =AB ·cos 30°=23 .第16题解图。
九年级数学中考复习第一轮复习基础训练三角函数(一)三角函数与解直角三角形 课时作业同步练习含答案解析

微专题8 三角函数(一)三角函数与解直角三角形考点1锐角三角函数的定义1.如图,在Rt △ABC 中,∠C =90°,AB =10,AC =8,则 sin A 等于( ) A.35 B.45 C.34 D.432.如图,边长为1的小正方形网格中, ⊙O 的圆心在格点上,cos ∠AED = .3.如图,在△ABC 中,CA=CB =4, cos C =14,则sinB 的值为 . 考点2 特殊角的三角函数值4.(1) sin 30°= ; cos 60°= ;tan 45"= ;(2)3sin 60"—2cos 30°—tan 60°= .5.在△ABC 中,∠A ,∠B 为锐角,若|sinA 一22|+(32-cosB )2=0,则∠C = 度. 考点3 解直角三角形及其实际应用6.如图,在△ABC 中,∠B =30°,AC=2,cosC =35.则AB 边的长为 .7.如图,某地修建高速公路,要从B 地向C 地修一座隧道(B,C 在同一水平面上),为了测量B ,C 两地之间的距离,某工程队员乘坐热气球从C 地出发垂直上升100m 到达A 处,在A 处观察B 地的俯角为30°,则B,C 两地间的距离为 m .8.如图,一艘船由A 港沿北偏东65°方向航行302km 至B 港,然后再沿北偏西40°方向航行至C 港,C 港在A 港北偏东20°方向,则A,C 两港之间的距离为 km.DOB AECAC ABCB第1题图第2题图第3题图30°30°B CC A CAB AB 第6题图 第7题图 第8题图9.如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,求山高AD.10.某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1.(1)求新坡面的坡角α的度数;(2)原天桥底部正前方8米处(PB的长)的文化墙PM是否需要拆除?请说明理由. :C BC微专题8 三角函数(一)三角函数与解直角三角形考点精练精练1锐角三角函数的定义1.如图,在Rt △ABC 中,∠C =90°,AB =10,AC =8,则 sin A 等于( A ) A.35 B.45 C.34 D.432.如图,边长为1的小正方形网格中, ⊙O 的圆心在格点上,cos ∠AED =255. 3.如图,在△ABC 中,CA=CB =4, cos C =14,则sinB 的值为104.精练2 特殊角的三角函数值4.(1) sin 30°=12; cos 60°=12;tan 45"= 1 ;(2)3sin 60"—2cos 30°—tan 60°= 32 .5.在△ABC 中,∠A ,∠B 为锐角,若|sinA 一22|+(32-cosB )2=0,则∠C =105度. 精练3 解直角三角形及其实际应用6.如图,在△ABC 中,∠B =30°,AC=2,cosC =35.则AB 边的长为165.DOB AECAC ABCB第1题图第2题图第3题图30°30°BC CACABAB第6题图第7题图第8题图7.如图,某地修建高速公路,要从B地向C地修一座隧道(B,C在同一水平面上),为了测量B,C两地之间的距离,某工程队员乘坐热气球从C地出发垂直上升100m到达A处,在A处观察B地的俯角为30°,则B,C两地间的距离为.8.如图,一艘船由A港沿北偏东65°方向航行至B港,然后再沿北偏西40°方向航行至C港,C港在A港北偏东20°方向,则A,C两港之间的距离为(30+km.9.如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,求山高AD.解:设AD=x米,则BDx米.CD=AD=xx-x=100.解得:x=50.答:山高为(50)米.10.某地的一座人行天桥如图所示,天桥高为6米,坡面BC的坡度为1:1,为了方便行人推车过天桥,有关部门决定降低坡度,使新坡面的坡度为1.(1)求新坡面的坡角α的度数;(2)原天桥底部正前方8米处(PB的长)的文化墙PM是否需要拆除?请说明理由. 解:(1)30°:(2)过点C作CD⊥AB于点D.则BD=CD=6.AD∴AB=AD-BD一6<8∴文化培PM不需要拆除.C B。
中考数学一轮复习专题训练:一元一次方程(附答案)

2020 年中考数学一轮复习专题训练:一元一次方程一.选择题(共 8 小题)1.以下四个式子中,是方程的是()A .3+2=5B .x= 1C. 2x﹣ 3< 022 D. a +2ab+b2.若对于 x 的方程 2x﹣( 2a﹣1) x+3=0 的解是 x=3,则 a=()A .1B .0C. 2D. 33.解是 x=2 的方程是()A .2( x﹣ 1)= 6B .C.D.4.以下等式变形正确的选项是()A .若﹣ 3x= 5,则 x=﹣B .若,则2x+3(x﹣1)=1C.若 5x﹣ 6=2x+8,则 5x+2x= 8+6D .若 3( x+1)﹣ 2x= 1,则 3x+3 ﹣2x= 15.在解方程 3x+5=﹣ 2x﹣ 1 的过程中,移项正确的选项是()A .3x﹣ 2x=﹣ 1+5B.﹣ 3x﹣ 2x= 5﹣ 1C. 3x+2x=﹣ 1﹣ 5D.﹣ 3x﹣ 2x=﹣ 1﹣ 56.解方程: 2﹣=﹣,去分母得()A .2﹣ 2 (2x﹣ 4)=﹣( x﹣ 7)B. 12﹣ 2 ( 2x﹣ 4)=﹣ x﹣7C. 2﹣( 2x﹣4)=﹣( x﹣ 7)D. 12﹣ 2 ( 2x﹣ 4)=﹣( x﹣ 7)7.有以下结论:①若 a+b+c= 0,则 abc≠ 0;②若 a( x﹣ 1)= b( x﹣ 1)有独一的解,则a≠b;③若 b=2a,则对于 x 的方程 ax+b= 0( a≠ 0)的解为 x=﹣;④若 a+b+c= 1,且 a≠ 0,则 x= 1 必定是方程 ax+b+c= 1 的解;此中结论正确的个数有()A.4 个B.3 个C.2 个D.1 个8.若对于x 的方程 |2x﹣3|+m= 0 无解, |3x﹣ 4|+n= 0 只有一个解, |4x﹣ 5|+k= 0 有两个解,A .m >n > kB .n > k > mC . k > m > nD . m > k > n二.填空题(共8 小题)9.比 a 的 3 倍大 5 的数等于 a 的 4 倍用等式表示为. 10.已知等式 5x m+2m =.+3= 0 是对于 x 的一元一次方程,则11.在 ① 2x ﹣ 1; ② 2x+1= 3x ; ③ |π﹣ 3|= π﹣ 3 ; ④ t+1 = 3 中,等式有,方程有.(填入式子的序号)12.已知 x =5 是方程 ax ﹣ 8= 20+a 的解,则 a = .13.小强在解方程时,不当心把一个数字用墨水污染成了x =1﹣ ,他翻阅了答案知道这个方程的解为 x = 1,于是他判断●应当是.14.已知代数式 与 互为相反数,则 x 的值是 .15.已知方程的解也是方程 |3x ﹣ 2|= b 的解,则b = .16.已知 x ﹣3y = 3,则 7+6y ﹣ 2x =.三.解答题(共 6 小题)17.解方程:( 1) 3x ﹣ 9= 6x ﹣1;( 2) x ﹣= 1﹣.18.若方程 3(x+1 )= 2+x 的解与对于 x 的方程 = 2( x+3)的解互为倒数,求 k 的值.19.已知对于 x 的方程( m+5) x|m|﹣4+18= 0 是一元一次方程.试求:( 1)m 的值;( 2)代数式 的值.20.依据题意设未知数,并列出方程(不用求解).( 1)有两个工程队,甲队人数30 名,乙队人数10 名,问如何调整两队的人数,才能使甲队的人数是乙队人数的7 倍.( 2)有一个班的同学准备去划船,租了若干条船,他们计算了一下,假如比原计划多租1 条船,那么正好每条船坐 6 人;假如比原计划少租 1 条船,那么正好每条船坐9 人.问这个班共有多少名同学?21.我们规定:若对于 x 的一元一次方程ax= b 的解为 b+a,则称该方程为“和解方程” .比如:方程 2x=﹣ 4 的解为 x=﹣ 2,而﹣ 2=﹣ 4+2,则方程 2x=﹣ 4 为“和解方程”.请依据上述规定解答以下问题:( 1)已知对于x 的一元一次方程3x= m 是“和解方程” ,求 m 的值;( 2)已知对于x 的一元一次方程﹣2x= mn+n 是“和解方程” ,而且它的解是x=n,求 m,n 的值.22.先阅读以下解题过程,而后解答问题(1)、( 2)、( 3).例:解绝对值方程:|2x|= 1.解:议论:①当 x≥ 0 时,原方程可化为2x= 1,它的解是x=.②当 x<0 时,原方程可化为﹣2x= 1,它的解是x=﹣.∴原方程的解为x=和﹣.问题( 1):依例题的解法,方程|的解是;问题( 2):试试解绝对值方程:2|x﹣2|= 6;问题( 3):在理解绝对值方程解法的基础上,解方程:|x﹣ 2|+|x﹣ 1|= 5.参照答案一.选择题(共8 小题)1.【解答】解:A、不是方程,由于不含有未知数,故本选项错误;B、是方程, x 是未知数,式子又是等式,故本选项正确;C、不是方程,由于它是不等式而非等式,故本选项错误;D、不是方程,由于它不是等式,故本选项错误;应选: B.2.【解答】解:把x=3 代入方程获得:6﹣ 3( 2a﹣ 1) +3= 0解得: a= 2.应选: C.3.【解答】解:将x=2 分别代入题目中的四个选项得:A、 2( x﹣ 1)= 2( 2﹣ 1)= 2≠ 6,因此, A 错误;B.= +1=2= X=2,因此, B 正确;C.==,因此,C错误;D .==≠1﹣x=1﹣2=﹣1,因此D错误;应选: B.4.【解答】解: A、若﹣ 3x=5,则 x=﹣,错误,故本选项不切合题意;B、若,则2x+3(x﹣1)=6,错误,故本选项不切合题意;C、若 5x﹣ 6=2x+8,则 5x﹣ 2x= 8+6,错误,故本选项不切合题意;D 、若 3( x+1)﹣ 2x= 1,则 3x+3 ﹣2x= 1,正确,故本选项切合题意;应选: D.5.【解答】解:方程3x+5=﹣ 2x﹣ 1 移项得: 3x+2 x=﹣ 1﹣ 5.应选: C.6.【解答】解:去分母得:12﹣2( 2x﹣ 4)=﹣( x﹣ 7),应选: D.7.【解答】解:① 错误,当a=0, b= 1, c=﹣ 1 时, a+b+c=0+1 ﹣ 1=0,可是 abc= 0;②正确,方程整理得:( a﹣ b) x= a﹣b,③ 错误,由 a ≠ 0, b = 2a ,方程解得: x =﹣ =﹣ 2;④ 正确,把 x = 1,a+b+c = 1 代入方程左侧得: a+b+c = 1,右侧= 1,故若 a+b+c = 1,且 a ≠ 0,则 x = 1 必定是方程 ax+b+c = 1 的解,应选: C .8.【解答】解: ( 1)∵ |2x ﹣ 3|+m = 0 无解,∴ m > 0.( 2)∵ |3x ﹣ 4|+n = 0 有一个解,∴ n = 0.( 3)∵ |4x ﹣ 5|+k = 0 有两个解,∴ k < 0.∴ m > n > k .应选: A .二.填空题(共 8 小题)9.【解答】解:依据题意得: 3a+5 = 4a .故答案为: 3a+5= 4.10.【解答】解:由于 5x m+2+3= 0 是对于 x 的一元一次方程,因此 m+2= 1,解得 m =﹣ 1.故填:﹣ 1.11.【解答】解:等式有 ②③④ ,方程有 ②④ .故答案为: ②③④ ,②④ .12.【解答】解:把 x = 5 代入方程 ax ﹣ 8= 20+a得: 5a ﹣ 8= 20+a ,解得: a = 7.故答案为: 7.13.【解答】解:●用 a 表示,把 x = 1 代入方程得 1= 1﹣,解得: a = 1.故答案是: 1.514.【解答】解:∵代数式与x﹣3 互为相反数,∴﹣=x﹣3,解得 x=.故答案为:.15.【解答】解:2(x﹣ 2)= 20﹣ 5( x+3),2x﹣ 4=20﹣ 5x﹣ 15,7x= 9,解得: x=.把 x=代入方程|3x﹣2|=b得:|3×﹣2|=b,解得: b=.故答案为:.16.【解答】解:x﹣ 3y= 3,方程两边都乘以﹣2,得6y﹣ 2x=﹣ 6,方程两边都加7,得7+6y﹣ 2x=﹣ 6+7= 1,故答案为: 1.三.解答题(共 6 小题)17.【解答】解:( 1)移项归并得:3x=﹣ 8,解得: x=﹣;(2)去分母得: 4x﹣ x+1=4﹣ 6+2x,移项归并得: x=﹣ 3.18.【解答】解:解3( x+1)= 2+x,得 x=﹣,∵双方程的解互为倒数,∴将 x=﹣ 2 代入=2(x+3)得=2,解得 k=0.19.【解答】解:( 1)由题意得,|m|﹣ 4= 1, m+5≠ 0,解得, m= 5;(2)当 m=5 时,原方程化为 10x+18 =0,解得, x=﹣,∴==﹣.20.【解答】解:(1)设从乙队调x 人去甲队,则乙队此刻有10﹣ x 人,甲队有30+x 人,由题意得30+x= 7( 10﹣ x);(2)设这个班共有 x 名同学,由题意得﹣1= +1.21.【解答】解:( 1)∵方程3x= m 是和解方程,∴= m+3,解得: m=﹣.(2)∵对于 x 的一元一次方程﹣ 2x= mn+n 是“和解方程” ,而且它的解是 x= n,∴﹣ 2n= mn+n,且 mn+n﹣2= n,解得 m=﹣ 3, n=﹣.22.【解答】解:( 1) |x|= 2,①当 x≥0 时,原方程可化为x= 2,它的解是x= 4;②当 x<0 时,原方程可化为﹣x=2,它的解是x=﹣ 4;∴原方程的解为x= 4 和﹣ 4,故答案为: x= 4 和﹣ 4.(2) 2|x﹣ 2|= 6,①当 x﹣ 2≥ 0 时,原方程可化为2(x﹣ 2)= 6,它的解是x= 5;②当 x﹣ 2< 0 时,原方程可化为﹣2(x﹣ 2)= 6,它的解是x=﹣ 1;∴原方程的解为x= 5 和﹣ 1.( 3) |x﹣ 2|+|x﹣ 1|= 5,①当 x﹣ 2≥ 0,即 x≥ 2 时,原方程可化为x﹣ 2+x﹣ 1= 5,它的解是x= 4;②当 x﹣ 1≤ 0,即 x≤ 1 时,原方程可化为2﹣ x+1﹣ x= 5,它的解是x=﹣ 1;③当 1< x< 2 时,原方程可化为2﹣x+x﹣ 1= 5,此时方程无解;∴原方程的解为x= 4 和﹣ 1.。
2021年中考复习数学一轮专练:矩形及其性质(一)及答案

2021年中考数学一轮专练:矩形及其性质(一)1.已知:如图,在矩形ABCD中,M,N分别是边AD、BC的中点,E,F分别是线段BM,CM的中点.(1)求证:△ABM≌△DCM;(2)判断四边形MENF是什么特殊四边形,并证明你的结论;(3)当AD:AB=时,四边形MENF是正方形(只写结论,不需证明)2.矩形ABCD的对角线交于O点,一条边的长为1,△AOB是正三角形,则这个矩形的周长为.3.如图,过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ,那么图中矩形AMKP的面积S1与矩形QCNK的面积S2的大小关系是S1S2;(填“>”或“<”或“=”)4.如图矩形ABCD中,AB=3cm,AD=4cm,过对角线BD的中点O作BD的垂直平分线EF,分别交AD、BC于点E、F,则AE的长为.5.在矩形ABCD中,AC、BD交于点O.过点O作OE⊥BD交射线BC于点E,若BE=2CE,AB=3,则AD的长为.6.如图,矩形ABCD被分割成一个菱形和两个三角形,如果其中一个三角形的面积是菱形面积的,那么AB:AD的值是.7.如图,在矩形ABCD中,E是直线BC上一点,且CE=CA,连结AE.若∠BAC=60°,则∠CAE的度数为.8.已知矩形ABCD,对角线AC、BD相交于点O,点E为BD上一点,OE=1,连接AE,∠AOB=60°,AB=2,则AE的长为.9.如图,在矩形ABCD中,点E是边AD上一点,EF⊥AC于点F.若tan∠BAC=2,EF =1,则AE的长为.10.如图,在矩形ABCD中,AB=4,BC=6,将△ABE沿着AE折叠至△AB'E,若BE=CE,连接B'C,则B′C的长为.11.如图,△ABC中,∠ABC=90°,O为AC的中点,连接BO并延长到D,连接AD,CD.添加一个条件,使四边形ABCD是矩形(填一个即可).12.如图,在平行四边形ABCD中,AC、BD相交于O,请添加一个条件,可得平行四边形ABCD是矩形.13.如图,平行四边形ABCD的对角线相交于点O,请你添加一个条件.(只添一个即可),使平行四边形ABCD是矩形.14.如图,在▱ABCD中,请再添加一个条件,使得四边形ABCD是矩形,你所添加的条件是.15.如图,四边形ABCD的对角线互相平分,请你添加一个条件,使它成为矩形,你添加的条件是.16.四边形ABCD的对角线AC、BD互相平分,要使它成为矩形,需要添加的条件是.17.用一刻度尺检验一个四边形是否为矩形,以下方法可行的有.(只要填序号即可)①量出四边及两条对角线,比较对边是否相等,对角线是否相等.②量出对角线的交点到四个顶点的距离,看是否相等.③量出一组邻边的长a、b以及和这两边组成三角形的那条对角线的长c,计算是否有a2+b2=c2.④量出两条对角线长,看是否相等.18.如图,在Rt△ABC中,∠BAC=90°,且BA=6,AC=8,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小值为.19.如图,△ABC是以AB为斜边的直角三角形,AC=4,BC=3,P为AB上一动点,且PE⊥AC于E,PF⊥BC于F,则线段EF长度的最小值是.20.如图,在菱形ABCD中,AC、BD交于点O,AC=6,BD=8,若DE∥AC,CE∥BD,则OE的长为.参考答案1.(1)证明:∵四边形ABCD是矩形,∴AB=DC,∠A=∠D=90°,∵M为AD中点,∴AM=DM,在△ABM和△DCM,∴△ABM≌△DCM(SAS);(2)答:四边形MENF是菱形.证明:∵N、E、F分别是BC、BM、CM的中点,∴NE∥CM,NE=CM,MF=CM,∴NE=FM,NE∥FM,∴四边形MENF是平行四边形,由(1)知△ABM≌△DCM,∴BM=CM,∵E、F分别是BM、CM的中点,∴ME=MF,∴平行四边形MENF是菱形;(3)解:当四边形MENF是正方形正方形时,则∠EMF=90°,∵△ABM≌△DCM,∴∠AMB=∠DMC=45°,∴△ABM、△DCM为等腰直角三角形,∴AM=DM=AB,∴AD=2AB,当AD:AB=2:1时,四边形MENF是正方形.故答案为:2:1.2.解:在矩形ABCD中,AC=2OB,∵△AOB是正三角形,∴OB=AB,∴AC=2AB,①AB=1时,AC=2,根据勾股定理,BC===,所以,矩形的周长=2(AB+BC)=2(1+)=2+2;②BC=1时,根据勾股定理,AB2+BC2=AC2,所以,AB2+12=(2AB)2,解得AB=,所以,矩形的周长=2(AB+BC)=2(+1)=+2;综上所述,矩形的周长为2+2或+2.故答案为:2+2或+2.3.解:∵四边形ABCD是矩形,四边形MBQK是矩形,四边形PKND是矩形,∴△ABD的面积=△CDB的面积,△MBK的面积=△QKB的面积,△PKD的面积=△NDK的面积,∴△ABD的面积﹣△MBK的面积﹣△PKD的面积=△CDB的面积﹣△QKB的面积=△NDK的面积,∴S1=S2.故答案为S1=S2.4.解:连接EB,∵EF垂直平分BD,∴ED=EB,设AE=xcm,则DE=EB=(4﹣x)cm,在Rt△AEB中,AE2+AB2=BE2,即:x2+32=(4﹣x)2,解得:x=,故答案为:cm.5.解:如图,当点E在BC的延长线上时,∵BE=2CE,∴BC=CE,∵OE⊥BD,∴OC=BC=CE,∵四边形ABCD是矩形,∴AO=CO=BO=DO,AD=BC;∴BO=CO=BC,∴△BOC是等边三角形,∴∠ACB=60°∴tan∠ACB=,∴BC==AD,如图,当点E在线段BC上时,设直线OE与直线AB,CD交于点F,点H,∵AB∥CD,∴,∴AF=CH,∵AB∥CD,∴△EBF∽△ECH,∴,∴BF=2CH=2AF,∴3+AF=2AF,∴AF=3=AB,且OE⊥BD,∴AO=AB=AF=3,∵AO=BO=CO=DO,∴AO=AB=BO,∴△ABO是等边三角形,∴∠ABD =60°, ∴tan ∠ABD =, ∴AD =3,故答案为:3或.6.解:∵四边形AECF 是菱形,∴AE =CE =CF ,∵四边形ABCD 是矩形,∴AD =BC ,∠B =∠D =90°,CD =AB∴Rt △AED ≌Rt △CFB (HL )∴S △ADE =S △CBF ,∵一个三角形的面积是菱形面积的,∴×AD ×DE =×AD ×EC , ∴EC =2DE ,∴AE =2DE ,DC =3DE =AB ,∴AD ==DE , ∴AB :AD =3DE :DE =:1,故答案为::1. 7.解:∵∠BAC =60°,∠ABC =90°, ∴∠ACB =30°,如图,当点E 在点B 左侧时,∵CE =CA ,∴∠CAE =∠AEC =75°,若点E '在点C 右侧时,∵AC =CE ',∴∠CAE '=∠CE 'A ,∵∠ACB=∠CAE'+∠CE'A=30°,∴∠CAE'=15°,综上所述:∠CAE的度数为75°或15°,故答案为75°或15°.8.解:如图,连接AE,∵四边形ABCD是矩形,∴OA=OB,且∠AOB=60°,∴△AOB是等边三角形,∴AO=OB=AB=2,若点E在BO上时,∵OE=1,∴BE=EO=1,且△ABO等边三角形,∴AE⊥BO,∴AE===,若点E'在OD上时,∴AE'===,故答案为:或.9.解:∵在矩形ABCD中,∠B=90°,tan∠BAC=2 ∴=2,∵AD=BC,CD=AB,∴=,∴tan∠EAF=,∵EF=1,∴AF=2,∴AE===,故答案为:.10.解:∵将△ABE沿着AE折叠至△AB'E,∴S△ABE =S△AB'E,BE=B'E,∵BE=CE,∴BE=EC=B'E=3,∴∠BB'C=90°,在Rt△ABE中,AE===5,∵×AE×BB'=2××AB×BE,∴BB'==,∴B'C===,故答案为:.11.解:添加BO=DO,理由:∵O为AC的中点,∴AO=CO,∵BO=DO,∴四边形ABCD是平行四边形,∵∠ABC=90°,∴四边形ABCD是矩形.故答案为:BO=DO.12.解:若使▱ABCD变为矩形,可添加的条件是:AC=BD;(对角线相等的平行四边形是矩形),∠ABC=90°等(有一个角是直角的平行四边形是矩形),故答案为:任意写出一个正确答案即可,如:AC=BD或∠ABC=90°.13.解:添加的条件是AC=BD,理由是:∵AC=BD,四边形ABCD是平行四边形,∴平行四边形ABCD是矩形,故答案为:AC=BD.答案不唯一.14.解:可添加AC=BD,在平行四边形ABCD中,∵AC=BD,∴四边形ABCD是矩形,故答案为:AC=BD(答案不唯一).15.解:可添加AC=BD,∵四边形ABCD的对角线互相平分,∴四边形ABCD是平行四边形,∵AC=BD,∴四边形ABCD是矩形,故答案为:AC=BD(答案不唯一).16.解:添加条件:AC=BD;理由如下:∵四边形ABCD的对角线AC、BD互相平分,∴四边形ABCD是平行四边形,又∵AC=BD,∴四边形ABCD是矩形;故答案为:AC=BD.17.解:①先测量两组对边是否相等,然后测量两条对角线是否相等;理由:两组对边分别相等的四边形是平行四边形,可以判定是否是矩形,故此选项正确;②根据对角线互相平分且相等的四边形是矩形,可知量出对角线的交点到四个顶点的距离,看是否相等,可判断是否是矩形,故此选项正确;③量出一组邻的长a、b以及和这两边组成三角形的那条对角线的长c,计算是否有a2+b2=c2.可以判断是否是直角,但不能判断是否是矩形;故此选项错误;④量出两条对角线长,看是否相等不能判定是矩形,必须两条对角线长相等气且互相平分才是矩形;故此选项错误;综上所述:用一刻度尺检验一个四边形是否为矩形,可行的方法有①②.故答案为:①②.18.解:∵∠BAC=90°,且BA=6,AC=8,∴BC==10,∵DM⊥AB,DN⊥AC,∴∠DMA=∠DNA=∠BAC=90°,∴四边形DMAN是矩形,∴MN=AD,∴当AD⊥BC时,AD的值最小,此时,△ABC的面积=AB×AC=BC×AD,∴AD==,∴MN的最小值为;故答案为:.19.解:连接PC.∵PE⊥AC,PF⊥BC,∴∠PEC=∠PFC=∠C=90°;又∵∠ACB=90°,∴四边形ECFP是矩形,∴EF=PC,∴当PC最小时,EF也最小,即当CP⊥AB时,PC最小,∵AC=4,BC=3,∴AB=5,∴AC•BC=AB•PC,∴PC=.∴线段EF长的最小值为;故答案是:.20.证明:∵四边形ABCD为菱形,∴AC⊥BD,OA=AC=3,OD=BD=4,∴∠AOD=90°,∴AD==5=CD∵DE∥AC,CE∥BD∴四边形OCED为平行四边形,又∵AC⊥BD∴四边形OCED为矩形∴CD=OE=5故答案为:5。
2021年九年级中考数学一轮复习专题 《四边形综合:动点与相似》高频考点训练(一)

2021年中考数学一轮复习专题《四边形综合:动点与相似》高频考点训练(一)1.如图1,在正方形ABCD中,点E是CD上一点(不与C,D两点重合),连接BE,过点C作CH⊥BE于点F,交对角线BD于点G,交AD边于点H,连接GE,(1)求证:△DHC≌△CEB;(2)如图2,若点E是CD的中点,当BE=8时,求线段GH的长;(3)设正方形ABCD的面积为S1,四边形DEGH的面积为S2,当的值为时,的值为.2.我们知道,有一个内角是直角的三角形是直角三角形,其中直角所在的两条边叫直角边,直角所对的边叫斜边(如图①所示).数学家还发现:在一个直角三角形中,两条直角边长的平方和等于斜边长的平方.即如果一个直角三角形的两条直角边长度分别是a和b,斜边长度是c,那么a2+b2=c2.(1)直接填空:如图①,若a=3,b=4,则c=;若a+b=4,c=3,则直角三角形的面积是.(2)观察图②,其中两个相同的直角三角形边AE、EB在一条直线上,请利用几何图形的之间的面积关系,试说明a2+b2=c2.(3)如图③所示,折叠长方形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8,BC=10,利用上面的结论求EF的长?3.四边形ABCD是矩形,点E是射线BC上一点,连接AC,DE.(1)如图1,点E在边BC的延长线上,BE=AC,若∠ACB=40°,求∠E的度数;(2)如图2,点E在边BC的延长线上,BE=AC,若M是DE的中点,连接AM,CM,求证:AM⊥MC;(3)如图3,点E在边BC上,射线AE交射线DC于点F,∠AED=2∠AEB,AF =4,AB=4,则CE=.(直接写出结果)4.如图.正方形ABCD的边长为4,点E从点A出发,以每秒1个单位长度的速度沿射线AD运动,运动时间为t秒(t>0),以AE为一条边,在正方形ABCD左侧作正方形AEFG,连接BF.(1])当t=1时,求BF的长度;(2)在点E运动的过程中,求D、F两点之间距离的最小值;(3)连接AF、DF,当△ADF是等腰三角形时,求t的值.5.如图,线段AB=4,射线BM⊥AB,P为射线BM上一点(0<BP<4),以AP为边作正方形APCD,且点C,D与点B在AP两侧,在线段DP上取一点E,使∠EAP=∠BAP.连接CE并延长交线段AB于点F.(1)求证:AE=CE;(2)求证:CF⊥AB;(3)试探究△AEF的周长是否是定值?若是定值,求出△AEF的周长;若不是定值,说明理由.6.四边形ABCD中,E为边BC上一点,F为边CD上一点,且∠AEF=90°.(1)如图1,若ABCD为正方形,E为BC中点,求证:=.(2)若ABCD为平行四边形,∠AFE=∠ADC,①如图2,若∠AFE=60°,求的值.②如图3,若AB=BC,EC=2CF,直接写出cos∠AFE值为.7.[阅读发现]如图①.在正方形ABCD的外侧.作两个等边三角形ABE和ADF,连接ED、FC,ED与FC交于点M,则图中△ADE≌△DFC(不用证明),可知ED=FC.∠DMC =°.[拓展应用]如图②,在矩形ABCD(AB>BC)的外侧,作两个等边三角形ABE和ADF,连接ED、FC,ED与FC交于点M.(1)求证:ED=FC;(2)若∠ADE=20°,直接写出∠DMC的度数.8.实践操作:第一步:如图1,将矩形纸片ABCD沿过点D的直线折叠,使点A落在CD上的点A'处,得到折痕DE,然后把纸片展平.第二步:如图2,将图1中的矩形纸片ABCD沿过点E的直线折叠,点C恰好落在AD 上的点C′处,点B落在点B'处,得到折痕EF,B'C′交AB于点M,C′F交DE于点N,再把纸片展平.问题解决:(1)如图1,填空:四边形AEA'D的形状是;(2)如图2,线段MC′与ME是否相等?若相等,请给出证明;若不等,请说明理由;(3)如图2,若AC′=2cm,DC'=4cm,求DN:EN的值.9.综合与实践问题情境在数学活动课上,老师提出了这样一个问题:如图①,已知正方形ABCD,点E是边上一点,连接AE,以AE为边在BC的上方作正方形AEFG.数学思考(1)连接GD,求证:△ABE≌△ADG;(2)连接FC,求∠FCD的度数;实践探究(3)如图②,当点E在BC的延长线上时,连接AE,以AE为边在BC的上方作正方形AEFG,连接FC,若正方形ABCD的边长为4,CE=2,则CF的长是.10.同学们:八年级下册第9章我们学习了一种新的图形变换旋转,图形旋转过程中蕴含着众多数学规律,以图形旋转为依托构建的解题方法是解决各类几何问题的常用方法.【问题提出】如图①,在正方形ABCD中,∠MAN=45°,点M、N分别在边BC、CD上.求证:MN=BM+DN.证明思路如下:第一步:如图②,将△ADN绕点A按顺时针方向旋转90°得到△ABE,再证明E、B、M三点在一条直线上.第二步:证明△AEM≌△ANM.请你按照证明思路写出完整的证明过程.【初步思考】如图③,四边形ABCD和CEFG为正方形,连接DG、BE,得到△DCG和△BCE.下列关于这两个三角形的结论:①周长相等;②面积相等;③∠CBE=∠CDG.其中所有正确结论的序号是.【深入研究】如图④,分别以▱ABCD的四条边为边向外作正方形,连接EF,GH,IJ,KL.若▱ABCD 的面积为8,则图中阴影部分(四个三角形)的面积之和为.参考答案1.证明(1)∵四边形ABCD是正方形,∴CD=BC,∠HDC=∠BCE=90°,∴∠DHC+∠DCH=90°,∵CH⊥BE,∴∠EFC=90°,∴∠ECF+∠BEC=90°,∴∠CHD=∠BEC,∴△DHC≌△CEB(AAS).(2)解:∵△DHC≌△CEB,∴CH=BE,DH=CE,∵CE=DE=CD,CD=CB,∴DH=BC,∵DH∥BC,∴.∴GC=2GH,设GH=x,则,则CG=2x,∴3x=8,∴x=.即GH=.(3)解:∵,∴,∵DH=CE,DC=BC,∴,∵DH∥BC,∴,∴,,设S△DGH=9a,则S△BCG=49a,S△DCG=21a,∴S△BCD=49a+21a=70a,∴S1=2S△BCD=140a,∵S△DEG:S△CEG=4:3,∴S△DEG=12a,∴S2=12a+9a=21a.∴.故答案为:.2.(1)解:若a=3,b=4,则由勾股定理得,c===5,若aa+b=4,c=3,则(a+b)2=42,a2+b2=32=9,即a2+2ab+b2=16,∴2ab+9=16,∴ab=,∴直角三角形的面积=ab=;故答案为:5;;(2)证明:图②的面积=S△DAE+S△CBE+S△DEC=ab+ab+c2,又图②的面积=S四边形ABCD=(a+b)(a+b)=(a+b)2,∴ab+ab+c2=(a+b)2,∴ab+ab+c2=a2+2ab+b2,即a2+b2=c2;(3)解:由折叠的性质得:AF=AD=10,DE=FE,∵四边形ABCD是矩形,∴BC=AD=10,CD=AB=8,∠B=∠C=90°,在Rt△ABF中,AB2+BF2=AF2,即82+BF2=102,解得:BF=6,∵BC=10,∴CF=BC﹣BF=10﹣6=4,设EF=x,则DE=x,∴EC=DC﹣DE=8﹣x,在Rt△ECF中,EC2+CF2=EF2,即(8﹣x)2+42=x2,解得:x=5,即EF=5.3.解:(1)如图1,连接BD,与AC交于点O,∵四边形ABCD是矩形,∴AC=BD,OB=OC∴∠DBC=∠ACB=40°∵BE=AC,∴BD=BE,∴∠BDE=∠E,∴∠E==70°;(2)如图2,延长CM交AD延长线于G,∵AG∥BE,∴∠GDM=∠E,∠G=∠GCE,∵M是DE的中点,∴DM=EM,∴△DMG≌△EMC(AAS),∴CE=DG,CM=MG,∴BC+CE=AD+DG,即AG=BE,由(1)知:BE=BD=AC,∴AG=AC,又∵CM=MG,∴AM⊥MC;(3)如图3,取AF的中点P,连接PD,则PD=AP=AF=2,∴∠PDA=∠PAD,在矩形ABCD中,∠AEB=∠PAD,∠AED=2∠AEB,∴∠DPE=∠PAD+∠PDA=2∠PAD=2∠AEB=∠AED,∴DE=PD=2,在△DEC中,∠DCE=90°,AB=DC=4,∴CE===2.故答案为:2.4.解:(1)当t=1时,AE=1,∵四边形AEFG是正方形,∴AG=FG=AE=1,∠G=90°,∴BF===,(2)如图1,延长AF,过点D作射线AF的垂线,垂足为H,∵四边形AGFE是正方形,∴AE=EF,∠AEF=90°,∴∠EAF=45°,∵DH⊥AH,∴∠AHD=90°,∠ADH=45°=∠EAF,∴AH=DH,设AH=DH=x,∵在Rt△AHD中,∠AHD=90°,∴x2+x2=42,解得x1=﹣2(舍去),x2=2,∴D、F两点之间的最小距离为2;(3)当AF=DF时,由(2)知,点F与点H重合,过H作HK⊥AD于K,如图2,∵AH=DH,HK⊥AD,∴AK==2,∴t=2.当AF=AD=4时,设AE=EF=x,∵在Rt△AEF中,∠AEF=90°,∴x2+x2=42,解得x 1=﹣2(舍去),x2=2,∴AE=2,即t=2.当AD=DF=4时,点E与D重合,t=4,综上所述,t为2或2或4.5.解:(1)证明:∵四边形APCD正方形,∴DP平分∠APC,PC=PA,∴∠APD=∠CPD=45°,∴△AEP≌△CEP(SAS),∴AE=CE;(2)CF⊥AB,理由如下:∵△AEP≌△CEP,∴∠EAP=∠ECP,∵∠EAP=∠BAP,∴∠BAP=∠FCP,∵∠FCP+∠CHP=90°,∠AHF=∠CHP,∴∠AHF+∠PAB=90°,∴∠AFH=90°,∴CF⊥AB;(3)△AEF的周长是定值,△AEF的周长为8.过点C作CN⊥PB于点N.∵CF⊥AB,BM⊥AB,∴FC∥BN,∴∠CPN=∠PCF=∠EAP=∠PAB,又AP=CP,∴△PCN≌△APB(AAS),∴CN=PB=BF,PN=AB,∵△AEP≌△CEP,∴AE=CE,∴△AEF的周长=AE+EF+AF,=CE+EF+AF,=BN+AF,=PN+PB+AF,=AB+CN+AF,=AB+BF+AF,=2AB,=8.6.(1)证明:如图1中,设正方形的边长为2a.∵四边形ABCD是正方形,∴∠B=∠C=90°,∵∠AEF=90°,∴∠AEB+∠FEC=90°,∠FEC+∠EFC=90°,∴∠AEB=∠EFC,∴△ABE∽△ECF,∴,∵BE=EC=a,AB=CD=2a,∴CF=a,DF=CD﹣CF=a,∴.(2)①在AD上截取DM=DF,连接MF.∵∠ADC=60°,∴△DMF是等边三角形,∴DF=MF,∠DMF=∠DFM=60°,∴∠AMF=120°,∵四边形ABCD为平行四边形,AD∥BC,∴∠ECF=120°,∴∠AMF=∠ECF,∵∠AFE=60°,∴∠AFM+∠EFC=60°,∵∠EFC+∠FEC=60°,∴∠AFM=∠FEC,∴△AMF∽△FCE,∴,∵∠AFE=60°,∠AEF=90°,∴,∴.②如图3,作FT=FD交AD于点T,作FH⊥AD于H,则∠FTD=∠FDT,∴180°﹣∠FTD=180°﹣∠D,∴∠ATF=∠C,又∵∠TAF+∠D=∠AFE+∠CFE,且∠D=∠AFE,∴∠TAF=∠CFE,∴△FCE∽△ATF,∴,设CF=2,则CE=4,可设AT=x,则TF=2x,AD=CD=2x+2,∴DH=DT=,且,由cos∠AFE=cos∠D,得,解得x=6,∴cos∠AFE=.故答案为:.7.解:如图①中,∵四边形ABCD是正方形,∴AD=AB=CD,∠ADC=90°,∵△ADE≌△DFC,∴DF=CD=AE=AD,∵∠FDC=∠FDA+∠ADC=60°+90°=150°,∴∠DFC=∠DCF=∠ADE=∠AED=15°,∴∠FDE=60°+15°=75°,∴∠MFD+∠FDM=90°,∴∠FMD=90°,故答案为:90°(1)∵△ABE为等边三角形,∴∠EAB=60°,EA=AB.∵△ADF为等边三角形,∴∠FDA=60°,AD=FD.∵四边形ABCD为矩形,∴∠BAD=∠ADC=90°,DC=AB.∴EA=DC.∵∠EAD=∠EAB+∠BAD=150°,∠CDF=∠FDA+∠ADC=150°,∴∠EAD=∠CDF.在△EAD和△CDF中,,∴△EAD≌△CDF(SAS).∴ED=FC;(2)∵△EAD≌△CDF,∴∠ADE=∠DFC=20°,∴∠DMC=∠FDM+∠DFC=∠FDA+∠ADE+∠DFC=60°+20°+20°=100°.8.解:(1)∵ABCD是矩形,∴∠A=∠ADC=90°,∵将矩形纸片ABCD沿过点D的直线折叠,使点A落在CD上的点A'处,得到折痕DE,∴AD=A′D,AE=A′E,∠ADE=∠A′DE=45°,∵AB∥CD,∴∠AED=∠A′DE=∠ADE,∴AD=AE,∴AD=AE=A′E=A′D,∴四边形AEA′D是菱形,∵∠A=90°,∴四边形AEA′D是正方形.故答案为:正方形;(2)MC′=ME.证明:如图1,连接C′E,由(1)知,AD=AE,∵四边形ABCD是矩形,∴AD=BC,∠EAC′=∠B=90°,由折叠知,B′C′=BC,∠B=∠B′,∴AE=B′C′,∠EAC′=∠B′,又EC′=C′E,∴Rt△EC′A≌Rt△C′EB′(HL),∴∠C′EA=∠EC′B′,∴MC′=ME;(3)∵Rt△EC′A≌Rt△C′EB′,∴AC′=B′E,由折叠知,B′E=BE,∴AC′=BE,∵AC′=2cm,DC′=4cm,∴AB=CD=2+4+2=8(cm),设DF=xcm,则FC′=FC=(8﹣x)cm,∵DC′2+DF2=FC′2,∴42+x2=(8﹣x)2,解得,x=3,即DF=3cm,如图2,延长BA、FC′交于点G,则∠AC′G=∠DC′F,∴tan∠AC′G=tan∠DC′F=,∴,∴,∵DF∥EG,∴△DNF∽△ENG,∴.9.(1)证明:∵四边形ABCD和四边形AEFG是正方形,∴AB=AD,AE=AG,∠ABE=∠ADG=90°,∴∠BAE+∠EAD=∠DAG+∠EAD,∴∠BAE=∠DAG,在△ABE和△ADG中,,∴△ABE≌△ADG(SAS);(2)解:如图①,过点F作FH⊥BC,交BC的延长线于点H,∵∠AEF=∠ABE=90°,∴∠BAE+∠AEB=90°,∠FEH+∠AEB=90°,∴∠FEH=∠BAE,又∵AE=EF,∠EHF=∠ABE=90°,∴△EHF≌△ABE(SAS),∴FH=EB,EH=AB=BC,∴CH=BE,∴CH=FH,∴∠FCH=45°,∴∠FCD=45°;(3)解:过点F作FH⊥BC,交BC的延长线于点H,如图②,由(2)知△EHF≌△ABE,∴EH=AB,FH=BE,∵AB=BC=4,CE=2,∴BE=FH=6,CH=CE+EH=6,∴CF==6.故答案为:6.10.【问题提出】(1)证明:将△ADN绕点A按顺时针方向旋转90°得到△ABE,在正方形ABCD中,∠BAD=∠ABM=∠D=90°,由旋转可知△ADN≌△ABE,∴∠D=∠ABE=90°,∠DAN=∠BAE,AN=AE,DN=BE,∴∠ABE+∠ABM=180°,∴E、B、M三点在一条直线上,∵∠MAN=45°,∴∠DAN+∠BAM=45°,∵∠DAN=∠BAE,∴∠BAE+∠BAM=∠EAM=45°,∴∠EAM=∠MAN,∵AN=AE,AM=AM,∴△AEM≌△ANM(SAS),∴ME=MN,∵ME=BE+BM,∴MN=DN+BM,【初步思考】解:∵BE≠DG,∴△DCG和△BCE的周长不一定相等,故①不正确;∵正方形CEFG绕点C旋转过程中,∠CBE≠∠CDG.∴③不正确;如图1,过点E作BC的平行线,过点B作CE的平行线,两线交于点H,连接CH.则四边形BHEC为平行四边形,∴BC=HE,S△BCE==S△CHE,∵四边形ABCD和四边形CEFG为正方形,∴CD=BC,CE=CG,∠BCD=∠ECG=90°,∴∠BCE+∠DCG=180°,∵∠HEC+∠BCE=180°,∴∠DCG=∠HEC,∵BC=HE=CD,∴△DCG≌△HEC(SAS),∴S△CHE=S△DCG,∴S△DCG=S△BCE.故②正确,故答案为:②.【深入研究】解:图中阴影部分(四个三角形)的面积之和为16.如图2,连接AC,BD,由【初步思考】的结论可知:S△AEF=S△ABD=,同理S△BHG=S△ABC,S△CIJ=S△CBD,S△DLK=S△DAC,∴阴影部分的面积S=S△AEF+S△BGH+S△CIJ+S△DLK=2S平行四边形ABCD=2×8=16.故答案为:16.。
2020中考数学一轮复习能力达标训练题1:有理数(附答案)

2020中考数学一轮复习能力达标训练题1:有理数(附答案)1.若|m+3|+(n ﹣2)2=0,则m ﹣n 的值为( )A .1B .﹣1C .5D .﹣52.下列说法正确的是( )①若m=n ,则|m|=|n|; ②若m=-n ,则|m|=|-n|;③若|-m|=|-n|,则m=-n ; ④若|-m|=|-n|,则m=n.A .①②B .③④C .①④D .②③3.如图,四个有理数m ,n ,p ,q 在数轴上对应的点分别为M ,N ,P ,Q ,若n+q=0,则m ,n ,p ,q 四个有理数中,绝对值最小的一个是( )A .pB .qC .mD .n4.在-32,▏-2▏,(-1)3,-(-2),-4这五个数中,负数的个数有( )A .1 个B .2个C .3个D .4个5.下列各对数中,互为相反数的是( ).A .+(-8)和(-8)B .-(-8)和+8C .-(-8)和+(+8)D .+8和+(-8)6.在-4,-6,0,7这四个数中最小的数是A .-4B .-6C .0D .77.下列各对数中,不是互为相反数的是( )A .()3--与3--B .23-与(-3)²C .100-与(-10)²D .3(2)-与32- 8.下面说法:①﹣a 一定是负数;②若|a |=|b |,则 a =b ;③一个有理数中不是整数就是分数;④一个有理数不是正数就是负数.⑤绝对值等于它本身的数是正数;其中正确的个数有( )A .1 个B .2 个C .3 个D .4 个9 )A B .C .D .310.实数 a ,b 在数轴上的位置如图所示,则下列结论正确的是( )A .a+b >0B .a ﹣b >0C .a•b >0D .a b>011.绝对值大于1而不大于4的整数有_________ ,它们的和是_____________.12.若|-x|=4,则x=____;若|x-3|=0,则x=____;若|x-3|=1,则x=____.133|27|b -=0,(a ﹣b )b ﹣1=_______。
2022年中考一轮复习数学几何专题:三角形 解答题训练(一)

2022年中考一轮复习数学几何专题:三角形解答题训练(一)1.如图,在平面直角坐标系中,已知点A(﹣1,m),点B(2,n),且|m﹣1|+=0.(1)求A,B两点的坐标;(2)在(1)的条件下,若直线AB交x轴于点C点,试求出C点坐标;不超过9,请求出a (3)在(2)的结论下,已知P(a,0)为x轴上一动点,若S△ABP的取值范围.2.如图,在△ABC中,AB=7,BC=14,M为AC的中点,OM⊥AC交∠ABC的平分线于O,OE ⊥AB交BA的延长线于E,OF⊥BC.垂足为F.(1)求证:AE=CF.(2)求线段BE的长.3.已知在△ACD中,P是CD的中点,B是AD延长线上的一点,连结BC,AP.(1)如图1,若∠ACB=90°,∠CAD=60°,BD=AC,AP=,求BC的长.(2)过点D作DE∥AC,交AP延长线于点E,如图2所示,若∠CAD=60°,BD=AC,求证:BC=2AP.(3)如图3,若∠CAD=45°,是否存在实数m,当BD=mAC时,BC=2AP?若存在,请直接写出m的值;若不存在,请说明理由.4.如图,在Rt△ABC中,∠BAC=90°,AB=AC,点D是BC中点,点E是AC边上一动点,连接DE,在DE左侧作Rt△DEF,满足∠DFE=90°,DF=EF,连接AF并延长,交BC于点G.(1)如图1,若AB=4,AE=1,求DE的长;(2)如图2,在点E的运动过程中,猜想AF与FG存在的数量关系,并证明你的结论;(3)如图3,在点E的运动过程中,将AF绕点F逆时针旋转90°,得到A′F,连接A'B,A'D,若AB=4,请直接写出当A'B+A′D取得最小值时,△A′DF的面积.5.如图,直线MN与直线PQ相交于O,∠POM=30°,点A在射线OP上运动,点B在射线OM上运动,AC、BC分别是∠BAO和∠ABO的角平分线.(1)若∠BAO=50°,试求出∠ACB的度数.(2)点A、B在运动的过程中,∠ACB的大小是否会发生变化?若发生变化,请说明理由;若不发生变化,试求出∠ACB的度数.(3)在(2)的条件下,在△ABC中,如果有一个角是另一个角的2倍,请直接写出∠BAC 的度数.6.如图,在平面直角坐标系中,已知点A的坐标是(a,0),点B的坐标是(b,0),其中a,b满足+(b﹣3)2=0.(1)填空:a=,b=;(2)在y轴有一点M(0,m),△ABM的面积为4.求m的值;(3)如图,若M在y轴负半轴,将线段AM沿x轴正方向平移,使得A的对应点为B,M 的对应点为N.若点P为线段AB上的任意一点(不与A,B重合),试写出∠MPN,∠PMA,∠PNB之间的数量关系,并说明理由.7.已知:DF∥BC,∠FDC=∠AEC.(1)如图1,已知CD⊥AB,CB平分∠NCE.求∠ABC的度数;(2)如图2,若∠ABC=∠ACF,AC=FC,DM=BE.求证:BC=MC.8.如图,在四边形ABCD中,∠DAB=∠DCB=90°,对角线AC与BD相交于点O,M、N分别是边BD、AC的中点.(1)求证:MN⊥AC;(2)当AC=30cm,BD=34cm时,求MN的长.9.如图,在等边△ABC中,点D是射线BC上一动点(点D在点C的右侧),CD=DE,∠BDE =120°.点F是线段BE的中点,连接DF、CF.(1)请你判断线段DF与AD的数量关系,并给出证明;(2)若AB=4,求线段CF长度的最小值.10.如图,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.填空:①∠AEB的度数为;②线段AD、BE之间的数量关系是.③当点A、D、E不在同一直线上,∠AEB的度数会发生变化吗?(填写“变化”或“不变”).11.在△ABC中,∠CAB=90°,AD是BC边上的中线,E是AD的中点,过点A作BC的平行线交BE的延长线于点F,连接CF.(1)求证:四边形ADCF是菱形.(2)连接CE,若CE=EF,直接写出长度等于的线段.12.如图,△ABC中,CD⊥AB,垂足为D.BE⊥AC,垂足为G,AB=CF,BE=AC.(1)求证:AE=AF;(2)求∠EAF的度数.13.如图,已知△ABC为等腰直角三角形,AB=AC且∠CAB=90°,E为BC上一点,且BE =AC,过E作EF⊥BC且EF=EC,连接CF.(1)如图1,已知AB=2,连接AE、AF,求△AEF的面积;(2)如图2所示,D为AB上一点,连接DB,作∠DBH=45°交EF于H点,求证:CD=HF+CE;(3)已知△ABC面积为8+4,D为射线AC上一点,作∠DBH=45°,交射线EF于H,连接DH,点M为DH的中点,当CM有最小值时,请直接写出△CMD的面积.14.直角三角形ABC中,∠ACB=90°,直线l过点C.(1)当AC=BC时,如图①,分别过点A、B作AD⊥l于点D,BE⊥l于点E.求证:△ACD ≌△CBE.(2)当AC=8,BC=6时,如图②,点B与点F关于直线l对称,连接BF,CF,动点M 从点A出发,以每秒1个单位长度的速度沿AC边向终点C运动,同时动点N从点F出发,以每秒3个单位的速度沿F→C→B→C→F向终点F运动,点M、N到达相应的终点时停止运动,过点M作MD⊥l于点D,过点N作NE⊥l于点E,设运动时间为t秒.①CM=,当N在F→C路径上时,CN=.(用含t的代数式表示)②直接写出当△MDC与△CEN全等时t的值.15.在△ABC和△DBE中,CA=CB,EB=ED,点D在AC上.(1)如图1,若∠ABC=∠DBE=60°,求证:∠ECB=∠A;(2)如图2,设BC与DE交于点F.当∠ABC=∠DBE=45°时,求证:CE∥AB;(3)在(2)的条件下,若tan∠DEC=时,求的值.16.阅读下列材料,完成相应任务.数学活动课上,老师提出了如下问题:如图1,已知△ABC中,AD是BC边上的中线.求证:AB+AC>2AD.智慧小组的证法如下:证明:如图2,延长AD至E,使DE=AD,∵AD是BC边上的中线∴BD=CD在△BDE和△CDA中∴△BDE≌△CDA(依据一)∴BE=CA在△ABE中,AB+BE>AE(依据二)∴AB+AC>2AD.任务一:上述证明过程中的“依据1”和“依据2”分别是指:依据1:;依据2:.归纳总结:上述方法是通过延长中线AD,使DE=AD,构造了一对全等三角形,将AB,AC,AD转化到一个三角形中,进而解决问题,这种方法叫做“倍长中线法”.“倍长中线法”多用于构造全等三角形和证明边之间的关系.任务二:如图3,AD是BC边上的中线,AB=3,AC=4,则AD的取值范围是;任务三:如图4,在图3的基础上,分别以AB和AC为边作等腰直角三角形,在Rt△ABE 中,∠BAE=90°,AB=AE;Rt△ACF中,∠CAF=90°,AC=AF.连接EF.试探究EF与AD的数量关系,并说明理由.17.(1)①如图1,△ABC、△ECF都是等腰直角三角形,点E在线段AB上,∠ACB=∠ECF =90°.求证:△ACF≌△BCE;②如图2,当AE=,BE=3AE时,求线段CG的长;(2)如图3,∠BDC=∠CAD=30°,∠BCD=90°,AB=2,AD=4,求AC的长.18.(1)如图①,△ABC和△CDE都是等边三角形,且点B,C,E在一条直线上,连接BD 和AE,直线BD,AE相交于点P.则线段BD与AE的数量关系为;BD与AE相交构成的锐角的度数为.(2)如图②,点B,C,E不在同一条直线上,其它条件不变,上述的结论是否还成立?请说明理由.(3)应用:如图③,点B,C,E不在同一条线上,其它条件依然不变,此时恰好有∠AEC =30°.设直线AE交CD于点Q,请把图形补全.若PQ=2,则DP=.19.如图,平面直角坐标系中,A(a,0),B(0,b),C(0,c),+|2﹣b|=0,c=(a﹣b).(1)求△ABC的面积;(2)如图2,点A以每秒m个单位的速度向下运动至A′,与此同时,点Q从原点出发,以每秒2个单位的速度沿x轴向右运动至Q′,3秒后,A′、C、Q′在同一直线上,求m 的值;(3)如图3,点D在线段AB上,将点D向右平移4个单位长度至E点,若△ACE的面积等于14,求点D坐标.20.在△ABC中,AC=BC,∠ACB=90°,AE平分∠BAC交BC于点E,BD⊥AE交AE延长线于点D,连接CD,过点C作CF⊥CD交AD于F.(Ⅰ)如图①,(1)求∠EBD的度数;(2)求证AF=BD;(Ⅱ)如图②,DM⊥AC交AC的延长线于点M,探究AB、AC、AM之间的数量关系,并给出证明.参考答案1.解:(1)∵|m﹣1|+=0,又∵|m﹣1|≥0,≥0,∴m=1,n=4,∴A(﹣1,1),B(2,4).(2)如图1中,过点B作BH⊥x轴于H,连接AH,设C(m,0).∵B(2,4),A(﹣1,1),∴H(2,0),BH=4,∵S△ABH =S△CBH﹣S△ACH,∴×4×3=×(2﹣m)×4﹣×(2﹣m)×1,∴m=﹣2,∴C(﹣2,0).(3)如图2中,当S△PAB=9时,•|a+2|•4﹣•|a+2|•1=9, 解得a=4或﹣8,∴满足条件的a的值为:﹣8≤a<﹣2或﹣2<a≤4.2.(1)证明:连接OA,∵OB平分∠ABC,又∵OE⊥AB,OF⊥BC,∴OE=OF.∵OM⊥AC,M为AC中点,∴OM垂直平分AC,∴OA=OC,在Rt△AEO与Rt△CFO中,,∴Rt△AEO≌Rt△CFO(HL),∴AE=CF;(2)解:在Rt△BEO与Rt△BFO中,,∴△BEO≌△BFO(HL),∴BE=BF,∵AB=7,BC=14,设AE=CF=x,∴x+7=14﹣x,∴,∴.3.解:(1)∵∠ACB=90°,∠CAD=60°,∴AB=,∵BD=AC,∴AD=AC,∴△ADC是等边三角形,∴∠ACD=60°,∵P是CD的中点,∴AP⊥CD,在Rt△APC中,AP=,∴,∴,(2)证明:连接BE,∵DE∥AC,∴∠CAP=∠DEP,在△CPA和△DPE中,∴△CPA≌△DPE(AAS),∴AP=EP=,DE=AC,∵BD=AC,∴BD=DE,又∵DE∥AC,∴∠BDE=∠CAD=60°,∴△BDE是等边三角形,∴BD=BE,∠EBD=60°,∵BD=AC,∴AC=BE,在△CAB和△EBA中,∴△CAB≌△EBA(SAS),∴AE=BC,∴BC=2AP,(3)存在这样的m,m=.理由如下:作DE∥AC交AP延长线于E,连接BE,由(2)同理可得DE=AC,∠EDB=∠CAD=45°,AE=2AP,当BD=时,∴BD=,作BF⊥DE于F,∵∠EDB=45°,∴BD=,∴DE=DF,∴点E,F重合,∴∠BED=90°,∴∠EBD=∠EDB=45°,∴BE=DE=AC,同(2)可证:△CAB≌△EBA(SAS),∴BC=AE=2AP,∴存在m=,使得BC=2AP4.(1)解:过点E作EH⊥DC,垂足为H,∵∠BAC=90°,AB=AC,AB=4,∴BC=4,∠C=45°,∵点D是BC中点,∴DB=DC=2,∵AE=1,∴CE=3,∵∠C=45°,∴HE=HC=,HD=CD﹣HC=,DE=,∴DE=.(2)AF=FG,证明如下:取AE的中点I,连接FI,DI,∵点D是BC中点,∴DI∥AB,∴△DIC是等腰直角三角形,∴,即,∠FDE=∠IDC=45°,∴∠FDI=∠BDC,∴△FDI∽△EDC,∴∠FID=∠C=45°,∴∠AIF=∠C=45°,∴FI∥CB,∴AF=FG.(3)延长DA′交AB于点M,取AM的中点N,连接DN,AD,AA′,∵△ADB和△AFA′是等腰直角三角形,∴=,∠BAD=∠A′AD=45°,∴∠BAA′=∠DAF,∴△BAA′∽△DBF,∴,由(2)可知,AF=FG,∠ADC=90°,∴AF=FD,∴BA′=AA′,∵BD=DA,∴DM垂直平分AB,BM=AM=DM=2,NM=1,∴DN=,sin,tam,过点A′作A′P⊥DN,垂足为P,∴sin,,当B、A′、P在同一条直线上时,A′B+A′D最小,∵∠BA′M=∠DA′P,∴∠MBP=∠MDN,∴,A′M=1,A′D=1,∵,A,∴,A,∵,∴,DP=,∴=.5.解:(1)如图1中,∵BC平分∠ABO,AC平分∠BAO,∴∠ABC=∠ABO,∠BAC=∠BAO,∵∠POM=30°,∴∠ABO+∠BAO=180°﹣30°=150°,∴∠CBA+∠CAB=(∠ABO+∠BAO)=×150°=75°,∴∠ACB=180°﹣(∠CBA+∠CAB)=180°﹣75°=105°;(2)∠ACB的大小不变,理由如下:由(1)知:点A、B在运动的过程中,∠ACB=105°;(3)由(2)可知,∠ACB=105°,∠BAC+∠ABC=75°,∵△ABC中有一个角是另一个角的2倍,∴∠ACB=2∠BAC或∠ACB=2∠ABC或∠ABC=2∠BAC或∠BAC=2∠ABC,∴∠BAC=52.5°或22.5°或25°或50°.6.解:(1)∵+(b﹣3)2=0,≥0,(b﹣3)2≥0,∴a+1=0,b﹣3=0,解得,a=﹣1,b=3,故答案为:﹣1;3;(2)由(1)可知A(﹣1,0),B(3,0),∴OA=1,OB=3,∴AB=OA+OB=4,由题意得,△ABM的面积=AB•OM=×4×OM=4,即×4×|m|=4,解得,m=±2;(3)∠MPN=∠PMA+∠PNB,理由如下:过点P作PE∥AM,则∠MPE=∠PMA,∵AM平移后得到BN,∴AM∥BN,∴PE∥BN,∴∠NPE=∠PNB,∴∠MPN=∠MPE+∠NPE=∠PMA+∠PNB.7.解:(1)∵DF∥BC,∴∠FDC=∠NCB,∵CB平分∠NCE,∴∠NCB=∠BCE,∵∠FDC=∠AEC,∴∠FDC=∠NCB=∠BCE=∠AEC,∵CD⊥AB,∴∠ENC=90°,∴∠AEC+∠NCE=∠AEC+∠BCE+∠NCB=3∠NCB=90°,∴∠NCB=30°,∴∠ABC=90°﹣∠NCB=60°;(2)∵DF∥BC,∴∠FMC=∠ACB,∵∠ABC=∠ACF,∴180°﹣∠FMC﹣∠ACF=180°﹣∠ACB﹣∠ABC,即∠F=∠BAC,在△DFC和△EAC中,,∴△DFC≌△EAC(AAS),∴CD=CE,在△MDC和△BEC中,,∴△MDC≌△BEC(SAS),∴MC=BC.8.解:(1)如图,连接AM,CM,∵∠DAB=∠DCB=90°,点M是BD的中点,∴AM=BD,CM=BD,∴AM=CM,∵点N是AC的中点,∴MN⊥AC;(2)∵BD=34cm,∴AM=CM=BD=17cm,∵AC=30cm,∴AN=AC=15cm,由(1)知,MN⊥AC,∴MN===8.9.解:(1)线段DF与AD的数量关系为:AD=2DF,理由如下:延长DF至点M,使DF=FM,连接BM、AM,如图1所示:∵点F为BE的中点,∴BF=EF,在△BFM和△EFD中,,∴△BFM≌△EFD(SAS),∴BM=DE,∠MBF=∠DEF,∴BM∥DE,∵线段CD绕点D逆时针旋转120°得到线段DE,∴CD=DE=BM,∠BDE=120°,∴∠MBD=180°﹣120°=60°,∵△ABC是等边三角形,∴AB=AC,∠ABC=∠ACB=60°,∴∠ABM=∠ABC+∠MBD=60°+60°=120°,∵∠ACD=180°﹣∠ACB=180°﹣60°=120°,∴∠ABM=∠ACD,在△ABM和△ACD中,,∴△ABM≌△ACD(SAS),∴AM=AD,∠BAM=∠CAD,∴∠MAD=∠MAC+∠CAD=∠MAC+∠BAM=∠BAC=60°,∴△AMD是等边三角形,∴AD=DM=2DF;(2)连接CE,取BC的中点N,连接作射线NF,如图2所示:∵△CDE为等腰三角形,∠CDE=120°,∴∠DCE=30°,∵点N为BC的中点,点F为BE的中点,∴NF是△BCE的中位线,∴NF∥CE,∴∠CNF=∠DCE=30°,∴点F的轨迹为射线NF,且∠CNF=30°,当CF⊥NF时,CF最短,∵AB=BC=4,∴CN=2,在Rt△CNF中,∠CNF=30°,∴CF=CN=1,∴线段CF长度的最小值为1.10.解:①如图1,∵△ACB和△DCE均为等边三角形,∴CA=CB,CD=CE,∠ACB=∠DCE=60°.∴∠ACD=∠BCE.在△ACD和△BCE中,∴△ACD≌△BCE(SAS).∴∠ADC=∠BEC.∵△DCE为等边三角形,∴∠CDE=∠CED=60°.∵点A,D,E在同一直线上,∴∠ADC=120°.∴∠BEC=120°.∴∠AEB=∠BEC﹣∠CED=60°.故答案为:60°.②∵△ACD≌△BCE,∴AD=BE.故答案为:AD=BE.③如图2,点A、D、E不在同一直线上,∠AEB的度数会发生变化;故答案为:变化.11.证明:(1)∵AF∥BC,∴∠FAE=∠BDE,∵E为AD中点,∴AE=DE,在△AEF和△DEB中,,∴△AEF≌△DEB(ASA),∴AF=BD,∵AD为Rt△ABC的斜边中线,∴AD=BD=CD,∴AF=AD=CD,又∵AF∥CD,∴四边形ADCF是菱形.(2)由(1)得E为BF中点,∵CE=EF,∴CE=BE,∴AD垂直平分BC,∴△ABC为等腰直角三角形,四边形CFAD为正方形,∴BD=AD=CD=CF=FA=AB.故答案为:BD,AD,CD,CF,FA.12.(1)证明:∵CD⊥AB,BE⊥AC,∴∠CAD+∠ACD=∠CAD+∠EBA=90°,∴∠ACD=∠EBA,在△AEB和△FAC中,,∴△AEB≌△FAC(SAS),∴AE=FA;(2)解:∵△AEB≌△FAC,∴∠E=∠CAF,∵∠E+∠EAG=90°,∴∠CAF+∠EAG=90°,即∠EAF=90°.13.解:(1)∵AB=AC=2,∠CAB=90°,∴BC===2,∠ACB=45°,如图1,过点A作AT⊥BC于点T,则BT=CT,AT=BC=,∵BE=AC=2,∴CE=BC﹣BE=2﹣2,∵EF⊥BC且EF=EC,∴∠ECF=45°,CF=CE=×(2﹣2)=4﹣2,∴∠ACF=∠ACB+∠ECF=45°+45°=90°,∴S△AEF =S△ACF﹣S△ACE﹣S△CEF=•AC•CF﹣•CE•AT﹣•CE•EF=×2×(4﹣2)﹣12×(2﹣2)×﹣×(2﹣2)×(2﹣2)=3﹣4;(2)如图2,∵∠DBH=45°=∠ABC,∴∠ABD+∠CBD=∠EBH+∠CBD,∴∠ABD=∠EBH,在△ABD和△EBH中,,∴△ABD≌△EBH(ASA),∴AD=EH,过点B作BR⊥AB交CF的延长线于点R,在RC上截取RK=AD,连接BK,BF,∴∠ABR=90°=∠A=∠ACF,∴四边形ABRC是矩形,∵AB=AC,∴四边形ABRC是正方形,∴BR=AB,∠R=90°=∠A,在△BRK和△BAD中,,∴△BRK≌△BAD(SAS),∴BK=BD,RK=AD,∠ABD=∠RBK,∵∠ABC=∠RBC=45°,∴∠ABC﹣∠ABD=∠RBC﹣∠RBK,即∠CBD=∠CBK,在△CBD和△CBK中,,∴△CBD≌△CBK(SAS),∴CD=CK=CF+FK,∵CF=CE,∴CD=FK+CE,在Rt△BRF和Rt△BEF中,,∴Rt△BRF≌Rt△BEF(HL),∴FR=FE,∵RK=AD=EH,∴FR﹣RK=FE﹣EH,即FK=FH,∴CD=FH+CE;(3)由(2)知,△ABD≌△EBH,∴AD=EH,根据瓜豆原理,点H的运动轨迹为射线EF,∵点M为DH的中点,点M的运动轨迹为射线AE,当CM有最小值时,CM⊥AE,∴∠AMC=90°,设AB=a,则BC=a,CE=()a,过点M作MK⊥AB于K,过点E作ET⊥AB于点T,∴∠BTE=∠BKM=∠AKM=∠ALM=∠BAC=90°,∵∠ABC=45°,∴ET=BT=BE•cos∠ABC=a•sin45°=a,∴AT=AB﹣BT=a﹣a=a,∴AE===a,∵ET∥AC,∴∠CAM=∠AET,∵∠AMC=∠ETA=90°,∴△AMC∽△ETA,∴==,即==,∴CM=a,AM=a,∵ET∥MK,∴△AET∽△AMK,∴=,即=,∴MK=a,∴S△ABM=AB•MK=•a•a=a2,∵∠AMD=∠BMD=90°,∴∠CMD+∠AMD=∠AMB+∠AMD,∴∠CMD=∠AMB,∵∠CAM+∠DCM=90°,∠CAM+∠BAM=90°,∴∠DCM=∠BAM,∴△CMD∽△AMB,∴===3﹣2,∴S△CMD =(3﹣2)•S△AMB=(3﹣2)•a2,∵S△ABC=a2=8+4,∴a2=16+8,∴S△CDM=(3﹣2)•a2=(3﹣2)××(16+8)=2.14.解:(1)△ACD与△CBE全等.理由如下:∵AD⊥直线l,∴∠DAC+∠ACD=90°,∵∠ACB=90°,∴∠BCE+∠ACD=90°,∴∠DAC=∠ECB,在△ACD和△CBE中,,∴△ACD≌△CBE(AAS);(2)①由题意得,AM=t,FN=3t,则CM=8﹣t,由折叠的性质可知,CF=CB=6,∴CN=6﹣3t.故答案为:8﹣t;6﹣3t.②由折叠的性质可知,∠BCE=∠FCE,∵∠MCD+∠CMD=90°,∠MCD+∠BCE=90°,∴∠NCE=∠CMD,∴当CM=CN时,△MDC与△CEN全等,当点N沿F→C路径运动时,8﹣t=6﹣3t,解得,t=﹣1(不合题意),当点N沿C→B路径运动时,8﹣t═3t﹣6,解得,t=3.5,当点N沿B→C路径运动时,由题意得,8﹣t=18﹣3t,解得,t=5,当点N沿C→F路径运动时,由题意得,8﹣t=3t﹣18,解得,t=6.5,综上所述,当t=3.5秒或5秒或6.5秒时,△MDC与△CEN全等.15.(1)证明:∵CA=CB,EB=ED,∠ABC=∠DBE=60°,∴△ABC和△DBE都是等边三角形,∴AB=BC,DB=BE,∠A=60°.∵∠ABC=∠DBE=60°,∴∠ABD=∠CBE,∴△ABD≌△CBE(SAS).∴∠A=∠ECB;(2)证明:∵∠ABC=∠DBE=45°,CA=CB,EB=ED,∴△ABC和△DBE都是等腰直角三角形,∴∠CAB=45°,∴,∴,∵∠ABC=∠DBE,∴∠ABD=∠CBE,∴△ABD∽△CBE,∴∠BAD=∠BCE=45°,∵∠ABC=45°,∴∠ABC=∠BCE,∴CE∥AB;(3)解:过点D作DM⊥CE于点M,过点D作DN∥AB交CB于点N,∵∠ACB=90°,∠BCE=45°,∴∠DCM=45°,∴∠MDC=∠DCM=45°,∴DM=MC,设DM=MC=a,∴a,∵DN∥AB,∴△DCN为等腰直角三角形,∴DN=DC=2a,∵tan∠DEC=,∴ME=2DM,∴CE=a,∴,∵CE∥DN,∴△CEF∽△NDF,∴.16.任务一:证明:延长AD至E,使DE=AD,∵AD是BC边上的中线,∴BD=CD,在△BDE和△CDA中,,∴△BDE≌△CDA(SAS),∴BE=CA,在△ABE中,AB+BE>AE(三角形任意两边之和大于第三边),∴AB+AC>2AD.故答案为:SAS,三角形任意两边之和大于第三边.任务二:解:如图1,延长AD至点E,使DE=AD,连接CE,∵AD是中线,∴BD=CD,在△ABD和△ECD中,,∴△ABD≌△CDE(SAS),∴AB=EC=4,在△ACE中,AC﹣CE<AE<AC+CE,∴4﹣3<2AD<4+3,∴1<2AD<7,∴.故答案为:<AD<.任务三:EF与AD的数量关系为EF=2AD.理由如下:如图2,延长AD至点M,使DM=AD,连接CM,∵AD是中线,∴BD=CD,在△ABD和△MCD中,,∴△ABD≌△CDM(SAS),∴AB=MC,∠ABD=∠DCM,∴AE=CM,AB∥CM,∴∠BAC+∠ACM=180°,∵∠BAE=∠CAF=90°,∴∠EAF+∠BAC=180°,∴∠EAF=∠ACM,又∵AF=AC,∴△EAF≌△MCA(SAS),∴AM=EF,∵AM=2AD,∴EF=2AD.17.解:(1)①证明:∵△ABC、△ECF都是等腰直角三角形,∴AC=BC,CE=CF,∠ACB=∠ECF=90°,∴∠BCE=∠ACF,在△ACF和△BCE中,,∴△ACF≌△BCE(SAS);②由①知△ACF≌△BCE,∴AF=BE,∠CBE=∠CAF,∵AC=BC,∠ACB=90°,∴∠B=∠BAC=45°,∴∠CAF=45°,∴∠EAF=90°,∵AE=,BE=3AE,∴AF=3,AB=BE+AE=4,∴AC=AB=4,EF==2,又∵△ECF为等腰直角三角形,∴∠CEF=45°,CE=EF=,∴∠CEG=∠EAC,又∵∠ECG=∠ACE,∴△ECG∽△ACE,∴,∴CE2=CG•AC,∴CG=;(2)过点A作AD的垂线,过点C作AC的垂线,两垂线交于点M,连接DM,∵∠CAD=30°,∴∠CAM=60°,∴∠AMC=30°,∴∠AMC=∠BDC,又∵∠ACM=∠BCD=90°,∴△BCD∽△ACM,∴,又∠BCD=∠ACM,∴∠BCD+∠BCM=∠ACM+∠BCM,即∠DCM=∠ACB,∴△DCM∽△BCA,∴,∵AB=2,∴DM=2=6,∴AM===2,∴AC=AM=.18.解:(1)∵△ABC和△CDE都是等边三角形,∴AB=AC,CD=CE,∠ACB=∠DCE=60°,∴∠ACB+∠ACD=∠DCE+∠ACD,即∠ACE=∠BCD,在△ACE和△BCD中,,∴△ACE≌△BCD(SAS),∴BD=AE,∠AEC=∠BDC,由三角形的外角性质,∠DPE=∠AEC+∠BDC,∠DCE=∠BDC+∠DBC,∴∠DPE=∠DCE=60°;故答案为:相等,60°;(2)成立.证明:∵△ABC和△CDE都是等边三角形,∴AB=AC,CD=CE,∠ACB=∠DCE=60°,∴∠ACB+∠ACD=∠DCE+∠ACD,即∠ACE=∠BCD,在△ACE和△BCD中,,∴△ACE≌△BCD(SAS),∴BD=AE,∠AEC=∠BDC,又∵∠DNA=∠ENC,∴∠DPE=∠DCE=60°.(3)补全图形如图③,由(1)(2)可知△AEC≌△BDC,∴∠AEC=∠BDC=30°,∵△DEC为等边三角形,∴∠DEC=∠EDC=60°,∴∠DEP=∠DEC﹣∠CEP=60°﹣30°=30°,∠PDE=∠BDC+∠EDC=60°+30°=90°,∴∠DPQ=60°,∴∠DQP=90°,∵PQ=2,∴DP=2PQ=2×2=4.故答案为:4.19.解:(1)∵+|2﹣b|=0,≥0,|2﹣b|≥0,∴=0.,|2﹣b|=0,∴a=﹣4,b=2,∴c=(a﹣b)=﹣3,∴A(﹣4,0),B(0,2),C(﹣3,0),∴BC=5,OA=4,∴S△ABC=×BC×OA=×5×4=10;(2)由题意知:OQ'=2×3=6,AA'=3m,∵S△A'Q'A =S△CQ'O+S梯形AA'CO,∴×6×3+×(3+3m)×4,∴m=.(3)连接OD,OE,设D(m,n),∵S△AOB =S△AOD+S△DOB,∴×2×(﹣m),∴m=2n﹣4,∵点D向右平移4个单位长度得到E点,∴E(2n,n),∵S△AOC +S△AOE+S△COE=S△ACE,∴×3×2n=14,∴n=,∴m=2n﹣4=﹣,∴D(﹣,).20.解:(Ⅰ)①∵AC=BC,∠ACB=90°,∴∠CAB=∠CBA=45°,∵AE平分∠BAC,∴∠CAE==,∵BD⊥AD,∴∠ADB=90°,∵∠AEC=∠BED,∴∠EBD=∠CAE=22.5°.②∵CF⊥CD,∴∠FCD=90°,∵∠ACB=90°,∴∠ACF+∠FCE=∠BCD+∠FCE,即∠ACF=∠BCD,由①得∠EBD=∠CAE=22.5°,在△ACF和△BCD中,,∴△ACF≌△BCD(ASA),∴AF=BD;(Ⅱ)AB、AC、AM之间的数量关系为AB+AC=2AM.证明:如图所示,过点D作DH⊥AB于点H,∵AD平分∠BAC,DM⊥AC,DH⊥AB,∴DM=DH,∵△ACF≌△BCD,∴CF=CD,又∵CF⊥CD,∴∠CFD=45°,∵∠CAE=22.5°,∴∠FCA=22.5°,∴AF=CF,由②得AF=BD,∴DC=DB,在Rt△CDM和Rt△BDH中,,∴Rt△CDM≌Rt△BDH(HL),∴CM=BH,在Rt△ADM和Rt△ADH中,,∴Rt△ADM≌Rt△ADH(HL),∴AM=AH,∴AB+AC=AH+BH+AC=AM+CM+AC=AM+AM=2AM.∴AB、AC、AM之间的数量关系为AB+AC=2AM.。
2021年九年级数学中考一轮复习专题突破训练(选择题专项):轴对称之线段最短问题(一)
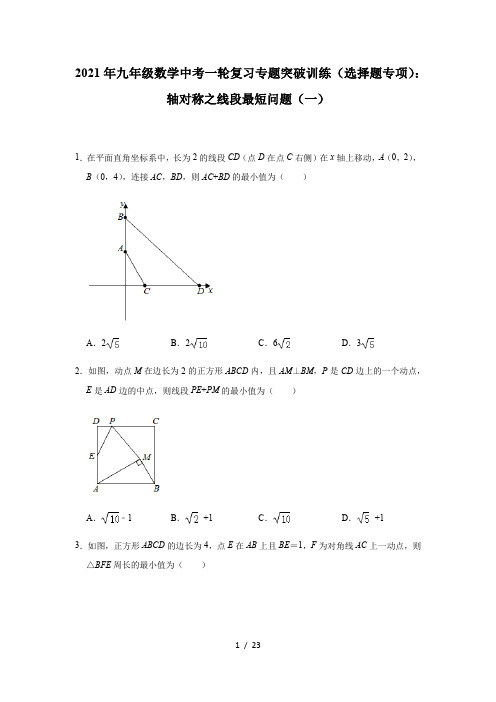
2021年九年级数学中考一轮复习专题突破训练(选择题专项):轴对称之线段最短问题(一)1.在平面直角坐标系中,长为2的线段CD(点D在点C右侧)在x轴上移动,A(0,2),B(0,4),连接AC,BD,则AC+BD的最小值为()A.2B.2C.6D.32.如图,动点M在边长为2的正方形ABCD内,且AM⊥BM,P是CD边上的一个动点,E是AD边的中点,则线段PE+PM的最小值为()A.﹣1B.+1C.D.+13.如图,正方形ABCD的边长为4,点E在AB上且BE=1,F为对角线AC上一动点,则△BFE周长的最小值为()A.5B.6C.7D.84.如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=4,以点O为圆心,2为半径的圆与OB交于点C,过点C作CD⊥OB交AB于点D,点P是边OA上的动点.当PC+PD 最小时,OP的长为()A.B.C.1D.5.如图,在矩形ABCD中,AB=6,AD=3,动点P满足S△P AB =S矩形ABCD,则点P到A、B两点距离之和P A+PB的最小值为()A.2B.2C.3D.6.如图,在Rt△ABO中,∠OBA=90°,A(4,4),点C在边AB上,且=,点D 为OB的中点,点P为边OA上的动点,当点P在OA上移动时,使四边形PDBC周长最小的点P的坐标为()A.(2,2)B.(,)C.(,)D.(3,3)7.如图,点P是边长为1的菱形ABCD对角线AC上的一个动点,点M,N分别是AB,BC边上的中点,则MP+PN的最小值是()A.B.1C.D.28.如图,在锐角三角形ABC中,BC=4,∠ABC=60°,BD平分∠ABC,交AC于点D,M,N分别是BD,BC上的动点,则CM+MN的最小值是()A.B.2C.2D.49.如图,在菱形ABCD中,AC=6,BD=6,E是BC边的中点,P,M分别是AC,AB 上的动点,连接PE,PM,则PE+PM的最小值是()A.6B.3C.2D.4.510.如图,∠AOB=60°,点P是∠AOB内的定点且OP=,若点M、N分别是射线OA、OB上异于点O的动点,则△PMN周长的最小值是()A.B.C.6D.311.如图,在正方形ABCD中,E,F分别为AD,BC的中点,P为对角线BD上的一个动点,则下列线段的长等于AP+EP最小值的是()A.AB B.DE C.BD D.AF12.如图,在正方形ABCD中,AB=9,点E在CD边上,且DE=2CE,点P是对角线AC 上的一个动点,则PE+PD的最小值是()A .3B .10C .9D .913.如图,在Rt △ABC 中,∠ACB =90°,AC =6,BC =8,AD 平分∠CAB 交BC 于D 点,E ,F 分别是AD ,AC 上的动点,则CE +EF 的最小值为( )A .B .C .D .614.如图,在△ABC 中,AB =AC ,AD 、CE 是△ABC 的两条中线,P 是AD 上一个动点,则下列线段的长度等于BP +EP 最小值的是( )A .BCB .CEC .AD D .AC15.如图,在矩形ABCD 中,AB =5,AD =3,动点P 满足S △P AB =S 矩形ABCD ,则点P 到A 、B 两点距离之和P A +PB 的最小值为( )A .B .C .5D .16.如图,在△ABC 中,AC =BC ,∠ACB =90°,点D 在BC 上,BD =3,DC =1,点P 是AB 上的动点,则PC +PD 的最小值为( )A.4B.5C.6D.717.如图,在矩形ABCD中,AD=4,∠DAC=30°,点P、E分别在AC、AD上,则PE+PD 的最小值是()A.2B.2C.4D.18.如图,矩形ABCD中,AB=10,BC=5,点E,F,G,H分别在矩形ABCD各边上,且AE=CG,BF=DH,则四边形EFGH周长的最小值为()A.5B.10C.10D.1519.如图,矩形ABOC的顶点A的坐标为(﹣4,5),D是OB的中点,E是OC上的一点,当△ADE的周长最小时,点E的坐标是()A.(0,)B.(0,)C.(0,2)D.(0,)20.如图,在Rt△ABC中,∠C=90°,AC=3,BC=4,D、E分别是AB、BC边上的动点,则AE+DE的最小值为()A.B.C.5D.参考答案1.解:设C(m,0),∵CD=2,∴D(m+2,0),∵A(0,2),B(0,4),∴AC+BD=+,∴要求AC+BD的最小值,相当于在x轴上找一点P(n,0),使得点P到M(0,2)和N(﹣2,4)的距离和最小,如图1中,作点M关于x轴的对称点Q,连接NQ交x轴于P′,连接MP′,此时P′M+P′N的值最小,∵N(﹣2,4),Q(0,﹣2)P′M+P′N的最小值=P′N+P′Q=NQ==2,∴AC+BD的最小值为2.故选:B.2.解:作点E关于DC的对称点E',设AB的中点为点O,连接OE',交DC于点P,连接PE,如图:∵动点M在边长为2的正方形ABCD内,且AM⊥BM,∴点M在以AB为直径的圆上,OM=AB=1,∵正方形ABCD的边长为2,∴AD=AB=2,∠DAB=90°,∵E是AD的中点,∴DE=AD=×2=1,∵点E与点E'关于DC对称,∴DE'=DE=1,PE=PE',∴AE'=AD+DE'=2+1=3,在Rt△AOE'中,OE'===,∴线段PE+PM的最小值为:PE+PM=PE'+PM=ME'=OE'﹣OM=﹣1.故选:A.3.解:如图,连接ED交AC于一点F,连接BF,∵四边形ABCD是正方形,∴点B与点D关于AC对称,∴BF=DF,∴△BFE的周长=BF+EF+BE=DE+BE,此时△BEF的周长最小,∵正方形ABCD的边长为4,∴AD=AB=4,∠DAB=90°,∵点E在AB上且BE=1,∴AE=3,∴DE=,∴△BFE的周长=5+1=6,故选:B.4.解:如图,延长CO交⊙O于点E,连接ED,交AO于点P,此时PC+PD的值最小.∵CD⊥OB,∴∠DCB=90°,又∠AOB=90°,∴∠DCB=∠AOB,∴CD∥AO∴∵OC=2,OB=4,∴BC=2,∴,解得,CD=;∵CD∥AO,∴=,即=,解得,PO=故选:B.5.解:设△ABP 中AB 边上的高是h .∵S △P AB =S 矩形ABCD ,∴AB •h =AB •AD ,∴h =AD =2,∴动点P 在与AB 平行且与AB 的距离是2的直线l 上,如图,作A 关于直线l 的对称点E ,连接AE ,BE ,则BE 的长就是所求的最短距离. 在Rt △ABE 中,∵AB =6,AE =2+2=4,∴BE ===2,即P A +PB 的最小值为2.故选:A .6.解:∵在Rt △ABO 中,∠OBA =90°,A (4,4),∴AB =OB =4,∠AOB =45°,∵=,点D 为OB 的中点, ∴BC =3,OD =BD =2,∴D (2,0),C (4,3),作D 关于直线OA 的对称点E ,连接EC 交OA 于P ,则此时,四边形PDBC 周长最小,E (0,2),∵直线OA的解析式为y=x,设直线EC的解析式为y=kx+b,∴,解得:,∴直线EC的解析式为y=x+2,解得,,∴P(,),故选:C.7.解:如图,作点M关于AC的对称点M′,连接M′N交AC于P,此时MP+NP有最小值,最小值为M′N的长.∵菱形ABCD关于AC对称,M是AB边上的中点,∴M′是AD的中点,又∵N是BC边上的中点,∴AM′∥BN,AM′=BN,∴四边形ABNM′是平行四边形,∴M′N=AB=1,∴MP+NP=M′N=1,即MP+NP的最小值为1,故选:B.8.解:如图,在BA上截取BE=BN,因为∠ABC的平分线交AC于点D,所以∠EBM=∠NBM,在△BME与△BMN中,所以△BME≌△BMN(SAS),所以ME=MN.所以CM+MN=CM+ME≥CE.因为CM+MN有最小值.当CE是点C到直线AB的距离时,即C到直线AB的垂线段时,CE取最小值为:4×sin60°=.故选:C.9.解:如图,作点E关于AC的对称点E′,过点E′作E′M⊥AB于点M,交AC于点P,则点P、M即为使PE+PM取得最小值,其PE+PM=PE′+PM=E′M,∵四边形ABCD是菱形,∴点E′在CD上,∵AC=6,BD=6,∴AB==3,=AC•BD=AB•E′M得×6×6=3•E′M,由S菱形ABCD解得:E′M=2,即PE+PM的最小值是2,故选:C.10.解:作P点分别关于OA、OB的对称点C、D,连接CD分别交OA、OB于M、N,如图,则MP=MC,NP=ND,OP=OD=OC=,∠BOP=∠BOD,∠AOP=∠AOC,∴PN+PM+MN=ND+MN+MC=DC,∠COD=∠BOP+∠BOD+∠AOP+∠AOC=2∠AOB =120°,∴此时△PMN周长最小,作OH⊥CD于H,则CH=DH,∵∠OCH=30°,∴OH=OC=,CH=OH=,∴CD=2CH=3.故选:D.11.解:如图,连接CP,由AD=CD,∠ADP=∠CDP=45°,DP=DP,可得△ADP≌△CDP,∴AP=CP,∴AP+PE=CP+PE,∴当点E,P,C在同一直线上时,AP+PE的最小值为CE长,此时,由AB=CD,∠ABF=∠CDE,BF=DE,可得△ABF≌△CDE,∴AF=CE,∴AP+EP最小值等于线段AF的长,故选:D.12.解:如图,连接BE,设BE与AC交于点P′,∵四边形ABCD是正方形,∴点B与D关于AC对称,∴P′D=P′B,∴P′D+P′E=P′B+P′E=BE最小.即P在AC与BE的交点上时,PD+PE最小,为BE的长度.∵直角△CBE中,∠BCE=90°,BC=9,CE=CD=3,∴BE==3.故选:A.13.解:如图所示:在AB上取点F′,使AF′=AF,过点C作CH⊥AB,垂足为H.在Rt△ABC中,依据勾股定理可知BA=10.CH==,∵EF+CE=EF′+EC,∴当C、E、F′共线,且点F′与H重合时,FE+EC的值最小,最小值为故选:C.14.解:如图连接PC,∵AB=AC,BD=CD,∴AD⊥BC,∴PB=PC,∴PB+PE=PC+PE,∵PE+PC≥CE,∴P、C、E共线时,PB+PE的值最小,最小值为CE的长度,故选:B.15.解:设△ABP中AB边上的高是h.∵S △P AB =S 矩形ABCD ,∴AB •h =AB •AD ,∴h =AD =2,∴动点P 在与AB 平行且与AB 的距离是2的直线l 上,如图,作A 关于直线l 的对称点E ,连接AE ,连接BE ,则BE 的长就是所求的最短距离.在Rt △ABE 中,∵AB =5,AE =2+2=4,∴BE ===,即P A +PB 的最小值为.故选:D .16.解:过点C 作CO ⊥AB 于O ,延长CO 到C ′,使OC ′=OC ,连接DC ′,交AB 于P ,连接CP .此时DP +CP =DP +PC ′=DC ′的值最小.∵BD =3,DC =1∴BC =4,∴BD =3,连接BC ′,由对称性可知∠C ′BA =∠CBA =45°,∴∠CBC ′=90°,∴BC′⊥BC,∠BCC′=∠BC′C=45°,∴BC=BC′=4,根据勾股定理可得DC′===5.故选:B.17.解:作D关于直线AC的对称点D′,过D′作D′E⊥AD于E,则D′E=PE+PD的最小值,∵四边形ABCD是矩形,∴∠ADC=90°,∵AD=4,∠DAC=30°,∵DD′⊥AC,∴∠CDD′=30°,∴∠ADD′=60°,∴DD′=4,∴D′E=2,故选:B.18.解:作点E关于BC的对称点E′,连接E′G交BC于点F,此时四边形EFGH周长取最小值,过点G作GG′⊥AB于点G′,如图所示.∵AE=CG,BE=BE′,∴E′G′=AB=10,∵GG′=AD=5,∴E′G==5,=2E′G=10.∴C四边形EFGH故选:B.19.解:作A关于y轴的对称点A′,连接A′D交y轴于E,则此时,△ADE的周长最小,∵四边形ABOC是矩形,∴AC∥OB,AC=OB,∵A的坐标为(﹣4,5),∴A′(4,5),B(﹣4,0),∵D是OB的中点,∴D(﹣2,0),设直线DA′的解析式为y=kx+b,∴,∴,∴直线DA′的解析式为y=x+,当x=0时,y=,∴E(0,),故选:B.20.解:如图,作点A关于BC的对称点A′,过点A′作A′D⊥AB交BC、AB分别于点E、D,则A′D的长度即为AE+DE的最小值,AA′=2AC=2×3=6,∵∠ACB=90°,BC=4,AC=3,∴AB=,∴sin∠BAC=,∴A′D=AA′•sin∠BAC=6×=,即AE+DE的最小值是.故选:B.。
中考数学第一轮复习坐标系专题训练

中考数学第一轮复习专题训练一、填空题:(每题3分,共36分)1、点A (3,-2)关于 x 轴对称的点是_____。
2、P (2,3)关于原点对称的点是_____。
3、P (-2,3)到 轴的距离是_____。
4、小红坐在第 5 排 24 号用(5,24)表示,则(6,27)表示小红坐在第__排___号。
5、以坐标平面内点A (2,4),B (1,0),C (-2,0)为顶点的三角形的面积是__。
6、如图1,△AOB 的顶点A 的坐标为_____。
7、如图1,△AOB 沿x 轴向右平移1个单位后,得到△A'O'B',则点A'的坐标为____。
8、如图2,矩形ABOC 的长OB =3,宽AB =2,则点A___。
9、如图3,正方形的边为2,则顶点C的坐标为_____。
10、如图4,△AOB 和它缩小后得到的△COD 。
则△AOB 和△COD 的相似比为____。
11、小东要在电话中告诉同学如图5的图形,他应当怎样描述。
_________________________。
12、如图6,一个机器人从O 点出以,向正东方走3米到达A 点,再向正北方走6米到达A 2点,再向正西方向走9米到达A 3点,再向正南方向走12米到达A 4点,再向正东走15米到达A 5点,按如此规律走下去,当机器人走到A 6点时,离O点的距离是_____米。
二、选择题:(每题 4 分,共 24 分) 1、若点A (m ,n )在第三象限,则点B (-m ,n),在( )A 、第一象限B 、第二象限C 、第三名象限D 、第四象限2、若P (m ,2)与点Q (3,n )关于 轴的对称,则m 、n 的值是( ) A 、-3,2 B 、3,-2 C 、-3,-2 D 、3,2 3、A 在B 的北偏东30°方向,则B 在A 的( )A 、北偏东30°B 、北偏东60°C 、南偏西30°D 、南偏西60°4、下列说法正确的是( )A 、两个等腰三角形必是位似图形B 、位似图形必是全等图形C 、两个位似图形对应点连线可能无交点D 、两个位似形对应点连线只有一个交点5、将△ABC 的三个顶点的纵坐标乘以-1,横坐标不变,则所得图形与原图形的关系是( )yy x 东 (6)x )A 、关于 x 轴对称B 、关于 轴对称C 、关于原点对称D 、原图形向 轴负方向平移1个单位6、如图,每个小正方形的边长为1个单位,对于A 、B 的位置,下列说法错误的是( )A 、B 向左平移 2 个单位再向下移 2 个单位与 A 重合B 、A 向左平移 2 个单位再向下移 2 个单位与 B 重合C 、B 在 A 的东北方向且相距 22 个单位D 、若点 B 的坐标为(0,0),则点 A 的坐标为(-2,-2)三、解答题:(每题 9 分,共 54 分)1、在如图所示的国际象棋棋盘中,双方四只子的位置分别是A (b ,3),B (d ,5),C (f ,7),D (h ,2),请在图中描出它们的位置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
闫家河镇中学20XX 年中考数学第一轮复习专题训练一方程 (2010.10.14)知识点提要(一)1.等式及其性质 ⑴ 等式:用等号“=”来表示 关系的式子叫等式.⑵ 性质:① 如果b a =,那么=±c a ;② 如果b a =,那么=ac ;如果b a =()0≠c ,那么=ca. 2. 方程、一元一次方程的概念⑴ 方程:含有未知数的 叫做方程;使方程左右两边值相等的 ,叫做方程的解;求方程解的 叫做解方程. 方程的解与解方程不同.⑵ 一元一次方程:在整式方程中,只含有 个未知数,并且未知数的次数是 ,系数不等于0的方程叫做一元一次方程;它的一般形式为 ()0≠a . 3. 解一元一次方程的步骤:①去 ;②去 ;③移 ;④合并 ;⑤系数化为1. 4.易错知识辨析:(1)判断一个方程是不是一元一次方程,首先在整式方程前提下,化简后满足只含有一个未知数,并且未知数的次数是1,系数不等于0的方程,像21=x,()1222+=+x x 等不是一元一次方程.(2)解方程的基本思想就是应用等式的基本性质进行转化,要注意:①方程两边不能乘以(或除以)含有未知数的整式,否则所得方程与原方程不同解;②去分母时,不要漏乘没有分母的项;③解方程时一定要注意“移项”要变号.(二)1.二元一次方程:含有 未知数(元)并且未知数的次数是 的整式方程.2. 二元一次方程组:由2个或2个以上的 组成的方程组叫二元一次方程组.3.二元一次方程的解: 适合一个二元一次方程的 未知数的值叫做这个二元一次方程的一个解,一个二元一次方程有 个解.4.二元一次方程组的解: 使二元一次方程组的 ,叫做二元一次方程组的解. 5. 解二元一次方程的方法步骤: 二元一次方程组 方程.消元是解二元一次方程组的基本思路,方法有 消元和 消元法两种. 6.易错知识辨析:消元转化(1)二元一次方程有无数个解,它的解是一组未知数的值;(2)二元一次方程组的解是两个二元一次方程的公共解,是一对确定的数值; (3)利用加减法消元时,一定注意要各项系数的符号.(三)1.一元二次方程:在整式方程中,只含 个未知数,并且未知数的最高次数是 的方程叫做一元二次方程.一元二次方程的一般形式是 .其中 叫做二次项, 叫做一次项, 叫做常数项; 叫做二次项的系数, 叫做一次项的系数. 2. 一元二次方程的常用解法:(1)直接开平方法:形如)0(2≥=a a x 或)0()(2≥=-a a b x 的一元二次方程,就可用直接开平方的方法.(2)配方法:用配方法解一元二次方程()02≠=++a o c bx ax 的一般步骤是:①化二次项系数为1,即方程两边同时除以二次项系数;②移项,使方程左边为二次项和一次项,右边为常数项,③配方,即方程两边都加上一次项系数一半的平方,④化原方程为2()x m n +=的形式,⑤如果是非负数,即0n ≥,就可以用直接开平方求出方程的解.如果n <0,则原方程无解.(3)公式法:一元二次方程20(0)ax bx c a ++=≠的求根公式是21,240)x b ac =-≥.(4)因式分解法:因式分解法的一般步骤是:①将方程的右边化为 ;②将方程的左边化成两个一次因式的乘积;③令每个因式都等于0,得到两个一元一次方程,解这两个一元一次方程,它们的解就是原一元二次方程的解.3.易错知识辨析: (1)判断一个方程是不是一元二次方程,应把它进行整理,化成一般形式后再进行判断,注意一元二次方程一般形式中0≠a .(2)用公式法和因式分解的方法解方程时要先化成一般形式. (3)用配方法时二次项系数要化1.(4)用直接开平方的方法时要记得取正、负.训练题一.填空题:1.22___)(_____6+=++x x x ⒎ 22____)(_____3-=+-x x x 22____)(_____+=++x x x ⒐ 22____)(_____-=+-x px x2.在选择方程082,0105,1,5)2)(1(42222=+=-=+=+-x x x y x x x ,12121,0432242+=+=+-x x x x x 中,应选一元二次方程的个数为-------------------( )A 3 个B 4 个C 5 个D 6 个 3、如果二次三项式226m x x +-是一个完全平方式,那么m 的值是_______________. 4、关于x 的方程03)3(7=+---x xm m 是一元二次方程,那么m =_______________.5、当n __________时,方程0)(2=+-n p x 有解,其解为_________________. 6、已知7532=++x x ,则代数式2932-+x x 的值为________________.7、解方程).51)(23()4)(32(x x x x --=+- 则它的根是 ; 8.如图,是一个正方形算法图,□里缺的数是____,并总结出规律:________________。
9、如图,四个一样大的小矩形拼成一个大矩形,如果大矩形的周长为 12cm ,那么小矩形的周长为____cm 。
10、一轮船从重庆到上海要 5 昼夜,而从上海到重庆要 7 昼夜,那么一个竹排从重庆顺流漂到上海要___昼夜。
11.如果方程2130m x-+=是一元一次方程,则m = .12.若5x -5的值与2x -9的值互为相反数,则x =_____. 13. 在方程yx 413-=5中,用含x 的代数式表示y 为y = ;当x =3时,y = . 14.如果x =3,y =2是方程326=+by x 的解,则b = . 15. 请写出一个适合方程13=-y x 的一组解: .16.若⎩⎨⎧-==11y x 是方程组⎩⎨⎧-=-=+1242a y x b y ax 的解,则⎩⎨⎧==______________b a .17. 在方程3x +4y =16中,当x =3时,y =___;若x 、y 都是正整数,这个方程的解为_____. 方程3(1)0x x +=的二次项系数是 ,一次项系数是 ,常数项是 . 18.关于x 的一元二次方程1(3)(1)30n n xn x n +++-+=中,则一次项系数是 .19.一元二次方程2230x x --=的根是 .20.某地20XX 年外贸收入为2.5亿元,20XX 年外贸收入达到了4亿元,若平均每年的增长率为x ,则可以列出方程为 .21. 方程 (5x -2) (x -7)=9 (x -7)的解是_________. 22.已知2是关于x 的方程23x 2-2 a =0的一个解,则2a -1的值是_________. 23.关于y 的方程22320y py p +-=有一个根是2y =,则关于x 的方程23x p -=的解为_____.二.选择题1.下列方程中,属于一元一次方程的是( )A 、x =y +1B 、1x=1 C 、x 2=x -1 D 、x =12、已知 3-x +2y =0,则 2x -4y -3 的值为( )A 、-3B 、3C 、1D 、03、若方程02=++n mx x 中有一个根为零,另一个根非零,则n m ,的值为---------( )(A ) 0,0==n m (B ) 0,0≠=n m (C ) 0,0=≠n m (D ) 0≠mn 4、方程0232=+-x x 的最小一个根的负倒数是-------------------------------( )(A ) 1 (B ) 2 (C ) 21 (D ) 45.下列方程中是一元二次方程的有( )①9 x 2=7 x ②32y=8 ③ 3y(y-1)=y(3y+1) ④ x 2-2y+6=0⑤ 2( x 2+1)=10 ⑥24x-x-1=0 A . ①②③ B. ①③⑤ C. ①②⑤ D. ⑥①⑤6. 一元二次方程(4x +1)(2x -3)=5x 2+1化成一般形式ax 2+bx +c =0(a ≠0)后a,b,c 的值为A .3,-10,-4 B. 3,-12,-2 C. 8,-10,-2 D. 8,-12,4 7.一元二次方程2x 2-(m +1)x +1=x (x -1) 化成一般形式后二次项的系数为1,一次项的系数为-1,则m 的值为( )A. -1B. 1C. -2D. 2 8. 如果x y y x b a b a 2427773-+-和是同类项,则x 、y 的值是( )A.x =-3,y =2B.x =2,y =-3C.x =-2,y =3D.x =3,y =-29. 下列方程组中,是二元一次方程组的是( )A .⎪⎩⎪⎨⎧=+=+9114y x y x B .⎩⎨⎧=+=+75z y y x C .⎩⎨⎧=-=6231y x x D .⎩⎨⎧=-=-1y x xy y x10. 关于x 、y 的方程组⎩⎨⎧=-=+m y x my x 932的解是方程3x +2y =34的一组解,那么m =( )A .2B .-1C .1D .-211.关于x 的一元二次方程225250x x p p -+-+=的一个根为1,则实数p =( ) A .4 B .0或2C .1D .1-三.解答题1.解方程(1)()()() 3175301x x x --+=+; (2)21101136x x ++-=.2 当m 取什么整数时,关于x 的方程1514()2323mx x -=-的解是正整数?3.苏州地处太湖之滨,有丰富的水产养殖资源,水产养殖户李大爷准备进行大闸蟹与河虾的混合养殖,他了解到如下信息:①每亩水面的年租金为500元,水面需按整数亩出租; ②每亩水面可在年初混合投放4公斤蟹苗和20公斤虾苗;③每公斤蟹苗的价格为75元,其饲养费用为525元,当年可获1400元收益; ④每公斤虾苗的价格为15元,其饲养费用为85元,当年可获160元收益; (1) 若租用水面 亩,则年租金共需__________元; (2) 水产养殖的成本包括水面年租金、苗种费用和饲养费用,求每亩水面蟹虾混合养殖的年利润(利润=收益-成本); (3) 李大爷现在奖金25000元,他准备再向银行贷不超过25000元的款,用于蟹虾混合养殖.已知银行贷款的年利率为8%,试问李大爷应该租多少亩水面,并向银行贷款多少元,可使年利润超过35000元?4. 解下列方程组:(1){4519323a b a b +=--= (2){2207441x y x y ++=-=-5.某厂工人小王某月工作的部分信息如下:信息一:工作时间:每天上午8∶20~12∶00,下午14∶00~16∶00,每月25元; 信息二:生产甲、乙两种产品,并且按规定每月生产甲产品的件数不少于60件.信息三:按件计酬,每生产一件甲产品可得1.50元,每生产一件乙产品可得2.80元.根据以上信息,回答下列问题:(1)小王每生产一件甲种产品,每生产一件乙种产品分别需要多少分? (2)小王该月最多能得多少元?此时生产甲、乙两种产品分别多少件?6. 若方程组{31x y x y +=-=与方程组{84mx ny mx ny +=-=的解相同,求m 、n 的值.7.解方程组:①⎩⎨⎧=-=+1392x y y x ②⎪⎩⎪⎨⎧=---=+1213343144y x y x8. 夏季,为了节约用电,常对空调采取调高设定温度和清洗设备两种措施.某宾馆先把甲、乙两种空调的设定温度都调高1℃,结果甲种空调比乙种空调每天多节电27度;再对乙种空调清洗设备,使得乙种空调每天的总节电量是只将温度调高1℃后的节电量的1.1倍,而甲种空调节电量不变,这样两种空调每天共节电405度.求只将温度调高1℃后两种空调每天各节电多少度?9. 某同学在A 、B 两家超市发现他看中的随身听的单价相同,书包单价也相同,随身听和书包单价之和是452元,且随身听的单价比书包单价的4倍少8元. ① 求该同学看中的随身听和书包单价各是多少元?② 某一天该同学上街,恰好赶上商家促销,超市A 所有商品打八折销售,超市B 全场购物满100元返购物券30元销售(不足100元不返券,购物券全场通用),但他只带了400元钱,如果他只在一家超市购买看中的这两样物品,你能说明他可以选择哪一家购买吗?若两家都可以选择,在哪一家购买更省钱?10. 已知一元二次方程0437122=-+++-m m mx x m )(有一个根为零,求m 的值.12.用22长的铁丝,折成一个面积是30㎝2的矩形,求这个矩形的长和宽.又问:能否折成面积是32㎝2的矩形呢?为什么?13. 如果方程①062=--bx ax 与方程②01522=-+bx ax 有一个公共根是3,求a ,b 的值,并求方程的另一个根.14、已知053)23(6522=+++-+-x x m m m m ,是关于x 的二次方程,求m 的值.17、已知方程06854234=+--+x x x x 有两根和为零,解这个方程.。
