高等数学典型例题与应用实例
高等数学应用案例讲解(精华版)

高 等 数 学 应 用 案 例案例 1,如何调整工人的人数而保证产量不变一工厂有 x 名技术工人和 y 名非技术工人,每天可生产的产品产 量为2(件)f ( x, y) x y现有 16 名技术工人和 32 名非技术工人,如何调整非技术工人的 人数,可保持产品产量不变?解:现在产品产量为 f (16,32) 8192 件,保持这种产量的函数曲线 为 f (x, y) 8192 ;对于任一给定值 x ,每增加一名技术工人时 y 的变化 量即为这函数曲线切线的斜率dy;而由隐函数存在定理,可得dxf dy dxx f y所以,当增加一名技术工人时,非技术工人的变化量为f dy dx2 y xx f y4 ;dydx当 x 32 时,可得 16, y 因此,要增加一个技术工人并要使产量不变,就要相应地削减约 4 名非技术工人;下面给出一个初等数学解法;令c :每天可生产的产品产量;x 0 ;技术工人数; y 0 ;非技术工人数;x ;技术工人增加人数;y ;在保持每天产品产量不变情形下,当技术工人由16 名增加到 17 名时,非技术人员要增加(或削减)的人数;由已知列方程:(1)当技术工人为 16 名,非技术工人为 32 名时, 每天的产品产 量为 c ,就有方程:(1)2 xy 0c(2)当技术工人增加了 1 名时,非技术工人应为( y )名,y 0且每天的产品产量为 c ,就有方程:2(2)( x 0x) ( y 0y) c联立方程组( 1),(2),消去 c 得:22y 0 ( x 0 x ) x( y 0y)2 x 0即2 2yx 0/( x 0x)y 0 y 0y 0 12( x 0x)1y 0 12x x 01代入 x ,得: 4 名,即削减4 名非技术工人;x 0 , y 0 , y比较这两种解法我们可以发觉,用初等数学方法运算此题的工作 量很大,究其缘由,我们留意到下面之绽开式:2n 11 x x 0x x 0x x 0n 1123( 1) n2x x 0n 11 从今绽开式我们可以看到,初等数学方法不能忽视掉高阶无穷小:2n1x x0xx0n 1 (3)3(1 ) n (x 0)n 4而高等数学方法却利用了隐函数求导,忽视掉高阶无穷小(3),所以运算较简单;案例2,征税的学问工厂想赚钱,政府要收税,一个怎样的税率才能使双方都受益?这是一个具有现实意义的问题;假设工厂以追求最大利润为目标而控制它的产量q,政府对其产品征税的税率(单位产品的税收金额)为t,我们的任务是,确定一个适当的税率,使征税收益达到最大;现已知工厂的总收益函数和总成本函数分别为R=R(q),C=C(q);由于每单位产品要纳税t,故平均成本要增加t,从而纳税后的总成本函数是C t C(q) tq利润函数是L t R(q) C t (q) R(q) C(q) tqdL tdq令0 ,有dR dq dCdq(1)t这就是在纳税的情形下获得最大利润的必要条件;政府征税得到的总收益是(2)T tq明显,总收益T 不仅与产量q 有关,而且与税率 f 有关;当税率t=0(免税)时,T=0 ;随着单位产品税率的增加,产品的价格也会提高,需求量就会降低,当税率 f 增大到使产品失去市场时,有q=0,从而也有T=0 ;因此,为了使征税收益最大,就必需恰当地选取t;我们利用一元函数极值的有关学问来解决本问题,下面看一个实例;例 1: 厂商的总收益函数和总成本函数分别为222q 2 ;R 30q 3q , Cq厂商追求最大利润,政府对产品征税,求1)征税收益的最大值及此时的税率 t ;2)厂商纳税前后的最大利润及价格.解: 1)由纳税后获得最大利润的必要条件 (1),得30 6q 2q 2 tq 1( 28 故t ) t8依据实际问题的判定, q t 就是纳税后厂商获得最大利润的产出水 平;于是,这时的征税收益函数1 (28t t 2) 80 ,得 T tq tdT dt 2t) 要使税收 T 取最大值,令 1( 28 0 ,即 t=14 8dT dt 依据实际问题可以肯定必有最大值,现在 0 只有一个根,所q 1(28 以当 t=14 时,T 的值最大;这时的产出水平 14) ,最大 t8征税收益为T tq t 142)简单算得纳税前, 当产出水平 时,可获得最大利润 L=47,此时价格 p ;将 q t , t =14 代入纳税后的利润函数4q 2L R( q) C (q) ( 28 t) q 2tt得最大利润 ,此时产品价格R(q) qp(30 3q) q q 1. 75可见,因产品纳税,产出水平由下降到;价格由上升到,最大利润由47 下降到;案例 3,隧道的车流量问题巴巴拉 (Barbara 接)受了纽约市隧道治理局的一份工作,她的第一 项任务就是打算每辆汽车以多大速度通过隧道可使车流量最大; 通过 大量的观看,她找到了一个很好的描述平均车速 (km/h) 与车流量 (辆/ 秒)关系的函数:35v 2f (v)v22(a)问平均车速多大时,车流量最大? (b)最大流量是多少?解: (a)这是一个极值的问题:2v v) 11) 2 df dv22v) 2 22df dv令 0 ,即 v 2得 v26.15(km / h)由实际问题知,当 /h 时,车流量最大; (b)最大车流量是 f (26.15)=8.8(辆/秒 )案例4,,核废料的处理问题以前,美国原子能委员会将放射性核废料装在密封的圆桶里扔到水深约91 米的海里;生态学家和科学家耽心这种做法担心全而提出疑问;原子能委员会向他们保证,圆桶决不会破漏;经过周密的试验,证明圆桶的密封性是很好的;但工程师们又问:圆桶是否会因与海底碰撞而发生破裂?原子能委员会说:决不会;但工程师们不放心;他们进行了大量的试验后发觉:当圆桶的速度超过每秒米时,圆桶会因碰撞而破裂;那末圆桶到达海底时的速度究竟是多少呢?它会因碰撞而破裂吗?下面是详细而真实的数据,你能依据它们解决这个问题吗?圆桶的重量 kg海水浮力为g/m33圆桶的体积圆桶下沉时的阻力:工程师们做了大量牵引试验后得出结论:这个阻力与圆桶的方位大致无关,而与下沉的速度成正比,比例系数;解:建立坐标系,设海平面为x 轴,y 轴的方向向下为正;由牛2d y ,F 为作用在圆桶上顿其次定律F=ma,其中m 为圆桶质量, adt 2的力:它由圆桶的重量W,海水作用在圆桶上的浮力×dy ;V=213.396(kg)及圆桶下沉时的阻力(其中v 为dt下沉速度)合成;即F=w-B-D=W-B- kv,这样就得到一个二阶微分方程2dy m d y W B k 2 dt dt(1)y(0) dy 0 v(0) 0dt t此微分方程是 ( y ) 型的;解此方程:y f 2dy dtd y dv dt由于 v,就代人( 1)得到一个一阶可分别变量的方程2dtm dvdtW B kv v(0) 0kW B(1 t 解得,mv(t )e)k至此,数学问题好像有了结果,得到了速度与时间的表达式,但实际 问题远没有解决;由于圆桶到达海底所需的时间t 并不知道,因而也就无法算出速度;这样,上述的表达式就没有实际意义;有人会说, W B;因而 虽然无法算出精确值但我们可以估量当 时, v(t)tkW B圆桶到达海底的速度不会超过;这个说法是对的,但惋惜 kW B/ s ,它太大了,毫无用处;这样,方程 (1)就需要用其它k2 dy dtd v, y 2 dvdy方法来解; y f ( y ) 型方程的另一种解法是:令,方 vdt 程(1)也化为一个一阶可分别变量的方程dvdy mv W B kv(2)v(0) y(0) 0 0v B 1m 解之, dv dyW kv1 m1 v kW k B ln(W B得y kv) C 2由初始条件得W B C ln(W B) 2k所以求当 y=91(米 )时,v=?好像这个 v 值也无法求得, 但我们用近似方法 例如牛顿法迭代可求出 v 的近似值;牛顿法介绍:如已知方程 g(v)=0,求 v 用迭代法:g(v n )g (v n ) v n v n, n 0,1,2, 1 在这里, (3)式可写成1m v k W k B ln W B kvy 02W B k mW B lnW B kv 取g (v)y vkW Bk a y WW B W B kv vlnkW Bk a W y W B其中 2,记 d0.447 ; b ,于是 kv bg (v) d v b ln 11 b v bv g ( v) 1 bb v1迭代格式为:g(v n ) g (v n )v n v n1b v n v nv nv n v n v n bv n d v nbln 1b b v n v n b(4)v v d b ln 1 n nv nb v n bbd b ln 1v n挑选一个好的初始值 v 0 ,就能很快算出结果;求 v 0 的粗略近似值:从 1 mv 2 2(2)中令 k=0( 即下沉时不计阻力 )得 C 由初始条件得(W B) y W B C=0; 2v2 y m / sm以 v 0 代入( 4)得13.64057.把 v 1代入(4)v 1 有v 2 13.632728.把v 2代入 (4) 这就够了,不用再迭代了;v 313.64m / s 12.2m / s ,因此这种处理核废料的方法是担心全的;v案例5,大气污染指数的影响因素一个城市的大气污染指数P 取决于两个因素,空气中固体废物的数量x 和空气中有害气体的数量y,在某种情形下x2 2 x y 4 x h2 ;PP P P P试说明的意义,并运算当x 增长10%或, ,x y x y( a,b ) (10,5)(a,b ) (10,5)y 增长10%时,用偏导数估算P 的转变量;P解:的意义:假如空气中有害气体的数量y 为一常数b,x( a,b )空气中固体废物的数量x 是变化的,那么当x=a 有一个单位的转变时,P大气污染指数P 大约转变个单位.x( a,b )P同样地,可以说明的意义.y(a ,b)P xPy22 x 2 y 4 y , 2 x8 x yP x 20 10 100 130(10,5)P20 400 420y(10,5)设空气中有害气体的量y=5,且固定不变,当空气中固体废物的量x=10 时,P 对x 的变化率等于130.当x 增长10%,即x 从10 到11,P 将增长大约130×1=130 个单位(事实上,P(10,5)=1200,P(11,5)=1331,P 增长了131 个单位);同样地,设空气中固体废物的量x=10 且固定不变,当空气中有害气体的量y=5 时,P 对Y 的变化率等于420.当Y 增长10%,即Y从5 到5.5,增长0.5 个单位时,P 大约增长420×0.5=210个单位(事实上,P(10,5)=1200,P(10,5.5)=1420,P 增长了220 个单位);因此,大气污染指数对有害气体增长10%比对固体废物增长10%更为敏锐;案例6,为什么不宜制造太大的核弹头核弹在与它的爆炸量(系指核裂变或聚变时释放出的能量,通常用相当于多少千吨T.N .T 炸药的爆炸威力来度量)的立方根成正比的距离内会产生每平方厘米千克的超压,这种距离算作有效距离;如记有效距离为 D ,爆炸量为x,就二者的函数关系为1D Cx 3其中C 是比例常数;又知当x 是100 千吨(T.N.T 当量)时,有效距离D 为3.2186千米.于是110033.2186=C11003即C所以这样,当爆炸量增至10 倍(变成1 00()千吨= 百万吨)时,有效距离增至10.6934(1000)36.93(4 km)差不多仅为100 千吨时的2 倍,说明其作用范畴( D 2 )并没因爆炸量的大幅度增加而显著增加;下面再来讨论爆炸量与相对效率的关系(这里相对效率的含义是,核弹的爆炸量每增加 1 千吨T.N .T 当量时有效距离的增量);2 32 3dD dx 1 3由x23知D x 如x 1 ,就x 100,23D0.2311(1000) 0.0107(km) 10.7(m)这就是说,对100千吨(10 万吨级)爆炸量的核弹来说,爆炸量每增加1 千吨,有效距离差不多增加米;如x x 1 ,就100,23D0.2311(1000) 0.0023(km) 2.3(m)即对百万吨级的核弹来说,每增加l 千吨的爆炸量,有效距离差不多仅增加米,相对效率是下降的;可见,除了制造,运载,投放等技术因素外,无论从作用范畴仍是从相对效率来说,都不宜制造当量级太大的核弹头;事实上,1945 年二战中美国投放在日本广岛,长崎的原子弹,其爆炸量为20 千吨,有效距离为千米;。
高等数学应用题.

第一章 函数 极限 连续问题1. 上岸点的问题有一个士兵P ,在一个半径为R 的圆形游泳池(图1—1)222x y R +≤内游泳,当他位于点(,02R-)时,听到紧急集 合号,于是得马上赶回位于A=(2R ,0)处的营房去,设该士 兵水中游泳的速度为1v ,陆地上跑步的速度为2v ,求赶回营房 所需的时间t 与上岸点M 位置的函数关系。
图1-1解:这里需要求的是时间t 与上岸点M 位置的函数关系,所以一定要先把上岸点M 的位置数字化,根据本题特点可设(cos ,sin )M R R θθ=其中θ为M 的周向坐标(即极坐标系中的极角),于是本题就成为了求函数关系()t f θ=的问题。
由对称性,我们可只讨论在上半圆周上岸的情况,即先确定函数()t f θ=的定义域为0θπ≤≤。
该士兵在水中游泳所花的时间为111PM t v === 而在陆地上跑步所需的时间,则要视上岸点位置的两种不同的情况要分别进行讨论:① 当03πθ≤≤时,有222M A t v '== ② 当3πθπ≤≤时,要先跑一段圆弧MB ,再跑一段且线段BA ,所以2221()(3R t MB BA v v πθ=+=-。
综上所述,可得121203(33t R v πθππθθπ≤≤=-≤≤问题2 外币兑换中的损失某人从美国到加拿大去度假,他把美元兑换成加拿大元时,币面数值增加12%,回国后他发现把加拿大元兑换成美元时,币面数值减少12%。
把这两个函数表示出来,并证明这两个函数不互为反函数,即经过这么一来一回的兑换后,他亏损了一些钱。
解:设1()f t 为将x 美元兑换成的加拿大元数,2()f t 为将x 加拿大元兑换成的美元数,则1()12% 1.12,0f t x x x x =+⋅=≥ 2()12%0.88,0f t x x x x =-⋅=≥而21(())0.880.120.9856,f f t x x x =⨯=<故1()f t ,2()f t 不互为反函数。
经典高数题举例

经典高数题举例1、函数f(x) = x^3 + 2x^2 - 5x + 3 的导数和二阶导数:解题思路:对f(x) 分别求导即可。
f'(x) = 3x^2 + 4x - 5 (一阶导数)f''(x) = 6x + 4 (二阶导数)2、函数f(x) = e^x * sin(x) 的导数:解题思路:使用乘积法则和链式法则进行求导。
f'(x) = e^x * sin(x) + e^x * cos(x)3、函数f(x) = ∫[1, x] (t^2 + 2t) dt 的原函数:解题思路:对被积函数进行积分,然后求出不定积分的原函数。
f(x) = ∫[1, x] (t^2 + 2t) dt = [(1/3)t^3 + t^2],其中x 是上限。
4、方程组的解:2x + 3y = 104x - 5y = -7解题思路:可以使用消元法或代入法来求解方程组。
解得x = 3,y = 2。
5、函数f(x) = ln(x) 在区间[1, e] 上的定积分:解题思路:计算定积分的值。
∫[1, e] ln(x) dx = [x ln(x) - x],在区间[1, e] 上。
6、曲线y = x^2 + 3x + 2 在点(1, 4) 处的切线方程:解题思路:求出曲线在给定点处的斜率,然后利用点斜式得到切线方程。
曲线的斜率为f'(x) = 2x + 3,在点(1, 4) 处的斜率为5。
切线方程为y - 4 = 5(x - 1),即y = 5x - 1。
7、函数f(x) = 3x^2 - 4x + 5 的极值点和极值:解题思路:计算函数的导数,并解方程找到导数为零的点。
f'(x) = 6x - 4,令f'(x) = 0,解得x = 2/3。
极值点为(2/3, f(2/3))。
极小值为f(2/3) = 19/3。
8、函数f(x) = sin^2(x) + cos^2(x) 的周期和振幅:解题思路:观察函数的性质,根据三角函数的性质得到周期和振幅。
高数中值定理总结典型例题

高数中值定理总结典型例题一、罗尔定理罗尔定理:如果函数f(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,且f(a)=f(b),则至少存在一点c∈(a,b),使得f′(c)=0。
典型例题:设f(x)=x3−3x+2,在区间[1,2]上应用罗尔定理。
解答:1.验证f(x)在[1,2]上连续,在(1,2)内可导。
f(x)=x3−3x+2是多项式函数,在R上连续且可导。
2.计算f(1)和f(2)。
f(1)=13−3×1+2=0f(2)=23−3×2+2=4(注意:虽然f(1)=f(2),但此步骤是为了展示如何应用定理的验证过程。
实际上,为了应用罗尔定理,我们需要找到一个包含x=1的区间,使得在该区间两端函数值相等。
但在这个例子中,我们直接考虑f(x)在x=1处的性质,并注意到f′(1)=0,这实际上是一个特例,因为罗尔定理的严格条件并未完全满足。
然而,为了教学目的,我们可以假设存在一个包含x=1且满足罗尔定理条件的小区间,或者直接观察f′(x)在x=1处的值。
)3.求导并找到导数为0的点。
f′(x)=3x2−3令f′(x)=0,解得x=±1。
在区间(1,2)内,只有x=1(虽然不在开区间内,但在此我们仅作为示例说明求导过程,并注意到x=1是临界点)。
注意:实际上,在这个例子中,由于f(1)=0且f′(1)=0,x=1是函数的一个零点也是一个驻点(即导数为零的点)。
虽然罗尔定理不能直接应用于这个区间,但我们可以观察到在x=1附近函数的行为符合罗尔定理的直观意义:函数在这一点附近先减后增(或先增后减),因此存在一点使得切线水平(即导数为零)。
二、拉格朗日中值定理拉格朗日中值定理:如果函数f(x)在闭区间[a,b]上连续,在开区间(a,b)内可导,那么在开区间(a,b)内至少存在一点c,使得f′(c)=b−af(b)−f(a)典型例题:证明:对于任意两个正数a和b(a=b),有2a+b>ab解答:1.定义函数f(x)=x。
高等数学实际应用案例

高等数学实际应用案例
案例名称:企业生产成本与利润的最优化问题
案例描述:
某企业生产一种产品,每月的生产成本随生产量的增加而增加,并且每月的销售利润随销售量的增加而增加。
企业希望通过确定最佳的生产量,使得每月的利润最大化。
数学模型:
设该企业每月生产量为x件,生产成本(C)与生产量(x)之间的关系为:C(x) = kx,其中k为生产成本与生产量之间的比例系数。
设该企业每月销售量为y件,销售利润(P)与销售量(y)之间的关系为:P(y) = py - F,其中p为销售利润与销售量之间的比例系数,F为固定费用(例如租金、工资等)。
问题:
该企业希望确定生产量x和销售量y的最佳组合,以最大化每月的利润P。
但生产量必须满足以下限制条件:
1. 生产量必须小于等于最大可生产量;
解决方法:
可以建立一个数学模型来求解该问题的最优解。
1. 分析最大生产量和最小生产量的限制条件,得出x的范围。
2. 根据利润最大化的目标,建立利润函数P(y)。
3. 建立约束条件x ≤ y。
4. 利用高等数学中的优化方法,将利润函数和约束条件进行数学求解,以确定最佳
的生产量和销售量组合。
实际应用:
该案例可以应用于各种生产型企业(例如制造业、农业等),帮助企业管理者在决策时确定最佳的生产量和销售量,从而最大化企业的利润。
注意事项:本案例为虚构案例,与实际企业无关。
如涉及任何真实企业或人物,纯属巧合。
高等数学在中学数学中的应用1000例

定理10 设函数f(x)在I 可导。
函数f(x)在区间I 是凸函数⇔I x x ∈∀21,,且21x x <,有))()()(()(22x f x f x f x f '≥''≤'。
推论 若函数f(x)在区间I 上存在二阶导数,且(1)I x ∈∀,有0)(>''x f ,则函数f(x)在区间I 严凸。
(2)I x ∈∀,有0)(<''x f ,则函数f(x)在区间I 严凹。
定理11(詹生不等式)若函数f(x)在区间I 是凸,则有不等式)()()()(22112211n n n n x f q x f q x f q x q x q x q f +⋅⋅⋅++≤+⋅⋅⋅++ 其中,,,2,1,0,n i q I x i i⋅⋅⋅=>∈且121=+⋅⋅⋅++n q q q 。
利用拉格朗日重要不等式证明不等式例33(101页) 证明:若函数)(x f 在闭区间[a,b]满足拉格朗日定理,且)(x f '在[a,b]上单调增加(减少),则 ∑∑-=+-='<-<'1110)()()()(n i i n i ixf h a f b f x f h( ∑∑-=+-='>->'10110)()()()(n i i n i ixf h a f b f x f h)其中a=0x ,ih x x i +=0(i=0,1,2,···,n),nab h b nh x x n -==+=,0 (此不等式称为拉格朗日重要不等式)证明 已知函数)(x f 在闭区间[a,b]满足拉格朗日定理,则)(x f 在[]1,+i i x x (i=0,1,2,···,n-1)上也满足拉格朗日定理,有))(()()(11i i i i i x x f x f x f -'=-++ξ ),(1+∈i i i x x ξ(i=0,1,2,···,n-1) 又已知)(x f '在[a,b]上单调增加,则)(x f '在[]1,+i i x x (i=0,1,2,···,n-1)上也单调增加,从而 <-'+))((1i i i x x x f ))(()()(111i i i i i x x x f x f x f -'<-+++ 或 <')(i x f h )()()(11++'<-i i i x f h x f x f (i=0,1,2,···,n-1) 于是 ∑∑∑-=+-=-=+'<-<'111011)())()(()(n i i n i n i i i ix f h x f xf x f h即 ∑∑-=+-='<-<'10110)()()()(n i i n i ixf h a f b f x f h类似可证,)(x f '为单调减少的情形 利用凸凹函数证明不等式例38 (105页)证明:当0>i a (i=0,1,2,····,n )时,有不等式na a a a a a a a a nnn n n+⋅⋅⋅++≤⋅⋅⋅≤+⋅⋅⋅++212121121(调和平均数) (几何平均数) (算术平均数)证明 分别证明两个不等式,首先证明右端不等式。
高等数学典型例题与应用实例(重积分B部分)

例 利用二重积分的性质,估计积分2222(2)d Dx y x y σ+-⎰⎰ 的值,其中D 为半圆形区域224,0x y y +≤≥.解 我们先求函数2222(,)2f x y x y x y =+-在区域22{(,)4,0}D x y x y y =+≤≥上的最大值和最小值.由22220,420,x yf x xy f y x y '⎧=-=⎪⎨'=-=⎪⎩解得D 内驻点为(2,1)±,(2,1)2f ±=. 在边界1:0L y =(22)x -≤≤上,2()(,0)g x f x x ==在1L 上(,)f x y 的最大值为4,最小值为0.在边界222:4L x y +=(0)y ≥上,242()(,4)58(22)h x f x x x x x =-=-+-≤≤由3()4100h x x x '=-=得驻点123550,,22x x x ==-=,(0)(0,2)8h f ==. 5537()(,)2224h f ±=±=. 综上,(,)f x y 在D 上的最大值为8,最小值为0.又D 的面积为2π,所以由二重积分的估值性质知222202(2)d 82Dx y x y πσπ⋅≤+-≤⋅⎰⎰,即22220(2)d 16Dx y x y σπ≤+-≤⎰⎰.例 设D 为xoy 平面上以(1,1),(1,1),(1,1)---为顶点的三角形区域,1D 为D 在第一象限的部分,则(cos sin )()Dxy x y dxdy +=⎰⎰.(A )12cos sin D x y dxdy ⎰⎰ (B )12D xy dxdy ⎰⎰(C )14(cos sin )D xy x y dxdy +⎰⎰ (D )0解 区域D 如图所示,并记0D 为以(1,1),(1,1),(0,0)-为顶点的三角形区域,则0D 关于y 轴对称,且1D 为0D 在y 轴右侧的部分区域,区域0D D -关于x 轴对称.又xy 关于x 和y 均为奇函数;而cos sin x y 关于x 为偶函数.关于y 为奇函数,由二重积分的奇偶对称性得0,0D D D xy dxdy xy dxdy -==⎰⎰⎰⎰,故0Dxy dxdy =⎰⎰;1cos sin 2cos sin ,cos sin 0D D D D x ydxdy x y dxdy x y dxdy -==⎰⎰⎰⎰⎰⎰,故1cos sin 2cos sin DD x y dxdy x y dxdy =⎰⎰⎰⎰.所以1(cos sin )cos sin 2cos sin DDDD xy x y dxdy xy dxdy x y dxdy x y dxdy +=+=⎰⎰⎰⎰⎰⎰⎰⎰.因此我们选(A ).例 设区域}0,0,4),{(22≥≥≤+=y x y x y x D ,()f x 为D 上的正值连续函数,,a b 为常数,则Dσ= .解 由题意知,D 关于直线y x =对称,由二重积分轮换对称性得DσDσ=12D d σ=⎰⎰ 211()π2π22242D D a b a b a b a b d d σσ+++=+==⋅⋅=⎰⎰⎰⎰. 因此,我们应填“π2a b+.”例 计算二次积分220sin xydx dy yππ⎰⎰解 积分区域如图,则 原式20sin yydy dx yπ=⎰⎰2200sin sin sin y dy ydy ydy ππππ==+-⎰⎰⎰4=;例设D为椭圆区域22(1)(2)149x y--+≤,计算二重积分()Dx y dxdy+⎰⎰.解令12cos,23sin,x ry r=+⎧⎨=+⎩θθ则D的极坐标表示为01,02r≤≤≤≤θπ,且(,)6(,)x yrrθ∂=∂.由式(10.2.8),可得2100()6(32cos3sin)Dx y dxdy d r r rdr+=++⎰⎰⎰⎰πθθθ2326(cos sin)1823d=++=⎰πθθθπ.例计算二重积分⎰⎰+Dyxyx dd)(,其中D为.122++≤+yxyx解解法1 D的边界曲线为,2/3212122=⎪⎭⎫⎝⎛-+⎪⎭⎫⎝⎛-yx这是一个以⎪⎭⎫⎝⎛21,21为圆心,23为半径的圆域,采用一般的变量代换,令⎪⎪⎩⎪⎪⎨⎧-=-=,21,21yvxu即作变换⎪⎪⎩⎪⎪⎨⎧+=+=,21,21vyux于是D变为.2/3:22≤+'vuD.111),(),(==∂∂=vuyxJ所以,()d d(1)1d dD Dx y x y u v u v'+=++⋅⋅⎰⎰⎰⎰(再用极坐标).23023d d )cos (sin d d d )1sin cos (d 222/30202/3020ππθθθθθθθππ=+⎪⎪⎭⎫ ⎝⎛⋅=++=++=⎰⎰⎰⎰⎰⎰r r r r rr r r D解法2 由于积分区域D :23212122≤⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-y x 关于21=x (即)021=-x 对称,故⎰⎰=⎪⎭⎫ ⎝⎛-D y x x .0d d 21 类似地,由于D 关于⎪⎭⎫⎝⎛=-=02121y y 即对称,故 ⎰⎰=⎪⎭⎫ ⎝⎛-D y x y .0d d 21 从而.2323d d d d 1d d 21d d 21d d )(2ππ=⎪⎪⎭⎫ ⎝⎛⋅===⋅+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=+⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰面积D y x y x y x y y x x y x y x D D D DD例 计算y x e I Dy xd d },max{22⎰⎰=,其中,}10,10|),{(≤≤≤≤=y x y x D解 D 由x y =分为D 2,D 2两部分,如图.⎪⎩⎪⎨⎧≤≤≤≤≤≤≤≤=1,10:,0,10:,21},max{2222y x x D e x y x D e e y x y x x e y y e x y x e y x e I yy xx D y D x d d d d d d d d 01010222212⎰⎰⎰⎰⎰⎰⎰⎰+=+=21110d d 2d d 2222x e x xe y e x x x xx ⎰⎰⎰⎰===.1102-==e e x例 利用二重积分计算定积分1(,0)ln b ax x I dx a b x-=>⎰解 因为1ln ln bb a btt aa x x x dt x x x-==⎰所以 ⎰⎰⎰⎰⎰⎪⎭⎫⎝⎛++=+=+===bab aba batta b t dt t dx x dt dx dt x I 11ln )1ln(11)(11例 ],[)(b a x f 为上的连续函数,且0)(>x f ,试利用二重积分证明.)()(1d )(2a b x f x x f baba-≥⎰⎰证 因为x x f y y f x x f x x f b a b a babad )(1d )(d )(1d )(⎰⎰⎰⎰=,d d )()(d d )()(y x y f x f y x x f y f DD⎰⎰⎰⎰≥= 其中 所以},,|),{(b y a b x a y x D ≤≤≤≤=⎰⎰⎰⎰⎰⎰+=DD bab ay x y f x f y x x f y f x x f x x f d d )()(d d )()(d )(1d )(2 y x y f x f y f x f y x y f x f x f y f DDd d )()()()(d d )()()()(22⎰⎰⎰⎰≥+=,)(2d d 22a b y x D-==⎰⎰亦即.)(d )(1d )(2a b x x f x x f baba-≥⎰⎰例 计算⎰1d )(x x xf ,其中⎰=21d int)(x t tS x f 解 当10,102≤≤≤≤x x 时⎰⎰⎰-===111222,d sin d sin d sin )(x x x y yy y y y t t tx f从而x y y y x x x xf x d d sin d )(101102⎰⎰⎰⎥⎦⎤⎢⎣⎡-= 图y x y yx y y y x x xDd d sin d sin d 1102⎰⎰⎰⎰-=⋅-=,其中D 曲线1,2==y x y ,和0=x 所围成,如图10-8。
高等数学实际应用案例

高等数学实际应用案例高等数学是一门抽象且理论性强的学科,但它在许多实际应用中发挥着重要的作用。
下面列举了10个高等数学的实际应用案例,从不同领域展示了数学在解决实际问题中的重要性。
1. 金融领域中的复利计算:在金融领域中,复利计算是非常重要的。
高等数学中的指数函数和对数函数可以帮助金融从业者计算复利的利率、本金和时间之间的关系,从而制定更加合理的投资策略。
2. 物理学中的运动方程:在物理学中,高等数学的微积分理论被广泛应用于描述物体的运动。
通过对位移、速度和加速度之间的关系进行微分和积分,可以精确地预测物体在不同时间点的位置和速度。
3. 工程学中的结构分析:在工程学中,高等数学的线性代数理论被用于解决结构分析问题。
通过矩阵和向量的运算,可以计算出工程结构的受力情况,从而确保结构的安全性和稳定性。
4. 经济学中的优化问题:在经济学中,高等数学的最优化理论被广泛应用于解决资源分配和决策问题。
通过对成本、收益和约束条件进行数学建模和优化,可以找到最优的经济决策方案。
5. 计算机科学中的图像处理:在计算机科学中,高等数学的线性代数和概率论理论被广泛应用于图像处理领域。
通过矩阵运算和概率模型,可以实现图像的压缩、增强和识别等功能。
6. 医学领域中的生物统计学:在医学领域中,高等数学的概率论和统计学理论被广泛应用于生物数据的分析和解释。
通过对大量的医学数据进行统计分析,可以为医学研究提供可靠的依据。
7. 生态学中的物种模型:在生态学中,高等数学的微分方程理论被用于构建物种的数量模型。
通过对物种数量随时间的变化进行微分方程建模,可以预测物种的增长和灭绝趋势,为生态保护提供参考。
8. 电力工程中的电路分析:在电力工程中,高等数学的复数理论被广泛应用于电路分析。
通过复数运算和电路等效原理,可以计算电路中电流、电压和功率之间的关系,为电力系统的设计和维护提供支持。
9. 地理学中的地形建模:在地理学中,高等数学的多元函数理论被用于地形的建模和分析。
高等数学案例集

高等数学案例集-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN《高等数学》案例集第一章 函数与极限(一)建立函数关系的的案例 1、零件自动设计要求,需确定零件轮廓线与扫过的面积的函数关系。
已知零件轮廓下部分为长a 2,宽a 22的矩形ABCD ,上部分为CD 圆弧,其圆心在AB 中点O 。
如下图所示。
M 点在BC 、CD 、DA 上移动,设BM =x ,OM 所扫过的面积OBM (或OBCM 或OBCDM )为y ,试求y=f(x)函数表达式,并画出它的图象。
解:⎪⎪⎪⎩⎪⎪⎪⎨⎧+≤≤++-+≤≤+≤≤==a x a ax a ax a axa a x ax x f y 2222242822222224122042)(22ππππ (二)极限1、一男孩和一女孩分别在离家2公理和1公理且方向相反的两所学校上学,每天同时放学后分别以4公理/小时和2公理/小时的速度步行回家,一小狗以6公理/小时的速度由男孩处奔向女孩,又从女孩奔向男孩,如此往返直至回家中,问小狗奔波了多少路程 若男孩和女孩上学时小狗也往返奔波在他们之间,问当他们到达学校时小狗在何处解:(1) 男孩和女孩到校所需时间是半小时,也即小狗奔波了半小时,故小狗共跑了3公里。
B C AD M MM(2)设x(t),y(t),z(t)分别表示t 时刻男孩、女孩、小狗距家的距离,(二)连续函数性质1、某甲早8时从山下旅店出发沿一条路径上山,下午5时到达山顶并留宿。
次日早8时沿同一路径下山,下午5时回到山下旅店。
某乙说,甲必在两天中的同一时刻经过路径中的同一地点.为什么第三章 中值定理与导数应用1、陈酒出售的最佳时机问题某个酒厂有一批新酿的好酒,如果现在就出售,可得总收入 R0=50万元。
如果窖藏起来待来年(第n 年)按陈酒价格出售,第n 年末可得总收入为R =R 0832n e 万元,而银行利率为r =0.05,试在各种条件下讨论这批好酒的出售方案。
高中数学知识点应用案例

高中数学知识点应用案例数学作为一门学科,不仅仅是为了在考试中取得好成绩,更重要的是它的应用性。
在高中阶段,学生们学习了许多数学知识点,这些知识点能够为我们解决现实生活中的问题提供有力的工具和方法。
在本文中,我们将通过一些案例来展示高中数学知识点的应用。
案例一:金融投资小明拥有一笔学费储蓄,希望将其投资到银行,以获得更高的回报。
他在一家银行选择了一个1年期定期存款,年利率为3%。
作为一名学生,小明需要计算一年后他的储蓄将会增加多少。
这个问题涉及到了简单的利息计算。
根据数学公式:利息 = 本金 ×利率 ×时间,我们可以计算出小明将获得的利息。
假设小明储蓄的本金为10000元,时间为1年,年利率为0.03。
代入公式计算,利息 = 10000 × 0.03 × 1 = 300元。
因此,一年后小明的储蓄将增加300元。
案例二:几何问题小红需要买一块地,该地是一个长方形,长为10米,宽为8米。
她想在该地周围建一个高度为2米的围墙。
现在她想知道需要多少材料来建造围墙。
这个问题涉及到了计算面积和周长的几何知识。
首先,我们计算围墙的总面积。
长方形的面积等于长乘以宽,即10 × 8 = 80平方米。
其次,我们计算围墙的周长。
长方形的周长等于两倍的长加上两倍的宽,即2 × 10 + 2 × 8 = 36米。
因此,小红需要购买36平方米的围墙材料。
案例三:函数图像小刚是一名数学爱好者,他对函数的图像非常感兴趣。
他选择了一个二次函数y = 2x² + 3x - 2,并画出了它的图像。
他想知道该函数的顶点坐标以及对称轴的方程。
这个问题涉及到了二次函数的性质。
对于二次函数y = ax² + bx + c,顶点的横坐标可以通过公式 -b/2a 计算得到。
在这个例子中, a = 2,b = 3,c = -2。
代入公式计算,顶点的横坐标为-3/(2*2)=-3/4。
高等数学应用案例(上)

2 根据题目提供的数据,设随着房价的 下降,住房率呈线性增长。
3 宾馆每间客房定价相等。
4 以x表示客房的定价,r表示宾馆的入 住率,y表示宾馆一天的总收入。
• 问题 一个星级宾馆有150间客房,经过一段时间的经营实践,该宾馆经理
得到一些数据:如果每间客房定价为160元,住房率为55%;定价为 140元,住房率为65%;定价为120元,住房率为75%;定价为100元, 住房率为85%。欲使每天收入最高,问每间客房的定价应是多少?
• 模型建立 根据条件,宾馆的入住率为
r 0.005x 1.35(70 x 160)
因而宾馆一天的总收入为 y 150x(0.005x 1.35) 202.5x 0.75x2
• 问题 一个星级宾馆有150间客房,经过一段时间的经营实践,该宾馆经理
得到一些数据:如果每间客房定价为160元,住房率为55%;定价为 140元,住房率为65%;定价为120元,住房率为75%;定价为100元, 住房率为85%。欲使每天收入最高,问每间客房的定价应是多少?
lim v
2 1 1
60
30 v
因此,有任何有限的返回速度情况下,往 返的平均速度都达不到每小时60km,除非
v .
星级宾馆的定价
• 问题
一个星级宾馆有150间客房,经过一段 时间的经营实践,该宾馆经理得到一些数 据:如果每间客房定价为160元,住房率为 55%;定价为140元,住房率为65%;定价 为120元,住房率为75%;定价为100元, 住房率为85%。欲使每天收入最高,问每 间客房的定价应是多少?
大学高等数学 第三章典型例题及小结

f ( x0 ) 0, 即方程有小于 1 的正根
2) 唯一性 .
f (x) 在以 x0 , x1 为端点的区间满足罗尔定理条件 , 在 x0 , x1 之间
证明 e x (ax 2 bx c ) 0 至多有三个实根 证 记
f ( x ) e x (ax2 bx c )
直接证明有困难,采用反证法
设 f ( x ) 0 有四个实根 x1 x2 x3 x4
记 f ( x ) e (ax bx c ) 连续、可导 对 f ( x ) 在[ x1 , x2 ],[ x2 , x3 ],[ x3 , x4 ] 用罗尔定理得
x ln(1 x) x ( x 0) . 例3. 证明不等式 1 x 证: 设 f (t ) ln(1 t ) ,
中值定理条件, 因此应有
即
因为
故
例4. 设
至少存在一点 证: 结论可变形为 使
证明
设 F ( x) x 2 , 则 f ( x) , F ( x) 在 [0, 1] 上满足柯西中值 定理条件, 因此在 ( 0 , 1 ) 内至少存在一点 , 使
x
lim
x2 x
2
x 1
lim
x
1 1 1 1 2
思考: 如何求 lim
2
arctan n
1 n
n
( n 为正整数) ?
例3. 求
高数典型例题期末总结

高数典型例题期末总结高数典型例题总结例题1:求函数f(x)=2x^2-3x-2的导数和导数的极值。
解析:首先,我们需要求出函数f的导数。
根据导数的定义和求导法则:f'(x)=(2x^2-3x-2)'=4x-3导数的极值需要满足导数等于0的条件,即4x-3=0,解得x=3/4。
接下来,我们需要判断导数的极值是极大值还是极小值。
根据二阶导数的定义和求导法则:f''(x)=(4x-3)'=4二阶导数大于0时,函数f在该点有极小值;二阶导数小于0时,函数f在该点有极大值;二阶导数等于0时,函数f的极值点需通过其他方法进行判断。
在本例中,f''(x)>0,所以f在x=3/4处有极小值。
例题2:求函数f(x)=x^3的不定积分。
解析:求函数的不定积分即求原函数,可以使用分部积分法。
设u=x^3,dv=dx,则du=3x^2dx,v=x。
根据分部积分法:∫f(x)dx=∫u dv=uv-∫v du=x^3*x-∫x*3x^2dx=x^4-3∫x^3dx∫x^3dx=x^4/4,代入得:∫f(x)dx=x^4-3*x^4/4=4x^4/4-3x^4/4=x^4/4所以,函数f(x)=x^3的不定积分为x^4/4。
例题3:已知函数f(x)=e^x,求函数f的定积分∫[0,1] f(x)dx。
解析:求函数的定积分即求函数在给定区间上的面积,可以使用定积分的性质和公式进行求解。
∫[0,1] f(x)dx=F(1)-F(0)其中,F(x)是函数f的原函数。
由于f(x)=e^x,F(x)的原函数是e^x。
代入得:∫[0,1] f(x)dx=F(1)-F(0)=e^1-e^0=e-1所以,函数f的定积分∫[0,1] f(x)dx=e-1。
综上所述,高等数学期末考试中的典型例题涉及到函数的导数、极值、不定积分和定积分的求解。
对于这类例题,我们需要熟悉基本的概念、原理和解题方法,并加强对相关定理和公式的理解和记忆。
《高等数学》应用实例

《高等数学》应用18例一、椅子能在不平的地面上放稳吗?二、磁盘的最大存储量三、有趣的Fibonacci数列四、分形几何中的Koch雪花五、工人上班何时效率最高?六、石油的消耗量七、捕鱼成本的计算八、飞出火星九、萃取问题十、最优化的产出水平十一、蚂蚁逃跑问题十二、资金配置问题十三、家庭教育基金问题十四、分针与时针重合问题十五、证明e是无理数十六、湖泊的污染问题十七、减肥问题十八、冷却定律和破案一、椅子能在不平的地面上放稳吗?要回答这个问题,我们先要做一些合理的假设:(1)椅子的四条腿长度相等,椅脚与地面接触处视为一个点,四脚的连线是一个正方形;(2)地面是一个连续曲面,没有象台阶那样的情况;(3)地面是相对平坦的,即在任何位置至少有三只脚着地;在以上假设下,问题就是四只脚A、B、C、D能否同时着地?为此我们以四脚的中心为原点建立坐标系(如图),再以原点为中心旋转椅子,用θ表示旋转的角度,并引入函数f(θ)表示A、C两腿与地面的距离之和,函数g(θ) 表示B、D两腿与地面的距离之和,且不妨假设f(θ)、g(θ)都是连续函数,又因在任何位置至少有三只脚着地,所以对任何θ,有f(θ)g(θ)=0。
于是,椅子能在不平的地面上放稳的问题就转化为:是否存在θ0,使f(θ0)=g(θ0)=0?回答是肯定的,下面是其证明。
不妨假设开始时f(0)>0,g(0)=0,现将椅子旋转900(π/2),对角线AC与BD互换,由f(0)>0,g(0)=0可知f(π/2)=0,g(π/2)>0。
令h(θ)= f(θ)-g(θ),则h(0)>0,而h(π/2)<0,根据连续函数的介值定理知,必存在θ0(0<θ0<π/2),使f(θ0)-g(θ0)=0。
最后,因为f(θ0)g(θ0)=0,所以f(θ0)=g(θ0)=0。
这种通过对实际问题先作合理的假设,最后转化成一个纯粹的数学问题并求解的方法就是数学建模。
高等数学典型例题与应用实例(重积分B部分)

例 利用二重积分的性质,估计积分2222(2)d Dx y x y σ+-⎰⎰ 的值,其中D 为半圆形区域224,0x y y +≤≥.解 我们先求函数2222(,)2f x y x y x y =+-在区域22{(,)4,0}D x y x y y =+≤≥上的最大值和最小值.由22220,420,x yf x xy f y x y '⎧=-=⎪⎨'=-=⎪⎩解得D内驻点为(,(2f =. 在边界1:0L y =(22)x -≤≤上,2()(,0)g x f x x ==在1L 上(,)f x y 的最大值为4,最小值为0.在边界222:4L x y +=(0)y ≥上,42()(58(22)h x f x x x x ==-+-≤≤由3()4100h x x x '=-=得驻点1230,x x x ===(0)(0,2)8h f ==.7((4h f ==. 综上,(,)f x y 在D 上的最大值为8,最小值为0.又D 的面积为2π,所以由二重积分的估值性质知222202(2)d 82Dx y x y πσπ⋅≤+-≤⋅⎰⎰,即22220(2)d 16Dx y x y σπ≤+-≤⎰⎰.例 设D 为xoy 平面上以(1,1),(1,1),(1,1)---为顶点的三角形区域,1D 为D 在第一象限的部分,则(cos sin )()Dxy x y dxdy +=⎰⎰.(A )12cos sin D x y dxdy ⎰⎰ (B )12D xy dxdy ⎰⎰(C )14(cos sin )D xy x y dxdy +⎰⎰ (D )0解 区域D 如图所示,并记0D 为以(1,1),(1,1),(0,0)-为顶点的三角形区域,则0D 关于y 轴对称,且1D 为0D 在y 轴右侧的部分区域,区域0D D -关于x 轴对称.又xy 关于x 和y 均为奇函数;而cos sin x y 关于x 为偶函数.关于y 为奇函数,由二重积分的奇偶对称性得0,0D D D xy dxdy xy dxdy -==⎰⎰⎰⎰,故0Dxy dxdy =⎰⎰;1cos sin 2cos sin ,cos sin 0D D D D x ydxdy x y dxdy x y dxdy -==⎰⎰⎰⎰⎰⎰,故1cos sin 2cos sin DD x y dxdy x y dxdy =⎰⎰⎰⎰.所以1(cos sin )cos sin 2cos sin DDDD xy x y dxdy xy dxdy x y dxdy x y dxdy +=+=⎰⎰⎰⎰⎰⎰⎰⎰.因此我们选(A ).例 设区域}0,0,4),{(22≥≥≤+=y x y x y x D ,()f x 为D 上的正值连续函数,,a b 为常数,则Dσ= .解 由题意知,D 关于直线y x =对称,由二重积分轮换对称性得DσDσ=12D d σ=⎰⎰ 211()π2π22242D D a b a b a b a b d d σσ+++=+==⋅⋅=⎰⎰⎰⎰. 因此,我们应填“π2a b+.”例 计算二次积分220sin xydx dy yππ⎰⎰解 积分区域如图,则 原式20sin yydy dx yπ=⎰⎰2200sin sin sin y dy ydy ydy ππππ==+-⎰⎰⎰4=;例 设D 为椭圆区域22(1)(2)149x y --+≤,计算二重积分()Dx y dxdy +⎰⎰. 解 令12cos ,23sin ,x r y r =+⎧⎨=+⎩θθ则D 的极坐标表示为01,02r ≤≤≤≤θπ,且(,)6(,)x y r r θ∂=∂.由式(10.2.8),可得21()6(32cos 3sin )Dx y dxdy d r r rdr +=++⎰⎰⎰⎰πθθθ20326(cos sin )1823d =++=⎰πθθθπ.例 计算二重积分⎰⎰+Dy x y x d d )(,其中D 为.122++≤+y x y x解 解法1 D 的边界曲线为,2/3212122=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-y x 这是一个以⎪⎭⎫ ⎝⎛21,21为圆心,23为半径的圆域,采用一般的变量代换,令⎪⎪⎩⎪⎪⎨⎧-=-=,21,21y v x u 即作变换⎪⎪⎩⎪⎪⎨⎧+=+=,21,21v y u x 于是D 变为.2/3:22≤+'v u D.11001),(),(==∂∂=v u y x J所以,()d d (1)1d d DD x y x y u v u v '+=++⋅⋅⎰⎰⎰⎰(再用极坐标).23023d d )cos (sin d d d )1sin cos (d 222/30202/3020ππθθθθθθθππ=+⎪⎪⎭⎫ ⎝⎛⋅=++=++=⎰⎰⎰⎰⎰⎰r r r r rr r r D解法2 由于积分区域D :23212122≤⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-y x 关于21=x (即)021=-x 对称,故⎰⎰=⎪⎭⎫ ⎝⎛-D y x x .0d d 21 类似地,由于D 关于⎪⎭⎫⎝⎛=-=02121y y 即对称,故 ⎰⎰=⎪⎭⎫ ⎝⎛-D y x y .0d d 21 从而.2323d d d d 1d d 21d d 21d d )(2ππ=⎪⎪⎭⎫ ⎝⎛⋅===⋅+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=+⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰面积D y x y x y x y y x x y x y x D D D DD例 计算y x e I Dy xd d },max{22⎰⎰=,其中,}10,10|),{(≤≤≤≤=y x y x D解 D 由x y =分为D 2,D 2两部分,如图.⎪⎩⎪⎨⎧≤≤≤≤≤≤≤≤=1,10:,0,10:,21},max{2222y x x D e x y x D e e y x y x x e y y e x y x e y x e I yy xx D y D x d d d d d d d d 01010222212⎰⎰⎰⎰⎰⎰⎰⎰+=+=21110d d 2d d 2222x e x xe y e x x x xx ⎰⎰⎰⎰===.1102-==e ex例 利用二重积分计算定积分1(,0)ln b ax x I dx a b x-=>⎰解 因为1ln ln bb a btt aa x x x dt x x x-==⎰所以 ⎰⎰⎰⎰⎰⎪⎭⎫⎝⎛++=+=+===bab aba batta b t dt t dx x dt dx dt x I 11ln )1ln(11)(11例 ],[)(b a x f 为上的连续函数,且0)(>x f ,试利用二重积分证明.)()(1d )(2a b x f x x f baba-≥⎰⎰证 因为x x f y y f x x f x x f b a b a babad )(1d )(d )(1d )(⎰⎰⎰⎰=,d d )()(d d )()(y x y f x f y x x f y f DD⎰⎰⎰⎰≥= 其中 所以},,|),{(b y a b x a y x D ≤≤≤≤=⎰⎰⎰⎰⎰⎰+=DD bab ay x y f x f y x x f y f x x f x x f d d )()(d d )()(d )(1d )(2 y x y f x f y f x f y x y f x f x f y f DDd d )()()()(d d )()()()(22⎰⎰⎰⎰≥+=,)(2d d 22a b y x D-==⎰⎰亦即.)(d )(1d )(2a b x x f x x f baba-≥⎰⎰例 计算⎰1d )(x x xf ,其中⎰=21d int)(x t tS x f 解 当10,102≤≤≤≤x x 时⎰⎰⎰-===111222,d sin d sin d sin )(x x x y yy y y y t t tx f从而x y y y x x x xf x d d sin d )(101102⎰⎰⎰⎥⎦⎤⎢⎣⎡-= 图y x y yx y y y x x xDd d sin d sin d 1102⎰⎰⎰⎰-=⋅-=,其中D 曲线1,2==y x y ,和0=x 所围成,如图10-8。
3.4 高等数学应用案例

放射性废物的处理【问题背景】美国原子能委员会早期是按以下方式处理浓缩放射性废物的. 他们将废物装入密封性能很好的圆桶中, 然后扔到水深300英尺的海里. 这种做法是否会造成放射性污染, 很自然地引起了生态学家及社会各界的关注. 原子能委员会一再保证, 圆桶非常坚固, 决不会破漏, 这种做法是绝对安全的. 然而一些工程师们却对此表示怀疑, 他们认为圆桶在海底相撞时有可能发生破裂. 由此双方展开了一场笔墨官司.究竟谁的意见正确呢? 只能让事实说话了!【问题分析】问题的关键在于圆桶到底能承受多大速度的碰撞? 圆桶和海底碰撞时的速度有多大?工程师们进行了大量破坏性的实验, 发现圆桶在直线速度为40 ft/s 的冲撞下会发生破裂, 剩下的问题就是计算圆桶沉入300 ft 深的海底时, 其末速度究竟有多大?1. 使用55加仑的圆桶; ( 1加仑 = 3.7854升 )2. 装满放射性废物时的圆桶重量为W = 527.436磅 (1 磅 = 0.4526公斤 )3. 在海水中圆桶受到的浮力 B = 470.327磅4. 圆桶下沉时受到海水的阻力 D = C v C 为常数, 经测算得: C = 0.08.5. 建立坐标系, 取垂直向下为坐标方向 y ,海平面为坐标原点. y0 【问题假设】根据牛顿第二定律, 圆桶下沉时应满足微分方程:22d d d ,,d :(0)0()(1)lim ()713.86(/) ()Cg t W y m W B D tW y m D Cv v g tdv m W Cv B dt v W B v t e CW B v t ft s t C-=----====--=-=--=≈→∞(重力浮力阻力)其中初值条件其解:容易计算出圆桶的极限速度:当时327 . 470 = B W = 527.436 C = 0.08 【建立模型】为了求出圆桶与海底的碰撞速度v(t), 需要求出圆桶下沉到海底300英尺时的时间 t , 再计算v(t),要做到这一点是十分困难的. 若将速度v 看成是海水深度y 的函数, 即:v y v t y y v t v t y t y v t v d d d d d d d d d d ))(()(22====由复合函数的求导法则()(1)Cg t W W B v t e C--=-【模型求解】2(0)0,(0)0ln v y v W B W B Cv gy C C W B W==-----=-初值条件:积分,得:借助数值方法求出 v (300)=45.1ft/s ,显然大于40ft/s 。
高数例题5

高数五例1 求 tan cos y y x x '+=通解例2 求微分方程 ln (ln )0x xdy y x dx +-=满足条件1==e x y的特解 例 3 已知函数 ()y y x =在任意点x 处的增量 21y x y x α∆∆=++,且当0x ∆→时,α是x ∆的高阶无穷小。
(0)y π=则 (1)y 等于(A )2π (B ) π (C ) 4e π (D )4e ππ例 4 若连续函数 ()f x 满足关系式 20()()ln 22x t f x f dt =+⎰ 则 ()f x 等于: (A ) ln 2x e (B )2ln 2x e(C )ln 2x e + (D )2ln 2x e + 例5 设曲线积分()[]()⎰--e xydy x f ydx e x f cos sin 与路径无关,其中()f x 具有一阶连续导数,且 (0)0f =则 ()f x 等于________例6 微分方程 22x y xy y '+= 满足初始条件 11x y ==的特解。
例7设()f x 具有二阶连续导数,(0),'(0)1f f =是[]2()()'()0xy x y f x y dx f x x y dy ⎡⎤+-++=⎣⎦为一全微分方程,求f(x)及微分方程的通解。
例8 设线性无关的函数123,,y y y 都是二阶非齐次线性方程()()()x f y x q y x p y =+'+''的解,12,c c 是任意常数,则该非齐次方程的通解为:(A )11223c y c y y ++ (B )()3212211y c c y c y c +-+(C )1122123(1)c y c y c c y +--- (D )1122123(1)c y c y c c y ++--例9."'323x y y y e-+-=通解 例10 "'244x y y y e-++=通解 例11 "'22x y y y e -+=通解例12 设0()sin ()()xf x x x t f t dt =--⎰,其中()f x 为连续函数。
高等数学案例
病房
床
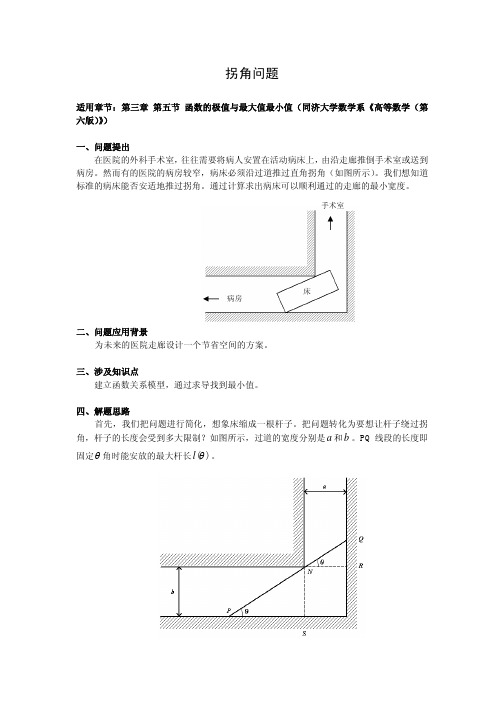
二、问题应用背景 为未来的医院走廊设计一个节省空间的方案。 三、涉及知识点 建立函数关系模型,通过求导找到最小值。 四、解题思路 首先,我们把问题进行简化,想象床缩成一根杆子。把问题转化为要想让杆子绕过拐 角,杆子的长度会受到多大限制?如图所示,过道的宽度分别是 a 和 b 。PQ 线段的长度即 固定 角时能安放的最大杆长 l ( ) 。
ቤተ መጻሕፍቲ ባይዱ
拐角问题
适用章节:第三章 第五节 函数的极值与最大值最小值(同济大学数学系《高等数学(第 六版) 》 ) 一、问题提出 在医院的外科手术室, 往往需要将病人安置在活动病床上, 由沿走廊推倒手术室或送到 病房。然而有的医院的病房较窄,病床必须沿过道推过直角拐角(如图所示) 。我们想知道 标准的病床能否安适地推过拐角。通过计算求出病床可以顺利通过的走廊的最小宽度。
五、解答过程 第 1 步,设杆长为 l ( ) 通过观察,我们发现 l ( ) PN NQ
SN csc RN sec b csc a sec
( 1)
l ( ) 在 0, 上的最小值,就是能顺利绕过拐角的最大杆长。 2
第 2 步,求出(1)式对 的导数 求导数得
dl a sec tan b csc cot d
第 3 步,求最值 令
dl 0 d
求得 tan
3
b a
, 代入(1)式得 l ( ) 的最小值为
2 2 3
l min (a 3 b 3 ) 2
这就是给定过道宽度 a 与 b ,能顺利绕过拐角的最大杆长。 六、问题延伸:假如杆子有一向上的倾角,走廊的高度对顺利通过直角拐角的最大杆长有什 么影响? 七、参考文献: 数学建模,电子科技大学出版社
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
v1.0 可编辑可修改例 利用二重积分的性质,估计积分2222(2)d D xy x y σ+-⎰⎰的值,其中D 为半圆形区域224,0x y y +≤≥.解 我们先求函数2222(,)2f x y x y x y =+-在区域22{(,)4,0}D x y x y y =+≤≥上的最大值和最小值.由22220,420,x yf x xy f y x y '⎧=-=⎪⎨'=-=⎪⎩解得D 内驻点为(2,1)±,(2,1)2f ±=. 在边界1:0L y =(22)x -≤≤上,2()(,0)g x f x x ==在1L 上(,)f x y 的最大值为4,最小值为0.在边界222:4L x y +=(0)y ≥上,242()(,4)58(22)h x f x x x x x =-=-+-≤≤由3()4100h x x x '=-=得驻点123550,,22x x x ==-=,(0)(0,2)8h f ==. 5537()(,)2224h f ±=±=. 综上,(,)f x y 在D 上的最大值为8,最小值为0.又D 的面积为2π,所以由二重积分的估值性质知222202(2)d 82Dx y x y πσπ⋅≤+-≤⋅⎰⎰,即22220(2)d 16Dx y x y σπ≤+-≤⎰⎰.例 设D 为xoy 平面上以(1,1),(1,1),(1,1)---为顶点的三角形区域,1D 为D 在第一象限的部分,则(cos sin )()Dxy x y dxdy +=⎰⎰.(A )12cos sin D x y dxdy ⎰⎰ (B )12D xy dxdy ⎰⎰(C )14(cos sin )D xy x y dxdy +⎰⎰ (D )0解 区域D 如图所示,并记0D 为以(1,1),(1,1),(0,0)-为顶点的三角形区域,则0D 关于y 轴对称,且1D 为0D 在y 轴右侧的部分区域,区域0D D -关于x 轴对称.又xy 关于x 和y 均为奇函数;而cos sin x y 关于x 为偶函数.关于y 为奇函数,由二重积分的奇偶对称性得0,0D D D xy dxdy xy dxdy -==⎰⎰⎰⎰,故0Dxy dxdy =⎰⎰;1cos sin 2cos sin ,cos sin 0D D D D x ydxdy x y dxdy x y dxdy -==⎰⎰⎰⎰⎰⎰,故1cos sin 2cos sin DD x y dxdy x y dxdy =⎰⎰⎰⎰.所以1(cos sin )cos sin 2cos sin DDDD xy x y dxdy xy dxdy x y dxdy x y dxdy +=+=⎰⎰⎰⎰⎰⎰⎰⎰.因此我们选(A ).例 设区域}0,0,4),{(22≥≥≤+=y x y x y x D ,()f x 为D 上的正值连续函数,,a b 为常数,则Dσ= .解 由题意知,D 关于直线y x =对称,由二重积分轮换对称性得DσDσ=12D d σ=⎰⎰ 211()π2π22242D D a b a b a b a b d d σσ+++=+==⋅⋅=⎰⎰⎰⎰. 因此,我们应填“π2a b+.”例 计算二次积分220sin xydx dy yππ⎰⎰解 积分区域如图,则 原式20sin yydy dx yπ=⎰⎰2200sin sin sin y dy ydy ydy ππππ==+-⎰⎰⎰4=;例 设D 为椭圆区域22(1)(2)149x y --+≤,计算二重积分()Dx y dxdy +⎰⎰. 解 令12cos ,23sin ,x r y r =+⎧⎨=+⎩θθ则D 的极坐标表示为01,02r ≤≤≤≤θπ,且(,)6(,)x y r r θ∂=∂.由式(10.2.8),可得21()6(32cos 3sin )Dx y dxdy d r r rdr +=++⎰⎰⎰⎰πθθθ20326(cos sin )1823d =++=⎰πθθθπ.例 计算二重积分⎰⎰+Dy x y x d d )(,其中D 为.122++≤+y x y x解 解法1 D 的边界曲线为,2/3212122=⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-y x 这是一个以⎪⎭⎫ ⎝⎛21,21为圆心,23为半径的圆域,采用一般的变量代换,令⎪⎪⎩⎪⎪⎨⎧-=-=,21,21y v x u 即作变换⎪⎪⎩⎪⎪⎨⎧+=+=,21,21v y u x 于是D 变为.2/3:22≤+'v u D.11001),(),(==∂∂=v u y x J所以,()d d (1)1d d DD x y x y u v u v '+=++⋅⋅⎰⎰⎰⎰(再用极坐标).23023d d )cos (sin d d d )1sin cos (d 222/30202/3020ππθθθθθθθππ=+⎪⎪⎭⎫ ⎝⎛⋅=++=++=⎰⎰⎰⎰⎰⎰r r r r rr r r D解法2 由于积分区域D :23212122≤⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-y x 关于21=x (即)021=-x 对称,故⎰⎰=⎪⎭⎫ ⎝⎛-D y x x .0d d 21 类似地,由于D 关于⎪⎭⎫⎝⎛=-=02121y y 即对称,故 ⎰⎰=⎪⎭⎫ ⎝⎛-D y x y .0d d 21 从而.2323d d d d 1d d 21d d 21d d )(2ππ=⎪⎪⎭⎫ ⎝⎛⋅===⋅+⎪⎭⎫ ⎝⎛-+⎪⎭⎫ ⎝⎛-=+⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰面积D y x y x y x y y x x y x y x D D D DD例 计算y x e I Dy xd d },max{22⎰⎰=,其中,}10,10|),{(≤≤≤≤=y x y x D解 D 由x y =分为D 2,D 2两部分,如图.⎪⎩⎪⎨⎧≤≤≤≤≤≤≤≤=1,10:,0,10:,21},max{2222y x x D e x y x D e e y x y x x e y y e x y x e y x e I yy xx D y D x d d d d d d d d 01010222212⎰⎰⎰⎰⎰⎰⎰⎰+=+=21110d d 2d d 2222x e x xe y e x x x xx ⎰⎰⎰⎰===.1102-==e ex例 利用二重积分计算定积分1(,0)ln b ax x I dx a b x-=>⎰解 因为1ln ln bb a btt aa x x x dt x x x-==⎰所以 ⎰⎰⎰⎰⎰⎪⎭⎫⎝⎛++=+=+===bab aba batta b t dt t dx x dt dx dt x I 11ln )1ln(11)(11例 ],[)(b a x f 为上的连续函数,且0)(>x f ,试利用二重积分证明.)()(1d )(2a b x f x x f baba-≥⎰⎰证 因为x x f y y f x x f x x f b a b a babad )(1d )(d )(1d )(⎰⎰⎰⎰=,d d )()(d d )()(y x y f x f y x x f y f DD⎰⎰⎰⎰≥= 其中 所以},,|),{(b y a b x a y x D ≤≤≤≤=⎰⎰⎰⎰⎰⎰+=DD bab ay x y f x f y x x f y f x x f x x f d d )()(d d )()(d )(1d )(2 y x y f x f y f x f y x y f x f x f y f DDd d )()()()(d d )()()()(22⎰⎰⎰⎰≥+=,)(2d d 22a b y x D-==⎰⎰亦即.)(d )(1d )(2a b x x f x x f baba-≥⎰⎰例 计算⎰1d )(x x xf ,其中⎰=21d int)(x t tS x f 解 当10,102≤≤≤≤x x 时⎰⎰⎰-===111222,d sin d sin d sin )(x x x y yy y y y t t tx f从而x y y y x x x xf x d d sin d )(101102⎰⎰⎰⎥⎦⎤⎢⎣⎡-= 图 y x y yx y y y x x xDd d sin d sin d 112⎰⎰⎰⎰-=⋅-=, 其中D 曲线1,2==y x y ,和0=x 所围成,如图10-8。
改变积分顺序,则)11(cos 21cos 21d sin 21d 2sin d sin d d d sin 1101002100-==-=⎥⎦⎤⎢⎣⎡-=⋅-==⎰⎰⎰⎰⎰⎰y y y y x y y xyyx y y x y y xyy D原积分例 设二元函数,⎪⎩⎪⎨⎧≤+<+≤+=.2||||111||||),(222y x y x y x x y x f计算⎰⎰=Dd y x f I σ),(,其中}.2||||),{(≤+=y x y x D 解:由区域的对称性和被积函数的奇偶性、有⎰⎰⎰⎰=DD d y x f d y x f 1),(4),(σσ其中,D 1为D 位于第一象限部分,D 1由1=+y x 分成两部分:}10,10|),{(11≤≤-≤≤=x x y y x D 图 }.0,0,21|),{(12≥≥≤+≤=y x y x y x D⎰⎰⎰⎰⎰⎰++=12111d d 1d d ),(222D D D y x yx y x x d y x f σ因为⎰⎰⎰⎰⎰=-==-11102102102121d )1(d d d d D xx x x y x x y x x⎰⎰⎰⎰⎰+=+==+++2sin cos 2sin cos 12022)12ln(2d cos sin 1d d d d 112πθθθθπθθθθr y x y x D所以 ).12ln(2431)12ln(21214d ),(++=⎥⎦⎤⎢⎣⎡++=⎰⎰Dy x f σ例 求∑∑==∞→n i nj n nj n i n112.2cos 1limπ 解 设平面区域D :,10,10≤≤≤≤y x 则二元函数y x y x f 2cos),(π=在D 上连续,二重积分⎰⎰Dy x y x f d d ),(存在,用平行于x 轴和y 轴的两组平行线把D 分成n 2个全等的正方形,如图,取,1,,2nn i n i ij i i =∆==σηξ则 .2cos 112cos ),(22nj n i nn n j n i f ij i i ππσηξ⋅=⋅⎪⎭⎫ ⎝⎛⋅⋅=故∑∑⎰⎰==→∞=ni nj D n y x y x n j n i n112d d 2cos 2cos 1lim ππ ⎰⎰=⋅=110.34d 2cosd ππy y x x 图例 设)(u f 有一阶导数且,9)0(,0)0(='=f f 求y x y x f t t y x t d d )(1lim 2230222+⎰⎰≤+→+。
