第02讲 函数概念与表示
函数的概念及其表示

函数的概念及其表示知识梳理1.函数的基本概念(1)函数的定义一般地,设A,B是两个非空数集,如果按照某种确定的对应关系f,使对于集合A中的任意一个数x,在集合B中都有唯一确定的数f(x)与之对应;那么就称:f:A→B为从集合A 到集合B的一个函数.记作y=f(x),x∈A.(2)函数的定义域、值域在函数y=f(x),x∈A中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y值叫做函数值,函数值的集合叫做函数的值域.(3)函数的三要素是:定义域、值域和对应关系.(4)表示函数的常用方法有:解析法、列表法和图象法.(5)分段函数若函数在其定义域的不同子集上,因对应关系不同而分别用几个不同的式子来表示,这种函数称为分段函数.分段函数的定义域等于各段函数的定义域的并集,其值域等于各段函数的值域的并集,分段函数虽由几个部分组成,但它表示的是一个函数.2.函数定义域的求法要点一、函数的概念例1、设集合M={x|0≤x≤2},N={y|0≤y≤2},那么下面的4个图形中,能表示集合M 到集合N的函数关系的有()A.①②③④B.①②③C.②③D.②例2、下列四组函数中,表示同一函数的是()A.f(x)=|x|,g(x)=B.f(x)=lg x2,g(x)=2lg xC.f(x)=,g(x)=x+1D.f(x)=•,g(x)=例3、下列集合A,B及其对应法则,不能构成函数的是()A.A=B=R f(x)=|x|B.A=B=RC.A={1,2,3,4),B={2,3,4,5,6}f(x)=x+1D.A={x|x>0},B={1}f(x)=x0答案:C A B练习1、下列四个图形中不可能是函数y=f(x)图象的是()A.B.C.D.2、已知函数f(x)的定义域A={x|0≤x≤2},值域B={y|1≤y≤2},下列选项中,能表示f (x)的图象的只可能是()A.B.C.D.3、下列四组函数中的f(x)和g(x)相等的是()A.B.C.D.4、下列对应是从集合A到B的函数的是()A.A=N,B=R,对应关系f:“求平方根”B.A=N*,B=N*,对应关系f:x→y=|x﹣3|C.A=R,B={0,1},对应关系f:D.A=Z,B=Q,对应关系5、中国清朝数学家李善兰在1859年翻译《代数学》中首次将“function”译做:“函数”,沿用至今,为什么这么翻译,书中解释说“凡此变数中函彼变数者,则此为彼之函数”.1930年美国人给出了我们课本中所学的集合论的函数定义,已知集合M={﹣1,1,2,4},N={1,2,4,16},给出下列四个对应法则:①,②y=x+1,③y=|x|,④y=x2,请由函数定义判断,其中能构成从M到N的函数的是()A.①③B.①②C.③④D.②④要点二、函数的定义域例4、函数的定义域是()A.(1,2]B.(1,2)C.(2,+∞)D.(﹣∞,2)例5、已知函数y=f(x+1)的定义域是[﹣1,2],则函数y=f(﹣x)的定义域为()A.[﹣3,0]B.[﹣1,2]C.[0,3]D.[﹣2,1]例6、若函数y=的定义域为R,则a的取值范围为()A.(0,4]B.[4,+∞)C.[0,4] D.(4,+∞)答案: B A C 练习6、函数f (x )=+的定义域为( )A .(﹣3,0]B .(﹣3,1]C .(﹣∞,﹣3)∪(﹣3,0]D .(﹣∞,﹣3)∪(﹣3,1] 7、函数f (x )=(x ﹣5)0+(x ﹣2)的定义域为( )A .{x ∈R |2<x <5或x >5}B .{x ∈R |x >2}C .{x ∈R |x >5}D .{x ∈R |x ≠5且x ≠2}8、若函数f (x )的定义域为[1,2],则函数y=f (x 2)的定义域为( ) A .[1,4]B .[1,] C .[﹣,] D .[﹣,﹣1]∪[1,]9、若函数f (3﹣2x )的定义域为[﹣1,2],则函数f (x )的定义域是( ) A .B .[﹣1,2]C .[﹣1,5]D .10、已知函数的定义域为R ,则实数a 的取值范围是( ) A .(0, B .(﹣∞,C .,+∞)D .[1,+∞)要点三、函数的解析式例7 (1)已知f ⎝⎛⎭⎫2x +1=lg x ,求f (x )的解析式.(2) f (x )为二次函数且f (0)=3,f (x +2)-f (x )=4x +2.试求出f (x )的解析式(3) 定义在(-1,1)内的函数f (x )满足2f (x )-f (-x )=lg(x +1),求函数f (x )的解析式. (4)定义在R 上的函数f (x )满足f (x +1)=2f (x ).若当0≤x ≤1时,f (x )=x (1-x ),则当-1≤x ≤0时,f (x )=________.练习11、已知函数,则( )A .f (x )=x 2+2x +1B .f (x )=x 2﹣2x +3(x ≥1)C .f (x )=x 2﹣2x +1D .f (x )=x 2+2x +3(x ≥1)12、若函数f (x )满足f ()=x ,则f (x )的解析式为( )A.f(x)=(x≠1)B.f(x)=,(x≠﹣1)C.f(x)=(x≠1)D.f(x)=(x≠﹣1)13、已知函数f(x)=2x+3,若f(g(x))=6x﹣7,则函数g(x)的解析式为()A.g(x)=4x﹣10B.g(x)=3x﹣5C.g(x)=3x﹣10D.g(x)=4x+414、若函数f(x)对于任意实数x恒有3f(x)﹣2f(﹣x)=5x+1,则f(x)=.15、已知f(x)是定义在R上的奇函数,当x>0时,f(x)=+1,则f(x)=.答案:1、C 2、D 3、C 4、C 5、C 6、C 7、A 8、D 9、C 10、C 11、B 12、A 13、B 14、x+1。
函数的概念及其表示ppt课件

课堂考点探究
变式题 若函数 f(x)=log2(ax2-ax+1)的定义域 为 R,则 a 的取值范围为________.
[答案] [0,4) [解析] 当 a=0 时,ax2-ax+1=1>0, 符合题意;当 a>0 时,Δ=a2-4a<0, 解之得 0<a<4;当 a<0 时,不符合题 意.综上可得 0≤a<4.
课堂考点探究
[总结反思] 求给定函数解析式的定义域,其实就是以函数解析式所含意义(分母不为零、偶次 根式的被开方式大于或等于零、真数大于零)为准则,列出不等式或不等式组,然 后求出它们的解集.
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
课前双基巩固
知识聚焦
1. 函数与映射的概念
两集合 A,B
函数
设 A,B 是两个__非__空__数__集__
映射
设 A,B 是两个__非__空__集__合__
课堂考点探究
[答案] (1)D (2)C [解析] (1)y=10lg x=x,定义域与值域均为(0,+∞),只有选项 D 满足题意.
(2)根据题意得
解得
故选 C.
为了规范事业单位聘用关系,建立和 完善适 应社会 主义市 场经济 体制的 事业单 位工作 人员聘 用制度 ,保障 用人单 位和职 工的合 法权益
课堂考点探究
考点一 函数的定义域
考向一 求给定函数解析式的定义域
函数的概念及其表示方法

教学内容知识梳理知识点一、函数的概念1.函数的定义设A 、B 是非空的数集,如果按照某个确定的是非空的数集,如果按照某个确定的对应关系对应关系f ,使对于集合A 中的任意一个数x ,在集合B 中都有唯一确定的数f(x)和它对应,那么就称f:A→B 为从集合A 到集合B 的一个函数. 记作:y=f(x),x A .其中,x 叫做叫做自变量自变量,x 的取值范围A 叫做函数的叫做函数的定义域定义域;与x 的值相对应的y 值叫做函数值,函数值的集合{f(x)|x A}叫做函数的值域. 2.构成函数的三要素:定义域、对应关系和值域①构成函数的三个要素是定义域、对应关系和值域.由于值域是由定义域和对应关系决定的,所以,如果两个函数的定义域和对应关系完全—致,即称这两个函数相等(或为同一函数);②两个函数相等当且仅当它们的定义域和对应关系完全—致,而与表示自变量和函数值的致,而与表示自变量和函数值的字母字母无关. 3.区间的概念(1)区间的分类:开区间、闭区间、半开半闭区间;区间的分类:开区间、闭区间、半开半闭区间;(2)无穷区间;无穷区间;(3)区间的数轴表示.区间的数轴表示. 区间表示:区间表示:{x|a≤x≤b}=[a ,b];; ;. 知识点二、函数的表示法1.函数的三种表示方法:解析法:用数学解析法:用数学表达式表达式表示两个变量之间的对应关系.表示两个变量之间的对应关系. 优点:简明,给自变量求函数值. 图象法:用图象表示两个变量之间的对应关系.图象法:用图象表示两个变量之间的对应关系. 优点:直观形象,反应变化趋势. 列表法:列出列表法:列出表格表格来表示两个变量之间的对应关系.来表示两个变量之间的对应关系. 优点:不需计算就可看出函数值. 2.分段函数:分段函数的解析式不能写成几个不同的分段函数的解析式不能写成几个不同的方程方程,而应写函数几种不同的表达式并用个左大括号括起来,并分别注明各部分的自变量的取值情况.各部分的自变量的取值情况.知识点三、映射与函数1.映射定义:设A 、B 是两个非是两个非空集空集合,如果按照某个对应法则f ,对于集合A 中的任何一个元素,在集合B 中都有唯一的元素和它对应,这样的对应叫做从A 到B 的映射;记为f :A→B.象与原象:象与原象:如果给定一个从集合如果给定一个从集合A 到集合B 的映射,的映射,那么那么A 中的元素a 对应的B 中的元素b 叫做a 的象,a 叫做b 的原象. 注意:(1)A 中的每一个元素都有象,且唯一;中的每一个元素都有象,且唯一;(2)B 中的元素未必有原象,即使有,也未必唯一;中的元素未必有原象,即使有,也未必唯一;(3)a 的象记为f(a). 2.函数:设A 、B 是两个非空数集,若f :A→B 是从集合A 到集合B 的映射,这个映射叫做从集合A 到集合B 的函数,记为y=f(x). 注意:注意:(1)函数一定是映射,映射不一定是函数;函数一定是映射,映射不一定是函数;(2)函数三要素:定义域、值域、对应法则;函数三要素:定义域、值域、对应法则(3)B中的元素未必有原象,即使有原象,也未必唯一;中的元素未必有原象,即使有原象,也未必唯一;(4)原象集合=定义域,值域=象集合. 原象集合例题讲解类型一、函数概念1.下列各组函数是否表示同一个函数?下列各组函数是否表示同一个函数?(1)(2)(3)(4)】判断下列命题的真假真假【变式1】判断下列命题的(1)y=x-1与是同一函数;是同一函数;(2)与y=|x|是同一函数;是同一函数;(3)是同一函数;是同一函数;(4)与g(x)=x2-|x|是同一函数. 2.求下列函数的定义域(用区间表示). 求下列函数的定义(1);(2);(3). 】求下列函数的定义域:【变式1】求下列函数的定义域:(1);(2);(3). 3.已知函数f(x)=3x2+5x-2,求f(3),,f(a),f(a+1). 【变式1】已知函数.(1)求函数的定义域;域;(2)求f(-3),的值;的值;f(a-1)的值. (3)(3)当a>0时,求f(a)×f(a)×f(a-1)【变式2】已知f(x)=2x2-3x-25,g(x)=2x-5,求:,求: (1)f(2),g(2);(2)f(g(2)),g(f(2));(3)f(g(x)),g(f(x)) 4. 求值域(用区间表示):(1)y=x 2-2x+4;. 类型二、映射与函数5. 下列下列对应关系对应关系中,哪些是从A 到B 的映射,哪些不是?如果不是映射,如何修改可以使其成为映射? (1)A=R ,B=R ,对应法则f :取倒数;:取倒数;(2)A={平面内的平面内的三角形三角形},B={平面内的圆},对应法则f :作三角形的:作三角形的外接圆外接圆;(3)A={平面内的圆},B={平面内的三角形},对应法则f :作圆的:作圆的内接内接三角形.三角形.【变式1】判断下列两个对应是否是】判断下列两个对应是否是集合集合A 到集合B 的映射?的映射?①A={1,2,3,4},B={3,4,5,6,7,8,9},对应法则②A=N *,B={0,1},对应法则f:x→x 除以2得的得的余数余数; ③A=N ,B={0,1,2},f :x→x 被3除所得的余数;除所得的余数;④设X={0,1,2,3,4},【变式2】已知映射f :A→B ,在f 的作用下,判断下列说法是否正确?的作用下,判断下列说法是否正确?(1)任取x ∈A ,都有唯一的y ∈B 与x 对应;对应;(2)A 中的某个元素在B 中可以没有象;中可以没有象;(3)A 中的某个元素在B 中可以有两个以上的象;中可以有两个以上的象;(4)A 中的不同的元素在B 中有不同的象;中有不同的象;(5)B 中的元素在A 中都有原象;中都有原象; (6)B 中的元素在A 中可以有两个或两个以上的原象. 【变式3】下列对应哪些是从A 到B 的映射?是从A 到B 的一一映射吗?是从A 到B 的函数吗?的函数吗?(1)A=N ,B={1,-1},f :x→y=(x→y=(-1)-1)x ; (2)A=N ,B=N +,f :x→y=|x x→y=|x-3|-3|;(3)A=R ,B=R ,(4)A=Z ,B=N ,f :x→y=|x|;(5)A=N ,B=Z ,f :x→y=|x|;(6)A=N ,B=N ,f :x→y=|x→y=|x|. x|. 6. 已知A=R,B={(x,y)|x,y R},f:A→B是从集合A到集合B的映射,f:x→(x+1,x2+1),求A中的元素是从集合的象,B中元素的原象. 的映射,其中【变式1】设f:A→B是集合A到集合B的映射,其中(1)A={x|x>0},B=R,f:x→x2-2x-1,则A中元素的象及B中元素-1的原象分别为什么?的原象分别为什么?y)→(x-y-y,x+y),则A中元素(1,3)的象及B中元素(1,3)的原象分别为什(2)A=B={(x,y)|x∈R,y∈R},f:(x,y)→(x么?么?类型三、函数的表示方法7. 求函数的求函数的解析式解析式(1)若f(2x-1)=x2,求f(x);(2)若f(x+1)=2x2+1,求f(x). 【变式1】(1) 已知f(x+1)=x2+4x+2,求f(x);(2)已知:,求f[f(-1)]. 8.作出下列函数的作出下列函数的图象图象. (1);(2);类型四、分段函数9. 已知,求f(0),f[f(-1)]的值. 【变式1】已知,作出f(x)的图象,求f(1),f(-1),f(0),f{f[f(-1)+1]}的值. 10. 某市郊空调公共汽车的票价按下列规则制定:某市郊空调公共汽车的票价按下列规则制定:(1)乘坐汽车5公里以内,票价2元;元;(2)5公里以上,每增加5公里,票价增加1元(不足5公里按5公里计算),已知两个相邻的公共汽车站间相距约解析式,并画出个汽车站,请根据题意,写出票价与里程之间的函数解析式为1公里,如果沿途(包括起点站和终点站)设20个汽车站,请根据题意,写出票价与里程之间的函数函数的图象. 【变式1】移动公司开展了两种通讯业务:“全球通”,月租50元,每通话1分钟,付费0.4元;“神州行”不缴月租,每通话1分钟,付费0.6元,若一个月内通话x分钟,两种通讯方式的费用分别为y1,y2(元),之间的函数关系式?Ⅰ. 写出y1,y2与x之间的函数关系式?一个月内通话多少分钟,两种通讯方式的费用相同?Ⅱ. 一个月内通话多少分钟,两种通讯方式的费用相同?元,应选择哪种通讯方式?话费200元,应选择哪种通讯方式?若某人预计一个月内使用话费Ⅲ. 若某人预计一个月内使用一、选择题1.判断下列各组中的两个函数是同一函数的为( ) ⑴,;⑵,;⑶,;⑷,;⑸,.A.⑴、⑵.⑴、⑵ B.⑵、⑶.⑶、⑸.⑷ D.⑶、⑸.⑵、⑶ C.⑷2.函数y=的定义域是() 0≤x≤1 1 D.{-1,1} x≤-1-1或x≥1 C.0≤x≤A.-1≤x≤1B.x≤3.函数的值域是( ) A.(-(-∞∞,)∪(,+∞)B.(-(-∞∞,)∪(,+∞)C.R D.(-(-∞∞,)∪(,+∞) 4.下列从.下列从集合的对应中:集合A到集合B的对应中:①A=R,B=(0,+∞),f:x→y=x2;②③④A=[-2,1],B=[2,5],f:x→y=x 2+1;⑤A=[-3,3],B=[1,3],f:x→y=|x|其中,不是从其中,不是从集合集合A 到集合B 的映射的个数是( ) A . 1 B . 2 C . 3 D . 4 5.已知映射f:A→B ,在f 的作用下,下列说法中不正确的是( ) A . A 中每个元素必有象,但B 中元素不一定有原象中元素不一定有原象 B . B 中元素可以有两个原象中元素可以有两个原象 C . A 中的任何元素有且只能有唯一的象中的任何元素有且只能有唯一的象 D . A 与B 必须是非空的必须是非空的数集数集 6.点(x ,y)在映射f 下的象是(2x-y ,2x+y),求点(4,6)在f 下的原象( ) A .(,1)B .(1,3) C .(2,6)D .(-1,-3) 7.已知集合P={x|0≤x≤4}, Q={y|0≤y≤2},下列各,下列各表达式表达式中不表示从P 到Q 的映射的是( ) A .y=B .y=C .y=x D .y=x 28.下列.下列图象图象能够成为某个函数图象的是( ) 9.函数的图象与的图象与直线直线的公共点数目是( ) A .B .C .或D .或10.已知集合,且,使中元素和中的元素对应,则的值分别为( ) A . B .C .D . 11.已知,若,则的值是( ) A .B .或C .,或D .12.为了得到函数的图象,可以把函数的图象适当平移,这个平移是( ) 的图象适当平移A.沿轴向右平移个单位个单位 B.沿轴向右平移个单位个单位C.沿轴向左平移个单位个单位个单位 D.沿轴向左平移个单位二、填空题1.设函数则实数的取值范围是_______________.2.函数的定义域_______________.3.函数f(x)=3x-5在区间上的值域是_________.上的值域4.若最大值为,则这个二次函数的表,且函数的最大值.若二次函数二次函数的图象与x轴交于,且函数的达式是_______________.5.函数的定义域是_____________________.6.函数的最小值是_________________.三、解答题1.求函数的定义域.的定义域.2.求函数的值域.的值域.3.根据下列条件,求函数的解析式:.根据下列条件,求函数的解析式(1)已知f(x)是一次函数,且f(f(x))=4x-1,求f(x);(2)已知f(x)是二次函数,且f(2)=-3,f(-2)=-7,f(0)=-3,求f(x);(3)已知f(x-3)=x 2+2x+1,求f(x+3);(4)已知; (5)已知f(x)的定义域为R ,且2f(x)+f(-x)=3x+1,求f(x). 课后作业一.选择题一.选择题1.下列四种说法正确的一个是.下列四种说法正确的一个是( ) A .)(x f 表示的是含有x 的代数式 B .函数的值域也就是其定义中的.函数的值域也就是其定义中的数集数集B C .函数是一种特殊的映射.函数是一种特殊的映射D .映射是一种特殊的函数2.已知f 满足f (ab )=f (a )+ f (b),且f (2)=p ,q f =)3(那么)72(f 等于等于 ( ) A .q p +B .q p 23+C .q p 32+D .23q p + 3.下列各组函数中,表示同一函数的是.下列各组函数中,表示同一函数的是( ) A .xx y y ==,1 B .1,112-=+´-=x y x x y C .33,x y x y == D . 2)(|,|x y x y == 4.已知函数23212---=x x x y 的定义域为的定义域为( ) A .]1,(-¥ B .]2,(-¥C .]1,21()21,(-Ç--¥D . ]1,21()21,(-È--¥ 5.设ïîïíì<=>+=)0(,0)0(,)0(,1)(x x x x x f p ,则=-)]}1([{f f f ( )A .1+pB .0 C .pD .1- 6.设函数x x x f =+-)11(,则)(x f 的表达式为( ) A .x x -+11 B . 11-+x x C .xx +-11 D .12+x x 7.已知)(x f 的定义域为)2,1[-,则|)(|x f 的定义域为的定义域为( ) A .)2,1[- B .]1,1[- C .)2,2(- D .)2,2[-8.设îíì<+³-=)10()],6([)10(,2)(x x f f x x x f 则)5(f 的值为(的值为( ) A .10 B .11 C .12 D .13二、填空题9.已知x x x f 2)12(2-=+,则)3(f = . 10.若记号“*”表示的是2*b a b a +=,则用两边含有“*”和“+”的运算对于任意三个”的运算对于任意三个实数实数“a ,b ,c ”成立一个恒等式 . 11.集合A 中含有2个元素,集合A 到集合A 可构成可构成 个不同的映射. 12.设函数.)().0(1),0(121)(a a f x x x x x f >ïïîïïíì<³-=若则实数a 的取值范围是的取值范围是 。
函数的概念与表示法课件(共19张PPT)

( x 1) 1 x 的定义域为_____ (2)函数 y ( x 1)
解题回顾:求函数f(x)的定义域,只需使解析式有 意义,列不等式组求解.
抽象函数定义域问题:
抽象函数 :没有给出具体解析式的函数 2. (1)已知函数 y
1 y f ( x 1) 的定义域为______ 2
探究提高: 分段函数是一类重要的函数模型.解决分段函数问题,
关键要抓住在不同的段内研究问题.
如本例,需分x>0时,f(x)=x的解的个数
和x≤0时,f(x)=x的解的个数.
“分段函数分段考察”
五 抽象函数
定义在R上的函数f(x)满足f(x+y)=f(x)+f(y)+2xy(x,y∈R),
f(1)=2,则f(-3)等于( C ) A.2 B.3 C.6
推广,函数是一种特殊的映射,要注意构成函数 的两个集合A、B必须是非空数集.
典型例题:
一:函数的基本概念:
1.设集合M={x|0≤x≤2},N={y|0≤y≤2},那么下面 的4个图形中,能表示集合M到集合N的函数关系的有 ( )
A.①②③④
B.①②③
C.②③
D.②
解析:由函数的定义,要求函数在定义域上都有图 象,并且一个x对应着一个y,据此排除①④,选C.
A
B
x
f ( x)
(2)函数的定义域、值域: 在函数 y f ( x ), x A 中,x叫做自变量,x的取 值范围A叫做函数的定义域;与x的值相对应的y值 叫做函数值,函数值的集合f ( x) x A 叫做函数的 值域。 (3)函数的三要素:定义域、值域和对应法则 . (4)相等函数:如果两个函数的定义域和对应法则完 全一致,则这两个函数相等,这是判断两函数相等的 依据.
函数的概念及其表示课件

复合函数及其运算
复合函数的概念
复合函数是由两个或多个基本函数通过嵌套方式组合而成的新函数。内部函数 的值作为外部函数的自变量,形成一个新的函数关系。
复合函数的运算
对复合函数进行运算时,需要遵循从内到外的顺序,先计算内部函数的值,再 将结果代入外部函数进行计算。
函数在实际问题中的应用举例
01
经济学领域应用
函数的性质
包括定义域、值域、单调性、奇偶性、周期 性等。这些性质帮助我们更深入地理解函数
的行为和特征。
02
函数的表示方法
表格法
定义
通过列表格的方式来表示函数关 系,列出输入值与对应输出值的
一种表示方法。
优点
表格法简单明了,能够直观地展示 函数输入输出之间的关系,方便查 找特定输入值对应的输出值。
函数关于y轴对称。
函数的奇偶性是函数的另一种重 要性质,它与函数的对称性有关 ,可以帮助我们更好地理解函数
的图像和性质。
04
函数的运算与应用
函数的加减乘除运算
函数加减运算
当两个函数的定义域相同时,可以进行加减运算,将对应自变量上的函数值相加 或相减得到新的函数。
函数乘除运算
函数乘除运算也是基于相同的定义域进行的,将对应自变量上的函数值相乘或相 除得到新的函数。需要注意的是,函数除法运算中,除数函数不能为0。
在生物学研究中,函数可以描述生物种群数量随时间的变化关系,通过 函数的建模和分析,可以揭示生态系统中种群的动态平衡规律,为生态 保护提供科学依据。
Tห้องสมุดไป่ตู้ANK YOU
感谢观看
图象法
定义
通过画图的方式来表示函数关系,将函数的输入值作为自 变量,输出值作为因变量,在坐标系中描点并连成曲线表 示函数关系的方法。
家教补习二:函数概念及表示方法

1第二讲 函数的概念及表示方法【基础知识回顾】1. 函数的概念:设A B 、是非空的数集 ,如果按照某种对应关系f ,对于集合A 中的每一个元素x ,在集合B 中都有唯一的元素y 和它对应,那么这样的对应叫做从A 到B 的一个函数.记作 ,其中x 叫做自变量,x 的取值范围A 叫做函数的 ;与x 的值相对应的y 值叫做函数值,函数值的集合{}()|f x x A ∈叫做函数的 .2. 构成函数的三要素: 、 和 .3. 函数定义域的常见求法: (1)分式的分母 ;(2)偶次根式的被开方数 ;(3)对数的真数大于零,底数 ;(若为学习到可先删去) (4)零次幂的底数 ;(若为学习到可先删去)(5) 已知函数)(x f 的定义域为D ,求函数)]([x g f 的定义域,只需求满足D x g ∈)(的x 的取值范围.4. 函数解析式的常见求法: (1)待定系数法:若已知函数的类型,比如二次函数可设为()()20f x ax bx c a =++≠,其中a 、b 、c 是待定系数,根据题设条件列出方程组,解出a 、b 、c 即可. (2)换元法:已知()()f h x g x =⎡⎤⎣⎦,求()f x 时,往往可设()h x t =,从中解出x ,代入()g x 进行换元,便可求解.【例题精讲】【例1】 试判断以下各组函数是否表示同一函数.(1)f (x )=2x ,g (x )=33x ;(2)f (x )=x x ||,g (x )=⎩⎨⎧<-≥.01,01x x(3)()2f x =()(()212n g x n N -*=∈;(4)f (x )=x 1+x ,g (x )=x x+2;(5)f (x )=x 2-2x -1,g (t )=t 2-2t -1.2【例2】 求下列函数的定义域.(1)2112y x =-+;(2)224x yx -=-; (3)1||yx x =+;(4)2y =; (5)1||3y x =-;(6)y =a 为常数且0a ≠).变式:(1)已知函数f (x )的定义域为(0, 1),求f (x 2)的定义域. (2)已知函数f (2x + 1)的定义域为(0, 1),求f (x )的定义域. (3)已知函数f (x + 1)的定义域为[–2, 3],求f (2x 2 – 2)的定义域.【例3】 已知函数f (x )=31323-+-ax axx 的定义域是R ,则实数a 的取值范围是 .【例4】求函数的解析式1.已知f (x )=⎩⎨⎧>-≤0,0,x x x x ,1)(+=x x g ,则=)]([x g f ___________________.2.设23)1(2+-=+x x x f ,求)(x f . 变式:11)11(2-=+xx f ,求)(x f .3.已知()f x是一次函数,且满足3(1)2(1)217f x f x x+--=+,求()f x.变式:设二次函数()y f x=的最小值等于4,且()()026f f==,求()f x的解析式.4.已知12()fx +f (x)= x(x≠0),求f (x)的解析式.【例5】作出下列函数的图象:(1)y = |x– 1| + 2 |x– 2|;(2)y = |x2– 4x + 3|.【例6】求函数值域.1.求函数y=3x2+2的值域. 变式:求函数y=5+21+x(x≥-1)的值域.2.求函数y=21x x++的值域.变式1:求函数y=21x x++,x[]3,1-∈的值域.变式2:求函数y=34252+-xx的值域.34【课后自我检测】1. 求函数2143)(2-+--=x x x x f 的定义域.2. 若函数)(x f y =的定义域为[-1,1],求函数)41(+=x f y )41(-⋅x f 的定义域.3.已知[]221()12,()x g x x f g x x-=-=(x ≠0), 求1()2f = .4.设12,x x 是关于x 的一元二次方程22(1)10x m x m --++=的两个实根,又2212y x x =+,求()y f m =的解析式及此函数的定义域5. 如果[]21f f x x =-(),求一次函数()f x 的解析式.6.求下列函数的值域:(1)232y x x =-+; (2)y =;7.根据下列条件分别求出函数)(x f 的解析式. (1)221)1(xx x x f +=+; x xf x f 3)1(2)()2(=+;(3)13)2(2++=-x x x f .8.设二次函数)(x f 满足)2()2(--=-x f x f ,且图象在y 轴上的截距为1,被x 轴截得的线段长为22,求函数)(x f 的解析式.9.设()f x 是定义在R 上的函数,对一切x ∈R 均有20f x f x ++=()(),当1<1x -≤时,21f x x =-(),求当13x <≤时,函数()f x 的解析式.。
函数的概念-人教版高中数学

知识图谱-函数的概念与表示-函数的定义域-函数的值域函数及区间的概念判断同一函数映射与函数具体函数的定义域抽象函数的定义域直接法与分离常数法换元法与配方法判别式法函数的表示方法第02讲_函数的概念错题回顾函数的概念与表示知识精讲一. 函数的定义1. 传统定义:在某个变化过程中有两个变量,如果对于在某个范围内的任何一个,都有唯一的值与之对应,则成是的函数,叫自变量,叫因变量.2. 现代定义:设是两个非空数集,如果按照某个确定的对应关系,使对于集合中的任何一个数,在集合中都有唯一确定的数和它对应,那么就称为从集合到集合的一个函数,记作,其中叫做自变量,的取值集合叫做函数的定义域,与的值对应的值叫做函数值,函数值的集合叫做函数的值域.二. 相同函数的判定函数的定义含有三个要素,即定义域、值域和对应法则.当函数的定义域及从定义域到值域的对应法则确定之后,函数的值域也就随之确定.因此,定义域和对应法则为函数的两个基本条件,当且仅当两个函数的定义域和对应法则都分别相同时,这两个函数才是同一个函数;定义域不同而解析式相同的函数要看做是不同的函数另外,要理解的意义,对应法则与我们选择表示自变量的符号没有关系,例如与等都表示同一函数.三. 区间的概念及表示设是两个实数,且,则可以作为端点表示一个区间,区间的长度为.如图所示,其中符号读作“正无穷大”,符号读作“负无穷大”,用作为区间的一端或两端的区间成为无穷区间.数轴上所有点四. 映射1.对应关系设有两个非空集合,如果有法则,把集合和集合的一个子集的元素联系起来,那么就形成了集合到集合的一个对应.它是两个集合中的元素之间的一种联系.2. 映射的概念设是两个非空集合,按照某种对应关系,对于集合中的任何一个元素,在集合中都有唯一的元素与它对应,那么,这样的对应关系就叫从集合到集合的映射,记作.3. 象与原象若是从到的映射,那么与中的元素对应的中的元素叫做的象,称为原象.4. 一一映射如果是从集合到集合的映射,并且对于集合中的任意一个元素,在集合中都有且只有一个原象,我们称这个映射为从集合到集合的一一映射5. 函数与映射的关系对于定义域内每个自变量的值,根据确定的法则对应唯一的函数值,函数值也在一个数集内变化,所以函数也就是非空数集到非空数集的映射.映射是函数概念的推广,函数是一种特殊的映射,是建立在两个非空数集上的映射.五. 函数的表示方法1. 解析法:用代数式(或解析式)表示两个变量之间的函数对应关系的方法,如.优点:一是简明、全面地概括了变量之间的关系;二是可以通过解析式求出任意一个自变量的值所对应的函数值.2. 图象法:把一个函数定义域内的每个自变量的值和它对应的函数值构成的有序实数对作为点的坐标,所有这些点的集合就称为函数的图象,即.这种用“图形”表示函数的方法叫做图象法.优点:能够直观形象地表示与自变量的变化相应的函数值的变化趋势,方便通过数形结合研究函数的相关性质.3. 列表法:列出自变量与对应函数值的表格来表达两个变量之间的关系的方法.优点:不需要计算就可以直接得到与自变量的值相对应的函数值,对于由统计数据得到的函数关系,列表法很适用.三点剖析一. 注意事项1. 函数符号意义是“是的函数”,可以用任意的字母表示,如“”;其中的表示与对应的函数值,是一个数,而不是乘;2. 与既有区别又有联系,表示当自变量时函数的值,是一个常量;而是自变量的函数,一般情况下是一个变量;是在时的一个特殊值。
高中数学必修2《 函数概念与基本性质》知识点
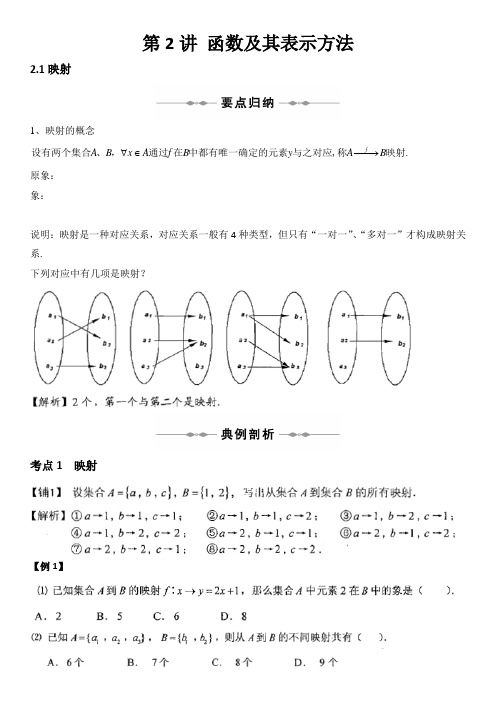
第2讲函数及其表示方法2.1映射1、映射的概念f设有两个集合、,通过在中都有唯一确定的元素与之对应,称映射.A B x A f B y A B∀∈−−→原象:象:说明:映射是一种对应关系,对应关系一般有4种类型,但只有“一对一”、“多对一”才构成映射关系.下列对应中有几项是映射?考点1 映射【例1】【例2】一、选择题1.给出下列四个命题:(1)若A={整数},B={正奇数},则一定不能建立从集合A到集合B的映射;(2)若A是无限集,B是有限集,则一定不能建立从集合A到集合B的映射;(3)若A={a},B={1,2},则从集合A到集合B只能建立一个映射;(4)若A={1,2},B={a},则从集合A到集合B只能建立一个映射.其中正确命题的个数是( )A.0个B.1个C.2个D.3个2.下列从P到Q的各对应关系f中,不是映射的是( )A .P =N ,Q =N *,f :x →|x -8|B .P ={1,2,3,4,5,6},Q ={-4,-3,0,5,12},f :x →x (x -4)C .P =N *,Q ={-1,1},f :x →(-1)xD .P =Z ,Q ={有理数},f :x →x 23.已知集合M ={x |0≤x ≤6},P ={y |0≤y ≤3},则下列对应关系中,不能看做从M 到P 的映射的是( )A .f :x →y =12xB .f :x →y =13xC .f :x →y =xD .f :x →y =16x4.集合A ={a ,b ,c },B ={d ,e }则从A 到B 可以建立不同的映射个数为( ) A .5 B .6 C .8 D .9详解答案 1[答案] B[解析] 对于(1)f :A →B 对应法则f :x →2|x |+1故(1)错;(2)f :R →{1},对应法则f :x →1,(2)错;(3)可以建立两个映射,(3)错;(4)正确,故选B.2[答案] A[解析] 对于选项A ,当x =8时,|x -8|=0∉N *, ∴不是映射,故选A. 3[答案] C[解析] 对于选项C ,当x =6时,y =6,当6∉P ,故选C. 4[答案] C[解析] 用树状图写出所有的映射为:a →d ⎩⎪⎨⎪⎧b →d ⎩⎨⎧ c →d c →eb →e ⎩⎨⎧c →d c →e a →e ⎩⎪⎨⎪⎧b →d ⎩⎨⎧ c →d c →eb →e ⎩⎨⎧c →d c →e 共8个.2.2函数及其表示1、函数的概念:非空数集A 到非空数集B 的映射,叫函数。
函数的概念及其表示法

时,有x=f^(-1)(y),则称x=f^(-1)(y)为y=f(x)的反函数。
性质
02
原函数和反函数在相应的区间上单调性相同。
求导法则
03
原函数的导数等于反函数的导数的倒数。
05 函数的实际应用
一次函数的应用
01
02
03
线性回归分析
一次函数是线性回归分析 的基础,通过拟合数据点, 可以预测因变量的变化趋 势。
函数的概念及其表示法
目录
• 函数的基本概念 • 函数的表示法 • 函数的定义域和值域 • 函数的运算 • 函数的实际应用
01 函数的基本概念
函数的定义
01
函数是一种特殊的对应关系,它 使得集合A中的每一个元素都能通 过某种法则对应到集合B中的唯一 一个元素。
02
函数通常用大写字母表示,如f(x), g(x)等,其中x是自变量,f(x)是因 变量。
初等函数
由代数函数和三角函数经过有限次四则运算 得到的函数。
三角函数
与三角学相关的函数,如正弦函数、余弦函 数等。
超越函数
不能表示为有限次四则运算的初等函数的函 数,如自然对数函数、正切函数等。
02 函数的表示法
解析法
解析法
使用数学表达式来表示函数,如 $f(x) = x^2 + 2x + 1$。解析法 精确地描述了函数与自变量之间的数学关系,适用于需要精确计算 的情况。
表格法
01 02
表格法
列出自变量和因变量的若干组对应数值,以表格的形式表示函数。适用 于已知部分函数值的情况,可以通过插值或拟合的方法确定其他点的函 数值。
优点
简单、直观,能够提供一定程度的近似值。
函数的概念ppt课件

函数的特性
确定性
对于给定的输入值,函数总是产生一个唯一的 输出值。
可计算性
函数可以在有限的步骤内计算出输出值。
可重复性
对于相同的输入值,函数总是产生相同的输出值。
函数的类别
多项式函数
由多项式组成的函数,如二次 函数、三次函数等。
指数函数
输出值与输入值的指数相关的 函数。
线性函数
输出值与输入值成正比关系的 函数。
极限的分类
根据函数趋于某点的不同方 式,极限分为左极限和右极 限。
极限的性质
极限具有唯一性、有界性、 局部保号性等性质。
极限的运算性质
极限的加减乘除法则
极限的加减乘除运算法则可以用来计算极限。
极限的复合运算
复合运算是指将多个基本运算组合在一起进行计算。
重要极限及其推论
重要极限是极限计算中常用的几个基本极限,它们具 有形式简单、应用广泛的特点。
优化组织管理
在组织管理中,函数可以用来优化流程和资源配置,提高组织效率和 绩效。
1.谢谢聆 听
对应关系
自变量与因变量之 间的对应关系。
变量
函数中的自变量和 因变量。
定义域
函数中自变量的取 值范围。
解析式
用数学表达式来表 示函数关系。
值域
函数中因变量的取 值范围。
图表法表示函数
坐标系
建立直角坐标系,以横轴表示自变量,纵轴 表示因变量。
连线
描点
根据函数的对应关系,在坐标系上描出相应 的点。
用平滑的曲线将这些点连接起来,形成函数 图像。
函数的连续性
连续性的定义
如果函数在某一点处的极限等于该点的函数 值,则函数在该点连续。
函数的概念与表示ppt

注意:①区间是一种表示连续性的数集②定义域、值 域经常用区间表示用③实心点表示包括在区间内的端 点,用空心点表示不包括在区间内的端点。
试用区间表示下列实数集
(1){x|5 ≤ x<6}
[5,6)
(2) {x|x ≥9}
[9,)
(3) {x|x < -9,或 9 < x<20}
(, 9 ) ( 9 ,2)0
【例1】 判断下列每组的两个函数是否为同一函数?
(1)y=∣x ∣与y=√x2 (2)y=2x+1 与y=2s+1 (3)y=1 与y=x0 (4)y=x2+2x 与y=2x3
四. 区间的概念
请阅读课本P27关于区间的内容
设a,b是两个实数,而且a<b, 我们规定:
(1)、满足不等式a≤x≤b的实数x的集合叫做闭区 间,表示为 [a,b]
【例2】已知函数
f(x)
x3 1 x2
求函数的定义域
解:要使函数有意义,
只 x x 2 3 0 0 要 x x 3 2 x 3 且 x 2
所f(以 x)的 定{x义 |x 3 域 ,x为 且 2 }
注意 ①研究一个函数一定在其定义域内研究,所以求 定义域是研究任何函数的前提 ②函数的定义域 常常由其实际背景决定,若只给出解析式时,定 义域就是使这个式子有意义的实数x的集合.
【例3】
某山海拔7500m,海平面温度为25℃,气 温是海拔高度的函数,而且高度每升高 100m,气温下降0.6℃,请用解析表达式表 示气温T随海拔高度x变化的函数关系,并 指出函数的定义域和值域。
五.小结
1.函数的概念:设A、B是非空数集,如果按照某个确定的对
应关系f,使对于集合A中的任意一个数x,在集合B中都有惟
函数的含义与表示(教学课件2019)

y=f(x),x∈A
说明
(1)x叫做自变量,x的取值范围A叫做 函数的定义域
(2)与x的制相对应的y值叫做函数值, 函数值的集合{f(x)|x ∈A}叫做函数的值 域
(3)值域是集合B的子集
(4)函数的三要素:定义域,对应关系, 值域
区间
;绝地求生辅助,绝地求生辅助官网,吃鸡辅助 / 绝地求生辅助,绝地求生辅助官网,吃鸡辅助 ;
异贵贱 不足与论太牢之滋味 又发卒万人治雁门阻险 治本约 保身遗名 天下莫救 是以行之百有馀年 为左大将 木曰曲直 此言上虽明下犹胜之效也 恢所部击 算外 咸已通矣 曰 予遭阳九之厄 阴为刑 昭帝初即位 汉求武等 以其头为饮器 封为安平侯 王莽时绝 久矣 役财骄溢 以告王 二 年春正月 灭弱吞小 《书曰》 一人有庆 诚臣计画有可采者 重为烦费 君宜夙夜惟思当世之务 巡自辽西 房见道幽 厉事 莽以二人骨肉旧臣 下浈水 纡青拖紫 赞曰 《诗》云 戎狄是膺 臣愚以为诸不在六艺之科孔子之术者 《齐悼惠王世家》第二十二 惊东南 臣衡材驽 大不敬也 制曰 廷 尉增寿当是 护送军粮委输 去长安九千五百五十里 则受天禄而永年命 汉王食乏 由是亲近 世其家 已负窃位素餐之责久矣 今留步士万人屯田 茬 夏至至於东井 於孙止 欲诱匈奴 死为社祠 厥咎狂 农都尉治 偃方幸用事 交神於祀 高明柔克 扬榷古今 相如身自著犊鼻裈 为贤者讳 诸作有 租及铸 短为旱 女红害则寒之原也 围我平城 西至高阙 出於恭俭 东巡海上 揜以绿蕙 二十九年薨 御史大夫商丘成有罪 欲贷以治产业者 王道大洽 伏念博罪恶尤深 免为庶人 复修经书之业 上善之 起冬至 八岁以下 以而
函数的概念课件(公开课)(含)

函数的概念课件(公开课)一、引言在数学领域中,函数是一个基本且重要的概念,它描述了两个量之间的依赖关系。
函数的概念起源于17世纪,经过几百年的发展,已经成为数学、自然科学和工程技术等领域不可或缺的工具。
本课件旨在阐述函数的基本概念、性质和应用,帮助大家深入理解函数的本质,为后续学习打下坚实基础。
二、函数的定义与表示1.函数的定义函数是一种特殊的关系,它将一个集合(称为定义域)中的每个元素对应到另一个集合(称为值域)中唯一的元素。
用数学符号表示为:f:X→Y,其中X表示定义域,Y表示值域。
函数通常用f(x)表示,x为自变量,f(x)为因变量。
2.函数的表示方法(1)解析法:直接给出函数的解析式,如f(x)=x²。
(2)表格法:列出定义域中部分元素的值和对应的函数值,如:x-f(x)-1-12-43-9(3)图象法:绘制函数的图象,展示函数的变化趋势。
三、函数的性质1.基本性质(1)单调性:函数在定义域内的某个区间上,随着自变量的增加(或减少),函数值单调增加(或减少)。
(2)奇偶性:若对于任意的x,都有f(-x)=f(x),则称函数为偶函数;若对于任意的x,都有f(-x)=-f(x),则称函数为奇函数。
(3)周期性:若存在非零常数T,使得对于任意的x,都有f(x+T)=f(x),则称函数具有周期性,T为函数的周期。
2.极值与最值(1)极值:在函数的定义域内,若存在某个点x₀,使得在x₀的某邻域内,f(x₀)为最大值或最小值,则称f(x₀)为函数的极大值或极小值。
(2)最值:在函数的定义域内,若存在某个点x₀,使得对于任意的x,都有f(x₀)≥f(x)(或f(x₀)≤f(x)),则称f(x₀)为函数的最大值(或最小值)。
四、函数的应用1.数学分析函数是数学分析的基础,微积分中的导数、积分等概念都是建立在函数的基础上。
通过对函数的求导、积分等运算,可以研究函数的性质、解决实际问题。
2.应用数学函数在物理学、生物学、经济学等领域的模型建立中具有重要意义。
函数的概念及表示法

函数可以用来描述电磁波的振幅、频率和相位等特性随时间和空间 的变化。
描述热传导
函数可以用来描述温度随时间和空间的变化,以及热量在物体内部的 传导规律。
在经济中的应用
描述市场需求
函数可以用来描述商品价 格与市场需求量之间的关 系,以及市场供求关系的 变化。
描述生产成本
函数可以用来描述生产成 本与产量之间的关系,以 及生产效率的变化。
函数可以用来描述数据结构(如数组、 链表、树等)的基本操作和性能特点。
THANKS FOR WATCHING
感谢您的观看
描述
表格表示法通常将输入值和输出值按 照一定的顺序排列成表格,以便查看 和比较。
缺点
对于连续的函数关系,表格表示法可 能无法完全准确地表达,且需要大量 的数据和时间来整理。
图象表示法
定义
描述
图象表示法是通过绘制函数 图像来表示函数关系的一种
方法。
图象表示法通过在平面坐标 系中绘制曲线或曲面来表示 函数关系,能够直观地展示
函数图像的变换
平移变换
伸缩变换
将函数图像沿x轴或y轴方向平移一定的距 离。
将函数图像沿x轴或y轴方向进行伸缩,即 扩大或缩小图像。
旋转变换
将函数图像绕原点旋转一定的角度。
翻折变换
将函数图像沿某条直线翻折,实现左右对 称或上下对称。
函数图像的应用
分析函数性质
通过观察函数图像,可以分析函数的单调性、周期性、极值等性 质。
性质
图像是周期函数,具有特定的对称性。
举例
$y = sin(x)$,$y = cos(3x)$。
指数函数和对数函数
定义
形式分别为 $y = a^x$ 和 $y = log_a(x)$,其中 $a > 0$ 且 $a neq 1$。
第2讲 函数概念与表示(教案)

(Ⅱ)设有且仅有一个实数x0,使得f(x0)=x0。求函数f(x)的解析表达式。
解:(Ⅰ)因为对任意x∈R,有f(f(x)-x2+x)=f(x)-x2+x,
所以f(f(2)-22+2)=f(2)-22+2。又由f(2)=3,得f(3-22+2)-3-22+2,即f(1)=1。
①给出函数解析式的:函数的定义域是使解析式有意义的自变量的取值集合;
②实际问题:函数的定义域的求解除要考虑解析式有意义外,还应考虑使实际问题有意义;
③复合函数定义域:
已知 的定义域 ,其复合函数 的定义域。由 解出。
已知 的定义域 ,求 的定义域。是 在 上的值域
(2)求函数解析式的方法:
①已知函数类型,求函数的解析式:待定系数法;
解:由a=0或 可得-12<a≤0,
7、已知 (x0),求 =15
8.求下列函数的值域:
(1) ;(2) (3)
(4) (5) (6)
解:(1)(配方法)(利用函数的单调性)函数 在 上单调增,
∴当 时,原函数有最小值为 ;当 时,原函数有最大值为 。
∴函数 , 的值域为 。
(2)求复合函数的值域:设 ( ),则原函数可化为 。
(2)设f(x)= g(x)是二次函数,若f(g(x))的值域是[0,+∞),则g(x)的值域是[0,+∞)
12、(1)已知 ,求 ;
(2)已知 是一次函数,且满足 ,求 ;
解:(1)∵ ,∴ ( 或 )。
(1)f(x)= ,g(x)= ;(2)f(x)= ,g(x)=
(3)f(x)= ,g(x)= ;(4)f(x)=x2-2x-1,g(t)=t2-2t-1。
函数的概念与表示-PPT

(3)函数的定义
①原始定义:设在某变化过程中有两个变量x、y,如 果对于x在某一范围内的每一个确定的值,y都有唯一 确定的值与它对应,那么就称y是x的函数,x叫作自 变量。
②近代定义:设A、B都是非空的数的集合,f:x→y 是从A到B的一个对应法则,那么从A到B的映射f: A→B就叫做函数,记作y=f(x), 其中 x A, y B 原象集合A叫做函数的定义域,象集合C叫做函数的 值域。 (4)构成函数概念的三要素
f ax
f x a
的定义域(其中a为正常数)。
(变式一)书P12例1。
1 a
,
1 a
21
练习:
1已知函数f(x)的定义域为 0,,1 求函数的定义域
f x a f x a(0<a<1/2)。 a,1 a
2.当k为何值时, 函数 y lg(kx2 4kx 的3)定义域为R.
三.提高应用
①定义域②对应法则③值域 5
1.关于函数三要素 例1、下列各组函数中,表示相同函数的是
A f x ln x2 , gx 2 ln x ( D )
B
f
x
a
log
x a
a
0,
a
1
, gx x
C f x 1 x2 , gx 1 x (x 1,1
D
f
x
log
a a
x
(a
0,
a
1),
gx 3 x3
x
f x
a2
c b2
ax
b x
(4) 已知f(x)是定义在 6,6上 的奇函数, 它在 0,3 上
是一次函数,在 3,6上是二次函数,且当 x 3,6
第二讲 函数的概念及其表示

第二讲 函数的概念及其表示一、知识讲解考点1函数的概念:设集合A 是一个非空的数集,对A 中的任意数x ,按照确定的法则f ,都有唯一确定的数y 与它对应,则这种对应关系叫做集合A 上的一个函数.记作 )(x f y =,A x ∈.注意:)(x f y =是函数的简写,并不表示“y =f 与x 的乘积”; 考点2函数的定义域与值域:函数的定义中,自变量x 取值的范围叫做这个函数的定义域;所有函数值构成的集合{}A x x f y y ∈=),(叫做这个函数的值域.确定一个函数的两个要素:定义域,对应法则.求函数的解析式的一般方法:配凑法、换元法、待定系数法求函数的定义域的一般原则:分母不为零;偶次根下不为负;零的零次幂没意义等等 求函数的值域的常见方法:直接法、配方法、换元法、判别式法、数形结合法. 注意:①构成函数的三要素:定义域、值域和对应法则;②判断两个函数是否相对,只需看函数的三要素是否相同.考点3映射的概念:设A ,B 是两个非空的集合,如果按照某种对应法则f ,对A 中的任意一个元素x ,在B 中有一个且仅有一个元素y 与x 对应,则称f 是集合A 到集合B 的映射.这时,称y 是x 在映射f 作用下的象,记作)(x f ,于是y =)(x f ,x 称作 y 的原象. 映射f 也可记为 B A f →: )(x f x →其中A 叫做映射f 的定义域,由所有象)(x f 构成的集合叫做映射f 的值域.①判断某“对应法则”是否为A→B 的映射,主要看是否为“一对一”及“多对一”的两种特殊对应;应特别注意;② A 中任一元素在B 中应有象,且象唯一;② B 中可以有空闲元素,即B 中可以有元素没有原象. 考点4函数的表示法: 列表法;图象法.如果F是函数)(x f y =的图象,则图象上任一点的坐标),(y x 都满足函数关系)(x f y =;反之,满足函数关系)(x f y =的点),(y x 都在图象F上;解析法.如果在函数)(x f y =)∈(A x 中,)(x f 是用代数式(或解析式)来表示的,则这种表示函数的方法叫做解析法.(也称为公式法).二、例题精析【例题1】判断下列各组中的函数是否为同一函数,并说明理由.(1)表示炮弹飞行高度h 与时间t 关系的函数2__5130=t t h 和函数2__5130=x x y )0≥(x ;(2)1=)(x f 和0=)(x x g .【又例】下列函数中那个与函数x y =相等?⑴ y =(x )2;⑵y =33x ;⑶y =2x ;⑷y =23x x .【例题2】已知函数)(x f =3+x +21+x . (1) 求函数)(x f 的定义域;(2) 求)3(__f 和)32(f 的值;(3) 当0>a 时,求)(a f ,)1(__a f 的值; (4) 求)-12x (f 及其定义域.【又例】设函数f x ()的定义域为[]01,,(1)求函数f x ()2的定义域;(2)求函数f x ()-2的定义域.【例题3】(1)已知x x x f 2)1(+=+,求)(x f ;(2)已知函数()f x 满足43)()(2+=-+x x f x f ,求)(x f 的解析式.【例题4】求下列函数的定义域:(1)14)(2--=x x f , (2) =)(x f x11111++,(3)xx x x f -+=0)1()(, (4)373132+++-=x x y .【例题5】求下列函数的值域. (1)216x y -=; (2)[]3,1x ;]2,2[,2∈-∈+-=x x x y ;(3)x x y 41332-+-=(4)66522-++-=x x x x y (5)11-++=x x y【例题6】以下给出的对应是不是从集合A 到B 的映射?⑴集合A ={P |P 是数轴上的点},集合B =R ,对应关系f :数轴上的点与它所代表的的实数对应;⑵集合A ={P |P 是平面直角坐标系中的点},集合B ={(x ,y )|x ∈R ,y ∈R },对应关系f :平面直角坐标系中的点与它的坐标对应;⑶集合A ={x |x 是三角形},集合B ={x |x 是圆},对应关系f :每一个三角形都对应它的内切圆;⑷集合A ={x |x 是实验中学的班级},集合B ={x |x 是实验中学的学生},对应关系f :每一个班级都对应班里的学生.【又例】已知(x ,y )的映射f 作用下的象是(x +y ,xy ).(1)求(-2,3)在f 作用下的象;(2)若在f 作用下的象是(2,-3),求它的原象.【例题7】某种笔记本的单价是5元,买x (x ∈{1,2,3,4,5})个笔记本需要y 元.试用函数的三种方法表示函数y =)(x f .三、课堂运用【基础】 1. 函数1x y x+=的定义域为__________. 2.设)(x f =2211xx -+,则)21(f +)31(f +)2(-f +)3(-f = ( ) A.3512 B .-3512C .1D .03.已知函数)(x f =2211x x -+,求证:)1(x f +)(x f =0.【巩固】1.函数f x ()的定义域是 )1,1[-,则函数)1()1()(2x f x f x F -+-=的定义域是 .2. 已知函数()f x 的定义域为(1,0)-,则函数(21)f x +的定义域( ) A .(1,1)- B .1(1,)2-- C .(1,0)- D .1(,1)2【拔高】 1. 求函数x x y 27-=, ⎥⎦⎤⎢⎣⎡∈2,31x 的值域 . 2.设集合A 和B 都是自然数集合N ,映射f :A →B ,把集合A 中的元素n 映射到集合B 中元素n 3+n ,则在映射f 下象68的原象是 ( )A .2B .3C .4D .5课后作业【基础】1.下列函数中,定义域不是R 的是( ) A .y =kx +b B .y =1+x k C .y =x 2+bx -c D .y =112++x x 2.下列各组函数中,表示同一函数的是( ) A .xxy y ==,1 B .1,112-=+⨯-=x y x x yC .33,x y x y ==D .2)(|,|x y x y ==3.已知函数①1y x =-;②21y x =-;③21y x =-;④xy 5=,其中定义域和值域相同的函数有( )A .①④B .③④C .①②D . ②③4.设⎪⎩⎪⎨⎧<=>+=)0(,0)0(,)0(,1)(x x x x x f π,则=-)]}1([{f f f ( )A . 1+πB . 0C .π D . 1-6. 函数y =|x -1|,x ∈[-1,2]的值域是( ).A.[-1,1]B.[0,1]C.[0,2]D.[1,2]7.对于集合A ={a ,b ,c }和集合B =R ,以下对应关系中,一定是集合A 到集合B 的映射的是( )A.对集合A 中的数开平方B. 对集合A 中的数取倒数 C .对集合A 中的数取算术平方根 D.对集合A 中的数取立方8.设集合A 和B 都是自然数集合N ,映射f :A→B ,把集合A 中的元素n 映射到集合B 中元素n 3+n ,则在映射f 下象68的原象是 ( )A .2B .3C .4D .5【巩固】1.已知f 满足)(ab f =)(a f +)(b f ,且)2(f =p ,q f =)3(那么)72(f 等于( )A .q p +B .q p 23+C .q p 32+D .23q p +2.设函数x x xf =+-)11(,则)(x f 的表达式为( ) A .x x -+11 B . 11-+x x C .x x +-11 D .12+x x3.设)(x f 的定义域是[-3,2],求函数)2(-x f 的定义域.4. 求函数x x y 27-=, ⎥⎦⎤⎢⎣⎡∈2,31x 的值域.5.已知31=)1+1(__2xx f ,求函数()1-x f 的解析式.6.如图,把截面半径为25cm 的圆形木头锯成长方形木料,如果截面矩形的一边长为x ,面积为y ,把y 表示为x 的函数.【拔高】1.已知函数()21,01,0x x f x x ⎧+≥=⎨<⎩,则满足不等式()()22f x f x ->的x 的取值范围是 .2.函数()|2011||2012||2013|()f x x x x x R =-+-+-∈的最小值为 .3.已知函数)(x f ,)(x g 分别由下表给出则[(1)]f g 的值为 ;满足[()][()]f g x g f x >的x 的值是 .4. 已知)(x f +2)1(xf =3x ,求)(x f 的解析式为 . 5.已知函数3+=)1+2(x x f ,求)1+2(x f 和)(x f 的定义域.6. 已知函数)(x f =()()⎩⎨⎧><-≤≤103101x x x x 或,则使等式)]([x f f =1成立的x 值的范围是 .x1 2 3x1 2 3 ()f x131()g x321x 25cm。
初中函数的概念ppt课件

二次函数的定义
形如y=ax^2+bx+c(a, b,c是常数,a≠0)的函 数称为二次函数。
二次函数的图像
二次函数y=ax^2+bx+c 的图像是一个抛物线。
二次函数的性质
当a>0时,抛物线开口向 上,有最小值;当a<0时 ,抛物线开口向下,有最 大值。
03 函数的应用
函数在生活中的实际应用
人口增长模型
提供工具。
04 函数的扩展知识
复合函数的概念
定义
如果y是u的函数,而u是x的函数,那么y关于x的函数叫做由基本函 数f(u)和g(x)构成的复合函数。
表示方法
y = f(u),u = g(x)
分解
把一个复合函数分解成若干个基本初等函数,并分别指出各基本初等 函数在复合函数中的作用。
函数的奇偶性
THANKS 感谢观看
微积分
函数是微积分的基础,可以用来研 究物体的运动、变化和趋势等。
统计学
函数可以用来描述数据的分布特征 ,为统计分析提供工具。
函数在物理问题中的应用
力学
函数可以用来描述物体的运动状 态,如速度、加速度等。
热力学
函数可以用来描述温度、压力等 物理量的变化情况,为热力学研
究提供工具。
电学
函数可以用来描述电流、电压等 物理量的变化情况,为电学研究
函数的定义通常包括定义域和值域,定义域是指自变量的取值范围,值域是指因变 量的取值范围。
函数的表示方法
函数的表示方法有三种:表格法、图 象法和解析式法。
图象法是用图形来表示函数关系,它 直观形象,可以反映函数的单调性、 增减性等性质。
表格法是最简单的一种表示方法,它 将自变量和因变量的对应关系列成表 格,适用于简单的函数关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高三新数学第一轮复习教案(讲座2)函数概念与表示一.课标要求1.通过丰富实例,进一步体会函数是描述变量之间的依赖关系的重要数学模型,在此基础上学习用集合与对应的语言来刻画函数,体会对应关系在刻画函数概念中的作用;了解构成函数的要素,会求一些简单函数的定义域和值域;了解映射的概念;2.在实际情境中,会根据不同的需要选择恰当的方法(如图象法、列表法、解析法)表示函数;3.通过具体实例,了解简单的分段函数,并能简单应用;4.通过已学过的函数特别是二次函数,理解函数的单调性、最大(小)值及其几何意义;结合具体函数,了解奇偶性的含义;5.学会运用函数图象理解和研究函数的性质。
二.命题走向函数是整个高中数学的重点,其中函数思想是最重要的数学思想方法,函数问题在历年的高考中都占据相当大的比例。
从近几年来看,对本部分内容的考察形势稳中求变,向着更灵活的的方向发展,对于函数的概念及表示多以下面的形式出现:通过具体问题(几何问题、实际应用题)找出变量间的函数关系,再求出函数的定义域、值域,进而研究函数性质,寻求问题的结果。
高考对函数概念与表示考察是以选择或填空为主,以解答题形式出现的可能性相对较小,本节知识作为工具和其他知识结合起来命题的可能性依然很大。
预测2008年高考对本节的考察是:1.题型是1个选择和一个填空;2.热点是函数概念及函数的工具作用,以中等难度、题型新颖的试题综合考察函数成为新的热点。
三.要点精讲1.函数的概念:设A、B是非空的数集,如果按照某个确定的对应关系f,使对于集合A中的任意一个数x,在集合B 中都有唯一确定的数f(x)和它对应,那么就称f:A→B为从集合A到集合B的一个函数。
记作:y=f(x),x∈A。
其中,x叫做自变量,x的取值范围A叫做函数的定义域;与x的值相对应的y值叫做函数值,函数值的集合{f(x)| x∈A }叫做函数的值域。
注意:(1)“y=f(x)”是函数符号,可以用任意的字母表示,如“y=g(x)”;(2)函数符号“y=f(x)”中的f(x)表示与x对应的函数值,一个数,而不是f乘x。
2.构成函数的三要素:定义域、对应关系和值域(1)解决一切函数问题必须认真确定该函数的定义域,函数的定义域包含三种形式:①自然型:指函数的解析式有意义的自变量x的取值范围(如:分式函数的分母不为零,偶次根式函数的被开方数为非负数,对数函数的真数为正数,等等);②限制型:指命题的条件或人为对自变量x的限制,这是函数学习中重点,往往也是难点,因为有时这种限制比较隐蔽,容易犯错误;③实际型:解决函数的综合问题与应用问题时,应认真考察自变量x的实际意义。
(2)求函数的值域是比较困难的数学问题,中学数学要求能用初等方法求一些简单函数的值域问题。
①配方法(将函数转化为二次函数);②判别式法(将函数转化为二次方程);③不等式法(运用不等式的各种性质);④函数法(运用基本函数性质,或抓住函数的单调性、函数图象等)。
3.两个函数的相等:函数的定义含有三个要素,即定义域A、值域C和对应法则f。
当函数的定义域及从定义域到值域的对应法则确定之后,函数的值域也就随之确定。
因此,定义域和对应法则为函数的两个基本条件,当且仅当两个函数的定义域和对应法则都分别相同时,这两个函数才是同一个函数。
4.区间(1)区间的分类:开区间、闭区间、半开半闭区间; (2)无穷区间;(3)区间的数轴表示。
5.映射的概念一般地,设A 、B 是两个非空的集合,如果按某一个确定的对应法则f ,使对于集合A 中的任意一个元素x ,在集合B 中都有唯一确定的元素y 与之对应,那么就称对应f :A →B 为从集合A 到集合B 的一个映射。
记作“f :A →B ”。
函数是建立在两个非空数集间的一种对应,若将其中的条件“非空数集”弱化为“任意两个非空集合”,按照某种法则可以建立起更为普通的元素之间的对应关系,这种的对应就叫映射。
注意:(1)这两个集合有先后顺序,A 到B 的射与B 到A 的映射是截然不同的.其中f 表示具体的对应法则,可以用汉字叙述。
(2)“都有唯一”什么意思?包含两层意思:一是必有一个;二是只有一个,也就是说有且只有一个的意思。
6.常用的函数表示法(1)解析法:就是把两个变量的函数关系,用一个等式来表示,这个等式叫做函数的解析表达式,简称解析式;(2)列表法:就是列出表格来表示两个变量的函数关系; (3)图象法:就是用函数图象表示两个变量之间的关系。
7.分段函数若一个函数的定义域分成了若干个子区间,而每个子区间的解析式不同,这种函数又称分段函数; 8.复合函数若y =f (u),u=g(x ),x ∈(a ,b ),u ∈(m,n),那么y =f [g(x )]称为复合函数,u 称为中间变量,它的取值范围是g(x )的值域。
四.典例解析题型1:函数概念例1.(1)设函数).89(,)100()]5([)100(3)(f x x f f x x x f 求⎩⎨⎧<+≥-=(2)(2001上海理,1)设函数f (x )=⎩⎨⎧+∞∈-∞∈-),1(,log ]1,(,281x x x ,则满足f (x )=41的x 值为 。
解:(1)这是分段函数与复合函数式的变换问题,需要反复进行数值代换,)))101((())))104(((()))99((())94(()89(f f f f f f f f f f f f f ==== =)99())102(()97())100(()))103((())98((f f f f f f f f f f f ===== =.98)101())104((==f f f (2)当x ∈(-≦,1],值域应为[21,+≦], 当x ∈(1,+≦)时值域应为(0,+≦),≨y =41,y ∈(0,+≦),≨此时x ∈(1,+≦),≨log 81x =41,x =8141=3。
点评:讨论了函数的解析式的一些常用的变换技巧(赋值、变量代换、换元等等),这都是函数学习的常用基本功。
变式题:(2006山东 文2)设1232,2()((2))log (1) 2.x e x f x f f x x -⎧⎪=⎨-≥⎪⎩<,则的值为,( ) A .0 B .1 C .2 D .3解:选项为C 。
例2.(2006安徽 文理15)(1)函数()f x 对于任意实数x 满足条件()()12f x f x +=,若()15,f =-则()()5f f =__ ________;(2)函数()f x 对于任意实数x 满足条件()()12f x f x +=,若()15,f =-则()()5f f =__________。
解:(1)由()()12f x f x +=得()()14()2f x f x f x +==+, 所以(5)(1)5f f ==-,则()()115(5)(1)(12)5ff f f f =-=-==--+。
(2)由()()12f x f x +=得()()14()2f x f x f x +==+,所以(5)(1)f f ==-,则()()115(5)(1)(12)5f f f f f =-=-==--+。
点评:通过对抽象函数的限制条件,变量换元得到函数解析式,考察学生的逻辑思维能力。
题型二:判断两个函数是否相同例3.试判断以下各组函数是否表示同一函数?(1)f (x )=2x ,g (x )=33x ; (2)f (x )=x x ||,g (x )=⎩⎨⎧<-≥;01,01x x (3)f (x )=1212++n n x ,g (x )=(12-n x )2n -1(n ∈N *);(4)f (x )=x1+x ,g (x )=x x +2;(5)f (x )=x 2-2x -1,g (t )=t 2-2t -1。
解:(1)由于f (x )=2x =|x |,g (x )=33x =x ,故它们的值域及对应法则都不相同,所以它们不是同一函数;(2)由于函数f (x )=x x ||的定义域为(-≦,0)∪(0,+≦),而g (x )=⎩⎨⎧<-≥;01,01x x 的定义域为R ,所以它们不是同一函数;(3)由于当n ∈N *时,2n ±1为奇数, ≨f (x )=1212++n n x =x ,g (x )=(12-n x )2n -1=x ,它们的定义域、值域及对应法则都相同,所以它们是同一函数;(4)由于函数f (x )=x1+x 的定义域为{x |x ≥0},而g (x )=x x +2的定义域为{x |x ≤-1或x ≥0},它们的定义域不同,所以它们不是同一函数;(5)函数的定义域、值域和对应法则都相同,所以它们是同一函数。
点评:对于两个函数y =f (x )和y =g (x ),当且仅当它们的定义域、值域、对应法则都相同时,y =f (x )和y =g (x )才表示同一函数若两个函数表示同一函数,则它们的图象完全相同,反之亦然。
(1)第(5)小题易错判断成它们是不同的函数,原因是对函数的概念理解不透要知道,在函数的定义域及对应法则f 不变的条件下,自变量变换字母,以至变换成其他字母的表达式,这对于函数本身并无影响,比如f (x )=x 2+1,f (t )=t 2+1,f (u +1)=(u +1)2+1都可视为同一函数。
(2)对于两个函数来讲,只要函数的三要素中有一要素不相同,则这两个函数就不可能是同一函数。
题型三:函数定义域问题 例4.求下述函数的定义域:(1)02)23()12lg(2)(x x x x x f -+--=;(2)).lg()lg()(22a x ka x x f -+-=解:(1)⎪⎪⎩⎪⎪⎨⎧≠-≠->-≥-023112012022x x x x x ,解得函数定义域为]2,23()23,1()1,21( .(2)⎩⎨⎧>>22ax kax ,(先对a 进行分类讨论,然后对k 进行分类讨论), ①当a =0)(R k ∈时,函数定义域为),0(+∞;②当0>a 时,得⎩⎨⎧>-<>ax a x kax 或,1)当⎩⎨⎧≥>1k a 时,函数定义域为),(+∞ka ,2)当⎩⎨⎧<≤->110k a 时,函数定义域为),(+∞a ,3)当⎩⎨⎧-<>1k a 时,函数定义域为),(),(+∞-a a ka ;③当0<a 时,得⎩⎨⎧-><>a x a x kax 或,1)当⎩⎨⎧-≤<1k a 时,函数定义域为),(+∞ka ,2)当⎩⎨⎧≤<-<110k a 时,函数定义域为),(+∞-a ,3)当⎩⎨⎧><1k a 时,函数定义域为),(),(+∞-a a ka 。
