抛物线及其性质知识点大全教学内容

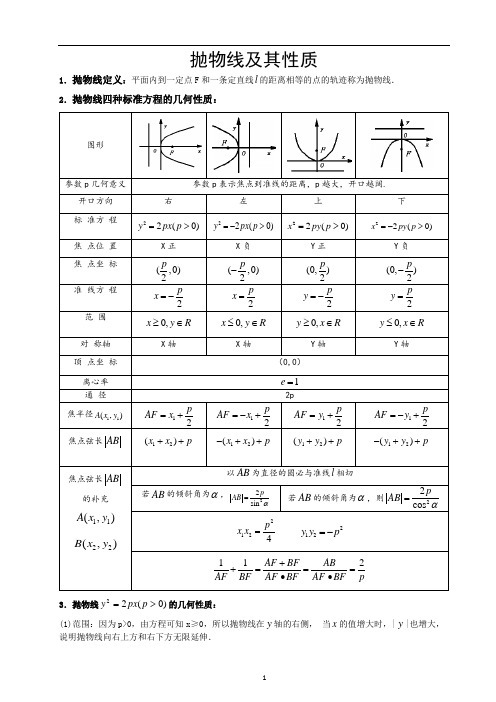
抛物线及其性质1．抛物线定义：平面内到一定点F 和一条定直线l 的距离相等的点的轨迹称为抛物线． 2．抛物线四种标准方程的几何性质：图形参数p 几何意义 参数p 表示焦点到准线的距离，p 越大，开口越阔.开口方向 右左上下 标 准方 程 22(0)y px p => 22(0)y px p =-> 22(0)x py p =>22(0)x py p =->焦 点位 置 X 正X 负Y 正Y 负焦 点坐 标 (,0)2p (,0)2p -(0,)2p(0,)2p -准 线方 程 2p x =-2p x =2p y =-2p y =范 围 0,x y R ≥∈0,x y R ≤∈0,y x R ≥∈0,y x R ≤∈对 称轴 X 轴X 轴Y 轴Y 轴顶 点坐 标 （0,0）离心率 1e =通 径 2p焦半径11(,)A x y 12p AF x =+12p AF x =-+12p AF y =+12p AF y =-+焦点弦长AB12()x x p ++ 12()x x p -++ 12()y y p ++ 12()y y p -++焦点弦长AB 的补充11(,)A x y22(,)B x y以AB 为直径的圆必与准线l 相切若AB 的倾斜角为α，22sin p AB α=若AB 的倾斜角为α，则22cos pAB α=2124p x x = 212y y p =-112AF BF AB AF BF AF BF AF BF p++===•• 3．抛物线)0(22>=p px y 的几何性质：(1)范围：因为p>0，由方程可知x ≥0，所以抛物线在y 轴的右侧， 当x 的值增大时，|y |也增大，说明抛物线向右上方和右下方无限延伸．(2)对称性：对称轴要看一次项，符号决定开口方向． (3)顶点（0，0），离心率：1=e ，焦点(,0)2p F ，准线2px -=，焦准距p ． (4) 焦点弦：抛物线)0(22>=p px y 的焦点弦AB ，),(11y x A ,),(22y x B ,则p x x AB ++=21||． 弦长|AB|=x 1+x 2+p,当x 1=x 2时，通径最短为2p 。

4．焦点弦的相关性质：焦点弦AB ，),(11y x A ,),(22y x B ，焦点(,0)2pF (1) 若AB 是抛物线22(0)y px p =>的焦点弦（过焦点的弦），且11(,)A x y ，22(,)B x y ，则：2124p x x =，212y y p =-。

(2) 若AB 是抛物线22(0)y px p =>的焦点弦，且直线AB 的倾斜角为α，则22sin P AB α=（α≠0）。

(3) 已知直线AB 是过抛物线22(0)y px p =>焦点F ,112AF BF AB AF BF AF BF AF BF p++===•• (4) 焦点弦中通径最短长为2p 。

通径：过焦点垂直于焦点所在的轴的焦点弦叫做通径．(5) 两个相切：○1以抛物线焦点弦为直径的圆与准线相切.○2过抛物线焦点弦的两端点向准线作垂线，以两垂足为直径端点的圆与焦点弦相切。

5．弦长公式：),(11y x A ,),(22y x B 是抛物线上两点，则221212()()AB x x y y =-+-||11||1212212y y k x x k -+=-+=6.直线与抛物线的位置关系 直线，抛物线，，消y 得：（1）当k=0时，直线l 与抛物线的对称轴平行，有一个交点； （2）当k ≠0时，Δ＞0，直线l 与抛物线相交，两个不同交点； Δ=0， 直线l 与抛物线相切，一个切点； Δ＜0，直线l 与抛物线相离，无公共点。

（3）若直线与抛物线只有一个公共点,则直线与抛物线必相切吗?（不一定）7.关于直线与抛物线的位置关系问题常用处理方法 直线l ：b kx y += 抛物线，)0(φp① 联立方程法：⎩⎨⎧=+=pxy bkx y 22⇒0)(2222=+-+b x p kb x k设交点坐标为),(11y x A ,),(22y x B ，则有0φ∆,以及2121,x x x x +，还可进一步求出b x x k b kx b kx y y 2)(212121++=+++=+，2212122121)())((b x x kb x x k b kx b kx y y +++=++=在涉及弦长，中点，对称，面积等问题时，常用此法，比如 a. 相交弦AB 的弦长2122122124)(11x x x x k x x k AB -++=-+=ak ∆+=21 或 2122122124)(1111y y y y k y y k AB -++=-+=ak ∆+=21 b. 中点),(00y x M , 2210x x x +=， 2210y y y += ② 点差法：设交点坐标为),(11y x A ，),(22y x B ，代入抛物线方程，得1212px y = 2222px y =将两式相减，可得)(2))((212121x x p y y y y -=+-2121212y y px x y y +=--a. 在涉及斜率问题时，212y y pk AB +=b. 在涉及中点轨迹问题时，设线段AB 的中点为),(00y x M ，021*******y py p y y p x x y y ==+=--， 即0y p k AB =， 同理，对于抛物线)0(22≠=p py x ，若直线l 与抛物线相交于B A 、两点，点),(00y x M 是弦AB 的中点，则有px p x p x x k AB 0021222==+=（注意能用这个公式的条件：1）直线与抛物线有两个不同的交点，2）直线的斜率存在，且不等于零）【经典例题】（1）抛物线——二次曲线的和谐线椭圆与双曲线都有两种定义方法，可抛物线只有一种：到一个定点和一条定直线的距离相等的所有点的集合.其离心率e=1，这使它既与椭圆、双曲线相依相伴，又鼎立在圆锥曲线之中.由于这个美好的1，既使它享尽和谐之美，又生出多少华丽的篇章.【例1】P 为抛物线px y 22=上任一点，F 为焦点，则以PF 为直径的圆与y 轴（ ）.A 相交 .B 相切 .C 相离 .D 位置由P 确定【解析】如图，抛物线的焦点为,02p F ⎛⎫⎪⎝⎭，准线是 :2pl x =-.作PH ⊥l 于H ，交y 轴于Q ，那么PF PH =， 且2pQH OF ==.作MN ⊥y 轴于N 则MN 是梯形PQOF 的中位线，()111222MN OF PQ PH PF =+==.故以PF 为直径的圆与y 轴相切，选B.【评注】相似的问题对于椭圆和双曲线来说，其结论则 分别是相离或相交的.（2）焦点弦——常考常新的亮点弦有关抛物线的试题，许多都与它的焦点弦有关.理解并掌握这个焦点弦的性质，对破解这些试题是大有帮助的.【例2】 过抛物线()022φp px y =的焦点F 作直线交抛物线于()()1122,,,A x y B x y 两点，求证：（1）12AB x x p =++ （2）pBF AF 211=+ 【证明】（1）如图设抛物线的准线为l ，作1AA l ⊥11111,2p A BB l B AA x ⊥==+于，则AF ， 122pBF BB x ==+.两式相加即得：12AB x x p =++（2）当AB ⊥x 轴时，有AF BF p ==，112AF BF p∴+=成立； 当AB 与x 轴不垂直时，设焦点弦AB 的方程为：2p y k x ⎛⎫=-⎪⎝⎭.代入抛物线方程：l XY FA(x,y)11B(x,y)22A 1B 1l2222p k x px ⎛⎫-= ⎪⎝⎭.化简得：()()222222014p k x p k x k -++=∵方程（1）之二根为x 1，x 2，∴1224k x x ⋅=.()122111212121111112224x x p p pp p AF BF AA BB x x x x x x +++=+=+=+++++ ()()121222121222424x x p x x p p p p pp x x p x x ++++===+++++. 故不论弦AB 与x 轴是否垂直，恒有pBF AF 211=+成立. （3）切线——抛物线与函数有缘有关抛物线的许多试题，又与它的切线有关.理解并掌握抛物线的切线方程，是解题者不可或缺的基本功.【例3】证明：过抛物线22y px =上一点M （x 0，y 0）的切线方程是：y 0y=p （x+x 0）【证明】对方程22y px =两边取导数：22.py y p y y''⋅=∴=，切线的斜率 00x x p k y y ='==.由点斜式方程：()()20000001p y y x x y y px px y y -=-⇒=-+20021y px =Q ，代入（）即得： y 0y=p （x+x 0）（4）定点与定值——抛物线埋在深处的宝藏抛物线中存在许多不不易发现，却容易为人疏忽的定点和定值.掌握它们，在解题中常会有意想不到的收获.例如：1.一动圆的圆心在抛物线x y 82=上，且动圆恒与直线02=+x 相切，则此动圆必过定点 （ ）()()()().4,0.2,0.0,2.0,2A B C D -显然.本题是例1的翻版，该圆必过抛物线的焦点，选B. 2.抛物线22y px =的通径长为2p ；3.设抛物线22y px =过焦点的弦两端分别为()()1122,,,A x y B x y ，那么：212y y p =-以下再举一例【例4】设抛物线22y px =的焦点弦AB 在其准线上的射影是A 1B 1，证明：以A 1B 1为直径的圆必过一定点【分析】假定这条焦点弦就是抛物线的通径，那么A 1B 1=AB=2p ，而A 1B 1与AB 的距离为p ，可知该圆必过抛物线的焦点.由此我们猜想：一切这样的圆都过抛物线的焦点.以下我们对AB 的一般情形给于证明.【证明】如图设焦点两端分别为()()1122,,,A x y B x y ，那么：22121112.y y p CA CB y y p =-⇒⋅==设抛物线的准线交x 轴于C ，那么.CF p =2111111.90A FB CF CA CB A FB ∴∆=⋅∠=︒中故.这就说明：以A 1B 1为直径的圆必过该抛物线的焦点.● 通法 特法 妙法（1）解析法——为对称问题解困排难解析几何是用代数的方法去研究几何，所以它能解决纯几何方法不易解决的几何问题（如对称问题等）.【例5】（10.四川文科卷.10题）已知抛物线 y=-x 2+3上存在关于直线x+y=0对称的相异两点A 、B ，则|AB|等于（ ）A.3B.4C.32D.42【分析】直线AB 必与直线x+y=0垂直，且线段 AB 的中点必在直线x+y=0上，因得解法如下.【解析】∵点A 、B 关于直线x+y=0对称，∴设直线AB 的方程为：y x m =+. 由()223013y x mx x m y x =+⎧⇒++-=⎨=-+⎩设方程（1）之两根为x 1，x 2，则121x x +=-. 设AB 的中点为M （x 0，y 0），则120122x x x +==-.代入x+y=0：y 0=12.故有11,22M ⎛⎫- ⎪⎝⎭. 从而1m y x =-=.直线AB 的方程为：1y x =+.方程（1）成为：220x x +-=.解得： 2,1x =-，从而1,2y =-，故得：A （-2，-1），B （1，2）.AB ∴=，选C.（2）几何法——为解析法添彩扬威虽然解析法使几何学得到长足的发展，但伴之而来的却是难以避免的繁杂计算，这又使得许多考生对解析几何习题望而生畏.针对这种现状，人们研究出多种使计算量大幅度减少的优秀方法，其中最有成效的就是几何法.【例6】（11.全国1卷.11题）抛物线24y x =的焦点为F ，准线为l ，经过F 且斜率XYABFA 1B 11MC XOYABMl x y +=ÿXYO F(1,0)AK60°M的直线与抛物线在x 轴上方的部分相交于点A ，AK l ⊥，垂足为K ，则AKF △的面积（ ）A ．4 B． C． D ．8 【解析】如图直线AFAFX=60°. △AFK 为正三角形.设准线l 交x 轴于M ，则2,FM p ==且∠KFM=60°，∴24,44AKF KF S ∆==⨯=选C. 【评注】（1）平面几何知识：边长为a 的正三角形的面积用公式2S ∆=计算. （2）本题如果用解析法，需先列方程组求点A 的坐标，，再计算正三角形的边长和面积.虽不是很难，但决没有如上的几何法简单.（3）定义法——追本求真的简单一着许多解析几何习题咋看起来很难.但如果返朴归真，用最原始的定义去做，反而特别简单. 【例7】（07.湖北卷.7题）双曲线22122:1(00)x y C a b a b-=>>，的左准线为l ，左焦点和右焦点分别为1F 和2F ；抛物线2C 的线为l ，焦点为21F C ；与2C 的一个交点为M ，则12112F F MF MF MF -等于（ ）A ．1-B ．1C ．12-D ．12【分析】 这道题如果用解析法去做，计算会特别繁杂，而平面几何知识又一时用不上，那么就从最原始的定义方面去寻找出路吧.如图，我们先做必要的准备工作：设双曲线的半 焦距c ，离心率为e ，作 MH l H ⊥于，令1122,MF r MF r ==.∵点M 在抛物线上，1112222,MF MF r MH MF r e MH MF r ∴=====故，这就是说：12||||MF MF 的实质是离心率e.其次，121||||F F MF 与离心率e 有什么关系？注意到：()1212111122111F F e r r c e a e e MF r r r e +⋅⎛⎫====-=- ⎪⎝⎭. 这样，最后的答案就自然浮出水面了：由于()12112||||11||||F F MF e e MF MF -=-+=-.∴选 A..（4）三角法——本身也是一种解析三角学蕴藏着丰富的解题资源.利用三角手段，可以比较容易地将异名异角的三角函数转化为同名同角的三角函数，然后根据各种三角关系实施“九九归一”——达到解题目的.因此，在解析几何解题中，恰当地引入三角资源，常可以摆脱困境，简化计算.【例8】（09.重庆文科.21题）如图，倾斜角为a 的直线经过抛物线x y 82=的焦点F ，且与抛物线交于A 、B 两点。