沪科版-全等三角形归类复习
沪科版八年级数学上册第14章 全等形和全等三角形 专题复习(解析版)
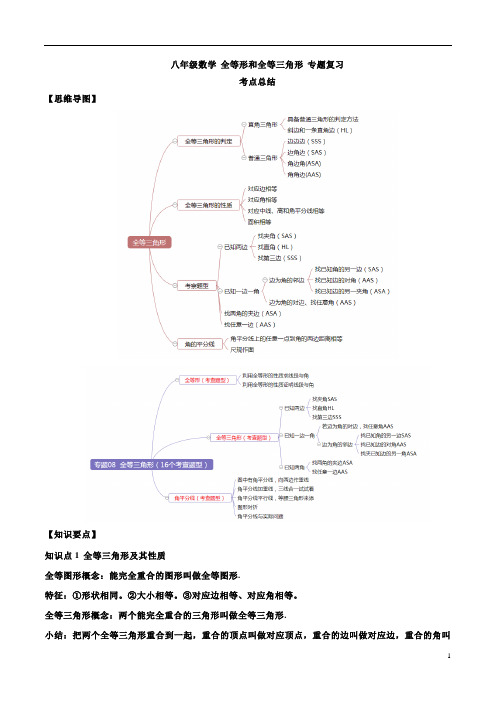
八年级数学全等形和全等三角形专题复习考点总结【思维导图】【知识要点】知识点1全等三角形及其性质全等图形概念:能完全重合的图形叫做全等图形.特征:①形状相同。
②大小相等。
③对应边相等、对应角相等。
全等三角形概念:两个能完全重合的三角形叫做全等三角形.小结:把两个全等三角形重合到一起,重合的顶点叫做对应顶点,重合的边叫做对应边,重合的角叫做对应角.表示方法:全等用符号“≌”,读作“全等于”。
书写三角形全等时,要注意对应顶点字母要写在对应位置上。
全等变换定义:只改变图形的位置,而不改变图形的形状和大小的变换。
变换方式(常见):平移、翻折、旋转。
全等三角形的性质:对应边相等,对应角相等。
1.(2017·四川中考模拟)已知四边形ABCD各边长如图所示,且四边形OPEF≌四边形ABCD.则PE的长为()A.3 B.5 C.6 D.10【答案】D【详解】∵四边形OPEF≌四边形ABCD∴PE=BC=10,故选D.2.(2019·福建中考模拟)如图,若△MNP≌△MEQ,则点Q应是图中的()A.点A B.点B C.点C D.点D【答案】D【详解】∵△MNP≌△MEQ,∴点Q应是图中的D点,如图,故选:D.3.(2018·广西中考模拟)下列说法中不正确的是()A.全等三角形的周长相等B.全等三角形的面积相等C.全等三角形能重合D.全等三角形一定是等边三角形【答案】D【详解】根据全等三角形的性质可知A,B,C命题均正确,故选项均错误;D.错误,全等三角也可能是直角三角,故选项正确.故选D.考查题型一利用全等三角形性质求线段与角1.(2019·武冈市第七中学中考模拟)如图,三角形纸片ABC,AB=10CM,BC=7CM,AC=6CM,沿过点B的直线折叠这个三角形,使顶点C落在AB边上的点E处,折痕为BD,则△AED的周长为()A.9CM B.13CM C.16CM D.10CM【答案】A【解析】解:由折叠的性质知,CD=DE,BC=BE=7CM.∵AB=10CM,BC=7CM,∴AE=AB﹣BE=3CM.△AED的周长=AD+DE+AE=AC+AE=6+3=9(CM).故选A.2.(2017·江苏南京溧水孔镇中学中考模拟)如图,△ABC≌△DEF,点A与D,B与E分别是对应顶点,且测得BC=5CM,BF=7CM,则EC长为()A.1CM B.2CM C.3CM D.4CM【答案】C【详解】解:∵△ABC≌△BAD,∴EF=BC=5CM,∵BF=7CM,BC=5CM,∴CF=EF-CF=3 CM,故选C.3.(2016·广东中考模拟)如图,△ACB≌△A′CB′,∠ACA′=30°,则∠BCB′的度数为()A.20°B.30°C.35°D.40°【答案】B【详解】∵△ACB≌△A′CB′,∴∠ACB=∠A′C′B′,∴∠ACB-∠A′CB=∠A′C′B′-∠A′CB,即∠BCB′=∠ACA′,又∠ACA′=30°,∴∠BCB′=30°,故选:B.4.(2019·沂源县中庄中学初一月考)如图,点B,C,D在同一条直线上,∠B=∠D=90°,△ABC≌△CDE,AB=6,BC=8,CE=10.(1)求△ABC的周长;(2)求△ACE的面积.【答案】(1)24;(2)50【详解】解:(1))∵△ABC≌△CDE∴AC=CE∴△ABC的周长=AB+BC+AC=24(2)∵△ABC≌△CDE∴AC=CE,∠ACB=∠CED,∠BAC=∠DCE又∠B=90°∴∠ACB+∠BAC=90°∴∠ACB+∠DCE=90°∴∠ACE=180°-(∠ACB+∠DCE)=90°×AC×CE=50∴△ACE的面积=12考查题型二利用全等三角形性质证明线段、角相等1.(2019·湖北黄石十四中初二期中)如图,点E在AB上,△ABC≌△DEC,求证:CE平分∠BED.【答案】见解析【详解】∵△ABC≌△DEC,∴∠B=∠DEC,BC=EC,∴∠B=∠BEC,∴∠BEC=∠DEC,∴CE平分∠BED.2.(2018·颍上县第五中学初二期中)若△ABC≌△DCB,求证:∠ABE=∠DCE.【答案】见解析【详解】证明:∵△ABC≌△DCB∴∠ABC=∠DCB,∠ACB=∠DBC∴∠ABC-∠DBC=∠DCB-∠ACB即∠ABE=∠DCE知识点2:全等三角形的判定(重点)注:①判定两个三角形全等必须有一组边对应相等;②全等三角形周长、面积相等.证题的思路(重点):考查题型三 已知一边一角(若边为角的对边,找任意角AAS )1.(2018·四川中考模拟)如图,AB=AE ,∠1=∠2,∠C=∠D .求证:AC=AD .【答案】见解析【解析】详解:∵∠1=∠2∴∠1+∠EAC=∠2+∠EAC∴∠BAC=∠EAD在ΔABC 和ΔAED 中{∠BAC =∠EAD∠C =∠D AB =AE∴ΔABC ≌ΔAED (AAS)∴AC=AD2.(2014·北京中考模拟)已知:如图,E 是AC 上一点,AB=CE ,AB ∥CD ,∠ACB =∠D .求证:BC =ED .【答案】证明见解析.【详解】∵AB∥CD,∴∠A=∠ECD.在△ABC和△ECD中,∵∠A=∠ECD,∠ACB=∠D,AB=CE,∴△ABC≌△ECD(AAS).∴BC=DE.3.(2018·四川中考模拟)已知,如图,E、F分别为□ABCD的边BC、AD上的点,且∠1=∠2,.求证:AE=CF.【答案】详见解析【详解】∵四边形ABCD为平行四边形∴∠B=∠D,AB=CD在△ABE与△CDF中,∠1=∠2,∠B=∠D,AB=CD∴△ABE≌△CDF∴AE=CF4.(2016·福建中考模拟)如图,∠ACB=90°,AC=BC,BE⊥CE,AD⊥CE.求证:△ACD≌△CBE.【答案】证明详见解析.【详解】∵AD⊥CE,BE⊥CE,∴∠ADC=∠E=90°,∵∠ACB=90°,∴∠BCE+∠ACD=90°,∵∠B+∠BCE=90°,∴∠B=∠ACD,在△BEC和△CDA中,∠ADC=∠E=90°,∠B=∠ACD,AC=BC,∴△ACD≌△CBE(AAS).考查题型四已知一边一角(边为角的邻边(找已知角的另一边SAS))1.(2016·四川中考真题)如图,C是线段AB的中点,CD=BE,CD∥BE.求证:∠D=∠E.【答案】见解析【详解】∵C是线段AB的中点,∴AC=CB,∵CD∥BE,∴∠ACD=∠B,在△ACD和△CBE中,∵AC=CB,∠ACD=∠B,CD=BE,∴△ACD≌△CBE(SAS),∴∠D=∠E.2.(2018·云南中考模拟)如图,点E,F在AB上,AD=BC,∠A=∠B,AE=BF.求证:∠C=∠D.【答案】证明见解析【详解】证明:∵AE=BF,∴AE+EF =BF+EF ,∴AF =BE ,在△ADF 与△BCE 中,AD BC A B AF BE =⎧⎪∠=∠⎨⎪=⎩∴△ADF ≌△BCE (SAS ),∴∠C =∠D .3.(2019·辽宁中考真题)如图,点E ,F 在BC 上,BE =CF ,AB =DC ,∠B =∠C ,求证:AF =DE .【答案】见解析;【详解】证明:∵BE =CF ,∴BE +EF =CF +EF ,即BF =CE ,在ΔABF 和ΔDCE 中,{AB =DC∠B =∠C BF =CE,∴ΔABF ≌ΔDCE (SAS)∴AF =DE .考查题型五 已知一边一角(边为角的邻边(找已知边的对角AAS ))1.(2013·浙江中考真题)如图,△ABC 与△DCB 中,AC 与BD 交于点E ,且∠A=∠D ,AB=DC .(1)求证:△ABE ≌DCE ;(2)当∠AEB=50°,求∠EBC 的度数。
沪科版数学八年级上册1全等三角形判定复习课件

B
D
C
课堂练习
5.如图:在四边形ABCD中,点E在边CD上,连接AE、BE并延长AE交BC
的延长线于点F,给出下列5个关系式::①AD∥BC,②,DE=EC③
∠1=∠2,④∠3=∠4,⑤AD+BC=AB。将其中三个关系式作为已知,
另外两个作为结论,构成正确的命题。请用序号写出两个正确的命
• 变式1:以上条件不变,将△ABC绕点C顺时
针旋转10度,以上的结论还成立吗?
A
E
B D
C
例3变式2
• 例4.已知,△ABC和△ECD都是等边三角形,且 点B,C,D在一条直线上求证:BE=AD
• 变式:以上条件不变,将△ABC绕点C顺时针旋
转60度,以上的结论还成立吗?
E
A
D C
例3变式3
• 例5.已知,△ABC和△ECD都是等边三
角形,当△ABC绕点C顺时针旋转ɑ时,
连接BE,DA;结论BE=AD还成立吗?
若成立请加以证明。
E
A
E
A
B
B
D
C
D C
例3变式4
引申:例6.已知,△ABC和△ECD都是等边三角形,且点
B交,于CN,,D试在判一定条△直C线M上N,的AC形与状BE相交于M,CE与EAD相
解:△CMN是等边三角形
A
M
课堂练习
3.已知点A,E,F,C在同一条直线上,且AE=CF,过
E F两点分别作DE⊥AC,BF⊥AC,且AB=CD,(
1)求证:BD平分 EF(2)若将△DEC的边EC沿AC方
向移动,变化为2时,其余条件不变,上述结论是否成立
,说明理由
沪科版八年级数学 14.1 全等三角形(学习、上课课件)

感悟新知
知1-练
方法点拨:确定两个图形全等的方法: 1. 条件判定法:(1)形状相同;(2)大小相等 . 是否是全 等形与位置无关 . 2. 重合判定法:通过平移、旋转、翻折等方法把两个 图形叠合在一起,看它们能否完全重合 .
感悟新知
知1-练
1-1. 下图所示的图形分割成两个全等的图形,正确的是 (B )
应边上的中线、对应边上的高、对应角的平分线、周长、 面积等.
感悟新知
知3-讲
要点提醒 1. 应用全等三角形性质时,要先确定两个条件:
(1)两个三角形全等; (2)找对应元素. 2. 全等三角形的性质是证明线段、角相等的常用方法.
感悟新知
例 4 如图14.1- 6,已知△ABC≌△EDF. (1)求证:DC=BF; (2)求证:AC∥EF. 解题秘方:利用全等三角形的 对应边相等和对应角相等解决 问题.
2. 全等变换的常见方式 平移、翻折、旋转 .
感悟新知
知1-讲
特别提醒 ◆完全重合说明两个图形周长和面积相等; ◆周长或面积相等的两个图形不一定是全等的.
感悟新知
例 1 如图14.1-1,下列图形是全等形的是( B )
知1-练
解题秘方:根据全等形的定义和特征进行判断 . 解:选项 A,C大小不同;选项 D形状不同,故选B.
②对应角的对边为对应边,两个对应角所夹的边是对应边.
③对应边的对角为对应角,两条对应边所夹的角是对应角.
(3)字母顺序法:
根据书写规范按照对应顶点确定对应边或对应角.
感悟新知
ቤተ መጻሕፍቲ ባይዱ知2-练
例 2 如图14.1-4,已知△ABD≌ △CDB,∠ABD= ∠CDB. 写出其对应边和对应角.
沪教版七年级下册第十四章 全等三角形单元复习 讲义
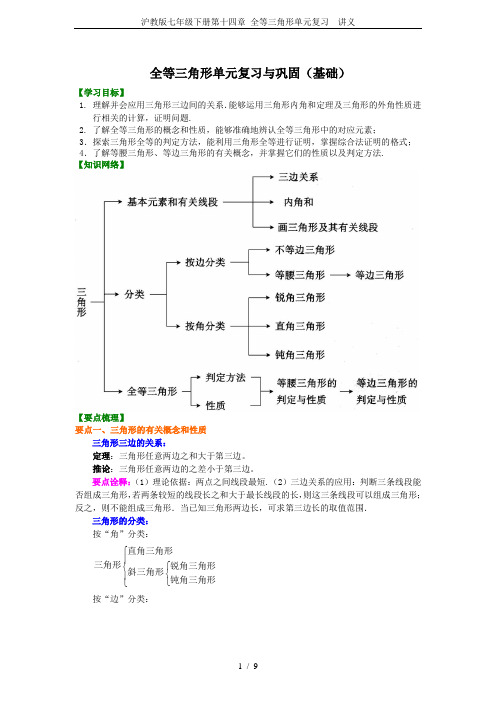
全等三角形单元复习与巩固(基础)【学习目标】1. 理解并会应用三角形三边间的关系.能够运用三角形内角和定理及三角形的外角性质进行相关的计算,证明问题.2. 了解全等三角形的概念和性质,能够准确地辨认全等三角形中的对应元素;3.探索三角形全等的判定方法,能利用三角形全等进行证明,掌握综合法证明的格式;4.了解等腰三角形、等边三角形的有关概念,并掌握它们的性质以及判定方法.【知识网络】【要点梳理】要点一、三角形的有关概念和性质三角形三边的关系:定理:三角形任意两边之和大于第三边。
推论:三角形任意两边的之差小于第三边。
要点诠释:(1)理论依据:两点之间线段最短.(2)三边关系的应用:判断三条线段能否组成三角形,若两条较短的线段长之和大于最长线段的长,则这三条线段可以组成三角形;反之,则不能组成三角形.当已知三角形两边长,可求第三边长的取值范围.三角形的分类:按“角”分类: ⎧⎪⎧⎨⎨⎪⎩⎩直角三角形三角形 锐角三角形斜三角形 钝角三角形 按“边”分类:⎧⎪⎧⎨⎨⎪⎩⎩不等边三角形三角形 底边和腰不相等的等腰三角形等腰三角形 等边三角形 三角形的重要线段:一个三角形有三条中线,它们交于三角形内一点.一个三角形有三条角平分线,它们交于三角形内一点.三角形的三条高所在的直线相交于一点的位置情况有三种:锐角三角形交点在三角形内;直角三角形交点在直角顶点;钝角三角形交点在三角形外.三角形的内角和与外角和:三角形内角和定理:三角形的内角和为180°.三角形外角性质:(1)三角形的一个外角等于与它不相邻的两个内角的和.(2)三角形的一个外角大于任意一个与它不相邻的内角.三角形的外角和: 三角形的外角和等于360°.要点二、全等三角形的判定与性质全等三角形对应边相等,对应角相等.全等三角形判定1——“边角边”:两边和它们的夹角对应相等的两个三角形全等(可以简写成“边角边”或“SAS ”).全等三角形判定2——“角边角”:两角和它们的夹边对应相等的两个三角形全等(可以简写成“角边角”或“ASA ”).全等三角形判定3——“角角边”:两个角和其中一个角的对边对应相等的两个三角形全等(可以简写成“角角边”或“AAS ”)全等三角形判定4——“边边边”:三边对应相等的两个三角形全等.(可以简写成“边边边”或“SSS ”).要点三、判定方法的选择1.选择哪种判定方法,要根据具体的已知条件而定,见下表:2.如何选择三角形证全等(1)可以从求证出发,看求证的线段或角(用等量代换后的线段、角)在哪两个可能全等的三角形中,可以证这两个三角形全等;(2)可以从已知出发,看已知条件确定证哪两个三角形全等;(3)由条件和结论一起出发,看它们一同确定哪两个三角形全等,然后证它们全等;(4)如果以上方法都行不通,就添加辅助线,构造全等三角形.要点四、等腰三角形等腰三角形的性质性质1:等腰三角形的两个底角相等(简称“等边对等角”).性质2:等腰三角形的顶角平分线、底边上的高、底边上的中线互相重合(简称“三线合一”).等腰三角形的性质的作用性质1证明同一个三角形中的两角相等.是证明角相等的一个重要依据.性质2用来证明线段相等,角相等,垂直关系等.等腰三角形是轴对称图形等腰三角形底边上的高(顶角平分线或底边上的中线)所在直线是它的对称轴,通常情况只有一条对称轴.等腰三角形的判定如果一个三角形中有两个角相等,那么这两个角所对的边也相等(简称“等角对等边”).要点诠释:等腰三角形的判定是证明两条线段相等的重要定理,是将三角形中的角的相等关系转化为边的相等关系的重要依据.等腰三角形的性质定理和判定定理是互逆定理.等边三角形的性质:等边三角形三个内角都相等,并且每一个内角都等于60°.等边三角形的判定:(1)三条边都相等的三角形是等边三角形;(2)三个角都相等的三角形是等边三角形;(3)有一个角是60°的等腰三角形是等边三角形.【典型例题】类型一、三角形的有关概念和性质1、如图,在△ABC中,∠B=67°,∠C=33°,AD是△ABC的角平分线,则∠CAD的度数为()A.40° B.45° C.50° D.55°【思路点拨】首先利用三角形内角和定理求得∠BAC的度数,然后利用角平分线的性质求得∠CAD的度数即可.【答案】A;【解析】解:∵∠B=67°,∠C=33°,∴∠BAC=180°-∠B-∠C=180°-67°-33°=80°∵AD是△ABC的角平分线,∴∠CAD=12∠BAC=12×80°=40°【总结升华】本题考查了三角形的内角和定理,属于基础题,比较简单.类型二、全等三角形的性质和判定2、两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,B,C,E在同一条直线上,连结DC.(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);(2)证明:DC⊥BE .【思路点拨】△ABE与△ACD中,已经有两边,夹角可以通过等量代换找到,从而证明△ABE ≌△ACD;通过全等三角形的性质,通过导角可证垂直.【答案与解析】解:(1)△ABE≌△ACD证明:∠BAC=∠EAD=90°∠BAC +∠CAE=∠EAD +∠CAE即∠BAE=∠CAD又AB=AC,AE=AD,△ABE≌△ACD(SAS)(2)由(1)得∠BEA=∠CDA,又∠COE=∠AOD∠BEA+∠COE =∠CDA+∠AOD=90°则有∠DCE=180°- 90°=90°,所以DC⊥BE.【总结升华】我们可以试着从变换的角度看待△ABE与△ACD,后一个三角形是前一个三角形绕着A点逆时针旋转90°得到的,对应边的夹角等于旋转的角度90°,即DC⊥BE.举一反三:【变式】如图,已知:AE⊥AB,AD⊥AC,AB=AC,∠B=∠C,求证:BD=CE.【答案】证明:∵AE⊥AB,AD⊥AC,∴∠EAB=∠DAC=90°∴∠EAB+∠DAE=∠DAC+∠DAE ,即∠DAB=∠EAC.在△DAB与△EAC中,DAB EAC AB AC B C ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△DAB ≌△EAC (ASA )∴BD =CE.类型三、巧引辅助线构造全等三角形3、 如图:在四边形ABCD 中,AD ∥CB ,AB ∥CD.求证:∠B =∠D.【思路点拨】∠B 与∠D 不包含在任何两个三角形中,只有添加辅助线AC ,根据平行线的性质,可构造出全等三角形.【答案与解析】证明:连接AC ,∵AD ∥CB ,AB ∥CD.∴∠1=∠2,∠3=∠4在△ABC 与△CDA 中1243AC CA ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ABC ≌△CDA (ASA )∴∠B =∠D【总结升华】添加公共边作为辅助线的时候不能割裂所给的条件,如果证∠A =∠C ,则连接对角线BD.4、己知:在ΔABC 中,AD 为中线.求证:AD <()12AB AC +【答案与解析】证明:延长AD 至E ,使DE =AD ,∵AD 为中线,∴BD =CD在△ADC 与△EDB 中DC DB ADC BDE AD ED =⎧⎪∠=∠⎨⎪=⎩∴△ADC ≌△EDB (SAS )∴AC =BE在△ABE 中,AB +BE >AE ,即AB +AC >2AD∴AD <()12AB AC +. 【总结升华】用倍长中线法可将线段AC ,2AD ,AB 转化到同一个三角形中,把分散的条件集中起来.倍长中线法实际上是绕着中点D 旋转180°.举一反三:【变式】若三角形的两边长分别为5和7, 则第三边的中线长x 的取值范围是( )A.1 <x < 6B.5 <x < 7C.2 <x < 12D.无法确定【答案】A ;提示:倍长中线构造全等三角形,7-5<2x <7+5,所以选A 选项.类型四、全等三角形动态型问题5、如图(1),AB ⊥BD 于点B ,ED ⊥BD 于点D ,点C 是BD 上一点.且BC =DE ,CD =AB .(1)试判断AC 与CE 的位置关系,并说明理由;(2)如图(2),若把△CDE 沿直线BD 向左平移,使△CDE 的顶点C 与B 重合,此时第(1)问中AC 与BE 的位置关系还成立吗?(注意字母的变化)【答案与解析】证明:(1)AC ⊥CE .理由如下:在△ABC 和△CDE 中,,90,,BC DE B D AB CD =⎧⎪∠=∠=︒⎨⎪=⎩∴ △ABC ≌△CDE (SAS ).∴ ∠ACB =∠E .又∵ ∠E +∠ECD =90°,∴ ∠ACB +∠ECD =90°.∴ AC ⊥CE .(2)∵ △ABC 各顶点的位置没动,在△CDE 平移过程中,一直还有AB C D '=,BC =DE ,∠ABC =∠EDC =90°,∴ 也一直有△ABC ≌△C DE '(SAS).∴ ∠ACB =∠E .而∠E +∠EC D '=90°,∴ ∠ACB +∠EC D '=90°.故有AC ⊥C E ',即AC 与BE 的位置关系仍成立.【总结升华】变还是不变,就看在运动的过程中,本质条件(本题中的两三角形全等)变还是没变.本质条件变了,结论就会变;本质条件不变,仅仅是图形的位置变了。
沪科版-全等三角形归类复习

全等三角形归纳复习常见辅助线的作法有以下几种:(1)遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变换中的“对折”.(2)遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全等变换中的“旋转”.(3)遇到角平分线,可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中的“对折”,所考知识点常常是角平分线的性质定理或逆定理.(4)过图形上某一点作特定的平分线,构造全等三角形,利用的思维模式是全等变换中的“平移”或“翻转折叠”(5)截长法与补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,是之与特定线段相等,再利用三角形全等的有关性质加以说明.这种作法,适合于证明线段的和、差、倍、分等类的题目.特殊方法:在求有关三角形的定值一类的问题时,常把某点到原三角形各顶点的线段连接起来,利用三角形面积的知识解答.顺口溜:人人都说几何难,难就难在辅助线;辅助线,如何添?构造全等很关键.图中有角平分线,可向两边作垂线;三角形中有中线,延长中线造全等;角平分线加平行,构造等腰三角形;角平分线加垂线,三线合一试试看;线段垂直平分线,常向两端把线连;还要刻苦加钻研,找出规律凭经验.一、倍长中线法△ABC 中,AD 是BC 边中线方式1: 延长AD 到E ,使DE=AD ,连接BE.方式2:间接倍长作CF ⊥AD 于F ,作BE ⊥AD 的延长线于E , 延长MD 到N ,使DN=MD ,连接CN. 连接BE.例1、已知:如图,△ABC 中,AB=5,AC=3,求中线AD 的取值范围.例2、如图,已知在△ABC中,AD是BC边上的中线,E是AD上一点,且BE=AC,延长BE交AC于F,求证:AF=EF.例3、如图所示,AD为△ABC的中线,∠ADB和∠ADC的平分线分别交AB、AC于点E、F.求证:BE+CF>EF.(提示:延长ED至M,使DM=DE,连接 CM,MF.)例4、已知在△ABC中,AB=AC,D在AB上,E在AC的延长线上,DE交BC于点F,且DF=EF.求证:BD=CE.练习1、如图,在△ABC 中,AB ≠AC ,D 、E 在BC 上,且DE=EC ,过D 作DF ∥BA 交AE 于点F ,DF=AC.求证:AE 平分∠BAC.练习2、如图,AD 为△ABC 的中线,求证:AB +AC >2AD.练习3、如图,△ABC 中,BD=DC=AC ,E 是DC 的中点,求证:AD 平分∠BAE.E D CB ACB二、借助角平分线造全等例1、已知,如图,在四边形ABCD 中,BC >AB ,AD=DC ,BD 平分∠ABC. 求证:∠BAD+∠BCD=180°.例2、如图,已知在△ABC 中,∠B=60°,△ABC 的角平分线AD 、CE 相交于点O ,求证:OE=OD.(有和角平分线垂直的线段时,通常把这条线段延长.)例3、已知:如图所示,在Rt △ABC 中,AB=AC,∠BAC=90°,∠1=∠2,CE ⊥BD 的延长于E.求证:BD=2CE.三、截长补短例1、如图,△ABC中,AB=2AC,AD平分∠BAC,且AD=BD,求证:CD⊥AC.例2、如图,AD∥BC,EA,EB分别平分∠DAB,∠CBA,CD过点E,求证:AB=AD+BC.练习1、如图,在△ABC中,∠BAC=60°,AD是∠BAC的平分线,且AC=AB+BD,求∠ABC的度数.练习2、如图,在△ABC中,∠ABC=60°,AD、CE分别平分∠BAC、∠ACB,求证:AC=AE+CD.四、连接已知点,构造全等三角形.例、已知:如图所示,AC、BD相交于O点,且AB=DC,AC=BD.求证:∠A=∠D.五、取线段中点构造全等三角形例、已知:如图所示,AB=DC,∠A=∠D.求证:∠ABC=∠DCB.六、证明线段不等关系例、如图,在△ABC的边上取两点D、E,且BD=CE,求证:AB+AC>AD+AE.FED CBA七、旋转例1、正方形ABCD 中,E 为BC 上的一点,F 为CD 上的一点,BE+DF=EF ,求∠EAF 的度数.例2、如图,在四边形ABCD 中,AC 平分∠BAD ,过C 作CE ⊥AB 于E ,并且1()2AE AB AD =+,求∠ABC+∠ADC 的度数.ED CBA八、直角三角形的全等问题[知识]:①直角三角形特有的HL判定定理;②SAS、AAS、ASA、SSS(转化为HL)也是完全适用直角三角形的,不要忘记;③同(等)角的余角相等应用非常广泛(重点).例1、如图,已知DO⊥BC,OC=OA,OB=OD,求证:△BCE是直角三角形.例2、把两个含有45°角的直角三角板如图放置,点D在BC上,连结BE、AD,AD的延长线交BE于点F.求证:AF⊥BE.例3、如图,在△ABC中,高AD与BE相交于点H,且AD=BD.问△BHD≌△ACD?九、等腰三角形、等边三角形的全等问题[知识]:①等腰三角形腰相等且底角相等,等边三角形三边相等且三个底角都是60度,即“等边对等角,等角对等边”;②如右图,由∠1=∠2,可得∠CBE=∠DBA ;反之也成立.例、如图1、2、3,过点A 分别作两个个大小不一样的等边三角形,连接BD ,CE.求证BD=CE.12BCAED练习、如图,四边形ABCD、DEFG都是正方形,连接AE、CG,AE与CG相交于点M,CG与AD 相交于点N.求证:AE=CG.GABDC题型:全等三角形在实际生活中的应用例1 如图所示,太阳光线AC和A′C′是平行的,同一时刻两个建筑物在太阳下的影子一样长,则建筑物是否一样高?说明理由.(注:太阳光线可看成是平行的)巩固1某游乐场有两个长度相同的滑梯,要想使左边滑梯BC的高度AC与右边滑梯EF的水平方向的长度DF相等,则两个滑梯的倾斜角∠ABC与∠DFE的大小必须满足什么关系?说明理由.。
沪科版八年级数学上册《全等三角形》知识总结和经典例题

沪科版八年级上册数学全等三角形复习[知识要点] 一、全等三角形 一般三角形直角三角形判定 边角边(SAS )、角边角(ASA ) 角角边(AAS )、边边边(SSS ) 具备一般三角形的判定方法 斜边和一条直角边对应相等(HL ) 性质对应边相等,对应角相等对应中线相等,对应高相等,对应角平分线相等② 全等三角形面积相等. 2.证题的思路:⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧⎪⎩⎪⎨⎧)找任意一边()找两角的夹边(已知两角)找夹已知边的另一角()找已知边的对角()找已知角的另一边(边为角的邻边)任意角(若边为角的对边,则找已知一边一角)找第三边()找直角()找夹角(已知两边AAS ASA ASA AAS SAS AAS SSS HL SAS 性质1、全等三角形的对应角相等、对应边相等。
2、全等三角形的对应边上的高对应相等。
3、全等三角形的对应角平分线相等。
4、全等三角形的对应中线相等。
5、全等三角形面积相等。
6、全等三角形周长相等。
(以上可以简称:全等三角形的对应元素相等) 7、三边对应相等的两个三角形全等。
(SSS)8、两边和它们的夹角对应相等的两个三角形全等。
(SAS) 9、两角和它们的夹边对应相等的两个三角形全等。
(ASA)10、两个角和其中一个角的对边对应相等的两个三角形全等。
(AAS)11、斜边和一条直角边对应相等的两个直角三角形全等。
(HL)运用1、性质中三角形全等是条件,结论是对应角、对应边相等。
而全等的判定却刚好相反。
2、利用性质和判定,学会准确地找出两个全等三角形中的对应边与对应角是关键。
在写两个三角形全等时,一定把对应的顶点,角、边的顺序写一致,为找对应边,角提供方便。
3,当图中出现两个以上等边三角形时,应首先考虑用SAS 找全等三角形。
4、用在实际中,一般我们用全等三角形测等距离。
以及等角,用于工业和军事。
有一定帮助。
5、角平分线的性质及判定性质:角平分线上的点到这个角的两边的距离相等 判定:到一个角的两边距离相等的点在这个角平分线上做题技巧一般来说考试中线段和角相等需要证明全等。
沪科版中考数学一轮复习第14章全等三角形复习课件

找这边的另一个邻角(ASA)
找这个角的另一个边(SAS) 找这边的对角 (AAS)
已知一边和它的对角
找一角(AAS) 已知角是直角,找一边(HL)
(3):已知两角--练习
找两角的夹边(ASA) 找夹边外的任意边(AAS)
例1:已知AC=FE,BC=DE,点A,D,B,F在一条直线上,AD=BF,
求证:∠E=∠C
∴ DC∥AB
练习2:已知,△ABC和△ECD都是等边三角形,且点B,C,D在
一条直线上求证:BE=AD 证明:
E
∵ △ABC和△ECD都是等边三角形
A
∴ AC=BC DC=EC ∠BCA=∠DCE=60°
∴ ∠BCA+∠ACE=∠DCE+ ∠ACE
B
D
即∠BCE=∠DCA
C
在△ACD和△BCE中
E
答: △CBF≌△FEC
A
F
B
C
D
证明: ∵ △ABF≌△DEC
∴ BF=EC ∵ △ABC≌△DEF ∴ BC=EF 在△CBF和△FEC中
BF=EC
BC=EF
CF=FC
∴ △CBF≌△FEC (SSS)
练习
2:如图,已知,EG∥AF,请你从下面三个条件中,再选出两 个作为已知条件,另一个作为结论,推出一个正确的命题。 (只写出一种情况)①AB=AC ②DE=DF ③BE=CF
(3):全等三角形的对应边上的对应中线、角平分线、 高线分别相等。
3:三角形全等的判定方法有哪些?
SSS、SAS、ASA、AAS、HL(RT△)
方法指引
证明两个三角形全等的基本思路:
(1):已知两边----
找第三边 (SSS) 找夹角 (SAS) 找是否有直角 (HL)
沪科版八年级上册全等三角形期末复习(包含答案)

期末复习四全等三角形类型一用尺规作三角形图QM4-11.如图QM4-1,点C在∠AOB的边OB上,利用∠NCB=∠O,用尺规作出了CN∥OA,作图中∠NCB=∠O的根据是()A.SASB.SSSC.ASAD.AAS2.如图QM4-2,已知线段a,b及直角∠α,且a>b,求作:△ABC,使∠C=∠α,AB=a,AC=b.图QM4-2类型二全等三角形的性质与判定图QM4-33.如图QM4-3,△ABC≌△ADE,∠DAC=60°,∠BAE=100°,BC,DE相交于点F,则∠DFB的度数是()A.15°B.20°C.25°D.30°4.要判定两个直角三角形全等,下列条件:(1)两条直角边对应相等;(2)两个锐角对应相等;(3)斜边和一条直角边对应相等;(4)一个锐角和一条边对应相等,其中正确的有() A.1个B.2个C.3个D.4个5.已知△ABC的三边长分别为3,5,7,△DEF的三边长分别为3,3x-2,2x-1,若这两个三角形全等,则x的值为()B.4C.3D.不能确定A.736.如图QM4-4,在△ABC中,∠B=∠C,BF=CD,BD=CE,则∠A与∠α的关系是()A.∠A=180°-∠αB.∠A=180°-2∠αC.∠A=90°-∠αD.∠A=90°-2∠α图QM4-4图QM4-57.如图QM4-5所示,AB=AC,AD=AE,∠BAC=∠DAE,∠1=25°,∠2=30°,则∠3=°.8.已知△ABC和△A'B'C',∠C=∠C'=90°,AC=A'C',要判定△ABC≌△A'B'C',必须添加条件①或②或③或④.9.如图QM4-6,△ABC的高BD,CE相交于点O,请你添加一对相等的线段或一对相等的角的条件,使BD=CE.你所添加的条件是.图QM4-6图QM4-710.如图QM4-7,已知C是∠AOB的平分线上的点,点P,P'分别在OA,OB上,若要得到OP=OP',则需要添加以下条件中的某一个即可:①∠OCP=∠OCP';②∠OPC=∠OP'C;③PC=P'C;④PP'⊥OC.请你写出所有正确的条件的序号:.11.如图QM4-8,D为锐角∠ABC内一点,点M在边BA上,点N在边BC上,且DM=DN,∠BMD+∠BND=180°.求证:BD平分∠ABC.图QM4-8类型三全等三角形的应用12.如图QM4-9,将两根钢条AA',BB'的中点O连在一起,使AA',BB'可以绕着点O自由转动,就做成了一个测量工件,由三角形全等得出A'B'的长等于内槽宽AB.那么判定△OAB≌△OA'B'的理由是()A.边角边B.角边角C.边边边D.角角边13.如图QM4-10,有两个长度相同的滑梯靠在一面墙上.已知左边滑梯的高度AC与右边滑梯水平方向的长度DF相等,则这两个滑梯与地面夹角∠ABC与∠DFE的度数和是() A.60°B.90°C.120°D.150°图QM4-9图QM4-10图QM4-1114.如图QM4-11,在东西走向的铁路上有A,B两站(视为直线上的两点)相距36千米,在A,B 的正北方向分别有C,D两个蔬菜基地,其中C到A站的距离为24千米,D到B站的距离为12千米,现要在铁路AB上建一个蔬菜加工厂E,使蔬菜基地C,D到E的距离相等,则E站应建在距A站千米的地方.15.如图QM4-12,有一块不规则土地ABCD,分别被甲、乙二人承包,一条公路GEFH穿过这块土地,EF左边被甲承包,右边被乙承包,AB∥CD.为方便通行,决定将这条公路尽量修直,但要求甲、乙二人的土地面积不变.请你设计一种方案,解决这个问题,并说明方案正确的理由.图QM4-12类型一综合运用三角形全等的判定与性质解决问题16.如图QM4-13,已知AD=BC,AB=CD,O是BD的中点,过点O作直线交BA的延长线于点E,交DC的延长线于点F.求证:OE=OF.图QM4-1317.如图QM4-14,AC平分∠EAB,DC=BC,CE⊥AD,交AD的延长线于点E,CF⊥AB,垂足为F.求证:AB+AD=2AF.图QM4-1418.如图QM4-15,在△ABC和△ABD中,现给出如下三个论断:①AD=BC;②∠C=∠D;③∠1=∠2.请选择其中两个论断为条件,另一个论断为结论,构造一个真命题.(1)写出所有的真命题(写成“}⇒”的形式,用序号表示):;(2)请选择一个真命题加以证明.图QM4-1519.如图QM4-16是某城市街道的示意图,已知△ABC与△ECD均是等边三角形(即三条边都相等,三个角都相等的三角形),点A,B,C,D,E,F,G,H为中巴车停靠站.(1)图中△ADC与△BEC全等吗?说明理由.(2)中巴车甲从A站出发,按照A→H→G→D→E→C→F的顺序达到F站;中巴车乙从B站出发,沿B→F→H→E→D→C→G的顺序到达G站.若甲、乙分别从A,B站同时出发,在各站耽误的时间相同,两车的平均速度也相同,试问哪一辆中巴车先到达指定站,为什么?图QM4-16类型二有关三角形全等的创新题展示20.已知△ABC的三边分别为a,b,c,△A'B'C'的三边分别为a',b',c',且有a2+a'2+b2+b'2+c2+c'2=2ab'+2bc'+2ca',则△ABC与△A'B'C'()A.一定全等B.不一定全等C.一定不全等D.无法确定21.全等三角形又叫合同三角形,平面内的合同三角形分为真正合同三角形与镜面合同三角形.假设△ABC和△A1B1C1是全等(合同)三角形,且点A与A1对应,点B与B1对应,点C与C1对应,当沿周界A→B→C→A及A1→B1→C1→A1环绕时,若运动方向相同,则称它们是真正合同三角形,如图QM4-17①;若运动方向相反,则称它们是镜面合同三角形,如图②.图QM4-17两个真正合同三角形,都可以在平面内通过平移或旋转使它们重合;而两个镜面合同三角形要重合,则必须将其中一个翻折180°,图QM4-18中的各组合同三角形中,是镜面合同三角形的是()图QM4-1822.我们知道,两边及其中一边的对角分别对应相等的两个三角形不一定全等,那么在什么情况下,它们会全等?(1)阅读与证明:对于这两个三角形均为直角三角形,显然它们全等(证明略);对于这两个三角形均为钝角三角形,可证它们全等(证明略);对于这两个三角形均为锐角三角形,它们也全等,可证明如下:已知:如图QM4-19,△ABC,△A1B1C1均为锐角三角形,AB=A1B1,BC=B1C1,∠C=∠C1,求证:△ABC≌△A1B1C1(请完成证明过程);(2)归纳与叙述:由(1)可得到一个正确的结论,请你写出这个结论.图QM4-19期末复习1.B2.解:如图.(1)作∠MCN=∠α;(2)在射线CM上截取CA=b;(3)以点A为圆心,a为半径画弧交CN于点B;(4)连接AB,则△ABC为所求作的直角三角形.3.B4.C5.C6.B7.558.AB=A'B'BC=B'C'∠A=∠A'∠B=∠B'9.∠DBC=∠ECB或∠EBC=∠DCB或AB=AC或AE=AD等10.①②④11.证明:如图所示,在AB上截取ME=BN,∵∠BMD+∠EMD=180°,∠BMD+∠BND=180°,∴∠EMD=∠BND.在△BND与△EMD中,∵{DN=DM,∠BND=∠EMD,BN=EM,∴△BND≌△EMD(SAS),∴∠DBN=∠MED,BD=DE,∴∠MBD=∠MED,∴∠MBD=∠DBN,∴BD平分∠ABC.12.A13.B14.1215.解:(答案不唯一)如图,取EF的中点O,连接GO并延长交FH于点M,GM就是修直后的公路.理由:设GM分别交AB,CD于点P,Q,由AB∥CD,可得∠PEO=∠QFO.又因为EO=FO,∠EOP=∠FOQ,所以△EOP≌△FOQ,所以这个方案能保持甲、乙二人的土地面积不变.16.证明:在△ABD和△CDB中,∵{AB=CD(已知), AD=CB(已知), BD=DB(公共边),∴△ABD≌△CDB(SSS),∴∠ABD=∠CDB(全等三角形的对应角相等).∵O是BD的中点,∴BO=DO.在△BOE和△DOF中,∵{∠ABO=∠CDO(已证),BO=DO(已证),∠BOE=∠DOF(对顶角相等),∴△BOE≌△DOF(ASA),∴OE=OF(全等三角形的对应边相等).17.证明:∵AC平分∠EAB,CE⊥AD,CF⊥AB,∴CE=CF.又∵DC=BC,∴Rt△DCE≌Rt△BCF,∴DE=BF.在Rt△ACE和Rt△ACF中,{CE=CF,AC=AC,∴Rt△ACE≌Rt△ACF,∴AE=AF.∴AB+AD=AF+BF+AD=AF+DE+AD=AF+AE=2AF.18.解:(1)∠∠}⇒②,∠∠}⇒①(2)选择命题一:∠∠}⇒②.证明:在△ABC和△BAD中,∵BC=AD,∠2=∠1,AB=BA,∴△ABC≌△BAD,∴∠C=∠D.选择命题二:∠∠}⇒①.证明:在△ABC和△BAD中,∵∠C=∠D,∠2=∠1,AB=BA,∴△ABC≌△BAD,∴AD=BC.19.解:(1)△ADC与△BEC全等.理由:∵△ABC与△ECD均是等边三角形,∴AC=BC,EC=DC,∠ACB=∠ECD,∴∠ACD=∠BCE.在△ADC与△BEC中,{AC=BC,∠ACD=∠BCE,DC=EC,∴△ADC≌△BEC(SAS).(2)甲的行驶路程为:AD+DE+EC+CF,乙的行驶路程为:BE+DE+DC+CG,∵△ADC≌△BEC,∴AD=BE,DC=EC(全等三角形的对应边相等),∠DAC=∠EBC(全等三角形的对应角相等).易得△BCF≌△ACG,∴CF=CG,∴两车行驶路程相等.∵两车同时出发,平均速度相同,∴两车同时到达指定站.20.A21.B22.解:(1)证明:分别过点B,B1作BD⊥AC于点D,B1D1⊥A1C1于点D1,如图,则∠BDC=∠B1D1C1=90°.∵BC=B1C1,∠C=∠C1,∴△BCD≌△B1C1D1,∴BD=B1D1.又∵AB=A1B1,∠ADB=∠A1D1B1=90°,∴△ADB≌△A1D1B1,∴∠A=∠A1.又∠C=∠C1,BC=B1C1,∴△ABC≌△A1B1C1.沪科版八年级上册全等三角形期末复习(包含答案)(2)若△ABC,△A1B1C1均为锐角三角形或均为直角三角形或均为钝角三角形,则当两边及其中一边的对角分别对应相等时,它们全等.11 / 11。
2024年沪科版八年级上册数学期末复习极速提分第10招全等三角形的四种基本模型

∴△ ABC ≌△ CDE ( ASA ).∴ AB = CD .
返回
1
2
3
4
AB = DE , BC = EF ,下列结论不一定正确的是(
A. △ ABC ≌△ DEF
B. ∠ B =∠ E
C. ∠ A =∠ F
D. BC ∥ EF
1
2
3
4
C )
返回
分类训练
翻折型
2. [2024·淮北五校联考模拟]如图, AB = AC ,∠ BAD =
∠ CAD ,求证: BD = CD .
【证明】在△ ABD 和△ ACD 中,
=,
ቐ∠=∠,
=,
所以△ ABD ≌△ ACD ( SAS ),
所以 BD = CD .
1
2
3
4
返回
分类训练
旋转型
3. 如图,在△ ABC 和△ ADE 中,∠ BAC =∠ DAE =
90°, AB = AC , AD = AE ,点 C , D , E 在一条直线
即 BC = EF .
∵ AB ∥ DE , AC ∥ DF ,
∴∠ B =∠ DEF ,∠ ACB =∠ F .
∠=∠,
在△ ABC 和△ DEF 中,ቐ=,
∠=∠,
Hale Waihona Puke ∴△ ABC ≌△ DEF ( ASA ).∴ AB = DE .
返回
分类训练
平移型
1. 如图,点 A , D , C , F 在同一条直线上, AD = CF ,
返回
1
2
3
4
分类训练
【证明】∵ AB ⊥ BD , ED ⊥ BD , AC ⊥ CE ,
最新沪科版八年级数学全等三角形复习

最新沪科版八年级数学全等三角形复习一、直角三角形的全等问题[知识]:①直角三角形特有的HL判定定理;②SAS、AAS、ASA、SSS(转化为HL)也是完全适用直角三角形的,不要忘记;③同(等)角的余角相等应用非常广泛(重点).例1、如图1,已知DO⊥BC,OC=OA,OB=OD,求证:△BCE是直角三角形例2、把两个含有45°角的直角三角板如图2放置,点D在BC上,连结BE、AD,AD的延长线交BE于点F.求证:AF⊥BE.,,在同例3、两个大小不同的等腰直角三角形三角板如图3-1所示放置,图3-2是由它抽象出的几何图形,B C E一条直线上,连接CD.(1)请找出图2中的全等三角形,并给予证明(说明:结论中不得含有未标识的字母);(2)证明:CD⊥BE例4、如图4,在△ABC中,高AD与BE相交于点H,且AD=BD,问△BHD≌△ACD,为什么?二、等腰三角形、等边三角形的全等问题[知识]:①等腰三角形腰相等且底角相等,等边三角形三边相等且三个底角都是60度,即“等边对等角,等角对等边”;②如右图,由∠1=∠2,可得∠CBE=∠DBA ;反之也成立;例5、已知在△ABC 中,AB=AC ,在△ADE 中,AD=AE ,且∠1=∠2,求证BD=CE.例6、如图6-1、6-2、6-3过点A 分别作两个个大小不一样的等边三角形,连接BD ,CE ,求证BD=CE.例7、如图7,四边形ABCD 、DEFG 都是正方形,连接AE 、CG ,AE 与CG 相交于点M ,CG 与AD 相交于点N .求证:CG AE ;图7 图88.如图,已知∠ABC=∠DBE=90°,DB=BE ,AB=BC .求证:AD=CE ,AD ⊥CEBC三、截长补短法.①特征:AB=CD+EF ;②在AB 上截取AG=CD ,再根据题意证明GB=EF 即可,即为“截长法”;③若将CD(或EF)延长至H ,使得CH=AB ,再根据题意证明DH=EF 即可,即为“补短法”例9、已知ABC ∆中,60A ∠=,BD 、CE 分别平分ABC ∠和.ACB ∠,BD 、CE 交于点O ,试判断BE 、CD 、BC 的数量关系,并加以证明.图9图10 例10、如图10,ABCD 是正方形,∠FAD =∠FAE . 求证:BE+DF=AE. 例11、如图11,在ABC ∆中,60BAC ∠=︒,AD 是BAC ∠的平分AC AB BD =+,求ABC ∠的度数.线,且图11 图12例12、如图12,在△ABC 中,∠ABC=60°,AD 、CE 分别平分∠BAC 、∠ACB ,求证:AC=AE+CD .四、倍长中线法△ABC 中 方式1: 延长AD 到E ,使DE=AD ,AD 是BC 边中线 连接BE方式2:间接倍长F ED C B A D OE C B A D C B A作CF ⊥AD 于F , 延长MD 到N ,作BE ⊥AD 的延长线于E 使DN=MD ,连接BE 连接CD例13、△ABC 中,AB=5,AC=3,求中线AD 的取值范围例14、如图14,已知在△ABC 中,AD 是BC 边上的中线,E 是AD 上一点,且BE=AC ,延长BE 交AC 于F ,求证:AF=EF图14 图15例15、如图15,在ABC ∆中,AC AB ≠,D 、E 在BC 上,且DE=EC ,过D 作BA DF //交AE 于点F ,DF=AC. 求证:AE 平分BAC ∠。
第14章全等三角形期末复习PPT课件(沪科版)

复习要点 1.全等三角形的定义
能够完全重合的两个三角形称为全等三角形. 2.全等三角形的性质:
全等三角形的对应边相等. 全等三角形的对应角相等. 全等三角形的对应边上的高相等. 全等三角形的对应边上的中线相等. 全等三角形的对应角的平分线相等.
复习要点 3.全等三角形的判定方法
C
D
∴BC=DC.
16. 如图,已知AC=BD, BC、AD相交于点E,且
BC⊥AC,BD⊥AD. AD 是∠BAC的平分线. 求证:BC
是∠ABD的平分线.
C
证明:∵ BC⊥AC,BD⊥AD,
D
∴∠C=∠D=90°.
在△RtABC和Rt△BAD中
AB=BA
A
B
AC=BD
∴ △RtABC ≌ Rt△BAD (HL)
要证:DE=AE-DC A 要证:AE=BD DC=BE 要证: △ABE≌△BCD
D 1E
∠ABE=∠BCD.
B
C
∠ABC=120° ∠D=60°
例2 如图,在△ABC中, ∠ABC=120°, AB=BC,
BD是∠ABC内的射线 ,若连接DC, ∠D=60°,点E是
线段BD上一点,且∠1=60°. 求证:DE=AE-DC.
一般三角形:SSS SAS ASA AAS 直角三角形:HL SAS ASA AAS
结论:判定两个三角形全等的条件中 至少有一组边对应相等.
复习要点
判定两个三角形全等的条件中至少有
一组边对应相等.
4. 判
S SSS
定
S
SAS
全 第一
等 的
找边S
A HL ASA
思
2024年中考数学(沪科版)二轮复习高频考点突破课件 全等三角形

延长C'D交AB'于点H.利用全等三角形的性质、平行线的性质、三角
形的外角的性质证明∠BFC=∠AHC'+∠C'+∠DAC,再求出∠C'+∠AHC'即
可解决问题.
规范解答
如图②,延长C'D交AB'于点H.∵ △AEB≌△AEB',∴ ∠ABE=∠AB’E.
∵ C'H∥EB',∴ ∠AHC'=∠AB'E.∴ ∠ABE=∠AHC'.∵ △ADC≌△ADC’,
(1) 如图①.
① 线段CD和BE之间的数量关系是
CD=BE
.
② 请写出线段AD,BE,DE之间的数量关系并证明.
即可得出结论.
规范解答
(1) ∵ AB⊥CD,
∴ ∠AFC=90°.
∴ ∠BAC+∠ACF=90°.
∵ ∠ACB=90°,
∴ ∠DCE+∠ACF=90°.
∴ ∠BAC=∠DCE.
在△ABC和△CDE中,
∠=∠,
∵ =,
∠=∠,
∴ △ABC≌△CDE(ASA).
(2) ∵ △ABC≌△CDE,
利用全等三角形的性质可以得到相等的角,再利用三角形的内角和定理及其推
论就可以求出相应的角的度数.同样,根据全等三角形的对应边相等可以得到相等
的线段,进而根据线段之间的和差关系就可以求出线段的长.
1. 如图,N,C,A三点在同一条直线上,N,B,M三点在同一条直线上,在△ABC
中,∠A:∠ABC:∠ACB=3:5:10,△MNC≌△ABC,则∠BCM的度数为
EF=160+140=240(海里).∴ 此时甲、乙两舰艇之间的距离是240海里.
沪科版数学八年级上册期末复习专题《全等三角形》PPT

1
2
3
4
5
6
7
8
9
10
11
12
13
14
14. 如图,在△ABC中,分别以AB,AC为边向外作△ABD和△ACE,且AD=AB,
AE=AC,∠DAB=∠CAE=α,CD与BE相交于点O,连接AO.
(1) 求证:BE=DC;
(1) ∵ ∠DAB=∠CAE,∴ ∠DAB+∠BAC=∠CAE
2
3
4
5
6
7
8
9
10
11
12
13
14
12. 如图,在五边形ABCDE中,∠B=∠E=90°,BC=ED,连接AC,AD,∠ACD
=∠ADC.
(1) 求证:△ABC≌△AED;
(1) ∵ ∠ACD=∠ADC,∴ AD=AC.在Rt△ABC
= ,
和Rt△AED中,∵
∴ Rt△ABC≌
= ,
C. (3,2)
D. (-3,2)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
7. 如图所示为一扇窗户的示意图,将窗户打开时,通常用风钩AB将窗户固
定.这样做的数学道理是 三角形具有稳定性 .
8. 如图,在△ABC和△DEF中,点B,E,C,F在同一条直线上,且AB=DE,BC=
EF,请你再添加一个适当的条件: 答案不唯一,如∠B=∠DEF ,使△ABC
C,D;再以点O为圆心,大于OC长为半径画弧,分别交OA,OB于点E,F;连接
CF,DE,则△EOD≌△FOC,其全等的依据是
沪科版八年级数学上册第14章-全等三角形知识例题讲解与练习

第14章 全等三角形【知识剖析】一、全等形:能够完全重合的两个图形,叫做全等形. 二、全等三角形的有关概念1、全等三角形的定义:能够完全重合的两个三角形,叫做全等三角形.2、全等三角形的对应元素:全等三角形中,互相重合的边叫做对应边;互相重合的角叫做对应角;互相重合的顶点叫做对应顶点.3、全等三角形的性质:全等三角形的对应边相等,对应角相等.注:用全等符号“≌”表示两个全等三角形时,通常把表示对应顶点的字母写在对应位置上.[例1] 如图,将△ABC 绕其顶点B 顺时针旋转一定角度后得到△DBE ,请说出图中两个全等三角形的对应边和对应角.[例2] (1)如图,△ABE 与△CED 是全等三角形,可表示为△ABE ≌_______,其中∠A=30°,∠B=70°,AB=3cm ,则∠D=_____,∠DEC =_____,CD=_____.(2)如图,△ABC ≌△DCB ,若CD=4cm ,∠A=28°,∠DBC=35°,则AB=_____,∠D=_____,∠ABC=_______.(3)如图,△AOB ≌△COD ,若CD=2cm ,∠B=45°,则AB=_____,∠D=______.[例3] 如图,△ACB ≌△A /CB /,∠A /CB=30°,∠ACB/=110°,则∠ACA/=______.[例4] 如图,在Rt △ABC 中,∠ACB=90°,且AC=BC=4cm ,已知△BCD ≌△ACE ,则四边形AECD 的面积是_________.[例5] 如图,将△ABC 沿直线DE 折叠后,使得点B 与点A 重合,已知AC=5cm ,△ADC 的周长为17cm ,则BC 的长为_______.[例6] 如图,将矩形纸片ABCD 折叠,使点D 与点B 重合,点C 落在点C /处,折痕为EF ,若∠EFC /=125°,那么∠ABE 的度数为________.三、全等三角形的判定 1、“边角边”定理:两边和它们的夹角对应相等的两个三角形全等.(SAS )ABC 和△DEF 中,AB DEB E BC EF =⎧⎪∠=∠⎨⎪=⎩ABC ≌△DEF 2、.(ASA ) 在△ABC 和△DEF 中,∵ B EBC EF C F ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△ABC ≌△DEF 3、“角角边”定理:两个角和其中一个角的对边对应相等的两个三角形全等.(AAS ) 在△ABC 和△DEF 中,∵B EC F AB DE ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ABC ≌△DEF4、“边边边”定理:三边对应相等的两个三角形全等.(SSS)在△ABC和△DEF中,∵AB DE BC EF AC DF=⎧⎪=⎨⎪=⎩∴△ABC≌△DEF另外,判定两个直角三角形全等还有另一种方法.:斜边和一条直角边对应相等的两个直角三角形全等.(HL)在Rt△ABC和Rt△DEF中,∵AB DEAC DF=⎧⎨=⎩∴ Rt△ABC≌Rt△DEF四、全等三角形的证明思路:⎪⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎪⎨⎧⎩⎨⎧⎪⎪⎩⎪⎪⎨⎧⎪⎩⎪⎨⎧⎪⎩⎪⎨⎧)找任意一边()找两角的夹边(已知两角)找夹已知边的另一角()找已知边的对角()找已知角的另一边(边为角的邻边)任意角(若边为角的对边,则找已知一边一角)找第三边()找直角()找夹角(已知两边AASASAASAAASSASAASSSSHLSAS[例7]如图,已知AB=AE,∠1=∠2,∠B=∠E,求证:BC=ED.[例8]如图,点A、B、C、D在同一条直线上,EA⊥AD,FD⊥AD,AE=DF,AB=DC.求证:∠ACE=∠DBF.[例9]如图,在Rt△ABC中,∠ACB=90°,CA=CB,D是AC上一点,E在BC的延长线上,且AE=BD,BD的延长线与AE交于点F.试通过观察、测量、猜想等方法来探索BF与AE有何特殊的位置关系,并说明你猜想的正确性.[例10] 如图,AC=DF,AD=BE,BC=EF.求证:AC∥DF.[例11]如图,AD是△ABC中BC边上的中线,求证:1()2AD AB AC<+[例12]如图,AB∥CD,EC、EB分别平分∠BCD和∠CBA,点E在AD上,求证:BC=AB+CD.[例13]如图,已知△ABC中,AC=BC=1,∠ABC=90°,把一块含30°角的直角三角板DEF 的直角顶点D放在AC的中点上(直角三角形的短直角边为DE,长直角边为DF),将直角三角板DEF绕D点按逆时针方向旋转.(1)在图(1)中,DE交AB于M,DF交BC于N.①证明DM=DN;②在这一旋转过程中,直角三角板DEF与△ABC的重叠部分为四边形DMBN,请说明四边形DMBN的面积是否发生变化?若发生变化,请说明是如何变化的.若不发生变化,求出其面积. (2)继续旋转至图(2)的位置,延长AB交DE于M,延长BC交DF于N,DM=DN是否仍然成立?若成立,请给出证明;若不成立,请说明理由.(3)继续旋转至图(3)的位置,延长FD交BC于N,延长ED交AB于M,DM=DN是否仍然成立?请写出结论,不用证明.【综合练习】一、选择题1、下列命题中:⑴形状相同的两个三角形是全等形;⑵在两个三角形中,相等的角是对应角,相等的边是对应边;⑶全等三角形对应边上的高、中线及对应角平分线分别相等.其中真命题的个数有( )A、3个B、2个C、1个D、0个2、下列说法正确的是()A.周长相等的两个三角形全等B.有两边和其中一边的对角对应相等的两个三角形全等C.面积相等的两个三角形全等D.有两角和其中一角的对边对应相等的两个三角形全等3、如果两个三角形中两条边和其中一边上的高对应相等,那么这两个三角形的第三条边所对的角的关系是()A. 相等B. 不相等C. 互余或相等D. 互补或相等4、已知△ABC≌△DEF,若∠A=50°,∠C=30°,则∠E等于()A. 30°B. 50°C.60°D.100°5、已知△ABC和△DEF中,∠B=∠E,∠C=∠F,若要△ABC≌△DEF,只要满足下列条件中的()A. AB=DFB.BC=DFC. AC=DED.BC=EF6、如图,AB=AC,EB=EC,那么图中的全等三角形共有()A. 1对B. 2对C.3对D.4对7、某同学不小心把一块三角形玻璃打碎,变成了如图所示的三块,现在要到玻璃店去配一块完全一样的玻璃,那么应带()去,才能配好.A. ①B.②C.③D.任意一块8、已知:的三边分别为,的三边分别为,且有,则与().A.一定全等 B.不一定全等 C.一定不全等 D.无法确定9、如图,已知点E在△ABC的外部,点D在BC边上,DE交AC于F,若∠1=∠2=∠3,AC=AE,则有( )A、△ABD≌△AFDB、△AFE≌△ADCC、△AEF≌△DFCD、△ABC≌△ADE(第9题)(第10题)(第11题)10、如图所示,∠E=∠F=90°,∠B=∠C,AE=AF,结论:①EM=FN;②CD=DN;③∠FAN=∠EAM;④△ACN≌△ABM.其中正确的有()A.1个 B.2个C.3个D.4个11、如图,在△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=64,且BD:CD=9:7,则点D到AB边的距离为( )A、18B、32C、28D、2412、如果D是△ABC中BC边上一点,并且△ADB≌△ADC,则△ABC是()A.锐角三角形 B.钝角三角形 C.直角三角形 D.等腰三角形二、填空题13、已知:△ABC ≌△A ′B ′C ′,∠A=∠A ′,∠B=∠B ′,∠C=70°,AB=15cm ,则∠C ′=_________,A ′B ′=__________.14、如图,在△ABC 和△FED ,AD=FC ,AB=FE ,当添加条件__________时,就可得到△ABC ≌△FED.(只需填写一个你认为正确的条件)(第14题) (第15题) (第16题)15、如图,BE ,CD 是△ABC 的高,且BD =EC ,判定△BCD ≌△CBE 的依据是 . 16、如图,在△ABC 中,AD=DE ,AB=BE ,∠A=80°,则∠CED=_____.17、如图,△ABC ≌△ADE ,BC 的延长线交DA 于点F ,交DE 于点G ,∠D=25°,∠E=105°,∠DAC=16°,则∠DGB=_________.18、如图是重叠的两个直角三角形,将其中一个直角三角形沿BC 方向平移得到△DEF.如果AB=8cm ,BE=4cm ,DH=3cm ,那么图中阴影部分面积为_______cm 2. 三、解答题19、如图,在△ABC 中,F 为AC 的中点,E 为AB 上一点,D 为EF 延长线上一点,∠A=∠ACD.求证://CD AE .20、如图,在△ABC 中,AD ⊥BC ,CE ⊥AB ,垂足分别为D 、E ,AD 、CE 交于点H ,已知EH=EB=3,AE=4,求CH 的长.21、如图,已知AD为△ABC的中线,试比较AB+AC与2AD的大小.22、如图,∠ABC=90°,AB=AC,D为AC上一点,分别过A、C作BD的垂线,垂足分别为E、F.求证:EF=CF-AE.23、(1)如图(1),A、E、F、C在同一条直线上,AE=CF,DE⊥AC,BF⊥AC,若AB=CD. 求证:BD平分EF;(2)若将图形变为图(2),其余条件不变,上述结论是否成立?请说明理由.24、如图(1),已知△ABC中,∠BAC=90°,AB=AC,AE是过点A的一条直线,且点B、C 在AE的两侧,BD⊥AE于点D,CE⊥AE于点E.(1)求证:BD=DE+CE;(2)若直线AE绕点A旋转到图(2)的位置(BD<CE)时,其余条件不变,问BD与DE、CE 的关系如何?请给予证明;(3)若直线AE绕点A旋转到图(3)的位置(BD>CE)时,其余条件不变,问BD与DE、CE 的关系如何?请直接写出结果,不需证明.。
最新沪科版八年级数学上第14章全等三角形复习课件

1、证明两个三角形全等 分析:现在我们已知
A→∠CAB=∠DAB
例1 :如图,点B在AE上 ,∠CAB=∠DAB,要使 ΔABC≌ΔABD,可补充的一 个条件是 ∠∠∠CACCBDB=A=E∠A==∠CD∠.DDBBAE
C
A
B E
S→ AB=AB(公共边) .
①用SAS,需要补充条件 AD=AC, ②用ASA,需要补充条件 ∠CBA=∠DBA, ③用AAS,需要补充条件 ∠C=∠D, ④此外,补充条件
∠CBE=∠DBE也可以 D___________________________
_______________________
1:如图,△AOB≌△COD,AB=7,∠C=60°则
CD= 7
,∠A= 60°
.
B
C
O
A
D
___________________________ _______________________
一、全等三角形性质应用
2:已知△ABC≌△DEF, ∠ A=60°,∠C=50°则
∠E= 70̊
.
A
D
B
(?)
练习1:如图,AE=AD,要使ΔABD≌ΔACE,请你增加一
个条件是
.
E A
D
B C
C
E 1 A 2
B
D
练习2:如图,已知∠1=∠2,AC=AD,增加下列件:①
AB=AE,②BC=ED,③∠C=∠D,④ ∠B=∠E,其中能使
ΔABC≌ΔAED的条件有( )个. B
B.3 C.2 D.1
沪科版 八年级数学课本 第十四章 全等三角形 复习题答案

P 114A 组复习题1.判断正误:(1)两边分别相等且其中一组等边所对的角相等的两个三角形全等.( )(2)两边分别相等的两个直角三角形全等.( )(3)一个锐角和一条直角边分别相等的两个直角三角形全等.( )解:(1)错误 (2)错误 (3)正确2.已知:如图,∠ABC =∠ACB ,BD ,CE 分别是∠ABC ,∠ACB 的平分线.求证:BD =CE.证明:∵∠ABC =∠ACB (已知)BD ,CE 分别是∠ABC ,∠ACB 的平分线,(已知)∴∠CBD =12∠ABC ,∠ECB =12∠ACB ,(角平分线定义)∴∠CBD =∠ECB.(等量代换)在△CBD 和△BCE 中{∠ABC =∠ACB ,(已知)BC =CB (公共边)∠CBD =∠ECB (已证)∴△CBD ≌△BCE ,(ASA)∴BD =CE.(全等三角形对应边相等)3.已知:如图,AB =AC ,DB =DC ,F 是AD 延长线上的一点.求证:∠BFA =∠CFA.证明:在△ABD 和△ACD 中{AB =AC (已知),BD =DC (已知),AD =AD (公共边),∴△ABD ≌△ACD (SSS ),∴∠BAF =∠CAF (全等三角形对应角相等).在△BAF 和△CAF 中{AB =AC (已知),∠BAF =∠CAF (已证),AF =AF (公共边),∴△BAF ≌△CAF ,(SAS)∴∠BFA =∠CFA (全等三角形对应角相等).4.已知:如图,在直角三角形ABC 中,∠ABC =90°,点D 在BC 的延长线上,且BD =AB ,过点B 作BE ⊥AC ,与BD 的垂线DE 交于点E.求证:△ABC ≌△BDE.证明:∵BE ⊥AC (已知)∴∠ACB +∠EBD =90°,(直角三角形两锐角互余)∵在直角三角形ABC 中,∠ABC =90°(已知)∴∠ACB +∠A =90°(直角三角形两锐角互余),∴∠A =∠EBD.(同角的余角相等)∵与BD 的垂线DE 交于点E (已知)∴∠D =90°(垂直的定义)在△ABC 和△BDE 中{∠ABC =∠D =90°(等量代换),AB =BD (已知),∠A =∠EBD (已证),∴△ABC ≌△BDE.(ASA)5.已知:如图,在Rt △ABC 中,∠ACB =90°,BC =2 cm ,CD ⊥AB ,在AC 上取一点E , 使EC =BC ,过点E 作EF ⊥AC ,交CD 的延长线于点F ,若EF =5 cm ,求AE 的长度.解:∵CD ⊥AB ,∴∠A +∠ACD =90°.又∵∠ACB =90°,∴∠A +∠B =90°,∴∠B =∠ACD ,即∠B =∠ECF.在△ACB 和△FEC 中,∵⎩⎪⎨⎪⎧∠ACB =∠FEC ,BC =CE ,∠B =∠ECF.∴△ACB ≌△FEC ,(ASA)∴AC =EF.∴AE =AC -CE =EF -BC =5-2=3.6.已知:如图,在△ABD和△CBE中,AD与BE交于点F,CE与BD交于点G,AB=CB,∠AFB =∠CGB,∠ABE=∠CBD.求证:AD=CE.证明:∵∠C=180°-∠CGB-∠CBD,∠A=180°-∠AFB-∠ABE,(三角形内角和等于180°)∠CGB=∠AFB,∠CBD=∠ABE.(已知)∴∠C=∠A.(等量代换)∵∠CBD=∠ABE.(已知)∴∠CBD+∠DBE=∠ABE+∠DBE(等式的性质),即∠CBE=∠ABD.在△CBE与△ABD中,{∠C=∠A(已证). AB=CB(已知)∠CBE=∠ABD(已证).∴△CBE≌△ABD,(ASA)∴AD=CE(全等三角形对应边相等).7.已知:如图,AB=AD,CB=CD.求证:∠B=∠D.证明:连结AC,在△ADC和△ABC中,{AD=AB(已知),DC=BC(已知),AC=AC(公共边),∴△ADC≌△ABC,(SSS)∴∠B=∠D(全等三角形对应角相等).8.已知:如图,AB=DC,AD=BC.求证:(1)AB∥DC,AD∥BC;(2)∠A=∠C,∠B=∠D.证明:连结AC.在△ADC和△ABC中,{DC=AB(已知),AD=BC(已知),AC=AC(共公边),∴△ADC≌△CBA,(SSS)∴∠D=∠B,∠DAC=∠BCA,∠DCA=∠BAC,(全等三角形对应角相等) (1)由∠DAC=∠BCA得AD∥BC,(内错角相等,两直线平行)由∠DCA=∠BAC得AB∥DC,(内错角相等,两直线平行)(2)由∠DAC=∠BCA,∠DCA=∠BAC,则∠DAC+∠BAC=∠BCA+∠DCA(等式的性质),∴∠DAB=∠DCB,即∠A=∠C.∴∠B=∠D(已证).9.如图,在雨伞的截面图中,伞骨AB =AC ,支撑杆OE =OF ,AE =13AB ,AF =13AC.当点O 沿AD 滑动时,雨伞开闭.问雨伞开闭过程中,∠BAD 与∠CAD 有什么关系?说明理由.解:∠BAD=∠CAD .理由:∵AB =AC ,AE =13AB ,AF =13AC , ∴AE =AF.在△AEO 和△AFO 中{AE =AF .(已证)OE =OF (已知)AO =AO (公共边)∴△AEO ≌△AFO ,(SSS)∴∠BAD =∠CAD (全等三角形对应角相等).10.已知:如图,AD 为△ABC 的中线,BE ⊥AD ,垂足为点E ,CF ⊥AD ,垂足为点F.求证:BE =CF.证明:∵AD 是BC 的中线(已知),∴BD =DC (中线的定义).∵BE ⊥AD ,CF ⊥AD (已知)∴∠E =∠DFC =90°(垂直的定义)在△BDE 和△CDF 中,{∠E =∠DFC =90°(已证)∠BDE =∠CDF (对顶角相等)BD =DC (已知)∴△BDE ≌△CDF ,(AAS)∴BE =CF.(全等三角形对应边相等)11.已知:如图,AB ⊥AC ,且AB =AC ,AD =AE ,BD =CE.试问:AD 与AE 是否垂直?若是,请给出证明;若不是,试说出理由.解:AD ⊥AE.证明:∵AB =AC ,AD =AE ,BD =CE ,(已知)∴△ABD ≌△ACE.(SSS)∴∠BAD =∠CAE (全等三角形对应角相等).∴∠BAD -∠DAC =∠CAE -∠DAC (等式的性质),即∠BAC =∠DAE又∵AB ⊥AC (已知)∴∠BAC=90°(垂直的定义),∴∠DAE=90°(等量代换)∴AD ⊥AE.(垂直的定义)12.已知:如图,在△ABC 中,∠BAC =90°,AB =AC ,直线MN 经过点A ,BD ⊥MN ,CE ⊥MN ,垂足分别为点D ,E.试判断BD +CE 与DE 的关系,并给出证明.解:BD +CE =DE.证明:∵∠BAC =90°(已知),∴∠BAD +∠CAE =90°(平角的定义),而∠BAD +∠ABD =90°(直角三角形两锐角互余),∴∠ABD =∠CAE (同角的余角相等).∵BD ⊥MN ,CE ⊥MN ,(已知)∴∠ADB =∠CEA =90°(垂直的定义),在△ABD 和△CAE 中,{∠ABD =∠CAE (已证),∠ADB =∠CEA =90°(已证)AB =AC (已知),∴△ABD ≌△CAE ,(AAS)∴BD =AE ,AD =CE (全等三角形对应边相等),∴BD +CE =AE +AD =DE.(等式的性质)即BD +CE =DE13.已知:如图,AB =AC ,AD =AE ,BD ,CE 相交于点O.(1)求证:OD =OE ;(2)AO 平分∠BAC 吗?为什么?解:(1)证明:在△ABD 和△ACE 中{AB =AC (已知),∠BAD =∠CAE (公共角),AD =AE (已知),∴△ABD ≌△ACE ,(SAS)∴∠B =∠C (全等三角形对应角相等).∵AB =AC ,BE =CD (已知).∴AB -AD =AC -AE (等式的性质)即BE=CD在△OBE 和△OCD 中{∠BOE =∠COD (对顶角相等),∠B =∠C (已证),BE =CD (已证)∴△OBE ≌△OCD ,(AAS)∴OD =OE (全等三角形对应边相等).(3) 平分.理由:∵AB =AC ,OB =OC(全等三角形对应边相等),∠B =∠C ,∴△AOB ≌△AOC ,(SAS)∴∠BAO =∠CAO ,即AO 平分∠BAC.P116B组复习题1.已知:如图,AB=CD,∠A=∠D,要使△AEC≌△DFB,还需增加一个什么条件?说出你增加的条件及理由.解:可以增加AE=DF或∠E=∠F或∠ACE=∠BDF,增加AE=DF的理由:∵AB=CD∴AB+BC=CD+BC即AC=BD,又∠A=∠D,故△AEC≌△DFB(SAS)增加∠E=∠F的理由:∵AB=CD∴AB+BC=CD+BC即AC=BD,又∠A=∠D,故△AEC≌△DFB(AAS)增加∠ACE=∠BDF的理由:∵AB=CD∴AB+BC=CD+BC即AC=BD,又∠A=∠D,故△AEC≌△DFB(ASA)2.已知:在△ABC中,CA=CB,∠C=90°,D为AB上任一点,AE⊥CD,垂足为点E,BF⊥CD,垂足为点F.求证:EF=|AE-BF|.证明:当点D靠近点A时,如图所示:∵在Rt△ACE中,∠CAE+∠ACE=90°(直角三角形两锐角互余),在Rt△ABC中,∠A CB=90°(已知)即∠BCD+∠ACE=90°,∴∠CAE=∠BCD(同角的余角相等).∵AE⊥CD,BF⊥CD,(已知)∴∠E=∠CFB=90°(垂直的定义)在△ACE和△CBF中,{∠CAE=∠BCD(已证),∠E=∠CFB=90°(已证)C A=C B(已知)∴△CAE≌△BCF.(AAS)∴AE=CF,CE=BF.(全等三角形对应边相等)∵EF=CE-CF,∴EF=BF-AE.同理,当点D靠近点B时,EF=AE-BF.所以EF=||AE-BF.。
2024年沪科版八年级上册数学期末复习极速提分第9招全等三角形判定的三种类型

BC , AE = BF , CE = DF . 求证:
(1)△ AEC ≌△ BFD ;
返回
1
2
3
4
5
6
7
分类训练
【证明】∵ AD = BC ,
∴ AD + DC = BC + DC ,即 AC = BD .
在△ AEC 和△ BFD 中,
=,
∴△ ABC ≌△ ADC ( SSS ).∴∠ B =∠ D .
返回
分类训练
已知一边一角型
方法1 一次全等型
1. 如图,在Rt△ ABC 中,∠ B =90°, CD ∥ AB , DE ⊥
AC 于点 E ,且 CE = AB .
求证:△ CED ≌△ ABC .
返回
1
2
3
4
5
6
7
分类训练
∴ BF + EF = CF + DF ,即 BE = CD .
∠=∠,
在△ ABE 和△ ACD 中,ቐ∠=∠,
=,
∴△ ABE ≌△ ACD ( AAS ).
∴ AB = AC ,即△ ABC 是等腰三角形.
返回
1
2
3
4
5
6
7
分类训练
3. 如图,在四边形 ABCD 中, E 是 AB 的中点, AD ∥ EC ,
∠ AED =∠ B .
(1)求证:△ AED ≌△ EBC ;
【证明】∵ AD ∥ EC ,
∴∠ A =∠ BEC .
∵ E 是 AB 的中点,∴ AE = EB = AB .
又∵∠ AED =∠ B ,∴△ AED ≌△ EBC ( ASA ).
沪科版八年级数学上册第14章 全等三角形单元复习讲义(含答案)
第14章全等三角形14.1全等三角形01基础题知识点1认识全等形1.下列图形是全等形的是(B)2.(芜湖无为县期末)下列说法正确的是(C)A.两个面积相等的图形一定是全等形B.两个长方形是全等形C.两个全等形形状一定相同D.两个正方形一定是全等形知识点2全等三角形及对应元素3.(合肥长丰县期末)下列说法正确的是(D)A.全等三角形是指形状相同的两个三角形B.全等三角形是指面积相等的两个三角形C.两个等边三角形是全等三角形D.全等三角形是指两个能完全重合的三角形4.如图,沿直线AC对折,△ABC与△ADC重合,则△ABC≌△ADC,AB的对应边是AD,AC的对应边是AC,∠BCA的对应角是∠DCA.5.(教材P95练习T2变式)如图,△ABC≌△CDA,AB与CD是对应边,请回答下列问题:(1)找出对应角和另外两组对应边;(2)用对应边找对应角,用对应角找对应边有何规律?解:(1)对应角:∠BAC与∠DCA,∠ACB与∠CAD,∠B与∠D.其他对应边:BC与DA,AC与CA.(2)对应边所对的角是对应角,对应角所对的边是对应边.知识点3全等三角形的性质6.(淮南期中)△ABC≌△DEF,下列结论中不正确的是(D)A .AB =DE B .BE =CFC .BC =EFD .AC =DE7.(马鞍山当涂县期末)如图,△ABC ≌△A ′B ′C ′,其中∠A =36°,∠C ′=24°,则∠B =120°.第7题图 第8题图8.如图所示,点C 为直线BE 上一点,△ABC ≌△ADC ,∠DCF =∠ECF ,则AC 和CF 的位置关系是互相垂直.9.(蚌埠期末)一个三角形的三边长为6,10,x ,另一个三角形的三边长为y ,6,12.如果这两个三角形全等,那么x +y =22.【变式】 变式点:对应边确定→对应边不确定已知△ABC 的三边长分别为3,5,7,△DEF 的三边长分别为3,3x -2,2x -1.若这两个三角形全等,则x 等于(C )A .73B .4C .3D .3或73易错点 忽略全等三角形中的对应关系10.(池州石台县期末)已知图中的两个三角形全等,则∠1等于(C)A .70°B .50°C .60°D .120°11.(合肥庐江县期中)已知△ABC ≌△FED ,若△ABC 的周长为32,AB =8,BC =12,则FD 的长为12.02 中档题12.如图,△ABC ≌△EBD ,AB =4 cm ,BD =7 cm ,则CE 的长度为(B) A .2 cm B .3 cm C .3.5 cm D .4 cm第12题图 第13题图13.(合肥肥东县期末)如图,△ABC ≌△DBE ,点D 在线段AC 上,线段BC 与DE 交于点F.下面各项中,不能推导出的结论是(D)A .∠EBF =∠ABDB .∠EBF =∠FDC C .∠ABD =∠FDC D .∠ABD =∠FBD14.(安庆期末)如图所示,△ABC ≌△ADE ,BC 的延长线交DA 于点F ,交DE 于点G.若∠ACB =105°,∠CAD =15°,∠B =30°,则∠1的度数为60°.15.如图所示,已知△ABC ≌△DEF ,且B ,E ,C ,F 在同一条直线上. (1)BE =CF 吗?试说明理由;(2)如果∠A =50°,求∠D 和∠EGC 的度数.解:(1)BE =CF.理由:∵△ABC ≌△DEF , ∴BC =EF.∴BC -EC =EF -EC ,即BE =CF.(2)∵△ABC ≌△DEF ,∴∠D =∠A =50°,∠B =∠DEF.∴AB ∥DE.∴∠EGC =∠A =50°.16.(教材P 96习题T 4变式)如图,△ABC ≌△ADE ,∠DAC =60°,∠BAE =100°,BC ,DE 相交于点F ,求∠DFB 的度数.解:∵△ABC ≌△ADE ,∴∠B =∠D ,∠BAC =∠DAE.又∵∠BAD =∠BAC -∠DAC ,∠CAE =∠DAE -∠DAC , ∴∠BAD =∠CAE.∵∠DAC =60°,∠BAE =100°, ∴∠BAD =12(∠BAE -∠DAC)=20°.∵在△ABG 和△FDG 中,∠B =∠D ,∠AGB =∠FGD , ∴∠DFB =∠BAD =20°.03 综合题17.如图所示,已知在△ABC 中,AB =AC =10 cm ,BC =8 cm ,D 为AB 的中点,点P 在线段BC 上以3 cm /s 的速度由点B 向点C 运动.同时,点Q 在线段CA 上由点C 向点A 以a cm /s 的速度运动,设运动的时间为t s .(1)求CP 的长;(用含t 的式子表示)(2)若以C ,P ,Q 为顶点的三角形和以B ,D ,P 为顶点的三角形全等,且∠B 和∠C 是对应角,求a 的值.解:(1)∵BP =3t cm ,BC =8 cm ,∴CP =(8-3t)cm .(2)①若△BDP ≌△CPQ ,则BD =CP ,BP =CQ. ∵AB =10 cm ,D 为AB 的中点,∴BD =5 cm .∴5=8-3t ,解得t =1.∵BP =CQ ,∴3t =at ,解得a =3;②若△BDP ≌△CQP ,则BP =CP ,BD =CQ , ∴3t =8-3t ,解得t =43.∵BD =CQ ,∴5=a ×43,解得a =154.综上所述,a 的值为3或154.14.2 三角形全等的判定14.2.1 两边及其夹角分别相等的两个三角形(SAS )01 基础题知识点1 用SAS 判定三角形全等1.下图中全等的三角形有(D )A .图1和图2B .图2和图3C .图2和图4D .图1和图32.如图,AC ,BD 相交于点O ,若OA =OD ,用“SAS ”证明△AOB ≌△DOC ,还需添加条件(B) A .∠AOB =∠DOC B .OB =OC C .∠C =∠D D .AB =CD第2题图 第3题图3.(教材P112习题4变式)已知:如图,点E ,A ,C 在同一条直线上,AB ∥CD ,AB =CE ,AC =CD ,可利用“SAS ”来判定△ABC ≌△CED .4.(南充中考)如图,已知AB =AD ,AC =AE ,∠BAE =∠DAC.求证:∠C =∠E.证明:∵∠BAE =∠DAC ,∴∠BAE -∠CAE =∠DAC -∠CAE , 即∠BAC =∠DAE.在△ABC 和△ADE 中,⎩⎨⎧AB =AD ,∠BAC =∠DAE ,AC =AE ,∴△ABC ≌△ADE(SAS ).∴∠C =∠E.5.(合肥瑶海区期末)已知:如图,AB =DE ,AB ∥DE ,BE =CF ,且点B ,E ,C ,F 都在一条直线上,求证:AC ∥DF.证明:∵AB ∥DE , ∴∠B =∠DEC.又∵BE =CF ,∴BC =EF.在△ABC 和△DEF 中,⎩⎨⎧AB =DE ,∠B =∠DEF ,BC =EF ,∴△ABC ≌△DEF(SAS ). ∴∠ACB =∠F. ∴AC ∥DF.知识点2 SAS 的应用6.【关注社会生活】如图所示,有一块三角形镜子,小明不小心将它打破成1、2两部分,现需配成同样大小的一面镜子.为了方便起见,需带上1号部分,其理由是有两边及其夹角对应相等的两个三角形全等.第6题图 第7题图7.把两根钢条AC ,BD 的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳).如图,若测得AB =5厘米,则槽宽CD 为0.05米.易错点1 考虑问题不全面而出错8.(合肥庐阳区校级月考)如图,AC ,BD 相交于点O ,且AO =CO ,BO =DO ,则图中全等的三角形有(A )A .4对B .3对C .2对D .1对易错点2 忽略两边一角中的角是两边的夹角这一特征而致错9.(铜陵义安区期末)如图,已知AB =DE ,BE =CF ,添加下列条件中哪一个能使△ABC ≌△DEF(B)A .∠A =∠DB .AB ∥DEC .BE =ECD .AC ∥DF02 中档题10.(教材P 100练习T 2变式)如图所示,O 为AC 的中点,如果要利用“SAS ”来判定△AOB ≌△COD ,那么应补充的一个条件是(D )A .∠A =∠CB .AB =CDC .∠B =∠CD .OB =OD11.(淮南潘集区期中)如图,在△ABC 中,∠A =∠B =50°,AK =BN ,AM =BK ,则∠MKN 的度数是(A )A .50°B .60°C .70°D .100°12.(宜昌中考)如图,在△ABC 中,D 是BC 边上的一点,AB =DB ,BE 平分∠ABC ,交AC 边于点E ,连接DE.(1)求证:△ABE ≌△DBE ;(2)若∠A =100°,∠C =50°,求∠AEB 的度数.解:(1)证明:∵BE 平分∠ABC , ∴∠ABE =∠DBE.在△ABE 和△DBE 中,⎩⎨⎧AB =DB ,∠ABE =∠DBE ,BE =BE ,∴△ABE ≌△DBE(SAS ).(2)∵∠A =100°,∠C =50°, ∴∠ABC =180°-∠A -∠C =30°. ∵BE 平分∠ABC ,∴∠ABE =∠DBE =12∠ABC =15°.∴∠AEB =180°-∠A -∠ABE =180°-100°-15°=65°.13.(教材P111习题T3变式)如图,点D ,E 分别是△ABC 的边AB ,AC 的中点,点F 在DE 的延长线上,且EF =DE .求证:(1)BD =FC ; (2)AB ∥CF .证明:(1)∵E 为AC 的中点, ∴AE =EC .在△AED 和△CEF 中,⎩⎨⎧AE =CE ,∠AED =∠CEF ,ED =EF ,∴△AED ≌△CEF (SAS). ∴AD =CF .又∵点D 为AB 的中点, ∴AD =BD .∴BD =CF .(2)由(1)知△AED ≌△CEF ,∴∠ADE =∠F .∴AB ∥FC .14.(亳州期末)如图,C 是线段AB 的中点,CD 平分∠ACE ,CE 平分∠BCD ,CD =CE. (1)求证:△ACD ≌△BCE ;(2)若∠D =50°,求∠B 的度数.解:(1)证明:∵点C 是线段AB 的中点, ∴AC =BC.又∵CD 平分∠ACE ,CE 平分∠BCD , ∴∠ACD =∠DCE ,∠DCE =∠BCE. ∴∠ACD =∠BCE.在△ACD 和△BCE 中,⎩⎨⎧CD =CE ,∠ACD =∠BCE ,AC =BC ,∴△ACD ≌△BCE(SAS ).(2)∵∠ACD +∠DCE +∠ECB =180°, ∠ACD =∠DCE =∠ECB , ∴∠ACD =∠DCE =∠ECB =60°. ∵△ACD ≌△BCE ,∴∠E =∠D =50°.∴∠B =180°-∠E -∠ECB =70°.03综合题15.(内江中考)如图,在Rt△ABC中,∠BAC=90°,AC=2AB,点D是AC的中点,将一块锐角为45°的直角三角板如图放置,使三角板斜边的两个端点分别与A,D重合,连接BE,EC.试猜想线段BE和EC的数量及位置关系,并证明你的猜想.解:BE=EC,BE⊥EC.证明:∵AC=2AB,点D是AC的中点,∴AB=AD=CD.∵∠EAD=∠EDA=45°,∴∠EAB=∠EDC=135°.∵EA=ED,∴△EAB≌△EDC(SAS).∴∠AEB=∠DEC,EB=EC.∴∠AEB+∠BED=∠DEC+∠BED.∴∠BEC=∠AED=90°.∴BE=EC,BE⊥EC.16.(淮南谢家集区期末)如图,已知方格纸中是4个相同的小正方形,则∠1+∠2的度数为90°.14.2.2 两角及其夹边分别相等的两个三角形(ASA)01 基础题知识点1 用ASA 判定三角形全等1.如图,已知△ABC 的三条边和三个角六个元素,则下面甲、乙、丙三个三角形中和△ABC 全等的图形是(D )A .只有乙B .只有丙C .甲和乙D .乙和丙2.下列能判定△ABC ≌△DEF 的条件是(D ) A .AB =DE ,BC =EF ,∠A =∠E B .AB =DE ,BC =EF ,∠C =∠E C .∠A =∠E ,AB =EF ,∠B =∠D D .∠A =∠D ,AB =DE ,∠B =∠E3.如图所示,已知∠ABC =∠DEF ,AB =DE ,若以“ASA”为依据说明△ABC ≌△DEF ,还需添加的一个条件为(A)A .∠A =∠DB .∠ACB =∠DFEC .BC =EFD .BE =CF第3题图 第4题图4.如图,点P 在∠AOB 的平分线上,∠APO =∠BPO ,则根据ASA 就可判定△AOP ≌△BOP. 5.(教材P 112习题T 5变式)(福州中考)如图,∠1=∠2,∠3=∠4,求证:AC =AD.证明:∵∠3=∠4, ∴∠ABC =∠ABD.在△ABC 和△ABD 中,⎩⎨⎧∠1=∠2,AB =AB ,∠ABC =∠ABD ,∴△ABC ≌△ABD(ASA ). ∴AC =AD.6.(教材P 102练习T 1变式)如图,∠1=∠2,∠ABC =∠DCB.求证:AB =DC.证明:∵∠ABC =∠DCB ,∠1=∠2, ∴∠ABC -∠1=∠DCB -∠2, 即∠DBC =∠ACB.在△ABC 和△DCB 中,⎩⎨⎧∠ACB =∠DBC ,BC =CB ,∠ABC =∠DCB ,∴△ABC ≌△DCB(ASA ).∴AB =DC.知识点2 ASA 的应用7.(教材P112习题T6变式)如图,一块三角形玻璃碎成了4块,现在要到玻璃店去配一块与原来的三角形玻璃完全一样的玻璃,那么最省事的办法是带________去(D)A .①B .②C .③D .④ 8.【关注热点信息】某同学沿一段笔直的人行道行走,在由A 步行到达B 处的过程中,通过隔离带的空隙O ,刚好浏览完对面人行道宣传墙上的社会主义核心价值观标语.其具体信息汇集如下:如图,AB ∥OH ∥CD ,相邻两平行线间的距离相等.AC ,BD 相交于点O ,OD ⊥CD ,垂足为D.已知AB =25m .根据上述信息,标语CD 的长度为25m .9.(教材P 102例4变式)如图,要测量水池的宽AB ,可过点A 作直线AC ⊥AB ,再由点C 观测,在BA 延长线上找一点B′,使∠ACB′=∠ACB ,这时只要量出AB′的长,就知道AB 的长,为什么?解:在测量过程中,∵AC ⊥AB , ∴∠CAB =∠CAB′=90°. 在△ACB 和△ACB′中,⎩⎨⎧∠CAB =∠CAB′,AC =AC ,∠ACB =∠ACB′,∴△CAB ≌△CAB ′(ASA ).∴AB =AB′.易错点 弄错全等三角形中对应元素而出错10.如图,∠B =∠ACD ,∠ACB =∠D =90°,AC 是△ABC 和△ACD 的公共边,所以就可以判定△ABC ≌△ACD.你认为正确吗?答:不正确.因为AC 虽是两三角形公共边但不是它们的对应边,所以不能全等.02 中档题11.如图,AB ∥CD ,点C 是BE 的中点,利用“ASA ”证明△ABC ≌△DCE ,还需要的条件是(C ) A .AB =DC B .∠A =∠D C .AC ∥DE D .AC =DE第11题图 第12题图 12.如图,AC =AE ,∠C =∠E ,∠CDE =55°,则∠ABE =125°.13.(池州石台县期末)如图,∠A =∠B ,AE =BE ,点D 在AC 边上,∠1=∠2,AE 和BD 相交于点O.求证:△AEC ≌△BED.证明:∵∠AOD =∠BOE ,∠A =∠B , ∴∠BEO =∠2. 又∵∠1=∠2, ∴∠1=∠BEO. ∴∠AEC =∠BED.在△AEC 和△BED 中,⎩⎨⎧∠A =∠B ,AE =BE ,∠AEC =∠BED ,∴△AEC ≌△BED(ASA ).14.(淮南谢家集区期中)如图,点B ,F ,C ,E 在一条直线l 上(点F ,C 之间不能直接测量),点A ,D 在直线l 的异侧,测得AB =DE ,AB ∥DE ,AC ∥DF.(1)求证:△ABC ≌△DEF ;(2)若BE =14 m ,BF =5 m ,求FC 的长度.解:(1)证明:∵AB ∥DE , ∴∠ABC =∠DEF. ∵AC ∥DF , ∴∠ACB =∠EFD. ∴∠A =∠D.在△ABC 和△DEF 中,⎩⎨⎧∠ABC =∠DEF ,AB =DE ,∠A =∠D ,∴△ABC ≌△DEF(ASA ). (2)∵△ABC ≌△DEF , ∴BC =EF.∴BF +FC =EC +FC. ∴BF =EC.∵BE =14 m ,BF =5 m ,∴FC =14-5-5=4(m ).15.(陕西中考)如图,已知:AB =AC ,D ,E 两点分别在AB ,AC 上,且AD =AE ,求证:△BDF ≌△CEF.证明:在△ABE 和△ACD 中,⎩⎨⎧AB =AC ,∠A =∠A ,AE =AD ,∴△ABE ≌△ACD(SAS ). ∴∠B =∠C.∵∠BDF =∠A +∠C ,∠CEF =∠A +∠B , ∴∠BDF =∠CEF.∵AB =AC ,AD =AE ,∴BD =CE. 在△BDF 和△CEF 中,⎩⎨⎧∠B =∠C ,BD =CE ,∠BDF =∠CEF ,∴△BDF ≌△CEF(ASA ).03 综合题16.(亳州涡阳县期末)如图,在Rt △ABC 中,∠ACB =90°,BC =2 cm ,CD ⊥AB ,在AC 上取一点E ,使EC =BC ,过点E 作EF ⊥AC 交CD 的延长线于点F ,若EF =5 cm ,求AE 的长.解:∵EF ⊥AC ,∴∠FEC =90°. ∵∠ACB =90°,∴∠ACB =∠FEC ,∠ECF +∠BCD =90°. ∵CD ⊥AB ,∴∠BCD +∠B =90°. ∴∠ECF =∠B.在△FCE 和△ABC 中,⎩⎨⎧∠ECF =∠B ,EC =CB ,∠FEC =∠ACB ,∴△FCE ≌△ABC(ASA ). ∴EF =AC.∵BC =2 cm ,EF =5 cm , ∴AE =AC -CE =EF -BC =3 cm .14.2.3 三边分别相等的两个三角形(SSS )01 基础题知识点1 用SSS 判定三角形全等1.如图,在△ABC 中,AB =AC ,EB =EC ,则由“SSS ”可以直接判定(B )A .△ABD ≌△ACDB .△ABE ≌△ACEC .△BDE ≌△CDED .以上答案都不对2.如图,AD =BC ,AC =BD ,用三角形全等的判定“SSS”可证明△ADC ≌△BCD 或△ABD ≌△BAC .第2题图 第3题图3.(教材P105练习T3变式)如图,在△ABC 中,AB =AC ,D ,E 两点在BC 上,且有AD =AE ,BD =CE .若∠BAD =30°,∠DAE =50°,则∠BAC 的度数为110°.4.(蒙城六中段考)如图,点B ,E ,C ,F 在同一条直线上,AB =DE ,AC =DF ,BE =CF.求证:∠A =∠D.证明:∵BE =CF ,BC =BE +EC ,EF =EC +CF. ∴BC =EF.在△ABC 和△DEF 中,⎩⎨⎧AB =DE ,BC =EF ,AC =DF ,∴△ABC ≌△DEF(SSS ). ∴∠A =∠D.5.(六安月考)如图,AB ⊥AC ,且AB =AC ,AD =AE ,BD =CE.求证:AD ⊥AE.证明:在△ABD 和△ACE 中,⎩⎨⎧AB =AC ,AD =AE ,BD =CE ,∴△ABD ≌△ACE(SSS ). ∴∠EAC =∠DAB. ∴∠DAE =∠BAC.∵AB ⊥AC ,∴∠BAC =90°. ∴∠DAE =90°,即AD ⊥AE.6.(教材P112习题T8变式)思考:一个平分角的仪器如图1所示,其中AB =AD ,BC =DC ,将点A 放在角的顶点,AB 和AD 沿着角的两边放下,沿AC 画一条射线AE ,AE 就是这个角的平分线,请说明理由.操作:如图2,利用直尺和圆规作已知角平分线的作法如下:①以点O 为圆心,适当长为半径画弧,交OA 于点M ,交OB 于点N .②分别以点M ,N 为圆心,大于12MN 的长为半径画弧在∠AOB 的内部相交于点C .③画射线OC ,射线OC 即为所求.根据以上作法可知,△OMC ≌△ONC 的依据是SSS .应用:工人师傅常用角尺平分一个任意角,作法如下:如图3,∠AOB 是一个任意角,在边AO ,OB 上分别取OM =ON ,移动角尺,使角尺两边相同的刻度分别与点M ,N 重合,过角尺顶点C 作射线OC ,求证:∠MCD =∠NCD .解:思考:在△ABC 和△ADC 中,⎩⎨⎧AB =AD ,BC =DC ,AC =AC ,∴△ABC ≌△ADC (SSS). ∴∠BAC =∠DAC .∴AE 是∠BAD 的平分线.应用:证明:在△OMC 和△ONC 中,⎩⎨⎧OM =ON ,MC =NC ,OC =OC ,∴△OMC ≌△ONC (SSS). ∴∠MCO =∠NCO .∵∠MCO +∠MCD =180°,∠NCO +∠NCD =180°, ∴∠MCD =∠NCD .知识点2 三角形的稳定性7.(合肥包河区期末)空调安装在墙上时,一般都会采用如图所示的方法固定,这种方法应用的几何原理是三角形具有稳定性.第7题图 第8题图8.(安徽期中)如图,要使四边形木架(用四根木条钉成)不变形,至少要再钉上的木条的根数为1条.02 中档题9.(蚌埠怀远县期末)如图,AB =AD ,CB =CD ,∠B =30°,∠BAD =50°,则∠BCD 的度数是(A ) A .110° B .100° C .120° D .80°第9题图 第10题图10.(蒙城段考)如图,AB =CD ,BC =DA ,点E ,F 在AC 上,且AE =CF ,则图中的全等三角形有(C) A .1对 B .2对 C .3对 D .4对11.(合肥庐阳区校级月考)如图,在①AB =AC ;②AD =AE ;③∠B =∠C ;④BD =CE 四个条件中,能证明△ABD 与△ACE 全等的条件顺序是(C)A .①②③B .②③④C .①②④D .③②④12.(安庆望江期末)如图,AC =BD ,AB =DC.求证:∠B =∠C.证明:连接AD ,在△ABD 和△DCA 中,⎩⎨⎧AB =DC ,AC =DB ,AD =DA ,∴△ABD ≌△DCA(SSS ). ∴∠B =∠C.13.(合肥长丰县期末)已知,如图,A ,D ,C ,B 在同一条直线上,AD =BC ,AE =BF ,CE =DF ,求证: (1)DF ∥CE ; (2)DE =CF.证明:(1)∵AD =BC , ∴AC =BD.又∵AE =BF ,CE =DF , ∴△ACE ≌△BDF(SSS ). ∴∠FDC =∠ECD. ∴DF ∥CE.(2)由(1)可得△ACE ≌△BDF , ∴∠A =∠B.又∵AD =BC ,AE =BF , ∴△ADE ≌△BCF(SAS ). ∴DE =CF.03 综合题14.(阜阳十九中月考)如图,在一个风筝ABCD 中,AB =AD ,BC =DC ,分别在AB ,AD 的中点E ,F 处挂两根彩线EC ,FC.求证:EC =FC.证明:连接AC.在△ABC 和△ADC 中,⎩⎨⎧AB =AD ,BC =DC ,AC =AC ,∴△ABC ≌△ADC(SSS ). ∴∠EAC =∠FAC.∵E ,F 分别是AB ,AD 的中点, ∴AE =12AB ,AF =12AD.∵AB =AD ,∴AE =AF.在△AEC 和△AFC 中,⎩⎨⎧AE =AF ,∠EAC =∠FAC ,AC =AC ,∴△AEC≌△AFC(SAS).∴EC=FC.15.(蚌埠淮上区期末)如图,已知△ABC(AC>AB),DE=BC,以D,E为顶点作三角形,使所作的三角形与△ABC全等,这样的三角形最多可以作出4个.14.2.4其他判定两个三角形全等的条件(AAS)01基础题知识点1用SSA和AAA不能判定三角形全等1.(马鞍山当涂县期末)如图,已知∠1=∠2,下列添加的条件不能使△ADC≌△CBA的是(B)A.AB∥DC B.AB=CDC.AD=BC D.∠B=∠D第1题图第2题图2.(蚌埠期末)如图,点B,F,C,E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是(C)A.AB=DE B.AC=DFC.∠A=∠D D.BF=EC3.(宣城期末)如图,在△ABC和△DEC中,AB=DE.若添加条件后使得△ABC≌△DEC,则在下列条件中,不能添加的是(D)A.BC=EC,∠B=∠EB.BC=EC,AC=DCC.∠B=∠E,∠A=∠DD.BC=EC,∠A=∠D知识点2用AAS判定三角形全等4.(百色中考)如图,已知AB=CD,∠B=∠C,AC和BD相交于点O,则能直接运用“AAS”判定全等的三角形是(D)A.△AOD≌△AOB B.△AOD≌△CODC.△ADC≌△DAB D.△AOB≌△DOC第4题图第5题图5.(阜阳颍上县期末)如图,在△ABC中,AC⊥BC,AE为∠BAC的平分线,ED⊥AB于点D,AB=7 cm,AC=3 cm,则BD的长为(B)A.3 cm B.4 cmC.1 cm D.2 cm6.如图,∠1=∠2,由“AAS”判定△ABD≌△ACD,则需添加的条件是∠B=∠C.第6题图 第7题图7.(合肥庐阳区校级月考)如图,AE =AD ,∠B =∠C ,BE =6,AD =4,则AC =10.8.(合肥包河区期末)如图,点F ,C 在BE 上,BF =CE ,∠A =∠D ,∠B =∠E.求证:AB =DE.证明:∵BF =CE , ∴BF +CF =CE +CF , 即BC =EF.在△ABC 和△DEF 中,⎩⎨⎧∠A =∠D ,∠B =∠E ,BC =EF ,∴△ABC ≌△DEF(AAS ). ∴AB =DE.9.(益阳中考)已知,如图,AB =AE ,AB ∥DE ,∠ECB =70°,∠D =110°,求证:△ABC ≌△EAD.证明:∵∠ECB =70°, ∴∠ACB =110°. 又∵∠D =110°, ∴∠ACB =∠D. ∵AB ∥DE ,∴∠CAB =∠E.在△ABC 和△EAD 中,⎩⎨⎧∠ACB =∠D ,∠CAB =∠E ,AB =EA ,∴△ABC ≌△EAD(AAS ).02 中档题10.如图所示,∠CAB =∠DBA ,∠C =∠D ,AC ,BD 相交于点E ,下列结论不正确的是(B )A .∠DAE =∠CBEB .△DEA 与△CEB 不全等C .CE =DED .EA =EB11.(安徽模拟)如图,AE ⊥AB 且AE =AB ,BC ⊥CD 且BC =CD ,请按照图中所标注的数据,计算图中实线所围成的图形的面积S 是(A )A .50B .62C .65D .6812.(教材P110练习T2变式)(阜阳期末)如图所示,∠E =∠F =90°,∠B =∠C ,AE =AF .给出下列结论:①∠1=∠2;②BE =CF ;③△ACN ≌△ABM ;④CD =DN .其中正确的结论是①②③.(将你认为正确的结论的序号都填上)13.(芜湖期中)如图,在△ABC 中,AD 是BC 边上的中线,过C 作AB 的平行线交AD 的延长线于E 点. (1)求证:AB =EC ;(2)若AB =6,AC =2,试求中线AD 的取值范围.解:(1)证明:∵AD 是BC 边上的中线, ∴BD =CD. ∵AB ∥CE ,∴∠BAD =∠E.在△ABD 和△ECD 中,⎩⎨⎧∠BAD =∠E ,∠BDA =∠CDE ,BD =CD ,∴△ABD ≌△ECD(AAS ).∴AB =EC.(2)由(1)得:△ABD ≌△ECD , ∴AB =EC =6,AD =DE.在△ACE 中,CE -AC <AE <CE +AC ,即6-2<2AD <6+2.∴4<2AD <8. ∴2<AD <4.14.(教材P113习题T12变式)(淮北烈山区期末)已知:如图,AB ,CD 相交于点O ,AC ∥DB ,OC =OD ,E ,F 为AB 上两点,且AE =BF .求证:CE ∥DF .证明:∵AC ∥BD , ∴∠A =∠B .在△ACO 和△BDO 中,⎩⎨⎧∠AOC =∠BOD ,∠A =∠B ,OC =OD ,∴△ACO ≌△BDO (AAS).∴OA =OB . ∵AE =BF ,∴OE =OF .在△COE 和△DOF 中,⎩⎨⎧OC =OD ,∠COE =∠DOF ,OE =OF ,∴△COE ≌△DOF (SAS). ∴∠OEC =∠OFD .∴CE ∥DF .03 综合题15.(芜湖期中)已知:如图,在锐角△ABC 中,BE ,CF 是高,在BE 的延长线上截取BQ =AC ,在CF 上截取CP =AB ,再分别过点P 作PM ⊥BC 于M 点,过点Q 作QN ⊥BC 于N 点.求证:(1)∠Q =∠ACB ; (2)PM +QN =BC.证明:(1)∵BE 是△ABC 的高, ∴∠ACB +∠EBC =90°. ∵QN ⊥BC ,∴∠Q +∠EBC =90°. ∴∠Q =∠ACB.(2)过点A 作AH ⊥BC 于点H.∵QN ⊥BC ,AH ⊥BC ,PM ⊥BC ,∴∠QNB =∠CHA =∠CMP =90°.∴∠BAH +∠ABC =90°,∠BCF +∠ABC =90°. ∴∠BAH =∠BCF.在△QNB 和△CHA 中,⎩⎨⎧∠Q =∠ACB ,∠QNB =∠CHA ,BQ =AC ,∴△QNB ≌△CHA(AAS ).∴QN =CH.在△PCM 和△BAH 中,⎩⎨⎧∠PCM =∠BAH ,∠CMP =∠AHB ,CP =AB ,∴△PCM ≌△BAH(AAS ).∴PM =BH. ∴PM +QN =BH +CH =BC.14.2.5 两个直角三角形全等的判定第1课时 斜边和一条直角边分别相等的两个直角三角形(HL )01 基础题知识点1 用HL 判定直角三角形全等1.(淮南田家庵区期中)如图,BE ,CD 是△ABC 的高,且BD =EC ,判定△BCD ≌△CBE 的依据是“HL ”.第1题图 第2题图2.如图,在△ABC 和△ABD 中,∠C =∠D =90°.若利用“HL ”证明△ABC ≌△ABD ,则需要添加条件AC =AD 或BC =BD.3.如图,D 是△ABC 的边BC 的中点,DE ⊥AC ,DF ⊥AB ,垂足分别为E ,F ,且BF =CE.求证:∠B =∠C.证明:∵DE ⊥AC ,DF ⊥AB , ∴∠DFB =∠DEC =90°. ∵点D 是BC 的中点, ∴BD =CD.在Rt △BDF 和Rt △CDE 中,⎩⎨⎧BD =CD ,BF =CE ,∴Rt △BDF ≌Rt △CDE(HL ). ∴∠B =∠C.知识点2 直角三角形全等判定的综合4.(淮南谢家集期中)下列判定直角三角形全等的方法,不正确的是(D ) A .两条直角边对应相等 B .斜边和一锐角对应相等 C .斜边和一直角边对应相等 D .两个直角三角形的面积相等5.如图所示,在△ABC 中,∠C =90°,ED ⊥AB 于点D ,BC =BD.如果AC =3 cm ,那么AE +DE 等于(B)A .2 cmB .3 cmC .4 cmD .5 cm6.(蚌埠期末)如图,∠ACB =90°,AC =BC ,AD ⊥CE ,BE ⊥CE ,垂足分别为D ,E.若AD =5 cm ,DE =3 cm ,则CD =2_cm _.7.(合肥庐江县期末)如图,点C ,E ,B ,F 在一条直线上,AB ⊥CF 于点B ,DE ⊥CF 于点E ,AC =DF ,AB =DE.求证:CE =BF.证明:∵AB ⊥CF ,DE ⊥CF , ∴∠ABC =∠DEF =90°. 在Rt △ABC 和Rt △DEF 中,⎩⎨⎧AC =DF ,AB =DE ,∴Rt △ABC ≌Rt △DEF(HL ). ∴BC =EF.∴BC -BE =EF -BE ,即CE =BF.知识点3 直角三角形全等的实际应用8.如图所示,要测量河两岸相对的两点A ,B 的距离,先在AB 的垂线BF 上取两点C ,D ,使CD =BC ,再定出BF 的垂线DE ,使点A ,C ,E 在一条直线上,利用△EDC ≌△ABC ,得ED =AB ,因此测得ED 的长度是AB 的长,判定△EDC ≌△ABC 的理由是(B)A .SASB .ASAC .SSSD .HL第8题图 第9题图9.如图,有两个长度相同的滑梯靠在一面墙的两侧,已知左边滑梯的高度AC 与右边滑梯水平方向的宽度DF 相等,则这两个滑梯与墙面的夹角∠ACB 与∠DEF 的度数和为(C)A .60°B .75°C .90°D .120°02 中档题10.如图,MN ∥PQ ,AB ⊥PQ ,点A ,D 在直线MN 上,点B ,C 在直线PQ 上,点E 在AB 上,AD +BC =7,AD =EB ,DE =EC ,则AB =7.11.(教材P109练习T3变式)如图,AD 为△ABC 的高,E 为AC 上一点,BE 交AD 于点F ,且有BF =AC ,FD =CD ,则BF 与AC 有何位置关系?请说明理由.解:BF ⊥AC ,理由如下: ∵AD 为△ABC 的高, ∴∠ADB =∠ADC =90°. 在Rt △BDF 和Rt △ADC 中,⎩⎨⎧BF =AC ,DF =CD ,∴Rt △BDF ≌Rt △ADC (HL). ∴∠EBC =∠DAC .∵∠DAC +∠C =90°,∴∠EBC +∠C =90°. ∴BF ⊥AC .12.(淮南潘集区校级月考)如图所示,点A ,E ,F ,C 在同一直线上,AE =CF ,过E ,F 分别作DE ⊥AC ,BF ⊥AC ,且AB =CD.(1)AB 与CD 平行吗?若平行,请说明理由;(2)求证:BD 平分EF.解:(1)AB 与CD 平行. 证明:∵AE =CF , ∴AE +EF =CF +EF , 即AF =CE.∵DE ⊥AC ,BF ⊥AC , ∴∠BFA =∠DEC =90°.在Rt △BFA 和Rt △DEC 中,⎩⎨⎧AB =CD ,AF =CE ,∴Rt △BFA ≌Rt △DEC(HL ).∴BF =DE ,∠A =∠C. ∴AB ∥CD.(2)在△BFG 和△DEG 中,⎩⎨⎧∠BGF =∠DGE ,∠BFG =∠DEG ,BF =DE ,∴△BFG ≌△DEG(AAS ). ∴FG =EG. ∴BD 平分EF.03 综合题13.(教材P 110例9变式)如图所示,△ABC 与△DEF 中,AB =DE ,AC =DF ,AH ,DG 分别是△ABC 和△DEF 的高,且AH =DG.(1)求证:△ABC ≌△DEF ;(2)你认为“有两边和第三边上的高分别对应相等的两个三角形全等”这句话对吗?为什么?解:(1)证明:在Rt △ABH 和Rt △DEG 中,⎩⎨⎧AB =DE ,AH =DG ,∴Rt △ABH ≌Rt △DEG(HL ). ∴BH =EG.在Rt △ACH 和Rt △DFG 中,⎩⎨⎧AC =DF ,AH =DG ,∴Rt △ACH ≌Rt △DFG(HL ). ∴CH =FG.∴BH +HC =EG +GF ,即BC =EF. 在△ABC 和△DEF 中,⎩⎨⎧AB =DE ,AC =DF ,BC =EF ,∴△ABC ≌△DEF(SSS ).(2)这句话不对,如图所示,在△ABC 和△ABD 中,AC =AD ,AB =AB ,AE =AE ,两个三角形同样具备两边及第三边上的高对应相等,但这两个三角形不全等,其中一个是锐角三角形,一个是钝角三角形.14.(合肥肥东县期末)如图,∠C=90°,AC=20,BC=10,AX⊥AC,点P和点Q同时从点A出发,分别在线段AC和射线AX上运动,且AB=PQ,当AP=10或20时,以点A,P,Q为顶点的三角形与△ABC全等.第2课时 灵活运用全等三角形的性质与判定定理01 基础题知识点1 全等三角形的性质1.如图,△ABC ≌△DCB ,点A 和点D 是对应点.若AB =3 cm ,BC =6 cm ,AC =5 cm ,则CD 的长为(D) A .6 cm B .5 cm C .4 cm D .3 cm第1题图 第2题图2.如图,在△ABC 中,∠B =∠C =65°,△DBE ≌△ECF ,则∠DEF 的度数是(C) A .75° B .70° C .65° D .60°3.如图,点D ,A ,E 在一条直线上,△ADC ≌△AEB ,∠BAC =40°,∠D =45°.求: (1)∠B 的度数; (2)∠BMC 的度数.解:(1)∵△ADC ≌△AEB , ∴∠BAE =∠CAD.∵D ,A ,E 在一条直线上,∴∠BAD =12(180°-∠BAC)=12×(180°-40°)=70°.∴∠CAD =∠BAD +∠BAC =70°+40°=110°.在△ACD 中,∠C =180°-∠CAD -∠D =180°-110°-45°=25°. 又∵△ADC ≌△AEB ,∴∠B =∠C =25°.(2)由三角形的外角性质,得∠BMC =∠BAC +∠C=40°+25°=65°.知识点2 全等三角形的判定4.(淮南潘集区期中)在△ABC 与△DEF 中,给出下列四组条件: (1)AB =DE ,AC =DF ,BC =EF ; (2)AB =DE ,∠B =∠E ,BC =EF ; (3)∠B =∠E ,BC =EF ,∠C =∠F ; (4)AB =DE ,∠B =∠E ,AC =DF.其中能使△ABC ≌△DEF 的条件共有(C ) A .1组 B .2组 C .3组 D .4组5.(邵阳中考)如图,已知AD =AE ,请你添加一个条件,使得△ADC ≌△AEB ,你添加的条件是AB =AC 或∠ADC =∠AEB 或∠ABE =∠ACD .(不添加任何字母和辅助线)第5题图 第6题图6.(教材P106例6变式)如图,已知AB ∥DE ,AB =DE ,以下四个条件:①AC =DF ;②∠A =∠D ;③AC ∥DF ;④BF =CE ,其中能判定△ABC ≌△DEF 的条件是②③④(请填写序号).知识点3 全等三角形的性质、判定的综合7.如图所示,D 是BC 的中点,AD ⊥BC ,那么下列结论中不一定成立的是(D) A .△ABD ≌△ACD B .∠B =∠C C .AD 平分∠BAC D .△ABC 的三边相等第7题图 第8题图8.(蚌埠月考)如图,AB 与CD 交于点O ,OA =OC ,OD =OB ,∠A =50°,∠B =30°,则∠D 的度数为(B) A .50° B .30° C .80° D .100°9.(六安裕安区期末)如图,已知在△ABC 和△AEF 中,AB =AC ,AE =AF ,∠CAB =∠EAF ,BE 交FC 于O 点.(1)求证:BE =CF ;(2)当∠BAC =70°时,求∠BOC 的度数.解:(1)证明:∵∠CAB =∠EAF , ∴∠CAB +∠CAE =∠EAF +∠CAE , 即∠BAE =∠CAF.在△BAE 和△CAF 中,⎩⎨⎧AB =AC ,∠BAE =∠CAE ,AE =AF ,∴△BAE ≌△CAF(SAS ). ∴BE =CF.(2)∵△BAE ≌△CAF ,∴∠EBA =∠FCA.∵∠BDA =∠ODC ,∴∠BOC =∠BAC =70°.02 中档题10.(淮北濉溪县期末)如图,AD =AE ,BE =CD ,∠ADB =∠AEC =100°,∠BAE =70°,下列结论错误的是(C )A .△ABE ≌△ACDB .△ABD ≌△ACEC .∠DAE =40°D .∠C =30°第10题图 第11题图11.(安徽月考)如图,在△ACB 中,∠ACB =90°,AC =BC ,点C 的坐标为(-2,0),点A 的坐标为(-6,3),则B 点的坐标是(B)A .(2,4)B .(1,4)C .(3,6)D .(1,5)12.(蚌埠淮上区期末)如图,AD =AE ,∠ADC =∠AEB ,BE 与CD 相交于点O.(1)在不添加辅助线的情况下,由已知条件可以得出许多结论,例如:△ABE ≌△ACD ,∠DOB =∠EOC ,∠DOE =∠BOC 等.请你动动脑筋,再写出3个结论(所写结论不能与题中举例相同,且只要写出3个即可).①△DBC ≌△ECB ,②∠ACD =∠ABE ,③BD =CE ;(答案不唯一) (2)请你从自己写出的结论中,选取一个说明其成立的理由.解:选择③BD =CE.理由:在△ABE 和△ACD 中,⎩⎨⎧∠A =∠A ,AE =AD ,∠AEB =∠ADC ,∴△ABE ≌△ACD(ASA ).∴AB =AC. ∴AB -AD =AC -AE.∴BD =CE. (答案不唯一).03 综合题13.(芜湖期中)已知:如图所示,在△ABC 中,∠BAC =60°,AD =AE ,BE ,CD 相交于点F ,且∠DFE =120°.在BE 的延长线上截取ET =DC ,连接A T.(1)求证:∠ADC =∠AET ; (2)求证:AT =AC ;(3)设BC 边上的中线AP 与BE 相交于Q.求证:∠QAB =∠QBA.证明:(1)∵∠BAC =60°,∠DFE =120°, ∴∠AEF +∠ADC =360°-60°-120°=180°. ∵∠AEF +∠AET =180°,∴∠ADC =∠AET.(2)在△AET 和△ADC 中,⎩⎨⎧AE =AD ,∠AET =∠ADC ,ET =DC ,∴△AET ≌△ADC(SAS ).∴AT =AC.(3)延长AP 至点G ,使得GP =AP ,连接BG. ∵AP 为BC 边上的中线,∴CP =BP.在△APC 和△GPB 中,⎩⎨⎧AP =GP ,∠APC =∠GPB ,CP =BP ,∴△APC ≌△GPB(SAS ).∴AC =GB. ∵AC =AT ,∴GB =AT.∵△AET ≌△ADC ,∴∠TAE =∠CAD =60°. ∴∠TAB =120°. ∵△APC ≌△GPB ,∴∠CAP =∠BGP.∴AC ∥BG.∴∠ABG =180°-∠BAC =180°-60°=120°=∠TAB.在△ABG 和△BAT 中,⎩⎨⎧AB =BA ,∠ABG =∠BAT ,BG =AT ,∴△ABG ≌△BAT(SAS ).∴∠QAB =∠QBA.小专题6 证明三角形全等的解题思路思路一:找边边相等呈现的方式:①公共边(包括全部公共和部分公共);②中点. 类型1 已知两边对应相等,找第三边相等1.如图,已知AB =ED ,AD =EC ,点D 是BC 的中点,求证:△ABD ≌△EDC.证明:∵点D 是BC 的中点, ∴BD =CD.在△ABD 和△EDC 中,⎩⎨⎧AB =ED ,AD =EC ,BD =DC ,∴△ABD ≌△EDC(SSS ).类型2 已知两角对应相等,找一边相等2.如图,∠ABD =∠CDB ,∠ADB =∠DBC ,求证:△ABD ≌△CDB.证明:在△ABD 和△CDB 中,⎩⎨⎧∠ABD =∠CDB ,BD =DB ,∠ADB =∠CBD ,∴△ABD ≌△CDB(ASA ).3.两块完全相同的三角形纸板ABC 和DEF ,按如图所示的方式叠放,阴影部分为重叠部分,点O 为边AC 和DF 的交点,不重叠的两部分△AOF 与△DOC 是否全等?为什么?解:全等.理由:∵两三角形纸板完全相同,∴BC =BF ,AB =BD ,∠A =∠D. ∴AB -BF =BD -BC , 即AF =DC.在△AOF 和△DOC 中,⎩⎨⎧∠A =∠D ,∠AOF =∠DOC ,AF =DC ,∴△AOF ≌△DOC(AAS ).类型3 已知直角三角形的直角边(或斜边)相等,找斜边(或直角边)相等4.如图,∠A =∠D =90°,AB =DF ,BE =CF.求证:△ABC ≌△DFE.证明:∵BE =CF , ∴BE +EC =CF +EC , 即BC =EF.在Rt △ABC 和Rt △DFE 中,⎩⎨⎧AB =DF ,BC =FE , ∴Rt △ABC ≌Rt △DFE(HL ).思路二:找角角相等呈现的方式:①公共角;②对顶角;③角平分线;④垂直;⑤平行.类型4 已知两边对应相等,找夹角相等5.如图,AB =AD ,AC =AE ,∠BAD =∠CAE.求证:△ABC ≌△ADE.证明:∵∠BAD =∠CAE ,∴∠BAD +∠DAC =∠CAE +∠DAC , 即∠BAC =∠DAE.在△ABC 和△ADE 中,⎩⎨⎧AB =AD ,∠BAC =∠DAE ,AC =AE ,∴△ABC ≌△ADE(SAS ).6.(安庆太湖县期末)两个大小不同的等腰直角三角形三角板如图1所示放置,图2是由它抽象出的几何图形,其中AB =AC ,AE =AD ,∠BAC =∠EAD =90°,∠ABC =∠ACB =∠AED =∠ADE =45°,B ,C ,E 在同一条直线上,连接DC.(1)请在图2中找出与△ABE 全等的三角形并给予证明(说明:结论中不得含有未标识的字母); (2)求证:DC ⊥BE.证明:(1)∵∠BAC =∠EAD =90°, ∴∠BAC +∠CAE =∠EAD +∠CAE , 即∠BAE =∠CAD.在△ABE 和△ACD 中,⎩⎨⎧AB =AC ,∠BAE =∠CAD ,AE =AD ,∴△ABE ≌△ACD(SAS ). (2)∵△ABE ≌△ACD , ∴∠ACD =∠ABE =45°.∴∠BCD =∠ACB +∠ACD =90°. ∴DC ⊥BE.类型5 已知一边一角对应相等,找另一角相等7.如图,D 是AC 上一点,AB =DA ,DE ∥AB ,∠B =∠DAE ,求证:△ABC ≌△DAE.证明:∵DE ∥AB , ∴∠CAB =∠EDA.在△ABC 和△DAE 中,⎩⎨⎧∠CAB =∠EDA ,AB =DA ,∠B =∠DAE ,∴△ABC ≌△DAE(ASA ).8.如图,已知∠BDC =∠CEB =90°,BE ,CD 相交于点O ,且AO 平分∠BAC ,求证: (1)△ADO ≌△AEO ; (2)△BDO ≌△CEO.证明:(1)∵AO 平分∠BAC , ∴∠DAO =∠EAO.∵∠BDC =∠CEB =90°, ∴∠ADO =∠AEO.在△ADO 和△AEO 中,⎩⎨⎧∠ADO =∠AEO ,∠DAO =∠EAO ,AO =AO ,∴△ADO ≌△AEO(AAS ). (2)∵△ADO ≌△AEO , ∴DO =EO.在△BDO 和△CEO 中,⎩⎨⎧∠BDO =∠CEO ,DO =EO ,∠DOB =∠EOC ,∴△BDO≌△CEO(ASA).小专题7 全等三角形的基本模型类型1 平移模型模型分析 此模型的特征是有一组边共线或部分重合,另两组边分别平行,常要在移动方向上加(减)公共线段,构造线段相等,或利用平行线性质找到对应角相等.1.(南充中考)如图,点O 是线段AB 的中点,OD ∥BC 且OD =BC. (1)求证:△AOD ≌△OBC ;(2)若∠ADO =35°,求∠DOC 的度数.解:(1)证明:∵点O 是线段AB 的中点, ∴AO =BO. ∵OD ∥BC , ∴∠AOD =∠OBC.在△AOD 和△OBC 中,⎩⎨⎧AO =OB ,∠AOD =∠OBC ,OD =BC ,∴△AOD ≌△OBC(SAS ). (2)∵△AOD ≌△OBC , ∴∠ADO =∠OCB =35°. ∵OD ∥BC ,∴∠DOC =∠OCB =35°. 类型2 对称模型模型分析 所给图形可沿某一直线折叠,直线两旁的部分能完全重合,重合的顶点就是全等三角形的对应顶点,解题时要注意其隐含条件,即公共边或公共角相等.2.(桂林中考)如图,AB =AD ,BC =DC ,点E 在AC 上.求证: (1)AC 平分∠BAD ; (2)BE =DE.证明:(1)在△ABC 和△ADC 中,⎩⎨⎧AB =AD ,AC =AC ,BC =DC ,∴△ABC ≌△ADC(SSS ). ∴∠BAC =∠DAC , 即AC 平分∠BAD.(2)由(1)知∠BAE =∠DAE.在△BAE 和△DAE 中,⎩⎨⎧BA =DA ,∠BAE =∠DAE ,AE =AE ,∴△BAE ≌△DAE(SAS ). ∴BE =DE.类型3 旋转模型3.如图,四边形ABCD 的对角线相交于点O ,AB ∥CD ,O 是BD 的中点. (1)求证:△ABO ≌△CDO ;(2)若BC =AC =4,BD =6,求△BOC 的周长.解:(1)证明:∵AB ∥CD ,∴∠BAO =∠DCO ,∠ABO =∠CDO. ∵O 是DB 的中点, ∴BO =DO.在△ABO 和△CDO 中,。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全等三角形归纳复习
常见辅助线的作法有以下几种:
(1)遇到等腰三角形,可作底边上的高,利用“三线合一”的性质解题,思维模式是全等变换中的“对折”.
(2)遇到三角形的中线,倍长中线,使延长线段与原中线长相等,构造全等三角形,利用的思维模式是全等变换中的“旋转”.
(3)遇到角平分线,可以自角平分线上的某一点向角的两边作垂线,利用的思维模式是三角形全等变换中的“对折”,所考知识点常常是角平分线的性质定理或逆定理.
(4)过图形上某一点作特定的平分线,构造全等三角形,利用的思维模式是全等变换中的“平移”或“翻转折叠”
(5)截长法与补短法,具体做法是在某条线段上截取一条线段与特定线段相等,或是将某条线段延长,是之与特定线段相等,再利用三角形全等的有关性质加以说明.这种作法,适合于证明线段的和、差、倍、分等类的题目.
特殊方法:在求有关三角形的定值一类的问题时,常把某点到原三角形各顶点的线段连接起来,利用三角形面积的知识解答.
顺口溜:
人人都说几何难,难就难在辅助线;辅助线,如何添?构造全等很关键. 图中有角平分线,可向两边作垂线;三角形中有中线,延长中线造全等; 角平分线加平行,构造等腰三角形;角平分线加垂线,三线合一试试看; 线段垂直平分线,常向两端把线连;还要刻苦加钻研,找出规律凭经验.
一、倍长中线法
△ABC 中,AD 是BC 边中线
方式1: 延长AD 到E ,使DE=AD ,连接BE.
方式2:间接倍长
作CF⊥AD于F,作BE⊥AD的延长线于E,
延长MD到N,使DN=MD,连接CN.
连接BE.
例1、已知:如图,△ABC中,AB=5,AC=3,求中线AD的取值范围.
例2、如图,已知在△ABC中,AD是BC边上的中线,E是AD上一点,且BE=AC,延长BE交AC于F,求证:AF=EF.
例3、如图所示,AD为△ABC的中线,∠ADB和∠ADC的平分线分别交AB、AC于点E、F. 求证:BE+CF>EF.(提示:延长ED至M,使DM=DE,连接 CM,MF.)
例4、已知在△ABC 中,AB=AC ,D 在AB 上,E 在AC 的延长线上,DE 交BC 于点F ,且DF=EF.求证:BD=CE.
练习1、如图,在△ABC 中,AB ≠AC ,D 、E 在BC 上,且DE=EC ,过D 作DF ∥BA 交AE 于点F ,DF=AC.求证:AE 平分∠BAC.
练习2、如图,AD 为△ABC 的中线,求证:AB +AC >2AD.
练习3、如图,△ABC 中,BD=DC=AC ,E 是DC 的中点,求证:AD 平分∠BAE.
E D C
B
A
C
B
二、借助角平分线造全等
例1、已知,如图,在四边形ABCD 中,BC >AB ,AD=DC ,BD 平分∠ABC. 求证:∠BAD+∠BCD=180°.
例2、如图,已知在△ABC 中,∠B=60°,△ABC 的角平分线AD 、CE 相交于点O ,求证:OE=OD.
(有和角平分线垂直的线段时,通常把这条线段延长.)
例3、已知:如图所示,在Rt △ABC 中,AB=AC ,∠BAC=90°,∠1=∠2,CE ⊥BD 的延长于E.求证:BD=2CE.
三、截长补短
例1、如图,△ABC
中,AB=2AC
,AD 平分∠
BAC ,且AD=BD ,求证:CD ⊥AC.
例2、如图,AD∥BC,EA,EB分别平分∠DAB,∠CBA,CD过点E,求证:AB=AD+BC.
练习1、如图,在△ABC中,∠BAC=60°,AD是∠BAC的平分线,且AC=AB+BD,求∠ABC的度数.
练习2、如图,在△ABC中,∠ABC=60°,AD、CE分别平分∠BAC、∠ACB,求证:AC=AE+CD.
四、连接已知点,构造全等三角形.
例、已知:如图所示,AC、BD相交于O点,且AB=DC,AC=BD.求证:∠A=∠D.
F
E
D C
B
A
五、取线段中点构造全等三角形
例、已知:如图所示,AB=DC ,∠A=∠D.求证:∠ABC=∠DCB.
六、证明线段不等关系
例、 如图,在△ABC 的边上取两点D 、E ,且BD=CE ,求证:AB+AC>AD+AE.
七、旋转
例1、正方形ABCD 中,E 为BC 上的一点,F 为CD 上的一点,BE+DF=EF ,求∠EAF 的度数.
例2、如图,在四边形ABCD 中,AC 平分∠BAD ,过C 作CE ⊥AB 于E ,并且1
()2
AE AB AD =+,求∠ABC+∠ADC 的度数.
E
D C
B
A
八、直角三角形的全等问题
[知识]:①直角三角形特有的HL判定定理;②SAS、AAS、ASA、SSS(转化为HL)也是完全适用直角三角形的,不要忘记;③同(等)角的余角相等应用非常广泛(重点).
例1、如图,已知DO⊥BC,OC=OA,OB=OD,求证:△BCE是直角三角形.
例2、把两个含有45°角的直角三角板如图放置,点D在BC上,连结BE、AD,AD的延长线交BE于点F.求证:AF⊥BE.
例3、如图,在△ABC中,高AD与BE相交于点H,且AD=BD.问△BHD≌△ACD?
九、等腰三角形、等边三角形的全等问题
[知识]:①等腰三角形腰相等且底角相等,等边三角形三边相等
且三个底角都是60度,即“等边对等角,等角对等边”; ②如右图,由∠1=∠2,可得∠CBE=∠DBA ;反之也成立.
例、如图1、2、3,过点A 分别作两个个大小不一样的等边三角形,连接BD ,CE.求证BD=CE.
练习、如图,四边形ABCD 、DEFG 都是正方形,连接AE 、CG ,AE 与CG 相交于点M ,CG 与AD
相交于点N .求证:AE=CG.
1
2
B
A
E
D A
B G D
F
E
C
题型:全等三角形在实际生活中的应用
例1 如图所示,太阳光线AC和A′C′是平行的,同一时刻两个建筑物在太阳下的影子一样长,那么建筑物是否一样高?说明理由.(注:太阳光线可看成是平
行的)
巩固1某游乐场有两个长度相同的滑梯,要想使左边滑梯BC的高度AC与右边滑梯EF的水平方向的长度DF相等,则两个滑梯的倾斜角∠ABC与∠DFE的大小必须满足什么关系?说明理由.。
