初二数学-反比例函数难题拓展(学生版)
初二数学-反比例函数难题拓展(学生版).doc
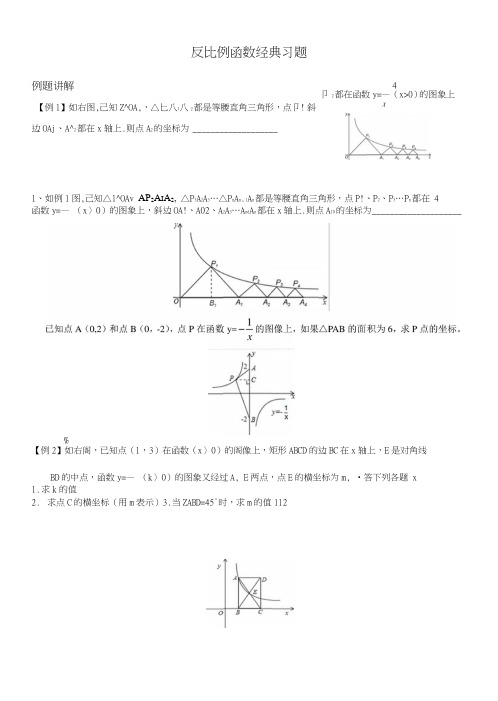
反比例函数经典习题例题讲解【例1】如右图,己知Z^OA,,△匕八|八2都是等腰直角三角形,点卩! 斜边OAj 、A^2都在x 轴上.则点A 2的坐标为 ___________________ 1、如例1图,己知△l^OAv AP 2A I A 2, △P 3A 2A 3…△P n A n .1A n 都是等腰直角三角形,点P!、P 2、P 3…P n 都在 4 函数y=— (x 〉0)的图象上,斜边OA!、A02、A 2A 3…A nd A n 都在x 轴上.则点A 10的坐标为 ____________________%【例2】如右阁,已知点(1,3)在函数(x 〉0)的阁像上,矩形ABCD 的边BC 在x 轴上,E 是对角线BD 的中点,函数y=— (k 〉0)的图象又经过A, E 两点,点E 的横坐标为m, •答下列各题 x1. 求k 的值2. 求点C 的横坐标(用m 表示)3.当ZABD=45°时,求m 的值1124 卩2都在函数y=— (x>0)的图象上, x21、已知:如图,矩形ABCD的边BC在x轴上,E是对角线AC、BD的交点,反比例函数y= —(x〉0)的图 x 象经过A, E两点,点E的纵坐标为m.(1)求点A坐标(用m表示)2、如图1,矩形ABCD的边BC在x轴的正半轴上,点E (m, 1)是对角线BD的中点,点A、E在反比例函数的阉象上.(1)求AB的长;b k(2)当矩形ABCD是正方形时,将反比例函数—的图象沿y轴翻折,得到反比例函数y= 2的图象(如图2),求卜的值;(3)直线y=-x上有一长为^动线段MN,作MH、NP都平行y轴交在条件(2)下,第一象限A的双曲线ky=—于点H、P,问四边形MHPN能否为平行四边形(如阁3) ?若能,请求出点M的坐标;若不能,请说明 x理由.【例3】在平面直角坐标系中,已知A(1,0),B(0,1),矩形OMPN的相邻两边OM, ON分别在x, y轴的正半轴上,O为原点,线段AB与矩形OMPN的两边MRNP的交点分别为E,F,AAOF^ ABOE (顶点依次对应)(1)求ZFOE;(2)求证:矩形OPMN的顶点P必在某个反比例函数图像上,并写出该函数的解析式。
反比例函数经典拓展难题

反比例函数难题拓展填空题1. (2011浙江金华,16,4分)如图,将一块直角三角板OAB 放在平面直角坐标系中,B (2,0),∠AOC =60°,点A 在第一象限,过点A 的双曲线为y= kx ,在x 轴上取一点P ,过点P作直线OA 的垂线l ,以直线l 为对称轴,线段OB 经轴对称变换后的像是O ′B ′. (1)当点O ′与点A 重合时,点P 的坐标是.(2)设P (t ,0)当O ′B ′与双曲线有交点时,t 的取值范围是 .2. (2011广东东莞,6,4分)已知反比例函数ky x=的图象经过(1,-2).则k = . 3. (2011山东滨州,18,4分)若点A(m ,-2)在反比例函数4y x=的图像上,则当函数值y ≥-2时,自变量x 的取值范围是___________. 4. (2011四川南充市,14,3分)过反比例函数y=xk(k ≠0)图象上一点A ,分别作x 轴,y 轴的垂线,垂足分别为B,C ,如果⊿ABC 的面积为3.则k 的值为 .5. (2011宁波市,18,3分)如图,正方形A 1B 1P 1P 2的顶点P 1、P 2在反比例函数y =2x (x >0)的图像上,顶点A 1、B 1分别在x 轴和y 轴的正半轴上,再在其右侧作正方形P 2P 3A 2B 2,顶点P 3在反比例函数y =2x(x >0)的图象上,顶点A 3在x 轴的正半轴上,则点P 3的坐标为6. (2011浙江衢州,5,4分)在直角坐标系中,有如图所示的t ,R ABO AB x ∆⊥轴于点B ,斜35=(0)ky xx=>的图像经过AO的中点C,且与AB交于的坐标为 .7. (2011浙江绍兴,13,5分) 若点12(1,),(2,)A yB y是双曲线3yx=上的点,则1y2y(填“>”,“<”“=”).8. (2011浙江丽水,16,4分)如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOC=60°,点A在第一象限,过点A的双曲线为y=kx,在x轴上取一点P,过点P 作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O′B′.(1)当点O′与点A重合时,点P的坐标是.(2)设P(t,0)当O′B′与双曲线有交点时,t的取值范围是 .9. (2011湖南常德,5,3分)如图1所示的曲线是一个反比例函数图象的一支,点A在此曲线上,则该反比例函数的解析式为_______________.10.(2011江苏苏州,18,3分)如图,已知点A的坐标为(3,3),AB⊥x轴,垂足为B,(第15题)xyCDBOIy1OAx3图1连接OA ,反比例函数y=xk(k>0)的图象与线段OA 、AB 分别交于点C 、D.若AB=3BD ,以点C 为圆心,CA 的45倍的长为半径作圆,则该圆与x 轴的位置关系是___________(填“相离”、“相切”或“相交”)11. (2011山东济宁,11,3分)反比例函数1m y x-=的图象在第一、三象限,则m 的取值范围是 .12. (2011四川成都,25,4分)在平面直角坐标系xOy 中,已知反比例函数2(0)ky k x=≠满足:当0x <时,y 随x 的增大而减小.若该反比例函数的图象与直线3y x k =-+都经过点P ,且7OP =,则实数k=_________.13. (2011安徽芜湖,15,5分)如图,在平面直角坐标系中有一正方形AOBC ,反比例函数ky x=经过正方形AOBC 对角线的交点,半径为(422-)的圆内切于△ABC ,则k 的值为 .14. (2011广东省,6,4分)已知反比例函数ky x=的图象经过(1,-2).则k = . 15. (2011江苏南京,15,2分)设函数2y x =与1y x =-的图象的交战坐标为(a ,b ),则11a b-的值为__________.16. (2011上海,11,4分)如果反比例函数k yx=(k是常数,k≠0)的图像经过点(-1,2),那么这个函数的解析式是__________.17. (2011湖北武汉市,16,3分)如图,□ABCD的顶点A,B的坐标分别是A(-1,0),B(0,-2),顶点C,D在双曲线y=xk上,边AD交y轴于点E,且四边形BCDE的面积是△ABE 面积的5倍,则k=_____.18. (2011湖北黄冈,4,3分)如图:点A在双曲线kyx=上,AB⊥x轴于B,且△AOB的面积S△AOB=2,则k=______.19. (2011湖北黄石,15,3分)若一次函数y=kx+1的图象与反比例函数y=x1的图象没有公共点,则实数k的取值范围是。
中考数学专题复习《反比例函数》拓展题(含答案)

《反比例函数》拓展题(含答案)知识点回顾由于反比例函数解析式及图象的特殊性,很多中考试题都将反比例函数与面积结合起来进行考察。
这种考察方式既能考查函数、反比例函数本身的基础知识内容,又能充分体现数形结合的思想方法,考查的题型广泛,考查方法灵活,可以较好地将知识与能力融合在一起。
下面就反比例函数中与面积有关的问题的四种类型归纳如下:一、利用反比例函数中|k|的几何意义求解与面积有关的问题设P为双曲线上任意一点,过点P作x轴、y轴的垂线PM、PN,垂足分别为M、N,则两垂线段与坐标轴所围成的的矩形PMON的面积为S=|PM|×|PN|=|y|×|x|=|xy|∴xy=k 故S=|k| 从而得结论1:过双曲线上任意一点作x轴、y轴的垂线,所得矩形的面积S为定值|k| 对于下列三个图形中的情形,利用三角形面积的计算方法和图形的对称性以及上述结论,可得出对应的面积的结论为:结论2:在直角三角形ABO中,面积S=结论3:在直角三角形ACB中,面积为S=2|k|结论4:在三角形AMB中,面积为S=|k|例题讲解【例1】如右图,已知△P10A1,△P2A1A2都是等腰直角三角形,点P1、P2都在函数y=4x(x>0)的图象上,斜边OA1、A1A2都在x轴上.则点A2的坐标为 .1、如例1图,已知△P1OA1,△P2A1A2,△P3A2A3…△P n A n-1A n都是等腰直角三角形,点P1、P2、P3…P n都在函数y=4x(x>0)的图象上,斜边OA1、A1A2、A2A3…A n-1A n都在x轴上.则点A10的坐标为2、已知点A(0,2)和点B(0,-2),点P在函数y=1x的图像上,如果△PAB的面积为6,求P点的坐标。
【例2】如右图,已知点(1,3)在函数y=kx(x>0)的图像上,矩形ABCD的边BC在x轴上,E是对角线BD的中点,函数y=kx(k>0)的图象又经过A,E两点,点E的横坐标为m,解答下列各题1.求k的值2.求点C的横坐标(用m表示)3.当∠ABD=45°时,求m的值1121、已知:如图,矩形ABCD的边BC在x轴上,E是对角线AC、BD的交点,反比例函数y=2 x(x>0)的图象经过A,E两点,点E的纵坐标为m.(1)求点A坐标(用m表示)(2)是否存在实数m,使四边形ABCD为正方形,若存在,请求出m的值;若不存在,请说明理由2、如图1,矩形ABCD的边BC在x轴的正半轴上,点E(m,1)是对角线BD的中点,点A、E在反比例函数y=kx的图象上.(1)求AB的长;(2)当矩形ABCD是正方形时,将反比例函数y=kx的图象沿y轴翻折,得到反比例函数y=1kx的图象(如图2),求k1的值;(3)直线y=-x上有一长为2动线段MN,作MH、NP都平行y轴交在条件(2)下,第一象限内的双曲线y=kx于点H、P,问四边形MHPN能否为平行四边形(如图3)?若能,请求出点M的坐标;若不能,请说明理由.【例3】在平面直角坐标系中,已知A(1,0),B(0,1),矩形OMPN的相邻两边OM,ON分别在x,y轴的正半轴上,O为原点,线段AB与矩形OMPN的两边MP,NP的交点分别为E,F,△AOF∽△BOE(顶点依次对应)(1)求∠FOE;(2)求证:矩形OPMN的顶点P必在某个反比例函数图像上,并写出该函数的解析式。
初二数学人教版(下册)反比例函数典型例题汇总(附答案)

例 下面函数中,哪些是反比例函数? (1)3x y -=;(2)x y 8-=;(3)54-=x y ;(4)15-=x y ;(5).81=xy 解:其中反比例函数有(2),(4),(5).说明:判断函数是反比例函数,依据反比例函数定义,xky =)0(≠k ,它也可变形为1-=kx y 及k xy =的形式,(4),(5)就是这两种形式.反比例函数的典型例题二例 在以下各小题后面的括号里填写正确的记号.若这个小题成正比例关系,填(正);若成反比例关系,填(反);若既不成正比例关系又不成反比例关系,填(非).(1)周长为定值的长方形的长与宽的关系 ( ); (2)面积为定值时长方形的长与宽的关系 ( ); (3)圆面积与半径的关系 ( ); (4)圆面积与半径平方的关系 ( );(5)三角形底边一定时,面积与高的关系 ( ); (6)三角形面积一定时,底边与高的关系 ( );(7)三角形面积一定且一条边长一定,另两边的关系 ( ); (8)在圆中弦长与弦心距的关系 ( );(9)x 越来越大时,y 越来越小,y 与x 的关系 ( ); (10)在圆中弧长与此弧所对的圆心角的关系 ( ). 答:说明:本题考查了正比例函数和反比例函数的定义,关键是一定要弄清出二者的定义.例 已知反比例函数62)2(--=a xa y ,y 随x 增大而减小,求a 的值及解析式.分析 根据反比例函数的定义及性质来解此题. 解 因为62)2(--=ax a y 是反比例函数,且y 随x 的增大而减小,所以⎩⎨⎧>--=-.02,162a a 解得⎩⎨⎧>±=.2,5a a所以5=a ,解析式为xy 25-=.反比例函数的典型例题四例 (1)若函数22)1(--=mx m y 是反比例函数,则m 的值等于( )A .±1B .1C .3D .-1(2)如图所示正比例函数0(>=k kx y )与反比例函数xy 1=的图像相交于A 、C 两点,过A 作x 轴的垂线交x 轴于B ,连结BC .若ABC ∆的面积为S ,则:A .1=SB .2=SC .3=SD .S 的值不确定解:(1)依题意,得⎩⎨⎧-=-≠-,12,012m m 解得1-=m .故应选D . (2)由双曲线x y 1=关于O 点的中心对称性,可知:O BC O BA S S ∆∆=. ∴12122=⋅=⨯⨯==∆AB OB AB OB S S OBA .故应选A .例 已知21y y y +=,1y 与x 成正比例,2y 与x 成反比例,当1=x 时,4=y ;当3=x 时,5=y ,求1-=x 时,y 的值.分析 先求出y 与x 之间的关系式,再求1-=x 时,y 的值.解 因为1y 与x 成正比例,2y 与x 成反比例,所以)0(,212211≠==k k xk y x k y . 所以xkx k y y y 2121+=+=.将1=x ,4=y ;3=x ,5=y 代入,得⎪⎩⎪⎨⎧=+=+.5313,42121k k k k 解得 ⎪⎪⎩⎪⎪⎨⎧==.821,81121k k 所以xx y 821811+=. 所以当1-=x 时,4821811-=--=y . 说明 不可草率地将21k k 、都写成k 而导致错误,题中给出了两对数值,决定了21k k 、的值.反比例函数的典型例题六例 根据下列表格x 与y x …… 1 2 3 456 …y…6 3 2 1.5 1.2 1 …(1x 的取值范围. 解:(1)图像如右图所示. (2)根据图像,设)0(≠=k xky ,取6,1==y x 代入,得16k=. ∴6=k .∴函数解析式为)0(6>=x xy . 说明:本例考查了函数的三种表示法之间的变换能力,即先由列表法通过描点画图转化为图像法,再由图像法通过待定系数法转化为解析法,题目新颖别致,有较强的趣味性.反比例函数的典型例题七例(1)一次函数1+-=x y 与反比例函数xy 3=在同一坐标系中的图像大致是如图中的( )(2)一次函数12--=k kx y 与反比例函数xky =在同一直角坐标系内的图像的大致位置是图中的( )解:1+-=x y 的图像经过第一、二、四象限,故排除B 、C ;又xy 3=的图像两支在第一、三象限,故排除D .∴答案应选A .(2)若0>k ,则直线)1(2+-=k kx y 经过第一、三、四象限,双曲线xky =的图像两支在第一、三象限,而选择支A 、B 、C 、D 中没有一个相符;若0<k ,则直线)1(2+-=k kx y 经过第二、三、四象限,而双曲线的两支在第二、四象限,故只有C 正确.应选C .例 已知函数24231-⎪⎭⎫ ⎝⎛+=mx m y 是反比例函数,且其函数图像在每一个象限内,y 随x 的增大而减小,求反比例函数的解析式.解:因为y 是x 的反比例函数,所以1242-=-m ,所以21=m 或.21-=m 因为此函数图像在每一象限内,y 随x 的增大而减小,所以031>+m ,所以31->m ,所以21=m ,所以反比例函数的解析式为.65xy = 说明:此题根据反比例函数的定义与性质来解反比例函数xky = )0(≠k ,当0>k 时,y 随x 增大而减小,当0<k 时,y 随x 增大而增大.例 一个长方体的体积是100立方厘米,它的长是y 厘米,宽是5厘米,高是x 厘米. (1)写出用高表示长的函数关系式; (2)写出自变量x 的取值范围; (3)当3=x 厘米时,求y 的值; (4)画出函数的图像.分析 本题依据长方体的体积公式列出方程,然后变形求出长关于高的函数关系式. 解 (1)因为长方体的长为y 厘米,宽为5厘米,高为x 厘米, 所以1005=xy ,所以xy 20=. (2)因为x 是长方体的高.所以0>x .即自变量x 的取值范围是0>x . (3)当3=x 时,326320==y (厘米) (4x … 0.525 1015…y … 40 10 4 2 311 …描点画图如图所示.例 已知力F 所作用的功是15焦,则力F 与物体在力的方向通过的距离S 的图象大致是( ).说明 本题涉及力学中作功问题,主要考查在力的作用下物体作功情况,由此,识别正、反比例函数,一次函数的图象位置关系.解 据S F W ⋅=,得15=S F ⋅,即SF 15=,所以F 与S 之间是反比例函数关系,故选(B ).例 一个圆台形物体的上底面积是下底面积的.32如果如下图所示放在桌上,对桌面的压强是Pa 200,翻过来放,对桌面的压强是多少?解:由物理知识可知,压力F ,压强p 与受力面积S 之间的关系是.SFp =因为是同一物体,F 的数值不变,所以p 与S 成反比例. 设下底面是0S ,则由上底面积是032S , 由SFp =,且0S S =时,200=p , 有.20020000S S pS F =⨯==因为是同一物体,所以0200S F =是定值.所以当032S S =时,).Pa (3003220000===S S SF p因此,当圆台翻过来时,对桌面的压强是300帕.说明:本题与物理知识结合考查了反比例函数,关键是清楚对于同一个物体,它对桌面的压力是一定的.例 如图,P 是反比例函数xky =上一点,若图中阴影部分的矩形面积是2,求这个反比例函数的解析式.分析 求反比例函数的解析式,就是求k 的值.此题可根据矩形的面积公式及坐标与线段长度的转化来解.解 设P 点坐标为),(y x .因为P 点在第二象限,所以0,0><y x . 所以图中阴影部分矩形的长、宽分别为y x ,-.又2=-xy ,所以2-=xy .因为xy k =,所以2-=k . 所以这个反比例函数的解析式为xy 2-=. 说明 过反比例函数图像上的一点作两条坐标轴的垂线,可得到一个矩形,这个矩形的面积等于xk y =中的k .例 当n 取什么值时,122)2(-++=n n x n n y 是反比例函数?它的图像在第几象限内?在每个象限内,y随x 增大而增大还是减小?分析 根据反比例函数的定义)0(≠=k x k y 可知,122)2(-++=n n x n n y 是反比例函数,必须且只需022≠+n n 且112-=-+n n .解 122)2(-++=n n xn n y 是反比例函数,则⎪⎩⎪⎨⎧-=-+≠+,11,0222n n n n ∴⎩⎨⎧-==-≠≠.10,20n n n n 或且即 1-=n .故当1-=n 时,122)2(-++=n nx n n y 表示反比例函数:xy 1-=. 01<-=k ,∴双曲线两支分别在二、四象限内,并且在每个象限内,y 随x 的增大而增大.11。
中考数学几何图形复习专题10 反比例函数的综合探究(数形结合)(学生版)

专题10 反比例函数的综合训练(数形结合)1.如图,一次函数4y x =-+的图象与反比例函数()0k y k x=≠在第一象限内的图象交于()1,A n 和()3,B m 两点.(1)求反比例函数的表达式.(2)在第一象限内,当一次函数4y x =-+的值大于反比例函数()0k y k x=≠的值时,写出自变量x 的取值范围(3)求△AOB 面积.2.如图,反比例函数2y x=的图象与一次函数y x b =+的图象交于(1, )A m ,(2, )B n -两点,一次函数图象与y 轴交于点C ,与x 轴交于点D .(1)求一次函数的表达式;(2)观察图象,写出2kx b x>+时自变量x 的取值范围; (3)连接OA ,在第三象限的反比例函数图象上是否存在一点P ,使得2OCP OCA S S =△△?若存在,请求出点P 的坐标;若不存在,请说明理由.3.如图,在平面直角坐标系xOy 中,已知正比例函数y =12x 的图象与反比例函数y =k x的图象交于A (a ,﹣2),B 两点.(1)求反比例函数的表达式和点B 的坐标;(2)P 是第一象限内反比例函数图象上一点,过点P 作y 轴的平行线,交直线AB 于点C ,连接PO ,若△POC 的面积为3,求点P 的坐标.4.如图,等腰Rt ABO 的直角顶点O 与平面直角坐标系的原点重合,反比例函数()0m y x x=<的图象经过点A ,反比例函数()0n y x x =>的图象经过点B .(1)试猜想m 与n 的数量关系,并说明理由;(2)若2n =,求当点B 的纵坐标分别为1和2时,等腰Rt ABO 的面积;(3)请直接写出当2n =时,等腰Rt ABO 的面积的最小值_________.5.如图,一次函数()=+0y mx n m ≠的图象与反比例函数()0k y k x =≠的图象相交于第二、四。
2023中考数学专项: 反比例函数与几何图形综合问题(重点突围)(学生版)

专题16反比例函数与几何图形综合问题【中考考向导航】目录【直击中考】 (1)【考向一反比例函数中K值的几何意义】 (1)【考向二反比例函数与三角形的综合问题】 (4)【考向三反比例函数与矩形的综合问题】 (6)【考向四反比例函数与菱形的综合问题】 (9)【考向五反比例函数与正方形的综合问题】 (11)【考向六反比例函数与圆的综合问题】 (15)【直击中考】【考向一反比例函数中K值的几何意义】【变式训练】1.(2023·安徽宿州·统考一模)如图,若反比例函数______在反比例函数3.(2022·黑龙江绥化·校考二模)如图,在过点A、C两点,点B在4.(2023秋·安徽池州·九年级统考期末)AC交y轴于点B,若点B是=【考向二反比例函数与三角形的综合问题】(1)求反比例函数的解析式;(2)过点A作AP垂直OA,交反比例函数的图象于点①求直线AC的解析式;②求点P的坐标.【变式训练】(1)求反比例函数的解析式;(2)坐标平面内有一点D,若以A(1)求反比例函数的表达式;(2)求等边△ACD的边长.【考向三反比例函数与矩形的综合问题】(1)直接写出B,C,D三点的坐标;(2)若将矩形向下平移,矩形的两个顶点值.【变式训练】上两点,的顶点【考向四反比例函数与菱形的综合问题】(1)求k的值及AB所在直线的函数表达式;(2)将这个菱形沿x轴正方向平移,当顶点【变式训练】是菱形,点(1)求一次函数与反比例函数的解析式;(2)设点P是直线AB上一动点,且ABCD(1)求双曲线y2的函数关系式及(2)判断点B是否在双曲线上,并说明理由;(3)若BA的延长线与双曲线【考向五反比例函数与正方形的综合问题】(1)求反比例函数的解析式;(2)若将正方形ABCD沿x轴向右平移得到正方形标,并判断点B′是否在该反比例函数的图象上,说明理由.【变式训练】在平面直角坐标系中,点(1)求反比例函数的解析式;(2)求四边形OAFM 的面积.2.(2022·山东济南·校考一模)如图,四边形35AE OE =.中点,以备用图4.(2022春·江苏苏州·八年级星海实验中学校考期中)如图,在平面直角坐标系中,四边形ABCD 为正方形,已知点()6,0A -、()7,3D -,点B 、C 在第二象限内.(1)点B 的坐标_________;(2)将正方形ABCD 以每秒2个单位的速度沿x 轴向右平移t 秒,若存在某一时刻t ,使在第一象限内点B 、D 两点的对应点B '、D ¢正好落在某反比例函数的图像上,请求出此时t 的值以及这个反比例函数的解析式;(3)在(2)的情况下,问是否存在y 轴上的点P 和反比例函数图像上的点Q ,使得以P 、Q 、B '、D ¢四个点为顶点的四边形是平行四边形?若存在,请直接写出符合题意的点Q 的坐标;若不存在,请说明理由.【考向六反比例函数与圆的综合问题】【变式训练】在反比例函数。
反比例函数压轴题经典培优好题难题(有答案)

B y A C
将y x 2
3 3 代入y 得, 2 x
D x
3 A(2, ) 2 3 C (2 , 0) 2 7 C ( , 0) 2
3 7 或C (2 , 0)即C ( , 0) 2 2 3 1 或C ( 2 , 0)即C ( , 0) 2 2
4 N 3 1 M 2
(2)若该反比例函数的图象与AB交于点Q,求直线PQ的 解析式.
∵AO=4 ∴A(-4,0) ∴Q的横坐标为-4 将x=-4代入y=-6/x得,y=3/2 ∴Q(-4,3/2) 设PQ:y=ax+b 将Q(-4,3/2)P(-2,3)代入得, -4a+b=3/2 -2a+b=3 a=3/4 解得 b=9/2 ∴PQ:y=3/4x+9/2
潮实:已知:如图,在直角坐标系xoy中,矩形OABC的边 OA在x轴的负半轴上,边OC在y轴的正半轴上,对角线AC 与OB相交于P,且BC=4,AB=6. (1)求过点P的反比例函数的解析式;
(1)如图,过P作PM⊥AO于M, PN⊥CO于N (ASA证明△BCP全等于△AOP, △OCP全等于△ABP) ∴AP=PO ∴∠1=∠2,∠3=∠4 ∴M是AO的中点,N是OC的中点 又∵OC=AB=6,AO=BC=4 ∴MO=1/2×4=2 ON=1/2×6=3 ∴P(-2,3) 设y=k/x 则k=xy=-2×3=-6 所以过P点的反比例函数解析式为 y=-6/x
6
Y
4
A
2
D E
-5
O B
-2
C
5
X
f x = 3 x
-4
【4】. 已知如图:点(1,3)在反比例函数y=
的图象上长方形ABCD的边BC在X轴上,E为对角线BD的中点, 反比例函数y= k (x > 0) 的图象又经过A,E两点,若E点的 x 横坐标为m. ①求反比例函数的解析式 ;
反比例函数经典拓展难题

1:(2007年浙江省初中数学竞赛)函数y =1x-图象的大致形状是( )A B C D3.已知y 与2x -3成反比例,且41=x 时,y =-2,求y 与x 的函数关系式.4.已知函数y =y 1-y 2,且y 1为x 的反比例函数,y 2为x 的正比例函数,且23-=x 和x =1时,y 的值都是1.求y 关于x 的函数关系式.5.作出反比例函数xy 12=的图象,并根据图象解答下列问题: (1)当x =4时,求y 的值;(2)当y =-2时,求x 的值;(3)当y >2时,求x 的范围.6.作出反比例函数xy 4-=的图象,结合图象回答: (1)当x =2时,y 的值;(2)当1<x ≤4时,y 的取值范围;(3)当1≤y <4时,x 的取值范围.7.作出函数xy 12=的图象,并根据图象回答下列问题: (1)当x =-2时,求y 的值;(2)当2<y <3时,求x 的取值范围; (3)当-3<x <2时,求y 的取值范围.8.如图,A 、B 是函数xy 2=的图象上关于原点对称的任意两点,BC ∥x 轴,AC ∥y 轴, △ABC 的面积记为S ,则(s= ).9.如图,点A 、B 是函数y =x 与xy 1=的图象的两个交点,作AC ⊥x 轴于C ,作BD ⊥x 轴于D ,则四边形ACBD 的面积为( ).10.已知:如图,在平面直角坐标系xOy 中,Rt △OCD 的一边OC 在x 轴上,∠C =90°,点D 在第一象限,OC =3,DC =4,反比例函数的图象经过OD 的中点A . (1)求该反比例函数的解析式;(2)若该反比例函数的图象与Rt △OCD 的另一边交于点B ,求过A 、B 两点的直线的解析式.11.如图,A 、B 两点在函数)0(>=x xmy 的图象上.(1)求m 的值及直线AB 的解析式;(2)如果一个点的横、纵坐标均为整数,那么我们称这个点是格点.请直接写出图中阴影部分(不包括边界)所含格点的个数.12.如图,已知点A 在反比例函数的图象上,AB ⊥x 轴于点B ,点C (0,1),若△ABC 的面积是3,则反比例函数的解析式为____________.13.如图,直线y =mx 与双曲线xky =交于A ,B 两点,过点A 作AM ⊥x 轴,垂足为M ,连结BM ,若S △ABM =2,则k 的值是( ).14.如图,双曲线xky =(k >0)经过矩形OABC 的边BC 的中点E ,交AB 于点D 。
反比例函数提高训练题(难)

反比例函数提高训练题(难)一、选择题:1、反比例函数的解析式为y=k/x,因此选项D正确。
2、根据反比例函数的性质可知,x越大,y越小,因此选项B正确。
3、根据反比例函数的性质可知,y=k/x,当x越大,y越小,因此选项D正确。
4、反比例函数y=k/x的图象是一个双曲线,开口朝右上方,因此选项C正确。
5、根据题目条件可知,XXX(x1y2-y1x2),因此选项B正确。
6、根据反比例函数的性质可知,y=k/x,当x越大,y越小,因此选项A正确。
二、填空题:1、反比例函数y=k/x的图象是一个双曲线,开口朝右上方,因此k>0.2、根据双曲线的性质可知,y=k/x的图象与x轴、y轴有渐近线,因此k≠0.3、根据反比例函数的性质可知,y=k/x,当x越大,y越小,因此m>0.4、根据双曲线的性质可知,y=k/x的图象与x轴、y轴有渐近线,因此k≠0.5、根据双曲线的性质可知,y=k/x的图象与x轴、y轴有渐近线,因此k≠0.6、根据反比例函数的性质可知,y=k/x,当x越大,y越小,因此m>0.7、根据双曲线的性质可知,y=k/x的图象与x轴、y轴有渐近线,因此k≠0.8、根据题目条件可知,点P关于y轴对称的点为(-a。
m/(a-1)),因此k=m/(a-1)。
9、根据反比例函数的性质可知,y=k/x,当x越大,y越小,因此m>0.10、根据题目条件可知,y2=8/(x-4),因此选项C正确。
11、根据题目条件可知,A1、A2、A3在x轴上,因此选项B正确。
1.将文章中的格式错误和明显有问题的段落删除,改写每段话如下:1.在图中,点B1、B2、B3分别交于x轴平行线,过点xB3、C2、C3、B1、B3,分别与y轴交于点C1、OB2、OB3.阴影部分的面积之和为连接OB1、OB2、OB3的三角形面积加上连接OB1、OB3、C3、C2、OB2的梯形面积。
2.已知点A(-1.y1)、B(1.y2)、C(2.y3)在反比例函数y=k/x 的图象上,其中ky2>y3.3.如图所示,点P在y=k1/x和y=k2/x的图象上,PC⊥x 轴于点C,交y=k1/x的图象于点A,PD⊥y轴于点D,交y=k2/x的图象于点B。
反比例函数经典拓展难题

反比例函数难题拓展填空题1. (2011浙江金华,16,4分)如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,k0), Z AOC= 60°,点A在第一象限,过点A的双曲线为y -,在x轴上取一点P,过点PX作直线0A的垂线I,以直线I为对称轴,线段0B经轴对称变换后的像是0B.(1)当点0'与点A重合时,点P的坐标是___________ .2. (2011广东东莞,6, 4分)已知反比例函数y=k的图象经过(1,—2).则k= ____________ .x6. (2011浙江衢州,5,4分)在直角坐标系中,有如图所示的 RHABO,AB_x 轴于点B ,斜3 k边AO =10, si n . AOB,反比例函数y 二―(x ■ 0)的图像经过AO 的中点C ,且与AB 交于 5 x点D ,则点D 的坐标为37. (2011浙江绍兴,13, 5分)若点A (1y ),B (2, y 2)是双曲线y 上上的点,贝Uxy 1 ____________ y 2 (填 > ,<=).8. (2011浙江丽水,16, 4分)如图,将一块直角三角板 OAB 放在平面直角坐标系中,B (2,k0),/AO G 60°,点A 在第一象限,过点A 的双曲线为y=-,在x 轴上取一点P,过点Px作直线0A 的垂线I ,以直线I 为对称轴,线段0B 经轴对称变换后的像是 0B. (1) 当点O'与点A 重合时,点P 的坐标是 __________ .(2) 设P (t ,0)当OB 与双曲线有交点时,t 的取值范围是 ——yICD Bx(第15题)9. (2011湖南常德,5,3分)如图1所示的曲线是一个反比例函数图象的一支,点A在此曲线上,则该反比例函数的解析式为 ____________________ .10. (2011江苏苏州,18,3分)如图,已知点 A 的坐标为(屈,3), AB 丄x 轴,垂足为B ,k连接0A 反比例函数y=# (k>0)的图象与线段OA AB 分别交于点C D.若AB=3BD 以点xC 为圆心,CA 的5倍的长为半径作圆,则该圆与x 轴的位置关系是 _______________ (填“相离”、4“相切”或“相交”)m — 111. ( 2011山东济宁,11,3分)反比例函数y=—— 的图象在第一、三象限,则 m 的取值x 范围是 ____________ .12. (2011四川成都,25,4分)在平面直角坐标系xOy 中,已知反比例函数丫二仝你=0)满x足:当x : 0时,y 随x 的增大而减小.若该反比例函数的图象与直线 y —X • Gk 都经过 点P ,且0P =万,则实数k= _____________ .13. ( 2011安徽芜湖,15,5分)如图,在平面直角坐标系中有一正方形 AOBC 反比例函数y=k 经过正方形AOBC 寸角线的交点,半径为(4-2血)的圆内切于△ ABC 则k 的值x 为 _________.14. (2011广东省,6, 4分)已知反比例函数y=^的图象经过(1,— 2).则k=.x2 1 115. (2011江苏南京,15,2分)设函数y=—与y=x-1的图象的交战坐标为(a, b ),则—-—x a b的值为 ___________ .k16. (2011上海,11, 4分)如果反比例函数y=k ( k 是常数,k 丸))的图像经过点(一1,x2),那么这个函数的解析式是 ____________ .17. (2011湖北武汉市,16, 3分)如图,□ ABCD 勺顶点A, B 的坐标分别是A (— 1, 0), B(0,— 2),顶点C, D 在双曲线y=-上,边AD 交y 轴于点E ,且四边形BCDE 勺面积是△ ABEx面积的5倍,则k= _____ .,, k18. (2011湖北黄冈,4, 3分)如图:点A 在双曲线y 二—上, AB 丄x 轴于B ,且SOB 的面x积S2AO=2,贝U k=_____ .x119.(2011湖北黄石,15, 3分)若一次函数y=kx+1的图象与反比例函数y=-的图象没有x 公共点,则实数k 的取值范围是 _____________ 。
初二数学反比例函数试题答案及解析

初二数学反比例函数试题答案及解析1.如图,在平面直角坐标系中,双曲线经过点B,连结OB.将OB绕点O按顺时针方向旋转90°并延长至A,使OA=2OB,且点A的坐标为(4,2).(1)求过点B的双曲线的函数关系式;(2)根据反比例函数的图像,指出当x<-1时,y的取值范围;(3)连接AB,在该双曲线上是否存在一点P,使得S△ABP =S△ABO,若存在,求出点P坐标;若不存在,请说明理由.【答案】(1)双曲线的函数关系式为y=﹣;(2)当x<﹣1时,0<y<2;(3)存在;点P坐标为(﹣,4).【解析】(1)作AM⊥x轴于点M,BN⊥x轴于点N,由相似三角形的判定定理得出△AOM∽△OBN,OA=2OB,再根据OA=2OB,点A的坐标为(4,2)可得出B点坐标,进而得出反比例函数的关系式;(2)由函数图象可直接得出结论;(3)根据AB两点的坐标可知AB∥x轴,S△ABP =S△ABO=5,再分当点P在AB的下方与当点P在x轴上方两种情况即可得出结论.试题解析:(1)作AM⊥x轴于点M,BN⊥x轴于点N,∵OB⊥OA,∠AMO=∠BNO=90°,∴∠AOM=∠NBO,∴△AOM∽△OBN.∵OA=2OB,∴,∵点A的坐标为(4,2),∴BN=2,ON=1,∴B(﹣1,2).∴双曲线的函数关系式为y=﹣;(2)由函数图象可知,当x<﹣1时,0<y<2;(3)存在.∵yA =yB,∴AB∥x轴,∴S△ABP =S△ABO=5,∴当点P在AB的下方时,点P恰好在x轴上,不合题意舍去;当点P在x轴上方时,点P在第二象限,得AB•(yP ﹣2)=5,即×5×(yP﹣2)=5,解得yP=4,∴点P坐标为(﹣,4).【考点】1、相似三角形的判定与性质;2、待定系数法;3、函数大小的比较;4、反比例函数2.已知点A(1,y1)、B(2,y2)、C(﹣3,y3)都在反比例函数的图象上,则y1、y2、y3的大小关系是____________________.【答案】y3<y2<y1.【解析】∵k=6>0,∴图象在一、三象限,且在每一象限内y随x的增大而减小.∵x1<x2,∴y1>y2>0,∵x3<0,∴y3<0,∴y3<y2<y1.故答案是y3<y2<y1.【考点】反比例函数图象上点的坐标特征.3.已知反比例函数y=的图象上有三个点(2,),(3,),(,),则,,的大小关系是()A.>>B.>>C.>>D.>>【答案】A.【解析】试题解析:∵-k2-1<0∴反比例函数y=的图象在第二、四象限∴>>故选A.【考点】反比例函数图象上点的坐标特征.4.已知长方形的面积为10,则它的长y与宽x之间的关系用图象大致可表示为图中的()A.B.C.D.【答案】A【解析】由长方形的面积公式得y=,且x>0,y>0,而B中有x<0,y<0的情况,C,D中有x=0或y=0的情况,据此即可得出结果.解:∵xy=10∴y=,(x>0,y>0)故选A.点评:现实生活中存在大量成反比例函数的两个变量,解答该类问题的关键是确定两个变量之间的函数关系,然后利用实际意义确定其所在的象限.5.已知反比列函数y=的图象在每一条曲线上,y都随x的增大而增大,(1)求k的取值范围;(2)在曲线上取一点A,分别向x轴、y轴作垂线段,垂足分别为B、C,坐标原点为O,若四边形ABOC面积为12,求此函数的解析式.【答案】(1)k<0 (2)y=﹣【解析】(1)直接根据反比例函数的性质求解即可,k<0;(2)直接根据k的几何意义可知:过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,所以|k|=12,而k<0,则k=﹣12.解:(1)∵反比列函数y=的图象在每一条曲线上,y都随x的增大而增大,∴k<0;(2)设A(x,y),由已知得,|xy|=|k|=12,∵k<0,∴k=﹣12,所以,反比例函数的解析式为y=﹣.点评:主要考查了反比例函数中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.6.在同一平面直角坐标系中,正比例函数y=(m﹣1)x与反比例函数y=的图象的大体位置不可能是()A.B.C.D.【答案】D【解析】根据题意,依次分析选项中的图象,根据图象,求出其参数的范围,并解看有无公共解,若有,则可能是它们的图象,若无解,则不可能是它们的图象;即可得答案.解:依次分析选项可得:A、4m>0,m﹣1>0;解可得m>1;故可能是它们的图象.B、4m>0,m﹣1<0;解可得0<m<1;故可能是它们的图象.C、4m<0,m﹣1<0;解可得m<1;故可能是它们的图象.D、4m<0,m﹣1>0;无解;故不可能是它们的图象.故选D.点评:本题考查正比例函数与反比例函数的图象性质,注意①正比例函数与反比例函数的图象与k的关系,②两个函数中参数的关系.7.若A(,b)、B(-1,c)是函数的图象上的两点,且<0,则b与c的大小关系为()A.b<c B.b>c C.b=c D.无法判断【答案】B【解析】反比例函数的性质:当时,图象在第一、三象限,在每一象限内,y随x的增大而减小;当时,图象在第二、四象限,在每一象限内,y随x的增大而增大.解:∵,∴故选B.【考点】反比例函数的性质点评:反比例函数的性质是初中数学的重点,是中考中比较常见的知识点,一般难度不大,需熟练掌握.8.如图,在直角坐标平面内,函数的图象经过A(1,4),B(a,b),其中a>1,过点B作轴垂线,垂足为C,连接AC、AB.(1)m= ;(2)若△ABC的面积为4,则点B的坐标为【答案】(1)4;(2)【解析】(1)把A的坐标代入反比例函数的解析式,即可求出m和得出反比例函数的解析式;(2)设B的坐标是(a,b),根据B在反比例函数上得出ab的值,再根据△ABC的面积为4求解即可.(1)把A(1,4)代入得;(2)设B的坐标是(a,b),∵B在反比例函数上,∴ab=4∵△ABC的面积为4,∴×a×(4-b)=4,∴2a ab=4,∴2a-2=4,a=3,∵ab=4,∴b=.则点B的坐标为(3,).【考点】反比例函数图象上点的坐标特征,用待定系数法求反比例函数的解析式,三角形的面积点评:待定系数法求函数的解析式是初中数学的重点,贯穿于整个初中数学的学习,是中考中比较常见的知识点,一般难度不大,需熟练掌握.9.如图,双曲线在第一象限内如图所示作一条平行y轴的直线分别交双曲线于A、B两点,连OA、OB,则S=。
反比例函数压轴题精选(含答案)

中考反比例函数经典结论:如图,反比例函数k 的几何意义: (I) 12AOB AOC S S k ∆∆==; (II) OBAC S k =矩形. 下面两个结论是上述结论的拓展.(1) 如图①,OPA OCD S S ∆∆=,OPC PADC S S ∆=梯形.(2)如图②,OAPB OBCA S S =梯形梯形,BPE ACE S S ∆∆=.经典例题例 1.(1)(兰州)如图,已知双曲线(0)k y x x=>经由矩形OABC 边AB 的中点F 且交BC 于点E ,四边形OEBF 的面积为2,则k = 2 ;(2)如图,点A B 、为直线y x =上的两点,过A B 、两点分离作y 轴的平行线交双曲线1(0)y x x=>于C D 、两点,若2BD AC =,则224OC OD -= 6 例2.(陕西)假如一个正比例函数的图象与一个反比例函数xy 6=的图象交),(),,(2211y x B y x A ,那么))((1212y y x x --值为 24 .解析:因为A,B 在反比例函数xy 6=上,所以611=y x ,我们知道正比例函数与反比例函数的交点坐标关于原点成中间对称,是以),(),,(2211y x B y x A 中有1212,y y x x -=-=,所以24644))(())((1111111212=⨯==----=--y x y y x x y y x x例3.(山东威海)如图,一次函数b kx y +=的图象与反比例函数xm y =的图象交于点A ﹙-2,-5﹚,C ﹙5,n ﹚,交y 轴于点B,交x 轴于点D .(1) 求反比例函数xm y =和一次函数b kx y +=(2) 衔接OA,OC .求△AOC 的面积.解:(1)∵反比例函数xm y =的图象经由点A ﹙-2,-5﹚,∴m=(-2)×( -5)=10.∴反比例函数的表达式为xy 10=.∵点C ﹙5,n ﹚在反比例函数的图象上,∴2510==n .∴C 的坐标为﹙5,2﹚.∵一次函数的图象经由点A,C,将这两个点的坐标代入b kx y +=,得⎩⎨⎧+=+-=-.5225b k b k ,解得⎩⎨⎧-==.31b k , ∴所求一次函数的表达式为y =x -3.(2) ∵一次函数y=x -3的图像交y 轴于点B,∴B 点坐标为﹙0,-3﹚.∴OB=3.∵A 点的横坐标为-2,C 点的横坐标为5,∴S△AOC= S△AOB+ S△BOC=()22152215212-21=+⋅⋅=⋅⋅+⋅⋅OB OB OB .例4.(福建福州)如图,已知直线12y x =与双曲线(0)k y k x=>交于A B ,两点,且点A 的横坐标为4. (1)求k 的值;(2)若双曲线(0)k y k x=>上一点C 的纵坐标为8,求AOC △的面积;(3)过原点O 的另一条直线l 交双曲线(0)k y k x=>于P Q ,两点(P 点在第一象面积为24,限),若由点A B P Q ,,,为极点构成的四边形求点P 的坐标. 解:(1)点A 横坐标为4,∴当4x =时,2y =.∴点A 的坐标为(42),. 点A 是直线12y x =与双曲线(0)k y k x=>的交点,428k ∴=⨯=.(2)解法一:如图1,点C 在双曲线上,当8y =时,1x =∴点C 的坐标为(18),. 过点A C ,分离做x 轴,y 轴的垂线,垂足为M N ,,得矩形DMON .32ONDM S =矩形,4ONC S =△,9CDA S =△,4OAM S =△.3249415AOC ONC CDA OAM ONDM S S S S S =---=---=△△△△矩形解法二:如图2,过点C A ,分离做x 轴的垂线,垂足为E F ,,点C 在双曲线8y x=上,当8y =时,1x =.∴点C 的坐标为(18),.点C ,A 都在双曲线8y x=上,4COEAOF S S ∴==△△COE COA AOF CEFA S S S S ∴+=+△△△梯形.COA CEFA S S ∴=△梯形.1(28)3152CEFA S =⨯+⨯=梯形,15COA S ∴=△.(3)反比例函数图象是关于原点O OP OQ ∴=,OA OB =.∴四边形APBQ 是平行四边形. 1124644POA APBQ S S ∴==⨯=△平行四边形. 设点P 横坐标为(04)m m m >≠且,得8()P m m,.过点P A ,分离做x 轴的垂线,垂足为E F ,, 点P A ,在双曲线上,4PQE AOF S S ∴==△△. 若04m <<,如图3,POE POA AOF PEFA S S S S +=+△△△梯形,6POA PEFA S S ∴==△梯形.182(4)62m m ⎛⎫+-= ⎪⎝⎭∴·. 解得2m =,8m =-(舍去).∴(24)P ,. 若4m >,如图4,AOF AOP POE AFEP S S S S +=+△△△梯形,图2图3图46POA PEFA S S ∴==△梯形.182(4)62m m ⎛⎫∴+-= ⎪⎝⎭,解得8m =,2m =-(舍去).(81)P ∴,. ∴点P 的坐标是(24)P ,或(81)P ,. 例 5.(山东淄博) 如图,正方形AOCB 的边长为4,反比例函数的图象过点E (3,4).(1)求反比例函数的解析式;(2)反比例函数的图象与线段BC 交于点D,直线1yx b 2过点D,与线段AB 订交于点F,求点F 的坐标;(3)衔接OF,OE,探讨∠AOF 与∠EOC 的数目关系,并证实. 【答案】解:(1)设反比例函数的解析式k yx , ∵反比例函数的图象过点E (3,4),∴k 43,即k=12.∴反比例函数的解析式12yx. (2)∵正方形AOCB 的边长为4,∴点D 的横坐标为4,点F 的纵坐标为4.∵点D 在反比例函数的图象上,∴点D 的纵坐标为3,即D (4,3). ∵点D 在直线1y x b 2上,∴134b 2,解得b=5.∴直线DF 为1yx 52.将y4代入1yx 52,得14x 52,解得x 2.∴点F 的坐标为(2,4).(3)∠AOF=12∠EOC.证实如下:在CD 上取CG=CF=2,衔接OG,衔接EG 并延伸交x轴于点H.∵AO=CO=4,∠OAF=∠OCG=900,AF=CG=2, ∴△OAF≌△OCG(SAS ).∴∠AOF=∠COG. ∵∠EGB=∠HGC,∠B=∠GCH=900,BG=CG=2,∴△EGB≌△HGC(AAS ).∴EG=HG. 设直线EG :ymxn ,∵E(3,4),G (4,2),∴43m n 24m n =+⎧⎨=+⎩,解得,m 2n=10=⎧⎨⎩-. ∴直线EG :y 2x10.令y2x10=0,得x 5.∴H(5,0),OH=5.在R t△AOF 中,AO=4,AE=3,依据勾股定理,得OE=5.∴OH=OE.∴OG 是等腰三角形底边EH 上的中线.∴OG 是等腰三角形顶角的等分线. ∴∠EOG=∠GOH.∴∠EOG=∠GOC=∠AOF,即∠AOF=12∠EOC.例 6.(山东威海)一次函数y ax b =+的图象分离与x 轴.y 轴交于点,M N ,与反比例函数ky x=的图象订交于点,A B .过点A 分离作AC x ⊥轴,AE y ⊥轴,垂足分离为,C E ;过点B 分离作BF x ⊥轴,BD y ⊥轴,垂足分离为F D ,,AC 与BD 交于点K ,衔接CD . (1)若点A B ,在反比例函数k y x=的图象的统一分支上,如图1,试证实: ①AEDK CFBK S S =四边形四边形; ②AN BM =.(2)若点A B ,分离在反比例函数k y=的图象的不合分支上,如图2,则AN 与BM还相等吗?试证实你的结论.解:(1)①AC x ⊥轴,AE y ⊥BF x ⊥轴,BD y ⊥轴,∴四边形AC x ⊥轴,BD y ⊥轴,∴四边形1111OC x AC y x y k ===,,,∴11AEOC S OC AC x y k ===矩形 2222OF x FB y x y k ===,,,∴22BDOF S OF FB x y k ===矩形.∴AEOC BDOF S S =矩形矩形.AEDK AEOC DOCK S S S =-矩形矩形矩形,CFBK BDOF DOCK S S S =-矩形矩形矩形,∴AEDK CFBK S S =矩形矩形)②由(1)知AEDK CFBK S S =矩形矩形.∴AK DK BK CK =.∴AK BKCK DK= 90AKB CKD ∠=∠=°,∴AKB CKD △∽△.∴CDK ABK ∠=∠.∴AB CD∥AC y ∥轴,∴四边形ACDN 是平行四边形.∴AN CD =.同理BM CD =.AN BM ∴=.(2)AN 与BM 仍然相等.AEDK AEOC ODKC S S S =+矩形矩形矩形,BKCF BDOF ODKC S S S =+矩形矩形矩形,又AEOC BDOF S S k ==矩形矩形,∴AEDK BKCF S S =矩形矩形∴AK DK BK CK =.∴CK DKAK BK=.K K ∠=∠,∴CDK ABK △∽△.∴CDK ABK ∠=∠.∴AB CD ∥.AC y ∥轴,∴四边形ANDC 是平行四边形.∴AN CD =.同理BM CD =.∴AN BM =.第一部分演习一.选择题1.(鄂州)如图,直线y=mx 与双曲线y=xk 交于A.B 两点,过点A 作AM⊥x 轴,垂足为M,贯穿连接BM,若ABM S ∆=2,则k 的值是2.(兰州) 如图,若正方形OABC 的极点B 和正方形ADEF 的极点E 都在函数1y x=(0x >)的图象上,则点E 的坐标是(,).3.(泰安)如图,双曲线)0(>k xk y =经由矩形OABC 的边BC 的中点E, 交AB 于点D.若梯形ODBC 的面积为3,则双曲线的解析式为A .xy 1=B .xy 2= C .x y 3=D .xy 6=OAB4.(仙桃)如图,已知双曲线)0k (xk y >=经由直角三角形斜边OB 的中点D,与直角边AB 订交于点C .若△OBC 的面积为3,则k =____________.OC D KF E N yxABM图2xyABO1S2Sy xO P 1P 2P 3P 4 P 5A 1 A 2 A 3 A 4 A 52x 5.(牡丹江市)如图,点A .B 是双曲线3y x=上的点,分离经由A .B 两点向x 轴.y 轴作垂线段,若1S =阴影,则12S S +=.6.(莆田)如图,在x 轴的正半轴上依次截取112233445OA A A A A A A A A ====,过点12345A A A A A 、、、、分离作x 轴的垂线与反比例函数()20y x x=≠的图象订交于点12345P P P P P 、、、、,得直角三角形1112233344455OPA A P A A P A A P A A P A 2、、、、,并设其面积分离为12345S S S S S 、、、、,则5S 的值为.. 第4题图 第5题图 第6题图7.(包头)已知一次函数1y x =+与反比例函数ky x =的图象在第一象限订交于点A ,与x 轴订交于点C AB x ,⊥轴于点B ,AOB △的面积为1,则AC 的长为8.( 嵊州市)如图,直线)0(<=k kx y 与双曲线xy 2-=交于),(),,(2211y x B y x A 两点,则122183y x y x -的值为A.-5 B.-10 C.5 D.10【答案】B9.(江苏无锡)如图,已知梯形ABCO 的底边AO 在x 轴上,BC∥AO,AB⊥AO,过点C 的双曲线ky x=交OB 于D,且OD :DB=1:2,若△OBC 的面积等于3,则k 的值A .等于2 B .等于34C .等于245D .无法肯定【答案】B第7题图 第8题图 第9题图10.(江苏盐城)如图,A.B 是双曲线y= kx(k>0) 上的点,A.B 两点的横坐标分离是a.2a,线段AB 的延伸线交x 轴于点C,若S△AOC=6.则k=.【答案】4 11.(安徽蚌埠二中)已知点(1,3)在函数)0(>=x xk y 的图像上.正方形ABCD 的边BC 在x 轴上,点E 是对角线BD 的中点,函数)0(>=x x k y 的图像又经由A .E 两点,则点E 的横坐标为__________.612.(四川内江)如图,反比例函数y =kx(x >0)的图象经由矩形OABC 对角线的交点M,分离与AB.BC 订交于点D.E .若四边形ODBE 的面积为6,则k 的值为y O AC B yBAoO ABCDxy图6yx O BC AAB C D E yxOMA .1B .2C .3D .4【答案】B第10题图 第11题图 第12题图13.(山东东营)如图,直线l 和双曲线(0)k y k x=>交于A.B 亮点,P 是线段AB 上的点(不与A.B 重合),过点A.B.P 分离向x 轴作垂线,垂足分离是C.D.E,衔接OA.OB.OP,设△AOC 面积是S1.△BOD 面积是S2.△POE 面积是S3.则 A. S1<S2<S3B. S1>S2>S3C. S1=S2>S3D. S1=S2<S3 【答案】D①x<0时,x2y =,②△OPQ 的面积为定值, ③x>0时,y 随x 的增大而增大 ④MQ=2PM⑤∠POQ 可以等于90°个中准确的结论是A .①②④B②④⑤C.③④⑤D.②③⑤ 【答案】B15.(甘肃兰州,15,4分)如图,矩形ABCD 的对角线BD 经由坐标原点,矩形的边分离平行于坐标轴,点C 在反比例函数221k k y x++=的图象上.若点A 的坐标为(-2,-2),则k 的值为A .1B .-3C .4D .1或-3【答案】D轴于A.B 16.(四川乐山)如图,直线6y x =-交x 轴.y 直线下两点,P 是反比例函数4(0)y x x=>图象上位于xyOABCD方的一点,过点P 作x 轴的垂线,垂足为点M,交AB 于点E,过点P 作y 轴的垂线,垂足为点N,交AB 于点F.则AF BE ⋅= A .8 B .6 C .4 D .62 【答案】A17.(•德州)如图,两个反比例函数和的图象分离是l1和l2.设点P在l1上,PC⊥x 轴,垂足为C,交l2于点A,PD⊥y 轴,垂足为D,交l2于点B,则三角形PAB 的面积为A . 3B . 4C .D .5 解解:∵点P 在y=上,∴设P 的坐标是(a,), ∵PA ⊥x 轴,∴A 的横坐标是a,∵A 在y=﹣上,∴A 的坐标是(a,﹣), ∵PB ⊥y 轴,∴B 的纵坐标是, ∵B 在y=﹣上,∴代入得:﹣, 解得:x=﹣2a,∴B 的坐标是(﹣2a,), ∴PA=﹣(﹣)=,PB=a ﹣(﹣2a )=3a, ∵PA ⊥x 轴,PB ⊥y 轴,x 轴⊥y 轴,∴PA ⊥PB,∴△PAB 的面积是:PA ×PB=××3a=.故选C .18.(福州)如图,过点C(1,2)分离作x 轴.y 轴的平行线,交直线y =-x +6于A. B 两点,若反比例函数y =kx (x >0)的图像与△ABC 有公共点,则k 的取值规模是A .2≤k≤9 B.2≤k≤8C .2≤k≤5D .5≤k≤8 解答:解:∵点C(1,2),BC∥y 轴,AC∥x 轴,ABCOxy∴当x =1时,y =-1+6=5,当y =2时,-x +6=2,解得x =4, ∴点A.B 的坐标分离为A(4,2),B(1,5),依据反比例函数系数的几何意义,当反比例函数与点C 订交时,k =1×2=2最小,设与线段AB 订交于点(x,-x +6)时k 值最大,则k =x(-x +6)=-x2+6x =-(x -3)2+9,∵ 1≤x≤4,∴当x =3时,k 值最大,此时交点坐标为(3,3), 是以,k 的取值规模是2≤k≤9.故选A .19.(临沂)如图,若点M 是x 轴正半轴上随意率性一点,过点M 作PQ∥y 轴,分离交函数1(0)k y x x =>和2(0)ky x x=>的图象于点P 和Q,衔接OP 和OQ .则下列结论准确的是A .∠POQ 不成能等于90°B.12k PM QM k = C .这两个函数的图象必定关于x 轴对称; D .△POQ 的面积是()1212k k + 故选:D .20.(湖北黄石)如图所示,已知11(,)2A y ,2(2,)B y 为反比例函数1y x=图像上的两点,动点(,0)P x 在x 正半轴上活动,当线段AP 与线段BP 之差达到最大时,点P 的坐标是DA. 1(,0)2B. (1,0)C. 3(,0)2D. 5(,0)2【解答】解:∵把A (1/2 ,y1),B (2,y2)代入反比例函数y=1/ x 得:y1=2,y2=1/2 ,yxOABP∴A(1/2 ,2),B (2,1/2 ),∵在△ABP 中,由三角形的三边关系定理得:|AP-BP|<AB,∴延伸AB 交x 轴于P′,当P 在P′点时,PA-PB=AB,即此时线段AP 与线段BP 之差达到最大,设直线AB 的解析式是y=kx+b,把 A.B 的坐标代入得: 2=1/2k+b ,1/2=2k+b,解得:k=-1,b=5/2 ,∴直线AB 的解析式是y=-x+5/2 ,当y=0时,x=5/2 ,即P (5/2 ,0),故选D .21.(湖北随州)如图,直线l 与反比例函数x y 2=的图象在第一象限内交于A.B 两点,交x 轴的正半轴于C 点,若AB :BC=(m 一l):1(m>l)则△OAB 的面积(用m 暗示)为A.m m 212-B.mm 12- C. m m )1(32- D.m m 2)1(32- 答案:B22.(江苏姑苏)如图,菱形OABC 的极点C 的坐标为(3,4),极点A 在x 轴的正半轴上.反比例函数y =k x(x >0)的图象经由极点B,则k 的值为A .12B .20C .24D .32【答案】D .解:过C 点作CD⊥x 轴,垂足为D .B AoxylO xyB A C∵点C 的坐标为(3,4),∴OD=3,CD=4.∴OC= OD2+CD2=32+42=5.∴OC=BC=5.∴点B 坐标为(8,4), ∵反比例函数y=k x(x >0)的图象经由极点B,∴k=32.23.(山东临沂)如图,等边三角形OAB 的一边OA 在x 轴上,双曲线y =3x在第一象限内的图象经由OB 边的中点C,则点B 的坐标是 A .(1,3)B .(3,1)C .(2,23)D .(23,2)【答案】:C .24.(湖北孝感)如图,函数y=﹣x 与函数的图象订交于A,B 两点,过A,B 两点分离作y 轴的垂线,垂足分离为点C,D .则四边形ACBD 的面积为A .2 B .4 C . 6 D .8 解答:解:∵过函数的图象上A,B 两点分离作y 轴的垂线,垂足分离为点C,D,∴S △AOC=S △ODB=|k|=2, 又∵OC=OD,AC=BD,∴S △AOC=S △ODA=S △ODB=S △OBC=2, ∴四边形ABCD 的面积为:S △AOC+S △ODA+S △ODB+S △OBC=4×2=8. 故选D .25.(四川内江)如图,反比例函数(x >0)的图象经由矩形OABC 对角线的交点M,分离于AB.BC 交于点D.E,若四边形ODBE 的面积为9,则k 的值为A . 1B .2 C .3 D .4 解答:解:由题意得:E.M.D 位于反比例函数图象上,则S △OCE=,S △OAD=,过点M 作MG ⊥y 轴于点G,作MN ⊥x 轴于点N,则S □ONMG=|k|,又∵M 为矩形ABCO 对角线的交点, ∴S 矩形ABCO=4S □ONMG=4|k|, 因为函数图象在第一象限,k >0,则++9=4k, 解得:k=3.故选C .26.(四川乐山)如图,已知第一象限内的点A 在反比例函数y = 2x 的图象上,第二象限内的点B 在反比例函数y = k x 的图象上,且OA⊥0B,cotA= 33,则k 的值为A .-3 B.-6 C.- 3 D.-2 3 在第一象27.(黔东南州)如图,直线y=2x 与双曲线y=限的交点为A,过点A 作AB⊥x 轴于B,将△ABO 绕点O 扭转90°,得到△A′B′O,则点A′的坐标为A.()1,0B. ()1,0或()1,0-C. ()2,0或()0,2-D. ()2,1-或()2,1-解答:解:联立直线与反比例解析式得:,消去y 得到:x2=1,解得:x=1或﹣1,∴y=2或﹣2, ∴A (1,2),即AB=2,OB=1,依据题意画出响应的图形,如图所示,可得A ′B ′=A ′′B ′′=AB=2,OB ′=OB ′′=OB=1,依据图形得:点A ′的坐标为(﹣2,1)或(2,﹣1). 故选D .Ox y ABC28. (•威海)如图,在平面直角坐标系中,∠AOB=90°,∠OAB=30°,反比例函数的图象经由点A,反比例函数的图象经由点B,则下列关于m,n 的关系准确的是( )A . m =﹣3nB . m =﹣nC .m=﹣nD .m=n解答: 解:过点B 作BE ⊥x 轴于点E,过点A 作AF ⊥x 轴于点F,设点B 坐标为(a,),点A 的坐标为(b,),∵∠OAB=30°,∴OA=OB,设点B 坐标为(a,),点A 的坐标为(b,),则OE=﹣a,BE=,OF=b,AF=,∵∠BOE+∠OBE=90°,∠AOF+∠BOE=90°, ∴∠OBE=∠AOF,又∵∠BEO=∠OFA=90°, ∴△BOE ∽△OAF,∴==,即==,解得:m=﹣ab,n=,故可得:m=﹣3n .故选A .二.填空题1.(湖北武汉)如图,直线y =33x b -+与y 轴交于点A,与双4,则k曲线y =k x在第一象限交于点B,C 两点,且AB ⋅AC ==. 答案:3(0x >)交2.( 福建德化)如图,直线43y x =与双曲线ky x =于点A .将直线43y x =向下平移个6单位后,与双曲线k y x=(0x >)交于点B ,与x 轴交于点C,则C 点的坐标为___________;若2AO BC=,则k =.【答案】()0,29,123.(湖南衡阳)如图,已知双曲线)0k (xk y >=经由直角三角形OAB 斜边OB 的中点D,与直角边AB 订交于点C .若△OBC 的面积为3, 则k =____________.【答案】24.(宁波市)如图,正方形A1B1P1P2的极点P1.P2在反比例函数y =2x (x >0)的图像上,极点A1.B1分离在x 轴和y 轴的正半轴上,再在其右侧作正方形P2P3A2B2,极点P3在反比例函数y =2x (x >0)的图象上,极点A3在x 轴的正半轴上,则点P3的坐标为 【答案】(3+1,3-1)5.(安徽芜湖)如图,在平面直角坐标系中有一正方形AOBC,半径为反比例函数k y x=经由正方形AOBC 对角线的交点,(422)的圆内切于△ABC,则k 的值为. 【答案】46.(湖北武汉市)如图,ABCD 的极点A,B 的坐标分离是A AD 交(-1,0),B (0,-2),极点C,D 在双曲线y=xk 上,边y 轴于点E,且四边形BCDE 的面积是△ABE 面积的5倍,则k=_____. 【答案】12在双曲7.(湖北孝感)如图,点A 在双曲线1y x上,点B ABCD 的线3yx上,且AB∥x 轴,C.D 在x 轴上,若四边形面积为矩形,则它的面积为. 【答案】2xy第16题图BCEDoQ PA xy第16题图HF BCEDoQ PA 8.(湖北荆州,16,4分)如图,双曲线2(0)yx x经由四边形OABC 的极点A.C,∠ABC=90°,OC等分OA 与x 轴正半轴的夹角,AB∥x 轴,将△ABC 沿AC 翻折后得到△AB'C,B '点落在OA 上,则四边形OABC 的面积是.【答案】29.(浙江温州)如图,已知动点A 在函数点C,延4=y x(x>o)的图象上,AB⊥x 轴于点B,AC⊥y 轴于伸CA 至点D,使AD=AB,延伸BA 至点E,使AE=AC.直线DE 分离交x 轴,y 轴于点P,Q.当QE :DP=4:9时,图中的暗影部分的面积等于____________. 如图,作EF⊥y 轴,DH⊥x 轴,由题意得:△QEF∽△DHP,∵QE:DP=4:9设AC= a,则AB=4a,49EF HP ,HP=94a ,∵△AED∽△DHP,∴424648==,==49934EA AD a a a a a DH HP a 得到:得:得:S暗影=2218+2a a=413+3=33) 10.(•聊城)如图,在直角坐标系中,正方形的中间在原点O,且正方形的一组对边与x 轴平行,点P (3a,a )是反比例函数y=(k >0)的图象上与正方形的一个交点.若图中暗影部分的面积等于9,则这个反比例函数的解析式为.解答: 解答:解:∵反比例函数的图象关于原点对称,∴暗影部分的面积和正好为正方形面积的,设正方形的边长为b ,则b 2=9,解得b =6,∵正方形的中间在原点O , ∴直线AB 的解析式为:x =3, ∵点P (3a ,a )在直线AB 上, ∴3a =3,解得a =1,∴P (3,1), ∵点P 在反比例函数y =(k >0)的图象上,∴k=3, ∴此反比例函数的解析式为:y=.故答案为:y=的图象交11.(•衢州)如图,已知函数y=2x和函数于A.B两点,过点A作AE⊥x轴于点E,若△AOE的面积为4,P是坐标平面上的点,且以点B.O.E.P为极点的四边形是平行四边形,则知足前提的P点坐标是P1(0,﹣4)P2(﹣4,﹣4)P3(4,4)解答:解:如图∵△AOE的面积为4,函数的图象过一.三象限,∴k=8,∵函数y=2x和函数的图象交于A.B两点,∴A.B两点的坐标是:(2,4)(﹣2,﹣4),∵以点B.O.E.P为极点的平行四边形共有3个,∴知足前提的P点有3个,分离为:P1(0,﹣4),P2(﹣4,﹣4),P3(4,4).故答案为:P1(0,﹣4),P2(﹣4,﹣4),P3(4,4).12.(甘肃兰州)如图,M为双曲线y=3x上的一点,过点M作x轴.y轴的垂线,分离交直线y=-x+m于点D.C两点,若直线y=-x+m与y轴交于点A,与x 轴订交于点B,则AD•BC的值为.解答:解:作CE⊥x轴于E,DF⊥y轴于F,如图,对于y=-x+m,令x=0,则y=m;令y=0,-x+m=0,解得x=m,∴A(0,m),B(m,0),∴△OAB等腰直角三角形,∴△ADF和△CEB都是等腰直角三角形,设M的坐标为(a,b),则ab=,CE=b,DF=a,∴AD=DF=a,BC=CE=b,∴AD•BC=a•b=2ab=2.故答案为2.13.(.深圳)如图,双曲线ky(k0)x=>与⊙O在第一象限内交于P.Q两点,分离过P.Q 两点向x 轴和y 轴作垂线,已知点P 坐标为(1,3),则图中暗影部分的面积为.【答案】4.【剖析】∵⊙O 在第一象限关于y=x 对称,k y (k 0)x=>也关于y=x 对称,P 点坐标是(1,3),∴Q 点的坐标是(3,1),∴S 暗影=1×3+1×3-2×1×1=4.14.(•扬州)如图,双曲线y =经由Rt△OMN 斜边上的点A,与直角边MN 订交于点B,已知OA =2AN,△OAB 的面积为5,则k 的值是 12 .解答: 过A 点作AC ⊥x 轴于点C,如图,则AC ∥NM,∴△OAC ∽△ONM,∴OC :OM =AC :NM =OA :ON,而OA =2AN,即OA :ON =2:3,设A 点坐标为(a,b),则OC =a,AC =b, ∴OM =a,NM =b,∴N 点坐标为(a,b), ∴点B 的横坐标为a,设B 点的纵坐标为y, ∵点A 与点B 都在y =图象上,∴k =ab =a •y, ∴y =b,即B 点坐标为(a,b),∵OA =2AN,△OAB 的面积为5,∴△NAB 的面积为, ∴△ONB 的面积=5+=,∴NB •OM =,即×(b -b)×a =,∴ab =12,∴k =12.故答案为12.15.(武汉)如图,点A 在双曲线y=的第一象限的那一支上,AB 垂直于x 轴与点B,点C 在x 轴正半轴上,且OC=2AB,点E 在线段AC 上,且AE=3EC,点D 为OB 的中点,若△ADE 的面积为3,则k 的值为. 解答:解:连DC,如图,C∵AE=3EC,△ADE 的面积为3,∴△CDE 的面积为1, ∴△ADC 的面积为4,设A 点坐标为(a,b ),则AB=a,OC=2AB=2a,而点D 为OB 的中点,∴BD=OD=b,∵S 梯形OBAC=S△ABO+S△ADC+S△ODC,∴(a+2a )×b=a×b+4+×2a×b,∴ab=, 把A (a,b )代入双曲线y=,∴k=ab=.16.(成都)如图,在平面直角坐标系xOy 中,直线AB 与x 轴.y 轴分离交于点A,B, 与反比例函数k y x=(k 为常数,且0k >)在第一象限的图象交于点E,F .过点E 作EM⊥y 轴于M,过点F 作FN⊥x 轴于N,直线EM 与FN 交于点C .若BE 1BF m=(m 为大于l的常数).记△CEF 的面积为1S ,△OEF 的面积为2S ,则12S S=________. (用含m 的代数式暗示) 答案:11m m (k 的几何意义,线段比的转化,面积的几种求法)17.(湖北黄冈)已知反比例函数y =6x在第一象限的图象如图所示,点A 在其图象上,点B 为x 轴正半轴上一点,衔接AO.AB,且AO =AB,则S△AOB=.【答案】6.【解析】如下图,过点A 作AC⊥OB 于点C,∵AO=AB,∴OC=BC .而AC =AC,AO =AB,∴△AOC≌△ABC.∴S△AOC=S△ABC.设点A 的坐标为(x,y)(x >0,y >0),则xy =6,AC =y,OC =x,∴S△AOB=2S△AOC=2×12×OC·AC=xy =6.18.(四川宜宾)如图,直线x y 34=与双曲线)0(>=x x k y 交于点A,将直线x y 34=向右平移29个单位后,与双曲线)0(>=x x k y 交于点B,与x 轴交于点C,若2=BCAO,则k=.【答案】12.【解析】起首求出平移后直线的解析式,然后直线x y 34=与双曲线)0(>=x xk y 两解析式联立方程组求出点A 的纵坐标,平移后的直线解析式x y 34=-6与双曲线)0(>=x xky 两解析式联立方程组,求出点B 的纵坐标,依据类似三角形对应边成比例的性质可得A.B 的纵坐标的比等于AO :BC,然后列出方程求解即可.19.(四川泸州)如图,()111P ,x y ,()222P ,x y ,……()P ,n n n x y 在函数()10y x x=>的图像上,11P OA ∆,212P A A ∆,323P A A ∆,……1P A A n n n -∆都是等腰直角三角形,斜边1OA .12A A .23A A ,……1A A n n -都在x 轴上(n是大于或等于2的正整数),则点3P 的坐标是;点n P 的坐标是(用含n 的式子暗示). 【答案】;【解析】过点P1作P1E⊥x 轴于点E,过点P2作P2F⊥x 轴于点F,过点P3作P3G⊥x 轴于点G,依据△P1OA1,△P2A1A2,△P3A2A3都是等腰直角三角形,可求出P1,P2,P3的坐标,从而总结出一般纪律得出点Pn 的坐标.21.(山东日照)如右图,直线AB 交双曲线xk y =于A.B,交x 轴于点C,B 为线段AC 的中点,过点B 作BM⊥x 轴于M,贯穿连接OA.若OM=2MC,S⊿OAC=12.则k 的值为___________. 【答案】8【解析】过点A 作AD⊥x 轴于点D,则△ADO 的面积为21k,∵BM⊥x 轴,∴AD∥BM, ∵B 为线段AC 的中点,∴BM 为△ADC 的中位线,∴DM=MC, ∵OM=2MC, ∴OD=DM=MC.∴S⊿OAC=3S⊿OAD,=12=k 23,∴k=8.22.(•宁波)如图,等腰直角三角形ABC极点A在x轴上,∠BCA=90°,AC=BC=2,反比例函数y=(x>0)的图象分离与AB,BC交于点D,E.贯穿连接DE,当△BDE∽△BCA时,点E的坐标为.【答案】.(,).【解析】如图,∵∠BCA=90°,AC=BC=2,反比例函数y=(x>0)的图象分离与AB,BC交于点D,E,∴∠BAC=∠ABC=45°,且可设E(a,),D(b,),∴C(a,0),B(a,2),A(2﹣a,0),∴易求直线AB的解析式是:y=x+2﹣a.又∵△BDE∽△BCA,∴∠BDE=∠BCA=90°,∴直线y=x与直线DE垂直,=,即ab=3.∴点D.E关于直线y=x对称,则又∵点D在直线AB上,∴=b+2﹣a,即2a2﹣2a﹣3=0,解得,a=,∴点E的坐标是(,).23.(•自贡)如图,在函数的图象上有点P1.P2.P3….Pn.Pn+1,点P1的横坐标为2,且后面每个点的横坐标与它前面相邻点的横坐标的差都是2,过点P1.P2.P3….Pn.Pn+1分离作x轴.y轴的垂线段,构成若干个矩形,如图所示,将图中暗影部分的面积从左至右依次记为S1.S2.S3….Sn,则S1=4 ,Sn=.(用含n的代数式暗示)解答: 解:当x=2时,P1的纵坐标为4,当x=4时,P2的纵坐标为2,当x=6时,P3的纵坐标为, 当x=8时,P4的纵坐标为1, 当x=10时,P5的纵坐标为:, 则S1=2×(4﹣2)=4=2[﹣]; S2=2×(2﹣)=2×=2[﹣]; S3=2×(﹣1)=2×=2[﹣];Sn=2[﹣]=;故答案为:4,.24.(•遵义)如图,已知直线y=x 与双曲线y=(k >0)交于A.B 两点,点B 的坐标为(﹣4,﹣2),C 为双曲线y=(k >0)上一点,且在第一象限内,若△AOC 的面积为6,则点C 的坐标为(2,4).解答:解:∵点B (﹣4,﹣2)在双曲线y=上,∴=﹣2,∴k=8, 依据中间对称性,点A.B 关于原点对称,所以,A (4,2), 如图,过点A 作AE ⊥x 轴于E,过点C 作CF ⊥x 轴于F,设点C 的坐标为(a,),则S △AOC=S △COF+S 梯形ACFE ﹣S △AOE=×8+×(2+)(4﹣a )﹣×8,=4+﹣4,=,∵△AOC 的面积为6,∴=6,整顿得,a2+6a ﹣16=0,解得a1=2,a2=﹣8(舍去),∴==4,∴点C 的坐标为(2,4).故答案为:(2,4).25.(武汉)如图,已知四边形ABCD 是平行四边形,BC =2AB,A,B 两点的坐标分离是(-1,0),(0,2),C,D 两点在反比例函数)0(<=x xk y 的图象上,则k 的值等于.答案:-12解析:如图,过C.D 两点作x 轴的垂线,垂足为F.G,CG 交AD于M 点,过D 点作DH⊥CG,垂足为H,∵CD∥AB,CD=AB,∴△CDH≌△ABO(AAS ),∴DH=AO=1,CH=OB=2,设C (m,n ),D (m -1,n -2), 则mn =(m -1)(n -2)=k,解得n=2-2m, 设直线BC 解析式为y=ax+b,将B.C 两点坐标代入得2b n am b=⎧⎨=+⎩,又n=2-2m, BC =22(2)m n +-=25m ,AB =5,因为BC =2AB,解得:m =-2,n =6,所以,k =mn =-12轴交于26.(咸宁)如图,一次函数y ax b =+的图像与x 轴.y两点,A B 、两点,与反比例函数k y x=的图象订交于C D、衔接分离过C D 、两点作y 轴.x 轴的垂线,垂足为E F 、,CF DE、.有以下四个结论:①CEF DEF S S ∆∆=;②AOB FOE ∆∆∽;③DCE CDF ∆∆≌;④AC BD =.个中准确的结论是 . 三.解答题1.(兰州) 如图,P1是反比例函数)0(>k x ky =在第一象限图像上的一点,点A1的坐标为(2,0). (1)当点P1的横坐标逐渐增大时,△P1OA1的面积将若何变更?(2)若△P1OA1与△P2A1A2均为等边三角形,求此反比例函数的解析式及A2点的坐标.FE D CB A o xyyx第15题图DCBAO2.(内蒙呼和浩特)在平面直角坐标系中,函数y=mx(x>0,m是常数)的图像经过点A(1,4).点B(a,b),个中a>1.过点A作x中的垂线,垂足为C,过点B 作y轴的垂线,垂足为D,AC与BD订交于点M,贯穿连接AD.DC.CB与AB.(1)求m的值;(2)求证:DC∥AB;(3)当AD=BC时,求直线AB的函数解析式.【答案】解:(1)∵点A(1,4)在函数y=mx的图像上,∴4=1m,得m=4.……………………………2分(2)∵点B(a,b)在函数y=mx的图像上,∴ab=4.又∵AC⊥x轴于C,BD⊥y轴于D交AC于M,∴AC⊥BD于M∴M(1,b),D(0,b),C(1,0)∴tan∠BAC=BMAM =14ab--=1aab b--=1b,tan∠DCM=DMMC=1b……………4分∴tan∠BAC=tan∠DCM,所以锐角∠BAC=∠DCM,DC∥AB………………………………………………6分(3)设直线AB的解析式为y=kx+b∵AB∥CD,AD=BC,∴四边形ABCD是平行四边形或等腰梯形.①四边形ABCD是平行四边形时,AC与BD互相等分,又∵AC⊥BD,∴B(2,2)∴422k b k b +=⎧⎨+=⎩,解得26k b =-⎧⎨=⎩∴直线AB 的解析式为:y =-2x +6.………………8分 ②当四边形ABCD 是等腰梯形时, BD 与AC 相等且垂直,∵AC=BD =4, ∴B(4,1)∴同理可求直线AB 的解析式为y =-x +5.…………………10分可以应用这一结论解决问题.如图,在统一向角坐标系中,正比例函数的图象可以看作是:将x 轴地点的直线绕着原点O xy 3=的图象分离交于第一.三象限的点B .D ,已知点)0,(m A -.)0,(mC .(1)直接断定并填写:不管α取何值,四边形ABCD 的外形必定是; (2)①当点B 为)1,(p 时,四边形ABCD 是矩形,试求p .α.和m 有值;②不雅察猜测:对①中的m 值,能使四边形ABCD 为矩形的点B 共有几个?(不必说理)(3)试探讨:四边形ABCD 能不克不及是菱形?若能, 直接写出B 点的坐标, 若不克不及, 解释来由. 【答案】解:(1)平行四边形 …………(3分)(2)①∵点)1,(p B 在xy 3=的图象上,∴p31=∴3=p ………………………………(4分) 过B 作E x BE 轴于⊥,则13==,BE OE 在BOE Rt ∆中,3331tan ===OE BE α α=30°∴2=OB又∵点B.D 是正比例函数与反比例函数图象的交点,∴点B.D 关于原点O 成中间对称∴OB=OD=2 ∵四边形ABCD 为矩形,且)0,(m A -)0,(m C ∴2====OD OC OB OA ∴2=m ;②能使四边形ABCD 为矩形的点B 共有2个; (3)四边形ABCD 不克不及是菱形. 法一:∵点A .C 的坐标分离为)0,(m -.)0,(m ∴四边形ABCD 的对角线AC 在x 轴上.又∵点B .D 分离是正比例函数与反比例函数在第一.三象限的交点. ∴对角线AC 与BD 不成能垂直. ∴四边形ABCD 不克不及是菱形法二:若四边形ABCD 为菱形,则对角线AC⊥BD,且AC 与BD 互相等分, 因为点A.C 的坐标分离为(-m,0).(m,0)所以点A.C 关于原点O 对称,且AC 在x 轴上. 所以BD 应在y 轴上,这与“点B.D 分离在第一.三象限”抵触,所以四边形ABCD 不成能为菱形.4.(广西柳州)如图,过点P(-4,3)作x 轴.y 轴的垂线,分离交x 轴.y 轴于A.B 两点,交双曲线xk y =(k≥2)于E.F 两点.(1)点E 的坐标是________,点F 的坐标是________;(均用含k 的式子暗示)(2)断定EF 与AB 的地位关系,并证实你的结论; 如有,(3)记OEF PEF S S S ∆∆-=,S 是否有最小值?求出其最小值;若没有,请解释来由.解:(1)E (-4,-4k ),F (3k ,3) ……3分(2)(证法一)结论:EF∥AB证实:∵P(-4,3)∴E(-4,-4k ),F (3k ,3),即得:PE=3+4k ,PF=3k +4 …∵1212433+=+=k k PEPA ,1212344+=+=k k PFPB ∠APB=∠EPF ∴△PAB∽△PEF∴∠PAB=∠PEF∴EF∥AB (证法二)结论:EF∥AB证实:∵P(-4,3)∴E(-4,-4k ),F (3k ,3),即得:PE=3+4k ,PF=3k +4 …在Rt△PAB 中,tan∠PAB=34=PAPB在Rt △PEF中,tan∠PEF=344343=++=k k PEPF ∴tan∠PAB= tan∠PEF∴∠PAB=∠PEF ∴ EF∥AB (3)(办法一)S 有最小值 ∵k S S S S FBO EAO PAOB PEDF +=++=∆∆12矩形四边形∴k S S S S PEF PEF PEDF EOF+-=-=∆∆∆12四边形由(2)知,)43)(43(2121++=⋅⋅=∆k k PF PE S PEF∴S=k S S S PEF OEFPEF --=-∆∆∆122=3)6(1211222-+=+k k k 又∵k≥2,此时S 的值随k 值增大而增大,∴当k=2时,37=最小S ∴S 的最小值是37(办法二)S 有最小值.分离过点E.F 作PF.PE 的平行线,交点为P′.由(2)知,P′⎪⎭⎫⎝⎛-43k k ,∵四边形PEP′为矩形,∴S△P′EF= S△PEF∴S=S△PEF- S△OEF = S△P′EF- S△OEF = S△OME +S 矩形OMP′N+ S△ONF=21222k k k ++=22k +k =3)6(1212-+k 又∵k≥2,此时S 的值随k 值增大而增大, ∴当k=2时,S 最小=37∴S 的最小值是37.5.( 四川绵阳)如图,已知正比例函数y = ax (a≠0)的图象与反比例函致另—个交xk y =(k≠0)的图象的一个交点为A (-1,2-k2),点为B,且A.B 关于原点O 对称,D 为OB 的中点,过点D 的线段OB 的垂直等分线与x 轴.y 轴分离交于C.E .(1)写出反比例函数和正比例函数的解析式; (2)试盘算△COE 的面积是△ODE 面积的若干倍.【答案】(1)由图知k >0,a >0.∵点A (-1,2-k2)在xk y =图象上,∴ 2-k2 =-k,即k2-k -2 = 0,解得k = 2(k =-1舍去),得反比例函数为xy 2=.此时A (-1,-2),代人y = ax,解得a = 2,∴正比例函数为y = 2x . (2)过点B 作BF⊥x 轴于F .∵A(-1,-2)与B 关于原点对称, ∴B(1,2),即OF = 1,BF = 2,得OB =5.由图,易知Rt△OBF∽Rt△OCD,∴OB : OC = OF : OD,而OD = OB∕2 =5∕2,∴OC = OB · OD∕OF = 2.5.由Rt△COE∽Rt△ODE 得5)5225()(22=⨯==∆∆OD OC S S ODE COE , 所以△COE 的面积是△ODE 面积的5倍. 7.(湖北荆州)已知:关于x 的一元二次方程()01222=+-+k x k x 的两根21,x x 知足02221=-x x ,双曲线xky 4=(x >0)经由Rt△OAB 斜边OB 的中点D,与直角边AB 交于C (如图),求OBC △S .【答案】解:()01222=+-+k x k x 有两根 ∴()041222≥--=∆k k 即41≤k 由02221=-x x 得:()()02121=+-x x x x当021=+x x 时,()012=--k 解得21=k ,不合题意,舍去 当021=-x x 时,21x x =,()041222=--=∆k k 解得:41=k 相符题意 ∴双曲线的解析式为:xy 1=过D 作DE⊥OA 于E,则21121S S OCA ODE =⨯==∆∆ ∵DE⊥OA,BA⊥OA∴DE∥AB∴△ODE∽△OBA∴42=⎪⎭⎫ ⎝⎛=∆∆OD OB S S ODE OBA ∴2214=⨯=∆OBA S∴23212=-=-=∆∆∆OCA OBA OBC S S S 8.(北京)已知反比例函数y= k x的图像经由点A (—3,1)(1)试肯定此反比例函数的解析式.(2)点O 是坐标原点,将线段OA 绕点O 顺时针扭转30°得到线段OB,断定点B 是否在反比例函数的图像上,并解释来由.(3)已知点P ()也在此反比例函数的图像上(个中m <0),过p点作x 轴的的垂线,交x 轴于点M,若线段PM 上消失一点Q,使得△OQM 的面积是12,设Q 点的纵坐标为n,求n2-的值.【答案】解:(1)由题意德k=∴反比例函数的解析式为y= (2)过点A 作x 轴的垂线交x 轴于点C,在Rt△AOC 中可得 由题意,∠AOC=30°,OB=OA=2,∴∠BOC=60°过点B 做x 轴的垂线交x 轴于点D,在Rt△BOD 中,可得∴点B 坐标(-x=-1代入y= ,得∴点B (-y= x-的图像上.(3)由y=得xy=∵点P ()在反比例函数的y= 的图像上,m <0)=210m ++= ∵PQ⊥x 轴∴Q 点的坐标(m,n ) ∵△OQM 的面积为12∴12OM.QM=12∵m<0 ∴m .n=-1 ∴22220m n n ++=∴21n -=-∴298n ++=.9.(广东广州市)已知Rt△ABC 的斜边AB 在平面直角坐标系的x 轴上,点C(1,3)在反比例函数y = k x 的图象上,且sin∠BAC= 35.(1)求k 的值和边AC 的长; (2)求点B 的坐标.【答案】(1)把C (1,3)代入y = kx 得k=3设斜边AB 上的高为CD,则sin∠BAC=CD AC =35∵C(1,3)∴CD=3,∴AC=5(2)分两种情形,当点B 在点A 右侧时,如图1有: AD=52-32=4,AO=4-1=3∵△ACD∽ABC∴AC2=AD·AB∴AB=AC2AD =254∴OB=AB-AO=254-3=134此时B 点坐标为(134,0)图1 图2当点B 在点A 左侧时,如图2此时AO=4+1=5OB= AB -AO=254-5=54此时B 点坐标为(-54,0)所以点B 的坐标为(134,0)或(-54,0).10.(山东聊城)如图,已知一次函数y =kx +b 的图象交反比例函数42my x-=(x>0)图象于点A.B,交x 轴于点C .x yB A CD O O xyB A CD(1)求m 的取值规模;(2)若点A 的坐标是(2,-4),且13BC AB =,求m 的值和一次函数的解析式;【答案】(1)因反比例函数的图象在第四象限,所以4-2m <0,解得m >2;(2)因点A(2,-4)在反比例函数图象上,所以-4=224m-,解得m =6,过点A.B分离作AM⊥OC 于点M,BN⊥OC 于点N,所以∠BNC=∠AMC =90°,又因为∠BCN =∠AMC,所以△BCN∽△ACM,所以ACBCAM BN =,因为31=AB BC ,所以41=AC BC ,即41=AM BN ,因为AM =4,所以BN =1,所以点B 的纵坐标为-1,因为点B 在反比例函数的图象上,所以当y =-1时,x =8,所以点B 的坐标为(8,-1),因为一次函数y =kx +b 的图象过点A(2,-4),B(8,-1),所以⎩⎨⎧-=+-=+1842b k b k ,解得⎪⎩⎪⎨⎧-==521b k ,所以一次函数的解析式为y =21x -511.(江苏南通)如图,直线l 经由点A(1,0),且与双曲线y =m x(x >0)交于点B(2,1),过点P(p,p -1)(p >1)作x 轴的平行线分离交曲线y =m x(x >0)和y=-m x(x <0)于M,N 两点.(1)求m 的值及直线l 的解析式;(2)若点P 在直线y =2上,求证:△PMB∽△PNA;(3)是否消失实数p,使得S△AMN=4S△APM?若消失,要求出所有知足前提的p 的值;若不消失,请解释来由.【答案】(1)∵点B(2,1)在双曲线y =m x上,∴12m =,得m =2.设直线l 的解析式为y =kx +b∵直线l 过A(1,0)和B(2,1) ∴021k b k b +=⎧⎨+=⎩,解得11k b =⎧⎨=-⎩∴直线l 的解析式为y =x -1.(2) 证实:当x =p 时,y =p -1,点P(p,p -1)(p >。
反比例函数经典拓展难题

反比例函数难题拓展填空题1. (2011浙江金华,16,4分)如图,将一块直角三角板OAB 放在平面直角坐标系中,B (2,0),∠AOC =60°,点A 在第一象限,过点A 的双曲线为y= kx ,在x 轴上取一点P ,过点P作直线OA 的垂线l ,以直线l 为对称轴,线段OB 经轴对称变换后的像是O ′B ′. (1)当点O ′与点A 重合时,点P 的坐标是.(2)设P (t ,0)当O ′B ′与双曲线有交点时,t 的取值范围是 .2. (2011广东东莞,6,4分)已知反比例函数ky x=的图象经过(1,-2).则k = . 3. (2011山东滨州,18,4分)若点A(m ,-2)在反比例函数4y x=的图像上,则当函数值y ≥-2时,自变量x 的取值范围是___________. 4. (2011四川南充市,14,3分)过反比例函数y=xk(k≠0)图象上一点A ,分别作x 轴,y 轴的垂线,垂足分别为B,C ,如果⊿ABC 的面积为3.则k 的值为 .5. (2011宁波市,18,3分)如图,正方形A 1B 1P 1P 2的顶点P 1、P 2在反比例函数y =2x (x >0)的图像上,顶点A 1、B 1分别在x 轴和y 轴的正半轴上,再在其右侧作正方形P 2P 3A 2B 2,顶点P 3在反比例函数y =2x(x >0)的图象上,顶点A 3在x 轴的正半轴上,则点P 3的坐标为6. (2011浙江衢州,5,4分)在直角坐标系中,有如图所示的t ,R ABO AB x ∆⊥轴于点B ,斜(0)ky xx=>的图像经过AO的中点C,且与AB交于7. (2011浙江绍兴,13,5分) 若点12(1,),(2,)A yB y是双曲线3yx=上的点,则1y2y(填“>”,“<”“=”).8. (2011浙江丽水,16,4分)如图,将一块直角三角板OAB放在平面直角坐标系中,B(2,0),∠AOC=60°,点A在第一象限,过点A的双曲线为y=kx,在x轴上取一点P,过点P 作直线OA的垂线l,以直线l为对称轴,线段OB经轴对称变换后的像是O′B′.(1)当点O′与点A重合时,点P的坐标是.(2)设P(t,0)当O′B′与双曲线有交点时,t的取值范围是 .9. (2011湖南常德,5,3分)如图1所示的曲线是一个反比例函数图象的一支,点A在此曲线上,则该反比例函数的解析式为_______________.10.(2011江苏苏州,18,3分)如图,已知点A的坐标为(3,3),AB⊥x轴,垂足为B,连接OA ,反比例函数y=xk(k>0)的图象与线段OA 、AB 分别交于点C 、D.若AB=3BD ,以点C 为圆心,CA 的45倍的长为半径作圆,则该圆与x 轴的位置关系是___________(填“相离”、“相切”或“相交”)11. (2011山东济宁,11,3分)反比例函数1m y x-=的图象在第一、三象限,则m 的取值范围是 .12. (2011四川成都,25,4分)在平面直角坐标系xOy 中,已知反比例函数2(0)ky k x=≠满足:当0x <时,y 随x 的增大而减小.若该反比例函数的图象与直线y x =-+都经过点P ,且OP =k=_________.13. (2011安徽芜湖,15,5分)如图,在平面直角坐标系中有一正方形AOBC ,反比例函数ky x=经过正方形AOBC 对角线的交点,半径为(4-ABC ,则k 的值为 .14. (2011广东省,6,4分)已知反比例函数ky x=的图象经过(1,-2).则k = . 15. (2011江苏南京,15,2分)设函数2y x =与1y x =-的图象的交战坐标为(a ,b ),则11a b-的值为__________.16. (2011上海,11,4分)如果反比例函数ky x=(k 是常数,k ≠0)的图像经过点(-1,2),那么这个函数的解析式是__________.17. (2011湖北武汉市,16,3分)如图,□ABCD 的顶点A ,B 的坐标分别是A (-1,0),B (0,-2),顶点C ,D 在双曲线y=xk上,边AD 交y 轴于点E ,且四边形BCDE 的面积是△ABE 面积的5倍,则k=_____.18. (2011湖北黄冈,4,3分)如图:点A 在双曲线ky x=上,AB ⊥x 轴于B ,且△AOB 的面积S △AOB =2,则k=______.19. (2011湖北黄石,15,3分)若一次函数y=kx+1的图象与反比例函数y=x1的图象没有公共点,则实数k 的取值范围是 。
反比例函数经典拓展难的题目

1:〔2007年某某省初中数学竞赛〕函数y =1x-图象的大致形状是〔 〕A B C D2.(2009年某某市)如图,点A 、B 是双曲线3y x=上的点,分别经过A 、B 两点向x 轴、y 轴作垂线段,假如1S =阴影,如此12S S +=.3.y 与2x -3成反比例,且41=x 时,y =-2,求y 与x 的函数关系式.4.函数y =y 1-y 2,且y 1为x 的反比例函数,y 2为x 的正比例函数,且23-=x 和x =1时,y 的值都是1.求y 关于x 的函数关系式.5.作出反比例函数xy 12=的图象,并根据图象解答如下问题: (1)当x =4时,求y 的值;(2)当y =-2时,求x 的值;(3)当y >2时,求x 的X 围.6.作出反比例函数xy 4-=的图象,结合图象回答: (1)当x =2时,y 的值;(2)当1<x ≤4时,y 的取值X 围;(3)当1≤y <4时,x 的取值X 围.7.作出函数xy 12=的图象,并根据图象回答如下问题: (1)当x =-2时,求y 的值;(2)当2<y <3时,求x 的取值X 围; (3)当-3<x <2时,求y 的取值X 围.xyABO1S2S8题图8.如图,A 、B 是函数xy 2=的图象上关于原点对称的任意两点,BC ∥x 轴,AC ∥y 轴, △ABC 的面积记为S ,如此(s= ).9.如图,点A 、B 是函数y =x 与xy 1=的图象的两个交点,作AC ⊥x 轴于C ,作BD ⊥x 轴于D ,如此四边形ACBD 的面积为( ).10.:如图,在平面直角坐标系xOy 中,Rt △OCD 的一边OC 在x 轴上,∠C =90°,点D 在第一象限,OC =3,DC =4,反比例函数的图象经过OD 的中点A .(1)求该反比例函数的解析式;(2)假如该反比例函数的图象与Rt △OCD 的另一边交于点B ,求过A 、B 两点的直线的解析式.11.如图,A 、B 两点在函数)0(>=x xmy 的图象上.(1)求m 的值与直线AB 的解析式;(2)如果一个点的横、纵坐标均为整数,那么我们称这个点是格点.请直接写出图影局部(不包括边界)所含格点的个数.12.如图,点A 在反比例函数的图象上,AB ⊥x 轴于点B ,点C (0,1),假如△ABC 的面积是3,如此反比例函数的解析式为____________.13.如图,直线y =mx 与双曲线xky =交于A ,B 两点,过点A 作AM ⊥x 轴,垂足为M ,连结BM ,假如S △ABM =2,如此k 的值是( ).14.如图,双曲线xky =(k >0)经过矩形OABC 的边BC 的中点E ,交AB 于点D 。
反比例函数经典拓展难题

反比例函数难题拓展填空题1. (2011浙江金华,16,4分)如图,将一块直角三角板OAB 放在平面直角坐标系中,B (2,0),∠AOC =60°,点A 在第一象限,过点A 的双曲线为y= kx ,在x 轴上取一点P ,过点P作直线OA 的垂线l ,以直线l 为对称轴,线段OB 经轴对称变换后的像是O ′B ′. (1)当点O ′与点A 重合时,点P 的坐标是.(2)设P (t ,0)当O ′B ′与双曲线有交点时,t 的取值范围是 .2. (2011广东东莞,6,4分)已知反比例函数ky x=的图象经过(1,-2).则k = . 3. (2011山东滨州,18,4分)若点A(m ,-2)在反比例函数4y x=的图像上,则当函数值y ≥-2时,自变量x 的取值范围是___________. 4. (2011四川南充市,14,3分)过反比例函数y=xk(k≠0)图象上一点A ,分别作x 轴,y 轴的垂线,垂足分别为B,C ,如果⊿ABC 的面积为3.则k 的值为 .5. (2011宁波市,18,3分)如图,正方形A 1B 1P 1P 2的顶点P 1、P 2在反比例函数y =2x (x >0)的图像上,顶点A 1、B 1分别在x 轴和y 轴的正半轴上,再在其右侧作正方形P 2P 3A 2B 2,顶点P 3在反比例函数y=2x(x >0)的图象上,顶点A 3在x 轴的正半轴上,则点P 3的坐标为6. (2011浙江衢州,5,4分)在直角坐标系中,有如图所示的t ,R ABO AB x ∆⊥轴于点B ,斜35=(0)ky x x =>的图像经过AO 的中点C ,且与AB 交于的坐标为 .7. (2011浙江绍兴,13,5分) 若点12(1,),(2,)A y B y 是双曲线3y x=上的点,则 1y 2y (填“>”,“<”“=”).8. (2011浙江丽水,16,4分)如图,将一块直角三角板OAB 放在平面直角坐标系中,B(2,0),∠AOC =60°,点A 在第一象限,过点A 的双曲线为y= kx ,在x 轴上取一点P ,过点P作直线OA 的垂线l ,以直线l 为对称轴,线段OB 经轴对称变换后的像是O ′B ′. (1)当点O ′与点A 重合时,点P 的坐标是.(2)设P(t ,0)当O ′B ′与双曲线有交点时,t 的取值范围是 .(第15题)xyCDBOI9. (2011湖南常德,5,3分)如图1所示的曲线是一个反比例函数图象的一支,点A 在此曲线上,则该反比例函数的解析式为_______________.10.(2011江苏苏州,18,3分)如图,已知点A 的坐标为(3,3),AB ⊥x 轴,垂足为B ,连接OA ,反比例函数y=xk(k>0)的图象与线段OA 、AB 分别交于点C 、D.若AB=3BD ,以点C 为圆心,CA 的45倍的长为半径作圆,则该圆与x 轴的位置关系是___________(填“相离”、“相切”或“相交”)11. (2011山东济宁,11,3分)反比例函数1m y x-=的图象在第一、三象限,则m 的取值范围是 .y1OAx3图112. (2011四川成都,25,4分)在平面直角坐标系xOy 中,已知反比例函数2(0)ky k x=≠满足:当0x <时,y 随x 的增大而减小.若该反比例函数的图象与直线3y x k =-+都经过点P ,且7OP =,则实数k=_________.13. (2011安徽芜湖,15,5分)如图,在平面直角坐标系中有一正方形AOBC ,反比例函数ky x=经过正方形AOBC 对角线的交点,半径为(422-)的圆内切于△ABC ,则k 的值为 .14. (2011广东省,6,4分)已知反比例函数ky x=的图象经过(1,-2).则k = . 15. (2011江苏南京,15,2分)设函数2y x =与1y x =-的图象的交战坐标为(a ,b ),则11a b-的值为__________.16. (2011上海,11,4分)如果反比例函数ky x=(k 是常数,k ≠0)的图像经过点(-1,2),那么这个函数的解析式是__________.17. (2011湖北武汉市,16,3分)如图,□ABCD 的顶点A ,B 的坐标分别是A (-1,0),B (0,-2),顶点C ,D 在双曲线y=xk上,边AD 交y 轴于点E ,且四边形BCDE 的面积是△ABE 面积的5倍,则k=_____.18. (2011湖北黄冈,4,3分)如图:点A 在双曲线ky x=上,AB ⊥x 轴于B ,且△AOB 的面积S △AOB =2,则k=______.19. (2011湖北黄石,15,3分)若一次函数y=kx+1的图象与反比例函数y=x1的图象没有公共点,则实数k 的取值范围是 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(x>0)的图象上,斜边OA
1
、A
1
A
2
、A
2
A
3
…A
n-1
A
n
都在x轴上.则点A
10
的坐标为
反比例函数经典习题
例题讲解
【例△1】如右图,已知P10A1,△P2A1A2都是等腰直角三角形,点P1、P2都在函数y=
4
x(x>0)的图象上,
斜边OA
1
、A
1
A
2
都在x轴上.则点A
2
的坐标为.
1、如例1图,已知△P
1
OA
△1
,P
2
A
1
A
△2
,P
3
A
2
A
△3
…P
n
A
n-1
A
n
都是等腰直角三角形,点P
1
、P
2
、P
3
…P
n
都在4
函数y=
x
2、已知点A(0,2)和点B(0,-2),点P在函数y=
1
x的图像上,如果△PAB的面积为6,求P点的坐标。
【例2】如右图,已知点(1,3)在函数y=
k
x(x>0)的图像上,矩形ABCD的边BC在x轴上,E是对角线BD的中点,函数y=
k
x(k>0)的图象又经过A,E两点,点E的横坐标为m,解答下列各题
1.求k的值
2.求点C的横坐标(用m表示)
3.当∠ABD=45°时,求m的值112
1、已知:如图,矩形ABCD的边BC在x轴上,E是对角线AC、BD的交点,反比例函数y=
2
x(x>0)的图象经过A,E两点,点E的纵坐标为m.
(1)求点A坐标(用m表示)
(2)是否存在实数m,使四边形ABCD为正方形,若存在,请求出m的值;若不存在,请说明理由
2、如图1,矩形ABCD的边BC在x轴的正半轴上,点E(m,1)是对角线BD的中点,点A、E在反比例函数y=
k
x的图象上.
(1)求AB的长;
(2)当矩形ABCD是正方形时,将反比例函数y=
k
x
k
的图象沿y轴翻折,得到反比例函数y=1的图象(如
x
图2),求k1的值;
(3)直线y=-x上有一长为2动线段MN,作MH、NP都平行y轴交在条件(2)下,第一象限内的双曲线y=
k
x于点H、P,问四边形MHPN能否为平行四边形(如图3)?若能,请求出点M的坐标;若不能,请说明理由.
【例3】在平面直角坐标系中,已知A(1,0),B(0,1),矩形OMPN的相邻两边OM,ON分别在x,y轴的正半轴上,O为原点,线段AB与矩形OMPN的两边MP,NP的交点分别为E,F,△AOF∽△BOE(顶点依次对应)
(1)求∠FOE;
(2)求证:矩形OPMN的顶点P必在某个反比例函数图像上,并写出该函数的解析式。
b(
b
如图,在平面直角坐标系中,直线y=-x+1分别交x轴、y轴于A,B两点,点P(a,b)是反比例函数y=
1
2x 在第一象限内的任意一点,过点P分别作PM⊥x轴于点M,PN⊥y轴于点N,PM,PN分别交直线AB于E,
F,有下列结论:①AF=BE;②图中的等腰直角三角形有4个;③△S
OEF
=
结论正确的序号是
1
2(a+b-1);④∠EOF=45°.其中【例4】已知:如右图,已知反比例函数y=
k
2x和一次函数y=2x-1,其中一次函数的图像经过(a,),a+1,
b+k).
(1)求反比例函数的解析式;
(2)如图,已知点A在第一象限,且同时在上述两个函数的图象上,求点A的坐标;
(3)利用(2)的结果,请问:在x轴上是否存在点P,使△AOP为等腰三角形?若存在,把符合条件的P
点坐标都求出来;若不存在,请说明理由.
已知反比例函数y=
k
2x和一次函数y=2x-1,其中一次函数的图象经过(a,),(a+k,b+k+2)
两点.
(1)求反比例函数的解析式;
(2)求反比例函数与一次函数两个交点A、B的坐标:
(3)根据函数图象,求不等式
k
2x>2x-1的解集;
(4)在(2)的条件下,x轴上是否存在点P,使△AOP为等腰三角形?若存在,把符合条件
的P点坐标都求出来;若不存在,请说明理由。
x
(1)反比例函数的解析式为y=-6
一、巩固练习:解答题
1、已知反比例函数y=k
x图象过第二象限内的点A(-2,m),作AB⊥x轴于B,△R t AOB面积为3;若直
k
线y=ax+b经过点A,并且经过反比例函数y=的图象上另一点C(n,-1).
x,m=3,n=6;
(2)求直线y=ax+b的解析式;
(3)设直线y=ax+b与x轴交于M,求AM的长;
(4)根据图象写出使反比例函数y=k
x值大于一次函数y=ax+b的值的x的取值范围。
2、已知如图:矩形ABCD的边BC在x轴上,E为对角线BD的中点,点B、D的坐标分别为B(1,0),D(3,3),反比例函
数y=k
x的图象经过A点,
(1)写出点A和点E的坐标;(2)求反比例函数的解析式;
3、如右图已知反比例函数y=k
x(k<0)的图像经过点A(-3,m),过A点作AB⊥x轴于点△B且AOB
的面积为3。
123
(1)求k和m的值
(2)若一次函数y=ax+1的图像经过点A,并且与x轴相交于点M,求∠AMO和|AO|:|AM|的值
2交x轴于C,交y轴于D,点P为反比例函数y=
k
拓展训练
4、已知反比例函数y=
k
2x和一次函数y=2x-1,其中一次函数的图象经过(a,b)、(a+1,b+k)两点.
(1)求反比例函数的解析式;
(2)若两个函数图象在第一象限内的交点为A(1,m),请问:在x轴上是否存在点B,使△AOB为直角三角形?若存在,
求出所有符合条件的点B的坐标;
(3)若直线y=-x+
1
2x
线CD于E,过P作x轴的平行线交直线CD于F,求证:DE•CF为定值.
(x>0)的图象上一点,过P作y轴的平行线交直
过手练习
1、已知:如右图已知反比例函数y=
12
x的图像与一次函数y=kx-7的图像都经过P(m,2)
(1)求这个一次函数的解析式;
(2)如果等腰梯形ABCD的顶点A、B在这个一次函数的图象上,顶点C、D在这个反比例函数的图象上,两底AD、BC与y轴平行,且A和B的横坐标分别为a和a+2,求a的值.。
