特殊角的三角函数函数值
特殊角的三角函数值记忆口诀
特殊角的三角函数值记忆口诀
一、特殊角的定义
在三角函数中，特殊角通常指的是0度、30度、45度、60度和90度这几个特殊角度。
这些角度具有特殊的三角函数值，对于学习和记忆这些数值，可以通过口诀来帮助记忆。
二、口诀的编制
为了方便记忆特殊角的三角函数值，可以借助以下口诀：
0度，一个圆缺一点，
sin为零，cos为一，
30度，一角箭头眉，
sin为一半，cos为根三分之一，
45度，锐角二等分，
sin为根二分之一，cos也然，
60度，钟头指牵引，
sin为根三分之一，cos为一半，
90度，劈腿分海洋，
sin是一，cos是零。
三、口诀的应用
借助这个口诀，我们可以轻松记忆0度、30度、45度、60度和90度这几个特殊角的正弦值和余弦值，从而在学习三角函数时更加得心应手。
四、总结
通过口诀的记忆方法，可以帮助我们更好地掌握特殊角的三角函数值，这对于学习三角函数和解题将大有裨益。
因此，在学习三角函数的过程中，可以尝试借助口诀这一记忆方法，以提高学习效率。
希望以上内容对特殊角的三角函数值的记忆有所帮助，更好地掌握知识。
三角函数特殊角值表
sin（－α）＝－sinα
——仅供参考
cos（－α）＝cosα
tan（－α）＝－tanα
公式四： 利用公式二和公式三可以得到π-α与α的三角函数值之间的关
系：
sin（π－α）＝sinα
cos（π－α）＝－cosα
tan（π－α）＝－tanα
公式五： 利用公式一和公式三可以得到 2π-α与α的三角函数值之间的
关系：
sin（2π－α）＝－sinα
cos（2π－α）＝cosα
பைடு நூலகம்
tan（2π－α）＝－tanα
公式六： π/2±α及 3π/2±α与α的三角函数值之间的关系：
sin（π/2＋α）＝cosα
sin（π/2－α）＝cosα
cos（π/2＋α）＝－sinα
cos（π/2－α）＝sinα
tan（π/2＋α）＝－cotα
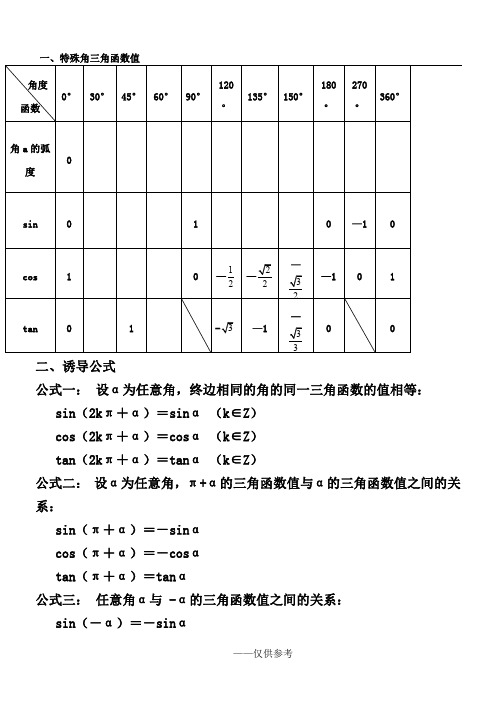
一、特殊角三角函数值
角度
120
180
0° 30° 45° 60° 90°
135° 150°
函数
°
°
270 360°
°
角 a 的弧 0
度
sin
0
1
0 —1 0
cos
1
0 —1 — 2
2
2
— 3
—1
0
1
2
tan
0
1
二、诱导公式
—
- 3 —1
0 3
0
3
公式一： 设α为任意角，终边相同的角的同一三角函数的值相等：
tan（π/2－α）＝cotα
sin（3π/2＋α）＝－cosα
sin（3π/2－α）＝－cosα
cos（3π/2＋α）＝sinα
特殊角的三角函数值
同角之间的三角函数的关系
1、如图,在Rt△ABC中,∠C=900,∠A,∠B,∠C的对边分别是a,b,c.
求证: sin2 A cos2 A 1.
a b 2 证明 : sin A , cos A , a b 2 c 2 , c c 2 2 a b a 2 b2 c 2 2 2 sin A cos A 2 1. 2 c c c c 即sin 2 A cos2 A 1.
cosA=sinB.
cotA=tanB.
sin 90 cos , cos 90 0 sin ,
0
tan 90 cot ,
0
cot 90 tan ,
0
如图,观察一副三角板: 它们其中有几个锐角?分别是多少度?
(1)sin30°等于多少?
则下底BC的长为 __________．
A 30° B D 60° C
【答案】10
24 4.计算： 2(2 cos 45 sin 60) 4 2 3 2 6 原式 2(2 ) 【解析】 2 2 4
6 6 2 2 2
2
【规律方法】 1.记住30°，45 °，60 °的特殊三角函数值及推导 方式，可以提高计算速度. 2.会构造直角三角形，充分利用勾股定理的有关知识结 合三角函数灵活运用.
(2)cos30°等于多少? (3)tan30°等于多少? (4)cot30°等于多少?
45° 45° ┌ 60°
30°
┌
请与同伴交流你是怎么想的?又是怎么做的?
(5)sin45°,sin60°等于多少? (6)cos45°,cos60°等于多少?
特殊角的三角函数值口诀
特殊角的三角函数值口诀
三角函数是数学中重要的概念，而特殊角的三角函数值口诀则是帮助我们快速记忆各种特殊角的三角函数值的方法。
下面将介绍一些有关特殊角的三角函数值口诀。
0度角
•正弦值：0
•余弦值：1
•正切值：0
30度角
•正弦值：1/2
•余弦值：√3/2
•正切值：√3/3
45度角
•正弦值：√2/2
•余弦值：√2/2
•正切值：1
60度角
•正弦值：√3/2
•余弦值：1/2
•正切值：√3
90度角
•不存在正弦值
•余弦值：0
•正切值：不存在
以上便是有关特殊角的三角函数值口诀，通过这些口诀，我们可以快速地了解各个特殊角的三角函数值，为解题提供便利。
希望这些口诀能够帮助你更加轻松地学习和记忆三角函数的知识。
要特别注意，这些口诀只适用于特殊角度，对于其他角度需要通过计算得出具体数值。
现实生活中，三角函数也被广泛应用于建筑、制图、物理等领域，深入了解三角函数将有助于更好地理解这些领域中的问题。
希望通过学习特殊角的三角函数值口诀，能够帮助我们更好地掌握三角函数的知识，提升数学能力，解决实际问题。
特殊角三角函数数值表
特殊角三角函数数值表
三角函数是数学中十分重要的一个分支，它在物理、工程、计算机等领域都有着广泛的应用。
特殊角是指 $0^\\circ$、$30^\\circ$、$45^\\circ$、$60^\\circ$、$90^\\circ$ 这几
个常见角度，它们的三角函数数值是一些基本常数，熟练掌握这些数值对于解决问题非常有帮助。
下面是特殊角 $0^\\circ$、$30^\\circ$、$45^\\circ$、$60^\\circ$、$90^\\circ$ 的正弦、余弦、正切数值表：
角度正弦值余弦值正切值
0°010
30°1/2√3/2√3/3
45°√2/2√2/21
60°√3/21/2√3
90°10无穷大
其中正弦值、余弦值、正切值分别代表相应角度下的正弦
函数值、余弦函数值、正切函数值。
特殊角的三角函数数值表可以帮助我们迅速计算出这几个角度下的三角函数值，进而解决一些数学和物理问题。
特殊角的三角函数数值表是数学学习的基础之一，熟练掌
握这些数值表可以为我们的学习和工作带来很多便利。
希望大家能够通过这个数值表熟练掌握特殊角下的三角函数值，提高自己的数学素养！。
特殊三角函数值
sin61=0.8746197071393957 sin62=0.8829475928589269 sin63=0.8910065241883678
sin40=0.6427876096865392 sin41=0.6560590289905073 sin42=0.6691306063588582
sin43=0.6819983600624985 sin44=0.6946583704589972 sin45=0.7071067811865475
正切值随着角度的增大（或减小）而增大（或减小）
余切值随着角度的增大（或减小）而减小（或增大）
（iii）当角度在0°≤α≤90°间变化时，
0≤sinα≤1, 1≥cosα≥0,
当角度在0°<α<90°间变化时，
tanα>0, cotα>0.
“锐角三角函数”属于三角学，是《数学课程标准》中“空间与图形”领域的重要内容。从《数学课程标准》看，中学数学把三角学内容分成两个部分，第一部分放在义务教育第三学段，第二部分放在高中阶段。在义务教育第三学段，主要研究锐角三角函数和解直角三角形的内容，本套教科书安排了一章的内容，就是本章“锐角三角函数”。在高中阶段的三角内容是三角学的主体部分，包括解斜三角形、三角函数、反三角函数和简单的三角方程。无论是从内容上看，还是从思考问题的方法上看，前一部分都是后一部分的重要基础，掌握锐角三角函数的概念和解直角三角形的方法，是学习三角函数和解斜三角形的重要准备。
cos7=0.992546151641322 cos8=0.9902680687415704 cos9=0.9876883405951378
特殊角的三角函数值
sin30°=
A的对边 斜边
1 2
cos30°=
A 的 邻 边 斜边
3 2
tan30°= A的对边 3 A的邻边 3
B
1 600
C
2
°A
3
sin60°= A斜的边对边
3 2
cos60°=
A 的邻边 斜边
1 2
tan60°=
A 的对边 A 的邻边
3
sin45°=A的对边 2
B
斜边
2
2
1
cos45°= A的邻边 2
3、 sin60°·cos60° 4、tan45°- sin30° 5、sin60°·tan30°-cos45° 6、tans45°- sin30°-cos60°
7、 cos 45 tan2 30
(1).2
sin
60°
3
tan
30°
1 3
0
(1)2009
(2). (
3
2)0
1 3
1
4
cos
30°
|
12 |
例2、(1)如图，在Rt△ABC中，∠C=90°， AB= 6 ， BC= 3 。求∠A的度数。
B
A
6
3
A
C
(1)
O B
(2)
(2)如图,已知圆锥的高AO等于圆锥的底面 半径OB的 3 倍,求α.
练习2：求锐角 的度数:
2sin 2 0
3 tan 1 0 2 sin( 15 ) 3
例3.求适合下列各式的锐角α
( 1 ) 3 t a n α 3
( 2 )2 c o s α 1 2
1
(3) 3tan2 4 tan 3 0
特殊角的三角函数值 表格
特殊角的三角函数值表格
在三角学中，特殊角的三角函数值是非常重要的知识点。
特殊角是指常见的角度值，如0度、30度、45度、60度和90度，它们的三角函数值是固定的，具有特殊性。
下表列出了这些特殊角的正弦、余弦和正切函数值：
角度正弦（sin）余弦（cos）正切（tan）
0度010
30度1/2√3/21/√3
45度√2/2√2/21
60度√3/21/2√3
90度10无穷大
这些特殊角的三角函数值是在解决三角函数问题时经常会用到的基本数值，对于计算各种三角函数式子和题目的解答都具有很大的帮助。
熟练掌握这些数值可以提高解题效率，并对理解三角函数的概念和性质有很大帮助。
三角函数特殊角值表
一、特殊角三角函数值
角度
120
180
0° 30° 45° 60° 90°
135° 150°
函数
°
°
270 360°
°
角 a 的弧 0
度
sin
0
1
0 —1 0
cos
1
0 —1 — 2
2
2
— 3
—1
0
1
2
tan
0
1
二、诱导公式
—
- 3 —1
0 3
0
3
公式一： 设α为任意角，终边相同的角的同一三角函数的值相等：
sin（2kπ＋α）＝sinα （k∈Z）
cos（2kπ＋α）＝cosα （k∈Z）
tan（2kπ＋α）＝tanα （k∈Z）
公式二： 设α为任意角，π+α的三角函数值与α的三角函数值之间的关
系：
sin（π＋α）＝－sinα
cos（π＋α）＝－cosα
tan（π＋α）＝tanα
公式三： 任意角α与 -α的三角函数值之间的关系：
关系：
sin（2π－α）＝－sinα
cos（2π－α）＝cosα
tan（2π－α）＝－tanα
公式六： π/2±α及 3π/2±α与α的三角函数值之间的关系：
sin（π/2＋α）＝cosα
sin（π/2－α）＝cosα
cos（π/2＋α）＝－sinα
cos（π/2－α）＝sinα
tan（π/2＋α）＝－cotα
sin（－α）＝－sinα
——仅供参考
cos（－α）＝cosα
tan（－α）＝－tanα