最迟完成时间
最迟完成时间计算公式

最迟完成时间计算公式最迟完成时间(Late Finish Time,LFT)是在项目管理中用于计算某项活动最晚可以完成的时间。
它是计算关键路径和项目完成时间的重要指标之一。
最迟完成时间是根据活动的最早开始时间(Early Start Time,EST)和活动的持续时间(Duration)来计算的。
最迟完成时间取决于后续活动的最迟开始时间(Late Start Time,LST),后续活动的最迟开始时间指的是在不影响项目完成时间的前提下,该活动最晚可以开始的时间。
最迟完成时间的计算公式如下:LFT = LST + Duration - 1其中LFT表示活动的最迟完成时间,LST表示后续活动的最迟开始时间,Duration表示活动的持续时间。
公式中的“-1”用于考虑到活动完成时间只能是整数。
最迟完成时间的计算需要遵循以下步骤:1. 首先,计算项目网络图和关键路径,确定每个活动的最早开始时间(EST)和最早完成时间(EFT)。
2. 然后,从最后一个活动开始,将其最迟完成时间(LFT)设置为与最早完成时间(EFT)相同的值。
3. 继续向前推算,计算前一个活动的最迟完成时间(LFT)。
4. 根据最后一个活动和前一个活动的持续时间,以及后续活动的最迟开始时间,使用上述公式计算最迟完成时间。
5. 重复上述步骤,一直计算到第一个活动,直到确定所有活动的最迟完成时间为止。
最迟完成时间的计算对于项目管理非常重要,它可以帮助项目团队确定任务的优先级和计划工期。
通过计算每个活动的最迟完成时间,项目经理可以识别出关键活动和关键路径,确保项目按计划完成。
最迟完成时间也可以用于确定项目的浮动时间。
浮动时间是指在不延误项目完成时间的情况下,某个活动可以推迟开始的时间。
通过比较最早完成时间和最迟完成时间,可以计算出每个活动的浮动时间,从而帮助项目团队有效利用项目资源。
总结起来,最迟完成时间是根据活动的最早开始时间和持续时间计算的指标,用于确定活动的最晚完成时间和项目的关键路径。
双代号网络计划时间参数的计算公式
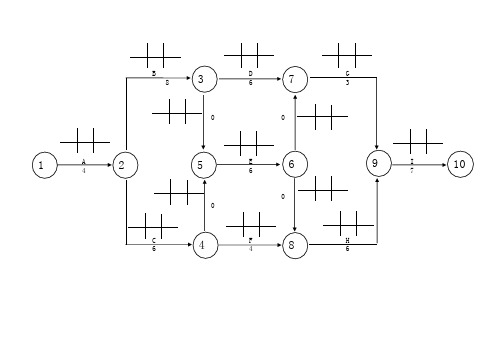
2、 TF=LF-EF
七、自由 时差的计 算: 1、FF=ES 后-ES前D或ES后EF前 2、FF=TES-D或TEF
B 8
3
0
D 6
7
0
1
A 4
2
C 6
5
0
E
6
6
0
4
F 4
8
G7
H 6
ES
EF
一、最早 开始时间 计算: 1、起 点:ES=0 2、只有 一项紧前 工作: ES=ES+D 3、有多 个紧前工 作:ES= 最大 (ES+D)
LS LF
TF
FF
五、最迟 开始时间 计算: 1、 LS=LF-D
六、总时 差的计 算: 1、 TF=LS-ES
ES-----工作最早开始时间 LS-----工作最迟开始时间 EF-----工作最早完成时间 LF-----工作最迟完成时间
TF-----工作总时差 FF-----工作自由时差
二、最早 完成时间 计算: EF=ES+D
三、网络 计划工期 的计算:
T=最大EF
双代号网络计划时间参数的计算公式
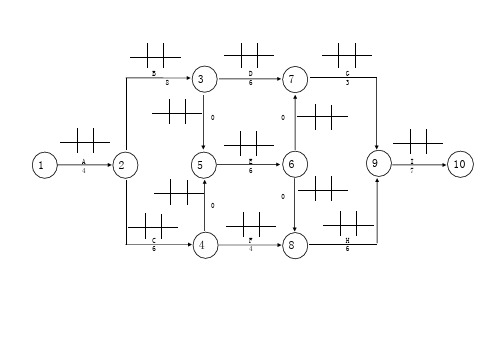
2、 TF=LF-EF
七、自由 时差的计 算: 1、FF=ES 后-ES前D或ES后EF前 2、FF=TES-D或TEF
六、总时 差的计 算: 1、 TF=LS-ES
ES-----工作最早开始时间 LS-----工作最迟开始时间 EF-----工作最早完成时间 LF-----工作最迟完成时间
TF-----工作总时差 FF-----工作自由时差
二、最早 完成时间 计算: EF=ES+D
三、网络 计划工期 的计算:
T=最大EF
B 8Βιβλιοθήκη 30D 6
7
0
1
A 4
2
C 6
5
0
E
6
6
0
4
F 4
8
G 3
9
I
10
7
H 6
ES
EF
一、最早 开始时间 计算: 1、起 点:ES=0 2、只有 一项紧前 工作: ES=ES+D 3、有多 个紧前工 作:ES= 最大 (ES+D)
LS LF
TF
FF
五、最迟 开始时间 计算: 1、 LS=LF-D
最迟开始时间和最迟完成时间例题

最迟开始时间和最迟完成时间例题最迟开始时间和最迟完成时间(LST/LLT)是项目管理中重要的概念,它们帮助确定项目活动的时间范围和项目进度。
在本文中,我将深入探讨最迟开始时间和最迟完成时间的定义、作用、计算方法以及其在项目管理中的重要性。
一、最迟开始时间和最迟完成时间的定义最迟开始时间(LST)指的是在不推迟项目完成日期的前提下,某项工作必须在何时开始。
而最迟完成时间(LLT)则是指在不推迟项目完成日期的前提下,某项工作必须在何时完成。
这两个时间点对于项目的进度控制和风险管理非常关键。
二、最迟开始时间和最迟完成时间的计算方法1. 最迟开始时间的计算方法:最迟开始时间 = 最迟完成时间 - 工作持续时间2. 最迟完成时间的计算方法:最迟完成时间 = 最迟开始时间 + 工作持续时间通过以上计算方法,可以很容易地得出最迟开始时间和最迟完成时间,从而帮助项目团队合理安排工作计划,以确保项目能够按时交付。
三、最迟开始时间和最迟完成时间在项目管理中的重要性1. 确保项目按时完成:通过合理计算最迟开始时间和最迟完成时间,项目团队可以有效控制项目进度,从而确保项目能够按时完成,提高项目的竞争力和客户满意度。
2. 风险管理:最迟开始时间和最迟完成时间还可以帮助项目团队更好地识别和管理项目进度风险。
一旦发现工作延迟,团队可以迅速调整工作计划,以避免项目延期。
4. 项目资源优化:通过合理安排最迟开始时间和最迟完成时间,项目团队可以更好地优化项目资源,避免资源闲置和浪费,提高工作效率。
五、个人观点和理解最迟开始时间和最迟完成时间是项目管理中非常重要的概念,对于项目的进度控制和风险管理至关重要。
合理计算最迟开始时间和最迟完成时间,可以帮助项目团队更好地安排工作计划,控制项目进度,提高工作效率,确保项目按时完成。
在项目管理中,我认为最迟开始时间和最迟完成时间的重要性不容忽视。
总结最迟开始时间和最迟完成时间是项目管理中的重要概念,它们对于项目的进度控制和风险管理至关重要。
网络图中的六个时间参数.doc

2.网络图中的六个时间参数(重点)网络图中的时间参数主要有六个:最早开始时间;最早完成时间;最迟开始时间;最迟完成时间;总时差和自由时差。
各时间参数的含义如下。
(1)工作最早开始时间ESii(EarliestStartTime)——是指在其所有紧前工作全部完成后,本工作有可能开始的最早时刻。
(2)工作最早完成时间EFii(EarliestFinishTime)——是指在其所有紧前工作全部完成后,本工作有可能完成的最早时刻。
工作的最早完成时间等于工作最早开始时间与其持续时间之和。
(3)工作最迟完成时间LFii(LatestFinishTime)——是指在不影响整个任务按期完成的前提下,本工作必须完成的最迟时刻。
(4)工作最迟开始时间LSii(LatestStartTime)——是指在不影响整个任务按期完成的前提下,本工作必须开始的最迟时刻。
工作的最迟开始时间等于工作最迟完成时间与其持续时间之差。
(5)总时差TFii(TotalFloatTime)——是指在不影响总工期的前提下,本工作可以利用的机动时间。
(6)自由时差FFii(FreeFloatTime)——是指在不影响其紧后工作最早开始时间的前提下,本工作可以利用的机动时间。
3.双代号网络图中时间参数的计算(1)时间参数计算数学模型:下面取一网络片断(图9-24)作为计算简图。
令整个计划的开始时间为第0天,则:工作最早开始时间等于其紧前工作最早完成时间的最大值。
令整个计划的总工期为一常数,则:工作最迟完成时间等于其紧后工作最迟开始时间的最小值。
在网络计划中,总时差最小的工作为关键工作。
特别地,当网络计划的计划工期等于计算工期时,总时差为零的工作就是关键工作。
由于工作的自由时差是总时差的构成部分,所以,当工作的总时差为零时,其自由时差必然为零。
即:如果网络计划中工作数量比较多,一般用项目管理软件进行计算。
如果数量不多也可用手工进行计算。
(2)计算步骤。
双代号网络计划时间参数计算

双代号网络计划时间参数计算网络计划指在网络图上标注时间参数而编制的进度计划。
网络计划的时间参数是确定工程计划工期、确定关键线路、关键工作的基础,也是判定非关键工作机动时间和进行优化,计划管理的依据。
时间参数计算应在各项工作的持续时间确定之后进行。
网络计划的时间参数主要有: ·工作的时间参数:最早开始时间 ES (Early start ) 最早完成时间 EF (Early finish ) 最迟开始时间 LS (Late start ) 最迟完成时间 LF (Late finish ) 总时差 TF (Total float ) 自由时差 FF (Free float ) ·节点的时间参数:最早开始时间 TE (Early event time ) 最早完成时间 TL (Late event time )在计算各种时间参数时,为了与数字坐标轴的规定一致,规定工作的开始时间或结束时间都是指时间终了时刻。
如坐标上某工作的开始(或完成)时间为第5天,是指第5个工作日的下班时,即第6个工作日的上班时。
在计算中,规定网络计划的起始工作从第0天开始,实际上指的是第1个工作日的上班开始。
一.双代号网络计划时间参数的计算双代号网络计划时间参数的计算有“按工作计算法”和“按节点计算法”两种。
(一)按工作计算法计算时间参数工作计算法是指以网络计划中的工作为对象,直接计算各项工作的时间参数。
计算程序如下:1.工作最早开始时间的计算工作的最早开始时间是指其所有紧前工作全部完成后,本工作最早可能的开始时刻。
工作j i -的最早开始时间以j i ES -表示。
规定:工作的最早开始时间应从网络计划的起点节点开始,顺着箭线方向自左向右依次逐项计算,直到终点节点为止。
必须先计算其紧前工作,然后再计算本工作。
(1)以网络计划起点节点为开始节点的工作的最早开始时间,如无规定时,其值等于零。
如网络计划起点节点代号为i ,则:(2)其它工作的最早开始时间等于其紧前工作的最早开始时间加上该紧前工作的工作历时所得之和的最大值,即:当工作j i -与其紧前工作i h -之间无虚工作时,有多项工作时取最大值:当工作j i -h-ii-j式中,()h g i h ES ES -- - 工作j i -的紧前工作i h -(h g -)的最早开始时间;()h g i h D D -- - 工作j i -的紧前工作i h -(h g -)的工作历时。
项目活动时间如何计算公式

项目活动时间如何计算公式在项目管理中,活动时间的计算是非常重要的一项工作。
活动时间的准确计算可以帮助项目团队合理安排资源和时间,提高项目的效率和质量。
本文将介绍项目活动时间如何计算的公式,并且通过实例来说明如何应用这些公式。
一、活动时间的计算公式。
1. 最早开始时间(ES)和最迟开始时间(LS)的计算公式:最早开始时间(ES)是指活动可以开始的最早时间,最迟开始时间(LS)是指活动必须开始的最迟时间。
它们的计算公式如下:ES = Max{所有紧前活动的最早完成时间}。
LS = 最早完成时间活动持续时间。
其中,Max{}表示取所有紧前活动的最早完成时间的最大值。
活动持续时间是指完成该活动所需的时间。
2. 最早完成时间(EF)和最迟完成时间(LF)的计算公式:最早完成时间(EF)是指活动可以完成的最早时间,最迟完成时间(LF)是指活动必须完成的最迟时间。
它们的计算公式如下:EF = ES + 活动持续时间。
LF = Min{所有紧后活动的最迟开始时间}。
其中,Min{}表示取所有紧后活动的最迟开始时间的最小值。
3. 活动总时差(Total Float)的计算公式:活动总时差是指活动可以延迟的时间,它的计算公式如下:Total Float = LF EF 或 Total Float = LS ES。
二、实例分析。
为了更好地说明活动时间的计算公式,我们通过一个实例来进行分析。
假设有一个项目,包括如下四个活动:A、B、C和D。
它们之间的关系如下图所示:A(3天)——> B(2天)——> C(4天)——> D(5天)。
其中,括号中的数字表示每个活动的持续时间。
现在我们来计算每个活动的最早开始时间(ES)、最迟开始时间(LS)、最早完成时间(EF)、最迟完成时间(LF)和活动总时差(Total Float)。
1. 计算A活动的ES和EF:A活动没有紧前活动,所以它的最早开始时间(ES)为0,最早完成时间(EF)为3。
总时差和自由时差的计算

3 自由时差=紧后最早开始时间—本工作 最早完成时间。
二、双代号网络图六时参数
最早开始时间ES 最迟开始时间LS 总时差TF 最早完成时间EF 最迟完成时间LF 自由时差FF
三、六时参数计算简易
A上(ES) B上(LS) 总时差(TF) A下(EF) B下(LF) 自由时差(FF)
双代号网络图参 数计算简易方法
一、非常有用的要点:
1、任何一个工作总时差≥自由时差 2、自由时差等于各时间间隔的最小 值(这点对六时参数的计算非常用)
3、关键线路上相邻工作的时间间隔 为零,且自由时差=总时差 4、在网络计划中,计算工期是根据 终点节点的最早完成时间的最大值
1 总时差=最迟完成时间—尚需完成时间。 计算结果若大于0,则不影响总工期。 若小于0则影响总工期。
最迟完成(LF)、最迟开始(LS)时间计算
0
3
1
A
3
3
8
2
B
5
88
15 15
3
D
5
7
02
68
C
4
6
C工作最迟完成(LF)=紧后D工作的最迟开 始时间=8 C工作最迟开始(LF)=本工作最迟完成-本 工作持续时间=8-6=2
最迟完成(LF)、最迟开始(LS)时间计算
0
3
1
A
3
33
88
2
B
5
88
15 15
最迟完成(LF)先计算最迟完成
从结束点往开始点做
1、终点工作的完成时间(LF)= 总工期=终点工作节点中最大的 最早完成时间(EF)
2、下一个工作最迟完成时间(LF) =上一个工作的最迟开始时间(LS)
双代号网络计划时间参数的计算方法

双代号网络计划时间参数的计算方法自认为对双代号网络图的知识掌握的差不多,也能够理解;只是在遇到这六个时间参数的时候,还是有些发怵,今天重新把这六个参数捋了捋,总结如下:1、最早开始时间、最早完成时间:从网络计划的起点节点开始,顺着箭头方向依次进行;以网络计划起点为开始节点的工作,当未规定其最早开始时间时,其最早开始时间为零;有多个紧前工作的工作,其最早开始时间等于其紧前工作最早完成时间的最大值。
2、最迟开始时间、最迟完成时间:从网络计划的终点节点开始,顺着箭头方向依次进行;以网络终点节点为完成节点的工作,其最迟完成时间等于网络计划的计划工期,即要先找出关键线路,求出计划总工期作为最后一项工作的最迟完成时间;有多个紧后工作的工作,其最迟完成时间等于其紧后工作最迟开始时间的最小值。
3、总时差:不影响总工期的时差,等于该工作最迟完成时间与最早完成时间之差,或该工作最迟开始时间与最早开始时间之差;总时差最小的工作为关键工作,当网络计划的计划工期等于计算工期时,总时差为零的工作就是关键工作;同一条线路上的总时差相等(同一条线路都可以共用的时间,谁用了是谁的,不影响总工期)。
4、自由时差不影响紧后工作的时间;对于有多个紧后工作的工作,其自由时差等于本工作之紧后工作最早开始时间-本工作最早完成时间所得之差的最小值;无紧后工作的工作,也就是以网络计划重点节点为完成节点的工作,其自由时差等于计划工期与本工作最早完成时间之差;对于网络计划中以重点节点为完成节点的工作,其自由时差与总时差相等;只有一项紧前工作的紧前工作,该紧前工作的自由时差为0;自由时差小于等于总时差,总时差为零自由时差必为0 。
呵呵,本来想用通俗的语言解释一下,可写下来还是有点绕,我觉得这东西贵在理解,好像只是专家们为了考试罗列了一些概念,把简单的问题弄复杂了;没办法为了考试,慢慢理解吧。
二、搭接网络计划时间参数的计算单代号搭接网络计划时间参数的计算与前述单代号网络计划和双代号网络计划时间参数的计算原理基本相同。
工作最早完成时间和最迟完成时间的计算

工作最早完成时间和最迟完成时间的计算最早完成时间是在各紧前工作全部完成后,本工作有可能完成的最早时刻。
工作i-j的最早完成时间用EFi-j表示。
工作最早完成时间等于工作最早开始时间加本工作持续时间。
工作最迟完成时间等于工作最迟开始时间加本工作持续时间最迟完成时间。
是在不影响整个任务按期完成的条件下,本工作最迟必须完成的时刻。
工作i-j的最迟完成时间用LEi-j表示。
自由时差的计算自由时差是在不影响其紧后工作最早开始的前提下,本工作可以利用的机动时间。
工作i-j的自由时差用FFi-j表示。
工作自由时差等于该工作的紧后工作的最早开始时间减本工作最早开始时间,再减本工作的持续时间所得之差的最小值。
工作的自由时差小于等于其总时差。
总时差的计算总时差是在不影响总工期的前提下,本工作可以利用的机动时间。
工作i-j的总时差用TFi-j表示。
工作总时差等于工作最迟开始时间减最早开始时间。
关键工作、关键节点和关键线路总时差最小的工作就是关键工作。
在计划工期Tp等于计算工期Tc时,总时差为0的工作就是关键工作。
关键工作两端的节点称为关键节点,关键节点具有如下规律。
①网络计划的起始节点和终点节点必为关键节点。
②以关键节点为完成节点的工作,当Tp=Tc 时,其总时差和自由时差必然相等。
其他非关键工作的自由时差小于等于总时差。
由关键工作组成的线路,且当每相邻的两项关键工作之间的时间间隔为0时,该条线路即为关键线路。
项目组织与管理和实物课程的考试都会涉及网络图的计算,双代号时标网络图自由时差和总时差的计算是经常考到的,我在学习中总结了一些简单的分析方法,希望可以帮助大家更快更准确的解决双代号时标网络图时间参数的计算。
一、自由时差,双代号时标网络图自由时差的计算很简单,就是该工作箭线上波形线的长度,但是有一种特殊情况,很容易忽略,如下图:其中E工作的箭线上没有波形线,但是E工作与其紧后工作之间都有时间间隔,此时E工作的自由时差为E与其紧后工作时间间隔的最小值,即E的自由时差为1。
总时差

总时差(用TFi-j表示),双代号网络图时间计算参数,指一项工作在不影响总工期的前提下所具有的机动时间。
用工作的最迟开始时间LSi-j与最早开始时间ESi-j之差表示。
自由时差,指一项工作在不影响后续工作的情况下所拥有的机动时间。
用紧后工作的最早开始时间与该工作的最早完成时间之差表示。
网络图时间参数相关概念包括:各项工作的最早开始时间、最迟开始时间、最早完成时间、最迟完成时间、节点的最早时间及工作的时差(总时差、自由时差)。
1 总时差=最迟完成时间—尚需完成时间。
计算结果若大于0,则不影响总工期。
若小于0则影响总工期。
2 拖延时间=总时差+受影响工期,与自由时差无关。
3 自由时差=紧后最早开始时间—本工作最早完成时间。
自由时差和总时差-----精选题解(免B)1、在双代号网络计划中,如果其计划工期等于计算工期,且工作i -j的完成节点j在关键线路上,则工作i-j的自由时差()。
A.等于零B.小于零C.小于其相应的总时差D.等于其相应的总时差答案:D解析:本题主要考察自由时差和总时差的概念。
由于工作i-j的完成节点j在关键线路上,说明节点j为关键节点,即工作i -j的紧后工作中必有关键工作,此时工作i-j的自由时差就等于其总时差。
2、在某工程双代号网络计划中,工作M的最早开始时间为第15天,其持续时间为7 天。
该工作有两项紧后工作,它们的最早开始时间分别为第27天和第30 天,最迟开始时间分别为第28天和第33 天,则工作M的总时差和自由时差()天。
A.均为5 B.分别为6和5 C.均为6 D.分别为11 和6答案:B解析:本题主要是考六时法计算方法1、工作M的最迟完成时间=其紧后工作最迟开始时间的最小值所以工作M的最迟完成时间等于[28,33]=282、工作M的总时差= 工作M的最迟完成时间- 工作M的最早完成时间等于28-(15+7)=63、工作M的自由时差= 工作M的紧后工作最早开始时间减工作M的最早完成时间所得之差的最小值:[27-22;30-22]= 5。
网络图中的六个时间参数

2.网络图中的六个时间参数(重点)网络图中的时间参数主要有六个:最早开始时间;最早完成时间;最迟开始时间;最迟完成时间;总时差和自由时差。
各时间参数的含义如下。
(1)工作最早开始时间ESii(EarliestStartTime)——是指在其所有紧前工作全部完成后,本工作有可能开始的最早时刻。
(2)工作最早完成时间EFii(EarliestFinishTime)——是指在其所有紧前工作全部完成后,本工作有可能完成的最早时刻。
工作的最早完成时间等于工作最早开始时间与其持续时间之和。
(3)工作最迟完成时间LFii(LatestFinishTime)——是指在不影响整个任务按期完成的前提下,本工作必须完成的最迟时刻。
(4)工作最迟开始时间LSii(LatestStartTime)——是指在不影响整个任务按期完成的前提下,本工作必须开始的最迟时刻。
工作的最迟开始时间等于工作最迟完成时间与其持续时间之差。
(5)总时差TFii(TotalFloatTime)——是指在不影响总工期的前提下,本工作可以利用的机动时间。
(6)自由时差FFii(FreeFloatTime)——是指在不影响其紧后工作最早开始时间的前提下,本工作可以利用的机动时间。
3.双代号网络图中时间参数的计算(1)时间参数计算数学模型:下面取一网络片断(图9-24)作为计算简图。
令整个计划的开始时间为第0天,则:工作最早开始时间等于其紧前工作最早完成时间的最大值。
令整个计划的总工期为一常数,则:工作最迟完成时间等于其紧后工作最迟开始时间的最小值。
在网络计划中,总时差最小的工作为关键工作。
特别地,当网络计划的计划工期等于计算工期时,总时差为零的工作就是关键工作。
由于工作的自由时差是总时差的构成部分,所以,当工作的总时差为零时,其自由时差必然为零。
即:如果网络计划中工作数量比较多,一般用项目管理软件进行计算。
如果数量不多也可用手工进行计算。
(2)计算步骤。
建设工程项目管理进度控制时间参数计算、关键线路的确定方法等考点汇总

建设工程项目管理进度控制时间参数计算、关键线路的确定方法等考点汇总双代号网络计划时间参数的计算方法可以用口诀来记忆:早时正向均取大,迟时逆向尽选小。
同点迟早差总差,自由时差定义找。
最早开始时间和最早完成时间的计算方法如下:起点节点为开始节点的工作,最早开始时间为0.对于其他工作,最早开始时间等于紧前工作的最早完成时间的最大值。
最早完成时间等于最早开始时间加上工作的持续时间。
确定计算工期的方法是以网络计划的终点节点为箭头节点的各个工作的最早完成时间的最大值。
最迟开始时间和最迟完成时间的计算方法如下:以网络计划的终点节点为箭头节点的工作的最迟完成时间等于计划工期。
对于其他工作,最迟完成时间等于紧后工作的最迟开始时间的最小值。
最迟开始时间等于最迟完成时间减去持续时间。
工作总时差和自由时差的计算方法如下:总时差是指在不影响总工期的前提下本工作可以利用的机动时间,可以通过最迟完成时间减去最早完成时间、最迟开始时间减去最早开始时间、或者紧后工作最迟开始时间减去本工作的最早完成时间来计算。
自由时差是指在不影响紧后工作最早开始时间的前提下,本工作可以利用的机动时间,可以通过紧后工作最早开始时间减去本工作的最早完成时间来计算。
关键工作是指总时差最小的工作,关键线路是指自始至终全部由关键工作组成的线路或线路上总的工作持续时间最长的线路,可以用双线或粗线标注。
标号法是一种快速寻求网络计算工期和关键线路的方法,具体步骤如下:1.网络计划起点节点的标号值为0.2.其他节点的标号值计算公式为:bjmax{biDi-j其中bi为源节点的标号值,Di-j为工作持续时间。
3.计算出节点的标号值后,应该用其标号值及其源节点对该节点进行双标号。
4.网络计划的计算工期为网络计划终点节点的标号值。
5.关键线路应从网络计划的终点节点开始,逆着箭线方向按源节点确定。
在双代号网络计划中,本题中有3条关键工作分别为ABCFI、ADEHI、ADEFI,关键线路长度为17,因此正确答案为C。
1、工作的最早开始时间

1、工作的最早开始时间(ES)顺着箭线的方向来计算,当有多条线路到达这项工作的时候,选取数值的最大值;(注意为加上各紧前工作的持续时间后的最大值);
最早完成时间EF=ES+D (D为本项工作的持续时间);
2、工作的最迟完成时间(LF),逆着箭线方向来计算,遇到多条线路到达这项工作时,选取数值的最小值。
(注意先应计算总工期,即为和终点节点相连的工作的最迟完成时间。
中间工作为减去紧后工作持续时间后的最小值);
最迟开始时间LS=LF-D (D为本工作的持续时间);
本公式中,持续时间D=EF-ES=LF-LS TF=LS-ES=LF-EF
记忆为:上-下=持续时间(D) ,右-左=总时差(TF)
后上1-前下1=自由时间(FF)
即为紧后工作的最早开始时间减去本工作的最早完成时间;
4、参数计算时可先从前往后计算工作最早开始时间(ES)和工作最早完成时间(EF)。
和起点节点相连的工作,最早开始时间都相等,且最早开始时间(ES)=0。
六时参数法公式

六时参数法公式
六时参数法是一种用于计算网络计划中工作在最迟开始时间
(最迟完成时间) 和总时差的方法。
以下是六时参数法公式的详细说明:
1. 最早开始时间 (最早完成时间):
最早开始时间 = 最早完成时间 - 持续时间 + 1
2. 最迟开始时间 (最迟完成时间):
最迟开始时间 = 最早开始时间 - 持续时间 + 1
最迟完成时间 = 最早完成时间 - 持续时间
3. 总时差:
总时差 = 最迟完成时间 - 最早完成时间
4. 自由时差:
自由时差 = 总时差 - 紧前工作的自由时差
其中,持续时间是指工作的实际持续时间,而不是计算持续时间。
最迟完成时间是指在没有任何延迟的情况下,该工作可以完成的最后时间。
最早完成时间是指在没有任何延迟的情况下,该工作可以完成的最早时间。
自由时差是指工作之间的时差,它反映了工作之间的先后顺序和持续时间的影响。
使用六时参数法计算网络计划中工作的最佳时间和总时差时,需要先确定每个工作的最早开始时间和最迟开始时间,以及持续时间和紧前工作的最早完成时间和最迟完成时间。
然后,根据公式计算出每个工作的最迟完成时间、总时差和自由时差。
最后,将这些值填入网络计划表格中,以便更好地分析网络计划中的任务优先级和顺序。
网络图中六个时参数

网络图中六个时参数————————————————————————————————作者:————————————————————————————————日期:2.网络图中的六个时间参数(重点)网络图中的时间参数主要有六个:最早开始时间;最早完成时间;最迟开始时间;最迟完成时间;总时差和自由时差。
各时间参数的含义如下。
(1)工作最早开始时间ESii(EarliestStartTime)——是指在其所有紧前工作全部完成后,本工作有可能开始的最早时刻。
(2)工作最早完成时间EFii(EarliestFinishTime)——是指在其所有紧前工作全部完成后,本工作有可能完成的最早时刻。
工作的最早完成时间等于工作最早开始时间与其持续时间之和。
(3)工作最迟完成时间LFii(LatestFinishTime)——是指在不影响整个任务按期完成的前提下,本工作必须完成的最迟时刻。
(4)工作最迟开始时间LSii(LatestStartTime)——是指在不影响整个任务按期完成的前提下,本工作必须开始的最迟时刻。
工作的最迟开始时间等于工作最迟完成时间与其持续时间之差。
(5)总时差TFii(TotalFloatTime)——是指在不影响总工期的前提下,本工作可以利用的机动时间。
(6)自由时差FFii(FreeFloatTime)——是指在不影响其紧后工作最早开始时间的前提下,本工作可以利用的机动时间。
3.双代号网络图中时间参数的计算(1)时间参数计算数学模型:下面取一网络片断(图9-24)作为计算简图。
令整个计划的开始时间为第0天,则:工作最早开始时间等于其紧前工作最早完成时间的最大值。
令整个计划的总工期为一常数,则:工作最迟完成时间等于其紧后工作最迟开始时间的最小值。
在网络计划中,总时差最小的工作为关键工作。
特别地,当网络计划的计划工期等于计算工期时,总时差为零的工作就是关键工作。
由于工作的自由时差是总时差的构成部分,所以,当工作的总时差为零时,其自由时差必然为零。
双代号网络计划时间参数含义及计算

双代号网络计划时间参数含义及计算江阴上元二建培训总结1.工作持续时间工作持续时间:是指一项工作从开始到完成的时间。
2.工期:是指完成一项任务所需要的时间。
①计算工期TC ;②要求工期TR;③计划工期TP当规定了要求工期TR 时,TP<TR ;上未规定要求工期时,TP=TC (计算工期为关键线路的总时间)【计算工期的计算】①计算工期为关键线路的总时间;②计算工期等于以网络计划的终点节点为箭头节点各个工作的最早完成时间的最大值。
【工作最早时间参数的计算】3.(1)最早开始(ES)、(2)最早完成(EF)(1)工作最早开始时间:工作的最早开始时间是指在各紧前工作全部完成后,本工作有可能开始的最早时刻。
(2)工作最早完成时间:工作的最早完成时间是指在各紧前工作全部完成后,本工作有可能完成的最早时刻。
(最早开始时间+持续时间)。
【工作最早时间参数的计算】①工作的最早时间参数受到紧前工作的约束,故其计算顺序应该是从起点节点开始,顺着箭线方向右逐项计算。
②以网络计划的起点节点为开始工作的最早开始时间为零。
③最早完成时间等于最早开始时间加上其持续时间。
④最早开始时间等于各紧前工作的最早完时间的最大值。
4.工作最迟时间:(1)工作最迟完成时间:是指在不影响整个任务按期(工期)完成的前提下,本工作必须完成的最迟时刻。
(2)工作最迟开始是指在不影响整个任务按期(工期)完成的前提下,本工作必须开始的最迟时刻。
(最迟完成时间-持续时间)。
工作最迟完成时间的计算:(受紧后工作制约)①以终点节点为完成节点的工作(最后一个工作):本工作最迟完成时间等于计划工期。
②不是以终点节点为完成节点的工作:(不是最后一个工作)本工作最迟完成时间等于其紧后工作最迟开始时间的最小值,或等于该工作的最早完成+总时差。
江阴上元教育报名地址:江阴市高巷路33号暨阳大厦14楼1401室(江阴市步行街东,江阴华地百货/大统华超市对面,江阴国际购物中心斜对面)江阴上元shangyuan1230公交线路(一):可乘1路、11路、12路、17路、19路、76路到高巷口站台下公交线路(二):可乘2路、21路、22路、23路、25路、32路、33路、37路到中山公园站台下,穿越中山公园到江阴市人民路步行街东头,江阴上元教育就在您旁边。
网络图中的六个时间参数

2.网络图中的六个时间参数(重点)网络图中的时间参数主要有六个:最早开始时间;最早完成时间;最迟开始时间;最迟完成时间;总时差和自由时差。
各时间参数的含义如下。
(1)工作最早开始时间ESii(EarliestStartTime)—-是指在其所有紧前工作全部完成后,本工作有可能开始的最早时刻.(2)工作最早完成时间EFii(EarliestFinishTime)—-是指在其所有紧前工作全部完成后,本工作有可能完成的最早时刻。
工作的最早完成时间等于工作最早开始时间与其持续时间之和。
(3)工作最迟完成时间LFii(LatestFinishTime)——是指在不影响整个任务按期完成的前提下,本工作必须完成的最迟时刻。
(4)工作最迟开始时间LSii(LatestStartTime)—-是指在不影响整个任务按期完成的前提下,本工作必须开始的最迟时刻.工作的最迟开始时间等于工作最迟完成时间与其持续时间之差.(5)总时差TFii(TotalFloatTime)——是指在不影响总工期的前提下,本工作可以利用的机动时间.(6)自由时差FFii(FreeFloatTime)-—是指在不影响其紧后工作最早开始时间的前提下,本工作可以利用的机动时间.3.双代号网络图中时间参数的计算(1)时间参数计算数学模型:下面取一网络片断(图9-24)作为计算简图。
令整个计划的开始时间为第0天,则:工作最早开始时间等于其紧前工作最早完成时间的最大值。
令整个计划的总工期为一常数,则:工作最迟完成时间等于其紧后工作最迟开始时间的最小值.在网络计划中,总时差最小的工作为关键工作。
特别地,当网络计划的计划工期等于计算工期时,总时差为零的工作就是关键工作。
由于工作的自由时差是总时差的构成部分,所以,当工作的总时差为零时,其自由时差必然为零.即:如果网络计划中工作数量比较多,一般用项目管理软件进行计算.如果数量不多也可用手工进行计算。
(2)计算步骤.时间参数的计算方法很多,可人工计算,也可通过计算机计算。
双代号网络图时间参数计算技巧
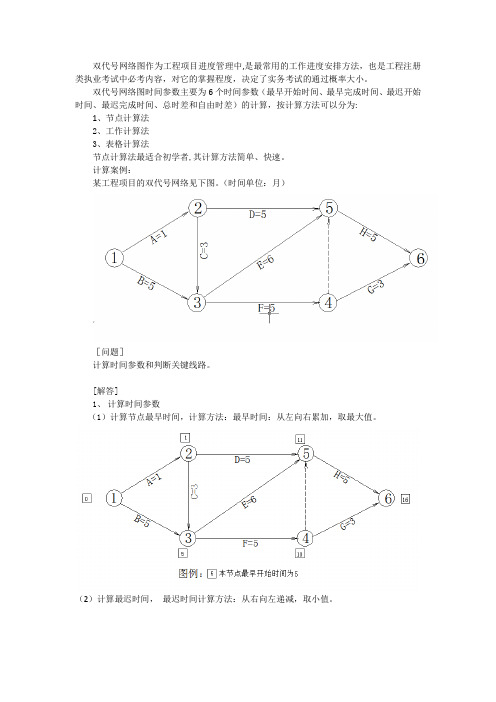
双代号网络图作为工程项目进度管理中,是最常用的工作进度安排方法,也是工程注册类执业考试中必考内容,对它的掌握程度,决定了实务考试的通过概率大小。
双代号网络图时间参数主要为6个时间参数(最早开始时间、最早完成时间、最迟开始时间、最迟完成时间、总时差和自由时差)的计算,按计算方法可以分为:1、节点计算法2、工作计算法3、表格计算法节点计算法最适合初学者,其计算方法简单、快速。
计算案例:某工程项目的双代号网络见下图。
(时间单位:月)[问题]计算时间参数和判断关键线路。
[解答]1、计算时间参数(1)计算节点最早时间,计算方法:最早时间:从左向右累加,取最大值。
(2)计算最迟时间,最迟时间计算方法:从右向左递减,取小值。
2、计算工作的六个时间参数自由时差:该工作在不影响其紧后工作最早开始时间的情况下所具有的机动时间。
总时差:该工作在不影响总工期情况下所具有的机动时间.通过前面计算节点的最早和最迟时间,可以先确定工作的最早开始时间和最迟完成时间,根据工作持续时间,计算出最早完成时间和最迟开始时间,以F工作为例,计算F工作的4个参数(以工作计算法标示)如下:注:EF=ES+工作持续时间LF=LS+工作持续时间接下来计算F工作的总时差TF,在工作计算法中,总时差TF=LS-ES或LF—EF,在节点计算法,总时差TF可以紧后工作的最迟时间—本工作的最早完成时间,或者是紧后工作最迟时间—最早时间,以F工作为例计算它的TF:接下来计算F工作的自由时差FF,根据定义:该工作在不影响其紧后工作最早开始时间的情况下所具有的机动时间,自由时差FF=紧后工作最早(或最小)开始时间—本工作最早完成时间ES,以F工作为例,F的紧后工作为G和H,G工作的最早开始时间为10(即4节点的最早时间),H工作的最早开始时间为11(即5节点的最早时间),G工作的时间最小,所以F的自由时差FF=G工作的最早开始时间ES—F工作的最早完成时间EF:最后计算所有工作的时间参数如图:通过上图我们得知:(1)关键线路为1-3-5-6,计算工期为16个月。
工作最早完成时间和最迟完成时间的计算

工作最早完成时间和最迟完成时间的计算最早完成时间是在各紧前工作全部完成后,本工作有可能完成的最早时刻。
工作i-j的最早完成时间用EFi-j表示。
工作最早完成时间等于工作最早开始时间加本工作持续时间。
工作最迟完成时间等于工作最迟开始时间加本工作持续时间最迟完成时间。
是在不影响整个任务按期完成的条件下,本工作最迟必须完成的时刻。
工作i-j的最迟完成时间用LEi-j表示。
自由时差的计算自由时差是在不影响其紧后工作最早开始的前提下,本工作可以利用的机动时间。
工作i-j 的自由时差用FFi-j表示。
工作自由时差等于该工作的紧后工作的最早开始时间减本工作最早开始时间,再减本工作的持续时间所得之差的最小值。
工作的自由时差小于等于其总时差。
总时差的计算总时差是在不影响总工期的前提下,本工作可以利用的机动时间。
工作i-j的总时差用T Fi-j 表示。
工作总时差等于工作最迟开始时间减最早开始时间。
关键工作、关键节点和关键线路总时差最小的工作就是关键工作。
在计划工期Tp等于计算工期Tc时,总时差为0的工作就是关键工作。
关键工作两端的节点称为关键节点,关键节点具有如下规律。
①网络计划的起始节点和终点节点必为关键节点。
②以关键节点为完成节点的工作,当Tp=Tc时,其总时差和自由时差必然相等。
其他非关键工作的自由时差小于等于总时差。
由关键工作组成的线路,且当每相邻的两项关键工作之间的时间间隔为0时,该条线路即为关键线路。
项目组织与管理和实物课程的考试都会涉及网络图的计算,双代号时标网络图自由时差和总时差的计算是经常考到的,我在学习中总结了一些简单的分析方法,希望可以帮助大家更快更准确的解决双代号时标网络图时间参数的计算。
一、自由时差,双代号时标网络图自由时差的计算很简单,就是该工作箭线上波形线的长度,但是有一种特殊情况,很容易忽略,如下图:其中E工作的箭线上没有波形线,但是E工作与其紧后工作之间都有时间间隔,此时E工作的自由时差为E与其紧后工作时间间隔的最小值,即E的自由时差为1。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
最迟完成时间=各紧后工作的最迟开始时间LS的最小值
最迟完成时间=各紧后工作的最迟开始时间LSj-k的最小值,其中最迟开始时间LSi-j是指在不影响整个任务按期完成的前提下,工作i-j必须开始的时间。
在最迟完成时间LSj-k是指在不影响整个任务按期完成的前提下,工作j-k必须完成的最后时刻。
工作i-j是工作j-k的紧后工作,在不影响紧后工作的前提下,工作j-k的最迟完成时间不能在工作i-j的最迟开始时间之后。
也就是说前序工作的最迟完成时间不能晚于后续工作的最晚开始时间。
若能理解望采纳!!
追问
说得有点罗嗦不过你提醒了我逆向来看在这里分享下我的理解以备有人来看其实也就一句话前项工作的最迟完成时间不可能比后项工作的最迟开始时间大就对了因为后项工作的开始时间逻辑上来说取决于前项工作的完成时间。
