(整理)恒定磁场的高斯定理和安培环路定理
§8-4 稳恒磁场的高斯定理与安培环路定理.

§8-4 稳恒磁场的高斯定理与安培环路定理
一. 稳恒磁场的高斯定理
由磁感应线的闭合性可知,对任意闭合曲面, 穿入的磁感应线条数与穿出的磁感应线条数相同, 因此,通过任何闭合曲面的磁通量为零。
静电场的高斯定理说明静电场为有源场,环 路定理又说明静电场无旋;稳恒磁场的环路 定理反映稳恒磁场有旋,高斯定理又反映稳 恒磁场无源。
安培环路定理
几点注意:
任意形状稳恒电流,安培环路定理都成立。
环流虽然仅与所围电流有关,但磁场却是所 有电流在空间产生磁场的叠加。
安培环路定理仅仅适用于恒定电流产生的恒 定磁场,恒定电流本身总是闭合的,因此安 培环路定理仅仅适用于闭合的载流导线。
L B (d l d l// )
B
L I d
r
dl
P
B
L
cos
90
dl
B
L
cos
dl//
0 LBr d 2 0 I r d
0 2 r
0I
结果一样!
长直电流的磁场
如果沿同一路径但改变
绕行方向积分:
B dl B cos( ) d l
的所有电流的代数和
安培环路定理
几点注意:
任意形状稳恒电流,安培环路定理都成立。
环流虽然仅与所围电流有关,但磁场却是所 有电流在空间产生磁场的叠加。
安培环路定理仅仅适用于恒定电流产生的恒 定磁场,恒定电流本身总是闭合的,因此安 培环路定理仅仅适用于闭合的载流导线。
B
2、磁场的高斯定理和安培环路定理

L
B dl o I i
L
S
B dS 0 j dS
S
B 0 j
安培环路定理的物理意义 磁场是有旋场(或磁场是非保守场,磁感应线 是闭合曲线)。
三、安培环路定理的应用
O
R
r
例3、求长直螺线管内的磁场。设螺线管的长度为 L,共有N匝线圈,单位长度上有 n = N/L匝线圈, 通过每匝线圈电流为I。管内中间部分的磁场是均 匀的,方向与管的轴线平行,在管的外侧磁场很 弱,可以忽略不计。
B
a
b
c d [解]: 若螺线管很长,则边缘效应可以忽略,螺 线管可看成是无限长,由对称性可知管内磁场是 均匀的,方向与管的轴线平行,并由右手螺旋定 则确定。在管的外侧磁场很弱,可以忽略不计。
B dl B 2πr μ0 I ,
j I / R2
且 I j s jπr 2 (r <R)
B
1 B μ0 jr 2
μ0 Ir B 2π R 2
0 I B 2R
μ0 I r = R处 B 2π R
B
0 Ir 1 0 jr, ( r R) 2 2 R 2 0 I 1 R2 0 j , r R ) ( 2 r 2 r
例2、求均匀载流无限长圆柱导体内外的磁场分布。
[解]:当r R时 B dl B 2r 0 I
L
I
R
μ0 I B 2π r
I 由 j πR 2
1 R2 B μ0 j 2 r
(r >R)
I jπR2
r
L
L
磁场的高斯定理和安培环路定理课件

03
安培环路定理的介绍与推导
安培环路定理的基本概念
总结词
安培环路定理是描述磁场散布的重要定理之一,它指出磁场线总是闭合的,且穿过任意一个封闭曲面的磁通量为 零。
详细描述
安培环路定理是电磁学中的基本定理之一,它描述了磁场线的性质和散布规律。根据安培环路定理,磁场线总是 闭合的,即磁场线不会中断或消失,而是形成一个完整的闭合曲线。此外,安培环路定理还指出,穿过任意一个 封闭曲面的磁通量为零,即磁场线不会从一个区域穿入另一个区域。
磁力线
磁感应强度
描述磁场强弱的物理量,单位是特斯 拉或高斯。
描述磁场散布的几何图形,磁力线闭 合且不相交,磁力线的疏密程度表示 磁场强弱。
高斯定理的背景与定义
高斯定理的背景
磁场在空间中的散布具有闭合性 ,即穿过某一封闭曲面S的磁通量 等于零或无穷大。
高斯定理的定义
穿过任意封闭曲面S的磁通量等于 该封闭曲面所包围的净磁荷量。
04
高斯定理与安培环路定理的比较与联系
两者之间的类似之处
闭合曲面的磁场通量
高斯定理和安培环路定理都涉及到闭合曲面的磁场通量。在高斯定理中,磁场 通量是通过闭合曲面进入或离开某一区域的量,而在安培环路定理中,磁场通 量与电流和闭合曲面的关系是关键。
无源磁场
高斯定理适用于无源磁场,即没有电流源的磁场。同样地,安培环路定理也适 用于无源磁场的情况。
高斯定理的应用场景
01
02
03
磁场散布分析
通过高斯定理可以分析磁 场在空间中的散布情况, 确定磁力线的走向和强弱 。
磁荷检测
高斯定理可以用于检测磁 场中的磁荷散布,例如磁 铁、发电机和电动机中的 磁荷散布。
磁场屏蔽
8-4 磁场高斯定理和安培环路定理

µ0 NI ≈ µ 0 nI B= 2π r
例3 无限大平面电流的磁场分布 r j -面电流密度矢量
Bz
By = 0
Bx = 0
Bx=0
By=0
l B
j
安培环流定理:2lB = µ 0 jl 安培环流定理:
B=
µ0 j
2
j
无限大均匀平面电流两侧的磁场是均匀磁 大小相等,方向相反。 场,大小相等,方向相反。
∫
L
ab
bc
cd
da
= B内 ab
N = µ0 ab I l
由安培环路定理
r ⊗ ⊗ ⊗ ⊗⊗ ⊗ ⊗ ⊗⊗ ⊗
N n= l
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅
c d
均匀场
b
B内
a
B = µ 0 nI
环形螺线管
. . . . .
. . . .. . .. . . . .
R
.
r . . .
..
. . . . .
.. . . . ...
.
I
∫ l B . dl µ I =∫ 2π r
o
=
∫l B r dϕ
∫0
2 π
ϕ =µ o I rd 2π
d ϕ =µ o I
结束
返回
3. 若改变积分绕行方向
∫ l B . dl = ∫l B cosα dl
=
µoI B= 2 r π l I O B r dϕ dl
∫l B cos(π θ )dl θ = ∫ l B cos dl
r r B⋅ dS = 0 ∫
S
高斯定理的积 分形式
穿过任意闭合曲面S的总磁通必然为零, 穿过任意闭合曲面 的总磁通必然为零,这就 的总磁通必然为零 高斯定理。 是稳恒磁场的高斯定理 是稳恒磁场的高斯定理。
11-4磁场的高斯定理和安培环路定理

闭合路径包围的电流为电流密度 沿所包围的曲面的积分
ห้องสมุดไป่ตู้
∑I =∫∫
i i
v v r r ∫∫S (∇×B)⋅ d S = µ0 ∫∫S j ⋅ dS v v 安培环路定理微分形式 ∇× B = µ j 0
S
v v j ⋅ dS
安培环路定理的存在说明磁场不是保守场 磁场不是保守场, 安培环路定理的存在说明磁场不是保守场,不 存在标量势函数。这是恒磁场不同于静电场的一 存在标量势函数。 个十分重要的性质。 个十分重要的性质。 安培环路定理可以用来处理电流分布具有一定 安培环路定理可以用来处理电流分布具有一定 对称性的恒磁场问题。 对称性的恒磁场问题。
dl ' o dl ' ' 垂线, 做 PO 垂线,取对称的长直 电流元,其合磁场方向平行于电流平面。 电流元,其合磁场方向平行于电流平面。无数对 点的总磁场方向平行于电流平面。 称元在 P点的总磁场方向平行于电流平面。 点的总磁场方向平行于电流平面
电流平面无限大, 电流平面无限大,故与电流平面等距离的各点 B 的大小相等。在该平面两侧的磁场方向相反。 14 的大小相等。在该平面两侧的磁场方向相反。
其磁场方向与电流满足右手螺旋。 其磁场方向与电流满足右手螺旋。
R2
R
L
R 1
L
同理可求得在螺绕管外部的磁场为零: 同理可求得在螺绕管外部的磁场为零:
∴B = 0
r ≤R 1
12
磁场的高斯定理
∫∫
∫L
S
v v B⋅ dS = 0
v ∇⋅ B = 0
安培环路定理
v v B⋅ dl = µ0 ∑Ii
i
v v ∇× B = µ0 j
磁场的高斯定理和 安培环路定理.ppt

B d S B d S
S1
磁通量仅由 的共同边界线所决定
S2
能否找到一个矢量A,它沿L作 线积分等于通过S的通量?
A dl B dS (a)
L
S
数学上可以证明,这样的矢量A的确存在,对
于磁感应强度B,A叫做磁矢势,A在空间的
分布也构成矢量场,简称矢势。
2π R
oR r
解 0 r R, B d l 0 l r R, l B d l 0I
B0 B 0I
2π r
§3 §4 磁场的高斯定理和安培环路定理
第二章 恒磁场
例5 无限长圆柱电缆的磁场(两空心圆筒)
解 0 r R1, B d l 0 B 0
第二章 恒磁场
例3 无限长载流圆柱体的磁场
I
解 1)对称性分析 2) 选取回路
RR
rR
Bdl l
0I
L
2π rB 0I
B 0I
2π r
r B
0 r R
l
B
d
l
0
π π
r2 R2
I
2π rB 0r2 I
R2
B
0Ir
2π R2
I . dB
ABLCDLA
B dl
AB B dl,
BLC
B dl
CD
DLA
B dl, B dl
B dl
AB
CD
BLC
CLB
DLA
L
B dl B dl 0,即 B dl B dl
磁场的高斯定理和安培环路定律

0I
是否成立???
设任意回路L在垂直于导线的平面内,与电流
成右手螺旋。
l B dl Bdl cos
0I
2πr
dlc
os
d
B
I
dl
r
0I
2πr
rd
0I
2π
d
l
B dl
l
0I
dl cos rd
闭合回路不环绕电流时
B1
0I
2 π r1
B2
0I
2 π r2
B1
B2
d
I
dl1
r1
dl2
I
I
解:取垂直纸面向里为法
B
线方向,以导线1所在位
置为坐标原点,建立如图 所示的坐标轴。
x
l
取细长条面元,面元内为
均匀磁场
a aa
B
0I 2x
2
0I
3a
x
o
x
窄条形面元的元磁通为
dm B dS BdS Bldx I
通过矩形面积内的磁通量
m
dm
2a
Bldx
a1
2a
a
0I 2x
2
0I
o
B 0I
2π x
B // S
x
方向垂直于纸面向里
dΦ BdS 0I ldx I
2π x
B
Φ
S
B dS
0Il
2π
d2
d1
dx x
l
Φ 0Il ln d2
2π d1
d1 d2
o
x
例2 两平行的无限长直导线通有电流 I , 相距3a,
矩形线框宽为a,高为l与直导线共面,求通过线框的
磁场的高斯定理和安培环路定理.
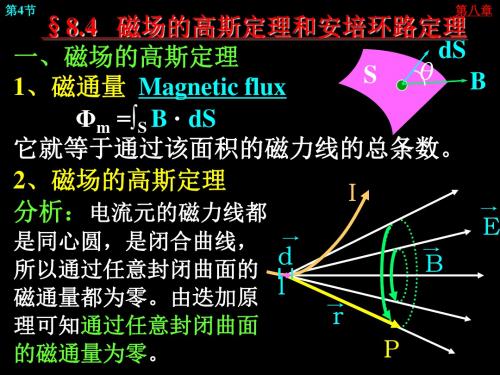
第二4节 、磁场的安培环路定理
第八章
1、真空中
根据闭合电流产生的磁场公式,即安
培 — 拉普拉氏定律,可证明真空中磁场 B
沿闭合回路 L
∮L B ·dl =μoΣI 此式称为真空中磁场的安培环流定理,式
中ΣI 是闭合回路 L 所包围的所有闭合电流
I 的代数和。
物理意义:磁场 B 是有旋场,非保守场
第4节
第八章
电流正负符号按右手螺旋定则:
电流方向与 L 的绕行方向符合右手螺
旋关系时,此电流为正,否则为负。
举例说明:
+I I
+ I1 + I2
- I3
L
第24、节 有磁介质
第八章
∮L B ·dl =μoΣI = μoΣIo +μoΣI’
式中ΣIo 和ΣI’ 分别是穿过安培环路 L 的自 由电流和束缚电流的总和。
其中 n = N/2R 为螺绕环单位长度的匝数。
2、环管外:ΣIo = 0,H// = 0,B// = 0 此式说明密绕螺绕环外部无磁场。
第特4节 例:当
R
第八章
时,即为无限长螺线管。
因此,长直螺线管内磁感应强度公式为:
B = o n I 此式表明,理想长直螺线管内部的磁感应强
注意:螺绕环和螺线管的外部磁场为零的结 论是在假定它们由许多不相连的圆环密集排 列组成的模型下得出的。实际上圆环以螺旋 线形式相连形成螺绕环和螺线管,沿螺绕环 和螺线管有一电流分量通过,即等效一圆电 流和长直载流导线,因此它们的外部磁场不 为零。但相比内部磁场而言,则相对很小。
2π R
μ 0I
2π R
第八章
I R
r
磁场的高斯定理和安培环路定理

dB
0dI
2(R2 r02 )3/ 2
dI=σωrdr
例18、电荷q均匀分布于一半径为R的圆盘上,圆 盘绕通过圆心且垂直于环面的轴匀速转动,角速度 为,求圆盘中心点的磁感应强度。
16
§11-5 磁场对载流导线的作用
一、 安培定律
安培力:载流导线在磁场中受到的磁场力
大小 dF IdlB sin
两个边bc、da 垂直于轴。
b
根据安培环路定理:
a
B
L B dl ab B dl bc B dl cd B dl da B dl
无垂直于轴的磁场分量,管外部磁场趋于零,
因此管内为均匀磁场,任一点的磁感应强度为:
B dl
dB' dB
dB''
l pd c
面平行,则有
dl' o dl''
L B dl B2l 0 jl
ab
B 0 j 方向如图所示。
2
结果:在无限大均匀平面电流的两侧的磁场都
为均匀磁场,并且大小相等,但方向相反。
15
例17、半径为R的圆片上均匀带电,电荷面密度为σ, 令该片以匀角速度ω绕它的轴旋转,求轴线上圆片中 心O为x处的磁场.
圆为安培环路
dB
B dl
L
2πrB
0
I
B 0I
rR
dl ''
dl '
2 πr
B dl
r
0
Ir 2 R2
B
0 Ir
磁场中的高斯定理及安培环路定理
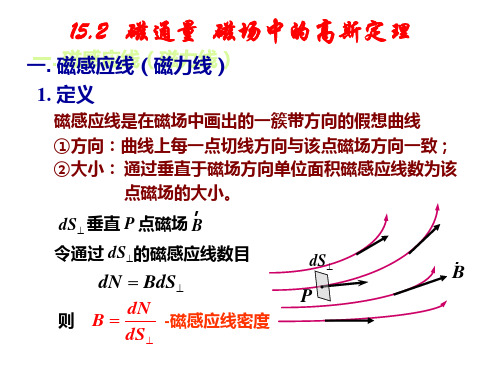
P
r B
则 B dN -磁感应线密度
dS
2. 几种典型的磁感应线
I
直线电流
圆电流
载流长螺线管
3. 磁感应线特性
磁感应线是环绕电流的无头尾的闭合曲线,无起点无终点; 磁感应线不相交。
二. 磁通量(magnetic flux)
1. 定义 通过磁场中任一给定面的
磁感线数目称为通过该面的 磁通量,用 表示。 2. 磁通量的计算 ① 磁场不均匀,S 为任意曲面
a
b
B
eeeeeeeeeeeee
Ñ B dl μ0 NI
l
B 0 NI
2 r
Amperian loop
B
o R1 R2 r
若 R1、R2 R2 R1
n N N
2 R1 2 r
则
B
μ 0
nI
B 0 NI 2 r
I
R2
R1
例题3 :
设在无限大导体薄板中有均匀电流沿平面流动, 在垂直于电流方向的单位长度上流过的电流为i (电流密度)。求此电流产生的磁场。
因而,同静电场中利用高斯定理确定已知电荷分 布的电场分布一样,需要满足一定的对称性。
例题1 :
已知:I 、R,电流沿轴向在截面上均匀分布, 求“无限长”载流圆柱导体内外磁场的分布
解: 首先分析对称性
电流分布——轴对称
I
磁场分布——轴对称
R
r
dS1
dB
dB2 dB1
O
l
P
dS2
电流及其产生的磁场具有轴对称分布时
B 0I 2 x
方向:
I
a
阴影部分通过的磁通量为:
rr B dS
6-2磁场的高斯定理和安培环路定理
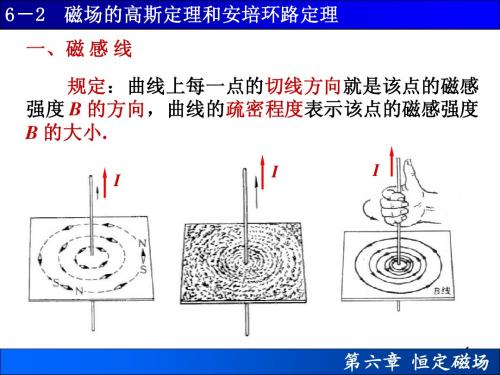
例6-3 如图所示,载流长直导线上的电流强度为 I , 它与边长分别为 a 和 b 矩形共面,边与长直导线平 行,两者之间的距离 d .求载流长直导线的磁场穿过 该平面的磁通量. 0 I 解 B 2π x B C B I
dΦ BdS
0
I
b
A dx D
2π x
bdx
o
x
d
a
0 Ib d a dx Φ 2 π d x 0 Ib d a ln 2π d
I2 I 3
l
B B1 B2 B3 B d l 0 ( I 2 I 3 )
l
L
I1
B d l 0 (I1 I1 I1 I 2 )
L
0 I1 I2) (
第六章 恒定磁场
11
6-2
磁场的高斯定理和安培环路定理
即在真空的稳恒磁场中,磁感应强度 B 沿任
0 乘以该闭合路径
I
电流 I 正负的规定 :I 与 为正;反之为负.
L 成右螺旋时,
第六章 恒定磁场
9
6-2
磁场的高斯定理和安培环路定理
注意
(1)环路定理中的磁感强度 B
为闭合路径 L 上的 磁感强度,它是由空间所有电流产生的。 (2)磁感强度沿闭合路径的环流,仅与闭合路径所包
6-2
磁场的高斯定理和安培环路定理
一、磁 感 线 规定:曲线上每一点的切线方向就是该点的磁感 强度 B 的方向,曲线的疏密程度表示该点的磁感强度 B 的大小.
I I I
第六章 恒定磁场
1
6-2
磁场的高斯定理和安培环路定理
I S S N I
N
11-4磁场的高斯定理和安培环路定理

单根导线产生的磁场
所有电流 的总场
L
L
Bn dl 0 I n
B1 dl 0 I1
L Bn1 dl 0 Bnk dl 0
L
任意回路
L
B dl 0 I i
i
穿过回路 的电流
7
在理解这个定理时,应注意以下几个问题 (1) 定理中的B是安培环路L上任意一点的磁感 应强度,它是由空间所有电流共同产生的。定理中 的 Ii则是安培环路L所包围的电流的代数和。 (2)矢量B的环路积分不恒等于零,说明稳恒磁 场不是保守力场,而是有旋场,所以在磁场中不 能引入势能(标量势)的概念。 (3)定理只适用于稳恒电流的磁场。由于稳恒电 流是闭合的,所以对于不闭合的有限长的载流导线, 安培环路定理不适用;
dl ' o dl ' ' 做 PO 垂线,取对称的长直 电流元,其合磁场方向平行于电流平面。无数对 称元在 P点的总磁场方向平行于电流平面。
电流平面无限大,故与电流平面等距离的各点
B 的大小相等。在该平面两侧的磁场方向相反。 16
作一安培回路如图: bc和 da两边被电流平面 等分。ab和cd 与电流平
B dl 0
根据安培环路定理,该安培环路一定包围电流。 由此可得结论:磁感应线总是与产生它的电流回 10 路套连在一起的。
3. 安培环路定理的应用 例1:求无限长载流圆柱体磁场分布。 解:圆柱体轴对称,以轴上一点为 I
圆心取垂直轴的平面内半径为 r 的 圆为安培环路
B dl 2πrB 0 I
8
边长为2a的正方形闭合回路 CDEFC,所通电流为I。现仅讨 论CD段,取中心处于其中点且 与其垂直的半径为r的圆为安培 环路,CD段所激发的磁场在圆 上各点的磁感应强度为 0 Ia BCD 2r (a 2 r 2 )1/ 2 BCD的方向与圆周相切,与电流的方向成右螺旋 关系。沿此圆周的环路积分为 0 Ia BCD dl 2 2 1/2 0I
磁场中的高斯定理及安培环路定理

0
l
l
μI
Ñl 2π0R dl
R
l
v B
r
μI 0
2πR=μ
I
2πR
0
若l 绕行方向与图示方向相反,则
B 0I 2R
dl
v
Ñ B
v dl
Ñ Bdl
cos
π=μ 0
(
I
)
Ñ l
l
赋予电流代数含义,则
v B
dlv=μ
I
0
l
2. 无限长直电流通过垂直平面内的任一回路
r
Ñ B
r dl
Ñ B
cosθdl
若 R1、R2 R2 R1
n N N
2 R1 2 r
则
B
μ 0
nI
B 0 NI 2 r
I
R2
R1
例题3 :
设在无限大导体薄板中有均匀电流沿平面流动, 在垂直于电流方向的单位长度上流过的电流为i (电流密度)。求此电流产生的磁场。
a
b
B
eeeeeeeeeeeee
d
c
讨论
关于安培环路定理的应用
BdS
0 I
adx
d x
2 x
通过矩形线圈的磁通量为:
dx
d
d b
0I adx
0Ia ln d b
d 2 x
2 d
15.4 安培环路定理
rv
一. 引言:稳恒磁场的环流 Ñl B dl ?
二. 定理推导
1. 无限长直电流通过圆形回路圆心且垂直于该回路
I
v
Ñ B
v dl
Ñ Bdl
cos
当电流分布以至于磁场分布具有高度对称性时, 可以应用安培环路定理计算磁感应强度的分布。
06磁场的高斯定理和安培环路定理

∫
∑
(4)安培环路定理说明磁场性质 磁场定理说明磁场性质 磁场是有旋场。
6
特例:以无限长载流直导线为例。 特例:以无限长载流直导线为例。 长直导线周围的磁力 线为一系列的同心圆, 长直导线周围的磁力 线为一系列的同心圆,选 取路径方向与磁感应强度方向相同; 感应强度方向相同 取路径方向与磁感应强度方向相同; 左边= 左边
dB ' '
dl '
o dl ' '
点的总磁场方向平行于电流平面。 无数对称元在 p点的总磁场方向平行于电流平面。 因为电流平面是无限大,故与电流平面等距离的各点 因为电流平面是无限大,故与电流平面等距离的各点B 的大小相等。在该平面两侧的磁场方向相反。 的大小相等。在该平面两侧的磁场方向相反。
13
. .. . .. . .. . .. . ..
a
b
B
B外 = 0
d
d a c d
c
∫ B ⋅ dl = ∫
b
a
B ⋅ dl + ∫ B ⋅ dl + ∫ B ⋅ dl + ∫ B ⋅ dl
b
c
∵ B ⊥ d l , cosθ = 0
B 螺线管外: 螺线管外: 外 = 0,
b
∫
c
b
B ⋅ dl = ∫ B ⋅ dl = 0,
∫ dl
B ⊥ dl , cosθ = 0
∫ B⋅ dl = 0
L
8
例1:长直密绕载流螺线管通有电流为 I,线圈密度 : 线圈密度 为 n,求管内一点的磁感应强度 。 ,求管内一点的磁感应强度 解:理想密绕螺线管,管内的磁 理想密绕螺线管, 场是均匀的, 场是均匀的,管外的磁场为 0 ; 作闭合环路 abcda,环路内的 环路内的 电流代数和为: 电流代数和为:∑ I = nabI
磁场高斯定理 安培环路定理

Amperian loop
µ0 NI ∴B = 2πr
磁场不均匀
B
µ0 NI B= 2π r
o
R1
R2
r
o
R1
R2
r
若 R1、R2 >> R2 − R1 N n= 2π R1
则:
B = µ0nI
当 2R >> d 时,螺绕环内可视为均匀场 。
已知: 例题 已知:I 、R,电流沿轴向在截面上均匀分 , 无限长”载流圆柱导体内外磁场的分布。 布,求“无限长”载流圆柱导体内外磁场的分布。 解: 首先分析对称性 电流分布——轴对称 电流分布 轴对称 磁场分布——轴对称 磁场分布 轴对称
r<R r>R
I
R
r<R 0 B = µ0 I r>R 2π r
µ0I B 2πR
r
O
R
无限大平板电流的磁场分布。 例题 无限大平板电流的磁场分布。设一无限大导体 薄平板垂直于纸面放置, 薄平板垂直于纸面放置,其上有方向垂直于纸面朝外 的电流通过,面电流密度( 的电流通过,面电流密度(即指通过与电流方向垂直 的单位长度的电流)到处均匀。 的单位长度的电流)到处均匀。大小为 j 。 解:视为无限多平行长 直电流的场。 直电流的场。 分析求场点p的对称性 垂线, 做 po 垂线,取对称的 长直电流元, 长直电流元,其合磁场 方向平行于电流平面。 方向平行于电流平面。
r r (3)要求环路上各点 B大小相等,B的方向与环路方向 要求环路上各点 r大小相等, r 一致,目的是将: B ⋅ dl = µ0 ∑ I 写成 B = µ0 ∑ I 一致,目的是将 ∫L r ∫ dl 的方向与环路方向垂直, 或 B 的方向与环路方向垂直, r r r r B ⊥ dl , cosθ = 0 ∫ B ⋅ dl = 0
磁场的高斯定理和安培环路定理
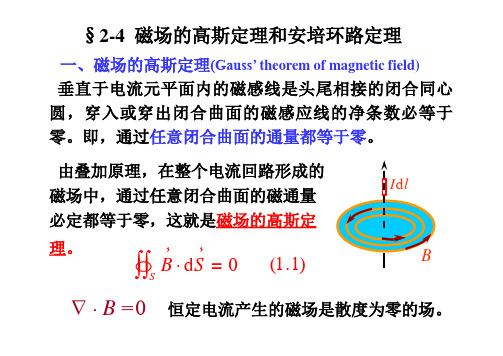
一、磁场的高斯定理(Gauss’ theorem of magnetic field) 垂直于电流元平面内的磁感线是头尾相接的闭合同心 圆,穿入或穿出闭合曲面的磁感应线的净条数必等于 零。即,通过任意闭合曲面的通量都等于零。
由叠加原理,在整个电流回路形成的
磁场中,通过任意闭合曲面的磁通量
L Bn dl 0In ,
L Bnk dl 0
任意回路
¸¸
n
B dl L
0
Ii
i1
穿过回路 的电流
闭合路径包围的电流为电
流 密度沿所包围的曲面的
¸
Ii
j dS
S
i
积分 安培环路定理说明磁场不是保守场,不存在标
量势函数。这是恒磁场不同于静电场的一个十分
重要的性质。
安培环路定理可以用来处理电流分布具有一定 对称性的恒磁场问题。
设 I1 , I 2 , … , I n电流过回路L,In 1 , I n 2 , … , I n k
电流不穿过回路L。令 B1 , B2 , … , Bn k 分别为单根
导线
I1
,
I
2
,
L
…
¸ B1
,
In
dl
பைடு நூலகம்
k产生的磁场,则有
¸
0I1 ,
L Bn1
dl
0
¸ #¸
# 所有电流的总¸ 场 ¸
小结
应用环路定理求解磁感应强度的步骤:
(1)根据通电电流产生的磁场的对称性,选 择合适的闭合曲线L,并规定计算方向;
(2)计算磁感应强度的环流以及通过曲线L 所包围的平面的电流的代数和;
高斯定理和安培环路定理

r R 时在圆柱面内做一圆周
B cos dl B dl B 2r 0
L L
dI ' dI
P
B0
例 无限大平面电流的磁场.有一无限大的导体平面,均匀地 流着自下而上的面电流.设其电流线密度(垂直于电流线的单 位长度上的电流)为a,求距平面为d的任一点的磁感应强度B.
(1)设闭合曲线L在垂直于无限长载流导线的平面内,电流I穿 过L. 设闭合回路 L为圆形回路( L 与 I 成右螺旋)
载流长直导线的磁感强 度为 0I B 2π R 0I l B d l 2 π R d l 0I l B d l 2 π R l d l
l
I
R R
L
r
2 π rB 0 I
0 r R
2 π rB
B
0I
2π r
B
2 π r l B d l 0 π R 2 I
I
.
dI
dB
0r
R
2
2
I
B
0 Ir
2π R
2
B
B 的方向与 I 成右螺旋
0 r R,
B
0 Ir
B dl μ 0 Ii
L
内
—— 安培环路定律
恒定电流的磁场中,磁感应强度沿一闭合路径 L 的线积分 等于路径 L 包围的电流强度的代数和的 μ 0 倍
安培环路定理
n B dl 0 Ii i 1
一闭合路径的积分的值,等于 0 乘以该闭合路径 所包围的各电流的代数和.
回路绕向化为逆时针时则对任意形状的回路设闭合回路l为圆形回路l与i不成右螺旋安培环路定律恒定电流的磁场中磁感应强度沿一闭合路径l的线积分等于路径l包围的电流强度的代数和的环路上各点的磁场为所有电流的贡献安培环路定理一闭合路径的积分的值等于乘以该闭合路径所包围的各电流的代数和
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
恒定磁场的高斯定理和安培环路定理1. 选择题题号:31011001分值:3分难度系数等级:1 1.磁场中高斯定理:⎰=∙ss d B 0 ,以下说法正确的是:( )A .高斯定理只适用于封闭曲面中没有永磁体和电流的情况B .高斯定理只适用于封闭曲面中没有电流的情况C .高斯定理只适用于稳恒磁场D .高斯定理也适用于交变磁场答案:D题号:31012002分值:3分难度系数等级:22.在地球北半球的某区域,磁感应强度的大小为5104-⨯T ,方向与铅直线成60度角。
则穿过面积为1平方米的水平平面的磁通量 ( )A .0B .5104-⨯WbC .5102-⨯WbD .51046.3-⨯Wb答案:C题号:31011003分值:3分难度系数等级:13.一边长为l =2m 的立方体在坐标系的正方向放置,其中一个顶点与坐标系的原点重合。
有一均匀磁场)3610(k j i B ++=通过立方体所在区域,通过立方体的总的磁通量有( )A .0B .40 WbC .24 WbD .12Wb答案:A题号:31013004分值:3分难度系数等级:34.无限长直导线通有电流I ,右侧有两个相连的矩形回路,分别是1S 和2S ,则通过两个矩形回路1S 、2S 的磁通量之比为:( )。
A .1:2B .1:1C .1:4D .2:1答案:B题号:31011005分值:3分难度系数等级:15.均匀磁场的磁感应强度B 垂直于半径为R 的圆面,今以圆周为边线,作一半球面S ,则通过S 面的磁通量的大小为()A .B R 22π B .B R 2πC .0D .无法确定答案:B题号:31012006分值:3分难度系数等级:2 6.在磁感强度为B 的均匀磁场中作一半径为r 的半球面S ,S 边线所在平面的法线方向单位矢量n 与B 的夹角为α,则通过半球面S 的磁通量为( )A .B r 2π B .B r 22πC .απsin 2B r -D .απcos 2B r - 答案:D题号:31011007分值:3分难度系数等级:17.若空间存在两根无限长直载流导线,空间的磁场分布就不具有简单的对称性,则该磁场分布( )A .不能用安培环路定理来计算B .可以直接用安培环路定理求出C .只能用毕奥-萨伐尔定律求出D .可以用安培环路定理和磁感应强度的叠加原理求出答案:D题号:31012008分值:3分难度系数等级:28.在图(a)和(b)中各有一半径相同的圆形回路L 1和L 2,圆周内有电流I 1和I 2,其分布相同,且均在真空中,但在(b)图中L 2回路外有电流I 3,P 2、P 1为两圆形回路上的对应点,则:()A .2121,P P L LB B l d B l d B =⋅=⋅⎰⎰ B .2121,P P L L B B l d B l d B ≠⋅≠⋅⎰⎰ C .2121,P P L L B B l d B l d B ≠⋅=⋅⎰⎰ D .2121,P P L L B B l d B l d B =⋅≠⋅⎰⎰答案:C题号:31012009分值:3分难度系数等级:29.一载有电流I 的导线分别均匀密绕在半径为R 和r 的长直圆筒上形成两个螺线管(R=2r ),两螺线管单位长度上的匝数相等,两螺线管中的磁感应强度大小B R 和B r 应满足()A .B R =2B r B .B R =B rC .2B R =B rD .B R =4B r答案:B题号:31012010分值:3分难度系数等级:210.无限长载流空心圆柱导体的内外半径分别为a,b,电流在导体截面上均匀分布,则空间各处的B的大小与场点到圆柱中心轴线的距离r 的关系定性地如图所示。
正确的图是( )(A) (B) (C) (D)答案:B题号:31012011分值:3分难度系数等级:211.如图所示,六根无限长导线互相绝缘,通过电流均匀为I ,区域Ⅰ、Ⅱ、Ⅲ、Ⅳ均为相等的正方形,哪一个区域指向纸内的磁通量最大 ( )A .Ⅰ区域B .Ⅱ区域C .Ⅲ区域D .Ⅳ区域答案:B题号:31012012分值:3分难度系数等级:212.如图所示,流出纸面的电流为2I ,流进纸面的电流为I ,则下述式中哪一个是正确的 ( ) A .I l d B L 012μ=∙⎰ B .I l d B L 02μ=∙⎰C .I l d B L 03μ-=∙⎰D .I l d B L 04μ-=∙⎰ 答案:D题号:31011013分值:3分难度系数等级:113.在一圆形电流I 所在的平面内,选取一个同心圆形闭合回路L ,则由安培环路定理可知 ( ) A .0=∙⎰l d B L,且环路上任意一点B=0B .0=∙⎰l d B L ,且环路上任意一点B ≠0C .0≠∙⎰l d B L,且环路上任意一点B ≠0D .0≠∙⎰l d B L ,且环路上任意一点B=常量答案:B题号:31013014分值:3分难度系数等级:314.如图,两根直导线ab 和cd 沿半径方向被接到一个截面处处相等的铁环上,稳恒电流I从a 端流入而从d 端流出,则磁感强度B 沿图中闭合路径L 的积分l d B L ∙⎰等于( )A .I 0μB .3/0I μC .4/0I μD .3/20I μ答案:D题号:31012015分值:3分难度系数等级:215.无限长直圆柱体,半径为R ,沿轴向均匀流有电流。
设圆柱体内(r<R )的磁感强度为i B ,圆柱体外(r>R )的磁感强度为e B ,则有 ( )A .iB 、e B 均与r 成正比 B .i B 、e B 均与r 成反比C .i B 与r 成反比,e B 与r 成正比D .i B 与r 成正比,e B 与r 成反比 答案:D题号:31011016分值:3分难度系数等级:116.若使半径为4⨯103-m 的裸铜线表面的磁感强度为5100.7-⨯T ,则铜线中需要通过的电流为 ( )A .0.14 AB .1.4 AC .2.8 AD .14 A答案:B题号:31012017分值:3分难度系数等级:217.取一闭合积分回路L ,使三根载流导线穿过它所围成的面。
现改变三根导线之间的相互间隔,但不越出积分回路,则 ( )A .回路L 内的∑I 不变,L 上各点的B 不变B .回路L 内的∑I 不变,L 上各点的B 改变C .回路L 内的∑I 改变,L 上各点的B 不变D .回路L 内的 I 改变,L 上各点的B 改变答案:B题号:31013018分值:3分难度系数等级:318.磁场由沿空心长圆筒形导体的均匀分布的电流产生,圆筒半径为R,X坐标轴垂直圆筒轴线,原点在中心轴线上,图(A )~(D )哪一条曲线表示B~X的关系? [ ]答案:B题号:31011019分值:3分难度系数等级:119.下列结论中你认为正确的是( )A .一根给定磁感应线上各点的B 的量值相同;B .用安培环路定理可以求出有限长一段直线电流周围的磁场;C .B 的方向是运动电荷所受磁力最大的方向(或试探载流线圈所受力矩最大的方向);D .一个不为零电流元在它的周围空间中任一点产生的磁感应强度也均不为零;答案:D题号:31011020分值:3分难度系数等级:120.下列可用环路定理求磁感应强度的是 ( )A .有限长载流直导体;B .C .有限长载流螺线管;D .无限长螺线管。
答案:D2. 判断题:题号:31021001分值:2分难度系数等级:11.可用安培环路定律推导出毕奥-萨伐尔定律。
()答案:错题号:31022002分值:2分难度系数等级:22.只有电流分布具有某种对称性时,才可用安培环路定理求解磁场问题。
()答案:对题号:31023003分值:2分难度系数等级:33.对于多个无限长平行载流直导线的磁场问题,由于总的磁场强度不具备对称性,求解过程中不可用安培环路定理。
()答案:错题号:31022004分值:2分难度系数等级:24.对于有限长、断面是圆形的载流直导线的磁场问题,由于圆形断面具有对称性,所以可用安培环路定理来求解此导线在周围产生的磁场。
()答案:错题号:31022005分值:2分难度系数等级:25.对于圆形载流螺线管,当螺线管只有一层密绕线圈时,由于单位长度上的电流密度相同,而且螺线管具有某些几何对称性,所以可用安培环路定理来求出螺线管两端的磁场。
()答案:错题号:31022006分值:2分难度系数等级:26.对于螺绕环,只有当环的孔径比环的平均半径小得多时,才可用安培环路定理来求解环内的磁场。
()答案:错题号:31022007分值:2分难度系数等级:27.对于载流螺线管内部,中部的磁感应线比两端的多。
()答案:对题号:31022008分值:2分难度系数等级:28.闭合曲线当中没有包含电流,说明闭合曲线中的磁感应强度处处为零。
( ) 答案:错题号:31023009分值:2分难度系数等级:39.磁场的高斯定理,说明磁场是发散式的场。
( )答案:错题号:31021010分值:2分难度系数等级:110.通过磁场的高斯定理可以说明,磁感应线是无头无尾,恒是闭合的。
( ) 答案:对3. 填空题题号:31032001分值:3分难度系数等级:21.一磁场的磁感应强度为k c j b i a B ++=,则通过一半径为R ,开口向Z 方向的半球壳,表面的磁通量大小为 Wb答案:c R 2π题号:31031002分值:3分难度系数等级:12.真空中有一载有稳恒电流I 的细线圈,则通过包围该线圈的封闭曲面S 的磁通量ϕ= 。
答案:0题号:31031003分值:3分难度系数等级:13.若通过S 面上某面元S d 的元磁通为d ϕ,而线圈中的电流增加为2I 时,通过同一面元的元磁通为φ'd ,则d ϕ:φ'd =答案:1:2题号:31032004分值:3分难度系数等级:24.均匀磁场的磁感应强度B 与半径为r 的圆形平面的法线n的夹角为α,今以圆周为边界,作一个半球面S ,S 与圆形平面组成封闭面如图,则通过S 面的磁通量ϕ= 。
答案:απcos 2B r -题号:31032005分值:3分难度系数等级:25.S 是一流有恒定电流的闭合线圈,电流强度为I ,方向如图,试求磁感应强度沿闭合曲线的环路积分⎰⋅l d B 为 。
答案:I 02μ-题号:31031006分值:3分难度系数等级:16.一根很长的铜导线,载有电流2A ,在距离此导线0.01m 处的磁感应强度为 。
答案:T 5104-⨯题号:31032007分值:3分难度系数等级:27.一根很长的圆形螺线管,沿圆周方向的面电流密度为i ,在线圈内部的磁感应强度为 。
答案:i 0μ题号:31031008分值:3分难度系数等级:18.一根很长的螺线管,总电阻20欧姆,两端连接在12V 的电源上,线圈半径2cm ,线圈匝数2000匝,在线圈内部距离轴线0.01m 处的磁场强度为 。
