2021人教A版高考数学总复习《导数与函数的零点》
2021版高考理科数学(人教A版)一轮复习 教师用书 数 第8讲 函数与方程
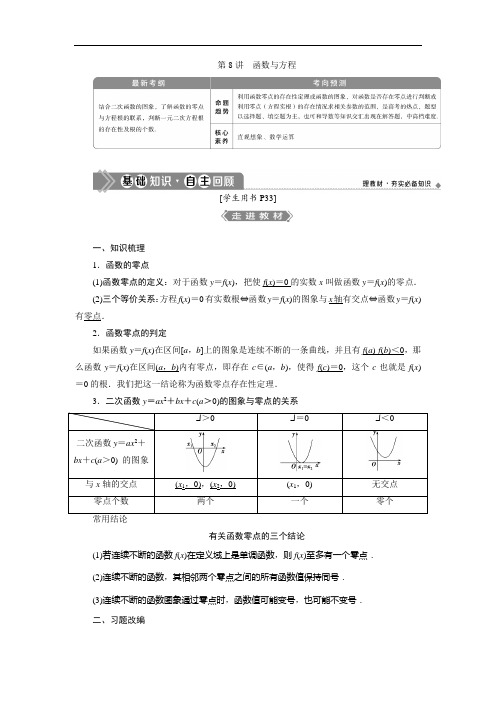
第8讲函数与方程[学生用书P33]一、知识梳理1.函数的零点(1)函数零点的定义:对于函数y=f(x),把使f(x)=0的实数x叫做函数y=f(x)的零点.(2)三个等价关系:方程f(x)=0有实数根⇔函数y=f(x)的图象与x轴有交点⇔函数y=f(x)有零点.2.函数零点的判定如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么函数y=f(x)在区间(a,b)内有零点,即存在c∈(a,b),使得f(c)=0,这个c也就是f(x)=0的根.我们把这一结论称为函数零点存在性定理.3.二次函数y=ax2+bx+c(a>0)的图象与零点的关系Δ>0Δ=0Δ<0二次函数y=ax2+bx+c(a>0) 的图象与x轴的交点(x1,0),(x2,0)(x1,0)无交点零点个数两个一个零个有关函数零点的三个结论(1)若连续不断的函数f(x)在定义域上是单调函数,则f(x)至多有一个零点.(2)连续不断的函数,其相邻两个零点之间的所有函数值保持同号.(3)连续不断的函数图象通过零点时,函数值可能变号,也可能不变号.二、习题改编1.(必修1P92A 组T2改编)已知函数y =f (x )的图象是连续曲线,且有如下的对应值表:x 1 2 3 4 5 6 y124.435-7414.5-56.7-123.6则函数y A .2个 B .3个 C .4个D .5个解析:选B.由零点存在性定理及题中的对应值表可知,函数f (x )在区间(2,3),(3,4),(4,5)内均有零点,所以y =f (x )在[1,6]上至少有3个零点.故选B.2.(必修1P92A 组T5改编)函数f (x )=ln x -2x 的零点所在的大致范围是( )A .(1,2)B .(2,3) C.⎝⎛⎭⎫1e ,1和(3,4)D .(4,+∞)解析:选B.易知f (x )为增函数,由f (2)=ln 2-1<0,f (3)=ln 3-23>0,得f (2)·f (3)<0.故选B.3.(必修1P88例1改编)函数f (x )=e x +3x 的零点个数是______.解析:由已知得f ′(x )=e x +3>0,所以f (x )在R 上单调递增,又f (-1)=1e -3<0,f (0)=1>0,因此函数f (x )有且只有一个零点.答案:1一、思考辨析判断正误(正确的打“√”,错误的打“×”) (1)函数的零点就是函数的图象与x 轴的交点.( )(2)函数y =f (x )在区间(a ,b )内有零点(函数图象连续不断),则f (a )·f (b )<0.( ) (3)只要函数有零点,我们就可以用二分法求出零点的近似值.( ) (4)二次函数y =ax 2+bx +c (a ≠0)在b 2-4ac <0时没有零点.( )(5)若函数f (x )在(a ,b )上连续单调且f (a )·f (b )<0,则函数f (x )在[a ,b ]上有且只有一个零点.( )答案:(1)× (2)× (3)× (4)√ (5)√ 二、易错纠偏常见误区|K(1)错用零点存在性定理; (2)误解函数零点的定义; (3)忽略限制条件;(4)错用二次函数在R 上无零点的条件.1.函数f (x )=x +1x的零点个数是______.解析:函数的定义域为{x |x ≠0},当x >0时,f (x )>0,当x <0时,f (x )<0,所以函数没有零点.答案:02.函数f (x )=x 2-3x 的零点是______. 解析:由f (x )=0,得x 2-3x =0, 即x =0和x =3. 答案:0和33.若二次函数f (x )=x 2-2x +m 在区间(0,4)上存在零点,则实数m 的取值范围是______. 解析:二次函数f (x )图象的对称轴方程为x =1.若在区间(0,4)上存在零点,只需f (1)≤0且f (4)>0即可,即-1+m ≤0且8+m >0,解得-8<m ≤1.答案:(-8,1]4.若二次函数f (x )=x 2+kx +k 在R 上无零点,则实数k 的取值范围是______. 解析:由题意得Δ=k 2-4k <0,解得0<k <4. 答案:(0,4)[学生用书P34]函数零点所在区间的判断(自主练透)1.设f (x )=ln x +x -2,则函数f (x )的零点所在的区间为( ) A .(0,1) B .(1,2) C .(2,3)D .(3,4)解析:选B.因为f (1)=ln 1+1-2=-1<0,f (2)=ln 2>0,所以f (1)·f (2)<0, 因为函数f (x )=ln x +x -2的图象是连续的,且为增函数,所以f (x )的零点所在的区间是(1,2).2.若a <b <c ,则函数f (x )=(x -a )(x -b )+(x -b )(x -c )+(x -c )(x -a )的两个零点分别位于区间( )A .(a ,b )和(b ,c )内B .(-∞,a )和(a ,b )内C .(b ,c )和(c ,+∞)内D .(-∞,a )和(c ,+∞)内解析:选A.因为a <b <c ,所以f (a )=(a -b )(a -c )>0, f (b )=(b -c )(b -a )<0,f (c )=(c -a )(c -b )>0,由函数零点存在性定理可知,在区间(a ,b ),(b ,c )内分别存在零点,又函数f (x )是二次函数,最多有两个零点.因此函数f (x )的两个零点分别位于区间(a ,b ),(b ,c )内,故选A.3.设函数y 1=x 3与y 2=⎝⎛⎭⎫12x -2的图象的交点为(x 0,y 0),若x 0∈(n ,n +1),n ∈N ,则x 0所在的区间是______.解析:令f (x )=x 3-⎝⎛⎭⎫12x -2,则f (x 0)=0,易知f (x )为增函数, 有f (1)<0,f (2)>0,所以x 0所在的区间是(1,2). 答案:(1,2)确定函数零点所在区间的方法(1)解方程法:当对应方程f (x )=0易解时,可先解方程,然后再看求得的根是否落在给定区间上.(2)图象法:把方程转化为两个函数,看它的交点所在区间.(3)利用函数零点的存在性定理:首先看函数y =f (x )在区间[a ,b ]上的图象是否连续,再看是否有f (a )·f (b )<0.若有,则函数y =f (x )在区间(a ,b )内必有零点.(4)数形结合法:通过画函数图象,观察图象与x 轴在给定区间上是否有交点来判断.函数零点的个数(师生共研)(1)函数f (x )=⎩⎪⎨⎪⎧x 2-2,x ≤0,2x -6+ln x ,x >0的零点个数是______.(2)函数f (x )=4cos 2x2·cos ⎝⎛⎭⎫π2-x -2sin x -|ln(x +1)|的零点个数为______. 【解析】 (1)当x ≤0时,令x 2-2=0,解得x =-2(正根舍去),所以在(-∞,0]上有一个零点;当x >0时,f ′(x )=2+1x >0恒成立,所以f (x )在(0,+∞)上是增函数.又因为f (2)=-2+ln 2<0,f (3)=ln 3>0,所以f (x )在(0,+∞)上有一个零点,综上,函数f (x )的零点个数为2.(2)f (x )=2(1+cos x )sin x -2sin x -|ln(x +1)|=sin 2x -|ln(x +1)|,x >-1,函数f (x )的零点个数即为函数y 1=sin 2x (x >-1)与 y 2=|ln(x +1)|(x >-1)的图象的交点个数.分别作出两个函数的图象,如图,可知有两个交点,则f (x )有两个零点.【答案】 (1)2 (2)2判断函数零点个数的方法(1)解方程法:所对应方程f (x )=0有几个不同的实数解就有几个零点. (2)零点存在性定理法:利用零点存在性定理并结合函数的性质进行判断.(3)数形结合法:转化为两个函数的图象的交点个数问题.先画出两个函数的图象,看其交点的个数,其中交点的个数,就是函数零点的个数.1.设函数f (x )是定义在R 上的奇函数,当x >0时,f (x )=e x +x -3,则f (x )的零点个数为( )A .1B .2C .3D .4解析:选C.因为函数f (x )是定义域为R 的奇函数,所以f (0)=0,所以0是函数f (x )的一个零点.当x >0时,令f (x )=e x +x -3=0. 则e x =-x +3.分别画出函数y =e x 和y =-x +3的图象,如图所示,有一个交点,所以函数f (x )在(0,+∞)上有一个零点.又根据对称性知,当x <0时函数f (x )也有一个零点. 综上所述,f (x )的零点个数为3.2.函数f (x )=2x |log 0.5x |-1的零点个数为______.解析:由f (x )=0,得|log 0.5x |=⎝⎛⎭⎫12x,作出函数y 1=|log 0.5x |和y 2=⎝⎛⎭⎫12x的图象, 由右图知两函数图象有2个交点, 故函数f (x )有2个零点. 答案:2函数零点的应用(多维探究)角度一 根据函数零点个数求参数(2020·安徽合肥二模)设函数f (x )=⎩⎪⎨⎪⎧|ln x |,x >0,e x (x +1),x ≤0.若函数g (x )=f (x )-b 有三个零点,则实数b 的取值范围是( )A .(1,+∞)B .⎝⎛⎭⎫-1e 2,0 C .(1,+∞)∪{0}D .(0,1]【解析】 令g (x )=f (x )-b =0,函数g (x )=f (x )-b 有三个零点等价于f (x )=b 有三个根,当x ≤0时,f (x )=e x (x +1),则f ′(x )=e x (x +1)+e x =e x (x +2 ),由f ′(x )<0得e x (x +2)<0,即x <-2,此时f (x )为减函数,由f ′(x )>0得e x (x +2)>0,即-2<x <0,此时f (x )为增函数,即当x =-2时,f (x )取得极小值f (-2)=-1e 2,作出f (x )的图象如图,要使f (x )=b 有三个根,则0<b ≤1,故选D.【答案】 D 角度二 根据函数有无零点求参数(1)函数f (x )=x 2-ax +1在区间⎝⎛⎭⎫12,3上有零点,则实数a 的取值范围是( )A .(2,+∞)B .[2,+∞) C.⎣⎡⎭⎫2,52 D .⎣⎡⎭⎫2,103 (2)已知函数f (x )=⎩⎪⎨⎪⎧0,x ≤0,e x ,x >0,则使函数g (x )=f (x )+x -m 有零点的实数m 的取值范围是( )A .[0,1)B .(-∞,1)C .(-∞,1]∪(2,+∞)D .(-∞,0]∪(1,+∞)【解析】 (1)由题意知方程ax =x 2+1在⎝⎛⎭⎫12,3上有解,即a =x +1x 在⎝⎛⎭⎫12,3上有解,设t =x +1x,x ∈⎝⎛⎭⎫12,3,则t 的取值范围是⎣⎡⎭⎫2,103.所以实数a 的取值范围是⎣⎡⎭⎫2,103. (2)函数g (x )=f (x )+x -m 的零点就是方程f (x )+x =m 的根,画出h (x )=f (x )+x =⎩⎪⎨⎪⎧x ,x ≤0,e x +x ,x >0的大致图象(图略).观察它与直线y =m 的交点,得知当m ≤0或m >1时,有交点,即函数g (x )=f (x )+x -m 有零点.【答案】 (1)D (2)D角度三 根据函数零点的范围求参数若函数f (x )=(m -2)x 2+mx +(2m +1)的两个零点分别在区间(-1,0)和区间(1,2)内,则m 的取值范围是______.【解析】 依题意,结合函数f (x )的图象分析可知m 需满足⎩⎪⎨⎪⎧m ≠2,f (-1)·f (0)<0,f (1)·f (2)<0, 即⎩⎪⎨⎪⎧m ≠2,[m -2-m +(2m +1)](2m +1)<0,[m -2+m +(2m +1)][4(m -2)+2m +(2m +1)]<0, 解得14<m <12.【答案】 ⎝⎛⎭⎫14,12根据函数零点的情况求参数的方法(1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围. (2)分离参数法:先将参数分离,转化成求函数值域问题加以解决.(3)数形结合法:先对解析式变形,在同一平面直角坐标系中画出函数的图象,然后数形结合求解.1.方程log 12(a -2x )=2+x 有解,则a 的最小值为______.解析:若方程log 12(a -2x)=2+x 有解,则⎝⎛⎭⎫122+x=a -2x有解,即14⎝⎛⎭⎫12x+2x =a 有解,因为14⎝⎛⎭⎫12x+2x ≥1,故a 的最小值为1. 答案:12.已知函数f (x )=⎩⎪⎨⎪⎧e x , x ≤0ln x , x >0,g (x )=f (x )+x +a .若g (x )存在2个零点,则a 的取值范围是______.解析:函数g (x )=f (x )+x +a 存在2个零点,即关于x 的方程f (x )=-x -a 有2个不同的实根,即函数f (x )的图象与直线y =-x -a 有2个交点,作出直线y =-x -a 与函数f (x )的图象,如图所示,由图可知,-a ≤1,解得a ≥-1.答案:a ≥-1[学生用书P267(单独成册)][基础题组练]1.(2020·河南商丘九校联考)函数f (x )=(x 2-1)·x 2-4的零点个数是( ) A .1 B .2 C .3D .4解析:选B.要使函数有意义,则x 2-4≥0,解得x ≥2或x ≤-2.由f (x )=0得x 2-4=0或x 2-1=0(不成立舍去),即x =2或x =-2.所以函数的零点个数为2.故选B.2.函数y =x -4·⎝⎛⎭⎫12x的零点所在的区间是( ) A .(0,1) B .(1,2) C .(2,3)D .(3,4)解析:选B.因为y =f (x )=x -4⎝⎛⎭⎫12x=x -⎝⎛⎭⎫12x -2是R 上连续递增的函数,且f (1)=1-2<0,f (2)=2-1>0,所以f (1)·f (2)<0,故函数y =x -4·⎝⎛⎭⎫12x的零点所在的区间为(1,2).故选B. 3.(2020·福建晋江四校联考)设函数y =log 3x 与y =3-x 的图象的交点为(x 0,y 0),则x 0所在的区间是( )A .(0,1)B .(1,2)C .(2,3)D .(3,4)解析:选C.令m (x )=log 3x +x -3,则函数m (x )=log 3x +x -3的零点所在的区间即为函数y =log 3x 与y =3-x 的图象的交点的横坐标所在的区间.因为m (x )=log 3x +x -3单调递增且连续,且满足m (2)m (3)<0,所以m (x )=log 3x +x -3的零点在(2,3)内,从而可知方程log 3x +x -3=0的解所在的区间是(2,3),即函数y =log 3x 与y =3-x 的图象交点的横坐标x 0所在的区间是(2,3).故选C.4.(2020·河南焦作统考)已知函数f (x )=⎩⎪⎨⎪⎧2x -x 2,x ≥0,1-ln (x +6),-6<x <0,则函数f (x )在(-6,+∞)上的零点个数为( )A .1B .2C .3D .4解析:选 C.由题知函数f (x )=⎩⎪⎨⎪⎧2x -x 2,x ≥0,1-ln (x +6),-6<x <0在(-6,+∞)上有零点,则⎩⎪⎨⎪⎧x ≥0,2x -x 2=0或⎩⎪⎨⎪⎧-6<x <0,1-ln (x +6)=0,解得x =2或x =4或x =e -6,即函数f (x )在(-6,+∞)上的零点个数为3.故选C.5.(2020·河北张家口模拟)已知函数f (x )=|ln x |,g (x )=f (x )-mx 恰有三个零点,则实数m 的取值范围是( )A.⎝⎛⎭⎫0,1e B .⎝⎛⎭⎫1e ,2e C .(0,1)D .⎝⎛⎭⎫1e ,+∞解析:选A.g (x )有三个零点,即y =f (x )与y =mx 的图象有三个交点,作出y =f (x )和y =mx 的图象如图.当y =mx 与y =f (x )相切时,设切点坐标为(x 0,ln x 0),则⎩⎪⎨⎪⎧mx 0=ln x 0,1x 0=m ,解得m =1e .则当0<m <1e 时,直线y =mx 与曲线y =f (x )有三个交点,即函数g (x )有三个零点.故选A.6.已知函数f (x )=log 2(x +1)+3x +m 的零点在(0,1]上,则实数m 的取值范围为______. 解析:由题意知函数f (x )=log 2(x +1)+3x +m 在定义域上单调递增,又由函数f (x )在(0,1]上存在零点,得⎩⎪⎨⎪⎧f (0)<0,f (1)≥0,即⎩⎪⎨⎪⎧log 2(0+1)+3×0+m <0,log 2(1+1)+3×1+m ≥0,解得-4≤m <0,即实数m 的取值范围为[-4,0).答案:[-4,0)7.已知函数f (x )=⎝⎛⎭⎫12x-cos x ,则f (x )在[0,2π]上的零点个数为________.解析:如图,作出g (x )=⎝⎛⎭⎫12x与h (x )=cos x 的图象,可知其在[0,2π]上的交点个数为3,所以函数f (x )在[0,2π]上的零点个数为3.答案:3 8.函数f (x )=⎝⎛⎭⎫12|x -1|+2cos πx (-4≤x ≤6)的所有零点之和为________.解析:可转化为两个函数y =⎝⎛⎭⎫12|x -1|与y =-2cos πx 在[-4,6]上的交点的横坐标的和,因为两个函数均关于x =1对称,所以两个函数在x =1两侧的交点对称,则每对对称点的横坐标的和为2,分别画出两个函数的图象易知两个函数在x =1两侧分别有5个交点,所以5×2=10.答案:109.关于x 的二次方程x 2+(m -1)x +1=0在区间[0,2]上有解,求实数m 的取值范围. 解:显然x =0不是方程x 2+(m -1)x +1=0的解,0<x ≤2时,方程可变形为1-m =x +1x ,又因为y =x +1x 在(0,1]上单调递减,在[1,2]上单调递增,所以y =x +1x 在(0,2]上的取值范围是[2,+∞),所以1-m ≥2,所以m ≤-1,故m 的取值范围是(-∞,-1].10.设函数f (x )=⎪⎪⎪⎪1-1x (x >0). (1)作出函数f (x )的图象;(2)当0<a <b ,且f (a )=f (b )时,求1a +1b的值;(3)若方程f (x )=m 有两个不相等的正根,求m 的取值范围.解:(1)如图所示. (2)因为f (x )=⎪⎪⎪⎪1-1x =⎩⎨⎧1x-1,x ∈(0,1],1-1x ,x ∈(1,+∞),故f (x )在(0,1]上是减函数,而在(1,+∞)上是增函数,由0<a <b 且f (a )=f (b ),得0<a <1<b ,且1a -1=1-1b ,所以1a +1b=2. (3)由函数f (x )的图象可知,当0<m <1时,方程f (x )=m 有两个不相等的正根.[综合题组练]1.已知[x ]表示不超过实数x 的最大整数,g (x )=[x ]为取整函数,x 0是函数f (x )=ln x -2x的零点,则g (x 0)等于( )A .1B .2C .3D .4解析:选B.f (2)=ln 2-1<0,f (3)=ln 3-23>0,故x 0∈(2,3),所以g (x 0)=[x 0]=2.故选B.2.(2020·湖南娄底二模)若x 1是方程x e x =1的解,x 2是方程x ln x =1的解,则x 1x 2等于( )A .1B .-1C .eD .1e解析:选A.考虑到x 1,x 2是函数y =e x 、函数y =ln x 与函数y =1x的图象的交点A ,B 的横坐标,而A ⎝⎛⎭⎫x 1,1x 1,B ⎝⎛⎭⎫x 2,1x 2两点关于y =x 对称,因此x 1x 2=1.故选A. 3.(2020·湘赣十四校联考)已知函数f (x )=⎩⎪⎨⎪⎧ax 2+2x +a (x ≤0)ax -3(x >0),有且只有1个零点,则实数a 的取值范围是______.解析:当a >0时,函数y =ax -3(x >0)必有一个零点,又因为-1a<0,故a ⎝⎛⎭⎫-1a 2+2⎝⎛⎭⎫-1a +a >0,解得a >1;当a =0时,f (x )=⎩⎪⎨⎪⎧2x (x ≤0),-3(x >0)恰有一个零点;当a <0时,若x >0,则f (x )=ax -3<0,若x ≤0,则f (x )=ax 2+2x +a ,此时,f (x )恒小于0,所以当a <0时,f (x )无零点,故答案为a =0或a >1.答案:a =0或a >14.已知函数f (x )=⎩⎪⎨⎪⎧|x 2+5x +4|,x ≤0,2|x -2|,x >0若函数y =f (x )-a |x |恰有4个零点,则实数a 的取值范围为________.解析:在同一平面直角坐标系内画出函数y =f (x )和y =a |x |的图象可知,若满足条件,则a >0. 当a ≥2时,在y 轴右侧,两函数图象只有一个公共点,此时在y 轴左侧,射线y =-ax (x ≤0)与抛物线y =-x 2-5x -4(-4<x <-1)需相切. 由⎩⎪⎨⎪⎧y =-x 2-5x -4,y =-ax 消去y , 得x 2+(5-a )x +4=0. 由Δ=(5-a )2-16=0,解得a =1或a =9.a =1与a ≥2矛盾,a =9时,切点的横坐标为2,不符合题意.当0<a <2,此时,在y 轴右侧,两函数图象有两个公共点,若满足条件,则-a <-1,即a >1.故1<a <2.答案:(1,2)5.已知函数f (x )=-x 2-2x ,g (x )=⎩⎪⎨⎪⎧x +14x ,x >0,x +1,x ≤0.(1)求g (f (1))的值;(2)若方程g (f (x ))-a =0有4个实数根,求实数a 的取值范围.解:(1)利用解析式直接求解得g (f (1))=g (-3)=-3+1=-2.(2)令f (x )=t ,则原方程化为g (t )=a ,易知方程f (x )=t 在(-∞,1)上有2个不同的解,则原方程有4个解等价于函数y =g (t )(t <1)与y =a 的图象有2个不同的交点,作出函数y =g (t )(t <1)的图象如图,由图象可知,当1≤a <54时,函数y =g (t )(t <1)与y =a 有2个不同的交点,即所求a 的取值范围是⎣⎡⎭⎫1,54. 6.设函数f (x )=x +1x -1,x ∈R 且x ≠1. (1)求f ⎝⎛⎭⎫110+f ⎝⎛⎭⎫18+f ⎝⎛⎭⎫16+f ⎝⎛⎭⎫14+f (4)+f (6)+f (8)+f (10)的值;(2)就m 的取值情况,讨论关于x 的方程f (x )+x =m 在x ∈[2,3]上解的个数.解:(1)根据题意,函数f (x )=x +1x -1,则f ⎝⎛⎭⎫1x =1x +11x-1=1+x 1-x =-1+x x -1, 则f (x )+f ⎝⎛⎭⎫1x =0,则f ⎝⎛⎭⎫110+f ⎝⎛⎭⎫18+f ⎝⎛⎭⎫16+f ⎝⎛⎭⎫14+f (4)+f (6)+f (8)+f (10)=f ⎝⎛⎭⎫110+f (10)+f ⎝⎛⎭⎫18+f (8)+f ⎝⎛⎭⎫16+f (6)+f ⎝⎛⎭⎫14+f (4)=0.(2)根据题意,设g (x )=f (x )+x =x +1x -1+x =(x -1)+2x -1+2, 令t =x -1,又由x ∈[2,3],则t ∈[1,2],则设h (t )=t +2t +2,有h ′(t )=1-2t 2=t 2-2t 2, 分析可得,在区间[1,2)上,h (t )单调递减,在区间[2,2]上,h (t )单调递增; 则h (t )在[1,2]有最小值h (2)=22+2,且h (1)=h (2)=5,则函数h (t )在区间[1,2]上有最大值5,最小值22+2,方程f (x )+x =m 的解的个数即为函数g (x )与直线y =m 的交点个数,分析可得,当m <22+2时,函数g (x )与直线y =m 没有交点,方程f (x )+x =m 无解; 当m =22+2时,函数g (x )与直线y =m 有1个交点,方程f (x )+x =m 有1个解; 当22+2<m ≤5时,函数g (x )与直线y =m 有2个交点,方程f (x )+x =m 有2个解; 当m >5时,函数g (x )与直线y =m 没有交点,方程f (x )+x =m 无解;综上可得,当m <22+2或m >5时,方程f (x )+x =m 无解;当m =22+2时,方程f (x )+x =m 有1个解;当22+2<m ≤5时方程f (x )+x =m 有2个解.快乐分享,知识无界!感谢您的下载!由Ruize收集整理!。
2021年新高考数学总复习讲义:函数零点

2021年新高考数学总复习讲义:函数零点知识讲解一、函数的零点1.零点的定义:对于函数()y f x ,使()0f x 的实数x 叫做函数()yf x 的零点.2.函数零点的等价关系函数()y f x =的零点就是方程()0f x =实数根,亦即函数()y f x =的图象与x 轴交点的横坐标.即方程()0f x =有实数根⇔函数()y f x =的图象与x 轴有交点⇔函数()y f x =有零点.3.零点存在性判定定理定理:如果函数()y f x =在区间[]a b ,上的图象是连续不断的一条曲线,且()()0f a f b ⋅<,则函()y f x =在区间()a b ,内有零点,即存在()c a b ∈,,使得()0f c =,这个c 就是方程()0f x =的根.4.对函数零点存在的判断中,必须强调:1)()f x 在[]a b ,上连续; 2)()()0f a f b <; 3)在()a b ,内存在零点. 这是零点存在的一个充分条件,但不是必要条件. 注意:函数()yf x 的零点就是方程()0f x 的实数根,也就是函数()yf x 的图象与x 轴交点的横坐标,所以函数的零点是一个数,而不是一个点.在写函数零点时,所写的一定是一个数字,而不是一个坐标.5. 二次函数零点的判定判别式2=4b ac △0△ 0△ 0△0)的图像2ax bx c 0a )的根2a2ax bxc0)的零点2ba2ax bxc0)的解集2ax bxc0)的解集1x 或2xx }2a6.一元二次方程20axbx c根的分布(下面对0a 进行讨论)20bk a △20bk a △1212()x x k k ,,1122k x k x )k ,内有且只有一根yyyky y1220b k a△23()0()0f k f k △且(2b k a经典例题一.选择题(共12小题)1.(2018•重庆模拟)函数f(x)=|x﹣2|﹣lnx在定义域内零点的个数为()A.0B.1C.2D.32.(2018•商洛模拟)函数f(x)=ln(x+1)﹣2x的零点所在的大致区间是()A.(3,4)B.(2,e)C.(1,2)D.(0,1)3.(2017秋•镇原县校级期末)函数f(x)=2x+7的零点为()A.7B.7 2C.﹣7D.−7 24.(2017秋•平罗县校级期末)方程2x=2﹣x的根所在区间是()A.(﹣1,0)B.(2,3)C.(1,2)D.(0,1)5.(2018春•番禺区校级月考)方程x3﹣3x﹣m=0在[0,1]上有实数根,则m的最大值是()A.0B.﹣2C.﹣118D.16.(2017•奉贤区二模)若f(x)为奇函数,且x0是y=f(x)﹣e x的一个零点,则﹣x0一定是下列哪个函数的零点()A.y=f(x)e x+1B.y=f(﹣x)e﹣x﹣1C.y=f(x)e x﹣1D.y=f(﹣x)e x+17.(2016秋•仙桃期末)函数f(x)=2x2﹣3x+1的零点个数是()A.0B.1C.2D.38.(2016秋•库尔勒市校级期末)下列函数中,既是奇函数又存在零点的函数是()A.y=sinx B.y=cosxC.y=lnx D.y=x3+19.(2016秋•黄山期末)函数f(x)=log2(x﹣1)的零点是()A.(1,0)B.(2,0)C.1D.210.(2016秋•东莞市校级期末)函数f(x)=x2﹣4x+4的零点是()A.(0,2)B.(2,0)C.2D.411.(2017秋•青冈县校级期中)函数f(x)=2x2﹣3x+1的零点是()A.﹣12,﹣1B.﹣12,1C.12,﹣1D.12,112.(2017春•江津区期中)设f(x)=ax+4,若f(1)=2,则a的值()A.2B.﹣2C.3D.﹣3二.填空题(共5小题)13.(2014秋•新沂市校级月考)已知集合A={x|ax2﹣3x+2=0,x∈R,a∈R}只有一个元素,则a=.14.(2014秋•涟水县校级期中)方程4x2﹣12x+k﹣3=0没有实根,则k的取值范围是.15.(2012秋•浦东新区校级月考)2﹣x+x2=5的实根个数为.16.(2012秋•金山区校级月考)函数y=x3﹣2x的零点是.17.已知x 38=234,则x=.三.解答题(共1小题)18.解方程:x3+x2=1.。
2021年高考数学总复习2.2函数的零点与方程课件理

017-2 017)=2
解析
答案
-18-
一
二
2 + 2 + , ≤ 0,
15.(2018 天津,理 14)已知 a>0,函数 f(x)= 2
若关
- + 2-2, > 0.
于x的方程f(x)=ax恰有2个互异.
解析:由f(x)=ax,可得
1
2
1
- + 4-4, < 2,
1
2
2
2
n
n
n
=1
i
i
于(
)
g(x)的图象也关于点(2,0)对称,即有
f(x)与 g(x)
A.4n
B.2n C.n D.0
的交点关于点(2,0)对称,
n
=1
i=1
=1
=1
则 ∑ (xi+yi)= ∑ xi+ ∑ yi,即有 ∑ yi=0,
可设 t=x1+x2+x3+…+xn,
则 t=xn+xn-1+ - +…+x1,
2
相加可得 2t=(x1+xn)+(x2+xn-1)+…+(xn+x1)=4+4+…+4=4n,
解得
t=2n.故选 B.
B
解析
关闭
答案
-11-
一
二
8.函数f(x)=x2-2x+a(ex-1+e-x+1)有唯一零点,那么a=(
1
1
A.-
B.
2
3
1
2021版新高考数学一轮复习高考大题专项(一)导数的综合应用新人教A版

e
10
........................ 优质文档..........................
........................ 优质文档..........................
(1)若 a=1,证明:当 x≥0 时,f(x)≥1; (2)略.
3.已知函数 f(x)=(x-k)ex. (1)求 f(x)的单调区间; (2)略.
2
........................ 优质文档..........................
........................ 优质文档..........................
高考大题专项(一) 导数的综合应用
突破 1 导数与函数的单调性 1.已知函数 f(x)=1x3-a(x2+x+1).
3
(1)若 a=3,求 f(x)的单调区间; (2)略.
2.已知函数 f(x)=ex-ax2. 1
........................ 优质文档..........................
(1)当 a=-1 时,求 f(x)的最大值; (2)若 f(x)在区间(0,e]上的最大值为-3,求 a 的值.
9
........................ 优质文档..........................
突破 4 导数与函数的零点 1.已知函数 f(x)=1x2-mln x.若 m≥1,令 F(x)=f(x)-x2+(m+1)x,试讨论函数 F(x)的零点个数.
2021届高考数学一轮复习第四章导数及其应用第4节导数与函数的零点含解析

第4节导数与函数的零点考试要求能利用导数解决函数的零点、方程的根、曲线的交点等问题。
知识梳理函数的零点、方程的根、曲线的交点,这三个问题本质上同属一个问题,它们之间可相互转化,这类问题的考查通常有两类:(1)讨论函数零点或方程根的个数;(2)由函数零点或方程的根的情况求参数的取值范围.[常用结论与易错提醒](1)注意构造函数;(2)注意转化思想、数形结合思想的应用。
诊断自测1.若函数f(x)=错误!在其定义域上只有一个零点,则实数a的取值范围是()A.(16,+∞)B。
[16,+∞)C。
(-∞,16) D.(-∞,16]解析①当x≤0时,f(x)=x+3x,∵y=x与y=3x在(-∞,0)上都单调递增,∴f(x)=x+3x在(-∞,0)上也单调递增,又f(-1)〈0,f(0)〉0,∴f(x)在(-1,0)内有一个零点。
②当x>0时,f(x)=错误!x3-4x+错误!,f′(x)=x2-4=(x+2)(x-2).令f′(x)=0得x=2或x=-2(舍),当x∈(0,2)时,f′(x)〈0,f(x)递减,当x∈(2,+∞)时,f′(x)〉0,f(x)递增,∴在x〉0时,f(x)最小=f(x)极小=233-8+错误!,要使f(x)在(0,+∞)上无零点,需错误!-8+错误!>0,∴a>16.答案A2。
已知函数f(x)=x2+e x-12(x〈0)与g(x)=x2+ln(x+a)的图象上存在关于y轴对称的点,则a的取值范围是() A。
错误! B.(-∞,错误!)C.错误!D。
错误!解析设点P(x0,y0)(x0〈0)在函数f(x)上,由题意可知,点P 关于y轴的对称点P′(-x0,y0)在函数g(x)上,所以错误!消y0可得x错误!+e x0-错误!=(-x0)2+ln(-x0+a),即e x0-ln(a-x0)-错误!=0(x0〈0),所以e x0-错误!=ln(a-x0)(x0〈0)。
21版高考数学人教A版浙江专用大一轮复习 3.4.2 导数与函数零点

温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word文档返回原板块。
核心考点·精准研析考点一判断函数零点(方程根)的个数1.已知函数f(x)=3ln x-x2+2x-3ln 3-,则方程f(x)=0的解的个数为________.2.已知函数f(x)=e x-ax-1(a∈R)(e=2.718 28…是自然对数的底数).(1)求f(x)的单调区间.(2)讨论g(x)=f(x)在区间[0,1]上零点的个数.【解题导思】序号联想解题1 由方程f(x)=0的解想到函数f(x)的零点序号题目拆解2(1)f(x)的单调区间求f′(x)并分析其正负确定单调区间(2)g(x)在区间[0,1]上零点的个讨论f(x)在[0,1]上的单调性,判断f(x)的零点个数,最后确定g(x)零点的个数.数【解析】1.因为f(x)=3ln x-x2+2x-3ln 3-(x>0),所以f′(x)=-x+2 ==,当x∈(0,3)时,f′(x)>0,f(x)单调递增;当x∈(3,+∞)时,f′(x)<0,f(x)单调递减,所以f(x)max=f(3)=3ln 3-+6-3ln 3-=0,因为当x→0时,f(x)→-∞;当x→+∞时,f(x)→-∞,所以方程f(x)=0只有一个解.答案:12.(1)因为f(x)=e x-ax-1,所以f′(x)=e x-a,当a≤0时,f′(x)>0恒成立,所以f(x)的单调递增区间为(-∞,+∞),无单调递减区间;当a>0时,令f′(x)<0,得x<ln a,令f′(x)>0,得x>ln a,所以f(x)的单调递减区间为(-∞,ln a),单调递增区间为(ln a,+∞).(2)令g(x)=0,得f(x)=0或x=,先考虑f(x)在区间[0,1]上的零点个数,①当a≤1时,f(x)在[0,1]上单调递增且f(0)=0,所以f(x)在[0,1]上有一个零点;②当a≥e时,f(x)在[0,1]上单调递减且f(0)=0,所以f(x)在[0,1]上有一个零点;③当1<a<e时,f(x)在[0,ln a)上单调递减,在(ln a,1]上单调递增,而f(1)=e-a-1,当e-a-1≥0,即1<a≤e-1时,f(x)在[0,1]上有两个零点, 当e-a-1<0,即e-1<a<e时,f(x)在[0,1]上有一个零点.当x=时,由f=0得a=2(-1).综上知,当a≤1或a>e-1或a=2(-1)时,g(x)在[0,1]上有两个零点;当1<a≤e-1且a≠2(-1)时,g(x)在[0,1]上有三个零点.利用导数研究方程根(函数零点)的技巧(1)研究方程根的情况,可以通过导数研究函数的单调性、最大值、最小值、变化趋势等.(2)根据题目要求,画出函数图象的走势规律,标明函数极(最)值的位置.(3)利用数形结合的思想去分析问题,可以使问题的求解有一个清晰、直观的整体展现.设函数f(x)=ln x+,m∈R.讨论函数g(x)=f′(x)-零点的个数. 【解析】由题设,g(x)=f′(x)-=--(x>0),令g(x)=0,得m=-x3+x(x>0).设φ(x)=-x3+x(x>0),则φ′(x)=-x2+1=-(x-1)(x+1),当x∈(0,1)时,φ′(x)>0,φ(x)在(0,1)上单调递增;当x∈(1,+∞)时,φ′(x)<0,φ(x)在(1,+∞)上单调递减.所以x=1是φ(x)的极大值点,也是φ(x)的最大值点.所以φ(x)的最大值为φ(1)=.由φ(0)=0,结合y=φ(x)的图象(如图),可知①当m>时,函数g(x)无零点;②当m=时,函数g(x)有且只有一个零点;③当0<m<时,函数g(x)有两个零点;④当m≤0时,函数g(x)有且只有一个零点.综上所述,当m>时,函数g(x)无零点;当m=或m≤0时,函数g(x)有且只有一个零点;当0<m<时,函数g(x)有两个零点.考点二已知函数零点个数求参数问题【典例】已知曲线f(x)=e x(ax+1)在x=1处的切线方程为y=bx-e.(1)求a,b.(2)若函数g(x)=f(x)-3e x-m有两个零点,求实数m的取值范围. 世纪金榜导学号【解题导思】序号题目拆解(1)曲线f(x)=e x(ax+1)在x=1处的切线方程为y=bx-e. 求导数,根据导数的几何意义,求出切线的斜率,解方程组,即可求出a和b的值(2)函数g(x)有两个零点求导数,利用导数确定函数的单调性,求出函数的极值,结合函数的零点与方程实数根的关系,数形结合,即可求出实数m的值.【解析】(1)f(x)=e x(ax+1),f′(x)=e x(ax+1)+e x·a=e x(ax+1+a),所以所以a=1,b=3e.(2)方法一:g(x)=f(x)-3e x-m=e x(x-2)-m,函数g(x)=e x(x-2)-m有两个零点,相当于曲线u(x)=e x·(x-2)与直线y=m有两个交点.u′(x)=e x·(x-2)+e x=e x(x-1),当x∈(-∞,1)时,u′(x)<0,所以u(x)在(-∞,1)上单调递减,当x∈(1,+∞)时,u′(x)>0,所以u(x)在(1,+∞)上单调递增,所以x=1时,u(x)取得极小值u(1)=-e,又x→+∞时,u(x)→+∞;x<2时,u(x)<0,所以-e<m<0.方法二:g(x)=f(x)-3e x-m=e x(x-2)-m,g′(x)=e x·(x-2)+e x=e x(x-1),当x∈(-∞,1)时,g′(x)<0,所以g(x)在(-∞,1)上单调递减,当x∈(1,+∞)时,g′(x)>0,所以g(x)在(1,+∞)上单调递增,所以x=1时,g(x)取得极小值g(1)=-e-m,又x→-∞时,g(x)→-m,所以-e<m<0.已知函数零点个数求参数的常用方法(1)分离参数法:首先分离出参数,然后利用求导的方法求出构造的新函数的最值,根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围.(2)分类讨论法:结合单调性,先确定参数分类的标准,在每个小范围内研究零点的个数是否符合题意,将满足题意的参数的各小范围并在一起,即为所求参数范围.已知函数f(x)=ln x+,a∈R.(1)若a=1,求曲线y=f(x)在点(1,f(1))处的切线方程.(2)若函数f(x)有且只有一个零点,求a的取值范围.【解析】(1)f(x)=ln x+的导数为f′(x)=-,得f(x)在x=1处的切线斜率为k=1-1=0,切点为(1,1),可得切线方程为y=1.(2)函数f(x)有且只有一个零点,即f(x)=0有且只有一个正实数根,可得-a=xln x,设g(x)=xln x,导数为g′(x)=1+ln x,可得x>时,g′(x)>0,g(x)单调递增;0<x<时,g′(x)<0,g(x)单调递减;即有x=时,g(x)取得最小值-,作出g(x)=xln x的图象,可得-a=-或-a≥0,解得a=或a≤0,则a的取值范围是∪(-∞,0].考点三可转化为函数零点个数的问题【典例】已知直线l:y=x+1,函数f(x)=ae x.(1)当a=1,x>0时,证明:曲线y=f(x)-x2在直线l的上方.(2)若直线l与曲线y=f(x)有两个不同的交点,求实数a的取值范围.世纪金榜导学号【解题导思】序号题目拆解(1)曲线y=f(x)-x2在直线l的上方证明曲线y=f(x)-x2在直线l的上方,转化为e x-x2-x-1>0恒成立.再利用导数判断函数单调性,从而求出最小值.(2)直线l与曲线y=f(x)有两个不同的交点令S(x)=ae x-x-1,直线l与曲线f(x)有两个不同的交点,既要判断S(x)在极值点两侧的单调性,又要判断极值点两侧的函数值的正负,即运用零点存在性定理,说明在极值点两侧零点各有一个.【解析】 (1)令J(x)=e x-x2-x-1,则J′(x)=e x-x-1,令g(x)=J′(x),则g′(x)=e x-1,当x>0时,g′(x)>0,所以在(0,+∞)上, J′(x)为增函数,所以J′(x)>J′(0)=0,从而J(x)也为增函数,得J(x)>J(0)=0. 故e x-x2>x+1,即曲线y=f(x)-x2在直线l的上方.(2)令S(x)=ae x-x-1,则S′(x)=ae x-1,当a≤0时,S′(x)<0,得S(x)在R上单调递减,不符合题意;当a>0时,令S′(x)=0,得x=ln ,所以S(x)在上为减函数,在上为增函数,由已知函数S(x)有两个零点,所以S(x)min=S=-ln <0,得0<a<1,此时S(-1)=>0,所以S(x)在上有且只有一个零点.由(1)得当x>0时,S(x)>a-x-1=ax2+(a-1)x+a-1,所以S>a+(a-1)+a-1=a+1>0.由(1)知,当x>0时,J′(x)>0得e x>x+1,令x+1=t,则ln t<t-1(t>1),所以>-1>ln ,所以S(x)在上有且只有一个零点,综上,0<a<1.处理函数y=f(x)与y=g(x)图象的交点问题的常用方法(1)数形结合,即分别作出两函数的图象,观察交点情况;(2)将函数交点问题转化为方程f(x)=g(x)根的个数问题,通过构造函数y=f(x)-g(x),利用导数研究函数的单调性及极值,并作出草图,根据草图确定根的情况.已知函数f(x)=x3-3x2+ax+2,曲线y=f(x)在点(0,2)处的切线与x轴交点的横坐标为-2.(1)求a.(2)证明:当k<1时,曲线y=f(x)与直线y=kx-2只有一个交点.【解析】 (1)f′(x)=3x2-6x+a,f′(0)=a.曲线y=f(x)在点(0,2)处的切线方程为y=ax+2,由题意得-=-2,所以a=1.(2)由(1)知,f(x)=x3-3x2+x+2.设g(x)=f(x)-kx+2=x3-3x2+(1-k)x+4.由题意知1-k>0,当x≤0时,g′(x)=3x2-6x+1-k>0,g(x)单调递增,g(-1)=k-1<0,g(0)=4,所以g(x)=0在(-∞,0]有唯一实根.当x>0时,令h(x)=x3-3x2+4,则g(x)=h(x)+(1-k)x>h(x),h′(x)=3x2-6x=3x(x-2),h(x)在(0,2)上单调递减,在(2,+∞)上单调递增,所以g(x)>h(x)≥h(2)=0.所以g(x)=0在(0,+∞)没有实根.综上,g(x)=0在R上有唯一实根,即当k<1时,曲线y=f(x)与直线y=kx-2只有一个交点.关闭Word文档返回原板块快乐分享,知识无界!感谢您的下载!由Ruize收集整理!。
2021年高考数学总复习2.4.3导数与函数的零点及参数范围课件理

-14-
考向一
考向二
考向三
1
综上所述,当 0≤a≤1 或 a=- 时,f(x)有一个零点;
1
1
2
当 a<-2时,f(x)无零点;当-2<a<0 时,f(x)有两个零点.
-15-
考向一
考向二
考向三
零点个数求参数范围
解题策略一 最小值法
例 3 已知函数 f(x)=x2-2 ln x 在点
解:(1)f(x)=x2-2 ln x 的定义域为(0,+∞),f'(x)=2x-2 .
因为 f'
1
2
f'(x)=2x-
1
=1-a=0,所以 a=1,f(x)=x2-2ln x,
1
2
=
(2-1)(2+1)
1
令 f'(x)>0,得 x>2,
2
.
1
令 f'(x)<0,得 0<x<2.
故函数 f(x)的单调递增区间是
的单调性、最大值、最小值、变化趋势等,并借助函数的大致图象
判断函数零点或方程根的情况.
-5-
考向一
考向二
考向三
对点训练1函数f(x)=(x2-3x+3)ex.
(1)试确定t的取值范围,使得函数f(x)在[-2,t](t>-2)上为单调函数;
'( 0 )
(2)当 x∈[-2,t],且 1<t<4 时,求满足
1
2 -1
(+1)(-1)
f'(x)=- +x=
由
21版高考数学人教A版浙江专用大一轮复习 十六 导数与函数零点

温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word文档返回原板块。
核心素养测评十六导数与函数零点1.设函数f(x)=x3+ax2+bx+c.(1)求曲线y=f(x)在点(0,f(0))处的切线方程.(2)设a=b=4,若函数f(x)有三个不同的零点,求c的取值范围.【解析】 (1)由f(x)=x3+ax2+bx+c,得f′(x)=3x2+2ax+b.因为f(0)=c,f′(0)=b,所以曲线y=f(x)在点(0,f(0))处的切线方程为y=bx+c.(2)当a=b=4时,f(x)=x3+4x2+4x+c,所以f′(x)=3x2+8x+4.令f′(x)=0,得3x2+8x+4=0,解得x=-2或x=-.当x变化时,f(x)与f′(x)在区间(-∞,+∞)上的变化情况如下: (--2 -x∞,-2)f′(x) + 0 - 0 +f(x) ↗ c ↘c-↗所以,当c>0且c-<0时,存在x1∈(-∞,-2),x2∈,x3∈,使得f(x1)=f(x2)=f(x3)=0.由f(x)的单调性知,当且仅当c∈时,函数f(x)有三个不同零点.【变式备选】设函数f(x)=xe x+a(1-e x)+1,a∈R.(1)求函数f(x)的单调区间.(2)若方程 f(x)=0在(0,+∞)上有解,证明:a>2.【解析】(1)因为f′(x)=[x-(a-1)]e x.所以x>a-1时,f′(x)>0,函数f(x)在(a-1,+∞)上单调递增,当 x<a-1时,f′(x)<0,函数f(x)在(-∞,a-1)上单调递减.(2)函数f(x)在(0,+∞)有零点,可得方程f(x)=0有解.a===x+,有解.令g(x)=x+,g′(x)=1+=,设函数h(x)=e x-x-2,h′(x)=e x-1>0,所以函数h(x)在(0,+∞)上单调递增,又h(1)=e-3<0,h(2)=e2-4>0,所以存在x0∈(1,2),使h(x)=0,故当x∈(0,x0)时,g′(x)<0;当x∈(x0,+∞)时,g′(x)>0,所以函数g(x)存在唯一最小值x0,满足=x0+2,所以g(x0)=x0+=x0+1∈(2,3),因为a=g(x)=x+有解,所以a≥g(x0)>2,所以a>2.2.(2020·揭阳模拟)已知函数f(x)=x-aln x-1.(1)若函数f(x)的极小值为0,求a的值.(2)∀t>0且a≤1,求证:f(e t)>t2.【解析】(1)因为f(x)=x-aln x-1,x∈(0,+∞),所以f′(x)=,当a≤0时,f′(x)>0,函数f(x)在定义域上递增,不满足条件; 当a>0时,函数f(x)在(0,a)上递减,在(a,+∞)上递增,故f(x)在x=a处取得极小值0,所以f(a)=a-aln a-1=0,令p(a)=a-aln a-1, p′(a)=-ln a,所以p(a)在(0,1)上单调递增,在(1,+∞)上单调递减,故p(a)≤p(1)=0,所以f(a)=0的解为a=1,故a=1.(2)方法一:由f(e t)>t2⇔e t-at-1>t2⇔e t-1>t2+at,因为a≤1,所以只需证当t>0时,e t-1>t2+t恒成立.令g(t)=e t-t2-t-1,g′(t)=e t-t-1,由(1)可知x-ln x-1≥0,令x=e t得e t-t-1≥0,所以g(t)在(0,+∞)上递增,故g(t)>g(0)=0,所以命题得证.方法二:f(e t)>t2⇔e t-at-1>t2⇔e t-t2-at-1>0,设g(t)=e t-t2-at-1(t>0),则g′(t)=e t-at-a,则g″(t)=e t-a,又e t>e0=1,a≤1,得g″(t)>0,所以g′(t) 单调递增,得g′(t)>g′(0)=1-a≥0,所以g(t)单调递增,得g(t)>g(0)=0,得证.关闭Word文档返回原板块快乐分享,知识无界!感谢您的下载!由Ruize收集整理!。
高考数学一轮复习导数与函数的零点课件

【训练2】 (2020·北京通州区一模)已知函数f(x)=xex,g(x)=a(ex-1).a∈R. (1)当a=1时,求证:f(x)≥g(x); (2)当a>1时,求关于x的方程f(x)=g(x)的实根个数. 解 设函数F(x)=f(x)-g(x)=xex-aex+a. (1)证明 当a=1时,F(x)=xex-ex+1,所以F′(x)=xex. 所以x∈(-∞,0)时,F′(x)<0;x∈(0,+∞)时,F′(x)>0. 所以F(x)在(-∞,0)上单调递减,在(0,+∞)上单调递增. 所以当x=0时,F(x)取得最小值F(0)=0. 所以F(x)≥0,即f(x)≥g(x).
(ⅰ)若 h(2)>0,即 a<e42,h(x)在(0,+∞)没有零点; (ⅱ)若 h(2)=0,即 a=e42,h(x)在(0,+∞)只有一个零点; (ⅲ)若 h(2)<0,即 a>e42,由于 h(0)=1,所以 h(x)在(0,2)有一个零点.
由(1)知,当 x>0 时,ex>x2,所以 h(4a)=1-1e64aa3=1-(1e62aa)3 2>1-(126aa)3 4=1-1a>0.
+∞),故 m>1;当 x≤1 时,f(x)=2x2-mx+m2 +58,要使得 g(x)=f(x)-m 有两个零
Δ=m2-858-m2 >0,
点,需满足m4 <1,
解得 m<-5 或 1<m≤74,综上可得1,74.
g(1)=2-m-m2 +58≥0,
答案 1,74
5.已知函数 f(x)=x+ln x-2e,g(x)=mx ,其中 e 为自然对数的底数,若函数 f(x)与 g(x) 的图象恰有一个公共点,则实数 m 的取值范围是________. 解析 因为 f′(x)=1+1x>0,所以函数在(0,+∞)上为增函数且 f1e=-1-1e<0,所以 当 m≥0 时,与 g(x)=mx 有一个公共点,当 m<0 时,令 f(x)=g(x),∴x2+xln x-2ex= m 有一解即可,设 h(x)=x2+xln x-2ex,令 h′(x)=2x+ln x+1-2e=0 得 x=1e,即当 x =1e时,h(x)有极小值-e+e21,故当 m=-e+e21时有一公共点,故填 m≥0 或 m=-e+e21. 答案 m≥0 或 m=-e+e21
第17讲第3课时导数与函数零点课件高三数学一轮复习

3.已知函数 f(x)=ex-a(a∈R),则函数 f(x)的零点个数最多为
x
A.0
B.1
C.2
() D.3
【解析】由 f(x)=ex-ax=0,得 xex=a(x≠0),设 h(x)=xex,则 h′(x)=(x+1)ex,当 x< -1 时,h′(x)<0,当-1<x<0 或 x>0 时,h′(x)>0,所以 h(x)=xex 在(-1,0),(0, +∞)上单调递增,在(-∞,-1)上单调递减,所以 h(x)min=h(-1)=-1e.
【答案】BC
6.已知函数f(x)=x3-x+1,则 ( )
A.f(x)有两个极值点
B.f(x)有三个零点
C.点(0,1)是曲线y=f(x)的对称中心D.直线y=2x是曲线y=f(x)的切线
【解析】由题知
配套精练
一、 单项选择题
A组 夯基精练
1.函数f(x)=ex与g(x)=x+1的图象的交点个数为
A.0
B.1
(B )
C.2
D.不确定
【解析】令h(x)=f(x)-g(x)=ex-x-1,则h′(x)=ex-1,令h′(x)=ex-1=0,得x=0.当
x<0时,h′(x)<0,当x>0时,h′(x)>0.所以当x=0时,h(x)取得最小值h(0)=0,即
线方程为 y=ex-e.
1
若函数
f(x)=
x-32
ex,g(x)=e. x
(2) 讨论函数 G(x)=f(x)-tg(x)(t∈R)的零点个数.
【解答】G(x)=x-32ex-ext,令 G(x)=0,得x-32ex=ext,即 t=x2-32xex-1(x≠0). 令 h(x)=x2-32xex-1,则 h′(x)=x+32(x-1)·ex-1,令 h′(x)=0,得 x=-32或 x=1.当 x∈
导数专题——导数与函数的零点(第二节)-人教版高中数学选修2-2课件

即a 0时,f (x)在(0, )上有1个零点,
0
a
2 时,f e
( x)在(0,e12
]上减,在(
1 e2
,
)上增,且x
0,
f
(x)
a, a
0,
x
时,
f
(x)
,
f
1 ( e2
)=a
2 e
0,
f
( x)在(0,e12
]上有且只有1个零点,在(
1 e2
,
)上有且(
1 e2
)
a
2 e
当a
2 时,由f(x) e
f
(
1 e2
)
a-
2 e
0得f(x)零点个数为0;
当a 2 时,显然f(x)在(0,+)上有1个零点; e
例1.已知函数f(x)=a+ x ln x(a R)
(2)求f(x)的零点个数,并说明你的理由.
当a
2 e
时,f
(
x)min
f
(
1 e2
x0
1, 0
1 x0
1,又由2ax02
x 0 1=0,得2a=
x 0 1 x02
1 x0
1 x02
(0, 2),0
a
1
下面验证0 a 1 时,函数f(x)有两个零点.
g(
1) a
2a a2
1 a
1
1 a a
0, g(1)
2(a
1)
0,1
x0
1 a
,
又由f
(1) e
a e2
1 e
)
a
2 e
0,又
2021届高三新高考数学人教A版一轮复习教学案:第三章第2节 第四课时 导数与函数的零点 Word

姓名,年级:时间:第四课时导数与函数的零点考点一判断零点的个数【例1】(2020·潍坊检测)已知函数f(x)=ln x-x2+ax,a∈R。
(1)证明ln x≤x-1;(2)若a≥1,讨论函数f(x)的零点个数。
(1)证明令g(x)=ln x-x+1(x>0),则g(1)=0,g′(x)=错误!-1=错误!,可得x∈(0,1)时,g′(x)>0,函数g(x)单调递增;x∈(1,+∞)时,g′(x)〈0,函数g(x)单调递减。
∴当x=1时,函数g(x)取得极大值也是最大值,∴g(x)≤g(1)=0,即ln x≤x-1。
(2)解即f′(x)=错误!-2x+a=错误!,x〉0.令-2x错误!+ax0+1=0,解得x0=错误!(负值舍去),在(0,x0)上,f′(x)>0,函数f(x)单调递增;在(x0,+∞)上,f′(x)<0,函数f(x)单调递减。
∴f(x)max=f(x0)。
当a=1时,x0=1,f(x)max=f(1)=0,此时函数f(x)只有一个零点x=1.当a>1时,f(1)=a-1>0,f错误!=ln 错误!-错误!+错误!<错误!-1-错误!+错误!=-错误!错误!-错误!<0,f(2a)=ln 2a-2a2〈2a-1-2a2=-2错误!错误!-错误!<0.∴函数f(x)在区间错误!和区间(1,2a)上各有一个零点.综上可得:当a=1时,函数f(x)只有一个零点x=1;当a>1时,函数f(x)有两个零点.规律方法1。
利用导数求函数的零点常用方法:(1)构造函数g(x)(其中g′(x)易求,且g′(x)=0可解),利用导数研究g(x)的性质,结合g(x)的图象,判断函数零点的个数. (2)利用零点存在定理,先判断函数在某区间有零点,再结合图象与性质确定函数有多少个零点.2。
根据参数确定函数零点的个数,解题的基本思想是“数形结合",即通过研究函数的性质(单调性、极值、函数值的极限位置等),作出函数的大致图象,然后通过函数图象得出其与x轴交点的个数,或者两个相关函数图象交点的个数,基本步骤是“先数后形”.【训练1】(2018·全国Ⅱ卷)已知函数f(x)=错误!x3-a(x2+x+1).(1)若a=3,求f(x)的单调区间;(2)证明:f(x)只有一个零点。
2021新高考数学二轮总复习专题二函数与导数2.2热点小专题一函数的零点及函数的应用学案含解析

2.2热点小专题一、函数的零点及函数的应用必备知识精要梳理1.零点存在性定理:如果函数y=f(x)在区间[a,b]上的图象是一条连续曲线,且有f(a)f(b)<0,那么函数y=f(x)在区间[a,b]内有零点,即存在c∈(a,b),使得f(c)=0,此时这个c就是方程f(x)=0的根.2.函数F(x)=f(x)-g(x)的零点就是方程f(x)=g(x)的根,即函数y=f(x)与y=g(x)的图象交点的横坐标.3.判断函数零点个数的方法:(1)利用零点存在性定理判断法;(2)代数法:求方程f(x)=0的实数根;(3)几何法:对于不易求根的方程,将它与函数y=f(x)的图象联系起来,利用函数的性质找出零点或利用两个函数图象的交点求解.在利用函数性质时,可用求导的方法判断函数的单调性.关键能力学案突破热点一判断函数零点所在的区间【例1】(1)如图是二次函数f(x)=x2-bx+a的部分图象,则函数g(x)=e x+f'(x)的零点所在的大致区间是()A.(-1,0)B.(0,1)C.(1,2)D.(2,3)(2)(2020湖北恩施高中月考,理11)已知单调函数f(x)的定义域为(0,+∞),对于定义域内任意x,f([f(x)-log2x])=3,则函数g(x)=f(x)+x-7的零点所在的区间为()A.(1,2)B.(2,3)C.(3,4)D.(4,5)解题心得判断函数y=f(x)在某个区间上是否存在零点,主要利用函数零点的存在性定理进行判断.首先看函数y=f(x)在区间[a,b]上的图象是否连续,然后看是否有f(a)·f(b)<0.若有,则函数y=f(x)在区间(a,b)内必有零点.【对点训练1】设定义域为(0,+∞)的单调函数f(x)对任意的x∈(0,+∞),都有f[f(x)-ln x]=e+1,若x0是方程f(x)-f'(x)=e的一个解,则x0可能存在的区间是() A.(0,1) B.(e-1,1) C.(0,e-1) D.(1,e)热点二判断函数零点的个数【例2】函数f(x)=2x|log0.5x|-1的零点个数为()A.1B.2C.3D.4 解题心得判断函数y=f(x)的零点个数时,常用以下方法:(1)解方程:当对应方程易解时,可通过解方程,判断函数零点的个数; (2)根据函数的性质结合已知条件进行判断;(3)通过数形结合进行判断,画函数图象,观察图象与x 轴交点的个数来判断. 【对点训练2】(2020山东滨州二模改编,16)设f (x )是定义在R 上且周期为6的周期函数,若函数y=f (x-1)的图象关于点(1,0)对称,函数y=f (x )在区间[-n ,n ](其中n ∈N *)上的零点的个数的最小值为a n ,则a 11= .热点三 已知函数零点个数求参数范围【例3】(2020山东潍坊二模,16)已知函数f (x )={lnx ,x ≥1,2x 3-3x 2+1,x <1,当x ∈[-1,e]时,f (x )的最小值为 ,设g (x )=[f (x )]2-f (x )+a ,若函数g (x )有6个零点,则实数a 的取值范围是 .解题心得已知函数有零点(方程有根),求参数的取值范围常用的方法:(1)直接法:直接根据题设条件构建关于参数的不等式,再通过解不等式确定参数范围. (2)分离参数法:先将参数分离,再转化成求函数值域问题加以解决.(3)数形结合法:先对解析式变形,在同一平面直角坐标系中画出函数的图象,再数形结合求解. 【对点训练3】(2020山东淄博4月模拟,7)已知函数f (x )={e x ,x ≤0,lnx ,x >0,g (x )=f (x )+x+a.若g (x )存在2个零点,则a 的取值范围是( ) A.[-1,0) B.[-1,+∞) C.[0,+∞) D.[1,+∞)热点四 函数的应用【例4】(2020山东,6)基本再生数R 0与世代间隔T 是新冠肺炎的流行病学基本参数.基本再生数指一个感染者传染的平均人数,世代间隔指相邻两代间传染所需的平均时间.在新冠肺炎疫情初始阶段,可以用指数模型:I (t )=e rt 描述累计感染病例数I (t )随时间t (单位:天)的变化规律,指数增长率r 与R 0,T 近似满足R 0=1+rT.有学者基于已有数据估计出R 0=3.28,T=6.据此,在新冠肺炎疫情初始阶段,累计感染病例数增加1倍需要的时间约为(ln 2≈0.69)( ) A.1.2天 B.1.8天 C.2.5天 D.3.5天 解题心得解决函数应用问题的步骤(1)审题:弄清题意,分清条件和结论,理顺数量关系,初步选择数学模型;(2)建模:将自然语言转化为数学语言,将文字语言转化为符号语言,利用数学知识,建立相应的数学模型;(3)解模:求解数学模型,得出数学结论;(4)还原:将数学结论还原为实际问题的意义.【对点训练4】(2020全国Ⅲ,理4)Logistic 模型是常用数学模型之一,可应用于流行病学领域.有学者根据公布数据建立了某地区新冠肺炎累计确诊病例数I (t )(t 的单位:天)的Logistic 模型:I (t )=K 1+e -0.23(t -53),其中K 为最大确诊病例数.当I (t *)=0.95K 时,标志着已初步遏制疫情,则t *约为(ln 19≈3)( ) A.60B.63C.66D.69核心素养微专题(一)例析“逻辑推理”在函数零点问题上的应用【例1】已知函数f (x )={|x +3|,x ≤0,x 3-12x +3,x >0,设g (x )=kx+1,且函数φ(x )=f (x )-g (x )的图象经过四个象限,则实数k 的取值范围为 . 核心素养分析解题的“逻辑推理”过程如下:函数φ(x )=f (x )-g (x )的图象经过四个象限等价于φ(x )在x>0和x<0时函数值有正有负,若φ(x )连续,则在y 轴两侧有变号的零点,即f (x )与g (x )的图象在y 轴两侧存在交点,且在交点处一个函数的图象穿过了另一个函数的图象.抓住临界情形:当k>0时,过定点(0,1)的直线g (x )要在y 轴左侧有交点,则k<13当k=13,且x<0时,f (x )≥g (x )恒成立,φ(x )不过第三象限,即此时k ∈(0,13);当k<0时,过定点(0,1)的直线要在y 轴右侧有交点,则k>-9(当k=-9时,直线g (x )与曲线f (x )相切,同样k=-9不符合题意),即k ∈(-9,0);k=0也符合题意.综上可知,k ∈(-9,13).【例2】已知函数f (x )={x 3-3x +2a ,x ≥a ,x 3+3x -4a ,x <a ,若存在x 0<0,使得f (x 0)=0,则实数a 的取值范围是 .核心素养分析解题的“逻辑推理”过程如下:函数f (x )={x 3-3x +2a ,x ≥a ,x 3+3x -4a ,x <a 的零点⇔f (x )=x 3-3|x-a|-a 的零点(分段函数⇒一般函数)⇔方程x 3=3|x-a|+a 的根⇔函数y=x 3与y=3|x-a|+a 的图象的交点的横坐标(零点⇒交点).所以由题意知,能让函数y=x 3与y=3|x-a|+a 的图象的交点的横坐标是负数的,a 的取值满足题意. 画图:y=3|x-a|+a 是顶点(a ,a )在第一、三象限角平分线上“移动”,且开口向上的“V 字形”,当a ≥0时,因为3|x-a|+a>0,所以不符合题意,当a<0时,若x ≥a ,则有x 3=3x-2a ,若x<a ,则有x 3=-3x+4a ,由图可知只需讨论射线y=3x-2a ,x ≥a 与y=x 3相切的临界情形即可.设切点为(m ,n )(m<0),由y=x 3,得y'=3x 2,所以有3m 2=3,得m=-1,所以n=(-1)3=-1,将切点坐标(-1,-1)代入直线方程y=3x-2a ,得a=-1.从而a 的取值范围是[-1,0).【跟踪训练】(2019浙江,9)设a ,b ∈R ,函数f (x )={x ,x <0,13x 3-12(a +1)x 2+ax ,x ≥0.若函数y=f (x )-ax-b 恰有3个零点,则( )A.a<-1,b<0B.a<-1,b>0C.a>-1,b<0D.a>-1,b>02.2 热点小专题一、函数的零点及函数的应用 关键能力·学案突破【例1】(1)B (2)C 解析(1)由图象知12<b2<1,得1<b<2,f'(x )=2x-b ,所以g (x )=e x +f'(x )=e x +2x-b ,则g (-1)=1e -2-b<0,g (0)=1-b<0,g (1)=e +2-b>0,所以g (0)g (1)<0.故选B .(2)因f (x )在(0,+∞)上单调,且f ([f (x )-log 2x ])=3,设t=f (x )-log 2x ,则f (x )=log 2x+t , 又由f (t )=3,∴f (t )=log 2t+t=3,观察易知t=2,所以f (x )=log 2x+2,所以g (x )=log 2x+x-5,因为g (3)<0,g (4)>0,所以零点所在的区间为(3,4). 对点训练1D 解析令f (x )-ln x=k ,则f (x )=ln x+k.由f [f (x )-ln x ]=e +1,得f (k )=e +1.又f (k )=ln k+k=e +1,可知k=e .故f (x )=ln x+e,所以f'(x )=1x ,x>0.所以f (x )-f'(x )=ln x-1x +e .令g (x )=ln x-1x +e -e =ln x-1x ,x ∈(0,+∞).因为g (x )=ln x-1x 在(0,+∞)内的图象是连续的,且g (1)=-1<0,g (e)=1-1e >0,所以存在x 0∈(1,e),使g (x 0)=0.故选D .【例2】B 解析函数f (x )=2x |log 0.5x|-1的零点也就是方程2x |log 0.5x|-1=0的根,即2x |log 0.5x|=1,整理得|log 0.5x|=(12)x.令g (x )=|log 0.5x|,h (x )=(12)x,画出g (x ),h (x )的图象如图所示.因为两个函数的图象有两个交点,所以f (x )有两个零点.故选B .对点训练27 解析由y=f (x-1)的图象关于点(1,0)对称,得y=f (x )为奇函数,易知f (0)=0.可令x=-3,则f (-3+6)=f (-3), 即f (3)=f (-3)=-f (3), 可得f (-3)=f (3)=0,当n=1,2时,f (x )在[-n ,n ]上,有f (0)=0;当n=3,4,5时,f (x )在[-n ,n ]上,有f (0)=0,f (3)=f (-3)=0;当n=6,7,8时,f (x )在[-n ,n ]上,有f (0)=0,f (3)=f (-3)=0,f (6)=f (-6)=0;当n=9,10,11时,f (x )在[-n ,n ]上,有f (0)=0,f (3)=f (-3)=0,f (6)=f (-6)=0,f (9)=f (-9)=0,即a 11=7. 【例3】-4 (0,14) 解析当x ∈[1,e]时,f (x )=ln x ,f (x )为增函数,所以,f (x )min =f (1)=ln1=0,当x ∈[-1,1)时,f (x )=2x 3-3x 2+1, 令f'(x )=6x 2-6x=0,解得x 1=1(舍)或x 2=0,且有f (x )在(-1,0)上单调递增,在(0,1)上单调递减, 因为f (-1)=-2-3+1=-4<f (1),故函数f (x )在[-1,e]上的最小值为-4;令t=f (x ),由g (x )=0,得t 2-t=-a ,作出函数y=f (x )的图象,如图所示:直线y=t 与函数y=f (x )的图象最多只有三个交点,所以0<t<1, 即说明方程t 2-t=-a 有两个(0,1)内的不等实根,亦即函数y=t 2-t 在(0,1)内的图象与直线y=-a 有两个交点, 因为y=t 2-t=(t -12)2−14,根据y=t 2-t 的图象可知,-14<-a<0,即实数a 的取值范围为0<a<14.对点训练3B 解析要使得方程g (x )=f (x )+x+a 有两个零点,等价于方程f (x )=-x-a 有两个实根,即函数y=f (x )的图象与直线y=-x-a 的图象有两个交点,从函数图象可知,必须使得直线y=-x-a 位于直线y=-x+1的下方,所以-a ≤1,即a ≥-1.故选B .【例4】B 解析由R 0=3.28,T=6,R 0=1+rT 得3.28=1+6r ,∴r=2.286=0.38,∴e 0.38t =2,即0.38t=ln2,0.38t ≈0.69,∴t ≈0.690.38≈1.8(天),故选B .对点训练4C 解析由K1+e -0.23(t *-53)=0.95K ,得e -0.23(t*-53)=119,两边取以e 为底的对数,得-0.23(t *-53)=-ln19≈-3,所以t *≈66.核心素养微专题(一)【例1】(-9,13) 【例2】[-1,0)跟踪训练C 解析当x<0时,由x=ax+b ,得x=b 1-a,最多一个零点取决于x=b1-a与0的大小,所以关键研究当x ≥0时,方程13x 3-12(a+1)x 2+ax=ax+b 的解的个数,令b=13x 3-12(a+1)x 2=13x 2x-32(a+1)=g (x ).画出三次函数g (x )的图象如图所示,可以发现分类讨论的依据是32(a+1)与0的大小关系.①若32(a+1)<0,即a<-1时,x=0处为偶重零点反弹,x=32(a+1)为奇重零点穿过,显然在x ≥0时g (x )单调递增,故与y=b 最多只能有一个交点,不符合题意.②若32(a+1)=0,即a=-1,0处为3次零点穿过,也不符合题意.③若32(a+1)>0,即a>-1时,x=0处为偶重零点反弹,x=32(a+1)为奇重零点穿过,当b<0时g (x )与y=b 可以有两个交点,且此时要求x=b1-a <0,故-1<a<1,b<0,选C .。
2024届高考一轮复习数学课件(新教材人教A版 ):利用导数研究函数的零点

∵f 1e=a-e<0,f(e)=a+1e>0, 且f(x)在(0,e)上单调递增, ∴f(x)在(0,e)上有且只有一个零点, 综上,f(x)有且只有一个零点.
1234
2.函数f(x)=ax+xln x在x=1处取得极值. (1)求f(x)的单调区间;
f(x)的定义域为(0,+∞),f′(x)=a+ln x+1, 由f′(1)=a+1=0,解得a=-1. 则f(x)=-x+xln x, ∴f′(x)=ln x,令f′(x)>0,解得x>1;令f′(x)<0,解得0<x<1. ∴f(x)的单调递增区间为(1,+∞),单调递减区间为(0,1).
因为函数f(x)的定义域为R, f(-x)=-xsin(-x)-1=f(x),所以函数f(x)为偶函数, 又 f′(x)=sin x+xcos x,且当 x∈0,π2时,f′(x)≥0, 所以函数 f(x)在0,π2上单调递增, 又函数 f(x)为偶函数,所以 f(x)在-π2,0上单调递减,
综上,函数 f(x)在0,π2上单调递增,在-π2,0上单调递减.
1234
f(x)=(x-1)ex-13ax3+13a=(x-1)ex-31ax2+x+1, 令f(x)=0, 则 x=1 或 ex-13a(x2+x+1)=0, 对于 ex-13a(x2+x+1)=0, 即x2+exx+1=13a, 构建 h(x)=x2+exx+1,
当x>e时,g′(x)<0,函数g(x)单调递减,
故 g(x)max=g(e)=1e, 且当 x>e 时,g(x)∈0,1e, 又 g(1)=0,所以 0<lnaa<1e,所以 a>1 且 a≠e, 即a的取值范围为(1,e)∪(e,+∞).
人教A版高考总复习数学精品课件 第四章 解答题专项 第3课时 利用导数研究函数的零点

当 ln(-2a)>0,即
1
a<-2时,在区间(-∞,0)和(ln(-2a),+∞)上,f'(x)>0,f(x)单调递增,在
1
区间(0,ln(-2a))上,f'(x)<0,f(x)单调递减.综上所述,当-2<a<0
时,函数 f(x)的单调
递增区间为(-∞,ln(-2a))和(0,+∞),单调递减区间为(ln(-2a),0);当
方法点拨利用单调性和函数零点存在定理确定零点个数
(1)讨论函数的单调性,确定函数的单调区间;
(2)在每个单调区间上,利用函数零点存在定理判断零点的个数;
(3)注意区间端点的选取技巧;
(4)含参数时注意分类讨论.
对点训练1(2021北京延庆高三模拟)已知函数f(x)=-ln x+2x-2.
(1)求曲线y=f(x)的斜率等于1的切线方程;
高 考
解答题
专项一
第3课时 利用导数研究函数的零点
考点一
确定函数零点的个数
考向1.利用单调性和函数零点存在定理确定零点个数
例1.(2021山东济南高三月考)若函数f(x)是R上的偶函数,g(x)是R上的奇函
数,且满足f(x)-g(x)=cos 2x+e-x-ex.
(1)求函数f(x),g(x)的解析式;
(2)求函数f(x)的极值;
(3)设g(x)=x2f(x)-2f(x),判断函数g(x)的零点个数,并说明理由.
解 (1)设切点为(x0,y0),因为
1
1
f'(x)=- +2,所以- +2=1,解得
高考文科数学专题复习《函数的零点PPT 课件

-10
1
(1,0)
一个零点 x=1
-12
-2
x2-2x+3=0 无实数根 y=x2-2x+3
4 -14
-24
-16
没有 交点
没有 零点
-15
-10
-5
-18 1
-6
结 论:函数的零点就是方程f(x)-2=-200的实数根,也就是函数y=f(x)的 --48 图象与x轴的交点的横坐标 -6
-10
结论:函数的零点就是方程f(x)=0的
(2)函数y=f(x)在区间(a,b)内有零点
函数y=f(x)在区间(a,b)内有零点
f(a)·f(b)<0 f(a)·f(b)<0。
f(a)·f(b)>0
(3)函数y=f(x)在单调区间(a,b)内有零点 f(a)·f(b)<0
a
a
b
b
a
b
析:
aRa0f (x)2x3判断零点是否[在 1,1]
2
a
x 1 b
a
-2
a b
b
注意:
函数y=f(x)在区间[a,b]上的图象是连续不 断的一条曲线:
(1) f(a)·f(b)<0 函数y=f(x)在区间
(a,b)内有零点;
(2)函数y=f(x)在区间(a,b)内有零点
f(a)·f(b)<0。
2
a
a
-10
b
-5
a
x 1 b
b
-2
(1)f(a)·f(b)<0 函数y=f(x)在区间(a,b)内有零点;
“f(x)在区间D上有不动点”当且仅当“F(x)=f(x)-x在区间D上有零点”
2021高考数学课件4.2.4导数与函数的零点

(2)令 g(x)=0,得 f(x)=0 或 x=12. 先考虑 f(x)在区间[0,1]上的零点个数, 当 a≤1 时,f(x)在(0,+∞)上单调递增且 f(0)=0, 所以 f(x)在[0,1]上有一个零点; 当 a≥e 时,f(x)在(-∞,1)上单调递减,且 f(0)=0, 所以 f(x)在[0,1]上有一个零点; 当 1<a<e 时,f(x)在(0,ln a)上单调递减,在(ln a,1)上单调递增. 而 f(1)=e-a-1,当 e-a-1≥0,即 1<a≤e-1 时,f(x)在[0,1] 上有两个零点,
由①②可得 ex0
-2x0=
e x0
x02 x0
1
即 x0 ex0 -2x02= ex0 -x20-1,(x0-1)( ex0 -x0-1)=0,
设 g(x)=ex-x-1,则 g′(x)=ex-1,
所以当 x>0 时,g′(x)>0,当 x<0 时,g′(x)<0,
所以 g(x)=ex-x-1 在(0,+∞)上单调递增,在(-∞,0)上单调 递减,
即当 a>e42时,函数 f(x)在(0,+∞)上有两个不同的零点. 所以,若函数 f(x)在(0,+∞)上有两个不同的零点,则实数 a 的 取值范围是e42,+∞.
有两个不同的零点.
综上,若函数 f(x)在(0,+∞)上有两个不同的零点,则实数 a 的 取值范围是e42,+∞.
解法二 由 f(x)=0 可得1a=xe2x, 令 k(x)=xe2x(x∈(0,+∞)),
则函数 f(x)在(0,+∞)上有两个不同的零点,即直线 y=1a与函数 k(x)的图象在(0,+∞)上有两个不同的交点,k′(x)=2x-ex x2=x2e-x x, 令 k′(x)=0 得 x=2,
2021版高考数学(人教A版理科)一轮复习攻略 十七 导数与函数零点

令 f′(x)=0,得 x=±2.
当 x 变化时,f′(x),f(x)的变化情况如下表:
x
(-∞,-2) -2 (-2,2) 2 (2,+∞)
f′(x)
+
0
-
0
+
f(x)
↗
↘-
↗
由此可得到 f(x)的大致图象(如图).
由图可知 f(x)有 3 个零点.
2.已知函数 f(x)=x3-12x+a,其中 a≥16,则 f(x)的零点的个数是
16
↘
-16
↗
所以 g(x)的图象如图所示:
因为 a≥16,所以 y=-a≤-16. 由图可知直线 y=-a 与 y=x3-12x 的图象有 1 个或 2 个交点.
3.若函数 f(x)=
恰有 2 个零点,则 a 的取值范围
为 () A.
B.
∪
C.
D.
∪
【解析】选 D.当 x>0 时,令 f(x)=0,可得 x3-x2-a=0,设 g(x)=x3-x2,则 g′(x) =x(3x-2),
满足 f(1)>0,f
<0,m<0,
解得 m>- , > ⇒ - <m<- . 答案: 8.若函数 f(x)=ln x-x-mx 在区间[1,e2]内有唯一的零点,则实数 m 的 取值范围是________. 【解析】函数 f(x)=ln x-x-mx 在区间[1,e2]内有唯一的零点, 得-x+ln x=mx,又 x>0,所以 m= -1,
()
A.4
B.4ln 2-3
C.2
D.5ln 2-4
【解析】选 D.函数 f(x)=ex+a-x3+2x2 在(0,+∞)上只有一个零点,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
当 a≤0 时,f′(x)<0,函数 f(x)在(0,+∞)上单调递减,
x+ 2 x- 2
当 a>0 时,f′(x)=a
a x3
a,
由 f′(x)≤0,解得 0<x≤ 2, a
∴此时函数 f(x)的单调递减区间为 0,
2a a.
综上可得:a≤0 时,函数 f(x)的单调递减区间为(0,+∞),
a>0 时,函数 f(x)的单调递减区间为 0,
在(0,x0)上,f′(x)>0,函数 f(x)单调递增;
在(x0,+∞)上,f′(x)<0,函数 f(x)单调递减.
∴f(x)max=f(x0).
当 a=1 时,x0=1,f(x)max=f(1)=0,此时函数 f(x)只有一个零点 x=1.
当 a>1 时,f(1)=a-1>0,
1 f 2a =ln 21a-41a2+12<21a-1-41a2+12
=-
1 -1 2a 2
2
-1<0,
4
f(2a)=ln
2a-2a2<2a-1-2a2=-2
a-1 2
2
-1<0.
2
Байду номын сангаас
∴函数
f(x)在区间
1 ,1 2a
和区间(1,2a)上各有一个零点.
综上可得:当 a=1 时,函数 f(x)只有一个零点 x=1;
当 a>1 时,函数 f(x)有两个零点.
规律方法 1.利用导数求函数的零点常用方法:
x
x
可得 x∈(0,1)时,g′(x)>0,函数 g(x)单调递增;
x∈(1,+∞)时,g′(x)<0,函数 g(x)单调递减.
∴当 x=1 时,函数 g(x)取得极大值也是最大值,
∴g(x)≤g(1)=0,即 ln x≤x-1.
(2)f′(x)=1-2x+a=-2x2+ax+1,x>0.
x
x
令-2x20+ax0+1=0,解得 x0=a+ a2+8(负值舍去), 4
递减.
(2)证明 由于 x2+x+1>0,所以 f(x)=0 等价于x2+xx3+1-3a=0.
设
g(x)=x2+xx3+1-3a,则
g′(x)=x2(x2+2x+3)≥0,仅当 (x2+x+1)2
x=0
时
g′(x)=0,
所以 g(x)在(-∞,+∞)单调递增.
故 g(x)至多有一个零点,从而 f(x)至多有一个零点.
第四课时 导数与函数的零点
考点一 判断零点的个数
【例 1】 (2020·潍坊检测)已知函数 f(x)=ln x-x2+ax,a∈R.
(1)证明 ln x≤x-1;
(2)若 a≥1,讨论函数 f(x)的零点个数.
(1)证明 令 g(x)=ln x-x+1(x>0),则 g(1)=0,
g′(x)=1-1=1-x,
2a a.
(2)由(1)可得若函数 f(x)有两个不同的零点,则必须满足 a>0,
且f
2 a
=a+aln 22
2<0, a
化为 ln 2<-1,解得 a>2e. a
所以实数 a 的取值范围是(2e,+∞).
考点三 函数零点的综合问题
函数的性质(单调性、极值、函数值的极限位置等),作出函数的大致图象,然后
通过函数图象得出其与 x 轴交点的个数,或者两个相关函数图象交点的个数,基
本步骤是“先数后形”.
【训练 1】 (2018·全国Ⅱ卷)已知函数 f(x)=1x3-a(x2+x+1). 3
(1)若 a=3,求 f(x)的单调区间;
(2)证明:f(x)只有一个零点.
又
f(3a-1)=-6a2+2a-1=-6
a-1 6
2
-1<0,
3
6
f(3a+1)=1>0,故 f(x)有一个零点. 3
综上,f(x)只有一个零点.
考点二 根据零点个数求参数的值(范围) 【例 2】 函数 f(x)=ax+xln x 在 x=1 处取得极值. (1)求 f(x)的单调区间; (2)若 y=f(x)-m-1 在定义域内有两个不同的零点,求实数 m 的取值范围. 解 (1)函数 f(x)=ax+xln x 的定义域为(0,+∞). f′(x)=a+ln x+1, 因为 f′(1)=a+1=0,解得 a=-1, 当 a=-1 时,f(x)=-x+xln x, f′(x)=ln x,令 f′(x)>0,解得 x>1; 令 f′(x)<0,解得 0<x<1. 所以 f(x)在 x=1 处取得极小值,f(x)的单调递增区间为(1,+∞),单调递减区间 为(0,1). (2)y=f(x)-m-1 在(0,+∞)内有两个不同的零点,可转化为 y=f(x)与 y=m+1 图象有两个不同的交点. 由(1)知,f(x)在(0,1)上单调递减,在(1,+∞)上单调递增,f(x)min=f(1)=-1, 当 0<x<e 时,f(x)=x(-1+ln x)<0;当 x>e 时,f(x)>0. 当 x>0 且 x→0 时,f(x)→0; 当 x→+∞时,显然 f(x)→+∞. 由图象可知,-1<m+1<0, 即-2<m<-1. 所以 m 的取值范围是(-2,-1). 规律方法 1.函数零点个数可转化为图象的交点个数,根据图象的几何直观求解. 2.与函数零点有关的参数范围问题,往往利用导数研究函数的单调区间和极值点, 并结合特殊点判断函数的大致图象,进而求出参数的取值范围. 【训练 2】 已知函数 f(x)=x12+aln x(a∈R). (1)求 f(x)的单调递减区间; (2)已知函数 f(x)有两个不同的零点,求实数 a 的取值范围. 解 (1)由题意可得,f′(x)=-x23+ax=ax2x-3 2(x>0),
(1)解 当 a=3 时,f(x)=1x3-3x2-3x-3,f′(x)=x2-6x-3. 3
令 f′(x)=0,解得 x=3-2 3或 x=3+2 3.
当 x∈(-∞,3-2 3)∪(3+2 3,+∞)时,f′(x)>0;
当 x∈(3-2 3,3+2 3)时,f′(x)<0.
故 f(x)在(-∞,3-2 3),(3+2 3,+∞)单调递增,在(3-2 3,3+2 3)单调
(1)构造函数 g(x)(其中 g′(x)易求,且 g′(x)=0 可解),利用导数研究 g(x)的性质,
结合 g(x)的图象,判断函数零点的个数.
(2)利用零点存在定理,先判断函数在某区间有零点,再结合图象与性质确定函
数有多少个零点.
2.根据参数确定函数零点的个数,解题的基本思想是“数形结合”,即通过研究
