专题5.1 任意角和弧度制(解析版)新教材第一册每节优质练(练出好成绩)

合集下载

人教版高中数学必修一精品讲义5.1 任意角和弧度制(精练)(解析版)

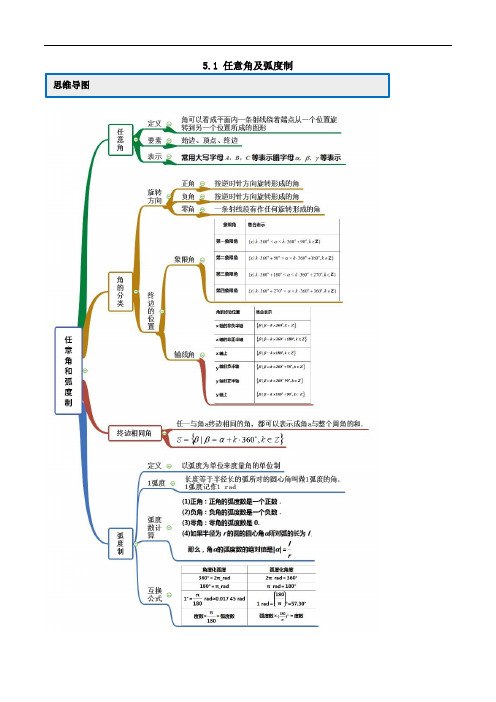
5.1 任意角和弧度制【题组一基本概念的辨析】1．（2020·河南林州一中高一月考）已知集合A ＝{α|α小于90°},B ＝{α|α为第一象限角},则A ∩B ＝( ) A ．{α|α为锐角} B ．{α|α小于90°} C ．{α|α为第一象限角} D ．以上都不对【正确答案】D【详细解析】∵A ＝{α|α小于90°},B ＝{α|α为第一象限角}, ∴A ∩B ＝{小于90°且在第一象限的角},对于A :小于90°的角不一定是第一象限的,不正确,比如﹣30°;对于B :小于90°的角且在第一象限的角不一定是0°～90°的角,不正确,例如﹣300°; 对于C :第一象限的角不一定是小于90°的角且在第一象限的角,不正确,例如380°, 故选D ．2．（2020·浙江高一课时练习）下列命题中正确的是（）． A ．第一象限角一定不是负角 B ．小于90°的角一定是锐角 C ．钝角一定是第二象限角 D ．终边和始边都相同的角一定相等【正确答案】C【详细解析】300︒-为第一象限角且为负角,故A 错误;5090-︒<︒,但50︒-不是锐角,故B 错误;终边与始边均相同的角不一定相等,它们可以相差360,k k Z ︒⋅∈,故D 错误．钝角一定是第二象限角,C 正确．故选:C ．3．（2020·汪清县汪清第六中学高一期中（文））下列结论中正确的是( ) A ．小于90°的角是锐角 B ．第二象限的角是钝角 C ．相等的角终边一定相同 D ．终边相同的角一定相等【正确答案】C【详细解析】对于A,小于90︒可能是负角,不是锐角;对于B,第二象限的角可能是负角,不是钝角;对于C,两个角相等,始边一致,则终边一定相同;对于D,终边相同的角,可能相差360°的倍数,不一定相等.故选C.4．（2020·全国高一课时练习）（1）给出下列说法: ①锐角都是第一象限角; ②第一象限角一定不是负角;③小于180°的角是钝角或直角或锐角.其中正确说法的序号为________.( 把正确说法的序号都写上) （2）将时钟拨快20分钟,则分针转过的度数是________. 【正确答案】② 120-︒【详细解析】（1）①锐角的范围为()0,90︒︒是第一象限的角,命题①正确;②第一象限角的范围为()()360,90360k k k Z ⋅︒︒+⋅︒∈,故第一象限角可以为负角,故②错误; ③根据任意角的概念,可知小于180°的角,可以为负角,故③错误; 故正确答案为:②（2）将时针拨快20分钟,则分针顺时针转过120︒,即转过的度数为120-︒ 故正确答案为:120-︒5．（2020·全国高一课时练习）给出下列说法: ①锐角都是第一象限角; ②第一象限角一定不是负角;③小于180°的角是钝角或直角或锐角．其中正确说法的序号为________．( 把正确说法的序号都写上) 【正确答案】①【详细解析】锐角指大于0°小于90°的角,都是第一象限角,所以①对;由任意角的概念知,第一象限角也可为负角,小于180°的角还有负角、零角,所以②③错误．故正确答案为:① 6．（2020·全国高一课时练习）下列命题正确的是____________( 填序号). ①－30°是第一象限角; ②750°是第四象限角; ③终边相同的角一定相等; ④－950°12′是第二象限的角. 【正确答案】④【详细解析】①30-︒是第四象限的角度,故①错误;②750°的终边与30︒的终边相同,故其为第一象限的角度,故②错误; ③终边相同的角度不一定相等,故③错误;④－950°12′与－950°12′108012948+︒=︒′的终边相同,其为第二象限的角,故④正确. 故正确答案为:④.【题组二角度与弧度转换】1．（2019·伊美区第二中学高一月考）300-化为弧度是（） A ．43π-B ．53π-C ．23π-D ．56π-【正确答案】B【详细解析】300530023603ππ-=-⨯=- 2．（2020·全国高一课时练习）把85π化为角度是( )A ．270°B ．280°C ．288°D ．318°【正确答案】C【详细解析】因为1801rad π⎛⎫=︒ ⎪⎝⎭,故8818028855πππ︒︒⎛⎫=⨯= ⎪⎝⎭.故选:C. 3．（2020·灵丘县豪洋中学高一期中）320-︒化为弧度是（） A ．43π-B ．169π-C ．76π-D ．56π-【正确答案】B【详细解析】320-︒化为弧度是16320=1809ππ-︒⨯-.故选:B 4．（2020·金华市江南中学高一期中）1500︒转化为弧度数为（） A ．253B ．163πC ．163D ．253π【正确答案】D【详细解析】由1180rad π︒=,所以15001550002318ππ︒=⨯=rad 故选:D 5．（2019·长沙铁路第一中学高一月考）将300o 化为弧度为（） A ．43πB ．53π C ．76π D ．74π 【正确答案】B【详细解析】53003001803ππ︒=⨯=．故选:B ． 6．（2020·通榆县第一中学校高一期末）512π=（）A ．70°B ．75°C ．80°D ．85°【正确答案】B【详细解析】因为1801rad π⎛⎫=︒⎪⎝⎭,故512π=51807512ππ⎛⎫⨯︒=︒ ⎪⎝⎭.故选:B. 7．（2020·全国高一课时练习）将下列角度与弧度进行互化. （1）20°;（2）－15°;（3）712π（4）－115π. 【正确答案】（1）20°＝9π;（2）－15°＝－12π;（3）712π＝105°;（4）－115π＝－396°.【详细解析】（1）20°＝20180π＝9π.（2）－15°＝－15180π＝－12π.（3）712π＝712×180°＝105°.( 4)－115π＝－115×180°＝－396°.【题组三终边相同】1．（2020·浙江高一课时练习）与405°角终边相同的角是（）． A ．45360,k k Z ︒︒-+⋅∈ B ．405360,k k Z ︒︒-+⋅∈ C ．45360,k k Z ︒︒+⋅∈ D ．45180,k k Z ︒︒+⋅∈【正确答案】C【详细解析】由于40536045︒︒︒=+,故与405°终边相同的角应为45360,k k Z ︒︒+⋅∈．故选:C 2．（2020·永州市第四中学高一月考）在0360~︒︒的范围内,与510︒-终边相同的角是（） A ．330︒ B ．210︒C ．150︒D ．30︒【正确答案】B【详细解析】因为510720210︒-=-+,则在0360~︒︒的范围内,与510︒-终边相同的角是210︒,故选:B. 3．（2020·合肥市第八中学高一月考）下列各个角中与2020°终边相同的是( ) A ．150︒- B ．680°C ．220°D ．320°【正确答案】C【详细解析】由题,20202205360︒=︒+⨯︒,故选:C4．（2020·汪清县汪清第六中学高一期中（文））在0°~360°范围内,与-1050°的角终边相同的角是（）A ．30°B ．150°C ．210°D ．330°【正确答案】A【详细解析】因为1050336030-︒=-⨯︒+︒所以在0°~360°范围内,与-1050°的角终边相同的角是30故选:A5．（2020·北京延庆·高一期末）与角196π终边相同的角为（） A ．6π-B ．6π C ．56π-D ．56π 【正确答案】C 【详细解析】与角196π终边相同的角可写成192,6παπ=+∈k k Z 令2k =-,则56πα=-故选:C6．（2020·辉县市第二高级中学高一期中）下列与的终边相同的角的表达式中正确的是( )A ．2k π＋45°( k ∈Z)B ．k ·360°＋π( k ∈Z)C ．k ·360°－315°( k ∈Z)D ．k π＋( k ∈Z)【正确答案】C 【详细解析】与的终边相同的角可以写成2k π＋( k ∈Z),但是角度制与弧度制不能混用,所以只有正确答案C 正确.故正确答案为C7．（2020·陕西大荔·高一月考）已知角2α是第一象限角,则α的终边位于（）A ．第一象限B ．第二象限C ．第一或第二象限D ．第一或第二象限或y 轴的非负半轴上【正确答案】D 【详细解析】∵由角2α是第一象限角,∴可得π2π2π,22k k k α<<+∈Z ,∴4π4ππ,k k k α<<+∈Z .即α的终边位于第一或第二象限或y 轴的非负半轴上.故选:D.8．（2020·宁县第二中学高一期中）已知角α的终边在图中阴影所表示的范围内（不包括边界）,那么α∈________.【正确答案】{}|180********,n n n αα⋅︒+︒<<⋅︒+︒∈Z . 【详细解析】在0360范围内,终边落在阴影内的角α满足:30150α<<或210330α<<∴满足题意的角α为:{}{}30360150360210360330360k k k k αααα+⋅<<+⋅⋃+⋅<<+⋅{}{}302180150218021021803302180k k k k αααα=+⋅<<+⋅⋃+⋅<<+⋅{}()(){}3021801502180302118015021180k k k k αααα=+⋅<<+⋅⋃++⋅<<++⋅{}30180150180n n αα=+⋅<<+⋅,k Z ∈,n Z ∈本题正确结果:{}30180150180,n n n Z αα+⋅<<+⋅∈ 【题组四象限的判断】1．（2020·广东高一期末）下列各角中,与2019°终边相同的角为（） A ．41° B ．129°C ．219°D ．﹣231°【正确答案】C【详细解析】因为20195360219=⨯+,所以219与2019°终边相同.故选:C. 2．（2020·湖南隆回·高一期末）下列各角中,与60终边相同的角为（）A ．30B ．120C ．420D ．300【正确答案】C【详细解析】与60终边相同的角的集合是{}60360,k k Z αα=+⋅∈,当1k =时,420α=.故选:C 3．（2020·河南项城市第三高级中学高一月考）设2α是第一象限角,且cos cos αα=-,则α是第（）象限角 A ．一 B ．二C ．三D ．四【正确答案】B【详细解析】∵2α是第一象限角,∴360903602k k α︒<<︒+︒,k Z ∈,∴720180720k k α︒<<︒+︒,k Z ∈,∴α为第一象限角或第二象限角或终边在y 轴正半轴上的轴线角, ∵cos cos αα=-,∴cos 0α<,∴α是第二象限角.故选:B .4．（2020·辉县市第二高级中学高一期中）角–2α=弧度,则α所在的象限是（） A ．第一象限 B ．第二象限C ．第三象限D ．第四象限【正确答案】C【详细解析】角–2α=弧度,2(,)2ππ-∈--,∴α在第三象限,故选:C .5．（2020·全国高一课时练习）若θ＝－5,则角θ的终边在（） A ．第四象限 B ．第三象限 C ．第二象限 D ．第一象限【正确答案】D【详细解析】2π－5与－5的终边相同,∵2π－5∈0,2π⎛⎫⎪⎝⎭,∴2π－5是第一象限角,则－5也是第一象限角. 故选:D6．（2020·浙江高一课时练习）若θ是第四象限角,则角2θ的终边在( ) A ．第一象限 B ．第一或第三象限 C ．第四象限D ．第二或第四象限【正确答案】D【详细解析】取80θ=-︒,则402θ=-︒,在第四象限;取320θ=︒,则1602θ=︒,在第二象限.故选:D .7．（2020·浙江高一课时练习）试求出终边在如图所示阴影区域内的角的集合．【正确答案】222,34k k k Zππβπβπ⎧⎫-++∈⎨⎬⎭⎩．【详细解析】因为42233πππ+=,所以43π的终边与23π-的终边相同,则终边在题图所示阴影区域内的角的集合为222,34k k k Zππβπβπ⎧⎫-++∈⎨⎬⎭⎩．8．（2020·上海高一课时练习）用弧度制写出终边在阴影部分的角的集合:（1）（2）【正确答案】（1）222,43k k k Zπαπαππ⎧⎫+<+∈⎨⎬⎩⎭;（2）,6k k k Zπαπαπ⎧⎫+∈⎨⎬⎩⎭【详细解析】（1）边界对应射线所在终边的角分别为222,() 43k k k Zππππ++∈，所以终边在阴影部分的角的集合为222,43k k k Zπαπαππ⎧⎫+<+∈⎨⎬⎩⎭（2）边界对应射线所在终边的角分别为222,2,()667k k k k k Z πππππππ+++∈，，所以终边在阴影部分的角的集合为722,22,66k k k Z k k k Z ππαπαπαππαπ⎧⎫⎧⎫≤+∈⋃+≤+∈⎨⎬⎨⎬⎩⎭⎩⎭=,6k k k Z παπαπ⎧⎫+∈⎨⎬⎩⎭【题组五扇形】1．（2020·山东潍坊·高一期末）已知某扇形的半径为4cm ,圆心角为2rad ,则此扇形的面积为（） A ．232cm B ．216cmC ．28cmD ．24cm【正确答案】B【详细解析】由题意,某扇形的半径为4cm ,圆心角为2rad , 根据扇形的面积公式,可得22211241622S r cm α==⨯⨯= 所以此扇形的面积为216cm .故选:B. 2．（2020·江西省铜鼓中学高一期末）一个扇形的圆心角为150°,面积为53π,则该扇形半径为（）A ．4B ．1C D ．2【正确答案】D【详细解析】圆心角为51506πα==,设扇形的半径为R ,2215152326S R R ππα=⋅⇒=⨯, 解得2R =.故选:D3．（2020·武威第八中学高一期末）已知扇形的周长为8cm ,圆心角为2弧度,则该扇形的面积为（） A ．24cm B ．26cmC ．28cmD ．216cm【正确答案】A【详细解析】设此扇形半径为r ,扇形弧长为l=2r 则2r +2r ＝8,r=2,∴扇形的面积为12l r=224r cm =故选A 4．（2020·辉县市第二高级中学高一期中）已知扇形的圆心角为2,周长为8,则扇形的面积为（） A ．2 B ．4C ．8D ．16【正确答案】B【详细解析】设该扇形的半径为r ,弧长为l ,则2lr =,且28l r +=,所以有42l r =⎧⎨=⎩,所以,该扇形的面积为142S lr ==.故选:B. 5．（2020·河南宛城·南阳中学高一月考）中国传统扇文化有着极其深厚的底蕴．一般情况下,折扇可看作是从一个圆面中剪下的扇形制作而成,设扇形的面积为1S ,圆面中剩余部分的面积为2S ,当1S 与2S 的比值为12时,扇面看上去形状较为美观,那么此时扇形的圆心角的弧度数为（）A ．(3πB ．1)πC ．1)πD ．2)π【正确答案】A【详细解析】1S 与2S 所在扇形圆心角的比即为它们的面积比,设1S 与2S 所在扇形圆心角分别为,αβ,则αβ=,又2αβπ+=,解得(3απ=- 故选:A6．（2020·永昌县第四中学高一期末）如图,已知扇形AOB 的圆心角为120°,半径长为6,求弓形ACB 的面积．【正确答案】12π-【详细解析】∵120°＝π＝π,∴l ＝6×π＝4π,∴AB 的长为4π.∵S 扇形OAB ＝lr ＝×4π×6＝12π,如图所示,作OD ⊥AB ,有S △OAB ＝×AB ×OD ＝×2×6cos 30°×3＝9.∴S 弓形ACB ＝S 扇形OAB －S △OAB ＝12π－9.∴弓形ACB 的面积为12π－9.【题组六生活中实际】 1．（2020·全国高一课时练习）将时钟拨快20分钟,则分针转过的度数是________．【正确答案】－120°【详细解析】将时针拨快20分钟,则分针顺时针转过120︒,即转过的度数为120-︒故正确答案为:120-︒ 2．（2020·全国高一课时练习）已知α＝30°,将其终边按逆时针方向旋转三周后的角度数为________.【正确答案】1110°【详细解析】一个角为30,其终边按逆时针方向旋转三周后的角的度数为:3603301110︒⨯+︒=︒．故正确答案为:1110︒．3．（2020·全国高一课时练习）写出下列说法所表示的角.（1）顺时针拧螺丝2圈;（2）将时钟拨慢2小时30分,分针转过的角．【正确答案】（1）－720°;（2）900°.【详细解析】（1）顺时针拧螺丝2圈,即旋转了2360=720⨯︒︒,顺时针旋转得到的角为负角,故转过的角是720-︒; （2）拨慢时钟需将分针按逆时针方向旋转,时针拨慢2小时30分,是2.5周角,角度数是2.5360900⨯︒=︒;又分针是逆时针旋转,转过的角是900︒．4．（2020·浙江高一课时练习）在一昼夜中,钟表的时针和分针有几次重合?几次形成直角?时针、分针和秒针何时重合?请写出理由．【正确答案】正确答案见详细解析.【详细解析】时针每分钟走0.5°,分针每分钟走6°,秒针每分钟走360°,（1）一昼夜有24601440⨯=（分钟）, 时针和分针每重合一次间隔的时间为36060.5-分钟, 所以一昼夜时针和分针重合14402236060.5=-（次）．（2）假设时针不动,分针转一圈与时针两次形成直角,但一昼夜时针转了两圈,则少了4次垂直,于是时针和分针一共有242444⨯-=（次）形成直角．（3）秒针与分针每重合一次间隔的时间为3603606-分钟,由3603606-和36060.5-的“最小公倍数”为720,而720分钟=12小时,所以一昼夜只有0:00与12:00这两个时刻“三针”重合．。

高一数学(必修一)《第五章-任意角和弧度制》练习题及答案解析-人教版

高一数学(必修一)《第五章任意角和弧度制》练习题及答案解析-人教版班级:___________姓名：___________考号：___________一、多选题1．已知扇形的周长是12，面积是8，则扇形的圆心角的弧度数可能是（） A ．1 B ．4C ．2D ．3二、单选题2．终边与直线y x =重合的角可表示为（） A ．45180,k k Z ︒︒+⋅∈ B ．45360,k k Z ︒︒+⋅∈ C ．135180,k k Z ︒︒+⋅∈ D ．225360,k k Z ︒︒+⋅∈3．下列角中与116π-终边相同的角是（） A ．30-︒B ．40-︒C ．20︒D ．390︒4．下列说法正确的是（）A ．长度等于半径的弦所对的圆心角为1弧度B ．若tan 0α≥，则()2k k k Z ππαπ≤≤+∈C ．若角α的终边过点()()3,40P k k k ≠，则4sin 5α D ．当()224k k k Z ππαπ<<+∈时，则sin cos αα<5．已知一个母线长为1的圆锥的侧面展开图的圆心角等于240︒，则该圆锥的侧面积为（）A B ．881πCD ．23π6．《掷铁饼者》取材于希腊的现实生活中的体育竞技活动，刻画的是一名强健的男子在掷铁饼过程中具有表现力的瞬间（如图）．现在把掷铁饼者张开的双臂近似看成一张拉满弦的“弓”，掷铁饼者的手臂长约为4πm肩宽约为8πm ，“弓”所在圆的半径约为5m 41.414≈和1.732）（）A ．1.012mB ．1.768mC ．2.043mD ．2.945m三、填空题7．6730'︒化为弧度，结果是______.8．已知扇形的周长为20cm ，面积为92cm ，则扇形的半径为________.9．折扇最早出现于公元五世纪的中国南北朝时代，《南齐书》上说：“褚渊以腰扇障日．”，据《通鉴注》上的解释，“腰扇”即折扇．一般情况下，折扇可以看作从一个圆面中剪下的扇形制作而成，设扇形的弧长为l ，扇形所在的圆的半径为r ，当l 与r 的比值约为2.4时，则折扇看上去的形状比较美观.若一把折扇所在扇形的半径为30cm ，在保证美观的前提下，此折扇所在扇形的面积是_______2cm ．10．设地球半径为R ，地球上北纬30°圈上有A ，B 两点，点A 在西经10°，点B 在东经110°，则点A 和B 两点东西方向的距离是___________.四、解答题11．将下列各角化成360,,0360k k βαα=+⋅︒∈︒≤<︒Z 的形式，并指出它们是第几象限的角：（1）1320︒；（2）315-︒；（3）1500︒；（4）1610-︒．12．根据角度制和弧度制的转化，已知条件：1690α=︒(1)把α表示成2k πβ+的形式[)()Z,02k βπ∈∈，；(2)求θ，使θ与α的终边相同，且()4,2θππ∈--．13．已知一扇形的圆心角是72°，半径为20，求扇形的面积． 14．已知一扇形的圆心角为α，半径为R ，弧长为l. (1)若α＝60°，R ＝10 cm ，求扇形的弧长l ；(2)已知扇形的周长为10 cm ，面积是4 cm 2，求扇形的圆心角；(3)若扇形周长为20 cm ，当扇形的圆心角α为多少弧度时，则这个扇形的面积最大？ 15．已知扇形的周长为c ，当扇形的圆心角为多少弧度时，则扇形的面积最大．16．某商场共有三层楼，在其圆柱形空间内安装两部等长的扶梯Ⅰ、Ⅱ供顾客乘用，如图，一顾客自一楼点A 处乘Ⅰ到达二楼的点B 处后，沿着二楼地面上的弧BM 逆时针步行至点C 处，且C 为弧BM 的中点，再乘Ⅱ到达三楼的点D 处，设圆柱形空间三个楼面圆的中心分别为半径为8m ，相邻楼层的间距为4m ，两部电梯与楼面所成角的正弦值均为13.(1)求此顾客在二楼地面上步行的路程； (2)求异面直线AB 和CD 所成角的余弦值.17．某地政府部门欲做一个“践行核心价值观”的宣传牌，该宣传牌形状是如图所示的扇形环面(由扇形OAD 挖去扇形OBC 后构成的)．已知2OA =米，OB x =米()02x <<，线段BA 、线段CD 与弧BC 、弧AD 的长度之和为6米，圆心角为θ弧度．(1)求θ关于x 的函数解析式；(2)记该宣传牌的面积为y ，试问x 取何值时，则y 的值最大?并求出最大值．参考答案与解析1．AB【分析】利用扇形的弧长与面积公式建立方程组求解，再利用圆心角公式.【详解】设扇形的半径为r ，弧长为l ，面积为S ，圆心角为α，则212l r +=，182S lr ==解得2r =和8l =或4r =和4l ，则4lrα==或1．故C ，D 错误. 故选：AB ． 2．A【分析】根据终边相同的角的概念，简单计算即可.【详解】终边与直线y x =重合的角可表示为45180,k k Z +⋅∈．故选：A. 3．D【分析】由角度制与弧度制的互化公式得到113306π-=-︒，结合终边相同角的表示，即可求解. 【详解】由角度制与弧度制的互化公式，可得113306π-=-︒ 与角330-︒终边相同的角的集合为{|330360,}A k k Z αα==-︒+⋅︒∈ 令2k =，可得390α=︒所以与角330α=-︒终边相同的角是390α=︒. 故选：D. 4．D【分析】利用弧度制、三角函数值的正负、三角函数的定义和三角函数线的应用逐一判断选项即可. 【详解】对于A ，长度等于半径的弦所对的圆心角为3π弧度，A 错误；对于B ，若tan 0α≥，则()2k k k ππαπ≤<+∈Z ，B 错误；对于C ，若角α的终边过点()()3,40P k k k ≠，则4sin 5α=±，C 错误；对于D ，当()224k k k ππαπ<<+∈Z 时，则sin cos αα<，D 正确.故选D.5．D【分析】根据扇形的圆心角、弧长和半径的关系以及扇形的面积求解. 【详解】解：将圆心角240︒化为弧度为：43π，设圆锥底面圆的半径为r 由圆心角、弧长和半径的公式得：4213r ππ=⨯，即23r =由扇形面积公式得：22133S ππ=⨯⨯=所以圆锥的侧面积为23π. 故选：D. 6．B【分析】由题意分析得到这段弓形所在的弧长，结合弧长公式求出其所对的圆心角，双手之间的距离，求得其弦长，即可求解.【详解】如图所示，由题意知“弓”所在的弧ACB 的长54488l ππππ=++=，其所对圆心角58524ππα==则两手之间的距离()522sin 1.768m 44AB AD π==⨯⨯≈．故选：B ．7．38π【解析】根据角度制与弧度制的关系180π︒=，转化即可. 【详解】180π︒= 1180π︒∴=36730'67.567.51808ππ︒∴︒==⨯=故答案为：38π 【点睛】本题主要考查了弧度制与角度制的转化，属于容易题. 8．9cm【分析】由题意设扇形的半径为r cm ，弧长为l cm ，由扇形的周长、面积可得1(202)92r r -=，解出r 后，验证即可得解.【详解】设扇形的半径为r cm ，弧长为l cm ，圆心角为θ ∵220l r +=，∴202l r =-∴192lr =，即1(202)92r r -=，解得1r =或9r = 当1r =时，则18l =，则181821l r θπ===>，不合题意，舍去；当9r =时，则2l =，则229l r θπ==<，符合题意. 故答案为：9cm.【点睛】本题考查了扇形弧长及面积公式的应用，考查了运算求解能力，属于基础题. 9．1080【分析】首先求出弧长，再根据扇形面积公式计算可得；【详解】解：依题意30r =cm ， 2.4lr=所以 2.472l r ==cm ，所以117230108022S lr ==⨯⨯=2cm ；故答案为：108010 【分析】求出,O A O B ''的长度，确定AO B ∠'的大小，再由弧长公式求得A,B 两地的东西方向的距离. 【详解】如图示，设O '为北纬30°圈的圆心，地球球心为O则60AOO '∠= ,故AO '=,即北纬30°R由题意可知2π1203AO B '∠==故点A 和B 两点东西方向的距离即为北纬30°圈上的AB 的长故AB 的长为2π3R =11．（1）132********︒=︒⨯+︒，第三象限；（2）()315360145-︒=︒⨯-+︒，第一象限；（3）1500360460︒=︒⨯+︒，第一象限；（4）()16103605190-︒=︒⨯-+︒，第三象限．【分析】先将各个角化为指定形式，根据通过终边相同的角的概念判断出角所在象限.【详解】（1）132********︒=︒⨯+︒，因为240︒的角终边在第三象限，所以1320︒是第三象限角；（2）()315360145-︒=︒⨯-+︒，因为45︒的角终边在第一象限，所以315-︒是第一象限角；（3）1500360460︒=︒⨯+︒，因为60︒的角终边在第一象限，所以1500︒是第一象限角；（4）()16103605190-︒=︒⨯-+︒，因为190︒的终边在第三象限，所以1610-︒是第三象限角. 12．(1)254218α=⨯π+π； (2)4718θπ=-.【分析】(1)先把角度数化成弧度数，再表示成符合要求的形式. (2)由(1)可得252,(Z)18k k θππ=+∈，再按给定范围求出k 值作答. (1)依题意，169251690169081801818παπππ=︒=⨯==+ 所以254218α=⨯π+π. (2)由(1)知252,(Z)18k k θππ=+∈，而(4,2)θππ∈--，则25422,()18k k Z ππππ-<+<-∈，解得2k =- 所以254741818θ=-π+π=-π. 13．80π【分析】先求出弧长，再利用扇形的面积公式直接求解. 【详解】设扇形弧长为l ，因为圆心角272721805ππ︒⨯=＝rad 所以扇形弧长2·2085l r παπ⨯=＝＝于是，扇形的面积S ＝12l ·r ＝12×8π×20＝80π. 14．（1）103π；（2）12；（3）=10,=2l α 【分析】（1）根据扇形的弧长公式进行计算即可．（2）根据扇形的周长公式以及面积公式建立方程关系进行求解（3）根据扇形的扇形公式结合基本不等式的应用进行求解即可．【详解】(1)α＝60°＝rad ，∴l ＝α·R ＝×10＝(cm).(2)由题意得解得 (舍去)，故扇形圆心角为. (3)由已知得，l ＋2R ＝20.所以S ＝lR ＝ (20－2R )R ＝10R －R 2＝－(R －5)2＋25，所以当R ＝5时，则S 取得最大值25 此时l ＝10，α＝2.【点睛】本题主要考查扇形的弧长公式和面积公式的应用，根据相应的弧长公式和面积公式建立方程关系是解决本题的关键．15．当扇形的圆心角为2rad 时，则扇形的面积最大.【解析】设扇形的半径为r ，弧长为l ，利用周长公式，求得2l c r =-，代入扇形的面积公式，结合二次函数的性质，即可求解.【详解】设扇形的半径为r ，弧长为l 则2l r c +=，即2(0)2c l c r r =-<<由扇形的面积公式12S lr =，代入可得222111(2)()22416c S c r r r cr r c =-=-+=--+当4c r =时，则即22cl c r =-=时，则面积S 取得最小值此时2l rad r α==，面积的最小值为2c 16.【点睛】本题主要考查了扇形的周长，弧长公式，以及扇形的面积公式的应用，其中解答中熟记扇形的弧长公式和面积公式，准确运算是解答的关键，着重考查了推理与运算能力，属于基础题. 16．(1)2πm【分析】（1）过点B 作一楼地面的垂线，垂足为B '，则B '落在圆柱底面圆上，结合题意计算出1BO M ∠的大小，再利用扇形的弧长公式即可得出结果.（2）建立空间直角坐标系，求出异面直线AB 和CD 的方向向量，再由异面直线所成角的向量公式代入即可得出答案. （1）如图，过点B 作一楼地面的垂线，垂足为B '，则B '落在圆柱底面圆上连接B A '，则B A '即为BA 在圆柱下底面上的射影故BAB '∠即为电梯Ⅰ与楼面所成的角，所以1sin 3BAB '∠=.因为4BB AM '==，所以AB '=在AOB '中8OA OB ='=，所以AOB '是等腰直角三角形连接1O ，B ，1O M ，则1π2BO M AOB '∠=∠= 因为BC CM =，所以BC 的长为π82π4⨯= 故此顾客在二楼地面上步行的路程为2π m . （2）连接2OO ，由（1）可知所在直线两两互相垂直.以O 为原点OB '，OA 和2OO 的方向分别为x ，y ，z 轴的正方向，建立空间直角坐标系，如图所示，则()8,0,4B ()0,8,0A 与()C 和()D -，所以()8,8,4AB =- ()4CD =-. 设异面直线AB 和CD 所成角为θ，则·42cos cos ,=9AB CD AB CD AB CDθ==故异面直线AB 和CD 17．(1)22(02)2x x x θ+=<<+； (2)当12x =时，则y 的值最大，最大值为94．【分析】(1)根据弧长公式和周长列方程得出θ关于x 的函数解析式；(2)根据面积公式求出y 关于x 的函数表达式，根据二次函数性质可得y 的最大值． (1)根据题意，弧BC 的长度为x θ米，弧AD 的长度2AD θ=米2(2)26x x θθ∴-++=∴22(02)2x x x θ+=<<+． (2)依据题意，可知2211222OAD OBC y S S x θθ=-=⨯-扇扇化简得：22y x x =-++ 02x <<∴当12x =，则2max 1192224y ⎛⎫=-++= ⎪⎝⎭．∴当12x =时，则y 的值最大，且最大值为94．。

2020年人教A版高中数学必修第一册5.1 任意角及弧度制(解析版)

5.1 任意角及弧度制运用一基础概念理解【例1】（2019·湖南高一期末）下列说法正确的是（） A.小于90︒的角是锐角B.钝角是第二象限的角C.第二象限的角大于第一象限的角D.若角α与角β的终边相同，则,απβ=+∈k k Z 【答案】B【解析】A ：负角不是锐角，比如“30-︒”的角，故错误； B ：钝角范围是“90180α︒<<︒”，是第二象限的角，故正确； C ：第二象限角取“91︒”，第一象限角取“361︒”，故错误； D ：当角α与角β的终边相同，则2,k k Z απβ=+∈.故选：B. 【触类旁通】1．已知A ={第一象限角}，B ={锐角}，C ={小于90°的角}，那么A ，B ，C 的关系是（） A.B =A ∩C B.B ∪C =C C.A ⊆B ∩C D.A =B =C【答案】B【解析】∵A ={第一象限角}={α|k ⋅360∘<α<k ⋅360∘+90∘,k ∈Z}；B ={锐角}={α|0∘<α<90∘}；C ={小于90°的角}={α|α<90∘}．∴B ∪C ＝{小于90°的角}＝C ，即B ⊂C ，且B ⊂A ，则B 不一定等于A ∩C ，A 不一定是C 的子集，三集合不一定相等，由集合间的关系可得B ∪C =C ．故选B ．运用二终边相同的角【例2】(1)如果α=−21∘，那么与终边相同的角可以表示为 A.{β|β=k ⋅360∘+21∘,k ∈Z } B.{β|β=k ⋅360∘−21∘,k ∈Z } C.{β|β=k ⋅180∘+21∘,k ∈Z }D.{β|β=k ⋅180∘−21∘,k ∈Z } (2)终边在直线y ＝－x 上的所有角的集合是( )A ．{α|α＝k ·360°＋135°，k ∈Z}B ．{α|α＝k ·360°－45°，k ∈Z}C ．{α|α＝k ·180°＋225°，k ∈Z}D ．{α|α＝k ·180°－45°，k ∈Z}(3)（2019春•南京期中）若角α＝m•360°+60°，β＝k•360°+120°，（m，k∈Z），则角α与β的终边的位置关系是（）A．重合B．关于原点对称C．关于x轴对称D．关于y轴对称【答案】(1)B(2)D(3)D【解析】根据终边相同的角相差360∘的整数倍，故与角α有相同终边的角为k⋅360∘+α(k∈Z)，所以α=−21∘，表示为k⋅360∘−21∘(k∈Z)，故选B.(2)直线y＝﹣x过原点，它是第二、四象限角的平分线所在的直线，故在0°～360°范围内终边在直线y＝﹣x上的角有两个：135°，315°．因此，终边在直线y＝﹣x上的角的集合S＝{α|α＝135°+k•360°，k∈Z}∪{α|α＝315°+k•360°，k∈Z}＝{α|α＝135°+2k•180°，k∈Z}∪{α|α＝135°+（2k+1）•180°，k∈Z}＝{α|α＝135°+k•180°，k∈Z}．或者表示为S＝{α|α＝k·180°－45°，k∈Z}．故选：D．(3)α的终边和60°的终边相同，β的终边与120°终边相同，∵180°﹣120°＝60°∴角α与β的终边的位置关系是关于y轴对称，故选：D．【触类旁通】1．与角－1 560°终边相同的角的集合中，最小正角是________，最大负角是________.【答案】240°－120°【解析】根据终边相同的角相差360°的整数倍，故与﹣1560°终边相同的角可表示为：{α|α＝k•360°﹣1560°，k∈Z}．则当k＝4时，α＝4×360°﹣1560°＝﹣120°，此时为最大的负角．当k＝5时，α＝5×360°﹣1560°＝240°，此时为最小的正角．故答案为：240°，﹣120°2.（2018春•武功县期中）下列各组角中，终边相同的角是（）A．﹣398°，1042°B．﹣398°，142°C．﹣398°，38°D．142°，1042°【答案】A【解析】由题意，﹣398°＝322°﹣2×360°，1042°＝322°+2×360°，142°，38°；这四个角中，终边相同的角是﹣398°和1042°．故选：A．3.已知α＝﹣30°，若α与β的终边关于直线x﹣y＝0对称，则β＝；若α与β的终边关于y轴对称，则β＝；若α与β的终边关于x轴对称，则β＝．【答案】见解析【解析】如图，设α＝﹣30°所在终边为OA，则关于直线x﹣y＝0对称的角β的终边为OB，终边在OB上的最小正角为120°，故β＝120°+k•360°，k∈Z；关于y轴对称的角β的终边为OC，终边在OC上的最小正角为210°，故β＝210°+k•360°，k∈Z；关于x轴对称的角β的终边为OD，终边在OD上的最小正角为30°，故β＝30°+k•360°，k∈Z．故答案为：120°+k •360°，k ∈Z ；210°+k •360°，k ∈Z ；30°+k •360°，k ∈Z ．运用三角所在象限【例3】（1）（2019·湖南高一期末）179︒是（） A ．第一象限角B ．第二象限角C ．第三象限角D ．第四象限角（2）（2019春•北碚区校级期中）已知α为第二象限角，则所在的象限是（） A ．第一或第二象限 B ．第二或第三象限 C ．第一或第三象限 D ．第二或第四象限【答案】（1）B （2）C【解析】（1）1791801︒︒︒=-，所以179︒表示第二象限角，故选B ．（2）∵α是第二象限角，∴k •360°+90°＜α＜k •360°+180°，k ∈Z ，则k •180°+45°＜＜k •180°+90°，k ∈Z ，令k ＝2n ，n ∈Z 有n •360°+45°＜＜n •360°+90°，n ∈Z ；在一象限；k ＝2n +1，n ∈z ，有n •360°+225°＜＜n •360°+270°，n ∈Z ；在三象限；故选：C ．【触类旁通】1.（2018•徐汇区校级模拟）若α是第二象限的角，则的终边所在位置不可能是（） A ．第一象限 B ．第二象限 C ．第三象限D ．笫象限【答案】C【解析】∵α是第二象限角，∴90°+k •360°＜α＜180°+k •360°，k ∈Z ．则30°+k •120°＜＜60°+k •120°，k ∈Z ．当k ＝0时，30°＜＜60°，α为第一象限角；2α3α当k ＝1时，150°＜＜180°，α为第二象限角；当k ＝2时，270°＜＜300°，α为第四象限角．由上可知，的终边所在位置不可能是第三象限角．故选：C ．2.（2019秋•宜城市校级月考）如果α是第三象限角，则是（）A ．第一象限角B ．第一或第二象限角C ．第一或第三象限角D ．第二或第四象限角【答案】C【解析】∵α是第三象限角，∴180°+k •360°＜α＜270°+k •360°，k ∈Z ， ∴﹣135°﹣k •180°＜﹣＜﹣90°﹣k •180°，∴﹣是第一或第三象限角．故选：C ．运用四弧度制的理解【例4】（2019春•历城区校级月考）下列命题中，真命题的是( ) A ．1弧度是一度的圆心角所对的弧 B ．1弧度是长度为半径的弧 C ．1弧度是一度的弧与一度的角之和D ．1弧度是长度等于半径长的弧所对的圆心角的大小【答案】D【解析】根据弧度的定义知：长度等于半径长的弧所对的圆心角叫做1弧度的角．故选：D ．2α-【触类旁通】1.（2019春•静安区期末）下列选项中，错误的是( ) A ．“度”与“弧度”是度量角的两种不同的度量单位B ．一度的角是周角的，一弧度的角是周角的 C ．根据弧度的定义，180度一定等于π弧度D ．不论是用角度制还是弧度制度量角，它们与圆的半径长短有关【答案】D【解析】“度”与“弧度”是度量角的两种不同的度量单位，判断正确；一度的角是周角的，一弧度的角是周角的，满足两种角的度量定义，正确；根据弧度的定义，180度一定等于π弧度，满足两种角的度量关系，正确；不论是用角度制还是弧度制度量角，它们与圆的半径长短有关，不正确；故选：D ．运用五角度与弧度的转化【例5-1】（2019春•微山县校级月考）将下列弧度转化为角度：角度化为弧度：（1）12π= ；（2）136π= ；（3）512π-= ．（4）36︒= rad ；（5）105-︒= rad ．【答案】：15°，390°，﹣75°，．【解析】∵π＝180°， ∴；；；36°＝36×；．【例5-2】（2019·榆林市第二中学高一期末）下列各角与3π终边相同的角是（） A ．43π B ．53π C ．43π-D ．53π-【答案】D 【解析】与3π终边相同的角可表示为()23k k Z πβπ=+∈，当1k =-时，53πβ=- 136012π136012π故选D【触类旁通】1．1 920°的角化为弧度数为( )A.163B.323C.163π D.323π【答案】D【解析】∵1°＝π180rad ，∴1 920°＝1 920×π180rad ＝323π rad.2．（2019·上海市三林中学高一月考）与角136π终边相同的最小正角大小是_________ 【答案】6π 【解析】所有与角136π终边相同的角是α =132,6k k Z ππ+∈ ，令1k =- 即得到最小的正角，即6π。

高考数学专题《任意角和弧度制及任意角的三角函数》习题含答案解析

专题5.1 任意角和弧度制及任意角的三角函数1．（2021·宁夏高三三模（文））已知角α终边经过点()1,2,P-则cosα=（）A．12B．12-C D．【答案】D【解析】直接利用三角函数的定义即可.【详解】由三角函数定义，cos5α==-.故选：D.2.（2021·中牟县教育体育局教学研究室高一期中）已知角α的终边经过点()3,1P-，则cosα=（）A B．C．D【答案】C【解析】由三角函数的定义即可求得cosα的值．【详解】角α的终边经过点(3,1)P-，cosα∴==故选：C．3．（2020·全国高一课时练习）若α＝－2，则α的终边在（）A．第一象限B．第二象限C．第三象限D．第四象限【答案】C【解析】练基础根据角的弧度制与角度制之间的转化关系可得选项.【详解】因为1 rad≈57.30°，所以－2 rad≈－114.60°，故α的终边在第三象限．故选：C.4．（2021·江苏高一期中）下列命题：①钝角是第二象限的角；②小于90︒的角是锐角；③第一象限的角一定不是负角；④第二象限的角一定大于第一象限的角；⑤手表时针走过2小时，时针转过的角度为60︒；⑥若5α=，则α是第四象限角．其中正确的题的个数是（）A．1个B．2个C．3个D．4个【答案】B【解析】结合象限角和任意角的概念逐个判断即可.【详解】对于①：钝角是大于90小于180的角，显然钝角是第二象限角. 故①正确；对于②：锐角是大于0小于90的角，小于90的角也可能是负角. 故②错误；对于③：359-显然是第一象限角. 故③错误；对于④：135是第二象限角，361是第一象限角，但是135361<. 故④错误；对于⑤：时针转过的角是负角. 故⑤错误；对于⑥：因为157.3rad≈，所以5557.3=286.5rad≈⨯，是第四象限角. 故⑥正确.综上，①⑥正确.故选：B.5．（2021·辽宁高三其他模拟）装饰公司制作一种扇形板状装饰品，其圆心角为23π，并在扇形弧上正面等距安装7个发彩光的小灯泡且在背面用导线将小灯泡串连（弧的两端各一个灯泡，导线接头忽略不计），已知扇形的半径为30厘米，则连接导线大致需要的长度约为（）A．55厘米B．63厘米C．69厘米D．76厘米【答案】B【解析】由于实际问题中扇形弧长较小，可将导线的长视为扇形弧长，利用弧长公式计算即可.【详解】因为在弧长比较短的情况下分成6等份，每部分的弦长和弧长相差很小，所以可以用弧长近似代替弦长，所以导线的长度为23020633ππ⨯=≈(厘米）．故选：B6．（2021·上海格致中学高三三模）半径为2，中心角为3π的扇形的面积等于（） A ．43π B ．πC ．23π D ．3π 【答案】C 【解析】根据扇形的面积公式即可求解. 【详解】解：因为扇形的半径2r ，中心角3πα=，所以扇形的面积2211222233S r ππα==⨯⨯=，故选：C.7．（2021·辽宁高三其他模拟）“数摺聚清风，一捻生秋意”是宋朝朱翌描写折扇的诗句，折扇出人怀袖，扇面书画，扇骨雕琢，是文人雅士的宠物，所以又有“怀袖雅物”的别号．如图是折扇的示意图，其中OA ＝20cm ，∠AOB ＝120°，M 为OA 的中点，则扇面（图中扇环）部分的面积是（）A ．50πcm 2B ．100πcm 2C ．150πcm 2D ．200πcm 2【答案】B 【解析】根据扇形面积公式计算可得；【详解】解：扇环的面积为22211332400100222883r S r r παααπ⎛⎫=-==⨯⨯= ⎪⎝⎭．故选：B8．（2021·重庆八中高三其他模拟）如图所示，扇环ABCD 的两条弧长分别是4和10，两条直边AD 与BC 的长都是3，则此扇环的面积为（）A ．84B ．63C ．42D ．21【答案】D 【解析】设扇环的圆心角为α，小圆弧的半径为r ，依题意可得4αr =且()310αr +=，解得α、r ，进而可得结果. 【详解】设扇环的圆心角为α，小圆弧的半径为r ，由题可得4αr =且()310αr +=，解得2α=，2r ，从而扇环面积()221252212S =⨯⨯-=. 故选：D ．9．（2021·浙江高二期末）已知角α的终边过点(1,)P y ，若sin 3α=，则y =___________．【答案】【解析】利用三角函数的定义可求y . 【详解】由三角函数的定义可得sin α==y =故答案为：10．（2021·山东日照市·高三月考）已知函数()3sin,06log ,0xx f x x x π⎧≤⎪=⎨⎪>⎩，则13f f ⎛⎫⎛⎫= ⎪ ⎪⎝⎭⎝⎭______．【答案】12- 【解析】利用分段函数直接进行求值即可．【详解】∵函数()3,06log ,0xsinx f x x x π⎧≤⎪=⎨⎪>⎩， ∴311log 133f ⎛⎫=- ⎪⎝⎭＝， ∴611(1)sin 32f f f π⎛⎫⎛⎫⎛⎫=-=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 故答案为：12-.1．（2021·河南洛阳市·高一期中（文））点P 为圆221x y +=与x 轴正半轴的交点，将点P 沿圆周逆时针旋转至点P '，当转过的弧长为2π3时，点P '的坐标为（）A ．1,2⎛ ⎝⎭B ．12⎛- ⎝⎭C ．21⎛⎫⎪ ⎪⎝⎭D ．122⎛⎫- ⎪ ⎪⎝⎭【答案】B 【解析】先求出旋转角，就可以计算点的坐标了. 【详解】设旋转角为θ，则22123θπππ⨯⨯=，得23πθ=，从而可得1(,22P '-. 故选：B.2．（2021·上海高二课时练习）若A 是三角形的最小内角，则A 的取值范围是（）练提升A ．0,2π⎛⎫⎪⎝⎭B ．0,3π⎛⎫ ⎪⎝⎭C ．,32ππ⎛⎫ ⎪⎝⎭D ．0,3π⎛⎤ ⎥⎝⎦【答案】D 【解析】由给定条件结合三角形三内角和定理即可作答. 【详解】设B ，C 是三角形的另外两个内角，则必有,A B A C ≤≤，又A B C π++=, 则3A A A A A B C π=++≤++=，即3A π≤，当且仅当3C B A π===，即A 是正三角形内角时取“=”，又0A >，于是有03A π<≤，所以A 的取值范围是(0,]3π.故选：D3．（2021·北京清华附中高三其他模拟）已知,R αβ∈．则“,k k Z αβπ=+∈”是“sin 2sin 2αβ=”的（） A ．充分而不必要条件 B ．必要而不充分条件 C ．充分必要条件 D ．既不充分也不必要条件【答案】A 【解析】求解出sin 2sin 2αβ=成立的充要条件，再与,k k Z αβπ=+∈分析比对即可得解. 【详解】,R αβ∈，sin 2sin 2sin[()()]sin[()()]αβαβαβαβαβ=⇔++-=+--⇔2cos()sin()0αβαβ+-=，则sin()0αβ-=或cos()0αβ+=，由sin()0αβ-=得,k k k Z αβπαβπ-=⇔=+∈，由cos()0αβ+=得,22k k k Z ππαβπαβπ+=+⇔=-+∈，显然s ,in 2sin 2k k Z απαββ=+∈=⇒，sin 2s ,in 2k k Z αβαβπ=+=∈，所以“,k k Z αβπ=+∈”是“sin 2sin 2αβ=”的充分不必要条件. 故选：A4．（2021·安徽池州市·池州一中高三其他模拟（理））已知一个半径为3的扇形的圆心角为()02θθπ<<，面积为98π，若()tan 3θϕ+=，则tan ϕ=（） A ．12-B ．34C ．12D ．43【答案】C 【解析】由扇形的面积公式得4πθ=,进而根据正切的和角公式解方程得1tan 2ϕ=. 【详解】解:由扇形的面积公式212S r θ=得9928πθ=,解得4πθ=, 所以()tan tan 1tan tan 31tan tan 1tan θϕϕθϕθϕϕ+++===--,解得1tan 2ϕ=故选:C5．（2021·新蔡县第一高级中学高一月考）一个圆心角为60的扇形，它的弧长是4π，则扇形的内切圆（与扇形的弧和半径的相切）的半径等于（） A ．2 B ．4 C ．2π D ．4π【答案】B 【解析】设扇形内切圆的半径为x ，扇形所在圆的半径为r ，求得3r x =，结合弧长公式，列出方程，即可求解. 【详解】如图所示，设扇形内切圆的半径为x ，扇形所在圆的半径为r ，过点O 作OD CD ⊥，在直角CDO 中，可得2sin 30ODCO x ==，所以扇形的半径为23r x x x =+=，又由扇形的弧长公式，可得343x ππ⨯=，解得4x =，即扇形的内切圆的半径等于4. 故选：B.6．（2021·安徽合肥市·合肥一中高三其他模拟（文））已知顶点在原点的锐角α，始边在x 轴的非负半轴，始终绕原点逆时针转过3π后交单位圆于1(,)3P y -，则sin α的值为（）A ．6B C ．16D ．16【答案】B 【解析】根据任意角的三角函数的定义求出1cos()33πα+=-，然后凑角结合两角差的正弦公式求出sin α. 【详解】由题意得1cos()33πα+=-(α为锐角) ∵α为锐角，∴5336πππα，∴sin()03πα+>sin()sin sin ()3333πππααα⎡⎤⇒+=⇒=+-⎢⎥⎣⎦1132326⎛⎫=⨯--⨯=⎪⎝⎭ 故选：B7．（2020·安徽高三其他模拟（文））已知角α的顶点与原点O 重合，始边与x 轴的非负半轴重合，它的终边经过点A (1，-3)，则tan()4πα+=（）A ．12B ．12-C ．1D ．-1【解析】根据终边上的点求出tan 3α=-，再结合正切和公式求解即可．【详解】由题知tan 3α=-，则tan tan3114tan()41321tan tan 4παπαπα+-++===-+-. 故选：B8．（2021·合肥一六八中学高三其他模拟（理））已知顶点在原点，始边在x 轴非负半轴的锐角α绕原点逆时针转π3后，终边交单位圆于P x ⎛ ⎝⎭，则sin α的值为（） ABCD．【答案】C 【解析】设锐角α绕原点逆时针转π3后得角β，由2113x +=，则x =，分x 的值结合三角函数的定义，求解即可，根据条件进行取舍. 【详解】设锐角α绕原点逆时针转π3后得角β，则3πβα=+，由α为锐角，根据题意角β终边交单位圆于,3P x ⎛ ⎝⎭，则2113x +=，则3x =±若3x =，则sin ,cos 33ββ==所以sin sin sin cos cos sin 03336πππαβββ⎛⎫=-=-=< ⎪⎝⎭，与α为锐角不符合.若x =，则sin ββ==所以sin sin sin cos cos sin 0333πππαβββ⎛⎫=-=-=> ⎪⎝⎭,满足条件.9．（2021·安徽宣城市·高三二模（文））刘徽是中国魏晋时期杰出的数学家，他提出“割圆求周”方法：当n 很大时，用圆内接正n 边形的周长近似等于圆周长，并计算出精确度很高的圆周率 3.1416π≈．在《九章算术注》中总结出“割之弥细，所失弥少，割之又割，以至于不可割，则与圆周合体而无所失矣”的极限思想．运用此思想，当π取3.1416时，可得sin 2︒的近似值为（）A ．0.00873B ．0.01745C ．0.02618D ．0.03491【答案】D 【解析】由圆的垂径定理，求得2sin 2AB =︒，根据扇形对应的弦长之和近似于单位圆的周长，列出方程，即可求解. 【详解】将一个单位圆分成90个扇形，则每个扇形的圆心角度数均为4︒由圆的垂径定理，可得每个圆心角所对的弦长221sin 22sin 2AB AC ==⨯⨯︒=︒，因为这90个扇形对应的弦长之和近似于单位圆的周长，所以9021sin 2180sin 22π⨯⨯⨯︒=︒≈，所以22 3.1416sin 20.03491180180π⨯︒≈=≈．故选：D ．10．（2021·江苏南通市·高三其他模拟）某设计师为天文馆设计科普宣传图片，其中有一款设计图如图所示.QRT 是一个以点O 为圆心､QT 长为直径的半圆，QT =.QST 的圆心为P ，2dm PQ PT ==.QRT与QST 所围的灰色区域QRTSQ 即为某天所见的月亮形状，则该月亮形状的面积为___________2dm .6π 【解析】连接PO ，可得PO QT ⊥，求出23QPT π∠=，利用割补法即可求出月牙的面积. 【详解】解：连接PO ，可得PO QT ⊥，因为sin 2QO QPO PQ ∠==，所以3QPO π∠=，23QPT π∠=，所以月牙的面积为2221121(21)dm 22326S πππ=⨯⨯-⨯⨯-⨯=.6π.1．（全国高考真题）已知角α的终边经过点(−4,3)，则cosα=（）A ．45B ．35C ．−35D ．−45 练真题【答案】D【解析】由题意可知x=-4，y=3，r=5，所以cosα=x r =−45.故选D. 2．（2020·全国高考真题（理））若α为第四象限角，则（）A ．cos2α>0B ．cos2α<0C ．sin2α>0D ．sin2α<0 【答案】D【解析】方法一：由α为第四象限角，可得3222,2k k k Z ππαππ+<<+∈，所以34244,k k k Z ππαππ+<<+∈此时2α的终边落在第三、四象限及y 轴的非正半轴上，所以sin 20α<故选：D. 方法二：当6πα=-时，cos 2cos 03πα⎛⎫=-> ⎪⎝⎭，选项B 错误；当3πα=-时，2cos 2cos 03πα⎛⎫=-< ⎪⎝⎭，选项A 错误；由α在第四象限可得：sin 0,cos 0αα<>，则sin 22sin cos 0ααα=<，选项C 错误，选项D 正确；故选：D.3.（2015·上海高考真题（文））已知点的坐标为，将绕坐标原点逆时针旋转至，则点的纵坐标为（）. A ． B ． C ． D ．【答案】D【解析】由题意，设OA 与x 轴所成的角为，显然，，故，故纵坐标为4．（2018·全国高考真题（文））已知角α的顶点为坐标原点，始边与x 轴的非负半轴重合，终边上有两点A(1 ， a)，B(2 ， b)，且cos2α=23，则|a −b |= A ．15 B ．√55 C ．2√55D ．1 【答案】B【解析】由O,A,B 三点共线，从而得到b =2a ，因为cos2α=2cos 2α−1=2⋅(√a 2+1)2−1=23，解得a 2=15，即|a |=√55，所以|a −b |=|a −2a |=√55，故选B.5.（2017·北京高考真题（理））在平面直角坐标系xOy 中，角α与角β均以Ox 为始边，它们的终边关于y 轴对称.若1sin 3α=，则()cos αβ-=___________. 【答案】79- 【解析】因为α和β关于y 轴对称，所以2,k k Z αβππ+=+∈，那么1sin sin 3βα==，cos cos 3αβ=-=（或cos cos 3βα=-=），所以()2227cos cos cos sin sin cos sin 2sin 19αβαβαβααα-=+=-+=-=-. 6．（2021·北京高考真题）若点(cos ,sin )P θθ与点(cos(),sin())66Q ππθθ++关于y 轴对称，写出一个符合题意的θ=___．【答案】512π（满足5,12k k Z πθπ=+∈即可）【解析】根据,P Q 在单位圆上，可得,6πθθ+关于y 轴对称，得出2,6k k Z πθθππ++=+∈求解. 【详解】(cos ,sin )P θθ与cos ,sin66Q ππθθ⎛⎫⎛⎫⎛⎫++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭关于y 轴对称，即,6πθθ+关于y 轴对称，2,6k k Z πθθππ++=+∈，则5,12k k Z πθπ=+∈，当0k =时，可取θ的一个值为512π. 故答案为：512π（满足5,12k k Z πθπ=+∈即可）.。

【2019版新教材】高中数学A版必修第一册第五章全章节教案教学设计+课后练习及答案(名师推荐精编版)

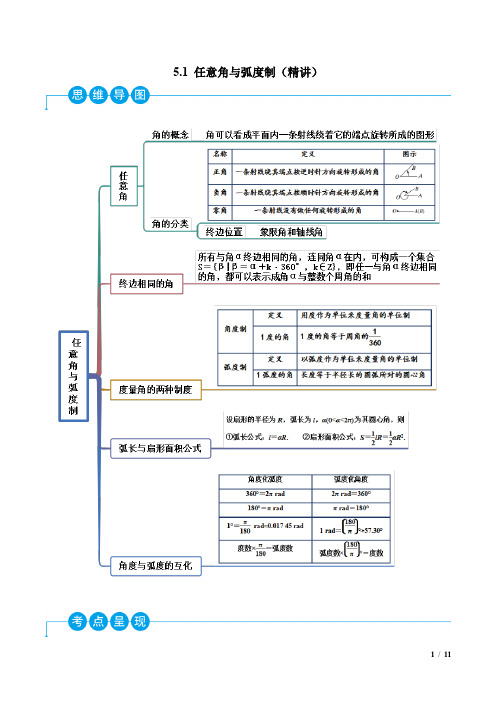
【新教材】人教统编版高中数学A版必修第一册第五章教案教学设计+课后练习及答案5.1.1《任意角和弧度制---任意角》教案教材分析：学生在初中学习了o 0～o 360，但是现实生活中随处可见超出o 0～o 360范围的角.例如体操中有“前空翻转体o 540”，且主动轮和被动轮的旋转方向不一致.因此为了准确描述这些现象，本节课主要就旋转度数和旋转方向对角的概念进行推广.教学目标与核心素养：课程目标1.了解任意角的概念.2.理解象限角的概念及终边相同的角的含义．3.掌握判断象限角及表示终边相同的角的方法．数学学科素养1.数学抽象：理解任意角的概念，能区分各类角；2.逻辑推理：求区域角；3.数学运算：会判断象限角及终边相同的角.教学重难点：重点：理解象限角的概念及终边相同的角的含义；难点：掌握判断象限角及表示终边相同的角的方法．课前准备：多媒体教学方法：以学生为主体，采用诱思探究式教学，精讲多练。

教学工具：多媒体。

教学过程：一、情景导入初中对角的定义是：射线OA 绕端点O 按逆时针方向旋转一周回到起始位置，在这个过程中可以得到o 0～o 360范围内的角.但是现实生活中随处可见超出o 0～o 360范围的角.例如体操中有“前空翻转体o 540”，且主动轮和被动轮的旋转方向不一致.请学生思考，如何定义角才能解决这些问题呢？要求：让学生自由发言，教师不做判断。

而是引导学生进一步观察.研探.二、预习课本，引入新课阅读课本168-170页，思考并完成以下问题1．角的概念推广后，分类的标准是什么？2．如何判断角所在的象限？3．终边相同的角一定相等吗？如何表示终边相同的角？要求：学生独立完成，以小组为单位，组内可商量，最终选出代表回答问题。

三、新知探究1．任意角(1)角的概念角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形．(2)角的表示如图，OA是角α的始边，OB是角α的终边，O是角的顶点．角α可记为“角α”或“∠α”或简记为“α”．(3)角的分类按旋转方向，角可以分为三类：名称定义图示正角按逆时针方向旋转形成的角负角按顺时针方向旋转形成的角零角一条射线没有作任何旋转形成的角2．象限角在平面直角坐标系中，若角的顶点与原点重合，角的始边与 x轴的非负半轴重合，那么，角的终边在第几象限，就说这个角是第几象限角；如果角的终边在坐标轴上，就认为这个角不属于任何一个象限．3．终边相同的角所有与角α终边相同的角，连同角α在内，可构成一个集合S＝{β|β＝α＋k·360°，k∈Z}，即任一与角α终边相同的角，都可以表示成角α与整数个周角的和．四、典例分析、举一反三题型一任意角和象限角的概念例1(1)给出下列说法：①锐角都是第一象限角；②第一象限角一定不是负角；③小于180°的角是钝角、直角或锐角；④始边和终边重合的角是零角．其中正确说法的序号为________(把正确说法的序号都写上)．(2)已知角的顶点与坐标原点重合，始边与x轴的非负半轴重合，作出下列各角，并指出它们是第几象限角．①420°，②855°，③－510°.【答案】（1）①（2）图略，①420°是第一象限角．②855°是第二象限角．③－510°是第三象限角．【解析】(1)①锐角是大于0°且小于90°的角，终边落在第一象限，是第一象限角，所以①正确；②－350°角是第一象限角，但它是负角，所以②错误；③0°角是小于180°的角，但它既不是钝角，也不是直角或锐角，所以③错误；④360°角的始边与终边重合，但它不是零角，所以④错误．(2) 作出各角的终边，如图所示：由图可知：①420°是第一象限角．②855°是第二象限角．③－510°是第三象限角．解题技巧：（任意角和象限角的表示）1．判断角的概念问题的关键与技巧．(1)关键：正确的理解角的有关概念，如锐角、平角等；(2)技巧：注意“旋转方向决定角的正负，旋转幅度决定角的绝对值大小．2．象限角的判定方法．(1)图示法：在坐标系中画出相应的角，观察终边的位置，确定象限．(2)利用终边相同的角：第一步，将α写成α＝k·360°＋β(k∈Z，0°≤β<360°)的形式；第二步，判断β的终边所在的象限；第三步，根据β的终边所在的象限，即可确定α的终边所在的象限．跟踪训练一1．已知集合A＝{第一象限角}，B＝{锐角}，C＝{小于90°的角}，则下面关系正确的是( )A．A＝B＝C B．A⊆CC．A∩C＝B D．B∪C⊆C【答案】D【解析】由已知得B C，所以B∪C⊆C，故D正确．2．给出下列四个命题：①－75°是第四象限角；②225°是第三象限角；③475°是第二象限角；④－315°是第一象限角．其中正确的命题有( )A．1个 B．2个 C．3个 D．4个【答案】D【解析】－90°＜－75°＜0°，180°＜225°＜270°，360°＋90°＜475°＜360°＋180°，－315°＝－360°＋45°且0°＜45°＜90°.所以这四个命题都是正确的．题型二终边相同的角的表示及应用例2(1)将－885°化为k·360°＋α(0°≤α＜360°，k∈Z)的形式是________．(2)写出与α＝－910°终边相同的角的集合，并把集合中适合不等式－720°＜β＜360°的元素β写出来．【答案】（1）(－3)×360°＋195°，（2）终边相同的角的集合为{β|β＝k·360°－910°，k∈Z}，适合不等式－720°＜β＜360°的元素－550°、－190°、170°.【解析】(1)－885°＝－1 080°＋195°＝(－3)×360°＋195°.(2)与α＝－910°终边相同的角的集合为{β|β＝k·360°－910°，k∈Z}，∵－720°＜β＜360°，即－720°＜k·360°－910°＜360°，k∈Z，∴k取1，2，3.当k＝1时，β＝360°－910°＝－550°；当k＝2时，β＝2×360°－910°＝－190°；当k＝3时，β＝3×360°－910°＝170°.解题技巧：(终边相同的角的表示)1．在0°到360°范围内找与给定角终边相同的角的方法(1)一般地，可以将所给的角α化成k·360°＋β的形式(其中0°≤β＜360°，k∈Z)，其中β就是所求的角．(2)如果所给的角的绝对值不是很大，可以通过如下方法完成：当所给角是负角时，采用连续加360°的方式；当所给角是正角时，采用连续减360°的方式，直到所得结果达到所求为止．2．运用终边相同的角的注意点所有与角α终边相同的角，连同角α在内可以用式子k·360°＋α，k∈Z表示，在运用时需注意以下四点：(1)k是整数，这个条件不能漏掉．(2)α是任意角．(3)k·360°与α之间用“＋”连接，如k·360°－30°应看成k·360°＋(－30°)，k∈Z.(4)终边相同的角不一定相等，但相等的角终边一定相同，终边相同的角有无数个，它们相差周角的整数倍．跟踪训练二1.下面与－850°12′终边相同的角是( )A ．230°12′B ．229°48′C ．129°48′D ．130°12′【答案】B【解析】与－850°12′终边相同的角可表示为α＝－850°12′＋k ·360°(k ∈Z)，当k ＝3时，α＝－850°12′＋1 080°＝229°48′.2．写出角α的终边落在第二、四象限角平分线上的角的集合为________．【答案】{α|α＝k ·180°＋135°，k ∈Z}．【解析】落在第二象限时，表示为k ·360°＋135°.落在第四象限时，表示为k ·360°＋180°＋135°，故可合并为{α|α＝k ·180°＋135°，k ∈Z}．题型三任意角终边位置的确定和表示例3 (1)若α是第一象限角，则α2是( )A ．第一象限角B ．第一、三象限角C ．第二象限角D ．第二、四象限角(2)已知，如图所示．①分别写出终边落在OA ，OB 位置上的角的集合；②写出终边落在阴影部分(包括边界)的角的集合．【答案】(1)B (2) ①终边落在OA 位置上的角的集合为{α|α＝135°＋k ·360°，k ∈Z}；终边落在OB 位置上的角的集合为{β|β＝－30°＋k ·360°，k ∈Z}．②故该区域可表示为{γ|－30°＋k ·360°≤γ≤135°＋k ·360°，k ∈Z}．【解析】(1) 因为α是第一象限角，所以k ·360°＜α＜k ·360°＋90°，k ∈Z ，所以k ·180°＜α2＜k ·180°＋45°，k ∈Z ，当k 为偶数时，α2为第一象限角；当k 为奇数时，α2为第三象限角．所以α2是第一、三象限角．(2) ①终边落在OA位置上的角的集合为{α|α＝90°＋45°＋k·360°，k∈Z}＝{α|α＝135°＋k·360°，k∈Z}；终边落在OB位置上的角的集合为{β|β＝－30°＋k·360°，k∈Z}．②由题干图可知，阴影部分(包括边界)的角的集合是由所有介于[－30°，135°]之间的与之终边相同的角组成的集合，故该区域可表示为{γ|－30°＋k·360°≤γ≤135°＋k·360°，k∈Z}．解题技巧：（任意角终边位置的确定和表示）1．表示区间角的三个步骤：第一步：先按逆时针的方向找到区域的起始和终止边界；第二步：按由小到大分别标出起始和终止边界对应的－360°～360°范围内的角α和β，写出最简区间{x|α<x<β}，其中β－α<360°；第三步：起始、终止边界对应角α，β再加上360°的整数倍，即得区间角集合．提醒：表示区间角时要注意实线边界与虚线边界的差异．2．nα或所在象限的判断方法：的范围；(1)用不等式表示出角nα或αn所在象限．(2)用旋转的观点确定角nα或αn跟踪训练三1．如图所示的图形，那么终边落在阴影部分的角的集合如何表示？【答案】角β的取值集合为{β|n·180°＋60°≤β<n·180°＋105°，n∈Z}．【解析】在0°～360°范围内，终边落在阴影部分(包括边界)的角为60°≤β<105°与240°≤β<285°，所以所有满足题意的角β为{β|k·360°＋60°≤β<k·360°＋105°，k∈Z}∪{β|k·360°＋240°≤β<k·360°＋285°，k∈Z}＝{β|2k·180°＋60°≤β<2k·180°＋105°，k∈Z}∪{β|(2k＋1)·180°＋60°≤β<(2k＋1)·180°＋105°，k∈Z}＝{β|n·180°＋60°≤β<n·180°＋105°，n∈Z}．故角β的取值集合为{β|n·180°＋60°≤β<n·180°＋105°，n∈Z}．五、课堂小结让学生总结本节课所学主要知识及解题技巧六、板书设计七、作业课本171页练习及175页习题5.1 1、2、7题.教学反思：本节课主要采用讲练结合与分组探究的教学方法，让学生从旋转方向和旋转度数熟悉角的概念，象限角，终边相同的角等，并且掌握其应用.5.1.2《任意角和弧度制---弧度制》教案教材分析：前一节已经学习了任意角的概念，而本节课主要依托圆心角这个情境学习一种用长度度量角的方法—弧度制，从而将角与实数建立一一对应关系，为学习本章的核心内容—三角函数扫平障碍，打下基础.教学目标与核心素养：课程目标1.了解弧度制,明确1弧度的含义.2.能进行弧度与角度的互化.3.掌握用弧度制表示扇形的弧长公式和面积公式.数学学科素养1.数学抽象：理解弧度制的概念；2.逻辑推理：用弧度制表示角的集合；3.直观想象：区域角的表示；4.数学运算：运用已知条件处理扇形有关问题.教学重难点：重点：弧度制的概念与弧度制与角度制的转化；难点：弧度制概念的理解．课前准备：多媒体教学方法：以学生为主体，采用诱思探究式教学，精讲多练。

高中数学新教材必修第一册第五章三角函数 5.1 任意角和弧度制(南开题库详解)

第五章三角函数 5.1 任意角和弧度制一、选择题（共60小题；共300分）1. 下列结论正确的是A. 终边相同的角一定相等B. 轴上的角均可表示为C. 第一象限的角都是锐角D. 钝角一定是第二象限的角2. 如果，，则是A. 第一或第三象限角B. 第一或第二象限角C. 第二或第四象限角D. 第三或第四象限角3. 已知角，的终边相同，那么的终边在A. 轴非负半轴上B. 轴非负半轴上C. 轴非正半轴上D. 轴非正半轴上4. 在半径不等的两个圆内，弧度的圆心角A. 所对弧长相等B. 所对的弦长相等C. 所对弧长等于各自半径D. 所对弦长等于各自半径5. 下列四个选项中，与角终边相同的角是A. B. C. D.6. 与的终边相同的角是A. B. C. D.7. 下列命题正确的是A. 第一象限角一定不是负角B. 小于的角一定是锐角C. 钝角一定是第二象限角D. 终边相同的角一定相等8. 若是第二象限角，则是A. 第一象限角B. 第二象限角C. 第三象限角D. 第四象限角9. 的弧度数是A. B. C. D.10. 已知一个扇形的圆心角的弧度数为，则该扇形的弧长与半径的比等于A. B. C. D.11. 半径为，中心角为的弧长为A. B. C. D.12. 下列各组角中，终边相同的是A. 与，B. 与，C. 与，D. 与，13. 一个扇形的圆心角为，半径为，则此扇形的面积为A. B. C. D.14. 与角终边相同的角是A. B. C. D.15. 圆弧长度等于圆弧所在圆的内接正三角形的边长，则圆弧所对圆心角的弧度数为A. B. C. D.16. 集合中，各角的终边都在A. 轴正半轴上B. 轴正半轴上C. 轴或轴上D. 轴正半轴或轴正半轴上17. 已知扇形的半径为，周长为，则扇形的圆心角等于A. B. C. D.18. 设集合，，那么A. B. C. D.19. 把表示成的形式，使最小的的值是A. B. C. D.20. 设小于的角，锐角，第一象限的角，小于但不小于的角，那么有A. B.C. D.21. 已知为第二象限角，则所在的象限是A. 第一或第二象限B. 第二或第三象限C. 第一或第三象限D. 第二或第四象限22. 下列命题正确的是A. 第一象限角一定不是负角B. 小于的角一定是锐角C. 钝角一定是第二象限角D. 终边相同的角一定相等23. 将表的分针拨快分钟，则分针旋转过程中形成的角的弧度数是A. B. C. D.24. 将化为弧度为A. B. C. D.25. 是A. 第一象限角B. 第二象限角C. 第三象限角D. 第四象限角26. 对于始边相同的角，下列命题正确的是A. 第一象限角必定为锐角B. 终边相同的角必定相等C. 相等的角，其终边位置必定相同D. 不相等的角，其终边位置必定不同27. 已知扇形的周长为，圆心角为弧度，则该扇形的面积为A. B. C. D.28. 下列选项中叙述正确的是A. 三角形的内角是第一象限角或第二象限角B. 锐角是第一象限的角C. 第二象限的角比第一象限的角大D. 终边不同的角同一三角函数值不相等29. 与角的终边相同的角是A. B. C. D.30. 角的终边所在的象限是A. 第一象限B. 第二象限C. 第三象限D. 第四象限31. ，则的终边在A. 第一象限B. 第二象限C. 第三象限D. 第四象限32. 已知集合，，则等于A.B.C.D. 或33. 将分针拨慢分钟，则分钟转过的弧度数是A. B. C. D.34. 下列说法正确的是A. 第二象限的角比第一象限的角大B. 若，则C. 三角形的内角是第一象限角或第二象限角D. 不论用角度制还是弧度制度量一个角，它们与扇形所对应的半径的大小无关35. 时钟经过一小时，时针转过了A. B. C. D.36. 若一扇形的圆心角为，半径为，则扇形的面积为A. B. C. D.37. 时钟经过一小时，时针转过了A. B. C. D.38. 已知第一象限角，锐角，小于的角，那么，，之间的关系是A. B. C. D.39. 周长为，圆心角为的扇形面积为A. B. C. D.40. 已知扇形的圆心角为，半径等于，则扇形的弧长为A. B. C. D.41. 在单位圆中，面积为的扇形所对的弧长为A. B. C. D.42. 集合中的角的终边所在的范围（阴影部分）是A. B.C. D.43. 已知扇形的周长是，面积是，则扇形的圆心角的弧度数是A. 或B.C.D.44. 给出下列命题：①第二象限角大于第一象限角；②三角形的内角是第一象限角或第二象限角；③不论用角度制还是用弧度制度量一个角，它们与扇形所对半径的大小无关；④若，则与的终边相同；⑤若，则是第二或第三象限的角．其中正确命题的个数是A. B. C. D.45. 已知扇形的周长为，圆心角为弧度，则该扇形的面积为A. B. C. D.46. 已知弧度的圆心角所对的弦长为，则这个圆心角所对的弧长是A. B. C. D.47. 一圆内切于圆心角为，半径为的扇形，则该圆的面积与扇形面积之比为A. B. C. D.48. 中心角为的扇形，它的弧长为，则三角形的内切圆半径为A. B. C. D.49. 若圆弧长度等于圆内接正三角形的边长，则其圆心角的弧度数为A. B. C. D.50. 设集合，，那么A. B. C. D.51. 下列结论中错误的是A. 若，则B. 若是第二象限角，则为第一象限或第三象限角C. 若角的终边过点，则D. 若扇形的周长为，半径为，则其中心角的大小为弧度52. 若角和角的终边关于轴对称，则角可以用角表示为A. B.C. D.53. 若角和角的终边关于轴对称，则角可以用角表示为A. B.C. D.54. 设，下列终边相同的角是A. 与B. 与C. 与D. 与55. 在一块顶角为，腰长为的等腰三角形钢板废料中裁剪扇形，现有如图所示两种方案，则A. 方案一中扇形的周长更长B. 方案二中扇形的周长更长C. 方案一中扇形的面积更大D. 方案二中扇形的面积更大56. 已知第一象限角，锐角，小于的角，那么，，关系是A. B. C. D.57. 设集合，集合，则．A. B. C. D.58. 下列命题中正确的是A. 若，则是第一或第三象限角B. 若，则C. 若，则与的终边相同D. 若角的终边在坐标轴上，则，59. 已知，则是A. 第一象限或第二象限的角B. 第二象限或第四象限的角C. 第一象限或第三象限的角D. 第二象限或第三象限的角60. 若是第二象限角，那么和都不是A. 第一象限角B. 第二象限角C. 第三象限角D. 第四象限角二、填空题（共30小题；共150分）61. 若角，则角的终边在第象限．62. 与角终边相同的角的集合是，它们中最小的正角是，最大的负角是，它们是第象限角．63. 某蒸汽机上的飞轮直径为，每分钟按顺时针方向旋转转，则飞轮每秒钟转过的弧度数是；轮周上的一点每秒钟经过的弧长为．64. 设，且角的终边与角的终边相同，则．65. 如图所示，用集合表示终边在阴影部分的角的集合为．66. 已知扇形的半径为，圆心角为弧度，则该扇形的面积为．67. 有下列四个结论：①角和的终边重合，则，；②角和的终边关于原点对称，则，；③角和的终边关于轴对称，则，；④角和的终边关于轴对称，则，．其中正确的有．（填序号）68. 若是第四象限，则是第象限角．69. 如果把化为（，）的形式，那么，．70. 已知角的终边经过点，且为第三象限角，则的取值范围是．71. 在集合中，属于区间的角的集合是．72. 终边与角的终边互相垂直的角的集合是．73. 若角的终边与角的终边关于直线对称，且，则．74. 已知扇形的面积为，扇形圆心角的弧度数是，那么扇形的周长为．75. 巳知一扇形的圆心角，那么此扇形的面积与其内切圆的面积之比为．76. 如图，已知扇形的圆心角为，半径为，则扇形中所含弓形的面积是．77. 已知扇形的周长为，那么当扇形的半径为时，扇形的面积最大．78. 已知圆心角为的扇形的弧长为，则它的内切圆半径是．79. 若某扇形的面积是，它的周长是，则该扇形圆心角的弧度数为．80. 若圆弧长度等于该圆内接正方形的边长，则其圆心角的弧度数是．81. 若将时钟拨慢，则时针转了；若将时钟拨快，则分针转了．82. 下列说法：①终边相同的角一定相等；②第二象限角大于第一象限角；③的角是第一象限角；④小于的角是钝角，直角或锐角．⑤弧度是的圆心角所对的弧；⑥弧度是长度等于半径的圆弧所对圆心角；⑦弧度等于．其中正确的序号为（把正确的序号都写出来）．83. 给出下列命题：第二象限角大于第一象限角；三角形的内角是第一象限角或第二象限角；不论是用角度制还是用弧度制度量一个角，它们与扇形的半径的大小无关；若，则与的终边相同；若，则是第二或第三象限的角．其中不正确的命题是．84. 若扇形的圆心角为，弧长为，则扇形的半径为．85. 如图，点，，是圆上的点，且，，则劣弧的长为．86. （）终边在直线上的角的集合是．（）若角的终边与角的终边相同，则在内终边与角的终边相同的角的个数为．87. 用弧度制表示终边在直线上的角的集合是．88. 有下列四个结论：①角和角的终边重合，则，；②角和角的终边关于原点对称，则，；③角和角的终边关于轴对称，则，；④角和角的终边关于轴对称，则，．其中正确的有．（填序号）89. 圆的半径为，为圆周上一点，现将如图放置的边长为的正方形（实线所示，正方形的顶点与点重合）沿圆周逆时针滚动，点第一次回到点的位置，则点走过的路径的长度为．90. 如图，在平面直角坐标系中，一单位圆的圆心的初始位置在，此时圆上一点的位置在，圆在轴上沿正向滚动．当圆滚动到圆心位于时，的坐标为．三、解答题（共10小题；共130分）91. 已知，若的终边与角的终边重合，求角．92. 试求出终边在如图所示阴影区域内的角的集合．93. 已知，求，并指出的终边位置．94. 今天是周日，那天后是周几?过多少天是周二?在数轴上表达：如图，周二是那些天?如何统一表达?95. （1）写出与下列各角终边相同的角的集合，并把中适合不等式的元素写出来：①；②（2）试写出终边在直线上的角的集合，并把中适合不等式的元素写出来．96. 已知扇形的圆心角是，半径是，弧长为．（1）若，，求扇形的面积；（2）若扇形的周长为，求扇形面积的最大值，并求此时扇形圆心角的弧度数．97. 如图，动点，从点出发，沿着圆周做匀速运动．点按逆时针方向每秒转，点按顺时针方向每秒转，求点，第一次相遇时所用的时间及点，各自走过的弧长．98. 己知弦长为，它所对的圆心角，求所夹的扇形面积以及所对的弓形的周长．99. 设是第二象限角，试比较，，的大小．100. 如图，在扇形中，，弧长为，求此扇形内切圆的面积．答案第一部分1. D2. A3. A4. C5. C6. D7. C8. A9. A10. C11. D12. D13. A 【解析】因为扇形的圆心角为，半径为，所以扇形的面积．14. D15. C16. C17. B18. B19. C20. D21. C22. C23. C 【解析】将表的分针拨快应按顺时针方向旋转，为负角.故A、B不正确，又因为拨快分钟，故转过的角的大小应为圆周的 .故所求角的弧度数为 .24. B25. B26. C27. A 【解析】设扇形的弧长为，扇形所在圆的半径为，由题意得解得．扇形28. B29. A30. C【解析】由，知角和角终边相同，在第三象限．31. C32. D33. C【解析】钟表的指针按顺时针方向转动，角为负角．．36. B 【解析】，所以扇形37. B 【解析】钟表的指针按顺时针方向转动，角为负角．38. A39. A40. A41. B42. C 【解析】当时，；当时，，应选C．43. A44. A 【解析】由于第一象限角不小于第二象限角，故①错；当三角形的内角为时，其既不是第一象限角，也不是第二象限角，故②错；③正确；由于，但与的终边不相同，故④错；当，时既不是第二象限角，又不是第三象限角，故⑤错．综上可知只有③正确．45. A【解析】由题意得解得所以．46. C 【解析】由题设，圆弧的半径，所以圆心角所对的弧长．47. B48. B49. D 【解析】如图，等边三角形是半径为的圆的内接三角形，则线段所对的圆心角，作，垂足为，在中，，，所以，，所以，由弧长公式得．50. B51. C52. B53. B【解析】因为为顶角为，腰长为的等腰三角形，所以，，，所以方案一中扇形的周长，方案二中扇形的周长，方案一中扇形的面积，方案二中扇形的面积．56. B 【解析】因为第一象限角，小于的角，锐角，所以．集合57. D 【解析】集合，所以．58. D 【解析】当时，，但不是第一或第三象限角，所以A不正确；当，时，，所以B不正确；当，时，，但是与的终边不相同，所以C不正确；D 正确．59. C 【解析】提示：由已知，所以，即．故是第一象限或第三象限的角．60. B【解析】因为是第二象限角，所以，，所以，，所以是第一或第三象限角，而是第三象限角，所以是第四象限角．第二部分61. 二62. ；，；，；，三63. ，64.65.【解析】由题图知，终边落在射线上的角为，以为终边的角与角的终边相同，所以终边落在图中阴影部分的角的集合为．66.【解析】根据扇形的弧长公式可得，根据扇形的面积公式可得．67. ①②③④68. 三69. 略，略70.71.72. 略73.74.【解析】设扇形的半径为，则，所以，所以扇形的周长为．75.【解析】设扇形的半径为，内切圆的半径为，则，即．又扇，内切圆，所以扇内切圆．76.【解析】因为扇形（），（），所以弓形扇形（）．77.【解析】设扇形的圆心角为，半径为，扇形的弧长．因为，，所以扇形当时，扇形的面积最大．78.【解析】如图，设内切圆半径为，则扇形的半径为，扇形弧长，解得．79.【解析】设扇形的半径为，弧长为，由题意知解得所以扇形的圆心角的弧度数为．80.【解析】设圆半径为，则圆内接正方形的对角线长为，所以正方形边长为，所以圆心角的弧度数是．81. ，【解析】将时针拨慢，时针按逆时针方向转动，转过的是正角，转过的度数为．将时针拨快，分针按顺时针方向转动，转过的是负角，转过的度数为．82. ⑥【解析】（1）明确各种角的定义，逐一判断即可．对于①，终边相同的角不一定相等，终边相同的角有无数多个，它们相差的整数倍，故①是错误的；对于②，角是第一象限角，角是第二象限角，，所以②错误；对于③，的角是指的角，其中角不是任何象限的角，为轴线角，故③错误；对于④，小于的角指满足的角，其中也包括负角和零角，故④错误．（2）弧度角的定义：把长度等于半径长的弧所对的圆心角叫做弧度的角．由此可知，只有⑥正确．⑤⑦错误．83.【解析】由于第一象限角不小于第二象限角，故错；当三角形的内角为时，其既不是第一象限角，也不是第二象限角，故错；正确；由于，但与的终边不相同，故错；当，时既不是第二象限角，又不是第三象限角，故错．综上可知只有正确．84.【解析】由，解得．85.【解析】．86. ，【解析】（）在内终边在直线上的角为，所以终边在直线上的角的集合为．（）因为，所以，依题意，，所以，所以＝，即在内与角的终边相同的角为，，共三个．87.【解析】，，，解得，又，故，，，角为，，．88. ①②③④89. ．【解析】每次转动一个边长时，圆心角转过，正方形有边，所以需要转动次，回到起点．在这次中，半径为的次，半径为的次，半径为的次，点走过的路径的长度= + = ．90.【解析】设，，由题意知劣弧长为，由于圆的半径为，所以．设，则，，所以的坐标为．第三部分91. 略92. 因为，所以终边在题图所示阴影区域内的角的集合为．93. 略94. 略．95. （1）①，其中适合不等式的元素为：，，；②，其中适合不等式的元素为：，，．（2）终边在直线上的角的集合其中适合不等式的元素为：，．96. （1）．（2）由题意知，即，，当时，的最大值为，当时，，．即扇形面积的最大值为，此时扇形圆心角的弧度数为．97. ，得秒，走过的弧长为，走过的弧长为．98. （）；（）．99. 因为是第二象限角，所以，，所以，，所以是第一或第三象限角（如图阴影部分）．结合单位圆上的三角函数线可得，（i）当是第一象限角时，，，，从而得；（ii）当是第三象限角时，，，，从而得．综上，当是第一象限角，即，时，；当是第三象限角，即，时，．100. 设扇形的半径为，其内切圆的半径为，由已知得，．又因为，所以．所以内切圆的面积为．。

高中数学新教材必修第一册第五章三角函数 5.1 任意角和弧度制(南开题库含详解)

第五章三角函数 5.1 任意角和弧度制一、选择题（共40小题；共200分）1. 下列四个选项中，与角终边相同的角是A. B. C. D.2. 已知一个扇形的圆心角的弧度数为，则该扇形的弧长与半径的比等于A. B. C. D.3. 的弧度数是A. B. C. D.4. 与的终边相同的角是A. B. C. D.5. 把表示成的形式，使最小的的值是A. B. C. D.6. 与角的终边相同的角是A. B. C. D.7. 将化为弧度为A. B. C. D.8. 是A. 第一象限角B. 第二象限角C. 第三象限角D. 第四象限角9. 一个扇形的圆心角为，半径为，则此扇形的面积为A. B. C. D.10. 已知为第二象限角，则所在的象限是A. 第一或第二象限B. 第二或第三象限C. 第一或第三象限D. 第二或第四象限11. 在单位圆中，面积为的扇形所对的弧长为A. B. C. D.12. 与角终边相同的角是A. B. C. D.13. 下列说法正确的是A. 第二象限的角比第一象限的角大B. 若，则C. 三角形的内角是第一象限角或第二象限角14. 将分针拨慢分钟，则分钟转过的弧度数是A. B. C. D.15. 已知扇形的周长为，圆心角为弧度，则该扇形的面积为A. B. C. D.16. 已知集合，，则等于A.B.C.D. 或17. ，则的终边在A. 第一象限B. 第二象限C. 第三象限D. 第四象限18. 圆弧长度等于圆弧所在圆的内接正三角形的边长，则圆弧所对圆心角的弧度数为A. B. C. D.19. 时钟经过一小时，时针转过了A. B. C. D.20. 集合中的角的终边所在的范围（阴影部分）是A. B.C. D.21. 下列命题中：①小于的角是锐角，②第二象限角是钝角，③终边相同的角相等，④若与有相同的终边，则必有，正确的个数是A. B. C. D.22. 时钟经过一小时，时针转过了A. B. C. D.23. 设小于的角，锐角，第一象限的角，小于但不小于的角，那么有A. B.C. D.A. 轴正半轴上B. 轴正半轴上C. 轴或轴上D. 轴正半轴或轴正半轴上25. 已知扇形的半径为，周长为，则扇形的圆心角等于A. B. C. D.26. 设集合，，那么A. B. C. D.27. 若一扇形的圆心角为，半径为，则扇形的面积为A. B. C. D.28. 已知扇形的周长为，圆心角为弧度，则该扇形的面积为A. B. C. D.29. 下列结论中错误的是A. 若，则B. 若是第二象限角，则为第一象限或第三象限角C. 若角的终边过点，则D. 若扇形的周长为，半径为，则其中心角的大小为弧度30. 给出下列命题：①第二象限角大于第一象限角；②三角形的内角是第一象限角或第二象限角；③不论用角度制还是用弧度制度量一个角，它们与扇形所对半径的大小无关；④若，则与的终边相同；⑤若，则是第二或第三象限的角．其中正确命题的个数是A. B. C. D.31. 设集合，集合，则．A. B. C. D.32. 若是第二象限角，那么和都不是A. 第一象限角B. 第二象限角C. 第三象限角D. 第四象限角33. 若圆弧长度等于圆内接正三角形的边长，则其圆心角的弧度数为A. B. C. D.34. 设集合，，那么A. B. C. D.35. 已知扇形的周长是，面积是，则扇形的圆心角的弧度数是A. 或B.C.D.36. 若角和角的终边关于轴对称，则角可以用角表示为A. B.C. D.37. 若角和角的终边关于轴对称，则角可以用角表示为A. B.C. D.38. 设，下列终边相同的角是A. 与B. 与C. 与D. 与39. 中心角为的扇形，它的弧长为，则三角形的内切圆半径为A. B. C. D.40. 一圆内切于圆心角为，半径为的扇形，则该圆的面积与扇形面积之比为A. B. C. D.二、填空题（共40小题；共200分）41. 若是第三象限的角，则是第象限角．42. 若角，则角的终边在第象限．43. 如图，射线绕顶点顺时针旋转到，再逆时针旋转到达，则的度数为．44. 将化为弧度为．45. 若是第四象限，则是第象限角．46. 已知扇形的半径为，圆心角为弧度，则该扇形的面积为．47. 已知角的终边经过点，且为第三象限角，则的取值范围是．48. 若扇形的中心角为，则扇形的内切圆的面积与扇形面积之比为．49. 终边与角的终边互相垂直的角的集合是．50. 某蒸汽机上的飞轮直径为，每分钟按顺时针方向旋转转，则飞轮每秒钟转过的弧度数是；轮周上的一点每秒钟经过的弧长为．51. 与角终边相同的角的集合是，它们中最小的正角是，最大的负角是，它们是第象限角．52. 的角化为角度制的结果为，的角化为弧度制的结果为．53. 已知扇形的周长为，圆心角为弧度，则该扇形的面积为．54. 设，且角的终边与角的终边相同，则．55. 如图所示，用集合表示终边在阴影部分的角的集合为．56. 已知，的终边所在的象限是．57. 有下列四个结论：①角和的终边重合，则，；②角和的终边关于原点对称，则，；③角和的终边关于轴对称，则，；④角和的终边关于轴对称，则，．其中正确的有．（填序号）58. 如果把化为（，）的形式，那么，．59. 在集合中，属于区间的角的集合是．60. 若圆弧长度等于该圆内接正方形的边长，则其圆心角的弧度数是．61. 把写成的形式为．62. 已知圆心角为的扇形的弧长为，则它的内切圆半径是．63. 如图，点，，是圆上的点，且，，则劣弧的长为．64. 如图，已知扇形的圆心角为，半径为，则扇形中所含弓形的面积是．65. 若将时钟拨慢，则时针转了；若将时钟拨快，则分针转了．66. 已知扇形的面积为，扇形圆心角的弧度数是，那么扇形的周长为．68. 巳知一扇形的圆心角，那么此扇形的面积与其内切圆的面积之比为．69. 下列说法：①终边相同的角一定相等；②第二象限角大于第一象限角；③的角是第一象限角；④小于的角是钝角，直角或锐角．⑤弧度是的圆心角所对的弧；⑥弧度是长度等于半径的圆弧所对圆心角；⑦弧度等于．其中正确的序号为（把正确的序号都写出来）．70. 给出下列命题：第二象限角大于第一象限角；三角形的内角是第一象限角或第二象限角；不论是用角度制还是用弧度制度量一个角，它们与扇形的半径的大小无关；若，则与的终边相同；若，则是第二或第三象限的角．其中不正确的命题是．71. 若扇形的圆心角为，弧长为，则扇形的半径为．72. （）终边在直线上的角的集合是．（）若角的终边与角的终边相同，则在内终边与角的终边相同的角的个数为．73. 若角的终边与角的终边关于直线对称，且，则．74. 有下列四个结论：①角和角的终边重合，则，；②角和角的终边关于原点对称，则，；③角和角的终边关于轴对称，则，；④角和角的终边关于轴对称，则，．其中正确的有．（填序号）75. 扇形的周长为，若这个扇形的面积为，则圆心角的大小为 .76. 已知扇形的周长为，那么当扇形的半径为时，扇形的面积最大．77. 若某扇形的面积是，它的周长是，则该扇形圆心角的弧度数为．78. 如图，在平面直角坐标系中，一单位圆的圆心的初始位置在，此时圆上一点的位置在，圆在轴上沿正向滚动．当圆滚动到圆心位于时，的坐标为．79. 圆的半径为，为圆周上一点，现将如图放置的边长为的正方形（实线所示，正方形的顶点和点重合）沿着圆周顺时针滚动，经过若干次滚动，点第一次回到点的位置，则点走过的路径的长度为．80. 圆的半径为，为圆周上一点，现将如图放置的边长为的正方形（实线所示，正方形的顶点与点重合）沿圆周逆时针滚动，点第一次回到点的位置，则点走过的路径的长度为．三、解答题（共20小题；共260分）81. 将集合中的角（角度制）在数轴上表达出来，并表示出第一象限角，锐角，负角的区间．82. 今天是周日，那天后是周几?过多少天是周二?在数轴上表达：如图，周二是那些天?如何统一表达?83. 已知角的终边与的终边相同，求在内与终边相同的角．84. 已知，若的终边与角的终边重合，求角．85. 用弧度制表达．写出终边在下列阴影部分内的角的集合（含边界）．（1）（2）86. 已知，求，并指出的终边位置．87. 集合，，试确定集合与之间的关系．88. （1）写出与下列各角终边相同的角的集合，并把中适合不等式的元素写出来：①；②（2）试写出终边在直线上的角的集合，并把中适合不等式的元素写出来．89. 试求出终边在如图所示阴影区域内的角的集合．90. 如图，三棱锥内接于一个圆锥（有公共顶点和底面，侧棱与圆锥母线重合）．已知，，，，（1）求圆锥的侧面积及侧面展开图的中心角；（2）求经过圆锥的侧面到点的最短距离．91. 如图，动点，从点出发，沿着圆周做匀速运动．点按逆时针方向每秒转，点按顺时针方向每秒转，求点，第一次相遇时所用的时间及点，各自走过的弧长．92. 请回答下列问题：（1）设，，用弧度制表示它们，并指出它们各自所在的象限．（2）设，，用角度制表示它们，并在～的范围内找出终边相同的所有角．93. 己知弦长为，它所对的圆心角，求所夹的扇形面积以及所对的弓形的周长．94. 已知是第二象限的角，求，是第几象限的角．95. 设是第二象限角，试比较，，的大小．96. 如图，在扇形中，，弧长为，求此扇形内切圆的面积．97. 如图所示，点在半径为且圆心在原点的圆上，．点从点出发，依逆时针方向匀速地沿圆周旋转，已知在内转过的角度为，经过到达第三象限，经过后又回到出发点，求，并判断其是第几象限角．98. 已知扇形的圆心角是，半径是，弧长为．（1）若，，求扇形的面积；（2）若扇形的周长为，求扇形面积的最大值，并求此时扇形圆心角的弧度数．99. （1）已知扇形的周长为，面积为，求扇形的圆心角的弧度数．（2）已知扇形的周长为，当它的半径和圆心角取什么值时，才能使扇形的面积最大?最大面积是多少?100. 如图，一个扇形的周长为，问它的圆心角取何值时，扇形的面积最大?并求出最大值．答案第一部分1. C2. C3. A4. D5. C6. A7. B8. B9. A 【解析】因为扇形的圆心角为，半径为，所以扇形的面积．10. C11. B12. D13. D14. C15. A【解析】设扇形的弧长为，扇形所在圆的半径为，由题意得解得．扇形16. D17. C18. C19. B 【解析】钟表的指针按顺时针方向转动，角为负角．20. C【解析】当时，；当时，，应选C．21. B22. B 【解析】钟表的指针按顺时针方向转动，角为负角．23. D24. C25. B26. B．27. B 【解析】，所以扇形28. A 【解析】由题意得解得所以．29. C30. A【解析】由于第一象限角不小于第二象限角，故①错；当三角形的内角为时，其既不是第一象限角，也不是第二象限角，故②错；③正确；由于，但与的终边不相同，故④错；当，时既不是第二象限角，又不是第三象限角，故⑤错．综上可知只有③正确．集合31. D 【解析】集合，所以．32. B 【解析】因为是第二象限角，所以，，所以，，所以是第一或第三象限角，而是第三象限角，所以是第四象限角．33. D 【解析】如图，等边三角形是半径为的圆的内接三角形，则线段所对的圆心角，作，垂足为，在中，，，所以，，所以，由弧长公式得．34. B35. A36. B37. B38. A39. B40. B第二部分41. 四42. 二43.44.45. 三46.【解析】根据扇形的弧长公式可得，根据扇形的面积公式可得．47.48.49. 略50. ，51. ；，；，；，三52. ，53.【解析】设扇形的半径为，所以，，所以，扇形的弧长为，半径为，扇形的面积为．54.55.【解析】由题图知，终边落在射线上的角为，以为终边的角与角的终边相同，所以终边落在图中阴影部分的角的集合为．56. 一、二象限57. ①②③④58. 略，略59.60.【解析】设圆半径为，则圆内接正方形的对角线长为，所以正方形边长为，所以圆心角的弧度数是．61.62.【解析】如图，设内切圆半径为，则扇形的半径为，扇形弧长，解得．63.【解析】．64.【解析】因为扇形（），（），所以弓形扇形（）．65. ，【解析】将时针拨慢，时针按逆时针方向转动，转过的是正角，转过的度数为．将时针拨快，分针按顺时针方向转动，转过的是负角，转过的度数为．66.【解析】设扇形的半径为，则，所以，所以扇形的周长为．67.【解析】，，，解得，又，故，，，角为，，．68.【解析】设扇形的半径为，内切圆的半径为，则，即．又扇，内切圆，所以扇内切圆．69. ⑥【解析】（1）明确各种角的定义，逐一判断即可．对于①，终边相同的角不一定相等，终边相同的角有无数多个，它们相差的整数倍，故①是错误的；对于②，角是第一象限角，角是第二象限角，，所以②错误；对于③，的角是指的角，其中角不是任何象限的角，为轴线角，故③错误；对于④，小于的角指满足的角，其中也包括负角和零角，故④错误．（2）弧度角的定义：把长度等于半径长的弧所对的圆心角叫做弧度的角．由此可知，只有⑥正确．⑤⑦错误．70.【解析】由于第一象限角不小于第二象限角，故错；当三角形的内角为时，其既不是第一象限角，也不是第二象限角，故错；正确；由于，但与的终边不相同，故错；当，时既不是第二象限角，又不是第三象限角，故错．综上可知只有正确．71.【解析】由，解得．72. ，【解析】（）在内终边在直线上的角为，所以终边在直线上的角的集合为．（）因为，所以，依题意，，所以，所以＝，即在内与角的终边相同的角为，，共三个．73.74. ①②③④75. 或76.【解析】设扇形的圆心角为，半径为，扇形的弧长．因为，，所以扇形当时，扇形的面积最大．77.【解析】设扇形的半径为，弧长为，由题意知解得所以扇形的圆心角的弧度数为．78.【解析】设，，由题意知劣弧长为，由于圆的半径为，所以．设，则，，所以的坐标为．79.【解析】由题意知，圆的半径，正方形的边长．由图可知，以正方形的边为弦时所对的圆心角为．正方形在圆上滚动时点的顺序依次为如图所示．当点首次回到点的位置时，正方形滚动了圈共次．设第次滚动，点的路程为，则；；；，因此，点所走过的路径的长度为．80. ．【解析】每次转动一个边长时，圆心角转过，正方形有边，所以需要转动次，回到起点．在这次中，半径为的次，半径为的次，半径为的次，点走过的路径的长度= + = ．第三部分81. 略．82. 略．83. 略84. 略85. （1）略．（2）略．86. 略87. 因为集合表示终边在四个象限的角平分线上角的集合，集合表示终边在坐标轴上（为偶数时）和四个象限的角平分线上（为奇数时）的角的集合，所以．88. （1）①，其中适合不等式的元素为：，，；②，其中适合不等式的元素为：，，．（2）终边在直线上的角的集合其中适合不等式的元素为：，．89. 因为，所以终边在题图所示阴影区域内的角的集合为．90. （1）因为，，，所以为底面圆的直径侧．圆锥的侧面展开图是一个扇形，设此扇形的中心角为，弧长为，则，所以，所以．（2）沿着圆锥的侧棱展开，在展开图中，，，．91. ，得秒，走过的弧长为，走过的弧长为．92. （1），所以在第二象限；，所以在第一象限．（2），与它终边相同的角可表示为，，由，得，所以，，即在～的范围内与终边相同的角是，．同理，在～范围内与终边相同的角是．93. （）；（）．94. ①因为为第二象限角，则，，所以，，所以是第三或第四象限角，以及终边落在轴的非正半轴上的角．②，．令，则，所以为第一象限角．令，则，所以为第二象限角．令，则，所以为第四象限角．所以是第一或第二或第四象限角．95. 因为是第二象限角，所以，，所以，，所以是第一或第三象限角（如图阴影部分）．结合单位圆上的三角函数线可得，（i）当是第一象限角时，，，，从而得；（ii）当是第三象限角时，，，，从而得．综上，当是第一象限角，即，时，；当是第三象限角，即，时，．96. 设扇形的半径为，其内切圆的半径为，由已知得，．又因为，所以．所以内切圆的面积为．97. 由题意，有．所以．又，即，所以，且所以或．故或．易知，故当，是第一象限角；当，是第二象限角．98. （1）．（2）由题意知，即，，当时，的最大值为，当时，，．即扇形面积的最大值为，此时扇形圆心角的弧度数为．99. （1）设扇形的圆心角的弧度数为，弧长为，半径为．由题意得：解得：，当时，，此时（舍）当时，，此时，∴扇形圆心角的弧度数是．（2）设扇形的圆心角为，半径为，弧长为，面积为，．所以当时，扇形的面积最大，这个最大值是，此时．当它的半径和圆心角分别取和弧度时，才能使扇形的面积最大，最大面积是．100. 设扇形的半径为，则周长，所以．．因为，当且仅当，即时等号成立．此时，所以当时，取得最大值为．。

专题5.1 任意角和弧度制及任意角的三角函数(练)(解析版)

专题5.1 任意角和弧度制及任意角的三角函数1．（浙江普通高校招生学业水平考试）若点(3,4)P -在角α的终边上，则cos α=（） A.35-B.35C.45-D.45【答案】A. 【解析】由任意角的三角函数的定义可知，3cos 5x r α==-，故选A. 2．（2020·永州市第四中学高一月考）点P 从(1,0)点出发，沿单位圆221x y +=逆时针方向运动π3弧长到达Q 点，则Q 点坐标为（）A ．13,2⎛⎫ ⎪ ⎪⎝⎭B ．31,2⎛⎫-- ⎪ ⎪⎝⎭C ．13,2⎛⎫-- ⎪ ⎪⎝⎭ D ．3,21⎛⎫- ⎪ ⎪⎝⎭【答案】A 【解析】由题意可知1r =，根据三角函数的定义可知1cos32x r π==，3sin 32y r π==，所以点Q 的坐标是13,22⎛⎫⎪ ⎪⎝⎭. 故选：A3.（2019·山东济南外国语学校高三开学考试（文））若圆弧长度等于圆内接正方形的边长，则该圆弧所对圆心角的弧度数为（） A ． B ． C ． D ．【答案】D 【解析】设圆的直径为，则圆内接正方形的边长为∵圆的圆弧长度等于该圆内接正方形的边长，∴圆弧的长度为∴圆心角弧度为故选D.4．已知角的终边在射线上，则等于（）A. B. C. D.【答案】A【解析】由题得在第四象限,且，所以故答案为：A.5.（2019·辽宁鞍山一中高考模拟（理））设，则“”是“”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件【答案】A【解析】当,可以得到,反过来若，至少有或，所以为充分不必要条件，故选A.6．（2020·安徽高三月考（文））达芬奇的经典之作《蒙娜丽莎》举世闻名，画中女子神秘的微笑，数百年来让无数观赏者入迷，现将画中女子的嘴唇近似的看作一个圆弧，设嘴角A、B间的圆弧长为l，嘴角间的距离为d，圆弧所对的圆心角为θ（θ为弧度角），则l、d和θ所满足的恒等关系为（）A．sin2=d lθθ B ．2sin2=d lθθC ．cos2=d lθθD ．2cos2=d lθθ【答案】B 【解析】设该圆弧所对应的圆的半径为r ，则2sin 2r d θ=，⋅=r l θ，两式相除得2sin2=d lθθ 故选：B .7．（2020·辽宁大连�高一期末）若42ππα<<，则点()cos sin ,sin tan P αααα--位于（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】C 【解析】由42ππα<<知：cos sin 1tan ααα<<<∴cos sin 0αα-<，sin tan 0αα-< 故，P 位于第三象限故选：C8.（2019·山东高三期中（文））圆心角为2弧度的扇形的周长为3，则此扇形的面积为 _____ ．【答案】【解析】设该扇形的半径为r ，根据题意，有，，，．故答案为：．9.（2018届浙江省杭州市第二次检测）已知角α 终边经过点()4sin 3sin θθ-，， 32πθπ⎛⎫∈ ⎪⎝⎭，，求sin α ， cos α ， tan α .【答案】见解析【解析】32θππ⎛⎫∈ ⎪⎝⎭，，∴sin 0θ< ，∵4sin x θ= ， 3sin y θ=- ， ∴225sin r x y θ=+=- ，∴3sin 5y r α== ， 4cos 5x r α== ， 3tan 4y x α==- 10.（2018届黑龙江省齐齐哈尔八中8月月考）已知角α的终边上有一点的坐标是()3,4P a a ，其中0a ≠，求sin α， cos α， tan α.【答案】434434 553553sin cos tan sin cos tan αθαααα＝，＝，＝或＝－，＝－，＝【解析】5r a ＝＝.当0a ＞时， 5r a ＝， ∴44335555y a x a sin cos ra r a αα＝＝＝，＝＝＝， 4433y a tan x a α＝＝＝；当a ＜0时，r ＝－5a ，∴sin α＝－45，cos α＝－35，tan α＝43. 综上可知， 434434.553553sin cos tan sin cos tan αααααα＝，＝，＝或＝－，＝－，＝1．（2020·黑龙江香坊�哈尔滨市第六中学校高三一模（理））《九章算术》是我国古代著名数学经典，其中对勾股定理的论述，比西方早一千多年，其中有这样一个问题：“今有圆材埋在壁中，不知大小；以锯锯之，深一寸，锯道长一尺，问径几何？”其意为：今有一圆柱形木材，埋在墙壁中，不知其大小，用锯去锯该材料，锯口深1寸，锯道长1尺，问这块圆柱形木料的直径是多少？长为0.5丈的圆柱形木材部分镶嵌在墙体中，截面图如图所示（阴影部分为镶嵌在墙体内的部分）.己知弦1AB =尺，弓形高1CD =寸，估算该木材镶嵌墙内部分的体积约为（）（注：一丈=10尺=100寸，53.14,sin 22.513π≈︒≈）A ．300立方寸B ．305.6立方寸C ．310立方寸D ．316.6立方寸【答案】D 【解析】设截面图中圆的半径为R （寸），则2251R R -+=，解得13R =. 如图，在截面图中连接,OA OB ，设AOB α∠=，则5sin213α=，故28απ≈即4πα≈.阴影部分的面积约为221116910135 6.3325242π⨯⨯-⨯-=，故木材镶嵌墙内部分的体积约为6.332550316.625⨯=（立方寸），故选：D.2．（2020·四川德阳�高三其他（理））将一条闭合曲线放在两条平行线之间，无论这条闭合曲线如何运动，只要它与两平行线中的一条直线只有一个交点，就必与另一条直线也只有一个交点，则称此闭合曲线为等宽曲线，这两条平行直线间的距离叫等宽曲线的宽比．如圆所示就是等宽曲线．其宽就是圆的直径．如图所示是分别以A 、B 、C 为圆心画的三段圆弧组成的闭合曲线Γ（又称莱洛三角形），下列关于曲线Γ的描述中，正确的有（）（1）曲线Γ不是等宽曲线；（2）曲线Γ是等宽曲线且宽为线段AB 的长；（3）曲线Γ是等宽曲线且宽为弧AB 的长；（4）在曲线Γ和圆的宽相等，则它们的周长相等；（5）若曲线Γ和圆的宽相等，则它们的面积相等．A ．1个B ．2个C ．3个D ．4个【答案】B 【解析】若曲线Γ和圆的宽相等，设曲线Γ的宽为1，则圆的半径为12，（1）根据定义，可以得曲线Γ是等宽曲线，错误；（2）曲线Γ是等宽曲线且宽为线段AB 的长，正确；（3）根据（2）得（3）错误；（4）曲线Γ的周长为1326ππ⨯⨯=，圆的周长为122ππ⨯=，故它们的周长相等，正确；（5）正三角形的边长为1，则三角形对应的扇形面积为2166ππ⨯=，正三角形的面积133112S =⨯⨯，则一个弓形面积36S π=则整个区域的面积为3333(62ππ+=，而圆的面积为2124ππ⎛⎫= ⎪⎝⎭，不相等，故错误；综上，正确的有2个，故选：B.3．（2019·历下�山东师范大学附中高三月考）【多选题】在平面直角坐标系xOy 中，角α顶点在原点O ，以x 正半轴为始边，终边经过点()()1,0P m m <，则下列各式的值恒大于0的是（）A ．sin tan ααB ．cos sin αα-C ．sin cos ααD ．sin cos αα+【答案】AB【解析】由题意知sin 0α<，cos 0α>，tan 0α<. 选项Asin 0tan αα>；选项B ，cos sin 0αα->；选项C ，sin cos 0αα<；选项D ，sin cos αα+符号不确定. 故选：AB.4．（2019·涟水县第一中学高一月考）【多选题】下列说法中正确的有（） A ．正角的正弦值是正的，负角的正弦值是负的，零角的正弦值是零B ．若三角形的两内角,αβ满足sin cos 0αβ⋅<，则此三角形必为钝角三角形C ．对任意的角α，都有sin cos sin cos αααα+=+D ．对任意角,2k k Z παα⎛⎫≠∈ ⎪⎝⎭，都有11tan tan tan tan αααα+=+ 【答案】BD 【解析】对于A ，正角和负角的正弦值都可正、可负，故A 错误；对于B ，∵sin cos 0αβ⋅<，(),0,αβπ∈，∴sin 0α>，cos 0β<，即,2πβπ⎛⎫∈ ⎪⎝⎭，∴三角形必为钝角三角形，故B 正确；对于C ，当sin α，cos α异号时，等式不成立，故C 错误；对于D ，∵tan α，1tan α的符号相同，∴11tan tan tan tan αααα+=+，故D 正确. 因此正确的有B ，D. 故选BD5.（2020·上海高一课时练习）扇形的圆心角为3π，它所对的弦长为20cm ，则此扇形的弧长为_________，面积为________. 【答案】203cm π 2200cm 3π 【解析】由题意，扇形的圆心角为3π，它所对的弦长为20cm ，可得扇形所在圆的半径为20r cm =，所以此扇形的弧长为2033l r cm ππ=⨯=，此扇形的面积为22120020233S cm ππ=⨯⨯=. 故答案为：203cm π，22003cm π. 6.（2018届河南省洛阳市高三第三次统考）已知角的始边与轴的非负半轴重合，顶点与坐标原点重合，终边过点，则__________．【答案】10. 【解析】根据角的终边过，利用三角函数的定义式，可以求得，所以有，故答案是10.7.（2018·山东高三期中（文））如图，在平面直角坐标系中，角的始边与轴的非负半轴重合且与单位圆相交于点，它的终边与单位圆相交于轴上方一点，始边不动，终边在运动.若，则弓形的面积的最大值为_______.【答案】【解析】易知OB=OA=r=1，S △AOB =，故弓形的面积=-，，导函数：S′=，∵，∴，∴S′ ，即=-在上是增函数，∴故填：.8.（2021·山西应县一中高三开学考试（文））已知点(),2P m -，()0m <为角α终边上一点，且cos 3mα=，求sin α和tan α.【答案】225sin ,tan 3αα=-=【解析】因为(),2P m -，则24=+r m ()0m <. 所以2cos 34α==+mm ，解得25m =，又因为0m <，所以5m =所以3r =，2sin3，5tan 5α=. 9. （2020·浙江高一课时练习）（1）已知θ是第二象限角，试判断tan(sin )tan(cos )θθ⋅的符号．（2）若sin(cos )cos(sin )0θθ⋅<，则θ为第几象限角？【答案】（1）tan(sin )tan(cos )0θθ⋅<；（2）θ为第二、三象限角或角θ终边在x 轴的非正半轴上．【解析】（1）∵θ是第二象限， ∴0sin 1,1cos 022ππθθ<<<-<-<<．∴tan(sin )0,tan(cos )0θθ><． ∴tan(sin )tan(cos )0θθ⋅<．（2）∵1cos 1,1sin 12222ππππθθ-<-<-<-<，∴cos(sin )0θ>，故要使sin(cos )cos(sin )0θθ⋅<，则必有sin(cos )0θ<．∴cos 0θ<，即θ为第二、三象限角或角θ终边在x 轴的非正半轴上．10．（2018·上海高考模拟）某企业欲做一个介绍企业发展史的铭牌，铭牌的截面形状是如图所示的扇形环面（由扇形OAD 挖去扇形OBC 后构成的）.已知10, (0<<10)OA=OB =x x ，线段BA 、CD 与弧BC 、弧AD 的长度之和为30米，圆心角为θ弧度.（1）求θ关于x 的函数解析式；（2）记铭牌的截面面积为y ，试问x 取何值时，y 的值最大？并求出最大值. 【答案】（1）210(010)10x x x θ+=<<+；（2）当52x =米时铭牌的面积最大，且最大面积为2254平方米.【解析】(1)根据题意，可算得弧BC x θ=⋅(m )，弧10AD θ=(m ). 又30BA CD BC CD +++=，于是，10101030x x x θθ-+-+⋅+=，所以，210(010)10x x x θ+=<<+.(2) 依据题意，可知22111022OAD OBC y S S x θθ=-=⨯-化简，得2550y x x =-++2522524x ⎛⎫=--+ ⎪⎝⎭.于是，当52x =(满足条件010x <<)时，max 2254y =(2m ). 答所以当52x =米时铭牌的面积最大，且最大面积为2254平方米.1．（2008·全国高考真题（文））若，且，则是（）A ．第一象限角B ．第二象限角C ．第三象限角D ．第四象限角【答案】C 【解析】，则的终边在三、四象限；则的终边在三、一象限，，，同时满足，则的终边在三象限.2．（2014·全国高考真题（文））已知角的终边经过点，则=（）A ．B ．C ．D ．【答案】D【解析】由题意可知x=-4，y=3，r=5，所以.故选D.3．（2020·全国高考真题（理））若α为第四象限角，则（） A ．cos2α>0 B ．cos2α<0C ．sin2α>0D ．sin2α<0【答案】D 【解析】方法一：由α为第四象限角，可得3222,2k k k Z ππαππ+<<+∈，所以34244,k k k Z ππαππ+<<+∈此时2α的终边落在第三、四象限及y 轴的非正半轴上，所以sin 20α< 故选：D. 方法二：当6πα=-时，cos 2cos 03πα⎛⎫=-> ⎪⎝⎭，选项B 错误；当3πα=-时，2cos 2cos 03πα⎛⎫=-< ⎪⎝⎭，选项A 错误；由α在第四象限可得：sin 0,cos 0αα<>，则sin 22sin cos 0ααα=<，选项C 错误，选项D 正确；故选：D.4.（2015·上海高考真题（文））已知点的坐标为，将绕坐标原点逆时针旋转至，则点的纵坐标为（）. A ．B ．C ．D ．【答案】D 【解析】由题意，设OA 与x 轴所成的角为，显然，，故，故纵坐标为5．（2018·全国高考真题（文））已知角的顶点为坐标原点，始边与轴的非负半轴重合，终边上有两点，，且，则（）A ．B ．C ．D ．【答案】B 【解析】由三点共线，从而得到，因为，解得，即，所以，故选B.6.（2017·北京高考真题（理））在平面直角坐标系xOy 中，角α与角β均以Ox 为始边，它们的终边关于y 轴对称.若1sin 3α=，则()cos αβ-=___________. 【答案】79-【解析】因为α和β关于y 轴对称，所以2,k k Z αβππ+=+∈，那么1sin sin 3βα==， 22cos cos αβ=-=22cos cos βα=-=），所以()2227cos cos cos sin sin cos sin 2sin 19αβαβαβααα-=+=-+=-=-.。

任意角和弧度制高中数学例题课后习题详解

第五章三角函数5.1任意角和弧度制例1在0°~360°范围内，找出与95012-︒'角终边相同的角，并判定它是第几象限角.解：95012129483360-︒'=︒'-⨯︒，所以在0°~360°范围内，与95012-︒'角终边相同的角是12948︒'，它是第二象限角.例2写出终边在y 轴上的角的集合.解：在0°~360°范围内，终边在y 轴上的角有两个，即90°，270°角（如图）.因此，所有与90°角终边相同的角构成集合{}1|90360,S k k ββ==︒+⋅︒∈Z ，而所有与270°角终边相同的角构成集合{}2|270360,S k k ββ==︒+⋅︒∈Z ，于是，终边在y 轴上的角的集合12S S S =⋃{}{}|902180,|901802180,k k k k ββββ==︒+⋅︒∈=︒+︒+⋅︒∈Z Z {}{}|902180,|90(21)180,k k k k ββββ==︒+⋅︒∈=︒++︒∈Z Z {}|90180,n n ββ==︒+⋅︒∈Z .例3写出终边在直线y x =上的角的集合S .S 中满足不等式360720β-︒≤<︒的元素β有哪些？解：如图，在直角坐标系中画出直线y x =，可以发现它与x 轴的夹角是45°，在0°~360°范围内，终边在直线y x =上的角有两个：45°，225°.因此，终边在直线y x =上的角的集合{}{}45360,2253|,|60S k k k k ββββ==︒+⋅︒∈=︒+⋅︒∈Z Z {}4518,|0n n ββ==︒+⋅︒∈Z .S 中适合不等式360720β-︒≤<︒的元素β有452180315︒-⨯︒=-︒，451180135︒-⨯︒=-︒，45018045︒+⨯︒=︒，451180225︒+⨯︒=︒，452180405︒+⨯︒=︒，453180585︒+⨯︒=︒.例4按照下列要求，把6730︒'化成弧度：（1）精确值；（2）精确到0.001的近似值.解：（1）因为13567302⎛⎫︒'=︒⎪⎝⎭，所以135π36730rad π rad 21808︒'=⨯=.（2）利用计算器有因此，6730 1.178rad ︒'≈.例5将3.14rad 换算成角度（用度数表示，精确到0.001）.解：利用计算器有因此， 3.14rad 179.909≈︒.例6利用弧度制证明下列关于扇形的公式：（1）l R α=；（2）212S R α=；（3）12S lR =.其中R 是圆的半径，α（02πα<<）为圆心角，l 是扇形的弧长，S 是扇形的面积.证明：由公式||l rα=可得l R α=.下面证明（2）（3）.半径为R ，圆心角为n °的扇形的弧长公式和面积公式分别是π180n R l =，2π360n R S =，将n °转换为弧度，得π180n α=，于是，212S R α=.将l R α=代入上式，即得12S lR =.5.1.1任意角练习1.锐角是第几象限角?第一象限角一定是锐角吗?再分别就直角、钝角来回答这两个问题.【答案】锐角是第一象角，第一象限角不一定是锐角；直角为终边在坐标轴上的角（不属于任何象限），但终边在坐标轴上的角不一定为直角；钝角为第二象角，但第二象角不一定为钝角.【解析】【分析】锐角是第一象角，第一象限角可以是锐角加360︒的整数倍，所以不一定是锐角；直角为终边在坐标轴上的角（不属于任何象限），但终边在坐标轴上的角不一定为直角，如180︒；钝角为第二象角，但第二象角不一定为钝角.【详解】锐角090α︒︒<<，是第一象限角，460503α︒︒<<是第一象限角不是锐角；直角的终边在坐标轴上（不属于任何象限），但终边在坐标轴上的角不一定为直角，如180︒；钝角90180α︒︒<<是第二象限角，450540α︒︒<<是第二象限角，但不是钝角，所以锐角是第一象角，第一象限角不一定是锐角；直角为终边在坐标轴上的角（不属于任何象限），但终边在坐标轴上的角不一定为直角；钝角为第二象角，但第二象角不一定为钝角.【点睛】此题考查象限角轴线角与锐角钝角和直角之间的关系，关键在于掌握终边相同的角的表示方式的辨析.2.今天是星期三，那么7()k k Z ∈天后的那一天是星期几?7()k k Z ∈天前的那一天是星期几?100天后的那一天是星期几?【答案】每周7天，呈周期性变化，今天是星期三，则7()k k ∈Z 天后的那一天是星期三；7()k k ∈Z 天前的那一天仍然是星期三；100天后的那一天是星期五.【解析】【分析】根据每周的周期性变化关系即可求解.【详解】每周7天，呈周期性变化，今天是星期三，则7()k k ∈Z 天后的那一天是星期三；7()k k ∈Z 天前的那一天仍然是星期三；1007142=⨯+，所以100天后的那一天是星期五.【点睛】此题考查周期性的实际应用，利用周期关系解决实际应用问题，关键在于准确建立模型将实际问题转化为数学问题.3.已知角的顶点与直角坐标系的原点重合，始边与x 轴的非负半轴重合，作出下列各角，并指出它们是第几象限角：（1）420︒；（2）75︒-；（3）855︒；（4）510︒-.【答案】（1）第一象限角，作图见解析；（2）第四象限角，作图见解析；（3）第二象限角，作图见解析；（4）第三象限角，作图见解析.【解析】【分析】（1）60360420︒︒︒=+，与60︒终边相同；（2）75︒-按照负角作图；（3）855720135︒︒︒=+与135︒终边相同；（4）510150360︒︒︒-=--与150︒-终边相同【详解】（1）如图①，是第一象限角；（2）如图②，是第四象限角；（3）如圈③，是第二象限角；（4）如图④，是第三象限角.①②③④【点睛】此题考查任意角的概念的辨析，作出角的终边位置判断其所在象限，关键在于对基本概念的熟练掌握.4.在0°~360°范围内，找出与下列各角终边相同的角，并指出它们是第几象限角：（1）5418-︒'；（2）3958︒'；（3）119030-︒'.【答案】（1）30542' ，第四象限角（2）358' ，第一象限角（3）24930' ，第三象限角【解析】【分析】（1）根据题意，通过对已知角加上或减去360 的整数倍后得到的角在0360 范围内，即可求解；（2）根据题意，通过对已知角加上或减去360 的整数倍后得到的角在0360 范围内，即可求解；（3）根据题意，通过对已知角加上或减去360 的整数倍后得到的角在0360 范围内，即可求解；【小问1详解】因为541836030542'-'+= ，所以在0360 范围内，与角5418-︒'终边相同的角为30542' ，是第四象限角.【小问2详解】因为3958360358''-= ，所以在0360 范围内，与角3958' 终边相同的角为358' ，是第一象限角.【小问3详解】因为119030436024930'-'=-⨯+ ，所以在0360 范围内，与角119030-' 终边相同的角为24930' ，是第三象限角.5.写出与下列各角终边相同的角的集合，并找出集合中适合不等式720360β︒︒-<≤的元素β：（1）130318︒'；（2）225︒-.【答案】（1）49642β︒'=-，13642︒-'，22318︒'；（2）585,225,135β︒︒︒=--【解析】【分析】（1）终边相同的角的集合{}|130318360,k k Z ββ︒︒'=+⋅∈，分别令5,4,3k =---，即可得解；（2）终边相同的角的集合{}|225360,k k Z ββ︒︒=-+⋅∈，分别令1,0,1k =-，即可得解.【详解】（1）{}|130318360,k k Z ββ︒︒'=+⋅∈，分别令5,4,3k =---，得49642β︒'=-，13642︒-'，22318︒'；（2）{}|225360,k k Z ββ︒︒=-+⋅∈，分别令1,0,1k =-，得585,225,135β︒︒︒=--.【点睛】此题考查终边相同的角的表示方法，以及找出在指定范围内的元素，关键在于准确表示，正确求解不等式.5.1.2弧度制练习6.把下列角度化成弧度：（1）2230︒'；（2）210-︒；（3）1200︒.【答案】（1）8π（2）76π-（3）203π【解析】【分析】（1）根据题意，结合弧度=角度180π⨯，即可求解；（2）根据题意，结合弧度=角度180π⨯，即可求解；（3）根据题意，结合弧度=角度180π⨯，即可求解.【小问1详解】由题意得，223022.51808ππ'=⨯= .【小问2详解】由题意得，()72102101806ππ-=⨯-=- .【小问3详解】由题意得，20120012001803ππ=⨯= .7.把下列弧度化成角度：（1）12π；（2）43π-；（3）310π.【答案】1）15 ；（2）240 ；（3）54o .【分析】(1)利用01rad 18π︒⎛⎫= ⎪⎝⎭转化即可(2)利用01rad 18π︒⎛⎫= ⎪⎝⎭转化即可(3)利用01rad 18π︒⎛⎫= ⎪⎝⎭转化即可【详解】(1)180151212πππ︒︒⎛⎫=⨯= ⎪⎝⎭.(2)4180424033πππ︒︒⎛⎫⎛⎫-=⨯-=- ⎪ ⎪⎝⎭⎝⎭.(3)31803541010πππ︒︒⎛⎫⎛⎫=⨯= ⎪ ⎪⎝⎭⎝⎭.【点睛】本题考查的是角度制和弧度制的相互转化，较简单.8.用弧度表示：（1）终边在x 轴上的角的集合；（2）终边在y 轴上的角的集合.【答案】（1）{|,}n n ααπ=∈Z ；（2）|,2n n πααπ⎧⎫=+∈⎨⎬⎩⎭Z .【解析】【分析】(1)将终边在x 轴正半轴上的角的集合与终边在x 轴负半轴上的角的集合取并集即可(2)将终边在y 轴正半轴上的角的集合与终边在y 轴负半轴上的角的集合取并集即可【详解】(1){|2,}{|2,}{|,}k k k k n n ααπααππααπ=∈⋃=+∈==∈Z Z Z ；(2)3|2,|2,|,222k k k k n n πππααπααπααπ⎧⎫⎧⎫⎧⎫=+∈⋃=+∈==+∈⎨⎬⎨⎬⎨⎬⎩⎭⎩⎭⎩⎭Z Z Z .【点睛】本题考查的是终边在坐标轴上的角的表示方法，较简单.9.利用计算工具比较下列各对值的大小：（1）cos0.75︒和cos0.75；（2）tan1.2︒和tan1.2.【答案】（1）cos0.75cos0.75︒>；（2）tan1.2tan1.2︒<.【分析】(1)利用计算器求出cos0.75︒和cos0.75的值即可(2)利用计算器求出tan1.2︒和tan1.2的值即可【详解】(1)由计算器可算出cos 0.75 1.000︒≈，cos0.750.712≈所以cos0.75cos0.75︒>(2)由计算器可算出tan1.20.021︒≈，tan1.2 2.572≈所以tan1.2tan1.2︒<【点睛】本题是一道比较三角函数值的题目，解答本题的关键是熟练掌握利用计算器求三角函数值的方法.10.分别用角度制、弧度制下的弧长公式，计算半径为1m 的圆中，60︒的圆心角所对的弧的长度（可用计算工具）.【答案】()3m π【解析】【分析】利用公式180n r l π=和l r α=分别计算即可【详解】角度制下：1r m =，60n ︒=，弧长()6011801803n r l m πππ⨯⨯===.弧度制下：1r m =，3πα=，弧长()3l r m πα==.【点睛】本题考查的是角度制和弧度制下弧长公式的应用，较简单.11.已知半径为120mm 的圆上，有一条弧的长是144mm ，求该弧所对的圆心角（正角）的弧度数.【答案】1.2【解析】【分析】利用公式l Rα=计算即可【详解】144 1.2120l R α===，即该弧所对的圆心角的张度数为1.2.【点睛】本题考查的是扇形有关公式的直接应用，较简单.习题5.1复习巩固12.在0°~360°范围内，找出与下列各角终边相同的角，并指出它们是哪个象限的角：（1）265-︒；（2）1000-︒；（3）84310-︒'；（4）3900︒.【答案】（1）95o ，第二象限角（2）80 ，第一象限角（3）23650' ，第三象限角（4）300o ，第四象限角【解析】【分析】（1）根据题意，结合与角α终边相同的角为360,k k Z α+⋅∈ ，即可求解；（2）根据题意，结合与角α终边相同的角为360,k k Z α+⋅∈ ，即可求解；（3）根据题意，结合与角α终边相同的角为360,k k Z α+⋅∈ ，即可求解；（4）根据题意，结合与角α终边相同的角为360,k k Z α+⋅∈ ，即可求解.【小问1详解】因为265136095-=-⨯+ ，所以在0360 范围内，与265- 终边相同的角为95o ，为第二象限角.【小问2详解】因为1000336080-=-⨯+ ，所以在0360 范围内，与1000- 终边相同的角为80 ，为第一象限角.【小问3详解】因为84310336023650''-=-⨯+ ，所以在0360 范围内，与84310'- 终边相同的角为23650' ，为第三象限角.【小问4详解】因为390010360300=⨯+ ，所以在0360 范围内，与3900 终边相同的角为300o ，为第四象限角.13.写出与下列各角终边相同的角的集合，并找出集合中适合不等式360360β-︒<≤︒的元素β：（1）60︒；（2）75-︒；（3）82430'-︒；（4）475︒；（5）90︒；（6）270︒；（7）180︒；（8）0︒.【答案】（1）{}|60360,S k k Z αα==︒+︒∈ ；300,60-︒︒.（2）{}|75360,S k k Z αα==-︒+︒∈ ；75,285-︒︒.（3）{}82430|360,S k k Z αα'-=+︒︒=∈ ；0,210543035'︒︒'-.（4）{}5|360,47S k k Z αα==+︒︒∈ ；245,115-︒︒.（5）{}0|360,9S k k Z αα==+︒︒∈ ；270,90-︒︒.（6）{}|270360,S k k Z αα==︒+︒∈ ；90,270-︒︒.（7）{}0|360,18S k k Z αα==+︒︒∈ ；180,180︒-︒.（8）{}|0360,S k k Z αα==︒+︒∈ ；0,360︒︒.【解析】【分析】根据终边相同的角的概念直接表示，并求出集合中适合不等式360360β-︒<≤︒的元素β.【小问1详解】{}|60360,S k k Z αα==︒+︒∈ ,其中适合不等式360360β-︒<≤︒的元素有：300,60-︒︒.【小问2详解】{}|75360,S k k Z αα==-︒+︒∈ ,其中适合不等式360360β-︒<≤︒的元素有：75,285-︒︒.【小问3详解】{}82430|360,S k k Z αα'-=+︒︒=∈ ,其中适合不等式360360β-︒<≤︒的元素有：0,210543035'︒︒'-.【小问4详解】{}5|360,47S k k Z αα==+︒︒∈ ,其中适合不等式360360β-︒<≤︒的元素有：245,115-︒︒.【小问5详解】{}0|360,9S k k Z αα==+︒︒∈ ,其中适合不等式360360β-︒<≤︒的元素有：270,90-︒︒.【小问6详解】{}|270360,S k k Z αα==︒+︒∈ ,其中适合不等式360360β-︒<≤︒的元素有：90,270-︒︒.【小问7详解】{}0|360,18S k k Z αα==+︒︒∈ ,其中适合不等式360360β-︒<≤︒的元素有：180,180︒-︒.【小问8详解】{}|0360,S k k Z αα==︒+︒∈ ,其中适合不等式360360β-︒<≤︒的元素有：0,360︒︒.14.分别用角度和弧度写出第一、二、三、四象限角的集合.【答案】第一象限角：{}|36036090,k k k ββ︒︒︒⋅<<⋅+∈Z ，|22,2k k k πβπβπ⎧⎫<<+∈⎨⎬⎩⎭Z ；第二象限角：{}|36090360180,k k k ββ︒︒︒︒⋅+<<⋅+∈Z ，|22,2k k k πβπβππ⎧⎫+<<+∈⎨⎬⎩⎭Z ；第三象限角：{}|360180360270,k k k ββ︒︒︒︒⋅+<<⋅+∈Z ，3|22,2k k k πβππβπ⎧⎫+<<+∈⎨⎬⎩⎭Z ；第四象限角：{}|36090360,k k k ββ︒︒︒⋅-<<⋅∈Z ，|22,2k k k πβπβπ⎧⎫-<<∈⎨⎬⎩⎭Z .【解析】【分析】先用角度制写出四个象限角的集合，再用弧度制写出这四个象限角的集合即可．【详解】解：用角度制写出象限角的集合是：第一象限角：{}|36036090,k k k ββ︒︒︒⋅<<⋅+∈Z ；第二象限角：{}|36090360180,k k k ββ︒︒︒︒⋅+<<⋅+∈Z ；第三象限角：{}|360180360270,k k k ββ︒︒︒︒⋅+<<⋅+∈Z ；第四象限角：{}|36090360,k k k ββ︒︒︒⋅-<<⋅∈Z .用弧度制写出象限角的集合是：第一象限角：|22,2k k k πβπβπ⎧⎫<<+∈⎨⎬⎩⎭Z ；第二象限角：|22,2k k k πβπβππ⎧⎫+<<+∈⎨⎬⎩⎭Z ；第三象限角：3|22,2k k k πβππβπ⎧⎫+<<+∈⎨⎬⎩⎭Z ；第四象限角：|22,2k k k πβπβπ⎧⎫-<<∈⎨⎬⎩⎭Z .【点睛】本题考查了象限角的角度制与弧度制的表示方法问题，解题时应熟练地写出来，是基础题．15.一条弦的长等于半径，这条弦所对的圆心角等于1弧度吗？为什么？【答案】不等于，原因见解析【解析】【分析】直接利用弧度数定义判断即可．【详解】解：不等于1弧度，这是因为等于半径长的弧所对的圆心角为1弧度的角，而等于半径长的弦所对的弧比半径长.【点睛】本题考查弧度制的应用，属于基础题．16.把下列角度化成弧度：（1）36︒；（2）150-︒；（3）1095︒；（4）1440︒.【答案】（1）5π（2）56π-（3）7312π（4）8π【解析】【分析】利用角度制与弧度制的转化公式直接计算即可.【小问1详解】解：36361805ππ︒=︒⨯=︒；【小问2详解】解：51501501806ππ︒=-︒⨯=-︒-；【小问3详解】解：731095109518012ππ︒=︒⨯=︒；【小问4详解】解：144014408180ππ︒=︒⨯=︒.17.把下列弧度化成角度（第（3）（4）题精确到0.01︒）：（1）76π-（2）103π-（3）1.4；（4）23.【答案】（1）210-（2）600-o（3）80.25（4）38.22【解析】【分析】（1）根据题意，结合180π= ，即可求解；（2）根据题意，结合180π= ，即可求解；（3）根据题意，结合180π= ，即可求解；（4）根据题意，结合180π= ，即可求解.【小问1详解】由题意得，7718021066π-=-⨯=- .【小问2详解】由题意得，101018060033π-=-⨯=- .【小问3详解】由题意得，1801.4 1.480.25π=⨯≈.【小问4详解】由题意得，2218038.2233π=⨯≈.综合运用18.已知α是锐角，那么2α是（）．A.第一象限角B.第二象限角C.小于180°的正角D.第一或第二象限角【答案】C【解析】【分析】由题知0,2πα⎛⎫∈ ⎪⎝⎭，故()20,απ∈，进而得答案.【详解】因为α是锐角,所以0,2πα⎛⎫∈ ⎪⎝⎭,所以()20,απ∈,满足小于180°的正角.其中D 选项不包括90 ，故错误.故选：C19.若α为第一象限角，则2α是（）A.第一象限角B.第二象限角C.第一或第二象限角D.第一或第三象限角【答案】D【解析】【分析】写出第一象限角α，得到2α的范围，再讨论k 的取值即可.【详解】因为α为第一象限角，所以22,2k k k Z ππαπ<<+∈，所以,24k k k Z απππ<<+∈，当0k =时，024απ<<，属于第一象限角，排除B ；当1k =时，524αππ<<，属于第三象限角,排除AC ；所以2α是第一或第三象限角故选：D20.要在半径100OA cm =的圆形金属板上截取一块扇形板，使其弧AB 的长为112cm ，那么圆心角AOB ∠是多少度（可用计算工具，精确到1°）？【答案】64︒【解析】【分析】由弧长公式变形可得112100AOB ∠=，化简即可．【详解】解：设AOB α∠=.方法1：由l R α=，得112100α=，解得112 1.12()64100rad α︒==≈，方法2：由180R l πα︒=，得100112180πα︒⨯=，解得64α︒≈.【点睛】本题考查弧长公式，属于基础题．21.已知弧长50cm 的弧所对圆心角为200︒，求这条弧所在的圆的半径（可用计算工具，精确到1cm ）.【答案】14cm【解析】【分析】利用弧长公式即可得出；【详解】解：方法一：102002001809ππ︒=⨯= ,由l aR =得10509R π=,14R cm ∴≈.方法二：由180n R l π=得20050180R π=，解得14R cm ≈.【点睛】本题考查了弧长公式，属于基础题．拓广探索22.每人准备一把扇形的扇子，然后与本小组其他同学的对比，从中选出一把展开后看上去形状较为美观的扇子，并用计算工具算出它的面积1S .（1）假设这把扇子是从一个圆面中剪下的，而剩余部分的面积为2S ，求1S 与2S 的比值；（2）要使1S 与2S 的比值为0.618，则扇子的圆心角应为几度（精确到1︒）？【答案】（1）12S S αβ=；（2）138︒【解析】【分析】（1）设1S 的圆心角为α，2S 的圆心角为β，从而由扇形的面积公式可计算12S S 的值．（2）由（1）可得0.6182θπθ=-，从而可求得0.764138θπ=≈︒．【详解】解：（1）设半径为12,,R S S 所对圆心角分别为,αβ，且2211222122,,12R S S S R S R αααβππββ+=+=∴==.（2）设扇子的圆心角为θ.由2122120.6181(2)2R S S R θπθ==-，得0.618(2)θπθ=-,则2.40138rad θ︒≈≈.【点睛】本题主要考查了扇形的面积公式，熟记公式是解题的关键，属于基础题．23.（1）时间经过4h （时），时针、分针各转了多少度？各等于多少弧度？（2）有人说，钟的时针和分针一天内会重合24次。

2021-2022年高一数学人教版A版(2019)必修第一册同步练习题5-1 任意角和弧度制含答案

2021-2022年高一数学人教版A版(2019)必修第一册同步练习题5-1 任意角和弧度制【含答案】一、选择题（本大题共8小题，每小题5分，共40分）在每小题所给出的四个选项中，只有一项是符合题目要求的．1．把一条射线绕着端点按顺时针方向旋转240°所形成的角是( )A．120°B．－120°C．240°D．－240°【答案】D【解析】按顺时针方向旋转形成的角是负角，排除A、C；又由题意知旋转的角度是240°，排除B.故选D.2．给出下列四个结论：①－15°角是第四象限角；②185°角是第三象限角；③475°角是第二象限角；④－350°角是第一象限角．其中正确的个数为( )A．1 B．2C．3 D．4【答案】D【解析】①－15°角是第四象限角；②因为180°<185°<270°，所以185°角是第三象限角；③因为475°＝360°＋115°，90°<115°<180°，所以475°角是第二象限角；④因为－350°＝－360°＋10°，所以－350°角是第一象限角．所以四个结论都是正确的．3．集合A＝{α|α＝k·90°－36°，k∈Z}，B＝{β|－180°<β<180°}，则A∩B＝( )A．{－36°，54°}B．{－126°，144°}C．{－126°，－36°，54°，144°}D．{－126°，54°}【答案】C【解析】令k ＝－1,0,1,2，则A ，B 的公共元素有－126°，－36°，54°，144°. 4．已知角α＝45°，β＝315°，则角α与β的终边( ) A ．关于x 轴对称 B ．关于y 轴对称 C ．关于直线y ＝x 对称 D ．关于原点对称【答案】A【解析】因为β＝315°＝360°－45°，所以315°角与－45°角的终边相同，所以α与β的终边关于x 轴对称．5．若α与β终边相同，则α－β的终边落在( ) A ．x 轴的非负半轴上 B ．x 轴的非正半轴上 C ．y 轴的非负半轴上 D ．y 轴的非正半轴上【答案】A【解析】∵α＝β＋k ·360°，k ∈Z ，∴α－β＝k ·360°，k ∈Z ，∴其终边在x 轴的非负半轴上． 6．(多选)已知角2α的终边在x 轴的上方，那么角α可能是( ) A ．第一象限角 B ．第二象限角 C ．第三象限角 D ．第四象限角【答案】AC【解析】因为角2α的终边在x 轴的上方，所以k ·360°<2α<k ·360°＋180°，k ∈Z ，则有k ·180°<α<k ·180°＋90°，k ∈Z.故当k ＝2n ，n ∈Z 时，n ·360°<α<n ·360°＋90°，n ∈Z ，α为第一象限角；当k ＝2n ＋1，n ∈Z 时，n ·360°＋180°<α<n ·360°＋270°，n ∈Z ，α为第三角限角．故选A 、C.7．若角α与角x ＋4π有相同的终边，角β与角x －4π有相同的终边，那么α与β间的关系为( ) A ．α＋β＝0B ．α－β＝0C ．α＋β＝2k π(k ∈Z)D ．α－β＝2π＋2k π(k ∈Z) 【答案】D【解析】∵α＝x ＋4π＋2k 1π(k 1∈Z)，β＝x －4π＋2k 2π(k 2∈Z)，∴α－β＝2π＋2(k 1－k 2)π(k 1∈Z ，k 2∈Z)．∵k 1∈Z ，k 2∈Z ，∴k 1－k 2∈Z.∴α－β＝2π＋2k π(k ∈Z)． 8.已知某机械采用齿轮传动，由主动轮M 带着从动轮N 转动(如图所示)，设主动轮M 的直径为150 mm ，从动轮N 的直径为300 mm ，若主动轮M 顺时针旋转2π，则从动轮N逆时针旋转( )A.8π B ．4π C.2π D ．π【答案】B【解析】设从动轮N 逆时针旋转θ rad ，由题意，知主动轮M 与从动轮N 转动的弧长相等，所以θπ⨯=⨯230022150，解得θ＝4π，选B. 二、填空题（本大题共4小题，每小题5分，共20分．不需写出解答过程，请把答案直接填写在横线上）9．若α满足180°<α<360°，5α与α有相同的始边，且又有相同的终边，则α＝________. 【答案】270°【解析】∵5α＝α＋k ·360°，k ∈Z ，∴α＝k ·90°，k ∈Z. 又∵180°<α<360°，∴α＝270°.10.集合{α|k ·180°≤α≤k ·180°＋45°，k ∈Z}中角表示的范围(用阴影表示)是图中的________(填序号)．【答案】②【解析】集合{α|k ·180°≤α≤k ·180°＋45°，k ∈Z}中，当k 为偶数时，此集合与{α|0°≤α≤45°}表示终边相同的角，位于第一象限；当k 为奇数时，此集合与{α|180°≤α≤225°}表示终边相同的角，位于第三象限．所以集合{α|k ·180°≤α≤k ·180°＋45°，k ∈Z}中角表示的范围为图②所示．11．（2020·浙江高一课时练习）一条铁路在转弯处呈圆弧形，圆弧的半径为2km ，一列火车以30km /h 的速度通过，10s 间转过_______弧度．【答案】124【解析】10s 间列车转过的弧长为10130(km)360012⨯=，转过的角1112224α==（弧度）．故答案为：12412.已知圆的一段弧长等于该圆外切正三角形的边长，则这段弧所对圆心角的弧度数的绝对值为______；若圆弧长等于其所在圆的内接正方形的周长，那么这段弧所对圆心角的弧度数的绝对_____. 【答案】23 42【解析】设圆半径为r ，这段弧所对圆心角的弧度数为θ，则圆外切正三角形的边长为23r ，∴23||23rθ==2r ，周长为42r ，即圆弧长为42r ，∴42||42rrθ==. 三、解答题（本大题共4小题，共40分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤）13．已知α，β都是锐角，且α＋β的终边与－280°角的终边相同，α－β的终边与670°角的终边相同，求角α，β的大小．【解析】由题意可知，α＋β＝－280°＋k ·360°，k ∈Z ， ∵α，β都是锐角，∴0°<α＋β<180°. 取k ＝1，得α＋β＝80°.①∵α－β＝670°＋k ·360°，k ∈Z ，α，β都是锐角， ∴－90°<α－β<90°.取k ＝－2，得α－β＝－50°.② 由①②，得α＝15°，β＝65°.14.如图，点A 在半径为1且圆心在原点的圆上，且∠AOx ＝45°，点P 从点A 处出发，以逆时针方向沿圆周匀速旋转．已知点P 在1秒内转过的角度为θ(0°<θ<180°)，经过2秒钟到达第三象限，经过14秒钟又回到出发点A ，求θ，并判断θ所在的象限．【解析】根据题意知，14秒钟后，点P 在角14θ＋45°的终边上，所以45°＋k ·360°＝14θ＋45°，k ∈Z.又180°<2θ＋45°<270°，即67.5°<θ<112.5°，∴67.5°<71800k <112.5°.又k ∈Z ，∴k ＝3或4，∴所求的θ的值为75400或77200.∵0°<75400<90°，90°<77200<180°，∴θ在第一象限或第二象限．15.已知扇形AOB 的圆心角α为23π，半径长R 为6，求：（1）弧AB 的长；（2）扇形所含弓形的面积. 【解析】（1）l ＝α·R ＝23π×6＝4π，所以弧AB 的长为4π. （2）S 扇形OAB ＝12lR ＝12×4π×6＝12π. 如图所示，过点O 作OD ⊥AB ，交AB 于点D ，23π＝120°，所以∠AOD ＝60°，∠DAO ＝30°，于是有S △OAB ＝12×AB ×OD ＝12×2×6cos 30°×3＝3所以弓形的面积为S 扇形OAB －S △OAB ＝12π－3所以弓形的面积是12π－316．（2020·浙江高一课时练习）如图，3dm ，宽为1dm 的长方形在桌面上作无滑动翻滚，翻滚到第四次时被小木块挡住，此时长方形的底边与桌面所成的角为6π，求点A 走过的路程及走过的弧所在扇形的总面积．【解析】如图:在扇形1ABA 中，圆心角为2π，弧长()131dm 22l AB πππ=⨯=+=，面积()21112dm 22S AB πππ=⨯⨯=⨯⨯=．在扇形12ACA 中，圆心角为2π，弧长()211dm 222l A C πππ=⨯=⨯=，面积()221111dm 2244S A C πππ=⨯⨯=⨯⨯=，在扇形23A DA 中，圆心角为263ππππ--=，弧长()3233dm 333l A D πππ=⨯==，面积()232131323dm 22S A D ππ===．综上，点A 走过的路程()()1239233dm 26l l l l ππππ+=++=++=，点A 走过的弧所在扇形的总面积()21237dm 424ππππ=++=++=S S S S。

专题5.1 任意角与弧度制(解析版)

专题5.1任意角与弧度制一、角的相关概念1.角可以看成平面内一条射线绕着它的端点从一个位置旋转到另一个位置所成的图形．2.角的表示：如图，OA是角α的始边，OB是角α的终边，O是角的顶点．角α可记为“角α”或“∠α”或简记为“α”．3.按照角的旋转方向可将角分为如下三类：4.相反角如图，我们把射线OA绕端点O按不同方向旋转相同的量所成的两个角叫做互为相反角．角α的相反角记为－α.二、象限角1.若角的顶点在原点，角的始边与x轴的非负半轴重合，则角的终边在第几象限，就称这个角是第几象限角．2.若角的终边在坐标轴上，则认为这个角不属于任何一个象限．3.象限角的判定方法(1)根据图象判定．依据是终边相同的角的概念，因为0°～360°之间的角的终边与坐标系中过原点的射线可建立一一对应的关系．(2)将角转化到0°～360°范围内．在直角坐标平面内，在0°～360°范围内没有两个角终边是相同的．(3)nα所在象限的判断方法确定nα终边所在的象限，先求出nα的范围，再直接转化为终边相同的角即可．(4)αn所在象限的判断方法4.已知角α所在象限，要确定角αn所在象限，有两种方法：①用不等式表示出角αn 的范围，然后对k 的取值分情况讨论：被n 整除；被n 除余1；被n除余2；…；被n 除余n －1.从而得出结论．②作出各个象限的从原点出发的n 等分射线，它们与坐标轴把周角分成4n 个区域．从x 轴非负半轴起，按逆时针方向把这4n 个区域依次循环标上1,2,3,4.α的终边在第几象限，则标号为几的区域，就是αn 的终边所落在的区域．如此，αn 所在的象限就可以由标号区域所在的象限直观地看出．三、终边相同的角1.设α表示任意角，所有与角α终边相同的角，包括α本身构成一个集合，这个集合可记为{β|β＝□01α＋k ·360°，k ∈Z }．2.对终边相同的角的理解(1)终边相同的角不一定相等，但相等的角终边一定相同；(2)k ∈Z ，即k 为整数，这一条件不可少；(3)终边相同的角的表示不唯一．四、角的单位制1.用度作为单位来度量角的单位制叫做角度制，规定1度的角等于周角的1360.2.长度等于半径长的圆弧所对的□03圆心角叫做1弧度的角，弧度单位用符号rad 表示，读作弧度，通常略去不写．以弧度作为单位来度量角的单位制叫做弧度制．3.弧度数的计算4.角度制和弧度制的比较(1)弧度制是以“弧度”为单位来度量角的单位制，而角度制是以“度”为单位来度量角的单位制．(2)1弧度的角是指等于半径长的弧所对的圆心角，而1度的角是指圆周角的1360的角，大小显然不同．(3)无论是以“弧度”还是以“度”为单位来度量角，角的大小都是一个与“半径”大小无关的值．(4)用“度”作为单位度量角时，“度”(即“°”)不能省略，而用“弧度”作为单位度量角时，“弧度”二字或“rad”通常省略不写．但两者不能混用，即在同一表达式中不能出现两种度量方法．五、角度与弧度的换算1.角度制与弧度制的换算2.一些特殊角的度数与弧度数的对应表度0°30°45°60°90°120°135°150°180°弧度π6π4π3π22π33π45π6π六、扇形的弧长及面积公式1.设扇形的半径为r ，弧长为l ，α(0<α<2π)为其圆心角的弧度数，n 为圆心角的角度数，则扇形的弧长：l ＝n πr 180＝αr ，扇形的面积：S ＝n πr 2360＝12lr ＝12α·r 2.一、单选题1．与525-角的终边相同的角可表示为（）A ．525360k k Z -⋅∈（）B ．185360k k Z +⋅∈（）C ．195360k k Z +⋅∈（）D ．195360k k Z -+⋅∈（）【答案】C【解析】解：525=1952360--⨯，所以525-角的终边与195角的终边相同，所以与525-角的终边相同的角可表示为195360k k Z +⋅∈（）.故选：C 2．下列与角23π的终边一定相同的角是（）A ．53πB ．()43k k Z ππ-∈C ．()223k k Z ππ+∈D ．()()2213k k Z ππ++∈【答案】C 【解析】对于选项C ：与角23π的终边相同的角为()223k k Z ππ+∈，C 满足.对于选项B ：当()2k n n Z =∈时，()442,33k n k Z n Z ππππ-=-∈∈成立；当()21k n n Z =+∈时，()()44212,333k n n k Z n Z ππππππ-=+-=-∈∈不成立.对于选项D ：()()2521233k k k Z ππππ++=+∈不成立.故选:C 3．在0°到360范围内，与405终边相同的角为（）A ．45-B ．45C ．135D ．225【答案】B【解析】：因为40536045=+，所以在0°到360范围内与405终边相同的角为45；故选：B 4．角76π所在的象限为（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】C 7362πππ<<，∴角76π位于第三象限.故选：C.5．已知角2022α=，则角α的终边落在（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】C【解析】因为20222225360α==+⨯，而222是第三象限角，故角α的终边落在第三象限.故选：C.6．下列说法正确的是（）A ．终边相同的角相等B ．相等的角终边相同C ．小于90︒的角是锐角D ．第一象限的角是正角【答案】B【解析】终边相同的角相差周角的整数倍，A 不正确；相等的角终边一定相同；所以B 正确；小于90︒的角是锐角可以是负角，C 错；第一象限的角是正角，也可以是负角，D 错误．故选：B.7．135-的角化为弧度制的结果为（）A ．32π-B ．35π-C ．34π-D ．34π【答案】C【解析】π3135π rad 1418035-⨯-==-．故选：C.8．中国传统折扇有着极其深厚的文化底蕴.《乐府诗集》中《夏歌二十首》的第五首曰：“叠扇放床上，企想远风来轻袖佛华妆，窈窕登高台.”如图所示，折扇可看作是从一个圆面中剪下的扇形制作而成若一把折扇完全打开时圆心角为67π，扇面所在大圆的半径为20cm ，所在小圆的半径为8cm ，那么这把折扇的扇面面积为（）A ．288πB ．144πC ．487πD ．以上都不对【答案】B【解析】由题意得，大扇形的面积为11612002020277S ππ=⨯⨯⨯=，小扇形的面积为21619288277S ππ=⨯⨯⨯=，所以扇面的面积为12120019214477S S πππ-=-=.故选：B 9．把375-︒表示成2πk θ+，k Z ∈的形式，则θ的值可以是（）A ．π12B ．π12-C ．5π12D ．5π12-【答案】B【解析】∵37515360-=-︒-︒︒，∴π3752πrad 12⎛⎫-︒=-- ⎪⎝⎭故选：B10．我国古代数学经典著作《九章算术》中记载了一个“圆材埋壁”的问题：“今有圆材埋在壁中，不知大小，以锯锯之，深一寸，锯道长一尺，问径几何?”现有一类似问题，不确定大小的圆柱形木材，部分埋在墙壁中，其截面如图所示.用锯去锯这木材，若锯口深2CD =锯道2AB =，则图中ACB 与弦AB 围成的弓形的面积为（）A ．2π-B ．23πC ．3πD ．33π-【答案】B【解析】解：设圆的半径为r ，则(2OD r CD r =-=--，112AD AB ==，由勾股定理可得222OD AD OA +=，即(2221r r ⎡⎤-+=⎣⎦，解得2r =，所以2OA OB ==，2AB =，所以3AOB π∠=，因此2212222343MBBAOB S S S ππ=-=⨯⨯-=-弓形扇形故选：B 11．《掷铁饼者》取材于希腊的现实生活中的体育竞技活动，刻画的是一名强健的男子在掷铁饼过程中最具有表现力的瞬间．现在把掷铁饼者张开的双臂近似看成一张拉满弦的“弓”，掷铁饼者的手臂长约为4π米，肩宽约为8π米，“弓”所在圆的半径约为1.25米，则掷铁饼者双手之间的距离约为（）A ．1.012米B ．1.768米C ．2.043米D ．2.945米【答案】B【解析】解：由题得：弓所在的弧长为：54488l ππππ=++=；所以其所对的圆心角58524ππα==；∴两手之间的距离2sin1.25 1.7684d R π=≈．故选：B ．12．“α是第四象限角”是“2α是第二或第四象限角”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】A【解析】当α是第四象限角时，3222,2k k k Z ππαππ+<<+∈，则3,42k k k Z παπππ+<<+∈，即2α是第二或第四象限角.当324απ=为第二象限角，但32πα=不是第四象限角，故“α是第四象限角”是“2α是第二或第四象限角”的充分不必要条件．故选：A13．在Rt POB 中，90PBO ∠=︒，以O 为圆心，OB 为半径作圆弧交OP 于点A ，若弧AB 等分POB 的面积，且AOB α∠=弧度，则（）A ．tan αα=B ．tan 2αα=C ．sin 2cos αα=D ．2sin cos αα=【答案】B【解析】设扇形的半径为r ，则扇形的面积为212r α.直角三角形POB 中，tan PB r α=，△POB 的面积为21tan 2r α⋅⋅.由题意得22112tan 22r r αα⨯=⋅⋅，所以tan 2αα=.故选：B14．砀山被誉为“酥梨之乡”，每逢四月，万树梨花开，游客八方来．如图1，梨花广场的标志性建筑就是根据梨花的形状进行设计的，建筑的五个“花瓣”中的每一个都可以近似看作由两个对称的弓形组成，图2为其中的一个“花瓣”平面图，设弓形的圆弧所在圆的半径为R ，，则一个“花瓣”的面积为（）A ．2π12R -B ．2π22R -C ．2π14R -D ．()2π1R-【答案】B【解析】因为弓形的圆弧所在圆的半径为R ，所以弓形的圆弧所对的圆心角的大小为2π，所以弓形的面积221142S R R π=⨯-，所以一个“花瓣”的面积为2π22R -，故选：B.15．设圆O 的半径为2，点P 为圆周上给定一点，如图，放置边长为2的正方形ABCD （实线所示，正方形的顶点A 与点P 重合，点B 在圆周上）.现将正方形ABCD 沿圆周按顺时针方向连续滚动，当点A 首次回到点P 的位置时，点A 所走过的路径的长度为（）A ．(1π-B ．(2πC ．4πD ．32π⎛+ ⎝⎭【答案】B【解析】由图可知，圆O 的半径为2r =，正方形ABCD 的边长为2a =，以正方形的边为弦所对的圆心角为3π，正方形在圆上滚动时点的顺序依次为如图所示，当点A 首次回到点P 的位置时，正方形滚动了3圈，共12次，设第i 次滚动时，点A 的路程为i m ，则163m AB ππ=⨯=，263m AC π=⨯=，363m AD ππ=⨯=，40m =，因此，点A 所走过的路程为()(123432m m m m π+++=+.故选：B.16．用半径为2，弧长为2π的扇形纸片卷成一个圆锥，则这个圆锥的体积等于（）A BC D ．4π【答案】B【解析】令圆锥底面半径为r ，则22ππ=r ，因此1r =∴圆锥的高为：h ==∴圆锥的体积21133π=⨯⨯=V 故选：B17．中国传统扇文化有着极其深厚的底蕴．一般情况下，折扇可看作是从一个圆面中剪下的扇形制作而成，设扇形的面积为1S ，圆面中剩余部分的面积为2S ，当1S 与2S 的比值为时，扇面看上去形状较为美观，那么此时扇形的圆心角的弧度数为（）A ．(35)π-B ．(51)πC ．(51)π+D ．(52)π【答案】A【解析】1S 与2S 所在扇形圆心角的比即为它们的面积比，设1S 与2S 所在扇形圆心角分别为,αβ，则512αβ=，又2αβπ+=，解得(35)απ=故选:A 18．《九章算木》是我国古代数学成就的杰出代表.其中《方田》章给出计算弧田面釈所用的经验公式为：弧田面积=12(弦×矢+矢²).弧田，由圆弧和其所对弦所围成.公式中“弦”指圆弧所对的弦长，“矢”等于半径长与圆心到弦的距离之差．现有圆心角为3π，弦长等于2米的弧田.按照《九章算木》中弧田面积的经验公式竍算所得弧田面积(单位，平方米)为A ．3πB ．33πC ．95322-D ．11332-【答案】D【解析】在圆心角为3π，弦长等于2米的弧田中，半径为23矢3=12(弦×矢+矢²)=((211122323322⎡⎤⨯-+-=-⎢⎥⎣⎦，故选D.19．将分针拨慢5分钟，则分钟转过的弧度数是（）A ．3πB ．3π-C ．6πD ．6π-【答案】C【解析】：分针转一周为60分钟，转过的角度为2π将分针拨慢是逆时针旋转∴钟表拨慢分钟，则分针所转过的弧度数为1 2.126ππ⨯=故选C ．20．一个圆锥的侧面展开图是圆心角为23π，弧长为2π的扇形，则该圆锥的体积为（）A ．3B ．C ．3D 【答案】A【解析】设圆锥的母线长为l ，底面半径为r ，则223l ππ=，解得3l =，又22ππ=r ，解得1r =，所以圆锥的高为h ==所以圆锥的体积为213V r h π==.故选：A .二、填空题21的体积为______【答案】2π3【解析】设该圆锥的母线长为l ，底面圆的半径为r ，由2125π25l ⨯=，得l =.因为2π5r =1r =，所以该圆锥的体积为212ππ133⨯⨯⨯.故答案为：2π322．《九章算术》是我国古代数学成就的杰出代表作，其中"方田"章给出了计算弧田面积时所用的经验公式，即弧田面积21(2弦矢矢)=⨯⨯+，弧田（如图）由圆弧和其所对弦围成，公式中“弦"指圆弧所对弦长，“矢"指圆弧顶到弦的距离（等于半径长与圆心到弦的距离之差），现有圆心角为23π，半径为6米的弧田，按照上述经验公式计算所得弧田面积是_________平方米．（结果保留根号）【答案】92【解析】设弧田的圆心为O ，弦为AB ，C 为AB 中点，连OC 交弧为D ，则OC AB ⊥，所以矢长为CD ，在Rt AOC △中，6AO =，3AOC π∠=，所以13,2OC OA AC ===，所以3,2CD OD OC AB AC =-===所以弧田的面积为()()2211933222AB CD CD ⋅+=+=.故答案为：92.23．中国折叠扇有着深厚的文化底蕴.如图（2），在半圆O （半径为20cm ）中作出两个扇形OAB 和OCD ，用扇环形ABDC （图中阴影部分）制作折叠扇的扇面.记扇环形ABDC 的面积为1S ，扇形OAB 的面积为2S，当1212S S =时，扇形的现状较为美观，则此时扇形OCD 的半径为__________cm【答案】1)【解析】设,AOB θ∠=，半圆O 的半径为r ，扇形OCD 的半径为1r，1212S S =，所以2212112212r r r θθθ-=，即2212512r r r -=，所以2212361()242r r -===，所以1r r =又20,r cm =，所以11)r cm =-，故答案为：1).24．“一湾如月弦初上，半壁澄波镜比明”描述的是敦煌八景之一的月牙泉.如图所示，月牙泉由两段在同一平面内的圆弧形岸连接围成.两岸连接点间距离为.其中外岸为半圆形，内岸圆弧所在圆的半径为60米.某游客绕着月牙泉的岸边步行一周，则该游客步行的路程为_______米.【答案】(40π+【解析】如图，是月牙湖的示意图，O 是QT 的中点，连结PO ，可得PO QT ⊥，由条件可知QT =，60PQ =所以sin QPO ∠=，所以3QPO π∠=，23QPT π∠=，所以月牙泉的周长(260403l πππ=⨯+⨯=+.故答案为：(40π+25．勒洛三角形是具有类似圆的“定宽性”的面积最小的曲线，它由德国机械工程专家，机构运动学家勒洛首先发现，其作法是：以等边三角形每个顶点为圆心，以边长为半径，在另两个顶点间作一段弧，三段弧围成的曲边三角形就是勒洛三角形．已知等边三角形的边长为1，则勒洛三角形的面积是_______．【来源】陕西省西安市莲湖区2021-2022学年高一下学期期末数学试题【解析】由题意得，勒洛三角形的面积为：三个圆心角和半径均分别为π3和1的扇形面积之和减去两个边长为1的等边三角形的面积，即221π1ππ33121sin 23232⨯⨯⨯-⨯⨯⨯=．故答案为：π2．26．若扇形的周长为定值l ，则当该扇形的圆心角()02ααπ<<=______时，扇形的面积取得最大值，最大值为______.【答案】22116l 【解析】设扇形的半径为r ，则扇形的弧长为rα故2r r lα+=扇形的面积22111(2)222S r r l r lr r α==-=-由二次函数的性质，当4l r =时，面积取得最大值为2116l 此时12r l α=，2α=故答案为：2，2116l。

任意角与弧度制(精讲)(解析版)

5.1 任意角与弧度制（精讲）考点一角度制与弧度制的互换【例1】（2022广东）把下列各角的弧度数化为度数，度数化为弧度数.（1）712π ；（2）136π- ；（3）1125° ；（4）-225°. 【答案】（1）105° （2）-390° （3）254π （4）- 54π 【解析】（1）根据弧度制与角度制的互化公式， 1801,1180rad rad ππ==，可得：771801051212πππ=⨯= ；（2）131318039066πππ-=-⨯=- （3） 25112511251804ππ=⨯=rad ；（4） 52252251804ππ-=-⨯=-rad .【一隅三反】1．（2022宿州）将210°化成弧度为（）A ．5π6-B ．5π6C ．4π3D ．7π6【答案】D【解析】π7210=210=π1806︒⨯。

故答案为：D. 2．（2022房山期中）将120°转化为弧度为（）A ．5π6B ．2π3C ．56D ．23【答案】B【解析】π2π1201201803︒=︒⨯=︒，故答案为：B. 3．（2022山西月考）角度20230︒化成弧度为（）A ．9π8B ．5π4C ．11π8D ．19π16【答案】A【解析】根据题意，π9π2023018022.50π88︒=︒+︒=+=。

故答案为：A. 考点二终边相同的角【例2】（2022·涟水）在与 530 角终边相同的角中，求满足下列条件的角．（1）最大的负角；（2）最小的正角；（3）在 {|720360}αα-≤<- 内的角．【答案】见解析【解析】（1）解：与 530 角终边相同的角为 360530k ⋅+ ， k Z ∈ .由 3603605300k -<⋅+< 且 k Z ∈ ，可得 2k =- ，故所求的最大负角为 190-（2）解：由 0360530360k <⋅+< 且 k Z ∈ ，可得 1k =- ，故所求的最小正角为 170 （3）解：由 720360530360k -≤⋅+<- 且 k Z ∈ ，可得 3k =- ，故所求的角为 550-【一隅三反】1．（2022陕西期末）在0~360°的范围内，下列与-510°终边相同的角是（）A ．330°B ．210°C ．150°D ．30°【答案】B【解析】因为-510°=-720°+210°，则在0°~360°的范围内，与-510°终边相同的角是210° .故选：B 2（2022房山月考）在230，320，310，310-中，与50终边相同的是（）A ．230B ．320C ．310D ．310-【答案】D【解析】与50终边相同的角为：()α50360k k Z =+⋅∈；当1k =-时，α310=-.故答案为：D. 3．（2022海东）下列各组角中，终边相同的是（）A ．43°和313°B ．37°和787°C ．65°和-655°D ．124°和-576°【答案】C【解析】 656552360︒=-︒+⨯︒ . 故答案为：C ． 4（20222怀化）（多选）与角 43π-终边相同的角是（） A ．3πB ．23πC ．43π D ．103π-【答案】BD 【解析】与角 43π-终边相同的角的集合是 4|23k k Z ααππ⎧⎫=-+∈⎨⎬⎩⎭，，当 1k = 时， 23απ=，当 1k =- 时， 103απ=- .故答案为：BD 考点三角象限的判断【例3-1】（2022南阳）已知角α2022=，则角α的终边落在（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】C【解析】因为α20222225360==+⨯，而222是第三象限角，故角α的终边落在第三象限.故答案为：C.【例3-2】（2022砀山月考）角 296π-的终边所在的象限是（） A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】C【解析】29367π666ππ-=-+，则296π-与 76π终边相同，故角 296π- 的终边所在的象限是第三象限.故答案为：C【一隅三反】1．（2022高一下·新余期末）410°角的终边落在（）A ．第一象限B ．第二象限C ．第三象限D ．第四象限【答案】A【解析】41036050=+，故为第一象限角。

新教材高中数学第五章任意角课后篇巩固提升含解析新人教A版必修第一册

新教材高中数学新人教A版选择性必修第一册：第五章三角函数5.1任意角和弧度制5.1.1任意角课后篇巩固提升合格考达标练1.(2021山西太原高一期末)475°角的终边所在的象限是()A.第一象限B.第二象限C.第三象限D.第四象限475°=360°+115°,又因为115°是第二象限角,而475°与115°终边相同,故475°角的终边所在的象限是第二象限.故选B.2.若θ是第四象限角,则90°+θ是()A.第一象限角B.第二象限角C.第三象限角D.第四象限角,将θ的终边按逆时针方向旋转90°得90°+θ的终边,则90°+θ是第一象限角.3.(2021广东潮州高一期末)下列角中终边与340°相同的角是()A.20°B.-20°C.620°D.-40°340°角终边相同的角的集合为{x|x=340°+k·360°,k∈Z},当k=-1时,可得x=-20°.故选B. 4.如图,终边在阴影部分(含边界)的角的集合是()A.{α|-45°≤α≤120°}B.{α|120°≤α≤315°}C.{α|-45°+k·360°≤α≤120°+k·360°,k∈Z}D.{α|120°+k·360°≤α≤315°+k·360°,k∈Z},终边落在阴影部分(含边界)的角的集合是{α|-45°+k·360°≤α≤120°+k·360°,k∈Z}.故选C.5.已知角α,β的终边关于直线x+y=0对称,且α=-60°,则β=.30°+k·360°,k∈Z-90°到0°的范围内,-60°角的终边关于直线y=-x对称的射线的对应角为-45°+15°=-30°,所以β=-30°+k·360°,k∈Z.6.与-2 020°角终边相同的最小正角是;最大负角是.°-220°-2020°=-6×360°+140°,140°-360°=-220°,所以最小正角为140°,最大负角为-220°. 7.已知角α的终边在图中阴影部分所表示的范围内(不包括边界),写出角α的集合.0°~360°范围内,终边落在阴影部分内的角为30°<α<150°与210°<α<330°,故所有满足题意的角α的集合为{α|k·360°+30°<α<k·360°+150°,k∈Z}∪{α|k·360°+210°<α<k·360°+330°,k∈Z}={α|n·180°+30°<α<n·180°+150°,n∈Z}.等级考提升练8.(2021北京西城高一期末)下列各角中,与27°角终边相同的是()A.63°B.153°C.207°D.387°27°角终边相同的角的集合为{α|α=27°+k·360°,k∈Z},取k=1,可得α=387°.故与27°角终边相同的是387°.故选D.9.射线OA绕端点O逆时针旋转120°到达OB位置,由OB位置绕端点O旋转到达OC位置,得∠AOC=-150°,则射线OB旋转的方向与角度分别为()A.逆时针,270°B.顺时针,270°C.逆时针,30°D.顺时针,30°,∠AOB=120°,设∠BOC=θ,所以∠AOC=∠AOB+∠BOC=120°+θ=-150°,解得θ=-270°,故需要射线OB绕端点O顺时针旋转270°.10.已知集合M={x|x=k·180°2±45°,k∈Z},P={x|x=k·180°4±90°,k∈Z},则M,P之间的关系为() A.M=P B.M⊆PC.M⊇PD.M∩P=⌀M,x=k·180°2±45°=k·90°±45°=(2k±1)·45°,k∈Z,对于集合P,x=k·180°4±90°=k·45°±90°=(k±2)·45°,k∈Z.∴M⊆P.11.(多选题)(2020海南临高高一期末)已知A={第一象限角},B={锐角},C={小于90°的角},那么A,B,C的关系是()A.B=A∩CB.B∪C=CC.B∩A=BD.A=B=CA,A∩C除了锐角,还包括其他角,比如-330°角,所以A选项错误.对B,锐角是小于90°的角,故B选项正确.对C,锐角是第一象限角,故C选项正确.对D,A,B,C中角的范围不一样,所以D选项错误.12.(多选题)已知角2α的终边在x轴的上方,那么角α可能是()A.第一象限角B.第二象限角C.第三象限角D.第四象限角2α的终边在x轴的上方,所以k·360°<2α<k·360°+180°,k∈Z,则有k·180°<α<k·180°+90°,k∈Z.故当k=2n,n∈Z时,n·360°<α<n·360°+90°,n∈Z,α为第一象限角;当k=2n+1,n∈Z时,n·360°+180°<α<n·360°+270°,n∈Z,α为第三象限角.故选AC.13.终边落在直线y=-√33x上的角的集合是.β|β=150°+k·180°,k∈Z}0°~360°范围内,终边落在直线y=-√33x上的角有两个,即150°角与330°角(如图),又所有与150°角终边相同的角构成的集合S1={β|β=150°+k·360°,k∈Z},所有与330°角终边相同的角构成的集合S2={β|β=330°+k·360°,k∈Z},于是,终边落在直线y=-√33x上的角的集合S=S1∪S2={β|β=150°+k·360°,k∈Z}∪{β|β=330°+k·360°,k∈Z}={β|β=150°+k·180°,k∈Z}.14.若α与288°角终边相同,则在0°~360°内终边与角α4终边相同的角是 .°,162°,252°,342°,得α=288°+k ·360°(k ∈Z ),α4=72°+k ·90°(k ∈Z ).又α4在0°~360°内,所以k=0,1,2,3,相应地有α4=72°,162°,252°,342°.15.已知α=-1 910°.(1)把α写成β+k ·360°(k ∈Z ,0°≤β<360°)的形式,并指出它是第几象限角; (2)求θ,使θ与α的终边相同,且-720°≤θ<0°.设α=β+k ·360°(k ∈Z ),则β=-1910°-k ·360°(k ∈Z ). 令-1910°-k ·360°≥0, 解得k ≤-1910360=-51136.k 的最大整数解为k=-6,求出相应的β=250°, 于是α=250°-6×360°,它是第三象限角. (2)令θ=250°+n ·360°(n ∈Z ),取n=-1,-2就得到符合-720°≤θ<0°的角. 250°-360°=-110°,250°-720°=-470°. 故θ=-110°或θ=-470°.新情境创新练16.已知α,β都是锐角,且α+β的终边与-280°角的终边相同,α-β的终边与670°角的终边相同,求角α,β的大小.,α+β=-280°+k ·360°,k ∈Z .∵α,β都是锐角,∴0°<α+β<180°. 取k=1,得α+β=80°. ①α-β=670°+k ·360°,k ∈Z . ∵α,β都是锐角,∴-90°<α-β<90°. 取k=-2,得α-β=-50°. ② 由①②,得α=15°,β=65°.。

5.1 任意角与弧度制(精练)(解析版)--人教版高中数学精讲精练必修一

5.1任意角与弧度制（精练）1．（2023春·上海静安·高一统考期末）在平面直角坐标系中，以下命题中所表述的角都是顶点在坐标原点，始边与x 轴的正半轴重合的角.①小于90︒的角一定是锐角；②第二象限的角一定是钝角；③终边重合的角一定相等；④相等的角终边一定重合.其中真命题的个数是（）A ．1B ．2C ．3D ．4【答案】A【解析】对于①，60-︒的角是小于90︒的角，但不是锐角，所以①错误，对于②，480︒的角是第二象限的角，但不是钝角，所以②错误，对于③，480︒的角和120︒的角终边相同，但不相等，所以③错误，对于④，因为角都是顶点在坐标原点，始边与x 轴的正半轴重合的角，所以若角相等，则终边一定重合，所以④正确，所以真命题的个数是1，故选：A2．（2023·全国·高三专题练习）集合ππππ,Z 42k k k αα⎧⎫+≤≤+∈⎨⎬⎩⎭中的角所表示的范围(阴影部分)是（）A ．B ．C ．D ．【答案】C【解析】当2(Z)k n n =∈时，ππ2π2π,Z 42n n n α+≤≤+∈，此时α表示的范围与ππ42α≤≤表示的范围一样；当21(Z)k n n =+∈时，ππ2ππ2ππ,Z 42n n n α++≤≤++∈，此时α表示的范围与ππππ42α+≤≤+表示的范围一样，故选：C ．3（2023·全国·高一专题练习）下列说法正确的是（）A ．角60o 和角600o 是终边相同的角B ．第三象限角的集合为3ππ2π2π,Z 2k k k αα⎧⎫+≤≤+∈⎨⎬⎩⎭∣C ．终边在y 轴上角的集合为ππ,Z 2k k αα⎧⎫=+∈⎨⎬⎩⎭∣D ．第二象限角大于第一象限角【答案】C【解析】600360240︒=︒+︒，与60︒终边不相，故A 错误；第三象限角的集合为3ππ2π2π,Z 2k k k αα⎧⎫+<<+∈⎨⎬⎩⎭∣，故B 错误；终边在y 轴上角的集合为π3π2π,Z 2π,Z 22n n n n αααα⎧⎫⎧⎫=+∈=+∈⎨⎬⎨⎬⎩⎭⎩⎭∣∣，即ππ2π,Z (21)π,Z 22n n n n αααα⎧⎫⎧⎫=+∈=++∈⎨⎬⎨⎬⎩⎭⎩⎭ ∣∣，即ππ,Z 2k k αα⎧⎫=+∈⎨⎬⎩⎭∣，故C 正确；120︒是第二象限角，390︒第一象限角，120390︒<︒，故D 错误；故选：C.4．（2023·全国·高一专题练习）已知α为第三象限角，则2α为第（）象限角.A ．二或四B ．三或四C ．一或二D ．二或三【答案】A【解析】因为α为第三象限角，所以360180360270Z,, k k k α︒︒︒︒⋅+<<⋅+∈所以180********Z,2, k k k α︒︒︒︒⋅+<<⋅+∈当k 为偶数时，记2,Z k n n =∈,所以36090360135Z 2,,n n n α︒︒︒︒⋅+<<⋅+∈所以2α为第二象限角，当k 为奇数时，记21,Z k n n =+∈,所以360270360315,Z,2n n n α︒︒︒︒⋅+<<⋅+∈所以2α为第四象限角，所以2α为第二或第四象限角，故选:A.5（2023秋·浙江·高二校联考开学考试）一只红蚂蚁与一只黑蚂蚁在一个圆（半径为1cm ）的圆周上爬动，且两只蚂蚁均从点()1,0A 同时逆时针匀速爬动，红蚂蚁以πrad /s 4的速度爬行，黑蚂蚁以πrad /s 12的速度爬行，则2秒钟后，两只蚂蚁之间的直线距离为（）A ．1BC ．π3D ．π6【答案】A【解析】如图所示，红蚂蚁以πrad /s 4的速度爬行，黑蚂蚁以πrad /s 12的速度爬行，则2秒钟后，红蚂蚁绕圆的角度为π2，到达B 处，黑蚂蚁绕圆的角度为π6，到达C 处，此时πππ-263BOC ∠==，即BOC 为正三角形，故1BC OB ==.故选：A6（2023秋·江西）《梦溪笔谈》是我国科技史上的杰作，其中收录了扇形弧长的近似计算公式：22ABl ⨯=+矢弦径.如图，公式中“弦”是指扇形中 AB 所对弦AB 的长，“矢”是指 AB 所在圆O 的半径与圆心O 到弦的距离之差，“径”是指扇形所在圆O 的直径.若扇形的面积为16π3，扇形的半径为4，利用上面公式，求得该扇形的弧长的近似值为（）A 1B ．1C ．1D ．1+【答案】D【解析】设该扇形的圆心角为α，由扇形面积公式得2116π423α⨯⨯=，所以2π3α=，取 AB 的中点C ，连接OC ，交AB 于点D ，则OC AB ⊥，则πcos 4cos23OD OA AOD ∠=⨯==，π224sin3AB AD ==⨯=，2CD OC OD =-=，所以扇形的弧长的近似值为22AB l ⨯=+矢弦径222CD AB OA=+2418⨯==+.故选：D7．（2023春·黑龙江绥化·高一校考阶段练习）中国扇文化有着深厚的文化底蕴，文人雅士喜欢在扇面上写字作画．如图是书画家唐寅（1470—1523）的《枯木寒鸦图》扇面，其尺寸如图所示，则该扇面的面积为（）A ．2280cm B ．2352cm C ．2528cm D ．2704cm 【答案】D【解析】如图，设AOB θ∠=，OA OB r ==，由弧长公式可得：2464(16)r r θθ=⎧⎨=+⎩，解得：485r =，扇形OCD 的面积211486416819.2cm 25S ⎛⎫=⨯⨯+= ⎪⎝⎭，扇形OAB 的面积2214824115.2cm 25S =⨯⨯=所以扇面的面积212704cm S S S =-=．故选：D ．8．（2023春·安徽·高一校联考期中）勒洛三角形是一种特殊三角形，指分别以正三角形的三个顶点为圆心，以其边长为半径作圆弧，由这三段圆弧组成的曲边三角形.如图，勒洛三角形ABC 的周长为π，则该勒洛三角形ABC 的面积为（）A ．4B ．2π4C ．π2D ．2π4+【答案】C【解析】因为勒洛三角形ABC 的周长为π，所以每段圆弧长为ππ33l r ==，解得1r =，即正三角形的边长为1，由题意可得21π32312123ABC C AB S S S -=-=⨯⋅⋅-⨯=△曲扇形故选：C9．（2023·全国·高一假期作业）下列说法正确的是（）A ．第一象限角一定是锐角B ．终边相同角一定相等C ．小于90°的角一定是锐角D ．钝角的终边在第二象限【答案】D【解析】对于A ，第一象限角是{}|36036090Z k k k αα︒︒︒⋅<<⋅+∈，，第一象限角不一定是锐角，故A 错误；对于B ，终边相同角不一定相等，它们可能差360Z k k ︒⋅∈，，故B 错误；对于C ，小于90°的角不一定是锐角，也可能是零角或者负角，故C 错误；对于D ，钝角是大于90°且小于180°的角，故D 正确；故选：D.10．（2023春·江西宜春·高一江西省宜丰中学校考期中）数学中处处存在着美，莱洛三角形就给人以对称的美感.莱洛三角形的画法如下：先画等边三角形ABC ，再分别以点,,A B C 为圆心，线段AB 长为半径画圆弧，便得到莱洛三角形（如图所示）.若莱洛三角形的周长为π2，则其面积是（）A．π4B．π8C．π8D．π4【答案】C【解析】莱洛三角形的周长为π2，可得弧长 6πA BC B AC ===，则等边三角形的边长π16π23AB BC AC ====，分别以点A 、B 、C 为圆心，圆弧,,AB BC AC 所对的扇形面积均为1π1π26224⨯⨯=，等边ABC的面积1122S =⨯所以莱洛三角形的面积是ππ3224168⨯-⨯=.故选：C.11．（2023春·云南曲靖·高一校考阶段练习）水滴是刘慈欣的科幻小说《三体II·黑暗森林》中提到的由三体文明使用强互作用力（SIM ）材料所制成的宇宙探测器，因为其外形与水滴相似，所以被人类称为水滴.如图所示，水滴是由线段,AB AC 和圆的优弧BC 围成，其中,AB AC 恰好与圆弧相切.若圆弧所在圆的半径为1，点A 到圆弧所在圆圆心的距离为2，则该封闭图形的面积为（）A 2π3B ．2π3C ．π3+D π3+【答案】A【解析】如图，设圆弧所在圆的圆心为O ，连接,,OA OB OC ，依题意得,OB AB OC AC ⊥⊥，且1,2OB OC OA ===，则π3AB AC BAC ∠===，所以2π3BOC ∠=，所以该封闭图形的面积为2112π2π212π12233⎛⎫⨯⨯+⨯-⨯+ ⎪⎝⎭.故选：A.12（2023秋·山东临沂·高一校考期末）设12ππππ,,2π,,2π,222S k k S k k S k k αααααα⎧⎫⎧⎫⎧⎫==+∈==+∈==-∈⎨⎬⎨⎬⎨⎬⎩⎭⎩⎭⎩⎭Z Z Z ∣∣∣，则下列结论错误的是（）A ．1S S ⊆B ．2S S ⊆C ．12S S S⋃=D ．12S S S⋂=【答案】D【解析】因为ππ,2S k k αα⎧⎫==+∈⎨⎬⎩⎭Z ∣表示终边落在y 轴上角的集合，1π2π,2S k k αα⎧⎫==+∈⎨⎬⎩⎭Z ∣表示终边落在y 轴正半轴上角的集合，2π2π,2S k k αα⎧⎫==-∈⎨⎬⎩⎭Z ∣表示终边落在y 轴负半轴上角的集合，所以1S S ⊆，2S S ⊆，12S S S ⋃=正确；12S S S ⋂=∅≠，故错误.故选：D13．（2023春·重庆长寿·高一重庆市长寿中学校校考期中）（多选）下列结论正确的是（）A ．7π6-是第二象限角B ．第三象限角的集合为3π|π2π2π,2k k k αα⎧⎫+≤≤+∈⎨⎬⎩⎭Z C ．终边在y 轴上的角的集合为π|π,2k k αα⎧⎫=+∈⎨⎬⎩⎭Z D ．若角α为锐角，则角2α为钝角【答案】AC【解析】对于选项A ：因为7π5π2π66-=-，且5π6为第二象限角，所以7π6-是第二象限角，故A 正确；对于选项B ：第三象限角的集合为3π|π2π2π,2k k k αα⎧⎫+<<+∈⎨⎬⎩⎭Z ，故B 错误；对于选项C ：终边在y 轴上的角的集合为π|π,2k k αα⎧⎫=+∈⎨⎬⎩⎭Z ，故C 正确；对于选项D ：若角α为锐角，即π02α<<，则02πα<<，所以角2α不一定为钝角，例如π4α=，则π22α=为直角，故D 错误；故选：AC.14（2023·全国·高一课堂例题）（多选）与457- 角终边相同的角的集合是（）A ．{}360457,k k αα=⋅-∈ZB ．{}36097,k k αα=⋅+∈ZC ．{}360263,k k αα=⋅+∈ZD ．{}360263,k k αα=⋅-∈Z【答案】AC【解析】与457- 终边相同的角可写为：()360457k k α=⋅-∈Z，()97360457k k ≠⋅-∈Z ，2632360457=⨯- ，()263360457k k -≠⋅-∈Z ，∴与457- 角终边相同的角的集合为：{}360457,k k αα=⋅-∈Z ，A 正确；{}360263,k k αα=⋅+∈Z ，C正确.故选：AC.15．（2022秋·河北石家庄·高一石家庄精英中学校考阶段练习）（多选）下列说法正确的有（）A ．1801πrad ⎛⎫=︒⎪⎝⎭B ．若角α是锐角，则2α是第一或第二象限角C ．若角α是第二象限角，则2a是第一或第三象限角D ．角α是第三或第四象限角的充要条件是sin 0α<【答案】AC【解析】由题意A 项，π1180rad ︒=∴1801πrad ⎛⎫=︒ ⎪⎝⎭故A 正确.B 项，若角α是锐角，∴π02α<<∴02πα<<∴2α不仅可能是第一或第二象限角，也可能在y 轴上，故B 错误.C 项，若角α是第二象限角，∴π2π2ππ2k k α+<<+()k ∈Z ∴ππππ422k k α+<<+()k ∈Z 则2a是第一或第三象限角故C 正确.D 项，若角α是第三或第四象限角则()2ππ21πk k α+<<+，且3π2π2k α¹+()k ∈Z ∴sin 0α<，必要性成立若sin 0α<，则()2ππ21πk k α+<<+()k ∈Z ∴角α是第三或第四象限角或在y 轴的负半轴上充分性不成立故D 错误.故选：AC.16．（2023秋·吉林长春·高一长春市实验中学校考期末）（多选）若角α是第二象限角，则下列各角中是第三象限角的是（）A ．α-B ．πα-C ．3π2α-D ．2α【答案】AC【解析】因为角α是第二象限角，所以π2π2ππ2k k α+<<+，Z k ∈，对于A ，ππ2π2π2k k α--<-<--，Z k ∈，故α-是第三象限角，故A 正确；对于B ，π2ππ2π+2k k α-<-<-，Z k ∈，故πα-是第一象限角，故B 不正确；对于C ，3πππ2π2π22k k α-+<-<-，Z k ∈，故3π2α-是第三象限角，故C 正确；对于D ，π4π24π2πk k α+<<+,Z k ∈,故2α是第三象限角或y 轴负半轴上的角或第四象限角，故D 不正确.故选：AC17（2022秋·陕西商洛·高一校考阶段练习）（多选）下列转化结果正确的是（）A ．6730︒＇化成弧度是3π8B ．10π3-化成角度是600-︒C ．150-︒化成弧度是7π6-D ．π12化成角度是15︒【答案】ABD【解析】对于A,6730︒＇化成弧度是π367.5π1808⨯=,故A 正确，对于B ，1010π=18060033--⨯=- ，故B 正确，对于C ，5π150150π1806︒=︒⨯--=- ，故C 错误，对于D ，π1=180151212⨯= ，故D 正确，故选：ABD18．（2023春·江西上饶·高一上饶市第一中学校考阶段练习）如图所示，终边落在阴影部分（包括边界）的角α的集合为．【答案】{}120360135360,Z k k k αα-︒+⋅︒≤≤︒+⋅︒∈．【解析】由图，阴影部分下侧终边相同的角为120360k -︒+︒，上侧终边相同的角为135360k ︒+︒且Z k ∈，所以阴影部分（包括边界）的角α的集合为{}120360135360,Z k k k αα-︒+⋅︒≤≤︒+⋅︒∈.故答案为：{}120360135360,Z k k k αα-︒+⋅︒≤≤︒+⋅︒∈19．（2023·全国·高三专题练习）若角α的顶点为坐标原点，始边在x 轴的非负半轴上，终边在直线y =上，则角α的取值集合是【答案】π{|π,Z}3k k αα=-∈【解析】直线y =的倾斜角是23π，所以终边落在直线y =上的角的取值集合为π{|π,Z}3k k αα=-∈故答案为：π{|π,Z}3k k αα=-∈20．（2023秋·江西抚州·高二江西省乐安县第二中学校考开学考试）若扇形的圆心角为120 ，半径32.则它的弧长为.【答案】π【解析】因为2π1203=o，又扇形的圆心角为120 ，半径为32，所以它的弧长为2π3π32l =⨯=，故答案为：π22．（2023春·江西上饶·高一统考期末）已知ABC 是边长为2的等边三角形.如图，将ABC 的顶点A 与原点重合，AB 在x 轴上，然后将三角形沿着x 轴正方向滚动，每当顶点A 再次回落到x 轴上时，将相邻两个点A 之间的距离称为“一个周期”，则完成“一个周期”时，顶点A 的路径长度为.【答案】83π/83π【解析】如图，顶点A 先以2为半径绕点B 顺时针旋转2π3弧度，再以2为半径绕点C 顺时针旋转2π3弧度，其路径长度为2π8π2233⨯⨯=.故答案为：8π323．（2023·全国·高一课堂例题）若角α是第二象限角，试确定角2α，3α是第几象限角．【答案】2α可能是第三象限角、第四象限角或终边在y 轴非正半轴上的角；3α可能是第一象限角、第二象限角或第四象限角【解析】因为α是第二象限角，所以90360180360(Z)k k k α︒+⋅︒<<︒+⋅︒∈，可得180236023602360,Z k k k α︒+⋅︒<<︒+⋅︒∈，所以2α可能是第三象限角、第四象限角或终边在y 轴非正半轴上的角．又由1203012060,Z 3k k k α⋅︒+︒<<⋅︒+︒∈，当3,Z k n k =∈时，3603036060,Z 3n n k α⋅︒+︒<<⋅︒+︒∈，此时3α是第一象限角；当31,Z k n k =+∈时，360150360180,Z 3n n k α⋅︒+︒<<⋅︒+︒∈，此时3α是第二象限角；当32,Z k n k =+∈时，360270360300,Z 3n n k α⋅︒+︒<<⋅︒+︒∈，此时3α是第四象限角．综上所述，3α可能是第一象限角、第二象限角或第四象限角．24．（2023·全国·高一假期作业）已知扇形的圆心角为α，所在圆的半径为r ．(1)若150,10r α=︒=，求扇形的弧长．(2)若扇形的周长为24，当α为多少弧度时，该扇形面积最大？求出最大面积．【答案】(1)25π3(2)max 2,36S α==【解析】（1）设扇形的弧长为l ．因为150α=︒，即5π,106r α==，所以5π2510π63l r α==⨯=．（2）由题设条件，知224l r +=，则242(012)l r r =-<<，所以扇形的面积()()22112421263622S lr r r r r r ==-=-+=--+．当6r =时，S 有最大值36，此时24212,2ll r rα=-===，所以当2α=时，扇形的面积最大，最大面积是36．25．（2023春·江西抚州·高一江西省抚州市第一中学校考期中）某地政府部门欲做一个“践行核心价值观”的宣传牌，该宣传牌形状是如图所示的扇形环面(由扇形OAD 挖去扇形OBC 后构成的)．已知2OA =米，OB x =米()02x <<，线段BA 、线段CD 与弧 BC 、弧 AD 的长度之和为6米，圆心角为θ弧度．(1)求θ关于x 的函数解析式；(2)记该宣传牌的面积为y ，试问x 取何值时，y 的值最大?并求出最大值．【答案】(1)22(02)2x x x θ+=<<+；(2)当12x =时，y 的值最大，最大值为94．【解析】（1）根据题意，弧 BC 的长度为x θ米，弧 AD 的长度2AD θ=米，2(2)26x x θθ∴-++=，∴22(02)2x x x θ+=<<+．（2）依据题意，可知2211222OAD OBC y S S x =-=⨯-扇扇，化简得：22y x x =-++，02x <<，∴当12x =，2max 1192224y ⎛⎫=-++= ⎪⎝⎭．∴当12x =时，y 的值最大，且最大值为94．26．（2022秋·陕西商洛·高一校考阶段练习）已知一扇形的圆心角为α，半径为R ，弧长为()0L α>．(1)已知扇形的周长为10cm ，面积是24cm ，求扇形的圆心角；(2)若扇形周长为20cm ，当扇形的圆心角α为多少弧度时，这个扇形的面积最大？并求此扇形的最大面积．【答案】(1)12(2)S 取得最大值25，此时2α=【解析】（1）由题意得2210142R R R αα+=⎧⎪⎨⋅=⎪⎩，解得18R α=⎧⎨=⎩(舍去)，412R α=⎧⎪⎨=⎪⎩．所以扇形圆心角12．（2）由已知得，220l R +=．所以()2112021022S lR R R R R ==-=-()2525R =--+，所以当5R =时，S 取得最大值25，21252R α⨯⨯=,解得2α=.当扇形的圆心角α为2多少弧度时，这个扇形的面积最大为25.27．（2023秋·高一课时练习）已知一扇形的中心角是α，所在圆的半径是R .（1）若45α=︒，10R =，求扇形的弧长l 及面积S ；（2）若扇形的周长是一定值C （0C >），当α为多少弧度时，该扇形有最大面积？并求最大面积；（3）若扇形的面积是一定值S （0S >），当α为多少弧度时，该扇形有最小周长？并求最小周长.【答案】13.（1）5π2l =，25π2S =；（2）当2α=弧度时，扇形面积最大，为216C ；（3）当2α=弧度时，扇形周长最小，为4S .【解析】（1）若45α=︒，10R =，则451804ππα=︒⨯=︒，所以扇形的弧长25104l R ππα==⨯=，扇形的面积21152510222S lR ππ==⨯⨯=；（2）扇形周长22C R l R R α=+=+，2CR α∴=+，2222111()42222164C C C S R ααααα∴=⋅==⋅+++扇．当且仅当24α=，即2α=时，扇形面积有最大值216C ．（3）扇形的面积212S R α=，所以2S R α=所以()()222222224222C S R l R SS S S ααααααααα+⎛⎫=⋅=⋅+≥⋅⋅= ⎭=+=⎪+⎝=+当且仅当2αα=即2α=时周长取得最小值4S1．（2023秋·江苏淮安·高一统考期末）如图，正六边形ABCDEF 的边长为2，分别以点,A B 为圆心，AF 长为半径画弧，两弧交于点G ，则 ,,AG BGAB 围成的阴影部分的面积为．【答案】43π【解析】如图，连接,GA GB .由题意知，线段,,GA GB AB 的长度都等于半径2，所以，GAB △为正三角形，则π3GBA GAB ∠=∠=，故GAB △的面积为212S =扇形GBA 的面积为2π22π33S =⨯=，由图形的对称性可知，扇形GAB 的面积与扇形GBA 的面积相等，所以阴影部分的面积2142π3S S S =-=-故答案为：4π32．（2023春·山东潍坊·高一校联考期中）某数学兴趣小组设计了一种螺线，作法如下：在水平直线m 上取长度为1的线段AB ，并作等边三角形ABC ，然后以点B 为圆心，BA 为半径逆时针画圆弧，交线段CB 的延长线于点D ；再以点C 为圆心，CD 为半径逆时针画圆弧，交线段AC 的延长线于点E ；再以点A 为圆心，AE 为半径逆时针画圆弧，交线段BA 的延长线于点F ；再以点B 为圆心，BF 为半径逆时针画圆弧，；以此类推，得到的螺线如图所示.当螺线与直线m 有4个交点（不含A 点）时，则螺线长度为（）A ．14πB ．30πC ．100π3D ．110π3【答案】A【解析】第1次画线：以点B 为圆心，扇形半径为1r =，旋转2π3，划过的圆弧长为2π2π133⨯=；第2次画线：以点C 为圆心，扇形半径为2r =，旋转2π3，划过的圆弧长为2π4π233⨯=，交m 累计1次；第3次画线：以点A 为圆心，扇形半径为3r =，旋转2π3，划过的圆弧长为32π6π2π33⨯==，交m 累计2次；第4次画线：以点B 为圆心，扇形半径为4r =，旋转2π3，划过的圆弧长为2π8π433⨯=；第5次画线：以点C 为圆心，扇形半径为=5r ，旋转2π3，划过的圆弧长为2π10π533⨯=，交m 累计3次；前5次累计画线2π4π6π8π10π10π33333++++=；第6次画线：以点A 为圆心，扇形半径为6r =，旋转2π3，划过的圆弧长为2π12π64π33⨯==，交m 累计4次，累计画线10π4π14π+=.故选：A.3．（2023春·河北张家口·高一统考期中）如图，已知扇形的周长为6，当该扇形的面积取最大值时，弦长AB =（）A ．3sin1B ．3sin 2C ．3sin1︒D ．3sin 2︒【答案】A【解析】设扇形的圆心角为α，半径为r ，弧长为l ，则26l r +=，62l r =-，由0620r l r >⎧⎨=->⎩可得03r <<，所以，扇形的面积为()21393224r r S lr r r ⎛⎫ ⎪⎝⎭-+==-≤=，当且仅当3r r -=，即32r =时，扇形的面积S 最大，此时623l r =-=．因为l r α=，则扇形的圆心角3232l r α===，取线段AB 的中点E ，由垂径定理可知OE AB ⊥，因为OA OB =，则112122AOE AOB ∠=∠=⨯=，所以，22sin13sin1AB AE OA ===.故选：A.4．（2023春·辽宁沈阳·高一沈阳二十中校联考期中）中国传统扇文化有着极其深厚的底蕴．一般情况下，折扇可看作是从一个圆面中剪下的扇形制作而成，如图，设扇形的面积为1S ，其圆心角为θ，圆面中剩余部分的面积为2S ，当1S 与2S时，扇面为“美观扇面”，则下列结论错误的是（）（参考数据：2.236≈）A ．122S S θπθ=-B ．若1212S S =，扇形的半径3R =，则13πS =C ．若扇面为“美观扇面”，则138θ≈︒D ．若扇面为“美观扇面”，扇形的半径20R =，则此时的扇形面积为(2003【答案】D【解析】扇形的面积为1S ，其圆心角为θ，半径为R ，圆面中剩余部分的面积为2S ，选项A ：()212212=12π2π2S R S R θθθθ=--.故A 正确；选项B ：由1212S S =，可得12π2θθ=-，解得2π3θ=，又扇形的半径3R =，则2112π33π23S =⨯⨯=.故B 正确；选项C ：若扇面为“美观扇面”，则1212π2S S θθ-==-，解得(()3π3 2.236180138θ⎡⎤=≈-⨯≈⎣⎦.故C 正确；选项D ：若扇面为“美观扇面”，则(3πθ=，又扇形的半径20R =，则此时的扇形面积为((213π202003π2⨯⨯=.故D 错误.故选：D5（2023春·北京海淀·高一北大附中校考期中）如图放置的边长为1的正PMN 沿x 轴滚动．设顶点(,)P x y 的运动轨迹对应的函数解析式为()y f x =，给出下列结论，其中正确结论的个数为（）①()y f x =的图象关于点3,02⎛⎫⎪⎝⎭对称；②()y f x =的图象关于直线32x =对称；③()y f x =在其两个相邻零点间的曲线长度为4π3；④()y f x =在其两个相邻零点间的图象与x 轴所围区域的面积为2π3．说明：“正PMN 沿x 轴滚动”包括沿x 轴正方向和负方向滚动．沿x 轴正方向滚动指的是先以顶点N 为中心顺时针旋转，当顶点M 落在x 轴上时，再以顶点M 为中心顺时针旋转，如此继续．类似地，正PMN 可以沿x 轴负方向滚动．A ．1B ．2C ．3D ．4【答案】B【解析】当正PMN 沿x 轴正方向滚动，绕N 旋转P 轨迹是以(1,0)N 为圆心，1为半径，圆心角为2π3的弧上，P 从(0,0)旋转到3(22；绕M 旋转P 轨迹是以(2,0)M 为圆心，1为半径，圆心角为2π3的弧上，P 从3(2旋转到(3,0)；绕P 旋转时P 点不动，后续继续旋转重复上述过程，只是圆心位置改变，同理，正PMN 沿x 轴负方向滚动，先绕P 旋转，然后绕M 旋转，再绕N 旋转，每次旋转角度、半径都相同，只是圆心不同；综上，P 在x 轴上部分轨迹如上图示，由图易知：区间[0,3]图象在x 轴上周期性出现，所以()y f x =的图象关于32x =对称，不关于3,02⎛⎫⎪⎝⎭对称，①错，②对；()y f x =在其两个相邻零点间的曲线长度为2π4π2133⨯⨯=，③对；()y f x =在其两个相邻零点间的图象与x 轴所围区域的面积为212π1π2π211sin 232334⨯⨯⨯+⨯⨯=+，④错.故选：B6．（2023秋·河南周口·高一校考开学考试）如图，等边三角形ABC 的边长为2，以A 为圆心，1为半径作圆分别交AB ，AC 边于D ，E ，再以点C 为圆心，CD 的长为半径作圆交BC 边于F ，连接E ，F ，那么图中阴影部分的面积为.【答案】π3124【解析】过A 作AM BC ⊥于,M EN BC ⊥于N ，∵等边三角形ABC 的边长为2,60,BAC B ACB ∠=∠=∠=2AM ∴===1,AD AE == ,,AD BD AE CE ∴==1,22EN AM ∴==∴图中阴影部分的面积为：ABC CEF ADE S S S 扇形－－－()BCD DCF S S - 扇形160π111130π32223602222360⋅⨯⋅⨯⎛⎫=⨯--⨯-⨯⨯- ⎪⎝⎭π31224=+-.故答案为:π31224+-.。

5.1任意角和弧度制-【新教材】人教A版(2019)高中数学必修第一册课后练习

2020-2021学年第一学期人教A 版（2019）必修第一册5.1任意角和弧度制课后练习一、单选题1．角2912π的终边所在的象限是（） A ．第一象限B ．第二象限C ．第三象限D ．第四象限 2．某扇形的面积为21cm ，它的周长为4cm ，那么该扇形圆心角的大小为（）A ．2B ．2C ．4D ．43．若一个扇形的周长与面积的数值相等，则该扇形所在圆的半径不可能等于( )A ．5B ．2C ．3D ．44．已知某扇形的半径为4cm ，圆心角为2rad ，则此扇形的面积为（）A ．232cmB ．216cmC ．28cmD ．24cm5．集合{|,}42k k k Z ππαπαπ+≤≤+∈中角所表示的范围(阴影部分)是( )A ．B ．C ．D ．6．若角αβ、的终边相同，则αβ-的终边在（）．A ．x 轴的非负半轴上B ．x 轴的非正半轴上C ．y 轴的非负半轴上D ．y 轴的非正半轴上7．下列各组角中，终边相同的角是( )A ．2029,33ππB ．22,33ππ- C ．33,22ππ- D ．725,99ππ-- 8．已知圆锥的母线长为5cm ，底面半径为53cm ，一只蚂蚁欲从圆锥的底面圆周上的点A 出发，沿圆锥侧面爬行一周回到点A .则蚂蚁爬行的最短路程长为（）A ．8cmB ．cmC ．10cmD ．5πcm二、填空题9．一个面积为1的扇形，所对弧长也为1，则该扇形的圆心角是________弧度 10．给出下列说法：①锐角都是第一象限角；②第一象限角一定不是负角；③小于180°的角是钝角或直角或锐角．其中正确说法的序号为________．(把正确说法的序号都写上) 11．若3604,5k k Z α=⋅+︒∈︒，则2α是第________象限角. 12．若扇形OAB 的面积是21cm ，它的弧所对的圆心角是2rad ，则它的弧长是_______cm ．三、解答题13.已知扇形AOB 的周长为8．（1）若这个扇形的面积为3，求其圆心角的大小。

5.1 任意角与弧度制(精讲)(解析版)--人教版高中数学精讲精练必修一

5.1任意角与弧度制（精讲）一．任意角1．角的定义及分类(1)角的概念：角可以看成平面内一条射线绕着它的端点旋转所成的图形．(2)角的表示：如图所示，角α可记为“α”或“∠α”或“∠AOB”，始边：OA，终边：OB，顶点O.(3)角的分类名称定义图示正角一条射线绕其端点按逆时针方向旋转形成的角负角一条射线绕其端点按顺时针方向旋转形成的角零角一条射线没有做任何旋转形成的角二．象限角与终边相同的角1.象限角与终边相同的角象限角把角放在平面直角坐标系中，使角的顶点与原点重合，角的始边与x 轴的非负半轴重合，那么，角的终边在第几象限，就说这个角是第几象限角；如果角的终边在坐标轴上，就认为这个角不属于任何一个象限终边相同的角所有与角α终边相同的角，连同角α在内，可构成一个集合S ＝{β|β＝α＋k ·360°，k ∈Z}，即任一与角α终边相同的角，都可以表示成角α与整数个周角的和k 有三层含义①特殊性：对k 每赋一个整数值就有一个具体对应的角．②一般性：表示所有与角α终边相同的角(包括α自身)．③从几何意义上看，k 表示角的终边按一定的方向转动的圈数．k 取正整数时，逆时针转动；k 取负整数时，顺时针转动；k ＝0时，没有转动．2．象限角的集合表示象限角象限角α的集合表示第一象限角{α|k ·360°<α<k ·360°＋90°，k ∈Z}第二象限角{α|k ·360°＋90°<α<k ·360°＋180°，k ∈Z}第三象限角{α|k ·360°＋180°<α<k ·360°＋270°，k ∈Z}第四象限角{α|k ·360°＋270°<α<k ·360°＋360°，k ∈Z}3．轴线角的集合表示角α终边的位置角α的集合表示在x 轴的非负半轴上{α|α＝k ·360°，k ∈Z}在x 轴的非正半轴上{α|α＝k ·360°＋180°，k ∈Z}在y 轴的非负半轴上{α|α＝k ·360°＋90°，k ∈Z}在y 轴的非正半轴上{α|α＝k ·360°＋270°，k ∈Z}在x 轴上{α|α＝k ·180°，k ∈Z}在y 轴上{α|α＝k ·180°＋90°，k ∈Z}在坐标轴上{α|α＝k ·90°，k ∈Z}三．度量角的两种单位制1.定义角度制定义用度作为单位来度量角的单位制1度的角周角的1360为1度的角，记作1°弧度制定义以弧度为单位来度量角的单位制1弧度的角长度等于半径长的圆弧所对的圆心角叫做1弧度的角.1弧度记作1rad2.弧度数(1)正角：正角的弧度数是一个正数.(2)负角：负角的弧度数是一个负数.(3)零角：零角的弧度数是0.(4)如果半径为r 的圆的圆心角α所对弧的长为l ，那么，角α的弧度数的绝对值是|α|＝lr .3.角度制与弧度制的换算四.设扇形的半径为R ，弧长为l ，α(0<α<2π)为其圆心角，则度量单位类别α为角度制α为弧度制扇形的弧长l ＝απR 180l ＝α·R 扇形的面积S ＝απR 2360S ＝12l ·R ＝12α·R 2一．表示区域角的三个步骤第一步：先按逆时针的方向找到区域的起始和终止边界.第二步：按由小到大分别标出起始和终止边界对应的－360°～360°范围内的角α和β，写出最简集合{x |α<x <β}，其中β－α<360°.第三步：起始、终止边界对应角α，β再加上360°的整数倍，即得区域角集合.二.已知α所在象限，确定nα或αn所在象限(1)用不等式表示α的范围，再确定nα或αn的范围，再判断角所在象限；(2)数形结合法，等分象限，确定角所在象限.三．角度与弧度互化在进行角度与弧度的换算时，抓住关系式πrad ＝180°是关键，由它可以得到：度数×π180＝弧度数，弧度数＝度数．角度与弧度互化的方法考点一与任意角有关的概念辨析【例1-1】（2023秋·高一课时练习）（多选）下列选项不正确的是（）A ．终边落在第一象限的角为锐角B ．锐角是第一象限的角C ．第二象限的角为钝角D ．小于90 的角一定为锐角【答案】ACD【解析】对于A ，终边落在第一象限的角不一定是锐角，如400 的角终边位于第一象限，但不是锐角，A 错误；对于B ，锐角是090 之间的角，终边位于第一象限，是第一象限角，B 正确；对于C ，终边落在第二象限的角不一定是钝角，如510 的角的终边位于第二象限，但不是钝角，C 错误；对于D ，小于90 的角不一定是锐角，如30- 的角小于90 ，但不是锐角，D 错误.故选：ACD.【例1-2】（2023·全国·高一课堂例题）每周一的早晨，我们都会在学校的操场上举行升国旗仪式，一般需要10分钟．这10分钟的时间，钟表的分针走过的角度是（）A ．30︒B ．30-︒C ．60︒D ．60-︒【答案】D【解析】分针是顺时针走的，∴形成的角度是负角，又分针走过了10分钟，∴走过的角度大小为103606060⨯︒=︒，综上，分针走过的角度是60-︒．故选：D ．【一隅三反】1．（2023福建厦门）（多选）下列说法错误的是（）A ．终边与始边重合的角是零角B ．终边与始边都相同的两个角一定相等C ．小于90°的角是锐角D ．若120α=-︒，则α是第三象限角【答案】ABC【解析】对于A.终边与始边重合的角的集合为{}360,Z k k αα=∈,故A 错误，对于B ，终边与始边都相同的两个角不一定相等，比如30,390 的终边和始边相同，但两个角不相等，故B 错误，对于C ，锐角为()0,90的角，所以小于90°的角不一定是锐角，故C 错误，对于D ，120α=-︒，则α是第三象限角，故D 正确，故选：ABC2．（2023秋·高一课时练习）（多选）下列说法，不正确的是（）A ．三角形的内角必是第一、二象限角B ．始边相同而终边不同的角一定不相等C ．钝角比第三象限角小D ．小于180°的角是钝角、直角或锐角【答案】ACD【解析】由题意，A 中，90°的角既不是第一象限角，也不是第二象限角，故A 错误；B 中，始边相同而终边不同的角一定不相等，故B 正确；C 中，钝角大于100-︒的角，而100-︒的角是第三象限角，故C 错误；D 中，零角或负角小于180︒，但它既不是钝角，也不是直角或锐角，故D 错误．故选：ACD.3．（2023上海）给出下列说法：①终边相同的角不一定相等；②第二象限的角大于第一象限的角；③0~90︒︒的角是第一象限的角；④小于180︒的角是钝角、直角和锐角.其中错误的序号是.【答案】②③④【解析】①终边相同的角不一定相等，终边相同的角有无数个，它们相差360︒的整数倍，故正确；②390︒角是第一象限角，120︒角是第二象限角，390120︒>︒，故错误；③0~90︒︒的角是指大于等于0︒小于90︒的角，其中0︒角不是象限角，故错误；④小于180︒的角还包括零角和负角，故错误；故答案为：②③④考点二终边相同的角【例2】（2023秋·吉林长春）下列各角中，与1850︒角终边相同的角是（）A ．40︒B ．50︒C ．320︒D ．400-︒【答案】B【解析】对选项A ，1850401810536010︒-==⨯+ ，故A 错误.对选项B ，因为18505018005360︒-=︒=⨯ ，故B 正确.对选项C ，18503201530436090︒-==⨯+ ，故C 错误.对选项D ，()18504002250636090︒--==⨯+，故D 错误.故选：B 【一隅三反】1．（2023秋·高一课时练习）与405°角终边相同的角是（）A ．k ·360°－45°，k ∈ZB ．k ·180°－45°，k ∈ZC ．k ·360°＋45°，k ∈ZD ．k ·180°＋45°，k ∈Z【答案】C【解析】∵405°＝360°＋45°，∴与405°终边相同的角是k ·360°＋45°，k ∈Z .故选：C 2．（2023秋·高一课时练习）与600 角终边相同的角可表示为（）A ．()360220k k ⋅+∈ZB ．()360240k k ⋅+∈ZC ．()36060k k ⋅+∈ZD ．()360260k k ⋅+∈Z【答案】B【解析】600360240=+ ，600∴ 角与240 角的终边相同，∴与600 角终边相同的角可表示为()360240k k ⋅+∈Z .故选：B.3．（2023·全国·高一课堂例题）已知角的顶点与直角坐标系的原点重合，始边与x 轴的非负半轴重合，作出下列各角，指出它们是第几象限角，并指出在0~︒360︒范围内与其终边相同的角．(1)405︒；(2)45-︒；(3)495︒；(4)520-︒．【答案】(1)45︒，第一象限角(2)315︒，第四象限角(3)135︒，第二象限角(4)200︒，第三象限角【解析】（1）405︒角是第一象限角，40545360︒=︒+︒，所以在0~360︒︒范围内，与405︒角终边相同的角是45︒角；（2）45-︒角是第四象限角，45315360-︒=︒-︒，所以在0~360︒︒范围内，与45-︒角终边相同的角是315︒角；（3）495︒角是第二象限角，495135360︒=︒+︒，所以在0~360︒︒范围内，与495︒角终边相同的角是135︒角；（4）520-︒角是第三象限角，5202002360-︒=︒-⨯︒，所以在0~360︒︒范围内，与520-︒角终边相同的角是200︒角；综上，（1）第一象限，与45︒角终边相同，（2）第四象限，与315︒角终边相同，（3）第二象限，与135︒角终边相同，（4）第三象限，与200︒角终边相同.考点三象限角和区间(域)角【例3-1】（2023·全国·高一课堂例题）写出终边在下图所示的直线上的角的集合．【答案】（1）{}45180,n n ββ=-︒+⋅︒∈Z ∣；（2）{}4590,n n ββ=︒+⋅︒∈Z ∣【解析】（1）由题图易知，在0360︒︒ 范围内，终边在直线y x =-上的角有两个，即135︒和315︒，因此，终边在直线y x =-上的角的集合为{}{}135360,315360,S k k k k ββββ==︒+⋅︒∈=︒+⋅︒∈Z Z ∣∣{}{}45(21)180,452(1)180,k k k k ββββ==-︒++⋅︒∈=-︒++⋅︒∈Z Z ∣∣U {}45180,n n ββ==-︒+⋅︒∈Z ∣；（2）同理可得终边在直线y x =上的角的集合为{}{}|45180,|45290,k k k k ββββ=︒+⋅︒∈==︒+⋅︒∈Z Z ，终边在直线y x =-上的角的集合为{}45180,S n n ββ==-︒+⋅︒∈Z ∣{}|45290,k k ββ==-︒+⋅︒∈Z {}|45(21)90,k k ββ==︒+-⋅︒∈Z ，所以终边在直线y x =上和在直线y x =-上的角的集合为{}{}|45290,|45(21)90,S k k k k ββββ==︒+⋅︒∈⋃=︒+-⋅︒∈Z Z{}|4590,n n ββ==︒+⋅︒∈Z .【例3-2】（2023·北京）（多选）已知α是锐角，则（）A ．180α︒+是第三象限角B ．2α是小于180︒的正角C ．2α是第一或第二象限角D ．2α是锐角【答案】ABD 【解析】由题知，因为α是锐角，所以090α<< ，对于A ：所以180180270α<+< ，故A 选项正确；对于BC ：02180α<< ，故B 选项正确，C 选项错误；对于D ：0452α<<，故D 选项正确；故选：ABD.【一隅三反】1．（2023春·山西朔州·高一怀仁市第一中学校校联考期末）集合{}18018060,k k k αα⋅≤≤⋅+∈Z ∣中的角所表示的范围（阴影部分）是（）A ．B ．C ．D ．【答案】C【解析】当2,Z k n n =∈时，{}36036060,Z n n k αα⋅≤≤⋅+∈ ∣，当21,Z k n n =+∈时，|360180360240,Z}n n k αα⋅+≤≤⋅+∈ ｛,所以选项C 满足题意.故选：C.2．（2023春·河南驻马店·高一校考阶段练习）用弧度表示终边落在如图所示的阴影部分内（不包括边界）的角的集合.【答案】（1）3ππ2π2π,Z 43k k k αα⎧⎫-<<+∈⎨⎬⎩⎭；（2）πππ,Z 62n n n παα⎧⎫+<<+∈⎨⎬⎩⎭【解析】（1）3ππ2π2π,Z 43k k k αα⎧⎫-<<+∈⎨⎬⎩⎭；（2）ππππ2π2π,Z 2ππ2ππ,Z 6262k k k k k k αααα⎧⎫⎧⎫+<<+∈⋃++<<++∈⎨⎬⎨⎬⎩⎭⎩⎭πππ,Z 62n n n παα⎧⎫=+<<+∈⎨⎬⎩⎭.3．（2023秋·高一课时练习）写出终边落在图中阴影区域内的角的集合．(1)(2)【答案】(1){}360135360300,k k k Zαα⋅+≤≤⋅+∈(2){}1806018045,k k k Zαα⋅-<<⋅+∈【解析】（1）在0~360︒︒范围内，图中终边在第二象限的区域边界线所对应的角为135︒，终边在第四象限的区域边界线所对应的角为300︒，因此，阴影部分区域所表示的集合为{}360135360300,k k k Z αα⋅+≤≤⋅+∈ ；（2）图中从第四象限到第一象限阴影部分区域表示的角的集合为{}6036045360,k k k Z αα-+⋅<<+⋅∈ {}218060218045,k k k Z αα=⋅-<<⋅+∈ ，图中从第二象限到第三象限阴影部分区域所表示的角的集合为{}120360225360,k k k Z αα+⋅<<+⋅∈()(){}21180602118045,k k k Z αα=+⋅-<<+⋅+∈ ，因此，阴影部分区域所表示角的集合为{}218060218045,k k k Z αα⋅-<<⋅+∈⋃ ()(){}21180602118045,k k k Z αα+⋅-<<+⋅+∈ {}1806018045,k k k Z αα=⋅-<<⋅+∈ .4．（2023春·四川眉山·高一校考期中）（1）如图，阴影部分表示角α的终边所在的位置，试写出角α的集合．（2）已知角1725α=-︒，将α改写成2π(,02π)k k ββ+∈≤<Z 的形式，并指出α是第几象限角．【答案】（1）答案见解析；（2）51012π-π+；是第一象限角．【解析】（1）①{}{}30360360,150360180360,k k k k k k αααα-︒+⋅︒≤≤⋅︒∈⋃︒+⋅︒≤≤︒+⋅︒∈Z Z {}30180180,k k k αα=-︒+⋅︒≤≤⋅︒∈Z ；②{}3036060360,k k k αα-︒+⋅︒<<︒+⋅︒∈Z ．（2）∵1725536075-︒=-⨯︒+︒，∴517251012π-︒=-π+．又5ππ0122<<，所以α与5π12终边相同，是第一象限角．5．（2023春·江西宜春·高一江西省丰城中学校考阶段练习）（镀锡）若α是第二象限角，则（）A ．α-是第一象限角B ．2α是第一或第三象限角C ．3π2α+是第二象限角D ．2α是第三象限角或2α是第四象限角或2α的终边在y 轴负半轴上【答案】BD【解析】因为α是第二象限角，所以可得22,Z 2k k k απ+π<<π+π∈．对于A ，ππ2π2π,Z 2k k k α--<-<--∈，则α-是第三象限角，所以A 错误;对于B ，可得,Z 422k k k αππ+π<<+π∈，当k 为偶数时，2α是第一象限角；当k 为奇数时，2α是第三象限角．所以B 正确;对于C ，3π5π2π2π2π,Z 22k k k α+<+<+∈，即()()3ππ21π21π,Z 22k k k α+<+<++∈，所以3π2α+是第一象限角，所以C 错误;对于D ，π4π22π4π,Z k k k α+<<+∈，所以2α的终边位于第三象限或第四象限或y 轴负半轴上，所以D 正确．故选：BD ．考点四角度与弧度的互化及应用【例4】（2022·广东广州）将下表中的角度和弧度互化：角度0°30°45°120°135°150°360°弧度3π2ππ32π【答案】答案见解析【解析】 180π=︒∴1180π︒=，1801π︒=故：角度0°30°45°60°90°120°135°150°180°270°360°弧度06π4π3π2π23π34π56ππ32π2π【一隅三反】1．（2023秋·高一课时练习）把下列角度与弧度进行互化．(1)72°；(2)－300°；(3)2；(4)2π9-.(5)780︒(6)1560-︒(7)67.5︒(8)103π-(9)12π(10)74π【答案】(1)2π5(2)5π3-(3)360π⎛⎫︒ ⎪⎝⎭(4)－40°.(5)133π弧度(6)263-π弧度(7)38π弧度(8)600-︒(9)15︒(10)315︒【解析】（1）π2π7272rad 1805︒=⨯=，（2）π5π300300rad rad 1803-︒=-⨯=-，（3）1803602rad 2ππ⎛⎫⎛⎫=⨯︒=︒ ⎪ ⎪⎝⎭⎝⎭，（4）2π2rad 1804099-=-⨯︒=-︒（5）780780180π︒=⨯弧度133π=弧度，（6）156********π-︒=-⨯弧度263π=-弧度，（7）67.567.5180π︒=弧度38π=弧度．（8）103π-弧度101806003=-⨯︒=-︒，（9）12π弧度1801512︒==︒，（10）74π弧度71803154=⨯︒=︒．考点五弧长公式与面积公式【例5-1】（2023·全国·高一假期作业）（多选）已知某扇形的周长为44，圆心角为2，则（）A ．该扇形的半径为11B ．该扇形的半径为22C ．该扇形的面积为100D ．该扇形的面积为121【答案】AD【解析】设该扇形的半径为r ，弧长为l ，则244l r +=，即2244r r +=，解得11r =．故该扇形的面积212111212S =⨯⨯=．故选：AD.【例5-2】（2023春·宁夏银川·高一宁夏育才中学校考开学考试）已知扇形的圆心角为α，所在圆的半径为.r (1)若60α=︒，3r =，求扇形的弧长;(2)若扇形的周长为16，当α为多少弧度时，该扇形面积最大?并求出最大面积．【答案】(1)π(2)当2α=时，扇形的面积最大，最大面积是16．【解析】（1）设扇形的弧长为l ．60α︒= ，即3πα=，3r =33l r παπ∴==⨯=.（2）由题设条件知，()216,16208l r l r r +==-<<,因此扇形的面积()()2211162841622S lr r r r r r ==-=-+=--+∴当4r =时，S 有最大值16，此时1628,2l l r r α=-===,∴当2α=时，扇形的面积最大，最大面积是16．【例5-3】（2023春·江西宜春·高一校考阶段练习）如图，点,,A B C 是圆O 上的点.(1)若4AB =，6ACB π∠=，求劣弧 AB 的长；(2)已知扇形AOB 的周长为8，求这个扇形的面积取得最大值时圆心角的大小.【答案】(1)43π(2)2【解析】（1）6ACB π∠= ，23AOB ACB π∴∠=∠=，又OA OB =，AOB ∴为等边三角形，4OA AB ∴==，则劣弧 AB 的长为433OA ππ⋅=.（2）设圆O 的半径为r ，扇形AOB 的弧长为l ，圆心角为α，扇形AOB 的周长为8，28r l ∴+=，方法一：扇形面积21112242442r l S l r l r +⎛⎫=⋅=⋅≤⋅= ⎪⎝⎭（当且仅当24r l ==时取等号），∴当扇形面积取得最大值时，圆心角2l r α==.方法二：扇形面积()()22118242422S l r r r r r r =⋅=-⋅=-+=--+，则当2r =时，S 取得最大值，此时824l r =-=，∴当扇形面积取得最大值时，圆心角2l rα==.【一隅三反】1．（2023·广东）已知扇形的半径为1，圆心角为60 ，则这个扇形的弧长为（）A ．π6B ．π3C ．2π3D ．60【答案】B 【解析】易知π603= ，由扇形弧长公式可得ππ133l =⨯=.故选：B2．（2023·全国·高一专题练习）已知扇形的周长为30．(1)若该扇形的半径为10，求该扇形的圆心角α，弧长l 及面积S ;(2)求该扇形面积S 的最大值及此时扇形的半径.【答案】(1)1α=，10l =，50S =；(2)2254，152.【解析】（1）由题知扇形的半径10r =，扇形的周长为30，∴22030l r l +=+=，∴10l =，10110l r α===，1110105022S lr ==⨯⨯=.（2）设扇形的圆心角α，弧长l ，半径为r ，则230l r +=，∴302l r =-，∴()()21522530112222154S lr r r r r r r -+⎛⎫--= ⎪=⎭≤⎝==当且仅当15r r -=，即152r =取等号，所以该扇形面积S 的最大值为2254，此时扇形的半径为152.3．（2023·广东揭阳）已知扇形OAB 的半径为r ，弧长为l ，圆心角为(02)ααπ<<.(1)若扇形OAB 的面积为定值S ，求扇形周长C 的最小值及对应的圆心角α的值；(2)若扇形OAB 的周长为定值C ，求扇形面积S 的最大值及对应的圆心角α的值.【答案】(1)2α=时C 的最小值为(2)2α=时S 的最大值为216C【解析】(1)由题设，l r α=，又222rl r S α==且2C l r =+，∴C =≥=2α=时等号成立，∴2α=时C的最小值为(2)由（1）知：(2)C r α=+，2222242(2)162(4)C C C S αααα===+++，当且仅当2α=时，S 的最大值为216C .。

第1节任意角和弧度制及任意角的三角函数(经典练习及答案详解)

第1节任意角和弧度制及任意角的三角函数知识梳理1.角的概念的推广(1)定义：角可以看成一条射线绕着它的端点旋转所形成的图形. (2)分类⎩⎨⎧按旋转方向不同分为正角、负角、零角Ｗ.按终边位置不同分为象限角和轴线角.(3)终边相同的角：所有与角α终边相同的角，连同角α在内，可构成一个集合S ＝{β|β＝α＋k ·360°，k ∈Z }. 2.弧度制的定义和公式(1)定义：长度等于半径长的圆弧所对的圆心角叫做1弧度的角，记作1 rad. (2)公式3.任意角的三角函数 (1)定义(2)定义的推广设P(x，y)是角α终边上异于原点的任一点，它到原点的距离为r(r>0)，那么sin α＝yr；cos α＝xr，tan α＝yx(x≠0).1.三角函数值在各象限的符号规律：一全正，二正弦，三正切，四余弦.2.角度制与弧度制可利用180°＝π rad进行互化，在同一个式子中，采用的度量制必须一致，不可混用.3.象限角4.轴线角诊断自测1.判断下列结论正误(在括号内打“√”或“×”)(1)小于90°的角是锐角.()(2)锐角是第一象限角，第一象限角也都是锐角.()(3)角α的三角函数值与其终边上点P 的位置无关.( ) (4)若α为第一象限角，则sin α＋cos α>1.( ) 答案 (1)× (2)× (3)√ (4)√ 解析 (1)锐角的取值范围是⎝ ⎛⎭⎪⎫0，π2.(2)第一象限角不一定是锐角.2.已知角θ的终边过点P (－12，m )，cos θ＝－1213，则m 的值为( ) A.－5 B.5C.±5D.±8答案 C解析由三角函数的定义可知cos θ＝－12（－12）2＋m2＝－1213，解得m ＝±5. 3.在－720°～0°范围内，所有与角α＝45°终边相同的角β构成的集合为________. 答案 {－675°，－315°}解析所有与角α终边相同的角可表示为：β＝45°＋k ×360°(k ∈Z )，则令－720°≤45°＋k ×360°<0°(k ∈Z )，得－765°≤k ×360°<－45°(k ∈Z ). 解得k ＝－2或k ＝－1，∴β＝－675°或β＝－315°.4.(2020·全国Ⅱ卷)若α为第四象限角，则( ) A.cos 2α>0 B.cos 2α<0 C.sin 2α>0D.sin 2α<0答案 D解析 ∵α是第四象限角，∴sin α<0，cos α>0，∴sin 2α＝2sin αcos α<0，故选D. 5.(多选题)(2021·武汉调研)下列说法正确的是( ) A.时钟经过两个小时，时针转过的角度是60° B.钝角大于锐角C.三角形的内角必是第一或第二象限角D.若α是第二象限角，则α2是第一或第三象限角答案 BD解析对于A ，时钟经过两个小时，时针转过的角是－60°，故错误；对于B ，钝角一定大于锐角，显然正确；对于C ，若三角形的内角为90°，则是终边在y 轴正半轴上的角，故错误；对于D ，∵角α的终边在第二象限， ∴2k π＋π2＜α＜2k π＋π，k ∈Z ， ∴k π＋π4＜α2＜k π＋π2，k ∈Z .当k ＝2n ，n ∈Z 时，2n π＋π4＜α2＜2n π＋π2，n ∈Z ，得α2是第一象限角；当k ＝2n ＋1，n ∈Z 时，(2n ＋1)π＋π4＜α2＜(2n ＋1)π＋π2，n ∈Z ，得α2是第三象限角，故正确.6.(2021·菏泽质检)密位广泛用于航海和军事，我国采取的“密位制”是6 000密位制，即将一个圆周分成6 000等份，每一等份是一个密位，那么60密位等于________rad. 答案 π50解析 ∵周角为2π rad ， ∴1密位＝2π6 000＝π3 000(rad)， ∴60密位＝π3 000·60＝π50(rad).考点一角的概念及其表示1.下列与角9π4的终边相同的角的表达式中正确的是( )A.2k π＋45°(k ∈Z )B.k ·360°＋9π4(k ∈Z ) C.k ·360°－315°(k ∈Z )D.k π＋5π4(k ∈Z )答案 C解析与9π4的终边相同的角可以写成2k π＋9π4(k ∈Z )，但是角度制与弧度制不能混用，排除A 、B ，易知D 错误，C 正确.2.(多选题)(2021·海南调研)已知α为第三象限角，则α2的终边所在的象限可能是( ) A.第一象限 B.第二象限 C.第三象限D.第四象限答案 BD解析 ∵α为第三象限角， ∴π＋2k π<α<3π2＋2k π，k ∈Z ， ∴π2＋k π<α2<3π4＋k π，k ∈Z ，当k ＝2m ，m ∈Z 时，π2＋2m π<α2<3π4＋2m π，m ∈Z ，此时α2在第二象限，当k ＝2m ＋1，m ∈Z 时，3π2＋2m π<α2<7π4＋2m π，m ∈Z ，此时α2在第四象限.综上，α2的终边在第二或第四象限.3.终边在直线y ＝3x 上，且在[－2π，2π)内的角α的集合为________________. 答案⎩⎨⎧⎭⎬⎫－5π3，－2π3，π3，4π3解析终边在直线y ＝3x 上的角α的集合为⎩⎨⎧⎭⎬⎫α|α＝π3＋k π，又由α∈[－2π，2π)，即－2π≤π3＋k π<2π，k ∈Z ，解得k ＝－2，－1，0，1，故满足条件的角α构成的集合为⎩⎨⎧⎭⎬⎫－5π3，－2π3，π3，4π3.感悟升华 1.确定nα，αn (n ∈N *)的终边位置的方法先用终边相同角的形式表示出角α的范围，再写出nα或αn 的范围，然后根据n 的可能取值讨论确定nα或αn 的终边所在位置(也可采用等分象限角的方法). 2.利用终边相同的角的集合求适合某些条件的角：先写出与这个角的终边相同的所有角的集合，然后通过对集合中的参数k 赋值来求得所需的角. 考点二弧度制及其应用【例1】已知一扇形的圆心角为α，半径为R ，弧长为l ，若α＝π3，R ＝10 cm ，求：(1)扇形的面积；(2)扇形的弧长及该弧所在弓形的面积. 解 (1)由已知得α＝π3，R ＝10， ∴S 扇形＝12α·R 2＝12·π3·102＝50π3(cm 2). (2)l ＝α·R ＝π3·10＝10π3(cm)，S 弓形＝S 扇形－S 三角形＝12·l ·R －12·R 2·sin π3 ＝12×10π3·10－12×102×32＝50π－7533(cm 2).感悟升华应用弧度制解决问题时应注意：(1)利用扇形的弧长和面积公式解题时，要注意角的单位必须是弧度.(2)求扇形面积最大值的问题时，常转化为二次函数的最值问题.(3)在解决弧长问题和扇形面积问题时，要合理地利用圆心角所在的三角形. 【训练1】 (1)(多选题)(2020·青岛质检)已知扇形的周长是6，面积是2，下列选项可能正确的有( ) A.圆的半径为2 B.圆的半径为1 C.圆心角的弧度数是1 D.圆心角的弧度数是2(2)已知扇形的周长为8 cm ，则该扇形面积的最大值为________cm 2. 答案 (1)ABC (2)4解析 (1)设扇形半径为r ，圆心角弧度数为α，则由题意得⎩⎨⎧2r ＋αr ＝6，12αr 2＝2，解得⎩⎪⎨⎪⎧r ＝1，α＝4或⎩⎪⎨⎪⎧r ＝2，α＝1，可得圆心角的弧度数是4或1. (2)设扇形半径为r cm ，弧长为l cm ，则2r ＋l ＝8，S ＝12rl ＝12r ×(8－2r ) ＝－r 2＋4r ＝－(r －2)2＋4，所以S max ＝4(cm 2).考点三三角函数的定义及应用角度1 求三角函数值【例2】已知角α的终边与单位圆的交点为P ⎝ ⎛⎭⎪⎫－12，y ，则sin α·tan α等于( )A.－33 B.±33C.－32D.±32答案 C解析由OP 2＝14＋y 2＝1，得y 2＝34，y ＝±32.当y ＝32时，sin α＝32，tan α＝－3，此时sin α·tan α＝－32.当y ＝－32时，sin α＝－32，tan α＝3，此时，sin α·tan α＝－32. 综上sin α·tan α＝－32. 角度2 由三角函数值求参数【例3】已知角α的终边过点P (－8m ，－6sin 30°)，且cos α＝－45，则m 的值为( ) A.－12 B.－32 C.12D.32答案 C解析由题意得点P (－8m ，－3)，r ＝64m 2＋9，所以cos α＝－8m64m 2＋9＝－45，所以m >0，解得m ＝12.角度3 三角函数值的符号【例4】 (多选题)(2021·重庆调研)已知|cos θ|＝cos θ，|tan θ|＝－tan θ，则角θ2的终边可能在( ) A.第二、四象限 B.第一、三象限 C.y 轴上D.x 轴上答案 AD解析∵|cos θ|＝cos θ，|tan θ|＝－tan θ，∴cos θ≥0，tan θ≤0，∴角θ的终边在第四象限或x轴正半轴上，∴角θ2的终边在第二、四象限或x轴上.故选AD.感悟升华 1.三角函数定义的应用(1)直接利用三角函数的定义，找到给定角的终边上一个点的坐标，及这点到原点的距离，确定这个角的三角函数值.(2)已知角的某一个三角函数值，可以通过三角函数的定义列出含参数的方程，求参数的值.2.要判定三角函数值的符号，关键是要搞清三角函数中的角是第几象限角，再根据正、余弦函数值在各象限的符号确定值的符号.如果不能确定角所在象限，那就要进行分类讨论求解.【训练2】(1)若sin θ·cos θ<0，tan θsin θ>0，则角θ是()A.第一象限角B.第二象限角C.第三象限角D.第四象限角(2)已知角θ的顶点与原点重合，始边与x轴非负半轴重合，若A(－1，y)是角θ终边上的一点，且sin θ＝－31010，则y＝________.答案(1)D(2)－3解析(1)由tan θsin θ>0，得1cos θ>0，所以cos θ>0.又sin θ·cos θ<0，所以sin θ<0，所以θ为第四象限角.故选D.(2)因为sin θ＝－31010<0，A(－1，y)是角θ终边上一点，所以y<0，由三角函数的定义，得yy2＋1＝－31010.解得y ＝－3.A 级基础巩固一、选择题1.小明出国旅游，当地时间比北京时间晚一个小时，他需要调整手表的时间，则时针转过的角的弧度数为( ) A.π3 B.π6C.－π3D.－π6答案 B解析因为当地时间比北京时间晚一个小时，所以时针应该是逆时针方向旋转，故时针转过的角的弧度数为π6.故选B.2.(多选题)(2021·淄博调研)下列四个命题正确的是( ) A.－3π4是第二象限角B.4π3是第三象限角C.－400°是第四象限角D.－315°是第一象限角答案 BCD解析－3π4是第三象限角，故A 错误；4π3＝π＋π3，从而4π3是第三象限角，B 正确；－400°＝－360°－40°，是第四象限角，从而C 正确；－315°＝－360°＋45°，是第一象限角，从而D 正确.3.(2020·天津期末)在平面直角坐标系中，若角α以x 轴的非负半轴为始边，且终边过点⎝ ⎛⎭⎪⎫－32，12，则sin α＝( )A.－32B.－12C.32D.12答案 D解析由任意角三角函数的定义得sin α＝12⎝ ⎛⎭⎪⎫－322＋⎝ ⎛⎭⎪⎫122＝12.故选D.4.已知扇形的面积为2，扇形圆心角的弧度数是4，则扇形的周长为( )A.2B.4C.6D.8答案 C解析设扇形的半径为r ，弧长为l ，则由扇形面积公式可得2＝12|α|r 2＝12×4×r 2，解得r ＝1，l ＝αr ＝4，所以所求扇形的周长为2r ＋l ＝6.5.若角α的终边在直线y ＝－x 上，则角α的取值集合为( )A.⎩⎨⎧⎭⎬⎫α⎪⎪⎪α＝k ·2π－π4，k ∈Z B.⎩⎨⎧⎭⎬⎫α⎪⎪⎪α＝k ·2π＋3π4，k ∈Z C.⎩⎨⎧⎭⎬⎫α⎪⎪⎪α＝k ·π－3π4，k ∈Z D.⎩⎨⎧⎭⎬⎫α⎪⎪⎪α＝k ·π－π4，k ∈Z 答案 D解析由图知，角α的取值集合为⎩⎨⎧⎭⎬⎫α⎪⎪⎪α＝2n π＋3π4，k ∈Z ∪ ⎩⎨⎧⎭⎬⎫α⎪⎪⎪α＝2n π－π4，k ∈Z ＝⎩⎨⎧⎭⎬⎫α⎪⎪⎪α＝（2n ＋1）π－π4，k ∈Z ∪ ⎩⎨⎧⎭⎬⎫α⎪⎪⎪α＝2n π－π4，k ∈Z ＝⎩⎨⎧⎭⎬⎫α⎪⎪⎪α＝k π－π4，k ∈Z . 6.设θ是第三象限角，且⎪⎪⎪⎪⎪⎪cos θ2＝－cos θ2，则θ2是( ) A.第一象限角B.第二象限角C.第三象限角D.第四象限角答案 B解析由θ是第三象限角知，θ2为第二或第四象限角，又⎪⎪⎪⎪⎪⎪cos θ2＝－cos θ2，所以cos θ2<0，综上可知，θ2为第二象限角.7.(2020·长沙模拟)已知角α的顶点在原点，始边与x 轴的非负半轴重合，终边上一点A (2sin α，3)(sin α≠0)，则cos α＝( )A.12B.－12C.32D.－32答案 A解析由三角函数定义得tan α＝32sin α，即sin αcos α＝32sin α，得3cos α＝2sin 2α＝2(1－cos 2α)，解得cos α＝12或cos α＝－2(舍去).故选A.8.(多选题)(2021·山东新高考模拟)如图，A ，B 是单位圆上的两个质点，点B 的坐标为(1，0)，∠BOA ＝60°，质点A 以1 rad/s 的角速度按逆时针方向在单位圆上运动，质点B 以2 rad/s 的角速度按顺时针方向在单位圆上运动，则( )A.经过1 s 后，∠BOA 的弧度数为π3＋3B.经过π12 s 后，扇形AOB 的弧长为7π12C.经过π6 s 后，扇形AOB 的面积为π3D.经过5π9 s 后，A ，B 在单位圆上第一次相遇答案 ABD解析经过1 s 后，质点A 运动1 rad ，质点B 运动2 rad ，此时∠BOA 的弧度数为π3＋3，故A 正确；经过π12 s 后，∠AOB ＝π12＋π3＋2×π12＝7π12，故扇形AOB 的弧长为7π12×1＝7π12，故B 正确；经过π6 s 后，∠AOB ＝π6＋π3＋2×π6＝5π6，故扇形AOB 的面积为S ＝12×5π6×12＝5π12，故C 不正确；设经过t s 后，A ，B 在单位圆上第一次相遇，则t (1＋2)＋π3＝2π，解得t ＝5π9(s)，故D 正确.二、填空题9.已知扇形的圆心角为π6，面积为π3，则扇形的弧长等于________. 答案 π3解析设扇形半径为r ，弧长为l ，则⎩⎪⎨⎪⎧l r ＝π6，12lr ＝π3，解得⎩⎨⎧l ＝π3，r ＝2. 10.在平面直角坐标系xOy 中，点P 在角2π3的终边上，且|OP |＝2，则点P 的坐标为________.答案 (－1，3)解析设点P 的坐标为(x ，y )，由三角函数定义得⎩⎪⎨⎪⎧x ＝|OP |cos 2π3，y ＝|OP |sin 2π3，所以⎩⎪⎨⎪⎧x ＝－1，y ＝3，所以点P 的坐标为(－1，3).11.(2021·河北九校联考)已知点P (sin 35°，cos 35°)为角α终边上一点，若0°≤α<360°，则α＝________.答案 55°解析由题意知cos α＝sin 35°＝cos 55°，sin α＝cos 35°＝sin 55°，P 在第一象限，所以α＝55°.12.已知角α的顶点为坐标原点，始边与x 轴的非负半轴重合，终边上有两点A (1，a )，B (2，b )，且cos 2α＝23，则|a －b |＝________.答案 55解析由O ，A ，B 三点共线，从而得到b ＝2a ，因为cos 2α＝2cos 2α－1＝2×⎝ ⎛⎭⎪⎫1a 2＋12－1＝23，解得a 2＝15，即|a |＝55，所以|a －b |＝|a －2a |＝|a |＝55.B 级能力提升13.设集合M ＝⎩⎨⎧⎭⎬⎫x |x ＝k 2·180°＋45°，k ∈Z ，N ＝{x |x ＝k 4·180°＋45°，k ∈Z }，那么( )A.M ＝NB.M ⊆NC.N ⊆MD.M ∩N ＝∅ 答案 B解析由于M 中，x ＝k 2·180°＋45°＝k ·90°＋45°＝(2k ＋1)·45°，2k ＋1是奇数；而N 中，x ＝k 4·180°＋45°＝k ·45°＋45°＝(k ＋1)·45°，k ＋1是整数，因此必有M ⊆N .14.(2019·北京卷)如图，A ，B 是半径为2的圆周上的定点，P 为圆周上的动点，∠APB 是锐角，大小为β.图中阴影区域的面积的最大值为( )A.4β＋4cos βB.4β＋4sin βC.2β＋2cos βD.2β＋2sin β 答案 B解析如图，设点O 为圆心，连接PO ，OA ，OB ，AB ，在劣弧上取一点C ，则阴影部分面积为△ABP 和弓形ACB 的面积和.因为A ，B 是圆周上的定点，所以弓形ACB 的面积为定值，故当△ABP 的面积最大时，阴影部分的面积最大.又AB 的长为定值，故当点P 为优弧的中点时，点P 到弦AB 的距离最大，此时△ABP 面积最大，即当P 为优弧的中点时，阴影部分面积最大.下面计算当P 为优弧的中点时阴影部分的面积.因为∠APB 为锐角，且∠APB ＝β，所以∠AOB ＝2β，∠AOP ＝∠BOP ＝180°－β，则阴影部分的面积S ＝S △AOP ＋S △BOP ＋S 扇形OAB ＝2×12×2×2sin(180°－β)＋12×22×2β＝4β＋4sin β.故选B.15.一扇形的圆心角为2π3，则此扇形的面积与其内切圆的面积的比值为________.答案 7＋439解析设扇形半径为R ，内切圆半径为r .则(R －r )sin π3＝r ，即R ＝⎝⎛⎭⎪⎫1＋233r . 又S 扇＝12|α|R 2＝12×2π3×R 2＝π3R 2＝7＋439πr 2，所以S 扇πr 2＝7＋439.16.在平面直角坐标系中，劣弧，，，是圆x 2＋y 2＝1上的四段弧(如图)，点P 在其中一段弧上，角α以Ox 为始边，OP 为终边.若tan α<cos α<sin α，则P 所在的圆弧是________.答案解析因为tan α<cos α，所以P 所在的圆弧不是，因为tan α<sin α，所以P 所在的圆弧不是，又cos α<sin α，所以P 所在的圆弧不是，所以P 所在的圆弧是.。

高中数学第五章三角函数5.1.1任意角学案含解析第一册

第五章三角函数5．1任意角和弧度制5．1.1任意角［目标] 1.理解任意角的概念，能区分各类角的概念;2.掌握象限角的概念，并会用集合表示象限角；3。

理解终边相同的角的含义及其表示，并能解决有关问题．[重点] 用集合的形式表示终边相同的角．［难点］会判断角的终边所在的象限．知识点一角的概念的推广和分类［填一填］1．任意角的概念角可以看成平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形．2．正角、负角和零角我们规定，一条射线绕其端点按逆时针方向旋转形成的角叫做正角，按顺时针方向旋转形成的角叫做负角．如果一条射线没有做任何旋转，我们称它形成了一个零角．这样,零角的始边与终边重合．如果α是零角，那么α＝0°.1．根据角的新的定义，角的范围有什么变化？提示：角的范围不再是以前学的锐角、直角以及钝角，而是任意的角．2．如图所示，图(1)中,角α的度数为330°，图（2）中，角β的度数为－150°，角γ的度数为570°。

解析：题图(1）中，α＝360°－30°＝330°；题图(2）中，β＝－360°＋60°＋150°＝－150°；γ＝360°＋60°＋（－β）＝360°＋60°＋150°＝570°.知识点二象限角[填一填］为了讨论问题的方便，我们在直角坐标系内使角的顶点与原点重合，角的始边与x轴的非负半轴重合．那么，角的终边在第几象限，我们就说这个角是第几象限角．如果角的终边在坐标轴上，就认为这个角不属于任何一个象限，称它为轴线角（或称为象限界角)．3．把角的顶点放在平面直角坐标系的原点，角的始边与x 轴的非负半轴重合,旋转该角，则其终边（除端点外）可能落在什么位置?提示：坐标轴上或四个象限内．4．“锐角”、“第一象限角"、“小于90°的角”三者有何不同？提示：锐角是第一象限角也是小于90°的角,而第一象限角可以是锐角，也可以大于360°，还可能是负角,小于90°的角可以是锐角,也可以是零角或负角．知识点三终边相同的角[填一填］所有与角α终边相同的角,连同角α在内，可构成一个集合S ＝｛β｜β＝α＋k·360°，k∈Z}，即任一与角α终边相同的角，都可以表示成角α与整数个周角的和．［答一答]5．终边相同的角相等吗？相等的角终边相同吗？提示：终边相同的角不一定相等，它们相差360°的整数倍；相等的角，终边相同．6．与－2 014°角终边相同的最小正角是146°。