刘鸿文版材料力学课件全套(4).ppt
合集下载
刘鸿文主编(第4版) 高等教育出版社《材料力学》课件全套

解: 用截面m-m将钻床截为两部分,取上半 部分为研究对象,
受力如图:
列平衡方程:
M
Y 0 FN P
Mo(F) 0
FN
Pa M 0
M Pa
目录
§1.4 内力、截面法和应力的概念
为了表示内力在一点处的强度,引入内力集度,
即应力的概念。
F A
pm
F A
—— 平均应力
C
p lim F A0 A
径20mm的圆截面杆,水平杆CB为 15×15的方截面杆。
B 解:1、计算各杆件的轴力。 (设斜杆为1杆,水平杆为2杆)
F 用截面法取节点B为研究对象
Fx 0 FN1 cos 45 FN2 0
x
Fy 0 FN1 sin 45 F 0
FN1 28.3kN
FN 2 20kN
目录
§2.2 轴向拉伸或压缩时横截面上的内力和应力
m
F m
F
FN
FN
Fx 0
FN F 0 FN F
2、轴力:截面上的内力
F
由于外力的作用线
与杆件的轴线重合,内
力的作用线也与杆件的
轴线重合。所以称为轴
力。 F 3、轴力正负号:
拉为正、压为负
4、轴力图:轴力沿杆 件轴线的变化
目录
§2.2 轴向拉伸或压缩时横截面上的内力和应力
例题2.1
A
F1
若:构件横截面尺寸不足或形状
不合理,或材料选用不当
___ 不满足上述要求,
不能保证安全工作.
若:不恰当地加大横截面尺寸或
选用优质材料
___ 增加成本,造成浪费
}均 不 可 取
研究构件的强度、刚度和稳定性,还需要了解材料的力学性能。因此在 进行理论分析的基础上,实验研究是完成材料力学的任务所必需的途径和 手段。
受力如图:
列平衡方程:
M
Y 0 FN P
Mo(F) 0
FN
Pa M 0
M Pa
目录
§1.4 内力、截面法和应力的概念
为了表示内力在一点处的强度,引入内力集度,
即应力的概念。
F A
pm
F A
—— 平均应力
C
p lim F A0 A
径20mm的圆截面杆,水平杆CB为 15×15的方截面杆。
B 解:1、计算各杆件的轴力。 (设斜杆为1杆,水平杆为2杆)
F 用截面法取节点B为研究对象
Fx 0 FN1 cos 45 FN2 0
x
Fy 0 FN1 sin 45 F 0
FN1 28.3kN
FN 2 20kN
目录
§2.2 轴向拉伸或压缩时横截面上的内力和应力
m
F m
F
FN
FN
Fx 0
FN F 0 FN F
2、轴力:截面上的内力
F
由于外力的作用线
与杆件的轴线重合,内
力的作用线也与杆件的
轴线重合。所以称为轴
力。 F 3、轴力正负号:
拉为正、压为负
4、轴力图:轴力沿杆 件轴线的变化
目录
§2.2 轴向拉伸或压缩时横截面上的内力和应力
例题2.1
A
F1
若:构件横截面尺寸不足或形状
不合理,或材料选用不当
___ 不满足上述要求,
不能保证安全工作.
若:不恰当地加大横截面尺寸或
选用优质材料
___ 增加成本,造成浪费
}均 不 可 取
研究构件的强度、刚度和稳定性,还需要了解材料的力学性能。因此在 进行理论分析的基础上,实验研究是完成材料力学的任务所必需的途径和 手段。
刘鸿文主编-材料力学课件

各向同性假设
总结词
各向同性假设认为材料在不同方向上具有相同的性质 和行为。
详细描述
各向同性假设是材料力学中的另一个重要假设。它意味 着材料在不同方向上具有相同的性质,如弹性模量、泊 松比等。这一假设使得我们可以用统一的数学模型来描 述材料的性质和行为,简化计算过程。在实际应用中, 对于一些各向同性较好的材料,可以采用统一的标准来 近似获得其整体性质。需要注意的是,各向同性材料并 不是指所有方向上的性质都完全相同,而是在一定范围 内可以近似认为各向同性。
机械零件设计
材料力学在机械领域中应用于各 种机械零件的设计,如轴、轴承
、齿轮等。
设备强度分析
对机械设备的强度进行分析,确保 设备在各种工况下的安全运行。
疲劳寿命预测
利用材料力学知识,预测机械零件 的疲劳寿命,提高设备的使用寿命 。
航空航天领域
飞行器结构分析
材料力学在航空航天领域 中应用于飞行器的结构分 析,确保飞行器的安全性 和稳定性。
详细描述
弹性力学理论是材料力学的基本理论之一,主要研究材料在弹性范围内受力时的变形和内力关系。该 理论基于胡克定律,即材料在弹性范围内受力时发生的形变与外力成正比,并引入了应变和应力等概 念来描述材料的变形和受力情况。
塑性力学理论
总结词
描述材料在超过弹性极限后发生塑性形 变时的应力-应变关系。
VS
根据船舶的工作环境和要求,选择具 有优良力学性能的材料。
05
材料力学的未来发展
新材料的研发
高强度轻质材料
如碳纤维复合材料、钛合金等, 在航空、汽车、体育器材等领域
有广泛应用前景。
智能材料
如形状记忆合金、压电陶瓷等, 具有自适应、自修复等特性,可 用于制造智能传感器、执行器等
材料力学(刘鸿文版)全套课件 PPT

850 750 650 550
104
105
106
107
108
N
从图可以得出三点结论:
(1)对于疲劳,决定寿命的 最重要因素是应力幅 。
(2)材料的疲劳寿命N 随应力幅 的增大而减小。
(3)存在这样一个应力幅,低于该应力幅,疲劳破坏不会发生,该应力幅
称为疲劳极限,记为 -1 。
目录
对于铝合金等有色金属,其S-N曲线没有明显的水平部分,一般规定
Δ
max
m in
O t
目录
通常用以下参数描述循环应力的特征
(1)应力比 r
r min max
r = -1 :对称循环 ; r = 0 :脉动循环 。
r < 0 :拉压循环 ; r > 0 :拉拉循环 或压压循环。
(2)应力幅
max min
(3)平均应力 m
B L
解: ⑴ 弯矩方程
F
A
M (x) M e Fx
Me
⑵ 变形能
V
L
M 2 (x) dx 2EI
L
1 2EI
(M
e
Fx)2 dx
M
2 e
L
M e FL2
F 2 L2
2EI 2EI 6EI
B L
F
⑶ 当F和M0分别作用时
A M0
V 1
MeL 2EI
F 2 L3 V 2 6EI
例:试求图示悬臂梁的应变能,并利用功
能原理求自由端B的挠度。
F
解:
l
x
M (x) F x
V
材料力学ppt(刘鸿文第四版含课后答案)

V
应力分布均匀 均匀时 应力分布均匀时
N Al N l U = uV = V = = 2 2E 2EA 2EA
Nl 推广到多杆系统 U = ∑ i=1 2E A i i
1 由能量守恒原理 U =W= P∆l 2 2 n 有 1 Ni li P∆l = ∑ 2 i=1 2E A i i
n 2 i i
关于静不定的基本概念
静定问题
静不定问题 —— 静不定次数 —— 多余约束 ——
求解静不定问题的基本方法
力的平衡关系。 静力平衡方程 -力的平衡关系。 变形与约束的协调关系。 变形协调方程 - 变形与约束的协调关系。 力与变形的关系。 物理关系 - 力与变形的关系。
例 1 (书p.50) 书 已知:1、2杆相同,抗拉 杆相同, 已知: 、 杆相同 刚度为E 刚度为 1A1 , 3杆的抗拉 杆的抗拉 长为l 角 刚度为E 刚度为 3A3 , 长为 , α角。 各杆的内力。 求:各杆的内力。 解: 静不定的次数? 静不定的次数?
(2) 变形协调方程 (3) 物理关系
∆l1 = ∆l2 = ∆l3 cosα (3) N1l N3l ∆l1 = ∆l3 = E1A cosα E3 A 1 3
(4)
物理关系代入变形协调方程
N1l N3l = cosα E A cosα E3 A 1 1 3
与平衡方程联立,可解出 与平衡方程联立,可解出:
D
C
B
2 l N2
3
1
αα
A P y N3
αα
∑X = 0 N1 sin α − N2 sinα = 0 N1 = N2 ∑Y = 0 N3 +2N1 cosα − P = 0
N1
x
P
应力分布均匀 均匀时 应力分布均匀时
N Al N l U = uV = V = = 2 2E 2EA 2EA
Nl 推广到多杆系统 U = ∑ i=1 2E A i i
1 由能量守恒原理 U =W= P∆l 2 2 n 有 1 Ni li P∆l = ∑ 2 i=1 2E A i i
n 2 i i
关于静不定的基本概念
静定问题
静不定问题 —— 静不定次数 —— 多余约束 ——
求解静不定问题的基本方法
力的平衡关系。 静力平衡方程 -力的平衡关系。 变形与约束的协调关系。 变形协调方程 - 变形与约束的协调关系。 力与变形的关系。 物理关系 - 力与变形的关系。
例 1 (书p.50) 书 已知:1、2杆相同,抗拉 杆相同, 已知: 、 杆相同 刚度为E 刚度为 1A1 , 3杆的抗拉 杆的抗拉 长为l 角 刚度为E 刚度为 3A3 , 长为 , α角。 各杆的内力。 求:各杆的内力。 解: 静不定的次数? 静不定的次数?
(2) 变形协调方程 (3) 物理关系
∆l1 = ∆l2 = ∆l3 cosα (3) N1l N3l ∆l1 = ∆l3 = E1A cosα E3 A 1 3
(4)
物理关系代入变形协调方程
N1l N3l = cosα E A cosα E3 A 1 1 3
与平衡方程联立,可解出 与平衡方程联立,可解出:
D
C
B
2 l N2
3
1
αα
A P y N3
αα
∑X = 0 N1 sin α − N2 sinα = 0 N1 = N2 ∑Y = 0 N3 +2N1 cosα − P = 0
N1
x
P
材料力学全ppt课件

x
切应变(角应变)
M点处沿x方向的应变: M点在xy平面内的切应变为:
x
lim
x0
s x
g lim ( LM N)
MN0 2
ML0
类似地,可以定义 y , z ,g 均为无量纲的量。
目录
§1.5 变形与应变
例 1.2
c
已知:薄板的两条边
4、稳定性:
在载荷 作用下,构 件保持原有 平衡状态的 能力。
强度、刚度、稳定性是衡量构件承载能力 的三个方面,材料力学就是研究构件承载能力 的一门科学。
目录
§1.1 材料力学的任务
三、材料力学的任务
材料力学的任务就是在满足强度、刚度 和稳定性的要求下,为设计既经济又安全的构 件,提供必要的理论基础和计算方法。
目录
§1.3 外力及其分类
按外力与时间的关系分类
静载: 载荷缓慢地由零增加到某一定值后,就保持不变或变动很不显著, 称为静载。
动载: 载荷随时间而变化。
如交变载荷和冲击载荷
交变载荷
冲击载荷
目录
§1.4 内力、截面法和应力的概念
内力:外力作用引起构件内部的附加相互作用力。 求内力的方法 — 截面法
传统具有柱、梁、檩、椽的木 制房屋结构
建于隋代(605年)的河北赵州桥桥 长64.4米,跨径37.02米,用石2800 吨
目录
§1.1 材料力学的任务
古代建筑结构
建于辽代(1056年)的山西应县佛宫寺释迦塔 塔高9层共67.31米,用木材7400吨 900多年来历经数次地震不倒,现存唯一木塔
目录
§1.1 材料力学的任务
架的变形略去不计。计算得到很大的简
化。
C
δ1
切应变(角应变)
M点处沿x方向的应变: M点在xy平面内的切应变为:
x
lim
x0
s x
g lim ( LM N)
MN0 2
ML0
类似地,可以定义 y , z ,g 均为无量纲的量。
目录
§1.5 变形与应变
例 1.2
c
已知:薄板的两条边
4、稳定性:
在载荷 作用下,构 件保持原有 平衡状态的 能力。
强度、刚度、稳定性是衡量构件承载能力 的三个方面,材料力学就是研究构件承载能力 的一门科学。
目录
§1.1 材料力学的任务
三、材料力学的任务
材料力学的任务就是在满足强度、刚度 和稳定性的要求下,为设计既经济又安全的构 件,提供必要的理论基础和计算方法。
目录
§1.3 外力及其分类
按外力与时间的关系分类
静载: 载荷缓慢地由零增加到某一定值后,就保持不变或变动很不显著, 称为静载。
动载: 载荷随时间而变化。
如交变载荷和冲击载荷
交变载荷
冲击载荷
目录
§1.4 内力、截面法和应力的概念
内力:外力作用引起构件内部的附加相互作用力。 求内力的方法 — 截面法
传统具有柱、梁、檩、椽的木 制房屋结构
建于隋代(605年)的河北赵州桥桥 长64.4米,跨径37.02米,用石2800 吨
目录
§1.1 材料力学的任务
古代建筑结构
建于辽代(1056年)的山西应县佛宫寺释迦塔 塔高9层共67.31米,用木材7400吨 900多年来历经数次地震不倒,现存唯一木塔
目录
§1.1 材料力学的任务
架的变形略去不计。计算得到很大的简
化。
C
δ1
刘鸿文版材料力学课件全套4ppt课件

解:(1)计算横截面的形心、 面积、惯性矩
F 350 F
F 350
M
y1 z0 y
FN
z1
150
A 15000mm2 z0 75mm z1 125 mm I y 5.31107 mm4
50 (2)立柱横截面的内力
FN F
M F 350 75103
50
150
425F 103 N m
10-1
压弯组合变形
目录
§8-1 组合变形和叠加原理
组合变形工程实例
拉弯组合变形
目录
§8-1 组合变形和叠加原理
组合变形工程实例
弯扭组合变形
目录
§8-1 组合变形和叠加原理
叠加原理
构件在小变形和服从胡克定理的条件下, 力的独立性原理是成立的。即所有载荷作用 下的内力、应力、应变等是各个单独载荷作 用下的值的叠加
r4
M8-4 扭转与弯曲的组合
r3
M 2 T 2
W
W d 3
32
d 3 32
M2 T2
3
32
1762 3002 100106
32.8103 m 32.8mm
目录
小结
1、了解组合变形杆件强度计算的基本方法 2、掌握斜弯曲和拉(压)弯组合变形杆件
0 -极限切应力,由单向拉伸实验测得
0 s /2
目录
7-11 四种常用强度理论
最大切应力理论(第三强度理论)
屈服条件 强度条件
1
3
s
ns
低碳钢拉伸
低碳钢扭转
目录
7-11 四种常用强度理论
最大切应力理论(第三强度理论) 实验表明:此理论对于塑性材料的屈服破坏能够得到 较为满意的解释。并能解释材料在三向均压下不发生
材料力学(刘鸿文第四版含课后答案)ppt课件
0.521 04(m)
lAC
N3l3 EA3
51030.5 1201094104
0.52104(m)
AB杆的变形
lAB lB D lC D lAC 1.051 04(m)
例 2 (书例2. 7) 已知: BC杆: d=20mm, BD杆: 8号槽钢。[]= 160 MPa, E=200GPa, P=60kN。 求:校核强度及B点位移。
dx
两面的力为:
dydz
x方向的伸长为: dx
当应力有一个增量d 时,
d 1
x方向伸长的增量为: ddx
则元功为:
dydz ddx
力所作的功为: dW 0 1dydzddx
dy
拉伸曲线
dz dx
1 d
则力所作的功为:
dW 0 1dydzddx
01ddV
(01d)dV
d
所以: dUdW(01d)dV
sin4/5, cos3/5, cot3/4
B1B3 1.56103m BB3 1.78103m
§2. 9 轴向拉伸或压缩的变形能
1 变形能 弹性体在外力作用下,因变形而储存
的能量称为变形能(或应变能)。
力的功 力的元功
P 拉伸曲线
dP
l
dWPd (l)
力的总功
P1
W0l1 Pd(l)
当应力小于 P
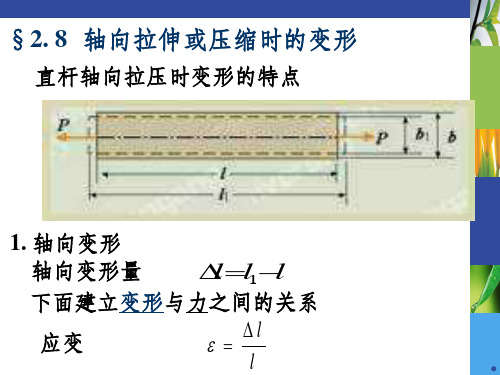
§2. 8 轴向拉伸或压缩时的变形
直杆轴向拉压时变形的特点
1. 轴向变形
轴向变形量
l l1l
下面建立变形与力之间的关系
应变
l
l
1. 轴向变形 轴向变形量
l l1l
应变 l
应力 N
l
材料力学课件全套刘鸿文版课件

杆件受力与变形的的几种形式
内容 种类
轴向拉伸 及 压缩
Axial Tension
剪切 Shear
外力特点
扭转 Torsion
平面弯曲 Bending
组合受力(Combined Loading)与变形
变形特点
材料力学
Mechanics of Materials
刚体静力学中关于平衡的理论和方法能否应用于材料力学?
符合假设1、2、3的构件称为理想变形体,符合小变形假设的理想变形体称为理想弹性体,这就是材料力 学的研究对象。
材料力学
§1-3 外力及其分类
Mechanics of Materials
外力按作用方式分: 体积力: 重力、惯性力; 表面力:水压力、面接触的力;
表面力分: 分布力:连续作用于表面的力; 集中力:火车车轮对钢轨、支座等。
材料力学
Mechanics of Materials
应力p可分解:
正应力—— ; 切应力——。
p
应 力 单 位 : 牛 / 米 2 ( N/m2 ) , 称 为 帕 斯 卡 或 简 称 帕 ( Pa ) 。 通 常 使 用 的 是 兆 帕 , 即 MPa ( 1MPa=106Pa)
2021/7/4
构件 的抗 变形 能力
Mechanics of Materials
2021年7月4日星期日
材料力学
▪ 3 稳定性
保持 原有 平衡 状态 的能 力
Mechanics of Materials
2021年7月4日星期日
材料力学
Mechanics of Materials
在满足上述强度、刚度和稳定性要求的同时,须尽可能合理选用材料和降低材料消耗量,以节 约投资。
内容 种类
轴向拉伸 及 压缩
Axial Tension
剪切 Shear
外力特点
扭转 Torsion
平面弯曲 Bending
组合受力(Combined Loading)与变形
变形特点
材料力学
Mechanics of Materials
刚体静力学中关于平衡的理论和方法能否应用于材料力学?
符合假设1、2、3的构件称为理想变形体,符合小变形假设的理想变形体称为理想弹性体,这就是材料力 学的研究对象。
材料力学
§1-3 外力及其分类
Mechanics of Materials
外力按作用方式分: 体积力: 重力、惯性力; 表面力:水压力、面接触的力;
表面力分: 分布力:连续作用于表面的力; 集中力:火车车轮对钢轨、支座等。
材料力学
Mechanics of Materials
应力p可分解:
正应力—— ; 切应力——。
p
应 力 单 位 : 牛 / 米 2 ( N/m2 ) , 称 为 帕 斯 卡 或 简 称 帕 ( Pa ) 。 通 常 使 用 的 是 兆 帕 , 即 MPa ( 1MPa=106Pa)
2021/7/4
构件 的抗 变形 能力
Mechanics of Materials
2021年7月4日星期日
材料力学
▪ 3 稳定性
保持 原有 平衡 状态 的能 力
Mechanics of Materials
2021年7月4日星期日
材料力学
Mechanics of Materials
在满足上述强度、刚度和稳定性要求的同时,须尽可能合理选用材料和降低材料消耗量,以节 约投资。
