北师大四份作业答案
北师大版五年级下册数学第六单元测试卷合集(4份)(有答案)
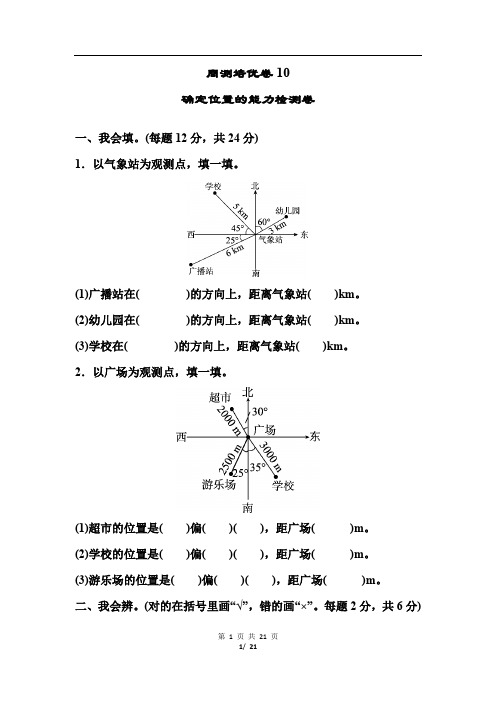
周测培优卷10确定位置的能力检测卷一、我会填。
(每题12分,共24分)1.以气象站为观测点,填一填。
(1)广播站在()的方向上,距离气象站()km。
(2)幼儿园在()的方向上,距离气象站()km。
(3)学校在()的方向上,距离气象站()km。
2.以广场为观测点,填一填。
(1)超市的位置是()偏()(),距广场()m。
(2)学校的位置是()偏()(),距广场()m。
(3)游乐场的位置是()偏()(),距广场()m。
二、我会辨。
(对的在括号里画“√”,错的画“×”。
每题2分,共6分)1.“北偏东45°”与“东偏北45°”表示的方向是一样的。
() 2.小美家在东东家的南方,所以说东东家在北方。
() 3.以不同学生的家为观测点,所描述的学校的位置是相同的。
()三、我会选。
(把正确答案的序号填在括号里。
每题2分,共6分) 1.北偏西20°,还可以说成()。
A.南偏西20°B.西偏北20°C.西偏北70° D.南偏东70°2.以学校为观测点,广场在东偏北30°的方向上,下图中正确的是()。
3.一架飞机向东偏北45°方向飞行,接到指令后,改向相反的方向飞行,那么这架飞机向()方向飞行。
A.东偏南45° B.西偏南45°C.西偏北45°四、动手操作,开发大脑。
(共20分)1.学校在小林家北偏西20°的方向上,距离小林家200 m。
你能在下图中找到学校的位置吗?画一画。
(10分)2.某勘探队在A城南偏西60°方向上约60 km处发现稀有金属矿。
请你在平面图上确定稀有金属矿的位置。
(10分)五、我会应用。
(共44分)1.小蜜蜂迷路了,你能告诉它回家的路吗?(10分)它应该向________偏________的方向飞________,再向________飞________,就可以到家了。
高中数学北师大版选修4-4课时分层作业 共9套含解析

∴B(x+2,0),C(x-2,0).
∵P也在AB的垂直平分线上,
∴|PA|=|PB|,
即 = ,
化简得x2-6y+5=0.
这就是所求的轨迹方程.
[能力提升练]
1.方程x2+xy=0的曲线是()
A.一个点B.一条直线
C.两条直线D.一个点和一条直线
[解析]x2+xy=x(x+y)=0,即x=0或x+y=0.
∴b2=c2-a2=4- = .
∴点P的轨迹方程为 - =1 .
由图可知,点P为双曲线与x轴的右交点时,|OP|最小,|OP|的最小值是 .
[答案]A
二、填空题
6.x轴上的单位长度为y轴上单位长度的2倍的平面直角坐标系中,以原点为圆心,4为半径的圆的图形变为________.
[解析]如果x轴上的单位长度不变,y轴上的单位长度缩小为原来的 ,圆x2+y2=16的图形变为中心在原点,焦点在x轴上的一个椭圆.
故方程x2+xy=0表示两条直线.
[答案]C
2.已知△ABC的底边BC长为12,且底边固定,顶点A是动点,且sinB-sinC= sinA,若以底边BC为x轴、底边BC的中点为原点建立平面直角坐标系,则点A的轨迹方程是()
A. - =1B. - =1(x<-3)
C. - =1D. - =1(x<-3)
8.如图所示,正方体ABCDA1B1C1D1的棱长为1,点M在AB上,且AM= AB,点P在平面ABCD上,且动点P到直线A1D1的距离的平方与P到点M的距离的平方差为1,在平面直角坐标系xAy中,动点P的轨迹方程是________.
[解析]过P作PQ⊥AD于Q,再过Q作QH⊥A1D1于H,连结PH,PM,可证PH⊥A1D1,设P(x,y),由|PH|2-|PM|2=1,得x2+1- =1,化简得y2= x- .
北师大版一年级数学上册第三单元测试卷4份

第三单元达标检测卷一、填一填,画一画。
(1题5分,3题6分,4题6分,其余每题8分,共41分)1.照样子填上合适的数。
2. 按规律,画一画,填一填。
(1) 每次多()个。
(2) 每次少()个。
3.在○里填上“+”或“-”。
3○3=6 4○4=0 4○3=16○3=9 10○4=6 5○0=54.在○里填上“>”“<”或“=”。
9-9○4 4+3○5 3+6○9-19-7○2 6-5○0 5-3○8-85.在□里填上合适的数。
□<8 7>□4<□9>□□=10 □<2 6<□5>□6.写出不同的算式。
二、连一连,算一算。
(1题8分,2题12分,3题6分,共26分) 1.连一连。
2.送小动物回家。
3.口算。
□+3=8 9-□=4 □-2=5□+5=9 9-□=7 □+6=8三、看图列式。
(12分)1.一共有多少个胡萝卜?2. 一共有多少个梨子?3.还剩几个?4. 一共有8本书。
5. 还剩多少根木头?6. 现在有多少只鸟?四、解决问题。
(3题5分,4题8分,其余每题4分,共21分) 1.一共有多少个小朋友?2.一共有8只蚂蚁,树叶下面有几只?3.原来车上有5名学生,现在车上有多少名学生?4.提出两个数学问题并解答。
4.10以内数的加减运算一、我wǒ会huì填tián一yi填tián,画huà一yi画huà。
(第3,4小题每题11分,其余每空1分,共32分)1.2.3.画一画,填一填。
○○○○______________________4+=10______________________□□□□□ +5=84.先画“○”表示下面的算式,再算出结果。
二、小xiǎo鸟niǎo送sònɡ信xìn,连lián一yi连lián。
(16分)三、细xì心xīn的de你nǐ,算suàn一yi算suàn。
北师大版高中数学必修必修课后习题答案

第一章 算法初步1.1算法与程序框图练习(P5) 1、算法步骤:第一步,给定一个正实数r .第二步,计算以r 为半径的圆的面积2S r π=.第三步,得到圆的面积S .2、算法步骤:第一步,给定一个大于1的正整数n .第二步,令1i =.第三步,用i 除n ,等到余数r .第四步,判断“0r =”是否成立. 若是,则i 是n 的因数;否则,i 不是n 的因数. 第五步,使i 的值增加1,仍用i 表示.第六步,判断“i n >”是否成立. 若是,则结束算法;否则,返回第三步.练习(P19)算法步骤:第一步,给定精确度d ,令1i =.的到小数点后第i 位的不足近似值,赋给a 的到小数点后第i 位的过剩近似值,赋给b .第三步,计算55ba m =-.第四步,若m d <,则得到5a;否则,将i 的值增加1,仍用i 表示.返回第二步. 第五步,输出5a.程序框图:习题1.1 A 组(P20)1、下面是关于城市居民生活用水收费的问题.为了加强居民的节水意识,某市制订了以下生活用水收费标准:每户每月用水未超过7 m 3时,每立方米收费1.0元,并加收0.2元的城市污水处理费;超过7m 3的部分,每立方收费1.5元,并加收0.4元的城市污水处理费.设某户每月用水量为x m 3,应交纳水费y 元,那么y 与x 之间的函数关系为 1.2,071.9 4.9,7x x y x x ≤≤⎧=⎨->⎩我们设计一个算法来求上述分段函数的值. 算法步骤:第一步:输入用户每月用水量x .第二步:判断输入的x 是否不超过7. 若是,则计算 1.2y x =;若不是,则计算 1.9 4.9y x =-.第三步:输出用户应交纳的水费y .程序框图:2、算法步骤:第一步,令i =1,S=0.第二步:若i ≤100成立,则执行第三步;否则输出S. 第三步:计算S=S+i 2. 第四步:i = i +1,返回第二步.程序框图:3、算法步骤:第一步,输入人数x ,设收取的卫生费为m 元.第二步:判断x 与3的大小. 若x >3,则费用为5(3) 1.2m x =+-⨯;若x ≤3,则费用为5m =.第三步:输出m .程序框图:B 组 1、算法步骤:第一步,输入111222,,,,,a b c a b c ..第二步:计算21121221b c b c x a b a b -=-.第三步:计算12211221a c a c y ab a b -=-.第四步:输出,x y .程序框图:2、算法步骤:第一步,令n=1第二步:输入一个成绩r,判断r与6.8的大小. 若r≥6.8,则执行下一步;若r<6.8,则输出r,并执行下一步.第三步:使n的值增加1,仍用n表示.第四步:判断n与成绩个数9的大小. 若n≤9,则返回第二步;若n>9,则结束算法.程序框图:说明:本题在循环结构的循环体中包含了一个条件结构.1.2基本算法语句练习(P24)13练习(P2912、本程序的运行过程为:输入整数x. 若x是满足9<x<100的两位整数,则先取出x的十位,记作a,再取出x的个位,记作b,把a,b调换位置,分别作两位数的个位数与十位数,然后输出新的两位数. 如输入25,则输出52.34练习(P32)12习题1.2 A组(P33)1、1(0)0(0)1(0)x xy xx x-+<⎧⎪==⎨⎪+>⎩23、程序:习题1.2 B组(P33)1、程序:23 41.3算法案例 练习(P45)1、(1)45; (2)98; (3)24; (4)17.2、2881.75.3、2200811111011000=() ,820083730=() 习题1.3 A 组(P48) 1、(1)57; (2)55. 2、21324.3、(1)104; (2)7212() (3)1278; (4)6315().4、习题1.3 B 组(P48)1、算法步骤:第一步,令45n =,1i =,0a =,0b =,0c =.第二步,输入()a i .第三步,判断是否0()60a i ≤<. 若是,则1a a =+,并执行第六步. 第四步,判断是否60()80a i ≤<. 若是,则1b b =+,并执行第六步. 第五步,判断是否80()100a i ≤≤. 若是,则1c c =+,并执行第六步. 第六步,1i i =+. 判断是否45i ≤. 若是,则返回第二步.第七步,输出成绩分别在区间[0,60),[60,80),[80,100]的人数,,a b c .2、如“出入相补”——计算面积的方法,“垛积术”——高阶等差数列的求和方法,等等.第二章 复习参考题A 组(P50)1、(1)程序框图: 程序: 1、(2)程序框图: 程序:2、见习题1.2 B 组第1题解答.3、45(1)向下的运动共经过约199.805 m (2)第10次着地后反弹约0.098 m (3)全程共经过约299.609 m13x 和它的位数n . n 是偶数,令2n m =;如果n 是奇数,令12n m -=. 1)i +-位上的数字是否相等. 若是,则使i 的值增加1,仍用i表示;否则,x不是回文数,结束算法.”是否成立. 若是,则n是回文数,结束算法;否则,返回第四步.第五步,判断“i m第二章统计2.1随机抽样练习(P57)1、.情况之间有误差. 如抽取的部分个体不能很好地代表总体,那么我们分析出的结果就会有偏差.2、(1)抽签法:对高一年级全体学生450人进行编号,将学生的名字和对应的编号分别写在卡片上,并把450张卡片放入一个容器中,搅拌均匀后,每次不放回地从中抽取一张卡片,连续抽取50次,就得到参加这项活动的50名学生的编号.(2)随机数表法:第一步,先将450名学生编号,可以编为000,001, (449)第二步,在随机数表中任选一个数. 例如选出第7行第5列的数1(为了便于说明,下面摘取了附表的第6~10行).16 22 77 94 39 49 54 43 54 82 17 37 93 23 78 87 35 20 96 43 84 26 34 91 6484 42 17 53 31 57 24 55 06 88 77 04 74 47 67 21 76 33 50 25 83 92 12 06 7663 01 63 78 59 16 95 55 67 19 98 10 50 71 75 12 86 73 58 07 44 39 52 38 7933 21 12 34 29 78 64 56 07 82 52 42 07 44 38 15 51 00 13 42 99 66 02 79 5457 60 86 32 44 09 47 27 96 54 49 17 46 09 62 90 52 84 77 27 08 02 73 43 28第三步,从选定的数1开始向右读,得到一个三位数175,由于175<450,说明号码175在总体内,将它取出;继续向右读,得到331,由于331<450,说明号码331在总体内,将它取出;继续向右读,得到572,由于572>450,将它去掉. 按照这种方法继续向右读,依次下去,直到样本的50个号码全部取出,这样我们就得到了参加这项活动的50名学生.3、用抽签法抽取样本的例子:为检查某班同学的学习情况,可用抽签法取出容量为5的样本. 用随机数表法抽取样本的例子:部分学生的心理调查等.抽签法能够保证总体中任何个体都以相同的机会被选到样本之中,因此保证了样本的代表性.4、与抽签法相比,随机数表法抽取样本的主要优点是节省人力、物力、财力和时间,缺点是所产生的样本不是真正的简单样本.练习(P59)1、系统抽样的优点是:(1)简便易行;(2)当对总体结构有一定了解时,充分利用已有信息对总体中的个体进行排队后再抽样,可提高抽样调查;(3)当总体中的个体存在一种自然编号(如生产线上产品的质量控制)时,便于施行系统抽样法.系统抽样的缺点是:在不了解样本总体的情况下,所抽出的样本可能有一定的偏差.2、(1)对这118名教师进行编号;(2)计算间隔1187.37516k==,由于k不是一个整数,我们从总体中随机剔除6个样本,再来进行系统抽样. 例如我们随机剔除了3,46,59,57,112,93这6名教师,然后再对剩余的112位教师进行编号,计算间隔7k=;(3)在1~7之间随机选取一个数字,例如选5,将5加上间隔7得到第2个个体编号12,再加7得到第3个个体编号19,依次进行下去,直到获取整个样本.3、由于身份证(18位)的倒数第二位表示性别,后三位是632的观众全部都是男性,所以这样获得的调查结果不能代表女性观众的意见,因此缺乏代表性.练习(P62)1、略2、这种说法有道理,因为一个好的抽样方法应该能够保证随着样本容量的增加,抽样调查结果会接近于普查的结果. 因此只要根据误差的要求取相应容量的样本进行调查,就可以节省人力、物力和财力.3、可以用分层抽样的方法进行抽样. 将麦田按照气候、土质、田间管理水平的不同而分成不同的层,然后按照各层麦田的面积比例及样本容量确定各层抽取的面积,再在各层中抽取个体(这里的个体是单位面积的一块地).习题2.1 A组(P63)1、产生随机样本的困难:(1)很难确定总体中所有个体的数目,例如调查对象是生产线上生产的产品.(2)成本高,要产生真正的简单随机样本,需要利用类似于抽签法中的抽签试验来产生非负整值随机数.(3)耗时多,产生非负整数值随机数和从总体中挑选出随机数所对的个体都需要时间.2、调查的总体是所有可能看电视的人群.学生A的设计方案考虑的人数是:上网而且登录某网址的人群,那些不能上网的人群,或者不登录某网址的人群就被排除在外了. 因此A方案抽取的样本的代表性差.学生B的设计方案考虑的人群是小区内的居民,有一定的片面性. 因此B方案抽取的样本的代表性差.学生C的设计方案考虑的人群是那些有电话的人群,也有一定的片面性. 因此C方案抽取的样本的代表性.所以,这三种调查方案都有一定的片面性,不能得到比较准确的收视率.3、(1)因为各个年级学习任务和学生年龄等因素的不同,影响各年级学生对学生活动的看法,所以按年级分层进行抽样调查,可以得到更有代表性的样本.(2)在抽样的过程中可能遇到的问题如敏感性问题:有些学生担心提出意见对自己不利;又如不响应问题:由于种种原因,有些学生不能发表意见;等等.(3)前面列举的两个问题都可能导致样本的统计推断结果的误差.(4)为解决敏感性问题,可以采用阅读与思考栏目“如何得到敏感性问题的诚实反应”中的方法设计调查问卷;为解决不响应问题,可以事先向全体学生宣传调查的意义,并安排专人负责发放和催收调查问卷,最大程度地回收有效调查问卷.4、将每一天看作一个个体,则总体由365天组成. 假设要抽取50个样本,将一年中的各天按先后次序编号为0~364天用简单随机抽样设计方案:制作365个号签,依次标上0~364. 将号签放到容器内充分搅拌均匀,从容器中任意不放回取出50个号签. 以签上的号码所对应的那些天构成样本,检测样本中所有个体的空气质量.用系统抽样设计抽样方案:先通过简单随机抽样方法从365天中随机抽出15天,再把剩下的350天重新按先后次序编号为0~349. 制作7个分别标有0~7的号签,放在容器中充分搅拌均匀. 从容器中任意取出一个号签,设取出的号签的编号为a ,则编号为7(050)a k k +≤<所对应的那些天构成样本,检测样本中所有个体的空气质量.显然,系统抽样方案抽出的样本中个体在一年中排列的次序更规律,因此更好实施,更受方案的实施者欢迎.5、田径队运动员的总人数是564298+=(人),要得到28人的样本,占总体的比例为27.于是,应该在男运动员中随机抽取256167⨯=(人),在女运动员中随机抽取281612-=(人).这样我们就可以得到一个容量为28的样本.6、以10为分段间隔,首先在1~10的编号中,随机地选取一个编号,如6,那么这个获奖者奖品的编号是:6,16,26,36,46.7、说明:可以按年级分层抽样的方法设计方案. 习题2.1 B 组(P64)1、说明:可以按年级分层抽样的方法设计方案,调查问卷由学生所关心的问题组成. 例如:(1)你最喜欢哪一门课程? (2)你每月的零花钱平均是多少? (3)你最喜欢看《新闻联播》吗? (4)你每天早上几点起床? (5)你每天晚上几点睡觉?要根据统计的结果和具体的情况解释结论,主要从引起结论的可能原因及结论本身含义来解释.2、说明:这是一个开放性的题目,没有一个标准的答案. 2.2用样本估计总体 练习(P71)1、说明:由于样本的极差为364.41362.51 1.90-=,取组距为0.19,将样本分为10组. 可以按照书上的方法制作频率分布表、频率分布直观图和频率折线图.2、说明:此题目属于应用题,没有标准的答案.3、茎叶图为:由该图可以看出30名工人的日加工零件个数稳定在120件左右. 练习(P74)这里应该采用平均数来表示每一个国家项目的平均金额,因为它能反应所有项目的信息. 但平均数会受到极端数据2000万元的影响,所以大多数项目投资金额都和平均数相差比较大. 练习(P79)1、甲乙两种水稻6年平均产量的平均数都是900,但甲的标准差约等于23.8,乙的标准差约等于41.6,所以甲的产量比较稳定.2、(1)平均重量496.86x ≈,标准差 6.55s ≈.(2)重量位于(,)x s x s -+之间有14袋白糖,所占的百分比约为66.67%.3、(1)略. (2)平均分19.25x ≈,中位数为15.2,标准差12.50s ≈.这些数据表明这些国家男性患该病的平均死亡率约为19.25,有一半国家的死亡率不超过15.2,15.2x >说明存在大的异常数据,值得关注. 这些异常数据使标准差增大. 习题2.2 A 组(P81) 1(2)汞含量分布偏向于大于1.00 ppm 的方向,即多数鱼的汞含量分布在大于1.00 ppm 的区域.(3)不一定. 因为我们不知道各批鱼的汞含量分布是否都和这批鱼相同. 即使各批鱼的汞含量分布相同,上面的数据只能为这个分布作出估计,不能保证平均汞含量大于1.00 ppm. (4)样本平均数 1.08x ≈,样本标准差0.45s ≈.(5)有28条鱼的汞含量在平均数与2倍标准差的和(差)的范围内.2度比较短,所以在这批棉花中混进了一些次品.3、说明:应该查阅一下这所大学的其他招生信息,例如平均数信息、最低录取分数线信息等. 尽管该校友的分数位于中位数之下,而中位数本身并不能提供更多录取分数分布的信息.在已知最低录取分数线的情况下,很容易做出判断;在已知平均数小于中位数很多,则说明最低录取分数线较低,可以推荐该校友报考这所大学,否则还要获取其他的信息(如标准差的信息)来做出判断.4、说明:(1)对,从平均数的角度考虑; (2)对,从标准差的角度考虑;(3)对,从标准差的角度考虑; (4)对,从平均数和标准差的角度考虑; 5、(1)不能. 因为平均收入和最高收入相差太多,说明高收入的职工只占极少数. 现在已知知道至少有一个人的收入为50100x =万元,那么其他员工的收入之和为4913.55010075ii x==⨯-=∑(万元)每人平均只有 1.53. 如果再有几个收入特别高者,那么初进公司的员工的收入将会很低.(2)不能,要看中位数是多少.(3)能,可以确定有75%的员工工资在1万元以上,其中25%的员工工资在3万元以上.(4)收入的中位数大约是2万. 因为有年收入100万这个极端值的影响,使得年平均收入比中位数高许多.6、甲机床的平均数=1.5x 甲,标准差=1.2845s 甲;乙机床的平均数 1.2z y =,标准差0.8718z s =. 比较发现乙机床的平均数小而且标准差也比较小,说明乙机床生产出的次品比甲机床少,而且更为稳定,所以乙机床的性能较好. 7、(1)总体平均数为199.75,总体标准差为95.26.(2)可以使用抓阄法进行抽样. 样本平均数和标准差的计算结果和抽取到的样本有关.(3) (4)略 习题2.2 B 组(P82)1、(1)由于测试1T 的标准差小,所以测试1T 结果更稳定,所以该测试做得更好一些. (2)由于2T 测出的值偏高,有利于增强队员的信心,所以应该选择测试2T .2、说明:此题需要在本节开始的时候就布置,先让学生分头收集数据,汇总所收集的数据才能完成题目.2.3变量间的相关关系 练习(P85)1、从已经掌握的知识来看,吸烟会损害身体的健康. 但除了吸烟之外,还有许多其他的随机因素影响身体健康,人体健康是很多因素共同作用的结果. 我们可以找到长寿的吸烟者,也更容易发现由于吸烟而引发的患病者,所以吸烟不一定引起健康问题. 但吸烟引起健康问题的可能性大,因此“健康问题不一定是由吸烟引起的,所以可以吸烟”的说法是不对的.2、从现在我们掌握的知识来看,没有发现根据说明“天鹅能够带来孩子”,完全可能存在既能吸引天鹅和又使婴儿出生率高的第3个因素(例如独特的环境因素),即天鹅与婴儿出生率之间没有直接的关系,因此“天鹅能够带来孩子”的结论不可靠.而要证实此结论是否可靠,可以通过试验来进行. 相同的环境下将居民随机地分为两组,一组居民和天鹅一起生活(比如家中都饲养天鹅),而另一组居民的附近不让天鹅活动,对比两组居民的出生率是否相同.(1)散点图如下:练习(P92)1、当0x =时,147.767y =,这个值与实际卖出的热饮杯数150不符,原因是:线性回归方程中的截距和斜率都是通过样本估计的,存在随机误差,这种误差可以导致预测结果的偏差;即使截距和斜率的估计没有误差,也不可能百分之百地保证对应于x ,预报值y 能够等于实际值y . 事实上:y bx a e =++. (这里e 是随机变量,是引起预报值y 与真实值y 之间的误差的原因之一,其大小取决于e 的方差.) 2、数据的散点图为:从这个散点图中可以看出,鸟的种类数与海拔高度应该为正相关(事实上相关系数为0.793). 但是从散点图的分布特点来看,它们之间的线性相关性不强. 习题2.3 A 组(P94)1、教师的水平与学生的学习成绩呈正相关关系. 又如,“水涨船高”“登高望远”等.2、 (3)基本成正相关关系,即食品所含热量越高,口味越好.(4)因为当回归直线上方的食品与下方的食品所含热量相同时,其口味更好. 3、(1)散点图如下:(2)回归方程为:0.66954.933y x =+.(3)加工零件的个数与所花费的时间呈正线性相关关系.(2)回归直线如下图所示:4、(1)散点图为:(2)回归方程为:0.546876.425y x =+.(3)由回归方程知,城镇居民的消费水平和工资收入之间呈正线性相关关系,即工资收入水平越高,城镇居民的消费水平越高. 习题2.3 B 组(P95)1、(1)散点图如下:(2)回归方程为: 1.44715.843y x =-.(3)如果这座城市居民的年收入达到40亿元,估计这种商品的销售额为42.037y ≈(万元).2、说明:本题是一个讨论题,按照教科书中的方法逐步展开即可.第二章 复习参考题A 组(P100)1、A .2、(1)该组的数据个数,该组的频数除以全体数据总数; (2)nm N.3、(1)这个结果只能说明A 城市中光顾这家服务连锁店的人比其他人较少倾向于选择咖啡色,因为光顾连锁店的人使一种方便样本,不能代表A 城市其他人群的想法. (2)这两种调查的差异是由样本的代表性所引起的. 因为A 城市的调查结果来自于该市光顾这家服装连锁店的人群,这个样本不能很好地代表全国民众的观点.4、说明:这是一个敏感性问题,可以模仿阅读与思考栏目“如何得到敏感性问题的诚实反应”来设计提问方法.5、表略. 可以估计出句子中所含单词的分布,以及与该分布有关的数字特征,如平均数、标准差等.6、(1)可以用样本标准差来度量每一组成员的相似性,样本标准差越小,相似程度越高.(2)A 组的样本标准差为 3.730A S ≈,B 组的样本标准差为11.789B S ≈. 由于专业裁判给分更符合专业规则,相似程度应该高,因此A 组更像是由专业人士组成的. 7、(1)中位数为182.5,平均数为217.1875.(2)这两种数字特征不同的主要原因是,430比其他的数据大得多,应该查找430是否由某种错误而产生的. 如果这个大数据的采集正确,用平均数更合适,因为它利用了所有数据的信息;如果这个大数据的采集不正确,用中位数更合适,因为它不受极端值的影响,稳定性好. 8、(1)略.(2)系数0.42是回归直线的斜率,意味着:对于农村考生,每年的入学率平均增长0.42%.(3)城市的大学入学率年增长最快.说明:(4)可以模仿(1)(2)(3)的方法分析数据.第二章 复习参考题B 组(P101)1、频率分布如下表:从表中看出当把 指标定为17.46千元 时,月65%的推销员经过努力才能完成销 售指标.2、(1)数据的散点图如下:(2)用y 表示身高,x 表示年龄,则数据的回归方程为6.y x =+.(3)在该例中,斜率6.317表示孩子在一年中增加的高度.(4)每年身高的增长数略. 3~16岁的身高年均增长约为6.323 cm. (5)斜率与每年平均增长的身高之间之间近似相等. 第三章 概率3.1随机事件的概率1、(1)试验可能出现的结果有3个,两个均为正面、一个正面一个反面、两个均为反面.(2)通过与其他同学的结果汇总,可以发现出现一个正面一个反面的次数最多,大约在50次左右,两个均为正面的次数和两个均为反面的次数在25次左右. 由此可以估计出现一个正面一个反面的概率为0.50,出现两个均为正面的概率和两个均为反面的概率均为0.25.2、略3、(1)例如:北京四月飞雪;某人花两元钱买福利彩票,中了特等奖;同时抛10枚硬币,10枚都正面朝上.(2)例如:在王府井大街问路时,碰到会说中文的人;去烤鸭店吃饭的顾客点烤鸭;在1~1000的自然数任选一个数,选到的数大于1.练习(P118)1、说明:例如,计算机键盘上各键盘的安排,公交线路及其各站点的安排,抽奖活动中各奖项的安排等,其中都用到了概率. 学生可能举出各种各样的例子,关键是引导他们正确分析例子中蕴涵的概率思想.2、通过掷硬币或抽签的方法,决定谁先发球,这两种方法都是公平的. 而猜拳的方法不太公平,因为出拳有时间差,个人反应也不一样.3、这种说法是错误的. 因为掷骰子一次得到2是一个随机事件,在一次试验中它可能发生也可能不发生. 掷6次骰子就是做6次试验,每次试验的结果都是随机的,可能出现2也可能不出现2,所以6次试验中有可能一次2都不出现,也可能出现1次,2次,…,6次.练习(P121)1、0.72、0.6153、0.44、D5、B习题3.1 A组(P123)1、D.2、(1)0;(2)0.2;(3)1.3、(1)430.067645≈;(2)900.140645≈;(3)7010.891645-≈.4、略5、0.136、说明:本题是想通过试验的方法,得到这种摸球游戏对先摸者和后摸者是公平的结论. 最好把全班同学的结果汇总,根据两个事件出现的频率比较近,猜测在第一种情况下摸到红球的概率为110,在第二种下也为110. 第4次摸到红球的频率与第1次摸到红球的频率应该相差不远,因为不论哪种情况,第4次和第1次摸到红球的概率都是1 10.习题3.1 B组(P124)1、D.2、略. 说明:本题是为了学生根据实际数据作出一些推断. 一般我们假定每个人的生日在12个月中哪一个月是等可能的,这个假定是否成立,引导学生通过收集的数据作出初步的推断.3.2古典概率练习(P130)1、110. 2、17. 3、16.1、38,38.2、(1)113;(2)1213;(3)14;(4)313;(5)0;(6)213;(7)12;(8)1.说明:模拟的方法有两种.(1)把1~52个自然数分别与每张牌对应,再用计算机做模拟试验.(2)让计算机分两次产生两个随机数,第一次产生1~4的随机数,代表4个花色;第二次产生1~13的随机数,代表牌号.3、(1)不可能事件,概率为0;(2)随机事件,概率为49;(3)必然事件,概率为1;(4)让计算机产生1~9的随机数,1~4代表白球,5~9代表黑球.4、(1)16;(2)略;(3)应该相差不大,但会有差异. 存在差异的主要原因是随机事件在每次试验中是否发生是随机的,但在200次试验中,该事件发生的次数又是有规律的,所以一般情况下所得的频率与概率相差不大.习题3.2 A组(P133)1、游戏1:取红球与取白球的概率都为12,因此规则是公平的.游戏2:取两球同色的概率为13,异色的概率为23,因此规则是不公平的.游戏3:取两球同色的概率为12,异色的概率为12,因此规则是公平的.2、第一位可以是1~9这9个数字中的一个,第二位可以是0~9这10个数字中的一个,所以(1)190;(2)18919090-=;(3)9919010-=3、(1)0.52;(2)0.18.4、(1)12;(2)16;(3)56;(4)16.5、(1)25;(2)825.6、(1)920;(2)920;(3)12.习题3.2 B组(P134)1、(1)13;(2)14.2、(1)35;(2)310;(3)910.说明:(3)先计算该事件的对立事件发生的概率会比较简单.3、具体步骤如下:①建立概率模型. 首先要模拟每个人的出生月份,可用1,2,…,11,12表示月份,用产生取整数值的随机数的办法,随机产生1~12之间的随机数. 由于模拟的对象是一个有10个人的集体,故把连续产生的10个随机数作为一组模拟结果,可模拟产生100组这样的结果.②进行模拟试验. 可用计算器或计算机进行模拟试验.如使用Excel软件,可参看教科书125页的步骤,下图是模拟的结果:其中,A,B,C,D,E,F,G,H,I,J的每一行表示对一个10人集体的模拟结果. 这样的试验一共做了100次,所以共有100行,表示随机抽取了100个集体.③统计试验的结果. K,L,M,N列表示统计结果. 例如,第一行前十列中至少有两个数相同,表示这个集体中至少有两个人的生日在同一月. 本题的难点是统计每一行前十列中至少有两个数相同的个数. 由于需要判断的条件态度,所以用K,L,M三列分三次完成统计.其中K列的公式为“=IF(OR(A1=B1,A1=C1,A1=D1,A1=E1,A1=F1,A1=G1,A1=H1,A1=I1,A1=J1,B1=C1,B1=D1,B1=E1,B1=F1,B1=G1,B1=H1,B1=I1,B1=J1,C1=D1,C1=E1,C1=F1,C1=G1,C1=H1,C1=I1,C1=J1,D1=E1,D1=F1,D1=G1,D1=H1,D1=I1,D1=J1),1,0)”,L列的公式为“=IF(OR(E1=F1,E1=G1,E1=H1,E1=I1,E1=J1,F1=G1,F1=H1,F1=I1,F1=J1,G1=H1,G1=I1,G1=J1,H1=I1,H1=J1,I1=J1),1,0)”,M列的公式为“=IF(OR(K1=1,L1=1),1,0)”,M列的值为1表示该行所代表的10人集体中至少有两个人的生日在同一个月. N1表示100个10人集体中至少有两个人的生日在同一个月的个数,其公式为“=SUM(M$1:M$100)”. N1除以100所得的结果0.98,就是用模拟方法计算10人集体中至少有两个人的生日在同一个月的概率的估计值. 可以看出,这个估计值很接近1.3.3几何概率练习(P140)1、(1)1;(2)38.2、如果射到靶子上任何一点是等可能的,那么大约有100个镖落在红色区域.说明:在实际投镖中,命中率可能不同,这里既有技术方面的因素,又是随机因素的影响,所以在投掷飞镖、射击或射箭比赛中不会以一枪或一箭定输赢,而是取多次成绩的总和,这就是为了减少随机因素的影响.习题3.3 A组(P142)1、(1)49;(2)13;(3)29;(4)23;(5)59.2、(1)126;(2)12;(3)326;(4)326;(5)12;(6)313.说明:(4)是指落在6,23,9三个相邻区域的情况,而不是编号为6,7,8,9,四个区域.3、(1)25;(2)115;(3)35. 说明:本题假设在任何时间到达路口是等可能的.习题3.3 B组(P142)。
《红对勾》2021届高三数学第一轮复习北师大版 课时作业4 Word版含解析

课时作业4 函数及其表示一、选择题(每小题5分,共40分)1.(2022·江西理,2)下列函数中,与函数y =13x定义域相同的函数为( )A .y =1sin x B .y =ln xx C .y =x e xD .y =sin xx解析:本题考查函数的定义域,由于y =13x的定义域为{x |x ≠0},满足条件的函数只有D ,故选D.答案:D2.(2022·北京海淀)假如f (1x )=x1-x ,则当x ≠0且x ≠1时,f (x )=________.( )A.1xB.1x -1C.11-xD.1x -1解析:令1x =t ,得x =1t . ∴f (t )=1t1-1t =1t -1∴f (x )=1x -1.答案:B3.设函数f (x )=⎩⎪⎨⎪⎧-x ,x ≤0x 2,x >0,若f (α)=4,则实数α=( )A. -4或-2B. -4或2 C .-2或4D .-2或2解析:本题主要考查分段函数求函数值等基础学问. 当α≤0时,f (α)=-α=4,∴α=-4; 当α>0时,f (α)=α2=4,∴α=2. 综之:α=-4或2,选B. 答案:B4.下列对应法则f 为A 上的函数的个数是( ) ①A =Z ,B =N +,f :x →y =x 2 ②A =Z ,B =Z ,f :x →y =x ③A =[-1,1],B ={0},f :x →y =0 A .0 B .1 C .2D .3解析:对于①,当0∈A 时,y =0∉B ,故①所给的对应法则不是A 到B 的映射,当然它不是A 上的函数关系;对于②,当2∈A 时,y =2∉B ,故②所给的对应法则不是A 到B 的映射,当然它不是A 上的函数关系;对于③,对于A 中的任一个数,依据对应法则,在B 中都有唯一元素0和它对应,故③所给的对应法则是A 到B 的映射,这两个数集之间的关系是集合A 上的函数关系.答案:B5.(2022·福建厦门3月模拟)已知函数f (x )=⎩⎪⎨⎪⎧3-x 2,x ∈[-1,2],x -3,x ∈(2,5],则方程f (x )。
北师大四下练习册答案

北师大四下练习册答案北师大版四年级下册数学练习册答案一、选择题1. 下列哪个数是最小的正整数?A. 0B. -1C. 1D. 2答案:C2. 一个数的平方是16,这个数是:A. 4B. -4C. 4或-4D. 16答案:C3. 以下哪个分数是最简分数?A. 4/8B. 5/10C. 3/4D. 6/9答案:C4. 一个数的倒数是1/4,这个数是:A. 4B. 1C. 1/4D. 4/1答案:A5. 一个数除以5的商是10,这个数是:A. 50B. 45C. 10D. 5答案:A二、填空题1. 一个数的平方等于81,这个数是______。
答案:±92. 一个数的立方等于27,这个数是______。
答案:33. 一个数的倒数是2/3,这个数是______。
答案:3/24. 一个数的平方根是5,这个数是______。
答案:255. 一个数的立方根是2,这个数是______。
答案:8三、计算题1. 计算下列各题:(1) 48 × 25答案:1200(2) 125 ÷ 25答案:5(3) 36 × 38答案:1368(4) 81 ÷ 9答案:92. 计算下列各题,并写出计算过程:(1) 56 × 78 - 45答案:4377(2) 98 ÷ 7 + 23答案:31四、解答题1. 一个长方形的长是20厘米,宽是15厘米,求它的周长和面积。
答案:周长= 2 × (20 + 15) = 70厘米面积= 20 × 15 = 300平方厘米2. 一个班级有40名学生,其中男生和女生的人数比是3:2。
求男生和女生各有多少人?答案:男生人数= 40 × (3/5) = 24人女生人数= 40 × (2/5) = 16人结束语:通过本练习册的练习,希望同学们能够更好地掌握四年级下册数学的知识点和解题技巧,提高数学思维能力和解决问题的能力。
【参考文档】北师大版数学暑假作业的参考答案-精选word文档 (3页)

本文部分内容来自网络整理,本司不为其真实性负责,如有异议或侵权请及时联系,本司将立即删除!== 本文为word格式,下载后可方便编辑和修改! ==北师大版数学暑假作业的参考答案(一)1.B2.B3.D4.B5.C6.C7.408.平行9.a=c>b10.13611.内错角相等,两直线平行;3;4;两直线平行,同位角相等12.(1)略(2)平行,理由略13.略14.(1)∠B+∠D=∠E(2)∠E+∠G=∠B+∠F+∠D(3)略(二)1.C2.B3.D4.D5.D6.C7.50°或65°8.49.平行10.9厘米或13厘米11.60°12.13.略14.略15.略16.(1)15°(2)20°(3)(4)有,理由略(三)1.20°2.厘米3.84.4.85.366.37.D8.C9.B10.B11.略12.FG垂直平分DE,理由略13.0.5米14.同时到达,理由略15.(1)城市A受影响(2)8小时(四)1.C2.D3.B4.A5.C6.A7.C8.B9.3010.611.,12.略13.略14.(1)直六棱柱(2)6ab15.3616.厘米(五)1.D2.D3.B4.D5.(1)抽样调查(2)普查6.8.07.178.50.49.31;3110.1711.冠军、亚军、季军分别为李扬、林飞、程丽12.略13.略(六)1.B2.C3.C4.50;105.0.1576米26.①②③7.略8.略9.略(七)1.B2.A3.C4.A5.C6.B7.D8.(1)<(2)>(3)≥(4)<(5)<9.410.a14.-2,-115.16.b<0(八)1.D2.C3.C4.C5.n≤76.238.9.0≤y≤510.11.x3(3)无解13.1,214.34,1615.(1)9≤m<12(2)9(九)1.C2.B3.C4.18≤t≤225.4.0米/秒6.5,7,97.8.大于201X0元9.2210.4人,13瓶11.当旅游人数为10~15人时选择乙旅行社;当旅游人数为16人时两家旅行社都可选择;当旅游人数为17~25人时选择甲旅行社12.(1)35元,26元(2)有3种方案;购买文化衫23件,相册27本的方案用于购买教师纪念品的资金更充足13.略(十)1.C2.C3.C4.C5.D6.C7.为任何实数;为08.a<-19.南偏西40°距离80米10.(6,6),(-6,6),(-6,-6),(6,-6)11.5或-112.(5,2)13.(x,6)(-3≤x≤2)14.略15.(-2,0)或(6,0)16.等腰直角三角形,917.略18.略。
【北师大版】高中数学必修四全册学案(全册共340页 附答案)

【北师大版】高中数学必修四全册学案(全册共340页附答案)目录§1周期现象§2角的概念的推广§3弧度制4.1 单位圆与任意角的正弦函数、余弦函数的定义4.2 单位圆与周期性4.3 单位圆与正弦函数、余弦函数的基本性质4.4 单位圆的对称性与诱导公式(一)4.4 单位圆的对称性与诱导公式(二)5.1 正弦函数的图像5.2 正弦函数的性质§6余弦函数的图像与性质7.1 正切函数的定义7.2 正切函数的图像与性质7.3 正切函数的诱导公式§8函数y=A sin(ωx+φ)的图像与性质(一)§8函数y=A sin(ωx+φ)的图像与性质(二)§9三角函数的简单应用章末复习课第二章平面向量§1从位移、速度、力到向量2.1 向量的加法2.2 向量的减法3.1 数乘向量3.2 平面向量基本定理§4平面向量的坐标§5从力做的功到向量的数量积§1周期现象内容要求 1.了解周期现象,能判断简单的实际问题中的周期(重点).2.初步了解周期函数的概念,能判断简单的函数的周期性(难点).知识点周期现象(1)概念:相同间隔重复出现的现象.(2)特点:①有一定的规律;②不断重复出现.【预习评价】1.(正确的打“√”,错误的打“×”)(1)地球上一年春、夏、秋、冬四季的变化是周期现象.(√)(2)钟表的分针每小时转一圈,它的运行是周期现象.(√)2.观察“2,0,1,7,2,0,1,7,2,0,1,7,…”寻找规律,则第25个数字是________.解析观察可知2,0,1,7每隔四个数字重复出现一次,具有周期性,故第25个数字为2. 答案 2题型一周期现象的判断【例1】判断下列现象是否为周期现象,并说明理由.(1)地球的自转;(2)连续抛掷一枚骰子,朝上一面的点数;(3)钟表的秒针的转动;(4)某段高速公路每天通过的车辆数.解(1)地球每天自转一圈,并且每一天内的任何时段总会重复前一天内相同时段的动作,因此是周期现象.(2)连续抛掷一枚骰子,朝上一面的点数有可能为1,2,…,6,并且前一次出现的点数,下一次可能出现,也可能不出现,故出现的点数是随机的,因此不是周期现象.(3)钟表的秒针的转动,每一分钟转一圈,并且每分钟总是重复前一分钟的动作,因此是周期现象.(4)某段高速公路每天通过的车辆数,会因时间、天气、交通状况等因素而发生变化,没有一个确定的规律,因此不是周期现象.规律方法周期现象的判断关键:首先要认真审题,明确题目的实际背景,然后应牢牢抓住“间隔相同,现象(或值)重复出现”这一重要特征进行判断.【训练1】判断下列现象是否为周期现象:(1)每届奥运会的举办时间;(2)北京天安门广场的国旗,日出时升旗,日落时降旗,则其每天的升旗时间;(3)中央电视台每晚7:00的新闻联播.解(1)奥运会每4年一届,所以其举办时间呈周期现象.(2)北京每天的日出、日落随节气变化,并非恒定,相邻两天的升旗时间间隔是变化的,不是常数,所以不是周期现象.(3)每24小时,新闻联播重复一次,所以是周期现象.题型二周期现象的应用【例2】一个地区不同日子里白昼的时长是不同的,所给表是某地一年中10天测量的白昼时间统计表(时间近似到0.1小时):坐标系中画出这些数据的散点图,并估计该地区一年中大约有多少天白昼时间大于15.9小时.(2)白昼时间的变化是否具有周期现象?你估计该地区来年6月21日的白昼时间是多少?解(1)散点图如图所示,因为从4月27日至8月13日的白昼时间均超过15.9小时,所以该地区一年白昼时间超过15.9小时的大约有3+31+30+31+12=107(天).(2)由散点图可知,白昼时间的变化是周期现象,该地区来年6月21日的白昼时间为19.4小时.规律方法收集数据、画散点图,分析、研究数据特点从而得出结论是用数学方法研究现实问题的常用方法.【训练2】受日月的引力,海水会发生涨落,这种现象叫做潮汐.已知某海滨浴场的海浪高度y(米)是时间t(0≤t≤24,单位:时)的函数,记作y=f(t),下表是某日各时的浪高数据:几次?时间最长的一次是什么时候?有多长时间?解由题中表可知,一天内能开放三次,时间最长的一次是上午9时至下午3时,共6个小时.【例3】2017年5月1日是星期一,问2017年10月1日是星期几?解按照公历记法,2017年5、7、8这三个月份都是31天,6、9月份各30天.从2017年5月1日到2017年10月1日共有153天,因为每星期有7天,故由153=22×7-1知,从2017年5月1日再过154天恰好与5月1日相同都是星期一,这一天是公历2017年10月2日,故2017年10月1日是星期日.【迁移1】试确定自2017年5月1日再过200天是星期几?解由200=28×7+4知自2017年5月1日再过200天是星期五.【迁移2】从2017年5月1日到2017年10月1日经过了几个星期五?几个星期一?解因为从2017年5月1日到2017年10月1日的153天中有21个完整的周期零6天,在每个周期中有且仅有一个星期五和一个星期一,故共经过了22个星期五,21个星期一.【迁移3】试确定自2017年5月1日再过7k+3(k∈Z)天后那一天是星期几?解每隔七天,周一至周日依次循环,故7k天后为周一,7k+3天后为星期四.规律方法应用周期性解决实际问题的两个要点特别提醒计算两个日期的间隔时间时要注意有的月份30天,有的月份31天,二月份有28天(或29天).课堂达标1.下列自然现象:月亮东升西落,气候的冷暖,昼夜变化,火山爆发.其中是周期现象的有( )A.1个B.2个C.3个D.4个解析月亮东升西落及昼夜变化为周期现象;气候的冷暖与火山爆发不是周期现象,故选B.答案 B2.如果今天是星期五,则58天后的那一天是星期( )A.五B.六C.日D.一解析每隔七天循环一次,58=7×8+2,故58天后为周日.答案 C3.共有50架飞机组成编队,按侦察机、直升机、轰炸机、歼击机的顺序轮换编队,则最后一架飞机是________飞机.解析周期为4,50=12×4+2,所以最后一架是直升机.答案直升机4.某物体作周期运动,如果一个周期为0.4秒,那么运动4秒,该物体经过了________个周期.解析4÷0.4=10,所以经过了10个周期.答案105.某班有48名学生,每天安排4名同学进行卫生值日,按一周上五天课,一学期二十周计算,该班每位同学一学期要值日几次?解共有48名学生,每天安排4名,则12个上课日就轮完一遍.一学期有5×20=100(个)上课日,而12×8=96(个)上课日,所以一个学期内该班每位同学至少值日8次,有部分同学要值日9次.课堂小结1.对于某些具有重复现象的事件,研究其规律,可预测未来在一定时间该现象发生的可能性及发生规律,具有一定的研究价值.2.利用散点图可以较直观地分析两变量之间的某种关系,然后再利用这种关系选择一种合适的函数去拟合这些散点,从而可以避免因盲目选择函数模型而造成的不必要的失误.基础过关1.下列是周期现象的为( ) ①闰年每四年一次;②某交通路口的红绿灯每30秒转换一次; ③某超市每天的营业额; ④某地每年6月份的平均降雨量. A .①②④B .②④C .①②D .①②③解析 ①②是周期现象;③中每天的营业额是随机的,不是周期现象;④中每年6月份的降雨量也是随机的,不是周期现象. 答案 C2.把17化成小数,小数点后第20位是( )A .1B .2C .4D .8解析 17=0.1·42857·,小数点后“142857”呈周期性变化,且周期为 6.∵20=3×6+2,∴第20位为4. 答案 C3.按照规定,奥运会每4年举行一次.2016的夏季奥运会在巴西举办,那么下列年份中不举办夏季奥运会的应该是( ) A .2020 B .2024 C .2026D .2028解析 C 中2026不是4的倍数,选C. 答案 C4.把一批小球按2个红色,5个白色的顺序排列,第30个小球是________色. 解析 周期为7,30=4×7+2,所以第30个小球与第2个小球颜色相同,为红色. 答案 红5.如图所示,变量y与时间t(s)的图像如图所示,则时间t至少隔________ s时y=1会重复出现1次.答案 26.若今天是星期一,则第7天后的那一天是星期几?第120天后的那一天是星期几?(注:今天是第一天)解每星期有7天,从星期一到星期日,呈周期性变化,其周期为7.∴第7天后的那一天是星期一.∵120=17×7+1,∴第120天后的那一天是星期二.7.水车上装有16个盛水槽,每个盛水槽最多盛水10升,假设水车5分钟转一圈,计算1小时内最多盛水多少升?解因为1小时=60分钟=12×5分钟,且水车5分钟转一圈,所以1小时内水车转12圈.又因为水车上装有16个盛水槽,每个盛水槽最多盛水10升,所以每转一圈,最多盛水16×10=160(升,)所以水车1小时内最多盛水160×12=1 920(升).能力提升8.钟表分针的运动是一个周期现象,其周期为60分钟,现在分针恰好指在2点处,则100分钟后分针指在( )A.8点处B.10点处C.11点处D.12点处解析由于100=1×60+40,所以100分钟后分针所指位置与40分钟后分针所指位置相同,现在分针恰好指在2点处,经过40分钟分针应指在10点处,故选B.答案 B9.设钟摆每经过1.8秒回到原来的位置.在图中钟摆达到最高位置A点时开始计时,经过1分钟后,钟摆的大致位置是( )A.点A处B.点B处C.O、A之间D.O、B之间解析 钟摆的周期T =1.8 秒,1分钟=(33×1.8+0.6)秒,又T 4<0.6<T2,所以经过1分钟后,钟摆在O 、B 之间. 答案 D10.今天是星期六,再过100天后是星期________. 解析 100=14×7+2,∴再过100天是星期一. 答案 一11.一个质点,在平衡位置O 点附近振动,如果不考虑阻力,可将此振动看作周期运动,从O 点开始计时,质点向左运动第一次到达M 点用了0.3 s ,又经过0.2 s 第二次通过M 点,则质点第三次通过M 点,还要经过的时间可能是________ s.解析 质点从O 点向左运动,O →M 用了0.3 s ,M →A →M 用了0.2 s ,由于M →O 与O →M 用时相同,因此质点运动半周期T2=0.2+0.3×2=0.8(s),从而当质点第三次经过M 时用时应为M →O →B →O →M ,所用时间为0.3×2+0.8=1.4(s). 答案 1.412.游乐场中的摩天轮匀速旋转,每转一圈需要12分钟,其中心O 距离地面40.5米,半径40米.如果你从最低处登上摩天轮,那么你与地面的距离将随时间的变化而变化,以你登上摩天轮的时刻开始计时,请解答下列问题:(1)你与地面的距离随时间的变化而变化,这个现象是周期现象吗? (2)转四圈需要多少时间?(3)你第四次距地面最高需要多少时间? (4)转60分钟时,你距离地面是多少? 解 (1)是周期现象,周期12分钟/圈. (2)转四圈需要时间为4×12=48(分钟).(3)第1次距离地面最高需122=6(分钟),而周期是12分钟,所以第四次距地面最高需12×3+6=42(分钟).(4)∵60÷12=5,∴转60分钟时你距离地面与开始时刻距离地面相同,即40.5-40=0.5(米).13.(选做题)下面是一个古希腊的哲学家、数学家、天文学家毕达哥拉斯的故事:有一次毕达哥拉斯处罚学生,让他来回数在黛安娜神庙的七根柱子(这七根柱子的标号分别为A,B,C,…,G),如图所示,一直到指出第1 999个数的柱子的标号是哪一个才能够停止.你能帮助这名学生尽快结束这个处罚吗?解通过观察可发现规律:数“2,3,4,…,1 997,1 998,1 999”按标号为“B,C,D,E,F,G,F,E,D,C,B,A”这12个字母循环出现,因此周期是12.先把1去掉,(1 999-1)÷12=166……6,因此第1 999个数的柱子的标号与第167个周期的第6个数的标号相同,故数到第1 999个数的柱子的标号是G.§2角的概念的推广内容要求 1.理解正角、负角、零角与象限角的概念(知识点1 角的概念(1)角的概念:角可以看成平面内一条射线绕着端点O从一个位置OA旋转到另一个位置OB 所形成的图形.点O是角的顶点,射线OA,OB分别是角α的始边和终边.(2)按照角的旋转方向,分为如下三类:(正确的打“√”,错误的打“×”)(1)按逆时针方向旋转所成的角是正角(√)(2)按顺时针方向旋转所成的角是负角(√)(3)没有作任何旋转就没有角对应(×)(4)终边和始边重合的角是零角(×)(5)经过1小时时针转过30°(×)知识点2 象限角如果角的顶点与坐标原点重合,角的始边与x轴的非负半轴重合,那么,角的终边(除端点外)在第几象限,就说这个角是第几象限角.如果角的终边在坐标轴上,就认为这个角不属于任何一个象限.【预习评价】1.锐角属于第几象限角?钝角又属于第几象限角?提示锐角属于第一象限角,钝角属于第二象限角.2.第二象限的角比第一象限的角大吗?提示不一定.如120° 是第二象限的角,390°是第一象限的角,但120°<390°.知识点3 终边相同的角所有与角α终边相同的角,连同角α在内,可构成一个集合S={β|β=α+k·360°,k∈Z},即任何一个与角α终边相同的角,都可以表示成角α与周角的整数倍的和.【预习评价】(正确的打“√”,错误的打“×”)(1)终边相同的角一定相等(×)(2)相等的角终边一定相同(√)(3)终边相同的角有无数多个(√)(4)终边相同的角它们相差180°的整数倍(×)题型一角的概念的推广【例1】写出下图中的角α,β,γ的度数.解要正确识图,确定好旋转的方向和旋转的大小,由角的概念可知α=330°,β=-150°,γ=570°.规律方法 1.理解角的概念的三个“明确”2.表示角时的两个注意点(1)字母表示时:可以用希腊字母α,β等表示,“角α”或“∠α”可以简化为“α”.(2)用图示表示角时:箭头不可以丢掉,因为箭头代表了旋转的方向,也即箭头代表着角的正负.【训练1】(1)图中角α=________,β=________;(2)经过10 min,分针转了________.解析(1)α=-(180°-30°)=-150°β=30°+180°=210°.(2)分针按顺时针过了周角的16,即-60°.答案(1)-150°210°(2)-60°题型二终边相同的角【例2】已知α=-1 910°.(1)把α写成β+k×360°(k∈Z,0°≤β<360°)的形式,并指出它是第几象限角;(2)求θ,使θ与α的终边相同,且-720°≤θ<0°.解(1)-1 910°=250°-6×360°,其中β=250°,从而α=250°+(-6)×360°,它是第三象限角.(2)令θ=250°+k×360°(k∈Z),取k=-1,-2就得到满足-720°≤θ<0°的角,即250°-360°=-110°,250°-720°=-470°.所以θ为-110°,-470°.规律方法将任意角化为α+k·360°(k∈Z,且0°≤α<360°)的形式,关键是确定k.可用观察法(α的绝对值较小时适用),也可用除以360°的方法.要注意:正角除以360°,按通常的除法进行,负角除以360°,商是负数,且余数为正值.【训练2】写出终边在阴影区域内(含边界)的角的集合.解 终边在直线OM 上的角的集合为M ={α|α=45°+k ·360°,k ∈Z }∪{α|α=225°+k ·360°,k ∈Z }={α|α=45°+2k ·180°,k ∈Z }∪{α|α=45°+(2k +1)·180°,k ∈Z } ={α|α=45°+n ·180°,n ∈Z }.同理可得终边在直线ON 上的角的集合为{α|α=60°+n ·180°,n ∈Z }, 所以终边在阴影区域内(含边界)的角的集合为 {α|45°+n ·180°≤α≤60°+n ·180°,n ∈Z }.【探究1】 在四个角-20°,-400°,-2 000°,1 600°中,第四象限角的个数是( ) A .0 B .1 C .2D .3解析 -20°是第四象限角,-400°=-360°-40°与-40°终边相同,是第四象限角,-2 000°=-6×360°+160°与160°终边相同,是第二象限角,1 600°=4×360°+160°与160°终边相同,是第二象限角,故第四象限角有2个. 答案 C【探究2】 写出终边落在第一象限和第二象限内的角的集合.解 根据终边相同的角一定是同一象限的角,又可以先写出第一象限锐角范围和第二象限钝角的范围,再加上360°的整数倍即可. 所以表示为:第一象限角的集合:S ={β|β=k ·360°+α,0°<α<90°,k ∈Z },或S ={β|k ·360°<β<k ·360°+90°,k ∈Z }.第二象限角的集合:S ={β|β=k ·360°+α,90°<α<180°,k ∈Z },或S ={β|k ·360°+90°<β<k ·360°+180°,k ∈Z }.【探究3】 已知α为第二象限角,那么2α,α2分别是第几象限角?解 ∵α是第二象限角,∴90+k ×360°<α<180°+k ×360°,180°+2k ×360°<2α<360°+2k ×360°,k ∈Z .∴2α是第三或第四象限角,或是终边落在y 轴的非正半轴上的角.同理45°+k 2×360°<α2<90°+k2×360°,k ∈Z .当k 为偶数时,不妨令k =2n ,n ∈Z ,则45°+n ×360°<α2<90°+n ×360°,此时,α2为第一象限角;当k 为奇数时,令k =2n +1,n ∈Z ,则225°+n ×360°<α2<270°+n ×360°,此时,α2为第三象限角.∴α2为第一或第三象限角. 【探究4】 已知α为第一象限角,求180°-α2是第几象限角.解 ∵α为第一象限角,∴k ·360°<α<k ·360°+90°,k ∈Z , ∴k ·180°<α2<k ·180°+45°,k ∈Z , ∴-45°-k ·180°<-α2<-k ·180°,k ∈Z ,∴135°-k ·180°<180°-α2<180°-k ·180°,k ∈Z .当k =2n (n ∈Z )时,135°-n ·360°<180°-α2<180°-n ·360°,为第二象限角;当k =2n +1(n ∈Z )时,-45°-n ·360°<180°-α2<-n ·360°,为第四象限角.∴180°-α2是第二或第四象限角.规律方法 1.象限角的判定方法(1)根据图像判定.利用图像实际操作时,依据是终边相同的角的概念,因为0°~360°之间的角与坐标系中的射线可建立一一对应的关系.(2)将角转化到0°~360°范围内,在直角坐标平面内,0°~360°范围内没有两个角终边是相同的.2.α,2α,α2等角的终边位置的确定方法不等式法:(1)利用象限角的概念或已知条件,写出角α的范围. (2)利用不等式的性质,求出2α,α2等角的范围.(3)利用“旋转”的观点,确定角终边的位置.例如,如果得到k ×120°<α3<k ×120°+30°,k ∈Z ,可画出0°<α3<30°所表示的区域,再将此区域依次逆时针或顺时针转动120°(如图所示).易错警示 由α的范围确定2α的范围时易忽视终边在坐标轴上的情况.课堂达标1.-361°的终边落在( ) A .第一象限 B .第二象限 C .第三象限D .第四象限解析 因为-361°的终边和-1°的终边相同,所以它的终边落在第四象限,故选D. 答案 D2.设A ={θ|θ为锐角},B ={θ|θ为小于90°的角},C ={θ|θ为第一象限的角},D ={θ|θ为小于90°的正角},则下列等式中成立的是( ) A .A =B B .B =C C .A =CD .A =D解析 直接根据角的分类进行求解,容易得到答案. 答案 D3.将-885°化为α+k ·360°(0°≤α<360°,k ∈Z )的形式是________________. 答案 195°+(-3)×360°4.与-1 692°终边相同的最大负角是________. 解析 ∵-1 692°=-5×360°+108°, ∴与108°终边相同的最大负角为-252°. 答案 -252°5.如图所示,写出终边落在阴影部分的角的集合.解设终边落在阴影部分的角为α,角α的集合由两部分组成.①{α|k·360°+30°≤α<k·360°+105°,k∈Z}.②{α|k·360°+210°≤α<k·360°+285°,k∈Z}.∴角α的集合应当是集合①与②的并集:{α|k·360°+30°≤α<k·360°+105°,k∈Z}∪{α|k·360°+210°≤α<k·360°+285°,k∈Z}={α|2k·180°+30°≤α<2k·180°+105°,k∈Z}∪{α|(2k+1)180°+30°≤α<(2k+1)180°+105°,k∈Z}={α|2k·180°+30°≤α<2k·180°+105°,或(2k+1)·180°+30°≤α<(2k+1)180°+105°,k∈Z}={α|n·180°+30°≤α<n·180°+105°,n∈Z}.课堂小结1.对角的理解,初中阶段是以“静止”的眼光看,高中阶段应用“运动”的观点下定义,理解这一概念时,要注意“旋转方向”决定角的“正负”,“旋转量”决定角的“绝对值大小”.2.区域角的表示形式并不唯一,如第二象限角的集合,可以表示为{α|90°+k×360°<α<180°+k×360°,k∈Z},也可以表示为{α|-270°+k×360°<α<-180°+k×360°,k∈Z}.基础过关1.下列各组角中,终边相同的是( )A.495°和-495°B.1 350°和90°C.-220°和140°D.540°和-810°解析-220°=-360°+140°,∴-220°与140°终边相同.答案 C2.设A={小于90°的角},B={锐角},C={第一象限角},D={小于90°而不小于0°的角},那么有( )A.B C A B.B A CC.D A∩C) D.C∩D=B解析锐角、0°~90°的角、小于90°的角及第一象限角的范围,如下表所示.答案 D3.若α是第四象限角,则180°-α是( )A.第一象限角B.第二象限角C.第三象限角D.第四象限角解析可以给α赋一特殊值-60°,则180°-α=240°,故180°-α是第三象限角.答案 C4.已知角α=-3 000°,则与角α终边相同的最小正角是______.解析∵-3 000°=-9×360°+240°,∴与-3 000°角终边相同的最小正角为240°.答案240°5.在-180°~360°范围内,与2 000°角终边相同的角是______.解析因为2 000°=200°+5×360°,2 000°=-160°+6×360°,所以在-180°~360°范围内与2 000°角终边相同的角有-160°,200°两个.答案-160°,200°6.在0°~360°范围内,找出与下列各角终边相同的角,并判定它们是第几象限角.(1)-150°;(2)650°;(3)-950°15′.解(1)因为-150°=-360°+210°,所以在0°~360°范围内,与-150°角终边相同的角是210°角,它是第三象限角.(2)因为650°=360°+290°,所以在0°~360°范围内,与650°角终边相同的角是290°角,它是第四象限角.(3)因为-950°15′=-3×360°+129°45′,所以在0°~360°范围内,与-950°15′角终边相同的角是129°45′角,它是第二象限角.7.写出与25°角终边相同的角的集合,并求出该集合中满足不等式-1 080°≤β<-360°的角β.解与25°角终边相同的角的集合为S={β|β=k·360°+25°,k∈Z}.令k=-3,则有β=-3×360°+25°=-1 055°,符合条件;令k=-2,则有β=-2×360°+25°=-695°,符合条件;令k =-1,则有β=-1×360°+25°=-335°,不符合条件. 故符合条件的角有-1 055°,-695°.能力提升8.以下命题正确的是( ) A .第二象限角比第一象限角大B .A ={α|α=k ·180°,k ∈Z },B ={β|β=k ·90°,k ∈Z },则ABC .若k ·360°<α<k ·360°+180°(k ∈Z ),则α为第一或第二象限角D .终边在x 轴上的角可表示为k ·360°(k ∈Z ) 解析 A 不正确,如-210°<30°.在B 中,当k =2n ,k ∈Z 时,β=n ·180°,n ∈Z . ∴AB ,∴B 正确.又C 中,α为第一或第二象限角或在y 轴的非负半轴上, ∴C 不正确.显然D 不正确. 答案 B9.集合M =⎩⎨⎧⎭⎬⎫x |x =k ·180°2±45°,k ∈Z ,P =⎩⎨⎧⎭⎬⎫x |x =k ·180°4±90°,k ∈Z ,则M 、P之间的关系为( ) A .M =P B .M P C .M PD .M ∩P =∅解析 对集合M 来说,x =(2k ±1)·45°,即45°的奇数倍;对集合P 来说,x =(k ±2)·45°,即45°的倍数. 答案 B10.已知角α、β的终边相同,那么α-β的终边在________. 解析 ∵α、β终边相同, ∴α=k ·360°+β(k ∈Z ).∴α-β=k ·360°,故α-β终边会落在x 轴非负半轴上. 答案 x 轴的非负半轴上11.若α为第一象限角,则k ·180°+α(k ∈Z )的终边所在的象限是第________象限. 解析 ∵α是第一象限角,∴k 为偶数时,k ·180°+α终边在第一象限;k 为奇数时,k ·180°+α终边在第三象限. 答案 一或三12.求终边在直线y =x 上的角的集合S .解 因为直线y =x 是第一、三象限的角平分线,在0°~360°之间所对应的两个角分别是45°和225°,所以S ={α|α=k ·360°+45°,k ∈Z }∪{α|α=k ·360°+225°,k∈Z }={α|α=2k ·180°+45°,k ∈Z }∪{α|α=(2k +1)·180°+45°,k ∈Z }={α|α=n ·180°+45°,n ∈Z }.13.(选做题)已知角α、β的终边有下列关系,分别求α、β间的关系式: (1)α、β的终边关于原点对称; (2)α、β的终边关于y 轴对称.解 (1)由于α、β的终边互为反向延长线,故α、β相差180°的奇数倍(如图1),于是α-β=(2k -1)·180°(k ∈Z ).(2)在0°~360°内,设α的终边所表示的角为90°-θ,由于α、β关于y 轴对称(如图2),则β的终边所表示的角为90°+θ.于是α=90°-θ+k 1·360°(k 1∈Z ),β=90°+θ+k 2·360°(k 2∈Z ).两式相加得α+β=(2k +1)·180°(k ∈Z ).§3 弧度制内容要求 1.了解弧度制的意义,能正确地进行弧度与角度的换算,熟记特殊角的弧度数(重点).2.掌握弧度制下的弧长公式,会用弧度解决一些实际问题(难点).知识点1 弧度制 (1)角度制与弧度制的定义(2)如果半径为r 的圆的圆心角α所对弧的长为l ,那么角α的弧度数的绝对值是|α|=lr. 【预习评价】(正确的打“√”,错误的打“×”)(1)“度”与“弧度”是度量角的两种不同的度量单位(√) (2)1°的角是周角的1360,1 rad 的角是周角的12π(√)(3)1°的角比1 rad 的角要大(×)(4)1 rad 的角的大小和所在圆的半径的大小有关(×) 知识点2 角度制与弧度制的换算 常见角度与弧度互化公式如下:请填充完整下表,一些特殊角的角度数与弧度数的对应关系有:设扇形的半径为R ,弧长为l ,α(0<α<2π)为其圆心角,则1.一个扇形的半径为2 cm ,圆心角为π6,则该扇形所对的弧长l =________cm.答案π32.一个扇形的半径为2 cm ,其对应的弧长为2.则该扇形的面积为________cm 2. 答案 2知识点4 利用弧度制表示终边相同的角在弧度制下,与α终边相同的角连同α在内可以表示为2k π+α(k ∈Z ),其中α的单位必须是弧度. 【预习评价】1.与30°终边相同的角为( ) A .2k π+π3(k ∈Z )B .2k π+π6(k ∈Z )C .360°k +π3(k ∈Z )D .2k π+30°(k ∈Z )答案 B2.终边在x 轴上的角的集合用弧度制表示为________. 答案 {α|α=k π,k ∈Z }题型一 角度与弧度的互化【例1】 将下列角度与弧度进行互化: (1)20°;(2)-15°;(3)7π12;(4)-115π.解 (1)20°=20×π180 rad =π9 rad.(2)-15°=-15×π180 rad =-π12 rad.(3)712π rad =712×180°=105°. (4)-115π rad =-115×180°=-396°.规律方法 角度制与弧度制互化的原则、方法以及注意点(1)原则:牢记180°=π rad ,充分利用1°=π180rad 和1 rad =⎝ ⎛⎭⎪⎫180π°进行换算.(2)方法:设一个角的弧度数为α,角度数为n ,则α rad =α·180°;n °=n ·π180rad.(3)注意点:①用“弧度”为单位度量角时,“弧度”二字或“rad”可以省略不写;②用“弧度”为单位度量角时,“常常把弧度数写成多少π的形式,如无特别要求,不必把π写成小数;③度化弧度时,应先将分、秒化成度,再化成弧度. 【训练1】 将下列各角度与弧度互化: (1)512π;(2)-76π;(3)-157°30′. 解 (1)512π=512×180°=75°;(2)-76π=-76×180°=-210°;(3)-157°30′=-157.5°=-157.5×π180rad=-78π rad.题型二 用弧度制表示终边相同的角【例2】 (1)把-1 480°写成α+2k π(k ∈Z )的形式,其中0≤α<2π; (2)若β∈[-4π,0),且β与(1)中α终边相同,求β. 解 (1)∵-1 480°=-74π9=-10π+16π9,0≤16π9<2π,∴-1 480°=16π9-2×5π=16π9+2×(-5)π.(2)∵β与α终边相同,∴β=2k π+16π9,k ∈Z .又∵β∈[-4π,0),∴β1=-2π9,β2=-209π.【训练2】 用弧度制表示终边在图中阴影区域内角的集合(包括边界)并判断 2 015°是不是这个集合的元素.解 因为150°=5π6.所以终边在阴影区域内角的集合为S =⎩⎪⎨⎪⎧⎭⎪⎬⎪⎫β⎪⎪⎪5π6+2k π≤β≤3π2+2k π,k ∈Z . 因为2 015°=215°+5×360°=43π36+10π,又5π6<43π36<3π2.所以2 015°=43π36∈S ,即2 015°是这个集合的元素.方向1 求弧长【例3-1】 已知扇形OAB 的圆心角α为120°,半径长为6.求的长;解 ∵α=120°=23π,r =6,∴的长l =23π×6=4π.方向2 求圆心角【例3-2】 已知扇形周长为10,面积是4,求扇形的圆心角. 解 设圆心角是θ,半径是r , 则⎩⎪⎨⎪⎧2r +r θ=10,12θ·r 2=4⇒⎩⎪⎨⎪⎧r =4,θ=12或⎩⎪⎨⎪⎧r =1,θ=8(舍).故扇形圆心角为12.方向3 求面积的最值【例3-3】 已知一扇形的周长为40 cm ,当它的半径和圆心角取什么值时,才能使扇形的面积最大?最大面积是多少?解 设扇形的圆心角为θ,半径为r ,弧长为l ,面积为S , 则l +2r =40,∴l =40-2r . ∴S =12lr =12×(40-2r )r =20r -r 2=-(r -10)2+100.∴当半径r =10 cm 时,扇形的面积最大,最大值为100 cm 2,此时θ=l r =40-2×1010rad =2 rad.∴当扇形的圆心角为2 rad ,半径为10 cm 时,扇形的面积最大为100 cm 2.规律方法 灵活运用扇形弧长公式、面积公式列方程组求解是解决此类问题的关键,有时运用函数思想、转化思想解决扇形中的有关最值问题,将扇形面积表示为半径的函数,转化为r 的二次函数的最值问题.课堂达标1.与120°角终边相同的角为( ) A .2k π-2π3(k ∈Z )B.11π3C .2k π-10π3(k ∈Z )D .(2k +1)π+2π3(k ∈Z )解析 120°=2π3且2k π-10π3=(2k -4)π+2π3(k ∈Z ),∴120°与2k π-10π3(k ∈Z ),终边相同.答案 C2.-23π12化为角度应为( )A .-345°B .-15°C .-315°D .-375°解析 -23π12=-2312×180°=-345°.答案 A3.已知扇形的半径为12,弧长为18,则扇形圆心角为________.解析 由弧长公式l =αR 得α=l R =1812=32.答案 324.下列结论不正确的是________(只填序号).①π3 rad =60°;②10°=π18 rad ;③36°=π5 rad ;④5π8 rad =115°. 解析5π8 rad =58×180°=112.5°,∴④错. 答案 ④5.一个扇形的面积为1,周长为4,求圆心角的弧度数. 解 设扇形的半径为R ,弧长为l ,则2R +l =4, ∴l =4-2R ,根据扇形面积公式S =12lR ,得1=12(4-2R )·R ,∴R =1,∴l =2,∴α=l R =21=2,即扇形的圆心角为2 rad.课堂小结1.角的概念推广后,在弧度制下,角的集合与实数集R 之间建立起一一对应的关系:每一个角都有唯一的一个实数(即这个角的弧度数)与它对应;反过来,每一个实数也都有唯一的一个角(即弧度数等于这个实数的角)与它对应.2.解答角度与弧度的互化问题的关键在于充分利用“180°=π rad”这一关系式. 3.在弧度制下,扇形的弧长公式及面积公式都得到了简化,具体应用时,要注意角的单位取弧度.基础过关1.在半径为10的圆中,240°的圆心角所对弧长为( )A.403πB.203π C.2003π D.4003π 解析 240°=240×π180 rad =43π rad ,∴弧长l =|α|·r =43π×10=403π,故选A.答案 A2.下列与9π4的终边相同的角的表达式中,正确的是( )A .2k π+45°(k ∈Z )B .k ·360°+9π4(k ∈Z )C .k ·360°-315°(k ∈Z )D .k π+5π4(k ∈Z )答案 C3.若α=-3,则角α的终边在( ) A .第一象限 B .第二象限 C .第三象限D .第四象限解析 ∵-π<-3<-π2,∴-3是第三象限角.答案 C4.若三角形三内角之比为4∶5∶6,则最大内角的弧度数是____________. 答案 25π5.如果一扇形的弧长变为原来的32倍,半径变为原来的一半,则该扇形的面积为原扇形面积的________.解析 由于S =12lR ,若l ′=32l ,R ′=12R ,则S ′=12l ′R ′=12×32l ×12R =34S .答案 346.把下列各角化为2k π+α(0≤α<2π,k ∈Z ) 的形式且指出它是第几象限角,并写出与它终边相同的角的集合.(1)-46π3;(2)-1 485°;(3)-20.解 (1)-46π3=-8×2π+2π3,它是第二象限角,终边相同的角的集合为。
北师大版四年级数学下册课本答案(可打印)

北师大版四年级数学下册课本习题答案(全)第1章小数的意义和加减法课本第3页练一练1、(说一说略)2、(1)7/10 0.7 47/100 0.47(2)61/1000 0.0613、略4、略第5页练一练1、略2、 1.600 2.1 0.1133、略4、 0.52 5 6 5.67 1 3 55、 18分钟第7-8页练一练1、(1)4 25 (2)4 一 4 0.012、10/100(或1/10) 60/100(或6/10)3、略4、5、1/10 0.7 0.3 9/10 1.7 2.8 0.03 6/100 0.3和0.7更接近0.5,1.7更接近2.6、(竖排)1 10 100 0.1 1 10 0.01 0.1 1(发现略)第10页练一练1、(涂一涂及交流略)出生时,淘气更高;其思更高。
< >2、< < < > < <3、(1)90.97 (2)30.974、略第12页练一练1、(1)略(2)25.2+21.6=46.8(元)2、(补图略)3.16+0.23=3.39(米)3.39-0.12=3.27(米)3、5 0.7 0.09 7 0.084、2 3.8 5.33 13.1 23.5 22.55、1.45+0.4=1.85(米) 1.85-0.05=1.8(米)6、分析:先求出半箱苹果的质量,然后求出一箱苹果的质量,最后求出箱子的质量。
解答:46.6-24.3=22.3(千克)苹果的质量:22.3+22.3=44.6(千克)箱子的质量:46.6-44.6=2(千克)第14-15页练一练1、(画一画略)(1)2.5-1.5=1(元)(2)1.5+0.5=2(元)2、10.2 4.8 7.63、(1)13.71-12.8=0.91(米)(2)13.71-0.24=13.47(米)4、5、(竖式略)6.06 18.37 4.26 1.25 16.64 3.646、8.10和15.00中的“0”都可以去掉;30.070和0.090的最后一个“0”可以去掉,其他的“0”不能去掉。
北师大版四年级数学暑假作业答案解析

北师大版四年级数学暑假作业答案解析为进一步提高孩子的学习能力,在暑假期间,您可以根据实际,让孩子在完成必做作业的基础上,去做相应的选做作业。
以下就是为大家分享的四年级数学暑假作业答案,希望对大家有帮助。
暑假作业一看谁算得又对又快。
(每题1分,共15分)450+360=810 720-390=330 423-299=124800×125=100000 300÷15=20 547+398=945850÷10=85 960÷60=16 990÷90=1116×50=800 58×5×2=580 921-123-77=721(37+43)÷40=2 720÷8÷9=10 24-24÷24+24=47二、判断题,对的打“√”、错的打“×”。
(每题1分,共7分)1.三万是三百个一百。
( √ )2.钝角大于90度。
( × )3.在同一平面内,两条直线如果不互相垂直,那么一定互相平行。
( × )4.学校操场占地面积是48000平方分米。
( × )暑假作业二一、看谁算得又对又快。
(每题1分,共15分)3250÷5=650 100-74.5=25.5 5.84+3.7=9.548×32×125=32019 4×17+8=76 5×55×2=550120÷40=3 20×47=940 125+75÷5=140490-90×2=310 660÷60=11 180-80÷20=176170+230=400 930÷30=31 60÷15+15=19暑假作业四一、看谁算得又对又快。
(每题1分,共12分)870-780=90 40×13=520 104÷13=854×99+54=5400 30×30=900 14×100=1400240÷15÷4=4 129+318+71=518 2×73×5=730700-300÷25=688 25+75÷75+25=51 40×200=8000二、填空题。
2020-2021学年新教材数学北师大版必修第一册课时分层作业4 全集与补集 Word版含解析

课时分层作业(四)全集与补集(建议用时:40分钟)一、选择题1.设U=R,A={x|x>0},B={x|x>1},则A∩(∁U B)=() A.{x|0≤x〈1} B.{x|0〈x≤1}C.{x|x〈0}D.{x|x〉1}B[∁U B={x|x≤1},∴A∩(∁U B)={x|0<x≤1}.]2.如图所示,U是全集,A,B是U的子集,则阴影部分所表示的集合是()A.A∩(∁U B)B.B∩(∁U A)C.∁U(A∩B)D.∁U(A∪B)B[阴影部分表示A以外的部分与B的交集,故阴影部分表示的集合为B∩(∁U A).故选B。
]3.设集合A={x∈N*|x≤6},B={2,4},则∁A B等于( ) A.{2,4} B.{0,1,3,5}C.{1,3,5,6} D.{x∈N*|x≤6}C[因为A={x∈N*|x≤6}={1,2,3,4,5,6},B={2,4},所以∁A B={1,3,5,6}.故选C.]4.设I为全集,S1、S2、S3是I的三个非空子集且S1∪S2∪S3=I,则下面论断不正确的是( )A.∁I S1∩(S2∪S3)=∅B.S1⊆(∁I S2∩∁1S3)C.∁I S1∩∁I S2∩∁I S3=∅D.S1⊆(∁I S2∪∁I S3)A[∁I S1∩(S2∪S3)=∁I S1∩∁I S1=∁I S1≠∅,故A错.]5.已知集合A={x|x〈a},B={x|1<x<2},且A∪(∁R B)=R,则实数a的取值范围是( )A.{a|a≤1} B.{a|a<1}C.{a|a≥2} D.{a|a〉2}C[∁R B={x|x≤1或x≥2},如图所示.∵A∪(∁R B)=R,∴a≥2.]二、填空题6.已知全集U={0,1,2,3,4},集合A={1,2,3},B={2,4},则(∁U A)∪B为________.{0,2,4}[∵∁U A={0,4},∴(∁U A)∪B={0,2,4}.]7.已知全集U={x|1≤x≤5},A={x|1≤x<a},若∁U A={x|2≤x≤5},则a=________.2[∵A∪(∁U A)=U,∴A={x|1≤x〈2}.∴a=2.]8.设U={0,1,2,3},A={x∈U|x2+mx=0},若∁U A={1,2},则实数m=________.-3[∵∁U A={1,2},∴A={0,3},∴9+3m=0,∴m=-3。
北师大版八年级数学暑假作业(四)及答案

初中八年级数学(北师大版)暑假作业(四)乐洋洋给我们送来了一组题目,(总共是30枚会标)赶快去收集吧。
1.2x+ 2y; 2 (x+y).2. 分解因式:x (x-2).3. 分解因式:=(a+2b)(a-2b).4. 分解因式:=(x-3)2.5、当时,=。
(答案写成真分数形式)不跟小马虎做朋友!二.基础训练之选择题:同学们,我是阿祥上面乐洋洋的题答的怎么样了?我可遇到难题了,老师给我出了一些选择题,我没达到老师的要求,没能收集到会标,全靠你们了(总共是30枚会标)。
1. 下列从左到右的变形是因式分解的是( D )A. B.C. D.2. 多项式各项的公因式是( C)A. B. C. D.3. 下列各式分解因式错误的是( D )A. B.C. D.4. 下列各多项式中能用提公因式法分解因式的是( A )A. B. C. D.5. 计算的结果为( C )A. B. C. D.好好想想再回答哦!三、能力训练阿和气喘嘘嘘得跑过来对大家说:“快点,亚运组委会招记分员和算分员呢,我们去看看吧。
”到那一看原来他们是有条件的,得答对下面的题,你能行吗?(总共是30枚会标)1.分解因式:(1)=2m (m-2n);(2)=-4xy (x2y+2);(3)=(a+b -2 )2。
2、利用分解因式进行计算:=76。
3.、小颖放假买了一个弹簧秤,说明书上这样写道:弹簧不挂物体时长10cm,挂上物体后会伸长,伸长的长度与所挂物体的质量成正比例,若挂上3kg物体后,弹簧总长是11.5cm,此弹簧总长最多为12.5cm.你能用所学数学知识帮小颖求出:所挂物体不得超过 2.5千克。
(答案写成小数形式)四、能力提升阿如发现下面这道题很难解答,你来帮她看看,应该怎么解答呢?(总共是10枚会标)小宝和爸爸、妈妈三人在公园玩跷跷板,爸爸体重80千克,坐在跷跷板的一端,妈妈的体重是小宝体重的3倍,与小宝同坐在另一端,这时,爸爸的一端着地,后来,小宝找来一块重为8千克的石头,加在他和妈妈坐的一端,结果,小宝一端下沉着地,猜猜小宝的体重为19千克(结果取整数)为你出色表现歌唱!同学们,我们一起努力把数学学好哦!。
北师大版五年级下册数学第七单元测试卷合集(4份)(有答案)

周测培优卷11用方程解决问题的能力检测卷一、我会填。
(每题3分,共18分)1.当a=0.4时,a×a=();当a=54时,3a=()。
2.甲数是x,乙数是甲数的3倍,乙、甲两数的和是(),乙、甲两数的差是()。
3.学校有老师x人,学生人数是老师的20倍,20x表示(),20x+x表示()。
4.圈圈和萌萌两家相距1540 m,两人相约同时从家出发相向而行。
圈圈每分走75 m,萌萌每分走65 m,她俩走()分后相遇。
5.聪聪过年收到压岁钱400元,明明收到的压岁钱比聪聪的2倍少100元,明明收到压岁钱()元。
6.希望村今年植树48棵,比去年的3倍少9棵,去年植树()棵。
二、我会辨。
(对的在括号里画“√”,错的画“×”。
每题2分,共6分) 1.5m+2m=10m() 2.4x-3x=x×x() 3.一个数比a的2倍多2.5,这个数是a÷2+2.5。
()三、我会选。
(把正确答案的序号填在括号里。
每题2分,共6分) 1.两列火车从两个车站同时出发,相向而行。
甲车每时行48 km,乙车每时行78 km,经过2.5时后两车相遇,两个车站之间的距离是()km。
A.75B.3150C.3152.王大爷用21.6 m的栅栏围了一个长方形鸡舍,如果鸡舍的长是6 m,宽是x m,根据题意可列方程为()。
A.6+x=21.6 B.x=21.6÷2+6 C.(6+x)×2=21.63.一场足球赛主队的球迷人数是客队球迷人数的7.5倍,客队的球迷比主队少39780人,客队有球迷()人。
A.6120 B.5304 C.4680四、计算挑战。
(共16分)1.直接写出结果。
(每题1分,共4分)3.4a-a=a-0.3a=15b-4.7b= 6.7t-t=2.解方程。
(每题3分,共12分)3x+5x=16 3.2x-9.8=9.4 12y-2y=3.5 24+6x=84五、看图列方程并解答。
2020-2021学年北师大版数学必修4课时作业:第一章 三角函数 单元质量评估2

第一章单元质量评估(二)时间:120分钟 满分:150分一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合要求的)1.已知角x 的终边上一点坐标为(sin 5π6,cos 5π6),则tan x 的值为( B ) A. 3 B .- 3 C.33D .-33解析:∵sin 5π6=sin(π-π6)=sin π6=12,cos 5π6=cos(π-π6)=-cos π6=-32,∴角x 的终边经过点(12,-32),根据正切函数的定义可知tan x =- 3. 2.在下列给出的函数中,以π为周期且在⎝ ⎛⎭⎪⎫0,π2内是增函数的是( D )A .y =sin x2 B .y =cos2x C .y =sin ⎝ ⎛⎭⎪⎫2x +π4 D .y =tan ⎝ ⎛⎭⎪⎫x -π4 解析:由函数周期为π可排除 A.x ∈⎝ ⎛⎭⎪⎫0,π2时,2x ∈(0,π),2x +π4∈⎝ ⎛⎭⎪⎫π4,54π,此时B 、C 中函数均不是增函数.故选D. 3.为了得到函数y =sin(2x -π3)的图像,只需把函数y =sin2x 的图像上所有的点( D )A .向左平行移动π3个单位长度B .向右平行移动π3个单位长度 C .向左平行移动π6个单位长度 D .向右平行移动π6个单位长度 解析:由题意,为了得到函数y =sin(2x -π3)=sin[2(x -π6)]的图像,只需把函数y =sin2x 的图像上所有的点向右平行移动π6个单位长度.4.若函数y =2cos(2x +φ)是奇函数,且在⎝⎛⎭⎪⎫0,π4上是增函数,则实数φ可能是( A )A .-π2B .0 C.π2 D .π解析:∵函数y =2cos(2x +φ)是奇函数,∴φ=k π+π2,k ∈Z , 又∵函数y =2cos(2x +φ)在⎝ ⎛⎭⎪⎫0,π4上是增函数,∴取⎝ ⎛⎭⎪⎫φ,π2+φ⊆[-π,0],可得φ=-π2,故应选A.5.已知ω>0,|φ|<π2,函数f (x )=sin(ωx +φ)的部分图像如图所示,为了得到函数g (x )=sin ωx 的图像,只要将f (x )的图像( B )A .向右平移π4个单位长度 B .向右平移π8个单位长度 C .向左平移π4个单位长度D .向左平移π8个单位长度解析:由图像知函数f (x )的周期T =4⎝ ⎛⎭⎪⎫5π8-3π8=π,所以2πω=π(ω>0),解得ω=2.因为函数f (x )过点⎝ ⎛⎭⎪⎫5π8,-1,所以sin ⎝ ⎛⎭⎪⎫2×5π8+φ=-1.因为|φ|<π2,所以φ=π4,即函数f (x )=sin ⎝ ⎛⎭⎪⎫2x +π4.要得到函数g (x )=sin2x ,只需将函数f (x )的图像向右平移π8个单位长度.故选B.6.设x 1,x 2为函数f (x )=sin(ωx -π6)(ω>0)的两个零点,且|x 2-x 1|的最小值为1,则ω=( A )A .πB.π2C.π3 D .π4解析:设函数f (x )的最小正周期为T ,则由题意得T2=1,解得T =2,∴2πω=2,解得ω=π.7.若函数f (x )=2cos ωx 在区间[0,2π3]上递减,且有最小值1,则ω的值可以是( B )A .2 B.12 C .3D .13解析:因为函数f (x )=2cos ωx 在区间[0,2π3]上递减,且有最小值1,所以f (2π3)=1,即2cos 2π3ω=1,cos 2π3ω=12,逐一检验各选项只有B 符合.8.若sin α-2cos α=5,则tan α=( C ) A.12 B .2 C .-12D .-2解析:∵sin α-2cos α=5,∴sin α>2cos α且sin 2α+4cos 2α-4sin αcos α=5,即得sin 2α+4cos 2α-4sin αcos αsin 2α+cos 2α=5,∴tan 2α-4tan α+4tan 2α+1=5,整理可得4tan 2α+4tan α+1=0,解得tan α=-12,故应选C.9.定义新运算“*”:a *b =⎩⎪⎨⎪⎧a (a ≤b ),b (a >b ),例如1]( A )A .[-1,22] B .[0,22] C .[-1,2]D .[-22,22]解析:由题意知f (x )=⎩⎪⎨⎪⎧sin x (sin x ≤cos x ),cos x (sin x >cos x ),画出函数在一个周期上的图像如图,可知A 正确.10.定义在R 上的函数f (x )满足f (x )=f (x +2),当x ∈[1,3]时,f (x )=2-|x -2|,则( B )A .f ⎝ ⎛⎭⎪⎫sin π3>f ⎝ ⎛⎭⎪⎫sin π6B .f ⎝ ⎛⎭⎪⎫sin 2π3<f ⎝ ⎛⎭⎪⎫cos 2π3C .f ⎝ ⎛⎭⎪⎫cos π3<f ⎝ ⎛⎭⎪⎫cos π4 D .f ⎝ ⎛⎭⎪⎫tan π6<f ⎝ ⎛⎭⎪⎫tan π4解析:x ∈[-1,1]时,x +2∈[1,3],f (x )=f (x +2)=2-|x |,所以f (x )在(0,1)上为减函数.由1>sin π3>sin π6>0知f ⎝ ⎛⎭⎪⎫sin π3<f ⎝ ⎛⎭⎪⎫sin π6,0<cos π3<cos π4<1,所以f ⎝ ⎛⎭⎪⎫cos π3>f ⎝ ⎛⎭⎪⎫cos π4,0<tan π6<tan π4=1,所以f ⎝ ⎛⎭⎪⎫tan π6>f ⎝ ⎛⎭⎪⎫tan π4.由于f ⎝ ⎛⎭⎪⎫32<f ⎝ ⎛⎭⎪⎫12 =f ⎝ ⎛⎭⎪⎫-12,所以f ⎝ ⎛⎭⎪⎫sin 2π3<f ⎝ ⎛⎭⎪⎫cos 2π3.故选B. 二、填空题(本大题共5小题,每小题5分,共25分,请把答案填写在题中横线上)11.函数y =1-cos x2sin x -1+log 2(2cos x +2)的定义域是⎝⎛⎭⎪⎫2k π+π6,2k π+3π4(k ∈Z ).解析:由⎩⎪⎨⎪⎧1-cos x 2sin x -1≥0,2cos x +2>0,解得2k π+π6<x <2k π+3π4,k ∈Z ,所以函数的定义域为⎝ ⎛⎭⎪⎫2k π+π6,2k π+3π4(k ∈Z ).12.设f (n )=sin n π6,则f (1)+f (2)+…+f (12)=0.解析:利用对称性,当n 从1取到12时,f (1)+f (2)+…+f (12)=0. 13.函数f (x )=-2tan x +m ,x ∈[-π4,π3]有零点,则实数m 的取值范围是[-2,23].解析:函数f (x )=-2tan x +m 有零点,即方程2tan x =m 有解.∵x ∈[-π4,π3],∴tan x ∈[-1,3],∴m ∈[-2,23].14.函数y =sin π3x 在区间[0,n ]上至少取得2个最大值,则正整数n 的最小值是8.解析:y =sin π3x 的周期T =2ππ3=6.在区间[0,n ]上至少取得2个最大值,说明在该区间上至少有54个周期,其区间长度为6×54=152,所以n ≥152,故正整数n 的最小值是8.15.给出下列命题:①函数y =cos ⎝⎛⎭⎪⎫23x +π2是奇函数;②存在实数α,使得2sin ⎝ ⎛⎭⎪⎫α+π4=32;③若α,β是第一象限角且α<β,则tan α<tan β;④x =π8是函数y =sin ⎝⎛⎭⎪⎫2x +5π4的一条对称轴方程;⑤函数y =sin ⎝⎛⎭⎪⎫2x +π3的图像关于点⎝ ⎛⎭⎪⎫π12,0成中心对称.把你认为正确的命题的序号都填在横线上①④.解析:对于①,y =cos ⎝ ⎛⎭⎪⎫23x +π2=-sin 23x ,故①正确,显然②③错误;对于④,x =π8时,y =sin ⎝⎛⎭⎪⎫2×π8+5π4=-1,故④正确;对于⑤,令2x +π3=k π,k ∈Z ,得x =-π6+k π2,k ∈Z ,显然⑤不正确. 三、解答题(本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤)16.(本小题12分)(1)已知扇形的面积为24π,弧长为8π,求该扇形的圆心角(用弧度制表示);(2)在平面直角坐标系中,角α的终边在直线3x +4y =0上,求sin α,cos α,tan α的值.解:(1)设扇形的半径为r ,圆心角为α弧度.由已知有,⎩⎨⎧12αr 2=24π,αr =8π,解得r =6,α=4π3.(2)①当α的终边在第二象限时,取终边上的点P (-4,3),|OP |=5,sin α=35,cos α=-45,tan α=-34.②当α的终边在第四象限时,取终边上的点P (4,-3),|OP |=5,sin α=-35,cos α=45,tan α=-34.17.(本小题12分)已知函数f (x )=2a sin(2x -π3)+b 的定义域为[0,π2],最大值为1,最小值为-5,求a 和b 的值.解:∵0≤x ≤π2,∴-π3≤2x -π3≤23π,∴-32≤sin(2x -π3)≤1,易知a ≠0. 当a >0时,f (x )max =2a +b =1,f (x )min =-3a +b =-5.由⎩⎪⎨⎪⎧ 2a +b =1,-3a +b =-5,解得⎩⎪⎨⎪⎧a =12-63,b =-23+12 3.当a <0时,f (x )max =-3a +b =1,f (x )min =2a +b =-5.由⎩⎪⎨⎪⎧ -3a +b =1,2a +b =-5,解得⎩⎪⎨⎪⎧a =-12+63,b =19-12 3.18.(本小题12分)已知函数f (x )=3sin ⎝ ⎛⎭⎪⎫ωx +π4(ω>0,x ∈R )的最小正周期为2π3.(1)求f (x )的解析式;(2)已知f ⎝ ⎛⎭⎪⎫23α+π12=-322,0<α<π2,求角α的大小.解:(1)∵函数f (x )=3sin(ωx +π4)的最小正周期为2π3,∴ω=3.∴f (x )=3sin ⎝ ⎛⎭⎪⎫3x +π4. (2)∵f ⎝ ⎛⎭⎪⎫23α+π12=-322,则由(1)知3sin ⎣⎢⎡⎦⎥⎤3⎝ ⎛⎭⎪⎫23α+π12+π4=3sin ⎝ ⎛⎭⎪⎫2α+π2=3cos2α=-322,∴cos2α=-22,又∵0<α<π2,∴0<2α<π,∴2α=34π.∴α=38π.19.(本小题12分)已知函数f (x )=A sin(ωx +φ)(A >0,ω>0,|φ|<π2)的部分图像如图所示.(1)试确定f (x )的解析式;(2)若f (α2π)=12,求cos(2π3+α2)的值.解:(1)由题图可知A =2,T 4=56-13=12,则T =2,ω=2πT =π. 将点(13,2)代入f (x )=2sin(πx +φ),得sin(π3+φ)=1,又|φ|<π2,所以φ=π6.故f (x )的解析式为f (x )=2sin(πx +π6)(x ∈R ).(2)因为f (α2π)=12,即2sin(α2+π6)=12,即sin(α2+π6)=14,所以cos(2π3+α2)=cos(π2+π6+α2)=-sin(π6+α2)=-14.20.(本小题13分)如果关于x 的方程sin 2x -(2+a )·sin x +2a =0在x∈⎣⎢⎡⎦⎥⎤-π6,5π6上有两个实数根,求实数a 的取值范围. 解:sin 2x -(2+a )sin x +2a =0,即(sin x -2)(sin x -a )=0.∵sin x -2≠0,∴sin x =a ,即求在x ∈⎣⎢⎡⎦⎥⎤-π6,5π6上sin x =a 有两根时a 的范围.由y =sin x ,x ∈⎣⎢⎡⎦⎥⎤-π6,5π6与y =a 的图像知12≤a <1.故实数a 的取值范围是⎣⎢⎡⎭⎪⎫12,1. 21.(本小题14分)已知函数f (x )=2cos(2x -π4),x ∈R . (1)求函数f (x )的最小正周期和单调递增区间;(2)求函数f (x )在区间[-π8,π2]上的最小值和最大值,并求出取得最值时自变量x 的值.解:(1)因为f (x )=2cos(2x -π4),所以函数f (x )的最小正周期为T =2π2=π.由-π+2k π≤2x -π4≤2k π(k ∈Z ),得-3π8+k π≤x ≤π8+k π(k ∈Z ),故函数f (x )的单调递增区间为[-3π8+k π,π8+k π](k ∈Z ).(2)因为f (x )=2cos(2x -π4)在区间[-π8,π8]上为增函数,在区间[π8,π2]上为减函数,又f (-π8)=0,f (π8)=2,f (π2)=2cos(π-π4)=-2cos π4=-1,故函数f (x )在区间[-π8,π2]上的最大值为2,此时x =π8;最小值为-1,此时x =π2.。
北师大版高中英语选择性必修第四册课时分层作业4含答案

课时分层作业(四)Ⅰ.单词拼写1.He recalled(回想) that she always came home late on Wednesdays.2.There is a limit to what one person can tolerate(容忍).3.We had to take out a second bond on the property(房产).4.The details of today's flights are displayed on the monitor(显示器).5.Landslides have cut off many villages in remote(偏远的) areas.6.The old woman ceased(停止) breathing the night before.7.I'd like to make a complaint(投诉) about the noise.8.The government will not negotiate(谈判) with terrorists.9.I called the station to inquire(询问) about train times.10.We are trying to detect(发现) and understand how the climates change.Ⅱ.阅读理解AFor several months,Cara has been working up the courage to approach her mom about what she saw on Instagram.Not long ago,the 11yearold girl,like all the other kids in this story,discovered that her mom had been posting her photos for much of her life.“I've wanted to bring it up.It's strange to see myself up there,and sometimes there are pictures I don't like of myself,”she said.Like most other modern kids,Cara grew up immersed(沉迷……之中) in social mediA.While many kids may not yet have accounts themselves,their parents,schools,sports teams,and organizations have been organizing an online presence for them since birth.The shock of realizing that details about your life have been shared online without your permission or knowledge has become an important experience in the lives of many teenagers.Recently a parenting blogger(博主) wrote in a Washington Post essay(散文) that despite(不顾) her 14-year-old daughter's horror at discovering that her mother had shared years of highly personal stories and information about her online,she simply could not stop posting on her blog and social mediA.The writer said that promising her daughter that she would stop posting herpublicly on the Internet would mean shutting down a vital part of herself,which isn't necessarily good for herself or her daughter.But it's not just crazy mommy bloggers who construct a child's online identity;plenty of average parents do the same.There's even a special word for it:sharenting.Almost a quarter of children begin their digital lives when parents upload their photos to the Internet,according to a study conducted by the Internetsecurity firm A VG.The study also found that 92 percent of kids under the age of 2 already have their own unique digital identity.【语篇解读】文章讲述了一些父母热衷于在互联网上发布自己孩子的照片以及文章,这让孩子们感到很烦恼。
四年级数学北师大版练习册答案

四年级数学北师大版练习册答案巻诸答案占构提§示一銀數的认识和加祓法1 •龙針的它丈儿盍①*筠° J 3 4 54. (DV CZ)V (3>X U)XS T(2>o.ua 0.D5 业(KJ Q. 12 fr.16£⑴他咔倍M仇M K即即・N3tnet 517 I.OQ& <»)«.772 W>0. U <niK_C3■k tl) X m〉X IJIX uj5 X49 3.S 5,?[JI 仇G8 &G氐⑴如耐占K2>1£^L i C灵叭真趴& &Cr v1 «2,333I, (t K (Di) (3>H (4>A克工」:.「叽心、5.如m MM. ・u」:2U)3Tfi.< 5. ^.0 -T ft < 5^2 乱於千魁轧主小拆直t監启 4加山护1歸■対觇09 mOQ乱。
k小空化”他3#4魁牺小■上H 2 li 2茁3S,(DDtR, n+ZI*7h■掘.邛(夢、1«, 13严£3—7 r<»6 X- I 一比川米*丙祷*旨十匸鬥-区承』3・】+鼻羽一企阳賊5. ■体看J. (1)0.03 2.54 0.405 3 0.78 0.009(UJ II. GOO 4.700 0.085 0.080 100. )004. (1>®28. 75+fl. 35-35.10(元》®50-3S. 10-14.90(X) (2*72.4-17.$(•!-)(3>12.S-fa. 79 X 81(千来》12.8+3.81 16. L1Q 千来> 6歌手次赛4. (1)41. 36+7. 36 3. 12-45. 60(儿) ⑵1W+0.話=2・S2(千木》千*(3>0. SG^O. 60+0・父0 — 2. 元b 4.95 4-1. 95 — 9・9"元》13.80+2.40+9.90- 26. IO(jt) 2«. 10<30 吗吗常30 JL^r.二认识田形】•圈形分矣千庁蚁沟形悅方形止方形 2)盘定卷定2. (I和® ②和⑤⑨和⑧2•三角老分矣分析.丰题所血的两边枚有描明建族还是怔力•所以决分情况讨论.(1) 当6为震反川为JK力时•二为8+6千3—20・(2) 当目为理匕(5为屁边吋•二角形的凭兴为84-43-6-223. 祥农与发现(-)Sft® 和2,⑴(1卅一肘》一2 =材Z>X18Q-4•榇姦与衣理(二)三角形边的呆务】•门■人T 小十以“ “《3,迪侑等腰< 1>»0 等5?2. (1> A O 人<3>C3. (Zem Zem Sem) (Z<m 3em 4cm) (3cm 3em 4en94H”傀曲7犷不»S.因为二危彤仃方两边之和人于饰=垃•这样走饶路了.5•四边彩分类2. (DA (2)B、・ 8 + 0+1:*4 + 44-3-30(EX>数图龙中的学问1. U>6 《2)6 L0 6 (3)6 5y 35三小數乘決1. 文具店2. (1 巾• 6X I ^)L5X5 ⑶30.2X33・ 4.4 8.44. (IU.«X5=24.( x) (2>3.4XI0—&4(无)50—34-I6C%)2•小散点鹰姦6. (1>1 吨1000 T 充0. 15Z1000 150( TX) (2>13 + 100-0. 13(T Jt> I4-1000 t A0. 13X1000-130(千克)7. (1)213 (2)1500^-10X0. 3 30(吨》3 •街心广圾3. (DA (2)G (a)A6. < > — > =7. <1)21X0. 9-<18. 9> 321 X0f 9~<28». 9> 1321 X 3.9~9) CS432IJXO. 0-& (654X21)X(0. 9)F&l磁H(Z)3.rx3-(114 1) X 7X6~(22a2> 3,7XO)~33.3 X?X(I2>-U.4(3.7>X<l$X-55.54倒黑2. = > < == <5. (1>Z.4XX.5~«(X> W-6-仁元、(Z>3.95X7-Z7 7Z(儿)(3H8.3XZ.1-3&. 06(»fe> 39. W+lB.6-57. 6机吨)5具行用慢的骗乳动物J ・(D5.07XC-XU2 (2)7.»X0.30-1&3(3)G.56X30-328S. (0550X1.8-630<ft)(2>i.5xa.fi 17.1( T7r*> 17.1XW 6B 血元)(3>® 1.2X30+2. 5X20-afi(儿》 ^100 <4”4+46・{00(千*注・打 100X4・3・430(•千米》6. 学竝手1. (IX 12.5X0. «)X0. 66 (2)( 1.2+0.8)X2. 5(3>( W+DXQ.45 (4X0. 25XUKCG. 125X31,• < 1 >3.98X3X30~3»8.Z(H> (ZX5S-bl3)X3. 25~325<元》 •肃XP5+ Z. 5X|5-fi^.5</t> 106 W.5-1? 5(/t>整理场复习(一)L(1>8L8 0.8L6 <2)407.3 100 100(3(D 玄彌② 饨危Q 蛻介 ")4、=6、7』、仏10都目以2. (D/2 (110>度 /3 (70)® Zt C110)ff (2>1.33 吨>1•號吨 >0. 75 盹 >0. 3F : <>35 千克^(1>G (2»R(1) 0.37X2 I 0.08X2 I 0.55 1. 46(米》(2) X5X2C 50«20(x>四现赛枷体1. 节日礼辂1. M I 2 22•茨安门广场1. (0小大 (2)大小2. ③①②4 ?比即久农•紙孚•曲%盘「门a.2. (1>—相雋<3)0.8 (5)2.55. : 6 3・7«元)17. 5 ; 5 3. 5(元》X7-J.5-0.Z<元〉咎.小军买伯出■實0.Z元.<Z>Z1.7 -21700 * 21700+50-434(*)^:略」6. <1>Z1.3 A; (2)0. 9 7L <3>2. 5 T 克仇门22.參现K鞭馆i. (2>$.$ ^.02 «3冲0 Ct)iXO.D-Lfe 】・8*2-0・9 (5>3.3«,5 放跆 1.d/5 33. <5X (DA (2) A <3)4$• <5>t4+(M+O-1. 7血元〉仇的+一・8机动 1.7S<l.oi答;走家塑血的牛笳便宜'施谁打电话的时何长1(1^ 80 <2>1.2 $7.2 i.;i,7 $e.2 応<3》大十•小十⑷ 15*3 «5 净大伽<e>$ 0,2X <DR (2》人(3>R <4>C4. (I>7 C<)X (4>V CJ>)V5. (I>a.C4X24-1. 2-14.昇千绎■略. <2)27. 36 A7. 2-9.8〈分忡》耳肚亠0・7・2饥分甘)样;略。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
学前卫生学答案1、一氧化碳中毒,中毒者的皮肤、粘膜可呈现__C.鲜艳的红色_________2、斜视可导致___A.弱视3、在以下食物中,含铁最多的是__A.猪肝4、骨折现象急救的原则是____A.固定____。
5、中枢神经系统,包括脑和__C.脊髓______。
6、以下几种退热方法中,属于物理降温的方法是_A.头部冷敷_________。
7、预防结核病的疫苗叫__C.卡介苗________。
8、八块腕骨,全部钙化,大约在__C.10岁左右______。
9、新生儿期是指从出生至__A.28天_______。
10、胡萝卜素在人体内可转变成C.维生素A。
11乳牙一般于2岁半出齐,共A.20_______颗。
12三大产热营养素为蛋白质、脂类和__B碳水化合物_________。
13、构成甲状腺素的原料是_B碘________。
14、前囟晚闭是指__B.前囟在1岁半尚未闭合。
________。
15、钩虫对患儿的最大危害,是使患儿___C贫血________。
1、什么是“婴儿扶触”?答:用双手对婴儿的皮肤进行有顺序、有手法技巧的扶触来达到保健的目的。
2.哪些因素可以影响人体对钙的吸收利用?答:维生素D可促进钙的吸收。
乳糖和氨基酸也可以促进钙的吸收。
植酸和草酸可与钙形成不溶解的钙盐,不利于钙的吸收。
对肥胖儿进行饮食管理的基本原则:①不宜使体重骤然减轻,最初,只要求制止体重速增,以后可使体重逐渐下降,至仅超过该年龄正常体重的10%左右时,即可不必严格限制食物,但仍需控制食量。
②在饮食管理期间,仍需照顾小儿的基本营养需要,蛋白质供给量不宜少于1~2克/公斤/日。
维生素及无机盐的供给量应充分。
为减少总热能摄入量,应限制脂肪。
③设法满足小儿食欲,不致因饥饿而感到痛苦,可补充体积大而供热能少的食物,如萝卜、芹菜等。
根据以上要求,食物应以蔬菜、水果、粮食为主,加适量的瘦肉、鱼、鸡蛋、豆类等。
④饮食管理须长期坚持才能获得满意的效果。
对幼儿进行安全教育的重点是什么?儿童可能生活在没有任何危险的世界中,经常对儿童进行安全教育,并非让他们整日提心吊胆,而是使他们逐渐积累生活经验,懂得危险,注意安全。
重点为:、1、遵守幼儿园的安全制度。
教育儿童不得随便离开自己的班级,有事必须得到老师的允许离开。
遵守规则,不做危险的活动或游戏等。
2、遵守交通规则。
走人行道,横过马路要走人行横道线,不要在马路上停留、玩耍、打闹。
3、懂得“水”“火”“电”的危险。
教育儿童不玩水,不摆弄电器。
在据水边较近的我玩耍时注意安全。
4、不要捡拾小物件。
更不能将放入口、鼻、耳中。
学前教育学答案1.在教学过程中,教师向儿童出示事先准备好的各种样品,如绘画、纸工、泥工样品,供儿童观察,模仿学习,该教师运用了(B范例法)2.在有关邻居关系的故事中,某教师让儿童对邻居王阿姨的心理状态进行分析,问:“王阿姨心里怎么想的?有什么感觉?”该教师运用了移情法中的(A认知提示)训练技术。
3.教师通过利用良好的班级气氛,亲密的师生关系,有安全感的平等发展的集体,让儿童深入其中,从而培养儿童关爱、互助等良好品质,该教师运用了(C环境体验法)4.幼儿园在某一阶段内要达到的教育目标是幼儿园的(B近期目标)5.在幼儿园实践中某些教师认为幼儿进餐、睡眠、午点等是保育,只有上课才是传授知识,发展智力的唯一途径,不注意利用各环节的教育价值,这种做法违反了(A发挥一日生活的整体功能原则)6.为托儿所婴儿选择玩具和游戏材料的注意事项,正确的描述是(C应根据婴儿年龄特点选择玩具)7.对待3岁前婴儿“口吃”现象(A这是学话初期常见的正常现象不必紧张)8.目前,我国幼儿园办园形式更加灵活,提供节假日临时收托孩子服务,早晚接送孩子服务,根据家长需要安排教师上下班时间等,主要是为了(D服务社会)9.对于入园初期适应困难的孩子,幼儿园教师可以B允许他们上半天,如中午午饭后由家长接回,再逐渐延长在园时间10.儿童身高和体重增长最为迅速的时期是(A出生的第一年)11.“玉不琢,不成器”说的是(C社会环境和教育)对心理发展的作用。
卢梭教育理论体系中一个最基本的思想是(A把儿童当作儿童来看待,把儿童看作教育中的一个积极因素13.皮亚杰把儿童心理发展过程划分为四个阶段,按顺序依次是(C感知运动阶段、前运算思维阶段、具体运算思维阶段、形式运算思维阶段14.“儿童中心论”的倡导者是(B杜威)15.创办了世界上第一所幼儿园,被世人誉为“幼儿教育之父”的人是(B福禄培尔)1、简述幼儿教师劳动的特点。
答:幼儿教师的劳动特点一、幼儿教师劳动的艰巨性二、幼儿教师劳动的细致性三、幼儿教师劳动的自主性四、幼儿教师劳动的创造性五、幼儿教师劳动的示范性和感染性六、幼儿教师劳动的整体性2、简述现代教育的特征。
答:现代教育的特征(1)教育的发展急剧增长;(2)教育体制和结构的显著变化;(3)教育的内涵扩大;(4)教育作用愈加重要;(5)教育的不平等依然存在。
二、论述题(每题5分,共2题)1、试述学前班教育小学化倾向的原因及危害。
答:(一)原因:(1)家长“望子成龙”的心态(2)师资力量薄弱(3)办学条件差(二)危害(1)影响幼儿身体的正常发育(2)制约幼儿智力的发展(3)压制幼儿良好个性的形成(4)不利于幼儿入学后良好学习习惯的养成2、结合实例说明游戏对儿童发展的重要作用。
答:作用(1)促进幼儿身体的发展(2)游戏能促进幼儿智力的发展(3)游戏促进了幼儿社会性的发展(4)游戏促进幼儿情感的发展《学前儿童语言教育》作业客观题部分:一、选择题(每题1分,共15题)1、认为儿童天生就有学习语言的能力且体现在一种语言获得装置(LAD)中的教育家是(A 斯金纳)2、儿童早期将“miao”的意义当作猫、狗、羊等,这种常见的错误属于词义的(C借代)3、从出生到一岁半左右的儿童语言学习现象通常被称为(D理解语言现象)4、谈话活动与日常交谈相比较而言,它具有(C自发性)5、教幼儿学英语应当始于培养幼儿的英语(B表达能力)6、能使学前儿童逐步获得独立构思和完整连贯表述的语言经验是(D早期阅读)为了培养有意识的倾听能力,不提倡教师采取的做法是教师可以通过手势、动作或其他体态语言来调动幼儿的积极性8、不符合幼儿园语言教育软件设计和选择原则的内容是(C同一个教学信息的呈现,要做到尽量不可重复)9、(D社会相互作用论)的语言学习模式认为,语言获得是在关键期内通过语言获得装置逐步掌握语法规则的过程。
10、根据凭借物的不同,幼儿园进述活动可分为实物讲述、看图讲述和(C情景表演讲述)11、幼儿出现比较严重的口吃现象,是一种(A言语流畅度障碍)12、语言内容不同于语言话题,主要表现在它是(B具体的)卡洛—乌尔福特和伦奇提出的“四范畴说”包括了语言规则范畴、语言内容认知范畴、语言操作范畴和语言理解范畴14、下列说法中不属于学前儿童语言教育整合观的是(A它包含了语言教育目标、内容、方式的整合)15、率先提出以系统性方式研究儿童语言构成的是(C乔姆斯基)主观题部分:一、简答题(每题2.5分,共2题)1、写出5种讲述活动的类型。
看图讲述生活经验讲述情境讲述绘图讲述续编故事2、构成幼儿良好语言环境的因素是什么?成人的言语范例,丰富的生活内容,多为幼儿提供自由交谈的机会二、论述题(每题5分,共2题)1、试述怎样才能使幼儿有健全的大脑和言语器官?为使婴幼儿的大脑和言语器官发育完善和保持健康呢?家长和幼儿园教师应注意以下两方面:(1)要优生(2)要保护好婴幼儿大脑及言语器官要有合理的生活制度;要注意不要让婴幼儿的头部受伤;尽量让婴幼儿少感冒,预防传染病;婴幼儿用药要十分小心;大人对婴幼儿讲话时声音不要过大,也要教育婴幼儿不要大喊大叫。
2、试述早期阅读对幼儿发展的作用。
(1)阅读能刺激大脑,是发展大脑神经组织的最好方式(2)阅读是儿童心理健康的重要条件(3)阅读增加了幼儿的经历与交往(4)阅读是幼儿个性发展的条件(5)阅读是幼儿学习成功的重要条件总之,早期阅读可以促进幼儿语言的全面发展。
儿童心理学一、简答题(每题2.5分,共2题)1、如何正确理解在心理发展上外因和内因的相互关系?(1)儿童心理的内部矛盾是在儿童主体和客观事物相互作用的过程中产生的。
2)所谓需要,也是一种反映形式。
3)所谓心理水平或心理状态,是过去反映活动的结果。
4新的需要和已有的水平之间的对立的统一和斗争,构成儿童心理发展的内部矛盾。
5)内部矛盾是儿童心理发展的内因,是儿童心理发展的根据,但内部矛盾的运动,任何时候都离不开一定的外因,教育就是儿童心理发展最主要的外因,是儿童心理发展的最主要条件。
2、少年期学生集体关系的变化。
本题可以从以下角度回答:1)在学校集体生活方面;2)在少年先锋队集体生活方面(3)在家庭集体生活方面二、论述题(每题5分,共2题)1、试述教学中儿童注意的培养。
(1)培养儿童对学习的自觉态度;2)培养儿童的组织性和纪律性;3)及时明确认识具体的学习目的任务;4)教材内容和教学方法力求丰富多彩;5)保持正常的工作速度;6)培养和利用儿童的学习兴趣;7)防止儿童过分疲劳;8)教师要照顾到全班儿童;9)考虑儿童的个别差异。
2、试述少年期学生思维的发展。
1)抽象逻辑思维日益占据主要地位,但是思维中的具体形象成分仍然起着重要作用。
2)思维的独立性和批判性有了显著发展,但容易产生片面性和表面性等缺点。
