存在性问题综合测试(三)(含答案)

合集下载

中考数学专题复习《勾股定理之折叠问题分类讨论、存在性问题》测试卷(附带答案)

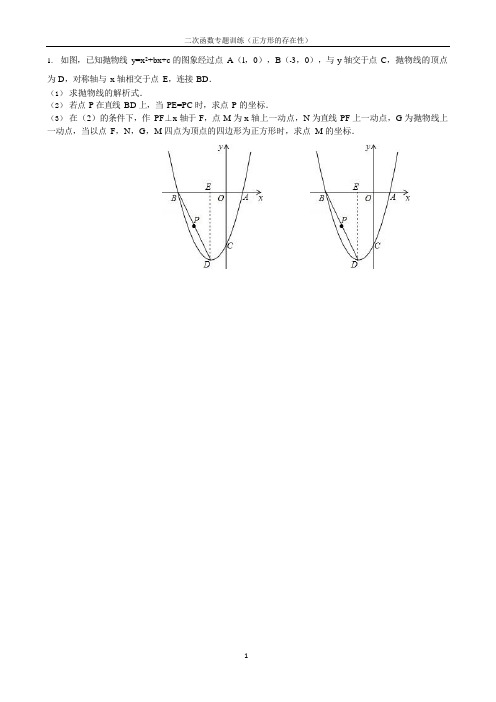
中考数学专题复习《勾股定理之折叠问题分类讨论存在性问题》测试卷（附带答案)学校:___________班级:___________姓名:___________考号:___________一单选题1．如图 ABC 中 90A ∠= 7AB = 24AC = 点D 为边AC 上一点将ABC 沿BD 折叠后点A 的对应点A '恰好落在BC 边上则线段AD 的长为（）A ．407B ．214C ．16825D ．3262．如图是一张直角三角形纸片已知6AC = 10AB = 将纸片沿AD 折叠使点C 落在AB 边上的点C '处则折痕AD 长为（）．A ．5B ．35C ．3D ．323．已知2OA = 2OB = 将AOB 沿着某直线CD 折叠后如图所示 CD 与x 轴交于点C 与AB 交于点D 则点C 坐标是（）A ．()0.4,0B ．()0.5,0C ．()0.6,0D ．()0.7,04．如图长方形纸片ABCD 中 6AB = 18AD = 将此长方形纸片折叠使点D 与点B 重合点C 落在点H 的位置折痕为EF 则ABE 的面积为（）A ．6B ．18C ．24D ．485．如图在平行四边形ABCD 中 60B ∠=︒ 4AB = 6AD = E 是AB 边的中点 F 是线段BC 上的动点将EBF 沿EF 所在直线折叠得到EB F ' 连接B D ' 则B D '的最小值是（）A ．4B ．6C ．2D ．26．将长方形纸片ABCD 如图折叠 B C 两点恰好重合在AD 边上的同一点P 处折痕分别是MH NG 若90MPN ∠=︒ 3PM = 5MN = 分别记PHM PNG PMN 的面积为1S 2S 3S 则1S 2S 3S 之间的数量关系是 ( )A ．312S S S =+B ．312322S S S =+C ．32155S S S =-D ．2123S S S =-7．如图直角ABC 中 90C ∠=︒ 3AC = 4BC = 将ABC 沿AB 折叠得ABD △ 点C 的对应点为点D 则点D 到BC 的距离为（）A ．125B ．245C ．9625D ．125或245 8．如图在Rt ABC △纸片中 9043A AB AC ∠=︒==，，将Rt ABC △纸片按图示方式折叠使点A 恰好落在斜边BC 上的点E 处 BD 为折痕则下列四个结论：①BD 平分ABC ∠①AD DE = ①DE EC = ①DEC 的周长为4 其中正确的个数有（）A ．1B ．2C ．3D ．4二填空题9．如图 Rt ABC △中 90ACB ∠=︒ 30B ∠=︒ 4AC = 点P 为AB 上一个动点以PC 为轴折叠APC △得到QPC 点A 的对应点为点Q 当点Q 落在ABC 内部（不包括边）上时 AP 的取值范围为 .10．如图在平面直角坐标系中长方形ABCO 的边OC OA 、分别在x 轴 y 轴上 3AB = 点E 在边BC 上将长方形ABCO 沿AE 折叠若点B 的对应点F 恰好是边OC 的三等分点则点E 的坐标是．11．如图有一个直角三角形纸片两直角边18cm AC = 24cm BC = 现将直角边AC 沿直线AD 折叠使它落在斜边AB 上且与AE 重合则BD = cm ．12．已知直线l 为长方形ABCD 的对称轴 5AD = 6AB = 点E 为射线DC 上一个动点把ADE 沿直线AE 折叠点D 的对应点D 恰好落在对称轴l 上．则点D 到边CD 的距离是．13．如图把长方形ABCD 沿直线BD 向上折叠使点C 落在C '的位置上 BC '交AD 于E 已知4CD = 8BC = 则EC D '的面积为．三解答题14．如图是一张直角三角形ABC 纸片 90C ∠=︒ 6AC = 8BC =．(1)在图1中将直角边AC 沿AD 折叠使点C 落在斜边AB 上的点E 处求CD 的长(2)在图2中将BFG 沿FG 折叠使点B 与点A 重合求BF 的长．15．一数学兴趣小组探究勾股定理在折叠中的应用如图将一张长方形纸片ABCD 放在平面直角坐标系中点A 与原点O 重合顶点B D 分别在x 轴 y 轴上 P 为边CD 上一动点连接BP 将BCP 沿BP 折叠点C 落在点C '处．(1)若4AB = 3AD = 如图1 连接BD 当点C '在线段BD 上时求点P 的坐标．(2)在（1）的条件下如图2 当点P 与点D 重合时沿BD 将BCD △折叠得BC D '△ DC '与x 轴交于E 点求BDE 的面积．(3)若8AB = 4BC = 当ADC '为等腰三角形时求点P 的坐标．16．如图1 ABC 中 90,BAC AB AC ∠=︒= D E 是直线BC 上两动点且45DAE =︒∠．探究线段BD DE EC 三条线段之间的数量关系：小明的思路是：如图2 将ABD △沿AD 折叠得ADF △ 连接EF 看能否将三条线段转化到一个三角形中 …请你参照小明的思路探究并解决下列问题：(1)猜想BD DE EC 三条线段之间的数量关系并证明(2)如图3 当动点E 在线段BC 上动点D 运动在线段CB 延长线上时其它条件不变（1）中探究的结论是否发生改变？请说明你的猜想并给予证明．17．已知ABC CDE △≌△ 且90B D ∠=∠=︒ 把ABC 和CDE 拼成如图所示的形状使点B C D 在同一条直线上若4AB = 3DE =．(1)求AE 的长(2)将ABC 沿AC 折叠点B 落在点F 处延长AF 与CE 相交于点G 求FG 的长．18．如图在ABC 中 90C ∠=︒ 把ABC 沿直线DE 折叠使ADE 与BDE 重合．(1)若38A ∠=︒ 则CBD ∠的度数为________(2)若6AC = 4BC = 求AD 的长(3)当(0)AB m m ABC =>，△的面积为24m +时求BCD △的周长．（用含m 的代数式表示）参考答案：1．B2．B3．B4．C5．C6．C7．C8．C9．234AP <<10．25⎛- ⎝⎭或2⎛- ⎝⎭11．1512．1或9/9或113．614．(1)3CD = (2)254BF15．(1)点P 的坐标为5,32⎛⎫ ⎪⎝⎭ (2)7516(3)当ADC '为等腰三角形时点P 的坐标为()44，或4⎫⎪⎪⎝⎭．16．(1)222DE BD EC =+(2)不变 222DE BD EC =+17．(1)AE =(2)9418．(1)14︒ (2)133AD =(3)BCD △的周长为4m +．。

二次函数,矩形的存在性问题,含答案(最新整理)

1. (2015 黑龙江省龙东地区) 如图，四边形OABC是矩形，点A、C在坐标轴上，△ODE是△OCB绕点O顺时针旋转90°得到的，点D在x轴上，直线BD交y轴于点F，交OE于点H，线段BC、OC的长是方程x2﹣6x+8=0的两个根，且OC＞BC．（1）求直线BD的解析式；（2）求△OFH的面积；（3）点M在坐标轴上，平面内是否存在点N，使以点D、F、M、N为顶点的四边形是矩形？若存在，请直接写出点N的坐标；若不存在，请说明理由．2. (2015 重庆市綦江县) 如图，抛物线与x 轴交与A ，B 两点（点A 在点B 的左侧），与y 轴223y x x =-++交于点C . 点D 和点C 关于抛物线的对称轴对称，直线AD 与y 轴相交于点E .（1）求直线AD 的解析式；（2）如图1，直线AD 上方的抛物线上有一点F ，过点F 作FG ⊥AD 于点G ，作FH 平行于x 轴交直线AD 于点H ，求△FGH 的周长的最大值；（3）点M 是抛物线的顶点，点P 是y 轴上一点，点Q 是坐标平面内一点，以A ，M ，P ，Q 为顶点的四边形是AM 为边的矩形，若点T 和点Q 关于AM 所在直线对称，求点T 的坐标.xxx26图图图图226图图图图126图图1（0，4）、3. (2016 山东省东营市) 】．】．C的坐标分别是（﹣1，0），将在平面直角坐标系中，平行四边形ABOC如图放置，点A、此平行四边形绕点O顺时针旋转90°，得到平行四边形A′B′OC′．（1）若抛物线经过点C、A、A′，求此抛物线的解析式；（2）点M时第一象限内抛物线上的一动点，问：当点M在何处时，△AMA′的面积最大？最大面积是多少？并求出此时M的坐标；（3）若P为抛物线上一动点，N为x轴上的一动点，点Q坐标为（1，0），当P、N、B、Q构成平行四边形时，求点P的坐标，当这个平行四边形为矩形时，求点N的坐标．4. (2016 贵州省毕节地区) 如图，已知抛物线y=x2+bx与直线y=2x+4交于A（a，8）、B两点，点P是抛物线上A、B之间的一个动点，过点P分别作x轴、y轴的平行线与直线AB交于点C和点E．（1）求抛物线的解析式；（2）若C为AB中点，求PC的长；（3）如图，以PC，PE为边构造矩形PCDE，设点D的坐标为（m，n），请求出m，n之间的关系式．5. (2013 湖南省常德市) 如图，已知二次函数的图象过点A (0，－3)，B ），对称轴为直线12x =-，点P 是抛物线上的一动点，过点P 分别作PM ⊥x 轴于点M ，PN ⊥y 轴于点N ，在四边形PMON 上分别截取1111,,,.3333PC MP MD OM OE ON NF NP ====（1）求此二次函数的解析式；（2）求证：以C ，D ，E ，F 为顶点的四边形CDEF 是平行四边形；（3）在抛物线上是否存在这样的点P ，使四边形CDEF 为矩形？若存在，请求出所有符合条件的P 点坐标；若不存在，请说明理由.6．如图所示，抛物线y=ax2+bx﹣3与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C．（1）求抛物线的解析式；（2）如图所示，直线BC下方的抛物线上有一点P，过点P作PE⊥BC于点E，作PF平行于x轴交直线BC 于点F，求△PEF周长的最大值；（3）已知点M是抛物线的顶点，点N是y轴上一点，点Q是坐标平面内一点，若点P是抛物线上一点，且位于抛物线的对称轴右侧，是否存在以P、M、N、Q为顶点且以PM为边的正方形？若存在，直接写出点P 的横坐标；若不存在，说明理由．参考答案1. (2015 黑龙江省龙东地区) 如图，四边形OABC是矩形，点A、C在坐标轴上，△ODE是△OCB绕点O顺时针旋转90°得到的，点D在x轴上，直线BD交y轴于点F，交OE于点H，线段BC、OC的长是方程x2﹣6x+8=0的两个根，且OC＞BC．（1）求直线BD的解析式；（2）求△OFH的面积；（3）点M在坐标轴上，平面内是否存在点N，使以点D、F、M、N为顶点的四边形是矩形？若存在，请直接写出点N的坐标；若不存在，请说明理由．1.分析：（1）解方程可求得OC、BC的长，可求得B、D的坐标，利用待定系数法可求得直线BD的解析式；（2）可求得E点坐标，求出直线OE的解析式，联立直线BD、OE解析式可求得H点的横坐标，可求得△OFH的面积；（3）当△MFD为直角三角形时，可找到满足条件的点N，分∠MFD=90°、∠MDF=90°和∠FMD=90°三种情况，分别求得M点的坐标，可分别求得矩形对角线的交点坐标，再利用中点坐标公式可求得N点坐标．解答：解：（1）解方程x2﹣6x+8=0可得x=2或x=4，∵BC、OC的长是方程x2﹣6x+8=0的两个根，且OC＞BC，∴BC=2，OC=4，∴B（﹣2，4），∵△ODE是△OCB绕点O顺时针旋转90°得到的，∴OD=OC=4，DE=BC=2，∴D（4，0），设直线BD解析式为y=kx+b，把B、D坐标代入可得，解得，∴直线BD的解析式为y=﹣x+；（2）由（1）可知E（4，2），设直线OE解析式为y=mx，把E点坐标代入可求得m=，∴直线OE解析式为y=x，令﹣x+=x，解得x=，∴H点到y轴的距离为，又由（1）可得F（0，），∴OF=，∴S△OFH=××=；（3）∵以点D、F、M、N为顶点的四边形是矩形，∴△DFM为直角三角形，①当∠MFD=90°时，则M只能在x轴上，连接FN交MD于点G，如图1，由（2）可知OF=，OD=4，则有△MOF∽△FOD，∴=，即=，解得OM=，∴M（﹣，0），且D（4，0），∴G（，0），设N点坐标为（x，y），则=，=0，解得x=，y=﹣，此时N点坐标为（，﹣）；②当∠MDF=90°时，则M只能在y轴上，连接DN交MF于点G，如图2，则有△FOD ∽△DOM ，∴=，即=，解得OM=6，∴M （0，﹣6），且F （0，），∴MG=MF=，则OG=OM ﹣MG=6﹣=，∴G （0，﹣），设N 点坐标为（x ，y ），则=0，=﹣，解得x=﹣4，y=﹣，此时N （﹣4，﹣）；③当∠FMD=90°时，则可知M 点为O 点，如图3，∵四边形MFND 为矩形，∴NF=OD=4，ND=OF=，可求得N （4，）；综上可知存在满足条件的N 点，其坐标为（，﹣）或（﹣4，﹣）或（4，）．2. (2015 重庆市綦江县) 如图，抛物线与x 轴交与A ，B 两点（点A 在点B 的左侧），与y 轴223y x x =-++交于点C . 点D 和点C 关于抛物线的对称轴对称，直线AD 与y 轴相交于点E .（1）求直线AD 的解析式；（2）如图1，直线AD 上方的抛物线上有一点F ，过点F 作FG ⊥AD 于点G ，作FH 平行于x 轴交直线AD 于点H ，求△FGH 的周长的最大值；（3）点M 是抛物线的顶点，点P 是y 轴上一点，点Q 是坐标平面内一点，以A ，M ，P ，Q 为顶点的四边形是AM 为边的矩形，若点T 和点Q 关于AM 所在直线对称，求点T 的坐标.xxx26图图图图226图图图图126图图1答案解：⑴AD ：1y x=+⑵过点F 作x 轴的垂线，交直线AD 于点M ，易证△FGH ≌△FGM 故FGH FGM C C =△△设2(,23)F m m m -++则FM =2223(1)2m m m m m -++-+=-++则 C=212(1(1)2FM FM m +==-+-⑶①若AP 为对角线如图，由△PMS ∽△MAR 可得由点的平移可知故Q 点关于直线AM 的对称点T 为9(0,)2P 1(2)2Q -，1(0,)2-②若AQ 为对角线如图，同理可知P 由点的平移可知Q 故Q 点关于直线AM 的对称点T 为1(0,)2-7(2,)29(0,)23. (2016 山东省东营市) 】．】．在平面直角坐标系中，平行四边形ABOC 如图放置，点A 、C 的坐标分别是（0，4）、（﹣1，0），将此平行四边形绕点O 顺时针旋转90°，得到平行四边形A ′B ′OC ′．（1）若抛物线经过点C 、A 、A ′，求此抛物线的解析式；（2）点M 时第一象限内抛物线上的一动点，问：当点M 在何处时，△AMA ′的面积最大？最大面积是多少？并求出此时M 的坐标；（3）若P 为抛物线上一动点，N 为x 轴上的一动点，点Q 坐标为（1，0），当P 、N 、B 、Q 构成平行四边形时，求点P 的坐标，当这个平行四边形为矩形时，求点N 的坐标．分析（1）由平行四边形ABOC 绕点O 顺时针旋转90°，得到平行四边形A ′B ′OC ′，且点A 的坐标是（0，4），可求得点A ′的坐标，然后利用待定系数法即可求得经过点C 、A 、A ′的抛物线的解析式；（2）首先连接AA ′，设直线AA ′的解析式为：y=kx+b ，利用待定系数法即可求得直线AA ′的解析式，再设点M 的坐标为：（x ，﹣x 2+3x+4），继而可得△AMA ′的面积，继而求得答案；（3）分别从BQ 为边与BQ 为对角线去分析求解即可求得答案．解答解：（1）∵平行四边形ABOC 绕点O 顺时针旋转90°，得到平行四边形A ′B ′OC ′，且点A 的坐标是（0，4），∴点A ′的坐标为：（4，0），∵点A 、C 的坐标分别是（0，4）、（﹣1，0），抛物线经过点C 、A 、A ′，设抛物线的解析式为：y=ax 2+bx+c ，∴，解得：，∴此抛物线的解析式为：y=﹣x 2+3x+4；（2）连接AA ′，设直线AA ′的解析式为：y=kx+b ，∴，解得：，∴直线AA ′的解析式为：y=﹣x+4，设点M 的坐标为：（x ，﹣x 2+3x+4），则S △AMA ′=×4×[﹣x 2+3x+4﹣（﹣x+4）]=﹣2x 2+8x=﹣2（x ﹣2）2+8，∴当x=2时，△AMA ′的面积最大，最大值S △AMA ′=8，∴M 的坐标为：（2，6）；（3）设点P的坐标为（x，﹣x2+3x+4），当P，N，B，Q构成平行四边形时，∵平行四边形ABOC中，点A、C的坐标分别是（0，4）、（﹣1，0），∴点B的坐标为（1，4），∵点Q坐标为（1，0），P为抛物线上一动点，N为x轴上的一动点，①当BQ为边时，PN∥BQ，PN=BQ，∵BQ=4，∴﹣x2+3x+4=±4，当﹣x2+3x+4=4时，解得：x1=0，x2=3，∴P1（0，4），P2（3，4）；当﹣x2+3x+4=﹣4时，解得：x3=，x2=，∴P3（，﹣4），P4（，﹣4）；②当PQ为对角线时，BP∥QN，BP=QN，此时P与P1，P2重合；综上可得：点P的坐标为：P1（0，4），P2（3，4），P3（，﹣4），P4（，﹣4）；如图2，当这个平行四边形为矩形时，点N的坐标为：（0，0）或（3，0）．4. (2016 贵州省毕节地区) 如图，已知抛物线y=x2+bx与直线y=2x+4交于A（a，8）、B两点，点P是抛物线上A、B之间的一个动点，过点P分别作x轴、y轴的平行线与直线AB交于点C和点E．（1）求抛物线的解析式；（2）若C为AB中点，求PC的长；（3）如图，以PC，PE为边构造矩形PCDE，设点D的坐标为（m，n），请求出m，n之间的关系式．分析（1）把A点坐标代入直线方程可求得a的值，再代入抛物线可求得b的值，可求得抛物线解析式；（2）联立抛物线和直线解析式可求得B点坐标，过A作AQ⊥x轴，交x轴于点Q，可知OC=AQ=4，可求得C点坐标，结合条件可知P点纵坐标，代入抛物线解析式可求得P点坐标，从而可求得PC的长；（3）根据矩形的性质可分别用m、n表示出C、P的坐标，根据DE=CP，可得到m、n的关系式．解：（1）∵A（a，8）是抛物线和直线的交点，∴A点在直线上，∴8=2a+4，解得a=2，∴A点坐标为（2，8），又A点在抛物线上，∴8=22+2b，解得b=2，∴抛物线解析式为y=x2+2x；（2）联立抛物线和直线解析式可得，解得，，∴B 点坐标为（﹣2，0），如图，过A 作AQ ⊥x 轴，交x 轴于点Q ，则AQ=8，OQ=OB=2，即O 为BQ 的中点，当C 为AB 中点时，则OC 为△ABQ 的中位线，即C 点在y 轴上，∴OC=AQ=4，∴C 点坐标为（0，4），又PC ∥x 轴，∴P 点纵坐标为4，∵P 点在抛物线线上，∴4=x 2+2x ，解得x=﹣1﹣或x=﹣1，∵P 点在A 、B 之间的抛物线上，∴x=﹣1﹣不合题意，舍去，∴P 点坐标为（﹣1，4），∴PC=﹣1﹣0=﹣1；（3）∵D （m ，n ），且四边形PCDE 为矩形，∴C 点横坐标为m ，E 点纵坐标为n ，∵C 、E 都在直线y=2x+4上，∴C （m ，2m+4），E （，n ），∵PC ∥x 轴，∴P 点纵坐标为2m+4，∵P 点在抛物线上，∴2m+4=x 2+2x ，整理可得2m+5=（x+1）2，解得x=﹣1或x=﹣﹣1（舍去），∴P 点坐标为（﹣1，2m+4），∴DE=﹣m ，CP=﹣1﹣m ，∵四边形PCDE 为矩形，∴DE=CP ，即﹣m=﹣1﹣m ，整理可得n 2﹣4n ﹣8m ﹣16=0，即m 、n 之间的关系式为n 2﹣4n ﹣8m ﹣16=0．5. (2013 湖南省常德市) 如图，已知二次函数的图象过点A (0，－3)，B ），对称轴为直线12x =-，点P 是抛物线上的一动点，过点P 分别作PM ⊥x 轴于点M ，PN ⊥y 轴于点N ，在四边形PMON 上分别截取1111,,,.3333PC MP MD OM OE ON NF NP ====（1）求此二次函数的解析式；（2）求证：以C ，D ，E ，F 为顶点的四边形CDEF 是平行四边形；（3）在抛物线上是否存在这样的点P ，使四边形CDEF 为矩形？若存在，请求出所有符合条件的P 点坐标；若不存在，请说明理由.解：（1）设二次函数的解析式为2y ax bx c =++,将点A （0，-3）、B）、对称轴方程分别代入可得：3,31.22c a c b a ⎧-=⎪=+⎪-=-⎩，解得1,1,3.a ab =⎧⎪=⎨⎪=-⎩∴此二次函数的解析式为23y x x =+-.（2）证明：如图连接CD ，DE ，EF ，FC.∵PM ⊥x 轴，PN ⊥y 轴，∴四边形OMPN 是矩形.∴MP =ON ，OM =PN.又1111,,,,3333PC MP MD OM OE ON NF NP ====∴,DM FN MC NE ==∴△CMD ≅△ENF,同理△ODE ≅△FPC(SAS),∴CF =ED ，CD =EF.,∴四边形CDEF 是平行四边形.（3）如图，作CQ ⊥y 轴于点Q ，设P 点坐标为()2,3x x x +-，则1.3QN PC OE MP ===∴()2133EQ x x =-+-.∴在Rt △ECQ 中，()22222213.9CE EQ CQ x x x =+=+-+当CD ⊥DE 时， ()()()()()()22222222222222222222222222221333413,99143,994114339999553.99DE OD OE x x x x x x CD DM CM x x x CE DE CD x x x x x x x x x =+⎛⎫⎡⎤=-+-+- ⎪⎢⎥⎝⎭⎣⎦=++-=+=++-∴=+=++-+++-=++- ()()()222222222215533,999443,993.x x x x x x x x x x x x ∴+-+=++-=+-+-=±(()()21212212123331,3 1.3311.x x x x y x x x x x y y P +-=====+-=-=-===-∴当时,此时，当时,，此时，，综上可知符合条件的点有四个，分别是，-，-，，，-本题用相似更简单！6．如图所示，抛物线y=ax2+bx﹣3与x轴交于A（﹣1，0），B（3，0）两点，与y轴交于点C．（1）求抛物线的解析式；（2）如图所示，直线BC下方的抛物线上有一点P，过点P作PE⊥BC于点E，作PF平行于x轴交直线BC 于点F，求△PEF周长的最大值；（3）已知点M是抛物线的顶点，点N是y轴上一点，点Q是坐标平面内一点，若点P是抛物线上一点，且位于抛物线的对称轴右侧，是否存在以P、M、N、Q为顶点且以PM为边的正方形？若存在，直接写出点P 的横坐标；若不存在，说明理由．【解答】解：（1）把A（﹣1，0），B（3，0）两点坐标代入抛物线y=ax2+bx﹣3，得到，解得，∴抛物线的解析式为y=x2﹣2x﹣3．（2）如图1中，连接PB、PC．设P（m，m2﹣2m﹣3），∵B（3，0），C（0，﹣3），∴OB=OC，∴∠OBC=45°，∵PF∥OB，∴∠PFE=∠OBC=45°，∵PE⊥BC，∴∠PEF=90°，∴△PEF是等腰直角三角形，∴PE最大时，△PEF的面积中点，此时△PBC的面积最大，则有S△PBC=S△POB+S△POC﹣S△BOC=•3•（﹣m2+2m+3）+•3•m﹣=﹣（m﹣）2+，∴m=时，△PBC的面积最大，此时△PEF的面积也最大，此时P（，﹣），∵直线BC的解析式为y=x﹣3，∴F（﹣，﹣），∴PF=，∵△PEF是等腰直角三角形，∴EF=EP=，∴C△PEF最大值=+．（3）①如图2中，当N与C重合时，点N关于对称轴的对称点P，此时思想MNQP是正方形，易知P（2，﹣3）．点P横坐标为2，②如图3中，当四边形PMQN是正方形时，作PF⊥y轴于N，ME∥x轴，PE∥y轴．易知△PFN≌△PEM，∴PF=PE，设P（m，m2﹣2m﹣3），∵M（1，﹣4），∴m=m2﹣2m﹣3﹣（﹣4），∴m=或（舍弃），∴P点横坐标为所以满足条件的点P的横坐标为2或．。

二次函数中的存在性问题(含答案及解析)

2018年8月4日初中数学试卷一、综合题（共9题；共135分）1.如图所示，抛物线y=ax2+bx+c的顶点为M（﹣2，﹣4），与x轴交于A、B两点，且A（﹣6，0），与y轴交于点C．（1）求抛物线的函数解析式；（2）求△ABC的面积；（3）能否在抛物线第三象限的图象上找到一点P，使△APC的面积最大？若能，请求出点P的坐标；若不能，请说明理由．2.（2017•乌鲁木齐）如图，抛物线y=ax2+bx+c（a≠0）与直线y=x+1相交于A（﹣1，0），B（4，m）两点，且抛物线经过点C（5，0）．（1）求抛物线的解析式；（2）点P是抛物线上的一个动点（不与点A、点B重合），过点P作直线PD⊥x轴于点D，交直线AB于点E．①当PE=2ED时，求P点坐标；②是否存在点P使△BEC为等腰三角形？若存在请直接写出点P的坐标；若不存在，请说明理由．3.（2017•赤峰）如图，二次函数y=ax2+bx+c（a≠0）的图象交x轴于A、B两点，交y轴于点D，点B的坐标为（3，0），顶点C的坐标为（1，4）．（1）求二次函数的解析式和直线BD的解析式；（2）点P是直线BD上的一个动点，过点P作x轴的垂线，交抛物线于点M，当点P在第一象限时，求线段PM长度的最大值；（3）在抛物线上是否存在异于B、D的点Q，使△BDQ中BD边上的高为2 √2？若存在求出点Q的坐标；若不存在请说明理由．4.（2017•广元）如图，已知抛物线y=ax2+bx+c过点A（﹣3，0），B（﹣2，3），C（0，3），其顶点为D．（1）求抛物线的解析式；（2）设点M（1，m），当MB+MD的值最小时，求m的值；（3）若P是抛物线上位于直线AC上方的一个动点，求△APC的面积的最大值；（4）若抛物线的对称轴与直线AC相交于点N，E为直线AC上任意一点，过点E作EF∥ND交抛物线于点F，以N，D，E，F为顶点的四边形能否为平行四边形？若能，求点E的坐标；若不能，请说明理由．5.（2017•巴中）如图，已知两直线l1， l2分别经过点A（1，0），点B（﹣3，0），且两条直线相交于y轴的正半轴上的点C，当点C的坐标为（0，√3）时，恰好有l1⊥l2，经过点A，B，C的抛物线的对称轴与l1、l2、x轴分别交于点G、E、F，D为抛物线的顶点．（1）求抛物线的函数解析式；（2）试说明DG与DE的数量关系？并说明理由；（3）若直线l2绕点C旋转时，与抛物线的另一个交点为M，当△MCG为等腰三角形时，请直接写出点M的坐标．6.如图，已知抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=﹣1，且抛物线经过A（1，0），C（0，3）两点，与x 轴交于点B．（1）若直线y=mx+n经过B、C两点，求直线BC和抛物线的解析式；（2）在抛物线的对称轴x=﹣1上找一点M，使点M到点A的距离与到点C的距离之和最小，求出点M的坐标；（3）设点P为抛物线的对称轴x=﹣1上的一个动点，求使△BPC为直角三角形的点P的坐标．7.如图，抛物线y=ax2+bx+c（a≠0）与x轴相交于A（﹣1，0），B（3，0），与y轴交于点C（0，3）．（1）求抛物线的解析式；（2）连接BC，点P为抛物线上第一象限内一动点，当△BCP面积最大时，求点P的坐标；（3）设点D是抛物线的对称轴上的一点，在抛物线上是否存在点Q，使以点B，C，D，Q为顶点的四边形为平行四边形？若存在，求出点Q的坐标；若不存在，说明理由．8.（2017•临沂）如图，抛物线y=ax2+bx﹣3经过点A（2，﹣3），与x轴负半轴交于点B，与y轴交于点C，且OC=3OB．（1）求抛物线的解析式；（2）点D在y轴上，且∠BDO=∠BAC，求点D的坐标；（3）点M在抛物线上，点N在抛物线的对称轴上，是否存在以点A，B，M，N为顶点的四边形是平行四边形？若存在，求出所有符合条件的点M的坐标；若不存在，请说明理由．答案解析部分一、综合题1.【答案】（1）解：设此函数的解析式为y=a（x+h）2+k，∵函数图象顶点为M（﹣2，﹣4），∴y=a（x+2）2﹣4，又∵函数图象经过点A（﹣6，0），∴0=a（﹣6+2）2﹣4解得a= 14，∴此函数的解析式为y= 14（x+2）2﹣4，即y= 14x2+x﹣3；（2）解：∵点C是函数y= 14x2+x﹣3的图象与y轴的交点，∴点C的坐标是（0，﹣3），又当y=0时，有y= 14x2+x﹣3=0，解得x1=﹣6，x2=2，∴点B的坐标是（2，0），则S△ABC= 12 |AB|•|OC|= 12×8×3=12；（3）解：假设存在这样的点，过点P作PE⊥x轴于点E，交AC于点F．设E（x，0），则P（x，14x2+x﹣3），设直线AC的解析式为y=kx+b，∵直线AC过点A（﹣6，0），C（0，﹣3），∴ {−6k+k=0−3=k，解得{k=−12k=−3，∴直线AC的解析式为y=﹣12x﹣3，∴点F的坐标为F（x，﹣12x﹣3），则|PF|=﹣12 x﹣3﹣（14x2+x﹣3）=﹣14x2﹣32x，∴S△APC=S△APF+S△CPF= 12 |PF|•|AE|+ 12|PF|•|OE|= 12 |PF|•|OA|= 12（﹣14x2﹣32x）×6=﹣34x2﹣92x=﹣34（x+3）2+ 274，∴当x=﹣3时，S△APC有最大值274，此时点P的坐标是P（﹣3，﹣154）．【考点】二次函数的应用【解析】【分析】（1）根据顶点坐标公式即可求得a、b、c的值，即可解题；（2）易求得点B、C的坐标，即可求得OC的长，即可求得△ABC的面积，即可解题；（3）作PE⊥x轴于点E，交AC于点F，可将△APC的面积转化为△AFP和△CFP的面积之和，而这两个三角形有共同的底PF，这一个底上的高的和又恰好是A、C两点间的距离，因此若设设E（x，0），则可用x来表示△APC的面积，得到关于x的一个二次函数，求得该二次函数最大值，即可解题．2.【答案】（1）解：∵点B（4，m）在直线y=x+1上，∴m=4+1=5，∴B（4，5），把A、B、C三点坐标代入抛物线解析式可得{k−k+k=016k+4k+k=525k+5k+k=0，解得{k=−1k=4k=5，∴抛物线解析式为y=﹣x2+4x+5（2）解：①设P（x，﹣x2+4x+5），则E（x，x+1），D（x，0），则PE=|﹣x2+4x+5﹣（x+1）|=|﹣x2+3x+4|，DE=|x+1|，∵PE=2ED，∴|﹣x2+3x+4|=2|x+1|，当﹣x2+3x+4=2（x+1）时，解得x=﹣1或x=2，但当x=﹣1时，P与A重合不合题意，舍去，∴P（2，9）；当﹣x2+3x+4=﹣2（x+1）时，解得x=﹣1或x=6，但当x=﹣1时，P与A重合不合题意，舍去，∴P（6，﹣7）；综上可知P点坐标为（2，9）或（6，﹣7）；②设P（x，﹣x2+4x+5），则E（x，x+1），且B（4，5），C（5，0），∴BE= √(k−4)2+(k+1−5)2 = √2 |x﹣4|，CE= √(k−5)2+(k+1)2 = √2k2−8k+26，BC= √(4−5)2+(5−0)2 = √26，当△BEC为等腰三角形时，则有BE=CE、BE=BC或CE=BC三种情况，当BE=CE时，则√2 |x﹣4|= √2k2−8k+26，解得x= 34，此时P点坐标为（34，11916）；当BE=BC时，则√2 |x﹣4|= √26，解得x=4+ √13或x=4﹣√13，此时P点坐标为（4+ √13，﹣4 √13﹣8）或（4﹣√13，4 √13﹣8）；当CE=BC时，则√2k2−8k+26 = √26，解得x=0或x=4，当x=4时E点与B点重合，不合题意，舍去，此时P 点坐标为（0，5）；综上可知存在满足条件的点P，其坐标为（34，11916）或（4+ √13，﹣4 √13﹣8）或（4﹣√13，4 √13﹣8）或（0，5）【考点】二次函数的应用，与二次函数有关的动态几何问题【解析】【分析】（1）由直线解析式可求得B点坐标，由A、B、C三点的坐标，利用待定系数法可求得抛物线解析式；（2）①可设出P点坐标，则可表示出E、D的坐标，从而可表示出PE和ED的长，由条件可知到关于P点坐标的方程，则可求得P点坐标；②由E、B、C三点坐标可表示出BE、CE和BC的长，由等腰三角形的性质可得到关于E点坐标的方程，可求得E点坐标，则可求得P点坐标．3.【答案】（1）解：∵抛物线的顶点C的坐标为（1，4），∴可设抛物线解析式为y=a（x﹣1）2+4，∵点B（3，0）在该抛物线的图象上，∴0=a（3﹣1）2+4，解得a=﹣1，∴抛物线解析式为y=﹣（x﹣1）2+4，即y=﹣x2+2x+3，∵点D在y轴上，令x=0可得y=3，∴D点坐标为（0，3），∴可设直线BD解析式为y=kx+3，把B点坐标代入可得3k+3=0，解得k=﹣1，∴直线BD解析式为y=﹣x+3（2）解：设P点横坐标为m（m＞0），则P（m，﹣m+3），M（m，﹣m2+2m+3），∴PM=﹣m2+2m+3﹣（﹣m+3）=﹣m2+3m=﹣（m﹣32）2+ 94，∴当m= 32时，PM有最大值94（3）解：如图，过Q作QG∥y轴交BD于点G，交x轴于点E，作QH⊥BD于H，设Q（x，﹣x2+2x+3），则G（x，﹣x+3），∴QG=|﹣x2+2x+3﹣（﹣x+3）|=|﹣x2+3x|，∵△BOD是等腰直角三角形，∴∠DBO=45°，∴∠HGQ=∠BGE=45°，当△BDQ中BD边上的高为2 √2时，即QH=HG=2 √2，∴QG= √2×2 √2 =4，∴|﹣x2+3x|=4，当﹣x2+3x=4时，△=9﹣16＜0，方程无实数根，当﹣x2+3x=﹣4时，解得x=﹣1或x=4，∴Q（﹣1，0）或（4，﹣5），综上可知存在满足条件的点Q，其坐标为（﹣1，0）或（4，﹣5）【考点】二次函数的应用，与二次函数有关的动态几何问题【解析】【分析】（1）可设抛物线解析式为顶点式，由B 点坐标可求得抛物线的解析式，则可求得D 点坐标，利用待定系数法可求得直线BD 解析式；（2）设出P 点坐标，从而可表示出PM 的长度，利用二次函数的性质可求得其最大值；（3）过Q 作QG∥y 轴，交BD 于点G ，过Q 和QH⊥BD 于H ，可设出Q 点坐标，表示出QG 的长度，由条件可证得△DHG 为等腰直角三角形，则可得到关于Q 点坐标的方程，可求得Q 点坐标． 4.【答案】（1）解：将A ，B ，C 点的坐标代入解析式，得 {9k −3k +k =04k −2k +k =3k =3 ，解得 {k =−1k =−2k =3，抛物线的解析式为y=﹣x 2﹣2x+3（2）解：配方，得y=﹣（x+1）2+4，顶点D 的坐标为（﹣1，4）作B 点关于直线x=1的对称点B′，如图1，则B′（4，3），由（1）得D （﹣1，4），可求出直线DB′的函数关系式为y=﹣ 15 x+ 195 ，当M （1，m ）在直线DN′上时，MN+MD 的值最小，则m=﹣ 15 ×1+ 195 = 185 ．（3）解：作PE⊥x 轴交AC 于E 点，如图2，AC 的解析式为y=x+3，设P （m ，﹣m 2﹣2m+3），E （m ，m+3）， PE=﹣m 2﹣2m+3﹣（m+3）=﹣m 2﹣3mS △APC = 12 PE •|x A |= 12 （﹣m 2﹣3m ）×3=﹣ 32 （m+ 32 ）2+ 278 ，当m=﹣32时，△APC的面积的最大值是278（4）解：由（1）、（2）得D（﹣1，4），N（﹣1，2）点E在直线AC上，设E（x，x+3），①当点E在线段AC上时，点F在点E上方，则F（x，﹣x2﹣2x+3），∵EF=DN∴﹣x2﹣2x+3﹣（x+3）=4﹣2=2，解得，x=﹣2或x=﹣1（舍去），则点E的坐标为：（﹣2，1）．②当点E在线段AC（或CA）延长线上时，点F在点E下方，则F（x，﹣x2﹣2x+3），∵EF=DN，∴（x+3）﹣（﹣x2﹣2x+3）=2，解得x= −3+√172或x= −3−√172，即点E的坐标为：（−3+√172，3+√172）或（−3−√172，3−√172）综上可得满足条件的点E为E（﹣2，1）或：（−3+√172，3+√172）或（−3−√172，3−√172）【考点】二次函数的性质，待定系数法求二次函数解析式，二次函数的应用，三角形的面积，轴对称-最短路线问题【解析】【分析】（1）根据待定系数法，可得答案.（2）利用轴对称求最短路径的知识，找到B点关于直线x=1的对称点B′，连接B′D，B′D与直线x=1的交点即是点M的位置，继而求出m的值.（3）根据平行于y轴的直线上两点间的距离最大的纵坐标减去较小的纵坐标，可得PE的长，根据三角形的面积，可得二次函数，根据二次函数的性质，可得答案.（4）设出点E的坐标，分情况讨论；①当点E再线段AC上时，点F在点E上方；②当点E再线段AC（或CA）延长线上时，点F在点E下方，根据平行四边形的性质，可得关于x的方程，继而求出点E的坐标.5.【答案】（1）解：设抛物线的函数解析式为y=ax2+bx+c．∵点A（1，0），点B（﹣3，0），点C（0，√3）在抛物线上，∴ {k+k+k=09k−3k+k=0k=√3，解得{k=−√33k=−2√33k=√3，∴抛物线的函数解析式为y=﹣√33 x2﹣2√33x+ √3（2）解：DG=DE．理由如下：设直线l 1的解析式为y=k 1x+b 1 ，将A （1，0），C （0， √3 ）代入，解得y=﹣ √3 x+ √3 ；设直线l 2的解析式为y=k 2x+b 2 ，将B （﹣3，0），C （0， √3 ）代入，解得y= √33x+ √3 ； ∵抛物线与x 轴的交点为A （1，0），B （﹣3，0）， ∴抛物线的对称轴为直线x=﹣1，又∵点G 、D 、E 均在对称轴上， ∴G（﹣1，2 √3 ），D （﹣1，4√33 ），E （﹣1， 2√33）， ∴DG=2 √3 ﹣ 4√33= 2√33，DE= 4√33﹣ 2√33= 2√33，∴DG=DE；（3）解：若直线l 2绕点C 旋转时，与抛物线的另一个交点为M ，当△MCG 为等腰三角形时，分三种情况： ①以G 为圆心，GC 为半径画弧交抛物线于点M 1、C ，点M 1与C 关于抛物线的对称轴对称，则M 1的坐标为（﹣2， √3 ）； ②以C 为圆心，GC 为半径画弧交抛物线于点M 2、M 3 ，点M 2与点A 重合，点A 、C 、G 在一条直线上，不能构成三角形，M 3与M 1重合；③作线段GC 的垂直平分线，交抛物线于点M 4、M 5 ，点M 4与点D 重合，点D 的坐标为（﹣1， 4√33），M 5与M 1重合；综上所述，满足条件的点M 只有两个，其坐标分别为（﹣2， √3 ），（﹣1， 4√33）．【考点】待定系数法求一次函数解析式，二次函数的性质，待定系数法求二次函数解析式，二次函数的应用，与二次函数有关的动态几何问题【解析】【分析】（1）设抛物线的函数解析式为y=ax 2+bx+c ．分别将A （1，0），B （﹣3，0），C （0， √3 ）三点坐标代入得到一个三元一次方程组，解之即可得到抛物线解析式.（2）DG=DE ．分别求出过A （1，0），C （0， 3 ）两点的直线l 1的解析式为y=﹣ √3 x+ √3 ；过B （﹣3，0），C （0， 3 ）两点的直线l 2的解析式为y= √33x+ √3 ；由二次函数的性质和已知条件求出DG 和DE 的长度即可. （3）若直线l 2绕点C 旋转时，与抛物线的另一个交点为M ，当△MCG 为等腰三角形时，分三种情况：①以G 为圆心，GC 为半径画弧交抛物线于点M 1（﹣2， √3 ）；②以C 为圆心，GC 为半径画弧交抛物线于点M 2、M 3 ，；③作线段GC 的垂直平分线，交抛物线于点M 4、M 5.6.【答案】（1）解：依题意得： {−k2k =−1k +k +k =0k =3，解之得： {k =−1k =−2k =3∴抛物线解析式为y=-x 2-2x+3∵对称轴为x=-1，且抛物线经过A （1，0）， ∴把B （-3，0）、C （0，3）分别代入直线y=mx+n ，得 {−3k +k =0k =3，解之得： {k =1k =3，∴直线y=mx+n 的解析式为y=x+3（2）解：设直线BC 与对称轴x=-1的交点为M ，则此时MA+MC 的值最小．把x=-1代入直线y=x+3得，y=2，∴M（-1，2），即当点M 到点A 的距离与到点C 的距离之和最小时M 的坐标为（-1，2）（3）解：如图：设P （-1，t ），又∵B（-3，0），C （0，3），∴BC 2=18，PB 2=（-1+3）2+t 2=4+t 2 ，PC 2=（-1）2+（t-3）2=t 2-6t+10，①若点B 为直角顶点，则BC 2+PB 2=PC 2即：18+4+t 2=t 2-6t+10解之得：t=-2；②若点C 为直角顶点，则BC 2+PC 2=PB 2即：18+t 2-6t+10=4+t 2解之得：t=4，③若点P 为直角顶点，则PB 2+PC 2=BC 2即：4+t 2+t 2-6t+10=18解之得：t 1= 3+√172 ，t 2= 3−√172；综上所述P 的坐标为（-1，-2）或（-1，4）或（-1， 3+√172 ）或（-1， 3−√172）．【考点】二次函数的应用，二次函数的实际应用-动态几何问题【解析】【分析】先把点A ，C 的坐标分别代入抛物线解析式得到a 和b ，c 的关系式，再根据抛物线的对称轴方程可得a 和b 的关系，再联立得到方程组，解方程组，求出a ，b ，c 的值即可得到抛物线解析式；把B 、C 两点的坐标代入直线y=mx+n ，解方程组求出m 和n 的值即可得到直线解析式；设直线BC 与对称轴x=-1的交点为M ，则此时MA+MC 的值最小．把x=-1代入直线y=x+3得y 的值，即可求出点M 坐标；设P （-1，t ），又因为B （-3，0），C （0，3），所以可得BC 2=18，PB 2=（-1+3）2+t 2=4+t 2 ， PC 2=（-1）2+（t-3）2=t 2-6t+10，再分三种情况分别讨论求出符合题意t 值即可求出点P 的坐标．7.【答案】（1）解：设抛物线解析式为y=a （x+1）（x ﹣3），把C （0，3）代入得a •1•（﹣3）=3，解得a=﹣1，所以抛物线解析式为y=﹣（x+1）（x ﹣3），即y=﹣x 2+2x+3（2）解：设直线BC 的解析式为y=kx+m ，把B （3，0），C （0，3）代入得 {3k +k =0k =3 ，解得 {k =−1k =3，所以直线BC的解析式为y=﹣x+3，作PM∥y轴交BC于M，如图1，设P（x，﹣x2+2x+3），（0＜x＜3），则M（x，﹣x+3），∴PM=﹣x2+2x+3﹣（﹣x+3）=﹣x2+3x，∴S△PCB= 12•3•PM=﹣32x2+ 92=﹣32（x﹣32）2+ 278，当x= 32时，△BCP的面积最大，此时P点坐标为（32，154）（3）解：如图2，抛物线的对称轴为直线x=1，当四边形BCDQ为平行四边形，设D（1，a），则Q（4，a﹣3），把Q（4，a﹣3）代入y=﹣x2+2x+3得a﹣3=﹣16+8+3，解得a=﹣2，∴Q（4，﹣5）；当四边形BCQD为平行四边形时，设D（1，a），则Q（﹣2，3+a），把Q（﹣2，3+a）代入y=﹣x2+2x+3得3+a=﹣4﹣4+3，解得a=﹣8，∴Q（﹣2，﹣5）；当四边形BQCD为平行四边形时，设D（1，a），则Q（2，3﹣a），把Q（2，3﹣a）代入y=﹣x2+2x+3得3﹣a=﹣4+4+3，解得a=0，∴Q（2，3），综上所述，满足条件的Q点坐标为（4，﹣5）或（﹣2，﹣5）或（2，3）．【考点】二次函数的应用，与二次函数有关的动态几何问题【解析】【分析】（1）设交点式y=a （x+1）（x ﹣3），然后把C 点坐标代入求出a 的值即可得到抛物线的解析式；（2）先利用待定系数法求出直线BC 的解析式为y=﹣x+3，作PM∥y 轴交BC 于M ，如图1，设P （x ，﹣x 2+2x+3），（0＜x ＜3），则M （x ，﹣x+3），利用三角形面积公式得到∴S △PCB = 12 •3•PM=﹣ 32 x 2+ 92 ，然后根据二次函数的性质求解；（3）如图2，分类讨论：当四边形BCDQ 为平行四边形，设D （1，a ），利用点平移的坐标规律得到Q （4，a ﹣3），然后把Q （4，a ﹣3）代入y=﹣x 2+2x+3中求出a 即可得到Q 点坐标；当四边形BCQD 为平行四边形或四边形BQCD 为平行四边形时，利用同样方法可求出对应Q 点坐标．8.【答案】（1）解：由y=ax 2+bx ﹣3得C （0．﹣3），∴OC=3，∵OC=3OB，∴OB=1，∴B（﹣1，0），把A （2，﹣3），B （﹣1，0）代入y=ax 2+bx ﹣3得 {4k +2k −3=−3k −k −3=0 ， ∴ {k =1k =−2， ∴抛物线的解析式为y=x 2﹣2x ﹣3（2）解：设连接AC ，作BF⊥AC 交AC 的延长线于F ，∵A（2，﹣3），C （0，﹣3），∴AF∥x 轴，∴F（﹣1，﹣3），∴BF=3，AF=3，∴∠BAC=45°，设D （0，m ），则OD=|m|，∵∠BDO=∠BAC，∴∠BDO=45°，∴OD=OB=1，∴|m|=1，∴m=±1，∴D 1（0，1），D 2（0，﹣1）（3）解：设M （a ，a 2﹣2a ﹣3），N （1，n ），①以AB 为边，则AB∥MN，AB=MN ，如图2，过M 作ME⊥对称轴y 于E ，AF⊥x 轴于F ，则△ABF≌△NME，∴NE=AF=3，ME=BF=3，∴|a﹣1|=3，∴a=3或a=﹣2，∴M（4，5）或（﹣2，11）；②以AB为对角线，BN=AM，BN∥AM，如图3，则N在x轴上，M与C重合，∴M（0，﹣3），综上所述，存在以点A，B，M，N为顶点的四边形是平行四边形，M（4，5）或（﹣2，11）或（0，﹣3）．【考点】二次函数的图象，二次函数的性质，二次函数的应用【解析】【分析】（1）待定系数法即可得到结论；（2）连接AC，作BF⊥AC交AC的延长线于F，根据已知条件得到AF∥x轴，得到F（﹣1，﹣3），设D（0，m），则OD=|m|即可得到结论；（3）设M（a，a2﹣2a﹣3），N（1，n），①以AB为边，则AB∥MN，AB=MN，如图2，过M作ME⊥对称轴y于E，AF⊥x轴于F，于是得到△ABF≌△NME，证得NE=AF=3，ME=BF=3，得到M（4，5）或（﹣2，11）；②以AB为对角线，BN=AM，BN∥AM，如图3，则N在x轴上，M与C重合，于是得到结论．。

与圆有关的存在性问题训练(含答案)

与圆有关的存在性问题训练例1：已知圆C :()2222=+-y x ，直线l ：2+=kx y .若直线l 上存在点P ，过点P 引圆的两条切线21,l l ，使得21l l ⊥，则实数k 的取值范围是（）A.[)()+∞-⋃-,3232,0B.[]3,232+-C.()0,∞-D.[)∞+，0答案：D例2：已知两点()0,a A ，()0,a B -()0>a ，若圆()()11322=-+-y x 上存在点P ，使得︒=∠90APB ，则正实数a 的取值范围为（）A.(]3,0 B.[]3,1 C.[]32， D.[]21，答案：B例3：在平面直角坐标系xOy中，圆C经过点()10，，()30，，且与x轴正半轴相切，若圆C上存在点M，使得直线OM与直线()0>=kkxy关于y轴对称，则k的最小值为（）A.332 B.3 C.32 D.34答案：D例4：已知圆()()1041:22=-+-y x C 和点()t M ,5，若圆C 上存在两点B A ,使得MB MA ⊥，则实数t 的取值范围是（）A.[]6,2- B.[]5,3- C.[]62， D.[]53，答案：C例5：已知点A 在圆2:22=+y x O 上，Q P ,是直线t x y +=上的两个不同的点，若存在Q P A ,,使得线段AQ AP ,的中点都在圆O 上，则t 的取值范围是________.答案：()6,6-∈t例6：在平面直角坐标系xOy 中，已知点()0,m A ，()0,4+m B ，若圆()83:22=-+m y x C 上存在点P ，使得︒=∠45APB ，则实数m 的取值范围是________.例7：已知A是圆C内异于圆心的一定点，动点P满足：在圆C上存在唯一点Q，使得0=QA，则动点P的轨迹为（）∙QPA.直线B.圆C.椭圆D.双曲线答案：C例8：在平面直角坐标系xOy 中，已知AB 是圆1:22=+y x O 的直径，若直线013:=+--k y kx l 上存在点P ，连接AP 与圆O 交于点Q ，满足OQ BP //，则实数k 的取值范围是________.例9：在平面直角坐标系xOy 中，点Q P ,分别为直线032:=-+y x l 与圆()()02:222>=+-r r y x M 上的动点，若存在点Q P ,，使得OPQ ∆是以O 为直角顶点的等腰直角三角形，则r 的取值范围为_________.例10：已知圆()43:221=++y x C ，圆()45:222=-+y x C ，若平面内存在点P 满足：过点P 有无数多对相互垂直的直线21,l l ，它们分别与圆1C ，圆2C 相交，且被圆1C ，圆2C 截得的弦长相等，求点P 的坐标.答案：()()1,1,4,421=-=P P例11：若圆()()22253r y x =++-上有且只有两个点到直线234=-y x 的距离等于1，则半径r 的取值范围是（）A.(]64， B.[)6,4 C.()64， D.[]64，答案：C例12：已知圆1:22=+y x O ，圆()()13:22=+-+-a y a x M .若圆M 上存在点P ，过点P 作圆O 的两条切线，切点为B A ,，使得︒=∠60APB ，则实数a 的取值范围是_______.答案：[]3,0∈a思考题：在平面直角坐标系xOy 中，已知圆()()03:222>=-+a a y x M ，点⎪⎭⎫ ⎝⎛-0,2a A ，()0,1B ，()2,3C ，若圆M 上存在点P ，使得︒=∠90BPC ，︒=∠45PAB ，则a 的值为________.。

人教版高一必修5第三章不等式专题含参数不等式恒成立与存在性问题教案含答案

专题-含参数不等式恒成立与存在性问题由任意性和存在性条件求参数的取值范围问题，一直是高考数学考试的重点和难点。

通过对近几年高考数学试题的研究，我们发现这类试题往往以压轴题的形式出现，所涉及的知识点内容覆盖面广，其中命题的核心在函数、方程、不等式等内容的交汇处。

下面就对这类问题进行详细的归类、归法，构建知识体系，希望对同学们有所帮助。

一、在不等式恒成立的条件下，求参数的取值范围问题在不等式恒成立条件下求参数的取值范围，一般原理是利用转化与化归思想将其转化为函数的最值或值域问题加以求解，方法可采用“分离参数法”或“不分离参数法”直接移项构造辅助函数的形式.类型1：对于一次函数，则有：],[,)(n m x b kx x f ∈+=（1）如果；()0()0()0f m f x f n >⎧>⇔⎨>⎩恒成立（2）如果.()0()0()0f m f x f n <⎧<⇔⎨<⎩恒成立例1、若不等式对满足的所有都成立，求的范围.)1(122->-x m x 22≤≤-m m x 解：我们可以用改变主元的办法，将视为主元，原不等式化为：，m 0)12()1(2<---x x m 令，则时，恒成立，所以只需)12()1()(2---=x x m m f 22≤≤-m 0)(<m f ⎩⎨⎧<<-0)2(0)2(f f 即，所以的范围是.⎪⎩⎪⎨⎧<---<----0)12()1(20)12()1(222x x x x x )231,271(++-∈x 说明：在给出的含有两个变量的不等式中，学生习惯把变量看成是主元（未知数），而把另一个变x 量看成参数，在有些问题中这样的解题过程繁琐。

如果把已知取值范围的变量作为主元，把要求取值范a 围的变量看作参数，则可简化解题过程。

类型2：设，)0()(2≠++=a c bx ax x f R x ∈（1）上恒成立；R x x f ∈>在0)(00<∆>⇔且a （2）上恒成立.R x x f ∈<在0)(00<∆<⇔且a 例2、已知关于的不等式对任意恒成立，求实数的取值范围.x 2210mx mx ++>x R ∈m 解：当时，原不等式化为显然成立；0m =10>当时，则需要满足条件：；0m ≠201440m m m m >⎧⇒<<⎨∆=-<⎩综上，实数的取值范围是.m [0,1)类型3：设)0()(2≠++=a c bx ax x f ],[βα∈x （1）当时，如果上恒成立；0>a ],[0)(βα∈>x x f 在⎪⎩⎪⎨⎧>>-⎪⎩⎪⎨⎧<∆≤-≤⎪⎩⎪⎨⎧><-⇔0)(2020)(2βββαααf aba b f a b 或或当时，如果上恒成立.0>a ],[0)(βα∈<x x f 在⎩⎨⎧<<⇔0)(0)(βαf f （2）当时，如果上恒成立；0<a ],[0)(βα∈>x x f 在⎩⎨⎧>>⇔0)(0)(βαf f 当时，如果上恒成立.0<a ],[0)(βα∈<x x f 在⎪⎩⎪⎨⎧<>-⎪⎩⎪⎨⎧<∆≤-≤⎪⎩⎪⎨⎧><-⇔0)(2020)(2βββαααf a bab f a b 或或例3、若时，不等式恒成立，求的取值范围。

学生综合素质评价存在的问题

学生综合素质评价的问题及思考付俊祥甘肃省武山县第一高级中学(741300)摘要:综合素质评价是新课程实验和高考改革的重要组成部分，但是学生综合素质评价目标取向偏移,标准缺乏统一,方案操作性不强, 权力分配不公平,导致学生综合素质评价实践中出现了形式主义倾向。

关键词:综合素质评价问题思考综合素质评价是新课程实验和高考改革方案的重要组成部分，是学生能否毕业和高校招生录取的重要依据。

用高考“指挥棒”促进学生、学校、家庭、社会重视道德品质、公民素养、身心发展等方面的状况，推动素质教育进一步深入开展，促进高中学生全面协调健康发展，是高考改革的一大进步，是推进素质教育的一大举措。

综合素质评价改革已经取得一定进展，各地的评价方案和评价指标体系具有一定的操作性，相关保障制度建设取得了一定的进展。

但是,学生综合素质评价的实践效果并不理想,遇到了一些困难和挑战，导致学生综合素质评价实践中出现了形式主义倾向,影响学生综合素质评价的质量与效果，影响新课程改革向纵深发展的进程。

一、评价目标取向偏移学生综合素质评价的目标是提高学生的综合素质、促进学生的全面发展，但在实施中评价目标却发生了偏移，放大了作为评价和考试制度所具有的筛选的工具性作用，造成了价值取向上的偏移。

家长、学生，甚至一部分教师将综合素质评价看做升学考试的一部分。

走访了学校领导、教师、学生和部分学生家长，普遍关注的是评价结果作为高考录取的依据。

对参加家长会的高一30名、高二30名、高三40名共100名家长，在随机选取高一30名、高二30名、高三40名共100名学生，抽取高一15名、高二15名、高三20名共50名教师，28名学校领导进行问卷调查，对综合素质评价关注点首选“高考录取取依据”，其次是“评价高中学业水平”，而“促进素质提高”最低。

学校领导、教师认为综合素质评价能“促进素质提高”达10%，是因为在评价过程中体现了“促进学生综合素质提高”的作用，强化了“不合格D等级”的管理。

存在自身存在问题原因分析及解决问题措施(最新)

存在自身存在问题、原因分析及解决问题措施(最新)通过学习文件和领导讲话精神，结合工作实际对照自查，我对个人进行了认真剖析，深刻感受到自己在学习、工作、生活中还存在很多问题与不足，现对自己在思想、政治、工作等方面存在的缺点和不足提出如下整改措施。

一、个人存在问题和不足1、对党的理论知识学习不够，不深。

在理论学习上存在浮燥情绪，在学习内容上，认为没有业务知识更实用。

在学习的方式上，理论联系实际还不够，不能融会贯通到真正的在干中学和学中干。

2、在思想上还缺乏开拓创新意识。

在思维方式上，有时习惯于凭经往常经验考虑问题，大胆探索的方式方法比较少。

3、工作作风有时不够扎实、不够深入、处理问题有时有时还存在不妥之处，工作中还缺乏足够的积极性、主动性、创造性。

自我思想有时还存在。

二、根据以上的不足之处，提出下一步的整改措施：1、努力强化学习，不断提高思想境界，全面提升自身素质。

自己越来越注意到在当今这个与时俱进、知识与信息不断更新的社会里，学习是提高自身素质的第一要务，充分认识到，在当前形式和环境中，只有不断的学习，才能不被这个社会所淘汰，这不但要学习应具备的相关业务知识和政治理论知识，还要学习更多的知识，目的就是为了今后游刃有余的工作打好一个坚实的基础。

在学习的过程中更重要的是要不断的提高自身的修养问题，还要强服务意识和责任意识，努力做一个有德有才的大家认可的机关人员，做一个高素质的人。

2、不断提高和改变工作思路，增强创新意识，提高工作水平。

我现在从事的工作，会面临许多新问题，新矛盾和新内容，这就要求我们要不断地更新知识，丰富自己的工作技能和实践本领的同时要善于在工作中开拓创新，提出新的思路和新见解，这样才能把良好的愿望和实际工作效果结合起来。

只有这样才能在工作中争创一流。

3、要在工作中埋头苦干，求真务实，提高效率。

在工作中脚踏实地地做好本职工作，模范地履行一个机关干部的职责。

树立高度的责任感和敬业精神，尽心尽力把工作做好。

【跨越一本线】高三数学问题：2.2函数中存在性与恒成立问题(含答案)

高三数学跨越一本线精品问题二函数中存在性与恒成立问题函数内容作为高中数学知识体系的核心,也是历年高考的一个热点.在新课标下的高考越来越注重对学生的综合素质的考察,恒成立与存在性问题便是一个考察学生综合素质的很好途径,它主要涉及到一次函数、二次函数、三角函数、指数函数和对数函数等常见函数的图象和性质,渗透着换元、化归、数形结合、函数与方程等思想方法,在培养思维的灵活性、创造性等方面起到了积极的作用.近几年的数学高考和各地的模考联考中频频出现存在性与恒成立问题,其形式逐渐多样化,但它们大都与函数、导数知识密不可分.与恒成立及存在性问题有关的知识如下：(1)恒成立问题①. ∀x∈D,均有f(x)>A恒成立,则f(x)min>A；②. ∀x∈D,均有f(x)﹤A恒成立,则 f(x)ma x<A；③. ∀x∈D,均有f(x) >g(x)恒成立,则F(x)= f(x)- g(x) >0,∴ F(x)min >0；④. ∀x∈D,均有f(x)﹤g(x)恒成立,则F(x)= f(x)- g(x) <0,∴ F(x) ma x <0；⑤. ∀x1∈D, ∀x2∈E,均有f(x1) >g(x2)恒成立,则f(x)min> g(x)ma x；⑥. ∀x1∈D, ∀x2∈E,均有f(x1) <g(x2)恒成立,则f(x) ma x < g(x) min.(2)存在性问题①. ∃x0∈D,使得f(x0)>A成立,则f(x) ma x >A；②. ∃x0∈D,使得f(x0)﹤A成立,则 f(x) min <A；③. ∃x0∈D,使得f(x0) >g(x0)成立,设F(x)= f(x)- g(x),∴ F(x) ma x >0；④. ∃x0∈D,使得f(x0) <g(x0)成立,设F(x)= f(x)- g (x),∴ F(x) min <0；⑤. ∃x1∈D, ∃x2∈E, 使得f(x1) >g(x2)成立,则f(x) ma x > g(x) min；⑥. ∃x1∈D, ∃x2∈E,均使得f(x1) <g(x2)成立,则f(x) min < g(x) ma x.(3)相等问题若f(x)的值域分别为A,B,则⊆；①. ∀x1∈D, ∃x2∈E,使得f(x1)=g(x2)成立,则A B②∃x 1∈D, ∃x2∈E, 使得f(x1)=g(x2)成立,则A B≠∅.(4)恒成立与存在性的综合性问题①∀x1∈D, ∃x2∈E, 使得f(x1) >g(x2)成立,则f(x)m in> g(x)m in；②∀x1∈D, ∃x2∈E, 使得f(x1) <g(x2)成立,则f(x)max < g(x)max.解决高中数学函数的存在性与恒成立问题常用以下几种方法：①函数性质法；②分离参数法；③主参换位法；④数形结合法等. 一、函数性质法【例1】已知函数f (x )＝x 3－ax 2＋10,若在区间1,2]内至少存在一个实数x ,使得f (x )<0成立,求实数a 的取值范围．【分析】本题实质是存在性问题【解析】解法一：f ′(x )＝3x 2－2ax ＝3x ⎝ ⎛⎭⎪⎫x －23a (1≤x ≤2),当23a ≤1,即a ≤32时,f ′(x )≥0,f (x )在1,2]上为增函数, 故f (x )m in ＝f (1)＝11－a ,所以11－a <0,a >11,这与a ≤32矛盾．当1<23a <2,即32<a <3时,当1≤x <23a ,f ′(x )<0；当23a <x ≤2,f ′(x )>0,所以x ＝23a 时,f (x )取最小值,因此有f ⎝ ⎛⎭⎪⎫23a <0,即827a 3－49a 3＋10＝－427a 3＋10<0,解得a >3352,这与32<a <3矛盾；当23a ≥2,即a ≥3时,f ′(x )≤0,f (x )在1,2]上为减函数,所以f (x )m in ＝f (2)＝18－4a ,所以18－4a <0,解得a >92,这符合a ≥3.综上所述,a 的取值范围为a >92.解法二：由已知得：a >x 3＋10x 2＝x ＋10x2,设g (x )＝x ＋10x 2(1≤x ≤2),g ′(x )＝1－20x3,∵1≤x ≤2,∴g ′(x )<0,所以g (x )在1,2]上是减函数．g (x )m in ＝g (2),所以a >92.【点评】解法一在处理时,需要用分类讨论的方法,讨论的关键是极值点与区间1,2]的关系；解法二是用的参数分离,由于ax 2>x 3＋10中x 2∈1,4],所以可以进行参数分离,而无需要分类讨论．【牛刀小试】【20xx 山西大学附中第二次模拟】设函数()()21xf x e x ax a =--+,其中1a <,若存在唯一的整数,使得()0f t <,则的取值范围是（） A ．3,12e ⎡⎫-⎪⎢⎣⎭ B ．33,24e ⎡⎫-⎪⎢⎣⎭ C ．33,24e ⎡⎫⎪⎢⎣⎭ D ．3,12e ⎡⎫⎪⎢⎣⎭【答案】D二、分离参数法【例2】已知函数()ln f x ax x x =+的图象在点e x =（为自然对数的底数）处的切线的斜率为．(1)求实数的值；(2)若2()f x kx ≤对任意0x >成立,求实数的取值范围.【分析】（1）由'()ln 1f x a x =++结合条件函数()ln f x ax x x =+的图象在点e x =处的切线的斜率为,可知'(e)3f =,可建立关于的方程：lne 13a ++=,从而解得1a =；（2）要使2()f x kx ≤对任意0x >恒成立,只需max 2()[]f x k x≥即可,而由（1）可知()ln f x x x x =+,∴问题即等价于求函数1ln ()xg x x+=的最大值,可以通过导数研究函数()g x 的单调性,从而求得其最值：221(1ln )ln '()x x xx g x x x⋅-+==-,令'()0g x =,解得1x =,当01x <<时,'()0g x >,∴()g x 在(0,1)上是增函数；当1x >时,'()0g x <,∴()g x 在(1,)+∞上是减函数,因此()g x 在1x =处取得最大值(1)1g =,∴1k ≥即为所求. 【解析】(1)∵()ln f x ax x x =+,∴'()ln 1f x a x =++, 又∵()f x 的图象在点e x =处的切线的斜率为,∴'(e)3f =, 即lne 13a ++=,∴1a =； (2)由（1）知,()ln f x x x x =+, ∴2()f x kx ≤对任意0x >成立1ln xk x+⇔≥对任意0x >成立, 令1ln ()xg x x +=,则问题转化为求()g x 的最大值, 221(1ln )ln '()x x xx g x x x ⋅-+==-,令'()0g x =,解得1x =,当01x <<时,'()0g x >,∴()g x 在(0,1)上是增函数；当1x >时,'()0g x <,∴()g x 在(1,)+∞上是减函数．故()g x 在1x =处取得最大值(1)1g =,∴1k ≥即为所求.【点评】在函数存在性与恒成立问题中求含参数范围过程中,当其中的参数（或关于参数的代数式）能够与其它变量完全分离出来并,且分离后不等式其中一边的函数（或代数式）的最值或范围可求时,常用分离参数法.此类问题可把要求的参变量分离出来,单独放在不等式的一侧,将另一侧看成新函数,于是将问题转化成新函数的最值问题.利用分离参数法来确定不等式(),0f x λ≥,（,x D λ∈为实参数）恒成立中参数λ的取值范围的基本步骤:(1)将参数与变量分离,即化为()()g f x λ≥（或()()g f x λ≤）恒成立的形式； (2)求()f x 在x D ∈上的最大（或最小）值；(3)解不等式()()max g f x λ≥ (或()()min g f x λ≤) ,得λ的取值范围. 【牛刀小试】【20xx 湖南省郴州市上学期第一次教学质量监测】已知函数()log a f x x =,()2log (22)a g x x t =+-,其中0a >且1a ≠,t R ∈．(1)若4t =,且1[,2]4x ∈时,()()()F x g x f x =-的最小值是－2,求实数的值； (2)若01a <<,且1[,2]4x ∈时,有()()f x g x ≥恒成立,求实数的取值范围. 【答案】(1)15；(2)[2,)+∞. 【解析】(1)∵4t =,∴24(1)()()()2log (22)log log a a a x F x g x f x x x x +=-=+-=1log 4(2)a x x=++ 易证1()4(2)h x x x =++在1[,1]4上单调递减,在[1,2]上单调递增,且1()(2)4h h >,∴min ()(1)16h x h ==,max 1()()254h x h ==,∴当1a >时,min ()log 16a F x =,由log 162a =-,解得14a =（舍去）当01a <<时,min ()log 25a F x =,由log 252a =-,解得15a =.综上知实数的值是15.三、主参换位法【例3】已知函数()ln()(x f x e a a =+为常数）是实数集R 上的奇函数,函数()()sin g x f x xλ=+是区间[]1,1-上的减函数,(1)求的值；(2)若[]2()11,1g x t t x λ≤++∈-在上恒成立,求的取值范围.【分析】在第二小题所给条件中出现了两个字母：及,那么解题的关键恰恰就在于该把其中哪个字母看成是一个变量,另一个作为常数.而根据本题中的条件特征显然可将视作自变量,则上述问题即可转化为在(],1-∞-内关于的一次函数大于等于0恒成立的问题,问题即可求解.【解析】(1)1a =(2)由(1)知：()f x x =,()sin g x x x λ∴=+,()g x 在[]11-，上单调递减, ()cos 0g x x λ'∴=+≤cos x λ∴≤-在[]11-，上恒成立,1λ∴≤-，[]max ()(1)sin1g x g λ=-=--, 只需2sin11t t λλ--≤++,2(1)sin110t t λ∴++++≥（其中1λ≤-）恒成立,由上述②结论：可令()2(1)sin110(1f t t λλλ=++++≥≤-）,则2t 101sin110t t +≤⎧⎨--+++≥⎩,21sin10t t t ≤-⎧∴⎨-+≥⎩,而2sin10t t -+≥恒成立,1t ∴≤-.【点评】某些函数存在性与恒成立问题中,当分离参数会遇到讨论的麻烦或者即使能容易分离出参数与变量,但函数的最值却难以求出时,可考虑变换思维角度.即把主元与参数换个位置,再结合其它知识,往往会取得出奇制胜的效果.此类问题的难点常常因为学生的思维定势,易把它看成关于的不等式讨论,从而因计算繁琐出错或者中途夭折；若转换一下思路,把待求的x 为参数,以为变量,构造新的关于参数的函数,再来求解参数应满足的条件这样问题就轻而易举的得到解决了.【牛刀小试】若不等式()2211x m x ->-对任意[]1,1m ∈-恒成立,求实数x 的取值范围.12x <<【解析】()2211x m x ->-可转化为()21210m x x --+<,设()()21210f m m x x =--+<,则()f m 是关于m 的一次型函数,要使()0f m <恒成立,只需()()221201220f x x f x x ⎧=-<⎪⎨-=--+<⎪⎩,解12x <<. 四、数形结合法【例4】已知函数()222f x x kx =-+,在1x ≥-恒有()f x k≥,求实数的取值范围.【分析】为了使题中的条件()f x k≥在[)1,x ∈-+∞恒成立,应能想到构造出一个新的函数()()F x f x k=-,则可把原题转化成所构造新的函数在区间[)1,-+∞时恒大于等于的问题,再利用二次函数的图象性质进行分类讨论,即可使问题得到圆满解决.【解析】令()()222F x f x k x kx k=-=-+-,则()0F x ≥对[)1,x ∈-+∞恒成立,而()F x 是开口向上的抛物线.当图象与x 轴无交点满足0∆<,即()24220k k ∆=--<,解得21k -<<.当图象与x 轴有交点,且在[)1,x ∈-+∞时()0F x ≥,则由二次函数根与系数的分布知识及图象可得：()010212F k ⎧⎪∆≥⎪⎪-≥⎨⎪-⎪-≤-⎪⎩解得32k -≤≤-, 故由①②知31k -≤<.【点评】如果题中所涉及的函数对应的图象、图形较易画出时,往往可通过图象、图形的位置关系建立不等式从而求得参数范围. 解决此类问题经常要结合函数的图象,选择适当的两个函数,利用函数图像的上、下位置关系来确定参数的范围.利用数形结合解决不等式问题关键是构造函数,准确做出函数的图象.常见的有两类函数：若二次函数()20y ax bx c a =++≠大于0恒成立,则有00a >⎧⎨∆<⎩,同理,若二次函数()20y ax bx c a =++≠小于0恒成立,则有00a <⎧⎨∆<⎩.若是二次函数在指定区间上的恒成立问题,还可以利用韦达定理以及根与系数的分布知识求解.【牛刀小试】【20xx 河北省武邑上学期第三次调研考试】已知定义在R 上的奇函数()f x 满足:当0x ≥时,()3f x x =,若不等式()()242f t f m mt ->+对任意实数恒成立,则实数m 的取值范围是（）A．(,-∞ B．()C. ()),0-∞⋃+∞ D．(),-∞⋃+∞【答案】A五、存在性之常用模型及方法【例5】设函数()21ln 2a f x a x x bx -=+-,a R ∈且1a ≠.曲线()y f x =在点()()1,1f 处的切线的斜率为. （1）求的值；（2）若存在[)1,x ∈+∞,使得()1af x a <-,求的取值范围. 【分析】（1）根据条件曲线()y f x =在点()()1,1f 处的切线的斜率为,可以将其转化为关于,的方程,进而求得的值：()()1af x a x b x'=+--,()10f '=⇒()101a a b b +--=⇒=；（2）根据题意分析可得若存在[1,)x ∈+∞,使得不等式()1a f x a <-成立,只需min()1af x a >-即可,因此可通过探求()f x 的单调性进而求得()f x 的最小值,进而得到关于的不等式即可,而由（1）可知()21ln 2a f x a x x x -=+-,则()()()11x a x a f x x ---⎡⎤⎣⎦'=,因此需对的取值范围进行分类讨论并判断()f x 的单调性,从而可以解得的取值范围是()()11,+∞.①当12a ≤时,11aa≤-, 在[)1,+∞上,()0f x '≥,()f x 为增函数,()()()min111122a a f x f ---==-=,令121a aa --<-,即2210a a +-<,解得11a <<. ②当11a <<时,1a >,()()()2minln 112111a a a a a f x f a a a a a a ⎛⎫==++> ⎪-----⎝⎭, 不合题意,无解,10分③当1a >时,显然有()0f x <,01a a >-,∴不等式()1af x a <-恒成立,符合题意,综上,的取值范围是()()11,+∞.【点评】解决函数中存在性问题常见方法有两种：一是直接法同上面所讲恒成立；二是间接法,先求其否定（恒成立）,再求其否定补集即可解决.它的逻辑背景：原命题为",()"x M P x ∀∈的否定为",()"x M P x ∃∈⌝；原命题为",()"x M P x ∃∈的否定为“,()"x M P x ∀∈⌝.处理的原则就是：不熟系问题转化为熟悉问题. 【牛刀小试】已知=)(x f x x +221,=)(x g a x -+)1ln(, (1)若存在]2,0[,21∈x x ,使得)()(21x g x f >,求实数的取值范围； (2)若存在]2,0[,21∈x x ,使得)()(21x g x f =,求实数的取值范围.【解析】()(),f x g x 在[]0,2上都是增函数,所以()f x 的值域，，]40[=A ()g x 的值域]3ln ,[a a B --=.(1) 若存在]2,0[,21∈x x ,使得)()(21x g x f >,则min max )()(x g x f >,即4a -,所以4->a . (2)若存在21,x x 使得)()(21x g x f =,则A B ≠∅,∴4a -≤且ln30a -≥,∴实数的取值围是[]4,ln3-.【迁移运用】1.【20xx 宁夏育才中学上学期第二次月考】设函数3()f x x x =+,x R ∈. 若当02πθ<<时,不等式0)1()sin (>-+m f m f θ恒成立,则实数m 的取值范围是（） A. 1(,1]2 B.1(,1)2C. [1,)+∞D.(,1]-∞ 【答案】D【解析】易得()f x 是奇函数,2()310()f x x f x '=+>⇒在R 上是增函数,又11(sin )(1)sin 1,0sin 111sin 1sin f m f m m m m m θθθθθ>-⇒>-⇒<<<⇒⇒≤--,故选D.2.【20xx 河北省武邑中学2高三上学期第三次调研】若对[),0,x y ∀∈+∞,不等式2242x y x y ax e e +---≤++,恒成立,则实数的最大值是（）A ．14B ． C. D ．12【答案】D3.【20xx 山西省孝义市高三上学期二轮模考】已知函数2ln ()()()x x b f x b R x +-=∈,若存在1[,2]2x ∈,使得()'()f x x f x >-⋅,则实数的取值范围是（）A ．(-∞B ．3(,)2-∞ C. 9(,)4-∞ D ．(,3)-∞ 【答案】C【解析】由题意,得2212()ln ()()x x b x x b f x x +----'=,则()()f x xf x +'＝2ln ()x x b x +-－212()ln ()x x b x x b x +----＝12()x x b x +-．若存在1[,2]2x ∈,使得()'()f x x f x >-⋅,则12()0x x b +->,所以12b x x <+．设1()2g x x x =+,则222121()122x g x x x -'=-=,当122x ≤≤时,()0g x '<；当22x ≤≤时,()0g x '>,所以()g x 在1[,22上单调递减,在2]上单调递增,所以当2x =,函数()g x 取最大值,最大值为19(2)244g =+=,所以max 9()4b g x <=,故选C ． 4.已知=)(x f x x +221,=)(x g a x -+)1ln(,若对任意123,,[0,2]x x x ∈,恒有()()()123f x f x g x +>,求实数的取值范围是 .【答案】[)ln3,+∞【解析】()(),f x g x 在[]0,2上都是增函数,所以()f x 的值域，，]40[=A ()g x 的值域]3ln ,[a a B --=.若对任意123,,[0,2]x x x ∈,恒有()()()123f x f x g x +>,则2max min )()(x g x f >,即a ->3ln 0,所以3ln >a . 5. 已知函数2(),([2,2])f x x x ∈-=,2()sin(2)3,[0,]62g x a x a x ππ=++∈, 1[2,2]x ∀∈-,001[0,],()()2x g x f x π∃∈=总使得成立,则实数的取值范围是．【答案】(,4][6,)-∞-+∞6.【20xx 江西省新余市高三第二次模拟考试】设函数x x e x f 1)(22+=,x ex e x g 2)(=,对),0(,21+∞∈∀x x ,不等式1)()(21+≤k x f k x g 恒成立,则正数的取值范围为 . 【答案】[)1,+∞【解析】对于函数()f x ,当0x >时, 22211()2e x f x e x e x x +==+≥=,所以当2(0,)x ∈+∞,函数()f x 有最小值2e ；对于函数2()x e x g x e =,2(1)'()xe x g x e-=,当01,'()0x g x <<>；当1,'()0x g x ><,所以当1x =时,函数()g x 有最大值(1)g e =.又不等式1)()(21+≤k x f k x g 恒成立,0k >,所以21e e k k ≤+,所以1k ≥. 7.设函数f (x )＝ax ＋sin x ＋cos x ．若函数f (x )的图象上存在不同的两点A ,B ,使得曲线y ＝f (x )在点A ,B 处的切线互相垂直,则实数a 的取值范围为．【答案】]1,1[-【解析】因为),4cos(2sin cos )(π++=-+='x a x x a x f则存在实数2,1x x ,使得1))4cos(2))(4cos(2(21-=++++ππx a x a 成立.不妨设11)(0,4k a x a π=+∈则22)[4k a x a π=+∈因此222120()2,12,1,1 1.k k a a a a <-≤-≤-≤-≤≤ 8.已知函数e ()ln ,()e xxf x mx a x mg x =--=,其中m ,a 均为实数． (1)求()g x 的极值；(2)设1,0m a =<,若对任意的12,[3,4]x x ∈12()x x ≠,212111()()()()f x f xg x g x -<-恒成立,求的最小值；(3)设2a =,若对任意给定的0(0,e]x ∈,在区间(0,e]上总存在1212,()t t t t ≠,使得120()()()f t f t g x == 成立,求m 的取值范围．【答案】(1)极大值为1,无极小值；(2) 3 -22e 3；(3)3[,)e 1+∞-．【解析】（1）e(1)()e xx g x -'=,令()0g x '=,得x = 1． ………………… 1分列表如下：∵g (1) = 1,∴y =()g x 的极大值为1,无极小值． …………………3分（2）当1,0m a =<时,()ln 1f x x a x =--,(0,)x ∈+∞．∵()0x af x x-'=>在[3,4]恒成立,∴()f x 在[3,4]上为增函数． …………………4分设1e ()()e xh x g x x ==,∵12e (1)()x x h x x --'=> 0在[3,4]恒成立, ∴()h x 在[3,4]上为增函数． …………………5分设21x x >,则212111()()()()f x f xg x g x -<-等价于2121()()()()f x f x h x h x -<-, 即2211()()()()f x h x f x h x -<-．设1e ()()()ln 1e xu x f x h x x a x x=-=---⋅,则u (x )在[3,4]为减函数．∴21e (1)()10e x a x u x x x -'=--⋅≤在（3,4）上恒成立． …………………6分 ∴11e ex x a x x---+≥恒成立．设11e ()ex x v x x x --=-+,∵112e (1)()1e x x x v x x ---'=-+=121131e [()]24x x ---+,x ∈3,4],∴1221133e [()]e 1244x x --+>>,∴()v x '< 0,()v x 为减函数．∴()v x 在3,4]上的最大值为v (3) = 3 -22e 3． ………………… 8分∴a ≥3 -22e 3,∴的最小值为3 -22e 3． …………………9分（3）由（1）知()g x 在(0,e]上的值域为(0,1]． …………………10分 ∵()2ln f x mx x m =--,(0,)x ∈+∞,当0m =时,()2ln f x x =-在(0,e]为减函数,不合题意． ………………… 11分当0m ≠时,2()()m x m f x x-'=,由题意知()f x 在(0,e]不单调,所以20e m <<,即2em >．① …………………12分此时()f x 在2(0,)m 上递减,在2(,e)m上递增, ∴(e)1f ≥,即(e)e 21f m m =--≥,解得3e 1m -≥．② 由①②,得3e 1m -≥． …………………13分 ∵1(0,e]∈,∴2()(1)0f f m =≤成立． …………………14分下证存在2(0,]t m∈,使得()f t ≥1．取e m t -=,先证e 2m m-<,即证2e 0m m ->．③ 设()2e x w x x =-,则()2e 10x w x '=->在3[,)e 1+∞-时恒成立． ∴()w x 在3[,)e 1+∞-时为增函数．∴3e ))01((w x w ->≥,∴③成立．再证()e m f -≥1． ∵e e 3()1e 1m m f m m m --+=>>-≥,∴3e 1m -≥时,命题成立．综上所述,m 的取值范围为3[,)e 1+∞-． …………………16分 9.【20xx 山西省孝义市高三上学期二轮模考】设函数2()ln f x ax a x =--,1()xe g x x e =-,其中a R ∈,e 2.718=为自然对数的底数.（1）讨论()f x 的单调性；（2）证明：当1x >时,()0g x >；（3）确定的所有可能取值,使得()()f x g x >在(1,)+∞区间内恒成立.【答案】（1）当x∈（时()f x 单调递减；当x∈+)∞时,()f x 单调递增；（2）详见解析；（3）a ∈1+)2∞[，．【解析】（1）由2()ln f x ax a x =--,得2121'()2(0)ax f x ax x x x-=-=>. 当0a ≤时,'()0f x <在(0,)+∞成立,则()f x 为(0,)+∞上的减函数；当0a >时,由'()0f x =,得2x a==±,∴当x ∈时,'()0f x <,当)x ∈+∞时,'()0f x >.则()f x 在(0,2a 上为减函数,在)2a+∞上为增函数. 综上,当0a ≤时,()f x 为(0,)+∞上的减函数；当0a >时,()f x 在(0,)2a上为减函数,在)+∞上为增函数. （2）证明：要证()0(1)g x x >>,即10x e x e ->,即证1x ex e >,也就是证x e e x >. 令()xe h x x=,则2(1)'()x e x h x x -=,∴()h x 在(1,)+∞上单调递增,则min ()(1)h x h e ==, 即当1x >时,()h x e >,∴当1x >时,()0g x >；综上所述,1x >,'()0x Φ>,()x Φ在区间(1,)+∞单调递增, ∴'()'(1)0t x t >≥,即()t x 在区间(1,)+∞单调递增,∴12a ≥.10.【20xx 四川省资阳市高三上学期第一次诊断】已知函数()()ln bf x a x b x x =++(其中a b ∈R ，).(Ⅰ) 当4b =-时,若()f x 在其定义域内为单调函数,求的取值范围；(Ⅱ) 当1a =-时,是否存在实数,使得当2[e e ]x ∈，时,不等式()0f x >恒成立,如果存在,求的取值范围,如果不存在,说明理由（其中是自然对数的底数,＝2.71828…）.【答案】(Ⅰ) (,0][1,)-∞+∞；(Ⅱ) 2e (,)e 1b ∈+∞-．【解析】(Ⅰ) 由题0x >,4()()4ln f x a x x x =--,2224444()(1)ax x a f x a x x x -+'=+-=.①当0a ≤时,知()0f x '<,则()f x 是单调递减函数；②当0a >时,只有对于0x >,不等式2440ax x a -+≥恒成立,才能使()f x 为单调函数,只需22(4)160a ∆=--≤,解之得11a a -或≤≥,此时1a ≥．综上所述,的取值范围是(,0][1,)-∞+∞． (Ⅱ) ()ln bf x b x x x=--,其中0x >,222()1b b x bx bf x x x x -++'=-+=． (ⅰ) 当0b ≤时,()0f x '<,于是()f x 在(0)+∞，上为减函数,则在2[e e ]，上也为减函数, 知max 1()(e)e (1)e 0e eb f x f b b ==--=--<恒成立,不合题意,舍去． (ⅱ) 当0b >时,由()0f x '=得x =．列表得知max1()(e)e (1)e e e b f x f b b ==--=--,而211e 2e(1)e (1)e 0e e e 1e 1b -----=<++≤,于是max()0f x <恒成立,不合题意,e >,即2e e 1b >+,则()f x 在上为增函数,在,+∞)上为减函数,要使在2[e e ]，恒有()0f x >恒成立,则必有2(e)0(e )0f f >⎧⎨>⎩，，则22e 0e 2e 0e b b b b ⎧-->⎪⎪⎨⎪-->⎪⎩，，所以243242e e e 1e e e .2e 1b b ⎧>=⎪⎪--⎨⎪>⎪-⎩，由于32232e e (2e 1)e 3e 10---=-+<,则244322e e e e 1e e 2e 1=>---,所以2e e 1b >-． 11. 【20xx 湖北省襄阳市四校高三上学期期中联考】已知函数21()(1)2x f x x e ax =--()a R ∈()I 当1a ≤时,求()f x 的单调区间；()II 当(0,+)x ∈∞时,()y f x '=的图象恒在32(1)y ax x a x =+--的图象上方,求的取值范围.【答案】（Ⅰ）当0a ≤时,单调增区间是(0,)+∞,单调减区间是(,0)-∞；当01a <<时,单调增区间是(,ln )a -∞,(0,)+∞,单调减区间是(ln ,0)a ；当1a =时,单调增区间是(,)-∞+∞,无减区间；（Ⅱ）1(,]2-∞．【解析】()I ()()xxf x xe ax x e a '=-=-当0a ≤时,0x e a ->,∴(,0)x ∈-∞时,()0f x '<,()f x 单调递减(0,)x ∈+∞时,()0f x '>,()f x 单调递增当01a <≤时,令()0f x '=得0ln x x a ==或． (i) 当01a <<时,ln 0a <,故：(,ln )x a ∈-∞时,()0f x '>,()f x 单调递增, (ln ,0)x a ∈ 时,()0f x '<,()f x 单调递减,(0,)x ∈+∞时,()0f x '>,()f x 单调递增；(ii) 当1a =时,ln 0a =, ()(1)x xf x xe ax x e '=-=-0≥恒成立,()f x 在(,)-∞+∞上单调递增,无减区间；综上,当0a ≤时,()f x 的单调增区间是(0,)+∞,单调减区间是(,0)-∞；当01a <<时,()f x 的单调增区间是(,ln )a -∞(0,)+∞和,单调减区间是(ln ,0)a ；当1a =时,()f x 的单调增区间是(,)-∞+∞,无减区间.()II 由()I 知()x f x xe ax '=-当(0,+)x ∈∞时,()y f x '=的图象恒在32(1)y ax x a x =+--的图象上方,即32(1)x xe ax ax x a x ->+--对(0,+)x ∈∞恒成立即 210x e ax x --->对(0,+)x ∈∞恒成立记 2()1x g x e ax x =--- (0)x >,∴()()21xg x e ax h x '=--=()'2x h x e a ∴=-(i) 当12a ≤时,()'20xh x e a =->恒成立,()g x '在(0,)+∞上单调递增, ∴()'(0)0g x g '>=, ∴()g x 在(0,)+∞上单调递增 ∴()(0)0g x g >=,符合题意；(ii) 当12a >时,令()'0h x =得ln(2)x a = (0,ln(2))x a ∴∈时,()'0h x <,∴()g x '在(0,ln(2))a 上单调递减∴(0,ln(2))x a ∈时,()'(0)0g x g '<= ∴()g x 在(0,ln(2))a 上单调递减, ∴ (0,ln(2))x a ∈时,()(0)0g x g <=,不符合题意综上可得的取值范围是1(,]2-∞.12. 【20xx 广东省惠州市第二次调研】已知函数()ln f x x =,()()h x a x a R =∈. （Ⅰ）函数()f x 的图象与()h x 的图象无公共点,求实数的取值范围；（Ⅱ）是否存在实数m ,使得对任意的1(,)2x ∈+∞,都有函数()my f x x=+的图象在()xe g x x=的图象的下方？若存在,请求出整数m 的最大值；若不存在,请说理由.（参考数据：ln 20.6931=,ln3 1.0986= 1.3956==）. 【答案】（Ⅰ）1(,)e+∞,（Ⅱ）1（Ⅱ）假设存在实数m 满足题意,则不等式ln x m e x x x +<对1(,)2x ∈+∞恒成立.即ln x m e x x <-对1(,)2x ∈+∞恒成立.令()ln xr x e x x =-,则'()ln 1xr x e x =--,令()ln 1xx e x ϕ=--,则1'()x x e x ϕ=-,∵'()x ϕ在1(,)2+∞上单调递增,121'()202e ϕ=-<,'(1)10e ϕ=->,且'()x ϕ的图象在1(,1)2上连续,∴存在01(,1)2x ∈,使得0'()0x ϕ=,即0010xe x -=,则00ln x x =-,∴ 当01(,)2x x ∈时,()x ϕ单调递减；当0(,)x x ∈+∞时,()x ϕ单调递增, 则()x ϕ取到最小值000001()ln 11xx e x x x ϕ=--=+-110≥=>, ∴ '()0r x >,即()r x 在区间1(,)2+∞内单调递增.11221111()ln ln 2 1.995252222m r e e ≤=-=+=,∴存在实数m 满足题意,且最大整数m 的值为.13.【20xx 河南省天一大联考】已知函数()ln f x b x =．（1）当1b =时,求函数2()()G x x x f x =--在区间1,2e ⎡⎤⎢⎥⎣⎦上的最大值与最小值；（2）若在[]1,e 上存在0x ,使得0001()bx f x x +-<-成立,求的取值范围．【答案】（1）21e e --,；（2）21(,2)(,)1e e +-∞-+∞-. 【解析】（1）当1b =时,2()()G x x xf x =--2ln (0)x x x x =-->,(21)(1)'()x x G x x+-=,令'()0G x =,得1x =,当变化时,()G x ,'()G x 的变化情况如下表：因为111()ln ln 212424G =--=-+<,(1)0G =, 2()1(1)11G e e e e e =--=-->,所以2()()G x x x f x =--在区间1,2e ⎡⎤⎢⎥⎣⎦上的最大值与最小值分别为：2max ()()1G x G e e e ==--,min ()(1)0G x G ==．（2）设1()ln bh x x b x x+=-+．若在[]1,e 上存在0x ,使得0001()b x f x x +-<-,即0001ln 0b x b x x +-+<成立,则只需要函数1()ln bh x x b x x+=-+在[]1,e 上的最小值小于零．又2221(1)'()1b b x bx b h x x x x +--+=--=[]2(1)(1)x x b x +-+=, 令'()0h x =,得1x =-（舍去）或1x b =+．①当1b e +≥,即1b e ≥-时,()h x 在[]1,e 上单调递减,故()h x 在[]1,e 上的最小值为()h e ,由1()0bh e e b e +=+-<,可得211e b e +>-．因为2111e e e +>--,所以211e b e +>-． ②当11b +≤,即0b ≤时,()h x 在[]1,e 上单调递增, 故()h x 在[]1,e 上的最小值为(1)h ,由(1)110h b =++<, 可得2b <-（满足0b ≤）．③当11b e <+<,即01b e <<-时,()h x 在(1,1)b +上单调递减,在(1,)b e +上单调递增,故()h x 在[]1,e 上的最小值为(1)2ln(1)h b b b b +=+-+．因为0ln(1)1b <+<,所以0ln(1)b b b <+<,所以2ln(1)2b b b +-+>,即(1)2h b +>,不满足题意,舍去．综上可得2b <-或211e b e +>-,所以实数的取值范围为21(,2)(,)1e e +-∞-+∞-． 14. 【20xx 江西省新余市模拟】已知函数a x x a xf xln )(2-+=（0>a ,且1≠a ）. （1）求函数)(x f 的单调区间；（2）若存在]1,1[,21-∈x x ,使得1|)()(|21-≥-e x f x f （是自然对数的底数）,求实数的取值范围.【答案】（1）函数)(x f 的单调增区间为),0(+∞,单调减区间为)0,(-∞；（2）),[]1,0(+∞∈e ea ．【解析】（1）a a x a x a a x f xxln )1(2ln 2ln )('-+=-+= ∵当1>a 时,0ln >a ,a a x ln )1(-在R 上是增函数, 当10<<a 时,0ln <a ,a a x ln )1(-在R 上也是增函数, ∴当1>a 或10<<a 时,总有)('x f 在R 上是增函数,又0)0('=f ,∴0)('>x f 的解集为),0(+∞,0)('<x f 的解集为)0,(-∞, 故函数)(x f 的单调增区间为),0(+∞,单调减区间为)0,(-∞. （2）∵存在]1,1[,21-∈x x ,使得1|)()(|21-≥-e x f x f 成立, 而当]1,1[-∈x 时,min max 21)()(|)()(|x f x f x f x f -≤-, ∴只要1)()(min max -≥-e x f x f 即可. 又∵,)('x f ,)(x f 的变化情况如下表所示：∴函数)(x f 在]0,1[-上是减函数,在]1,0[上是增函数, ∴当]1,1[-∈x 时,)(x f 的最小值1)0()(min ==f x f ,)(x f 的最大值max )(x f 为)1(-f 和)1(f 中的最大者.∵a a a a a a a f f ln 21)ln 11()ln 1()1()1(--=++--+=--, 令a aa a g ln 21)(--=)0(>a , ∵0)11(211)('22>-=-+=a a a a g ,∴a aa a g ln 21)(--=在),0(+∞∈a 上是增函数. 而0)1(=g ,故当1>a 时,0)(>a g ,即)1()1(->f f ；当10<<a 时,0)(<a g ,即)1()1(-<f f .∴当1>a 时,1)0()1(-≥-e f f ,即1ln -≥-e a a ,函数a a y ln -=在),1(+∞∈a 上是增函数,解得e a ≥；当10<<a 时,1)0()1(-≥--e f f ,即1ln 1-≥+e a a, 函数a a y ln 1+=在)1,0(∈a 上是减函数,解得ea 10≤<. 综上所述,所求的取值范围为),[]1,0(+∞∈e e a . 15.【20xx 浙江省绍兴市柯桥区二模】设函数()2k k f x a xb =-+,其中{}0,1,2a k >∈.（1）若()2f x 在(],1a a +上有最小值, 求实数的取值范围；（2）当2a ≥,92b =-时, 记()()1g x f x =,若对任意[]12,,1x x a a ∈+,总存在[]0,1x a a ∈+,使得()()()1202g x g x g x +≤,求0x 的取值范围.【答案】(1)()0,2；(2)[)[)2,34,+∞.()()(){}22max 9999max ,1max 2,1max 2,2222g x g a g a a a a a a a a a ⎧⎫⎧⎫=+=----=----⎨⎬⎨⎬⎩⎭⎩⎭()()22223299223932322a a a a a a a a a a -----=-++=--+；∴当3a ≥时,222299222a a a a --≤--, 即2299222a a a a --≤--,即()()1g a g a ≤+, 故()()max 1g x g a =+,从而[)014,x a =+∈+∞；当23a ≤<时,222299222a a a a -->--, 即2299222a a a a -->--,即()()1g a g a >+,故()()max g x g a =,从而[)02,3x a =∈；综上所述,0x 的取值范围为[)[)2,34,+∞。

圆锥曲线综合问题—5. 存在性问题

圆锥曲线综合问题—5. 存在性问题（一）存在性问题是近几年高考试题对解析几何考查的一种热点题型，以判断满足条件的点、直线、参数是否存在，证明直线与圆锥曲线的位置关系，数量关系(等量或不等量)为主要呈现方式，多以解答题的形式考查；对这类问题，若存在，需要找出来，若不存在，需说明理由，其解法有：一、假设法假设法的一般解法是，先假定存在，然后根据已知条件或其他定理、公理、法则等推导下去，如与已知定理、公理、法则等不发生矛盾，即推出的结果合理，并经验证成立，那么结论成立，若发生矛盾，则结论不成立。

1.（2015届湖南省浏阳一中、攸县一中、醴陵一中三校高三联考）已知椭圆:C 22221(0)x y a b a b +=>>的焦距为，且过点31(,)22A .（1）求椭圆的方程；（2）已知:1l y kx =-，是否存在k 使得点A 关于l 的对称点B （不同于点A ）在椭圆C 上？若存在求出此时直线l 的方程，若不存在说明理由.【答案】（1）2213x y +=；（2）不存在k 满足条件2. 【2015届吉林省实验中学高三上学期第四次模拟考试数学（理）】已知椭圆C 的中心在原点O ，焦点在x 轴上，离心率为12，右焦点到右顶点的距离为1；（Ⅰ）求椭圆C 的标准方程；（Ⅱ）是否存在与椭圆C 交于,A B 两点的直线l ：()y kx m k =+∈R ，使得22OA OB OA OB +=-成立？若存在，求出实数m 的取值范围，若不存在，请说明理由.【答案】（1）22143x y +=（2）(-∞，-7]∪[7，+∞)3. （河北省容城中学2014届高三上学期第一次月考数学（理）试题）已知点A (-2,0),B (2,0),直线P A 与直线PB 的斜率之积为34-，记点P 的轨迹为曲线C .(1)求曲线C 的方程.(2)设M ,N 是曲线C 上任意两点,且OM ON OM ON -=+，问是否存在以原点为圆心且与MN 总相切的圆?若存在,求出该圆的方程;若不存在,请说明理由.【答案】（1）221(0)43x y y +=≠(2) 存在以原点为圆心且与MN 总相切的圆，其方程为22127x y +=4. 【浙江省温州八校2014届高三10月期初联考数学(理)】如图，椭圆2222+=1(>>0)x y C a b a b ：经过点3(1,),2P 离心率1=2e ，直线l 的方程为=4x .(Ⅰ)求椭圆C 的方程；(Ⅱ)AB 是经过右焦点F 的任一弦(不经过点P )，设直线AB 与直线l 相交于点M ，记,,PA PB PM 的斜率分别为123,,.k k k 问:是否存在常数λ，使得123+=.k k k λ若存在求λ的值；若不存在，说明理由.【答案】（1）22143x y +=（2）2λ=5. 【中原名校联盟2013-2014学年高三上期第一次摸底考试理】（本小题满分12分）已知椭圆长轴的左右端点分别为A ，B ，短轴的上端点为M ，O 为椭圆的中心，F 为椭圆的右焦点，且AF u u u r ·FB uur ＝1，｜OF uu u r｜＝1．（Ⅰ）求椭圆的标准方程；（2）若直线l 交椭圆于P ，Q 两点，问：是否存在直线l ，使得点F 恰为△PQM 的垂心?若存在，求出直线l 的方程；若不存在，请说明理由．【答案】（1）2212x y +=（2）存在，方程为43y x =-6. 【河北省邯郸市2014届高三9月摸底考试数学理科】（本题满分12分）已知定点(3,0)G -，S 是圆22:(3)72C x y -+=（C 为圆心）上的动点，SG 的垂直平分线与SC 交于点E .设点E 的轨迹为M . (1),求M 的方程； (2)是否存在斜率为1的直线l ，使得直线l 与曲线M 相交于A ，B 两点，且以AB 为直径的圆恰好经过原点？若存在，求出直线l 的方程；若不存在，请说明理由．【答案】（1）221189x y +=（2）y x y x =+=-7. 直线1ax y -= 与曲线2221x y -=相交于P 、Q 两点。

2021高中同步创新课堂生物优化方案人教版必修1习题：第三章章末综合检测(三) Word版含答案

章末综合检测(三)1．下列有关细胞膜制备及观看的叙述，正确的是()A．家鸡的红细胞是最佳的试验材料B．若选用洋葱鳞片叶表皮细胞作试验材料，则应先用蛋白酶处理以去除细胞壁C．制备细胞膜应先利用吸水涨破法，再利用离心法猎取D．可以直接用高倍镜进行观看解析：选C。

家鸡的红细胞中含有细胞核和众多的细胞器，制备的细胞膜中会有核膜和细胞器膜；植物细胞壁的主要成分是纤维素和果胶，用蛋白酶处理无法去掉细胞壁；用显微镜观看时应先用低倍镜，再用高倍镜。

2．对细胞内各种生物膜的结构和组成的叙述，错误的是()A．主要由蛋白质、脂质和少量糖类组成B．蛋白质在细胞膜行使功能时起重要作用C．不同生物膜上的蛋白质的种类和数量不同D．细胞膜与各种细胞器膜的化学组成完全相同解析：选D。

细胞膜主要由脂质(50%)和蛋白质(40%)组成，糖类较少，约占2%～10%。

蛋白质在细胞膜行使功能时起重要作用，因此，不同生物膜的蛋白质种类和数量不同。

细胞膜与各种细胞器膜的功能不同，所含的蛋白质种类和数量不同。

3．(2022·宿迁高一检测)下图为细胞间信息沟通的一种方式，下列有关叙述不正确的是()A．图示反映了细胞膜具有细胞间信息沟通的功能B．图中乙细胞表示靶细胞C．图中a表示信号分子(如激素)D．图中b表示细胞膜上的载体蛋白解析：选D。

由图可知，甲细胞分泌的信号分子通过血液运送作用于乙细胞，实现细胞间的信息沟通，体现了细胞膜具有细胞间信息沟通的功能，A项正确；乙细胞为接受信号分子的细胞，即靶细胞，B项正确；a由甲细胞产生，而后经体液运输作用于乙细胞，则a应为信号分子，C项正确；乙细胞通过其细胞膜上的b 物质与a物质识别，则b应为靶细胞膜上的受体，D项错误。

4．争辩显示，台湾乳白蚁粪便具有一种特殊的功效，即其所含有的起爱护作用的细菌能阻挡并杀死入侵乳白蚁的真菌。

下列相关的说法不正确的是()A．台湾乳白蚁、细菌和真菌三种生物都存在以核膜为界限的细胞核B．对台湾乳白蚁具有爱护作用的细菌的遗传物质是暴露的DNAC．台湾乳白蚁在咀嚼木材时所需要的能量主要由线粒体供应D．台湾乳白蚁、细菌和真菌都含有合成蛋白质的机器——核糖体解析：选A。

高考数学(文)二轮复习专题三不等式第2讲三个二次关系与恒成立问题、存在性问题 Word版含答案

第2讲三个二次关系与恒成立问题、存在性问题【课前热身】第2讲三个二次关系与恒成立问题、存在性问题(本讲对应学生用书第21~22页)1.(必修5 P69练习3改编)不等式x2+x-2<0的解集为.【答案】(-2，1)【解析】方程x2+x-2=0的根为x1=-2，x2=1，故不等式x2+x-2<0的解集为(-2，1).2.(必修5 P73习题6改编)已知不等式ax2+bx-1<0的解集为{x|x<3或x>4}，则a=，b=.【答案】-112712【解析】由题意知3和4是方程ax2+bx-1=0的两根，所以a(x-3)(x-4)=0，所以a=-1 12，b=7 12.3.(必修5 P94习题11改编)已知关于x的不等式x2-ax+2a>0在R上恒成立，则实数a 的取值范围是.【答案】(0，8)【解析】因为x2-ax+2a>0在R上恒成立，所以Δ=a2-4×2a<0，所以0<a<8.4.(必修5 P71练习5改编)在R上定义运算：x*y=x(1-y)，若不等式(x-a)*(x+a)<1对任意实数x恒成立，则实数a的取值范围是.【答案】13 -22⎛⎫ ⎪⎝⎭，【解析】依题意知x-a-x2+a2<1恒成立，即21-2x⎛⎫⎪⎝⎭+23-4a a⎛⎫+⎪⎝⎭>0恒成立，于是a2-a-34<0恒成立，解得-12<a<32.5.(必修1 P32习题7改编)若定义在R上的二次函数f(x)=ax2-4ax+b在区间[0，2]上是增函数，且f(m)≥f(0)，则实数m的取值范围是.【答案】{m|0≤m≤4}【解析】由函数的对称轴为x=2，且在[0，2]上为增函数，知a<0，根据函数图象可得实数m的取值范围是{m|0≤m≤4}.【课堂导学】含参一元二次不等式的解法例1解关于x的一元二次不等式(x-2)(ax-2)>0.【解答】当a=0时，原不等式可化为x-2<0，所以x<2.当a≠0时，原不等式化为a(x-2)x-2a>0，①当a>1时，2a<2，原不等式化为(x-2)2-xa⎛⎫⎪⎝⎭>0，所以x<2a或x>2.②当a=1时，2a=2，原不等式化为(x-2)2>0，所以x∈R且x≠2.③当0<a<1时，2a>2，原不等式化为(x-2)2-xa⎛⎫⎪⎝⎭>0，则x<2或x>2a.④当a<0时，2a<2，原不等式化为(x-2)2-xa⎛⎫⎪⎝⎭<0，所以2a<x<2.综上所述，当a=0时，原不等式的解集为{x|x<2}；当a>1时，原不等式的解集为2|2x x xa⎧⎫<>⎨⎬⎩⎭或；当a=1时，原不等式的解集为{x|x∈R且x≠2}；当0<a<1时，原不等式的解集为22x x xa⎧⎫<>⎨⎬⎩⎭或；当a<0时，原不等式的解集为22x xa⎧⎫<<⎨⎬⎩⎭.变式解关于x的一元二次不等式ax2+(a-1)x-1>0. 【解答】由ax2+(a-1)x-1>0，得(ax-1)(x+1)>0.当a>0时，(ax-1)(x+1)>0⇔1-xa⎛⎫⎪⎝⎭(x+1)>0⇔x<-1或x>1a；当-1<a<0时，(ax-1)(x+1)>0⇔1-xa⎛⎫⎪⎝⎭(x+1)<0⇔1a<x<-1；当a=-1时，(ax-1)(x+1)>0⇔-(x+1)2>0⇔(x+1)2<0⇔x∈∅；当a<-1时，(ax-1)(x+1)>0⇔1-xa⎛⎫⎪⎝⎭(x+1)<0⇔-1<x<1a.综上所述，当a>0时，不等式的解集为1|-1x x xa⎧⎫<>⎨⎬⎩⎭或；当-1<a<0时，不等式的解集为1|-1x xa⎧⎫<<⎨⎬⎩⎭；当a=-1时，不等式的解集为∅；当a<-1时，不等式的解集为1|-1x xa⎧⎫<<⎨⎬⎩⎭.三个二次之间的关系例2 (2016·苏州调研测试)已知函数f (x )=x|x-a|，a ∈R ，g (x )=x 2-1. (1)当a=1时，解不等式f (x )≥g (x )；(2)记函数f (x )在区间[0，2]上的最大值为F (a )，求F (a )的表达式. 【解答】(1)由f (x )≥g (x )，当a=1时，即解不等式x|x-1|≥x 2-1. 当x ≥1时，不等式为x 2-x ≥x 2-1，解得x ≤1，所以x=1；当x<1时，不等式为x-x 2≥x 2-1，解得-12≤x ≤1，所以-12≤x<1.综上，不等式f (x )≥g (x )的解集为1-12⎡⎤⎢⎥⎣⎦，. (2)因为x ∈[0，2]，当a ≤0时，f (x )=x 2-ax ，则f (x )在区间[0，2]上是增函数，所以F (a )=f (2)=4-2a.当0<a<2时，f (x )=22-0-2x ax x a x ax a x ⎧+≤<⎨≤≤⎩，，，，则f (x )在区间02a ⎡⎤⎢⎥⎣⎦，上是增函数，在区间2a a ⎡⎤⎢⎥⎣⎦，上是减函数，在区间[a ，2]上是增函数，所以F (a )=max (2)2a f f ⎧⎫⎛⎫⎨⎬ ⎪⎝⎭⎩⎭，，而f 2a ⎛⎫ ⎪⎝⎭=24a ，f (2)=4-2a ，令f 2a ⎛⎫ ⎪⎝⎭<f (2)，即24a <4-2a ，解得-4-42<a<-4+42，所以当0<a<2-4时，F (a )=4-2a ；令f 2a ⎛⎫ ⎪⎝⎭≥f (2)，即24a ≥4-2a ，解得a ≤-4-42或a ≥-4+2，所以当42-4≤a<2时，F (a )=24a . 当a ≥2时，f (x )=-x 2+ax ，当1≤2a <2，即2≤a<4时，f (x )在区间02a ⎡⎤⎢⎥⎣⎦，上是增函数，在22a ⎡⎤⎢⎥⎣⎦，上是减函数，则F (a )=f 2a ⎛⎫ ⎪⎝⎭=24a ；当2a≥2，即a ≥4时，f (x )在区间[0，2]上是增函数，则F (a )=f (2)=2a-4；综上，F (a )=24-242-442-4442-4 4.a a aa a a ⎧<⎪⎪≤<⎨⎪≥⎪⎩，，，，，变式 (2016·苏锡常镇一调)已知函数f (x )=2x-1+a ，g (x )=bf (1-x )，其中a ，b ∈R .若关于x 的不等式f (x )≥g (x )的解的最小值为2，则实数a 的取值范围是 .【答案】(-∞，-2]∪1-4∞⎛⎫+ ⎪⎝⎭，【解析】因为g (x )=b (2-x +a )，所以f (x )≥g (x )，即2x-1+a ≥2xb+ab ，即(2x )2-2a (b-1)2x -2b ≥0.由二次不等式与二次方程的根的关系知，关于2x 的方程(2x )2-2a (b-1)2x -2b=0的2x 的值分别为4，-2b .因为2x 取正值，要想2x 最小为4，所以-2b≤0，即b ≥0.又因为4-2b =2a (b-1)，所以b=4(2)41a a ++≥0，解得a ≤-2或a>-14.恒成立问题与存在性问题例3已知函数f(x)=x2+2ax-a+2.(1)若对于任意的x∈R，f(x)≥0恒成立，求实数a的取值范围；(2)若对于任意的x∈[-1，1]，f(x)≥0恒成立，求实数a的取值范围；(3)若对于任意的a∈[-1，1]，x2+2ax-a+2>0恒成立，求实数x的取值范围. 【点拨】恒成立问题中注意变更主元法的运用.【解答】(1)若对于任意的x∈R，f(x)≥0恒成立，需满足Δ=4a2-4(-a+2)≤0，解得-2≤a≤1.故实数a的取值范围是[-2，1].(2)由题知对称轴方程为x=-a，当-a<-1，即a>1时，f(x)min=f(-1)=3-3a≥0，解得a≤1，与已知矛盾，舍去；当-a>1，即a<-1时f(x)min=f(1)=3+a≥0，解得-3≤a<-1；当-1≤a≤1时，f(x)min=f(-a)=-a2-a+2≥0，解得-1≤a≤1.综上，实数a的取值范围是[-3，1].(3)对于任意的a∈[-1，1]，x2+2ax-a+2>0恒成立，等价于g(a)=(2x-1)a+x2+2>0，所以222-120-2120x xx x⎧++>⎨++>⎩，，解得x≠-1，所以x的取值范围是{x|x ≠-1}.变式(2016·盐城中学)已知函数f(x)=22x x ax++，x∈[1，+∞).(1)若对任意的x∈[1，+∞)，f(x)>0恒成立，求实数a的取值范围；(2)若对任意的a∈[-1，1]，f(x)>4恒成立，求实数x的取值范围.【解答】(1)若对任意的x∈[1，+∞)，f(x)>0恒成立，即22 x xax++>0，x∈[1，+∞)恒成立，亦即x2+2x+a>0，x∈[1，+∞)恒成立，即a>-x2-2x，x∈[1，+∞)恒成立，即a>(-x2-2x)max，x∈[1，+∞)，而(-x2-2x)max=-3，x∈[1，+∞)，所以a>-3.所以实数a的取值范围为{a|a>-3}.(2)因为a∈[-1，1]时，f(x)>4恒成立，即22x x ax++>4，x∈[1，+∞)恒成立，所以x2-2x+a>0对a∈[-1，1]恒成立，把g(a)=a+x2-2x看成a的一次函数，则使g(a)>0对a∈[-1，1]恒成立的条件是(1)0(-1)0gg>⎧⎨>⎩，，即22-210-2-10x xx x⎧+>⎨>⎩，，解得x<1-2或x>2+1.又x≥1，所以x>2+1，故所求x的取值范围是(2+1，+∞).【课堂评价】1.(2016·全国卷Ⅰ)设集合A={x|x2-4x+3<0}，B={x|2x-3>0}，则A∩B=. 【答案】332⎛⎫⎪⎝⎭，【解析】因为集合A=(1，3)，B=32∞⎛⎫+ ⎪⎝⎭，，所以A ∩B=332⎛⎫ ⎪⎝⎭，.2.(2016·启东调研测试)已知偶函数f (x )在[0，+∞)上单调递增，且f (3)=0，则不等式f (x 2-2x )<0的解集为 . 【答案】(-1，3)【解析】根据偶函数的性质，可得-3<x 2-2x<3，解得-1<x<3，从而不等式的解集为(-1，3).3.(2016·扬州中学)已知函数f (x )=13x 3+2x ，对任意的t ∈[-3，3]，f (tx-2)+f (x )<0恒成立，则实数x 的取值范围是 .【答案】51--33⎛⎫⎪⎝⎭，【解析】易知函数f (x )=13x 3+2x 是R 上的奇函数且单调递增，f (tx-2)+f (x )<0化为f (tx-2)<f (-x )，即tx-2<-x ，问题变为g (t )=(x+1)t-2<0在t ∈[-3，3]上恒成立，故有(-3)0(3)0g g <⎧⎨<⎩，，解得-53<x<-13.4.(2016·徐州、连云港、宿迁三检)已知对满足x+y+4=2xy 的任意正实数x ，y ，都有x 2+2xy+y 2-ax-ay+1≥0，则实数a 的取值范围是 .【答案】17-4∞⎛⎤⎥⎝⎦，【解析】对于正实数x ，y ，由x+y+4=2xy ，得x+y+4=2xy ≤2()2x y +，解得x+y ≥4.不等式x 2+2xy+y 2-ax-ay+1≥0可化为(x+y )2-a (x+y )+1≥0，令t=x+y (t ≥4)，则该不等式可化为t 2-at+1≥0，即a ≤t+1t 对于任意的t ≥4恒成立，令u (t )=t+1t (t ≥4)，则u'(t )=1-21t =22-1t t >0对于任意的t ≥4恒成立，从而函数u (t )=t+1t (t ≥4)为单调增函数，所以u (t )min =u (4)=4+14=174，于是a ≤174.5.(2015·宿迁一模)已知函数f (x )=x 2-2ax+a 2-1，若关于x 的不等式f (f (x ))<0的解集为空集，则实数a 的取值范围是 . 【答案】(-∞，-2]【解析】因为f (x )=[x-(a+1)][x-(a-1)]，所以f (f (x ))<0等价于[f (x )-(a+1)][f (x )-(a-1)]<0，从而a-1<f (x )<a+1，要使f (f (x ))<0的解集为空集，根据函数的图象，则需y=a+1与y=f (x )至多有一个交点.又因为f (x )=(x-a )2-1≥-1，所以a+1≤-1，解得a ≤-2.温馨提示：趁热打铁，事半功倍.请老师布置同学们完成《配套检测与评估》第11~12页.【检测与评估】第2讲三个二次关系与恒成立问题、存在性问题一、填空题1.若关于x 的不等式ax 2+2x+a>0的解集为R ，则实数a 的取值范围是 .2.(2016·安徽省六校联考)若正实数x，y满足x+y=2，且1xy≥M恒成立，则M的最大值为.3.(2016·南师附中)若当x>-3时，不等式a≤x+23x 恒成立，则实数a的取值范围是.4.若对任意实数x∈[-1，1]，不等式x2+ax-3a<0恒成立，则实数a的取值范围是.5.(2016·常州中学)当x∈(-∞，-1]时，不等式(m2-m)·4x-2x<0恒成立，则实数m的取值范围是.6.(2016·启东中学)已知f(x)=x2+2x+a ln x，若f(x)在区间(0，1]上恒为单调函数，则实数a的取值范围为.7.(2016·江苏信息卷)若对任意实数x>1，y>12，不等式p≤22-1xy+24-1yx恒成立，则实数p的最大值为.8.(2016·苏大考前卷)已知不等式(ax+3)(x2-b)≤0对任意x∈(0，+∞)恒成立，其中a，b是整数，则a+b的取值集合为.二、解答题9.(2016·江苏怀仁中学)设函数f(x)=ax2+(b-2)x+3(a≠0).(1)若不等式f(x)>0的解集为(-1，3)，求a，b的值；(2)若f(1)=2，a>0，b>0，求1a+4b的最小值.10.(2016·泰州中学)已知函数f(x)=ax2+2x+c(a，c∈N*)满足①f(1)=5；②6<f(2)<11.(1)求函数f(x)的表达式；(2)若对任意的x∈[1，2]，都有f(x)-2mx≥0恒成立，求实数m的取值范围.11.(2015·浙江卷)设函数f(x)=x2+ax+b(a，b∈R).(1)当b=24a+1时，求函数f(x)在区间[-1，1]上的最小值g(a)的表达式；(2)已知函数f(x)在区间[-1，1]上存在零点，且0≤b-2a≤1，求实数b的取值范围.【检测与评估答案】第2讲三个二次关系与恒成立问题、存在性问题一、填空题1. (1，+∞)【解析】当a=0时，易知条件不成立；当a≠0时，要使不等式ax2+2x+a>0的解集为R，必须满足24-40aa>⎧⎨∆=<⎩，，解得a>1.2.1【解析】因为正实数x，y满足x+y=2，所以xy≤2()4x y+=224=1，所以1xy≥1.又1xy≥M恒成立，所以M≤1，即M的最大值为1.3. (-∞，-3]【解析】设f(x)=x+23x+=(x+3)+23x+-3，因为x>-3，所以x+3>0，故f(x)≥23=2-3，当且仅当-3时等号成立，所以a的取值范围是(-∞，-3].4.12∞⎛⎫+⎪⎝⎭，【解析】设f(x)=x2+ax-3a.因为对任意实数x∈[-1，1]，不等式x2+ax-3a<0恒成立，所以(-1)1--30(1)1-30f a af a a=<⎧⎨=+<⎩，，解得a>12.5.(-1，2)【解析】原不等式变形为m2-m<12x⎛⎫⎪⎝⎭，因为函数y=12x⎛⎫⎪⎝⎭在(-∞，-1]上是减函数，所以12x⎛⎫⎪⎝⎭≥-112⎛⎫⎪⎝⎭=2.当x∈(-∞，-1]时，m2-m<12x⎛⎫⎪⎝⎭恒成立等价于m2-m<2，解得-1<m<2.6. (-∞，-4]∪[0，+∞)【解析】由题意知f'(x)=2x+2+ax=222x x ax++，因为f(x)在区间(0，1]上恒为单调函数，所以f'(x)在区间(0，1]上恒大于等于0或恒小于等于0，所以2x2+2x+a≥0或2x2+2x+a≤0在区间(0，1]上恒成立，即a≥-(2x2+2x)或a≤-(2x2+2x)，而函数y=-2x2-2x在区间(0，1]上的值域为[-4，0)，所以a≥0或a≤-4.7. 8【解析】令a=2y-1，b=x-1，则22-1xy+24-1yx=2(1)ba++2(1)ab+，问题转化为求2(1)ba++2(1)ab+的最小值.又2(1)b a ++2(1)a b +≥2×ab =2×ab =2ab ab ab ⎛++ ⎪⎭≥2×(2+2)=8，当且仅当a=b=1，即x=2，y=1时取等号.8. {8，-2} 【解析】当b ≤0时，由(ax+3)(x 2-b )≤0得ax+3≤0在x ∈(0，+∞)上恒成立，则a<0，且a ·0+3≤0，矛盾，故b>0.当b>0时，由(ax+3)(x 2-b )≤0可设f (x )=ax+3，g (x )=x 2-b ，又g (x )的大致图象如图所示，那么由题意可知03-a b a <⎧⎪⎨=⎪⎩，，再由a ，b 是整数得到-19a b =⎧⎨=⎩，或-31a b =⎧⎨=⎩，，因此a+b=8或-2.(第8题)二、解答题9. (1) 由题意得(-1)0(3)0f f =⎧⎨=⎩，，即-5093-30a b a b +=⎧⎨+=⎩，，解得-14.a b =⎧⎨=⎩，(2) 因为f (1)=2，所以a+b=1，所以1a +4b =(a+b )14a b ⎛⎫+ ⎪⎝⎭=5+b a +4a b ≥9，当且仅当b=2a=12时取等号.10. (1) 由题知5=a+c+2，即c=3-a.又6<4a+c+4<11，所以-13<a<43.又a∈N*，所以a=1，c=2. 所以f(x)=x2+2x+2.(2) 由已知得2(m-1)≤x+2x在x∈[1，2]上恒成立.因为当x∈[1，2]时，x+2x∈3⎡⎤⎣⎦，所以2(m-1)≤2，即m+1，所以实数m的取值范围为(-∞+1].11. (1) 当b=24a+1时，函数f(x)=22ax⎛⎫+⎪⎝⎭+1，故其图象的对称轴为直线x=-2a.当a≤-2时，g(a)=f(1)=24a+a+2；当-2<a≤2时，g(a)=f-2a⎛⎫⎪⎝⎭=1；当a>2时，g(a)=f(-1)=24a-a+2.综上，g(a)=222-2 41-22-2 2.4aa aaaa a⎧++≤⎪⎪⎪<≤⎨⎪⎪+>⎪⎩，，，，，(2) 设s，t为方程f(x)=0的解，且-1≤t≤1，则-.s t a st b+=⎧⎨=⎩，因为0≤b-2a≤1，所以-22tt+≤s≤1-22tt+(-1≤t≤1).当0≤t≤1时，2-22tt+≤st≤2-22t tt+，由于-23≤2-22tt+≤0和-13≤2-22t tt+≤9-4，所以-23≤b≤9-.当-1≤t<0时，2-22t tt+≤st≤2-22tt+，由于-2≤2-22tt+<0和-3≤2-22t tt+<0，所以-3≤b<0.故b的取值范围是-3⎡⎣，.。

2023年中考数学压轴题专题10 二次函数与圆存在性问题【含答案】

专题10二次函数与圆存在性问题二次函数是初中数学代数部分最重要的概念之一，是中考数学的重难点；而圆是初中几何中综合性最强的知识内容，它与二次函数都在中考中占据及其重要的地位，两者经常作为压轴题综合考查，能够很好的考查学生的数学综合素养以及分析问题、解决问题的能力.圆心与抛物线的关系、圆上的点和抛物线的关系，其本质就是把位置关系向数量化关系转化.二次函数与圆的综合要数形结合，在读题之前要想到圆中的相关概念、性质及定理，比如圆的定义、垂径定理、圆周角、圆心角、内心、外心、切线、四点共圆的、隐藏圆等；对于二次函数，要熟练掌握解析式的求法和表达形式、顶点、最值、与方程之间的关系，线段长与点的坐标之间的数量转化等.【例1】（2022•闵行区二模）如图，在平面直角坐标系xOy中，抛物线y＝ax2+bx+4与x轴相交于点A（﹣1，0），B（3，0），与y轴交于点C．将抛物线的对称轴沿x轴的正方向平移，平移后交x轴于点D，交线段BC于点E，交抛物线于点F，过点F作直线BC的垂线，垂足为点G．（1）求抛物线的表达式；（2）以点G为圆心，BG为半径画⊙G；以点E为圆心，EF为半径画⊙E．当⊙G与⊙E内切时．①试证明EF与EB的数量关系；②求点F的坐标．【例2】（2022•福建模拟）如图，已知抛物线y＝ax2+bx+c与x轴相交于A，B两点，点C（2，﹣4）在抛物线上，且△ABC是等腰直角三角形．（1）求抛物线的解析式；（2）过点D（2，0）的直线与抛物线交于点M，N，试问：以线段MN为直径的圆是否过定点？证明你的结论．【例3】（2022•武汉模拟）已知抛物线y＝﹣2x2+bx+c（c＞0）．（1）如图1，抛物线与直线l相交于点M（﹣1，0），N（2，6）．①求抛物线的解析式；②过点N作MN的垂线，交抛物线于点P，求PN的长；（2）如图2，已知抛物线y＝﹣2x2+bx+c与x轴交于A、B两点，与y轴交于点C，点A，B，C，D（0，n）四点在同一圆上，求n的值．【例4】（2022•上海模拟）在平面直角坐标系xOy中，抛物线y＝ax2﹣3ax+2（a＜0）交y轴于点A，抛物线的对称轴交x轴于点P，联结PA．（1）求线段PA的长；（2）如果抛物线的顶点到直线PA的距离为3，求a的值；（3）以点P为圆心、PA为半径的⊙P交y轴的负半轴于点B，第一象限内的点Q在⊙P上，且劣弧＝2．如果抛物线经过点Q，求a的值．1．（2021•广元）如图1，在平面直角坐标系xOy中，抛物线y＝ax2+bx+c与x轴分别相交于A、B两点，与y轴相交于点C，下表给出了这条抛物线上部分点（x，y）的坐标值：x…﹣10123…y…03430…（1）求出这条抛物线的解析式及顶点M的坐标；（2）PQ是抛物线对称轴上长为1的一条动线段（点P在点Q上方），求AQ+QP+PC的最小值；（3）如图2，点D是第四象限内抛物线上一动点，过点D作DF⊥x轴，垂足为F，△ABD的外接圆与DF 相交于点E．试问：线段EF的长是否为定值？如果是，请求出这个定值；如果不是，请说明理由．2．（2021•张家界）如图，已知二次函数y＝ax2+bx+c的图象经过点C（2，﹣3），且与x轴交于原点及点B （8，0）．（1）求二次函数的表达式；（2）求顶点A的坐标及直线AB的表达式；（3）判断△ABO的形状，试说明理由；（4）若点P为⊙O上的动点，且⊙O的半径为2，一动点E从点A出发，以每秒2个单位长度的速度沿线段AP匀速运动到点P，再以每秒1个单位长度的速度沿线段PB匀速运动到点B后停止运动，求点E的运动时间t的最小值．3．（2021•宜宾）如图1，在平面直角坐标系中，抛物线与x轴分别交于A、B两点，与y轴交于点C（0，6），抛物线的顶点坐标为E（2，8），连结BC、BE、CE．（1）求抛物线的表达式；（2）判断△BCE的形状，并说明理由；（3）如图2，以C为圆心，为半径作⊙C，在⊙C上是否存在点P，使得BP+EP的值最小，若存在，请求出最小值；若不存在，请说明理由．4．（2020•雨花区校级一模）如图1，已知抛物线y＝ax2﹣12ax+32a（a＞0）与x轴交于A，B两点（A在B 的左侧），与y轴交于点C．（1）连接BC，若∠ABC＝30°，求a的值．（2）如图2，已知M为△ABC的外心，试判断弦AB的弦心距d是否有最小值，若有，求出此时a的值，若没有，请说明理由；（3）如图3，已知动点P（t，t）在第一象限，t为常数．问：是否存在一点P，使得∠APB达到最大，若存在，求出此时∠APB的正弦值，若不存在，也请说明理由．5．（2020•汇川区三模）如图，在平面直角坐标系上，一条抛物线y＝ax2+bx+c（a≠0）经过A（1，0）、B （3，0）、C（0，3）三点，连接BC并延长．（1）求抛物线的解析式；（2）点M是直线BC在第一象限部分上的一个动点，过M作MN∥y轴交抛物线于点N．1°求线段MN的最大值；2°当MN取最大值时，在线段MN右侧的抛物线上有一个动点P，连接PM、PN，当△PMN的外接圆圆心Q在△PMN的边上时，求点P的坐标．6．（2021•开福区模拟）如图，在平面直角坐标系中，抛物线y＝x2﹣bx+c交x轴于点A，B，点B的坐标为（4，0），与y轴于交于点C（0，﹣2）．（1）求此抛物线的解析式；（2）在抛物线上取点D，若点D的横坐标为5，求点D的坐标及∠ADB的度数；（3）在（2）的条件下，设抛物线对称轴l交x轴于点H，△ABD的外接圆圆心为M（如图1），①求点M的坐标及⊙M的半径；②过点B作⊙M的切线交于点P（如图2），设Q为⊙M上一动点，则在点运动过程中的值是否变化？若不变，求出其值；若变化，请说明理由．7．（2020•天桥区二模）如图，抛物线y＝ax2+bx+c（a≠0），与x轴交于A（4，0）、O两点，点D（2，﹣2）为抛物线的顶点．（1）求该抛物线的解析式；（2）点E为AO的中点，以点E为圆心、以1为半径作⊙E，交x轴于B、C两点，点M为⊙E上一点．①射线BM交抛物线于点P，设点P的横坐标为m，当tan∠MBC＝2时，求m的值；②如图2，连接OM，取OM的中点N，连接DN，则线段DN的长度是否存在最大值或最小值？若存在，请求出DN的最值；若不存在，请说明理由．8．（2020•百色）如图，抛物线的顶点为A（0，2），且经过点B（2，0）．以坐标原点O为圆心的圆的半径r＝，OC⊥AB于点C．（1）求抛物线的函数解析式．（2）求证：直线AB与⊙O相切．（3）已知P为抛物线上一动点，线段PO交⊙O于点M．当以M，O，A，C为顶点的四边形是平行四边形时，求PM的长．9．（2020•西藏）在平面直角坐标系中，二次函数y＝x2+bx+c的图象与x轴交于A（﹣2，0），B（4，0）两点，交y轴于点C，点P是第四象限内抛物线上的一个动点．（1）求二次函数的解析式；＝，求点P的坐标；（2）如图甲，连接AC，PA，PC，若S△P AC（3）如图乙，过A，B，P三点作⊙M，过点P作PE⊥x轴，垂足为D，交⊙M于点E．点P在运动过程中线段DE的长是否变化，若有变化，求出DE的取值范围；若不变，求DE的长．10．（2020•宜宾）如图，已知二次函数的图象顶点在原点，且点（2，1）在二次函数的图象上，过点F（0，1）作x轴的平行线交二次函数的图象于M、N两点．（1）求二次函数的表达式；（2）P为平面内一点，当△PMN是等边三角形时，求点P的坐标；（3）在二次函数的图象上是否存在一点E，使得以点E为圆心的圆过点F和点N，且与直线y＝﹣1相切．若存在，求出点E的坐标，并求⊙E的半径；若不存在，说明理由．11．（2021•嘉兴二模）定义：平面直角坐标系xOy中，过二次函数图象与坐标轴交点的圆，称为该二次函数的坐标圆．（1）已知点P（2，2），以P为圆心，为半径作圆．请判断⊙P是不是二次函数y＝x2﹣4x+3的坐标圆，并说明理由；（2）已知二次函数y＝x2﹣4x+4图象的顶点为A，坐标圆的圆心为P，如图1，求△POA周长的最小值；（3）已知二次函数y＝ax2﹣4x+4（0＜a＜1）图象交x轴于点A，B，交y轴于点C，与坐标圆的第四个交点为D，连结PC，PD，如图2．若∠CPD＝120°，求a的值．12．（2021•常州二模）如图1：抛物线y＝﹣x2+bx+c过点A（﹣1，0），点B（3，0），与y轴交于点C．动点E（m，0）（0＜m＜3），过点E作直线l⊥x轴，交抛物线于点M．（1）求抛物线的解析式及C点坐标；（2）连接BM并延长交y轴于点N，连接AN，OM，若AN∥OM，求m的值．（3）如图2．当m＝1时，P是直线l上的点，以P为圆心，PE为半径的圆交直线l于另一点F（点F在x 轴上方），若线段AC上最多存在一个点Q使得∠FQE＝90°，求点P纵坐标的取值范围．13．（2021•乐山模拟）如图，抛物线y＝ax2+bx+2与直线AB相交于A（﹣1，0），B（3，2），与x轴交于另一点C．（1）求抛物线的解析式；（2）在y上是否存在一点E，使四边形ABCE为矩形，若存在，请求出点E的坐标；若不存在，请说明理由；（3）以C为圆心，1为半径作⊙O，D为⊙O上一动点，求DA+DB的最小值14．（2021•河北区二模）如图，在平面直角坐标系中，抛物线y＝﹣x2+bx+3的对称轴是直线x＝2，与x 轴相交于A，B两点（点A在点B的左侧），与y轴交于点C．（Ⅰ）求抛物线的解析式及顶点坐标；（Ⅱ）M为第一象限内抛物线上的一个点，过点M作MN⊥x轴于点N，交BC于点D，连接CM，当线段CM＝CD时，求点M的坐标；（Ⅲ）以原点O为圆心，AO长为半径作⊙O，点P为⊙O上的一点，连接BP，CP，求2PC+3PB的最小值．15．（2021•长沙模拟）如图，在平面直角坐标系中，抛物线y＝ax2+bx+c（a＞0）的顶点为M，经过C（1，1），且与x轴正半轴交于A，B两点．（1）如图1，连接OC，将线段OC绕点O顺时针旋转，使得C落在y轴的负半轴上，求点C的路径长；（2）如图2，延长线段OC至N，使得ON＝，若∠OBN＝∠ONA，且，求抛物线的解析式；（3）如图3，抛物线y＝ax2+bx+c的对称轴为直线，与y轴交于（0，5），经过点C的直线l：y＝kx+m （k＞0）与抛物线交于点C、D，若在x轴上存在P1、P2，使∠CP1D＝∠CP2D＝90°，求k的取值范围．16．（2021秋•上城区校级期中）如图，已知抛物线y＝﹣x2+bx+c与x轴交于A、B两点（点A在点B左边），与y轴交于点C，⊙M是△ABC的外接圆．若抛物线的顶点D的坐标为（1，4）．（1）求抛物线的解析式，及A、B、C三点的坐标；（2）求⊙M的半径和圆心M的坐标；（3）如图2，在x轴上有点P（7，0），试在直线BC上找点Q，使B、Q、P三点构成的三角形与△ABC相似．若存在，请直接写出点坐标；若不存在，请说明理由．17．（2021秋•西湖区校级期中）我们把一个半圆与抛物线的一部分合成的封闭图形称为“蛋圆”．如图所示，点A、B、C、D分别是“蛋圆”与坐标轴的交点，已知点D的坐标为（0，﹣3），AB为半圆的直径，半圆圆心M的坐标为（1，0），半圆半径为2．（1）求“蛋圆”抛物线部分的解析式及“蛋圆”的弦CD的长；（2）已知点E是“蛋圆”上的一点（不与点A，点B重合），点E关于x轴的对称点是点F，若点F也在“蛋圆”上，求点E坐标；（3）点P是“蛋圆”外一点，满足∠BPC＝60°，当BP最大时，直接写出点P的坐标．18．（2021•雨花区二模）如图1，已知圆O的圆心为原点，半径为2，与坐标轴交于A，C，D，E四点，B 为OD中点．（1）求过A，B，C三点的抛物线解析式；（2）如图2，连接BC，AC．点P在第一象限且为圆O上一动点，连接BP，交AC于点M，交OC于点N，当MC2＝MN•MB时，求M点的坐标；（3）如图3，若抛物线与圆O的另外两个交点分别为H，F，请判断四边形CFEH的形状，并说明理由．19．（2020•东海县二模）如图，△AOB的三个顶点A、O、B分别落在抛物线C1：y＝x2+x上，点A的坐标为（﹣4，m），点B的坐标为（n，﹣2）．（点A在点B的左侧）（1）则m＝，n＝．（2）将△AOB绕点O逆时针旋转90°得到△A'OB'，抛物线C2：y＝ax2+bx+4经过A'、B'两点，延长OB'交抛物线C2于点C，连接A'C．设△OA'C的外接圆为⊙M．①求圆心M的坐标；②试直接写出△OA'C的外接圆⊙M与抛物线C2的交点坐标（A'、C除外）．20．（2022•绿园区二模）在平面直角坐标系中，已知某二次函数的图象同时经过点A（0，3）、B（2m，3）、C（m，m+3）．其中，m≠0．（1）当m＝1时．①该二次函数的图象的对称轴是直线．②求该二次函数的表达式．（2）当|m|≤x≤|m|时，若该二次函数的最大值为4，求m的值．（3）若同时经过点A、B、C的圆恰好与x轴相切时，直接写出该二次函数的图象的顶点坐标．21．（2022•炎陵县一模）抛物线：y＝﹣x2+bx+c与y轴的交点C（0，3），与x轴的交点分别为E、G两点，对称轴方程为x＝1．（1）求抛物线的解析式；（2）如图1，过点C作y轴的垂线交抛物线于另一点D，F为抛物线的对称轴与x轴的交点，P为线段OC 上一动点．若PD⊥PF，求点P的坐标．（3）如图1，如果一个圆经过点O、点G、点C三点，并交于抛物线对称轴右侧x轴的上方于点H，求∠OHG的度数；（4）如图2，将抛物线向下平移2个单位长度得到新抛物线L，点B是顶点．直线y＝kx﹣k+4（k＜0）与抛物线L交于点M、N．与对称轴交于点G，若△BMN的面积等于2，求k的值．22．（2022•杨浦区二模）如图，已知在平面直角坐标系xOy中，抛物线y＝﹣+bx+c与x轴相交于点A （4，0），与y轴相交于点B（0，3），在x轴上有一动点E（m，0）（0＜m＜4），过点E作x轴的垂线交线段AB于点N，交抛物线于点P，过P作PM⊥AB，垂足为点M．（1）求这条抛物线的表达式；（2）设△PMN的周长为C1，△AEN的周长为C2，如果，求点P的坐标；（3）如果以N为圆心，NA为半径的圆与以OB为直径的圆内切，求m的值．【例1】（2022•闵行区二模）如图，在平面直角坐标系xOy中，抛物线y＝ax2+bx+4与x轴相交于点A（﹣1，0），B（3，0），与y轴交于点C．将抛物线的对称轴沿x轴的正方向平移，平移后交x轴于点D，交线段BC于点E，交抛物线于点F，过点F作直线BC的垂线，垂足为点G．（1）求抛物线的表达式；（2）以点G为圆心，BG为半径画⊙G；以点E为圆心，EF为半径画⊙E．当⊙G与⊙E内切时．①试证明EF与EB的数量关系；②求点F的坐标．【分析】（1）根据点A、B的坐标，设抛物线y＝a（x+1）（x﹣3），再将点C代入即可求出a的值，从而得出答案；（2）①分两种情形，当r⊙G＞r⊙E时，则GB﹣EF＝GE，则EF＝EB，当r⊙G＜r⊙E时，则EF﹣GB＝GE，设EF＝5t，FG＝3t，GE＝4t，则5t﹣GB＝4t，则GB＝t＜GE＝4t，从而得出矛盾；②由．设BD＝t，则DE＝，利用勾股定理得BE＝，则F坐标为（3﹣t，3t），代入抛物线解析式，从而解决问题．【解答】解：（1）∵点A坐标为（﹣1，0），点B坐标为（3，0）．设抛物线y＝a（x+1）（x﹣3）（a≠0），∵抛物线经过点C（0，4），∴4＝﹣3a．解得．∴抛物线的表达式是；（2）①由于⊙G与⊙E内切，当r⊙G＜r⊙E时，则EF﹣GB＝GE，设EF＝5t，FG＝3t，GE＝4t，则5t﹣GB＝4t，∴GB＝t＜GE＝4t，∴点E在线段CB的延长线上．又∵已知点E在线段BC上，∴矛盾，因此不存在．当r⊙G＞r⊙E时，则GB﹣EF＝GE，又∵GE＝GB﹣EB，∴EF＝EB；②∵OC⊥OB，FD⊥OB，∴∠COB＝∠EDB＝90°．∴．∴设BD＝t，则DE＝；在Rt△BED中，由勾股定理得，．∴，∴F坐标为（3﹣t，3t），∵F点在抛物线上，∴，∴解得，t＝0（点F与点B重合，舍去）．∴F坐标为（，）．【例2】（2022•福建模拟）如图，已知抛物线y＝ax2+bx+c与x轴相交于A，B两点，点C（2，﹣4）在抛物线上，且△ABC是等腰直角三角形．（1）求抛物线的解析式；（2）过点D（2，0）的直线与抛物线交于点M，N，试问：以线段MN为直径的圆是否过定点？证明你的结论．【分析】（1）等腰直角三角形斜边中线等于斜边一半，点的坐标，不难求出A、B两点坐标，把点A、B、C 代入二次函数解析式，解三元一次方程组就可得到函数解析式．（2））通过设过点D（2，0）的直线MN解析式为y＝k（x﹣2）＝kx﹣2k，得到关于x、关于y的方程，利用跟与系数的关系，再得到圆的解析式，待定系数法确定定点的x、y的值，确定定点的坐标．【解答】解：连接AC、BC，过点C作CP垂直于x轴于点P．在Rt△CAB中，AC＝BC，CP⊥AB，点C（2，﹣4），∴CP＝AP＝PB＝4，OP＝2，∴OA＝AP﹣OP＝4﹣2＝2，OB＝OP+PB＝4+2＝6，∴点A（﹣2，0），点B（6，0），把点A（﹣2，0），点B（6，0），点C（2，﹣4）代入函数解析式得，解得，∴抛物线的解析式为：y＝x2﹣x﹣3．故答案为：y＝x2﹣x﹣3．（2）设过点D（2，0）的直线MN解析式为y＝k（x﹣2）＝kx﹣2k，联立直线与抛物线解析式得关于x的等式：kx﹣2k＝x2﹣x﹣3，化简得＝0，x N+x M＝﹣＝4（k+1），x N x M＝＝8k﹣12..........①，联立直线与抛物线解析式得关于y的等式：y＝（+2）2﹣（+2）﹣3，化简得y2+（﹣﹣1）y﹣4＝0，y M+y N＝4k2，y M y N＝﹣16k2................②，线段MN的中点就是圆的圆心，∴x O＝（x N+x M）＝2（K+1），代入直线方程得y O＝2k2，∴圆心坐标为（2k+2，2k2），直径MN＝＝，把①、②代入上式化简整理得直径MN＝，设圆上某一点（x，y）到圆心的距离等于半径，∴＝，化简整理得16k2+12﹣8k＝x2﹣4kx﹣4x+y2﹣4k2y＝﹣4yk2﹣4kx+x2﹣4x+y2，圆过定点，所以与k值无关，看作是关于k的二次等式，k2、k的系数，常量对应相等，得﹣8＝﹣4x，x＝2，16＝﹣4y，y＝﹣4，由以上分析，所以以MN为直径的圆过定点（2，﹣4）．故答案为：以线段MN为直径的圆过定点（2，﹣4）．【例3】（2022•武汉模拟）已知抛物线y＝﹣2x2+bx+c（c＞0）．（1）如图1，抛物线与直线l相交于点M（﹣1，0），N（2，6）．①求抛物线的解析式；②过点N作MN的垂线，交抛物线于点P，求PN的长；（2）如图2，已知抛物线y＝﹣2x2+bx+c与x轴交于A、B两点，与y轴交于点C，点A，B，C，D（0，n）四点在同一圆上，求n的值．【分析】（1）①把点M（﹣1，0），N（2，6）代入到y＝﹣2x2+bx+c中，可得b和c的值．②设P（a，﹣2a2+4a+6），再利用M（﹣1，0），N（2，6），得到MN、PM、PN的表达式，最后利用勾股定理求得a的值．（2）令C（0，c），当y＝0时，代入抛物线得x A x B＝﹣，根据两角对应相等，可得△AOC∽△DOB，然后再找到对应线段成比例，即得到n的值．【解答】解：（1）①把M（﹣1，0）N（2，6）代入y＝﹣2x2+bx+c，得，解得，∴抛物线的解析式为y＝﹣2x2+4x+6；②由①，抛物线解析式为：y＝﹣2x2+4x+6，设P（a，﹣2a2+4a+6）∵M（﹣1，0），N（2，6），∴MN＝＝3，∴PM＝，PN＝，又∵PN⊥MN，则PM2＝MN2+PN2，（﹣1﹣a）2+（2a2﹣4a﹣b）2＝（3）2+（2﹣a）2+（2a2﹣4a）2．整理得：4a2﹣9a+2＝0，∴（a﹣2）（4a﹣1）＝0．∴a1＝2，a2＝．当a＝2时，P与N重合，∴a＝，PN＝．（2）证明：设OA＝﹣x A，OB＝x B，OD＝﹣n当y＝0时，﹣2x2+bx+c＝0，∴x A x B＝﹣，∴OA•OB＝﹣x A x B＝．∵∠CAO＝∠BDO，∠ACO＝∠DBO∴△AOC∽△DOB∴＝∴OA•OB＝OC•OD∴＝c•（﹣n）．∵c≠0∴n＝﹣．【例4】（2022•上海模拟）在平面直角坐标系xOy中，抛物线y＝ax2﹣3ax+2（a＜0）交y轴于点A，抛物线的对称轴交x轴于点P，联结PA．（1）求线段PA的长；（2）如果抛物线的顶点到直线PA的距离为3，求a的值；（3）以点P为圆心、PA为半径的⊙P交y轴的负半轴于点B，第一象限内的点Q在⊙P上，且劣弧＝2．如果抛物线经过点Q，求a的值．【分析】（1）分别求出P（，0），A（0，2），由两点间距离公式可求；＝×PM×OP＝×AP×3，可得a＝﹣；（2）抛物线的顶点为M（，2﹣a），由S△APM（3）连接PQ，BP，AM，设Q（t，at2﹣3at+2），求出M（﹣1，0），由垂径定理可得AM＝AQ，＝①，PQ＝AP，得②，联立①②可得a＝．【解答】解：（1）y＝ax2﹣3ax+2＝a（x﹣）2+2﹣a，∴抛物线的对称轴为x＝，∴P（，0），令x＝0，则y＝2，∴A（0，2），∴PA＝；（2）由（1）可知抛物线的顶点为M（，2﹣a），∵a＜0，∴2﹣a＞0，∴S △APM ＝×PM ×OP ＝×AP ×3，∴（2﹣a ）×＝×3，解得a ＝﹣；（3）连接PQ ，BP ，AM ，∵MP ⊥AB ，∴＝，∵＝2，∴＝，∴AM ＝AQ ，设Q （t ，at 2﹣3at +2），∵AP ＝，P （，0），∴M （﹣1，0），∴＝①，∵PQ ＝AP ，∴②，联立①②可得t ＝或t ＝﹣1（舍），将t ＝代入①，可得a ＝．1．（2021•广元）如图1，在平面直角坐标系xOy中，抛物线y＝ax2+bx+c与x轴分别相交于A、B两点，与y轴相交于点C，下表给出了这条抛物线上部分点（x，y）的坐标值：x…﹣10123…y…03430…（1）求出这条抛物线的解析式及顶点M的坐标；（2）PQ是抛物线对称轴上长为1的一条动线段（点P在点Q上方），求AQ+QP+PC的最小值；（3）如图2，点D是第四象限内抛物线上一动点，过点D作DF⊥x轴，垂足为F，△ABD的外接圆与DF 相交于点E．试问：线段EF的长是否为定值？如果是，请求出这个定值；如果不是，请说明理由．【分析】（1）运用待定系数法即可求出抛物线解析式，再运用配方法求出顶点坐标；（2）如图1，将点C沿y轴向下平移1个单位得C′（0，2），连接BC′交抛物线对称轴x＝1于点Q′，过点C作CP′∥BC′，交对称轴于点P′，连接AQ′，此时，C′、Q′、B三点共线，BQ′+C′Q′的值最小，运用勾股定理即可求出答案；（3）如图2，连接BE，设D（t，﹣t2+2t+3），且t＞3，可得DF＝t2﹣2t﹣3，BF＝t﹣3，AF＝t+1，运用圆内接四边形的性质可得∠DAF＝∠BEF，进而证明△AFD∽△EFB，利用＝，即可求得答案．【解答】解：（1）根据表格可得出A（﹣1，0），B（3，0），C（0，3），设抛物线解析式为y＝a（x+1）（x﹣3），将C（0，3）代入，得：3＝a（0+1）（0﹣3），解得：a＝﹣1，∴y＝﹣（x+1）（x﹣3）＝﹣x2+2x+3＝﹣（x﹣1）2+4，∴该抛物线解析式为y＝﹣x2+2x+3，顶点坐标为M（1，4）；（2）如图1，将点C沿y轴向下平移1个单位得C′（0，2），连接BC′交抛物线对称轴x＝1于点Q′，过点C作CP′∥BC′，交对称轴于点P′，连接AQ′，∵A、B关于直线x＝1对称，∴AQ′＝BQ′，∵CP′∥BC′，P′Q′∥CC′，∴四边形CC′Q′P′是平行四边形，∴CP′＝C′Q′，Q′P′＝CC′＝1，在Rt△BOC′中，BC′＝＝＝，∴AQ′+Q′P′+P′C＝BQ′+C′Q′+Q′P′＝BC′+Q′P′＝+1，此时，C′、Q′、B三点共线，BQ′+C′Q′的值最小，∴AQ+QP+PC的最小值为+1；（3）线段EF的长为定值1.如图2，连接BE，设D（t，﹣t2+2t+3），且t＞3，∵EF⊥x轴，∴DF＝﹣（﹣t2+2t+3）＝t2﹣2t﹣3，∵F（t，0），∴BF＝OF﹣OB＝t﹣3，AF＝t﹣（﹣1）＝t+1，∵四边形ABED是圆内接四边形，∴∠DAF+∠BED＝180°，∵∠BEF+∠BED＝180°，∴∠DAF＝∠BEF，∵∠AFD＝∠EFB＝90°，∴△AFD∽△EFB，∴＝，∴＝，∴EF＝＝＝1，∴线段EF的长为定值1．2．（2021•张家界）如图，已知二次函数y＝ax2+bx+c的图象经过点C（2，﹣3），且与x轴交于原点及点B （8，0）．（1）求二次函数的表达式；（2）求顶点A的坐标及直线AB的表达式；（3）判断△ABO的形状，试说明理由；（4）若点P为⊙O上的动点，且⊙O的半径为2，一动点E从点A出发，以每秒2个单位长度的速度沿线段AP匀速运动到点P，再以每秒1个单位长度的速度沿线段PB匀速运动到点B后停止运动，求点E 的运动时间t的最小值．【分析】（1）运用待定系数法即可求出答案；（2）运用配方法将抛物线解析式化为顶点式，得出顶点坐标，运用待定系数法求出直线AB的函数表达式；（3）方法1：如图1，过点A作AF⊥OB于点F，则F（4，0），得出△AFO、△AFB均为等腰直角三角形，即可得出答案，方法2：由△ABO的三个顶点分别是O（0，0），A（4，﹣4），B（8，0），运用勾股定理及逆定理即可得出答案；（4）以O为圆心，2为半径作圆，则点P在圆周上，根据t＝AP+PB＝PD+PB，可知当B、P、D三点共线时，PD+PB取得最小值，过点D作DG⊥OB于点G，由t＝DB＝即可求出答案．【解答】解：（1）∵二次函数y＝ax2+bx+c（a≠0）的图象经过C（2，﹣3），且与x轴交于原点及点B（8，0），∴c＝0，二次函数表达式可设为：y＝ax2+bx（a≠0），将C（2，﹣3），B（8，0）代入y＝ax2+bx得：，解得：，∴二次函数的表达式为；（2）∵＝（x﹣4）2﹣4，∴抛物线的顶点A（4，﹣4），设直线AB的函数表达式为y＝kx+m，将A（4，﹣4），B（8，0）代入，得：，解得：，∴直线AB的函数表达式为y＝x﹣8；（3）△ABO是等腰直角三角形．方法1：如图1，过点A作AF⊥OB于点F，则F（4，0），∴∠AFO＝∠AFB＝90°，OF＝BF＝AF＝4，∴△AFO、△AFB均为等腰直角三角形，∴OA＝AB＝4，∠OAF＝∠BAF＝45°，∴∠OAB＝90°，∴△ABO是等腰直角三角形．方法2：∵△ABO的三个顶点分别是O（0，0），A（4，﹣4），B（8，0），∴OB＝8，OA＝＝＝，AB＝＝＝，且满足OB2＝OA2+AB2，∴△ABO是等腰直角三角形；（4）如图2，以O为圆心，2为半径作圆，则点P在圆周上，依题意知：动点E的运动时间为t＝AP+PB，在OA上取点D，使OD＝，连接PD，则在△APO和△PDO中，满足：＝＝2，∠AOP＝∠POD，∴△APO∽△PDO，∴＝＝2，从而得：PD＝AP，∴t＝AP+PB＝PD+PB，∴当B、P、D三点共线时，PD+PB取得最小值，过点D作DG⊥OB于点G，由于，且△ABO为等腰直角三角形，则有DG＝1，∠DOG＝45°∴动点E的运动时间t的最小值为：t＝DB＝＝＝5．3．（2021•宜宾）如图1，在平面直角坐标系中，抛物线与x轴分别交于A、B两点，与y轴交于点C（0，6），抛物线的顶点坐标为E（2，8），连结BC、BE、CE．（1）求抛物线的表达式；（2）判断△BCE的形状，并说明理由；（3）如图2，以C为圆心，为半径作⊙C，在⊙C上是否存在点P，使得BP+EP的值最小，若存在，请求出最小值；若不存在，请说明理由．【分析】（1）运用待定系数法即可求得答案；（2）△BCE是直角三角形．运用勾股定理逆定理即可证明；（3）如图，在CE上截取CF＝（即CF等于半径的一半），连结BF交⊙C于点P，连结EP，则BF的长即为所求．【解答】解：（1）∵抛物线的顶点坐标为E（2，8），∴设该抛物线的表达式为y＝a（x﹣2）2+8，∵与y轴交于点C（0，6），∴把点C（0，6）代入得：a＝﹣，∴该抛物线的表达式为y＝x2+2x+6；（2）△BCE是直角三角形．理由如下：∵抛物线与x轴分别交于A、B两点，∴令y＝0，则﹣（x﹣2）2+8＝0，解得：x1＝﹣2，x2＝6，∴A（﹣2，0），B（6，0），∴BC2＝62+62＝72，CE2＝（8﹣6）2+22＝8，BE2＝（6﹣2）2+82＝80，∴BE2＝BC2+CE2，∴∠BCE＝90°，∴△BCE是直角三角形；（3）⊙C上存在点P，使得BP+EP的值最小且这个最小值为．理由如下：如图，在CE上截取CF＝（即CF等于半径的一半），连结BF交⊙C于点P，连结EP，则BF的长即为所求．理由如下：连结CP，∵CP为半径，∴＝＝，又∵∠FCP＝∠PCE，∴△FCP∽△PCE，∴＝＝，即FP＝EP，∴BF＝BP+EP，由“两点之间，线段最短”可得：BF的长即BP+EP为最小值．∵CF＝CE，E（2，8），∴由比例性质，易得F（，），∴BF＝＝．4．（2020•雨花区校级一模）如图1，已知抛物线y＝ax2﹣12ax+32a（a＞0）与x轴交于A，B两点（A在B 的左侧），与y轴交于点C．（1）连接BC，若∠ABC＝30°，求a的值．（2）如图2，已知M为△ABC的外心，试判断弦AB的弦心距d是否有最小值，若有，求出此时a的值，若没有，请说明理由；（3）如图3，已知动点P（t，t）在第一象限，t为常数．问：是否存在一点P，使得∠APB达到最大，若存在，求出此时∠APB的正弦值，若不存在，也请说明理由．【分析】（1）令y＝0，求得抛物线与x轴的交点A、B的坐标，令x＝0，用a表示C点的坐标，再由三角函数列出a的方程，便可求得a的值；（2）过M点作MH⊥AB于点H，连接MA、MC，用d表示出M的坐标，根据MA＝MC，列出a、d的关系式，再通过关系式求得结果；（3）取AB的中点T，过T作MT⊥AB，以M为圆心，MA为半径作⊙M，MT与直线y＝x交于点S，P′为直线y＝x上异于P的任意一点，连接AP′，交⊙M于点K，连接BK，MP，AP，BP，MB，MA，当P 为直线y＝x与⊙M的切点时，∠APB达到最大，利用圆圆周角性质和解直角三角形的知识求得结果便可．【解答】解：（1）连接BC，令y＝0，得y＝ax2﹣12ax+32a＝0，解得，x＝4或8，∴A（4，0），B（8，0），令x＝0，得y＝ax2﹣12ax+32a＝32a，∴C（0，32a），又∠ABC＝30°，∴tan∠ABC＝，解得，a＝；（2）过M点作MH⊥AB于点H，连接MA、MC，如图2，∴AH＝BH＝＝2，∴OH＝6，设M（6，d），∵MA＝MC，∴4+d2＝36+（d﹣32a）2，得2ad＝32a2+1，∴d＝16a+＝，∴当4时，有，即当a＝时，有；（3）∵P（t，t），∴点P在直线y＝x上，如图3，取AB的中点T，过T作MT⊥AB，以M为圆心，MA为半径作⊙M，MT与直线y＝x交于点S，P′为直线y＝x上异于P的任意一点，连接AP′，交⊙M于点K，连接BK，MP，AP，BP，MB，MA，当⊙M与直线y＝x相切时，有∠APB＝∠AKB＞∠AP′B，∴∠APB最大，此时相切点为P，设M（6，d），而T（6，0），∴S（6，6），∴∠PSM＝90°﹣∠SOT＝45°，又MP＝MB＝，∴MS＝＝，∵MS+MT＝ST＝6，∴，解得，d＝2（负根舍去），经检验，d＝2是原方程的解，也符合题意，∴M（6，2），∴MB＝2，∵∠AMB＝2∠APB，MT⊥AB，MA＝MB，∴∠AMT＝∠BMT＝∠AMB＝∠APB，∴sin∠APB＝sin∠BMT＝．5．（2020•汇川区三模）如图，在平面直角坐标系上，一条抛物线y＝ax2+bx+c（a≠0）经过A（1，0）、B （3，0）、C（0，3）三点，连接BC并延长．（1）求抛物线的解析式；（2）点M是直线BC在第一象限部分上的一个动点，过M作MN∥y轴交抛物线于点N．1°求线段MN的最大值；2°当MN取最大值时，在线段MN右侧的抛物线上有一个动点P，连接PM、PN，当△PMN的外接圆圆心Q在△PMN的边上时，求点P的坐标．【分析】（1）将三个已知点坐标代入抛物线的解析式中列出方程组求得a、b、c，便可得抛物线的解析式；（2）1°用待定系数法求出直线BC的解析式，再设M的横坐标为t，用t表示MN的距离，再根据二次函数的性质求得MN的最大值；2°分三种情况：当∠PMN＝90°时；当∠PNM＝90°时；当∠MPN＝90°时．分别求出符合条件的P点坐标便可．【解答】解：（1）把A、B、C三点的坐标代入抛物线y＝ax2+bx+c（a≠0）中，得，解得，，∴抛物线的解析式为：y＝x2﹣4x+3；（2）1°设直线BC的解析式为y＝mx+n（m≠0），则，解得，，∴直线BC的解析式为：y＝﹣x+3，设M（t，﹣t+3）（0＜t＜3），则N（t，t2﹣4t+3），∴MN＝﹣t2+3t＝﹣，∴当t＝时，MN的值最大，其最大值为；2°∵△PMN的外接圆圆心Q在△PMN的边上，∴△PMN为直角三角形，由1°知，当MN取最大值时，M（），N（），①当∠PMN＝90°时，PM∥x轴，则P点与M点的纵坐标相等，∴P点的纵坐标为，当y＝时，y＝x2﹣4x+3＝，解得，x＝，或x＝（舍去），∴P（）；②当∠PNM＝90°时，PN∥x轴，则P点与N点的纵坐标相等，∴P点的纵坐标为﹣，当y＝﹣时，y＝x2﹣4x+3＝﹣，解得，x＝，或x＝（舍去），∴P（，）；③当∠MPN＝90°时，则MN为△PMN的外接圆的直径，∴△PMN的外接圆的圆心Q为MN的中点，∴Q（），半径为，过Q作QK∥x轴，与在MN右边的抛物线图象交于点K，如图②，令y＝，得y＝x2﹣4x+3＝，解得，x＝＜（舍），或x＝，∴K（，），∴QK＝＞，即K点在以MN为直径的⊙Q外，设抛物线y＝x2﹣4x+3的顶点为点L，则l（2，﹣1），连接LK，如图②，则L到QK的距离为，LK＝，设Q点到LK的距离为h，则，∴＝，∴直线LK下方的抛物线与⊙Q没有公共点，∵抛物线中NL部分（除N点外）在过N点与x轴平行的直线下方，∴抛物线中NL部分（除N点外）与⊙Q没有公共点，∵抛物线K点右边部分，在过K点与y轴平行的直线的右边，∴抛物线K点右边部分与⊙Q没有公共点，综上，⊙Q与MN右边的抛物线没有交点，∴在线段MN右侧的抛物线上不存在点P，使△PMN的外接圆圆心Q在MN边上；综上，点P的坐标为（）或（）．6．（2021•开福区模拟）如图，在平面直角坐标系中，抛物线y＝x2﹣bx+c交x轴于点A，B，点B的坐标为（4，0），与y轴于交于点C（0，﹣2）．（1）求此抛物线的解析式；（2）在抛物线上取点D，若点D的横坐标为5，求点D的坐标及∠ADB的度数；（3）在（2）的条件下，设抛物线对称轴l交x轴于点H，△ABD的外接圆圆心为M（如图1），①求点M的坐标及⊙M的半径；②过点B作⊙M的切线交于点P（如图2），设Q为⊙M上一动点，则在点运动过程中的值是否变化？若不变，求出其值；若变化，请说明理由．【分析】（1）c＝﹣2，将点B的坐标代入抛物线表达式得：0＝﹣4b﹣2，解得：b＝﹣，即可求解；。

存在性问题专题

存在性问题是指判断满足某种条件的事物是否存在的问题，这类问题的知识覆盖面较广，综合性较强，题意构思非常精巧，解题方法灵活，对学生分析问题和解决问题的能力要求较高，是近几年来各地中考的“热点”。

这类题目解法的一般思路是：假设存在→推理论证→得出结论。

若能导出合理的结果，就做出“存在”的判断，导出矛盾，就做出不存在的判断。

由于“存在性”问题的结论有两种可能，所以具有开放的特征，在假设存在性以后进行的推理或计算，对基础知识，基本技能提出了较高要求，并具备较强的探索性，正确、完整地解答这类问题，是对我们知识、能力的一次全面的考验。

例1（2011广东）22．如图，抛物线2517144y x x =-++与y 轴交于A 点，过点A 的直线与抛物线交于另一点B ，过点B作BC ⊥x 轴，垂足为点C(3，0).（1）求直线AB 的函数关系式；（2）动点P 在线段OC 上从原点出发以每秒一个单位的速度向C 移动，过点P 作PN ⊥x 轴，交直线AB 于点M ，交抛物线于点N. 设点P 移动的时间为t 秒，MN 的长度为s 个单位，求s 与t 的函数关系式，并写出t 的取值范围；（3）设在（2）的条件下（不考虑点P 与点O ，点C 重合的情况），连接CM ，BN ，当t 为何值时，四边形BCMN 为平行四边形？问对于所求的t 值，平行四边形BCMN 是否菱形？请说明理由.【答案】解：（1）∵A 、B 在抛物线2517144y x x =-++上， ∴当=01x y = 时，当5=32x y = 时。

即A 、B 两点坐标分别为（0，1），（3，52）。

设直线AB 的函数关系式为=y kx b +， ∴ 得方程组：1532b k b =+= ，解之，得 121k b ==。

直线AB 的解析式为1=12y x +。

（2）依题意有P 、M 、N 的坐标分别为P （t ，0），M （t ，112t +），N （t ，2517144t t -++） ()225171515110344244s MN NP MPt t t t t t ∴==-⎛⎫++-+=+≤≤ ⎪⎝⎭=--（3）若四边形BCMN 为平行四边形，则有MN=BC ，此时，有25415452=+-t t ，解得11=t ，22=t 所以当t=1或2时，四边形BCMN 为平行四边形。

二次函数专题训练(正方形的存在性问题)含答案(可编辑修改word版)

1.如图，已知抛物线y=x2+bx+c 的图象经过点A（l，0），B（﹣3，0），与y 轴交于点C，抛物线的顶点为D，对称轴与x 轴相交于点E，连接BD．（1）求抛物线的解析式．（2）若点P 在直线BD 上，当PE=PC 时，求点P 的坐标．（3）在（2）的条件下，作PF⊥x 轴于F，点M 为x 轴上一动点，N 为直线PF 上一动点，G 为抛物线上一动点，当以点F，N，G，M 四点为顶点的四边形为正方形时，求点M 的坐标．2.如图，抛物线y=﹣x2+bx+c 与x 轴交于点A 和点B，与y 轴交于点C，点B 坐标为（6，0），点C 坐标为（0，6），点D 是抛物线的顶点，过点D 作x 轴的垂线，垂足为E，连接BD．（1）求抛物线的解析式及点D 的坐标；（2）点F 是抛物线上的动点，当∠FBA=∠BDE 时，求点F 的坐标；（3）若点M 是抛物线上的动点，过点M 作MN∥x 轴与抛物线交于点N，点P 在x 轴上，点Q 在坐标平面内，以线段MN 为对角线作正方形MPNQ，请写出点Q 的坐标．3.如图，已知抛物线y=ax2+bx﹣3 过点A（﹣1，0），B（3，0），点M、N 为抛物线上的动点，过点M 作MD∥y 轴，交直线BC 于点D，交x 轴于点E．过点N 作NF⊥x 轴，垂足为点 F（1）求二次函数y=ax2+bx﹣3 的表达式；（2）若M 点是抛物线上对称轴右侧的点，且四边形MNFE 为正方形，求该正方形的面积；（3）若M 点是抛物线上对称轴左侧的点，且∠DMN=90°，MD=MN，请直接写出点M 的横坐标．4.(2015 贵州省毕节地区) 如图，抛物线y=x2+bx+c 与x 轴交于A（﹣1，0），B（3，0）两点，顶点M 关于x 轴的对称点是M′．（1）求抛物线的解析式；（2）若直线AM′与此抛物线的另一个交点为C，求△CAB 的面积；（3）是否存在过A，B 两点的抛物线，其顶点P 关于x 轴的对称点为Q，使得四边形APBQ 为正方形？若存在，求出此抛物线的解析式；若不存在，请说明理由．5.(2016 辽宁省铁岭市) ．如图，抛物线y=﹣x2+bx+c 与x 轴交于点A，点B，与y 轴交于点C，点B 坐标为（6，0），点C 坐标为（0，6），点D 是抛物线的顶点，过点D 作x 轴的垂线，垂足为E，连接BD．（1）求抛物线的解析式及点D 的坐标；（2）点F 是抛物线上的动点，当∠FBA=∠BDE 时，求点F 的坐标；（3）若点M 是抛物线上的动点，过点M 作MN∥x 轴与抛物线交于点N，点P 在x 轴上，点Q 在平面内，以线段MN 为对角线作正方形MPNQ，请直接写出点Q 的坐标．6.(2016 广东省茂名市) ．如图，抛物线y=﹣x2+bx+c 经过A（﹣1，0），B（3，0）两点，且与y 轴交于点C，点D 是抛物线的顶点，抛物线的对称轴DE 交x 轴于点E，连接BD．（1）求经过A，B，C 三点的抛物线的函数表达式；（2）点P 是线段BD 上一点，当PE=PC 时，求点P 的坐标；（3）在（2）的条件下，过点P 作PF⊥x 轴于点F，G 为抛物线上一动点，M 为x 轴上一动点，N 为直线PF 上一动点，当以F、M、G 为顶点的四边形是正方形时，请求出点M 的坐标．二次函数专题训练（正方形的存在性问题）参考答案1.如图，已知抛物线y=x2+bx+c 的图象经过点A（l，0），B（﹣3，0），与y 轴交于点C，抛物线的顶点为D，对称轴与x 轴相交于点E，连接BD．（1）求抛物线的解析式．（2）若点P 在直线BD 上，当PE=PC 时，求点P 的坐标．（3）在（2）的条件下，作PF⊥x 轴于F，点M 为x 轴上一动点，N 为直线PF 上一动点，G 为抛物线上一动点，当以点F，N，G，M 四点为顶点的四边形为正方形时，求点M 的坐标．【解答】解：（1）∵抛物线y=x2+bx+c 的图象经过点A（1，0），B（﹣3，0），∴，∴，∴抛物线的解析式为y=x2+2x﹣3；（2）由（1）知，抛物线的解析式为y=x2+2x﹣3；∴C（0，﹣3），抛物线的顶点D（﹣1，﹣4），∴E（﹣1，0），设直线BD 的解析式为y=mx+n，∴，∴，∴直线BD 的解析式为y=﹣2x﹣6，设点P（a，﹣2a﹣6），∵C（0，﹣3），E（﹣1，0），根据勾股定理得，PE2=（a+1）2+（﹣2a﹣6）2，PC2=a2+（﹣2a﹣6+3）2，∵PC=PE，∴（a+1）2+（﹣2a﹣6）2=a2+（﹣2a﹣6+3）2，∴a=﹣2，∴y=﹣2×（﹣2）﹣6=﹣2，∴P（﹣2，﹣2），（3）如图，作PF⊥x 轴于F，∴F（﹣2，0），设M（d，0），∴G（d，d2+2d﹣3），N（﹣2，d2+2d﹣3），∵以点F，N，G，M 四点为顶点的四边形为正方形，必有FM=MG，∴|d+2|=|d2+2d﹣3|，∴d= 或d=，∴点M 的坐标为（，0），（，0），（，0），（，0）．2.如图，抛物线y=﹣x2+bx+c 与x 轴交于点A 和点B，与y 轴交于点C，点B 坐标为（6，0），点C 坐标为（0，6），点D 是抛物线的顶点，过点D 作x 轴的垂线，垂足为E，连接BD．（1）求抛物线的解析式及点D 的坐标；（2）点F 是抛物线上的动点，当∠FBA=∠BDE 时，求点F 的坐标；（3）若点M 是抛物线上的动点，过点M 作MN∥x 轴与抛物线交于点N，点P 在x 轴上，点Q 在坐标平面内，以线段MN 为对角线作正方形MPNQ，请写出点Q 的坐标．【解答】解：（1）把B、C 两点坐标代入抛物线解析式可得，解得，∴抛物线解析式为y=﹣x2+2x+6，∵y=﹣x2+2x+6=﹣（x﹣2）2+8，∴D（2，8）；（2）如图1，过F 作FG⊥x 轴于点G，设F（x，﹣x2+2x+6），则FG=|﹣x2+2x+6|，∵∠FBA=∠BDE，∠FGB=∠BED=90°，∴△FBG∽△BDE，∴=，∵B（6，0），D（2，8），∴E（2，0），BE=4，DE=8，OB=6，∴BG=6﹣x，∴= ，当点F 在x 轴上方时，有=，解得x=﹣1 或x=6（舍去），此时F 点的坐标为（﹣1，）；当点F 在x 轴下方时，有=﹣，解得x=﹣3 或x=6（舍去），此时F 点坐标为（﹣3，﹣）；综上可知F 点的坐标为（﹣1，）或（﹣3，﹣）；（3）如图2，设对角线MN、PQ 交于点O′，∵点M、N 关于抛物线对称轴对称，且四边形MPNQ 为正方形，∴点P 为抛物线对称轴与x 轴的交点，点Q 在抛物线的对称轴上，设Q（2，2n），则M 坐标为（2﹣n，n），∵点M 在抛物线y=﹣x2+2x+6 的图象上，∴n=﹣（2﹣n）2+2（2﹣n）+6，解得n=﹣1+ 或n=﹣1﹣，∴满足条件的点Q 有两个，其坐标分别为（2，﹣2+2）或（2，﹣2﹣2）．3.如图，已知抛物线y=ax2+bx﹣3 过点A（﹣1，0），B（3，0），点M、N 为抛物线上的动点，过点M 作MD∥y 轴，交直线BC 于点D，交x 轴于点E．过点N 作NF⊥x 轴，垂足为点 F（1）求二次函数y=ax2+bx﹣3 的表达式；（2）若M 点是抛物线上对称轴右侧的点，且四边形MNFE 为正方形，求该正方形的面积；（3）若M 点是抛物线上对称轴左侧的点，且∠DMN=90°，MD=MN，请直接写出点M 的横坐标．【解答】解：（1）把A（﹣1，0），B（3，0）代入y=ax2+bx﹣3，得：，解得，故该抛物线解析式为：y=x2﹣2x﹣3；（2）由（1）知，抛物线解析式为：y=x2﹣2x﹣3=（x﹣1）2﹣4，∴该抛物线的对称轴是x=1，顶点坐标为（1，﹣4）．如图，设点M 坐标为（m，m2﹣2m﹣3），其中m＞1，∴ME=|﹣m2+2m+3|，∵M、N 关于x=1 对称，且点M 在对称轴右侧，∴点N 的横坐标为2﹣m，∴MN=2m﹣2，∵四边形MNFE 为正方形，∴ME=MN，∴|﹣m2+2m+3|=2m﹣2，分两种情况：①当﹣m2+2m+3=2m﹣2 时，解得：m1=、m2=﹣（不符合题意，舍去），当m=时，正方形的面积为（2﹣2）2=24﹣8 ；②当﹣m2+2m+3=2﹣2m 时，解得：m3=2+，m4=2﹣（不符合题意，舍去），当m=2+时，正方形的面积为[2（2+）﹣2]2=24+8 ；综上所述，正方形的面积为24+8或24﹣8．（3）设BC 所在直线解析式为y=px+q，把点B（3，0）、C（0，﹣3）代入表达式，得：，解得：，∴直线BC 的函数表达式为y=x﹣3，设点M 的坐标为（t，t2﹣2t﹣3），其中t＜1，则点N（2﹣t，t2﹣2t﹣3），点D（t，t﹣3），∴MN=2﹣t﹣t=2﹣2t，MD=|t2﹣2t﹣3﹣t+3|=|t2﹣3t|．∵MD=MN，∴|t2﹣3t|=2﹣2t，分两种情况：①当t2﹣3t=2﹣2t 时，解得t1=﹣1，t2=2（不符合题意，舍去）．②当3t﹣t2=2﹣2t 时，解得t3=，t2=（不符合题意，舍去）．综上所述，点M 的横坐标为﹣1 或．4.(2015 贵州省毕节地区) 如图，抛物线y=x2+bx+c 与x 轴交于A（﹣1，0），B（3，0）两点，顶点M 关于x 轴的对称点是M′．（1）求抛物线的解析式；（2）若直线AM′与此抛物线的另一个交点为C，求△CAB 的面积；（3）是否存在过A，B 两点的抛物线，其顶点P 关于x 轴的对称点为Q，使得四边形APBQ 为正方形？若存在，求出此抛物线的解析式；若不存在，请说明理由．分析：（1）根据待定系数法，可得函数解析式；（2）根据轴对称，可得M′的坐标，根据待定系数法，可得AM′的解析式，根据解方程组，可得B 点坐标，根据三角形的面积公式，可得答案；（3）根据正方形的性质，可得P、Q 点坐标，根据待定系数法，可得函数解析式．解答：解：（1）将A、B 点坐标代入函数解析式，得，解得，抛物线的解析式y=x2﹣2x﹣3；（2）将抛物线的解析式化为顶点式，得y=（x﹣1）2﹣4，M 点的坐标为（1，﹣4），M′点的坐标为（1，4），设AM′的解析式为y=kx+b，将A、M′点的坐标代入，得，解得，AM′的解析式为y=2x+2，联立AM′与抛物线，得，解得，C 点坐标为（5，12）．S△ABC=×4×12=24；（3）存在过A，B 两点的抛物线，其顶点P 关于x 轴的对称点为Q，使得四边形APBQ 为正方形，由ABPQ 是正方形，A（﹣1，0）B（3，0），得P（1，﹣2），Q（1，2），或P（1，2），Q（1，﹣2），①当顶点P（1，﹣2）时，设抛物线的解析式为y=a（x﹣1）2﹣2，将A 点坐标代入函数解析式，得a（﹣1﹣1）2﹣2=0，解得a= ，抛物线的解析式为y=（x﹣1）2﹣2，②当P（1，2）时，设抛物线的解析式为y=a（x﹣1）2+2，将A 点坐标代入函数解析式，得a（﹣1﹣1）2+2=0，解得a=﹣，抛物线的解析式为y=﹣（x﹣1）2+2，综上所述：y=（x﹣1）2﹣2 或y=﹣（x﹣1）2+2，使得四边形APBQ 为正方形．5.(2016 辽宁省铁岭市) ．如图，抛物线y=﹣x2+bx+c 与x 轴交于点A，点B，与y 轴交于点C，点B 坐标为（6，0），点C 坐标为（0，6），点D 是抛物线的顶点，过点D 作x 轴的垂线，垂足为E，连接BD．（1）求抛物线的解析式及点D 的坐标；（2）点F 是抛物线上的动点，当∠FBA=∠BDE 时，求点F 的坐标；（3）若点M 是抛物线上的动点，过点M 作MN∥x 轴与抛物线交于点N，点P 在x 轴上，点Q 在平面内，以线段MN 为对角线作正方形MPNQ，请直接写出点Q 的坐标．分析（1）由点B、C 的坐标利用待定系数法即可求出抛物线的解析式，再利用配方法将抛物线解析式变形成顶点式即可得出结论；（2）设线段BF 与y 轴交点为点F′，设点F′的坐标为（0，m），由相似三角形的判定及性质可得出点F′的坐标，根据点B、F′的坐标利用待定系数法可求出直线BF 的解析式，联立直线BF 和抛物线的解析式成方程组，解方程组即可求出点F 的坐标；（3）设对角线MN、PQ 交于点O′，如图2 所示．根据抛物线的对称性结合正方形的性质可得出点P、Q 的位置，设出点Q 的坐标为（2，2n），由正方形的性质可得出点M 的坐标为（2﹣n，n）．由点M 在抛物线图象上，即可得出关于n 的一元二次方程，解方程可求出n 值，代入点Q 的坐标即可得出结论．解答解：（1）将点B（6，0）、C（0，6）代入y=﹣x2+bx+c 中，得：，解得：，∴抛物线的解析式为y=﹣x2+2x+6．∵y=﹣x2+2x+6=﹣（x﹣2）2+8，∴点D 的坐标为（2，8）．（2）设线段BF 与y 轴交点为点F′，设点F′的坐标为（0，m），如图1 所示．∵∠F′BO=∠FBA=∠BDE，∠F′OB=∠BED=90°，∴△F′BO∽△BDE，∴．∵点B（6，0），点D（2，8），∴点E（2，0），BE=6﹣4=4，DE=8﹣0=8，OB=6，∴OF′=•OB=3，∴点F′（0，3）或（0，﹣3）．设直线BF 的解析式为y=kx±3，则有0=6k+3 或0=6k﹣3，解得：k=﹣或k=，∴直线BF 的解析式为y=﹣x+3 或y=x﹣3．联立直线BF 与抛物线的解析式得：①或②，解方程组①得：或（舍去），∴点F 的坐标为（﹣1，）；解方程组②得：或（舍去），∴点F 的坐标为（﹣3，﹣）．综上可知：点F 的坐标为（﹣1，）或（﹣3，﹣）．（3）设对角线MN、PQ 交于点O′，如图2 所示．∵点M、N 关于抛物线对称轴对称，且四边形MPNQ 为正方形，∴点P 为抛物线对称轴与x 轴的交点，点Q 在抛物线对称轴上，设点Q 的坐标为（2，2n），则点M 的坐标为（2﹣n，n）．∵点M 在抛物线y=﹣x2+2x+6 的图象上，∴n=﹣+2（2﹣n）+6，即n2+2n﹣16=0，解得：n1=﹣1，n2=﹣﹣1．∴点Q 的坐标为（2，﹣1）或（2，﹣﹣1）．6.(2016 广东省茂名市) 】．如图，抛物线y=﹣x2+bx+c 经过A（﹣1，0），B（3，0）两点，且与y 轴交于点C，点D 是抛物线的顶点，抛物线的对称轴DE 交x 轴于点E，连接BD．（1）求经过A，B，C 三点的抛物线的函数表达式；（2）点P 是线段BD 上一点，当PE=PC 时，求点P 的坐标；（3）在（2）的条件下，过点P 作PF⊥x 轴于点F，G 为抛物线上一动点，M 为x 轴上一动点，N 为直线PF 上一动点，当以F、M、G 为顶点的四边形是正方形时，请求出点M 的坐标．分析（1）利用待定系数法求出过A，B，C 三点的抛物线的函数表达式；（2）连接PC、PE，利用公式求出顶点D 的坐标，利用待定系数法求出直线BD 的解析式，设出点P 的坐标为（x，﹣2x+6），利用勾股定理表示出PC2和PE2，根据题意列出方程，解方程求出x 的值，计算求出点P 的坐标；（3）设点M 的坐标为（a，0），表示出点G 的坐标，根据正方形的性质列出方程，解方程即可．解答解：（1）∵抛物线y=﹣x2+bx+c 经过A（﹣1，0），B（3，0）两点，∴，解得，，∴经过A，B，C 三点的抛物线的函数表达式为y=﹣x2+2x+3；（2）如图1，连接PC、PE，x=﹣=﹣=1，当x=1 时，y=4，∴点D 的坐标为（1，4），设直线BD 的解析式为：y=mx+n，则，解得，，∴直线BD 的解析式为y=﹣2x+6，设点P 的坐标为（x，﹣2x+6），则PC2=x2+（3+2x﹣6）2，PE2=（x﹣1）2+（﹣2x+6）2，∵PC=PE，∴x2+（3+2x﹣6）2=（x﹣1）2+（﹣2x+6）2，解得，x=2，则y=﹣2×2+6=2，∴点P 的坐标为（2，2）；（3）设点M 的坐标为（a，0），则点G 的坐标为（a，﹣a2+2a+3），∵以F、M、G 为顶点的四边形是正方形，∴FM=MG，即|2﹣a|=|﹣a2+2a+3|，当2﹣a=﹣a2+2a+3 时，整理得，a2﹣3a﹣1=0，解得，a=，当2﹣a=﹣（﹣a2+2a+3）时，整理得，a2﹣a﹣5=0，解得，a= ，∴当以F M、G、为顶点的四边形是正方形时点，M 的坐标（0，）（0，）（0，）（，0）．为，，，。

复查测验：综合测试3

复查测验：综合测试3.txt“恋”是个很强悍的字。

它的上半部取自“变态”的“变”，下半部取自“变态”的“态”。

复查测验：综合测试3 审计学基础(023********) > ■测试评价■ > 综合测试 > 复查测验：综合测试3问题 1 得 0 分，满分 2 分审计的独立性表现为双向独立的是( )。

正确答案： D. 注册会计师审计问题 2 得 0 分，满分 2 分不以会计报表为直接审计对象的审计业务是( )。

正确答案： B. 验证企业资本问题 3 得 0 分，满分 2 分会计师事务所对无法胜任的或不能按时完成的业务，应( )。

正确答案： D. 拒绝接受委托问题 4 得 0 分，满分 2 分在整个审计过程中处于中心环节的是( )。

正确答案： B. 实施阶段问题 5 得 0 分，满分 2 分一般而言，要证实被审计单位对某项资产“存在性”，注册会计师应获取的审计证据为( )。

正确答案： A. 实物证据问题 6 得 0 分，满分 2 分在分析程序的系统性步骤中，你认为最核心的步骤是( )。

正确答案： C. 分析数据及确认重大差异问题 7 得 0 分，满分 2 分双重目的的测试是指( )。

正确答案： D. 在控制测试的同时进行实质性程序问题 8 得 0 分，满分 2 分注册会计师希望从2000张编号为0001至2000的支票中抽取100张进行审计，随机确定的抽样起点为1955，采用系统抽样法下，抽取到的第四个样本号为( )。

正确答案： B. 0015问题 9 得 0 分，满分 2 分在资产负债表试算平衡表中，左方“调整金额”栏中( )的金额应等于右方同栏中的金额。

正确答案： B. 借方合计数－贷方合计数问题 10 得 0 分，满分 2 分在以下书面文件中，( )没有明确提及注册会计师的审计责任。

正确答案： B. 管理建议书问题 11 得 0 分，满分 2 分关于独立审计的表述正确的是( )。

中考数学第二轮专题复习第41课存在性问题、定值问题(含答案)

∴MC的解析式为：y＝－x－3，令y＝0，则x＝－3，
∴E点坐标为(－3，0)，
∴OE＝OB＝3，且OC⊥BE，
∴CE＝CB，∴∠B＝∠E，设P(x，－x－3)，
(1)证明：如图1中， ∵AE∥DF，AD∥EF，∴四边形ABCD是平行四边形， ∵四边形ABOC是正方形， ∴AC＝AB＝OC＝OB，∠ACE＝∠ABD＝90°， ∵E，D分别是OC，OB的中点， ∴CE＝BD， ∴△CAE≌△ABD(SAS)， ∴AE＝AD， ∴四边形AEFD是菱形．
(2)解：如图1中，连接DE. ∵S△SE△ODA＝DB＝12 S×△4A×CE＝4＝12 8×，8×4＝16， ∴S△AED＝S正方形ABOC－2S△ABD－S△EOD＝64－2×16－8＝24， ∴S菱形AEFD＝2S△AED＝48.
y y
2x 2 2x2 8x
6
，
解得：
x1 y1
10，
x2 y2
4 6
，
∴S△ABD＝
1 2
×2×6＝6，
设点E(m，2m－2)，
∵直线BE将△ABD的面积分为1∶2两部分，
∴ ∴S1△×ABE2＝×(132mS△－AB2D)＝＝22或或S1△×ABE2＝×23(2mS△－AB2D)＝＝44，，
(2)∵y＝2x2－8x＋6＝2(x－2)2－2，
∴顶点M的坐标为(2，－2)，
∵抛物线的顶点M与对称轴l上的点N关于x轴对称，
∴点N(2，2)，
设直线AN解析式为：y＝kx＋b，
由题意可得
0 2
k b 2k b
，解得：bk
2 2
，
∴直线AN解析式为：y＝2x－2，
联立方程组得：点D(4，6)，