二面角习题及答案
高考数学试卷二面角

一、选择题1. 下列关于二面角的叙述中,正确的是()A. 二面角是由两个平面相交形成的角B. 二面角是由两个平面相交形成的两条线段所夹的角C. 二面角是由两个平面相交形成的两条射线所夹的角D. 二面角是由两个平面相交形成的两条直线所夹的角答案:C2. 在二面角中,一个平面内两条相交直线与另一个平面所成的角分别为α和β,则二面角的度数是()A. α + βB. α - βC. |α - β|D. 90°答案:C3. 若二面角的平面角为θ,那么这个二面角的度数范围是()A. 0° < θ < 90°B. 0° ≤ θ ≤ 180°C. 0° < θ ≤ 180°D. 90° < θ ≤ 180°答案:C4. 下列图形中,能表示二面角的是()A. 一个等腰三角形B. 一个等边三角形C. 一个矩形D. 一个正方形答案:C5. 若二面角的平面角为60°,则其补角的度数是()A. 60°B. 120°C. 180°D. 240°答案:B二、填空题6. 在二面角中,若一个平面内两条相交直线与另一个平面所成的角分别为α和β,则二面角的平面角为______。
答案:|α - β|7. 若二面角的平面角为θ,那么这个二面角的度数范围是______。
答案:0° < θ ≤ 180°8. 若一个二面角的平面角为45°,则其补角的度数是______。
答案:135°三、解答题9. 已知二面角的平面角为60°,求这个二面角的补角的度数。
解答过程:根据题意,设二面角的平面角为θ,则有:θ = 60°由补角的定义可知,二面角的补角为180° - θ,因此:补角= 180° - 60° = 120°所以,这个二面角的补角的度数是120°。
高二数学二面角专项练习题及参考答案(精品)

高二数学二面角专项练习题及参考答案班级_____________姓名_____________一、定义法:直接在二面角的棱上取一点,分别在两个半平面内作棱的垂线,得出平面角. 例1 在四棱锥P-ABCD 中,ABCD 是正方形,PA ⊥平面ABCD ,PA=AB=a ,求二面角B-PC-D 的大小。
二、垂线法:已知二面角其中一个面内一点到一个面的垂线,用三垂线定理或逆定理作出二面角的平面角;例2 在四棱锥P-ABCD 中,ABCD 是平行四边形,PA ⊥平面ABCD ,PA=AB=a ,∠ABC=30°,求二面角P-BC-A 的正切。
三、垂面法:作棱的垂直平面,则这个垂面与二面角两个面的交线所夹的角就是二面角的平面角 例3 在四棱锥P-ABCD 中,ABCD 是正方形,PA ⊥平面ABCD ,求B-PC-D 的大小。
四、投影面积法:一个平面α上的图形面积为S ,它在另一个平面β上的投影面积为S',这两个平面的夹角为θ,则S'=Scos θ或cos θ=/SS .例4 在四棱锥P-ABCD 中,ABCD 为正方形,PA ⊥平面ABCD ,PA =AB =a ,求平面PBA 与平面PDC 所成二面角的大小。
五、补形法:对于一类没有给出棱的二面角,应先延伸两个半平面,使之相交出现棱,然后再选用上述方法(尤其要考虑射影法)。
例5、在四棱锥P-ABCD 中,ABCD 为正方形,PA ⊥平面ABCD ,PA =AB =a ,求平面PBA 与平面PDC 所成二面角的大小。
方法归纳:二面角的类型和求法可用框图展现如下: [基础练习]1. 二面角是指 ( ) A 两个平面相交所组成的图形B 一个平面绕这个平面内一条直线旋转所组成的图形C 从一个平面内的一条直线出发的一个半平面与这个平面所组成的图形D 从一条直线出发的两个半平面所组成的图形2.平面α与平面β、γ都相交,则这三个平面可能有 ( ) A 1条或2条交线 B 2条或3条交线C 仅2条交线D 1条或2条或3条交线3.在300的二面角的一个面内有一个点,若它到另一个面的距离是10,则它到棱的距离是( )A 5B 20C 210 D225 4.在直二面角α-l-β中,RtΔABC 在平面α内,斜边BC 在棱l 上,若AB 与面β所成的角为600,则AC 与平面β所成的角为 ( ) A 300 B 450 C 600 D 1200 5.如图,射线BD 、BA 、BC 两两互相垂直,AB=BC=1,BD=26, 则弧度数为3的二面角是( ) A D-AC-B B A-CD-BC A-BC-D D A-BD-C6.△ABC 在平面α的射影是△A 1B 1C 1,如果△ABC 所在平面和平面α成θ,则有( ) A S △A1B1C1=S △ABC ·sinθ B S △A1B1C1= S △ABC ·cosθC S △ABC =S △A1B1C1·sinθD S △ABC =S △A1B1C1·cosθ7.如图,若P 为二面角M-l-N 的面N 内一点,PB ⊥l ,B 为垂足,A 为l 上一点,且∠PAB=α,PA 与平面M 所成角为β,二面角M-l-N 的 大小为γ,则有 ( )A.sinα=sinβsinγB.sinβ=sinαsinγC.sinγ=sinαsinβ D 以上都不对AB C DAB M NP l C1A1B1D8.在600的二面角的棱上有两点A 、B ,AC 、BD 分别是在这个二面角的两个面内垂直于AB 的线段,已知:AB=6,AC=3,BD=4,则CD= 。
二面角真题

二面角(2010-2012真题)1.(2012年全国高考课标卷)如图,直三棱柱111ABC A B C -中112AC BC AA ==,D 是棱1AA 的中点,BD DC ⊥1。
(1)证明:BC DC ⊥1;(2)求二面角11C BD A --的大小。
2.(2012年全国高考全国卷一)如图,四棱锥P ABCD -中,底面ABCD 为菱形,PA ⊥底面ABCD ,22AC =,2,PA E =是PC 上的一点,2PE EC =。
(1)证明:PC ⊥平面BED ;(2)设二面角A PB C --为90︒,求PD 与平面PBC 所成角的大小。
3.(2011年全国高考课标卷)如图,四棱锥P —ABCD 中,底面ABCD 为平行四边形,∠DAB=60°,AB=2AD,PD ⊥底面ABCD 。
(Ⅰ)证明:PA ⊥BD ;(Ⅱ)若PD=AD ,求二面角A-PB-C 的余弦值。
ECBDAP4.(2011年全国高考全国卷一)如图,四棱锥S ABCD -中, //AB CD ,BC CD ⊥,侧面SAB 为等边三角形,2,1AB BC CD SD ====。
(Ⅰ)证明:SD ⊥平面SAB ;(Ⅱ)求AB 与平面SBC 所成角的大小。
5.(2010年全国高考全国卷一)如图,四棱锥S-ABCD 中,SD ⊥底面ABCD ,AB//DC ,AD ⊥DC ,AB=AD=1,DC=SD=2,E 为棱SB 上的一点,平面EDC ⊥平面SBC 。
(Ⅰ)证明:SE=2EB ;(Ⅱ)求二面角A-DE-C 的大小。
6.(2010年全国高考全国卷二)如图,直三棱柱111ABC A B C -中,AC BC =,1AA AB =,D 为1BB 的中点,E 为1AB 上的一点,13AE EB =。
(Ⅰ)证明:DE 为异面直线1AB 与CD 的公垂线;(Ⅱ)设异面直线1AB 与CD 的夹角为45°,求二面角111A AC B --的大小。
二面角习题含详细答案

又AP⊥PC,PB∩PC=P, ∴AP⊥平面PBC①.…………………………………………2分 又BC⊂平面PBC,∴AP⊥BC. 又AC⊥BC,AP∩AC=A, ∴BC⊥平面PAC①.
又BC⊂平面ABC,∴平面PAC⊥平面ABC.…………………4分
(2)∵PA⊥PC,且PA⊥PB,
∴∠BPC是二面角D-AP-C的平面角②. 由(1)知BC⊥平面PAC,则BC⊥PC, ∴sin∠BPC= BC 2 . ……………………………………8分
通过分析条件,鉴别已知角是否为二面角的 平面角,否则就需利用垂直关系作辅助线得 到其平面角. 证明且点明某平面角是所求二面角的平面角. 把角放在三角形内求值,要注意的是二面角 的范围.
作图
定性
求解
【典例训练】
1.如图所示,在三棱锥P-ABC中,PA⊥平面ABC,∠BAC=90°,
则二面角B-PA-C的大小为( )
证明
求值
【想一想】找二面角的平面角的方法有哪些?
提示:(1)垂面法:由二面角的平面角的定义,只需作与棱垂 直的平面,则该平面与两半平面所成交线构成的角就是二面角 的平面角. (2)平移法:先分别在两半平面内找一条垂直于棱的射线,然 后平移到一起找到二面角的平面角.
【规范解答】线面垂直的综合应用
【典例】(12分)如图所示,已知三
(A)90°
(B)60°
(C)45°
(D)30°
2.如图所示,在△ABC中,AB⊥BC,SA⊥平面ABC,DE垂直平分 SC,且分别交AC,SC于点D,E,又SA=AB,SB=BC,求二面角
E-BD-C的大小.
【解析】1.选A.∵PA⊥平面ABC,BA,CA⊂平面ABC,
∴BA⊥PA,CA⊥PA,因此,∠BAC即为二面角B-PA-C的平面角.
二面角2练习及答案

⼆⾯⾓2练习及答案⼆⾯⾓练习2班级姓名1.如图,已知AB⊥平⾯BCD,BC⊥CD,M是CD的中点.则⼆⾯⾓A-CD-B的平⾯⾓是() A.∠ADB B.∠BDC C.∠AMB D.∠ACB【答案】D【解析】已知AB⊥平⾯BCD,可知AB⊥CD,⼜BC⊥CD,AB∩BC=B,∴CD⊥平⾯ABC.AC?平⾯ABC,∴CD⊥AC,由⼆⾯⾓的平⾯⾓的定义可知,⼆⾯⾓A-CD-B的平⾯⾓是∠ACB.故选D.2.在⼆⾯⾓α-l-β中,A∈α,AB⊥平⾯β于B,BC⊥平⾯α于C,若AB=6,BC=3,则⼆⾯⾓α-l-β的平⾯⾓的⼤⼩为()A.30°B.60°C.30°或150°D.60°或120°【答案】D【解析】如图,∵AB⊥β,∴AB⊥l,∵BC⊥α,∴BC⊥l,∴l⊥平⾯ABC,设平⾯ABC∩l=D,则∠ADB为⼆⾯⾓α-l-β的平⾯⾓或补⾓.∵AB=6,BC=3,∴∠BAC=30°,∴∠ADB=60°,∴⼆⾯⾓⼤⼩为60°或120°.3.如图所⽰,在三棱锥P-ABC中,PA⊥平⾯ABC,∠BAC=90°,则⼆⾯⾓B-PA-C的⼤⼩为()A.90°B.60°C.45°D.30°【答案】A【解析】∵PA⊥平⾯ABC,BA,CA?平⾯ABC,∴BA⊥PA,CA⊥PA,因此,∠BAC即为⼆⾯⾓B-PA-C的平⾯⾓.⼜∠BAC=90°,即⼆⾯⾓B-PA-C的⼤⼩为90°,故选A.4.从空间⼀点P向⼆⾯⾓α-l-β的两个⾯α,β分别作垂线PE,PF,E,F为垂⾜,若∠EPF =60°,则⼆⾯⾓的平⾯⾓的⼤⼩是()A.60°B.120°C.60°或120°D.不确定【答案】C【解析】若点P在⼆⾯⾓内,则⼆⾯⾓的平⾯⾓为120°;若点P在⼆⾯⾓外,则⼆⾯⾓的平⾯⾓为60°.5.过边长为1的正⽅形ABCD的顶点A,作线段EA⊥平⾯ABCD,若EA=1,则平⾯ADE与平⾯BCE所成⼆⾯⾓的⼤⼩为()A.30°B.45°C.60°D.150°【答案】B【解析】如图所⽰.已知EA⊥平⾯ABCD,所以平⾯EAB⊥平⾯ABCD,则平⾯ADE与平⾯BCE所成⼆⾯⾓的平⾯⾓即为∠AEB,⼜EA=1,AB=1,∠EAB=90°,所以∠AEB =45°.故选B.6.如图,四棱锥P-ABCD中,底⾯ABCD是矩形,PD⊥平⾯ABCD,且PD=AD=1,AB=2,点E是AB上⼀点,当⼆⾯⾓P -EC-D为45°时,AE等于()A.1B.12C.2-2D.2-3【答案】D【解析】过点D作DF⊥CE于点F,连接PF,因为PD⊥平⾯ABCD,所以DF是PF在平⾯ABCD内的投影,因为DF⊥CE,所以PF⊥CE,可得∠PFD为⼆⾯⾓P-EC-D的平⾯⾓,即∠PFD=45°.在Rt△PDF中,PD=DF=1,因为在矩形ABCD中,△EBC∽△CFD,所以DFBC =CDEC,得EC=CD·BCDF=2.在Rt△BCE中,根据勾股定理,得BE=2?BC2=3,所以AE=AB-BE=2-3,故选D.7.已知PA垂直于矩形ABCD所在平⾯,PA=3,AB=2,BC=23,则⼆⾯⾓P-BD-A的正切值为()A.1B.2C.212D.3【答案】D【解析】过A作AH⊥BD于H,连接PH,因为PA⊥平⾯ABCD,所以∠PHA即为⼆⾯⾓P-BD-A的平⾯⾓.在直⾓△PHB中,因为PA=3,AH=AB×ADBD =2×234=3所以tan∠PHA=PAAH =3=3.故选D.8.在平⾯四边形ABCD中,AB=AD=1,BC=CD=2,AB⊥AD,沿BD将△ABD折起,使得AC=1,则⼆⾯⾓A-BD-C的平⾯⾓的正弦值为________.【答案】63【解析】在平⾯四边形ABCD中,取BD的中点E,由条件知A、E、C共线,且为BD的垂直平分线,⼜在△ABD中,AB⊥AD,AB=AD=1,∴BD=2,∴AE=12BD=22.在△CBD中,BC=DC=2,∴CE=62,沿BD折叠后,∠AEC为⼆⾯⾓A-BD-C的平⾯⾓,⼜AC=1,∴在△AEC中,AE2+AC2=CE2,∠EAC=90°,∴sin∠AEC=ACEC =6=63.9.三棱锥P-ABC的两侧⾯PAB、PBC都是边长为2的正三⾓形,AC=3,则⼆⾯⾓A-PB -C的⼤⼩为________.【答案】60°【解析】如图所⽰,取PB的中点M,连接MA、MC,由于△PAB、△PBC都是边长为2的正三⾓形,∴PB⊥MA,PB⊥MC,且MA=MC=3,∴∠AMC即为⼆⾯⾓A-PB-C的平⾯⾓.⼜AC=3,∴△MAC为正三⾓形,∠AMC=60°.10.在三棱柱ABC-A1B1C1中,侧棱都与底⾯垂直,且有AA1=AB=BC=AC,点E是线段BB1的中点,则平⾯C1EA与底⾯ABC所成的⼆⾯⾓的⼤⼩(锐⾓)是________.【答案】45°【解析】在平⾯BCC1B1中,延长C1E与直线BC交于D点,则AD为平⾯C1EA 与平⾯ABC的交线.∵AA1=AB =BC=AC,点E是线段BB1的中点,∴BD=BC=AB,∴△CAD是直⾓三⾓形,∠CAD=90°,∴AC⊥AD.⼜CC1⊥平⾯ABC,∴CC1⊥AD,CC1∩AC=C,∴AD⊥平⾯AA1C1C,∴AC1⊥AD,∴∠CAC1是平⾯C1EA与底⾯ABC所成的⼆⾯⾓的平⾯⾓.在直⾓三⾓形ACC1中,CC1=AC,∴tan∠C1AC=CC1AC=1,即∠CAC1=45°.故答案为45°.11.在正⽅体ABCD-A1B1C1D1中,截⾯A1BD与底⾯ABCD所成的⼆⾯⾓A1-BD-A的正切值为________.【答案】2【解析】连接AC交BD于点O,如图所⽰.因为A1O⊥BD,AO⊥BD,所以∠A1OA即为⼆⾯⾓A1-BD-A的平⾯⾓,在△A1OA中,设AA1=a,则AO=22a,所以⼆⾯⾓A1-BD-A的正切值为2.12.如图,已知四边形ABCD是正⽅形,PA⊥平⾯ABCD.(1)求⼆⾯⾓B-PA-D的平⾯⾓的度数;(2)求⼆⾯⾓B-PA-C的平⾯⾓的度数.【答案】(1)∵PA⊥平⾯ABCD,∴AB⊥PA,AD⊥PA.∴∠BAD为⼆⾯⾓B-PA-D的平⾯⾓.⼜由题意知∠BAD=90°,∴⼆⾯⾓B-PA-D的平⾯⾓的度数为90°.(2)∵PA⊥平⾯ABCD,∴AB⊥PA,AC⊥PA.∴∠BAC为⼆⾯⾓B-PA-C的平⾯⾓.⼜四边形ABCD为正⽅形,∴∠BAC=45°.即⼆⾯⾓B-PA-C的平⾯⾓的度数为45°. 13.如图,直三棱柱ABC-A1B1C1中,AC=BC=1AA1,D是棱AA1的中点,DC1⊥BD.2(1)证明:DC1⊥BC;(2)求⼆⾯⾓A1-BD-C1的⼤⼩.【答案】(1)证明由题设知,三棱柱的侧⾯为矩形.由于D为AA1的AA1,可得D C12+DC2=C C12,中点,故DC=DC1.⼜AC=12所以DC1⊥DC.⽽DC1⊥BD,CD∩BD=D,所以DC1⊥平⾯BCD.因为BC?平⾯BCD,所以DC1⊥BC.(2)解DC1⊥BC,CC1⊥BC?BC⊥平⾯ACC1A1?BC⊥AC,取A1B1的中点O,过点O作OH⊥BD于点H,连接C1O,C1H,A1C1=B1C1?C1O⊥A1B1,⾯A1B1C1⊥⾯A1BD?C1O⊥⾯A1BD,⼜∵DB?⾯A1DB,∴C1O⊥BD,⼜∵OH⊥BD,∴BD⊥⾯C1OH,C1H?⾯C1OH,∴BD⊥C1H,得点H与点D重合,且∠C1DO是⼆⾯⾓a,C1D=2a=2C1O?∠C1DO=30°,A1-BD-C1的平⾯⾓,设AC=a,则C1O=22故⼆⾯⾓A1-BD-C1的⼤⼩为30°.14.如图所⽰,三棱锥P-ABC中,D是AC的中点,PA=PB=PC=5,AC=22,AB=2,BC=6.(1)求证:PD⊥平⾯ABC;(2)求⼆⾯⾓P-AB-C的正切值.【答案】(1)证明连接BD,∵D是AC的中点,PA=PC=5,∴PD⊥AC.∵AC=22,AB=2,BC=6,∴AB2+BC2=AC2,∴∠ABC=90°,即AB⊥BC.∴BD =12AC=2=AD.∵PD2=PA2-AD2=3,PB=5,∴PD2+BD2=PB2.∴PD⊥BD.∵AC∩BD=D,∴PD⊥平⾯ABC.(2)解取AB的中点E,连接DE、PE,由E为AB的中点,知DE∥BC,∵AB⊥BC,∴AB⊥DE.∵PD⊥平⾯ABC,∴PD⊥AB.⼜DE∩PD=D,∴AB⊥平⾯PDE,∴PE⊥AB.∴∠PED是⼆⾯⾓P-AB-C的平⾯⾓.在Rt△PED中,DE=12BC=62,PD=3,∠PDE=90°,∴tan∠PED=PDDE=2.∴⼆⾯⾓P-AB-C的正切值为2.15.如图所⽰,四棱锥P-ABCD的底⾯ABCD是边长为1的菱形,∠BCD=60°,E是CD的中点,PA⊥底⾯ABCD,PA=3.求⼆⾯⾓A-BE-P的⼤⼩.【答案】如图所⽰,连接BD,由ABCD是菱形且∠BCD=60°,知△BCD是等边三⾓形.因为E是CD的中点,所以BE⊥CD.⼜AB∥CD,所以BE⊥AB.⼜因为PA⊥平⾯ABCD,BE?平⾯ABCD,所以PA⊥BE.⽽PA∩AB=A,因此BE⊥平⾯PAB.因为PB?平⾯PAB,所以PB⊥BE.⼜AB⊥BE,所以∠PBA是⼆⾯⾓A-BE-P的平⾯⾓.在Rt△PAB中,tan∠PBA=PAAB=3,则∠PBA=60°.故⼆⾯⾓A-BE-P的⼤⼩是60°.16.如图,在三棱锥P-ABC中,PA⊥底⾯ABC,∠BCA=90°,点D、E分别在棱PB、PC上,且DE∥BC.(1)求证:BC⊥平⾯PAC.(2)是否存在点E,使得⼆⾯⾓A—DE—P为直⼆⾯⾓?并说明理由.【答案】(1)∵PA⊥底⾯ABC,∴PA⊥BC.⼜∠BCA=90°,∴AC⊥BC.⼜∵AC∩PA=A,∴BC⊥平⾯PAC.(2)∵DE∥BC,⼜由(1)知,BC⊥平⾯PAC,∴DE⊥平⾯PAC.⼜∵AE?平⾯PAC,PE?平⾯PAC,∴DE⊥AE,DE⊥PE.∴∠AEP 为⼆⾯⾓A-DE-P的平⾯⾓.∵PA⊥底⾯ABC,∴PA⊥AC,∴∠PAC=90°.∴在棱PC上存在⼀点E,使得AE⊥PC.这时∠AEP=90°,故存在点E,使得⼆⾯⾓A-DE-P为直⼆⾯⾓.17.如图,在直三棱柱(侧棱垂直于底⾯的棱柱)ABC-A1B1C1中,AB=4,AC=BC=3,D为AB的中点.(1)求点C到平⾯A1ABB1的距离;(2)若AB1⊥A1C,求⼆⾯⾓A1-CD-C1的平⾯⾓的余弦值.【答案】(1)由AC=BC,D为AB的中点,得CD⊥AB,⼜CD⊥AA1,故CD⊥平⾯A1ABB1,所以C到平⾯A1ABB1的距离CD=2?BD2=5.(2)如图,取D1为A1B1的中点,连接DD1,则DD1∥AA1∥CC1.⼜由(1)知CD⊥平⾯A1ABB1,故CD⊥A1D,CD⊥DD1,所以∠A1DD1为所求的⼆⾯⾓A1-CD-C1的平⾯⾓.因为CD⊥平⾯A1ABB1,AB1?平⾯A1ABB1,所以AB1⊥CD,⼜已知AB1⊥A1C,A1C∩CD=C,所以AB1⊥平⾯A1CD,故AB1⊥A1D,从⽽∠A1AB1、∠A1DA都与∠B1AB互余,因此∠A1AB1=∠A1DA,所以Rt△A1AD∽Rt△B1A1A.因此AA1AD =A1B1AA1,即AA12=AD·A1B1=8,得A1A=22.从⽽A1D= AA12+AD2=23,所以,在Rt△A1DD1中,cos∠A1DD1=DD1A1D =AA1A1D =6 3.。
二面角专项训练(人教A版)(含答案)

二面角专项训练(人教A版)一、单选题(共7道,每道10分)1.等于90°的二面角内有一点P,过P有PA⊥α于点A,PB⊥β于点B,如果PA=PB=a,则P 到交线的距离为( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:与二面角有关的点、线、面间的距离计算2.如图,在三棱锥F-ABC中,FC⊥底面ABC,CA=CB=CF,∠ACB=120°,则二面角F-AB-C的正切值为( )A. B.C. D.答案:C解题思路:试题难度:三颗星知识点:二面角的平面角及求法3.如图,在四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其他四个侧面都是腰长为的等腰三角形,则二面角V-AB-C的平面角为( )A.30°B.45°C.60°D.90°答案:C解题思路:试题难度:三颗星知识点:二面角的平面角及求法4.如图,在三棱锥P-ABC中,PA⊥平面ABC,AC⊥AB,PA=AB=2,AC=1,则二面角A-PC-B的正弦值为( )A. B.C. D.答案:D解题思路:试题难度:三颗星知识点:二面角的平面角及求法5.如图,在直三棱柱ABC-A1B1C1中,AC=BC=AA1,∠ACB=90°,D是棱AA1的中点,则二面角B-DC1-C的余弦值为( )A. B.C. D.答案:B解题思路:试题难度:三颗星知识点:二面角的平面角及求法6.如图,在直三棱柱ABC-A1B1C1中,AC=BC=AA1,D是棱AA1的中点,DC1⊥BD,则二面角A1-BD-C1的大小为( )A.30°B.45°C.60°D.90°答案:A解题思路:试题难度:三颗星知识点:二面角的平面角及求法7.如图,在直三棱柱ABC-A1B1C1中,AB1⊥A1C,AB=4,AC=BC=3,D为AB的中点,则二面角A1-CD-C1的平面角的余弦值为( )A. B. C. D.答案:D解题思路:试题难度:三颗星知识点:二面角的平面角及求法。
二面角习题
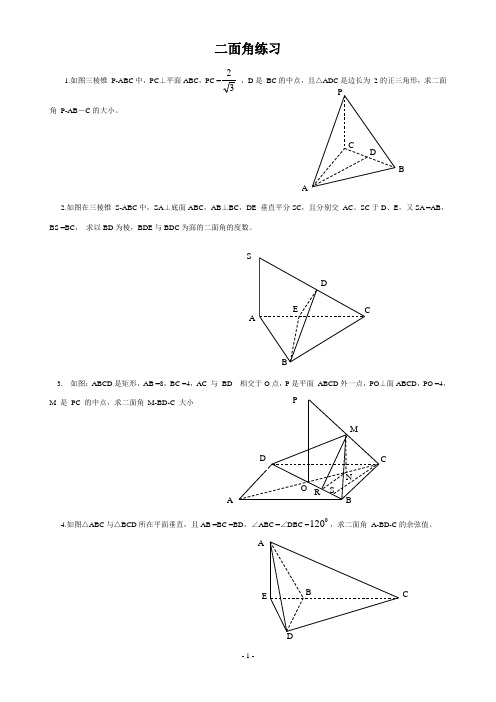
二面角练习1.如图三棱锥 P-ABC 中,PC ⊥平面ABC ,PC =32 ,D 是 BC 的中点,且△ADC 是边长为 2的正三角形,求二面角 P-AB -C 的大小。
2.如图在三棱锥 S-ABC 中,SA ⊥底面ABC ,AB ⊥BC ,DE 垂直平分SC ,且分别交 AC 、SC 于D 、E ,又SA =AB ,BS =BC , 求以BD 为棱,BDE 与BDC 为面的二面角的度数。
3. 如图:ABCD 是矩形,AB =8,BC =4,AC 与 BD 相交于O 点,P 是平面 ABCD 外一点,PO ⊥面ABCD ,PO =4,M 是 PC 的中点,求二面角 M-BD-C 大小4.如图△ABC 与△BCD 所在平面垂直,且AB =BC =BD ,∠ABC =∠DBC =0120,求二面角 A-BD-C 的余弦值。
DPCABEDBASCSR NMOBDPACBAEC5.已知正方体 AC',M 、N 分别是BB',DD'的中点,求截面 AMC'N 与面ABCD ,CC'D'D 所成的角。
6. 如图,设ABC —A1B1C1是直三棱柱,E 、F 分别为AB 、A1B1的中点,且AB =2AA1=2a,AC =BC =3a.(1)求证:AF ⊥A1C(2)求二面角C —AF —B 的大小7.如图1111D C B A ABCD -是长方体,AB=2,11==AD AA ,求二平面C AB 1与1111D C B A 所成二面角的大小.8.在正方体1111D C B A ABCD -中,1BB K ∈,1CC M ∈,且141BB BK =,143CC CM =..求:平面AKM与ABCD 所成角的大小.D ’ B ’D AC ’B A ’CMN答案:1解:由已知条件,D 是BC 的中点 ∴ CD =BD =2 又△ADC 是正三角形 ∴ AD =CD =BD =2∴ D 是△ABC 之外心又在BC 上 ∴ △ABC 是以∠BAC 为直角的三角形, ∴ AB ⊥AC , 又 PC ⊥面ABC ∴ PA ⊥AB (三垂线定理)∴∠PAC 即为二面角 P-AB-C 之平面角, 易求 ∠PAC =30°2.解:∵ BS =BC ,又DE 垂直平分SC∴ BE ⊥SC ,SC ⊥面BDE ∴ BD ⊥SC ,又SA ⊥面ABC ∴ SA ⊥BD ,BD ⊥面SAC ∴ BD ⊥DE ,且BD ⊥DC 则 ∠EDC 就是所要求的平面角 设 SA =AB =a , 则 BC =SB =2a 且 AC = 3易证 △SAC ∽△DEC ∴ ∠CDE =∠SAC =60° 3.解:取OC 之中点N ,则 MN ∥PO ∵ PO ⊥面ABCD∴ MN ⊥面ABCD 且 MN =PO/2 =2, 过 N 作 NR ⊥BD 于 R ,连MR ,则 ∠MRN 即为二面角 M-BD-C 的平面角过 C 作 CE ⊥BD 于S 则 RN =21CE 在 Rt △BCD 中,CD ·BC =BD ·CE∴58BD BC CD CE =⋅=∴54RN =25RN MN MRN tan ==∠ EDBASCSR NMOBDPAC∴25a r c t a nM R N =∠4.解:过 A 作 AE ⊥CB 的延长线于E , 连结 DE , ∵ 面ABC ⊥面BCD ∴ AE ⊥面BCD∴ E 点即为点A 在面BCD 内的射影∴ △EBD 为△ABD 在面BCD 内的射影设 AB =a 则AE =DE =ABsin60°=a 23 ∴ AD =41ABD cos 26=∠, ∴ sin ∠ABD =415∴22A B D a 815415a 21S =⨯=∆ 又 a 21BE =∴2B D E a 83a 21a 2321S =⋅⋅=∆ ∴55S S c o s A B D B D E ==θ∆∆考虑到我们求的是二面角 A-BD-E ,而二面角 A-BD-C 与A-BD-C 互补∴ 二面角 A-BD-C 的余弦值为55-。
二面角习题及标准答案

二面角习题及答案————————————————————————————————作者:————————————————————————————————日期:二面角1.如图三棱锥 P-ABC 中,PC ⊥平面ABC ,PC =32 ,D 是 BC 的中点,且△ADC是边长为 2的正三角形,求二面角 P-AB -C 的大小。
解2.如图在三棱锥 S-ABC 中,SA ⊥底面ABC ,AB ⊥BC ,DE 垂直平分SC ,且分别交 AC 、SC 于D 、E ,又SA =AB ,BS =BC , 求以BD 为棱,BDE 与BDC 为面的二面角的度数。
解:3. 如图:ABCD 是矩形,AB =8,BC =4,AC 与 BD 相交于O 点,P 是平面 ABCD 外一点,PO ⊥面ABCD ,PO =4,M 是 PC 的中点,求二面角 M-BD-C 大小。
解:4.如图△ABC 与△BCD 所在平面垂直,且AB =BC =BD ,∠ABC =∠DBC =0120,求二面角 A-BD-C 的余弦值。
解:DPC A BE DB ASCS R NMO B DPA CB A EC5.已知正方体 AC',M 、N 分别是BB',DD'的中点,求截面 AMC'N 与面ABCD ,CC'D'D 所成的角。
解:6.如图 AC ⊥面BCD ,BD ⊥面ACD ,若AC =CD =1,∠ABC =30°,求二面角D AB C --的大小。
解:7. 三棱锥 A-BCD 中,∠BAC =∠BCD =90°,∠DBC =30°,AB =AC =6,AD =4,求二面角 A-BC-D 的度数。
解:9. 如图所示,四棱锥P —ABCD 的底面是边长为a 的菱形,∠A =60°,PC ⊥平面ABCD ,PC =a,E 是PA 的中点.(1)求证平面BDE ⊥平面ABCD.(2)求点E 到平面PBC 的距离.(3)求二面角A —EB —D 的平面角大小. 解析:D BD ACBAC M N B F E ACDDOA BC10. 如图,已知正方体ABCD —A1B1C1D1的棱长为1,E 、F 分别在棱AB 、BC 上,G 在对角线BD1上,且AE =41,BF =21,D1G ∶GB =1∶2,求平面EFG 与底面ABCD 所成的二面角的大小.11. 如图,设ABC —A1B1C1是直三棱柱,E 、F 分别为AB 、A1B1的中点,且AB =2AA1=2a,AC =BC =3a. (1)求证:AF ⊥A1C(2)求二面角C —AF —B 的大小12.如图1111D C B A ABCD -是长方体,AB=2,11==AD AA ,求二平面C AB 1与1111D C B A 所成二面角的大小.13. 在正方体1111D C B A ABCD -中,1BB K ∈,1CC M ∈,且141BB BK =,143CC CM =..求:平面AKM 与ABCD 所成角的大小.14. 如图,将边长为a 的正三角形ABC 按它的高AD 为折痕折成一个二面角C AD C --'. (1)若二面角C AD C --'是直二面角,求C C '的长; (2)求C A '与平面CD C '所成的角;(3)若二面角C AD C --'的平面角为120°,求二面角D C C A -'-的平面角的正切值.参考答案解:由已知条件,D 是BC 的中点∴ CD =BD =2 又△ADC 是正三角形 ∴ AD =CD =BD =2∴ D 是△ABC 之外心又在BC 上 ∴ △ABC 是以∠BAC 为直角的三角形, ∴ AB ⊥AC , 又 PC ⊥面ABC ∴ PA ⊥AB (三垂线定理)∴∠PAC 即为二面角 P-AB-C 之平面角, 易求 ∠PAC =30°2、解:∵ BS =BC ,又DE 垂直平分SC ∴ BE ⊥SC ,SC ⊥面BDE ∴ BD ⊥SC ,又SA ⊥面ABC ∴ SA ⊥BD ,BD ⊥面SAC ∴ BD ⊥DE ,且BD ⊥DC 则 ∠EDC 就是所要求的平面角 设 SA =AB =a ,则 BC =SB =2a 且 AC = 3易证 △SAC ∽△DEC ∴ ∠CDE =∠SAC =60° 3、解:取OC 之中点N ,则 MN ∥PO ∵ PO ⊥面ABCD∴ MN ⊥面ABCD 且 MN =PO/2 =2, 过 N 作 NR ⊥BD 于 R ,连MR , 则 ∠MRN 即为二面角 M-BD-C 的平面角 过 C 作 CE ⊥BD 于S则 RN =21CE 在 Rt △BCD 中,CD ·BC =BD ·CE ∴ 58BD BC CD CE =⋅=DPCA BE DBASCS R N MO B DPA C∴ 54RN =25RN MN MRN tan ==∠ ∴ 25arctanMRN =∠ 4. 解:过 A 作 AE ⊥CB 的延长线于E , 连结 DE , ∵ 面ABC ⊥面BCD ∴ AE ⊥面BCD∴ E 点即为点A 在面BCD 内的射影∴ △EBD 为△ABD 在面BCD 内的射影设 AB =a 则AE =DE =ABsin60°=a 23 ∴ AD =41ABD cos 26=∠, ∴ sin ∠ABD =415∴ 22ABD a 815415a 21S =⨯=∆ 又 a 21BE = ∴ 2BDE a 83a 21a 2321S =⋅⋅=∆ ∴ 55S S cos ABD BDE ==θ∆∆ 5. 解:设边长为a ,易证 ANC'N 是菱形 且MN =a 2,A'C =a 3 ∴S□AMC'N = 2a 26'AC 21MN =⋅由于AMC'N 在面ABCD 上的射影即 为正方形ABCD ∴ S□ABCD =2aD B D AC BAC MN∴ 36a 26a cos 221==θ ∴ 36arccos1=θ 取CC'的中点M',连结DM'则平行四边形DM'C'N 是四边形AMC'N 在CC'D'D 上的射影,S□DM'C'M =2a 21 ∴ 66a 26a21cos 222==θ ∴66arccos2=θ 6. 解:作DF ⊥AB 于F ,CE ⊥AB 于E , ∵ AC =CD =1 ∠ABC =30° ∴ AD =2,BC =3 , AB =2, BD =2 在Rt △ABC 中, 23231AB BC AC CE =⨯=⋅=,同理 1222ABBDAD DF =⨯=⋅= ∴ 1DF BD BF 22=-=21CE AC AE 22=-= ∴ 212112EF =--= ∴ θ⋅-++=cos DF EF 2EF DF CE CD 2222∴ 33cos =θ BF E ACD即所求角的大小为33arccos。
二面角1练习及答案

二面角练习1班级姓名1.从二面角内一点分别向二面角的两个面引垂线,则这两条垂线所夹的角与二面角的平面角的关系是()A.互为余角B.相等C.其和为周角D.互为补角【答案】D【解析】画图知从二面角内一点分别向二面角的两个面引垂线,则这两条垂线所夹的角与二面角的平面角互为补角,所以选D.2.如图,四棱锥V-ABCD中,底面ABCD是边长为2的正方形,其他四个侧面都是侧棱长为的等腰三角形,则二面角V-AB-C的大小为()A.30°B.45°C.60°D.120°【答案】C【解析】如图所示,由题意可得四棱锥V-ABCD是正四棱锥,连接AC,BD,相交于点O,连接VO,则VO⊥平面ABCD.取AB的中点M,连接VM,OM,则AB⊥OM,∴AB⊥VM.∴∠OMV是二面角V-AB-C的平面角.由正方形可得OB=BD=×2=,∴VO==.在Rt△VOM中,tan∠VMO===,∴∠VMO=60°.3.如图在长方体中,AB=AD=2,CC1=,则二面角C1-BD-C的大小为()A.30°B.45°C.60°D.90°【答案】A【解析】连接AC,交BD于点O,连接OC1,⊥平面ABCD,因为ABCD为正方形,则AC⊥BD,又CC所以CC1⊥BD,则BD⊥平面CC1O,所以BD⊥OC1,所以∠COC1是二面角C1-BD-C的平面角.又OC=AC=×AB=.在Rt△OCC1中,CC1=,所以tan∠COC1==,所以∠COC1=30°,故选A.4.在四面体ABCD中,已知棱AC的长为,其余各棱长都为1,则二面角A-CD-B的余弦值为()A.B.C.D.【答案】C【解析】取AC的中点E,取CD的中点F,连接BE,EF,BF.∵△BCD为等边三角形,F为CD中点,∴CD⊥BF.∵CD=AD=1,AC=,∴△ACD为等腰直角三角形,∴CD⊥AD.又EF∥AD,∴EF⊥CD.∴∠EFB为A-CD-B的平面角.又EF=,BE=,BF=,∴△BEF为直角三角形,cosθ==.5.如图所示,将等腰直角△ABC沿斜边BC上的高AD折成一个二面角,此时∠B′AC=60°,那么这个二面角的大小是()A.90°B.60°C.45°D.30°【答案】A【解析】连接B′C,则△AB′C为等边三角形.设AD=a,则B′C=AC=a,B′D=DC=a,所以∠B′DC=90°.6.如图所示,在△ABC中,AD⊥BC,△ABD的面积是△ACD的面积的2倍.沿AD将△ABC翻折,使翻折后BC⊥平面ACD,此时二面角B-AD-C的大小为()A.30°B.45°C.60°D.90°7.若P是△ABC所在平面外一点,而△PBC和△ABC都是边长为2的正三角形,PA=,那么二面角P-BC-A的大小为________.【答案】90°【解析】取BC的中点O,连接OA,OP,则∠POA为二面角P-BC-A的平面角,OP=OA=,PA=,所以△POA为直角三角形,∠POA=90°.8.如图,长方体ABCD-A1B1C1D1中,ABCD是边长为1的正方形,D1B与平面ABCD所成的角为45°,则棱AA的长为________;二面角B-DD1-C的大小为________.【答案】45°【解析】因为ABCD是边长为1的正方形,所以对角线BD=.又因为D1B与平面ABCD所成的角为45°,即∠D1BD=45°.所以AA1=DD1=.由于CD⊥DD1,BD⊥DD1.所以二面角B-DD1-C的平面角为∠CDB.又因为△CDB为等腰直角三角形,所以二面角B-DD1-C的平面角∠CDB=45°.9.如图,在正方体ABCD-A1B1C1D1中,截面C1D1AB与底面ABCD所成的二面角C1-AB-C的大小为________.【答案】45°【解析】∵AB⊥BC,AB⊥BC1,∴∠C1BC为二面角C1-AB-C的平面角,大小为45°.10.在边长为1的菱形ABCD中,∠ABC=60°,把菱形沿对角线AC折起,使折起后BD=,则二面角B-AC-D的余弦值为________.【答案】【解析】如图所示,由二面角的定义,知∠BOD即为二面角的平面角.∵DO=OB=BD=,∴∠BOD=60°.∴cos∠BCD=.11.如图所示,在长方体ABCD-A1B1C1D1中,BC=2,AA1=1,E,F分别在AD和BC上,且EF∥AB,若二面角C1-EF-C等于45°,则BF=________.,C1F⊂平面BC1,CF⊂平面BC1,【答案】1【解析】∵AB⊥平面BC∴AB⊥C1F,AB⊥CF,又EF∥AB,∴C1F⊥EF,CF⊥EF,∴∠C1FC是二面角C1-EF-C的平面角,∴∠C1FC=45°,∴△FCC1是等腰直角三角形,∴CF=CC1=AA1=1.又BC=2,∴BF=BC-CF=2-1=1. 12.如图,已知三棱锥A-BCD的各棱长均为2,求二面角A-CD-B的余弦值.13.如图,AB是⊙O的直径,PA垂直于⊙O所在的平面,C是圆周上的一点,且PA=AC,求二面角P-BC-A的大小.14.如图,已知VA,VB,VC两两垂直,VA=VB=VC=a.(1)求平面ABC和平面ABV所成的二面角的余弦值;(2)求三棱锥V-ABC的体积.【答案】(1)∵VA,VB,VC两两垂直,VA=VB=VC=a,∴AB=BC=AC=a,∴S△ABV=a2,S△ABC=a2.∴平面ABC和平面ABV所成的二面角的余弦值为=.(2)三棱锥V-ABC的体积为××a×a×a=a3.15.如图所示,已知Rt△ABC,斜边BC⊂α,点A∉α,AO⊥α,O为垂足,∠ABO=30°,∠ACO=45°,求二面角A-BC-O的大小.【答案】如图所示,在平面α内,过O作OD⊥BC,垂足为D,连接AD.∵AO⊥α,BC⊂α,∴AO⊥BC.又∵AO∩OD=O,∴BC⊥平面AOD.而AD⊂平面AOD,∴AD⊥BC.∴∠ADO是二面角A-BC-O的平面角.由AO⊥α,OB⊂α,OC⊂α,知AO⊥OB,AO⊥OC.又∠ABO=30°,∠ACO=45°,∴设AO=a,则AC=a,AB=2a.在Rt△ABC中,∠BAC=90°,∴BC==a,∴AD===.在Rt△AOD中,sin∠ADO===,∴∠ADO=60°.即二面角A-BC-O的大小是60°.16.如图,在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点E在棱AB上移动. (1)证明:DE⊥A1D;(2)求AE等于何值时,二面角D1-EC-D的大小为45°?。
二面角习题与答案

∴ 又
∴
∴
5.解:设边长为a,易证ANC'N是菱形
且MN = ,A'C =
∴S□AMC'N=
由于AMC'N在面ABCD上的射影即
为正方形ABCD
∴S□ABCD=
∴
∴
取CC'的中点M',连结DM'
则平行四边形DM'C'N是四边形AMC'N在CC'D'D上的射影,
S□DM'C'M=
∴
5.已知正方体AC',M、N分别是BB',DD'的中点,求截面AMC'N与面ABCD,CC'D'D所成的角。
解:
6.如图AC⊥面BCD,BD⊥面ACD,若AC =CD =1,∠ABC =30°,求二面角 的大小。
解:
7.三棱锥A-BCD中,∠BAC =∠BCD =90°,∠DBC =30°,AB =AC = ,AD =4,求二面角A-BC-D的度数。
14.如图,将边长为a的正三角形ABC按它的高AD为折痕折成一个二面角 .
(1)若二面角 是直二面角,求 的长;
(2)求 与平面 所成的角;
(3)若二面角 的平面角为120°,求二面角 的平面角的正切值.
参考答案
解:由已知条件,D是BC的中点
∴CD =BD =2又△ADC是正三角形
∴AD =CD =BD =2
∴CE= a,OE= a,∴tan∠COE= =2.
∴二面角C—AF—B的大小是arctan2.
12、解析:∵ 平面ABCD∥平面 ,∴ 平面 与平面 的交线l为过点 且平行于AC的直线.直线l就是二平面 与 所成二面角的棱.又 ⊥平面 ,过 作AH⊥l于H,连结AH.则 为二面角 的平面角.可求得 .因此所求角的大小为 或
高一寒假作业(8)——立体几何二面角专题(含答案)

高一寒假作业(8)—二面角专题1、正三棱柱ABC —A 1B 1C 1中,D 是BC 的中点,AA 1=AB =1. (1)求证:A 1C //平面AB 1D ;(2)求二面角B —AB 1—D 的正切值;2、如图,在长方体1111ABCD A B C D -中,11,2,AD AA AB ===点E 在线段AB 上.(1)求异面直线1D E 与1A D 所成的角;(2)若二面角1D EC D --的大小为45︒,求点B 到平面1D EC 的距离.3. 如图,四边形ABCD 是正方形,PB ⊥平面ABCD ,MA//PB ,PB=AB=2MA , (1)证明:AC//平面PMD ;(2)求直线BD 与平面PCD 所成的角的大小;(3)求平面PMD 与平面ABCD 所成的二面角(锐角)的正切值。
4、 已知斜三棱柱111ABC A B C -,90BCA ∠=,2AC BC ==,1A 在底面ABC 上的射影恰为AC 的中点D ,又知11BA AC ⊥。
(1)求证:1AC ⊥平面1A BC ; (2)求1CC 到平面1A AB 的距离; (3)求二面角1A A B C --的正弦值。
5、 如图,已知正三棱柱ABC —A 1B 1C 1的各棱长都为a ,P 为A 1B 上的点。
(1)试确定PBP A 1的值,使得PC ⊥AB ;(2)若321=PBP A ,求二面角P —AC —B 的大小;(3)在(2)条件下,求C 1到平面PAC 的距离。
6、如图所示,四棱锥P -ABCD 的底面ABCD 是边长为1的菱形,∠BCD =60°,E 是CD 的中点,PA ⊥底面ABCD ,PA =2.(1)证明:平面PBE ⊥平面PAB ;(2)求平面PAD 和平面PBE 所成二面角(锐角)的正弦值.7、如图7-29,在四棱锥P —ABCD 中,底面ABCD 是平行四边形,,32=BD ,AB=4,AD=2,侧棱PB=15,PD=3。
高中数学例题:二面角

高中数学例题:二面角例6.已知Rt△ABC,斜边BCα⊂,点Aα∉,AO⊥α,O为垂足,∠ABO=30°,∠ACO=45°,求二面角A-BC-O的大小。
【答案】60°【解析】如图所示,在平面α内,过O作OD⊥BC,垂足为D,连接AD。
设OC=a,∵AO⊥α,BC⊂α,∴AO⊥BC。
又∵AO∩OD=O,∴BC⊥平面AOD。
而AD⊂平面AOD,∴AD⊥BC,∴∠ADO是二面角A-BC-O的平面角。
由AO⊥α,OB⊂α,OC⊂α知AO⊥OB,AO⊥OC。
又∠ABO=30°,∠ACO=45°,∴AO=a,AC=,AB=2a。
在Rt△ABC中,∠BAC=90°,∴BC==,∴3AB ACADBC⋅===。
在Rt△AOD中,sin AOADOAD∠===。
∴∠ADO=60°,即二面角A-BC-O的大小是60°。
【总结升华】本题是用垂线法作二面角的平面角,求二面角的平面角关键是找出(或作出)平面角,再把平面角放到三角形中求解。
举一反三:【变式1】如图,在五面体ABCDEF中,四边形ADEF是正方形,FA⊥平面ABCD,BC∥AD,CD=1,AD ∠BAD=∠CDA=45°。
(1)求异面直线CE与AF所成角的余弦值;(2)证明:CD⊥平面ABF;(3)求二面角B—EF—A的正切值。
【答案】(1)3(2)略(3)14【解析】(1)因为//FA DE,所以CE与DE所成的角就是异面直线CE与AF所成角,余弦值为3。
(2)如右图,过点B作BG∥CD,交AD于点G,则∠BGA=∠CDA=45°。
由∠BAD=45°,可得BG⊥AB。
从而CD⊥AB。
又CD⊥FA,FA∩AB=A,所以CD⊥平面ABF。
(3)如图,MN与NG所成的角即为二面角B—EF—A的平面角,所以二面角B—EF—A的正切值为14。
(完整)二面角习题及答案
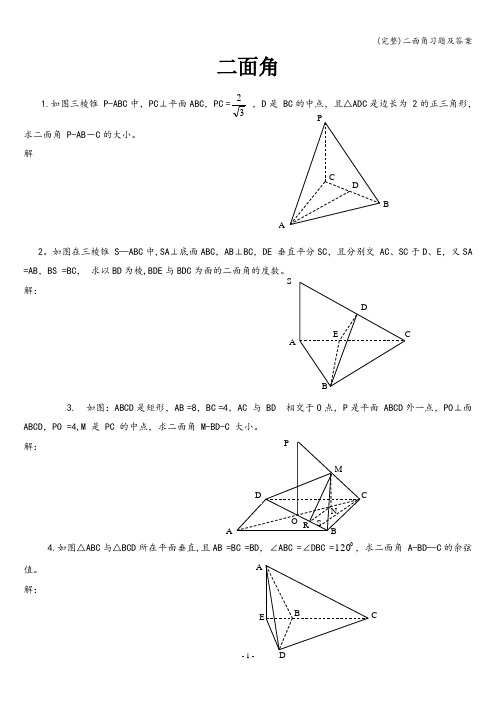
二面角1.如图三棱锥 P-ABC 中,PC ⊥平面ABC ,PC =32 ,D 是 BC 的中点,且△ADC 是边长为 2的正三角形,求二面角 P-AB -C 的大小。
解2。
如图在三棱锥 S —ABC 中,SA ⊥底面ABC ,AB ⊥BC ,DE 垂直平分SC ,且分别交 AC 、SC 于D 、E ,又SA =AB ,BS =BC , 求以BD 为棱,BDE 与BDC 解:3. 如图:ABCD 是矩形,AB =8,BC =4,AC 与 BD 相交于O 点,P 是平面 ABCD 外一点,PO ⊥面ABCD ,PO =4,M 是 PC 的中点,求二面角 M-BD-C 大小。
解:4.如图△ABC 与△BCD 所在平面垂直,且AB =BC =BD ,∠ABC =∠DBC =,求二面角 A-BD —C 的余弦值。
解:ABAC5.已知正方体 AC ’,M 、N 分别是BB ’,DD'的中点,求截面 AMC'N 与面ABCD ,CC'D ’D 所成的角. 解:6。
如图 AC ⊥面BCD ,BD ⊥面ACD ,若AC =CD =1,∠ABC =30°,求二面角D AB C --的大小。
解:7。
三棱锥 A —BCD 中,∠BAC =∠BCD =90°,∠DBC =30°,AB =AC =6,AD =4,求二面角 A-BC-D 的度数。
解:9。
如图所示,四棱锥P-ABCD 的底面是边长为a 的菱形,∠A =60°,PC ⊥平面ABCD,PC =a ,E 是PA 的中点。
(1)求证平面BDE ⊥平面ABCD 。
(2)求点E 到平面PBC 的距离。
(3)求二面角A —EB —D 的平面角大小. 解析:10。
如图,已知正方体ABCD —A1B1C1D1的棱长为1,E 、F 分别在棱AB 、BC上,G 在对角线BD1上,且AE =41,BF =21,D1G ∶GB =1∶2,求平面EFG 与底面ABCD 所成的二面角的大小.D ’B ’DAC ’BA ’CMNBF EACDDOABC11。
解二面角问题三种方法(习题及答案)

C A B DA A 1B DC C 1 B 1 解二面角问题(一)寻找有棱二面角的平面角的方法和求解。
(1)定义法:利用二面角的平面角的定义,在二面角的棱上取一点,过该点在两个半平面内作垂直于棱的射线,两射线所成的角就是二面角的平面角,这是一种最基本的方法。
要注意用二面角的平面角定义的三个“主要特征”来找出平面角,当然这种找出的角要有利于解决问题。
下面举几个例子来说明。
例1:如图,立体图形V -ABC 的四个面是全等的正三角形,画出二面角V -AB -C 的平面角并求出它的度数.例2:在三棱锥P —ABC 中,APB=BPC=CPA=600,求二面角A-PB —C 的余弦值。
这样的类型是不少的,如下列几道就是利用定义法找出来的:1、在正方体ABCD -A 1B 1C 1D 1中,找出二面角B -AC -B 1的平面角并求出它的度数。
2、.边长为a 的菱形ABCD ,∠ACB=600,现沿对角线BD 将其折成才600的二面角,则A 、C 之间的距离为 。
(菱形两条对角线互相垂直,对折后的一条对角线成两条线段仍都垂直于另一条对角线,则所成的角是二面角的平面角)3、正三棱柱ABC —A 1B 1C 1的底面边长是4,过BC 的一个平面与AA 1交于D ,若AD =3,求二面角D ―BC ―A 的正切值。
总之,能用定义法来找二面角的平面角的,一般是图形的性质较好,能够较快地找到满足二面角的平面角的三个主要特征。
并且能够很快地利用图形的一些条件来求出所要求的。
在常见的几何体有正四面体,正三棱柱,正方体,以及一些平面图形,正三角形,等腰三角形,正方形,菱形等等,这些有较好的一些性质,可以通过它们的性质来找到二面角的平面角。
至于求角,通常是把这角放在一个三角形中去求解.由图形及题目的已知条件来求这个三角形的边长或者角,再用解三角形的知识去求解。
(2)三垂线法:是利用三垂线的定理及其逆定理来证明线线垂直,来找到二面角的平面角的方法。
二面角习题及答案之欧阳家百创编

二面角欧阳家百(2021.03.07)1.如图三棱锥 P-ABC 中,PC ⊥平面ABC BC 的中点,且△ADC 是边长为 2-C 的大小。
解2.如图在三棱锥 S-ABC 中,SA ⊥底面ABC ,直平分SC ,且分别交 AC 、SC 于D 、E ,又求以BD 为棱,BDE 与BDC 解:3. 如图:ABCD 是矩形,AB =8,BC =4,AC 点,P 是平面 ABCD 外一点,PO ⊥面ABCD ,的中点,求二面角 M-BD-C 大小。
解:4.如图△ABC 与△BCD ABC =∠DBC =0120,求二面角解:5.已知正方体 AC',M 、N 分别是AMC'N 与面ABCD ,CC'D'D 解:6.如图 AC ⊥面BCD ,BD ⊥面ACDCA ’=30°,求二面角D AB C --的大小。
解:7. 三棱锥 A-BCD 中,∠BAC =∠BCD =90°,∠DBC =30°,AB =AC =6,AD =4,求二面角 A-BC-D 的度数。
解:9. 如图所示,四棱锥P —ABCD =60°,PC ⊥平面ABCD ,PC =a,E 是PA 的中点(1)求证平面BDE ⊥平面ABCD.(2)求点E 求二面角A —EB —D 的平面角大小. 解析:10. 如图,已知正方体ABCD —A1B1C1D1的棱长为1,E 、F 分别在棱AB 、BC 上,G 在对角线BD1上,且AE =41,BF =21,D1G ∶GB =1∶2,求平面EFG 与底面ABCD 所成的二面角的大小.11. 如图,设ABC —A1B1C1是直三棱柱,E 、F 分别为AB 、A1B1的中点,且AB =2AA1=2a,AC =BC =3a. (1)求证:AF ⊥A1C(2)求二面角C —AF —B 的大小12.如图1111D C B A ABCD -是长方体,AB=2,11==AD AA ,求二平面C AB 1与1111D C B A 所成二面角的大小.13.在正方体1111D C B A ABCD -中,1BB K ∈,1CC M ∈,且141BB BK =,B143CC CM =..求:平面AKM 与ABCD 所成角的大小.14.如图,将边长为a 的正三角形ABC 按它的高AD 为折痕折成一个二面角C AD C --'.(1)若二面角C AD C --'是直二面角,求C C '的长; (2)求C A '与平面CD C '所成的角;(3)若二面角C AD C --'的平面角为120°,求二面角D C C A -'-的平面角的正切值.参考答案解:由已知条件,D 是BC 的中点 ∴ CD =BD =2 又△ADC 是正三角形 ∴ AD =CD =BD =2∴ D 是△ABC 之外心又在BC 上∴△ABC 是以∠BAC 为直角的三角形, ∴ AB ⊥AC , 又 PC ⊥面ABC ∴ PA ⊥AB (三垂线定理)∴∠PAC 即为二面角 P-AB-C 之平面角, 易求 ∠PAC =30°2、解:∵ BS =BC ,又DE ∴ BE ⊥SC ,SC ⊥面BDE ∴ BD ⊥SC ,又SA ⊥面ABC ∴ SA ⊥BD ,BD ⊥面SAC ∴ BD ⊥DE ,且BD ⊥DCAB则 ∠EDC 就是所要求的平面角 设 SA =AB =a ,则 BC =SB =2a 且 AC = 3 易证 △SAC ∽△DEC ∴∠CDE =∠SAC =60°3、解:取OC 之中点N ,则 MN∵ PO ⊥面ABCD∴ MN ⊥面ABCD 且 过 N 作 NR ⊥BD 于 R ,连MR 则 ∠MRN 即为二面角 M-BD-C 过 C 作 CE ⊥BD 于S则 RN =21CE 在 Rt △BCD 中,CD ·BC =BD ·CE ∴58BD BC CD CE =⋅=∴54RN =25RN MN MRN tan ==∠ ∴25arctanMRN =∠ 4.解:过 A 作 AE ⊥CB 的延长线于E , 连结 DE , ∵ 面ABC ⊥面BCD ∴ AE ⊥面BCD∴ E 点即为点A 在面BCD 内的射影∴△EBD 为△ABD 在面BCD 内的射影A设 AB =a 则AE =DE =ABsin60°= a 23 ∴ AD =41ABD cos 26=∠, ∴ sin ∠ABD =415∴22ABD a 815415a 21S =⨯=∆ 又 a 21BE = ∴2BDE a 83a 21a 2321S =⋅⋅=∆ ∴55S S cos ABD BDE ==θ∆∆ 5.解:设边长为a ,易证 ANC'N且MN =a 2,A'C =a 3∴S□AMC'N = 2a 26'AC 21MN =⋅由于AMC'N 在面ABCD 为正方形ABCD ∴ S□ABCD =2a ∴36a 26a cos 221==θ ∴36arccos1=θ 取CC'的中点M',连结DM'则平行四边形DM'C'N 是四边形AMC'N 在CC'D'D 上的射影,AC ’A ’CS□DM'C'M =2a 21∴66a 26a21cos 222==θ ∴66arccos2=θ 6.解:作DF ⊥AB 于F ,CE ⊥AB 于∵ AC =CD =1 ∠ABC =30° ∴ AD =2,BC =3 ,AB =2, BD =2在Rt △ABC 中,23231AB BC AC CE =⨯=⋅=,同理 1222AB BDAD DF =⨯=⋅=∴1DF BD BF 22=-=21CE AC AE 22=-=∴212112EF =--= ∴θ⋅-++=cos DF EF 2EF DF CE CD 2222 ∴33cos =θ 即所求角的大小为33arccos。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二面角1.如图三棱锥 P-ABC 中,PC ⊥平面ABC ,PC =32 ,D 是 BC 的中点,且△ADC 是边长为 2的正三角形,求二面角 P-AB -C 的大小。
解:由已知条件,D 是BC 的中点∴ CD =BD =2 又△ADC 是正三角形 ∴ AD =CD =BD =2∴ D 是△ABC 之外心又在BC 上 ∴ △ABC 是以∠BAC 为直角的三角形, ∴ AB ⊥AC , 又 PC ⊥面ABC∴ PA ⊥AB (三垂线定理)∴∠PAC 即为二面角 P-AB-C 之平面角, 易求 ∠PAC =30°2.如图在三棱锥 S-ABC 中,SA ⊥底面ABC ,AB ⊥BC ,DE 垂直平分SC ,且分别交 AC 、SC 于D 、E ,又SA =AB ,BS =BC , 求以BD 为棱,BDE 与BDC 为面的二面角的度数。
解:∵ BS =BC ,又DE 垂直平分SC∴ BE ⊥SC ,SC ⊥面BDE ∴ BD ⊥SC ,又SA ⊥面ABC ∴ SA ⊥BD ,BD ⊥面SAC ∴ BD ⊥DE ,且BD ⊥DC 则 ∠EDC 就是所要求的平面角 设 SA =AB =a ,则 BC =SB =2a 且 AC = 3易证 △SAC ∽△DEC ∴ ∠CDE =∠SAC =60°3. 如图:ABCD 是矩形,AB =8,BC =4,AC 与 BD 相交于O 点,P 是平面 ABCD 外一点,PO ⊥面ABCD ,PO =4,M 是 PC 的中点,求二面角 M-BD-C 大小。
DPCABEDBASC解:取OC 之中点N ,则 MN ∥PO ∵ PO ⊥面ABCD∴ MN ⊥面ABCD 且 MN =PO/2 =2, 过 N 作 NR ⊥BD 于 R ,连MR ,则 ∠MRN 即为二面角 M-BD-C 的平面角 过 C 作 CE ⊥BD 于S 则 RN =21CE 在 Rt △BCD 中,CD ·BC =BD ·CE ∴ 58BD BC CD CE =⋅=∴ 54RN =25RN MN MRN tan ==∠ ∴ 25a r c t a n M R N=∠ 4.如图△ABC 与△BCD 所在平面垂直,且AB =BC =BD ,∠ABC =∠DBC =0120,求二面角 A-BD-C 的余弦值。
解:过 A 作 AE ⊥CB 的延长线于E , 连结 DE , ∵ 面ABC ⊥面BCD ∴ AE ⊥面BCD∴ E 点即为点A 在面BCD 内的射影∴ △EBD 为△ABD 在面BCD 内的射影设 AB =a 则AE =DE =ABsin60°=a 23 ∴ AD =41ABD cos 26=∠, ∴ sin ∠ABD =415∴ 22A B D a 815415a 21S =⨯=∆ 又 a 21BE =SR NMOBDPA CDBAEC∴ 2B D E a 83a 21a 2321S =⋅⋅=∆ ∴ 55S S c o s A B D B D E ==θ∆∆ 考虑到我们求的是二面角 A-BD-E ,而二面角 A-BD-C 与A-BD-C 互补 ∴ 二面角 A-BD-C 的余弦值为55-。
5.已知正方体 AC',M 、N 分别是BB',DD'的中点,求截面 AMC'N 与面ABCD ,CC'D'D 所成的角。
解:设边长为a ,易证 ANC'N 是菱形 且MN =a 2,A'C =a 3 ∴S□AMC'N = 2a 26'AC 21MN =⋅由于AMC'N 在面ABCD 上的射影即 为正方形ABCD∴ S□ABCD =2a ∴ 36a 26a cos 221==θ ∴ 36a r c c o s 1=θ 取CC'的中点M',连结DM'则平行四边形DM'C'N 是四边形AMC'N 在CC'D'D 上的射影,S□DM'C'M =2a 21 ∴ 66a 26a21c o s 222==θ D ’B ’DAC ’BA ’C MN∴66arccos2=θ 6.如图 AC ⊥面BCD ,BD ⊥面ACD ,若AC =CD =1,∠ABC =30°,求二面角D AB C --的大小。
解:作DF ⊥AB 于F ,CE ⊥AB 于E , ∵ AC =CD =1 ∠ABC =30° ∴ AD =2,BC =3 , AB =2, BD =2 在Rt △ABC 中, 23231AB BC AC CE =⨯=⋅=, 同理 1222ABBDAD DF =⨯=⋅= ∴ 1DF BD BF 22=-=21CE AC AE 22=-= ∴ 212112EF =--= ∴ θ⋅-++=c o s DF EF 2EF DF CE CD 2222∴ 33c o s =θ即所求角的大小为33arccos 。
7. 三棱锥 A-BCD 中,∠BAC =∠BCD =90°,∠DBC =30°,AB =AC =6,AD =4,求二面角 A-BC-D 的度数。
解:由已知条件∠BAC =90°,AB =AC , 设BC 的中点设为O ,则OA =OC =3BC =32BF EACDOABC2333230tan BC DC 0=⨯== ∴ θ⋅-++=cos CD AO 2CD OC AO AD 2222解之得:21cos -=θ ∴150=θ8. 如图,四面体ABCD 的棱BD 长为2,其余各棱的长均是2,求:二面角A —BD —C 、A —BC —D 、B —AC —D 的大小.解析:(1)取BD 的中点O ,连AO 、OC.在ΔABD 中,∵AB =AD =2,BD =2,∴ΔABD 是等腰直角三角形,AO ⊥BD ,同理OC ⊥BD. ∴∠AOC 是二面角A —BD —C 的平面角又AO =OC =1,AC =2,∴∠AOC =90°.即二面角A —BD —C 为直二面角.(2)∵二面角A —BD —C 是直二面角,AO ⊥BD ,∴AO ⊥平面BCD. ∴ΔABC 在平面BCD 内的射影是ΔBOC.∵S ΔOCB =21,S ΔABC =23,∴cos θ=33.即二面角A —BC —D 的大小是arccos 33.(3)取AC 的中点E ,连BE 、DE.∵AB =BC ,AD =DC , ∴BD ⊥AC ,DE ⊥AC ,∴∠BED 就是二面角的平面角.在ΔBDE 中,BE =DE =26,由余弦定理,得cos α=-31 ∴二面角B —AC —D 的大小是π-arccos 31.评析 本例提供了求二面角大小的方法:先作出二面角的平面角,再利用其所在的三角形算出角的三角函数值,或利用面积的射影公式S ′=S ·cos θ求得.又EG ∥AB ,故易得tan ∠AEG=tan ∠BAE=22=AB BE .9. 如图所示,四棱锥P —ABCD 的底面是边长为a 的菱形,∠A =60°,PC ⊥平面ABCD ,PC =a,E 是PA 的中点.(1)求证平面BDE ⊥平面ABCD.(2)求点E 到平面PBC 的距离.(3)求二面角A —EB —D 的平面角大小.解析:(1)设O 是AC ,BD 的交点,连结EO. ∵ABCD 是菱形,∴O 是AC 、BD 的中点,∵E 是PA 的中点,∴EO ∥PC ,又PC ⊥平面ABCD ,∴EO ⊥平面ABCD ,EO ⊂平面BDE ,∴平面BDE ⊥平面ABCD. (2)EO ∥PC ,PC ⊂平面PBC ,∴EO ∥平面PBC ,于是点O 到平面PBC 的距离等于E 到平面PBC 的距离. 作OF ⊥BC 于F ,∵EO ⊥平面ABCD ,EO ∥PC ,PC ⊂平面PBC ,∴平面PBC ⊥平面ABCD ,于是OF ⊥平面PBC ,OF 的长等于O 到平面PBC 的距离.由条件可知,OB =2a ,OF =2a ×23=43a ,则点E 到平面PBC 的距离为43a.(3)过O 作OG ⊥EB 于G ,连接AG ∵OE ⊥AC ,BD ⊥AC ∴AC ⊥平面BDE ∴AG ⊥EB(三垂线定理) ∴∠AGO 是二面角A —EB —D 的平面角∵OE =21PC =21a,OB =23a ∴EB =a.∴OG =EB OB OE ⋅=43a 又AO =21a.∴tan ∠AGO =OG AO =332∴∠AGO =arctan 332.评析 本题考查了面面垂直判定与性质,以及利用其性质求点到面距离,及二面角的求法,三垂线定理及逆定理的应用.10. 如图,已知正方体ABCD —A1B1C1D1的棱长为1,E 、F 分别在棱AB 、BC 上,G 在对角线BD1上,且AE =41,BF =21,D1G ∶GB =1∶2,求平面EFG 与底面ABCD 所成的二面角的大小.解析:设G 在底面ABCD 上的射影为H ,H ∈BD ,∵D D GH 1=B D GB 1=32 ∴GH =32作HM ⊥EF 于M ,连GM ,由三垂线定理知GM ⊥EF ,则∠GMH =θ就是平面BFG 与底面ABCD 所成的二面角的平面角,tan θ=HM GH.下面求HM 的值.建立如图所示的直角坐标系,据题设可知.H(31,32)、E(41,0)、F(1,21)∴直线EF 的方程为0210--y =41141--x , 即 4x-6y-1=0.由点到直线的距离公式可得|HM |=22641326314+-⨯-⨯=13611,∴tg θ=32·11136=11134,θ=arctg 11134.说明 运用解析法来求HM 的值是本例的巧妙所在.11. 如图,设ABC —A1B1C1是直三棱柱,E 、F 分别为AB 、A1B1的中点,且AB =2AA1=2a,AC =BC =3a. (1)求证:AF ⊥A1C(2)求二面角C —AF —B的大小分析 本小题考查空间几何垂直的概念和二面角的度量等知识. 解 (1)∵AC =BC ,E 为AB 中点,∴CE ⊥AB 又∵ABC —A1B1C1为直棱柱,∴CE ⊥面AA1BB 连结EF ,由于AB =2AA1 ∴AA1FE 为正方形∴AF ⊥A1E ,从而AF ⊥A1C(2)设AF 与A1E 交于O ,连结CO ,由于AF ⊥A1E ,知AF ⊥面CEA1 ∴∠COE 即为二面角C —AF —B 的平面角 ∵AB =2AA1=2a,AC =BC =3a∴CE =2a,OE =22a,∴tan ∠COE =aa 222=2.∴二面角C —AF —B 的大小是arctan2.12.如图1111D C B A ABCD -是长方体,AB=2,11==AD AA ,求二平面C AB 1与1111D C B A所成二面角的大小.解析:∵ 平面ABCD ∥平面1111D C B A ,∴ 平面C AB 1与平面1111D C B A 的交线l 为过点1B 且平行于AC 的直线.直线l 就是二平面C AB 1与1111D C B A 所成二面角的棱.又1AA ⊥平面1111D C B A ,过1A 作AH ⊥l 于H ,连结AH .则1AHA ∠为二面角1A l A --的平面角.可求得25tan 1=∠AHA .因此所求角的大小为25arctan 或25arctanπ-13. 在正方体1111D C B A A B C D -中,1BB K ∈,1CC M ∈,且141BB BK =,143CC CM =..求:平面AKM 与ABCD 所成角的大小.解析:由于BCMK 是梯形,则MK 与CB 相交于E .A 、E 确定的直线为l ,过C 作CF ⊥l 于F ,连结MF ,因为MC ⊥平面ABCD ,CF ⊥l ,故MF ⊥l .∠MFC 是二面角M-l-C 的平面角.设正方体棱长为a ,则a CM 43=,a BK 41=.在△ECM 中,由BK ∥CM 可得a EB 21=,a CF 53=,故45t a n =∠M F C .因此所求角的大小为45arctan或45arctanπ-.14. 如图,将边长为a 的正三角形ABC 按它的高AD 为折痕折成一个二面角C AD C --'. (1)若二面角C AD C --'是直二面角,求C C '的长; (2)求C A '与平面CD C '所成的角;(3)若二面角C AD C --'的平面角为120°,求二面角D C C A -'-的平面角的正切值.解析: (1)若︒='∠90DC C ,∵ AC=a ,∴a C D DC 21='=,∴ a C C 22='.(2)∵ C D AD '⊥,AD ⊥DC ,∴ AD ⊥平面C C D '.∴ D C A '∠为C A '与平面C C D '所成的角,在Rt △C AD '中,AC DC C D 21==',∴ ︒='∠30C DA ,于是︒='∠60D C A .(3)取C C '的中点E ,连结AE 、DE ,∵ DC C D =',AC C A =',∴ C C AE '⊥,C C DE '⊥,∴ ∠AED 为二面角D C C A -'-的平面角,∵ ︒='∠120DC C ,aCD D C 21==',∴a DE 41=,在Rt △AED 中,a AD 23=,∴.324123tan ===∠a aDE AD AED。
