勾股定理专题

合集下载

专题勾股定理及其逆定理【九大题型】

专题2.6勾股定理及其逆定理【九大题型】【浙教版】【题型1勾股定理的运用】 (1)【题型2直角三角形中的分类讨论思想】 (2)【题型3勾股定理解勾股树问题】 (3)【题型4勾股定理解动点问题】 (4)【题型5勾股定理的验证】 (6)【题型6直角三角形的判定】 (8)【题型7勾股数问题】 (9)【题型8格点图中求角的度数】 (10)【题型9勾股定理及其逆定理的运用】 (11)【题型1勾股定理的运用】【例1】（2022•和平区三模）如图，在△ABC中，∠C＝90°，AD平分∠CAB，CD＝1.5，BD＝2.5，则AC的长为（）A．5B．4C．3D．2【变式1-1】（2022春•上杭县期中）如图在Rt△ABC中，∠B＝90°，AB＝8，AC＝10，AC的垂直平分线DE分别交AB、AC于D、E两点，则BD的长为（）A．32B．74C．2D．52【变式1-2】（2022春•汉阳区期中）如图，在△ABC中AB＝AC＝10，BC＝16，若∠BAD＝3∠DAC，则CD ＝．【变式1-3】（2021秋•朝阳区校级期末）如图，在△ABC中，∠C＝90°，AB＝30，D是AC上一点，AD：CD ＝25：7，且DB＝DA，过AB上一点P，作PE⊥AC于E，PF⊥BD于F，则PE+PF长是．【题型2直角三角形中的分类讨论思想】【例2】（2022春•长沙月考）已知△ABC中，AB＝13，AC＝15，BC边上的高为12．则△ABC的面积为（）A．24或84B．84C．48或84D．48【变式2-1】（2022春•宁津县期中）△ABC中，AB＝15，AC＝13，高AD＝12，则△ABC的周长是（）A．42B．32C．42或32D．42或37【变式2-2】（2022春•香河县期中）已知直角三角形两边的长为5和12，则此三角形的周长为（）A．30B．119+17C．119+17或30D．36【变式2-3】（2022春•海淀区校级期中）在Rt△ABC中，∠ACB＝90°，AC＝4，AB＝5．点P在直线AC上，且BP＝6，则线段AP的长为．【题型3勾股定理解勾股树问题】【例3】（2021秋•南关区期末）如图，所有阴影部分四边形都是正方形，所有三角形都是直角三角形，若正方形A、B、D的面积依次为6、10、24，则正方形C的面积为（）A．4B．6C．8D．12【变式3-1】（2021秋•高新区校级期末）如图，在四边形ABCD中，∠DAB＝∠BCD＝90°，分别以四边形的四条边为边向外作四个正方形，若S1+S4＝135，S3＝49，则S2＝（）A．184B．86C．119D．81【变式3-2】（2022春•泗水县期中）有一个边长为1的正方形，经过一次“生长”后，在它的左右肩上生出两个小正方形，其中，三个正方形围成的三角形是直角三角形，再经过一次“生长”后，变成了如图，如果继续“生长”下去，他将变得“枝繁叶茂”，请你计算出“生长”了2022次后形成的图形中所有正方形的面积之和为（）A．2020B．2021C．2022D．2023【变式3-3】（2022春•张湾区期中）如图①，在△ABC中，∠ACB＝90°，AC：BC＝4：3，这个直角三角形三边上分别有一个正方形．执行下面的操作：由两个小正方形向外分别作直角边之比为4：3的直角三角形，再分别以所得到的直角三角形的直角边为边长作正方形．图②是1次操作后的图形，图③是2次操作后的图形．如果图①中的直角三角形的周长为12，那么10次操作后的图形中所有正方形的面积和为（）A．225B．250C．275D．300【题型4勾股定理解动点问题】【例4】（2021秋•开福区校级期末）如图，Rt△ACB中，∠ACB＝90°，AB＝25cm，AC＝7cm，动点P从点B 出发沿射线BC以2cm/s的速度运动，设运动时间为ts，当△APB为等腰三角形时，t的值为（）A．62596或252B．252或24或12C．62596或24或12D．62596或252或24【变式4-1】（2021秋•宛城区期末）如图，在Rt△ABC中，∠ACB＝90°，BC＝40cm，AC＝30cm，动点P从点B出发沿射线BA以2cm/s的速度运动．则当运动时间t＝s时，△BPC为直角三角形．【变式4-2】（2022春•蚌山区校级期中）如图，在△ABC中，∠ACB＝90°，AB＝10，AC＝8，点P从点A出发，以每秒2个单位长度的速度沿折线A﹣B﹣C运动．设点P的运动时间为t秒（t＞0）．（1）BC的长是．（2）当点P刚好在∠BAC的角平分线上时，t的值为．【变式4-3】（2022春•河东区期中）如图，已知△ABC中，∠B＝90°，AB＝16cm，BC＝12cm，P、Q是△ABC 边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，同时停止．（1）P、Q出发4秒后，求PQ的长；（2）当点Q在边CA上运动时，出发几秒钟后，△CQB能形成直角三角形？【题型5勾股定理的验证】【例5】勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪以灵感，他惊喜的发现，当两个全等的直角三角形如图1或图2摆放时，都可以用“面积法”来证明，下面是小聪利用图1证明勾股定理的过程：将两个全等的直角三角形按图1所示摆放，其中∠DAB＝90°，求证：a2+b2＝c2证明：连接DB，过点D作BC边上的高DF，则DF＝EC＝b﹣a＝S△ACD+S△ABC=12b2+12ab．∵S四边形ADCB＝S△ADB+S△DCB=12c2+12a（b﹣a）又∵S四边形ADCB∴12b2+12ab=12c2+12a（b﹣a）∴a2+b2＝c2请参照上述证法，利用图2完成下面的证明．将两个全等的直角三角形按图2所示摆放，其中∠DAB＝90°．求证：a2+b2＝c2．【变式5-1】（2022春•巢湖市校级期中）学习勾股定理之后，同学们发现证明勾股定理有很多方法．某同学提出了一种证明勾股定理的方法：如图1点B是正方形ACDE边CD上一点，连接AB，得到直角三角形ACB，三边分别为a，b，c，将△ACB裁剪拼接至△AEF位置，如图2所示，该同学用图1、图2的面积不变证明了勾股定理．请你写出该方法证明勾股定理的过程．【变式5-2】（2021秋•朝阳区期末）【阅读理解】我国古人运用各种方法证明勾股定理，如图①，用四个直角三角形拼成正方形，通过证明可得中间也是一个正方形．其中四个直角三角形直角边长分别为a、b，斜边长为c．图中大正方形的面积可表示为（a+b）2，也可表示为c2+4×12ab，即（a+b）2＝c2+4×12ab，所以a2+b2＝c2．【尝试探究】美国第二十任总统伽菲尔德的“总统证法”如图②所示，用两个全等的直角三角形拼成一个直角梯形BCDE，其中△BCA≌△ADE，∠D＝90°，根据拼图证明勾股定理．【定理应用】在Rt△ABC中，∠C＝90°，∠A、∠B、∠C所对的边长分别为a、b、c．求证：a2c2+a2b2＝c4﹣b4．【变式5-3】（2022春•寿光市期中）如图①，美丽的弦图，蕴含着四个全等的直角三角形．（1）弦图中包含了一大，一小两个正方形，已知每个直角三角形较长的直角边为a，较短的直角边为b，斜边长为c，结合图①，试验证勾股定理．（2）如图②，将这四个直角三角形紧密地拼接，形成飞镖状，已知外围轮廓（粗线）的周长为24，OC＝3，求该飞镖状图案的面积．（3）如图③，将八个全等的直角三角形紧密地拼接，记图中正方形ABCD，正方形EFGH，正方形MNKT的面积分别为S1，S2，S3，若S1+S2+S3＝40，则S2＝．【题型6直角三角形的判定】【例6】（2022春•绥宁县期中）若△ABC的三边长分别为a、b、c，下列条件中能判断△ABC是直角三角形的有（）①∠A＝∠B﹣∠C，②∠A：∠B：∠C＝3：4：5，③∠A＝90°﹣∠B，④∠A＝∠B=12∠C，⑤a2＝（b+c）（b﹣c），⑥a：b：c＝5：12：13．A．3个B．4个C．5个D．6个【变式6-1】（2022春•赣州月考）下列满足条件的三角形中，不是直角三角形的是（）A．在△ABC中，若a=35c，b=45c．则△ABC为直角三角形B．三边长的平方之比为1：2：3C．三内角之比为3：4：5D．三边长分别为a，b，c，c＝1+n2，a＝n2﹣1，b＝2n（n＞1）【变式6-2】（2022春•汉滨区期中）若△ABC的三边长a，b，c满足（a﹣c）2＝b2﹣2ac，则（）A．∠A为直角B．∠B为直角C．∠C为直角D．△ABC不是直角三角形【变式6-3】（2022春•开州区期中）下列是直角三角形的有（）个①△ABC中a2＝c2﹣b2②△ABC的三内角之比为3：4：7③△ABC的三边平方之比为1：2：3④三角形三边之比为3：4：5A．1B．2C．3D．4【题型7勾股数问题】【例7】（2022春•滑县月考）在学习“勾股数”的知识时，小明发现了一组有规律的勾股数，并将它们记录在如下的表格中．a68101214…b815243548…c1017263750…则当a＝24时，b+c的值为（）A．162B．200C．242D．288【变式7-1】（2022•湖北）勾股定理最早出现在商高的《周髀算经》：“勾广三，股修四，经隅五”．观察下列勾股数：3，4，5；5，12，13；7，24，25；…，这类勾股数的特点是：勾为奇数，弦与股相差为1．柏拉图研究了勾为偶数，弦与股相差为2的一类勾股数，如：6，8，10；8，15，17；…，若此类勾股数的勾为2m（m≥3，m为正整数），则其弦是（结果用含m的式子表示）．【变式7-2】（2022春•白云区期末）（1）3k，4k，5k（k是正整数）是一组勾股数吗？如果是，请证明；如果不是，请说明理由；（2）如果a，b，c是一组勾股数，那么ak，bk，ck（k是正整数）也是一组勾股数吗？如果是，请证明；如果不是，请说明理由．【变式7-3】（2022•石家庄三模）已知：整式A＝n2+1，B＝2n，C＝n2﹣1，整式C＞0．（1）当n＝1999时，写出整式A+B的值（用科学记数法表示结果）；（2）求整式A2﹣B2；（3）嘉淇发现：当n取正整数时，整式A、B、C满足一组勾股数，你认为嘉淇的发现正确吗？请说明理由．【题型8格点图中求角的度数】【例8】（2021秋•伊川县期末）如图，正方形ABCD是由9个边长为1的小正方形组成的，点E，F均在格点（每个小正方形的顶点都是格点）上，连接AE，AF，则∠EAF的度数是．【变式8-1】（2022•惠山区一模）如图所示的网格是由相同的小正方形组成的网格，点A，B，P是网格线的交点，则∠PAB+∠PBA＝°．【变式8-2】（2022春•武侯区校级期末）如图，在正方形网格中，每个小正方形的边长均为1，点A，B，C，D，P都在格点上，连接AP，CP，CD，则∠PAB﹣∠PCD＝．【变式8-3】（2022春•孝南区期中）如图所示的网格是正方形网格，△ABC和△CDE的顶点都是网格线交点，那么∠BCA+∠DCE＝．【题型9勾股定理及其逆定理的运用】【例9】（2021秋•蓝田县校级期末）如图，在△ABC中，AB＝AC，D是CA的延长线上一点，连接BD．（1）若AC＝8，AD＝17，BD＝15，判断AB与BD的位置关系，并说明理由；（2）若∠D＝28°，∠DBC＝121°，求∠DAB的度数．【变式9-1】（2022春•陵城区期中）如图，在△ABC中，AD、BE分别为边BC、AC的中线，分别交BC、AC于点D、E．（1）若CD＝4，CE＝3，AB＝10，求证：∠C＝90°；（2）若∠C＝90°，AD＝6，BE＝8，求AB的长．【变式9-2】（2021春•当涂县期末）如图，在△ABC中．D是AB边的中点，DE⊥AB于点D，交AC于点E，且AE2﹣CE2＝BC2，（1）试说明：∠C＝90°；（2）若DE＝6，BD＝8，求CE的长．【变式9-3】（2022春•汉阳区校级月考）如图，在四边形ABCD中，∠ABC＝90°，AB＝6，BC＝8，CD＝10，AD＝102．（1）求四边形ABCD的面积．（2）求对角线BD的长．。

勾股定理专题

ABC勾股定理专题例1.如图,在四边形ABCD 中,∠BAD=90o,∠DBC=90o,AD=3,AB=4,BC=12,求CD.例2.已知0)10(862=-+-+-z y x ,则由此z y x ,,为三边的三角形是什么三角形?例3.印度数学家什迦逻(1141年-1225年)曾提出过“荷花问题”:“平平湖水清可鉴,面上半尺生红莲; 出泥不染亭亭立,忽被强风吹一边,渔人观看忙向前,花离原位二尺远;能算诸君请解题,湖水如何知深浅?”请用学过的数学知识回答这个问题.例4.如图,有一块直角三角形纸片,两直角边AC ＝6cm,BC ＝8cm,现将直角边AC 沿直线AD 折叠,使它恰好落在斜边AB 上,且与AE 重合,求CD 的长. 例5.如图,在长方体ABCD-A 1B 1C 1D 1中,AB=BB 1=2,AD=3,一只蚂蚁从A 点出发,沿长方体表面爬到C 1点,求蚂蚁怎样走路程最短,最短路程是多少?例6.如图,折叠长方形(四个角都是直角,对边相等)的一边AD,使点D 落在BC 边的点F 处,已知AB=8cm,BC=10cm,求EC 的长; 练习1.如图,AD ＝4,CD ＝3,∠ADC ＝90o,AB ＝13,BC ＝12,求该图形的面积.2.如图,正方形网格中的△ABC,若小方格边长为1,则△ABC 是什么三角形?3.小明想知道学校旗杆的高,他发现旗杆顶端的绳子垂到地面还多1米,当他把绳子的下端拉开5米后,发现下端刚好接触地面,求旗杆的高度.4.已知,如图,在Rt △ABC 中,∠C=90o ,∠1=∠2,CD=1.5,BD=2.5,求AC 的长.5.如图,一圆柱高8cm,底面半径为2cm,一只蚂蚁从点A 爬到点B 处吃食,从圆侧面爬行的最短路程是多少?(π取3)6.已知,如图,长方形ABCD 中,AB=3cm,AD=9cm,将此长方形折叠,使点B 与点D 重合,折痕为EF,则△ABE 的面积为多少?C DABA CD DAABCD AB EFDBADE13cmm5mD CBA AAOBAB CD检测题一.填空题:1.在Rt △ABC 中,斜边AB=2,则AB 2+BC 2+CA 2= ;2.如图1,图1中正方形A 的面积是_______,图2中正方形B 的面积是 ;3.在Rt ⊿ABC 中,斜边AB 上的高为CD,若AC=3,BC=4,则CD=_______;4.在高5m,长13m 的一段台阶上铺上地毯,台阶的剖面图如图,地毯的长度至少需要___________m.5.在Rt △ABC 中,∠C=90o,①若a=5,b=12,则c=_____;②若a=15,c=25,则b=_____;③若c=61,b=60,则a=_____;④若a:b=3;4,c=10则S Rt△ABC =____.6.在△ABC 中,AC=17cm,BC=10cm,AB=9cm,这是一个三角形(按角分).7.直角三角形两直角边长分别为5和12,则它斜边上的高为__________.8.在平静的湖面上,有一支红莲,高出水面1米,阵风吹来,红莲被吹到一边, 花朵齐及水面,已知红莲移动的水平距离为2米,问这里水深是________m.9.已知两条线段的长为5c m 和12c m,当第三条线段的长为 c m 时,这三条线段能组成一个直角三角形. 10.有一个长为12c m,宽为4c m,高为3c m 的长方体形铁盒,在其内部要放一根笔直的铁丝,则铁丝最长达到 c m.11.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7cm,则正方形A,B,C,D 的面积之和为______cm 2. 二.选择题:1.一直角三角形的斜边比直角边大2,另一直角边为6,则斜边长为( )A.4 B.8 C.10 D.122.CD 是直角三角形ABC 斜边AB 上的高,若AB=10,AC:BC=3:4,则这个直角三角形的面积是( )A.6 B.8 C.12 D.243.斜边为17cm,一条直角边长为15cm 的直角三角形的面积是( )A.60 B.30 C.90 D.1204.下列数组中,是勾股数的是( )A.1,1,3 B.5,3,2 C.0.2,0.3,0.5 D.514131,,5.下列各组数中,以a,b,c 为边的三角形不是Rt △的是( )A.a=1.5,b=2,c=3 B.a=7,b=24,c=25 C.a=6,b=8,c=10 D.a=3,b=4,c=56.已知一个Rt △的两边长分别为3和4,则第三边长的平方是( )A.25 B.14 C.7D.7或257.若线段a,b,c 组成Rt △,则它们的比可以是( )A.2:3:4 B.3;4;6 C.5;12:13 D.4:6;78.Rt △一直角边的长为11,另两边为自然数,则Rt △的周长为( )A.121 B.120 C.132 D.不能确定 9.等腰三角形底边长10cm,腰长为13,则此三角形的面积为( )A.40 B.50 C.60 D.70 10.已知,如图,一轮船以16海里/时的速度从港口A 出发向东北方向航行,另一轮船以12海里/时的速度同时从港口A 出发向东南方向航行,离开港口2小时后,则两船相距( )A.25海里 B.30海里 C.35海里 D.40海里三.解答题:1.如图,一根旗杆在离地面9m 处断裂,旗杆顶部落在离旗杆底部12m 处,旗杆折断之前有多高?2.种盛饮料的圆柱形杯(如图),测得内部底面半径为2.5㎝,高为12㎝,吸管放进杯里,杯口外面至少要露出4.6㎝,问吸管要做多长?3.如图,一个长方形的操场,今不绕长方形操场的两邻边(即不A →B →C)走,而取捷径沿对角线(A →C)走,省去21长方形长边的距离,求长方形的短边和长边的比是多少?4.在一棵树的10米高处有两只猴子,一只猴子爬下树走到离树20米处的池塘的A 处.另一只爬到树顶D ,距离以直线计算,如果两只猴子所经过的距离相等,则这棵树高多少米?5.如图,在四边形ABCD 中,AB=BC=2,CD=3,AD=1,且∠ABC=90o,试求∠A 的度数.6.如图,沿OA 将圆锥侧面剪开,展开成平面图形是扇形OAB.(1)扇形的弧AB 和点B 在圆锥的侧面上是怎样的位置关系?(2)若角∠AOB=90o ,则圆锥底面圆半径r 与扇形OAB 的半径R ? (3)若点A 在圆锥侧面上运动一圈后又回到原位,则点A 运动的最短路程应该怎样设计?若r 2=0.5,且∠动的最短路程.B 22581图2A225400图19m12m北南 A东D BA AB CD7c。

勾股定理专题

专题复习勾股定理（郑默言）本章常用知识点：1、勾股定理：直角三角形两直角边的等于斜边的。

如果用字母a,b,c 分别表示直角三角形的两直角边和斜边，那么勾股定理可以表示为：。

2、勾股数：满足a 2+b 2=c 2的三个，称为勾股数。

常见勾股数如下：3、常见平方数：121112=； 144122=； 169132=； 196142=； 225152=；256162=289172=； 324182=； 361192=； 400202=；441212=； 484222= 529232=； 576242=； 625252=； 676262=；729272=专题一、勾股定理与面积1、、在Rt ▲ABC 中，∠C=︒90,a=5,c=3.，则Rt ▲ABC 的面积S= 。

2、一个直角三角形周长为12米，斜边长为5米，则这个三角形的面积为：3、直线l 上有三个正方形a 、b 、c ，若a 和c 的面积分别为5和11，则b 的面积为4、在直线l 上依次摆放着七个正方形(如图所示)。

已知斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是S 1、S 2、S 3、S 4，则S 1＋S 2＋S 3＋S 4等于。

5、三条边分别是5,12,13的三角形的面积是。

6、如果一个三角形的三边长分别为a,b,c 且满足：a2+b 2+c 2+50=6a+8b+10c,则这个三角形的面积为。

7、如图，︒=∠90ACB ，BC=8,AB=10,CD 是斜边的高，求CD 的长？l321S 4S 3S 2S 18、如下图，在∆ABC 中，︒=∠90ABC ，AB=8cm ，BC=15cm ，P 是到∆ABC 三边距离相等的点，求点P 到∆ABC 三边的距离。

9、如右图：在四边形ABCD 中，AB=2，CD=1，∠A=60°，求四边形ABCD 的面积。

10、如图①，分别以直角三角形ABC 三边为直径向外作三个半圆，其面积分别用S 1、S 2、S 3表示，则不难证明S 1=S 2+S 3 .(1) 如图②，分别以直角三角形ABC 三边为边向外作三个正方形，其面积分别用S 1、S 2、S 3表示，那么S 1、S 2、S 3之间有什么关系？(不必证明)(2) 如图③，分别以直角三角形ABC 三边为边向外作三个正三角形，其面积分别用S 1、S 2、S 3表示，请你确定S 1、S 2、S 3之间的关系并加以证明；(3) 若分别以直角三角形ABC 三边为边向外作三个正多边形，其面积分别用S 1、S 2、S 3表示，请你猜想S 1、S 2、S 3之间的关系?.专题二、勾股定理与折叠1、如图，矩形纸片ABCD 的边AB=10cm,BC=6cm,E 为BC 上一点，将矩形纸片沿AE 折叠，点B 恰好落在DC 边上的点G 处，求BE 的长。

勾股定理的培优专题

勾股定理的培优专题勾股定理培优专题一、基础知识1.勾股定理的逆定理是：如果三角形的三边长 a、b、c 满足 a+b=c，那么这个三角形是直角三角形。

2.勾股定理的逆定理和勾股定理的题设和结论相反，被称为互逆命题。

3.如果一个定理的逆命题经过证明是正确的，它也是一个定理，称这两个定理互为逆定理。

4.能够成为直角三角形三条边长的三个正整数3、4、5 等，称为勾股数。

巩固练：1.如果三角形的三边长 a、b、c 满足 a+b=c，那么这个三角形是直角三角形，这个定理叫做勾股定理的逆定理。

2.如果两个命题中，第一个命题的题设是第二个命题的结论，而第一个命题的结论是第二个命题的题设，那么这两个命题叫做互逆命题。

如果把其中一个命题叫做原命题，那么另一个命题叫做它的逆命题。

3.分别以下列四组数为一个三角形的边长：(1)6、8、10，(2)5、12、13，(3)8、15、17，(4)4、5、6，其中能构成直角三角形的有 1、2、3 号。

4.若△ABC 中，(b-a)(b+a)=c，则∠B=90°。

5.如图，正方形网格中，每个小正方形的边长为1，则网格上的△ABC 是直角三角形。

6.若一个三角形的三边长分别为1、a、8(其中a为正整数)，则以 a-2、a、a+2 为边的三角形的面积为 6(a-1)。

7.写出下列命题的逆命题，并判断逆命题的真假。

1) 两直线平行，同位角相等。

逆命题为：同位角相等，则两直线平行。

真。

2) 若 a>b，则 a>b。

逆命题为：若a≤b，则a≤b。

假。

二、例题和训练考点一：证明三角形是直角三角形例1：已知：如图，在△ABC 中，CD 是 AB 边上的高，且 CD=AD·BD。

求证：△ABC 是直角三角形。

训练：已知：在△ABC 中，∠A、∠B、∠C 的对边分别是 a、b、c，满足a+b+c+3√3=10a+24b+26c。

试判断△ABC 的形状。

例2：如图，在直角△ABC 中，∠B=90°，BD 垂直于AC，且 AD=CD。

勾股定理专题

3、勾股数：满足a2+b2=c2的三个正整数，称为勾股数。
二、典型例题与强化练习
题型一关于勾股定理的考察
例1（1）在Rt△ABC中，∠C=90°，AC=5，BC=12，求AB；
（2）在Rt△ABC中，∠C=90°，AB=25，AC=20，求BC的长；
例2如图，已知△ABC中，∠ACB=90°，以△ABC的各边为边在
△ABC外作三个正方形，S1、S2、S3分别表示这三个正方形的面积，
S1=81、S3=225，则S2=_________．
强化练习
1、一个直角三角形两直角边长分别为3和4，下列说法正确的是( )
A、斜边长为25 B、三角形的周长为25ቤተ መጻሕፍቲ ባይዱ
C、斜边长为5 D、三角形面积为20
2、若直角三角形两直角边长分别为8和15，则其斜边长是____．
且∠A=90°，求四边形ABCD的面积。
强化练习
1、强大的台风使得一根旗杆在离地面9米处折断倒下，旗杆顶部落在离旗杆底部12米的地方，请问旗杆折断之前有多长？
2、已知，如图，四边形ABCD中，AB=3cm，AD=4cm，BC=13cm，CD=12cm，且∠A=90°，求四边形ABCD的面积．
课后作业
4、如图,64、400分别为所在正方形的面积，则图中字母所代表的正方形面积是。
5、下列三条线段不能组成直角三角形的是（）
A、a=8，b=15，c=17B、a=9，b=12，c=15
C、a=9，b=40，c=41D、a：b：c=2：3：4
6、若正整数a、b、c是一组勾股数，则下列各组数仍是勾股数的是（）
9、有一只小鸟在一棵高4m的小树梢上捉虫子，它的伙伴在离该树12m，高20m的一棵大树的树梢上发出友好的叫声，它立刻以4m/s的速度飞向大树树梢，那么这只小鸟至少几秒才可能到达大树和伙伴在一起？

勾股定理专题知识点+常考题型+重难点题型

勾股定理专题知识点+常考题型+重难点题型（含详细答案）一、目录一、目录 (1)二、基础知识点 (3)1.勾股定理： (3)2.勾股定理的逆定理： (3)3.勾股定理的证明 (3)4.含特殊角的直角三角形三边的关系 (3)5.逆命题与逆定理 (4)三、常考题型 (5)1.勾股定理在几何计算中的应用-求线段的长 (5)2. 勾股定理在几何计算中的应用-坐标平面内两点的距离 (6)3. 勾股定理在几何计算中的应用-面积问题 (8)4.构造直角三角形 (9)5.勾股定理的逆定理的应用 (11)四、重难点题型 (14)1.利用勾股定理解计算问题 (14)2勾股数组 (15)3.与线段平方关系有关的证明题 (16)4.矩形和直角三角形中的折叠问题 (18)二、基础知识点1.勾股定理：如果直角三角形的两条直角边长分别为a，b，斜边长为c，那么a2+b2=c2注：1）仅在直角三角形中存在勾股定理2）由于直角三角形的斜边最长，故运用勾股定理时，一定要抓住直角三角形最长边(即斜边)的平方等于两短边两直角边的平方和，避免出现这样的错误2.勾股定理的逆定理：如果三角形三边长分别为a，b，c，且满足a2+b2=c2，那么这个三角形是以c为斜边的直角三角形。

注：在同一个三角形中，大边对大角，小角对小边3.勾股定理的证明方法一：方法二：4.含特殊角的直角三角形三边的关系勾股数：1）a=3，b=4，c=52）a=5，b=12，c=13特殊直角三角形①a=x，c=2x，b=√3x②a=x，b=x，c=√2x③AC=x，DC=x，AD=√2x，BD=√2x④AC=x，AF=2x，DC=√3x，BD=2x5.逆命题与逆定理命题与定理命题：判断一件事的语句定理：经过我们一定推理，得到的真命题互逆命题：两个命题的题设、结论正好相反的命题。

若将其中一个叫做原命题，则另一个就是它的逆命题逆定理：若一个定理的逆命题成立，则这个定理与原定理互为逆定理三、常考题型1.勾股定理在几何计算中的应用-求线段的长解析：应用勾股定理，在直角三角形中，“知二求一”。

《勾股定理》专题复习(含答案)

第一章《勾股定理》专项练习专题一：勾股定理考点分析：勾股定理单独命题的题目较少，常与方程、函数，四边形等知识综合在一起考查，在中考试卷中的常见题型为填空题、选择题和较简单的解答题典例剖析例1．（1）如图1是一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸（单位：mm ），计算两圆孔中心A 和B 的距离为______mm ．（2）如图2，直线l 上有三个正方形a b c ，，，若a c ，的面积分别为5和11，则b 的面积为（）Ａ．4 Ｂ．6Ｃ．16Ｄ．55分析：本题结合图中的尺寸直接运用勾股定理计算即可．解：（1）由已知得：AC=150-60=90，BC=180—60=120，由勾股定理得: AB 2=902+1202=22500,所以AB=150（mm ）（2)由勾股定理得：b=a+c=5+11=16，故选C ．点评：以上两例都是勾股定理的直接运用，当已知直角三角形的两边,求第三边时，往往要借助于勾股定理来解决．例2．如图3，正方形网格的每一个小正方形的边长都是1，试求122424454A E A A E C A E C ++∠∠∠的度数．解：连结32A E ．32122222A A A A A E A E ==，，32212290A A E A A E ∠=∠=，322122Rt Rt A A E A A E ∴△≌△（SAS ）．322122A E A A E A ∴∠=∠．由勾股定理,得:4532C E C E ===，4532A E A E ===,44332A C A C ==,445332A C E A C E ∴△≌△（SSS ）．323454A E C A E C ∴∠=∠图1 图21A2A3A 4A 5A 5E 2E 1E 1D 1C 1B 4C1A 2A 3A4A 5A 5E2E 1E1D 1C 1B 4C 3C 2C图3122424454324424323224A E A A E C A E C A E C A E C A E C A E C ∴∠+∠+∠=∠+∠+∠=∠．由图可知224E C C △为等腰直角三角形．22445A E C ∴∠=．即12242445445A E A A E C A E C ∠+∠+∠=．点评：由于在正方形网格中，它有两个主要特征：（1）任何格点之间的线段都是某正方形或长方形的边或对角线，所以格点间的任何线段长度都能求得．（2）利用正方形的性质，我们很容易知道一些特殊的角，如450、900、1350，便一目了然．以上两例就是根据网格的直观性，再结合图形特点，运用勾股定理进行计算，易求得线段和角的特殊值，重点考查学生的直觉观察能力和数形结合的能力．专练一：1、△ABC 中，∠A ：∠B ：∠C=2:1：1,a ，b ，c 分别是∠A 、∠B 、∠C 的对边，则下列各等式中成立的是（）（A ）222a b c +=；（B ）222a b =; （C)222c a =； (D ）222b a = 2、若直角三角形的三边长分别为2，4,x,则x 的可能值有（）（A ）1个；（B ）2个； (C ）3个； (D ）4个3、一根旗杆在离底面4.5米的地方折断，旗杆顶端落在离旗杆底部6米处，则旗杆折断前高为（）（A ）10.5米；（B ）7。

(完整版)勾股定理知识点+对应类型

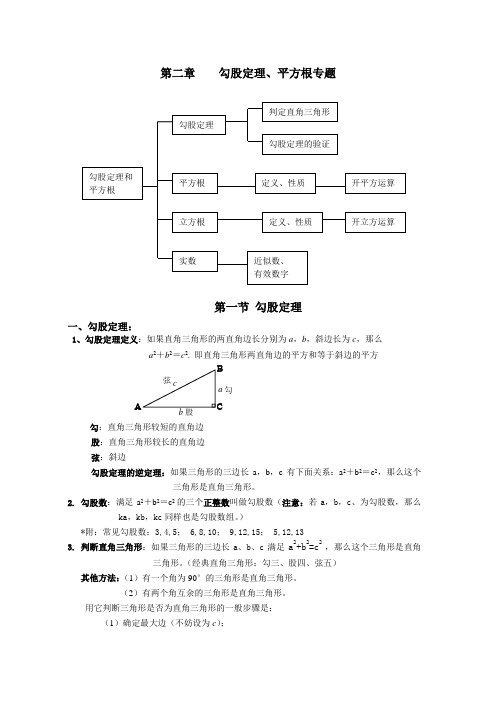
第二章勾股定理、平方根专题第一节勾股定理一、勾股定理：1、勾股定理定义：如果直角三角形的两直角边长分别为a，b，斜边长为c，那么a2＋b2＝c2. 即直角三角形两直角边的平方和等于斜边的平方ABCabc弦股勾勾：直角三角形较短的直角边股：直角三角形较长的直角边弦：斜边勾股定理的逆定理：如果三角形的三边长a，b，c有下面关系：a2＋b2＝c2，那么这个三角形是直角三角形。

2. 勾股数：满足a2＋b2＝c2的三个正整数叫做勾股数（注意：若a，b，c、为勾股数，那么ka，kb，kc同样也是勾股数组。

）*附：常见勾股数：3,4,5； 6,8,10； 9,12,15； 5,12,133. 判断直角三角形：如果三角形的三边长a、b、c满足a2+b2=c2 ，那么这个三角形是直角三角形。

（经典直角三角形：勾三、股四、弦五）其他方法：（1）有一个角为90°的三角形是直角三角形。

（2）有两个角互余的三角形是直角三角形。

用它判断三角形是否为直角三角形的一般步骤是：（1）确定最大边（不妨设为c）；（2）若c 2＝a 2＋b 2，则△ABC 是以∠C 为直角的三角形；若a 2＋b 2＜c 2，则此三角形为钝角三角形（其中c 为最大边）；若a 2＋b 2＞c 2，则此三角形为锐角三角形（其中c 为最大边）4.注意：（1）直角三角形斜边上的中线等于斜边的一半（2）在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半。

（3）在直角三角形中，如果一条直角边等于斜边的一半，那么这条直角边所对的角等于30°。

5. 勾股定理的作用：（1）已知直角三角形的两边求第三边。

（2）已知直角三角形的一边，求另两边的关系。

（3）用于证明线段平方关系的问题。

（4）利用勾股定理，作出长为n 的线段二、平方根：（11——19的平方）1、平方根定义：如果一个数的平方等于a ，那么这个数就叫做a 的平方根。

勾股定理专题(含答案)

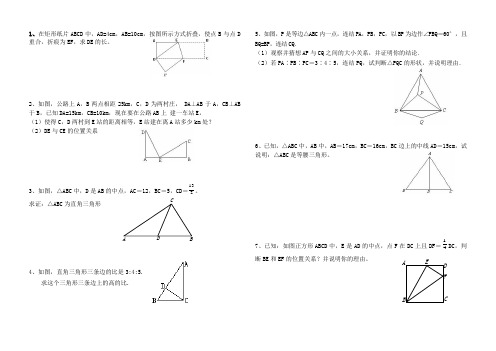
C DAB CFDE1、在矩形纸片ABCD中，AD=4cm，AB=10cm，按图所示方式折叠，使点B与点D重合，折痕为EF，求DE的长。

2、如图，公路上A，B两点相距25km，C，D为两村庄， DA⊥AB于A，CB⊥AB于B，已知DA=15km，CB=10km，现在要在公路AB上建一车站E，（1）使得C，D两村到E站的距离相等，E站建在离A站多少km处？（2）DE与CE的位置关系3、如图，△ABC中，D是AB的中点，AC＝12，BC＝5，CD＝132。

求证：△ABC为直角三角形4、如图，直角三角形三条边的比是3:4:5.求这个三角形三条边上的高的比.5、如图，P是等边△ABC内一点，连结PA，PB，PC，以BP为边作∠PBQ＝60°，且BQ=BP，连结CQ．（1）观察并猜想AP与CQ之间的大小关系，并证明你的结论．（2）若PA∶PB∶PC＝3∶4∶5，连结PQ，试判断△PQC的形状，并说明理由．6、已知，△ABC中，AB中，AB＝17cm，BC＝16cm，BC边上的中线AD＝15cm，试说明：△ABC是等腰三角形。

7、已知：如图正方形ABCD中，E是AD的中点，点F在DC上且DF＝14DC，判断BE和EF的位置关系？并说明你的理由。

4cm5cm1、已知一个Rt △的两边长分别为3和4，则第三边长是；2、左边是一个正方形，则此正方形的面积是 ( )A. 1cm 2B. 3cm 2C. 6cm 2D. 9cm 23、一圆柱高8cm,底面半径2cm,一只蚂蚁从点A 爬到点B 处吃食,要爬行的最短路程( 取3)是 . 4、在△ABC 中，∠A ，∠B ，∠C 的对边分别为a ，b ，c ，∠C=90°，且c 2=2b 2，则这个三角形有一个锐角为；5、如图，已知AB⊥CD，△ABD，△BCE 都是等腰三角形，CD=8，BE=3，则AC 的长等于；6、直角三角形两直角边长为6cm 和8cm,7、旗杆顶端的绳子垂到地面还多1米，把绳子的下端拉开绳子下端刚好接触地面，旗杆的高度为。

勾股定理专题训练

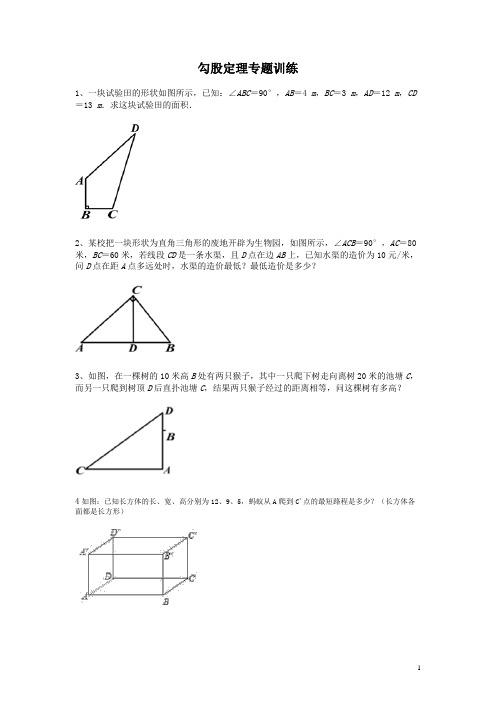
勾股定理专题训练1、一块试验田的形状如图所示，已知：∠ABC＝90°，AB＝4 m，BC＝3 m，AD＝12 m，CD ＝13 m．求这块试验田的面积．2、某校把一块形状为直角三角形的废地开辟为生物园，如图所示，∠ACB＝90°，AC＝80米，BC＝60米，若线段CD是一条水渠，且D点在边AB上，已知水渠的造价为10元/米，问D点在距A点多远处时，水渠的造价最低？最低造价是多少？3、如图，在一棵树的10米高B处有两只猴子，其中一只爬下树走向离树20米的池塘C，而另一只爬到树顶D后直扑池塘C，结果两只猴子经过的距离相等，问这棵树有多高？4如图：已知长方体的长、宽、高分别为12、9、5，蚂蚁从A爬到C'点的最短路程是多少？（长方体各面都是长方形）5、如图，在长方体上有一只蚂蚁从项点A出发，要爬行到顶点B去找食物，一只长方体的长、宽、高分别为4、1、2，如果蚂蚁走的是最短路径，你能画出蚂蚁走的路线吗？6、如图所示，圆柱形的玻璃容器，高18cm，底面周长为24cm，在外侧距下底1cm的点S处有一蜘蛛，与蜘蛛相对的圆柱形容器的上口外侧距开口处1cm的点F处有一只苍蝇，试求急于捕获苍蝇充饥的蜘蛛所走的最短路径．7、如图，在海上观察所A，我边防海警发现正北6km的B处有一可疑船只正在向东方向8km的C处行驶．我边防海警即刻派船前往C处拦截．若可疑船只的行驶速度为40km/h，则我边防海警船的速度为多少时，才能恰好在C处将可疑船只截住？8、定义：三边长和面积都是整数的三角形称为“整数三角形”．数学学习小组的同学从32根等长的火柴棒（每根长度记为1个单位）中取出若干根，首尾依次相接组成三角形，进行探究活动．小亮用12根火柴棒，摆成如图所示的“整数三角形”；小颖分别用24根和30根火柴棒摆出直角“整数三角形”；小辉受到小亮、小颖的启发，分别摆出三个不同的等腰“整数三角形”．（1）请你画出小颖和小辉摆出的“整数三角形”的示意图；（2）你能否也从中取出若干根，按下列要求摆出“整数三角形”，如果能，请画出示意图；如果不能，请说明理由．①摆出等边“整数三角形”；②摆出一个非特殊（既非直角三角形，也非等腰三角形）“整数三角形”．9、张老师在一次“探究性学习”课中,设计了如下表:n 2 3 4 5 …a 22-1 32-1 42-1 52-1 …b 4 6 8 10 …c 22+1 32+1 42+1 52+1 …(1)请你分别观察a、b、c与n之间的关系,并用含自然数n (n>1)的代数式表示:a =" ______,b" =" ______,c" = ______.(2)猜想:以a、b、c为边的三角形是否为直角三角形?并说明你的猜想.10、如图,在四边形ABCD中，AB=BC=2，CD=3，AD=1，且∠ABC=900，试求∠A的度数｡11、求图中的字母A、B所代表的正方形的面积．12、如图，Rt△ABC中，∠C=90°，AD平分∠CAB，DE⊥AB于E，若AC=6，BC=8，CD=3．（1）求DE的长；（2）求△ADB的面积．13、如图，已知长方形ABCD中AB="8" cm,BC="10" cm,在边CD上取一点E，将△ADE折叠使点D恰好落在BC边上的点F，求CE的长.14、如图：要修建一个育苗棚，棚高h="1.8" m,棚宽a="2.4" m,棚的长为12 m,现要在棚顶上覆盖塑料薄膜，试求需要多少平方米塑料薄膜？15、如图，一个牧童在小河的南4km的A处牧马，而他正位于他的小屋B的西8km北7km 处，他想把他的马牵到小河边去饮水，然后回家.他要完成这件事情所走的最短路程是多少？16、如图，E 、F 分别是正方形ABCD 中BC 和CD 边上的点，且，，F 为CD 的中点，连接AF 、AE ，问△AEF 是什么三角形？请说明理由.17、勾股数又称商高数，它有无数组，是有一定规律的.比如有一组求勾股数的式子：，，（其中为正整数，且）.你能验证它吗？利用这组式子，完成下表，通过表格，你会发现勾股数有哪些规律？请查阅有关资料，相信你将有更多收获.12 3 4 5 6 …2 3 4 5 6 … … … … … … … …18、已知长方体的长为2cm 、宽为1cm 、高为4cm ，一只蚂蚁如果沿长方体的表面从A 点爬到B ′点,那么沿哪条路最近,最短的路程是多少?19、一个直立的火柴盒在桌面上倒下，启迪人们发现了勾股定理的一种新的验证方法.如图，火柴盒的一个侧面ABCD倒下到AB′C′D′的位置，连接CC′，设AB=a,BC=b,AC=c，请利用四边形BCC′D′的面积验证勾股定理：a2+b2=c2.20、利用四个全等的直角三角形可以拼成如图所示的图形，这个图形被称为弦图．观察图形，验证：试卷答案1,四边形ABCD的面积是36 m22,D点在距A点64米的地方，水渠的造价最低，其最低造价为480元3,这棵树有15米高．4,解：①如图展开得：根据题意得：AB=12，BC'=5+9=14，在△ABC′中，由勾股定理得：AC′===2．②如图AC=12+9=21，C C′=5，由勾股定理得：AC'=＞2答：蚂蚁从A爬到C′点的最短路程是2．5,解：线段AB的长就是蚂蚁走的最短距离，分为两种情况：如图1：AC=4，BC=2+1=3，∠C=90°，由勾股定理得：AB=5；如图2：AC=4+1=5，BC=2，∠C=90°，在△ABC中，由勾股定理得：AB=＞5，∴沿图1路线走时最短，即能画出蚂蚁走的最短路线：如图从A到C′再到B．6,解：如图展开后连接SF，求出SF的长就是捕获苍蝇充饥的蜘蛛所走的最短路径，过S作SE⊥CD于E，则BC=SE=×24cm=12cm，EF=18cm﹣1cm﹣1cm=16cm，在Rt△FES中，由勾股定理得：SF===20（cm），答：捕获苍蝇充饥的蜘蛛所走的最短路径的长度是20cm．7,解：∵AB=6，BC=8∴AC==10km，∵可疑船只的行驶速度为40km/h，∴可疑船只的行驶时间为8÷40=0.2小时，∴我边防海警船的速度为10÷0.2=50km/小时，∴我边防海警船的速度为50km/h时，才能恰好在C处将可疑船只截住．8,解：（1）小颖摆出如图1所示的“整数三角形”：小辉摆出如图2所示三个不同的等腰“整数三角形”：（2）①不能摆出等边“整数三角形”．理由如下：设等边三角形的边长为a，则等边三角形面积为．因为，若边长a为整数，那么面积一定非整数．所以不存在等边“整数三角形”；②能摆出如图3所示一个非特殊“整数三角形”：9,(1)n2-1，2n，n2+1；（2）是直角三角形10,135011,字母A所代表的正方形的面积是225；字母 B所代表的正方形的面积是22512,解：（1）∵A D平分∠CAB，DE⊥AB，∠C=90°，∴CD=DE。

勾股定理专题复习课

勾股定理可以用于计算直角三角形的面积。
详细描述
根据勾股定理，直角三角形的面积可以通过两条直角边的长度和斜边的高来计算。面积 = (1/2) × 直角边1 × 直角边2 = (1/2) × 斜边 × 高。
示例
在直角三角形ABC中，已知直角边a=3和b=4，斜边c=5，斜边上的高h可以通过面积公式计算为h=12/5。
等。
05 勾股定理的易错点解析
勾股定理适用条件的误解
总结词
理解不准确
01
总结词
应用范围限制
03
总结词
忽视前提条件
05
02
详细描述
勾股定理适用于直角三角形，但学生常常误以为它适用于所有三角形，导致在解题时出现错误。
04
详细描述
勾股定理只适用于直角三角形，对于非直角三角形，需要使用其他定理和公式进行计算。
06
详细描述
勾股定理的前提是三角形必须是直角三角形，如果忽视这个前提，会导致计算结果不准确。
勾股定理计算中的常见错误
在此添加您的文本17字
总结词：计算错误
在此添加您的文本16字
详细描述：学生在使用勾股定理进行计算时，常常因为粗心或对公式理解不准确而出现计算错误。
在此添加您的文本16字
总结词：单位不统一
勾股定理与三角函数的关系
总结词
勾股定理与三角函数之间存在密切关系，可以通过三角函数来求解相关问题。
详细描述
在解决与直角三角形相关的三角函数问题时，勾股定理常常被用来计算边长或角度。例如，在求解三角函数的实际应用问题时，可以使用勾股定理来计算相关物体的长度或距离。
示例
在解决与航海、测量和几何学相关的实际问题时，常常需要使用勾股定理和三角函数来求解角度和距离。

勾股定理专题(附问题详解,全面、精选)

勾股定理一、探索勾股定理【知识点1】勾股定理定理内容：在RT△中，勾股定理的应用：在RT△中，知两边求第三边，关键在于确定斜边或直角典型题型1、对勾股定理的理解〔1〕直角三角形的两条直角边长分别为a, b，斜边长c，如此如下关于a,b,c的关系不成立的是〔〕A、c²- a²=b²B、c²- b²=a²C、a²- c²=b²D、 a²+b²= c²〔2〕在直角三角形中，∠A=90°，如此如下各式中不成立的是〔〕A、BC²- AB²=AC²B、BC²- AC²=AB ²C、AB²+AC²= BC²D、AC²+BC²= AB ²2、应用勾股定理求边长〔3〕在直角三角形ABC中，AB=10 cm, BC=8 cm, 求AC的长.〔4〕在直角△中，假如两直角边长为a、b，且满足，如此该直角三角形的斜边长为．3、利用勾股定理求面积〔5〕以直角△的三边为直径作半圆，其中两个半圆的面积为25π，16π，求另一个半圆的面积。

〔6〕如图〔1〕，图中的数字代表正方形的面积，如此正方形A的面积为。

〔7〕如图〔2〕，三角形中未知边x与y的长度分别是x= ,y=。

〔8〕在Rt△ABC中，∠C＝90°，假如AC＝6，BC＝8，如此AB的长为〔〕A、6B、8C、10D、12〔9〕在直线l上依次摆放着七个正方形〔如图4所示〕。

斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是S S12、、S S S S S S341234、，则+++=_____________。

【知识点2】勾股定理的验证推导勾股定理的关键在于找面积相等，由面积之间的等量关系并结合图形利用代数式恒等变形进展推导。

专题01 勾股定理(考点清单)解析版

专题01讲勾股定理（考点清单）【聚焦考点】题型一：用勾股定理解三角形题型二：勾股数问题题型三：以直角三角形三边为边长的图形面积题型四：勾股定理和网格问题题型五：勾股定理和折叠问题题型六：利用勾股定理求两条线段的平方和题型七：以炫图为背景的计算题题型八：勾股定理的应用题型九：勾股定理的证明题型十：勾股定理的综合问题【题型归纳】题型一：用勾股定理解三角形A ．13【答案】A 【专训1-1】（2023下·河南新乡·八年级校考期末）如图，在Rt ABC △中，90B Ð=°，6AB =，10AC =，以边BC 为直径作一个半圆，则半圆(阴影部分)的面积为（）A ．4πB ．8πC ．12πD ．16π【专训1-2】（2023下·四川宜宾·八年级统考期末）如图，菱形OABC 的边长为2，45AOC Ð=°，则点B 的坐标是( ) A ．()22,2B ．(2【答案】D 【分析】过点B 作x 轴的垂线，可证OH BH 与就是点B 的横坐标与纵坐标．因为菱形OABC 的边长为2，∴2OA AB ==．由菱形的对边AB OC ∥可得：又90BHA Ð=°，题型二：勾股数问题，，是勾股数的是（）【专训2-1】（2023下·安徽合肥·八年级统考期末）下列各组a b c【专训2-2】（2023下·贵州铜仁·八年级统考期末）成书于大约公元前1世纪的《周髀算经》是中国现存最早的一部数学典籍，里面记载的勾股定理的公式与证明相传是在西周由商高发现，故又称之为商高定理．观察下列勾股数：3，4，5；5，12，13；7，24，25；…，这类勾股数的特点是：勾为奇数，弦与股相差为1；古希腊哲学家m³，m为正整数），弦与股相差为2的一类勾股数，柏拉图（公元前427年—公元前347年）研究了勾为2m（3如：6，8，10；8，15，17；…，若此类勾股数的勾为12，则其股为（）A ．14B ．16C ．35D ．37【答案】C 【分析】依题意，设斜边为x ，则股为2x -，根据勾股定理即可求出x 的值．【详解】解：依题意，设斜边为x ，则股为2x -，∴()222122x x +-=，解得：37x =，∴股为237235x -=-=，故选：C ．题型三：以直角三角形三边为边长的图形面积【典例3】2023下·云南红河·八年级统考期末）如图，直线l 上有三个正方形,,a b c ，若,a c 的面积分别为6和9，则b 的面积为（）A ．9B ．12C ．15D ．20【答案】C 【分析】先根据AAS 证明ABC CDE △△≌，由此得BC DE =，在Rt ABC △中，根据勾股定理可得222AC AB BC =+，等量代换可得222AC AB DE =+，即可求出b 的面积．【详解】如图，ABC QV 中90ABC Ð=°，90ACB BAC \Ð+Ð=°．90ACE Ð=°Q ，90ACB ECD \Ð+Ð=°，BAC ECD \Ð=Ð．又90,ABC CDE AC CE Ð=Ð=°=Q ，AAS ()ABC CDE \≌V V ，BC DE \=．90,ABC ABC Ð=°QV ，222AC AB BC \=+，222AC AB DE \=+，即6915b a c S S S =+=+=．故选：C【专训3-1】（2023下·安徽马鞍山·八年级校考期末）ABC V 中，90ACB Ð=°，分别以ABC V 的三边作为边长向形外作正方形，并把各正方形的面积分别记作1S ，2S ，3S ，如图，若126S =，29S =，则3S 的值为（）A ．13B ．17C ．20D ．35【答案】B 【分析】由2=26AB ，29BC =，再根据勾股定理即可得到结论．【详解】解：∵126S =，29S =，∴2=26AB ，29BC =，∵90ACB Ð=°，∴22226917AC AB BC =-=-=，∴2317S AC ==．故选：B ．【专训3-2】（2023下·广西柳州·八年级统考期末）如图，在Rt ABC △中，90ACB Ð=°，分别以AC 、BC 为边作正方形，若12AB =，则正方形ADEC 和正方形BCFG 的面积和为（）A ．144B ．120C ．100D ．无法计算【答案】A 【分析】根据勾股定理即可进行解答．【详解】解：∵四边形ADEC 和四边形BCFG 为正方形，∴2ADEC S AC =形正方，2BCFG S BC =形正方，∵在Rt ABC △中，90C Ð=°，∴222212144AC BC AB +===，∴22144ADEC BCFG S S BC AC +=+=正方正方形形，故选：A ．题型四：勾股定理和网格问题【典例4】（2023下·河北保定·八年级统考期末）如图，在34´的正方形网格（每个小正方形的边长都是1）中，标记格点A ，B ，C ，D 的是（）A ．线段ABB ．线段BC C ．线段ACD ．线段BD【答案】B 【分析】根据勾股定理分别求解AB ，BC ，AC ，BD ，从而可得答案．【详解】解：由勾股定理可得：【专训4-1】（2023下·湖北武汉·八年级统考期中）如图，由单位长度为1的4个小正方形拼成的一个大正方形网格，连接三个小格点，可得ABCV，则AC边上的高是（）A．32 2【答案】C【分析】设AC边上的高为【专训4-2】（2022上·山西运城·八年级统考期末）如图，ABCV的顶点A，B，C在边长为1的正方形网格的格点上，则BC边上的高为（）题型五：勾股定理和折叠问题【典例5】（2023下·湖北荆州·八年级统考期末）如图，在Rt ABC △中，90,8,6A AB AC Ð=°==，将ABC V 沿CD 翻折，使点A 与BC 边上的点CDA ．5【答案】D 【分析】利用勾股定理求得【专训5-1】（2023下·山东济宁·八年级统考期末）如图所示，有一块直角三角形纸片，90C Ð=°，2AC =，32BC =，将斜边AB 翻折，使点B 落在直角边AC 的延长线上的点E 处，折痕为AD ，则CE 的长为（） A ．1B ．34【答案】C 【分析】根据勾股定理求出AB 【专训5-2】（2023下·天津和平·八年级天津市第五十五中学校考期末）如图，有一个直角三角形纸片，两直角边6cm AC =，8cm BC =，现将直角边AC 沿直线AD 折叠，使它落在斜边AB 上，且与AE 重合，则CD 的长为（）题型六：利用勾股定理求两条线段的平方和【典例6】（2021上·江苏扬州·八年级统考期末）如图，在△ABC 中，AB ＝6，AC ＝9，AD⊥BC 于D ，M 为AD 上任一点，则MC 2－MB 2等于（）A ．29B ．32C ．36D ．45【答案】D 【分析】在Rt △ABD 及Rt △ADC 中可分别表示出BD 2及CD 2，在Rt △BDM 及Rt △CDM 中分别将BD 2及CD 2的表示形式代入表示出BM 2和MC 2，然后作差即可得出结果．【详解】解：在Rt △ABD 和Rt △ADC 中，BD 2＝AB 2−AD 2，CD 2＝AC 2−AD 2，在Rt △BDM 和Rt △CDM 中，BM 2＝BD 2＋MD 2＝AB 2−AD 2＋MD 2，MC 2＝CD 2＋MD 2＝AC 2−AD 2＋MD 2，∴MC 2−MB 2＝（AC 2−AD 2＋MD 2）−（AB 2−AD 2＋MD 2）＝AC 2−AB 2＝45．故选：D ．【专训6-1】（2020上·浙江杭州·八年级统考期末）如图，在Rt ABC D 中， 90ACB °Ð=，以AB ，AC ，BC 为边作等边ABD D ，等边ACE D .等边CBF D .设AEH D 的面积为1S ，ABC D 的面积为2S ，BFG D 的面积为3S ，四边形DHCG 的面积为4S ，则下列结论正确的是（）【专训6-2】（2018上·辽宁沈阳·八年级校考期末）如图OP=1，过P 作PP 1⊥OP 且PP 1=1，得OP 1P 1作P 1P 2⊥OP 1且P 1P 2=1，得OP 2P 2作P 2P 3⊥OP 2且P 2P 3=1，得OP 3=2，依此法继续作下去，得OP 2017等于（）题型七：以炫图为背景的计算题【典例7】（2023下·安徽·八年级统考期末）“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，如图所示的“赵爽弦图”是由四个全等的直角三角形和一个小正方形拼成的一个大正方形．设直角三角形较长直角边长为a ，较短直角边长为b ，若168ab =，大正方形的面积为625，则小正方形的边长为（）A ．7B ．24C ．17D ．25【答案】C 【分析】勾股定理得：22625a b +=，又222()26252168289a b a b ab -=+-=-´=，由此即可求出17()a b a b -=>，因此小正方形的边长为17．【详解】解：由题意知小正方形的边长是a b -，由勾股定理得：22625a b +=，222()26252168289a b a b ab -=+-=-´=Q ，17()a b a b \-=>，\小正方形的边长为17．故选：C ．【专训7-1】（2023下·青海西宁·八年级统考期末）如图，“赵爽弦图”巧妙地利用面积关系证明了勾股定理，是我国古代数学的骄傲，它是由四个全等的直角三角形和一个小正方形拼成的一个大正方形．设直角三角形两直角边为a ，b ．斜边为c ，若85ab c ==，，则小正方形的边长为（）A．3B【答案】A【分析】由题意可知：中间小正方形的边长为：边长．【详解】解：由题意可知：中间小正方形的边长为：【专训7-2】（2023下·北京房山·八年级统考期末）如图，四个全等的直角三角形围成一个大正方形，中间是个小正方形，这个图形是我国汉代赵爽在注解《周髀算经》时给出的，人们称它为“赵爽弦图”，如果图中勾3a=，弦c=，则小正方形的面积为（）5A．1B．2【答案】A【分析】首先根据勾股定理求出c=，【详解】∵勾3a=，弦5∴224=-=b c a2()(题型八：勾股定理的应用【典例8】（2023下·辽宁葫芦岛·八年级统考期末）如图是楼梯的一部分，若2AD =，1BE =，3AE =，一只蚂蚁在A 处发现C 处有一块糖，则这只蚂蚁吃到糖所走的最短路程为（） A ．25B ．【答案】A 【分析】将台阶展开得到的是一个矩形，蚂蚁要从【专训8-1】（2023下·广东广州·八年级统考期末）如图，一个工人拿一个2.5米长的梯子，底端A 放在距离墙根C 0.7米处，另一头B 点靠墙，如果梯子的顶部下滑0.4米，梯子的底部向外滑多少米？（）A ．0.4B ．0.6C ．0.7D ．0.8【专训8-2】（2023下·北京怀柔·八年级统考期末）如图，在我军某次海上演习中，两艘航母护卫舰从同一港口O 同时出发，1号舰沿东偏南60°方向以9节（1节=1海里/小时）的速度航行，2号舰沿南偏西60°方向以12节的速度航行，离开港口2小时后它们分别到达A ，B 两点，此时两舰的距离是（）A ．9海里B ．12海里C ．15海里D ．30海里【答案】D 【分析】由60EOA Ð=°，60BOM Ð=°，求得30MOA Ð=°，90AOB Ð=°，再利用勾股定理的逆定理计算求解．【详解】解：由题意可得：60EOA Ð=°，60BOM Ð=°∴30MOA Ð=°，90AOB Ð=°又∵9218AO =´=（海里），12224BO =´=（海里），题型九：勾股定理的证明【典例9】（2023下·四川绵阳·八年级统考期末）如图，是2002年8月在北京召开的第24届国际数学家大会会标，创作的灵感来源于我国三国时代东吴数学家赵爽所注的著作《周髀算经》中的一个数学知识，这个数学知识是（）A ．黄金分割【答案】D 【分析】如图，边长为为()b a -的小正方形的面积，即可求解．由题意得：边长为c 的大正方形的面积的小正方形的面积，即：214(2c ab b =´+-整理得：222c a b =+，【专训9-1】（2023下·河北廊坊·八年级统考期末）勾股定理是数学定理中证明方法最多的定理之一，也是用代数思想解决几何问题最重要的工具之一．下列图形中可以证明勾股定理的有（）A ．①③B ．②③C ．②④D ．①④【答案】D 【分析】利用同一个图形的面积的不同表示方法进行验证即可．【详解】解：①()()22211222S a b a ab b =+=++梯形，(2111122222S ab ab c ab c =++=+梯形【专训9-2】（2023上·河北保定·八年级统考期末）勾股定理是几何中的一个重要定理，在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载．如图1是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理．图2是由图1放入长方形内得到的， 90610BAC AB BC Ð=°==，，，点D ，E ，F ，G ，H ，I 都在长方形KLMJ 的边上，则长方形KLMJ 的面积为（）A ．420B ．440C ．430D ．410【答案】B 【分析】延长AB 交KL 于P ，延长AC 交LM 于Q ，可得ABC PFB QCG V V V 、、全等，根据全等三角形对应边相等可得PB AC CQ AB ==，，然后求出IP 和DQ 的长，再根据长方形的面积公式列式计算即可得解．【详解】解：如图，延长AB 交KL 于P ，延长AC 交LM 于Q ，由题意得，90BAC BPF FBC BC BF ===°=∠∠∠，，∴90ABC ACB PBF ABC +=°=+∠∠∠∠，∴ACB PBF =∠∠，∴()AAS ABC PFB △≌△，同理可证()AAS ABC QCG △≌△，∴86PB AC CQ AB ====，，∵图2是由图1放入长方形内得到，∴86822IP =++=，68620DQ =++=，∴长方形KLMJ 的面积2220440=´=．故选：B ．题型十：勾股定理的综合问题【典例10】（2023下·内蒙古呼伦贝尔·八年级校考期末）如图，某自动感应门的正上方A 处装着一个感应器，离地的高度AB 为2.5米，当人体进入感应器的感应范围内时，感应门就会自动打开．一个身高1.6米的学生CD 正对门，缓慢走到离门1.2米的地方时( 1.2BC =米），感应门自动打开，AD 为多少米？【答案】2.5米【分析】过点D 作DE 【详解】解：如图，过点2.5AB =Q 米，BE =答：AD为2.5米．【点睛】本题考查了勾股定理的应用，解题的关键是作出辅助线，构造直角三角形，利用勾股定理求得线段AD的长度．【专训10-1】．（2023上·河南周口·八年级校考期末）图1为“弦图”，最早是由三国时期的数学家赵爽在为《周髀算经》作注时给出的，它标志着中国古代的数学成就．根据该图，赵爽用两种不同的方法计算正方形的面积，通过正方形面积相等，从而证明了勾股定理．现有4个全等的直角三角形（图2中灰色部分），直角边长分别为a，b，斜边长为c，将它们拼合为图2的形状．(1)小诚同学在图2中加了相应的虚线，从而轻松证明了勾股定理，请你根据小诚同学的思路写出证明过程；b=时，求图2中空白部分的面积．(2)当3a=，4【答案】(1)见解析(2)13【分析】（1）根据图形可得，图2中图形的总面积可以表示为：以【专训10-2】（2023上·河北承德·八年级统考期末）如图，已知在ABC V 中，90ACB Ð=°，8AC =，16BC =，点D 在线段AC 上，且3CD =，点P 从点B 出发沿射线BC 方向以每秒2个单位长度的速度向右运动．设点P 的运动时间为t 秒，连接AP ． (1)当3t =时，求AP 的长度；(2)当ABP V 是以BP 为腰的等腰三角形时，求t 的值；(3)连接PD ，在点P 的运动过程中，当PD 平分APC Ð时，直接写出【答案】(1)241则90AED PED Ð=Ð=°．90PED ACB \Ð=Ð=°．PD Q 平分APC Ð，DE AP ^3ED CD \==，PE PC ==同①得3ED CD ==，PE PC =835AD AC CD \=-=-=，AE \=2225AD DE -=-。

专题13勾股定理(知识点串讲)(解析版)

专题13 勾股定理知识框架重难突破一、勾股定理1、勾股定理直角三角形两直角边的平方和等于斜边的平方.如果直角三角形的两直角边长分别为，斜边长为，那么.备注：（1）勾股定理揭示了一个直角三角形三边之间的数量关系.（2）利用勾股定理，当设定一条直角边长为未知数后，根据题目已知的线段长可以建立方程求解，这样就将数与形有机地结合起来，达到了解决问题的目的.（3）理解勾股定理的一些变式：，，2、勾股定理的证明方法一：将四个全等的直角三角形拼成如图（1）所示的正方形.图（1）中，所以.方法二：将四个全等的直角三角形拼成如图（2）所示的正方形.图（2）中，所以.方法三：如图（3）所示，将两个直角三角形拼成直角梯形.，所以.3、勾股定理的应用1. 已知直角三角形的任意两条边长，求第三边；2. 用于解决带有平方关系的证明问题；3. 利用勾股定理，作出长为的线段.例1．（2019·安徽省定远县第二初级中学初二月考）如图，在Rt △ABC 中，∠C ＝90°，AC ＝9，BC ＝12，则点C 到AB 的距离是（）A ．365B ．1225C ．94D ．4【答案】A【解析】设点C 到AB 距离为h ．在Rt ABC ∆中，90C ∠=︒，∴222AC BC AB +=∵9AC =，12BC =∴15AB == ∵1122∆==ABC S AC BC AB h ∴12936==155⨯h ．故选：A ．练习1．（2019·安徽省初二期末）如果一个直角三角形的两条边长分别为6和10，那么这个三角形的第三边长为（）A ．8B ．10C ．D ．8或【答案】D【解析】当6和10是两条直角边时，第三边324 ，当6和10分别是一斜边和一直角边时，第三边=8，所以第三边可能为8或．故选：D ．例2．（2019·安徽省初二期中）下列各组数中，是勾股数的为（）A ．1，1，2B ．1.5，2，2.5C ．7，24，25D ．6，12，13【答案】C【解析】解：A 、∵12+12≠22，∴不是勾股数，此选项错误；B 、1.5和2.5不是整数，此选项错误；C 、∵72+242=252，∴是勾股数，此选项正确；D 、∵62+122≠132，∴不是勾股数，此选项错误．故选C ．练习1．（2018·合肥市第四十二中学初二期中）如图，在四边形ABCD 中，∠DAB =∠BCD = 90°，分别以四边形的四条边为边向外作四个正方形，若S 1+ S 4= 100，S 3= 36，则S 2=（）A ．136B ．64C ．50D ．81【答案】B 【解析】由题意可知：S 1=AB 2，S 2=BC 2，S 3=CD 2，S 4=AD 2，如果连接BD ，在直角三角形ABD 和BCD 中，BD 2=AD 2+AB 2=CD 2+BC 2，即S 1+S 4=S 3+S 2，因此S 2=100-36=64，故选B ．例3．（2019·安徽省初二期末）在平面直角坐标系中，点()43P ,-到坐标原点O 的距离是______.【答案】5【解析】点P 到原点O 5．故答案为：5练习1．（2019·安徽省初二期末）如图，在Rt △ABC 中，∠ACB=90°．AC=BC ．边AC 落在数轴上，点A 表示的数是1，点C 表示的数是3，负半轴上有一点B₁，且AB₁=AB ，点B₁所表示的数是（）A ．-2B ．-C ．-1D ．1-【答案】D 【解析】解：根据题意，AC=3-1=2，∵∠ACB=90°，AC=BC ，∴AB ==，∴B 1到原点的距离是-1．又∵B′在原点左侧，∴点B1表示的数是1-．故选D．例4．（2018·安徽省初二期末）如图，将长方形纸片ABCD折叠，使边DC落在对角线AC上，折痕为CE，且D点落在对角线D′处．若AB=3，AD=4，则ED的长为（）A．32B．3C．1D．43【答案】A【解析】∵AB=3，AD=4，∴DC=3∴根据勾股定理得AC=5根据折叠可得：△DEC≌△D′EC，∴D′C=DC=3，DE=D′E设ED=x，则D′E=x，AD′=AC﹣CD′=2，AE=4﹣x，在Rt△AED′中：（AD′）2+（ED′）2=AE2，即22+x2=（4﹣x）2，解得：x=3 2故选A.练习1．（2018·安徽省初二期末）如图，Rt△ABC中，AB=6，BC=4，∠B=90°，将△ABC折叠，使A点与BC的中点D重合，折痕为MN，则线段BN的长为（）A．53B．52C．83D．5【答案】C【解析】解：设NB=x，则AN=6−x由翻折的性质可知：ND=AN=6−x ∵点D是BC的中点，∴BD=12BC=12×4=2在Rt△NBD中，由勾股定理可知：ND²=NB²+DB²，即(6−x) ²=x²+2²，解得：x=8 3∴BN=8 3故选C例5．（2019·安徽省初二期末）我国古代数学家赵爽的弦图，它是由四个全等的直角三角形和中间的小正方形拼成的大正方形，如图所示，如果大正方形的面积是13，小正方形的面积为1，直角三角形的较短直角边长为a，较长直角边长为b，那么(a＋b)2的值为()A．13B．19C．25D．169【答案】C【解析】解：小正方形面积开方,得边长1,则有b-a=1大正方形边长的平方为其面积即13,则在三角形中有a2+b2=13将b-a=1两边平方,得a2+b2−2ab=1将a2+b2=13代入,得13-2ab=1故ab=6由a2+b2=13与2ab=12两式相加,得a2+b2+2ab=25(a+b)2=25故选C练习1．（2019·安徽省初一期末）用图1中四个完全一样的直角三角形可以拼成图2的大正方形。

勾股定理专题

专题 勾股定理及其逆定理【九大题型】

勾股定理专题

勾股定理专题

勾股定理的培优专题

勾股定理专题

勾股定理专题知识点+常考题型+重难点题型

《勾股定理》专题复习(含答案)

(完整版)勾股定理知识点+对应类型

勾股定理专题(含答案)

勾股定理专题训练

勾股定理专题复习课

勾股定理专题(附问题详解,全面、精选)

专题01 勾股定理(考点清单)解析版

专题13勾股定理(知识点串讲)(解析版)

专题勾股定理及其逆定理【九大题型】