2007苍南县“姜立夫”杯数学竞赛
07高等数学竞赛获奖表

学校 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院 浙江建设职业技术学院
姓名 陈达盛 徐和正 陈才华 柳孟垒 诸葛飞 郦泽辉 应高飞 罗家耀 吴寿龙 陈斌武 张金海 柳可可 张明 余伊飞 朱建强 黄辉 李文辉 徐艳沄 王立波 邱建华 盛烨栋 王健 裘登良 杨宇 曹益星 包睿 励建丰 仇强 蒋超安 陆忠浩 卢建波 杨文攀 刘海洋 钟连芝 黄荣进 张挺 陈成 王麒 陈品全 陈飞 邢卫娣 扬志伟
评奖 一等奖 一等奖 一等奖 二等奖 二等奖 二等奖 二等奖 二等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖 三等奖
804037 804046 804007 804030 804042 804031 804033 804044 804024 804038 804051
2014苍南县姜立夫杯数学竞赛

苍教研函[2014] 309号
关于公布2014年苍南县“姜立夫杯”
高中数学竞赛结果的通知
各高级中学:
2014年苍南县“姜立夫杯”高中数学竞赛于12月14日在苍南中学举行,全县共有1001名高一、高二学生参加竞赛,竞赛结果已经揭晓,吴姝瑶等258名学生分获不同组别的一、二、三等奖。
现将获奖名单予以公布。
附件:获奖学生和指导师名单
二○一四年十二月十六日
附件:获奖学生和指导师名单
1.一类高中组
1.1高一段:
一等奖(8名)
二等奖(10名)
三等奖(21名)
1.2高二段:
一等奖(7名)
二等奖(11名)
三等奖(23名)
2.二类高中组
2.1高一段:
一等奖(9名)
二等奖(18名)
三等奖(26名)
2.2高二段:
一等奖(8名)
二等奖(15名)
三等奖(30名)
3.三类高中组
3.1高一段:
一等奖(7名)
二等奖(11名)
三等奖(19名)
3.2高二段:
一等奖(6名)
二等奖(10名)
三等奖(19名)。
甬教研200743号

甬教研〔2007〕43号关于公布2007年全国初中数学竞赛获奖名单的通知各县(市)区教育局教研室、城区各中学:2007年全国初中数学竞赛的初、复赛工作,已圆满结束。
现将我市获2007年全国初中数学竞赛(浙江赛区)优胜团体奖和2007年全国初中数学竞赛(浙江赛区)一、二、三等奖,(宁波赛区)一、二、三等奖,(宁波城区)一、二、三等奖名单,予以公布。
附件1:2007年全国初中数学竞赛(浙江赛区)优胜团体名单附件2:2007年全国初中数学竞赛(浙江赛区)获奖名单附件3:2007年全国初中数学竞赛(宁波赛区)获奖名单附件4:2007年全国初中数学竞赛(宁波城区)获奖名单宁波市教育局教研室二○○七年五二十二日附件1:2007年全国初中数学竞赛(浙江赛区)优胜团体名单余姚市实验学校镇海区蛟川书院附件2:2007年全国初中数学竞赛(浙江赛区)获奖名单一等奖(26人)胡俊杰余姚实验学校黄杰余姚实验学校顾焱芸余姚实验学校朱林源宁波惠贞书院张凯北仑东海实验贺争盛北仑东海实验张朝俊北仑东海实验王远瞻奉化锦溪书院蔡西文镇海蛟川书院马雪环余姚实验学校岑武斌慈溪实验中学岑凯路慈溪实验中学岑健慈溪西门中学董羽婕奉化锦溪书院柴嘉文宁波兴宁中学沈世民宁海桃源中学韩志涛象山文峰学校马雨航余姚实验学校陈凯伦余姚实验学校姚皓籍余姚舜水中学张逸尘镇海蛟川书院邵冰蕾镇海蛟川书院李挺镇海蛟川书院朱凯镇海蛟川书院严晓芳镇海仁爱中学孙群超镇海蛟川书院二等奖(44人)徐骞北仑东海实验王博韬北仑东海实验傅霞君慈溪上林中学翁佳莉慈溪阳光实验学校王晗晟奉化锦溪书院薛傲宁波七中隋新宁波曙光中学忻恺宁波外国语学校李淇竹宁波外国语学校叶晗捷宁波外国语学校孙逸帆宁波外国语学校王淳宁波外国语学校金帅宁波外国语学校徐挺宁波外国语学校俞益峰宁波外国语学校竺可林宁波兴宁中学陈斌象山滨海学校计羽象山港书院励磊象山文峰学校丁逸涵象山文峰学校周瑜潇象山文峰学校毛丁益鄞州古林镇中学张婧倩鄞州古林中学俞屠娜鄞州蓝青学校项嘉南鄞州宋诏桥中学谢杰鄞州占岐中学沈佳烨余姚实验学校陆倩未余姚实验学校陈冕余姚实验学校施琴儿余姚实验学校徐彬彬余姚实验学校顾淑霞余姚实验学校陈飞翔余姚舜水中学王文权余姚舜水中学黄玮余姚舜水中学章童立川余姚舜水中学罗灵余姚阳明中学徐彬彬余姚阳明中学顾宇伟余姚阳明中学倪雪皎余姚阳明中学韩位峤镇海蛟川书院乐华彪镇海蛟川书院曹怡镇海蛟川书院王陈镇海仁爱中学三等奖(56人)曹崇浩北仑东海实验周凯峰北仑东海实验傅小天北仑东海实验李建元北仑东海实验朱航漫北仑东海实验董巧北仑顾国和外国语学校陈旭北仑松花江中学胡晨慈溪实验中学余泽辉慈溪阳光实验学校朱璐烨慈溪阳光实验学校华凯慈溪阳光实验学校徐松杰慈溪育才中学江志炳奉化锦屏中学董浩奉化实验中学胡时涛奉化实验中学卢楠宁波惠贞书院王井宁波惠贞书院章少杰宁波惠贞书院张琦宁波惠贞书院康健宁波十五中俞翔宁波外国语学校傅超宁波外国语学校沈逸磊宁波外国语学校周若余宁波外国语学校宋晨翔宁波外国语学校夏腾宁波兴宁中学施凯翔宁海长街中学沈海芸宁海大佳何中学魏守乐宁海跃龙中学章肖楠宁海跃龙中学张祺祯宁海跃龙中学王梦云宁海跃龙中学张一帆象山港书院陈磊象山文峰学校孙世春鄞州东钱湖中学虞天明鄞州古林镇中学郑文杰鄞州集仕港中学陈娟鄞州集仕港中学张超鄞州邱隘实验中学李莹莹鄞州望春初中水叶灵鄞州云龙中学陈恺豪鄞州占岐中学王齐辉余姚梨洲中学林倩颖镇海蛟川书院谢伯奇镇海蛟川书院周嘉杰镇海蛟川书院乐静镇海蛟川书院陈洋镇海蛟川书院潘东腾镇海蛟川书院孙宇凌镇海蛟川书院李顿镇海仁爱中学顾旭晨镇海仁爱中学康世勇镇海外语实验学校石珂奕镇海外语实验学校郑磊镇海外语实验学校伍晨熙镇海蛟川书院附件3:2007年全国初中数学竞赛(宁波赛区)获奖名单一等奖(共16人)金宾斌镇海外语实验学校刘波镇海仁爱中学陈超洋镇海蛟川书院陈雪婷镇海蛟川书院王佳颖镇海蛟川书院郑海滨余姚实验学校张文杰余姚实验学校张若伊慈溪实验中学叶振超慈溪上林中学郑益辉北仑顾国和外国语学校徐程婕镇海蛟川书院徐周余姚阳明中学岑少杰慈溪育才中学张宇北仑东海实验朱隽慧北仑东海实验虞祎北仑东海实验二等奖(共67人)方怡轩镇海外语实验学校陈薇娜镇海仁爱中学郑凯文镇海蛟川书院吴丹辉镇海蛟川书院叶旻渊镇海蛟川书院蔡佳彬余姚舜水中学郑燕志余姚实验学校罗一洋慈溪上林中学胡施超慈溪锦纶中学钱哲冰慈溪凤湖中学贝嘉杰北仑顾国和外国语学校沈方平北仑东海实验陈臻晗镇海外语实验学校黄凯镇海仁爱中学张杰镇海仁爱中学董力镇海仁爱中学张继镇海蛟川书院陈晓颖镇海蛟川书院陈佳斌镇海蛟川书院毛雅澜余姚实验学校章柳慰余姚实验学校孙凯凯慈溪育才中学周鑫慈溪实验中学陶杨懿慈溪实验中学赖赤松慈溪实验中学马城飞慈溪实验中学罗豪鑫慈溪实验中学孙雪晨慈溪上林中学胡凯益北仑芦江书院邬银杰北仑芦江书院顾海艇北仑联合实验学校王奇唯北仑联合实验学校毛舒存北仑东海实验陈佳妮镇海蛟川书院刘元镇海蛟川书院邵靓余姚舜水中学周易余姚实验学校郑梦焱余姚实验学校孙咏雷余姚梨洲中学俞时峰慈溪阳光实验学校丁凌云慈溪锦纶中学柳洋宁波兴宁中学邵辉宁波外国语学校朱羽张扬宁波外国语学校陈梓舒宁波外国语学校张晨宁波东恩中学吴苗杰北仑联合实验学校柴科斌北仑顾国和外国语学校梅彧翀北仑东海实验胡楚楚镇海仁爱中学王开立镇海蛟川书院郭嘉羽镇海蛟川书院李乐镇海蛟川书院许昕镇海蛟川书院蔡聪余姚子陵中学赵泽榆余姚实验学校赵柯超余姚实验学校徐晓艳慈溪实验中学沈旭晨慈溪实验中学赵扬慈溪金山中学陈巍巍慈溪观海卫中学黄础熠慈溪白河初中沈灵超慈溪庵东中学裘今宁波外国语学校李何东宁波外国语学校郑斌北仑芦江书院周琪北仑顾国和外国语学校三等奖(共104人)林森镇海外语实验学校徐俊杰镇海仁爱中学王昳镇海蛟川书院虞思祎镇海蛟川书院韩鑫豪镇海蛟川书院平方炯余姚阳明中学蒋垚余姚舜水中学俞柯达余姚实验学校罗焕棋慈溪实验中学章婧文宁波外国语学校陈安琪宁波曙光中学郑贤彬宁波十九中学洪祥来宁波惠贞书院韩宇超宁波惠贞书院宋雪祺宁波东恩中学王析镭宁波东恩中学林世杰大榭中学茅磊北仑东海实验王涵怡镇海蛟川书院李凯舟余姚舜水中学罗乐威余姚舜水中学俞晓婧余姚实验学校陈凯余姚实验学校张宇舟余姚梨洲中学沈群策慈溪阳光实验学校胡乔宇慈溪西门中学徐洁慈溪实验中学沈启杰慈溪实验中学吴天宇宁波兴宁中学徐晓望宁波外国语学校李黎明宁波外国语学校张骞宁波四眼矸中学沈凌峰宁波翠柏中学方萌镇海仁爱中学雷宇洋镇海蛟川书院沈启涛镇海蛟川书院陈琳琳余姚实验学校钟已承余姚实验学校苗婷如余姚实验学校包磊余姚兰江中学许宜哲象山港书院张熊慈溪天元中学叶婧宁波外国语学校周鑫一宁波外国语学校俞申远宁波曙光中学严峥晖宁波七中蔡倩宁波华茂外国语学校包扬宁波东恩中学顾张璐北仑顾国和中学林佳毅北仑东海实验徐晟琛北仑东海实验夏海亮镇海蛟川书院胡丹丹镇海蛟川书院周寅镇海蛟川书院薛亮亮宁海跃龙中学罗未萌奉化实验中学方立奉化锦溪书院陈策辉慈溪阳光实验学校茅琦杰慈溪阳光实验学校陈徐慈溪实验中学严凯宁波外国语学校张神玮宁波七中孙可人宁波李兴贵中学张维宁波惠贞书院林世廷宁波华茂外国语学校冯雪灵宁波东恩中学丁俊杰大榭中学赵经北仑东海实验吴梦天镇海蛟川书院金泽成镇海蛟川书院黄诗婷镇海蛟川书院范志巍镇海蛟川书院毛芸婷余姚阳明中学张超杰余姚历山中学毕天昊鄞州东钱湖中学邬锦彬宁波外国语学校汪洲宁波外国语学校刘全杰宁波外国语学校胡骏宁波外国语学校应启迪宁波华茂外国语学校冯鹏飞北仑联合实验学校朱佳敏镇海仁爱中学楼凌霄镇海蛟川书院毛守迪余姚阳明中学李振宇象山文峰学校高洁象山港书院董佳伊象山滨海学校蔡昀宁宁海城关中学严洪泽慈溪新城中学黄雷生慈溪观海卫中学朱文渊宁波庄桥中学沈沁波宁波兴宁中学朱恩泽宁波万里学校史佳豪宁波外国语学校李倩婷宁波外国语学校郑晖宁波曙光中学林澄昱宁波曙光中学汤琦宁波七中刘珉宁波惠贞书院方雁宁波华茂外国语学校张东哲象山文峰学校武子皓象山文峰学校王行宇象山文峰学校李忠宇象山文峰学校附件4:2007年全国初中数学竞赛(宁波城区)获奖名单一等奖(共10人)屠佳蕾宁波第十五中学包馨馨宁波李兴贵中学朱甬宁波惠贞书院曹彦俊宁波惠贞书院杨明宁波华茂外国语学校张士俊宁波东恩中学茹楷宁波东恩中学林蔚宁波第十五中学胡恬粼宁波惠贞书院陈伦宁波惠贞书院二等奖(20人)陈阳宁波万里学校汪溯滢宁波市第七中学尚宇萌宁波惠贞书院顾晨光宁波华茂外国语学校柴婧婧宁波惠贞书院陈佳乐宁波华茂外国语学校曹肖阳宁波华茂外国语学校傅立甬宁波东恩中学王川川宁波市第七中学黄虹宁波惠贞书院俞晓非宁波东方中学施志浩宁波万里学校张野宁波曙光中学孔树宇宁波第十五中学施经天宁波市第七中学汪梦宁宁波明楼中学王鹤宁波李兴贵中学顾佳莹宁波李兴贵中学张闻起宁波惠贞书院童阳洋宁波惠贞书院三等奖(56人)王维宁波庄桥中学余磊宁波惠贞书院江涵宁波惠贞书院包超杰宁波东恩中学郑福浩宁波万里学校姚超玲宁波万里学校杨炀宁波第十五中学毛佳拓宁波第十五中学吴文雄宁波东恩中学袁波宁波东恩中学杨晓冬宁波第十九中学任侃宁波曙光中学刘扬宁波曙光中学竺婷婷宁波明楼中学钱丰瑜宁波惠贞书院周莓莓宁波李兴贵中学刘悦宁波四眼矸中学鲁斌宁波幸福苑中学章逸磊宁波惠贞书院潘梦迪宁波市华茂外国语学校王天宇宁波市华茂外国语学校顾重建宁波大榭中学潘靖南宁波第十五中学王俏宁波第十五中学臧思聪宁波东恩中学陈震宇宁波东恩中学胡迪昆宁波李兴贵中学刘晓霏宁波明楼中学冯佳琪宁波惠贞书院范晨虹宁波惠贞书院周洋宁波万里学校杜坚存宁波万里学校徐见仁宁波万里学校许群凯宁波市华茂外国语学校徐天麟宁波东恩中学刘畅宁波东恩中学张雨星宁波东恩中学钱峰宁波翠柏中学卢怡阗宁波市第七中学童峰宁波明楼中学林舒怡宁波惠贞书院钱雪聪宁波市华茂外国语学校胡立波宁波第十五中学李珅宁波第十五中学华昀宁波东恩中学陈瑾涵宁波李兴贵中学徐松宁波曙光中学李甬芸宁波曙光中学傅博平宁波至诚学校张序佳宁波曙光中学茅呈琳宁波四眼矸中学周俊翔宁波四眼矸中学张嘉璐宁波惠贞书院杨佑佑宁波惠贞书院倪丽莎宁波惠贞书院孙小天宁波惠贞书院。
浙江省苍南县姜立夫杯2015年高一上学期数学竞赛试卷

2015年苍南县“姜立夫杯”数学竞赛高一试卷考生注意事项:1本卷共有17道题目,全卷满分100分,考试时间120分钟.2答题前,务必在试题卷、答题卷的密封线内填写好自己的学校、姓名和准考证号. 3本卷所有试题都必须用蓝色或黑色签字笔在答题卷上书写,在试题卷上作答无效. 4本卷解答一律不准使用计算器.一、选择题(本大题共8小题,每小题4分,满分32分,每小题有且仅有一个正确的答案)1.已知a 为给定的实数,那么集合{}22320=-+-=M x x x a 的子集的个数为( ) A .1 B .2 C .4 D .不确定 2.函数()212()log 23f x x x =--的单调递增区间是( )A .)1,(--∞B .)1,(-∞C .),1(+∞D .),3(+∞ 3.函数221)(xx x f x --=( )A 是偶函数但不是奇函数B 是奇函数但不是偶函数C 既是偶函数又是奇函数D 既不是偶函数也不是奇函数 4.设3log 2=a ,ln 2=b ,125-=c ,则( )A .c b a <<B .a c b <<C .<<c a bD .<<c b a5.设函数()()2log 2xf x m =+,则满足函数()f x 的定义域和值域都是实数集R 的实数m构成的集合为( )A .{}0m m =B .{}0m m ≤C .{}0m m ≥D .{}1m m = 6.已知函数21,0,()log ,0,x x f x x x +≤⎧=⎨>⎩则函数[]()1=-y f f x 的零点个数是( )A. 1B. 2C. 3D. 47.如果不等式21x x a <-+的解集是区间()3,3-的子集,则实数a 的取值范围是( )A .(,7)-∞B .(],7-∞C .(,5)-∞D .(],5-∞ 8.已知(),(),()f x g x h x 为一次函数,若对实数x 满足1,1()()()32,1022,0x f x g x h x x x x x -<-⎧⎪-+=+-≤<⎨⎪-+≥⎩,则()h x 的表达式为( )A.1()2h x x =-B.1()2h x x =--C.1()2h x x =-+D.1()2h x x =+ 二、填空题(本大题共6个小题,每小题6分,满分36分.)9.已知点(在幂函数()y f x =的图象上,则()4f = ▲ .10.设,a b 为不相等的两个实数,若二次函数()2f x x ax b =++满足()()f a f b =,则()2f 的值为 ▲ .11.已知函数()315(1)()(1)x a x x f x ax ì--<ï=í³ïî是实数集R 上的增函数,则实数a 的取值范围为 ▲ .12.已知奇函数)(x f 在定义域[]3,3-上是减函数,且()2(2)20-+-<f x x f x ,则实数x 的取值范围是 ▲13.已知()f x 为R 上增函数,且对任意∈x R ,都有()34⎡⎤-=⎣⎦xf f x ,则(2)f 的值等于▲14.已知自然数a b c d e 、、、、满足1100a b c d e ≤<<<<≤,则当b da c e++取最小值时,a b c d e ++++=____▲ ___2015年苍南县“姜立夫杯”数学竞赛高一答题卷一、选择题(本大题共8小题,每小题4分,满分32分.每小题有且仅有一个正确的答案)二、填空题(本大题共6个小题,每小题6分,满分36分. 请将正确的答案填在横线上)9.________________________ 10._____________________________ 11._______________________ 12._____________________________ 13._______________________ 14._____________________________三、解答题(本大题共3小题,第15、16题各10分,第17题12分,满分32分.要求写出必要的解答过程)15.设集合}023|{2≤++=x x x A ,}0|{2≤++=b ax x x B , (1) 若R B A C x x B A C R R =≤<-= )(},21|{)(,求b a ,的值; (2) 若1=b ,且A B A = ,求实数a 的取值范围.16.已知函数()(1)(01)xxf x a k a a a -=-->≠且是定义域为R 上的奇函数.(1)求k 的值; (2)若23)1(=f ,且)(2)(22x f m a a x g x x ⋅-+=-在),1[∞+上的最小值为2-, 求m 的值.17.设二次函数c bx ax x f ++=2)((0,,,≠∈a R c b a )满足条件: ①当R x ∈时,(1)(3)-=-f x f x ;②不等式241()21--≤≤+x f x x 对一切实数x 都成立。
2012年苍南县“姜立夫杯”数学竞赛高二试卷

2012年苍南县“姜立夫杯”数学竞赛高二试卷考生注意事项:1本卷共有17道题目,全卷满分100分,考试时间120分钟.2答题前,务必在试题卷、答题卷的密封线内填写好自己的学校、姓名和准考证号. 3本卷所有试题都必须用蓝色或黑色签字笔在答题卷上书写,在试题卷上作答无效. 4本卷解答一律不准使用计算器.一、 选择题(本大题共8小题,每小题4分,满分32分,每小题有且仅有一个正确的答案)1、已知+∈∈R y R x ,,集合}1,2,{},1,,1{2+--=---++=y yy B x x x x A ,若A=B ,则22y x +的值是( )A. 5B. 4C. 25D. 10 2、命题P :6πα≠, 命题q :1sin 2α≠,则p 是q 的( ) A. 充分且必要条件 B. 充分不必要条件 C. 必要不充分条件 D. 既不充分又不必要条件3、如图,四边形ABCD 中,1AB AD CD ===,BD =BD CD ⊥.将四边形ABCD 沿对角线BD 折成四面体A BCD '-,使平面A BD '⊥平面BCD ,则下列结论正确的是( )A. A C BD '⊥B. 90BA C'∠=C. CA '与平面A BD '所成的角为30D. 四面体A BCD '-的体积为134、多面体ABCD A BC D -的直观图,正视图,俯视图,侧视图如下所示. ) A .31112a B .312a C .334a D .356aABCD正视图侧视图5、设()11xf x x +=-,又记()()()()()11,,1,2,,k k f x f x f x f f x k +=== 则()2012f x =( ) A .11x x +- B .11x x -+ C .x D .1x-6、设点(1,0)A ,(2,1)B ,如果直线1ax by +=与线段AB 有一个公共点,那么22a b +有( )A. 最小值为15 B.最大值为15 D.7、已知函数21,0,()log ,0,x x f x x x +≤⎧=⎨>⎩则函数1)]([+=x f f y 的零点个数是( )A. 1B. 2C. 3D. 48、,,a b c 为互不相等的正数,222a c bc +=,则下列关系中可能成立的是( )A .a b c >>B .b c a >>C .b a c >>D .a c b >>二、填空题(本大题共6个小题,每小题6分,满分36分.)9、已知点(2,)P t 在不等式组40,30x y x y --≤⎧⎨+-≤⎩表示的平面区域内,则点(2,)P t 到直线34100x y ++=距离的最大值为____________.10、如图,在边长为1的正方形ABCD 中,E 为BC 的中点,若F 为正方形内(含边界)任意一点,则AE AF ⋅的最大值为 .11、已知长方体的三条面对角线的长分别为5,4,x ,则x 的取值范围为 .12、在平面直角坐标系中,定义1212(,)d P Q x x y y =-+-为两点11(,)P x y ,22(,)Q x y 之间的“折线距离”. 则圆221x y +=上一点与直线20x y +-上一点的“折线距离”的最小值是____________________. 13、对任意x ∈R ,函数()f x 满足1(1)2f x +=,设)()]([2n f n f a n -=, 数列}{n a 的前15项的和为3116-,则(15)f = . 14、设()f x 是定义在R上的奇函数,且满足(2)()f x f x +=-;又当01x ≤≤时,1()2f x x =,则1()2x f x ⎧⎫=-⎨⎬⎩⎭= 。
甬教研〔2007〕43号(精)

甬教研〔2007〕43号关于公布2007年全国初中数学竞赛获奖名单的通知各县(市)区教育局教研室、城区各中学:2007年全国初中数学竞赛的初、复赛工作,已圆满结束。
现将我市获2007年全国初中数学竞赛(浙江赛区)优胜团体奖和2007年全国初中数学竞赛(浙江赛区)一、二、三等奖,(宁波赛区)一、二、三等奖,(宁波城区)一、二、三等奖名单,予以公布。
附件1:2007年全国初中数学竞赛(浙江赛区)优胜团体名单附件2:2007年全国初中数学竞赛(浙江赛区)获奖名单附件3:2007年全国初中数学竞赛(宁波赛区)获奖名单附件4:2007年全国初中数学竞赛(宁波城区)获奖名单宁波市教育局教研室二○○七年五二十二日附件1:2007年全国初中数学竞赛(浙江赛区)优胜团体名单余姚市实验学校镇海区蛟川书院附件2:2007年全国初中数学竞赛(浙江赛区)获奖名单一等奖(26人)胡俊杰余姚实验学校黄杰余姚实验学校顾焱芸余姚实验学校朱林源宁波惠贞书院张凯北仑东海实验贺争盛北仑东海实验张朝俊北仑东海实验王远瞻奉化锦溪书院蔡西文镇海蛟川书院马雪环余姚实验学校岑武斌慈溪实验中学岑凯路慈溪实验中学岑健慈溪西门中学董羽婕奉化锦溪书院柴嘉文宁波兴宁中学沈世民宁海桃源中学韩志涛象山文峰学校马雨航余姚实验学校陈凯伦余姚实验学校姚皓籍余姚舜水中学张逸尘镇海蛟川书院邵冰蕾镇海蛟川书院李挺镇海蛟川书院朱凯镇海蛟川书院严晓芳镇海仁爱中学孙群超镇海蛟川书院二等奖(44人)徐骞北仑东海实验王博韬北仑东海实验傅霞君慈溪上林中学翁佳莉慈溪阳光实验学校王晗晟奉化锦溪书院薛傲宁波七中隋新宁波曙光中学忻恺宁波外国语学校李淇竹宁波外国语学校叶晗捷宁波外国语学校孙逸帆宁波外国语学校王淳宁波外国语学校金帅宁波外国语学校徐挺宁波外国语学校俞益峰宁波外国语学校竺可林宁波兴宁中学陈斌象山滨海学校计羽象山港书院励磊象山文峰学校丁逸涵象山文峰学校周瑜潇象山文峰学校毛丁益鄞州古林镇中学张婧倩鄞州古林中学俞屠娜鄞州蓝青学校项嘉南鄞州宋诏桥中学谢杰鄞州占岐中学沈佳烨余姚实验学校陆倩未余姚实验学校陈冕余姚实验学校施琴儿余姚实验学校徐彬彬余姚实验学校顾淑霞余姚实验学校陈飞翔余姚舜水中学王文权余姚舜水中学黄玮余姚舜水中学章童立川余姚舜水中学罗灵余姚阳明中学徐彬彬余姚阳明中学顾宇伟余姚阳明中学倪雪皎余姚阳明中学韩位峤镇海蛟川书院乐华彪镇海蛟川书院曹怡镇海蛟川书院王陈镇海仁爱中学三等奖(56人)曹崇浩北仑东海实验周凯峰北仑东海实验傅小天北仑东海实验李建元北仑东海实验朱航漫北仑东海实验董巧北仑顾国和外国语学校陈旭北仑松花江中学胡晨慈溪实验中学余泽辉慈溪阳光实验学校朱璐烨慈溪阳光实验学校华凯慈溪阳光实验学校徐松杰慈溪育才中学江志炳奉化锦屏中学董浩奉化实验中学胡时涛奉化实验中学卢楠宁波惠贞书院王井宁波惠贞书院章少杰宁波惠贞书院张琦宁波惠贞书院康健宁波十五中俞翔宁波外国语学校傅超宁波外国语学校沈逸磊宁波外国语学校周若余宁波外国语学校宋晨翔宁波外国语学校夏腾宁波兴宁中学施凯翔宁海长街中学沈海芸宁海大佳何中学魏守乐宁海跃龙中学章肖楠宁海跃龙中学张祺祯宁海跃龙中学王梦云宁海跃龙中学张一帆象山港书院陈磊象山文峰学校孙世春鄞州东钱湖中学虞天明鄞州古林镇中学郑文杰鄞州集仕港中学陈娟鄞州集仕港中学张超鄞州邱隘实验中学李莹莹鄞州望春初中水叶灵鄞州云龙中学陈恺豪鄞州占岐中学王齐辉余姚梨洲中学林倩颖镇海蛟川书院谢伯奇镇海蛟川书院周嘉杰镇海蛟川书院乐静镇海蛟川书院陈洋镇海蛟川书院潘东腾镇海蛟川书院孙宇凌镇海蛟川书院李顿镇海仁爱中学顾旭晨镇海仁爱中学康世勇镇海外语实验学校石珂奕镇海外语实验学校郑磊镇海外语实验学校伍晨熙镇海蛟川书院附件3:2007年全国初中数学竞赛(宁波赛区)获奖名单一等奖(共16人)金宾斌镇海外语实验学校刘波镇海仁爱中学陈超洋镇海蛟川书院陈雪婷镇海蛟川书院王佳颖镇海蛟川书院郑海滨余姚实验学校张文杰余姚实验学校张若伊慈溪实验中学叶振超慈溪上林中学郑益辉北仑顾国和外国语学校徐程婕镇海蛟川书院徐周余姚阳明中学岑少杰慈溪育才中学张宇北仑东海实验朱隽慧北仑东海实验虞祎北仑东海实验二等奖(共67人)方怡轩镇海外语实验学校陈薇娜镇海仁爱中学郑凯文镇海蛟川书院吴丹辉镇海蛟川书院叶旻渊镇海蛟川书院蔡佳彬余姚舜水中学郑燕志余姚实验学校罗一洋慈溪上林中学胡施超慈溪锦纶中学钱哲冰慈溪凤湖中学贝嘉杰北仑顾国和外国语学校沈方平北仑东海实验陈臻晗镇海外语实验学校黄凯镇海仁爱中学张杰镇海仁爱中学董力镇海仁爱中学张继镇海蛟川书院陈晓颖镇海蛟川书院陈佳斌镇海蛟川书院毛雅澜余姚实验学校章柳慰余姚实验学校孙凯凯慈溪育才中学周鑫慈溪实验中学陶杨懿慈溪实验中学赖赤松慈溪实验中学马城飞慈溪实验中学罗豪鑫慈溪实验中学孙雪晨慈溪上林中学胡凯益北仑芦江书院邬银杰北仑芦江书院顾海艇北仑联合实验学校王奇唯北仑联合实验学校毛舒存北仑东海实验陈佳妮镇海蛟川书院刘元镇海蛟川书院邵靓余姚舜水中学周易余姚实验学校郑梦焱余姚实验学校孙咏雷余姚梨洲中学俞时峰慈溪阳光实验学校丁凌云慈溪锦纶中学柳洋宁波兴宁中学邵辉宁波外国语学校朱羽张扬宁波外国语学校陈梓舒宁波外国语学校张晨宁波东恩中学吴苗杰北仑联合实验学校柴科斌北仑顾国和外国语学校梅彧翀北仑东海实验胡楚楚镇海仁爱中学王开立镇海蛟川书院郭嘉羽镇海蛟川书院李乐镇海蛟川书院许昕镇海蛟川书院蔡聪余姚子陵中学赵泽榆余姚实验学校赵柯超余姚实验学校徐晓艳慈溪实验中学沈旭晨慈溪实验中学赵扬慈溪金山中学陈巍巍慈溪观海卫中学黄础熠慈溪白河初中沈灵超慈溪庵东中学裘今宁波外国语学校李何东宁波外国语学校郑斌北仑芦江书院周琪北仑顾国和外国语学校三等奖(共104人)林森镇海外语实验学校徐俊杰镇海仁爱中学王昳镇海蛟川书院虞思祎镇海蛟川书院韩鑫豪镇海蛟川书院平方炯余姚阳明中学蒋垚余姚舜水中学俞柯达余姚实验学校罗焕棋慈溪实验中学章婧文宁波外国语学校陈安琪宁波曙光中学郑贤彬宁波十九中学洪祥来宁波惠贞书院韩宇超宁波惠贞书院宋雪祺宁波东恩中学王析镭宁波东恩中学林世杰大榭中学茅磊北仑东海实验王涵怡镇海蛟川书院李凯舟余姚舜水中学罗乐威余姚舜水中学俞晓婧余姚实验学校陈凯余姚实验学校张宇舟余姚梨洲中学沈群策慈溪阳光实验学校胡乔宇慈溪西门中学徐洁慈溪实验中学沈启杰慈溪实验中学吴天宇宁波兴宁中学徐晓望宁波外国语学校李黎明宁波外国语学校张骞宁波四眼矸中学沈凌峰宁波翠柏中学方萌镇海仁爱中学雷宇洋镇海蛟川书院沈启涛镇海蛟川书院陈琳琳余姚实验学校钟已承余姚实验学校苗婷如余姚实验学校包磊余姚兰江中学许宜哲象山港书院张熊慈溪天元中学叶婧宁波外国语学校周鑫一宁波外国语学校俞申远宁波曙光中学严峥晖宁波七中蔡倩宁波华茂外国语学校包扬宁波东恩中学顾张璐北仑顾国和中学林佳毅北仑东海实验徐晟琛北仑东海实验夏海亮镇海蛟川书院胡丹丹镇海蛟川书院周寅镇海蛟川书院薛亮亮宁海跃龙中学罗未萌奉化实验中学方立奉化锦溪书院陈策辉慈溪阳光实验学校茅琦杰慈溪阳光实验学校陈徐慈溪实验中学严凯宁波外国语学校张神玮宁波七中孙可人宁波李兴贵中学张维宁波惠贞书院林世廷宁波华茂外国语学校冯雪灵宁波东恩中学丁俊杰大榭中学赵经北仑东海实验吴梦天镇海蛟川书院金泽成镇海蛟川书院黄诗婷镇海蛟川书院范志巍镇海蛟川书院毛芸婷余姚阳明中学张超杰余姚历山中学毕天昊鄞州东钱湖中学邬锦彬宁波外国语学校汪洲宁波外国语学校刘全杰宁波外国语学校胡骏宁波外国语学校应启迪宁波华茂外国语学校冯鹏飞北仑联合实验学校朱佳敏镇海仁爱中学楼凌霄镇海蛟川书院毛守迪余姚阳明中学李振宇象山文峰学校高洁象山港书院董佳伊象山滨海学校蔡昀宁宁海城关中学严洪泽慈溪新城中学黄雷生慈溪观海卫中学朱文渊宁波庄桥中学沈沁波宁波兴宁中学朱恩泽宁波万里学校史佳豪宁波外国语学校李倩婷宁波外国语学校郑晖宁波曙光中学林澄昱宁波曙光中学汤琦宁波七中刘珉宁波惠贞书院方雁宁波华茂外国语学校张东哲象山文峰学校武子皓象山文峰学校王行宇象山文峰学校李忠宇象山文峰学校附件4:2007年全国初中数学竞赛(宁波城区)获奖名单一等奖(共10人)屠佳蕾宁波第十五中学包馨馨宁波李兴贵中学朱甬宁波惠贞书院曹彦俊宁波惠贞书院杨明宁波华茂外国语学校张士俊宁波东恩中学茹楷宁波东恩中学林蔚宁波第十五中学胡恬粼宁波惠贞书院陈伦宁波惠贞书院二等奖(20人)陈阳宁波万里学校汪溯滢宁波市第七中学尚宇萌宁波惠贞书院顾晨光宁波华茂外国语学校柴婧婧宁波惠贞书院陈佳乐宁波华茂外国语学校曹肖阳宁波华茂外国语学校傅立甬宁波东恩中学王川川宁波市第七中学黄虹宁波惠贞书院俞晓非宁波东方中学施志浩宁波万里学校张野宁波曙光中学孔树宇宁波第十五中学施经天宁波市第七中学汪梦宁宁波明楼中学王鹤宁波李兴贵中学顾佳莹宁波李兴贵中学张闻起宁波惠贞书院童阳洋宁波惠贞书院三等奖(56人)王维宁波庄桥中学余磊宁波惠贞书院江涵宁波惠贞书院包超杰宁波东恩中学郑福浩宁波万里学校姚超玲宁波万里学校杨炀宁波第十五中学毛佳拓宁波第十五中学吴文雄宁波东恩中学袁波宁波东恩中学杨晓冬宁波第十九中学任侃宁波曙光中学刘扬宁波曙光中学竺婷婷宁波明楼中学钱丰瑜宁波惠贞书院周莓莓宁波李兴贵中学刘悦宁波四眼矸中学鲁斌宁波幸福苑中学章逸磊宁波惠贞书院潘梦迪宁波市华茂外国语学校王天宇宁波市华茂外国语学校顾重建宁波大榭中学潘靖南宁波第十五中学王俏宁波第十五中学臧思聪宁波东恩中学陈震宇宁波东恩中学胡迪昆宁波李兴贵中学刘晓霏宁波明楼中学冯佳琪宁波惠贞书院范晨虹宁波惠贞书院周洋宁波万里学校杜坚存宁波万里学校徐见仁宁波万里学校许群凯宁波市华茂外国语学校徐天麟宁波东恩中学刘畅宁波东恩中学张雨星宁波东恩中学钱峰宁波翠柏中学卢怡阗宁波市第七中学童峰宁波明楼中学林舒怡宁波惠贞书院钱雪聪宁波市华茂外国语学校胡立波宁波第十五中学李珅宁波第十五中学华昀宁波东恩中学陈瑾涵宁波李兴贵中学徐松宁波曙光中学李甬芸宁波曙光中学傅博平宁波至诚学校张序佳宁波曙光中学茅呈琳宁波四眼矸中学周俊翔宁波四眼矸中学张嘉璐宁波惠贞书院杨佑佑宁波惠贞书院倪丽莎宁波惠贞书院孙小天宁波惠贞书院。
苍南县“姜立夫杯”高中数学竞赛高一苍南县“姜立夫杯”高中数学竞赛高一准考证准考证

试场_______________准考证号________________ 试场_______________准考证号________________竞赛时间:2020年12月13日(星期日)上午9:00~11:00 竞赛时间:2020年12月13日(星期日)上午9:00~11:00 竞赛地点:苍南中学竞赛地点:苍南中学苍南县教师发展中心制苍南县教师发展中心制苍南县“姜立夫杯”高中数学竞赛(高一)苍南县“姜立夫杯”高中数学竞赛(高一)准考证准考证学校_______________姓名________________ 学校_______________姓名________________试场_______________准考证号________________ 试场_______________准考证号________________竞赛时间:2020年12月13日(星期日)上午9:00~11:00 竞赛时间:2020年12月13日(星期日)上午9:00~11:00 竞赛地点:苍南中学竞赛地点:苍南中学苍南县教师发展中心制苍南县教师发展中心制苍南县“姜立夫杯”高中数学竞赛(高一)苍南县“姜立夫杯”高中数学竞赛(高一)准考证准考证学校_______________姓名________________ 学校_______________姓名________________试场_______________准考证号________________ 试场_______________准考证号________________竞赛时间:2020年12月13日(星期日)上午9:00~11:00 竞赛时间:2020年12月13日(星期日)上午9:00~11:00 竞赛地点:苍南中学竞赛地点:苍南中学苍南县教师发展中心制苍南县教师发展中心制苍南县“姜立夫杯”高中数学竞赛(高一)苍南县“姜立夫杯”高中数学竞赛(高一)准考证准考证学校_______________姓名________________ 学校_______________姓名________________试场_______________准考证号________________ 试场_______________准考证号________________竞赛时间:2020年12月13日(星期日)上午9:00~11:00 竞赛时间:2020年12月13日(星期日)上午9:00~11:00 竞赛地点:苍南中学竞赛地点:苍南中学苍南县教师发展中心制苍南县教师发展中心制苍南县“姜立夫杯”高中数学竞赛(高一)苍南县“姜立夫杯”高中数学竞赛(高一)准考证准考证学校_______________姓名________________ 学校_______________姓名________________试场_______________准考证号________________ 试场_______________准考证号________________竞赛时间:2020年12月13日(星期日)上午9:00~11:00 竞赛时间:2020年12月13日(星期日)上午9:00~11:00 竞赛地点:苍南中学竞赛地点:苍南中学苍南县教师发展中心制苍南县教师发展中心制试场_______________准考证号________________ 试场_______________准考证号________________竞赛时间:2020年12月13日(星期日)上午9:00~11:00 竞赛时间:2020年12月13日(星期日)上午9:00~11:00 竞赛地点:苍南中学竞赛地点:苍南中学苍南县教师发展中心制苍南县教师发展中心制苍南县“姜立夫杯”高中数学竞赛(高二)苍南县“姜立夫杯”高中数学竞赛(高二)准考证准考证学校_______________姓名________________ 学校_______________姓名________________试场_______________准考证号________________ 试场_______________准考证号________________竞赛时间:2020年12月13日(星期日)上午9:00~11:00 竞赛时间:2020年12月13日(星期日)上午9:00~11:00 竞赛地点:苍南中学竞赛地点:苍南中学苍南县教师发展中心制苍南县教师发展中心制苍南县“姜立夫杯”高中数学竞赛(高二)苍南县“姜立夫杯”高中数学竞赛(高二)准考证准考证学校_______________姓名________________ 学校_______________姓名________________试场_______________准考证号________________ 试场_______________准考证号________________竞赛时间:2020年12月13日(星期日)上午9:00~11:00 竞赛时间:2020年12月13日(星期日)上午9:00~11:00 竞赛地点:苍南中学竞赛地点:苍南中学苍南县教师发展中心制苍南县教师发展中心制苍南县“姜立夫杯”高中数学竞赛(高二)苍南县“姜立夫杯”高中数学竞赛(高二)准考证准考证学校_______________姓名________________ 学校_______________姓名________________试场_______________准考证号________________ 试场_______________准考证号________________竞赛时间:2020年12月13日(星期日)上午9:00~11:00 竞赛时间:2020年12月13日(星期日)上午9:00~11:00 竞赛地点:苍南中学竞赛地点:苍南中学苍南县教师发展中心制苍南县教师发展中心制苍南县“姜立夫杯”高中数学竞赛(高二)苍南县“姜立夫杯”高中数学竞赛(高二)准考证准考证学校_______________姓名________________ 学校_______________姓名________________试场_______________准考证号________________ 试场_______________准考证号________________竞赛时间:2020年12月13日(星期日)上午9:00~11:00 竞赛时间:2020年12月13日(星期日)上午9:00~11:00 竞赛地点:苍南中学竞赛地点:苍南中学苍南县教师发展中心制苍南县教师发展中心制。
最新-2018年度苍南县“姜立夫杯”数学竞赛高二试题答

2018年苍南县“姜立夫杯”数学竞赛高二试题参考答案二、填空题9、(1,1)- 10、2004 11 12 13、0x =14、10a -<< 三、解答题15、解:设l 方程为1(1)y m x -=--,则1(1,0)P m +,(0,1)Q m +-----------------1分 从而可得直线PR 和QS 的方程分别为120m x y m+--=和22(1)0x y m -++=--------2分 又||PRQS,11|221|32||m m RS +++++∴== 又22|||PR QS +==-----------------------------------------------------------------------5分 所以四边形PRSQ 的面积为:2123212PRSQ m S +++==21191()5480m m ++--------------------------------8分 219118(2)54805≥+-=。
所以四边形PRSQ 面积的最小值为185--------------------------------------------------------------10分16、解:设椭圆的离心率为e ,则1||MF e d=,即1||MF de =,--------------------------1分 又12||||2MF MF a +=,所以2||2MF a de =-,---------------------------------------3分由题意可得212||||MF d MF =,所以22(2)d e d a de =-,故22a d e e=+,------5分 由d 不小于左顶点到左准线的距离且不大于右顶点到左准线的距离,即2222222112a a a a a e e ca d a e c c a a ae e c⎧≥-⎪⎪+-≤≤+⇒⇒≤<⎨⎪≤+⎪+⎩-----------------------------9分 11e ≤<时,符合条件的点M 存在, 当01e <<时,点M 不存在。
通知

林炜
镇海中学
A组
绍兴
111
姚元
诸暨中学
A组
宁波
150
虞华艇
镇海中学
A组
绍兴
112
刘于绰
诸暨中学
A组
宁波
151
陈培文
镇海中学
A组
绍兴
113
张家怡
诸暨中学
A组
宁波
152
杨根茂
象山中学
A组
杭州
114
杨嘉胤
杭州二中
A组
宁波
153
杨起帆
镇海中学
A组
嘉兴
115
陆范菲
嘉善高级中学
A组
绍兴
154
徐远
新昌中学
A组
郦润华
诸暨中学
A组
宁波
94
井永乐
效实
A组
温州
133
叶立早
温州中学
A组
宁波
95
叶荔
余姚中学
A组
湖州
134
郑欣
湖州中学
A组
宁波
96
马潇辉
慈溪中学
A组
金华
135
陈赞迪
兰溪一中
A组
宁波
97
丁雪成
慈溪中学
A组
台州
136
杨羲
路桥中学
A组
宁波
98
陈超丰
慈溪中学
A组
嘉兴
137
皮学锋
嘉兴一中
A组
宁波
99
陈硕冰
镇海中学
杭州二中
A组
金华
65
华佳驹
东阳中学
2007年浙江省数学夏令营获奖名单公布如下
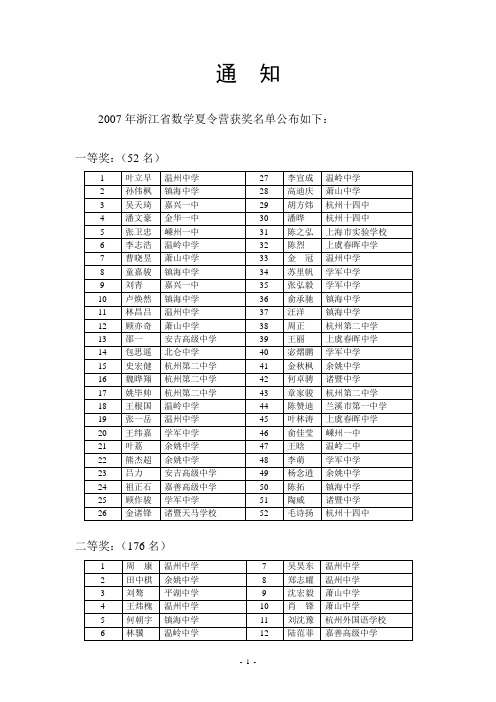
裘欣融
嘉兴一中
92
何袁
富阳中学
135
谢俊
平阳中学
93
崔德琦
海盐元济高级中学
136
郑伟
平阳中学
94
汪晨骅
杭州第二中学
137
陈亨键
瑞安市第十中学
95
吴俊佳
杭州第二中学
138
虞明杭
瑞安市第十中学
96
鲁福韬
杭州第二中学
139
阮高威
瑞安市第十中学
97
王婧
黄岩中学
140
何骏
上海市曹杨二中
98
陶蕴哲
金华一中
海盐元济高级中学
133
戚人杰
诸暨中学
172
岑蔚之
杭州第二中学
134
朱钰锋
富阳中学
173
沈涛
绍兴县柯桥中学
135
沈普霖
富阳中学
174
吴刚
嵊州一中
136
顾宇阳
富阳中学
175
何文军
富阳中学
137
金凌
富阳中学
176
王飞翔
富阳中学
三等奖:(194名)
1
李挺
温州中学
43
吴凯杰
镇海中学
2
陈波
安吉高级中学
44
裘露萍
王圳勋
镇海中学
84
温丽健
平阳中学
85
吴钟伟
嵊州一中
128
徐俊
海盐元济高级中学
86
陈浩洋
台州中学
129
袁斐
海盐元济高级中学
87
王凌霄
台州中学
2007年全国初中数学联赛成绩已于近日揭晓

男 八年级 什邡马井中学
男 八年级 什邡中学实验学校
男 八年级 什邡外国语学校
女 八年级 什邡外国语学校
男 八年级 什邡中学实验学校
男 八年级 什邡中学实验学校
女 八年级 什邡方亭中学
男 八年级 什邡中学实验学校
男 八年级 什邡隐丰中学
女 八年级 什邡禾丰中学
男 八年级 什邡雍城中学
男 八年级 什邡雍城中学
实验中学
女 八年级
实验中学
男 八年级 绵竹中学实验学校
男 八年级
实验中学
男 八年级 绵竹中学实验学校
男 八年级 绵竹中学实验学校
男 八年级
实验中学
女 八年级 绵竹中学实验学校
缪世莉 苏先君 陈道胜 肖开芝 罗先勇 唐华文 唐华文 唐华文 雷志铭 缪世莉 赖志良 唐华文 毛曦曜 陈道英 杨建 雷志铭 曾本强 陈道胜 曾本强 王礼东 郭文湘 钟基团
女 八年级 什邡外国语学校
女 八年级 什邡中学实验学校
男 八年级 什邡外国语学校
女 八年级 什邡中学实验学校
女 八年级 什邡中学实验学校
男 八年级 什邡双盛中学
男 八年级 什邡马祖中学
男 八年级 什邡外国语学校
女 八年级 什邡方亭中学
女 八年级 什邡外国语学校
男 八年级 什邡禾丰中学
女 八年级 什邡双盛中学
九年级
德阳中学
九年级
孝泉中学
广汉市(33人)
男 九年级 广汉中学实验学校
女 九年级 广汉连山中学
男 九年级 广汉中学实验学校
女 九年级 广汉南兴中学
男 九年级 广汉光华双语学校
女 九年级 广汉连山中学
男 九年级 广汉雒城三中
关于公布2007年苍南县中小学科学学生实验操作竞赛获奖...

关于公布2007年苍南县中小学科学学生实验操作竞赛获奖名单的通知苍南县教育局教育技术装备站苍教技通〔2007〕12号苍教研通〔2007〕320号各学区、直属各类学校,各乡镇中小学:根据苍教技通〔2007〕7号《关于举行全县中小学生科学实验操作竞赛的通知》要求,县教育局教育技术装备站、教研室于11月3、4日组织举办全县中小学《科学》学生实验操作竞赛,共评出中小学城镇组、农村组集体奖第一、二、三名,城镇组、农村组学生一、二、三等奖169名,优秀指导师17名。
现将获奖学区、学生和优秀指导师奖名单予以公布(见附件)。
附件1:2007年苍南县初中学生科学实验操作竞赛获奖名单附件2:2007年苍南县小学学生科学实验操作竞赛获奖名单附件3:2007年苍南县中小学学生科学实验操作竞赛优秀指导师名单苍南县教育局教育技术装备站苍南县教育局教学研究室二○○七年十一月十日附件1:2007年苍南县初中学生科学实验操作竞赛获奖名单城镇组集体奖:第一名:金乡学区第二名:灵溪学区第三名:桥墩学区个人奖:一等奖9名二等奖14名三等奖21名农村组集体奖:第一名:矾山学区第二名:宜山学区第三名:灵溪学区个人奖:一等奖7名二等奖17名三等奖24名附件2:2007年苍南县小学学生科学实验操作竞赛获奖名单城镇组集体奖:第一名:矾山学区第二名:灵溪学区第三名:宜山学区个人奖:一等奖6名二等奖15名农村组集体奖:第一名:金乡学区第二名:钱库学区第三名:灵溪学区个人奖:一等奖6名二等奖11名三等奖17名附件3:2007年苍南县中小学学生科学实验操作竞赛优秀指导师名单优秀指导师(17名):王成周(民族中学)温怀良(金乡二中)黄光水(金乡二中)张亦清(灵溪三中)陈荣部(灵溪三中)屠昌满(灵溪九中)陈明明(云岩中学)林允闯(南宋中学)吕明抽(巴曹一中)郑义杰(灵溪一小)高健(龙港四小)李孝钊(实验二小)雷政春(矾山一小)缪心聪(巴曹一小)张招鹏(巴曹一小)黄银花(望里二小)黄小华(藻溪小学)。
2007年全国高中数学联合竞赛温州市级奖

瑞安三中 龙湾中学 乐清市柳市中学 平阳鳌江中学 泰顺一中 永嘉上塘中学 平阳鳌江中学 温州八中 文成中学 苍南龙港高级中学 瓯海第二高级中学 苍南狮山中学 平阳浙鳌高中 龙湾中学 龙湾中学 乐清市柳市中学 乐清市虹桥中学 温州国际育英实验学校 苍南龙港二高 苍南县求知中学 乐清市第三中学 平阳浙鳌高中 瑞安三中 龙湾中学 苍南县求知中学 乐清市乐成公立寄宿学校 温州二十二中 苍南龙港高级中学 龙湾中学 苍南龙港高级中学 乐清市柳市中学 乐清市第二中学 永嘉上塘中学 苍南灵溪二高 苍南狮山中学 温州市教师教育院附校 永嘉上塘中学 温州八中 温州十五中 苍南狮山中学 温州八中 瑞安十中 龙湾永强中学 乐清市第三中学 龙湾中学
高三 高三 高二 高三 高三 高三 高三
池仁访 陈华云
谢逢楷 倪文洁
高三 高三 高三 高三 高三 高二 高二 高三 高三 高三 高二 高三 高三 高三 高三 初三 高三 高三 高三 高三 高二 高二 高三 高三 高三 高三 高三
王巨才 李威武 陈华云 陈华云
刘艳阳 肖若茂 庞应征 池仁访 陈华云 肖若茂
赵大藏
市二等奖(33名 市二等奖 (33名 )
姓名 陈涵逸 胡文建 黄邦印 李士棣 林大进 王啸威 吴圣杰 谢浩然 叶鹭 张峰 陈建疆 陈如通 季林坤 肖艺涵 徐成浩 薛迪秀 张亮亮 张也 郑 南 周杰 庄孟杰 郑小驹 冯启雯 黄石慧 金道伟 金逸凡 吕诗宁 缪仁梁 邵建北 童影贝 王亚纳 曾强 指导师 胡云华 苏亦滔 陈陆巧 陈陆巧 陈陆巧 陈陆巧 陈陆巧 苏亦滔 胡浩鑫 赵大藏
高三 高三 高三 高三 高三 高三 高三 高二 高三
戴光森
钱祥隆 张海阔 张贤菲 张业允 蔡旺利 陈赛丰 林常栩 吕瞻远 王家其 温时米 翁晓锋 夏孟鹏 蔡廷廷 高张引 叶锐睿 张程 郑鹏 周辉 方孝仲 陈进取 陈志辉 范坚坚 洪威迪 黄扩伟 林甲品 沈 阳 项剑乔 杨象爽 余建国 张维笑 赵威 朱晓海 诸 斌 陈批 陈庆勇 陈旭强 胡永奇 金圣洁* 金小飞 潘夏兰 施 霖 王奇思 王世才 徐健敏 张凌浩
年苍南县“姜立夫杯”高中数学竞赛高一试卷

年苍南县“姜立夫杯”高中数学竞赛高一试卷一、选择题(每题5分,共40分)1、三元实数集A=},,{y x xy x +,B=},||,0{y x ,且A=B ,则20062006xy +=( )A 、0B 、1C 、2D 、-12、若某等差数列{a n }中,1662a a a ++是一个确定的常数,则其前n 项和S n 中也为确定的常数的是( )A 、 15SB 、 14SC 、 8SD 、7S 3、设函数121(1)()lg (1)x x f x x x -⎧-<=⎨≥⎩,若1)(0>x f ,则x 0的取值范围是( ) A 、(0,10) B 、(-1,+∞) C 、(-∞,-2) D 、(-∞,0)∪(10,+∞)4、等差数列}{n a 的前n 项和为S n ,且3184=S S ,则=168S S ( ) A 、81 B 、31 C 、91 D 、103 5、已知集合{|1284,,,}P u u m n l m n l Z ==++∈,集合{|201612,,,}Q u u p q r p q r Z ==++∈,则P 与Q 的关系为( )A 、P =QB 、P ∩Q =φC 、 P ∪Q =RD 、P ∪Q =Z6、数列1,2,2,3,3,3,4,4,4,4……,则这个数列的第个数是( )A 、62B 、63C 、64D 、657、已知函数f(x)是R 上的减函数,A (0,-2),B (-3,2)是其图象上的两点,则不等式|f(x+2)|>2的解集是( )A 、(-1,2)B 、(-∞,-1)∪(2,+∞)C 、(-∞,-5)∪(-2,+∞)D 、(-∞,-3)∪(0,+∞)8、某火车站在节日期间的某个时刻候车旅客达到高峰,此时旅客还在按一定的流量到达。
如果只打开3个检票口,需要30分钟才能使所有滞留旅客通过检票口。
如果打开6个检票口,只需要10分钟就能让所有滞留旅客通过。
2017年苍南县“姜立夫杯”高二数学竞赛

2017年苍南县“姜立夫杯”数学竞赛高二试卷考生注意事项:1本卷共有17道题目,全卷满分100分,考试时间120分钟.2答题前,务必在试题卷、答题卷的密封线内填写好自己的学校、姓名和准考证号. 3本卷所有试题都必须用蓝色或黑色签字笔在答题卷上书写,在试题卷上作答无效. 4本卷解答一律不准使用计算器.一、选择题(本大题共8小题,每小题4分,满分32分,每小题有且仅有一个正确的答案)1.已知集合{}13A x x x Z =-≤∈,,{}21B y y x x R ==-+∈,,则A B ⋂的非空真子集.....有( ) A .31个 B .30个 C .15个 D .14个2.设正项等比数列{}n a 的前n 项和为n S ,且()10302020102S S S S -=-,则数列{}n a 的公比为( ) A .18 B .14 C .12D .13.若函数2243()2log 3a x x x f x x x ⎧-+≤=⎨+>⎩,,,,(0a >且1a ≠)的值域为[)3+∞,,则实数a 的取值范围为( )A .(]13,B .(13),C .(3)+∞,D .[)3+∞,4.方程201625375112017x x x -+-+-=共有( )实根 A .0个 B .1个 C .2个 D .3个或3个以上5.如图,在三棱锥P ABC -中,PAB △,PBC △均为等边三角形,且AB BC ⊥。
则二面角A PC B --的余弦值为( ) A.3 B.3 C.3 D .136.若实数a b ,满足20101a b b a a +-≥⎧⎪--≤⎨⎪≤⎩,则22a b a b ++的最大值为( )A . 1B .54 C . 75D . 2 ABCP(第5题)7.已知正方体1111D C B A ABCD -的棱长为1,在对角线D A 1上取点M ,在1CD 上取点N ,使得线段MN 平行于对角面11A ACC ,则MN 的最小值为( )A B .1 C D .28.已知共面向量a ,b ,c 满足||3a =,=2b c a +且||||b b c =-.若对每一个确定的向量b ,记||b ta -(t ∈R)的最小值为min d ,则当b 变化时,min d 的最大值为( )A .43B .2C .4D .6二、填空题(本大题共6个小题,每小题6分,满分36分.)9.设()f x 是定义在R 上的函数,对任意实数x 有()()341f x f x +⋅-=-。
2009年苍南县姜立夫杯高中数学竞赛准考证编号规则概要
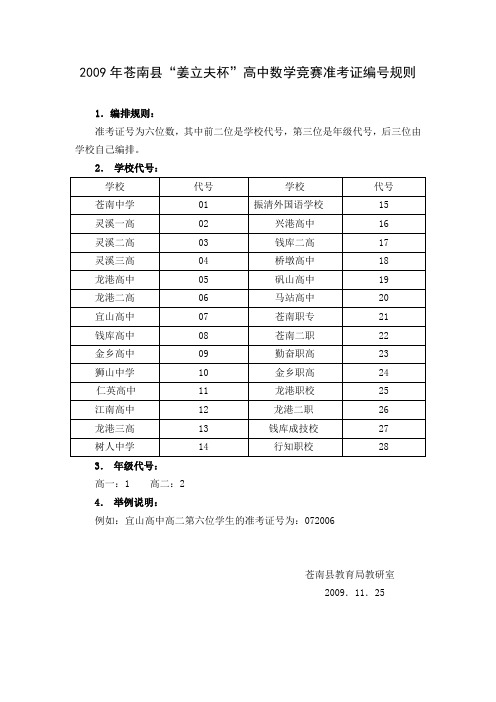
2009.11.25
19
龙港二高
06
马站高中
20
宜山高中
07
苍南职专
21
钱库高中
08
苍南二职
22
金乡高中
09
勤奋职高
23
狮山中学
10
金乡职高
24
仁英高中
11
龙港职校
25
江南高中
12
龙港二职
26
龙港三高
13
钱库成技校
27
树人:
高一:1高二:2
4.举例说明:
例如:宜山高中高二第六位学生的准考证号为:072006
2009年苍南县“姜立夫杯”高中数学竞赛准考证编号规则
1.编排规则:
准考证号为六位数,其中前二位是学校代号,第三位是年级代号,后三位由学校自己编排。
2.学校代号:
学校
代号
学校
代号
苍南中学
01
振清外国语学校
15
灵溪一高
02
兴港高中
16
灵溪二高
03
钱库二高
17
灵溪三高
04
桥墩高中
18
龙港高中
05
矾山高中
浙江省苍南县“姜立夫杯”2018年高二数学上学期竞赛试题

浙江省苍南县“姜立夫杯”2018年高二数学上学期竞赛试题考生注意事项:1本卷共有17道题目,全卷满分100分,考试时间120分钟.2答题前,务必在试题卷、答题卷的密封线内填写好自己的学校、姓名和准考证号. 3本卷所有试题都必须用蓝色或黑色签字笔在答题卷上书写,在试题卷上作答无效. 4本卷解答一律不准使用计算器.一、选择题(本大题共8小题,每小题4分,满分32分,每小题有且仅有一个正确的答案) 1.若集合{0}A x x =≥,且A B B ⋂=,则集合B 可能是( ) A.{}1,2 B.{1}x x ≤ C.{1,0,1}- D.R2.若对任意实数x 都有x x x f x f sin cos 3)(2)(-=-+,则函数()y f x =的图象的对称轴方程为( ) A .Z k k x ∈+=,4ππ B .Z k k x ∈-=,4ππ C . Z k k x ∈+=,8ππ D .Z k k x ∈-=,6ππ3.一个水平放置的一个的正三棱锥,其底面是边长为6的正三角形、侧棱长均为5, 其主视图,俯视图如图所示,则其侧视图( )A.形状是等腰三角形,面积为133B.形状是等腰三角形,面积为2393 C.不是等腰三角形,面积为 133 D.不是等腰三角形,面积为2393 4.已知在△ABC 中,∠ACB=,AB=2BC ,现将△ABC 绕BC 所在直线旋转到△PBC ,设二面角P﹣BC ﹣A 大小为θ,PB 与平面ABC 所成角为α,PC 与平面PAB 所成角为β,若0<θ<π,则α、sin β的范围分别是( ))33,0(],3,0(.πA ]33,0(],3,0(.πB)21,0(],3,0(.πC 1.(0,],(0,)62D π 5.202,()342x f x x x x ≤≤=+-函数的最大值是( )A. 5B. 6C.7D.86.已知点()1,1A --.若曲线T 上存在两点,B C ,使ABC ∆为正三角形,则称T 为“正三角形”曲线.给定下列三条曲线:①222x y +=;②()3003x y x +-=≤≤;③1(0)y x x=->. 其中,“正三角形”曲线的个数是( ) A . 0 B . 1 C . 2 D . 37.如图,圆C 分别与x 轴、y 轴正半轴相切于A 、B ,过劣弧AB 上一点T 作圆C 的切线,分别交x 轴、y 轴正半轴于M 、N 两点,若点Q (2,1)是 切线上一点,则∆MON 周长的最小值为( ) A . 8 B . 10 C . 12 D . 548.已知平面向量a ,b ,|a |=1,|b |=2, e r 为平面单位向量且|a ·e r |+|b r ·e r|的最大值为7,则下列结论成立的是( )A .|a +b r |=|a -b r | B.b r ·(a -b )=0 C. a ·(a -b )=0 D. min ,||3t R b ta ∈-=r r二、填空题(本大题共6个小题,每小题6分,满分36分.) 9. 在ABC △中,2a =,3b =,4c =,则sin 2sin AC= ▲ . 10. 设{}n a 的公比为q 的等比数列,其前n 项和为n S ,且32420192018,S S S =+ 则q = ▲11. 432(1)0[0,)x x x a x a x -+-++≥∈+∞对恒成立,则a= ▲12.2()3,|(())0}|()0},xf x x ax b x f f x x f x a b φ=++⋅===≠+函数若{{则取值范围是 ▲ 13.在三棱锥ABC P -中,BC AB ⊥,32,2,AB BC PA PB ===当三棱锥ABC P -体积取最大时,锐二面角P-AC-B 的大小=θθtan ,则 ▲ .14. 22224560,24x y x y xy x y x y x y +--++=+-+、是实数,则的取值范围是▲三、解答题(本大题共3小题,第15、16题各10分,第17题12分,满分32分.要求写出必要的解答过程)15.已知圆22-(2)40)2x a y a a y kx +-=>=+C:()(与直线交于M 、N 两点,其中C 为圆心,=2a (1)若, 125CM CN ⋅=-uuu r uuu r ,求k 的值;=1,k (2)若当CMN ∆面积取最大时,求a 的值.16. 已知函数()2f x x ax b =++.(1) 0a ≠且1b =,求()y f x =在区间0,a ⎡⎤⎣⎦上的最大值; (2) 若,a b Z ∈,且()a b f x +是的零点,求所有可能b 的值.17. 已知{a n }满足,++∈+==N n a a a a n n n ,144,812211 (1)证明:;811≤<+n n a a(2)证明:1211121119n n a a a +++>-+++L2018年苍南县“姜立夫杯”数学竞赛高二答题卷一、选择题(本大题共8小题,每小题4分,满分32分.每小题有且仅有一个正确的答案)二、填空题(本大题共6个小题,每小题6分,满分36分. 请将正确的答案填在横线上)9.________________ 10.________________ 11.________________ 12.________________ 13.________________ 14.________________三、解答题(本大题共3小题,第15、16题各10分,第17题12分,满分32分.要求写出必要的解答过程)15.已知圆22-(2)40)2x a y a a y kx +-=>=+C:()(与直线交于M 、N 两点, 其中C 为圆心,=2a (1)若, 125CM CN ⋅=-uuu r uuu r , 求k 的值;=1,k (2)若当CMN ∆面积取最大时,求a 的值.16. 已知函数()2f x x ax b =++.(1) 0a ≠且1b =,求()y f x =在区间0,a ⎡⎤⎣⎦上的最大值; (2) 若,a b Z ∈,且()a b f x +是的零点,求所有可能b 的值.17.已知{a n }满足,++∈+==N n a a a a n n n ,144,812211 (1)证明:;811≤<+n n a a (2)证明:9211111121->++++++n a a a n Λ2018年苍南县“姜立夫杯”数学竞赛高二试题参考答案一、 选择题(本大题共8小题,每小题4分,满分32分.每小题有且仅有一个正确的答案)二、填空题(本大题共6个小题,每小题6分,满分36分. 请将正确的答案填在横线上)9.8710. 12018 11.212.[0,4) 13.2 14. ]3,313[-- 三、解答题(本大题共3小题,第15、16题各10分,第17题12分,满分32分.要求写出必要的解答过程)15.已知圆22-(2)40)2x a y a a y kx +-=>=+C:()(与直线交于M 、N 两点 其中C 为圆心,=2a (1)若,125CM CN ⋅=-uuu r uuu r , 求k 的值; =1,k (2)若当CMN ∆面积取最大时,求a 的值.解析:(1)125CM CN⋅=-uuu r uuu r得3cos,5MCN∠=-……2分……2分1=22k=或……1分(其他方法酌情给分)(2)设圆心到直线的距离为d,S==……2分当CMN∆面积取最大时d (2)=4a=……1分(其他方法酌情给分)16. 已知函数()2f x x ax b=++.(1) 0a≠且1b=,求()y f x=在区间0,a⎡⎤⎣⎦上的最大值;(2) 若,a b Z∈,且()a b f x+是的零点,求所有可能b的值.解析:(1)当a>0时,()222max1[1,21],|()|21f x x ax a f x a=++∈+=+……2分当a<0时, ()222max4-4-1[,1],|()|max||,144a af x x ax f x⎧⎫=++∈=⎨⎬⎩⎭……2分=2441,0aa-≤-<⎧⎪⎨⎪⎩,a……1分(2)()()()20f a b a b a a b b+=++++=得22230a ab b b+++=……1分2=b-8b∆必为完全平方数……1分2222=b-8b=,()16m N m∆∈-=令m得(b-4){{{{42444-44-848444-44-2b m b m b m b mb m b m b m b m--=--=--=--=-+=-+=-+=-+=或或或所有可能b的值为9、8、-1、0 ……3分17. 已知{a n}满足,++∈+==Nnaaaannn,144,812211(1)证明:;811≤<+n n a a (2)证明:9211111121->++++++n a a a n Λ 解析:(1)0>n a 易得=-+n n a a 1014)12(141441442223222≤+--=+--=-+n n n n n n n n n a a a a a a a a a ……2分∴≤≤∴+,811n n a a 014)12(22<+--n n n a a a ;811≤<∴+n n a a ……2分 (用nnn n n n a a a a a a 14114421+=+=+同样给分) (2)284414422221+=+≤+=+nnn n n n n n a a a a a a a a ……2分 12211+=+≥+n n n n a a a a ,)11(2111+≥++nn a a 111292)11(11--⋅=⋅+≥+n n n a a ,1)21(911-⋅≤+n n n a a ……3分 =+11n a 1)21(91111-⋅-≥+-n n n a a ……2分 92])21()21(211[911111111221->+++-≥++++++-n n a a a n n ΛΛ…1分。
2007年浙江省苍南县“姜立夫杯”高一数学竞赛试题及答案

2007年苍南县“姜立夫杯”数学竞赛高一试卷考生注意事项:1.本卷共有17道题目,全卷满分100分,考试时间120分钟.2.答题前,务必在试题卷、答题卷的密封线内填写好自己的学校、姓名和准考证号. 3.本卷所有试题都必须用兰色或黑色签字笔在答题卷上书写,在试题卷上作答无效. 4.本卷解答一律不允许用计算器.一、选择题:(共8小题,每小题4分,共32分,每小题只有一个正确答案)1.函数()()211f x x R x=∈+的值域是 ( ) A.[0, 1] B.[0, 1)C .(0, 1] D.(0, 1)2.设集合S={x |2x -3|x |+2=0}, T={x | (a -4)x =4}, 则满足T ⊂ ≠S 的a 的值共有( ) A.5 B.4 C.3 D.23.函数()()44222x x x x f x --=+-+的最小值是 ( ) A.1 B.2 C.-3 D .-24.函数()y f x =的图象为C , 而C 关于直线2x =对称的图象为1C , 将1C 向左平移2个 单位后得到的图象为2C ,则2C 所对应的函数为 ( ) A.y =f (-x ) B .y =f (2-x ) C.y = f (4-x ) D.y =f (6-x ) 5.若函数()()()2log 201a f x x xa a =+>≠且在区间(0,21)内恒有()0f x >,则()f x 的单调递增区间为 ( ) A.(-∞, -41) B.(-41, +∞) C.(0, +∞) D.(-∞, -21)6.若()33sin cos cos sin 02θθθθθπ-≥-≤<, 则θ的取值范围是 ( )A.[0,4π] B.[4π,π] C .[4π,45π] D.[2π,23π)7.已知集合{}{}50,60,,A x x a B x x b a b N =-≤=-≥∈, 且{}2,3,4AB N =,则a b +的取值范围是 ( )A.{z ∈R |27≤z ≤36}B.{z ∈N |27≤z ≤36}C.{z ∈N |28≤z ≤35}D.{z ∈N |26≤z ≤37} 8.若()g x 是不恒等于零的偶函数, 函数()()21221x f x g x ⎛⎫=+⋅+ ⎪-⎝⎭在()0,+∞上有最大值5,则()f x 在(),0-∞上有 ( ) A.最小值-1 B.最小值-5 C.最小值-3 D.最大值-3二、填空题(共6小题,每小题6分, 共36分)9.函数f (x )=2|1|432-+-+x x x 的定义域为____________________.10.已知函数()f x =⎩⎨⎧≤<+-<≤---20 ,202 ,2x x x x , 则()f x -()f x ->-2的解集为_____________.11.函数2log y x =与函数3cos y x =的图象的交点个数共有 .12.已知函数()224f x x x =--, 若()0f x a -<在R 上恒成立, 实数a 的取值范围为.13.若2351xyz==>, 则2,3,5x y z 从小到大的排列顺序是____________.14.实数(),,a b c a b ≠满足())()30a b c b c a --+-=, 则2)())((b a a c c b ---=_______.三、解答题(第15题8分, 第16, 17题各12分, 共32分)15.设函数()226f x x ax a =-++的值域为集合B .(1)若[)0,B =+∞, 求实数a 的所有取值的集合A ;(2)若[)0,B ⊆+∞,求实数a 所有取值的集合D ,并求函数()()42g a a a a D =-+∈的值域.16.设()()2,,f x ax bx c a b c =++为实常数, ()01f =,()()(),0,0f x xg x f x x <⎧⎪=⎨->⎪⎩.(1)若()20f -=, 且对任意实数x 均有()0f x ≥成立, 求()g x 的表达式;(2)在(1)的条件下, 若()()h x f x kx =+不是[-2, 2]上的单调函数, 求实数k 的取值范围; (3)设0,0,0a m n >><且0m n +>, 当()f x 为偶函数时, 求证: ()()0g m g n +<.17.设函数()2243,f x ax x a a =+--是实常数, 如果函数()y f x =在区间(-1, 1)上有零点, 求实数a 的取值范围.2007年苍南县“姜立夫杯”数学竞赛高一答题卷一、选择题:(共8小题,每小题4分,共32分,每小题只有一个正确答案)二、填空题(共6小题,每小题6分, 共36分)9. (-∞,-4]∪(1,+∞) 10. [-2, -1)∪(0, 2] 11. 3 12. a >4 13. 3y , 2x , 5z 14. 3-三、解答题(第15题8分, 第16, 17题各12分, 共32分)15.设函数()226f x x ax a =-++的值域为集合B . (1)若[)0,B =+∞, 求实数a 的所有取值的集合A ;(2)若[)0,B ⊆+∞,求实数a 所有取值的集合D ,并求函数()()42g a a a a D =-+∈的值域. 15.解: f (x )=(x -a )2+a +6-a 2(1)∵B =[0, +∞), 故f (x )min =0, 即a +6-a 2=0 即a 2-a -6=0 解得a =3或-2, ∴A ={3, -2}(2)∵B ⊆[0, +∞), 故f (x )min ≥0, 即a +6-a 2≥0 即a 2-a -6≤0 解得 -2≤a ≤3, ∴ D =[-2, 3]故g (a )= -a 2-2a +4=5 -(a +1)2, a ∈[-2, 3],∴当a = -1时, g (a )有最大值为5, 当a =3时, g (a )有最小值-11 因此, g (x )的值域为[-11, 5]16.设()()2,,f x ax bx c a b c =++为实常数, ()01f =,()()(),0,0f x xg x f x x <⎧⎪=⎨->⎪⎩.(1)若()20f -=, 且对任意实数x 均有()0f x ≥成立, 求()g x 的表达式;(2)在(1)的条件下, 若()()h x f x kx =+不是[-2, 2]上的单调函数, 求实数k 的取值范围; (3)设0,0,0a m n >><且0m n +>, 当()f x 为偶函数时, 求证: ()()0g m g n +<. 16.解:由f (0)=1得c =1(1)由f (-2)=0得4a -2b +1=0, 又由f (x )≥0对x ∈R 恒成立, 知a >0且△=b 2-4a c ≤0即b 2-2b +1=(b -1)2≤0 ∴b =1, a =41从而f (x )=41x 2+x +1∴g (x )=⎪⎪⎩⎪⎪⎨⎧>---<++0,1410,14122x x x x x x(2)由(1)知h (x )=41x 2+(k +1) x +1, 其图象的对称轴为x = -2(k +1) ,再由h (x )在 [-2, 2]上不是单调函数, 故得-2<-2(k +1)<2 解得-2<k <0(3)当f (x )为偶函数时, f (-x )=f (x ), ∴b =0, ∴f (x )=ax 2+1, a >0 故f (x )在(0, +∞)上为增函数, 从而, g (x )在(0, +∞)上为减函数, 又m >0, n <0, m +n >0 ∴ m >-n >0, 从而g (m )<g (-n )且g (-n )= -f (-n )= -f (n )= - g (n ) 故得g (m )< -g (n ), 因此, g (m )+g (n )<0 17.设函数()2243,f x ax x a a =+--是实常数, 如果函数()y f x =在区间(-1, 1)上有零点, 求a 的取值范围.17.解:当a =0时, 则f (x )=4x -3, 此时f (x )的零点为43∈(-1, 1), 故a =0满足题设. 当a ≠0时, 令△=16+8a (3+a )=0, 即a 2+3a +2=0 解得a = -1或-2(1)当a = -1时, 此时f (x )= -2x 2+4x -2= -2(x -1)2, 它有一个零点-1∉(-1, 1) 当a = -2时, 此时f (x )= -4x 2+4x -1= -4(x -21)2, 它有一个零点21∈( -1, 1), 故 a = -2满足题设(2)当f (-1)f (1)= (a -7)( a +1)<0即 -1<a <7时, f (x )有唯一一个零点在(-1, 1)内(3)当f (x )在(-1, 1)上有两个零点时, 则⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧<-<->>->++=∆>1110)1(0)1(0)23(802a f f a a a 或⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧<-<-<<->++=∆<1110)1(0)1(0)23(802a f f a a a解得a >7或a <-2综上所述, a 的取值范围是a ≤-2或-1<a <7或a >7。
2007年全国高中数学联赛及山东省数学竞赛

2007年全国高中数学联赛及山东省数学竞赛济南赛区通报2007年全国高中数学联赛预赛和决赛已分别于2007年9月16日上午和2007年10月14日上午分别进行.我市有11081人参加了预赛,有227人参加了决赛.在此次竞赛中,我市选手取得了十分优异成绩,获全国一等奖人数和全国一、二、三等奖人数均列全省各参赛单位前列,其中全省获全国一等奖的43人中就有我市的15人,达到全省的近30%.有4人进入全国冬令营,达到最高水平,现将此次竞赛的情况通报如下:一、全国奖(共63人)1.全国一等奖共15人韦东奕(240分,山师附中) 王颖婓(206分,实验中学)安传恺(201分,山师附中)王储(190分,实验中学) 刘青阳 (177分, 山师附中) 鲁悦(172分,山师附中)冯龙(152分,实验中学) 禹泽西(150分, 实验中学) 方延博(150分,实验中学)路若洲(143分,实验中学) 刘宁(141分, 实验中学) 高茉人(130分,实验中学)楚天翔(124分,实验中学) 孙晨正(123分, 山师附中) 姜晖(122分,山师附中)2.全国二等奖共 27人梅潇(119分, 实验中学) 隋春宁(117分,山师附中)贺兆印(116分,历城一中)丁寰宇(114分,实验中学)刘光强(110分,山师附中)王哲(110分,实验中学)王振中(105分,山师附中) 徐硕(105分,实验中学)申晓斌(104分,实验中学)丛亚(103分,实验中学)李凤麟 (103分,山师附中) 曲焜 (101分, 实验中学)宋超逸(101分, 实验中学) 窦欣元(101分, 实验中学) 韩谡越( 99分,章丘四中)牟象禹(97分,山师附中)胡颖凯(96分,山师附中)马万里 ( 94分, 实验中学)王飞(94分,山师附中)孔陆洋(94分,山师附中)孟庆迪 ( 93分, 实验中学)丁晋(93分,实验中学)翟晓辉(138分,山师附中)张赛峥(92分,实验中学)顾然(92分,山师附中)刘筱宁(92分,外语学校)杨晓婉(92分,实验中学)3.全国三等奖共 21人孙振宇(91分,实验中学)陈邦锐(91分,实验中学)王越(91分,实验中学)李鑫业(89分,山师附中)秦立煜(88分,实验中学)刘毅(87分,实验中学)岑昊(86分,山师附中)栾义龙 (86分, 实验中学) 石敬玉(86分,章丘四中)张天宇(86分,实验中学)姜怡然(86分,山师附中)吕林超(85分,实验中学)陈诚(85分,济南中学)孙染(84分,实验中学)王元(84分,实验中学)张棋(84分,山师附中)郝克(83分,外语学校)黄杨(83分,山师附中)王雨(82分,外语学校)王梁(82分,实验中学)杨云钊(81分,山师附中)二、此次竞赛的预赛也是山东省数学竞赛,根据竞赛成绩,学生获奖情况如下:(注:根据济南市数学竞委会规定,获全国二等奖以上不在给予省级奖励)1.省一等奖共158人(排名不分先后)实验中学(6人):夏靓116分王晓熙113分王冬雨111分刘毅110分钟睿106分梁健102分,山师附中(9人):董跃振111分刘苏方108分李鑫业102分曲士眹 99分黄杨 96分韩蕾 94分刘海 93分罗荣钧 90分姜怡然90分济南一中(1 人):陈双 94分济南二中( 5人):宫庆凯 76分于昌灏 70分郭晓宁 64分姜玉玺 63分李祺龙58分济南三中( 6人):蒋丽 84分孙新利 71分张虎 67分卫成林 66分商和宁 66分张婷婷 66分济南七中(2人): 肖玉淼 49分陈晨 45分济南九中(2人):鞠佳 69分王紫辉 66分济十一中(2人):李中华 70分王春喜 63分济南52中(1人):赵芳亮 57分济南中学(13人):王瑞 90分邹世俊83分外语学校( 2人):杨金龙100分郝克 98分英才高中( 6人):孟宇 73分张译文 56分王路 54分高建辉50分陈徭 50分济钢中学( 7人):李泳江 90分陈琛 88分李霖 85分刘一畅 83分刘梦晨 82分马长琳 81分秦汉唐 79分三职高中(4人):王阿冉53分李强51分徐桂亮 49分王珂 49分历城区(14人):历城一中:曹芳106分贺兆印97分胡春晖93分王超 90分陈磊 90分历城二中:李双江102分高昊鸥99分张广乐96分刘红霞95分李延龙 93分历城四中:蔡荣峰 94分刘振83分历城五中:马业兴84分洪楼高中:张金花98分章丘市(32人):章丘一中:赵蕾蕾87分徐帅 81分刘波80分章丘四中:李喆 140分马宪进104分王增辉97分陈成成96分朱福兴 94分索金召 93分党灿93分柏杨93分许昊93分章丘五中:郭乐田104分田春钊108分李虎100分刘杰100分张方瑞96分韩成龙 90分靳丰晨 89分刘洋槐84分王海景 83分郭红 80分郑伟 80分鲁家刚80分章丘七中:高兵孟娜袭苗苗姜树浩章丘中学:王俊荣99分宁纪森95分宋涛93分甄爱香93分平阴县( 8人):张文选119分刘聪102分许昌斌98分孙朝阳96分张明达96分张子键 93分路文高 93分马世杰81分,长清区(16人):李娇102分安玮100分孟强97分钟涵94分朱有云93分焦裕龙 88分段学苇87分张越86分赵鹏85分朱存良85分段益雪100分张毓胜98分兰英新87分齐本明87分田德洲83分杨洪伟83分商河县( 4人):王光龙87分于和善86分李良金85分周祥政83分济阳县(18人):王钊114分盛华英110分郭富明101分周亚凡 99分胥燕燕 95分菅秀峰 95分冯涛 93分李超119分齐震112分卢乾坤101分李国栋100分韩涛104分闫宁101分李晓阳106分菅庆圣102分崔月 98分霍纯森 96分华震 96分2.省二等奖共202人实验中学(13人):祁海洋100分秦立煜101分李骥100分韩祥冬100分李文硕98分王越 98分栾义龙 98分李可扬96分孙棋 96分孙振宇96分叶梦醒 96分邹宗航 96分栗榛96分山师附中(13人):杜宏 87分宋建浩 87分张志浩 86分付强 85分曹旭 85分赵玉祯 84分杨云钊 82分宋晓楠 81分刘青华 79分王聪 79分李丹蕾 78分陈飞 78分刘雯 78分济南二中(9人):韩长龙 57分李丽丽 57分李征 56分丘化凯 55分姚运华 55分吕诚哲 54分杨霖 54分崔然旭 54分孙波 54分济南三中(4人):孙志超 64分朱婷婷 60分王振坤 60分龙玉梅60分济南七中( 3人):胡勇超 44分崔燕 43分孙彬 43分济南九中( 3人):周淑灿 60分隋宏远 60分马宝强60分济十一中( 2人):唐智55分宋怀杰 54分济52中( 2人):王淑芬 53分朱婷婷53分济南中学( 3人):杨晓煜 82分吴凌雪81 分王芯 81分外语学校( 5人):万伟 90分宋瑞雪 89分袁心 88分罗丁 85分张庆辰 85分济钢高中( 9人):冯博宇 78分赵晓丹 78分朱鑫鹏 77分潘红 76分金岩76分王智飞 75分周婷婷75分李璐 75分宿波75分英才高中( 8人):韩晓松 48分肖剑辉 48分赵院 48分张天佑 48分薛桐 48分李晓 47分李晓明 44分苏志勇 44分三职高中( 4人):赵殿龙 48分毛文靓 45分季淑玉 45分王梅梅44分历城区(17人):历城一中:金增奇89分陈荣荣89分柴柏晓87分杨小龙85分张强84分历城二中:颜庆87分杜文帅85分翟凤婷85分靳若安85分杨登平85分历城四中:孙光军64分李明64分钱宇63分历城五中:王兴英78分苏志南78分洪楼高中:赵志勇88分王金振78分章丘市(41人):章丘一中:孙月红77分蒋全芝75分刘乃龙72分张永亮71分张强70分刘凤翔70分章丘四中:石敬玉92分张学超92分蔡云云92分陈龙桥92分李娜 88分李臣88分陈光鹏88分刘敏87分徐家昌86分董彤阳85分孙广帅85分高云逸85分章丘五中:冯业飞79分张瑞谦79分黄立臣78分胡继伟78分徐昭萌78分孙盟 78分于巍巍78分柳庆娓78分吴鹏77分韩福芸77分范士凯 76分韩春超76分刘延清76分章丘七中:程宗越孟超高玲刘娇龙杨兵贾超章丘中学:张硕90分董晓越90分曹林丽87分侯东明86分巩敏86分李鹏86分平阴县(8人):乔珂欣91分王文华90分沙宗国90分张德水88分陈涛87分刘德福86分苏本民80分杜言铭75分长清区(26人):王帅84分杜杰84分李君朋83分王华83分于晓菲82分卢婧82分王岩81分戴伟81分宋丙亮81分庄卫卫81分马晓81分杨仁俊80分韩传刚80分李珊80分邢庆涛80分孟维昌81分周恒80分王斌80分李修源78分孙传海78分段好新77分赵婷婷77分贾丹78分王倩74分蒋艳66分范升涛66分商河县(5人):展长伟81分卢培义81分王伟81分孙发鲁79分张旭78分济阳县(27人):罗宾甲 90分牛法富 90分牛佳瑞 90分裴建梁 89分张刚峰 89分李道通 87分艾杰 87分陈新斌 86分孙云飞 86分刘文静 95分王莉 93分刘超 93分杨骁 93分温明强 92分张元炜 91分李振 90分王彬 90分张蕊88分徐春花 88分李凯 88分吴鹏 87分张龙87分秦婷婷 87分张勇87分刘贵奇87分张滨 87分徐囡 87分3.省三等奖218人实验中学(5人):孙染 95分王梁 95分李翔宇 94分陈邦锐 94分陈茜茜94分山师附中(13人):杨晓星 76分翟毅 76分冯君淑 77分袁源 76分夏冰 75分孙晴川 75分张河慧 75分王睿 75分崔赛飞 75分陈琛 74分王尧 74分王迪 74分赵越 74分济南一中( 1人):李晨光 78分济南二中(5人):陶然 51分赵元圆 50分孙吉隆 50分王越50分陈安 50分济南三中( 6人):崔丙伟 59分王官玲 57分李璐 57分刘海洋 57分商广义 57分杨润蕊56 分济南七中( 2人):胡尊飞 42分成龙 42分济南九中( 5人):史良 58分王明 58分刘讳58分刘帅帅 57分贾杰 57分济十一中(3人):董丽君 51分牛邦龙 51分徐永龙 49分济南中学(2人):陈栋 80分张望80分外语学校(5人):于东宁 81分欧阳82分李千81分黄一成 81分郦龙 81分钢厂高中(13人):彭高飞 74分赵冲 74分李辉73分耿浩 72分杨紫娇 71分李延文 71分张楠 72分柴宝臣 72分郭琦 72分林尧 72分刘爽 73分蒋薇 71分徐涛 70分英才高中( 9人):王华琳 42分金传铭 42分李超42分陈娜 42分李佳倩42分张鹏 42分王翰林 42分段晨彤42分玉叶 41分三职高中(5人):付磊 43分于鸿 43分王硕 42分叶鑫42分宋晓艳 42分历城区(20人):历城一中:王俊国83分刘丹82分张凤82分陈哲81分马超81分历城二中:张良82分韩豹81分杜磊81分李洪燕81分侯程广81分,李敏81分王曰儒81分历城四中:周晓琼59分彭延杰59分韩娟59分历城五中:陈世军76分赵成75分范圣男75分洪楼高中:刘玉娟70分卢长瑞68分章丘市(47人):章丘一中:韩超69分张帅69分孙秀婷69分郭盼69分丁帅69分李豪杰69分宁建69分章丘四中:董道江84分李广84分马永岩84分鹿苗苗84分陈慧颖84分赵春雷84分程彬84分卢国华84分张晓彤84分韩继雷84分韩慧梅83分宁超众83分吕素华82章丘五中:王福荣75分牛凯峰75分韩强75分吕晓萌75分王沛阳75分孙方杰75分李中雨75分宋梅玲75分杨志敏75分李杰74分张运涛74分黄文娟74分郑兴花74分闫广霞74分冯业芝74分章丘七中:赵静刘群陈样高娟柏文王瑶章丘中学:党义鹏85分彭绍辉85分赵静84分郭嘉宾81分李跃81分刘元康80分平阴县(13人):杨其资84分李霞84分丁姗姗84分李浩84分白哲84分刘兵83分高璇82分陈阳82分王蒙82分刘涛82分吴庆存82分王超82分王龙江72分长清区(28人):于海龙78分苏军78分张晓旭78分刘天燕78分庄庆鹏78分田娜78分邵继美78分刘文雪78分李柱杰77分王佳77分韩聪77分李照垒76分张伟76分张其昌76分孔令燕76分杨崭76分薛德宝74分王东东74分李婷婷74分刘东73分孟凡荣73分赵双73分李善刚73分韩胜涛73分王元腾69分柴茂青72分张双双63分赵玉芹63分商河县(6人):金冉78分芮法莹77分车召堂75分赵富燕75分赵华安75分徐超74分济阳县(30人):王闯 85分高迪 85分呼燕 85分周讯 85分李三九 84分徐小青 84分孙志凌 84分李方吉 84分杜学知 84分王浩 84分刘志远 84分刘喆 84分袁新超 84分姚麒麟86分高帅 86分张强 86分杨吉伟 86分高扬 86分张震 84分高翠萍 85分王忠华 84分张传凯 84分朱学亮84分高荣祥 84分张红梅84分江继宽 84分李连玉84分陈国良84分常超 84分刘非84分注: 1.获山东省一、二、三等奖的学生如获全国奖的奖次高于或等于省奖,则不再发省奖。
2007年苍南县“姜立夫杯”数学竞赛高一试卷(浙江省)

2007年苍南县“姜立夫杯”数学竞赛高一试卷(浙江省)D(A )-5 (B )-3 (C )3(D )随a,b,c 而变4、若函数f(x)=a 2sin2x +(a -2)cos2x 的图象关于直线x =-π对称,则a 的值等于5 (D )226、已知在数列{a n }满足,a 1=2+3,a n +2(1-a n )=1+a n ,则a 2005的值为 ( )(A)2+ 3 (B)2- 3 (C)3-2 (D)-2- 3二、填空题(每小题9分,共54分)+和,则Sf(x)最小值是.12、已知正整数n不超过2005, 并且能表示成不少于60个连续正整数之和,那么,这样的正整数n有个.三、解答题(每小题20分,共60分)13、已知函数y=sinx+asin2xcosx..(1)当sinx=1时,求y的值;(2分)(2)若函数的最大值为1,求实数a的取值范围. (18分)14、n2(n≥4)个正数排成n行n列a11a12a13 (1)a21a22a23 (2)a31a32a33 (3)a24=nn.15、某公司离火车站40千米,有12名该公司的职员出差,须从公司出发赶到火车站,他们步行的速度为4千米/时,当时公司仅有一辆同时可送4人的轿车,其速度为52千米/时. 要求在3小时内将12名职员送到车站,还希望轿车第一批送的职员能尽早地到车站买票. 试问第一批职员最早能比3小时提前多少时间赶到车站.江苏省苏州实验中学2005年暑期竞赛数学情况调查测试卷(参考答案)1、 B 原函数即为y =2+2(x -1)+1x 3、C 容易判断f(x)+f(-x)=8,且lglog 310= lg lg10lg3 = -lg lg3lg10= -lglg3,故有f(lglog 310)+ f(lglg3)=8,从而f(lglg3)=3. 选C4、C 函数f(x)=a 2sin2x +(a -2)cos2x 的图象关于直线x = -π8对称,则f(-π8)应取得函数的最大值或最小值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2007苍南县“姜立夫”杯数学竞赛高二试卷2007年苍南县“姜立夫杯”数学竞赛高二试卷考生注意事项:1.本卷共有17道题目,全卷满分100分,考试时间120分钟.2.答题前,务必在试题卷、答题卷的密封线内填写好自己的学校、姓名和准考证号. 3.本卷所有试题都必须用兰色或黑色签字笔在答题卷上书写,在试题卷上作答无效. 4.本卷解答一律不允许用计算器.一、选择题:(共8小题,每小题4分,共32分,每小题只有一个正确答案)1.已知数列{}na 的前n 项和28nSn n=-, 若4<ka <7,则k = ( ) A.9 B.8 C.7D.62.设集合S={x |x 2-5|x |+6=0}, T={x |(a -2)x =2}, 则满足T ⊂ ≠S 的a 的值共有 ( ) A.5 B.4 C.3D.2 3.已知,,a b c为三条不同的直线, 且,,a M b N MN c ⊂⊂=平面平面(1)若a 与b 是异面直线, 则c 至少与a , b 中的一条相交;(2)若a //b , 则必有a //c ;(3)若a 不垂直于c , 则a 与b 一定不垂直; (4)若a ⊥b , a ⊥c , 则必有M N ⊥. 其中正确的命题的个数是( ) A.3 B.2 C.1D.04.为使关于实数x 的不等式()2121x x aa a R -+-≤-+∈的解集是空集, 则实数a 的 取值范围是( )A. a >1B. -1<a <0C.0<a <1D. 1<a <25.在△ABC 中, 如果2228a b c +=, 则(BA tan 1tan 1+) tan C 的值等于 ( )A.72B.71C.92D.91 6.若点A(1,3)关于直线y kx =的对称点落在x 轴上, 则k = ( )A.33B.22C.33或-3D.22或-27.已知x , y 满足⎪⎩⎪⎨⎧≤≥+≥+-3006x y x y x , 若z ax y =+的最大值为39a +, 最小值为33a -, 则a 的取值范围是( )A.a ≤-1或a ≥1B.0≤a ≤1C.-1≤a ≤0D.-1≤a ≤18.若()()()sin 232f x x x θθ=++为奇函数, 且在[0,4π]为增函数, 则θ的一个值为( )A.32πB. -3πC.65πD. -6π二、填空题(共6小题,每小题6分, 共36分)9.设向量OA 绕点O 逆时针旋转2π, 得向量OB , 且2OA +OB =(8, 9), 则向量OB =_____.10.从3名男生和n 名女生中, 任选3人参加比赛, 已知3人中至少有1名女生的概率为3534, 则n =______.11.若sin 2(x +125π)-sin 2(x -125π)= -43, 且x ∈(43π,π), 则tan x =_______.12.设na 是(3 +x )n的展开式中x 项的系数(n =2, 3,4,… ), 则当n >100时, 223a +333a +…+nn a 3的整数部分的值为 .13.若集合A 中的每个元素都可表为1, 2, 3,…,8中两个不同的数之积, 则集合A 中元素个数的最大值为______14.定义: 区间[](),c d c d <的长度为d c -. 已知函数3log y x=的定义域为[],a b , 值域为[]0,2,则区间[],a b 长度的最大值与最小值的差等于________.2007年苍南县“姜立夫杯”数学竞赛高二答题卷一、选择题:(共8小题,每小题4分,共32分,每小题只有一个正确答案)题号 1 2 3 4 5 6 7 8答案二、填空题(共6小题,每小题6分, 共36分)9. 10.11. 12.13. 14.三、解答题(第15题8分, 第16, 17题各12分, 共32分)15.设a为实数, 且函数()2=-+-的最2111f x a x x x小值为()g a.(1)设11=+-, 求t的取值范围, 并把()t x xf x表示为t的函数()m t.(2)求1()g的值.816.直线l 过点(1,1), 交x 轴, y 轴的正半轴分别于A , B , 过A , B 作直线330x y ++=的垂线, 垂足分别为C , D .(1)当AB //CD 时, 求CD 中点M 的坐标; (2)当|CD |最小时, 求直线l 的方程.17.设函数()f x 的定义域为R, 当x <0时, ()f x >1, 且对于任意的实数,x y R ∈, 有()()()f x y f x f y +=⋅成立. 又数列{}na 满足()10a f =, 且()()*11(2)n nf a n N f a +=∈--(1)求证: ()f x 是R 上的减函数; (2)求2007a 的值;(3)若不等式)11()11)(11(21na a a +++ ≥k ·12+n 对一切*n N ∈均成立, 求k 的最大值.2007年苍南县“姜立夫杯”数学竞赛高二答题卷一、选择题:(共8小题,每小题4分,共32分,每小题只有一个正确答案) 题号 1 2 3 4 5 6 7 8 答案CABCACDB二、填空题(共6小题,每小题6分, 共36分)9. (-2,5) 10. 4 11.312.17 13. 24 14.8三、解答题(第15题8分, 第16, 17题各12分, 共32分)15.设a 为实数, 且函数()22111f x a x x x =-+-的最小值为()g a .(1)设11t x x =+-, 求t 的取值范围, 并把()f x 表示为t 的函数()m t . (2)求1()8g 的值. 15.解:(1)∵xx t -++=11, ∴要使t 有意义, 必须⎩⎨⎧≥-≥+0101x x , 解得-1≤x ≤1∵]4,2[12222∈-+=x t, 且t ≥0 ∴t 的取值范围是]2,2[又121122-=-t x, ∴t ta t m --=)121(2)(2at at 22--=, ]2,2[∈t(2)由题意知g (81)即为函数m (t )41812--=t t=49)4(812--x , ]2,2[∈t 的最小值.此时, m (t )在[2,2]上是减函数, 故得g (81)=m (2)= -4716.直线l 过点(1,1), 交x 轴, y 轴的正半轴分别于A , B , 过A , B 作直线330x y ++=的垂线, 垂足分别为C , D .(1)当AB //CD 时, 求CD 中点M 的坐标; (2)当|CD |最小时, 求直线l 的方程. 16.解: 依题意, 设A (a , 0), B (0, b ), a >0, b>0, 则直线AB 的方程为1=+bya x ∵点(1, 1)在AB 上, ∴111=+ba ① (1)当AB //CD 时, 则可得k AB = -3, 即-3-=ab ∴b =3a 结合①解得a =34, b =4 设AB 的中点为N , 则N (31, 2). 又∵AC , BD ⊥垂直于CD , M 是CD 的中点∴MN ⊥CD ,从而直线MN 的方程为y =31(x -32)+2与方程3x +y +3=0联立, 可解得M (1013,3043-) (2)∵AC , BD ⊥垂直于直线y = -3x -3, ∴直线AC 的方程为y =31(x -a ), 即x -3y -a =0, 且点B 到直线AC 的距离就等于|CD |, 故得|CD |=10331|3|2b a a b +=+--(b a 11+)=)34(101b a a b ++≥)324(101+ 等号成立当且仅当⎪⎩⎪⎨⎧=+=1113ba b a 即⎪⎩⎪⎨⎧+=+=33131b a 因此, 所求的直线l 的方程为x +3y -3-1=017.设函数()f x 的定义域为R, 当x <0时, ()f x >1, 且对于任意的实数,x y R ∈, 有()()()f x y f x f y +=⋅成立. 又数列{}na 满足()10a f =, 且()()*11(2)n nf a n N f a +=∈-- (1)求证: ()f x 是R 上的减函数; (2)求2007a 的值;(3)若不等式)11()11)(11(21na a a +++ ≥k ·12+n 对一切*n N ∈均成立, 求k 的最大值.17.解(1)由题设, 令x = -1, y =0, 可得f (-1)=f (-1)f (0), ∴ f (0)=1. 故a 1=f (0)=1 当x >0时, -x <0, ∴ f (-x )>1, 且 1=f (0)=f (x )f (-x ), 故得 0<f (x )<1 从而可得f (x )>0, x ∈R设x 1, x 2∈R, 且x 1<x 2, 则x 2-x 1>0, 故f (x 2-x 1)<1, f (x 1)>0 从而f (x 1) -f (x 2)=f (x 1) -f (x 1+x 2-x 1)=f (x 1) -f (x 1)f (x 2-x 1)=f (x 1)[1-f (x 2-x 1)]>0即f (x 1)>f (x 2), ∴函数f (x )在R 上是减函数.(2)由f (a n +1)=)2(1na f --, 得f (a n +1)f ( -2-a n )=1,即f (a n +1-a n -2)=f (0)由f (x )的单调性, 故a n +1-a n -2=0 即a n +1-a n =2 (n ∈N *) 因此, {a n }是首项是1, 公差为2的等差数列, 从而a n =2n -1, ∴ a 2007=4013(3)设g (n )=12)11()11)(11(21++++n a a a n, 则g (n )>0, 且k ≤g (n )对n ∈N *恒成立.由1)1(4)1(23212)11()()1(21-++=+++=++n n n n a n g n g n >1, 即g (n +1)>g (n ),∴ g (n )在N *上为单调递增函数, 故g (n )≥g (1)=323 因此, k ≤323, 即k 的最大值为323。
