南充市高 2021 届第一次高考适应性考试理科数学试题
四川省南充市2024届高三高考适应性考试(一诊)考试数学(理)试题(含答案)

注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其他答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将答题卡交回。
一、单项选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的四川省南充市高2024届高考适应性考试(一诊)理科数学。
1.抛物线24x y =的准线方程为()A .1x =-B .1x =C .1y =-D .1y =2.当12m <<时,复数1(2)m m i -+-在复平面内对应的点位于()A .第一象限B .第二象限C .第三象限D .第四象限3.已知正方形ABCD 的边长为1,则AB BC CA +-=()A .0BC.D .44.已知直线m ,n 和平面α,n α⊂,m α⊂/,则“m n ∥”是“m α∥”的()条件A .充分不必要B .必要不充分C .充分必要D .既不充分也不必要5.已知全集U R =,集合{}3log (1)1A x x =->,2214x B x y ⎧⎫=+=⎨⎬⎩⎭,则能表示A ,B ,U 关系的图是()A .B.C.D .6.某商品的地区经销商对2023年1月到5月该商品的销售情况进行了调查,得到如下统计表.发现销售量y (万件)与时间x (月)成线性相关,根据表中数据,利用最小二乘法求得y 与x 的回归直线方程为:0.480.56y x =+.则下列说法错误的是()时间x (月)12345销售量y (万件)11.62.0a3A .由回归方程可知2024年1月份该地区的销售量为6.8万件B .表中数据的样本中心点为()3,2.0C . 2.4a =D .由表中数据可知,y 和x 成正相关7.二项式62x ⎫-⎪⎭的展开式中常数项为()A .60-B .60C .210D .210-8.已知:123a +=,3123b -=,则下列说法中错误的是()A .2a b +=B .312b <<C .1b a -<D .1ab >9.如图,正方体1111ABCD A B C D -的棱长为2,E ,F 分别为BC ,1CC 的中点,则平面AEF 截正方体所得的截面面积为()A .32B .92C .9D .1810.如图1是函数()cos 2f x x π⎛⎫= ⎪⎝⎭的部分图象,经过适当的平移和伸缩变换后,得到图2中()g x 的部分图象,则()图1图2A .1()22g x f x ⎛⎫=-⎪⎝⎭B .202332g ⎛⎫=-⎪⎝⎭C .方程14()log g x x =有4个不相等的实数解D .1()2g x >的解集为152,266k k ⎛⎫++ ⎪⎝⎭,k Z ∈11.已知双曲线2213y x -=的左右焦点分别为1F ,2F ,左右顶点分别为1A ,2A ,P 为双曲线在第一象限上的一点,若211cos 4PF F ∠=,则12PA PA ⋅= ()A .2-B .2C .5D .5-12.已知函数2()ln 2f x x m x=-+-(03m <<)有两个不同的零点1x ,2x (12x x <),下列关于1x ,2x 的说法正确的有()个①221m x e x <②122x m >+③3233m e x m<<-④121x x >A .1B .2C .3D .4二、填空题:本题共4小题,每小题5分,共20分。
四川省南充市高第一次高考适应性考试试卷

20XX年中学测试中学试题试卷科目:年级:考点:监考老师:日期:2021届四川省南充市高第一次高考适应性考试试卷第Ⅰ卷(选择题共30分)一、(12分,每小题3分)1.下列词语中,加点字的读音全部正确的一组是A.庇.护(pì) 欢谑.(xuè) 称.心如意(chēng) 鳞次栉.(zhì)比B.剽.窃(piáo) 坍圮.(pǐ) 锲.而不舍(qì) 悄.(qiǎo)然无声C.信笺.(qiān) 盘桓.(huán) 量.体裁衣(liáng) 饮鸩.(zhèn)止渴D.框.(kuàng)架勾.当(gòu) 杀一儆.(jǐng)百长歌当.(dàng)哭2.下列词语中没有错别字的一组是A.贸然吊胃口愤世疾俗凭心而论B.亲睐敲竹杠唇枪舌箭震古烁今C.讫今过干瘾误八歧途风烛残年D.洽谈打圆场卑躬屈膝激浊扬清3.下列各句中,加点的成语使用不恰当的一句是A.近年来,中东的局部战争接连不断,造成大量难民毁家纾难....,流离失所,这一现象已引起国际社会的极大关注。
B.读者读了欧·亨利的(麦琪的礼物)后,总会觉得一股人生的苦味猛地涌上心头,使人对那对相濡以沫....的夫妻充满了同情。
C.随着城市犬患的日益突出,市民反对养犬的呼声与日俱增....,治理犬患已刻不容缓。
D.在传统教育中,不唯书,不唯上,大胆怀疑等思想和行为往往被视为出格,但在创造性教育中必须开禁,否则创造性教育就是叶公好龙....。
4.下列各句中,没有语病的一句是A.本报《没有苗圃的园丁》一文,报道了宁夏海原县一位代课教师每月只拿50元工资、在没有校舍的情况下挤出自家一间房坚持办学的感人事迹。
B.占人类学家贾兰坡早期及国家文物局近期分别主持的两项重大考古发现表明,,永定河这条天然走廊是“占人类移动的路线”。
C.侵入我国的寒潮的路径,不是每次都一样的,这要看北极地带和西伯利亚的冷空气哪一部分气压最高,我国哪一邢分气压最低所决定的。
四川省南充市高2021届第一次高考适应性考试(含答案)

南充市高2021届第一次高考适应性考试英语试题第1卷第一部分听力(共两节,满分30分)第一节(共5小题:每小题1.5分,满分7.5分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C三个远项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下小题。
每段话一读遍。
例: How much is the shirt?A.£ 19.15B.£ 9.18C.£ 9.15答案是CI. Where does the conversation probably take place?A. In a drugstore.B. At a zoo.C. In a library.2. What will the man do nextA .Sit and eat his meal.B .Change some money. C.Take the food home.3. what does the woman suggest!A. Starting a business.B.Buying a computer.C.Hiring an assistant.4. What are the speakers talking about?A. The traffic.B.The weather.C.The scenery.5. When did the man see the film'A. On SaturdayB. On Wednesday.C.On Thursday.第二节(共15小题:每小题1.5分,满分22.5分)听下面5段对话或独白, 每段对话或独自后有几个小题,从题中所给的A、B、C三个选项中选出最佳选, 并标在试卷的相应位置。
听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟: 听完后, 各小题将给出5秒钟的作答时间。
2021-2022学年四川省南充市高三(上)适应性数学试卷(理科)(一诊)(附答案详解)
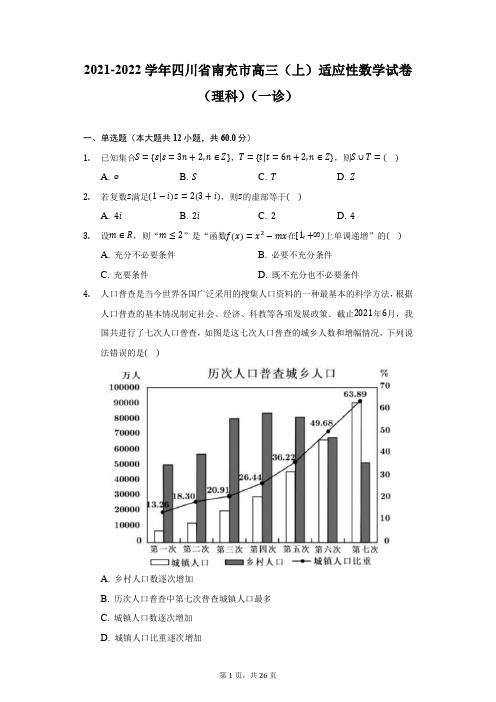
2021-2022学年四川省南充市高三(上)适应性数学试卷(理科)(一诊)一、单选题(本大题共12小题,共60.0分)1.已知集合S={s|s=3n+2,n∈Z},T={t|t=6n+2,n∈Z},则S∪T=()A. ⌀B. SC. TD. Z2.若复数z满足(1−i)z=2(3+i),则z的虚部等于()A. 4iB. 2iC. 2D. 43.设m∈R,则“m≤2”是“函数f(x)=x2−mx在[1,+∞)上单调递增”的()A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件4.人口普查是当今世界各国广泛采用的搜集人口资料的一种最基本的科学方法,根据人口普查的基本情况制定社会、经济、科教等各项发展政策.截止2021年6月,我国共进行了七次人口普查,如图是这七次人口普查的城乡人数和增幅情况,下列说法错误的是()A. 乡村人口数逐次增加B. 历次人口普查中第七次普查城镇人口最多C. 城镇人口数逐次增加D. 城镇人口比重逐次增加5. 农业农村部于2021年2月3日发布信息:全国按照主动预防、内外结合、分类施策、有效处置的总体要求,全面排查蝗灾隐患.为了做好蝗虫防控工作,完善应急预案演练,专家假设蝗虫的日增长率为6%,最初有N 0只,则大约经过( )天能达到最初的1800倍.(参考数据:ln1.06≈0.0583,ln1.6≈0.4700,ln1800≈7.4955,ln8000≈8.9872.)A. 129B. 150C. 197D. 1996. 函数f(x)=(e x +e −x )ln|x|的图象大致是( )A.B.C.D.7. 设数列{b n }前n 项的乘积T n =b 1⋅b 2⋅…⋅b n ,若数列{b n }的通项公式为b n =4010−n ,则下面的等式中正确的是( )A. T 1=T 19B. T 8=T 11C. T 5=T 12D. T 3=T 178. 双曲线C :x 2a 2−y 2b2=1(a >0,b >0)的离心率为√5,抛物线y 2=2px(p >0)的准线与双曲线C 的渐近线交于A ,B 点,若△OAB(O 为坐标原点)的面积为2,则抛物线的方程为( )A. y 2=4xB. y 2=6xC. y 2=8xD. y 2=16x9. 已知函数f(x)=acos(x −π3)+√3sin(x −π3)(a ∈R)是偶函数.g(x)=f(2x +π6)+1,若关于x 的方程g(x)=m 在[0,7π12]有两个不相等实根,则实数m 的取值范围是( )A. [0,3]B. [0,3)C. [2,3)D. [√2+1,3)10. 若A ,B 是⊙O :x 2+y 2=4上两个动点,且OA⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ =−2,A ,B 到直线l :√3x +y −4=0的距离分别为d 1,d 2,则d 1+d 2的最大值是( )A. 3B. 4C. 5D. 611. 如图,某人在垂直于水平地面ABC 的墙面前的点A 处进行射击训练,已知点A 到墙面的距离为AB ,某目标点P 沿墙面上的射线CM 移动,此人为了准确瞄准目标点P ,需计算由点A 观察点P 的仰角θ的大小,若AB =15cm ,AC =25cm ,∠BCM =45°,则tanθ的最大值是( ).(仰角θ为直线AP 与平面ABC 所成的角)A. 259B. 53C. 45D. 3512. 设函数f(x)的定义域为R ,f(x −1)为奇函数,f(x +1)为偶函数,当x ∈[1,3]时,f(x)=kx +m ,若f(0)−f(3)=−2,则f(2022)=( )A. −2B. 0C. 2D. 4二、单空题(本大题共4小题,共20.0分)13. 若直线y =2x +t 与曲线y =2lnx 相切,则实数t 的值为______.14. 已知平面向量a ⃗ =(2,0),b ⃗ =(−1,2),若向量c ⃗ =a ⃗ +(a ⃗ ⋅b ⃗ )b ⃗ ,则c⃗ =______.(其中c⃗ 用坐标形式表示) 15. 已知△ABC 的内角A ,B ,C 的对应边分别为a ,b ,c.若A =π3,c =4,若△ABC 的面积为2√3,则△ABC 的外接圆的半径为______.16. 已知O 为坐标原点,抛物线C :y 2=2px(p >0)上一点A 到焦点F 的距离为4,设点M为抛物线C 准线l 上的动点,给出以下命题:①若△MAF 为正三角形时,则抛物线C 方程为y 2=4x ; ②若AM ⊥l 于M ,则抛物线在A 点处的切线平分∠MAF ; ③若MF ⃗⃗⃗⃗⃗⃗ =3FA⃗⃗⃗⃗⃗ ,则抛物线C 方程为y 2=6x ; ④若|OM|+|MA|的最小值为2√13,则抛物线C 方程为y 2=8x . 其中所有正确的命题序号是______.三、解答题(本大题共7小题,共82.0分)17. 已知数列{a n }的前n 项和为S n ,且S n+1=S n +a n +1,______.请在①a 4+a 7=13;②a 1,a 3,a 7成等比数列;③S 10=65,这三个条件中任选一个补充在上面题干中,并解答下面问题. (Ⅰ)求数列{a n }的通项公式;(Ⅱ)设数列{an2n }的前n 项和T n ,求证:1≤T n <3.18.在全球抗击新冠肺炎疫情期间,我国医疗物资生产企业加班加点生产防疫物品,保障抗疫一线医疗物资供应.某口罩生产厂商在加大生产的同时,狠抓质量管理,不定时抽查口罩质量,质检人员从某日所生产的口罩中随机抽取了100个,将其质量指标值分成以下五组:[100,110),[110,120),[120,130),[130,140),[140,150],得到如下频率分布直方图.(Ⅰ)规定:口罩的质量指标值越高,说明该口罩质量越好,其中质量指标值低于130的为二级口罩,质量指标值不低于130的为一级口罩.现从样本口罩中利用分层抽样的方法随机抽取8个口罩,再从中抽取3个,记其中一级口罩个数为X,求X的分布列及数学期望E(X);(Ⅱ)在2021年“双十一”期间,某网络购物平台推出该型号口罩订单“秒杀”抢购活动,甲,乙两人分别在A、B两店参加一次抢购活动.假定甲、乙两人在A、B两店抢购成功的概率分别为P1,P2,记甲、乙两人抢购成功的总次数为Y,求Y的分布列及数学期望E(Y).19.如图1,在矩形ABCD中,AB=4,AD=2,E是CD的中点,将△ADE沿AE折起,得到如图2所示的四棱锥D1−ABCE,其中平面D1AE⊥平面ABCE.(Ⅰ)设F为CD1的中点,在AB上是否存在一点M,使得MF//平面D1AE.若存在,请证明;若不存在,请说明理由;(Ⅱ)求直线BD1与平面CD1E所成角的正弦值.20.已知椭圆C:x2a2+y2b2=1(a>b>0)的离心率为√22,椭圆C的下顶点和上顶点分别为B1,B2且|B1B2|=2,过点P(0,2)且斜率为k的直线l与椭圆C交于M,N两点.(1)求椭圆C的标准方程;(2)当k=2时,求△OMN的面积;(3)求证:直线B1M与直线B2N的交点T恒在一条定直线上.21.已知函数f(x)=12x2−ax+x−a+1e x,其中a∈R.(Ⅰ)讨论f(x)的单调性;(Ⅱ)若a∈(0,1),设g(x)=f(x)−f(0),(ⅰ)证明:函数g(x)在区间(0,+∞)内有唯一的一个零点;(ⅱ)记(ⅰ)中的零点为x 0,求证:e x 0<x1−a+1.22. 在平面直角坐标系xOy 中,曲线C 1:{x =a +acosϕy =asinϕ(φ为参数,实数a >0),曲线C 2:{x =bcosϕy =b +bsinϕ(φ为参数,实数b >0),在以O 为极点,x 轴的正半轴为极轴的极坐标系中,射线1:θ=α(ρ≥0,0≤α≤π2)与C 1交于O ,A 两点,与C 2交于O ,B 两点,当α=0时,|OA|=1;当α=π2时,|OB|=2. (Ⅰ)求a ,b 的值;(Ⅱ)求2|OA|2+√3|OA|⋅|OB|的最大值.23. 记函数f(x)=|x +1|+|2x −1|的最小值为m .(Ⅰ)求m 的值:(Ⅱ)若正数a ,b ,c 满足abc =2m 3,证明:(ab +bc +ca)(a +b +c)≥9.答案和解析1.【答案】B【解析】解:集合S={s|s=3n+2,n∈Z},T={t|t=6n+2,n∈Z},∴T⫋S,∴S∪T=S.故选:B.推导出T⫋S,从而S∪T=S.本题考查集合的运算,考查并集定义等基础知识,考查运算求解能力,是基础题.2.【答案】D=(3+i)(1+i)=2+4i,【解析】解:由题意,可知z=2(3+i)1− i所以复数z的虚部为4,故选:D.利用复数的运算性质,直接求解即可.本题考查了复数的运算性质,属于基础题.3.【答案】C【解析】解:若函数f(x)=x2−mx在[1,+∞)上单调递增,≤1,∴m≤2,则m2∴m≤2是函数f(x)=x2−mx在[1,+∞)上单调递增的充要条件,故选:C.先求出函数f(x)=x2−mx在[1,+∞)上单调递增的等价条件,再利用充要条件的定义判断即可.本题考查二次函数的单调性,充要条件的判断,属于基础题.4.【答案】A【解析】解:乡村人口第6次,比第5次少,人口不是逐渐递增的,故A 错误, 历次人口普查中第七次普查城镇人口为63.89(万人),为最多,故B 正确, 城镇人口数从第1次到第7次,人口数逐次增加,故C 正确, 城镇人口比重函数图象为递增图象,故D 正确, 故选:A .根据函数图象直接进行判断即可.本题主要考查简单的合情推理,根据函数图象直接进行判断是解决本题的关键,是基础题.5.【答案】A【解析】解:设经过n 天后蝗虫数量达到原来的1800倍, 则N 0(1+6%)nN 0=1800,即1.06n =1800,所以n =log 1.061800=ln1800ln1.06≈129.故选:A .根据已知条件,结合对数函数的公式,即可求解.本题主要考查函数的实际应用,掌握对数函数的公式是解本题的关键,属于基础题.6.【答案】C【解析】解:函数的定义域为{x|x ≠0},排除A ,D ,f(−x)=(e −x +e x )ln|−x|=(e x +e −x )ln|x|=f(x),则f(x)是偶函数,图象关于y 轴对称,当0<x <1时,f(x)<0,排除B , 故选:C .判断函数的奇偶性和对称性,利用当0<x <1时,f(x)<0进行判断即可.本题主要考查函数图象的识别和判断,利用函数的奇偶性和对称性以及排除法是解决本题的关键,是基础题.7.【答案】B【解析】解:∵数列{b n}的通项公式为b n=4010−n,∴T n=b1⋅b2⋅…⋅b n,=409⋅408⋅407⋅......⋅4010−n=409+8+....+(10−n),∵9+8+.....+(10−n)=n(9+10−n)2=−12n2+192n,开口向下,对称轴为n=192,∴四个选项中只有B成立,故选:B.根据条件求出T n的表达式,结合二次函数的性质即可求解结论.本题主要考查数列递推关系式的应用以及二次函数的性质,属于基础题.8.【答案】C【解析】解:双曲线C:x2a2−y2b2=1(a>0,b>0)的离心率为√5,可得e=ca =√1+b2a2=√5,可得2a=b,渐近线方程为y=±12x,抛物线y2=2px(p>0)的准线方程为x=−p2,求得A(−p2,−p4),B(−p2,p4),△OAB(O为坐标原点)的面积为2,可得12×p2×p2=2,解得p=4,即有抛物线的方程为y2=8x.故选:C.由双曲线的离心率,可得2a=b,求得渐近线方程和抛物线的准线方程,联立解得A,B,再由三角形的面积公式,解方程可得p,进而得到所求抛物线的方程.本题考查双曲线的方程和性质,主要是离心率和渐近线方程,考查抛物线的方程和性质,以及运算能力,属于中档题.9.【答案】C【解析】解:函数f(x)=acos(x−π3)+√3sin(x−π3)=(a2cosx+√32asinx)+√3(12sinx−√32cosx)=(a 2−32)cosx +(√32a +√32)sinx 是偶函数(a ∈R),∵f(x)=f(−x),∴√32a +√32=0,∴a =−1,故f(x)=−2cosx ,∴g(x)=−2cos(2x +π6)+1, 若关于x 的方程g(x)=m 在[0,7π12]有两个不相等实根, 则cos(2x +π6)=1−m 2在[0,7π12]有两个不相等实根,∵x ∈[0,7π12],∴2x +π6∈[π6,4π3],∵cos4π3=−12,∴−1<1−m 2≤−12,∴2≤m <3,∴实数m 的取值范围是[−2,3). 故选:C .由利用三角恒等变换化简f(x)的解析式,根据函数的奇偶性求得a ,可得f(x)的解析式,再得g(x)的解析式,再利用余弦函数的图象和性质,求得实数m 的取值范围. 本题主要考查三角恒等变换,函数的奇偶性,函数y =Asin(ωx +φ)的图象变换规律,余弦函数的图象和性质,属于中档题.10.【答案】D【解析】解:因为A ,B 是⊙O :x 2+y 2=4上两个动点,且OA ⃗⃗⃗⃗⃗ ⋅OB ⃗⃗⃗⃗⃗⃗ =−2, 所以2×2×cos∠AOB =−2, 故cos∠AOB =−12, 所以∠AOB =120°, 设AB 中点为P ,在等腰三角形AOB 中,OP =1, 所以P 在以O 为圆心,以1为半径的圆上, 设P 到直线l 的距离为d ,由梯形的中位线定理可知2d =d 1+d 2, 因为O 到直线l :√3x +y −4=0的距离为42=2, 所以P 到直线l 的距离的最大值为2+1=3, 所以d 1+d 2的最大值为6, 故选:D .根据条件可得∠AOB=120°,设AB中点为P,由等腰三角形的性质可知P在以O为圆心,以1为半径的圆上,而由梯形的中位线定理可知P到直线l的距离为d1+d2的一半,故求出P点到直线l的距离的最大值即可.本题考查了平面向量数量积的性质,动点轨迹的问题,属于中档题.11.【答案】B【解析】解:过点P作PP′⊥BC交BC于点P′,连接AP′,则tanθ=PP′AP′,设BP′=x,则CP′=20−x,由∠BCM=45°,PP′=CP′tan45°=20−x,在RtΔABP中,AP′=√225+x2,∴tanθ=√225+x2,令y=√225+x2,则y′=−√225+x 2−(20−x)⋅2√225+x2225+x2=√225+x2,当0≤x≤20时,y′<0,所以函数在[0,20]单调递减,∴x=0时,取得最大值为2015=43,当P′在CB的延长线上,PP′=CP′tan45°=20+x,在RtΔABP中,AP′=√225+x2,∴tanθ=√225+x2,令y=(20+x)2225+x2,则y′=0可得x=454,此时函数的最大值为53,综上可知,函数的最大值为53,故选:B.过点P作PP′⊥BC交BC于点P′,连接AP′,设BP′=x,可得tanθ=PP′AP′=√225+x2,分P′在BC之间和P′在CB的延长线上两种情况求最值,比较可得结果.本题考查了三角形中的几何计算及三角函数的最值问题,属于中档题.12.【答案】C【解析】解:∵f(x−1)为奇函数,∴f(−x−1)=−f(x−1),当x=0时,f(−1)=−f(−1),即f(−1)=0,∵f(x+1)为偶函数,∴f(−x+1)=f(x+1),则f(−x−2)=−f(x),f(−x+2)=f(x),即f(−x−2)=−f(−x+2),则f(x−2)=−f(x+2),即f(x)=−f(x+4),则f(x+8)=−f(x+4)=f(x),即f(x)的周期是8,f(0)=f(2),∵当x∈[1,3]时,f(x)=kx+m,若f(0)−f(3)=−2,∴f(2)−f(3)=−2,即2k+m−3k−m=−k=−2,得k=2,此时f(x)=2x+m,又f(3)=f(2+1)=f(−2+1)=f(−1)=0,即6+m=0,得m=−6,即f(x)=2x−6,则f(2022)=f(252×8+6)=f(6)=f(2+4)=−f(4−2)=−f(2)=−(4−6)=2,故选:C.根据函数奇偶性建立方程求出函数f(x)是周期为8的周期函数,利用函数的周期性进行转化求解即可.本题主要考查函数值的计算,根据函数奇偶性和周期性的关系求出函数的周期是解决本题的关键,是中档题.13.【答案】−2【解析】解:∵y=2lnx,∴y′=2x ,设切点为(m,2lnm),得切线的斜率为2m,∴曲线在点(m,2lnm)处的切线方程为:y−2lnm=2m×(x−m).即y=2mx−2+2lnm,由2m=2,得m=1,∴t=−2+2ln1=−2.故答案为:−2.欲求t的值,只须求出切线的方程即可,故先利用导数求出在切点处的导函数值,再结合导数的几何意义即可求出切线的斜率,进一步求解t值.本题主要考查直线的方程、导数的几何意义、利用导数研究曲线上某点切线方程等基础知识,考查运算求解能力.属于基础题.14.【答案】(4,−4)【解析】解:因为a⃗=(2,0),b⃗ =(−1,2),所以c⃗=a⃗+(a⃗⋅b⃗ )b⃗ =(2,0)+(2,−4)=(4,−4).故答案为:(4,−4).根据向量的运算性质计算即可.本题考查了平面向量数量积的性质及其运算,属于基础题.15.【答案】2【解析】解:根据题意得12bcsinA=2√3,把A=π3,c=4代入得b=2,由余弦定理得a=√b2+c2−2bccosA=√22+42−2×2×4×12=2√3,设△ABC的外接圆的半径为R,由正弦定理得asinA =2R,∴R=√32×√32=2.故答案为:2.由△ABC的面积为2√3可求得b值,然后由余弦定理求得a值,再由正弦定理求得△ABC的外接圆的半径.本题考查正、余弦定理及三角形面积公式,考查数学运算能力,属于基础题.16.【答案】①②③④【解析】解:对于①,当△MAF 为正三角形时,|AF|=|AM|,故A M 与x 轴平行,∵|AF|=|AM|=4,∴F 到准线的距离等于12|AM|=2,即p =2,故①正确; 对于②,设A(x 0,y 0),不妨设点A 在第一象限,则y 0=√2px 0, 由y =√2px.得y′=√2p 2√x,所以抛物线在A 的切线的斜率k =√2p 2√x 0,所以抛物线在A 处的切线方程为y −√2px 0=√2p 2√x 0(x −x 0),∵F(p2,0),M(−p 2,√2px 0),所以MF 的中点为H(0,√2px 02) 显然点H 在直线y −√2px 0=√2p 2√x 0(x −x 0)上,即AH 为△AFM 的一条中线,又由抛物线的定义,知|AF|=|AM|,所以△AFM 为等腰三角形, 所以AH 平分∠MAF ;故②正确;对于③,若MF ⃗⃗⃗⃗⃗⃗ =3FA⃗⃗⃗⃗⃗ ,则A ,M ,F 三点共线,且|MF|=12,由三角形的相似比可得1216=p4,得p=3,故③正确;对于④,设B(−p,0),则O,B关于准线对称,故|MO|=|MB|,∵|AF|=4,∴A点横坐标为4−p2,不妨设A在第一象限,则A点纵坐标为√8p−p2,故|OM|+|MA|的最小值为|AB|=√(4+p2)2+8p−p2=2√13,解得p=4或p=12,由4−p2≥0,p≤8,故p=4,故④正确.故答案为:①②③④.根据等边三角形性质判断①,根据三线合一判断②,利用相似三角形判断③,根据最短距离列方程计算p,判断④.本题考查抛物线的几何性质,考查数学转化思想,考查运算求解能力,是中档题.17.【答案】解:数列{a n}的前n项和为S n,且S n+1=S n+a n+1,整理得a n+1−a n=1(常数),故数列{a n}是以1为公差的等差数列;选条件①时,(Ⅰ)由于①a4+a7=13;2a1+9=13,解得a1=2,故a n=2+(n−1)=n+1;证明:(Ⅱ)设b n=n+12n,所以T n=221+322+423+...+n+12n①,1 2T n=222+323+424+...+n+12n+1②,①−②得:12T n=12+122+....+12n−n+12n+1+12,整理得T n=3−n+32n.所以T n<3,由于设f(n)=f(n)=3−n+32n,满足f(n)−f(n−1)>0,故函数f(x)为单调递增函数,由于T1=1,所以1≤T n<3.选条件②a1,a3,a7成等比数列所以a32=a1⋅a7,解得a1=2,故a n=2+(n−1)=n+1;证明:(Ⅱ)设b n=n+12n,所以T n=221+322+423+...+n+12n①,1 2T n=222+323+424+...+n+12n+1②,①−②得:12T n=12+122+....+12n−n+12n+1+12,整理得T n=3−n+32n.所以T n<3,由于设f(n)=f(n)=3−n+32n,满足f(n)−f(n−1)>0,故函数f(x)为单调递增函数,由于T1=1,所以1≤T n<3.选条件③S10=65时,10a1+10×92=65,解得a1=2,故a n=2+(n−1)=n+1;证明:(Ⅱ)设b n=n+12n,所以T n=221+322+423+...+n+12n①,1 2T n=222+323+424+...+n+12n+1②,①−②得:12T n =12+122+....+12n −n+12n+1+12, 整理得T n =3−n+32n.所以T n <3,由于设f(n)=f(n)=3−n+32n,满足f(n)−f(n −1)>0,故函数f(x)为单调递增函数,由于T 1=1, 所以1≤T n <3.【解析】首先确定数列{a n }为等差数列,进一步选条件①②③时, (Ⅰ)直接求出数列的通项公式;(Ⅱ)利用乘公比错位相减法和放缩法及函数的单调性的应用求出结果.本题考查的知识要点:数列的通项公式的求法,数列的求和,数列的单调性,乘公比错位相减法在数列求和中的应用,放缩法,主要考查学生的运算能力和数学思维能力,属于中档题.18.【答案】(I)解:按分层抽样的方法抽取8个口罩,则其中二级、一级口罩的个数分别为6个和2个,所以随机变量X 的可能取值为0,1,2, 则P(X =0)=C 63C 83=514,P(X =1)=C 62C 21C 83=1528,P(X =2)=C 61C 22C 83=328,所以随机变量X 的分布列为:所以期望为E(X)=0×514+1×1528+2×328=34. (II)解:由题意,随机变量Y 的可能取值为0,1,2, 则P(Y =0)=(1−p 1)(1−p 2)=1−(p 1+p 2)+p 1p 2, P(Y =1)=p 1(1−p 2)+(1−p 1)p 2=p 1+p 2−2p 1p 2, P(Y =2)=p 1p 2,所以随机变量Y 的分布列为:E(Y)=p1+p2−2p1p2+2×p1p2=1+p2p1+p2.【解析】(I)按分层抽样得到二级、一级口罩的个数分别为6个和2个,得出X的可能取值为0,1,2,求得相应的概率,列出分布列,利用期望的公式,即可求解;(II)根据题意得到随机变量Y的可能取值为0,1,2,结合相互对立事件的概率公式,求得相应的概率,列出分布列,利用期望的公式,即可求解.本题考查离散型随机变量的分布列与期望,考查学生的运算能力,属于中档题.19.【答案】解:(Ⅰ)存在,且AM=14AB,取D1E的中点L,连接AL,FL,∵FL//EC,EC//AB,∴FL//AB且FL=14AB,∴FL//AM,FL=AM∴AMFL为平行四边形,∴MF//AL,因为MF⊄平面AD1E,AL⊂平面AD1E,所以MF//平面AD1E.故线段AB上存在满足题意的点M,且AMAB =14.(Ⅱ)取AB的中点K,AE的中点O,连接OK,D1O⊥AE,OK⊥AK,因为平面D1AE⊥平面ABCE,则D1O⊥平面ABCE,故以O为坐标原点,OA,OK,OD1为x,y,z轴建立空间直角坐标系,如图所示,可得B(−√2,2√2,0),C(−2√2,√2,0),E(−√2,0,0),D 1(0,0,√2), EC ⃗⃗⃗⃗⃗ =(−√2,√2,0),ED 1⃗⃗⃗⃗⃗⃗⃗ =(√2,0,√2),BD 1⃗⃗⃗⃗⃗⃗⃗⃗ =(√2,−2√2,√2) 设平面CD 1E 的一个法向量为m⃗⃗⃗ =(x,y,z), 由{m ⃗⃗⃗ ⋅EC ⃗⃗⃗⃗⃗ =0m ⃗⃗⃗ ⋅ED 1⃗⃗⃗⃗⃗⃗⃗ =0,即{−√2x +√2y =0√2x +√2z =0, 令x =1,解得y =1,z =−1,所以m ⃗⃗⃗ =(1,1,−1), 设直线BD 1与平面CD 1E 所成角为θ,sinθ=|cos〈m ⃗⃗⃗ ,BD 1⃗⃗⃗⃗⃗⃗⃗⃗ 〉|=|m ⃗⃗⃗ ⋅BD1⃗⃗⃗⃗⃗⃗⃗⃗ ||m ⃗⃗⃗ ||BD1⃗⃗⃗⃗⃗⃗⃗⃗ |=√2√3×√12=√23, 所以直线BD 1与平面CD 1E 所成角的正弦值为√23.【解析】(Ⅰ)先分析确定点M 位置,再取D 1E 的中点L ,根据平面几何知识得AMFL 为平行四边形,最后根据线面平行判定定理得结果.(Ⅱ)取AB 的中点K ,AE 的中点O ,连接OK ,以O 为坐标原点,OA ,OK ,OD 1为x ,y ,z 轴建立空间直角坐标系,利用空间向量的数量积即可求解.本题主要考查线面平行的证明,空间向量及其应用,线面角的计算等知识,属于中等题.20.【答案】解:(1)由题意可得{e =ca =√222b =2c 2=a 2−b 2,解得:a 2=2,b 2=1, 所以椭圆的方程为:x 22+y 2=1;(2)由题意可得直线MN 的方程为:y =2x +2,设M(x 1,y 2),N(x 2,y 2), 联立{x 22+y 2=1y =2x +2,整理可得:9x 2+16x +6=0,x 1+x 2=−169,x 1x 2=69=23,所以弦长|MN|=√1+22⋅√(x 1+x 2)2−4x 1x 2=√5⋅√16281−4×23=√5⋅2√109,O 到直线MN 的距离d =√5, 所以S △MON =12×|MN|⋅d =12×√5⋅2√109√5=2√109; (3)证明:设直线MN 的方程为:y =kx +2,设M(x 1,y 2),N(x 2,y 2), 联立{y =kx +2x 22+y 2=1,整理可得:(1+2k 2)x 2+8kx +6=0,所以△=64k 2−4×6×(1+2k 2)>0,可得:k 2>32, 且x 1+x 2=−8k1+2k 2,x 1x 2=61+2k 2, 由(1)可得B 1(0,−1),B 2(0,1),设T(m,n), 由T ,M ,B 1三点共线,所以n+1m=y 1+1x 1=kx 1+3x 1=k +3x 1,①由T ,M ,B 2三点共线:n−1m=y 2−1x 2=kx 2+1x 2=k +1x 2,②由①+②×3可得:n+1m +3n−3m=4k +3(x 1+x 2)x 1x 2=4k +3⋅−8k 1+2k 261+2k 2=0,所以可得4n −2=0,解得:n =12, 所以点T 恒在直线y =12上.【解析】(1)由离心率和短轴的值即a ,b ,c 的关系求出a ,b 的值,进而求出椭圆的方程; (2)由题意设直线MN 的方程,与椭圆联立求出两根之和及两根之积,进而求出弦长|MN|的值,再求O 到直线MN 的距离,代入面积公式求出三角形的面积;(3)由(1)可得B 1,B 2的坐标,设T 的坐标,由直线B 1M 与直线B 2N 的交点T 可得T 与B 1,B 2的坐标的关系,将直线MN 的方程与椭圆联立求出两根之和及两根之积,进而可得T 的纵坐标为定值,即可证得结论.本题考查求椭圆的方程及直线与椭圆的综合,三角形面积的求法,及直线恒过定点的证明,属于中档题.21.【答案】解:(Ⅰ)求导f′(x)=(x −a)−x−a e x=(x −a)e x −1e x,令f′(x)=0,解得x =a 或x =0,当a >0时,由f′(x)>0,解得x >a 或x <0,由f′(x)<0,解得0<x <a , 所以f(x)在(−∞,0)和(a,+∞)上单调递增,在(0,a)上单调递减,当a=0时,由f′(x)=x(e x−1)e x>0,得x>0,f′(x)<0,x>0,所以f(x)在(−∞,+∞)上单调递增;当a<0时,由f′(x)>0,解得x<a或x>0,f′(x)<0,解得a<x<0,f(x)在(−∞,a)和(0,+∞)上单调递增,在(a,0)上单调递减,综上所述,当a>0时,f(x)在(−∞,0)和(a,+∞)上单调递增,在(0,a)上单调递减,当a=0时,f(x)在(−∞,+∞)上单调递增,当a<0时,f(x)在(−∞,a)和(0,+∞)上单调递增,在(a,0)上单调递减;(Ⅱ)(ⅰ)证明:由(Ⅰ)可知,当a∈(0,1)时,g(x)在(0,a)上单调递减,在(a,+∞)上单调递增,所以g(a)<g(0)=f(0)−f(0)=0,解法一:g(a+√a2+2(1−a))>12[a+√a2+2(1−a)]2−a[a+√a2+2(1−a)]−(1−a)=0,存在唯一的x0∈(a,a+√a2−2a+2),使得g(x0)=0,故函数g(x)在区间(0,+∞)内有唯一的一个零点.解法二:g(x)=f(x)−f(0)=12x2−ax+x−a+1e x−(1−a)>12x2−ax−(1−a)>1 2x2−ax−1=12x(x−2a)−1,g(2a+2)>12(2a+2)×2−1=2a+1>0,存在唯一的x0∈(a,2a+2),使得g(x0)=0,故函数g(x)在区间(0,+∞)内有唯一的一个零点.解法三:g(x)=f(x)−f(0)=12x2−ax+x−a+1e x−(1−a)>12x2−ax+a−1,g(2)>12×22−2a+a−1=1−a>0,存在唯一的x0∈(a,2),使得g(x0)=0,故函数g(x)在区间(0,+∞)内有唯一的一个零点.说明:若给出解法当a∈(0,1)时,g(x)=f(x)−f(0)=f(x)+a−1,g(x)与f(x)的单调性相同,由(Ⅰ)可知,当a∈(0,1)时,g(x)在(0,a)上单调递减,在(a,+∞)上单调递增,所以g(a)<g(0)=f(0)−f(0)=0,当x>a时,x→+∞,g(x)→∞.(扣2分)(ⅱ)证明:e x0<x01−a+1,只需证:x0+1−ae x0>1−a,由于g(x0)=0,得f(x0)=f(0),故12x02−ax0+x0+1−ae x0=1−a,只需证12x02−ax0+x0+1−ae x0<x0+1−ae x0,只需证x0<2a,因为f(x)在(a,+∞)上单调递增,所以f(x0)<f(2a),因为f(x0)=f(0),所以只需证明f(2a)>f(0),解法一:由f(2a)−f(0)=a+1e2a −(1−a)=a+1e2a+a−1,设ℎ(a)=a+1e2a+a−1,a∈(0,1),则ℎ′(a)=e2a−2a−1e2a,设2a=t,则t∈(0,2),设k(t)=e t−t−1,则k′(t)=e t−1>0,所以k(t)=e t−t−1在(0,2)单调递增,所以k(t)>k(0)=0,则ℎ′(a)=e2a−2a−1e2a>0,所以ℎ(a)=a+1e2a+a−1在(0,1)上单调递增,所以ℎ(a)>ℎ(0)=0,所以f(2a)>f(0),故原不等式得证.解法二:由f(2a)−f(0)=a+1e2a −(1−a)=(1−a)[a+1(1−a)e2a−1],φ(a)=a+1(1−a)e2a−1,a∈(0,1),φ′(a)=(1−a)e2a−(a+1)[−e2a+2(1−a)e2a](1−a)2e2a =2a2(1−a)2e2a>0,所以φ(a)在(0,1)上单调递增,所以φ(a)>φ(0)=0,所以f(2a)>f(0),原不等式得证.解法三:由f(2a)−f(0)=a+1e2a −(1−a)=1−ae2a⋅(1+a1−a−e2a)=1−ae2a(e ln1+a1−a−e2a),设p(a)=ln1+a1−a−2a=ln(1+a)−ln(1−a)−2a,a∈(0,1),则p′(a)=11+a +11−a−2=2−2(1−a2)(1+a)(1−a)2a2(1+a)(1−a)>0,因此p(a)=ln1+a1−a−2a在(0,1)单调递增,因为1>a>0,所以p(a)>p(0)=0,所以f(2a)>f(0),故原不等式得证.【解析】(Ⅰ)求导,根据导数与函数单调性的关系,即可判断f(x)的单调性;(Ⅱ)当a∈(0,1),求得g(x)的单调性,解法一:由g(a)<0,及g(a+√a2+2(1−a))>0,利用函数的零点存在定理可得:函数g(x)在区间(0,+∞)内有唯一的一个零点; 解法二:利用放缩法,可得g(2a +2)>12(2a +2)×2−1=2a +1>0,结合g(a)<0,因此存在唯一的x 0∈(a,2a +2),使得g(x 0)=0,函数g(x)在区间(0,+∞)内有唯一的一个零点;解法三:利用放缩可得g(x)=f(x)−f(0)=12x 2−ax +x−a+1e x−(1−a)>12x 2−ax +a −1,因此g(2)>0,同理可得函数g(x)在区间(0,+∞)内有唯一的一个零点. (ⅱ)原不等式可转化为x 0<2a ,由f(x)在(a,+∞)上单调递增,因此f(x 0)<f(2a),进而f(2a)>f(0). 解法一:构造函数ℎ(a)=a+1e 2a+a −1,a ∈(0,1),求导根据导数与函数单调性的关系,求得最小值,即可证明f(2a)>f(0);解法二:设φ(a)=a+1(1−a)e 2a −1,a ∈(0,1),求导可得,φ(a)在(0,1)上单调递增,所以φ(a)>φ(0)=0,因此可得f(2a)>f(0);解法三:设p(a)=ln 1+a 1−a −2a =ln(1+a)−ln(1−a)−2a,a ∈(0,1),求得,可得p(a)=ln 1+a1−a −2a 在(0,1)单调递增,因为p(a)>p(0)=0,即可得到f(2a)>f(0). 本题考查导数的综合应用,导数与函数单调性的关系,函数的零点问题,函数的隐零点,放缩法的应用,考查转化思想,分类讨论思想,属于难题.22.【答案】解:(Ⅰ)曲线C 1:{x =a +acosϕy =asinϕ(φ为参数,实数a >0),转换为直角坐标方程为(x −a)2+y 2=a 2,根据{x =ρcosθy =ρsinθx 2+y 2=ρ2转换为极坐标方程为ρ=2acosθ;当α=0时,|OA|=1;故a =12.曲线C 2:{x =bcosϕy =b +bsinϕ(φ为参数,实数b >0),转换为直角坐标方程为x 2+(y −b)2=b 2,根据{x =ρcosθy =ρsinθx 2+y 2=ρ2转换为极坐标方程为ρ=2bsinθ;当α=π2时,|OB|=2.故b =1. 故a =12,b =1.(Ⅱ)由于曲线C 1和曲线C 2的方程为ρ=cosθ和ρ=2sinθ;所以2|OA|2+√3|OA|⋅|OB =1+cos2θ+√3sin2θ=2sin(2θ+π6)+1;由于0≤θ≤π2, 所以2θ+π6∈[π6,7π6],故2|OA|2+√3|OA|⋅|OB 的最大值为3,当2θ+π6=π2,即θ=π6时取得最大值.【解析】(Ⅰ)直接利用参数方程、极坐标方程和直角坐标方程之间的转换进一步求出a 和b 的值;(Ⅱ)利用极径的应用和三角函数的关系式的变换和正弦型函数的性质的应用求出最大值.本题考查的知识要点:参数方程、极坐标方程和直角坐标方程之间的转换,三角函数的关系式的变换,正弦型函数的性质的应用,主要考查学生的运算能力和数学思维能力,属于中档题.23.【答案】(Ⅰ)解:由题意得,f(x)={−3x,x ≤−1−x +2,−1<x <123x,x ≥12,作出函数f(x)图像如图所示,由图可知,当x =12时,函数f(x)取最小值,f(x)min =−12+2=32,故m =32. (Ⅱ)证明:由(Ⅰ)得abc =1,故ab +bc +ca =1c +1a +1b ,因为a ,b ,c 均为正数,所以要证明不等式(ab +bc +ca)(a +b +c)≥9, 只需证明(1a +1b +1c )(a +b +c)≥9,由柯西不等式得:(1a +1b +1c )(a +b +c)≥(√a √a √b √b √c √c )2=9,当且仅当a=b=c=1时,取等号,所以原不等式成立.【解析】(Ⅰ)将函数f(x)化简为分段函数形式,并作出函数图像,由图像判断并计算最小值;(Ⅱ)由(Ⅰ)得abc=1,可得ab+bc+ca=1c +1a+1b,将证明不等式(ab+bc+ca)(a+b+c)≥9转化为证明(1a +1b+1c)(a+b+c)≥9成立,利用柯西不等式证明即可.本题主要考查绝对值函数的最值,柯西不等式的应用等知识,属于基础题.。
四川省南充市2023届高三上学期高考适应性考试(一诊)理科数学试题

一、单选题二、多选题1. 将三角函数向左平移个单位后,得到的函数解析式为A.B.C.D.2. 已知全集,集合,,则如图中阴影部分所表示的集合为A.B.C.D.3. 已知函数,的定义域均为,且,,若的图象关于直线对称,,则( )A.B.C .0D .24.复数的虚部为( )A .3B.C .2D.5. 已知集合,,则为( )A.B.C.D.6. 小说《三体》中的“水滴”是三体文明派往太阳系的探测器,由强相互作用力材料制成,被形容为“像一滴圣母的眼泪”.小刘是《三体》的忠实读者,他利用几何作图软件画出了他心目中的水滴(如图),由线段AB ,AC 和优弧BC 围成,其中BC 连线竖直,AB ,AC 与圆弧相切,已知“水滴”的水平宽度与竖直高度之比为,则().A.B.C.D.7. 蹴鞠,又名蹴球,踢圆等,蹴有用脚蹴、踢、蹋的含义,鞠最早系外包皮革、内实米糠的球.因而蹴鞠就是指古人以脚蹴,蹋、踢皮球的活动,类似今日的足球.2006年5月20日,蹴鞠已作为非物质文化遗产经国务院批准列入第一批国家非物质文化遗产名录.已知某鞠的表面上有五个点、、、、恰好构成一正四棱锥,若该棱锥的高为8,底面边长为,则该鞠的表面积为( )A.B.C.D.8.已知,将函数的图象向右平移个单位得到,则使得函数是偶函数的的最小值是( )A.B.C.D.9. 已知直线与函数的图象相交,A ,B ,C 是从左到右的三个相邻交点,设,四川省南充市2023届高三上学期高考适应性考试(一诊)理科数学试题四川省南充市2023届高三上学期高考适应性考试(一诊)理科数学试题三、填空题四、解答题,则下列结论正确的是( ).A.将的图象向右平移个单位长度后关于原点对称B.若,则C .若在上无最值,则的最大值为D.10.已知函数,则下列结论正确的是( )A.对于任意的,存在偶函数,使得为奇函数B.若只有一个零点,则C .当时,关于的方程有3个不同的实数根的充要条件为D .对于任意的,一定存在极值11. 已知向量满足,则可能成立的结果为( )A.B.C.D.12. 已知全集U 的两个非空真子集A ,B 满足,则下列关系一定正确的是( )A.B.C.D.13. 定义在R 上的奇函数f (x )以2为周期,则f (1)=________.14. 已知函数则________;方程的解为________.15. 已知,若,则_____.16. 已知函数,其中a 为实数.(1)讨论函数的单调性;(2)令,若恒成立,求实数a 的取值范围.17. 安庆某农场主拥有两个面积都是220亩的农场——加盟“生态农场”与“智慧农场”,种植的都是西瓜,西瓜根据品相和质量大小分为优级西瓜、一级西瓜、残次西瓜三个等级.农场主随机抽取了两个农场的西瓜各100千克,得到如下数据:“生态农场”优级西瓜和一级西瓜共95千克,两个农场的残次西瓜一共20千克,优级西瓜数目如下:“生态农场”20千克,“智慧农场”25千克.(1)根据所提供的数据,完成下列列联表,并判断是否有95%的把握认为残次西瓜率与农场有关?农场非残次西瓜残次西瓜总计生态农场智慧农场总计(2)种植西瓜的成本为0.5元/千克,且西瓜价格如下表:等级优级西瓜一级西瓜残次西瓜价格(元/千克) 2.5 1.5(无害化处理费用)①以样本的频率作为概率,请分别计算两个农场每千克西瓜的平均利润;②由于农场主精力有限,决定售卖其中的一个农场,请你根据以上数据帮他做出决策.(假设两个农场的产量相同)参考公式:,其中.附表:0.1000.0500.0100.0012.7063.841 6.63510.82818. 如图,直三棱柱的所有棱长都是2,D、E分别是AC、的中点.(1)求证:平面;(2)求三棱锥的体积.19.已知圆:,定点,如图所示,圆上某一点恰好与点关于直线对称,设直线与直线的交点为.(1)求证:为定值,并求出点的轨迹方程;(2)设,为曲线上一点,为圆上一点(,均不在轴上).直线,的斜率分别记为,,且.求证:直线过定点,并求出此定点的坐标.20. 某职业中专开设的一门学科的考试分为理论考试和实践操作考试两部分,当理论考试合格才能参加实践操作考试,只有理论考试与实践操作考试均合格,才能获得技术资格证书,如果一次考试不合格有1次补考机会.学校为了掌握该校学生对该学科学习情况,进行了一次调查,随机选取了100位同学的一次考试成绩,将理论考试与实践操作考试成绩折算成一科得分(百分制),制成如下表格:分段[40,50)[50,60)[60,70)[70,80)[80,90)[90,100]人数510a30a+510(1)①求表中a的值,并估算该门学科这次考试的平均分(同一组数据用该组区间的中点值代表);②在[40,50), [50,60), [60,70)这三个分数段中,按频率分布情况,抽取7个学生进行教学调研,学校的教务主任要在这7名学生中随机选2人进行教学调查,求这2人均来自[60,70)的概率;(2)该校学生小明在历次该学科模拟考试中,每次理论合格的概率均为,每次考实践操作合格的概率均为,这个学期小明要参加这门学科的结业考试,小明全力以赴,且每次考试互不影响.如果小明考试的次数的期望不低于2.5次,求的取值范围.21. 已知,是椭圆的左,右顶点,,过椭圆的右焦点的直线交椭圆于点,,交直线于点,且直线,,的斜率成等差数列,和是椭圆上的两动点,和的横坐标之和为2,的中垂线交轴于点.(1)求椭圆的方程;(2)求的面积的最大值.。
四川省南充市2021届新高考第一次适应性考试数学试题含解析

四川省南充市2021届新高考第一次适应性考试数学试题一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设函数()f x 定义域为全体实数,令()(||)|()|g x f x f x =-.有以下6个论断:①()f x 是奇函数时,()g x 是奇函数;②()f x 是偶函数时,()g x 是奇函数;③()f x 是偶函数时,()g x 是偶函数;④()f x 是奇函数时,()g x 是偶函数⑤()g x 是偶函数;⑥对任意的实数x ,()0g x ….那么正确论断的编号是( )A .③④B .①②⑥C .③④⑥D .③④⑤ 【答案】A【解析】【分析】根据函数奇偶性的定义即可判断函数()g x 的奇偶性并证明.【详解】当()f x 是偶函数,则()()f x f x -=,所以()()(||)|()|(||)|()|g x f x f x f x f x g x -=---=-=,所以()g x 是偶函数;当()f x 是奇函数时,则()()f x f x -=-,所以()()(||)|()|(||)|()|g x f x f x f x f x g x -=---=-=,所以()g x 是偶函数;当()f x 为非奇非偶函数时,例如:()5f x x =+, 则()27f -=,()23f -=,此时(2)0g ->,故⑥错误;故③④正确.故选:A【点睛】本题考查了函数的奇偶性定义,掌握奇偶性定义是解题的关键,属于基础题.2.已知函数2()ln(1)f x x x -=+-,则函数(1)=-y f x 的图象大致为( ) A . B .C .D .【答案】A 【解析】 【分析】用排除法,通过函数图像的性质逐个选项进行判断,找出不符合函数解析式的图像,最后剩下即为此函数的图像.【详解】设2()(1)ln 1g x f x x x -=-=-+,由于120112ln 22g -⎛⎫=> ⎪⎝⎭+,排除B 选项;由于()2222(e),e 2e 3e g g --==--,所以()g e >()2e g ,排除C 选项;由于当x →+∞时,()0>g x ,排除D 选项.故A 选项正确.故选:A【点睛】本题考查了函数图像的性质,属于中档题.3.某市政府决定派遣8名干部(5男3女)分成两个小组,到该市甲、乙两个县去检查扶贫工作,若要求每组至少3人,且女干部不能单独成组,则不同的派遣方案共有( )种A .240B .320C .180D .120【答案】C【解析】【分析】在所有两组至少都是3人的分组中减去3名女干部单独成一组的情况,再将这两组分配,利用分步乘法计数原理可得出结果.【详解】两组至少都是3人,则分组中两组的人数分别为3、5或4、4,又因为3名女干部不能单独成一组,则不同的派遣方案种数为432882221180C C A A ⎛⎫+-= ⎪⎝⎭. 故选:C.【点睛】本题考查排列组合的综合问题,涉及分组分配问题,考查计算能力,属于中等题.4.函数()sin x y x-=([),0x π∈-或(]0,x π∈)的图象大致是( ) A . B . C .D .【答案】A【解析】【分析】确定函数的奇偶性,排除两个选项,再求x π=时的函数值,再排除一个,得正确选项.【详解】分析知,函数()sin x y x -=([),0x π∈-或(]0,x π∈)为偶函数,所以图象关于y 轴对称,排除B ,C , 当x π=时,sin 0x x =,排除D , 故选:A .【点睛】本题考查由函数解析式选择函数图象,解题时可通过研究函数的性质,如奇偶性、单调性、对称性等,研究特殊的函数的值、函数值的正负,以及函数值的变化趋势,排除错误选项,得正确结论.5.若复数12z i =+,2cos isin ()z ααα=+∈R ,其中i 是虚数单位,则12||z z -的最大值为( ) A 51B .512C 51D .512【答案】C由复数的几何意义可得12z z -表示复数12z i =+,2cos sin z i αα=+对应的两点间的距离,由两点间距离公式即可求解.【详解】由复数的几何意义可得,复数12z i =+对应的点为()2,1,复数2cos sin z i αα=+对应的点为()cos ,sin αα,所以121z z -=,其中tan φ2=,故选C【点睛】本题主要考查复数的几何意义,由复数的几何意义,将12z z -转化为两复数所对应点的距离求值即可,属于基础题型.6.已知复数z 满足:34zi i =+(i 为虚数单位),则z =( )A .43i +B .43i -C .43i -+D .43i -- 【答案】A【解析】【分析】利用复数的乘法、除法运算求出z ,再根据共轭复数的概念即可求解. 【详解】由34zi i =+,则3434431i i z i i +-===--, 所以z =43i +.故选:A【点睛】本题考查了复数的四则运算、共轭复数的概念,属于基础题. 7.如果实数x y 、满足条件10{1010x y y x y -+≥+≥++≤,那么2x y -的最大值为( )A .2B .1C .2-D .3-【答案】B【解析】解:当直线2x y z -=过点()0,1A -时,z 最大,故选B8.已知斜率为2-的直线与双曲线()2222:10,0x y C a b a b-=>>交于,A B 两点,若()00,M x y 为线段AB 中点且4OM k =-(O 为坐标原点),则双曲线C 的离心率为( )A 5B .3C 3D .324【答案】B【解析】【分析】设1122(,),(,)A x y B x y ,代入双曲线方程相减可得到直线AB 的斜率与中点坐标之间的关系,从而得到,a b 的等式,求出离心率.【详解】 004OM y k x ==-, 设1122(,),(,)A x y B x y ,则22112222222211x y a b x y a b ⎧-=⎪⎪⎨⎪-=⎪⎩, 两式相减得1212121222()()()()0x x x x y y y y a b +-+--=, ∴2121221212()()AB y y b x x k x x a y y -+==-+220220124b x b a y a ⎛⎫==⋅-=- ⎪⎝⎭,22228,13b b e a a∴=∴=+=. 故选:B .【点睛】本题考查求双曲线的离心率,解题方法是点差法,即出现双曲线的弦中点坐标时,可设弦两端点坐标代入双曲线方程相减后得出弦所在直线斜率与中点坐标之间的关系.9.已知正方体1111ABCD A B C D -的棱长为1,平面α与此正方体相交.对于实数()03d d <<,如果正方体1111ABCD A B C D -的八个顶点中恰好有m 个点到平面α的距离等于d ,那么下列结论中,一定正确的是A .6m ≠B .5m ≠C .4m ≠D .3m ≠ 【答案】B【解析】【分析】此题画出正方体模型即可快速判断m 的取值.【详解】如图(1)恰好有3个点到平面α的距离为d ;如图(2)恰好有4个点到平面α的距离为d ;如图(3)恰好有6个点到平面α的距离为d .所以本题答案为B.【点睛】本题以空间几何体为载体考查点,面的位置关系,考查空间想象能力,考查了学生灵活应用知识分析解决问题的能力和知识方法的迁移能力,属于难题.10.()()()cos 0,0f x A x A ωϕω=+>>的图象如图所示,()()sin g x A x ωϕ=--,若将()y f x =的图象向左平移()0a a >个单位长度后所得图象与()y g x =的图象重合,则a 可取的值的是( )A .112πB .512πC .712πD .11π12【答案】B【解析】【分析】根据图象求得函数()y f x =的解析式,即可得出函数()y g x =的解析式,然后求出变换后的函数解析式,结合题意可得出关于a 的等式,即可得出结果.【详解】由图象可得1A =,函数()y f x =的最小正周期为23471T πππ⎛⎫-= ⎪⎝⎭=⨯,22T πω∴==, 777cos 2cos 112126f πππϕϕ⎛⎫⎛⎫⎛⎫=⨯+=+=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭Q , 则()726k k Z πϕππ+=+∈,()26k k Z πϕπ∴=-+∈,取6πϕ=-, ()cos 26f x x π⎛⎫∴=- ⎪⎝⎭,则()2sin 2cos 263g x x x ππ⎛⎫⎛⎫=-+=+ ⎪ ⎪⎝⎭⎝⎭, ()()cos 226g x f x a x a π⎛⎫∴=+=+- ⎪⎝⎭,22263a k πππ-=+,可得()512a k k Z ππ=+∈, 当0k =时,512a π=. 故选:B.【点睛】本题考查利用图象求函数解析式,同时也考查了利用函数图象变换求参数,考查计算能力,属于中等题. 11.在ABC ∆中,D 在边AC 上满足13AD DC =u u u r u u u r ,E 为BD 的中点,则CE =u u u r ( ). A .7388BA BC -u u u r u u u r B .3788BA BC -u u u r u u u r C .3788BA BC +u u u r u u u r D .7388BA BC +u u u r u u u r 【答案】B【解析】【分析】 由13AD DC =u u u r u u u r ,可得34CD CA =u u u r u u u r ,1()2CE CB CD =+u u u r u u u r u u u r 13()24CB CA =+u u u r u u u r ,再将CA BA BC =-u u u r u u u r u u u r 代入即可.【详解】 因为13AD DC =u u u r u u u r ,所以34CD CA =u u u r u u u r ,故1()2CE CB CD =+=u u u r u u u r u u u r 13()24CB CA +=u u u r u u u r 133()244BC BA BC -+-=u u u r u u u r u u u r 3788BA BC -u u u r u u u r . 故选:B.【点睛】本题考查平面向量的线性运算性质以及平面向量基本定理的应用,是一道基础题.12.已知EF 为圆()()22111x y -++=的一条直径,点(),M x y 的坐标满足不等式组10,230,1.x y x y y -+≤⎧⎪++≥⎨⎪≤⎩则ME MF ⋅u u u r u u u r 的取值范围为( )A .9,132⎡⎤⎢⎥⎣⎦ B .[]4,13 C .[]4,12D .7,122⎡⎤⎢⎥⎣⎦【答案】D【解析】【分析】 首先将ME MF ⋅u u u r u u u r 转化为21MT -u u u r ,只需求出MT 的取值范围即可,而MT 表示可行域内的点与圆心(1,1)T -距离,数形结合即可得到答案.【详解】作出可行域如图所示设圆心为(1,1)T -,则()()ME MF MT TE MT TF ⋅=+⋅+=u u u r u u u u r u u u r u u r u u u r u u u r22()()MT TE MT TE MT TE +⋅-=-u u u r u u r u u u r u u r u u u r u u r 21MT =-u u u r ,过T 作直线10x y -+=的垂线,垂足为B ,显然MB MT MA ≤≤,又易得(2,1)A -,所以22[1(2)](11)13MA =--+--=22321(1)TB ==+- 故ME MF ⋅u u u r u u u r 271[,12]2MT =-∈u u u r . 故选:D.【点睛】本题考查与线性规划相关的取值范围问题,涉及到向量的线性运算、数量积、点到直线的距离等知识,考查学生转化与划归的思想,是一道中档题.二、填空题:本题共4小题,每小题5分,共20分。
四川省南充市高中2021届高三数学第一次适应性考试试题 理(含解析)

四川省南充市高中2021届高三数学第一次适应性考试试题 理(含解析)一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}|10A x x =-≥,{}2|1B x x =≤,则AB =( )A. {}|1x x ≥B. {}1|x x ≥-C. {}|1x x ≤D.{}|1x x ≤-【答案】B 【解析】 【分析】化简集合B ,按照并集定义,即可得出答案. 【详解】{}{}2|1|11B x x x x =≤=-≤≤,A B ={}1|x x ≥-.故选:B【点睛】本题考查集合的运算,属于基础题. 2.12i=-( ) A. 2155i -+ B. 2155i -- C.2551i + D.2155i - 【答案】C 【解析】 【分析】分母实数化,即可求得结果. 【详解】12212(2)(2)55i i i i i +==+--+. 故选:C【点睛】本题考查复数的除法,属于基础题. 3.“60A =︒”是“1cos 2A =”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件 【答案】A 【解析】 【分析】根据充分必要条件判断方法,即可得出结论. 【详解】若060A =,则1cos 2A =成立; 若1cos 2A =,则00006036060360()A k k k Z =+⋅-+⋅∈或, 故60A =︒不成立, 所以“60A =︒”是“1cos 2A =”的充分不必要条件. 故选:A【点睛】本题考查充分必要条件的判断,要注意三角函数值与角之间的关系,属于基础题. 4.一个与球心距离为1的平面截球所得的圆面积为π,则球的表面积为( )A. B. 8πC.D. 4π【答案】B 【解析】试题分析:设球的半径为R ,截面小圆半径为r 21r r ππ∴=∴=R ∴=248S R ππ==考点:圆的截面小圆性质及球的表面积点评:球的半径为R ,截面小圆半径为r ,球心到截面的距离为d,则有222R r d =+,球的表面积24S R π= 5.函数1()sin cos 2f x x x =的最小值是( ) A.14B. 12C. 12-D. 14-【答案】D 【解析】 【分析】利用二倍角化简1()sin cos 2f x x x =,即可得答案. 【详解】111()sin cos sin 2244f x x x x ==≥-.故选:D【点睛】本题考查二倍角公式的应用以及三角函数的有界性,属于基础题.6.10112x ⎛⎫+ ⎪⎝⎭的展开式中3x 的系数为( )A. 5B. 10C. 15D. 20【答案】C 【解析】 【分析】根据二项展开式定理写出通项,即可求出结果.【详解】10112x ⎛⎫+ ⎪⎝⎭展开式的通项为1010101101011()(),0,1,2,,1022k k k k kk T C x C x k ---+===,3x 的系数是733101011()1528C C =⨯= 故选:C【点睛】本题考查展开式的系数,掌握通项公式是解题的关键,属于基础题.7.若过点(4,0)A 的直线l 与曲线22(2)1x y -+=有公共点,则直线l 的斜率的取值范围为( )A. ⎡⎣B. (C. 33⎡-⎢⎣⎦D.⎛ ⎝⎭【答案】C 【解析】设直线方程为(4)y k x =-,即40kx y k --=,直线l 与曲线22(2)1x y -+=有公共点,圆心到直线的距离小于等于半径22411k kdk-=≤+,得222141,3k k k≤+≤,选择C另外,数形结合画出图形也可以判断C正确.8.函数()21,1,1x xf xx x⎧-≤⎪=⎨>⎪⎩,若方程()f x a=有且只有一个实数根,则实数a满足()A. 1a= B. 1a> C. 01a≤< D. 0a<【答案】A【解析】【分析】作出函数()f x图像,数形结合,即可求出答案.【详解】做出函数()f x图像,如下图所示:()1f x=有且只有一个实数根.故选:A【点睛】本题考查函数零点的个数,考查数形结合思想,属于基础题.9.设点M是线段BC的中点,点A在直线BC外,若2BC=,AB AC AB AC+=-,则AM =( )A.12B. 1C. 2D. 4【答案】B 【解析】 【分析】||||AB AC AB AC +=-两边平方,可得0AB AC ⋅=,即AB AC ⊥,利用直角三角形斜边中线与斜边长度的关系,即可求出||AM . 【详解】||||AB AC AB AC +=-,两边平方得,222222AB AB AC AC AB AB AC AC +⋅+=-⋅+,0,AB AC AB AC ∴⋅=∴⊥,M 是线段BC的中点,1||||12AM BC ∴==. 故选:B【点睛】本题考查向量的模长以及向量的数量积运算,属于基础题. 10.ABC ∆的内角A ,B ,C 的对边分别为a ,b ,c .若tan tan a ba b A B+=+,则角C =( ) A.6π B.4π C.3π D.2π 【答案】D 【解析】 【分析】利用正弦定理边化角,化切为弦,整理求出A B +值,即可求出结果.【详解】tan tan a b a b A B+=+,sin sin sin sin cos cos sin sin cos cos A BA B A BA B A B+=+=+, sin cos sin cos A A B B -=-+,平方得2sin cos 2sin cos ,sin 22sin 2A A B B A B -=-∴=, 22(0,2),22A B A B π∈∴=、或22A B π+=,,A B ∴=或2A B π+=,若,A B =则sin cos ,tan 1,(0,)A A A A π∴=∴=∈,42A B C ππ∴==∴=,若2A B π+=,则2C π=.故选:D【点睛】本题考查正弦定理边角互化,考查同角间的平方关系和三角函数值与角的关系,属于中档题. 11.设'()f x 是函数()f x 的导函数,且'()2()()f x f x x R >∈,12f e ⎛⎫= ⎪⎝⎭(e 为自然对数的底数),则不等式2(ln )f x x <的解集为( ) A. 0,2e ⎛⎫ ⎪⎝⎭B.C. 1,2e e ⎛⎫⎪⎝⎭D. 2e ⎛⎝ 【答案】B 【解析】 【分析】 构造函数F (x )=()2xf x e,求出导数,判断F (x )在R 上递增.原不等式等价为F (lnx )<F(12),运用单调性,可得lnx <12,运用对数不等式的解法,即可得到所求解集. 【详解】可构造函数F (x )=()2xf x e,F′(x )=()()22222()x xx f x e f x e e -=()()2'2xf x f x e -,由f′(x )>2f (x ),可得F′(x )>0,即有F (x )在R 上递增. 不等式f (lnx )<x 2即为()2f lnx x<1,(x >0),即()2lnxf lnx e<1,x >0.即有F (12)=12f e⎛⎫⎪⎝⎭=1,即为F (lnx )<F (12),由F (x )在R 上递增,可得lnx <12,解得0<x. 故不等式的解集为(0), 故选B .【点睛】利用导数解抽象函数不等式,实质是利用导数研究对应函数单调性,而对应函数需要构造. 构造辅助函数常根据导数法则进行:如()()f x f x '<构造()()xf xg x e =, ()()0f x f x '+<构造()()x g x e f x =, ()()xf x f x '<构造()()f xg x x=, ()()0xf x f x '+<构造()()g x xf x =等12.已知14m <<,1F ,2F 为曲线22:144x y C m +=-的左、右焦点,点P 为曲线C 与曲线22:11E y x m -=-在第一象限的交点,直线l 为曲线C 在点P 处的切线,若三角形12F PF 的内心为点M ,直线1F M 与直线l 交于N 点,则点M ,N 横坐标之差为( ) A. 1- B. 2-C. 3-D. 随m 的变化而变化 【答案】A 【解析】 【分析】先求出P 点坐标,得出切线方程,求出三角形12F PF 的内切圆的半径、直线1F M 的方程,联立求出N 的横坐标,即可得出结论.【详解】联立222214411x y m y x m ⎧+=⎪⎪-⎨⎪-=⎪-⎩消去y,得24,0,x x x m =>∴= 设00(,)P x y ,直线l 方程为00144x xy y m①设三角形12F PF 内切圆半径为r ,则由等面积可得002(42),2M my my m r r y m=+∴==+ ②直线1F M 的方程为()1My x m m=++ ③联立①②③,化简可得36,2N mx m x =∴=,在12F PF ∆中,内切圆圆心M ,各边的切点分别为,,A D E , 由圆的切线性质可得1122||||,||||,||||F A F D EF AF PD PE ===,121212||||||||||||2F P F P F D F E F A F A ∴-=-=-=,. 121||||2,||1M F A F A m F A m x m +=∴=+=+, 1,1M M N x x x =∴-=-.故选:A【点睛】本题考查双曲线方程的性质以及焦点三角形的内切圆,考查直线与椭圆的位置关系,考查计算能力,属于综合题.二、填空题:本大题共4小题,每小题5分,共20分.13.已知()1,1A ,()2,4B -,(),9C x -,且//AB AC ,则x =__________. 【答案】3 【解析】 【分析】根据向量平行的坐标关系,即可求解, 【详解】()1,1A ,()2,4B -,(),9C x -(1,5),(1,10)AB AC x =-=--, //,5(1)100,3AB AC x x ∴--+==.故答案为:3【点睛】本题考查向量的坐标表示、平行向量的坐标形式的充要条件,属于基础题.14.函数()sin f x x x =在区间0,2π⎡⎤⎢⎥⎣⎦上的最大值为_________. 【答案】2 【解析】 【分析】化简函数()f x ,根据自变量的范围,即可求出结论.【详解】()sin 2sin()3f x x x x π=+=+,50,2336x x ππππ≤≤∴≤+≤, ()f x ∴的最大值为2.故答案为:2【点睛】本题考查三角函数的化简,以及三角函数最值,属于基础题.15.已知函数()2sin 1x xxe x f x x e ++=++,则()()()()()()()()()()()54321012345f f f f f f f f f f f -+-+-+-+-++++++的值是________. 【答案】11 【解析】 【分析】根据所求值的自变量的关系,先求()()f x f x +-的值,即可求出结果.【详解】()()f x f x +-=22sin sin()11x x x xxe x xe x x x e e --++-++++-+-+22211x x x x x xe x x xe e e e ++-+-+=+=+,(5)(5)(4)(4)(1)(1)2f f f f f f ∴-+=-+==-+=,(0)1f =,()()()()()()()()()()()54321012345f f f f f f f f f f f -+-+-+-+-++++++=11故答案为:11【点睛】本题考查函数的对称性的应用,关键要转化为研究()()f x f x +-的值,属于中档题. 16.过抛物线()220x py p =>的焦点作斜率为1的直线与该抛物线交于A ,B 两点,又过A ,B 两点作x 轴的垂线,垂足分别为D ,C .若梯形ABCD的面积为p =__________.【解析】 【分析】设1122(,),(,),A x y B x y ,联立直线与抛物线方程求出121,2,,x x y y ,代入12121||()2ABCD S x x y y =-+梯形,即可求出p 的值. 【详解】设1122(,),(,)A x y B x y ,抛物线的焦点(0,)2p F , 直线AB 方程为2p y x =+, 联立222x py p y x ⎧=⎪⎨=+⎪⎩,消去y ,得2220x px p --=,解得121233,,,,22x p x p y p y p -+==+==,212121||()2ABCD S x x y y =-+==梯形p ∴=.故答案为【点睛】本题考查直线与圆锥曲线的位置关系,以及梯形的面积公式,考查计算能力,属于中档题.三、解答题:共70分。
四川省南充市2021届新第一次高考模拟考试数学试卷含解析

四川省南充市2021届新第一次高考模拟考试数学试卷一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知函数()y f x =在R 上可导且()()f x f x '<恒成立,则下列不等式中一定成立的是( ) A .3(3)(0)f e f >、2018(2018)(0)f e f > B .3(3)(0)f e f <、2018(2018)(0)f e f > C .3(3)(0)f e f >、2018(2018)(0)f e f < D .3(3)(0)f e f <、2018(2018)(0)f e f < 【答案】A 【解析】 【分析】 设()()x f x g x e=,利用导数和题设条件,得到()0g x '>,得出函数()g x 在R 上单调递增, 得到()0(3)(2018)g g g <<,进而变形即可求解. 【详解】由题意,设()()x f x g x e =,则()2()()()()()x x x xf x e f x e f x f xg x e e '''--'==, 又由()()f x f x '<,所以()()()0xf x f xg x e '-'=>,即函数()g x 在R 上单调递增, 则()0(3)(2018)g g g <<,即032018(0)(3)(2018)(0)f f f f e e e =<<,变形可得32018(3)(0),(2018)(0)f e f f e f >>.故选:A. 【点睛】本题主要考查了利用导数研究函数的单调性及其应用,以及利用单调性比较大小,其中解答中根据题意合理构造新函数,利用新函数的单调性求解是解答的关键,着重考查了构造思想,以及推理与计算能力,属于中档试题.2.已知函数()f x 在R 上都存在导函数()f x ',对于任意的实数都有2()e ()x f x f x -=,当0x <时,()()0f x f x '+>,若e (21)(1)a f a f a +≥+,则实数a 的取值范围是( )A .20,⎡⎤B .2,0⎡⎤-C .[0,)+∞D .(,0]-∞【解析】 【分析】先构造函数,再利用函数奇偶性与单调性化简不等式,解得结果. 【详解】令()()x g x e f x =,则当0x <时,()[()()]0xg x e f x f x ''=+>,又()()()()xx g x ef x e f xg x --=-==,所以()g x 为偶函数,从而()()211ae f a f a +≥+等价于211(21)(1),(21)(1)a a ef a e f ag a g a +++≥++≥+, 因此22(|21|)(|1|),|21||1|,3200.3g a g a a a a a a -+≥-+-+≥-++≤∴-≤≤选B. 【点睛】本题考查利用函数奇偶性与单调性求解不等式,考查综合分析求解能力,属中档题.3.抛物线24y x =的焦点为F ,点(,)P x y 为该抛物线上的动点,若点(1,0)A -,则PFPA的最小值为( )A .12B .C .2D 【答案】B 【解析】 【分析】通过抛物线的定义,转化PF PN =,要使||||PF PA 有最小值,只需APN ∠最大即可,作出切线方程即可求出比值的最小值. 【详解】解:由题意可知,抛物线24y x =的准线方程为1x =-,(1,0)A -,过P 作PN 垂直直线1x =-于N ,由抛物线的定义可知PF PN =,连结PA ,当PA 是抛物线的切线时,||||PF PA 有最小值,则APN ∠最大,即PAF ∠最大,就是直线PA 的斜率最大, 设在PA 的方程为:(1)y k x =+,所以2(1)4y k x y x=+⎧⎨=⎩, 解得:2222(24)0kx k x k -++=,所以224()2440k k ∆=--=,解得1k =±,||2cos ||2PF NPA PA =∠=. 故选:B .【点睛】本题考查抛物线的基本性质,直线与抛物线的位置关系,转化思想的应用,属于基础题.4.2-31ii =+( ) A .15-22i B .15--22iC .15+22i D .15-+22i 【答案】B 【解析】 【分析】利用复数代数形式的乘除运算化简得答案. 【详解】()()()()231231515111222i i i i z i i i i -----====--++-.故选B . 【点睛】本题考查复数代数形式的乘除运算,考查了复数的基本概念,是基础题.5.已知双曲线C :22221x y a b-=(0a >,0b >)的焦距为2c .点A 为双曲线C 的右顶点,若点A 到双曲线C 的渐近线的距离为12c ,则双曲线C 的离心率是( ) A 2 B 3C .2D .3【答案】A 【解析】【详解】由题意(,0)A a ,一条渐近线方程为b y x a =,即0bx ay -=,∴2212d c a b ==+, 222214a b c c =,即22222()14a c a c c -=,42440e e -+=,2e =. 故选:A . 【点睛】本题考查求双曲线的离心率,掌握渐近线方程与点到直线距离公式是解题基础. 6.已知111M dx x =+⎰,20cos N xdx π=⎰,由程序框图输出的S 为( )A .1B .0C .2πD .ln 2【答案】D 【解析】试题分析:1011ln(1)|ln 201M dx x x ==+=+⎰,20cos sin |120N xdx x ππ===⎰,所以M N <,所以由程序框图输出的S 为ln 2.故选D . 考点:1、程序框图;2、定积分. 7.已知复数21aibi i-=-,其中a ,b R ∈,i 是虚数单位,则a bi +=( ) A .12i -+ B .1C .5D 5【答案】D 【解析】 试题分析:由21aibi i-=-,得()21,1,2ai i bi b i a b -=-=+∴=-=,则8.若[]0,1x ∈时,|2|0x e x a --≥,则a 的取值范围为( ) A .[]1,1- B .[]2,2e e --C .[]2e,1-D .[]2ln 22,1-【答案】D 【解析】 【分析】由题得22x x x e a x e -≤≤+对[]0,1x ∀∈恒成立,令()()2g 2,xxf x x e x x e =-=+,然后分别求出()()max min ,f xg x 即可得a 的取值范围.【详解】由题得22x x x e a x e -≤≤+对[]0,1x ∀∈恒成立,令()()2g 2,xxf x x e x x e =-=+, ()2x f x e '=-Q 在[]0,1单调递减,且()ln 20f '=, ()f x ∴在()0,ln 2上单调递增,在()ln 2,1上单调递减, ()()max ln 22ln 22a f x f ∴≥==-,又()g 2xx x e =+在[]0,1单调递增,()()min 01a g x g ∴≤==,∴a 的取值范围为[]2ln 22,1-.故选:D 【点睛】本题主要考查了不等式恒成立问题,导数的综合应用,考查了转化与化归的思想.求解不等式恒成立问题,可采用参变量分离法去求解.9.直三棱柱111ABC A B C -中,12CA CC CB ==,AC BC ⊥,则直线1BC 与1AB 所成的角的余弦值为( )A B .C D .35【答案】A 【解析】 【分析】设122CA CC CB ===,延长11A B 至D ,使得111A B B D =,连1,BD C D ,可证1//AB BD ,得到1C BD ∠(或补角)为所求的角,分别求出111,,BC AB C D ,解1C BD V 即可.设122CA CC CB ===,延长11A B 至D ,使得111A B B D =,连1,BD C D ,在直三棱柱111ABC A B C -中,1111//,AB A B AB A B =,11//,AB B D AB B D ∴=,四边形1ABDB 为平行四边形,1//AB BD ∴,1C BD ∴∠(或补角)为直线1BC 与1AB 所成的角,在1Rt BCC △中,22115BC CC BC =+=,在111Rt A B C △中,221111111115,cos 5A B AC B C B AC =+=∠=, 在11AC D V 中,22211111111112cos 420168C D A C A D A C A D B A C =+-⋅∠=+-=,在11Rt AA B △中,22111113,3AB AA A B BD AB =+=∴==,在1BC D V 中,22211115cos 2565BC BD C D C BD BC BD +-∠===⋅. 故选:A.【点睛】本题考查异面直线所成的角,要注意几何法求空间角的步骤“做”“证”“算”缺一不可,属于中档题. 10.设i 是虚数单位,a R ∈,532aii a i+=-+,则a =( ) A .2- B .1-C .1D .2【答案】C 【解析】 【分析】 由532aii a i+=-+,可得()()()5323232ai a i i a a i +=+-=++-,通过等号左右实部和虚部分别相等解:532aii a i+=-+Q,()()()5323232ai a i i a a i ∴+=+-=++- 53232a a a =+⎧∴⎨-=⎩,解得:1a =.故选:C. 【点睛】本题考查了复数的运算,考查了复数相等的涵义.对于复数的运算类问题,易错点是把2i 当成1进行运算. 11.已知抛物线C :()220y px p =>,直线()02p y k x k ⎛⎫=-> ⎪⎝⎭与C 分别相交于点A ,M 与C 的准线相交于点N ,若AM MN =,则k =( )A .3B .3C .D .13【答案】C 【解析】 【分析】根据抛物线的定义以及三角形的中位线,斜率的定义表示即可求得答案. 【详解】显然直线()02p y k x k ⎛⎫=-> ⎪⎝⎭过抛物线的焦点,02p F ⎛⎫ ⎪⎝⎭如图,过A,M 作准线的垂直,垂足分别为C ,D ,过M 作AC 的垂线,垂足为E根据抛物线的定义可知MD=MF ,AC=AF ,又AM=MN ,所以M 为AN 的中点,所以MD 为三角形NAC 的中位线,故MD=CE=EA=12AC 设MF=t ,则MD=t ,AF=AC=2t ,所以AM=3t ,在直角三角形AEM 中,==所以tan ME k MAE AE t=∠===故选:C 【点睛】本题考查求抛物线的焦点弦的斜率,常见于利用抛物线的定义构建关系,属于中档题.12.已知点(25,310A 在双曲线()2221010x y b b-=>上,则该双曲线的离心率为( )A 10B 10C 10D .210【答案】C 【解析】 【分析】将点A 坐标代入双曲线方程即可求出双曲线的实轴长和虚轴长,进而求得离心率. 【详解】将5x =310y =()2221010x y b b-=>得310b =,而双曲线的半实轴10a =,所以2210c a b =+=,得离心率10ce a==故选C. 【点睛】此题考查双曲线的标准方程和离心率的概念,属于基础题. 二、填空题:本题共4小题,每小题5分,共20分。
四川省南充市高中2021届高考数学第一次适应性考试试题 理

四川省南充市高中2021届高考数学第一次适应性考试试题 理本试卷分第I 卷(选择题)和第II 卷(非选择题)。
第I 卷1至2页,第II 卷3至4页,共4页,满分150分,考试时间120分钟。
考生作答时,须将答案答在答题卡上,在本试卷、草稿纸上答题无效,考试结束后,只将答题卡交回。
第I 卷 选择题(共60分)注意事项:必须使用2B 铅笔在答题卡上将所选答案对应的标题涂黑。
第I 卷共12小题。
一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
.1.已知集合A ={x|x -1≥0},B ={x|x 2≤1},则A ∪B =A.{x|x ≥1}B.{x|x ≥-1}C.{x|x ≤1}D.{x|x ≤-1}2.12i -= A.2155i -+ B.2155i -- C.2155i + D.2155i -3.“A =60°”是“cosA =12”的A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件 4.用与球心距离为1的平面去截球,所得的截面圆面积为π,则球的表面积为πC.8πD.4π5.函数f(x)=12sinxcosx 的最小值是 A.14 B.12 C.-12 D.14 6.101(1)2x +的展开式中x 3的系数为A.5B.10C.15D.207..过点A(4,0)的直线l 与圆(x -2)2+y 2=1有公共点,则直线l 的斜率的取值范围是 A.(] C.(] 8.函数1(),1x f x x x ≤=⎨>⎪⎩,若方程f(x)=a 有且只有一个实数根,则实数a 满足A.a =1B.a>1C.0≤a<1D.a<09.设点M 是线段BC 的中点,点A 在直线BC 外,若2,BC AB AC AB AC =+=-,则AM = A.12B.1C.2D.4 10.△ABC 的内角A ,B ,C 的对边分别为a ,b ,c 。
四川省南充市届高三第一次高考适应性考试

四川省南充市届高三第一次高考适应性考试数学试卷(理科)第Ⅰ卷(选择题 共分)一、选择题:本大题共个小题,每小题分,共分.在每小题给出的四个选项中,只有一项是符合题目要求的..若集合()(){}140M x x x =--=,()(){}130N x x x =+-<,则M N =( ).∅ .{}1 .{}4 .{}1 4,.若复数1z i =+,则21z z =-( ).2 .2- .2i .2i -.已知向量1 sin 2a α⎛⎫= ⎪⎝⎭,,()sin 1b α=,,若a b ∥,则锐角α为( ) .30︒ .60︒ .45︒ .75︒ .设33log 10 log 7a b ==,,则3a b -=( ) .1049 .4910 .710 .107.已知等差数列{}n a 的公差为,若134 a a a ,,成等比数列,则2a 等于( ) .4- .6- .8- .10-.如图是一个几何体的正视图与侧视图,其俯视图是面积为82的矩形,则该几何体的表面积是( ).2082+ .2482+ ..某程序框图如图所示,执行该程序,若输入,则输出S =( ). . ..已知点()() 0P a b ab ≠,是圆222x y r +=内的一点,直线m 是以P 点为中点的弦所在的直线,直线l 的方程为2ax by r +=,那么( ).m l ∥,且l 与圆相交 .m l ⊥,且l 与圆相切 .m l ∥,且l 与圆相离 .m l ⊥,且l 与圆相离 .设1sin 43πθ⎛⎫+= ⎪⎝⎭,则sin 2θ=( ).19 .79 .19- .79- .如果一个球的外切圆锥的高是这个球的半径的倍,则圆锥的侧面积和球的表面积之比为( ) .9:4 .4:3 .3:1 .3:2.已知抛物线()220y px p =>,过其焦点且斜率为的直线交抛物线于 A B ,两点,若线段AB 的中点的纵坐标为,则该抛物线的准线方程为( ).1x = .1x =- .2x = .2x =-.已知 αβ,是三次函数()3211232f x x ax bx =++的两个极值点,且()0 1α∈,,()1 2β∈,, a b R ∈,,则21b a --的取值范围是( ) .1 14⎛⎫ ⎪⎝⎭,.1 12⎛⎫ ⎪⎝⎭, .11 24⎛⎫- ⎪⎝⎭, .11 22⎛⎫- ⎪⎝⎭, 第Ⅱ卷(非选择题 共分)二、填空题(每题分,满分分,将答案填在答题纸上).512x x ⎛⎫+ ⎪⎝⎭的展开式中,3x 的系数是 (用数学填写答案);.若1a >,则11a a +-的最小值是 ..如果函数()()sin 2f x x θ=+,函数()()'f x f x +为奇函数,()'f x 是()f x 的导函数,则tan θ= . .已知正数数列{}n a 的前n 项和()2114n n S a =+,则n a = . 三、解答题 (本大题共小题,共分.解答应写出文字说明、证明过程或演算步骤.). (本小题满分分)ABC △的内角 A B C ,,的对边分别为 a b c ,,,已知()cos 2cos b C a c B =-. (Ⅰ)求B ;(Ⅱ)若2c =,3b =,求ABC △的面积. . (本小题满分分)某示范高中为了推进新课程改革,满足不同层次学生的需求,决定从高一年级开始,在每周周一、周三、周五的课外活动期间同时开设数学、物理、化学、生物和信息技术辅导讲座,每位有兴趣的同学可以在期间任何一天参加任何一门科目的辅导讲座,也可以放弃任何一门科目的辅导讲座.(规定:各科达到预先设定的人数时称为满座,否则称为不满座)统计数据表明,各讲座各天的满座概率如下表: 信息技术生物化学物理数学周一 14 14 14 14 12周三 12 12 12 12 23 周五1313131323(Ⅰ)求数学辅导在周一、周三、周五都不满座的概率;(Ⅱ)设周三各辅导讲座满座的科目数为X ,求X 的分布列和数学期望()E X . . (本小题满分分)如图,ABCD 是菱形,PA ⊥平面ABCD ,2PA AD ==,60BAD ∠=︒. (Ⅰ)求证:平面PBD ⊥平面PAC ; (Ⅱ)求二面角D PB C --的余弦值.PODCBA. (本小题满分分)已知椭圆()222210x y a b a b +=>>的离心率为12,两焦点之间的距离为.(Ⅰ)求椭圆的标准方程;(Ⅱ)过椭圆的右顶点作直线交抛物线24y x =于 A B ,两点,求证:OA OB ⊥(O 为坐标原点). . (本小题满分分)已知函数()()2ln 22x f x x a =--(a 为常数,0a ≠).(Ⅰ)当1a =时,求函数()f x 在点()()3 3f ,的切线方程 (Ⅱ)求()f x 的单调区间;(Ⅲ)若()f x 在0x 处取得极值,且30 2 2x e e ⎡⎤∉++⎣⎦,,而()0f x ≥在32 2e e ⎡⎤++⎣⎦,上恒成立,求实数a 的取值范围.(其中e 为自然对数的底数)请考生在、两题中任选一题作答,如果多做,则按所做的第一题记分.. (本小题满分分)在直角坐标系xOy 中,直线l 的参数方程为3x a ty t ⎧=+⎪⎨=⎪⎩,(t 为参数),在极坐标系(与直角坐标系xOy 取相同的单位长度,且以原点O 为极点,以x 轴正半轴为极轴)中,圆C 的方程为4cos ρθ=. (Ⅰ)求圆C 在直角坐标系中的方程; (Ⅱ)若圆C 与直线l 相切,求实数a 的值. . (本小题满分分)已知函数()()21f x x a x a R =---∈.(Ⅰ)当3f x的最大值;a=时,求函数()(Ⅱ)解关于x的不等式()0f x≥.四川省南充市届高三第一次高考适应性考试数学试卷(理科)参考答案及评分意见一、选择题、:二、填空题.2- .21n -三、解答题.解:(Ⅰ)由已知及正弦定理得()sin cos 2sin sin cos 2sin cos sin cos B C A C B A B C B =-⋅=-.………………分则sin cos sin cos 2sin cos B C C B A B +=.………………分 ()sin 2sin cos B C A B +=,故sin 2sin cos A A B =. 因为,在ABC △中,sin 0A ≠.所以1cos 2B =,3B π=.…………………………分(Ⅱ)由已知及余弦定理得 2944cos a a B =+-,又3B π=,.解:(Ⅰ)设数学辅导讲座在周一、周三、周五都不满座为事件A ,则 ()122111123318A P ⎛⎫⎛⎫⎛⎫=---= ⎪⎪⎪⎝⎭⎝⎭⎝⎭.……………………分(Ⅱ)X 的可能取值为,,,,,. ()40121112348X P =⎛⎫⎛⎫=--=⎪ ⎪⎝⎭⎝⎭.……………………分()34141112121111223238X P C =⎛⎫⎛⎫⎛⎫=⋅-⋅-+-⋅= ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭.……………………分 ()22321442112112711122322324X P C C =⎛⎫⎛⎫⎛⎫⎛⎫=⋅⋅-⋅-+⋅-⋅= ⎪⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭.………………分 ()3223244311211211112232233X P C C =⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=⋅-⋅-+⋅-⋅= ⎪⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭.…………分 ()43344121123112322316X P C =⎛⎫⎛⎫⎛⎫⎛⎫=⋅-+⋅-⋅=⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭. ()451212324X P =⎛⎫=⋅= ⎪⎝⎭.……………………分 XP148 18 724 13 316 124数学期望()117131801234548824316243E X =⨯+⨯+⨯+⨯+⨯+⨯=.………………分 .(Ⅰ)证明:由ABCD 是菱形可得BD AC ⊥, 因为PA ⊥平面ABCD ,BD ⊂平面ABCD , 所以PA BD ⊥,又PAAC A =,所以BD ⊥平面PAC ,又BD ⊂平面PBD , 故平面PBD ⊥平面PAC .……………………分(Ⅱ)解:以OA 为x 轴的正方向,OB 为y 轴的正方向,建立如图所示的直角坐标系,则()0 0 0O ,,,()0 1 0B ,,,()3 0 2P ,,,()3 0 0C -,,.……分设平面PBD 的一个法向量()1111 n x y z =,,,由1n OB ⊥,1n OP ⊥,可得11111101003020x y z x y z ⋅+⋅+⋅=⎧⎪⎨+⋅+=⎪⎩,即111320y x z =⎧⎪⎨+=⎪⎩, 所以可取131 0 2n ⎛⎫=- ⎪ ⎪⎝⎭,,.……………………分 同理可得平面PBC 的一个法向量()2 13 3n =--,,.………………分 所以1212125cos 7n n n n n n ⋅<>==,. 故二面角D PB C --的余弦值为57.………………分 .(Ⅰ)解:由题意可得24c =,12c a =.所以 4 2a c ==,. 由222b a c =-可得212b =,所以椭圆标准方程为:2211612x y +=.……………………分(Ⅱ)证明:由(Ⅰ)可得椭圆的右顶点为()4 0,,由题意得,可设过()4 0,的直线方程为: 4x my =+.………………………………………………分 由244x my y x=+⎧⎨=⎩消去x 得:24160y my --=. 设()11 A x y ,,()22 B x y ,,则1212416y y my y +=⎧⎨=-⎩.………………分所以()()()()21212121212124414160OA OB x x y y my my y y m y y m y y ⋅=+=+++=++++=, 故OA OB ⊥.………………………………………………分 .解:()1'2xf x x a=--(2x >) (Ⅰ)当1a =时,()1'2f x x x =-,()'32f =-.()932f =-, 所以,函数()f x 在点()()3 3f ,处的切线方程为: ()9232y x +=--,即4230x y +-=.…………………………分 (Ⅱ)()()212'22x x x a f x x a a x --=-=---()()()21112x a a x ⎡⎤=---+⎣⎦-, 因为2x >,所以20x ->,①当0a <时,()()()21120x a x x a --+=-->在2x >上成立, 所以()'f x 当2x >恒大于,故()f x 在()2 +∞,上是增函数.………………………………分 ②当0a >时,()()()()1'11112f x x a x a a x =--++--+-,因为2x >,所以110x a -++>,()20a x ->,当11x a ≥++时,()'0f x ≤,()f x 为减函数;当211x a ≤≤++时,()'0f x ≥,()f x 为增函数.………………分 综上:当0a <时,()f x 在()2 +∞,上为增函数; 当0a >时,()f x 在()2 11a ++,上为增函数,在()1 1 a +++∞,上为减函数.…………分 (Ⅲ)由(Ⅱ)知0x 处有极值,故0a >,且011x a =++,因为30 2 2x e e ⎡⎤∉++⎣⎦,且22e +>,所以()f x 在32 2e e ⎡⎤++⎣⎦,上单调.……………………分 当32 2e e ⎡⎤++⎣⎦,为增区间时,()0f x ≥恒成立,则有()363211220e a a e ef e ⎧+<++⎪⇒>+⎨+≥⎪⎩. 当32 2e e ⎡⎤++⎣⎦,为减区间时,()0f x ≥恒成立,则有 ()2633221144206a e e e a e e f e a ⎧<+⎧+>++⎪⎪⇒⎨⎨+++≥≥⎪⎪⎩⎩解集为空集. 综上:当632a e e >+时满足条件.…………………………分 .解:(Ⅰ)由4cos ρθ=得24cos ρρθ=, 结合极坐标与直角坐标的互化公式cos sin x y ρθρθ=⎧⎨=⎩,得224x y x +=,即()2224x y -+=.…………………………分(Ⅱ)由3x a t y t ⎧=+⎪⎨=⎪⎩(t 为参数)化为普通方程,得30x y a --=,l 与圆C 相切,2213a -=+.所以2a =-或.…………………………分.解:(Ⅰ)当3a =时,()()()()133********x x f x x x x x x x --≥⎧⎪=---=-+<<⎨⎪+≤⎩,所以,当1x =时,()f x 取得最大值.……………………分 (Ⅱ)由()0f x ≥,得21x a x -≥-, 两边平方得()()2241x a x -≥-, ()()2320x a x a ---+≤⎡⎤⎡⎤⎣⎦⎣⎦,所以①当1a >,不等式解集为22 3a a +⎛⎫- ⎪⎝⎭,;②当1a =,不等式解集为{}1x x =;③当1a <,不等式解集为2 23a a +⎛⎫- ⎪⎝⎭,.……………………分。
四川省南充市2021届新高考数学第一次调研试卷含解析

四川省南充市2021届新高考数学第一次调研试卷一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.若实数,x y 满足的约束条件03020y x y x y ≥⎧⎪+-≤⎨⎪-≥⎩,则2z x y =+的取值范围是( )A .[)4+∞,B .[]06,C .[]04,D .[)6+∞,【答案】B【解析】【分析】 根据所给不等式组,画出不等式表示的可行域,将目标函数化为直线方程,平移后即可确定取值范围.【详解】实数,x y 满足的约束条件03020y x y x y ≥⎧⎪+-≤⎨⎪-≥⎩,画出可行域如下图所示:将线性目标函数2z x y =+化为2y x z =-+,则将2y x =-平移,平移后结合图像可知,当经过原点()0,0O 时截距最小,min 0z =;当经过()3,0B 时,截距最大值,max 2306z =⨯+=,所以线性目标函数2z x y =+的取值范围为[]0,6,故选:B.【点睛】本题考查了线性规划的简单应用,线性目标函数取值范围的求法,属于基础题.2.已知实数x ,y 满足约束条件220220x y x y +-≥⎧⎪-+≥⎨⎪,则22x y +的取值范围是( )A .25,22⎡⎤⎢⎥⎣B .4,85⎡⎤⎢⎥⎣⎦C .2,85⎡⎤⎢⎥⎣⎦D .[]1,8【答案】B【解析】【分析】画出可行域,根据可行域上的点到原点距离,求得22xy +的取值范围. 【详解】由约束条件作出可行域是由(2,0)A ,(0,1)B ,(2,2)C 三点所围成的三角形及其内部,如图中阴影部分,而22x y +可理解为可行域内的点到原点距离的平方,显然原点到AB 所在的直线220x y +-=的距离是可行域内的点到原点距离的最小值,此时222245OA OB x y OD AB ⋅⎛⎫+=== ⎪⎝⎭,点C 到原点的距离是可行域内的点到原点距离的最大值,此时2222228x y +=+=.所以22x y +的取值范围是4,85⎡⎤⎢⎥⎣⎦.故选:B【点睛】本小题考查线性规划,两点间距离公式等基础知识;考查运算求解能力,数形结合思想,应用意识. 3.已知某几何体的三视图如图所示,则该几何体的体积是( )A .643B .64C .323D .32【解析】【分析】根据三视图,还原空间几何体,即可得该几何体的体积.【详解】由该几何体的三视图,还原空间几何体如下图所示:可知该几何体是底面在左侧的四棱锥,其底面是边长为4的正方形,高为4, 故()16444433V =⨯⨯⨯=.故选:A【点睛】本题考查了三视图的简单应用,由三视图还原空间几何体,棱锥体积的求法,属于基础题.4.如图是国家统计局公布的年入境游客(单位:万人次)的变化情况,则下列结论错误的是()A .2014年我国入境游客万人次最少B .后4年我国入境游客万人次呈逐渐增加趋势C .这6年我国入境游客万人次的中位数大于13340万人次D .前3年我国入境游客万人次数据的方差小于后3年我国入境游客万人次数据的方差【答案】D【解析】【分析】ABD 可通过统计图直接分析得出结论,C 可通过计算中位数判断选项是否正确.A.由统计图可知:2014年入境游客万人次最少,故正确;B.由统计图可知:后4年我国入境游客万人次呈逐渐增加趋势,故正确;C.入境游客万人次的中位数应为13340.13与13604.33的平均数,大于13340万次,故正确;D.由统计图可知:前3年的入境游客万人次相比于后3年的波动更大,所以对应的方差更大,故错误. 故选:D.【点睛】本题考查统计图表信息的读取以及对中位数和方差的理解,难度较易.处理问题的关键是能通过所给统计图,分析出对应的信息,对学生分析问题的能力有一定要求.5.已知双曲线2221xya-=的一条渐近线方程是3y x=,则双曲线的离心率为()AB.3CD.3【答案】D 【解析】双曲线的渐近线方程是1y xa=±,所以1a=1a b==,2224c a b=+=,即2c=,cea== D.6.《九章算术》是我国古代数学名著,书中有如下问题:“今有勾六步,股八步,问勾中容圆,径几何?”其意思为:“已知直角三角形两直角边长分别为6步和8步,问其内切圆的直径为多少步?”现从该三角形内随机取一点,则此点取自内切圆的概率是()A.12πB.3πC.6πD.9π【答案】C【解析】【分析】利用直角三角形三边与内切圆半径的关系求出半径,再分别求出三角形和内切圆的面积,根据几何概型的概率计算公式,即可求解.【详解】10=,利用等面积法,可得其内切圆的半径为6826810⨯==++r,所以向次三角形内投掷豆子,则落在其内切圆内的概率为2216682ππ⋅=⨯⨯.【点睛】本题主要考查了面积比的几何概型的概率的计算问题,其中解答中熟练应用直角三角形的性质,求得其内切圆的半径是解答的关键,着重考查了推理与运算能力.7.如图是一个算法流程图,则输出的结果是( )A .3B .4C .5D .6【答案】A【解析】【分析】 执行程序框图,逐次计算,根据判断条件终止循环,即可求解,得到答案.【详解】由题意,执行上述的程序框图:第1次循环:满足判断条件,2,1x y ==;第2次循环:满足判断条件,4,2x y ==;第3次循环:满足判断条件,8,3x y ==;不满足判断条件,输出计算结果3y =,故选A .【点睛】本题主要考查了循环结构的程序框图的结果的计算与输出,其中解答中执行程序框图,逐次计算,根据判断条件终止循环是解答的关键,着重考查了运算与求解能力,属于基础题.8.设i 为虚数单位,若复数(1)22z i i -=+,则复数z 等于( )A .2i -B .2iC .1i -+D .0【答案】B【解析】根据复数除法的运算法则,即可求解. 【详解】22(1)22,21iz i i z ii+-=+==-.故选:B.【点睛】本题考查复数的代数运算,属于基础题.9.对两个变量进行回归分析,给出如下一组样本数据:()0.675,0.989-,()1.102,0.010-,()2.899,1.024,()9.101,2.978,下列函数模型中拟合较好的是()A.3y x=B.3xy=C.()21y x=--D.3logy x=【答案】D【解析】【分析】作出四个函数的图象及给出的四个点,观察这四个点在靠近哪个曲线.【详解】如图,作出A,B,C,D中四个函数图象,同时描出题中的四个点,它们在曲线3logy x=的两侧,与其他三个曲线都离得很远,因此D是正确选项,故选:D.【点睛】本题考查回归分析,拟合曲线包含或靠近样本数据的点越多,说明拟合效果好.10.已知函数2,0()4,0x xf xx x-⎧⎪=+>…,若()02f x<,则x的取值范围是()A.(,1)-∞-B.(1,0]-C.(1,)-+∞D.(,0)-∞【答案】B【解析】【分析】对0x 分类讨论,代入解析式求出0()f x ,解不等式,即可求解.【详解】 函数2,0()4,0x x f x xx -⎧⎪=⎨+>⎪⎩„,由()02f x < 得00220x x -⎧<⎪⎨⎪⎩„或00420x x ⎧+<⎪⎨>⎪⎩ 解得010-<x „.故选:B.【点睛】本题考查利用分段函数性质解不等式,属于基础题.11.在三棱锥S ABC -中,4SB SA AB BC AC =====,26SC =,则三棱锥S ABC -外接球的表面积是( )A .403πB .803πC .409πD .809π 【答案】B【解析】【分析】取AB 的中点D ,连接SD 、CD ,推导出90SDC ∠=o ,设设球心为O ,ABC ∆和SAB ∆的中心分别为E 、F ,可得出OE ⊥平面ABC ,OF ⊥平面SAB ,利用勾股定理计算出球O 的半径,再利用球体的表面积公式可得出结果.【详解】取AB 的中点D ,连接SD 、CD ,由SAB ∆和ABC ∆都是正三角形,得SD AB ⊥,CD AB ⊥,则34232SD CD ==⨯=,则222222,由勾股定理的逆定理,得o .设球心为O ,ABC ∆和SAB ∆的中心分别为E 、F .由球的性质可知:OE ⊥平面ABC ,OF ⊥平面SAB , 又312343OE DF OE OF ====⨯⨯=,由勾股定理得2226OD OE DE =+=. 所以外接球半径为22222660233R OD BD ⎛⎫=+=+= ⎪ ⎪⎝⎭. 所以外接球的表面积为2260804433S R πππ⎛⎫===⎪ ⎪⎝⎭. 故选:B.【点睛】本题考查三棱锥外接球表面积的计算,解题时要分析几何体的结构,找出球心的位置,并以此计算出球的半径长,考查推理能力与计算能力,属于中等题.12.某地区教育主管部门为了对该地区模拟考试成进行分析,随机抽取了200分到450分之间的2000名学生的成绩,并根据这2000名学生的成绩画出样本的频率分布直方图,如图所示,则成绩在[250,350]内的学生人数为( )A .800B .1000C .1200D .1600【答案】B【解析】【分析】 由图可列方程算得a ,然后求出成绩在[250,350]内的频率,最后根据频数=总数×频率可以求得成绩在[250,350]内的学生人数.【详解】所以成绩在[250,350]内的频率(0.0040.006)500.5=+⨯=,所以成绩在[250,350]内的学生人数20000.51000=⨯=.故选:B【点睛】本题主要考查频率直方图的应用,属基础题.二、填空题:本题共4小题,每小题5分,共20分。
四川省南充市高三高考适应性考试(一诊)考试数学(理)答案

2024届南充一诊理科数学参考答案一、选择题:本题共12小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项符合题目要求.题号123456789101112选项CDCABABDBDCD二.填空题:本大题共4小题,每小题5分,共20分.把答案填在答题卡上.13.1 14.3 -15.87 π16.21 三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17―21题必考题,每个试题考生必须作答.第22、23题为选考题,考试根据要求作答.(一)必考题17.解:(1) 数列{}n a 是等比数列且4a 是26a 和3a 的等差中项21131 3246262q a q a q a a a a +=+=∴即0622=--q q 整理得:解得:2=q 或23-=q .2211n n n q a a q =⋅==-时,当.)23(2231-11n n n q a a q -⋅=⋅=-=-时,当*).( 23(221-N n a a n n n n ∈-⋅==∴或(2):由(1)得,若0>q ,nn a 2=111)1(12log 2log 1log log 1122122+-=+=⋅=⋅=++n n n n a a b n n n n n .20242023202411 2024120231()2023120221()3121()211( 20232022212023=-=-+-++-+-=++++= b b b b T 18解:(1).由题意得60140100100)40802060(200))()()(()(222⨯⨯⨯⨯-⨯=++++-=d b c a d c b a bc ad n K 879.7524.921200>≈=分4 分6 分8 分12 分4故有99.5%的把握认为70岁以上老人感染支原体肺炎与自身有慢性疾病有关.(2).现从感染支原体肺炎的60位老人中按分层抽样的方式抽出6人,则6人中有慢性疾病4人,无有慢性疾病2人.再从6人中随机抽出4人,则抽出的4人中可能有以下3种组合:①有慢性疾病4人;此时8=ξ万元②有慢性疾病3人,无有慢性疾病1人;此时7=ξ万元③有慢性疾病2人,无有慢性疾病2人;此时6=ξ万元所以ξ的可能取值为6 7 8,,故151)8(4644===C C P ξ;158)7(461234===C C C P ξ;156)6(462224===C C C P ξ故ξ的分布列为:ξ876P15115852则ξ的数学期望32052615871518)(=⨯+⨯+⨯=ξE (万元)19(1).方法一:证明:取BD 的中点F ,连结AF22 232 422=-==∴==⊥∴=DF AD AF DF AD BD BDAF AB AD DEAF DE AF DE BD DE BCD DE =∴=⊥∴⊥,平面//22 FDEA 四边形∴为矩形BDAE //∴BCD AE BCDBD BCD AE 平面平面平面// ∴⊂⊄ 分5 分6 分8 分11 分12 分6 分2 分4方法二:证明:取BD 的中点F ,连结AF22 4 3222=-=∴⊥∴===DF AD AF BD AF BD AB AD , BCD AF BDBCD ABDE ABDE AF BCDABDE ABDE DE BCD DE 平面平面平面,平面平面平面平面,平面⊥∴=⊂⊥∴⊂⊥ DEAF DE AF =∴,//FDEA 四边形∴为矩形BDAE //∴BCD AE BCDBD BCD AE 平面平面平面// ∴⊂⊄ (2)取BC 的中点M ,连结FM AM ,.90=∠BCD 2==∴FB CF ,BCD DE DE AF 平面,⊥// BCD AF 平面⊥∴CFAF ⊥∴222==AF CF ,又3222=+=∴CF AF AC AB AC =∴的平面角为二面角的中点为D BC A AMF AMBC MF BC BC M --∠∴⊥⊥∴, 22tan ==∠∆∴MFAFAMF AFM Rt 中,3221==∴=∴BC CD FM ,分2 分5 分6 分4 分8方法一:以轴,为轴,为为坐标原点,y CB x CD C 建立如图所示的空间直角坐标系xyz C -,()() 0,0,2 0,0,0,,D C ∴ )22,3,1( )22,0,2(,,A E ).0,32,0(B )0,32,0( )22,3,1( )22,0,2(===∴CB CA CE ,,设平面ABC 的法向量),,( z y x n =, 0 0⎪⎩⎪⎨⎧=⋅=⋅CB n CA n 由 0320223⎩⎨⎧==++y z y x 得1-=z 取得:)1,0,22( -=n 设直线CE 与平面ABC 所成角为θ,9633222222 , cos sin =⨯-⨯=⋅⋅=><=CEn CE n CE n θ则∴直线CE 与平面ABC 所成角的正弦值为96.方法二:过C 作BD 的垂线交BD 于HBDCH ⊥∴BCD CH BCD DE 平面,平面⊂⊥ CH DE ⊥∴D DE BD = 又ABDECH 平面⊥∴在BCD ∆中,3 , 2121=⨯=⨯=∆CH CH BD CD BC S BCD 得由又2221=⨯==∆∆DE AE S S DAE BAE 3623223131=⨯⨯=⨯=∴∆-CH S V BAE BAE C 32===CA BC AB 又ABC ∆∴为等边三角形,33=∆ABC S 设点E 到平面ABC 的距离为h ,由BAE C ABC E V V --=得:322=h .故点E 到平面ABC 的距离为322.222==∆CD DE CDE Rt ,中,又分12 分10 分10 分11分12 分2 分6 分1 分4 32=∴CE 所以直线CE 与平面ABC 所成角的正弦值为96=CE h 注:以下方法酌情给分的距离相等到平面、知,平面由ABC F E ABC EF //,如右图,取,中点M BC .,FN ABC E ABC FN N AM FN F 的距离等于到平面,即平面则可证于作过⊥⊥20题:(1).由2sin )( 2)(≥≥x x mf x h 得:恒成立时xexm x sin 2 ),0(≥∈∴π)0( sin 2)(πϕ<<=x exx x令xe x x x )sin (cos 2)(-='∴ϕππϕπϕ<<<'<<>'x x x x 4:0)(40:0)(得;由得由上单调递减,上单调递增;在,在)4()4 0()(πππϕx 4 max )4()(ππϕϕ-==∴e x 所以),[ 4+∞-πem 的取值范围为(2).由已知)(x f 与)(x g 的图像关于直线x y =对称x x g ln )(=∴设公切线与),()(s x e s e x f 相切于点=,)ln ,(ln )(t t x x g 相切于点与=:知公切线可分别表示为,由xx g e x f x 1)()(='=')1()(s e x e y s x e e y ssss-+=-=-,即或1ln 1)(1ln -+=-=-t x ty t x t t y ,即⎪⎩⎪⎨⎧-=-=∴②①1ln )1( 1t s e te s s 1)1(s s e t s --=-得:由①②消去01)1( =---s s e s 即则令 ,1)1()(---=x e x x F x1)(,-='x xe x F 显然0)(0<'≤x F x 时,时,当0>x ,令1)()(-='=x xe x F x μ上单调递增,在故)0()(,0)1()(∞+>+='∴x e x x x μμ分5 (*)8 分分11 分10 分5 分12 分1 分6 又01)1(01)0(>-='<-='e F F ,01)( )1 0(0000=-='∈∃∴x e x x F x 使得,单调递减,时,当)(0)(0x F x F x x <'<∴;单调递增,时,当)(0)(0x F x F x x >'>02)1(013)2(2<-=->+-=-eF e F ,又;03)2(02)1(2>-=<-=e F F ,所以)(x F 有且仅有两个零点 ,21x x ,且).2,1( ),1,2(21∈--∈x x 知:由01)1()(1111=---=x e x x F x 01)1(1)1()(11111111=---=-+--=--x x x e x e x x ex x F 111)1,2(x x x -≠--∈知由02121=+=-∴x x x x 即)(x f ∴与)(x g 有且仅有两条公切线,且)(x f 图像上两切点横坐标互为相反数.处理的解法,评分标准酌情题过程可参照文科再构造函数证明,具体或得:或由①②消去或得:处由①②消去注:)2(20 011ln 01ln )1( 11011 (*) =-+-=----+==-+-t t t t t t s s s e s s e t s s 21解:(1).显然四边形ABCD 为菱形,故其内切圆以O 为圆心,半径为r 的距离到直线AD O )1,0()05(D A ,又由-055=+-y x AD 的方程为:得直线r d AD ==+=65515的距离故原点到直线6522=+y x ABCD 内切圆的标准方程为:故四边形(2).方法一:由题意可知,, )0 2(1-F 故MN 方程为:)2(+=x k y ),(),(2211y x N y x M ,设则直线MP 的方程为:)1(111--=x x y y )(05105510])1(5[ )1(1 151212121221211122*=-+-+--+⎪⎪⎩⎪⎪⎨⎧--==+ x x y x y x x y x x yy y x 得:联立分4 分3分7 分8 分6 又上,故在椭圆E y x M ),(11152121=+y x ,即212155x y -=代入)(*式整理得:0355)3(2112121=-+--x x x y x x 0031>∆≠-,显然x33512111x x x x x P --=⋅∴3)2(232)1(1 35311111111-+=-=--=--=∴x x k x y x x y y x x x P P P ,3)2(2,3531111⎪⎪⎭⎫⎝⎛-+--x x k x x P 故同理: 3)2(2,3532222;⎪⎪⎭⎫⎝⎛-+--x x k x x Q 2544)55(2 )3)(53()3)(53()]3)(2()3)(2[(23533533)2(23)2(212121221122122112211kx x x x k x x x x x x x x k x x x x x x k x x k k =--=------+--+=------+--+='∴故25k k =',即k k '=52所以:存在常数52=λ满足题意.方法二:由题意可知,, )0 2(1-F 故MN 方程为:)2(+=x k y ),( ),( ),( ),(44332211y x Q y x P y x N y x M ,,,设),1( ),1(3311y x t y x RPt MR -=--∴=设)( 01 )1(131313131*⎩⎨⎧=++=+⎩⎨⎧=--=- ty y t tx x ty y x t x 得:23131313122322123*********1211))((5))((151515t ty y ty y tx x tx x t y t y x t x t y x y x -=-++-+∴-=-+-⨯-⎪⎪⎩⎪⎪⎨⎧=+=+得:②由①②① 分9 分12 分11分9 分10 分11 分12 分5 分7 分8 分9 分10 ttx x t tx x t 55 105))(1()(31231-=--=+-+*即:带入上式得:将tx t x t tx x 23 2313131-=-=∴+=+,又 )52()2(11113t k x k t y t y -=+-=-=∴)52( 23 44μμμ-=-==k y x RQ NR ,,同理可得:设kt t k t k t k x x y y k 25)11(211(5)23()23()52(52(4343=--=------=--='∴μμμμ故25k k =',即k k '=52所以:存在常数52=λ满足题意.22.解:(1).显然1C 是过原点且倾斜角为α的直线∴1C 的极坐标方程为αθ=)20(R ∈<<ρπα2C 的极坐标方程为2παθ+=)20(R ∈<<ρπα.(2).由⎩⎨⎧== sin 8αθθρ得A 的极坐标为()αα,sin 8由⎪⎩⎪⎨⎧+==2sin 8παθθρ得B 的极坐标为⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛++2 cos 82 )2sin(8πααπαπα,,即,.ααcos 8 sin 8==∴OB OA ,AOB ∆∴的面积为:ααα2sin 16cos sin 3221==⋅=OB OA S 又20(πα,∈AOB ∆=∴ 4时,πα面积的最大值为16.分3 分1分2 分3 分5 分6 分8 分9 分10 分8 分9 分10 23.解:(1)⎪⎩⎪⎨⎧≥-<≤-+--<=+--=4 642 222 624)(x x x x x x x f 6)(4min -=≥∴x f x 时,当05)(2≥+-a a x f 恒成立0562≥+--∴a a 即0652≤+-a a 32≤≤∴a 故a 的取值范围为[]32,.(2)由(1)知:6 .6=++=c b a M 即法1:3618)(3)3()2()3()1()2()1(6 )3)(2(2)3)(1(2)2)(1(23213212=+++=+++++++++++++++≤++++++++++++++=+++++∴c b a c b c a b a c b a c b c a b a c b a c b a (当且仅当⎩⎨⎧=+++=+=+ 6321c b a c b a ,即⎪⎩⎪⎨⎧===123c b a 时等号成立321+++++∴c b a 的最大值为6.法2:(柯西不等式)[]363)6()111()3()2()1()131211(00 02222222=⨯+++=++⋅+++++≤⋅++⋅++⋅+∴>>>c b a c b a c b a c b a 当且仅当⎪⎩⎪⎨⎧=+++=+=+6131211c b a c b a ,即⎪⎩⎪⎨⎧===123c b a 时等号成立321+++++∴c b a 的最大值为6.。
四川省南充市高高三上学期第一次高考适应性考试数学(

所以抽中的从事礼宾接待的志愿者有人,从事语言翻译的志愿者有人。
用事件表示“至少有1名从事礼宾接待的志愿者被选中”,则它的对立事件表示“没有1名从事礼宾接待的志愿者被选中”, 则23257()1()110C P A P A C =-=-=………………………………………………………6分 (2)由题意:的可能取值为0,1,2,3.则,124831228(1)55C C P C ξ===, 214831212(2)55C C P C ξ===, , 因此,(2)方法一:利用等体积法可求到面的距离为,则直线与平面所成的角的正弦值为,从而方法二:设为平面的一个法向量,则 100n CN n NB ⎧⋅=⎪⎨⋅=⎪⎩ 即,令,则。
又则1sin |cos ,|n C N θ=<>=从而……………………………12分 19.解:(1)R x x x x x f ∈++-=,5102731)(23,则. 因为,是函数5102731)(23++-=x x x x f 的两个极值点,则20.解:(1)设椭圆的标准方程)0(12222>>=+b a by a x 由已知可得⎪⎪⎪⎩⎪⎪⎪⎨⎧+====2222222c b a b a c e解得.故椭圆的标准方程.………………………………………4分(2)联立方程⎪⎩⎪⎨⎧=++=1222y x m kx y ,消得:0224)21(222=-+++m kmx x k . 当0)12(822>+-=∆m k ,即①时,,.所以,. 又k x x y y 102)21(22121-=-+--+,化简整理得:②. ……………………………9分 (3)代②入①得:.又原点到直线的距离为.22222122122412||1||km k k x x k AB ++-+=-+=. 所以22221224||||21k m k m d AB S AOB ++-=⋅=∆. 而且,则2024212<<-=∆m m m S AOB ,. 所以当,即时,取得最大值. ……………………………13分若,函数在上单调递增,则函数在上无最大值,不满足条件.若,函数在上单调递减,在上单调递增,则函数在上无最大值,不满足条件. ⅲ)当时,由01))12(2()(<+-+='x a ax x x g ,函数在上单调递减,故成立. 综上:实数的取值范围是. …………………………………9分。
四川省南充市高三数学第一次高考适应性考试试题 理(含解析)新人教A版

高考数学一模试卷(理科)参考答案与试题解析一、选择题(每题5分,共50分)1.(5分)(2011•天津)i是虚数单位,复数=()解:复数=2.(5分)(2013•南充一模)已知全集U=R,集合A={x|0<2x<1},B={x|log3x>0},则A∩3.(5分)(2013•南充一模)设a,b,c是三条不同的直线,α,β是两个不同的平面,则4.(5分)(2013•南充一模)已知命题是()5.(5分)(2013•南充一模)为了得到函数y=sin(2x﹣)的图象,只需把函数y=sin(2x+)向左平移个长度单位向右平移向左平移个长度单位向右平移)x+)))的图象向右平移个长度单位得到)B C D7.(5分)(2013•南充一模)执行如图所示的程序框图,则输出的S的值是()是是是是.8.(5分)(2013•南充一模)设等差数列{a n} 的前n项和为S n,a2、a4是方程x2﹣2x+b=0 5==9.(5分)(2013•南充一模)已知三角形ABC中,点D是BC的中点,过点D的直线分别交直线AB,AC于E、F两点,若=(λ>0),=μ(μ>0),则的最小值==x三点共线可设=,==x(=当且仅当时取等号10.(5分)(2013•南充一模)已知F1(﹣c,0),F2(c,0)为椭圆的两个焦点,P为椭圆上一点且,则此椭圆离心率的取值范围是(),由求得,得=,∴.,∴≥0,∴≤≤≤,二、填空题(每题5分,共25分)11.(5分)(2013•南充一模)已知某个几何体的三视图如图所示(正视图弧线是半圆),根据图中标出的尺寸(单位:cm),可得这个几何体的体积是8+πcm3.12.(5分)(2013•南充一模)若(ax﹣1)5的展开式中x3的系数是80,则实数a的值是 2 .13.(5分)(2013•南充一模)在体积为V的三棱锥S﹣ABC的棱AB上任取一点P,则三棱锥P﹣SBC的体积大于的概率是.的体积大于的面积大于等于即可.},则有BC•PE>×BC•AD;>,>AP=S=故答案为:.14.(5分)(2002•北京)已知P是直线3x+4y+8=0上的动点,PA,PB是圆x2+y2﹣2x﹣2y+1=0的两条切线,A,B是切点,C是圆心,那么四边形PACB面积的最小值为.故答案为:15.(5分)(2013•南充一模)对于三次函数f(x)=ax3+bx2+cx+d,定义y=f″(x)是函数y=f′(x)的导函数.若方程f″(x)=0有实数解x0,则称点(x0,f(x0))为函数y=f(x)的“拐点”.有同学发现:任何一个三次函数既有拐点,又有对称中心,且拐点就是对称中心.根据这一发现,对于函数g(x)=x3﹣x2+3x++,则…+的值为3018 .,解得,又,即=…+,可知其图象关于点=…+…+三、解答题(共6小题,共75分)16.(12分)(2013•南充一模)已知△ABC的三个内角A,B,C所对的边分别为a,b,c.,,且.(Ⅰ)求A的大小;(Ⅱ)若a=1,.求S△ABC.(Ⅰ)由.求得结果.)∵,∴,∴17.(12分)(2013•南充一模)某班级举行一次知识竞赛活动,活动分为初赛和决赛两个阶段、现将初赛答卷成绩(得分均为整数,满分为100分)进行统计,制成如下频率分布表.(1)填充频率分布表中的空格(在解答中直接写出对应空格序号的答案);(2)决赛规则如下:参加决赛的每位同学依次口答4道小题,答对2道题就终止答题,并获得一等奖.如果前三道题都答错,就不再答第四题.某同学进入决赛,每道题答对的概率P的值恰好与频率分布表中不少于80分的频率的值相同.①求该同学恰好答满4道题而获得一等奖的概率;②记该同学决赛中答题个数为X,求X的分布列及数学期望.)根据样本容量,频率和频数之间的关系得到①0.16×50=8②=0.44﹣14=6④=0.1218.(13分)(2013•南充一模)如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.(Ⅰ)求证:AC⊥平面BDE;(Ⅱ)求二面角F﹣BE﹣D的余弦值;(Ⅲ)设点M是线段BD上一个动点,试确定点M的位置,使得AM∥平面BEF,并证明你的结论.,可知,,.,即为平面的法向量,的余弦值为=019.(12分)(2013•南充一模)设数列{a n}的各项都为正数,其前n项和为S n,已知对任意n∈N*,S n是和a n的等差中项.(Ⅰ)证明数列{a n}为等差数列,并求数列{a n}的通项公式;(Ⅱ)证明.是,则,故(和+a(﹣)+…+(﹣20.(12分)(2013•南充一模)已知椭圆的中心在原点,焦点在x轴上,一个顶点为B(0,﹣1),且其右焦点到直线的距离为3.(1)求椭圆的方程;(2)是否存在斜率为k(k≠0),且过定点的直线l,使l与椭圆交于两个不同的点M、N,且|BM|=|BN|?若存在,求出直线l的方程;若不存在,请说明理由.)设椭圆的方程为,由已知得y=kx++9kx+=0得,则的坐标为)设椭圆的方程为,由已知得,∴.y=kx+=0得的坐标为,化简,得,∴或.21.(14分)(2013•南充一模)已知函数f(x)=x(1nx+1)(x>0).(I)求函数f(x)的最小值;(II)设F(x)=ax2+f′(x)(a∈R),讨论函数F(x)的单调性;(III)若斜率为k的直线与曲线y=f′(x)交于A(x1,y1)、B(x2,y2)(x1<x2)两点,求证:.=2ax+=(,可得)单调增区间为,单调减区间为;>。
2021届四川省南充市高三上学期第一次高考适应性考试数学(理)试卷解析

绝密★启用前2021届四川省南充市高三上学期第一次高考适应性考试数学(理)试题注意事项:1、答题前填写好自己的姓名、班级、考号等信息 2、请将答案正确填写在答题卡上一、单选题1.已知集合{}250A x x x =+>,{}34A x x =-<<,则A B =()A .(5-,0)B .(3-,0)C .(0,4)D .(5-,4)答案:C思路:解一元二次不等式,化简集合A ,再由交集的概念,即可得出结果. 解:因为{}{2505A x x x x x =+>=<-或}0x >,又{}34A x x =-<<,所以{}04A B x x ⋂=<<. 故选:C.2.若()11z i i -=+,则z =() A .2i -+ B .2i --C .2i +D .2i -答案:D思路:根据()11z i i -=+,利用复数除法运算求解. 解:因为()11z i i -=+,所以()111121i i i z i i ++=+=+=--, 故选:D3.我国南宋数学家秦九韶所著《数学九章》中有“米谷粒分”问题:粮仓开仓收粮,粮农送来米1512石,验得米内夹谷,抽样取米一把,数得216粒内夹谷27粒,则这批米内夹谷约() A .164石 B .178石C .189石D .196石答案:C【解析】试题分析:由已知,抽得样本中含谷27粒,占样本的比例为271=2168,则由此估计总体中谷的含量约为11512=1898⨯石.故选C.【解析】抽样中的用样本去估计总体.4.10202111x x ⎛⎫-+ ⎪⎝⎭的展开式中2x 的系数为() A .45 B .45-C .120D .120-答案:A思路:因为()1010202120211111x x x x =⎛⎫⎡⎤++++ ⎪⎢⎥⎝⎭⎣⎦,故展开式特点可知2x 的系数即为()101x +的2x 的系数,再结合二项式定理通项公式即可求解解:()1010202120211111x x x x =⎛⎫⎡⎤++++ ⎪⎢⎥⎝⎭⎣⎦()()()()012101010101098202120212202110011111111x x x x xC C C C xx⨯⨯+++++++=+,故在10202111x x ⎛⎫++ ⎪⎝⎭的展开式中,2x 的系数即为()101x +的2x 的系数,又()101x +展开式的通项为10110r rr T C x -+=,令102r -=,故8r =,所以2x 的系数为81045C =.故选:A.点评:本题考查三项展开式中指定项的系数,解决此类问题的关键在于把三项整合成两项的和,即将问题转化为()101x +的2x 的系数,再利用二项展开式求相关项的系数,注意这些相关项的系数与指定项的系数的关系.5.已知各项均为正数的等比数列{}n a 的前3项和为21,且13a =,则35a a +=() A .36 B .60C .84D .92答案:B思路:设各项均为正数的等比数列{}n a 的公比为()0q q >,根据题中条件,求出公比,再由等比数列的基本量运算,即可得出结果.解:设各项均为正数的等比数列{}n a 的公比为()0q q >, 因为数列{}n a 的前3项和为21,且13a =, 所以()21233121a a q a q ++++==,解得2q或3q =-(舍),则()()24351341660a a a q q+=+=+=.6.已知直线420x my m -+-=与圆224x y +=相切,则m =() A .0 B .43-C .0或43-D .0或43答案:D思路:根据题意,由直线与圆相切的判断方法可得2421m m-=+2,解可得m 的值,即可得答案.解:根据题意,圆x 2+y 2=4的圆心为(0,0),半径r =2, 直线x ﹣my+4m ﹣2=0与圆x 2+y 2=4相切,则有2421m m-=+2,解可得:m =0或43, 故选:D .点评:直线与圆相切只需满足圆心到直线的距离等于半径即可.7.函数331x x y =-的图象大致是()A .B .C .D .答案:C思路:通过求函数的定义域,自变量与函数值的变化情况,利用排除法可求解 解:解:因为函数的定义域为{}0x x ≠,所以A 不符合题意, 当0x <时,30x <,310x -<,则0y >,所以B 不符合题意,当x 趋向于无穷大时,31x -的增长速度快于3x 的增长速度,所以对的y 趋向于零,所以D 不符合题意,C 符合题意,8.执行如图的程序框图,若输入k 的值为3,则输出S 的值为()A .10B .15C .18D .21答案:B解:由题意可得,2,3;n S ==3,6;n S == 4,10;n S == 5,15n S ==程序结束,故选B.9.已知二面角AB αβ--的平面角是锐角θ,M α∈,N β∈,MN β⊥,C AB ∈,MCB ∠为锐角,则()A .MCN θ∠<B .MCN θ∠=C .MCN θ∠>D .以上三种情况均有可能答案:A思路:过MO 作MO⊥AB,交AB 于O ,连结NO ,则NO⊥AB,从而∠MON=θ,由此能求出结果.解:二面角α﹣AB ﹣β的平面角是锐角θ,M∈α,MN⊥β,C∈AB,∠MCB 为锐角 过MO 作MO⊥AB,交AB 于O ,连结NO , 则NO⊥AB,∴∠MON=θ,∵在直角三角形MNO 中,有sin MNMON MO∠=,在直角三角形MNC 中,有sin MNMCN MC∠=, 又MO<MC ,所以sin sin MON MCN ∠>∠ 所以∠MON>∠MCN, 即θ>∠MCN. 故选:A .点评:关键点点睛:利用定义作出二面角和线面角,再在直角三角形中利用正弦值比较大小.10.双曲线C :22221x y a b-=(0a >,0b >)的左焦点为F ,A ,B 分别为C 的左,右支上的点,O 为坐标原点,若四边形ABOF 为菱形,则C 的离心率为() A 5B .3C 31D 32答案:C思路:由题意可得AB OB OF c ===且//AB OF ,从而求出点B 的坐标,将其代入双曲线方程中,即可得出离心率.解:由题意(),F c o -,四边形ABOF 为菱形,如图,则AB OB OF c === 且//AB OFA ,B 分别为C 的左,右支上的点,设A 点在第二象限,B 在第一象限.由双曲线的对称性,可得2B cx =,过点B 作BH x ⊥交x 轴于点H ,则11,222cOB c OH AB OB ====所以60BOH ∠=︒,则32BH =,所以32c B ⎛⎫ ⎪ ⎪⎝⎭所以22223144c c a b-=,则22222234c b c a a b -=,即42840e e -+=解得2423e =+,或2423e =-由双曲线的离心率1e >,所以取2423e =+,则31e =+ 故选:C11.已知定义在R 上的函数()f x 满足()()f x f x -=,且当0x <时,()31xf x =+,若432a =,254b =,1325c =,则() A .()()()f a f b f c << B .()()()f b f c f a << C .()()()f b f a f c << D .()()()f c f a f b <<答案:D思路:根据指数与幂函数的单调性,得到1b a c <<<;再由题中条件,得到函数()f x 在()0,∞+上单调递减,进而可得出结果. 解:因为24413355331422162525<=<=<=,则1b a c <<<;因为定义在R 上的函数()f x 满足()()f x f x -=,所以()f x 为偶函数; 又当0x <时,()31xf x =+显然单调递增,所以当0x >时,()f x 单调递减;因此()()()f b f a f c >>. 故选:D.12.已知函数()312ln 2x x e axf x e x---=+只有一个零点,则a =() A .31e + B .31e -C .eD .1e答案:A思路:由题意()f x 只有一个零点,等价于函数()22ln 2e xg x ex e x x=-+的图象与函数y a =的图象只有一个交点,利用导数得到()g x 的单调区间和极值,作出函数()g x的大致图象,由数形结合可得答案.解:由函数()312ln 2x x e axf x e x---=+只有一个零点, 所以方程312ln 20x x e axe x---+=只有一个实数根. 即方程32222ln 2ln 2e x ex e x e xa ex e x x x-+==-+只有一个实数根.即函数()22ln 2e xg x ex e x x=-+的图象与函数y a =的图象只有一个交点. 由()()()2221ln ln 222e x e e x g x ex e e e x x x --'=-+=+- 当0x e <<时,1ln 0,0x e x ->->,则()0g x '>. 当x e >时,1ln 0,0x e x -<-<,则()0g x '<. 所以()g x 在()0e ,上单调递增,在(),e +∞上单调递减. 又0x →时,ln e xx→-∞,所以()g x →-∞ x →+∞时,ln 0e xx→,222ex e x -+→-∞,所以()g x →-∞,且()333121g e e e e =-+=+作出()g x 的大致图象如图.如图,当31a e =+时,函数()22ln 2e xg x ex e x x=-+的图象与函数y a =的图象只有一个交点. 所以31a e =+ 故选:A点评:方法点睛:已知函数零点个数(方程根的个数)求参数值(取值范围)常用的方法: (1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数范围; (2)分离参数法:先将参数分离,转化成求函数的值域问题加以解决;(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出函数的图象,利用数形结合的方法求解 二、填空题13.已知向量a ,b →的夹角为3π,且1b →=,2a b →-=a =______.答案:3思路:把模用数量积表示后可求得a .解:∵2a b →-=∴222222(2)444cos 473a b a b a a b b a a π→→→→-=-=-⋅+=-+=,解得3a =(-1舍去). 故答案为:3.14.记n S 是等差数列{}n a 的前n 项和.若333a S ==,则5a =______. 答案:7思路:设等差数列{}n a 的公差为d ,根据条件可得112320a d a d +=⎧⎨+=⎩,求出通项公式,可得答案.解:设等差数列{}n a 的公差为d由333a S ==,可得31230a a a =⎧⎨+=⎩,即112320a d a d +=⎧⎨+=⎩ 解得112a d =-⎧⎨=⎩,所以()11223n a n n =-+-⨯=-所以52537a =⨯-= 故答案为:715.设F 为椭圆C :22143x y +=的右焦点,不垂直于x 轴且不过点F 的直线l 与C 交于M ,N 两点,在MFN △中,若MFN ∠的外角平分线与直线MN 交于点P ,则P的横坐标为______. 答案:4思路:根据椭圆方程221 43x y+=,设()()1122,,,M x y N x y,由椭圆的第二定义得到12112,222MF x NF x=-=-,设()P m n,,然后根据外角平分线定理,由MF MPNF NP=求解.解:如图所示:因为椭圆方程为22143x y+=,所以2,3,1a b c===,所以椭圆的右焦点是()1,0F,所以离心率为12cea==,设()()1122,,,M x y N x y,由椭圆的第二定义得:2212MF NFea ax xc c==--,所以12112,222MF x NF x=-=-,设()P m n,,由外角平分线定理得MF MPNF NP=,即1122122122xx mx m x--=--,化简得()()1212122x x m x x -=-, 解得4m =所以P 的横坐标为4 故答案为:4点评:关键点点睛:本题关键是外角平分线定理的应用.16.已知函数()21,02,0x x f x x x ⎧-≥=⎨-<⎩,则关于x 的方程()()0f f x k +=,给出下述四个结论:①存在实数k ,使得方程恰有1个实根;②存在实数k ,使得方程恰有2个不相等的实根;③存在实数k ,使得方程恰有3个不相等的实根;④存在实数k ,使得方程恰有4个不相等的实根.其中所有正确结论的编号是______. 答案:①②③ 思路:根据题意得出()()f f x 的解析式,作出函数()()f f x 的大致图象,根据函数图象与yk =-的交点个数情况得出对应的k 范围,可得出各个命题的真假.解:由函数()21,02,0x x f x x x ⎧-≥=⎨-<⎩可得,当1≥x 或0x <时,()0f x ≥,当01x ≤<时,()0f x <,所以()()()()()()20102f x f x f f x f x f x ⎧≥⎡⎤-⎪⎣⎦=⎨<-⎪⎩,即()()422221220141x x x f f x x x x x ⎧-≥⎪=-+≤<⎨⎪-<⎩当1≥x 时,422y x x =-,则()()3444110y x x x x x '=-=-+>恒成立.所以422y x x =-在[)1+∞,上单调递增. 则函数()()ff x 的大致图象如图所示.由方程方程()()0ff x k +=,得方程()()f f x k =-当1k -=-即1k =是,方程恰有1个实数根. 当10k -<-≤时,方程恰有2个不等实数根. 当02k <-≤时,方程恰有3个不等实数根. 当2k <-时,方程恰有2个不等实数根. 当1k -<-时,方程无实数根. 所以①②③正确. 故答案为:①②③点评:方法点睛:已知函数有零点(方程有根)求参数值(取值范围)常用的方法: (1)直接法:直接求解方程得到方程的根,再通过解不等式确定参数范围; (2)分离参数法:先将参数分离,转化成求函数的值域问题加以解决;(3)数形结合法:先对解析式变形,进而构造两个函数,然后在同一平面直角坐标系中画出函数的图象,利用数形结合的方法求解 三、解答题17.手机运动计步已成为一种时尚,某学校统计了该校教职工一天行走步数(单位:百步).根据数据得到如图所示的直方图:(1)求频率分布直方图中a 的值,并由频率分布直方图估计该校教职工一天行走步数的中位数m ;(2)若该校有教职工175人,试估计一天行走步数不大于130的人数. 答案:(1)0.008=a ,125;(2)98.思路:(1)由频率和为1即可计算a 的值,结合中位数计算公式即可得结果; (2)用人数175与行走步数不大于130的频率相乘即可.解:(1)由题意得()0.0020.0060.0120.0100.0020.002201a a +++++++⨯=, 解得0.008=a ,设中位数110m x =+,则0.002200.006200.008200.0120.5x ⨯+⨯+⨯+⋅=,解得15x =,所以11015125m =+=.(2)因为()1750.002200.006200.008200.0122098⨯⨯+⨯+⨯+⨯=, 所以,估计一天行走步数不大于130的人数为98.18.ABC ∆中,角,,A B C 的对边分别为,,a b c ,2cos 2b C c a -=. (1)求B 的大小;(2)若3a =,且AC 边上的中线长为192,求c 的值. 答案:(1)23B π=;(2)5c =. 【解析】试题分析:(1)由余弦定理化简等式可知:222a c b ac +-=-,进而求出角B ,结合B 的范围,可求出B.(2)由(1)知222239b a c ac c c =++=++,取AC 的中点D ,连接BD,由余弦定理可求cos C ,从而联立方程求出结果 试题解析:解:(1)因为2cos 2b C c a -=,所以由余弦定理可得,2222?22a b c b c a ab+--=,化简得222a c b ac +-=-,所以2221cos 22a cb B ac +-==-,因为()0,B π∈,所以23B π=. (2)由(1)得,222239b a c ac c c =++=++,①又因为在ABC ∆中,222cos 2a b c C ab+-=,取AC 中点D ,连结BD . 因为193,a BD ==在CBD ∆中,222221944cos 2?b a BC CD BD C BC CD ab+-+-==, 所以2221992944b b c ⎛⎫+-=+- ⎪⎝⎭,② 把①代入②,化简得23100c c --=, 解得5c =,或2c =-(舍去),所以5c =.19.在五边形AEBCD 中,BC CD ⊥,C //D AB ,22AB CD BC ==,AE BE ⊥,AE BE =(如图).将△ABE 沿AB 折起,使平面ABE⊥平面ABCD ,线段AB 的中点为O(如图).(1)求证:平面ABE⊥平面DOE ;(2)求平面EAB 与平面ECD 所成的锐二面角的大小. 答案:(1)见解析(2)45°思路:(1)根据矩形的性质,求得AB OD ⊥,再由等腰三角形的性质,证得EO AB ⊥,由线面垂直的判定,可得AB⊥平面EOD ,再由面面垂直的判定定理,即可证得平面AB E⊥平面EOD ;(2)由(1)以O 为坐标原点,以OB ,OD ,OE 所在直线分别为,,x y z 轴建立如图所示的空间直角坐标系O xyz -,求得平面ECD 和平面ABE 的法向量,利用向量的夹角公式,即可求解.解:(1)由题意2AB CD =,O 是线段AB 的中点,则OB CD =.又//CD AB ,则四边形OBCD 为平行四边形,又BC CD ⊥,则AB OD ⊥, 因AE BE =,OB OA =,则EO AB ⊥.EO DO O ⋂=,则AB⊥平面EOD.又AB平面ABE ,故平面ABE⊥平面EOD.(2)由(1)易知OB ,OD ,OE 两两垂直,以O 为坐标原点,以OB ,OD ,OE 所在直线分别为,,x y z 轴建立如图所示的空间直角坐标系O xyz -, △EAB 为等腰直角三角形,且AB=2CD=2BC ,则OA OB OD OE ===,取1CD BC ==,则O (0,0,0),A (-1,0,0),B (1,0,0),C (1,1,0),D (0,1,0), E (0,0,1),则1CD =-(,0,0),011DE =-(,,), 设平面ECD 的法向量为n x y z =(,,), 则有取0,0,n CD n DE ⎧⋅=⎨⋅=⎩0,0,x y z -=⎧⎨-+=⎩1z =,得平面ECD 的一个法向量011n =(,,), 因OD⊥平面ABE.则平面ABE 的一个法向量为010OD =(,,), 设平面ECD 与平面ABE 所成的锐二面角为θ,则221112,2cos cos OD n θ⨯==+=, 因为0(0,90)θ∈,所以045θ=,故平面ECD 与平面ABE 所成的镜二面角为45°.点评:本题考查了面面垂直的判定与证明,以及空间角的求解问题,意在考查学生的空间想象能力和逻辑推理能力,解答本题关键在于能利用直线与直线、直线与平面、平面与平面关系的相互转化,通过严密推理,同时对于立体几何中角的计算问题,往往可以利用空间向量法,通过求解平面的法向量,利用向量的夹角公式求解.20.已知函数()3x x x n f m =+-的图象在点()()1,1f 处的切线方程为9480x y +-=.(1)求m ,n ;(2)设02t <≤,已知函数()()16f x g x t=,若对于任意1x ,[]22,x t t ∈-,都有()()121g x g x -≤,求t 的取值范围.答案:(1)12m =,50n =;(2)4,23⎡⎤⎢⎥⎣⎦.思路:(1)根据点()()1,1f 在切线上,以及导数的几何意义即可求解;(2)利用()f x 的导数确定()f x 在区间[]22-,上的单调性,将不等式恒成立转化为()()max min 16x x f t f -≤,利用()f x 的单调性求出最值,得到关于t 的不等关系,即可求解.解:(1)由题意得()23f x x m '=-,所以()31f m '=-,因为()f x 在点()()1,1f 处的切线方程为9480x y +-=, 所以39m -=-,解得:12m =, 因为点()()1,1f 在切线9480x y +-=上, 所以()911480f ⨯+-=,解得:()139f =, 所以3391121n =-⨯+,解得:50n =, 故12m =,50n =.(2)由(1)得()31250x f x x =-+,由()()()23123220x x x x f =-=+-<',可得:22x -<<,所以()f x 在[]22-,上单调递减, 当02t <≤时,对任意1x ,[]22,x t t ∈-, 都有()()121g x g x -≤,即当[]2,x t t ∈-时,()()max min 16x x f t f -≤.因为[][]2,22,t t -⊇-,所以()f x 在[]2,t t -上单调递减, 所以()()()()3max 2212250f f x t t t =-=---+,()()3min 1250x t t f f t ==-+则()()2max min 6121616f f x x t t t -=-++≤,即23280t t +-≥,解得:2t ≤-或43≥t ,又02t <≤ 所以423t ≤≤,故t 的取值范围是4,23⎡⎤⎢⎥⎣⎦.点评:方法点睛:利用导数研究函数单调性的方法(1)确定函数()f x 的定义域;求导函数()'f x ,由()0f x '>(或()0f x '<)解出相应的x 的范围,对应的区间为()f x 的增区间(或减区间);(2)确定函数()f x 的定义域;求导函数()'f x ,解方程()0f x '=,利用()0f x '=的根将函数的定义域分为若干个子区间,在这些子区间上讨论()'f x 的正负,由符号确定()f x 在子区间上的单调性.21.在平面直角坐标系xOy ,已知点M (2,1),动点P 到直线1y =-的距离为d ,满足2226PMd PO +=+.(1)求动点P 的轨迹C 的方程;(2)过轨迹C 上的纵坐标为2的点Q 作两条直线QA ,QB ,分别与轨迹C 交于点A ,B ,且点D (3,0)到直线QA ,QB 的距离均为m (02m <≤),求线段AB 中点的横坐标的取值范围.答案:(1)24y x =;(2)(]9,37.思路:(1)设动点(),P x y ,用坐标由两点间的距离公式表示出2226PM d PO +=+化简即可得到答案.(2)设直线QA 的方程为()112y k x =-+,由点到直线的距离公式可得到点D 到QA 的距离m =QB 的方程为()212y k x =-+,分析点D 到QB 的距离,可得1k ,2k 是方程()2224840m k k m --+-=的两根,得到1k ,2k 的关系,设()11,A x y ,()22,B x y ,联立直线QA 与抛物线的方程,得出1y ,同理得出2y ,得到线段AB 中点的横坐标为0x ,从而得出答案. 解:(1)设动点(),P x y ,则()()22221M P x y =-+-,222PO x y =+,1d y =+,由2226PMd PO +=+,得()()222222116x y y x y -+-++=++,化简得24y x =,故动点P 的轨迹C 的方程为24y x =.(2)由题意知直线QA ,QB 的斜率存在且不为0,由(1)知点Q (1,2),所以设直线QA 的方程为()112y k x =-+,(10k ≠), 则D 到QA的距离m =(0m <≤整理得()222114840m k k m --+-=.设直线QB 的方程为()212y k x =-+,(20k ≠), 同理可得()222224840m k k m --+-=,所以1k ,2k 是方程()2224840m k k m --+-=的两根, 因为()22464443240m m m ∆=--=->, 所以12284k k m +=-,121k k =. 设()11,A x y ,()22,B x y , 由()1212,4,y k x y x ⎧=-+⎨=⎩得2114480k y y k --+=.()11164480k k ∆=--+>,所以111842k y k -=,1214242y k k =-=-, 同理可得11242y k =-,设线段AB 中点的横坐标为0x ,则221212028x x y y x ++==()()()()()()22221221212121242422212238k k k k k k k k k k -+-==+-++=+-+-,设[)12284,24t k k m =+=∈---,所以20223x t t =--,(42t -≤<-),函数2223y x x =--在[)4,2--为单调递减,所以0937x <≤,故线段AB 中点的横坐标的取值范围是(]9,37.点评:关键点睛:本题考查抛物线的方程,直线与抛物线的问题关系问题,解答本题的关键是由点到直线的距离公式得到1k ,2k 是方程()2224840m k k m --+-=的两根,从而得到12284k k m +=-,121k k =,将直线方程与抛物线方程联立,从而求出线段AB 中点的横坐标,属于中档题.22.在平面直角坐标系xOy 中,曲线1C的参数方程为12x t y ⎧=+⎪⎪⎨⎪=⎪⎩(t 为参数).以O 为极点,x 轴的非负半轴为极轴建立极坐标系,曲线2C 的极坐标方程为2(cos sin )ρθθ=+.(1)求曲线1C 的极坐标方程和曲线2C 的直角坐标方程; (2)设曲线1C 与曲线2C 交于,P Q 两点,求||||OP OQ ⋅的值答案:(1)cos sin 1ρθρθ-=,22220x y x y +--=;(2)2思路:(1)曲线1C 参数方程消去参数t ,可得到1C 的普通方程,进而将其转化为极坐标方程即可,利用极坐标方程与直角坐标方程间的关系,可将2C 的极坐标方程化为直角坐标方程;(2)结合曲线1C 、2C 的极坐标方程,可得()()22221cos sin cos sin 4++-=+ρθθθθρ,展开并整理得42840ρρ-+=,设,P Q 两点所对应的极径分别为12,ρρ,可求得12ρρ的值,进而可得到||||OP OQ ⋅的值.解:(1)由122x y t ⎧=+⎪⎪⎨⎪=⎪⎩消去参数t ,得1x y -=,由cos ,sin x y ρθρθ==,可得曲线1C 的极坐标方程为cos sin 1ρθρθ-=.由2(cos sin )ρθθ=+,可得曲线2C 的直角坐标方程为()222x y x y +=+,即22220x y x y +--=.(2)由2(cos sin )ρθθ=+,得cos sin 2ρθθ+=,由cos sin 1ρθρθ-=,得1cos sin θθρ-=,则()()22221cos sin cos sin 4++-=+ρθθθθρ,即22124ρρ+=,整理得42840ρρ-+=,设,P Q 两点所对应的极径分别为12,ρρ,则()2124ρρ=, 所以12||||2OP OQ ρρ⋅==.点评:极坐标与参数方程是高考选修部分的重要考点,应熟练掌握极坐标方程,直角坐标方程以及普通方程的互化,理解极坐标中ρ的含义,属于基础题. 23.已知函数()2x x a af x -++=,其中0a >. (1)若1a =,求不等式()5f x ≤的解集;(2)若存在0x ,使得()03f x ≤成立,求a 的取值范围. 答案:(1){}23x x -≤≤;(2)[1,2].思路:(1)利用零点分段法,去绝对值,解不等式;(2)首先利用绝对值三角不等式求()f x 的最小值,再利用不等式()min 3f x ≤,求a 的取值范围.解:(1)()21,1,213,12,21,2,x x f x x x x x x -+<-⎧⎪=-++=-≤≤⎨⎪->⎩由()5f x ≤可得1,215,x x <-⎧⎨-+≤⎩或12,35,x -≤≤⎧⎨≤⎩或2,215,x x >⎧⎨-≤⎩解得21x -≤<-或12x -≤≤或23x <≤ 所以原不等式的解集为{}23x x -≤≤.(2)若存在0x ,使得()03f x ≤,则只需要()min 3f x ≤. 因为()222x x a x x a a a a a ⎛⎫-++≥--+=+ ⎪⎝⎭,(0a >)当且仅当()20x x a a ⎛⎫-⋅+≤ ⎪⎝⎭即2a x a -≤≤时等号成立,所以只需23aa+≤,即2320a a-+≤,解得12a≤≤故a的取值范围是[1,2].点评:方法点睛:本题考查了分段函数的最值、证明不等式,常见方法有以下几种. (1)去绝对值,将函数化为分段函数,利用分段函数的图像可求最值.(2)利用绝对值三角不等式求最值.(3)证明不等式的方法:作差法、作商法.(4)构造函数,利用导函数证明不等式.。
全国卷四川省南充市仪陇宏德中学2021届高考数学模拟卷一理

(全国卷)四川省南充市仪陇宏德中学2021届高考数学模拟卷(一)理1、已知集合21{|2740},{|2}x A x x x B y y +=--≤==,则()R A B ⋃=( ) A.{|4}x x ≤ B.{|04}x x ≤≤C.{|0}x x ≤D.1{|}2x x ≤-2、复数()1iR 1ia z a +=∈+在复平面内对应的点在虚轴上,则a 等于( ) A .2B .1-C .1D .2-3、设样本数据1210,,,x x x 的平均数和方差分别为1和4,若i i y x a =+(a 为非零常数, 1,2,10)i =,则1210,,,y y y 的平均数和方差分别为( )A. 1,4a +B. 1,4a a ++C. 1,4D. 1,4a +4、已知定义在R 上的函数()f x 对于任意的实数x 都满足()()3f x f x +=-,且 当[]0,3x ∈时,()1e 3x f x -=+,则()1228f =( ) A .4-B .4C .3e 3+D .1227e 3+5、平面向量a 与b 的夹角为()60,2,0,1a b ==,则2a b + 等于( ) A. 22B. 23C. 12D. 106、已知数列{}n a ,满足111n a a +=-,若112a =,则2020a =( )A .2B .2C .-1D .17、6(2)()x y x y +⋅-的展开式中,43x y 的系数是( )A.-10B.-50C.50D.108、执行如图所示的程序框图,若输出结果为2019505,则中可填( )A.2019?i <B.2019?i >C.2019?i ≥D.2019?i ≤9、已知奇函数()()()3cos ,02f x x x πωφωφφω⎛⎫=+-+<> ⎪⎝⎭对任意R x ∈都有()02f x f x π⎛⎫++= ⎪⎝⎭,现将()f x 图象向右平移3π个单位长度得到()g x 图象,则下列判断错误的是( )A .函数()g x 在区间,122ππ⎡⎤⎢⎥⎣⎦上单调递增 B .()g x 图象关于直线712x π=对称C .函数()g x 在区间,63ππ⎡⎤-⎢⎥⎣⎦上单调递减 D .()g x 图象关于点,03π⎛⎫⎪⎝⎭对称10、在各棱长均相等的直三棱柱111ABC A B C -中,已知M 是棱1BB 的中点,N 是棱AC 的中点,则异面直线1A M 与BN 成角的正切值为( )3 B.1 6211、已知函数1()sin 2sin 3f x x a x =-,且对于任意的12,(,)x x ∈-∞+∞,121212()(),1f x f x x x x x -≠<-恒成立,则实数a 的取值范围是( )A.11[,]44-B.11[,]33-C.11[,]22-D.[1,1]-12、已知椭圆2222:1(0)x y C a b a b+=>>的左,右顶点分别为12,A A ,c 为椭圆C 的半焦距,过1A的直线与圆222x y c +=切与点N ,与双曲线2222:1x y E a b-=在第一象限交于点M ,满足12MA MA ⊥,若椭圆C 的离心率为1e ,双曲线E 的离心率为2e ,则211e e +的值为( )A.165B.5C.655D.2513、如图是一个射击靶的示意图,圆形靶的靶心为O ,半径为2米,一个运动员在练习射击的时候,在靶上画出了一个标志胜利的"V "形轴对称图案AOBC ,其中,60AOB ∠=︒,点,A B 在圆形靶的边缘上,点C 距离靶的边缘的最短距离为1米.现他朝靶上任意射击一次,没有脱靶,则其命中靶中"V "形图案的概率为__________.14、已知直线()(:2480)l x y λμμλμλ++---=交22:25O x y +=于A B ,两点,C 为l 外一动点,且2AC BC =,则AB 的最小值为 ;当AB 最小时,ABC △面积的最大值为 .15、已知数列{}n a 的前n 项和122n n n S a +=-,若不等式()2235n n n a --<-λ对n +∀∈N 恒成立,则整数λ的最大值为_________________.16、已知某个机械零件是由两个有公共底面的圆锥组成的,且这两个圆锥有公共点的母线互相垂直,把这个机械零件打解成球形,该球的半径最大为1,设这两个圆锥的高分别为12,h h ,则12h h +的最小值为________.17、在ABC ∆中,内角A B C ,,所对的边分别为a b c ,,,若2a =,cos cos 2cos 0a C c A b B ++=.(1)求B ;(2)若BC 边的中线AM 长为5,求ABC ∆的面积.18、在如图所示的几何体中,四边形ABCD 是菱形,ADNM 是矩形,平面ADNM ⊥平面ABCD .2AD =,1AM =,DE AB ⊥ 且点E 为AB 的中点.MECABDN(1) 求证: //AN 平面MEC ;(2) 求ME 与平面MBC 所成角的正弦值;(3) 在线段AM 上是否存在点P ,使二面角P EC D --的大小为π3?若存在,求出AP 的长;若不存在,请说明理由.19、如图,已知抛物线2x y =,点11,24A ⎛⎫- ⎪⎝⎭,39,24B ⎛⎫⎪⎝⎭,抛物线上的点13(,)22P x y x ⎛⎫-<<⎪⎝⎭.过点B 作直线AP 的垂线,垂足为Q .(1)求直线AP 斜率的取值范围; (2)求AP PQ ⋅的最大值.20、高铁和航空的飞速发展不仅方便了人们的出行,更带动了我国经济的巨大发展,据统计,在2018年这一年内从A 市到B 市乘坐高铁或飞机出行的成年人约为50万人次.为了解乘客出行的满意度,现从中随机抽取100人次作为样本.得到下表(单位:人次):(1)在样本中任取1个,求这个出行人恰好不是青年人的概率;(2)在2018年从A 市到B 市乘坐高铁的所有成年人中,随机选取2人次,记其中老年人出行的人次为X .以频率作为概率.求X 的分布列和数学期望;(3)如果甲将要从A 市出发到B 市,那么根据表格中的数据,你建议甲是乘坐高铁还是飞机?并说明理由.21、已知函数()πcos 2f x x ⎛⎫ ⎪⎝=⎭-,()()x g x e f x '=⋅,其中e 为自然对数的底数.(1)求曲线()y g x =在点()(0)0g ,处的切线方程.(2)若对任意π,02x ⎡⎤∈-⎢⎥⎣⎦不等式()()g x x f x m ≥⋅+恒成立,求实数m 的取值范围.(3)试探究当ππ,42x ⎡⎤∈⎢⎥⎣⎦时,方程()()g x x f x =⋅的解的个数,并说明理由.22、在平面直角坐标系xOy 中,直线l 的参数方程为11x y ⎧=⎪⎪⎨⎪=⎪⎩(t 为参数).在以原点O 为极点,x 轴正半轴为极轴的极坐标系中,圆C 的方程为4cos ρθ=.(Ⅰ)写出直线l 的普通方程和圆C 的直角坐标方程.(Ⅱ)若点P 坐标为()1,1,圆C 与直线l 交于,A B 两点,求PA PB +的值. 23、已知函数()22121f x x x =--+.(1)画出函数()f x 的大致图象,并求出函数()f x 的值域;(2)若不等式()321f x a x >-+恒成立,求实数a 的取值范围.答案以及解析1答案及解析: 答案:A解析:21{|2740}{|4}2A x x x x x =--≤=-≤≤,1{|2}{|0}xB y y y y +===>{|0}RB y y =≤,所以(){|4}R A B x x ⋃=≤,故选A.2答案及解析: 答案:D 解析:()()()()()()2i 1i 222i 1i 1i 1i 2a a a a z +-++-+===++-在复平面内对应的点的坐标为22,22a a +-⎛⎫⎪⎝⎭且在虚轴上,所以20a +=,即2a =-.3答案及解析: 答案:A解析:由题得:121010110x x x +++=⨯=;()()()222121011110440x x x -+-++-=⨯=,1210,,,y y y 的均值和方差分别为:均值121010y y y y +++=12101210()()()()1010101101010x a x a x a x x x a a a +++++++++++====+方差()()()222121010y y y y y y -+-++-=[][][]2221210()(1)()(1)()(1)10x a a x a a x a a +-+++-++++-+=2221210(1)(1)(1)4041010x x x -+-++-=== 故选A.4答案及解析: 答案:A解析:定义在R 上的函数()f x 对于任意的实数x 都满足()()3f x f x +=-, ∴()()()63f x f x f x +=-+=, 当[]0,3x ∈时,()1e 3x f x -=+, ∴()()()1228204644f f f =⨯+= ()()111e 34f -=-=-+=-.故选:A.5答案及解析: 答案:B解析:2a b +=== B6答案及解析: 答案:A解析:数列{}n a 满足1111,12n n a a a +==-, ()23411112,1,11211212a a a ====-==----,512112a ==-7答案及解析: 答案:D解析:6()x y -展开式中33x y 的系数为336(1)20C -=-,42x y 的系数为226(1)15C -=,6(2)()x y x y ∴+⋅-展开式中,43x y 的系数为2021510-+⨯=,故选D.8答案及解析: 答案:B解析:21224114()(1)2(1)1i i i i a i i i i i i -+===-+⋅++,由程序框图知S 表示数列12{}ii a +的前i 项和,于是111111144(1)4()4()...4()2233411i S i i i =-+-+-++-=++.因为输出结果为2019505,所以420191505i i =+,2019i =,故选B.9答案及解析: 答案:C解析:()()()cos f x x x ωϕωϕ=+-+2sin 6x πωϕ⎛⎫=+- ⎪⎝⎭,()f x ∵是奇函数, ,6k k z πϕπ-=∈∴ ,,6k k z πϕπ=+∈∴, 2πϕ<∵,6πϕ=∴ ,()2sin f x x ω=∴.()02f x f x π⎛⎫++= ⎪⎝⎭∵,()2f x fx π⎛⎫=-+ ⎪⎝⎭∴ ,()()2f x f x f x ππ⎛⎫+=-+= ⎪⎝⎭,()f x ∴的最小周期为2,2Tππω==∴, ()2sin 2f x x =∴,()22sin 23g x x π⎛⎫=-⎪⎝⎭∴. 易知()g x 在7,1212ππ⎡⎤⎢⎥⎣⎦上单调递增,在5,1212ππ⎡⎤-⎢⎥⎣⎦上单调递减,所以A 正确,C 错误; 由22,32x k k z πππ-=+∈,得()g x 的对称轴方程为7,122k x k z ππ=+∈, 所以B 正确; 由22,3x k k z ππ-=∈,得,32k x k z ππ=+∈, ()g x ∴的对称中心为,023k ππ⎛⎫+⎪⎝⎭ (k z ∈), 所以D 正确.10答案及解析: 答案:C解析:如图,取1AA 得中点P ,连接,PN PB ,则由直三棱柱的性质可知1//A M PB ,则PBN ∠为异面直线1A M 与BN 所成的角(或其补角).设三棱柱的棱长为2,则2,5,3PN PB BN ===,所以222PN BN PB +=,所以90PNB ∠=︒.在Rt PBN△中,26tan 33PN PBN BN ∠===,故选C.11答案及解析: 答案:B解析:因为对于任意的12,(,)x x ∈-∞+∞,121212()(),1f x f x x x x x -≠<-恒成立.所以1211221212()()()(())10f x f x f x x f x x x x x x -----=<--恒成立,则1()()sin 2sin 3g x f x x x a x x =-=--在(,)-∞+∞上单调递减,故2245'()cos2cos 1cos cos 0333g x x a x x a x =--=--≤在(,)-∞+∞上恒成立,令cos x t =,则245[1,1],033t t at ∈---≤在[1,1]-上恒成立令245()([1,1])33h t t at t =---,则(1)0(1)0h h -≤⎧⎨≤⎩,解得1133a -≤≤12答案及解析: 答案:D解析:如图 ,由已知得222a b c =+, 则12,A A 分別为双曲线2222:1x y E c b-=的左、石焦点.连接ON ,由直线1A M与圆222x y c +=切于点N ,得ON c =,从而1A N b =,12A M b =,222A M ON c ==. 由双曲线的定义,得122A M A M c -=,即222b c c -=,2b c =, 从而椭圆的离心率11e 5c a ==,双曲线的离心率2e 5ac ==, 所以211e 25e +=,故选D.13答案及解析: 答案:14π解析:连接OC ,由题意可知,2,1,150OA OC AOC ==∠=︒,由三角形面积公式得1121sin15022AOC S =⨯⨯⨯︒=△,由对称性可知,靶中“V”形图案的面积为1.又圆形靶的面积为4π,所以由几何概型的概率计算公式得命中靶中“V”形图案的概率为14π.14答案及解析: 答案:6;12解析:由()()2480x y λμμλμλ++---=得()()4280x y x y λμ+-+--=,则40280x y x y +-=⎧⎨--=⎩,得40x y =⎧⎨=⎩, 所以直线()()2480x y λμμλμλ++---=经过定点0(4)M ,,设O 为坐标原点,若AB 最小,则OM AB ⊥,此时6AB ==. 设3(4)A ,,3(4,)B -,()C x y ,,由2AC BC =,,化简得点C 的轨迹方程为()()224516x y -++=,则点C 的轨迹是圆心为(4)5-,,半径为4的圆,易知圆心(4)5-,在直线AB 上,因而C 点到AB 的最大距离为4,故ABC △面积的最大值为164122⨯⨯=.15答案及解析: 答案:4解析:当1n =时,21122S a =-得14a =,122n n n S a +=-;当2n ≥时,122n n n S a -=-,两式相减得1222n n n n a a a -=--,得122n n n a a -=+,所以11122n n n n a a ---=. 又1122a =,所以数列2n n a ⎧⎫⎨⎬⎩⎭是以2为首项,1为公差的等差数列,12n na n =+,即()12nn a n =+⋅. 因为0n a >,所以不等式()2235n n n a --<-λ,等价于2352nn -->λ. 记232n nn b -=,2n ≥时,112121223462n n n nn b n n b n ++--==--.所以3n ≥时,()13max 31,8n n n b b b b +<==. 所以33375,5888-><-=λλ,所以整数λ的最大值为4.16答案及解析: 答案:解析:由题意可知,打磨后所得半径最大的球是由这两个圆锥构成的组合体的内切球,内切球的半径1R =,如图为这个组合体的轴截面示意图,圆O 为内切球的轴截面,,,,E F G H 分别为切点,连接,,,,,,,OA OB OC OD OE OF OG OH ,由题意可知,AB BC AD DC ⊥⊥,12,1AC h h R OE OF OG OH =+=====,则AOB BOC COD AOD ABCD S S S S S =+++四边形△△△△即11111(22)()22222AB BC R AB R BC R CD R AD R AB BC R AB BC ⨯=⨯+⨯+⨯+⨯=+=+所以AB BC AB BC ⨯=+,由基本不等式可得2AB BC AB BC AB BC ⨯=+≥⨯,则4AB BC ⨯≥,当且仅当AB BC =时等号成立,所以222212()28h h AC AB BC AB BC +==+≥⨯≥,当且仅当AB BC =时等号成立,故12h h +的最小值为22.17答案及解析: 答案:(1)在ABC ∆中,sin sin sin a b cA B C==,且cos cos 2cos 0a C c A b B +=, ∴sin cos sin cos 2cos 0A C C A B B +=,∴()sin 120B B ⋅=, 又∵sin 0B ≠,∴2cos B =. ∵B 是三角形的内角, ∴3π4B =. (2)在ABM ∆中,3π154BM AM B AB c ===,,,, 由余弦定理得()2222cos AM c BM c BM B =+-⋅⋅,∴2240c c +-=, ∵0c >,∴2c =在ABC ∆中,2a =,2c =,3π4B =, ∴ABC ∆的面积1sin 12S ac B ==.解析:18答案及解析:答案:(1)设CM 与BN 交于F ,连接EF由已知可得四边形BCNM 是平行四边形,所以F 是BN 的中点. 因为E 是AB 的中点,所以//AN EF 又EF ⊂平面MEC ,AN ⊄平面MEC ,所以//AN 平面MEC(2)ADNM 是矩形,平面ADNM ⊥平面ABCD ,平面ADNM 平面ABCD AD =∴DN ⊥平面ABCD如图建立空间直角坐标系D xyz -,则(0,0,0)D ,(3,0,0)E ,(0,2,0)C ,(3,1,1)M -,(3,1,0)B ,(0,0,1)N 设平面MBC 的法向量为1111(,,)n x y z =(0,2,1)MB =-(3,1,0)BC =-1100MB n BC n ⎧⋅=⎪⎨⋅=⎪⎩∴200y z y -=⎧⎪⎨+=⎪⎩∴1(1,n =(0,1,1)ME =-111cos ,||||2ME n ME n ME n ⋅-<>===∴ME 与平面MBC 所成角的正弦值(3)设1,)P h -,(3,2,0)CE =-,(0,1,)EP h =- 设平面PEC 的法向量为1(,,)n x yz =则1100CE n EP n ⎧⋅=⎪⎨⋅=⎪⎩,∴200y y hz -=-+=⎪⎩令y , 1(2n h = 又平面ADE 的法向量2(0,0,1)n = 1212121cos,2||||7n n n n n n⋅<>===解得,h =∵1>∴在线段AM 上不存在点P ,使二面角P EC D --的大小为π3. 解析:19答案及解析:答案:(1)由题易得()2,P x x ,1322x -<<, 故()21141,1122APx k x x -==-∈-+,故直线AP 斜率的取值范围为()1,1-. (2)由题(1)知()2,?P x x ,1322x -<<, 故211,24PA x x ⎛⎫=--- ⎪⎝⎭,设直线AP 的斜率为k , 则11:24AP y kx k =++,139:24BP y x k k =-++, 由1124{13924y kx k y x k k =++=-++ 222234981,2244k k k k Q k k ⎛⎫+-++⇒ ⎪++⎝⎭, 故23432221,11k k k k k k k PQ k k ⎛⎫+----++= ⎪++⎝⎭, 又()21,PA k k k =----,故323322(1)(1)(1)(1)(1)(1)11k k k k k PA PQ PA PQ k k k k +-+--⋅=⋅=+=+-++, 即3(1)(1)PA PQ k k ⋅=+-,令3()(1)(1)f x x x =+-,11x -<<,则22()(1)(24)2(1)(21)f x x x x x =+-+'=--, 当112x -<<时, '()0f x >, 当112x <<时, '()0f x <, 故max 127()216f x f ⎛⎫==⎪⎝⎭, 即PA PQ ⋅的最大值为2716. 解析:20答案及解析:答案:(1)设事件:“在样本中任取1个,这个出行人恰好不是青年人”为M ,由表可得:样本中出行的老年人、中年人、青年人人次分别为19,39,42, 所以在样本中任取1个,这个出行人恰好不是青年人的概率193929()10050P M +==(2)由题意,X 的所有可能取值为:0,1,2.因为在2018年从A 市到B 市乘坐高铁的所有成年人中,随机选取1人次,此人为老年人概率是151755=. 所以022116(0)(1)525P X C ==⨯-=, 12118(1)(1)5525P X C ==⨯⨯-=,22211(2)()525P X C ==⨯=所以随机变量X 的分布列为:故16812()0122525255E X =⨯+⨯+⨯=. (3)答案不唯一,言之有理即可.如可以从满意度的均值来分析问题,参考答案如下: 由表可知,乘坐高铁的人满意度均值为:521012511011652121115⨯+⨯+⨯=++, 乘坐飞机的人满意度均值为:410145702241475⨯+⨯+⨯=++, 因为11622155>,所以建议甲乘坐高铁从A 市到B 市. 解析:21答案及解析:答案:(1)依题意得()sin f x x =,()cos x g x e x =⋅.()00cos01g e ==,()cos sin x x g x e e x '=-,()01g '=,所以曲线()y g x =在点()(0)0g ,处的切线方程为1y x =+.(2)原题等价于对任意π,02x ⎡⎤∈-⎢⎥⎣⎦,()()min m g x x f x ≤-⋅⎡⎤⎣⎦ 设()()()h x g x x f x =-⋅,π,02x ⎡⎤∈-⎢⎥⎣⎦.则()cos sin sin cos x x h x e x e x x x '=---()()cos 1sin x xe x x e x =-+,因为π,02x ⎡⎤∈-⎢⎥⎣⎦,所以()cos 0x e x x -≥,()1sin 0xe x +≤,所以()0h x '≥,故()h x 在π,02⎡⎤-⎢⎥⎣⎦上单调递增,因此当π2x =-时函数()h x 取得最小值,ππ22h ⎛⎫⎪⎭=-⎝-;所以π2m ≤-,即实数m 的取值范围是π,2⎛⎤-∞- ⎥⎝⎦.(3)设()()()H x g x x f x =-⋅,ππ,42x ⎡⎤∈⎢⎥⎣⎦,当ππ,42x ⎡⎤∈⎢⎥⎣⎦时,()()cos sin sin cos 0x H x e x x x x x '=---<,所以函数()H x 在ππ,42⎡⎤⎢⎥⎣⎦上单调递减,故函数()H x 在ππ,42⎡⎤⎢⎥⎣⎦上至多只有一个零点,又π4ππ044H e ⎛⎫=-⎫⎪⎝ ⎪⎭⎭⎪>⎝,0π2π2H ⎛⎫ ⎪⎝⎭=-<,而且函数()H x 在ππ,42⎡⎤⎢⎥⎣⎦上是连续不断的, 因此,函数()H x 在ππ,42⎡⎤⎢⎥⎣⎦上有且只有一个零点即方程()()g x x f x =⋅只有一个解.解析:22答案及解析:答案:(1)直线l的参数方程为11x y ⎧=⎪⎪⎨⎪=+⎪⎩(t 为参数). 消去参数t 可得:直线l 的普通方程为:20x y +-= 圆C 的方程为4cos ρθ=.即24cos ρρθ=, 可得圆C 的直角坐标方程为:22(2)4x y -+=. (2)将11x y ⎧=⎪⎪⎨⎪=⎪⎩代入22(2)4x y -+=得:220t +-=得1212220,*20,t t t t +=-<=-< 则2121212()4 4.PA PB t t t t t t +=-=+-= 解析:23答案及解析:答案:(1)因为()22121f x x x =--+ 所以123,211()61,22123,2x x f x x x x x ⎧-+<-⎪⎪⎪=-+-≤≤⎨⎪⎪->⎪⎩作出函数()f x 的大致图象如图所示由图可知,函数()f x 的值域为[2,)-+∞(2)()321f x a x >-+,即22121321x x a x --+>-+即221221x x a -++> 即21212ax x -++>因为2121(21)(21)2x x x x -++≥--+= 所以22a<,即4a < 所以实数a 的取值范围为(,4)-∞ 解析:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
南充市高 2021 届第一次高考适应性考试
理科数学
第 I 卷(共60 分)
一、单项选择题:本大题共 10 小题,每小题 6分,共 60 分。
1. 已知集合 A = {x | x 2 +5x >0} ,B ={x |-3<x <4} ,则 A ∩B =
A. (-5,0)
B. (-3,0)
C. (0,4)
D. (-5,4)
2. 若( z -1) i = i+1,则 z =
A. -2+i
B. -2-i
C. 2+i
D. 2-i
3. 我国南宋数学家秦九韶所著《数学九章》中有“米谷粒分”问题:粮仓开仓收粮,粮农送来米1512石,验得米内夹谷,抽样取米一把,数得 216 粒内夹谷 27 粒,则这批米内夹谷约
A. 164 石
B. 178 石
C. 189 石
D. 196 石 4. (1-x +1 x 2021 )10 的展开式中 x 2 的系数为 A. 45
B. -45
C. 120
D. -120 5. 已知各项均为正数的等比数列{a n } 的前 3 项和为 21,且 a 1 = 3,则 a 3 +a 5 =
A. 36
B. 60
C. 84
D. 92
6. 已知直线 x -my +4m -2 = 0 与圆 x 2 +y 2 = 4 相切,则 m =
A. 0
B. -43
C. 0 或-43
D. 0 或 43
7. 函数3
31
x x y =-的图象大致为
8. 执行如图所示的程序框图,如果输入 k 的值为 3,则输出 S 的值为
A. 10
B. 15
C. 18
D. 21
9. 已知二面角 α-AB -β 的平面角是锐角θ,M ∈α,N ∈β,MN ⊥β,
C ∈AB ,∠MCB 为锐角,则
A. ∠MCN <θ
B. ∠MCN = θ
C. ∠MCN >θ
D. 以上三种情况均有可能 10. 双曲线2222:1x y C a b -=( a >0,b >0) 的左焦点为 F ,A ,B 分别为C 的左,右支上的点,O 为坐标 原点,若四边形 ABOF 为菱形,则 C 的离心率为
A. 5
B. 2 3
C. 3 +1
D. 3 +2
第 II 卷(共90 分)
二、填空题:本大题共 4 小题,每小题 5 分,共 20 分。
11.已知向量a ,b 的夹角为π3
,且|b | = 1, |a -2b |=7 ,则|a |= . 12. 记 S n 是等差数列{a n } 的前 n 项和. 若 a 3 = S 3 = 3,则 a 5 = .
13. 设 F 为椭圆 C :22
143
x y +=的右焦点,不垂直于 x 轴且不过点 F 的直线 l 与 C 交于 M ,N 两点,在△MFN 中,若∠MFN 的外角平分线与直线 MN 交于点 P ,则 P 的横坐标为 .
14. 已知函数21,0,()2,0,x x f x x x ⎧-⎪=⎨-<⎪⎩
≥,则关于 x 的方程 f ( f ( x )) +k = 0,给出下述四个结论: ①存在实数 k ,使得方程恰有 1 个实根;
②存在实数 k ,使得方程恰有 2 个不相等的实根;
③存在实数 k ,使得方程恰有 3 个不相等的实根
;
④存在实数 k ,使得方程恰有 4 个不相等的实根.
其中所有正确结论的编号是 . 三、解答题:共 70 分。
解答应写出文字说明、证明过程或演算步骤。
第 15 ~ 19 题为必
考题,每个试题考生都必须作答。
第 20、21题为选考题,考生根据要求作答。
(一) 必考题:共 60 分
15. ( 本题满分 12 分)
手机运动计步已成为一种时尚,某学校统计
了该校教职工一天行走步数( 单位:百步) .
根据数据得到如右直方图:
(1) 求频率分布直方图中 a 的值,并由频
率分布直方图估计该校教职工一天行走步
数的中位数 m ;
.
(2) 若该校有教职工175 人,试估计一天行走步数不大于130 的人数.
16.( 本题满分12 分)
△ABC 的内角A,B,C 的对边分别为a,b,c,已知2b cos C-c = 2a.
(1) 求B;
(2) 若a = 3,且AC 边上的中线长为
19
2,求c.
17.( 本题满分12 分)
在五边形AEBCD中,BC⊥CD,CD//AB,AB
= 2CD = 2BC,AE⊥BE,AE = BE(如图1),将
△ABE 沿AB 折起使得平面ABE ⊥平面
ABCD,线段AB 的中点为O(如图2) .
(1) 求证:平面ABE⊥平面DOE;
(2) 求平面EAB 与平面ECD 所成的锐二面角的大小.
18.( 本题满分12 分)
已知函数f( x)= x3-mx+n 的图象在点(1,f(1)) 处的切线方程为9x+y-48 = 0.
(1) 求m,n;
(2) 设0 < t≤2,已知函数g (x)=
f( x)
16t,若对于任意x1,x2∈ [ t- 2,t ],都有|g(x1)-g(x2)|≤1,求t 的取值范围.
19.( 本题满分12分)
在平面直角坐标系xOy ,已知点M ( 2, 1 ),动点P 到直线y =-1 的距离为d,满足|PM|2 +d2 =|PO |2 +6.
(1) 求动点P 的轨迹C 的方程;
(2) 过轨迹C 上的纵坐标为2 的点Q 作两条直线QA,QB,分别与轨迹C 交于点
A,B,且点D(3,0) 到直线QA,QB 的距离均为m(0<m≤ 2 ),求线段AB 中点的横坐标的取值范围.
( 二) 选考题:共10 分。
请考生在20、21题中任选一题作答,如果多做,则按所做的第一题计分。
20. ( 本题满分10 分) 选修 4-4:坐标系与参数方程
在平面直角坐标系xOy 中,曲线 C 1
的参数方程为1,,x y ⎧=+⎪⎪⎨⎪=⎪⎩
( t 为参数),以 O 为极
点,x 轴的非负半轴为极轴建立极坐标系,曲线 C 2 的极坐标方程为2(cos sin )ρθθ=+ .
(1) 求 C 1 的极坐标方程和 C 2 的直角坐标方程;
(2) 设 C 1 与 C 2 交于 P ,Q 两点,求| OP |·| OQ | 的值.
21. ( 本题满分 10 分) 选修 4-5:不等式选讲 已知函数2()||||f x x x a a =-
++,其中 a >0. (1) 若 a = 1,求不等式 f ( x )≤5 的解集;
(2) 若存在 x 0 ,使得 f ( x 0 )≤3 成立,求 a 的取值范围.。
