六组诱导公式的应用
诱导公式的应用

诱导公式的应用诱导公式是数学中常见的一种方法,用于推导出未知变量之间的关系。
它在科学研究、工程设计、经济分析等领域都有广泛的应用。
本文将介绍诱导公式的一些应用案例。
一、物理学中的应用1. 牛顿第二定律:F=ma牛顿第二定律描述了物体受力和加速度之间的关系。
通过应用诱导公式,我们可以得到加速度和力、质量之间的关系。
2. 化学反应速率:v=k[A]^m[B]^n在化学反应中,反应速率与反应物浓度之间存在一定的关系。
通过实验数据的分析,可以利用诱导公式推导出反应速率与反应物浓度的关系。
二、工程学中的应用1. 电阻与电流、电压之间的关系:R=V/I在电路中,电阻的大小与电流和电压之间存在一定的关系。
通过应用诱导公式,可以推导出电阻与电流、电压之间的关系。
2. 压力与流量之间的关系:P=Q/A在流体力学中,压力与流量之间存在一定的关系。
通过应用诱导公式,可以推导出压力与流量和截面积之间的关系。
三、经济学中的应用1. 边际效用递减定律:MU=ΔU/ΔQ经济学中的边际效用递减定律描述了消费者对于每一单位商品的边际效用递减的情况。
通过应用诱导公式,可以推导出边际效用与总效用之间的关系。
2. 生产函数:Y=f(K,L)在宏观经济学中,生产函数描述了生产产出与资本和劳动力之间的关系。
通过应用诱导公式,可以推导出生产产出与资本、劳动力之间的关系。
四、统计学中的应用1. 相关系数:r=(Σxy-ΣxΣy/n)/[√(Σx^2- (Σx)^2/n) √(Σy^2- (Σy)^2/n)]相关系数用于衡量两个变量之间的相关程度。
通过应用诱导公式,可以推导出相关系数的计算公式。
2. 回归分析:Y=β0+β1X+ε在统计学中,回归分析用于建立变量之间的数学模型。
通过应用诱导公式,可以推导出回归方程中的系数和误差项之间的关系。
总结起来,诱导公式在物理学、工程学、经济学和统计学等领域都有广泛的应用。
通过应用诱导公式,可以推导出未知变量之间的关系,帮助我们理解问题和解决问题。
诱导公式总结大全

诱导公式1诱导公式的本质所谓三角函数诱导公式,就是将角n·(π/2)±α的三角函数转化为角α的三角函数。
常用的诱导公式公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinαcos(2kπ+α)=cosαtan(2kπ+α)=tanαcot(2kπ+α)=cotα公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotα公式三:任意角α与 -α的三角函数值之间的关系:sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα公式六:π/2±α与α的三角函数值之间的关系:sin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanα诱导公式记忆口诀奇变偶不变,符号看象限。
“奇、偶”指的是整数n的奇偶,“变与不变”指的是三角函数的名称的变化:“变”是指正弦变余弦,正切变余切。
(反之亦然成立)“符号看象限”的含义是:把角α看做锐角,不考虑α角所在象限,看n·(π/2)±α是第几象限角,从而得到等式右边是正号还是负号。
一全正;二正弦;三两切;四余弦这十二字口诀的意思就是说:第一象限内任何一个角的四种三角函数值都是“+”;第二象限内只有正弦是“+”,其余全部是“-”;第三象限内只有正切和余切是“+”,其余全部是“-”;第四象限内只有余弦是“+”,其余全部是“-”。
诱导公式总结大全

tan3am(3tan—tan八3(a))/(1-3ta门八2(a))
sin3 om sin(2(+a msin2acos+cos2asina
m2sinacosA2(+)1—2sin八2(a))sina
m2sina—2si门八3(a+sin—2sin八3(a)
=3sina—4si门八3(a)
tan( a+ B)=(tan+tanB)/(1—tana •tanB)
tan( a— B) =(tan—tanB)/(1+tana •tanB)
二倍角的正弦、余弦和正切公式
sin2a2sinacosa
cos2aCOSA2(a—SinA2(a¥2COSA2(a—1a1—2sinA2(a)
tan2a2tana/(1—tan八2(a))
变”是指正弦变余弦,正切变余切。(反之亦然成立)符号看象限”的含
义是:把角a看做锐角,不考虑a角所在象限,看n•(n/2)是第几象限角, 从而得到等式右边是正号还是负号。一全正;二正弦;三两切;四余弦
这十二字口诀的意思就是说:第一象限内任何一个角的四种三角函数值都
是+”第二象限内只有正弦是+”其余全部是第三象限内只有
sin—sin#2cos((r B)/2)•sin((帥/2)
cosa+cosB=2cos((rB)/2)•cos— B)/2) cosa—cosB=—2sin((+B)/2)•sin— B)/2)
三角函数的积化和差公式
sina・cosBsin(+ B +sin(— B)]
cosa・si牛Bsin(+ B —sin(— B)]
常用的诱导公式有以下六组

常用的诱导公式有以下六组一、导数的四则运算公式:1.两个函数的和(差)的导数等于这两个函数的导数之和(差)。
例如,若f(x)和g(x)分别是可导函数,则(f+g)'(x)=f'(x)+g'(x);(f-g)'(x)=f'(x)-g'(x)。
2.一个函数与一个常数的乘积的导数等于这个函数的导数乘以该常数。
例如,若f(x)是可导函数,c为常数,则(c*f(x))'=c*f'(x)。
3.两个函数的乘积的导数等于第一个函数的导数与第二个函数的乘积加上第一个函数与第二个函数的导数的乘积。
例如,若f(x)和g(x)分别是可导函数,则(f*g)'(x)=f'(x)*g(x)+f(x)*g'(x)。
4.一个函数除以另一个函数的导数等于分子函数的导数乘以分母函数减去分子函数乘以分母函数的导数的商再除以分母函数的平方。
例如,若f(x)和g(x)分别是可导函数,则(f/g)'(x)=(f'(x)*g(x)-f(x)*g'(x))/g^2(x)。
二、复合函数的导数计算公式:5.若y=f(u)和u=g(x)都是可导函数,则复合函数y=f(g(x))的导数可以通过链式法则计算。
即,(f(g(x)))'=f'(g(x))*g'(x)。
6.若y=f(x)是可导函数,且u=g(y)是可导函数,则复合函数u=g(f(x))的导数可以通过链式法则计算。
即,(g(f(x)))'=g'(f(x))*f'(x)。
这六个常用的导数计算公式在求解函数的导数时经常使用,可以用于简化计算,提高效率。
根据这些公式,可以对各种类型的函数进行导数计算,如多项式函数、三角函数、指数函数等。
在实际的应用中,这些公式能够帮助我们求解函数的极值、拐点、切线等问题,具有非常重要的意义。
六组诱导公式的应用

诱导公式一、六组公式一: 公式二:公式三: 公式四:公式五: 公式六:记忆口诀:奇变偶不变,符号看象限。
一、求值:例1、求下列各三角函数的值(1)sin 0120 (2)cos 0300 (3)tan 0240 (4)sin45π(5)sin(-0600) (6)cos(-317π) (7)tan(-67π) (8)sin(-12000)例2、已知sin(∂+π)=53,求(1)cos(π2-∂) (2)sin(∂+2π)例3、已知cos(∂-6π)=33,求cos(∂+65π)-sin 2)6(π-∂的值。
例4、已知cos(-800)=k,求tan1000的值。
三、化简:例5、(1))5sin()cos()2tan()6cos()2sin(θππθθπθπθπ+-----(2)[][]),)cos()sin()1(cos )1(sin z k k k k k ∈+--+++(其中θπθπθπθπ例6、ABC ∆中,证明下列各式:(1)sin(A+B)=sinC (2)cos(A+B)=-cosC(3)sin(2B A +)=cos 2C (4)cos )2(B A +=sin 2C四、综合题:例7、已知∂是第三象限角,f(∂)=)sin()tan()tan()2cos()sin(∂--∂++-∂∂-∂-πππππ, (1)化简f()∂(2)若cos(∂23π-)=51,求f(∂)的值。
(3)若01860-=∂,求f(∂)的值。
例8、已知函数f(x)=asin(∂+x π)+bcos(βπ+x ),其中a,b βα,都是非零实数,又知f(2010)=-1,求f(2011)例9、已知f(n)=sin)102(...)3()2()1(),(6f f f f z n n +++∈求π例10、已知tan ∂,1tan ∂是方程22(2)0x k x k -++=的两根,求sin()cos()ππ-∂++∂的值。
三角函数的诱导公式知识点

三角函数的诱导公式知识点三角函数的诱导公式知识点数学是人类对事物的抽象结构与模式进行严格描述的一种通用手段,可以应用于现实世界的任何问题,所有的数学对象本质上都是人为定义的。
下面是店铺整理的三角函数的诱导公式知识点,欢迎大家借鉴与参考,希望对大家有所帮助。
三角函数的诱导公式诱导公式的本质所谓三角函数诱导公式,就是将角n·(π/2)±α的三角函数转化为角α的三角函数。
常用的诱导公式公式一:设α为任意角,终边相同的角的同一三角函数的值相等:sin(2kπ+α)=sinα k∈zcos(2kπ+α)=cosα k∈ztan(2kπ+α)=tanα k∈zcot(2kπ+α)=cotα k∈z公式二:设α为任意角,π+α的三角函数值与α的三角函数值之间的关系:sin(π+α)=-sinαcos(π+α)=-cosαtan(π+α)=tanαcot(π+α)=cotα公式三:任意角α与 -α的三角函数值之间的关系:sin(-α)=-sinαcos(-α)=cosαtan(-α)=-tanαcot(-α)=-cotα公式四:利用公式二和公式三可以得到π-α与α的三角函数值之间的关系:sin(π-α)=sinαcos(π-α)=-cosαtan(π-α)=-tanαcot(π-α)=-cotα公式五:利用公式一和公式三可以得到2π-α与α的三角函数值之间的关系:sin(2π-α)=-sinαcos(2π-α)=cosαtan(2π-α)=-tanαcot(2π-α)=-cotα公式六:π/2±α与α的三角函数值之间的关系:sin(π/2+α)=cosαcos(π/2+α)=-sinαtan(π/2+α)=-cotαcot(π/2+α)=-tanαsin(π/2-α)=cosαcos(π/2-α)=sinαtan(π/2-α)=cotαcot(π/2-α)=tanα推算公式:3π/2±α与α的三角函数值之间的关系:sin(3π/2+α)=-cosαcos(3π/2+α)=sinαtan(3π/2+α)=-cotαcot(3π/2+α)=-tanαsin(3π/2-α)=-cosαcos(3π/2-α)=-sinαtan(3π/2-α)=cotαcot(3π/2-α)=tanα诱导公式记忆口诀:“奇变偶不变,符号看象限”。
《诱导公式的应用》课件

角度范围
诱导公式适用于特定角度 范围内的三角函数计算, 超出范围应考虑其他方法 。
函数类型
确保所涉及的三角函数类 型适用于该公式,避免因 函数类型不匹配而出现错 误。
注意公式的正误使用
公式来源
确保所使用的诱导公式来 源可靠,避免使用错误的 公式或来源不明的公式。
符号判断
在使用诱导公式时,应注 意符号的正负判断,确保 计算结果的准确性。
THANKS
感谢观看
03
诱导公式的应用场景
三角函数的化简
总结词
利用诱导公式简化复杂的三角函数表达式。
详细描述
在解决三角函数问题时,经常会遇到一些复杂的表达式,如 分母含有三角函数、三角函数嵌套等。通过应用诱导公式, 可以将这些复杂的表达式进行化简,使其更易于处理。
三角函数的求值
总结词
利用诱导公式计算三角函数的值。
《诱导公式的应用》 ppt课件
目录
• 诱导公式简介 • 诱导公式的分类 • 诱导公式的应用场景 • 诱导公式的推导方法 • 诱导公式的使用注意事项
01
诱导公式简介
诱导公式的基本公式将角度变换为0度到360度 之间的等价形式,从而简化三角 函数的计算和化简。
04
诱导公式的推导方法
利用三角函数的周期性推导
周期性定义
应用实例
三角函数具有周期性,即对于任意整 数k,函数y=sin(x)和y=cos(x)的图像 都关于直线x=kπ对称。
例如,可以利用周期性推导出 sin(17π/6)=sin(π/6),因为17π/6和 π/6相差一个周期。
推导过程
利用三角函数的周期性,我们可以将 任意角度x转化为0到π/2之间的角度 ,从而利用已知的三角函数值进行计 算。
学案5:5.3 诱导公式(二)

5.3 诱导公式(二)必备知识·探新知基础知识知识点1 诱导公式五思考1:(1)角π2-α与角α的终边有什么样的位置关系? (2)点P 1(a ,b )关于y =x 对称的对称点坐标是什么?知识点2 诱导公式六思考2:如何由公式四及公式五推导公式六?知识点3 对诱导公式的理解1.对诱导公式五、六的两点说明(1)诱导公式五、六反映的是角π2±α与α的三角函数值之间的关系.可借用口诀“函数名改变,符号看象限”来记忆.(2)诱导公式是三角变换的基本公式,其中角可以是一个单角,也可以是一个复角,应用时要注意整体把握,灵活变通.2.对诱导公式一~六的两点说明(1)诱导公式一~六揭示了终边具有某种对称关系的两个角的三角函数之间的关系.(2)公式一~六的记忆口诀和说明①口诀:奇变偶不变,符号看象限.②说明:思考3:六组诱导公式各有什么作用?基础自测1.已知sin α=35,则sin(π2+α)的值为( ) A .-35B .-45C .45D .±452.已知sin(7π2+α)=15,那么cos α=( ) A .-25B .-15C .15D .253.下列与sin(θ-π2)的值相等的式子为( ) A .sin(π2+θ) B .cos(π2+θ) C .cos(3π2-θ) D .sin(3π2+θ) 4.化简:1+cos(π2+α)·sin(π2-α)·tan(π+α)= .5.化简:sin (π-α)cos (π2+α)cos (π+α)sin (3π2-α)cos (3π2+α)= . 关键能力·攻重难题型探究题型一 利用诱导公式进行化简、求值例1 计算:(1)sin 2120°+cos180°+tan45°-cos 2(-330°)+sin(-210°);(2)1+cos100°sin170°cos370°+1-sin 2170°.[归纳提升] 利用诱导公式化简三角函数式的步骤用诱导公式可把任意角的三角函数转化为锐角三角函数,即口诀是:“负化正,大化小,化到锐角再查表”.【对点练习】❶ sin (-α-3π2)·sin (3π2-α)·tan 2(2π-α)cos (π2-α)·cos (π2+α)·cos 2(π-α).题型二 三角恒等式的证明例2 求证:2sin (θ-32π)cos (θ+π2)-11-2sin 2(π+θ)=tan (9π+θ)+1tan (π+θ)-1.[归纳提升] 对于恒等式的证明,应遵循化繁为简的原则,从左边推到右边或从右边推到左边,也可以用左右归一、变更论证的方法.常用定义法、化弦法、拆项拆角法、“1”的代换法、公式变形法,要熟练掌握基本公式,善于从中选择巧妙简捷的方法.【对点练习】❷ 求证:sin (θ-5π)cos (π2-θ)sin (π2+θ)cos (3π-θ)cos (3π2+θ)sin (-4π-θ)=-1.题型三 诱导公式与函数结合的运用例3 已知f (α)=cos (π2+α)·cos (2π-α)·sin (-α+3π2)sin (-π-α)·sin (3π2+α). (1)化简f (α);(2)若α是第三象限角,且cos(α-3π2)=15,求f (α)的值.[归纳提升] 用诱导公式化简求值的方法(1)解决与函数有关问题的关键就是利用诱导公式对表达式进行化简.(2)运用诱导公式时要特别注意三角函数在各象限的符号.【对点练习】❸ 已知角α的终边在第二象限,且与单位圆交于点(m ,223). (1)求tan α的值;(2)求2sin (π-α)+sin (π2+α)32cos (-α)-sin (π+α)的值.误区警示 对诱导公式理解不透彻而致错例4 已知sin(x +π6)=14,则sin(5π6-x )+sin 2(π3-x )= .[方法点拨] 利用诱导公式解题时,只有在利用诱导公式时才视公式中的角为锐角,变换前后原来是什么角就是什么角.学科素养 分类讨论思想在三角函数化简中的应用例5 化简:sin ⎝⎛⎭⎫4n -14π-α+cos ⎝⎛⎭⎫4n +14π-α(n ∈Z ).[归纳提升] 1.本题的化简过程,突出体现了分类讨论的思想,当然除了运用分类讨论的思想将n 分两类情况来讨论外,在解答过程中还处处体现了化归思想和整体思想.2.在转化过程中,缺乏整体意识,是出错的主要原因.课堂检测·固双基1.若cos65°=a ,则sin25°的值是( )A .-aB .aC .1-a 2D .-1-a 22.若sin(π2+θ)<0,且cos(π2-θ)>0,则θ是( )A .第一象限角B .第二象限角C .第三象限角D .第四象限角3.已知cos ⎝⎛⎭⎫π2+α=-35,且α是第二象限角,则sin ⎝⎛⎭⎫α-3π2的结果是( )A .45B .-45C .±45D .354.若α∈(π,3π2),则1-sin 2(3π2-α)=( )A .sin αB .-sin αC .cos αD .-cos α5.已知角α的终边上有一点P (1,3),则sin (π-α)-sin (π2+α)cos (3π2-α)+2cos (-π+α)的值为() A .-25 B .-45C .-47 D .-4【参考答案】必备知识·探新知基础知识知识点1 诱导公式五思考1:提示:(1)如图,角π2-α与角α的终边关于y =x 对称.(2)点P 1(a ,b )关于y =x 对称的对称点坐标是P 2(b ,a ). 知识点2 诱导公式六思考2: 提示:sin(π2+α)=sin[π-(π2-α)]=sin(π2-α)=cos α, cos(π2+α)=cos[π-(π2-α)]=-cos(π2-α)=-sin α. 知识点3 对诱导公式的理解思考3:提示:公式一:将角化为0~2π内的角求值;公式二:将0~2π内的角转化为0~π内的角求值;公式三:将负角转化为正角求值;公式四:将π2~π内的角转化为0~π2内的角求值; 公式五、公式六:实现正弦与余弦的相互转化.基础自测1.[答案] D[解析] ∵sin α=35,∴cos α=±45,∴sin(π2+α)=cos α=±45,故选D . 2.[答案] B[解析] 因为sin(72π+α)=sin(2π+3π2+α)=sin(3π2+α)=-cos α,所以cos α=-15,故选B . 3.[答案] D[解析] sin(θ-π2)=-sin(π2-θ)=-cos θ.对于A ,sin(π2+θ)=cos θ;对于B ,cos(π2+θ)=-sin θ;对于C ,cos(3π2-θ)=cos[π+(π2-θ)]=-cos(π2-θ)=-sin θ;对于D ,sin(3π2+θ)=sin[π+(π2+θ)]=-sin(π2+θ)=-cos θ.故选D . 4.[答案] cos 2α[解析] 原式=1-sin α·cos α·tan α=1-sin 2α=cos 2α.5.[答案] -sin α[解析] ∵32π-α=π+π2-α,32π+α=π+π2+α, ∴原式=sin α(-sin α)(-cos α)(-cos α)·sin α=-sin α. 关键能力·攻重难题型探究题型一 利用诱导公式进行化简、求值例1[解] (1)原式=sin 260°-cos0°+tan45°-cos 230°+sin30°=34-1+1-34+12=12. (2)原式=1+cos (180°-80°)sin (90°+80°)cos (360°+10°)+1-sin 2(180°-10°)=1+(-cos80°)cos80°cos10°+1-sin 210°=1-cos 280°2cos10° =sin80°2cos10°=cos10°2cos10°=12. 【对点练习】❶ [解] 原式=sin (-α+π2)·[-sin (π2+α)]·tan 2(2π-α)cos (π2-α)·cos (π2+α)·cos 2(π-α) =cos α·(-cos α)·tan 2αsin α·(-sin α)·cos 2α=tan 2αsin 2α=1cos 2α. 题型二 三角恒等式的证明例2[证明] 左边=-2sin (32π-θ)·(-sin θ)-11-2sin 2θ=2sin[π+(π2-θ)]sin θ-11-2sin 2θ=-2sin (π2-θ)sin θ-11-2sin 2θ=-2cos θsin θ-1cos 2θ+sin 2θ-2sin 2θ=(sin θ+cos θ)2sin 2θ-cos 2θ=sin θ+cos θsin θ-cos θ. 右边=tan (9π+θ)+1tan (π+θ)-1=tan θ+1tan θ-1=sin θ+cos θsin θ-cos θ. ∴左边=右边,故原式得证.【对点练习】❷ [证明] 左边=-sin (5π-θ)sin θcos θcos (π-θ)sin θ[-sin (4π+θ)]=-sin (π-θ)sin θcos θ-cos θsin θ(-sin θ)=-sin θsin θ=-1=右边, 故原式得证.题型三 诱导公式与函数结合的运用例3[解] (1)f (α)=-sin α·cos (-α)·[-sin (π2-α)]sin (π+α)·sin (π2+α) =sin α·cos α·cos α-sin α·cos α=-cos α. (2)因为cos(α-3π2)=-sin α=15,所以sin α=-15, 又α是第三象限角,所以cos α=-1-sin 2α=-1-(-15)2=-265, 所以f (α)=-cos α=265. 【对点练习】❸ [解] (1)由题得m 2+(223)2=1,所以m =±13, 因为角α的终边在第二象限,所以m =-13,所以tan α=223-13=-2 2. (2)2sin (π-α)+sin (π2+α)32cos (-α)-sin (π+α)=2sin α+cos α32cos α+sin α=2tan α+132+tan α=2×(-22)+132-22=-322. 误区警示 对诱导公式理解不透彻而致错例4[错解] ∵sin(x +π6)=14, ∴cos[π2-(x +π6)]=cos(π3-x )=sin(x +π6)=14, ∴sin(5π6-x )+sin 2(π3-x )=sin[π-(x +π6)]+[1-cos 2(π3-x )] =-sin(x +π6)+[1-cos 2(π3-x )]=-14+[1-(14)2]=1116. [错因分析] 在利用诱导公式sin(π-α)时,没能正确利用“符号看象限”来判断符号.[正解] ∵sin(x +π6)=14, ∴cos[π2-(x +π6)]=cos(π3-x )=sin(x +π6)=14, ∴sin(5π6-x )+sin 2(π3-x )=sin[π-(x +π6)]+[1-cos 2(π3-x )] =sin(x +π6)+[1-cos 2(π3-x )]=14+[1-(14)2]=1916. 学科素养分类讨论思想在三角函数化简中的应用例5[解] 当n 为偶数时,设n =2k (k ∈Z ),则原式=sin ⎝⎛⎭⎫8k -14π-α+cos ⎝⎛⎭⎫8k +14π-α =sin[2k π+(-π4-α)]+cos[2k π+(π4-α)] =sin(-π4-α)+cos(π4-α) =-sin(π4+α)+cos[π2-(π4+α)] =-sin(π4+α)+sin(π4+α)=0. 当n 为奇数时,设n =2k +1(k ∈Z ),则原式=sin ⎝⎛⎭⎫8k +34π-α+cos ⎝⎛⎭⎫8k +54π-α=sin[2k π+(3π4-α)]+cos[2k π+(5π4-α)] =sin(3π4-α)+cos(5π4-α) =sin[π-(π4+α)]+cos[π+(π4-α)] =sin(π4+α)-cos(π4-α) =sin(π4+α)-cos[π2-(π4+α)] =sin(π4+α)-sin(π4+α)=0. 故sin(4n -14π-α)+cos(4n +14π-α)=0. 课堂检测·固双基1.[答案] B[解析] sin 25°=sin(90°-65°)=cos 65°=a .2.[答案] B[解析] 因为cos θ<0,sin θ>0,∴θ是第二象限角.3.[答案] B[解析] ∵cos ⎝⎛⎭⎫π2+α=-35,∴-sin α=-35,∴sin α=35, 又α是第二象限角,∴cos α=-45,∴sin ⎝⎛⎭⎫α-3π2=cos α=-45. 4.[答案] B[解析] ∵α∈(π,32π),∴sin α<0,∴1-sin 2(32π-α)=1-cos 2α=-sin α. 5.[答案] A[解析] ∵角α的终边上有一点P (1,3),在第一象限, ∴由三角函数的定义知sin α=310,cos α=110. ∵sin (π-α)-sin (π2+α)cos (32π-α)+2cos (-π+α)=sin α-cos α-sin α-2cos α=310-110-310-210=-25. ∴选A .。
六组诱导公式

六组诱导公式随着社会的发展,人们在不断探索如何做出正确的决定以及如何改善其他人的行为。
其中,一种被广泛应用的理论是“六组诱导公式”(Six-Group Persuasion Formula),它是由美国心理学家卡洛斯科森(Carlos Cosson)提出的一种理论。
六组诱导公式是一种以分析、理解和应用情感来帮助人们进行决策和行动的指南。
它的基本思想是,当一个人要说服另一个人时,必须关注六个不同的因素。
这六个因素分别是:信念、知识、愿望、压力、进展和体验。
它们组成了一个称为“诱导公式”的框架,可以帮助人们更好地把握影响他们立场和改变行为的因素。
首先,信念是指一个人对某种可能性的态度。
它是由一个人获得的知识或信仰所形成的。
这通常基于一个人过去的经验或教育,也可能是基于社会上流行的信仰或观念。
其次,知识是指一个人拥有的具体信息。
它可以从社会媒体、广播、新闻传播等来源获得,也可以通过研究、研讨会或实习等方式获取。
第三,愿望是指一个人想要实现某种目标的动机。
愿望可以来自其他人的要求、惩罚或者自我设定的目标,也可以来自对自己未来的期望。
然后,压力是指一个人可能面临的外部和内部压力。
外部压力往往来自其他人,比如社会舆论、传统、政府制度等;而内部压力则通常来自自己,比如紧张、恐惧、焦虑、害怕失败等。
第五,进展是指一个人实现目标的步骤和进程。
这些步骤和进程往往可以帮助一个人更清楚地了解自己的目标和方向,也可以帮助他们发现并克服阻碍他们前进的障碍。
最后,体验是指一个人在实现目标过程中获得的有意义的情感反应。
这种情感反应通常可以激发更多的动力,从而促使他们不断前进。
六组诱导公式主要用于帮助人们学习如何有效地影响他人,同时也可以用于改善自身行为。
它可以帮助人们认清和理解影响他们决策和行为的不同因素,并让他们能够更有效地审视决策和采取行动的原因。
它还可以帮助人们促进沟通,更好地理解其他人的情感和观点,从而改善自身的行为。
诱导公式(原卷版)

5.3 诱导公式【知识点梳理】 知识点一:诱导公式 诱导公式一: sin(2)sin k απα+=, cos(2)cos k απα+=,tan(2)tan k απα+=,其中k Z ∈诱导公式二: sin()sin αα-=-, cos()cos αα-=,tan()tan αα-=-,其中k Z ∈诱导公式三:sin[((21)]sin k απα++=-, cos[(21)]cos k απα++=-, tan[(21)]tan k απα++=,其中k Z ∈诱导公式四:sin cos 2παα⎛⎫+= ⎪⎝⎭,cos sin 2παα⎛⎫+=- ⎪⎝⎭. sin cos 2παα⎛⎫-= ⎪⎝⎭,cos sin 2παα⎛⎫-= ⎪⎝⎭,其中k Z ∈ 知识点诠释:(1)要化的角的形式为90k α⋅±(k 为常整数); (2)记忆方法:“奇变偶不变,符号看象限”;(3)必须对一些特殊角的三角函数值熟记,做到“见角知值,见值知角”;(4)sin cos cos 444x x x πππ⎛⎫⎛⎫⎛⎫+=-=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭;cos sin 44x x ππ⎛⎫⎛⎫+=- ⎪ ⎪⎝⎭⎝⎭.知识点二:诱导公式的记忆诱导公式一~三可用口诀“函数名不变,符号看象限”记忆,其中“函数名不变”是指等式两边的三角函数同名,“符号”是指等号右边是正号还是负号,“看象限”是指把α看成锐角时原三角函数值的符号.诱导公式四可用口诀“函数名改变,符号看象限”记忆,“函数名改变”是指正弦变余弦,余弦变正弦,为了记忆方便,我们称之为函数名变为原函数的余名三角函数.“符号看象限”同上.因为任意一个角都可以表示为90(||45)k αα︒︒⋅+<的形式,所以这六组诱导公式也可以统一用“口诀”:“奇变偶不变,符号看象限”,意思是说角90k α⋅±(k 为常整数)的三角函数值:当k 为奇数时,正弦变余弦,余弦变正弦;当k 为偶数时,函数名不变,然后α的三角函数值前面加上当视α为锐角时原函数值的符号.用诱导公式进行化简时的注意点: (1)化简后项数尽可能的少; (2)函数的种类尽可能的少; (3)分母不含三角函数的符号; (4)能求值的一定要求值;(5)含有较高次数的三角函数式,多用因式分解、约分等.知识点三:利用诱导公式求任意角三角函数值的步骤用诱导公式可将任意角的三角函数化为锐角的三角函数,其一般方向是: ①化负角的三角函数为正角的三角函数; ②化为[0,2π]内的三角函数; ③化为锐角的三角函数.可概括为:“负化正,大化小,化到锐角为终了”(有时也直接化到锐角求值). 【题型归纳目录】题型一:利用诱导公式求解给角求值问题 题型二:利用诱导公式求解给值求值问题 题型三:诱导公式在三角函数式化简中的应用 题型四:诱导公式在三角函数证明中的应用 题型五:诱导公式的综合应用 题型六:利用互余互补关系求值 【典型例题】题型一:利用诱导公式求解给角求值问题 例1.(2022·全国·高一专题练习)172053sin cos tan 636πππ⎛⎫⎛⎫⎛⎫-+-+-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭______.例2.(2022·全国·高一)()8cos330sin 30tan cos903π︒+-︒++︒=______.例3.(2022·西藏拉萨·高一期末)11cos6π=( )A 2B 3C .12D .1变式1.(2022·全国·高一课时练习)设sin 25a ︒=,则sin65cos115tan 205︒︒︒=( ) A 221a-B .221a- C .2a - D .2a变式2.(2022·全国·高一课时练习)()sin 660-的值是( ) A .12B .12-C 3D .3变式3.(2022·广西桂林·高一期末)sin 405=( ) A .1 B .12-C 3D 2变式4.(2022·云南昆明·高一期末)35πsin 6=( ) A .12B .12-C 3D .3【方法技巧与总结】利用诱导公式求任意角三角函数值的步骤 (1)“负化正”:用公式一或三来转化.(2)“大化小”:用公式一将角化为0︒到360︒间的角. (3)“小化锐”:用公式二或四将大于90︒的角转化为锐角. (4)“锐求值”:得到锐角的三角函数后求值. 题型二:利用诱导公式求解给值求值问题 例4.(2022·安徽阜阳·高一期末)已知12cos 13θ=-,若θ是第二象限角,则()tan πθ+的值为( ) A .512B .125C .-512D .-125例5.(2022·安徽省舒城中学高一开学考试)若()4sin ,5πα+=-且α是第二象限角,则cos α=( )A .45-B .35 C .35D .45例6.(2022·广东·饶平县第二中学高一阶段练习)设02πα⎛⎫∈ ⎪⎝⎭,,若3sin ,5α=则cos 2πα⎛⎫+= ⎪⎝⎭( )A .35B .45C .35 D .45-变式5.(2022·全国·高一课时练习)在ABC 中,()7sin sin 2213A A ππ⎛⎫+++= ⎪⎝⎭,则tan A 的值是( )A .125- B .125C .512-D .512变式6.(2022·全国·高一课时练习)若()4sin 5πα+=-,则3cos 2πα⎛⎫-=⎪⎝⎭( ) A .45-B .35 C .45D .35变式7.(2022·江西上饶·高一阶段练习)已知5sin α=,则πcos 2α⎛⎫-= ⎪⎝⎭( )A 5B .5C .25D 25变式8.(2022·辽宁·辽师大附中高一阶段练习)已知()113sin cos 2013cos 22ππαπαα⎛⎫⎛⎫-+-=-- ⎪ ⎪⎝⎭⎝⎭,则22sin sin cos ααα-=( )A .2110 B .32C 3D .2变式9.(2022·河南南阳·高一期中)已知角,02πα⎛⎫∈- ⎪⎝⎭,且22tan 3tan sin 4sin 0αααα--=,则()cos 2021απ+=( ) A .14-B .15C .14D 15【方法技巧与总结】 解决条件求值问题的方法(1)解决条件求值问题,首先要仔细观察条件与所求式之间的角、函数名及有关运算之间的差异及联系.(2)可以将已知式进行变形向所求式转化,或将所求式进行变形向已知式转化.题型三:诱导公式在三角函数式化简中的应用例7.(2022·陕西·蒲城县蒲城中学高一期末)(1)计算:203π13373cos πtan π1144tan π3⎛⎫- ⎪⎛⎫⎝⎭-⋅- ⎪⎝⎭; (2)已知4tan 3α=,求222sin 2sin cos 2cos sin ααααα+-的值.例8.(2022·西藏拉萨·高一期末)已知α为第三象限角,且sin cos()tan()2()cos()f πααπααπα⎛⎫--+ ⎪⎝⎭=-. (1)化简()f α; (2)若25()f α=,求cos α的值.例9.(2022·浙江·杭州高级中学高一期末)(1)化简()3sin()cos tan()2cos tan(2)2f ππααπααπαπα⎛⎫---- ⎪⎝⎭=⎛⎫--+ ⎪⎝⎭;(2)已知关于x 的方程21204x bx -+=的两根为sin θ和cos θ,,42ππθ⎛⎫∈ ⎪⎝⎭.求实数b 以及sin cos θθ-的值.变式10.(2022·安徽省舒城中学高一开学考试)已知α是第三象限角,且sin(π)cos(2π)tan(2π)tan(π)sin(3π)()f αααααα---+-+-=.(1)化简()f α;(2)若3sin 5α=-,求()f α;(3)若1860α︒=-,求()f α.变式11.(2022·全国·高一课时练习)已知()1sin 1sin 1sin 1sin f ααααα+-=-+α为第二象限角.(1)若()3f α=,求224sin cos 3αα+的值;(2)若()21cos 2f αα=,求()3cos 2023cos 2ππαα⎛⎫+++⎪⎝⎭的值.变式12.(2022·全国·高一课时练习)已知()()()()()()sin cos 2tan tan sin f πβπββπββππβ--+=----.(1)若角β是第三象限角,且()1sin 5βπ-=,求()f β的值; (2)若2220β=︒,求()f β的值.变式13.(2022·全国·高一课时练习)已知角α的顶点在坐标原点,始边与x 轴非负半轴重合,终边经过函数()33x f x a -=--(0a >且1a ≠)的定点M .(1)求sin 2cos αα-的值;(2)求()()()()πsin πcos 2tan 5πcos 2πsin ααααα⎛⎫+++ ⎪⎝⎭-+++-的值.【方法技巧与总结】 三角函数式化简的常用方法(1)合理转化:①将角化成2k πα±,πα±,k Z ∈的形式.②依据所给式子合理选用诱导公式将所给角的三角函数转化为角α的三角函数. (2)切化弦:一般需将表达式中的切函数转化为弦函数.(3)注意“1”的应用:221sin cos tan4παα=+=.(4)用诱导公式进行化简时,若遇到k πα±的形式,需对k 进行分类讨论,然后再运用诱导公式进行化简.题型四:诱导公式在三角函数证明中的应用例10.(2022·全国·高一课时练习)(1)求证:tan(2)sin(2)cos(6)tan 33sin()cos()22παπαπααππαα----=-++; (2)设8tan()7m πα+=,求证1513sin()3cos()37720221sin()cos()77m m ππααππαα++-+=+--+.例11.(2022·全国·高一专题练习)求证:3πtan(2π)cos cos(6π)2tan 3π3πsin cos 22a a a a a a ⎛⎫--- ⎪⎝⎭=-⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭例12.(2022·上海·高一课时练习)已知A 、B 、C 是ABC 的三个内角,求证; (1)cos(2)cos 0A B C A +++=; (2)3πtan tan 044A B C+++=.变式14.(2022·上海·高一)若k ∈Z ,求证:sin(π)cos(π)1sin[(1)π]cos[(1)π]k k k k αααα-+=-+++-.变式15.(2022·全国·高一课时练习)求证:()()()()()()()()()sin 3cos 4sin 4cos 2cos cos sin tan sin απαππαπααππααπαπαπ-+---=--++---.【方法技巧与总结】 三角恒等式的证明策略对于恒等式的证明,应遵循化繁为简的原则,从左边推到右边或从右边推到左边,也可以用左右归一、变更论证的方法.常用定义法、化弦法、拆项拆角法、“1”的代换法、公式变形法,要熟练掌握基本公式,善于从中选择巧妙简捷的方法.题型五:诱导公式的综合应用例13.(2022·全国·高一课时练习)在①()3sin 2sin 2ππαα⎛⎫-=- ⎪⎝⎭,②()2tan 3πα-=-这两个条件中任选一个,补充在下面横线中,并解答.已知α为第一象限角,且___________,求sin α,cos α,tan α的值.例14.(2022·全国·高一课时练习)已知函数()π5π10πcos 2cos 2tan 26334π4πtan 2sin 233x x x f x x x ⎛⎫⎛⎫⎛⎫--+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=⎛⎫⎛⎫+-- ⎪ ⎪⎝⎭⎝⎭. (1)化简()f x ; (2)若()0310f x =,求00π2πsin 2cos 263x x ⎛⎫⎛⎫-+- ⎪ ⎪⎝⎭⎝⎭的值.例15.(2022·江西上饶·高一阶段练习)在平面直角坐标系xOy 中,OAB 的顶点O 与坐标原点重合,点A 在x 轴的正半轴上,点B 在第二象限,且1OA OB ==,记AOB α=∠,满足4sin 5α=. (1)求点B 的坐标;(2)求()()()22cos 3cos 12sin cos παπααπα⎛⎫-+++ ⎪⎝⎭--的值.变式16.(2022·陕西渭南·高一期末)已知α为第二象限角,π4sin 25α⎛⎫-=- ⎪⎝⎭.(1)求sin α的值;(2)若cos tan()cos(2)2()tan(19)sin(5)sin()f αααααααπ⎛⎫--π+π- ⎪⎝⎭=--π-π-π+,求()f α的值.变式17.(2022·陕西渭南·高一期末)已知角α的顶点在原点,始边与x 轴的非负半轴重合,终边经过点()3,4P -.(1)求cos()cos 2ππαα⎛⎫-++ ⎪⎝⎭的值;(2)求sin()cos sin()tan()2cos(2)sin cos()tan()2πααπαπαππααπαπα⎛⎫---+ ⎪⎝⎭⎛⎫-++- ⎪⎝⎭的值.变式18.(2022·陕西渭南·高一期末)已知角θ的终边经过点()(),220P m m m >. (1)求tan θ的值;(2)求()()()()()sin sin sin tan 2cos 2cos cos 2ππθθπθπθππθθπθ⎛⎫++-+ ⎪⎝⎭⎛⎫--+ ⎪⎝⎭的值.变式19.(2022·广西·桂林市奎光学校高一期末)已知点(,22P m 是角α终边上的一点,且1cos 3α=-.(1)求tan α的值;(2)求()()sin cos 3cos sin 22αππαππαα--+⎛⎫⎛⎫++- ⎪ ⎪⎝⎭⎝⎭的值.【方法技巧与总结】解决此类问题时,可先用诱导公式化简变形,将三角函数的角度统一后再用同角三角函数关系式,这样可避免公式交错使用时导致的混乱.题型六:利用互余互补关系求值例16.(2022·广西·桂林市奎光学校高一期末)已知2sin 33πα⎛⎫+=- ⎪⎝⎭,则2sin cos 36ππαα⎛⎫⎛⎫-+-=⎪ ⎪⎝⎭⎝⎭________.例17.(2022·内蒙古大学满洲里学院附属中学高一期末)已知π3sin 65x ⎛⎫-= ⎪⎝⎭,则πcos 3x ⎛⎫+ ⎪⎝⎭的值是___________.例18.(2022·贵州·遵义四中高一期中)已知3sin 35πα⎛⎫+= ⎪⎝⎭,则7cos 6πα⎛⎫-=⎪⎝⎭__________.变式20.(2022·江苏省灌南高级中学高一阶段练习)已知cos(45°+α)=513,则cos(135°-α)=________.变式21.(2022·江西省万载中学高一期中)若3sin 6πθ⎛⎫- ⎪⎝⎭,则2cos 3πθ⎛⎫- ⎪⎝⎭的值为_____.变式22.(2022·全国·高一课时练习)当0,2πθ⎛⎫∈ ⎪⎝⎭时,若51cos 62πθ⎛⎫-=- ⎪⎝⎭,则sin 6πθ⎛⎫+ ⎪⎝⎭的值为_________.变式23.(2022·黑龙江·大庆实验中学高一期末)已知cos 6πθ⎛⎫- ⎪⎝⎭=a (|a |≤1),则cos 56πθ⎛⎫+⎪⎝⎭+sin 23πθ⎛⎫- ⎪⎝⎭的值是________.【方法技巧与总结】巧用相关角的关系会简化解题过程.观察所求角与已知角是否具有互余、互补等特殊关系.在转化过程中可以由已知到未知,也可以由未知索已知.常见的互余关系有3πα-,6πα+;3πα+,6πα-;4πα+,4πα-等.常见的互补关系有3πθ+,23πθ-;4πθ+,34πθ-等. 【同步练习】一、单选题1.(2022·全国·高一课时练习)已知sin 37a =,则cos 593=( ) A .aB .a -C 21a -D .21a --2.(2022·全国·高一课时练习)设()()()sin πcos πx f x a b x αβ++=+,其中,,,a b αβ∈R ,若()20215f =,则()2022f =( ) A .4B .3C .-5D .53.(2022·辽宁葫芦岛·高一期末)已知α为锐角,()2sin π3α-=,则cos α的值为( ) A .13B .23-C 5D .54.(2022·全国·高一专题练习)在ABC 中,下列等式一定成立的是( ) A .sin sin A B CB .()cos cos A BC += C .cossin 22B C A+= D .sinsin 22B C A+= 5.(2022·全国·高一单元测试)在平面直角坐标系xOy 中,角α的终边与单位圆交于点734⎫-⎪⎪⎝⎭,则3πsin 2α⎛⎫+= ⎪⎝⎭( ) A .34B .34-C 7D .76.(2022·全国·高一课时练习)已知()0,απ∈,()tan 3sin παα-=,则tan α=( ) A .22B 2C .24-D .22-7.(2022·陕西渭南·高一期末)若33sin 25πα⎛⎫+= ⎪⎝⎭,且α是第三象限角,则2021cos 2πα⎛⎫+=⎪⎝⎭( ) A .35B .35 C .45D .45-8.(2022·北京市第十九中学高一期中)若α为任意角,则满足cos cos 2k παα⎛⎫+⋅=- ⎪⎝⎭的一个k 的值为( )A .1B .2C .3D .4二、多选题9.(2022·新疆·柯坪湖州国庆中学高一期末)下列与sin θ的值一定相等的是( )A .πcos 2θ⎛⎫+ ⎪⎝⎭B .πsin 2θ⎛⎫- ⎪⎝⎭C .πcos 2θ⎛⎫- ⎪⎝⎭D .()sin πθ-10.(2022·全国·高一课时练习)在ABC 中,下列等式一定成立的是( ) A .sincos 22A B C+=- B .()sin 22cos2A B C +=- C .()tan tan A B C +=-D .()sin sin A B C +=11.(2022·全国·高一课时练习)已知函数()cos 2xf x =,则( )A .()()f x f x -=B .()()f x f x -=-C .()()2f k x f x π+=,k ∈ZD .()()()21kf k x f x π-=-,k ∈Z12.(2022·全国·高一课时练习)定义:角θ与ϕ都是任意角,若满足2πθϕ+=,则称θ与ϕ“广义互余”.已知()1sin 4πα+=-,则下列角β中,可能与角α“广义互余”的是( )A .15sin β=B .()1cos 4πβ+=C .tan 15β=D .15tan β=三、填空题13.(2022·天津·高一期末)已知1tan 2α=,则cos()3cos 23sin sin()2ππααπαα⎛⎫--+ ⎪⎝⎭=⎛⎫--- ⎪⎝⎭_________. 14.(2022·天津·高一期末)已知函数3()sin 2(0)f x ax b x ab =++≠,若(2019)f k =,则(2019)f -=_________.15.(2022·江苏·南京市第一中学高一阶段练习)若()()2sin πcos π2πsin 2ααα+-=⎛⎫+ ⎪⎝⎭,则22sin sin cos 1cos αααα+=+______. 16.(2022·北京·牛栏山一中高一阶段练习)已知角α的终边经过点()3,4,将角α的终边绕原点O 顺时针旋转2π得到角β的终边,则tan β=___________. 17.(2022·安徽·砀山中学高一期中)已知π3cos 64α⎛⎫+=- ⎪⎝⎭,则5ππcos sin 63αα⎛⎫⎛⎫-+-= ⎪ ⎪⎝⎭⎝⎭______.四、解答题18.(2022·江西省万载中学高一期中)(1)化简:222cos(4)cos ()sin (3)sin(4)sin(5)cos ()θπθπθπθππθθπ+++-+-- (2)已知()sin 3n f n π=(n ∈Z ),求(1)f +(2)f +(3)f +…+(2012)f 的值.19.(2022·江西省万载中学高一阶段练习)已知3sin()cos()tan()22()tan()sin()f ππααπααπαπα-+-=---- (1)化简()f α (2)若31cos()25πα-=,α为第三象限角,求()f α的值.20.(2022·安徽省舒城中学高一开学考试)(1)已知3sin 5α=-,求tan cos αα+的值(2()2382cos225sin tan 204033π⎛⎫---- ⎪⎝⎭21.(2022·全国·高一课时练习)已知A 、B 、C 为ABC 的三个内角,求证:ππsin cos 2424A B C +⎛⎫⎛⎫+=- ⎪⎪⎝⎭⎝⎭22.(2022·全国·高一课时练习)如图,锐角α和钝角β的终边分别与单位圆交于A ,B 两点,且OA OB ⊥.(1)求()()πsinπcos23πcosπsin2αββα⎛⎫++⎪⎝⎭⎛⎫-+⎪⎝⎭的值;(2)若点A的横坐标为35,求2sin cosαβ的值.。
诱导公式及应用

九组诱导公式总结及应用题型:九组诱导公式总结及其应用【知识链接】1.公式内容:2.文字概括:奇变偶不变,符号看象限.其中,“奇、偶”是指:.3.诱导公式对三角函数式的求值、化简、证明等具有重要作用,须熟练掌握,灵活运用,运用顺序:负化正,大化小,化到锐角再查表.注:以上各公式的推导思路及过程不需掌握,若有兴趣,详见后面附录.【巩固与应用】③这些关系式就是以上三个公式.例1化简sin()cos[(1)]sin[(1)]cos()kπαkπαkπαkπα-⋅--++⋅+(Z)k∈.结果:分2(Z)k n n=∈、21(Z)k n n=+∈化简,得1-.1.sin210=DAB.C.1D.12-2.sin(300)-=CA.12B.12-CD.3.已知sin(3)13απ-=,则cos()πα+= BA.13B.13-C.D.-4.已知sin(14απ-=,则cos(3)sin(56)παπα+++=.5sin(22)cos1cos()πθθθπθ--⋅=+,(0,)θπ∈,求θ的值.结果:3π,23π6.(05湖南文2)tan600=DA.BC.D7.(08陕西)sin 330= BA .B .12-C .12 D8.tan 2010= .例2 已知sin(3)2sin(32)παπα+=+,求下列各式的值.(1)sin 4cos 5sin 2cos αααα-+; 结果:16- (2)2sin sin 2αα+. 结果:85例3 化简tan(27)tan(49)tan(63)tan(139)αβαβ--+- . 1-1.若cos(5)x π+,[,]x ππ∈-,则x = BA .56π,7πB .56π±C .7π±D .2π±2.已知sin(6)14x π+=,则2sin(56)sin (3)πx πx -+-= .3.已知(2,32)αππ∈,tan(7)34απ-=-,则sin cos αα+=A .1±B .15-C .1D .7-4.若cos()12πα+=-,322παπ<<,则sin(2)πα+= DA .12B .CD .5.若sin()sin(32)πθπθ-+-=(02)θπ≤≤,则sin cos(2)θπθ+-= .结果:46.若cos(6)πα-=,则cos(56)πα+= . 7.cos(174)sin(17ππ---= AA B . C .0 D8.已知cos31m = ,则sin 239tan149= BA .2(1)m m -BC .2(1)m m -D .9.化简:332sin ()cos()cos()tan ()cos ()πααπαπααπ+-++--. 3cos α 10.若Z n ∈,则在下列各式 ①sin(3)n ππ+;②sin(23)n ππ±;③sin[(1)3]n n ππ+-;④cos[2(1)n n ππ+-中, 与sin 3π相等的是 .(写上所有符合要求的式子的序号). ③④11=. 1。
诱导公式五六课件

[变式训练 1] 若 sin(180°+α)+cos(90°+α)=m,则 cos(270°
-α)+2sin(360°-α)的值为( D )
A.-12m
Байду номын сангаас
B.-32m
1 C.2m
3 D.2m
解析:由题意得-sinα-sinα=m,所以 sinα=-m2 . cos(270°-α)+2sin(360°-α)=-sinα-2sinα=-3sinα=32m. 故选 D.
2.诱导公式反映了各种不同形式的角的三角函数之间的相 互关系,并具有一定的规律性,“奇变偶不变,符号看象限”, 是记住这些公式的有效方法.
3.诱导公式是三角变换的基本公式,其中角 α 可以是一个 单角,也可以是一个复角,应用时要注意整体把握、灵活变通.
温馨 提 示
请 做:课时作业 44
PPT文稿 〔点击进入〕
第五章
三角函数
5.3 诱导公式
第2课时 诱导公式五、六
[目标] 1.能够借助单位圆中的三角函数线推导出诱导公式 五、六;2.能灵活地利用诱导公式进行化简、求值.
[重点] 诱导公式五、六的应用. [难点] 诱导公式的推导与证明.
要点整合夯基础 课堂达标练经典
典例讲练破题型 课时作业
知识点一
D.- 1-a2
解析:cos130°=cos(90°+40°)=-sin40°=-a.
2.已知 sin(α-π4)=13,则 cos(π4+α)的值等于( D )
22 A. 3
B.-2 3 2
1 C.3
D.-13
解析:∵π4+α-(α-π4)=π2, ∴cos(π4+α)=cos[π2+(α-π4)]=-sin(α-π4)=-13.
三角函数恒等变换

三角函数恒等变换三角函数恒等变换 一、三角函数的诱导公式1、下列各角的终边与角α的终边的关系 角2k π+α(k ∈Z)π+α-α图示与α角终边的关系相同 关于原点对称关于x 轴对称角 π-α2π-α 2π+α图示与α角终边的关系 关于y 轴对称关于直线y=x 对称2、六组诱导公式 组数 一 二 三 四 五 六 角2k π+απ+α-απ-α2π-α2π+α(k∈Z)正弦sinα-sinα-sinαsinαcosαcosα余弦cosα- cosαcosα- cosαsinα-sinα正切tanαtanα- tanα- tanα口诀函数名不变符号看象限函数名改变符号看象限注:诱导公式可概括为的各三角函数值的化简公式。
记忆规律是:奇变偶不变,符号看象限。
其中的奇、偶是指的奇数倍和偶数倍,则函数名称变为相应的余名函数;若是偶数倍,则函数名称不变,符号看象限是指把α看成锐角时原函数值的符号作为结果的符号。
二、两角和与差的正弦、余弦和正切公式1、两角和与差的正弦、余弦和正切公式2、二倍角的正弦、余弦、正切公式.sinα=22tan21tan2αα+, cosα=221tan21tan2αα-+3、形如asinα+bcosα的化简asinα+bcosα=22a b+α+β).其中cos β22a b+,sinβ22a b+三、简单的三角恒等变换1、用cosα表示sin22α,cos22α,tan22αsin22α=1cos2α-;cos22α=1cos2α+;tan 22α=1cos 1cos αα-+ 注:上述三组公式从左到右起到一个扩角降幂的作用;从右到左起到一个缩角升幂的作用。
2、用cos α表示sin 2α,cos 2α,tan 2αsin 2α=cos 2α=tan 2α= 3、用sin α,cos α表示tan 2α tan 2α=sin 1cos 1cos sin αααα-=+ 四、常用数据: 30456090、、、的三角函数值 6sin15cos 75-==,42615cos 75sin +==3275cot 15tan -== ,3215cot 75tan +==注: ⑴以上公式务必要知道其推导思路,从而清晰地“看出”它们之间的联系,它们的变化形式.如tan()(1tan tan )tan tan αβαβαβ+-=+221cos 1cos cos,sin 2222αααα+-==等.从而可做到:正用、逆用、变形用自如使用各公式.⑵三角变换公式除用来化简三角函数式外,还为研究三角函数图象及性质做准备. ⑶三角函数恒等变形的基本策略。
高中数学诱导公式大全

高中数学诱导公式大全数学中有众多的诱导公式,本文为大家整理了高中数学中的常见诱导公式,方便大家在复习学习时使用。
1. 平方差公式(a + b)(a - b) = a² - b²这个公式通常用于把一个含有两个数的算式转化为两个平方数之差的形式。
例如:19 × 21 = (20 - 1)(20 + 1) = 400 - 1 = 399。
2. 同底数幂相除的规律a^m ÷ a^n = a^(m-n)这个公式通常用于简化同底数幂的除法计算,只需要将指数相减即可。
例如:4³ ÷ 4² = 4^(3-2) = 4。
3. 牛顿莱布尼兹公式f(b) - f(a) = ∫a^b f'(x) dx这个公式是微积分中的重要定理,用于计算曲线下的面积或弧长。
它将原函数的值与导数之间建立了联系,方便进行积分计算。
4. 余弦定理c² = a² + b² - 2ab cosC这个公式通常用于求解三角形的边长或角度,可以根据三边长度或两边一夹角的余弦值来计算第三边长度或夹角大小。
5. 正弦定理a/sinA = b/sinB = c/sinC这个公式通常用于求解三角形的边长或角度,可以根据三角形的一个角和这个角的对边的长度,以及任意两个角或者边长之比来计算其他角或者边长的值。
6. 勾股定理a² + b² = c²这个公式通常用于求直角三角形中三条边中未知边的长度或判定一个三角形是否为直角三角形。
7. 毕达哥拉斯定理若a、b、c都是正整数,且a² + b² = c²,则称该三组数为毕达哥拉斯数。
8. 相反数的性质a + (-a) = 0一个数加上它的相反数等于零,即a和-a互为相反数。
9. 分配律a(b + c) = ab + ac这个公式通常用于计算多项式的乘法。
诱导公式大全

诱导公式大全诱导公式是数学中的一个重要概念,它可以帮助我们简化复杂的表达式,解决各种数学问题。
在本文中,我们将为大家详细介绍各种常见的诱导公式,希望能够帮助大家更好地理解和运用这些公式。
一、三角函数的诱导公式。
1. sin(A ± B) = sinAcosB ± cosAsinB。
2. cos(A ± B) = cosAcosB ∓ sinAsinB。
3. tan(A ± B) = (tanA ± tanB) / (1 ∓ tanAtanB)。
这些诱导公式可以帮助我们简化三角函数的加减运算,特别是在解决三角函数的复合运算问题时,能够起到很大的作用。
二、指数函数的诱导公式。
1. e^x ± e^(-x) = 2coshx。
2. e^x ∓ e^(-x) = 2sinhx。
3. (e^x + e^(-x)) / 2 = coshx。
4. (e^x e^(-x)) / 2 = sinhx。
这些诱导公式是指数函数的一些常见运算公式,通过这些公式,我们可以将指数函数的运算转化为双曲函数的运算,从而简化计算过程。
三、对数函数的诱导公式。
1. ln(xy) = ln x + ln y。
2. ln(x/y) = ln x ln y。
3. ln(x^n) = nlnx。
对数函数的诱导公式主要是针对对数的乘除运算和指数的换底运算,这些公式在解决对数函数的复合运算问题时非常有用。
四、微积分中的诱导公式。
1. (x^n)' = nx^(n-1)。
2. (e^x)' = e^x。
3. (lnx)' = 1/x。
4. (sinx)' = cosx。
5. (cosx)' = -sinx。
6. (tanx)' = sec^2x。
这些微积分中的诱导公式是我们在求导过程中经常会用到的公式,通过这些公式,我们可以快速求得各种函数的导数,解决各种微积分问题。
《诱导公式五、六》三角函数

利用诱导公式五、六证明三角恒等式
总结词
在一些情况下,可以利用诱导公式五、六来证明一些三角恒等式。
详细描述
在一些情况下,要证明的三角恒等式形式可能较为复杂,此时可以利用诱导公式五、六来进行化简和 变形,从而证明该恒等式。例如,可以利用诱导公式五、六来证明一些涉及到正弦、余弦、正切函数 的恒等式,如两角和与差的三角函数公式等。
乘积化和差或和差化积的三角函数式。
利用诱导公式五、六求三角函数的值
总结词
在求解一些三角函数值的问题中,可以利用诱导公式五、六来得到所需的值。
详细描述
在一些情况下,直接使用三角函数的定义来求解其值可能较为繁琐。此时,可以利用诱导公式五、六来简化求 解过程。例如,可以利用诱导公式五来求得一个在第二象限的角的正弦值或余弦值,也可以利用诱导公式六来 求得一个在第四象限的角的正切值。
记忆口诀:对于初学者来说,可以借助口诀来记忆诱导 公式五、六。例如,“奇变偶不变,符号看象限;一全 正,二正弦,三正切,四余弦;五正割,六余切”这个 口诀就能够很好地帮助记忆诱导公式五、六。
诱导公式五、六的变种及应对方法
变种一
已知三角函数值求角。对于已知三角函数值求角的问 题,可以利用三角函数的反函数或者三角函数的和差 倍角公式来解决。
三角函数是一种在直角坐标系中表示角度的数学函数,它们具有周期性和对称性 等性质,这些性质可以用来推导诱导公式五、六。
诱导公式五、六的内容
诱导公式五
$\sin(k\pi+\alpha)=\sin\alpha$,其中$k$是整数。
诱导公式六
$\cos(k\pi+\alpha)=(-1)^{k}\cos\alpha$,其中$k$是整数。
变种二
诱导公式的应用

=
tan +1
tan -1
.
(2)已知 cos x+sin x∈[- 2, 2],求函数 y=cos x+sin x+sin xcos x 的最大值.
方法指导
(1)“1”用 sin2α+cos2α 代换,再化简;(2)令 t=cos x+sin x,整体换元
求二次函数的最值.
课堂导学
课前预学
cos (6π-)结
证明三角恒等式的常用方法:①由左边推至右边或由右边推至左边,遵循
的是化繁为简的原则;②证明左边=A,右边=A,则左边=右边,这里的 A 起着桥梁的作用;③
通过作差或作商证明,即左边-右边=0 或
左边
右边
右边
=1 或
左边
=1.
课堂导学
课前预学
【针对训练 3】求证:
=
si n 2 αtan cos
cos sin tan
6
=sin α.
3
(2)因为 f(α)=sin α= ,且 α 是锐角,所以 cos α= 1-sin2 α= ,
3
所以 tan α=
sin
cos
3
= 2,
则 sin α+ 2sin αcos α-cos α+
2
=
=
2
si n 2 α+ 2sin cos -co s 2 α
(2)若 α 的终边经过点 P(-3,4),求 f(α)的值.
解析
=
(1)f(α)=
sin (cos -sin )
sin
-sin sin +cos sin
tan cos
第二讲 诱导公式的应用
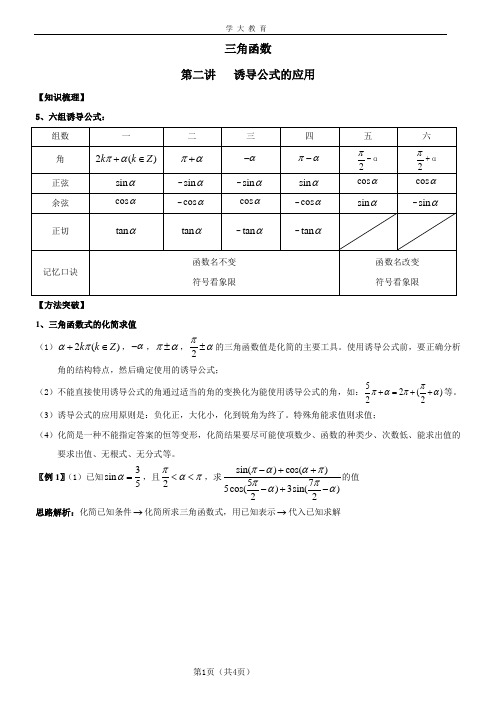
三角函数第二讲 诱导公式的应用【知识梳理】 5、六组诱导公式:【方法突破】1、三角函数式的化简求值(1)2()k k Z απ+∈,α-,πα±,2πα±的三角函数值是化简的主要工具。
使用诱导公式前,要正确分析角的结构特点,然后确定使用的诱导公式;(2)不能直接使用诱导公式的角通过适当的角的变换化为能使用诱导公式的角,如:52()22ππαπα+=++等。
(3)诱导公式的应用原则是:负化正,大化小,化到锐角为终了。
特殊角能求值则求值;(4)化简是一种不能指定答案的恒等变形,化简结果要尽可能使项数少、函数的种类少、次数低、能求出值的要求出值、无根式、无分式等。
〖例1〗(1)已知3sin 5α=,且2παπ<<,求sin()cos()575cos()3sin()22πααπππαα-++-+-的值思路解析:化简已知条件→化简所求三角函数式,用已知表示→代入已知求解(2)已知sin()2cos(2)απαπ-=-,求3333sin ()5cos (4)3cos (5)sin ()πααππαα-+-+--的值2、三角函数的简单综合应用问题:〖例2〗已知sin θ是方程25760x x --=的根,且θ是第三象限角,求233sin()cos()tan ()22cos()sin()22ππααπαππαα-----+的值【精题精练】 1. 1sin()2πα+=-,则cos α的值为;若cos()2πθ+=,且2πθ<,则tan θ= 2.已知0cos100m =,0tan 80的值是 (用含m 的代数式表示结果) 3. 已知31tan(5)1a aπθ-+=+,若θ为第二象限角,则a 的取值范围是 4.已知角sin()112πθ-⎛⎫< ⎪⎝⎭,则θ是第 象限角5.化简2sin()cos()21cos ππααα--=- 6.化简sin(5)cos()cos(8)23sin()sin(4)2πθπθπθπθθπ-⋅--⋅-=-⋅-- 7.已知4sin()5πα+=,且sin cos 0αα<,则2sin()3tan(3)4cos(3)αππααπ-+--的值为 8.若tan 3α=,则2sin 3cos sin 2cos αααα-+= ;224sin 3sin cos 5cos αααα-- =9.若sin cos 2sin cos αααα+=-;则3sin(5)sin()2παπα-⋅- 的值是 10.已知角α的终边过点(1P ,则sin()sin()2ππαα--+=11.设222sin()cos()cos()()31sin (3)cos()sin ()22f παπααπαπππααα+----=+-++-+,则23()6f π-= 12.已知(cos )cos3f x x =,则0(sin30)f = 13.已知A 为锐角,1lg(1cos ),lg1cos A m n A+==-,则lgsin A =14.已知()sin()cos()4f x a x b x παπβ=++++(a 、b 、α、β均为非零实数),若(2011)6f =,则(2012)f =15.设α是第三象限角,且sin 2α=,则2α是第几象限角?16.已知1sin()64x π+=,求275sin()cos ()66x x ππ++-的值17.若sin cos 2sin cos αααα+=-,求sin(5)cos(2)sin()cos()2αππαπαπα---+18.已知α是第三象限角,且3sin()cos(2)tan()2()cot()sin()f παπααπααππα---+=----(1)化简()f α; (2)若31cos()25απ-=,求()f α的值; (3)若01860α=-,求()f α的值;19.若()sin()3n f n n Z π=∈ (1)求证:()(6)f n f n =+; (2)求(1)(2)(2012)f f f +++ 的值;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
诱导公式
一、六组
公式一: 公式二:
公式三: 公式四:
公式五: 公式六:
记忆口诀:奇变偶不变,符号看象限。
一、求值:
例1、求下列各三角函数的值
(1)sin 0120 (2)cos 0300 (3)tan 0240 (4)sin
45π
(5)sin(-0600) (6)cos(-
317π) (7)tan(-67π) (8)sin(-12000)
例2、已知sin(∂+π)=
53,求(1)cos(π2-∂) (2)sin(∂+2π)
例3、已知cos(
∂-6π)=3
3,求cos(∂+65π)-sin 2)6(π-∂的值。
例4、已知cos(-800)=k,求tan1000的值。
三、化简:
例5、(1)
)5sin()cos()2tan()6cos()2sin(θππθθπθπθπ+-----
(2)
[][]),)cos()sin()1(cos )1(sin z k k k k k ∈+--+++(其中θπθπθπθπ
例6、ABC ∆中,证明下列各式:
(1)sin(A+B)=sinC (2)cos(A+B)=-cosC
(3)sin(2B A +)=cos 2C (4)cos )2(B A +=sin 2
C
四、综合题:
例7、已知∂是第三象限角,f(∂)=)
sin()tan()tan()2cos()sin(∂--∂++-∂∂-∂-πππππ, (1)化简f()∂
(2)若cos(∂23π-)=5
1,求f(∂)的值。
(3)若01860-=∂,求f(∂)的值。
例8、已知函数f(x)=asin(∂+x π)+bcos(βπ+x ),其中a,b βα,都是非零实数,又知f(2010)=-1,求f(2011)
例9、已知f(n)=sin
)102(...)3()2()1(),(6f f f f z n n +++∈求π
例10、已知tan ∂,
1tan ∂是方程22(2)0x k x k -++=的两根,求sin()cos()ππ-∂++∂的值。
课后作业:
1、 求值:
(1)sin 0600 (2)cos3300 (3)tan(
53π) (4)sin(176π-)
2
3
4 12cos(),sin()633ππαα+=+=则sin 280,cos10m = 则等于12sin(2)cos(2)22ππ+-+=。
