专题：解二元一次方程组(含答案)

专题：解二元一次方程组

——学会选择最优的解法

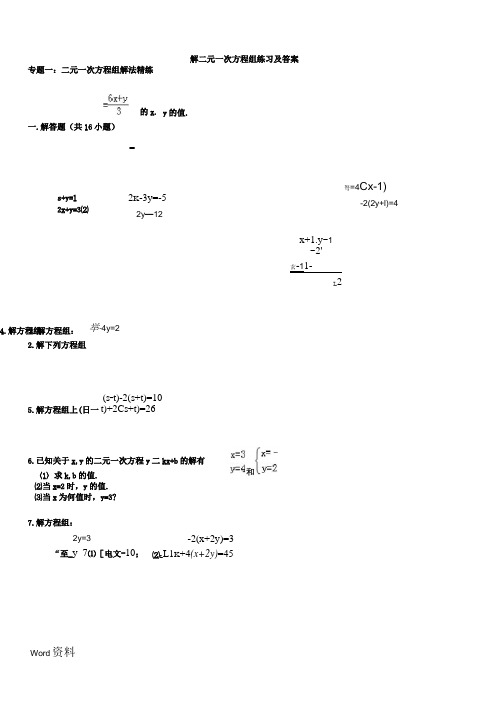
◆类型一 解未知数系数含有1或－1的方程组

1.已知a ，b 满足方程组⎩

⎪⎨⎪⎧a －b ＝2，a ＋b ＝6，则3a ＋b 的值为（ ） A.14 B.4 C.－4 D.－14

2.以方程组⎩

⎪⎨⎪⎧y ＝－x ＋2①，y ＝x －1②的解为坐标的点（x ，y ）在平面直角坐标系中的位置在（ ） A.第一象限 B.第二象限

C.第三象限

D.第四象限

3.若3x m ＋2n y 与－13

y m －n x 4是同类项，则m ＝ ，n ＝ Ｗ. 4.解方程组：

（1）⎩

⎪⎨⎪⎧x －y ＝0①，2x ＋y ＝6②；

（2）（2017·桂林中考）⎩

⎪⎨⎪⎧2x ＋y ＝3①，5x ＋y ＝9②.

◆类型二 解同一未知数系数互为倍数关系的方程组

5.二元一次方程组⎩

⎪⎨⎪⎧2x ＋3y ＝7，2x －3y ＝1的解为（ ） A.⎩⎪⎨⎪⎧x ＝4，y ＝3 B.⎩⎪⎨⎪⎧x ＝2，y ＝1 C.⎩⎪⎨⎪⎧x ＝－4，y ＝3 D.⎩

⎪⎨⎪⎧x ＝2，y ＝－1 6.解方程组：

（1）⎩⎪⎨⎪⎧5x ＋2y ＝25①，3x ＋4y ＝15②； （2）⎩

⎪⎨⎪⎧8x ＋9y ＝73①，17x －3y ＝74②.

◆类型三 解两个方程中未知数系数成对称关系的方程组

7.若x ，y 满足方程组⎩

⎪⎨⎪⎧x ＋3y ＝7，3x ＋y ＝5，则x －y 的值等于（ ） A.－1 B.1 C.2 D.3

8.方程组⎩

⎪⎨⎪⎧2x ＋3y ＝3，3x ＋2y ＝11的解为 Ｗ. 9.已知方程组⎩

⎪⎨⎪⎧3x ＋y ＝1＋3a ①，x ＋3y ＝1－a ②的解满足x ＋y ＝0，求a 的值.

◆类型四 含字母系数的方程组的运用

10.（2017·余干县校级期末）已知x ，y 满足方程组⎩

⎪⎨⎪⎧x ＋m ＝4，y －5＝m ，则无论m 取何值，x ，y 恒有关系式是（ ）

A.x ＋y ＝1

B.x ＋y ＝－1

C.x ＋y ＝9

D.x ＋y ＝－9

11.（2017·枣庄中考）已知⎩⎪⎨⎪⎧x ＝2，y ＝－3是方程组⎩⎪⎨⎪⎧ax ＋by ＝2，bx ＋ay ＝3

的解，则a 2－b 2＝ Ｗ. 12.已知方程组⎩⎪⎨⎪⎧2x ＋y ＝－2，ax ＋by ＝－4和方程组⎩

⎪⎨⎪⎧3x －y ＝12，bx ＋ay ＝－8的解相同，求（5a ＋b ）2的值.

参考答案与解析

1．A 2.A 3.2 1

4．解：(1)①＋②，得3x ＝6，解得x ＝2.把x ＝2代入①得y ＝2，∴原方程组的解为⎩

⎪⎨⎪⎧x ＝2，y ＝2. (2)②－①，得3x ＝6，解得x ＝2，把x ＝2代入①得y ＝－1，∴原方程组的解为⎩

⎪⎨⎪⎧x ＝2，y ＝－1. 5．B

6．解：(1)①×2－②，得10x －3x ＝50－15，解得x ＝5.把x ＝5代入②得y ＝0.∴原方

程组的解为⎩

⎪⎨⎪⎧x ＝5，y ＝0. (2)①＋②×3，得8x ＋51x ＝73＋74×3，解得x ＝5.把x ＝5代入②得17×5－3y ＝74，

解得y ＝113，∴原方程组的解为⎩⎪⎨⎪⎧x ＝5，y ＝113.

7．A 8.⎩

⎨⎧x ＝275，y ＝－135 9．解：①＋②，得4x ＋4y ＝2＋2a ，∴x ＋y ＝1＋a 2.∵x ＋y ＝0，∴1＋a 2

＝0，解得a ＝－1.

10．C 11.1

12．解：解方程组⎩⎪⎨⎪⎧2x ＋y ＝－2，3x －y ＝12，得⎩⎪⎨⎪⎧x ＝2，y ＝－6.将⎩⎪⎨⎪⎧x ＝2，y ＝－6代入⎩

⎪⎨⎪⎧ax ＋by ＝－4，bx ＋ay ＝－8，得

⎩⎪⎨⎪⎧2a －6b ＝－4，2b －6a ＝－8.解得⎩⎨⎧a ＝74

，b ＝54，∴(5a ＋b )2＝102＝100.