小学奥数- 带余除法(一)
小学奥数 余数性质(一)

1. 学习余数的三大定理及综合运用2. 理解弃9法,并运用其解题一、三大余数定理:1.余数的加法定理 a 与b 的和除以c 的余数,等于a ,b 分别除以c 的余数之和,或这个和除以c 的余数。
例如:23,16除以5的余数分别是3和1,所以23+16=39除以5的余数等于4,即两个余数的和3+1.当余数的和比除数大时,所求的余数等于余数之和再除以c 的余数。
例如:23,19除以5的余数分别是3和4,所以23+19=42除以5的余数等于3+4=7除以5的余数为22.余数的加法定理a 与b 的差除以c 的余数,等于a ,b 分别除以c 的余数之差。
例如:23,16除以5的余数分别是3和1,所以23-16=7除以5的余数等于2,两个余数差3-1=2. 当余数的差不够减时时,补上除数再减。
例如:23,14除以5的余数分别是3和4,23-14=9除以5的余数等于4,两个余数差为3+5-4=43.余数的乘法定理a 与b 的乘积除以c 的余数,等于a ,b 分别除以c 的余数的积,或者这个积除以c 所得的余数。
例如:23,16除以5的余数分别是3和1,所以23×16除以5的余数等于3×1=3。
当余数的和比除数大时,所求的余数等于余数之积再除以c 的余数。
例如:23,19除以5的余数分别是3和4,所以23×19除以5的余数等于3×4除以5的余数,即2.乘方:如果a 与b 除以m 的余数相同,那么n a 与n b 除以m 的余数也相同.二、弃九法原理在公元前9世纪,有个印度数学家名叫花拉子米,写有一本《花拉子米算术》,他们在计算时通常是在一个铺有沙子的土板上进行,由于害怕以前的计算结果丢失而经常检验加法运算是否正确,他们的检验方式是这样进行的:例如:检验算式1234189818922678967178902889923++++=1234除以9的余数为11898除以9的余数为818922除以9的余数为4678967除以9的余数为7178902除以9的余数为0这些余数的和除以9的余数为2而等式右边和除以9的余数为3,那么上面这个算式一定是错的。
小学奥数教程:带余除法(一)全国通用(含答案)

【关键词】走美杯,五年级,初赛,第13题
【解析】由题意,“用去尾法,10个商的和为30;用四舍五入法,l0个商的和为34”可知,10个数中除以3余2的数有34-30=4(个),又知道10个自然数的和为100,设除以3余1的数有 个,那么根据用去尾法后十个商的和与10个自然数的和,可得关系式: ,解得, 。
【考点】除法公式的应用【难度】2星【题型】解答
1【解析】除以7的余数只能是0~6,所以商只能是0~6,满足大于7的数只有商和余数都为5、6,所以只能是40、48。
【答案】40、48
【例 8】已知2008被一些自然数去除,所得的余数都是10,那么这样的自然数共有多少个?
【考点】除法公式的应用【难度】2星【题型】解答
【关键词】希望杯,四年级,复赛,第3题
【解析】因为最大的三位数为 , ,所以满足题意的三位数最大为:
【答案】
【巩固】计算口÷△,结果是:商为10,余数为▲。如果▲的值是6,那么△的最小值是_____。
【考点】除法公式的应用【难度】1星【题型】填空
【关键词】希望杯,五年级,复赛,第4题,6分
【解析】根据带余除法的性质,余数必须小于除数,则有△的最小值为7。
现在要求被11除余8,我们可以这样考虑:这样的数加上3后,就能被11整除了.所以我们得到“一个数被11除余8”的判定法则:将偶位数字相加得一个和数,再将奇位数字相加再加上3,得另一个和数,如果这两个和数之差能被11除尽,那么这个数是被11除余8的数;否则就不是.
要把1、9、8、8排成一个被11除余8的四位数,可以把这4个数分成两组,每组2个数字.其中一组作为千位和十位数,它们的和记作A;另外一组作为百位和个位数,它们之和加上3记作B.我们要适当分组,使得能被11整除.现在只有下面4种分组法:
小学奥数精讲:带余除法(同余式和同余方程)知识点及典型例题

小学奥数精讲:带余除法(同余式和同余方程)一、基本性质的复习1、带余数除法算式:a÷b=q……r(a、b、q、r 均为整数) 从中我们应该得到:(1)b>r 除数大于余数(2)a-r=b×q 被除数减去余数则会出现整除关系,则带余数问题就可以转化为整数问题。
2、余数的性质:(1)可加性:和的余数等于余数的和。
即:两数和除以m 的余数等于这两个数分别除以m 的余数和。
例:7÷3=2……1 5÷3=1……2,则(7+5)÷3 的余数就等于(1+2)÷3 的余数0。
(2)可减性:差的余数等于余数的差。
即:两数差除以m 的余数等于这两个数分别除以m 的余数差。
例:17÷3=5……2 5÷3=1……2,则(17-5)÷3 的余数就等于(2-2)÷3 的余数0。
(3)可乘性:积的余数等于余数的积。
即:两数积除以m 的余数等于这两个数分别除以m 的余数积。
例:64÷7=9……1 45÷7=6……3,则(64×45)÷3 的余数就等于(1×3)÷7 的余数3。
二、同余式在生活中,若两个自然数 a 和 b 都除以同一个除数m 时,余数相同该如何表示呢?在代数中我们称之为同余。
即:a 与b 同余于模m。
意思就是自然数a 和b 关于m 来说是余数相同的。
用同余式表达为:a≡b(modm).注:若a 与b 同余于模m,则a 与b 的差一定被m 整除。
(余数的可减性)三、例题。
例1、当2011 被正整数N 除时,余数为16,请问N 的所有可能值有多少个?例2、(1)求多位数1234567891011…20102011除以9的余数?(2)将1开始到103的连续奇数依次写成一个多位数:a=135791113…9799101103,则数a共有多少位?数a除以9 的余数为几?(3)一个多位数1234567……979899,问除以11 的余数是多少?例3、(1)用一个数除200 余5,除300 余1,除400 余10,求这个数?(2)甲、乙、丙、丁四个旅行团分别有游客69 人,85 人、93 人、97 人。
小学奥数带余除法

2.6带余除法2.6.1相关概念在整数围,整数a除以整数b(b≠0),若有a÷b=q……r,(即a=bq+r),0≤r<b。
当r=0时,我们称a能被b整除;当r≠0时,我们称a不能被b整除,r为a除以b的余数,q为a除以b的商。
2.6.2余数的性质⑴被除数=除数×商+余数,除数=(被除数-余数)÷商,商=(被除数-余数)÷除数。
⑵余数小于除数。
2.6.3同余定理(1)如果a,b除以c的余数相同,就称a、b对于除数c来说是同余的,且有a与b 的差能被c整除。
(a、b、c均为正整数)例如,17与11除以3的余数都是2,所以17-11能被3整除。
(2)a与b的和除以c的余数,等于a,b分别除以c的余数之和(或这个和除以c的余数)。
例如,23,16除以5的余数分别是3和1,所以(23+16)除以5的余数等于3+1=4。
注意:当余数之和大于除数时,所求余数等于余数之和再除以c的余数。
例如,23,19除以5的余数分别是3和4,所以(23+19)除以5的余数等于(3+4)除以5的余数。
(3)a与b的乘积除以c的余数,等于a,b分别除以c的余数之积(或这个积除以c 的余数)。
例如,23,16除以5的余数分别是3和1,所以(23×16)除以5的余数等于3×1=3。
注意:当余数之积大于除数时,所求余数等于余数之积再除以c的余数。
例如,23,19除以5的余数分别是3和4,所以(23×19)除以5的余数等于(3×4)除以5的余数。
性质(2)(3)都可以推广到多个自然数的情形。
2.6.4典型例题例1 5122除以一个两位数得到的余数是66,求这个两位数。
分析与解:由性质(2)知,除数×商=被除数-余数。
5122-66=5056,5056应是除数的整数倍。
将5056分解质因数,得到5056=26×79。
由性质(1)知,除数应大于66,再由除数是两位数,得到除数在67~99之间,符合题意的5056的约数只有79,所以这个两位数是79。
小学奥数:带余除法(一).专项练习及答案解析

1.能够根据除法性质调整余数进行解题2.能够利用余数性质进行相应估算3.学会多位数的除法计算4.根据简单操作进行找规律计算带余除法的定义及性质1、定义:一般地,如果a是整数,b是整数(b≠0),若有a÷b=q……r,也就是a=b×q +r,0≤r<b;我们称上面的除法算式为一个带余除法算式。
这里:(1)当0r=时:我们称a可以被b整除,q称为a除以b的商或完全商(2)当0r≠时:我们称a不可以被b整除,q称为a除以b的商或不完全商一个完美的带余除法讲解模型:如图这是一堆书,共有a本,这个a就可以理解为被除数,现在要求按照b本一捆打包,那么b就是除数的角色,经过打包后共打包了c捆,那么这个c就是商,最后还剩余d本,这个d就是余数。
这个图能够让学生清晰的明白带余除法算式中4个量的关系。
并且可以看出余数一定要比除数小。
2、余数的性质⑴被除数=除数⨯商+余数;除数=(被除数-余数)÷商;商=(被除数-余数)÷除数;⑵余数小于除数.3、解题关键理解余数性质时,要与整除性联系起来,从被除数中减掉余数,那么所得到的差就能够被除数整除了.在一些题目中因为余数的存在,不便于我们计算,去掉余数,回到我们比较熟悉的整除性问题,那么问题就会变得简单了.除法公式的应用例题精讲知识点拨教学目标5-5-1.带余除法(一)【例 1】某数被13除,商是9,余数是8,则某数等于。
【考点】除法公式的应用【难度】1星【题型】填空【关键词】希望杯,四年级,复赛,第2题,5分【解析】125【答案】125【例 2】一个三位数除以36,得余数8,这样的三位数中,最大的是__________。
【考点】除法公式的应用【难度】1星【题型】填空【关键词】希望杯,四年级,复赛,第3题【解析】因为最大的三位数为999,999362727÷=L,所以满足题意的三位数最大为:⨯+=36278980【答案】980【巩固】计算口÷△,结果是:商为10,余数为▲。
小学五年级奥数题带余数的除法【五篇】

小学五年级奥数题带余数的除法【五篇】导读:本文小学五年级奥数题带余数的除法【五篇】,仅供参考,如果觉得很不错,欢迎点评和分享。
【第一篇】一个两位数去除251,得到的余数是41.求这个两位数。
分析这是一道带余除法题,且要求的数是大于41的两位数.解题可从带余除式入手分析。
解:∵被除数÷除数=商…余数,即被除数=除数×商+余数,∴251=除数×商+41,251-41=除数×商,∴210=除数×商。
∵210=2×3×5×7,∴210的两位数的约数有10、14、15、21、30、35、42、70,其中42和70大于余数41.所以除数是42或70.即要求的两位数是42或70。
【第二篇】用一个自然数去除另一个整数,商40,余数是16.被除数、除数、商数与余数的和是933,求被除数和除数各是多少? 解:∵被除数=除数×商+余数,即被除数=除数×40+16。
由题意可知:被除数+除数=933-40-16=877,∴(除数×40+16)+除数=877,∴除数×41=877-16,除数=861÷41,除数=21,∴被除数=21×40+16=856。
答:被除数是856,除数是21。
【第三篇】某年的十月里有5个星期六,4个星期日,问这年的10月1日是星期几? 解:十月份共有31天,每周共有7天,∵31=7×4+3,∴根据题意可知:有5天的星期数必然是星期四、星期五和星期六。
∴这年的10月1日是星期四【第四篇】3月18日是星期日,从3月17日作为第一天开始往回数(即3月16日(第二天),15日(第三天),…)的第1993天是星期几? 解:每周有7天,1993÷7=284(周)…5(天),从星期日往回数5天是星期二,所以第1993天必是星期二. 【第五篇】一个数除以3余2,除以5余3,除以7余2,求适合此条件的最小数。
小学奥数题库《数论》余数问题带余除法1星题(含解析)全国通用版

数论-余数问题-带余除法-1星题课程目标知识提要带余除法•定义一般的,如果a是整数,b是整数(b≠0),若有a÷b=q⋯⋯r,也就是说a=b×q+r,0≦r<b,我们称上面的除法算式为一个带余除法算式。
(1)当r=0时,我们称a可以被b整除,q称为a除以b的商或完全商;(2)当r≠0时,我们称a不可以被b整除,q称为a除以b的商或不完全商。
精选例题带余除法1. 有一个除法算式,被除数和除数的和是136,商是7,则除数是.【答案】17【分析】(1)被除数÷除数=7,因此我们能得到被除数是除数得7倍.(2)如果设除数是1份,那么被除数就是7份,它们的和是136.所以每份量为:136÷8=17.即除数是17.2. 在一个除法算式中,被除数是12,除数小于12,则可能出现的不同的余数之和是.【答案】15【分析】除数小于12且有不同余数,除数可能是11、10、9、8、7.余数分别是1、2、3、4、5.余数之和是1+2+3+4+5=15.3. 已知2008被一些自然数去除,得到的余数都是10.那么这些自然数共有个.【答案】11个【分析】2008−10=1998一定能被这些数整除,且这些数一定大于10,1998=2×3×3×3×37.1998的因数一共有:(1+1)×(3+1)×(1+1)=16个.其中小于10的有:1,2,3,6,9那么大于10的因数有16−5=11个.即这些自然数共有11个.4. 买一支水彩笔需要1元7角,用15元钱最多可以买这样的水彩笔支.【答案】8【分析】1元7角相当17角,15元相当于150角.可列出如下算式:150÷17=8⋯14.故最多可以买这样的水彩笔8支.5. 两数相除,商4余8,被除数、除数两数之和等于73,则被除数是.【答案】60【分析】被除数=4×除数+8,被除数减去8后是除数的4倍,所以根据和倍问题可知,除数为(73−8)÷(4+1)=13,所以,被除数为13×4+8=60.6. 有两个自然数相除,商是17,余数是13,已知被除数、除数、商与余数之和为2113,则被除数是.【答案】1968【分析】设除数为a,被除数为17a+13,即可得到(17a+13)+a+17+13=2113,那么除数=115,被除数=115×17+13=1968.7. 在一个除法算式中,如果商是16,余数是8,那么被除数最小是.【答案】152【分析】根据余数小于除数,得到除数最小为9,那么被除数的最小值为16×9+8=152.8. 在一个除法算式中,如果商是16,余数是8,那么被除数与除数的和最小是.【答案】161【分析】由上题152+9=161.9. (1)34÷4=8⋯⋯2,则[34÷4]=,{34÷4}=;(2)已知a÷125=b⋯⋯10,[a÷125]=6,求{a÷125} = ;(3)已知a÷20=3⋯⋯b,{a÷20}=0.45,求[a÷20] = ,a = .【答案】(1)8,0.5;(2)0.08;(3)3,69【分析】(1)34÷4的整数部分就是商,因此为8,{34÷4}相当于余数除以4,因此为0.5.(2)如果a÷b=q⋯⋯r,[a÷b]=q,{a÷b}=r÷b方法1:b=6,a=6×125+10=760,{760÷125}=0.08;方法2:b=6,{a÷125}=10÷125=0.08.(3)如果a÷b=q⋯⋯r,[a÷b]=q,{a÷b}=r÷b,所以[a÷20]=3,b=0.45×20=9,a=3×20+9=69.10. 用一个自然数去除另一个自然数,商为5.被除数、除数的和是36,求这两个自然数各是多少?【答案】被除数为30,除数为6.【分析】被除数÷除数=5,所以根据和倍问题可知,除数为36÷(5+1)=6,所以被除数为5×6=30.11. 若a÷b=7⋯⋯9,则a的最小值是多少?【答案】79【分析】根据余数小于除数,得到除数最小为10,那么a的最小值为7×10+9=79.12. (1)25÷6=4⋯⋯1;34÷6=5⋯⋯4,那么(25+34)÷6=( )⋯⋯( ).(2)45÷7=6⋯⋯3;26÷7=3⋯⋯5,那么(45+26)÷7=( )⋯⋯( ).(3)a÷8⋯⋯5;b÷8⋯⋯6,那么(a+b)÷8⋯⋯( ).(4)a÷8⋯⋯5;b÷8⋯⋯6;c÷8⋯⋯7,那么(a+b+c)÷8⋯⋯( ).【答案】(1)(25+34)÷6=(9)⋯⋯(5);(2)(45+26)÷7=(10)⋯⋯(1).(3)(a+b)÷8⋯⋯(3).(4)(a+b+c)÷8⋯⋯(2).【分析】(1)(25+34)÷6=9⋯⋯5;(2)(45+26)÷7=10⋯⋯1.(3)所以余数的和为5+6=11,11÷8=1⋯⋯3,余数为3.(4)余数的和为5+6+7=18,18÷8=2⋯⋯2,余数为2.13. 请在下列括号中填上适当的数.(1)a÷8⋯⋯6;b÷8⋯⋯7,那么(a+b)÷8⋯⋯( ).(2)a÷10⋯⋯5;b÷10⋯⋯6;c÷10⋯⋯7,那么(2a+b+c)÷10⋯⋯( ).【答案】(1)5;(2)3【分析】(1)余数的和为6+7=13,13÷8=1⋯⋯5,余数为5.(2)2a+b+c=a+a+b+c,所以余数的和为5+5+6+7=23,23÷10=2⋯⋯3,余数为3.14. 1013除以一个两位数,余数是12.求出符合条件的所有的两位数.【答案】13,77,91【分析】1013−12=1001,1001=7×11×13,那么符合条件的所有的两位数有11,13,77,91,因为“余数小于除数”,所以舍去11,答案只有13,77,91.15. 1013除以一个两位数,余数是12.求出所有符合条件的两位数.【答案】13,77,91【分析】1013−12=1001,1001=7×11×13,那么符合条件的所有的两位数有11,13,77,91,因为“余数小于除数”,所以舍去11,答案只有13,77,91.16. 甲、乙两数的和是16,甲数除以乙数商是2余1,求甲数和乙数各是多少?【答案】乙=5,甲=11【分析】设乙数为a,即甲为2a+1,可得到(2a+1)+a=16,那么乙=5,甲=11.17. 2025除以一个两位数,余数是75,这个两位数是多少?【答案】78【分析】这个两位数是2025−75=1950的约数,其中比75大的只有78.18. 一个数除以另一个数,商是3,余数是3.如果除数和被除数都扩大10倍,那么被除数、除数、商、余数的和是263,求这2个自然数各是多少?【答案】5、18【分析】设除数为a,被除数为3a+3,即可得到10(3a+3)+10a+3+30=263,那么除数=5,被除数=5×3+3=18.19. 甲、乙两数的差是113,甲数除以乙数商7余5,则甲数和乙数各是多少?【答案】乙=18,甲=131【分析】设乙数为a,即甲为7a+5,可得到(7a+5)−a=113,那么乙=18,甲= 131.20. 两数相除,商4余8,被除数、除数、商数、余数四数之和等于415,则被除数是_______.【答案】324【分析】设被除数和除数分别为x,y,可以得到\[ \begin{cases} x = 4y + 8\hfill \\ x + y + 4 + 8= 415 \hfill \\ \end{cases} \]解方程组得\[ \left\{ \begin{gathered} x = 324 \hfill\\ y = 79 \hfill\\ \end{gathered} \right. \]即被除数为324.21. 78除以一个数得到的商是8,并且除数与余数的差是3,求除数和余数.【答案】除数为9,余数为6.【分析】78÷除数=8⋯⋯(余数−3),81÷除数=9⋯⋯0被除数加上除数与余数的差3的和刚好是除数的9倍,则除数为(78+3)÷9=9,余数为6.22. 用某自然数a去除1992,得到商是46,余数是r,求a和r.【答案】a=43,r=14【分析】由1992是a的46倍还多r,得到1992÷46=43......14,得1992=46×43+ 14,所以a=43,r=14.23. 甲、乙两个数,甲数除以乙数商2余17,乙数的10倍除以甲数商3余45.求甲、乙二数.【答案】乙=24,甲=65【分析】设乙数为a,即甲为2a+17,可得到10a÷(2a+17)=3⋯⋯45,整理为10a= 3(2a+17)+45,那么乙=24,甲=65.24. 一个三位数除以43,商是a余数是b,求a+b的最大值.【答案】64【分析】试除法:999÷43=23⋯⋯10;999−10−1=988;988÷43=22⋯⋯42.余数最大为42,所以a+b的最大值为42+22=64.25. (1)82÷6=13⋯⋯4;50÷6=8⋯⋯2,那么(82−50)÷6=( )⋯⋯( ).(2)74÷6=12⋯⋯2;22÷6=3⋯⋯4,那么(74−22)÷6=( )⋯⋯( ).(3)a÷6余5;b÷6余1,那么(a−b)÷6余几呢?(4)a÷6余3;b÷6余5,那么(a−b)÷6余几呢?【答案】(1)(82−50)÷6=(5)⋯⋯(2).(2)(74−22)÷6=(8)⋯⋯(4).(3)余4.(4)余4.【分析】(1)(82−50)÷6=5⋯⋯2.(2)(74−22)÷6=8⋯⋯4.(3)余数的差是4,所以余数是4.(4)余数不够减时借1当6用来减,3+6=9,9−5=4,所以余数是4.26. 用一个自然数去除另一个自然数,商为8,余数是3.被除数、除数的和是48,求这两个自然数各是多少?【答案】被除数为43,除数为5.【分析】因为被除数减去3后使除数的8倍,所以根据和倍问题可知,除数为(48−3)÷(8+1)=5,所以被除数为5×8+3=43.27. 50除以一个一位数,余数是2.求出符合条件的一位数.【答案】3,4,6,8【分析】50÷除数=商⋯⋯2,50−2=48,48=除数×商,48=1×48=2×24=3×16=4×12=6×8,因为“余数小于除数且除数是一位数“那么符合条件的所有的数有3,4,6,8.28. 一个两位数除310,余数是37,求这样的两位数.【答案】39;91【分析】本题为余数问题基础题型,需要学生明白一个重要知识点,就是把余数问题---即“不整除问题”转化为整除问题.方法为用被除数减去余数,即得到一个除数的倍数;或者是用被除数加上一个“除数与余数的差”,也可以得到一个除数的倍数.本题中310−37=273,说明273是所求余数的倍数,而273=3×7×13,所求的两位数约数还要满足比37大,符合条件的两位数有39,91.29. 一个两位数除以13的商是6,除以11所得的余数是6,求这个两位数.【答案】83【分析】因为一个两位数除以13的商是6,所以这个两位数一定大于78,并且小于13×(6+1)=91;又因为这个两位数除以11余6,而78除以11余1,这个两位数为78+5=83.30. 43除以一个数得到的商是8,并且除数与余数的差是2,求除数和余数.【答案】除数为5,余数为3.【分析】43=8×除数+余数,被除数加上除数与余数的差2的和刚好是除数的9倍,则除数为(43+2)÷(8+1)=5,余数为3.31. 用一个自然数去除另一个自然数,商为7.被除数、除数的和是48,求这两个自然数各是多少?【答案】除数为6,被除数为42.【分析】被除数÷除数=7,所以根据和倍问题可知,除数为48÷(7+1)=6,所以被除数为6×7=42.32. 计算:(1)已知a÷25=b⋯⋯5,[a÷20]=4,求a=;(2)已知a÷10=7⋯⋯b,{a÷10}=0.5,求[a÷10]=,a=.【答案】(1)105;(2)7,75【分析】(1)b =4,a=4×25+5=105(2)a÷b=q⋯⋯r,[a÷b]=q,{a÷b}=r÷b,所以[a÷10]=7,b=0.5×10=5,a=7×10+5=75.33. 46除以一个一位数,余数是1.求出符合条件的一位数.【答案】3,5,9【分析】46÷除数=商⋯⋯1,46−1=45,45÷除数=商⋯⋯0,45=除数×商,45=3×15=5×9,因为“余数小于除数且除数是一位数”那么符合条件的所有的一位数有3,5,9.34. 博士要给小朋友们分糖,一共128块,如果每人分5块,最多可以分给几个小朋友?【答案】25【分析】128÷5=25⋯⋯3,最多分给25个小朋友,还剩3块.35. 128除以一个数得到的商是9,并且除数与余数的差是2,求除数和余数.【答案】除数为13,余数为11.【分析】128÷除数=9⋯⋯(余数−2),130÷除数=10⋯⋯0被除数加上除数与余数的差2的和刚好是除数的10倍,则除数为(128+2)÷10=13,余数为11.36. 有一个整数,39,51,147被它除所得的余数都是3,求这个数.【答案】4;6;12【分析】方法一:39−3=36,147−3=144,(36,144)=12,12的约数是1,2,3,4,6,12,因为余数为3要小于除数,这个数是4,6,12.方法二:由于所得的余数相同,得到这个数一定能整除这三个数中的任意两数的差,也就是说它是任意两数差的公约数.51−39=12,147−39=108,(12,108)=12,所以这个数是4,6,12.37. 一个除法算式中,被除数、除数、商与余数都是自然数,并且商与余数相等.若被除数是47,则除数是多少?【答案】46【分析】设除数为b,商和余数都是c,这个算式就可以表示为:47÷b=c⋯⋯c,即b×c+c=47;c×(b+1)=47,所以c一定是47的因数,47的因数只有1和47;c为47肯定不符合条件,所以c=1,即除数是46,余数是1.38. 已知2012被一些正整数去除,得到的余数为10,则这样的正整数共有多少个?【答案】13个【分析】2012−10=2002一定能被这些数整除,2002=2×7×11×13.因为2002中一共有(1+1)×(1+1)×(1+1)×(1+1)=16个,排除小于10的因数1、2、7,满足条件的正整数共有16−3=13个.39. 188+288+388+…+2088除以9、11的余数各是多少?【答案】8;11.【分析】根据等差数列求和列式:188+288+388+…+2088=22760,所以22760÷9⋯⋯8;22760÷11⋯1.40. 著名的斐波那契数列是这样的:1,1,2,3,5,8,13,21,⋯,这串数列当中第2008个数除以3所得的余数为多少?【答案】0【分析】斐波那契数列的构成规则是从第三个数起每一个数都等于它前面两个数的和,由此可以根据余数定理将斐波那契数列转换为被3除所得余数的数列:1,1,2,0,2,2,1,0,1,1,2,0,⋯,第九项和第十项连续两个是1,与第一项和第二项的值相同且位置连续,所以斐波那契数列被3除的余数每8个一个周期循环出现,由于2008除以8的余数为0,所以第2008项被3除所得的余数为第8项被3除所得的余数为0.。
小学奥数 余数性质(一) 精选练习例题 含答案解析(附知识点拨及考点)

1. 学习余数的三大定理及综合运用2. 理解弃9法,并运用其解题一、三大余数定理:1.余数的加法定理 a 与b 的和除以c 的余数,等于a ,b 分别除以c 的余数之和,或这个和除以c 的余数。
例如:23,16除以5的余数分别是3和1,所以23+16=39除以5的余数等于4,即两个余数的和3+1.当余数的和比除数大时,所求的余数等于余数之和再除以c 的余数。
例如:23,19除以5的余数分别是3和4,所以23+19=42除以5的余数等于3+4=7除以5的余数为22.余数的加法定理a 与b 的差除以c 的余数,等于a ,b 分别除以c 的余数之差。
例如:23,16除以5的余数分别是3和1,所以23-16=7除以5的余数等于2,两个余数差3-1=2. 当余数的差不够减时时,补上除数再减。
例如:23,14除以5的余数分别是3和4,23-14=9除以5的余数等于4,两个余数差为3+5-4=43.余数的乘法定理a 与b 的乘积除以c 的余数,等于a ,b 分别除以c 的余数的积,或者这个积除以c 所得的余数。
例如:23,16除以5的余数分别是3和1,所以23×16除以5的余数等于3×1=3。
当余数的和比除数大时,所求的余数等于余数之积再除以c 的余数。
例如:23,19除以5的余数分别是3和4,所以23×19除以5的余数等于3×4除以5的余数,即2. 乘方:如果a 与b 除以m 的余数相同,那么n a 与n b 除以m 的余数也相同.二、弃九法原理在公元前9世纪,有个印度数学家名叫花拉子米,写有一本《花拉子米算术》,他们在计算时通常是在一个铺有沙子的土板上进行,由于害怕以前的计算结果丢失而经常检验加法运算是否正确,他们的检验方式是这样进行的:例如:检验算式1234189818922678967178902889923++++=1234除以9的余数为11898除以9的余数为818922除以9的余数为4678967除以9的余数为7知识点拨教学目标5-5-3.余数性质(三)178902除以9的余数为0这些余数的和除以9的余数为2而等式右边和除以9的余数为3,那么上面这个算式一定是错的。
小学奥数余数问题完整版教案带解析和答案

⼩学奥数余数问题完整版教案带解析和答案数论问题之余数问题教学⽬标余数问题是数论知识板块中另⼀个内容丰富,题⽬难度较⼤的知识体系,也是各⼤杯赛⼩升初考试必考的奥数知识点,所以学好本讲对于学⽣来说⾮常重要。
余数问题主要包括了带余除法的定义,三⼤余数定理(加法余数定理,乘法余数定理,和同余定理),及中国剩余定理和有关弃九法原理的应⽤。
三⼤余数定理:1、余数的加法定理a与b的和除以c的余数,等于a,b分别除以c的余数之和,或这个和除以c的余数。
例如:23,16除以5的余数分别是3和1,所以23+16=39除以5的余数等于4,即两个余数的和3+1.当余数的和⽐除数⼤时,所求的余数等于余数之和再除以c的余数。
例如:23,19除以5的余数分别是3和4,所以23+19=42除以5的余数等于3+4=7除以5的余数,即2.2、余数的乘法定理a与b的乘积除以c的余数,等于a,b分别除以c的余数的积,或者这个积除以c所得的余数。
例如:23,16除以5的余数分别是3和1,所以23×16除以5的余数等于3×1=3。
当余数的和⽐除数⼤时,所求的余数等于余数之积再除以c的余数。
例如:23,19除以5的余数分别是3和4,所以23×19除以5的余数等于3×4除以5的余数,即2.3.同余定理若两个整数a、b被⾃然数m除有相同的余数,那么称a、b对于模m同余,⽤式⼦表⽰为:a ≡b ( mod m ),左边的式⼦叫做同余式。
同余式读作:a同余于b,模m。
由同余的性质,我们可以得到⼀个⾮常重要的推论:若两个数a,b除以同⼀个数m得到的余数相同,则a,b的差⼀定能被m整除⽤式⼦表⽰为:如果有a≡b ( mod m ),那么⼀定有a-b=mk,k是整数,即m|(a-b)三、弃九法原理⽽我们在求⼀个⾃然数除以9所得的余数时,常常不⽤去列除法竖式进⾏计算,只要计算这个⾃然数的各个位数字之和除以9的余数就可以了,在算的时候往往就是⼀个9⼀个9的找并且划去,所以这种⽅法被称作“弃九法”。
小学数学奥数知识点《有余数的除法》例题讲解

小学奥数《有余数的除法》例题讲解在有余数除法中,要记住:(1)余数<除数;(2)被除数=商×除数+余数例1(1)()÷7=8……(),根据余数写出被除数最大是几?最小是几?(2)()÷()=()……6,除数最小是几?【思路点拨】(1)根据余数一定要比除数小的原理,余数可以取1,2,3,4,5,6。
最大的余数确定最大的被除数,最小的余数确定最小的被除数。
(2)根据余数一定要比除数小的原理,除数要大于6,而大于6的数有很多,其中最小的是。
【模仿练习】1.算式()÷()=8……()中,被除数最小是几?2.下题中被除数最大可填几,最小可填几?()÷8=3……()3.你能写出下面题中最大的被除数和最小的被除数吗?()÷4=7……()例2算式28÷()=()……4中,除数和商各是多少?【思路点拨】根据“被除数=商×除数+余数”,商×除数=被除数-余数,即,商×除数=28-4=24。
而24=×=×=×=×,再根据除数>余数就可以确定对应的除数和商。
【模仿练习】下列算式中,除数和商各是几?(1)22÷()=() (4)(2)65÷()=() (2)(3)37÷()=() (7)(4)48÷()=() (6)例3算式()÷7=()……()中,商和余数相等,被除数可以是哪些数?【思路点拨】要求出被除数,必须确定商和余数,而商等于余数,所以可以先根据除数是7来确定余数的值,根据余数小于除数,所以得到余数可以取,,,,,,从而得到对应的商,然后再求出被除数。
例4算式()÷()=()……6,除数和商相等,被除数最小是几?【思路点拨】通过余数等于6可以确定除数应该大于6,大于6的数有无数个,但是要想使被除数最小,则除数应该尽量小,这样一来除数就只能取,再根据商和除数相等确定商,最后根据“被除数=商×除数+余数”求出最小的被除数。
小学五年奥数-带余除法

带余除法【知能大展台】如果a是一个整数,b是一个自然数,那么一定有两个整数q和r,使得:a=b×q+r(0≤r﹤b)当r=0时,则称 a能被b整除当r≠0时,r叫做a除以b的余数,q叫做a除以b的不完全商.如果a、b两个整数除以自然数m后所得的余数相同,就称整数a、b对于除数m来说就是同余的。
如果两个整数a、b对于除数m(m为自然数)来说就是同余的,那么a与b 的差一定能被m整除。
这是同余的一条重要性质。
根据余数相同,可以对整数进行分类。
例如一个整数a被3除时,余数只能有0、1、2这三种可能,因此所有整数可以分为3k,3k+1,3k+2(k为整数)这三种类型。
【试金石】例1 两个数相除,商是22,余数是8,被除数、除数、商与余数的和是866,求被除数和除数。
【分析】“两个数相除,商是22,余数是8”,可以理解为“被除数比除数的22倍还多8”。
如果把除数看做1倍数,那么本题可转化成一道和倍应用题。
【解答】除数为:(866-22-8×2)÷(22+1)=36被除数为:36×22+8=800答:被除数是800,除数是36。
【智力加油站】两个数相除,商是40,余数是16,被除数与除数的和是877,求除数。
【试金石】例2 一个整数分别除442、297和210,得到相同的余数,这个整数是多少?【分析】根据已知条件可知,本题是要求除数的,并且442、297和210这三个数对于除数来说是同余的。
根据同余的性质,这三个数中任意两个数的差,都应是除数的倍数,即除数是题中三个数中任意两个数的差的公因数。
【解答】442-297=145297-210=87(145,87)=29所求除数应是29的约数,29=1×29,但1不符合题意。
所以,29是所求的整数。
答:这个整数是29。
【智力加油站】【针对性训练】一个整数分别除300、254和185,得到相同的余数,这个整数是多少?【试金石】例3 在大于1999的自然数中,被66除后,商与余数相等的数共有多少个?这些数的总和是多少?【分析】在带余除法中,由于余数<除数,故本题中的商与余数最大不超过65,又由于被除数>1999,故商数>1999÷66,这就限定了商的余数,从而本题可解。
苏教版奥数二下 第一讲 有余数的除法(认识余数)

苏教版奥数二下第一讲有余数的除法(认识余数)第一讲有余数的除法(认识余数)例1:有一堆苹果,总数不到50个,把这堆苹果平均分给7个人,还余下3个苹果,这堆苹果有多少个?类似的问题还有:1.一次跳绳比赛,奖品是圆珠笔,获奖选手有4人,每人得到几支圆珠笔,就余下几支圆珠笔。
准备好的圆珠笔共有多少支?2.有一批桃子,不到30个,把这些桃子平均分给6只小猴吃,每只小猴分的个数比3多,结果每只小猴分别的个数与剩下的个数不相等,这堆桃子有多少个?3.希望小学把买来的小足球平均分给5个班,买来的小足球不足20个,结果每个班分到的个数与剩下的个数不相等。
学校买来最少多少个小足球?最多多少个小足球?例2:下面这道除法竖式题,余数是7,要你填相应的商、除数和被除数,你最多可以填出多少道?类似的问题还有:1.下面这道算式,你最多可以写出多少道?2.在□里填上适当的数,使算式成立。
你最多可以写出多少道?6=□ (1)3.幼儿园XXX拿来一包饼干,不够40块,比35块多,她从左到右依次发给XXX、XXX、小方、XXX,每人1块发完,再从左到右发起,直到分完为止。
每人拿到的饼干块数相同。
每人拿到几块饼干?饼干一共有多少块?例3:二(1)班学生排练团体操,班主任让全班排队,要求每行站8人,学生排成了5行,还多余几个学生不够排成一行。
二(1)班有学生多少人?类似的问题还有:1.二(1)班小朋友到玄武湖划船,每船坐4人,还余下小朋友,不够租一条船。
二(1)班最少有多少小朋友去划船?2.幼儿园XXX发小人书给6个小朋友看,小人书本数小于30,每人分到的小人书一样多,而且剩下的本数可以正好再分给1个小朋友看,XXX原来有多少本小人书?3.小白兔从山上采回一篮蘑菇,比20个多,比40个少。
如果按5个一组来数,则余4个。
如果按3个一组来数,则余1个。
小白兔一共采了多少个蘑菇?例4:下面两题中的△,□各代表一个数字,△、□各代表数字几算式成立?类似的问题还有:1.下面除法算式中,有些数字用□、△代替,你能求出□、△各代表什么数字吗?1)△6÷△=8 (4)2)□5÷7=7……△2.用什么数字代替下面算式中的“※”,得到的商为9,并且有最大的余数,余数是几,被除数是多少?9÷9=9……()。
小学奥数-带余除法-求余数
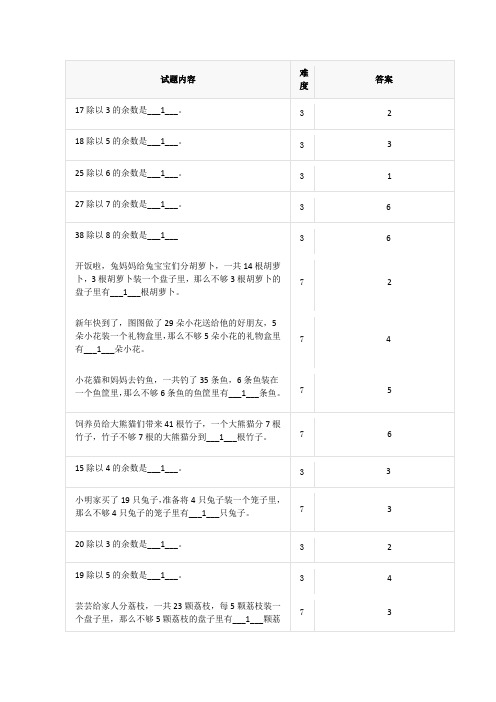
2
新年快到了,图图做了29朵小花送给他的好朋友,5朵小花装一个礼物盒里,那么不够5朵小花的礼物盒里有___1___朵小花。
7
4
小花猫和妈妈去钓鱼,一共钓了35条鱼,6条鱼装在一个鱼筐里,那么不够6条鱼的鱼筐里有___1___条鱼。
7
5
饲养员给大熊猫们带来41根竹子,一个大熊猫分7根竹子,竹子不够7根的大熊猫分到___1___根竹子。
试题内容
难度
答案
17除以3的余数是___1___。
3
2
18除以5的余数是___1___。
3
3
25除以6的余数是___1___。
3
1
27除以7的余数是___1___。
3
6
38除以8的余数是___1___
3
6
开饭啦,兔妈妈给兔宝宝们分胡萝卜,一共14根胡萝卜,3根胡萝卜装一个盘子里,那么不够3根胡萝卜的盘子里有___1___根胡萝卜。
7
6
15除以4的余数是___1___。
3
3
小明家买了19只兔子,准备将4只兔子装一个笼子里,那么不够4只兔子的笼子里有___1___只兔子。
7
3
20除以3的余数是___1___。
3
2
19除以5的余数是_____。
3
4
芸芸给家人分荔枝,一共23颗荔枝,每5颗荔枝装一个盘子里,那么不够5颗荔枝的盘子里有___1___颗荔枝。
7
3
孙悟空回到花果山,一共带回去62根香蕉,分给小猴子们。一个小猴子分9根,香蕉不够9根的小猴子分到___1___根香蕉。
7
8
16除以6的余数是___1___。
3
4
小学奥数 数论 余数问题 带余除法(一).题库版

1. 能够根据除法性质调整余数进行解题2.能够利用余数性质进行相应估算3. 学会多位数的除法计算4. 根据简单操作进行找规律计算带余除法的定义及性质 1、定义:一般地,如果a 是整数,b 是整数(b ≠0),若有a ÷b =q ……r ,也就是a =b ×q +r ,0≤r <b ;我们称上面的除法算式为一个带余除法算式.这里:(1)当0r =时:我们称a 可以被b 整除,q 称为a 除以b 的商或完全商(2)当0r ≠时:我们称a 不可以被b 整除,q称为a 除以b 的商或不完全商一个完美的带余除法讲解模型:如图这是一堆书,共有a 本,这个a 就可以理解为被除数,现在要求按照b 本一捆打包,那么b 就是除数的角色,经过打包后共打包了c 捆,那么这个c 就是商,最后还剩余d 本,这个d 就是余数.这个图能够让学生清晰的明白带余除法算式中4个量的关系.并且可以看出余数一定要比除数小.2、余数的性质⑴ 被除数=除数⨯商+余数;除数=(被除数-余数)÷商;商=(被除数-余数)÷除数;⑵ 余数小于除数.知识点拨教学目标5-5-1.带余除法(一)3、解题关键理解余数性质时,要与整除性联系起来,从被除数中减掉余数,那么所得到的差就能够被除数整除了.在一些题目中因为余数的存在,不便于我们计算,去掉余数,回到我们比较熟悉的整除性问题,那么问题就会变得简单了.除法公式的应用【例 1】 某数被13除,商是9,余数是8,则某数等于 .【考点】除法公式的应用 【难度】1星 【题型】填空【关键词】2009年,希望杯,第七届,四年级,复赛,第2题,5分【解析】 125【答案】125【例 2】 一个三位数除以36,得余数8,这样的三位数中,最大的是__________.【考点】除法公式的应用 【难度】1星 【题型】填空【关键词】2008年,希望杯,第六届,四年级,复赛,第3题【解析】 因为最大的三位数为999,999362727÷=,所以满足题意的三位数最大为:36278980⨯+=【答案】980【巩固】 计算口÷△,结果是:商为10,余数为▲.如果▲的值是6,那么△的最小值是_____.【考点】除法公式的应用 【难度】1星 【题型】填空【关键词】2005年,希望杯,第三届,五年级,复赛,第4题,6分【解析】 根据带余除法的性质,余数必须小于除数,则有 △的最小值为7.【答案】7【例 3】 除法算式÷□□=208中,被除数最小等于 .【考点】除法公式的应用 【难度】1星 【题型】填空【关键词】2007年,第5届,希望杯,4年级,初赛,4题【解析】 本题的商和余数已经知道了,若想被除数最小,则需要除数最小即可,除数最小是819+=,所以本题答案为:20×(8+1)+8=188.【答案】188【例 4】 71427和19的积被7除,余数是几?【考点】除法公式的应用 【难度】1星 【题型】填空【关键词】第一届,华杯赛,初赛,第14题【解析】 71427被7除,余数是6,19被7除,余数是5,所以71427×19被7除,余数就是6×5被7除所得的余数2.【答案】2例题精讲【例 5】 1013除以一个两位数,余数是12.求出符合条件的所有的两位数.【考点】除法公式的应用 【难度】1星 【题型】解答【解析】 1013121001-=,100171113=⨯⨯,那么符合条件的所有的两位数有11,13,77,91,因为“余数小于除数”,所以舍去11,答案只有13,77,91.【答案】13,77,91共三个【巩固】 一个两位数除310,余数是37,求这样的两位数.【考点】除法公式的应用 【难度】1星 【题型】解答【解析】 本题为余数问题的基础题型,需要学生明白一个重要知识点,就是把余数问题---即“不整除问题”转化为整除问题.方法为用被除数减去余数,即得到一个除数的倍数;或者是用被除数加上一个“除数与余数的差”,也可以得到一个除数的倍数.本题中310-37=273,说明273是所求余数的倍数,而273=3×7×13,所求的两位数约数还要满足比37大,符合条件的有39,91.【答案】39或者97【巩固】 在下面的空格中填上适当的数.3124774002【考点】除法公式的应用 【难度】2星 【题型】填空【关键词】2004年,第2届,走美杯,3年级,决赛,第10题,12分【解析】 本题的被除数、商和余数已经给出,根据除法的计算公式:被除数÷除数=商余数,逆推计算得到:除数=(20047—13)÷742=27.【答案】27【例 6】 一个两位奇数除1477,余数是49,那么,这个两位奇数是多少?【考点】除法公式的应用 【难度】1星 【题型】解答【解析】 这个两位奇数能被1477-49=1428整除,且必须大于49,1428=2×2×3×7×17,所以这样的两位奇数只有51.【答案】51【例 7】 大于35的所有数中,有多少个数除以7的余数和商相等?【考点】除法公式的应用 【难度】2星 【题型】解答【解析】 除以7的余数只能是0~6,所以商只能是0~6,满足大于7的数只有商和余数都为5、6,所以只能是40、48.【答案】40、48【例 8】 已知2008被一些自然数去除,所得的余数都是10,那么这样的自然数共有多少个?【考点】除法公式的应用 【难度】2星 【题型】解答【解析】 本题为一道余数与约数个数计算公式的小综合性题目.由题意所求的自然数一定是2008-10即1998的约数,同时还要满足大于10这个条件.这样题目就转化为1998有多少个大于10的约数,319982337=⨯⨯,共有(1+1)×(3+1)×(1+1)=16个约数,其中1,2,3,6,9是比10小的约数,所以符合题目条件的自然数共有11个.【答案】11【巩固】 写出全部除109后余数为4的两位数.【考点】除法公式的应用 【难度】2星 【题型】解答【关键词】美国长岛,小学数学竞赛,第五届【解析】 1094105357-==⨯⨯.因此,这样的两位数是:15;35;21.【答案】两位数是:15;35;21【例 9】 甲、乙两数的和是1088,甲数除以乙数商11余32,求甲、乙两数.【考点】除法公式的应用 【难度】2星 【题型】解答【关键词】清华附中,小升初分班考试【解析】 (法1)因为 甲=乙1132⨯+,所以 甲+乙=乙1132⨯++乙=乙12321088⨯+=;则乙(108832)1288 =-÷=,甲1088=-乙1000=.(法2)将余数先去掉变成整除性问题,利用倍数关系来做:从1088中减掉32以后,1056就应当是乙数的(111)+倍,所以得到乙数10561288=÷=,甲数1088881000=-=.【答案】乙数10561288=÷=,甲数1088881000=-=【例 10】 用某自然数a 去除1992,得到商是46,余数是r ,求a 和r .【考点】除法公式的应用 【难度】2星 【题型】解答【关键词】第五届,小数报,决赛【解析】 因为1992是a 的46倍还多r ,得到19924643......14÷=,得1992464314=⨯+,所以43a =,14r =.【答案】43a =,14r =【例 11】 当1991和1769除以某个自然数n ,余数分别为2和1.那么,n 最小是多少?【考点】除法公式的应用 【难度】2星 【题型】解答【解析】 如果用1990和1769去除这个自然数n 时,余数是1.而1901769211317-==⨯,我们不妨取13n =,再验证一下:1991131532÷=,1769131361÷=,所以n 最小为13.【答案】13【例 12】 有三个自然数a ,b ,c ,已知b 除以a ,得商3余3;c 除以a ,得商9余11.则c 除以b ,得到的余数是 .【考点】除法公式的应用 【难度】2星 【题型】填空【关键词】2010年,第8届,希望杯,5年级,初赛,第4题,6分【解析】 33b a =+911c a =+(99)232c a b =++=+所以应该余2.【答案】2【例 13】 有两个自然数相除,商是17,余数是13,已知被除数、除数、商与余数之和为2113,则被除数是多少?【考点】除法公式的应用 【难度】3星 【题型】解答【关键词】2003年,小学数学奥林匹克【解析】 被除数+除数+商+余数=被除数+除数+17+13=2113,所以被除数+除数=2083,由于被除数是除数的17倍还多13,则由“和倍问题”可得:除数=(2083-13)÷(17+1)=115,所以被除数=2083-115=1968.【答案】1968【巩固】 两数相除,商4余8,被除数、除数、商数、余数四数之和等于415,则被除数是_______.【考点】除法公式的应用 【难度】3星 【题型】填空【关键词】2002年,小学数学奥林匹克【解析】 因为被除数减去8后是除数的4倍,所以根据和倍问题可知,除数为4154884179---÷+=()(),所以,被除数为7948324⨯+=.【答案】324【巩固】 用一个自然数去除另一个自然数,商为40,余数是16.被除数、除数、商、余数的和是933,求这2个自然数各是多少?【考点】除法公式的应用 【难度】3星 【题型】解答【解析】 本题为带余除法定义式的基本题型.根据题意设两个自然数分别为x ,y ,可以得到40164016933x y x y =+⎧⎨+++=⎩,解方程组得85621x y =⎧⎨=⎩,即这两个自然数分别是856,21. 【答案】两个自然数分别是856,21【例 14】 有一个三位数,其中个位上的数是百位上的数的3倍.且这个三位数除以5余4,除以11余3.这个三位数是_【考点】除法公式的应用 【难度】3星 【题型】填空【解析】 首先个位数不是4就是9,又因为它是百位的3倍所以一定是9,那么百位就是3,又因为它被11除余3,因此十位是9,答案是399【答案】399【例 15】 一个自然数,除以11时所得到的商和余数是相等的,除以9时所得到的商是余数的3倍,这个自然数是_________.【考点】除法公式的应用 【难度】3星 【题型】填空【关键词】2004年,福州市,迎春杯【解析】设这个自然数除以11余a (011)a ≤<,除以9余b (09)b ≤<,则有1193a a b b +=⨯+,即37a b =,只有7a =,3b =,所以这个自然数为12784⨯=.【答案】84【例 16】 盒子里放有编号1到10的十个球,小红先后三次从盒子中共取出九个球,如果从第二次起,每次取出的球的编号的和都比上一次的两倍还多一,那么剩下的球的编号为____.【考点】除法公式的应用 【难度】3星 【题型】填空【关键词】第五届,走美杯,四年级,初赛,第11题【解析】 令第1次取的编号为a ,第二次取的编号为2a+1,第三次取的编号为:2(2a+1)+1=4a+3;还剩下的编号为:55-7a-4=51-7a ,当a 为6时,余下的是9;当a 为7时,余下的是2.【答案】9或者2【例 17】 10个自然数,和为100,分别除以3.若用去尾法,10个商的和为30;若用四舍五入法,l0个商的和为34.10个数中被3除余l 的有________个.【考点】除法公式的应用 【难度】3星 【题型】填空【关键词】2008年,第六届,走美杯,五年级,初赛,第13题【解析】 由题意,“用去尾法,10个商的和为30;用四舍五入法,l0个商的和为34”可知,10个数中除以3余2的数有34-30=4(个),又知道10个自然数的和为100,设除以3余1的数有x 个,那么根据用去尾法后十个商的和与10个自然数的和,可得关系式:2410030333x ⨯+=-,解得,2x =. 【答案】2【例 18】 3782除以某个整数后所得的商恰好是余数的21倍,那么除数最小可能是 .【考点】除法公式的应用 【难度】3星 【题型】填空【关键词】2008年,学而思杯,4年级,第2题【解析】 设除数为a ,商为b ,余数为c ,则3782a b c ÷=,且21b c =.可以将除式转化为213782a c c ⨯+=,所以2113782c a +=(),所以c 和211a +()是3782的约数,378223161=⨯⨯,在3782的约数中只有31611891⨯=被21除所得的余数为1,所以2111891a +=,90a =.【答案】90【例 19】 在大于2009的自然数中,被57除后,商与余数相等的数共有______个.【考点】除法公式的应用 【难度】4星 【题型】填空【关键词】2009年,第14届,华杯赛,初赛,第10题【解析】 根据题意,设这样的数除以57所得的商和余数都为a (a ﹤57),则这个数为57×a +a =58a .所以58a﹥2009,得到a ﹥2009÷58=373458,由于a 为整数,所以a 至少为35.又由于a ﹤57,所以a 最大为56,则a可以为35,36,37,…,56.由于每一个a的值就对应一个满足条件的数,所以所求的满足条件的数共有56-35+1=22个.【答案】22【例 20】用1、9、8、8这四个数字能排成几个被11除余8的四位数?【考点】除法公式的应用【难度】5星【题型】填空【关键词】第二届,华杯赛,初赛,第14题【解析】用1、9、8、8可排成12个四位数,即1988,1898,1889,9188,9818,9881,8198,8189,8918,8981,8819,8891它们减去8变为1980,1890,1881,9180,9810,9873,8190,8181,8910,8973,8811,8883其中被11整除的仅有1980,1881,8910,8811,即用1、9、8、8可排成4个被1除余8的四位数,即1988,1889,8918,8819.【又解】什么样的数能被11整除呢?一个判定法则是:比较奇位数字之和与偶位数字之和,如果它们之差能被11除尽,那么所给的数就能被11整除,否则就不能够.现在要求被11除余8,我们可以这样考虑:这样的数加上3后,就能被11整除了.所以我们得到“一个数被11除余8”的判定法则:将偶位数字相加得一个和数,再将奇位数字相加再加上3,得另一个和数,如果这两个和数之差能被11除尽,那么这个数是被11除余8的数;否则就不是.要把1、9、8、8排成一个被11除余8的四位数,可以把这4个数分成两组,每组2个数字.其中一组作为千位和十位数,它们的和记作A;另外一组作为百位和个位数,它们之和加上3记作B.我们要适当分组,使得能被11整除.现在只有下面4种分组法:经过验证,第(1)种分组法满足前面的要求:A=1+8,B=9+8+3=20,B-A=11能被11除尽.但其余三种分组都不满足要求.根据判定法则还可以知道,如果一个数被11除余8,那么在奇位的任意两个数字互换,或者在偶位的任意两个数字互换,得到的新数被11除也余8.于是,上面第(1)分组中,1和8中任一个可以作为千位数,9和8中任一个可以作为百位数.这样共有4种可能的排法:1988,1889,8918,8819.答:能排成4个被11除余8的数【答案】4。
小学奥数知识名师点拨 例题精讲 带余除法(一).教师版

数的 17 倍还多 13,则由“和倍问题”可得:除数=(2083-13)÷(17+1)=115,所以被除数=2083-115=1968. 【答案】1968
【巩固】计算口÷△,结果是:商为 10,余数为▲。如果▲的值是 6,那么△的最小值是_____。 【考点】除法公式的应用 【难度】1 星 【题型】填空 【关键词】希望杯,五年级,复赛,第 4 题,6 分 【解析】根据带余除法的性质,余数必须小于除数,则有 △的最小值为 7。 【答案】 7
【例 3】 除法算式 □ □ = 208 中,被除数最小等于
5-5-1.带余除法(一).题库
教师版
page 4 of 6
【解析】令第 1 次取的编号为 a,第二次取的编号为 2a+1,第三次取的编号为:2(2a+1)+1=4a+3;还剩下 的编号为:55-7a-4=51 7a,当 a 为 6 时,余下的是 9;当 a 为 7 时,余下的是 2.
【巩固】一个两位数除 310,余数是 37,求这样的两位数。
【考点】除法公式的应用 【难度】1 星 【题型】解答 【解析】本题为余数问题的基础题型,需要学生明白一个重要知识点,就是把余数问题---即“不整除问题”转
化为整除问题。方法为用被除数减去余数,即得到一个除数的倍数;或者是用被除数加上一个“除数 与余数的差”,也可以得到一个除数的倍数。 本题中 310-37=273,说明 273 是所求余数的倍数,而 273=3×7×13,所求的两位数约数还要满足比 37 大,符合条件的有 39,91. 【答案】39 或者 97
小学奥数 带余除法(一) 精选练习例题 含答案解析(附知识点拨及考点)

1. 能够根据除法性质调整余数进行解题2. 能够利用余数性质进行相应估算3. 学会多位数的除法计算4. 根据简单操作进行找规律计算带余除法的定义及性质1、定义:一般地,如果a 是整数,b 是整数(b ≠0),若有a ÷b =q ……r ,也就是a =b ×q +r ,0≤r <b ;我们称上面的除法算式为一个带余除法算式。
这里: (1)当0r =时:我们称a 可以被b 整除,q 称为a 除以b 的商或完全商 (2)当0r ≠时:我们称a 不可以被b 整除,q 称为a 除以b 的商或不完全商 一个完美的带余除法讲解模型:如图这是一堆书,共有a 本,这个a 就可以理解为被除数,现在要求按照b 本一捆打包,那么b 就是除数的角色,经过打包后共打包了c 捆,那么这个c 就是商,最后还剩余d 本,这个d 就是余数。
这个图能够让学生清晰的明白带余除法算式中4个量的关系。
并且可以看出余数一定要比除数小。
2、余数的性质⑴ 被除数=除数⨯商+余数;除数=(被除数-余数)÷商;商=(被除数-余数)÷除数; ⑵ 余数小于除数. 3、解题关键知识点拨教学目标5-5-1.带余除法(一)理解余数性质时,要与整除性联系起来,从被除数中减掉余数,那么所得到的差就能够被除数整除了.在一些题目中因为余数的存在,不便于我们计算,去掉余数,回到我们比较熟悉的整除性问题,那么问题就会变得简单了.例题精讲除法公式的应用【例1】某数被13除,商是9,余数是8,则某数等于。
【考点】除法公式的应用【难度】1星【题型】填空【关键词】希望杯,四年级,复赛,第2题,5分【解析】125【答案】125【例2】一个三位数除以36,得余数8,这样的三位数中,最大的是__________。
【考点】除法公式的应用【难度】1星【题型】填空【关键词】希望杯,四年级,复赛,第3题【解析】因为最大的三位数为999,999362727÷=,所以满足题意的三位数最大为:36278980⨯+=【答案】980【巩固】计算口÷△,结果是:商为10,余数为▲。
奥数余数问题带余除法

精心整理
页脚内容
带余除法
被除数=除数×商+余数
被除数—余数=除数×商
余数=被除数—除数×商
商=(被除数—余数)÷除数
要注意以下几点:
1. 余数总是小于除数的整数。
2. 只要
3. 整除例1、 例2、 数是多
1、 被
2、一个
3、两个
4、1705
5、如果例3、 1、被除2、被除3、两个4、一个5、1492
6、从
7、两个例4、 1、一个
2、一个
3、有一个两位数被3除或被4除,余数都是1,符合这一条件的最大三位数和最小三位数各是多少?
4、有一个最小的两位数,除以5余数是3,除以13余数是5,这个最小的两位数除以11余数是多少?
5、一个两位数除以一个一位数,商仍是两位数,余数是8.被除数、除数、商及余数的和是多少?
6、一个两位数除329,这个两位数与商相等,余数是5,求这个两位数。
7、一个三位数,它除以19,所得的商和余数相等,符合这个条件的三位数有多少个?其中最大的是多少?最小的是多少?
精心整理
页脚内容
8、五年级同学去西湖划船,若每船坐8人,则余下7人;若每船坐12人,则余下11人,若每船坐14人,则余下13人,五年级至少有同学多少人?
9、实验小学五年级的同学在操场上做游戏,每组5人则多1人,每组6人则多1人,每组7人则多1人,五年级做游戏的同学至少有多少人?
10、筐子里有一些皮球,三个三个地数余2个,四个四个地数余3个,五个五个地数余4个,筐子里至少有多少个皮球?。
小学五年级奥数专题——带余除法问题

小学五年级奥数:专题三——带余除法1 、5122除以一个两位数取得的余数是66,求这个两位数。
2、被除数、除数、商与余数之和是2143,已知商是33,余数是52,求被除数和除数。
3、甲、乙两数的和是1088,甲数除以乙数商11余32,求甲、乙两数。
4、有一个整数,用它去除70,110,160取得的三个余数之和是50。
求这个数。
5、求478×296×351除以17的余数。
6、甲、乙两个代表团搭车去参观,每辆车可乘36人。
两代表团坐满若干辆车后,甲代表团余下的11人与乙代表团余下的成员正好又坐满一辆车。
参观完,甲代表团的每一个成员与乙代表团的每一个成员两两合拍一张照片留念。
若是每一个胶卷可拍36张照片,那么拍完最后一张照片后,相机里的胶卷还可拍几张照片?7 、9437569与8057127的乘积被9除,余数是__。
8 、在1、2、3、4、……、1993、1994这1994个数中,选出一些数,使得这些数中的每两个数的和都能被26整除,那么这样的数最多能选出_______个。
9 、一个整数,除300、262、205,取得相同的余数(余数不为0)。
这个整数是_____。
10、小张在计算有余数的除法时,把被除数113错写成131,结果商比原来多3,但余数刚巧相同。
那么该题的余数是多少?11、五只猴子找到一堆桃子,怎么也平分不了,于是大家同意去睡觉,明天再说。
夜里,一只猴子偷偷起来,吃掉一只桃子,剩下的桃子正好平分五等份,它拿走自己的一份,然后去睡觉;第二只猴子起来,也吃掉一只桃子,剩下的桃子也正好分成五等份,它也拿走了自己的一份,然后去睡觉。
第三、四、五只猴子也都这样做。
问:最初至少有______个桃子。
12 、在1、2、3、……、30这30个自然数中,最多能掏出______个数,使掏出的这些数中,任意两个不同的数的和都不是7的倍数。
13、一个数除以3余2,除以5余3,除以7余2。
求知足条件的最小自然数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5-5-1.带余除法(一)
教学目标
1.能够根据除法性质调整余数进行解题
2.能够利用余数性质进行相应估算
3.学会多位数的除法计算
4.根据简单操作进行找规律计算
知识点拨
带余除法的定义及性质
1、定义:一般地,如果a是整数,b是整数(b≠0),若有a÷b=q……r,也就是a=b×q+r,
0≤r<b;我们称上面的除法算式为一个带余除法算式。
这里:
(1)当0
r=时:我们称a可以被b整除,q称为a除以b的商或完全商
(2)当0
r≠时:我们称a不可以被b整除,q称为a除以b的商或不完全商
一个完美的带余除法讲解模型:如图
这是一堆书,共有a本,这个a就可以理解为被除数,现在要求按照b本一捆打包,那么b就是除数的角色,经过打包后共打包了c捆,那么这个c就是商,最后还剩余d本,这个d就是余数。
这个图能够让学生清晰的明白带余除法算式中4个量的关系。
并且可以看出余数一定要比除数小。
2、余数的性质
⑴被除数=除数⨯商+余数;除数=(被除数-余数)÷商;商=(被除数-余数)÷除数;
⑵余数小于除数.
3、解题关键
理解余数性质时,要与整除性联系起来,从被除数中减掉余数,那么所得到的差就能够被除数整除了.在一些题目中因为余数的存在,不便于我们计算,去掉余数,回到我们比较熟悉的整除性问题,那么问题就会变得简单了.
例题精讲
除法公式的应用
【例1】某数被13除,商是9,余数是8,则某数等于。
【例2】一个三位数除以36,得余数8,这样的三位数中,最大的是__________。
【巩固】计算口÷△,结果是:商为10,余数为▲。
如果▲的值是6,那么△的最小值是_____。
【例3】除法算式
□□=208中,被除数最小等于。
【例4】71427和19的积被7除,余数是几?
【例5】1013除以一个两位数,余数是12.求出符合条件的所有的两位数.
【巩固】一个两位数除310,余数是37,求这样的两位数。
【巩固】在下面的空格中填上适当的数。
【例6】一个两位奇数除1477,余数是49,那么,这个两位奇数是多少?
【例7】大于35的所有数中,有多少个数除以7的余数和商相等?
【例8】已知2008被一些自然数去除,所得的余数都是10,那么这样的自然数共有多少个?
【巩固】写出全部除109后余数为4的两位数.
【例9】甲、乙两数的和是1088,甲数除以乙数商11余32,求甲、乙两数.
【例10】用某自然数a去除1992,得到商是46,余数是r,求a和r.
【例11】当1991和1769除以某个自然数n,余数分别为2和1.那么,n最小是多少?
【例12】有三个自然数a,b,c,已知b除以a,得商3余3;c除以a,得商9余11。
则c除以b,得到的余数是。
【例13】有两个自然数相除,商是17,余数是13,已知被除数、除数、商与余数之和为2113,则被除数是多少?
【巩固】两数相除,商4余8,被除数、除数、商数、余数四数之和等于415,则被除数是_______.
【巩固】用一个自然数去除另一个自然数,商为40,余数是16.被除数、除数、商、余数的和是933,求这2个自然数各是多少?
【例14】有一个三位数,其中个位上的数是百位上的数的3倍。
且这个三位数除以5余4,除以11余3。
这个三位数是_
【例15】一个自然数,除以11时所得到的商和余数是相等的,除以9时所得到的商是余数的3倍,这个自然数是_________.
【例16】盒子里放有编号1到10的十个球,小红先后三次从盒子中共取出九个球,如果从第二次起,每次取出的球的编号的和都比上一次的两倍还多一,那么剩下的球的编号为____。
【例17】10个自然数,和为100,分别除以3。
若用去尾法,10个商的和为30;若用四舍五入法,l0个商的和为34.10个数中被3除余l的有________个.
【例18】3782除以某个整数后所得的商恰好是余数的21倍,那么除数最小可能是。
【例19】在大于2009的自然数中,被57除后,商与余数相等的数共有______个.
【例20】用1、9、8、8这四个数字能排成几个被11除余8的四位数?。
