线性代数 第一章、矩阵
合集下载
线性代数知识点汇总1
第一章 矩阵矩阵的概念：n m A *（零矩阵、负矩阵、行矩阵、列矩阵、n 阶方阵、相等矩阵) 矩阵的运算：加法（同型矩阵）---------交换、结合律 数乘n m ij ka kA *)(=---------分配、结合律乘法nm lkj ik n l kj l m ik b a b a B A *1**)()(*)(*∑==（一般AB=BA ，不满足消去律；由AB=0，不能得A=0或B=0） 转置：A A T T =)( TT T B A B A +=+)( T T kA kA =)( TT T A B AB =)( 方幂：2121k k k kA AA += 2121)(k k k k A A +=逆矩阵：设A 是N 阶方阵，若存在N 阶矩阵B 的AB=BA=I 则称A 是可逆的， 且B A=-1矩阵的逆矩阵满足的运算律：1、可逆矩阵A 的逆矩阵也是可逆的，且A A =--11)(2、可逆矩阵A 的数乘矩阵kA 也是可逆的，且111)(--=A kkA 3、可逆矩阵A 的转置TA 也是可逆的，且T T A A )()(11--=4、两个可逆矩阵A 与B 的乘积AB 也是可逆的，且111)(---=A B AB ，但是两个可逆矩阵A 与B 的和A+B 不一定可逆，即使可逆，但11)(--+≠+B A B A 。
A 为N 阶方阵，若|A|=0，则称A 为奇异矩阵，否则为非奇异矩阵。
5、若A 可逆，则11--=A A逆矩阵注：①AB=BA=I 则A 与B 一定是方阵 ②BA=AB=I 则A 与B 一定互逆； ③不是所有的方阵都存在逆矩阵；④若A 可逆，则其逆矩阵是唯一的。
分块矩阵：加法，数乘，乘法都类似普通矩阵转置：每块转置并且每个子块也要转置注：把分出来的小块矩阵看成是元素初等变换：1、交换两行（列）2.、非零k 乘某一行（列）3、将某行（列）的K 倍加到另一行（列） 初等变换不改变矩阵的可逆性，初等矩阵都可逆 初等矩阵：单位矩阵经过一次初等变换得到的矩阵等价标准形矩阵⎪⎪⎭⎫⎝⎛=O O O I D r r第二章 行列式N 阶行列式的值：行列式中所有不同行、不同列的n 个元素的乘积的和n nn nj j j j j j j j j nij a a a a ...)1(21212121)..(∑-=τ行列式的性质：①行列式行列互换，其值不变。
线性代数 第一章、矩阵
张一 98 90 87 72 李二 89 90 86 98 王三 97 84 75 87 刘六 85 88 85 88
解： 用矩阵表示为
98
89
90 90
87 86
72
98
97 84 75 87
85 88 85 88
11
几种比较特殊的矩阵：
行矩阵：只有一行的矩阵
列矩阵：只有一列的矩阵
L
L L L
称为线性变换的系数矩阵。
am1
am 2
0 0 3
14
数量矩阵：对角矩阵中当 1 2 n时
例如：
5 0 0 0
0
5
0
0
就是一个数量矩阵
0 0 5 0
0
0
0
5
也就是说，数量矩阵是对角矩阵的一种特例
15
单位矩阵：当数量矩阵中对角线上的常数为1，
称为单位矩阵，用字母 E 或 En 表示
1 0 L 0
即
M M O M
ym am1 x1 am2 x2 amn xn .
称为由变量x1 ,x2 , ... ,xn到变量y1 ,y2 , ... ,ym的
变换为线性变换。线性变换由 m 个 n元函数
组成，每个函数都是变量的一次幂，故而称
之为线性变换。
17
a11 a12 L
其中,由系数构成的矩阵
A
a21
a22
0
0
L
1
特点:从左上角到右下角的直线(主对角线)上
的元素都是1，其他元素都是0。
16
定义1.4
线性变换：
如果变量y1 ,y2 ,... ,ym可由变量x1 ,x2 ,... ,xn线性表示,
第一章线性代数
2. 初等矩阵的性质 定理1.1. 定理1.1. 对m×n矩阵A施行一次初等行变换 矩阵A施行一次初等行 相当于在A 相当于在A的左边乘以相应的初等 矩阵; 施行一次初等列 矩阵; 对A施行一次初等列变换相 当于在A 当于在A的右边乘以相应的初等矩 阵.
第一章 矩阵
§1.5 方阵的逆矩阵
§1.5 方阵的逆矩阵 一. 逆矩阵的概念 1. 定义: 设A为方阵, 若存在方阵B, 使得 定义: 为方阵, 若存在方阵B AB = BA = E, 则称A可逆, 并称B 则称A可逆, 并称B为A的逆矩阵. 逆矩阵. 2. 逆矩阵是唯一的， A−1. 逆矩阵是唯一的， 记为A 记为 3. 性质:设A, B为同阶可逆方阵, 数k ≠ 0. 则 性质: 为同阶可逆方阵, (1) (A−1)−1 = A. (2) (AT)−1 = (A−1)T. (A (3) (kA)−1 = k−1A−1. (4) (AB)−1 = B−1A−1.
则λA =
λA11 λA12 … λA1r λA21 λA22 … λA2r
… … … … . λAs1 λAs2 … λAsr
第一章 矩阵
§1.3 分块矩阵
3. 分块乘法
设A为m×l矩阵, B为l ×n矩阵, 将它们分块如下 矩阵, 矩阵, A11 A12 … A1t B11 B12 … B1r A21 A22 … A2t B21 B22 … B2r A= … … … … , B= … … … … , As1 As2 … Ast Bt1 Bt2 … Btr 其中A 的列数分别与B 其中Ai1, Ai2, …, Ait的列数分别与B1j, B2j, …, Btj的 行数相等. 行数相等. C11 C12 … C1r t C21 C22 … C2r 其中C 则AB = … … … … , 其中Cij = Σ AikBkj , k=1 Cs1 Cs2 … Csr (i = 1, 2, …, s; j = 1, 2, …, r.)
《线性代数》课后习题集与答案第一章B组题
《线性代数》课后习题集与答案第一章B组题基础课程教学资料第1章矩阵习题一(B)1、证明：矩阵A 与所有n 阶对角矩阵可交换的充分必要条件是A 为n 阶对角矩阵. 证明：先证明必要性。
若矩阵A 为n 阶对角矩阵. 即令n 阶对角矩阵为：A =??n a a a 00000021,任何对角矩阵B 设为n b b b0000021，则AB=??n n b a b a b a000002211，而BA =??n n a b a b a b000002211，所以矩阵A 与所有n 阶对角矩阵可交换。
再证充分性，设 A =??nn n n n n b b b b b b b b b 212222111211，与B 可交换，则由AB=BA ，得：nn n n n n n n n b a b a b a b a b a b a b a b a b a 221122222111122111=nn n n n n n n n b a b a b a b a b a b a b a b a b a 212222221211121111，比较对应元素，得0)(=-ij j i b a a ，)(j i ≠。
又j i a a ≠，)(j i ≠，所以0=ij b ，)(j i ≠，即A 为对角矩阵。
2、证明：对任意n m ?矩阵A ，T AA 和A A T均为对称矩阵. 证明：(TAA )T =(A T )T A T =AA T，所以，TAA 为对称矩阵。
(A A T)T =A T (A T )T =A T A ，所以，A A T 为对称矩阵。
3、证明：如果A 是实数域上的一个对称矩阵，且满足O A =2 ，则A =O . 证明：设A =??nn n n n n a a a a a a a a a 212222111211，其中，ij a 均为实数，而且ji ij a a =。
由于O A =2，故A 2=AA T =nn n n n n a a a a a a a a a 212222111211nn nnn n a a a a a a a a a 212221212111=0。
线性代数第一章矩阵的转置
矩阵转置的性质
矩阵转置具有一些重要的性质，如$(A+B)^T=A^T+B^T$、$(AB)^T=B^TA^T$、$(A^T)^T=A$等，这 些性质在基变换过程中具有重要作用。
实例分析：利用矩阵转置进行向量空间基变换
实例描述
基变换过程
结果分析
考虑二维平面上的一个向量空间，其 原基为$begin{bmatrix} 1 0 end{bmatrix}$和$begin{bmatrix} 0 1 end{bmatrix}$，现需要将其变换为 新基$begin{bmatrix} 1 1 end{bmatrix}$和$begin{bmatrix} -1 1 end{bmatrix}$。
线性代数第一章矩阵的转置
• 矩阵转置基本概念 • 矩阵转置与线性变换 • 特殊类型矩阵的转置 • 矩阵转置在方程组求解中应用 • 矩阵转置在向量空间中应用 • 总结与回顾
01
矩阵转置基本概念
矩阵转置定义
01
将矩阵的行和列互换得到的新矩 阵称为原矩阵的转置矩阵。
02
对于任意矩阵A，其转置矩阵记为 AT或A'，满足AT=A'。
关键知识点总结
01
02
03
04
$(kA)^T = kA^T$，其中$k$ 是常数
$(AB)^T = B^TA^T$
对称矩阵：若矩阵$A$满足 $A^T = A$，则称$A$为对称
矩阵。
反对称矩阵：若矩阵$A$满足 $A^T = -A$，则称$A$为反
对称矩阵。
常见误区提示
误区一
认为只有方阵才能进行转 置操作。实际上，任何形 状的矩阵都可以进行转置。
误区二
错误地认为$(AB)^T = A^TB^T$。正确的公式是 $(AB)^T = B^TA^T$。
矩阵转置具有一些重要的性质，如$(A+B)^T=A^T+B^T$、$(AB)^T=B^TA^T$、$(A^T)^T=A$等，这 些性质在基变换过程中具有重要作用。
实例分析：利用矩阵转置进行向量空间基变换
实例描述
基变换过程
结果分析
考虑二维平面上的一个向量空间，其 原基为$begin{bmatrix} 1 0 end{bmatrix}$和$begin{bmatrix} 0 1 end{bmatrix}$，现需要将其变换为 新基$begin{bmatrix} 1 1 end{bmatrix}$和$begin{bmatrix} -1 1 end{bmatrix}$。
线性代数第一章矩阵的转置
• 矩阵转置基本概念 • 矩阵转置与线性变换 • 特殊类型矩阵的转置 • 矩阵转置在方程组求解中应用 • 矩阵转置在向量空间中应用 • 总结与回顾
01
矩阵转置基本概念
矩阵转置定义
01
将矩阵的行和列互换得到的新矩 阵称为原矩阵的转置矩阵。
02
对于任意矩阵A，其转置矩阵记为 AT或A'，满足AT=A'。
关键知识点总结
01
02
03
04
$(kA)^T = kA^T$，其中$k$ 是常数
$(AB)^T = B^TA^T$
对称矩阵：若矩阵$A$满足 $A^T = A$，则称$A$为对称
矩阵。
反对称矩阵：若矩阵$A$满足 $A^T = -A$，则称$A$为反
对称矩阵。
常见误区提示
误区一
认为只有方阵才能进行转 置操作。实际上，任何形 状的矩阵都可以进行转置。
误区二
错误地认为$(AB)^T = A^TB^T$。正确的公式是 $(AB)^T = B^TA^T$。
第一章 矩阵
1、数乘
阳光普照
定义3 规定数 与矩阵 A [ai j ]mn 的乘积 A 为
A A [ai j ]m n .
显然
0 A O, 1 A A. A (1) A [ai j ]m n 称为矩阵A的负矩阵。
数乘满足运算律：
1 A A; 2 A A A;
二、矩阵的乘法运算
显然可考虑定义矩阵的乘法和除法为：
A B [ai j bi j ]mn
和
A B [ai j bi j ]mn ,
这是个著名的病态矩阵，称为Hilbert矩阵。
例 4 （图的邻接矩阵） 某航空公司在A,B,C,D四城市之间开辟了若干 航线 ,如图所示表示了四城市间的航班图,如果 从A到B有航班,则用箭头从 A指向 B.
到达城市
A
出 发 城 市
B
C
D
A
B
C
A B C D
D
我们先用表格来表示航班图（见前页） 。表格中
太繁琐了，得换个思路！！
注意到二元一次方程组的解完全由未知数系数
a11、a12、a21、a22
及常数项 b1、b2 所确定。
三元一次方程组的解完全由未知数系数
a11、a12、a13、a21、a22、a23、a31、a32、a33
及常数项 b1、b2、b3 所确定。
一般地，归纳可知，n元的线性方程组
将上式回代入
(1)
中，并整理，可得
b1a22 b2a12 x1 a11a22 a12a21
对于三元一次线性方程组
a11 x1 a12 x2 a13 x3 b1 a21 x1 a22 x2 a23 x3 b2 a x a x a x b 32 2 33 3 3 31 1
阳光普照
定义3 规定数 与矩阵 A [ai j ]mn 的乘积 A 为
A A [ai j ]m n .
显然
0 A O, 1 A A. A (1) A [ai j ]m n 称为矩阵A的负矩阵。
数乘满足运算律：
1 A A; 2 A A A;
二、矩阵的乘法运算
显然可考虑定义矩阵的乘法和除法为：
A B [ai j bi j ]mn
和
A B [ai j bi j ]mn ,
这是个著名的病态矩阵，称为Hilbert矩阵。
例 4 （图的邻接矩阵） 某航空公司在A,B,C,D四城市之间开辟了若干 航线 ,如图所示表示了四城市间的航班图,如果 从A到B有航班,则用箭头从 A指向 B.
到达城市
A
出 发 城 市
B
C
D
A
B
C
A B C D
D
我们先用表格来表示航班图（见前页） 。表格中
太繁琐了，得换个思路！！
注意到二元一次方程组的解完全由未知数系数
a11、a12、a21、a22
及常数项 b1、b2 所确定。
三元一次方程组的解完全由未知数系数
a11、a12、a13、a21、a22、a23、a31、a32、a33
及常数项 b1、b2、b3 所确定。
一般地，归纳可知，n元的线性方程组
将上式回代入
(1)
中，并整理，可得
b1a22 b2a12 x1 a11a22 a12a21
对于三元一次线性方程组
a11 x1 a12 x2 a13 x3 b1 a21 x1 a22 x2 a23 x3 b2 a x a x a x b 32 2 33 3 3 31 1
线性代数 第一章矩阵 参考答案
0 A2
0 A1
0 I A11r1 , A21r2 I 0 I 0 0 I
0 A11
A2 1 0
P31 习题 1.4 1.按上课要求做，则此题中行阶梯形答案不唯一，行最简形和标准形答案唯一
1 1 1 （1） 0 2 1 0 0 0
法一
2 1 1 B ( A 2 I ) A ，求出 ( A 2 I ) 1 1 1 4 3 4 2 3 3 8 B 1 5 3 1 1 0 2 9 1 6 4 1 2 3 2 12
4.解： 4 X
4 0 0 4 8 (3) 2 14 2 (4) 3 11 5 11 5 4 10 1 1 0 1 7.解: AB ; BA 1 2 0 0 1 2
1 0 （2） 0 0 1 0 （3） 0 0 1 0 （4） 0 0
1 1 0 0 3 2 0 0 1 1 0 0
1 1 0 0 3 1 1 0 2 1 0 0
1 0 1 ，0 1 2 1 0 0 1 1 0 0 0 1 1 1 ， 0 0 0 1 0 0 0 0 7 0 1 5 1 , 0 1 1 0 0 0 0 2 1 1 0 5 1 ，0 1 1 0 0 0 0 0 0 0
（法二）
A1 X1 X 2 的逆阵为 B ，则有 0 X 3 X4 A1 X 1 X 2 I 0 0 X X I 0 4 3
A21 。 0
I 0 r1 r2 A2 0 I 0 0 A21 1 所以 A 1 0 A1 A1 0
第一章 矩阵
⎛ 250 500 190 10 ⎞ ⎜ ⎟ C = ⎜ 300 500 300 410 ⎟ ⎜ 600 310 110 400 ⎟ ⎝ ⎠
表示，其中矩阵 C 的第 i 行第 j 列（ i =1，2，3； j =1，2，3，4）元素恰好是矩阵 A 与 B 的 第 i 行第 j 列元素之和． 定义 2 设有两个 m × n 矩阵 A = (aij ) 与 B = (bij ) ，那么 m × n 矩阵
a12 a 22 # am2
a1n ⎞ ⎟ " a 2n ⎟ " # ⎟ ⎟ " a mn ⎟ ⎠ "
(1.1)
称为一个 m 行 n 列矩阵，简称 m × n 矩阵．这 m × n 个数称为矩阵 A 的元素，其中 aij 表示 矩阵 A 的第 i 行第 j 列元素． 元素是实数的矩阵称为实矩阵， 元素是复数的矩阵称为复矩阵． 本书中的矩阵都指实矩 阵． （1.1）式可以简记为
设矩阵 A = (aij ) ，记 − A = ( −aij ) ，那么 − A 称为矩阵 A 的负矩阵，显然有
A + (− A) = (− A) + A = 0 ．
从而规定矩阵的减法为
A − B = A + (− B) ．
如果三个门市部销售四种计算机（单位：台）在第一月内的销售情况矩阵为
⎛ 150 200 100 0 ⎞ ⎜ ⎟ A = ⎜ 170 300 50 210 ⎟ ， ⎜ 320 160 10 230 ⎟ ⎝ ⎠
第一章 矩 阵
矩阵是线性代数的主要研究对象之一，它在数学、物理学，工程技术以及社会科学等领 域都有广泛的应用．本章主要介绍矩阵及其应用．
§1
矩阵的概念
主要知识点：矩阵的定义；矩阵的例子（线性方程组的系数矩阵及增广矩阵） ；矩阵相
线性代数复习提纲
第一章 矩阵1 矩阵的概念特殊矩阵：行矩阵、列矩阵、对角矩阵、上三角阵、下三角矩阵、单位矩阵、对称矩阵、反对称矩阵。
2 矩阵的运算：（1）矩阵的线性运算及其运算规律－矩阵的加法（减法）和数乘。
（2）矩阵的乘法：能够进行乘法运算必须具备的条件，运算方法，左乘与右乘的区别。
乘法的运算规律（应用较为普遍的是矩阵乘法满足结合律） （3）矩阵的转置：(AB)T =B T A T（4）矩阵的逆：AB=BA=I →A -1=B 矩阵的逆唯一 运算规律： (A -1) -1= A ；(λA) -1= λ-1A -1；(AB) -1=B -1A -1；(A T ) -1=(A -1) T 矩阵逆的计算方法：待定系数法、初等变换法、伴随矩阵法。
3 分块矩阵及其运算第二章 线性方程组与矩阵初等变换 1 线性方程组与矩阵的一一对应关系2 高斯消元法：线性方程组的三种变换→阶梯形方程组。
3 利用矩阵初等变换解线性方程组：三种初等变换→行阶梯形矩阵→行最简形矩阵4 非齐次线性方程组解的三种情形的讨论⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎭⎫ ⎝⎛++++0000000000000000000011,221,2222111,111211r r rn r r rr nr r nr r d d c c c d c c c c d c c c c c（1）无解（2）唯一解（3）无数解 5矩阵等价的概念 6 初等矩阵的概念7 初等矩阵与矩阵初等变换的关系8 逆矩阵定理：设A 是n 阶矩阵，那么下列各命题等价： （1）A 是可逆矩阵；（2）齐次线性方程组Ax ＝0只有零解； （3）A 可以经过有限次初等行变换化为In ； （4）A 可表示为有限个初等矩阵的乘积。
9 利用矩阵初等变换求矩阵的逆 A 可以经过一系列初等行变换化为I ； I 经过这同一系列初等行变换化为A -1P s …P 2P 1 (A | I n )=(I n |A -1)第三章 行列式1 n 阶行列式的定义（1）全排列及其奇偶性：逆序数的概念，对换，相邻对换。
线性代数第一章、矩阵PPT课件
矩阵的秩的计算方法
可以通过初等行变换或初等列变换将矩阵转化为行阶梯形或列阶梯形，然后数非零行的个数即为矩阵的秩。
矩阵的秩的定义
矩阵的秩是其行向量组或列向量组的一个极大线性无关组中向量的个数。
矩阵的秩
通过初等行变换将增广矩阵化为行阶梯形，然后回代求解。
高斯消元法
克拉默法则
迭代法
适用于线性方程组系数行列式不为0的情况，通过解方程组求出方程的解。
n阶方阵A的行列式记为det(A)，是一个n阶的方阵，其值是一个实数。
行列式与转置矩阵的行列式相等，即det(A^T) = det(A)；行列式的乘法性质，即det(kA) = k^n * det(A)；行列式的初等变换性质，即行列式在初等变换下保持不变。
行列式的定义与性质
行列式的性质
行列式的定义
线性代数第一章、矩阵ppt课件
目录
CONTENTS
矩阵的定义与性质 矩阵的逆与行列式 矩阵的秩与线性方程组 矩阵的特征值与特征向量 矩阵的分解与正交矩阵 矩阵在实际问题中的应用
01
矩阵的定义与性质
CHAPTER
矩阵的定义与性质
about the subject matter here refers to the subject matter here.
相似法
如果存在可逆矩阵P，使得P^(-1)AP=B，则矩阵A的特征值和特征向量可以通过矩阵B的特征值和特征向量来求解。
特征值与特征向量的计算方法
如果矩阵A的所有特征值都是实数且没有重复，则矩阵A可以对角化。
判断矩阵是否可对角化
求解线性方程组
判断矩阵是否相似
优化问题
通过将线性方程组Ax=b转化为特征值问题，可以求解线性方程组。
可以通过初等行变换或初等列变换将矩阵转化为行阶梯形或列阶梯形，然后数非零行的个数即为矩阵的秩。
矩阵的秩的定义
矩阵的秩是其行向量组或列向量组的一个极大线性无关组中向量的个数。
矩阵的秩
通过初等行变换将增广矩阵化为行阶梯形，然后回代求解。
高斯消元法
克拉默法则
迭代法
适用于线性方程组系数行列式不为0的情况，通过解方程组求出方程的解。
n阶方阵A的行列式记为det(A)，是一个n阶的方阵，其值是一个实数。
行列式与转置矩阵的行列式相等，即det(A^T) = det(A)；行列式的乘法性质，即det(kA) = k^n * det(A)；行列式的初等变换性质，即行列式在初等变换下保持不变。
行列式的定义与性质
行列式的性质
行列式的定义
线性代数第一章、矩阵ppt课件
目录
CONTENTS
矩阵的定义与性质 矩阵的逆与行列式 矩阵的秩与线性方程组 矩阵的特征值与特征向量 矩阵的分解与正交矩阵 矩阵在实际问题中的应用
01
矩阵的定义与性质
CHAPTER
矩阵的定义与性质
about the subject matter here refers to the subject matter here.
相似法
如果存在可逆矩阵P，使得P^(-1)AP=B，则矩阵A的特征值和特征向量可以通过矩阵B的特征值和特征向量来求解。
特征值与特征向量的计算方法
如果矩阵A的所有特征值都是实数且没有重复，则矩阵A可以对角化。
判断矩阵是否可对角化
求解线性方程组
判断矩阵是否相似
优化问题
通过将线性方程组Ax=b转化为特征值问题，可以求解线性方程组。
第一章(第一二节)矩阵的概念及基本运算PPT课件
没有得到老一辈数学家们的重视。如：他曾五次将一篇
代 “五次方程不能由公式给出其解”的论文寄给在格廷根的
高斯，但都没有得到回音。由于他的不断出外求学，致使
数 经济状况十分糟糕，最后只得回到自己的故乡—挪威。没
过多久，他就在忧郁中结束了自己年仅27岁的短暂生命。
就在他死后的第三天，他的朋友通知他，他已被柏林大学
代 们称之为维是 m×n 的矩阵，简称为 m×n 矩阵，简记为
。其表[ a示ij ]形m 式n （通式）为：
数
a11 a12 a1n
a
21
a 22
a2n
a m1 a m 2 a mn 7
一、矩阵的定义
a11 a12 a1n
a
21
a 22
a2n
线
a m1 a m 2 a mn
线 们满足
(1)m = p 且n = q；
性 (2)aij=bij，其中i=1,2,…,m；j=1,2,…,n。
代
则称A与B相等，记为A=B。
数
即： A 与B 两个矩阵的维和相对应的
元均一一对应相等。
24
二、矩阵的和
定义 设A=[aij]m×n ，B=[bij]m×n ，令C= [aij+ bij]m×n , 称矩
22 35 31 21
14 61 14 45
数
49 55 45 62
5
6
59
67
a21=2； a22=12； a23=24； a31=3； a32=11； a33=27。
9
试问： 6 3 1
332
B= 8 4 3 C= 4 7 分别是否为矩阵？
线
952
3 6 1 为什么？
线性代数(复旦大学) 第一章矩阵
注: 反对称矩阵的对角元素都为零.
马和平 (理学院 数学系) 线性代数 B
2013–2014学年秋季学期
9月29日
8 / 71
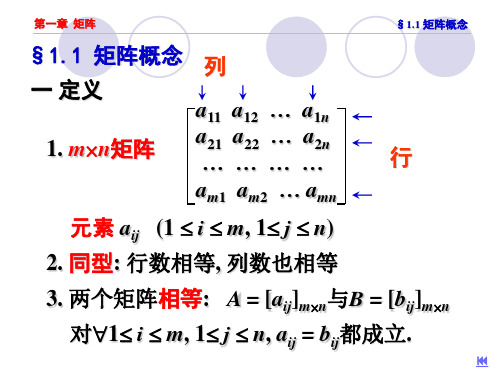
1.1.3 矩阵的线性运算 定义 1.3 (矩阵相等) 若 ������ = (������������������ )������×������ 和 ������ = (������������������ )������×������ , 且 ������������������ = ������������������ (������ = 1, 2, · · · , ������;
线性代数 B
2013–2014学年秋季学期
9月29日
3 / 71
例 线性代数方程组 ⎧
⎪ ⎪ ������11 ������1 + ������12 ������2 + · · · + ������1������ ������������ = ������1 , ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ������21 ������1 + ������22 ������2 + · · · + ������2������ ������������ = ������2 , ⎪ ⎪ ······························ , ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ ������������1 ������1 + ������������2 ������2 + · · · + ������������������ ������������ = ������������
解： 因为 所以
2 − ������ = ������, 2 = ������, 5������ = ������ − 8, ������ = 1, ������ = 2, ������ = −2.
《线性代数》第1章-矩阵(张小向2014黑白打印版)
c 3
同型
20 16
50 20
30 16
与
20 50 30
16 20 16
不同型
5. 两个矩阵相等(equal)
大前提: 同型
A = (aij)m×n与B = (bij)m×n相等:
对∀1≤ i ≤ m, 1≤ j ≤ n, aij = bij都成立 记为A = B.
第一章 矩阵
§1.1 矩阵的基本概念
0 0
0 0
2
3
10 1 0
从i市经一次中转到达j市航线的条数=?
bij = ai1a1j + ai2a2j + ai3a3j + ai4a4j .
1
21 1 0
i
2
j
B = (bij) =
01 10
1 0
1 0
3 4
02 1 1
第一章 矩阵
§1.2 矩阵的基本运算
2. 定义: A = (aij)m×s与B = (bij)s×n的乘积(product)
a1
列向量(row vector):
a2 …
n–维
(n–dimensional)
an
第i分量 (ith component): ai (i = 1, …, n)
第一章 矩阵
§1.1 矩阵的基本概念
4. 同型(same-sized): 行数相等, 列数也相等
20 16
50 20
30 16
与
a 1
b 2
注: ① 设矩阵A = (aij)m×n , 记−A = (−aij)m×n , ——A的负矩阵(additive inverse of A).
② 设A, B是同型矩阵, 则它们的差
矩阵理论课件-第一章 线性代数引论
推论2 V中任意一个元素y, 均可由V的一个基底 x1, … , xn唯一表出.
坐标：
n
设 dim V=n, x1, , xn为一组基，y V , 令y= ai xi ,称 i 1
有序数组(a1, , an )T 为y在基x1, , xn下的坐标，它由 y与基x1, , xn唯一确定.
n
例如Pn(x)={ ai xi | ai R}为n+1维空间，1，x, ,xn可作为 i0
2 0 -2 1
注：实际上即
1
0
1 2
1 1
3 1
是标准基(1
,
2
,
3
,
4
)到
1
2
2
2
(1,2,3,4 )的过渡矩阵. 第二问也可用前面讲的公式.
四、子空间和维数定理
子空间：设V是数域F上的线性空间，W V，W非空， 若W中向量关于V的加法和数乘运算也构成F上的线性 空间，则称W为V的子空间.
例1 恒等变换 T：V V，Tx=x,x V. 零变换 T：V V，Tx=0,x V.
例2 伸缩变换：取定k 0,令 T： R3 R3， Tx=kx,x R3. T将R3中任一向量拉伸(k>1)或 压缩(k<1)k倍.
例3 平面旋转变换：取定 （0,2）,x (x1, x2 )
令
cos
W1 W2不一定为子空间，例如两个坐标轴之并.
定理 3 设W1，W2为V的两个子空间，则
dim(W1 W2 ) dim W1 dim W2 dim(W1 W2 ).
直和：如果和空间W1 W2中的任一向量均可唯一的表成W1中 的一个向量和W2中的一个向量之和，则称W1 W2是W1与W2的 直和，记为W1 W（2 或W1 W2）.
坐标：
n
设 dim V=n, x1, , xn为一组基，y V , 令y= ai xi ,称 i 1
有序数组(a1, , an )T 为y在基x1, , xn下的坐标，它由 y与基x1, , xn唯一确定.
n
例如Pn(x)={ ai xi | ai R}为n+1维空间，1，x, ,xn可作为 i0
2 0 -2 1
注：实际上即
1
0
1 2
1 1
3 1
是标准基(1
,
2
,
3
,
4
)到
1
2
2
2
(1,2,3,4 )的过渡矩阵. 第二问也可用前面讲的公式.
四、子空间和维数定理
子空间：设V是数域F上的线性空间，W V，W非空， 若W中向量关于V的加法和数乘运算也构成F上的线性 空间，则称W为V的子空间.
例1 恒等变换 T：V V，Tx=x,x V. 零变换 T：V V，Tx=0,x V.
例2 伸缩变换：取定k 0,令 T： R3 R3， Tx=kx,x R3. T将R3中任一向量拉伸(k>1)或 压缩(k<1)k倍.
例3 平面旋转变换：取定 （0,2）,x (x1, x2 )
令
cos
W1 W2不一定为子空间，例如两个坐标轴之并.
定理 3 设W1，W2为V的两个子空间，则
dim(W1 W2 ) dim W1 dim W2 dim(W1 W2 ).
直和：如果和空间W1 W2中的任一向量均可唯一的表成W1中 的一个向量和W2中的一个向量之和，则称W1 W2是W1与W2的 直和，记为W1 W（2 或W1 W2）.
线性代数教学课件：矩阵的概念
代
当i>j时, aij 0
数
2 3 0 1
如
0
1
1
1
=
0 0 0 2 0 0 0 1
=
▪下三角矩阵
a11 0
0
a21
a22
0
线
an1 , aij 0
1 0 0 0
数
如
2
4
0
0
=
3 0 1 0
1 2 1 1
=
可以建立线性方程组与矩阵的一一对应：
=
0 0 1
可以建立线性方程组与矩阵的一一对应：
如，称 A 2 1 1
线
1 0 1
为线性代数方程组
2 x1 x1
x2
x3 x3
1 的系数矩阵； 2
性 代
系数及常数项组成的矩阵
—
A
2
1
1
1
数
1 0 1 2
称为方程组的增广矩阵.
=
=
1.1 矩阵及其运算
同型矩阵： Amn , Bmn
例1.2 某企业生产4种产品，各种产品的季度产值
（单位：万元）如下表：
线
产值
季节 产品1 产品2 产品3 产品4
性
1 80 58 75 78
代
2 98 70 85 84
3 90 75 90 90
数
4 88 70 82 80
80
这个数表 98
90
58 70 75
75 85 90
78 84
具体描述了这家企业各种产品 各季度的产值，同时也揭示了
代
▪行矩阵或行向量
a1 a2 an 如（1 0 1 2） 数
线性代数第一章
a1n aM2n , amn
称为m行n 列矩阵, 简称m n 矩阵. 其中aij称为矩阵
的第i行第 j 列元素, 也称为矩阵的(i, j)元.
矩阵常用大写英文字母表示，如 A, B,C,L . 有时记作 [aij ], Amn，或[aij ]mn .
a11 a12 L
A
a21 M
a22 M
65 3 2
6 0
r2 2r1
r3 r1 r3 4r1
0 0
1 1
2 2
0 0
3 3
2 2
4 7 6 14 5 12
0 1 2 2 1 4
1 2 1 3 1 2
1 2 1 0 5 7
r3 r2
r3 r2
0
1
2 0 3 2 12r3 0 1
20
3
2
r3 r4 0 0 0 2 4 6 r13r3 0 0 0 1 2 3
L
am1 am2 L
a1n aM2n aij amn
当P = R时 , 矩阵A称为实矩阵； 当P = C时 , 矩阵A称为复矩阵.
特殊矩阵
(1)零矩阵：元素全为零的矩阵，记作 Osn , 或O .
(2)行向量(矩阵)：只有一行的矩阵. (3)列向量(矩阵)：只有一列的矩阵.
同型矩阵：行数、列数均相等的两个矩 阵.
转置矩阵
定义1.2.3 将一个m n矩阵
a11 a12 L
A
a21
a22
L
M M
am1 am2 L
a1n
a2
n
M
amn
的行依次变列(或列依次变行)所得到的n m 矩阵
a11 a21 L
a12
北京科技大学线性代数课件1
0 0 1 O a 0 0 0 b 1 B 1 1 b
0 0 0 a 0 0 A2 A3 A4 其中 A1 0 1 b 1 1 1 b 0
Ait Btj Aik Bkj
线性代数1-2
例2 设 1 0 0 1 A 1 2 1 1 2 解： 1 0 E 0 1 A 1 2 1 A1 1
0 0 0 0 , 1 0 0 1
1 A1 0 1 1 1 0 1 2 1 B B 1 21 0 14 1 1 2
线性代数1-2
例
a 0 A 1 0 a 0 A 1 0
1 0 0 a A a 0 0 A O 0 , 0 b 1 E B 1 E 1 1 b 0 1 0 0 a 0 0 ( A1 , A2 , A3 , A4 ) 0 b 1 1 1 b a 1
0 2 4 1
1 0 3 3
0 1 . 3 1
线性代数1-2
例2 设 1 0 0 1 A 1 2 1 1 2 解 1 0 E 0 1 A 1 2 1 A1 1
0 0 1 0 0 0 1 2 , B 1 0 1 0 1 1 0 1
线性代数1-2
第一章 矩阵
1.2分块矩阵
分块矩阵的概念 分块矩阵的运算规则
线性代数1-2
2.分块矩阵的运算规则 分块的原则： (1)分块的目的是为了简化矩阵运算； (2)矩阵分块后必须使子块能够运)分块对角阵
线性代数1-2
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
bm
零矩阵：元素都是零的矩阵 记作O。
12
a11 a12 L
上三角矩阵：形如
0
a22 L
L L L
0
0L
a1n
a2n
的方阵
L
ann
a11 0 L
下三角矩阵：形如
a21
L
a22 L
L L
an1
an 2
L
0
0 L
的方阵
ann
线性运算
24
三. 矩阵与矩阵相乘(矩阵的乘法)
引例 设变量 x1, x2 , x3 到变量 y1, y2 的线性变换为
y1 y2
a11x1 a21x1
a12 x2 a13x3 a22 x2 a23x3
变量 t1, t2到变量 x1, x2 , x3 的线性变换为
98
89
90 90
87 86
72
98
97 84 75 87
85 88 85 88
11
几种比较特殊的矩阵：
行矩阵：只有一行的矩阵
列矩阵：只有一列的矩阵
有多少个？它们都 相等吗？
A (a1, a2 , L , an )
b1
B
b2
M
1 0 L 0
如：单位矩阵
En
0
M
1 M
L
0
M
0
0
L
1
对应的线性变换为
y1 x1
y2 L
x2
称为恒等变换
yn xn
18
再如: 线性变换
y1 1 x1 ,
y2
2
x2
,
yn n xn .
对应n阶系数矩阵为
1 0 L 0
A
0
2
L
0
M M
M
0
0L
n
是一个对角矩阵。
也就是说，线性变换和系数矩阵是一一对应的。
19
§2 矩阵的运算
背景: 矩阵之所以有用,不在于把一组数能排成矩形 数表,而在于能进行有实际意义的运算。
一. 矩阵的加法
定义2.1 设有两个mn矩阵A=(aij), B=(bij),那么A
实际上，一阶矩阵就是一个数。
(3)若两个矩阵行数和列数分别相等，则称这 两个矩阵是同型矩阵，否则称为非同型矩阵。
(4)若两个矩阵不但是同型矩阵，而且对应的元 素也相等，则称这两个矩阵相等。
9
矩阵应用举例：
例1：把下图中四个城市之间的航线用矩阵表示出来
城市2
城市1
城市4
城市3
解:设 aij 10,，从从城城市市ii到到城城市市jj有没一有条航航线线（1 i，j 4）
由m×n 个数 aij ( i = 1, 2, …, m ; j = 1, 2, …, n)按一 定次序排成 m 行 n 列的矩形数表
a11 a12 L
a21
a22
L
L L L
am1 am2 L
a1n
a2n
L
amn
Amn
称为一个 m 行 n 列的矩阵，简记为 (aij)m×n
定义2.3 设A=(aij)ms，B=(bij)sn ，那么规定矩阵A与
B的乘积是C=(cij) m n,
s
其中 cij ai1b1 j ai 2b2 j aisbsj aikbkj k 1
并把此乘积记作C=AB。
a11
ai1
a
m1
a12 ai2 am2
单位矩阵：当数量矩阵中对角线上的常数为1，
称为单位矩阵，用字母 E 或 En 表示
1 0 L 0
即
E
0
1
L
0
M M O M
0
0
L
1
特点:从左上角到右下角的直线(主对角线)上
的元素都是1，其他元素都是0。
16
定义1.4
线性变换：
如果变量y1 ,y2 ,... ,ym可由变量x1 ,x2 ,... ,xn线性表示,
x1 x2
b11t1 b12t2 b21t1 b22t2
x3 b31t1 b32t2
那么，变量 t1, t2到变量 y1, y2 的线性变换应为
y1 y2
a11 a21
b11t1 b12t2 b11t1 b12t2
例如:
diag
(1,
2,
3)
0
2
0 是一个三阶对角矩阵
0 0 3
14
数量矩阵：对角矩阵中当 1 2 n时
例如：
5 0 0 0
0
5
0
0
就是一个数量矩阵
0 0 5 0
0
0
0
5
也就是说，数量矩阵是对角矩阵的一种特例
15
变换为线性变换。线性变换由 m 个 n元函数
组成，每个函数都是变量的一次幂，故而称
之为线性变换。
17
a11 a12 L
其中,由系数构成的矩阵
A
a21
a22
L
L L L
称为线性变换的系数矩阵。
am1
am 2
L
a1n
a2n
L
amn
可以看出给定一个矩阵必定对应于一个线性变换
23
例2ห้องสมุดไป่ตู้
设
4
A
2
3 0
1
5
,
B
1 1
2 0
0 3
求 A－3B
解：
3 6 0
3B
3
0
9
4 3 1 3 6 0
A
3B
2
0
5
3
0
9
1 5
9 0
1
4
说明：矩阵的加法运算和数乘运算统称为矩阵的
1
§1 矩阵的概念
背景： 数的发展：自然数 整数 有理数
实数 复数 对于这些数一般用集合的观点讨论,通常只 是研究它们的一些运算法则和运算规律。例 如加、减、乘、除等。
2
在研究某些问题时，常常和所研究对象的取值范围 有关。
如求方程 x2 1 0 的根，
此方程不仅在有理数范围内无解，就是在实数范围 内也无解，只在复数范围内有解。
b12 b22 b32
a11b11 a21b11
a12b21 a22b21
a13b31 a23b31
a11b12 a12b22 a13b32
a21b12
a22b22
a23b32
按上述方法定义的矩阵乘法有实际意义。 由此推广得到一般的定义：
27
第一章 矩阵
矩阵是线性代数的一个最基本的概念，是线性代 数的研究对象和重要工具，许多理论问题和实际问题 都可以用矩阵表示并且可以运用有关理论得到解决。 例如 ：学生各科考试成绩，企业销售产品的数量和 单价，超市物品配送路径等。本章就是讨论最简单的 由数形成的矩形数表—矩阵及其运算。
1.1 矩阵的概念 1.2 矩阵的运算 1.3 可逆矩阵 1.4 矩阵的初等变换和初等方阵
定义2.2 数与矩阵A的乘积记作 A,规定为
a11 a12 L
A
a21
M
a22
M
L
am1
am 2
L
a1n
a2n
M
a
mn
数与矩阵相乘满足运算规律:
(1)()A (A)
(2)( )A A A
(3)( A B) A B
为了在以后的讨论中能把具有共同运算性质的数集 统一处理
下面引入一个一般的概念
3
定义1.1
设F是复数集C的一个子集合，如果F满 足下列两个条件： （1）0和1都在 F 中 （2） F 中任意两个数(可以相等)的和、差、积、 商（除数不为零）仍然在该集合中
则称集合 F 构成一个数域
例如: 有理数集、实数集、复数集都构成数域。 但整数集不构成数域。
加法满足运算规律: (1) A+B= B + A; (2) (A + B)+C= A +(B +C) .
(交换律) (结合律)
特别的: (3) A + O = O + A = A
(4) A + (-A) = (-A) + A = O
A是A的负矩阵
A (aij )mn
21
类似的，也可以定义矩阵的减法。
注意: （1）本书中涉及到的数都是指某个数域中的数 （2）若没有特别说明涉及到的数域一般是指实数域