应力、应力状态分析(习题解答)
周建方版材料力学习题解答[第八章9]分析
![周建方版材料力学习题解答[第八章9]分析](https://img.taocdn.com/s3/m/cbb06210a417866fb94a8e07.png)
8-49现用某种黄铜材料制成的标准圆柱形试件做拉伸试验。
已知临近破坏时,颈缩中心部位的主应力比值为113321::::=σσσ;并已知这种材料当最大拉应力达到770MPa 时发生脆性断裂,最大切应力达到313MPa 时发生塑性破坏。
若对塑性破坏采用第三强度理论,试问现在试件将发生何种形式的破坏?并给出破坏时各主应力之值。
解: 令主应力分别为:σσ31=,σσσ==32脆性断裂时,由第一强度理论=1r σσσ31==770MPa所以,塑性破坏时,由第三强度理论 所以故,试件将发生脆性断裂。
破坏时MPa 7701=σ,MPa 25732==σσ8-50 钢制圆柱形薄壁压力容器(参见图8-13),其平均直径mm d 800=,壁厚mm 4=δ,材料的M P a ][120=σ,试根据强度理论确定容器的许可内压p 。
解:在压力容器壁上取一单元体,其应力状态为二向应力状态。
p pd 504'==δσ ,p pd1002"==δσ 其三个主应力为p 100"1==σσ, p 50'2==σσ,03=σ据第三强度理论所以 ,MPa p 2.13≤,许可内压MPa p 2.13= 据第四强度理论所以,MPa p 39.14≤,许可内压MPa p 39.14=8-51 空心薄壁钢球,其平均内径mm d 200=,承受内压MPa p 15=,钢的MPa ][160=σ。
试根据第三强度理论确定钢球的壁厚δ。
解:钢球上任一点应力状态如图示 其三个主应力为:σσσ==21,03=σ而 MPa MPa d p R R p δδδδππσ4342.0152222=⨯=⋅=⋅⋅=据第三强度理论 所以 mm m 69.41069.41601433=⨯=⨯≥-δ 8-52 图8-77所示两端封闭的铸铁圆筒,其直径mm d 100=,壁厚mm 10=δ,承受内压MPa p 5=,且在两端受压力kN F 100=和外扭矩m kN T ⋅=3作用,材料的许用拉应力MPa ][40=+σ,许用压应力MPa ][160=-σ,泊松比250.=ν,试用莫尔强度理论校核其强度。
刘鸿文《材料力学》复习笔记和课后习题(含考研真题)详解(应力和应变分析强度理论)【圣才出品】

平面的外法线方向。
7 / 135
圣才电子书 十万种考研考证电子书、题库视频学习平台
三、三向应力状态分析 1.三向应力圆 如图 7-1-4 所示,以三个主应力表示的单元体,由三个相互垂直的平面分别作应力圆, 将三个平面的应力圆绘在同一平面上得到三向应力状态下的应力圆,如图 7-1-5 所示。与 每一主应力所对应的应力圆可由与该主平面相正交的其余面上的应力作出。 注意:作三向应力圆应至少知道一个主应力的大小和方向。
1 / 135
圣才电子书 十万种考研考证电子书、题库视频学习平台
实例:在滚珠轴承中,滚珠与外圈接触点处的应力状态,可以作为三向应力状态的实例。 二、二向应力状态分析 1.解析法 如图 7-1-1(a)所示,一单元体 abcd 处于平面应力状态,采用截面法取左边部分单 元体 eaf 为研究对象,如图 7-1-1(b)所示。
5 / 135
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 7-1-3(a)
图 7-1-3(b) ③求主应力数值和主平面位置 a.求主应力数值的方法 如图 7-1-3(b)所示,点 A1 和点 B1 分别为代表最大主应力和最小主应力,其大小为
6 / 135
圣才电子书 十万种考研考证电子书、题库视频学习平台
圣才电子书 十万种考研考证电子书、题库视频学习平台
第 7 章 应力和应变分析强度理论
7.1 复习笔记
一、应力状态 一点的应力状态:过一点不同方向面上应力的集合。 应力状态的研究对象是单元体,其特征为:①单元体的尺寸无限小,每个面上应力均匀 分布;②任意一对平行平面上的应力相等。 主单元体是指各侧面上切应力均为零的单元体。其中,单元体上切应力为零的面称为主 平面,主平面上的正应力称为主应力。 说明:一点处必定存在一个单元体,使得三个相互垂直的面均为主平面,三个互相垂直 的主应力分别记为 σ1、σ2、σ3,且规定按代数值大小的顺序来排列,即 σ1≥σ2≥σ3。 应力状态分类及实例 (1)单向应力状态:也称为简单应力状态,三个主应力 σ1、σ2、σ3 中只有一个不等 于零。 实例:简单的拉伸或压缩。 (2)平面(二向)应力状态:三个主应力 σ1、σ2、σ3 中有两个不等于零。 实例:薄壁圆筒横截面上的点和圆形容器包含直径的任意横截面上的点。 (3)空间(三向)应力状态:和平面应力状态统称为复杂应力状态,三个主应力 σ1、 σ2、σ3,均不等于零。
应力状态例题(整合全部)

A
45
B
得:
q
2m
XA YA NB B
(2)选择等边角钢型号
N B 56.6 103 2 A 353 . 75 mm [ ] 160 106
查附录Ⅲ
A q
选择40 5角钢, 其横截面面积为379.1mm 2
拉伸与压缩/拉(压)时的强度计算 例题4 应力 图示结构,钢杆1:圆形截面,直径d=16 mm,许用
F
b
F
L
L
材料力学
剪切实用计算
解:剪切面如图所示。剪
F/2 F
切面面积为:
A Lb
由剪切强度条件:
剪切面
F/2
Fs F / 2 [ ] A Lb
由挤压强度条件:
F L 100mm 2b[ j ]
jy
Fb F /2 [ jy ] A jy b
材料力学
0.022 160 106
由平衡条件:
M
A
0
[ F ] AB [ FN ] ADsin
[ FN ] ADsin 50.24 1 0.75 / 0.752 1 12.06 kN [F ] 2 .5 AB
拉伸与压缩/轴向拉(压)时的变形 C 0.75m A 1m D D
[ ]1 150MPa ;杆2:方形截面,边长 a=100 mm, [ ]2 4.5MPa ,(1)当作用在B点的载荷 F=2 吨时,校核强 度;(2)求在B点处所 1.5m 能 承受的许用载荷。 B A 1 解: 一般步骤:
2m F 外力 内力 应力
2
C
利用强度条 件校核强度
3-1-1 应力状态分析

设ABC为主平面,在主平面上有τ=0 由于τ2= S2-σ2 即可得S=σ 所以Sx=Sl=σl Sy=σm Sz=σn 因此有: (σx-σ)l+τyxm+τzxn =0
τxyl+(σy-σ)m+τzyn =0 τxzl+τyzm+(σz-σ)n=0 而:l2+m2+n2=1 此为隐含条件 所以有:
第13章 应力分析stress analysis
本章内容:应用塑性力学分析金属在外力作用下的变形行为 本章重点:点的应力状态分析
应力stress:单位面积上的内力。
材料力学方法:切面法,将物体切开, 利用内力外力平衡条件求切面上 的应力分布。
:把物体切成无数个微六面体(或其他形状),称微元体或单元体,根据 单元体静力平衡条件写出平衡微分方程,再考虑其他条件求解。
13.1 应力状态分析
目标:任意一点的应力状态stress state —— 整个变形体的应 力状态
13.1.1 应力分析截面法
外力outside forces—— 产生内力 应力:正应力(stress)σ,切应力(shear stress)τ 要点:截开物体后,内力变外力。 13.1.1.1 单向拉伸uniaxial tensile应力分析
13.1.4.2 主轴坐标系
若以主应力(σ1 σ2 σ3方向即主轴方向)作坐标系,则坐标轴 为1,2,ห้องสมุดไป่ตู้方向轴。
此时, 在此坐标系下的任意斜面(l, m, n)上有:
S1=σ1l S2=σ2m S3=σ3n 以及:S2=σ12 l2+ σ22 m2 +σ32n2
σ=σ1 l2+ σ2 m2 +σ3n2 τ2= S2-σ2 而且:J1=σ1 + σ2 +σ3 J2=-(σ1σ2 + σ2σ3 +σ3σ1) J3=σ1σ2σ3 又由于:l2+m2+n2=1 所以有: 此方程为一椭球面方程,称应力椭球面。 其中S1 S2 S3分别表示全应力S在1,2,3轴向上的投影。
材料力学典型例题及解析7.应力应变状态典型习题解析

应力、应变状态分析典型习题解析1 已知矩形截面梁,某截面上的剪力F S =120 kN 及弯矩m kN 10⋅=M 。
绘出表示1、2、3及4点应力状态的微体,并求出各点的主应力。
b = 60 mm ,h = 100 mm 。
解题分析:从图中可分析1、4点是单向应力状态,2点在中性轴上为纯剪切应力状态,31取平行和垂直与梁横截面的六个平面,构成微体。
则各点处的应力状态如图示。
2、梁截面惯性矩为点微体上既有正应力又有切应力。
解:、画各点处微体的应力状态图计算各点处主应力4843333m 1050012m 10100(106012−−−×=×××==)bh I z 1点处弯曲正应力(压应力)MPa 100Pa 10100m10500m 1050m N 101064833−=×=×××⋅×==−−z I My σ1点为单向压缩受力状态,所以021==σσ,MPa 1003−=σ2点为纯剪切应力状态,MPa 30Pa 1030m10100602N1012036263=×=×××××=−τ(向下)容易得到,MPa 301=σ,02=σ,MPa303−=σ3点为一般平面应力状态弯曲正应力MPa50Pa 1050m 10500m 1025m N 101064833=×=×××⋅×==−−z I My σ弯曲切应力σ14τ2F S =120 kN题图1中性轴324hστ25 mm 31b M =10 kN·mσ3150 mm 1MPa 5.22Pa 1050.22m10500m 1060m 105.372560N 101206483393*S =×=××××××××==−−−zz bI S F τMPa6.8MPa6.58Pa)10522()2Pa 1050(2Pa 1050)2(22626622minmax −=×+×±×=+−±+=x y x yx τσσσσσσ所以 MPa 6.581=σ,02=σ,MPa 6.83−=σ4点为单向拉伸应力状态,拉伸正应力的大小与1点相等。
应力应变分析习题解答

402
94.72 5.28
MPa
习题解答
根据大小来确定主应力的次序如下:
1 94.72MPa, 2 50MPa, 3 5.28MPa
于是该单元体的形状改变比能为:
uf
1 6E
(1
2)2
(2
3 ) 2
(3
1)2
1 0.3106
6 200103
[(94.72
50)2
(50
5.28)2
y
m x
n
y
y
x
n
x
习题解答
x
2
y
x
2
y
cos2
x
sin
2
x
2
y
sin
2
x
cos2
A
2
Bo
x
y
习题解答
3、各单元体各面上的应力如图所示(应力单位MPa)。试利用应力圆: 1)求指定截面上的应力; 2)求主应力的数值; 3)在单元体上绘出主平面的位置及主应力的方向。
30
30
30
60o
30
解:1)由以下应力公式 可得
y 30MPa
解:要想求单元体的形状改变比能,必须先求出
该单元体的三个主应力,由右图可知 z 50
为该单元体的一主应力,于是可只计算垂直于z轴的
70MPa
平面上的主应力。由平面应力公式可得
m a x
min
x
y 2
x
2
y
2
2x
40MPa x z 50MPa
70 30 2
70 30 2 2
2
y
2
2x
70 30 2
应力状态分析及强度理论习题讲解

答案:
D
四、计算
1. 构件内危险点应力状态如图所示,试作强度校核: 1)材料为铸铁,已知许用拉应力 t 30MPa,压应力 90MPa;3)材料仍为铸铁,应力分量中 为压应力。
15MPa
c 90MPa,泊松比 =0.25;2)材料为铝合金,
15MPa
45 , 45
90 90
45 45
45
x
O
45 , 45
(b)
45
45
x
(c)
(d)
4.用电阻应变仪测得空心钢轴表面一点与母线成45 方向 上的正应变 45 200 103。已知该轴转速为120r / min , 外径D 120mm,内径d 80mm,钢材E 210GPa, =0.28, 求轴传递的功率。
45
a b
1
45
1
3
O
45 3
x
(b)
4 WP D 1 12 10 1 8 /12 16 16 272.3 106 m 3 n E 所以 N WP 45 9550 1 120 210 109 272.3 106 200 103 112kW 9550 1 0.28 3 4 3 6
n
dA
y
30
120
1
t
30
20
1 2
x
2
40 30
(b)
4 5,26 B C
68
240
3)作应力圆(图(c)) (1)取比例尺,1cm-20MPa,在 - 坐标平 面内作点1(+20,0)、2(-40,0);
材料力学习题应力状态和强度理论

应力状态分析与强度理论基 本 概 念 题一、选择题1. 三种应力状态分别如图(a )、(b )、(c )所示,则三者间的关系为( )。
A .完全等价B .完全不等价C .图(b )、图(c )等价D .图(a )、图(c )等价题1图2. 已知应力情况如图所示,则图示斜截面上的应力为( )。
(应力单位为 MPa)。
A .70-=ασ,30-=ατB .0=ασ,30=ατC .70-=ασ,30=ατD .0=ασ,30-=ατ3. 在纯剪切应力状态中,其余任意两相互垂直截面上的 正应力,必定是( )。
A .均为正值B .一为正值一为负值C .均为负值 题2图D .均为零值4. 单元体的应力状态如图所示,由x 轴至1σ方向的夹角为( )。
A .︒5.13 B .︒-5.76 C .︒5.76 D .︒-5.13题4图 题5图5. 单元体的应力状态如图所示,则主应力1σ、2σ分别为( )。
(应力单位MPa). -33-A .901=σ,102-=σB .1001=σ,102-=σC .901=σ,02=σD .1001=σ,02=σ 6. 如图6所示单元体最大剪应力max τ为( )。
A .100 MPaB .50 MPaC .25 MPaD .0题6图 题7图7. 单元体如图所示,关于其主应力有下列四种答案,正确的是( )。
A .1σ>2σ,03=σ B .3σ<2σ<0,03=σ01=σ C .1σ>0,2σ= 0,3σ<0,1σ<3σ D .1σ>0,2σ= 0,3σ<0,1σ>3σ8. 已知应力圆如图7-22所示,图(a )、(b )、(c )、(d )分别表示单元体的应力状态和A 截面的应力,则与应力圆所对应的单元体为( )。
A .图(a )B .图(b )C .图(c )D .图(d )题8图9. 在图示四种应力状态中,其应力圆具有相同的圆心和相同的半径是( )。
-34-题9图A .图(a )、图(d )B .图(b )、图(c )C .图(a )、图(b )、图(c ) 、图(d )D .图(a )、图(d )、图(b )、图(c )10. 如图所示,较大体积的钢块上开有一贯穿的槽,槽内嵌入一铝质立方体,铝块受到均布压力P 作用,假设钢块不变形,铝块处于( )。
工程力学(静力学与材料力学)习题及答案 )-正应力分析
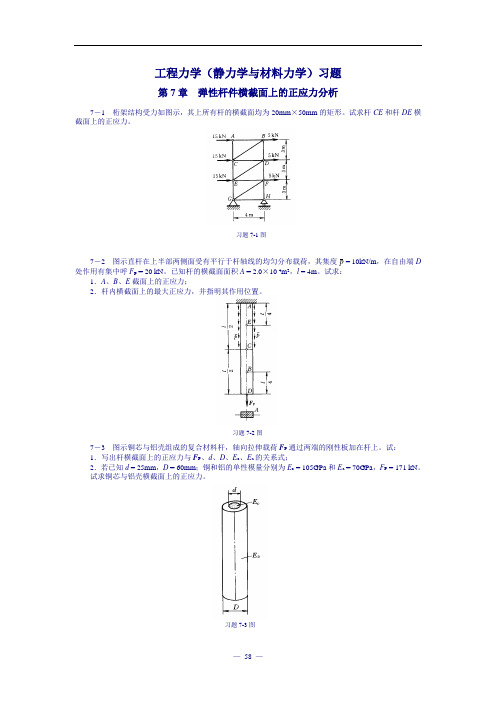
习题7-1图习题7-2图 习题7-3图工程力学(静力学与材料力学)习题第7章 弹性杆件横截面上的正应力分析7-1 桁架结构受力如图示,其上所有杆的横截面均为20mm ×50mm 的矩形。
试求杆CE 和杆DE 横截面上的正应力。
7-2 图示直杆在上半部两侧面受有平行于杆轴线的均匀分布载荷,其集度p = 10kN/m ,在自由端D 处作用有集中呼F P = 20 kN 。
已知杆的横截面面积A = 2.0×10-4m 2,l = 4m 。
试求:1.A 、B 、E 截面上的正应力;2.杆内横截面上的最大正应力,并指明其作用位置。
7-3 图示铜芯与铝壳组成的复合材料杆,轴向拉伸载荷F P 通过两端的刚性板加在杆上。
试:1.写出杆横截面上的正应力与F P 、d 、D 、E c 、E a 的关系式;2.若已知d = 25mm ,D = 60mm ;铜和铝的单性模量分别为E c = 105GPa 和E a = 70GPa ,F P = 171 kN 。
试求铜芯与铝壳横截面上的正应力。
习题7-4图 习题7-5图 习题7-6图习题7-7图 7-4 图示由铝板钢板组成的复合材料柱,纵向截荷F P 通过刚性平板沿着柱的中心线施加在其上。
试:1.导出复合材料柱横截面上正应力与F P 、b 0、b 1、h 和E a 、E s 之间的关系式;2.已知F P = 385kN ;E a = 70GPa ,E s = 200GPa ;b 0 = 30mm ,b 1 = 20mm ,h = 50mm 。
求铝板与钢板横截面上的最大正应力。
7-5 从圆木中锯成的矩形截面梁,受力及尺寸如图所示。
试求下列两种情形下h 与b 的比值:1.横截面上的最大正应力尽可能小;2.曲率半径尽可能大。
7-6 梁的截面形状为正方形去掉上、下角,如图所示。
梁在两端力偶M z 作用下发生弯曲。
设正方形截面时,梁内最大正应力为0σ;去掉上、下角后,最大正应力变为0max σσk =,试求:1.k 值与h 值之间的关系;2.max σ为尽可能小的h 值,以及这种情形下的k 值。
材料力学习题 应力状态分析答案详解

13、在图示梁的A点测得梁在弹性范围内的纵横方向的线应变 、 后,所能算出的材料常数有( D )。
(A)只有E;(B)只有v;(C)只有G;(D)E、v和G均可算出。
解析:中间段为纯弯曲,A点为单向拉伸,
则
14、纯剪应力状态下,各向同性材料单元体的体积改变有四种答案,正确答案是( C )。
解答:
确定 , 确定
6、 物体内某一点,载荷系统Ⅰ和载荷系统Ⅱ单独作用时产生的应力状态分别如图(a)和(b)所示。试求两载荷系统同时作用时(仍处于弹性小变形)的主单元体和主应力。
解答:
7、构件上某点处的应力状态如图所示。试求该点处的主应力及最大切应力之值,并画出三向应力状态的应力圆。
解答:
8、图示单元体,已知 、 及该点的最大主应力 。求该点的另外两个主应力 、 及最大切应力 。
解答:
确定
确定
2、已知应力状态如图。试求主应力及其方向角,并确定最大切应力值。
解答:
确定
所以 确定
3、图示单元体,求:(1)指定斜截面上的应力:(2)主应力大小,并将主平面标在单元体图上。
解答:
确定
所以 确定
4、用解析法求图示单元体ab面上的应力( ),并求 及主应力。
解答:
5、试求图示单元体主应力及最大切应力,并将主平面在单元体上标出。
由第三强度理论 安全
10、直径为20mm的圆截面折杆受力情况如图所示,已知:F=0.2kN,材料的许用应力为 。试用第三强度理论确定折杆的长度a的许用值。
解答:
在危险截面A上危险点在七上下边缘
由第三强度理论
取
11、AB、CD两杆互相垂直,在水平面内,C点的集中力2F及D点的集中力F与刚架平面垂直。已知F=20kN,l=1m,各杆直径相同d=10cm, 。试按最大切应力强度理论校核强度。
家电公司研发部资料材料力学习题答案(七)
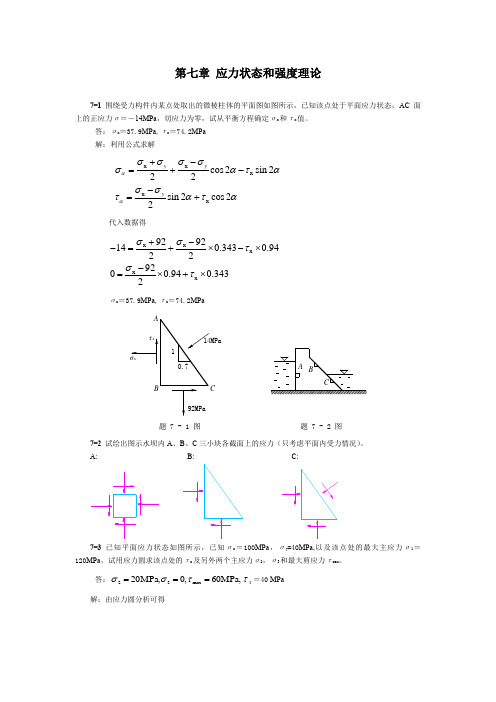
第七章 应力状态和强度理论7-1 围绕受力构件内某点处取出的微棱柱体的平面图如图所示,已知该点处于平面应力状态,AC 面上的正应力σ=-14MPa ,切应力为零,试从平衡方程确定σx 和τx 值。
答:σx =37.9MPa ,τx =74.2MPa 解:利用公式求解x x x x x cos 2sin 222sin 2cos 22yyyαασσσσσατασστατα+-=+--=+代入数据得x x x x x 9292140.3430.94229200.940.3432σστστ+--=+⨯-⨯-=⨯+⨯σx =37.9MPa ,τx =74.2MPa7-2 试绘出图示水坝内A 、B 、C 三小块各截面上的应力(只考虑平面内受力情况)。
A: B: C:7-3 已知平面应力状态如图所示,已知σx =100MPa ,σy =40MPa,以及该点处的最大主应力σ1=120MPa ,试用应力圆求该点处的τx 及另外两个主应力σ2,σ3和最大剪应力τmax。
答:MPa,60,0MPa,20max 32===τσσx τ=40 MPa 解:由应力圆分析可得A BC题 7 - 2 图题 7 - 1 图111(100,),(40,),(,0)x x c D D C ττσ'-x 121004070MPa221207050MPa 705020MPayc c c r r σσσσσσσ++====-=-=∴=-=-=是平面应力状态3=0σ∴222x x 13max (100)40MPa120060MPa 22c r σττσστ∴=-+⇒=--===7-4 已知平面应力状态一点处互相垂直平面上作用有拉应力90MPa 和压应力50MPa ,这些面上还有剪应力,如果最大主应力为拉应力100MPa ,试求:(1) 上述面上的切应力; (2) 此平面上另一主应力; (3) 最大切应力平面上的正应力; (4) 最大切应力。
材料力学习题应力状态分析答案详解

1、图示应力状态,按第三强度理论的强度条件为 。
(注: )
解答:
2、第三强度理论和第四强度理论的相当应力分别为 及 ,对于纯剪切应力状态,恒有 / = 。
解答:纯剪应力状态
3、一般情况下,材料的塑性破坏可选用最大剪应力或形状改变能密度强度理论;而材料的脆性破坏则选用最大拉应力或最大伸长线应变强度理论(要求写出强度理论的具体名称)。
解答:
17、一体积为10×10×10mm3的立方铝块,将其放入宽为10mm的刚性槽中,已知v(铝)=0.33,求铝块的三个主应力。
解答:
18、外径为D、内径为d的空心圆轴受扭转时,若利用一电阻应变片作为测力片,用补偿块作为温度补偿,采用半桥接线。问:(1)此测力电阻片如何粘贴可测出扭矩;(2)圆轴材料的E、v均为已知, 为测得的应变值,写出扭矩计算式。
解答:
7、构件上某点处的应力状态如图所示。试求该点处的主应力及最大切应力之值,并画出三向应力状态的应力圆。
解答:
8、图示单元体,已知 、 及该点的最大主应力 。求该点的另外两个主应力 、 及最大切应力 。
解答:
9、试确定图示单元体的最大切应力,以及图示斜截面上的正应力和切应力。
解答:
10、已知受力构件某处的 , , ,材料的E=200GPa,v=0.3。试求该点处的 、 。
解答:在危险截面A上危险点在七上下边缘
由第三强度理论
不安全
12、图示齿轮传动轴内电机带动,作用在齿轮上的力如图示,已知轴的直径d=30mm,P=0.8kN,Q=2kN,l=50mm,齿轮节圆直径D=200mm。试用第三强度理论校核轴的强度。已知轴的 。
13、图示传动轴,皮带轮Ⅰ直径D1=80cm,皮带轮Ⅱ直径D2=40cm,已知轴的许用应力 。试以第四强度理论设计轴的直径d,并指出危险截面位置,画出危险点的应力状态。
(4-6)部分习题及其解答

本教材习题和参考答案及部分习题解答第四章已知物体内一点的六个应力分量为:50x a σ=,0y σ=,30z a σ=-,75yz a τ=-,80zx a τ=,50xy a τ= 试求法线方向余弦为112n =,122n =,3n 的微分面上的总应力T 、正应力n σ和剪应力n τ。
解:应力矢量T 的三个分量为11106.57i i T n a σ==,228.033T a =-,318.71T a =-总应力111.8T a 。
]正应力26.04n i i T n a σ==。
剪应力108.7n a τ。
过某点有两个面,它们的法向单位矢量分别为n 和m ,在这两个面上的应力矢量分别为1T 和2T ,试证12⋅=⋅T m T n 。
证:利用应力张量的对称性,可得12()()ij i j ji i j n m n m σσ⋅=⋅⋅===⋅⋅=⋅T m n σm m σn T n 。
证毕。
某点的应力张量为01211210x xy xz yx y yz y zx zy z στττστσττσ=⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦且已知经过该点的某一平面上的应力矢量为零,求y σ及该平面的单位法向矢量。
…解:设要求的单位法向矢量为i n ,则按题意有 0ij j n σ=即2320n n +=,1230y n n n σ++=,1220n n += (a)上面第二式的两倍减去第一式和第三式,得 2(22)0y n σ-=上式有两个解:20n =或1yσ=。
若20n =,则代入式(a)中的三个式子,可得1n =30n =,这是不可能的。
所以必有1y σ=。
将1y σ=代入式(a),利用1i i n n =,可求得=n基础的悬臂伸出部分具有三角柱体形状,见图,下部受均匀压力作用,斜面自由,试验证应力分量 、22(arctg )x y xyA C x x yσ=--++ 22(arctg )yy xyA B x x yσ=-+++0z yz xz σττ===,222xy y A x y τ=-+满足平衡方程,并根据面力边界条件确定常数A 、B 和C 。
应力、应力状态分析(习题解答)

8-9 矩形截面梁如图所示,绘出1、2、3、4点的应力单元体,并写出各点的应力计算式。
解:(1)求支反力R A =,R B = (2)画内力图如图所示。
xPl(-)(+)PlMkN ·m)PPy(-)(-)(+)VkN)题8-9图(3) 求梁各点的正应力、剪应力:(4)画各点的应力单元体如图所示。
9-1 试用单元体表示图示构件的A 、B 的应力单元体。
(a )解:(1)圆轴发生扭转变形,扭矩如图所示。
111max 222222333333max 442330,22(')[()]448114()121200(0,0)16ZZZ ZzV pA b hh h hP P b M V S Pl hy I I bb h b h b M SM PlW b h σττστστστ==-=-⋅=-⋅⋅-⋅⨯⨯-⋅=⋅=⋅==⋅⨯⨯⨯⨯⋅=====-=-=⨯⨯80A-+16080T (kN ·m )(2)绘制A 、B 两点的应力单元体:A 、B 两点均在圆轴最前面的母线上,横截面上应力沿铅垂方向单元体如图所示:331601020.21680510.216A A t bB t T Pa kPa W T Pa kPaW τπτπ===⨯===-⨯(b )解:(1)梁发生弯曲变形,剪力、弯矩图如图所示。
-+120VkN)40MkN ·m)+120402060题9-1(b )(2)绘制A 、B 两点的应力单元体:A 点所在截面剪力为正,A 点横截面的剪力为顺时针,同时A 点所在截弯矩为正下拉,而A 点是压缩区的点。
B 点所在截面剪力为负,B 点横截面的剪力为逆时针,同时B 点所在截弯矩为正下拉,而B 点是拉伸区的点。
单元体如图所示:333.3333.60100.0537.50.1200.21212010(0.1200.050.075) 5.6250.1200.20.1201220100.0512.50.1200.2124010(0.1200.05A A A tA z A A tB B B t B z B B t M y Pa MPaI V S Pa MPaI b M y Pa MPaI V S I bστστ⨯=-⋅=-⨯=-⨯⋅⨯⨯⨯⨯=⋅==⋅⨯⨯⨯=⋅=⨯=⨯⋅-⨯⨯⨯⨯=⋅=⋅g g 30.075) 1.8750.1200.20.12012Pa MPa=-⨯⨯9-2(c解:(1)由题意知:30,20.5030ox x y MP MPa MP στσα==-==,,。
第七章应力状态习题答案

( 2 )图解法作应力圆如题 7 . 4 图( d 1)所示。应力圆与 σ 轴的两个交点的坐标,即是 σ 1 、 σ 3 的数 值。由 CDx ,顺时针旋转 2α 0 ,可确定主平面的方位。 CDx 的长度即为最大切应力的数值。主应力单 元体如题 7 . 4 图(d2)所示。
5
( e )如题 7 . 4 图( e )所示。
τα =
σ x −σ y
2
⎛ 100 − 50 ⎞ sin 2α + τ xy cos 2α = ⎜ sin120D + 0 ⎟ MPa = 21.7 MPa 2 ⎝ ⎠
( 2 )图解法 作应力圆如题 7 . 3 图( cl )所示。从图中可量得 Dα 点的坐标,此坐标便是 σ α 和 τ α 数值。 ( d )如题 7 . 3 图( d )所示。
按照主应力的记号规定
σ 1 =4.7MPa, σ 2 =0, σ 3 =-84.7MPa
tan 2α 0 = − 2τ xy
σ x −σ y
=
=
−2 × 20 = −0.5 , α 0 =-13.3° 0 + 80
τ max =
σ1 − σ 3
2
4.7 + 84.7 MPa = 44.7 MPa 2
。
1
斜截面 AB 与 x 平面的夹角 a2 = 105 ,其上应力 σ a2=45MPa,τ a = 25 3MPa 。将这些数据代入斜截面
。
2
上应力公式中,对 AB 斜截面有
σx +σ y
2
+
σ x −σ y
2
cos 210。− τ xy sin 210。= 45 ①
σ x −σ y
工程力学 第9章 应力状态分析 习题及解析
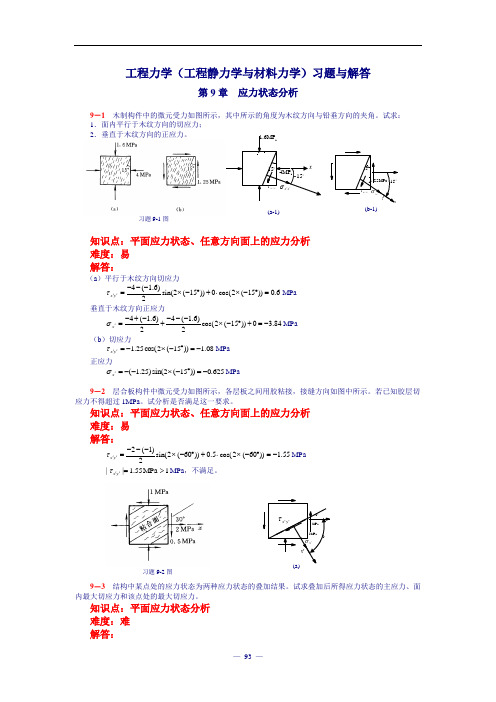
习题9-1图 x15-'x x'σy'x'τ 1.25MPa15 (b-1)15a 4MP15-y'x'τx'x'σa1.6MP x (a-1) 习题9-2图302MPa 0.5MPa-60x'σ'x ''y x τ 工程力学(工程静力学与材料力学)习题与解答第9章 应力状态分析9-1 木制构件中的微元受力如图所示,其中所示的角度为木纹方向与铅垂方向的夹角。
试求: 1.面内平行于木纹方向的切应力;2.垂直于木纹方向的正应力。
知识点:平面应力状态、任意方向面上的应力分析 难度:易 解答:(a )平行于木纹方向切应力6.0))15(2cos(0))15(2sin(2)6.1(4=︒-⨯⋅+︒-⨯---=''y x τMPa 垂直于木纹方向正应力84.30))15(2cos(2)6.1(42)6.1(4-=+︒-⨯---+-+-='x σMPa (b )切应力08.1))15(2cos(25.1-=︒-⨯-=''y x τMPa正应力625.0))15(2sin()25.1(-=︒-⨯--='x σMPa9-2 层合板构件中微元受力如图所示,各层板之间用胶粘接,接缝方向如图中所示。
若已知胶层切应力不得超过1MPa 。
试分析是否满足这一要求。
知识点:平面应力状态、任意方向面上的应力分析 难度:易 解答:55.1))60(2cos(5.0))60(2sin(2)1(2-=︒-⨯⋅+︒-⨯---=''y x τMPa 1MPa 55.1||>=''y x τMPa ,不满足。
9-3 结构中某点处的应力状态为两种应力状态的叠加结果。
试求叠加后所得应力状态的主应力、面内最大切应力和该点处的最大切应力。
知识点:平面应力状态分析 难度:难 解答:习题9-2图yσxσxyτ=yσxσxyτx=yσxσxyτ=左微元⎪⎪⎪⎩⎪⎪⎪⎨⎧-='-='-=-='+=--+='000000022cos 122sin )2sin(222cos 10)2cos(22σθσσσσθθστσθθσσσx y xy x 叠加 ⎪⎪⎪⎩⎪⎪⎪⎨⎧-=+'=-=+=+=+'=''000022cos 1022sin 022cos 3σθσσσθττσθσσσy y y x xy x x0)cos 1()cos 1( )22sin (4)22cos 122cos 3(21222cos 122cos 330020202021=⎩⎨⎧-+=-+--+±-++=⎭⎬⎫σσθσθσθσθθσθθσσ 面内最大切应力:θσσστcos 2021max=-='该点最大切应力:031max2cos 12σθσστ+=-=左微元0023))30(2sin()(ττσ=︒-⨯-='x ,0230τσσ-='-='x y ,2))30(2cos(00τττ=︒-⨯='xy 右微元0023)302sin()(ττσ=︒⨯-=''x,0230τσσ-=''-=''x y ,2))30(2cos()(00τττ-=︒⨯-=''xy 叠加 03τσσσ='+'=y x x ,03τσσσ-=''+'=y y y ,0=''+'=xyxy xy τττ 013τσ=,02=σ,033τσ-= 面内031max32||τσστ=-='xABOσOσαα(a)习题9-4图A60CB60100-x σxσyxτxyτ92MPa(a)习题9-5图该点031max 32||τσστ=-=叠加[]⎪⎪⎪⎩⎪⎪⎪⎨⎧=⎥⎦⎤⎢⎣⎡︒-⨯--+==--+==⎥⎦⎤⎢⎣⎡︒-⨯--+-++=MPa 30))45(2sin(2)30(5070MPa 1010)3050(0MPa 90))45(2cos(2)30(502)30(5080xy y x σσσ主应力0MPa 0MPa100304)]100(90[212109022231=⎩⎨⎧=⨯+-±+=⎭⎬⎫σσσ面内及该点:5021002||||31max max=-=-=='σσττMPa9-4 已知平面应力状态的最大正应力发生在与外力作用的自由表面AB 相垂直的面上,其值为0σ。
《工程力学(工程静力学与材料力学)(第3版)》习题解答:第9章 应力状态分析

MPa
MPa
2.
MPa
MPa
9-13图示外径为300mm的钢管由厚度为8mm的钢带沿20°角的螺旋线卷曲焊接而成。试求下列情形下,焊缝上沿焊缝方向的切应力和垂直于焊缝方向的正应力。
1.只承受轴向载荷FP = 250kN;
2.只承受内压p=5.0MPa(两端封闭)
3.同时承受轴向载荷FP = 250kN和内压p=5.0MPa(两端封闭)
难度:一般
解答:
(1)当 = 40℃
mm<
mm<
所以铝板内无温度应力,
(2)当 = 80℃
mm>
mm>
∴ (1)
(2)
所以解得qx = qy=70MPa(压)
, MPa
MPa
9-18对于一般平面应力状态,已知材料的弹性常数E、 ,且由实验测得 和 。试证明:
知识点:广义胡克定律、 三者之间的关系
难度:一般
难度:一般
解答:
正确答案是C。
(A)不满足切应力互等定律;
(B)不满足平衡;
(C)既可满足切应力互等,又能达到双向的平衡;
(D)不满足两个方向的平衡。
9-27微元受力如图所示,图中应力单位为MPa。试根据不为零主应力的数目,它是:
(A)二向应力状态;
(B)单向应力状态;
(C)三向应力状态;
(D)纯切应力状态。
MPa
9-7受力物体中某一点处的应力状态如图所示(图中p为单位面积上的力)。试求该点处的主应力。
知识点:应力圆的应用
难度:难
解答:
应力圆半径
9-8从构件中取出的微元,受力如图所示。试:
1.求主应力和最大切应力;
2.确定主平面和最大切应力作用面位置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8-9 矩形截面梁如图所示,绘出1、2、3、4点的应力单元体,并写出各点的应力计算式。
解:(1)求支反力R A =,R B = (2)画内力图如图所示。
xPl(-)(+)PlMkN ·m)PPy(-)(-)(+)VkN)题8-9图(3) 求梁各点的正应力、剪应力:(4)画各点的应力单元体如图所示。
9-1 试用单元体表示图示构件的A 、B 的应力单元体。
(a )解:(1)圆轴发生扭转变形,扭矩如图所示。
111max 222222333333max 442330,22(')[()]448114()121200(0,0)16ZZZ ZzV pA b hh h hP P b M V S Pl hy I I bb h b h b M SM PlW b h σττστστστ==-=-⋅=-⋅⋅-⋅⨯⨯-⋅=⋅=⋅==⋅⨯⨯⨯⨯⋅=====-=-=⨯⨯80A-+16080T (kN ·m )(2)绘制A 、B 两点的应力单元体:A 、B 两点均在圆轴最前面的母线上,横截面上应力沿铅垂方向单元体如图所示:331601020.21680510.216A A t bB t T Pa kPa W T Pa kPaW τπτπ===⨯===-⨯(b )解:(1)梁发生弯曲变形,剪力、弯矩图如图所示。
-+120VkN)40MkN ·m)+120402060题9-1(b )(2)绘制A 、B 两点的应力单元体:A 点所在截面剪力为正,A 点横截面的剪力为顺时针,同时A 点所在截弯矩为正下拉,而A 点是压缩区的点。
B 点所在截面剪力为负,B 点横截面的剪力为逆时针,同时B 点所在截弯矩为正下拉,而B 点是拉伸区的点。
单元体如图所示:333.3333.60100.0537.50.1200.21212010(0.1200.050.075) 5.6250.1200.20.1201220100.0512.50.1200.2124010(0.1200.05A A A tA z A A tB B B t B z B B t M y Pa MPaI V S Pa MPaI b M y Pa MPaI V S I bστστ⨯=-⋅=-⨯=-⨯⋅⨯⨯⨯⨯=⋅==⋅⨯⨯⨯=⋅=⨯=⨯⋅-⨯⨯⨯⨯=⋅=⋅g g 30.075) 1.8750.1200.20.12012Pa MPa=-⨯⨯9-2(c解:(1)由题意知:30,20.5030ox x y MP MPa MP στσα==-==,,。
(2)求30o 斜截面上的应力cos 2sin 22230503050cos 60(20)sin 6052.32()223050sin 2cos 2sin 60(20)cos 6018.67()22x x x xx o o o o x x x MPa MPa αασσσσσατασστατα+-=+-+-=+--⨯=--=+=+-⨯=- (e) 试用解析法求出(1)图示应力单元体-30o 斜截面的应力。
(2)主应力与主方向,以及面内的剪应力极值;(2)在单元体上标出主平面。
解:(1)由题意知:oMPa MP x x 30.20,10-=-=-=ατσ。
见图(a )(MP a )σ3=-.62O(a) (b)题9-2e 图(2)求α斜截面上的应力。
cos 2sin 222100100cos(60)(20)sin(60) 6.16()22100sin 2cos 2sin(60)(20)cos(60)0.67()22xy x yx o o x yo o x MPa MPa αασσσσσατασστατα+-=+--+--=+---⨯-=---=+=-+-⨯-=- (3) 求梁的主应力及主平面方位角:max min 1002215.62520.62()25.62x y MPa σσσσ+⎫-+=±=±⎬⎭⎧=-±=⎨-⎩故,MPa MPa 62.25,0,62.15321-===σσσ0022(20)tan 24100=-37.98x x yoτασσα-⨯-==-=---- (4)求最大剪应力)(62.20231max MPa =-=σστ(4)画点的主应力单元体如图(b )所示。
9-3c 对图示应力单元体,试用解析法求解:(1)主应力与主方向,以及面内的剪应力极值;(2)在单元体上标出主平面、主应力和剪应力极值及其作用面。
解:(1)由题意知: 40,20,40x y x MP MP MPa σστ=-=-=-。
(2) 求梁的主应力及主平面方位角:max min 40202211.233041.23()71.23x y MPa σσσσ+⎫--=±=±⎬⎭⎧=-±=⎨-⎩故,12311.23,0,71.23MPa MPa σσσ===- 0022(40)tan 24-37.9840+20o x x y ταασσ-⨯-==-=-→=--(4)求最大剪应力13max 11.23+71.23=41.23()22MPa σστ-==-37.98457o o o s α=+=(4)画点的主应力单元体、剪应力极值及其作用面如图所示。
9-8 梁如图示,试求:(1)A 点处指定斜截面上的应力;(2)A 点处的主应力及主平面位置。
V kN)40-+M k N ·m)(c)题9-8140(d )++(d )(c)(b)M k N ·m)140题9-8+-40V kN)解:(1)根据对称性可知,两约束反力均为70kN,并绘出剪力和弯矩图如图示。
A 点在跨中稍左或稍右截面上,70140V M ==⋅中中kN ,kN m(2)求跨中稍左横截面上A 点的应力。
①查表得36a 工字钢的几何参数:4343360,136,15.8,10,15800cm ()42224436015.8360336015.813615.815.810464116.68mm 4.6410m2482z z h b t d I h t h t h h S bt t d *-=====⎛⎫- ⎪⎛⎫⎛⎫=⋅-+-⋅⋅+ ⎪ ⎪ ⎪⎝⎭⎝⎭ ⎪⎝⎭-⨯⎛⎫⎛⎫=⨯⨯+-⨯⨯-==⨯ ⎪ ⎪⎝⎭⎝⎭mm mm mm mm ②求跨中稍左横截面上A 点的应力33,81401036010Pa 79.7MPa 41580010A xA z M y I σ--⨯⨯=⋅=⨯=⨯ 纵向纤维间无挤压:,0A y σ=3,4,837010 4.6410Pa 20.56MPa 158********z AA xz VS I d τ*---⨯==⨯⨯=⋅⨯⨯⨯ (3)绘制A 点的应力单元体。
(4)求A 点600斜截面上的应力。
cos 2sin 22279.779.7cos(260)20.56sin(260) 2.12()2279.7sin 2cos 2sin(260)20.56cos(260)24.23()22x yx yx o o x y o o x MPa MPa αασσσσσατασστατα+-=+-=+⨯-⨯⨯=-=+=⨯+⨯⨯=(5)求梁A 点处的主应力及主平面位置。
max min 79.72284.6939.8544.84()4.99x y MPa σσσσ+⎫=±=±⎬⎭⎧=±=⎨-⎩故,12384.69,0, 4.99MPa MPa σσσ===- 002220.56tan 20.516-13.679.7o x x y ταασσ-⨯==-=-→=-9-9试求图示杆件A 点处的主应力。
题9-9z τ2π4π+-+60πM k N ·m)T kN)N kN)kN解:(1)外力分析:构件发生拉弯扭组合变形。
(2)内力分析:轴力图、扭矩图、弯矩图如图所示。
A 所在横截面的内力为:6042N T M πππ===⋅固固固kN,kN ,kN m(3)应力分析:A 点在上边缘点,无弯曲剪应力。
A 点所在横截面各点具有均匀分布的轴力引起的拉的正应力N σ,A 点在上下弯的拉伸区的边缘点W σ,该点正应力33,236010210=Pa=88MPa 0.10.1432A x N W zN M AW ππσσσππ⨯⨯=+=++⨯⨯固固 ,0A z σ=同时,该点还有扭转剪应力3,3410=Pa=64MPa 0.116A x tT W πτπ⨯=⨯固。
应力单元体如图所示。
(4)求梁A 点处的主应力及主平面位置。
max min 8822121.674477.67()33.67x z MPa σσσσ⎫+=±=±⎬⎭⎧=±=⎨-⎩故,123121.67,0,33.67MPa MPa σσσ===- 002264tan 2 1.4546-27.788o x x z ταασσ-⨯==-=-→=-9-5 试用图解法求解题9-3d7°7°解:(1)由图可知:20,30,20x y xMP MP MPaσστ=-==-。
故:x、y面所对应的点分别为T(-20,-20),T‘(30,20)(2)定比例尺,建立坐标系σ-τ(3)先在建立坐标系内作出x、y面所对应的点,连接该两点与σ坐标轴交于C点。
再以C点为圆心,T T‘为直径作出应力圆如图所示。
(4)过T点作水平线与应力圆交于P点,以P点为极点建立极坐标Px。
(5)连接P和应力圆最右点A、最左点A‘,分别得13σσ、的大小和方向,=-19.33αo。
(6)连接P和应力圆最上点B、最下点B‘,分别得max minττ、的大小和方向,=25.67sαo。
(7)画点的主应力单元体、剪应力极值及其作用面如图所示。
9-11a 求图示单元体的主应力。
解:(1)由单元体可知:z面为主面60MPazσ=(2)建立应力坐标系如图,画应力圆如图,则:123110MPa,60,10MPa σσσ===,主应力单元体如图所示。
9-13:图示薄壁圆筒受拉伸和扭转同时作用。
若T 20kN,600kN m P M ==⋅,且50mm,2mm d δ==。
试求:(1)A 点指定截面的应力;(2)A 点主应力及其方位角,并绘制主应力单元体。
解:(1)由题意知:如图(a )构件发生拉扭组合变形,构件横截面上既有拉伸引起的正应力,又有扭转引起的剪应力.。
其原始单元体如图(c )、(d)所示:(b)(d)题9-13图[]MPaPa d W M MPaPa AP d d Tx x 24.73])(1[)2(1660021.6105.0)002.0205.0(41020423223-=-+⨯-=-==-⨯+⨯==+δδπτπσ (2)求A 点指定-60O 斜截面上的应力。
