运筹学模拟题及答案(5套)
运筹模拟试题及答案

运筹模拟试题及答案
一、选择题
1. 进行运筹学研究时,下列哪种不是需要考虑的因素?
A. 成本
B. 时间
C. 资源
D. 颜色
答案:D
2. 运筹学中常用的优化方法包括以下哪种?
A. 贪心算法
B. 冒泡排序
C. 快速排序
D. 二分查找
答案:A
3. 下列哪种不是传统运筹学方法的代表性问题?
A. 线性规划
B. 背包问题
C. 旅行商问题
D. 贪心算法
答案:D
二、填空题
1. 运筹学最早是在(古代/近代)开始发展的。
答案:近代
2. 线性规划是运筹学中经典的(优化/排列)方法。
答案:优化
3. 旅行商问题是求解搜索过程中的最短(路径/时间)问题。
答案:路径
三、解答题
1. 请简要说明什么是线性规划,以及线性规划的基本原理。
答:线性规划是一种数学优化方法,用于找到使某种目标函数达到
最优的变量取值。
其基本原理是通过建立数学模型,确定决策变量和
约束条件,然后求解最优解,以达到最大化或最小化某项指标的目的。
2. 请简要介绍一下运筹学中的模拟方法以及其应用领域。
答:运筹学中的模拟方法是通过模拟系统的运行过程来进行决策分析和优化设计。
其应用领域包括生产调度、物流管理、金融风险分析等领域,在实际问题中具有广泛的应用。
以上为运筹模拟试题及答案,希望对您的学习和工作有所帮助。
如果还有其他问题,欢迎随时与我们联系。
祝您学习进步!。
《运筹学》试题及答案大全

《运筹学》试题及参考答案一、填空题(每空2分,共10分)1、在线性规划问题中,称满足所有约束条件方程和非负限制的解为可行解。
2、在线性规划问题中,图解法适合用于处理变量为两个的线性规划问题。
3、求解不平衡的运输问题的基本思想是设立虚供地或虚需求点,化为供求平衡的标准形式。
4、在图论中,称无圈的连通图为树。
5、运输问题中求初始基本可行解的方法通常有最小费用法、西北角法两种方法。
二、(每小题5分,共10分)用图解法求解下列线性规划问题:1)max z =6x 1+4x 2⎪⎪⎩⎪⎪⎨⎧≥≤≤+≤+0781022122121x x x x x x x ,解:此题在“《运筹学》复习参考资料.doc ”中已有,不再重复。
2)min z =-3x 1+2x 2⎪⎪⎪⎩⎪⎪⎪⎨⎧≥≤-≤-≤+-≤+0,137210422422121212121x x x x x x x x x x 解:可行解域为abcda ,最优解为b 点。
⑴⑵⑶⑷⑸⑹、⑺由方程组⎩⎨⎧==+02242221x x x 解出x 1=11,x 2=0∴X *=⎪⎪⎭⎫⎝⎛21x x =(11,0)T∴min z =-3×11+2×0=-33三、(15分)某厂生产甲、乙两种产品,这两种产品均需要A 、B 、C 三种资源,每种产品的资源消耗量及单位产品销售后所能获得的利润值以及这三种资源的储备如下表所示:AB C 甲94370乙46101203602003001)建立使得该厂能获得最大利润的生产计划的线性规划模型;(5分)2)用单纯形法求该问题的最优解。
(10分)解:1)建立线性规划数学模型:设甲、乙产品的生产数量应为x 1、x 2,则x 1、x 2≥0,设z 是产品售后的总利润,则max z =70x 1+120x 2s.t.⎪⎪⎩⎪⎪⎨⎧≥≤+≤+≤+0300103200643604921212121x x x x x x x x ,2)用单纯形法求最优解:加入松弛变量x 3,x 4,x 5,得到等效的标准模型:max z =70x 1+120x 2+0x 3+0x 4+0x 5s.t.⎪⎪⎩⎪⎪⎨⎧=≥=++=++=++5,...,2,1,03001032006436049521421321j x x x x x x x x x x j 列表计算如下:四、(10分)用大M 法或对偶单纯形法求解如下线性规划模型:min z =5x 1+2x 2+4x 3⎪⎩⎪⎨⎧≥≥++≥++0,,10536423321321321x x x x x x x x x 解:用大M 法,先化为等效的标准模型:max z /=-5x 1-2x 2-4x 3s.t.⎪⎩⎪⎨⎧=≥=-++=-++5,...,2,1,010********214321j y x x x x x x x x j增加人工变量x 6、x 7,得到:max z /=-5x 1-2x 2-4x 3-M x 6-M x 7s.t⎪⎩⎪⎨⎧=≥=+-++=+-++7,...,2,1,010*********2164321j x x x x x x x x x x x j大M 法单纯形表求解过程如下:五、(15分)给定下列运输问题:(表中数据为产地A i 到销地B j 的单位运费)B 1B 2B 3B 4s iA 1A 2A 312348765910119108015d j82212181)用最小费用法求初始运输方案,并写出相应的总运费;(5分)2)用1)得到的基本可行解,继续迭代求该问题的最优解。
数学:运筹学试题及答案

数学:运筹学试题及答案1、判断题求最小值问题的目标函数值是各分支函数值的下界。
正确答案:对2、填空题动态规划大体上可以分为()、()、()、()四大类。
正确答案:离散确定型;离散随机型;连续确定型;连续随机(江南博哥)型3、多选系统模型按照抽象模型形式可以分为()A.数学模型B.图象模型C.模糊性模型D.逻辑模型E.仿真模型正确答案:A, B, D, E4、单选线性规划一般模型中,自由变量可以代换为两个非负变量的()A.和B.差C.积D.商正确答案:B5、填空题运筹学的目的在于针所研究的系统求得一个合理应用人才,物力和财力的最佳方案。
发挥和提高系统的(),最终达到系统的()。
正确答案:效能及效益;最优目标6、填空题采用人工变量法时,若基变量中出现了()的人工变量,表示在原问题有解。
正确答案:非零7、填空题满足()的基本解称为基本可行解。
正确答案:非负条件8、填空题在箭线式网络图中从始点出发,由各个关键活动连续相接,直到终点的费时最长的线路称为()。
正确答案:关键线路9、单选在求解运输问题的过程中可运用到下列哪些方法()。
A.西北角法B.位势法C.闭回路法D.以上都是正确答案:D10、问答题请简要回答一般系统模型的三个特征。
正确答案:①它是现实世界一部分的抽象和模仿;②它由那些与分析的问题有关的要素所构成;③它表明了系统有关要素间的逻辑关系或定量关系。
11、名词解释初始基本可行解正确答案:多个基本可行解中一个,一般情况下在求最大时取最小的基本可行解,求最小时取最大的基本可行解。
12、名词解释不确定条件下的决策正确答案:指在需要决策的问题中,只估测到可能出现的状态,但状态发生的概率,由于缺乏资源和经验而全部未知。
它属于不确定情况下的决策.13、名词解释时间优化正确答案:时间优化是在人力材料设备资金等资源基本上有保证的条件下寻求最短的工程周期14、填空题企业在采购时,供应方根据批发量的大小定出不同的优惠价格,这种价格上的优惠称为()正确答案:数量折扣15、填空题常用的两种时差是工作总时差和工作()正确答案:自由时差16、多选根据对偶理论,在求解线性规划的原问题时,可以得到以下结论()A.对偶问题的解B.市场上的稀缺情况C.影子价格D.资源的购销决策E.资源的市场价格正确答案:A, C, D17、问答题运用单纯形法求解线性规划问题的步骤是什么?正确答案:(1)确定初始基可行解(2)检验初始基可行解是否最优(3)无解检验(4)进行基变换(5)进行旋转运算,之后回到步骤2,循环直到完成整个问题的求解18、单选设一个线性规划问题(P)的对偶问题为(D),则关于它们之间的关系的陈述不正确的是()。
《运筹学》试题及答案(四)

《运筹学》试题及答案一、单选题1. μ是关于可行流f的一条增广链,则在μ上有(D)A.对一切B.对一切C.对一切D.对一切2.不满足匈牙利法的条件是(D)A.问题求最小值B.效率矩阵的元素非负C.人数与工作数相等D.问题求最大值3.从甲市到乙市之间有—公路网络,为了尽快从甲市驱车赶到乙市,应借用()CA.树的逐步生成法B.求最小技校树法C.求最短路线法D.求最大流量法4.串联系统可靠性问题动态规划模型的特点是()DA.状态变量的选取B.决策变量的选取C.有虚拟产地或者销地D.目标函数取乘积形式5.当基变量x i的系数c i波动时,最优表中引起变化的有(B)A.最优基BB.所有非基变量的检验数C.第i 列的系数D.基变量X B6.当非基变量x j的系数c j波动时,最优表中引起变化的有(C)A.单纯形乘子B.目标值C.非基变量的检验数D. 常数项7.当线性规划的可行解集合非空时一定(D)A.包含点X=(0,0,···,0)B.有界C.无界D.是凸集8.对偶单纯形法的最小比值规划则是为了保证(B)A.使原问题保持可行B.使对偶问题保持可行C.逐步消除原问题不可行性D.逐步消除对偶问题不可行性9.对偶单纯形法迭代中的主元素一定是负元素()AA.正确B.错误C.不一定D.无法判断10.对偶单纯形法求解极大化线性规划时,如果不按照最小化比值的方法选取什么变量则在下一个解中至少有一个变量为正()BA.换出变量B.换入变量C.非基变量D.基变量11.对LP问题的标准型:max,,0Z CX AX b X==≥,利用单纯形表求解时,每做一次换基迭代,都能保证它相应的目标函数值Z必为()BA.增大B.不减少C.减少D.不增大12. 单纯形法迭代中的主元素一定是正元素( )AA.正确B.错误C.不一定D.无法判断13.单纯形法所求线性规划的最优解()是可行域的顶点。
AA.一定B.一定不C.不一定D.无法判断14.单纯形法所求线性规划的最优解()是基本最优解。
运筹学试题及详细答案

运筹学试题及详细答案
一、选择题
1、Nash均衡的定义是:
A、每位参与者的行为均达到最佳利益的状态
B、每位参与者的行为均达到得到最大胜利的状态
C、每位参与者的行为均达到合作的最佳状态
D、每位参与者的行为均达到合作的最大胜利的状态
答案:A
2、决策就是参与者用来实现选择的:
A、计划
B、机构
C、程序
D、工具
答案:D
3、运筹学可以分为:
A、组合数学
B、运动学
C、博弈论
D、概率论
答案:A、B、C、D
4、非线性规划有:
A、分支定界法
B、梯度下降法
C、基于格法的解法
D、对偶法
答案:A、B、C、D
5、关于迭代法,下列表述正确的有:
A、可以求解非凸优化问题
B、单次迭代过程简单
C、收敛性较好
D、用于非线性规划
答案:A、B、C
二、填空题:
1、博弈论是研究__参与者之间的__的科学。
答案:多,竞争。
运筹学试卷及答案完整版

《运筹学》模拟试题及参考答案一、判断题(在下列各题中,你认为题中描述的内容为正确者,在题尾括号内写“√”,错误者写“×”。
)1. 图解法提供了求解线性规划问题的通用方法。
( )2. 用单纯形法求解一般线性规划时,当目标函数求最小值时,若所有的检验数C j-Z j ≥0,则问题达到最优。
( )3. 在单纯形表中,基变量对应的系数矩阵往往为单位矩阵。
( )4. 满足线性规划问题所有约束条件的解称为基本可行解。
( )5. 在线性规划问题的求解过程中,基变量和非基变量的个数是固定的。
( )6. 对偶问题的目标函数总是与原问题目标函数相等。
( )7. 原问题与对偶问题是一一对应的。
( )8. 运输问题的可行解中基变量的个数一定遵循m+n-1的规则。
( )9. 指派问题的解中基变量的个数为m+n。
( )10. 网络最短路径是指从网络起点至终点的一条权和最小的路线。
( )11. 网络最大流量是网络起点至终点的一条增流链上的最大流量。
( )12. 工程计划网络中的关键路线上事项的最早时间和最迟时间往往不相等。
( )13. 在确定性存贮模型中不许缺货的条件下,当费用项目相同时,生产模型的间隔时间比订购模型的间隔时间长。
( )14. 单目标决策时,用不同方法确定的最佳方案往往是一致的。
( )15. 动态规划中运用图解法的顺推方法和网络最短路径的标号法上是一致的。
( )三、填空题1. 图的组成要素;。
2. 求最小树的方法有、。
3. 线性规划解的情形有、、、。
4. 求解指派问题的方法是。
5. 按决策环境分类,将决策问题分为、、。
6. 树连通,但不存在。
A 111四、下列表是线性规划单纯形表(求Z max ),请根据单纯形法原理和算法。
1. 计算该规划的检验数2. 计算对偶问题的目标函数值3. 确定上表中输入,输出变量五、已知一个线性规划原问题如下,请写出对应的对偶模型21max 6x x S +=⎪⎩⎪⎨⎧≥≥+≤+0,16327212121x x x x x x六、下图为动态规划的一个图示模型,边上的数字为两点间的距离,请用逆推法求出S 至F 点的最短路径及最短路长。
运筹学考试试卷及答案

运筹学考试试卷及答案一、选择题(每题2分,共20分)1. 线性规划问题的标准形式是:A. 所有变量都非负B. 目标函数是最大化C. 所有约束条件都是等式D. 所有约束条件都是不等式答案:A2. 单纯形法中,如果某个变量的检验数为负数,那么:A. 该变量可以增大B. 该变量可以减小C. 该变量保持不变D. 该变量不能进入基答案:A3. 在运输问题中,如果某种资源的供应量大于需求量,那么应该:A. 增加供应量B. 减少需求量C. 增加需求量D. 减少供应量答案:C4. 动态规划的基本原理是:A. 递归B. 迭代C. 回溯D. 分解答案:D5. 决策树中,每个节点代表:A. 一个决策B. 一个状态C. 一个结果D. 一个概率答案:A6. 排队论中,M/M/1队列的特点是:A. 到达时间服从泊松分布,服务时间服从指数分布,且只有一个服务台B. 到达时间服从指数分布,服务时间服从泊松分布,且只有一个服务台C. 到达时间服从泊松分布,服务时间服从指数分布,且有两个服务台D. 到达时间服从指数分布,服务时间服从泊松分布,且有两个服务台答案:A7. 网络流问题中,最大流最小割定理说明:A. 最大流等于最小割B. 最大流小于最小割C. 最大流大于最小割D. 最大流与最小割无关答案:A8. 整数规划问题中,分支定界法的基本思想是:A. 将问题分解为多个子问题B. 将问题转化为线性规划问题C. 将问题转化为非线性规划问题D. 将问题转化为动态规划问题答案:A9. 在多目标决策中,如果目标之间存在冲突,通常采用的方法是:A. 目标排序B. 目标加权C. 目标合并D. 目标替换答案:B10. 敏感性分析的目的是:A. 确定最优解的稳定性B. 确定最优解的唯一性C. 确定最优解的可行性D. 确定最优解的最优性答案:A二、填空题(每题2分,共20分)1. 线性规划问题的可行域是由所有_________约束条件构成的集合。
答案:可行2. 在单纯形法中,如果目标函数的系数都是正数,则该问题为_________问题。
最全运筹学习题及答案

最全运筹学习题及答案共1 页运筹学习题答案)1.1用图解法求解下列线性规划问题,并指出问题是具有唯一最优解、无穷多最优解、无界解还是无可行解。
(1)max z?x1?x25x1+10x2?50x1+x2?1x2?4x1,x2?0(2)min z=x1+1.5x2x1+3x2?3x1+x2?2x1,x2?0(3)+2x2x1-x2?-0.5x1+x2x1,x2?0(4)max z=x1x2x1-x2?03x1-x2?-3x1,x2?0(1)(图略)有唯一可行解,max z=14(2)(图略)有唯一可行解,min z=9/4(3)(图略)无界解(4)(图略)无可行解1.2将下列线性规划问题变换成标准型,并列出初始单纯形表。
共2 页(1)min z=-3x1+4x2-2x3+5x4 4x1-x2+2x3-x4=-2x1+x2+3x3-x4?14 -2x1+3x2-x3+2x4?2x1,x2,x3?0,x4无约束(2zk?i??xk?1mxik?(1Max s. t .-4x1xx1,x2共3 页(2)解:加入人工变量x1,x2,x3,…xn,得:Max s=(1/pk)? i?1n?k?1m?ikxik-Mx1-Mx2-…..-Mxnm(1)max z=2x1+3x2+4x3+7x4 2x1+3x2-x3-4x4=8x1-2x2+6x3-7x4=-3x1,x2,x3,x4?0(2)max z=5x1-2x2+3x3-6x4共4 页x1+2x2+3x3+4x4=72x1+x2+x3+2x4=3x1x2x3x4?0(1)解:系数矩阵A是:?23?1?4??1?26?7? ??令A=(P1,P2,P3,P4)P1与P2线形无关,以(P1,P2有2x1+3x2=8+x3+4x4x1-2x2=-3-6x3+7x4令非基变量x3,x4解得:x1=1;x2=2基解0,0)T为可行解z1=8(2)同理,以(P=(45/13,0,-14/13,0)T是非可行解;3以(P1,P4X(3)=,,7/5)T是可行解,z3=117/5;(4)以(P2,P=(,45/16,7/16,0)T是可行解,z4=163/16;3以(P2,P4)为基,基解X(5)0,68/29,0,-7/29)T是非可行解;(6)TX以(P4,P)为基,基解=(0,0,-68/31,-45/31是非可行解;)3最大值为z3=117/5;最优解X(3)=(34/5,0,0,7/5)T。
运筹学试题及答案

运筹学试题及答案考试时间:120分钟命题人:XXX一、选择题(共60分)1. 运筹学的核心思想是:A. 尽可能地满足需求B. 确定最优决策C. 提高运营效率D. 预测未来趋势答案:B2. 下列哪个不是运筹学的应用领域?A. 生产调度B. 金融风险管理C. 市场营销D. 交通规划答案:C3. 线性规划是研究下列问题的数学方法:A. 最大化目标函数B. 最小化目标函数C. 求解等式系统D. 优化约束条件答案:D4. 整数规划是线性规划的扩展,其特点是:A. 变量只能取整数值B. 变量可以取任意实数值C. 目标函数必须是整数D. 约束条件必须是整数答案:A5. 运筹学中的最短路径问题是指:A. 在有向图中找到从起点到终点的最短路径B. 在无向图中找到连接所有节点的最短路径C. 在网络中找到连接所有节点的最短路径D. 在带权图中找到权值最小的路径答案:A二、计算题(共40分)1. 某工厂有3个生产车间,分别需要完成4个任务。
完成每个任务所需时间如下:车间1:10小时车间2:8小时车间3:6小时为了提高效率,每个车间只能同时进行一个任务。
请问应如何分配任务,才能使得所有任务完成的时间最短?答案:将任务按照时间从大到小排序分配,先将任务分配给车间1和车间2,然后再将任务分配给车间3。
具体分配如下:车间1:10小时(任务1)车间2:8小时(任务2)车间3:6小时(任务3)车间1:18小时(任务1+任务4)车间2:16小时(任务2+任务4)车间3:12小时(任务3)总时间为18小时。
2. 某物流公司需要将货物从发货仓库A送至目的地仓库B。
货物可通过3条不同的路径运送,分别需要的运输时间为:路径1:6小时路径2:8小时路径3:10小时若考虑各路径的运输成本,路径1的运输成本为100元/小时,路径2的运输成本为150元/小时,路径3的运输成本为120元/小时。
请问应如何选择路径,使得运输成本最低?答案:计算各路径的单位成本,并选择单位成本最低的路径。
数学:运筹学试题及答案(强化练习)

数学:运筹学试题及答案(强化练习)1、单选不属一般系统,特别是人造系统特征的是()A.整体性B.集合性C.目的性D.规模性正确答案:D2、名词解释概率向量正确答案:任意一个向量u=(u1,u2,…,un),如果(江南博哥)它内部的各种元素为非负数,且总和等于1,则此向量称为概率向量。
3、填空题影子价格实际上是与原问题各约束条件相联系的()的数量表现。
正确答案:对偶变量4、单选关于线性规划和其对偶规划的叙述中,正确的是()A.极大化问题(原始规划)的任意一个可行解所对应的目标函数值是对偶问题最优目标函数值的一个下界B.极小化问题(对偶规划)的任意一个可行解所对应的目标函数值是原始问题最优目标函数值的一个下界C.若原始问题可行,则其目标函数无界的充要条件是对偶问题有可行解D.若对偶问题可行,则其目标函数无界的充要条件是原始问题可行正确答案:A5、单选为建立运输问题的改进方案,在调整路线中调整量应为()。
A.奇数格的最小运量B.奇数格的最大运量C.偶数格的最小运量D.偶数格的最大运量正确答案:A6、单选下述选项中结果一般不为0的是()。
A.关键结点的结点时差B.关键线路的线路时差C.始点的最早开始时间D.活动的专用时差正确答案:D7、填空题动态规划中,把所给问题的过程,分为若干个相互联系的()正确答案:阶段8、多选系统评价常用的理论有()A.数量化理论B.效用理论C.最优化理论D.不确定性理论E.模糊理论正确答案:A, B, C, D9、填空题常用的两种时差是工作()和工作自由时差。
正确答案:总时差10、填空题()(EOQ)是使总的存货费用达到最低的某种存货台套的最佳订货量。
正确答案:经济订货量11、填空题分枝定界法一般每次分枝数量为()正确答案:2个12、单选用单纯形法求解线性规划时,不论是极大化或是极小化问题,均用最小比值原则确定出基变量,该说法()。
A.正确B.不正确C.可能正确D.以上都不对正确答案:A13、名词解释安全库存量正确答案:也称保险库存量,是为了预防可能出现的缺货现象而保持的额外库存量14、填空题若线性规划问题有(),必在某顶点上得到。
运筹学模拟试卷及详细答案解析填空(含答案)

运筹学模拟试卷及详细答案解析填空(含答案)一、填空题(每题2分,共40分)1. 线性规划问题中,若决策变量为非负约束,则该约束条件可以表示为______。
2. 在线性规划中,若目标函数为最大化问题,则其标准形式中目标函数的系数应为______。
3. 线性规划问题中,若约束条件为等式约束,则该约束条件对应的松弛变量为______。
4. 在运输问题中,若产地A到销地B的运输成本为2元/吨,则对应的运输成本矩阵中的元素为______。
5. 对偶问题的最优解是原问题的______。
6. 在指派问题中,若甲完成某项工作的时间为3小时,则对应的效率矩阵中的元素为______。
7. 网络图中,若两个节点之间的距离为5,则对应的弧长为______。
8. 在排队论中,若服务时间为负指数分布,则其平均服务时间为______。
9. 随机规划问题中,目标函数和约束条件的参数都是______。
10. 在库存管理中,若每次订购成本为100元,则对应的订购成本系数为______。
11. 在动态规划中,最优策略是______。
12. 在非线性规划中,若目标函数为凹函数,则该问题为______。
13. 线性规划问题中,若目标函数为最小化问题,则其标准形式中目标函数的系数应为______。
14. 在整数规划中,若决策变量为整数变量,则该约束条件可以表示为______。
15. 在排队论中,若到达率为λ,则单位时间内的平均到达人数为______。
16. 在指派问题中,若乙完成某项工作的时间为2小时,则对应的效率矩阵中的元素为______。
17. 在运输问题中,若产地A的供应量为100吨,则对应的供应量矩阵中的元素为______。
18. 在非线性规划中,若目标函数为凸函数,则该问题为______。
19. 在动态规划中,最优子策略是______。
20. 在随机规划问题中,目标函数和约束条件的参数都是______。
二、详细答案解析1. 答案:x ≥ 0解析:线性规划问题中,决策变量通常为非负约束,表示为x ≥ 0。
《运筹学》模拟试题及答案

^高等教育《运筹学》模拟试题及答案一、名词解释运筹学:运筹学主要运用数学方法研究各种系统的优化途径及方案。
为决策者提供科学的决策依据线性规划:一般地,如果我们要求出一组变量的值,使之满足一组约束条件,这组约束条件只含有线性不等式或线性方程,同时这组变量的值使某个线性的目标函数取得最优值(最大值或最小值)。
这样的数学问题就是线性规划问题可行解:在线性规划问题的一般模型中,满足约束条件的一组12,,.........n x x x 值称为此线性规划问题的可行解, 最优解:在线性规划问题的一般模型中,使目标函数f达到最优值的可行解称为线性规划问题的最优解。
运输问题:将一批物资从若干仓库(简称为发点)运往若干目的地(简称为收点),通过组织运输,使花费的费用最少,这类问题就是运输问题闭回路:如果在某一平衡表上已求得一个调运方案,从一个空格出发,沿水平方向或垂直方向前进,遇到某个适当的填有调运量的格子就转向前进.如此继续下去,经过若干次,就一定能回到原来出发的空格.这样就形成了一个由水平线段和垂直线段所组成的封闭折线,我们称之为闭回路二、单项选择1、最早运用运筹学理论的是( A )A 二次世界大战期间,英国军事部门将运筹学运用到军事战略部署B 美国最早将运筹学运用到农业和人口规划问题上C 二次世界大战期间,英国政府将运筹学运用到政府制定计划D 50年代,运筹学运用到研究人口,能源,粮食,第三世界经济发展等问题上2、下列哪些不是运筹学的研究范围( D )A 质量控制B 动态规划C 排队论D 系统设计3、对于线性规划问题,下列说法正确的是( D )A 线性规划问题可能没有可行解B 在图解法上,线性规划问题的可行解区域都是“凸”区域C 线性规划问题如果有最优解,则最优解可以在可行解区域的顶点上到达D 上述说法都正确4、下面哪些不是线性规划问题的标准形式所具备的( C )A 所有的变量必须是非负的B 所有的约束条件(变量的非负约束除外)必须是等式C 添加新变量时,可以不考虑变量的正负性D 求目标函数的最小值5、在求解运输问题的过程中运用到下列哪些方法( D )A 西北角法B 位势法C 闭回路法D 以上都是6、在用单纯形法求解线性规划问题时,下列说法错误的是( D )A 如果在单纯形表中,所有检验数都非正,则对应的基本可行解就是最优解B 如果在单纯形表中,某一检验数大于零,而且对应变量所在列中没有正数,则线性规划问题没有最优解C 利用单纯形表进行迭代,我们一定可以求出线性规划问题的最优解或是判断线性规划问题无最优解D 如果在单纯形表中,某一检验数大于零,则线性规划问题没有最优解三、填空1、 运筹学的主要研究对象是各种有组织系统的管理问题及生产经营活动,其主要研究方法是量化和模型化方法,2、 运筹学的目的在于针对所研究的系统求得一个合理应用人才,物力和财力的最佳方案.发挥和提高系统的效能及效益,最终达到系统的最优目标。
运筹练习题及答案

运筹练习题及答案运筹学是应用数学的一个分支,它主要研究如何在有限资源下,通过合理规划和决策来达到最优效果。
以下是一些运筹练习题及答案,供学习者练习和参考。
练习题1:线性规划问题某工厂生产A和B两种产品,每种产品都需要使用机器和劳动力。
生产1单位A产品需要1小时机器时间和2小时劳动力,生产1单位B产品需要2小时机器时间和1小时劳动力。
工厂每天有10小时机器时间和15小时劳动力。
如果A产品的利润是3元,B产品的利润是5元,问如何安排生产计划以使总利润最大化?答案:设生产A产品的数量为x,B产品的数量为y。
目标函数:最大化利润 Z = 3x + 5y约束条件:1. 机器时间:x + 2y ≤ 102. 劳动力时间:2x + y ≤ 153. 非负性:x ≥ 0, y ≥ 0通过图解法或单纯形法,我们可以得到最优解为x = 4, y = 3,此时最大利润为34元。
练习题2:整数规划问题一家公司需要安排10名员工在5个不同的部门工作。
每个部门至少需要1名员工,且每个员工只能在一个部门工作。
部门A需要至少3名员工,部门B需要至少2名员工,部门C需要1名员工,部门D和E 各需要至少1名员工。
问如何分配员工以满足所有部门的需求?答案:设部门A、B、C、D、E分别分配的员工数为x1, x2, x3, x4, x5。
目标函数:满足所有部门需求,无直接利润最大化。
约束条件:1. x1 + x2 + x3 + x4 + x5 = 102. x1 ≥ 33. x2 ≥ 24. x3 = 15. x4 = 16. x5 = 1通过枚举法或整数规划算法,我们可以得到一种分配方案为:部门A 分配3人,B分配2人,C、D、E各分配1人。
练习题3:网络流问题某公司有3个仓库和4个销售点,每个销售点每天对产品的需求量已知。
公司需要决定如何从仓库向销售点分配产品,以满足所有销售点的需求,同时使总运输成本最小。
答案:设仓库i向销售点j的运输量为x_ij,运输成本为c_ij。
运筹学题库及详解答案

运筹学题库及详解答案1. 简述线性规划的基本假设条件。
答案:线性规划的基本假设条件包括目标函数和约束条件都是线性的,所有变量的取值范围都是连续的,并且目标函数和约束条件都是确定的。
2. 解释单纯形法的基本原理。
答案:单纯形法是一种求解线性规划问题的算法。
它从一个初始可行解开始,通过迭代的方式,每次选择一个非基变量,通过行操作将其变为基变量,同时保持解的可行性,直到达到最优解。
3. 什么是对偶问题?请给出一个例子。
答案:对偶问题是指一个线性规划问题与其对应的另一个线性规划问题之间的关系。
它们共享相同的技术系数矩阵,但目标函数和约束条件互换。
例如,如果原问题是最大化目标函数 \( c^T x \) 受约束\( Ax \leq b \),对偶问题则是最小化 \( b^T y \) 受约束 \( A^T y \geq c \)。
4. 如何确定一个线性规划问题的最优解?答案:确定线性规划问题的最优解通常需要满足以下条件:(1) 所有约束条件都得到满足;(2) 目标函数的值达到可能的最大值(最大化问题)或最小值(最小化问题);(3) 存在至少一个基解,使得所有非基变量的值都为零。
5. 解释灵敏度分析在运筹学中的作用。
答案:灵敏度分析用于评估当线性规划问题中的参数发生变化时,对最优解的影响。
它可以帮助决策者了解哪些参数的变化对结果影响最大,从而在实际应用中做出更灵活的决策。
6. 什么是运输问题,它与一般线性规划问题有何不同?答案:运输问题是线性规划的一个特例,它涉及将一种或多种商品从一个地点运输到另一个地点,以满足不同地点的需求,同时最小化运输成本。
与一般线性规划问题不同,运输问题通常具有特定的结构,可以通过特定的算法(如西北角法或最小元素法)来求解。
7. 描述网络流问题的基本特征。
答案:网络流问题涉及在网络中流动的资源或商品,目标是最大化或最小化流的总价值或成本。
网络由节点和边组成,节点代表资源的供应点或需求点,边代表资源流动的路径。
运筹学 考题与答案

一、填空题:1. 表1中给出某线性规划问题计算过程中的一个单纯形表,目标函数为654228max x x x z ++=,约束条件为≤,表中321,,x x x 为松弛变量,表中解的目标函数值为14=z 。
(1)a =______,b =______,c =______,d =______,e =______,f =______,g =______; (2)表中给出的解为___________(提示:最优解,满意解,可行解……)。
2.在单纯形法的计算中,按照最小比值θ来确定换出基的变量时,有时出现存在两个以上相同的最小比值,从而出现_______现象。
3.使用动态规划方法解决多阶段决策问题,首先要将实际问题写成动态规划模型,此时要用到5个概念:_______、_______、_______、状态转移方程和指标函数。
二、判断题1.图解法同单纯形法虽然求解的形式不同,但从几何上理解,两者是一致的。
( )2.根据对偶问题的性质,当原问题为无界解时,其对偶问题无可行解;反之,当对偶问题无可行解时,其原问题具有无界解。
( )3.运输问题时一种特殊的线性规划模型,因而求解结果也可能出现下列四种情况之一:唯一最优解、无穷多最优解、无界解、无可行解。
( )4.动态规划中,定义状态时应保证在各个阶段中所作决策的相互独立性。
( )5.求图的最小支撑树以及求图中一点至另一点的最短路问题,都可以归结为求解整数规划问题。
( )三、简答题1.简述影子价格的经济意义。
2.简述不确定型决策方法中的悲观准则。
四、计算题1.用图解法求解下列线性规划问题,并指出问题是具有唯一最优解、无穷多最优解、无界解或无可行解。
(8分)⎪⎩⎪⎨⎧≥≥+≥++=0,5.14312.46min 21212121x x x x x x st x x z 2.已知表2为求解某线性规划问题的最终单纯形表,表中4x ,5x 为松弛变量,问题的约束为≤形式。
运筹学模拟题及答案(5套)
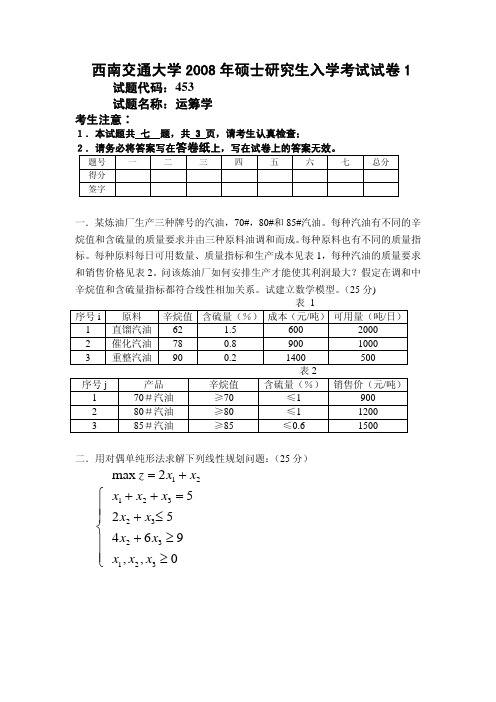
4 66 66 76
七.用单纯形法解线性规划问题,如何判断下列问题: (15 分) 1. 无可行解; 2. 有多重解; 3. 有无界解。
西南交通大学 2008 年硕士研究生入学考试试卷 2
试题代码:453 试题名称:运筹学
考生注意∶
1.本试题共 七 题,共 3 页,请考生认真检查; 2.请务必将答案写在答卷纸上,写在试卷上的答案无效。
文学 50 40 60 30 10 艺术 40 30 20 30 20 音乐 40 30 30 20 10 美术 20 30 20 30 30 问:应如何安排一周的讲座日程,使不能出席讲座的学生总数最少,并计算不能 出席讲座的学生总数。 六.某飞行队有 5 名正驾驶员和 5 名副驾驶员。由于种种原因,某些正、副驾驶 员不能同机飞行,某些则可以,如下表所示。每架飞机出航时需正,副驾驶员各 一人。问最多能有几架飞机同时出航?应如何安排正,副驾驶员?用图论方法求 解。 (20 分)
x5 x 6 17 x1 4 x 2 8x 3 2x3 2x4 x 6 3x 7 2 x 4x 10x 4 2 x 7 9 1 2 x j 0 j 1, ,7
max z 5 x1 12 x 2 4 x3 x 2x x 5 2 3 1 2 x1 x 2 3 x3 2 x1 , x 2 , x3 0 用单纯形法求解,得其终表如下: 5 12 c
j
4
0
-M
CB X B
12 5
x1
0 1 0
x2
x
; ;
2.用表上作业法求解某运输问题,若已计算出某空格的检验数为-2,则其经 济意义是 该空格出发进行调整,设调整量为 2,则调后可使总运费下降 10 动态规划中的 Bellman 最优性原理是 。 ,若从 ;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x5 x 6 17 x1 4 x 2 8x 3 2x3 2x4 x 6 3x 7 2 x 4x 10x 4 2 x 7 9 1 2 x j 0 j 1, ,7
max z x1 (1 x2 ) x3 x1 x2 x3 1 xj 0 j 1,2,3
四.用隐枚举法求解下列 0-1 规划问题(20 分)
五.用动态规划方法求解下列问题(25 分)
六. 今有三个仓库运送某种产品到四个市场上去, 仓库的供应量是 20, 20 和 100, 市场需求量是 20,20,60 和 20,仓库与市场之间的路线上的容量如下表(容量 零表示两点间无直接的路线可通) 。用图论方法确定现有路线容量能否满足市场 的需求,若不能,应修改哪条线路的容量。 (20 分)
max z 5x1 7 x2 10 x3 3x4 x5 x1 3x2 5x3 x4 4 x5 2 2 x1 6 x2 3x3 2 x4 2 x5 0 2 x2 2 x3 x4 x5 1 1 j 1, ,5 xj 0
四.从甲, 乙, 丙, 丁, 戊五人中挑选四人去完成四项工作,已知每人完成各项工 作的时间如下表所示。规定每项工作只能由一个人去单独完成,每个人最多承担 一项工作,假定甲必须保证分配到工作,丁因某种原因不同意承担第四项工作。 在满足上述条件下, 如何分配工作, 使完成四项工作总的花费时间最少。 (20 分) 人 一 二 三 四 工作 甲 10 5 15 20 乙 2 10 5 15 丙 3 15 14 13 丁 15 2 7 6 戊 9 4 15 8 五.求 V1 到各点的最短路及最短路径。 (20 分)
副 正
B1 * *
B2
B3 *
B4
B5 *
A1 A2 A3 A4 A5
*
* *
* *
七.填空: (20 分) 1.某工程公司拟从四个项目中选择若干项目,若令 1,第i个项目被选中; i 1,2,3,4 xi 0,第i个项目未被选中;
=
用 i 的线性表达式表示下列要求: (1)从 1,2,3 项目中至少选 2 个: (2)只有项目 2 被选中,项目 4 才能被选中:
一.用单纯形法求解下述线性规划问题(20 分)
max z 4 x1 x 2 x1 x 2 2 x1 4 x 2 4 x1 2 x 2 8 x1 , x 2 0
二.设一线性规划问题为(25 分)
max z 2 x1 7 x2 x3 x1 x2 x3 6 x 2x 4 2 x 1 j 0 j 1, ,3
西南交通大学 2008 年硕士研究生入学考试试卷 1
试题代码:453 试题名称:运筹学
考生注意∶
1.本试题共 七 题,共 3 页,请考生认真检查; 2.请务必将答案写在答卷纸上,写在试卷上的答案无效。
题号 得分 签字 一 二 三 四 五 六 七 总分
一.某炼油厂生产三种牌号的汽油,70#,80#和 85#汽油。每种汽油有不同的辛 烷值和含硫量的质量要求并由三种原料油调和而成。 每种原料也有不同的质量指 标。每种原料每日可用数量、质量指标和生产成本见表 1,每种汽油的质量要求 和销售价格见表 2。问该炼油厂如何安排生产才能使其利润最大?假定在调和中 辛烷值和含硫量指标都符合线性相加关系。试建立数学模型。 (25 分) 表 1 序号 i 原料 辛烷值 含硫量(%) 成本(元/吨) 可用量(吨/日) 1 直馏汽油 62 1.5 600 2000 2 催化汽油 78 0.8 900 1000 3 重整汽油 90 0.2 1400 500 表2 序号 j 产品 辛烷值 含硫量(%) 销售价(元/吨) 1 70#汽油 ≥70 ≤1 900 2 80#汽油 ≥80 ≤1 1200 3 85#汽油 ≥85 ≤0.6 1500 二.用对偶单纯形法求解下列线性规划问题: (25 分)
1 0 0
x3
-1/5 7/5 -3/5
x4
2/5 1/5
x5
-1/5 2/5
B b
-1
x2
x1
8/5 9/5
cj z j
-29/5 -M+2/5
X4 为松弛变量,X5 为人工变量, 1.上述模型的对偶模型为:
; 2.对偶模型的最优解为: 3.当两种资源分别单独增加一个单位时,目标函数值分别增加 ; ;
4 增加一个约束条件
x1 2x3 2
三.某种产品今后四周的需求量分别为 300,700,900,600 件,必须得到满足。ห้องสมุดไป่ตู้已知每件产品的成本在起初两周是 10 元,以后两周是 15 元。工厂每周能生产这 种产品 700 件,且在第二、三周能加班生产。加班后,每周可增产 200 件产品, 但成本每件增加 5 元。产品如不能在本周交货,则每件每周存贮费是 3 元。问如 何安排生产计划,使总成本最小,要求建立运输问题数学模型求解。 (25 分) 四.某校蓝球队准备从以下 6 名预备队员中选拔 3 名为正式队员,并使平均身高 尽可能高,这 6 名预备队员情况如下表所示,试建立数学模型。 (20 分) 队员的挑选要满足下列条件: 2 3 4 5 少补充一名后卫队员; 大李或小田中间只能入选一名; 最多补充一名中锋; 如果大李或小赵入选,小周就不能入选。
市场 仓库
1 30 0 20 20
2 10 0 10 20
3 0 10 40 60
4 40 50 5 20
供应量 20 20 100
1 2 3 需求量
七.下列叙述中正确的是 ( ) (20 分) 4 图解法与单纯形法,虽然求解的形式不同,但从几何上理解,两者是一致的; 5 若线性规划的原问题有多重最优解,则其对偶问题也一定具有多重最优解; 6 如果运输问题单位运价表的某一行(或某一列)元素分别加上一个常数 k, 最优调运方案将不会发生变化; 7 对于极大化问题 max Z =
max z 5 x1 12 x 2 4 x3 x 2x x 5 2 3 1 2 x1 x 2 3 x3 2 x1 , x 2 , x3 0 用单纯形法求解,得其终表如下: 5 12 c
j
4
0
-M
CB X B
12 5
x1
0 1 0
x2
x
; ;
2.用表上作业法求解某运输问题,若已计算出某空格的检验数为-2,则其经 济意义是 该空格出发进行调整,设调整量为 2,则调后可使总运费下降 10 动态规划中的 Bellman 最优性原理是 。 ,若从 ;
西南交通大学 2008 年硕士研究生入学考试试卷 4
试题代码:453 试题名称:运筹学
min W bij xij
n
n
重复部分后,恰好构成该图的最小支撑树。
西南交通大学 2008 年硕士研究生入学考试试卷 3
试题代码:453 试题名称:运筹学
考生注意∶
1.本试题共 七 题,共 3 页,请考生认真检查; 2.请务必将答案写在答卷纸上,写在试卷上的答案无效。
题号 得分 签字 一 二 三 四 五 六 七 总分
和
-1 4.最优基的逆矩阵 B =
5.如果原问题增加一个变量,则对偶问题的可行域将可能变大还是变小? . 三.求解下列各题(解题方法自选)(20 分)
min z 5x11 6x12 10x13 8x21 10x22 12x23
预备队员 大张 大李 小王 小赵 小田 小周
号码 4 5 6 7 8 9
身高(厘米) 193 191 187 186 180 185
位置 中锋 中锋 前锋 前锋 后卫 后卫
五.某高校拟开设文学、艺术、音乐、美术四个学术讲座。每个讲座每周下午举 行一次。 经调查知, 每周星期一至星期五不能出席某一讲座的学生数如下表: (20 分) 星期 讲座 一 二 三 四 五
max z 2 x1 x2
x1 x2 x3 5 2 x2 x3 5 4 x2 6 x3 9 x1 , x2 , x3 0
三.已知某运输问题的产销平衡表与单位运价表如下表所示,B2 地区需要的 115 单位必须满足,试确定最优调拨方案。 (20 分) Bj Ai B1 B2 B3 A1 10 15 20 A2 20 40 15 A3 30 35 40 销量 25 115 60 B4 20 30 55 30 B5 40 30 25 70 产量 50 100 130
4 66 66 76
七.用单纯形法解线性规划问题,如何判断下列问题: (15 分) 1. 无可行解; 2. 有多重解; 3. 有无界解。
西南交通大学 2008 年硕士研究生入学考试试卷 2
试题代码:453 试题名称:运筹学
考生注意∶
1.本试题共 七 题,共 3 页,请考生认真检查; 2.请务必将答案写在答卷纸上,写在试卷上的答案无效。
六.某公司有资金 4 百万元向 A,B,C 三个项目追加投资,各个项目可以有不 同的投资额(以百万元为单位) ,相应的效益值如下表。问怎样分派资金,使总 效益值最大,试用动态规划方法求解。 (25 分) 项目 A B C 0 38 40 38 1 41 42 64 投资额 2 48 50 68
3 60 60 78
考生注意∶
1.本试题共 七 题,共 3 页,请考生认真检查; 2.请务必将答案写在答卷纸上,写在试卷上的答案无效。
题号 得分 签字 一.对约束条件(20 分) 一 二 三 四 五 六 七 总分
说明解 X=(1,2,1,0,0,0,0)T 是不是基可行解,假定不是,试找出一个基可 行解。 二.已知线性规划问题(20 分)
