上海版教材矩阵与行列式习题(有答案)

沪教版(上海)高三年级新高考辅导与训练第七章矩阵与行列式、算法初步、复数三、复数

沪教版（上海）高三年级新高考辅导与训练第七章矩阵与行列式、算法初步、复数三、复数学校:___________姓名：___________班级：___________考号：___________一、解答题1．已知复数226(310)z m m m m i =--+--.当实数m 为何值时，复数z 为 (1)实数；(2)纯虚数；(3)零.2．设复数z 满足4z R z+∈，且22z -=，求z .3．若z 为虚数，且||1z =，求证11z z -+为纯虚数. 4．已知||1z =.求21z z -+的模的最大值与最小值.5．关于x 的方程()222150x ax a a R --+=∈的两个根分别是α、β，且8αβ+=，求a 的值，并求方程的根. 6．计算下列各题：(1)55(1)(1)11i i i i +-+-+；(2)201920191111i i i i +-⎛⎫⎛⎫- ⎪ ⎪-+⎝⎭⎝⎭；；(4) 23201920202320192020i i i i i +++++.7．已知复数()2262153m m z m m i m --=++-+，当m 为何实数时，复数z 是：（1）实数；（2）虚数；（3）纯虚数；（4）对应点在实轴的上方.8．若关于x 的方程22470x zx i -++=有实根，求复数z 的模的最小值和此时z 的值. 9．解答下列各题：(1)已知|2|z -=， |3|4z -=，求z ； (2)已知11z z +-为纯虚数，|1|1z -=，求z . 10．下列方程至少有一个实根，求实数t 的值与相应方程的根.（1）2(2)(2)0x t i x ti ++++=；（2）2(21)(3)0x i x t i --+-=.11．方程21(4)02x m x m --+=的两根为α，β，且||||αβ+=，求实数m 的值.二、单选题12．复数z 满足22|2||1|5z i z ---=，则它在复平面内对应点的轨迹是（）. A ．圆B ．直线C ．双曲线D ．椭圆13．复数3z ai =+满足条件|2|2-<z ，则实数a 的取值范围是（）. A ．(1,1)-B．(-C ．(2,2)-D．(14．若复数z 满足|34|2z i +-=，则|||z 的最小值和最大值分别是（）. A ．1和9B ．4和10C ．5和11D ．3和715．使11+⎛⎫ ⎪-⎝⎭ni i 为正实数的最小自然数n 是（）.A ．2B ．4C ．6D ．816．若复数312a ii++（a R ∈，i 为虚数单位）是纯虚数，则实数a 的值为（） A ．-6B ．13C ．32D17．满足条件12011z i ii+=-+的复数z 对应的点在（）.A ．第一象限B ．第二象限C ．第三象限D ．第四象限三、填空题18．如果复数z 满足关系式2z z i +=+,那么z 等于． 19．已知复数z 满足||1z i -=，则|1|z -的取值范围是________. 20．若z a bi =+，21zR z∈+，则实数a ，b 应满足的条件为________. 21．在复数范围内分解因式：44x y +=________.22．方程2(12)2(1)0ax i x a i ++--=有实根，则实数a 的取值为________. 23．复数z 满足0zz z z ++=，则z 对应点的轨迹是________.参考答案1．(1)2m =-或5m =；(2)3m =；(3)2m =-. 【分析】(1)根据z 为实数，则虚部为0，即可求出m ；(2)根据z 为纯虚数，则虚部不为0，而实部为0，即可求出m ； (3)根据z 为零，则实部与虚部同时为零，即可求出m . 【详解】(1)z 为实数的充要条件是z 的虚部为0，即23100m m --=，解得2m =-或5m =，所以当2m =-或5m =时，z 为实数.(2)z 为纯虚数的充要条件是z 的虚部不为0，而实部为0，即22603100m m m m ⎧--=⎨--≠⎩，解得3m =，所以当3m =时，z 为纯虚数.(3)z 为零的充要条件是z 的实部与虚部同时为零，即22603100m m m m ⎧--=⎨--=⎩，解得2m =-，所以当2m =-时，0z =. 【点睛】本题主要考查复数的概念，复数的分类，属于基础题.2．4z =，1z =-或1=+z 【分析】设(),z a bi a b R =+∈，利用复数的四则运算将复数4z z+化为一般形式，可得其虚部为零，再由22z -=，可得出关于实数a 、b 的方程组，解出a 、b 的值，由此可得出复数z . 【详解】设(),z a bi a b R =+∈，则0z ≠，即a 、b 不同时为零，224444a bi z a bi a bi R z a bi a b -+=++=++∈++，2240b b a b∴-=+，① 由22z -=，得()2224a b -+=.②解由①、②所组成的联立方程组()22224024b b a b a b ⎧-=⎪+⎨⎪-+=⎩，解得40a b =⎧⎨=⎩或1a b =⎧⎪⎨=⎪⎩1a b =⎧⎪⎨=⎪⎩4z ∴=，1=+z或1z =-.【点睛】本题考查复数的求解，考查复数的概念以及复数的模等基础知识，根据题意列出方程组是解答的关键，考查计算能力，属于中等题. 3．证明见解析【分析】设(,)z a bi a b R =+∈，可得221a b +=，且0b ≠，代入11z z -+化简即可得证. 【详解】证法1：设(,)z a bi a b R =+∈，则221a b +=，且0b ≠.所以2211(1)(1)11(1)z a bi a bi a bi z a bi a b -+--++-==+++++22221(1)(1)2(1)22()a b a bi a bi bi a b a+-++--==+++. 因为0b ≠，221a b +=，所以1a ≠-，所以11z z -+为纯虚数. 证法2：由||1z =，得1=zz .所以11111111z z zz z z z z z zz z z z -----⎛⎫===-=- ⎪+++++⎝⎭.因为||1z =，z 为虚数，所以1z ≠±，由非零复数z 为纯虚数的充要条件证明了11z z -+为纯虚数. 【点睛】本题主要考查复数的模，复数的代数形式的乘除运算及纯虚数的概念，属于基础题. 4．最大值为3，最小值为0 【分析】设(1,1)z a bi a b =+-≤≤，则221a b +=，代入21z z -+，可得2221(21)z z a -+=-，根据a 的范围即可得最值. 【详解】设(1,1)z a bi a b =+-≤≤，则221a b +=，即221b a =-，222221()()11(2)2(2)z z a bi a bi a b a ab b i a a ab b i-+=+-++=--++-=-+-，∴()222222222212(2)(21)(21)(21)z z a aab b a a b a a -+=-+-=-+-=-，因为11a -≤≤，所以3211a -≤-≤，所以22019z z ≤-+≤，即21z z -+的模最大为3，最小为零. 【点睛】本题考查复数的代数运算及模的运算，考查学生的计算能力，是基础题.5．当4a =时，方程的根为11x =，27x =；当12a =-时，方程的根为1x =，2x =. 【分析】分0∆≥和∆<0两种情况讨论，在0∆≥时，由8αβ+=结合韦达定理可求得实数a 的值，并可求得原方程的根；在∆<0时，由8αβ+=结合韦达定理求得实数a 的值，进而求得原方程的根. 【详解】对于二次方程()222150x ax a a R --+=∈，()()()244152435a a a a ∆=--=-+.（1）当0∆≥，即5a ≤-或3a ≥时，由韦达定理得2a αβ+=，152a αβ=-.又αβ+==当1520a αβ=->时，即当5a ≤-或1532a ≤<时，则28a αβαβ+=+==，解得4a =，此时原方程为2870x x -+=，该方程的两根分别为11x =，27x =；当1520a αβ=-≤时，即当152a ≥时，则αβ+===8==，整理得22310a a +-=，解得1a =-±；（2）当∆<0，即53a -<<时，由韦达定理得2a αβ+=，152a αβ=-.28αβα+=====，解得12a =-，此时，原方程为2160x x ++=，解得1x =，2x =.综上，当4a =时，方程的根为11x =，27x =；当12a =-时，方程的根为1x =，2x =. 【点睛】本题考查实系数一元二次方程的求解，考查了韦达定理的应用，考查计算能力，属于中等题. 6．(1)0；(2)2i -；(3)516；(4)10101010i - 【分析】根据复数的乘除运算法则及乘方运算，即可计算出(1)(2)的值；利用复数模的运算性质可求出(3)的值；利用分组求和及i 的运算性质可求出(4)的值. 【详解】(1) 5566232322(1)(1)(1)(1)[(1)][(1)]11(1)(1)(1)(1)11i i i i i i i i i i i i i i +-+-+-+=+=+-+-++---3333(2)(2)44022i i i i -=+=-=.(2)因为21(1)21(1)(1)2i i ii i i i ++===--+，21(1)21(1)(1)2i i i i i i i ---===-++-，所以20192019201945043201920319111(22221)i i i i i i i i i i ⨯+-=--==+-⎛⎫⎛⎫ ⎪ ⎪-+=⎝⎭=-⎝⎭.(3) ==5454845252516⨯====⨯. (4) 23201920202320192020i i i i i +++++(234)(5678)(2017201820192020)i i i i i i =--++--+++--+(22)(22)(22)+i i i =-+-+-505(22)i =⨯-10101010i =-.【点睛】本题主要考查复数的乘除运算，乘方运算，复数的模的运算性质及i 的运算性质，属于中档题.7．（1）5m =-或3；（2）5m ≠-且3m ≠±；（3）2m =-；（4）3m >或5m <-. 【分析】（1）根据题意得出复数z 的虚部为零，进而可求得实数m 的值；（2）根据题意得出复数z 的虚部不为零，由此可解得实数m 的取值范围；（3）根据题意得出复数z 的实部为零，虚部不为零，由此可解得实数m 的值；（4）根据题意得出复数z 的虚部为正数，由此可解得实数m 的取值范围. 【详解】（1）若复数z 为实数，则2215030m m m ⎧+-=⎨+≠⎩，解得5m =-或3；（2）若复数z 为虚数，则2215030m m m ⎧+-≠⎨+≠⎩，解得5m ≠-且3m ≠±；（3）若复数z 为纯虚数，则226032150m m m m m ⎧--=⎪+⎨⎪+-≠⎩，解得2m =-；（4）若复数z 在复平面内对应的点位于实轴的上方，则2215030m m m ⎧+->⎨+≠⎩，解得5m <-或3m >.【点睛】本题考查利用复数的类型求参数，解题时要结合已知条件对复数的实部和虚部进行限制，考查计算能力，属于基础题. 8．49755z i ⎛⎫=±+ ⎪⎝⎭，||z最小值为【分析】设z a bi =+，根据复数运算得到224070x ax bx ⎧-+=⎨-=⎩，利用均值不等式计算模的最值得到答案. 【详解】22470x zx i -++=，设z a bi =+，则()22470x a bi x i -+++=，即()22470x ax bx i -++-=，x ∈R ，则224070x ax bx ⎧-+=⎨-=⎩，则2497240a b b -+=，即7247b a b =+，222222272449625484898749b b z a b b b b ⎛⎫=+=++=++≥= ⎪⎝⎭，当且仅当224962549b b =，即75b =±时等号成立，min z =75b =时，495a =，75b =-时，495a =-，故49755z i ⎛⎫=±+⎪⎝⎭. 【点睛】本题考查了复数的运算，复数的模，均值不等式，意在考查学生的计算能力和综合应用能力.9．(1)34i ±；(2)12z =± 【分析】(1)设(,)z a bi a b R =+∈代入已知求出复数的模，解方程组即可求出,a b ； (2)设(,)z a bi a b R =+∈代入11z z +-及|1|1z -=化简，联立方程即可求出,a b . 【详解】(1) 设(,)z a bi a b R =+∈，则z a bi =-，所以|2||(2)|z a bi -=-+=|3||(3)|4z a bi -=--= 所以22(2)17a b -+=，22(3)()16a b -+-= 解得3a =，4b =±，所以34z i =±. (2) 设(,)z a bi a b R =+∈，则2222222211(1)(1)(1)1211(1)(1)(1)(1)z a bi a bi a bi a bi a b biz a bi a bi a bi a b a b +++++---++--====--+-+---+-+ 22222212(1)(1)a b b i a b a b +-=--+-+为纯虚数，所以2210a b +-=且0b ≠，①由|1|1z -=得|1|1a bi -+=，所以22(1)1a b -+=，②由①②解得12a =，2b =±，所以122z =±. 【点睛】本题主要考查复数的概念，复数代数形式的乘除运算，复数的模及共轭复数，考查运算求解能力，属于中档题.10．（1）t =，1x =22x i =，或t =-1x =，22x i =-；（2）112t =，112x =-，2122x i =- 【分析】（1）根据复数运算得到22020x tx x t ⎧++=⎨+=⎩，解得t =±.（2）根据复数运算得到230210x x t x ⎧++=⎨+=⎩，解得112t =，再代入原方程解得答案.【详解】（1）2(2)(2)0x t i x ti ++++=，则()2202x x t i tx +++=+，则22020x tx x t ⎧++=⎨+=⎩，则222042t t -+=，解得t =±当t =时，(2202x x i +++=+即()20x x i =，解得1x =22x i =-；当t =-(2202x x i +-+=-即()20x x i =，解得1x =，22x i .（2）2(21)(3)0x i x t i --+-=，则2(2103)x x x t i +-+=+，则230210x x t x ⎧++=⎨+=⎩，则12112x t ⎧=-⎪⎪⎨⎪=⎪⎩，当112t =时，2(21014)x x x i ++-=+，即112022x x i ⎛⎫⎛⎫++-= ⎪⎪⎝⎭⎝⎭，故112x =-，2122x i =-. 【点睛】本题考查了复数范围内解方程，意在考查学生的计算能力和应用能力，漏解是容易发生的错误.11．4m =-72m =．【分析】由韦达定理得出,αβαβ+，把||||αβ+=平方后用,αβαβ+表示并代入后可求得m ．【详解】由题意若方程有两个实数根，则21(4)402m m ∆=--⨯≥，解得2m ≤或8m ≥， 4m αβ+=-，12m αβ=，又||||αβ+=，∴()2222||||2()227αβααββαβαβαβ+=++=+-+=，即2(4)7m m m --+=，0m ≥时，2(4)7m -=，4m =4m =+0m <时，2(4)27m m --=，21090m m -+=，解得1m =或9m =．全舍去．所以4m =-若方程是两个虚数根，4m αβ+=-，12m αβ=，设(,)a bi a b R α=+∈，则a bi β=- αβ=2212a b m +=，αβ+==2274a b +=，2272()2m a b =+=．综上4m =-72m =．【点睛】本题考查韦达定理，属于基础题，解题时要注意如果是实系数二次方程的实数解，则判别式0≥，如果是虚数根，则可设根为(,)a bi a b R +∈，代入后用实数的知识求解（或用复数相等的定义转化）．12．B【分析】设(,)z x yi x y R =+∈，代入已知式化简整理后，由方程可得轨迹曲线．【详解】设(,)z x yi x y R =+∈，则222222221(2)(1|2)||1|5z i x yi i x yi x y x z y ⎡⎤=+--+-=+--+--⎣-=⎦-，整理得210x y --=，它是一条直线．故选：B ．【点睛】本题考查复数的几何意义，设(,)z x yi x y R =+∈，代入计算得出轨迹方程，由方程得轨迹是求复平面上点的轨迹的常用方法．13．D【分析】由模长公式和已知条件可得a 的不等式，解不等式可得.【详解】解：∵3z ai =+满足条件|2|2-<z ，|1|2ai ∴+<2<，平方可得23a <，解得a <<故选：D.【点睛】本题考查复数的模长公式，涉及不等式的解法，属基础题.14．D【分析】由342z i +-=可得z 在复平面内的轨迹是以()3,4-为圆心，以2为半径的圆，利用z 表示圆上的点到原点的距离,结合圆的几何性质可得结果.【详解】因为复数z 满足，342z i +-=，所以z 在复平面内的轨迹是以()3,4-为圆心，以2为半径的圆， z 表示圆上的点到原点的距离，5=，所以z 的最大值是527+=,z 的最小值是523-=，故选：D.【点睛】本题考查复数的模的几何意义，点的轨迹，复数的模的几何意义是复平面内两点间的距离，所以若z x yi =+，则z a bi --表示点(),x y 与点(),a b 的距离，z a bi r --=表示以(),a b 为圆心，以r 为半径的圆，属于中档题.15．B【分析】化简得11nn i i i +⎛⎫ ⎪⎭=-⎝，再逐个分析即可.【详解】因为()()()()111111n n n i i i i i i i ⎡⎤+++⎛⎫⎢⎥ ⎪--+⎝⎭⎣⎦==，又1234,1,,1i i i i i i ==-=-=，故使11+⎛⎫ ⎪-⎝⎭n i i 为正实数的最小自然数n 是4.故选：B【点睛】本题主要考查了n i 的周期性.属于基础题.16．A【解析】解答： ∵()()()()312363212121255a i i a i a a i i i i +-++-==+++-是纯虚数， ∴605{3205a a +=-≠，解得a=−6. 本题选择A 选项.17．A【分析】根据行列式可得(1)(1)(12)0z i i i +--+=，再根据复数的乘除运算即可出复数z ，进而可求出z 即可得到答案.【详解】由已知得(1)(1)(12)0z i i i +--+=，所以(1)3z i i +=+，所以3(3)(1)4221(1)(1)2i i i i z i i i i ++--====-++-，所以2z i =+，所以复数z 对应的点坐标为(2,1)在第一象限.故选：A【点睛】本题主要考查二阶行列式的运算，复数的乘除运算及共轭复数，属于基础题.18．34i + 【解析】试题分析：设(,)z a bi a b R =+∈，则z a bi =-，z =2a bi i +=+，所以得：2{1a b ==，解得：3{41a b ==，所以34z i =+．考点：复数的运算．19．1]【分析】利用复数的几何意义求解，||1z i -=表示复平面内到点(0,1)距离为1的所有复数对应的点，|1|z -表示复平面内到点(1,0)的距离，结合两点间距离公式可求范围.【详解】因为在复平面内，||1z i -=表示到点(0,1)距离为1的所有复数对应的点，即复数z 对应的点都在以(0,1)为圆心，半径为1的圆上；|1|z -表示复数z 对应的点到点(1,0)11=，11=，所以|1|z -的取值范围是1].故答案为：1].【点睛】本题主要考查复数的几何意义，明确几何意义是求解的关键，侧重考查直观想象的核心素养. 20．0b =或221a b +=【分析】根据复数的运算得出21+z z ()()()222222222212114a a b ab b b a i a b a b +-++--=+--，再由复数是实数的条件得出实数a ，b 应满足的条件.【详解】()22222211()1212z a bi a bi a bi z a bi a abi b a b abi +++===+++++-+-+()()222222212()14ab abi a bi a b a b +--=++-- ()()()22222222222112214a a b b a b i a bi ab a b a b+-++--+=+-- ()()()2222322222212214a a b ab b a b b a b i a b a b+-+++--=+-- ()()()222222222212114a a b ab b b a i a b a b+-++--=+-- 因为21z R z ∈+，故有()2210b b a --=,所以0b =或2210b a --=，即0b =或221a b +=是a ，b 应满足的条件.故答案为：0b =或221a b +=.【点睛】本题考查复数的运算和复数的概念，属于中档题.21．2222x y x y x y x y ⎛⎫⎛⎫⎛⎫⎛⎫+---++ ⎪⎪⎪⎪ ⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭【分析】利用2222()x y x yi +=-分解因式．【详解】2244222222()()22x y x y i x y i x yi x y ⎡⎤⎡⎤⎛⎫⎛⎫⎢⎥⎢⎥+=+-=-⋅-⋅ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎣⎦⎣⎦2222x y x y x y x y ⎛⎫⎛⎫⎛⎫⎛⎫=-+-+ ⎪⎪⎪⎪ ⎪⎪⎪⎪⎝⎭⎝⎭⎝⎭⎝⎭．【点睛】本题考查在复数范围内因式分解．在复数范围内每个n 次多项式都可以分解成n 个一次因式之积．22．0或【分析】根据方程2(12)2(1)0ax i x a i ++--=有实根，设实根为x ，转化为()22220ax x a x a i +-++=，利用复数相等求解.【详解】因为方程2(12)2(1)0ax i x a i ++--=有实根，设实根为x ，则()22220ax x a x a i +-++=，所以220220ax x a x a ⎧+-=⎨+=⎩，化简得：()230a a -=，解得0a =或a =故答案为：0或【点睛】本题主要考查复系数方程的解法以及复数相等的应用，还考查了运算求解的能力，属于基础题.23．圆2220x y x ++=【分析】设z x yi =+，代入0zz z z ++=整理化简即可.【详解】解：设z x yi =+，则()()()()0x yi x yi x yi x yi +--+++=，整理得2220x y x ++=，即z 对应点的轨迹是圆2220x y x ++=. 故答案为：圆2220x y x ++=.【点睛】本题考查共轭复数的概念，复数的运算及复数的几何意义，是基础题.。

上海版矩阵与行列式基础练习题

矩阵与行列式习题本试卷共18题，时间60分钟，总分值100分〕班级：：一、填空选择题：〔每题3分，共36分〕1、46x A y ⎛⎫= ⎪⎝⎭，13u B v ⎛⎫= ⎪⎝⎭，且A B =，那么A+AB= 。

2、设231001252437A B -⎛⎫⎛⎫⎪⎪==- ⎪⎪ ⎪ ⎪-⎝⎭⎝⎭，那么3A –4B 为。

3、设A 为二阶矩阵，其元素满足，0a a ji ij =+，i=1，2，j=1，2，且2a a 2112=-，那么矩阵 A= .4、设2442,1221A B -⎛⎫⎛⎫== ⎪ ⎪-⎝⎭⎝⎭則32A B - = ,=AB ，=BA5、假设点A 在矩阵1222-⎡⎤⎢⎥-⎣⎦对应的变换作用下得到的点为〔3，- 4〕，那么点A 的坐标为 .6、假设202137x y -⎛⎫⎛⎫⎛⎫=⎪⎪ ⎪-⎝⎭⎝⎭⎝⎭，那么x y +=___________. 7、1212a a b b =1,那么12122233b b a a =-- _____ 。

8、〔1〕行列式z kc c y kb b xka a = ；〔2〕211121__________112-= 9、124221342D -=---，那么21a 的代数余子式21A = 。

10、2413201x x 的代数余子式012=A ，那么代数余子式=21A11、设A 为3阶方阵，且3A =，那么2A -=______________12、如果方程组⎩⎨⎧=++=++0101dy cx by ax 的系数行列式1=d c b a ，那么它的解为二、简答题〔每题8分，共64分〕1、⎪⎪⎭⎫⎝⎛-=533201A ⎪⎪⎪⎭⎫⎝⎛-=013164245B 求()AB .2.1011A ⎛⎫= ⎪⎝⎭，分别计算23A A 、，猜想*(2)n A n n ≥∈N ，；3. 将以下线性方程组写成矩阵形式，并用矩阵变换的方法求解:⑴ 32110250x y x y --=⎧⎨+-=⎩；⑵111612102113x y z ⎛⎫⎛⎫⎛⎫⎪⎪ ⎪-= ⎪⎪ ⎪ ⎪⎪ ⎪-⎝⎭⎝⎭⎝⎭.4、函数f(x)=xa x+1111111 ，其中a 是实数，求函数f(x)在区间[2,5]上的最小值。

2020届上海(沪教版)高考考典——第8章-矩阵和行列式初步教师版

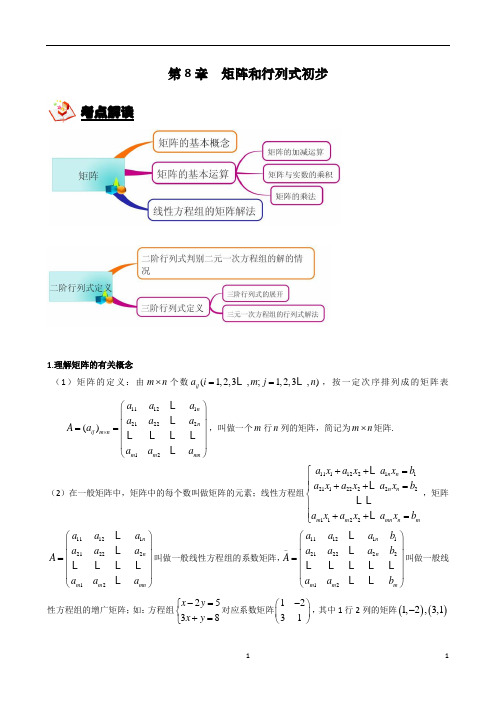
第8章矩阵和行列式初步考点解读1.理解矩阵的有关概念（1）矩阵的定义：由m n⨯个数(1,2,3,;1,2,3,)ija i m j n==L L，按一定次序排列成的矩阵表111212122212()nnij m nm m mna a aa a aA aa a a⨯⎛⎫⎪⎪==⎪⎪⎝⎭LLL L L LL，叫做一个m行n列的矩阵，简记为m n⨯矩阵.（2）在一般矩阵中，矩阵中的每个数叫做矩阵的元素；线性方程组11112211211222221122n nn nm m mn n ma x a x a x ba x a x a x ba x a x a x b++=⎧⎪++=⎪⎨⎪⎪++=⎩LLL LL，矩阵A=111212122212nnm m mna a aa a aa a a⎛⎫⎪⎪⎪⎪⎝⎭LLL L L LL叫做一般线性方程组的系数矩阵，A-=11121121222212nnm m ma a a ba a a ba a b⎛⎫⎪⎪⎪⎪⎝⎭LLL L L L LL L叫做一般线性方程组的增广矩阵；如：方程组2538x yx y-=⎧⎨+=⎩对应系数矩阵1231-⎛⎫⎪⎝⎭，其中1行2列的矩阵()()1,2,3,1-叫做系数矩阵的两个行向量；2行1列的矩阵12,31-⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭叫做系数矩阵的列向量；（3）当矩阵的行数与列数相等时，该矩阵称为方矩阵，简称方阵；我们把主对角线元素为1、其余元素均为零的方矩阵，如1001⎛⎫⎪⎝⎭，叫做单位矩阵.2.矩阵的运算及其性质（1）矩阵的加法，若111212122212()n n ij m nm m mn a a a a a a A a a a a ⨯⎛⎫⎪ ⎪== ⎪⎪⎝⎭L L L L L L L，111212122212()n n ij m n m m mn b b b b b b B b b b b ⨯⎛⎫ ⎪⎪== ⎪ ⎪⎝⎭LL L LL L L，则C A B =+=111112121121212222221122n n n n m m m m mn mna b a b a b a b a b a b a b a b a b +++++++++L LL L L L L.（2）矩阵的加法满足性质: 交换律,结合律.（3）数与矩阵乘法定义：以数k 乘矩阵()ij A a =的每个元素所得的矩阵()ij ka 叫做数k 与矩阵A 相乘的积，记作kA ；（4）设矩阵111211121112212221222122,,a a b b c c A B C a a b b c c ⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.如果它们元素间的关系可以用下列等式表示：1122(1,2;1,2)ij i j i j c a b a b i j =+==，则C 叫做矩阵A 和矩阵B 的积，记作C =AB（5）矩阵A 的初等变换，指的是对A 实施如下变换：3．行列式的有关概念与性质（1）初中代数中，二元线性方程组111222,a x b y c a x b y c +=⎧⎨+=⎩当12210a b a b -≠时，二元线性方程组有唯一解：1221122112211221c b c b x a b a b a c a c y a b a b -⎧=⎪-⎪⎨-⎪=⎪-⎩，为了方便记忆，引入定义a c b d =ad bc -，a c b d 叫做二阶行列式， ad bc -叫做二阶行列式的展开式；设1122a b D a b =，1122x c b D c b =，1122y a c D a c =，则方程组的唯一解可表示为：xy D x D D y D⎧=⎪⎪⎨⎪=⎪⎩. （i ）0D ≠，方程组有唯一解；（ii ）0D =：①x y D D 、中至少有一个不为零，方程组无解； ②0x y D D ==，方程组有无穷多解.（3）三阶行列式的两种展开方法：①按对角线展开.123123123a b c b c a c a b=++321123132a b c b a c a b c---②按一行（或一列）展开.111222333a b ca b ca b c=123231312321213132a b c a b c a b c a b c a b c a b c++---123321322312332()()()a b c b c b a c a c c a b a b=-+-+-(4)把三阶行列式某元素所在的行和列划去，剩下的元素组成的二阶行列式，叫做这个元素的余子式；如果用,i j分别表示某个元素所在的行数和列数，那么这个元素的余子式．补充与提高：行列式运算性质：①把行列式的某一行的所有元素乘以一个数k，等于用k乘以这个行列式；②行列式中某一行所有元素的公因子可以提到行列式记号的外边；③如果行列式中某一行的元素全为0，那么这个行列式的值为0；④交换行列式的任意两行，行列式的绝对值不变，符号相反；⑤如果行列式有两行的对应元素相同，那么这个行列式的值为0；⑥如果行列式有两行的对应元素成比例，那么这个行列式的值为0；⑦如果行列式的某一行的元素都是二项式，那么这个行列式等于把这些二项式各取一项组成相应的行，而其余行不变的两个行列式的和；例如：111222222333a b ca ab bc ca b c'''+++=111222333a b ca b ca b c+111222333a b ca b ca b c'''.注意：红线上三元素的乘积均为正，蓝线上三元素的乘积均为负.乘以(1)i j+-所得的式子，叫做这个元素的代数余子式.（5）三阶行列式D 等于它的任意一行（或列）的所有元素分别和它们的代数余子式的乘积的和.例如：111222333a b c D a b c a b c ==222222a A b B c C ++.(6)三元线性方程组111122223333a x b y c z d a x b y c z d a x b y c z d ++=⎧⎪++=⎨⎪++=⎩，对应系数行列式111222333a b c D a b c a b c =,111222333x d b c D d b c d b c =，111222333y a d c D a d c a d c =，111222333z a b d D a b d a b d =.①当0D ≠时，方程组有唯一解x y z D x D D y D D z D ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩；②当0=0x y D D D =且，时，方程组有无穷多解；③当0x y D D D =且，不全为0时，方程组无解.(7)①三角形的面积公式: △ABC 的三个顶点坐标分别为112233(,),(,),(,)A x y B x y C x y ，则ABC S =△11223311121x y x y x y .②同一平面上A B C 、、三点共线的充要条件为112233111x y x y x y =0.8.1矩阵的概念例题精讲【例1】写出下列线性方程组的系数矩阵和增广矩阵：（1）3560437x y x y ++=⎧⎨=-⎩（2）214625x z y z x y z -=⎧⎪+=⎨⎪-+=⎩一个元素的代数余子式通常用这个元素相应的大写字母并附加相同的下标来表示【参考答案】（1）35356,43437-⎛⎫⎛⎫ ⎪ ⎪---⎝⎭⎝⎭ （2）1021021014,01462112115--⎛⎫⎛⎫⎪ ⎪⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭8.2矩阵的运算例题精讲【例1】已知矩阵 3 0-2 1A ⎛⎫= ⎪⎝⎭，矩阵-2 1 2 2B ⎛⎫= ⎪⎝⎭，求矩阵X ，使其满足B X A =-32．【参考答案】813320⎛⎫-⎪ ⎪ ⎪-⎝⎭【例2】已知下列矩阵⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫ ⎝⎛--=3110146,602413,591732C B A ，计算：（1）A(B+C) (2)(B+C)A (3)BA+CA (4)从（1）（2）（3）的计算结果你能得出什么结论？【参考答案】（1）1198245⎛⎫ ⎪⎝⎭ （2）151842234610131133---⎛⎫ ⎪-- ⎪ ⎪---⎝⎭ （3）151842234610131133---⎛⎫ ⎪-- ⎪ ⎪---⎝⎭（4）(B+C)A= BA+CA8.3二阶行列式例题精讲【例1】展开并化简下列行列式：（1）3423- （2）245lg 2lg - 【参考答案】（1）17- （2）2lg 24lg5+【例2】判断m 取什么值时，下列关于x,y 的线性方程组（1）有唯一解？（2）无解？（3）有无穷解？⎪⎩⎪⎨⎧=+-+-=--1)1()1(1)5(22y m x m y m x【参考答案】221(5)(1)(2)(3)1(1)m D m m m m m --==++-+-+221(5)2(1)(2)1(1)x m D m m m ---==-+-+11211y D m m -==++（1）1,2,3m ≠--时，方程组有唯一解；（2）13m =-或方程组无解；（3）2m =-方程组有无穷解．8.4三阶行列式例题精讲【例1】按要求计算下列行列式（1）直接化简计算行列式D=412101423--的值；（2）按照第一行展开；（3）按照第一列展开．【参考答案】（1）19D = （2）011110324142421D --=-+（3）01242431214141D ---=-+-【例2】通过对课本知识的学习，我们知道，对于三元一次方程组⎪⎩⎪⎨⎧=++=++=++333322221111dz c y b x a d z c y b x a d z c y b x a ，其中x ，y ，z是未知数，系数)3,2,1(=i c b a i i i 、、不全为零，当系数行列式D=0时，方程组无解或有无穷多解．以下是几位同学在D =0的条件下，类比二元一次方程组的解的情况，对三元一次方程组的解的情况的一些探索结论：结论一：当D=0，且0===z y x D D D 时，方程组有无穷多解结论二：当D=0，且都z y x D D D ,,不为零时，方程组有无穷多解结论三：当D=0，且0===z y x D D D 时，方程组无解．可惜的是这些结论都不正确，下面分别给出了一些反例，现在请你分析一下，这些给出的方程组分别是哪个错误结论的反例，并说出你的理由．（A ）⎪⎩⎪⎨⎧=++=++=++232132032z y x z y x z y x （B ）⎪⎩⎪⎨⎧=+=++=+0420202y x z y x y x （C ）⎪⎩⎪⎨⎧=++=++-=+230212z y x z y x y x【参考答案】（A ）x y z D D D D ====而方程组无解，是结论一的反例．（B ）x y z D D D D ====而方程组无穷多解，是结论三的反例．（C ）0125x y z D D D D ====- 而方程无解，是结论二的反例．过关演练2020年一模汇编——矩阵、行列式一、填空题【宝山2】已知5124=--λλ，则=λ . 【答案】3【解析】由行列式的运算得：524=---)()(λλ，即3=λ【杨浦2】关于x ，y 的方程组2130x y x y -=⎧⎨+=⎩的增广矩阵为【答案】211130-⎛⎫⎪⎝⎭【解析】根据增广矩阵的含义，所以是211130-⎛⎫⎪⎝⎭【长宁，嘉定，金山3】行列式12 31-的值为_______.【答案】7【解析】行列式的化简，12 31-=711--32=⨯⨯）（【浦东4】若关于y x 、的方程组为12x y x y +=⎧⎨-=⎩，则该方程组的增广矩阵为____________．【答案】111112⎛⎫⎪-⎝⎭【解析】矩阵行列式定义【松江6】若关于x y 、的二元一次方程组42mx y m x my m+=+⎧⎨+=⎩无解，则实数m =【答案】2- 【解析】令24401m D m m==-=，2m ∴=±；令22420x m D m m mm+==-=，得0m =或2；令22201y m m D m m m+==--=，得2m =或1-；因为方程组无解，0D ∴=，x D 、y D 不同时为0，2m ∴=-二、选择题【黄浦13】方程2153x x=的解集是（）【A 】{2} 【B 】{2,2}- 【C 】{1,1}- 【D 】{i,i}- 【答案】B【解析】2235,2x x -==±，解集是{2,2}-2020届高三数学一轮复习典型题专项训练6、（2019届嘉定长宁区高三二模）若线性方程组的增广矩阵为2012m n ⎛⎫⎪⎝⎭，则m n +=7、（2019届普陀区高三二模）行列式中第2行第1列元素的代数余子式的值为﹣10，则k＝．8、（2019届徐汇区高三二模）函数cos2sin ()3cos x xf x x-=在区间(0,]2π上的最小值为9、（宝山区2018高三上期末）关于x y ，的二元一次方程组x y x y 341310+=⎧⎨-=⎩1、（2019届黄浦区高三二模）行列式1247的值为 2、（2019届闵行松江区高三二模）若x 、y 的方程组10240x my x y n +-=⎧⎨-+=⎩有无穷多组解，则11m n 的值为3、（2019届浦东新区高三二模）若行列式128012x -=，则x =4、（2019届杨浦区高三二模）函数arcsin 211xx y =-的值域是5、（2019届宝山区高三二模）方程sec 301sin x x=的解集为__________的增广矩阵为（）（A ）3411310-⎛⎫⎪-⎝⎭ （B ）3411310⎛⎫ ⎪--⎝⎭ （C ）3411310⎛⎫⎪-⎝⎭ （D ）3411310⎛⎫ ⎪⎝⎭10、（奉贤区2018高三上期末）关于x 、y 的二元一次方程组的增广矩阵是⎪⎪⎭⎫⎝⎛222111c b a c b a ，则方程组存在唯一解的条件是（）．A ．⎪⎪⎭⎫⎝⎛21a a 与⎪⎪⎭⎫ ⎝⎛21b b 平行 B ．⎪⎪⎭⎫ ⎝⎛21a a 与⎪⎪⎭⎫ ⎝⎛21c c 不平行 C ．⎪⎪⎭⎫ ⎝⎛21a a 与⎪⎪⎭⎫⎝⎛21b b 不平行 D ．⎪⎪⎭⎫ ⎝⎛21b b 与⎪⎪⎭⎫ ⎝⎛21c c 不平行 11、（杨浦区2018高三上期末）已知一个关于x 、y 的二元一次方程组的增广矩阵是112012-⎛⎫⎪⎝⎭，则x y += 12、（虹口区2019届高三一模）若复数sin i 1cos iz θθ-=（i 为虚数单位），则||z 的最大值为 13、（宝山区2019届高三上期末（一模））关于,x y 的二元一次方程组的增广矩阵为12-3015⎛⎫⎪⎝⎭，则x y += ．14、（奉贤区2019届高三上期末（一模））下列以行列式表达的结果中，与sin()αβ-相等的是（）A.sin sin cos cos αβαβ- B.cos sin sin cos βαβα C. sin sin cos cos αβαβ D. cos sin sin cos ααββ-15、（黄浦区2019届高三上期末（一模））已知三阶行列式123456789，元素8的余子式的值与代数余子式的值之和为16、（闵行区2019届高三上期末（一模））方程110322x =-的解为17、（浦东新区2019届高三上期末（一模））不等式2log 1021x >的解为18、（松江区2019届高三上期末（一模））若增广矩阵为1112m m m m +⎛⎫⎪⎝⎭的线性方程组无解，则实数m 的值为19、（徐汇区2019届高三上期末（一模））若数列{}n a 的通项公式为*2()111n na n N n n=∈+，则lim n n a →∞=___________.20、（杨浦区2019届高三上期末（一模））在行列式274434651xx--中，第3行第2列的元素的代数余子式记作()f x ，则1()y f x =+的零点是参考答案：二、行列式1、－12、33、34、14[,]22ππ-+ 5、,3x x k k Z ππ⎧⎫=-+∈⎨⎬⎩⎭6、37、－148、9、C 10、ｃ 11、－16012、1213、－8 14、C 15、0 16、2log 5x = 17、(4,)+∞ 18、－1 19、－1 20、－1。

上海高二数学矩阵及其运算有详细答案精品

版高二上数学矩阵及其运算一．初识矩阵（一）引入：引例1：已知向量()1,3OP =，如果把OP 的坐标排成一列，可简记为13⎛⎫ ⎪⎝⎭；引例2：2008记为：512128363836232128⎛⎫ ⎪ ⎪ ⎪⎝⎭；我们可将上表奖牌数简231324244x y mz x y z x y nz ++=⎧⎪-+=⎨⎪+-=⎩中未知数引例3：将方程组z y x ,,的系数按原来的次序排列，可简记为2332441m n ⎛⎫ ⎪- ⎪ ⎪-⎝⎭；若将常数项增加进去，则可简记为：2313242414m n ⎛⎫⎪- ⎪ ⎪-⎝⎭。

（二）矩阵的概念1、上述形如13⎛⎫ ⎪⎝⎭、512128363836232128⎛⎫ ⎪ ⎪ ⎪⎝⎭、2332441m n ⎛⎫ ⎪- ⎪ ⎪-⎝⎭、2313242414m n ⎛⎫⎪- ⎪ ⎪-⎝⎭这样的矩形数表叫做矩阵。

2、在矩阵中，水平方向排列的数组成的向量()12,,n a a a ⋅⋅⋅称为行向量；垂直方向排列的数组成的向量12n b b b ⎛⎫⎪ ⎪ ⎪⋅⋅⋅ ⎪⎝⎭称为列向量；由m 个行向量与n 个列向量组成的矩阵称为m n ⨯阶矩阵，m n ⨯阶矩阵可记做m n A ⨯，如矩阵13⎛⎫ ⎪⎝⎭为21⨯阶矩阵，可记做21A ⨯；矩阵512128363836232128⎛⎫ ⎪⎪ ⎪⎝⎭为33⨯阶矩阵，可记做33A ⨯。

有时矩阵也可用A 、B 等字母表示。

3、矩阵中的每一个数叫做矩阵的元素，在一个m n ⨯阶矩阵m n A ⨯中的第i （i m ≤）行第j （j n ≤）列数可用字母ij a 表示，如矩阵512128363836232128⎛⎫ ⎪⎪ ⎪⎝⎭第3行第2个数为3221a =。

4、当一个矩阵中所有元素均为0时，我们称这个矩阵为零矩阵。

如000000⎛⎫⎪⎝⎭为一个23⨯阶零矩阵。

5、当一个矩阵的行数与列数相等时，这个矩阵称为方矩阵，简称方阵，一个方阵有n 行（列），可称此方阵为n阶方阵，如矩阵512128363836232128⎛⎫ ⎪ ⎪ ⎪⎝⎭、2332441m n ⎛⎫⎪- ⎪ ⎪-⎝⎭均为三阶方阵。

上海高二数学矩阵及其运算(有详细答案)精品

上海版高二上数学矩阵及其运算一．初识矩阵（一）引入：引例1：已知向量()1,3OP =，如果把OP 的坐标排成一列，可简记为13⎛⎫⎪⎝⎭；引例2：2008我们可将上表奖牌数简记为：512128363836232128⎛⎫ ⎪⎪ ⎪⎝⎭；引例3：将方程组231324244x y mz x y z x y nz ++=⎧⎪-+=⎨⎪+-=⎩中未知数z y x ,,的系数按原来的次序排列，可简记为2332441m n ⎛⎫⎪- ⎪ ⎪-⎝⎭；若将常数项增加进去，则可简记为：2313242414m n ⎛⎫⎪- ⎪ ⎪-⎝⎭。

（二）矩阵的概念1、上述形如13⎛⎫ ⎪⎝⎭、512128363836232128⎛⎫ ⎪ ⎪ ⎪⎝⎭、2332441m n ⎛⎫ ⎪- ⎪ ⎪-⎝⎭、2313242414m n ⎛⎫⎪- ⎪ ⎪-⎝⎭这样的矩形数表叫做矩阵。

2、在矩阵中，水平方向排列的数组成的向量()12,,n a a a ⋅⋅⋅称为行向量；垂直方向排列的数组成的向量12n b b b ⎛⎫⎪ ⎪ ⎪⋅⋅⋅ ⎪⎝⎭称为列向量；由m 个行向量与n 个列向量组成的矩阵称为m n ⨯阶矩阵，m n ⨯阶矩阵可记做m n A ⨯，如矩阵13⎛⎫ ⎪⎝⎭为21⨯阶矩阵，可记做21A ⨯；矩阵512128363836232128⎛⎫ ⎪⎪ ⎪⎝⎭为33⨯阶矩阵，可记做33A ⨯。

有时矩阵也可用A 、B 等字母表示。

3、矩阵中的每一个数叫做矩阵的元素，在一个m n ⨯阶矩阵m n A ⨯中的第i （i m ≤）行第j （j n ≤）列数可用字母ij a 表示，如矩阵512128363836232128⎛⎫ ⎪⎪ ⎪⎝⎭第3行第2个数为3221a =。

4、当一个矩阵中所有元素均为0时，我们称这个矩阵为零矩阵。

如000000⎛⎫⎪⎝⎭为一个23⨯阶零矩阵。

5、当一个矩阵的行数与列数相等时，这个矩阵称为方矩阵，简称方阵，一个方阵有n 行（列），可称此方阵为n阶方阵，如矩阵512128363836232128⎛⎫ ⎪ ⎪ ⎪⎝⎭、2332441m n ⎛⎫⎪- ⎪ ⎪-⎝⎭均为三阶方阵。

上海版矩阵与行列式基础练习题

上海版矩阵与行列式基础练习题换的方法求解:⑴32110250x y x y --=⎧⎨+-=⎩； ⑵111612102113x y z ⎛⎫⎛⎫⎛⎫ ⎪⎪ ⎪-= ⎪⎪ ⎪ ⎪⎪ ⎪-⎝⎭⎝⎭⎝⎭.4、已知函数f(x)=x a x +1111111 ，其中a 是实数，求函数f(x)在区间[2,5]上的最小值。

5、计算D=a a aaa -----1101101的值6. 用行列式解下列方程组：（1）⎩⎨⎧=++=+-0162032y x y x ；（2）⎩⎨⎧=+=++5lg 4lg 301lg 5lg 2y x x y ．7. 若关于x 、y 、z 的方程组：⎪⎩⎪⎨⎧=+=++=++m z x mz m y x z y x 212有唯一解，求m 所满足的条件，并求出唯一解．8. 解关于x 、y 、z 的三元一次方程组⎪⎩⎪⎨⎧=+-=++=++31z y x a z ay x az y x ，并讨论解的情况．1． (上海 3) 若行列式417 5 x x 38 9中，元素4的代数余子式大于0，则x 满足的条件是______ 2．（2010年高考上海市理科4）行列式的值是。

3．（2010年上海市春季高考11) 方程的解集为。

4.(2011·上海)行列式⎪⎪⎪⎪⎪⎪a b c d (a ，b ，c ，d ∈{－1,1,2})所有可能的值中，最大的是________．5．(2012年高考上海卷理科3)函数1sin cos 2)(-= x x x f 的值域是 .6．【上海市青浦区2013届高三上学期期末文】若=642531222c b a 222222C c B b A a ++，则2C 化简后的最后结果等于____ _______．7．【上海市松江区2013届高三上学期期末文】若行列式,021421=-x 则=x ．计数原理(20131220)作业[1]10个人走进只有6把不同椅子的屋子，若每把椅子必须且只能坐一人，共有多少种不同的坐法？[2]从－3，－2，－1,0，1,2，3，4八个数字中任取3个不同的数字作为二次函数c+=2axbxy+的系数a，ｂ，ｃ的取值，问共能组成多少个不同的二次函数？[3]以三棱柱的顶点为顶点共可组成多少个不同的三棱锥？[4]4名男生和3名女生并坐一排，分别回答下列问题：（1）男生必须排在一起的坐法有多少种？（2）女生互不相邻的坐法有多少种？（3）男生相邻、女生也相邻的坐法有多少种？（4）男女生相间的坐法有多少种？（5）女生顺序已定的坐法有多少种？[5]某运输公司有7个车队，每个车队的车均多于4辆，现从这个车队中抽调出10辆车，并且每个车队至少抽调一辆，那么共有多少种不同的抽调方法？[6]用0,1，2，…，9这十个数字组成无重复数字的四位数，若千位数字与个位数字之差的绝对值是2，则这样的四位数共有多少个？7．某一天的课程表要排入语文、数学、英语、物理、体育、音乐6节课，如果第一节不排体育，最后一节不排数学，一共有多少种不同的排法？8.在7名运动员中选出4人组成接力队，参加4×10 0米接力赛，那么甲、乙两人都不跑中间两棒的安排方法有多少种？9．有5双不同型号的皮鞋，从中任取4只有多少种不同的取法？所取的4只中没有2只是同型号的取法有多少种？所取的4只中有一双是同型号的取法有多少种？10.一个五棱柱的任意两个侧面都不平行，且底面内的任意一条对角线与另一底面的边也不平行，以它的顶点为顶点的四面体有多少个？11.4名男生5名女生，一共9名实习生分配到高一的四个班级担任见习班主任，每班至少有男、女实习生各1名的不同分配方案共有多少种？12.有6本不同的书，分给甲、乙、丙三人.（1）甲、乙、丙三人各得2本，有多少种分法？（2）一人得1本，一人得2本，一人得3本，有多少种分法？（3）甲得1本，乙得2本，丙得3本，有多少种分法？（4）平均分成三堆，每堆2本，有多少种分法？矩阵与行列式(20131220)课后作业答案本试卷共18题，时间60分钟，满分100分）班级：姓名：一、填空选择题：（每题3分，共36分）1、已知46xAy⎛⎫= ⎪⎝⎭，13uBv⎛⎫= ⎪⎝⎭，且A B=，那么A+AB=⎪⎪⎭⎫ ⎝⎛36302026 。

行列式习题及答案

行列式习题及答案【篇一：上海版教材矩阵与行列式习题(有答案)】lass=txt>姓名成绩一、填空题cos1.行列式?3sincos?6sinac?3bd?6的值是 .2.行列式（a,b,c,d?{?1,1,2}）的所有可能值中，最大的是 .?2x?0?3.将方程组?3y?z?2写成系数矩阵形式为 .?5x?y?3?4.若由命题a:“2x31-x20”能推出命题b:“x?a”，则a的取值范围是．?a1x?b1y?c15.若方程组?的解为x?1,y?2，则方程组ax?by?c?222?2b1x?5a1y?3c1?0的解为x? ，y? . ?2bx?5ay?3c?022?26.方程2x4x2?0的解集为.?39?2x1 y1x3 y3?4x1 y1x2 y27.把x2 y2x3 y3表示成一个三阶行列式为. 8.若?abc的三个顶点坐标为a(1,?2),b(?2,3),c(?4,?5)，其面积为 .2x9.在函数f?x???x1?x2?1x中x3的系数是 x110.若执行如图1所示的框图，输入x1?1,x2?2,x3?4,x4?8,则输出的数等于111.矩阵的一种运算???ab??x??ax?by??ab??????????,该运算的几何意义为平面上的点在矩阵的作用下(x,y)????????cd??y??cx?dy??cd??1a???的作用下变换成曲线x?y?1?0，则a?b的b1??变换成点(ax?by,cx?dy)，若曲线x?y?1?0在矩阵??值为 .12.在集合?1,2,3,4,5?中任取一个偶数a和奇数b构成以原点为起点的向量???a,b?.从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形，记所有作成的平行四边形的个数为n，其中面积不超过．．．4的平行四边形的个数为m，则m?n二.选择题13.系数行列式d?0是三元一次方程组无解的（） a. 充分非必要条件 b. 必要非充分条件c. 充分必要条件d. 既非充分也非必要条件 14.下列选项中错误的是（）. a.abccacbdd??caddbb.abcd?dcbac.a?3cb?3d?acbdd.???a?c?b?d15.若a,b,c表示?abc的三边长，aa2且满足ba?b?ca?b?c?0， a?b?cb2c2c则?abc是（）.a. 等腰三角形b. 直角三角形c. 等腰直角三角形d. 等边三角形 16. 右边（图2）的程序框图输出结果s?（） a．20 b. 35 c. 40 d .45 2图2三、解答题：1?|x|?5?1??mx?217. 已知p：矩阵?|x|?1的某个列向量的模不小于，行列式q：2?01?余子式的值不小于2.若p是q成立的充分条件，求实数m的取值范围. ．．．．18.已知等比数列{an}的首项a1?1，公比为q，（1）求二阶行列式?10?24?3中元素?1的代数1a1a2a3a4的值；（2）试就q的不同取值情况，讨论二元一次方程组??a1x?a3y?3何时无解，何时有无穷多解？?a2x?a4y??2119.已知函数f(x)?0sinxsinx0xsinx0的定义域为?0,2m???，最大值为4.试求函数g(x)?msinx?2cosx?2??（x?r）的最小正周期和最值．320. 将等差数列an?2n?1(n?n)中n2个项依次排列成下列n行n列的方阵,在方阵中任取一个元素,记为x1,划去x1所在的行与列,将剩下元素按原来得位置关系组成(n-1)行(n-1)列方阵,任取其中一元素x2,划去x2所在的行与列?,将最后剩下元素记为xn,记sn?x1?x2??xn，求lim*n??sn的值。

（完整版）第一章行列式与矩阵的计算的练习（含答案）

（完整版）第一章行列式与矩阵的计算的练习（含答案）行列式及矩阵的计算（课堂练习）一、填空1．已知三阶方阵A 的行列式为3，则2A -= -242. 设12,01A -??= 1()32x g x x -=-+，则()g A =0800-??3．设,,αβγ为3维列向量，记矩阵(,,),(,,)A B αβγαββγγα==+++，若3,A B =则=,,,,6αβγβγα+=4.行列式11111111---x 的展开式中,x 的系数是 2 . 5．设???? ??=1201A 则=kA 1021k ??。

（k 为正整数）. 6．设321,,ααα,21,ββ都是四维列向量，且四阶行列式1123,,,m αααβ=，1232,,,n αααβ=,则12312,,,2αααββ-=16m n +解：11231232,,,2,,,Dαααβαααβ=+-14412312322,,,(1),,,16m n αααβαααβ=+-=+7. 已知四阶行列式D 中第三列元素分别为1，3，-2，2，它们对应的余子式分别为3，-2，1，1，则行列式D =－3 .解：D ＝1×3＋3×（－2）＋（－2）×1＋2×1＝－3二、判断题1．设A 、B 均为n 阶方阵，则A B A B =.（× ）2．设A 、B 均为n 阶方阵，则AB A B =. （√ ）三、行列式计算（1）4333343333433334ΛΛΛΛΛΛΛΛΛ=n D 解：nD n c c c c c c +++13121M 43313343133341333313ΛΛΛΛΛΛΛΛΛ++++n n n n 11312r r r r r r n ---M 10100001033313ΛΛΛΛΛΛΛΛΛ+n =13+n （2）11111231149118271D --=--解：（范得蒙行列式）＝（－1－3）（－1＋2）（－1－1）（3＋2）（3－1）（－2－1）＝－240五、a 为何值时，线性方程组：-=++=++=++aax x x x ax x x x x a 322321321321有唯一解？解：2)1)(2(111111det -+==a a aa a A ，2-≠a 且1≠a 时，有唯一解.。

专题14 矩阵与行列式(习题)-2021届沪教版高考数学一轮复习(上海专用)

2021届高考数学一轮复习专题14 矩阵与行列式一、填空题1．（2020·上海普陀·三模）满足sin 0cos xx =的实数x 的取值范围是______．【答案】,3x k k Z ππ=+∈【解析】试题分析：sin 0x x =，即，∴,3x k k Z ππ=+∈．2．（2020·宝山·上海交大附中高三其他）已知方程102x b x -=-的一个根是2a i +（其中a R ∈，i 是虚数单位），则实数b =______. 【答案】5 【解析】解：()212202x x x b x x b b x -=-+=-+=-，因为2a i +是方程的一个根，所以()()22220a i a i b +-++=，即()224440a a b a i -+-+-=，所以，解得，故答案为:5.3．（2020·上海杨浦·复旦附中高三期末）在行列式21406532020x--中，第三行第二列的元素3的代数余子式的值为4，则实数x 的值为______. 【答案】2 【解析】在行列式21406532020x--中，第三行第二列的元素3的代数余子式的值为4，则2124446xx --=-=-，解得2x =.故答案为：2.4．（2020·上海高三专题练习）当实数m ________时，方程组有唯一解．【答案】1m ≠- 【解析】因为有唯一解，所以，即22(1)(1)(1)0101m m m m m m --+++≠⇒+≠⇒≠-. 故答案为：1m ≠-5．（2020·上海高三专题练习）若行列式，则．【答案】2或3- 【解析】由题意得，所以260x x +-=，解得2或3-．6．（2020·上海高三专题练习）关于x ，y 的方程组无实数解，则m =________．【答案】【解析】解：列出行列式系数：114a =，12a m =，21b m =， 21a m =，221a =，22b =，则()()244221mD m m m m ==-=+-， ()222212x m m D m m m m ==-=-，()()232482422y m D m m m m m ==-=-++，当0D =，0x D ≠时，原方程组无解，即当2m =-时，成立，则当2m =-时，方程组无实数解. 故答案为：.7．（2018·上海交通大学附属中学嘉定分校高三其他）设函数()312xxf x ==，则x =_______.【答案】94【解析】()231x f x x ==-=，即230x =，即，0x ≥，32=，解得94x =. 故答案为：94. 8．（2020·上海高三一模）已知4251λλ-=-，则λ=________ 【答案】3 【解析】解：4251λλ-=-，解得3λ=，故答案为：3．9．（2020·上海闵行·高三一模）设函数 11-，则方程()1f x =的解为____________【答案】2x = 【解析】由题意得，即22x x -=，解得2x =或1x =-，由函数定义域可知2x =. 故答案为：2x =.10．（2016·上海徐汇·高三一模（文））若三条直线30ax y ++=，20x y ++=和210x y -+=相交于一点，则行列式111a 的值为________________.【答案】1 【解析】先由三条直线30ax y ++=，20x y ++=和210x y -+=相交于一点，求出a ，再由二阶行列式的计算法则可计算出行列式111a 的值.联立，解得，由于三条直线30ax y ++=，20x y ++=和210x y -+=相交于一点，所以，直线30ax y ++=过点，则130a --+=，解得2a =，因此，212111111=⨯-⨯=. 故答案为：1.11．（2020·上海杨浦·高三二模）行列式120235580=_______.【答案】10 【解析】．故答案为：10．12．（2020·上海虹口·高三二模）设复数cos sin i z iαα=（i 为虚数单位），若，则tan 2α=________.【答案】1 【解析】因为，又，所以，所以22cos 1sin 20αα--=，即cos 2sin 20αα-=，所以. 故答案为：113．（2018·上海徐汇·高二期末）行列式63125142k --中元素3-的代数余子式的值为5，则k =________．【答案】1 【解析】行列式63125142k --中元素3-的代数余子式为()()12214512kk +-=---=-，解得1k =.故答案为：1.14．（2019·上海市建平中学高三月考）已知数列满足()1*12452n n nn a a n N a a ++--=∈-，则使20192019a >成立的正整数1a 的最小值为__________. 【答案】2019 【解析】由题可知，()()21245n n n a a a +---=，变形可得，即数列{}2n a -是一个首项为，公差是1的等差数列，故有故答案为：2019二、单选题15．（2020·上海高三专题练习）已知，(3,1)AC =-，则△ABC 的面积为（）． A ．5631-B ．3516- C ． D ．【答案】C 【解析】设的夹角为α，先求出sin α=232ABCS =，又，即得解. 设的夹角为α，所以5cos ||||AB AC AB ACα⨯===所以，所以12322ABCS==.又.所以△ABC 的面积为. 故选：C.16．（2020·上海高三专题练习）三阶行列式中，1b 的代数余子式是（）． A ．1122a c a c B ． C ． D ．1122c a c a【答案】C 【解析】行列式1b 的代数余子式是()222222333313321a c a c c a a c a c c a +=-=-.故选：C.17．（2020·上海高三专题练习）已知()11,AB x y =，，则三个不同点A ，B ，C 共线是11220x y x y =的（）．A ．充要条件B ．充分非必要条件C ．必要非充分条件D ．既非充分又非必要条件【答案】A 【解析】解：∵()11,AB x y =，，由A ，B ，C 共线得，， ∴12210x y x y -=，又由11220x y x y =得，12210x y x y -=，∴三个不同点A ，B ，C 共线是11220x y x y =的充要条件，故选：A ．18．（2020·上海高二课时练习）已知ABC 的三边长为,,a b c ，且，则ABC 的形状为（）. A ．等腰三角形 B ．等边三角形C ．直角三角形D ．等腰直角三角形【答案】B 【解析】2221101a cb a a bc ac ab bc c b =++---=，所以222()()()0a b b c c a -+-+-=，所以a b c ==，所以ABC 是等边三角形．故选：B ．三、解答题19．（2020·上海高三专题练习）已知三角形三边的和6a b c ++=，又0a b cca b b c a=，求各边之长．【答案】2a b c === 【解析】因为0a b cca b b ca=，所以3333a b c abc ++=，又因为3333a b c abc +≥+，当且仅当a b c ==时，取等号，又因为6a b c ++=，所以2a b c ===，20．（2020·上海高三专题练习）判别关于x ，y 的二元一次方程组解的情况，并解方程组：．【答案】当0m =时，0x =，y R ∈，有无穷多解；当1m =时，无解；当0m ≠且1m ≠时，有唯一解22(2)(1)m m x m -=-，【解析】因为，所以22221(1)(1)(1)1m m m D m m m m m m m--==---=-233322(1)(2)x m m m D m m m m m m m -==--=-，32221(1)1y m m D m m m m m m m -==--=--，当0m ≠且1m ≠时，0D ≠，方程组有唯一解22(2)(1)m m x m -=-，；.当0m =时，0,0x y D D D ===，方程组有无穷多解0x =，y R ∈；当1m =时，0,0x D D =≠，方程组无解；综合得：当0m =时，0x =，y R ∈，有无穷多解；当1m =时，无解；当0m ≠且1m ≠时，有唯一解22(2)(1)m m x m -=-，. 21．（2020·上海高三专题练习）化简：．【答案】0 【解析】由三阶行列式的计算方法，可得：原式sin()sin cos sin sin cos()cos 2cos sin cos βϕβββααϕϕϕϕϕ-=-+cos sin()cos sin cos 2ββϕαϕϕ-+cos [cos cos 2sin()sin ]αβϕβϕϕ+--.22．（2020·上海高三专题练习）直线y x =与双曲线221x y -=交于点B ，C ，点A 的坐标为，求ABC 的面积．【答案】2【解析】由题意联立方程组可得(B ，(2,C -，进而可得(1,1)AB =-，(3,1)AC =--，再利用111231ABCS -=--△即可得解.由，得2114x =,解得2x =±,不妨设(B，(2,C -，则(1,1)AB =-，(3,1)AC =---， ∴.23．（2018·cos 0.5sin 0(0)1cos A x A A xA x>按第一列展开得1121312M M -+，记函数1121()f x M M =+，且()f x 的最大值是4. (1)求A ；(2)将函数的图像向左平移12π个单位，再将所得图像上各点的横坐标扩大为原来的2倍，纵坐标不变，得到函数()y g x =的图像，求()g x 在上的值域. 【答案】（1）A =2）【解析】（1）先根据行列式，求出函数()f x ，再利用二倍角公式，辅助角公式化简，结合()f x 的最大值是4，即可求A ；（2）向左移12π得4sin 212y x π⎛⎫=- ⎪⎝⎭，横坐标变为原来2倍得()4sin 12g x x π⎛⎫=-⎪⎝⎭因为，所以，所以. 解(1)11sin 0sin cos 1cos A x M A x x x==，221cos cos 221cos AA x A M A x x=-=-+，max 4f ==，所以A =(2)向左移12π得4sin 212y x π⎛⎫=- ⎪⎝⎭，横坐标变为原来2倍得()4sin 12g x x π⎛⎫=- ⎪⎝⎭因为，所以，所以24．（2018·上海静安·高三二模）设函数（a 为实数）. （1）若1a =-，解不等式()0f x ≥；（2）若当01xx>-时，关于x 的不等式()1f x ≥成立，求a 的取值范围；（3）设，若存在x 使不等式成立，求a 的取值范围. 【答案】(1)8{|3x x ≤或6}x ≥;(2)[5,)-+∞;(3)[4,)-+∞ 【解析】(1)代入1a =-直接解不等式即可; (2)由01xx>-解得01x <<,故可将()1f x ≥化为,从而求出a 的范围; (3)化简()g x ,故可将题设条件变为:存在x 使成立,因此求出2722x x ---的最小值即可得出结论. (1)若1a =-,则由()0f x ≥得, 即或,解得6x ≥或83x ≤, 故不等式的解集为8{|3x x ≤或6}x ≥; (2)由01xx>-解得01x <<, 由()1f x ≥得,当01x <<时,该不等式即为, 设()(2)7F x a x =-+,则有解得5a ≥-,因此实数a 的取值范围为[5,)-+∞; (3),若存在x 使不等式()()f x g x ≤成立, 即存在x 使271x ax -++成立, 即存在x 使成立, 又, 所以,所以15a -≥-,即4a ≥-, 所以a 的取值范围为:[4,)-+∞。

上海高二数学矩阵及其运算(有详细答案)精品-推荐下载

叫做方程组的系数矩阵；而矩阵
（三）、应用举例：

4z

2
中未知数
2 3 m 1

3 4
2 1
x,
4 n
y,
z
2 4
的系数按原来的次序排列所得的矩阵

叫做方程组的增广矩阵。
例 1、下表是我国第一位奥运会射箭比赛金牌得主张娟娟与对手韩国选手朴成贤在决赛中的各阶段成绩表：
（1）将两人的成绩各阶段成绩用矩阵表示；
0 1

2 1 0 2

0 3
3 0
为单位矩阵，且
2 2
13
,

（四）、课堂练习：
1、请根据游戏“剪刀、石头、布”的游戏规则，作出一个 3 阶方阵（胜用 1 表示，输用 1 表示，相同则为 0）。
2、奥运会足球比赛中国队所在 C 组小组赛单循环比赛结果如下：

2
,

比利时胜新西兰 0∶1
，求
sin

的值。
（1）试用一个 4 阶方阵表示这 4 个队之间的净胜球数；（以中国、巴西、比利时、新西兰为顺序排列）（2）若胜一场可得 3 分，平一场得 1 分，负一场得 0 分，试写出一个 4 阶方阵表示各队的得分情况；（排列顺
一．初识矩阵
（一）引入：
引例
1：已知向量
OP

1,
3，如果把
引例 2：2008 年北京奥运会奖牌榜前三位成绩如下表：
引例
我们可将上表奖牌数简记为：
3：将方程组
2x 3y mz 1
3x 4x
将常数项增加进去，则可简记为：
（二）矩阵的概念

上海版教材矩阵与行列式习题(有答案)

上海版教材矩阵与行列式习题（有答案）矩阵、行列式和算法（20221224）姓名成绩一、填空题co1.行列式3inco6in36的值是.2.行列式ab（a,b,c,d{1,1,2}）的所有可能值中，最大的是.cd2某03.将方程组3yz2写成系数矩阵形式为.5某y34.若由命题A:“2某>0”能推出命题B:“某a”，则a的取值范围是．31-某2开始a1某b1yc15.若方程组的解为某1,y2，则方程组a某byc2222b1某5a1y3c10的解为某，y.2b2某5a2y3c2016.方程1输入某1,某2,某3,某4i1,某024某某20的解集为.139某某某iii1i4是否某某47.把某2y2某3y32某1y1某3y34某1y1某2y2表示成一个三阶行列式为.8.若ABC的三个顶点坐标为A(1,2),B(2,3),C(4,5)，其面积为.2某9.在函数f某某1某21某中某3的系数是.某输出某1结束图110.若执行如图1所示的框图，输入某11,某22,某34,某48,则输出的数等于.11.矩阵的一种运算ab某a某byab该运算的几何意义为平面上的点在矩阵的作用下(某,y),cdyc某dycd1a的作用下变换成曲线某y10，则ab的b1变换成点(a某by,c某dy)，若曲线某y10在矩阵值为.12.在集合1,2,3,4,5中任取一个偶数a和奇数b构成以原点为起点的向量a,b.从所有得到的以原点为起点的向量中任取两个向量为邻边作平行四边形，记所有作成的平行四边形的个数为n，其中面积不超过．．．4的平行四边形的个数为m，则mn二.选择题13.系数行列式D0是三元一次方程组无解的（）A.充分非必要条件B.必要非充分条件C.充分必要条件D.既非充分也非必要条件14.下列选项中错误的是（）.A.abcdcdababdbB.cdcaa3cb3dabC.cdcdD.开始ababcdcdi0S015.若a,b,c表示ABC的三边长，aa22且满足bbcc2abcabc0，abcSS2i1ii2否则ABC是（）.A.等腰三角形B.直角三角形C.等腰直角三角形D.等边三角形16.右边（图2）的程序框图输出结果S（）A．20B.35C.40D.45三、解答题：i8是输出S结束图21|某|51m2某217.已知P：矩阵|某|1的某个列向量的模不小于，行列式Q：012余子式的值不小于2.若P是Q成立的充分条件，求实数m的取值范围.．．．．18.已知等比数列{an}的首项a11，公比为q，（1）求二阶行列式1403中元素1的代数21a1a2a3a4的值；（2）试就q的不同取值情况，讨论二元一次方程组a1某a3y3何时无解，何时有无穷多解？a2某a4y2119.已知函数f(某)0in某3co某in某0in某2m0的定义域为0,，最大值为4.试求函数g(某)min某2co某2（某R）的最小正周期和最值．20.将等差数列an2n1(nN)中n个项依次排列成下列n行n列的方阵,在方阵中任取一个元素,记为某1,某2划去某1所在的行与列,将剩下元素按原来得位置关系组成(n-1)行(n-1)列方阵,任取其中一元素某2,划去某2所在的行与列,将最后剩下元素记为某n,记Sn某1某2某n，求limnSn的值。

上海矩阵与行列式基础练习题

上海版矩阵与行列式基础练习题————————————————————————————————作者：————————————————————————————————日期：矩阵与行列式习题本试卷共18题，时间60分钟，满分100分）班级：姓名：一、填空选择题：（每题3分，共36分）1、已知46x A y ⎛⎫= ⎪⎝⎭，13u B v ⎛⎫= ⎪⎝⎭，且A B =，那么A+AB= 。

2、设231001252437A B -⎛⎫⎛⎫⎪⎪==- ⎪⎪ ⎪ ⎪-⎝⎭⎝⎭，则3A –4B 为。

3、设A 为二阶矩阵，其元素满足，0a a ji ij =+，i=1，2，j=1，2，且2a a 2112=-，那么矩阵 A= .4、设2442,1221A B -⎛⎫⎛⎫== ⎪ ⎪-⎝⎭⎝⎭則32A B - = ,=AB ，=BA5、若点A 在矩阵1222-⎡⎤⎢⎥-⎣⎦对应的变换作用下得到的点为（3，- 4），那么点A 的坐标为 .6、若202137x y -⎛⎫⎛⎫⎛⎫=⎪⎪ ⎪-⎝⎭⎝⎭⎝⎭，则x y +=___________. 7、1212a a b b =1,则12122233b b a a =-- _____ 。

8、（1）行列式z kc c y kb b xka a = ；（2）211121__________112-= 9、已知124221342D -=---，则21a 的代数余子式21A = 。

10、已知2413201x x 的代数余子式012=A ，则代数余子式=21A11、设A 为3阶方阵，且3A =，则2A -=______________12、如果方程组⎩⎨⎧=++=++0101dy cx by ax 的系数行列式1=d c b a ，那么它的解为二、简答题（每题8分，共64分）1、已知⎪⎪⎭⎫⎝⎛-=533201A ⎪⎪⎪⎭⎫⎝⎛-=013164245B 求()AB .2.已知1011A ⎛⎫= ⎪⎝⎭，分别计算23A A 、，猜测*(2)n A n n ≥∈N ，；3. 将下列线性方程组写成矩阵形式，并用矩阵变换的方法求解:⑴ 32110250x y x y --=⎧⎨+-=⎩；⑵111612102113x y z ⎛⎫⎛⎫⎛⎫⎪⎪ ⎪-= ⎪⎪ ⎪ ⎪⎪ ⎪-⎝⎭⎝⎭⎝⎭.4、已知函数f(x)=xa x+1111111 ，其中a 是实数，求函数f(x)在区间[2,5]上的最小值。

2020届上海(沪教版)高考考典——第8章-矩阵和行列式初步教师版

第8章矩阵和行列式初步考点解读1.理解矩阵的有关概念（1）矩阵的定义：由m n⨯个数(1,2,3,;1,2,3,)ija i m j n==L L，按一定次序排列成的矩阵表111212122212()nnij m nm m mna a aa a aA aa a a⨯⎛⎫⎪⎪==⎪⎪⎝⎭LLL L L LL，叫做一个m行n列的矩阵，简记为m n⨯矩阵.（2）在一般矩阵中，矩阵中的每个数叫做矩阵的元素；线性方程组11112211211222221122n nn nm m mn n ma x a x a x ba x a x a x ba x a x a x b++=⎧⎪++=⎪⎨⎪⎪++=⎩LLL LL，矩阵A=111212122212nnm m mna a aa a aa a a⎛⎫⎪⎪⎪⎪⎝⎭LLL L L LL叫做一般线性方程组的系数矩阵，A-=11121121222212nnm m ma a a ba a a ba a b⎛⎫⎪⎪⎪⎪⎝⎭LLL L L L LL L叫做一般线性方程组的增广矩阵；如：方程组2538x yx y-=⎧⎨+=⎩对应系数矩阵1231-⎛⎫⎪⎝⎭，其中1行2列的矩阵()()1,2,3,1-叫做系数矩阵的两个行向量；2行1列的矩阵12,31-⎛⎫⎛⎫⎪ ⎪⎝⎭⎝⎭叫做系数矩阵的列向量；（3）当矩阵的行数与列数相等时，该矩阵称为方矩阵，简称方阵；我们把主对角线元素为1、其余元素均为零的方矩阵，如1001⎛⎫⎪⎝⎭，叫做单位矩阵.2.矩阵的运算及其性质（1）矩阵的加法，若111212122212()n n ij m nm m mn a a a a a a A a a a a ⨯⎛⎫⎪ ⎪== ⎪⎪⎝⎭L L L L L L L，111212122212()n n ij m n m m mn b b b b b b B b b b b ⨯⎛⎫ ⎪⎪== ⎪ ⎪⎝⎭LL L LL L L，则C A B =+=111112121121212222221122n n n n m m m m mn mna b a b a b a b a b a b a b a b a b +++++++++L LL L L L L.（2）矩阵的加法满足性质: 交换律,结合律.（3）数与矩阵乘法定义：以数k 乘矩阵()ij A a =的每个元素所得的矩阵()ij ka 叫做数k 与矩阵A 相乘的积，记作kA ；（4）设矩阵111211121112212221222122,,a a b b c c A B C a a b b c c ⎛⎫⎛⎫⎛⎫=== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.如果它们元素间的关系可以用下列等式表示：1122(1,2;1,2)ij i j i j c a b a b i j =+==，则C 叫做矩阵A 和矩阵B 的积，记作C =AB（5）矩阵A 的初等变换，指的是对A 实施如下变换：3．行列式的有关概念与性质（1）初中代数中，二元线性方程组111222,a x b y c a x b y c +=⎧⎨+=⎩当12210a b a b -≠时，二元线性方程组有唯一解：1221122112211221c b c b x a b a b a c a c y a b a b -⎧=⎪-⎪⎨-⎪=⎪-⎩，为了方便记忆，引入定义a c b d =ad bc -，a c b d 叫做二阶行列式， ad bc -叫做二阶行列式的展开式；设1122a b D a b =，1122x c b D c b =，1122y a c D a c =，则方程组的唯一解可表示为：xy D x D D y D⎧=⎪⎪⎨⎪=⎪⎩. （i ）0D ≠，方程组有唯一解；（ii ）0D =：①x y D D 、中至少有一个不为零，方程组无解； ②0x y D D ==，方程组有无穷多解.（3）三阶行列式的两种展开方法：①按对角线展开.123123123a b c b c a c a b=++321123132a b c b a c a b c---②按一行（或一列）展开.111222333a b ca b ca b c=123231312321213132a b c a b c a b c a b c a b c a b c++---123321322312332()()()a b c b c b a c a c c a b a b=-+-+-(4)把三阶行列式某元素所在的行和列划去，剩下的元素组成的二阶行列式，叫做这个元素的余子式；如果用,i j分别表示某个元素所在的行数和列数，那么这个元素的余子式．补充与提高：行列式运算性质：①把行列式的某一行的所有元素乘以一个数k，等于用k乘以这个行列式；②行列式中某一行所有元素的公因子可以提到行列式记号的外边；③如果行列式中某一行的元素全为0，那么这个行列式的值为0；④交换行列式的任意两行，行列式的绝对值不变，符号相反；⑤如果行列式有两行的对应元素相同，那么这个行列式的值为0；⑥如果行列式有两行的对应元素成比例，那么这个行列式的值为0；⑦如果行列式的某一行的元素都是二项式，那么这个行列式等于把这些二项式各取一项组成相应的行，而其余行不变的两个行列式的和；例如：111222222333a b ca ab bc ca b c'''+++=111222333a b ca b ca b c+111222333a b ca b ca b c'''.注意：红线上三元素的乘积均为正，蓝线上三元素的乘积均为负.乘以(1)i j+-所得的式子，叫做这个元素的代数余子式.（5）三阶行列式D 等于它的任意一行（或列）的所有元素分别和它们的代数余子式的乘积的和.例如：111222333a b c D a b c a b c ==222222a A b B c C ++.(6)三元线性方程组111122223333a x b y c z d a x b y c z d a x b y c z d ++=⎧⎪++=⎨⎪++=⎩，对应系数行列式111222333a b c D a b c a b c =,111222333x d b c D d b c d b c =，111222333y a d c D a d c a d c =，111222333z a b d D a b d a b d =.①当0D ≠时，方程组有唯一解x y z D x D D y D D z D ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩；②当0=0x y D D D =且，时，方程组有无穷多解；③当0x y D D D =且，不全为0时，方程组无解.(7)①三角形的面积公式: △ABC 的三个顶点坐标分别为112233(,),(,),(,)A x y B x y C x y ，则ABC S =△11223311121x y x y x y .②同一平面上A B C 、、三点共线的充要条件为112233111x y x y x y =0.8.1矩阵的概念例题精讲【例1】写出下列线性方程组的系数矩阵和增广矩阵：（1）3560437x y x y ++=⎧⎨=-⎩（2）214625x z y z x y z -=⎧⎪+=⎨⎪-+=⎩一个元素的代数余子式通常用这个元素相应的大写字母并附加相同的下标来表示【参考答案】（1）35356,43437-⎛⎫⎛⎫ ⎪ ⎪---⎝⎭⎝⎭ （2）1021021014,01462112115--⎛⎫⎛⎫⎪ ⎪⎪ ⎪ ⎪ ⎪---⎝⎭⎝⎭8.2矩阵的运算例题精讲【例1】已知矩阵 3 0-2 1A ⎛⎫= ⎪⎝⎭，矩阵-2 1 2 2B ⎛⎫= ⎪⎝⎭，求矩阵X ，使其满足B X A =-32．【参考答案】813320⎛⎫-⎪ ⎪ ⎪-⎝⎭【例2】已知下列矩阵⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎪⎭⎫ ⎝⎛--=⎪⎪⎭⎫ ⎝⎛--=3110146,602413,591732C B A ，计算：（1）A(B+C) (2)(B+C)A (3)BA+CA (4)从（1）（2）（3）的计算结果你能得出什么结论？【参考答案】（1）1198245⎛⎫ ⎪⎝⎭ （2）151842234610131133---⎛⎫ ⎪-- ⎪ ⎪---⎝⎭ （3）151842234610131133---⎛⎫ ⎪-- ⎪ ⎪---⎝⎭（4）(B+C)A= BA+CA8.3二阶行列式例题精讲【例1】展开并化简下列行列式：（1）3423- （2）245lg 2lg - 【参考答案】（1）17- （2）2lg 24lg5+【例2】判断m 取什么值时，下列关于x,y 的线性方程组（1）有唯一解？（2）无解？（3）有无穷解？⎪⎩⎪⎨⎧=+-+-=--1)1()1(1)5(22y m x m y m x【参考答案】221(5)(1)(2)(3)1(1)m D m m m m m --==++-+-+221(5)2(1)(2)1(1)x m D m m m ---==-+-+11211y D m m -==++（1）1,2,3m ≠--时，方程组有唯一解；（2）13m =-或方程组无解；（3）2m =-方程组有无穷解．8.4三阶行列式例题精讲【例1】按要求计算下列行列式（1）直接化简计算行列式D=412101423--的值；（2）按照第一行展开；（3）按照第一列展开．【参考答案】（1）19D = （2）011110324142421D --=-+（3）01242431214141D ---=-+-【例2】通过对课本知识的学习，我们知道，对于三元一次方程组⎪⎩⎪⎨⎧=++=++=++333322221111dz c y b x a d z c y b x a d z c y b x a ，其中x ，y ，z是未知数，系数)3,2,1(=i c b a i i i 、、不全为零，当系数行列式D=0时，方程组无解或有无穷多解．以下是几位同学在D =0的条件下，类比二元一次方程组的解的情况，对三元一次方程组的解的情况的一些探索结论：结论一：当D=0，且0===z y x D D D 时，方程组有无穷多解结论二：当D=0，且都z y x D D D ,,不为零时，方程组有无穷多解结论三：当D=0，且0===z y x D D D 时，方程组无解．可惜的是这些结论都不正确，下面分别给出了一些反例，现在请你分析一下，这些给出的方程组分别是哪个错误结论的反例，并说出你的理由．（A ）⎪⎩⎪⎨⎧=++=++=++232132032z y x z y x z y x （B ）⎪⎩⎪⎨⎧=+=++=+0420202y x z y x y x （C ）⎪⎩⎪⎨⎧=++=++-=+230212z y x z y x y x【参考答案】（A ）x y z D D D D ====而方程组无解，是结论一的反例．（B ）x y z D D D D ====而方程组无穷多解，是结论三的反例．（C ）0125x y z D D D D ====- 而方程无解，是结论二的反例．过关演练2020年一模汇编——矩阵、行列式一、填空题【宝山2】已知5124=--λλ，则=λ . 【答案】3【解析】由行列式的运算得：524=---)()(λλ，即3=λ【杨浦2】关于x ，y 的方程组2130x y x y -=⎧⎨+=⎩的增广矩阵为【答案】211130-⎛⎫⎪⎝⎭【解析】根据增广矩阵的含义，所以是211130-⎛⎫⎪⎝⎭【长宁，嘉定，金山3】行列式12 31-的值为_______.【答案】7【解析】行列式的化简，12 31-=711--32=⨯⨯）（【浦东4】若关于y x 、的方程组为12x y x y +=⎧⎨-=⎩，则该方程组的增广矩阵为____________．【答案】111112⎛⎫⎪-⎝⎭【解析】矩阵行列式定义【松江6】若关于x y 、的二元一次方程组42mx y m x my m+=+⎧⎨+=⎩无解，则实数m =【答案】2- 【解析】令24401m D m m==-=，2m ∴=±；令22420x m D m m mm+==-=，得0m =或2；令22201y m m D m m m+==--=，得2m =或1-；因为方程组无解，0D ∴=，x D 、y D 不同时为0，2m ∴=-二、选择题【黄浦13】方程2153x x=的解集是（）【A 】{2} 【B 】{2,2}- 【C 】{1,1}- 【D 】{i,i}- 【答案】B【解析】2235,2x x -==±，解集是{2,2}-2020届高三数学一轮复习典型题专项训练6、（2019届嘉定长宁区高三二模）若线性方程组的增广矩阵为2012m n ⎛⎫⎪⎝⎭，则m n +=7、（2019届普陀区高三二模）行列式中第2行第1列元素的代数余子式的值为﹣10，则k＝．8、（2019届徐汇区高三二模）函数cos2sin ()3cos x xf x x-=在区间(0,]2π上的最小值为9、（宝山区2018高三上期末）关于x y ，的二元一次方程组x y x y 341310+=⎧⎨-=⎩1、（2019届黄浦区高三二模）行列式1247的值为 2、（2019届闵行松江区高三二模）若x 、y 的方程组10240x my x y n +-=⎧⎨-+=⎩有无穷多组解，则11m n 的值为3、（2019届浦东新区高三二模）若行列式128012x -=，则x =4、（2019届杨浦区高三二模）函数arcsin 211xx y =-的值域是5、（2019届宝山区高三二模）方程sec 301sin x x=的解集为__________的增广矩阵为（）（A ）3411310-⎛⎫⎪-⎝⎭ （B ）3411310⎛⎫ ⎪--⎝⎭ （C ）3411310⎛⎫⎪-⎝⎭ （D ）3411310⎛⎫ ⎪⎝⎭10、（奉贤区2018高三上期末）关于x 、y 的二元一次方程组的增广矩阵是⎪⎪⎭⎫⎝⎛222111c b a c b a ，则方程组存在唯一解的条件是（）．A ．⎪⎪⎭⎫⎝⎛21a a 与⎪⎪⎭⎫ ⎝⎛21b b 平行 B ．⎪⎪⎭⎫ ⎝⎛21a a 与⎪⎪⎭⎫ ⎝⎛21c c 不平行 C ．⎪⎪⎭⎫ ⎝⎛21a a 与⎪⎪⎭⎫⎝⎛21b b 不平行 D ．⎪⎪⎭⎫ ⎝⎛21b b 与⎪⎪⎭⎫ ⎝⎛21c c 不平行 11、（杨浦区2018高三上期末）已知一个关于x 、y 的二元一次方程组的增广矩阵是112012-⎛⎫⎪⎝⎭，则x y += 12、（虹口区2019届高三一模）若复数sin i 1cos iz θθ-=（i 为虚数单位），则||z 的最大值为 13、（宝山区2019届高三上期末（一模））关于,x y 的二元一次方程组的增广矩阵为12-3015⎛⎫⎪⎝⎭，则x y += ．14、（奉贤区2019届高三上期末（一模））下列以行列式表达的结果中，与sin()αβ-相等的是（）A.sin sin cos cos αβαβ- B.cos sin sin cos βαβα C. sin sin cos cos αβαβ D. cos sin sin cos ααββ-15、（黄浦区2019届高三上期末（一模））已知三阶行列式123456789，元素8的余子式的值与代数余子式的值之和为16、（闵行区2019届高三上期末（一模））方程110322x =-的解为17、（浦东新区2019届高三上期末（一模））不等式2log 1021x >的解为18、（松江区2019届高三上期末（一模））若增广矩阵为1112m m m m +⎛⎫⎪⎝⎭的线性方程组无解，则实数m 的值为19、（徐汇区2019届高三上期末（一模））若数列{}n a 的通项公式为*2()111n na n N n n=∈+，则lim n n a →∞=___________.20、（杨浦区2019届高三上期末（一模））在行列式274434651xx--中，第3行第2列的元素的代数余子式记作()f x ，则1()y f x =+的零点是参考答案：二、行列式1、－12、33、34、14[,]22ππ-+ 5、,3x x k k Z ππ⎧⎫=-+∈⎨⎬⎩⎭6、37、－148、9、C 10、ｃ 11、－16012、1213、－8 14、C 15、0 16、2log 5x = 17、(4,)+∞ 18、－1 19、－1 20、－1。

(沪教版高二上)数学第九章矩阵和行列式初步

37
3) 0;
3n
5) 0
0
4) 1A2E;
3
0 0
0
1 0 ; 6) 0
0
4n
1 8
2) 4;
0 1 2 1 5 0 ; 0 0
2 1 0
三.
X 1 3 4.
1 0 2
谢谢观赏！
2020/11/5
40
kk
即 A k AAA 。规定 A0 E
k个
易证 AkAl Akl, Ak l Ak.l k,l为正整数
转置矩阵:
把 mn 矩阵
A 的行与列依次互换得到另
nm 一个
矩阵，称为
A 的转置矩阵，记作
AT
转置矩阵的运算性质
1A TTA ;
2 A B T A T B T ;
3kA TkT A ;
4 AT B B T A T .
对称阵:
A n 设为阶方阵，如果满足
，即.
AAT
a ij a jii,j 1 ,2 , ,n
A 则称为对称阵.
反对称阵: 伴随方阵:
如果 ATA则矩 A称阵为反.对称
A 设
是行列式
ij
A a ij 中元素
a 的代数 ij
余子式,称方阵
A 为方阵的伴随方阵.
3 5 3
t
.
3) 已知
A 23 31 , f(x)x25x3,
则 f(A)
.
4 )若 n 阶A 矩满阵足 A 2 2 A 方 3 E 程 0 ,则
A1
.
3 0 0
5) 设A0 1 0,则An
.
0 0 4
0 0 2

上海高二数学行列式初步(有详细答案)绝对精品

2013年暑期高二数学行列式初步§ 二阶行列式(1)——二阶行列式一．引入观察二元一次方程组的解法，设二元一次方程组()()11122212a x b y c a x b y c +=⎧⎪⎨+=⎪⎩ 用加减消元法来解，()()()211221122112b b a b a b x c b c b ⨯-⨯⇒-=-; ()()()121221122121a a a b a b y a c a c ⨯-⨯⇒-=-当12210a b a b -≠时，有12211221221122c b c b x a b a b a c a c y a b a b -⎧=⎪-⎪⎨-⎪=⎪-⎩.二. 定义二阶行列式及展开用记号1122a b a b 来表示算式122a b a b -,即1112222a b a b a b a b =-.说明:二阶行列式表示的是四个数的一种特定的算式思考与运用 1. 解方程:3621x x =-.解:()231661204321x x x x x x orx x =⋅--=⇒--=⇒==-.2. 求函数()2212sin 22cos 12xf x x =的值域.解: ()[]2222212sin 212sin cos 1sin cos 0,1222cos 12xx x f x x x x ⎛⎫==-=-=∈ ⎪⎝⎭. 3．行列式⎪⎪⎪⎪⎪⎪a b c d (a ，b ，c ，d ∈{－1,1,2})所有可能的值中，最大的是________．解析：⎝⎛⎭⎪⎫a b c d ＝ad －bc ，则a ＝d ＝2，bc ＝－2时，取最大值为6. 答案：6三. 利用二阶行列式解二元一次方程组将1221c b c b -和1221a c a c -分别用行列式来表示,可以表示为1122c b c b 和1122a c a c ,即11220a b D a b =≠,1122x c b D c b =,1122y a c D a c =,于是上述二元一次方程组的解可以表示为xy D x DD y D⎧=⎪⎪⎨⎪=⎪⎩(0D ≠).§ 二阶行列式(2)——作为判别式的二阶行列式一．练习与复习 (一)展开下列行列式: 1. 21111a a a --++()()()231111a a a a =-++-⨯-=;2.22cos sin cos sin 1sin cos θθθθθθ=--=--;5=;4.sin cos sin cos 2cos sin 2sin sin 2cos 2ααααααααα=-=-.(二)解下列方程组1. 12103214515x x y x y y ⎧=⎪-=⎧⎪⇒⎨⎨+=⎩⎪=-⎪⎩;2. 791313313312177135132x x y x y y x y⎧⎧⎧+===⎪⎪⎪⎪⎪⎪⇒⇒⎨⎨⎨⎪⎪⎪=+==⎪⎪⎪⎩⎩⎩;3. 231232x y x y +=⎧⎨+=⎩ 无解; 4. 231462x y x y +=⎧⎨+=⎩ 无穷多解.二. 作为判别式的二阶行列式通过加减消元法将二元一次方程组111222a x b y c a x b y c +=⎧⎨+=⎩化为xy D x D D y D ⋅=⎧⎪⎨⋅=⎪⎩,(1) 当0D ≠时,方程组有唯一解(2) 当0D =时,若x D ,y D 中至少有一个不为零,则方程组无解;若0x y D D ==,则方程组有无穷多解. 感受与体验 P10 练习(2) 1; P10 习题 3 思考与运用例解关于,x y 的二元一次方程组,并对解的情况进行讨论:1323mx y mx my m +=-⎧⎨-=+⎩.解: ()133m D m m m m==-+-,()11323x D m m m-==-++-,11323y D m m m -==+-+,当0D ≠,即0m ≠且3m ≠-时有唯一解11,x y m m==-; 当0m =时,0D =,而30x D =-≠,方程组无解;当3m =-时,0D =,且0x y D D ==,方程组有无穷多解. □三. 拓展与提高例1 已知三角形的三个顶点坐标分别为()0,0,()11,x y ,()22,x y ,试用行列式表示三角形的面积.()()1121212211111222S x y x x y y x y x y =++--- 11222112112211111111222222x y x y x y x y x y x y x y =+-+--- ()111221221122x y x y x y x y =-=. □例2 （1）计算行列式2346、792127、34-912-的值；（2）从上述结果中得出一个一般的结论，并证明. 解: (1) 均为0; (2) 0a bka kb=,证明:0a bkab kab ka kb=-=.同理0a ka b kb= □§ 三阶行列式(1)——三阶行列式的展开(1)一. 三阶行列式的概念用记号111222333a b c a b c a b c 表示算式123231312321213132a b c a b c a b c a b c a b c a b c ++---,称为三阶行列式.二. 三阶行列式的展开 (一) 按对角线展开例计算三阶行列式124221342D -=---.解: ()()()()122213424D =⨯⨯-+⨯⨯-+-⨯-⨯()()()()11422242314-⨯⨯-⨯-⨯---⨯⨯-=-. 感受与体验 P12 练习(1)(二)按一行(或一列)展开1. 余子式把三阶行列式中某个元素所在的行和列划去,将剩下的元素按原来的位置关系组成的二阶行列式称为该元素的余子式.例如1133a c a c 和1133a b a b 分别是111222333a b c a b c a b c 中元素2b 和2c 的余子式. 2. 代数余子式把余子式添上相应的符号,某元素所在行列式中的位置第i 行第j 列,该元素的代数余子式的符号为()1i j+-例如()2211331a c a c +-和()2311331a b a b +-分别是111222333a b c a b c a b c 中元素2b 和2c 的代数余子式. 注：各元素代数余子式的符号如图所示:+-+-+-+-+3. 按一行(或一列)展开111222111111333a b c a b c a A b B c C a b c =++112233a A a A a A =++=L例按第一行和第一列展开行列式124221342D -=---.a 11a 22a 33a 12a 23a 31a 13a 21a 32a 11a 23a 32a 12a 21a 33a 13a 22a 31解: 按第一行展开:124212122221124423234342D -⎛-⎫-=-=⋅+⋅-- ⎪----⎝⎭--14=-; 按第一列展开: 12421242422112314424221342D -⎛-⎫-=-=⋅-⋅--=- ⎪--⎝⎭--. 感受与体验 P15 练习(2) 1; 2§ 三阶行列式(2)——三阶行列式的展开(2)一.复习按对角线或按一行（一列）展开三阶行列式的方法完成练习 P21 习题 1 (用适当的方法) 二.例题与练习例1 若行列式0021040938k=,求k 的值.解: 002108405938kk k ==⇒=.□例2 已知行列式11110211λλ-=-,求λ的值. 解: 2111134041211or λλλλλλ-=--=⇒==--. □ 例3 已知()2112150f x x x=,若()0f x >,求x 的取值范围.解:()22211212121522527505550f x x xx x x x x xx x==-+=-+-=-+>()5,1,2x ⎛⎫⇒∈-∞+∞ ⎪⎝⎭U . □ 例4 把下面的算式写成一个三阶行列式:(1)023*******22132313113312-----=-; (2)112211112233332233111x y x y x y xy x y x y x y x y x y -+=. (答案不唯一) □ 例5 验证三阶行列式的某一行(列)的元素与另一行(列)的对应元素的代数余子式的乘积之和为零.解: 例如三阶行列式111222333a b c a b c a b c 的第二行元素222,,a b c 分别与第一行的元素111,,a b c 的代数余子式相乘,即222222212121222333333b c a c a b a A b B c C a b c b c a c a b ++=-+2112222222223332222223330a b c b c a c ab a bc a b c b c a c a b a b c ==-+=. □ 例5 在直角坐标系中,不在一直线的三点:()11,A x y ,()22,B x y ,()33,C x y 依逆时针顺序排列. (1)探求用行列式表示ABC V 的面积公式;(2)当,,A B C 三点依顺时针顺序排列式, ABC V 的面积公式有何变化解: (1)记梯形,,EBCF EBAD DACF 的面积分别为123,,S S S ,()()()123321122S EB FC EF x x y y =+⋅=+-,同理有 ()()2121212S x x y y =+-,()()3313112S x x y y =+-,则 ()()()12323321331122112S S S S x y x y x y x y x y x y =--=---+-⎡⎤⎣⎦ 1122111122333322331111221x y xy x y xy x y x y x y x y x y ⎛⎫=-+= ⎪ ⎪⎝⎭ (2)11223311121x y S x y x y =-. [说明] 本例可得两个结论:(1) 定点坐标分别为()11,A x y ,()22,B x y ,()33,C x y 的ABC V 的面积为11223311121x y S x y x y =; (2) 平面上三点()11,A x y ,()22,B x y ,()33,C x y 共线的充要条件为1122331101x y x y x y =. 三.布置作业§ 三阶行列式(3)——三元一次方程组的行列式解法一. 复习二元一次方程组的行列式解法及解的情况的判别方法对于二元一次方程组xy D x D D y D ⋅=⎧⎪⎨⋅=⎪⎩当0D ≠时,方程组有唯一解;当0D =时,若x D ,y D 中至少有一个不为零,则方程组无解;若0x y D D ==,则方程组有无穷多解.二. 三元一次方程组的行列式解法对于三元一次方程组111122223333a x b y c z d a x b y c z d a x b y c z d ++=⎧⎪++=⎨⎪++=⎩,记其系数行列式为111222333a b c D a b c a b c =, 用D 中第一列元素的代数余子式123,,A A A 依次乘以方程组的各方程,得11111111a A x b A y c A z d A ++=, 22222222a A x b A y c A z d A ++=, 33333333a A x b A y c A z d A ++=,将上述三个等式相加,得()()()112233112233112233112233a A a A a A x b A b A b A y c A c A c A d A d A d A ++++++++=++，其中记111112233222333x d b c D d A d A d A d b c d b c =++=，则x D x D ⋅=,同理可得 y D y D ⋅=，z D z D ⋅=，于是方程组x y z D x D D y D D z D ⎧⋅=⎪⋅=⎨⎪⋅=⎩当0D ≠时有惟一解x y z D x D D y D D z D ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩.例解三元一次方程组:632752215x y z x y z x y z ++=⎧⎪-+=⎨⎪++=⎩.解: 1113129522D =-=,61171291522x D =-=,161372185152y D ==,116317275215z D =-=,1,2,3x y z ∴===. □感受与体验 P19练习(3) 用行列式解下列方程组三. 当系数行列式0D =的情况当0D =时三元一次方程组可能无解,也可能有无穷多解.例求关于,,x y z 的方程组13x y mz x mu z m x y z ++=⎧⎪++=⎨⎪-+=⎩有惟一解的条件,并在此条件下写出该方程组的解.解: ()()11111101111mD m m m m ==-+-≠⇒≠±-, 又()()111411311x mD mmm m ==-+--,()()31y D m m =---,()41z D m =-,所以当1m ≠±时,方程组的解为43141x m y m z m ⎧⎪=⎪-⎪=⎨+⎪⎪=-⎪+⎩. □注意与二元一次方程组解的情况相区别。

上海版教材 矩阵与行列式习题(有答案)

沪教版(上海)高三年级新高考辅导与训练第七章矩阵与行列式、算法初步、复数三、复数

上海版矩阵与行列式基础练习题

2020届上海(沪教版)高考考典——第8章-矩阵和行列式初步教师版

上海高二数学矩阵及其运算有详细答案精品

上海高二数学矩阵及其运算(有详细答案)精品

上海版矩阵与行列式基础练习题

行列式习题及答案

（完整版）第一章行列式与矩阵的计算的练习（含答案）

专题14 矩阵与行列式(习题)-2021届沪教版高考数学一轮复习(上海专用)

上海高二数学矩阵及其运算(有详细答案)精品-推荐下载

上海版教材矩阵与行列式习题(有答案)

上海矩阵与行列式基础练习题

2020届上海(沪教版)高考考典——第8章-矩阵和行列式初步教师版

(沪教版高二上)数学第九章矩阵和行列式初步

上海高二数学行列式初步(有详细答案)绝对精品

上海版教材矩阵与行列式习题(有答案)