数学13《算法案例---秦九韶算法》测试
13算法案例(二)

v5=v4x+7=534×5+7=2677
例1:用秦九韶算法求多项式 f(x)=2x5-5x4-4x3+3x2-6x+7当x=5时的值. 解法一:首先将原多项式改写成如下形式 : f(x)=((((2x-5)x-4)x+3)x-6)x+7 然后由内向外逐层计算一次多项式的值,即
v0=2
v1=v0x-5=2×5-5=5
例2:把89化为二进制的数. 我们可以用下面的除法算式表示除2取余法: 余数 1 0 0 1 1 0 1
2 89 2 44 2 22 2 11 2 5 2 2 21 0
把算式中各步所得的余数 从下到上排列,得到 89=1011001(2).
这种方法也可以推广为把 十进制数化为k进制数的 算法,称为除k取余法.
二进制:可使用的数字有0和1,基数是2;
十进制:可使用的数字有0,1,2,…,8,9等十个数字, 基数是10; 注意:为了区分不同的进位制,常在数字的右 下脚标明基数,. 如111001(2)表示 ? 进制数,34(5)表示?进制数. 十进制数一般不标注基数.
练习.下列有可能是 4 进制数的是( A.5 123 C.3 103
3 -6 0 605 3040 15170 608 3034 15170 所以,当x=5时,多项式的值是15170. 注意:n次多项式有n+1项,因此缺少哪一项 应将其系数补0. 列表 2 x=5 2 -5 10 5 0 -4 25 125 25 121
一般地,对于一个n次多项式 f(x)=anxn+an-1xn-1+an-2xn-2+……+a1x+a0. 我们可以改写成如下形式: f(x)=(…(anx+an-1)x+an-2)x+…+a1)x+a0. 求多项式的值时,首先计算最内层括号内一 次多项式的值,即 v1=anx+an-1,
高中数学之算法案例

算法案例(讲义)➢ 知识点睛典型算法举例: 1. 辗转相除法①方法概述:两数相除,较大数除以较小数,得商和余数,继而较小数除以余数,重复操作,直至除尽,此时除数即为最大公约数.②原理:在a =bq +r 中,除数b 和余数r 能被同一个数整除,那么被除数a 也能被这个数整除.或者说,除数与余数的最大公约数,就是被除数与除数的最大公约数. 2. 秦九韶算法把一个n 次多项式改写成如下形式:1110121102312101210()()(())((()))n n n n n n n n n n n n n n n f x a x a x a x a a x a x a x a a x a x a x a x a a x a x a x a x a ----------=++++=++++=+++++==+++++……………… 记0n v a =,11n n v a x a -=+,…,10n n v v x a -=+.求多项式的值时,首先计算最内层括号内一次多项式的值,即v 1,然后由内向外逐层计算. 3. 进位制①k 进制:若k 是一个大于1的整数,那么以k 为基数的k 进制数可以表示为一串数字连写在一起的形式.110()n n k a a a a -…11011000n n n n a a a a N a k a a a k --∈<<<≤(,,…,,,,,…,,)②进位制数相互转化:k 进制转十进制,计算k 进制数a 的右数第i 位数字i a 与1i k -的乘积1i i a k -⋅,再将其累加,重复操作求和.十进制数转k 进制数(除k 取余法): 如右图,十进制数化为二进制数, 89=1011001(2).➢ 精讲精练1. 用“辗转相除法”求下列数的最大公约数:(1)459和357的最大公约数是____________;余数2222222012511224489(2)三个数324243135,,的最大公约数是____________.2. 用秦九韶算法求多项式的值:(1)计算多项式x x x x x x x f 876543)(23456+++++=在1.0=x 时的值时,需要做乘法和加法的次数分别是_______,_______;(2)求多项式23456()1235879653f x x x x x x x =+-++++在x =-4的值时,4v 的值为_______;(3)计算多项式5432()853261f x x x x x x =+++++,当2x =时的值为________. 3. 完成下列进制的转化:(3)(10)10202____=; (10)__________(8)101=;1231(5)=_____________(7).4. 三位七进制的数表示的最大的十进制的数是( )A .322B .402C .342D .3655. 在下列各数中,最小的数是( )A .)9(85B .)6(210C .)4(1000D .(2)1111116. 已知三个数12(16),25(7),33(4),按照从小到大的顺序排列为________________.7. 已知()175r =(10)125,则r =________.8. 如图所示的程序框图的算法思路来源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的a ,b 的值分别为14,18,则输出的a 的值为( ) A .0B .2C .4D .149. 如图所示的程序框图给出了利用秦九韶算法求多项式值的一个实例,若输入n ,x 的值分别为3,2,则输出v 的值为( ) A .35B .20C .18D .910.下面是把二进制数(2)11111化为十进制数的一个程序框图,判断框内应填入的条件是()A.5i>?B.4i≤?C.4i>?D.5i≤?11.执行如图所示的程序框图后,输出的值为4,则P的取值范围是()A.715816P<≤B.1516P>C.3748P<≤D.715816P<≤12.设a是一个各位数字都不是0且没有重复数字的三位数.将组成a的3个数字按从小到大排成的三位数记为I(a),按从大到小排成的三位数记为D(a)(例如a=815,则I(a)=158,D(a)=851).阅读如图所示的程序框图,运行相应的程序,任意输入一个a,输出的结果b=________.13. 已知函数232 1 01 012 1x x y x x x x x -<⎧⎪=+<⎨⎪+⎩≤≥()()(),写出求该函数的函数值的算法,并画出程序框图.14. 设计一算法,求使20063212222>++++n Λ成立的最小正整数n 的值.15.设计算法计算:1112131415167S=++++++,画出程序框图.【参考答案】1. (1)51;(2)272. (1)6;5;(2)220;(3)3813. 101 145 3624. C5. D6. (4)(16)(7)331225<<7. 88. B9. C 10. C 11. C 12. 495 13. 略 14. 略 15. 略算法案例(随堂测试)1. 372和684的最大公约数是( )A .36B .186C .12D .5892. 用秦九韶算法计算多项式65432()3567983512f x x x x x x x =+++-++在x =-4时的值时,v 2的值为( )A .-57B .-22C .34D .743. 1234(8)=________(10);300=________(5);300=_______(6).4. 设计一个算法,输入正整数n ,输出111123n++++….【参考答案】1. C2. C3. 668;2 200;1 2204. 略算法案例(习题)➢ 巩固练习5. 求下列数的最大公约数:(1)1 443与999的最大公约数是_____________;(2)319,377,116的最大公约数是___________.6. 用秦九韶算法求n 次多项式1110()n n n n f x a x a x a x a --=++++…,当x =x 0时,0()f x 需要算乘法、加法的次数分别为( ) A .n 2,nB .2n ,nC .n ,2nD .n ,n7.已知532=++++,运用秦九韶算法计算x=3时的值时,v3的值为()()231f x x x x xA.27 B.11 C.109 D.368.用秦九韶算法求多项式765432=++++++在x=3时的值为________.()765432f x x x x x x x x9.把21化为二进制数,则此数为()A.10011(2)B.10110(2)C.10101(2)D.11001(2)10.一个k进制的三位数与某六进制的二位数等值,则k不可能是()A.3 B.4 C.5 D.711.下列各数中,最小的数是()A.75B.210(6)C.111111(2)D.85(9)12.若a=33(10),b=52(6),c=11111(2),则三个数的大小关系是()A.c>b>a B.b>c>a C.c>a>b D.a>b>c13.中国古代有计算多项式值的秦九韶算法,如图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=()A.7B.12C.17D.34第9题图第10题图14.如图是一个算法的程序框图,该算法所输出的结果是()A.11112310++++…B.11113519++++…C.111124620++++…D.231011112222++++…15.某程序框图如图所示,若输出的S=57,则判断框内为()A.k>4?B.k>5?C.k>6?D.k>7?11第11题图 第12题图16. 执行如图所示的程序框图,若输入k 的值为8,则判断框图可填入的条件是( )A .S ≤34?B .S ≤56?C .S ≤1112? D .S ≤1524?17. 设计一个算法,输入两个数,输出两个数中较大的一个.18.已知函数21111131x x y x x x x ⎧-<-⎪=+-⎨⎪+>≤≤()()(),试画出求函数值的程序框图.19. 对任意给定的正整数n ,写出一个求13+23+33+…+n 3的算法程序框图.20.设计算法求111112233499100++++⨯⨯⨯⨯…的值,要求画出程序框图.【参考答案】1.(1)111 (2)292.D3.D4.213245.C6.D7.C8.D9.C10.C11.A12.C13.略14.略15.略16.略12。
数学13《算法案例---秦九韶算法》测试(新人教A版必修3)
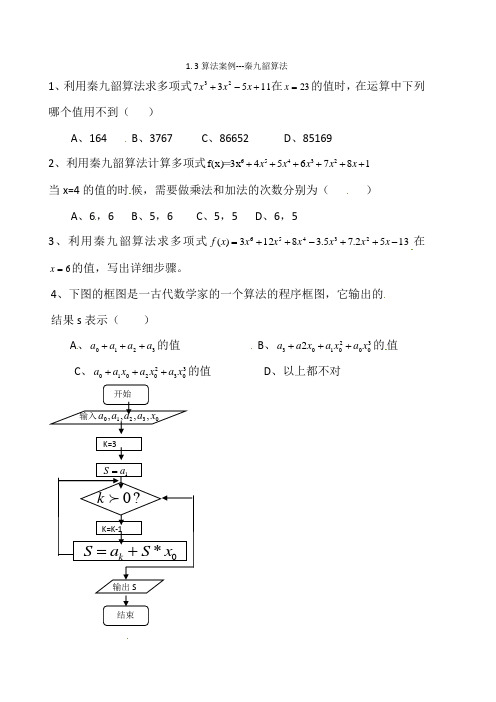
1. 3算法案例---秦九韶算法1、利用秦九韶算法求多项式1153723+-+x x x 在23=x 的值时,在运算中下列哪个值用不到( )A 、164B 、3767C 、86652D 、851692、利用秦九韶算法计算多项式1876543x f(x)23456++++++x x x x x = 当x=4的值的时候,需要做乘法和加法的次数分别为( )A 、6,6B 、5,6C 、5,5D 、6,53、利用秦九韶算法求多项式1352.75.38123)(23456-++-++=x x x x x x x f 在6=x 的值,写出详细步骤。
4、下图的框图是一古代数学家的一个算法的程序框图,它输出的 结果s 表示( ) A 、3210a a a a +++的值 B 、300201032x a x a x a a +++的值 C 、303202010x a x a x a a +++的值 D 、以上都不对开始K=31a S =?0 kK=K-10*x S a S k +=输入03210,,,,x a a a a输出S结束5、已知n 次多项式1011()n n n n n P x a x a x a x a --=++++,如果在一种算法中,计算0k x (k =2,3,4,…,n )的值需要k -1次乘法,(1)计算30()P x 的值需要9次运算(6次乘法,3次加法),那么计算0()n P x 的值需要多少次运算?(2)若采取秦九韶算法:0011(),()()k k k P x a P x xP x a ++==+(k =0, 1,2,…,n -1),计算30()P x 的值只需6次运算,那么计算0()n P x 的值共需要多少次运算?(3)若采取秦九韶算法,设a i =i+1,i=0,1,…,n ,求P 5(2)(写出采取秦九韶算法的计算过程)答案:1、D2、A3、解:13)5)2.7)5.3)8)123((((()(-++-++=x x x x x x x f2.243168)6(2.2431681362.40530562.67542.765.11245.36188863012635645342312010==-⨯==+⨯==+⨯==-⨯==+⨯==+⨯==f v v v v v v v v v v v v v4、C5、n +3)(2)2n ;(3)∵0011(),()()k k k P x a P x xP x a ++==+, ∴P 0(2)=1,P 1(2)=2P 0(2)+2=4;P 2(2)=2P 1(2)+3=11; P 3(2)=2P 2(2)+4=26;P 4(2)=2P 3(2)+5=57;P 5(2)=2P 4(2)+6=120。
算法案例—辗转相除、更相减损、秦九韶

v1=1×(-2)+5=3 v2=3×(-2)+10=4 v3=4×(-2)+10=2 v4=2×(-2)+5=1 v5=1×(-2)+1=-1
比比谁算得快!
例2 已知一个5次多项式为 f (x )
= 5x + 3.5x + 1.7x - 0.8
5ห้องสมุดไป่ตู้
3
用秦九韶算法求当x=5时,V1,V3的值及求f(5)的值做多少次乘法运算.
v1 an x an1
v2 v1 x an2
最后的一 项是什么?
v3 v2 x an3 vn vn1 x a0
最第 i 个等 式是什么?
这种将求一个n次多项式f(x)的值转化成求n个一 次多项式的值的方法,称为秦九韶算法。
特征: 对于一个n次n+1项多项式,
观察括号的特点?做几次加法,几次乘法?
an1 x
n4
a3 ) x a2 ) x a1 ) x a0
f ( x) ((an x an1 ) x an2 ) x a1 ) x a0
要求多项式的值,应该先算最内层的一次多项式的值,即 然后,由内到外逐层计算一次多项式的值,即
〖创设情景,揭示课题〗
[问题2]:我们都是利用找公约数的方法来求
最大公约数,如果两个数比较大而且根据我
们的观察又不能得到一些公约数,我们又应
该怎样求它们的最大公约数?比如求8251与
6105的最大公约数?
1.辗转相除法:
例1 求两个正数8251和6105的最大公约数。
分析:8251与6105两数都比较大,而且没 有明显的公约数,如能把它们都变小一点,根据 已有的知识即可求出最大公约数.
数学人教B版必修3教案1.3算法案例——秦九韶算法与排序含答案

1.3算法案例——秦九韶算法与排序
总课时
1
教学要求
1.了解秦九韶算法的计算过程,并理解利用秦九韶算法可以减少计算次数提高计算效率的实质;
2.掌握数据排序的原理能使用直接排序法与冒泡排序法给一组数据排序,进而能设计冒泡排序法的程序框图及程序,理解数学算法与计算机算法的区别,理解计算机对数学的辅助作用.
教学重点难点
重点:1.秦九韶算法的特点;2.两种排序法的排序步骤及计算机程序设计
难点:1.秦九韶算法的先进性理解;2.排序法的计算机程序设计
教法
讲练
教学过程
一、复习引入
我们已经学过了多项式的计算,下面我们计算一下多项式
当 时的值,并统计所做的计算的种类及计算次数.
根据我们的计算统计可以得出我们共需要10次乘法运算,5次加法运算.
阅读课本P30—P31面的内容,回答下面的问题:
பைடு நூலகம்(1)排序法中的直接插入排序法与冒泡排序法的步骤有什么区别?
(2)冒泡法排序中对5个数字进行排序最多需要多少趟?
(3)在冒泡法排序对5个数字进行排序的每一趟中需要比较大小几次?
游戏:5位同学每人拿一个数字牌在讲台上演示冒泡排序法对5个数据4,11,7,9,6排序的过程,让学生通过观察叙述冒泡排序法的主要步骤.并结合步骤解决例3的问题.
当 时的值的程序框图.
解:程序框图如下:
例3用冒泡排序法对数据7,5,3,9,1从小到大进行排序
解:P32
例4设计冒泡排序法对5个数据进行排序的程序框图.
解:程序框图如下:
(三)课堂练习
1.利用秦九韶算法计算 .
2.写出用冒泡排序法对5个数据4,11,7,9,6排序的过程中每一趟排序的结果.
高二数学算法案例试题答案及解析

高二数学算法案例试题答案及解析1. 两个二进制数101(2)与110(2)的和用十进制数表示为( ) A .12 B .11 C .10D .9【答案】B【解析】101(2)=22+0×21+1×20=5,110(2)=1×22+1×21+0×20=6. 【考点】二进制数与十进制数的互相转化.2. 用辗转相除法求294和84的最大公约数时,需要做除法的次数是 A .1 B .2 C .3D .4【答案】B【解析】由辗转相除法可知:,所以需要做除法的次数是2.【考点】算法的应用.3. 将十进制数102转化为三进制数结果为:【答案】10210.【解析】将十进制数转化为3进制数的方法为除3取余法,再把各步所得的余数从下到上排列即得10210.【考点】算法的应用.4. 设、、为整数(),若和被除得的余数相同,则称和对模同余,记为()。
已知,则的值可以是( ) A .2015 B .2011 C .2008 D .2006【答案】B 【解析】因为的余数为1, 的值可以是2011,故选B. 【考点】新定义的应用点评:主要是理解同余的概念,然后借助于二项式定理来得到结论,属于基础题。
5. (本题满分12分)将101111011(2)转化为十进制的数; 【答案】379【解析】解: 101111011(2)=1×28+0×27+1×26+1×25+1×24+1×23+0×22+1×21+1=379. 【考点】本试题考查了进位制的转换运算。
点评:将k 进位制转化内十进制,只要将各个数位上的数乘以k 的次幂即可,注意n 位数的最好次幂为n-1次幂,然后依次类推相加得到结论。
属于基础题。
6. 阅读上图的程序框图, 若输出的值等于,那么在程序框图中的判断框内应填写的条件是( )A.?B.?C.?D.?【答案】A【解析】第一次循环:S=1+1=2,i=2,不满足条件,执行循环;第二次循环:S=2+2=4,i=3,不满足条件,执行循环;第三次循环:S=4+3=7,i=4,不满足条件,执行循环;第四次循环:S=7+4=11,i=5,不满足条件,执行循环;第五次循环:S=11+5=16,i=6,满足条件,退出循环体,输出S=16,故判定框中应填i>5或i≥6,故选:A。
2020学年高中数学第一章算法初步1.3.2秦九韶算法练习(含解析)新人教A版必修3(最新整理)

第9课时秦九韶算法知识点一秦九韶算法的原理1.用秦九韶算法计算f(x)=6x5-4x4+x3-2x2-9x当x=x0时的值,需要加法(或减法)与乘法运算的次数分别为( )A.5,4 B.5,5 C.4,4 D.4,5答案D解析n次多项式需进行n次乘法;若各项均不为零,则需进行n次加法,缺一项就减少一次加法运算.f(x)中无常数项,故加法次数要减少一次,为5-1=4.故选D.2.用秦九韶算法求多项式f(x)=1+2x+x2-3x3+2x4在x=-1时的值,v2的结果是( )A.-4 B.-1 C.5 D.6答案D解析n=4,a4=2,a3=-3,a2=1,a1=2,a0=1,由秦九韶算法的递推关系式得v0=2,v1=v0x+a3=-5,v2=v1x+a2=6.3.用秦九韶算法求多项式f(x)=7x6+6x5+3x2+2当x=4时的值时,先算的是( )A.4×4=16 B.7×4=28C.4×4×4=64 D.7×4+6=34答案D解析因为f(x)=a n x n+a n-1x n-1+…+a1x+a0=(…((a n x+a n-1)x+a n-2)x+…+a1)x +a0,所以用秦九韶算法求多项式f(x)=7x6+6x5+3x2+2当x=4时的值时,先算的是7×4+6=34.4.用秦九韶算法求多项式f(x)=x4-2x3+3x2-7x-5,当x=4时的值,给出如下数据.①0 ②2 ③11 ④37 ⑤143其中运算过程中(包括最终结果)会出现的数有________.(只填序号)答案②③④⑤解析将多项式改写成f(x)=(((x-2)x+3)x-7)x-5.v=1;v=1×4-2=2;1v=2×4+3=11;2v=11×4-7=37;3v=37×4-5=143.4知识点二利用秦九韶算法计算多项式的值5.用秦九韶算法求多项式f(x)=7x7+6x6+5x5+4x4+3x3+2x2+x当x=3时的值.解f(x)=((((((7x+6)x+5)x+4)x+3)x+2)x+1)x,所以有v=7;v=7×3+6=27;1v=27×3+5=86;2v=86×3+4=262;3v=262×3+3=789;4v=789×3+2=2369;5v=2369×3+1=7108;6v=7108×3=21324.7故当x=3时,多项式f(x)=7x7+6x6+5x5+4x4+3x3+2x2+x的值为21324.易错点利用秦九韶算法求含空项的n次多项式的值时易出现错误6.已知f(x)=3x4+2x2+4x+2,利用秦九韶算法求f(-2)的值.易错分析由于没有抓住秦九韶算法原理的关键,没有正确改写多项式并使每一次计算只含有x的一次项而致误.正解f(x)=3x4+0·x3+2x2+4x+2=(((3x+0)x+2)x+4)x+2,v=3×(-2)+0=-6;1v=-6×(-2)+2=14;2v=14×(-2)+4=-24;3v=-24×(-2)+2=50.4故f(-2)=50.一、选择题1.用秦九韶算法计算多项式f(x)=3x6+9x5+5x4+6x3+12x2+8x-7在x=2时的值,需要做乘法和加法的次数分别是( )A.5,5 B.5,6 C.6,6 D.6,5答案C解析因为f(x)的最高次数是6,所以需要做乘法和加法的次数都是6.2.用秦九韶算法求多项式f(x)=12+35x-8x2+79x3+6x4+5x5+3x6在x=-4时,v4的值为()A.-57 B.220 C.-845 D.3392答案B解析v0=3,v1=3×(-4)+5=-7,v=-7×(-4)+6=34,2v=34×(-4)+79=-57,3v=-57×(-4)-8=220.43.已知多项式f(x)=4x5+3x4+2x3-x2-x-错误!,用秦九韶算法求f(-2)等于()A.-错误! B.错误! C.错误! D.-错误!答案A解析∵f(x)=((((4x+3)x+2)x-1)x-1)x-错误!,∴f(-2)=((((4×(-2)+3)×(-2)+2)×(-2)-1)×(-2)-1)×(-2)-错误!=-错误!.4.秦九韶算法的先进性主要体现在减少运算次数,下列说法正确的是( )A.可以减少加法运算次数B.可以减少乘法运算次数C.同时减少加法和乘法的运算次数D.加法次数和乘法次数都有可能减少答案B解析秦九韶算法可以把至多n n+12次乘法运算减少为至多n次乘法运算.加法运算次数不变.5.用秦九韶算法计算函数y=2x3-3x2+2x-1在x=2时的函数值,则下列各式正确的是()A.v0=2 B.v0=1 C.v1=4 D.v2=7答案A解析根据秦九韶算法,把多项式改写成y=((2x-3)x+2)x-1,从内到外依次计算:v0=2,v1=2×2-3=1,v2=1×2+2=4,v3=4×2-1=7.二、填空题6.已知f(x)=x5+2x3+3x2+x+1,用秦九韶算法计算x=3时的值,v3的值为________.答案36解析v0=1,v1=1×3+0=3,v2=3×3+2=11,v3=11×3+3=36,….7.用秦九韶算法求多项式f(x)=5x5+3x3+2x2+10,当x=3时f(x)的值为________.答案1324解析f(x)=5x5+0x4+3x3+2x2+0x+10=((((5x+0)x+3)x+2)x+0)x+10=((((5x)x+3)x+2)x)x+10,当x=3时,有v0=5,v1=5×3=15,v2=15×3+3=48,v3=48×3+2=146,v4=146×3=438,v5=438×3+10=1324,∴f(3)=1324.8.用秦九韶算法求多项式f(x)=1-5x-8x2+10x3+6x4+12x5+3x6当x=-4时的值时,v0,v1,v2,v3,v4中最大值与最小值的差是________.答案62解析多项式变形为f(x)=3x6+12x5+6x4+10x3-8x2-5x+1=(((((3x+12)x+6)x+10)x-8)x-5)x+1,v=3,v=3×(-4)+12=0,1v=0×(-4)+6=6,2v=6×(-4)+10=-14,3v=-14×(-4)-8=48,4∴v4最大,v3最小.∴v4-v3=48-(-14)=62.三、解答题9.利用秦九韶算法求多项式f(x)=3x6+12x5+8x4-3.5x3+7.2x2+5x-13,当x=6时的值,写出详细步骤.解f(x)=(((((3x+12)x+8)x-3.5)x+7.2)x+5)x-13,v=3,v=v0×6+12=30,1v=v1×6+8=188,2v=v2×6-3.5=1124.5,3v=v3×6+7.2=6754.2,4v=v4×6+5=40530.2,5v=v5×6-13=243168.2.6f(6)=243168.2.10.用秦九韶算法计算多项式f(x)=5x7+x6-x3+x+3当x=-1时的值,并判断f(x)在区间[-1,0]内有没有零点.解∵f(x)=5x7+x6-x3+x+3=((((((5x+1)x+0)x+0)x-1)x+0)x+1)x+3,∴当x=-1时,v0=5,v=5×(-1)+1=-4,1v=-4×(-1)+0=4,2v=4×(-1)+0=-4,3v=-4×(-1)-1=3,4v=3×(-1)+0=-3,5v=-3×(-1)+1=4,6v=4×(-1)+3=-1,7∴f(-1)=-1.又f(0)=3,∴f(0)·f(-1)<0,由零点存在定理,知f(x)在区间[-1,0]内有零点.尊敬的读者:本文由我和我的同事在百忙中收集整编出来,本文档在发布之前我们对内容进行仔细校对,但是难免会有不尽如人意之处,如有疏漏之处请指正,希望本文能为您解开疑惑,引发思考。
高一数学算法案例试题答案及解析

高一数学算法案例试题答案及解析1.用辗转相除法求得数98与63的最大公约数是____________;【答案】7【解析】98=63×1+35,63=35×1+28,35=28×1+7,28=7×4.∴98与63的最大公约数是7.【考点】辗转相除.2.已知函数,用秦九韶算法计算__________;【答案】4485【解析】则;故答案为:4485.【考点】秦九韶算法.3.用秦九韶算法求多项式f(x)=x5+3x4-5x3+7x2-9x+11当x=4时的值为.【答案】1559【解析】,当x=4时f(x)=1559.【考点】秦九韶算法.4.已知,应用秦九韶算法计算时的值时,的值为()A.27B.11C.109D.36【答案】D【解析】根据秦九韶算法,把多项式改写成,所以,,,,故选D.【考点】秦九韶算法.5.用辗转相除法求得228和1995的最大公约数是【答案】57【解析】∵1995÷228=1…171,228÷171=1…57,171÷57=3,∴228与1995的最大公约数是57。
【考点】本题主要考查辗转相除法。
点评:简单题,思路清晰,细心计算即得。
6.下表提供了某工厂节能降耗技术改造后生产甲产品过程中记录的产量(吨)与相应的生产能耗(吨标准煤)的几组对照数据。
(2)请根据上表提供的数据,用最小二乘法求出关于的线性回归方程;(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤。
试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)【答案】(1)如图(2)(3)预测生产100吨甲产品的生产能耗比技术改造前降低19.65吨标准煤。
【解析】(1)如图(2)由系数公式可知,,,所以线性回归方程为(3)时,所以预测生产100吨甲产品的生产能耗比技术改造前降低19.65吨标准煤。
算法案例(秦九韶算法)

算法的步骤和流程
01
02
03
04
2. 将 $a_{i+1}$ 加到 $v$ 中。 3. 将 $v$ 存储在变量 $P$ 中。
步骤3:返回 $P$ 作为多项 式的值。
通过以上步骤,秦九韶算法可以 在 $O(n)$ 的时间内计算出一元 多项式的值,其中 $n$ 是多项式 的次数。与直接使用常规的求值 方法相比,秦九韶算法可以显著 减少乘法的次数,从而提高计算
缺点
对大系数多项式不适用
秦九韶算法适用于系数和次数都很大的多项式,但如果多项式的 系数非常大,可能会导致数值溢出或下溢,影响计算精度。
需要额外的存储空间
秦九韶算法需要存储中间结果,如果多项式的次数很大,需要额外 的存储空间。
对某些特殊多项式不适用
秦九韶算法不适用于某些特殊的多项式,如常数、一次多项式等。
秦九韶算法的应用场景
数值分析
秦九韶算法在数值分析中广泛应用于求解多项式方程的根,以及进行 数值积分和微分等计算。
科学计算
在科学计算领域,秦九韶算法被用于计算物理、化学、工程等领域中 的多项式函数值,以及进行数据拟合和插值等操作。
计算机图形学
在计算机图形学中,秦九韶算法被用于计算光线追踪和纹理映射等算 法中的多项式函数值,以提高渲染效率和精度。
05
秦九韶算法的优缺点
优点
高效性
秦九韶算法是一种快速算法,可以在多项式 时间内完成计算,比直接计算更高效。
易于编程实现
秦九韶算法的步骤明确,易于编程实现,可 以方便地应用于计算机程序中。
数值稳定性
秦九韶算法在计算过程中可以减少舍入误差, 提高数值稳定性。
适用范围广
秦九韶算法适用于多项式的系数和次数都很 大的情况,具有较广的适用范围。
1[1].3算法案例(第二课时) 秦九韶算法
![1[1].3算法案例(第二课时) 秦九韶算法](https://img.taocdn.com/s3/m/f05c5a203169a4517723a30a.png)
满二进一,就是二进制; 满十进一,就是十进制;
满十二进一,就是十二进制; 满六十进一,就是六十进制
基数:
“满几进一”就是几进制,几进制的基数就是几.
k进制 (表示方法)
十进制数:用0,1,2,3,4,5,6,7,8,9来表示; 二进制只有0和1两个数字,七进制用0—6七个数字
十六进制有0—9十个数字及ABCDEF六个字母.
算法二:先计算x2的值,然后依次计算x2· x、( x2· x、 x)· ( ( x2· x)· x)· x的值。 共做了 4 次乘法运算,5 次加法运算。
秦九韶算法
例如:把一个5次多项式f(x)=a5x5+a4x4+a3x3+a2x2+a1x+a0 改写成如下形式:
f ( x) (a5 x a4 x a3 x a2 x a1 ) x a0 3 2 (( a5 x a4 x a3 x a2 ) x a1 ) x a0
751 7 162 5 161 1160 1873 (16) (10)
2361 2 83 3 82 6 81 1 80 (8)
进制转化
1. k进制数化成十进制数
an an 1 a1a0( k ) (0 an k , 0 an 1 ,, a1 , a0 k ).
+5x5+3x6,当x=-4时,v3的值为( C )
A -845 B 220 C -57 D 34
3.用秦九韶算法计算多项式f(x)=x6-12x5+60x4-160x3
+240x2-192x+64,当x=2时的值?
算法案例 (第二课时)
一、进位制
课时作业27:1.3 算法案例(一)

1.3 算法案例(一)学业水平合格练1.秦九韶算法与直接计算相比较,下列说法错误的是()A.秦九韶算法与直接计算相比,大大节省了做乘法的次数,使计算量减少,并且逻辑结构简单B.秦九韶算法减少了做乘法的次数,在计算机上也就加快了计算的速度C.秦九韶算法减少了做乘法的次数,在计算机上也就降低了计算的速度D.秦九韶算法避免了对自变量x单独做幂的计算,而且与系数一起逐次增长幂次,从而提高计算的精度2.下列说法中正确的个数为()①辗转相除法也叫欧几里得算法;②辗转相除法的基本步骤是用较大的数除以较小的数;③求最大公约数的方法,除辗转相除法之外,没有其他方法;④编写辗转相除法的程序时,要用到循环语句.A.1 B.2C.3 D.43.利用秦九韶算法求f(x)=1+2x+3x2+…+6x5当x=2时的值时,下列说法正确的是() A.先求1+2×2B.先求6×2+5,第二步求2×(6×2+5)+4C.f(2)=1+2×2+3×22+4×23+5×24+6×25直接运算求解D.以上都不对4.中国古代有计算多项式值的秦九韶算法,下图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a为2,2,5,则输出的s=()A .7B .12C .17D .345.用更相减损术求117和182的最大公约数时,需做减法的次数是( ) A .8 B .7 C .6D .56.用秦九韶算法求n 次多项式f (x )=a n x n +a n -1x n -1+…+a 1x +a 0当x =x 0时的值,求f (x 0)需要乘方、乘法、加法的次数分别为( ) A .n (n +1)2,n ,nB .n,2n ,nC .0,2n ,nD .0,n ,n7.用秦九韶算法求多项式f (x )=12+35x -8x 2+79x 3+6x 4+5x 5+3x 6当x =-4的值时,其中v 1的值为________.8.378和90的最大公约数为________. 9.求1356和2400的最小公倍数.10.用秦九韶算法求多项式f (x )=7x 7+6x 6+5x 5+4x 4+3x 3+2x 2+x 当x =3时的值.应试能力等级练11.下列哪组的最大公约数与1855,1120的最大公约数不同()A.1120,735 B.385,350C.385,735 D.1855,32512.用秦九韶算法计算多项式f(x)=3x6+4x5+5x4+6x3+7x2+8x+1,当x=0.4时的值时,需要做乘法和加法的次数分别是()A.6,6B.5,6C.5,5D.6,513.已知a=333,b=24,则使得a=bq+r(q,r均为自然数,且0≤r≤b)成立的q和r的值分别为________.14.用秦九韶算法求多项式f(x)=1-5x-8x2+10x3+6x4+12x5+3x6当x=-4时的值时,v0,v1,v2,v3,v4中最大值与最小值的差是________.15.用辗转相除法和更相减损术两种方法求三个数72,120,168的最大公约数.参考答案学业水平合格练1.【答案】C【解析】秦九韶算法减少了做乘法的次数,在计算机上也就加快了计算的速度,故选项C 错误.2.【答案】C【解析】①、②、④正确,③错误.3.【答案】B【解析】利用秦九韶算法应先算a n x+a n-1,再算(a n x+a n-1)x+a n-2,故选B.4.【答案】C【解析】该题考查程序框图的运行及考生的识图能力.由程序框图知,第一次循环:x=2,n=2,a=2,s=0×2+2=2,k=1;第二次循环:a=2,s=2×2+2=6,k=2;第三次循环:a=5,s=6×2+5=17,k=3.结束循环,输出s的值为17,故选C.5.【答案】C【解析】∵182-117=65,117-65=52,65-52=13,52-13=39,39-13=26,26-13=13,∴13是117和182的最大公约数,需做减法的次数是6.6.【答案】D【解析】因为f(x)=(…((a n x+a n-1)x+a n-2)x+…+a1)x+a0,所以乘方、乘法、加法的次数分别为0,n,n.7.【答案】-7【解析】∵f(x)=12+35x-8x2+79x3+6x4+5x5+3x6,∴v0=a6=3,v1=v0x+a5=3×(-4)+5=-7.8.【答案】18【解析】378=90×4+18,90=18×5+0,∴378与90的最大公约数是18.9.解:2400=1356×1+1044,1356=1044×1+312,1044=312×3+108,312=108×2+96,108=96×1+12,96=12×8.所以1356与2400的最大公约数为12.则1356与2400的最小公倍数为(1356×2400)÷12=271200.10.解:f(x)=((((((7x+6)x+5)x+4)x+3)x+2)x+1)·x,所以v0=7,v1=7×3+6=27,v2=27×3+5=86,v3=86×3+4=262,v4=262×3+3=789,v5=789×3+2=2369,v6=2369×3+1=7108,v7=7108×3=21324.故x=3时,多项式f(x)=7x7+6x6+5x5+4x4+3x3+2x2+x的值为21324.应试能力等级练11.【答案】D【解析】∵(1855,1120)→(735,1120)→(735,385)→(350,385)→(350,35),∴1855与1120的最大公约数是35,由以上计算过程可知选D.12.【答案】A【解析】根据秦九韶算法,把多项式改写为f(x)=(((((3x+4)x+5)x+6)x+7)x+8)x+1,∴需要做6次加法运算,6次乘法运算,故选A.13.【答案】13,21【解析】用333除以24,商即为q,余数就是r.333÷24的商为13,余数是21.∴q=13,r=21.14.【答案】62【解析】多项式变形为f(x)=3x6+12x5+6x4+10x3-8x2-5x+1=(((((3x+12)x+6)x+10)x-8)x-5)x+1,v0=3,v1=3×(-4)+12=0,v2=0×(-4)+6=6,v3=6×(-4)+10=-14,v4=-14×(-4)-8=48,所以v4最大,v3最小,所以v4-v3=48+14=62.15.解:(辗转相除法):先求120,168的最大公约数.因为168=120×1+48,120=48×2+24,48=24×2,所以120,168的最大公约数是24.再求72,24的最大公约数.因为72=24×3,所以72,24的最大公约数为24,即72,120,168的最大公约数为24.(更相减损术):先求120,168的最大公约数.168-120=48,120-48=72,72-48=24,48-24=24,所以120,168的最大公约数为24.再求72,24的最大公约数.72-24=48,48-24=24,所以72,24的最大公约数为24,即72,120,168的最大公约数为24.。
第一章 1.3 算法案例:辗转相除法、秦九韶算法

3,答案:C
返回
• 4.用秦九韶算法求f(x)=3x?+4x?+5x? +6x?+7x?+8x+1,当x=0.4时的值, 需进行乘法运算和加法运算的次数分别为 ( ) • A. 6 6 B. 5 6 • C.6 5 D.6 12 • 解析:改写多项多f(x)=(((((3x+4)x+5)x+ 6)x+7)x+8)x+1,则需要6次乘法和6次加 法. • 答案:A
返回
课堂练习
2.用辗转相除法求294和84的最大公约数时,需要 做除法的次数是( ) A.1 B. 2 C.3 D. 4 3.用秦九韶算法求多项式的值,可用哪种结构的算 法实现( ) A.顺序结构 B.条件结构 C.循环结构 D.A、B两种 • 2,解析:由294=84×3+42,84=42×2知,共需 做2次除法. • 答案:B
返回
法二:更相减损术:
因为378与90都是偶数. 所以用2约简得189和45. 189-45=144,144-45=99, 99-45=54,54-45=9, 45-9=36,36-9=27, 27-9=18,18-9=9.
所以378与90的最大公约数为2×9=18.
返回
[例2]
用秦九韶算法求多项式
1.3 算法案例 辗转相除法、秦九韶算法
返回
预习思考
• 1,用辗转相除法求80和36的最大公约数, 并用更相减损术检验所得结果.
• 2,用秦九韶算法求多项式f(x)=2x4-6x3 -5x2+4x-6在x=5时的值.
返回
[例1]
用辗转相除法求80和36的最大公约数,并
用更相减损术检验所得结果. [自主解答] 用辗转相除法:
返回
1.秦九韶算法的步骤
返回
2.应用秦九韶算法计算多项式的值应注意的问题 (1)要正确将多项式的形式进行改写. (2)计算应由内向外依次计算. (3)当多项式函数中间出现空项式,要以系数为零的
1.3 等值算法、割圆术、秦九韶案例

1.3 中国古代数学中的算法案例【学习目标】通过学习中国古代数学中的算法案例,进一步体会“算法”概念,了解中国古代数学对世界数学发展的贡献,增强民族自豪感。
【知识网络】【学路导引】学习重点:等值算法、割圆术、秦九韶算法的原理和优越性学习难点:将等值算法、割圆术、秦九韶算法转化为程序语言学法指导:通过模仿、操作、探索,将三种算法转变为程序语言,进一步理解几种基本算法语句,熟悉算法的三种基本结构,多动手,多动脑,多上机。
【范例精析】例1:求两个正整数的最大公约数。
精析:利用while循环语句和if-else条件语句编写。
解:a=input("please give zhe first number")b=input("please give zhe second number")while a<>bif a>=ba=a-b;elseb=b-a;endendprint(%io(2),a,b)点评:求两个正整数的最大公约数有等值法和辗转相除法两种方法,但是等值算法更优越。
例2:任给一个数,精确到小数点后第n位。
精析:利用取整函数floorx=input("x=")n=input("qing shu ru jing que dao xiao shu dian hou de wei shu");a=x*10^n;x=floor(a+0.5);x=x/(10^n)点评:取整函数floor是取不超过实数本身的最大整数。
例3:(1)、写出求圆周率不足近似值的程序。
(2)、写出求圆周率的过剩近似值的程序。
精析:根据祖冲之的割圆术编写。
解:(1)m=input("m=")n=6;x=1;s=6*sqrt(3)/4;for i=1:mh=sqrt(1-(x/2)^2);s=s+n*x*(1-h)/2;n=2*n;x=sqrt((x/2)^2+(1-h)^2);endprint(%io(2),n,s)(2)m=input("m=")n=6;x=1;s=6*sqrt(3)/4;for i=1:mh=sqrt(1-(x/2)^2);t=s;s=s+n*x*(1-h)/2;n=2*n;x=sqrt((x/2)^2+(1-h)^2);end$=2*s-t;print(%io(2),n,$)点评:我国古代的算法,非常适合编写成现在的计算机程序。
秦九韶算法与K进制练习题(含详细解答)

秦九韶算法与K进制练习题(含详细解答)秦九韶与k进制练习题一.选择题(共16小题)1.把77化成四进制数的末位数字为()A.4 B.3 C.2 D.12.用秦九韶算法求多项式f(x)=x+2x+x3x1,当x=2时的值,则v3=()A.4 B.9 C.15 D.293.把67化为二进制数为()A.__ B.__-__ C.__-__ D.__-__4.用秦九韶算法计算多项式f(x)=3x+4x+5x+6x+7x+8x+1当x=0.4时的值时,需要做乘法和加法的次数分别是()A.6,6 B.5,6 C.5,5 D.6,55.使用秦九韶算法计算x=2时f(x)=6x+4x2x+5x7x2x+5的值,所要进行的乘法和加法的次数分别为()A.6,3 B.6,6 C.21,3 D.21,66.把27化为二进制数为()A.1011(2)B.__(2)__-__C.__(2)432D.__(2)7.用秦九韶算法计算多项式f (x)=5x+4x+3x2__1在x=4时的值时,需要进行的乘法、加法的次数分别是()A.14,5 B.5,5 C.6,5 D.7,58.二进制数__-__(2)对应的十进制数是()A.401 B.385 C.201 D.2589.小明中午放学回家自己煮面条吃,有下面几道工序:①洗锅盛水2分钟;②洗菜6分钟;③准备面条及佐料2分钟;④用锅把水烧开10分钟;⑤煮面条和菜共3分钟.以上各道工序,除了④之外,一次只能进行一道工序.小明要将面条煮好,最少要用()分钟.A.13 B.14 C.15 D.2310.用秦九韶算法在计算f(x)=2x+3x2x+4x6时,要用到的乘法和加法的次数分别为()A.4,3 B.6,4 C.4,4 D.3,411.用秦九韶算法求多项式f(x)=1+2x+x3x+2x在x=1时的值,v2的结果是()A.4 B.1 C.5 D.612.下列各数85(9)、210(6)、1000(4)、__(2)中最大的数是()A.85(9)B.210(6)C.1000(4)D.__(2)__13.十进制数89化为二进制的数为()A.__-__(2)B.__-__(2)C.__-__(2)D.__-__(2)14.烧水泡茶需要洗刷茶具(5min)、刷水壶(2min)、烧水(8min)、泡茶(2min)等个步骤、从下列选项中选最好的一种算法()A.第一步:洗刷茶具;第二步:刷水壶;第三步:烧水;第四步:泡茶B.第一步:刷水壶;第二步:洗刷茶具;第三步:烧水;第四步:泡茶C.第一步:烧水;第二步:刷水壶;第三步:洗刷茶具;第四步:泡茶D.第一步:烧水;第二步:烧水的同时洗刷茶具和刷水壶;第三步:泡茶15.在下列各数中,最大的数是()A.85(9)B.210(6)16.把23化成二进制数是()A.00110 B.__二.填空题(共11小题)C.1000(4)D.__(2)C.__ D.__ 17.用秦九韶算法求多项式f(x)=12+35x8x+79x+6x+5x+3x在x=4的值时,其中V1的值= _________ .18.把5进制的数412(5)化为7进制是_________ .19.用秦九韶算法计算多项式f(x)=8x+5x+3x+2x+1在x=2时的值时,v2=.20.用秦九韶算法计算多项式f(x)=3x+4x+5x+6x+7x+8x+1当x=0.4时的值时,至多需要做乘法和加法的次数分别是_________ 和_________ .21.军训基地购买苹果慰问学员,已知苹果总数用八进位制表示为abc,七进位制表示为cba,那么苹果的总数用十进位制表示为_________ .22.若六进制数Im05(6)(m为正整数)化为十进数为293,则m= _________ .23.用秦九韶算法求多项式f(x)=5x+2x+3.5x2.6x+1.7x0.8当x=5时的值的过程中v3=.24.完成下列进位制之间的转化:1234=(4).25.把十进制数51化为二进制数的结果是26.进制转化:403(6)= _________(8)__-__-__2.27.完成右边进制的转化:1011(2)= _________ (10)= _________ (8).三.解答题(共3小题)3228.将多项式x+2x+x1用秦九韶算法求值时,其表达式应写成29.写出将8进制数__转化为7进制数的过程.30.已知一个5次多项式为f(x)=4x3x+2x+5x+1,用秦九韶算法求这个多项式当x=2时的值.532答案与评分标准一.选择题(共16小题)1.把77化成四进制数的末位数字为()A.4 B.3 C.2 D.1考点:排序问题与算法的多样性。
2021高中数学-秦九韶算法(精选试题)

高中数学-秦九韶算法1、用秦九韶算法求多项式fx=2x7+x6-3x5+2x4+4x3-8x2-5x+6的值时,V4=V3x+__________.2、已知n次多项式Pnx=a0xn+a1xn-1+⋅⋅⋅+an-1x+an.如果在一种算法中,计算x0k(k=2,3,4,⋅⋅⋅,n)的值需要k-1次乘法,计算P3x0的值共需要9次运算(6次乘法,3次加法),那么计算Pnx0的值共需要______次运算.下面给出一种减少运算次数的算法:P0x0=a0,Pk+1x=xPkx+ak+1(k=0,1,2,⋅⋅⋅,n-1).利用该算法,计算P3x0的值共需要6次运算,计算Pnx0的值共需要_______次运算.3、用``秦九韶算法’’计算多项式fx=5x5+4x4+3x3+2x2+x+1,当x=2时的值的过程中,要经过_____________次乘法运算和________次加法运算.4、(1)用辗转相除法求282与470的最大公约数.(2)用秦九韶算法求多项式fx=7x7+6x6+5x5+4x4+3x3+2x2+x,当x=3时的值.5、用秦九韶算法求多项式fx=7x7+6x6+5x5+4x4+3x3+2x2+x,当x=3时,v3的值为()A.27B.86C.262D.786、用秦九韶算法求多项式fx=7x7+6x6+5x5+4x4+3x3+2x2+x,当x=3时的值_______.7、用秦九韶算法计算fx=3x6+4x5+5x4+6x3+7x2+8x+1当x=0.4时的值,需要进行乘法运算和加法运算的次数分别为()A.6,6B.5,6C.6,5D.6,128、用秦九韶算法计算函数fx=2x4+3x3+5x-4在x=2时的函数值.9、用秦九韶算法求多项式fx=3x5+x2-x+2,当x=-2时的值时,需要进行的乘法运算和加法运算的次数分别为()A.4,2B.5,3C.5,2D.6,210、用秦九韶算法求多项式fx=x6-5x5+6x4+x2-3x+2,当x=3时的值.11、用秦九韶算法计算fx=6x5-4x4+x3-2x2-9x,需要加法(或减法)与乘法运算的次数分别为()A.5,4B.5,5C.4,4D.4,512、用秦九韶算法求多项式fx=x5+5x4+10x3+10x2+5x+1当x=-2时的值为_________.13、用秦九韶算法求多项式fx=x7-2x6+3x3-4x2+1当x=2时的函数值.14、用秦九韶算法求多项式fx=12+35x-8x2+79x3+6x4+5x5+3x6在x=-4的值时,v4的值为()A.-57B.220C.-845D.339215、用秦九韶算法计算多项式fx=x6-12x5+60x4-160x3+240x2-192x+64,当x=2时的值.16、用秦九韶算法计算多项式fx=6x6+5x5+4x4+3x3+2x2+x+7在x=0.4时的值时,需做加法和乘法的次数的和为()A.10B.9C.12D.817、已知fx=x5+2x3+3x2+x+1,应用秦九韶算法计算x=3时的值时,v3的值为()A.27B.11C.109D.3618、用秦九韶算法计算多项式fx=x6-12x5+60x4-160x3+240x2-192x+64当x=2时的值.19、已知n次多项式Pnx=a0xn+a1xn-1+⋯+an-2x2+an-1x+an,如果在一种算法中,计算x0kk=234⋯n的值需要k-1次乘法,计算P3x0的值共需要9次运算(6次乘法,3次加法),那么计算Pnx0的值共需要____________次运算.下面给出一种减少运算次数的算法:P0x=a0,Pk+1x=xPkx+ak+1k=012⋯n-1.利用该算法,计算P3x0的值共需要6次运算,计算Pnx0的值共需要____________次运算.20、中国古代有计算多项式的秦九韶算法,下图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入a为2,2,5,则输出的s=()A.7B.12C.17D.3421、用秦九韶算法求多项式fx=x6+2x5+3x4+4x3+5x2+6x当x=2时的值.22、用秦九韶算法计算fx=2x4+3x3+5x-4在x=2时的值.23、秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求多项式值的一个实例,若输入n,x的值分别为3,2,则输出v的值为()A.35B.20C.18D.924、秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数学九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的计算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为3,2,则输出v的值为()A.9B.18C.20D.3525、用秦九韶算法计算多项式fx=1+8x+7x2+5x4+4x5+3x6在x=5时所对应的v4的值为()A.1 829B.1 805C.2 507D.2 54326、用秦九韶算法求多项式fx=7x7+6x6+5x5+4x4+3x3+2x2+x当x=3时的值.27、用秦九韶算法计算多项式fx=12+35x-8x2+79x3+6x4+5x5+3x6,在x=-4时的值时,v3的值为()A.-845B.220C.-57D.3428、已知多项式fx=4x5+3x4+2x3-x2-x-12,用秦九韶算法求f-2等于()A.-1972B.1972C.1832D.-183229、用秦九韶算法计算多项式fx=3x6+4x5+5x4+6x3+7x2+8x+1,当x=0.4时的值,需要做乘法和加法的次数分别是()A.6,6B.5,6C.5,5D.6,530、用秦九韶算法求n次多项式fx=anxn+an-1xn-1+⋯+a1x+a0,当x=x0时,求fx0需要算乘方、乘法、加法的次数分别为()A.nn+12,n,nB.n,2n,nC.0,2n,nD.0,n,nfx=1+2x+x2-3x3+2x4,当x=-1的值时,v2的结果是____________.32、阅读程序框图,利用秦九韶算法计算多项式fx=anxn+an-1xn-1+⋯+a1x+a0,当x=x0时,框图中A处应填入____________.33、用秦九韶算法求多项式fx=x5+5x4+10x3+10x2+5x+1,当x=-2时的值.34、用秦九韶算法,求y=7.5x6+8.65x5-3.7x4+4.2x3+2.1x2+x-5.5在x=0.5时的值,写出详细计算过程.35、已知函数fx=x3-2x2-5x+6,用秦九韶算法求f10的值.36、用秦九韶算法求多项式fx=12-8x2+6x4+5x5+3x6在x=-4时,v4的值为()A.-57B.220C.-845D.53637、下面关于算法的说法正确的是()A.秦九韶算法是求两个数的最大公约数B.更相减损术是求多项式的值的方法C.辗转相除法是求多项式的值的方法D.以上皆错38、在利用秦九韶算法求当x=2时,fx=1+2x+3x2+4x3+5x4+6x5的值时,下列说法正确的是()A.先求1+2×2B.先求6×2+5,第二步求2×6×2+5+4C.f2=1+2×2+3×22+4×23+5×24+6×25直接运算求解D.以上皆错39、用秦九韶算法求多项式fx=anxn+an-1xn-1+⋯+a1x+a0时,求fx0需要算乘方、乘法、加法的次数分别为()A.12nn+1,n,nB.n,2n,nC.0,2n,nD.0,n,n40、秦九韶算法与直接计算相比较,下列说法错误的是()A.秦九韶算法与直接计算相比,大大节省了乘法的次数,使计算量减小,并且逻辑结构简单B.秦九韶算法减少计算乘法的次数,在计算机上也就加快了计算的速度C.秦九韶算法减少计算乘法的次数,在计算机上也就降低了计算的速度D.秦九韶算法避免对自变量x单独作幂的计算,而是与系数一起逐次增长幂次,从而可提高计算的精确度41、已知n次多项式Pnx=a0xn+a1xn-1+⋯+an-1x+an,如果在一种算法中,计算x0k(k=2,3,4,⋯,n)的值需要k-1次乘法,计算P3x0的值共需要9次运算(6次乘法,3次加法),那么计算P10x0的值共需要_________次运算.下面给出一种减少运算次数的算法:P0x=a0,Pk+1x=xPkx+ak+1(k=0,1,2,⋯,n-1).利用该算法,计算P3x0的值共需要6次运算,计算P10x0的值共需要___________次运算.42、用秦九韶算法求多项式fx=8x7+5x6+3x4+2x+1,当x=2时的值.43、秦九韶是我国南宋时期的数学家,普州(现四川省安岳县)人,他在所著的《数学九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法.如图所示的程序框图给出了利用秦九韶算法求某多项式值的一个实例,若输入n,x的值分别为3,2,则输出v的值为()A.18B.35C.65D.13044、已知8次多项式fx=a8x8+a7x7+⋯+a1x+a0,用秦九韶算法求fx0的值,需要进行的乘法运算,加法运算的次数分别是()A.8,8B.16,8C.36,8D.9,945、用秦九韶算法求多项式fx=5x5+4x4-3x2+x-1,当x=13时的值时,先算的是()A.13×13B.5×135C.5×13+4D.5×13+4×346、用秦九韶算法求多项式fx=x5+0.11x3-0.15x-0.04当x=0.3时的值.47、用秦九韶算法求多项式fx=12+35x-8x2+79x3+6x4+5x5+3x6在x=-4时的值时,v4的值为()A.-57B.220C.-845D.339248、用秦九韶算法计算多项式fx=5x7+x6-x3+x+3当x=-1时的值,并判断多项式fx在区间-10内是否有零点.49、用秦九韶算法计算多项式fx=2x7+2x6+3x5+6x4+5x3-x2-5x+8当x=2的值时,其中v3的值为()A.15B.36C.41D.77。
算法案例 习题(含答案)

算法案例 习题(含答案)一、单选题1.给出下列命题:①命题“ ”的否定是“ ”;②命题“若 ,则 ”的逆命题是真命题;③把 化为十进制为11;④“方程 表示椭圆”的充要条件是“ ”.其中正确命题的个数为( )A . 1B . 2C . 3D . 42.用秦九韶算法计算多项式65432692351712)(x x x x x x x f ++++-+=在4-=x 时的值时,3V 的值为( )A .-307B .-81C .19D .13.《周易》历来被人们视作儒家之首,它表现了古代中华民族对万事万物的深刻而不朴素的认识,是中华人文文化的基础,它反映出中国古代的二进制计数的思想方法,我们用近代术语解释为:把阳“—”当作数字“1”,把阴“——”当作数字“0”,则八卦所代表的数表示如下:依次类推,则六十四卦“屯”卦,符号“”表示的十进制是( )A . 18B . 17C . 16D . 154.在下列各数中,最大的数是( )A . 85(9)B . 210(6)C . 1000(4)D . 11111(2)5.二位进制数 化为十位进制数是( )A .B .C .D .6.“结绳计数”是远古时代的人最常用的计数方法,就是用打绳结的办法来计算物体的数量.如图所示的是一位猎人记录自己捕获猎物的个数,在从右向左依次排行的不同绳子上打结,满五进一.根据图示可知,猎人捕获猎物的个数是( )A . 123B . 86C . 66D . 387.我国南宋时期的数学家秦九韶是普州(现四川省安岳县)人,秦九韶在所著的《数书九章》中提出的多项式求值的秦九韶算法,至今仍是比较先进的算法,其算法如下:多项式函数 写为,即可用如图所示的程序框图来求某多项式的值.若输入 及 ,运行程序可以输出16,则 的值为( )A .B . 1或C . 1D . 2或8.下列各数中,最大的是( )A .B .C .D .9.用秦九韶算法计算多项式()f x = 653225238103,x x x x x x ++-+-=4-时, 4V 的值为A . 92B . 1529C . 602D . 148-二、填空题10.辗转相除法与更相减损术都是求两个正整数的最大公约数的有效算法,用这两种方法均可求得 和 的最大公约数为__________.11.请将以下用“更相减损术”求两个正整数a,b 的最大公约数的程序补充完整:INPUT “a,b=”;a,bWHILE a<>bIF a>b THENa=a-bELSE_________END IFWENDPRINT aEND12.把八进制数()()8102转化为三进制数为______________.13.11 001 ()2101=__________()10.14.用秦九韶算法求多项式f(x)=x 4-2x 3+3x 2-7x-5当x=4时的值,给出如下数据:①0 ②2 ③11 ④37 ⑤143其运算过程中(包括最终结果)会出现的数有____(只填序号).15.二进制数()210对应的十进制数是__________.16.把“五进制”数转化为“七进制”数: ()5321=__________()717.用“秦九韶算法”计算多项式()543254321f x x x x x x =+++++,当2x =时的值的过程中,要经过____________次乘法运算和_________次加法运算.18.三个数72,120,168的最大公约数是 ;三、解答题19.把110(5)转化为二进制数.20.(本题满分13分)已知一个5次多项式为f (x )=4x 5﹣3x 3+2x 2+5x+1,用秦九韶算法求这个多项式当x=2时的值21.某高中男子体育小组的50米跑成绩(单位:s )为:6.4,6.5,7.0,6.8,7.1,7.3,6.9,7.4,7.5,6.7,画出程序框图,从这些成绩中搜索出小于6.8s的成绩.22.试分别用辗转相除法和更相减损术求840与1764、440与556的最大公约数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学13《算法案例---秦九韶算法》测试《算法案例---秦九韶算法》测试
1.请简述秦九韶算法的原理和应用领域。
(200字)
秦九韶算法是一种用于求解多项式的算法,其原理是利用多项式的迭代运算,通过不断累加、相乘的方式快速计算多项式的值。
在秦九韶算法中,我们可以将多项式表示为P(x) = a0 + a1 * x + a2 * x^2 + ... + an * x^n,其中a0、a1、a2 ... an分别为多项式的系数,n为多项式的最高次数。
秦九韶算法的关键在于利用迭代运算,通过反复累加和相乘的操作,将多项式的求解过程化简为一个简单的数值计算。
具体来说,我们可以将多项式P(x)的求解过程表示为以下形式:P(x) = (...((an * x + an-1) * x + an-2) * x + ...) * x + a0。
秦九韶算法的应用领域十分广泛。
在数学领域,它可以用于高等代数学、微积分和数值分析等方面的多项式计算。
在计算机科学领域,秦九韶算法可以用于实现多项式的编程计算和求解,例如图像处理、信号处理、数据压缩等方面的应用。
2.请说明秦九韶算法的时间复杂度和空间复杂度,并分析其优势和劣势。
(400字)
秦九韶算法的时间复杂度为O(n),其中n为多项式的最高次数。
它的空间复杂度为O(1),因为该算法只需要少量的变量对计算过程进行临时存储,并不需要额外的空间。
秦九韶算法的优势在于其计算速度快,尤其适用于对多项式进行大量计算的情况。
通过不断累加和相乘的运算,可以在较短的时间内得到多项式的值。
相比传统的直接计算法,秦九韶算法具有更高的效率。
然而,秦九韶算法也存在一些劣势。
首先,该算法需要事先知道多项式的系数,如果系数未知或需要动态获取,则无法使用该算法。
其次,秦九韶算法对于多项式次数较高的情况,计算过程中可能会有较大的误差累积,从而影响计算结果的准确性。
此外,秦九韶算法只适用于一维的多项式计算,对于多维的多项式计算并不适用。
综上所述,秦九韶算法是一种简单且高效的多项式计算方法,适用于多项式次数较低且系数已知的情况。
它能够在短时间内快速计算多项式的值,具有较大的应用潜力。
然而,在应用实践中,需要根据具体情况评估其可行性和适用性,避免出现误差累积和精度问题。
