数字信号卷积的计算例题

合集下载

数字信号处理各章测试题

第一章1、设某线性时不变离散系统的差分方程为)()1()(310)1(n x n y n y n y =++--,试求它的单位抽样响应。

它是不是因果的？是不是稳定的？2、用两种方法计算下面两个序列的线性卷积：x(n)= δ(n)+2δ(n+2)-δ(n-4) , y(n)= 3δ(n-1)+δ(n-3) 。

3、一阶因果系统的差分方程为 y(n)-ay(n-1)=x(n), a 是实数，求：（1）、该系统的系统函数H （z ）和收敛域；（2）、分0<a<1, a=0, a>1三种情况写出h(n)及稳定性，画出零极点分布图。

4、下列是系统的单位脉冲响应表达式，试指出这些系统的因果、稳定性。

（1）、 e R n anN ()（2）、 2nU n ()- （3）、)2()2(++-n n δδ （4）、)(2n U n （5）、 )1(3--n U n (6)、)1(1+n U n5、若azaz z X --=--111)(，1->az ，试求)(z X 的反z 变换。

6、已知某线性时不变系统的单位脉冲响应为()()n h n a u n =，10<<a ，输入序列为()()nx n b u n =，10<<b ，（1）请用z 域关系式计算该系统的输出序列y (n )；（2）请分析该系统的因果稳定性。

7、已知某系统的差分方程为)()2(2)1(3)(n x n y n y n y +---=，求：（1）、系统函数（2）、系统频响（3）、系统零极点（4）、收敛域为1<|z|<2时的单位脉冲响应。

8、序列的Z 变换)21)(5.01(5.1)(111------=z zzz X 。

在以下三种收敛域下，哪一种是左边序列？哪一种是右边序列？哪一种是双边序列？并求出各对应的序列。

（1）、| z | > 2 （2）、| z | < 0.5 （3）、0.5 < | z | < 29、已知一线性移不变因果系统，可用如下差分方程描述：)1(21)()1(21)(-+=--n x n x n y n y求：（1）该系统的冲激响应；（2）系统对输入n j e n x ω=)(的响应；（3）系统的频响。

卷积的几种计算方法以及程序实现FFT算法

因为输油管道不是很长可以考虑设计滤波器器通过信号测量来测试管道的损伤当有焊缝时所接受的信号会有所损失当管道式腐蚀时由于管壁变得不再是平滑的时候信号的频率就会有所改变
数字信号处理
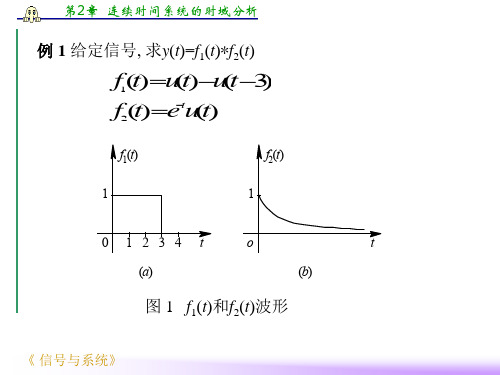
用一个例子说明计算卷积的基本方法。例子：设函数 f1（t）=u(t) – u(t-3),f2(t)=e-tu(t),试计算其卷积 y(t)= f1（t）* f2(t)。
e ( t 1) )u(t 2)
Made by 霏烟似雨
数字信号处理
ht 1
e

t 2
u (t ) u (t 2)
e t 1
e t u (t )
O
t
波形
O
2
t
2. 今有一输油管道，长 12 米，请用数字信号处理的方法探测管道内部的损伤，管道的损伤可能为焊缝，腐蚀。叙述你的探测原理，方法与结果。（不是很清楚）探测原理：因为输油管道不是很长，可以考虑设计滤波器器通过信号测量来测试管道的损伤，当有焊缝时，所接受的信号会有所损失，当管道式腐蚀时，由于管壁变得不再是平滑的时候，信号的频率就会有所改变。
1 e 2

u( ) u( 2) e (t ) u(t ) d

e t e 2 u ( )u (t )d e t e 2 u ( 2)u (t )d

4) 定积分限（关键）
3 当 t>3 时，f1（τ ）与 f2(t-τ )的图形的图形仅在[0,3]内有重叠，如图 c,所以
综上所述有：
3、利用卷积的特性计算
卷积作为一种数学运算方法，具有某些特殊的有用特性。在卷积运算中要注意应用卷积的特性简化运算，尤其要重视应用奇异函数的卷积特性。（1）微积分等效特性

数字信号处理卷积计算

1 f 1( k ) 0 0 k 2 其它

1 2 f 2(k ) 3 0
k 1 k 2 k 3 其它
调用conv()函数求上述两序列的卷积和

题三：编写计算两离散序列卷积和
f(k)=f1(k)*f2(k)的实用函数dconv().要求该程序在计算出卷积和f(k)的同时，还绘出序列f1(k),f2(k) 和f(k)的时域波形图。 function[f,k]=dconv(f1,f2,k1,k2) %f1(k),f2(k)及f(k)的对应序号向量分别为k1，k2 和k。

f 1( i ) f 2 ( k i )
在离散信号与系统分析中有两个与卷积和相关的重要结论： f （1）( k ) f ( i ) ( k i ) f ( k ) * ( k )，即离散序列可分解为一系列幅度由f(k)决定的单位序列δ(k)及其平移序列之积。 (2)对线性时不变系统，设其输入序列为f(k)，单位响应为h(k)，其零状态响应为y(k)，则有：

i
y (k )

i

f (i ) h ( k i )
涉及的函数
1.画图函数：plot,stem,subplot,title, xlable,ylable
2.卷积函数conv.m用来实现两个离散序列的线性卷积。其调用格式是： y=conv(x,h) 若x的长度为N，h的长度为M，则y的长度L=N+M-1。
注意：conv默认两个信号的时间序列从n=0开始，因此默认y对应的时间序号也从n=0开始。
3. 长度函数 length 4.产生1数组函数ones
实验内容

题一：令x(n)={1，2，3，4，5} ，h(n)＝{6，2， 3，6，4，2}，y(n)=x(n)*h(n)，求y(n)。要求用subplot和stem画出x(n),h(n),y(n)与n的离散序列图形。题二：已知序列

数字信号的卷积运算

（14）（15）
那么 x[n]和 h[n]的卷积 y[n]仍然是以 N 为周期的序列，在 matlab 里面可以借助 conv() 函数来计算，代码如下：代码 1： % matlab 计算周期为 N 的 x[n]和 h[n]的卷积
temp=conv(x,h); temp(1:N-1)=temp(1:N-1)+temp(N+1:2*N-1); y=temp(1:N); 对于上述的卷积运算，可以等效于矩阵的运算，例如，设 x，h，y 是长度为 N 的行矩阵，分别对应于 x[n]，h[n]，y[n]的一个周期，表示如下：
由（9）（12）可得
1 N
N 1
X [k ]e
k 0
j nk
, 0 n N 1
（12）
0 0 0 1 1 1 R exp j nk N 0 ( N 2) 1 0 ( N 1) 1
x [ x1 , x2 , x3 ,..., xN 1 , xN ], h [h1 , h2 , h3 ,..., hN 1 , hN ], y [ y , y , y ,..., y , y ]. 1 2 3 N 1 N
并假设
（16）
y xA y[ n] x[n]* h[n]
（13）
由（7）（13）也可以验证（11）的结果。
3 周期序列的卷积
设 x[n],h[n]是以长度 N 为周期的序列，即
x[n] x[n kN ],(k ... 2, 1,0,1, 2...) h[ n] h[ n kN ], ( k ... 2, 1, 0,1, 2...)
那么，A 就是对应于 h 的矩阵，它是 N 阶方阵，表示如下：

数字信号处理习题及答案解析

==============================绪论==============================1. A/D 8bit 5V 00000000 0V 00000001 20mV 00000010 40mV 00011101 29mV==================第一章时域离散时间信号与系统==================1.①写出图示序列的表达式答：3)1.5δ(n 2)2δ(n 1)δ(n 2δ(n)1)δ(n x(n)-+---+++= ②用δ(n) 表示y (n )={2,7,19,28,29,15}2. ①求下列周期)54sin()8sin()4()51cos()3()54sin()2()8sin()1(n n n n n ππππ-②判断下面的序列是否是周期的; 若是周期的，确定其周期。

（1）A是常数 8ππn 73Acos x(n)⎪⎪⎭⎫ ⎝⎛-= （2）)81(j e )(π-=n n x 解：（1）因为ω=73π, 所以314π2=ω, 这是有理数，因此是周期序列，周期T =14。

（2）因为ω=81, 所以ωπ2=16π, 这是无理数，因此是非周期序列。

③序列)Acos(nw x(n)0ϕ+=是周期序列的条件是是有理数2π/w 0。

3.加法乘法序列{2，3，2，1}与序列{2，3，5，2，1}相加为__{4，6，7，3，1}__，相乘为___{4，9，10，2} 。

移位翻转：①已知x(n)波形，画出x(-n)的波形图。

②尺度变换：已知x(n)波形，画出x(2n)及x(n/2)波形图。

卷积和：①h(n)*求x(n)，其他02n 0n 3，h(n)其他03n 0n/2设x(n) 例、⎩⎨⎧≤≤-=⎩⎨⎧≤≤= }23,4,7,4，23{0,h(n)*答案：x(n)=②已知x (n )={1,2,4,3},h (n )={2,3,5}, 求y (n )=x (n )*h (n )x (m )={1,2,4,3},h (m )={2,3,5}，则h (-m )={5,3,2}(Step1:翻转)解得y (n )={2,7,19,28,29,15}③(n)x *(n)x 3)，求x(n)u(n u(n)x 2),2δ(n 1)3δ(n δ(n)2、已知x 2121=--=-+-+=}{1,4,6,5,2答案：x(n)=4.如果输入信号为，求下述系统的输出信号。

数字信号处理习题集大题与答案

1设序列x(n)={4，3，2，1} ，另一序列h(n) ={1，1，1，1}，n=0,1,2,3 （1）试求线性卷积 y(n)=x(n)*h(n) （2）试求6点圆周卷积。

（3）试求8点圆周卷积。

解：1．y(n)=x(n)*h(n)={4,7,9,10,6,3,1}2．6点圆周卷积={5,7,9,10,6,3}3．8点圆周卷积={4,7,9,10,6,3,1,0}2二．数字序列 x(n)如图所示. 画出下列每个序列时域序列： (1) x(n-2); (2)x(3-n); (3)x[((n-1))6],(0≤n ≤5); (4)x[((-n-1))6],(0≤n ≤5);n12340.543210-1-2-3x(3-n)x[((n-1))6]n54321043210.5n12340.5543210x[((-n-1))6]3．已知一稳定的LTI 系统的H(z)为)21)(5.01()1(2)(111------=z z z z H试确定该系统H(z)的收敛域和脉冲响应h[n]。

解:0.52ReIm系统有两个极点，其收敛域可能有三种形式，|z|<0.5, 0.5<|z|<2, |z|>2 因为稳定，收敛域应包含单位圆，则系统收敛域为：0.5<|z|<211111213/25.013/4)21)(5.01()1(2)(--------=---=z z z z z z H )1(232)()5.0(34)(--+=n u n u n h n n4．设x(n)是一个10点的有限序列x （n ）={ 2,3,1,4,-3,-1,1,1,0,6}，不计算DFT ，试确定下列表达式的值。

(1) X(0), (2) X(5), (3)∑=9)(k k X,（4）∑=-95/2)(k k j k X eπ解：（1）（2）（3）（4）5． x(n)和h(n)是如下给定的有限序列 x(n)={5, 2, 4, -1, 2}， h(n)={-3, 2, -1 }(1) 计算x(n)和h(n)的线性卷积y(n)= x(n)* h(n)； (2) 计算x(n)和h(n)的6 点循环卷积y 1(n)= x(n)⑥h (n)； (3) 计算x(n)和h(n)的8 点循环卷积y 2(n)= x(n)⑧h (n)；比较以上结果，有何结论？14][]0[19===∑=n N n x X W 12][][]5[119180510-=-===⎩⎨⎧-=∑∑====奇偶奇数偶数n n n n n n x n x X n n W20]0[*10][][101]0[99===∑∑==x k X k X x k k 0]8[*10][][101]))210[((][]))[((2)10/2(92)10/2(9010)/2(===-⇔--=-=-∑∑x k X ek X ex k X e m n x k j k k j k m N k j N πππ解：（1）5 2 4 -1 2-3 2 15 2 4 -1 210 4 8 -2 4-15 -6 -12 3 -6-15 4 -3 13 -4 3 2y(n)= x(n)* h(n)={-15,4,-3,13,-4,3,2}(2)5 2 4 -1 2-3 2 15 2 4 -1 210 4 8 -2 4-15 -6 -12 3 -6-15 4 -3 13 -4 3 22-13 4 -3 13 -4 3 2y1(n)= x(n)⑥h(n)= {-13,4,-3,13,-4,3}(3)因为8>(5+3-1),所以y3(n)= x(n)⑧h(n)＝{-15,4,-3,13,-4,3,2，0}y3(n)与y(n)非零部分相同。

数字信号处理试题和答案

数字信号处理试题和答案⼀. 填空题1、⼀线性时不变系统，输⼊为 x（n）时，输出为y（n）；则输⼊为2x（n）时，输出为 2y(n) ；输⼊为x（n-3）时，输出为y(n-3) 。

2、从奈奎斯特采样定理得出，要使实信号采样后能够不失真还原，采样频率fs与信号最⾼频率fmax 关系为： fs>=2fmax。

3、已知⼀个长度为N的序列x(n)，它的离散时间傅⽴叶变换为X（e jw），它的N点离散傅⽴叶变换X（K）是关于X（e jw）的N 点等间隔采样。

4、有限长序列x(n)的8点DFT为X（K），则X（K）= 。

5、⽤脉冲响应不变法进⾏IIR数字滤波器的设计，它的主要缺点是频谱的交叠所产⽣的现象。

6．若数字滤波器的单位脉冲响应h（n）是奇对称的，长度为N，则它的对称中⼼是 (N-1)/2 。

7、⽤窗函数法设计FIR数字滤波器时，加矩形窗⽐加三⾓窗时，所设计出的滤波器的过渡带⽐较窄，阻带衰减⽐较⼩。

8、⽆限长单位冲激响应（IIR）滤波器的结构上有反馈环路，因此是递归型结构。

9、若正弦序列x(n)=sin(30nπ/120)是周期的,则周期是N= 8 。

10、⽤窗函数法设计FIR数字滤波器时，过渡带的宽度不但与窗的类型有关，还与窗的采样点数有关11．DFT与DFS有密切关系，因为有限长序列可以看成周期序列的主值区间截断，⽽周期序列可以看成有限长序列的周期延拓。

12．对长度为N的序列x(n)圆周移位m位得到的序列⽤xm (n)表⽰，其数学表达式为xm(n)=x((n-m))N RN (n)。

13．对按时间抽取的基2-FFT流图进⾏转置，并将输⼊变输出，输出变输⼊即可得到按频率抽取的基2-FFT流图。

14.线性移不变系统的性质有交换率、结合率和分配律。

15.⽤DFT近似分析模拟信号的频谱时，可能出现的问题有混叠失真、泄漏、栅栏效应和频率分辨率。

16.⽆限长单位冲激响应滤波器的基本结构有直接Ⅰ型，直接Ⅱ型，串联型和并联型四种。

2.5 用DFT计算线性卷积-数字信号处理

2．5 用DFT计算线性卷积
这种利用DFT技术来计算两个有限长序列线性卷积的方法称为快速卷积。 2.长序列卷积计算对于x（n）序列很长问题，（不能实现信号实时处理），可将x（n）分成较小的段，如每段长为 L，得xi（n），i=1，2，…N/L，N是信号的总长度，将xi（n）与h（n）作卷积，得到相应的输出 yi（n），然后把yi（n）按一定规则首尾相加，即可得到完整的输出y（n）。
2．5 用DFT计算线性卷积
(1)设x（n）为M点序列，h（n）为L点序列，y（n） =x（n）＊h（n）即y（n）是x（n）和h（n）的线性卷积，那么y（n）是一个（M+L-1）点的序列，而DFT对应循环卷积而不对应线性卷积。对于循环卷积：
x(n) h(n) IDFT[X(k)H(k)]
2．5 用DFT计算线性卷积
(1)原序列按长度L≥N1+N2-1补零得x1（k），x2 （k） (2)求DFT得x1（n）→X1（k），x2（n）→X2（k）
(3)计算DFT得乘积Y（k）=X1（k）X2（k） (4)求IDFT得y（n）=IDFT[Y（k）]
2．5 用DFT计算线性卷积
把长序列分成短序列作卷积的方法有两种，一是叠接相加法，二是叠接舍去法。作业1：设信号x·求系统的输出y（n）=x（n）＊h（n） ·试用循环卷积计算y（n） ·简述通过DFT来计算y（n）的思路
2．5 用DFT计算线性卷积式中x（n）和h（n）都是N点序列，所以循环卷积也是N点序列，而线性卷积结果为2N-1点序列。所以如果让两个结果相同，必须让x（n）为2N-1 点序列，h（n）也为2N-1点序列才可，补零策略。
2．5 用DFT计算线性卷积
习题：例：对于x（n）={2，1，1}， h（n） ={2，2，1} 2*3-1=5 循环卷积 y（n）= x(n) h(n) {7,7,6} 补零后 x'（n）={2，1，1，0，0}， h'（n）={2， 2，1，0，0} 循环卷积y'（n）={4，6，6，3，1}= 线性卷积

数字信号处理实验报告——离散系统的差分方程、冲激响应和卷积分析

实验2 离散系统的差分方程、冲激响应和卷积分析实验目的：加深对离散系统的差分方程、冲激响应和卷积分析方法的理解。

实验原理：离散系统其输入、输出关系可用以下差分方程描述：∑=∑=-=-M k k N k k k n x p k n y d 0][][输入信号分解为冲激信号，∑-=∞-∞=m m n m x n x ][][][δ。

记系统单位冲激响应][][n h n →δ，则系统响应为如下的卷积计算式：∑∞-∞=-=*=m m n h m x n h n x n y ][][][][][当Nk d k ,...2,1,0==时，h[n]是有限长度的（n ：[0，M]），称系统为FIR 系统；反之，称系统为IIR 系统。

在MATLAB 中，可以用函数y=Filter(p,d,x) 求解差分方程，也可以用函数 y=Conv(x,h)计算卷积。

实验内容：编制程序求解下列两个系统的单位冲激响应和阶跃响应，并绘出其图形。

[]0.6[1]0.08[2][][1]y n y n y n x n x n +-+-=--[]0.2{[1][2][3][4][5][6]}y n x n x n x n x n x n x n =-+-+-+-+-+-实验要求：给出理论计算结果和程序计算结果并讨论。

实验过程：[]0.6[1]0.08[2][][1] +-+-=--y n y n y n x n x n （1）单位冲激响应：>> a=[1,0.6,0.08];>> b=[1,-1];>> N=20;>> x=[1,zeros(1,N)];>> y=filter(b,a,x);>> stem(y);>> xlabel('时间序列n');>> ylabel('信号幅度');>> title('单位冲激响应h(n)');>>（2）单位阶跃响应：>> a=[1,0.6,0.08];>> b=[1,-1];>> N=20;>> x=[ ones(1,N)];>> y=filter(b,a,x);>> stem(y);>> xlabel('时间序号');>> ylabel('信号幅度');>> title('单位阶跃响应h （n ）'); >>理论分析：由差分方程得系统函数为：1121()10.60.08zH z zz----=++利用分部分式法可得：1176()10.410.2H z zz--=-++，z 反变换得：()[7(0.4)6(0.2)nnh n u n =⋅--⋅- h(n)即为单位冲击响应。

数字信号处理期末考题

(b)X[m]和H[m]相乘得Y[m]
(c)对Y[m]做8点IDFT得y[k]。
3．X=fft(x,8);
H=fft(y,8);
y=real(ifft(X.*H));
四、
(1) ，
(2)Tmax=1/8秒。
(3)
五、
1．。
2．加窗，分段求平均。
六、周期序列：无误差。
非周期序列：泄漏误差，加非矩形窗；栅栏效应，补零；谱分辨率，增加所取序列长度。
2.平滑周期图和平均周期图改善了周期图的方差性能，但却降低了谱分辨率和增大了偏差。
3.可能使短序列的功率谱估计出现错误的结果。
现代功率谱估计的基本思想：根据所研究信号的先验知识，对观测数据以外的数据作出某种比较合理的假设，以达到提高谱估计质量的目的。
六、
（1）类型：Ⅰ型或Ⅱ型
（2）采用Ⅰ型时，M=8
(3)用MATLAB函数fftshift对DFT的结果X[m]进行重新排序，试确定重新排序后的序列中,m=300点和m=1200点所对应的连续信号频谱X(j)中的频率点。
八、已知某因果稳定离散LTI系统的系统函数为
(1)试画出系统的零极点分布图，确定系统的收敛域；
(2)试判断该系统是IIR系统还是FIR系统，求出系统的单位脉冲响应h[k]；
(4)画出(3)中数字滤波器的直接型结构图。
六、利用矩形窗函数法设计一个线性相位FIR数字低通滤波器，使其逼近截频为C=rad的理想低通数字滤波器。
(1)确定可选用的线性相位FIR系统的类型（I，II，III，IV）；
(2)若FIR数字滤波器的阶数M=8，试求h[k]的表达式；
(3)画出该滤波器的线性相位直接型结构图，不带h[k]的具体值。
2．简述x(t), ,x[k]和四类信号频谱的特点，及它们之间的对应关系。

《数字信号处理》圆周卷积和与线性卷积和实验

《数字信号处理》圆周卷积和与线性卷积和实验一、实验目的1. 掌握用MTALAB软件实现有限长序列的圆周移位和圆周翻褶的方法；2. 掌握在MATLAB中圆周卷积和的时域和频域计算方法；3. 理解圆周卷积和与线性卷积和的关系，掌握用FFT计算线性卷积和的方法。

二、实验原理和实验内容1. 圆周移位和圆周翻褶（1）求余数（模运算）函数mod(n，N)调用方法：n1=mod(n,N)功能：n1=n + KN，0≤ n1≤ N-1，K为整数，余数n1在0至N-1之间将模运算用到位置向量上，可实现有限长序列的周期延拓，即1(mod)(())Nn n N n==。

设x的起始位置为0，长度为N，坐标为：n=0:K*N-1 % N为延拓周期，K为周期数延拓后序列的值为：x=x(mod(n, N)+1)由于MATLAB中数组x的下标是为nx=[1:N]，而mod(n, N)的值在0到N-1之间，因此要将mod( )函数的结果加1。

➢练习调用该函数mod( )将序列()[1,2,3,4,5]x n=延拓5个周期得到序列y(n)。

程序x=[1,2,3,4,5]nx=[0:1:4];n=[0:1:24];N=5;y=x(mod(n,N)+1)subplot(121),stem(nx,x);title('原序列');subplot(122),stem(n,y);title('延拓后序列');结果x =1 2 3 4 5y =Columns 1 through 151 2 3 4 5 1 2 3 4 5 1 2 3 4 5 Columns 16 through 251 2 3 4 5 1 2 3 4 5（2）圆周移位N 点有限长序列的m 点移位可以看成将()x n 以N 为周期，延拓成周期序列()(())N x n x n =，将(())N x n 做m 点线性移位后，再取主值区间中的序列，即可得到()x n 的m 点圆周移位序列()m x n ，即()(())()m N N x n x n m R n =+注意：只能计算有限长序列的DTFT ，对于无限长序列，要进行截取。

数字信号处理第四章9 线性卷积和线性相关的FFT算法

比较直接计算和FFT法计算的运算量
Km md mF ML 2 N (1 3 / 2 * lo g 2 N )
讨论：
1）当
M L
则 N M L 1 2M
Km
M
2
4 M [1 3 / 2 * (1 lo g 2 M )]

M 1 0 6 lo g 2 M
4） y i ( n ) IF F T [ Y i ( k )]
2） H ( k ) F F T [ h ( n )]
3） Y i ( k ) X i ( k ) H ( k )
2012-10-11
5） y ( n )

i
yi (n )
数字信号处理
2012-10-11
数字信号处理
N 1
2012-10-11
数字信号处理
思考题：
下列DFT应用中，能否将x(n)补零点使
1）频谱分析 2）计算线性卷积
3）计算 X ( z )
z re
j 2 N k
N 2
m
2012-10-11
数字信号处理
md LM / 2
数字信号处理
FFT法：以圆周卷积代替线性卷积
令 N 2
m
M L 1
x(n) x(n) 0 h(n) h(n) 0
0 n L 1 L n N 1 0 n M 1 M n N 1
则 y (n ) x(n ) * h (n ) x (n ) N h (n )
舍弃yi(n)的前M-1个点，再将yi(n)顺次连接，即得y(n)。
2012-10-11 数字信号处理

数字信号处理例题

而
T [ax1 (n) + bx2 (n)] = [ax1 (n) + bx2 (n)]2 =[ax1 (n)]2 + [bx2 (n)]2 + 2abx1 (n) x2 (n)
即
T [ax1 (n) + bx2 (n)] ≠ ay1 (n) + by2 (n)
所以，系统不是线性系统。
7
又因为
T [ x(n − m)] = [ x(n − m)]2 , y (n − m) = [ x(n − m)]2
n = −∞
∑
∞
h( n) =
p<∞
9
根据单位抽样序列的性质，可得
α n h( n) = 0
∞
0 ≤ n ≤ N −1 其它
N −1 n= 0
S 由此得 =
n = −∞
h( n) ∑ α ∑=
n
<∞
因为 α 0 , α1 , , α N −1为常数.
所以系统是稳定的。
10
例5、以下序列是系统的单位抽样响应h(n)，判断该系统是否因果的、稳定的。（1） n2 （5）
所以x(n)是非周期序列。
5
例3、判断系统
y (n) = [ x(n)]2
是否为线性系统、是否为移不变系统。
分析：利用定义来判断：（1）线性：满足可加性和比例性：
T [a1 x1 (n) + a2 x2 (n)] = a1T [ x1 (n)] + a2T [ x2 (n)]
（2）移不变性：输入和输出的移位相同：
为双边序列。为左边序列。为右边序列。
23
例3 用长除法，留数定理法，部分分式法求下列X(z)的z反变换。

数字信号处理卷积公式

数字信号处理卷积公式一、离散序列的卷积公式。

1. 定义。

- 设离散序列x(n)和h(n)，它们的卷积y(n)定义为：y(n)=∑_m =-∞^∞x(m)h(n - m)- 这里m是求和变量，n表示卷积结果y(n)的序列序号。

2. 计算步骤示例。

- 例如，已知x(n)={1,2,3}（n = 0,1,2时的值，其他n时x(n)=0），h(n)={2,1}（n = 0,1时的值，其他n时h(n)=0）。

- 当n = 0时：- y(0)=∑_m =-∞^∞x(m)h(0 - m)=x(0)h(0)=1×2 = 2- 当n = 1时：- y(1)=∑_m =-∞^∞x(m)h(1 - m)=x(0)h(1)+x(1)h(0)=1×1+2×2=1 + 4=5- 当n = 2时：- y(2)=∑_m =-∞^∞x(m)h(2 - m)=x(0)h(2)+x(1)h(1)+x(2)h(0)=1×0+2×1+3×2=0 + 2+6 = 8- 当n = 3时：- y(3)=∑_m =-∞^∞x(m)h(3 - m)=x(1)h(2)+x(2)h(1)=2×0+3×1 = 3- 当n>3时，y(n)=0。

所以y(n)={2,5,8,3}。

3. 卷积的性质。

- 交换律：x(n)*h(n)=h(n)*x(n)，即∑_m =-∞^∞x(m)h(n - m)=∑_m =-∞^∞h(m)x(n - m)。

- 结合律：(x(n)*h_1(n))*h_2(n)=x(n)*(h_1(n)*h_2(n))。

- 分配律：x(n)*(h_1(n)+h_2(n))=x(n)*h_1(n)+x(n)*h_2(n)。

二、连续信号的卷积公式。

1. 定义。

- 设连续时间信号x(t)和h(t)，它们的卷积y(t)定义为：y(t)=∫_-∞^∞x(τ)h(t-τ)dτ- 这里τ是积分变量，t表示卷积结果y(t)的时间变量。

计算卷积的方法

总结词
详细描述了系统传递函数的计算过程，包括系统传递函数的定义、系统函数的表示、系统传递函数的计算步骤以及计算实例。
详细描述
系统传递函数是描述线性时不变系统动态特性的数学模型，可以通过系统的输入输出关系来计算。具体来说，假设有一个线性时不变系统，其输入为x(t)，输出为y(t)，系统的传递函数可以通过以下步骤得到：首先根据系统的输入输出关系列出微分方程，然后通过拉普拉斯变换求解微分方程，得到传递函数H(s)。
04
卷积的特性
时移性
总结词
卷积的结果可以通过将其中一个信号进行时间平移来获得。
VS
详细描述
卷积运算具有时移性，即当一个信号在时间上平移时，其与另一个信号的卷积结果也会相应地发生平移。这种特性在信号处理和控制系统等领域中非常重要，因为它允许我们通过改变输入信号的时间位置来控制输出信号的时间响应。
滤波器
滤波器
卷积在信号处理中常常用于实现滤波器功能。通过设计特定的滤波器系数（相当于冲激响应），可以对输入信号进行滤波处理，提取出需要的信号成分或者抑制不需要的噪声干扰。
IIR滤波器和FIR滤波器
在数字信号处理中，滤波器可以分为无限冲激响应（IIR）滤波器和有限冲激响应（FIR）滤波器。IIR滤波器具有反馈结构，可以实现对信号的递归处理；而FIR滤波器没有反馈结构，只能实现线性相位响应。
计算卷积的方法
• 卷积的定义 • 卷积的物理意义 • 计算卷积的方法 • 卷积的特性 • 卷积的计算实例
01
卷积的定义
数学定义
数学上，卷积是一种二元运算，表示为 *。对于两个函数 f 和 g，它们的卷积定义为
(f * g)[n] = sum_{k=-infty}^{+infty} f[k] g[n-k])

数字信号处理计算题库

计算与证明题信号与系统的时域分析与处理1.判断下列系统是否为线性移不变系统，并说明理由。

（假定x(n)为实序列）（1）y(n) = T ［x(n) ］= nx(n) （2）y(n) = T ［x(n) ］= 2x(n)2．设h(n)=3n)21(u(n)为线性移不变系统的单位抽样响应，若输入x(n)=u(n)，求∞→n lim y(n)，其中y(n)为输出。

3．系统（其中y(n)为输出序列，x(n)为输入序列）输入输出关系为y(n)=∑∞-∞=-i i n x i h ),()(其中，h(n)为一确定序列。

证明此系统为线性移不变。

离散时间傅里叶变换（DTFT ）1. 证明实序列x(n)的傅里叶变换X(e j ω)有如下对称性质：Re ［X(e j ω)］=Re ［X(e -j ω)］； Im ［X(e j ω)］=-Im ［X(e -j ω)］。

2. 设DTFT ［x(n)］=X(e j ω)，求DTFT ［x(n)*x *(-n)］.3. 设DTFT ［x(n)］=X(e j ω)，y(n)=⎩⎨⎧±±=其它,0,L 2,L ,0n ),L /n (x，求DTFT ［y(n)］。

4．设线性移不变系统的单位采样响应为()()21()23n h n u n +=-，求其频率响应。

Z 变换1. 求x(n)=cos(ω0n)u(n)的Z 变换。

2．用Z 变换求下列两个序列的卷积：h(n)=⎪⎪⎩⎪⎪⎨⎧-+=≤≤其它0)1()()(,10)21(n n n x n nδδ3.已知系统输入输出方程为y(n)=x(n)-x(n-1)（1）证明该系统为线性移不变。

（2）求系统函数H(z)的形式。

2．(10分)求序列x(n)=2-n u(-n)的Z 变换。

4．(10分)考虑一个具有系统函数44116()1116z H z z ---+=-的稳定系统。

1）求系统的零点和极点，并作出图表示； 2）画出系统的级联型结构图。

卷积例题-PPT课件

《信号与系统》
(2) 0<t<3时，f2(t-τ)波形如图1(d)所示。
《信号与系统》
第2章连续时间系统的时域分析
(3) t>3时，f2(t-τ)波形如图1(e)所示，此时，仅在
0<τ<3范围内，乘积f1(τ)f2(t-τ) 不为零，故有
《信号与系统》
第2章连续时间系统的时域分析
例2
设系统的冲激响应为h(t)=δ(t+T)+δ(t-T)，如图2
例4 已知某线性时不变系统如图3所示。已知图中 h1(t)=u(t) ， h2(t)=δ(t-1) ， h3(t)=e-3(t-2)u(t-2) ，求该系统的冲激响应h(t)。解： h(t)=h1(t)*h2(t)+h3(t)
=h(t)*δ(t-1)+e-3(t-2)u(t-2)
=u(t-1)+e-3(t-2)u(t-2)
t
o (b)
t
图 1 f1(t)和f2(t)波形
《信号与系统》
第2章连续时间系统的时域分析
f1 ( ) 1 f2 ( － ) 1
0
1
2 (a )
3
4

(b )
o

f 2 ( t － )
1
f1 ( ) f2 ( t － )
1
f1 ( )
t 0 (c ) t＜ 0
3
《信号与系统》
第2章连续时间系统的时域分析
h ( t ) 1 f( t ) 系统 h ( t ) 3
h ( t ) 2
∑
y ( t )
图3 例4 系统框图
《信号与系统》
第2章连续时间系统的时域分析