2018中考复习-图形的对称与折叠练习题.docx
近年中考数学专题复习折叠问题(扫描(2021年整理)

2018中考数学专题复习折叠问题(扫描版)
编辑整理:
尊敬的读者朋友们:
这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2018中考数学专题复习折叠问题(扫描版))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2018中考数学专题复习折叠问题(扫描版)的全部内容。
中考折叠专题。
2018年中考数学一轮复习专题 图形折叠问题及答案

2018年中考数学一轮复习专题图形折叠问题综合复习一选择题:1.如图,E是矩形ABCD中BC边的中点,将△ABE沿AE折叠到△AFE,F在矩形ABCD内部,延长AF交DC于G点,若∠AEB=55°,则∠DAF=( )A.40° B.35° C.20° D.15°2.如图,把一个长方形纸片沿EF折叠后,点D、C分别落在D′、C′的位置,若∠EFB=65°,则∠AED′等于()A.50° B.55° C.60° D.65°3.如图,把矩形ABCD沿EF翻折,点B恰好落在AD边的B′处,若AE=2,DE=6,∠EFB=60°,则矩形ABCD的面积是()A.12 B.24 C.12 D.164.如图,已知矩形ABCD沿着直线BD折叠,使点C落在C′处,BC′交AD于E,AD=8,AB=4,则DE长为()A.3 B.4 C.5 D.65.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=3,则BC的长为()A.1 B.2 C. D.6.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,则重叠部分△AFC的面积为()A.12 B.10 C.8 D.67.如图,矩形ABCD中,点E在边AB上,将矩形ABCD沿直线DE折叠,点A恰好落在边BC的点F处.若AE=5,BF=3,则CD的长是()A.7B.8 C.9 D. 108.如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠DEC的大小为()A.78° B.75° C.60° D.45°9.如图,将边长为12cm的正方形ABCD折叠,使得点A落在CD边上的点E处,折痕为MN.若CE的长为7cm,则MN的长为()A. 10 B. 13 C. 15 D. 1210.如图,将矩形纸片ABCD的四个角向内翻折,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=12厘米,EF=16厘米,则边AD的长是 ( )A.12厘米 B.16厘米 C.20厘米 D.28厘米11.如图,在矩形 OABC 中,OA=8,OC=4,沿对角线 OB 折叠后,点 A 与点 D 重合,OD 与 BC交于点 E,则点 D 的坐标是()A.(4,8)B.(5,8)C.(,) D.(,)12.将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为()A. B. 2 C. 3 D.13.如图,矩形纸片ABCD中,AD=3cm,点E在BC上,将纸片沿AE折叠,使点B落在AC上的点F处,且∠AEF=∠CEF,则AB的长是( )A.1 cm B.cm C.2 cm D. cm14.如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰好落在∠BCD的平分线上时,CA1的长为()A.3或4 B.4或3C.3或4 D.3或415.如图,在矩形ABCD中,点E、F分别在边AB,BC上,且AE=AB.将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q.对于下列结论:①EF=2BE,②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )A.①② B.②③C.①③ D.①④16.如图,点M、N分别在矩形ABCD边AD、BC上,将矩形ABCD沿MN翻折后点C恰好与点A重合,若此时=,则△AMD′的面积与△AMN的面积的比为( )A.1:3 B.1:4 C.1:6 D.1: 917.图,矩形ABCD中,点E是AD的中点,将△ABE折叠后得到△GBE,延长B G交CD于点F,若CF=1,FD=2,则BC的长为( )A.3B.2C.2D.218.如图,矩形ABCD边AD沿拆痕AE折叠,使点D落在BC上的F处,已知AB=6,△ABF的面积是24,则FC等于().A.2 B.3 C.4 D.519.如图,在菱形纸片ABCD中,∠A=60°,将纸片折叠,点A、D分别落在点A′、D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD时,的值为()A.B.C.D.20.如图,在矩形纸片ABCD中,AB=3,AD=5.折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC 边上移动时,折痕的端点P,Q也随之移动。
精品-2018年中考数学真题分类汇编第一期专题18图形的展开与叠折试题含解析

图形的展开与叠折一、选择题1.(2018•四川凉州•3分)一个正方体的平面展开图如图所示,将它折成正方体后“建”字对面是()A.和B.谐C.凉D.山【分析】本题考查了正方体的平面展开图,对于正方体的平面展开图中相对的面一定相隔一个小正方形,据此作答.【解答】解:对于正方体的平面展开图中相对的面一定相隔一个小正方形,由图形可知,与“建”字相对的字是“山”.故选:D.【点评】注意正方体的空间图形,从相对面入手,分析及解答问题.2.(2018·天津·3分)如图,将一个三角形纸片沿过点的直线折叠,使点落在边上的点处,折痕为,则下列结论一定正确的是()A. B.C. D.【答案】D【解析】分析:由折叠的性质知,BC=BE.易得.详解:由折叠的性质知,BC=BE.∴..故选:D.点睛:本题利用了折叠的性质:折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.3 (2018·新疆生产建设兵团·5分)如图,矩形纸片ABCD中,AB=6cm,BC=8cm.现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为()A.6cm B.4cm C.3cm D.2cm【分析】根据翻折的性质可得∠B=∠AB1E=90°,AB=AB1,然后求出四边形ABEB1是正方形,再根据正方形的性质可得BE=AB,然后根据CE=BC﹣BE,代入数据进行计算即可得解.【解答】解:∵沿AE对折点B落在边AD上的点B1处,∴∠B=∠AB1E=90°,AB=AB1,又∵∠BAD=90°,∴四边形ABEB1是正方形,∴BE=AB=6cm,∴CE=BC﹣BE=8﹣6=2cm.故选:D.【点评】本题考查了矩形的性质,正方形的判定与性质,翻折变换的性质,判断出四边形ABEB1是正方形是解题的关键.4 (2018·台湾·分)如图为一直棱柱,其底面是三边长为5、12、13的直角三角形.若下列选项中的图形均由三个矩形与两个直角三角形组合而成,且其中一个为如图的直棱柱的展开图,则根据图形中标示的边长与直角记号判断,此展开图为何?()A.B.C.D.【分析】三棱柱的侧面展开图是长方形,底面是三角形,据此进行判断即可.【解答】解:A选项中,展开图下方的直角三角形的斜边长为12,不合题意;B选项中,展开图上下两个直角三角形中的直角边不能与其它棱完全重合,不合题意;C选项中,展开图下方的直角三角形中的直角边不能与其它棱完全重合,不合题意;D选项中,展开图能折叠成一个三棱柱,符合题意;故选:D.【点评】本题主要考查了几何体的展开图,从实物出发,结合具体的问题,辨析几何体的展开图,通过结合立体图形与平面图形的转化,建立空间观念,是解决此类问题的关键.5. (2018•河南•3分)某正方体的每个面上那有一个汉字,如图是它的一种展开图,那么在原正方体中,与“国”字所在面相对的面上的汉字是()A.厉B.害C.了D.我6.(2018·浙江衢州·3分)如图,将矩形ABCD沿GH折叠,点C落在点Q处,点D落在AB 边上的点E处,若∠AGE=32°,则∠GHC等于()A.112°B.110°C.108°D.106°【考点】平行线的性质【分析】由折叠可得:∠DGH=∠DGE=74°,再根据AD∥BC,即可得到∠GHC=180°﹣∠DGH=106°.【解答】解:∵∠AGE=32°,∴∠DGE=148°,由折叠可得:∠DGH=∠DGE=74°.∵AD∥BC,∴∠GHC=180°﹣∠DGH=106°.故选D.【点评】本题主要考查了平行线的性质,解题时注意:两直线平行,同旁内角互补.7. (2018·浙江舟山·3分)将一张正方形纸片按如图步骤①,②沿虚线对折两次,然后沿③中平行于底边的虚线剪去一个角,展开铺平后的图形是()A. B.C. D.【考点】剪纸问题【解析】【解答】解:沿虚线剪开以后,剩下的图形先向右上方展开,缺失的部分是一个等腰直角三角形,用直角边与正方形的边是分别平行的,再沿着对角线展开,得到图形A。
初中数学中考模拟复习专题20 几何三大变换问题之轴对称(折叠)问题考试卷及答案.docx

xx学校xx学年xx学期xx试卷姓名:_____________ 年级:____________ 学号:______________题型选择题填空题简答题xx题xx题xx题总分得分一、xx题(每空xx 分,共xx分)试题1:如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是点E,F,连接EF,交AD于点G,求证:AD⊥EF.试题2:如图,在Rt△ABC中,∠C=900,∠B=300,BC=,点D是BC边上一动点(不与点B、C重合),过点D作DE⊥BC交AB边于点E,将∠B沿直线DE翻折,点B落在射线BC上的点F处,当△AEF为等腰三角形时,BD的长为。
试题3:如图①是3×3菱形格,将其中两个格子涂黑,并且使得涂黑后的整个图案是轴对称图形,约定绕菱形ABCD的中心旋转能重合的图案都视为同一种,例②中四幅图就视为同一种,则得到不同共有【】评卷人得分A.4种B.5种 C.6种 D.7种试题4:如图,△ABC中,已知∠BAC=45°,AD⊥BC于D,BD=2,DC=3,求AD的长。
小萍同学灵活运用了轴对称知识,将图形进行翻折变换,巧妙地解答了此题。
(1)分别以AB、AC为对称轴,画出△ABD、△ACD的轴对称图形,D、C点的对称点分别为E、F,延长EB、FC相交于G 点,求证:四边形AEGF是正方形;(2)设AD=x,利用勾股定理,建立关于x的方程模型,求出x的值。
试题5:菱形ABCD中,∠ABC=450,点P是对角线BD上的任一点,点P关于直线AB、AD、CD、BC的对称点分别是点E、F、G、H,BE与DF相交于点M,DG与BH相交于点N,证明:四边形BMDN是正方形。
试题6:如图,已知⊙O的直径CD为4,弧AC的度数为120°,弧BC的度数为30°,在直径CD上作出点P,使BP+AP的值最小,若BP+AP的值最小,则BP+AP的最小值为。
试题7:已知A,B,C为⊙O上相邻的三个六等分点,点E在劣弧AC上(不与A,B,C重合),EF为⊙O的直径,将⊙O沿EF折叠,使点A与A′重合,点B与B′重合,连接EB′,EC,EA′。
7.4图形翻折问题(第1部分)-2018年中考数学试题分类汇编(word解析版)

第七部分专题拓展7.4 图形翻折问题【一】知识点清单翻折变换(折叠问题)1、翻折变换(折叠问题)实质上就是轴对称变换.2、折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.3、在解决实际问题时,对于折叠较为复杂的问题可以实际操作图形的折叠,这样便于找到图形间的关系.首先清楚折叠和轴对称能够提供给我们隐含的并且可利用的条件.解题时,我们常常设要求的线段长为x,然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案.我们运用方程解决时,应认真审题,设出正确的未知数.【二】分类试题及参考答案与解析一、选择题1.(2018年天津-第10题-3分)如图,将一个三角形纸片ABC沿过点B的直线折叠,使点C落在AB边上的点E处,折痕为BD,则下列结论一定正确的是()A.AD=BD B.AE=AC C.ED+EB=DB D.AE+CB=AB【知识考点】翻折变换(折叠问题).【思路分析】先根据图形翻折变换的性质得出BE=BC,根据线段的和差,可得AE+BE=AB,根据等量代换,可得答案.【解答过程】解:∵△BDE由△BDC翻折而成,∴BE=BC.∵AE+BE=AB,∴AE+CB=AB,故D正确,故选:D.【总结归纳】本题考查的是翻折变换,熟知图形翻折不变性的性质是解答此题的关键.2.(2018年宁夏-第7题-3分)将一个矩形纸片按如图所示折叠,若∠1=40°,则∠2的度数是()A.40°B.50°C.60°D.70°【知识考点】平行线的性质.【思路分析】结合平行线的性质得出:∠1=∠3=∠4=40°,再利用翻折变换的性质得出答案.【解答过程】解:由题意可得:∠1=∠3=∠4=40°,则∠2=∠5==70°.故选:D.【总结归纳】本题考查的是平行线的性质,用到的知识点为:两直线平行,内错角相等.3.(2018年青海省-第19题-3分)如图,把直角三角形ABO放置在平面直角坐标系中,已知∠OAB=30°,B点的坐标为(0,2),将△ABO沿着斜边AB翻折后得到△ABC,则点C的坐标是()A.(4)B.(2,C.3)D.【知识考点】坐标与图形性质;翻折变换(折叠问题).【思路分析】过点C作CD⊥y轴,垂直为D,首先证明△BOA≌△BCA,从而可求得BC的长,然后再求得∠DCB=30°,接下来,依据在Rt△BCD中,求得BD、DC的长,从而可得到点C的坐标.【解答过程】解:∵∠OAB=∠ABC=30°,∠BOA=∠BCA=90°,AB=AB,∴△BOA≌△BCA.∴OB=BC=2,∠CBA=∠OBA=60°,过点C作CD⊥y轴,垂直为D,则∠DCB=30°.∴DB=BC=1,DC=BC=.∴C(,3).故选:C.【总结归纳】本题主要考查的是全等三角形的性质和判定、含30°直角三角形的性质,熟练掌握相关知识是解题的关键.4.(2018年吉林省-第5题-2分)如图,将△ABC折叠,使点A与BC边中点D重合,折痕为MN,若AB=9,BC=6,则△DNB的周长为()A.12 B.13 C.14 D.15【知识考点】翻折变换(折叠问题).【思路分析】由D为BC中点知BD=3,再由折叠性质得ND=NA,从而根据△DNB的周长=ND+NB+BD=NA+NB+BD=AB+BD可得答案.【解答过程】解:∵D为BC的中点,且BC=6,∴BD=BC=3,由折叠性质知NA=ND,则△DNB的周长=ND+NB+BD=NA+NB+BD=AB+BD=3+9=12,故选:A.【总结归纳】本题主要考查翻折变换,解题的关键是掌握翻折变换的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.5.(2018年新疆-第7题-5分)如图,矩形纸片ABCD中,AB=6cm,BC=8cm.现将其沿AE对折,使得点B落在边AD上的点B1处,折痕与边BC交于点E,则CE的长为()A.6cm B.4cm C.3cm D.2cm【知识考点】翻折变换(折叠问题);矩形的性质.【思路分析】根据翻折的性质可得∠B=∠AB1E=90°,AB=AB1,然后求出四边形ABEB1是正方形,再根据正方形的性质可得BE=AB,然后根据CE=BC﹣BE,代入数据进行计算即可得解.【解答过程】解:∵沿AE对折点B落在边AD上的点B1处,∴∠B=∠AB1E=90°,AB=AB1,又∵∠BAD=90°,∴四边形ABEB1是正方形,∴BE=AB=6cm,∴CE=BC﹣BE=8﹣6=2cm.故选:D.【总结归纳】本题考查了矩形的性质,正方形的判定与性质,翻折变换的性质,判断出四边形ABEB1是正方形是解题的关键.二、填空题1.(2018年重庆A卷-第16题-4分)如图,把三角形纸片折叠,使点B、点C都与点A重合,折痕分别为DE,FG,得到∠AGE=30°,若AE=EG=则△ABC的边BC的长为厘米.【知识考点】翻折变换(折叠问题).【思路分析】根据折叠的性质和含30°的直角三角形的性质解答即可.【解答过程】解:∵把三角形纸片折叠,使点B、点C都与点A重合,折痕分别为DE,FG,∴BE=AE,AG=GC,∵∠AGE=30°,AE=EG=2厘米,∴AG=6,∴BE=AE=2,GC=AG=6,∴BC=BE+EG+GC=6+4,故答案为:6+4,【总结归纳】此题考查翻折问题,关键是根据折叠的性质和含30°的直角三角形的性质解答.2.(2018年重庆B卷-第16题-4分)如图,在Rt△ABC中,∠ACB=90°,BC=6,CD是斜边AB 上的中线,将△BCD沿直线CD翻折至△ECD的位置,连接AE.若DE∥AC,计算AE的长度等于.【知识考点】平行线的性质;直角三角形斜边上的中线;翻折变换(折叠问题).【思路分析】根据题意、解直角三角形、菱形的性质、翻折变化可以求得AE的长.【解答过程】解:由题意可得,DE=DB=CD=AB,∴∠DEC=∠DCE=∠DCB,∵DE∥AC,∠DCE=∠DCB,∠ACB=90°,∴∠DEC=∠ACE,∴∠DCE=∠ACE=∠DCB=30°,∴∠ACD=60°,∠CAD=60°,∴△ACD是等边三角形,∴AC=CD,∴AC=DE,∵AC∥DE,AC=CD,∴四边形ACDE是菱形,∵在Rt△ABC中,∠ACB=90°,BC=6,∠B=30°,∴AC=,∴AE=.【总结归纳】本题考查翻折变化、平行线的性质、直角三角形斜边上的中线,解答本题的关键是明确题意,找出所求问题需要的条件,利用数形结合的思想解答.三、解答题1.(2018年江西省-第19题-8分)图1是一种折叠门,由上下轨道和两扇长宽相等的活页门组成,整个活页门的右轴固定在门框上,通过推动左侧活页门开关.图2是其俯视简化示意图,已知轨道AB=120cm,两扇活页门的宽OC=OB=60m,点B固定,当点C在AB上左右运动时,OC与OB的长度不变.(所有的结果保留小数点后一位)(1)若∠OBC=50°,求AC的长;(2)当点C从点A向右运动60cm时,求点O在此过程中运动的路径长.参考数据:sn50°≈0.77.cos50°≈0.64,tan50°≈1.19,π取3.14.【知识考点】轨迹;翻折变换(折叠问题);解直角三角形的应用.【思路分析】(1)作OH⊥BC于H,如图2,利用等腰三角形的性质得BH=CH,在Rt△OBH中利用余弦定义计算出BH,从而得到BC的长,然后计算AB﹣BC即可;(2)先判断△OBC为等边三角形得到∠OBC=60°,再根据圆的定义得到点O在此过程中运动路径是以B点为圆心,BO为半径,圆心角为60°的弧,然后根据弧长公式计算即可.【解答过程】解:(1)作OH⊥BC于H,如图2,∵OB=OC,∴BH=CH,在Rt△OBH中,∵cos∠OBH=,∴BH=60•cos50°=60×0.64=38.4,∴BC=2BH=2×38.4=76.8,∴AC=AB﹣BC=120﹣76.8=43.2.答:AC的长为43.2cm;(2)∵OB=OC=60,而BC=60,∴△OBC为等边三角形,∴∠OBC=60°,∴当点C从点A向右运动60cm时,点O在此过程中运动路径是以B点为圆心,BO为半径,圆心角为60°的弧,∴点O在此过程中运动的路径长==20π≈62.8(cm).【总结归纳】本题考查了轨迹:灵活运用几何性质确定图形运动过程中不变的几何量,从而判定轨迹的几何特征,然后进行几何计算.也考查了解直角三角形的运用.2.(2018年广东省-第22题-7分)如图,矩形ABCD中,AB>AD,把矩形沿对角线AC所在直线折叠,使点B落在点E处,AE交CD于点F,连接DE.(1)求证:△ADE≌△CED;(2)求证:△DEF是等腰三角形.【知识考点】翻折变换(折叠问题);全等三角形的判定与性质;矩形的性质.(1)根据矩形的性质可得出AD=BC、AB=CD,结合折叠的性质可得出AD=CE、AE=CD,【思路分析】进而即可证出△ADE≌△CED(SSS);(2)根据全等三角形的性质可得出∠DEF=∠EDF,利用等边对等角可得出EF=DF,由此即可证出△DEF是等腰三角形.【解答过程】证明:(1)∵四边形ABCD是矩形,∴AD=BC,AB=CD.由折叠的性质可得:BC=CE,AB=AE,∴AD=CE,AE=CD.在△ADE和△CED中,,∴△ADE≌△CED(SSS).(2)由(1)得△ADE≌△CED,∴∠DEA=∠EDC,即∠DEF=∠EDF,∴EF=DF,∴△DEF是等腰三角形.【总结归纳】本题考查了全等三角形的判定与性质、翻折变换以及矩形的性质,解题的关键是:(1)根据矩形的性质结合折叠的性质找出AD=CE、AE=CD;(2)利用全等三角形的性质找出∠DEF=∠EDF.。
初中数学中考二轮复习重难突破专题04 折叠问题(含答案)

专题04 折叠问题重点分析在中考,这是必考内容,主要考查形式包括:单纯判断对称图形的识别;利用对称图形的性质求点坐标;利用折叠的对称性性质的相关计算与证明。
难点解读考点:轴对称图形与轴对称轴对称图形轴对称图形定义如果一个图形沿着某条直线对折后,直线两旁的部分能够完全重合,那么这个图形就叫做轴对称图形,这条直线叫做对称轴如果两个图形对折后,这两个图形能够完全重合,那么我们就说这两个图形成轴对称,这条直线叫做对称轴对应线段相等AB=ACAB=A′B′,BC=B′C′,AC=A′C′对应角相等∠B=∠C∠A=∠A′,∠B=∠B′,∠C=∠C′性质对应点所连的线段被对称轴垂直平分区别(1)轴对称图形是一个具有特殊形状的图形,只对一个图形而言;(2)对称轴不一定只有一条(1)轴对称是指两个图形的位置关系,必须涉及两个图形;(2)只有一条对称轴关系(1)沿对称轴对折,两部分重合;(2)如果把轴对称图形沿对称轴分成“两个图形”,那么这“两个图形”就关于这条直线成轴对称(1)沿对称轴翻折,两个图形重合;(2)如果把两个成轴对称的图形拼在一起,看成一个整体,那么它就是一个轴对称图形1.常见的轴对称图形: 等腰三角形、矩形、菱形、正方形、圆.2.折叠的性质:折叠的实质是轴对称,折叠前后的两图形全等,对应边和对应角相等.3.作某点关于某直线的对称点的一般步骤1)过已知点作已知直线(对称轴)的垂线,标出垂足;2)在这条直线另一侧从垂足除法截取与已知点到垂足的距离相等的线段,那么截点就是这点关于该直线的对称点.4.作已知图形关于某直线的对称图形的一般步骤1)作出图形的关键点关于这条直线的对称点;2)把这些对称点顺次连接起来,就形成了一个符合条件的对称图形.真题演练1.如图,在矩形中,,将此矩形折叠,使点C与点A重合,点D落在点处,折痕为,则的长为____,的长为____.【答案】①. ②.【解析】由折叠得,,,设DF=x,则AF=8-x,,由勾股定理得DF=,,过作,过D作DM⊥于M,根据面积法可得,,再由勾股定理求出,根据线段的和差求出,最后由勾股定理求出;【详解】解:∵四边形ABCD是矩形,∴CD=AB=6,由折叠得,,设DF=x,则AF=8-x,又Rt中,,即解得,,即DF=∴过作,过D作DM⊥于M,∵∴,解得,∵∴,解得,∴∴∴;故答案为:6;.【点拨】此题主要考查了矩形的折叠问题,勾股定理等知识,正确作出辅助线构造直角三角形运用勾股定理是解答此题的关键.2.如图,在中.,点是边上一动点.连接,将沿折叠,点落在处,当点在内部(不含边界)时,长度的取值范围是___________.【答案】【解析】分别求出当落在AC和BC上时的长度即可.【详解】∵∠ABC=90°,AB=2,BC=4,∴,当点落在AC上时,如图,∵将△ABD沿BD折叠,点A落在处,∴∠ADB==90°,∵,∴,当点落在BC上时,如图,过点D作DH⊥AB于H,∵将△ABD沿BD折叠,点A落在处,∴∠ABD=∠DBC=45°,∵DH⊥AB,∴∠HDB=∠HBD=45°,∴BH=DH,∵,∴HD=2AH=BH,∵AB=AH+BH=2AH+AH=2,∴,,∴,∴当点在△ABC内部(不含边界)时,AD长度的取值范围为.【点拨】本题考查折叠问题,解题的关键是考虑两种极端情况.还可以利用相似来解题.3.如图,长方形ABCD中,AD=BC=8,AB=CD=17,∠DAB=∠B=∠C=∠D=90°.点E为射线DC上的一个动点,△ADE与△AD′E关于直线AE对称,当△AD′B为直角三角形时,DE的长为______.【答案】或【解析】分两种情况:点E在DC线段上,点E为DC延长线上的一点,进一步分析探讨得出答案即可.【详解】如图1,∵折叠,∴△AD′E≌△ADE,∴∠AD′E=∠D=90°,∵∠AD′B=90°,∴B.D′、E三点共线,又∵ABD′∽△BEC,AD′=BC,∴ABD′≌△BEC,∴BE=AB=17,∵BD′==15,∴DE=D′E=17﹣15=2;如图2,∵∠ABD″+∠CBE=∠ABD″+∠BAD″=90°,∴∠CBE=∠BAD″,在△ABD″和△BEC中,∠D″=∠BCE,AD″=BC,∠CBE=∠BAD″,∴△ABD″≌△BEC,∴BE=AB=17,∴DE=D″E=17+15=32.综上所知,DE=2或32.故答案为2或32.【点拨】本题考查翻折的性质,三角形全等的判定与性质,勾股定理,掌握翻折的性质,分类探讨的思想方法是解决问题的关键.4.在菱形ABCD中,∠B=60°,BC=2 cm,M为AB的中点,N为BC上一动点(不与点B重合),将△BMN 沿直线MN折叠,使点B落在点E处,连接DE,CE,当△CDE为等腰三角形时,线段BN的长为_____.【答案】或2【解析】分两种情况:①如图1,当DE=DC时,连接DM,作DG⊥BC于G,由菱形的性质得出AB=CD=BC=2,AD ∥BC,AB∥CD,得出∠DCG=∠B=60°,∠A=120°,DE=AD=2,求出DG=,CG=,BG=BC+CG=3,由折叠的性质得:EN=BN,EM=BM=AM,∠MEN=∠B=60°,证明△ADM≌△EDM,得出∠A=∠DEM=120°,证出D.E.N三点共线,设BN=EN=x,则GN=3-x,DN=x+2,在Rt△DGN中,由勾股定理得出方程,解方程即可;②如图2,当CE=CD上,CE=CD=AD,此时点E与A重合,N与点C重合,CE=CD=DE=DA,△CDE是等边三角形,BN=BC=2(含CE=DE这种情况).【详解】解:分两种情况,①如图1,当DE=DC时,连接DM,作DG⊥BC于G,∵四边形ABCD是菱形,∴AB=CD=BC=2,AD∥BC,AB∥CD,∴∠DCG=∠B=60°,∠A=120°,∴DE=AD=2,∵DG⊥BC,∴∠CDG=90°-60°=30°,∴CG=CD=1,∴DG=CG=,BG=BC+CG=3,∵M为AB的中点,∴AM=BM=1,由折叠的性质得:EN=BN,EM=BM=AM,∠MEN=∠B=60°,在△ADM和△EDM中,AD=ED,AM=EM,DM=DM,∴△ADM≌△EDM(SSS),∴∠A=∠DEM=120°,∴∠MEN+∠DEM=180°,∴D.E.N三点共线,设BN=EN=x,则GN=3-x,DN=x+2,在Rt△DGN中,由勾股定理得:(3-x)²+()² =(x+2)²,解得:x=,即BN=;②当CE=CD时,CE=CD=AD,此时点E与A重合,N与点C重合,如图2所示:CE=CD=DE=DA,△CDE是等边三角形,BN=BC=2(符合题干要求);综上所述,当△CDE为等腰三角形时,线段BN的长为或2;故答案为或2.【点拨】本题考查了折叠变换的性质、菱形的性质、全等三角形的判定与性质、三点共线、勾股定理、直角三角形的性质、等腰三角形的性质等知识,熟练掌握并灵活运用是解题的关键.5.如图,在矩形ABCD中,AB=4,BC=3,点P是AB上(不含端点A,B)任意一点,把△PBC沿PC折叠,当点B′的对应点落在矩形ABCD的对角线上时,BP=__________________________.【答案】或.【解析】分两种情况探讨:①点B落在矩形对角线BD上,②点B落在矩形对角线AC上,由三角形相似得出比例式,即可得出结果.【详解】①点A落在矩形对角线BD上,如图1所示.∵矩形ABCD中,AB=4,BC=3∴∠ABC=90°,AC=BD,∴AC=BD==5.根据折叠的性质得:PC⊥BB′,∴∠PBD=∠BCP,∴△BCP∽△ABD,∴,即,解得:BP=.②点A落在矩形对角线AC上,如图2所示.根据折叠的性质得:BP=B′P,∠B=∠PB′C=90°,∴∠AB′A=90°,∴△APB′∽△ACB,∴,即,解得:BP=.故答案为或.【点拨】本题考查了折叠问题、勾股定理,矩形的性质以及三角形相似的判定与性质;熟练掌握矩形的性质,由三角形相似得出比例式是解决问题的关键.6.如图,在矩形ABCD中,AD=5,AB=8,点E为射线DC上一个动点,把△ADE沿直线AE折叠,当点D的对应点F刚好落在线段AB的垂直平分线上时,则DE的长为_____.【答案】或10【解析】【详解】试题分析:根据题意,可分为E点在DC上和E在DC的延长线上,两种情况求解即可:如图①,当点E在DC上时,点D的对应点F刚好落在线段AB的垂直平分线QP上,易求FP=3,所以FQ=2,设FE=x,则FE=x,QE=4-x,在Rt△EQF中,(4-x)2+22=x2,所以x=.(2)如图②,当,所以FQ=点E在DG的延长线上时,点D的对应点F刚好落在线段AB的垂直平分线QP上,易求FP=3,所以FQ=8,设DE=x,则FE=x,QE=x-4,在Rt△EQF中,(x-4)2+82=x2,所以x=10,综上所述,DE=或10.7.如图,在矩形纸片中,,,点是的中点,点是边上的一个动点,将沿所在直线翻折,得到,连接,,则当是以为腰的等腰三角形时,的长是________.【答案】或【解析】存在两种情况:当=DC时,连接ED,根据勾股定理可得ED的长,可判断E,A´,D三点共线,根据勾股定理即可得出结论;当=时,证明AEA´F是正方形,于是得出结论.【详解】解:①当=DC时,如图1,连接ED,∵点是的中点,,,四边形是矩形,∴AD=BC=,∠A=90°,∴DE=,∵将沿所在直线翻折,得到,∴A´E=AE=2,A´D=DC=AB=4,∴DE=A´E+A´D=6,∴点E,A´,D三点共线,∵∠A=90°,∴∠FA´E=∠FA´D=90°,设AF=x,则A´F=x,FD=-x,在Rt△FA´D中,,解得x=,∴FD=3;②当=时,如图2,∵=,∴点A´在线段CD的垂直平分线上,∴点A´在线段AB的垂直平分线上,∵点是的中点,∴EA´是AB的垂直平分线,∴∠AEA´=90°,∵将沿所在直线翻折,得到,∴∠A=∠EA´F=90°,AF=FA´,∴四边形AEA´F是正方形,∴AF=AE=2,∴DF=.故答案为或.【点拨】本题考查了翻折变换,矩形的性质,等腰三角形的性质,正方形的判定与性质,勾股定理.分类讨论思想的运用是解题的关键.8.如图,在Rt△ABC中,∠C=90°,BC=2,AC=2,点D是BC的中点,点E是边AB上一动点,沿DE 所在直线把△BDE翻折到△B′DE的位置,B′D交AB于点F.若△AB′F为直角三角形,则AE的长为____或___【答案】3或【解析】△AB′F为直角三角形,应分两种情况进行讨论.当∠AFB′为直角时,利用勾股定理求出B′E,也就是BE的长,便求出AE.当∠AB′F为直角时,过A作AN⊥EB′,交EB′的延长线于N,构造Rt△B′EF,利用勾股定理便可求出AE.【详解】解:①当B′D⊥AE时,△AB′F为直角三角形,如下图:根据题意,BE=B′E,BD= B′D=BC=. ∠B=∠EB′F∵在Rt△ABC中,∠C=90°,BC=2,AC=2∴AB===4∴∠B=∠EB′F =30°.∵在Rt△BDF中,∠B=30°∴DF=BD=∴B′F=B′D-DF=-=∵在Rt△B′EF中,∠EB′F =30°∴EF=B′E,∵B′F===EF,即=EF,∴EF=,则BE=1,∴AE=AB-BE=4-1=3.②当D B′⊥A B′时,△AB′F为直角三角形,如下图:连接AD,过A作AN⊥EB′,交EB′的延长线于N.根据题意,BE=B′E,BD=CD=B′D=BC=. ∠B=∠EB′F ∵在Rt△ABC中,∠C=90°,BC=2,AC=2∴AB===4∴∠B=∠EB′F =30°.∵∠AB′F=90°∴∠AB′E=∠AB′F+∠EB′F=120°∴Rt△AB′N中,∠AB′N=60°,∠B′AN=30°在Rt△AB′D和Rt△ACD中∴Rt△AB′D≌Rt△ACD(H L)∴AB′=AC=2∴B′N=1,AN=设AE=x,则BE= B′E=4-x∵在Rt△AEN中,∴()2+(4-x+1)2=x2∴x=综上,AE的长为3或.【点拨】本题是一道综合题,涉及到直角三角形全等的判定,30°角的直角三角形的性质,勾股定理等知识.9.如图,在矩形中,,,将点绕点逆时针旋转,点的对应点为.的平分线交于,且.若点落在矩形的边上,则的值为______.【答案】或【解析】分两种情况:①点B′落在AD边上,根据矩形与折叠的性质易得AB=BE,即可求出a的值;②点B′落在CD 边上,证明△ADB′∽△B′CE,根据相似三角形对应边成比例即可求出a的值.【详解】解:分两种情况:①当点B′落在AD边上时,如图1.∵四边形ABCD是矩形,∴∠BAD=∠B=90°,∵将△ABE沿AE折叠,点B的对应点B′落在AD边上,∴∠BAE=∠B′AE=∠BAD=45°,∴AB=BE,∴a=;②当点B′落在CD边上时,如图2.∵四边形ABCD是矩形,∴∠BAD=∠B=∠C=∠D=90°,AD=BC=a.∵将△ABE沿AE折叠,点B的对应点B′落在CD边上,∴∠B=∠AB′E=90°,AB=AB′=1,EB=EB′=a,∴DB′==,EC=BC−BE=a−a=a.∵∠B′AD=∠EB′C=90°−∠AB′D,∠D=∠C=90°,∴△ADB′∽△B′CE,∴,即,解得a1=,a2=−(舍去).综上,所求a的值为或.故答案为或.【点拨】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质,勾股定理,相似三角形的判定与性质.进行分类讨论与数形结合是解题的关键。
八年级初二数学 图形的对称-翻折变换(折叠问题) 含答案
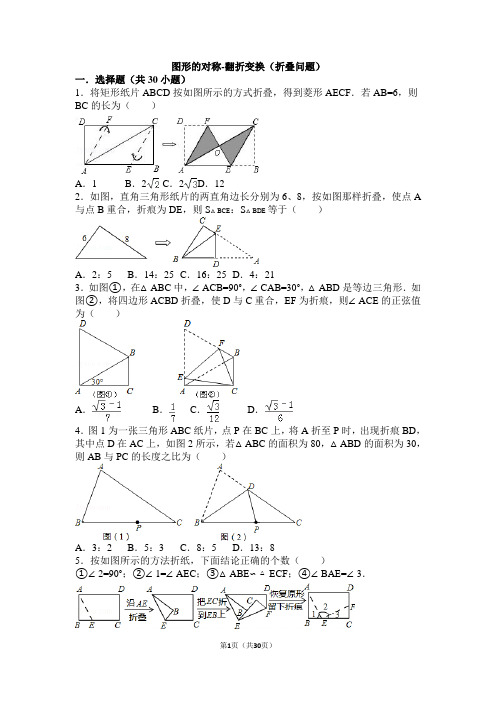
图形的对称-翻折变换(折叠问题)一.选择题(共30小题)1.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=6,则BC的长为()A.1 B.2 C.2D.122.如图,直角三角形纸片的两直角边长分别为6、8,按如图那样折叠,使点A 与点B重合,折痕为DE,则S△BCE:S△BDE等于()A.2:5 B.14:25 C.16:25 D.4:213.如图①,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形.如图②,将四边形ACBD折叠,使D与C重合,EF为折痕,则∠ACE的正弦值为()A.B.C.D.4.图1为一张三角形ABC纸片,点P在BC上,将A折至P时,出现折痕BD,其中点D在AC上,如图2所示,若△ABC的面积为80,△ABD的面积为30,则AB与PC的长度之比为()A.3:2 B.5:3 C.8:5 D.13:85.按如图所示的方法折纸,下面结论正确的个数()①∠2=90°;②∠1=∠AEC;③△ABE∽△ECF;④∠BAE=∠3.A.1个B.2个C.3个D.4个6.如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠AED′=40°,则∠EFB等于()A.70°B.65°C.80°D.35°7.如图,把矩形ABCD沿EF折叠,使点C落在点A处,点D落在点G处,若∠CFE=60°,且DE=1,则边BC的长()A.3 B.4 C.3.5 D.68.如图,四边形ABCD是矩形,AB=4,AD=3,把矩形沿直线AC折叠,点B 落在点E处,AE交CD于点F.连接DE,则DF的长是()A.B.C.D.9.张萌和小平两人打算各用一张正方形的纸片ABCD折出一个等边三角形,两人作法如下:张萌:如图1,将纸片对折得到折痕EF,沿点B翻折纸片,使点A落在EF上的点M处,连接CM,△BCM即为所求;小平:如图2,将纸片对折得到折痕EF,沿点B翻折纸片,使点C落在EF上的点M处,连接BM,△BCM 即为所求,对于两人的作法,下列判断正确的是()A.小平的作法正确,张萌的作法不正确B.两人的作法都不正确C.张萌的作法正确,小平的作法不正确D.两人的作法都正确10.如图,折叠矩形纸片ABCD的一边AD,使点D落在BC边上的点F处,若AB=8,BC=10,则△CEF的周长为()A.12 B.16 C.18 D.2411.如图,在矩形ABCD中,AB=3,BC=5,点E在边CD上,连接BE,将△BCE 沿BE折叠,若点C恰好落在AD边上的点F处,则CE的长为()A.B.C.D.12.如图,在△ABC中,∠C=90°,AB=5cm,AC=4cm,点D在AC上,将△BCD 沿着BD所在直线翻折,使点C落在斜边AB上的点E处,则DC的长为()A.cm B.cm C.2cm D.cm13.如图,在平面直角坐标系中,点A(0,4)、B(3,0),连接AB,将△AOB 沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,则直线BC的解析式为()A.y=﹣B.y=﹣x+C.y=﹣D.y=﹣2x+14.如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,点O落在BC边上的点E处.则直线DE的解析式为()A.y=x+5 B.y=x+5 C.y=x+5 D.y=x+515.如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,当DE=2时,BC的长为()A.3 B.4 C.5 D.616.如图,将平行四边形ABCD沿对角线AC折叠,点B的对应点落在点E处,且点B、A、E在同一条直线上,CE交AD于点F,连接ED.下列结论中错误的是()A.AF=B.四边形ACDE是矩形C.图中与△ABC全等的三角形有4个D.图中有4个等腰三角形17.如图,有一张直角三角形纸片ABC,边AB=6,AC=10,∠ABC=90°,将该直角三角形纸片沿DE折叠,使点C与点B重合,则四边形ABDE的周长为()A.16 B.17 C.18 D.1918.如图,梯形ABCD中,AD∥BC,AB=DC,∠DBC=45°,点E在BC上,点F在AB上,将梯形ABCD沿直线EF翻折,使得点B与点D重合.如果,那么的值是()A.B.C.D.19.如图,在边长为12的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G.则BG的长为()A.5 B.4 C.3 D.220.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(﹣1,0),B(﹣2,3),C(﹣3,1).将△ABC沿y轴翻折得到△A′B′C′,则点B′的坐标为()A.(2,1)B.(2,3)C.(4,1)D.(0,2)21.如图,△ABC周长为36cm,把其边AC对折,使点C、A重合,折痕交BC 边于点D,交AC边于点E,连结AD,若AE=6cm,则△ABD的周长是()A.24cm B.26cm C.28cm D.30cm22.如图,矩形ABCD中,AB=8,把矩形沿直线AC折叠,点B落在点E处,AE交CD于点F,若AF=,则AD的长为()A.3 B.4 C.5 D.623.如图的实线部分是由Rt△ABC经过两次折叠得到的,首先将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,再沿DE折叠使点A落在DC′延长线上的点A′处,若图中,∠A=30°,BC=5cm,则折痕DE的长为()A.B.2C.2D.24.如图一直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于()A.2cm B.3cm C.4cm D.5cm25.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为()A.6 B.8 C.10 D.1226.如图,矩形ABCD中,AB=3,AD=9,将此矩形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为()A.6 B.8 C.10 D.1227.如图所示,有一块直角三角形纸片,∠C=90°,AC=2,BC=,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为()A.B.C.1 D.28.如图所示,折叠平行四边形的一边AD,使点A落在DC边上的点E处,已知AB=6,BC=4,则EC的长为()A.1 B.2 C.3 D.1.529.如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出以下结论:①△DAG≌△DFG;②BG=2AG;③S△DGF=120;④S△BEF=.其中所有正确结论的个数是()A.4 B.3 C.2 D.130.如图,将矩形纸片ABCD沿EF折叠,使D点与BC边的中点D重合,若BC=8,CD=6,则CF的长为()A.B.C.2 D.1图形的对称-翻折变换(折叠问题)参考答案与试题解析一.选择题(共30小题)1.将矩形纸片ABCD按如图所示的方式折叠,得到菱形AECF.若AB=6,则BC的长为()A.1 B.2C.2D.12【考点】翻折变换(折叠问题);勾股定理的应用;菱形的性质;矩形的性质.【分析】根据菱形AECF,得∠FCO=∠ECO,再利用∠ECO=∠ECB,可通过折叠的性质,结合直角三角形勾股定理求解.【解答】解:∵菱形AECF,AB=6,∴假设BE=x,∴AE=6﹣x,∴CE=6﹣x,∵四边形AECF是菱形,∴∠FCO=∠ECO,∵∠ECO=∠ECB,∴∠ECO=∠ECB=∠FCO=30°,2BE=CE,∴CE=2x,∴2x=6﹣x,解得:x=2,∴CE=4,利用勾股定理得出:BC2+BE2=EC2,BC===2,故选:C.【点评】此题主要考查了折叠问题以及勾股定理等知识,解题过程中应注意折叠是一种对称变换,它属于轴对称,根据轴对称的性质,折叠前后图形的形状和大小不变,如本题中折叠前后角相等.2.如图,直角三角形纸片的两直角边长分别为6、8,按如图那样折叠,使点A 与点B重合,折痕为DE,则S△BCE:S△BDE等于()A.2:5 B.14:25 C.16:25 D.4:21【考点】翻折变换(折叠问题).【分析】在Rt△BEC中利用勾股定理计算出AB=10,根据折叠的性质得到AD=BD=5,EA=EB,设AE=x,则BE=x,EC=8﹣x,在Rt△BEC中根据勾股定理计算出x=,则EC=8﹣=,利用三角形面积公式计算出S△BCE=BC•CE=×6×=,在Rt△BED中利用勾股定理计算出ED==,利用三角形面积公式计算出S△BDE=BD•DE=×5×=,然后求出两面积的比.【解答】解:在Rt△BAC中,BC=6,AC=8,∴AB==10,∵把△ABC沿DE使A与B重合,∴AD=BD,EA=EB,∴BD=AB=5,设AE=x,则BE=x,EC=8﹣x,在Rt△BEC中,∵BE2=EC2+BC2,即x2=(8﹣x)2+62,∴x=,∴EC=8﹣x=8﹣=,∴S△BCE=BC•CE=×6×=,在Rt△BED中,∵BE2=ED2+BD2,∴ED==,∴S△BDE=BD•DE=×5×=,∴S△BCE:S△BDE=:=14:25.故选B.【点评】本题考查了折叠问题:折叠前后两图形全等,即对应线段相等,对应角相等.也考查了勾股定理.3.如图①,在△ABC中,∠ACB=90°,∠CAB=30°,△ABD是等边三角形.如图②,将四边形ACBD折叠,使D与C重合,EF为折痕,则∠ACE的正弦值为()A.B.C.D.【考点】翻折变换(折叠问题).【分析】在Rt△ABC中,设AB=2a,已知∠ACB=90°,∠CAB=30°,即可求得AB、AC的值,由折叠的性质知:DE=CE,可设出DE、CE的长,然后表示出AE的长,进而可在Rt△AEC中,由勾股定理求得AE、CE的值,即可求∠ACE 的正弦值.【解答】解:∵△ABC中,∠ACB=90°,∠BAC=30°,设AB=2a,∴AC=a,BC=a;∵△ABD是等边三角形,∴AD=AB=2a;设DE=EC=x,则AE=2a﹣x;在Rt△AEC中,由勾股定理,得:(2a﹣x)2+3a2=x2,解得x=;∴AE=,EC=,∴sin∠ACE==.故选:B.【点评】本题考查的是翻折变换,熟知折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等是解答此题的关键.4.图1为一张三角形ABC纸片,点P在BC上,将A折至P时,出现折痕BD,其中点D在AC上,如图2所示,若△ABC的面积为80,△ABD的面积为30,则AB与PC的长度之比为()A.3:2 B.5:3 C.8:5 D.13:8【考点】翻折变换(折叠问题).【分析】如图,作辅助线;首先求出△BDP的面积,进而求出△DPC的面积;借助三角形的面积公式求出的值;由旋转变换的性质得到AB=PB,即可解决问题.【解答】解:如图,过点D作DE⊥BC于点E;由题意得:S△ABD=S△PBD=30,∴S△DPC=80﹣30﹣30=20,∴=,由题意得:AB=BP,∴AB:PC=3:2,故选A.【点评】该题主要考查了翻折变换的性质及其应用问题;解题的方法是作高线,表示出三角形的面积;解题的关键是灵活运用翻折变换的性质来分析、判断、推理或解答.5.按如图所示的方法折纸,下面结论正确的个数()①∠2=90°;②∠1=∠AEC;③△ABE∽△ECF;④∠BAE=∠3.A.1个B.2个C.3个D.4个【考点】翻折变换(折叠问题);相似三角形的判定与性质.【分析】根据翻折变换的性质、相似三角形的判定定理解答即可.【解答】解:由翻折变换的性质可知,∠AEB+∠FEC=×180°=90°,则∠AEF=90°,即∠2=90°,①正确;由图形可知,∠1<∠AEC,②错误;∵∠2=90°,∴∠1+∠3=90°,又∠1+∠BAE=90°,∴∠BAE=∠3,④正确;∵∠BAE=∠3,∠B=∠C=90°,∴△ABE∽△ECF,③正确.故选:C.【点评】本题考查的是翻折变换的性质,翻折变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.6.如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置.若∠AED′=40°,则∠EFB等于()A.70°B.65°C.80°D.35°【考点】翻折变换(折叠问题).【分析】根据平角的知识可求出∠DED′的度数,再由折叠的性质可得出∠D′EF=∠DEF=∠DED′,从而根据平行线的性质可得出∠EFB的度数.【解答】解:∵∠AED′=40°,∴∠DED′=180°﹣40°=140°,又由折叠的性质可得,∠D′EF=∠DEF=∠DED′,∴∠DEF=70°,又∵AD∥BC,∴∠EFB=70°.故选:A.【点评】此题考查了翻折变换的知识,解答本题的关键是根据折叠的性质得出∠D′EF=∠DEF=∠DED′,难度一般.7.如图,把矩形ABCD沿EF折叠,使点C落在点A处,点D落在点G处,若∠CFE=60°,且DE=1,则边BC的长()A.3 B.4 C.3.5 D.6【考点】翻折变换(折叠问题).【分析】由矩形的性质得到∠1=∠CFE=60°,由折叠可得∠2=60°,从而求得∠4的度数,得到AE=EC,在Rt△CDE中利用勾股定理可求得EC的长度,即可得到答案.【解答】解:∵矩形ABCD,∴BC∥AD,∴∠1=∠CFE=60°,∵EF为折痕,∴∠2=∠1=60°,AE=EC,∴∠3=180°﹣60°﹣60°=60°,Rt△CDE中,∠4=90°﹣60°=30°,∴EC=2×DE=2×1=2,∴BC=AE+ED=EC+ED=2+1=3.故选:A.【点评】本题考查了翻折问题;由折叠得到角相等,得到AE=EC利用勾股定理求解是正确解答本题的关键.8.如图,四边形ABCD是矩形,AB=4,AD=3,把矩形沿直线AC折叠,点B 落在点E处,AE交CD于点F.连接DE,则DF的长是()A.B.C.D.【考点】翻折变换(折叠问题).【分析】由四边形ABCD是矩形与△AEC由△ABC翻折得到,AD=CE,∠ADF=∠CEF,由AAS证得△ADF≌△CEF,的长FA=FC,设DF=x,则FA=4﹣x,由勾股定理得:DA2+DF2=AF2,即可求出DF的长.【解答】解:∵四边形ABCD是矩形,∴AD=BC,AB=DC=4,∠ADF=90°,∵△AEC由△ABC翻折得到,∴BC=EC,∠CEF=∠ABC=90°,∴AD=CE,∠ADF=∠CEF,在△ADF与△CEF中,,∴△ADF≌△CEF(AAS),∴FA=FC,设DF=x,则FA=FC=DC﹣DF=4﹣x,在Rt△DFA中,由勾股定理得:DA2+DF2=AF2,即32+x2=(4﹣x)2,解得:x=,即DF的长是.故选C.【点评】本题主要考查了折叠的性质、矩形的性质、全等三角形的判定与性质、勾股定理等知识;熟练掌握折叠的性质,得到相等的线段与角是解决问题的关键.9.张萌和小平两人打算各用一张正方形的纸片ABCD折出一个等边三角形,两人作法如下:张萌:如图1,将纸片对折得到折痕EF,沿点B翻折纸片,使点A落在EF上的点M处,连接CM,△BCM即为所求;小平:如图2,将纸片对折得到折痕EF,沿点B翻折纸片,使点C落在EF上的点M处,连接BM,△BCM 即为所求,对于两人的作法,下列判断正确的是()A.小平的作法正确,张萌的作法不正确B.两人的作法都不正确C.张萌的作法正确,小平的作法不正确D.两人的作法都正确【考点】翻折变换(折叠问题).【分析】在图1中,由BM=2BF推出∠BMF=30°,所以∠MBF=60°,再根据等边三角形的判定方法即可证明.在图2中,证明方法类似.【解答】解:图1中,∵四边形ABCD是正方形,∴AB=AD=BC∵AE=ED=BF=FC,AB=BM,∴BM=2BF,∵∠MFB=90°,∴∠BMF=30°,∴∠MBF=90°﹣∠BMF=60°,∵MB=MC,∴△MBC是等边三角形,∴张萌的作法正确.在图2中,∵BM=BC=2BF,∠MFB=90°,∴∠BMF=30°,∴∠MBF=90°﹣∠BMF=60°,∵MB=MC∴△MBC是等边三角形,∴小平的作法正确.故选D.【点评】本题考查正方形的性质、翻折不变性、直角三角形的性质,解题的关键是在一个直角三角形中如果斜边是直角边的两倍那么这条直角边所对的锐角是30度.10.如图,折叠矩形纸片ABCD的一边AD,使点D落在BC边上的点F处,若AB=8,BC=10,则△CEF的周长为()A.12 B.16 C.18 D.24【考点】翻折变换(折叠问题).【分析】先根据矩形的性质得AD=BC=10,AB=CD=8,再根据折叠的性质得AF=AD=10,EF=DE,在Rt△ABF中,利用勾股定理计算出BF=6,则CF=BC ﹣BF=4,易得△CEF的周长.【解答】解:∵四边形ABCD为矩形,∴AD=BC=10,AB=CD=8,∵矩形ABCD沿直线AE折叠,顶点D恰好落在BC边上的F处,∴AF=AD=10,EF=DE,在Rt△ABF中,∵BF==6,∴CF=BC﹣BF=10﹣6=4,∴△CEF的周长为:CE+EF+CF=CE+DE+CF=CD+CF=8+4=12.故选A.【点评】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了矩形的性质和勾股定理,利用勾股定理得CF的长是解答此题的关键.11.如图,在矩形ABCD中,AB=3,BC=5,点E在边CD上,连接BE,将△BCE 沿BE折叠,若点C恰好落在AD边上的点F处,则CE的长为()A.B.C.D.【考点】翻折变换(折叠问题).【分析】设CE=x,由矩形的性质得出AD=BC=5,CD=AB=3,∠A=∠D=90°.由折叠的性质得出BF=BC=5,EF=CE=x,DE=CD﹣CE=3﹣x.在Rt△ABF中利用勾股定理求出AF的长度,进而求出DF的长度;然后在Rt△DEF中根据勾股定理列出关于x的方程,即可解决问题.【解答】解:设CE=x.∵四边形ABCD是矩形,∴AD=BC=5,CD=AB=3,∠A=∠D=90°.∵将△BCE沿BE折叠,使点C恰好落在AD边上的点F处,∴BF=BC=5,EF=CE=x,DE=CD﹣CE=3﹣x.在Rt△ABF中,由勾股定理得:AF2=52﹣32=16,∴AF=4,DF=5﹣4=1.在Rt△DEF中,由勾股定理得:EF2=DE2+DF2,即x2=(3﹣x)2+12,解得:x=.故选B.【点评】本题考查了折叠的性质:折叠是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.也考查了勾股定理、矩形的性质、方程思想等知识,关键是熟练掌握勾股定理,找准对应边.12.如图,在△ABC中,∠C=90°,AB=5cm,AC=4cm,点D在AC上,将△BCD 沿着BD所在直线翻折,使点C落在斜边AB上的点E处,则DC的长为()A.cm B.cm C.2cm D.cm【考点】翻折变换(折叠问题).【分析】首先由勾股定理求出BC,由折叠的性质可得∠BED=∠C=90°,BE=BC=3cm,得出AE=AB﹣BE=2cm,设DC=xcm,则DE=xcm,AD=(4﹣x)cm,由勾股定理得出方程,解方程即可.【解答】解:∵∠C=90°,AB=5cm,AC=4cm,∴BC==3cm,∵将△BCD沿着直线BD翻折,使点C落在斜边AB上的点E处,∴△BED≌△BCD,∴∠BED=∠C=90°,BE=BC=3cm,∴AE=AB﹣BE=2cm,设DC=xcm,则DE=xcm,AD=(4﹣x)cm,由勾股定理得:AE2+DE2=AD2,即22+x2=(4﹣x)2,解得:x=.故选:B.【点评】本题主要考查翻折变换的性质,全等三角形的性质,勾股定理;熟练掌握翻折变换的性质,由勾股定理得出方程是解决问题的关键.13.如图,在平面直角坐标系中,点A(0,4)、B(3,0),连接AB,将△AOB 沿过点B的直线折叠,使点A落在x轴上的点A′处,折痕所在的直线交y轴正半轴于点C,则直线BC的解析式为()A.y=﹣B.y=﹣x+C.y=﹣D.y=﹣2x+【考点】翻折变换(折叠问题);待定系数法求一次函数解析式.【分析】由点A(0,4)、B(3,0),可求得AB的长,然后由折叠的性质,求得OA′的长,且△A′OC∽△AOB,再由相似三角形的性质,求得OC的长,继而利用待定系数法求得直线BC的解析式.【解答】解:∵点A(0,4)、B(3,0),∴OA=4,OB=3,∴AB==5,由折叠的性质可得:A′B=AB=5,∠OA′C=∠OAB,∴OA′=A′B﹣OB=2,∵∠A′OC=∠AOB=90°,∴△A′OC∽△AOB,∴,即,解得:OC=,∴点C的坐标为:(0,),设直线BC的解析式为:y=kx+b,则,解得:,∴直线BC的解析式为:y=﹣x+.故选C.【点评】此题考查了折叠的性质、勾股定理、相似三角形的判定与性质以及待定系数法求一次函数的解析式.注意求得点C的坐标是解此题的关键.14.如图,四边形OABC是一张放在平面直角坐标系中的矩形纸片,O为原点,点A在x轴的正半轴上,点C在y轴的正半轴上,OA=10,OC=8,在OC边上取一点D,将纸片沿AD翻折,点O落在BC边上的点E处.则直线DE的解析式为()A.y=x+5 B.y=x+5 C.y=x+5 D.y=x+5【考点】翻折变换(折叠问题);待定系数法求一次函数解析式.【分析】首先在RT△ABE中,求出EB,再在RT△CDE中利用勾股定理即可解决问题.【解答】解:∵△ADE是由△ADO翻折,∴DE=DO,AO=AE=10,∵四边形OABC是矩形,∴OC=AB=8,AO=BC=10,∠B=∠BCO=∠BAO=90°,在RT△ABE中,∵AE=10,AB=8,∴EB===6,∴EC=4,设DO=DE=x,在RT△DCE中,∵CD2+CE2=DE2,∴(8﹣a)2+42=a2,∴a=5,∴点D(0,5),点E(4,8),设直线DE为y=kx+b,∴解得,∴直线DE为:y=+5.故选A.【点评】本题考查翻折变换、待定系数法确定一次函数的解析式,解题的关键是巧妙利用勾股定理,用方程的思想去思考问题,属于中考常考题型.15.如图,将三角形纸片ABC沿DE折叠,使点A落在BC边上的点F处,且DE∥BC,当DE=2时,BC的长为()A.3 B.4 C.5 D.6【考点】翻折变换(折叠问题).【分析】首先由DE∥BC与折叠的性质,可证得DE是△ABC的中位线,继而求得答案.【解答】解:∵DE∥BC,∴∠ADE=∠B,∠EDF=∠BFD,由折叠的性质可得:∠ADE=∠EDF,AD=DF,∴∠B=∠BFD,∴BD=DF,∴AD=BD,同理:AE=EC,∴DE=BC,即BC=2DE=4.故选B.【点评】此题考查了折叠的性质以及三角形中位线的性质.注意证得DE是△ABC的中位线是关键.16.如图,将平行四边形ABCD沿对角线AC折叠,点B的对应点落在点E处,且点B、A、E在同一条直线上,CE交AD于点F,连接ED.下列结论中错误的是()A.AF=B.四边形ACDE是矩形C.图中与△ABC全等的三角形有4个D.图中有4个等腰三角形【考点】翻折变换(折叠问题);平行四边形的性质.【分析】由四边形ABCD是平行四边形,得到AB=CD,AB∥CD,AD=BC,由折叠的性质得到AB=AE,BC=CE,等量代换得到AE=CD,AD=CE,推出四边形ACDE是平行四边形,于是得到AF=BC,四边形ACDE是矩形,故A,B 正确;根据平行四边形和矩形的性质得到△ACD≌△ACE≌△CDE≌△ADE≌△ABC,于是得到图中与△ABC全等的三角形有4个,故C正确;推出△BCE是等腰三角形,△AEF,△ACF,△CDF,△DEF是等腰三角形,于是得到图中有5个等腰三角形,故D错误.【解答】解:∵四边形ABCD是平行四边形,∴AB=CD,AB∥CD,AD=BC,由折叠的性质得到AB=AE,BC=CE,∴AE=CD,AD=CE,∵点B、A、E在同一条直线上,∴AE∥CD,∴四边形ACDE是平行四边形,∴AF=BC,四边形ACDE是矩形,故A,B正确;∵四边形ABCD是平行四边形,四边形ACDE是矩形,∴△ACD≌△ACE≌△CDE≌△ADE≌△ABC,∴图中与△ABC全等的三角形有4个,故C正确;∵BC=CE,∴△BCE是等腰三角形,∵四边形ACDE是矩形,∴AF=EF=CF=DF,∴△AEF,△ACF,△CDF,△DEF是等腰三角形,∴图中有5个等腰三角形,故D错误;故选D.【点评】本题考查了平行四边形的性质、折叠的性质以及等腰三角形的判定和性质,解题的关键是熟记等腰三角形和矩形的判定方法.17.如图,有一张直角三角形纸片ABC,边AB=6,AC=10,∠ABC=90°,将该直角三角形纸片沿DE折叠,使点C与点B重合,则四边形ABDE的周长为()A.16 B.17 C.18 D.19【考点】翻折变换(折叠问题).【分析】根据勾股定理得到BC=8,由折叠的性质得到BD=CD=BC=4,DE⊥BC,根据三角形的中位线的性质得到DE=AB=3,AE=AC=5,于是得到结论.【解答】解:∵AB=6,AC=10,∠ABC=90°,∴BC=8,∵将该直角三角形纸片沿DE折叠,使点C与点B重合,∴BD=CD=BC=4,DE⊥BC,∵∠ABC=90°,∴DE∥AB,∴DE=AB=3,AE=AC=5,∴四边形ABDE的周长=AB+AE+DE+BD=6+5+3+4=18,故选C.【点评】此题考查了折叠的性质,勾股定理,三角形的中位线的性质,注意掌握折叠前后图形的对应关系.18.如图,梯形ABCD中,AD∥BC,AB=DC,∠DBC=45°,点E在BC上,点F在AB上,将梯形ABCD沿直线EF翻折,使得点B与点D重合.如果,那么的值是()A.B.C.D.【考点】翻折变换(折叠问题).【分析】根据对称的性质得到△BFE≌△DFE,得到DE=BE.根据已知条件得到∠DEB=90°,设AD=1,BC=4,过A作AG⊥BC于G,根据矩形的性质得到GE=AD=1,根据全等三角形的性质得到BG=EC=1.5,根据勾股定理得到AB=CD==5,通过△BDC∽△DEF,得到,求出BF=,于是得到结论.【解答】解:∵EF是点B、D的对称轴,∴△BFE≌△DFE,∴DE=BE.∵在△BDE中,DE=BE,∠DBE=45°,∴∠BDE=∠DBE=45°.∴∠DEB=90°,∴DE⊥BC.在等腰梯形ABCD中,∵,∴设AD=1,BC=4,过A作AG⊥BC于G,∴四边形AGED是矩形.∴GE=AD=1,∵Rt△ABG≌Rt△DCE,∴BG=EC=1.5,∴AG=DE=BE=2.5∴AB=CD==5,∵∠ABC=∠C=∠FDE,∵∠CDE+∠C=90°,∴∠FDE+∠CDE=90°∴∠FDB+∠BDC+∠FDB=∠FDB+∠DFE=90°,∴∠BDC=∠DFE,∵∠DEF=∠DBC=45°,∴△BDC∽△DEF,∴,∴DF=,∴BF=,∴AF=AB﹣BF=,∴=.故选B.【点评】此题考查等腰梯形的性质,翻折的性质,三角形全等的判定与性质,等腰直角三角形的性质,相似三角形的判定和性质等知识,注意结合图形,作出常用辅助线解决问题.19.如图,在边长为12的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G.则BG的长为()A.5 B.4 C.3 D.2【考点】翻折变换(折叠问题).【分析】利用翻折变换对应边关系得出AB=AF,∠B=∠AFG=90°,利用HL定理得出△ABG≌△AFG即可;利用勾股定理得出GE2=CG2+CE2,进而求出BG 即可;【解答】解:在正方形ABCD中,AD=AB=BC=CD,∠D=∠B=∠BCD=90°,∵将△ADE沿AE对折至△AFE,∴AD=AF,DE=EF,∠D=∠AFE=90°,∴AB=AF,∠B=∠AFG=90°,又∵AG=AG,在Rt△ABG和Rt△AFG中,,∴Rt△ABG≌Rt△AFG(HL),∴BG=GF,∵E是边CD的中点,∴DE=CE=6,设BG=x,则CG=12﹣x,GE=x+6,∵GE2=CG2+CE2∴(x+6)2=(12﹣x)2+62,解得x=4∴BG=4.故选B.【点评】此题主要考查了全等三角形的判定和性质,勾股定理的综合应用以及翻折变换的性质,根据翻折变换的性质得出对应线段相等是解题关键.20.如图,在平面直角坐标系中,△ABC的三个顶点的坐标分别为A(﹣1,0),B(﹣2,3),C(﹣3,1).将△ABC沿y轴翻折得到△A′B′C′,则点B′的坐标为()A.(2,1)B.(2,3)C.(4,1)D.(0,2)【考点】翻折变换(折叠问题);坐标与图形性质.【分析】根据关于y轴对称的点的特点找到B',结合直角坐标系可得出点B′的坐标.【解答】解:∵将△ABC沿y轴翻折得到△A′B′C′,∴点B与点B′关于y轴对称,∴B′(2,3),故选B.【点评】本题考查了翻折变换﹣折叠问题,坐标与图形的关系,熟记关于y轴对称的点的特点是解答本题的关键.21.如图,△ABC周长为36cm,把其边AC对折,使点C、A重合,折痕交BC 边于点D,交AC边于点E,连结AD,若AE=6cm,则△ABD的周长是()A.24cm B.26cm C.28cm D.30cm【考点】翻折变换(折叠问题).【分析】根据翻折变换的性质可得AE=EC,AD=CD,然后求出△ABD的周长=AB+BC,代入数据计算即可得解.【解答】解:∵△ABC的边AC对折顶点C和点A重合,∴AE=EC,AD=CD,∴△ABD的周长=AB+BD+AD=AB+BD+CD=AB+BC,∵AE=6cm,∴AC=AE+EC=6+6=12,∵△ABC的周长为36cm,∴AB+BC=36﹣12=24cm,∴△ABD的周长是24cm.故选A.【点评】本题考查了翻折变换的性质,熟记翻折前后的两个图形能够完全重合得到相等的边是解题的关键.22.如图,矩形ABCD中,AB=8,把矩形沿直线AC折叠,点B落在点E处,AE交CD于点F,若AF=,则AD的长为()A.3 B.4 C.5 D.6【考点】翻折变换(折叠问题).【分析】根据平行线的性质和翻转变换的性质得到FD=FE,FA=FC,根据勾股定理计算即可.【解答】解:∵DC∥AB,∴∠FCA=∠CAB,又∠FAC=∠CAB,∴∠FAC=∠FCA,∴FA=FC=,∴FD=FE,∵DC=AB=8,AF=,∴FD=FE=8﹣=,∴AD=BC=EC==6,故选:D.【点评】本题考查的是翻转变换的性质,翻转变换是一种对称变换,它属于轴对称,折叠前后图形的形状和大小不变,位置变化,对应边和对应角相等.23.如图的实线部分是由Rt△ABC经过两次折叠得到的,首先将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,再沿DE折叠使点A落在DC′延长线上的点A′处,若图中,∠A=30°,BC=5cm,则折痕DE的长为()A.B.2C.2D.【考点】翻折变换(折叠问题).【分析】根据直角三角形两锐角互余求出∠ABC=60°,翻折前后两个图形能够互相重合可得∠BDC=∠BDC′,∠CBD=∠ABD=30°,∠ADE=∠A′DE,然后求出∠BDE=90°,再解直角三角形求出BD,然后求出DE即可.【解答】解:∵△ABC是直角三角形,∠A=30°,∴∠ABC=90°﹣30°=60°,∵将Rt△ABC沿BD折叠,使点C落在斜边上的点C′处,∴∠BDC=∠BDC′,∠CBD=∠ABD=∠ABC=30°,∵沿DE折叠点A落在DC′的延长线上的点A′处,∴∠ADE=∠A′DE,∴∠BDE=∠ABD+∠A′DE=×180°=90°,在Rt△BCD中,BD=BC÷cos30°=5÷=cm,在Rt△BDE中,DE=BD•tan30°=×=cm.故选:D.【点评】本题考查了翻折变换的性质,解直角三角形,熟记性质并分别求出有一个角是30°角的直角三角形是解题的关键.24.如图一直角三角形纸片,两直角边AC=6cm,BC=8cm,现将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,则CD等于()A.2cm B.3cm C.4cm D.5cm【考点】翻折变换(折叠问题).【分析】首先根据题意得到:△AED≌△ACD;进而得到AE=AC=6,DE=CD;根据勾股定理求出AB=10;再次利用勾股定理列出关于线段CD的方程,问题即可解决.【解答】解:由勾股定理得:==10,由题意得:△AED≌△ACD,∴AE=AC=6,DE=CD(设为x);∠AED=∠C=90°,∴BE=10﹣6=4,BD=8﹣x;由勾股定理得:(8﹣x)2=42+x2,解得:x=3(cm),故选B.【点评】该命题主要考查了翻折变换及其应用问题;解题的关键是借助翻折变换的性质,灵活运用勾股定理、全等三角形的性质等几何知识来分析、判断、推理或解答.25.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,点D落在点D′处,则重叠部分△AFC的面积为()A.6 B.8 C.10 D.12【考点】翻折变换(折叠问题).【分析】因为BC为AF边上的高,要求△AFC的面积,求得AF即可,求证△AFD′≌△CFB,得BF=D′F,设D′F=x,则在Rt△AFD′中,根据勾股定理求x,于是得到AF=AB﹣BF,即可得到结果.【解答】解:易证△AFD′≌△CFB,∴D′F=BF,设D′F=x,则AF=8﹣x,在Rt△AFD′中,(8﹣x)2=x2+42,解之得:x=3,∴AF=AB﹣FB=8﹣3=5,∴S△AFC=•AF•BC=10.故选C.【点评】本题考查了翻折变换﹣折叠问题,勾股定理的正确运用,本题中设D′F=x,根据直角三角形AFD′中运用勾股定理求x是解题的关键.26.如图,矩形ABCD中,AB=3,AD=9,将此矩形折叠,使点B与点D重合,折痕为EF,则△ABE的面积为()A.6 B.8 C.10 D.12【考点】翻折变换(折叠问题).【分析】根据折叠的条件可得:BE=DE,在直角△ABE中,利用勾股定理就可以求解.【解答】解:将此长方形折叠,使点B与点D重合,∴BE=ED.∵AD=AE+DE=AE+BE=9.∴BE=9﹣AE,根据勾股定理可知AB2+AE2=BE2.解得AE=4.∴△ABE的面积为3×4÷2=6.故选:A.【点评】本题考查了利用勾股定理解直角三角形的能力,即:直角三角形两直角边的平方和等于斜边的平方.27.如图所示,有一块直角三角形纸片,∠C=90°,AC=2,BC=,将斜边AB翻折,使点B落在直角边AC的延长线上的点E处,折痕为AD,则CE的长为()A.B.C.1 D.【考点】翻折变换(折叠问题).【分析】由有一块直角三角形纸片,∠C=90°,AC=2,BC=,利用勾股定理即可求得AB的长,然后由折叠的性质,求得AE的长,继而求得答案.【解答】解:∵∠C=90°,AC=2,BC=,∴AB==,由折叠的性质可得:AE=AB=,∴CE=AE﹣AC=.故选A.【点评】此题考查了折叠的性质以及勾股定理.注意掌握折叠前后图形的对应关系是解此题的关键.28.如图所示,折叠平行四边形的一边AD,使点A落在DC边上的点E处,已知AB=6,BC=4,则EC的长为()A.1 B.2 C.3 D.1.5【考点】翻折变换(折叠问题).【分析】利用平行四边形的对边相等得到AD=BC=4,DC=AB=6,再由折叠的性质得到DE=AD,由DC﹣DE求出EC的长即可.【解答】解:由折叠及平行四边形的性质得:AE=AD=BC=4,DC=AB=6,则EC=DC﹣DE=6﹣4=2,故选B.【点评】此题考查了翻折变换(折叠问题),以及平行四边形的性质,熟练掌握折叠的性质是解本题的关键.29.如图,正方形ABCD中,AB=12,点E在边BC上,BE=EC,将△DCE沿DE对折至△DFE,延长EF交边AB于点G,连接DG、BF,给出以下结论:。
江西省2018年中考数学总复习第1部分基础过关第七单元图形与变换课时27对称与折叠作业2018041

课时27对称与折叠(时间:45分钟分值:60分)评分标准:选择填空每题3分基础过关1.(2017天津)在一些美术字中,有的汉字是轴对称图形.下面4个汉字中,可以看作是轴对称图形的是()2.(2017黑龙江)下列图形中,既是轴对称图形又是中心对称图形的是()3.如图1所示的下列四组图形中,左边的图形与右边的图形成中心对称的有()图1A.1组B.2组C.3组D.4组4.如图2,网格是由边长为1的正方形组成的,若△A′B′C′与△ABC关于直线AB对称,则点C的对称点C′的坐标是()图2A.(0,1) B.(0,-3)C.(3,0) D.(2,1)5.(2017呼和浩特)如图3所示,序号(1)(2)(3)(4)对应的四个三角形,都是△ABC这个图形进行了一次变换之后得到的,其中是通过轴对称得到的是()图3A.(1) B.(2)C.(3) D.(4)6.(2017赤峰)如图4,将边长为4的菱形ABCD纸片折叠,使点A恰好落在对角线的交点O处,若折痕EF=2 3,则∠A=()图4A.120°B.100°C.60°D.30°7.(2017乌鲁木齐)如图5,在矩形ABCD中,点F在AD上,点E在BC上,把这个矩形沿EF折叠后,使点D恰好落在BC边上的G点处,若矩形面积为4 3且∠AFG=60°,GE=2BG,则折痕EF的长为()图5A.1 B.3C.2 D.2 318.如图6,在矩形ABCD中,点E,F分别在边AB,BC上,且AE=AB,将矩形沿直线EF3折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q,对于下列结论:①EF=2BE;②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是()图6A.①②B.②③C.①③D.①④9.请写出一个平面几何图形,使它满足“把一个图形沿某一条直线翻折过来,直线两旁的部分能够相互重合”这一条件,这个图形可以是__________.10.如图7,直线m是正五边形ABCDE的对称轴,且直线m过点A,则∠1的度数为________.图711.如图8(a),ABCD是一矩形纸片,AB=6 c m,AD=8 c m,E是AD上一点,且AE=6 c m. 操作:(1)将AB向AE折过去,使AB与AE重合,得折痕AF,如图8(b);(2)将△AFB以BF为折痕向右折过去,得图8(c).则△GFC的面积是________cm2.图812.如图9,已知△ABC中,∠B=90°,BC=3,AB=4,D是边AB上一点,DE∥BC交AC于点E,将△ADE沿DE翻折得到△A′DE,若△A′EC是直角三角形,则AD长为__________.图913.(6分)如图10,在平面直角坐标系中,A(-3,2),B(-4,-3),C(-1,-1).图10(1)在图中作出△ABC关于y轴对称的△A1B1C1;(2)写出点△A1,B1,C1的坐标(直接写答案):A1__________;B1__________;C1__________;(3)△A1B1C1的面积为________;(4)在y轴上画出点P,使PB+PC最小.14.(8分)如图11,在Rt△ACB中,∠ACB=90°,AB=c,BC=a,D是AB上一点,将Rt △ABC沿CD折叠,使B点落在AC边上的B′处,若此时满足AB′=B′D,求证:c=2a.图11拓展提升1.(10分)(背景)某班在一次数学实践活动中,对矩形纸片进行折叠实践操作,并将其产生的数学问题进行相关探究.(操作)如图12,在矩形ABCD中,AD=6,AB=4,点P是BC边上一点,现将△APB沿AP 对折,得△APM,显然点M位置随P点位置变化而发生改变.(问题)试求下列几种情况下点M到直线CD的距离.图12(1)∠APB=75°;(2)P与C重合.课时27对称与折叠基础过关 1.C 2.C 3.C 4.D 5.A 6.A7.C8.D7 259.圆(答案不唯一)10.72°11.212. 或8 813.解:(1)如图1所示,△A1B1C1即为所求;(2)A1(3,2);B1(4,-3);C1(1,-1);(3)6.5;(4)如图1所示,P点即为所求.图114.证明:由折叠的性质得∠B=∠CB′D,又AB′=B′D,∴∠A=∠ADB′,∠CB′D=2∠A.∴∠B=2∠A.∵∠ACB=90°,∴3∠A=90°.∴∠A=30°.∴c=2a.拓展提升 1.解:(1)当∠APB=75°时,如图2,过M作EF⊥AD,则EF⊥BC,图2∵∠AMP=∠B=∠MFP=90°,∴∠AME=∠MPF.∴△AEM∽△MFP.∵∠APB=75°,∴∠BPM=2∠APB=150°.∴∠MPF=30°.∴∠AME=30°.∵AM=AB=4,∴AE=2.∴DE=4.(2)当P与C重合的,如图3,过M作GH∥AD交BA,CD的延长线于G,H,则四边形ADHG是矩形,图3∵∠ABC=∠AMC=90°,∴∠AMG=∠MCH.。
中考数学(贵阳专版)总复习训练:第6章 第1节 图形的对

第六章 图形的变化 第一节 图形的对称与折叠一、选择题1.如图所示图形中,是轴对称图形的是( B ),A ) ,B ) ,C ) ,D )2.如图是一个正方体展开图,把展开图折叠成正方体后,“我”字一面的相对面上的字是( D ) A .的 B .中 C .国 D .梦(第2题图)(第3题图)3.如图,在矩形ABCD 中,AB =8,BC =12,点E 是BC 的中点,连接AE ,将△ABE 沿AE 折叠,点B 落在点F 处,连接FC ,则sin ∠ECF =( D )A .34B .43C .35D .454.如图,点O 是圆形纸片的圆心,将这个圆形纸片按下列顺序折叠,使AB ︵和AC ︵都经过圆心O ,则阴影部分的面积是⊙O 面积的( B )A .12B .13C .23D .355.如图,在平面直角坐标系中,直线AB 与x 轴交于点A(-2,0),与x 轴夹角为30°,将△ABO 沿直线AB 翻折,点O 的对应点C 恰好落在双曲线y =kx(k ≠0)上,则k 的值为( D )A .4B .-2C . 3D .- 3(第5题图)(第6题图)6.如图,点P 是∠AOB 内任意一点,OP =5 cm ,点M 和点N 分别是射线OA 和射线OB 上的动点,△PMN 周长的最小值是5 cm ,则∠AOB 的度数是( B )A .25°B .30°C .35°D .40°7.如图,在△ABC 中,AB =10,AC =8,BC =12,AD ⊥BC 于点D ,点E ,F 分别在AB ,AC 边上,把△ABC 沿EF 折叠,使点A 与点D 恰好重合,则△DEF 的周长是( B )A .14B .15C .16D .17 二、填空题8. 已知点P(3,a)关于y 轴的对称点为Q(b ,2),则ab =__-6__ .9.如图,在矩形ABCD 中,AB =3,BC =5,在CD 上任取一点E ,连接BE ,将△BCE 沿BE 折叠,使点C 恰好落在AD 边上的点F 处,则CE 的长为__53__.(第9题图)(第10题图)10.如图,在▱ABCD 中,点E 为边CD 上一点,将△ADE 沿AE 折叠至△AD′E 处,AD ′与CE 交于点F.若∠B =52°,∠DAE =20°,则∠FED′的大小为__36°__.11.在三角形纸片ABC 中,∠C =90°,∠B =30°,点D(不与B ,C 重合)是BC 上任意一点,将此三角形纸片按下列方式折叠,若EF 的长度为a ,则△DEF 的周长为__3a __.(用含a 的式子表示)12.如图,在平面直角坐标系中,点A(0,4),B(3,0),连接AB ,将△AOB 沿过点B 的直线折叠,使点A 落在x 轴上的点A′处,折痕所在的直线交y 轴正半轴于点C ,则直线BC 的表达式为__y =-12x +32__.三、解答题13.如图,将平行四边形ABCD 沿对角线BD 进行折叠,折叠后点C 落在点F 处,DF 交AB 于点E.(1)求证:∠EDB =∠EBD ;(2)判断AF 与DB 是否平行,并说明理由. 解:(1)由折叠可知:∠CDB =∠EDB. ∵四边形ABCD 是平行四边形,∴DC ∥AB , ∴∠CDB =∠EBD ,∴∠EDB =∠EBD ; (2)AF ∥DB.理由:∵∠EDB =∠EBD ,∴DE =BE , 由折叠可知:DC =DF , ∵四边形ABCD 是平行四边形, ∴DC =AB ,∴DF =AB , ∴AE =EF ,∴∠EAF =∠EFA ,在△BED 中,∠EDB +∠EBD +∠DEB =180°, ∴2∠EDB +∠DEB =180°,同理,在△AEF 中,2∠EFA +∠AEF =180°, ∵∠DEB =∠AEF ,∴∠EDB =∠EFA , ∴AF ∥DB.14.下列3×3网格图都是由9个相同小正方形组成,每个网格图中有3个小正方形已涂上阴影,请在余下的6个空白小正方形中,按下列要求涂上阴影:(1)在图①中选取1个涂上阴影,使4个阴影小正方形组成一个轴对称图形,但不是中心对称图形; (2)在图②中选取1个涂上阴影,使4个阴影小正方形组成一个中心对称图形,但不是轴对称图形; (3)在图③中选取2个涂上阴影,使5个阴影小正方形组成一个轴对称图形.解:(1)画出下列其中一种即可:(2)画出下列其中一种即可:(3)画出下列其中一种即可:15.如图,在平面直角坐标系xOy 中,△ABC 三个顶点坐标分别为A(-2,4),B(-2,1),C(-5,2).(1)请画出△ABC 关于x 轴对称的△A 1B 1C 1;(2)将△A 1B 1C 1的三个顶点的横坐标与纵坐标同时乘以-2,得到对应的点A 2,B 2,C 2,请画出△A 2B 2C 2; (3)求△A 1B 1C 1与△A 2B 2C 2的面积比,即S △A 1B 1C 1∶S △A 2B 2C 2=____.(不写解答过程,直接写出结果) 解:(1)如图所示,△A 1B 1C 1即为所求; (2)如图所示,△A 2B 2C 2即为所求; (3)1∶4 16.问题背景:如图①,点A ,B 在直线l 的同侧,要在直线l 上找一点C ,使AC 与BC 的距离之和最小,我们可以作出点B 关于l 的对称点B′,连接AB′与直线l 交于点C ,则点C 即为所求.(1)实践运用:如图②,已知,⊙O 的直径CD 为4,点A 在⊙O 上,∠ACD =30°,B 为AD ︵的中点,P 为直径CD 上一动点,则BP +AP 的最小值为____;(2)知识拓展:如图③,在Rt△ABC中,AB=10,∠BAC=45°,∠BAC的平分线交BC于点D,E,F分别是线段AD和AB上的动点,求BE+EF的最小值,并写出解答过程.解:(1)22;(2)如题图③,过点B作BH⊥AC于点H,BH交AD于点E′,过点E′作E′F′⊥AB于点F′.∵AD为∠BAC的平分线,∴E′H=E′F′,∴BE′+E′F′=BE′+E′H=BH,在Rt△ABH中,AB=10,∠BAC=45°,∴BC=AB=10,∴BH=BCsin45°=22AB=5 2.∴当E点在E′的位置时,BE+EF有最小值,最小值为5 2.。
2018中考数学专题04 图形折叠问题(选填题重难点题型)(解析版)

1中考指导:近年来,图形折叠问题特别是矩形折叠问题一直是各地中考试题中一道靓丽的风景线.将矩形按不同要求进行折叠可以产生丰富多彩的几何问题.其中,创设开放的折叠情境,使矩形的顶点在折叠后的图形中的落点位置不固定,形成两解类中考压轴填空题的命题形式正悄然兴起. 折叠矩形纸片是轴对称变换,属于全等图形的范畴.可以先从边、角、形三方面思考折叠前后有哪些相等的线段、角和全等三角形,然后联想已知条件,看看又能产生哪些新的结论.这当中,尤其要注意将矩形折叠中产生的角平分线与矩形的两组对边分别平行结合在一起思考,往往会发现等腰三角形.面对折叠后的“静止”图形,你会发现解决这类折叠问题的关键有二点:一是在折叠操作(或“凭空想象”)中,弄清楚各种情况,画出相应状态下的静态图形;二是利用轴对称知识将分散的几何条件(边长)集中到某一个直角三角形中,再设未知数,运用勾股定理构建方程求解.典型例题解析:【例1】(2017年内蒙古赤峰二中中考数学二模)如图,在矩形ABCD 中,E 、F 分别是AD 、CD 的中点,沿着BE 将△ABE 折叠,点A 刚好落在BF 上,若AB=2,则AD=________.【答案】22∴Rt △EA′F ≌Rt △EDF (HL ), ∴A′F=DF=1,∴BF=BA′+A′F=AB +DF=2+1=3, 在Rt △BCF 中,22223122BF CF -=-=∴2 .点睛:本题考查了翻折变换的知识,解答本题的关键是连接EF ,证明Rt △EA′F ≌Rt △EDF ,得出BF 的长,再利用勾股定理解答即可.【例2】(河南省周口市西华县2018届九年级第一次模拟)如图,在Rt △ABC 中,∠ACB=90°,AB=5,AC=3,点D 是BC 上一动点,连接AD ,将△ACD 沿AD 折叠,点C 落在点E 处,连接DE 交AB 于点F ,当△DEB 是直角三角形时,DF 的长为_____.3【答案】或.∴DE=;如图2所示:∠EDB=90时,4由翻折的性质可知:AC=AC′,∠C=∠C′=90°, ∵∠C=∠C′=∠CDC′=90°, ∴四边形ACDC′为矩形,【点睛】本题考查了翻折变换、勾股定理、相似三角形的判定与性质等,结合题意,正确地进行分类讨论并画出相应的图形是解题的关键.*网【例3】(2018年河南省驻马店市实验中学第一次中考模拟)如图,在矩形ABCD 中,AB =83,AD =10,点E 是CD 的中点,将这张纸片依次折叠两次:第一次折叠纸片使点A 与点E 重合,如图②,折痕为MN ,连接ME ,NE ;第二次折叠纸片使点N 与点E 重合,如图③,点B 落到B′处,折痕为HG ,连接HE ,则下列结论:①ME ∥HG ;②△MEH 是等边三角形;③∠EHG =∠AMN ;④tan ∠EHG =53.其中正确的个数是( )A. 1个B. 2个C. 3个D. 4个【答案】C点睛:本题属于四边形综合题,主要考查翻折变换、勾股定理、相似三角形的判定和性质等知识的综合应用,解题的关键是作辅助线构造相似三角形,依据相似三角形对应边成比例,求得EN的长度.解决折叠问题时,常常设要求的线段长为x,然后根据折叠和轴对称的性质用含x的代数式表示其他线段的长度,选择适当的直角三角形,运用勾股定理列出方程求出答案.强化训练1.(2018年浙江省宁波市鄞州区中考数学模拟)在矩形纸片A BCD中,AD=8,AB=6,E是边BC上的点,将纸片沿5AE折叠,使点B落在点F处,连接FC,当△EFC为直角三角形时,BE的长为()A. 3B. 5C. 3或5D. 3或6【答案】D点睛:本题考查了翻折变换、矩形的性质、角平分线的性质、正方形的判定与性质以及勾股定理,分∠EFC=90°和∠FEC=90°两种情况寻找BE的长度是解题的关键.2.如图是一张矩形纸片ABCD,AD=10cm,若将纸片沿DE折叠,使DC落在DA上,点C的对应点为点F,若BE=6cm,则CD=( )A. 4cmB. 6cmC. 8cmD. 10cm67【答案】A【解析】由题意可知∠DFE=∠CDF=∠C=90°,DC=DF , ∴四边形ECDF 是正方形, ∴DC=EC=BC-BE , ∵四边形ABCD 是矩形, ∴BC=AD=10, ∴DC=10-6=4(cm ). 故选A.3.如图,矩形ABCD 沿着AE 折叠,使D 点落在BC 边上的F 点处,如果60BAF ∠=o ,则DAE ∠等于 ( )A. 15°B. 30°C. 45°D. 60° 【答案】A4.(陕西省宝鸡市凤翔县2017-2018学年九年级期末)如图,在矩形ABCD 中,AB=8,BC=4,将矩形沿AC 折叠,则重叠部分△AFC 的面积为( )8A. 12B. 10C. 8D. 6 【答案】B【解析】四边形ABCD 是矩形,,,,,,点睛:本题考查了图形的翻折问题、矩形的性质、三角形的面积及勾股定理;利用勾股定理求得AF 的大小,从而求得叠部分△AFC 的面积是正确解答本题的关键. *网95.(辽宁省大石桥市水源镇九年一贯制学校2018届九年级下学期月考)如图,矩形纸片ABCD 中,G 、F 分别为AD 、BC 的中点,将纸片折叠,使D 点落在GF 上,得到△HAE ,再过H 点折叠纸片,使B 点落在直线AB 上,折痕为PQ .连接AF 、EF ,已知HE=HF ,下列结论:①△MEH 为等边三角形;②AE ⊥EF ;③△PHE ∽△HAE ;④ 23AD AB ,其中正确的结论是( )A. ①②③B. ①②④C. ①③④D. ①②③④ 【答案】D【解析】试题解析:∵矩形纸片ABCD 中,G 、F 分别为AD 、BC 的中点, ∴GF ⊥AD ,由折叠可得,AH=AD=2AG ,∠AHE=∠D=90°, ∴∠AHG=30°,∠EHM=90°-30°=60°, ∴∠HAG=60°=∠AED=∠MEH ,∴△EHM 中,∠EMH=60°=∠EHM=∠MEH , ∴△MEH 为等边三角形,故①正确; ∵∠EHM=60°,HE=HF , ∴∠HEF=30°,∴∠FEM=60°+30°=90°,即AE ⊥EF ,故②正确; ∵∠PEH=∠MHE=60°=∠HEA ,∠EPH=∠EHA=90°,10∴△PHE ∽△HAE ,故③正确;6.(安徽合肥市2018届初三名校大联考一)如图,矩形ABCD 中,AB=4,BC=2,把矩形ABCD 沿过点A 的直线AE 折叠,点D 落在矩形ABCD内部的点D 处,则CD 的最小值是A. 2B. 5C. 252D. 252【答案】C【解析】根据题意,点D′在以点A 为圆心,AD 为半径且在矩形ABCD 内部的圆弧上,连接AC 交圆弧于点D′,由勾股定理得2242+=5CD′的最小值为5,故选C.7.(广东省广州三中2017年中考数学一模)如图,把一矩形纸片OABC 放入平面直角坐标系xoy 中,使OA ,OC 分别落在x 轴、y 轴上,现将纸片OABC 沿OB 折叠,折叠后点A 落在点A'的位置,若OA=1,OB=2,则点A'的坐标为( )11A. 132⎛⎫⎪⎪⎝⎭, B. 132⎛⎫- ⎪ ⎪⎝⎭, C. 3455⎛⎫- ⎪⎝⎭, D. ( ()31-, 【答案】B【解析】点睛:(1)折叠问题充分利用对应的边相等,角相等.12(2)通过三角函数值能推出角的度数;(3)已知线段的长度,表示坐标的时候注意符号问题.8.(2018年广东省深圳市中考数学突破模拟二)如图,将矩形ABCD 沿AE 折叠,点D 的对应点落在BC 上点F处,过点F 作FG ∥CD ,连接EF ,DG ,下列结论中正确的有( )①∠ADG=∠AFG ;②四边形DEFG 是菱形;③DG 2=12AE•EG ;④若AB=4,AD=5,则CE=1.A. ①②③④B. ①②③C. ①③④D. ①② 【答案】B(3)如图所示,连接DF 交AE 于O ,∵四边形DEFG为菱形,∴GE⊥DF,OG=OE=12 GE,∵∠DOE=∠ADE=90°,∠OED=∠DEA,∴△DOE∽△ADE,∴OE DEDE AE,即DE2=EO•AE,∵EO=12GE,DE=DG,∴DG2=12AE•EG,故③正确;9.如图,矩形ABCD中,E是AD的中点,将△ABE沿直线BE折叠后得到△GBE,延长BG交CD于点F.若AB=4,BC= 6,则FD的长为()1314A.85 B. 4 C. 94D. 23 【答案】C【解析】试题解析:∵E 是AD 的中点,∴AE =DE ,∵△ABE 沿BE 折叠后得到△GBE , ∴AE =EG ,AB =BG , ∴ED =EG ,∵在矩形ABCD 中, ∴90A D ∠=∠=o , ∴90EGF ∠=o ,1510.(2018年湖北省咸宁市咸安区中考数学模拟)如图,有一矩形纸片ABCD ,AB=6,AD=8,将纸片折叠使AB 落在AD 边上,折痕为AE ,再将△ABE 以BE 为折痕向右折叠,AE 与CD 交于点F ,则CFCD的值是( )A. 1B.12 C. 13 D. 14【答案】C【解析】由题意知:AB=BE=6,BD=AD ﹣AB=2(图2中),AD=AB ﹣BD=4(图3中); ∵CE∥AB, ∴△ECF∽△ADF,得12CE CF AD DF ==, 即DF=2CF ,所以CF :CD=1:3,16故选C .【点睛】本题考查了矩形的性质,折叠问题,相似三角形的判定与性质等,准确识图是解题的关键. *网11.如图,在矩形ABCD 中,AB =3,AD =5,点E 在DC 上,将矩形ABCD 沿AE 折叠,点D 恰好落在BC 边上的点F 处,那么cos ∠EFC 的值是( )A.35 B. 45 C. 12D. 32【答案】A点睛:本题考查的是翻折变换的性质、余弦的概念,掌握翻折变换是一种对称变换,折叠前后图形的形状和大小不变,位置变换,对应边和对应角相等时解题的关键.1712.如图,在矩形ABCD 中,点F 在AD 上,点E 在BC 上,把这个矩形沿EF 折叠后,使点D 恰好落在BC 边上的G 点处,若矩形面积为43且∠AFG =60°,GE =2BG ,则折痕EF 的长为( )A. 1B. 3C. 2D. 23【答案】C13.(2017年安徽省安庆一中中考数学三模)如图,小亮拿一张矩形纸图(1),沿虚线对折一次得图(2),下将对角两顶点重合折叠得图(3),按图(4)沿折痕中点与重合顶点的连线剪开,得到三个图形,这三个图形分别是( )A. 都是等腰梯形B. 都是等边三角形C. 两个直角三角形,一个等腰三角形D. 两个直角三角形,一个等腰梯形【答案】C【解析】严格按照图中的顺序向上对折,对角顶点对折,沿折痕中点与重合顶点的连线剪开展开可得到两个直角三角形,一个等腰三角形.故选C.14.如图,将一张三角形纸片折叠,使点落在边上,折痕,得到;再继续将纸片沿的对称轴折叠,依照上述做法,再将折叠,最终得到矩形,若中,和的长分别为和,则矩形的面积为().A. B. C.D.【答案】B15.(山东省临朐县沂山风景区2018届九年级上期末模拟)如图,矩形纸片ABCD中,AB=4,BC=8,将纸片折叠,1819使点C 与点A 重合,折痕为EF ,点D 的对应点为G ,连接DG ,则图中阴影部分面积是( )A. 5B. 3C.365 D. 185【答案】D【解析】过点G 作GH ⊥AD 于点H ,由题意知,AF=FC ,AB=CD=AG=4,BC=AD=8,在Rt △ABF 中,由勾股定理知AB 2+BF 2=AF 2 , 即42+(8﹣AF )2=AF 2 , 解得AF=5,2016.如图,在矩形ABCD 中,AD=5,AB=8,点E 为射线DC 上一个动点,把△ADE 沿直线AE 折叠,当点D 的对应点F 刚好落在线段AB 的垂直平分线上时,则DE 的长为________.A. 3或4B.52或10 C. 52或53 D. 25或53【答案】B【解析】试题解析:①如图1,当点F 在矩形内部时, ∵四边形ABCD 为矩形, 58AD AB ==,, ∴AB CD =,②如图2,当点F在矩形外部时,2122∵四边形ABCD 为矩形, 58AD AB ==,,∴AB CD =,设DE EF y ==,则4ME y =-, 在Rt EMF V 中, ∴222ME MF EF +=, 即()22248y y -+=,∴10.y =即DE =10. 故选B.17.(河南省濮阳市2018届九年级第一次模拟)如图,在Rt△ABC 中,∠C=90°,AC=3,BC=4,点D ,E 为AC ,BC 上两个动点,若将∠C 沿DE 折叠,点C 的对应点'C 恰好落在AB 上,且'ADC∆恰为直角三角形,则此时CD 的长为___________.23【答案】12473或 【解析】试题解析: 9034C AC BC ∠=︒==,,,225,AB AC BC ∴=+=由折叠可知: .DC DC =' 若90,ADC ∠='oDC '∥,CB,ADC ACB '∴V V ∽,AD DC AC CB ∴='3,34DC DC-∴= 解得: 12.7CD =点睛:两组角对应相等,两个三角形相似.18.(河北省唐山市路南区2017年中考数学三模)如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落在点B′AD=3,则△EB′C的周长为________.的位置,AB′与CD交于点E,若AB=8,【解析】试题分析:根据翻折图形的性质可得:B′C=BC=AD,∠B′=∠B=∠D=90°,结合对顶角得出△ADE和△CB′E 全等,则B′E=DE,则△EB′C的周长=B′C+B′E+CE=BC+DE+EC=BC+CD=AD+AB=3+8=11.*网19.(2018年咸宁市通城县北港镇初级中学数学中考模拟)如图,在矩形ABCD中,把∠A沿DF折叠,点A恰好落E处,则tan∠ADF=_______.在矩形的对称中心2420.(安徽省蚌埠市2017届九年级下学期中考一模)如图,在一张矩形纸片ABCD中,AB=4,BC=8,点E,F分别在AD,BC上,将纸片ABCD沿直线EF折叠,点C落在AD上的一点H处,点D落在点G处,有以下四个结论:①四边形CFHE是菱形;②线段BF的取值范围为3≤BF≤4;③EC平分∠DCH;④当点H与点A重合时,EF=25.以上结论中,你认为正确的有______.(填序号)【答案】①②④.【解析】试题解析:①∵FH与EG,EH与CF都是原来矩形ABCD的对边AD、BC的一部分,∴FH//CG,EH//CF,∴四边形CFHE是平行四边形,由翻折的性质得,CF=FH,2526∴四边形CFHE 是菱形, 故①正确;③∴∠BCH =∠ECH ,∴只有30DCE ∠=o 时EC 平分∠DCH , 故③错误;过点F 作FM ⊥AD 于M ,则ME =(8−3)−3=2,由勾股定理得, 2225EF MF ME =+=, 故④正确,综上所述,结论正确的有①②④, 故答案为:①②④.27。
自学初中数学资料 折叠问题 图形的翻折、轴对称(资料附答案)

自学资料一、图形的翻折、轴对称【知识探索】1.如果把一个图形沿某一条直线翻折,能与另一个图形重合,那么叫做这两个图形关于这条直线成轴对称,这条直线叫做对称轴,两个图形中的对应点叫做关于这条直线的对称点.【说明】(1)两个图形关于一条直线成轴对称,这两个图形对应线段的长度和对应角的大小相等,它们的形状相同,大小不变;(2)在成轴对称的两个图形中,分别联结两对对应点,取中点,联结两个中点所得的直线就是对称轴.2.把一个图形沿某一条直线翻折过来,直线两旁的部分能够相互重合,这个图形叫做轴对称图形,这条直线就是它的对称轴.【错题精练】第1页共26页自学七招之日计划护体神功:每日计划安排好,自学规划效率高非学科培训第2页 共26页 自学七招之提前完卷飞刀:考场控时莫紧张,跳跃答卷心不慌 非学科培训例1.如图,在△ABC 中,∠ACB=90°,AB=5,BC=3,P 是AB 边上的动点(不与点B 重合),将△BCP 沿CP 所在的直线翻折,得到△B′CP ,连接B′A ,则下列判断:①当AP=BP 时,AB′∥CP ;②当AP=BP 时,∠B′PC=2∠B′AC③当CP ⊥AB 时,AP=175;④B′A 长度的最小值是1.其中正确的判断是______ (填入正确结论的序号)【解答】解:①∵在△ABC 中,∠ACB=90°,AP=BP ,∴AP=BP=CP ,∠BPC=12(180°-∠APB′),由折叠的性质可得:CP=B′P ,∠CPB′=∠BPC=12(180°-∠APB′),∴AP=B′P ,∴∠AB′P=∠B′AP=12(180°-∠APB′),∴∠AB′P=∠CPB′,∴AB′∥CP ;故①正确;②∵AP=BP ,∴PA=PB′=PC=PB ,∴点A ,B′,C ,B 在以P 为圆心,PA 长为半径的圆上,∵由折叠的性质可得:BC=B′C , ∴BC ̂=B′C ̂,∴∠B′PC=2∠B′AC ;故②正确;③当CP ⊥AB 时,∠APC=∠ACB ,∵∠PAC=∠CAB ,∴△ACP ∽△ABC ,∴APAC =ACAB ,∵在Rt △ABC 中,由勾股定理可知:AC=√AB 2−BC 2=√52−32=4,∴AP=AC 2AB =165;故③错误;④由轴对称的性质可知:BC=CB′=3,∵CB′长度固定不变,∵AB'≥AC-CB'∴AB′的长度有最小值.AB′有最小值=AC-B′C=4-3=1.故④正确.故答案为:①②④.【答案】①②④例2.如图所示,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.现给出以下四个命题(1)∠APB=∠BPH;(2)当点P在边AD上移动时,△PDH的周长不发生变化;(3)∠PBH=45°;(4)BP=BH.其中正确的命题是______.【解答】(1)证明:如图1,∵PE=BE,∴∠EBP=∠EPB.又∵∠EPH=∠EBC=90°,∴∠EPH-∠EPB=∠EBC-∠EBP.即∠PBC=∠BPH.又∵AD∥BC,∴∠APB=∠PBC.∴∠APB=∠BPH.故(1)正确;(2))△PHD的周长不变为定值8.第3页共26页自学七招之举一反三剑:总结归纳典型题,多种解法开脑洞非学科培训第4页 共26页 自学七招之提前完卷飞刀:考场控时莫紧张,跳跃答卷心不慌 非学科培训证明:如图2,过B 作BQ ⊥PH ,垂足为Q .由(1)知∠APB=∠BPH ,在△ABP 和△QBP 中,{∠APB =∠BPH∠A =∠BQP BP =BP∴△ABP ≌△QBP (AAS ).∴AP=QP ,AB=BQ .又∵AB=BC ,∴BC=BQ .又∵∠C=∠BQH=90°,BH=BH ,∴△BCH ≌△BQH .∴CH=QH .∴△PHD 的周长为:PD+DH+PH=AP+PD+DH+HC=AD+CD=8.故(2)正确;(3)解:∵△ABP ≌△QBP (AAS )、△BCH ≌△BQH .∴∠QBH=∠HBC ,∠ABP=∠PBQ ,∴∠PBH=∠PBQ+∠QBH=12∠ABC=45°.故(3)正确;(4)解:∵∠PBH=45°固定不变,∴当点P 在AD 上移动时,∠BPH 的度数不断发生变化,∴∠BPH 的度数与∠BHP 不一定相等,故BP 与BH 不一定相等.故答案为:(1)(2)(3).【答案】(1)(2)(3)例3.如图,把某矩形纸片ABCD 沿EF ,GH 折叠(点E ,H 在AD 边上,点F ,G 在BC 边上),使点B 和点C 落在AD 边上同一点P 处,A 点的对称点为A′点,D 点的对称点为D′点,若∠FPG =90°,△A′EP 的面积为4,△D′PH 的面积为1,则矩形ABCD 的面积等于【答案】例4.如图,在菱形紙片ABCD中,AB=2.将纸片折叠,使点B落在AD边上的点B′处(不与A,D重合),点C落在C′处,线段B′C′与直线CD交于点G,折痕为EF,则下列说法①若∠A=90,B′为AD中点时,AE=34②若∠A=60°,B′为AD中点时,点E恰好是AB的中点③若∠A=60°,C′F⊥CD时,CFFD =√3−12其中正确的是()第5页共26页自学七招之举一反三剑:总结归纳典型题,多种解法开脑洞非学科培训第6页 共26页 自学七招之提前完卷飞刀:考场控时莫紧张,跳跃答卷心不慌 非学科培训A. ①②B. ①③C. ②③D. ①②③【解答】解:①∵∠A=90°,四边形ABCD 是菱形,∴四边形ABCD 是正方形,∴AB=AD ,∵B′为AD 中点时,∴AB'=1,设AE=x ,则B'E=BE=2-x ,在Rt △AB'E 中,由勾股定理得:12+x 2=(2-x )2,解得:x=34,①正确; ②连接BD 、BE',如图:∵∠A=60°,AB=AD ,∴△ABD 是等边三角形,∴∠ABD=60°,∵B′为AD 中点,∴∠AB'B=90°,∠ABB'=30°∵BE=B'E ,∴∠BB'E=∠ABB'=30°,∴∠AB'E=60°,∴△AB'E 是等边三角形,∴AE=B'E=BE ,∴点E 是AB 的中点,②正确;③设CF=x ,由折叠的性质得:C'F=CF=x ,∠C'=∠C=∠A=60°,∵C′F ⊥CD ,∴∠C'GF=30°,∴C'G=2C'F=2x ,GF=√3C'F=√3x ,∴DG=CD-GF-CF=2-√3x-x ,∵∠D=180°-∠A=120°,∠DGB'=∠C'GF=30°,∴∠DB'G=30°,∴DB'=DG ,设BD 交B'C'于H ,则B'H=GH=12B'G=12(2-2x )=1-x ,∴DG=2(1−x )√3,∴2(1−x )√3=2-√3x-x , 解得:x=4-2√3,∴CF=4-2√3,FD=2-(4-2√3)=2√3-2,∴CF FD =√3−12,③正确; 故选:D .【答案】D例5.如图,以半圆的一条弦BC为对称轴将弧BC折叠后与直径AB交于点D,若AD=4,BD=8,则CB的长为__________【解答】第7页共26页自学七招之举一反三剑:总结归纳典型题,多种解法开脑洞非学科培训【答案】例6.如图,矩形ABCD中,BC=3,且BC>AB,E为AB边上任意一点(不与A,B重合),设BE=t,将△BCE沿CE对折,得到△FCE,延长EF交CD的延长线于点G,则tan∠CGE= (用含t的代数式表示).【解答】解:如图连接BF交EC于O,作EM⊥CD于M,∵∠EMC=∠EBC=∠BCM=90°,∴四边形EBCM是矩形,∴CM=EB=t,EM=BC=3,在RT△EBC中,∵EB=t,BC=3,∴EC=√t2+32=√t2+9,∵EB=EF,CB=CF,∴EC垂直平分BF,∵12•EC•BO=12•EB•BC,∴BO=3t√t2+9,BF=2BO=6t√t2+9∵∠AEF+∠BEF=180°,∠BEF+∠BCF=180°,∴∠AEF=∠BCF,∵AB∥CD,∴∠BEC=∠ECG=∠CEF,∠AEF=∠G=∠BCF ∴GE=GC,∴∠GCE=∠GEC=∠CFB=∠CBF,∴△CBF∽△GCE,∴GCBC =ECBF,第8页共26页自学七招之提前完卷飞刀:考场控时莫紧张,跳跃答卷心不慌非学科培训∴GC=t 2+92t,GM=GC-CM=9−t22t,∴tan∠CGE=EMGM =6t9−t2.故答案为6t9−t2.【答案】6t9−t2例7.阅读下面材料:在学习小组活动中,小明探究了下面问题:菱形纸片ABCD的边长为2,折叠菱形纸片,将B、D两点重合在对角线BD上的同一点处,折痕分别为EF、GH.当重合点在对角线BD上移动时,六边形AEFCHG的周长的变化情况是怎样的?小明发现:若∠ABC=60°,①如图1,当重合点在菱形的对称中心O处时,六边形AEFCHG的周长为______;②如图2,当重合点在对角线BD上移动时,六边形AEFCHG的周长______(填“改变”或“不变”).请帮助小明解决下面问题:如果菱形纸片ABCD边长仍为2,改变∠ABC的大小,折痕EF的长为m.(1)如图3,若∠ABC=120°,则六边形AEFCHG的周长为______;(2)如图4,若∠ABC的大小为2α,则六边形AEFCHG的周长可表示为______.【解答】解:①如图1,当重合点在菱形的对称中心O处时,由题意可知△BEF和△DGH是等边三角形,∴EF+AE+AG+GH+CH+CF=BE+AE+AG+GD+DH+CH=2+2+2=6.∴六边形AEFCHG的周长为6;②如图2,当重合点在对角线BD上移动时,由题意可知△BEF和△DGH是等边三角形,∴EF+AE+AG+GH+CH+CF=BE+AE+AG+GD+DH+CH=2+2+2=6.∴六边形AEFCHG的周长为6.故六边形AEFCHG的周长不变.(1)如图3,若∠ABC=120°,由题意可知EF+GH=AC,则六边形AEFCHG的周长为2×2+2×sin60°×2=4+2√3;(2)如图4,若∠ABC的大小为2α,由题意可知EF+GH=AC,则六边形AEFCHG的周长可表示为2×2+2×sinα×2=4+4sinα.故答案为:①6;②不变.(1)4+2√3;(2)4+4sinα.第9页共26页自学七招之举一反三剑:总结归纳典型题,多种解法开脑洞非学科培训【答案】6不变4+2√34+4sinα例8.已知边长为3的正方形ABCD中,点E在射线BC上,且BE=2CE,连接AE交射线DC于点F,若△ABE沿直线AE翻折,点B落在点B1处.(1)如图1,若点E在线段BC上,求CF的长;(2)求sin∠DAB1的值;(3)如果题设中“BE=2CE”改为“BECE=x”,其它条件都不变,试写出△ABE翻折后与正方形ABCD公共部分的面积y与x的关系式及自变量x的取值范围(只要写出结论,不需写出解题过程).【解答】(1)解:∵AB∥DF,∴ABCF =BECE,∵BE=2CE,AB=3,∴3CF =2CECE,∴CF=32;(2)解:①若点E在线段BC上,如图1,设直线AB1与DC相交于点M.由题意翻折得:∠1=∠2.∵AB∥DF,∴∠1=∠F,∴∠2=∠F,∴AM=MF.设DM=x,则CM=3−x.又∵CF=1.5,∴AM=MF=92−x,在Rt△ADM中,AD2+DM2=AM2,∴32+x2=(92−x)2,∴x=54,∴DM=54,AM=134,第10页共26页自学七招之提前完卷飞刀:考场控时莫紧张,跳跃答卷心不慌非学科培训∴sin∠DAB1=DMAM =513;②若点E在边BC的延长线上,如图2,设直线AB1与CD延长线相交于点N.同理可得:AN=NF.∵BE=2CE,∴BC=CE=AD.∵AD∥BE,∴ADCE =DFFC,∴DF=FC=32,设DN=x,则AN=NF=x+32.在Rt△ADN中,AD2+DN2=AN2,∴32+x2=(x+32)2,∴x=94.∴DN=94,AN=154sin∠DAB1=DNAN=35;(3)解:若点E在线段BC上,y=9x2x+2,定义域为x>0;若点E在边BC的延长线上,y=9x−92x,定义域为x>1.【答案】(1)32;(2)①513,②35;(3)略.【举一反三】1.如图,已知△ABC中,AB=8,BC=7,AC=6,E是AB的中点,F是AC边上一个,综上所述,EF的长为72或143.72或1432.如图,在菱形纸片ABCD中,AB=4,∠A=60°,将菱形纸片翻折,使点A落在CD边的中点E处,折痕为FG,点F、G分别在边AB、AD上,则GE=______,EF=______.【解答】解:如图过点E作EH⊥AD于H,EN⊥AB于N,过点A作AM⊥CD于M∵ABCD是菱形,∴AB∥CD,AD=AB=CD=AB=4∴∠ADM=∠BAD=∠HDE=60°∵E是CD中点∴DE=2在Rt△DHE,中,DE=2,HE⊥DH,∠HDE=60°∴DH=1,HE=√3∵折叠∴AG=GE,AF=EF在Rt△HGE中,GE2=GH2+HE 2∴GE2=(4-GE+1)2+3∴GE=2.8在Rt△AMD中,AD=4,AM⊥DM,∠ADM=60°∴MD=2,AM=2√3∵AB∥CD,AM∥EN∴AMEN是平行四边形且AM⊥CD∴AMEN是矩形∴AN=ME=2+2=4,(即N与B重合)AM=EN=2√3在Rt△FBE中,EF2=EN2+FB 2EF2=(4-EF)2+12EF=3.5【答案】2.83.53.折叠矩形纸片ABCD时,发现可以进行如下操作:①把△ADE翻折,点A落在DC边上的点F处,折痕为DE,点E在AB边上;②把纸片展开并铺平;③把△CDG翻折,点C落在线段AE上的点H处,折痕为DG,点G在BC边上,若AB=AD+2,EH=1,则AD=______.【解答】解:设AD=x,则AB=x+2,∵把△ADE翻折,点A落在DC边上的点F处,∴DF=AD,EA=EF,∠DFE=∠A=90°,∴四边形AEFD为正方形,∴AE=AD=x,∵把△CDG翻折,点C落在线段AE上的点H处,折痕为DG,点G在BC边上,∴DH=DC=x+2,∵HE=1,∴AH=AE-HE=x-1,在Rt△ADH中,∵AD2+AH2=DH2,∴x2+(x-1)2=(x+2)2,整理得x2-6x-3=0,解得x1=3+2√3,x2=3-2√3(舍去),即AD的长为3+2√3.故答案为3+2√3.【答案】3+2√34.小明尝试着将矩形纸片 ABCD (如图①, AD>CD )沿过 A 点的直线折叠,使得 B 点落在 AD 边上的点 F 处,折痕为 AE (如图②);再沿过 D 点的直线折叠,使得 C 点落在 DA 边上的点 N 处, E 点落在 AE 边上的点 M 处,折痕为 DG (如图③).如果第二次折叠后, M 点正好在 ∠ NDG 的平分线上,那么矩形 ABCD 长与宽的比值为.【答案】√2:1 .5.如图,AC是矩形ABCD的对角线,⊙O是△ABC的内切圆,现将矩形ABCD按如图所示的方式折叠,使点D与点O重合,折痕为FG,点F,G分别在AD,BC上,连接OG,DG,若OG⊥DG,且⊙O 的半径长为1,则下列结论不成立的是()A. CG=1B. 矩形ABCD的面积为6+4√3C. ∠ACB=30°D. AF=2√3【解答】解:如图,设⊙O 与BC 的切点为M ,连接MO 并延长MO 交AD 于点N ,∵将矩形ABCD 按如图所示的方式折叠,使点D 与点O 重合,折痕为FG ,∴OG=DG ,∵OG ⊥DG ,∴∠MGO+∠DGC=90°,∵∠MOG+∠MGO=90°,∴∠MOG=∠DGC ,在△OMG 和△GCD 中,{∠OMG =∠DCG =90°∠MOG =∠DGC OG =DG,∴△OMG ≌△GCD ,∴OM=GC=1,CD=GM=BC-BM-GC=BC-2.故A 正确,∵AB=CD ,∴BC-AB=2.设AB=a ,BC=b ,AC=c ,⊙O 的半径为r ,⊙O 是Rt △ABC 的内切圆可得r=12(a+b-c ),∴c=a+b-2.在Rt △ABC 中,由勾股定理可得a 2+b 2=(a+b-2)2,整理得2ab-4a-4b+4=0,又∵BC-AB=2即b=2+a ,代入可得2a (2+a )-4a-4(2+a )+4=0,解得a 1=1+√3,a 2=1-√3(舍去),∴a=1+√3,b=3+√3,∴S 矩形ABCD =AB•BC=6+4√3,故B 正确,∴tan ∠ACB=AB BC =√33,∴∠ACB=30°,故C 正确,再设DF=x ,在Rt △ONF 中,FN=3+√3-1-x ,OF=x ,ON=1+√3-1=√3,由勾股定理可得(2+√3-x )2+(√3)2=x 2,解得x=4-√3,∴AF=AD-DF=2√3-1,故D 错误,故选:D .【答案】D6.如图,在⊙O 中,将AB̂沿弦AB 翻折交半径AO 的延长线于点D ,延长BD 交⊙O 于点C ,AC 切ADB ̂所在的圆于点A ,则tan ∠C 的值是( )A. √3B. 43C. 2+√3D. 1+√2【解答】解:作点D关于AB的对称点H,连接AH,BH,CH.根据对称性可知,ADB̂所在圆的圆心在直线AH上,∵AC切ADB̂所在的圆于点A,∴AC⊥AH,∴∠CAH=90°,∴CH是⊙O的直径,∴∠CBH=90°,∴∠ABD=∠ABH=45°,∴∠AHC=∠ABC=45°,∴∠ACH=∠AHC=45°,∴AC=AH,∵OC=OH,∴AD垂直平分线段CH,∴DC=DH,∴∠DCH=∠DHC,∵BD=BH,∴∠BDH=∠BHD=45°,∵∠BDH=∠DCH+∠DHC,∴∠DCH=22.5°,∴∠ACD=∠CHB=67.5°,设BD=BH=a,则CD=DH=√2a,∴tan∠ACB=tan∠CHB=BCBH =a+√2aa=1+√2,故选:D.【答案】D7.半径为2的圆弧形纸片按如图方式折叠,使对折后半圆弧的中点M与圆心O重合,则图中阴影部分的面积是______.【解答】解:如图,连接OM交AB于点C,连接OA、OB,由题意知,OM⊥AB,且OC=MC=1,在Rt△AOC中,∵OA=2,OC=1,∴cos∠AOC=OCOA =12,AC=√OA2−OC2=√3∴∠AOC=60°,AB=2AC=2√3,∴∠AOB=2∠AOC=120°,则S弓形ABM=S扇形OAB-S△AOB=120π×22360-12×2√3×1=4π3-√3,S阴影=S半圆-2S弓形ABM=1 2π×22-2(4π3-√3)=2√3−23π.故答案为:2√3−23π.【答案】2√3−23π8.如图,将矩形ABCD沿EF折叠,使顶点C恰好落在AB边的C1处,点D落在点D1处,C1D1交线段AE于点G.(1)求证:△BC1F∽△AGC1;(2)若C1是AB的中点,AB=6,BC=9,求AG的长.1.如图,在四边形纸片ABCD中,AB=BC,AD=CD,∠A=∠C=90°,∠B=150°,将纸片先沿直线BD 对折,再将对折后的图形沿从一个顶点出发的直线裁剪,剪开后的图形打开铺平,若铺平后的图形中有一个是面积为2的平行四边形,则BC= .【解答】解:如图1所示:作AE∥BC,延长AE交CD于点N,过点B作BT⊥EC于点T,当四边形ABCE为平行四边形,∵AB=BC,∴四边形ABCE是菱形,∵∠A=∠C=90°,∠B=150°,BC∥AN,∴∠ADC=30°,∠BAN=∠BCE=30°,则∠NAD=60°,∴∠AND=90°,∵四边形ABCE面积为2,∴设BT=x,则BC=EC=2x,故2x×x=2,解得:x=1(负数舍去),故BC=2;如图2,当四边形BEDF是平行四边形,∵BE=BF,∴平行四边形BEDF是菱形,∵∠A=∠C=90°,∠B=150°,∴∠ADB=∠BDC=15°,∵BE=DE,∴∠AEB=30°,∴设AB=y,则BE=2y,∵四边形BEDF面积为2,∴AB×DE=2y2=2,解得:y=1,故BC=1,综上所述:BC=2或1.故答案为:2或1.【答案】2或1̂沿BD翻折,点C的对称点C′恰好落在AB 2.如图,已知半圆的内接四边形ABCD,AB是直径,DCB上.若AC′=4,C′B=5,则BD的长是()A. 4√3B. 3√7C. 7D. 8【解答】解:作DE⊥AB于E,连接DC′,由折叠的性质可知,CD=C′D,∠CBD=∠C′BD,∴DA=DC,∴AD=C′D,又DE⊥AB,∴AE=EC′=2,∴EB=7,由射影定理得,DE2=AE•EB=14,在Rt△DEB中,BD2=DE2+BE2=63,∴BD=3√7,故选:B.【答案】B3.如图,正方形ABCD中,AB=3,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE,延长EF交边BC于点G,连接AG、CF.下列结论:①点G是BC中点;②FG=FC;③与∠AGB相等的角有5个;④S△FGC=910.其中正确的是()A. ①③B. ②③C. ①④D. ②④【解答】解:∵正方形ABCD中,AB=3,CD=3DE,∴DE=13×3=1,CE=3-1=2,∵△ADE沿AE对折至△AFE,∴AD=AF,EF=DE=1,∠AFE=∠D=90°,∴AB=AF=AD,在Rt△ABG和Rt△AFG中,{AG=AGAB=AF,∴Rt△ABG≌Rt△AFG(HL),∴BG=FG,设BG=FG=x,则EG=EF+FG=1+x,CG=3-x,在Rt△CEG中,EG2=CG2+CE2,即(1+x)2=(3-x)2+22,解得,x=32,∴CG=3-32=3 2,∴BG=CG=32,即点G是BC中点,故①正确;∵tan∠AGB=ABBG =332=2,∴∠AGB≠60°,∴∠CGF≠180°-60°×2≠60°,又∵BG=CG=FG,∴△CGF不是等边三角形,∴FG≠FC,故②错误;由(1)知Rt △ABG ≌Rt △AFG ,∴∠AGB=∠AGF=12∠BGF ,根据三角形的外角性质,∠GCF+∠GFC=∠AGB+∠AGF ,∴∠GCF=∠GFC=∠AGB ,∵AD ∥BC ,∴∠AGB=∠GAD ,∴与∠AGB 相等的角有4个,故③错误;△CGE 的面积=12CG•CE=12×32×2=32, ∵EF :FG=1:32=2:3,∴S △FGC =32+3×32=910,故④正确; 综上所述,正确的结论有①④.故选:C .【答案】C4.如图,在矩形ABCD 中,AB=2,AD=5,点P 在线段BC 上运动,现将纸片折叠,使点A 与点P 重合,得折痕EF (点E 、F 为折痕与矩形边的交点),设BP=x ,当点E 落在线段AB 上,点F 落在线段AD 上时,x 的取值范围是______.【解答】解:如图;①当F 、D 重合时,BP 的值最小;根据折叠的性质知:AF=PF=5;在Rt △PFC 中,PF=5,FC=2,则PC=√21;∴BP 的最小值为5-√21;②当E 、B 重合时,BP 的值最大;由折叠的性质可得AB=BP=2,即BP的最大值为2.所以x的取值范围是5-√21≤x≤2.故答案为:5-√21≤x≤2.【答案】5-√21≤x≤25.如图,现有边长为5的正方形纸片ABCD,点P为AD边上的一点(不与点A、点D重合)将正方形纸片折叠,使点B落在点P处,点C落在点G处,PG交DC于点H,折痕为EF连结BP,BH.当AP=2时,PH=______.【解答】解:设AE=x,则BE=5-x.由翻折的性质可知:BE=PE=x,∠APG=∠ABC=90°.∴∠APE+∠DPH=90°.∵∠AEP+∠APE=90°,∴∠AEP=∠DPH.又∵∠A=∠D=90°,∴△APE∽△DHP.在Rt△APE中,PE2=AE2+AP2,即(5-x)2=x2+22,解得x=2.1.则PE=5-2.1=2.9.∵△APE∽△DHP,∴EPPH =AEPD,即2.9PH=2.13,解得:PH=297.故答案为:297.【答案】2976.如图,矩形纸片ABCD中,AD=15cm,AB=10cm,点P、Q分别为AB、CD的中点,E、G分别为BC、PQ上的点,将这张纸片沿AE折叠,使点B与点G重合,则△AGE的外接圆的面积为______.【解答】解:由翻折的性质得,AG=AB,∠GAE=∠BAE,∵点P、Q分别为AB、CD的中点,∴AP=12AB,∴AP=12AG,∴∠AGP=30°,∴∠PAG=90°-∠AGP=90°-30°=60°,∴∠BAE=12∠PAG=12×60°=30°,在Rt△ABE中,AE=AB÷cos30°=10÷√32=20√33cm,∴△AGE的外接圆的面积=π(AE2)2=π(12×20√33)2=1003πcm2.故答案为:1003πcm2.【答案】1003πcm27.如图,矩形ABCD中,AD=10,AB=8,点E为边DC上一动点,连接AE,把△ADE沿AE折叠,使点D落在点D′处,当△DD′C是直角三角形时,DE的长为______.【解答】解:∵△ADE沿AE折叠,使点D落在点D′处,∴DE=D′E,AD=AD′=10,当∠DD′C=90°时,如图1,∵DE=D′E,∴∠1=∠2,∵∠1+∠4=90°,∠2+∠3=90°,∴∠3=∠4,∴ED′=EC,CD=4;∴DE=EC=12当∠DCD′=90°时,则点D′落在BC上,如图2,设DE=x,则ED′=x,CE=8-x,∵AD′=AD=10,∴在Rt△ABD′中,BD′=√102−82=6,∴CD′=4,在Rt△CED′中,(8-x)2+42=x2,解得x=5,即DE的长为5,综上所述,当△DD′C是直角三角形时,DE的长为4或5.故答案为4或5.【答案】4或5。
【中考专题】2018年 九年级数学中考专题 折叠问题(含答案)
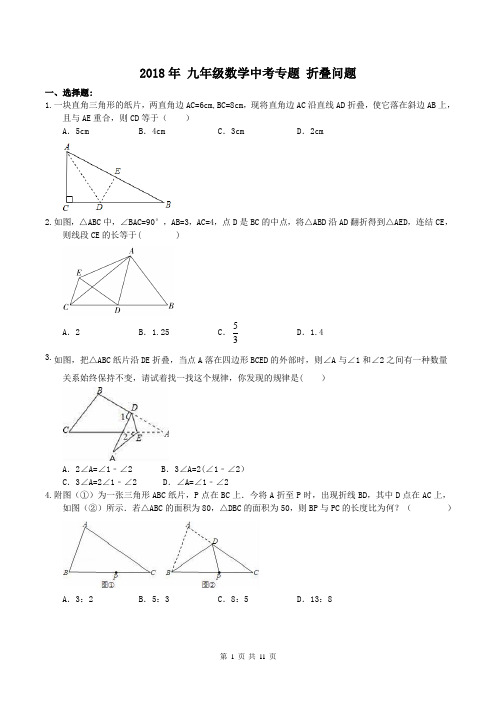
2018年 九年级数学中考专题 折叠问题一、选择题:1.一块直角三角形的纸片,两直角边AC=6cm,BC=8cm ,现将直角边AC 沿直线AD 折叠,使它落在斜边AB 上,且与AE 重合,则CD 等于( )A .5cmB .4cmC .3cmD .2cm2.如图,△ABC 中,∠BAC=90°,AB=3,AC=4,点D 是BC 的中点,将△ABD 沿AD 翻折得到△AED ,连结CE ,则线段CE 的长等于( )A .2B .1.25C .35D .1.43.如图,把△ABC 纸片沿DE 折叠,当点A 落在四边形BCED 的外部时,则∠A 与∠1和∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )A .2∠A=∠1﹣∠2B .3∠A=2(∠1﹣∠2)C .3∠A=2∠1﹣∠2D .∠A=∠1﹣∠24.附图(①)为一张三角形ABC 纸片,P 点在BC 上.今将A 折至P 时,出现折线BD ,其中D 点在AC 上,如图(②)所示.若△ABC 的面积为80,△DBC 的面积为50,则BP 与PC 的长度比为何?( )A .3:2B .5:3C .8:5D .13:85.如图,直角三角形纸片两直角边长分别为6,8,按如图折叠,使A与B重合,折痕为DE,则S:S△BDE等于△BCE ()A.2:5 B.14:25 C.16:25 D.4:216.如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为()A.B.2.5 C.4 D.57.如图,将一个矩形纸片ABCD,沿着BE折叠,使C、D点分别落在点C,D1处.若∠C1BA=50°,则∠ABE的1度数为()A.15°B.20°C.25°D.30°8.如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=6cm,则tan∠EAF的值是()A.0.5 B.0.75 C.2 D.59.如图,把长方形纸片ABCD折叠,使其对角顶点C与A重合.若长方形的长BC为8,宽AB为4,则折痕EF的长度为()A.5 B.3C.2D.310.如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD边交于点F,则B′F的长度为()A.1 B.C.2-D.2﹣211.将一张宽为4cm的长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形,则这个三角形面积的最小值是()A. cm2B.8cm2C. cm2D.16cm212.如图,将一个等腰Rt△ABC对折,使∠A与∠B重合,展开后得折痕CD,再将∠A折叠,使C落在AB上的点F处,展开后,折痕AE交CD于点P,连接PF、EF,下列结论:①tan∠CAE=﹣1;②图中共有4对全等三角形;③若将△PEF沿PF翻折,则点E一定落在AB上;④PC=EC;⑤S四边形DFEP=S△APF.正确的个数是()A.1个B.2个C.3个D.4个二、填空题:13.矩形纸片ABCD中,AD=4cm,AB=10cm,按如图方式折叠,使点B与点D重合,折痕为EF,则DE= cm.14.如图,把等边三角形ABC沿着DE折叠,使点A恰好落在BC边上的点P处,且DP⊥BC,若BP=4 cm,则EC= cm.15.如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.当△CEB′为直角三角形时,BE的长为16.如图,矩形ABCD中,AB=1,E、F分别为AD、CD的中点,沿BE将△ABE折叠,若点A恰好落在BF上,则AD= .17.如图,在Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC上,以AD为折痕,△ABD折叠得到△AB′D,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是 .18.如图所示,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A.点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.现给出以下四个命题(1)∠APB=∠BPH;(2)当点P在边AD上移动时,△PDH的周长不发生变化;(3)∠PBH=450 ; (4)BP=BH.其中正确的命题是.三、解答题:19.如图①,将矩形ABCD沿DE折叠使点A落在点A′处,然后将矩形展平,如图②沿EF折叠使点A落在折痕DE上的点G处,再将矩形ABCD沿CE折叠,此时顶点B恰好落在DE上的点H处.(1)求证:EG=CH;(2)已知AF=2,求AD和AB的长.20.如图,四边形ABCD表示一张矩形纸片,AB=10,AD=8.E是BC上一点,将△ABE沿折痕AE向上翻折,点B恰好落在CD边上的点F处,⊙O内切于四边形ABEF.求:(1)折痕AE的长;(2)⊙O的半径.21.在正方形ABCD中,E、F分别为BC、CD的中点,AE与BF相交于点G.(1)如图1,求证:AE⊥BF;(2)如图2,将△BCF沿BF折叠,得到△BPF,延长FP交BA的延长线于点Q,若AB=4,求QF的值.22.阅读材料,在平面直角坐标系中,已知x轴上两点A(x,0),B(x2,0)的距离记作AB=|x1﹣x2|;若A,B1是平面上任意两点,我们可以通过构造直角三角形来求AB间的距离,如图,过A,B分别向x轴、y轴作垂线AM1、AN1和BM2、BN2,垂足分别是M1、N1、M2、N2,直线AN1交BM2于点Q,在Rt△ABQ中,AQ=|x1﹣x2|,BQ=|y1﹣y2|,∴AB2=AQ2+BQ2=|x1﹣x2|+|y1﹣y2|2=(x1﹣x2)2+(y1﹣y2)2,由此得到平面直角坐标系内任意两点A(x1,y1),B(x2,y2)间的距离公式为:(1)AB= .(2)直接应用平面内两点间距离公式计算点A(1,﹣3),B(﹣2,1)之间的距离为;(3)根据阅读材料并利用平面内两点间的距离公式,求代数式+的最小值.23.如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的B′处,得到折痕EC,将点A落在直线EF上的点A′处,得到折痕EN.(1)若∠BEB′=110°,则∠BEC= °,∠AEN= °,∠BEC+∠AEN= °.(2)若∠BEB′=m°,则(1)中∠BEC+∠AEN的值是否改变?请说明你的理由.(3)将∠ECF对折,点E刚好落在F处,且折痕与B′C重合,求∠DNA′.24.如图,已知矩形OABC在坐标系中,A(0,4),C(6,0),直线y=x与AB交于D点,E为BC上一点.(1)如图1,若△OCE沿OE翻折,当C恰好与D点重合时,求此时E点坐标;(2)如图2,若△OCE与BDE相似,求E点坐标;(3)如图,3,已知线段GH开始时在矩形OABC内壁与BC重合(不考虑厚度),M为GH中点,将线段GH 沿矩形内壁滑动,G在BC上滑动,H在CO上滑动,线段GH长度始终保持不变,当G与C点重合时,停止运动.在滑动的过程中,当DM长度最小值时,求此时M点坐标.参考答案1.C2.D;3.A.4.A5.A6.B7.D8.C.9.D.10.A.11.B.12.D.13.答案为:5.8.14.答案为:2+23;15.答案为: 3或616.答案为: .17.答案为:2或5;解析:∵在Rt△ABC纸片中,∠C=90°,AC=6,BC=8,∴AB=10,∵以AD为折痕,△ABD折叠得到△AB′D,∴BD=DB′,AB′=AB=10.如答图①,当∠B′DE=90°时,过点B′作B′F⊥AC的延长线于点F.设BD=DB′=x,则AF=6+x,FB′=8-x.在Rt△AFB′中,由勾股定理,得AB′2=AF2+FB′2,即(6+x)2+(8-x)2=102,解得x1=2,x2=0(舍去),∴BD=2;如答图②,当∠B′ED=90°时,点C与点E重合.∵AB′=10,AC=6,∴B′E=4.设BD=DB′=x,则CD=8-x.在Rt△B′DE中,DB′2=DE2+B′E2,即x2=(8-x)2+42,解得x=5,∴BD=5.综上所述,BD的长是2或5.18.答案为:(1)(2)(3).19.解:(1)证明:由折叠知△AEF≌△GEF,△BCE≌△HCE,∵AE=A′E=BC,∠AEF=∠BCE,∴△AEF≌△BCE,∴△GEF≌△HCE,∴EG=CH;(2)∵AF=FG=2,∠FDG=45°,∴FD=2,AD=2+2;∵AF=FG=HE=EB=2,AE=AD=2+2,∴AB=AE+EB=2+2+2=2+22.20.21.1)证明:∵E,F分别是正方形ABCD边BC,CD的中点,∴CF=BE,在△ABE和△BCF中,∴Rt△ABE≌Rt△BCF(SAS),∴∠BAE=∠CBF,又∵∠BAE+∠BEA=90°,∴∠CBF+∠BEA=90°,∴∠BGE=90°,∴AE⊥BF;(2)解:∵将△BCF沿BF折叠,得到△BPF,∴FP=FC,∠PFB=∠BFC,∠FPB=90°,∵CD∥AB,∴∠CFB=∠ABF,∴∠ABF=∠PFB,∴QF=QB,设QF=x,PB=BC=AB=4,CF=PF=2,∴QB=x,PQ=x﹣2,在Rt△BPQ中,∴x2=(x﹣2)2+42,解得:x=5,即QF=5.22.解:(1)∵AB2=AQ2+BQ2=|x﹣x2|2+|y1﹣y2|2=(x1﹣x2)2+(y1﹣y2)2,1∴AB=.故答案为.(2)∵A(1,﹣3),B(﹣2,1),∴AB==5.故答案为5.(3)代数式+的最小值表示在x轴上找一点P(x,0),到A(0,2),B(3,1)的距离之和最小.如图,作A关于x轴的对称点A′,连接BA′与x轴的交点即为所求的点P.此时PA+PB最小,∵A′(0,﹣2),B(3,1),∴PA+PB=PA′+PB=BA′==3.∴代数式+的最小值为3.23.解:(1)由折叠的性质可得,∠BEC=∠B'EC,∠AEN=∠A'EN,∵∠BEB′=110°,∴∠AEA'=180°﹣110°=70°,∴∠BEC=∠B'EC=0.5∠BEB′=55°,∠AEN=∠A'EN=0.5∠AEA'=35°.∴∠BEC+∠AEN=55°+35°=90°;(2)不变.由折叠的性质可得:∠BEC=∠B'EC,∠AEN=∠A'EN,∵∠BEB′=m°,∴∠AEA'=180°﹣m°,可得∠BEC=∠B'EC=0.5∠BEB′=0.5m°,∠AEN=∠A'EN=0.5∠AEA'=0.5(180°﹣m°),∴∠BEC+∠AEN=0.5m°+0.5(180°﹣m°)=90°,故∠BEC+∠AEN的值不变;(3)由折叠的性质可得:∠B'CF=∠B'CE,∠B'CE=∠BCE,∴∠B'CF=∠B'CE=∠BCE=×90°=30°,在Rt△BCE中,∵∠BEC与∠BCE互余,∴∠BEC=90°﹣∠BCE=90°﹣30°=60°,∴∠B'EC=∠BEC=60°,∴∠AEA'=180°﹣∠BEC﹣∠B'EC=180°﹣60°﹣60°=60°,∴∠AEN=0.5∠AEA'=30°,∴∠ANE=90°﹣∠AEN=90°﹣30°=60°,∴∠ANE=∠A'NE=60°24.解:(1)E(6,2.5);(2)E(6,3);(3)M ().第11 页共11 页。
贵州中考数学总复习34——图形的对称(含折叠)

命题点 2 与折叠有关的计算(遵义2019.15,2018.18)
5.(2017黔西南州19题3分)如图,将边长为6 cm的正方形纸片ABCD折叠,使点D落
9
在AB边中点E处,点C落在点Q处,折痕为FH,则线段AF的长是___4___cm.
第5题图
6. (2019遵义15题4分)如图,平行四边形纸片ABCD的边AB,BC的长分别是10 cm和7.5 cm,将其四个角向内对折后,点B与点C重合于点C′,点A与点D重合于 点A′.四条折痕围成一个“信封四边形”EHFG,其顶点分别在平行四边形ABCD 的四条边上,则EF=____1_0___cm.
第9题图
10.(2017黔南州7题4分)如图,在正方形ABCD中,AB=9,点E在CD边上,且DE
=2CE,点P是对角线AC上的一个动点,则PE+PD的最小值是( A )
A. 3 10
B. 10 3
C. 9
D. 9 2
第10题图
贵州其他地市真题精选
11. (2017毕节15题3分)如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,AD平
分∠CAB交BC于D点,E,F分别是AD,AC上的动点,则CE+EF的最小值为( C )
A. 40
B. 15
C. 24
D. 6
3
4
5
第11题图
12. (2017安顺17题4分)如图所示,正方形ABCD的边长为6,△ABE是等边三角形, 点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最 小值为____6____.
作图方法 (1)找出原图形的关键点(各顶点),作出它们关于对称轴(或对称中心)的对称点; (2)根据原图形依次连接各对称点即可
中考数学一轮图形折叠问题专题复习题(有答案)

20XX年中考数学一轮图形折叠问题专题复习题(有答案)6.如图,在矩形ABCD中,AB=8,BC=4,将矩形沿AC折叠,则重叠部分△AFC的面积为()A.12 B.10 C.8 D.67.如图,矩形ABCD中,点E在边AB上,将矩形ABCD 沿直线DE折叠,点A恰好落在边BC的点F处.若AE=5,BF=3,则CD的长是()A.7B.8 C.9 D.108.如图,菱形纸片ABCD中,∠A=60°,折叠菱形纸片ABCD,使点C落在DP(P为AB中点)所在的直线上,得到经过点D的折痕DE.则∠DEC的大小为()A.78° B.75° C.60° D.45°9.如图,将边长为12cm的正方形ABCD折叠,使得点A落在CD边上的点E处,折痕为MN.若CE的长为7cm,则MN的长为()A.10 B.13 C.15 D.1210.如图,将矩形纸片ABCD的四个角向内翻折,恰好拼成一个无缝隙无重叠的四边形EFGH,若EH=12厘米,EF=16厘米,则边AD的长是( )A.12厘米B.16厘米C.20厘米D.28厘米11.如图,在矩形OABC 中,OA=8,OC=4,沿对角线OB 折叠后,点 A 与点 D 重合,OD 与BC交于点E,则点 D 的坐标是()A.(4,8)B.(5,8)C.(,)D.(,)12.将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为()A. B. 2 C. 3 D.13.如图,矩形纸片ABCD中,AD=3cm,点E在BC上,将纸片沿AE折叠,使点B落在AC上的点F处,且∠AEF=∠CEF,则AB的长是( )A.1 cm B.cm C.2 cm D.cm14.如图,在矩形ABCD中,AB=5,BC=7,点E是AD上一个动点,把△BAE沿BE向矩形内部折叠,当点A的对应点A1恰好落在∠BCD的平分线上时,CA1的长为()A.3或4 B.4或3 C.3或4 D.3 或415.如图,在矩形ABCD中,点E、F分别在边AB,BC上,且AE= AB.将矩形沿直线EF折叠,点B恰好落在AD边上的点P处,连接BP交EF于点Q.对于下列结论:①EF=2BE,②PF=2PE;③FQ=4EQ;④△PBF是等边三角形.其中正确的是( )A.①②B.②③C.①③D.①④16.如图,点M、N分别在矩形ABCD边AD、BC上,将矩形ABCD沿MN翻折后点C恰好与点A重合,若此时= ,则△AMD′ 的面积与△AMN的面积的比为( )A.1:3 B.1:4 C.1:6 D.1: 917.图,矩形ABCD中,点E是AD的中点,将△ABE折叠后得到△GBE,延长B G交CD于点F,若CF=1,FD=2,则BC的长为( )A.3B.2C.2D.218.如图,矩形ABCD边AD沿拆痕AE折叠,使点D落在BC上的F处,已知AB=6,△ABF的面积是24,则FC等于().A.2 B.3 C.4 D.519.如图,在菱形纸片ABCD中,∠A=60°,将纸片折叠,点A、D分别落在点A′、D′处,且A′D′经过点B,EF为折痕,当D′F⊥CD 时,的值为()A.B.C.D.20.如图,在矩形纸片ABCD中,AB=3,AD=5.折叠纸片,使点A落在BC边上的A′处,折痕为PQ,当点A′在BC边上移动时,折痕的端点P,Q也随之移动。
轴对称作图折叠剪纸专项练习30题(有答案)ok

轴对称作图折叠剪纸专项练习30题(有答案)ok轴对称作图折叠剪纸专项练习30题(有答案)1.如图,在正方形网格上有一个△DEF.(1)作△DEF关于直线HG的轴对称图形;(2)作△DEF的EF边上的高;(3)若网格上的最小正方形边长为1,求△DEF的面积.2.△ABC在平面直角坐标系中的位置如图所示.(1)作出△ABC关于y轴对称的△A1B1C1,并写出△A1B1C1各顶点的坐标;(2)将△ABC向右平移6个单位,作出平移后的△A2B2C2,并写出△A2B2C2各顶点的坐标;(3)观察△A1B1C1和△A2B2C2,它们是否关于某直线对称?若是,请在图上画出这条对称轴.注:考察学生通过对几何图形做不同变换,作出几何对象的大小,位置,特征的变化情况,理解图形的对称,掌握数形结合思想.3.如图,△ABC中,A(﹣2,3),B(﹣3,1),C(﹣1,2).(1)将△ABC向右平移4个单位长度,画出平移后的△A1B1C1;(2)画出△ABC关于x轴对称的△A2B2C2;(3)将△ABC绕原点O旋转180°,画出旋转后的△A3B3C3;(4)在△A1B1C1,△A2B2C2,△A3B3C3中,△_________与△_________成轴对称,对称轴是_________;△_________与△_________成中心对称,对称中心的坐标是_________.4.已知:如图,△ABC、直线m、点M在网格中如图所示的位置,请按以下要求作图:(1)将△ABC向上平移6个单位得△A1B1C1;第1 页共1 页(2)作出△ABC关于直线m的轴对称图形△A2B2C2;(3)作出△A2B2C2绕点M顺时针旋转90°的图形△A3B3C3.5.△ABC在平面直角坐标系中如图所示,(1)作出△ABC关于x轴对称的图形△A1B1C1;若P(a,b)是△ABC内一点,请用a,b表示出点P关于x轴对称的点P1的坐标;(2)作出△ABC关于原点对称的图形△A2B2C2,写出点C2的坐标.(3)△A2B2C2能否由△A1B1C1通过某种变换而得到?若能,请指出是何种变换.6.在平面直角系中,已知△ABC和△DEF的顶点分别为A(1,0)、B(3,0)、C(2,1)、D(4,3)、E(6,5)、F(4,7).按下列要求画图:(1)画出△ABC以点O为位似中心,在y轴异侧放大2倍后得到的△A1B1C1,并写出点C1的坐标;(2)画出△A1B1C1关于x轴的对称图形△A2B2C2.并写出点C2的坐标;(3)指出△A2B2C2经过哪些变换,可以与△DEF拼成一个正方形.第 2 页共2 页。
【中考专题】2018年 九年级数学中考专题 折叠问题(含答案)

2018年 九年级数学中考专题 折叠问题一、选择题:1.一块直角三角形的纸片,两直角边AC=6cm,BC=8cm ,现将直角边AC 沿直线AD 折叠,使它落在斜边AB 上,且与AE 重合,则CD 等于( )A .5cmB .4cmC .3cmD .2cm2.如图,△ABC 中,∠BAC=90°,AB=3,AC=4,点D 是BC 的中点,将△ABD 沿AD 翻折得到△AED ,连结CE ,则线段CE 的长等于( )A .2B .1.25C .35D .1.43.如图,把△ABC 纸片沿DE 折叠,当点A 落在四边形BCED 的外部时,则∠A 与∠1和∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,你发现的规律是( )A .2∠A=∠1﹣∠2B .3∠A=2(∠1﹣∠2)C .3∠A=2∠1﹣∠2D .∠A=∠1﹣∠24.附图(①)为一张三角形ABC 纸片,P 点在BC 上.今将A 折至P 时,出现折线BD ,其中D 点在AC 上,如图(②)所示.若△ABC 的面积为80,△DBC 的面积为50,则BP 与PC 的长度比为何?( )A .3:2B .5:3C .8:5D .13:85.如图,直角三角形纸片两直角边长分别为6,8,按如图折叠,使A与B重合,折痕为DE,则S:S△BDE等于△BCE ()A.2:5 B.14:25 C.16:25 D.4:216.如图,Rt△ABC中,AB=9,BC=6,∠B=90°,将△ABC折叠,使A点与BC的中点D重合,折痕为MN,则线段BN的长为()A.B.2.5 C.4 D.57.如图,将一个矩形纸片ABCD,沿着BE折叠,使C、D点分别落在点C,D1处.若∠C1BA=50°,则∠ABE的1度数为()A.15°B.20°C.25°D.30°8.如图,折叠矩形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=6cm,则tan∠EAF的值是()A.0.5 B.0.75 C.2 D.59.如图,把长方形纸片ABCD折叠,使其对角顶点C与A重合.若长方形的长BC为8,宽AB为4,则折痕EF的长度为()A.5 B.3C.2D.310.如图,在边长为2的菱形ABCD中,∠B=45°,AE为BC边上的高,将△ABE沿AE所在直线翻折得△AB′E,AB′与CD边交于点F,则B′F的长度为()A.1 B.C.2-D.2﹣211.将一张宽为4cm的长方形纸片(足够长)折叠成如图所示图形,重叠部分是一个三角形,则这个三角形面积的最小值是()A. cm2B.8cm2C. cm2D.16cm212.如图,将一个等腰Rt△ABC对折,使∠A与∠B重合,展开后得折痕CD,再将∠A折叠,使C落在AB上的点F处,展开后,折痕AE交CD于点P,连接PF、EF,下列结论:①tan∠CAE=﹣1;②图中共有4对全等三角形;③若将△PEF沿PF翻折,则点E一定落在AB上;④PC=EC;⑤S四边形DFEP=S△APF.正确的个数是()A.1个B.2个C.3个D.4个二、填空题:13.矩形纸片ABCD中,AD=4cm,AB=10cm,按如图方式折叠,使点B与点D重合,折痕为EF,则DE= cm.14.如图,把等边三角形ABC沿着DE折叠,使点A恰好落在BC边上的点P处,且DP⊥BC,若BP=4 cm,则EC= cm.15.如图,矩形ABCD中,AB=6,BC=8,点E是BC边上一点,连接AE,把∠B沿AE折叠,使点B落在点B′处.当△CEB′为直角三角形时,BE的长为16.如图,矩形ABCD中,AB=1,E、F分别为AD、CD的中点,沿BE将△ABE折叠,若点A恰好落在BF上,则AD= .17.如图,在Rt△ABC纸片中,∠C=90°,AC=6,BC=8,点D在边BC上,以AD为折痕,△ABD折叠得到△AB′D,AB′与边BC交于点E.若△DEB′为直角三角形,则BD的长是 .18.如图所示,现有一张边长为4的正方形纸片ABCD,点P为正方形AD边上的一点(不与点A.点D重合)将正方形纸片折叠,使点B落在P处,点C落在G处,PG交DC于H,折痕为EF,连接BP、BH.现给出以下四个命题(1)∠APB=∠BPH;(2)当点P在边AD上移动时,△PDH的周长不发生变化;(3)∠PBH=450 ; (4)BP=BH.其中正确的命题是.三、解答题:19.如图①,将矩形ABCD沿DE折叠使点A落在点A′处,然后将矩形展平,如图②沿EF折叠使点A落在折痕DE上的点G处,再将矩形ABCD沿CE折叠,此时顶点B恰好落在DE上的点H处.(1)求证:EG=CH;(2)已知AF=2,求AD和AB的长.20.如图,四边形ABCD表示一张矩形纸片,AB=10,AD=8.E是BC上一点,将△ABE沿折痕AE向上翻折,点B恰好落在CD边上的点F处,⊙O内切于四边形ABEF.求:(1)折痕AE的长;(2)⊙O的半径.21.在正方形ABCD中,E、F分别为BC、CD的中点,AE与BF相交于点G.(1)如图1,求证:AE⊥BF;(2)如图2,将△BCF沿BF折叠,得到△BPF,延长FP交BA的延长线于点Q,若AB=4,求QF的值.22.阅读材料,在平面直角坐标系中,已知x轴上两点A(x,0),B(x2,0)的距离记作AB=|x1﹣x2|;若A,B1是平面上任意两点,我们可以通过构造直角三角形来求AB间的距离,如图,过A,B分别向x轴、y轴作垂线AM1、AN1和BM2、BN2,垂足分别是M1、N1、M2、N2,直线AN1交BM2于点Q,在Rt△ABQ中,AQ=|x1﹣x2|,BQ=|y1﹣y2|,∴AB2=AQ2+BQ2=|x1﹣x2|+|y1﹣y2|2=(x1﹣x2)2+(y1﹣y2)2,由此得到平面直角坐标系内任意两点A(x1,y1),B(x2,y2)间的距离公式为:(1)AB= .(2)直接应用平面内两点间距离公式计算点A(1,﹣3),B(﹣2,1)之间的距离为;(3)根据阅读材料并利用平面内两点间的距离公式,求代数式+的最小值.23.如图,长方形纸片ABCD,点E、F分别在边AB、CD上,连接EF,将∠BEF对折,点B落在直线EF上的B′处,得到折痕EC,将点A落在直线EF上的点A′处,得到折痕EN.(1)若∠BEB′=110°,则∠BEC= °,∠AEN= °,∠BEC+∠AEN= °.(2)若∠BEB′=m°,则(1)中∠BEC+∠AEN的值是否改变?请说明你的理由.(3)将∠ECF对折,点E刚好落在F处,且折痕与B′C重合,求∠DNA′.24.如图,已知矩形OABC在坐标系中,A(0,4),C(6,0),直线y=x与AB交于D点,E为BC上一点.(1)如图1,若△OCE沿OE翻折,当C恰好与D点重合时,求此时E点坐标;(2)如图2,若△OCE与BDE相似,求E点坐标;(3)如图,3,已知线段GH开始时在矩形OABC内壁与BC重合(不考虑厚度),M为GH中点,将线段GH 沿矩形内壁滑动,G在BC上滑动,H在CO上滑动,线段GH长度始终保持不变,当G与C点重合时,停止运动.在滑动的过程中,当DM长度最小值时,求此时M点坐标.参考答案1.C2.D;3.A.4.A5.A6.B7.D8.C.9.D.10.A.11.B.12.D.13.答案为:5.8.14.答案为:2+23;15.答案为: 3或616.答案为: .17.答案为:2或5;解析:∵在Rt△ABC纸片中,∠C=90°,AC=6,BC=8,∴AB=10,∵以AD为折痕,△ABD折叠得到△AB′D,∴BD=DB′,AB′=AB=10.如答图①,当∠B′DE=90°时,过点B′作B′F⊥AC的延长线于点F.设BD=DB′=x,则AF=6+x,FB′=8-x.在Rt△AFB′中,由勾股定理,得AB′2=AF2+FB′2,即(6+x)2+(8-x)2=102,解得x1=2,x2=0(舍去),∴BD=2;如答图②,当∠B′ED=90°时,点C与点E重合.∵AB′=10,AC=6,∴B′E=4.设BD=DB′=x,则CD=8-x.在Rt△B′DE中,DB′2=DE2+B′E2,即x2=(8-x)2+42,解得x=5,∴BD=5.综上所述,BD的长是2或5.18.答案为:(1)(2)(3).19.解:(1)证明:由折叠知△AEF≌△GEF,△BCE≌△HCE,∵AE=A′E=BC,∠AEF=∠BCE,∴△AEF≌△BCE,∴△GEF≌△HCE,∴EG=CH;(2)∵AF=FG=2,∠FDG=45°,∴FD=2,AD=2+2;∵AF=FG=HE=EB=2,AE=AD=2+2,∴AB=AE+EB=2+2+2=2+22.20.21.1)证明:∵E,F分别是正方形ABCD边BC,CD的中点,∴CF=BE,在△ABE和△BCF中,∴Rt△ABE≌Rt△BCF(SAS),∴∠BAE=∠CBF,又∵∠BAE+∠BEA=90°,∴∠CBF+∠BEA=90°,∴∠BGE=90°,∴AE⊥BF;(2)解:∵将△BCF沿BF折叠,得到△BPF,∴FP=FC,∠PFB=∠BFC,∠FPB=90°,∵CD∥AB,∴∠CFB=∠ABF,∴∠ABF=∠PFB,∴QF=QB,设QF=x,PB=BC=AB=4,CF=PF=2,∴QB=x,PQ=x﹣2,在Rt△BPQ中,∴x2=(x﹣2)2+42,解得:x=5,即QF=5.22.解:(1)∵AB2=AQ2+BQ2=|x﹣x2|2+|y1﹣y2|2=(x1﹣x2)2+(y1﹣y2)2,1∴AB=.故答案为.(2)∵A(1,﹣3),B(﹣2,1),∴AB==5.故答案为5.(3)代数式+的最小值表示在x轴上找一点P(x,0),到A(0,2),B(3,1)的距离之和最小.如图,作A关于x轴的对称点A′,连接BA′与x轴的交点即为所求的点P.此时PA+PB最小,∵A′(0,﹣2),B(3,1),∴PA+PB=PA′+PB=BA′==3.∴代数式+的最小值为3.23.解:(1)由折叠的性质可得,∠BEC=∠B'EC,∠AEN=∠A'EN,∵∠BEB′=110°,∴∠AEA'=180°﹣110°=70°,∴∠BEC=∠B'EC=0.5∠BEB′=55°,∠AEN=∠A'EN=0.5∠AEA'=35°.∴∠BEC+∠AEN=55°+35°=90°;(2)不变.由折叠的性质可得:∠BEC=∠B'EC,∠AEN=∠A'EN,∵∠BEB′=m°,∴∠AEA'=180°﹣m°,可得∠BEC=∠B'EC=0.5∠BEB′=0.5m°,∠AEN=∠A'EN=0.5∠AEA'=0.5(180°﹣m°),∴∠BEC+∠AEN=0.5m°+0.5(180°﹣m°)=90°,故∠BEC+∠AEN的值不变;(3)由折叠的性质可得:∠B'CF=∠B'CE,∠B'CE=∠BCE,∴∠B'CF=∠B'CE=∠BCE=×90°=30°,在Rt△BCE中,∵∠BEC与∠BCE互余,∴∠BEC=90°﹣∠BCE=90°﹣30°=60°,∴∠B'EC=∠BEC=60°,∴∠AEA'=180°﹣∠BEC﹣∠B'EC=180°﹣60°﹣60°=60°,∴∠AEN=0.5∠AEA'=30°,∴∠ANE=90°﹣∠AEN=90°﹣30°=60°,∴∠ANE=∠A'NE=60°24.解:(1)E(6,2.5);(2)E(6,3);(3)M ().第11 页共11 页。
中考数学专题复习:对称与折叠

中考数学专题复习:对称与折叠基础巩固1.下列图形是轴对称图形而不是中心对称图形的是( )2.如图,在Rt△ABC中,∠BAC=90°,∠B=50°,AD⊥BC,垂足为D,△ADB与△ADB′关于直线AD对称,点B的对称点是点B′,则∠CAB′的度数为( )第2题图A.10°B.20°C.30°D.40°3.剪纸是我国传统的民间艺术.将一张纸片按图1,2的方式沿虚线依次对折后,再沿图3中的虚线裁剪,最后将图4中的纸片打开铺平,所得图案应该是( )第3题图4.在如图所示3×3的正方形网格中,有三个小方格被涂上了阴影,请在图中再选择两个空白的小正方形并涂成阴影,使得图中的阴影部分成为轴对称图形,不同的填涂方法共有( )第4题图A.4种B.5种C.6种D.7种5.如图,在正方形ABCD中,AB=3,点E,F分别在边AB,CD上,∠EFD=60°.若将四边形EBCF沿EF折叠,点B恰好落在AD边上,则BE的长度为( )第5题图A.1 B.2C.3D.26.如图,在▱ABCD中,∠A=50°,AD⊥BD,沿直线DE将△ADE翻折,使点A落在点A′处,A′E交BD于点F,则∠FDE=( )第6题图A.15°B.20°C.25°D.30°7.如图,三角形纸片ABC,点D是BC边上一点,连接AD,把△ABD沿着AD翻折,得到△AED,DE与AC交于点G,连接BE交AD于点F.若DG=GE,AF=3,BF=2,△ADG 的面积为2,则点F到BC的距离为( )第7题图A.55B.255C.455D.4338.如图,D是等边三角形ABC边AB上的一点,且AD∶DB=2∶3,现将△ABC折叠,使点C与D重合,折痕为EF,点E,F分别在AC和BC上,则CE∶CF=( )第8题图A.78B .45C .56D .679.如图,在矩形ABCD 中,AB =2,BC =25 ,E 是BC 的中点,将△ABE 沿直线AE 翻折,点B 落在点F 处,连接CF ,则cos ∠ECF 的值为( )第9题图A .23B .104C .53 D .25510.点M (1,2)关于原点对称的点的坐标为__________.11.如图,在平面直角坐标系xOy 中,已知点C (3,2),△A 1B 1C 1与△ABC 关于直线x =4对称,则点C 的对应点C 1的坐标为__________.第11题图12.如图,矩形ABCD 中,E 为边AB 上一点,将△ADE 沿DE 折叠,使点A 的对应点F 恰好落在边BC 上,连接AF 交DE 于点N ,连接BN .若BF ·AD =15,tan ∠BNF =52,则矩形ABCD 的面积为__________.第12题图13.如图,矩形ABCD中,AD=12,AB=8,E是AB上一点,且EB=3,F是BC上一动点,若将△EBF沿EF对折后,点B落在点P处,则点P到点D的最短距离为__________.第13题图14.用四块大正方形地砖和一块小正方形地砖拼成如图所示的实线图案,每块大正方形地砖面积为a,小正方形地砖面积为b,依次连接四块大正方形地砖的中心得到正方形ABCD.则正方形ABCD的面积为__________.(用含a,b的代数式表示)第14题图15.如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处.求证:B′E=BF.第15题图16.如图,四边形ABCD的对角线AC,BD相交于点O,OA=OC,OB=OD+CD.第16题图(1)如图1,过点A作AE∥DC交BD于点E,求证:AE=BE.(2)如图2,将△ABD 沿AB 翻折得到△ABD ′. ①求证:BD ′∥CD ;②若AD ′∥BC ,求证:CD 2=2OD ·BD .拓展提升1.如图,把某矩形纸片ABCD 沿EF ,GH 折叠(点E ,H 在AD 边上,点F ,G 在BC 边上),使点B 和点C 落在AD 边上同一点P 处,A 点的对称点为A ′,D 点的对称点为D ′,若∠FPG =90°,S △A ′EP =8,S △D ′PH =2,则矩形ABCD 的长为( )第1题图A .65 +10B .610 +52C .35 +10D .310 +522.如图,在平面直角坐标系中,已知A (3,6),B (-2,2),在x 轴上取两点C ,D (点C 在点D 左侧),且始终保持CD =1,线段CD 在x 轴上平移,当AD +BC 的值最小时,点C 的坐标为__________.第2题图3.在矩形ABCD 中,AB =1,BC =a ,点E 在边BC 上,且BE =35 a ,连接AE ,将△ABE沿AE 折叠.若点B 的对应点B ′落在矩形ABCD 的边上,则折痕的长为__________. 4.实践操作如图1,将矩形纸ABCD沿对角线AC翻折,使点B′落在矩形ABCD所在平面内,B′C和AD相交于点E,连接B′D.第4题图解决问题(1)在图1中,①B′D和AC的位置关系为__________;②将△AEC剪下后展开,得到的图形形状是__________.(2)如图2,若图1中的矩形变为平行四边形(AB≠BC),则结论①和结论②是否成立?若成立,请挑选其中的一个结论加以证明;若不成立,请说明理由.拓展应用(3)小红沿对角线折叠一张矩形纸片,发现所得图形是轴对称图形,沿对称轴再次折叠后,得到的仍是轴对称图形,则小红折叠的矩形纸片的长宽之比为__________.参考答案基础巩固10.(-1,-2)11. (5,2)12. 1513. 1014. a+b15.证明:在矩形ABCD中,AD∥BC,∴∠B′EF=∠EFB.根据折叠的性质,可得∠B′FE=∠EFB,BF=B′F,∴∠B′FE=∠B′EF.∴B′E=B′F.∴B′E=BF.16.证明:(1)∵AE∥DC,∴∠AEO=∠CDO,∠EAO=∠DCO.又OA=OC,∴△AOE≌△COD(AAS).∴CD=AE,OD=OE.∵OB=OE+BE,OB=OD+CD,∴BE=CD.∴AE=BE.(2)①如图1,过点A作AG∥CD交BD于点G.图1由(1)可知AG=BG,∴∠ABG=∠BAG.∵将△ABD 沿AB 翻折得到△ABD ′, ∴∠ABD ′=∠ABD . ∴∠ABD ′=∠BAG . ∴BD ′∥AG .又AG ∥CD ,∴BD ′∥CD . ②如图1,延长AG 交BC 于点F . ∵AD ′∥BC ,∴∠D ′AB =∠ABC .由翻折可知∠D ′AB =∠DAB ,∴∠ABC =∠DAB . 由(1)可知AG =BG ,∴∠GAB =∠ABD . ∴∠DAB -∠GAB =∠ABC -∠ABD . ∴∠DAG =∠DBC .∵AG ∥CD ,∴∠AGD =∠BDC . ∴△ADG ∽△BCD . ∴BD AG =CD DG .由(1)知AG =CD ,OD =GO , ∴DG =2OD . ∴CD 2=2OD ·BD . 拓展提升1.D2.(-1,0)3.35或354.解:(1)①B ′D ∥AC ;②菱形.(2)结论①,②都成立. 若选择①,证明如下:∵四边形ABCD 是平行四边形, ∴AD =BC ,AD ∥BC .∴∠DAC =∠ACB . ∵将△ABC 沿AC 翻折至△AB ′C ,∴B ′C =BC ,∠ACB =∠ACB ′.∴B ′C =AD ,∠DAC =∠ACB ′. ∴AE =CE .∴B ′E =DE .∴∠CB ′D =∠ADB ′.∵∠AEC =∠B ′ED ,∠ACB ′=∠CAD ,∴∠ADB ′=∠DAC .∴B′D∥AC.若选择②,证明如下:∵四边形ABCD是平行四边形,∴AD∥BC.∴∠DAC=∠ACB.∵将△ABC沿AC翻折至△AB′C,∴∠ACB′=∠ACB.∴∠DAC=∠ACB′.∴AE=CE.∴△AEC是等腰三角形.∴将△AEC剪下后展开,得到的图形四边相等.∴将△AEC剪下后展开,得到的图形是菱形.(3)1∶1或∶1.。
中考数学试题-2018年中考数学复习同步检测(23)轴对称

2018年中考数学复习同步检测(23)轴对称、中心对称、折叠知识网络一、(1)(2)(3)→→对称轴轴对称图象性质:、、 二、(1)(2)(3)→→中心对称中心对称图象性质:、、 三、⎧⎫⎨⎬⎩⎭性质定理角平分线“集合”语言逆定理 四、⎧⎫⎨⎬⎩⎭性质定理线段垂直平分线“集合”语言逆定理五、→折叠轴对称图象一、选择题1.【18浙江】下列图形中,既是轴对称图形,又是中心对称图形的是 ( )2.【18嘉兴】下列图形中,轴对称图形是( )3.【18温州】下列图形中,既是轴对称图形又是中心对称图形的是( )4.【18丰台】下列多边形中,既是轴对称图形又是中心对称图形的是( ) A. 平行四边形 B. 正方形 C. 等腰梯形 D. 等边三角形5.【18北京】下列图形中,不是中心对称图形的是( )A. 圆B. 菱形C. 矩形D. 等边三角形 6.【18深圳】图所列图形中是中心对称图形的为()(D)x(B)(C)A B C D7.【18河北】等边三角形、正方形、菱形和等腰梯形这四个图形中,是中心对称图形的有( ) A .1个 B .2个 C .3个 D .4个 8.【18常德】在下列图形中,既是中心对称图形又是轴对称图形的是 ( )A .等腰三角形B .圆C .梯形D .平行四边形9.【18南平】如图,将一块边长为12的正方形纸片ABCD 的顶点A 折叠至DC 边上的点E ,使DE=5,这痕为PQ ,则PQ 的长为( )A.12B.13C.14D.1510.【18宿迁】如图,将一个边长分别为4、8的长方形纸片ABCD 折叠,使C 点与A 点重合,则折痕EF的长是( )AB. CD.11.【18锦州】一张正方形纸片经过两次对折,并在如图位置上剪去一个小正方形,打开后是( )12.【18泰州】用折纸的方法,可以直接剪出一个正五边形(如下图).方法是:拿一张长方形纸对折,折痕为AB ,以AB 的中点O 为顶点将平角五等份,并沿五等份的线折叠,再沿CD 剪开,使展开后的图形为正五边形,则∠OCD 等于( )A .118°B .90°C .72°D .60°13.【18泸州】下列图形中,是中心对称图形的是( )A .等边三角形B .平行四边形C .梯形D .正五边形FEDCBA第10题图DOA .B .C .D . 14.【18包头】下列图形中对称轴最多的图形是( )15.【18太原】下列图形中,只有两条对称轴的是( )A .正六边形B .矩形C .等腰梯形D .圆16.【18黄石】下列图案中,既是轴对称图形,又是中心对称图形的是( )17.【18梅山】下列图形中,既不是中心对称图形,又不是轴对称图形的是( )A.射线B.两条相交直线C.正五边形D.把一张纸对折后任意剪成一个形状,把它打开所得到的图形18.【18重庆课改】下列图形中,既是轴对称图形,又是中心对称图形的是( )A B C D二、填空题1.【18丽水】在平行四边形、矩形、菱形、正方形、等腰梯形的五种图形中,既是轴对称、又是中心对称的图形是 .2.【18漳州】写出一个你所学过的既是轴对称又是中心对称图形 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、(2017玉林)五星红旗上的每一个五角星(A.是轴对称图形,但不是中心对称图形B.是屮心对称图形,但不是轴对称图形C.既是轴对称图形,又是中心对称图形D.既不是轴对称图形,也不是中心对称图形【考点】R5:中心对称图形;P3:轴对称图形.【分析】根据轴对称与中心对称图形的性质即可得出结论.【解答】解:・・•五星红旗上的五角星是等腰三角形,・••五星红旗上的每-个五角星是轴对称图形,但不是中心对称图形. 故选A.2、(2017无锡)下列图形中,是中心对称图形的是()【考点】R5:中心对称图形.【分析】根据中心对称图形的定义逐个判断即可.【解答】解:A、不是屮心对称图形,故本选项不符合题意;B、不是中心对称图形,故本选项不符合题意;C、是中心对称图形,故木选项符合题意;D、不是中心对称图形,故本选项不符合题意;故选C.3、(2017江西)下列图形中,是轴对称图形的是(【考点】P3:轴对称图形.【分析】根据轴对称图形的概念求解.【解答】解:A 、不是轴对称图形,故A 不符合题意;B 、 不是轴对称图形,故B 不符合题意;C 、 是轴对称图形,故C 符合题意;D 、 不是轴对称图形,故D 不符合题意;故选:C.4、(2017泰州)把卜列英文字母看成图形,既是轴对称图形又是中心对称图形的 【考点】R5:中心对称图形;P3:轴对称图形.【分析】根据轴对称图形和中心对称图形的概念对各选项分析判断即可得解.【解答】解:A 、是轴对称图形,不是中心对称图形,故木选项错误;B 、 既不是轴对称图形,又不是中心对称图形,故本选项错误;C 、 既是轴对称图形又是中心对称图形,故本选项正确;A. E B .F c.Hn.S)D、不是轴对称图形,是屮心对称图形,故本选项错误. 故选C.【点评】木题考查了中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,旋转180度后两部分重合.5、下列图形屮既是屮心对称图形又是轴对称图形的有儿个(B )正六边形A. B. C. D.6.(2016宜昌)如图,若要添加一条线段,使之既是轴对称图形又是中心对称图形,.正确【考点】中心对称图形;轴对称图形.【分析】根据轴对称图形与中心对称图形的概念求解.【解答】解:A、是轴对称图形,也是中心对称图形;B、不是轴对称图形,也不是屮心对称图形;C、不是轴对称图形,也不是屮心对称图形;D、是轴对称图形,不是中心对称图形.故选A.【点评】本题考查了中心对称图形与轴对称图形的概念.轴对称图形的关键是寻找对称轴, 图形两部分折叠后可重合,中心对称图形的关键是要寻找对称中心,旋转180度后两部分重合.7、(2016义乌)我国传统建筑中,窗框(如图1)的图案玲珑剔透、千变万化,窗框一部分 如图2,它是一个轴对称图形,其对称轴有( )A. 1条B. 2条C. 3条D. 4条【考点】轴对称图形.【分析】直接利用轴对称图形的定义分析得出答案.【解答】解:如图所示: 其对称轴有2条.故选:B.【点评】此题主要考查了轴对称图形的定义,正确把握定义是解题关键. 8、(2017枣庄)如图,把正方形纸片ABCD 沿对边中点所在的直线对折后展开, 折痕为MN,再过点B 折叠纸片,使点A 落在MN 上的点F 处,折痕为BE.若 AB 的长为2,则FM 的长为( )【考点】PB :翻折变换(折叠问题).【分析】根据翻折不变性,AB=FB=2, BM=1,在RtABFM 屮,可利用勾股定 理求出FM 的值.【解答】解「・•四边形ABCD 为正方形,AB=2,过点B 折叠纸片,使点A 落 在MN 上的点F 处,Z.FB=AB=2, BM=1,则在RtABMF 中,FM=^BF 2-BM2 =^22-12 二翻, 故选:B. OS}— —图2 图29、(2016南充)如图,对折矩形纸片ABCD,使AB 与DC 重合得到折痕EF,将纸 片展平;再一次折叠,使点D 落到EF 上点G 处,并使折痕经过点A,展平纸片 后ZDAG 的大小为( )【分析】直接利用翻折变换的性质以及直角三角形的性质得出Z2=Z4,再利用平行线的性 质得出Z1=Z2=Z3,进而得出答案.【解答】解:如图所示:由题意可得:Z1=Z2, AN=MN, ZMGA=90°,NG=-AM,故 AN 二NG, 2则 Z2=Z4,・・・EF 〃AB, AZ4=Z3,.\Z1=Z2=Z3=-x90°=30°, 3A ZDAG=60°.故选:C.【点评】此题主要考查了翻折变换的性质以及平行线的性质,正确得出Z2=Z4是解题关键. 10、如图,把菱形ABCD 沿AH 折叠,B 落在BC 边上的点E 处.若ZBAE=40°, 则ZEDC 的大小为( )A. 10。
B. 15。
C ・ 18。
D ・ 20°【考点】翻折变换(折叠问题);菱形的性质.折叠问题【分析】根据翻折变换的性质可得AB=AE,然后根据等腰三角形两底角相等求 岀ZB=ZAEB=70°,根据菱形的四条边都相等可得AB=AD,菱形的对角相等求 出ZADC,再求出ZDAE,然后根据等腰三角形两底角相等求出ZADE,然后根 据Z EDC= Z ADC-Z ADE 计算即可得解.【解答】解:・・•菱形ABCD 沿AH 折叠,B 落在BC 边上的点E 处,・•・ AB=AE,•・・ ZBAE=40°,・•・ ZB=Z AEB=- ( 180°-40°) =70°, 2在菱形 ABCD 中,AB=AD, ZADC=ZB=70°,AD//BC,・・・ ZDAE=ZAEB=70°,V AB=AE, AB=AD,/• AE=AD,,."DE=*(18O“DAE)=*(I8OW55。
,••• ZEDC=ZADC -ZADE=70°-55°=15°.故选:B.B. 45°C. 60°D. 75°A. 30°11、如图,在RtAABC 中,ZACB=90°, AC=2 ^3 , BC=6,动点P、Q 分别在边AB, BC ±,则则CP+PQ的最小值为()A. 3A/3 B・ 3+型一C. 2A/3 D. 2+^32【考点】轴对称■最短路线问题;勾股定理.利用轴对称变换解决最短问题【分析】作C关于AB的对称点C\过C,作C,Q丄BC于Q,交AB于P,则CQ=CP+PQ的最小值,解直角三角形得到AB=4V3 ,根据三角形的面积公式得到CC"等=2x鲁= 6=6,根据相似三角形的性质即可得到结论.【解答】解:作C关于AB的对称点CT,过C,作C7Q丄BC于Q,交AB于P, 则C'Q=CP+PQ的最小值,•••在RtAABC 屮,ZACB=90°, AC=2 馆,A AB=4 V3 ,•••cs 竺空= 2X^1斗, AB4^3・.・ ZB=ZC\ ZC z QC=ZACB=90o,・•・△CC'Qs/XBAC,・・・竺=空,即斗空AB BC 4V3 6・・・CQ=3 VL故选:A.12、(2017天水)如图所示,在矩形ABCD中,ZDAO65。
,点E是CD上一点, BE交AC于点F,将ABCE沿BE折叠,点C恰好落在AB边上的点C处,则【考点】PB:翻折变换(折叠问题);LB:矩形的性质.【分析】根据直角三角形两锐角互余求出ZACD,再根据翻折变换的性质判断出四边形BCEC是正方形,根据正方形的性质可得ZBEO45。
,然后根据三角形的一个外角等于与它不相邻的两个内角的和求出ZBFC,再根据翻折变换的性质可得ZBFC^ZBFC,然后根据平角等于180。
列式计算即可得解.【解答】解:・・•矩形ABCD, ZDAC=65°,・・・ ZACD=90° - ZDAC=90° - 65°=25°,V ABCE沿BE折叠,点C恰好落在AB边上的点C处,・・・四边形BCEC是正方形,・・・ZBEC=45°,由三角形的外角性质,ZBFC=ZBEC+ZACD=45°+25°=70°,由翻折的性质得,ZBFC』ZBFC=70。
,・・・ ZAFC'=180。
一ZBFC ・ ZBFC'=180。
・ 70°・ 70°=40°.故答案为:40。
・13、如图.将正方形纸片ABCD 折叠,使边AB 、CB 均落在对角线BD ±,得折【考点】翻折变换(折叠问题).折叠问题试题讲解&……・……B【分析】首先根据正方形的性质可得Z l + Z2+Z3+Z4=ZABC=90°,再根据折叠可得Z1 = Z2=—ZABD, Z3 = Z4=— 2 2ZDBC,进而可得 Z2+Z3=45°,即 ZEBF=45°.【解答】解:・・•四边形ABCD 是正方形,・•・ ZABC=90°,根据折叠可得Z1 = Z2=—ZABD, Z3 = Z4=—ZDBC, 2 2・.・ Z l + Z2+Z3 + Z4=ZABC=90°,・•・ Z2+Z3=45。
,即 ZEBF=45°,故答案为:45°.【点评】此题主要考查了图形的翻折变换,关键是找准图形翻折后,哪些角是相 14、如图,△ ABC 屮,ZB=40°, ZC=30°,点 D 为边 BC ±一点,将厶ADC 沿 直线AD 折叠后,点C 落到点E 处,若DE 〃AB,则ZADC 的度数为110。
.【考点】三角形内角和定理;平行线的性质.三角形内角和定理【分析】根据三角形的内角和得到ZBAO110。
,由折叠的性质得到ZE=ZC=30°, ZEAD=ZCAD,根据平行线的性质得到ZBAE=ZE=30°,根据三角形的内角和即可得到结论.【解答】解:V ZB=40°, ZC=30°,・•・ ZBAC=110°,由折叠的性质得,ZE=ZC=30°, ZEA D=ZC AD,•・・DE 〃 AB,・•・ ZBAE=ZE=30°,・•・ ZCAD=40°,・•・ ZADC=180°-ZCAD-ZC=l 10°,故答案为:110。
.痕BE 、BF,则ZEBF 的大小为45。
. D【点评】本题考查了三角形的内角和,折叠的性质,平行线的性质,熟练掌握折叠的性质是解题的关键.15、如图,菱形ABCD 的对角线相交于点O, AC=2, BD=2 A /3 ,将菱形按如图 方式折叠,使点B 与点0重合,折痕为EF,则五边形AEFCD 的周长为7.【考点】翻折变换(折叠问题);菱形的性质. 折叠问题【分析】根据菱形的性质得到ZAB0=ZCB0, AC 丄BD,得到ZABC=60°,由折叠的性质得到EF 丄BO, 0E=BE, ZBEF=Z0EF,推出△ BEF 是等边三角形,得到ZBEF=60°,得到AAEO 是等边三角形,推出EF 是厶ABC 的中位线,求得EF=-AC=1, AE=OE=1,同理 CF=OF=1,于是得到结论. 2【解答】解:•・•四边形ABCD 是菱形,AC=2, BD=2A /3 ,・・・ ZABO=ZCBO, AC 丄 BD,V AO=1, B0=A /3 ,A ZABO=30°, AB=2,・•・ ZABC=60°,山折叠的F 生质得,EF 丄BO, OE=BE, ZBEF=ZOEF,A BE=BF, EF# AC,•••△BEF 是等边三角形,・•・ ZBEF=60°,・•・ ZOEF=60°,・•・ ZAEO=60°,•••△AEO 是等边三角形,・•・ AE=OE,・•・ BE=AE,・•・EF 是厶ABC 的中位线,1A EF=-AC=1, AE=OE=1, 2同理 CF=OF=1,・•・五边形AEFCD 的周长为= l + l + l+2+2=7.故答案为:7.16、如图,在平行四边形ABCD 屮,E 为AB 边上的点,BE=BC,将厶ADE 沿DE 翻折,点A 的对应点F 恰好落在CE ±・ZADF=84°,则ZBEC=32°/.tanZABO= — BO V3 3【考点】翻折变换(折叠问题);等腰三角形的性质;平行四边形的性质. 折叠问题试题讲解【分析】由折叠的性质:ZDFE=ZA,设ZBEC=x,由等腰三角形的性质得出ZBCE=ZBEC=x,与平行四边形的性质得出ZA=ZBCD, AB〃CD,得出ZDCF=ZBEC=x, ZDFE= ZA= ZBCD=2x,在四边形ADFE中,由四边形内角和定理得出方程,解方程即可.【解答】解:由折叠的性质可得:ZDFE=ZA,设ZBEC=x,VBE=BC,・•・ ZBCE=ZBEC=x,・・・四边形ABCD是平行四边形,・・・ ZA=ZBCD, AB〃CD,・・・ ZDCF=ZBEC=x,・・・ ZDFE=ZA=ZBCD=2x,在四边形ADFE 中,ZA+Z ADF+ZDFE+ZAEF=360°,・・・ 2x+84°+2x+180°-x=360°,解得:x=32°,・・・ZBEC=32°;故答案为:32°.【点评】此题考查了平行四边形的性质、折叠的性质、等腰三角形的性质以及四边形内角和定理.熟练掌握平行四边形的性质和折叠的性质,由四边形内角和定理得出方程是解决问题的关键.17、(237・滨州)如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在AB 边上的E处,EQ与BC相交于点F,若AD=8, AB=6, AE=4,则AEBF周长的大小为8【考点】翻折变换(折叠问题);矩形的性质. 》折叠问题~【分析】设AH=a,贝IJ DH=AD-AH=8-a,通过勾股定理即可求出a值,再根据同角的余角互补可得出ZBFE=ZAEH,从而得出厶EBF^ AHAE,根据相似三角形的周长比等于对应比即可求出结论.【解答】解:设AH=a,贝IJ DHH=8・a,在RtAAEH 中,ZEAH=90°, AE=4, AH=a, EH=DH=8-a,A EH2=AE2+AH2,即(8・a)2=42+a2,解得:a=3.V ZBFE+ZBEF=90°, Z BEF+Z AEH=90°,・•・ ZBFE=ZAEH.又J ZEAH=ZFBE=90°,・•・ ZXEBFsAHAE,.C_ BE _ AB — AE _ 2••石;=乔=AH•・•C AHAE=AE+EH+AH=AE+AD=12,2故答案为:8.【点评】本题考查了翻折变换、矩形的性质、勾股定理以及相似三角形的判定及性质,解题的关键是找出△ EBF-AHAE.本题属于屮档题,难度不大,解决该题型题日时,通过勾股定理求出三角形的边长,再根据相似三角形的性质找出周长间的比例是关键.18、如图,将一张长方形纸片的一角斜折过去,顶点D落在D处,AB为折痕, 再将BE翻折过去与BD,重合,E落在CF上E,处:(1)AB与BQ的位置关系;戈(2)当折角ZABD=30°时,求ZCE Z C/的度数.【考点】翻折变换(折叠问题);平行线的性质.隐形的翅膀一一折叠解题实例【分析】(1)根据折叠的性质,得岀ZABD,+ ZE,BQ=- ZDBE*+- ZEBE'=-2 2 2ZDBE=90°,即可得到AB与BQ的位置关系;(2)根据折叠的性质得出ZDBEJ60。
