现代时间序列分析模型讲义.pptx
合集下载
时间序列分析模型课件(PPT108张)

确定性时序分析的目的
• 克服其它因素的影响,单纯测度出某一个 确定性因素对序列的影响 • 推断出各种确定性因素彼此之间的相互作 用关系及它们对序列的综合影响
4-3-2 时间序列趋势分析
• 目的
–有些时间序列具有非常显著的趋势,我们分析 的目的就是要找到序列中的这种趋势,并利用 这种趋势对序列的发展作出合理的预测
随机性变化分析: AR、MA、ARMA模型
Cramer分解定理(1961)
• 任何一个时间序列 { x t }都可以分解为两部分的叠 加:其中一部分是由多项式决定的确定性趋势成 分,另一部分是平稳的零均值误差成分,即
x t t t
d j0
jt j
(B)at
随机性影响
确定性影响
对两个分解定理的理解
(2)季节性周期变化 受季节更替等因素影响,序列依一固 定周期规则性的变化,又称商业循环。 采用的方法:季节指数; (3)循环变化 周期不固定的波动变化。
(4)随机性变化
由许多不确定因素引起的序列变化。 随机性变化分析: AR、MA、ARMA模型
确定性变化分析 时间序列分析
趋势变化分析 周期变化分析 循环变化分析
(1 )
0 1 , 2 j
j0
2 ~ WN ( 0 , (2) t )
( V , ) 0 , t s (3 ) E t s
确定性序列与随机序列的定义
• 对任意序列 而言,令 序列值作线性回归 关于q期之前的
2 ( t ) q 其中{ t } 为回归残差序列, Var
参数估计方法
线性最小二乘估计
Tt ab
t
a ln a b ln b
b t T t a
《时间序列模型 》课件

《时间序列模型》ppt 课件
目录
Contents
• 时间序列模型概述 • 时间序列模型的基础 • 时间序列模型的建立 • 时间序列模型的预测 • 时间序列模型的应用 • 时间序列模型的未来发展
01 时间序列模型概述
时间序列的定义
01 时间序列是指按照时间顺序排列的一系列观测值 。
02 时间序列数据可以是数值型、分类型或混合型。 03 时间序列数据可以用于描述和预测时间变化的现
详细描述
通过分析历史经济数据的时间序列特性,时间序列模型能够预 测未来经济走势,为政策制定者和企业决策者提供重要参考。
举例说明
例如,利用ARIMA模型分析国内生产总值(GDP)的时间 序列数据,可以预测未来一段时间的GDP增长趋势。
股票预测
01
总结词
时间序列模型在股票市场中具有实际应用价值。
02 03
SARIMA、VAR等。
识别模型阶数
02
确定模型的参数,如自回归阶数、差分阶数和移动平均阶数。
考虑季节性和趋势性
03
如果时间序列数据存在季节性和趋势性,需要在模型中加以考
虑。
参数估计
01
使用最小二乘法或最大似然法等统计方法估计模型 的参数。
02
考虑使用软件包或编程语言进行计算,如Python的 statsmodels库或R语言的forecast包。
象。
时间序列的特点
时序性
时间序列数据是按照时间顺序排列的,具有 时间上的连续性。
趋势性
时间序列数据通常具有一定的趋势,如递增 、递减或周期性变化。
季节性
一些时间序列数据呈现季节性变化,如年度 、季度或月度的变化规律。
不确定性
时间序列数据受到多种因素的影响,具有不 确定性,难以精确预测。
目录
Contents
• 时间序列模型概述 • 时间序列模型的基础 • 时间序列模型的建立 • 时间序列模型的预测 • 时间序列模型的应用 • 时间序列模型的未来发展
01 时间序列模型概述
时间序列的定义
01 时间序列是指按照时间顺序排列的一系列观测值 。
02 时间序列数据可以是数值型、分类型或混合型。 03 时间序列数据可以用于描述和预测时间变化的现
详细描述
通过分析历史经济数据的时间序列特性,时间序列模型能够预 测未来经济走势,为政策制定者和企业决策者提供重要参考。
举例说明
例如,利用ARIMA模型分析国内生产总值(GDP)的时间 序列数据,可以预测未来一段时间的GDP增长趋势。
股票预测
01
总结词
时间序列模型在股票市场中具有实际应用价值。
02 03
SARIMA、VAR等。
识别模型阶数
02
确定模型的参数,如自回归阶数、差分阶数和移动平均阶数。
考虑季节性和趋势性
03
如果时间序列数据存在季节性和趋势性,需要在模型中加以考
虑。
参数估计
01
使用最小二乘法或最大似然法等统计方法估计模型 的参数。
02
考虑使用软件包或编程语言进行计算,如Python的 statsmodels库或R语言的forecast包。
象。
时间序列的特点
时序性
时间序列数据是按照时间顺序排列的,具有 时间上的连续性。
趋势性
时间序列数据通常具有一定的趋势,如递增 、递减或周期性变化。
季节性
一些时间序列数据呈现季节性变化,如年度 、季度或月度的变化规律。
不确定性
时间序列数据受到多种因素的影响,具有不 确定性,难以精确预测。
现代时间序列分析模型

PPT文档演模板
现代时间序列分析模型
ADF检验在Eviews中的实现—△GDPP
PPT文档演模板
现代时间序列分析模型
ADF检验在Eviews中的实现—△GDPP
•从△GDPP(-1)的 参数值看,其t统 计量的值大于临界 值(单尾),不能 拒绝存在单位根的 零假设。同时,由 于时间项项T的t统 计量也小于AFD 分布表中的临界值 (双尾),因此不 能拒绝不存在趋势 项的零假设。需进 一步检验模型2 。 在1%置信度下。
1、问题的提出
• 经典回归模型(classical regression model)是建立在 平稳数据变量基础上的,对于非平稳变量,不能使用经典 回归模型,否则会出现虚假回归等诸多问题。
PPT文档演模板
现代时间序列分析模型
• ADF检验模型
•零假设 H0:=0 备择假设 H1:<0
PPT文档演模板
•模型 1 •模型2 •模型3
现代时间序列分析模型
• 检验过程
–实际检验时从模型3开始,然后模型2、模型1。 –何时检验拒绝零假设,即原序列不存在单位根,为
平稳序列,何时停止检验。 –否则,就要继续检验,直到检验完模型1为止。
PPT文档演模板
现代时间序列分析模型
ADF检验在Eviews中的实现—GDPP
PPT文档演模板
•从GDPP(-1) 的参数值看, 其t统计量的 值大于临界值 (单尾),不 能拒绝存在单 位根的零假设。 同时,由于常 数项的t统计 量也小于ADF 分布表中的临 界值(双尾), 因此不能拒绝 不存在趋势项 的零假设。需 进一步检验模 型1。
– 只要其中有一个模型的检验结果拒绝了零假设,就 可以认为时间序列是平稳的;
时间序列分析课件讲义

7
3.5E+09 3.0E+09 2.5E+09 2.0E+09 1.5E+09 1.0E+09
5.0E+08 99:01 99:07 00:01 00:07 01:01 01:07 02:01 02:07
Y
8
单变量时间序列分析
趋势模型
确定型趋势模型
平滑模型 季节模型
水平模型
加法模型
9
乘法模型
ARMA模型 ARIMA模型 (G)ARCH类模型
42
(2)ADF检验 DF检验只对存在一阶自相关的序列适用。 ADF检验 适用于存在高阶滞后相关的序列。 y = y t 1 + t
表述为
y t = y t 1 + t
t
存在高阶滞后相关的序列,经过处理可以表述为 y t = y t 1 + 1yt 1+ 2yt 2 + ....... + p1yt p1 + t 上式中,检验假设为
34
特别地,若 其中,{ t }为独立同分布,且E( t ) = 0,
D( t )
2 = <
yt= y t 1+ t
t = 1,2,......
,则{
(random waik process) 。可以看出,随机游动过程是 单位根过程的一个特例。
yt }为一随机游动过程
(2) 季节差分
3. 随机性
23
(四)ARMA模型及其改进 1. 自回归模型 AR(p) 模型的一般形式
( B) yt
=
et
AR (p) 序列的自相关和偏自相关 rk :拖尾性 k :截尾性
3.5E+09 3.0E+09 2.5E+09 2.0E+09 1.5E+09 1.0E+09
5.0E+08 99:01 99:07 00:01 00:07 01:01 01:07 02:01 02:07
Y
8
单变量时间序列分析
趋势模型
确定型趋势模型
平滑模型 季节模型
水平模型
加法模型
9
乘法模型
ARMA模型 ARIMA模型 (G)ARCH类模型
42
(2)ADF检验 DF检验只对存在一阶自相关的序列适用。 ADF检验 适用于存在高阶滞后相关的序列。 y = y t 1 + t
表述为
y t = y t 1 + t
t
存在高阶滞后相关的序列,经过处理可以表述为 y t = y t 1 + 1yt 1+ 2yt 2 + ....... + p1yt p1 + t 上式中,检验假设为
34
特别地,若 其中,{ t }为独立同分布,且E( t ) = 0,
D( t )
2 = <
yt= y t 1+ t
t = 1,2,......
,则{
(random waik process) 。可以看出,随机游动过程是 单位根过程的一个特例。
yt }为一随机游动过程
(2) 季节差分
3. 随机性
23
(四)ARMA模型及其改进 1. 自回归模型 AR(p) 模型的一般形式
( B) yt
=
et
AR (p) 序列的自相关和偏自相关 rk :拖尾性 k :截尾性
时间序列分析PPT授课课件

2.3 181 323.625 5.1 324 432.125 7.3 390 525.500
2.4 753 341.750 5.2 224 426.000 7.4 978 542.750
3.1 269 357.875 5.3 284 417.000 8.1 483
20232./23/23 214 374.875 5.4 822 427.000 8.2 320
2.乘法模型(时间序列的变化在每周期有与趋 势相同的比例时适用)
假定四种变动因素之间存在着交互作用 y=T×S × C × R
同样可简化为: y=T×S × R y=T×S
2022/3/23
5
第二节 长期趋势的测定
一.数学模型法
设时间序列的数据为(ti,yi)
设直线趋势方程为:
yt a bt
1.4 733 283.699 2.584 3.4 860 363.819 2.364
2.1 224 293.714 0.763 4.1 345 373.834 0.923
2.2 114 303.729 0.375 4.2 203 383.849 0.529
2.3 181 313.744 0.577 4.3 233 393.864 0.592
(2)求周期每一点的算术平均数(或几何平均数)得 到一个周期的季节因子
(3)对季节因子进行修正
若为季度数据,则S1+S2+S3+S4=4;
若为月度数据,则S1+S2+ …+S12=12。
2022/3/23
19
第三节 季节变动的测定
(资料见例1)
年.
季 度
销售 额Y
趋势值T
季节因子 Y/T
时间序列分析课件.pptx
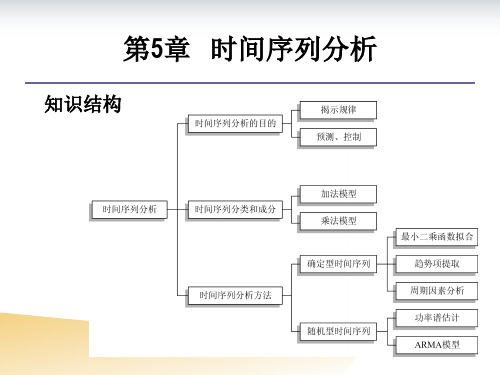
第5章 时间序列分析
知识结构
第5章 时间序列分析
What is time series analysis?
Why to do ?
How to do?
日行迹
第5章 时间序列分析
时间序列
➢ 时间序列的概念 ➢ 时间序列的表示 ➢ 时间序列分析 ➢ 时间序列的分类 ➢ 时间序列的组合成分
时间序列分析方法
时间序列分析方法
时间序列分析的一般步骤: (1) 序列的预处理:如果原始序列为非等间隔序列,通常采用 曲线拟合及等距化重采样得到等距序列。 (2) 描述性时序分析:通过直观的数据比较或绘图观测,寻找 序列中蕴含的发展规律,往往可直观地判断序列是否具有趋势 项、周期变化等特性。 (3) 统计时序分析:计算时间序列的各种统计量,如均值,方 差,正态性检验等。利用统计特性剔除不符合统计规律的异常 样本。 (4) 判断时间序列的组合成分,对不同的成分采用不同的分析 方法。 (5) 利用不同成分的模型进行预测后叠加,得到最终的时间序 列预测值。
时间序列可能是应用最普遍的数据表现形式和数据存储格式。 在生物医学领域也存在着大量的时间序列,
人体从清晨到深夜的体温记录 人体餐后血糖浓度的变化 不同睡眠阶段的脑电波形等都是时间序列 。。。。。。
绝大多数情况下时间序列被看作为随机序列。
时间序列
时间序列的表示
X {x(T ), x(2T ),, x(kT )} {x[n]}
时间序列
时间序列分析
时间序列分析的实现是通过对观察值序列的性质进行推断,即 通过对历史观察值的分析预测而得出未来观察值的预测值。
cool! What will be next?
汽车发展的时间序列
时间序列
时间序列分析 时间序列分析的目的主要在于: (1) 描述事物在过去时间的状态。 (2) 分析事物发展变化的规律。 (3) 对事物的发展变化趋势进行预测或施加控制。
知识结构
第5章 时间序列分析
What is time series analysis?
Why to do ?
How to do?
日行迹
第5章 时间序列分析
时间序列
➢ 时间序列的概念 ➢ 时间序列的表示 ➢ 时间序列分析 ➢ 时间序列的分类 ➢ 时间序列的组合成分
时间序列分析方法
时间序列分析方法
时间序列分析的一般步骤: (1) 序列的预处理:如果原始序列为非等间隔序列,通常采用 曲线拟合及等距化重采样得到等距序列。 (2) 描述性时序分析:通过直观的数据比较或绘图观测,寻找 序列中蕴含的发展规律,往往可直观地判断序列是否具有趋势 项、周期变化等特性。 (3) 统计时序分析:计算时间序列的各种统计量,如均值,方 差,正态性检验等。利用统计特性剔除不符合统计规律的异常 样本。 (4) 判断时间序列的组合成分,对不同的成分采用不同的分析 方法。 (5) 利用不同成分的模型进行预测后叠加,得到最终的时间序 列预测值。
时间序列可能是应用最普遍的数据表现形式和数据存储格式。 在生物医学领域也存在着大量的时间序列,
人体从清晨到深夜的体温记录 人体餐后血糖浓度的变化 不同睡眠阶段的脑电波形等都是时间序列 。。。。。。
绝大多数情况下时间序列被看作为随机序列。
时间序列
时间序列的表示
X {x(T ), x(2T ),, x(kT )} {x[n]}
时间序列
时间序列分析
时间序列分析的实现是通过对观察值序列的性质进行推断,即 通过对历史观察值的分析预测而得出未来观察值的预测值。
cool! What will be next?
汽车发展的时间序列
时间序列
时间序列分析 时间序列分析的目的主要在于: (1) 描述事物在过去时间的状态。 (2) 分析事物发展变化的规律。 (3) 对事物的发展变化趋势进行预测或施加控制。
c14时间序列分析入门.pptx

tN
作用:消除干扰,显示序列的趋势性变化;并通 过加权因子的选取,增加新数据的权重,使趋势 预测更准确
(3) 二次滑动平均模型
yˆˆt
yˆt
yˆt1 N
yˆtN 1
tN
对经过一次滑动平均产生的序列再进行滑动平均
(4) 指数平滑模型
yˆt yˆt1 ( yt1 yˆt1) yˆt yt1 (1 ) yˆt1
结论: 1 时,一阶自回归序列渐进平稳
③ AR(p)的自相关函数
• 自协方差函数
rk E(xt xtk )
Ext (1xtk1 2 xtk2 p xtk p tk ) Ext1xtk1 Ext2 xtk2 Ext xp tk p 1 rk1 2rk2 prk p
两边同除以r0 • 自相关函数
k
rk r0
1k1 2 k2 p k p
AR(p)的自相关函数
k
rk r0
1k1 2 k2
p k p
k k , 0 1
耶尔-瓦克尔(Yule-Walker)方程
1 1 2 1 p p1 2 11 2 p p2
p 1 p1 2 p2 p
2)
Varxt
2 (与t无关的有限常数) x
3) 对任意整数t和k, r t,t+k只和k有关rt,tk rk
• 随机序列的特征量随时间而变化,称为非平 稳序列
xt t
xt t
平稳序列的特性
• 方差
rt ,t
r0
E[( xt
)
2
]
2 x
• 自相关函数:
k
rk
2 x
rk r0
0 1, k k , k 1
xt t t1 2t2 3t3
时间序列分析课程.pptx

(3)经济内容应当一致。对于指标名称相同,而前 后时期的经济内容不一致的指标也需进行调整。
(4)计算方法、计算价格和计算单位要一致。
描述性时序分析
• 通过直观的数据比较或绘图观测,寻 找序列中蕴含的发展规律,这种分析 方法就称为描述性时序分析
• 描述性时序分析方法具有操作简单、 直观有效的特点,它通常是人们进行 统计时序分析的第一步。
描述性时序分析案例
• 例1 德国业余天文学家施瓦尔发现太阳黑 子的活动具有11年左右的周期
例2 1964年——1999年中国纱年产量序列
例3 1962年1月——1975年12月平均每头奶 牛月产奶量序列
例4 1949年——1998年北京市每年最高气温序列
二、时间序列的分类
绝对数序列
派生
时期序列 时点序列
反映现象发展水平的指标数值
140 120 100
80 60 40 20
0 1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47
要素一:时间t 要素二:指标数值a
研究意义
1、能够描述社会经济现象的发展状况和结果;
2、能够研究社会经济现象的发展速度、发展趋势 和平均水平,探索社会经济现象发展变化的规律, 并据以对未来进行统计预测;
统计学
STATISTICS
第8 章
时间序列分析
学习内容
8. 1 时间序列的描述性分析 8. 2 时间序列及其构成因素 8. 3 时间序列趋势变动分析 8. 4 季节变动分析 8. 5 循环变动分析(自学)
统计学
STATISTICS
8.1 时间序列的描述性分析
一、时间序列的含义 二、时间序列的分类 三、时间序列的图形描述 四、时间序列的速度分析
(4)计算方法、计算价格和计算单位要一致。
描述性时序分析
• 通过直观的数据比较或绘图观测,寻 找序列中蕴含的发展规律,这种分析 方法就称为描述性时序分析
• 描述性时序分析方法具有操作简单、 直观有效的特点,它通常是人们进行 统计时序分析的第一步。
描述性时序分析案例
• 例1 德国业余天文学家施瓦尔发现太阳黑 子的活动具有11年左右的周期
例2 1964年——1999年中国纱年产量序列
例3 1962年1月——1975年12月平均每头奶 牛月产奶量序列
例4 1949年——1998年北京市每年最高气温序列
二、时间序列的分类
绝对数序列
派生
时期序列 时点序列
反映现象发展水平的指标数值
140 120 100
80 60 40 20
0 1 3 5 7 9 11 13 15 17 19 21 23 25 27 29 31 33 35 37 39 41 43 45 47
要素一:时间t 要素二:指标数值a
研究意义
1、能够描述社会经济现象的发展状况和结果;
2、能够研究社会经济现象的发展速度、发展趋势 和平均水平,探索社会经济现象发展变化的规律, 并据以对未来进行统计预测;
统计学
STATISTICS
第8 章
时间序列分析
学习内容
8. 1 时间序列的描述性分析 8. 2 时间序列及其构成因素 8. 3 时间序列趋势变动分析 8. 4 季节变动分析 8. 5 循环变动分析(自学)
统计学
STATISTICS
8.1 时间序列的描述性分析
一、时间序列的含义 二、时间序列的分类 三、时间序列的图形描述 四、时间序列的速度分析
时间序列分析方法概论.pptx

• “遗失数据”的现象是经常发生的,在中国,经济体 制和核算体系都处于转轨之中。在出现“遗失数据” 时,如果样本容量足够大,样本点之间的联系并不紧 密的情况下,可以将“遗失数据”所在的样本点整个 去掉
• 如果样本容量有限,或者样本点之间的联系紧密,去 掉某个样本点会影响模型的估计质量,则要采取特定 的技术将“遗失数据”补上
查资料。
样本数据的质量
• 完整性(不能有遗失数据,必要时,采用插值技术补 上)
• 准确性(准确真实且数据口径方面也符合建模要求)
• 可比性(将范围口径和价格口径调整一致)
• 一致性——同质性(样本与母体一致),用31个省市 的数据作为全国总量模型的数据就违反了一致性
完整性
• 指模型中包含的所有变量都必须得到相同容量的样本 观测值。这既是模型参数估计的需要,也是经济现象 本身应该具有的特征
可比性
• 是通常所说的数据口径问题
• 得到的经济统计数据,一般可比性较差,其原因在于 统计范围口径的变化和价格口径的变化,必须进行处 理后才能用于模型参数的估计
• 计量经济学方法,是从样本数据中寻找经济活动本身 客观存在的规律性,如果数据是不可比的,得到的规 律性就难以反映实际
• 不同的研究者研究同一个经济现象,采用同样的变量 和数学形式,选择的样本点也相同,但可能得到相差 甚远的结果。原因在于样本数据的可比性
时间数列的编制原则
• 基本原则是保证可比性,主要包括:
̶ 时 间 上可 比 ̶ 总体范围可比 ̶ 计算口径可比 ̶ 经济内容可比
一致性
• 指母体与样本的一致性
• 违反一致性的情况经常会发生
– 用企业的数据作为行业生产函数模型的样本数据, 用人均收人与消费的数据作为总量消费函数模型的 样本数据,用31个省份的数据作为全国总量模型的 样本数据,等等。
• 如果样本容量有限,或者样本点之间的联系紧密,去 掉某个样本点会影响模型的估计质量,则要采取特定 的技术将“遗失数据”补上
查资料。
样本数据的质量
• 完整性(不能有遗失数据,必要时,采用插值技术补 上)
• 准确性(准确真实且数据口径方面也符合建模要求)
• 可比性(将范围口径和价格口径调整一致)
• 一致性——同质性(样本与母体一致),用31个省市 的数据作为全国总量模型的数据就违反了一致性
完整性
• 指模型中包含的所有变量都必须得到相同容量的样本 观测值。这既是模型参数估计的需要,也是经济现象 本身应该具有的特征
可比性
• 是通常所说的数据口径问题
• 得到的经济统计数据,一般可比性较差,其原因在于 统计范围口径的变化和价格口径的变化,必须进行处 理后才能用于模型参数的估计
• 计量经济学方法,是从样本数据中寻找经济活动本身 客观存在的规律性,如果数据是不可比的,得到的规 律性就难以反映实际
• 不同的研究者研究同一个经济现象,采用同样的变量 和数学形式,选择的样本点也相同,但可能得到相差 甚远的结果。原因在于样本数据的可比性
时间数列的编制原则
• 基本原则是保证可比性,主要包括:
̶ 时 间 上可 比 ̶ 总体范围可比 ̶ 计算口径可比 ̶ 经济内容可比
一致性
• 指母体与样本的一致性
• 违反一致性的情况经常会发生
– 用企业的数据作为行业生产函数模型的样本数据, 用人均收人与消费的数据作为总量消费函数模型的 样本数据,用31个省份的数据作为全国总量模型的 样本数据,等等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
零假设 H0:=0 备择假设 H1:<0
模型1 模型2 模型3
• 检验过程
–实际检验时从模型3开始,然后模型2、模型1。 –何时检验拒绝零假设,即原序列不存在单位根,为
平稳序列,何时停止检验。 –否则,就要继续检验,直到检验完模型1为止。
• 检验原理与DF检验相同,只是对模型1、2、3 进行检验时,有各自相应的临界值表。
• 如果时间序列含有明显的随时间变化的某种趋 势(如上升或下降),也容易导致DF检验中的 自相关随机误差项问题。
• ADF检验模型
m
X t X t1 i X ti t i 1
m
X t X t1 i X ti t i 1
m
X t t X t1 i X ti t i 1
一、时间序列的平稳性 二、单整序列 三、单位根检验
一、时间序列的平稳性 Stationary Time Series
⒈问题的提出
• 经典计量经济模型常用到的数据有:
– 时间序列数据(time-series data); – 截面数据(cross-sectional data) – 平行/面板数据(panel data/time-series cross-section data)
–例如:如果有两列时间序列数据表现出一致的变化趋势 (非平稳的),即使它们没有任何有意义的关系,但进 行回归也可表现出较高的可决系数。
2、平稳性的定义
• 假定某个时间序列是由某一随机过程
(stochastic process)生成的,即假定时间序
列{Xt}(t=1, 2, …)的每一个数值都是从一个 概率分布中随机得到,如果满足下列条件:
第六讲 现代时间序列分析模型
§1 时间序列平稳性和单位根检验 §2 协整与误差修正模型
• 经典时间序列分析模型:
– MA、AR、ARMA – 平稳时间序列模型 – 分析时间序列自身的变化规律
• 现代时间序列分析模型:
– 分析时间序列之间的关系 – 单位根检验、协整检验 – 现代宏观计量经济学
§1 时间序列平稳性和单位根检验
量Xt有一个单位根。
X t ( 1) X t1 t X t1 t
等价于通过该式判断 是否存在δ=0。
• 通过上式判断Xt是否有单位根,就是时间序列 平稳性的单位根检验。
• 一般检验模型
X t X t1 t X t X t1 t
零假设 H0:=0 备择假设 H1:<0
可通过OLS法下的t检验完成。
0.01 0.05 0.10
样本容量
25 50
100
500
-3.75 -3.58 -3.51 -3.44 3.00 -2.93 -2.89 -2.87 2.63 -2.60 -2.58 -2.57
∝ t分布临界值
(n=∝)
-3.43
-2.33
-2.86
-1.65
-2.57
-1.28
• 如果t<临界值,则拒绝零假设H0: =0,认为 时间序列不存在单位根,是平稳的。
• I(0)代表一平稳时间序列。
• 现实经济生活中只有少数经济指标的时间序列 表现为平稳的,如利率等;
• 大多数指标的时间序列是非平稳的,例如,以 当年价表示的消费额、收入等常是2阶单整的, 以不变价格表示的消费额、收入等常表现为1 阶单整。
• 大多数非平稳的时间序列一般可通过一次或多 次差分的形式变为平稳的。
• 时间序列数据是最常见,也是最常用到的数据。 • 经典回归分析暗含着一个重要假设:数据是平稳的。
• 数据非平稳,大样本下的统计推断基础——“一致 性”要求——被破怀。
• 数据非平稳,往往导致出现“虚假回归” (Spurious Regression)问题。
–表现为两个本来没有任何因果关系的变量,却有很高的 相关性。
• 但也有一些时间序列,无论经过多少次差分, 都不能变为平稳的。这种序列被称为非单整的 (non-integrated)。
三、平稳性的单位根检验
(unit ro
X t X t1 t X t X t1 t
随机游走,非平稳
对该式回归,如果确实 发现ρ=1,则称随机变
• 但是,在零假设(序列非平稳)下,即使在大样 本下t统计量也是有偏误的(向下偏倚),通常的 t 检验无法使用。
• Dicky和Fuller于1976年提出了这一情形下t统计 量服从的分布(这时的t统计量称为统计量), 即DF分布。
• 由于t统计量的向下偏倚性,它呈现围绕小于零均 值的偏态分布。
显著性水平
单尾检验
2、ADF检验(Augment Dickey-Fuller test)
• 为什么将DF检验扩展为ADF检验?
• DF检验假定时间序列是由具有白噪声随机误差 项的一阶自回归过程AR(1)生成的。但在实际检 验中,时间序列可能由更高阶的自回归过程生 成,或者随机误差项并非是白噪声,用OLS法 进行估计均会表现出随机误差项出现自相关, 导致DF检验无效。
宽平稳、广义平稳
• 白噪声(white noise)过程是平稳的: Xt=t , t~N(0,2)
• 随机游走(random walk)过程是非平稳的: Xt=Xt-1+t , t~N(0,2) Var(Xt)=t2
• 随机游走的一阶差分(first difference)是平稳 的: Xt=Xt-Xt-1=t ,t~N(0,2)
– 均值E(Xt)=是与时间t 无关的常数;
– 方差Var(Xt)=2是与时间t 无关的常数;
– 协方差Cov(Xt,Xt+k)=k 是只与时期间隔k有关,与 时间t 无关的常数;
• 则称该随机时间序列是平稳的(stationary),
而该随机过程是一平稳随机过程(stationary
stochastic process)。
• 如果一个时间序列是非平稳的,它常常可通过 取差分的方法而形成平稳序列。
二、单整序列 Integrated Series
• 如果一个时间序列经过一次差分变成平稳的, 就称原序列是一阶单整(integrated of 1)序列, 记为I(1)。
• 一般地,如果一个时间序列经过d次差分后变 成平稳序列,则称原序列是d 阶单整 (integrated of d)序列,记为I(d)。
模型1 模型2 模型3
• 检验过程
–实际检验时从模型3开始,然后模型2、模型1。 –何时检验拒绝零假设,即原序列不存在单位根,为
平稳序列,何时停止检验。 –否则,就要继续检验,直到检验完模型1为止。
• 检验原理与DF检验相同,只是对模型1、2、3 进行检验时,有各自相应的临界值表。
• 如果时间序列含有明显的随时间变化的某种趋 势(如上升或下降),也容易导致DF检验中的 自相关随机误差项问题。
• ADF检验模型
m
X t X t1 i X ti t i 1
m
X t X t1 i X ti t i 1
m
X t t X t1 i X ti t i 1
一、时间序列的平稳性 二、单整序列 三、单位根检验
一、时间序列的平稳性 Stationary Time Series
⒈问题的提出
• 经典计量经济模型常用到的数据有:
– 时间序列数据(time-series data); – 截面数据(cross-sectional data) – 平行/面板数据(panel data/time-series cross-section data)
–例如:如果有两列时间序列数据表现出一致的变化趋势 (非平稳的),即使它们没有任何有意义的关系,但进 行回归也可表现出较高的可决系数。
2、平稳性的定义
• 假定某个时间序列是由某一随机过程
(stochastic process)生成的,即假定时间序
列{Xt}(t=1, 2, …)的每一个数值都是从一个 概率分布中随机得到,如果满足下列条件:
第六讲 现代时间序列分析模型
§1 时间序列平稳性和单位根检验 §2 协整与误差修正模型
• 经典时间序列分析模型:
– MA、AR、ARMA – 平稳时间序列模型 – 分析时间序列自身的变化规律
• 现代时间序列分析模型:
– 分析时间序列之间的关系 – 单位根检验、协整检验 – 现代宏观计量经济学
§1 时间序列平稳性和单位根检验
量Xt有一个单位根。
X t ( 1) X t1 t X t1 t
等价于通过该式判断 是否存在δ=0。
• 通过上式判断Xt是否有单位根,就是时间序列 平稳性的单位根检验。
• 一般检验模型
X t X t1 t X t X t1 t
零假设 H0:=0 备择假设 H1:<0
可通过OLS法下的t检验完成。
0.01 0.05 0.10
样本容量
25 50
100
500
-3.75 -3.58 -3.51 -3.44 3.00 -2.93 -2.89 -2.87 2.63 -2.60 -2.58 -2.57
∝ t分布临界值
(n=∝)
-3.43
-2.33
-2.86
-1.65
-2.57
-1.28
• 如果t<临界值,则拒绝零假设H0: =0,认为 时间序列不存在单位根,是平稳的。
• I(0)代表一平稳时间序列。
• 现实经济生活中只有少数经济指标的时间序列 表现为平稳的,如利率等;
• 大多数指标的时间序列是非平稳的,例如,以 当年价表示的消费额、收入等常是2阶单整的, 以不变价格表示的消费额、收入等常表现为1 阶单整。
• 大多数非平稳的时间序列一般可通过一次或多 次差分的形式变为平稳的。
• 时间序列数据是最常见,也是最常用到的数据。 • 经典回归分析暗含着一个重要假设:数据是平稳的。
• 数据非平稳,大样本下的统计推断基础——“一致 性”要求——被破怀。
• 数据非平稳,往往导致出现“虚假回归” (Spurious Regression)问题。
–表现为两个本来没有任何因果关系的变量,却有很高的 相关性。
• 但也有一些时间序列,无论经过多少次差分, 都不能变为平稳的。这种序列被称为非单整的 (non-integrated)。
三、平稳性的单位根检验
(unit ro
X t X t1 t X t X t1 t
随机游走,非平稳
对该式回归,如果确实 发现ρ=1,则称随机变
• 但是,在零假设(序列非平稳)下,即使在大样 本下t统计量也是有偏误的(向下偏倚),通常的 t 检验无法使用。
• Dicky和Fuller于1976年提出了这一情形下t统计 量服从的分布(这时的t统计量称为统计量), 即DF分布。
• 由于t统计量的向下偏倚性,它呈现围绕小于零均 值的偏态分布。
显著性水平
单尾检验
2、ADF检验(Augment Dickey-Fuller test)
• 为什么将DF检验扩展为ADF检验?
• DF检验假定时间序列是由具有白噪声随机误差 项的一阶自回归过程AR(1)生成的。但在实际检 验中,时间序列可能由更高阶的自回归过程生 成,或者随机误差项并非是白噪声,用OLS法 进行估计均会表现出随机误差项出现自相关, 导致DF检验无效。
宽平稳、广义平稳
• 白噪声(white noise)过程是平稳的: Xt=t , t~N(0,2)
• 随机游走(random walk)过程是非平稳的: Xt=Xt-1+t , t~N(0,2) Var(Xt)=t2
• 随机游走的一阶差分(first difference)是平稳 的: Xt=Xt-Xt-1=t ,t~N(0,2)
– 均值E(Xt)=是与时间t 无关的常数;
– 方差Var(Xt)=2是与时间t 无关的常数;
– 协方差Cov(Xt,Xt+k)=k 是只与时期间隔k有关,与 时间t 无关的常数;
• 则称该随机时间序列是平稳的(stationary),
而该随机过程是一平稳随机过程(stationary
stochastic process)。
• 如果一个时间序列是非平稳的,它常常可通过 取差分的方法而形成平稳序列。
二、单整序列 Integrated Series
• 如果一个时间序列经过一次差分变成平稳的, 就称原序列是一阶单整(integrated of 1)序列, 记为I(1)。
• 一般地,如果一个时间序列经过d次差分后变 成平稳序列,则称原序列是d 阶单整 (integrated of d)序列,记为I(d)。
