2.角含半角模型

半角模型定理公式

半角模型定理公式【原创实用版】目录1.半角模型定理的概述2.半角模型定理的公式表示3.半角模型定理的证明4.半角模型定理的应用正文一、半角模型定理的概述半角模型定理是数学领域中的一个重要定理，主要应用于解决三角函数、微积分等数学问题的计算与求解。

该定理以其独特的视角和简便的计算方法，为数学研究带来了很大的便利。

二、半角模型定理的公式表示半角模型定理的公式表示如下：设角 A 的半角为 B，则有：sin(B) = ±√((1 - cos(A))/2)cos(B) = ±√((1 + cos(A))/2)tan(B) = ±√((1 - cos(A))/(1 + cos(A)))三、半角模型定理的证明为了证明半角模型定理，我们可以利用三角函数的和角公式进行推导。

以 sin(B) 为例，根据和角公式，有：sin(B) = sin(A/2) * √(1 - cos(A/2))由于 A = 2B，所以 A/2 = B，代入上式得：sin(B) = sin(B) * √(1 - cos(B))进一步化简，得：√(1 - cos(A)) = √(1 - cos(B))由于√(1 - cos(A)) 和√(1 + cos(A)) 的正负号不确定，所以需要加上±号。

同理，可以证明 cos(B) 和 tan(B) 的公式。

四、半角模型定理的应用半角模型定理在实际应用中具有很高的价值，尤其在解决一些复杂数学问题时，可以大大简化计算过程。

例如，在求解三角函数的值、计算微积分等问题时，都可以利用半角模型定理进行简化。

总之，半角模型定理以其独特的公式表示和简便的计算方法，为数学研究带来了很大的便利。

角含半角模型结论的证明

角含半角模型结论的证明角含半角模型结论的证明引言在几何学中，我们经常需要证明一些结论，其中一个重要的结论就是角含半角模型。

本文将对这一结论进行详细的证明。

一、定义和基本概念1. 角：由两条射线共同起点所组成的图形称为角。

2. 半角：若一个角被平分，则其被平分后形成的两个角是等角，且每个等角都是原来角的半角。

3. 角含半角模型：如果一个点P在∠ABC内部，则有∠ABP≥∠CBP；如果一个点P在∠ABC外部，则有∠ABP≤∠CBP。

二、证明过程1. 证明内部情况下的模型（1）当点P在∠ABC内部时，如图1所示：图1由于AP和BP都在∠ABC内部，因此有：∠ABP+∠CBP=∠ABC（全等三角形）因为AP和BP都在∠ABC内部，所以有：m<ABP+m<CBP<m<ABC（夹逼定理）又因为m<ABP+m<CBP=m<ABC/2（半角公式），所以有：m<ABP≥m<ABC/2-m<CBP即：m<ABP≥m<CBP所以∠ABP≥∠CBP。

（2）当点P在∠ABC外部时，如图2所示：图2由于AP和BP都在∠ABC外部，所以有：∠ABP+∠CBP=360°-∠ABC（补角）因为AP和BP都在∠ABC外部，所以有：m<ABP+m<CBP>m<ABC（夹逼定理）又因为m<ABP+m<CBP=m<ABC/2（半角公式），所以有：m<ABP≤180°-m<CBP-m<ABC/2即：m<ABP≤m<CBP所以∠ABP≤∠CBP。

三、总结通过上述证明，我们可以得出结论：如果一个点在一个角的内部，则这个点到角的两边的距离相等；如果一个点在一个角的外部，则这个点到角的两边的距离不相等。

这一结论被称为角含半角模型。

它是几何学中非常重要的一个基本结论，在许多几何问题中都有广泛应用。

旋转模型-角含半角模型

旋转模型-角含半角模型【内容介绍】本次资料主要包含数学科目，重点指导学生了解旋转模型相关知识，掌握不同旋转模型的解题方法；主要是通过要点梳理，帮助大家综合掌握角含半角模型的含义和解题方法，再通过典型例题的分析，帮助大家了解常考题型。

建议大家深入学习掌握要点梳理，认真研读例题，并在日常学习中注重练习，实现对学习目标的综合把握。

【要点梳理】1）半角模型概念：过多边形一个顶点作两条射线，使这两条射线夹角等于该顶角一半2）思想方法：通过旋转构造全等三角形，实现线段的转化3）基本模型要点一、正方形含半角图1 图2△△△△AEF AEB AFDS S +S ）4（；BEF 分平 EA ，DFE 分平 FA ）3（；半一的长周形方正是长周的(2) CEF EF=BE+DF;）1（：论结的下以明证，EAF=45，点的上边CD 、BC 是别分F 、E ，中ABCD 形方正在：1图如：题例=∠∠∠︒。

化转的角和段线现实，形角三等全造构转旋过通，型模角半合符，角45有含中角90：析分︒︒△△△△△△△△△AEG AEF AEG AEF G AFE AFD CEF BE BG BE DF AEF AEG AEB AEG AEB AFD 证得S S =S S S S ；证得；证得EF+CE+CF=BE+CE+DF+CF=BC+CD,(2)长周的。

立成=+=+≅∴∠=∠∠=∠=∠∴∴+=+,(4),,,(3)=(1),△△△△△EF EG AEG AEF AE AE AEG AEF EAG EAF AG AF EAG EAF EAF G B C GBC ABG ABC ABG AG AF ABG D BG DF ABCD AD AB ，，中和在，，线共点三、、则，到得，转旋针时顺点沿将，中形方正在，图如：答解∴==∴≅⎩=⎪⎨∠∠⎪⎧=∴∠∠︒∠︒∴∴∠∠+∠︒∠︒∆=∠=∠=︒=∠=︒=︒,===45=45==180ABC =90,90,,GAF 90,2,ADF A 90。

第5讲角含半角模型(解析版)

中考数学几何模型5：角含半角模型TH 名师点睛拨开云雾开门见山角含半角模型，顾名思义即一个角包含着它的一半大小的角。

它主要包含：等腰直角三角形角含半角模型；正方形中角含半角模型两种类型。

解决类似问题的常见办法主要有两种：旋转目标三角形法和翻折目标三角形法。

类型一：等腰直角三角形角含半角模型（1）如图，在△ABC中，AB=AC，∠BAC=90°，点D，E在BC上，且∠DAE=45°，则：BD2+CE2=DE2.图示（1）作法1：将△ABD旋转90°作法2：分别翻折△ABD,△ACE（2）如图，在△ABC中，AB=AC，∠BAC=90°，点D在BC上，点E在BC延长线上，且∠DAE=45°，则：BD2+CE2=DE2.图示（2）（3）如图，将等腰直角三角形变成任意等腰三角形时，亦可以进行两种方法的操作处理..任意等腰三角形类型二：正方形中角含半角模型（1）如图，在正方形ABCD中，点E，F分别在边BC，CD上，∠EAF=45°，连接EF，过点A作AG⊥于EF于点G，则：EF=BE+DF，AG=AD.图示（1）作法：将△ABE绕点A逆时针旋转90°（2）如图，在正方形ABCD中，点E，F分别在边CB，DC的延长线上，∠EAF=45°，连接EF，则：EF=DF-BE.图示（2）作法：将△ABE绕点A逆时针旋转90°（3）如图，将正方形变成一组邻边相等，对角互补的四边形，在四方形ABCD中，AB=AD，∠BAD+∠C=180°，点E，F分别在边BC，CD上，∠EAF=12∠BAD，连接EF，则：EF=BE+DF.图示（3）作法：将△ABE绕点A逆时针旋转∠BAD的大小典题探究启迪思维探究重点例题1. 如图，正方形ABCD的边长为4，点E，F分别在AB，AD上，若CE＝5，且∠ECF＝45°，则CF 的长为4．【解答】解：如图，延长FD到G，使DG＝BE；连接CG、EF；∵四边形ABCD为正方形，在△BCE与△DCG中，，∴△BCE≌△DCG（SAS），∴CG＝CE，∠DCG＝∠BCE，∴∠GCF＝45°，在△GCF与△ECF中，，∴△GCF≌△ECF（SAS），∴GF＝EF，∵CE＝5，CB＝4，∴BE＝3，∴AE＝1，设AF＝x，则DF＝4﹣x，GF＝1+（4﹣x）＝5﹣x，∴EF＝＝，∴（5﹣x）2＝1+x2，∴x＝，即AF＝，∴DF＝4﹣＝，∴CF＝＝＝4，故答案为：4．变式练习>>>1．如图四边形ABCD中，AD∥BC，∠BCD＝90°，AB＝BC+AD，∠DAC＝45°，E为CD上一点，且∠BAE＝45°．若CD＝4，则△ABE的面积为（）A．B．C．D．【解答】解法一：作AF⊥CB交CB的延长线于F，在CF的延长线上取一点G，使得FG＝DE．∵AD∥BC，∴∠BCD+∠ADC＝180°，∴∠ADC＝∠BCD＝∠AFC＝90°，∴四边形ADCF是矩形，∵∠CAD＝45°，∴AD＝CD，∴四边形ADCF是正方形，∴AF＝AD，∠AFG＝∠ADF＝90°，∴△AFG≌△ADE，∴AG＝AE，∠F AG＝∠DAE，∴∠F AG+∠F AB＝∠EAD+∠F AB＝45°＝∠BAE，∴△BAE≌△BAG，∴BE＝BG＝BF+GF＝BF+DE，设BC＝a，则AB＝4+a，BF＝4﹣a，在Rt△ABF中，42+（4﹣a）2＝（4+a）2，解得a＝1，∴BC＝1，BF＝3，设BE＝b，则DE＝b﹣3，CE＝4﹣（b﹣3）＝7﹣b．在Rt△BCE中，12+（7﹣b）2＝b2，解得b＝，∴BG＝BE＝，∴S△ABE＝S△ABG＝××4＝．例题2. 在正方形ABCD中，连接BD．（1）如图1，AE⊥BD于E．直接写出∠BAE的度数．（2）如图1，在（1）的条件下，将△AEB以A旋转中心，沿逆时针方向旋转30°后得到△AB′E′，AB′与BD交于M，AE′的延长线与BD交于N．①依题意补全图1；②用等式表示线段BM、DN和MN之间的数量关系，并证明．（3）如图2，E、F是边BC、CD上的点，△CEF周长是正方形ABCD周长的一半，AE、AF分别与BD 交于M、N，写出判断线段BM、DN、MN之间数量关系的思路．（不必写出完整推理过程）【解答】解：（1）∵BD是正方形ABCD的对角线，∴∠ABD＝∠ADB＝45°，∵AE⊥BD，∴∠ABE＝∠BAE＝45°，（2）①依题意补全图形，如图1所示，②BM、DN和MN之间的数量关系是BM2+MD2＝MN2，将△AND绕点D顺时针旋转90°，得到△AFB，∴∠ADB＝∠FBA，∠BAF＝∠DAN，DN＝BF，AF＝AN，∵在正方形ABCD中，AE⊥BD，∴∠ADB＝∠ABD＝45°，∴∠FBM＝∠FBA+∠ABD＝∠ADB+∠ABD＝90°，在Rt△BFM中，根据勾股定理得，FB2+BM2＝FM2，∵旋转△ANE得到AB1E1，∴∠E1AB1＝45°，∴∠BAB1+∠DAN＝90°﹣45°＝45°，∵∠BAF＝DAN，∴∠BAB1+∠BAF＝45°，∴∠F AM＝45°，∴∠F AM＝∠E1AB1，∵AM＝AM，AF＝AN，∴△AFM≌△ANM，∴FM＝MN，∵FB2+BM2＝FM2，∴DN2+BM2＝MN2，变式练习>>>2. （1）【探索发现】如图1，正方形ABCD中，点M、N分别是边BC、CD上的点，∠MAN＝45°，若将△DAN绕点A顺时针旋转90°到△BAG位置，可得△MAN≌△MAG，若△MCN的周长为6，则正方形ABCD的边长为3．（2）【类比延伸】如图（2），四边形ABCD中，AB＝AD，∠BAD＝120°，∠B+∠D＝180°，点M、N分别在边BC、CD 上的点，∠MAN＝60°，请判断线段BM，DN，MN之间的数量关系，并说明理由．（3）【拓展应用】如图3，四边形ABCD中，AB＝AD＝10，∠ADC＝120°，点M，N分别在边BC，CD上，连接AM，MN，△ABM是等边三角形，AM⊥AD，DN＝5（﹣1），请直接写出MN的长．【解答】解：（1）如图1中，∵△MAN≌△MAG，∴MN＝GM，∵DN＝BG，GM＝BG+BM，∴MN＝BM+DN，∵△CMN的周长为：MN+CM+CN＝6，∴BM+CM+CN+DN＝6，∴BC+CD＝6，∴BC＝CD＝3，故答案为3．（2）如图2中，结论：MN＝NM+DN．延长CB至E，使BE＝DN，连接AE，∵∠ABC+∠D＝180°，∠ABC+∠ABE＝180°，∴∠D＝∠ABE，在△ABE和△ADN中，，∴△ABE≌△ADN，∴AN＝AE，∠DAN＝∠BAE，∵∠BAD＝2∠MAN，∴∠DAN+∠BAM＝∠MAN，∴∠MAN＝∠EAM，在△MAN和△MAE中，，∴△MAN≌△MAE，∴MN＝EM＝BE+BM＝BM+DN，即MN＝BM+DN；（3）解：如图3，把△ABM绕点A逆时针旋转150°至△ADG，连接AN．作NH⊥AD于H，在AH上取一点K，使得∠NKH＝30°在Rt△DHN中，∵∠NDH＝60°DN＝5（﹣1），∴DH＝DN＝，HN＝DH＝，在Rt△KNH中，KN＝2HN＝15﹣5，HK＝HN＝，∴AK＝AH﹣HK＝15﹣5，∴AK＝KN，∴∠KAN＝∠KNA，∵∠NKH＝∠KAN+∠KNA，∴∠NAK＝15°，∴∠MAN＝75°＝∠BAD，由（2）得，MN＝BM+DN＝10+5（﹣1）＝5+5．例题3. 如图，在四边形ABCD中，AB=BC，∠A=∠C=90°，∠B=135°，K，N分别是AB，BC上的点，若△BKN的周长为AB的2倍，求∠KDN的度数.变式练习>>>3. 如图，正方形被两条与边平行的线段EF，GH分割成四个小矩形，P是EF与GH的交点，若矩形PFCH 的面积恰是矩形AGPE面积的2倍，试确定∠HAF的大小并证明你的结论.例题4. 如图，在四边形ABCD中，AB＝AD，BC＝CD，∠ABC＝∠ADC＝90°，∠MAN＝∠BAD．（1）如图1，将∠MAN绕着A点旋转，它的两边分别交边BC、CD于M、N，试判断这一过程中线段BM、DN和MN之间有怎样的数量关系？直接写出结论，不用证明；（2）如图2，将∠MAN绕着A点旋转，它的两边分别交边BC、CD的延长线于M、N，试判断这一过程中线段BM、DN和MN之间有怎样的数量关系？并证明你的结论；（3）如图3，将∠MAN绕着A点旋转，它的两边分别交边BC、CD的反向延长线于M、N，试判断这一过程中线段BM、DN和MN之间有怎样的数量关系？直接写出结论，不用证明．【解答】解：（1）证明：延长MB到G，使BG＝DN，连接AG．∵∠ABG＝∠ABC＝∠ADC＝90°，AB＝AD，∴△ABG≌△ADN．∴AG＝AN，BG＝DN，∠1＝∠4．∴∠1+∠2＝∠4+∠2＝∠MAN＝∠BAD．∴∠GAM＝∠MAN．又AM＝AM，∴△AMG≌△AMN．∴MG＝MN．∵MG＝BM+BG．∴MN＝BM+DN．（2）MN＝BM﹣DN．证明：在BM上截取BG，使BG＝DN，连接AG．∵∠ABC＝∠ADC＝90°，AD＝AB，∴△ADN≌△ABG，∴AN＝AG，∠NAD＝∠GAB，∴∠MAN＝∠NAD+∠BAM＝∠DAB，∴∠MAG＝∠BAD，∴∠MAN＝∠MAG，∴△MAN≌△MAG，∴MN＝MG，∴MN＝BM﹣DN．（3）MN＝DN﹣BM．达标检测领悟提升强化落实1. 请阅读下列材料：问题：正方形ABCD中，M，N分别是直线CB、DC上的动点，∠MAN＝45°，当∠MAN交边CB、DC 于点M、N（如图①）时，线段BM、DN和MN之间有怎样的数量关系？小聪同学的思路是：延长CB至E使BE＝DN，并连接AE，构造全等三角形经过推理使问题得到解决．请你参考小聪同学的思路，探究并解决下列问题：（1）直接写出上面问题中，线段BM，DN和MN之间的数量关系；（2）当∠MAN分别交边CB，DC的延长线于点M/N时（如图②），线段BM，DN和MN之间的又有怎样的数量关系？请写出你的猜想，并加以证明；（3）在图①中，若正方形的边长为16cm，DN＝4cm，请利用（1）中的结论，试求MN的长．【解答】解：（1）BM+DN＝MN；（2）DN﹣BM＝MN．理由如下：如图，在DC上截取DF＝BM，连接AF．∵AB＝AD，∠ABM＝∠ADF＝90°，∴△ABM≌△ADF（SAS）∴AM＝AF，∠MAB＝∠F AD．∴∠MAB+∠BAF＝∠F AD+∠BAF＝90°，即∠MAF＝∠BAD＝90°．又∠MAN＝45°，∴∠NAF＝∠MAN＝45°．∵AN＝AN，∴△MAN≌△F AN．∴MN＝FN，即MN＝DN﹣DF＝DN﹣BM；（3）∵正方形的边长为16，DN＝4，∴CN＝12．根据（1）可知，BM+DN＝MN，设MN＝x，则BM＝x﹣4，∴CM＝16﹣（x﹣4）＝20﹣x．在Rt△CMN中，∵MN2＝CM2+CN2，∴x2＝（20﹣x）2+122．解得x＝13.6．∴MN＝13.6cm．2. （1）如图1，在四边形ABCD中，AB＝AD，∠B＝∠D＝90°，E、F分别是边BC、CD上的点，且∠EAF＝∠BAD．试探究图中线段BE、EF、FD之间的数量关系．（1）小王同学探究此问题的方法是：延长EB到点G，使BG＝DF，连结AG，先证明△ABG≌△ADF，再证明△AEG≌△AEF，可得出结论，他的结论应是EF＝BE+FD．（2）如图2，在四边形ABCD中，AB＝AD，∠B+∠D＝180°，E、F分别是边BC、CD上的点，且∠EAF＝∠BAD，上述结论是否仍然成立，并说明理由．（3）如图3，在四边形ABCD中，AB＝AD，∠B+∠ADC＝180°，E、F分别是边BC、CD延长线上的点，且∠EAF＝∠BAD，（1）中的结论是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明．【解答】解：（1）由△ABG≌△ADF，△AEG≌△AEF可知，BG＝DF，EF＝EG＝BG+EF＝DF+EF，故答案为EF＝BE+FD.（2）（1）中的结论EF＝BE+FD仍然成立．理由：延长EB到点G，使BG＝DF，连结AG．∵∠ABD+∠D＝180°，∠ABD+∠ABG＝180°，∴∠ABG＝∠D，∴AB＝AD，BG＝DF，∴△ABG≌△ADF，∴∠BAG＝∠DAF，AG＝AF，∵∠EAF＝∠BAD，∴∠BAE+∠DAF＝∠BAD＝∠BAE+∠BAG，∴∠EAG＝∠EAF，∵AE＝AE，AG＝AF，∴△EAG≌△EAF，∴EG＝EF，∵EG＝BG+BE＝DF+BE，∴EF＝BE+DF．3. 小曼和他的同学组成了“爱琢磨”学习小组，有一次，他们碰到这样一道题：“已知正方形ABCD，点E、F、G、H分别在边AB、BC、CD、DA上，若EG⊥FH，则EG＝FH．”为了解决这个问题，经过思考，大家给出了以下两个方案：方案一：过点A作AM∥HF交BC于点M，过点B作BN∥EG交CD于点N；方案二：过点A作AM∥HF交BC于点M，过点A作AN∥EG交CD于点N．…（1）对小曼遇到的问题，请在甲、乙两个方案中任选一个加以证明（如图（1））．（2）如果把条件中的“正方形”改为“长方形”，并设AB＝2，BC＝3（如图（2）），是探究EG、FH之间有怎样的数量关系，并证明你的结论．（3）如果把条件中的“EG⊥FH”改为“EG与FH的夹角为45°”，并假设正方形ABCD的边长为1，FH的长为（如图（3）），试求EG的长度．【解答】解：（1）证明：过点A作AM∥HF交BC于点M，作AN∥EG交CD的延长线于点N，∴AM＝HF，AN＝BC，在正方形ABCD中，AB＝AD，∠ABM＝∠BAD＝∠ADN＝90°∵EG⊥FH，∴∠NAM＝90°，∴∠BAM＝∠DAN，在△ABM和△ADN中，∠BAM＝∠DAN，AB＝AD，∠ABM＝∠ADN∴△ABM≌△ADN∴AM＝AN，即EG＝FH（2）结论：EG：FH＝3：2证明：过点A作AM∥HF交BC于点M，作AN∥EC交CD的延长线于点N，∴AM＝HF，AN＝EC，在长方形ABCD中，BC＝AD，∠ABM＝∠BAD＝∠ADN＝90°，∵EG⊥FH，∴∠NAM＝90°，∴∠BAM＝∠DAN．∴△ABM∽△ADN．，∵AB＝2，BC＝AD＝3，∴．（3）解：过点A作AM∥HF交BC于点M，过点A作AN∥EG交CD于点N，∵．∴在Rt△ABM中，BM＝．将△AND绕点A顺时针旋转90°到△APB．∵EG与FH的夹角为45°，∴∠MAN＝45°，∴∠DAN+∠MAB＝45°，即∠P AM＝∠MAN＝45°，从而△APM≌△ANM，∴PM＝NM．设DN＝x，则NC＝1﹣x，MN＝PM＝．在Rt△CMN中，解得．∴．4. 已知：如图，正方形ABCD的边长为a，BM，DN分别平分正方形的两个外角，且满足∠MAN=45°，连接MC，NC，MN．（1）填空：与△ABM相似的三角形是_________，BM•DN=_________；（用含a的代数式表示）（2）求∠MCN的度数；（3）猜想线段BM，DN和MN之间的等量关系并证明你的结论.。

第5讲角含半角模型(原卷版) 2020年中考数学几何模型能力提升篇(全国通用)

中考数学几何模型5：角含半角模型st●模型1：截长补短模型●模型2：共顶点模型●模型3：对角互补模型●模型:4：中点模型●模型5：角含半角模型●模型6：弦图模型●模型7：轴对称最值模型●模型8：费马点最值模型●模型9：隐圆模型●模型10：胡不归最值模型●模型11：阿氏圆最值模型●模型12：主从联动模型名师点睛拨开云雾开门见山角含半角模型，顾名思义即一个角包含着它的一半大小的角。

它主要包含：等腰直角三角形角含半角模型；正方形中角含半角模型两种类型。

解决类似问题的常见办法主要有两种：旋转目标三角形法和翻折目标三角形法。

类型一：等腰直角三角形角含半角模型（1）如图，在△ABC中，AB=AC，∠BAC=90°，点D，E在BC上，且∠DAE=45°，则：BD2+CE2=DE2.图示（1）作法1：将△ABD旋转90°作法2：分别翻折△ABD,△ACE（2）如图，在△ABC中，AB=AC，∠BAC=90°，点D在BC上，点E在BC延长线上，且∠DAE=45°，则：BD2+CE2=DE2.图示（2）（3）如图，将等腰直角三角形变成任意等腰三角形时，亦可以进行两种方法的操作处理..任意等腰三角形类型二：正方形中角含半角模型（1）如图，在正方形ABCD中，点E，F分别在边BC，CD上，∠EAF=45°，连接EF，过点A作AG⊥于EF于点G，则：EF=BE+DF，AG=AD.图示（1）作法：将△ABE绕点A逆时针旋转90°（2）如图，在正方形ABCD中，点E，F分别在边CB，DC的延长线上，∠EAF=45°，连接EF，则：EF=DF-BE.图示（2）作法：将△ABE绕点A逆时针旋转90°（3）如图，将正方形变成一组邻边相等，对角互补的四边形，在四方形ABCD中，AB=AD，∠BAD+∠C=180°，点E，F分别在边BC，CD上，∠EAF=12∠BAD，连接EF，则：EF=BE+DF.图示（3）作法：将△ABE绕点A逆时针旋转∠BAD的大小典题探究启迪思维探究重点例题1. 如图，正方形ABCD的边长为4，点E，F分别在AB，AD上，若CE＝5，且∠ECF＝45°，则CF 的长为．变式练习>>>1．如图四边形ABCD中，AD∥BC，∠BCD＝90°，AB＝BC+AD，∠DAC＝45°，E为CD上一点，且∠BAE＝45°．若CD＝4，则△ABE的面积为（）A．B．C．D．例题2. 在正方形ABCD中，连接BD．（1）如图1，AE⊥BD于E．直接写出∠BAE的度数．（2）如图1，在（1）的条件下，将△AEB以A旋转中心，沿逆时针方向旋转30°后得到△AB′E′，AB′与BD交于M，AE′的延长线与BD交于N．①依题意补全图1；②用等式表示线段BM、DN和MN之间的数量关系，并证明．（3）如图2，E、F是边BC、CD上的点，△CEF周长是正方形ABCD周长的一半，AE、AF分别与BD 交于M、N，写出判断线段BM、DN、MN之间数量关系的思路．（不必写出完整推理过程）变式练习>>>2. （1）【探索发现】如图1，正方形ABCD中，点M、N分别是边BC、CD上的点，∠MAN＝45°，若将△DAN绕点A顺时针旋转90°到△BAG位置，可得△MAN≌△MAG，若△MCN的周长为6，则正方形ABCD的边长为3．（2）【类比延伸】如图（2），四边形ABCD中，AB＝AD，∠BAD＝120°，∠B+∠D＝180°，点M、N分别在边BC、CD 上的点，∠MAN＝60°，请判断线段BM，DN，MN之间的数量关系，并说明理由．（3）【拓展应用】如图3，四边形ABCD中，AB＝AD＝10，∠ADC＝120°，点M，N分别在边BC，CD上，连接AM，MN，△ABM是等边三角形，AM⊥AD，DN＝5（﹣1），请直接写出MN的长．例题3. 如图，在四边形ABCD中，AB=BC，∠A=∠C=90°，∠B=135°，K，N分别是AB，BC上的点，若△BKN的周长为AB的2倍，求∠KDN的度数.变式练习>>>3. 如图，正方形被两条与边平行的线段EF，GH分割成四个小矩形，P是EF与GH的交点，若矩形PFCH 的面积恰是矩形AGPE面积的2倍，试确定∠HAF的大小并证明你的结论.例题4. 如图，在四边形ABCD中，AB＝AD，BC＝CD，∠ABC＝∠ADC＝90°，∠MAN＝∠BAD．（1）如图1，将∠MAN绕着A点旋转，它的两边分别交边BC、CD于M、N，试判断这一过程中线段BM、DN和MN之间有怎样的数量关系？直接写出结论，不用证明；（2）如图2，将∠MAN绕着A点旋转，它的两边分别交边BC、CD的延长线于M、N，试判断这一过程中线段BM、DN和MN之间有怎样的数量关系？并证明你的结论；（3）如图3，将∠MAN绕着A点旋转，它的两边分别交边BC、CD的反向延长线于M、N，试判断这一过程中线段BM、DN和MN之间有怎样的数量关系？直接写出结论，不用证明．达标检测领悟提升强化落实1. 请阅读下列材料：问题：正方形ABCD中，M，N分别是直线CB、DC上的动点，∠MAN＝45°，当∠MAN交边CB、DC 于点M、N（如图①）时，线段BM、DN和MN之间有怎样的数量关系？小聪同学的思路是：延长CB至E使BE＝DN，并连接AE，构造全等三角形经过推理使问题得到解决．请你参考小聪同学的思路，探究并解决下列问题：（1）直接写出上面问题中，线段BM，DN和MN之间的数量关系；（2）当∠MAN分别交边CB，DC的延长线于点M/N时（如图②），线段BM，DN和MN之间的又有怎样的数量关系？请写出你的猜想，并加以证明；（3）在图①中，若正方形的边长为16cm，DN＝4cm，请利用（1）中的结论，试求MN的长．2. （1）如图1，在四边形ABCD中，AB＝AD，∠B＝∠D＝90°，E、F分别是边BC、CD上的点，且∠EAF＝∠BAD．试探究图中线段BE、EF、FD之间的数量关系．（1）小王同学探究此问题的方法是：延长EB到点G，使BG＝DF，连结AG，先证明△ABG≌△ADF，再证明△AEG≌△AEF，可得出结论，他的结论应是．（2）如图2，在四边形ABCD中，AB＝AD，∠B+∠D＝180°，E、F分别是边BC、CD上的点，且∠EAF＝∠BAD，上述结论是否仍然成立，并说明理由．（3）如图3，在四边形ABCD中，AB＝AD，∠B+∠ADC＝180°，E、F分别是边BC、CD延长线上的点，且∠EAF＝∠BAD，（1）中的结论是否仍然成立？若成立，请证明；若不成立，请写出它们之间的数量关系，并证明．3. 小曼和他的同学组成了“爱琢磨”学习小组，有一次，他们碰到这样一道题：“已知正方形ABCD，点E、F、G、H分别在边AB、BC、CD、DA上，若EG⊥FH，则EG＝FH．”为了解决这个问题，经过思考，大家给出了以下两个方案：方案一：过点A作AM∥HF交BC于点M，过点B作BN∥EG交CD于点N；方案二：过点A作AM∥HF交BC于点M，过点A作AN∥EG交CD于点N．…（1）对小曼遇到的问题，请在甲、乙两个方案中任选一个加以证明（如图（1））．（2）如果把条件中的“正方形”改为“长方形”，并设AB＝2，BC＝3（如图（2）），是探究EG、FH之间有怎样的数量关系，并证明你的结论．（3）如果把条件中的“EG⊥FH”改为“EG与FH的夹角为45°”，并假设正方形ABCD的边长为1，FH的长为（如图（3）），试求EG的长度．4. 已知：如图，正方形ABCD的边长为a，BM，DN分别平分正方形的两个外角，且满足∠MAN=45°，连接MC，NC，MN．（1）填空：与△ABM相似的三角形是_________，BM•DN=_________；（用含a的代数式表示）（2）求∠MCN的度数；（3）猜想线段BM，DN和MN之间的等量关系并证明你的结论.。

初中几何模型角含半角模型

几何模型：角含半角模型角含半角模型，顾名思义即一个角包含着它的一半大小的角。

它主要包含：等腰直角三角形角含半角模型；正方形中角含半角模型两种类型。

解决类似问题的常见办法主要有两种：旋转目标三角形法和翻折目标三角形法。

类型一：等腰直角三角形角含半角模型（1）如图，在△ABC中，AB=AC，∠BAC=90°，点D，E在BC上，且∠DAE=45°，则：BD2+CE2=DE2.图示（1）作法1：将△ABD旋转90°作法2：分别翻折△ABD,△ACE（2）如图，在△ABC中，AB=AC，∠BAC=90°，点D在BC上，点E在BC延长线上，且∠DAE=45°，则：BD2+CE2=DE2.图示（2）（3）如图，将等腰直角三角形变成任意等腰三角形时，亦可以进行两种方法的操作处理..任意等腰三角形类型二：正方形中角含半角模型（1）如图，在正方形ABCD中，点E，F分别在边BC，CD上，∠EAF=45°，连接EF，过点A作AG⊥于EF于点G，则：EF=BE+DF，AG=AD.图示（1）作法：将△ABE绕点A逆时针旋转90°（2）如图，在正方形ABCD中，点E，F分别在边CB，DC的延长线上，∠EAF=45°，连接EF，则：EF=DF-BE.图示（2）作法：将△ABE绕点A逆时针旋转90°（3）如图，将正方形变成一组邻边相等，对角互补的四边形，在四方形ABCD中，AB=AD，∠BAD+∠C=180°，点E，F分别在边BC，CD上，∠EAF=12∠BAD，连接EF，则：EF=BE+DF.图示（3）作法：将△ABE绕点A逆时针旋转∠BAD的大小典题探究启迪思维探究重点例题1. 如图，正方形ABCD的边长为4，点E，F分别在AB，AD上，若CE＝5，且∠ECF＝45°，则CF 的长为4．【解答】解：如图，延长FD到G，使DG＝BE；连接CG、EF；∵四边形ABCD为正方形，在△BCE与△DCG中，，∴△BCE≌△DCG（SAS），∴CG＝CE，∠DCG＝∠BCE，∴∠GCF＝45°，在△GCF与△ECF中，，∴△GCF≌△ECF（SAS），∴GF＝EF，∵CE＝5，CB＝4，∴BE＝3，∴AE＝1，设AF＝x，则DF＝4﹣x，GF＝1+（4﹣x）＝5﹣x，∴EF＝＝，∴（5﹣x）2＝1+x2，∴x＝，即AF＝，∴DF＝4﹣＝，∴CF＝＝＝4，故答案为：4．变式练习>>>1．如图四边形ABCD中，AD∥BC，∠BCD＝90°，AB＝BC+AD，∠DAC＝45°，E为CD上一点，且∠BAE＝45°．若CD＝4，则△ABE的面积为（）A．B．C．D．【解答】解法一：作AF⊥CB交CB的延长线于F，在CF的延长线上取一点G，使得FG＝DE．∵AD∥BC，∴∠BCD+∠ADC＝180°，∴∠ADC＝∠BCD＝∠AFC＝90°，∴四边形ADCF是矩形，∵∠CAD＝45°，∴AD＝CD，∴四边形ADCF是正方形，∴AF＝AD，∠AFG＝∠ADF＝90°，∴△AFG≌△ADE，∴AG＝AE，∠F AG＝∠DAE，∴∠F AG+∠F AB＝∠EAD+∠F AB＝45°＝∠BAE，∴△BAE≌△BAG，∴BE＝BG＝BF+GF＝BF+DE，设BC＝a，则AB＝4+a，BF＝4﹣a，在Rt△ABF中，42+（4﹣a）2＝（4+a）2，解得a＝1，∴BC＝1，BF＝3，设BE＝b，则DE＝b﹣3，CE＝4﹣（b﹣3）＝7﹣b．在Rt△BCE中，12+（7﹣b）2＝b2，解得b＝，∴BG＝BE＝，∴S△ABE＝S△ABG＝××4＝．例题2 如图，在四边形ABCD中，AB=BC，∠A=∠C=90°，∠B=135°，K，N分别是AB，BC上的点，若△BKN的周长为AB的2倍，求∠KDN的度数.变式练习>>>2. 如图，正方形被两条与边平行的线段EF，GH分割成四个小矩形，P是EF与GH的交点，若矩形PFCH 的面积恰是矩形AGPE面积的2倍，试确定∠HAF的大小并证明你的结论.。

角含半角模型

角含半角模型第九章：半角模型模型1：倍长中线或类中线构造全等三角形，已知如下条件：①∠2=1/2∠AOB；②OA=OB。

连接F′B，将△FOB绕点O旋转至△FOA的位置，连接F′E、FE，可得△OEF′≌△OEF。

分析：1）半角模型的命名：存在两个角度是一半关系，并且这两个角共顶点；2）通过先旋转全等再轴对称全等，一般结论是证明线段和差关系；3）常见的半角模型是90°含45°，120°含60°。

实例：例1：在四边形ABCD中，∠B+∠D=180°，AB=AD，E、F分别是线段BC、CD上的点，且BE+FD=EF。

求证：∠EAF=1/2∠BAD。

例2：在四边形ABCD中，∠B+∠ADC=180°，AB=AD，E、F分别是BC、CD延长线上的点，且∠EAF=1/2∠BAD。

求证：EF=BE-FD。

例3：在等边△ABC的两边AB、AC上分别有两点M、N，D为△ABC外一点，且∠MDN=60°，∠BDC=120°，BD=DC。

探究：当M、N分别在线段AB、AC上移动时，BM、NC、MN之间的数量关系。

1）当DM=DN时，BM、NC、MN之间的数量关系是；2）当DM≠DN时，猜想（1）的结论是否成立，需要证明；例4：在等边△ABC中，点O是边AC、BC的垂直平分线的交点，M、N分别在直线AC、BC上，且∠MON=60°。

1）当CM=CN时，M、N分别在边AC、BC上时，AM、CN、MN三者之间的数量关系是；2）当CM≠CN时，需要证明（1）中的结论是否成立；3）当点M在边AC上，点N在BC的延长线上时，AM、CN、MN三者之间的数量关系是。

例5：在正方形ABCD中，∠MAN=45°，它的两边分别交线段CB、DC于点M、N。

求证：BM+DN=MN。

2作AH⊥XXX于点H，证明AH=AB。

在直角三角形ABH中，由勾股定理可得：AH²=AB²-BH²。

专题相似三角形中的半角模型(学生版)

专题10相似三角形中的半角模型相似三角形在中考数学几何模块中占据着重要地位。

相似三角形与其它知识点结合以综合题的形式呈现，其变化很多，难度大，是中考的常考题型。

如果大家平时注重解题方法，熟练掌握基本解题模型，再遇到该类问题就信心更足了。

本专题就半角模型进行梳理及对应试题分析，方便掌握。

模型1.半角模型（相似模型）【常见模型及结论】1）半角模型（正方形中的半角相似模型）条件：已知，如图，在正方形ABCD 中，∠EAF 的两边分别交BC 、CD 边于M 、N 两点，且∠EAF ＝45°结论：如图1，△AMN ∽△AFE 且AF AE EF AM AN MN===．（思路提示：∠ANM=∠AEF ，∠AMN=∠AFE ）；图1图2结论：如图2，△MAN ∽△MDA ，△NAM ∽△NBA ；结论：如图3，连接AC ，则△AMB ∽△AFC ，△AND ∽△AEC ．且AF AC AM AB==；图3图4结论：如图4，△BME ∽△AMN ∽△DFN.（2）半角模型（特殊三角形中的半角相似模型）（1）含45°半角模型图1条件：如图1，已知∠BAC ＝90°，45ABC ACB DAE ∠=∠=∠=︒；结论：①△ABE ∽△DAE ∽△DCA ；②AB AD CD BE AE AC==；③AB AC BE CD ⋅=⋅（2AB BE CD =⋅）（2）含60°半角模型条件：如图2，已知∠BAC ＝120°，60ADE DAE ∠=∠=︒；结论：①△ABD ∽△CAE ∽△CBA ；②AD CE AC BD AE AB==；③AD AE BD CE ⋅=⋅（2DE BD CE =⋅）图2分别是分别在边M例7．（2022·广东深圳·统考二模）【教材呈现】（1）如图1，在同一平面内，将两个全等的等腰直角三角形ABC 和AFG 摆放在一起，点A 为公共顶点，90BAC G ∠=∠=︒，若ABC 固定不动，将AFG 绕点A 旋转，边AF ，AG 与边BC 分别交于点D ，E （点D 不与点B 重合，点E 不与点C 重合），则结论2BE CD AB ⋅=是否成立______（填“成立”或“不成立”）；【类比引申】（2）如图2，在正方形ABCD 中，EAF ∠为BAD ∠内的一个动角，两边分别与BD ，BC 交于点E ，F ，且满足EAF ADB ∠=∠，求证：ADE ACF ∽；【拓展延伸】（3）如图3，菱形ABCD 的边长为12cm ，120BAD ∠=︒，EAF ∠的两边分别与BD ，BC 相交于点E ，F ，且满足EAF ADB ∠=∠，若9cm BF =，则线段DE 的长为______cm ．A ．4B ．32．（2022·广东深圳·统考一模）如图，正方形与对角线BD 交于点M ，N ，连接④::2:5:3DN MN BM =3．如图，正方形ABCD 中，ABC 绕点A 逆时针旋转到AB C ''△，AB '、AC '分别交对角线BD 于点E 、F ，若4AE =，则EF ED ⋅的值为（）A ．4B ．6C ．8D ．164．如图，菱形ABCD 的边长为4，E ，F 分别是AB ，AD 边上的动点，BE AF =，120BAD ∠=︒，则下列结论：①BEC AFC ∆∆≌；②ECF ∆为等边三角形；③AGE AFC ∠=∠；④若1AF =，则12GF GE =．其中正确个数为（）A ．4B ．3C ．2D ．16．（2023·成都市·九年级专题练习）如图，在将△ADC 绕点A 顺时针旋转90°后，得到△的面积等于四边形AFBD 的面积；④BE 7．（2023·上海宝山·校考一模）如图，在△么DE BC 的值是．8．（2023春·辽宁沈阳·八年级统考期中）通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的.下面是一个案例，请补充完整．原题：如图1，点E ，F 分别在正方形ABCD 的边BC ，CD 上，45EAF ∠=︒，连接EF ，则EF BE DF =+，试说明理由．(1)思路梳理AB CD =，∴把ABE 绕点A 逆时针旋转90︒至ADG △，可使AB 与AD 重合.90180ADC B FDG ∠=∠=︒∠=︒，，∴点F ，D ，G 共线.根据______(从“SSS ，ASA ，AAS ，SAS ”中选择填写)，易证AFG ≌△______，得EF BE DF =+．(2)类比引申如图2，四边形ABCD 中，AB AD =，90BAD ∠=︒，点E ，F 分别在边BC ，CD 上，45.EAF ∠=︒若B ∠，D ∠都不是直角，则当B ∠与D ∠满足等量关系______时，仍有EF BE DF =+．(3)联想拓展如图3，在ABC 中，90BAC ∠=︒，AB AC =，点D ，E 均在边BC 上，且45.DAE ∠=︒猜想BD ，DE ，EC 应满足的等量关系，并写出推理过程．(4)思维深化如图4，在ABC 中，60BAC ∠=︒，AB AC =，点D ，E 均在直线BC 上，点D 在点E 的左边，且30DAE ∠=︒，当4AB =，1BD =时，直接写出CE 的长．9．（2023·陕西西安·九年级校考期中）问题研究，如图，在等腰ABC 中，AB AC =，点D 、E 为底边BC 上的两个动点（不与B 、C 重合），且DAE B ∠=∠．（1）请在图中找出一个与ABE 相似的三角形，这个三角形是__________；（2）若90BAC ∠=︒，分别过点D 、E 作AB 、AC 的垂线，垂足分别为F 、G ，且DF 、EG 的反向延长线交于点M ，若1AB =，求四边形AFMG 的面积；问题解决（3）如图所示，有一个矩形仓库ABCD ，其中40AB =米，30AD =米，现计划在仓库的内部的E 、F 两处分别安装监控摄像头，其中点E 在边BC 上，点F 在边DC 上．设计要求45EAF ∠=︒且CE CF =，则CE 的长应为多少米？12．（2022秋·广东·九年级深圳市福田区北环中学校考期中）如图①，在正方形ABCD中，点N、M分别在边BC、CD上，连接AM、AN、MN．∠MAN＝45°，将△AMD绕点A顺时针旋转90°，点D与点B重合，得到△ABE．易证：△ANM≌△ANE，从而得DM＋BN＝MN．【实践探究】(1)在图①条件下，若CN＝6，CM＝8，则正方形ABCD的边长是______．(2)如图②，点M、N分别在边CD、AB上，且BN＝DM．点E、F分别在BM、DN上，∠EAF＝45°，连接EF，猜想三条线段EF、BE、DF之间满足的数量关系，并说明理由．(3)【拓展应用】如图③，在矩形ABCD中，AB＝6，AD＝8，点M、N分别在边DC、BC上，连接AM，AN，已知∠MAN＝45°，BN＝2，求DM的长．13．（2023春·江苏·八年级专题练习）问题背景：如图1，在正方形ABCD 中，点E F 、分别在边BC CD 、上，45EAF ∠=︒，求证：EF BE DF =+．洋洋同学给出了部分证明过程，请你接着完成剩余的证明过程．证明：延长FD 到点P 使DP BE =，连接AP ，正方形ABCD ，90AB AD ADP ABE ∴∠∠︒=，==，在 Rt ABE △和Rt ADP △中，AB AD ABE ADP BE DP =⎧⎪∠=∠⎨⎪=⎩()Rt ABE Rt ADP SAS ∴△≌△迁移应用：如图2，在正方形ABCD 中，QA QB 、交CD 于点G H 、，若45AQB ∠=︒，31CH GH ==，，求AG 的长．联系拓展：如图3，在矩形ABCD 中，点E F 、分别在边BC CD 、上，45EAF ∠=︒，若::1:2:4DF AD AB =，探究BE 与EC 的数量关系，并给出证明．14．（2023·浙江杭州·九年级期中）已知正方形ABCD 的边长为4，一个以点A 为顶点的45°角绕点A 旋转，角的两边分别与边BC 、DC 的延长线交于点E 、F ，连接EF ．设,CE a CF b ==．（1）如图1，当EAF ∠被对角线AC 平分时，求a 、b 的值；（2）当AEF △是直角三角形时，求a 、b 的值；（3）如图3，探索EAF ∠绕点A 旋转的过程中，CEF △的面积是否发生变化？请说明理由．统考中考真题）数学兴趣小组探究了以下几何图形．如图【探究一】如图②，把CDM V 绕点C 逆时针旋转90︒得到CBH ，同时得到点H 在直线AB 上．求证：CNM CNH ∠=∠【探究二】在图②中，连接BD ，分别交CM ，CN 于点E ，F ．求证：CEF CNM △∽△；【探究三】把三角尺旋转到如图③所示位置，直线BD 与三角尺45︒角两边CM ，CN 分别交于点E ，F ．连接AC 交BD 于点O ，求EF NM 的值．。

(完整版)初中数学九大几何模型

初中数学九大几何模型一、手拉手模型----旋转型全等（1）等边三角形【条件】：△OAB 和△OCD 均为等边三角形；【结论】：①△OAC ≌△OBD ；②∠AEB=60°；③OE 平分∠AED （2）等腰直角三角形【条件】：△OAB 和△OCD 均为等腰直角三角形；【结论】：①△OAC ≌△OBD ；②∠AEB=90°；③OE 平分∠AED （3）顶角相等的两任意等腰三角形【条件】：△OAB 和△OCD 均为等腰三角形；且∠COD=∠AOB【结论】：①△OAC ≌△OBD ； ②∠AEB=∠AOB ； ③OE 平分∠AEDOABC DE图 1OABC D E图 2OABCDE图 1OABCDE图 2OABC DEOABCD E图 1图 2二、模型二：手拉手模型----旋转型相似（1）一般情况【条件】：CD ∥AB ，将△OCD 旋转至右图的位置【结论】：①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ； ②延长AC 交BD 于点E ，必有∠BEC=∠BOA （2）特殊情况【条件】：CD ∥AB ，∠AOB=90°将△OCD 旋转至右图的位置【结论】：①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ； ②延长AC 交BD 于点E ，必有∠BEC=∠BOA ； ③===OAOBOC OD AC BD tan ∠OCD ；④BD ⊥AC ； ⑤连接AD 、BC ，必有2222CD AB B C AD +=+；⑥BD AC 21S △BCD ⨯=三、模型三、对角互补模型（1）全等型-90°【条件】：①∠AOB=∠DCE=90°；②OC 平分∠AOB【结论】：①CD=CE ；②OD+OE=2OC ；③2△OCE △OCD △DCE OC 21S S S =+= 证明提示：①作垂直，如图2，证明△CDM ≌△CEN②过点C 作CF ⊥OC ，如图3，证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时（如图4）：以上三个结论：①CD=CE ；②OE-OD=2OC ； ③2△OCD △OCE OC 21S S =-OB CO ACDEOB CDEOA C DAO BCDE图 1A OBCDE M N 图 2A OBCDEF图 3A O BCDEMN 图 4（2）全等型-120°【条件】：①∠AOB=2∠DCE=120°；②OC 平分∠AOB【结论】：①CD=CE ；②OD+OE=OC ；③2△OCE △OCD △DCE OC 43S S S =+=证明提示：①可参考“全等型-90°”证法一；②如右下图：在OB 上取一点F ，使OF=OC ，证明△OCF 为等边三角形。

2023年中考数学常见几何模型之全等模型-半角模型

专题02 全等模型--半角模型全等三角形在中考数学几何模块中占据着重要地位，也是学生必须掌握的一块内容，本专题就半角模型进行梳理及对应试题分析，方便掌握。

模型1.半角模型【模型解读】过等腰三角形顶点两条射线，使两条射线的夹角为等腰三角形顶角的一半这样的模型称为半角模型。

【常见模型及证法】常见的图形为正方形，正三角形，等腰直角三角形等，解题思路一般是将半角两边的三角形通过旋转到一边合并成新的三角形，从而进行等量代换，然后证明与半角形成的三角形全等，再通过全等的性质得到线段之间的数量关系。

半角模型（题中出现角度之间的半角关系）利用旋转——证全等——得到相关结论.1．（2022·湖北十堰·中考真题）【阅读材料】如图①，四边形ABCD 中，AB AD =，180B D ∠+∠=︒，点E ，F 分别在BC ，CD 上，若2BAD EAF ∠∠=，则EF BE DF =+．【解决问题】如图②，在某公园的同一水平面上，四条道路围成四边形ABCD ．已知100m CD CB ==，60D ∠=︒，120ABC ∠=︒，150BCD ∠=︒，道路AD ，AB 上分别有景点M ，N ，且100m DM =，)501m BN =，若在M ，N 之间修一条直路，则路线M N →的长比路线M A N →→的长少_________m （结果取整数，参考数据：1.7≈）．【答案】370【分析】延长,AB DC 交于点E ，根据已知条件求得90E ∠=︒,进而根据含30度角的直角三角形的性质，求得,EC EB ，,AE AD ，从而求得AN AM +的长，根据材料可得MN DM BN =+，即可求解．【详解】解：如图，延长,AB DC 交于点E ，连接,CM CN ，Q 60D ∠=︒，120ABC ∠=︒，150BCD ∠=︒，30A ∴∠=︒，90E ∠=︒，100DC DM ==Q ∴△DCM 是等边三角形，60DCM ∴∠=︒,90BCM ∴∠=︒,在Rt BCE V 中，100BC =，18030ECB BCD ∠=︒−∠=︒，1502EB BC ==，EC =100DE DC EC ∴=+=+Rt ADE △中，2200AD DE ==+150AE =， ∴200100100AM AD DM =−=+=+()AN AB BN AE EB BN =−=−−())15050501=−−150=，100150250AM AN ∴+=+=+Rt CMB △中，BM ==Q )50501EN EB BN EC =+=+==∴△ECN 是等腰直角三角形()1752NCM BCM NCB BCM NCE BCE DCB ∴∠=∠−∠=∠−∠−∠=︒=∠由阅读材料可得))100501501MN DM BN =+=+=，∴路线M N →的长比路线M A N →→的长少)250501200370+=+≈m ．答案：370．【点睛】本题考查了含30度角的直角三角形的性质，勾股定理，理解题意是解题的关键．2．（2022·河北邢台·九年级期末）学完旋转这一章，老师给同学们出了这样一道题： “如图1，在正方形ABCD 中，∠EAF ＝45°，求证：EF ＝BE ＋DF ．”小明同学的思路：∵四边形ABCD 是正方形，∴AB ＝AD ，∠B ＝∠ADC ＝90°．把△ABE 绕点A 逆时针旋转到ADE '△的位置，然后证明AFE AFE '≌△△，从而可得=EF E F '．E F E D DF BE DF ''=+=+，从而使问题得证．(1)【探究】请你参考小明的解题思路解决下面问题：如图2，在四边形ABCD 中，AB ＝AD ，∠B ＝∠D ＝90°，12EAF BAD ∠=∠，直接写出EF ，BE ，DF 之间的数量关系． (2)【应用】如图3，在四边形ABCD 中，AB ＝AD ，∠B ＋∠D ＝180°，12EAF BAD ∠=∠，求证：EF ＝BE ＋DF ．(3)【知识迁移】如图4，四边形ABPC 是⊙O 的内接四边形，BC 是直径，AB ＝AC ，请直接写出PB ＋PC 与AP 的关系． ADE ，证明△逆时针旋转，旋转角等于∠BAD ）将△ABP 绕点可知ABE ADE '≌△△，∴由∠ADC +∠ADE =180°知，∵12EAF BAD ∠=∠，∴∠BAF ∴∠DAE '+∠DAF =∠EAF =∴△AEF ≌△AE F '，∴EF =（2）证明：将△ABE 绕点A E '由旋转可知ABE ADE '≌△△，∴BE ∵∠B ＋∠ADC ＝180°，∴ADC ∠+∵12EAF BAD ∠=∠，∴BAE DAF ∠+∠∴12DAE DAF BAD '∠+∠=，∴FAE ∠由圆内接四边形性质得：∠AC 即P ，C ，P '在同一直线上．∴∵BC 为直径，∴∠BAC =90°=∠∴△PAP '为等腰直角三角形，∴【点睛】本题考查了旋转与全等三角形的综合应用、直径所对的圆周角是直角、圆内接四3．（2022·福建·龙岩九年级期中）（1）【发现证明】如图1，在正方形ABCD 中，点E ，F 分别是BC ，CD 边上的动点，且45EAF ∠=︒，求证：EF DF BE =+．小明发现，当把ABE △绕点A 顺时针旋转90°至ADG V ，使AB 与AD 重合时能够证明，请你给出证明过程．（2）【类比引申】①如图2，在正方形ABCD 中，如果点E ，F 分别是CB ，DC 延长线上的动点，且∠EAF =45°，则（1）中的结论还成立吗？若不成立，请写出EF ，BE ，DF 之间的数量关系______（不要求证明）②如图3，如果点E ，F 分别是BC ，CD 延长线上的动点，且45EAF ∠=︒，则EF ，BE ，DF 之间的数量关系是_____（不要求证明）.（3）【联想拓展】如图1，若正方形ABCD 的边长为6，AE =AF 的长．4．（2022·山东省青岛第二十六中学九年级期中）【模型引入】当几何图形中，两个共顶点的角所在角度是公共大角一半的关系，我们称之为“半角模型”【模型探究】（1）如图1，在正方形ABCD中，E、F分别是AB、BC边上的点，且∠EDF ＝45°，探究图中线段EF，AE，FC之间的数量关系．【模型应用】（2）如图2，如果四边形ABCD中，AB＝AD，∠BAD＝∠BCD＝90°，∠EAF ＝45°，且BC＝7，DC＝13，CF＝5，求BE的长．【拓展提高】（3）如图3，在四边形ABCD中，AB＝AD，∠ABC与∠ADC互补，点E、F∠BAD．当BC＝4，DC＝7，CF＝1时，△CEF的周分别在射线CB、DC上，且∠EAF=12长等于．（4）如图4，正方形ABCD中，V AMN的顶点M、N分别在BC、CD边上，AH⊥MN，且AH＝AB，连接BD分别交AM、AN于点E、F，若MH＝2，NH＝3，DF＝EF的长．（5）如图5，已知菱形ABCD中，∠B=60°，点E、F分别是边BC，CD上的动点（不与端点重合），且∠EAF=60°．连接BD分别与边AE、AF交于M、N，当∠DAF＝15°时，求证：MN2+DN2=BM2．∵△ADF绕A顺时针旋转得△ABG，∴∠BAG=∠DAF，又AH=AN，AB=AD，∴△ABH≌△ADN（SAS），∴DN=BH，∠ABH=∠ADN，∵∠B=60°，且∠EAF=60°．∴∠BAD=120°，∴∠DAF+∠BAE=∠EAF=60°，∴∠BAG+∠BAE=∠EAF，即∠MAH=∠MAN，而AH=AN，AM=AM，∴△AMH≌△AMN（SAS），∴MN=MH，∠AMN=∠AMH，∵菱形ABCD，∠B=60°，∴∠ABD=∠ADB=30°，∴∠HBD=∠ABH+∠ABD=60°，∵∠DAF=15°，∠EAF=60°，∴△ADM中，∠DAM=∠AMD=75°，∴∠AMN=∠AMH=75°，∴∠HMB=180°-∠AMN-∠AMH=30°，∴∠BHM=90°，∴BH2+MH2=BM2，∴DN2+MN2=BM2．【点睛】本题是四边形综合题，主要考查了旋转的性质、正方形的性质、等腰直角三角形的性质、全等三角形的判定和性质、勾股定理等知识，解题关键是学会用旋转法添加辅助线，构造全等三角形解决问题，学会利用探究的结论解决新的问题，属于中考压轴题．课后专项训练：1．（2022·重庆市育才中学二模）回答问题（1）【初步探索】如图1：在四边形ABCD中，AB=AD，∠B=∠ADC=90°，E、F分别是BC、CD上的点，且EF=BE+FD，探究图中∠BAE、∠F AD、∠EAF之间的数量关系．小王同学探究此问题的方法是：延长FD到点G，使DG=BE．连接AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是_______________；（2）【灵活运用】如图2，若在四边形ABCD中，AB=AD，∠B+∠D=180°．E、F分别是BC、CD上的点，且EF=BE+FD，上述结论是否仍然成立，并说明理由；（3）【拓展延伸】知在四边形ABCD中，∠ABC+∠ADC=180°，AB=AD，若点E在CB的延长线上，点F在CD的延长线上，如图3所示，仍然满足EF=BE+FD，请直接写出∠EAF与∠DAB的数量关系．（2）仍成立，理由：如图2，延长FD 到点G ，使DG =BE ，连接AG ，∵∠B +∠ADF =180°，∠ADG +∠ADF =180°，∴∠B =∠ADG ，又∵AB =AD ，∴△ABE ≌△ADG （SAS ），∴∠BAE =∠DAG ，AE =AG ，∵EF =BE +FD =DG +FD =GF ，AF =AF ，∴△AEF ≌△AGF （SSS ），∴∠EAF =∠GAF =∠DAG +∠DAF =∠BAE +∠DAF ；1∠DAB ．证明：如图3，在DC 延长线上取一点G ，使得2．（2022·江西九江·一模）如图（1），在四边形ABCD 中，180B D ∠+∠=︒，AB AD =，以点A 为顶点作EAF ∠，且12EAF BAD ∠=∠，连接EF ．(1)观察猜想如图（2），当90BAD B D ∠=∠=∠=︒时，①四边形ABCD 是______（填特殊四边形的名称）；②BE ，DF ，EF 之间的数量关系为______．(2)类比探究如图（1），线段BE ，DF ，EF 之间的数量关系是否仍然成立？若成立，请加以证明；若不成立，请说明理由．(3)解决问题如图（3），在ABC V 中，90BAC ∠=︒，4AB AC ==，点D ，E 均在边BC 上，且45DAE ∠=︒，若BD =，求DE 的长．Rt ECM 中，由勾股定理可解得ABCD 是矩形，又∵（2）如下图，延长CD 至点H 同（1）②的证明方法得ABE △BE FD EF +=．（3）如图过点C 作CM BC ⊥在ABC V 中，由90BAC ∠=︒，Rt ECM 中，由勾股定理得，523，即DE 【点睛】本题考查了特殊的平行四边形的判定、全等三角形的性质和判定及勾股定理的应用，熟练应用相关定理和性质是解决本题的关键．3．（2022·山东聊城·九年级期末）（1）如图1，点E ，F 分别在正方形ABCD 的边BC ，CD 上，45EAF ∠=︒，连接EF ，求证：EF BE DF =+，试说明理由．（2）类比引申：如图2，四边形ABCD 中，AB AD =，90BAD ∠=︒，点E ，F 分别在边BC ，CD 上，∠EAF =45°，若B 、D ∠都不是直角，则当B 与D ∠满足等量关系______时，仍有EF BE DF =+，试说明理由．（3）联想拓展：如图3，在△ABC 中，90BAC ∠=︒，AB AC =，点D ，E 均在边BC 上，且∠DAE =45，若1BD =，2EC =，求DE 的长．AB AD =Q ，∴把△ABE 绕点A 逆时针旋转90︒至△ADG ，AB 与AD 重合． ∠ADC =∠B =90°∠FDG =180°，点F 、D 、G 三点共线，则DAG BAE ∠∠=，AE AG =，∠F AG =∠F AD +∠GAD =∠F AD +∠BAE =90°-45°=45°=∠EAF 即∠EAF =∠F AG ，在△EAF 和△GAF 中，AF AF EAF GAF AE AG =⎧⎪∠=∠⎨⎪=⎩， ∴△AFG ≌△()AFE SAS ，∴EF =FG =BE +DF ；()2当180B D ∠+∠=︒，仍有EF BE DF =+．理由：AB AD =Q ，∴把△ABE 绕点A 逆时针旋转90︒至△ADG ，可使AB 与AD 重合，如图2，BAE DAG ∴∠=∠，∠B =∠ADG90BAD ∠=︒，45EAF ∠=︒，∴∠BAE +∠DAF =45°，∴∠F AG =45°∴∠EAF =∠F AG ， 180ADC B ∠+∠=︒Q ，∴∠ADC +∠ADG =180°∴∠FDG =180°，点F 、D 、G 共线．在△AFE 和△AFG 中，AE AG FAE FAG AF AF =⎧⎪∠=∠⎨⎪=⎩∴△AFE ≌△AFG (SAS)．EF FG ∴=，即：EF BE DF =+．故答案为：180B D ∠+∠=︒．()3将△ACE 绕点A 旋转到△ABF 的位置，连接DF ，则∠F AB =∠CAE90BAC ∠=︒Q ，45DAE ∠=︒，∴∠BAD +∠CAE =45°．又∵∠F AB =∠CAE ，∴∠F AB +∠BAD =45°，∴∠F AD =∠DAE =45°．则在△ADF 和△ADE 中， AD AD =，∠F AD =∠DAE ，AF AE =，4．（2022·黑龙江九年级阶段练习）已知：正方形ABCD 中，∠MAN=45°，∠MAN 绕点A 顺时针旋转，它的两边分别交CB 、DC （或它们的延长线）于点M 、N ．当∠MAN 绕点A 旋转到BM =DN 时，（如图1），易证BM +DN =MN ．(1)当∠MAN 绕点A 旋转到BM ≠DN 时（如图2），线段BM 、DN 和MN 之间有怎样的数量关系？写出猜想，并加以证明；(2)当∠MAN 绕点A 旋转到如图3的位置时，线段BM 、DN 和MN 之间又有怎样的数量关系？请直接写出你的猜想．【答案】(1)BM DN MN +=，理由见解析；(2)DN BM MN −=，理由见解析【分析】（1）把ADN ∆绕点A 顺时针旋转90︒，得到ABE ∆，然后证明得到AEM ANM ∆∆≌，从而证得ME MN =，可得结论；（2）首先证明ADQ ABM ∆∆≌，得DQ BM =，再证明AMN AQN ∆∆≌，得MN QN =，可得结论；（1）解：BM DN MN +=．理由如下：如图2，把ADN ∆绕点A 顺时针旋转90︒，得到ABE ∆，90ABE ADN ∴∠=∠=︒，AE AN =，BE DN =，180ABE ABC ∴∠+∠=︒，∴点E ，点B ，点C 三点共线，90904545EAM NAM ∴∠=︒−∠=︒−︒=︒，又45NAM ∠=︒Q ，在AEM ∆与ANM ∆中，AE AN EAM NAM AM AM =⎧⎪∠=∠⎨⎪=⎩，AEM ANM ∴∆∆≌（SAS ），ME MN ∴=， ME BE BM DN BM =+=+Q ，DN BM MN ∴+=；（2）解：DN BM MN −=．理由如下：在线段DN 上截取DQ BM =，在ADQ ∆与ABM ∆中，AD AB ADQ ABM DQ BM =⎧⎪∠=∠⎨⎪=⎩，ADQ ABM ∴∆∆≌（SAS ）， DAQ BAM ∴∠=∠，QAN MAN ∴∠=∠．在AMN ∆和AQN ∆中，AQ AM QAN MAN AN AN =⎧⎪∠=∠⎨⎪=⎩，AMN AQN ∴∆∆≌（SAS ）， MN QN ∴=，DN BM MN ∴−=．【点睛】本题是四边形综合题，考查正方形的性质，旋转变换，全等三角形的判定和性质，勾股定理等知识，解题的关键是学会利用旋转法添加辅助线，构造全等三角形解决问题．5．（2022·重庆南川·九年级期中）如图，正方形ABCD 中，45MAN ∠=︒，MAN ∠绕点A 顺时针旋转，它的两边分别交BC 、DC （或它们的延长线）于点M 、N ．(1)当MAN ∠绕点A 旋转到BM DN =时（如图1），证明：2MN BM =；(2)绕点A 旋转到BM DN ≠时（如图2），求证：MN BM DN =+；(3)当MAN ∠绕点A 旋转到如图3位置时，线段BM 、DN 和MN 之间有怎样的数量关系？请写出你的猜想并证明．【答案】(1)见解析(2)见解析(3)DN BM MN −=，见解析【分析】（1）把ADN △绕点A 顺时针旋转90︒，得到ABE △，证得B 、E 、M 三点共线，即可得到AEM △≌ANM V ，从而证得ME MN =；（2）证明方法与（1）类似；（3）在线段DN 上截取DQ BM =，判断出ADQ △≌ABM V ，同（2）的方法，即可得出结论．（1）证明：如图1，∵把ADN △绕点A 顺时针旋转90︒，得到ABE △，ABE ∴V ≌ADN △，AE ANM ∴=，ABE D ∠=∠，Q 四边形ABCD 是正方形，90ABC D ∴∠=∠=︒，90ABE ABC ∴∠=∠=︒，∴点E 、B 、M 三点共线．90904545EAM NAM ∴∠=︒−∠=︒−︒=︒，又45NAM ∠=︒Q ，在AEM △与ANM V 中，AE AN EAM NAM AM AM =⎧⎪∠=∠⎨⎪=⎩，AEM ∴△≌()ANM SAS V ，ME MN ∴=，ME BE BM DN BM =+=+Q ，DN BM MN ∴+=，BM DN =Q ，2MN BM ∴=．（2）证明：如图2，把ADN △绕点A 顺时针旋转90︒，得到ABE △，ABE ∴V ≌ADN △，AE ANM ∴=，ABE D ∠=∠，Q 四边形ABCD 是正方形，90ABC D ∴∠=∠=︒，90ABE ABC ∴∠=∠=︒，∴点E 、B 、M 三点共线．90904545EAM NAM ∴∠=︒−∠=︒−︒=︒，又45NAM ∠=︒Q ，在AEM △与ANMV 中，AE AN EAM NAM AM AM =⎧⎪∠=∠⎨⎪=⎩，AEM ∴△≌()ANM SAS V ，ME MN ∴=，ME BE BM DN BM =+=+Q ，DN BM MN ∴+=．（3）解：DN BM MN −= 理由如下：如图3，在线段DN 上截取DQ BM =，连接AQ ，在ADQ △与ABM V 中，AD AB ADQ ABM DQ BM =⎧⎪∠=∠⎨⎪=⎩，ADQ ∴≌()ABM SAS V ，DAQ BAM ∴∠=∠，QAN MAN ∴∠=∠．在AMN V 和AQN △中，AQ AM QAN MAN AN AN =⎧⎪∠=∠⎨⎪=⎩，AMN ∴V ≌()AQN SAS V ，MN QN ∴=，DN BM MN ∴−=．【点睛】本题是四边形综合题，考查正方形的性质，旋转变换，全等三角形的判定和性质，勾股定理等知识，学会利用旋转法添加辅助线，构造全等三角形是解题的关键．6．（2022·江西景德镇·九年级期中）（1）【特例探究】如图1，在四边形ABCD 中，AB AD =，90ABC ADC ∠=∠=︒，100BAD ∠=︒，50EAF ∠=︒，猜想并写出线段BE ，DF ，EF 之间的数量关系，证明你的猜想；（2）【迁移推广】如图2，在四边形ABCD 中，AB AD =，180ABC ADC ∠+∠=︒，2BAD EAF ∠∠=．请写出线段BE ，DF ，EF 之间的数量关系，并证明；（3）【拓展应用】如图3，在海上军事演习时，舰艇在指挥中心（O 处）北偏东20°的A处．舰艇乙在指挥中心南偏西50°的B 处，并且两舰艇在指挥中心的距离相等，接到行动指令后，舰艇甲向正西方向以80海里/时的速度前进，同时舰艇乙沿北偏西60°的方向以90海里/时的速度前进，半小时后，指挥中心观测到甲、乙两舰艇分别到达C ，D 处，且指挥中心观测两舰艇视线之间的夹角为75°．请直接写出此时两舰艇之间的距离．【答案】（1）EF =BE +DF ，理由见解析；（2）EF =BE +DF ，理由见解析；（3）85海里【分析】（1）延长CD 至点G ，使DG =BE ，连接AG ，可证得△ABE ≌△ADG ，可得到AE =AG ，∠BAE =∠DAG ，再由100BAD ∠=︒，50EAF ∠=︒，可证得△AEF ≌△AGF ，从而得到EF =FG ，即可求解；（2）延长CD 至点H ，使DH =BE ，连接AH ，可证得△ABE ≌△ADH ，可得到AE =AH ，∠BAE =∠DAH ，再由2BAD EAF ∠∠=，可证得△AEF ≌△AHF ，从而得到EF =FH ，即可求解；（3）连接CD ，延长AC 、BD 交于点M ，根据题意可得∠AOB =2∠COD ，∠OAM +∠OBM =70°+110°=180°，再由（2）【迁移推广】得：CD =AC +BD ，即可求解．【详解】解：（1）EF =BE +DF ，理由如下：如图，延长CD 至点G ，使DG =BE ，连接AG ，∵90ABC ADC ∠=∠=︒，∴∠ADG =∠ABC =90°，∵AB =AD ，∴△ABE ≌△ADG ，∴AE =AG ，∠BAE =∠DAG ，∵100BAD ∠=︒，50EAF ∠=︒，∴∠BAE +∠DAF =50°，∴∠F AG =∠EAF =50°，∵AF =AF ，∴△AEF ≌△AGF ，∴EF =FG ，∵FG =DG +DF ，∴EF =DG +DF =BE +DF ；（2）EF =BE +DF ，理由如下：如图，延长CD 至点H ，使DH =BE ，连接AH ，∵180ABC ADC ∠+∠=︒，∠ADC +∠ADH =180°，∴∠ADH =∠ABC ，∵AB =AD ，∴△ABE ≌△ADH ，∴AE =AH ，∠BAE =∠DAH ，∵2BAD EAF ∠∠=∴∠EAF =∠BAE +∠DAF =∠DAF +∠DAH ，∴∠EAF =∠HAF ， ∵AF =AF ，∴△AEF ≌△AHF ，∴EF =FH ，∵FH =DH +DF ，∴EF =DH +DF =BE +DF ；（3）如图，连接CD ，延长AC 、BD 交于点M ，根据题意得： ∠AOB =20°+90°+40°=150°，∠OBD =60°+50°=110°，∠COD =75°，∠OAM =90°-20°=70°，OA =OB ，∴∠AOB =2∠COD ，∠OAM +∠OBM =70°+110°=180°，∵OA =OB ，∴由（2）【迁移推广】得：CD =AC +BD ，∵AC =80×0.5=40，BD =90×0.5=45，∴CD =40+45=85海里．即此时两舰艇之间的距离85海里．【点睛】此题是三角形综合题，主要考查了全等三角形的判定和性质、勾股定理的运用、等腰直角三角形的性质，题目的综合性较强，难度较大，解题的关键是正确的作出辅助线构造全等三角形，解答时，注意类比思想的应用．7．（2022·上海·九年级专题练习）小明遇到这样一个问题：如图1，在Rt △ABC 中，∠BAC＝90°，AB ＝AC ，点D ，E 在边BC 上，∠DAE ＝45°．若BD ＝3，CE ＝1，求DE 的长．小明发现，将△ABD 绕点A 按逆时针方向旋转90º，得到△ACF ，联结EF （如图2），由图形旋转的性质和等腰直角三角形的性质以及∠DAE ＝45°，可证△F AE ≌△DAE ，得FE ＝DE ．解△FCE ，可求得FE （即DE ）的长．(1)请回答：在图2中，∠FCE 的度数是，DE 的长为．参考小明思考问题的方法，解决问题：(2)如图3，在四边形ABCD 中，AB ＝AD ，∠B ＋∠D ＝180°．E ，F 分别是边BC ，CD 上的点，且∠EAF ＝12∠BAD ．猜想线段BE ，EF ，FD 之间的数量关系并说明理由．）根据旋转的性质，可得ADB AFC ≌，勾股定理解按逆时针方向旋转，使AB 与AD 重合，得到△AEF ≌△AGF ，EF ＝∴ADB AFC ≌ACF ∴∠,90AB AC BAC ∠==45ACF ABD ∴∠=∠=︒Rt FCE 中，Q BD ＝2EF CF =+猜想：EF =BE 如图，将△ABE8．（2022·黑龙江·哈尔滨市九年级阶段练习）已知四边形ABCD是正方形，一个等腰直角三角板的一个锐角顶点与A点重合，将此三角板绕A点旋转时，两边分别交直线BC，CD 于M，N．(1)如图1，当M，N分别在边BC，CD上时，求证：BM+DN=MN(2)如图2，当M，N分别在边BC，CD的延长线上时，请直接写出线段BM，DN，MN之间的数量关系(3)如图3，直线AN与BC交于P点，MN=10，CN=6，MC=8，求CP的长．【答案】（1）见解析；（2）BM DN MN −=；（3）3【分析】（1）延长CB 到G 使BG DN =，连接AG ，先证明AGB AND ≅△△，由此得到AG AN =，GAB DAN ∠=∠，再根据45MAN ∠=︒，90BAD ∠=︒，可以得到45GAM NAM ∠=∠=︒，从而证明AMN AMG △≌△，然后根据全等三角形的性质即可证明BM DN MN +=；（2）在BM 上取一点G ，使得BG DN =，连接AG ，先证明AGB AND ≅△△，由此得到AG AN =，GAB DAN ∠=∠，由此可得90GAN BAD ∠=∠=︒，再根据45MAN ∠=︒可以得到45GAM NAM ∠=∠=︒，从而证明AMN AMG △≌△，然后根据全等三角形的性质即可证明BM DN MN −=；（3）在DN 上取一点G ，使得DG BM =，连接AG ，先证明ABM ADG V V ≌，再证明AMN AGN △≌△，设DG BM x ==，根据DC BC =可求得2x =，由此可得6AB BC CD CN ====，最后再证明ABP NCP △≌△，由此即可求得答案．【详解】（1）证明：如图，延长CB 到G 使BG DN =，连接AG ，∵四边形ABCD 是正方形，∴AB AD =，90ABG ADN BAD ∠=∠=∠=︒，在ABG V 与ADN △中，AB AD ABG ADN BG DN =⎧⎪∠=∠⎨⎪=⎩， ()AGB AND SAS ∴△≌△，AG AN ∴=，GAB DAN ∠=∠，45MAN ∠=︒Q ，90BAD ∠=︒，∴45DANBAM BAD MAN ∠+∠=∠−∠=︒，45GAM GAB BAM DAN BAM ∴∠=∠+∠=∠+∠=︒，GAM NAM ∴∠=∠，在AMN V 与AMG V 中，AM AM GAM NAM AN AG =⎧⎪∠=∠⎨⎪=⎩， ()AMN AMG SAS ∴△≌△，MN GM ∴=，又∵BM GB GM +=，BG DN =，BM DN MN ∴+=；（2）BM DN MN −=，理由如下：如图，在BM 上取一点G ，使得BG DN =，连接AG ，∵四边形ABCD 是正方形，∴AB AD =，90ABG ADN BAD ∠=∠=∠=︒，在ABG V 与ADN △中，AB AD ABG ADN GB DN =⎧⎪∠=∠⎨⎪=⎩，()AGB AND SAS ∴△≌△，AG AN ∴=，GAB DAN ∠=∠，∴GAB GAD DAN GAD ∠+∠=∠+∠，∴90GAN BAD ∠=∠=︒，又45MAN ∠=︒Q ，45GAM GAN MAN MAN ∴∠=∠−∠=︒=∠，在AMN V 与AMG V 中，AM AM GAM NAM AN AG =⎧⎪∠=∠⎨⎪=⎩，()AMN AMG SAS ∴△≌△，MN GM ∴=，又∵BM BG GM −=，BG DN =，∴BM DN MN −=，故答案为：BM DN MN −=；（3）如图，在DN 上取一点G ，使得DG BM =，连接AG ，9．（2022·浙江·九年级阶段练习）如图1，等腰直角三角板的一个锐角顶点与正方形ABCD的顶点A重合，将此三角板绕点A旋转，使三角板中该锐角的两条边分别交正方形的两边BC，DC于点E，F，连接EF．（1）猜想BE、EF、DF三条线段之间的数量关系，并证明你的猜想；（2）在图1中，过点A作AM⊥EF于点M，请直接写出AM和AB的数量关系；（3）如图2，将Rt△ABC沿斜边AC翻折得到Rt△ADC，E，F分别是BC，CD边上的∠BAD，连接EF，过点A作AM⊥EF于点M，试猜想AM与AB之间的数点，∠EAF=12量关系．并证明你的猜想．10．（2022·北京四中九年级期中）如图，在△ABC中，∠ACB=90°，CA=CB，点P在线段AB上，作射线CP（0°＜∠ACP＜45°)，射线CP绕点C逆时针旋转45°，得到射线CQ，过点A作AD⊥CP于点D，交CQ于点E，连接BE．(1)依题意补全图形；(2)用等式表示线段AD，DE，BE之间的数量关系，并证明．【答案】(1)作图见解析．(2)结论：AD+BE=DE．证明见解析．【分析】（1）根据要求作出图形即可．（2）结论：AD +BE =DE ．延长DA 至F ，使DF=DE ，连接CF ．利用全等三角形的性质解决问题即可．（1）解：如图所示：（2）结论：AD +BE =DE ．理由：延长DA 至F ，使DF =DE ，连接CF ．∵AD ⊥CP ，DF =DE ，∴CE =CF ，∴∠DCF =∠DCE =45°，∵∠ACB =90°，∴∠ACD +∠ECB =45°，∵∠DCA +∠ACF =∠DCF =45°，∴∠FCA =∠ECB ，在△ACF 和△BCE 中，CA CB ACF BCE CF CE =⎧⎪∠=∠⎨⎪=⎩，∴△ACF ≌△BCE （SAS ），∴AF =BE ，∴AD +BE =DE ．【点睛】本题考查作图-旋转变换，全等三角形的判定和性质，等腰直角三角形的判定和性质等知识，解题的关键是正确寻找全等三角形解决问题，属于中考常考题型．。

初三数学几何专题旋转--“对角互补角含半角”模型

“对角互补+角含半角”旋转模型知识点：1. 旋转的定义及其性质；2. 旋转对称图形和中心对称图形；3. 旋转的对角互补模型；4. 旋转的角含半角模型．教学目标：1. 理解旋转的定义和性质；2. 熟记旋转的模型；3. 知道旋转对角互补模型和角含半角模型的特点；4. 会根据旋转的对角互补模型和角含半角模型解决几何问题．教学重点：1. 会根据旋转的对角互补模型和角含半角模型解决几何问题．教学难点：1. 会根据旋转的对角互补模型和角含半角模型解决几何问题．难度 ★1、如图，在等腰直角三角形ABC 中，∠ABC=90°，D 为AC 边上的中点，过点D 作DE ⊥DF ，交AB 于点D ，交BC 于点F ，若AE=4，FC=3，则EF 的长为．【思路点拨】连接BD ，根据的等腰直角三角形的性质证明△BED ≌△CFD （ASA ），得出AE=BF 、BE=CF ，由AE=BF=4，FC=BE=3，由勾股定理就可以求得EF 的长．【解析】解：连接BD ．∵D 是AC 中点，∴∠ABD=∠CBD=45°，BD=AD=CD ，BD ⊥AC ∵∠EDB+∠FDB=90°，∠FDB+∠CDF=90°，∴∠EDB=∠CDF ，在△BED 和△CFD 中，⎪⎩⎪⎨⎧∠∠CDF ＝EDB ∠CD ＝BD C＝EBD ∠，∴△BED ≌△CFD （ASA ），∴BE=CF ；∵AB=BC ，BE=CF=3，∴AE=BF=4，在Rt △BEF 中，EF=22BF BE +=2243+=5；故答案为：5．难度 ★2、如图，正方形ABCD 的边长为1，AB 、AD 上各存一点P 、Q ，若△APQ 的周长为2，求∠PCQ 的度数．【思路点拨】角含半角模型的倒推，需要旋转，将△APQ 的周长转化成正方形两边长之和，可得∠PCQ的度数．【解析】解：如图所示，△APQ 的周长为2，即AP+AQ+PQ=2①，正方形ABCD 的边长是1，即AQ+QD=1，AP+PB=1， ∴AP+AQ+QD+PB=2②， ①－②得，PQ －QD －PB=0， ∴PQ=PB+QD ．延长AB 至M ，使BM=DQ ．连接CM ，△CBM ≌△CDQ （SAS ）， ∴∠BCM=∠DCQ ，CM=CQ ，∵∠DCQ+∠QCB=90°，∴∠BCM+∠QCB=90°，即∠QCM=90°， PM=PB+BM=PB+DQ=PQ ．在△CPQ 与△CPM 中，CP=CP ，PQ=PM ，CQ=CM ， ∴△CPQ ≌△CPM （SSS ）， ∴∠PCQ=∠PCM=12∠QCM=45°．“图形的旋转”是近几年中考的必考内容，也是中考的热点和重点．运用旋转的全等变换，证明线段与角相等或和、差、倍、分关系，以及在旋转中探索图形的变化，进行图案中心对称选择是近几年中考的常见题型，研究图形旋转变换的变化规律，证明线段之间的数量关系是中考的重点题型，对Q PDCBA角互补和角含半角的旋转模型相对手拉手模型虽少些，但也是旋转模型的考查方向，所以要关注．知识点一旋转（1）定义：在平面内，一个图形绕着一个定点旋转一定的角度得到另一个图形的变化叫作旋转，定点叫作旋转中心，旋转的角度叫作旋转角，如果一个图形上的点A 经过旋转变为A ’，那么这两个点叫做旋转的对应点．（2）性质：①对应点到旋转中心的距离相等； ②旋转前后图形的大小和形状没有改变；③两组对应点分别与旋转中心的连线所成的角相等，都等于旋转角； ④旋转中心是唯一不动的点．（3）旋转三要素：①定点﹣﹣﹣﹣旋转中心 ②旋转方向 ③旋转角度（4）旋转对称图形：在平面内，一个图形绕着一个定点旋转一定的角度后，能够与原图形重合，这样的图形叫旋转对称图形．中心对称图形：在平面内，一个图形绕某一定点旋转180°，能够和原来的图形完全重合，那么这个图形叫作中心对称图形，这个定点叫作对称中心．中心对称：把一个图形绕某一个点旋转180°。

相似三角形中的基本模型-半角模型(解析版)

相似三角形中的基本模型--半角模型相似三角形在中考数学几何模块中占据着重要地位。

相似三角形与其它知识点结合以综合题的形式呈现，其变化很多，难度大，是中考的常考题型。

如果大家平时注重解题方法，熟练掌握基本解题模型，再遇到该类问题就信心更足了。

本专题就半角模型进行梳理及对应试题分析，方便掌握。

模型1.半角模型(相似模型)【常见模型及结论】1)半角模型(正方形中的半角相似模型)条件：已知，如图，在正方形ABCD中，∠EAF的两边分别交BC、CD边于M、N两点，且∠EAF=45°结论：如图1，△AMN∽△AFE且AFAM=AEAN=EFMN=2．(思路提示：∠ANM=∠AEF，∠AMN=∠AFE)；图1图2结论：如图2，△MAN∽△MDA，△NAM∽△NBA；结论：如图3，连接AC，则△AMB∽△AFC，△AND∽△AEC．且AFAM=ACAB=2；图3图4结论：如图4，△BME∽△AMN∽△DFN.2)半角模型(特殊三角形中的半角相似模型)(1)含45°半角模型图1图2条件：如图1，已知∠BAC=90°，∠ABC=∠ACB=∠DAE=45°；结论：①△ABE∽△DAE∽△DCA；②ABBE=ADAE=CDAC；③AB⋅AC=BE⋅CD(AB2=BE⋅CD)(2)含60°半角模型条件：如图1，已知∠BAC=120°，∠ADE=∠DAE=60°；结论：①△ABD∽△CAE∽△CBA；②ADBD=CEAE=ACAB；③AD⋅AE=BD⋅CE(DE2=BD⋅CE)1(2023·山东济南·九年级期中)如图，在正方形ABCD中，点E、F分别是BC、DC边上的两点，且∠EAF=45°，AE、AF分别交BD于M，N．下列结论：①AB2=BN⋅DM；②AF平分∠DFE；③AM⋅AE=AN⋅AF；④BE+DF=2MN．其中正确的结论是()A.①②③④B.①②③C.①③D.①②【答案】A【分析】①转证AB:BN=DM:AB，因为AB=AD，所以即证AB:BN=DM:AD．证明△ABN∽△MDA；②把△ABE绕点A逆时针旋转90°，得△ADH证明△AFH≌△AFE(SAS)；③即证AM:AN=AF:AE，证明△AMN∽△AFE(两角相等)；④由②得BE十DF=EF，当E点与B点重合、F与C重合时，根据正方形的性质，结论成立．【详解】①∵∠BAN=∠BAM+∠MAN=∠BAM+45°，∠AMD=∠ABM+∠BAM=45°+∠BAM，∴∠BAN=∠AMD．又∠ABN=∠ADM=45°，∴△ABN∽△MDA，∴AB:BN=DM:AD，∵AD=AB，∴AB2=BN⋅DM．故①正确；②如图，把△ABE绕点A逆时针旋转90°，得到△ADH，∵∠BAD=90°，∠EAF=45°，∴∠BAE+∠DAF=45°．∴∠EAF=∠HAF，∵AE=AH，AF=AF，∴△AEF≌△AHF，∴∠AFH =∠AFE ，即AF 平分∠DFE ，故②正确；③∵AB ∥CD ，∴∠DFA =∠BAN ，∵∠AFE =∠AFD ，∠BAN =∠AMD ，∴∠AFE =∠AMN ，又∠MAN =∠FAE ，∴△AMN ∽△AFE ，∴AM :AF =AN :AE ，即AM ·AE =AN ·AF ，故③正确；④由②得BE +DF =DH +DF =FH =FE ，过A 作AO ⊥BD ，作AG ⊥EF ，则△AFE 与△AMN 的相似比就是AG :AO ，易证△ADF ≌△AGF (AAS )，则可知AG =AD =2AO ，从而得证，故④正确，故选：A ．【点睛】此题考查了正方形的性质、相似(包括全等)三角形的判定和性质、旋转的性质等知识点，综合性极强，难度较大．2(2023·山东滨州·统考中考模拟)如图，在矩形ABCD 中，AB =2，BC =4，点E 、F 分别在BC 、CD 上，若AE =5，∠EAF =45°，则AF 的长为．【答案】4103【分析】取AB 的中点M ，连接ME ，在AD 上截取ND =DF ，设DF =DN =x ，则NF =2x ，再利用矩形的性质和已知条件证明△AME ∽△FNA ，利用相似三角形的性质：对应边的比值相等可求出x 的值，在直角三角形ADF 中利用勾股定理即可求出AF 的长．【详解】解：取AB 的中点M ，连接ME ，在AD 上截取ND =DF ，设DF =DN =x ，∵四边形ABCD 是矩形，∴∠D =∠BAD =∠B =90°，AD =BC =4，∴NF =2x ，AN =4-x ，∵AB =2，∴AM =BM =1，∵AE =5，AB =2，∴BE =1，∴ME =BM 2+BE 2=2，∵∠EAF =45°，∴∠MAE +∠NAF =45°，∵∠MAE +∠AEM =45°，∴∠MEA =∠NAF ，∴△AME ∽△FNA ，∴AM FN =ME AN ，∴12x=24-x ，解得：x =43∴AF =AD 2+DF 2=4103故答案为4103．【点睛】本题考查了矩形的性质、相似三角形的判断和性质以及勾股定理的运用，正确添加辅助线构造相似三角形是解题的关键．3(2023·福建龙岩·统考一模)如图，∠ACB =90°,AC =BC ,∠DCE =45°，如果AD =3,BE =4，则BC 的长是( )．A.5B.52C.62D.7【答案】C【详解】分析：由于△ABC中，AC=BC，∠ACB=90°，设DE=x，则AB=7+x，可以得出△ACE∽△CDE∽△BDC，根据相似三角形的性质，列出关于x方程，解出x，再计算BC的长．详解：设DE=x，则AB=7+x．∵∠ACB=90°，AC=BC，∴∠DCE=∠CAE=∠DBC=45°∴△ACE∽△CDE∽△BDC，设CD=a，CE=b，则有以下等式：x：b=b：3+x，x：a=a：4+x，x：a=b：AC，整理得：b2=x(x+3)，a2=x(x+4)，x•AC=ab，x2(x+3)(x+4)=a2b2=x2•AC2=x2(x+7)22，解得：x=5；∴AB=12，∴AC=BC=62．故选C．点睛：本题主要考查了三角形相似的性质和判定、等腰直角三角形的性质，以及列方程求解的能力．4(2023·广东·九年级专题练习)如图，ΔABC中，∠BAC=120°，AB=AC，点D为BC边上的点，点E为线段CD上一点，且CE=1，AB=23，∠DAE=60°，则DE的长为．【答案】7 3【分析】利用含30°角的直角三角形的性质及图形的相似可求DE的长．【详解】解：如图，作AF⊥BC于F，作EG⊥AC于G．∵ΔABC中，∠BAC=120°，AB=AC．∴∠B=∠C=30°．在R tΔCEG中，∠C=30°．∴EG=12CE=12，CG=32．∴AG=23-32=332．∵AF⊥BC．∴∠AFC=90°．∴AF=12AC=3．∵∠DAE=60°=∠FAC．∴∠DAF=∠EAG．∵∠AFD=∠AGE=90°．∴ΔADF∽ΔAGE．∴AF AG =DFEG，即3332=DF12．∴DF=13．由勾股定理得：AE2=AG2+EG2=AF2+EF2．∴EF2=3322+12 2-(3)2=4．∴EF=2．DE=2+13=73故答案为：73【点睛】本题考查含30°角的直角三角形的性质及相似三角形的判定，作辅助线构造直角三角形是求解本题的关键．5(2023·辽宁沈阳·统考二模)在菱形ABCD中，∠B=60°．点E，F分别在边BC，CD上，且BE= CF．连接AE，AF．(1)如图1，连接EF ，求证：△AEF 是等边三角形；(2)AG 平分∠EAF 交BC 于点G ．①如图2，AG 交EF 于点M ，点N 是BC 的中点，当BE =4时，求MN 的长．②如图3，O 是AC 的中点，点H 是线段AG 上一动点(点H 与点A ，点G 不重合)．当AB =12，BE =4时，是否存在直线OH 将△ACE 分成三角形和四边形两部分，其中三角形的面积与四边形的面积比为1∶3．若存在，请直接写出AH AG 的值；若不存在，请说明理由．【答案】(1)见解析；(2)①MN =23；②12或57【分析】(1)证△ABE ≌△ACF ，根据有一个角是60°的等腰三角形是等边三角形证明即可；(2)①连接AN ，证△NAM ∽△BAE ，列出比例式，根据相似比即可求解；②分点H 为AG 中点和点N 为EC 中点两种情况，根据相似比，求出比值即可．【详解】解：(1)∵四边形ABCD 是菱形，∴AB =BC ，∵∠B =60°，∴△ABC 是等边三角形，∴AB =AC ，∠ACB =∠ACD =∠BAC =60°，∵BE =CF ，∴△ABE ≌△ACF ；∴AE =AF ，∴∠BAE =∠CAF ，∴∠EAF =60°，∴△AEF 是等边三角形；(2)①连接AN ，∵点N 是BC 的中点，∴∠ANB =90°，∵∠B =60°，∴∠BAN =30°，∴cos ∠BAN =AN AB=32，由(1)知，△AEF 是等边三角形，∠EAF =60°，AG 平分∠EAF∴∠AME =90°，∠EAM =30°，∴cos ∠EAM =AM AE=32，∠BAN -∠EAN =∠EAM -∠EAN ，即∠BAE =∠NAM ，∴△NAM ∽△BAE∴MN BE =AM AE，∴MN 4=32，∴MN =23②如图，当点H 为AG 中点时，即AH AG=12；∵O 是AC 的中点，∴OH ∥EC ，∴△AMO ∽△AEC ,∵AO AC =12，∴S △AMO S △AEC =14，即S △AMO S 四边形MECO=13；同理，如图所示，当点N 为EC 中点时，ON ∥AE ，S △CON S 四边形NEAO=13；连接FG ，作FP ⊥BC ，交BC 延长线与点P ，∵BE =CF =4，AB =BC =12，∴CE =8,∵CD ∥AB ，∴∠B =∠DCP =60°，∴∠CFP =30°，∴CP =2，FP =CF 2-CP 2=23，∵AE =AF ，AG =AG ，∠EAG =∠FAG ，∴△EAG ≌△FAG ，∴EG =FG ，设EG =x ,CG =8-x ，PG =10-x ，(10-x )2+(23)2=x 2，解得，x =5.6，∵EN =CN =4，AH AG =EN EG =45.6=57；综上，AH AG的值为：12或57．【点睛】本题考查了菱形的性质，等边三角形的判定与性质，解直角三角形，相似三角形的判定与性质，解题关键是熟练运用相关几何知识，构建几何模型证明相似或全等．6(2023山东九年级期中)如图，正方形ABCD 的对角线相交于点O ，点M ，N 分别是边BC ，CD 上的动点(不与点B ，C ，D 重合)，AM ，AN 分别交BD 于点E ，F ，且∠MAN 始终保持45°不变．(1)求证：AF AM=22；(2)求证：AF ⊥FM ；(3)请探索：在∠MAN 的旋转过程中，当∠BAM 等于多少度时，∠FMN =∠BAM ？写出你的探索结论，并加以证明．【答案】(1)证明见解析；(2)证明见解析；(3)∠BAM =22.5．【分析】(1)先证明A 、B 、M 、F 四点共圆，根据圆内接四边形对角互补即可证明∠AFM =90°，根据等腰直角三角形性质即可解决问题．(2)由(1)的结论即可证明．(3)由：A ．B 、M 、F 四点共圆，推出∠BAM =∠EFM ，因为∠BAM =∠FMN ，所以∠EFM =∠FMN ，推出MN ∥BD ，得到CMCB =CN CD，推出BM =DN ，再证明△ABM ≌△ADN 即可解决问题．【详解】解：(1)∵四边形ABCD 是正方形，∴∠ABD =∠CBD =45°，∠ABC =90°，∵∠MAN =45°，∴∠MAF =∠MBE ，∴A 、B 、M 、F 四点共圆，∴∠ABM +∠AFM =180°，∴∠AFM =90°，∴∠FAM =∠FMA =45°，∴AM =2AF ，∴AF AM=22．(2)由(1)可知∠AFM =90°，∴AF ⊥FM ．(3)结论：∠BAM =22.5时，∠FMN =∠BAM理由：∵A 、B 、M 、F 四点共圆，∴∠BAM =∠EFM ，∵∠BAM =∠FMN ，∴∠EFM =∠FMN ，∴MN ∥BD ，∴CM CB =CN CD，∵CB =DC ，∴CM =CN ，∴MB =DN ，在△ABM 和△ADN 中，∵AB =AD ，∠ABM =∠ADN ，BM =DN ，∴△ABM ≌△ADN ，∴∠BAM =∠DAN ，∵∠MAN =45°，∴∠BAM +∠DAN =45°，∴∠BAM =22.5°．7(2022·广东深圳·统考二模)【教材呈现】(1)如图1，在同一平面内，将两个全等的等腰直角三角形ABC 和AFG 摆放在一起，点A 为公共顶点，∠BAC =∠G =90°，若△ABC 固定不动，将△AFG 绕点A 旋转，边AF ，AG 与边BC 分别交于点D ，E (点D 不与点B 重合，点E 不与点C 重合)，则结论BE ⋅CD =AB 2是否成立(填“成立”或“不成立”)；【类比引申】(2)如图2，在正方形ABCD 中，∠EAF 为∠BAD 内的一个动角，两边分别与BD ，BC 交于点E ，F ，且满足∠EAF =∠ADB ，求证：△ADE ∽△ACF ；【拓展延伸】(3)如图3，菱形ABCD 的边长为12cm ，∠BAD =120°，∠EAF 的两边分别与BD ，BC 相交于点E ，F ，且满足∠EAF =∠ADB ，若BF =9cm ，则线段DE 的长为cm ．【答案】(1)成立；(2)证明见解析；(3)53cm ．【分析】(1)根据等腰三角形性质得出∠DAC =∠AEB ，再证△BEA ∽△CAD 即可；(2)根据正方形性质得出∠CAF =∠DAE 即可；(3)如图3，在DE 上取一点M ，使∠MAD =30°，过M 作MN ⊥AD 于N ，根据四边形ABCD 为菱形，且∠BAD =120°，证出∠MAD =∠MDA =30°，再证△ACF ∽△AME ，求出AC =3AM ，利用菱形ABCD 的边长为12cm ，求出CF =3ME =3cm 即可．【详解】解：(1)结论BE ⋅CD =AB 2成立理由：如图1，∵△ABC 和△AFG 都是等腰直角三角形，∴∠B =∠C =∠FAG =45°∵∠DAC =∠CAE +45°，∠AEB =∠CAE +45°，∴∠DAC =∠AEB又∵∠B =∠C ，∴△BEA ∽△CAD ，∴BE AC =AB CD ，∵AC =AB ，∴BE ⋅CD =AB 2，故答案为：成立(2)证明：如图2，∵四边形ABCD 是正方形，∴∠CAD =∠ACB =∠ADB =45°，∵∠EAF =∠ADB ，∴∠EAF =∠CAD =45°，∴∠ACF +∠CAE =∠DAE +∠CAE ，∴∠CAF =∠DAE ，又∵∠ACB =∠ADB ，∴△ADE ∽△ACF ；(3)线段DE 的长为53cm理由：如图3，在DE 上取一点M ，使∠MAD =30°，过M 作MN ⊥AD 于N ，又∵四边形ABCD 为菱形，且∠BAD =120°，∴∠CAD =∠ACB =∠ADC =60°，∴∠MDA =12∠ADC =30°∴∠MAD =∠MDA =30°，∴∠AME =60°，∴∠AME =∠ACB =60°，∵∠CAD =60°，∠MAD =30°，∴∠CAM =30°，∵∠EAF =∠ADB ，∴∠EAF =∠CAM =30°，∴∠CAF =∠MAE ，∴△ACF ∽△AME ，∴CF ME =AC AM，∵AN =12AD ，AN =AM cos30°=32AM ，∴2AN =3AM ，2AN =AD ，∴MA =MD =33AD ，∵AD =AC ，∴AC =3AM ，∴CF ME =ACAM=3，∵菱形ABCD的边长为12cm，∴BC=AD=12cm，∵BF=9cm，∴CF=3ME=3cm，∴ME=3cm，∵MD=33AD，∴MD=33×12=43cm ，∴DE=ME+MD=43+3=53cm，∴线段DE的长为53cm．故答案为53．【点睛】本题考查等腰直角三角形性质，正方形性质，三角形相似判定与性质，菱形性质，锐角三角形函数，掌握等腰直角三角形性质，正方形性质，三角形相似判定与性质，菱形性质，锐角三角形函数是解题关键．课后专项训练1(2023·广东深圳·九年级校考阶段练习)如图，在正方形ABCD中，点E，F分别在边BC，DC上，AE、AF分别交BD于点M，N，连接CN、EN，且CN=EN．下列结论：①AN=EN，AN⊥EN；②BE+DF=EF；③∠DFE=2∠AMN；④EF2=2BM2+2DN2．其中正确结论的个数是()A.4B.3C.2D.1【答案】A【分析】将△ABE绕点A逆时针旋转90°，得到△ADH，则∠1=∠4，AE=AH，BE=DH，可证得△BNA ≌△BNC，从而得到AN=CN，∠NCE=∠BAN，进而得到∠NEC=∠NCE=∠BAN，再由四边形内角和定理可得AN=NE,AN⊥NE，故①正确；再证明△AFE≌△AFH，可得EF=FH=DF+DH=DF+ BE,∠AFH=∠AFE，故②正确；再由∠MAN=∠NDF=45°,∠ANM=∠DNF，可得∠AMN=∠AFD=∠AFE，从而得到∠DFE=2∠AMN，故③正确；再证明△AMN∽△AFE，△AEN是等腰直角三角形，可得AE=2AN，从而得到EF=2MN，将△ABM绕点A逆时针旋转90°，得到△ADG，则∠DAG=∠BAM,AM=AG，∠ADG=∠ABM=45°，证明△ANG≌△ANM，可得MN=GN，再由勾股定理，可得故④正确，即可求解．【详解】解：如图，将△ABE绕点A逆时针旋转90°，得到△ADH，则∠1=∠4，AE=AH，BE=DH，∵四边形ABCD是正方形，∴AB=BC=AD,∠BAD=∠ABC=90°,∠ABD=∠CBD=45°，在△BNA和△BNC中，BN=BN ∠NBA=∠BA=BCNBC∴△BNA≌△BNC，∴AN=CN，∠NCE=∠BAN，∵CN=EN，∴∠NEC=∠NCE=∠BAN，∵∠NEC+∠BEN=180°，∴∠BAN+∠BEN=180°，∴∠ABC+∠ANE=180°，∴∠ANE=90°，∴AN=NE,AN⊥NE，故①正确；∴∠3=∠AEN=45°，∵∠1=∠4，∴∠2+∠4=∠2+∠1=45°，∴∠3=∠FAH=45°，∵AF=AF,AE=AH，∴△AFE≌△AFH，∴EF=FH=DF+DH=DF+BE,∠AFH=∠AFE，故②正确；∵∠MAN=∠NDF=45°,∠ANM=∠DNF，∴∠AMN=∠AFD=∠AFE，又∵∠AFE=∠AFD,∠DFE=∠AFE+∠AFD，∴∠DFE=2∠AMN，故③正确；∵∠MAN=∠EAF,∠AMN=∠AFE，∴△AMN∽△AFE，∴NMEF =ANAE，∵AN=NE,AN⊥NE，∴△AEN是等腰直角三角形，∴AE=2AN，∴NMEF =ANAE=12，∴EF=2MN，如图，将△ABM绕点A逆时针旋转90°，得到△ADG，则∠DAG=∠BAM,AM=AG，∠ADG=∠ABM=45°，∴∠NDG=90°，即△GDN是直角三角形，∵∠MAN=45°，∴∠BAM+∠DAN=∠DAG+∠DAN=∠GAN=45°=∠MAN，∵AN=AN，∴△ANG≌△ANM，∴MN=GN，∴MN2=DN2+DG2=DN2+BM2，∴EF2=2MN2=2DN2+2BM2，故④正确；故选A．【点睛】本题考查正方形的性质、全等三角形的判定和性质、勾股定理、相似三角形的判定和性质等知识，解题的关键是灵活运用所学知识解决问题，学会利用旋转法，添加辅助线构造全等三角形解决问题．2(2022·广东深圳·统考一模)如图，正方形ABCD中，E是BC的中点，F在CD上，CF=2DF，连接AE，AF与对角线BD交于点M，N，连接MF，EN．给出结论：①∠EAF=45°；②AN⊥EN；③tan∠AMN=3；④DN:MN:BM=2:5:3．其中正确的是()A.①②③B.①②④C.①③④D.②③④【答案】A【分析】将△ABE顺时针旋转，使得AB与AD重合，此时得△ADG，将△AFD逆时针旋转，使得AD与AB 重合，此时得△ABH，根据∠HAF=∠GAE=90°，即可求得∠HAE=∠FAE=45°，①正确；根据∠HAE=∠FAE=45°可得△AMN∼△DFN，即可求tan∠AMN=tan∠DFN=ADDF =63=3，即可得③正确；根据如图正方形构造直角坐标系，求出直线AE、AF、BD的解析式，再联立解析式，即可求得M、N两点的坐标，再根据坐标求出DN、MN、BM、AN、NE，即可知AN=NE=3102，则有∠EAN=∠AEN=45°，则有∠ANE=90°，AN⊥NE，②正确；根据DN、MN、BM长度可知DN:MN:BM=3:5:4，④错误．【详解】将△ABE顺时针旋转，使得AB与AD重合，此时得△ADG，将△AFD逆时针旋转，使得AD与AB 重合，此时得△ABH，链接EF，如图所示：为了方便计算，设正方形的边长为6，则有AB=BC=CD=AD=6，则有BE=EC=3=DG，CF=4，DF=2=BH，∠BAE=∠DAG，则有：HE=5=FG，利用勾股定理，易求得：AH=AF=210，AE=AG=35，EF=5，BD=62，根据图形的旋转，可知∠HAB=∠FAD，∠BAE=∠DAG，∴∠HAF=∠GAE=90°，∵AH=AF，HE=5=FG，AE=AE，∴△AHE≅△AFE，同理可证得△AEF≅△AGF，∴∠HAE=∠FAE，又∵∠HAF=∠GAE=90°，∴∠HAE=∠FAE=45°，故①正确；∵∠HAE=∠FAE=45°，∠ANM=∠DNF，∴△AMN∼△DFN，同理可证△AMN∼△BME，∴∠AMN=∠DFN，∴tan∠AMN=tan∠DFN=ADDF =62=3，故③正确；以B为坐标原点O，AB所在的直线为y轴，以BC所在的直线为x轴，构建直角坐标系，则有A点坐标为(0,6)，B点坐标为(0,0)，C点坐标为(6,0)，D点坐标为(6,6)，F点坐标为(6,4)，E点坐标为(3,0)，则直线AF的解析式为：y=-13x+6，BD的解析式为y=x，AE的解析式为y=-2x+6，联立：y=-13x+6 y=x，得到N点坐标为：92,9 2，同理的M点坐标为(2,2)，过M点作MP垂直于BC，交BC于P点，过N点作NQ垂直于DC，交DC于Q点，则有MP=2，DQ=DC-QC=6-92=32，则有BM=(2-0)2+(2-0)2=22，DN=6-9 22+6-922=322，则有MN=BD-BM-DN=62-22-322=522，则有：DN:MN:BM=322:522:22=3:5:4，故④错误；根据N点坐标为：92 ,92，A点坐标为：(0,6)，E点坐标为：(3,0)，可得AN=0-9 22+6-922=NE=3-922+0-922=3102，则在△AEN中，∠EAN=∠AEN=45°，∴∠ANE=90°，∴AN⊥NE，故②正确；故选：A．【点睛】本题考查了直角坐标系的构建、相似三角形以及坐标系中求解两点间距离等知识．准确作出辅助线并构建直角坐标系是解答本题的关键．3如图，正方形ABCD中，△ABC绕点A逆时针旋转到△AB C ，AB 、AC 分别交对角线BD于点E、F，若AE=4，则EF⋅ED的值为()A.4B.6C.8D.16【答案】D【分析】先根据正方形的性质、旋转的性质可得∠EAF=∠EDA=45°，再根据相似三角形的判定与性质即可得．【详解】∵四边形ABCD是正方形，∴∠BAC=∠EDA=45°，由旋转的性质得：∠B AC =∠BAC，∴∠B AC =∠EDA，即∠EAF=∠EDA，在△AEF和△DEA中，∠EAF=∠EDA ∠AEF=∠DEA，∴△AEF∼△DEA，∴EF AE =AEDE，即EF4=4DE，∴EF⋅DE=16，故选：D．【点拨】本题考查了正方形的性质、旋转的性质、相似三角形的判定与性质，熟练掌握相似三角形的判定与性质是解题关键．4如图，菱形ABCD的边长为4，E，F分别是AB，AD边上的动点，BE=AF，∠BAD=120°，则下列结论：①ΔBEC≌ΔAFC；②ΔECF为等边三角形；③∠AGE=∠AFC；④若AF=1，则GFGE=12．其中正确个数为()A.4B.3C.2D.1【答案】B【分析】由SAS证明△BEC≌△AFC，①正确；由全等三角形的形状得CE=CF，∠BCE=∠ACF，再由∠BCE+∠ECA=∠BCA=60°，得∠ACF+∠ECA=60°，得△CEF是等边三角形，②正确；由∠AGE=∠CAF+∠AFG=60°+∠AFG，∠AFC=∠CFG+∠AFG=60°+∠AFG，得∠AGE=∠AFC，故③正确；④过点E 作EM ∥BC 交AC 下点M 点，易证△AEM 是等边三角形，则EM =AE ，由AF ∥EM ，则△AFG ∽△MEG ，得④错误．【详解】解：①∵四边形ABCD 是菱形，∴AB =AD =4，∠BAC =∠CAD ．∵∠BAD =120°，∴∠BAC =∠CAD =60°，∴ΔABC 和ΔACD 都是等边三角形，∴∠B =∠CAD =60°，BC =AC ．∵BE =AF ，∴ΔBEC ≌ΔAFC SAS ，故①正确．②∵ΔBEC ≌ΔAFC ，∴CE =CF ，∠BCE =∠ACF ．∵∠BCE +∠ECA =∠BCA =60°，∴∠ACF +∠ECA =60°，∴ΔCEF 是等边三角形，故②正确．③∵∠AGE =∠CAF +∠AFG =60°+∠AFG ，∠AFC =∠CFG +∠AFG =60°+∠AFG ，∴∠AGE =∠AFC ，故③正确．④过点E 作EM ∥BC 交AC 于点M ，∴∠AEM =∠B =60°，∠AME =∠ACB =60°，∴ΔAEM 是等边三角形，∴EM =AE ．∵BE =AF =1，∴AE =AB -BE =4-1=3，∴EM =AE =3．∵AF ∥EM ，∴ΔAFG ~ΔMEG ，∴GF GE=AF EM =13﹐故④错误，正确个数为3．故选B ．【点拨】本题考查了菱形的性质、等边三角形性质、全等三角形的判定与性质、相似三角形的判定与性质等知识；熟练掌握菱形的性质、全等三角形的判定与性质、相似三角形的判定与性质是解题的关键．5(2023·浙江绍兴·校联考三模)矩形ABCD 中，AB =6，AD =12，连接BD ，E ，F 分别在边BC ，CD 上，连接AE ，AF 分别交BD 于点M ，N ，若∠EAF =45°，BE =3，则DN 的长为．【答案】1255【分析】根据矩形的性质，由勾股定理得出BD ，延长AB 至P ，使PB =AB =6，过P 作BC 的平行线交DC 的延长线于Q ，得正方形APQD ，延长AE 交PQ 于H ，连接HF ，将△ADF 绕点A 顺时针旋转90°，点D 与点P 重合，得到△APG ，由旋转的性质可得PG =PF ，∠APG =∠ADF =90°，AG =AF ，∠PAG =∠DAF ，证出∠GAF =90°，得出∠GAH =∠FAH =45°，可证△AGH ≌△AFH ，得出GH =FH ，证出FH =DF +PH ，设DF =x ，则FQ =12-x ，利用勾股定理列出方程求出x =4，然后由DF ∥AB ，得△DFN ∽△BAN ，所以DF AB=DN BN =23，即可求出DN 的长．【详解】解：在矩形ABCD 中，∵∠BAD =90°，AB =6，AD =12，∴BD =AB 2+AD 2=62+122=65，如图，延长AB 至P ，使PB =AB =6，过P 作BC 的平行线交DC 的延长线于Q ，得正方形APQD ，延长AE交PQ于H，连接HF，将△ADF绕点A顺时针旋转90°，点D与点P重合，得到△APG，∵四边形APQD是正方形，∴AP=PQ=DQ=AD，∠PAD=∠APH=∠Q=∠ADQ=90°，由旋转得：△APG≌△ADF，∴PG=DF，∠APG=∠ADF=90°，AG=AF，∠PAG=∠DAF，∴∠PAG+∠PAF=∠PAF+∠DAF=90°，即∠GAF=90°，C ，P，H三点共线，∵∠HAF=45°，∴∠GAH=90°-45°=45°，∴∠GAH=∠FAH=45°，在△AGH和△AFH中，AG=AF∠GAH=∠FAH AH=AH，∴△AGH≌△AFH SAS ，∴GH=FH，∵GH=PG+PH=DF+PH，∴FH=DF+PH，设DF=x，则FQ=DQ-DF=12-x，∵AB=BP=6，BE∥PQ，∴AEEH =ABBP=1，∴AE=EH，∴PH=2BE=2×3=6，∴FH=DF+PH=6+x，HQ=12-6=6，在Rt△QFH中，由勾股定理得：FQ2+HQ2=FH2，∴(12-x2+62=x+62，解得：x=4，∴DF=4，∵DF∥AB，∴△DFN∽△BAN，∴DFAB =DN BN=23，∴DN=25BD=25×65=1255．故答案为：1255．【点睛】本题考查了正方形的性质，全等三角形的判定与性质，勾股定理，相似三角形的判定与性质等知识；证明三角形全等和由勾股定理得出方程是解题的关键．6(2023·成都市·九年级专题练习)如图，在Rt△ABC中，AB=AC，D、E是斜边BC上两点，且∠DAE=45°，将△ADC绕点A顺时针旋转90°后，得到△AFB，连接EF，下列结论：①△AED≌△AEF；②AEBE=ADCD；③△ABC的面积等于四边形AFBD的面积；④BE2+DC2=DE2；⑤BE=EF-DC；其中正确的选项是(填序号)【答案】①③④【分析】①根据旋转的性质知∠CAD=∠BAF，AD=AF，因为∠BAC=90°，∠DAE=45°，所以∠CAD+∠BAE=45°，可得∠EAF=45°=∠DAE，由此即可证明△AEF≌△AED；②当△ABE∽△ACD时，该比例式成立；③根据旋转的性质，△ADC ≌△ABF ，进而得出△ABC 的面积等于四边形AFBD 的面积；④据①知BF =CD ，EF =DE ，∠FBE =90°，根据勾股定理判断．⑤根据①知道△AEF ≌△AED ，得CD =BF ，DE =EF ；由此即可确定该说法是否正确．【详解】解：①根据旋转的性质知∠CAD =∠BAF ，AD =AF ．∵∠BAC =90°，∠DAE =45°，∴∠CAD +∠BAE =45°，∴∠EAF =45°，∴△AED ≌△AEF ；故本选项正确；②∵AB =AC ，∴∠ABE =∠ACD ；∴当∠BAE =∠CAD 时，△ABE ∽△ACD ，∴AE BE =AD CD ；当∠BAE ≠∠CAD 时，△ABE 与△ACD 不相似，即AE BE ≠AD CD；∴此比例式不一定成立，故本选项错误；③根据旋转的性质知△ADC ≌△AFB ，∴S △ABC =S △ABD +S △ABF =S 四边形AFBD ，即三角形ABC 的面积等于四边形AFBD 的面积，故本选项正确；④∵∠FBE =45°+45°=90°，∴BE 2+BF 2=EF 2．∵△ADC 绕点A 顺时针旋转90°后，得到△AFB ，∴△AFB ≌△ADC ，∴BF =CD ．又∵EF =DE ，∴BE 2+DC 2=DE 2，故本选项正确；⑤根据①知道△AEF ≌△AED ，得CD =BF ，DE =EF ，∴BE +DC =BE +BF >DE =EF ，即BE +DC >FE ，故本选项错误．综上所述：正确的说法是①③④．故答案为：①③④．【点睛】本题考查了图形的旋转变换以及全等三角形的判定等知识，三角形三边的关系，相似三角形的性质与判定，解题时注意旋转前后对应的相等关系．7(2023·上海宝山·校考一模)如图，在△ABC 中，AB =AC ，点D 、E 在边BC 上，∠DAE =∠B =30°，且AD AE=32，那么DE BC 的值是．【答案】13318-1．【分析】由已知可得△ABE ∼△DAE ，从而可知AB BE =AD AE=32，AE 2=BE ∙DE ，设AB =3x ，则BE =2x ，再利用勾股定理和等腰三角形性质用x 表示DE 和BC ，从而解答【详解】解：∵∠BAE =∠DAE +∠BAD ，∠ADE =∠B +∠BAD ，又∵∠DAE =∠B =30°，∴∠BAE =∠ADE ，∴△ABE ∼△DAE ，∴AB BE =AD AE =32，AE 2=BE ∙DE ，过A 点作AH ⊥BC ，垂足为H ，设AB =3x ，则BE =2x ，∵∠B =30°，∴AH =12AB =32x ，BH =332AB =332x ，∴EH =BH -BE =332-2 x ，在Rt △AHE 中，AE 2=AH 2+EH 2=32x 2+332x -2x 2=13-63 x 2，又∵AE 2=BE ∙DE ，∴13-63 x 2=2x ∙DE ，∴DE =13-632x ，∵AB =AC ，AH ⊥BC ，∴BC =2BH =33x ，∴DE BC=13-632x 33x =13318-1，故答案为：DE BC =13-632x 33x=13318-1 .【点睛】本题考查了相似三角形的判定和性质、等腰三角形的性质以及勾股定理，利用三角形相似得到AB 与BE 的关系是解题的关键．8(2023春·辽宁沈阳·八年级统考期中)通过类比联想、引申拓展研究典型题目，可达到解一题知一类的目的.下面是一个案例，请补充完整．原题：如图1，点E ，F 分别在正方形ABCD 的边BC ，CD 上，∠EAF =45°，连接EF ，则EF =BE +DF ，试说明理由．(1)思路梳理∵AB =CD ，∴把△ABE 绕点A 逆时针旋转90°至△ADG ，可使AB 与AD 重合.∵∠ADC =∠B =90°，∠FDG =180°，∴点F ，D ，G 共线.根据(从“SSS ，ASA ，AAS ，SAS ”中选择填写)，易证△AFG ≌，得EF =BE +DF ．(2)类比引申如图2，四边形ABCD 中，AB =AD ，∠BAD =90°，点E ，F 分别在边BC ，CD 上，∠EAF =45°.若∠B ，∠D 都不是直角，则当∠B 与∠D 满足等量关系时，仍有EF =BE +DF ．(3)联想拓展如图3，在△ABC 中，∠BAC =90°，AB =AC ，点D ，E 均在边BC 上，且∠DAE =45°.猜想BD ，DE ，EC 应满足的等量关系，并写出推理过程．(4)思维深化如图4，在△ABC 中，∠BAC =60°，AB =AC ，点D ，E 均在直线BC 上，点D 在点E 的左边，且∠DAE =30°，当AB =4，BD =1时，直接写出CE 的长．【答案】(1)SAS，△AFE(2)∠B+∠D=180°(3)DE2=BD2+EC2，理由见解析(4)CE的长为87或83【分析】(1)把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合，再证明△AFE≌△AFG进而得到EF=FG，即可证明结论；(2)∠B+∠D=180°时，EF=BE+DF与(1)的证法类同；(3)把△AEC绕点A顺时针旋转90°得到△ABE ，连接DE ，根据旋转的性质，可知△AEC≌△ABE 得到BE =EC、AE =AE、∠C=∠ABE 、∠EAC=∠E AB，，根据Rt△ABC中的，AB=AC得到∠E BD=90°，所以E B2+BD2=E D2，证△AE D≌△AED，利用DE =DE 得到DE2=BD2+EC2；(4)分两种情况：点D在BC边上或点D在BC的延长线上，①当点D在BC边上时，过点A作AF⊥BC于点F，过点D作DG⊥AB于点G，利用三角函数求出BG，DG，AF，再证明△AFE∽△AGD，运用相似三角形性质即可求出EF，再由CE=CF-EF可求得CE；②当点D在CB的延长线上时，过点A作AF⊥BC于点F，过点D作DG⊥AB于点G，与①同理可求得EF，再由CE=CF+EF求出CE即可．【详解】(1)解：∵AB=AD，∴把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合．∴∠BAE=∠DAG，∵∠BAD=90°，∠EAF=45°，∴∠BAE+∠DAF=45°，∴∠EAF=∠FAG，∵∠ADC=∠B=90°，∴∠FDG=180°，点F、D、G共线，在△AFE和△AFG中，AE=AG∠EAF=∠FAG AF=AF，∴△AFE≌△AFG SAS ，∴EF=FG，即：EF=BE+DF．故答案为：SAS，△AFE；(2)解：∠B+∠D=180°时，EF=BE+DF，理由如下：∵AB=AD，∴如图2:把△ABE绕点A逆时针旋转90°至△ADG，可使AB与AD重合，∴∠BAE=∠DAG，∵∠BAD=90°，∠EAF=45°，∴∠BAE+∠DAF=45°，∴∠EAF=∠FAG，∵∠ADC+∠B=180°，∴∠FDG=180°，点F、D、G共线，在△AFE和△AFG中，AE=AG∠FAE=∠FAG AF=AF，∴△AFE≌△AFG SAS ，∴EF=FG，即：EF=BE+DF．故答案为：∠B+∠D=180°；(3)解：猜想：DE2=BD2+EC2．理由如下：如图3：把△AEC绕点A顺时针旋转90°得到△ABE ，连接DE ，∴△AEC≌△ABE ，∴BE =EC，AE =AE，∠C=∠ABE ，∠EAC=∠E AB，在Rt△ABC中，AB=AC，∴∠ABC=∠ACB=45°，∴∠ABC+∠ABE'=90°，即∠E BD=90°，∴E B2+BD2=E D2，又∵∠DAE=45°，∴∠BAD+∠EAC=45°，∴∠E AB+∠BAD=45°，即∠E AD=45°，在△AE D和△AED中，AE =AE∠E AD=∠DAE AD=AD，∴△AE D≌△AED SAS ，∴DE=DE ，∴DE2=BD2+EC2；(4)解：点D，E均在直线BC上，点D在点E的左侧，BD=1，∴分两种情况：点D在BC边上或点D在CB的延长线上，①当点D在BC边上时，如图4-1，过点A作AF⊥BC于点F，过点D作DG⊥AB于点G，∵AB=AC=4，∠BAC=60°，∴BF=CF=2，∠BAF=∠CAF=30°，AF=3BF=23，∵∠AGD=90°，∠B=60°，BD=1，∴BG=12BD=12，DG=3BG=32，∴AG=AB-BG=4-12=72，∵∠DAE=30°，∴∠DAF+∠BAD=∠DAF+∠FAE=30°，∴∠BAD=∠FAE，∵∠AFE=∠AGD=90°，∴△AFE∽△AGD，∴EFDG =AFAG，∴EF32=2372，∴EF=67，∴CE=CF-EF=2-67=87；②当点D在CB的延长线上时，如图4-2，过点A作AF⊥BC于点F，过点D作DG⊥AB于点G，由①知，BF=CF=2，∠BAF=∠CAF=30°，∵∠DGB=90°，∠DBG=∠ABC=60°，∴BG=12BD=12，DG=3BG=32，∴AG=AB+BG=4+12=92，∵∠DAE=∠BAF=30°，∴∠DAG+∠BAE=∠BAE+∠EAF，∴∠DAG=∠EAF，∴△DAG∽△EAF，∴EFDG =AF AG，∴EF32=2392，∴EF=23，∴CE=CF+EF=2+23=83．综上所述，CE的长为87或83．【点睛】本题主要考查了全等三角形的判定和性质、相似三角形的判定和性质、旋转变换的性质、三角函数定义、勾股定理的应用等知识点，掌握全等三角形的判定定理和性质定理、相似三角形的判定和性质，合理添加辅助线并灵活运用分类讨论思想是解题的关键．9(2023·陕西西安·九年级校考期中)问题研究，如图，在等腰△ABC中，AB=AC，点D、E为底边BC 上的两个动点(不与B、C重合)，且∠DAE=∠B．(1)请在图中找出一个与△ABE相似的三角形，这个三角形是；(2)若∠BAC=90°，分别过点D、E作AB、AC的垂线，垂足分别为F、G，且DF、EG的反向延长线交于点M，若AB=1，求四边形AFMG的面积；问题解决(3)如图所示，有一个矩形仓库ABCD，其中AB=40米，AD=30米，现计划在仓库的内部的E、F两处分别安装监控摄像头，其中点E在边BC上，点F在边DC上．设计要求∠EAF=45°且CE=CF，则CE的长应为多少米？【答案】(1)ΔDAE；(2)四边形的面积为12；(3)CE的长为70+45385米．【分析】(1)根据已知条件及相似三角形的判定可直接得出；(2)把ΔABD绕点A逆时针旋转90°得到ΔACH，连接EH，根据旋转可得ΔABD≅ΔACH，利用三角形全等的性质得出BD=CH，AD=AH，∠ACH=∠B，利用角和边之间的关系可得：ΔCEH为直角三角形，根据勾股定理及等量代换得出CE2+BD2=EH2，根据全等三角形的判定得出ΔHAE≅ΔDAE，得EH=DE，再求出各三角形的面积确定SΔCGE+SΔBDF=SΔDEM，再根据图形中三角形的关系得出S四边形AFMG=SΔABC，即可求得四边形面积；(3)根据(2)中思路，作图：延长AD到S，延长BC到G，使AS=BG=AB，连接SG，延长AF交SG于点H，连接EH，延长GS到T，使ST=BE，连接AT，则四边形ABGS为正方形，根据全等三角形的判定定理得出ΔATH≅ΔAEH，根据全等三角形的性质及等量代换得出∠HAT=∠HAE，再利用三角形全等的判定证明ΔATH≅ΔAEH，设CE=CF=x，可得出ST=30-x，GE=x+10，DF=40-x，在根据相似三角形的判定和性质得出ADAS=DFSH，将各边代入得出SH，HE，GH，在RtΔADF中，利用勾股定理得出方程求解即可．【详解】解：(1)∵∠AEB=∠DEA，∠B=∠DAE，∴ΔDAE~ΔABE，故答案为：ΔDAE；(2)如图所示：把ΔABD绕点A逆时针旋转90°得到ΔACH，连接EH，∴ΔABD≅ΔACH，∠DAH=90°，∴BD=CH，AD=AH，∠ACH=∠B，∵∠BAC=90°，AB=AC，∴∠B=∠ACB=45°，∴∠ACH=45°，∴∠ECH=∠ACB+∠ACH=90°，∴CE2+CH2=EH2，∴CE2+BD2=EH2，∵∠DAE=∠B，∴∠DAE=45°，∵∠DAH=90°，∴∠HAE=∠DAE=45°，在ΔHAE和ΔDAE中，AH=AD∠HAE=∠DAE AE=AE，∴ΔHAE≅ΔDAE，∴EH=DE，∴CE2+BD2=DE2，∵MG⊥AC于点G，∠ACB=45°，∴∠DEM=∠CEG=∠ACB=45°，∴CG=EG，∴CE2=2CG2，∵SΔCGE=12×CG×CE=CG22，∴SΔCGE=CE24，同理可得：SΔBDF =BD24，在ΔDEM中，∠DEM=∠EDM=45°，∴∠M=90°，同理可得：SΔDEM=DE2 4，∵CE2+BD2=DE2，∴SΔCGE+SΔBDF=SΔDEM，∴S四边形AFMG =S五边形AFDEG+SΔCGE+SΔBDF，即S四边形AFMG=SΔABC，∵SΔABC=12×AB×AC=12，∴S四边形AFMG=12，即四边形的面积为12；(3)如图，延长AD到S，延长BC到G，使AS=BG=AB，连接SG，延长AF交SG于点H，连接EH，延长GS到T，使ST=BE，连接AT，则四边形ABGS为正方形，∴BG=GS=AS=AB=40，DS=CG=40-30=10，在ΔABE和ΔAST中，AB=AS∠ABE=∠ASTBE=ST，∴∠BAE=∠SAT，AB=AT，∴∠HAT=∠HAS+∠SAT=∠HAS+∠BAE=45°，，∴∠HAT=∠HAE，在ΔATH和ΔAEH中，AT=AE∠HAT=∠HAEAH=AH，∴ΔATH≅ΔAEH，∴HT=HE，设CE=CF=x，则ST=BE=BC-CE=30-x，GE=x+10，DF=40-x，∵DF∥SH，∴ΔADF~ΔASH，∴ADAS=DFSH，即：3040=40-xSH，解得：SH=160-4x3，∴HE=HT=HS+ST=160-4x3+30-x=250-7x3，GH=GS-SH=40-160-4x3=4x-403，∴在Rt ΔADF 中，x +10 2+4x -4032=250-7x 3 2，解得：x 1=70+45385，x 2=70-45385(舍去)，即CE 的长为70+45385米．【点睛】题目主要考查相似三角形的判定和性质、全等三角形的判定和性质、勾股定理、一元二次方程的运用求解等，根据题意作出相应辅助线，融会贯通综合运用这些知识点是解题关键．10(2023·陕西汉中·九年级统考期末)如图，△ABC 中，∠BAC =120°，AB =AC ，点D 为BC 边上一点．(1)如图1，若AD =AM ，∠DAM =120°．①求证：BD =CM ；②若∠CMD =90°，求BD CD的值．(2)如图2，点E 为线段CD 上一点，且CE =4，AB =63，∠DAE =60°，求DE 的长．【答案】(1)①见解析，②BD CD=12(2)6.5【分析】(1)①通过证明△ABD ≌△ACM ，即可求证；②由①可得BD =CM ，再根据等边对等角求出∠ACM 和∠ACB 的度数，即可得出∠MCD =60°，最后根据直角三角形中30°角所对的边是斜边的一半即可求证；(2)过点E 作EG ⊥AC 于G ，过A 作AF ⊥BC 于F ，证明△ADF ∽△AEG ，可以求出DF ，利用勾股定理可以求出EF 的长，从而可以求解．【详解】(1)证明：①∵∠BAC =120°，∠DAM =120°，∴∠BAC -∠CAD =∠DAM -∠CAD ，即∠BAD =∠MAC ，在△ABD 和△ACM 中，AB =AC∠BAD =∠MAC AD =AM，∴△ABD ≌△ACM SAS ，∴BD =CM ；②∵∠BAC =120°，AB =AC ，∴∠ACB =12180°-120° =30°，由①可得：△ABD ≌△ACM ，∴∠ACM =∠ACB =30°，∴∠DCM =∠ACM +∠ACB =60°，∵∠CMD =90°，∴在△CDM 中，∠CDM =180°-90°-60°=30°，∴CM =12CD ，整理得：CM CD =12，由①可得BD =CM ，∴BD CD=12．(2)过点A 作AF ⊥BC 于点F ，过点E 作EG ⊥AC 于点G ，∵AB =AC ，∠BAC =120°，∴∠C =12180°-120° =30°，∵EG ⊥AC ，AB =AC =63，∴AF =12AC =33，在Rt △ACF 中，根据勾股定理可得：CF =AB 2-AF 2=9，∵CE =4，∴EF =CF -CE =9-4=5，∵EG ⊥AC ，∠C =30°，∴EG =12EC =2，在Rt △CEG 中，根据勾股定理可得：CG =CE 2-EG 2=23，∴AG =AC -CG =63-23=43，∵AB =AC ，∠BAC =120°，AF ⊥BC ，∴∠CAF =12∠BAC =60°，∵∠DAE =60°，∴∠DAE -∠EAF =∠CAF -∠EAF ，即∠DAF =∠EAG ，∵∠AFD =∠AGE =90°，∴△ADF ∽△AEG ，∴DF EG =AF AG ，即DF 2=3343，解得：DF =32，∴DE =DF +EF =32+5=6.5．【点睛】本题主要考查了全等三角形的性质与判定，等腰三角形的性质，含30度角的直角三角形的性质，勾股定理等等，解题的关键在于能够熟练掌握相关知识进行求解．11(2023·辽宁沈阳·九年级统考期末)【教材呈现】(1)如图1，在同一平面内，将两个全等的等腰直角三角形ABC 和AFG 摆放在一起，A 为公共顶点，∠BAC =∠G =90°，BC =6，若△ABC 固定不动，将△AFG 绕点A 旋转，边AF 、AG 与边BC 分别交于点D ，E (点D 不与点B 重合，点E 不与点C 重合)①求证：AE 2=DE •BE ；②求BE •CD 的值；【拓展探究】(2)如图2，在△ABC 中，∠C =90°，点D ，E 在边BC 上，∠B =∠DAE =30°，且AD =34AE ，请直接写出DE BC 的值．【答案】(1)①证明见解析；②18；(2)25318-2【分析】(1)①只需要证明△ABE ∽△DAE ，得到AE DE =BE AE，即可推出AE 2=DE ∙BE ；②先证明∠AEB =∠DAC ，则可证△AEB ∽△DAC ，推出BE ∙CD =AB ∙CA ，然后利用勾股定理求出AB =AC =32，即可得到BE ∙CD =AB ∙CA =18；(2)设AD =3x ，AE =4x ，先证明△ADE ∽△BDA ，推出BD AB =AD AE =34，设BD =3y ，AB =4y ，得到DE =AE ⋅AD AB=3x 2y ，求出AC =2y ，BC =23y ，则CD =BC -BD 23-3 y 在直角△ACD 中，AD 2=CD 2+AC 2，则9x 2=23-3 2y 2+4y 2，即可推出x 2y2=25-1239，由此求解即可．【详解】解：(1)①∵△ABC 和△AGF 都是等腰直角三角形，∠BAC =∠G =90°，∴∠B =∠C =∠GAF =。

中考数学复习：几何模型-半角旋转导学案

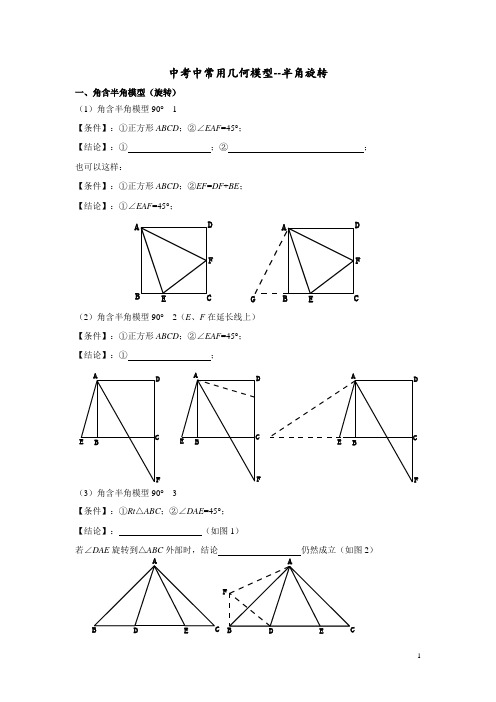
中考中常用几何模型--半角旋转一、角含半角模型（旋转）（1）角含半角模型90°---1【条件】：①正方形ABCD ；②∠EAF =45°；【结论】：① ；② ；也可以这样：【条件】：①正方形ABCD ；②EF =DF +BE ；【结论】：①∠EAF =45°；ABCDEF AB CDEFG（2）角含半角模型90°---2（E 、F 在延长线上）【条件】：①正方形ABCD ；②∠EAF =45°；【结论】：① ；（3）角含半角模型90°---3【条件】：①Rt △ABC ；②∠DAE =45°；【结论】：（如图1）若∠DAE 旋转到△ABC 外部时，结论仍然成立（如图2）ABCDEFABCDEFABCDEFAB C D EABCD EF（4）角含半角模型90°（变形）【条件】：①正方形ABCD ；②∠EAF =45°；【结论】：；【例题讲解】例1.如图,在平面直角坐标系中,边长为2的正方形OABC 的两顶点A 、C 分别在y 轴、x 轴的正半轴上,顶点O 在原点(如图1).现将正方形OABC 绕O 点顺时针旋转一定角度，当A 点第一次落在直线y =x 上时停止旋转。

旋转过程中，AB 边交直线y =x 于点M ，BC 边交x 轴于点N .(1)当点A 第一次落在直线y =x 上时停止旋转，此时图形旋转了___度； (2)旋转过程中,当MN 和AC 平行时(如图2)，求旋转角∠NOC 的度数；(3)设△MBN 的周长为P ,在旋转正方形OABC 的过程中(如图3)，P 值是否变化?请判断并证明你的结论。

例2.如图,△ABC 是边长为3的等边三角形,△BDC 是等腰三角形,且∠BDC =120°,以D 为顶A B C DG H F EA B CD GHFE点作一个60°角,使其两边分别交AB于M交AC于点N,连接MN,则△AMN的周长为.例3.如图,将Rt△ABC沿斜边翻折得到△ADC,点E,F分别为DC,BC边上的点,且∠DAB=2∠EAF.试猜想DE，BF，EF之间有何数量关系，并证明你的猜想。

角含半角模型(完整版)

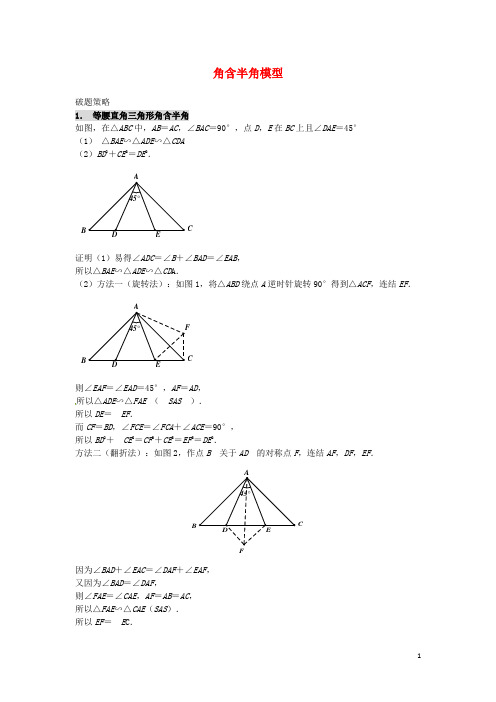
第九章半角模型模型1 已知如图： ② ∠2=12∠AOB ；②OA=OB 。

连接F ′B ，将△FOB 绕点O 旋转至△FOA 的位置，连接F ′E 、FE ，可得△OEF ′≌△OEF 。

模型分析（1）半角模型的命名：存在两个角度是一半关系，并且这两个角共顶点；（2）通过先旋转全等再轴对称全等，一般结论是证明线段和差关系；（3）常见的半角模型是90°含45°，120°含60°。

【模型图解】模型必备条件：AD=DC,对角互补，角含半角; 结论：短边之和=长边1.M点在线段AB上原图旋转全等结论：AM+NC=MN2.M点在线段AB延长线上，N在BC延长线上原图旋转全等结论：AM-CN=MN注意：旋转对象=△ADM（同M的位置无关）旋转终止条件=两个相等的边重合特例_1 直角三角形角含半角——点在AB上原图结论：旋转全等特例_1 直角三角形角含半角——点在AB延长线上原图旋转全等特例_2 正方形角含半角——点在AB上原图旋转全等特例_2 正方形角含半角——点在AB延长线上原图旋转全等AFEBCD模型实例【模型分析】例1．如图，在四边形ABCD 中，∠B+∠ADC=180°，AB=AD,E 、F 分别是BC 、CD 延长线上的点，且∠EAF=12∠BAD 。

求证：EF=BE-FD 。

图2AMBDCN 1图BACDMN 例2．在等边△ABC 的两边AB 、AC 上分别有两点M 、N ，D 为△ABC 外一点，且∠MDN=60°，∠BDC=120°，BD=DC 。

探究：当M 、N 分别在线段AB 、AC上移动时，BM 、NC 、MN 之间的数量关系。

（1）如图①，当DM=DN 时，BM 、NC 、MN 之间的数量关系是；（2）如图②，当DM ≠DN 时，猜想（1）问的结论还成立吗？写出你的猜想并加以证明。

A MCNOB A BMOCN图32图图1ACBOMN例3．已知，在等边△ABC中，点O是边AC、BC 的垂直平分线的交点，M、N 分别在直线AC、BC上，且∠MON=60°。

角含半角模型破题策略1．等腰直角三角形角含半角如图，在△ABC 中，AB ＝AC ，∠BAC ＝90°，点D ，E 在BC 上且∠DAE ＝45° （1） △BAE ∽△ADE ∽△CDA（2）BD 2＋CE 2＝DE 2．45°EA BCD证明（1）易得∠ADC ＝∠B ＋∠BAD ＝∠EAB ，所以△BAE ∽△ADE ∽△CD A ．（2）方法一（旋转法）：如图1，将△ABD 绕点A 逆时针旋转90°得到△ACF ，连结EF ．45°FEA BCD则∠EAF ＝∠EAD ＝45°，AF ＝AD ，所以△ADE ∽△FAE （ SAS ）．所以DE ＝ EF ．而CF ＝BD ，∠FCE ＝∠FCA ＋∠ACE ＝90°，所以BD 2＋ CE 2＝CF 2＋CE 2＝EF 2＝DE 2．方法二（翻折法）：如图2，作点B 关于AD 的对称点F ，连结AF ，DF ，EF ．45°EA BCD因为∠BAD ＋∠EAC ＝∠DAF ＋∠EAF ，又因为∠BAD ＝∠DAF ，则∠FAE ＝∠CAE ，AF ＝AB ＝AC ，所以△FAE ∽△CAE （SAS ）．所以EF ＝ E C ．而DF ＝BD ， ∠DFE ＝∠AFD ＋ ∠AFE ＝90°，所以BD 2＋ EC 2＝ FD 2＋ EF 2＝ DE 2．【拓展】①如图，在△ ABC 中，AB ＝AC ，∠BAC ＝90°，点D 在BC 上，点E 在BC 的延长线上，且∠DAE ＝45°，则BD 2＋CE 2＝DE 2．ED可以通过旋转、翻折的方法来证明，如图：EADFEAD②将等腰直角三角形变成任意的等腰三角形：如图，在△ABC 中，AB ＝AC ，点D ，E 在BC 上，且∠DAE ＝12∠BAC ，则以BD ，DE ，EC 为三边长的三角形有一个内角度数为180°－∠BA C ．B可以通过旋转、翻折的方法将BD ，DE ，EC 转移到一个三角形中，如图：BCEBD2．正方形角含半角如图1，在正方形ABCD 中，点E ，F 分别在边BC ，CD 上，∠EAF ＝45°，连结EF ，则：45°图1ABCD E图2GF E A B 45°图3H F EABDC（1）EF ＝BE ＋DF;（2）如图2，过点A 作AG ⊥EF 于点G ，则AG ＝AD ;（3）如图3，连结BD 交AE 于点H ，连结FH ．则FH ⊥AE ．（1）如图4，将△ABE 绕点A 逆时针旋转90°得到△ADI 证明．图4IEAB D则∠IAF ＝∠EAF ＝45°，AI ＝AE ，所以△AEF ∽△AIF （SAS ），所以EF ＝IF ＝DI ＋DF ＝BE ＋DF ．（2）因为△AEF ∽△AIF ，AG ⊥EF ，AD ⊥IF ，所以AG ＝A D ．（3）由∠HAF ＝∠HDF ＝45°可得A ，D ，F ，H 四点共圆，从而∠AHF ＝180°－∠ADF ＝90°，即FH ⊥AE ．【拓展】①如图，在正方形ABCD 中，点E ，F 分别在边CB ，DC 的延长线上，∠EAF ＝45°，连结EF ，则EF ＝DF －BE ．F BC E可以通过旋转的方法来证明.如图:EBA②如图，在一组邻边相等、对角互补的四边形ABCD 中，AB =AD ，∠BAD +∠C =180 °，点E ，F 分别在BC 、CD 上，∠EAF =12∠BAD ，连结EF ，则EF=BE+DF. ADCE可以通过旋转的方法来证明.如图:AFDCE G例题讲解例1 如图1，点E 、F 分别在正方形ABCD 的边BC 、CD 上，∠EAF ＝45°.（1）试判断BE 、EF 、FD 之间的数量关系.（2）如图2，在四边形ABCD 中，∠BAD ≠90°，AB ＝AD ．∠B ＋∠D ＝180°，点E 、F 分别在BC 、CD 上，则当∠EAF 与∠BAD 满足关系时，仍有EF ＝BE ＋FD .（3）如图3．在某公园的同一水平面上，四条通道围成四边形ABCD .已知AB ＝AD ＝80m ，∠B ＝60°，∠ADC ＝120°，∠BAD ＝150°，道路BC ，CD 上分别有景点 E ，F ，且AE ⊥AD ．DF ＝40（3－1）m ．现要在E 、F 之间修一条笔直的道路，求这条道路EF 的长．（结果取整数，参考数据：2＝1.41，3＝1.73）图1FA D CBE图2AD CF图3FCA EBD解：（1）由“正方形内含半角模型”可得EF ＝BE ＋FD ．（2）∠BAD ＝2∠EAF ，理由如下：如图4，延长CD 至点G ，使得DG ＝BE ．连结AG. 易证△ABE ≌△ADG （SAS ）. 所以AE ＝AG ，即EF ＝BE ＋DF ＝DG ＋DF ＝GF . 从而证得△AEF ≌△AGF （ SSS ）．所以∠EAF ＝∠GAF ＝12∠EAG ＝12∠BAD . 图4AD F图5HFCGA BED（3）如图5，将△ABE 绕点A 逆时针旋转1 50°至△ADG ．连结AF ．由题意可得∠BAE ＝60°所以△ABE 和△ADG 均为等腰直角三角形. 过点A 作 AH ⊥DG 于点H ．则DH ＝12AD ＝40m ，AH ＝32 AD ＝3 m.而DF ＝4031）m. 所以∠EAF ＝∠GAF ＝45°.可得△EAF ≌△GAF （SAS ）．所以EF ＝GF ＝80m+403l ）m ≈109. 2m.例2如图，正方形ABCD 的边长为a ，BM 、DN 分别平分正方形的两个外角，且满足∠MA N ＝45°．连结MC 、NC 、MN ．（1）与△ABM 相似的三角形是，BM g DN ＝（用含有a 的代数式表示）；（2）求∠MCN 的度数；（3）请你猜想线段BM 、DN 和MN 之间的等量关系，并证明你的结论. NAC B解：（1）△NDA ，2a . （2）由（1）可得BM ABAD ND=，所以BM DCBC DN=．易证∠CBM ＝∠NDC ＝45°，所以△BCM ∽△DNC ．则∠BCM ＝∠DNC ，所以∠MCN =360°一∠BCD 一∠BCM 一∠DCN ＝270°－（∠DNC +∠DCN ）＝270°－（180°－∠DNC ）＝135°．（3） 222BM DN MN +=，证明如下：如图，将△ADN 绕点A 顺时针旋转90°，得到△ABE ，连结EM. 易得AE ＝AN . ∠MAE ＝∠MAN ＝45°，∠EBM ＝90°，所以△A ME ≌△AMN .（SAS ）. 则ME ＝MN ．在Rt △BME 中，222BM BE EM += 所以222BM DN EM +=.ENBC AM倒3 如图，在四边形ABCD 中，AD ∥BC ，∠BCD ＝90°，AB ＝BC ＋AD ，∠DAC ＝45°，E 为CD 上一点，且∠BAE ＝45°.若CD ＝4，求△ABE 的面积.图1BADCE解：如图1．过点A 作CB 的垂线，交CB 的延长线于点F .由∠DAC =45°，∠ADC ＝90°，可得AD ＝CD.所以四边形ADCF 为正方形. 从而AF ＝ FC ＝4．令BC ＝m ，则AB ＝4＋m ，BF ＝4－m ．在Rt △AFB 中，有16＋（4－m ）2一（4＋m ）2所以AB ＝5，BF ＝3．如图2．将△ADE 绕点A 逆时针旋转90°至△AFG. 易证△AGH ≌△AEB ．令DE ＝n ，则CE ＝4 －n ，BE ＝BG ＝3＋n在Rt △BCE 中，有1+（4－n ）2＝（3＋n ）2，解得n ＝47. 所以BG ＝257. 从而15027ABE ABG S S AF BG ∆∆===g . 图2FADCEG进阶训练1.如图，等边△ABC 的边长为1，D 是△ABC 外一点且∠BDC ＝120°，BD ＝CD ，∠MDN ＝60°，求△AMN 的周长．NDABCM2．如图，在正方形ABCD 中，连结BD ，E 、F 是边BC ，CD 上的点，△CEF 的周长是正方形ABCD 周长的一半，AE 、AF 分别与BD 交于M 、N ，试判断线段BM 、DN 和MN 之间的数量关系，并证明．NMC DFEBA3．如图，在△ABC 中，∠ACB ＝90°，点D 在边AB 上，DE ⊥BC 于点E ，且DE ＝BC ，点F 在边AC 上，连结BF 交DE 于点G ，若∠DBF ＝45°，DG ＝275，BE ＝3，求CF 的长． G F EDCBA。

2.角含半角模型

半角模型定理公式

最新中考数学教材全册知识点梳理复习专题7.角含半角模型课件PPT

角含半角模型结论的证明

旋转模型-角含半角模型

第5讲角含半角模型(解析版)

第5讲角含半角模型(原卷版) 2020年中考数学几何模型能力提升篇(全国通用)

初中几何模型角含半角模型

角含半角模型

专题相似三角形中的半角模型(学生版)

最新中考数学压轴题破解策略专题15《角含半角模型》

(完整版)初中数学九大几何模型

2023年中考数学常见几何模型之全等模型-半角模型

初三数学几何专题旋转--“对角互补角含半角”模型

相似三角形中的基本模型-半角模型(解析版)

中考数学复习：几何模型-半角旋转导学案

角含半角模型(完整版)