第五章周转轮系及其传动比资料
合集下载
机械设计基础课件第五章轮系

第二节 定轴轮系及其传动
机械设计基础课件第五章轮系
第二节 定轴轮系及其传动比
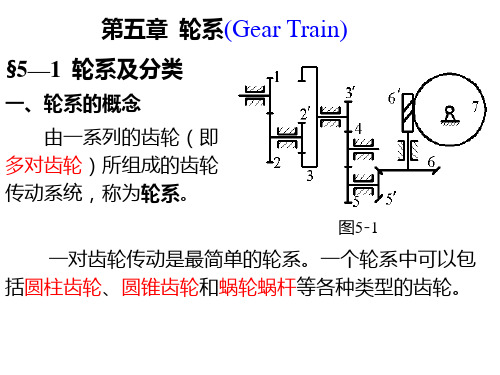
一对圆锥齿轮传动时,在节点具有相同速度, 故表示转向的箭头或同时指向节点(图c),或同时 背离节点。
蜗轮的转向不仅与蜗杆 转向有关,而且与其螺旋线 方向有关。判断时可采用左 手或右手定则。
请注意蜗杆旋向的表示 方法。
机械设计基础课件第五章轮系
第六节 几种特殊的行星传动简介
• 四、活齿传动
• 随着原动机和工作机向着多样化方向的发展,对 传动装置的性能要求也日益苛刻。为了适应这一 要求,除对齿轮、蜗杆蜗轮等传统的传动装置作 大量的研究和改进外,近20多年来人们还研究出 了多种新型传动装置如谐波传动、摆线针轮传动 等。这些传动都成功地应用于许多行业的各种机 械装置中。
机械设计基础课件第五章轮系
第二节 定轴轮系及其传动比
机械设计基础课件第五章轮系
第三节 周转轮系及其传动比
周转轮系中行星轮的运动不是绕固定轴线的 简单转动(包括自转和公转),所以周转轮系各 构件间的传动比就不能直接用定轴轮系的方法来 计算了。
机械设计基础课件第五章轮系
第三节 周转轮系及其传动比
• 周转轮系和定轴轮系的根本区别在于周转轮系中 有转动着的系杆。为了解决周转轮系的传动比的 计算问题,我们应当设法将周转轮系转化成定轴 轮系。也就是说应当使系杆静止不动。
机械设计基础课件第五章轮系
第六节 几种特殊的行星传动简介
二、摆线针轮行星传动 摆线针轮行星传动与渐开线少齿差行星传动的
不同处在于齿廓曲线各异。在摆线针轮行星传动中, 轮1的内齿是带有套筒的圆柱销形针齿,行星轮2的 齿廓曲线则是短幅外摆线的等距曲线。
摆线针轮行星传动除具有传动比大、结构紧凑、 体积小、重量轻及传动效率高的优点外,还因为同时 承担载荷的齿数多,以及齿廓间为滚动摩擦,所以传 动平稳、承载能力大、轮齿磨损小、使用寿命长。
第五章_轮系

若两轮转向相同,转速同号;
若两轮转向相反,转速异号。
正负号问题
iGHK
G K H
iGK
3、周轮系传动比计算实例
例1 已知各轮齿数为z1=100,z2=101, z2=100,z3=99。1)试求传
动比iH1;2)若z3=100,其它各轮齿数不变,iH1又为多少?
解:i1H
1
1
i1H3 1
101 99
z2 z1
平面成立!
2′ H
3
K-H-V 型
i1H2
n1 nH n2 nH
z2 z1
0 nH z2 n2 nH z1
n2
三、混合轮系的传动比
1、混合轮系传动比的计算
复合轮系传动比计算
H ?
复合轮系既不能将其 视为定轴轮系来计算 其传动比,也不能将 其视为单一的周转轮 系来计算其传动比。
按自由度分
行星轮系(F=1)
2
3
H
差动轮系(F=2)
2
3
H
1
1
中心轮是转动, 还是固定?
二、周转轮系的传动比计算
周转轮系
周转轮系
定轴轮系
?
转化
原周转轮系 的转化机构
假想的定轴轮系
1、周转轮系传动比计算反转法原理
32
O2
O1 O3
H OH
1
32
O2
O1
H
O3
1
绕固定轴线转动的系杆
反转法原理:
对整个周转轮系叠加上一个绕固定轴转动的系杆反向角速 度,各构件间的相对运动不变,但系杆相对静止,周转轮 系就变成定轴轮系。
z2z3 z1 z 2
2
2
3
若两轮转向相反,转速异号。
正负号问题
iGHK
G K H
iGK
3、周轮系传动比计算实例
例1 已知各轮齿数为z1=100,z2=101, z2=100,z3=99。1)试求传
动比iH1;2)若z3=100,其它各轮齿数不变,iH1又为多少?
解:i1H
1
1
i1H3 1
101 99
z2 z1
平面成立!
2′ H
3
K-H-V 型
i1H2
n1 nH n2 nH
z2 z1
0 nH z2 n2 nH z1
n2
三、混合轮系的传动比
1、混合轮系传动比的计算
复合轮系传动比计算
H ?
复合轮系既不能将其 视为定轴轮系来计算 其传动比,也不能将 其视为单一的周转轮 系来计算其传动比。
按自由度分
行星轮系(F=1)
2
3
H
差动轮系(F=2)
2
3
H
1
1
中心轮是转动, 还是固定?
二、周转轮系的传动比计算
周转轮系
周转轮系
定轴轮系
?
转化
原周转轮系 的转化机构
假想的定轴轮系
1、周转轮系传动比计算反转法原理
32
O2
O1 O3
H OH
1
32
O2
O1
H
O3
1
绕固定轴线转动的系杆
反转法原理:
对整个周转轮系叠加上一个绕固定轴转动的系杆反向角速 度,各构件间的相对运动不变,但系杆相对静止,周转轮 系就变成定轴轮系。
z2z3 z1 z 2
2
2
3
机械设计基础第五章轮系

2. 根据周转轮系的组合方式,利用周转轮系传动比计算公式求
03
出周转轮系的传动比。
实例分析与计算
1
3. 将定轴轮系和周转轮系的传动比相乘,得到复 合轮系的传动比。
2
4. 根据输入转速和复合轮系的传动比,求出输出 转速。
3
计算结果:通过实例分析和计算,得到了复合轮 系的输出转速。
05 轮系应用与实例分析
仿真结果输出
将仿真结果以图形、数据等形式输出,以便 进行后续的分析和处理。
实验与仿真结果对比分析
01
数据对比
将实验数据和仿真数据进行对比 ,分析两者之间的差异和一致性 。
结果分析
02
03
优化设计
根据对比结果,分析轮系设计的 合理性和可行性,找出可能存在 的问题和改进方向。
针对分析结果,对轮系设计进行 优化和改进,提高轮系的性能和 稳定性。
04 复合轮系传动比计算
复合轮系构成及特点
构成
由定轴轮系和周转轮系(或几个周转轮系)组合而成,称为复合轮系。
特点
复合轮系的传动比较复杂,其传动比的计算需结合定轴轮系和周转轮系的传动比计算公式进行。
复合轮系传动比计算公式
对于由定轴轮系和周转轮系组成的复合轮系,其传动比计算 公式为:i=n1/nK=(Z2×Z4×…×Zk)/(Z1×Z3×…×Zk-1)×(1)m,其中n1为输入转速,nK为输出转速,Z为各齿轮齿数 ,m为从输入轴到输出轴外啮合齿轮的对数。
火车车轮与轨道
通过轮系保证火车在铁轨 上的平稳运行和导向作用 。
船舶推进器
利用轮系将主机的动力传 递给螺旋桨,推动船舶前 进。
军事装备中轮系应用举例
坦克传动系统
采用轮系实现坦克发动机的动力 输出与行走机构的连接,确保坦 克在各种地形条件下的机动性。
周转轮系混合轮系传动比计算例题培训资料

例4:如图所示的周转轮系中,已知各轮齿 (lún chǐ)数为Z1=100, Z2=99, Z3=100, Z4=101 ,行星架H为原动件,试求传动比 iH1=?
解: iH1=n H / n 1
i1H4=(n 1 - n H )/ (n 4 - n H ) =1- n 1 / n H =-Z2Z4/Z1Z3
=1- i1H
i1H =-(1-99x101/100x100)=-1/10000
iH1=n H / n 1 =1/i1H =-10000
传动比为负,表示行星架H与齿轮(chǐlún)1的转向 相反。
用画箭头法标出转化(zhuǎnhuà)轮系中各构件的转向关系,如
第二页,共4页。
例5: 如图所=0 ,n2= n2 `
i12
n1 n2
z2 z1
=-2
i1H = n1 /nH = -10
负号说明行星架H与齿轮1转向相反。
第四页,共4页。
负号表示行星(xíngxīng)架与齿轮1转向相反。
2.求n3
:(n3 =
H
i12
n2n)1- n H n 2- n H
Z2 Z1
n 2 = - 133 r/min = n3
负号表示轮3与齿轮(c第h三ǐ页,l共ú4页n。 )1转向相反。
混合轮系传动比的计算
先将混合轮系分解成基本周转轮系和定轴轮系,然后分 别列出传动比计算式,最后(zuìhòu)联立求解。
Z2=25, Z3=20, Z4=60,n1=200r/min,
n4=50r/min,且两太阳轮1、4转向相反。试
求行星(xíngxīng)架转速n H及行星(xíngxīng)
轮解转:速n3。
1.求n H i1H4
解: iH1=n H / n 1
i1H4=(n 1 - n H )/ (n 4 - n H ) =1- n 1 / n H =-Z2Z4/Z1Z3
=1- i1H
i1H =-(1-99x101/100x100)=-1/10000
iH1=n H / n 1 =1/i1H =-10000
传动比为负,表示行星架H与齿轮(chǐlún)1的转向 相反。
用画箭头法标出转化(zhuǎnhuà)轮系中各构件的转向关系,如
第二页,共4页。
例5: 如图所=0 ,n2= n2 `
i12
n1 n2
z2 z1
=-2
i1H = n1 /nH = -10
负号说明行星架H与齿轮1转向相反。
第四页,共4页。
负号表示行星(xíngxīng)架与齿轮1转向相反。
2.求n3
:(n3 =
H
i12
n2n)1- n H n 2- n H
Z2 Z1
n 2 = - 133 r/min = n3
负号表示轮3与齿轮(c第h三ǐ页,l共ú4页n。 )1转向相反。
混合轮系传动比的计算
先将混合轮系分解成基本周转轮系和定轴轮系,然后分 别列出传动比计算式,最后(zuìhòu)联立求解。
Z2=25, Z3=20, Z4=60,n1=200r/min,
n4=50r/min,且两太阳轮1、4转向相反。试
求行星(xíngxīng)架转速n H及行星(xíngxīng)
轮解转:速n3。
1.求n H i1H4
《机械设计基础》第5章 轮系

3’ Z4 × 2’ × Z1 Z1 Z2’ Z3’ nn =n1 ( -) ) ) = 21( - Z ( 2 Z (- Z )2× × Z 3 2 4 4 Z3 3 n2’ (代入) i2’3= n = Z 5 (代入) 5 n3 4 Z2’ Z4 n5 =n4 (i45= n = ) Z1 Z Z2’ Z4 5 Z2’ ( - Z (5 Z ) ) n3 =n2’ Z ) = n1 ( Z1 Z2’ Z23’ 3 Z4 () n5 = n1 ( - Z3 ( Z ) ) () Z4 Z5 2 3
H 1 3
再代入公式计算
混合轮系及其传动比
混合轮系: =定轴轮系+周转轮系
H
求解思路: 1 区分轮系 (定轴,周转) 2 分别求传动比 3 联立求解
周转轮系 定轴轮系
(差动)
2 1
3 2’ 4
5
3’
3 已知: 例,联立求解 Z1=24, Z2=52, n5= nH Z2’=21, Z3=78, Z3’=18,
V=
60×1000
(m/s)
ω1 ω2
ω1
Fa1
v2 ω2
(左右手法则)
1 2 3 2’ 4
解1: 求:1 欲使猴子上升,
D 2 因猴子有心脏病, 例:图示电梯, 试确定电机轴 D 3’ 要求:V≤0.1m/s。 已知: 的转向;V 试校核安全性 4 Z1=16 , Z2=32 , V4 ω (D=600mm);倘若 Z2’=20, Z3=40 , 不安全,从机构运 Z3’= 2 , Zω=40 , 4 3’ 动角度出发,可采 n1 =800 rpm 取哪些措施。
轮系的分类:
——分类的方法是按照轮系传动时各 轮轴心线的位置是否运动进行分类的。
第5章 轮系(基础) (2)

§5-4 复合轮系及其传动比
在差动轮系中:
H i13
Z2Z3 n1H n1 n H 52 78 H ( ) ( ) (a) n3 n H 24 21 n3 ZZ
1 2
在定轴轮系中
n3 Z5 78 13 i35 ( ) n5 18 3 Z
§5-3
周转轮系及其传动比
一、周转轮系的组成
1.行星轮:轴线位置变动的齿轮,即既作自转又作公转的齿轮; 2.行星架(转臂或系杆):支持行星轮作自转和公转的构件; 3.中心轮(或太阳轮):轴线位置固定并与行星轮啮合的齿轮。 上图: 行星轮-- 齿轮2; 行星架– H杆; 中心轮-- 齿轮1、3 。
§5-3
图中1、3二轮虚线箭头反向,故取“-”,由 此得
n1 n H 61 () 0 nH 27
解得:
i1H
n1 61 1 3.26 nH 27
n1 6000 nH 1840r / min i1H 3.26
设n1的转向为正,则
nH的转向和n1相同。
§5-3
四、例题
周转轮系及其传动比
例5-3 在图5-6所示圆锥齿轮组成的差动轮系中,已知Z1=60,Z2=40, Z2′=Z3=20,若n1和n3均为120r/min,但转向相反(如图中实线箭头 所示),求nH的大小和方向。 解 将H固定,画出转化轮系各 轮的转向,如虚线箭头所示。 由通式可得:
H i13
Z2Z3 n1H n1 n H H () n3 n H n3 ZZ
在周转轮系中,设ωH为行星架H的角速度。根据相对运动原 理,当给整个周转轮系加上一个绕轴线OH转动的公共转速(-ωH) 后,行星架H便静止不动了,而各构件间的相对运动并不改变。这 样,所有齿轮的几何轴线的位置全部固定,原来的周转轮系便成 了定轴轮系),这一定轴轮系称为原来周转轮系的转化轮系。
周转轮系的传动比计算

图示轮系中,已知:Z 1 Z 2 30, Z 3 90, 例2. 轮1与系杆转速均为n1 nH 1rpm , 且转向相 反。求: n3 ?
Z2
H
n1 nH Z3 解: i n3 nH Z1 n1 nH 90 3 n3 nH 30
H 13
令n1 转向为正 , n 为负。 转向为正 , n H H 1
Z1 Z3
1 1 ( 1 ) 1 则 :: 则 33 n3 ( 1) n 3 1 5 5 ((与 与n nH 同向)) n3 3 H同向 3 3
例3.图示轮系中, 已知: Z1 Z 3 40, Z 2 30. 求: i1 H ? 解:
作业:
P 196197
65 66 6 11
周转轮系的动比计算
赵 爽
上海电机学院
知识回顾
一、定轴轮系传动比计算公式:
i AB
A 所有从动齿轮齿数的乘积 B 所有主动齿轮齿数的乘积
注: 公式中齿数比前符号的确定
二、周转轮系传动比的计算
(Transmission ratio of epicyclic gear train)
基本思想: 给整个周转轮系加上一个与系杆 H的角速度大小相等,方向相反的公 设法把周转轮系转化成定轴轮 共角速度 H ,系杆的角速度变为0 系,然后间接利用定轴轮系的传动 ,即系杆静止,整个周转轮系转化 比公式来求解。 为假想的定轴轮系。
i13 H
Z 2 Z3 Z3 1H 1 H H 3 H Z1Z 2 3 Z1
H H H H o
1H 1 H 2H 2 H 3H 3 H
转化机构 转化机构
周转轮系的传动比计算公式:
【机械设计基础】第五章 轮系

轮
系
三个运动件中,有两个构件为主动件 一个为从动 三个运动件中 有两个构件为主动件,一个为从动, 运动复合的差动轮系 有两个构件为主动件 一个为从动, 三个运动件中,有一件主动,两件从动, 三个运动件中,有一件主动,两件从动,运动分解的差动轮系 三个运动件中,两个中心轮之一固定, 三个运动件中,两个中心轮之一固定, 行星轮系 系杆H固定 演变为定轴轮系。 固定, 系杆 固定,演变为定轴轮系。
第五章
轮
系
重点学习内容
1.定轴轮系和周转轮系的传动比计算 2.轮系中从动轮转动方向的判定
机 械 设 计 基 础
第五章
轮
系
第一节 定轴轮系及其传动比计算 第二节 周转轮系及其传动比计算 第三节 轮系的功用
机 械 设 计 基 础
第五章
轮
系
现代机械中, 现代机械中,为了满足不同的工作要求只用一对齿轮传 动往往是不够的,通常用一系列齿轮共同传动。 动往往是不够的,通常用一系列齿轮共同传动。这种由一系列 齿轮(包括蜗杆蜗轮)组成的传动系统称为齿轮系(简称轮系)。 齿轮(包括蜗杆蜗轮)组成的传动系统称为齿轮系(简称轮系)。 齿轮系
机 械 设 计 基 础
周转轮系的分类: 周转轮系的分类:
第五章
轮
系
1、行星轮系:自由度为1的周转轮系,需要两个原动 、行星轮系:自由度为 的周转轮系 的周转轮系, 件才能有确定的运动。 件才能有确定的运动。 2、差动轮系:自由度为2的周转轮系,需要一个原动 、差动轮系:自由度为 的周转轮系 的周转轮系, 件才能有确定的运动。 件才能有确定的运动。
第五章
转化后的定轴轮系 的传动比为: 的传动比为:
H 13
n1 n1 − nH i = H = n3 n3 − nH
周转轮系的传动比

第5章 轮 系
(2) 对于包含有圆锥齿轮或蜗杆传动的定轴轮系,由于是各 轮的轴线不平行,则只能采用画箭头的方法确定传动比的符号。
对于圆锥齿轮传动,表示齿轮副转向的箭头同时指向或同时 背离啮合处。对于蜗杆传动,从动蜗轮转向的判定方法是: 对 右旋蜗杆用右手定则,四指弯曲顺着主动蜗杆的转向,与拇指 指向相反的方向,就是蜗轮在啮合处圆周速度的方向。对左旋 蜗杆用左手定则,方法同上。
第5章 轮 系
【例5-1】图5-3所示的电动卷扬机减速器中,齿轮1为主动 轮,动力由卷筒H输出。各轮齿数为z1=24,z2=33,z2′=21, z3 =78,z3′=18,z4=30,z5=78。求i1H。
解 (1) 分解轮系。
在该轮系中,双联齿轮2-2′的几何轴线是绕着齿轮1和3的轴 线转动的,所以是行星轮; 支持它运动的构件(卷筒H)就是系杆; 和行星轮相啮合且绕固定轴线转动的齿轮1和3是两个中心轮。 这两个中心轮都能转动,所以齿轮1、2-2′,3和系杆H组成一个 2K-H型双排内外啮合的差动轮系。剩下的齿轮3′,4, 5是一个 定轴轮系。二者合在一起便构成一个混合轮系。
第5章 轮 系
图5-6 实现分路传动
第5章 轮 系
4. 实现运动的合成和分解
在图5-7所示的由圆锥齿轮组成的行星轮系中,中心轮1与3
都可以转动,而且z1=z3。根据式(5-2)并且用画虚箭头的方法判 定中心轮1与3的相转向后得到
i1H3
n1H n3H
n1 nH n3 nH
z3 z1
n3' n5
z5 z3'
78 18
13 3
(a)
对差动轮系的转化机构,根据式(5-2)得到
机械设计基础.第五章_轮系机构

z2 zn 1 H n H z1 z n 1
各轮齿数已知,就可以确定1、n、H之间的关系; 如果其 中两个转速已知,就可以计算出第三个,进而可以计算周转轮系 的传动比。
1、i1H 是转化机构中齿轮1为主动轮、齿轮n为从动轮时的传动 n
比,其大小和方向可以根据定轴轮系的方法来判断; 2、表达式中 1、n、H的正负号问题。若基本构件的实际 转速方向相反,则 的正负号应该不同。
1 z 2 z 3 z 4 z 5 i15 5 z1 z 2' z 3' z 4
1 2 3 4 1 i15 2 3 4 5 5
大小:
i1 k
1 m 从 动 轮 齿 数 连 乘 积 ( 1) k 主动轮齿数连乘积
m: 外 啮 合 的 次 数
3 要在 先计 学算 会传 分动 析比 传大 动小 路之 线前 Ⅱ 1 2 Ⅲ
动力输出
4
传动路线 动力输入
Ⅰ
两级齿轮传动装置
例1
如图所示轮系,分析该轮系传动路线。
Ⅴ Ⅰ
z1
z7 z8
Ⅲ
z9
Ⅵ
n1 z2
Ⅱ
z5 Ⅳ z6
z3
z4
n9
解
该轮系传动路线为:
Ⅰ
n1
z1 z2
Ⅱ
z3 z4
Ⅲ
z5 z6
Ⅳ
z7 z8
z 2 z3 z5 1 z 2 z 3 z 4 z 5 i15 5 z1 z 2' z 3' z 4 z1 z 2 ' z 3'
?
转向?
平面定轴轮系(各齿轮轴线相互平行)
例 1:
《机械设计基础》第5章 轮系
解:差动轮系:1—2—3(H)
i13
H
=
n1 n3
nH nH
=
-
z2 z1
•
z3 z2
=
-
z3 z1
设轮1的转向为正(即n1=10 ) , 则轮3的转向为负(即n3= -10) 。故
n1 n3
10 nH = -90/30 =-3
10 nH
解得:nH = -5rpm(与轮1的转向相反) i1H = n1 / nH =10/-5= -2(轮1与行星架H的转向相反)
如图a:整个轮系加上 “-nH” ,周转轮
系部分
定轴轮系,但定
图a
轴轮系部分
周转轮系;
如图b:由于各个周转轮系有不同的nH, 无法加上一个公共角速度“-
nH1”或“-nH2”来将整个轮系转 化为定轴轮系。
图b
计算复合轮系传动比的正确方法是:(计算步骤) 1、首先分析轮系,正确区分各个基本轮系(即单一的定
而是绕其它齿轮的固定轴线回转;
2)再找行星架(1个) :支承行星轮的构件(注:其形 状不一定是简单的杆件,有时是箱体或齿 轮,同一行星架上可能有几个行星轮);
3)最后找太阳轮(1~2个):与行星轮啮合且几何轴线是 固定的、并与行星架的轴线重合。
则:每个行星架 + 此行星架上的行星轮 +与行星轮啮合的太阳轮 = 1个周转轮系。
2、5的转向相同)
∴
i17=
z2 z1
•
z3 z 2
•
z4 z3
•
z5 z4
•
z6 z5
•
z7 z6
上例中的轮4,其齿数多少不影响传动比的大小,只
起改变转向的作用,在轮系中的这种齿轮称为惰轮(过桥
周转轮系传动比计算

周转轮系传动比计算
周转轮系(传动轮系)是指由两个或多个齿轮组成的传动装置,用于实现转矩和转速的变换。
在机械传动中,计算周转轮系的传动比是非常重要的,下面是关于周转轮系传动比的计算方法及相关参考内容。
1. 传动比的定义:
传动比是指输入轴(或驱动轴)的转速与输出轴(或从动轴)的转速之间的比值。
根据不同的周转轮系类型和传动方式,传动比可以通过不同的计算公式来计算。
2. 计算方法:
(1)直线齿轮传动:对于直线齿轮传动,传动比等于从动轮
的齿数除以驱动轮的齿数。
传动比 = 从动轮的齿数 / 驱动轮的齿数
(2)斜齿轮传动:对于斜齿轮传动,传动比等于从动轮的齿
数除以驱动轮的齿数乘以斜齿轮的传动比。
传动比 = (从动轮的齿数 / 驱动轮的齿数) * 斜齿轮的传动比
(3)带传动:对于带传动,传动比等于从动轮的转速除以驱
动轮的转速。
传动比 = 从动轮的转速 / 驱动轮的转速
3. 相关参考内容:
(1)《机械设计手册(第3版)》中关于周转轮系传动比的计算方法和相关公式。
(2)《机械设计基础(第3版)》中关于直线齿轮传动、斜齿轮传动和带传动的传动比计算方法和实例。
(3)《机械工程设计手册(第4版)》中关于周转轮系传动比的计算和设计原则。
(4)《机械设计手册(第4版)》中关于各种传动方式的传动比计算方法和设计指导。
(5)机械学术论文和研究报告中关于传动比计算方法和应用的内容。
以上是关于周转轮系传动比计算方法及相关参考内容的简要介绍。
通过合理计算和选择传动比,可以确保传动装置的性能和效率,满足各种工程需求。
机械设计-周转轮系的传动比计算

方法确定。GK 是周转轮系中轮G与轮K的绝对转速之比,其大小与正负号必须由计算结果确定。
2. 周转轮系的传动比计算
【例1】在右图所示的行星轮系中,已知z1=100,z2=99,z2′=100,z3=101。试求 iH1 。
解:由周转轮系转化机构的传动比计算公式得
13 =
即
1 −
3 −
行星架 H
= − =
周转轮系的转化机构
2. 周转轮系的传动比计算
对于转化机构的传动比 13 ,可用定轴轮系传动比的计算方法求出:
13 =
1
3
=
1 −
3 −
=−
3
1
推广到一般情况,单级周转轮系中任意两轮 G、K 以及行星架 H 的
转速与齿数的关系为
解:
13 =
1 −
3 −
=−
3
1
式中表示转化机构中轮 1 与轮 3 反向。由题意知,轮 1 与轮 3 同向回转,
故 n1 与 n3 以同号代入上式,则有
110−
200−
解之可得
=−
= 170
70
35
= −2
r/min
由计算得 nH 为正,故 nH 与 n1 转向相同。
= −3000/
1 =
1
=−
1
3
式中的负号表示行星架的转向与齿轮1的转向相反,与齿轮3相同。
差动轮系
2. 周转轮系的传动比计算
【例3】在右图所示的锥齿轮差动轮系中,已知齿数z1=35,z3=70,两太阳轮同向回转,转速
n1=110 r/mim,n3=200r/mim。试求转臂的转速nH 。
速分别为: n1=100r/mim,n3=400r/mim。试求nH和 iH1。
2. 周转轮系的传动比计算
【例1】在右图所示的行星轮系中,已知z1=100,z2=99,z2′=100,z3=101。试求 iH1 。
解:由周转轮系转化机构的传动比计算公式得
13 =
即
1 −
3 −
行星架 H
= − =
周转轮系的转化机构
2. 周转轮系的传动比计算
对于转化机构的传动比 13 ,可用定轴轮系传动比的计算方法求出:
13 =
1
3
=
1 −
3 −
=−
3
1
推广到一般情况,单级周转轮系中任意两轮 G、K 以及行星架 H 的
转速与齿数的关系为
解:
13 =
1 −
3 −
=−
3
1
式中表示转化机构中轮 1 与轮 3 反向。由题意知,轮 1 与轮 3 同向回转,
故 n1 与 n3 以同号代入上式,则有
110−
200−
解之可得
=−
= 170
70
35
= −2
r/min
由计算得 nH 为正,故 nH 与 n1 转向相同。
= −3000/
1 =
1
=−
1
3
式中的负号表示行星架的转向与齿轮1的转向相反,与齿轮3相同。
差动轮系
2. 周转轮系的传动比计算
【例3】在右图所示的锥齿轮差动轮系中,已知齿数z1=35,z3=70,两太阳轮同向回转,转速
n1=110 r/mim,n3=200r/mim。试求转臂的转速nH 。
速分别为: n1=100r/mim,n3=400r/mim。试求nH和 iH1。
周转轮系及其传动比

3) 式中nG、nK、nH均为代数值,在计算中必须同时代入 正、负号,求得的结果也为代数值,即同时求得了构 件转速的大小和转向。
§5-3
4)
周转轮系及其传动比
注意iHGK与iGK是完全不同的两 个概念。iHGK是转化轮系中G、 K两轮相对于行星架H的相对 转速之间的传动比;而iGK是周 转轮系中G、K两轮绝对转速 之间的传动比。
H i13
z 2 z 3 图9-9 n1H n1 n H n1 n H H n3 n H 0 nH z 1 z 2' n3
转化轮系齿轮1和齿 轮3的转向相同。
§5-3
得 所以
i1 H
周转轮系及其传动比
z z n1 101 99 1 1 2 3 1 nH z 1 z 2' 100 100 10000
n1 n1 n2 n3' n4 n5' n6' z2 z3 z4 z5 z6 z7 i17 n7 n2 n3 n4 n5 n6 n7 z1 z2 z3' z4 z5 z6' z 2 z 3 z4 z5 z6 z7 i12i23 i3'4 i45i56 i6'7 z1 z2 z3' z4 z5 z6'
iH1
1 i1 H
10000
传动比iH1为正,表示行星架H与齿轮1转向相同。 该例说明行星轮系可以用少数几个齿轮获得很大的传
动比。但要注意,这种类型的行星轮系传动,减速比
愈大,其机械效率愈低。一般不宜用来传递大功率。 如将其用作增速传动 (即齿轮1低速输入,行星架H高
速输出),则可能产生自锁。
复合轮系
第五章 轮系-3

13
ω
H 3
ω3i−ωH ω1 =z1− i H 1 z2 =
1H
ωH
1K
3
§5—3周转轮系传动比计算 3
周转轮系传动比计算方法 周转轮系 上角标 H
- ωH
转化机构: 转化机构:假想的定轴轮系
i1H n
正负号问题
ω1 ωn ω H i1n
计算转化机构的传动比
ω1H ω1 − ω H z2 … zn H i1n = H = =± ωn ωn − ωH z1 … z n −1
§5—3周转轮系传动比计算 3
6)任何时候都不能用箭头或(- )m来 )任何时候都不能用箭头或(-1) (- 直观的判断周转轮系中从动件的真实 转向,只能按 转向,只能按i1k计算结果与原假定方 向来确定 ; 7)无论行星轮数目为多少,只要转化轮系 )无论行星轮数目为多少, 是串联式轮系, 是串联式轮系, 此行星轮系仍旧是一个 单一行星轮系。 单一行星轮系。
z2 ⋅ ⋅ ⋅ zk i = (−1) z1 1⋅ ⋅− zω −1 ω 1H ω ⋅ k H H
m
§5—3周转轮系传动比计算 3
3)ω1H、ωkH、i1kH为转化机构的角速度、 ) 为转化机构的角速度、 传动比,按定轴轴轮系公式计算; 传动比,按定轴轴轮系公式计算; 4)ω1、ωk、 ωH为周转轮系的角速度,均 ) 为周转轮系的角速度, 为代数值,公式中要带相应的“+”、 代数值,公式中要带相应的“ 、 “-” ; 5)对于周转轮系,若已知公式中 1、ωk、 )对于周转轮系,若已知公式中ω z3 ω 1H ω1 −ωH H ωH13 = i 三个角速度中任意两个的大小和方 = = − H z1 ω3 ω3 −ωH 可求第三个的大小和方向; 向,可求第三个的大小和方向;
ω
H 3
ω3i−ωH ω1 =z1− i H 1 z2 =
1H
ωH
1K
3
§5—3周转轮系传动比计算 3
周转轮系传动比计算方法 周转轮系 上角标 H
- ωH
转化机构: 转化机构:假想的定轴轮系
i1H n
正负号问题
ω1 ωn ω H i1n
计算转化机构的传动比
ω1H ω1 − ω H z2 … zn H i1n = H = =± ωn ωn − ωH z1 … z n −1
§5—3周转轮系传动比计算 3
6)任何时候都不能用箭头或(- )m来 )任何时候都不能用箭头或(-1) (- 直观的判断周转轮系中从动件的真实 转向,只能按 转向,只能按i1k计算结果与原假定方 向来确定 ; 7)无论行星轮数目为多少,只要转化轮系 )无论行星轮数目为多少, 是串联式轮系, 是串联式轮系, 此行星轮系仍旧是一个 单一行星轮系。 单一行星轮系。
z2 ⋅ ⋅ ⋅ zk i = (−1) z1 1⋅ ⋅− zω −1 ω 1H ω ⋅ k H H
m
§5—3周转轮系传动比计算 3
3)ω1H、ωkH、i1kH为转化机构的角速度、 ) 为转化机构的角速度、 传动比,按定轴轴轮系公式计算; 传动比,按定轴轴轮系公式计算; 4)ω1、ωk、 ωH为周转轮系的角速度,均 ) 为周转轮系的角速度, 为代数值,公式中要带相应的“+”、 代数值,公式中要带相应的“ 、 “-” ; 5)对于周转轮系,若已知公式中 1、ωk、 )对于周转轮系,若已知公式中ω z3 ω 1H ω1 −ωH H ωH13 = i 三个角速度中任意两个的大小和方 = = − H z1 ω3 ω3 −ωH 可求第三个的大小和方向; 向,可求第三个的大小和方向;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
当外啮合次数为奇数时,始末两轮反向,传 动比为-;当外啮合次数为偶数时,始末两轮同向, 传动比+。传动比也可用公式表示为:
i1K
n1 nK
(1)m
z2 z3z4 zK z1 z2 z3 z(K 1)
式中m为全平行轴定轴轮系齿轮1至齿轮K之间
外啮合次数。
例题5-1 已知各轮齿数Z1=18、Z2=36、Z3=80、 Z3’=20、Z4=18、Z5=30、Z5’=15、Z6’=2(右旋)、 Z7=60、n1=1440r/min,其转向如图,求传动比i17、 i15、i25及涡轮的转速和转向。
i25
n2 n5
z3z4 z5 z 2 z3 z 4
6
n7
n1 i17
1440 720
2r / min
第三节 周转轮系及其传动比
一、周转轮系的组成
在图所示轮系中,齿轮1 和3以及构件H各绕固定的几 何 轴 线 O1 、 O3 、 OH 转 动 (O1、O3、OH 重合),齿 轮2空套在构件H的小轴上, 当构件H转动时,齿轮2一方 面绕自己的几何轴线O2自转, 同时又随构件H绕固定的几 何轴线OH公转。
周转轮系,两个中心轮都能 转动,该机构自由度 F=3×4-2×4-2=2 , 需 要 两 个原动件,这种周转轮系称 为差动轮系。 差动轮系
周转轮系,只有一个中心轮 能转动,该机构自由度 F=3×3-2×3-2=1 , 需 要 一 个原动件,这种周转轮系称 为行星轮系。 行星轮系
二、周转轮系传动比计算
向有关。
蜗杆右旋用右手,
左旋用左手,四指握
向蜗杆转动方向,拇
指方向为蜗杆前进方
向,根据相对运动原
理,蜗轮的运动方向
应与此相反。
锥齿轮机构
蜗轮蜗杆机构
定轴轮系传动比计算
Z1、Z2、Z2’ 表示各轮的齿数 n1、n2、n2’ … 表示各轮的转速。 同一轴上的齿轮转速相同,n2=n2’、n3=n3’、n5=n5’、
第5章 轮系
第一节 轮系的类型 第二节 定轴轮系及其传动比 第三节 周转轮系及其传动比 第四节 符合轮系及其传动比 第五节 轮系的应用 第六节 几种特殊的行星传动简介
第一节 轮系的类型
由一对齿轮组成的机构是齿轮传动的最简单形
式。但是在机械中,为了获得很大的传动比,或者
为了将输入轴的一种转速变换为输出轴的多种转速
周转轮系中行星轮的运动 不是绕固定轴的转动,所以其 传动比不能直接用定轴轮系传 动比计算方法来计算。
但是,如果是行星架固定 不动,并保持各构件间相对运 动不变,则就转化为一个定轴 轮系。
等原因,常采用一系列互相啮合的齿轮将输入轴和
输出轴连接起来。这种一系类齿轮组成的传动系统
称为轮系。
轮系的分类
定轴轮系
周转轮系 行星轮系(F=1) 差动轮系(F=2)
定轴轮系:传动时每个齿轮的几何轴线都是固定的。
开始 停止
周转轮系:轮系中有齿轮的几何轴线位置不固定。 至少有一齿轮的几何轴线绕另一齿轮的几何轴线转 动的轮系。
解: 从轮2开始,依次标出各对啮合齿轮的转动方
向。 1、7两轮的轴线不平行,1、5两轮转向相反,
2、5两轮转向相同。
i17
n1 n7
z2 z3 z4 z5 z6 z7 z1 z 2 z3 z 4 z5 z6
720
(↑
)
i15
n1 n5
z2 z3z4 z5 z1 z 2 z3 z 4
12
定轴轮系各轮的相对转向可以通过逐对齿轮 标注箭头的方法来确定。
一对平行轴外啮合齿轮,两轮转向相反。用方 向相反的箭头表示
一对平行轴内啮合齿轮,两轮转向相同。用方 向相同的箭头表示。 两齿轮内啮合传动过程
一对圆锥齿轮传动时,在节点具有相同速度, 故表示转向的箭头或同时指向节点,或同时背离节 点。
蜗轮与蜗杆的啮合,与蜗杆的转向和螺旋线的旋
周转轮系由行星轮、行星架和中心轮组成。 行星轮:周转轮系中轴线位置变动的齿轮,即做自 转又做公转的齿轮。 行星架:或叫转臂,支持行星轮做自转或公转的构 件。 中心轮:或叫太阳轮, 轴线位置固定的齿轮。
中心轮有时两个, 有时一个。行星架与中 心轮的几何轴线必须重 合,否则不能传动。
为了使传动时惯性 力平衡及减轻齿轮上载 荷,常采用几个完全相 同的行星轮均布在中心 轮周围,属于虚约束, 在机构运动简图中只需 画出一个。
齿数Z4在分子分母各出现一次,不影响传动比 大小,只起改变转动方向。称为惰轮或过桥齿轮。
推广至一般情况,轮1为起始主动轮,轮K为最 末从动轮,则定轴轮系始末两轮传动比数值计算 的一般公式为:
i1K
n1 nK
轮1至轮K间所有从动轮齿数的乘积 轮1至轮K间所有主动轮齿数的乘积
z2 z3z4 zK z1 z2 z3 z(K 1)
上式所求为传动比数值大小,通常以绝对值
表示。两轮相对转动方向则由图中箭头表示。
当起始主动轮1和最末从动轮K的轴线相平行时,两轮转的同异可用传动比的正负表示。两
轮转向相同时,传动比为+;两轮转向相反时,传
动比为-。
因此,平行两轴间的定轴轮系传动比计算公
式为:
i1K
n1 nK
() z2 z3 z4 zK z1z2 z3 z(K 1)
开始
停止
第二节 定轴轮系及其传动比
定轴轮系传动比:输入轴与输出轴角速度(或转 速)之比。
iab表示:a代表输入轴,b代表输出轴。
iab
a b
na nb
传动比等于两轮角速度之比,等于两轮转速
(转/分)之比。
传动比不仅要确定数值,而其要两轴的相对
转动方向。这样才能完整的表达输入轴与输出轴
之间的关系。
n6=n6’
i12
n1 n2
z2 z1
i23
n2 n3
n2 n3
z3 z2'
i34
n3 n4
n3 n4
z4 z3
i45
n4 n5
z5 z4
i56
n5 n6
n5 n6
z6 z5
i67
n6 n7
n6 n7
z7 z 6
设与轮1固联的为输入轴,与轮7固联的为输出 轴,则输入轴与输出轴的传动比数值为:
i17
n1 n7
n1 n2
n2 n3 n3 n4
n4 n5
n5 n6
n6 n7
i12i23i34i45i56i67
z2 z3z4 z5 z6 z7 z1 z 2 z3 z 4 z5 z6
上式表明:定轴轮系传动比的数值等于各对啮合齿
轮传动比的连乘积,也等于所有从动轮齿数的乘积
与所有主动轮齿数的乘积之比。
