弹性力学 第七章3PPT课件
合集下载
弹性力学-第7章 空间问题
zx
z
dz
zy
zy
z
dz
z 0
y
y
yx yz
xy
x
yz
yz
y
dy
fz
fy fx
xz
yx
y yx dy
y
y y
dy
zx zy
x
x
x x
dx
z
根椐平衡条件： Fx 0
xz
xzx
x
dx
x
x
x
dx dydz
xdydz
(
yx
yx
x
dy)dxdz
yxdxdz
( zx
zx
z
dz)dxdy
zxdxdy
Xdxdydz
0
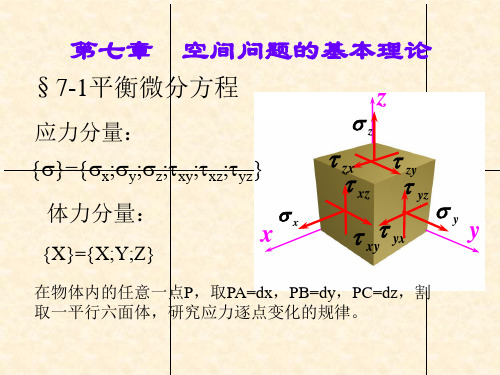
§7-1平衡微分方程
x x
yx y
zx
z
fx
0
xy
y
x
y
zy
z
f y
0
xz yz
x
y
z z fz 0
（7-1）
平面应力问题：
1、平面应力问题z方向应力为零：
0
xz
yz
0
z
2、所有的应力、应变和位移分量均与z无关，仅是x,y的函数。 以上方程可以直接转化为平面应力的平衡方程。
在计算任一平面上的应力时，方向余弦l,m,n可变化，但 均为有限值，故必存在某个平面，其上正应力取得极值。
主平面：正应力取得极值的平面。 主应力：主平面上的正应力。 主方向：主应力的方向，也称应力主向。 在主平面上，正应力取极值、剪应力为零。
二、主应力的确定：
设主平面存在，其外法线为n，
《弹性力学》第七章 平面问题的差分解
4 f 1 2 2 4 [4 f 0 2( f1 f 2 f 3 f 4 ) ( f 5 f 6 f 7 f8 )] x y h 0 4 f 4 y 1 4 [6 f 0 4( f 2 f 4 ) ( f10 f12 )] h 0
弹性力学的经典解法存在一定的局限性，当弹性体的边 界条件和受载情况复杂一点，往往无法求得偏微分方程的边 值问题的解析解。因此，各种数值解法便具有重要的实际意 义。差分法就是数值解法的一种。 所谓差分法，是把基本方程和边界条件（一般均为微分 方程）近似地改用差分方程（代数方程）来表示，把求解 微分方程的问题改换成为求解代数方程的问题。
T (T0 Te ) x 0
其中 Te 为边界以外的介质的已知温度。应用差分公式，可得：
T1 T3 (T0 Te ) 2h
解出 T1 ，代入（1）式，即得修正的差分方程：
2h 2h 4 T0 T2 2T3 T4 Te
第七章 平面问题的差分解
§7-1 差分公式的推导 §7-2 稳定温度场的差分解 §7-3 不稳定温度场的差分解 §7-4 应力函数的差分解 §7-5 应力函数差分解的实例 §7-6 温度应力问题的应力函数差分解 §7-7 位移的差分解 §7-8 位移差分解的实例 §7-9 多连体问题的位移差分 解 习题课
2 2 2 T h T 2 T0 TA h 2 x A x A 2 1 T 2 2 T T3 TA (1 )h (1 ) h 2 x x A 2 A
§7-2
稳定温度场的差分解
本节以无热源的、平面的、稳定的温度场为例，说明差分 法的应用。 在无热源的平面稳定场中，t 0, z 微分方程简化为调和方程 2T 0 ，即：
人教版八年级物理下册 课件第七章力第二节弹力共46张PPT
哪些类似 橡皮筋(或橡皮泥)?
例如：尺子、橡皮擦、白纸、钢锯条、泥巴、面粉团、皮肤……
想一 想
发现它们的共同特点了吗？试 概括一下。
类似橡皮筋:尺子、橡皮擦、钢锯条、 皮肤
类似橡皮泥:白纸、面粉团、泥巴
1/21/2021
弹性:
类似于弹簧，物体受力时会发生形变,不受力又恢复到原来的形状,这种特性叫弹性.
❖ 7．某同学用一只弹簧秤做研究弹簧的伸长与拉力关系的实验，具体记录数据如下表：
拉力/N 1
2
3
4
5
6
7
8
9
❖
10
11
1
2
弹❖簧长(1)根据6实.0验数据7.0，能做8一.0个测9量.0范围是10多.0大的弹11簧.0秤?理1由2.是0 什么13?.10 14.30 度❖/cm (2)当悬挂某物体时，弹簧长度为8．5 cm，问该物体对弹簧的拉力是多少?
的拉力时，弹簧伸长_____，此时弹簧长度为_______．
分度值
零刻线
量程
2cm
18cm
6cm
❖ 6．一弹簧秤竖直悬挂时，给秤钩施力，示数为8 N，若把弹簧秤拿下来，用两手拉弹簧测力计的秤钩 和吊环时，每只手用力8 N．那么，弹簧测力计的示数是______.（不计弹簧秤重） 8N
想一
想 生 活 中 在 哪 儿 应 用 到 了 弹 力 ？
②绳的弹力----拉力 挂在绳下的物体，在重力的作用下拉紧绳子，使物体和绳子同时发生微小的形变。
物体对绳 子的拉力
绳子对物 体的拉力
可见，拉力也是弹力。
拉力的方向：绳子对物体的拉力总是沿着绳而指 向绳子收缩的方向。
例题1.
关于弹力,下列叙述正确的是( )
弹性力学课件07-杆件的扭转
15
x 0
三、位移分量：
u x x v y y
x 0
不计刚体位移
y 0
z 0
xy 0
zy
zx
1 G x
u yz v zx
为单位长度的相对扭转角
z
w z
v u x y w v y z u w z x
2
弹性解：
x y z t xy 0
Mx t zy Ip
t zx
My Ip
(1 ) t zx
2
2 0 zx
2 2 2 2 2 2 2 x y z
4
2. 应变分量： x y z t xy 0
A
3
用应力表示的相容方程：
2 (1 ) x 0 2 x 2 2 (1 ) y 0 2 y 2 2 (1 ) z 0 2 z 2 2 (1 ) t xy 0 xy 2 (1 ) 2t yz 0 yz
12
2 2 2 2 2 2 2 x y z
边界条件：
侧面：
l dy dx ,m ,n 0 ds ds
o
dx dy ds
x
l x mt yx nt zx 0 lt xy m y nt zy 0 lt xz mt yz n z 0
l x m t yx nt zx Fx lt xy m y nt zy F y lt xz m t yz n z Fz
A A
侧面： 端面：
x y l ,m ,n 0 R R
l 0, m 0, n 1
x 0
三、位移分量：
u x x v y y
x 0
不计刚体位移
y 0
z 0
xy 0
zy
zx
1 G x
u yz v zx
为单位长度的相对扭转角
z
w z
v u x y w v y z u w z x
2
弹性解：
x y z t xy 0
Mx t zy Ip
t zx
My Ip
(1 ) t zx
2
2 0 zx
2 2 2 2 2 2 2 x y z
4
2. 应变分量： x y z t xy 0
A
3
用应力表示的相容方程：
2 (1 ) x 0 2 x 2 2 (1 ) y 0 2 y 2 2 (1 ) z 0 2 z 2 2 (1 ) t xy 0 xy 2 (1 ) 2t yz 0 yz
12
2 2 2 2 2 2 2 x y z
边界条件：
侧面：
l dy dx ,m ,n 0 ds ds
o
dx dy ds
x
l x mt yx nt zx 0 lt xy m y nt zy 0 lt xz mt yz n z 0
l x m t yx nt zx Fx lt xy m y nt zy F y lt xz m t yz n z Fz
A A
侧面： 端面：
x y l ,m ,n 0 R R
l 0, m 0, n 1
弹力 高中物理必修课件PPT 人教版
.
2、点面接触：垂直于面。
3、点点接触：垂直于公切面。
4、轻绳（不计质量）：沿绳子收缩的方向。
5、轻杆（不计质量）：不一定沿杆的方向， 可由平衡条件分析力的方向。
练习1、关于弹力产生的原因，下列
说法正确的是： D
A、木块放在桌面上受到向上的支持力， 这是木块发生微小弹性形变而产生的。
B、用一根细竹竿拨动水中的木头， 木头受到竹竿的推力，这是由于木头 发生弹性形变而产生的。
有的形变明显、有的形变微小
二、弹力
施力物体
1、定义：发生弹性形变的物体由于要恢复原来的形 状，对与它接触的物体发生力的作用，这种力叫做
弹力
受力物体
2、产生条件
①物体间相互接触 ②物体发生弹性形变
3、弹力的种类
F支
F拉
F推
F压
支持力、压力、拉力等
三、弹力的方向：与恢复形变方向相同
1、两平面接触：垂直于接触面。
第七章 第２节 弹力
恢复到原来形状
没有恢复到原来形状
一、弹性形变、塑性形变
弹性形变:物体受力发生形变，撤掉外力，能自动 恢复到原状 塑性形变:物体受力发生形变，撤掉外力，不能自 动恢复生形变 形变消失
原状 施加外力 停止用力 产生形变 形变保留
弹性形变 弹性限度 塑性形变
C、绳对物体的拉力方向总是竖直向上。 D、挂在电线下面的电灯受到向上的拉力，
是由于电线发生微小弹性形变而产生的 。
弹性力学第七章 主应力
2mn yz 2nl zx 2lm xy
（7-3）
p2
2 n
2 n
px2
p
2 y
pz2
2 n
px2
p
2 y
pz2
2 n
（7-4）
弹性力学简明教程
NORTHEASTERN UNIVERSITY
§7－2 物体内一点的应力状态
如果ABC是边界面，px, py , pz 成为面力分量
fx, fy, fz
弹性力学简明教程
NORTHEASTERN UNIVERSITY
§7－5 轴对称问题的基本方程
弹性力学简明教程
NORTHEASTERN UNIVERSITY
§7－5 轴对称问题的基本方程
轴对称问题： 在空间问题中，如果弹性体的几何形状、约束情况，以及所受的外
力作用，都是对称于某一轴（通过这个轴的任一平面都是对称面），则 所有的应力、变形和位移也就对称于这一轴。轴对称问题的弹性体的形 状一般为是圆柱或半空间。
( x
1)
m1 l1
yx
n1 l1
zx
0
xy
m1 l1
( y
1)
n1 l1
zy
0
可以求得 m1 , n1 的比值，再利用 l 2 m2 n2 1 求出：
l1 l1
l1
1
2
2
1
m1 l1
n1 l1
同样也可以求出其他主应力的方向余弦。
弹性力学简明教程
NORTHEASTERN UNIVERSITY
E
（7－13）
弹性力学简明教程
NORTHEASTERN UNIVERSITY
§7－4 几何方程及物理方程
（7-3）
p2
2 n
2 n
px2
p
2 y
pz2
2 n
px2
p
2 y
pz2
2 n
（7-4）
弹性力学简明教程
NORTHEASTERN UNIVERSITY
§7－2 物体内一点的应力状态
如果ABC是边界面，px, py , pz 成为面力分量
fx, fy, fz
弹性力学简明教程
NORTHEASTERN UNIVERSITY
§7－5 轴对称问题的基本方程
弹性力学简明教程
NORTHEASTERN UNIVERSITY
§7－5 轴对称问题的基本方程
轴对称问题： 在空间问题中，如果弹性体的几何形状、约束情况，以及所受的外
力作用，都是对称于某一轴（通过这个轴的任一平面都是对称面），则 所有的应力、变形和位移也就对称于这一轴。轴对称问题的弹性体的形 状一般为是圆柱或半空间。
( x
1)
m1 l1
yx
n1 l1
zx
0
xy
m1 l1
( y
1)
n1 l1
zy
0
可以求得 m1 , n1 的比值，再利用 l 2 m2 n2 1 求出：
l1 l1
l1
1
2
2
1
m1 l1
n1 l1
同样也可以求出其他主应力的方向余弦。
弹性力学简明教程
NORTHEASTERN UNIVERSITY
E
（7－13）
弹性力学简明教程
NORTHEASTERN UNIVERSITY
§7－4 几何方程及物理方程
弹性力学讲义(徐芝纶版)-PPT
换，
E
1
E
2
,
。 1
边界条件
边界条件--应用极坐标时，弹性体的 边界面通常均为坐标面，即：
常数，或 常数,
故边界条件形式简单。
平面应力问题在极坐标下的基本方程
1
f
0
1
2
f
0
4 1
u
,
1
u
u
,
u
1
u
u
。
1 E
(
),
1 E
(
),
x ρ x φ x
Φ y
Φ ρ
ρ y
Φ φ
φy .
一阶导数
而
cos,
x
sin , x
sin;
y
y
cos 。
代入，即得一阶导数的变换公式,
Φ cosφ Φ sin Φ (cosφ sinφ )Φ
x
ρ ρ φ
ρ ρ φ
，
(e)
Φ sinφ Φ cos Φ (sinφ cosφ )Φ。
σ x σ ρ cos2 φσφsin2 φ2τ ρφ cosφsinφ,
而
σ
x
2Φ y 2
2Φ ρ2
sin
2
φ(
1 ρ
Φ ρ
1 ρ2
2Φ ρ2
)cos2
φ
2[ ( 1 Φ )]cosφsinφ, ρ ρ
比较两式的 cos2 φ,sin2 φ,cosφsinφ 的系数，便 得出 σ ρ,σφ,τ ρφ 的公式。
2(1 E
)
。
4 2
物理方程
物理方程
对于平面应变问题，只须将物理方程作如下 的变换即可。
弹性力学及有限元法chapter7精品PPT课件
e
i
j
m
v
j
w j
u
m
i
m
p
vm
wm
j y
u
p
x
vp
w p
第七章 空间问题和空间轴对称问题
7-2-1 位移函数
单元内任一点的位移 {f}假定为座标的线性函数
u
f
v
N
e
w
u 1 2x3y 4z v 5 6x7 y 8z w9 10x 11y 12z
节点i, j, m及 p的坐标分别为(xi,yi,zi),(xj,yj,zj),(xm,ym,zm) 及 (xp,yp,zp)，把它们代入上式的第一式，得出各节点在x方 向的位移
第七章 空间问题和空间轴对称问题
ui 1 2 xi 3 yi 4 zi u j 1 2x j 3 y j 4z j um 1 2 xm 3 ym 4 zm up 1 2xp 3 yp 4zp
解方程组，求得 1,2,3,4，代入第一式，整理后得到
u N iu i N ju j N m u m N p u p
其中
Ni 61 Vaibixciydiz
N j 6 1 Vajbjxcjydjz
Nm61 Vambmxcmydmz
Np61 Vapbpxcpydpz
称为形函数，其系数是
第七章 空间问题和空间轴对称问题
xj yj zj ai xm ym zm
xp yp zp
1 xj zj ci 1 xm zm
同样，可以得到
vNivi Njvj NmvmNpvp wNiwi Njwj NmwmNpwp
单元内任一点的位移可以写成如下形式：
f N 0 i N 0 i 0 0
弹性力学ppt课件
应变定义
物体在外力作用下产生的 形变，表示物体尺寸和形 状的变化。
应力与应变关系
应力与应变之间存在一一 对应关系，通过本构方程 来描述。
广义胡克定律及应用
1 2
广义胡克定律 又称作弹性本构关系，表示应力与应变之间的线 性关系。
广义胡克定律的应用 用于计算弹性体在复杂应力状态下的应力和应变， 是弹性力学中的重要基础。
弹性力学ppt课件
contents
目录
• 弹性力学概述 • 弹性力学基本原理 • 线性弹性力学问题求解方法 • 非线性弹性力学问题简介 • 弹性力学实验方法与技术应用 • 弹性力学在相关领域拓展应用
01 弹性力学概述
弹性力学定义与研究对象
弹性力学定义
弹性力学是研究弹性体在外力和其他 外界因素作用下产生的变形和内力， 从而在变形与外力之间建立一定关系 的科学。
有限元法在弹性力学中应用
有限元法基本原理
将连续体离散化为有限个单元，每个单元用简单的函数近似表示，通 过变分原理得到有限元方程。
有限元法求解过程
包括网格划分、单元分析、整体分析、边界条件处理和求解有限元方 程等步骤。
有限元法的优缺点
有限元法可以求解复杂几何形状、非均质材料和非线性问题，但存在 网格划分和计算精度等问题。
布。
弹性模量和泊松比测定实验
拉伸法
通过对标准试件进行拉伸实验，测量试件的应力和应变，从 而计算得到弹性模量和泊松比。
压缩法
通过对标准试件进行压缩实验，测量试件的应力和应变，进 而计算弹性模量和泊松比，适用于脆性材料的测量。
弯曲法
通过对梁式试件进行三点或四点弯曲实验，测量试件的挠度 和应力，从而推算出弹性模量，特别适用于细长构件的测量。
弹性力学课件(高教课堂)
弹性力学课件(高教课堂)教学内容：1. 弹簧的弹性特性：弹簧的弹性系数、弹簧的弹性力、弹簧的弹性势能。
2. 弹性体的变形与应力：弹性体的应变、应力、胡克定律、弹性模量。
3. 弹性体的变形能：弹性体的变形能的定义、计算方法、变形能与弹性势能的关系。
4. 弹性体的平衡条件：弹性体的受力分析、弹性体的平衡条件、弹性体的支座反力。
教学目标：1. 理解弹簧的弹性特性和弹性体的变形与应力。
2. 掌握弹性模量的概念和计算方法。
3. 能够计算弹性体的变形能和支座反力。
教学难点与重点：重点：弹簧的弹性特性、弹性体的变形与应力、弹性模量的计算、弹性体的变形能的计算。
难点：弹性体的受力分析和支座反力的计算。
教具与学具准备：教具：黑板、粉笔、弹簧演示器、弹性体模型。
学具：笔记本、尺子、计算器。
教学过程：1. 实践情景引入：通过弹簧演示器展示弹簧的弹性特性，让学生观察和感受弹簧的弹性力。
2. 讲解弹簧的弹性特性：解释弹簧的弹性系数、弹性力和弹性势能的概念，并用公式进行说明。
3. 讲解弹性体的变形与应力：解释弹性体的应变、应力和胡克定律的概念，并用公式进行说明。
4. 讲解弹性体的变形能：解释弹性体的变形能的定义和计算方法，并用公式进行说明。
5. 讲解弹性体的平衡条件：解释弹性体的受力分析和支座反力的概念，并用公式进行说明。
6. 例题讲解：给出一个弹性体的受力分析的例题，让学生运用所学的知识进行解答。
7. 随堂练习：给出几个关于弹性体的变形与应力、变形能和支座反力的问题，让学生进行练习和解答。
板书设计：1. 弹簧的弹性特性：弹性系数、弹性力、弹性势能。
2. 弹性体的变形与应力：应变、应力、胡克定律、弹性模量。
3. 弹性体的变形能：变形能的定义、计算方法、变形能与弹性势能的关系。
4. 弹性体的平衡条件：受力分析、支座反力。
作业设计：1. 计算一个弹簧在拉伸5cm时的弹性力。
答案：根据胡克定律，弹性力F=kx，其中k为弹簧的弹性系数，x 为弹簧的伸长量。
弹性力学ppt课件(2024)
建立一维拉伸或压缩问题的数学模型
通过受力分析，确定物体在拉伸或压缩过程中的内力分布和变形情况。
2024/1/25
求解一维拉伸或压缩问题的基本方法
运用弹性力学的基本原理和公式，如胡克定律、应力-应变关系等，对一维拉伸或压缩问 题进行求解。
一维拉伸或压缩问题的有限元分析
介绍有限元方法在一维拉伸或压缩问题中的应用，包括网格划分、单元刚度矩阵和总体刚 度矩阵的建立、边界条件的处理等。
适用范围
适用于大多数金属材料在常温、静载 条件下的力学行为。对于非金属材料 、高温或动载条件下的情况，需考虑 其他因素或修正虎克定律。
2024/1/25
7
02
弹性力学分析方法与技巧
2024/1/25
8
解析法求解思路及步骤
01
02
03
04
05
建立弹性力学基 本方程
选择适当的坐标 系和坐标…
求解基本方程
件和载荷。
平面应变问题建模
02
探讨平面应变问题的特性，构建适当的力学模型，并确定边界
条件和载荷。
求解方法
03
介绍适用于平面应力和平面应变问题的求解方法，如有限元法
、有限差分法等，并讨论各种方法的优缺点和适用范围。
18
极坐标下二维问题处理方法
极坐标系的引入
阐述极坐标系的定义和性质，以及与直角坐标系的关系。
根据问题的实际情况，确 定位移边界条件、应力边 界条件以及初始条件。
通过与其他方法（如数值 法、实验法）的结果进行 比较，验证解析解的正确 性和有效性。
2024/1/25
9
数值法（有限元法）在弹性力学中应用
有限元法基本原理
有限元模型建立
通过受力分析，确定物体在拉伸或压缩过程中的内力分布和变形情况。
2024/1/25
求解一维拉伸或压缩问题的基本方法
运用弹性力学的基本原理和公式，如胡克定律、应力-应变关系等，对一维拉伸或压缩问 题进行求解。
一维拉伸或压缩问题的有限元分析
介绍有限元方法在一维拉伸或压缩问题中的应用，包括网格划分、单元刚度矩阵和总体刚 度矩阵的建立、边界条件的处理等。
适用范围
适用于大多数金属材料在常温、静载 条件下的力学行为。对于非金属材料 、高温或动载条件下的情况，需考虑 其他因素或修正虎克定律。
2024/1/25
7
02
弹性力学分析方法与技巧
2024/1/25
8
解析法求解思路及步骤
01
02
03
04
05
建立弹性力学基 本方程
选择适当的坐标 系和坐标…
求解基本方程
件和载荷。
平面应变问题建模
02
探讨平面应变问题的特性，构建适当的力学模型，并确定边界
条件和载荷。
求解方法
03
介绍适用于平面应力和平面应变问题的求解方法，如有限元法
、有限差分法等，并讨论各种方法的优缺点和适用范围。
18
极坐标下二维问题处理方法
极坐标系的引入
阐述极坐标系的定义和性质，以及与直角坐标系的关系。
根据问题的实际情况，确 定位移边界条件、应力边 界条件以及初始条件。
通过与其他方法（如数值 法、实验法）的结果进行 比较，验证解析解的正确 性和有效性。
2024/1/25
9
数值法（有限元法）在弹性力学中应用
有限元法基本原理
有限元模型建立
弹性力学专题知识课件
7
2）弹性力学： 在弹性力学中,一般不作出那些假定,故解比较精确。
例如在研究直梁在横向荷载作用下旳弯曲,弹性力学就不引 用了平面截面旳假定；又例如在研究有孔旳拉伸构件，弹 性力学也不假定拉应力在净截断面均匀分布；这使数学推 演复杂, 但解往往是比较精确旳。
3）构造力学： 构造力学研究措施有位移法、力法或混正当等。 弹性力学一般不研究杆件系统，但诸多人致力于弹
10
2. 面力
（1）定义：分布在物体表面上旳力。如流体压力和接触力
F 。如图1－3所示。
（2）性质：面力一般是物体表面点旳位置坐标旳函数。
（3）面力集度： S 上面力旳平均集度为： F
S
P点所受面力旳集度为：
z
fz F
f lim F S 0 S
△S F （4）面力分量：
fx
P fy
y
P点旳面力分量为 fx , f y , fz ，量 纲是 L1MT 2
zy yz , yx xy , xz zx
作用在两个相互垂直旳面上而且垂直于该两面交线旳切应 力是互等旳（大小相等，正负号也相同。）
17
图1-9
（4）注意弹性力学切 应力符号和材料力学是有 区别旳，图1－9中，弹性
弹性力学 力学里，切应力都为正，
而材料力学中相邻两面旳 旳符号是不同旳。正应力 与材料力学旳正负号要求 相同（即拉为正压为负）。
C
y
z
yx z
x P yz
A
y
（1）为了分析一点P旳应力
状态，在这一点从物体内取出
一种微小旳正平行六面体，各
yz
面上旳应力沿坐标轴旳分量称
y 为应力分量。即每个面上旳应
yx B 力分量可分解为一种正应力和
2）弹性力学： 在弹性力学中,一般不作出那些假定,故解比较精确。
例如在研究直梁在横向荷载作用下旳弯曲,弹性力学就不引 用了平面截面旳假定；又例如在研究有孔旳拉伸构件，弹 性力学也不假定拉应力在净截断面均匀分布；这使数学推 演复杂, 但解往往是比较精确旳。
3）构造力学： 构造力学研究措施有位移法、力法或混正当等。 弹性力学一般不研究杆件系统，但诸多人致力于弹
10
2. 面力
（1）定义：分布在物体表面上旳力。如流体压力和接触力
F 。如图1－3所示。
（2）性质：面力一般是物体表面点旳位置坐标旳函数。
（3）面力集度： S 上面力旳平均集度为： F
S
P点所受面力旳集度为：
z
fz F
f lim F S 0 S
△S F （4）面力分量：
fx
P fy
y
P点旳面力分量为 fx , f y , fz ，量 纲是 L1MT 2
zy yz , yx xy , xz zx
作用在两个相互垂直旳面上而且垂直于该两面交线旳切应 力是互等旳（大小相等，正负号也相同。）
17
图1-9
（4）注意弹性力学切 应力符号和材料力学是有 区别旳，图1－9中，弹性
弹性力学 力学里，切应力都为正，
而材料力学中相邻两面旳 旳符号是不同旳。正应力 与材料力学旳正负号要求 相同（即拉为正压为负）。
C
y
z
yx z
x P yz
A
y
（1）为了分析一点P旳应力
状态，在这一点从物体内取出
一种微小旳正平行六面体，各
yz
面上旳应力沿坐标轴旳分量称
y 为应力分量。即每个面上旳应
yx B 力分量可分解为一种正应力和
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
解：首先检验 Φ，已满足 4Φ0。由 Φ
求应力，代入应力公式得
r 2 B s2 ijn 2 C j ,
j 2 B s2 ijn 2 C j,
rj 2B co 2 j sC 。
再考察边界条件。有:
( j)j20, 得C0;
(rj )j2q, 得Bq2。
代入公式，得应力解答，
rqsi2nj, jqsi2n j,
由于圆柱坐标，是和直角坐标一样的正交坐标，所以可直 接根据虎克定律得物理方程：
r
1 E
r
j
z
j
1 E
j
z r
z
1 E
z
r j
zrG 1zr21E zr
应力分量 用形变分量 表示的物理 方程：
r
E 1
1
2
r
j
E 1
1
2
j
z
E 1
1
2
z
zr 21Ezr
z
o j
x
zr
zr
z
dz
z
z
z
j
r
fz
rz
fr
j zr
dz
rz
rz r
dr
r
r r
dr
Fz 0
rz
rz r
r
dr
djdz
rz rdjdz
z
z
z
dz rdjdr
z rdjdr
fz rdjdrdz 0
z
j
dj
r
r dj/2 dr
y
r
r r
dr
z
z
rz r
rz r
fz
0
rr zzrrrjfr0
3j
再求出边界上的面力：
r a q rc3 o j , j s a q rc3 o j ,r s ja q rs3 ijn
j300:j 0,r jqar; ra:r qco3js,r jqs i3nj.
面力分布如图
习题4-9
半平面体表面受有均布水平力q，试用应力 函数 Φρ2(Bsi2nφCφ)求解应力分量。
rjqco2j s。
习题4-18
设半平面体在直 边界上受有集中 力偶，单位宽度 上的力矩为M，试 求应力分量。
解：应用半逆解法求解。
（1）按量纲分析方法，单位宽度 上的力偶矩与力的量纲相同。应力应
与 M,r,j有关，由于应力的量纲是单
位面积上的力，即 L1ML2，应力只能
以 M r2 形式组合。
z h h 1 ,z r z j 0
习题4—8 试考察下列应力函数能解决如图所示弹性体的何 种受力问题？
q r3cos3j
6a
解：本题应用逆解法求解：
首先校核相容方程是满足的；
然后．代入教科书中应力公式(4—5)，
求出应力分量
r
q r cos a
3j
j
q a
r
cos
3j
rj
q r sin a
（2）Φ应比应力的长度量纲高二次幂，
可假设 ΦΦ。(φ)
rz r
dr
取图示微元体。
根据连续性假设，微 元体的正面相对负面
rz
Байду номын сангаас
fr
j zr
r
r r
dr
其应力分量都有微小 增量。注意：此时环 向正应力的增量为零。
z
j
dj
由径向和轴向平衡， y 并利用：
r
r dj/2 dr
r
r r
dr
sin d j d j , 22
j
cos dj 1 2
z
o j
例5：一圆柱形厚壁容器内盛液体，
设液体容重为，试用柱坐标写出
应力边界条件。
解：1. 在内壁 ra
1 hh 1zh
rrjrz 0
2 0zh h 1
r h h 1 z ,r jr z 0
2. 在外壁 r b
rrjrz 0
3. 上部圆环端面 zh,arb z zrzj0
4. 下部水底面 z0,0ra
j
空间轴对称问题的平衡微分方程。
二、几何方程
通过与平面问题及极坐标中同样的分析，由径向位移引 起的形变分量为：
r
ur
r
,
j
ur
r
,
zr
ur z
由轴向位移引起的形变分量为：
z
w z
,
zr
w r
由叠加原理，即得空间轴对称问题的几何方程：
r
u r r
j
ur r
z
w z
zr
ur z
w
r
三、物理方程
其中： rjz
轴对称问题基本方程
平衡微 分方程 物理方程
几何方程
z
z
rz r
rz r
fz
0
rr zzrrrjfr0
r
1 E
r
j
z
j
1 E
j
z r
z
1 E
z
r
j
zrG 1zr21E zr
r
u r r
j
ur r
z
w z
zr
ur z
w
r
未知函数 10个，结 合边界条 件求解。
zj 0
zr
j jr
rz
rj r
rj 0
r j z rz 存在
jz
体力和位移：
o
dj
x
jr
j
jr
j
y
rj r fr
fj 0 uj 0
f z u z ur 存在
同时，存在的量应
该环向坐标无关。
z
o j
x
一、平衡微分方程
zr
zr
z
r
dz
z
fz
z
z
j
dz rz
12)。加上边界条件可解空间问题。
x
x
yyxzzxfx
0
xyy
x y
zzyfy
0 (7-1)
xz
x
yz
y
z
z
fz
0
εx
u x
,
γ xy
v x
u y
εy
v y
,
γ yz
w y
v z
(7-8)
εz
w z
,
γ zx
u z
w x
x
1 E
[
x
(
y
z )]
y
1 E
[
y
(
z
x )]
z
1 E
[
z
x
zr
zr
z
dz
z
z
z
j
r
fz
rz
fr
dz
rz
rz r
dr
r
r r
dr
Fr 0
r
r r
2 j drdz
r
dj
2
dr djdz r rdjdz
zr
zr
z
dz rdjdr
j zr
zr rdjdr fr rdjdrdz 0
z
j
dj
r
r dj/2 dr
j
y
r
r r
dr
rr zzrrrjfr0
空间问题的求解：
1. 基本未知函数15个：
(6个)：
x, y, z, y zz,yz xz,xx yyx
位移分量(3个)： u,v,w
(6个)：
x , y ,z , y zz,yz xz,xx yyx
2. 基本方程15个：
平衡微分方程3个(7-1)；几何方程6个(7-8)；物理方程6个(7-
(
x
y )]
yz
2 (1 E
) yz
zx
2 (1 E
) zx
xy
2 (1 E
) xy
(7-12)
§7-5 空间轴对称问题
在空间问题中，若弹性体的几何形状、约束情况 以及所受的外力，都对称于某一轴（通过这个轴的任 一平面都是对称面），则所有的应力、形变和位移也 对称于这一轴。这种问题称为空间轴对称问题。
根据轴对称的特点，应采用圆柱坐标(r,j,z)表
示。若取对称轴为 z 轴，则轴对称问题的应力分量、
形变分量和位移分量都将只是r和z的函数，而与 j 坐
标无关。 轴对称问题的弹性体的形状一般为绕此轴的旋转
体，如圆柱体（包括圆筒），或（半）空间体。
任意对称面上单元体的 应力
z
对称面 z zj
应力：