支导线终点位置误差公式新的推导方法.
支导线测量与计算学习

Y2 Y1 y12 702.999 161.439 864.438m
支导线没有多余观测值,因此没有角度检核条件,不产生角度闭合 差,因此观测值的差错不易发觉,计算时必须再次检核。
导线边长测量
导线边长一般用电磁波测距仪或全 站仪观测,同时观测垂直角将斜距 化为平距。
平距=斜距*sin垂直角
导线转折角测量
导线的转折角是在导线点上由相邻 两导线边构成的水平角。(导线的转 折角分为左角和右角,在导线前进 方向左侧的水平角称为左角,在右 侧的称右角)。)
三、导线测量内业计算
目的:计算各导线点的坐标。 要求:合理分配测量误差,并评定
2 2 D2
X= D cos Y= D sin
1
D1 1
AB
B
(XB,YB)
A
xB1 D1 cos B1 297.26 cos 770025 66.834m
y B1 D1 sin B1 297.26 sin 770025 289.649m
x12 D2 cos 12 187.82 cos 591555 95.988m y12 D2 sin 12 187.82 sin 591555 161.439m
导线测量的精度。
导线测量内业三种基本运算
1.推算各边方位角:
前 后 左 180
2.计算各边坐标增量: X=D cos Y=D sin
3.推算各点坐标 X前= X后+X Y前= Y后+Y
支导线的计算步骤(一)
根据已知点坐标反 算起始边的方位角 例如已知:
1 D1
2 D2
2
XA = 664.20 m YA = 213.30 m XB = 864.22 m YB = 413.35 m
全站仪支导线在井下测量中的精度估算与布测

全站仪支导线在井下测量中的精度估算与布测摘要:目前,地下矿山勘测的主要方法是导线测量,全站仪同时具有角度测量和测距功能,目前生产的全站仪内置了多种测量软件,因此负责人的勘测方式根据要求的不同测量方法也不同。
全站仪广泛应用于各个测量领域,在煤矿,铁矿石等的生产和建设中,特别是在地下测量时,全站仪是最常用的测量仪器,而横移测量则是最多的。
全站仪线测量技术被广泛用于采矿勘测中,因为它可以同时测量地下目标的三维位置。
基于全站仪测量,边缘测量以及全站仪分支遍历端点误差的估计和分析,本文对全站仪遍历点布局提出了一些警告。
它为矿井中全站仪分支电缆的布局,测量和最终点误差估计提供了参考。
关键词:全站仪;全站仪支导线;精度;角度测量误差;测量边缘误差;布局;注意事项引言全站仪支导线是矿山开发,准备和采矿中最常见,分布最广泛的铺设线。
由于在分全站仪支导线上没有多余的观测值,因此没有检查角度或边长的条件。
其中,完全机械化的洞穴勘探工作面的设计和开挖相应地提高了对渗透率测量的要求,《煤矿勘查规程》通常要求点位置误差小于±0.3m。
因此,估算已铺设全站仪支导线终点的精度尤为重要,并且在布置和测量全站仪支导线过程中需要注意相关问题。
1地质勘测的重要性矿物质是我国最基本,最重要的能源之一,不仅为我国提供了丰富的矿产资源,而且还促进了各行各业的发展,提高了我国的经济效率。
由于我国有多种类型的矿山,因此在采矿过程中极有可能发生安全事故,例如极有可能发生的倒塌事故,不仅造成巨大的经济损失,而且造成很多破坏,这也给建筑企业造成巨大损失,甚至给建筑工人造成严重的伤害和致命的事故,并对一些家庭造成致命的伤害。
因此,从安全生产的角度来看,地质勘测非常重要。
另一方面,矿山勘测会执行矿山生产和建设的全过程,并在监督项目质量方面发挥作用,这样可以使各种项目根据工程设计要求顺利进行。
同时,按矿山测量的矿石产量,矿产流失数据统计数据可以设计出最合理采矿计划,以促进矿山的可持续发展。
矿山测量-6.3.1支导线终点的点位误差(精)

1 1 y1 K
北京工业职业技术学院
将上式代入终点坐标误差公式得:
2 Mx
1
2 2 R m 2 yi i 1
2
北京工业职业技术学院
3、支导线终点K在x轴及y轴方向上的点位误差
4、支导线终点的点位误差
M M M
2 K 2 xK
2 yK
北京工业职业技术学院
分析上式可知: (1)起始点点位误差对导线终点点位误差的影响,与 导线的长度和形状无关,且保持常量。 (2)起始边方位角误差对导线终点点位误差的影响, 与导线的形状有关,当起始边方位角误差一定时,对 直伸型导线影响最大,曲折型导线次之,闭合导线则 不受影响。 (3)测角误差对导线终点点位误差的影响随测角误差 的增大和测站数目的增多而增大,当几条导线的测角 精度相同、测站数和总长度相近时,其影响取决于导 线的形状,对直伸型导线影响最大,曲折型导线次之, 闭合导线最小。
在实际工作中,经常需要的是沿某一指定方向上的 点位误差。如,在巷道贯通测量时,就需要估算垂直 于巷道中线方向上的误差。 在解决上述问题时,只需设一个假定坐标系的x’、y’ 与某指定方向重合 : 当用光电测距时:
M
2 x 'K
2 My '
K
L 2 R m cos 1 1 2 n 2 n m 2 m Lx ' 2 Rx2' ml2 sin 2 1 1 m
2 2 y' 2 m n 2 y' n 2 l 2
北京工业职业技术学院
导线计算误差计算公式

导线计算误差计算公式导线计算是土木工程中的重要内容,它涉及到测量、勘测和工程设计等方面。
在实际的工程中,导线计算的准确性对工程的施工和质量都有着重要的影响。
因此,导线计算误差的计算是非常重要的,它可以帮助工程师们了解到导线计算的准确性,从而对工程进行合理的设计和施工。
误差的来源。
在导线计算中,误差主要来源于测量仪器的精度、环境条件的影响、人为操作的不准确等因素。
其中,测量仪器的精度是误差的主要来源之一。
在测量过程中,由于测量仪器的精度限制,会导致测量结果的误差。
此外,环境条件的影响也是导致误差的重要因素之一。
比如,在恶劣的天气条件下,如风雨、高温等,都会对测量结果产生一定的影响。
此外,人为操作的不准确也是导致误差的一个重要因素。
在测量过程中,如果操作人员没有按照标准的操作流程进行操作,就会导致误差的产生。
误差的分类。
在导线计算中,误差可以分为系统误差和随机误差两种。
系统误差是指在测量过程中由于测量仪器的精度、环境条件等因素引起的偏差,它是可以被纠正的。
而随机误差是指在测量过程中由于人为操作不准确等因素引起的偏差,它是无法被纠正的。
误差的计算公式。
在导线计算中,误差的计算是非常重要的。
通常情况下,我们可以使用以下的公式来计算误差:总误差 = 系统误差 + 随机误差。
其中,系统误差可以通过对测量仪器的精度进行评估来得到,而随机误差则可以通过对测量结果的重复测量来得到。
通过以上的公式,我们可以计算出导线计算的总误差,从而对工程进行合理的设计和施工。
误差的控制。
在导线计算中,误差的控制是非常重要的。
为了保证导线计算的准确性,我们需要采取一系列的措施来控制误差。
首先,我们需要对测量仪器进行定期的校准,以确保测量仪器的精度。
其次,我们需要对测量过程中的环境条件进行评估,并采取相应的措施来减小环境条件对测量结果的影响。
此外,我们还需要对操作人员进行培训,以确保操作人员按照标准的操作流程进行操作。
总结。
导线计算误差的计算是非常重要的,它可以帮助工程师们了解到导线计算的准确性,从而对工程进行合理的设计和施工。
支导线的计算

7.3.4 支导线的计算由于支导线是由一个已知点出发,即不同到原出发点,也不附和到另外已知点上,故这种导线无法检验。
计算时,根据已知点坐标,方位角及测得的转角,;利用坐标在正算公式得支点的坐标。
如图7-11所示,起算数据M(P0)~A(P1)的方位角α01,A(P1)的坐标(x1,y1)。
观测数据为各转角βi,导线边长Di(i+1)(i=1,2,…,n-1),n为导线点的最大编号,对于支导线,一般n≤3.其计算步骤如下:(1)推算坐标方位角利用起算坐标方位角α01和观测转折角βi计算各边的坐标方位角,即αi(i+1)= α(i-1)±βi±180°(i=1,2,…,n-1) (7-19) Βi前的符合:以i-1→i→i+1为前进方向,当βi为左角时取“+”,当βi为右角时取“-”,所谓“左加右减”;180°前的符号:等式右边前两项之和小于180°时取“+”,反之取“-”。
(2)计算坐标增量利用上步计算的坐标方位角和观测得到的各边长Di(i+1),计算相邻导线的坐标增量为△xi(i+1)=Di(i+1)cosαi(i+1)△yi(i+1)=Di(i+1)sinαi(i+1)i=1,2,…,n-1(3)推算坐标利用起算坐标(xi, yi)和坐标增量计算结果,依次推算各导线点的坐标为Xi+1= xi+△xi(i+1)Yi+1=yi+△yi(i+1)7.3.5控制点的加密当已知控制点的数量不能满足测图或施工的要求时,需要对控制点进行加密。
常用的加密方法是交会法,交会法分为前方交会法,后方交会法和边长交会法。
1.前方交会法如图7-12—(a)所示,由两个(或两个)已知点A.B来确定未知点P的坐标的方法称为前方交会法,即用经纬仪在已知点A.B上分别向新点P观测.水平角α和β,从而计算P点的坐标。
计算步骤如下:。
工程测量平差支导线改正数公式

工程测量平差支导线改正数公式工程测量中,平差是指通过对测量结果进行处理,使其更加准确和可靠。
而平差支导线改正数则是平差计算中一个非常重要的步骤。
平差支导线改正数的计算需要考虑以下几个因素:1.支导线长度的改正支导线长度的改正是指将实测的支导线长度改正到理论长度。
由于实测支导线长度受到环境条件、测量仪器精度等因素的影响,与理论长度之间存在一定的误差。
改正支导线长度可以提高精度,从而提高测量结果的准确性。
支导线长度的改正公式为:L’=L+ΔL其中,L’为改正后的支导线长度,L为实测支导线长度,ΔL为长度改正数。
2.支导线方位角的改正支导线的方位角也需要进行改正,以纠正由于测量仪器、观测者等原因引起的误差。
支导线方位角的改正数也是平差计算中的一个重要参数。
支导线方位角的改正公式为:α’=α+Δα其中,α’为改正后的支导线方位角,α为实测支导线方位角,Δα为方位角改正数。
3.支导线垂直角的改正垂直角也需要进行改正,以消除由于测量仪器、测量环境等因素引起的误差。
支导线垂直角的改正也是平差计算中一个重要的环节。
支导线垂直角的改正公式为:β’=β+Δβ其中,β’为改正后的支导线垂直角,β为实测支导线垂直角,Δβ为垂直角改正数。
根据以上的改正公式,可以对支导线进行长度、方位角和垂直角的改正。
然后,将改正后的支导线数据应用于平差计算中,获得更准确、可靠的测量结果。
总之,工程测量平差支导线改正数是对支导线长度、方位角和垂直角进行改正,以提高测量结果的准确性和可靠性。
改正数的计算公式是根据实测数据和理论公式进行推导和计算的。
通过平差支导线改正数的计算,可以获得更加准确的测量结果,提高测量的精度和可靠性。
(贯通误差预计用)

225.104 621.2324
693.303 309.7826
945.954 225.7104
704.695 804.3179
161.63 843.6319
547.916 102.4951
5.998 459.7529
174.263 761.4508
815.728 513.3588
0.0
0.0
图6 加测两条陀螺定向边
图8 加测一条陀螺定向边
1 11 7 4 0.000000 0.000000 70.000000 3.000000 140.000000 7.000000 149.000000 45.000000 164.000000 114.000000 179.000000 182.000000 194.000000 250.000000 209.000000 319.000000 223.000000 387.000000 238.000000 456.000000 253.000000 524.000000 268.000000 592.000000 0.000000 0.000000 -70.000000 -4.000000 -140.000000 -7.000000 -209.000000 -11.000000 -279.000000 -14.000000 -349.000000 -18.000000 -419.000000 -21.000000 -489.000000 -25.000000
225.104 621.2324
693.303 309.7826
945.954 225.7104
704.695 804.3179
736.725 964.2209
563.173 895.3012
井下支导线终点位置误差预计问题探讨

井下支导线终点位置误差预计问题探讨廖志平(广东省一五二地质队 ,广东 广州 510440)摘 要 :井下控制导线分基本控制导线和采区控制导线 。
预计井下支导线终点的位置误差时 ,由于基本控制导线终点坐标 、终边方位角不是相互独立变量 ,此时不能以此作为起算边 、起算点 ,按有关公式…1 ,2‟来预计采空区控制导线终点位 置误差 。
关健词 :矿山测量 ;导线误差预计 ;误差传播定律1 问题的提出某矿布设了如图 1 所示的井下控制导线 ,其中 1~ t 为基本 控制导线点 , ( t + 1) ~ K 为采区控制导线点 。
现对导线终点 K 的位置误差进行预计 。
M βB ———采区控制导线测角中误差 ; m li ———i 边量边误差 。
1 . 2 分段预计(1) 基本控制导线终点 t 也就是采区控制导线起算点的位置误差为 :22t - 1 M α0Mβs Σ t - 1 M 2 22 2 2 t= M 1 + ρ2 R (l ,t)+ ρ2 i = 1R (i ,t)+ Σ m li (2)i = 1 (2) 基本控制导线最后一条边 ( t - 1 ,t ) 也就是采区控制导线 起算边的方位角误差为 :M 2 2 2α( t - 1 ,t ) = M α0 + ( t - 1) M βs(3)(3) 采区控制导线终点 K 的位置误差由基本控制导线终点 t的位置误差 M t , 终 边 方 位 角 误 差 M α( t - 1 ,t ) , 采 区 导 线 测 角 误 差 M βB ,量边误差 mli 等四项组成 。
22 k - 1 M β( t - 1 ,t ) M βsΣ k - 1M 222 2 2 k= M t + R ( t ,k) +ρ2 j = tR (j ,k) + Σ m li(4)ρ2i = t将式 (2) 、式 (3) 代入式 (4) 得 :图 1 井下控制导线终点 K 位置误差预计图22 t - 1 2 2 M α0 M βs M α0 + (t - 1) m βst - 1M 2 2k= M 1 + R 1 + ΣR 2 2 + Σ m 2 + R 2+ (i ,t )li ( t ,k ) ρ2ρ2 i = 1一般说来 ,预计 K 点误差有两种思路 :思路 1 :直接预计 ,即由起算点 1 直接预计终点 K 点误差 。
毕业设计__两种贯通方法误差预计程序设计

摘要现在市场上没有一款正式发布的软件明确支持地下贯通误差预计,并且实际工作中使用图解法或者Excel计算繁琐复杂,在特大型贯通中又有些力所不足。
基于此,本文主要使用C++语言,设计井下两种贯通方法(一井贯通和两井贯通)误差预计程序。
程序直接读取点数据文件和按约定原则的贯通信息数据文件(txt文本格式文件),计算贯通点在重要方向上的误差值,极大的减少处理数据和计算繁琐度。
并且改变了在增添或者删除加测陀螺定向边情况下就需要大规模重新计算的局面,使贯通测量设计提高效率。
整个使用的误差预计公式,为现在贯通误差预计中使用最久最成熟的导线法误差预计公式。
程序主要由两个大类,一是支导线误差预计类,二是加测陀螺定向边的方向附合导线误差预计类组成。
通过main主函数的调用,简单组合,实现程序最大的灵活性。
而每个类由主要的五个成员函数构成,使程序简明。
最后以文本格式输出贯通误差预计详细结果和预计处理过程的相关数据。
不仅对实际误差预计工作有现实意思,也为编制测量程序积累了经验。
关键字:导线法贯通误差预计程序AbstractNowadays,We can’t find a software tha t released officially supporting estimation of through error underground in the surveying and mapping market.Besides,using graphical method or Excel to calculate during the practical work is complicated.It’s inefficient in the large-scale break through survey.Therefore,this article will design program to solve error prediction of two back through ways(single shaft orientation and two shaft orientation).The program can directly read data files andbreak through information data files (.txt) according to the contract.It can calculate the error value of holing point on the important direction which greatly simplify the process. It also change the situation where need to a large scale recalculate in the case of adding or deleting gyroscopic directed edges which can improve efficiency in through survey.The error prediction formula the program use is the most longer and mature formula in break through error prediction.The program concludetwo parts: error prediction of branch conductor and direction-connecting traverse which has gyroscopic directed edges.By calling mainfunction,simply combining,the program achieve great flexibility.Each class has five member function makes the program simple andclear.Finally it can output the result and related data of error prediction process.This article is not only meaningful to the actual work,but also a useful experience for measurement program writing.Keywords: Wire ; error prediction ; through ; software目录1.绪论 11.1研究的背景及意义 11.2国内外研究现状 21.3研究的内容与方法 42.贯通误差预计公式 62.1支导线误差公式 62.2方向附合导线误差公式 92.3导线最远点高程中误差的误差预计公式 12 3.贯通误差预计程序总体设计 133.1数据格式设计 133.2贯通情况讨论与程序灵活性设计 173.3预计过程可视性设计 244.程序详细设计 274.1读入数据类设计 274.2支导线误差预计类设计 314.3加测陀螺定向边误差预计类设计 364.4 main主函数体现程序灵活简单特性 39 5.程序在实际案例中应用 415.1 某煤矿开采面最弱点误差预计 415.2某煤矿两井贯通误差预计 456.结论与展望 47参考文献 50致谢 52附录 531. 绪论1.1研究背景及意义随着国际隧道协会(IAT)提出“大力发展地下空间,开始人类新的穴居时代“的倡议和中国国家发展改革委、外交部、商务部2015年3月28日联合发布了《推动共建丝绸之路经济带和21世纪海上丝绸之路的愿景与行动》。
导线测量对贯通影响的误差预计新公式(精)
2 公式推导
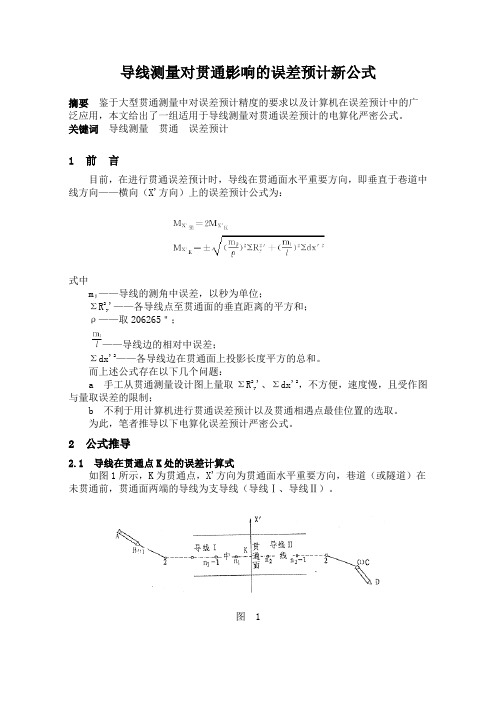
2.1 导线在贯通点K处的误差计算式
如图1所示,K为贯通点,X'方向为贯通面水平重要方向,巷道(或隧道)在未贯通前,贯通面两端的导线为支导线(导线Ⅰ、导线Ⅱ)。
图 1
a 支导线I在贯通点K处的方差及协方差计算式
把K点看作为支导线I的终点,则有:
(1)
而导线任意边i的方位角是所测角度的函数,即
(2)
上列两式中
XB——支导线I起算点B的已知X坐标;
YB——支导线I起算点B的已知Y坐标;
αAB——支导线I起算边AB的已知坐标方位角;
βj——支导线I各转折角;
li——支导线I各边的边长,如ln1表示导线点n1至贯通点K的边长;
(5)
c 导线在贯通点K处的方差及协方差计算式
因,由支导线Ⅰ、Ⅱ分别推算到K点时,在X与Y方向上的偏差为:
将上式写成矩阵形式,为:
F=AX
式中
而,
所以,运用协方差传播定律,得支导线Ⅰ、Ⅱ对K点综合影响的方差及协方差为:
(6)
上式中
n——导线Ⅰ、Ⅱ的导线点数之总和,即n=n1+n2。
d 导线在贯通点K处的误差计算式
式中
mβ——导线的测角中误差,以秒为单位;
ΣR2y'——各导线点至贯通面的垂直距离的平方和;
ρ——取206265";
——导线边的相对中误差;
Σdx'2——各导线边在贯通面上投影长度平方的总和。
而上述公式存在以下几个问题:
a 手工从贯通测量设计图上量取ΣR2y'、Σdx'2,不方便,速度慢,且受作图与量取误差的限制;
αi——支导线I各边的坐标方位角,如αn1表示导线点n1至贯通点K的坐标方位角;
导线测量的精度.ppt

u u1 u2 un
ns d1 n 1s d2 s dn
则终点n的横向中误差:
mu
m s
n2 n 12 12
m s nn 12n 1
6
m L n 1.5
3
3. 终点n的点位中误差:
Mn
mt2 mu2
2L
m2 L2
2
n
1.5 3
或:M n L
mK
1 2
0.0012 6000 6000122 10 6
206265 48
0.22m m
本节重点
1. 直伸形支导线终点中误差公式(纵向——量 边误差影响;横向—— 测角误差影响);
2. 直伸形附和导线闭合差的中误差公式; 3.直伸形附和导线最弱点的中误差。
作业:
复习本节内容。
位移。 3. 导线横向误差:
由于测角误差影响而使导线在垂直方向上产生 的位移。
1. 量边误差影响:
设:量距单位权中误差μ,终点n距起点
A的长度L=ns,则终点n的量距中误差:
ms L
终点n的纵向中误差即:
mt ms L 2. 测角误差影响:
横向位移
u1
ns
d1
u2
n 1s
d 2
终点n横向位移中误差:
1.终点纵向(量边)中误差:
与支导线相同
mt ms L
2. 终点横向中误差:
i i vi
i
f n
i
1 n
MA i n 1800
BN
di
d i
1 n
di
终点横向位移真误差:
u
ns d1
n 1s
d 2
s
单一导线误差理论

– 2、导线边数相同时,支导线、方位附合、坐 标附合、方位坐标附合他们的最弱方位角中误 差之比为4:2:2.3:1,应布设附合导线
4.4 单一误差理论
• 综合以上对各种单一导线点位误差的讨论, 对比分析得出如下结论:
– 1、导线直伸时,纵向中误差由测距引起, 横向中误差由测角引起 – 2、在不考虑起始数据时,单导线最弱点位 置中误差与导线总长度L、边长D,点数n有 关。当平均边长一定时,点位中误差与L近 似成正比;而当L一定时,点位中误差与 n 的平方根近似成正比 – 3、见表4-6,P125
2
mTo n( n 1)( 2n 1) L2 6
2
4.4 单一误差理论
• 从上式可以看出
–在直伸形支导线中,终点的纵向误 差主要是由于测距误差所引起的, 终点的横行误差主要是由于测角误 差和起始方位角误差所引起的
4.4 单一误差理论
• 附合导线的分类:
4.4 单一误差理论
• 2、支导线终点位置误差
如上图建立坐标系,终点坐标公式为:
x n 1 Di cosT y n 1 [ Di s in T ]
n i 1
n i 1
4.4 单一误差理论
• 为导出终点沿x方向和y方向的误差公式,建立终点 坐标与直接观测值βi和Di的微分关系:
dTi 1 n n n dxn 1 cosTidDi 1 Di s in Ti cosTidDi 1 yidTi 1 1
3.任一点的纵横坐标中误差
mt m D k k 2 ( n 1)
第五章导线测量

n 1
mT m 4
控制测量技术
福建信息职业技术学院
5
2.方位附合导线终点位置误差
对于“等边直伸”的方位符合导线, Ti=0,D1=D2=…=Dn。此时终点纵向、横向 位置误差公式:
mt mu
m
2 D
n
m
2 L2
2
D
nn
1n
12
2
控制测量技术
福建信息职业技术学院
11
关于单一导线点位误差的讨论:
(1)导线直伸时,纵向中误差由测距误差引起,横 向中误差由测角误差引起。
(2)在不考虑起始数据误差影响的情况下,单导线 最弱点位置中误差与导线的总长度L、导线边长D及 导线点数n有关。当平均边长一定时,导线的点位 中误差与L近似成正比;而当L一定时,点位中误差 与√n近似成正比。
福建信息职业技术学院
10
关于单一导线方位角中误差的讨论:
(1)在不考虑起始数据误差情况下,导线推算边方 位角中误差与 √n 成正比,而与导线形状关系不大。 为了保证导线边方位角精度,应当限制导线转折角 数目。在导线长度一定时,适当加长导线边,可以 减少转折角个数。
(2)在导线边数目相同时,以上所述4种导线:支导 线、方位附合导线、坐标附合导线、方位坐标附合 导线,它们的最弱边方位角中误差之比是4 :2 : 2.3 :1。
mT m
n1 16
控制测量技术
福建信息职业技术学院
7
4.方位和坐标附合导线中点位置误差
对于两端均有方位角和坐标控制点的等边直伸附合 导线,最弱点位于导线中点。 方位和坐标附合导线中点(最弱点)位置误差:
等边直伸形附合导线终点的点位误差推算

等边直伸形附合导线的点位误差推算附合导线是导线测量的一种,通过测量夹角和边长计算点的平面坐标的方法称为导线测量,它还包括闭合导线和支导线。
附合导线是由一个已知点出发开始测量,经过若干未知点,到达另一个已知点,然后通过平差计算得到未知点平面坐标的导线测量。
其特点是两端的坐标,方位角均为已知,所以需要进行角度平差及坐标平差。
等边直伸形附合导线终点的点位误差推算过程如下:kx t M =k y u M = 2222222'22222222222'2222[]{[]}[cos ]1[]{[]}[sin ]1l l y x x y x x y y x y M R t M M R a l b L n M R u M M R a l b L n ββββαραρ=+=-+++=+=-+++其中因为0i α≈,所以cos 1i α≈,sin 0i α≈,0i y R ≈,'x L L ≈,0y L ≈'1n L L n =+222'22222222[][]{[]}1ll x x y x t M a l b L M R u M R n βρ==+==-+ 经过边长改正12(1)''''1(1)(1)1......21n n x x x x n R n l n l n n R n l n l n R l R l -=⋅=⋅+=-⋅=-⋅+=⋅=⋅ 2222222222(1)(21)(21)[][(1)2]1166x n n n n n l n n R n l n l l l l n n +++=+-+++=⋅=++3222(1)[][(121)]14x n n n l R l n n n +=⋅⋅+++-+=+222222222[](2){[]}112x x M M R n l n u R n ββρρ+=-=⋅+ 212M n u L βρ+=±⋅⋅当n 很大时,12M n u L βρ≈ '22'22222[]11n n t a l b L a L b L n n =+=⋅+⋅++ 当n 很大时,边长经过平差之后系统误差项随闭合差的影响已经被消除,t a L ≈±其中最大横向误差的点,并不是附合导线终点,而是其中点,若分别从导线起始点和其中点测量,得121L 2=u =212u ==832n M u M n u L ββρρ⋅±±中中中中1122t t a L ±=±中中= 由此可见经过角度和坐标平差后的附合导线的最大横向误差是支导线的18,最大纵向误差也有明显的提高。
导线测边比例误差计算公式

导线测边比例误差计算公式导线测量是土地测量中常用的一种测量方法,它通过测量导线的长度和角度来确定地面上各点的位置。
在实际的测量过程中,由于各种因素的影响,导线测量中会存在一定的误差。
其中,导线测边比例误差是导线测量中一个重要的误差来源,它直接影响着测量结果的准确性。
因此,了解导线测边比例误差的计算公式对于提高测量准确性具有重要意义。
导线测边比例误差是指在导线测量中,由于测量仪器、环境条件等因素的影响,导致实际测量长度与理论测量长度之间的误差。
通常情况下,导线测边比例误差可以通过测量结果的比较来确定。
具体来说,设导线测量的实际长度为L,理论长度为l,则导线测边比例误差可以用以下公式来表示:误差 = (L l) / l 100%。
其中,误差表示导线测边比例误差的大小,L表示实际测量长度,l表示理论测量长度。
该公式可以直观地反映导线测边比例误差的大小,通过对误差的计算,可以及时发现和纠正测量中的问题,保证测量结果的准确性。
在实际的导线测量中,导线测边比例误差的计算通常需要考虑多种因素。
首先,由于测量仪器的精度和稳定性不同,不同的仪器在测量过程中会存在一定的误差。
其次,测量环境的影响也是导致导线测边比例误差的重要因素。
例如,气温、湿度、风力等环境条件的变化都会对测量结果产生影响。
此外,测量人员的经验和技术水平也会对导线测边比例误差产生影响。
因此,在进行导线测量时,需要综合考虑以上因素,合理选择测量仪器、控制测量环境,并且培训和提高测量人员的技术水平,以减小导线测边比例误差的大小。
在实际的工程测量中,导线测边比例误差的大小通常需要符合一定的要求。
一般来说,对于一般的测量工程,导线测边比例误差的允许范围为1:10000,而对于高精度的测量工程,导线测边比例误差的允许范围则更为严格,通常为1:20000。
因此,在进行导线测量时,需要根据具体的测量要求,合理控制导线测边比例误差的大小,以确保测量结果的准确性。
为了减小导线测边比例误差的大小,可以采取一些措施。
导线全长闭合差公式

导线全长闭合差公式导线全长闭合差公式是在测量工程领域被广泛运用的公式,用于计算导线测量中断面起点与回点的距离差。
导线全长闭合差公式的推导及应用,为测量工程领域的各项工作提供了便利,极大地提高了工程测量的精度和效率。
一、导线全长闭合差公式的推导过程1.1 闭合差的概念在测量中,由于各种误差的原因,所测得的闭合路线长度往往与实际的闭合路线长度有一定的差别,这种差别被称为闭合差。
1.2 导线全长的定义导线全长是指导线闭合后的总长度,即断面起点至回点的距离和。
导线全长是测量的一个基本概念,也是测量计算的重要参数。
1.3 闭合差公式的推导设A为断面起点,B为回点,AB段的实际长度为L,测量长度为Lm,闭合差为δ,则有:Lm = L + δδ = Lm - L将所有断面的实际长度及闭合差相加,得到测量全长Ls和测量全长闭合差Σδ:Ls = ΣL + Σδ其中,ΣL表示所有断面长度的总和。
将上述公式代入导线全长的定义式中,得到导线全长的闭合差公式:LC = Ls - LLC = ΣL + Σδ - L二、导线全长闭合差公式的应用2.1 测量中线的全长闭合差计算测量中线是测量工程中使用最广泛的测量方法之一。
测量中线的全长闭合差可以通过上述公式进行计算。
首先,需要测量出每个断面的实际长度L,然后根据测量数据计算出每个断面的测量长度Lm。
最后,将所有断面的测量长度和闭合差相加,即可得到测量中线的全长闭合差。
2.2 工程施工中的应用在建筑、道路和桥梁等工程施工中,需要精确测量土地和道路的长度和宽度。
导线全长闭合差公式可以帮助测量工程师更准确地计算工程测量参数,从而保证工程施工的品质和效率。
2.3 对测量精度的影响导线全长闭合差公式在测量工程中广泛应用,其精度对于工程测量结果的准确性起到决定性作用。
测量过程中,闭合差越小,说明测量精度越高;反之,闭合差越大,测量精度就越低。
三、总结导线全长闭合差公式是测量工程领域广泛应用的公式之一。
等边直伸形附和导线误差推算及精度分析

等边直伸形附和导线误差推算及精度分析附和导线是测量导线的一种,它是一个有已知点出发测量经过若干未知点到达另一个一直到,然后通过平差计算的到未知点平面坐标的测量导线。
其特点是两端坐标和方位角均为已知。
若附和导线的边长都相等,则称为等边直伸形导线。
若要计算等边直伸形导线的误差,需先从等边直伸形支导线终点的坐标误差和角度平差后的等边直伸形导线终点误差算起。
1.等边直伸形支导线终点的坐标误差设错误!未找到引用源。
为导线终点K沿直伸方向错误!未找到引用源。
的误差,简称“纵向误差”错误!未找到引用源。
为垂直于导线直伸方向错误!未找到引用源。
的误差,简称“横向误差”则错误!未找到引用源。
;错误!未找到引用源。
错误!未找到引用源。
(1-1)错误!未找到引用源。
(1-2)由于采用了假定坐标系统错误!未找到引用源。
,错误!未找到引用源。
,则错误!未找到引用源。
≈0,故cosα′i≈1,sinα′i≈0,Ry′i≈0,L x′≈L,L y′≈0因此错误!未找到引用源。
(1-3)错误!未找到引用源。
(1-4)错误!未找到引用源。
;错误!未找到引用源。
;错误!未找到引用源。
;错误!未找到引用源。
故错误!未找到引用源。
同时闭合线错误!未找到引用源。
则错误!未找到引用源。
(1-5)当边很多时,错误!未找到引用源。
(1-6)2.角度平差后导线终点的误差错误!未找到引用源。
(2-1)错误!未找到引用源。
(2-2)此处选择《矿山测量学.第一分册.生产矿井测量》中的公式进行推导计算上面两个公式是在原坐标系统下估算导线角度平差后的终点误差的公式,为了简化起见,将坐标原点移动到导线平均坐标点上,通常称此点为导线的重点或中心点,它的坐标为错误!未找到引用源。
;错误!未找到引用源。
此时公式2-1和2-2可化为错误!未找到引用源。
(2-3)错误!未找到引用源。
(2-4)公式中错误!未找到引用源。
;错误!未找到引用源。
显然错误!未找到引用源。
;错误!未找到引用源。
支导线终点位置误差公式新的推导方法.

支导线终点位置误差公式新的推导方法论文导读:本文引用科学实验法中的“控制变量法”来推导支导线终点位置误差。
控制变量法”是指在分析每一个影响因素对结果产生的影响的时候。
但仍少不了复杂的公式推导。
公式推导,毕业论文,支导线终点位置误差公式新的推导方法。
关键词:支导线,位置误差,控制变量法,公式推导0.引言由于测角和量边误差的积累,必然会使导线点的位置产生误差。
毕业论文,公式推导。
测角和量边误差是使导线点产生误差的根本因素。
本文引用科学实验法中的“控制变量法”来推导支导线终点位置误差。
“控制变量法”是指在分析每一个影响因素对结果产生的影响的时候,假设其它的影响因素对结果是没有影响或暂且不考虑其影响,这样得出的结果即为某一影响因素对结果产生影响的大小。
1.经典的理论方法推导支导线终点误差《矿山测量》教科书用了大量的篇幅,依据误差传播的基本规律对支导线点位误差公式进行了推导,其思路清晰、理论易懂,推导测角误差所引起的终点点位误差。
图1-1支导线终点误差示意图导线终点k 的坐标是所有角度及边长的函数。
根据偶然误差传播律,可得利用钢尺量距时终点k的坐标误差公式:(1-1)式中为导线各到导线终点K的连线长度a为偶然误差系数,b为系统误差系数为导线各边长L为导线始点与终点的连线的长度。
2.相邻点法推导支导线终点误差科教书中的推导方法经典,但是推导过程复杂繁琐,不易记忆。
所以有学者提出了自己的推导方法来简化该推导过程,这样跟容易理解。
以下为该方法的主要介绍。
2.1 经纬仪支导线任意相邻两点间误差传递公式由经纬仪支导线测量知,导线点的位置误差主要是由于测角误差和量边误差的积累而产生的,而支导线测量的特点是依此传递的,每测站的测角和量边都是独立完成,对于任意相邻两导线点,假定其中一点为起算点,则另一点的坐标可表示为:(2-2)其中:为相邻两导线点间的水平距离;n为两导线点之间的方位角。
由误差传播规律知,任意相邻两导线点之间测角误差和量边误差对纵坐标的点位误差的影响为:(2-3)同理可求出对横坐标的点位误差 2.2 方位角传递误差引起的相邻导线点点位误差导线任意边的方位角是测角的函数,其公式可表示为:(2-4)式中——起算导线边的方位角;——所测导线各左角。
单一导线误差理论..

n
1
2 mD
x
n 1
xi
2
n
2 m
1
2
L2
2 mT 0
对于等边直伸形支导线,Ti=0,D1=D2=……=Dn,nD=L, yi=0 ,
xn1 xi n 1 i D.
n 1
x
x
2 n i 1
2 D D 2 (12 2 2 n 2 ) n(n 1)(2n 1) 6
n i 1
yn1 y1 0 • 坐标轴转换后上式:
4.4 单一误差理论
• 在测距中,除偶然误差mD的影响外,应包括系 统误差的影响,系统误差对导线终点位置误差影 响为:
Di cosT L
n i 1
m cos Ti 1 m L yn1 y
2 t 2 n 2 D 2 2
3.任一点的纵横坐标中误差
mt m D k k 2 ( n 1)
k 1 2 mu {[( Lx i x k xi ) 2 ]1 xk [( x B xi ) 2 ] n k } m L 1 2
4.4 单一误差理论
• 综合以上对各种单一导线的方位角中误差 的讨论,分析对比可得到如下结论:
mT m
1 af ff aa PF
1 PF
1 n 1 PT 4
2
mT m
n 1 4
4.4 单一误差理论
对于等边直伸导线,Ti=0,D1=D2=……=Dn,此时 终点纵横坐标权函数式为:
dx n 1 vD1 vD 2 vD n dy n 1 nD v 1
井下经纬仪支导线误差估算公式简便推导方法

井下经纬仪支导线误差估算公式简便推导方法
王德利
【期刊名称】《矿山测量》
【年(卷),期】1998(000)003
【摘要】井下经纬仪支导线的误差估算公式是通过求偏导的方法推导而采,需掌握微积分知识,本文用微量关系和几何关系分析这一问题,得出相同的估算公式.用于教学,学生容易接受,理解更加深刻.
【总页数】3页(P11-13)
【作者】王德利
【作者单位】北京煤炭工业学校
【正文语种】中文
【中图分类】TD1
【相关文献】
1.井下支导线终点位置误差预计问题探讨 [J], 廖志平
2.用低等级陀螺经纬仪导线代替井下基本控制导线的探讨 [J], 刘小生
3.井下导线网陀螺经纬仪定向检测与误差分析 [J], 陈君翊
4.井下经纬仪导线对中误差分析 [J], 徐忠军
5.方向附合导线终点误差的严密估算公式 [J], 马振利
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
支导线终点位置误差公式新的推导方法
论文导读:本文引用科学实验法中的“控制变量法”来推导支导线终点位置误差。
控制变量法”是指在分析每一个影响因素对结果产生的影响的时候。
但仍少不了复杂的公式推导。
公式推导,毕业论文,支导线终点位置误差公式新的推导方法。
关键词:支导线,位置误差,控制变量法,公式推导
0.引言由于测角和量边误差的积累,必然会使导线点的位置产生误差。
毕业论文,公式推导。
测角和量边误差是使导线点产生误差的根本因素。
本文引用科学实验法中的“控制变量法”来推导支导线终点位置误差。
“控制变量法”是指在分析每一个影响因素对结果产生的影响的时候,假设其它的影响因素对结果是没有影响或暂且不考虑其影响,这样得出的结果即为某一影响因素对结果产生影响的大小。
1.经典的理论方法推导支导线终点误差《矿山测量》教科书用了大量的篇幅,依据误差传播的基本规律对支导线点位误差公式进行了推导,其思路清晰、理论易懂,推导测角误差所引起的终点点位误差。
图1-1支导线终点误差示意图导线终点k 的坐标是所有角度及边长的函数。
根据偶然误差传播律,可得利用钢尺量距时终点k的坐标误差公式:(1-1)式中为导线各到导线终点K的连线长度a为偶然误差系数,b为系统误差系数为导线各边长L
为导线始点与终点的连线的长度。
2.相邻点法推导支导线终点误差
科教书中的推导方法经典,但是推导过程复杂繁琐,不易记忆。
所以有学者提出了自己的推导方法来简化该推导过程,这样跟容易理解。
以下为该方法的主要介绍。
2.1 经纬仪支导线任意相邻两点间误差传递公式由经纬仪支导线测量知,导线点的位置误差主要是由于测角误差和量边误差的积累而产生的,而支导线测量的特点是依此传递的,每测站的测角和量边都是独立完成,对于任意相邻两导线点,假定其中一点为起算点,则另一点的坐标可表示为:(2-2)其中:为相邻两导线点间的水平距离;n为两导线点之间的方位角。
由误差传播规律知,任意相邻两导线点之间测角误差和量边误差对纵坐标的点位误差的影响为:(2-3)同理可求出对横坐标的点位误差 2.2 方位角传递误差引起的相邻导线点点位误差导线任意边的方位角是测角的函数,其公式可表示为:(2-4)式中——起算导线边的方位角;——所测导线各左角。
毕业论文,公式推导。
由式(2-1)式不难看出,式中的第二项是方位角传递误差引起的相邻导线点点位误差假定起算方位角无误差,当测角精度相同,,根据误差传播规律有:将上式代入方位角传递误差的公式推得:(2-5) 2.3 终点点位误差的公式推导将(2-4)式代入到(2-5)式得
同理令以上各式相加从而推出横坐标的点位误差
(2-6)上式中第一项为起算点中误差,第二项为量边中误差。
假定起算点无误差,量边误差采用教科书中推导值,则推出公式如公式(1-1)所示。
3.直接分析图形的方法,推导出公式以上方法虽然比经典的方法简单一些,但仍少不了复杂的公式推导。
我们在学习过程中,认真分析,从图形着手总结出新的方法,更加直观简便,以供大家参考研究。
3.1测角误差引起的支导线终点的位置误差假设所测量的所有转角中,只有第一个转角有误差,其他的转角是完全正确的。
那么在图形上表现为,所测量的导线绕着已知点1,以为半径整体发生了旋转,如图3-1所示。
图3-1 由图1可
知,支导线终点K偏离真实位置的线量大小为=。
其中为导线各到导线终点K的连线长度。
假设所测量的所有转角中,只有第二个转角有误差,其他的转角是完全正确的。
那么在图形上表现为,所测量的导线绕着导线点2,以为半径整体发生了旋转.,如图3-2所示。
图3-2 由图2可知,支导线终点K偏离真实位置的线量大小为 =。
同理,我们可以求出第i个转角的误差使导线终点偏离真实位置的线量大小为在实际的测量过程中,在没有明显错误的情况下,我们认为每个转角的测量都有误差,且测量中误差大小相等,都会对导线的终点产生,使其偏离真实的位置。
所以综合考虑测角误差使终点偏离真实位置的大小为。
3.2量边误差引起的支导线终点的位置误差对于光电测距导线来说,测距误差为式中A为固定误差,B为比例误差,为个导线边长。
对于钢尺量距而言,测距误差为式中a为偶然误差系数,b 为系统误差系数。
由于钢尺量边常有系统误差存在,因此需要进一步分析量边偶然误差与系统误差对于终点K的坐标影响。
这里我们只讨论钢尺量距
(1)量边偶然误差的影响当无明显的系统误差时,即b=0,则。
这是第i 条边的误差对最终点位置的影响大小。
综合考虑,当b=0时,量边对最终点的影响大小为(2)量边系统误差的影响当量边存在明显的系统误差时,由于它对边长的影响是单方面的,其大小与边长成正比。
如图3-3所示,ABCDE为正确导线,假设在这条导线中没有其他误差的影响,只考虑量边系统误差的影响,而且假设所有边长均按相同比例伸,从而使导线变成
A′B′C′D′E′,不难看出,它与正确导线的形状相似,因而导线各点的位置都从原来的正确位置,沿着该点与起始点A的连线方向移动了一段距离,其大小为相应连线的长度乘以系统误差影响系数b。
BB′=b×ABCC′=b×AC D D′=b×ADEE′=b×AE 由此可见,由量边系统误差所引起的支导线终点的位置误差为EE′=b×AE=bL 式中L为导线始点与终点的连线(叫做闭合线)的长度。
所以量边误差所引起的导线终点误差为图3-3量边系统误差的影响由以上分析可知,测角量边误差对导线终点的影响大小与公式(1-1)一样。
无论用那种方法进行研究,得出的结果肯定是统一的。
4 总结在井下测量作业过程中,无论是井下基本控制导线最弱点的误差精度估计还是贯通测量误差预计,经纬仪支导线都应用相当广泛。
工作人员和学者对其特点进行了大量的研究,得出许多宝贵的理论和经验。
这些经验给我们以后的实践带来了诸多的方便,我们可以直接应用于工作和研究中,这也有利用我们以后学习和工作。
由以上的分析可以得出以下结论:
(1)导线的精度与测角量边的精度、测站数目和导线的形状有关,而测角误差的影响对导线的精度起决定性作用。
毕业论文,公式推导。
(2)为了提高导线精度,减小导线点点位误差,首先应注意提高测角精度,同时应适当增大边长,已减小测站个数。
(3)有条件时,要尽量将导线布设成闭合图形,闭合导线可以消除系统误差的影响。
(4) R越大,误差越大,故有直伸型导线误差最大,曲折型导线较小。
参考文献: [1]张国良,朱家钰,顾和和.矿山测量学[M].徐州:中国矿业大学出版社,2008:215-219 [2]周立吴,张国良,林家聪编.生产矿井测量[M]//矿山测量学(第一分册).北京:中国矿业学院出版社,1987. [3]付金峰,高洁等.相邻点法推导支导线终点误差[J].矿山测量.2004,1:49-50 [4]李洪涛,王磊,法惟刚.解析法分析支导线终点误差[J].有色金属(矿山部分).2009,61(2):19-
21。
