相似多边形精品PPT教学课件
合集下载
《相似多边形》相似图形4精品 课件

•
九、没有人不想和你同坐一辆豪华轿车 ,但你 需要的 ,却是 轿车坏 了还会 和你一 起搭巴 士的人 。
•
十、我喜欢你的意思就是:从现在起, 你已经 具备伤 害我的 能力, 以及不 好意思 我看谁 都像情 敌。
•
十一、不相信下辈子,只想善待你今生 。因为 我不知 道,下 一辈子 是否还 能遇见 你,所 以我今 生才会 那么努 力把最 好的给 你。
人生如逆水行舟,不进则退。
•
优胜劣汰的世界里,你必须不断提升 自己的 价值。 一、放下大概就是这样,即使我们没在 一起, 我也会 好好的 ,谢谢 时间惊 艳了那 段有你 的记忆 ,也谢 谢现在 更努力 变好的 自己。
•
二、抱歉啊,不能为你金戈铁马,也不 能许你 一世繁 华,不 过我能 给你一 个小家 ,里面 温了杯 暖茶。
E
C 22 30 48
D
自主练习 书 P129
2.在下面的图形中,有两个相似三
角形,试确定 y、m、n的值。
△ABC∽△DEF A
D
n°
3a
10
y 2a 50°
B
45°
85° C 45°m°F
E
尝试解决 例1:有一块呈三角形形
状的草坪,其中一边的长是 20m,在这个草坪的图纸上,这条 边长 5cm,其他两边的长度都是3.5cm。 求该草坪其他两边的实际长度。
毕业八年的她被迫重返人才市场,但 彼时的 她与毕 业时相 比毫无 长进, 面试屡 屡碰壁 。
李尚龙曾说:
真正的安稳是历经世事后的淡薄,你 还没有 见过世 界,就 想隐退 山林, 到头来 只会是 井底之 蛙。”
人生如逆水行舟,不进则退。
•
优胜劣汰的世界里,你必须不断提升 自己的 价值。 一、放下大概就是这样,即使我们没在 一起, 我也会 好好的 ,谢谢 时间惊 艳了那 段有你 的记忆 ,也谢 谢现在 更努力 变好的 自己。
《相似多边形》图形的相似PPT精品课件

∵正三角形的三边都相等,
∴
.
B
C
D
E
F
4.3 相似多边形
例1 下列每组图形形状相同,它们的对应角有怎样的关系?对应边呢?
(2) 正方形 ABCD 与正方形 EFGH.
A
B
解:(1)∵正方形的每个角都是直角,
∴
D
C
∵正方形的四边相等,
E
F
∴
H
G
4.3 相似多边形
归纳
相似多边形:各角分别相等、各边对应成比例的两个多边形叫做相似 多边形. 相似比:相似多边形对应边的比叫做相似比 .
教案下载: . /jiaoan/
ppt论坛: . .cn
ppt课件: . /kejian/
语文课件: . /kejian/yuwen/ 数学课件: . /kejian/shuxue/
英语课件: . /kejian/yingyu/ 美术课件: . /kejian/meishu/
科学课件: . /kejian/kexue/ 物理课件: . /kejian/wuli/
4.3 相似多边形
思考 1:任意两个正 n 边形相似吗? 答:任意两个正 n 边形都相似.
思考 2:任意两个菱形相似吗? 答:任意两个菱形不一定相似.
4.3 相似多边形
1. 观察下面两组图形,图中的两个图形相似吗?为什么?
10 正方形
12
菱形
10
12
答:不相似. 因为虽然它们对应边是成比例的,但它们的对应角不相等.
与 F1A1 的比都相等,称为对应边.
A1
B1
A
B
F
C
F1
C1
ED
E1
相似多边形 ppt课件

重
难
题
型
突
破
思路点拨
4.3 相似多边形
重
难
题
型
突
破
解题通法
解决此类问题,一般是根据对应边成比例,列出比例
式求解,注意结果要符合实际.
4.3 相似多边形
易 ■ 判定相似多边形时忽略条件
错
例 下列各组图形中一定是相似多边形的是 (
易
混
A. 两个直角三角形
分
析
B. 两个等边三角形
C. 两个菱形
D. 两个矩形
A. 甲和乙
B. 甲和丙
C. 乙和丙
D. 甲、乙和丙
4.3 相似多边形
[解题思路]
考
点
矩形已经满足各角分别相等,判断各边是否成比例即可
清
单
≠
,∴ 甲与乙不相似;∵ =
,∴ 甲与丙
解 .∵
.
.
.
读
.
≠
[答案]
B
相似;∵
.
.
,∴ 乙与丙不相似.
4.3 相似多边形
考 ■考点二 相似多边形的性质
读
∴BC=12.
[答案]
48 12
4.3 相似多边形
重 ■题型 相似多边形性质与判定的应用
难
例 如图,一个矩形广场的长为 90 m,宽为 60 m,广
题
型 场内有两横、两纵四条小路,如果两条横向小路的宽均为
突
破 1.2 m,那么每条纵向小路的宽为多少时小路内外边缘所围
成的两个矩形相似?
4.3 相似多边形
)
4.3 相似多边形
[解题思路]
难
题
型
突
破
思路点拨
4.3 相似多边形
重
难
题
型
突
破
解题通法
解决此类问题,一般是根据对应边成比例,列出比例
式求解,注意结果要符合实际.
4.3 相似多边形
易 ■ 判定相似多边形时忽略条件
错
例 下列各组图形中一定是相似多边形的是 (
易
混
A. 两个直角三角形
分
析
B. 两个等边三角形
C. 两个菱形
D. 两个矩形
A. 甲和乙
B. 甲和丙
C. 乙和丙
D. 甲、乙和丙
4.3 相似多边形
[解题思路]
考
点
矩形已经满足各角分别相等,判断各边是否成比例即可
清
单
≠
,∴ 甲与乙不相似;∵ =
,∴ 甲与丙
解 .∵
.
.
.
读
.
≠
[答案]
B
相似;∵
.
.
,∴ 乙与丙不相似.
4.3 相似多边形
考 ■考点二 相似多边形的性质
读
∴BC=12.
[答案]
48 12
4.3 相似多边形
重 ■题型 相似多边形性质与判定的应用
难
例 如图,一个矩形广场的长为 90 m,宽为 60 m,广
题
型 场内有两横、两纵四条小路,如果两条横向小路的宽均为
突
破 1.2 m,那么每条纵向小路的宽为多少时小路内外边缘所围
成的两个矩形相似?
4.3 相似多边形
)
4.3 相似多边形
[解题思路]
中小学精品课件相似多边形的性质课件ppt

• (1)设法求出图上外环路的长度,并由此求出外环路的 实际长度;
• (2)估计外环路所围成的区域的面积.你是怎么做的?与
同伴交流. • 点拨
平坦立交桥
• (1)用一根线绳沿图中的外环路
重叠放置,此时线绳的长度就是
外环路的图上距离;
大阳泉
• (2)把图上的外环路近似地看作 一个矩形.
义井桥
• 某市城市广场,是一个因周边环境设计 建造的一个不规则多边形,具有和谐的 自然美.设计图的比例尺是1∶10 000. 图上多边形与实际多边形相似吗?如果 相似,它们的相似比是多少?图上多边形 与实际多边形的周长比是多少?面积呢?
么? • (2).求正方形PQRSR的边长.
B P DQ C 设正方形PQRS的边长
四• 解边:形(1)P△QRASS是R正∽方△形ABC.理RS由∥是B:C 为x cm, 则AE=(40-x)cm,
∠ASR= ∠B ∠ARS= ∠C
40 x x . 40 60
△ASR∽△ABC. • (2).由(1)可知, △ASR∽△ABC.
BM EN
BC . AB BM . EF DE EN
且∠B =∠E.
MD C
∴△AMB∽△DNE.(两边对应成比
例且夹角相等的两个三角形相似).
AM DN
AB DE
.(相似三角形对应边成比E 例).
N
F
即,相似三角形对应中线的比等于相似比.
你还记得相似三角形周长的比与相似比的关系 及其理由吗?
判定两个三角形相似的方法:
两角对应相等的两个三角形相似.
三边对应成比例的两个三角形相似.
两边对应成比例,且夹角相等的两个三角
形相似.
斜边直角边对应成比例的两个三角形相
相似多边形的性质课件

使用哪个定理来判断多边形是否相似。
三边对应成比例判定定理
总结词
通过两个多边形的三边对应成比例,可以判定两个多 边形相似。
详细描述
三边对应成比例判定定理是相似多边形判定定理的一 种,它基于两个多边形的三边对应成比例,从而判定 两个多边形相似。这个定理在实际应用中非常有用, 因为它只需要比较三个边的长度就可以判断两个多边 形是否相似,相对于其他判定定理更为简便。然而, 需要注意的是,这个定理只适用于三边对应成比例的 情况,对于更多边的多边形,需要使用其他判定定理 进行判断。
总结词
通过比较相似多边形的面积和相似比, 证明面积比等于相似比的平方。
详细描述
首先,计算两个相似多边形的面积。 然后,计算它们的相似比。最后,比 较面积和相似比的关系,如果面积比 等于相似比的平方,则证明了面积比 等于相似比的平方。
THANKS
感谢观看
多边形相似。
02
相似多边形的性质
相似多边形的对应角相等
总结词
相似多边形的对应角是相等的,这是相似多边形的基本性质之一。
详细描述
根据相似多边形的定义,如果两个多边形相似,则它们的对应角必定相等。这 意味着无论多边形的大小如何变化,只要它们是相似的,它们的对应角就会保 持不变。
相似多边形的对应边成比例
角-角-边判定定理
总结词
通过两个多边形的对应角相等,且对应边成比例,可以判定两个多边形相似。
详细描述
角-角-边且对应边成比例,从而判定 两个多边形相似。在几何学中,这个定理是非常重要的,因为它提供了一种简单而有效的方法来判断两个多边形 是否相似。
相似多边形的性质
相似多边形的面积之 比等于对应边长的平 方之比。
相似多边形的对应角 相等,对应边成比例。
三边对应成比例判定定理
总结词
通过两个多边形的三边对应成比例,可以判定两个多 边形相似。
详细描述
三边对应成比例判定定理是相似多边形判定定理的一 种,它基于两个多边形的三边对应成比例,从而判定 两个多边形相似。这个定理在实际应用中非常有用, 因为它只需要比较三个边的长度就可以判断两个多边 形是否相似,相对于其他判定定理更为简便。然而, 需要注意的是,这个定理只适用于三边对应成比例的 情况,对于更多边的多边形,需要使用其他判定定理 进行判断。
总结词
通过比较相似多边形的面积和相似比, 证明面积比等于相似比的平方。
详细描述
首先,计算两个相似多边形的面积。 然后,计算它们的相似比。最后,比 较面积和相似比的关系,如果面积比 等于相似比的平方,则证明了面积比 等于相似比的平方。
THANKS
感谢观看
多边形相似。
02
相似多边形的性质
相似多边形的对应角相等
总结词
相似多边形的对应角是相等的,这是相似多边形的基本性质之一。
详细描述
根据相似多边形的定义,如果两个多边形相似,则它们的对应角必定相等。这 意味着无论多边形的大小如何变化,只要它们是相似的,它们的对应角就会保 持不变。
相似多边形的对应边成比例
角-角-边判定定理
总结词
通过两个多边形的对应角相等,且对应边成比例,可以判定两个多边形相似。
详细描述
角-角-边且对应边成比例,从而判定 两个多边形相似。在几何学中,这个定理是非常重要的,因为它提供了一种简单而有效的方法来判断两个多边形 是否相似。
相似多边形的性质
相似多边形的面积之 比等于对应边长的平 方之比。
相似多边形的对应角 相等,对应边成比例。
相似多边形 公开课精品课件

2cm,那么它们的相似比是( ) 6 9 3 3 A. B. C. D. 5 4 4 2 2 已知正方形ABCD与正方形DEFG的边长分别是2
3
cm和4cm,则正方形ABCD与正方形DEFG的相似比 是_______.
(来自《典中点》)
知识总结 知识方 法要点 关键总结 注意事项
相 似 多 边 形
(来自《典中点》)
知3-导
知识点
3 相似比
两个图形相似,其中一个图形可以看作由另一个 图形放大或缩小得到.例如,放映电影时,投在屏幕上 的画面就是胶片上图形的放大;用复印机把一个图形 放大或缩小后所得的图形,都与原来的图形相似.下图 中有2对图形,每对图形中的两个图形相似.其中较大 (小)的图形可以看成是由较小 (大)的图形放大(缩小)得 到的.
知3-讲
例3 如图,把矩形ABCD对折,折痕为MN,矩形DMNC与矩
形ABCD相似,已知AB=4.
(1) 求AD的长; (2)求矩形DMNC与矩形ABCD的相似比. 相似多边形的对应边的比相等, 导引: A 其比值就是相似比.
M
D
B
E
C
知3-讲
x 解: (1)设AD=x,则 DM . 2 ∵矩形DMNC与矩形ABCD相似, AD CD ∴ . DC DM x 4 ∴ ,∴x 2 32. 4 x 2 ∴x 4 2或x 4 2 舍去,即AD的长为4 2. 4 2 . (2)矩形DMNC与矩形ABCD的相似比为 2 4 2
第二十五章
图形的相似
25.7
相似多边形和图形的位似
第1课时
相似多边形
1
课堂讲解
相似多边形的定义 相似多边形的性质 相似比
2
《相似多边形》相似图形PPT精品教学课件

做相似多边形。
相似比概念: 相似多边形对应边的比叫做相似比。
如:六边形ABCDEF与六边形A1B1C1D1E1F1相似, 记作六边形ABCDEF 六边形A1B1C1D1E1F1,其中 AB:A1B1的值就是相似比.
注:1、相似符号“∽ ”读作“相似于” 2、在记两个多边形相似时,要把表示对应角顶点 的字母写在对应的位置上。
六边形ABCDEF与六边形A1B1C1D1E1F1 是形状相同的图形;其中∠A与∠A1, ∠B与∠B1, ∠C与∠C1, ∠D与∠D1, ∠E 与∠E1, ∠F与∠F1对应相等,称为对应 角;AB与A1B1,BC与B1C1,CD与C1D1, DE与 D1E1,EF与E1F1,FA与F1A1的比都相等, 称 为对应边.
10 正方形
8 矩形
10
(2)
12
答:不相似。因为虽然它们对应角相等, 但它们对应边不成比例。
2. 如果两个多边形不相似,那么它们的对应 角可能都相等吗? 对应边可能都成比例 吗?
答:如果两个多边形不相似,它们的对应角 可能都相等;如果两个多边形不相似,对应边 也可能成比例。
但如果两个多边形不相似,那么它们不可 能各角对应相等且各边对应成比例.
身边的友人渐渐地脱单,越来越多的走进婚姻的殿堂,而我依然在殿堂外独自行走,关心自己的人,都在为自己着急,挑选各种各样认为好的女孩,而我却总是无动于衷。我不知道是因为自己对爱情的惧怕,还是对婚姻的恐惧,还是已无力与一个陌生人去从相识开始,也以无心去接受这一切,所以独自逃离的远远地,不提不问不想不念。 我不知道,未来,谁与我并肩看人间烟火。只是,在内心深处,有一股浓浓的思念萦绕心尖,剪不断,理还乱,或许,是一年,或许,是两年,或许,一辈子。刚刚结束了班夫的自驾游,去之前一点没做攻略,除了传说中对美景的盛赞,对那里几乎一无所知。 头一次毫无准备地上路,得益于同行的友人一家,他们已是三顾班夫了,轻车熟路,所以我放心地当了甩手掌柜,从装备到路线、酒店、景点、美食,统统不必操心,乐得轻松自在。 这是一片广袤的天地,无一处不风景,无一眼不风情。 最喜欢峡谷里的瀑布,清凉的冰水摧枯拉朽般从高耸的岩壁奔流而下,无止无休,千年万年,冲刷出今日的残岩断壁。伫立在水边,俯仰之间,山水交融,仿佛看到了久远的一幕,子在川上曰:逝者如斯夫。 而友人一家之所以乐此不疲地到此三游,则是为了一座岛——精灵岛,位于嘉士伯国家公园的马琳湖。 精灵岛已经成了他们心中的一份执念。 第一次慕名而至,临近冬季,一场大雪扑灭了他们通往精灵岛的梦幻之旅。 第二次避开了雪季,却不想又被大雾遮望眼,再一次与精灵岛失之交臂。 此行已是第三次了,虽然沿途的景致百看不厌,却比不上心系精灵岛的一眼。 遗憾的是,又一次天公不作美,明明之前连日的晴空万里,偏偏这一日阴雨绵绵云雾缭绕,注定又要错失梦想中的小岛了。 我的心情还好,因为没有过多的期待,入目皆是美景,撑起雨伞欣赏了一圈雨中湖景朦胧岛影,后来在湖边的礼品店里看到了清晰的精灵岛图片,权当完成了心愿。 友人静静地站在湖边,望着面前的雨幕,一言不发。 我向她提议,“不如我们多呆一天,或许明天就放晴了。” “天气预报说今天下午才有雨,本以为早上赶过来还能来得及看一眼的。”她失落地说。 “那明天呢?”我暗自惭愧,自己连天气预报都没看。 “明天也有雨。”她皱眉道。 “那--”我不知该说什么安慰好了。 “走吧,这就是人生,总要有点遗憾的,就让它永远留在我的心里,偶尔想念一下,作为求而不得的最美风景吧!”她甩甩头,最后看了一眼她的梦想,然后潇洒地往回走了。 她的一番话似乎把所有的不悦都带走了,突然觉得这样的遗憾竟比睛天还美。 风景自在人心,有时候不完美也是一种完美。 于是想起另一个故事。 一次聚会,有个朋友刚从张家界旅游回来,大赞那里风景绝美,堪称人间仙境。 在看过她晒出的自拍后,所有人都开始兴致勃勃地憧憬起来,相约什么时侯有假期可以同行。 只有闺蜜沉默不语。 我后知后觉地记起来,她和初恋男友分手的那年暑假,正是她男友从张家界回来之后不久。 她曾经说过,此生都不会去那个地方,因为在她心里,那是世界上最美的地方,是他曾经承诺要带她一起去看的风景,因为少了他,再美的风景都是泡影。 难道这么多年过去了,她还没能放下? 她看出我的疑惑,淡淡地笑了,“不是因为他,纯粹是不想去。我相信它是最美的,就因为相信,所以不想破坏了它在我心里的那份完美,一旦真正去了,总会有遗憾,现实永远没有想象的完美。” 她把初恋放下了,却放不下他为她描绘的那片风景。还是因为太在意啊,没有期盼,何来遗憾? 人生需要遗憾,因为遗憾,所以真实;因为遗憾,所以美丽。 就象张家界之于闺蜜,精灵岛之于友人一家,每个人的遗憾都源于心中所念。 心有所系,故有所憾。引导语:傻孩子,你记住,可以哭,可以恨,但是不可以不坚强。心若在,梦就在,你必须非常努力,因为后面还有一群人在等着看你的笑话。即便是躺着中枪,也要姿势漂亮! 傻孩子,你记住:我们有许多的梦想,不一定都能实现,有些梦想甚至要摒弃。不要把自己太当回事,也不要把自己太不当回事。好好地呵护自己,对自己好点,就要有好的心态,有了好的心态就会心胸宽广,就会豁达,就会有好的心境。 傻孩子,你记住:爱一个人不容易,忘记一个人更难。是啊,爱一个人是很苦的很苦的事,想一个人是很累的很累的事,等一个人是很傻的很傻的事,为什么我们却不能拒绝这样的相思?为什么我们心甘情愿无怨无悔?为什么我们却如此依然痴迷不悟?
相似比概念: 相似多边形对应边的比叫做相似比。
如:六边形ABCDEF与六边形A1B1C1D1E1F1相似, 记作六边形ABCDEF 六边形A1B1C1D1E1F1,其中 AB:A1B1的值就是相似比.
注:1、相似符号“∽ ”读作“相似于” 2、在记两个多边形相似时,要把表示对应角顶点 的字母写在对应的位置上。
六边形ABCDEF与六边形A1B1C1D1E1F1 是形状相同的图形;其中∠A与∠A1, ∠B与∠B1, ∠C与∠C1, ∠D与∠D1, ∠E 与∠E1, ∠F与∠F1对应相等,称为对应 角;AB与A1B1,BC与B1C1,CD与C1D1, DE与 D1E1,EF与E1F1,FA与F1A1的比都相等, 称 为对应边.
10 正方形
8 矩形
10
(2)
12
答:不相似。因为虽然它们对应角相等, 但它们对应边不成比例。
2. 如果两个多边形不相似,那么它们的对应 角可能都相等吗? 对应边可能都成比例 吗?
答:如果两个多边形不相似,它们的对应角 可能都相等;如果两个多边形不相似,对应边 也可能成比例。
但如果两个多边形不相似,那么它们不可 能各角对应相等且各边对应成比例.
身边的友人渐渐地脱单,越来越多的走进婚姻的殿堂,而我依然在殿堂外独自行走,关心自己的人,都在为自己着急,挑选各种各样认为好的女孩,而我却总是无动于衷。我不知道是因为自己对爱情的惧怕,还是对婚姻的恐惧,还是已无力与一个陌生人去从相识开始,也以无心去接受这一切,所以独自逃离的远远地,不提不问不想不念。 我不知道,未来,谁与我并肩看人间烟火。只是,在内心深处,有一股浓浓的思念萦绕心尖,剪不断,理还乱,或许,是一年,或许,是两年,或许,一辈子。刚刚结束了班夫的自驾游,去之前一点没做攻略,除了传说中对美景的盛赞,对那里几乎一无所知。 头一次毫无准备地上路,得益于同行的友人一家,他们已是三顾班夫了,轻车熟路,所以我放心地当了甩手掌柜,从装备到路线、酒店、景点、美食,统统不必操心,乐得轻松自在。 这是一片广袤的天地,无一处不风景,无一眼不风情。 最喜欢峡谷里的瀑布,清凉的冰水摧枯拉朽般从高耸的岩壁奔流而下,无止无休,千年万年,冲刷出今日的残岩断壁。伫立在水边,俯仰之间,山水交融,仿佛看到了久远的一幕,子在川上曰:逝者如斯夫。 而友人一家之所以乐此不疲地到此三游,则是为了一座岛——精灵岛,位于嘉士伯国家公园的马琳湖。 精灵岛已经成了他们心中的一份执念。 第一次慕名而至,临近冬季,一场大雪扑灭了他们通往精灵岛的梦幻之旅。 第二次避开了雪季,却不想又被大雾遮望眼,再一次与精灵岛失之交臂。 此行已是第三次了,虽然沿途的景致百看不厌,却比不上心系精灵岛的一眼。 遗憾的是,又一次天公不作美,明明之前连日的晴空万里,偏偏这一日阴雨绵绵云雾缭绕,注定又要错失梦想中的小岛了。 我的心情还好,因为没有过多的期待,入目皆是美景,撑起雨伞欣赏了一圈雨中湖景朦胧岛影,后来在湖边的礼品店里看到了清晰的精灵岛图片,权当完成了心愿。 友人静静地站在湖边,望着面前的雨幕,一言不发。 我向她提议,“不如我们多呆一天,或许明天就放晴了。” “天气预报说今天下午才有雨,本以为早上赶过来还能来得及看一眼的。”她失落地说。 “那明天呢?”我暗自惭愧,自己连天气预报都没看。 “明天也有雨。”她皱眉道。 “那--”我不知该说什么安慰好了。 “走吧,这就是人生,总要有点遗憾的,就让它永远留在我的心里,偶尔想念一下,作为求而不得的最美风景吧!”她甩甩头,最后看了一眼她的梦想,然后潇洒地往回走了。 她的一番话似乎把所有的不悦都带走了,突然觉得这样的遗憾竟比睛天还美。 风景自在人心,有时候不完美也是一种完美。 于是想起另一个故事。 一次聚会,有个朋友刚从张家界旅游回来,大赞那里风景绝美,堪称人间仙境。 在看过她晒出的自拍后,所有人都开始兴致勃勃地憧憬起来,相约什么时侯有假期可以同行。 只有闺蜜沉默不语。 我后知后觉地记起来,她和初恋男友分手的那年暑假,正是她男友从张家界回来之后不久。 她曾经说过,此生都不会去那个地方,因为在她心里,那是世界上最美的地方,是他曾经承诺要带她一起去看的风景,因为少了他,再美的风景都是泡影。 难道这么多年过去了,她还没能放下? 她看出我的疑惑,淡淡地笑了,“不是因为他,纯粹是不想去。我相信它是最美的,就因为相信,所以不想破坏了它在我心里的那份完美,一旦真正去了,总会有遗憾,现实永远没有想象的完美。” 她把初恋放下了,却放不下他为她描绘的那片风景。还是因为太在意啊,没有期盼,何来遗憾? 人生需要遗憾,因为遗憾,所以真实;因为遗憾,所以美丽。 就象张家界之于闺蜜,精灵岛之于友人一家,每个人的遗憾都源于心中所念。 心有所系,故有所憾。引导语:傻孩子,你记住,可以哭,可以恨,但是不可以不坚强。心若在,梦就在,你必须非常努力,因为后面还有一群人在等着看你的笑话。即便是躺着中枪,也要姿势漂亮! 傻孩子,你记住:我们有许多的梦想,不一定都能实现,有些梦想甚至要摒弃。不要把自己太当回事,也不要把自己太不当回事。好好地呵护自己,对自己好点,就要有好的心态,有了好的心态就会心胸宽广,就会豁达,就会有好的心境。 傻孩子,你记住:爱一个人不容易,忘记一个人更难。是啊,爱一个人是很苦的很苦的事,想一个人是很累的很累的事,等一个人是很傻的很傻的事,为什么我们却不能拒绝这样的相思?为什么我们心甘情愿无怨无悔?为什么我们却如此依然痴迷不悟?
相似多边形ppt课件五

内角和的概念
多边形的内角和是指其所有内角的度数之和。对于任意一个n边形,其内角和为(n-2)×180°。
外角和的概念
多边形的外角和是指其所有外角的度数之和。对于任意一个n边形,其外角和为360°。
相似多边形内角和与外角和的性质
相似多边形的内角和与外角和都与其对应边的长度无关,只与其边的数量有关。因此,无 论相似多边形的边长如何变化,其内角和与外角和都不会发生变化。
举例:两个三角形如果两个角相等, 并且它们所夹的边成比例,则这两个 三角形相似。
边边角相似判定定理
两个对应边成比例,且夹的对应角相等,则两多边形相似。
举例:两个三角形如果两边成比例,并且它们夹的角相等, 则这两个三角形相似。
边边边相似判定定理
所有对应边的比相等,则两多边形相似。 举例:两个矩形如果所有边的比相等,则这两个矩形相似。
练习题二:求两个多边形的面积比
题目
已知两个多边形,一个是正方形, 边长为a,另一个是矩形,长为a, 宽为b。求两个多边形的面积比。
解答
正方形的面积为 $a^2$,矩形的 面积为 $ab$。因此,两个多边形 的面积比为 $frac{a^2}{ab} = frac{a}{b}$。
练习题三:判断两个多边形是否相似
04
相似多边形的扩展知识
相似多边形的面积比
01
面积比的概念
相似多边形的面积比是它们的对应边的平方之比,即如果两个多边形相
似,那么它们的面积之比等于它们的对应边长之比的平方。
02
面积比的性质
相似多边形的面积比具有传递性,即如果两个多边形与第三个多边形相
似,那么它们的面积比等于它们与第三个多边形的面积比的乘积。
相似多边形的周长比具有传递性,即如果两个多边形与第 三个多边形相似,那么它们的周长比等于它们与第三个多 边形的周长比的乘积。
多边形的内角和是指其所有内角的度数之和。对于任意一个n边形,其内角和为(n-2)×180°。
外角和的概念
多边形的外角和是指其所有外角的度数之和。对于任意一个n边形,其外角和为360°。
相似多边形内角和与外角和的性质
相似多边形的内角和与外角和都与其对应边的长度无关,只与其边的数量有关。因此,无 论相似多边形的边长如何变化,其内角和与外角和都不会发生变化。
举例:两个三角形如果两个角相等, 并且它们所夹的边成比例,则这两个 三角形相似。
边边角相似判定定理
两个对应边成比例,且夹的对应角相等,则两多边形相似。
举例:两个三角形如果两边成比例,并且它们夹的角相等, 则这两个三角形相似。
边边边相似判定定理
所有对应边的比相等,则两多边形相似。 举例:两个矩形如果所有边的比相等,则这两个矩形相似。
练习题二:求两个多边形的面积比
题目
已知两个多边形,一个是正方形, 边长为a,另一个是矩形,长为a, 宽为b。求两个多边形的面积比。
解答
正方形的面积为 $a^2$,矩形的 面积为 $ab$。因此,两个多边形 的面积比为 $frac{a^2}{ab} = frac{a}{b}$。
练习题三:判断两个多边形是否相似
04
相似多边形的扩展知识
相似多边形的面积比
01
面积比的概念
相似多边形的面积比是它们的对应边的平方之比,即如果两个多边形相
似,那么它们的面积之比等于它们的对应边长之比的平方。
02
面积比的性质
相似多边形的面积比具有传递性,即如果两个多边形与第三个多边形相
似,那么它们的面积比等于它们与第三个多边形的面积比的乘积。
相似多边形的周长比具有传递性,即如果两个多边形与第 三个多边形相似,那么它们的周长比等于它们与第三个多 边形的周长比的乘积。
《相似多边形》相似图形PPT精选教学课件

07 产品经理看到你登陆都要哭了,你 是海军 陆战队 吗?是 登录啦 。 08 “唉”和“哎”是完全不同的两个字,如 果当话 头的话 可以用 “诶”。
09 “优惠券”打成“优惠卷”的商家我是不 会买的 。 10 娱乐新闻也是要严谨的,“曝光”写成 “暴光” 就勉勉 强强了 ,“爆 光”是什 么啦。
11 你们真的是一群很有品位的读者, 一定不 会分不 清品位 和品味 的。 04 语言习惯
06 同理还有能把确凿读成 quezuo 而不是 quezao 的。 07 太多流行歌手唱“在午夜徘回……”, 以至于 听到哪 个歌手 唱对“ 徘徊”都 很让人 感动。
08 除了周杰伦以外,很难接受任何人 念出“瓜 牛”这两 个字。 03 文字
#3 typo 01 分不清“哪”和“那”,会真的造成语意 理解上 的困惑 。
如:六边形ABCDEF与六边形A1B1C1D1E1F1相似, 记作六边形ABCDEF 六边形A1B1C1D1E1F1,其中 AB:A1B1的值就是相似比.
注:1、相似符号“∽ ”读作“相似于” 2、在记两个多边形相似时,要把表示对应角顶点 的字母写在对应的位置上。
S
如果两个多边形相似,那 么它们的对应角有什么关系? 对应边呢?
02 读音
#2 pronouncation 01 想邀请把弹幕(danmu)读成 tanmu 的朋友,当场给我弹弹看。 02 阈 Yù值,这个词很难读,当然最简单的办 法就是 ……不 用这个 词。 03 接电话时请用“唯”,用“胃”我勉强能 忍,但 用“ why”的是 不是过 分了。 04 一旦把“崩溃”说成“奔溃”,就会给人 一种在 大雨里 含泪嚎 叫奔跑 的即视 感。 05 给予现在也可以读作 gei yu 了,但我听到有人读 ji yu,我还是会忍不住投去赞赏的 目光。
09 “优惠券”打成“优惠卷”的商家我是不 会买的 。 10 娱乐新闻也是要严谨的,“曝光”写成 “暴光” 就勉勉 强强了 ,“爆 光”是什 么啦。
11 你们真的是一群很有品位的读者, 一定不 会分不 清品位 和品味 的。 04 语言习惯
06 同理还有能把确凿读成 quezuo 而不是 quezao 的。 07 太多流行歌手唱“在午夜徘回……”, 以至于 听到哪 个歌手 唱对“ 徘徊”都 很让人 感动。
08 除了周杰伦以外,很难接受任何人 念出“瓜 牛”这两 个字。 03 文字
#3 typo 01 分不清“哪”和“那”,会真的造成语意 理解上 的困惑 。
如:六边形ABCDEF与六边形A1B1C1D1E1F1相似, 记作六边形ABCDEF 六边形A1B1C1D1E1F1,其中 AB:A1B1的值就是相似比.
注:1、相似符号“∽ ”读作“相似于” 2、在记两个多边形相似时,要把表示对应角顶点 的字母写在对应的位置上。
S
如果两个多边形相似,那 么它们的对应角有什么关系? 对应边呢?
02 读音
#2 pronouncation 01 想邀请把弹幕(danmu)读成 tanmu 的朋友,当场给我弹弹看。 02 阈 Yù值,这个词很难读,当然最简单的办 法就是 ……不 用这个 词。 03 接电话时请用“唯”,用“胃”我勉强能 忍,但 用“ why”的是 不是过 分了。 04 一旦把“崩溃”说成“奔溃”,就会给人 一种在 大雨里 含泪嚎 叫奔跑 的即视 感。 05 给予现在也可以读作 gei yu 了,但我听到有人读 ji yu,我还是会忍不住投去赞赏的 目光。
人教版九年级下册数学27.1:相似多边形 课件(共16张PPT)

对于图中两个相似的四边形,它们的对应角、对应边是否有同样的结论?
∠C=∠G= 900, ∠D=∠H= 900
在比例尺为1:10 000 000的地图上,量得甲、乙两地的距离是30cm,求两地的实际距离
相似多边形的判定方法:
(2)正方形ABCD与正方形EFGH. ∴AB=BC=CD=DA
x
∴∠A=∠E= 900, ∠B=∠F= 900
D
∴AB=BC=CD=DA
EF=FG=GH=HE
B
C
∴ ABBCCDDA.
E
H
EF FGGHHE
F
G
探究
1. 下图是两个相似的三角形,猜想它们的对 应角、对应边的比是否相等?
2. 对于图中两个相似的四边形,它们的对应 角、对应边是否有同样的结论?
问题:任意两个相似的多边形有什么性质?
相似多边形性质: 相似多边形对应角相等,对应边的比相等.
118°
18cm 例 如图,四边形ABCD和EFGH相似,求角α,β的大小和EH的长度x
x = 300000000 答: 甲,乙两地的实际距离为30000千米
解:四边形ABCD和EFGH相似,它们的对应角相等.由此可得
78° 83° ∠β=360°-(78°+83°+118°)=81°.
我们把相似多边形对应边的比称为相似比.
EF=FG=GH=HE ∠α=∠C=83°,∠A=∠E=118°
的比相等,那么这两个多边形相似. 解得 x=28(cm)
四边形ABCD和EFGH相似,它们的对应边的比相等.由此可得 我们把相似多边形对应边的比称为相似比.
答: 甲,乙两地的实际距离为30000千米 答: 甲,乙两地的实际距离为30000千米 (2)正方形ABCD与正方形EFGH. ∴∠A=∠E= 900, ∠B=∠F= 900
相似多边形-完整版PPT课件
相似多边形
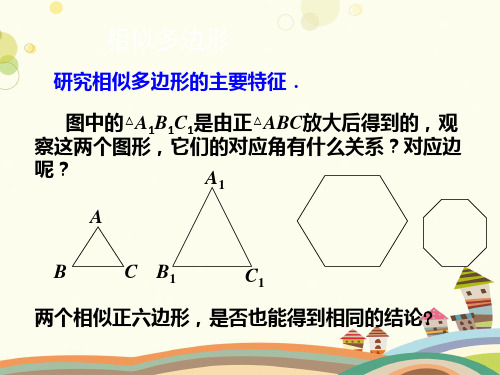
研究相似多边形的主要特征.
图中的△A1B1C1是由正△ABC放大后得到的,观 察这两个图形,它们的对应角有什么关系?对应边
呢?
A1
A
B
C B1
C1
两个相似正六边形,是否也能得到相同的结论?
相似多边形
对比图中的△A1B1C1和△ABC,由于正三角形的每 个角都等于60 ° ,可得
∠A=∠A1,∠B=∠B1,∠C=∠C1
由△ABC和△A1B1C1是正三角形可得:
AB=BC=AC, A1B1=B1C1=A1C1
这说明:正三角形都是相似的,它们的对应角 相等,对应边的比相等.
图中的两个相似的正六边形,也有类似的结论.
相似多边形
对于四条线段a、b、c、d,如果其中两条线段的比 (即它们长度的比)与另两条线段的比相等,如 (即baad=bcdc)我们就说这四条是成比例线段,简称 比例线段.
相似的正多边形对应角相等, 对应边的比相等.
这个结论对于一般的相似多边形是否成立呢?
相似多边形
1. 图是两个相似的三角形,它们的对应角有什么们的对应角、对 应边是否有同样的结论?
(1)对应角相等 对应成比例
(2) 具有同样的结论
为验证你的猜想,可 以用刻度尺和量角器 量一量.
研究相似多边形的主要特征.
图中的△A1B1C1是由正△ABC放大后得到的,观 察这两个图形,它们的对应角有什么关系?对应边
呢?
A1
A
B
C B1
C1
两个相似正六边形,是否也能得到相同的结论?
相似多边形
对比图中的△A1B1C1和△ABC,由于正三角形的每 个角都等于60 ° ,可得
∠A=∠A1,∠B=∠B1,∠C=∠C1
由△ABC和△A1B1C1是正三角形可得:
AB=BC=AC, A1B1=B1C1=A1C1
这说明:正三角形都是相似的,它们的对应角 相等,对应边的比相等.
图中的两个相似的正六边形,也有类似的结论.
相似多边形
对于四条线段a、b、c、d,如果其中两条线段的比 (即它们长度的比)与另两条线段的比相等,如 (即baad=bcdc)我们就说这四条是成比例线段,简称 比例线段.
相似的正多边形对应角相等, 对应边的比相等.
这个结论对于一般的相似多边形是否成立呢?
相似多边形
1. 图是两个相似的三角形,它们的对应角有什么们的对应角、对 应边是否有同样的结论?
(1)对应角相等 对应成比例
(2) 具有同样的结论
为验证你的猜想,可 以用刻度尺和量角器 量一量.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020/12/6
11
感谢你的阅览
Thank you for reading
温馨提示:本文内容皆为可修改式文档,下载后,可根据读者的需求 作修改、删除以及打印,感谢各位小主的阅览和下载
日期:
演讲者:蒝味的薇笑巨蟹
2020/12/6
3m (300+2×7.5)cm
(150+2×7.5)cm 1.5m
7.5cm
F B C
H
9
题型2 求相似多边形的对应角或对应边
F
已知,如图,五边形ABCDE∽五边形FGHIJ,
且
A
G
AB=2cm,CD=3cm,DE=2.2cm,GH=6cm, HI =5cm,FJ=4cm, ∠A=120o,∠H=90o B
解得FG=10/3cm,BC=18/5cm,IJ=11/3cm,AE=12/5cm
2020/12/6
10
课外作业:1、P112 习题4.5
2、请预习第四节《相似三角形》
预习提示:
1 什么是三角形? 2 相似三角形的对应边和对应角有什么关系? 3 两个全等三角形,直角三角形,等腰三角形,等边三角形, 等腰直角三角形,哪些肯定相似,哪些不一定相似,为什么?
∴AB/DE = BC/EF = CA/FD
2020/12∴/6这两个正三角形的对应边的比相等(即对应边成比例)
5
(2)正方形ABCD与正方EFGH它们的对应角有怎样的关系?对应边呢?
E
F
A
D
B
C
H
G
解:∵正方形每个角都等于90o, ∴∠A =∠E = 90o, ∠B =∠F = 90o, ∠C =∠G = 90o, ∠D =∠H = 90o ∴这两个正方形的对应角相等
∵正方形的四个 内角均为直角, 而菱形的内角有钝角有锐角
∴它们的对应角不相等 2020∴/12这/6 一组图形不相似
5 (2)
10
(2) ∵正方形和矩形的四个内角都是直角
∴它们的对应角相等
∵对应边 5/6≠5/10
∴对应边不成比例
∴这一组图形也不相似
8
E
A
2 一块长3m,宽1.5m的矩形黑板如图,镶其 外围的木质边宽7.5cm.边框内外边缘所组 成的矩形相似吗?为什么?
GD
7.5cm
解: ∵矩形的每个内角都等于90o
∴∠A=∠E=900, ∠B=∠F=90o, ∠H=90o,∠D=∠G=90o
∴它们的对应角相等 ∵AB/EF=300/(300+2×7.5)=20/21
BC/FH=150/(150+2×7.5)=10/11 ∴AB/EF≠BC/FH ∴ 矩形ABCD和矩形EFGH不相似
又∵正方形的四边相等 ∴AB/EF = BC/FG = CD/GH = DA/HE ∴这两个正方形的对应边的比相等(即对应边成比例)
2020/12/6
6
重要问题学法指导
问题 相似多边形 对应角相等,对应边成比例的两个多边形叫做相似
多边形,相似多边形的对应边的比叫做相似比.
#若四边形ABCD与四边形EFGH相似,可记作: 四边形ABCD∽四边形EFGH
数学(八年级下)
第四章 相似图形
2020/12/6
1
2.3 形状相似的图形
知识点框架
经历相似多边形概念的形成过程,了解相似 多边形的含义
知道相似多边形的对应角相等,对应边成比 例
在探索相似多边形的过程中,进一步发展自 身类比,反思\交流等方面的能力,提高数学思 维水平,体会公例的作用
2020/12/6
2
复习旧课
问题:用同一张底片洗出不同尺寸的
照片,两张图片相似吗?
2020/12/6
3
新课进行
观察以下两个多边形,并回答如下问题:
(1)在下图中两个多边形中,是否有相等的内角?设法验证. (2)在下图中两个多边形中,相等内角的两边是否成比例?
A F
B C
A1 F1
B1 C1
E
D
2020/12/6
E1
证明两个多边形相似的条件:
{ 1 对应角相等 2 对应边成比例
2020/12/6
7
解题方法 技巧 策略
题型1 判断两个多边形相似
1 判断下列每组图形是否相似,为什么?
5 正方形
6 菱形
6 5 正方形
长方形
5
(1)
6
解:(1)∵正方形,菱形的四条边都相等
∴它们的对应边一定成比例
(如上图对边应的比是 5/6)
D1
4
例题讲解
e.g. 下列每组图形形状相同,它们的对应角有怎样的关系? 对应边呢?
E B
A
C
D
F
(1)正三角形ABC与正三角形DEF;
解:∵正三角形每个角都等于60o,
∴∠A =∠D = 60o, ∴∠B =∠E = 60o, ∴∠C =∠F = 60o,
∴这三边相等
J
E
求:(1)相似比等于多少?
(2)FG,IJ,BC,AE, ∠F, ∠C
C
DH
I
解:(1)相似比=CD/HI=3/5
(2) ∵五边形ABCDE∽五边形FGHIJ
∴ ∠F =∠A=120o, ∠C= ∠H=90o,
∴AB/FG=BC/GH=CD/HI=DE/IJ=EA/JF
即2/FG=BC/6=3/5=2.2/IJ=AE/4
