简明材料力学(刘鸿文)第二版 第8章课后答案
物理学简明教程马文蔚第1至8章课后习题答案详解

For personal use only in study and research; not for commercial use1 -1 质点作曲线运动,在时刻t 质点的位矢为r ,速度为v ,速率为v ,t 至(t +Δt )时间内的位移为Δr , 路程为Δs , 位矢大小的变化量为Δr ( 或称Δ|r |),平均速度为v ,平均速率为v .(1) 根据上述情况,则必有( )(A) |Δr |= Δs = Δr(B) |Δr |≠ Δs ≠ Δr ,当Δt →0 时有|d r |= d s ≠ d r(C) |Δr |≠ Δr ≠ Δs ,当Δt →0 时有|d r |= d r ≠ d s(D) |Δr |≠ Δs ≠ Δr ,当Δt →0 时有|d r |= d r = d s(2) 根据上述情况,则必有( )(A) |v |= v ,|v |= v (B) |v |≠v ,|v |≠ v(C) |v |= v ,|v |≠ v (D) |v |≠v ,|v |= v分析与解 (1) 质点在t 至(t +Δt )时间内沿曲线从P 点运动到P′点,各量关系如图所示, 其中路程Δs =PP′, 位移大小|Δr |=PP ′,而Δr =|r |-|r |表示质点位矢大小的变化量,三个量的物理含义不同,在曲线运动中大小也不相等(注:在直线运动中有相等的可能).但当Δt →0 时,点P ′无限趋近P 点,则有|d r |=d s ,但却不等于d r .故选(B).(2) 由于|Δr |≠Δs ,故ts t ΔΔΔΔ≠r ,即|v |≠v . 但由于|d r |=d s ,故ts t d d d d =r ,即|v |=v .由此可见,应选(C). 1 -2 一运动质点在某瞬时位于位矢r (x,y )的端点处,对其速度的大小有四种意见,即 (1)t r d d ; (2)t d d r ; (3)t s d d ; (4)22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x . 下述判断正确的是( )(A) 只有(1)(2)正确 (B) 只有(2)正确(C) 只有(2)(3)正确 (D) 只有(3)(4)正确分析与解 tr d d 表示质点到坐标原点的距离随时间的变化率,在极坐标系中叫径向速率.通常用符号v r 表示,这是速度矢量在位矢方向上的一个分量;td d r 表示速度矢量;在自然坐标系中速度大小可用公式t s d d =v 计算,在直角坐标系中则可由公式22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=t y t x v 求解.故选(D). 1 -3 一个质点在做圆周运动时,则有( )(A) 切向加速度一定改变,法向加速度也改变(B) 切向加速度可能不变,法向加速度一定改变(C) 切向加速度可能不变,法向加速度不变(D) 切向加速度一定改变,法向加速度不变分析与解 加速度的切向分量a t起改变速度大小的作用,而法向分量a n 起改变速度方向的作用.质点作圆周运动时,由于速度方向不断改变,相应法向加速度的方向也在不断改变,因而法向加速度是一定改变的.至于a t是否改变,则要视质点的速率情况而定.质点作匀速率圆周运动时, a t恒为零;质点作匀变速率圆周运动时, a t为一不为零的恒量,当a t改变时,质点则作一般的变速率圆周运动.由此可见,应选(B).1 -4 质点的运动方程为23010t t x +-=和22015t t y -=,式中x ,y 的单位为m,t 的单位为s。
刘鸿文材料力学

分布力:体积力、表面力; 集中力:火车车轮对钢轨、支座等。
2019/9/20
材料力学 第一章 绪论
§1-3 外力及其分类
外力按随时间变化分:
静载荷:自重,变化相对较慢; 动载荷:交变载荷、冲击;
2019/9/20
材料力学 第一章 绪论
§1-4 内力、截面法和应力的概念
内力:受外力作用引起的相互作用; 材料力学中的内力:物体内部各部分之间因外力而 引起的附加相互作用力,即“附加内力”;
d
m
aa 0.025125106 ab 200
a a’
tgm
aa 0.025100106ra ad 250
d
2019/9/20
材料力学 第一章 绪论
小变形假设
δ远小于构件的最小尺
A
寸,在研究构件的平衡和运动 时按变形前的原始尺寸进行计
算,以保证问题在几何上是线
δ1
2019/9/20
材料力学 第一章 绪论
刚体静力学中关于平衡的理论和方法能否应用于 材料力学?
上述两种情形下对弹性杆的平衡和变形将会产 生什么影响?
2019/9/20
材料力学 第一章 绪论
第一章结束
2019/9/20
2019/9/20
材料力学 第一章 绪论
§1-1 材料力学的任务
强度问题:
美国的Tacoma老桥于 1940年11月7日因风力引 起的振动而产生断裂
2019/9/20
材料力学 第一章 绪论
§1-1 材料力学的任务
强度问题:
垮塌后的彩虹桥
1999年1月4日,我
国重庆市綦江县彩虹桥 发生垮塌,造成:
在满足上述强度、刚度和稳定性要求的同时, 须尽可能合理选用材料和降低材料消耗量,以节约 投资。
简明材料力学全套精品课件

受力如图:
列平衡方程:
M
Y 0 FN P
Mo(F) 0
FN
Pa M 0
M Pa
目录
§1.4 内力、截面法和应力的概念
为了表示内力在一点处的强度,引入内力集度,
即应力的概念。
F
pm
F A
—— 平均应力
A
C
目录
§1.1 材料力学的任务
四、材料力学的研究对象 构件的分类:杆件、板壳、块体
材料力学主要研究杆件
{ 直杆—— 轴线为直线的杆 曲杆—— 轴线为曲线的杆
{等截面杆——横截面的大小 形状不变的杆 变截面杆 ——横截面的大小 或形状变化的杆 等截面直杆 ——等直杆
目录
§1.2 变形固体的基本假设
在外力作用下,一切固体都将发生变形, 故称为变形固体。在材料力学中,对变形固体 作如下假设: 1、连续性假设: 认为整个物体体积内毫无空隙地充满物质 灰口铸铁的显微组织 球墨铸铁的显微组织
杆切开
F1
(2)留下左半段或右半段
F2
(3)将弃去部分对留下部
F5
分的作用用内力代替 F1
(4)对留下部分写平衡方
F2
程,求出内力的值。
m F4
m
F3
F4
F3
目录
§1.4 内力、截面法和应力的概念 例如
F
a
a
F
M FS
FS=F M Fa
目录
§1.4 内力、截面法和应力的概念
例 1.1 钻床 求:截面m-m上的内力。
古代建筑结构
传统具有柱、梁、檩、椽的木 制房屋结构
简明材料力学习题答案
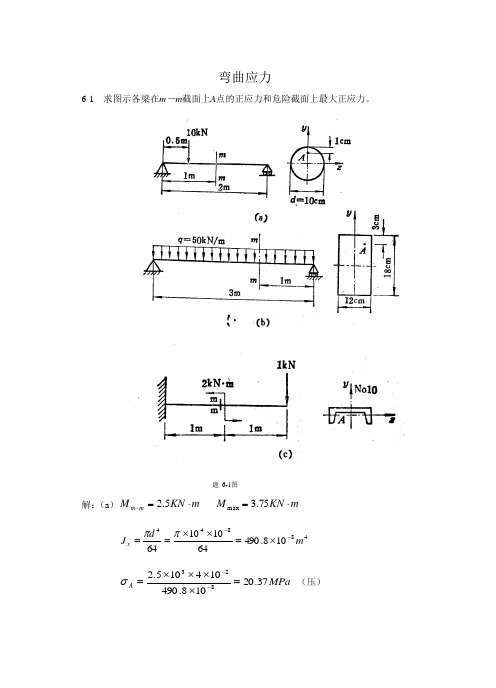
弯曲应力6-1 求图示各梁在m -m 截面上A 点的正应力和危险截面上最大正应力。
题 6-1图解:(a )m KN M m m ⋅=-5.2 m KN M ⋅=75.3max48844108.49064101064m d J x --⨯=⨯⨯==ππMPa A 37.20108.490104105.2823=⨯⨯⨯⨯=--σ (压)MPa 2.38108.4901051075.3823max =⨯⨯⨯⨯=--σ (b )m KN M m m ⋅=-60 m KN M ⋅=5.67max488331058321210181212m bh J x --⨯=⨯⨯== MPa A 73.611058321061060823=⨯⨯⨯⨯=--σ (压) MPa 2.104105832109105.67823max =⨯⨯⨯⨯=--σ (c )m KN M m m ⋅=-1 m KN M ⋅=1max48106.25m J x -⨯=36108.7m W x -⨯=cm y A 99.053.052.1=-=MPa A 67.38106.251099.0101823=⨯⨯⨯⨯=--σ (压) MPa 2.128106.2510183max =⨯⨯=-σ 6-2 图示为直径D =6 cm 的圆轴,其外伸段为空心,内径d =4cm ,求轴内最大正应力。
解:)1(32431απ-=D W x⎪⎭⎫ ⎝⎛-⨯⨯⨯=-463)64(110326π 361002.17m -⨯=3463321021.213210632m D W x --⨯=⨯⨯==ππMPa 88.521002.17109.0631=⨯⨯=-σ MPa 26.551021.2110172.1631=⨯⨯=-σ MPa 26.55max =σ6-3 T 字形截面铸铁梁的尺寸与所受载荷如图示。
试求梁内最大拉应力与最大压应力。
已知I z =10170cm 4,h 1=9.65cm ,h 2=15.35cm 。
刘鸿文《材料力学》复习笔记和课后习题(含考研真题)详解(应力和应变分析强度理论)【圣才出品】

平面的外法线方向。
7 / 135
圣才电子书 十万种考研考证电子书、题库视频学习平台
三、三向应力状态分析 1.三向应力圆 如图 7-1-4 所示,以三个主应力表示的单元体,由三个相互垂直的平面分别作应力圆, 将三个平面的应力圆绘在同一平面上得到三向应力状态下的应力圆,如图 7-1-5 所示。与 每一主应力所对应的应力圆可由与该主平面相正交的其余面上的应力作出。 注意:作三向应力圆应至少知道一个主应力的大小和方向。
1 / 135
圣才电子书 十万种考研考证电子书、题库视频学习平台
实例:在滚珠轴承中,滚珠与外圈接触点处的应力状态,可以作为三向应力状态的实例。 二、二向应力状态分析 1.解析法 如图 7-1-1(a)所示,一单元体 abcd 处于平面应力状态,采用截面法取左边部分单 元体 eaf 为研究对象,如图 7-1-1(b)所示。
5 / 135
圣才电子书 十万种考研考证电子书、题库视频学习平台
图 7-1-3(a)
图 7-1-3(b) ③求主应力数值和主平面位置 a.求主应力数值的方法 如图 7-1-3(b)所示,点 A1 和点 B1 分别为代表最大主应力和最小主应力,其大小为
6 / 135
圣才电子书 十万种考研考证电子书、题库视频学习平台
圣才电子书 十万种考研考证电子书、题库视频学习平台
第 7 章 应力和应变分析强度理论
7.1 复习笔记
一、应力状态 一点的应力状态:过一点不同方向面上应力的集合。 应力状态的研究对象是单元体,其特征为:①单元体的尺寸无限小,每个面上应力均匀 分布;②任意一对平行平面上的应力相等。 主单元体是指各侧面上切应力均为零的单元体。其中,单元体上切应力为零的面称为主 平面,主平面上的正应力称为主应力。 说明:一点处必定存在一个单元体,使得三个相互垂直的面均为主平面,三个互相垂直 的主应力分别记为 σ1、σ2、σ3,且规定按代数值大小的顺序来排列,即 σ1≥σ2≥σ3。 应力状态分类及实例 (1)单向应力状态:也称为简单应力状态,三个主应力 σ1、σ2、σ3 中只有一个不等 于零。 实例:简单的拉伸或压缩。 (2)平面(二向)应力状态:三个主应力 σ1、σ2、σ3 中有两个不等于零。 实例:薄壁圆筒横截面上的点和圆形容器包含直径的任意横截面上的点。 (3)空间(三向)应力状态:和平面应力状态统称为复杂应力状态,三个主应力 σ1、 σ2、σ3,均不等于零。
工程材料力学性能 第二版 课后习题答案

《工程材料力学性能》(第二版)课后答案第一章材料单向静拉伸载荷下的力学性能一、解释下列名词滞弹性:在外加载荷作用下,应变落后于应力现象。
静力韧度:材料在静拉伸时单位体积材科从变形到断裂所消耗的功。
弹性极限:试样加载后再卸裁,以不出现残留的永久变形为标准,材料能够完全弹性恢复的最高应力。
比例极限:应力—应变曲线上符合线性关系的最高应力。
包申格效应:指原先经过少量塑性变形,卸载后同向加载,弹性极限(ζP)或屈服强度(ζS)增加;反向加载时弹性极限(ζP)或屈服强度(ζS)降低的现象。
解理断裂:沿一定的晶体学平面产生的快速穿晶断裂。
晶体学平面--解理面,一般是低指数,表面能低的晶面。
解理面:在解理断裂中具有低指数,表面能低的晶体学平面。
韧脆转变:材料力学性能从韧性状态转变到脆性状态的现象(冲击吸收功明显下降,断裂机理由微孔聚集型转变微穿晶断裂,断口特征由纤维状转变为结晶状)。
静力韧度:材料在静拉伸时单位体积材料从变形到断裂所消耗的功叫做静力韧度。
是一个强度与塑性的综合指标,是表示静载下材料强度与塑性的最佳配合。
二、金属的弹性模量主要取决于什么?为什么说它是一个对结构不敏感的力学姓能?答案:金属的弹性模量主要取决于金属键的本性和原子间的结合力,而材料的成分和组织对它的影响不大,所以说它是一个对组织不敏感的性能指标,这是弹性模量在性能上的主要特点。
改变材料的成分和组织会对材料的强度(如屈服强度、抗拉强度)有显著影响,但对材料的刚度影响不大。
三、什么是包辛格效应,如何解释,它有什么实际意义?答案:包辛格效应就是指原先经过变形,然后在反向加载时弹性极限或屈服强度降低的现象。
特别是弹性极限在反向加载时几乎下降到零,这说明在反向加载时塑性变形立即开始了。
包辛格效应可以用位错理论解释。
第一,在原先加载变形时,位错源在滑移面上产生的位错遇到障碍,塞积后便产生了背应力,这背应力反作用于位错源,当背应力(取决于塞积时产生的应力集中)足够大时,可使位错源停止开动。
材料力学性能-第2版课后习题答案-11页文档资料

第一章 单向静拉伸力学性能1、 解释下列名词。
1弹性比功:金属材料吸收弹性变形功的能力,一般用金属开始塑性变形前单位体积吸收的最大弹性变形功表示。
2.滞弹性:金属材料在弹性范围内快速加载或卸载后,随时间延长产生附加弹性应变的现象称为滞弹性,也就是应变落后于应力的现象。
3.循环韧性:金属材料在交变载荷下吸收不可逆变形功的能力称为循环韧性。
4.包申格效应:金属材料经过预先加载产生少量塑性变形,卸载后再同向加载,规定残余伸长应力增加;反向加载,规定残余伸长应力降低的现象。
5.解理刻面:这种大致以晶粒大小为单位的解理面称为解理刻面。
6.塑性:金属材料断裂前发生不可逆永久(塑性)变形的能力。
韧性:指金属材料断裂前吸收塑性变形功和断裂功的能力。
7.解理台阶:当解理裂纹与螺型位错相遇时,便形成一个高度为b 的台阶。
8.河流花样:解理台阶沿裂纹前端滑动而相互汇合,同号台阶相互汇合长大,当汇合台阶高度足够大时,便成为河流花样。
是解理台阶的一种标志。
9.解理面:是金属材料在一定条件下,当外加正应力达到一定数值后,以极快速率沿一定晶体学平面产生的穿晶断裂,因与大理石断裂类似,故称此种晶体学平面为解理面。
10.穿晶断裂:穿晶断裂的裂纹穿过晶内,可以是韧性断裂,也可以是脆性断裂。
沿晶断裂:裂纹沿晶界扩展,多数是脆性断裂。
11.韧脆转变:具有一定韧性的金属材料当低于某一温度点时,冲击吸收功明显下降,断裂方式由原来的韧性断裂变为脆性断裂,这种现象称为韧脆转变12.弹性不完整性:理想的弹性体是不存在的,多数工程材料弹性变形时,可能出现加载线与卸载线不重合、应变滞后于应力变化等现象,称之为弹性不完整性。
弹性不完整性现象包括包申格效应、弹性后效、弹性滞后和循环韧性等2、 说明下列力学性能指标的意义。
答:E 弹性模量 G 切变模量 r σ规定残余伸长应力 2.0σ屈服强度 gt δ金属材料拉伸时最大应力下的总伸长率 n 应变硬化指数 【P15】3、 金属的弹性模量主要取决于什么因素?为什么说它是一个对组织不敏感的力学性能指标?答:主要决定于原子本性和晶格类型。
材料力学第五版(刘鸿文主编)课后答案解析

幻灯片296
幻灯片297
幻灯片298
幻灯片299
幻灯片300
幻灯片301
幻灯片302
幻灯片303
幻灯片304
幻灯片305
幻灯片306
幻灯片307
幻灯片308
幻灯片309
幻灯片310
幻灯片311
幻灯片312
幻灯片313
幻灯片314
幻灯片315
幻灯片316
幻灯片317
幻灯片318
幻灯片319
幻灯片93
幻灯片94
幻灯片95
幻灯片96
幻灯片97
幻灯片98
幻灯片99
幻灯片100
幻灯片101
幻灯片102
幻灯片103
幻灯片104
幻灯片105
幻灯片106
幻灯片107
幻灯片108
幻灯片109
幻灯片110
幻灯片111
幻灯片112
幻灯片113
幻灯片114
幻灯片115
幻灯片116
幻灯片117
幻灯片118
幻灯片119
幻灯片220
幻灯片221
幻灯片222
幻灯片223
幻灯片224
幻灯片225
幻灯片226
幻灯片227
幻灯片228
幻灯片229
幻灯片230
幻灯片231
幻灯片232
幻灯片233
幻灯片234
幻灯片235
幻灯片236
幻灯片237
幻灯片238
幻灯片239
幻灯片240
幻灯片241
幻灯片242
幻灯片243
幻灯片244
幻灯片145
幻灯片146
幻灯片147
简明材料力学(刘鸿文)第二版 第8章课后答案

λ(3) =
μ l3
i
= λ(1) ×
l3 = 31.25 ≺ λ2 l1
∴σ cr = σ s 1 ∴ Pcr (3) = σ S A = 240 × 106 × × π × 0.162 = 4825 kN 4
10.8. 无缝钢管厂的穿孔顶杆如图所示。杆长l=4.5 m,横截面直径d=150 mm。材料为低合金 钢,E=210GPa,σp=200MPa。顶杆两端可简化为铰支座,规定稳定安全系数nst=3.3。 试求顶杆的许可载荷。
λ1=100, λ2=62。 10.15. 某厂自制简易起重机如图所示。 压杆BD为 20 号槽钢, 材料为Q235 钢, 最大起重量P=40kN。若规定nst=5,试校核杆BD的稳定性。
A 1.5m 30
o
0.5m B C
XA
YA
z y
P
RBD
D
解:(1) 受力分析 以整体为研究对象,由平衡方程可求得
π d 22 [σ ]
4 × 0.281
π × 0.0252 × 160 × 106
4 × 0.281
= 279.5 kN
(3) 杆 AD 受压,考虑稳定问题 AD 杆的柔度
λ=
柔度极限值
μl
i
=
1 × 1.2 = 120 0.04 / 4
上海理工大学 力学教研室
5
λ1 = π λ λ1
E
σP
=π
C
解:由铰 B 的平衡可得 P
θ B
o
P1
90
P2
P1 θ P P2
P2 = P1tgθ
由已知条件可知,
l BC = l AB tg β
AB 和 BC 皆为细长压杆
材料力学考研刘鸿文《材料力学》考研真题与考点笔记

材料力学考研刘鸿文《材料力学》考研真题与考点笔记一、选择题真题解析1根据均匀、连续性假设,可以认为()。
[北京科技大学2012年研] A.构件内的变形处处相同B.构件内的位移处处相同C.构件内的应力处处相同D.构件内的弹性模量处处相同【答案】D @@【解析】连续性假设认为组成固体的物质不留空隙地充满固体的体积,均匀性假设认为在固体内到处有相同的力学性能。
均匀、连续的构件内的各截面成分和组织结构一样,弹性模量处处相同。
2反映固体材料强度的两个指标一般是指()。
[北京科技大学2010年研] A.屈服极限和比例极限B.弹性极限和屈服极限C.强度极限和断裂极限D.屈服极限和强度极限【答案】D @@【解析】衡量塑性材料的强度指标为屈服极限,衡量脆性材料强度的指标为强度极限。
3根据小变形假设,可以认为()。
[西安交通大学2005年研]A.构件不变形B.构件不破坏C.构件仅发生弹性变形D.构件的变形远小于构件的原始尺寸【答案】D @@【解析】小变形假设即原始尺寸原理认为无论是变形或因变形引起的位移,其大小都远小于构件的最小尺寸。
4对于没有明显屈服阶段的塑性材料,通常以产生()所对应的应力值作为材料的名义屈服极限。
[西安交通大学2005年研]A.0.2的应变B.0.2%的应变C.0.2的塑性应变D.0.2%的塑性应变【答案】D @@【解析】对于没有屈服阶段的塑性材料,是将卸载后产生的0.2%的塑性应变所对应的应力值作为屈服极限,称为名义屈服极限或条件屈服极限,用σ0.2表示。
5韧性材料应变硬化之后,经卸载后再加载,材料的力学性能发生下列变化()。
[北京科技大学2010年研]A.比例极限提高,弹性模量降低B.比例极限提高,韧性降低C.比例极限不变,弹性模量不变D.比例极限不变,韧性不变【答案】B @@【解析】材料冷作硬化后,比例极限得到了提高,但塑性变形和伸长率却有所降低,而弹性模量是材料的特性,与此无关。
6现有钢、铸铁两种棒材,其直径相同(不计失稳可能)。
材料力学刘鸿文第六版最新课件第八章 组合变形

F c 160 106 171300N
934 934
许 可 压 力 为 F 45000N 45kN
§8-2 拉伸或压缩与弯曲的组合
例2图 示一夹具。在夹紧零件时, 夹 具受到的P = 2KN的力作用 。已知: 外力作用线与夹具竖杆轴线间的距离
e = 60 mm, 竖杆横截面的尺寸为b = 10 mm ,h = 22 mm,材料许用应力 [] = 170 MPa 。 试校核此夹具竖杆 的强度。
4、拉(压)弯组合变形下的强度计算
拉弯组合变形下的危险点 处于单向应力状态
t ,max
Fl Wy
F A
[ t ]
c ,max
Fl Wy
F A
[ c ]
4、中性轴位置
由中性轴上各点的正应力均为零;
FN
My
Байду номын сангаас
|z| 0
A
Iy
| z | FN I y A M y
+_
(-z y)
y -_
z
_
_
+
|z|
第三组
圆截面、弯扭组合变形
§8-4 扭转与弯曲的组合
扭转+双向弯曲
求合弯矩
M
2
M
2 y
M
2 z
§8-4 扭转与弯曲的组合
例题1 传动轴左端的轮子由电机带动,传入的扭转力偶矩
Me=300Nm。两轴承中间的齿轮半径R=200mm,径向啮合 力F1=1400N,轴的材料许用应力〔σ 〕=100MPa。试按 第三强度理论设计轴的直径d。
§8-1 组合变形和叠加原理
基本变形 构件只发生一种变形;
轴向拉压、扭转、平面弯曲、剪切;
物理学简明教程马文蔚第1至8章课后习题答案详解

For personal use only in study and research; not for commercial use1 -1 质点作曲线运动,在时刻t 质点的位矢为r ,速度为v ,速率为v ,t 至(t +Δt )时间内的位移为Δr , 路程为Δs , 位矢大小的变化量为Δr ( 或称Δ|r |),平均速度为v ,平均速率为v .(1) 根据上述情况,则必有( )(A) |Δr |= Δs = Δr(B) |Δr |≠ Δs ≠ Δr ,当Δt →0 时有|d r |= d s ≠ d r(C) |Δr |≠ Δr ≠ Δs ,当Δt →0 时有|d r |= d r ≠ d s(D) |Δr |≠ Δs ≠ Δr ,当Δt →0 时有|d r |= d r = d s(2) 根据上述情况,则必有( )(A) |v |= v ,|v |= v (B) |v |≠v ,|v |≠ v(C) |v |= v ,|v |≠ v (D) |v |≠v ,|v |= v分析与解 (1) 质点在t 至(t +Δt )时间内沿曲线从P 点运动到P′点,各量关系如图所示, 其中路程Δs =PP′, 位移大小|Δr |=PP ′,而Δr =|r |-|r |表示质点位矢大小的变化量,三个量的物理含义不同,在曲线运动中大小也不相等(注:在直线运动中有相等的可能).但当Δt →0 时,点P ′无限趋近P 点,则有|d r |=d s ,但却不等于d r .故选(B).(2) 由于|Δr |≠Δs ,故ts t ΔΔΔΔ≠r ,即|v |≠v . 但由于|d r |=d s ,故ts t d d d d =r ,即|v |=v .由此可见,应选(C). 1 -2 一运动质点在某瞬时位于位矢r (x,y )的端点处,对其速度的大小有四种意见,即 (1)t r d d ; (2)t d d r ; (3)t s d d ; (4)22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛t y t x . 下述判断正确的是( )(A) 只有(1)(2)正确 (B) 只有(2)正确(C) 只有(2)(3)正确 (D) 只有(3)(4)正确分析与解 tr d d 表示质点到坐标原点的距离随时间的变化率,在极坐标系中叫径向速率.通常用符号v r 表示,这是速度矢量在位矢方向上的一个分量;td d r 表示速度矢量;在自然坐标系中速度大小可用公式t s d d =v 计算,在直角坐标系中则可由公式22d d d d ⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=t y t x v 求解.故选(D). 1 -3 一个质点在做圆周运动时,则有( )(A) 切向加速度一定改变,法向加速度也改变(B) 切向加速度可能不变,法向加速度一定改变(C) 切向加速度可能不变,法向加速度不变(D) 切向加速度一定改变,法向加速度不变分析与解 加速度的切向分量a t起改变速度大小的作用,而法向分量a n 起改变速度方向的作用.质点作圆周运动时,由于速度方向不断改变,相应法向加速度的方向也在不断改变,因而法向加速度是一定改变的.至于a t是否改变,则要视质点的速率情况而定.质点作匀速率圆周运动时, a t恒为零;质点作匀变速率圆周运动时, a t为一不为零的恒量,当a t改变时,质点则作一般的变速率圆周运动.由此可见,应选(B).1 -4 质点的运动方程为23010t t x +-=和22015t t y -=,式中x ,y 的单位为m,t 的单位为s。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
λ1 = π
E
σP
=π
200 × 109 = 99.3 200 × 106
λ2 =
a − σ S 304 − 240 = = 57 1.12 b
(2) 求各杆的临界压力Pcr 1 杆:
λ(1) =
1× 5 = 125 λ1 i 0.16 / 4 π d 4 π × 0.164 I= = = 3.22 × 10−5 m 4 64 64 2 π EI π 2 × 200 × 109 × 3.22 × 10−5 Pcr (1) = = = 2542 kN 2 2 (μl ) (1 × 5) =
上海理工大学 力学教研室
2
2
垂直的xz平面内,两端则可认为是固定支座。试确定其工作安全系数。
x z 3100 I I 14 96 85 140 y y
解:(1) 计算截面的几何性质
A = 0.14 × 0.096 − 0.085 × ( 0.096 − 0.014 ) = 6.47 × 10−3 m 2 Iy = 1 1 × 0.085 × 0.0143 + × ( 0.14 − 0.085) × 0.0963 = 4.0745 × 10−6 m 4 12 12 1 1 I z = × 0.096 × 0.143 − × ( 0.096 − 0.014 ) × 0.0853 = 1.7755 × 10 −5 m 4 12 12 Iy 4.0745 × 10−6 = = 0.025 m iy = 6.47 × 10−3 A iz = Iz 1.7755 × 10−5 = = 0.052 m A 6.47 × 10−3
λ=
μl
i
=
4 μ l 4 × 1 × 0.257 = = 128.5 d 0.008 =π 210 × 109 = 92.9 240 × 106
λ1 = π
∴λ
E
σP λ1
挺杆是细长压杆,使用欧拉公式计算临界压力 (2) 校核挺杆的稳定性
I=
πd4
64
=
π × 0.0084
π 2 EI = Pcr = 2 (μl )
D 1.2m A B C
P
1.2m G
1m
1m
解:(1) 分析 ABC 受力 RAD
A B C
P
RAG 列平衡方程
RB
∑M
变形谐调条件
B
=0
( RAD + RAG ) × 1 − P × 1 = 0
Δl AD = Δl AG
RAD + RAG = P
RAD × 1.2 RAG × 1.2 = EAAD EAAG
C
解:由铰 B 的平衡可得 P
θ B
o
P1
90
P2Leabharlann P1 θ P P2P2 = P1tgθ
由已知条件可知,
l BC = l AB tg β
AB 和 BC 皆为细长压杆
E AB = EBC
I AB = I BC
μ AB = μ BC = 1
Pcr1 =
π 2 E AB I AB
2 l AB
Pcr 2 =
a − σ s 304 − 235 = = 61.6 1.12 b ∴ λ2 ≺ λ xz ≺ λ1
连杆为中长杆,用直线公式计算临界压力
Pcr = σ cr A = ( a − bλ xz ) A = ( 304 − 1.12 × 62) × 106 × 6.47 × 10−3 = 1517.6 kN
p
A l
B
P 解:(1) 求柔度极限值
P
λ1 = π
压杆的柔度
E
σP
=π
210 × 109 = 92.9 240 × 106
λ=
压杆是大柔度杆 (2) 压杆的临界压力
μl
i
==
1 × 1.8 = 96 0.075 / 4
λ1
I=
πd4
64
=
π × 0.0754
π 2 EI = Pcr = 2 (μl )
π d 22 [σ ]
4 × 0.281
π × 0.0252 × 160 × 106
4 × 0.281
= 279.5 kN
(3) 杆 AD 受压,考虑稳定问题 AD 杆的柔度
λ=
柔度极限值
μl
i
=
1 × 1.2 = 120 0.04 / 4
上海理工大学 力学教研室
5
λ1 = π λ λ1
E
σP
=π
206 × 109 = 100.8 200 × 106
压杆是大柔度杆,用欧拉公式计算临界压力
I=
π d14
64
=
π × 0.044
64
= 1.257 × 10−7 m 4
Pcr =
根据稳定性条件
π 2 EI π 2 × 206 × 109 × 1.257 × 10−7 = = 177.5 kN 2 2 (μl ) (1 × 1.2)
工作安全系数
= 2.01 × 10−10 m 4 64 π 2 × 210 × 109 × 2.01 × 10−10
(1 × 0.257 )
n=
2
= 6.31KN
Pcr 6.31 = = 3.59 Pmax 1.76
所以挺杆满足稳定性要求。 10.4. 图示蒸汽机活塞杆AB所受压力为P=120 kN,l=1.8 m,截面为圆形d=75 mm。材料为 Q275 钢,E=210 GPa,σs=240 MP。规定nst=8。试校核活塞杆的稳定性。
I y = 144cm 4
μ = 1, λ=
iy
l BD = 1.5 / cos 300 = 1.732m
μ l BD
=
1 × 1.732 = 82.87 2.09 × 10−2
∴ λ2 ≺ λ ≺ λ1
BD 杆为中长杆 (3) 计算临界压力
Pcr = σ cr A = ( a − bλ ) A = ( 304 − 1.12 × 82.87 ) × 106 × 32.837 × 10−4 = 693.5 kN
λ1=100, λ2=62。 10.15. 某厂自制简易起重机如图所示。 压杆BD为 20 号槽钢, 材料为Q235 钢, 最大起重量P=40kN。若规定nst=5,试校核杆BD的稳定性。
A 1.5m 30
o
0.5m B C
XA
YA
z y
P
RBD
D
解:(1) 受力分析 以整体为研究对象,由平衡方程可求得
(4) 稳定性校核
n=
Pcr 693.5 = = 6.5 RBD 106.7
4
nst
上海理工大学 力学教研室
满足稳定要求。 10.17 图示结构中的杆AD和AG材料均为Q235 钢,E=206 GPa,σp=200 MPa,σs =235 MPa, a=304 MPa,b=1.12 MPa,[σ]=160 MPa。两杆均为圆截面,杆AD的直径为d1=40 mm 杆AG的直径为d2=25 mm。横梁ABC可视为刚体,规定的稳定安全系数nst=3,试求P 的许可值。
3 杆:
λ(3) =
μ l3
i
= λ(1) ×
l3 = 31.25 ≺ λ2 l1
∴σ cr = σ s 1 ∴ Pcr (3) = σ S A = 240 × 106 × × π × 0.162 = 4825 kN 4
10.8. 无缝钢管厂的穿孔顶杆如图所示。杆长l=4.5 m,横截面直径d=150 mm。材料为低合金 钢,E=210GPa,σp=200MPa。顶杆两端可简化为铰支座,规定稳定安全系数nst=3.3。 试求顶杆的许可载荷。
2 2
RAD AAD ⎛ d1 ⎞ ⎛ 40 ⎞ = = ⎜ ⎟ = ⎜ ⎟ = 2.56 RAG AAG ⎝ d 2 ⎠ ⎝ 25 ⎠
解方程组得
RAD = 0.719 P
(2) 杆 AG 受拉,考虑强度条件
RAG = 0.281P
σ AG =
P≤
RAG 0.281P = ≤ [σ ] 2 AAG π d 2 /4 =
3
解:(1) 求柔度极限值
λ1 = π
压杆的柔度
E
σP
=π
10 × 109 = 70.25 20 × 106
λ=
μl
i
==
1× 4 = 115.5 0.12 / 12
λ1
压杆是大柔度杆 (2) 用欧拉公式计算压杆的临界应力
Pcr =
π 2 E π 2 × 10 × 109 = = 7.40 MPa 115.52 λ2
顶杆 d
P
l 上海理工大学 力学教研室
1
解:(1) 求顶杆的临界载荷
λ1 = π
I=
E
σP
=
=π
210 × 109 = 101.8 200 × 106 = 2.485 × 10−5 m 4
λ=
μl
i
=
1 × 4.5 = 120 0.15 / 4
λ1
πd4
64
2
π × 0.154
64
π EI π 2 × 210 × 109 × 2.485 × 10−5 Pcr = = = 2543.4 kN 2 2 (μl ) (1 × 4.5)
∑M
A
=0
RBD cos30o × AD − P × AC = 0
RBD =
P × AC 40 × 2.0 = = 106.7 kN o cos30 × AD cos30o × 1.5 × tg 30o
(2) BD 压杆的柔度 查型钢表,20 号槽钢:
A = 32.837cm 2
