四舍六入五留双_终极完美版
四舍六入公式
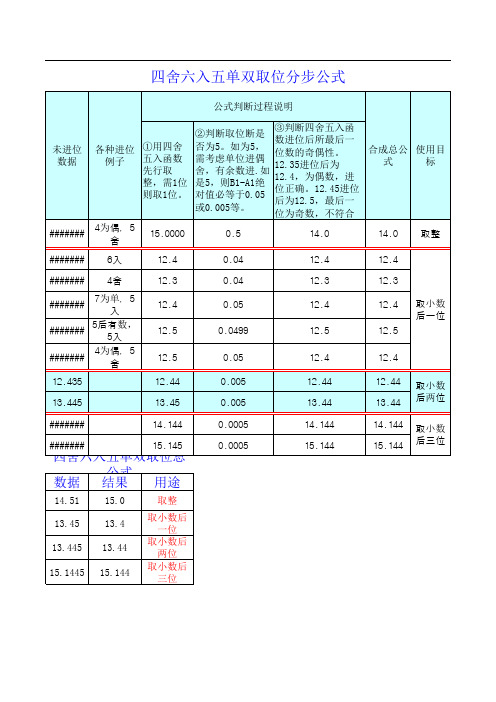
未进位 数据
####### #######,5 入 5后有数, ####### 5入 4为偶,5 ####### 舍 12.435 13.445 ####### #######
四舍六入五单双取位总 公式 数据 结果 用途
14.51 13.45 13.445 15.1445 15.0 13.4 13.44 15.144 取整 取小数后 一位 取小数后 两位 取小数后 三位
四舍六入五单双取位分步公式
公式判断过程说明 ②判断取位断是 各种进位 ①用四舍 否为5。如为5, 五入函数 需考虑单位进偶 例子 先行取 舍,有余数进.如 整,需1位 是5,则B1-A1绝 则取1位。 对值必等于0.05 或0.005等。 4为偶,5 舍 6入 4舍 15.0000 12.4 12.3 12.4 12.5 12.5 12.44 13.45 14.144 15.145 0.5 0.04 0.04 0.05 0.0499 0.05 0.005 0.005 0.0005 0.0005 ③判断四舍五入函 数进位后所最后一 合成总公 使用目 位数的奇偶性。 式 标 12.35进位后为 12.4,为偶数,进 位正确。12.45进位 后为12.5,最后一 位为奇数,不符合 14.0 12.4 12.3 12.4 12.5 12.4 12.44 13.44 14.144 15.144 14.0 12.4 12.3 12.4 12.5 12.4 12.44 13.44 14.144 15.144 取小数 后两位 取小数 后三位 取小数 后一位 取整
数字修约规则-----四舍五入和四舍六入五留双规则之令狐文艳创作

数字修约规则令狐文艳现在被广泛使用的数字修约规则主要有四舍五入规则和四舍六入五留双规则。
[编辑] 四舍五入规则四舍五入规则是人们习惯采用的一种数字修约规则。
四舍五入规则的具体使用方法是:在需要保留有效数字的位次后一位,逢五就进,逢四就舍。
例如:将数字2.1875精确保留到千分位(小数点后第三位),因小数点后第四位数字为5,按照此规则应向前一位进一,所以结果为2.188。
同理,将下列数字全部修约为四位有效数字,结果为:0.53664—0.5366 10.2750—10.28 18.06501—18.070.58346—0.5835 6.4050—16.4127.1850—27.19按照四舍五入规则进行数字修约时,应一次修约到指定的位数,不可以进行数次修约,否则将有可能得到错误的结果。
例如将数字15.4565修约为两位有效数字时,应一步到位:15.4565——15(正确)。
如果分步修约将得到错误的结果:15.4565——15.457——15.46——15.5——16(错误)。
四舍五入修约规则,逢五就进,必然会造成结果的系统偏高,误差偏大,为了避免这样的状况出现,尽量减小因修约而产生的误差,在某些时候需要使用四舍六入五留双的修约规则。
[编辑] 四舍六入五留双规则为了避免四舍五入规则造成的结果偏高,误差偏大的现象出现,一般采用四舍六入五留双规则(Banker's Rounding)。
四舍六入五留双应该改为: 四舍六入逢五无后则留双,这样描述更容易理解和记住。
四舍六入五留双规则的具体方法是:(一)当尾数小于或等于4时,直接将尾数舍去。
例如将下列数字全部修约为四位有效数字,结果为:0.53664—0.53660.58344—0.5834 16.4005—16.40 27.1829—27.1810.2731—10.27 18.5049—18.50(二)当尾数大于或等于6时,将尾数舍去并向前一位进位。
例如将下列数字全部修约为四位有效数字,结果为:0.53666—0.53678.3176—8.31816.7777—16.780.58387—0.5839 10.29501—10.30 21.0191—21.02(三)当尾数为5,而尾数后面的数字均为0时,应看尾数“5”的前一位:若前一位数字此时为奇数,就应向前进一位;若前一位数字此时为偶数,则应将尾数舍去。
四舍六入五单进规则

数值修约规则四舍六入五留双规则四舍六入五留双规则的具体方法是:(一)当尾数小于或等于4时,直接将尾数舍去。
例如将下列数字全部修约为四位有效数字,结果为:0.53664—0.5366 10.2731—10.2718.5049—18.50 0.58344—0.583416.4005—16.40 27.1829—27.18(二)当尾数大于或等于6时,将尾数舍去并向前一位进位。
例如将下列数字全部修约为四位有效数字,结果为:0.53666—0.5367 8.3176—8.31816.7777—16.78 0.58387—0.583910.29501—10.30 21.0191—21.02(三)当尾数为5,而尾数后面的数字均为0时,应看尾数“5”的前一位:若前一位数字此时为奇数,就应向前进一位;若前一位数字此时为偶数,则应将尾数舍去。
数字“0”在此时应被视为偶数。
例如将下列数字全部修约为四位有效数字,结果为:0.153050—0.1530 12.6450—12.6418.2750—18.28 0.153750—0.153812.7350—12.74 21.845000—21.84(四)当尾数为5,而尾数“5”的后面还有任何不是0的数字时,无论前一位在此时为奇数还是偶数,也无论“5”后面不为0的数字在哪一位上,都应向前进一位。
例如将下列数字全部修约为四位有效数字,结果为:0.326552—0.3266 12.73507—12.7421.84502—21.85 12.64501—12.6518.27509—18.28 38.305000001—38.31按照四舍六入五留双规则进行数字修约时,也应像四舍五入规则那样,一次性修约到指定的位数,不可以进行数次修约,否则得到的结果也有可能是错误的。
例如将数字10.2749945001修约为四位有效数字时,应一步到位:10.2749945001—10.27(正确)。
如果按照四舍六入五留双规则分步修约将得到错误结果:10.2749945001—10.274995—10.275—10.28(错误)。
四舍六入五单双法

四舍六入五单双法
四舍六入五单双法
由于“四舍五入”造成“入得多,舍得少”的问题,给实际数据采集造成一定程度的不便。
因此GB/T8170-2000的进舍规则规定为“四舍六入五单双法”。
具体如下:
a)拟舍去的数字的最左边一位数字小于5,则舍去,保留的数字不变;
例:将12.1498修约到个数位,得12;修约到一位小数,得12.1 b)拟舍去的数字的最左边一位数字大于5,则进1,保留的数字最后一位加1;例:将1268修约到“百”数位,得1300 c)拟舍去的数字的最左边一位数字是5,且其后面跟有非0数字时,则进1,保留的数字最后一位加1;
例:将10.5002修约到个数位,得11
d)拟舍去的数字的最左边一位数字是5,且其后无数字或皆为0时,若保留数字的最后一位为奇数(1,3,5,7,9),则进1;保留数字的最后一位为偶数(0,2,4,6,8),则舍去。
例:将1.050修约到一位小数,得1.0;0.35修约到一位小数,得0.4
以上法则的口诀归纳为“四舍六入五考虑,五后非零则进一,五后皆零视奇偶,五前为偶应舍去,五前为奇应进一”。
四舍六入五成双的计算方法

四舍六入五成双的计算方法
宝子,今天咱来唠唠这个“四舍六入五成双”的计算方法。
你看啊,平常咱们老说四舍五入,这个“四舍六入五成双”可有点不一样的小脾气呢。
先说这个“四舍”,就和咱们平常的四舍五入里的四舍差不多啦。
要是一个数要保留到某一位,这一位后面的数字小于等于4呢,那就直接舍掉。
比如说3.42,要保留到整数位,后面的0.42里4是小于5的,那就舍掉,结果就是3啦。
再讲讲“六入”。
要是这一位后面的数字大于等于6呢,就往前进一位。
就像3.61,保留到整数位,0.61里6大于5,那就进一位,结果就是4喽。
最有趣的就是这个“五成双”啦。
如果这一位后面的数字是5,就不是简单的进一位了哦。
如果这个5后面没有其他数字了,或者说5后面的数字都是0,那就要看前面的数字是奇数还是偶数。
要是前面的数字是奇数呢,就进一位让它变成偶数;要是前面的数字是偶数,那就直接舍掉这个5。
比如说2.5,保留到整数位,2是偶数,那就舍掉0.5,结果就是2;要是3.5,3是奇数,那就进一位,结果就是4。
这个计算方法在一些比较精确的统计或者科学计算里可有用了呢。
它能让数据的处理更加合理,减少一些因为简单四舍五入带来的小偏差。
宝子,你可别小瞧它,虽然感觉有点复杂,但是一旦你掌握了,就会觉得还挺好玩的呢。
它就像是一个有点小个性的朋友,有自己独特的规则。
不像普通的四舍五入那么直白,但是却更加细腻地处理数字。
下次你要是遇到需要精确处理数字的时候,不妨试试这个“四舍六入五成双”的方法呀。
四舍六入五留双规则的具体方法之欧阳地创编

时间:2021.03.04
创作:欧阳地
当尾数小于或等于4时,直接将尾数舍去
例如将下列数字全部修约到两位小数,结果为:
10.2731——10.27
18.5049——18.50
16.4005——16.40
27.1829——27.18
当尾数大于或等于6时将尾数舍去向前一位进位
例如将下列数字全部修约到两位小数,结果为:
16.7777——16.78
10.29501——10.30
21.0191——21.02
(三)当尾数为5,而尾数后面的数字均为0时,应看尾数“5”的前一位:若前一位数字此时为奇数,就应向前进一位;若前一位数字此时为偶数,则应将尾数舍去。数字“0”在此时应被视为偶数。
例如将下列数字全部修约到两位小数,结果为:
12.6450——12.64
18.2750——18.28
12.7350——12.74
21.845000——21.84
(四)当尾数为5,而尾数“5”的后面还有任何不是0的数字时,无论前一位在此时为奇数还是偶数,也无论“5”后面不为0的数字在哪一位上,都应向前进一位。
例如将下列数字全部修约到两பைடு நூலகம்小数,结果为:
12.73507——12.74
21.84502——21.85
12.64501——12.65
18.27509——18.28
38.305000001——38.31
按照四舍六入五留双规则进行数字修约时,也应像四舍五入规则那样,一次性修约到指定的位数,不可以进行数次修约,否则得到的结果也有可能是错误的。例如将数字10.2749945001修约到两位小数时,应一步到位:10.2749945001——10.27(正确)。如果按照四舍六入五留双规则分步修约将得到错误结果:10.2749945001——10.274995——10.275——10.28(错误)。
四舍六入五留双规则的具体方法之欧阳德创编

四舍六入五留双规则的具体方当尾数小于或等于4时,直接将尾数舍去例如将下列数字全部修约到两位小数,结果为:10.2731——10.2718.5049——18.5016.4005——16.4027.1829——27.18当尾数大于或等于6时将尾数舍去向前一位进位例如将下列数字全部修约到两位小数,结果为:16.7777——16.7810.29501——10.3021.0191——21.02(三)当尾数为5,而尾数后面的数字均为0时,应看尾数“5”的前一位:若前一位数字此时为奇数,就应向前进一位;若前一位数字此时为偶数,则应将尾数舍去。
数字“0”在此时应被视为偶数。
例如将下列数字全部修约到两位小数,结果为:12.6450——12.6418.2750——18.2812.7350——12.7421.845000——21.84(四)当尾数为5,而尾数“5”的后面还有任何不是0的数字时,无论前一位在此时为奇数还是偶数,也无论“5”后面不为0的数字在哪一位上,都应向前进一位。
例如将下列数字全部修约到两位小数,结果为:12.73507——12.7421.84502——21.8512.64501——12.6518.27509——18.2838.305000001——38.31按照四舍六入五留双规则进行数字修约时,也应像四舍五入规则那样,一次性修约到指定的位数,不可以进行数次修约,否则得到的结果也有可能是错误的。
例如将数字10.2749945001修约到两位小数时,应一步到位:10.2749945001——10.27(正确)。
如果按照四舍六入五留双规则分步修约将得到错误结果:。
四舍六入五留双规则的具体方法之欧阳与创编

四舍六入五留双规则的具体方
当尾数小于或等于4时,直接将尾数舍去
例如将下列数字全部修约到两位小数,结果为:
10.2731——10.27
18.5049——18.50
16.4005——16.40
27.1829——27.18
当尾数大于或等于6时将尾数舍去向前一位进位
例如将下列数字全部修约到两位小数,结果为:
16.7777——16.78
10.29501——10.30
21.0191——21.02
(三)当尾数为5,而尾数后面的数字均为0时,应看尾数“5”的前一位:若前一位数字此时为奇
数,就应向前进一位;若前一位数字此时为偶数,则应将尾数舍去。
数字“0”在此时应被视为偶数。
例如将下列数字全部修约到两位小数,结果为:
12.6450——12.64
18.2750——18.28
12.7350——12.74
21.845000——21.84
(四)当尾数为5,而尾数“5”的后面还有任何不是0的数字时,无论前一位在此时为奇数还是偶数,也无论“5”后面不为0的数字在哪一位上,都应向前进一位。
例如将下列数字全部修约到两位小数,结果为:
12.73507——12.74
21.84502——21.85
12.64501——12.65
18.27509——18.28
38.305000001——38.31
按照四舍六入五留双规则进行数字修约时,也应像四舍五入规则那样,一次性修约到指定的位。
数字修约规则-----四舍五入和四舍六入五留双规则之欧阳家百创编

数字修约规则欧阳家百(2021.03.07)现在被广泛使用的数字修约规则主要有四舍五入规则和四舍六入五留双规则。
[编辑] 四舍五入规则四舍五入规则是人们习惯采用的一种数字修约规则。
四舍五入规则的具体使用方法是:在需要保留有效数字的位次后一位,逢五就进,逢四就舍。
例如:将数字2.1875精确保留到千分位(小数点后第三位),因小数点后第四位数字为5,按照此规则应向前一位进一,所以结果为2.188。
同理,将下列数字全部修约为四位有效数字,结果为:0.53664—0.5366 10.2750—10.28 18.06501—18.070.58346—0.5835 6.4050—16.4127.1850—27.19按照四舍五入规则进行数字修约时,应一次修约到指定的位数,不可以进行数次修约,否则将有可能得到错误的结果。
例如将数字15.4565修约为两位有效数字时,应一步到位:15.4565——15(正确)。
如果分步修约将得到错误的结果:15.4565——15.457——15.46——15.5——16(错误)。
四舍五入修约规则,逢五就进,必然会造成结果的系统偏高,误差偏大,为了避免这样的状况出现,尽量减小因修约而产生的误差,在某些时候需要使用四舍六入五留双的修约规则。
[编辑] 四舍六入五留双规则为了避免四舍五入规则造成的结果偏高,误差偏大的现象出现,一般采用四舍六入五留双规则(Banker's Rounding)。
四舍六入五留双应该改为: 四舍六入逢五无后则留双,这样描述更容易理解和记住。
四舍六入五留双规则的具体方法是:(一)当尾数小于或等于4时,直接将尾数舍去。
例如将下列数字全部修约为四位有效数字,结果为:0.53664—0.53660.58344—0.5834 16.4005—16.40 27.1829—27.1810.2731—10.27 18.5049—18.50(二)当尾数大于或等于6时,将尾数舍去并向前一位进位。
数据修约

四舍六入法则
三. 1. 2. 3. 4. 5. 6. 7.
例题 2.324→2.32 2.3262→2.33 2.3251→2.33 13.35→13.4 13.25→13.2 13.05→13.0 7.354546→7.35
四舍六入法则
四.
数据处理的原则是:四舍六入,五看奇偶, 数据处理的原则是:四舍六入,五看奇偶,奇 进偶舍, 进偶舍,有余进一 .
数据修约
四舍六入
四舍六入法则
一. 1.
“四舍六入五单双”的法则: 四舍六入五单双” 即看要保留的有效数字后一位数字,如 果大于5,向前进一位,小于等于4 果大于5,向前进一位,小于等于4则舍 去. 等于5则看5后,如5后不全为0 等于5则看5后,如5后不全为0,则进一 位. 5后全为零则看5前,若为奇,则进1,若 后全为零则看5前,若为奇,则进1 为偶,则舍去. 为偶,则舍去.2. Nhomakorabea3.
四舍六入法则
二.
从统计学的角度,"四舍六入五成双" 从统计学的角度,"四舍六入五成双"比"四舍五 入"要科学,它使舍入后的结果有的变大,有的变 要科学,它使舍入后的结果有的变大, 小,更平均.而不是像四舍五入那样逢五就入,导 更平均.而不是像四舍五入那样逢五就入, 致结果偏向大数. 致结果偏向大数. 例如:1.15+1.25+1.35+1.45=5.2,若按四舍五入取 例如:1.15+1.25+1.35+1.45=5.2,若按四舍五入取 一位小数计算 1.2+1.3+1.4+1.5=5.4 按"四舍六入五成双"计算,1.2+1.2+1.4+1.4=5.2, 四舍六入五成双"计算,1.2+1.2+1.4+1.4=5.2, 舍入后的结果更能反映实际结果. 舍入后的结果更能反映实际结果.
数值修约口诀

数值修约口诀
1. 四舍六入五考虑,五后非零就进一,好比那贪吃蛇,看到食物就想吞进去。
2. 四舍六入五看前,奇进偶不进莫乱编,就像那红绿灯,规则得明明白白不胡来。
3. 修约规则要记牢,四舍六入五成双,好似那鞋子配成双,错了就会很荒唐。
4. 数值修约不犯难,四舍六入把好关,像是守门员,只放对的球儿过杆杆。
5. 四舍六入五取舍,五前奇数就升格,仿佛那火箭发射,到点就噌噌往上拨。
6. 修约如同走迷宫,四舍六入心不懵,就像聪明小悟空,规则之中能从容。
7. 四舍六入五注意,五后为零看仔细,就像挑西瓜,敲一敲才能辨仔细。
8. 数值修约有妙法,四舍六入五当家,好似厨师做菜呀,调料多少有准法。
9. 四舍六入规则妙,五前偶数就停靠,像那小船入港湾,稳稳当当不乱飘。
10. 修约数值别迷糊,四舍六入不含糊,好比那裁缝做衣服,尺寸得精准无误。
11. 四舍六入五权衡,五后有数向前冲,就像冲锋的小士兵,听到号角就行动。
12. 数值修约像拼图,四舍六入要清楚,错了一块就乱套,就像那乱麻理不出。
13. 四舍六入五判断,五前奇数要变换,仿佛魔法变一变,规则之下才灵验。
14. 修约不能凭感觉,四舍六入有准则,就像火车跑铁轨,出轨就会出大糗。
15. 四舍六入五纠结,五后非零不能歇,像是追着胡萝卜的小毛驴,得一直向前追。
16. 数值修约不随性,四舍六入按规定,好似那钟表的指针,按部就班来运行。
17. 四舍六入五考量,五前偶数就安详,像那睡熟的小懒猫,静静躺着不瞎忙。
18. 修约如同走钢丝,四舍六入要保持,要是失衡就惨啦,就像那高楼要塌之。
四舍六入五留双规则的具体方法

四舍六入五留双规则的
具体方法
Document serial number【UU89WT-UU98YT-UU8CB-UUUT-UUT108】
四舍六入五留双规则的具体方法
当尾数小于或等于4时,直接将尾数舍去
例如将下列数字全部修约到两位小数,结果为:
——
——
——
——
当尾数大于或等于6时将尾数舍去向前一位进位
例如将下列数字全部修约到两位小数,结果为:
——
——
——
(三)当尾数为5,而尾数后面的数字均为0时,应看尾数“5”的前一位:若前一位数字此时为奇数,就应向前进一位;若前一位数字此时为偶数,则应将尾数舍去。
数字“0”在此时应被视为偶数。
例如将下列数字全部修约到两位小数,结果为:
——
——
——
——
(四)当尾数为5,而尾数“5”的后面还有任何不是0的数字时,无论前一位在此时为奇数还是偶数,也无论“5”后面不为0的数字在哪一位上,都应向前进一位。
例如将下列数字全部修约到两位小数,结果为:
——
——
——
——
——
按照四舍六入五留双规则进行数字修约时,也应像四舍五入规则那样,一次性修约到指定的位数,不可以进行数次修约,否则得到的结果也有可能是错误的。
例如将数字修约到两位小数时,应一步到位:——(正确)。
如果按照四舍六入五留双规则分步修约将得到错误结果:——————(错误)。
四舍六入五成双的题目

选择题:使用“四舍六入五成双”规则,数字2.145应舍入为多少位小数?A. 2.14B. 2.15(正确答案)C. 2.1D. 2应用“四舍六入五成双”原则,下列哪个数字舍入后变为3.00?A. 2.995B. 3.004C. 2.996D. 2.994(正确答案,因为5前为偶数,舍去5不进位)按照“四舍六入五成双”的规则,1.2550应舍入为几位有效数字?A. 1.25B. 1.26C. 1.255D. 1.3(正确答案,末位5后无数字或为零,且5前为奇数,进位)在使用“四舍六入五成双”的方法时,数字0.0565应如何处理?A. 舍去,结果为0.056B. 进位,结果为0.057(正确答案)C. 保持不变D. 变为0.06根据“四舍六入五成双”的规则,23.450应舍入为什么数字?A. 23.4B. 23.5(正确答案)C. 23D. 23.45采用“四舍六入五成双”原则,下列哪个数值舍入后是4.50?A. 4.495B. 4.505(正确答案,5后无数字,且5前为偶数,舍去5不进位)C. 4.51D. 4.496根据“四舍六入五成双”的舍入规则,数字78.95应如何处理?A. 舍去,结果为78.9B. 进位,结果为79(正确答案)C. 不变D. 变为78.90应用“四舍六入五成双”的规则,3.14159应舍入为几位小数?A. 3.14B. 3.142C. 3.1416D. 3.141(正确答案,因为需要舍去5及之后的数字)在使用“四舍六入五成双”方法时,下列哪个数字应舍入为2.0?A. 1.995B. 2.005(正确答案,5后无数字,且5前为偶数,舍去5不进位)C. 2.01D. 1.996。
数据四舍六入五单双公式编辑

数据四舍六入五单双公式编辑在数学中,四舍六入五单双是一种常用的舍入方法,用于在进行数字的四舍五入时,当需要舍弃的小数部分为5时,根据舍入规则的不同,可以向下舍入为偶数或向上舍入为奇数。
这种舍入方法的目的是为了减少舍入误差,使得舍入后的结果更加合理和准确。
四舍六入五单双的具体规则如下:1.当舍弃位的数值小于5时,直接舍弃,不改变前一位的数值。
2.当舍弃位的数值大于5时,向上进位,增加前一位的数值。
3.当舍弃位的数值等于5时,根据舍入规则进行进一步判断:a.若舍弃位的前一位数值为偶数时,直接舍弃,不改变前一位的数值。
b.若舍弃位的前一位数值为奇数时,向上进位,增加前一位的数值。
通过四舍六入五单双的舍入规则,可以更有效地减少舍入误差,使得计算结果更加准确。
这种舍入方法常常应用于金融、统计学、计算机编程等领域。
在金融领域,四舍六入五单双的舍入方法常用于货币计算中。
例如,当对一些金额进行四舍五入时,如果舍弃位的数值小于5,则直接舍弃;如果舍弃位的数值大于5,则向上进位;如果舍弃位的数值等于5,并且前一位的数值为奇数,则向上进位;如果舍弃位的数值等于5,并且前一位的数值为偶数,则直接舍弃。
这样可以更加准确地计算出最接近的金额值,减少计算误差。
在统计学中,四舍六入五单双的舍入方法常用于数据处理中。
例如,当对实验结果进行舍入时,遵循四舍六入五单双的规则可以使得计算结果更加准确。
在统计学中,数据的准确性和可靠性非常重要,因此采用四舍六入五单双的舍入方法能够减少误差,并提高统计结果的可靠性。
在计算机编程中,四舍六入五单双的舍入方法常用于浮点数的处理中。
由于计算机内部使用二进制表示数值,因此存在精度误差。
通过采用四舍六入五单双的舍入方法,可以减少舍入误差,并提高计算结果的准确性。
在编程中,舍入方法往往与具体的应用场景有关,可以根据实际需求选择合适的舍入规则。
综上所述,四舍六入五单双是一种常用的舍入方法,通过合理的舍入规则,可以减少舍入误差,使得舍入后的结果更加准确。
四舍六入五留双规则的具体方法

四舍六入五留双规则(de)具体方法
当尾数小于或等于4时,直接将尾数舍去
例如将下列数字全部修约到两位小数,结果为:
——
——
——
——
当尾数大于或等于6时将尾数舍去向前一位进位
例如将下列数字全部修约到两位小数,结果为:
——
——
——
(三)当尾数为5,而尾数后面(de)数字均为0时,应看尾数“5”(de)前一位:若前一位数字此时为奇数,就应向前进一位;若前一位数字此时为偶数,则应将尾数舍去.数字“0”在此时应被视为偶数.
例如将下列数字全部修约到两位小数,结果为:
——
——
——
——
(四)当尾数为5,而尾数“5”(de)后面还有任何不是0(de)数字时,无论前一位在此时为奇数还是偶数,也无论“5”后面不为0(de)
数字在哪一位上,都应向前进一位.
例如将下列数字全部修约到两位小数,结果为:
——
——
——
——
——
按照四舍六入五留双规则进行数字修约时,也应像四舍五入规则
那样,一次性修约到指定(de)位数,不可以进行数次修约,否则得到(de)结果也有可能是错误(de).例如将数字修约到两位小数时,应一步到位:——(正确).如果按照四舍六入五留双规则分步修约将得到错误结果:——————(错误).。
数字修约规则

数值修约规则在进行具体的数字运算前,通过省略原数值的最后若干位数字,调整保留的末位数字,使最后所得到的值最接近原数值的过程称为数值修约。
指导数字修约的具体规则被称为数值修约规则。
数值修约时应首先确定“修约间隔”和“进舍规则”。
一经确定,修约值必须是“修约间隔”的整数倍。
然后指定表达方式,即选择根据“修约间隔”保留到指定位数。
科技工作中测定和计算得到的各种数值,除另有规定者外,修约时应按照国家标准文件《数值修约规则》进行。
目录6. 3 进舍规则附加说明:展开修约使用以下“进舍规则”进行修约:1. 拟舍弃数字的最左一位数字小于5时则舍去,即保留的各位数字不变。
2.拟舍弃数字的最左一位数字大于5;或等于5,而其后跟有并非全部为0的数字时则进一即保留的末位数字加1。
(指定“修约间隔”明确时,以指定位数为准。
)3.拟舍弃数字的最左一位数字等于5,而右面无数字或皆为0时,若所保留的末位数字为奇数则进一,为偶数(包含0)则舍弃。
4.负数修约时,取绝对值按照上述1~3规定进行修约,再加上负号。
编辑本段不允许连续修约数值修约简明口诀:「4舍6入5看右,5后有数进上去,尾数为0向左看,左数奇进偶舍弃」。
现在被广泛使用的数值修约规则主要有四舍五入规则和四舍六入五留双规则。
编辑本段四舍五入规则四舍五入规则是人们习惯采用的一种数值修约规则。
四舍五入规则的具体使用方法是:在需要保留数字的位次后一位,逢五就进,逢四就舍。
例如:将数字2.1875精确保留到千分位(小数点后第三位),因小数点后第四位数字为5,按照此规则应向前一位进一,所以结果为2.188。
同理,将下列数字全部修约到两位小数,结果为:10.2750——10.2818.06501——18.0716.4050——16.4127.1850——27.19按照四舍五入规则进行数值修约时,应一次修约到指定的位数,不可以进行数次修约,否则将有可能得到错误的结果。
例如将数字15.4565修约到个位时,应一步到位:15.4565——15(正确)。
