湖南省2014年高中数学竞赛
湖南省十三校2014届高三第二次联考数学理试题Word版含解析

湖南省2014届高三·十三校联考 第二次考试理科数学试卷考试时间:2014年4月12日15:00~17:00得分:【试卷综析】 本套试卷是湖南省13校第二次联考试题,试卷在题型、题量、分值、难度、知识点分布及覆盖面上都和高考试题比较接近。
从整体上看,试卷难度适当,具有较好的区分度、效度和信度。
试题注重考查了基础知识、基本技能和基本方法,突出了对学生数学能力的考查。
例如第6题,第8题,9题都很好地考查了学生的数学能力。
在学生熟悉的背景下进行命题,进行创新,这是高考的要求,也是中学教学的要求。
在本套试卷中,有所体现,这是一大亮点。
一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的,请将所选答案填在答题卡中对应位置. 1.已知集合1{|1}1A x x =≤-,{|ln 0}B x x =≤,则A B =( ) A. (,1)-∞ B. (0,1] C. [0,1) D. (0,1) 【知识点】借助分式不等式和对数不等式考查集合的运算。
【答案解析】D {|1A x x =<或2}x ≥,{|01}B x x =<<,所以AB =(0,1)【思路点拨】解分式不等式时,要时刻注意,移项通分。
利用数轴求集合的交集。
2.已知a R ∈,则“”是“复数2(2)(1)(z a a a i i =--++为虚数单位)为纯虚数”的( ) A. 充分不必要条件 B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件 【知识点】本题考查了复数知识和充分必要条件的判断。
【答案解析】C 复数2(2)(1)(z a a a i i =--++为虚数单位)为纯虚数的充要条件是22010a a a ⎧--=⎨+≠⎩,所以2a =。
【思路点拨】复数为纯虚数,必须保证实部等于0,虚部不等于0.先求出充要条件,然后再把充要条件的范围放大或缩小。
3.(2013·肇庆二模改编)若某程序框图如图所示,则该程序运行 后输出的值是( )A. 4B. 5C. 6D. 7【知识点】程序框图问题。
2014年全国高中数学联赛试题及答案详解(A卷)

2013
解:由题设
an
2(n 1) n
an1
2(n 1) n
2n n 1 an2
2(n 1) n
2n n 1
23 2
a1
2n1 (n
1)
.
记数列{an} 的前 n 项和为 Sn ,则
Sn =
2 + 2 × 3 + 22 × 4 + + 2n−1(n +1)
2015 2013
2015
.
2013
5. 正四棱锥 P ABCD 中,侧面是边长为 1 的正三角形,M , N 分别是边 AB, BC 的中
点,则异面直线 MN 与 PC 之间的距离是
.
答案: 2 . 4
解:设底面对角线 AC, BD 交于点 O ,过点 C 作直
线 MN 的垂线,交 MN 于点 H . 由 于 PO 是 底 面 的 垂 线 , 故 PO CH , 又
解:记 f (z) (z )2 z .则
f (z1) f (z2 ) (z1 )2 z1 (z2 )2 z2
(z1 z2 2)(z1 z2 ) z1 z2 .
①
假如存在复数 z1, z2 ( z1 , z2 1, z1 ≠ z2 ) ,使得 f (z1) f (z2 ) ,则由①知,
连接的情况数.
(1) 有 AB 边:共 25 32 种情况.
(2) 无 AB 边,但有 CD 边:此时 A , B 可用折线连接当且仅当 A 与 C , D 中至少一
点相连,且 B 与 C , D 中至少一点相连,这样的情况数为 (22 1)(22 1) 9 .
湖南省师大附中、长沙市一中等六校2014届高三4月联考数学(理)试题-含答案

C .等边三角形
D .等腰直角三角形
6.设 {a n} 是等比数列,则 “a1<a2 <a4”是 “数列 {a n} 是递增数列 ”的
A .充分而不必要条件
B .必要而不充分条件
C .充分必要条件
D .既不充分也不必要条件
7.一个几何体的三视图如图所示,则该几何体的外接球的体积为
A.4 3
a 的取值范围;
(2)当 a=1 时,若 f ( x) >n 恒成立,求满足条件的正整数 n 的最大值;
3 2n
(3)求证:( 1+1 ×3)×( 1+3 ×5)×… ×[1+ ( 2n- l)( 2n+l ) ]>e 2 .
参考答案
uuur ⊥ OB ?若存在, 写出该圆的方程, 并求该切线在 y 轴上截距的取值范围及 | AB| 的取值范围; 若
不存在,说明理由.
22.(本小题满分 13 分)
x(1 a1nx)
已知函数 f(x) =
(x 1).
x1
(1)若 g( x ) =( x-l ) 2f ′( x )在( 1, +
)是增函数,求实数
息中按一定规则对信息加密,设定原信息为
A 0=a1a2… an, ai∈{0 , 1} ( i=1 , 2, 3… n),传输当
中原信息中的 1 都转换成 01,原信息中的 0 转换成 10,定义这种数字的转换为变换丁,在多次
的加密过程中,满足 A k=T( A k-1), k=1, 2, 3,….
( 1)若 A 2: 10010110,则 A 0 为 ____
;
( 2)若 A 0 为 10,记 A K 中连续两项都是 l 的数对个数为 l K,k=l ,2,3,…,则 l K=
湖南省高中数学竞赛试题及答案

2016年湖南省高中数学竞赛试题及答案一、选择题(本大题共6个小题,每小题5分,满分30分.每小题所提供的四个选项中只有一项是符合题目要求的)1.设集合{}0123,,,S A A A A =,在S 上定义运算“⊕”为:i j k A A A ⊕=,其中k 为i j +被4除的余数,,0,1,2,3.i j =则满足关系()20x x A A ⊕⊕=的()x x S ∈的个数为( )A .1B .2C .3D .4 答案:B .提示:因为()20,x x A A ⊕⊕=,设kx x A ⊕=,所以20,2,k A A a k ⊕==即2x x A ⊕=,故1x A =或3.x A =答案:A .2.一个骰子由1-6六个数字组成,根据如图所示的三种状态显示的数字,可推得“?”的数字是 ( )A .6B .3C .1D .2 3.设函数()2c o s ,fx x x =-{}n a 是公差为8π的等差数列,()()12f a f a +++()n f a 5,π=则()2315f a a a -=⎡⎤⎣⎦ ( )A .0B .116π C .18π D .21316π答案:D .提示:因为{}n a 是公差为8π的等差数列,且 ()()12f a f a +++()5f a()()()1122552cos 2cos 2cos 5,a a a a a a π=-+-++-=即()()1251252cos cos cos 5a a a a a a π+++-+++=,所以33333310cos cos cos cos cos 5.4884a a a a a a πππππ⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫--+-+++++= ⎪ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦即33102cos2cos1cos 5.48a a πππ⎛⎫-++= ⎪⎝⎭记()102cos2cos1cos 548g x x x πππ⎛⎫=-++- ⎪⎝⎭,则 ()102cos 2cos 1sin 048g x x ππ⎛⎫'=+++> ⎪⎝⎭,即()g x 在R 为增函数,有唯一零点2x π=,所以3.2a π=所以()2223151320.2242416f a a a ππππππ⎛⎫⎛⎫⎛⎫-=⨯---+=⎡⎤ ⎪ ⎪⎪⎣⎦⎝⎭⎝⎭⎝⎭ 4.设,m n 为非零实数,i 为虚数单位,z C ∈,则方程z ni z mi n ++-=与方程z ni z mi m+--=-在同一复平面内的图形(其中12,F F 是焦点)是( )答案:B . 提示:z n i z m i n ++-=表示以()()120,,0,F n F m -为焦点的椭圆且0.n >z ni z mi m +--=-表示以()()120,,0,F n F m -为焦点的双曲线的一支.由n z ni z mi m n =++-≥+,知0.m <故双曲线z ni z mi m +--=-的一支靠近点2F .5.给定平面向量()1,1,那么,平面向量11,22⎛+ ⎝⎭是将向量()1,1经过 变换得到的,答案是 ( )A .顺时针旋转60所得B .顺时针旋转120所得C .逆时针旋转60所得D .逆时针旋转120所得 答案:C .提示:设两向量所成的角为θ,则()1,11cos ,2θ⋅==又0,180θ⎡⎤∈⎣⎦,所以60θ=.又110,022<>,所以C 正确. 6.在某次乒乓球单打比赛中,原计划每两名选手各比赛一场,但有3名选手各比赛了两场之后就退出了,这样全部比赛只进行了50场,那么上述3名选手之间比赛场数是( )A .0B .1C .2D .3 答案:B .提示:设这3名选手之间比赛的场数是r ,共n 名选手参赛,依题意有23650n Cr -+-=,即()()3444.2n n r --=+因为03r ≤≤,所以分4种情况讨论:①当0r =时,有()()3488n n --=,即27760n n --=,但它没有正整数解,故0r ≠;②当1r =时,有()()3490n n --=,解得13n =,故1r =符合题意;③当2r =时,有()()3492n n --=,即27800,n n --=但它没有正整数解,故2r ≠; ④当3r =时,有()()3494n n --=,即27820n n --=,但它没有正整数解,故 3.r ≠二、填空题(本大题共6个小题,每小题8分,满分48分,解题时只需将正确答案直接填在横线上.)7.规定:对于x R ∈,当且仅当()*1n n n n N ≤<+∈时,[]x n =.则不等式[][]2436450x x -+≤的解集是 .答案:28.x ≤≤。
2014年全国高中数学联赛湖南赛区预赛_黄仁寿

分 共
,
3 0
分 5 如图
)
.
. }
1
,
在 三 棱 F
、
1
.
设似
2
2
=
|
a
l
a = ?
y
,
a
:
、
y
G Z
则 选 柱中 已 知点 ^
,
册
,
,
的
‘
项正 确 的是 中 点
(
)
.
M
及AC 的中
(
A)
B
)
9 9
G M 迗 M M
,
1
0 £
M 点
i
V
所 决 定 的 平面
:
若不 等 式
则 实数
三
1
+
2
y
)
^
(
^ +
2
r)
恒成立
,
数组
(
a
,
6
)
,
使得
A
、
巧
均 为 不 动 点 并证 明
?
a
的 最 大 值为
(
、
解答 题 共
1
7 2
你 的 结 论 分 I 6 2 0 分 已 知 数列 W 满 足
?
.
)
.
(
)
3 (
.
6
2
,
已知
一
0
iC 内 为AAf
,
丨
处
.
…厂
r
,
则
P
、
P
1
'
关于圆 周
2014年全国高中数学联赛获奖名单
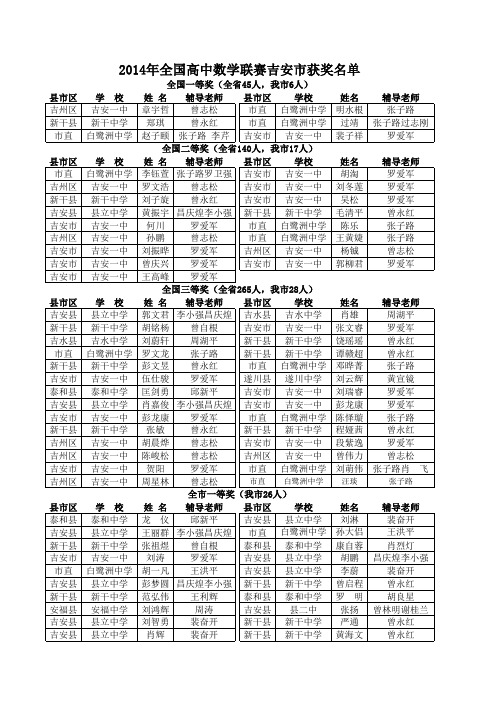
县市区 新干县 万安县 新干县 新干县 吉安县 永新县 吉水县 永丰县
吉水中学 万安中学 白鹭洲中学
学校 新干中学 县立中学 县立中学 县立中学 万安中学 吉水中学 新干中学 新干中学
吉水中学
县立中学 吉水中学 吉安一中 吉安一中 新干中学 新干二中 县立中学 峡江中学 吉安一中 吉水中学 吉安一中 白鹭洲中学 安福中学 永丰中学 峡江中学 吉安一中 吉安一中 白鹭洲中学 白鹭洲中学 吉水二中
市直 市直 市直 吉州区 安福县 吉安县 吉安县 吉水县 吉水县 吉水县 井冈山
吉水中学 县立中学 县立中学 县立中学 县立中学 县立中学 白鹭洲中学 县立中学 县立中学 县立中学 县立中学 县立中学 县立中学 县立中学 县立中学 县立中学 县立中学 县立中学 峡江中学 泰和中学 吉安一中 吉安一中 吉安一中 吉安一中 白鹭洲中学 白鹭洲中学
彭慧翔 曾永红
吉安县 县立中学
李祖文 傅新彪
永新县 任弼时中学
汤景泰 裴奋开
吉州区 吉安一中
习剑坤
王虎
吉州区 吉安一中
康佳
罗爱军
吉安县 县立中学
宋蕾 周湖平刘秋华 吉安县 县立中学
罗玉畦 曾志松
吉安县 县立中学
曾昭呼 张子路
泰和县 泰和中学
谢志伟
周涛
吉安市 吉安一中
陈雨轩 傅伟鑫
市直 白鹭洲中学
李双智 廖冬平
吉州区 吉安一中 杨铖
吉安一中 曾庆兴 罗爱军
吉安市 吉安一中 郭柳君
吉安一中 王高峰 罗爱军
全国三等奖(全省265人,我市28人)
学 校 姓 名 辅导老师 县市区 学校
姓名
县立中学 郭文君 李小强昌庆煌 吉水县 吉水中学 肖雄
2014年全国高中数学联合竞赛试题及解答.(A卷)

1 。 100
,a n 1 arctan(sec a n ) , (n N ) 求正整数 m , 6 , ) ,且 tan a n 1 sec a n 2 2
★解析:由已知条件可知,对任意正整数 n , a n 1 ( 由于 sec a n 0 ,故 a n 1 (0,
2014 年全国高中数学联合竞赛试题(A 卷)
第 2 页 共 11 页
2a | QF1 | | QF2 || PF1 | | PF2 | 2c 4
于是 | QF2 || PF1 | | PF2 | | QF1 | 2c 1 设 H 为线段 PF1 的中点,则 | F1 H | 2, | QH | 5 ,且有 F2 H PF1 。由勾股定理知,
① ②
2014 年全国高中数学联合竞赛试题(A 卷)
第 4 页 共 11 页
而点 P 的坐标 ( a, b) 同时满足①,②。故 A , B 的坐标均满足方程
by 2( x a )
③ ( x1 , y1 ) , ( x 2 , y 2 )
故③就是直线 AB 的方程。 直线 PO 与 AB 的斜率分别为 从而③即为 y
tan a m tan a1 tan a 2 … sec a1 sec a 2 sec a m
tan a m tan a1 tan a 2 … (利用①) tan a 2 tan a3 tan a m 1
2014 年全国高中数学联合竞赛试题(A 卷)
第 5 页 共 11 页
2 2 2 2 2 2 5
48 3 。 64 4
二、解答题:本大题共 3 小题,共 56 分。解答应写出文字说明、证明过程或演算步骤。 2014A 9、 (本题满分 16 分)平面直角坐标系 xOy 中, P 是不在 x 轴上的一个动点,满足条件:过 P 可作抛物线 y 4 x 的两条切线,两切点连线 l P 与 PO 垂直.设直线 l P 与直线 PO , x 轴的交点分别 为 Q, R 。 ⑴证明: R 是一个定点; ⑵求
湖南省岳阳市部分省重点高中2014级高一期考联考数学试题(含详细解答)
1 / 15
湖南省岳阳市部分省重点高中
2014级高一期考联考数学试题
时量:120分钟
总分:100分
命题:周军才
审题:彭志龙
一、本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合
题目要求的. 1、函数x
x x f 2
11
)
(的定义域是
(
)
A .|1x x
B .|12
x x x 且C .
|12
x x
x
且D .|1
x x
2、下列函数中,在
(1, 1)-内有零点且在定义域内单调递增的是
(
)
A .12
log y x
=B .21
x
y =-C .2
12
y x =-
D .3
y x
=-3、关于循环结构的论述正确的是
(
)
A .①是直到型循环结构④是当型循环结构
B .①是直到型循环结构③是当型循环结构
C .②是直到型循环结构④是当型循环结构
D .④是直到型循环结构①是当型循环
结构
4、下列选项中不是..右图中几何体的三种视图之一的是
(
)
满足条件?
循环体
是
否
①
满足条件?
循环体
否
是
②满足条件?
循环体是
否
③满足条件?
循环体
否
是
④。
年湖南省高中数学竞赛试卷A及答案

年湖南省高中数学竞赛试卷A及答案考生注意:1、本试卷共三大题(16个小题),全卷满分150分。
2、用钢笔、签字笔或圆珠笔作答。
3、解题书写不要超出装订线。
4、不能使用计算器。
一、选择题(本大题共6小题,每小题6分,满分36分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1.记[x]为不大于x的最大整数,设有集合,,则 ( ) A.(-2,2) B.[-2,2] C. D.2.若,则 = ( )A.-1 B. 1 C. D.3.四边形的各顶点位于一个边长为1的正方形各边上,若四条边长的平方和为t,则t的取值区间是 ( )A.[1,2] B.[2,4] C.[1,3] D.[3,6]4.如图,在正方体ABCD-A1B1C1D1中,P为棱AB上一点,过点P在空间作直线l,使l与平面ABCD和平面ABC1D1均成角,则这样的直线条数是 ( )A. 1 B. 2C. 3 D. 45.等腰直角三角形 ABC中,斜边BC= ,一个椭圆以C为其焦点,另一个焦点在线段AB上,且椭圆经过A,B两点,则该椭圆的标准方程是(焦点在x轴上) ( )A. B.C. D.(注:原卷中答案A、D是一样的,这里做了改动)6.将正方形的每条边8等分,再取分点为顶点(不包括正方形的顶点),可以得到不同的三角形个数为 ( )A.1372 B. 2024 C. 3136 D.4495二、填空题(本大题共6小题,每小题6分,满分36分,请将正确答案填在横线上。
)7.等差数列的前m项和为90,前2 m项和为360,则前4m项和为_____.8.已知,,且,则的值为______ ___.9.100只椅子排成一圈,有n个人坐在椅子上,使得再有一个人坐入时,总与原来的n个人中的一个坐在相邻的椅子上,则n的最小值为__________.10.在 ABC中,AB= ,AC= ,BC= ,有一个点D使得AD平分BC并且是直角,比值能写成的形式,这里m、n是互质的正整数,则m-n=______ __.11.设ABCD-A1B1C1D1是棱长为1的正方体,则上底面ABCD的内切圆上的点P与过顶点A,B,C1,D1的圆上的点Q之间的最小距离是___________.12.一项“过关游戏”的规则规定:在第n关要抛一颗骰子n次,如果这n次抛掷所出现的点数之和大于,则算过关。
数学奥赛

通知
2014年湖南省高中数学竞赛有关事项通知如下:
一、时间:2014年6月28日9:00-11:00
二、考场安排
第一考室:4201
497班黎沁刘其邵立轲林盛何占魁郭晋彤李雨农黄蕊
邹锦胡翌灵陈应翔张志宏范雄翔于荣杰王雅馨龙南岳
498班郑景仁程健杨颖李乔威常东来赵青云周映雪吴琪禹思琪杨斌袁宇薇胡羽妙赵紫怡
499班陈鹤语沈琰婷许定誉周惟渭欧楠青陈宇豪沈瀚翔李文锋王斯盛陈沫龙杰锋
第二考室:4202
500班王伊严澍周天乐周子凌罗光宇郝小可高扬姜煜
喻伏剑张咏鼎
501班陈宇王绪普李藴佚王芷郁曾奕谢润东贺羽汶
502班刘艺璇杨名宇邓望权李熙悦周立立李苇珂罗聪刘浏陈坤503班毛雨范知礼尹伊姚云岫李平天胡显东陈昱蓉夏昳轩陈权周楚琪胡汝俊李若章卢沁瑶邓一维吴晗李粤湘孔锦文
第三考室:4203
504班李根严立能晏小静徐思诚李宇琛龙玉婷彭雪琪罗晔周子琪黄慧婧任雪荻王子恬刘洪菘
494班刘旭周威彭宇
495班佘林度田家君
496班旷昊恒谭时锴欧阳华超杨俊杰彭一凡
506班刘雨璇徐荣婧何文韬
506班李江游希佳钟吉琳赵升曼肖博文伍嘉辉彭欣怡
508班任术李高洁方芷萱李伊雨周林萱周典潘昱函。
湖南省岳阳市部分省重点高中2014级高一期考联考数学试题(含详细解答)

湖南省岳阳市部分省重点高中2014级高一期考联考数学试题时量:120分钟 总分:100分 命题:周军才 审题:彭志龙一、本大题共10个小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1、函数xx x f -++=211)(的定义域是( ) A .{}|1x x ≥-B .{}|12x x x ≥-≠且C . {}|12x x x >-≠且D .{}|1x x >-2、下列函数中,在(1, 1)-内有零点且在定义域内单调递增的是( )A .12log y x = B .21xy =-C .212y x =-D .3y x =-3A .①是直到型循环结构④是当型循环结构B .①是直到型循环结构③是当型循环结构C .②是直到型循环结构④是当型循环结构D .④是直到型循环结构①是当型循环结构4、下列选项中不是..右图中几何体的三种视图之一的是( )①② ③ ④5、一条直线经过点()2,3A -,并且它的倾斜角是直线3y x =的倾斜角的两倍,则这条直线的点斜式方程是( )A.)32y x +=- B.)32y x -+ C.)32y x +=-D.)32y x -=+6、已知菱形ABCD 的边长为2,60BAD ∠=︒,现沿BD 将ABD折起并使得AC (如右图所示),则二面角A BD C --的大小为( )A .30︒B .60︒C .90︒D .120︒7、圆心在曲线2(0)y x x=>上,与直线210x y ++=相切且面积最小的圆的方程为( ) A .22(1)(2)5x y -+-=B .22(2)(1)5x y -+-=C .22(1)(2)25x y -+-=D .22(2)(1)25x y -+-=8、将参加夏令营的600名学生编号为:001,002,…,600,采用系统抽样的方法抽取一个容量为50的样本,且随机抽得的编号为003.这600名学生分住在3个营区,从001到300住在第1营区,从301到495住在第2营区,从496到600住在第3营区,则3个营区被抽中的人数依次为( )A .26,16,8B .25,16,9C .25,17,8D .24,17,9 9、已知函数()f x 是定义在R 上的奇函数,且对任意x 都有(2)()f x f x +=.当[)0,1x ∈时,()21x f x =-,则12log 6f ⎛⎫⎪⎝⎭的值为( ) A .52-B .-5C .12-D .-6DCBACDBA10、用)(A C 表示非空集合A 中的元素个数,定义⎩⎨⎧<-≥-=-)()(),()()()(),()(||B C A C A C B C B C A C B C A C B A .若}2,1{=A ,}|32||{2a x x x B =-+=,且1||=-B A ,由a 的所有可能值构成的集合为S ,那么()C S 等于( )A .1B .2C .3D .4 二、填空题:本大题共5小题,每小题4分,共20分,把正确答案填在横线上. 11、点()2,6A 到直线342x y -=的距离是 . 12、若4log 3x =,则44x x -+= .13、在空间直角坐标系Oxyz 中有四点()()()()0,0,0,0,0,3,0,3,0,2,3,4O A B C ,则多面体OABC 的体积是 .14、如右下图所示的程序框图,输入98,63m n ==时,程序运行结束后输出的,m i 值的和. 为 .15、甲、乙、丙、丁四个物体同时从某一点出发向同一个方向运动,其路程()()1,2,3,4i f x i =.关于时间()0x x ≥的函数关系式分别为:()()()()()21234221,,,log 1x f x f x x f x x f x x =-===+.有以下结论:① 当1x >时,甲走在最前面; ② 当1x >时,乙走在最前面;③ 当01x <<时,丁走在最前面,当1x >时,丁走在最后面; ④ 丙不可能走在最前面,也不可能走在最后面; ⑤ 如果它们一直运动下去,最终走在最前面的是甲。
湖南省2014年高中数学竞赛

湖南省2014年高中数学竞赛湘西自治州赛区学生获奖情况通报湖南省2014年高中数学竞赛分为高二年级和高三年级两个组别于六月二十八日进行。
湘西自治州赛区的有关工作已经完成。
本次竞赛实行交叉巡考,集中评卷,各项工作认真、严格、有序。
全州评出高三年级一等奖32人,二等奖 50人,三等奖 80人;高二年级一等奖 52人,二等奖 74人,三等奖 132人。
现将学生获奖情况(见附件)通报如下,望获奖同学再接再厉。
湘西州教育科学研究院2014年7月5日附件:2014年湖南省高中数学竞赛湘西自治州赛区学生获奖情况通报高三组一等奖(32人)姓名单位成绩杨子谦州民中130田铖永顺一中107龙坤龙山皇仓中学104鲁鹏云古丈一中103彭瑞州民中101覃帅州民中101郭佳龙山皇仓中学99沈芳羽州民中96刘宣敏州民中94符津铭龙山皇仓中学93张晓龙龙山皇仓中学93田志富州民中91邓归航龙山皇仓中学91廖旺冬凤凰高级中学91全翔永顺一中89石平安花垣边高89邹凡莹州民中88向启保靖民中88张林林保靖民中88徐昊花垣边高88喻与越州民中87付小萍泸溪一中87杨东龙州民中86周倩嘉保靖民中86崔小凤永顺一中85徐航州民中85龙喜涛州民中85罗佳峰龙山高级中学85胡成龙山皇仓中学85黄力平泸溪一中85李湘麓泸溪一中85吴玉良凤凰华鑫中学84二等奖(50人)姓名单位成绩郭露龙山皇仓中学83 龙春鹏花垣边高83 龙林静古丈一中83 梁大星永顺一中82 彭恩泽永顺一中82 张亚苹州民中82 杜雨钊泸溪一中82 罗涛州民中81 黄德华龙山皇仓中学81 邓昊泸溪一中81 陈俊伟保靖民中81 龙华强凤凰华鑫中学81 彭林军州民中80 谭肖卓龙山高级中学80 彭霄龙山皇仓中学80 向文钊泸溪一中80 田卓琛保靖民中80 韩承远凤凰华鑫中学80 张向驰州民中79 向金眀州民中79 田政鳞州民中79 杨文杰龙山高级中学79 向子能州民中78 张凯轩州民中78 田根龙山高级中学78 谭必成泸溪一中78 杨童泸溪一中78 杨道鹏保靖民中78 谢瑶姬保靖民中78 雷琳琳花垣边高78 田春贤凤凰高级中学78 田曜铭凤凰华鑫中学78 龙媛凤凰华鑫中学78 覃芬芬永顺一中77 熊恒州民中77 滕雨龙山皇仓中学77张笛泸溪一中77 向鹏飞保靖民中77 李左胜花垣边高77 田粒花垣边高77 曾理古丈一中77 韩永成凤凰华鑫中学77 肖诗舟永顺一中76 吴康分州民中76 石维瑞州民中76 冯家桢龙山皇仓中学76 张朝勇泸溪一中76 梁榕榕泸溪一中76 彭顺麒麟保靖民中76 田瞿阳保靖民中76三等奖(80人)姓名单位成绩龙伟永顺一中75 包文吉州民中75 吕宇州民中75 鲁爱平龙山皇仓中学75 张鹏龙山皇仓中学75 田昌发泸溪一中75 张子悦泸溪一中75 彭虹达保靖民中75 杨晓凤凰华鑫中学75 秦欣欣凤凰华鑫中学75 吴宗荣凤凰华鑫中学75 曾韬泸溪一中74 李岱键泸溪一中74 张水艳花垣边高74 麻利园花垣边高74 覃潇州二民中73 向渊州二民中73 田滢紫州民中73 陈祺州民中73 孙天翔州民中73 张维龙山高级中学73刘钟秦龙山高级中学73 彭茜龙山皇仓中学73 刘贾泸溪一中73 杨智文泸溪一中73 罗义杰花垣边高73 石桓宇花垣边高73 麻清雪花垣边高73 杨宁欣凤凰华鑫中学73 胡文苏永顺一中72 黄立宇永顺一中72 曹阳州民中72 李秋阳州民中72 梁鑫州民中72 孙崧育龙山高级中学72 徐靖杰龙山高级中学72 彭暾豪龙山高级中学72 向俊宇龙山高级中学72 聂作永龙山皇仓中学72 唐智健泸溪一中72 田胜泸溪一中72 姚静泸溪一中72 宋晓婷泸溪一中72 彭雅洁保靖民中72 田子蕾保靖民中72 宋丽保靖民中72 罗勇花垣边高72 田庚凤凰高级中学72 石祥州民中71 黄林州民中71 王彬泽龙山高级中学71 孙瑞华龙山高级中学71 孙盼龙山皇仓中学71 向庭宇龙山皇仓中学71 张越泸溪一中71 杜梦瑶泸溪一中71 李杰泸溪一中71 梁绪庆花垣边高71 石凤芝花垣边高71 周典坤州民中70韩玉叶州民中70 莫凝州民中70 杨佳州民中70 钟金燕泸溪二中70 谭国江龙山皇仓中学70 代德发泸溪一中70 杨斌泸溪一中70 黄棽泸溪一中70 吴笛剑保靖民中70 石靖媛保靖民中70 曾书勋保靖民中70 李函保靖民中70 贾光进花垣边高70 石楠花垣边高70 龙子红古丈一中70 彭展志古丈一中70 冯晶凤凰高级中学70 张波吉首市一中69 莫芳艳泸溪二中68 符辰桂永顺二中55高二组一等奖(52人)姓名单位成绩周子杰州民中132 李映辉泸溪一中130 严梓文龙山皇仓中学125 田奥升龙山皇仓中学123 向冶泸溪一中123 田峰州民中122 欧晓娟凤凰华鑫中学122 刘宇恒凤凰高级中学122 李月华龙山高级中学121 田野永顺一中120 高香玉州民中119 瞿水香龙山皇仓中学119 彭苏樊州民中118肖康州二民中118 黄智超吉首市一中118 李昌盛龙山皇仓中学118 向少聪州民中117 彭归燕吉首市一中117 李斌泸溪一中117 陈晨曦州民中116 肖知秋州民中116 田雪州民中115 范欧永顺一中115 雷桓凤凰高级中学115 刘一鸣州民中114 叶杰伟龙山皇仓中学114 张钊瑞龙山高级中学114 杨良策泸溪一中114 吴迎刚凤凰华鑫中学114 龙欣宇州民中113 贾雪韵州民中113 龙钊涣州民中113 李思君州民中113 彭鑫龙山高级中学113 龙海柳凤凰华鑫中学113 龙晓慧州民中112 张倖僖龙山高级中学112 向淑珍永顺一中112 李宸泸溪一中112 屈骏杰凤凰华鑫中学112 麻洁东凤凰华鑫中学112 田红飞凤凰华鑫中学112 李晓强州二民中111 易世彬龙山皇仓中学111 熊俊永顺一中111 聂金耀凤凰高级中学111 邓茹烨州民中110 王俊武龙山皇仓中学110 燕道德龙山皇仓中学110 龙芳琦凤凰华鑫中学110 石文林泸溪二中110 欧玮古丈一中110二等奖(74人)姓名单位成绩田丰州民中109 向恬靓州民中109 彭峥龙山高级中学109 邢琪凤凰华鑫中学109 陈思源州民中108 杨悦涵州民中108 程琛州民中108 向刚州民中108 尚晔龙山高级中学108 彭佳星龙山高级中学108 向陶钧永顺一中108 鲁文君永顺一中108 洪维古丈一中108 肖宇永顺一中107 彭路赢保靖民中107 段雷鸣州民中106 刘双盈州民中106 张诗语龙山皇仓中学106 刘钆瑶龙山高级中学106 刘艳玲龙山高级中学106 张杰龙山高级中学106 彭清萍永顺一中106 向梦州民中105 石峰情州民中105 段召亲龙山皇仓中学105 马锡明龙山高级中学105 李丹永顺一中105 田园轩州民中104 黄家望州民中104 袁馨雨州民中104 邹凤敏州民中104 滕思慧州民中104 郑世杰龙山皇仓中学104 田志豪龙山皇仓中学104 董良海龙山皇仓中学104 周梓涵龙山高级中学104黄玉萍永顺一中104 杨骐锲泸溪一中104 徐青州民中103 付麟永顺一中103 包洪源泸溪一中103 谭喜凤凰华鑫中学103 吴吉胜凤凰高级中学103 吴静凤凰高级中学103 秦鹏州民中102 瞿玲州民中102 杨开坤龙山皇仓中学102 姚莞永顺一中102 彭爽永顺一中102 唐旭泸溪一中102 滕冬凤凤凰高级中学102 吴边凤凰华鑫中学102 刘洋古丈一中102 贾雪艳州民中101 向阳春州二民中101 田小艳龙山皇仓中学101 宋建平龙山高级中学101 何晶晶龙山高级中学101 罗恺泸溪一中101 石晓琪州民中100 张光茸州民中100 欧阳青云州民中100 杜子悻州民中100 戴付昕州民中100 蔡宜霏龙山皇仓中学100 肖运芬龙山皇仓中学100 薛蓉龙山高级中学100 陈炫杉永顺一中100 周子轩永顺一中100 刘雪伶永顺一中100 蒋慧永顺一中100 唐玮祺泸溪一中100 廖化化凤凰华鑫中学100 蒋忠魁凤凰华鑫中学100三等奖(132人)姓名单位成绩王菊凤凰高级中学100 杨丹州民中99 向功坤州民中99 罗云刚州民中99 舒琳州民中99 李明妍龙山皇仓中学99 吴良宵龙山高级中学99 王鹏永顺一中99 李辉泸溪一中99 陈娟凤凰高级中学99 彭玉彬州民中98 陈曦州民中98 侯森泉州民中98 田清烨州民中98 王浩然州民中98 刘继汉龙山高级中学98 郭艳君龙山高级中学98 杨冰龙山高级中学98 向宏程永顺一中98 宋泽学永顺一中98 符森泸溪一中98 孙碧岳泸溪一中98 隆森凤凰华鑫中学98 林姝凤凰华鑫中学98 唐吉英凤凰华鑫中学98 王俊芝凤凰华鑫中学98 王小霞古丈一中98 向千秋古丈一中98 麻顺跃州民中97 向承雨州民中97 彭祝龙山皇仓中学97 田庆华龙山高级中学97 彭博龙山高级中学97 邓依恒龙山高级中学97 尹泉玲永顺一中97 孔骥永顺一中97罗一夫泸溪一中97 曹必阳泸溪一中97 李定奇古丈一中97 胡慧君州民中96 王紫麟州民中96 滕征轩州民中96 谢菱州民中96 吴骞州民中96 陈邻州二民中96 陈浪吉首市一中96 陈鸿龙山皇仓中学96 张慧龙山高级中学96 谢易生永顺一中96 向月华永顺一中96 杨帆泸溪一中96 谢伯全泸溪一中96 王胜泸溪一中96 邓鑫泸溪一中96 龙智星凤凰华鑫中学96 杨港凤凰高级中学96 麻林珍凤凰华鑫中学96 宋子静州民中95 秦渊明州民中95 符鑫龙山高级中学95 邹昕龙山高级中学95 张发泸溪一中95 唐静泸溪一中95 李向媛泸溪一中95 张宇花垣边高95 张强古丈一中95 黄德强州民中94 田扑龙州民中94 彭梦圆州民中94 田红艳州民中94 李思龙州民中94 陈建朝州民中94 彭文婕州民中94 熊锦涛州民中94 周家豪州民中94林湘渝州二民中94 彭钊龙山皇仓中学94 田杰龙山高级中学94 尹志翔永顺一中94 秦海峰永顺一中94 丁超润永顺一中94 向爽永顺一中94 陈宜妥保靖民中94 代警坤泸溪一中94 杨雨凡凤凰华鑫中学94 龙秀位凤凰华鑫中学94 吴金鑫凤凰华鑫中学94 李水宽泸溪二中94 吴糠花垣边高94 石梦杨州民中93 李向阳州民中93 向灵柯州民中93 周熙洋州民中93 肖霁颖吉首市一中93 隆慧芝吉首市一中93 骆癸帆龙山皇仓中学93 付均永顺一中93 史枭航永顺一中93 田周纯古丈一中93 唐先澍州民中92 唐群青龙山皇仓中学92 彭元华龙山皇仓中学92 杨升龙山高级中学92 胡钊源龙山高级中学92 马宏国永顺一中92 符竟予永顺一中92 彭光钊保靖民中92 黄炜泸溪一中92 杨兴东泸溪一中92 谭海月泸溪一中92 杨颜菲泸溪一中92 刘岳凤凰华鑫中学92 刘欢花垣边高92 谢源州民中92田邵君州民中91 向泓霖州民中91 杨琳玢州民中91 梁婷州民中91 田仲毓州民中91 余渊州民中91 彭红娇州二民中91 张慧龙山皇仓中学91 向海容永顺一中91 杨洵永顺一中91 麻雷保靖民中91 龙建芝凤凰华鑫中学91 龙俊凤凰华鑫中学91 张祖英凤凰华鑫中学91 彭文文古丈一中91 吴中玉凤凰文昌中学90 田廷忠永顺二中78 李镇华吉首市民中54。
2014年长沙市首届中学数学教师解题能力大赛_高中试题)答案

(I)有人被调剂的概率;
(II)停业的店铺数 ξ 的分布列和数学期望。
解:设某人所开的两家小店分别为 A、B,A 店有 i 人请假记为事件 Ai (i = 0,1,2),B 店有 i 人请假记为事件 Bi (i = 0,1,2).
则有
.
sin PF1F2 sin PF2F1
( ) 【答案】 2 −1,1
.
解法
1,因为在
ΔPF1F2
中,由正弦定理得
PF2 sin PF1F2
=
PF1 sin PF2F1
则由已知,得
sin
a PF1F2
=
c sin PF2F1
,即 aPF1
= cPF2
设点 (x0 , y0 ) 由焦点半径公式,得 PF1 = a + ex0 , PF2 = a − ex0
22 3322
33
3
2
由几何概型知 cos π x 的值介于 0 到 1 之间的概率为 3 = 1 .
2
2
23
三、本大题共 6 小题,共 75 分. 解答应写出文字说明,证明过程或演算步骤.
16.(满分 12 分)
在△ABC 中,角 A、B、C 的对边分别为 a、b、c,且满足 a2 − ab + b2 = c2 .
故椭圆的离心率 e ∈ ( 2 −1,1)
解法 2
由解析 1 知 PF1
=
c a
PF2 由椭圆的定义知
PF1
+
PF2
=
2a则
c a
PF2
+
PF2
=
2a即PF2
2014年湖南隆回二中竞赛数学

2014年隆回县第二中学竞赛考试卷数 学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,全卷满分150分,考试时间120分钟.第I 卷(选择题共48分)一、选择题:本大题共8小题,每小题6分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若22{228}{log 1}xA xB x x -=∈<=∈>Z R ≤,,则()AB R ð的元素个数为( ) A .0B .1C .2D .32.在四边形ABCD 中,120A =︒,90B =︒,3AD =,BC =7BD =,求CD =( )A .3 B. C .7 D. 3.若对任意x ∈R ,不等式x ax ≥恒成立,则实数a 的取值范围是( ) A .1a <-B .1a ≤C .1a <D .1a ≥4.函数()3sin 2f x x π⎛⎫=- ⎪3⎝⎭的图象为C , ①图象C 关于直线1112x =π对称; ②函数()f x 在区间5ππ⎛⎫-⎪1212⎝⎭,内是增函数; ③由3sin 2y x =的图象向右平移π3个单位长度可以得到图象C . 以上三个论断中,正确论断的个数是( ) A .0 B .1 C .2D .35.如果点P 在平面区域22021020x y x y x y -+⎧⎪-+⎨⎪+-⎩≥≤≤上,点Q 在曲线22(2)1x y ++=上,那么PQ 的最小值为( ) A1B1- C.1 D16.若锐角α满足2sin 3αα+= ,则2tan 23πα⎛⎫+⎪⎝⎭的值是 A.- B. C.7D.7-7.定义在R 上的函数()f x 既是奇函数,又是周期函数,T 是它的一个正周期.若将方程()0f x =在闭区间[]T T -,上的根的个数记为n ,则n 可能为( )A .0B . 1C .3D .58.已知等差数列{}n a 中,27a =,4a 15= ,则前10项的和10S = ( ) A .100 B .210 C .380 D .400 9. 若等比数列{}n a 的前n 项和为13n n S a +=+,则常数a 的值等于( ) A .13- B .1- C .13D .3- 10.()f x =的最大值为( )A .1B .3C .4D .5第Ⅱ卷(非选择题 共102分)二、填空题:本大题共4小题,每小题6分,共24分.把答案填在答题卡的相应位置. 11.下列命题:①a c b c ⋅=⋅,则a b =;②若a 与b 是共线向量,c 与b 是共线向量,则a与c 也是共线向量;③若a b a b +=-,则0a b =;④若a 与b 是单位向量,则 1a b =12.在四面体O ABC -中,OA OB OC D ===,,,a b c 为BC 的中点,E 为AD 的中点,则OE = (用,,a b c 表示).13.如图,抛物线21y x =-+与x 轴的正半轴交于点A , 将线段OA 的n 等分点从左至右依次记为121n P P P -,,,, 过这些分点分别作x 轴的垂线,与抛物线的交点依次为 121n Q Q Q -,,,,从而得到1n -个直角三角形11Q OP △,212121n n n Q PP Q P P ---△,,△.当n →∞时,这些三角形 的面积之和的极限为 .yx1Q 2Q1n Q +21y x =+1P 2P2n P - 1n P - O第14题图14.在ABC ∆中,角A ,B ,C 的对边分别为a ,b ,c ,若A ,B ,C 成等差数列,2a ,2b ,3c 成等比数列,则cos cos A B =15. 设a ,b ,c 满足1a =,3b =,32a b =-,,60a b b c --=︒,则c 的最大值是三、解答题:本大题共6小题,共64分.解答应写出文字说明、证明过程或演算步骤. 15.(本小题满分12分)已知0αβπ<<4,为()cos 2f x x π⎛⎫=+ ⎪8⎝⎭的最小正周期,1tan 1(cos 2)4αβα⎛⎫⎛⎫=+-= ⎪ ⎪⎝⎭⎝⎭,,,a b ,且m =∙.求22cos sin2()cos sin ααβαα++-的值.16.(本小题满分14分)已知向量 )1,1(=m 和向量 和的夹角为43π,1-=∙。
数学--2014年全国高中数学联赛模拟试题(湖南师大附中)

2014年全国高中数学联赛模拟试题第一试一、填空题:本大题共8小题,每小题8分,共64分. 1、设127()3x f x x +=-+,11()(())n n f x f f x +=,2,3x x ≠-≠-,则2013(2014)f =______.答案:2012. 注意到 11()23f x x =--+,211()2312233f x x x =--=--+--++, 31()31223f x x x =--=--++.故20133(2014)(2014)2014f f ==. 2、设实数10x >,则函数()()()lglglg lglg lg lglg xxf x x x =-的值域为 .答案:{}0设lg lg y x =,则lg 10yx =, 则()()()()lg lglglg lglg lg lg lg lg 10100yyxxy yyy x x y y -=-=-=.3、设R 是满足00[][]5x y x y x y ≥⎧⎪≥⎨⎪+++≤⎩,,的点(),x y 构成的区域,则区域R 的面积为_______.(其中[]x 表示不超过实数x 的最大整数).答案:92一方面,当3x y +<时,有[][]3x y x y +≤+<,则[][]2x y +≤, 满足[][]5x y x y +++≤;另一方面,当3x y +>时,有[][]{}{}3x y x y +++>,而{}{}2x y +<, 则[][]1x y +>,从而[][]2x y +≥,于是[][]5x y x y +++>,这与条件矛盾.故区域R 的面积为92.4、二元函数()f x y ,的最大值为___________.答案:设2cos x a =,2cos y b =,则0,1a b ≤≤.f =由于0,1a b ≤≤,则2a a ≤1≤1≤,1≤=≤,故f ≤当1a b ==,或0,1a b ==或1,0a b ==时,f 取到最大值. 5、在等差数列{}n a 中,若11101a a <-,且它的前n 项n S 有最大值,那么当n S 取得最小正值时,n = .答案:19由于等差数列{}n a 的前n 项n S 有最大值和有最大值,则首项10a >,公差0d <.由11101a a <-,知道100a >,110a <,10110a a +<. 于是()()120201*********a a S a a +==+<,()1191910191902a a S a +==>,()()219191*********a a S S a a +-==+<.故那么当n S 取得最小正值时,19n =.6、甲、乙两人玩游戏,规则如下:第奇数局,甲赢的概率为34,第偶数局,乙赢的概率为34.每一局没有平局,规定:当其中一人赢的局数比另一人赢的局数多2次时游戏结束.则游戏结束时,甲乙两人玩的局数的数学期望为________.答案:163设游戏结束时,甲乙两人玩的局数的数学期望为E ,则()352288E E =⨯+⨯+解得163E =. 7、设五边形ABCDE 满足120A B C D ∠=∠=∠=∠=, 则AC BDAE ED⋅⋅的最小值为 .答案:34延长AB 与DC 相交于点H ,延长EA 与CB 相交于点F ,延长ED 与BC 相交于点G . 则,,AFB DCG BCH ∆∆∆均为正三角形. 设AB x =,BC y =,CD z =.容易得到四边形EAHD 为平行四边形,则EA HD y z ==+.在ABC ∆中,由余弦定理, AC =于是ACAE=.同理,BDED =故AC BDAE ED⋅=⋅.注意到,2)()02x y x y ≥+⇔-≥.有34AC BDAE ED⋅=≥⋅.等号成立,当且仅当x y z ==.即所求的最小值为34. 8、过正四面体ABCD 的顶点A 作一个形状为等腰三角形的截面,且使截面与底面BCD 所成的角为075.这样的截面共可作出 个 .答案:18设正BCD ∆中心为O ,以O为圆心,cot 753为半径作圆.则圆O 在BCD ∆的内部,且所求截面与平面BCD 的交线是该圆的切线.有三种情况:(1) 切线与BCD ∆的一边平行时,有6个这样的截面;(2) 切线11B C (其中1B 在边BC 上,1C 在边CD 上)且11CB C D =,则截面11AB C ∆为等腰三角形.这样的截面有6个;(3) 作BE 切圆O ,交CD 于E ,由BCE ACE ∆∆,有BE AE =,对应ABE ∆是等腰三角形,这样的截面共有6个.故满足条件的截面共有18个.二、解答题:本大题共3小题,共56分.9、(本小题满分16分)、试求实数a 的取值范围,使得2是不等式22log (23)21log x x a a+->+的最小整数解.首先 230xa ->,0a >,且12a ≠. 原不等式等价于22223log 201log x a x a a-+->+. (1)当 21log 0a +>,即12a >时,有 2223log 20x a x a-+->,整理有 2223240x x a a -⋅->. 解得 24xa >,2xa <-(舍去). 从而 2log 4x a >. 注意到当12a >时,2log 41a >.故要使2是不等式22log (23)21log x x a a+->+的最小整数解,有2log 42a <,解得1a <,于是112a <<. (2)当21log 0a +<,即102a <<时,注意到343422a ->->,有 2222log (23)01log a a+-<+不合题设条件.即102a <<不满足条件. 综上所述,a 的取值范围为1(,1)2.10、(本小题满分20分)、数列{}1n n a ≥定义为11a =,24a =,)2n a n ≥.⑴ 求证:数列{}1n n a ≥为整数列;⑵ 求证:121n n a a ++()1n ≥是完全平方数. 证明:⑴ 定义00a =.当1n ≥时,2111n n n a a a -+=+,2121n n n a a a ++=+,两式相减,整理得:()()1112n n n n n n a a a a a a ++-++=+, 即2111n n n n n na a a a a a ++-+++=()1,0n n a ∀≥≠.因此2112201114n n n n n n n n n a a a a a a a a a a a a ++--+-++++=====. 故 214n n n a a a ++=-.(1n ≥)由此二阶递推式及11a =,24a =,容易得到数列{}1n n a ≥为整数列. ⑵ 对1n ≥,()21111111044n n n n n n n n n a a a a a a a a a ++-+++-=-+=-+()()22211114121n n n n n n n n a a a a a a a a ++++=-+-=--+.因此()21121n n n n a a a a +++=-. 故命题得证!11、(本小题满分20分)、若1l 与2l 是两条互相平行的直线,其中1l 与抛物线:C 2(0)y ax bx c a =++≠交于,A B 两点,2l 与抛物线C 相切于D 点,记ABD ∆的面积为1S ,弓形ADB 的面积为2S .求证:12S S 为定值,并求这个定值.(即与,,a b c 无关). 证明:不妨设抛物线2(0)y ax bx c a =++>.直线1l ,2l 的方程分别为y kx m =+,y kx n =+.设()()()112233,,,,,A x y B x y D x y ,其中12x x <.联立直线1l 与抛物线方程,有2()0ax b k x c m +-+-=,依题设,2()4()0b k a c m ∆=--->.由韦达定理,12b k x x a -+=-,12c mx x a-=.容易得到21x x a-=.于是AB =.联立直线2l 与抛物线方程,有2()0ax b k x c n +-+-=,依题设,2()4()0b k a c n '∆=---=,所以()244ac b k n a--=.又两条平行直线之间的距离为d =ABD ∆的面积为112S AB d =⋅⋅=. 对弓形ADB 的面积为()2122()()x x S kx m axbx c dx =+-++⎰2322322222211111111111232232kx mx ax bx cx kx mx ax bx cx ⎛⎫⎛⎫⎛⎫⎛⎫=+-++-++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭()()()()()221121212111332x x a x x ax x b k x x c m ⎡⎤=--++--+--⎢⎥⎣⎦将12b k x x a -+=-及12c m x x a-=代入上式, 2S =. 从而1234S S =.加试一、(本小题满分40分)一、如图,设A 为12,O O 的一个交点,直线l 切12,O O 分别于,B C ,3O 为ABC∆的外心,3O 关于A 的对称点为D ,M 为12O O 的中点.求证:12O DM O DA ∠=∠. 证明:易得31O O 是AB 的中垂线,32O O 是AC 的中垂线.连接12,AO AO .则31112O O A BO A CBA ∠=∠=∠,MDO 2O 1O 3CBAMDO 2O 1O 3CBA13312O O A BO A BCA ∠=∠=∠,故 31O O ACBA ∆∆.同理,3213O O ABCAO O A ∆∆∆.做312O O O ∆的外接圆Γ,设3O A 交Γ于另一点E ,则123213EO O AO O AO O ∠=∠=∠,213123EO O AO O AO O ∠=∠=∠,故121332O EO O AO O AO ∆∆∆.从而133122O O O A O O EO =,233121O O O AO O EO =, 因此 312132321O A O O O O EO O O EO ⋅=⋅=⋅,于是四边形132O O O E 是调和四边形. 由托勒密定理,()3121323213121122O A O O O O EO O O EO O E O O ⋅=⋅+⋅=⋅, 所以, 3312O A O E =,从而E 与D 重合. 再由 ()2313232113212MO O D O O EO O O O E O O O D ⋅=⋅+⋅=⋅,知道312O O D O MD ∆∆.所以,213O DM O DO ∠=∠. 故12O DM O DA ∠=∠.二、(本小题满分40分)设1101n n a a a -<<<<<.求证:()2221212121211112n n n a a a a a na a a a +++>+++----.证明:令211ni i i ia L a a =-=-∑,约定01a =,1n i i R ia ==∑,1ni i S a ==∑.由柯西不等式,(2221121ni i L i ==⎛⎫=≥+∑∑()()()()()()()()221122221011212219232121n i i nn i i i ni i i a R S i aa a i i a n a =--==⎛⎫+ ⎪+⎝⎭==+-++-+-+∑∑∑()()2222124444889889988n ii R S R RS S R RSR S R S i a =++++>=>++++++∑ 19191121616182162R R R R R S =->->-++. 故原不等式得证!三、(本小题满分50分)试求所有的正整数n ,使得存在正整数数列12n a a a <<<,使得和()1i j a a i j n +≤<≤互不相同,且模4意义下各余数出现的次数相同.解:所求的n 为4k ,其中k 为正整数. 我们用i m 表示12,,,n a a a 中模4余i 的个数,1,2,3,4i =.注意到,若12,,,n a a a 满足题设条件,则121,1,,1n a a a +++也满足题设条件,故可不妨设 1324m m m m +≥+.记214n T C =,考察()i j a a i j +<模4不同类中的项数,有13242224221314231234m m m m C C m m T C C m m Tm m m m T m m m m T⎧++=⎪++=⎪⎨+=⎪⎪+=⎩ ……(*) 所以 ()()13242213242m m m m T m m m m C C ++=++=+故 ()()()()()213241324m m m m m m mm +++=+-+.令()()13240k m m m m =+-+≥,则有2132k k m m ++=,2242k k m m -+=,2n k =.另一方面,由(*)知,()()13240m m m m --=,()()221324m m m m k -=-+,由于n 为正整数,则1k ≥,从而 240m m -=,且 ()213m m k -=,令13l m m =-,则2k l =,42244l l m m -==,()42421322,,44l l l l l l m m ⎛⎫+++-= ⎪⎝⎭或424222,44l l l l l l ⎛⎫+-++ ⎪⎝⎭,满足条件(*). 故24n k l ==满足题设条件.综上所述,所求的n 为4k ,其中k 为正整数.四、(本小题满分50分)集合S 是由空间内2014个点构成,满足任意四点不共面.正整数m 满足下列条件:将任意两点连成一条线段,并且在此线段上标上一个m ≤的非负整数,使得由S 中顶点构成的任何一个三角形,一定有两边上的数字是相同的,且这个数字小于第三边上的数字.试求m 的最小值.解:考虑一般情形,集合S 由4n ≥个点构成,满足任意四点不共面.正整数m 满足条件:在任意线段上标上一个m ≤的非负整数,使得由S 中顶点构成的任何一个三角形,一定有两边上的数字是相同的,且这个数字小于第三边上的数字.记r 为线段上被标数字不同的数目,则1r m ≤+.高中数学打印版校对版本 下面我们用数学归纳法证明:2log r n ≥.当4n =时,结论平凡;对4n >,取标上数字最小的边AB ,记为数字d .任取异于,A B 的点C S ∈,则AC 或BC 边上的数字恰有一个为d .记{}{}|,P C AC d C S A ==∈,{}{}|,Q C BC d C S B ==∈. 不妨设2n P ≥. 由归纳假设知,对P 中被标数字的数目22log log 12n n ≥=-,因为d 是被标记数字中最小的,故()22log 11log r n n ≥-+=.故结论成立.特别地,当2014n =时,有2log 2014r ≥,从而11r ≥.从而10m ≥.下证,m 的最小值为10.记这2014个点分别为1,2,,2014,我们标记线段()ij i j >上的数字为t ,其中t 为满足2|t i j -的最大非负整数.因为,2014i j ≤,所以10t ≤.现设,,i j k 为任意不同的三点,若线段,ij ik 被标记为同一数字s ,则2s i j a -=,2s i k b -=,这里,a b 均为奇数,于是()()2()s j k i k j k b a -=---=-,由于b a -为偶数,知线段jk 上标记的数字大于s ,满足题设条件;若线段,ij ik 标记为不同的数字,()t s t s <,则2t i j a -=,2s i k b -=,这里,a b 均为奇数,于是()()2(2)t s t j k i k j k b a --=---=-,由于2s t b a --为奇数,知线段jk 上标记的数字为t ,满足题设条件.综上所述,m 的最小值为10.。
2014年全国高中数学联赛湖南赛区初赛试题(word版)

2014年全国高中数学联赛湖南赛区初赛试题(6月28日9:00至11:00)一.选择题(本大题共6小题,每小题5分,满分30分)1.设{}22,,M a a x y x y ==-∈Z ,则( ) A .9,10M M∈∈ B .9,10M M ∉∈ C .9,10M M ∈∉ D .9,10M M ∉∉2.设条件p :实数,m n 满足24,03;m n mn <+<⎧⎨<<⎩ 条件q :实数,m n 满足01,2 3.m n <<⎧⎨<<⎩,则() A .p 是q 的充分不必要条件 B .p 是q 的必要不充分条件C .p 是q 的充要条件D .p 既不是q 的充分条件又不是q 的必要条件3.若{}n a 是等差数列,首项10a >,201320140a a +>,201320140a a ⋅<,则使前n 项和0n S >成立的最大自然数n 是( ) A .4025 B .4026 C .4027D .40284.给定平面向量(1,1)=a ,那么,平面向量=b 是向量a 经过( ) A .顺时针旋转o 60所得 B .顺时针旋转o 120所得C .逆时针旋转o 60所得D .逆时针旋转o 120所得5.在如图所示的三棱柱中,点A 、1BB 的中点M 以及11B C 的中点N 所决定的平面把三棱柱割成体积不同的两部分,则较小部分的体积和原三棱柱的体积之比为( )A .2336 B .1336 C .1323 D .12236.已知圆222:C x y r +=,两点P 、*P 在以O 为起点的射线上,并且满足*2OP OP r ⋅=,则称P 、*P 关于圆周C 对称,那么双曲线221x y -=上的点(,)P x y 关于单位圆周22:1C x y +=的对称点*P 所满足的方程是( )A .2244x y x y -=+B .22222()x y x y -=+C .22442()x y x y -=+ D .222222()x y x y -=+二.填空题(本大题共6小题,每小题8分,满分48分)7.已知函数22()5319653196f x x x x x =-++-+,则(20)(14)f f += .8.已知02x π<<,πsin cos 4x x -=,若1tan tan x x +可以表示成πc a b -的形式(a ,b ,c 是正整数),则a b c ++= .9.不等式322430x x x --+<的解集是 .10.已知一无穷等差数列中有3项(顺次排列但不一定相连):13,25,41,则可以判断得出2013 (填“是”、“不是”、“不能确定”)数列中的一项.11.随机挑选一个三位数I ,则I 含有因子5的概率为 .12.已知实数,x y 满足0,50,30,x y x y y -⎧⎪+-⎨⎪-⎩≤≥≤若不等式222()()a x y x y ++≤恒成立,则实数a 的最大值是 .三.解答题(本大题共4小题,满分72分)13.(本小题满分16分)已知O 为ABC △的内部一点,BAO CAO CBO ACO ∠=∠=∠=∠,试探究ABC △的三边满足的关系,并证明你的结论.14.(本小题满分16分)某旅游区每年各个月接待游客的人数近似地满足周期性规律,即第n 个月从事旅游服务工作的人数()f n 可近似地用函数()100[cos()]f n A n k ωα=++来刻画,其中正整数n 表示月份且*n ∈N ,例如1n =表示1月份,A 和k 是正整数,0ω>,π(,π)2α∈.统计发现,该地区每年各个月份从事旅游服务工作的人数有以下规律:每年相同的月份,该地区从事旅游服务工作的人数基本相同;该地区从事旅游服务工作的人数最多的8月份和最少的2月份相差约400人;2月份该地区从事旅游服务工作的人数约为100人,随后逐月递增直到8月份达到最多.(1)试根据已知信息,确定一个符合条件的()f n 的表达式;(2)一般地,当该地区从事旅游服务工作的人数在400或400以上时,该地区也进入了一年中的旅游“旺季”,那么,一年中的哪几个月是该地区的旅游“旺季”?请说明理由.15.(本小题满分20分)若实数0x 满足00()f x x =,则称0x x =为函数()f x 的一个不动点.已知32()3f x x ax bx =+++(其中a ,b 为常数)有互异的两个极值点1x 和2x .试判断是否存在实数组(,)a b ,使得1x 和2x 皆为不动点,并证明你的结论.16.(本小题满分20分)已知数列{}n x 满足:212n n n x x x ++=+,12x =,26x =;数列{}n y 满足:212n n n y y y ++=+,13y =,29y =.求证:存在正整数0n ,使得对任意0n n >都有n n x y >.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
湖南省2014年高中数学竞赛
湘西自治州赛区学生获奖情况通报
湖南省2014年高中数学竞赛分为高二年级和高三年级两个组别于六月二十八日进行。
湘西自治州赛区的有关工作已经完成。
本次竞赛实行交叉巡考,集中评卷,各项工作认真、严格、有序。
全州评出高三年级一等奖32人,二等奖 50人,三等奖 80人;高二年级一等奖 52人,二等奖 74人,三等奖 132人。
现将学生获奖情况(见附件)通报如下,望获奖同学再接再厉。
湘西州教育科学研究院
2014年7月5日
附件:2014年湖南省高中数学竞赛湘西自治州赛区学生获奖情况通报
高三组
一等奖(32人)
二等奖(50人)
三等奖(80人)
高二组
一等奖(52人)
三等奖(132人)。
