无理根式的不定积分
不定积分求解方法

不定积分求解方法本页仅作为文档封面,使用时可以删除This document is for reference only-rar21year.March探讨不定积分的解题方法班级学号姓名51 杨洁珊摘要在数学分析中,不定积分占有非常重要的地位,是高等数学教学的难点和重点.具有很高的灵活性,可以开拓学生的思路,培养学生灵活的思维能力,同时还存在一题多解的方法使学生能过做到举一反三、触类旁通的教学效果。
为了正确使用各种积分方法求解不定积分,我们必须掌握它的概念和性质以及积分的基本公式,才能够在以后的解题中做题自如,进行同类迁移。
研究不定积分要重在提高自己的逻辑思维能力、科学分析能力、运用数学语言能力、联想运算能力以及应用能力。
求解不定积分的过程对学生的科学思维和文化素质的培养所起的作用极为明显。
求解不定积分的方法主要有直接积分法(即直接利用积分公式求解)、换元积分法(第一换元积分法、第二换元积分法)、分部积分法。
关键词不定积分、直接积分法、换元积分法、分部积分法、分解积分法。
前言正如假发有逆运算减法,乘法有其逆运算除法一样,微分法也有它的逆运算——积分法。
我们已经知道微分法的基本问题是研究如何从已知函数求出它的导函数,相反:求一个未知函数使其导函数恰好是某一已知函数。
提出这个逆问题,首先是因为它出现在许多实际问题之中,如:已知速度求路程;已知加速度求速度;已知曲线上每一点处的,求曲线方程等等这些都是积分在生活中的应用,特别是在物理学中的应用,变力做功,质点做变速直线运动的路程以及引力问题。
所以掌握不定积分的求法,在我们的数学物理科学研究工作中显得尤为重要。
标题一、直接积分法我们已经知道积分法是微分的逆运算,即直接积分法就是利用最基本的积分公式求解积分。
要掌握这一方法首先就应该熟记,并懂得灵活运用。
下面的基本积分表就必须掌握1.0dx c=⎰2adx ax c=+⎰3.()10,01aaxx dx c a xa+=+≠>+⎰4() 1ln||0 dx x c xx=+≠⎰5.x xe e c=+⎰6.(0,1)ln x x a a dx c a a x=+>≠⎰17.cos sin axdx ax c a=+⎰ ()18sin cos 0axdx ax c a a=-+≠⎰ ()29sec tan 0xdx x c a =+≠⎰210.csc tan xdx x c =+⎰11.sec tan sec x xdx x c =+⎰12.csc cot csc x xdx x c =-+⎰13.arcsin arccos 'dxx c x c =+=-+⎰ 214.arctan cot '1dx dx x c arc x c x=+=-++⎰ 22115.ln ||2dx x a c x a a x a-=+-+⎰ 16.sec ln |sec tan |xdx x x c =++⎰在实际计算中最重要的是要把复杂的运算转化为熟悉的积分公式,如下几种情况(1).假分式化为真分式方法:分母不改变,对分子进行拼凑,转化为真分式。
浅谈无理函数不定积分的求解方法

浅谈无理函数不定积分的求解方法摘要:我们将自变量包含在根式之下的函数称为无理函数。
这样的特点使得无理函数不定积分,在通常情况下求解较为复杂。
对于一个无理函数来说,大多数情况下,较常见的情况是同一个无理函数有多个求不定积分的方法,如何从多种不定积分求解方法中选出最优的解法,就是一个我们需要考虑的问题了。
本文旨在将以往的无理函数不定积分求解方法进行综述,探讨各个方法在求解上的应用与具体使用过程。
同时,总结了对一些常见的无理函数不定积分类型的常用解法。
为无理函数不定积分的求解提供一种思路。
关键字:无理函数不定积分计算方法Abstract:We usually call the function which have one or more arguments under the radical as irrational function. The feature of irrational function makes the irrational function integral become tough problem for we to solve. For an irrational function, in most cases, the more common situation is the same irrational function with multiple indefinite integral method. So, how to select an optimal solution from a variety of indefinite integral method, is a problem that we need to consider.This article aims to past the irrational function of indefinite integral solution method to carry on the summary, discusses the application of various methods on solving the use with specific process. At the same time, summarizes the irrational function of some common indefinite integral types of commonly used method. In order to provide a way to solve the irrational function indefinite integral problems.key words:irrational function indefinite integral method1.无理函数不定积分的求解方法通常情况下,我们对无理函数不定积分的求解通常都会先对无理函数部分做前置处理工作。
有理函数的积分
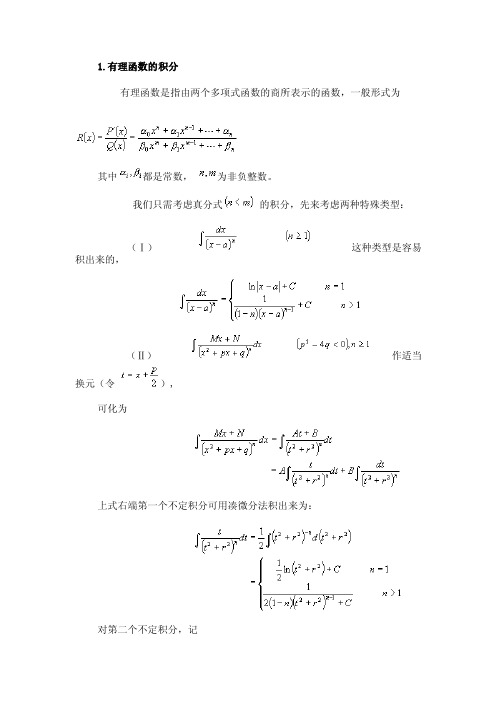
1.有理函数的积分有理函数是指由两个多项式函数的商所表示的函数,一般形式为其中都是常数,为非负整数。
我们只需考虑真分式的积分,先来考虑两种特殊类型:(Ⅰ)这种类型是容易积出来的,(Ⅱ)作适当换元(令),可化为上式右端第一个不定积分可用凑微分法积出来为:对第二个不定积分,记用分部积分法可导出递推公式:整理得重复使用递推公式,最终归结为计算而可积出来为这样就可完成对不定积分(Ⅱ)的计算。
对任一个有理函数而言,均可写成一个多项式与一个有理真分式的和,而多项式的积分问题已经解决,下面主要考虑有理真分式(不妨设)的积分问题。
为叙述简便,不妨设.其方法是将化成许多简单分式(即类型(Ⅰ)、(Ⅱ))的代数和然后逐项积分。
由于类型(Ⅰ)、(Ⅱ)总是可“积出来”的,从面有理函数总是可以“积出来”。
下面简述分解有理真分式()的步骤:第一步按代数学的结论,将分母分解成实系数的一次因式与二次因式的乘幂之积。
其中均为自然数。
第二步根据因式分解结构,写出的部分分式的待定形式:对于每个形如的因式,所对应的部分分式为对于每个形如的因式,所对应的部分分式为把各个因式所对应的部分分式加起来,就完成了对的部分分式分解。
第三步确定待定系数:通分后比较分子上的多次式的系数,得待定系数的线性方程组,由此解得待定系数的值。
例8.13 求2.三角函数有理式和积分由及常数经过有限次四则运算所得的函数称为关于的有理式(或三角函数有理式)。
用表示对于这种函数的不定积分我们总可通过代换,化为以为变量的有理函数的积分。
理由是,,,又,故从而上面的讨论说明:三角函数有理式也总是可以“积出来”的,但对具体问题而言,用上述方法往往计算量太大,因此,有时要考虑用其它简便方法。
(1)如果是的奇函数时,即则设即可。
例如求(1);(2).(2)如果是的奇函数时,即则设即可。
例如求.(3)如果是关于与的偶函数时,即则设即可。
例如求(1);(2).(4)请研究被积函数为(为自然数)时的情况。
有理函数、三角函数及一些无理函数的不定积分

1 x 1 1 2 J n 1 2 [ dx] 2 2 n 1 2 2 n 1 n 1 (x a ) a 2a n 1 ( x a ) Jn 1
2 2
x
2 n 1
2( n 1)a ( x a )
2n 3 2( n 1)a
2
J n 1 .
分解后的部分分式必须是最简分式.
1 dx . 例4 求积分 2 x( x 1) 1 1 1 1 dx 解 dx 2 2 x ( x 1) x ( x 1) x 1 1 1 1 dx dx dx 2 x ( x 1) x 1
2u 1 u 2 1 u 2 du 2 (1 u)(1 u )
(1 u)2 (1 u2 ) 1 u 1 du du du 2 2 (1 u)(1 u ) 1 u 1 u
1 = arctanu ln(1 u2 ) ln | 1 u | C 2
§有理函数、三角函数及一些无理函 数的不定积分
1、 有理函数的积分 2、 三角函数有理式的积分 3、 无理函数的积分
一、有理函数的积分
有理函数的定义: 两个多项式的商表示的函数.
P ( x ) a0 x n a1 x n1 an1 x an Q( x ) b0 x m b1 x m 1 bm 1 x bm
A B 1, A 5 , ( 3 A 2 B ) 3, B 6 x3 5 6 . 2 x 5x 6 x 2 x 3
A B C 1 , 例2 2 2 x ( x 1 ) x ( x 1) x 1
= -d (cotx )
(2021年整理)不定积分解题方法及技巧总结

不定积分解题方法及技巧总结(推荐完整)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(不定积分解题方法及技巧总结(推荐完整))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为不定积分解题方法及技巧总结(推荐完整)的全部内容。
不定积分解题方法及技巧总结(推荐完整)编辑整理:张嬗雒老师尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布到文库,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是我们任然希望不定积分解题方法及技巧总结(推荐完整)这篇文档能够给您的工作和学习带来便利。
同时我们也真诚的希望收到您的建议和反馈到下面的留言区,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请下载收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为〈不定积分解题方法及技巧总结(推荐完整)〉这篇文档的全部内容。
⎰不定积分解题方法总结摘要:在微分学中,不定积分是定积分、二重积分等的基础,学好不定积分十分重要。
然而在学习过程中发现不定积分不像微分那样直观和“有章可循”.本文论述了笔者在学习过程中对不定积分解题方法的归纳和总结. 关键词:不定积分;总结;解题方法不定积分看似形式多样,变幻莫测,但并不是毫无解题规律可言.本文所总结的是一般规律,并非所有相似题型都适用,具体情况仍需要具体分析。
1.利用基本公式。
(这就不多说了~)2.第一类换元法.(凑微分)设f(μ)具有原函数F (μ)。
则C x F x d x f dx x x f +==⋅⎰⎰)]([)()]([)(')]([ϕϕϕϕϕ其中)(x ϕ可微。
高数同济44有理函数三角函数及一些无理函数的不定积分

例4 求积分
1 x(x 1)2dx.
解 x(x11)2dx1 x(x 11)2x1 1dx
1 xd x(x 11)2d xx1 1dx
ln x1ln x (1)C . x1
1
例5 求积分 (12x)(1x2)dx.
解 (12x)1(1x2)dx1542xdx152xx215dx
5 2 ln 1 2 ( x ) 1 5 1 2 x x 2d x 1 5 1 1 x 2 dx
由代数学定理:
Q(x)=b0(x-a) …(x-b) (x2 +px+q) …(x2+rx+s)
Q(x)=b0(x-a) …(x-b) (x2 +px+q) …(x2+rx+s)
难点 将有理函数化为最简分式之和.
设 Q P((x x))b a 00 x x m n b a 1 1x xm n 1 1 b am n 1 1x x a bn m是真 . 分
例12
求积分
x 3x1
d.x 2x1
解 先对分母进行有理化
原式 (3 x 1 x (2 3 x x 1 1 ) (3 2 x x 1 1 )2 x 1 )dx
(3x 12x 1 )dx
1 3 3x1d(3x1)1 2 2x1d(2x1)
2(3x1)2 31(2x1)2 3C .
例1 x3 x2 5x6
化为最简分式之和.
x3 A B ,
待
(x2)(x3) x2 x3
定
x 3 A ( x 3 ) B ( x 2 ),系
数
x 3 ( A B ) x ( 3 A 2 B ), 法
A(3A B21,B)3,
第四节 三角函数有理式与某些无理根式的不定积分

原式 t6 2t4 1.12t11dt 12 t14 2t12 t8 dt 4 t15 24 t13 4 t9 C
t3
5 13 3
4
5
x4
24
13
x12
4
3
x4
C.
5 13 3
6
3、形如 R x, ax2 bx c dx, a 0, ax2 bx c 0, 在一般的
的积分公式。
5)、形如:
dx , (n N , 且 n 3), 则令 x 1, 再利
xn x2 a2
t
用凑微分法或由已知公式;当 n 3 时,则一般用第二换元法
(作三角函数变换去根号)
10
R(sin x, cos x)dx 才考虑用万能置换法?
一般地,不满足上述2)的各种特殊情形的,才考虑用万 能置换法。
4
三、某些无理(根式)函数的不定积分 一般的无理(根式)函数的不定积分并不一定能求得出来,而对于 一些简单的无理函数则可通过适当的代换可化为有理函数的不定积 分,作代换的目的就是去掉根号。以下是一些常见无理(根式)函 数的不定积分的求法:
2
2
cos( ),
cos.cos 1 cos( ) cos( ). 求出其积分。
2
m
n
c、对于 sin x cos x dx, 当m、n中有一奇数时,可拆开它,然后用
凑微分法求其积分;
当m、n均为偶数时,可利用倍角公式:sin x cos x 1 sin 2x; 2
n1 ax b ,L cx d
,
nk
ax cx
积分运算法则

不定积分的运算法则;包含如下两个性质注意性质适用条件:1、设函数fx的原函数存在即fx可积;下同;k是常数;则:1k≠02k=02、设fx;gx两个函数存在原函数;则:3、常见积分几种运算法换元积分法:①设fu具有原函数Fu ;如果u是中间变量:u=x;且x可微;那么;根据复合函数微分法;有dF=x=fx'xdx;从而根据不定积分的定义就得:若要求;若可化为的形式;那么:这种方法称为第一类换元法..②利用第二类换元法化简不定积分的关键仍然是选择适当的变换公式x = φt..此方法主要是求无理函数带有根号的函数的不定积分..由于含有根式的积分比较困难;因此我们设法作代换消去根式;使之变成容易计算的积分.. 下面简单介绍第二类换元法中常用的方法:1根式代换:被积函数中带有根式;可直接令t =2三角代换:利用三角函数代换;变根式积分为有理函数积分;有三种类型:被积函数含根式;令被积函数含根式;令;被积函数含根式;令..注:记住三角形示意图可为变量还原提供方便..3倒代换即令:设m;n 分别为被积函数的分子、分母关于x 的最高次数;当n-m>1时;用倒代换可望成功4指数代换:适用于被积函数由指数所构成的代数式;5万能代换半角代换:被积函数是三角函数有理式;可令;则:分部积分法:设函数u=ux及v=vx具有连续导数;则其乘积的导数为:;移项得:对两边求不定积分;得:也可写为:如果求有困难;而求比较容易时;分部积分公式就可以发挥作用了..。
数学分析8.3有理函数可化为有理函数的不定积分

第八章 不定积分3 有理函数可化为有理函数的不定积分一、有理函数的不定积分有理函数:由两个多项式函数的商所表示的函数,其一般形式为:R(x)=)(Q )P(x x =n1-m 1m 0n1-n 1n 0βx βx βαx αx α+⋯+++⋯++, 其中n,m 为非负整数,α0,α1,…αn 与β0,β1,…βn 都是常数,且α0β0≠0. 若m>n ,则称它为真分式;若m ≤n ,则称它为假分式.注:1、假分式可化为整式与真分式的和;2、真分式可表示为若干个部分分式之和(称为部分分式分解);3、分解部分分式的一般步骤:第一步:对分母Q(x)在实系数内作标准分解:(分解前先化β0=1) Q(x)=(x-a 1)1λ…(x-a s )sλ(x 2+p 1+q 1)1μ…(x 2+p t +q t )tμ,其中λi ,μj (i=1,2,…,s ;j=1,2,…,t)均为自然数,而且∑=s1i iλ+2∑=t1j j μ=m ;p j 2-4q j <0, j=1,2,…,t.第二步:根据分母各因式分别写出与之相应的部分分式。
对于每个形如(x-a)k 的因式,它所对应的部分分式是:a -x A 1+22a)-(x A +…+k k a)-(x A ;对于每个形如(x 2+px+q)k 的因式,它所对应的部分分式是:q px x C x B 211++++2222q)px (x C x B ++++…+k2kk q)px (x C x B +++.第三步:确定待定系数。
将所有部分分式通分相加,所得分式的分母即为原分母Q(x),分子与原分子P(x)恒等。
根据同幂项系数相等,可得一组关于待定系数的线性方程,方程组的解就是需要确定的系数。
例1:对R(x)=8-x 4x 2x 5x x 10-x 9x 4x 2x 2345234+--+++-作部分分式分解.解:Q(x)=x 5+x 4-5x 3-2x 2+4x-8=(x-2)(x+2)2(x 2-x+1), R(x)=2-x A 0+2x A 1++222)(x A ++1x x C Bx 2+-+,两边乘以Q(x)得:2x 4-x 3+4x 2+9x-10 ≡A 0(x+2)2(x 2-x+1)+A 1(x 2-4)(x 2-x+1)+A 2(x-2)(x 2-x+1)+(Bx+C)(x-2)(x+2)2. 根据等式两边同幂项系数相等,得到线性方程组:⎪⎪⎪⎩⎪⎪⎪⎨⎧-10.=8C -2A -4A -4A ,9=4C -8B -3A +4A ,4=2C +4B -3A -3A -A ,-1=C +2B +A +A -3A ,2=B +A +A 2102121021010 解得:A 0=1, A 1=2, A 2=-1, B=-1, C=1. ∴对R(x)作部分分式分解的结果为:R(x)=2-x 1+2x 2+-22)(x 1+-1x x 1-x 2+-.注:对以上待定系数法有时可运用简便方法,如将x=2代入恒等式得: 32-8+16+18-10≡A 0·(2+2)2(4-2+1),∴A 0=1,将x=-2代入恒等式得: 32+8+16-18-10≡A 2(-2-2)(4+2+1),∴A 2=-1,于是化简恒等式得: x 4-3x 3+12+16≡A 1(x 2-4)(x 2-x+1)+(Bx+C)(x-2)(x+2)2,分别令x=0,1,-1可得:⎪⎩⎪⎨⎧+ 8.=C +B -3A 2,=3C 3B +A 4,=2C +A 111 解得:A 1=2, B=-1, C=1.小结:求有理真分式的不定积分可归为以下两种形式的不定积分:(1)∫k a)-(x dx =⎪⎩⎪⎨⎧>+=+ 1.k ;C a)-k)(x -(111,k C ;|a -x |ln 1-k (2)∫k 2q)px (x M Lx +++dx=∫k 22)r (t N Lt ++dt=L ∫k 22)r (t t +dt+N ∫k22)r (t dt+,其中 t=x+2p ,r 2=q-4p 2,N=M-4p L.当k=1时,原式=L ∫22r t t +dt+N ∫22rt dt +=2L ln(t 2+r 2)+ r N arctan r t +C. 当k ≥2时,∫k 22)r (t t +dt =1-k 22)r (t )k 1(21+-+C. I k =∫k 22)r (t dt +=2r 1∫k 22222)r (t t -)r (t ++dt=2r 1I k-1-2r 1∫k 222)r (t t +dt=2r 1I k-1+)1k (2r 12-∫td ⎥⎦⎤⎢⎣⎡+1-k 22)r (t 1=2r 1I k-1+)1k (2r 12-⎥⎦⎤⎢⎣⎡-+1-k 1-k 22I )r (t t=1-k 21-k 222I )1k (2r 3-2k )r (t )1k (2r t -++-.重复计算直至归为计算I 1. 最后换元为x ,就得到最终的结果.例2:求∫2222)2x -(x 1x ++dx. 解:2222)2x -(x 1x ++=2222)2x -(x 1)-x 2(2)x 2(x +++-=22x -x 12++222)2x -(x 1-x 2+∫22x -x dx2+=∫11)-(x 1)-d(x 2+dx=arctan(x-1)+C.∫222)2x -(x 1-x 2+dx=∫2222)2x -(x 2)2x -d(x +++∫221)]1)-[(x 1)-d(x +=-222)2x -(x 1++∫22)1t (dt +. ∫22)1t (dt +=1)2(t t 2++21∫1t dt 2+=1)2(t t 2++21arctant+C=2)2x -2(x 1-x 2++21arctan(x-1)+C. ∴原式= arctan(x-1)-222)2x -(x 1++2)2x -2(x 1-x 2++21arctan(x-1)+C=2)2x -2(x 3-x 2++23arctan(x-1)+C.二、三角函数有理式的不定积分:由u(x),v(x)及常数经过有限次四则运算所得到的函数称为关于u(x),v(x)的有理式,并用R(u(x),v(x))表示.∵sinx=2x tan 12x2tan2+=2t12t +, cosx=2x tan 12xtan -122+=22t 1t -1+, (t=tan 2x ); ∴∫R(sinx,cosx)dx=∫R(2t 12t +,22t 1t -1+)d(2arctant)=∫R(2t 12t +,22t 1t -1+)2t12+d(t). 例3:求∫cosx )sinx (1sinx1++dx.解:∫cosx )sinx (1sinx 1++dx=∫22222t 12)t1t -1(1t 12t t 12t 1+⋅+++++dt =21∫(t+2+t 1)dt=4t 2+t+21ln|t|+C=41tan 22x + tan 2x +21ln|tan 2x|+C.例4:求∫xcos b x sin a dx2222+(ab ≠0).解:∫x cos b x sin a dx 2222+=∫2222b x tan a x sec +dx=∫222b x tan a dtanx +=∫222b t a dt+=ab 1∫1b at bat d 2+⎪⎭⎫ ⎝⎛⎪⎭⎫ ⎝⎛=ab 1arctan b at +C=ab 1arctan batanx +C.三、某些无理根式的不定积分: 1、∫R(x,nd cx b ax ++)dx 型不定积分(ad-bc ≠0),只需令t=n dcx bax ++,化为有理函数的不定积分. 例5:求∫2x 2x x1-+dx. 解:令t=2x 2x -+,则x=1t 22t 22-+,原式=∫22t 1)t(t 22+-d 1t 22t 22-+=∫2222221)2)(t (2t 2)]2t(2t -1)1)[4t(t t(t -++--dt=-2∫1)1)(t (t 2t 222-+dt=-2∫(1t 12++1t 12-)dt=-2arctant-∫(1t 1--1t 1+)dt=ln 1t 1t -+-2arctant +C =ln12x 2x 12x 2x --++-+-2arctan 2x 2x -++C=ln 2x 2x 2x 2x --+-++-2arctan2x 2x -++C =ln 44x 2x 22-+-2arctan 2x 2x -++C=ln|2x+24x 2-|-2arctan 2x 2x -++C.例6:求∫2xx 2x)(1dx-++.解:∫2x x 2x)(1dx-++=∫)x 1)(x 2(x)(1dx+-+=∫x2x1x)(112-++dx. 令t=x 2x 1-+,则x=1t 1-2t 22+,dx=22221)(t 1)-2t(2t -1)4t(t ++dt=221)(t t 6+dt. 1+x=1+1t 1-2t 22+=1t 3t 22+,2x )(11+=422t 91)(t +.原式=∫224221)(t t6t 91)t(t +⋅+dt=32∫t -2dt=-t 32+C=x 1x 232+--+C.2、∫R(x,c bx ax 2++)dx 型不定积分(a>0时b 2-4ac ≠0, a<0时b 2-4ac>0),由于ax 2+bx+c=a[(x+a 2b )2+22a 4b -4ac ],若记u=x+a 2b , k 2=22a4b -4ac ,则此二次三项式必属于以下三种情形之一:|a|(u 2±k 2),|a|(k 2-u 2). 因此上述无理根式的不定积分可化为以下三种类型之一:∫R(u,22k u ±)du ,∫R(u,22u k -)du.分别令u=ktant, u=ksect, u=ksint ,则都化为三角有理式的不定积分.例7:求I=∫3x 2x x dx 2--.解法一:令u=x-1=2sec θ, t=tan 2θ, 则t=1x 3-x +. I=∫41)-(x x 1)-d(x 2-=∫4u )1(u du 2-+=∫1θsec )1(2sec θdsec θ2-+=∫)1θ(2secθtan tan θanθs+d θ=∫12sec θsec θ+d θ=∫cos θ21+d θ=∫222t 1t -12t 12+++dt=2∫3t 12+dt=32∫13t 12+⎪⎪⎭⎫ ⎝⎛d ⎪⎪⎭⎫ ⎝⎛3t=32arctan ⎪⎪⎭⎫⎝⎛3t +C=32arctan ⎪⎪⎭⎫ ⎝⎛+33x 3-x +C. 解法二:令3x 2x 2--=x-t, 则x=)1t (23t 2-+, dx=22)1t (23-t 2t --dt. I=∫⎪⎪⎭⎫ ⎝⎛--+-+--t )1t (23t )1t (23t )1t (23-t 2t 2222dt=-2∫3t 12+dt=-32arctan ⎪⎪⎭⎫ ⎝⎛3t +C =32arctan ⎪⎪⎭⎫⎝⎛---3x 3x 2x 2+C.注:一般地,二次三项式ax 2+bx+c 中若a>0,则可令c bx ax 2++=a x ±t ;若c>0,也可令c bx ax 2++=xt ±a ,这类变换称为欧拉变换.习题求下列不定积分:(1)∫1-x x 3dx ;(2)∫127x -x 2-x 2+dx ;(3)∫3x 1dx +;(4)∫4x1dx+;(5)∫221)1)(x -(x dx +; (6)∫22)1x 2(2x 2-x ++dx ;(7)∫x cos 35dx -;(8)∫xsin 2dx 2+;(9)∫x tan 1dx+; (10)∫22x x 1x -+dx ;(11)∫xx dx 2+;(12)∫x1x-1x 12+dx. 解:(1)∫1-x x 3dx=∫1-x 11x 3+-dx=∫(x 2+x+1)dx+∫1-x 1dx=3x 3+2x 2+x+ln|x-1|+C.(2)127x -x 2-x 2+=4)-3)(x -(x 2-x ≡3-x A +4-x B ;∴x-2≡A(x-4)+B(x-3).当x=3时,解得A=-1;当x=4时,解得B=2.∴原式=∫4-x 2dx-∫3-x 1dx=2ln|x-4|-ln|x-3|+C=ln 3-x 4)-(x 2+C.(3)3x11+=1)x 1)(x (x 12+-+≡1x A ++1x -x C Bx 2++;∴A(x 2-x+1)+(Bx+C)(x+1)≡1. 当x=-1时,解得A=31;由A+B=0,得B=-31;由A+C=1,得C=32. ∴原式=31∫1x 1+dx-31∫1x -x 2-x 2+dx=31ln|x+1|-61∫1x -x 3-1-2x 2+dx=31ln|x+1|-61∫1x -x 1)x -d(x 22+++21∫1x -x 12+dx=61ln 1x -x 1)+(x 22++21∫4321-x 12+⎪⎭⎫ ⎝⎛dx =61ln 1x -x 1)+(x 22++31∫121-x 3221-x 32d 2+⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛=61ln 1x -x 1)+(x 22++31arctan 31-x 2+C. (4)∫4x 1dx +=21∫422x 11x -1x +++dx=21∫42x 11x ++dx -21∫42x 11x +-dx=21∫222x 1x x 11++dx-21∫222x 1x x 11+-dx=21∫2x 1x x 1x d 2+⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛--21∫2x 1x x 1x d 2-⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+ =42arctan x 21-x 2-82∫)2x 1(x x 1x d ++⎪⎭⎫ ⎝⎛++82∫)2x 1(x x 1x d -+⎪⎭⎫ ⎝⎛+=42arctan x 21-x 2-82ln 1x 2x 1x 2x 22+-+++C. (5)由221)1)(x -(x 1+≡1-x A +1x C Bx 2+++221)(x EDx ++得:A(x 2+1)2+(Bx+C)(x-1)(x 2+1)+(Dx+E)(x-1)≡1. 当x=1时,解得A=41. ∴41x 4+21x 2+41+Bx 4-Bx 3+Cx 3+Bx 2-Cx 2-Bx+Cx-C+Dx 2-Dx+Ex-E=(41+B)x 4-(B-C)x 3+(21+B-C+D)x 2-(B-C+D-E)x-(C+E-41)≡1. ∴B=-41,C =-41,D=-21,E=-21. 原式=41∫1-x dx -41∫1x 1x 2++dx-21∫221)(x 1x ++dx =41ln|x-1|-81∫1x 1)d(x 22++-41∫1x dx 2+-41∫2221)(x 1)d(x ++-21∫221)(x dx + =81ln 1x 1)(x 22+--41arctanx+)1x (412+-21∫221)(x dx +又∫221)(x dx +=∫221)t (tan dtant +=∫cos 2tdt=21∫(cos2t+1)dt=41∫cos2td2t +21∫dt =41sin2t+21t+C=)1t (tan 2tant 2++21arctanx+C=)1x (2x 2++21arctanx+C.∴原式=81ln 1x 1)(x 22+--41arctanx+)1x (412+-)1x (4x 2+-41arctanx+C=81ln 1x 1)(x 22+--21arctanx+)1x (4x -12++C.(6)∫22)1x 2(2x 2-x ++dx=41∫222)1x 2(2x )1x 2d(2x ++++-25∫22)1x 2(2x dx ++=-)1x 24(2x 12++-5∫22)]11)[(2x 1)d(2x +++=-)1x 24(2x 12++-45[1x 22x 12x 2++++2arctan(2x+1)]+C =-)1x 22(2x 3x 52+++-25arctan(2x+1)+C.(7)∫x cos 35dx -=∫222t 1)t 3(15t 12+--+dt=21∫1t)2(d2t 2+=21arctan2t+C=21arctan(2tan 2x )+C.(8)方法一:∫x sin 2dx 2+=∫22t 1t 22t 12+++dt=∫1t t dt 2++=32∫13132t 3132t d 2+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+ =32arctan ⎪⎭⎫ ⎝⎛+3132t +C=32arctan ⎪⎪⎪⎪⎭⎫ ⎝⎛+3132x 2tan +C. 方法二:∫x sin 2dx 2+=∫x tan x sec 2x dx sec 222+=∫2x tan 3dtanx 2+dt=66∫1x tan 23tanx23d2+=66arctan(tanx 23)+C.(9)∫x tan 1dx +=∫x tanx sec x sec x dx sec 222+=∫1tanx x tan x tan dtanx23+++ =21(∫1tanx dtanx +-∫1x tan tanxdtanx 2++∫1x tan dtanx 2+)=21(ln|tanx+1|-21∫1x tan )1x d(tan 22+++x) =21(ln 1x tan |1tanx |2+++x)+C=21(ln|cosx+sinx|+x)+C. (10)I=∫22xx 1x -+dx=-∫22xx 1x x 1-+-+dx+∫2xx 11)dx (x -++=-∫2x x 1-+dx+∫2xx 11)dx (x -++=-x 2x x 1-+-∫22xx 12x -x 2-+dx+∫2xx 11)dx (x -++=-x 2xx 1-+-I+21∫2xx 1x -+dx+∫2xx 11)dx (x -++=-x 2x x 1-+-I+23∫2xx 132x -++dx. ∴I=-2x x 12x -++43∫2x x 132x -++dx.又∫2x x 132x -++dx=-21∫2x x 1x 21-+-dx+67∫2x x 1dx -+ =-2x x 1-++67∫251-2x 151-2x d ⎪⎪⎭⎫ ⎝⎛-⎪⎪⎭⎫ ⎝⎛=-2x x 1-++67∫arcsin 51-2x +C. ∴原式=-2x x 12x -+-432x x 1-++87∫arcsin 51-2x +C. (11)令t-x=x x 2+,则x=12t t 2+,dx=d 12t t 2+=21)(2t 1)t(t 2++dt. ∫x x dx 2+=∫12t t t 1)(2t 1)t(t 222+-++dt=∫12t 1)d(2t ++=ln|2t+1|+C=ln|2x x 2++2x+1|+C. (12) ∫x 1x -1x 12+dx=-∫1x11-x 1+d x 1=-∫1t 1-t +dt=-∫1t 1-t 2-dt=-∫1t tdt 2-+∫1t dt 2- =-1t 2-+ln|t+1t 2-|+C=-x x 12-+ln x x 112-++C.。
有理函数和可化为有理函数的不定积分

2
2
其中 i , j N + , 且
2 i 2 j m , p j 4q j 0, j 1,2,, t .
i 1 j 1
s
t
命题2 如果多项式Q ( x )能分解为(1)式, 则 P( x ) 有理真分式 能唯一地分解为下列部分分式之和 Q( x)
例3 求下列不定积分
x3 1 (1) 2 dx (2) 3 dx 2 x 5x 6 x 2x x 1 x (3) 3 dx (4) 3 dx 2 2x x 2x 1 x 1 x3 5 6 x3 解 (1) , 2 x 2 x 3 x 5 x 6 ( x 2)( x 3)
p Lp p2 (令t x , M N, q r2) 2 2 4
Lx M t 1 (7 ) 2 dx L 2 2 n dt N 2 2 n dt n (t r ) (t r ) ( x px q)
x 1 1 1 (3) 2 dx 2 d ( x 2 a 2 ) ln( x 2 a 2 ) C. x a2 2 x a2 2 x 1 1 1 2 2 n 2 2 2 2 (4) 2 dx 2 d (x a ) (x a ) d (x a ) ( x a 2 )n 2 2 ( x a 2 )n
例1.求下列不定积分
1 (1) dx n ( x a)
(5) 1 I2 2 dx 2 2 (x a ) I3 1 dx 2 2 3 (x a )
( 2)
1 dx 2 2 x a x dx 2 2 x a
(3)
In
无理根式的不定积分PPT课件

1
x
x2
. 1
有理真分式必定可以表示成若干个部分分
式之和(称为部分分式分解)
有理函数化为部分分式之和的一般步骤:
第一步 对分母 Qx 在实系数内作标准分解:
Qxxa11Lxass x2p1xq1 1
Lx2ptxqt t
其中b0 1,i, j i 1,2,L ,t 均为自然数,而且
s
t
i 2 jm ;p 2 j 4 q j 0 ,j 1 ,2 , ,t.
其中m、n都是非负整数;a0 ,a1 , ,an及 b0 ,b1 , ,bm都是实数,并且a0 0,b0 0.
假定分子与分母之间没有公因式
(1) nm , 这有理函数是真分式; (2) nm , 这有理函数是假分式;
利用多项式除法, 假分式可以化成一个多 项式和一个真分式之和.
例
x3 x 1 x2 1
8.3 有理函数和可化为有理函数的不定积分
一、有理函数的不定积分 二、三角函数有理式的不定积分 三、某些无理根式的不定积分
一、有理函数的积分
有理函数的定义: 两个多项式的商表示的函数称之为有理
函数.其一般形式为
Q P ( (x x ) ) b a 0 0 x x m n b a 1 1 x x m n 1 1 b a m n 1 1 x x a b n m (1)
6 t1 3t3 1tt3 2dt
6lnt 3ln1t 3 2
d(11tt22)311t2dt
6 ln t 3 ln 1 t 3 ln (1 t2) 3 a r c ta n t C 2
x 3 ln 1 e (6 x) 3 ln 1 e (3 x) 3 are c 6 x) tC a . n 2
简单无理函数的不定积分方法小结

学法教法研究课程教育研究高等教育简单无理函数的不定积分方法小结窦林立杜二玲(中国地质大学长城学院基础课教学部河北保定071000)【摘要】总结了几种简单的无理函数的不定积分的计算方法,并举出实例。
【关键词】高等数学不定积分无理函数【基金资助】中国地质大学长城学院校级科研项目(ZDCYK014017)。
【中图分类号】G64【文献标识码】A 【文章编号】2095-3089(2015)16-0034-01微积分是高等数学的核心,不定积分的计算又是微积分学的主要内容。
无理函数的不定积分是考研数学和高等数学竞赛中的常见题型。
本文给出了几种简单常见无理函数的不定积分的计算方法。
1.几种简单的无理函数的不定积分无理函数不定积分的一般方法是:用换元积分法,去掉根号,将无理函数转化为有理函数,再进行积分。
应注意根据被开方数的次数进行不同的变量替换。
1.1被积函数为ax+b n√型(即被开方数最高次数为1)方法:令ax+b n√=t例1求∫x 22x-1√dx解:令2x-1√=t ,即x=12(t 2+1),dx=tdt,则∫x 22x-1√dx=∫1t ·14(t 2+1)2·tdt=14∫(t 4+2t 2+1)dt=120t 5+16t 3+14t+c=120(2x-1)52+16(2x-1)32+14(2x-1)12+c 例2求∫dx(1+x 3√)x√解:令x 6√=t ,即x=t 6,dx=6t 5dt ,则∫dx (1+x 3√)x√=∫6t 5(1+t 2)t 3dt=6∫t 21+t 2dt =6∫1-11+t2()dt=6(t-arctant)+c=6(x 6√-arctan x 6√)+c1.2被积函数为ax 2+bx+c √型(即被开方数最高次数为2)方法:利用三角代换例3求∫dxx 2+2x+2√)解:∫dx x 2+2x+2√)=∫dx (x+1)2+1√令x+1=tant ,即x=tant-1,dx=sec 2tat 则∫dx (x+1)2+1√=∫sec 2t sect dt=∫sectdt=ln|sect+tant|+c画出辅助三角形,如图ln|sect+tant|+c=ln|x 2+2x+2√+x+1|+c 若感觉三角代换步骤太繁,以下两种情况可避免使用三角代换。
不定积分总结

不定积分一、原函数定义1 如果对任一I x ∈,都有)()(x f x F =' 或 dx x f x dF )()(= 则称)(x F 为)(x f 在区间I 上的原函数。
例如:x x cos )(sin =',即x sin 是x cos 的原函数。
2211)1ln([xx x +='++,即)1ln(2x x ++是211x+的原函数。
原函数存在定理:如果函数)(x f 在区间I 上连续,则)(x f 在区间I 上一定有原函数,即存在区间I 上的可导函数)(x F ,使得对任一I x ∈,有)()(x f x F ='。
注1:如果)(x f 有一个原函数,则)(x f 就有无穷多个原函数。
设)(x F 是)(x f 的原函数,则)(])([x f C x F ='+,即C x F +)(也为)(x f 的原函数,其中C 为任意常数。
注2:如果)(x F 与)(x G 都为)(x f 在区间I 上的原函数,则)(x F 与)(x G 之差为常数,即C x G x F =-)()((C 为常数)注3:如果)(x F 为)(x f 在区间I 上的一个原函数,则C x F +)((C 为任意常数)可表达)(x f 的任意一个原函数。
二、不定积分定义2 在区间I 上,)(x f 的带有任意常数项的原函数,成为)(x f 在区间I 上的不定积分,记为⎰dx x f )(。
如果)(x F 为)(x f 的一个原函数,则 C x F dx x f +=⎰)()(,(C 为任意常数)三、不定积分的几何意义图 5—1设)(x F 是)(x f 的一个原函数,则)(x F y =在平面上表示一条曲线,称它为)(x f 的一条积分曲线.于是)(x f 的不定积分表示一族积分曲线,它们是由)(x f 的某一条积分曲线沿着y 轴方向作任意平行移动而产生的所有积分曲线组成的.显然,族中的每一条积分曲线在具有同一横坐标x 的点处有互相平行的切线,其斜率都等于)(x f .在求原函数的具体问题中,往往先求出原函数的一般表达式C x F y +=)(,再从中确定一个满足条件 00)(y x y = (称为初始条件)的原函数)(x y y =.从几何上讲,就是从积分曲线族中找出一条通过点),(00y x 的积分曲线.四、不定积分的性质(线性性质)[()()]()()f x g x dx f x dx g x dx ±=±⎰⎰⎰()() kf x dx k f x dx =⎰⎰k (为非零常数)五、基本积分表∫ a dx = ax + C,a和C都是常数∫ x^a dx = [x^(a + 1)]/(a + 1) + C,其中a为常数且a ≠ -1∫ 1/x dx = ln|x| + C∫ a^x dx = (1/lna)a^x + C,其中a > 0 且a ≠ 1∫ e^x dx = e^x + C∫ cosx dx = sinx + C∫ sinx dx = - cosx + C∫ cotx dx = ln|sinx| + C = - ln|cscx| + C∫ tanx dx = - ln|cosx| + C = ln|secx| + C∫ secx dx =ln|cot(x/2)| + C= (1/2)ln|(1 + sinx)/(1 - sinx)| + C= - ln|secx - tanx| + C = ln|secx + tanx| + C∫ cscx dx = ln|tan(x/2)| + C= (1/2)ln|(1 - cosx)/(1 + cosx)| + C= - ln|cscx + cotx| + C = ln|cscx - cotx| + C∫ sec^2(x) dx = tanx + C∫ csc^2(x) dx = - cotx + C∫ sec xtanx dx = secx + C∫ cscxcotx dx = - cscx + C∫ dx/(a^2 + x^2) = (1/a)arctan(x/a) + C ∫ dx/√(a^2 - x^2) = arcsin(x/a) + C ∫ dx/√(x^2 + a^2) = ln|x + √(x^2 + a^2)| + C ∫ dx/√(x^2 - a^2) = ln|x + √(x^2 - a^2)| + C∫ √(x^2 - a^2) dx = (x/2)√(x^2 - a^2) - (a^2/2)ln|x + √(x^2 - a^2)| + C ∫ √(x^2 + a^2) dx = (x/2)√(x^2 + a^2) + (a^2/2)ln|x + √(x^2 + a^2)| + C ∫ √(a^2 - x^2) dx = (x/2)√(a^2 - x^2) + (a^2/2)arcsin(x/a) + C六、第一换元法(凑微分)设)(u F 为)(u f 的原函数,即)()(u f u F =' 或 ⎰+=C u F du u f )()(如果 )(x u ϕ=,且)(x ϕ可微,则)()]([)()()()()]([x x f x u f x u F x F dxdϕϕϕϕϕ'='=''= 即)]([x F ϕ为)()]([x x f ϕϕ'的原函数,或)()(])([])([)]([)()]([x u x u du u f C u F C x F dx x x f ϕϕϕϕϕ==⎰⎰=+=+='因此有定理1 设)(u F 为)(u f 的原函数,)(x u ϕ=可微,则)(])([)()]([x u du u f dx x x f ϕϕϕ=⎰⎰=' (2-1)公式(2-1)称为第一类换元积分公式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 5
.
,
例4
求积分
1 x( x 1)2dx.
解
1 x(x
1)2dx
1 x
(x
1 1)2
1 x
1
dx
1
1
1
dx x
(
x
1)2
dx
x
dx 1
ln x 1 ln x 1 C. x 1
1
例5 求积分 (1 2x)(1 x2 ) dx.
解
1
(1
2 x )(1
an bm
(1)
其中m、n都是非负整数;a0 ,a1 ,,an及 b0 ,b1 ,,bm都是实数,并且a0 0,b0 0.
假定分子与分母之间没有公因式
(1) n m, 这有理函数是真分式;
(2) n m, 这有理函数是假分式;
利用多项式除法, 假分式可以化成一个多 项式和一个真分式之和.
2u 1 u2 2
R
1
u2
,
1
u2
1
u2
du.
例8
1
dx cos
x
2
解法一:
t tg x 2
I
1
1
1
1
t2 t
t
2 2
dt
dt
t
c
tg
x 2
c
解法二: ( 用初等化简 )
I
1 2
dx cos2
x
sec2
x d( x) 22
tan
x 2
c
2
解法三: ( 用初等化简, 并凑微 )
d (cos
x)
1 4
1 sin
x
dx
1 4
1 cos2
x
dx
1 4cos
x
1 ln tan 4
x 2
1 tan 4
x
C.
三、简单无理函数的积分
1、讨论类型 R( x,n ax b),
R( x, n ax b ), (ad bc 0)
cx e
令t n ax b
解决方法
作代换去掉根号.
]
C
24
1 tan
x 2
3
3 8 tan
x 2
3 tan 8
x 2
1 24
tan
x 2
3
C.
解(二) 修改万能置换公式, 令 u tan x
sin x
u, 1 u2
dx
1
1 u2
du,
1
sin4
dx x
1 u
4
1
1 u2
du
1
u2 u4 du
1
u2
1 3u3
1 u
C
1 cot3 3
其中b0 1,i, j i 1,2, ,t 均为自然数,而且
s
t
i 2
j
m;
p
2 j
4q j
0,
j
1,2,, t .
i 1
j 1
第二步 根据分母的各个因式分别写出与之 相应的部分分式:
(1)分母中若有因式 ( x a)k ,则分解后为
(x
A1 a)k
(x
A2 a)k1
Ak , xa
t
1
x
e2
1
x
e3
x
e6
dx
1
t3
1
t2
t
6 dt t
6
t(1
t
1 )(1
t
2
dt )
6 t
1
3
t
3t 3 1 t2
dt
6 t
1
3
t
3t 1 t
3
2
dt
6ln t 3ln 1 t 3
2
d
(1 t 2 1 t2
)
3
1
1 t
2
dt
6ln t 3ln 1 t 3 ln(1 t 2 ) 3arctan t C 2
说明 无理函数去根号时, 取根指数的最小公倍数.
例14 求积分
x 3x 1
dx. 2x 1
解 先对分母进行有理化
原式 (
x( 3x 1 2x 1) 3x 1 2x 1)( 3x 1
dx 2x 1)
(t2
t r2)k
dt
2(1
1 k)(t 2
r 2 )k1
c
令
Ik
dt 1 (t2 r2)k r2
(t 2 (t
r 2
2)t r 2 )k
2
dt
1 r2
Ik 1
1 r2
t2 (t 2 r 2 )k dt
1
1
1
r 2 Ik1 2r 2 (k 1) td ((t 2 r 2 )k1 )
)
1
A 2x
Bx C 1 x2
,
1 A(1 x2 ) (Bx C )(1 2x),
整理得 1 ( A 2B)x2 (B 2C )x C A,
A 2B 0,
B 2C 0, A C 1,
1
(1 2x)(1
A x2 )
1
4, B 5 4
5 2x
2,C 5
2
u tan x 2
x 2
ln | sec x | ln | 1 tan x | C.
2
2
例10
求积分
1 sin 4
x
dx.
解(一) u tan x , 2
sin
x
1
2u u2
,
dx
1
2 u2
du,
1 sin4
x
dx
1
3u2 3u4 8u4
u6du
1[ 8
1 3u3
3 u
3u
u3 3
例7
dx
x( x10 1)
解
dx x( x10 1)
=
x9
x10 (
x10
dx 1)
1 10
(
1 x10
1 x10
1
)d
(
x10
)
1 ln 10
x10 x10 1
C
二、三角函数有理式的不定积分 三角有理式的定义 由三角函数和常数经过有限次四则
运算构成的函数称之为三角有理式. 一般记为 R(sin x,cos x)
x
cot
x
C.
注 当被积函数是sin2 x ,cos2 x 及sin x cos x 的有理式时,采用变换t tan x往往较为简便.
解(三) 可以不用万能置换公式.
1 sin4
x
dx
csc2
x(1
cot2 x)dx
csc2 xdx cot2 xdc(sc2cxodt xx)
cot x 1 cot3 x C. 3
特殊地:k
1,
分解后为
x
Mx 2
N px
q
;
第三步 确定待定系数 。一般方法是将
所有部分分式通分相加,所得分式的分母即
为 原 分 母 Q x , 而 其 分 子 亦 应 与 原 分 子 P x 恒等.
于是,按同幂项系数必定相等,得到一
组关于待定系数的线性方程,这组方程的
解就是需要确定的系数.
真分式化为部分分式之和的待定系数法
1 r2
I k 1
1 2r2 (k
1)
(t
2
t r 2 )k1
Ik1
所以
t
2k 3
Ik 2r 2 (k 1)(t 2 r 2 )k1 2r 2 (k 1) Ik1
结论 有理函数的原函数都是初等函数.
注 用求有理真分式的最简分式分解式的方 法求其积分往往很麻烦。所以,当我们求有 理函数的积分时,应尽可能地考虑是否有其 它更简便的解法。
例12
求积分
1 x
1 xdx x
或t
n
ax cx
b d
解 令 1 x t 1 x t2,
x
x
x
t
2
1
, 1
dx
2tdt t2 1
2,
1 x
1
x
xdx
t
2
1t
t
2
2t
12dt
2
t 2dt t 2 1 2
1
t
2
1
1
dt
2t ln t 1 C t 1
2
1 x
三角有理函数的积分,一般有如下规律
(一) R(sinx)cosxdx 令t sin X R(cosx)sinxdx 令t cos X R(tanx)sec2xdx 令t tan X
(二)万能代换
x
x
sin x 2sin x cos x 22
2 tan 2
sec2 x
2 tan
1
tan
8.3 有理函数和可化为有理函数的不定积分
一、有理函数的不定积分 二、三角函数有理式的不定积分 三、某些无理根式的不定积分
一、有理函数的积分
有理函数的定义:
两个多项式的商表示的函数称之为有理 函数.其一般形式为
P( Q(
x) x)
a0 xn b0 xm
a1 xn1 b1 xm1
an1 x bm1 x
I
1 cos 1 cos2
x x
dx
csc2
xdx
d sin x sin2 x
cot x 1 c csc x cot x c sin x
