教大家反求INV函数(渐开线函数)

合集下载

反三角函数公式

反三角函数公式反三角函数是指反向计算三角函数的值的一组函数。

反三角函数有正弦的反函数，余弦的反函数，正切的反函数，以及它们的反函数的逆函数（例如：逆正弦、逆余弦、逆正切等）。

在数学中，反三角函数可以用来解决三角函数的方程，以及在三角函数的运算和分析中的一些问题。

1. 反正弦函数 (arcsin 或 sin^(-1))：反正弦函数将给定的值的正弦值作为输入，并返回其角度。

其定义域为[-1,1]，值域为[-π/2,π/2]。

反正弦函数的性质：-定义域：[-1,1]-值域：[-π/2,π/2]- 奇函数：arcsin(-x) = -arcsin(x)- 奇函数的区间性质：arcsin(x)在[-1, 1]上是递增的- 奇对称性：arcsin(x) = arcsin(-x)- 反函数：sin(arcsin(x)) = x2. 反余弦函数 (arccos 或 cos^(-1))：反余弦函数将给定的值的余弦值作为输入，并返回其角度。

其定义域为[-1,1]，值域为[0,π]。

反余弦函数的性质：-定义域：[-1,1]-值域：[0,π]- 偶函数：arccos(-x) = arccos(x)- 奇对称性：arccos(x) = -arccos(-x)- 反函数：cos(arccos(x)) = x3. 反正切函数 (arctan 或 tan^(-1))：反正切函数将给定的值的正切值作为输入，并返回其角度。

其定义域为(-∞,+∞)，值域为(-π/2,π/2)。

反正切函数的性质：-定义域：(-∞,+∞)-值域：(-π/2,π/2)- 奇函数：arctan(-x) = -arctan(x)- 奇对称性：arctan(x) = arctan(-x)- 反函数：tan(arctan(x)) = x4. 反余切函数 (arccot 或 cot^(-1))：反余切函数将给定的值的余切值作为输入，并返回其角度。

其定义域为(-∞,+∞)，值域为(0,π)。

渐开线函数inv（a）的计算方法

渐开线函数inv（a）的计算⽅法渐开线函数inv(a)的计算⽅法inv函数不是标准函数，没有统⼀算法。

inv 是英⽂ inverse，倒序，反变换。

MATLAB 中的 Y = inv(X)，是矩阵求逆。

密码学中遇到的这个函数，也可能只是定性说明，表⽰反算解密，或者表⽰逆运算。

在圆柱齿轮⾓变位计算中, 会遇到渐开线函数 invα的计算。

invα在⼿册中有表可查, 当⼿头没有⼿册, 则可按下式计算:invα=tgα-α等号右边第⼀项的α是⾓度值, ⽽第⼆项, α是弧度值, 计算时很不⽅便。

为此, 将此式改为invα=tgα- απ/180则可直接利⽤计算器来计算, 很为⽅便。

今举例计算如下。

⼀⾓度变位直齿圆柱齿轮⼩齿轮齿数 z1=40, ⼤齿轮齿数z2=66, 模数 m=3mm, 压⼒⾓α=20°, 变位中⼼距 a'=162.70mm。

1.计算标准齿轮副的中⼼距 aa=( z1+z)2 m2=( 40+60) ×32=159mm2.变位齿轮副的啮合⾓α'α'=cos-1cosα?aa'=cos-1cos20?°159162.70=23.317888°3.节圆上的渐开线函数 invα'invα'=tga'- α?'π180°=tg23.317888°- 23.317888°×π180°=0.024064 W06.05-2 6————————!"#$:&’()*+,-./0( 2345235) 78&’9:;<=>?@2-303 116023〔BC DEF〕渐开线函数 invα的简便计算⽅法。

反渐开线函数计算

齿数
模数压力角已知中心距未变位时中心距中心距变动系数
Z1 Z2 m α° a′
a
y
角变位外啮合直齿渐开线函数计算 16 23
3.25 20 65
a=(z1+z2)*m/2
63.375
y=(a′-a)/m
0.5
齿数模数压力角已知中心距未变位时中心距
中心距变动系数
啮合角
a′
acosa′=acos(a/a′ *cosα)
0.025069042 0.014904
0.54460035
ΔY=xΣ-y
查表x1=0.18 xΣ=x2-x1
d1=z1*m d2=z2*m ha1=(ha*+x1+Δy-Δy02)*m ha2=(ha*-x2+Δy-k2)*m x2≥2 k2=0 hf1=(ha*+c*-x1)*m hf2=(ha*+c*+x2)*m h=ha+hf da1=d1+2ha1 da2=d2-2ha2 df1=d1-2hf1 df2=d2+*hf2 db1=d1*cosa db2=d2*cosa u=z2/z1 d′1=2a′/(u-1)
6.575239662 4.239391304
Ω=asin(ha/d)
6.575239662 4.239391304
k=a*z/180+0.5+2*x* cosa/pi()
2.495891516
3
Wk=(Wk*+ΔW)*m
25.52491027
ΔW=2x*sina
0.249401328
Wk*=cosa*(pi()*(k0.5)+z*inva)

反三角函数公式大全

反三角函数公式大全反三角函数是三角函数的逆运算，它们是一组用来描述角度的函数，与三角函数相对应。

在数学中，反三角函数广泛应用于三角函数的逆运算、三角方程的求解以及在物理、工程等领域的实际问题中。

本文将为您详细介绍反三角函数的各种公式，帮助您更好地理解和应用反三角函数。

1. 反正弦函数公式。

反正弦函数通常表示为arcsin(x)，其定义域为[-1,1]，值域为[-π/2,π/2]。

其公式如下：arcsin(x) = y, 当且仅当sin(y) = x, -π/2 ≤ y ≤π/2。

2. 反余弦函数公式。

反余弦函数通常表示为arccos(x)，其定义域为[-1,1]，值域为[0,π]。

其公式如下：arccos(x) = y, 当且仅当cos(y) = x, 0 ≤ y ≤π。

3. 反正切函数公式。

反正切函数通常表示为arctan(x)，其定义域为实数集，值域为(-π/2,π/2)。

其公式如下：arctan(x) = y, 当且仅当tan(y) = x, -π/2 < y < π/2。

4. 反余切函数公式。

反余切函数通常表示为arccot(x)，其定义域为实数集，值域为(0,π)。

其公式如下：arccot(x) = y, 当且仅当cot(y) = x, 0 < y < π。

5. 反正割函数公式。

反正割函数通常表示为arcsec(x)，其定义域为(-∞,-1]∪[1,+∞)，值域为[0,π]。

其公式如下：arcsec(x) = y, 当且仅当sec(y) = x, 0 ≤ y ≤π或 y < 0。

6. 反余割函数公式。

反余割函数通常表示为arccsc(x)，其定义域为(-∞,-1]∪[1,+∞)，值域为[-π/2,π/2]。

其公式如下：arccsc(x) = y, 当且仅当csc(y) = x, -π/2 ≤ y ≤π/2 或 y ≠ 0。

以上是反三角函数的基本公式，通过这些公式我们可以求出给定数值的反三角函数值，从而解决实际问题中的角度计算、三角方程求解等问题。

初中数学如何求解三角函数的逆函数

初中数学如何求解三角函数的逆函数求解三角函数的逆函数是解决三角函数相关问题的重要内容。

逆函数是指将函数的输入和输出互换的函数，通过求解三角函数的逆函数，我们可以得到原函数对应的角度值。

下面我将详细介绍求解三角函数的逆函数的方法。

1. 求解sin(x)的逆函数：要求解sin(x)的逆函数，我们首先需要了解sin(x)函数在一个周期内的性质。

sin(x)函数在区间[-π/2, π/2]上是单调递增的，并且在这个区间上是一一对应的。

因此，我们可以将sin(x)的定义域限定在[-π/2, π/2]上。

对于sin(x)的逆函数sin^(-1)(x)，我们可以用符号y表示，即y = sin^(-1)(x)。

这表示y是sin(x)的逆函数的值，即y是对应于x的角度值。

求解sin(x)的逆函数的一种常用方法是利用三角函数的定义和性质。

根据sin(x)在[-π/2, π/2]上的性质，我们可以得到以下等式：sin(y) = x根据这个等式，我们可以通过求解y来求解sin(x)的逆函数。

具体的求解方法可以使用反三角函数，即利用反正弦函数arcsin(x)。

2. 求解cos(x)的逆函数：求解cos(x)的逆函数的方法与求解sin(x)的逆函数类似。

cos(x)函数在区间[0, π]上是单调递减的，并且在这个区间上是一一对应的。

因此，我们可以将cos(x)的定义域限定在[0, π]上。

对于cos(x)的逆函数cos^(-1)(x)，我们可以用符号y表示，即y = cos^(-1)(x)。

这表示y是cos(x)的逆函数的值，即y是对应于x的角度值。

求解cos(x)的逆函数的方法也是利用三角函数的定义和性质。

根据cos(x)在[0, π]上的性质，我们可以得到以下等式：cos(y) = x根据这个等式，我们可以通过求解y来求解cos(x)的逆函数。

具体的求解方法可以使用反三角函数，即利用反余弦函数arccos(x)。

3. 求解tan(x)的逆函数：求解tan(x)的逆函数的方法与求解sin(x)和cos(x)的逆函数有所不同。

反正弦函数公式

反正弦函数公式：解析求解正弦函数逆运算正弦函数在数学中广泛应用，在实际问题中也经常出现。

但有时我们需要求解正弦函数的逆运算，即求解反正弦函数。

本文将从反正弦函数的定义、性质和求解公式三个方面，详细介绍反正弦函数的相关知识。

一、反正弦函数的定义反正弦函数是指一个函数，其定义域为[-1, 1]，值域为[-π/2, π/2]，满足以下条件：对于任意y在值域内，都存在一个对应的x在定义域内，使得sinx=y。

这个对应的x即为反正弦函数的值，记作arcsin(y)。

二、反正弦函数的性质（1）反正弦函数在定义域内是单调递增的函数。

（2）反正弦函数的导数为1/√(1-y²)，即arcsin'(y)=1/√(1-y²)。

（3）反正弦函数的图像关于y轴对称。

（4）反正弦函数属于奇函数，即arcsin(-y)=-arcsin(y)。

三、求解反正弦函数的公式求解反正弦函数可以使用泰勒级数、牛顿迭代法等方法。

其中，最常用的是求解反正弦函数的公式：arcsin(y)=sin⁻¹(y)=x，即y=sin(x)。

下面介绍反正弦函数的一些常用公式：（1）arcsin(0)=0（2）arcsin(1)=π/2（3）arcsin(-1)=-π/2（4）arcsin(√2/2)=π/4（5）arcsin(-√3/2)=-π/3需要注意的是，反正弦函数在定义域内不是一个全局单射函数，因此在求解反正弦函数时需要注意：当y=±1时，由于sin(-π/2)=sin(π/2)=±1，无法确定x的值，因此反正弦函数在y=±1时没有定义。

总结起来，反正弦函数的定义、性质和求解公式都非常重要，对于求解正弦函数的逆运算具有重要指导意义。

在数学和工程学科中，反正弦函数也有广泛的应用和研究。

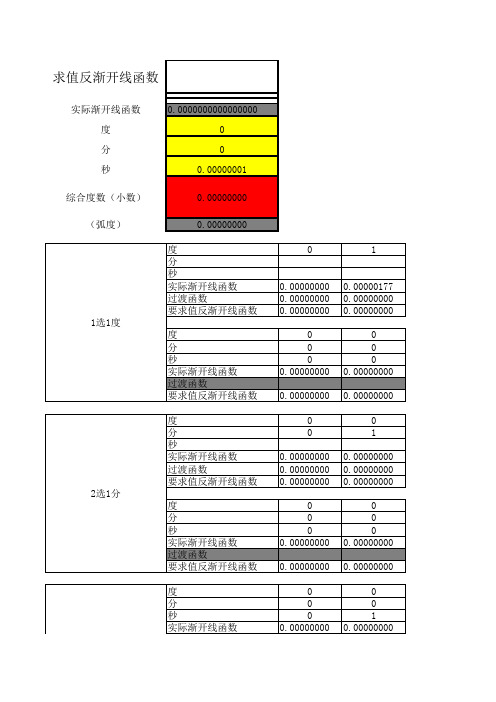
(反)渐开线函数角度换算(高精度)

0 0 0 0.00000000 0.00000000 0.00000000
0 0 0.1 0.00000000 0.00000000 0.00000000
0 0 0 0.00000000
0 0 0 0.00000000
0.00000000 0.00000000
0 0 0 0.00000000 0.00000000 0.00000000
0 0 0.0001 0.00000000 0.00000000 0.00000000
0 0 0 0.00000000
0 0 0 0.00000000
0.00000000 0.00000000
0 0 0 0.00000000 0.00000000 0.00000000
0 0 0.00001 0.00000000 0.00000000 0.00000000
0 0 0.002 0.00000000 0.00000000 0.00000000
0 0 0.003 0.00000000 0.00000000 0.00000000
0 0 0.004 0.00000000 0.00000000 0.00000000
0 0 0.005 0.00000000 0.00000000 0.00000000
0 0 0.006 0.00000000 0.00000000 0.00000000
0 0 0.007 0.00000000 0.00000000 0.00000000
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0
0.00000000 0.00000000 0.00000000 0.00000000 0.00000000 0.00000000

渐开线函数inv的反函数

渐开线函数inv的反函数1.引言1.1 概述概述部分的目标是为读者提供关于本文主题的背景和整体情况的概括。

在这一部分，我们将引言渐开线函数inv的反函数的概念和研究意义，以及本文的结构和目的。

渐开线函数inv的反函数是指在数学领域中与渐开线函数相对应的一种函数。

渐开线函数是一种特殊的曲线，其特点是在任意一点上，曲线上该点的切线与一个定点之间的距离保持相等。

渐开线函数在工程学、物理学和计算机图形学等领域有着广泛的应用。

本文的目标是研究渐开线函数inv的反函数，并探讨它的特点和应用。

我们将首先介绍渐开线函数的基本定义和一些特点，以帮助读者对该函数有一个清晰的认识。

然后，我们将重点讨论渐开线函数的反函数，包括其定义、性质和计算方法等方面。

通过对反函数的研究，我们可以更好地理解渐开线函数的特点和结构。

文章的结构如下：在引言之后，我们将进入正文部分。

在正文的第一部分，我们将详细介绍渐开线函数的定义和特点，包括其几何性质和数学表达式等方面。

在第二部分，我们将重点讨论渐开线函数的反函数，包括如何求解和应用等方面。

最后，在结论部分，我们将总结渐开线函数inv的反函数的特点和应用，并展望未来关于该领域的研究方向。

通过本文的阅读，读者将能够全面了解渐开线函数inv的反函数，并在实际问题中应用它的相关知识和方法。

通过对渐开线函数inv的反函数的研究，我们可以更好地理解和应用渐开线函数，同时也为数学和工程学等学科的发展提供了新的思路和方法。

希望本文能够对相关领域的学者和研究人员提供一些启发和参考。

1.2文章结构文章结构的目的是为了组织和呈现文章的内容，使读者能够清晰地理解文章的逻辑和论述。

在本文中，文章结构主要分为引言、正文和结论三个部分。

引言部分（1.1）旨在引述渐开线函数inv的问题并概述本文的目的。

它将简要介绍渐开线函数的背景和特点，以及为什么需要讨论渐开线函数inv的反函数。

此外，引言中还可以提及渐开线函数在实际应用中的重要性和影响。

三角函数的反函数与解三角方程

三角函数的反函数与解三角方程在高中数学中，我们学习过三角函数及其性质。

三角函数包括正弦函数、余弦函数、正切函数等。

而与之对应的反函数，即反三角函数，是用来解决一些三角方程的重要工具。

本文将详细介绍三角函数的反函数以及如何利用反函数来解决三角方程。

一、正弦函数的反函数正弦函数的反函数称为反正弦函数，常用符号为sin^(-1)，也可用arcsin表示。

反正弦函数可以表示为y = sin^(-1)(x)，其中x的取值范围为[-1, 1]，y的取值范围为[-π/2, π/2]。

反正弦函数的求值方法如下：1. 将给定的x值代入反正弦函数的表达式中；2. 计算得到的y值即为所求的反正弦函数的值。

二、余弦函数的反函数余弦函数的反函数称为反余弦函数，常用符号为cos^(-1)，也可用arccos表示。

反余弦函数可以表示为y = cos^(-1)(x)，其中x的取值范围为[-1, 1]，y的取值范围为[0, π]。

反余弦函数的求值方法如下：1. 将给定的x值代入反余弦函数的表达式中；2. 计算得到的y值即为所求的反余弦函数的值。

三、正切函数的反函数正切函数的反函数称为反正切函数，常用符号为tan^(-1)，也可用arctan表示。

反正切函数可以表示为y = tan^(-1)(x)，其中x的取值范围为(-∞, +∞)，y的取值范围为(-π/2, π/2)。

反正切函数的求值方法如下：1. 将给定的x值代入反正切函数的表达式中；2. 计算得到的y值即为所求的反正切函数的值。

四、解三角方程利用三角函数的反函数可以解决一些三角方程。

一般来说，解三角方程的步骤如下：1. 将方程转化为三角函数的方程；2. 利用三角函数的性质和恒等式进行等式变形，将方程化简为形如sin^(-1)(x) = a或cos^(-1)(x) = a的形式；3. 根据反函数的定义，得到x的值。

需要注意的是，在解三角方程时，需要根据具体的题目要求确定解的范围，并且考虑到周期性的特点。

常用反三角函数公式表

反三角函数公式arc sin x + arc sin y = arc sin x – arc sin y = arc cos x + arc cos y = arc cos x – arc cos y = arc tan x + arc tan y = arc tan x – arc tan y = 2 arc sin x = 2 arc cos x =2 arc tanx = cos (n arc cos x) =反三角函数图像与特征反正弦曲线图像与特征反余弦曲线图像与特征拐点(同曲线对称中心)：，该点切线斜率为1拐点(同曲线对称中心)：，该点切线斜率为－1 反正切曲线图像与特征反余切曲线图像与特征拐点(同曲线对称中心)：，该点切线斜率为1 拐点：，该点切线斜率为－1渐近线：渐近线：名称反正割曲线反余割曲线方程图像顶点渐近线反三角函数的定义域与主值范围函数主值记号定义域主值范围反正弦若，则反余弦若，则反正切若，则反余切若，则反正割若，则反余割若，则一般反三角函数与主值的关系为式中n为任意整数.反三角函数的相互关系arc sin x = arc cos x = arc tan x = arc cot x =sin x = x-x3/3!+x5/5!-...(-1)k-1*x2k-1/(2k-1)!+... (-∞<x<∞)cos x = 1-x2/2!+x4/4!-...(-1)k*x2k/(2k)!+... (-∞<x<∞)arcsin x = x + 1/2*x3/3 + 1*3/(2*4)*x5/5 + ... (|x|<1)arccos x = π - ( x + 1/2*x3/3 + 1*3/(2*4)*x5/5 + ... ) (|x|<1)arctan x = x - x^3/3 + x^5/5 - ... (x≤1)ArcSin(x) 函数功能：返回一个指定数的反正弦值，以弧度表示，返回类型为Double。

反三角函数导数公式及推导过程

反三角函数导数公式及推导过程反三角函数导数公式及推导过程：反三角函数即为三角函数的反函数，将x和y的位置互换，此时y为自变量（即角度），x为y的函数，在将其化为x为自变量，y为x的函数的形式，得到的即是反三角函数。

反三角函数导数公式及推导过程反函数求导方法:若F(X),G(X)互为反函数,则: F'(X)*G'(X)=1E.G.:y=arcsinx x=sinyy'*x'=1 (arcsinx)'*(siny)'=1y'=1/(siny)'=1/(cosy)=1/根号(1-sin^2y)=1/根号(1-x^2)其余依此类推反正弦函数正弦函数y=sin x在[-π/2，π/2]上的反函数，叫做反正弦函数。

记作arcsinx，表示一个正弦值为x的角，该角的范围在[-π/2，π/2]区间内。

定义域[-1，1] ，值域[-π/2，π/2]。

反余弦函数余弦函数y=cos x在[0，π]上的反函数，叫做反余弦函数。

记作arccosx，表示一个余弦值为x的角，该角的范围在[0，π]区间内。

定义域[-1，1] ，值域[0，π]。

反正切函数正切函数y=tan x在（-π/2，π/2）上的反函数，叫做反正切函数。

记作arctanx，表示一个正切值为x的角，该角的范围在（-π/2，π/2）区间内。

定义域R，值域（-π/2，π/2）。

反余切函数余切函数y=cot x在（0，π）上的反函数，叫做反余切函数。

记作arccotx，表示一个余切值为x的角，该角的范围在（0，π）区间内。

定义域R，值域（0，π）。

三角函数的逆运算与应用三角函数

三角函数的逆运算与应用三角函数三角函数是数学中的重要概念，它在各个领域都有广泛的应用。

在三角函数中，除了正弦、余弦和正切等常见函数外，还存在逆运算，即反函数。

这篇文章将介绍三角函数的逆运算以及其在实际问题中的应用。

一、三角函数的逆运算三角函数中的逆运算是指由一个三角函数的值反推出该角度的过程。

三角函数的逆运算有反正弦函数、反余弦函数和反正切函数。

1. 反正弦函数（arcsin）反正弦函数是指已知一个三角函数值，求出对应的角度。

符号表示为：y = arcsin(x)，其中 x 为正弦函数的值，y 为角度值。

反正弦函数的定义域为 [-1, 1]，值域为 [-π/2, π/2]。

2. 反余弦函数（arccos）反余弦函数是指已知一个三角函数值，求出对应的角度。

符号表示为：y = arccos(x)，其中 x 为余弦函数的值，y 为角度值。

反余弦函数的定义域为 [-1, 1]，值域为[0, π]。

3. 反正切函数（arctan）反正切函数是指已知一个三角函数值，求出对应的角度。

符号表示为：y = arctan(x)，其中 x 为正切函数的值，y 为角度值。

反正切函数的定义域为 (-∞, +∞)，值域为 (-π/2, π/2)。

二、三角函数逆运算的应用三角函数的逆运算在实际问题中有着广泛的应用，下面将介绍其中几个典型的应用场景。

1. 几何应用三角函数的逆运算广泛应用于几何问题中，例如在给定三角形的边长或两个角度的情况下，可以使用反正弦函数或反余弦函数求解缺失的边长或角度。

这在解题过程中非常常见，有助于解决各种与三角形相关的问题。

2. 物理应用三角函数的逆运算在物理学中也有着重要的应用。

例如，在物体投射运动中，通过已知的初速度、投射角度和高度等信息，可以使用反正切函数求解出物体在空中的飞行时间、射程等相关数据。

此外，在波动和振动问题中，反正弦函数和反余弦函数都可以帮助求解各种周期性运动的相关参数。

3. 工程应用在工程领域中，三角函数的逆运算也被广泛应用。

教大家反求INV函数（渐开线函数）

教大家反求INV函数（渐开线函数）教大家反求INV函数(渐开线函数)liuhong860211 11级分类：理工学科被浏览93次 2013.09.09 请微博专家回答检举齿轮计算中需要使用到的。

wildhouser采纳率：53% 11级 2013.09.10鉴于百度知道尚没有教如何反解INV函数方法，我准备写一个方法，方便大家搜索。

---------------------------------- 解法需要使用编程软件(我个人使用的是VB6.0) 思路是使用试凑法，用黄金分割法优化。

Dim IP1, OP2, R1, R2, Mate, PN, i As Double Private Sub Command1_Click() IP1 = Val(Text1.Text) ‘你手上需要查的数值 R1 = 0 ’左值域R2 = 90 ‘右值域Mate = (R2 - R1) * 0.6180339887498 + R1 ’试凑一个角度(55.62°) For i = 1 To 1000 ’循环(迭代1000次) OP2 = Tan(Mate * 3.1415926535898 / 180) - Mate * 3.1415926535898 / 180 ‘求出试求角度的INV值 PN = OP2 - IP1 ‘试求值与目标值比大小If PN > 0 Then ’如果大于0，说明试求值大了。

那么应该把把右值域R2减小到试求角度。

R2 = Mate Mate = (R2 - R1) * 0.3819660112502 + R1 ‘从右端取0.618的点Else R1 = Mate ’如果小于0，说明试求值小了。

那么应该把把左值域R1增大到试求角度。

Mate = (R2 - R1) * 0.6180339887498 + R1 ‘从左端取0.618点 End If 退出if Next 退出循环 Text2.Text = Mate 显示最终试凑角度(精度在0.0001以内) End Sub GUI界面，大家自己随便写。

三角函数的反函数求解

三角函数的反函数求解在数学中，三角函数是常见的一类函数，包括正弦函数、余弦函数、正切函数等。

而三角函数的反函数则是指对应于三角函数的逆运算，用来求解原函数的输入值。

本文将对三角函数的反函数求解进行详细介绍。

一、正弦函数的反函数求解正弦函数是数学中最基本的三角函数之一，通常表示为sin(x)，其中x为自变量，sin(x)的值范围在-1到1之间。

要求解正弦函数的反函数，可以使用反正弦函数，记作arcsin(x)或者sin^(-1)(x)。

反正弦函数的定义域为[-1, 1]，值域为[-π/2, π/2]。

例如，当sin(x) = 1时，可以得到反正弦函数的解为arcsin(1) = π/2。

二、余弦函数的反函数求解余弦函数是三角函数中的另一个重要函数，通常表示为cos(x)，其中x为自变量，cos(x)的值范围也在-1到1之间。

要求解余弦函数的反函数，可以使用反余弦函数，记作arccos(x)或者cos^(-1)(x)。

反余弦函数的定义域为[-1, 1]，值域为[0, π]。

例如，当cos(x) = 0时，可以得到反余弦函数的解为arccos(0) = π/2。

三、正切函数的反函数求解正切函数是三角函数中的又一个常见函数，通常表示为tan(x)，其中x为自变量，tan(x)的值可以在整个实数范围内取值。

要求解正切函数的反函数，可以使用反正切函数，记作arctan(x)或者tan^(-1)(x)。

反正切函数的定义域为整个实数范围，值域为(-π/2, π/2)。

例如，当tan(x) = 1时，可以得到反正切函数的解为arctan(1) = π/4。

四、其他三角函数的反函数求解除了正弦函数、余弦函数和正切函数，还有其他的三角函数，如余切函数、正割函数和余割函数等。

这些函数的反函数求解与前面介绍的方法类似，只需要使用对应的反函数，如反余切函数、反正割函数和反余割函数等。

五、使用反函数求解实际问题三角函数的反函数求解在实际问题中具有广泛的应用。

反三角函数arcsin 计算

反三角函数arcsin 计算
反三角函数是数学中非常重要的一类函数，其中比较常见的就是反正弦函数arcsin。

arcsin函数是将一个实数作为参数，然后返回一个角度，表示这个角度的正弦值为这个实数。

换句话说，它是正弦函数的反函数，它的定义域是[-1,1]，值域是[-π/2,π/2]。

要计算一个实数的arcsin函数值，我们可以采用以下方法：
1. 确定这个实数的值域是[-1,1]。

如果给定的实数不在这个区间内，那么它就没有arcsin函数值。

2. 找到这个实数在单位圆上的对应点，即以这个实数为正弦值的那个角度。

3. 计算这个角度的弧度值，即将这个角度转化为以弧度为单位的值。

4. 得到这个实数的arcsin函数值，即这个角度的弧度值。

举个例子，假设给定一个实数x，我们想要求它的arcsin函数值。

首先我们需要确认x在[-1,1]之间，然后可以通过反三角函数的定义确定以x为正弦值的角度。

然后我们将这个角度转化为弧度值，并得到这个实数的arcsin函数值。

反三角函数在数学、物理、工程等领域中都有着广泛的应用。

在物理学中，反三角函数被用于计算物理量和角度之间的相互关系；在工程中，反三角函数被用于解决各种实际问题。

因此，学好反三角函数对于理解和应用数学知识具有重要的意义。

渐开线函数速效求解

渐开线函数速效求解《渐开线函数速效求解》一、渐开线函数概述渐开线函数是一种复杂的实值函数，它有着与普通函数不同的函数特性，并且成功的模拟出来的物理过程如运动轨迹、传动特性等。

渐开线函数被广泛应用于机械设计、仿真设计、调节系统等工程领域。

它们具有下列优点：（1）参数量少，曲线简洁。

（2）可以实现复杂的运动轨迹和传动特性，有效模拟复杂物理系统。

（3）可以极其精确地定义动作时序，能够满足许多非线性场景的需要。

二、渐开线函数求解渐开线函数的求解是渐开线函数计算的核心问题，也是其应用的关键。

渐开线函数求解可以分为两步：首先构造一组形状函数，然后通过拟合简化求解。

（1）构造形状函数从数学角度来看，渐开线函数是一组单调函数的有限组合，它有着函数集合中每个函数必须严格满足一定的性质，这些性质称之为形状函数。

渐开线函数中的形状函数包括线性函数、指数函数、乘积函数、二次函数等，每个形状函数的参数必须满足特定的数学关系，形成渐开线函数的系数。

（2）拟合简化求解拟合简化求解是渐开线函数求解的另一大环节，它是と基于惯性有关变量对应要求曲线函数来实现的。

渐开线函数求解会首先以矩阵结构存储输入、输出数据，然后使用拟合算法，配合最小二乘法拟合曲线函数，最后通过运算公式，简化得到渐开线函数的系数，最后再曲线分析法实现复杂数学计算。

三、渐开线函数速效求解渐开线函数的求解通常需要运用比较复杂的数据处理算法，其中服务器消耗大量的时间在求解过程中，为了降低渐开线函数的求解时间，市场上出现了很多通过应用多核心、GPU 计算技术等优化技术来减少求解时间的解决方案，称之为渐开线函数速效求解。

（1）基于多核心计算技术基于多核心计算技术，将传统的求解方法进行重新编写，将复杂的求解问题分成小的任务，再分发到多个核心来计算。

在这样的多核心环境下，每个核心只需要处理较少的计算任务，所以渐开线函数求解的计算速度大大提高，大大提高了渐开线函数求解的性能。

（2）基于GPU计算技术GPU计算技术则是基于对运算负载的低效性，采用GPU计算卡来完成计算，每一个GPU计算卡有着成百上千个处理核心，而这些处理核心可以同时处理大量的渐开线函数系数，极大提升了渐开线函数求解的计算速度。