七年级数学上册天天练试题
七年级上册数学计算题每日一练

七年级上册数学计算题每日一练七年级上册数学计算题每日一练 30 题一、有理数运算1. 计算:(5) + 7解析:异号两数相加,取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值。
所以(5) + 7 = 22. 计算:(8) (3)解析:减去一个数,等于加上这个数的相反数。
所以(8) (3) = 8 + 3 = 53. 计算:(6)×(5)解析:两数相乘,同号得正,异号得负,并把绝对值相乘。
所以(6)×(5) = 304. 计算:(18)÷(6)解析:两数相除,同号得正,异号得负,并把绝对值相除。
所以(18)÷(6) = 35. 计算:(2)^3解析:(2)^3 = (2)×(2)×(2) = 86. 计算:3^2解析:先计算指数运算,再取相反数。
所以3^2 = 97. 计算:\left(\dfrac{1}{2}\right) +\left(\dfrac{1}{3}\right)解析:通分计算,\left(\dfrac{1}{2}\right) +\left(\dfrac{1}{3}\right) = \dfrac{3}{6} + \dfrac{2}{6} =\dfrac{1}{6}8. 计算:\left(\dfrac{2}{3}\right)\left(\dfrac{1}{2}\right)解析:通分计算,\left(\dfrac{2}{3}\right)\left(\dfrac{1}{2}\right) = \dfrac{4}{6} + \dfrac{3}{6} =\dfrac{1}{6}9. 计算:\left(\dfrac{3}{4}\right)×\dfrac{8}{9}解析:约分计算,\left(\dfrac{3}{4}\right)×\dfrac{8}{9} = \dfrac{2}{3}10. 计算:\left(\dfrac{4}{5}\right)÷\dfrac{2}{3}解析:将除法转化为乘法,\left(\dfrac{4}{5}\right)÷\dfrac{2}{3} =\dfrac{4}{5}×\dfrac{3}{2} = \dfrac{6}{5}二、整式运算11. 化简:3x + 2x解析:合并同类项,3x + 2x = 5x12. 化简:5y 3y解析:合并同类项,5y 3y = 2y13. 化简:2a^2 + 3a^2解析:合并同类项,2a^2 + 3a^2 = 5a^214. 化简:4xy 3xy + 5xy解析:合并同类项,4xy 3xy + 5xy = 6xy15. 化简:3m^2n 2mn^2 + 5m^2n 3mn^2解析:合并同类项,3m^2n 2mn^2 + 5m^2n 3mn^2 = 8m^2n 5mn^216. 计算:(2x + 3y) (x 2y)解析:去括号,2x + 3y x + 2y = x + 5y17. 计算:3a^2 (2a^2 + 5a 1)解析:去括号,3a^2 2a^2 5a + 1 = a^2 5a + 118. 计算:2(3x 2y) 3(2x + y)解析:去括号,6x 4y 6x 3y = 7y19. 计算:(3a + 2b) + (4a b)解析:去括号,3a + 2b + 4a b = 7a + b20. 计算:(2x^2 3x + 1) (3x^2 2x 5)解析:去括号,2x^2 3x + 1 3x^2 + 2x + 5 = x^2 x + 6三、综合运算21. 计算:2(3x + 1) 3(2 x)解析:去括号,6x + 2 6 + 3x = 9x 422. 计算:3(x 2) + 2(2x 1)解析:去括号,3x 6 + 4x 2 = 7x 823. 计算:5 3(2x 1) = 4x + 7解析:去括号,5 6x + 3 = 4x + 7移项,6x 4x = 7 5 3合并同类项,10x = 1系数化为 1,x = \dfrac{1}{10}24. 计算:\dfrac{2x 1}{3} \dfrac{x + 2}{2} = 1解析:去分母,2(2x 1) 3(x + 2) = 6去括号,4x 2 3x 6 = 6移项,4x 3x = 6 + 2 + 6合并同类项,x = 1425. 计算:2(x 1) + 3(x + 2) = 5(x 1)解析:去括号,2x 2 + 3x + 6 = 5x 5移项,2x + 3x 5x = 5 + 2 6合并同类项,0 = 9(无解)26. 计算:\dfrac{3x + 1}{2} \dfrac{4x 2}{5} = 1解析:去分母,5(3x + 1) 2(4x 2) = 10去括号,15x + 5 8x + 4 = 10移项,15x 8x = 10 5 4合并同类项,7x = 1系数化为 1,x = \dfrac{1}{7}27. 计算:3[2(x 1) 3(x + 2)] = 6(x 1)解析:去括号,3(2x 2 3x 6) = 6x 63(x 8) = 6x 63x 24 = 6x 6移项,3x 6x = 24 6合并同类项,9x = 18系数化为 1,x = 228. 计算:\dfrac{x + 1}{3} \dfrac{x 2}{6} = 2解析:去分母,2(x + 1) (x 2) = 12去括号,2x + 2 x + 2 = 12移项,2x x = 12 2 2合并同类项,x = 829. 计算:4 3(2 x) = 5x解析:去括号,4 6 + 3x = 5x移项,3x 5x = 6 4合并同类项,2x = 2系数化为 1,x = 130. 计算:\dfrac{2x 1}{4} = \dfrac{1 x}{3} + 1解析:去分母,3(2x 1) = 4(1 x) + 12去括号,6x 3 = 4 4x + 12移项,6x + 4x = 4 + 12 + 3合并同类项,10x = 19系数化为 1,x = \dfrac{19}{10}。
初一数学上册计算题天天练(强烈推荐)60

1、在数轴上将下列各数表示出来。
2-3—, 3 ,0 , 7.252、写出下列各数的相反数。
1—, 18 ,6 ,-0.833、写出下列各数的绝对值。
51—, 3.05 ,-1 , 0.2474、比较下列各组数的大小。
(1)-11与-3 (2)-3与-1.25 (3)|-6.5|与|-1.5|1 2(4)-—与-—(5)13与-|-6| (6)|-56.3|与|-1.2|2 55、计算。
1 117+—+—21×(-13)-20×(-13)6 156 1 7(---)×-(-60)÷8×(-12)7 6 86 6 1-(—+—-—)×343 1×[7+(-2)3]7 7 76、合并同类项。
6m-(9m-4) m+(4m+7z)+(3z+7m)-4(7n+9)-2n 10+(6n+8)+(8n+4)2(ab-5a)-(3a-7b) 16(abc+6a)-8(6a+9abc)6(xy-4z)-(-xy-3z) -5(pq+pr)+(8pq-pr)7、解方程。
5 x 1—x-—=—0.6x-0.2=5.4-8.4x3 4 32 1—-6x=9+—x 5(x-7)-9(x+3)=123 81 1—(6x-8)=—x+3 9x+8(8+x)=-73 5y-1 y-3——=7+—— 4.5x+7.5(x+7)=203 61 2—(5-4x)=—(4x-2) 8(6x+9)=195 71、在数轴上将下列各数表示出来。
41—, 1 ,0 , 3.252、写出下列各数的相反数。
1—, -22 ,-6 ,-0.753、写出下列各数的绝对值。
24—, -3.85 ,3 ,-0.2494、比较下列各组数的大小。
(1)-20与-1 (2)-3与-0.25 (3)|-8.6|与|0.2|1 2(4)-—与-—(5)6与-|-6| (6)|-38.7|与|-4|2 95、计算。
七年级上册数学整式的加减天天练 13.14 .15.16

1. 已知关于x 、y 的单项式234x y 与单项式1218m n x y ---的和为一个单项式,求mn .2已知关于x 、y 的单项式4b c x y 与单项式1218m n x y ---的和为4n m ax y ,求abc .4. 已知133m x y +与42n mx y +-是同类项,则m = ,n = ,13423m n x y mx y ++-= .5. 若代数式221322xy y xa a -+-)(是五次二项式,求a 的值6. 多项式5)13(72++-+x n kx x m 是关于x 的三次三项式,并且一次项系数为−7,求m+n−k 的值。
7. 已知一个多项式52381m +++xy yx m )(是个四次三项式,那么m 的值1.先化简,再求值:2(a 2-ab )-3(23a 2-ab )-5,其中a =-2,b =3.2.先化简,再求值:(3x 2-xy +7)-(5xy -4x 2+7),其中x ,y 满足(x -2)2+|3y -1|=0.3.2,322=+=+ab b ab a 已知,求多项式)(22222b b 2233+--+-a a b ab a 的值4.先化简,再求值:(3x 2+5x -2)-2(2x 2+2x -1)+2x 2-5,其中x 2+x -3=05.如果210a a +-=,求3222a a ++的值6. 若331x x -=,求432912372003x x x x +--+的值.7、已知多项式3223(3)(2)5m x x x n x x x -++++-是关于x 的二次多项式,当x =2时的值为-17,求当x =-2时,此多项式的值.8.已知a +2b =-3,则3(2a -3b )-4(a -3b )+b 的值为_____9.已知xy =1,x +y =12,那么代数式y -(xy -4x -3y )的值等于 10.当x =1时,多项式ax 3+bx +1的值为5,则当x =-1时,多项式12ax 3+12bx +1的值为 .1.已知多项式(4x 2+ax -y +6)-(2bx 2-3x +5y -1),若多项式的值与字母x 的取值无关,则a b 的值2.已知多项式2324x x --与多项式A 的和为6x -1,且式子(1)A mx ++的计算结果中不含关于x 的一次项,求m 的值.3.已知多项式2x ax y b +-+与2363bx x y -+-的差的值与字母x 的取值无关,求代数式22223(2)(4)a ab b a ab b ---++的值.4. 已知多项式)15(2323223++-+-+y x y y x x a )()中不含x3项,计算)(1421223-+-a a a 的值。
七年级数学上册天天练试题
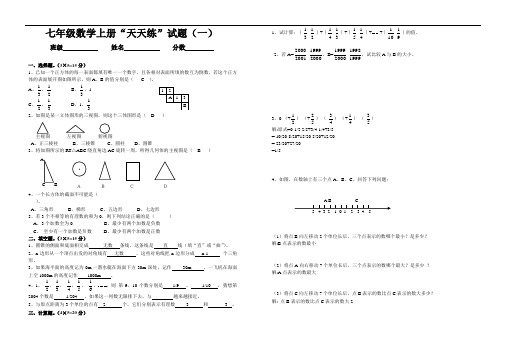
七年级数学上册“天天练”试题(一)班级姓名 分数一、选择题。
(3×5=15分)1、已知一个正方体的每一表面都填有唯一一个数字,且各相对表面所填的数互为倒数,若这个正方体的表面展开图如图所示,则A 、B 的值分别是( C )。
A 、31,21 B 、31,1 C 、21,31 D ,1,312、如图是某一立体图形的三视图,则这个三体图形是( D )左视图A 、正三棱柱 B、三棱锥 C 、圆柱 D 、圆锥3、将如图所示的RT △ABC 绕直角边AC 旋转一周,所得几何体的主视图是( B )A B C D 4、一个长方体的截面不可能是( )。
A 、三角形B 、梯形C 、五边形D 、七边形 5、若3个不相等的有理数的和为0,则下列结论正确的是( ) A 、3个加数全为0 B 、最少有两个加数是负数 C 、 至少有一个加数是负数 D 、最少有两个加数是正数 二、填空题。
(3×5=15分)1、圆锥的侧面和底面相交成 无数 条线,这条线是 直 线(填“直”或“曲”)。
2、n 边形从一个顶点出发的对角线有 无数 ,这些对角线把n 边形分成 n-1 个三角形。
3、如果海平面的高度记为0m,一潜水艇在海面下方30m 深处,记作 -30m ,一飞机在海面上空1000m 的高度记作 1000m 。
4、1,-21,31,-41,51,-61, ,则 第9、10个数分别是 1/9 , - 1/10 ,猜想第2004个数是 - 1/204 ,如果这一列数无限排下去,与 越来越接近。
5、与原点距离为3个单位的点有 2 个,它们分别表示有理数 -3 和 3 。
三、计算题。
(4×5=20分)1、试计算:|31-21|+|41-31|+|51-41|+ +|101-91|的值。
2、若A=20012000-20001999,B=20001999-19991998,试比较A 与B 的大小。
3、0-(+21)-(+52)-(-43)-(+41)-(-53) 解:原式=0-1/2-2/5+3/4-1/4+3/5=-10/20-8/20+15/20-5/20+12/20 =-23/20+27/20 =1/54、如图,在数轴上有三个点A 、B 、C 。
(完整word版)初一数学全册计算题天天练

初一数学上册计算题天天练第1天一、有理数口算(直接写出得数)1、)8()16(-+-=2、122+- =3、 )85(78-+ =4、)15()14(+-- =5、)16(4--=6、)6()4(-⨯-=7、)31(84-⨯=8、3)48(÷- =9、⎪⎭⎫ ⎝⎛-÷-316)( = 10、)2(3--= 11、42- = 12、42)(- = 13、20121)(- = 14、20131)(- = 15、20121- 16、 =二、整式的加减——去括号、合并同类型(1))(2)(2b a b a a +-++ (2))32(2[)3(1yz x x xy +-+--]三、整式的加减——先化简、再求值233(4333)(4),2;a a a a a a +----+=-其中四、解一元一次方程(1)2x+5=5x-7 (2) 4-3(2-x)=5x()32--一、有理数混合运算1、31277⎛⎫÷- ⎪⎝⎭85513)64(⨯÷-⨯2、22128(2)2⎛⎫-⨯-+÷- ⎪⎝⎭3、 9181739⨯⎪⎭⎫ ⎝⎛-二、整式的加减——去括号、合并同类型(3))32(3)23(4)(5b a b a b a -+--+; (4))377()5(322222a b ab b ab a a ---+--三、整式的加减——先化简、再求值 22222222(22)[(33)(33)],1, 2.x y xy x y x y x y xy x y ---++-=-=其中四、解一元一次方程(3)3(x-2)=2-5(x-2) (4) 2(x+3)-5(1-x)=3(x -1)一、有理数混合运算4、⎪⎭⎫ ⎝⎛-++-÷41312112415、()31-6612131⨯⎪⎭⎫ ⎝⎛+-- 6、)43(411)43()411(-------二、整式的加减——去括号、合并同类型(5) )45()54(3223--++-x x x x (6))324(2)132(422+--+-x x x x三、整式的加减——先化简、再求值 ()()()2222223224b ab a ab b a b ab a +-+-+---- 其中4.0,41=-=b a四、解一元一次方程(5) 3(1)2(2)23x x x +-+=+ (6) 3(2)1(21)x x x -+=--一、有理数混合运算7、⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛--⎪⎭⎫ ⎝⎛+--318216315414 8、173115321176.0324-⎪⎭⎫ ⎝⎛-⨯⎪⎭⎫ ⎝⎛-+÷+⨯-二、整式的加减——去括号、合并同类型(7))69()3(522x x x +--++-. (8))35()2143(3232a a a a a a ++--++-三、整式的加减——先化简、再求值 2(a 2b +2b 3-ab 3)+3a 3-(2ba 2-3ab 2+3a 3)-4b 3,其中a =-3,b =2四、解一元一次方程(7)2x =3x-1 (8) 2x -13 =x+22 +1一、有理数混合运算9、108524835)16(+⎪⎭⎫ ⎝⎛-++⎪⎭⎫ ⎝⎛-+- 10、()()631)2(42+--⨯--+-二、整式的加减——去括号、合并同类型(9))(4)(2)(2n m n m n m -++-+ (10)]2)34(7[522x x x x ----三、整式的加减——先化简、再求值21x 2-2212- (x + y )2⎡⎤⎢⎥⎣⎦-23(-32x 2+31y 2),其中x =-2, y =-34四、解一元一次方程(9)12131=--x (10) x x -=+38一、有理数混合运算11、20112012)2(21-⨯⎪⎭⎫ ⎝⎛- 12、⎪⎭⎫ ⎝⎛-+-127659521()36-⨯ 13、()1-⎪⎭⎫ ⎝⎛-÷⎪⎭⎫ ⎝⎛-÷3114310二、整式的加减——去括号、合并同类型(1)(2)(3)x y y x --- (2)()()()b a b a b a 4227523---+-三、整式的加减——先化简、再求值21x -2(x -31y 2)+(-23x +31y 2),其中x =-2,y =-32.四、解一元一次方程(11) 12542.13-=-x x (12 ) 310.40.342x x -=+一、有理数混合运算14、()2332-÷-()2-⨯ 15、81)4(2033--÷- 16、100()()222---÷⎪⎭⎫ ⎝⎛-÷32二、整式的加减——去括号、合并同类型(3)()[]22222223ab b a ab b a --- (4) 2213[5(3)2]42a a a a ---++三、整式的加减——先化简、再求值 x x x x x x 5)64(213223312323-++-⎪⎭⎫ ⎝⎛--- 其中x =-121四、解一元一次方程(13) 1111248x x x x -=++ (14) 3142125x x -+=-一、有理数混合运算17、)()(32312115--+--- 18、)()()(846592-÷---⨯+-二、整式的加减——去括号、合并同类型(5) 2x -(3x -2y +3)-(5y -2); (6) -(3a +2b )+(4a -3b +1)-(2a -b -3)三、整式的加减——先化简、再求值21x 2-2⎪⎭⎫ ⎝⎛+--⎪⎭⎫ ⎝⎛-222231322331y x y x ,其中x =-2,y =-34四、解一元一次方程1512 (15)=-+x x 312121 (16)-=-x x一、有理数混合运算19、100512161004----÷+)( 20、()()()201321111-+-+-二、整式的加减——去括号、合并同类型(1)(8xy -x 2+y 2)+(-y 2+x 2-8xy ); (2)(2x 2-21+3x )-4(x -x 2+21)三、整式的加减——先化简、再求值 x x x x x x 5)64(213223312323-++-⎪⎭⎫ ⎝⎛--- 其中x =-121;四、解一元一次方程 (17) 31257243y y +-=- (18) 576132x x -=-+一、有理数混合运算 21、)43(65)531(42-⨯--÷- 22、4)28.0(5)2(43÷--⨯-+ 23、2)6543187(36-+-⨯-二、整式的加减——去括号、合并同类型(3)()[]22222223ab b a ab b a --- (4) 2213[5(3)2]42a a a a ---++三、整式的加减——先化简、再求值21x 2-2⎪⎭⎫ ⎝⎛+--⎪⎭⎫ ⎝⎛-222231322331y x y x ,其中x =-2,y =-34四、解一元一次方程(19)143321=---m m (20) 52221+-=--y y y一、有理数混合运算24、419932(4)(1416)41313⎡⎤--⨯-÷-⎢⎥⎣⎦)22- 25、()⎪⎭⎫⎝⎛-⨯÷-++-31324323二、整式的加减——去括号、合并同类型 (5)()()()xy yx xy yxy x -+---+-22222322 (6) 3x 2-[7x -(4x -3)-2x 2].三、整式的加减——先化简、再求值2(a 2b +2b 3-ab 3)+3a 3-(2ba 2-3ab 2+3a 3)-4b 3,其中a =-3,b =2四、解一元一次方程 (21)12136x x x -+-=- (22) 38123x x ---=一、有理数混合运算24、⎪⎪⎭⎫ ⎝⎛--⨯+-2323221)21(2 25、()⎥⎦⎤⎢⎣⎡-÷⎪⎭⎫ ⎝⎛⨯-+---2512.01452二、整式的加减——去括号、合并同类型(3) 2x -(3x -2y +3)-2(5y -2); (4) -2(3a +2b )+(4a -3b +1)-(2a -b -3)三、整式的加减——先化简、再求值已知2-a +(b +1)2=0,求5ab 2-[2a 2b -(4ab 2-2a 2b )]的值四、解一元一次方程 (23) 12(x-3)=2-12(x-3) (24)35.012.02=+--x x一、实数混合运算二、解一元一次不等式(组)1、 136155-+x x >2、⎩⎨⎧++-x x xx 423215三、解方程组1、503217x y x y -=⎧⎨+=⎩ 2、四、先化简、再求值:)31(6)31(322y x y x x +-+--,其中2-=x ,1-=y)512(5)1-)313(3)2-一、实数混合运算二、 解一元一次不等式(组)1、 x x 4923+≥-2、⎩⎨⎧-≤+>+145321x x xx三、解方程组1、 2、四、先化简、再求值:3x 2y ﹣[2xy ﹣2(xy ﹣x 2y )+x 2y 2],其中x=3,y=﹣33271816)3-+--31433)4---⨯一、实数混合运算二、解一元一次不等式(组)1、)1(5)32(2+<+x x2、⎪⎩⎪⎨⎧--≤--x x x x 14214)23(三、解二元一次方程组1、 2、四、先化简、再求值: )3(2)52(4222xy x y xy x xy ++-+-其中 x =-2,y =133364271)6-+---2)3(223)5-----π()()()9-214-4-2-23323⎪⎭⎫ ⎝⎛⨯+⨯一、实数混合运算1、()22-错误!未找到引用源。
七年级上册数学每日一练

七年级上册数学每日一练一、有理数的运算。
1. 计算:- ( - 2)+( - 3)- 解:( - 2)+( - 3)=-(2 + 3)=-5- 4+( - 7)- 解:4+( - 7)=4 - 7=-3- ( - 1)+0- 解:( - 1)+0=-12. 计算:- ( - 3)×4- 解:( - 3)×4=-12- ( - 2)×( - 5)- 解:( - 2)×( - 5)=10- 0×( - 6)- 解:0×( - 6)=03. 计算:- ( - 8)÷4- 解:( - 8)÷4=-2- ( - 15)÷( - 3)- 解:( - 15)÷( - 3)=5- 0÷( - 2)- 解:0÷( - 2)=0二、整式的加减。
1. 化简:- 3a+2b - 5a - b- 解:(3a - 5a)+(2b - b)=-2a + b- 4x^2 - 3x+7 - 3x^2+4x - 5- 解:(4x^2 - 3x^2)+(-3x + 4x)+(7 - 5)=x^2+x + 22. 先化简,再求值:- 已知a = 2,b=-1,求2(a^2 - ab)-3(a^2 - ab)的值。
- 解:- 先化简2(a^2 - ab)-3(a^2 - ab)=(2 - 3)(a^2 - ab)=-(a^2 - ab)=-a^2+ab。
- 当a = 2,b=-1时,原式=-2^2+2×(-1)=-4 - 2=-6三、一元一次方程。
1. 解方程:- 2x+3 = 5x - 1- 解:移项得2x - 5x=-1 - 3,合并同类项得-3x=-4,系数化为1得x=(4)/(3) - 3(x - 2)=2x+1- 解:去括号得3x - 6 = 2x+1,移项得3x - 2x=1 + 6,解得x = 72. 列方程解应用题:- 某班有学生45人,会下象棋的人数是会下围棋人数的3.5倍,两种棋都会及两种棋都不会的人数都是5人,求只会下围棋的人数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
__________________________________________________大山教育每日练习试题(一)姓名出题人:陈老师一、选择题。
(3×5=15分)1、已知一个正方体的每一表面都填有唯一一个数字,且各相对表面所填的数互为倒数,若这个正方体的表面展开图如图所示,则A 、B 的值分别是( )。
A 、31,21 B 、31,1 C 、21,31 D ,1,312、如图是某一立体图形的三视图,则这个三体图形是( )主视图 左视图A 、正三棱柱B 、三棱锥C 、圆柱D 、圆锥3、将如图所示的RT △ABC 绕直角边AC 旋转一周,所得几何体的主视图是( )A B C D 4、一个长方体的截面不可能是( )。
A 、三角形B 、梯形C 、五边形D 、七边形 5、若3个不相等的有理数的和为0,则下列结论正确的是( ) A 、3个加数全为0 B 、最少有两个加数是负数 C 、 至少有一个加数是负数 D 、最少有两个加数是正数 二、填空题。
(3×5=15分)1、圆锥的侧面和底面相交成条线,这条线是线(填“直”或“曲”)。
2、n 边形从一个顶点出发的对角线有,这些对角线把n 边形分成 个三角形。
3、如果海平面的高度记为0m,一潜水艇在海面下方30m 深处,记作,一飞机在海面上空1000m 的高度记作。
4、1,-21,31,-41,51,-61,,则 第9、10个数分别是,,猜想第2004个数是,如果这一列数无限排下去,与越来越接近。
5、与原点距离为3个单位的点有个,它们分别表示有理数和。
三、计算题。
(4×5=20分) 1、试计算:|31-21|+|41-31|+|51-41|++|101-91|的值。
2、若A=20012000-20001999,B=20001999-19991998,试比较A 与B 的大小。
3、0-(+21)-(+52)-(-43)-(+41)-(-53)4、如图,在数轴上有三个点A、B、C。
回答下列问题:(1)将点B向左移动2个单位长后,三个点表示的数哪个最小?是多少?(2)将点A向右移动7个单位长后,三个点表示的数哪个最大?是多少?(3)将点C向左移动7个单位长后,点B表示的数比点C表示的数大多少?(4)怎样移动A、B、C中的两个点,才能使三个点表示的数相同,有几种移动方法____________________________________________________________________________________________________大山教育 试题(二)姓名出题人:陈老师一、选择题。
(3’×5=15’)1、5个数相乘,积为负,那么其中负因数的个数是( )A 、1B 、3C 、5D 、1或3或52、-243的相反数的倒数为( )A 、243B 、234 C 、114D 、113 3、如果aa ||=-1,则a 的取值范围是( ) A 、 a <0 B 、a ≤0 C 、a ≥0 D 、a >04、如果一个有理数的偶次幂是正数,那么这个有理数( )A 、一定是正数B 、是正数或负数C 、一定是负数D 、可以是任意有理数 5、(-0.125)2004×(-8)2005 的值为( )A 、-4B 、4C 、-8D 、8二、填空题(3’×5=15’)1、倒数是它本身的数是,相反数是它本身的数是,绝对值是它本身的数是。
2、如果a 2=(-3)2,那么a=3、若|a+5|+(b-2)2=0 ,则a b =4、-(-2)的倒数是;-(32)的相反数是。
5、若一个数的平方是4,则这个数是;若一个数的立方是8,则这个数是;一个数的立方是-271,这个数是。
三、计算题。
(4×5’=20分)__________________________________________________1、105×(31-75-52)2、已知:(x+y )2+|y-3|=0,求xyyx 的值。
3、(-3)2-(121)3×92-6÷|-32|34、a 、b 、c 在数轴上的位置如图所示,化简|a |+|a-b|-|b-c-a|大山教育 每日练习试题(三)姓名出题人:陈老师选择题。
(5×3’=15’)__________________________________________________(1)如果甲数为x ,且甲数为乙数的3倍,那么乙数是( )A 、31x B 、3x C 、x+3 D 、x+31 (2)下列各组中是同类项的是( )A 、2x 2,3 xB 、3xy ,4x 2yC 、a 2b ,b 2aD 、5(x-y ),3(x-y )(3)七年级进行体能测试,一班有m 个学生,平均成绩是a 分,二班有n 个学生,平均成绩是b 分,则一、二班的平均成绩为( ) A 、 B 、 C 、 D 、 (4)如果x 2+x-10=-9,那么代数式2x 2+2x-6的值为( ) A 、4 B 、5 C 、-4 D 、-5 (5)按F 图所示的程序计算,若开始输入的值为x=3,则最后输出的结果是( )二、填空题。
(5×3’=15’) (6)“数a 的2倍与10的和” 用代数式数字表示为。
(7)小英对代数式3a 给出了这样的解释,西瓜每千克3元,那么买a 千克西瓜共需要3a 元,请你对该代数式作出另外的解释:。
(8)某市出租车收费标准为:起价10元,3千米后每千米1.8元,是某人乘坐出租车x (x >3)千米时的付费为元。
(9|a-b|-|a-c|=(10)按规律填空:1、3、7、15、……(第n 个数) 三、解答题。
(4×5’=20’)(11)化简下列式子:3x 2+2(x 2-y 2)-(x 2+y 2)(12)已知x+y=5,xy=4,求代数式2xy-2x+1的值。
a+b 2 a+b m+n am+bn m+n am+bn a+b__________________________________________________(13)已知小明的年龄为m 岁,小红的年龄比小明的年龄的2倍少4岁,小华的年龄比小红的年龄的21还多1岁,求这三个同学的年龄之和。
(14)一根长80cm 的弹簧,一端固定,如果另一端挂上物体,那么在正常情况下物体的质量每增加1千克可使弹簧增长2cm 。
(1)正常情况下,当挂着x 千克的物体时,弹簧的长度是多少厘米?大山教育每日练习试题(四)姓名出题人:陈老师一、选择题。
(3’×5=15’)__________________________________________________1、用代数式表示“x 的3倍与y 的平方的和”正确的是( )A 、(3x+y )2B 、(3x )2+y 2C 、3x+y 2D 、3(x 2+y 2)2、化简m-n-(m+n )的结果( )A 、0B 、2mC 、-2nD 、2m-2n3、已知M 是线段AB 上一点,不能确定M 是AB 中点的条件是( )A 、AM=BMB 、AM=21AB C 、AB=2BM D 、AM+BM=AB4、平面上AB 两点间的距离是指( )A 、经过A 、B 两点的直线 B 、射线ABC 、线段ABD 、线段AB 的长度5、12点10分时,时针和分针的夹角是( ) A 、500 B 、540 C 、550 D 、600 二、填空题:(3’×5=15’)6、a-b-c 的相反数是。
7、代数式6xy-3y 2+3x ,共有项,分别是。
8、1、4、9、16、、、……(第n 个数)9、平面内的三点可确定直线。
10、根据图填空:AB=AC+CD+=+DB=AC+ 三、计算题:(4×5’=20’) 11、化简:3a 2+2(a 2-y 2)-(x 2+y 2)12、先化简再求值:9a+6a 2-3(a-32a 2),其中a=-2。
13、如图,已知点C 在线段AB 上,且AC=6cm ,BC=4 cm ,点M 、N 分别是AC 和BC 的中点。
求线段MN 的长。
AC D BAM N B__________________________________________________14、将连续的偶数2、4、6、8、……排成如下的数表,用十字框框住5个数,如下图,回答下列问题: 2 4 6 8 10 12 14 16 18 20 22 24 26 28 30 32 34 36 38 40 42 44 46 48(1)十字框内5个数的和与框内中间数30有什么关系? (2)若设中间数为a ,用代数式表示十字框内的5个数以及5个数之和。
大山教育每日练习试题(五)姓名出题人:陈老师一、选择:(3’×5=15’)1、如图:图中线段共有( )A 、4条B 、5条C 、6条D 、7条 2、如图:从A 点到F 点的最短路线是( )A 、A →D →E →FA B C DEF__________________________________________________B 、A →C →E →F C 、A →B →E →FD 、无法确定3、小敏用一个10倍放大镜观察一个100的角,她看到的角的度数是( )A 、100B 、200C 、1000D 、无法确定4、如图,∠PQR 等于1380,SQ ⊥QR (即∠SQR 是直角)QT ⊥PQ (即∠PQT 是直角),则∠SQT 等于( )A 、420B 、640C 、480D 、240 5、线段AB=5cm 、BC=4 cm 。
P 为AC 的中点, 则AP 的长为( )A 、4.5 cmB 、0.5 cmC 、4.5 cm 或0.5 cmD 、不能确定 二、填空:(3’×6=18’)6、将弯曲的河道改直,可以缩短航程,是因为。
7、已知线段AC=6cm ,在直线AC 上截取CB=2 cm ,则AB=cm 。
8、138.40-49036’=。
9、在同一平面内三条直线a 、b 、c , 且有a ⊥c ,b ⊥c ,那么a 与b 的位置关于。
10、轮船航行到A 处测得小岛B 的方向为北偏西360,那么从B 观察A 处的方向为。
11、延长线段AB 到点C ,使BC=31AB ,D 为AC 的中点,且DC=6 cm ,则AB 的长是cm 。
三、解答题。
(7’+10’)12、如图所示,B 、C 两点把线段AD 分成2:4:3三部分,M 是AD 的中点,CD=6,求线段MC 的长。
13、如图,O 是直线AB 上一点,∠AOC=31∠BOC ,OC 是∠AOD 的平分线。
