小学数学六年级易错题库 - 易错题库含答案
六年级计算(易错题)20条(含答案)

六年级计算(易错题)20条(含答案)1、计算2.5÷(1-25%)时,可以先算出25%的值为0.25,然后用1减去0.25得到0.75,最后将2.5除以0.75,得到3.33.2、计算4.6÷8 + 5.4×12.5%时,可以先算出12.5%的值为0.125,然后将5.4乘以0.125得到0.675,再将4.6除以8得到0.575,最后将0.575和0.675相加,得到1.25.3、计算980×120%-980×20%时,可以先算出120%的值为1.2,20%的值为0.2,然后将980乘以1.2得到1176,再将980乘以0.2得到196,最后将1176减去196,得到980.4、计算(xxxxxxxx35—×)÷时,需要知道缺少的数是多少。
这里无法计算,需要更多信息。
5、计算(38+19)÷时,需要知道缺少的数是多少。
这里无法计算,需要更多信息。
6、计算(+-)×88÷时,需要知道缺少的数是多少。
这里无法计算,需要更多信息。
7、计算2×3÷(4÷(5-2)+1)时,可以先算出5-2的值为3,然后将4除以3加1得到2.3333,最后将2乘以3除以2.3333,得到2.5714.8、计算5/8×37+5/8×62+5/8时,可以先将5/8乘以37得到23.125,再将5/8乘以62得到38.75,最后将这两个数相加再加上5/8,得到62.375.9、计算89÷(23÷12)×6时,可以先将23÷12的值计算出来,得到1.9167,然后将89除以1.9167,再将结果乘以6,得到279.10、计算/36÷(3+24-9)时,可以先将3+24-9的值计算出来,得到18,然后将除以36再除以18,得到392.5.12、计算25×(1+40%)÷37.5%时,可以先将40%的值计算出来,得到0.4,然后将1加上0.4得到1.4,再将25除以37.5%的值,即0.375,最后将结果乘以1.4,得到37.3333.13、计算158-58÷87.5%时,可以先将87.5%的值计算出来,得到0.875,然后将58除以0.875,得到66.2857,最后将158减去66.2857,得到91.7143.14、计算15×(215/15+15/17)×17时,可以先将215/15的值计算出来,得到14.3333,然后将15/17的值计算出来,得到0.8824,再将14.3333加上0.8824得到15.2157,最后将15.2157乘以17,得到258.999.15、计算4÷44/5-5÷4时,可以先将4除以44/5,即将4乘以5/44,得到0.4545,然后将5除以4得到1.25,最后将0.4545减去1.25,得到-0.7955.18、计算4/5:X=2/5时,可以先将等式两边的分数转化为小数,即4/5转化为0.8,2/5转化为0.4,然后将0.4除以0.8,得到0.5,即X的值为0.5.。
最新小学数学六年级易错题难题题库 - 易错题难题题库含答案

最新小学数学六年级易错题难题题库 - 易错题难题题库含答案一、培优题易错题1.如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走均为正,向下向左走均为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(﹣1,﹣4),其中第一个数表示左右方向,第二个数表示上下方向.(1)图中A→C(________,________),B→C(________,________),C→________(+1,﹣2);(2)若这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+2,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出P的位置;(3)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程.(4)若图中另有两个格点M、N,且M→A(3﹣a,b﹣4),M→N(5﹣a,b﹣2),则N→A应记为什么?【答案】(1)+3;+4;+2;0;D(2)解:P点位置如图1所示;(3)解:如图2,根据已知条件可知:A→B表示为:(1,4),B→C记为(2,0)C→D记为(1,﹣2);则该甲虫走过的路线长为:1+4+2+1+2=10(4)解:由M→A(3﹣a,b﹣4),M→N(5﹣a,b﹣2),所以,5﹣a﹣(3﹣a)=2,b﹣2﹣(b﹣4)=2,所以,点A向右走2个格点,向上走2个格点到点N,所以,N→A应记为(﹣2,﹣2)【解析】【解答】解:(1)图中A→C(+3,+4),B→C(+2,0),C→D(+1,﹣2);故答案为:(+3,+4),(+2,0),D;【分析】(1)根据向上向右走均为正,向下向左走均为负确定数据即可;(2)根据所给的路线确定点的位置即可;(3)根据表示的路线确定长度相加可得结果;(4)观察点的变化情况,根据(1)即可确定点走了格数,从而确定结论.2.某工厂一周计划每天生产电动车80辆,由于工人实行轮休,每天上班人数不同,实际每天生产量与计划量相比情况如表(增加的为正数,减少的为负数):(2)本周总生产量是多少辆?比原计划增加了还是减少了?增加或减少多少辆?【答案】(1)解:生产量最多的一天比生产量最少的一天多生产6-(-5)=6+5=11辆;(2)解:总产量4+(-1)+2+(-2)+6+(-3)+(-5)+80×7=561辆,比原计划增加了,增加了561-560=1辆.【解析】【分析】(1)根据列表得到生产量最多的一天是星期五,是(80+6)辆,产量最少的一天是星期日是(80-5)辆,生产量最多的一天比生产量最少的一天多生产6-(-5)辆;(2)根据题意总产量是80×7+4+(-1)+2+(-2)+6+(-3)+(-5),找出相反数,再由减去一个数等于加上这个数的相反数,求出本周总生产量,得到比原计划增加或减少了的值.3.在抗洪抢险中,人民解放军的冲锋舟沿东西方向的河流抢救灾民,早晨从A地出发,晚上到达B地,规定向东为正方向.当天航行路程记录如下:(单位:千米)14,﹣9,-18,﹣7,13,﹣6,10,﹣5问:(1)B地在A地的何位置;(2)若冲锋舟每千米耗油0.5升,油箱容量为29升,求途中需补充多少升油?【答案】(1)解:∵14-9-18-7+13-6+10-5=-8,∴B在A正西方向,离A有8千米(2)解:∵|14|+|-9|+|-18|+|-7|+|13|+|-6|+|10|+|-5|=82千米,∴82×0.5-29=12升.∴途中要补油12升【解析】【分析】(1)根据题意得到B地在A地14-9-18-7+13-6+10-5=-8处,即正西方向,离A有8千米;(2)根据距离的意义得到各个数的绝对值的和,再求出耗油量,得到途中需补充的油量.4.在一条东西走向的马路旁,有青少年宫、学校、商场、医院四家公共场所.已知青少年宫在学校东300m处. 商场在学校西200m处,医院在学校东500m处.若将马路近似地看做一条直线,以学校为原点,向东方向为正方向,用1个单位长度表示100m.(1)在数轴上表示出四家公共场所的位置.(2)列式计算青少年宫与商场之间的距离.【答案】(1)解:如图所示:(2)解:由题意可得:300-(-200)=500或︱-200-300︱=500.答:青少年宫与商场之间的距离是500 m【解析】【分析】(1)根据题意画出学校为原点的数轴,在数轴上表示出四家公共场所的位置;(2)根据题意青少年宫与商场之间的距离是300-(-200),再根据减去一个数等于加上这个数的相反数,求出青少年宫与商场之间的距离.5.如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.(结果保留π)(1)把圆片沿数轴向左滚动1周,点A到达数轴上点C的位置,点C表示的数是________数(填“无理”或“有理”),这个数是________;(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是________;(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,+3,﹣4,﹣3①第几次滚动后,A点距离原点最近?第几次滚动后,A点距离原点最远?②当圆片结束运动时,A点运动的路程共有多少?此时点A所表示的数是多少?【答案】(1)无理;﹣2π(2)4π或﹣4π(3)解:①∵圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,+3,﹣4,﹣3,∴第4次滚动后,A点距离原点最近;第3次滚动后,A点距离原点最远;②∵|+2|+|﹣1|+|+3|+|﹣4|+|﹣3|=13,∴13×2π×1=26π,∴A点运动的路程共有26π;∵(+2)+(﹣1)+(+3)+(﹣4)+(﹣3)=﹣3,(﹣3)×2π=﹣6π,∴此时点A所表示的数是:﹣6π【解析】【解答】解:(1)把圆片沿数轴向左滚动1周,点A到达数轴上点C的位置,点C表示的数是无理数,这个数是﹣2π;故答案为:无理,﹣2π;(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是4π或﹣4π;故答案为:4π或﹣4π;【分析】(1)利用圆的半径以及滚动周数即可得出滚动距离;(2)利用圆的半径以及滚动周数即可得出滚动距离;(3)①利用滚动的方向以及滚动的周数即可得出A点移动距离变化;②利用绝对值的性质以及有理数的加减运算得出移动距离和A表示的数即可.6.、、三瓶盐水的浓度分别为、、,它们混合后得到克浓度为的盐水.如果瓶盐水比瓶盐水多克,那么瓶盐水有多少克?【答案】解:设C瓶盐水有x克,则B瓶盐水为(x+30)克,A瓶盐水为100-(x+x+30)=70-2x克。
最新小学数学六年级易错题库 - 易错题库含答案

最新小学数学六年级易错题库 - 易错题库含答案一、培优题易错题1.某工艺品厂计划一周生产工艺品2100个,平均每天生产300个,但实际每天生产量与计划相比有出入.下表是某周的生产情况 (超产记为正,减产记为负):(1)写出该厂星期一生产工艺品的数量.:(2)本周产量最多的一天比最少的一天多生产多少个工艺品?(3)请求出该工艺品厂在本周实际生产工艺品的数量.(4)已知该厂实行每周计件工资制,每生产一个工艺品可得60元,若超额完成任务,则超过部分每个可得50元,少生产一个扣80元.试求该工艺厂在这一周应付出的工资总额.【答案】(1)解:由表格可得周一生产的工艺品的数量是:300+5=305(个),答:该厂星期一生产工艺品的数量是305个.(2)解:本周产量最多的一天是星期六,最少的一天是星期五,∴(16+300)-【(-10)+300】=26(个),答:本周产量最多的一天比最少的一天多生产26个工艺品.(3)解:2100+【5+(-2)+(-5)+15+(-10)+16+(-9)】=2100+10=2110(个).答:该工艺品厂在本周实际生产工艺品的数量是2110个.(4)解:(+5)+(-2)+(-5)+(15)+(-10)+(+16)+(-9)=10(个).根据题意得该厂工人一周的工资总额为:2100×60+50×10=126500(元).答:该工艺厂在这一周应付出的工资总额是126500元.【解析】【分析】(1)根据表格中将300与5相加可求得周一的产量.(2)由表格中的数字可知星期六产量最高,星期五产量最低,用星期六对应的数字与300相加求出产量最高的量;同理用星期五对应的数字与300相加求出产量最低的量,两者相减即可求出所求的个数.(3)由表格中的增减情况,把每天对应的数字相加,利用互为相反数的两数和为0,且根据同号及异号两数相加的法则计算后,再加上2100即可得到工艺品一周的生产个数.(4)用计划的2100乘以单价60元,加超额的个数乘以50元,即为一周工人工资的总额. 2.已知:如图,这是一种数值转换机的运算程序.(1)若第1次输入的数为2,则第1次输出的数为1,那么第2次输出的数为;若第1次输入的数为12,则第5次输出的数为________.(2)若输入的数为5,求第2016次输出的数是多少.(3)是否存在输入的数x,使第3次输出的数是x?若存在,求出所有x的值;若不存在,请说明理由.【答案】(1)4、6(2)解:5+3=8,8× =4,4× =2,2× =1,1+3=4,∴若输入的数为5,则每次输出的数分别是8、4、2、1、4、2、1,…,(2016−1)÷3=2015÷3=671 (2)∴第2016次输出的数是2(3)解:当x为奇数时,有 (x+3)+3=x,解得x=9(舍去),× (x+3)=x,解得x=1,当x为偶数时,有 × × x=x,解得x=0,× x+3=x,解得x=4,×( x+3)=x,解得x=2,综上所述,x=0或1或2或4【解析】【解答】解:(1)∵1+3=4,∴第1次输出的数为1,则第2次输出的数为4.×12=6,6× =3,3+3=6,6× =3,3+3=6,∴第1次输入的数为12,则第5次输出的数为6.【分析】(1)根据运算程序得到第1次输出的数为1,第2次输出的数为3+1,第1次输入的数为12,则第5次输出的数(12÷2÷2+3)÷2+3;(2)根据题意由输入的数为5,每次输出的数分别是8、4、2、1、4、2、1···,得到3次一循环,求出第2016次输出的数;(3)根据运算程序得到当x为奇数时和为偶数时,求出所有x的值.3.古希腊著名的毕达哥拉斯学派把1,3,6,10,…这样的数称为“三角形数”,而把1,4,9,16,…这样的数称为“正方形数”.(1)第5个“三角形数”是________,第n个“三角形数”是________,第5个“正方形数”是________,第n个“正方形数”是________.(2)除“1”以外,请再写一个既是“三角形数”,又是“正方形数”的数________.(3)经探究我们发现:任何一个大于1的“正方形数”都可以看做两个相邻“三角形数”之和. 例如:①4=1+3;②9=3+6;③16=6+10;④________;⑤________;…请写出上面第4个和第5个等式.(4)在(3)中,请探究n2=________+________。
小学六年级数学易错题经典练习(附答案)

六年级数学易错题一、填空题。
1、一种盐水的含盐率是20%,盐与水的比是( )。
2、生产同样多的零件,小张用了4小时,小李用了6小时,小张和小李工作效率的最简比是( )。
3、从甲地到乙地,客车要行驶4时,货车要行驶5时,客车的速度与货车的速度比是( ),货车的速度比客车慢( )%。
4、100克糖溶在水里,制成的糖水的含糖率为12.5%,如果再加200克水,这时糖与糖水的比是( )。
5、若从六(1)班调全班人数的1/10到六(2)班,则两班人数相等,原来六(1)班与六(2)班的人数比是( )。
6、把甲队人数的1/4调入乙队,这时两队人数相等,甲队与乙队原人数的比为( )。
7、六(1)班今天到校40人,请病假的5人,该班的出勤率是( )。
8、把一个半径是10cm的圆拼成接成一个近似的长方形后,长方形的周长是( ),面积是( )。
9、两个数的差相当于被减数的40%,减数与差的比是( )。
10、( )米比9米多40% , 9米比( )少55% ,200千克比160千克多()%;160千克比200千克少( )%;16米比( )米多它的60%;()比32少30% 。
11、钟面上时针的长1dm,一昼夜时针扫过的面积是( )。
12、一根水管,第一次截去全长的1/4,第二次截去余下的2/3,两次共截去全长的( )。
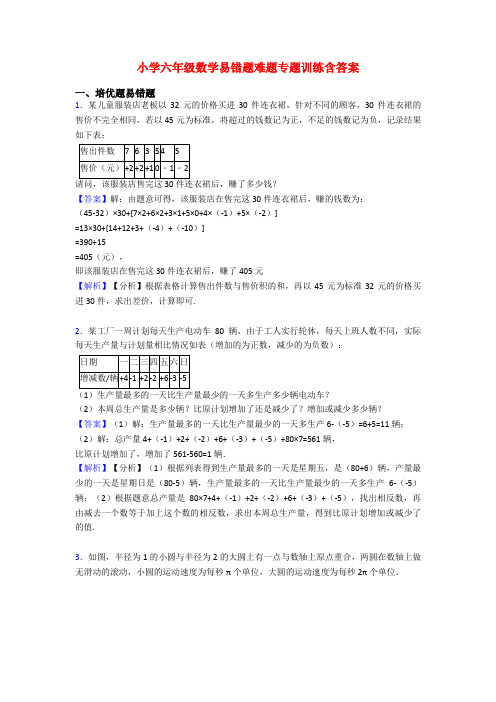
13、某种皮衣价格为1650元,打八折出售可盈利10%.那么若以1650元出售,可盈利( )元。
14、正方形边长增加10%,它的面积增加( )% 。
二、判断题。
1、某商品先提价5%,后又降阶5%,这件商品的现价与原价相等。
( )2、在含盐20%的盐水中加入同样多的盐和水后,盐水的含盐率不变。
()3、如果甲数比乙数多25%,那么乙数就比甲数少25%。
( )4、半径是2厘米的圆,它的周长和面积相等。
( )5、直径相等的两个圆,面积不一定相等。
( )6、比的前项和后项都乘或除以同一个数,比值大小不变。
全国小学六年级数学高频易错题(附答案)

全国小学六年级数学高频易错题一、选择题(每题5分,共30分)1.60秒与1分钟的比值是()。
A. 1∶1B. 1∶2C. 2∶1D. 1∶602.如果一个长方形的长是8厘米,宽是4厘米,那么长与宽的比是()。
A. 2∶1B. 1∶2C. 4∶1D. 1∶43.小明有20元钱,他把这些钱分成两份,第一份是第二份的2倍,那么第一份的钱是()。
A. 10元B. 12元C. 8元D. 14元4.一辆车行驶120公里耗油6升,平均每升油可以行驶多少公里?正确的列式为()。
A. 120÷6B. 6÷120C. 120×6D. 6×1205.在一个三角形中,三个内角的度数比是2∶3∶4,这个三角形的内角分别是()。
A. 40°, 60°, 80°B. 30°, 45°, 75°C. 20°, 30°, 50°D. 40°, 60°, 80°6.一杯盐水中含盐20克,水的质量为80克,盐与水的比是()。
A. 1∶4B. 1∶5C. 1∶3D. 1∶27.一条绳子长120厘米,剪去30厘米后,剩下的绳子与剪去的绳子的比是()。
A. 4∶1B. 3∶1C. 2∶1D. 5∶18.如果A∶B=3∶5,B∶C=2∶3,那么A∶B∶C=()。
A. 6∶10∶15B. 3∶5∶7.5C. 6∶10∶9D. 3∶5∶4.59.一块长方形的土地,长与宽的比是5∶3,周长是80米,这块土地的面积是()。
A. 200平方米B. 300平方米C. 400平方米D. 500平方米10.一个比的比值是4,后项是8,这个比的前项是()。
A. 2B. 4C. 6D. 12二、判断题(每题2分,共20分)1.一个分数乘以整数,积一定不小于这个分数。
()2.甲数是乙数的3倍,乙数与甲数的比是1∶3。
小学六年级数学易错题难题训练含答案

小学六年级数学易错题难题训练含答案一、培优题易错题1.纽约、悉尼与上海的时差如下表(正数表示同一时刻比上海时间早的时数,负数表示同一时刻比上海晚的时数):1日上午10时,悉尼时间是________.(2)上海、纽约与悉尼的时差分别为________(正数表示同一时刻比悉尼时间早的时数,负数表示同一时刻比悉尼晚的时数).(3)王老师2018年9月1日,从纽约Newwark机场,搭乘当地时间上午10:45的班机,前往上海浦东国际机场,飞机飞行的时间为14小时55分钟,问飞机降落上海浦东国际机场的时间.【答案】(1)12(2)-2,-14(3)解:10时45分+14时55分+12时=37时40分.故飞机降落上海浦东国际机场的时间为2018年9月2日下午1:40【解析】【解答】(1)10+(+2)=12时,即当上海是10月1日上午10时,悉尼时间是12时.( 2 )12-10=2;-12-2=-14;故上海、纽约与悉尼的时差分别为-2,-14.【分析】(1)根据表格得到悉尼时间是10+(+2);(2 )由表格得到上海与悉尼的时差是2,纽约与悉尼的时差-12-2;(3)根据题意得到10时45分+14时55分+12时,得到飞机降落上海浦东国际机场的时间.2.规定一种新的运算:a★b=a×b-a-b2+1,例如3★(-4)=3×(-4)-3-(-4)2+1.请计算下列各式的值。
(1)2★5;(2)(-2)★(-5).【答案】(1)解:2★5=2×5-2-52+1=-16(2)解:(-2)★(-5)=(-2)×(-5)-(-2)-(-5)2+1=-12【解析】【分析】根据新运算定义得到算式,再根据有理数的运算法则计算即可,先算乘方,再算乘除,再算加减,如果有括号先算括号里面的.3.已知:如图,这是一种数值转换机的运算程序.(1)若第1次输入的数为2,则第1次输出的数为1,那么第2次输出的数为;若第1次输入的数为12,则第5次输出的数为________.(2)若输入的数为5,求第2016次输出的数是多少.(3)是否存在输入的数x,使第3次输出的数是x?若存在,求出所有x的值;若不存在,请说明理由.【答案】(1)4、6(2)解:5+3=8,8× =4,4× =2,2× =1,1+3=4,∴若输入的数为5,则每次输出的数分别是8、4、2、1、4、2、1,…,(2016−1)÷3=2015÷3=671 (2)∴第2016次输出的数是2(3)解:当x为奇数时,有 (x+3)+3=x,解得x=9(舍去),× (x+3)=x,解得x=1,当x为偶数时,有 × × x=x,解得x=0,× x+3=x,解得x=4,×( x+3)=x,解得x=2,综上所述,x=0或1或2或4【解析】【解答】解:(1)∵1+3=4,∴第1次输出的数为1,则第2次输出的数为4.×12=6,6× =3,3+3=6,6× =3,3+3=6,∴第1次输入的数为12,则第5次输出的数为6.【分析】(1)根据运算程序得到第1次输出的数为1,第2次输出的数为3+1,第1次输入的数为12,则第5次输出的数(12÷2÷2+3)÷2+3;(2)根据题意由输入的数为5,每次输出的数分别是8、4、2、1、4、2、1···,得到3次一循环,求出第2016次输出的数;(3)根据运算程序得到当x为奇数时和为偶数时,求出所有x的值.4.如图,已知数轴上点A表示的数为8,B是数轴上一点,且AB=14,动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒。
小学六年级上册数学易错题(含答案)

1、在一个长8CM,宽6CM的长方形里剪一个半圆,它的最大直径是()CM2、在同一个平面内,两个大小不同的圆可以组成的图形最多可能有()条对称轴,最少可能有()条对象轴。
3、半径的长度是直径的1/2(对或错)4、因为D=2R,所以同一个的两要半径一定能组成直径(对或错)1、有一种浓度为18%的农药200kg,为了得到浓度为10%的农药,需要加水多少千克?2、少年共有两个合唱队,甲队有50人,如果从甲队调出10%到乙队,甲队人数比乙队的92%少1人,乙队现有多少人?3、修一座厂房,用了34万元,比计划节约百分之15,节约了多少万元4、少年宫有两个合唱队,甲队有50人,如果从甲队调出10/100到乙队,甲队比乙队的92/100少1人,乙队原有学生多5、一件大衣,现价320元,比原价降低了80元,现价比原价降低了百分之几?6、甲数的25%比乙数多20%,乙数是40,甲数是多少?7、一根电线剪下2/5后,又接上18米,这样比原来长1/5,这根电线原来长多少米?8、一个圆环铁片,外直径是6分米,环宽1分米,这个圆环铁片的面积是多少平方分米?9、粮仓运来320千克大米,第一次卖了3/8,第二次卖余下的1/6,这批大米比原来少了()千克。
10、把一根9/10米的绳子平均分成3段,每段是全长的(),每段是3米的(—)。
11、7/50平方米=()平方分米1、在面积是20平方厘米的正方形内画一个最大的圆,这个圆的面积是()平方厘米。
2、小圆的半径是4厘米,大圆的半径是12厘米,小圆周长是大圆周长的(-)。
3、在一块长10分米,宽6分米的长方形木板上锯出一个最大的半圆,这个半圆的面积是()平方分米。
4、水结成冰,体积增加水的1/11,150立方米的冰化成水后,体积是多少。
列式()5、甲乙两个工程队,甲队的人数比乙队少30人,从甲队抽5人到乙队,这时甲队的人数是乙队的3/8,甲乙两人原来各有多少人?6、把一个直径为4CM的圆分成两个半圆,这两半圆的周长和是()CM。
小学六年级数学易错题难题专题训练含答案
(1)若大圆沿数轴向左滚动 1 周,则该圆与数轴重合的点所表示的数是________; (2)若大圆不动,小圆沿数轴来回滚动,规定小圆向右滚动时间记为正数,向左滚动时间 记为负数,依次滚动的情况记录如下(单位:秒):﹣1,+2,﹣4,﹣2,+3,﹣8 ①第几次滚动后,小圆离原点最远? ②当小圆结束运动时,小圆运动的路程共有多少?此时两圆与数轴重合的点之间的距离是 多少?(结果保留 π) (3)若两圆同时在数轴上各自沿着某一方向连续滚动,滚动一段时间后两圆与数轴重合的 点之间相距 6π,求此时两圆与数轴重合的点所表示的数. 【答案】(1)-4π (2)解:①第 1 次滚动后,|﹣1|=1, 第 2 次滚动后,|﹣1+2|=1, 第 3 次滚动后,|﹣1+2﹣4|=3, 第 4 次滚动后,|﹣1+2﹣4﹣2|=5, 第 5 次滚动后,|﹣1+2﹣4﹣2+3|=2, 第 6 次滚动后,|﹣1+2﹣4﹣2+3﹣8|=10, 则第 6 次滚动后,小圆离原点最远; ②1+2+4+3+2+8=20, 20×π=20π, ﹣1+2﹣4﹣2+3﹣8=﹣10, ∴ 当小圆结束运动时,小圆运动的路程共有 20π,此时两圆与数轴重合的点之间的距离是 10π (3)解:设时间为 t 秒, 分四种情况讨论: i)当两圆同向右滚动, 由题意得:t 秒时,大圆与数轴重合的点所表示的数:2πt, 小圆与数轴重合的点所表示的数为:πt, 2πt﹣πt=6π, 2t﹣t=6, t=6, 2πt=12π,πt=6π, 则此时两圆与数轴重合的点所表示的数分别为 12π、6π. ii)当两圆同向左滚动, 由题意得:t 秒时,大圆与数轴重合的点所表示的数:﹣2πt, 小圆与数轴重合的点所表示的数:﹣πt,
六年级小学数学毕业考试易错题目集锦带完整答案(易错题)

六年级小学数学毕业考试易错题目集锦一.选择题(共10题,共20分)1.圆柱的高一定时,体积与底面积()。
A.成正比例B.成反比例C.不成比例2.一种画册原价每本6.9元,现在按每本4.83元出售,这种画册按原价打了()折。
A.八五B.七C.八D.七五3.用一定的钱买地砖,每块砖的价钱和买砖块数()。
A.成正比例B.成反比例C.不成比例D.不成反比例4.一块长方形的菜地,周长是240米,长和宽的比是4∶2.这块地的面积是()。
A.6400平方米B.1600平方米C.3200平方米5.下面说法正确的是()。
A.一条直线长10m。
B.圆锥的体积比与它等底等高的圆柱的体积小。
C.一年中有6个大月、6个小月。
D.把一根木头锯成7段,若锯每一段所用的时间都相等,那么锯每一段的时间是锯完这根木头所用时间的。
6.在一次考试中,小明的分数比全班平均分高出5分,记作(+5)分,小红的分数记作(-3)分,小明比小红多()。
A.-8分B.8分C.5分D.-3分7.ab=c(a、b、c均不为0),当a一定时,b与c()。
A.成正比例B.成反比例C.不成比例8.沿长方形的一条边旋转一周得到一个()。
A.圆锥B.圆柱C.长方体9.根据下表中的两种相关联的量的变化情况,判断它们成不成比例?成什么比例?总价一定,单价和数量()。
A.成正比例B.成反比例C.不成比例D.不成反比例10.已知点A和点B在同一条数轴上,点A表示数-2,点B与点A相距3.5个单位长度,那么点B表示的数是()。
A.-1.5B.5.5C.1.5或-5.5D.-1.5或3.5二.判断题(共10题,共20分)1.比例尺一定,图上距离和实际距离成正比例。
()2.最大的负数是-1。
()3.如果两个圆柱的侧面积相等,那么它们的底面周长也相等。
()4.圆柱体的底面积与底面半径成正比例。
()5.如果a×2=b×3,那么a:b=2:3。
()6.把15:14写成分数的形式是。
小学数学六年级易错题难题题库 - 易错题难题题库含答案

小学数学六年级易错题难题题库 - 易错题难题题库含答案一、培优题易错题1.下列图表是2017 年某校从参加中考体育测试的九年级学生中随机调查的10 名男生跑1000 米和 10 名女生跑 800米的成绩.(1)按规定,女生跑 800 米的时间不超过 3'24"就可以得满分.该校九年级学生有 490 人,男生比女生少 70 人.请你根据上面成绩,估计该校女生中有多少人该项测试成绩得满分? (2)假如男生 1 号和男生 10 号被分在同组测试,请分析他俩在 400 米的环形跑道测试的过程中能否相遇。
若能,求出发多长时间才能相遇;若不能,说明理由.【答案】(1)解:设男生有x人,女生有(x+70)人,由题意得:x+x+70=490,解得:x=210,则女生x+70=210+70=280(人).故女生得满分人数: (人)(2)解:不能;假设经过x分钟后,1号与10号在1000米跑中能首次相遇,根据题意得:解得又∵∴考生1号与10号不能相遇。
【解析】【分析】(1)通过男生、女生的人数关系列出方程,得出女生的人数;(2)根据题意表达出1号跟10号的速度,两位若相遇,相减的路程为400米,得出的时间为4.8, 但是4.8分钟大于3分钟,所以两位在测试过程中不会相遇。
2.如图,已知数轴上点A表示的数为8,B是数轴上一点,且AB=14,动点P从点A出发,以每秒5个单位长度的速度沿数轴向左匀速运动,设运动时间为t(t>0)秒。
(1)写出数轴上点B表示的数________,点P表示的数________(用含t的代数式表示);(2)动点Q从点B出发,以每秒3个单位长度的速度沿数轴向左匀速运动,若点P、Q同时出发,问点P运动多少秒时追上点Q?(3)若M为AP的中点,N为PB的中点.点P在运动的过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请你画出图形,并求出线段MN的长;(4)若点D是数轴上一点,点D表示的数是x,请你探索式子|x+6|+|x-8|是否有最小值?如果有,直接写出最小值;如果没有,说明理由.【答案】(1)-6;8-5t(2)解:设点P运动x秒时,在点C处追上点Q(如图)则AC=5x,BC=3x,∵AC-BC=AB∴5x-3x=14解得:x=7,∴点P运动7秒时,在点C处追上点Q(3)解:没有变化.分两种情况:①当点P在点A、B两点之间运动时:MN=MP+NP= AP+ BP= (AP+BP)= AB=7②当点P运动到点B的左侧时:MN=MP-NP= AP- BP= (AP-BP)= AB=7综上所述,线段MN的长度不发生变化,其值为7(4)解:式子|x+6|+|x-8|有最小值,最小值为14.【解析】【解答】解:(1)点B表示的数是-6;点P表示的数是8-5t,【分析】(1)点B表示的数是-6;点P表示的数是8-5t,【分析】(1)根据点A的坐标和AB之间的距离即可得出B点的坐标和P点的坐标;(2)设点P运动x秒时,在点C处追上点Q,则AC=5x,BC=3x,根据距离的差为14列出方程即可求解;(3)分类讨论:①当点P在点A、B两点之间运动时,根据MN=MP+NP进行计算即可;②当点P运动到点B的左侧时,根据MN=MP-NP计算即可;(4)分三种情况去绝对值符号:x8时,原式=x+6+x-8=2x-214; -6x8时,原式=x+6+8-x=14; x-6时,原式=-x-6-x+8=-2x+214,综上所述得出最小值。
小学六年级数学易错题集锦(附答案)

六年级数学易错题集锦一、填空题。
1、一种盐水的含盐率是20%,盐与水的比是()。
2、生产同样多的零件,小张用了4小时,小李用了6小时,小张和小李工作效率的最简比是()。
3、从甲地到乙地,客车要行驶4时,货车要行驶5时,客车的速度与货车的速度比是(),货车的速度比客车慢()%。
4、100克糖溶在水里,制成的糖水的含糖率为12.5%,如果再加200克水,这时糖与糖水的比是()。
5、若从六(1)班调全班人数的1/10到六(2)班,则两班人数相等,原来六(1)班与六(2)班的人数比是()。
6、把甲队人数的1/4调入乙队,这时两队人数相等,甲队与乙队原人数的比为()。
7、六(1)班今天到校40人,请病假的5人,该班的出勤率是()。
8、把一个半径是10cm的圆拼成接成一个近似的长方形后,长方形的周长是(),面积是()。
9、()米比9米多40% , 9米比()少55% ,200千克比160千克多()%;160千克比200千克少()%;16米比()米多它的60%;( )比32少30% 。
10、钟面上时针的长1dm,一昼夜时针扫过的面积是()。
11、一根水管,第一次截去全长的1/4,第二次截去余下的2/3,两次共截去全长的()。
12、某种皮衣价格为1650元,打八折出售可盈利10%.那么若以1650元出售,可盈利()元。
13、正方形边长增加10%,它的面积增加()% 。
二、判断题。
1、某商品先提价5%,后又降阶5%,这件商品的现价与原价相等。
()2、在含盐20%的盐水中加入同样多的盐和水后,盐水的含盐率不变。
()3、如果甲数比乙数多25%,那么乙数就比甲数少25%。
()4、半径是2厘米的圆,它的周长和面积相等。
()5、直径相等的两个圆,面积不一定相等。
()6、比的前项和后项都乘或除以同一个数,比值大小不变。
()三、选择题。
A、6︰1B、5︰1C、5︰6D、6︰53、一杯牛奶,牛奶与水的比是1︰4,喝掉一半后,牛奶与水的比是()。
小学六年级数学易错题难题专题训练含答案

小学六年级数学易错题难题专题训练含答案一、培优题易错题1.甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费.设小红在同一商场累计购物x元,其中x>100.(1)根据题意,填写下表(单位:元):(2)当x取何值时,小红在甲、乙两商场的实际花费相同?(3)当小红在同一商场累计购物超过100元时,在哪家商场的实际花费少?【答案】(1)271;0.9x+10;278;0.95x+2.5(2)解:根据题意,有0.9x+10=0.95x+2.5,解得x=150,∴当x=150时,小红在甲、乙两商场的实际花费相同。
(3)解:由0.9x+10<0.95x+2.5,解得x>150,由0.9x+10>0.95x+2.5,解得x<150.∴当小红累计购物超过150元时,在甲商场的实际花费少.当小红累计购物超过100元而不到150元时,在乙商场的实际花费少.当小红累计购物150元时,甲、乙商场花费一样【解析】【解答】解:(1)在甲商场:271,0.9x+10;在乙商场:278,0.95x+2.5.【分析】(1)根据提供的方案列出代数式;(2)根据(1)中的代数式利用费用相同可得关于x的方程,解方程即可;(3)列不等式得出x的范围,可选择商场.2.在一条东西走向的马路旁,有青少年宫、学校、商场、医院四家公共场所.已知青少年宫在学校东300m处. 商场在学校西200m处,医院在学校东500m处.若将马路近似地看做一条直线,以学校为原点,向东方向为正方向,用1个单位长度表示100m.(1)在数轴上表示出四家公共场所的位置.(2)列式计算青少年宫与商场之间的距离.【答案】(1)解:如图所示:(2)解:由题意可得:300-(-200)=500或︱-200-300︱=500.答:青少年宫与商场之间的距离是500 m【解析】【分析】(1)根据题意画出学校为原点的数轴,在数轴上表示出四家公共场所的位置;(2)根据题意青少年宫与商场之间的距离是300-(-200),再根据减去一个数等于加上这个数的相反数,求出青少年宫与商场之间的距离.3.某手机经销商购进甲,乙两种品牌手机共 100 部.(1)已知甲种手机每部进价1500 元,售价2000 元;乙种手机每部进价3500 元,售价4500 元;采购这两种手机恰好用了 27 万元 .把这两种手机全部售完后,经销商共获利多少元?(2)已经购进甲,乙两种手机各一部共用了5000 元,经销商把甲种手机加价50%作为标价,乙种手机加价 40%作为标价.从 A,B 两种中任选一题作答:A:在实际出售时,若同时购买甲,乙手机各一部打九折销售,此时经销商可获利1570 元.求甲,乙两种手机每部的进价.B:经销商采购甲种手机的数量是乙种手机数量的 1.5 倍.由于性能良好,因此在按标价进行销售的情况下,乙种手机很快售完,接着甲种手机的最后10 部按标价的八折全部售完.在这次销售中,经销商获得的利润率为 42.5%.求甲,乙两种手机每部的进价.【答案】(1)解:设购进甲种手机部,乙种手机部,根据题意,得解得:元.答:销商共获利元.(2)解:A: 设每部甲种手机的进价为元,每部乙种手机的进价元,根据题意,得解得:答:求甲,乙两种手机每部的进价分别为:3000元,2000元.B:乙种手机:部,甲种手机部,设每部甲种手机的进价为元,每部乙种手机的进价元,根据题意,得解得:答:求甲,乙两种手机每部的进价分别为:2000元,3000元.【解析】【分析】(1)甲的单价乘以部数加上乙的单价乘以部数等于总数,根据题意列出,然后解方程得到结果。
六年级数学易错题含答案

六年级数学易错题含答案一、培优题易错题1.如果一个正整数能表示为两个连续偶数的平方差,那么称这个正整数为“神秘数”.如:4=22-02,12=42-22,20=62-42,因此4,12,20这三个数都是神秘数.(1)28和2012这两个数是神秘数吗?为什么?(2)设两个连续偶数为2k+2和2k(其中k取非负整数),由这两个连续偶数构造的神秘数是4的倍数吗?为什么?(3)两个连续奇数的平方差(取正数)是神秘数吗?为什么?【答案】(1)解:找规律:4=4×1=22-02, 12=4×3=42-22, 20=4×5=62-42, 28=4×7=82-62,…,2012=4×503=5042-5022,所以28和2012都是神秘数(2)解:(2k+2) 2-(2 k) 2=4(2k +1),因此由这两个连续偶数构造的神秘数是4的倍数(3)解:由(2)知,神秘数可以表示成4(2k+1),因为2 k +1是奇数,因此神秘数是4的倍数,但一定不是8的倍数.另一方面,设两个连续奇数为2 n +1和2 n -1,则(2 n +1) 2-(2n-1)2=8n,即两个连续奇数的平方差是8的倍数.因此,两个连续奇数的平方差不是神秘数.【解析】【分析】(1)根据规律得到28=4×7=82-62, 2012=4×503=5042-5022,得到28和2012这两个数是神秘数;(2)由(2k+2)2-(2k)2=(2k+2+2k)(2k+2-2k)=4(2k +1),因此由这两个连续偶数构造的神秘数是4的倍数;(3)神秘数可以表示成4(2k+1),因为2k +1是奇数,因此神秘数是4的倍数,但一定不是8的倍数;两个连续奇数的平方差是8的倍数,因此这两个连续奇数的平方差不是神秘数.2.下列图表是2017 年某校从参加中考体育测试的九年级学生中随机调查的10 名男生跑1000 米和 10 名女生跑 800米的成绩.(1)按规定,女生跑 800 米的时间不超过 3'24"就可以得满分.该校九年级学生有 490 人,男生比女生少 70 人.请你根据上面成绩,估计该校女生中有多少人该项测试成绩得满分? (2)假如男生 1 号和男生 10 号被分在同组测试,请分析他俩在 400 米的环形跑道测试的过程中能否相遇。
最新小学数学六年级易错题难题题库 - 易错题难题题库含详细答案

最新小学数学六年级易错题难题题库 - 易错题难题题库含详细答案一、培优题易错题1.对于实数a、b,定义运算:a▲b= ;如:2▲3=2﹣3= ,4▲2=42=16.照此定义的运算方式计算[2▲(﹣4)]×[(﹣4)▲(﹣2)]=________.【答案】1【解析】【解答】解:根据题意得:2▲(﹣4)=2﹣4= ,(﹣4)▲(﹣2)=(﹣4)2=16,则[2▲(﹣4)]×[(﹣4)▲(﹣2)]= ×16=1,故答案为:1【分析】先利用定义计算括号中的值,再进行计算即可.在利用新运算的时候需要先判断两个数的大小关系,根据其选择算式.2.某手机经销商购进甲,乙两种品牌手机共 100 部.(1)已知甲种手机每部进价1500 元,售价2000 元;乙种手机每部进价3500 元,售价4500 元;采购这两种手机恰好用了 27 万元 .把这两种手机全部售完后,经销商共获利多少元?(2)已经购进甲,乙两种手机各一部共用了5000 元,经销商把甲种手机加价50%作为标价,乙种手机加价 40%作为标价.从 A,B 两种中任选一题作答:A:在实际出售时,若同时购买甲,乙手机各一部打九折销售,此时经销商可获利1570 元.求甲,乙两种手机每部的进价.B:经销商采购甲种手机的数量是乙种手机数量的 1.5 倍.由于性能良好,因此在按标价进行销售的情况下,乙种手机很快售完,接着甲种手机的最后10 部按标价的八折全部售完.在这次销售中,经销商获得的利润率为 42.5%.求甲,乙两种手机每部的进价.【答案】(1)解:设购进甲种手机部,乙种手机部,根据题意,得解得:元.答:销商共获利元.(2)解:A: 设每部甲种手机的进价为元,每部乙种手机的进价元,根据题意,得解得:答:求甲,乙两种手机每部的进价分别为:3000元,2000元.B:乙种手机:部,甲种手机部,设每部甲种手机的进价为元,每部乙种手机的进价元,根据题意,得解得:答:求甲,乙两种手机每部的进价分别为:2000元,3000元.【解析】【分析】(1)甲的单价乘以部数加上乙的单价乘以部数等于总数,根据题意列出,然后解方程得到结果。
小学数学六年级易错题难题题库 - 易错题难题题库含详细答案

小学数学六年级易错题难题题库 - 易错题难题题库含详细答案一、培优题易错题1.“△”表示一种新的运算符号,已知:2△3=2﹣3+4,7△2=7﹣8,3△5=3﹣4+5﹣6+7,…;按此规则,计算:(1)10△3=________.(2)若x△7=2003,则x=________.【答案】(1)11(2)2000【解析】【解答】(1)10△3=10-11+12=11;(2)∵x△7=2003,∴x-(x+1)+(x+2)-(x+3)+(x+4)-(x+5)+(x+6)=2003,解得x=2000.【分析】(1)首先弄清楚定义新运算的计算法则,从题目中给出的例子来看,第一个数表示从整数几开始,后面的数表示几个连续整数相加减,根据发现的运算规则,即可由10△3列出算式,再根据有理数加减法法则,即可算出答案;(2)根据定义新运算的计算方法,由x△7=2003,列出方程,求解即可。
2.如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走均为正,向下向左走均为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(﹣1,﹣4),其中第一个数表示左右方向,第二个数表示上下方向.(1)图中A→C(________,________),B→C(________,________),C→________(+1,﹣2);(2)若这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+2,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出P的位置;(3)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程.(4)若图中另有两个格点M、N,且M→A(3﹣a,b﹣4),M→N(5﹣a,b﹣2),则N→A应记为什么?【答案】(1)+3;+4;+2;0;D(2)解:P点位置如图1所示;(3)解:如图2,根据已知条件可知:A→B表示为:(1,4),B→C记为(2,0)C→D记为(1,﹣2);则该甲虫走过的路线长为:1+4+2+1+2=10(4)解:由M→A(3﹣a,b﹣4),M→N(5﹣a,b﹣2),所以,5﹣a﹣(3﹣a)=2,b﹣2﹣(b﹣4)=2,所以,点A向右走2个格点,向上走2个格点到点N,所以,N→A应记为(﹣2,﹣2)【解析】【解答】解:(1)图中A→C(+3,+4),B→C(+2,0),C→D(+1,﹣2);故答案为:(+3,+4),(+2,0),D;【分析】(1)根据向上向右走均为正,向下向左走均为负确定数据即可;(2)根据所给的路线确定点的位置即可;(3)根据表示的路线确定长度相加可得结果;(4)观察点的变化情况,根据(1)即可确定点走了格数,从而确定结论.3.如图,一只甲虫在5×5的方格(每小格边长为1)上沿着网格线运动.它从A处出发去看望B、C、D处的其它甲虫,规定:向上向右走均为正,向下向左走均为负.如果从A到B记为:A→B(+1,+4),从B到A记为:B→A(﹣1,﹣4),其中第一个数表示左右方向,第二个数表示上下方向.(1)图中A→C(________,________),B→C(________,________),C→________(+1,﹣2);(2)若这只甲虫从A处去甲虫P处的行走路线依次为(+2,+2),(+2,﹣1),(﹣2,+3),(﹣1,﹣2),请在图中标出P的位置;(3)若这只甲虫的行走路线为A→B→C→D,请计算该甲虫走过的路程.(4)若图中另有两个格点M、N,且M→A(3﹣a,b﹣4),M→N(5﹣a,b﹣2),则N→A应记为什么?【答案】(1)+3;+4;+2;0;D(2)解:P点位置如图1所示;(3)解:如图2,根据已知条件可知:A→B表示为:(1,4),B→C记为(2,0)C→D记为(1,﹣2);则该甲虫走过的路线长为:1+4+2+1+2=10(4)解:由M→A(3﹣a,b﹣4),M→N(5﹣a,b﹣2),所以,5﹣a﹣(3﹣a)=2,b﹣2﹣(b﹣4)=2,所以,点A向右走2个格点,向上走2个格点到点N,所以,N→A应记为(﹣2,﹣2)【解析】【解答】解:(1)图中A→C(+3,+4),B→C(+2,0),C→D(+1,﹣2);故答案为:(+3,+4),(+2,0),D;【分析】(1)根据向上向右走均为正,向下向左走均为负确定数据即可;(2)根据所给的路线确定点的位置即可;(3)根据表示的路线确定长度相加可得结果;(4)观察点的变化情况,根据(1)即可确定点走了格数,从而确定结论.4.某工厂一周计划每天生产电动车80辆,由于工人实行轮休,每天上班人数不同,实际每天生产量与计划量相比情况如表(增加的为正数,减少的为负数):日期一二三四五六日增减数/辆+4-1+2-2+6-3-5(2)本周总生产量是多少辆?比原计划增加了还是减少了?增加或减少多少辆?【答案】(1)解:生产量最多的一天比生产量最少的一天多生产6-(-5)=6+5=11辆;(2)解:总产量4+(-1)+2+(-2)+6+(-3)+(-5)+80×7=561辆,比原计划增加了,增加了561-560=1辆.【解析】【分析】(1)根据列表得到生产量最多的一天是星期五,是(80+6)辆,产量最少的一天是星期日是(80-5)辆,生产量最多的一天比生产量最少的一天多生产6-(-5)辆;(2)根据题意总产量是80×7+4+(-1)+2+(-2)+6+(-3)+(-5),找出相反数,再由减去一个数等于加上这个数的相反数,求出本周总生产量,得到比原计划增加或减少了的值.5.规定两数a,b之间的一种运算,记作(a,b):如果,那么(a,b)=c.例如:因为23=8,所以(2,8)=3.(1)根据上述规定,填空:(3,27)=________,(5,1)=________,(2,)=________.(2)小明在研究这种运算时发现一个现象:(3n,4n)=(3,4)小明给出了如下的证明:设(3n, 4n)=x,则(3n)x=4n,即(3x)n=4n,所以3x=4,即(3,4)=x,所以(3n, 4n)=(3,4).请你尝试运用这种方法证明下面这个等式:(3,4)+(3,5)=(3,20)【答案】(1)3;0;-2(2)解:设(3,4)=x,(3,5)=y,则, =5,∴,∴(3,20)=x+y ,∴(3,4)+(3,5)=(3,20)【解析】(1)∵33=27,50=1,2-2= ,∴(3,27)=3,(5,1)=0,(2,)=-2.故答案依次为:3,0,-2【分析】根据新定义的运算得到幂的运算规律,由幂的运算规律得到相等的等式.6.有、、三种盐水,按与数量之比为混合,得到浓度为的盐水;按与数量之比为混合,得到浓度为的盐水.如果、、数量之比为,混合成的盐水浓度为,问盐水的浓度是多少?【答案】解:B盐水浓度:(14%×6-13%×3)÷(4-1)=(0.84-0.39)÷3=0.45÷3=15%A盐水浓度:14%×3-15×2=12%C盐水浓度:[10.2%×(1+1+3)-12%×1-15×1]÷3=(0.51-0.27)÷3=0.24÷3=8%答:盐水C的浓度为8%。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学数学六年级易错题库 - 易错题库含答案一、培优题易错题1.某手机经销商购进甲,乙两种品牌手机共 100 部.(1)已知甲种手机每部进价1500 元,售价2000 元;乙种手机每部进价3500 元,售价4500 元;采购这两种手机恰好用了 27 万元 .把这两种手机全部售完后,经销商共获利多少元?(2)已经购进甲,乙两种手机各一部共用了5000 元,经销商把甲种手机加价50%作为标价,乙种手机加价 40%作为标价.从 A,B 两种中任选一题作答:A:在实际出售时,若同时购买甲,乙手机各一部打九折销售,此时经销商可获利1570 元.求甲,乙两种手机每部的进价.B:经销商采购甲种手机的数量是乙种手机数量的 1.5 倍.由于性能良好,因此在按标价进行销售的情况下,乙种手机很快售完,接着甲种手机的最后10 部按标价的八折全部售完.在这次销售中,经销商获得的利润率为 42.5%.求甲,乙两种手机每部的进价.【答案】(1)解:设购进甲种手机部,乙种手机部,根据题意,得解得:元.答:销商共获利元.(2)解:A: 设每部甲种手机的进价为元,每部乙种手机的进价元,根据题意,得解得:答:求甲,乙两种手机每部的进价分别为:3000元,2000元.B:乙种手机:部,甲种手机部,设每部甲种手机的进价为元,每部乙种手机的进价元,根据题意,得解得:答:求甲,乙两种手机每部的进价分别为:2000元,3000元.【解析】【分析】(1)甲的单价乘以部数加上乙的单价乘以部数等于总数,根据题意列出,然后解方程得到结果。
(2)A 根据进价加利润等于甲和乙的售价,列出方程B 先求出甲乙的部数,表示出甲乙的标价,列出关系式,50部甲×甲的标价+10部甲×甲标价的八折+40部乙×乙的标价=利润率乘以成本,即可解出结果。
2.已知:如图,这是一种数值转换机的运算程序.(1)若第1次输入的数为2,则第1次输出的数为1,那么第2次输出的数为;若第1次输入的数为12,则第5次输出的数为________.(2)若输入的数为5,求第2016次输出的数是多少.(3)是否存在输入的数x,使第3次输出的数是x?若存在,求出所有x的值;若不存在,请说明理由.【答案】(1)4、6(2)解:5+3=8,8× =4,4× =2,2× =1,1+3=4,∴若输入的数为5,则每次输出的数分别是8、4、2、1、4、2、1,…,(2016−1)÷3=2015÷3=671 (2)∴第2016次输出的数是2(3)解:当x为奇数时,有 (x+3)+3=x,解得x=9(舍去),× (x+3)=x,解得x=1,当x为偶数时,有 × × x=x,解得x=0,× x+3=x,解得x=4,×( x+3)=x,解得x=2,综上所述,x=0或1或2或4【解析】【解答】解:(1)∵1+3=4,∴第1次输出的数为1,则第2次输出的数为4.×12=6,6× =3,3+3=6,6× =3,3+3=6,∴第1次输入的数为12,则第5次输出的数为6.【分析】(1)根据运算程序得到第1次输出的数为1,第2次输出的数为3+1,第1次输入的数为12,则第5次输出的数(12÷2÷2+3)÷2+3;(2)根据题意由输入的数为5,每次输出的数分别是8、4、2、1、4、2、1···,得到3次一循环,求出第2016次输出的数;(3)根据运算程序得到当x为奇数时和为偶数时,求出所有x的值.3.如图,半径为1的小圆与半径为2的大圆上有一点与数轴上原点重合,两圆在数轴上做无滑动的滚动,小圆的运动速度为每秒π个单位,大圆的运动速度为每秒2π个单位.(1)若大圆沿数轴向左滚动1周,则该圆与数轴重合的点所表示的数是________;(2)若大圆不动,小圆沿数轴来回滚动,规定小圆向右滚动时间记为正数,向左滚动时间记为负数,依次滚动的情况记录如下(单位:秒):﹣1,+2,﹣4,﹣2,+3,﹣8①第几次滚动后,小圆离原点最远?②当小圆结束运动时,小圆运动的路程共有多少?此时两圆与数轴重合的点之间的距离是多少?(结果保留π)(3)若两圆同时在数轴上各自沿着某一方向连续滚动,滚动一段时间后两圆与数轴重合的点之间相距6π,求此时两圆与数轴重合的点所表示的数.【答案】(1)-4π(2)解:①第1次滚动后,|﹣1|=1,第2次滚动后,|﹣1+2|=1,第3次滚动后,|﹣1+2﹣4|=3,第4次滚动后,|﹣1+2﹣4﹣2|=5,第5次滚动后,|﹣1+2﹣4﹣2+3|=2,第6次滚动后,|﹣1+2﹣4﹣2+3﹣8|=10,则第6次滚动后,小圆离原点最远;②1+2+4+3+2+8=20,20×π=20π,﹣1+2﹣4﹣2+3﹣8=﹣10,∴当小圆结束运动时,小圆运动的路程共有20π,此时两圆与数轴重合的点之间的距离是10π(3)解:设时间为t秒,分四种情况讨论:i)当两圆同向右滚动,由题意得:t秒时,大圆与数轴重合的点所表示的数:2πt,小圆与数轴重合的点所表示的数为:πt,2πt﹣πt=6π,2t﹣t=6,t=6,2πt=12π,πt=6π,则此时两圆与数轴重合的点所表示的数分别为12π、6π.ii)当两圆同向左滚动,由题意得:t秒时,大圆与数轴重合的点所表示的数:﹣2πt,小圆与数轴重合的点所表示的数:﹣πt,﹣πt+2πt=6π,﹣t+2t=6,t=6,﹣2πt=﹣12π,﹣πt=﹣6π,则此时两圆与数轴重合的点所表示的数分别为﹣12π、﹣6π.iii)当大圆向右滚动,小圆向左滚动时,同理得:2πt﹣(﹣πt)=6π,3t=6,t=2,2πt=4π,﹣πt=﹣2π,则此时两圆与数轴重合的点所表示的数分别为4π、﹣2π.iiii)当大圆向左滚动,小圆向右滚动时,同理得:πt﹣(﹣2πt)=6π,t=2,πt=2π,﹣2πt=﹣4π,则此时两圆与数轴重合的点所表示的数分别为﹣4π、2π【解析】【解答】解:(1)若大圆沿数轴向左滚动1周,则该圆与数轴重合的点所表示的数是﹣2π•2=﹣4π,故答案为:﹣4π;【分析】(1)该圆与数轴重合的点所表示的数,就是大圆的周长;(2)①分别计算出第几次滚动后,小圆离原点的距离,比较作答;②先计算总路程,因为大圆不动,计算各数之和为﹣10,即小圆最后的落点为原点左侧,向左滚动10秒,距离为10π;(3)分四种情况进行讨论:大圆和小圆分别在同侧,异侧时,表示出各自与数轴重合的点所表示的数.根据两圆与数轴重合的点之间相距6π列等式,求出即可.4.在平面直角坐标系中,若点P(x,y)的坐标x、y均为整数,则称点P为格点.若一个多边形的面积记为S,其内部的格点数记为N,边界上的格点数记为L.例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.(1)写出图中格点四边形DEFG对应的S,N,L.(2)已知任意格点多边形的面积公式为S=N+aL+b,其中a,b为常数.当某格点多边形对应的N=82,L=38,求S的值.【答案】(1)解:根据图形可得:S=3,N=1,L=6(2)解:根据格点三角形ABC及格点四边形DEFG中的S、N、L的值可得,,解得a ,∴S=N+ L﹣1,将N=82,L=38代入可得S=82+ ×38﹣1=100【解析】【分析】(1)按照所给定义在图中输出S,N,L的值即可;(2)先根据(1)中三角形与四边形中的S,N,L的值列出关于a,b的二元一次方程组,解方程组求得a,b的值,从而求得任意格点多边形的面积公式,代入所给N,L的值即可求得相应的S的值.5.十字交叉法的证明过程:设甲、乙两瓶溶液的质量分别为和,浓度分别为和(),将两瓶溶液混合后所得的溶液浓度为,求证:.【答案】证明:甲溶液中溶质的质量为,乙溶液中的溶质质量为,则混和溶液中的溶质质量为,所以混合溶液的浓度为,所以,即,,可见。
【解析】【分析】溶液的浓度=溶质的质量÷溶液的质量,溶质的质量=溶液质量×浓度。
根据计算方法分别表示出两个容器中溶质的质量和混合后的浓度,得到等式后用十字交叉法证明这个等式即可。
6.有两种溶液,甲溶液的酒精浓度为,盐浓度为,乙溶液中的酒精浓度为,盐浓度为.现在有甲溶液千克,那么需要多少千克乙溶液,将它与甲溶液混和后所得的溶液的酒精浓度是盐浓度的3倍?【答案】解:假设把水都蒸发掉,则甲溶液盐占盐和酒精的:10%÷(15%+10%)=40%,乙溶液中盐占盐和酒精的:5%÷(45%+5%)=10%;需要配的溶液盐占盐和酒精的:1÷(1+3)=25%;则:(0.25-0.1):(0.4-0.25)=0.15:0.15=1:1,1千克甲溶液中盐和酒精:1×(15%+10%)=0.25(千克),1千克乙溶液中盐和酒精:1×(5+45%)=0.5(千克)。
答:需要0.5千克乙溶液,将它与甲溶液混和后所得的溶液的酒精浓度是盐浓度的3倍。
【解析】【分析】可以这样来看,将溶液中的水剔出或者说蒸发掉,那么所得到的溶液就是盐溶在酒精中。
(事实上这种情况不符合物理规律,但这只是假设)。
这样就能分别求出甲、乙溶液中盐占盐和酒精的百分之几。
根据配制成溶液中酒精是盐的3倍先计算出配制后盐占盐和酒精的百分之几。
分别求出1千克甲、乙溶液中盐和酒精的质量,然后确定需要加入的乙溶液的重量即可。
7.、、三瓶盐水的浓度分别为、、,它们混合后得到克浓度为的盐水.如果瓶盐水比瓶盐水多克,那么瓶盐水有多少克?【答案】解:设C瓶盐水有x克,则B瓶盐水为(x+30)克,A瓶盐水为100-(x+x+30)=70-2x克。
(70-2x)×20%+(x+30)×18%+16%x=100×18.8%14-0.4x+0.18x+5.4+0.16x=18.80.06x=19.4-18.8x=0.6÷0.06x=1070-2×10=50(克)答:A瓶盐水有50克。
【解析】【分析】设C瓶盐水有x克,则B瓶盐水为(x+30)克,A瓶盐水为100-(x+x+30)=70-2x克。
等量关系:A瓶中盐的重量+B瓶中盐的重量+C瓶中盐的重量=混合后盐的总重量。
根据等量关系列方程求出x的值,进而求出A瓶盐水的重量。
8.已知三种混合物由三种成分、、组成,第一种仅含成分和,重量比为;第二种只含成分和,重量比为;第三种只含成分和,重量之比为 .以什么比例取这些混合物,才能使所得的混合物中、和,这三种成分的重量比为?【答案】解:D:C=(3+5):2=4:1;第二种混合物不含,的含量为,第三种混合物不含,的含量为,所以倍第三种混合物含为,倍第二种混合物含为,即第二种、第三种混合物的重量比为;于是此时含有,,即,而最终混合物中,所以第一种混合物的质量与后两种混合质量和之比为,所以三种混合物的重量比为。
