第四章 习题解答
第4章 习题解答

第4章 习题与答案4-1作简谐振动的物体,每次通过同一位置时,不一定相同的量是 [ ] (A) 位移 ; (B) 速度 ; (C) 加速度; (D) 能量。
[答案:B ]4-2 把单摆摆球从平衡位置向位移正方向拉开,使摆线与竖直方向成一微小角度θ ,然后由静止放手任其振动,从放手时开始计时。
若用余弦函数表示其运动方程,则该单摆振动的初相为 [ ](A) π; (B) π/2; (C) 0; (D) θ [答案:C ]4-3 谐振动的振动曲线如题4-3图所示,则有[ ] (A )A 超前π/2; (B )A 落后π/2; (C )A 超前π; (D )A 落后π。
[答案:A ]4-4 一个质点作简谐振动,振辐为A ,在起始时刻质点的位移为A /2,且向x 轴的正方向运动,代表此简谐振动的旋转矢量图为题4-4图 中哪一个? [ ][答案:B ]4-5 两个质点各自作简谐振动,它们的振幅相同、周期相同。
第一个质点的振动方程为x 1 = A cos(ωt + α)。
当第一个质点从相对于其平衡位置的正位移处回到平衡位置时,第二个质点恰在最大负位移处。
则第二个质点的振动方程为 [ ] (A) )π21cos(2++=αωt A x ; (B) )π21cos(2-+=αωt A x ; (C) )π23cos(2-+=αωt A x ; (D) )cos(2π++=αωt A x 。
[答案:A ]4-6 已知某简谐振动的振动曲线如题4-6图所示。
则此简谐振动的振动方程(SI )为 [ ](A) 题4-4图题4-3图(A )220.02cos()33x t =π+π;(B )220.02cos()33x t =π-π;(C )420.02cos()33x t =π+π;(D )420.02cos()33x t =π-π。
[答案:C ]4-7 弹簧振子作简谐振动,先后以相同的速度依次通过A 、B 两点,历时1秒,质点通过B 点后再经过1秒又第二次通过B 点,在这2秒内质点通过的总路程为12cm ,则质点的振动周期和振幅分别为 [ ](A )3s 、12cm ; (B )4s 、6cm ; (C )4s 、9cm ; (D )2s 、8cm 。
功和能习题解答

第四章 功和能一 选择题1. 一辆汽车从静止出发,在平直公路上加速前进时,若发动机功率恒定,则正确的结论为:( )A. 加速度不变B. 加速度随时间减小C. 加速度与速度成正比D. 速度与路径成正比 解:答案是B 。
简要提示:在平直公路上,汽车所受阻力恒定,设为F f 。
发动机功率恒定,则P =F v ,其中F 为牵引力。
由牛顿运动定律得a m F F =-f ,即:f F P/m -v a =。
所以,汽车从静止开始加速,速度增加,加速度减小。
2. 下列叙述中正确的是: ( ) A. 物体的动量不变,动能也不变. B. 物体的动能不变,动量也不变. C. 物体的动量变化,动能也一定变化. D. 物体的动能变化,动量却不一定变化. 解:答案是A 。
3. 一颗卫星沿椭圆轨道绕地球旋转,若卫星在远地点A 和近地点B 的角动量与动能分别为L A 、E k A 和L B 、E k B ,则有:( )A. L B > L A , E k B > E k AB. L B > L A , E k B = E k AC. L B = L A , E k B > E k A地球BA选择题3图D. L B = L A , E k B = E k A 解:答案是C 。
简要提示:由角动量守恒,得v B > v A ,故E k B > E k A 。
4. 对功的概念有以下几种说法:(1) 保守力作正功时,系统内相应的势能增加. (2) 质点运动经一闭合路径,保守力对质点作的功为零.(3) 作用力和反作用力大小相等、方向相反,所以两者所作功的代数和必为零. 在上述说法中: ( )A. (1)、(2)是正确的;B. (2)、(3)是正确的;C. 只有(2)是正确的;D. 只有(3)是正确的. 解:答案是C 。
5. 如图所示,足够长的木条A 置于光滑水平面上,另一木块B 在A 的粗糙平面上滑动,则A 、B 组成的系统的总动能:( )A. 不变B. 增加到一定值C. 减少到零D. 减小到一定值后不变 解:答案是D 。
量子力学周世勋习题解答第四章

第四章习题解答4.1.求在动量表象中角动量x L 的矩阵元和2x L 的矩阵元。
解:⎰⋅⋅'-'-=τπd e p z p y e L r p i y z rp i p p x)ˆˆ()21()(3 ⎰⋅⋅'--=τπd e zp yp e r p i y z rp i)()21(3 ⎰⋅⋅'-∂∂-∂∂-=τπd e p p p p i e rp i zy y z r p i))(()21(3⎰⋅'-∂∂-∂∂-=τπd e p p p p i r p p i z y y z)(3)21)()(()()(p p p p p p i y z z y'-∂∂-∂∂= δ ⎰''=τψψd L x L p x p p p x 2*2)()( ⎰⋅⋅'--=τπd e p z p y e r p i y z r p i23)ˆˆ()21( ⎰⋅⋅'---=τπd e p z p y p z p y e r p i y z y z rp i)ˆˆ)(ˆˆ()21(3 ⎰''-∂∂-∂∂-=τπd e p p p p i p z p y e rp i yz z y y z r p i))()(ˆˆ()21(3 ⎰⋅⋅'--∂∂-∂∂=τπd e p z p y e p p p p i r p i y z rp i y z z y)ˆˆ()21)()((3 ⎰⋅'-∂∂-∂∂-=τπd e p p p p r p p i y z z y)(322)21()()()(22p p p p p p yz z y'-∂∂-∂∂-= δ #4.2 求能量表象中,一维无限深势阱的坐标与动量的矩阵元。
解:基矢:x a n a x u n πsin 2)(=能量:22222a n E n μπ =对角元:2sin 202a xdx a m x a x a mm ==⎰π 当时,n m ≠ ⎰⋅⋅=a mn dx ax x a m a x 0)(sin )(sin 2π[][]1)1()(4)(1)(11)1(])(sin )()(cos )([])(sin )()(cos )([1)(cos )(cos 12222222022202220---=⎥⎦⎤⎢⎣⎡+----=⎥⎥⎦⎤+++++-⎢⎢⎣⎡--+--=⎥⎦⎤⎢⎣⎡+--=--⎰n m n m a aa n m mnan m n m a x a n m n m ax x a n m n m a x a n m n m ax x a n m n m a a dx x a n m x a n m x a ππππππππππππ[][]a n m mn i n m n m a a n i x a n m n m a x a n m n m a a n i dxx a n m x a n m a n i xdxa n x a m an i xdxan dx d x a m a i dx x u p x u p n m nm aa a a n m mn )(21)1(]1)1()(1)(1 )(cos)()(cos )()(sin )(sin cos sin 2sin sin 2)(ˆ)(2220202020*---=--⎥⎦⎤⎢⎣⎡-++=⎥⎦⎤⎢⎣⎡--+++=⎥⎦⎤⎢⎣⎡-++-=⋅-=⋅-==--⎰⎰⎰⎰πππππππππππππππ#4.3 求在动量表象中线性谐振子的能量本征函数。
仪器分析第四章课后习题答案24页PPT

敏化电极是指气敏电极、酶电极、细菌电极及生物电极等。 这类电极的结构特点是在原电极上覆盖一层膜或物质,使得 电极的选择性提高。典型电极为氨电极。
以氨电极为例,气敏电极是基于界面化学反应的敏化电极, 事实上是一种化学电池,由一对离子选择性电极和参比电极 组成。试液中欲测组分的气体扩散进透气膜,进入电池内部, 从而引起电池内部某种离子活度的变化。而电池电动势的变 化可以反映试液中欲测离子浓度的变化。
14.以0.03318mol.l-1的硝酸镧溶液电位滴定100.0mL氟化物溶 液,滴定反应为:
L3a 3F La3 F
滴定时用氟离子离子选择性电极为指示电极,饱和甘汞电极 为参比电极,得到下列数据:
加入La(NO)3 的体积/mL
电动势/V
加入La(NO)3 的体积/mL
电动势/V
0.00 29.00 30.00 30.30 30.60 30.90
00) 01)1
故:Cx = 2.73 × 10-3 mol.L-1
13.下面是用0.1000mol.L-1NaOH 溶液电位滴定50.00mL某一元 弱酸的数据:
V/mL pH V/mL pH V/mL pH
0.00
2.90 14.00 6.60 17.00
11.30
1.00
4.00 15.00 7.04 18.00
Dp H/DV
12
10
8
6
4
2
0
11
12
13
14
15
16
17
V/m L
(c) 从(b)表数据可以计算如下的二阶微商,可以看出终 点应该介于15.60-15.70之间.
弹性力学(徐芝纶)第四章习题答案

第四章 习题解答4-14-2、解:本题为轴对称应力问题,相应的径向位移为: ()()()()()θ+θ+⎥⎦⎤⎢⎣⎡υ-+υ-+-υ-+υ+-=sin cos ln K I Cr 12Br 311r Br 12r A 1E 1u r (1) 轴对称应力通式为()()02ln 232ln 2122=+++-=+++=θθτσσr r C r B rAC r B r A由应力边界条件()()()()0,00,===-=====b r r b r r a r r a r r q θθτστσ并结合位移单值条件可知B=0,求得:22222222ab qa C a b qb a A -=--= 因半径的改变与刚体位移I ,K 无关,且为平面应变问题,将A 、B 、C 代入(1)式,并将υυυυ-→-→1,12EE 得:内半径的改变:()()()⎪⎪⎭⎫⎝⎛-+-+-=⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛--+-⎪⎭⎫ ⎝⎛-+-=∆=υυυυυυυυ11*111112222222222222a b a b Eqa a a b qa a a b q b a E u ar r外半径的改变:()()()2222222222221*11111a b ab E qa b a b qa b a b q b a Eu br r --=⎥⎦⎤⎢⎣⎡-⎪⎭⎫ ⎝⎛--+-⎪⎭⎫ ⎝⎛-+-=∆=υυυυυυ 圆筒厚度的改变:()()()⎪⎪⎭⎫⎝⎛-++---=∆-∆=∆==υυυ112a b a b E qa u u R ar r b r r4-2另解:半径为r 的圆筒周长为r π2,受载后周长则为 ()θθεπεππ+=+1222r r r , 于是半径为 ()θε+1r ,半径的改变量则为:⎥⎦⎤⎢⎣⎡⎪⎭⎫ ⎝⎛+--⎪⎭⎫ ⎝⎛+--=⎪⎭⎫⎝⎛---=C r A C rA r E E r r r 212111*2222υυυσυυσυεθθ将对应的A 、C 及r=a,b 分别代入,可求出内外半径的改变及圆筒厚度的改变。
第4章 习题解答
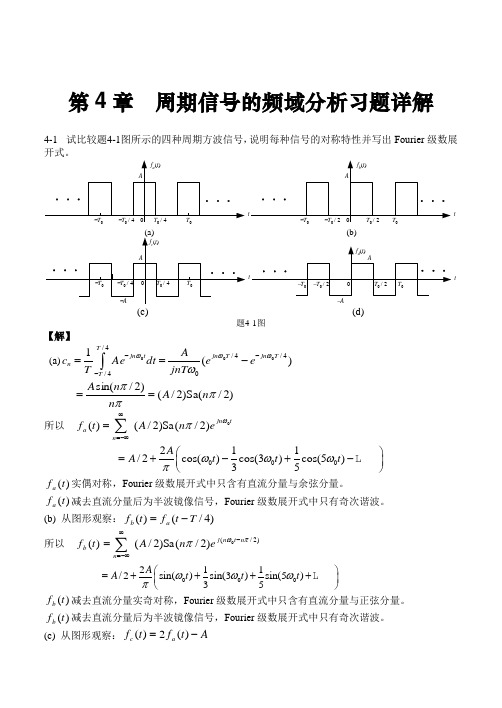
第4章 周期信号的频域分析习题详解4-1 试比较题4-1图所示的四种周期方波信号,说明每种信号的对称特性并写出Fourier 级数展开式。
tt(b)tt-A(c) (d)题4-1图【解】 (a))(14/4/04/4/000T jn T jn tjn T T n eejnT A dt AeTc ωωωω----==⎰)2/(Sa )2/()2/sin(πππn A n n A ==所以 tjn n a e n A t f 0)2/(Sa )2/()(ωπ∑∞-∞==000211/2cos()cos(3)cos(5)35A A t t t ωωωπ⎛⎫=+-+- ⎪⎝⎭)(t f a 实偶对称,Fourier 级数展开式中只含有直流分量与余弦分量。
)(t f a 减去直流分量后为半波镜像信号,Fourier 级数展开式中只有奇次谐波。
(b) 从图形观察:)4/()(T t f t f a b -=所以 )(t f b )2/(0)2/(Sa )2/(πωπn t n j n en A -∞-∞=∑=000211/2sin()sin(3)sin(5)35A A t t t ωωωπ⎛⎫=++++ ⎪⎝⎭)(t f b 减去直流分量实奇对称,Fourier 级数展开式中只含有直流分量与正弦分量。
)(t f b 减去直流分量后为半波镜像信号,Fourier 级数展开式中只有奇次谐波。
(c) 从图形观察:A t f t f a c -=)(2)(第4章 周期信号的频域分析 83所以 tjn n n c en A t f 0)2/(Sa )(0,ωπ∑∞≠-∞==000411c o s ()c o s (3)c o s (5)35A t t t ωωωπ⎛⎫=-+- ⎪⎝⎭)(t f c 实偶对称,且是半波镜像信号,Fourier 级数展开式中只含有奇次谐波的余弦分量。
(d) 从图形观察:)4/()(T t f t f c d -=所以 )2/(0,0)2/(Sa )(πωπn t n j n n d en A t f -∞≠-∞=∑=000411sin()sin(3)sin(5)35A t t t ωωωπ⎛⎫=++- ⎪⎝⎭)(t f d 实奇对称,且是半波镜像信号,Fourier 级数展开式中只含有奇次谐波的正弦分量。
应用多元统计分析课后习题答案高惠璇部分习题解答(00004)市公开课金奖市赛课一等奖课件

[(
y1
aˆ0
)2
]
0
可得
ˆ
2
1 3
( y1
aˆ0 )2
( y2
aˆ0 )2
( y3
3aˆ0 )2
drf
ˆ
2 0
似然比统计量分子为
L(aˆ0
, ˆ 0 2
)
(2
)
3 2
(ˆ 0 2
)
3 2
exp[
3 2
].
第5页
5
第四章 回归分析
似然比统计量为
L(aˆ0 ,ˆ02 ) L(aˆ,bˆ,ˆ 2 )
第18页 18
第四章 回归分析
第19页 19
第四章 回归分析
等号成立 C(ˆ ) 0 (CC)1C • C(ˆ ) 0 ˆ.
第20页 20
第四章 回归分析
第21页 21
第四章 回归分析
第22页 22
第四章 回归分析
见附录P394定理7.2(7.5)式
第23页 23
第四章 回归分析
证实:(1)预计向量为 Yˆ Cˆ C(CC)1CY HY
yˆ
1 n
n i 1
yˆi
1 n
1n
Yˆ
1 n
1n
HY
1 n
(H1n )Y
1 n
1n
Y
y.
(因1n C张成的空间,这里有H1n 1n )
(2) 因 n ( yi y)( yˆi yˆ ) n ( yi yˆi yˆi y)( yˆi y)
0
ln
L
2
n
2
2
1
2( 2 )2
(Y
大学电路习题第4章
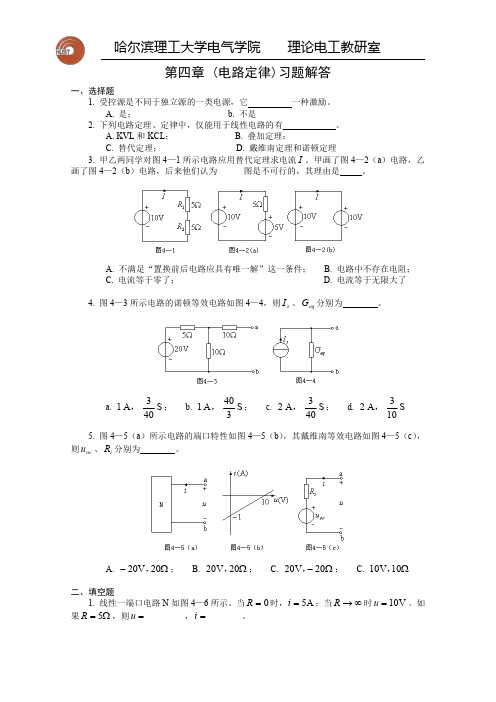
第四章(电路定律)习题解答一、选择题1.受控源是不同于独立源的一类电源,它一种激励。
A.是; b.不是2.下列电路定理、定律中,仅能用于线性电路的有。
A.KVL 和KCL ; B.叠加定理;C.替代定理; D.戴维南定理和诺顿定理3.甲乙两同学对图4—1所示电路应用替代定理求电流I 。
甲画了图4—2(a )电路,乙画了图4—2(b )电路,后来他们认为图是不可行的,其理由是。
A.不满足“置换前后电路应具有唯一解”这一条件;B.电路中不存在电阻;C.电流等于零了;D.电流等于无限大了4.图4—3所示电路的诺顿等效电路如图4—4,则s I 、eq G 分别为。
a.S 403A 1,;b.S 340A 1,;c.S 403A 2,;d.S 103A 2,5.图4—5(a )所示电路的端口特性如图4—5(b ),其戴维南等效电路如图4—5(c ),则oc u 、i R 分别为。
A.Ω-20V 20,;B.Ω20V 20,;C.Ω-20V 20,; C.Ω10V 10,二、填空题1.线性一端口电路N 如图4—6所示。
当0=R 时,A 5=i ;当∞→R 时V 10=u 。
如果Ω=5R ,则=u ,=i 。
2.图4—7所示电路中,N 为线性电路,且Ω=10R 。
当0=s u ,0=s i 时,V 5=u ;当A 2=s i ,0=s u 时,V 8=u ;当0=s i ,V 10=s u 时,V 6=u 。
那么,当A 6=s i ,V 4=s u 时,=i 。
3.图4—8(a )所示电路的戴维南等效电路如图4—8(b ),那么=s U ,=eq R 。
4.图4—9(a )所示电路的戴维南等效电路如图4—9(b ),则=s U ,=eq R 。
5.在图4—10(a )所示的电路中,i u 1024-=(i 的单位用安培时,u 的单位为伏特),其戴维南等效电路如图4—10(b ),则=s u ,=0R 。
三、计算题1.用叠加定理计算图4—11所示电路中的u 。
《运筹学》 第四章习题及 答案

《运筹学》第四章习题一、思考题1.运输问题的数学模型具有什么特征?为什么其约束方程的系数矩阵的秩最多等于1-+n m ?2. 用左上角法确定运输问题的初始基本可行解的基本步骤是什么?3. 最小元素法的基本思想是什么?为什么在一般情况下不可能用它直接得到 运输问题的最优方案?4. 沃格尔法(V ogel 法)的基本思想是什么?它和最小元素法相比给出的运输问题的初始基本可行解哪一个更接近于最优解?为什么?5. 试述用闭回路法检验给定的调运方案是否最优的原理,其检验数的经济意义是什么?6. 用闭回路法检验给定的调运方案时,如何从任意空格出发去寻找一条闭回路?这闭回路是否是唯一的?7. 试述用位势法求检验数的原理、步骤和方法。
8. 试给出运输问题的对偶问题(对产销平衡问题)。
9. 如何把一个产销不平衡的运输问题(产大于销或销大于产)转化为产销平衡的运输问题。
10.一般线性规划问题应具备什么特征才可以转化为运输问题的数学模型? 11.试述在表上作业法中出现退化解的涵义及处理退化解的方法。
二、判断下列说法是否正确1.运输问题模型是一种特殊的线性规划模型,所以运输问题也可以用单纯形方法求解。
2.因为运输问题是一种特殊的线性规划模型,因而求其解也可能出现下列四种情况:有唯一最优解;有无穷多个最优解;无界解;无可行解。
3.在运输问题中,只要给出一组(1-+n m )个非零的{}j i x ,且满足∑==nj i j i a x 1,∑==mi j j i b x 1,就可以作为一个基本可行解。
4.表上作业法实质上就是求解运输问题的单纯形法。
5.按最小元素法或元素差额法给出的初始基本可行解,从每一空格出发都可以找到一闭回路,且此闭回路是唯一的。
6.如果运输问题单位运价表的某一行(或某一列)元素分别加上一个常数k ,最优调运方案将不会发生变化。
7.如果运输问题单位运价表的某一行(或某一列)元素分别乘上一个常数k ,最优调运方案将不会发生变化。
组合数学第四章习题解答

4.23 凸多面体中与一个顶点相关的各角之和与2 的差称为该顶点的欠角,证明凸多面体各顶点欠 角之和为4
证:设V,S,E分别为顶点集,面集,边(棱)集。 由欧拉定理 |V|+|S|-|E|=2. 设aij为与顶点vi, 面Sj为相关的面角,ej为Sj的的边数, 给定Sj则∑aij=(ej-2)π 欠角和为∑(2π-∑aij)=∑2π-∑ ∑aij =2|V|π-∑ ∑aij=2|V|π-∑(ej-2)π =2|V|π-∑ejπ+2|S|π =2|V|π+2|S|π-2|E|π=4π
G×G’的单位元素是(e,e’),试证G×G’是群 (1)封闭性显然 (2)结合律显然 (3)逆元素显然
(4)单位元显然
4.27 一个项链由7颗珠子装饰成的,其中两颗珠 子是红的,3颗是蓝的,其余两颗是绿的,问有多少 种装饰方案,试列举之。
G (1)(2)(3)(4)(5)(6)(7) (1234567),(1357246), (1473625),(1526374), (1642753),(1765432)
4.24 足球由正五边形与正六边形相嵌而成 (a)一个足球由多少正五边形与正六边形组成 (b)把一个足球所有的正六边形都着以黑色,正五 边形则着以其它各色,每个正五边形着色各不相 同,有多少种方案?
4.25 若G和G是两个群
G G ' {( g ,g ')g G ,g ' G ' }, ( g ,g ')( g ,g ') ( g g ,g 'g '), 1 1 2 2 1 2 1 2
4.21 在正四面体的每个面上都引一条高,有多少 种方案?
解:除了绕顶点-对面的中心轴旋转均不会 产生不变的图象外, 绕其他轴的旋转相当于正 4面体的面3着色。参照讲义4.6例3可得不同的 方案数为 M=[34+3·32]/12=9
概率论习题及解答-第四章特征函数

的一个新分割, 且
∑n ∑ m
ξ +η =
(xi + yj )1AiBj .
i=1 j=1
所以由数学期望的定义和概率的有限可加性得
∑n ∑ m
∑n ∑ m
∑n ∑ m
E(ξ + η) =
(xi + yj)P(AiBj) =
xiP(AiBj) +
yj P(AiBj )
i=1 j=1
i=1 j=1
i=1 j=1
概率论习题解答
李勇 张余辉
May 30, 2018
1 第四章 数字特征与特征函数
§4.1.4 练习题
练习4.1.1 设 ξ 和 η 均为简单随机变量, 试证明 E(ξ + η) = E(ξ) + E(η).
证明: 不妨假设
∑n ξ = xi1Ai ,
i=1
∑ m η = yj 1Bj ,
j=1
其中 {Ai} 和 {Bj} 均为样本空间的分割. 记 Cij = AiBj, 则 {Cij : 1 i n, 1 j m} 构成样本空间
解: 记 ξ = min{ξ1, ξ2, · · · , ξn}, η = max{ξ1, ξ2, · · · , ξn}, 则 (ξ, η) 的联合密度函数
p(ξ,η)(x, y) = n(n − 1)(y − x)n−2, 0 < x < y < 1,
所以 ξ 和 η 的边缘密度函数分别为 ∫∞
∑n
∑ m
= xiP(Ai) + yjP(Bj) = E(ξ) + E(η).
i=1
j=1
练习4.1.2 假设简单随机变量 ξ 和 η 相互独立, 试证明
离散数学_第_4_章习题解答讲解

第四章归结法原理习题与解答1. 用归结法证明:(1)(2)(3)(4)(5)(6)解(1) 首先将p→q,p→r,¬(p→q∧r)化为合取范式。
p→q⇔¬p∨qp→r⇔¬p∨r¬(p→q∧r)⇔¬(¬p∨(q∧r))⇔p∧(¬q∨¬r) 给出子句集{¬p∨q,¬p∨r,p,¬q∨¬r}的反驳如下。
⑴ ¬p∨q⑵ ¬p∨r⑶ p⑷ ¬q∨¬r⑸ q 由⑴和⑶由⑵和⑶⑹ r⑺ ¬r 由⑷和⑸⑻ □ 由⑹和⑺因此,p→q,p→r|=p→q∧r(2) 首先将p→r,q→r,¬(p∨q→r)化为合取范式。
p→r⇔¬p∨rq→r⇔¬q∨r¬(p∨q→r)⇔(p∨q)∧¬r给出子句集{¬p∨r,¬q∨r,p∨q,¬r}的反驳如下。
⑴ ¬p∨r⑵ ¬q∨r⑶ p∨q⑷ ¬r⑸ q∨r 由⑴和⑶ p→q,p→r|=p→q∧r p→r,q→r|=p∨q→r p→q∨r|=(p→q)→(p→r)p∧q→r|=(p→r)∨(q→r) p∨q∨r,p→r|=q∨r (p→q)→(p→r)|=p→(q→r)由⑵和⑸⑹ r⑺ □由⑷和⑹因此,p→r,q→r|=p∨q→r(3) 首先将p→q∨r,¬((p→q)∨(p→r))化为合取范式。
p→q∨r⇔¬p∨q∨r¬((p→q)∨(p→r))⇔¬((¬p∨q)∨(¬p∨r))⇔p∧¬q∧¬r 给出子句集{¬p∨q∨r,p,¬q,¬r}的反驳如下。
⑴ ¬p∨q∨r⑵ p⑶ ¬q⑷ ¬r⑸ q∨r 由⑴和⑵⑹ r 由⑶和⑸⑺ □ 由⑷和⑹因此,p→q∨r|=(p→q)∨(p→r)(4) 首先将p∧q→r,¬((p→r)∨(q→r))化为合取范式。
运筹学习题答案(第四章)(课堂PPT)

Ⅰ
1500
6
Ⅱ
2000
4.5
Ⅲ
1000
3
page 9 28 April 2020
School of Management
运筹学教程
第四章习题解答
表4-14
商标
兑制要求
售价(元/kg)
红
Ⅲ少于10% Ⅰ多于50%
5.5
黄
Ⅲ少于70% Ⅰ多于20%
5.0
蓝
Ⅲ少于50% Ⅰ多于10%
4.8
解:x11 1125, x12 300, x13 75, x21 1125,
x2
d1
d
2
d3
d1
d
2
d3
150 40 40
x1
,
x2
,
d
i
,
d
i
0, i
1,2,3
解:x1
55, x2
40,
d
2
15
满足P1,不满足P2
page 3 28 April 2020
School of Management
运筹学教程
第四章习题解答
min
P1
(d
3
d
4
第四章习题解答
解:目标规划模型如下:
min
P1d1
,
P2
(d
2
d
3
d
4
),
P3d
5
,
P4
d
6
x1 x2 x3 1000
x1
d1
d1
300,
x2
d
3
d
3
350,
x1
第4章习题解答

第4章 习题讲解 章
为变址寄存器, R1为基址寄存器 PC为程序计数器 为基址寄存器, 【题4-6 】 R为变址寄存器, R1为基址寄存器,PC为程序计数器 OP I
寻址 方式 (1) ) (2) ) (3) ) (4) ) (5) ) (6) ) I 0 0 0 0 1 1 X 00 01 10 11 00 11
【题4-5】指令格式结构如下所示,试分析指令格式及 】指令格式结构如下所示, 寻址方式的特点 的特点。 寻址方式的特点。
15 12 11 9 8 6 5 3 2 0
OP
寻址方式
寄存器
寻址方式
寄存器
答: ① 所示指令是单字长二地址指令。 所示指令是单字长二地址指令 单字长二地址指令。
操作码字段OP有 可以指定2 16条指令 ② 操作码字段 有4位,可以指定24=16条指令。 可以是RR RS或SS型指令 RR、 型指令。 寻址方式有2 ③ 寻址方式有23=8种,可以是RR、RS或SS型指令。
第4章 典型例题 章
为操作码字段, 【例4.2】指令格式如下所示,OP为操作码字段,试分 】 指令格式如下所示, 为操作码字段 析指令格式特点。 析指令格式特点。
15 10 7 4 3 0
OP
——
源寄存器
变址寄存器
位移量 (16位) 位
答:
双字长二地址指令; ① 双字长二地址指令; 操作码字段OP OP为 可以指定2 64种操作 种操作; ② 操作码字段OP为6位,可以指定26=64种操作; 一个操作数在源寄存器( 16个 ③ 一个操作数在源寄存器(共16个)中,另一个操作数在内存储 器中(有效地址由变址寄存器和位移量决定) 所以是RS 指令。 RS型 器中 ( 有效地址由变址寄存器和位移量决定 ) , 所以是 RS 型 指令 。
有机化学第四章习题答案

p941.解释下列名词。
共轭效应互变异构1,4-加成亲核加成乙烯基化反应氢化热离域能(共轭能)超共轭效应双烯合成亲双烯体红外活性键的伸缩振动键的弯曲振动解:共轭效应:由于结构的原因,双键π电子云不再只定域在双键上,也有部分离域到分子的其它部分,即发生了键的离域。
这种离域效应叫共轭效应。
互变异构:在一般条件下,两个构造异构体可以迅速地相互转变的异构现象。
1,4-加成:一分子试剂加在共轭双键两端的加成反应。
亲核加成:由亲核试剂进攻而引起的加成反应。
乙烯基化反应:反应物分子中的氢原子被乙烯基取代的反应。
氢化热:每一摩尔烯烃催化加氢时放出的能量叫氢化热。
离域能(共轭能):共轭分子中由于键的离域而导致分子的额外的稳定能,称为离域能。
超共轭效应:σ轨道与π轨道相互作用而引起的离域效应。
双烯合成:共轭二烯和某些具有碳碳双键的化合物发生1,4-加成,生成环状化合物的反应。
亲双烯体:在双烯合成中能和共轭二烯反应的重键化合物叫做亲双烯体。
红外活性:能吸收红外辐射的性质。
键的伸缩振动:只改变键长,而不改变键角的振动。
键的弯曲振动:只改变键角,而不改变键长的振动。
2.用系统命名法命名下列化合物:(1) (CH3)3CC≡CCH2CH3(2) HC≡CCH2Br (3) CH2=CHC≡CH (4)CH2=CHCH2CH2C≡CH (5) CH3CHClC≡CCH2CH3(6) CH3C≡CC(CH=CH2)=CHCH2CH3(7)解:(1) 2,2-二甲基-3-己炔(2) 3-溴丙炔(3) 1-丁烯-3-炔(4) 1-己烯-5-炔(5) 2-氯-3-己炔(6) 4 –乙烯基-4 –庚烯-2-炔(7) 1,3,5-己三烯3.写出下列化合物的构造式。
(1) 4 –甲基-1-戊炔(2) 3 –甲基-3-戊烯-1-炔(3) 二异丙基乙炔(4) 1,5 –己二炔(5) 异戊二烯(6) 丁苯橡胶(7) 乙基叔丁基乙炔解:(1) CH≡CCH2CH(CH3)CH3(2) CH≡CC(CH3)=CHCH3(3) (CH3)2CHC≡CCH(CH3)2(4) CH≡CCH2CH2C≡CH (5) CH2=C(CH3)CH=CH2(6) -[-CH2CH=CHCH2CH(C6H5)CH2-〕n- (7)CH3CH2C≡CC(CH3)34.写出1-丁炔与下列试剂作用的反应式。
线性代数练习4

T
S ABC
x1 1 x2 2 x3
y1 1 y2 1 . y3 1
证明:因为 AB x2 x1 , y 2 y1 ,0
AC x3 x1 , y3 y1 ,0,从而
x x1 AB AC 0,0 2 x3 x1
y 2 y1 y3 y1
y 5 x 1, 点,直线 y 2 x 3 .
2
2、 将 xOz 坐标面上的抛物线 z 5 x 绕 x 轴旋转一周,求生成的旋转曲面的方程. 解:抛物线 z 5 x 绕 x 轴旋转一周所生成的曲面方程为:
2
( y 2 z 2 ) 5x
3、 将 xOy 坐标面上的双曲线 4 x 9 y 36 分别绕 x 轴及 y 轴旋转一周,求生成的两个旋
6 求下列直线的方程: (1) 经过 A( 1,0,-1),B( 1,1,3)两点.
ቤተ መጻሕፍቲ ባይዱ
(2) 过点 A( 1,-1,2)与直线
x y 2z 1 0 平行. x 2 y 3z 2 0
解: (1)方向向量为 AB 0,1,4 所以直线的方程为
x 1 y z 1 0 1 4
4、 说明下列旋转曲面是怎样形成的: (1) x
2
y2 z2 1; 4 4
5,1,0 ,
也即点 M0( 4,-3,1)在平面 x+2y -z-3=0 上的投影点.
习题 4—5
1、 指出下列方程在平面直角坐标系与空间直角坐标系中各表示什么图形: (1) x y 2 y 0 ;圆,圆柱面
2 2
(2) x 2 y ;抛物线,抛物柱面
2
(3) 4 x 2 y 1;直线,平面 (4)
管理运筹学第四章习题答案

管理运筹学第四章习题答案管理运筹学第四章习题答案管理运筹学是一门研究如何有效管理和运用资源的学科,它涉及到决策、优化和模型等方面的知识。
第四章是管理运筹学中的重要章节,主要讲述了线性规划的基本概念和解法。
在本文中,我们将针对第四章的习题进行回答,并给出详细的解析和思路。
1. 线性规划的基本概念线性规划是一种数学建模方法,用于解决在给定约束条件下的最优化问题。
它的目标是通过线性函数的最大化或最小化来实现资源的有效利用。
线性规划的基本要素包括决策变量、目标函数和约束条件。
决策变量是问题中需要决策的变量,通常用x1、x2等表示。
目标函数是需要最大化或最小化的线性函数,可以是利润、成本等。
约束条件是问题中的限制条件,可以是资源的限制、技术要求等。
2. 线性规划的解法线性规划可以通过图形法、单纯形法和对偶理论等方法进行求解。
其中,单纯形法是最常用的解法之一。
单纯形法的基本思想是通过不断地移动解空间中的顶点,逐步接近最优解。
它的步骤包括初始化、选择进入变量、选择离开变量、计算新的基变量等。
3. 习题解答以下是第四章习题的答案和解析:习题1:某公司生产两种产品A和B,每单位产品A的利润为3万元,产品B 的利润为4万元。
产品A的生产需要2台机器和3名工人,产品B的生产需要1台机器和4名工人。
机器和工人的数量分别为6台和18名。
如何安排生产,使得利润最大化?解析:设生产产品A的数量为x,产品B的数量为y。
根据题意,可以列出以下线性规划模型:目标函数:Maximize 3x + 4y约束条件:2x + y ≤ 63x + 4y ≤ 18x, y ≥ 0通过求解上述线性规划模型,可以得到最优解x=2,y=4,利润最大化为22万元。
习题2:某公司生产两种产品A和B,产品A的利润为2万元,产品B的利润为3万元。
产品A的生产需要1台机器和2名工人,产品B的生产需要1台机器和3名工人。
机器和工人的数量分别为5台和10名。
如何安排生产,使得利润最大化?解析:设生产产品A的数量为x,产品B的数量为y。
水力学 第四章课后题答案

4.7 水平突然扩大管路,如图所示,已知:直径 d1=5cm,直径d2=10cm,管中流量Q=20l/s,试 求:U形水银比压计中的压差读数Δh。
解:以管轴中心线为基准面,写1-1,2-2断面
的能量方程
p1
g
1v12
2g
p2
g
2v22
2g
hj
p1 p2 v22 v12 (v1 v2 )2
(2)经2分钟流入量水箱的水量为0.329m3。试 求弯管的局部水头损失系数ζ值。
解:流量 Q V 0.329 0.00274m3 / s
T 120
v Q 1.4m / s
A
hf
l d
v2 2g
0.6m
hj hw hf 0.629 0.6 0.029m
hj
v2 2g
2ghj v2
4.1 雷诺数的物理意义?为什么可以判别流态?说明由层流到湍流的物理过程。
答:在流体运动中惯性力对黏滞力比值的无量纲数。Re=UL/ν .其中U为速度特 征尺度,L为长度特征尺度,ν为运动学黏性系数.
P116.P118 4.2 层流有什么特点?如何判别? 答:P116,雷诺数判别 4.3 何谓粘性底层?它的厚度对沿程水头损失有何影响? 答:在湍流中,紧靠固体边界附近的地方,因脉动流速很小,由脉动流速产生 的附加切应力也很小,而流速梯度却很大,所以粘滞切应力起主导作用,其流态 基本上属于层流。因此湍流中不是整个液流都是湍流,在紧靠固体边界表面有一 层极薄的层流层存在,该层流层就叫粘性底层。
0
1
0.023
[2 lg(3.7 d )]2
求出的λ值与假设相符合
通过上述计算说明同一个管径的水管中流过不同 的流量Q,其管壁可以是光滑区,或过渡粗糙区, 也可以是粗糙区。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1 第四章 习题解答3/150、试用实验方法鉴别晶体SiO 2、SiO 2 玻璃、硅胶和SiO 2 熔体。
它们的结构有什么不同?解答:利用X-射线粉末衍射检测。
晶体SiO 2——质点在三维空间做有规律的排列,各向异性。
SiO 2 熔体——内部结构为架状,近程有序,远程无序。
SiO 2 玻璃——各向同性。
硅胶——疏松多孔。
7/151、SiO 2 熔体的粘度在1000℃时为1014 Pa·s ,在1400℃时为107 Pa·s 。
SiO 2 玻璃粘滞流动的活化能是多少?上述数据为恒压下取得,若在恒容下获得,你认为活化能会改变吗?为什么?解答:(1)根据公式:)exp(0RTE ∆=ηη 1000℃时,η=1014 Pa·s ,T=1000+273=1273K , )1273314.8exp(10014⨯∆=E η (1) 1400℃时,η=107 Pa·s ,T =1400+273=1673K ,)1673314.8exp(1007⨯∆=E η (2) 联立(1)和(2)式解得:η0 = 5.27×10-16 Pa·s ,△E = 713.5 kJ/mol(2)若在在恒容下获得,活化能不会改变。
因为活化能是液体质点作直线运动所必需的能量。
它与熔体组成和熔体[SiO 4]聚合程度有关。
212/151、一种用于密封照明灯的硼硅酸盐玻璃,它的退火点是544℃,软化点是780℃。
求:(1)这种玻璃粘性流动的活化能;(2)它的工作范围;(3)它的熔融范围。
解答:(1)根据公式:)exp(0RTE ∆=ηη 退火点544℃, η=1012Pa·s ,T=544+273=817K , )817314.8exp(10012⨯∆=E η (1) 软化点为780℃,η=4.5×106 Pa·s ,T=780+273=1053K ,)1053314.8exp(104.506⨯∆=⨯E η (2)联立(1)和(2)式解得:η0 = 1.39×10-12 Pa·s ,△E = 373.13 kJ/mol 。
(2)工作温度范围粘度一般为103~107Pa.s 根据公式:)(Ln 0ηηR ET ∆=当η=103 Pa·s 时,T =373.13×1000/8.314×Ln(103/1.39×10-12)=1311.9K= 1038.9℃当η=107 Pa·s 时,T =373.13×1000/8.314×In(107/1.39×10-12)=1033.6K= 760.6℃所以工作温度范围是:1038.9℃~760.6℃。
(3)熔融范围粘度一般是10~100 Pa.s当η=10 Pa·s 时,T=1516.0K= 1243.0℃3 当η=100 Pa·s 时,T=1406.6K= 1133.6℃所以熔融温度范围是1243.0℃~1133.6℃。
15/151、试计算下列玻璃的结构参数及非桥氧分数。
(1)Na 2O·SiO 2;(2)Na 2O·CaO·Al 2O 3·SiO 2;(3)Na 2O·1/3Al 2O 3·SiO 2;(4)18Na 2O·10CaO·72SiO 2 (wt %)。
解答:(1)Z=4,R=3/1=3,X=2R-Z=6-4=2,Y=8-2R=8-6=2; 非桥氧%=%1002⨯+X Y X= 2/(1+2)×100% = 66.7%。
(2)因 (Na 2O+CaO)/Al 2O 3 = 2 > 1,所以 Al 3+被视为网络形成离子 Z=4,R= (1+1+3+2)/(2+1) = 2.33,X=2R-Z=4.66-4=0.66,Y=4-0.66=3.34;非桥氧%=%1002⨯+X Y X= 0.66/(1.67+0.66)×100% = 28.3%。
(2)因 Na 2O/Al 2O 3 = 3 > 1,所以 Al 3+被视为网络形成离子Z=4,R= (1+1+2)/(2/3+1) = 2.4,X=2R-Z=4.8-4=0.8,Y=4-0.8=3.2,非桥氧%=%1002⨯+X Y X= 0.8/(1.6+0.8)×100% = 33.3%。
(4)质量百分比转化为摩尔百分比:Na 2O CaOSiO 2 wt% 18 10 72mol 0.290 0.1791.2004 mol% 17.4% 10.7% %Z=4,R=(17.4+10.7+71.9×2)/71.9=2.39,X=2R-Z=0.78,Y=4-0.78=3.22非桥氧%=%1002⨯+X Y X= 0.78/(1.61+0.78)×100% = 32.6%。
21/151、以下三种物质,哪个最容易形成玻璃?哪个最不容易形成玻璃,为什么?(1) Na 2O·2SiO 2;(2)Na 2O ·SiO 2;(3)NaCl 。
解:(1)最容易形成玻璃,(3)最不容易形成玻璃。
经计算可知R 1=2.5,R 2=3,Y 1=3,Y 2=2,Y 1>Y 2,高温下(1)粘度大,容易形成玻璃,NaCl 不具备网络结构,为典型的离子晶体很难形成玻璃。
24/150、在100g 的SiO 2中要加入多少CaO ,才能使O :Si 达2.5? 解:设要加入Xg 的CaO ,M CaO =56g/mol ,M SiO2=60g/mol , 则:(X/56+100×2/60)/(100/60)=2.5解得:X=46.672/211、何谓表面张力和表面能?在固态和液态这两者有何差别? 解:表面张力:垂直作用在单位长度线段上的表面紧缩力或将物体5 表面增大一个单位所需作的功;σ=力/总长度(N/m );表面能:恒温、恒压、恒组成情况下,可逆地增加物系表面积须对物质所做的非体积功称为表面能;J/m 2=N/m ;液体:不能承受剪应力,外力所做的功表现为表面积的扩展,因为表面张力与表面能数量是相同的;固体:能承受剪切应力,外力的作用表现为表面积的增加和部分的塑性形变,表面张力与表面能不等。
5/211、什么是吸附和粘附?当用焊锡来焊接铜丝时,用挫刀除去表面层,可使焊接更加牢固,请解释这种现象?解:吸附:固体表面力场与被吸附分子发生的力场相互作用的结果,发生在固体表面上,分物理吸附和化学吸附;粘附:指两个发生接触的表面之间的吸引,发生在固液界面上; 铜丝放在空气中,其表面层被吸附膜(氧化膜)所覆盖,焊锡焊接铜丝时,只是将吸附膜粘在一起,锡与吸附膜粘附的粘附功小,锉刀除去表面层露出真正铜丝表面(去掉氧化膜),锡与铜相似材料粘附很牢固。
7/211、在20℃及常压下,将半径为10-3m 的汞分散成半径为10-9m 的小汞滴,求此过程所需作的功是多少?已知20℃时汞的表面张力0.47N/m 。
解:此过程所需作的功应等于系统表面能的增加,即J 9.51014.34101047.0434341827923231=⨯⨯⨯⨯=⨯⨯=---r r r W πππγ 8/211、在2080℃的Al 2O 3(L )内有一半径为10-8m 的小气泡,求该气泡6 所受的附加压力是多大?已知2080℃时Al 2O 3(L )的表面张力为0.700N/m 。
解:根据公式rP γ2=∆,可算得△P=2×0.7/10-8=1.4×108 N 。
12/211、试解释粘土结构水和结合水(牢固结合水、松结合水)、自由水的区别,分析后两种水在胶团中的作用范围及其对工艺性能的影响。
解:粘土结构水是粘土结构中的水;由于粘土颗粒一般带负电,因水是极性分子,当粘土颗粒分散于水中时,在粘土表面负电场的作用下,水分子以一定取向分布在粘土颗粒周围以氢键与其表面上的氧和氢氧基结合,负电端向外。
在第一层水分子的外围形成一个负电表面,因而又吸引第二层水分子。
负电场对水分子的引力作用,随着离开粘土表面距离的增加而减弱,因此水分子的排列也有定向逐渐过渡到混乱。
靠近内层形成的定向排列的水分子层称为牢固结合水,围绕在粘土颗粒周围,与粘土颗粒形成一个整体,一起在介质中运动,其厚度约为3-10 个水分子厚。
在牢固结合水的外围吸引着一部分定向程度较差的水分子层称为松结合水,由于离开粘土颗粒表面较远,他们之间的结合力较小。
在松结合水以外的水叫自由水。
结合水的密度大,热容小,界电常数小,冰点低等,在物理性质上与自由水不同。
粘土和水结合的数量可以用测量润湿热来判断。
粘土与这三种水结合的状态与数量将会影响粘土-水系统的工艺性能。
在粘土含水量一定的情况下,若结合水减少,则自由水就多,此时粘土胶的体积减小,容易移动,因而泥浆粘度小,流动性好;当结合水量多时,水膜厚,利于粘土胶粒间的滑动,则可塑性好。
14/211、粘土的很多性能与吸附阳离子种类有关。
指出粘土吸附下列不同阳离子后的性能变化规律,(以箭头表示:小→大)H+Al3+Ba2+Sr2+Ca2+Mg2+NH4+K+Na+Li+(l)离子交换能力;(2)粘土的ζ电位;(3)粘土的结合水量;(4)泥浆稳定性;(5)泥浆流动性;(6)泥浆触变性;(7)泥团可塑性;(8)泥浆滤水性;(9)泥浆浇注时间(10)坯体形成速率。
解答:(l)离子交换能力:Li+→Na+→K+→NH4+→Mg2+→Ca2+→S r2+→Ba2+→Al3+→H+(2)粘土的ζ电位:H+→Li+→Na+→K+→NH4+→Mg2+→Ca2+→Sr2+→Ba2+→ Al3+(3)粘土的结合水量:NH4+→Al3+→Ba2+→Sr2+→Ca2+→Mg2+→K+→Na+→Li+→H+(4)泥浆稳定性:H+→Al3+→Ba2+→Sr2+→Ca2+→Mg2+→NH4+→K+→Na+→Li+(5)泥浆流动性:H+→Li+→Na+→K+→Mg2+→Ca2+→Sr2+→Ba2+→Al3+→NH4+(6)泥浆触变性:H+→Li+→Na+→K+→Mg2+→Ca2+→Sr2+→Ba2+→Al3+→NH4+(7)泥团可塑性:Li+→Na+→K+→NH4+→Mg2+→Ca2+→Sr2+→Ba2+→Al3+→ H+(8)泥浆滤水性:H+→Al3+→Ba2+→Sr2+→Ca2+→Mg2+→NH4+→K+→Na+→Li+(9)泥浆浇注时间:Li+→Na+→K+→NH4+→Mg2+→Ca2+→Sr2+→Ba2+→Al3+→H+10)坯体形成速率:H+→Al3+→Ba2+→Sr2+→Ca2+→Mg2+→NH4+→ K+→Na+→Li+7。
