图的邻接表表示法

合集下载

数据结构-邻接表

for(i=0;i<NumOfVertices() ;i++) if(!visited[i]) BroadFirstSearch(i, visited, Visit);
delete [ ] visited; }
8.4 图的遍历（续）
图的生成树
定义：G的所有顶点加上遍历过程中经过的边所构成的子图称作图G的生成树G’
visited[v]=1;
/*标记第v个顶点已访问*/
/*访问第v个顶点邻接的未被访问过的顶点w，并从w出发递归地按照深度优先的方式进行遍历*/
w= GetFirstNeighbor (v); /*得到第v个顶点的第一个邻接顶点w*/
while(w!= -1)
{ if(!visited[w]) DepthFirstSearch(w,visited,Visit); //递归调用
void BroadFirstSearch(const int v, int visited[ ], void visit(VT Vertex));
public:
AdjTWGraph(void);
~AdjTWGraph(void);
int NumOfVertices(void)const;
int NumOfEdges(void)const;
(2) 无向图：第i个链表中的表结点数为TD(vi)；能逆求邻有I接向D表(图vi。)：。第为i个便链于表求中ID的(v表i) 可结另点外数建为立OD有(v向i)，图不的
(3) 容易寻找顶点的邻接点，但判断两顶点间是否有边或弧，需搜索两结点对应的单链表。
(4) 邻接表多用于稀疏图的存储（e<<n2)
void Visit(VT item))

邻接表表示法的特点

邻接表表示法的特点
邻接表表示法是一种用于表示无向图的数据结构，它是一种非常灵活、实用的方法，可以有效地表达图中的信息。

这种表示法也可以应用于表示有向图和有权图。

邻接表表示法的一个特点是，它可以有效地表示图的结构，使得对图的操作（如查找某个顶点的邻接点、计算边的权重等）变得非常容易。

首先，邻接表表示法可以方便地表示有向图和有权图。

在邻接表表示法中，每个节点都有一个节点表，其中包含有关该节点的所有信息，包括其邻接点以及到达相邻节点所需要的边的权重。

这使得查找某个节点的邻接点和计算边的权重变得非常容易。

其次，邻接表表示法可以非常有效地表示无向图的连接信息。

它可以方便地表示图的结构，使得查找邻接点和计算边的权重变得非常容易。

此外，邻接表表示法的另一个特点是它的实现较为简单。

它是由数组和链表组成的，因此实现起来非常容易，也可以节省大量内存空间。

同时，它的操作速度也相对较快，简单高效。

最后，邻接表表示法还可以用来表示一些特殊图，比如带有环的图，树图，二维坐标图等。

它能够有效地表示对应数据结构，从而使得查找、检索和操作变得容易。

总之，邻接表表示法是一种非常实用的表示无向图和有向图的技术手段，它的特点是：可以有效地表示图的结构，实现较为简单，操
作速度较快，而且能够有效地表示一些特殊图，树图，二维坐标图等。

它对查找某个顶点的邻接点和计算边的权重来说，都非常有效。

因此，邻接表表示法在表示图结构以及进行图处理方面都有很大的优势。

图基本算法图的表示方法邻接矩阵邻接表

图基本算法图的表⽰⽅法邻接矩阵邻接表要表⽰⼀个图G=(V,E)，有两种标准的表⽰⽅法，即邻接表和邻接矩阵。

这两种表⽰法既可⽤于有向图，也可⽤于⽆向图。

通常采⽤邻接表表⽰法，因为⽤这种⽅法表⽰稀疏图（图中边数远⼩于点个数）⽐较紧凑。

但当遇到稠密图（|E|接近于|V|^2）或必须很快判别两个给定顶点⼿否存在连接边时，通常采⽤邻接矩阵表⽰法，例如求最短路径算法中，就采⽤邻接矩阵表⽰。

图G=<V，E>的邻接表表⽰是由⼀个包含|V|个列表的数组Adj所组成，其中每个列表对应于V中的⼀个顶点。

对于每⼀个u∈V，邻接表Adj[u]包含所有满⾜条件（u，v）∈E的顶点v。

亦即，Adj[u]包含图G中所有和顶点u相邻的顶点。

每个邻接表中的顶点⼀般以任意顺序存储。

如果G是⼀个有向图，则所有邻接表的长度之和为|E|，这是因为⼀条形如（u，v）的边是通过让v出现在Adj[u]中来表⽰的。

如果G是⼀个⽆向图，则所有邻接表的长度之和为2|E|，因为如果（u，v）是⼀条⽆向边，那么u会出现在v的邻接表中，反之亦然。

邻接表需要的存储空间为O（V+E）。

邻接表稍作变动，即可⽤来表⽰加权图，即每条边都有着相应权值的图，权值通常由加权函数w：E→R给出。

例如，设G=<V，E>是⼀个加权函数为w的加权图。

对每⼀条边（u，v)∈E，权值w（u，v）和顶点v⼀起存储在u的邻接表中。

邻接表C++实现:1 #include <iostream>2 #include <cstdio>3using namespace std;45#define maxn 100 //最⼤顶点个数6int n, m; //顶点数，边数78struct arcnode //边结点9 {10int vertex; //与表头结点相邻的顶点编号11int weight = 0; //连接两顶点的边的权值12 arcnode * next; //指向下⼀相邻接点13 arcnode() {}14 arcnode(int v,int w):vertex(v),weight(w),next(NULL) {}15 arcnode(int v):vertex(v),next(NULL) {}16 };1718struct vernode //顶点结点，为每⼀条邻接表的表头结点19 {20int vex; //当前定点编号21 arcnode * firarc; //与该顶点相连的第⼀个顶点组成的边22 }Ver[maxn];2324void Init() //建⽴图的邻接表需要先初始化，建⽴顶点结点25 {26for(int i = 1; i <= n; i++)27 {28 Ver[i].vex = i;29 Ver[i].firarc = NULL;30 }31 }3233void Insert(int a, int b, int w) //尾插法，插⼊以a为起点，b为终点，权为w的边，效率不如头插，但是可以去重边34 {35 arcnode * q = new arcnode(b, w);36if(Ver[a].firarc == NULL)37 Ver[a].firarc = q;38else39 {40 arcnode * p = Ver[a].firarc;41if(p->vertex == b) //如果不要去重边，去掉这⼀段42 {43if(p->weight < w)44 p->weight = w;45return ;46 }47while(p->next != NULL)48 {49if(p->next->vertex == b) //如果不要去重边，去掉这⼀段50 {51if(p->next->weight < w);52 p->next->weight = w;53return ;54 }55 p = p->next;56 }57 p->next = q;58 }59 }60void Insert2(int a, int b, int w) //头插法，效率更⾼，但不能去重边61 {62 arcnode * q = new arcnode(b, w);63if(Ver[a].firarc == NULL)64 Ver[a].firarc = q;65else66 {67 arcnode * p = Ver[a].firarc;68 q->next = p;69 Ver[a].firarc = q;70 }71 }7273void Insert(int a, int b) //尾插法，插⼊以a为起点，b为终点，⽆权的边，效率不如头插，但是可以去重边74 {75 arcnode * q = new arcnode(b);76if(Ver[a].firarc == NULL)77 Ver[a].firarc = q;78else79 {80 arcnode * p = Ver[a].firarc;81if(p->vertex == b) return; //去重边，如果不要去重边，去掉这⼀句82while(p->next != NULL)83 {84if(p->next->vertex == b) //去重边，如果不要去重边，去掉这⼀句85return;86 p = p->next;87 }88 p->next = q;89 }90 }91void Insert2(int a, int b) //头插法，效率跟⾼，但不能去重边92 {93 arcnode * q = new arcnode(b);94if(Ver[a].firarc == NULL)95 Ver[a].firarc = q;96else97 {98 arcnode * p = Ver[a].firarc;99 q->next = p;100 Ver[a].firarc = q;101 }102 }103void Delete(int a, int b) //删除以a为起点，b为终点的边104 {105 arcnode * p = Ver[a].firarc;106if(p->vertex == b)107 {108 Ver[a].firarc = p->next;109 delete p;110return ;111 }112while(p->next != NULL)113if(p->next->vertex == b)114 {115 p->next = p->next->next;116 delete p->next;117return ;118 }119 }120121void Show() //打印图的邻接表（有权值）122 {123for(int i = 1; i <= n; i++)124 {125 cout << Ver[i].vex;126 arcnode * p = Ver[i].firarc;127while(p != NULL)128 {129 cout << "->(" << p->vertex << "," << p->weight << ")";130 p = p->next;131 }132 cout << "->NULL" << endl;133 }134 }135136void Show2() //打印图的邻接表(⽆权值）137 {138for(int i = 1; i <= n; i++)140 cout << Ver[i].vex;141 arcnode * p = Ver[i].firarc;142while(p != NULL)143 {144 cout << "->" << p->vertex;145 p = p->next;146 }147 cout << "->NULL" << endl;148 }149 }150int main()151 {152int a, b, w;153 cout << "Enter n and m：";154 cin >> n >> m;155 Init();156while(m--)157 {158 cin >> a >> b >> w; //输⼊起点、终点159 Insert(a, b, w); //插⼊操作160 Insert(b, a, w); //如果是⽆向图还需要反向插⼊161 }162 Show();163return0;164 }View Code 邻接表表⽰法也有潜在的不⾜之处，即如果要确定图中边（u,v）是否存在，只能在顶点u邻接表Adj[u]中搜索v，除此之外没有其他更快的办法。

图论基础图的表示与常见算法

图论基础图的表示与常见算法图论是数学的一个分支，研究的是图这种数学结构。

图由节点（顶点）和边组成，是研究网络、关系、连接等问题的重要工具。

在图论中，图的表示和算法是非常重要的内容，本文将介绍图的表示方法以及一些常见的图算法。

一、图的表示1. 邻接矩阵表示法邻接矩阵是表示图的一种常见方法，适用于稠密图。

对于一个有n 个节点的图，邻接矩阵是一个n×n的矩阵，其中第i行第j列的元素表示节点i到节点j是否有边相连。

如果有边相连，则该元素的值为1或边的权重；如果没有边相连，则该元素的值为0或者无穷大。

邻接矩阵的优点是可以方便地进行边的查找和修改，但缺点是对于稀疏图来说，会浪费大量的空间。

2. 邻接表表示法邻接表是表示图的另一种常见方法，适用于稀疏图。

对于一个有n 个节点的图，邻接表是一个长度为n的数组，数组中的每个元素是一个链表，链表中存储了与该节点相连的其他节点。

邻接表的优点是节省空间，适用于稀疏图，但缺点是查找边的时间复杂度较高。

3. 关联矩阵表示法关联矩阵是表示图的另一种方法，适用于有向图。

对于一个有n个节点和m条边的图，关联矩阵是一个n×m的矩阵，其中第i行第j列的元素表示节点i和边j的关系。

如果节点i是边j的起点，则该元素的值为-1；如果节点i是边j的终点，则该元素的值为1；如果节点i与边j无关，则该元素的值为0。

关联矩阵适用于有向图，可以方便地表示节点和边之间的关系。

二、常见图算法1. 深度优先搜索（Depth First Search，DFS）深度优先搜索是一种用于遍历或搜索图的算法。

从起始节点开始，沿着一条路径一直向下搜索，直到到达叶子节点，然后回溯到上一个节点，继续搜索其他路径。

DFS可以用递归或栈来实现。

2. 广度优先搜索（Breadth First Search，BFS）广度优先搜索是另一种用于遍历或搜索图的算法。

从起始节点开始，先访问起始节点的所有邻居节点，然后再依次访问邻居节点的邻居节点，以此类推。

邻接表

数据结构在信息学竞赛中的应用图形结构——邻接表引出：在介绍完邻接矩阵之后，我们发现，邻接矩阵还是无法储存过大的图，例如一旦图的顶点数超过6000，就可能有内存溢出的危险。

所以，我们需要找到一种新的方式来满足我们的需求。

定义：邻接表，实际上就是一种由链表组成的图形数据结构，对于其每一个顶点，都用链表来记录它的出边。

我们需要记录以下信息来储存图：1、对于每一个顶点，需要记录从该顶点连出的最后一条边。

2、对于每一条边，需要记录由同一顶点连出的上一条边，以及该边所连向的顶点。

例如，在像下面这样的图中：AaObB像这样一张图，我们就可以这样来储存：1、O点连出的最后一条边记为b，而A和B都没有连出边，所以记为0。

2、a是O连出的第一条边，连向A，所以上一条边记为0，连向的点记为A；而b的上一条变记为a，连向的点记为B。

这就是这个邻接表的信息，如果我们需要加入一条由O连向C的边c，只需要：1、记录边c的信息：指向的点为C，上一条边为原本O点连出的最后一条边b。

2、更新O点的最后一边为c。

这样我们就可以完整维护邻接表。

C++代码如下：struct Adjlist{int prev; //上一条边int node; //连向的点} adjlist[E]; //定义邻接表的边int last[N]; //记录顶点连出的最后一条边int num; //记录边的数量void addline(int p1,int p2){++num;adjlist[num].node = p2; //更新边adjlist[num].prev = last[p1];last[p1] = num; //维护顶点连出的最后一条边}PS：如果边带权值只需要加入权值元素就好了。

分析：空间上，一个邻接表只需要占用的单元数目为N+2E。

时间上，在结合了深度、广度优先算法之后，实际上，每访问一条边的时间复杂度只有O(1)。

应用：总结：。

邻接表表示法的特点

邻接表表示法的特点
邻接表表示法是一种把图结构的存储结构。

它的空间使用效率高，操作效率也比较高，而且相对来说存储结构比较清楚方便管理。

首先，邻接表存储结构最大的优点就是空间复杂度极小，因为它只需要存储图中的顶点信息和边信息就可以描述图中的结构，此外，每个顶点只需要存储其相邻节点的序号而不需要存储两顶点之间的
距离，所以节点所占的内存空间少，也减少了图中属性的存储。

其次，邻接表存储结构的操作效率也比较高，因为在邻接表存储结构中，每个顶点都有相应的链表来存储其相邻节点的序号，所以在查找和更新操作中，只需要找到顶点的链表，就可以很方便地查找或更新其邻接节点的信息，也十分提高了操作效率。

此外，邻接表存储结构的结构也比较清晰，在建立时只需要用一个数据结构把图的顶点和邻接边按照一定的顺序存储起来，就可以把图中的结构信息全部存储起来。

这样，程序员就可以非常快速地定位顶点的相邻边，也方便管理。

总之，邻接表表示法优化了图的存储，使得程序员可以更加快速准确地定位顶点的相邻边，并且使得管理变得更加简单方便。

邻接表表示法也在图的可视化中有着广泛的应用，有助于更好地提高图的存储效率和操作效率。

因此，邻接表表示法的特点是空间使用效率高，操作效率也比较高，相对来说存储结构比较清晰方便管理，且有着广泛的应用。

未来，会有更多的算法和应用技术来提高图的效率，并且在使用邻接表表示
法时，还有很多细节需要更新和思考，以更加优雅地描述图结构。

有向图的邻接表表示法

有向图的邻接表表⽰法图的邻接表表⽰法类似于树的孩⼦链表表⽰法。

对于图G中的每个顶点vi，该⽅法把所有邻接于vi的顶点vj链成⼀个带头结点的单链表，这个单链表就称为顶点vi的邻接表(Adjacency List)。

1．邻接表的结点结构（1）表结点结构┌────┬───┐│adjvex │next │└────┴───┘　邻接表中每个表结点均有两个域:　①邻接点域adjvex 存放与vi相邻接的顶点vj的序号j。

　②链域next 将邻接表的所有表结点链在⼀起。

注意：　若要表⽰边上的信息(如权值)，则在表结点中还应增加⼀个数据域。

（2）头结点结构┌────┬─────┐│vertex │firstedge │└────┴─────┘　顶点vi邻接表的头结点包含两个域：　①顶点域vertex 存放顶点vi的信息　②指针域firstedge vi的邻接表的头指针。

注意：　①为了便于随机访问任⼀顶点的邻接表，将所有头结点顺序存储在⼀个向量中就构成了图的邻接表表⽰。

　②有时希望增加对图的顶点数及边数等属性的描述，可将邻接表和这些属性放在⼀起来描述图的存储结构。

代码实例2.{输出结果为：int VexNum,ArcNum;//定义图的顶点数和边数VertexNode vertex[MAX_VERTEX_NUM];//定义头结点数组。

}AdjList;void CreateGraph(AdjList *adj,int *n){int e,s,d;cout<<"输⼊顶点数和边数"<<endl;cin>>*n>>e;//输⼊顶点数和边数。

adj->VexNum=*n;adj->ArcNum=e;EdgeNode *q=NULL;//初始化表头结点int i;for(i=1;i<=*n;i++){输⼊第2条边的起点和终点2 4输⼊第3条边的起点和终点2 1输⼊第4条边的起点和终点4 3输⼊第5条边的起点和终点3 6输⼊第6条边的起点和终点3 53.代码实例2(ps:补充于2011-6-14) 总体⽽⾔，邻接表表⽰法中主要含有两种结点，分别是头结点和表结点(也叫做边结点)，在头结点(s)到表结点(d)之间存在着⼀条边。

《数据结构之图》相关知识点总结

第5章图●图的定义①图由顶点集V和边集E组成，记为G=（V，E），V(G)是图G中顶点的有穷非空集合，E(G)是图G中顶点之间变得关系集合，|V|表示顶点个数，也称图的阶，|E|表示边数（线性表和树都可以是空的，但图可以只有一个顶点没有边）②有向图：弧是顶点的有序对，记为<v,w>，v,w是顶点,v是弧尾，w是弧头，从顶点v到顶点w的弧。

无向图：边是顶点的无序对，记为(v,w)③简单图：一个图满足：不存在重复边；不存在顶点到自身的边。

多重图相对于简单图定义④完全图：无向图中，任意两顶点之间存在边，称为完全无向图。

N个顶点的无向完全图有n(n-1)/2条边。

在有向图中，任意两顶点之间存在方向相反的两条弧，称为有向完全图，N 个顶点的有向完全图有n(n-1)条边。

⑤连通图：在无向图中任意两顶点都是连通的。

无向图中的极大连通子图称为连通分量。

极大要求连通子图包含其所有的边和顶点，极小连通子图既要保持图连通，又要保持边数最少⑥在有向图中任意两顶点v,w，存在从顶点v到顶点w和从顶点w到顶点v两条路径，这种图称为强连通图。

有向图的极大强连通子图称为有向图的强连通分量。

⑦生成树：①包含图中所有顶点n，②生成树有n-1条边, ③任意两点连通。

对生成树而言，砍去一条边变成非连通图，加上一条边形成一个回路。

在非连通图中，连通分量的生成树构成了非连通图的生成森林。

⑧顶点的度：以该顶点为端点的边的数目。

无向图的全部顶点的度之和等于边数的两倍。

有向图的度等于出度和入度之和，入度是以该顶点为终点的有向边的数目，出度是以该顶点为起点的有向边的数目。

有向图的全部顶点的入度之和和出度之和相等且等于边数。

⑨图中每条边可以标上具有某种含义的数值，该数值称为边的权值。

带有权值的图称为网。

○10对于无向图G=(V, {E})，如果边(v，v’)∈E，则称顶点v，v’互为邻接点，即v，v’相邻接。

边(v，v’)依附于顶点v 和v’，或者说边(v, v’)与顶点v 和v’相关联。

图的表示方法

图的表示方法图是一种常用的数据结构，用于描述事物之间的关系或连接。

在计算机科学和信息技术领域，图的表示方法是研究和应用的关键。

本文将介绍图的常见表示方法，并探讨它们的特点和适用场景。

1. 邻接矩阵表示法邻接矩阵是一种使用二维矩阵表示图的方式。

其中矩阵的行和列分别对应图中的顶点，而矩阵的元素表示图中顶点之间的边。

如果两个顶点之间存在边，则矩阵对应位置的元素为1，否则为0。

如果图是有权重的，则可以将权重值存储在矩阵的元素中。

邻接矩阵的优点是简单直观，易于理解和实现。

它可以快速检查两个顶点之间是否存在边，时间复杂度为O(1)。

然而，邻接矩阵的缺点是占用空间较大，特别是对于稀疏图而言，大量的0元素浪费了存储空间。

2. 邻接表表示法邻接表是一种使用链表表示图的方式。

其中每个顶点都对应一个链表，链表中存储与该顶点相邻的顶点。

如果图是有权重的，则链表节点可以包含权重值。

邻接表的优点是占用空间较小，特别适用于表示稀疏图。

它可以快速访问和遍历某个顶点相邻的顶点，时间复杂度为O(k)，其中k是顶点相邻的边的数量。

然而，邻接表的缺点是不方便检查两个顶点之间是否存在边，需要遍历链表。

3. 关联矩阵表示法关联矩阵是一种使用二维矩阵表示图的方式，其中矩阵的行对应顶点，列对应边。

关联矩阵中，如果顶点与边相连，则对应位置元素为1，否则为0。

关联矩阵的优点是可以较为直观地表示图的结构和关系。

它适用于表示有向图和无向图，以及多重图。

然而，关联矩阵的缺点是占用空间较大，尤其对于有大量顶点和边的图而言。

4. 边列表表示法边列表是一种使用列表表示图的方式。

其中列表中的每个元素存储边的信息，包括起点、终点和权重等。

对于有向图，边列表包含有向边的信息。

边列表的优点是比较节省存储空间，特别适合表示稀疏图。

它便于遍历和访问边的信息，但相应地，检查两个顶点之间是否有边的操作较为耗时。

综上所述，图的表示方法有邻接矩阵、邻接表、关联矩阵和边列表等多种形式，每种方法都有自己的特点和适用场景。

图的邻接表表示法及顶点入度、出度的计算方法

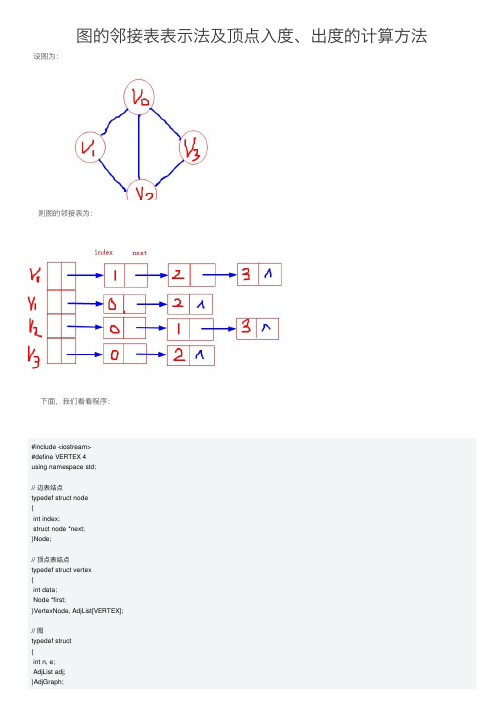
图的邻接表表⽰法及顶点⼊度、出度的计算⽅法设图为：则图的邻接表为：下⾯，我们看看程序：#include <iostream>#define VERTEX 4using namespace std;// 边表结点typedef struct node{int index;struct node *next;}Node;// 顶点表结点typedef struct vertex{int data;Node *first;}VertexNode, AdjList[VERTEX];// 图typedef struct{int n, e;AdjList adj;}AdjGraph;// 创建图void createAdjGraph(AdjGraph &g){g.n = VERTEX;g.e = VERTEX + 1;// 下⾯创建AdjGraph的代码很丑陋，仅供⽰意Node *p1, *p2, *p3;p1 = new Node;p2 = new Node;p3 = new Node;p1->index = 1;p2->index = 2;p3->index = 3;g.adj[0].first = p1;p1->next = p2;p2->next = p3;p3->next = NULL;Node *q0, *q2;q0 = new Node;q2 = new Node;q0->index = 0;q2->index = 2;g.adj[1].first = q0;q0->next = q2;q2->next = NULL;Node *r0, *r1, *r3;r0 = new Node;r1 = new Node;r3 = new Node;r0->index = 0;r1->index = 1;r3->index = 3;g.adj[2].first = r0;r0->next = r1;r1->next = r3;r3->next = NULL;Node *s0, *s2;s0 = new Node;s2 = new Node;s0->index = 0;s2->index = 2;g.adj[3].first = s0;s0->next = s2;s2->next = NULL;}// 求图中顶点的⼊度void inDegree(AdjGraph g){Node *p;int i, inD;for(i = 0; i < g.n; i++){inD = 0;p = g.adj[i].first;while(NULL != p){inD++;p = p->next;}cout << "顶点" << i << "的⼊度为:" << inD << endl;cout << "顶点" << i << "的⼊度为:" << inD << endl;}}// 求图中顶点的出度void outDegree(AdjGraph g){Node *p;int i, outD;for(i = 0; i < g.n; i++){outD = 0;p = g.adj[i].first;while(NULL != p){outD++;p = p->next;}cout << "顶点" << i << "的出度为:" << outD << endl;}}int main(){AdjGraph g;createAdjGraph(g);inDegree(g); // 打印⼊度cout << endl;outDegree(g); // 打印出度return 0;}结果为：顶点0的⼊度为:3顶点1的⼊度为:2顶点2的⼊度为:3顶点3的⼊度为:2顶点0的出度为:3顶点1的出度为:2顶点2的出度为:3顶点3的出度为:2值得⼀提的是，对于有向图⽽⾔，我们⼀般采⽤的邻接表是正邻接表，在这种情况下，求图的各顶点的出度相对较易，⽽⼊度则不好直接求。

邻接表表示法的特点

邻接表表示法的特点
邻接表表示法是一种常用的图的存储方式，它是表示两个顶点之间连接关系的一种数据结构，它通过一种“键”和“值”的关系来表示图中各个结点和它们之间的边。

因此，邻接表表示法在图论以及图算法方面是非常有用的。

本文将介绍邻接表表示法的特点，并归纳总结出邻接表表示法的优点和缺点。

首先，邻接表表示法的特点之一就是存储利用率比较高。

邻接表表示法只需要存储节点和边的关系，而不需要存储节点的额外信息，因此它只需要占用少量的存储空间，而它可以表示图中所有的边，因此它支持非常大的图。

其实，它也可以支持连通图的存储，这一点极大的方便了读写操作，使得它可以被用来存储大型图。

此外，邻接表表示法还具有操作简单快捷的特点。

它可以把图中任意两个点之间的关系表示出来，并且可以简便地查找任意两个节点之间的路径，这对于寻找最短路径以及路径搜索来说非常有用。

邻接表表示法也可以很方便地操作权重边，所以它也可以用来表示容量图，带权图和特殊图。

最后，邻接表表示法的一个显著特点就是灵活的应用。

它可以用于表示不同类型的图，如无向图、有向图、带权图和容量图，这一点对于实际应用非常有用。

由于它可以表示图中任意两个点之间的边，因此它可以被用来表示一些复杂的网络，比如互联网和电话网络。

综上所述，邻接表表示法具有较高的存储利用率、操作简单快捷的特点和灵活的应用，因此它在数据结构与图算法方面是非常有用的
存储方式。

当前，邻接表表示法已经被广泛应用于实际的网络系统以及图算法开发中，它也一直在不断发展，一定会把图算法研究带到一个新的高度。

图算法表示及遍历方法详解

图算法表示及遍历方法详解图是计算机科学中常用的数据结构之一，用于表示和解决各种实际问题。

本文将详细介绍图的算法表示以及遍历方法，帮助读者更深入了解和应用图算法。

一、图的定义和表示方法图是由节点（顶点）和边构成的一种数据结构。

常见的图表示方法有两种：邻接矩阵和邻接表。

1. 邻接矩阵表示法邻接矩阵是一个二维矩阵，其中的元素表示图中各个节点之间的连接关系。

对于一个有n个节点的图，邻接矩阵是一个n x n的矩阵，用0和1表示节点之间是否有边相连。

例如，对于一个有4个节点的图，邻接矩阵可以表示为：1 2 3 41[0, 1, 1, 0]2[1, 0, 0, 1]3[1, 0, 0, 0]4[0, 1, 0, 0]邻接矩阵表示法简单直观，适用于节点数量相对较小、边的数量相对较大时。

2. 邻接表表示法邻接表是通过链表的形式，将每个节点的邻接顶点存储起来，用于表示图的连接关系。

对于一个有n个节点的图，可以使用一个长度为n 的数组，数组中的每个元素都是一个链表，链表中存储了与该节点相连的其他节点。

例如，对于一个有4个节点的图，邻接表可以表示为：1->2->32->1->43->14->2邻接表表示法相对节省存储空间，适用于节点数量较大、边的数量相对较小的情况。

二、图的遍历方法图的遍历是指按一定规则依次访问图中的每个节点，以达到查找、搜索或其他操作的目的。

常见的图遍历方法有深度优先搜索（DFS）和广度优先搜索（BFS）。

1. 深度优先搜索（DFS）深度优先搜索从某个节点开始，沿着一条路径一直访问到最后一个节点，然后回溯到上一个节点，再选择另一条未访问过的路径，重复上述过程，直到遍历完整个图。

DFS可以使用递归或栈来实现。

以下是使用递归实现DFS的示例代码：```pythondef dfs(graph, start, visited):visited[start] = Trueprint(start)for neighbor in graph[start]:if not visited[neighbor]:dfs(graph, neighbor, visited)```2. 广度优先搜索（BFS）广度优先搜索从某个节点开始，先访问其所有邻接节点，然后再访问邻接节点的邻接节点，依次类推，直到遍历完整个图。

邻接表表示法的特点

邻接表表示法的特点
邻接表是图或网络数据结构的一种重要表示方法，它可以有效地表示网络拓扑结构，在图论和网络分析中有着重要的应用。

邻接表的特点主要有以下几点：
一、数据存储的方便性
邻接表的表示方法能够以很方便的方式存储复杂的图数据，其中每个顶点会有非常多的相邻顶点，而邻接表可以有效地表示每个顶点的所有邻接点，使得数据的存储更加方便。

二、操作的便捷性
在操作邻接表时，可以实现对复杂的图网络数据的快速查询、统计，这样使得在处理大规模图数据时，变得更加方便。

三、图计算的效率
在使用邻接表来描述网络拓扑结构时，可以更加关注每个顶点之间的邻接关系，特别是在计算机图形学中，可以使用邻接表来快速计算图形网络的最佳路径等，极大地提升了图计算的效率。

四、实现的简易性
邻接表的实现比较简单，只需要实现一组简单的操作语句，就可以完成对图的描述，而且邻接表只需要一个数组，节省了存储空间，使实现变得更加简单。

总结：邻接表是图或网络数据结构的一种重要表示方法，其特点包括：（1）数据存储的方便性；（2）操作的便捷性；（3）图计算的效率；（4）实现的简易性。

邻接表在图论和网络分析中有着广泛的应用，
为复杂的图网络数据的快速查询和统计提供了可靠而有效的解决方案。

邻接表表示法的特点

邻接表表示法的特点
邻接表表示法是表示静态图的一种常用数据结构，特点如下：
1. 节约空间：邻接表表示法只存储了图中节点有
边相连的相关信息，以节约内存空间；
2. 直观性强：邻接表表示法可以直观地将图的节
点与边进行映射；
3. 搜索容易：邻接表表示法使用“指针”原理，来
记录某一个顶点的所有相邻顶点，这样给搜索带
来极大便利；
4. 更新可控：邻接表表示法可以让图的更新操作更加可控，比如，增加或者删除节点时，只需要更改相关联的邻接表即可；
5. 实现简单：邻接表表示法的实现非常简单，它可以使用数组或者有序链表进行数据的存储；
6. 无序：邻接表表示的图是无序的，无法通过线性结构进行搜索；
7. 不支持超级节点：邻接表表示的图仅支持一层
节点间的连接，不支持超级节点的连接，以及多层节点间的路径搜索。

图的两种存储方式---邻接矩阵和邻接表

图的两种存储⽅式---邻接矩阵和邻接表图：图是⼀种数据结构，由顶点的有穷⾮空集合和顶点之间边的集合组成，表⽰为G(V,E)，V表⽰为顶点的集合，E表⽰为边的集合。

⾸先肯定是要对图进⾏存储，然后进⾏⼀系列的操作，下⾯对图的两种存储⽅式邻接矩阵和邻接表尽⾏介绍。

（⼀）、邻接矩阵存储：⽤两个数组分别进⾏存储数据元素（顶点）的信息和数据元素之间的关系（边或弧）的信息。

存储顶点：⽤⼀个连续的空间存储n个顶点。

存储顶点之间的边：将由n个顶点组成的边⽤⼀个n*n的矩阵来存储，如果两个顶点之间有边，则表⽰为1，否则表⽰为0。

下⾯⽤代码来实现邻接矩阵的存储：#define SIZE 10class Graph{public:Graph(){MaxVertices = SIZE;NumVertices = NumEdges = 0;VerticesList = new char[sizeof(char)*MaxVertices];Edge = new int*[sizeof(int*)*MaxVertices];int i,j;for(i = 0;i<MaxVertices;i++)Edge[i] = new int[sizeof(int)*MaxVertices];for(i = 0;i<MaxVertices;i++){for(j = 0;j<MaxVertices;++j)Edge[i][j] = 0;}}void ShowGraph(){int i,j;cout<<"";for(i = 0;i<NumVertices;i++)cout<<VerticesList[i]<<"";cout<<endl;for(i = 0;i<NumVertices;i++){cout<<VerticesList[i]<<"";for(j = 0;j<NumVertices;j++)cout<<Edge[i][j] <<"";cout<<endl;}cout<<endl;}int GetVertexPos(char v){int i;for(i = 0;i<NumVertices;i++){if(VerticesList[i] == v)return i;}return -1;}~Graph(){Destroy();}void Insert(char v){if(NumVertices < MaxVertices){VerticesList[NumVertices] = v;NumVertices++;}}void InsertEdge(char v1,char v2){int i,j;int p1 = GetVertexPos(v1);int p2 = GetVertexPos(v2);if(p1 == -1 || p2 == -1)return ;Edge[p1][p2] = Edge[p2][p1] = 1;NumEdges++;}void RemoveEdge(char v1,char v2){int p1 = GetVertexPos(v1);int p2 = GetVertexPos(v2);if(p1 == -1 || p2== -1)return;if(Edge[p1][p2] == 0)return;Edge[p1][p2] = Edge[p2][p1] = 0;NumEdges--;}void Destroy(){delete[] VerticesList;VerticesList = NULL;for(int i = 0;i<NumVertices;i++){delete Edge[i];Edge[i] = NULL;}delete[] Edge;Edge = NULL;MaxVertices = NumVertices = 0;}void RemoveVertex(char v){int i,j;int p = GetVertexPos(v);int reNum = 0;if(p == -1)return;for(i = p;i<NumVertices-1;i++){VerticesList[i] = VerticesList[i+1];}for(i = 0;i<NumVertices;i++){if(Edge[p][i] != 0)reNum++;}for(i = p;i<NumVertices-1;i++){for(j = 0;j<NumVertices;j++){Edge[i][j] = Edge[i+1][j];}}for(i = p;i<NumVertices;i++){for(j = 0;j<NumVertices;j++)Edge[j][i] = Edge[j][i+1];}NumVertices--;NumEdges = NumEdges - reNum;}private:int MaxVertices;int NumVertices;int NumEdges;char *VerticesList;int **Edge;};上⾯的类中的数据有定义最⼤的顶点的个数（MaxVertices），当前顶点的个数（NumVertices），当前边的个数（NumEdges），保存顶点的数组，保存边的数组。

邻接表

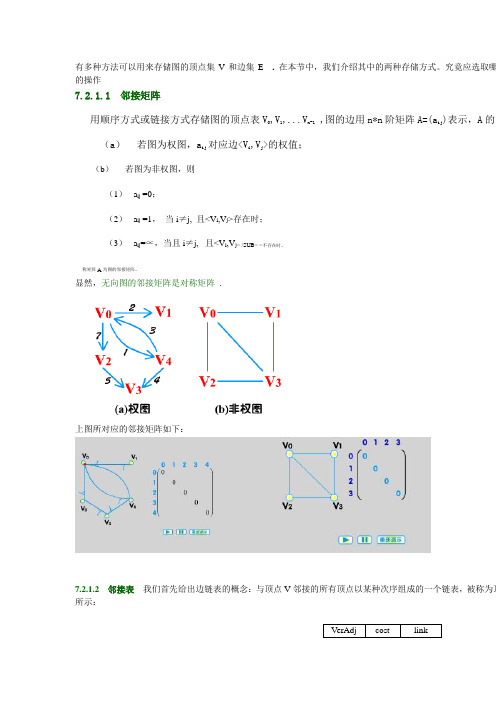
VerAdj cost
link
图 7.4 边结点其中，VerAdj 域存放 V 的某个邻接顶点在顶点表中的序号；cost 域存放边<V,VerAdj>的权值；link 域存放指向点显示的是边<V,VerAdj>的信息，因此称之为边结点。
对于无权图，边没有权值，边结点也就不需要包含 cost 域，所以边结点由两个域 VerAdj 和 l
（b）若图为非权图，则（1） aij =0；（2） aij =1，当 i≠j, 且<Vi,Vj>存在时；（3） aij=∝，当且 i≠j, 且<Vi,Vj< /SUB> >不存在时。
称矩阵 A 为图的邻接矩阵。
显然，无向图的邻接矩阵是对称矩阵 .
上图所对应的邻接矩阵如下：
7.2.1.2 邻接表我们首先给出边链表的概念：与顶点 V 邻接的所有顶点以某种次序组成的一个链表，被称为顶所示：
对于无权图，边没有权值，边结点也就不需要包含 cost 域，所以边结点由两个域 VerAdj 和 l 用顺序存储方式存储图的顶点表 n-1，每个顶点的结构如图 7.5 所示
7.5 顶点结点
VerName adjacent
其中，VerName 域存放该顶点的名称，adjacent 域是指针域，存放指向 VerName 的边链表的头 adjacent 域存放的是顶点 VerName 的边链表的头指针。
info
头结点
data
firstarc
二、无向图的邻接表
ห้องสมุดไป่ตู้
图 7-5
三、有向图的邻接表和逆邻接表（一）在有向图的邻接表中，第 i 个单链表链接的边都是顶点 i
发出的边。（二）为了求第 i 个顶点的入度，需要遍历整个邻接表。因此可

名词解释邻接表

邻接表邻接表（Adjacency List）是一种用于表示图的数据结构。

图是由节点（顶点）和边组成的数据结构，它们之间的关系可以用邻接表来表示和存储。

1. 图的基本概念在介绍邻接表之前，我们先简单了解一下图的基本概念。

•顶点（Vertex）：也称为节点，是图中的一个元素。

顶点可以有一个或多个相关联的边。

•边（Edge）：连接两个顶点的线段，表示两个顶点之间的关系。

•有向图（Directed Graph）：每条边都有一个方向，从一个顶点指向另一个顶点。

•无向图（Undirected Graph）：边没有方向，可以从任意一个顶点到达另一个顶点。

2. 邻接表的定义邻接表是一种用于表示图的数据结构，它使用链表来存储每个顶点及其相邻顶点之间的关系。

具体来说，对于每个顶点，我们使用一个链表来存储与该顶点相邻的其他顶点。

3. 邻接表的实现3.1 数据结构定义为了表示邻接表，我们需要定义两个数据结构：•节点（VertexNode）：表示图中的一个顶点，包含一个指向第一个相邻顶点的指针。

•边（EdgeNode）：表示图中的一条边，包含一个指向与之相邻的顶点的指针。

// 节点结构struct VertexNode {int vertex; // 顶点数据EdgeNode* firstEdge; // 指向第一条边的指针};// 边结构struct EdgeNode {int adjVertex; // 相邻顶点数据EdgeNode* nextEdge; // 指向下一条边的指针};3.2 邻接表的创建创建邻接表需要遍历图中每个顶点，并为每个顶点创建一个节点。

对于每个节点，我们需要遍历其相邻顶点，并为每个相邻顶点创建一条边。

// 创建邻接表void createAdjList(VertexNode*& adjList, int numOfVertices) {adjList = new VertexNode[numOfVertices]; // 创建节点数组for (int i = 0; i < numOfVertices; i++) {adjList[i].vertex = i + 1; // 给每个节点赋值cout << "请输入与" << adjList[i].vertex << "相邻的顶点（以0结束）：" << endl;EdgeNode* pre = nullptr;EdgeNode* cur;int adjVertex;cin >> adjVertex;while (adjVertex != 0) {cur = new EdgeNode;cur->adjVertex = adjVertex;if (pre == nullptr) {adjList[i].firstEdge = cur;} else {pre->nextEdge = cur;}pre = cur;cin >> adjVertex;}}}3.3 邻接表的遍历遍历邻接表可以获取图中所有顶点及其相邻顶点的信息。