小学奥数简单逻辑推理习题

合集下载

小学奥数---逻辑推理

小学奥数---逻辑推理一．选择题（共6小题）1．现在从甲、乙、丙、丁四个人中选出两个人参加一项活动．规定：如果甲去，那么乙也去；如果丙不去，那么乙也不去；如果丙去；那么丁不去．最后去参加活动的两个人是（）A．甲、乙B．乙、丙C．甲、丙D．乙、丁2．森林里举行比赛，要派出狮子、老虎、豹子、大象中的两个动物去参加，如果派狮子去，那么也要派老虎去；如果不派豹子去，那么也不能派老虎去；要是豹子参加的话，大象可不愿意去．那么，最后能去参加比赛的是（）A．狮子、老虎B．老虎、豹子C．狮子、豹子D．老虎、大象3．6人参加乒乓球赛，每两人都要比赛一场，胜者的2分，负者的0分，比赛结果有两人并列第二名，两人并列第5名，那么，第4名得（）分．A．3 B．4 C．5 D．64．六名同学参加围棋比赛，每两个人都要比赛一场，胜者得2分，负者得0分，比赛结果有两个并列第二名，两个并列第五名，则第一名得了（）分．A．10 B．12 C．8 D．65．甲、乙、丙、丁四人比赛乒乓球，每两人要赛一场，结果甲胜了丁，并且甲、乙、丙三人胜的场数相同，则丁胜了（）场．A．1 B．2 C．3 D．06．甲、乙、丙、丁坐在同一排1号至4号的座位上，小红看着他们说：“甲的两边不是乙，丙的两边不是丁，甲的座位号比丙大．”那么，坐在1号座位的是（）A．甲B．乙C．丙D．丁二．填空题（共5小题）7．甲、乙、丙、丁4人站成一排，从左至右依次编号是1、2、3、4号，他们有如下对话：甲：我左右两人都比我高．乙：我左右两人都比我矮．丙：我是最高的．丁：我右边没有人．如果他们4人都是诚实的好孩子，那么甲、乙、丙、丁的编号按顺序组成的4位数是．8．小明、小亮、小光三人昨天和今天连续两天去肯德基吃饭．吃饭时，他们每人要的不是鸡块就是汉堡，并且（1）如果小明要的是鸡块，那么小亮要的就是汉堡；（2）小明或小光要的是鸡块，但是不会两人都要鸡块；（3）小亮和小光不会两人都要汉堡．已知三人中有一人昨天要鸡块，今天要汉堡．这个人是．9．小明碰到了三个人，其中一位是牧师、一位是骗子、一位是疯子．牧师只说真话，骗子只说假话，疯子有时说真话，有时说假话．第一位说：“我是疯子．”第二位说：“你胡说，你才不是疯子呢！”第三位说：“别说了，我是疯子．”一那么．这三个人中第位是疯子．10．有排成一排的四张扑克牌，正好是四种花色都有，A、K、Q、J各一张．并且已知（1）A的左边是红桃，右边是J；（2）K在Q的左边；（3）黑桃的左边是J，并且与方块不相邻．这四张牌分别是黑桃，红桃，方块，梅花．11．甲、乙、丙、丁四人中只有1人会开汽车．甲说：“我会开”．乙说：“我不会开”．丙说：“甲不会开”．丁什么也没说．已知甲、乙、丙三人的话中只有一句是真话．会开车的是．三．解答题（共4小题）12．小力比小強小兩歲，小強比小傑大4歲，小虎比小傑大3歲．小虎和小力誰大？13．动物大会上，小兔、小鹿、乌龟比高矮．小鹿说：“我比小兔高!”，乌龟说：“我不比小兔高!”猜一猜，三个小动物谁高谁矮．14．有四个嫌疑犯；甲、乙、丙、丁，他们的话如下，甲说，我不是罪犯乙说，丁是罪犯丙说，乙说罪犯丁说，我不是罪犯以上四人只有一个人说假话，请问：谁是罪犯？15．甲、乙、丙、丁四个小朋友在楼下玩球，不小心把王奶奶家的玻璃打碎了，王奶奶问他们四人是谁打碎的，甲说：“是乙打碎了玻璃”．乙说：“是丁打的．”丙说：“不是我打的．”丁说：“乙说得不对．”如果这四人中只有丁说了实话，那么是谁打碎了玻璃？小学奥数---逻辑推理参考答案与试题解析一．选择题（共6小题）1．现在从甲、乙、丙、丁四个人中选出两个人参加一项活动．规定：如果甲去，那么乙也去；如果丙不去，那么乙也不去；如果丙去；那么丁不去．最后去参加活动的两个人是（）A．甲、乙B．乙、丙C．甲、丙D．乙、丁【分析】①根据如果甲去，那么乙也去，可得甲在，乙必然也在；②又根据如果丙不去，那么乙也不去，可得如果乙去了，丙也一定去了，同时满足①②的条件和“如果丙去；那么丁不去”只能是乙、丙参加了活动，据此解答即可．【解答】解：根据如果甲去，那么乙也去，可得甲在，乙必然也在，又根据如果丙不去，那么乙也不去，可得如果乙去了，丙也一定去了，如果丙去；那么丁不去，可得：如果丙不去；那么丁去，同时乙也不去，则根据“甲去，那么乙也去”可得甲也不去，这样只有丁去，这与两个人参加一项活动相矛盾．同时满足条件只能是乙、丙参加了活动．故选：B．2．森林里举行比赛，要派出狮子、老虎、豹子、大象中的两个动物去参加，如果派狮子去，那么也要派老虎去；如果不派豹子去，那么也不能派老虎去；要是豹子参加的话，大象可不愿意去．那么，最后能去参加比赛的是（）A．狮子、老虎B．老虎、豹子C．狮子、豹子D．老虎、大象【分析】通过分析可知：从题意出发：（1）狮子去则老虎去，逆否命题：老虎不去则狮子也不去，（2）不派豹子则不派老虎，逆否命题：派老虎则要派豹子，（3）派豹子则大象不愿意去，逆否命题：大象去则不能派豹子从（2）出发可以看出答案为B．据此解答即可．【解答】解：题目要求有两个动物去，可以使用假设法，若狮子去，则老虎去，老虎去则豹子也去．三个动物去，矛盾，所以狮子不去．若豹子不去则老虎不去，那么只有大象去，矛盾，所以豹子去．豹子去则大象不去，由两种动物去得到结论，老虎要去．所以答案是B，豹子和老虎去．故选：B．3．6人参加乒乓球赛，每两人都要比赛一场，胜者的2分，负者的0分，比赛结果有两人并列第二名，两人并列第5名，那么，第4名得（）分．A．3 B．4 C．5 D．6【分析】6人参加乒乓球赛，每两人都要比赛一场，即每人都要与另外5人赛一场，又比赛是在两人之间进行的，所以共需要赛6×（6﹣1）÷2=15场，所以总分是15×2=30分，最高分为一人五场全胜5×2=10分，又比赛结果有两人并列第二名，两人并列第5名，由于30=10+6+6+4+2+2，所以第四名是4分．【解答】解：共需要赛6×（6﹣1）÷2=15场，所以总分是15×2=30分，最高分5×2=10分，由于30=10+6+6+4+2+2，所以第四名是4分．故选：B．4．六名同学参加围棋比赛，每两个人都要比赛一场，胜者得2分，负者得0分，比赛结果有两个并列第二名，两个并列第五名，则第一名得了（）分．A．10 B．12 C．8 D．6【分析】第一名胜五场，得10分；第二名两人并列，都是胜3场，得6分；第四名胜2场，得4分；第五名两人并列，只胜一场，得2分．【解答】解：第一名胜五场，得10分；第二名两人并列，都是胜3场，得6分；第四名胜2场，得4分；第五名两人并列，只胜一场，得2分．因此第一名得了胜五场，因此得2×5=10（分）故选：A．5．甲、乙、丙、丁四人比赛乒乓球，每两人要赛一场，结果甲胜了丁，并且甲、乙、丙三人胜的场数相同，则丁胜了（）场．A．1 B．2 C．3 D．0【分析】四人比赛乒乓球，每两人要赛一场，则每人都要和其他三人赛一场，每人要赛三场，共比赛4×3÷2=6场，由于没有平局，则每场都有一队胜，一队负．由于甲，乙，丙三人胜的场数相同，若甲，乙，丙各胜1场，则丁胜6﹣1×3=3场，即丁全胜，不合题意（甲胜了丁）．若甲，乙，丙各胜2场，则丁胜6﹣2×3=0场，即丁全输，符合题意．【解答】解：由题意可知，每人要赛三场，共比赛4×3÷2=6场，由于甲，乙，丙三人胜的场数相同，若甲，乙，丙各胜1场，则丁胜6﹣1×3=3场，即丁全胜，不合题意（甲胜了丁）．若甲，乙，丙各胜2场，则丁胜6﹣2×3=0场，即丁全输，符合题意．故选：D．6．甲、乙、丙、丁坐在同一排1号至4号的座位上，小红看着他们说：“甲的两边不是乙，丙的两边不是丁，甲的座位号比丙大．”那么，坐在1号座位的是（）A．甲B．乙C．丙D．丁【分析】由题意知，一排1号至4号的座位上分别坐一人，由“甲的两边不是乙”可知甲跟丙、丁相邻，由“丙的两边不是丁”可知丙的两边是甲和乙，由此可得甲和丙是紧挨着的，再由“甲的座位号比丙大”可得甲和丙的位置关系应是“丙﹣甲”，再结合“丙的两边是甲和乙”可得：“乙﹣丙﹣甲”，由于甲跟丙、丁相邻，所以丁只能在4号座位上，这样四人在1号至4号的座位上的顺序就是：“乙﹣丙﹣甲﹣丁”，所以坐在1号座位的是乙；据此解答．【解答】解：由“甲的两边不是乙”可知甲跟丙、丁相邻，由“丙的两边不是丁”可知丙的两边是甲和乙，由此可得甲和丙是紧挨着的，再由“甲的座位号比丙大”可得甲和丙的位置关系应是“丙﹣甲”，再结合“丙的两边是甲和乙”可得：“乙﹣丙﹣甲”，由于甲跟丙、丁相邻，所以丁只能在4号座位上，这样四人在1号至4号的座位上的顺序就是：“乙﹣丙﹣甲﹣丁”，所以坐在1号座位的是乙；故选：B．二．填空题（共5小题）7．甲、乙、丙、丁4人站成一排，从左至右依次编号是1、2、3、4号，他们有如下对话：甲：我左右两人都比我高．乙：我左右两人都比我矮．丙：我是最高的．丁：我右边没有人．如果他们4人都是诚实的好孩子，那么甲、乙、丙、丁的编号按顺序组成的4位数是2314．【分析】4人都是诚实的好孩子，也就是4人都是说真话，丁说它的右边没有人，那么丁排在4号；再从甲乙的话可知甲乙都不排在1号，那么丙排在1号；又丙是最高的，所以他比排在2号的人要高，甲符合这个特征，所以甲排在2号，从而求解．【解答】解：首先根据“丁：我右边没有人”可以得出丁在4号；再根据“甲：我左右两人都比我高．乙：我左右两人都比我矮．”可知，甲乙两边都有人，那么丙排在1号；又丙是最高的，所以他比排在2号的人要高，甲符合这个特征，所以甲排在2号；剩下的乙排在3号；综上可知：甲、乙、丙、丁的编号按顺序组成的4位数是2314．故答案为：2314．8．小明、小亮、小光三人昨天和今天连续两天去肯德基吃饭．吃饭时，他们每人要的不是鸡块就是汉堡，并且（1）如果小明要的是鸡块，那么小亮要的就是汉堡；（2）小明或小光要的是鸡块，但是不会两人都要鸡块；（3）小亮和小光不会两人都要汉堡．已知三人中有一人昨天要鸡块，今天要汉堡．这个人是小亮．【分析】若小明要的是鸡块，则小亮与小光都要了汉堡，与（3）矛盾，所以小明要的是汉堡；则小光要的是鸡块，然后进一步解答即可．【解答】解：若小明要的是鸡块，则小亮与小光都要了汉堡，与（3）矛盾，所以小明要的是汉堡；则根据（1）小光只要的是鸡块，那么小亮要的是汉堡，也可以是鸡块；所以，已知三人中有一人昨天要鸡块，今天要汉堡．这个人是小亮．故答案为：小亮．9．小明碰到了三个人，其中一位是牧师、一位是骗子、一位是疯子．牧师只说真话，骗子只说假话，疯子有时说真话，有时说假话．第一位说：“我是疯子．”第二位说：“你胡说，你才不是疯子呢！”第三位说：“别说了，我是疯子．”一那么．这三个人中第3位是疯子．【分析】按题意，运用假设法，（1）假设第一位是疯子，则第二位是骗子，第三位也是骗子，矛盾；（2）假设第二位是疯子，则第一位是骗子，第三位也是骗子，矛盾；（3）假设第三位是疯子，则第一位是骗子，第二位是牧师，成立，最后不难得出结论．【解答】解：根据分析，（1）假设第一位是疯子，则第二位是骗子，第三位也是骗子，矛盾；（2）假设第二位是疯子，则第一位是骗子，第三位也是骗子，矛盾；（3）假设第三位是疯子，则第一位是骗子，第二位是牧师，成立，所以第三位是疯子．故答案是：3．10．有排成一排的四张扑克牌，正好是四种花色都有，A、K、Q、J各一张．并且已知（1）A的左边是红桃，右边是J；（2）K在Q的左边；（3）黑桃的左边是J，并且与方块不相邻．这四张牌分别是黑桃A，红桃Q，方块K，梅花J．【分析】由（1）（2）（3）先排出个别扑克牌的顺序，再根据它们之间的位置关系，推出问题的答案．【解答】解：由（1）可知顺序为：红桃，A，J；由（2）可知顺序：Q，K由（3）可知顺序：黑桃，J由（1）（3）知，A是黑桃．由（1）（2）（3）可知顺序：K，Q，A，J，由A的左边是红桃，可知Q是红桃．又因为黑桃与方块不相邻，因此J不是方块，只能是梅花，因此，K是方块．黑桃是A 红桃是Q，方块是K，梅花是J．故答案为：A，Q，K，J．11．甲、乙、丙、丁四人中只有1人会开汽车．甲说：“我会开”．乙说：“我不会开”．丙说：“甲不会开”．丁什么也没说．已知甲、乙、丙三人的话中只有一句是真话．会开车的是乙．【分析】据题意，假设结论（即会开车的分别是甲、乙或丙），然后根据他们所说的话，推出与题意矛盾的即为错误结论，从而得出正确答案．【解答】解：假设甲会开车，那么，甲和乙说的是真话，所以和已知矛盾，所以甲不会开车，假设乙会开车，那么甲和乙说的是假话，丙说的是真话，符合题意，假设丙会开车，那么乙和丙说的是真话，也和题意矛盾，所以，乙会开车．故答案为：乙．三．解答题（共4小题）12．小力比小強小兩歲，小強比小傑大4歲，小虎比小傑大3歲．小虎和小力誰大？【分析】小强比小杰大4岁，小虎比小杰大3岁，则小强比小虎大4﹣3=1岁，又小力比小强小两岁，2＞1，所以小虎大．【解答】解：小强比小虎大4﹣3=1岁，又小力比小强小两岁，2＞1，答：小虎大．13．动物大会上，小兔、小鹿、乌龟比高矮．小鹿说：“我比小兔高!”，乌龟说：“我不比小兔高!”猜一猜，三个小动物谁高谁矮．【分析】由小鹿说：“我比小兔高!”，乌龟说：“我不比小兔高!”，我们用大于号进行排列，小鹿＞小兔，小兔＞乌龟，所以，小鹿＞小兔＞乌龟．据此解答即可．【解答】解：由题意可知：小鹿＞小兔小兔＞乌龟所以小鹿＞小兔＞乌龟．所以小鹿最高，乌龟最矮．答：小鹿最高，乌龟最矮．14．有四个嫌疑犯；甲、乙、丙、丁，他们的话如下，甲说，我不是罪犯乙说，丁是罪犯丙说，乙说罪犯丁说，我不是罪犯以上四人只有一个人说假话，请问：谁是罪犯？【分析】因为他们中只有一个人讲的话错了，也就是只有一个人说了假话，从题中分析，因为乙、丙说的相矛盾，所以肯定乙和丙中有一人说了假话，如果是乙说真话，则和丁说的相矛盾，不符合题意，所以是乙说了假话，那么就说明其他三人说了真话，所以推断是乙是罪犯．【解答】解：乙、丙说的相矛盾，所以肯定乙和丙中有一人说了假话，如果是乙说真话，则和丁说的相矛盾，不符合题意，所以是乙说了假话，那么就说明其他三人说了真话，所以推断乙是罪犯．综上所述，罪犯一定是乙．答：乙是罪犯．15．甲、乙、丙、丁四个小朋友在楼下玩球，不小心把王奶奶家的玻璃打碎了，王奶奶问他们四人是谁打碎的，甲说：“是乙打碎了玻璃”．乙说：“是丁打的．”丙说：“不是我打的．”丁说：“乙说得不对．”如果这四人中只有丁说了实话，那么是谁打碎了玻璃？【分析】这四人中只有丁说了实话，那么根据“乙说是丁打的”可得：不是丁打的，那么只能是甲、乙、丙三个人中的一个，然后根据甲和丙说的话进行判断（甲丙说谎），从而得出结论．【解答】解：这四人中只有丁说了实话，那么根据丁说：“乙说得不对．”、乙说：“是丁打的．”可得：不是丁打的，那么只能是甲、乙、丙三个人中的一个；又因为甲说谎，所以可能是甲或丙；又因为丙也说谎，且丙说：“不是我打的．”，从而可以肯定是丙打碎了玻璃．答：是丙打碎了玻璃．第11页（共11页）。

小学奥数思维训练-逻辑推理问题(通用,含答案)

小学奥数思维训练-逻辑推理问题学校:___________姓名：___________班级：___________考号：___________一、填空题1．填数使下列竖式成立：（1）（2）二、排序题2．200米赛跑，张强比李军快0.2秒，王明的成绩是39.4秒，赵刚的成绩比王明慢0.9秒，但比张强快0.1秒，林林比张强慢3秒，请你给这五人排出名次来。

三、解答题3．有三个和尚，一个讲真话，一个讲假话，另外一个有时讲真话，有时讲假话。

一天，一位智者遇到这三个和尚，他先问左边的那个和尚：“你旁边的是哪一位？”和尚回答说“讲真话的。

”他又问中间的和尚：“你是哪一位？”和尚答：“我是半真半假的。

”他最后问右边的和尚：“你旁边是哪一位？”答：“讲假话的。

”根据他们的回答，智者马上分清了他们，你能分清吗？4．一次全校数学竞赛，A、B、C、D、E五位同学取得了前五名，发奖后有人问他们的名次，回答是：A说：“B是第三名，C是第五名．”B说：“D是第二名，E是第四名．”C说：“A是第一名，E是第四名．”D说：“C是第一名，B是第二名．”E说：“D是第二名，A是第三名．”最后，他们都补充说：“我们的话半真半假．”请你判断一下他们每个人的名次．5．老师有一黑两白三顶帽子，给两个学生看后，让他们闭上眼睛，从中取出两顶给他们戴上，然后让他们睁开眼睛，互相看清对方戴的帽子，并立即说出自己头上戴的帽子是什么颜色，两位同学都不能立即说出，请问你知道这两位学生戴的各是什么颜色的帽子吗？6．曾实、张晓、毛梓青在一起，一位是工程师、一位是医师、一位是教师。

现在只知道：（1）毛梓青比教师年龄大；（2）曾实和医师不同岁；（3）医师比张晓年龄小。

你能确定谁是工程师？谁是医师？谁是教师吗？7．某公安人员需查清甲、乙、丙三人谁先进办公室，三人口供如下：甲：丙第二个进去，乙第三个进去。

乙：甲第三个进去，丙第一个进去。

丙：甲第一个进去，乙第三个进去。

小学奥数逻辑推理题及答案

【导语】逻辑推理能⼒是⼀种以敏锐的思考分析、快捷的反应、迅速地掌握问题的核⼼，在最短时间内作出合理正确选择的能⼒。

以下是⽆忧考整理的《⼩学奥数逻辑推理题及答案》相关资料，希望帮助到您。

1.⼩学奥数逻辑推理题及答案 A、B、C、D四⼈进⾏象棋⽐赛，每两⼈都要赛⼀场，结果A胜了D，并且A、B、C三⼈⽣的场数相同。

问D胜了机场？解答： D⼀场没胜：每两⼈都要赛⼀场，共有6场⽐赛。

A、B、C三⼈胜的场数相同，因此，A、B、C不可能全胜。

也不可能只胜⼀场，否则，D就胜了三场。

因此，A、B、C只可能各胜2场。

因此，D胜场数=6-2-2-2=0　2.⼩学奥数逻辑推理题及答案 1、张、王、吴三位⽼师都在某校任教，他们分别教⾳乐、体育、美术中的⼀科，其中：（1）张⽼师不教美术（2）吴⽼师不会画画也不会唱歌。

你能说出三位⽼师各教什么课程吗？ 2、三个盒⼦中有⼀个盒⼦放着珍珠，每个盒⼦上各写着⼀句话，但只有⼀句真话，其余都是谎话。

第⼀个盒⼦是红⾊的，上⾯写着：“珍珠在这⾥”；第⼆个盒⼦是蓝⾊的，上⾯写着“珍珠不在红盒⼦⾥”；第三个盒⼦是黄⾊的，上⾯写着：“珍珠不在这⾥”请问，珍珠到底在哪个盒⼦⾥？答案解析： 1、吴⽼师教体育，张⽼师教⾳乐，王⽼师教美术。

2、珍珠在第三个盒⼦中；假设法，通过分析，第⼀个盒⼦与第⼆个盒⼦写的正好相反，说明⼀个是真话，⼀个是假话。

假设第⼀个盒⼦说的是对的，则第三个盒⼦“珍珠不在这⾥”也是对的，所以⽭盾，所以第⼀个盒⼦错的，第⼆个盒⼦对的，那么第三个盒⼦是错的，所以珍珠在第三个盒⼦中。

3.⼩学奥数逻辑推理题及答案四年级有三个班，每班有两个班长，开班会时，每次每班只要⼀个班长参加。

第⼀次到会的有A，B，C；第⼆次到会的`有B，D，E；第三次到会的有A，E，F。

请问哪两位班长是同班的？⽤数字"1"表⽰到会，⽤数字"0"表⽰没到会，可列下表从第⼀次到会的情况看，A只能和D，E，F同班从第⼆次到会的情况看，A只能和D，E同班从第三次到会的情况看，A只能和D同班利⽤上述表格，仿照上述⽅法，推出与B，C分别同班的同学。

小学奥数逻辑推理知识点+例题+练习 (分类全面)

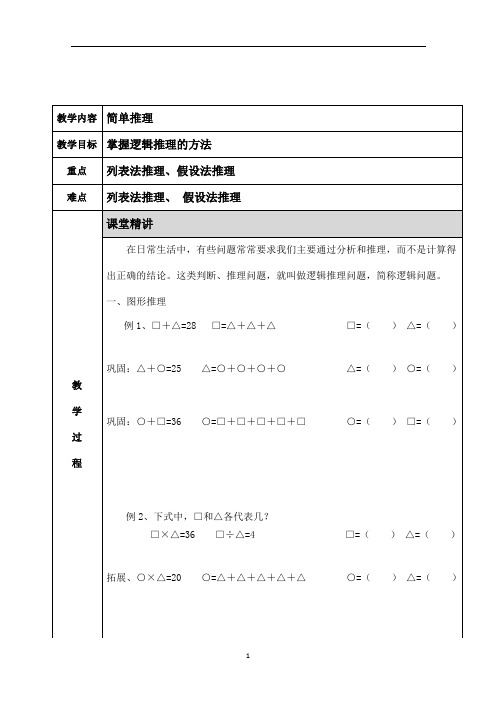
拓展、□=○＋○＋○＋○○×□=16 □=（）○=（）
例3、下面三块正方体的六个面都是按相同的规律涂有红、黄、蓝、白、绿、黑六种颜色。

请判断黄色的对面是什么颜色？白色的对面是什么颜色？红色的对面是什么颜色？
（A）
黄
黑
白
（B）
红
白
绿
（C）
红
蓝
黄
拓展：一个正方体6个面上分别写着1、2、3、4、5、6。

根据下图摆放的三种情况，判断每个数字对面上的数字是几。

二、文字推理
例1、小王、小张和小李一位是工人，一位是农民，一位是教师，现在只知道：小李比教师年龄大；小王与农民不同岁；农民比小张年龄小。

问：谁是工人？谁是农民？谁是教师？
课后作业
1、☆＋○=18 ☆=○＋○☆=（）○=（）
2、○×□=16 □÷○=4 ○=（）□=（）
3、甲、乙、丙分别是来自中国、日本和英国的小朋友。

甲不会英文，乙不懂日语却与英国小朋友热烈交谈。

问：甲、乙、丙分别是哪国的小朋友？
4、根据一个正方体的三种不同的摆法，判断出相对的两个面上的字母各是什么？。

小学奥数之逻辑推理专题训练(附详解)

三年级奥数之逻辑推理专题训练：1、在三只盒子里，一只装有两个黑球，一只装有两个白球，还有一只装有黑球和白球各一个．现在三只盒子上的标签全贴错了．你能否仅从一只盒子里拿出一个球来，就确定这三只盒子里各装的是什么球?从标签为（黑+白）箱子里抽出一个球来，如果是黑球（白球），那么这个箱子里应该是两个黑球（白球），贴了（2黑）标签的箱子里应该是2白球（白+黑），贴了（2白）的箱子里应该是黑+白（2黑）2．甲、乙、丙、丁4位同学的运动衫上印有不同的号码．赵说：“甲是2号，乙是3号．”钱说：“丙是4号，乙是2号．”孙说：“丁是2号，丙是3号．”李说：“丁是l号，乙是3号．”又知道赵、钱、孙、李每人都只说对了一半．那么丙的号码是几号?应该是4号，假设甲是2号，则丁是1号，丙是3号，乙是2号，与甲重复，假设不成立。

假设乙是3号，则丙是4号，丁是2号，甲是1号。

符合要求。

3．某校数学竞赛，A，B，C，D，E，F，G，H这8位同学获得前8名．老师让他们猜一下谁是第一名．A说：“或者F是第一名，或者H是第一名．”B说：“我是第一名．”C说：“G 是第一名．”D说：“B不是第一名．”E说：“A说得不对．”F说：“我不是第一名，H也不是第一名．”G说：“C不是第一名．”H说：“我同意A的意见．”老师指出：8个人中有3人猜对了．那么第一名是谁?B和D两个人中一个对一个错，假设A对则H对E和F错，并且C、G错。

那么C是第一名，这样就和A说的矛盾，所以假设不成立。

所以A错且H错，则E 对F对，C、G也错，同样推出C是第一名。

4．某参观团根据下列条件从A，B，C，D，E这5个地方中选定参观地点：①若去A地，则也必须去B地；②B，C两地中至多去一地；③D，E两地中至少去一地；④C，D两地都去或者都不去；⑤若去E地，一定要去A，D两地．那么参观团所去的地点是哪些?假设C、D两地都去，则没去B地，再假设去了E地，则一定去了A地，也必须去B地，矛盾，所以没去E地，同样也没有去A地；假设C、D两地都不去，则去了E地，去了E地，一定要去A、D地，矛盾。

小学奥数逻辑推理题及答案

几道逻辑推理题（含答案）1．世界级的马拉松选手每天跑步不超过6公里。

因此，如果一名选手每天跑步超过6公里，它就不是一名世界级马拉松选手。

以下哪项与上文推理方法相同？（A）跳远运动员每天早晨跑步。

如果早晨有人跑步，则他不是跳远运动员。

（B）如果每日只睡4小时，对身体不利。

研究表明，最有价值的睡眠都发生在入睡后第5小时。

（C）家长和小孩做游戏时，小孩更高兴。

因此，家长应该多做游戏。

（D）如果某汽车早晨能起动，则晚上也可能起动。

我们的车早晨通常能启动，同样，它晚上通常也能启动。

（E）油漆三小时之内都不干。

如果某涂料在三小时内干了，则不是油漆。

2．19世纪有一位英国改革家说，每一个勤劳的农夫，都至少拥有两头牛。

那些没有牛的，通常是好吃懒做的人。

因此它的改革方式便是国家给每一个没有牛的农夫两头牛，这样整个国家就没有好吃懒做的人了。

这位改革家明显犯了一个逻辑错误。

下列选项哪个与该错误相类似？（A）天下雨，地上湿。

现在天不下雨，所以地也不湿。

（B）这是一本好书，因为它的作者曾获诺贝尔奖。

（C）你是一个犯过罪的人，有什么资格说我不懂哲学？（D）因为他躺在床上，所以他病了。

（E）你说谎，所以我不相信你的话；因为我不相信你的话，所以你说谎。

3．有一天，某一珠宝店被盗走了一块贵重的钻石。

经侦破，查明作案人肯定在甲、乙、丙、丁之中。

于是，对这四个重大嫌疑犯进行审讯。

审讯所得到的口供如下：甲：我不是作案的。

乙：丁是罪犯。

丙：乙是盗窃这块钻石的罪犯。

丁：作案的不是我。

经查实：这四个人的口供中只有一个是假的。

那么，以下哪项才是正确的破案结果？（A）甲作案。

（B）乙作案。

（C）丙作案。

（D）丁作案。

（E）甲、乙、丙、丁共同作案。

4．古代一位国王和他的张、王、李、赵、钱五位将军一同出外打猎，各人的箭上都刻有自己的姓氏。

打猎中，一只鹿中箭倒下，但不知是何人所射。

张说："或者是我射中的，或者是李将军射中的。

"王说："不是钱将军射中的。

小学奥数逻辑推理题集含答案

小学奥数逻辑推理题集含答案一、填空题1. 甲、乙、丙三人进行跑步比赛.A、B、C三人对比赛结果进行预测.A说:“甲肯定是第一名.”B说:“甲不是最后一名.”C说:“甲肯定不是第一名.”其中只有一人对比赛结果的预测是对的.预测对的是 .2. A、B、C、D、E和F六人一圆桌坐下.B是坐在A右边的第二人.C是坐在F右边的第二人.D坐在E的正对面,还有F和E不相邻.那么,坐在A和B之间的是 .3. 甲、乙、丙、丁与小明五位同学进入象棋决赛.每两人都要比赛一盘,每胜一盘得2分,和一盘得1分,输一盘得0分.到现在为止,甲赛了4盘,共得了2分；乙赛了3盘,得了4分；丙赛了2盘，得了1分；丁赛了1盘，得了2分.那么小明现在已赛了盘，得了分.4. 曹、钱、刘、洪四个人出差，住在同一个招待所.一天下午,他们分别要找一个单位去办事.甲单位星期一不接待,乙单位星期二不接待,丙单位星期四不接待,丁单位只在星期一、三、五接待，星期日四个单位都不接待.曹:“两天前,我去误了一次,今天再去一次,还可以与老洪同走一条路.”钱:“今天我一定得去,要不明天人家就不接待了.”刘:“这星期的前几天和今天我去都能办事.”洪:“我今天和明天去,对方都接待.”那么,这一天是星期 ,刘要去单位,钱要去单位,曹要去单位,洪要去单位.5. 四位外国朋友住在十八层高的饭店里,他们分别来自埃及、法国、朝鲜和墨西哥.(1)A住的层数比C住的层数高,但比D住的层数低；(2)B住的层数比朝鲜人住的层数低；(3)D住的层数恰好是法国人住的层数的5倍；(4)如果埃及人住的层数增加2层,他与朝鲜人相隔的层数,恰好和他与墨西哥人相隔的层数一样；(5)埃及人住的层数是法国人和朝鲜人住的层数的和.根据上述情况,请你确定A是人,住在层；B是人,住在层；C是人,住在层；D是人,住在层.6. 小赵的电话号码是一个五位数,它由五个不同的数字组成.小张说：“它是84261.”小王说：“它是26048.”小李说：“它是49280.”小赵说：“谁说的某一位上的数字与我的电话号码上的同一位数字相同，就算谁猜对了这个数字.现在你们每人都猜对了位置不相邻的两个数字.”这个电话号码是 .7. 小赵的电话号码是一个五位数,它由五个不同的数字组成.小王说：“它是93715.”小张说：“它是79538.”小李说：“它是15239.”小赵说：“谁说的某一位上的数字与我的电话号码上的同一位数字相同，就算谁猜对了这个数字.现在你们三人猜对的数字个数都一样,并且电话号码上的每一个数字都有人猜对.而每个人猜对的数字的数位都不相邻”.这个电话号码是 .8. A、B、C、D四人定期去图书馆，四人中A、B二人每隔8天(中间空7天,下同)、C每隔6天、D每隔4天各去一次，在2月份的最后一天，四人刚好都去了图书馆，那么从3月1日到12月31日只有一个人来图书馆的日子有____ 天.9. 六年级六个班组织乒乓球单打比赛,每班派甲、乙两人参赛，根据规则每两人之间至多赛一场，且同班的两人之间不进行比赛.比赛若干场后发现,除一班队员甲以外,其他每人已比赛过的场数各不相同,那么一班队员乙已赛过____场.10. 人的血型通常为A型,B型,O型,AB型.子女的血型与其父母血型间的关系如下表所示:父母的血型子女可能的血型O,O OO,A A,OO,B B,OO,AB A,BA,A A,OA,B A,B,AB,OA,AB A,B,ABB,B B,OB,AB A,B,ABAB,AB A,B,AB现有三个分别身穿红,黄,蓝上衣的孩子,他们的血型依次为O,A,B.每个孩子的父母都戴着同颜色的帽子,颜色也分红,黄,蓝三种,依次表示所具有的血型为AB,A,O.那么穿红、黄、蓝上衣的孩子的父母戴帽子的颜色是、、 .二、解答题11. 刘毅、马宏明、张健三个男孩都有一个妹妹,六人在一起打乒乓球,进行男女混合双打,事先规定:兄妹不搭档.第一盘:刘毅和小萍对张健和小英；第二盘:张健和小红对刘毅和马宏明的妹妹.小萍、小红和小英各是谁的妹妹？12. 四位运动员分别来自北京、上海、浙江和吉林,在游泳、田径、乒乓球和足球四项运动中,每人只参加了一项,且四人的运动项目各个不相同,除此以外,只知道一些零碎情况：(1)张明是球类运动员,不是南方人；(2)胡老纯是南方人,不是球类运动员；(3)李勇和北京运动员、乒乓球运动员三人同住一个房间；(4)郑永禄不是北京运动员,年龄比吉林运动员和游泳运动员两人的年龄小；(5)浙江运动员没有参加游泳比赛.根据这些条件,请你分析一下:这四名运动员各来自什么地方?各参加什么运动?13. 老吴、老周、老杨分别是工程师、会计师和农艺师，还分别是业余作家、画家和音乐家,但不知道每人的职业及业余爱好,只知道：(1)业余音乐家、作家常和老吴一起看电影；(2)画家常请会计师讲经济学的道理；(3)老周一点也不爱好文学；(4)工程师埋怨自己对绘画、音乐一窍不通. 请你指出每个人的职业和爱好.14. 四个人聚会,每人各带了2件礼品,分赠给其余三个人中的二人,试证明:至少有两对人,每对人是互赠过礼品的.———————————————答案——————————————————————1. CA 、C 的预测截然相反,必一对一错.因为只有一人对,不论A 、C 谁对,B 必错,所以甲是最后一名,C 对. 2. E如右图,E 坐在A 、B 之间.3. 2,3.由题意可画出比赛图,已赛过的两人之间用线段引连(见右图).由图看出小明赛了2盘.因为一共赛了六盘,共得12分,所以小明得了12-(2+4+1+2)=3(分).4. 三,丙,丁,甲,乙.由刘的讲话,知这一天是星期三,刘要去丙单位.钱要去丁单位,曹去的是甲单位,洪去的是乙单位.5. 埃及,8；法国，3；朝鲜，5；墨西哥，15.容易知道,墨西哥人住得最高,埃及人次之,朝鲜人又次之,法国人最低,各层次分别15,8,5和3.由(2)知B 是法国人,由(3)和D 是墨西哥人,由(1)知A 是埃及人,而C 是朝鲜人.6. 86240.因为每人猜对两个数字,三人共猜对张:842±1 2⨯3=6(个)数字,而电话号码只有5位, 王:26048 所以必有一位数字被两人同对猜对.如右李:49↑80图所示,猜对的是左起第三位数字2.因为每人猜对的两个数字不相邻,所以张、李猜对的另一个数字分别在两端,推知王猜对的数字是6和4,进一步推知张猜对8,李猜对0.电话号码是86240. 7. 19735.因为每个数字都有人猜对,所以每人至少猜对两个数字.下页右上图中,同一甲丁小明位数中只有方框中的两个数相同,如果每人猜对的数字多于两位,相同的数字至少有3⨯3-5=4(组),所以每人恰好猜对两个数字. 王: 9 3 7 1 5三人共猜对2⨯3=6(个)数字,因为电话号码只有张: 7 9 5 3 85位,所以相同的一组是正确的,即左起第四位是李: 1 5 2 3 93.因为每人猜对的数字不相邻,所以张、李猜对的另一个数字都在前两位,王猜对的两个数字是7和5,进而推知张猜对9,李猜对1.电话号码是19735.8. 51天.):天, 306÷24=12…18，所以所求天数为4⨯12+3=51(天).9. 5根据题意,有11名队员比赛场数各不相同,并且每人最多比赛10场,所以除甲外的11名队员比赛的场数分别为0~10.已赛10场的队员与除已赛0场外的所有队员都赛过,所以已赛10场的队员与已赛0场的队员同班；已赛9场的队员与除已赛0、1场外的所有队员都赛过,所以已赛9场的队员与已赛1场的队员同班；同理,已赛8、7、6场的队员分别与已赛2、3、4场的队员同班；所以甲与已赛5场的队员同班,即乙赛过5场.注本题可以求出甲也赛了5场,分别与已赛10、9、8、7、6场的队员各赛1场.10. 蓝、黄、红.解法一题中表明,每个孩子的父母是同血型的.具有B型血的孩子,其父母同血型时,由表中可见,只能是B型或AB型,但题中没有同具B型血的父母,所以戴红帽子的父母的孩子穿蓝上衣.具有A型血的孩子的同血型的父母,只可能同为A型血或同为AB型血.今已知有一对父母为AB型血者,所以穿黄上衣的孩子的父母戴黄帽子.由表中可见,其孩子为O型血时,父母血型只能同为A型或B型或O型.今已知不具有同为B型血的父母,而同为A型血的父母的孩子已知具有A型血.把代表孩子的点与他的可能双亲的代表点之间连一直线段,便可得下面的图；由于孩子与其父母之间是唯一搭配的,所以,保存下来的只有连着红、蓝；黄，黄及蓝，红的三条边.所以,穿红上衣(O型血)孩子的父母戴蓝帽子.孩子衣服颜色父母帽子颜色(O型血)(AB型血)(A型血)(A型血)(B型血)(O型血)所以,穿红上衣的孩子的父母戴蓝帽子；穿黄上衣的孩子的父母戴黄帽子；穿蓝上衣的孩子的父母戴红帽子.,张健和小萍分别是兄妹.12.13.表解如下:由(3)北京运动员是乒乓球运动员, 故张是足球运动员郑是乒乓球运动员由(4)吉林运动员不是游泳运动员,故李是田径运动员,而胡是游泳运动员由(5)知胡是上海运动员而郑是浙江运动员.张明是北京选手李勇是吉林选手14. 设此四人为甲、乙、丙、丁并用画在平面上的四个点分别表示他们，称为它们的代表点,当某人(例如甲)赠了1件礼品给另一个(例如乙)时,就由甲向乙的代表点画一条有指向的线,无非有以下两个可能:(1)甲、乙、丙、丁每人各收到了2件礼品.(2)上面的情形不发生.这时只有以下一个可能,即有一个人接受了3件礼品 (即多于2件礼品；因为一人之外总共还有三个人，所以至多收到3件礼品).(或许会有人说,还有两个可能:有人只收到1件礼品及有人什么礼品也没收到.其实,这都可归以“有一人接受了3件礼品”这个情形.因为,当有一人(例如甲)只接受了1件礼品的情形发生时,四人共带来的8件礼品中还剩下7件在甲以外的三个人中分配,如果他们每人至多只收到2件礼品,则收受礼品数将不超过6件,这不可能,所以至少有一人收到2件以上(即3件)礼品,同样,当甲未收到礼品时,8件礼品分给乙、丙、丁三人，也必定有人收到3件礼品).当(1)发生时,例如甲收到乙、丙的礼品,由于甲发出的礼品中至少有1件给了乙或丙,为确切计,设乙收到了甲的礼品,于是我们先有了一对人:(甲、乙),他们互赠了礼品，如果丙也收到甲的礼品,那么又有了第二对互赠了礼品的人(甲、丙)；如果收到甲礼品的另一人是丁(如右图)丁的2件礼品必定分赠了乙及丙(甲已收足了本情形中限定的2件礼品)丙或乙的另一件礼品给了丁,则问题也解决(这时另一对互赠了礼品的人便是(乙、丁)或(丙、丁)但丙的另一件礼品只能给丁,因为这时乙已收足了2件礼品,所以，当本情形发生时,至少能找到两对互赠过1件礼品的人.当(2)发生时,不失一般性,设甲收到了来自乙、丙、丁的各1件礼品，但甲又应向他们之中的某两人(例如乙、丙)各赠送1件礼品,于是(甲、乙),(甲、丙)便是要找的两对人.总上可知,证明完毕.老吴是业余画家,老周是业余音乐家,老杨是业余作家.工程师是老杨,会计师是老周农艺师是老吴.十八逻辑推理(B)一、填空题1. 从前一个国家里住着两种居民,一个叫宝宝族,他们永远说真话；另一个叫毛毛族,他们永远说假话.一个外地人来到这个国家,碰见三位居民,他问第一个人：“请问,你是哪个民族的人？”“匹兹乌图”.那个人回答.外地人听不懂,就问其他两个人：“他说的是什么意思？”第二个人回答：“他说他是宝宝族的.”第三个人回答：“他说他是毛毛族的.”那么,第一个人是族,第二个人是族,第三个人是族.2. 有四个人各说了一句话.第一个人说：“我是说实话的人.”第二个人说：“我们四个人都是说谎话的人.”第三个人说：“我们四个人只有一个人是说谎话的人.”第四个人说：“我们四个人只有两个人是说谎话的人.”请你确定第一个人说话,第二个人说话,第三个人说___ 话,第四个人说话.3. 某地质学院的三名学生对一种矿石进行分析.甲判断:不是铁,不是铜.乙判断:不是铁,而是锡.丙判断:不是锡,而是铁.经化验证明,有一个人判断完全正确,有一人只说对了一半,而另一人则完全说误了.那么,三人中是对的, 是错的, 只对了一半.4. 甲、乙、丙、丁四人参加一次数学竞赛.赛后,他们四个人预测名次的谈话如下:甲:“丙第一名，我第三名.”乙：“我第一名，丁第四名.”丙：“丁第二名，我第三名.”丁没说话.最后公布结果时,发现他们预测都只对了一半.请你说出这次竞赛的甲、乙、丙、丁四人的名次.甲是第名,乙是第名,丙是第名,丁是第名.5. 王春、陈则、殷华当中有一人做了件坏事，李老师在了解情况中,他们三人分别说了下面几句话：陈：“我没做这件事.殷华也没做这件事.”王：“我没做这件事.陈刚也没做这件事.”殷：“我没做这件事.也不知道谁做了这件事.”当老师追问时,得知他们都讲了一句真话,一句假话,则做坏事的人是 .6. 三个班的代表队进行N(N 2)次篮班比赛,每次第一名得a分,第二名得b分,第三名得c分(a、b、c为整数，且a>b>c>0).现已知这N次比赛中一班共得20分，二班共得10分，三班共得9分，且最后一次二班得了a分，那么第一次得了b分的是班.7. A、B、C、D四个队举行足球循环赛(即每两个队都要赛一场),胜一场得3分,平一场得1分,负一场得0分.已知:(1)比赛结束后四个队的得分都是奇数；(2)A队总分第一；(3)B队恰有两场平局,并且其中一场是与C队平局.那么,D队得分.8. 六个足球队进行单循环比赛,每两队都要赛一场.如果踢平,每队各得1分,否则胜队得3分,负队得0分.现在比赛已进行了四轮(每队都已与4个队比赛过),各队4场得分之和互不相同.已知总得分居第三位的队共得7分,并且有4场球赛踢成平局,那么总得分居第五位的队最多可得分,最少可得分.9. 甲、乙、丙、丁四个队参加足球循环赛,已知甲、乙、丙的情况列在下表甲与丁的比分为 ,丙与丁的比分为 .10. 某俱乐部有11个成员,他们的名字分别是A~K.这些人分为两派,一派人总说实话,另一派人总说谎话.某日,老师问:“11个人里面，总说谎话的有几个人？”那天,J和K休息,余下的9个人这样回答：A说：“有10个人.”B说：“有7个人.”C说：“有11个人.”D说：“有3个人.”E说：“有6个人.”F说：“有10个人.”G说：“有5个人.”H说：“有6个人.”I 说：“有4个人.”那么,这个俱乐部的11个成员中,总说谎话的有个人.二、解答题11. 甲、乙、丙三人,一个姓张,一个姓李和一个姓王,他们一个是银行职员,一个是计算机程序员,一个是秘书.又知甲既不是银行职员也不是秘书；丙不是秘书；张不是银行职员；王不是乙,也不是丙.问:甲、乙、丙三人分别姓什么?12. ←世界杯足球小组赛,每组四个队进行单循环比赛.每场比赛胜队得3分,败队记0分.平局时两队各记1分.小组全赛完以后,总积分最高的两个队出线进入下轮比赛.如果总积分相同,还要按小分排序.问:一个队至少要积几分才能保证本队必然出线?简述理由.↑在上述世界杯足球小组赛中,若有一个队只积3分,问:这个队有可能出线吗?为什么?13.有一个如图那样的方块网,每1个小方块里有1个人,在这些人中间,有人戴着帽子,有人没戴.每一个人都只能看见自己前方,后方和斜方的人的头,如图1所示A 方块里的人能看见8个人的头,B 方块里的人能看见5个人的头,C 方块里的人能看见3个人的头,自己看不见自已的头.在图2的方格中,写着不同方块里的人能看见的帽子的数量,那么,请在图中找出有戴帽子的人的方块,并把它涂成黑色.14. 某校学生中,没有一个学生读过学校图书馆的所有图书,又知道图书馆内任何两本书至少被一个同学都读过,问:能不能找到两个学生甲、乙和三本书A 、B 、C ，甲读过A 、B ，没读过C ，乙读过B 、C ，没读过A ?说明判断过程.———————————————答案——————————————————————1. 宝宝,宝宝,毛毛.如果第一个人是宝宝族的,他说真话,那么他说的是“我是宝宝族的”.如果这个人是毛毛族的,他说假话,他说的还是“我是宝宝族的”.所以第二个人是宝宝族的,第三个人是毛毛族的.”2. 真,假,假,不确定.第二个人显然说的是假话.如果第三个人说的是真话,那么第四个人说的也是真话,产生矛盾.所以第三个人说假话.如果第四个人说真话,那么第一个人也说真话.如果第四个人说假话,那么只有第一个人说真话.所以可以确定第一个人主真话,第二、第三个人说假话，第四个人不能确定.3. 丙,乙,甲.如果甲的判断完全正确,那么乙说对了一半“不是铁，”所以这矿石也不是锡,这样丙也说对了一半,矛盾.如果乙的判断完全正确,那么甲对了一半,这矿石应是铜,丙也说对了一半,矛盾.所以丙的判断完全正确,而乙完全错了,甲只说对了一半.图1 图24. 三,一,四,二.假设甲说的“丙是第一名”正确，结果推出丙是第三名，矛盾，故甲说的第二句话是正确.由表中可知乙第一名,丁第二名,甲第三名,则第四名是丙.×5. 陈刚.如果王春做了坏事,则陈刚的两句话都是真话,不合题意；如果殷华做了坏事，则王春的两句话都是真话，不合题意；如果陈刚做了坏事，符合题意.所以陈刚做了坏事.6. 三.N次比赛共得20+10+9=39(分),39=3⨯13,所以共进行了3次比赛,每次比赛共得13分,即a+b+c=13.因为一班3次比赛共得20分,20÷3=6…2,所以a≥7,a,b,c可能组合为7、5、1；7、4、2；8、4、1；8、3、2；9、3、1，考虑到3次比赛得20分，只有a=8、b=4、c=1时才有可能,由此推知三个班3次比赛7. 3B队得分是奇数,并且恰有两场平局,所以B队是平2场胜1场,得5分.A队总分第1,并且没有胜B队,只能是胜2场平1场(与B队平),得7分.因为C队与B队平局,负于A队,得分是奇数,所以只能得1分.D队负于A、B队,胜C队,得3分.8. 3,1.共赛了4⨯6÷2=12(场),其中平了4场,分出胜负的8场,共得3⨯8+2⨯4=32(分).因为前三位的队至少共得7+8+9=24(分),所以后三位的队至多共得32-24=8(分).又因为第四位的队比第五位的队得分多,所以第五位的队至多得3分.因为第六位的队可能得0分,所以第五位的队至少得1分(此时这两队之间必然没有赛过).9. 3:2,3:4.由乙队共进2球,胜2场平1场推知,乙队胜的两场都是1:0,平的一场是0:0.由甲队与乙队是0:0,甲队与丙队未赛,推知甲队所有的进球都来自与丁队的比赛,所以甲队与丁队是3:2.由丙队与乙队是0:1,丙队与甲队未赛,所以丙队与丁队是3:4.10 9.因为9个人回答出了7种不同的人数,所以说谎话的不少于7人.若说谎话的有7人,则除B外,其他回答问题的8人均说了谎话,与假设出现矛盾；若说谎话的有8人,则回答问题的9人均说了谎话,出现矛盾；若说谎话的有10人,则只能1人说实话,而A和F都说了实话,出现了矛盾；若说谎话的有11人,则没有说实话的，而E说了实话,出现矛盾；显然说谎话的有9人,回答问题的9人均说谎话,休息的两人说实话.11. 根据题意有关条件,用“√”表示是、“Х”表示不是,列表所示.这样,可12. ←四个队单循环赛共6场比赛,每场均有胜负,6场最多共计18分.若该队积7分,剩下的11分被3个队去分,那么,不可能再有两个队都得7分,即至多再有一个队可得7分以上.这样该队可以出线.其次,如果该队积6分,则剩下12分,可能有另两队各得6分.如果这另两队小分都比该队高,该队就不能出线了.所以,一个队至少要积7分才能保证必然出线.↑有可能出线.当6场比赛都是平局时,4个队都得3分,这时两个小分最高的队可以出线.如果这个队恰属于两个小分最高的队,那么这个队就会出线.13.答案如右图所示←站在第一行第五列的人能看见1顶帽子,说明他周围的3人中有2人没戴帽子.↑站在第二行第四列的人能看见7顶帽子,说明他周围的8人中只有1人没戴帽子,综合结论←可知他本人没有戴帽子.→站在第二行第五列的人能看到4顶帽子,且他周围的五人中已有1人没戴帽子,说明其余4人均戴帽子,根据结论←可知他本人没戴帽子.↓利用上下对称原理可以分析出:站在第四行、第五行后三列的6个人中,只有第四行第四列、第五列两人没戴帽子,其他人均戴帽子.︒站在第四行第二列的人能看到7顶帽子,说明他周围的8人中只有1人没戴帽子.±站在第三行第1列的人能看见1顶帽子,说明他周围的5人中只有1人戴帽子.综合结论︒可知:这1人不可能是第二行第1、2列的人,也不可能是第四行第二列的人.所以只能是站在第三行第二列的人或第四行第1列的人."站在第五行第1列的人能看到2顶帽子,说明结论±所说戴帽子的人站在第四行第一列.≥站在第二行第二列的人能看到6顶帽子,说明站在第一行第1、2列的2人都戴帽子.14. 解法一首先从读书数最多的学生中找一人叫他为甲,由题设,甲至少有一本书C未读过,设B是甲读过的书中的一本,根据题设,可找到学生乙,乙读过B、C.由于甲是读书数最多的学生之一,乙读书数不能超过甲的读书数,而乙读过C书,甲未读过C书,所以甲一定读过一本书A,乙没读过A书,否则乙就比甲至少多读过一本书,这样一来,甲读过A、B,未读过C；乙读过B、C，未读过A.因此可以找到满足要求的两个学生.解法二将全体同学分成两组.若某丙学生所读的所有的书,都被另一同学全部读过,而后一同学读过的书中,至少有一本书,丙未读过,则丙同学就分在第一组.另外,凡一本书也未读过的同学也分在第一组,其余的同学就分在第二组.按照以上分组方法,不可能将全体同学都分在第一组,因为读书数最多的同学一定在第二组.在第二组中,任找一位同学叫做甲,由题设有书C,甲未读过.再从甲读过的书中任找一本书叫做B,由题设,可找到同学乙,乙读过B、C书,由于甲属于第二组,所以甲一定读过一本书A,乙未读过A,否则甲只能分在第一组.这样,甲读过A、B,未读过C；乙读过B、C,未读过A.。

趣味奥数题6年级逻辑推理

趣味奥数题6年级逻辑推理一、题目。

1. 甲、乙、丙三人进行跑步比赛。

甲说：“我跑得不是最快的，但比丙快。

”请你说出他们三人的跑步速度顺序。

- 解析：根据甲说的话，甲不是最快的且比丙快，那么最快的只能是乙，其次是甲，最后是丙。

所以三人的速度顺序为乙＞甲＞丙。

2. 有A、B、C、D四位同学参加数学竞赛。

他们对自己的成绩进行了预测。

A 说：“我肯定得第一名。

”B说：“我不会得最后一名。

”C说：“我不可能得第一名。

”D说：“我肯定得最后一名。

”竞赛结果出来后，发现他们四人中只有一人预测错误。

那么谁预测错误了呢？- 解析：假设A预测错误，那么A不是第一名，C说自己不可能得第一名是正确的，D说自己肯定得最后一名是正确的，B说自己不会得最后一名也是正确的，这样就符合只有一人预测错误；假设B预测错误，那么B就是最后一名，可是D说自己是最后一名，这样就矛盾了；假设C预测错误，那么C就是第一名，这与A说自己是第一名矛盾；假设D预测错误，那么D不是最后一名，B说自己不是最后一名，这样就没有人是最后一名了，也矛盾。

所以A预测错误。

3. 张、王、李三位老师分别教语文、数学、英语。

已知：张老师不教英语；王老师不教语文；教英语的老师不教数学；教语文的老师和王老师是好朋友。

请问三位老师分别教什么科目？- 解析：由可知张老师不教英语；由可知王老师不教语文；由可知王老师不教语文。

从知道教英语的老师不教数学，那么英语老师只能教语文或者英语。

假设张老师教语文，因为王老师不教语文，教英语的老师不教数学，所以王老师教数学，李老师教英语；假设张老师教数学，因为张老师不教英语，王老师不教语文，所以王老师教英语，李老师教语文。

4. 有红、黄、蓝、白、黑五种颜色的小球，它们之间的关系是：红色球比白色球大；蓝色球比黄色球大且比黑色球小；黄色球比白色球大；黑色球比红色球小。

请按照球的大小顺序排列这五种颜色的球。

- 解析：由可知黄＜蓝＜黑；由可知白＜红；由可知白＜黄；由可知黑＜红。

小学奥数逻辑推理题及答案

小学奥数逻辑推理题及答案1.世界级的马拉松选手每天跑步不超过6公里。

因此，如果一名选手每天跑步超过6公里，它就不是一名世界级马拉松选手。

推理方法相同的选项是：(E) 油漆三小时之内都不干。

如果某涂料在三小时内干了，则不是油漆。

改写：油漆一般需要三小时以上才能干透，如果某种涂料在三小时内干了，那么它就不是油漆。

2.19世纪有一位英国改革家说，每一个勤劳的农夫，都至少拥有两头牛。

那些没有牛的，通常是好吃懒做的人。

因此它的改革方式便是国家给每一个没有牛的农夫两头牛，这样整个国家就没有好吃懒做的人了。

相类似的选项是：(B) 这是一本好书，因为它的作者曾获诺贝尔奖。

改写：这本书的作者曾获得诺贝尔奖，因此它是一本好书。

3.有一天，某一珠宝店被盗走了一块贵重的钻石。

经侦破，查明作案人肯定在甲、乙、丙、丁之中。

于是，对这四个重大嫌疑犯进行审讯。

审讯所得到的口供如下：甲：我不是作案的。

___：丁是罪犯。

丙：乙是盗窃这块钻石的罪犯。

___：作案的不是我。

经查实：这四个人的口供中只有一个是假的。

那么，以下哪项才是正确的破案结果？正确的破案结果是：(B) 乙作案。

改写：在四个嫌疑犯的口供中，只有一个是假的，而乙嫌疑犯说丁是罪犯，因此乙是作案人。

4.古代一位国王和他的___、___、___、___、钱五位将军一同出外打猎，各人的箭上都刻有自己的姓氏。

打猎中，一只鹿中箭倒下，但不知是何人所射。

___说："或者是我射中的，或者是___射中的。

"___："不是___射中的。

"___："如果不是___射中的，那么一定是王将军射中的。

"___："既不是我射中的，也不是___射中的。

"钱说："既不是___射中的，也不是___射中的。

"国王让人把射中鹿的箭拿来，看了看，说："你们五位将军的猜测，只有两个人的话是真的。

"正确的结论是：(A) ___射中此鹿。

小学奥数之逻辑推理题(详细解析)

小学奥数之逻辑推理题（详细解析）1、有500人聚会，其中至少有一人说假话，这500人里任意两个人总有一个（即总有人）说真话。

说真话的有多少人？说假话的有多少人？分析：任意2个人都有人说真话，说明说假话的必须≤1人，又因为题目说了，至少有一人说假话即说假话的人≥1人，所以满足≤1和人≥1，可见说假话的只能是1人，所以说真话的有500-1=499人。

2、某次考试考完后，A、B、C、D四个同学猜测他们的考试成绩。

A说：“我肯定考得最好”。

-------（1）|B说：“我不会是最差的”。

-------（2）C说：“我没有A考得好，但也不是最差的”。

--------（3）D说：“可能我考得最差。

”-------（4）成绩一公布，只有一人说错了。

请你按照考试分数由高到低排出他们的顺序。

分析：假设法。

假设A是最差的，那么第（1）和（2）都是错的话。

矛盾了。

假设B是最差的，那么第（2）和（4）都是错的话。

矛盾了。

假设C是最差的，那么第（3）和（4）都是错的话。

矛盾了。

、所以证明了D是最差的。

那么第（4）句话是对的。

第（2）句话也是对的，第（1）句话和第（3）句话必须一个对一个错，如果第（1）是对的，那么第（3）一定对，那么四个都是对的话，矛盾了。

所以：第（1）句话是错的，第（3）必须对的。

根据D是最差的，A不是最好的，C是对的，C比A差，所以只有B才是最好的。

所以A 是第二好，C是第三好，D是最差的。

由高到低排列为：B、A、从、D。

3、王涛、李明、江兵三人在一起谈话。

他们当中一位是校长，一位是老师，一位是学生家长。

现在只知道：（1）江兵比家长年龄大。

（2）王涛和老师不同岁。

（3）老师比李明年龄小。

你能确定谁是校长、谁是老师、谁是家长吗？:分析：第（2）和第（3）中，老师不是李明也不是王涛，所以老师是江兵。

因为江兵是老师，所以第（3）句话中证明了：江兵比李明小，结合第（1）句话中“江兵比家长大”，说明“李明”不是家长，是校长。

小升初数学奥数必考(逻辑推理题)

小升初数学奥数必考（逻辑推理题）
1.有三个盒子，分别标有“苹果”、“橙子”、“苹果和橙子”，但实际上每个盒
子的标签都错了。

你只能打开一个盒子看里面的东西，然后重新贴上正确的标签，怎么做？
2.有三个开关，分别控制三盏灯，你只能进入房间一次，如何确定哪个开关
控制哪盏灯？
3.有10个球，其中9个重量相同，1个较重，用天平称三次，找出那个较重
的球。

4.有100个囚犯和100个盒子，每个盒子里有一张纸条，上面写着一个囚犯
的名字。

每个囚犯可以打开最多50个盒子，如果所有囚犯都能找到自己的名字，他们就能全部获释。

设计一种策略，使他们获胜的概率尽可能大。

5.有100个瓶子，其中一瓶有毒，毒药在24小时内会致死。

你有10只小白
鼠，如何在24小时内找出那瓶有毒的瓶子？
6.甲乙两人同时从A地出发前往B地，甲的速度是每小时5公里，乙的速度
是每小时4公里，甲比乙早到1小时，求AB两地的距离。

7.一辆汽车以每小时60公里的速度行驶，行驶了3小时后，速度提高到每
小时80公里，再行驶2小时，求总行驶距离。

8.一个水池有两个进水管，单独开第一个管需要4小时注满水池，单独开第
二个管需要6小时注满水池，两个管同时开需要多少时间注满水池？9.一家商店打折销售商品，原价100元的商品打8折后再打9折，最终售价
是多少？
10.一个长方体的长、宽、高分别为3、4、5，求其体积和表面积。

小学奥数逻辑推理练习题及答案

小学奥数逻辑推理练习题及答案1. 问题：下列是一道逻辑推理题，请选择正确的答案。

问题：蓝色、黄色和红色的旗帜分别代表国家A、B和C，以下是三个旗帜的信息：- A国的旗帜不是蓝色。

- B国的旗帜不是黄色。

- C国的旗帜不是红色。

结论：根据以上信息，以下结论正确的是：A. A国的旗帜是黄色。

B. B国的旗帜是蓝色。

C. C国的旗帜是红色。

D. A国的旗帜是蓝色。

答案：B. B国的旗帜是蓝色。

2. 问题：下列是一道逻辑推理题，请选择正确的答案。

问题：五位老师正在一起讨论他们教的学科和身高的关系，以下是一些信息：- 老师A比老师B矮，但比老师C高。

- 老师D比老师C矮，但比老师E高。

结论：根据以上信息，以下结论正确的是：A. 老师B比老师E矮。

B. 老师A比老师D矮。

C. 老师C比老师B高。

D. 老师A比老师C高。

答案：C. 老师C比老师B高。

3. 问题：下列是一道逻辑推理题，请选择正确的答案。

问题：请根据下面的数字序列推断下一个数字：1, 4, 9, 16, 25, __结论：根据以上数字序列，下一个数字应该是：A. 30B. 36C. 42D. 49答案：B. 364. 问题：下列是一道逻辑推理题，请选择正确的答案。

问题：小明、小红、小李和小刚四人排成一排，以下是一些信息： - 小明在小李的左边。

- 小红在小刚的右边。

结论：根据以上信息，以下结论正确的是：A. 小刚在小红的左边。

B. 小红在小李的右边。

C. 小明在小刚的左边。

D. 小红在小明的左边。

答案：C. 小明在小刚的左边。

5. 问题：下列是一道逻辑推理题，请选择正确的答案。

问题：请根据下面的图形选择正确的图形以继续图形序列：图形序列：△, ▢, ◯, __结论：根据以上图形序列，以继续序列的正确图形是：A. △B. ▢C. ◯D. ■答案：D. ■通过以上五个小学奥数逻辑推理练习题及答案的讲解，我们可以锻炼孩子们的逻辑思维和推理能力。

这些题目涵盖了不同类型的逻辑推理问题，包括旗帜推理、身高排列、数字序列推断、人物排列和图形推理。

小学生奥数逻辑推理练习题(精选)

1.小学生奥数逻辑推理练习题1、有三个小朋友们在谈论谁做的好事多。

冬冬说：“兰兰做的比静静多。

”兰兰说：“冬冬做的比静静多。

”静静说：“兰兰做的比冬冬少。

”这三位小朋友中，谁做的好事最多？谁做的好事最少？分析与解答：我们用“>”来表示每个小朋友之间做好事多少的关系。

兰兰>静静冬冬>静静冬冬>兰兰所以，冬冬>兰兰>静静，冬冬做的好事最多，静静做的最少。

2、甲、乙、丙、丁四个人同时参加数学竞赛。

最后：甲说：“丙是第一名，我是第三名。

”乙说：“我是第一名，丁是第四名。

”丙说：“丁是第一名，我是第三名。

”丁没有说话。

成绩揭晓时，大家发现甲、乙、丙三个人各说对了一半。

你能说出他们的名次吗？分析与解答：推理时，必须以“他们都只说对了一半”为前提。

为了帮助分析，我们可以借助图表进行分析。

（1）乙说“我是第一名”也是错的，而乙说“丁是第四名”是对的。

（2）由丁是第四名推出丙说“丁是第二名”是错的，根据条件，丙说“我是第三名”是对的。

（3）这样，丙既是第一名，又是第三名，自然是错的。

重新推理：（1）由甲说的“我是第一名”推出丙说的“我是第三名”是错的，而丙说的“我是第一名”是对的。

2.小学生奥数逻辑推理练习题A、B、C、D四人在一场比赛中得了前4名。

已知D的名次不是，但它比B、C 都高，而C的名次也不比B高。

问：他们各是第几名？解答：D名次不是，但比B、C高，所以它是第2名，A是第1名。

C的名次不比B 高，所以B是第3名，C是第4名。

3.小学生奥数逻辑推理练习题甲乙丙丁各自参加篮球、排球、足球和象棋。

现在知道：（1）甲的身材比排球运动员高。

（2）几年前，丁由于事故，失去了双腿。

（3）足球运动员比丙和篮球运动员都矮。

猜猜就甲乙丙丁各参加什么项目？解：由（2）可知丁肯定是象棋运动员，由（1）（3）可知甲不是排球和足球运动员，那么甲只能是篮球运动员，由（3）可知丙不是足球运动员，那么只能是排球运动员了，剩下的乙就是足球运动员了。

小学生奥数逻辑推理练习题5篇

【导语】逻辑思维是指将思维内容联结、组织在⼀起的⽅式或形式。

思维是以概念、范畴为⼯具去反映认识对象的。

以下是⽆忧考整理的《⼩学⽣奥数逻辑推理练习题5篇》相关资料，希望帮助到您。

1.⼩学⽣奥数逻辑推理练习题 1．有五个⼈各说了⼀句话。

第⼀个⼈说：“我们中间每个⼈都说谎”。

第⼆个⼈说：“我们中间只有⼀个⼈说谎”。

第三个⼈说：“我们中间有两个⼈说谎”。

第四个⼈说：“我们中间有三个⼈说谎”。

第五个⼈说：“我们中间有四个⼈说谎”。

请问，他们谁说谎话，谁说真话？ 2．某地质学院的三名学⽣对⼀种矿⽯进⾏分析。

甲判断：不是铁，不是铜。

⼄判断：不是铁，不是锡。

丙判断：不是锡，⽽是铁。

经化验证明，有⼀个⼈判断完全正确，有⼀个⼈只说对了⼀半，⽽另⼀个则完全说错了。

你知道三⼈中谁是对的，谁是错的，谁是只对了⼀半的吗？　2.⼩学⽣奥数逻辑推理练习题 1．五个旅游者在海滨交谈。

甲：“我从A城来，⼄A城来，丙从B城来”。

⼄：“我从C城来，戊从C城来，丙从B城来”。

丙：“我不从B城来，甲不从D城来，丁从E城来”。

丁：“我⽗亲从A城来，我母亲从D城来，我从F城来”。

戊：“甲从A城来，⼄从A城来，我从F城来”。

如果他们每⼈都说了两句真话，⼀句假话，你能判断每⼀个⼈各来⾃哪个城市吗？ 2．在⼀次有3⼈参加的讲话中，⼩张指责⼩王和⼩李：“你们都在说谎。

”⼩李却说：“⼩张正在说谎。

”⼩王则说：“⼩李正在说谎。

”试判断他们谁讲的是真话，谁讲的是假话？前⼋名，⽼师让他们猜⼀下谁是第⼀名。

A：“或者F是第⼀名，或者H是第⼀名。

” B：“我是第⼀名。

” C：“G是第⼀名。

” D：“B不是第⼀名。

” E：“A说的不对。

” F：“我不是第⼀名，H也不是第⼀名”。

G：“C不是第⼀名。

” H：“我同意A的意见。

” ⽼师指出，⼋⼈中有三⼈猜对了，那么谁是第⼀名？3.⼩学⽣奥数逻辑推理练习题 1．A、B、C、D、E、F六年⾜球队进⾏⽐赛，每队都已赛过三场。

小学奥数部分—简单的逻辑推理及习题答案全解

简单的逻辑推理1、A、B、C、D四人，已知B不是最高的，但他比A、D高，而A不比D高，请把他们按高矮排列。

2、甲、乙、丙、丁四人同时参加了读书竞赛，赛后他们各自预测名次，甲说：“丙第一名，我第三名。

”乙说：“我第一名，丁第四名。

”丙说：“丁第二名，我第三名。

”丁没说话。

最后成绩公布时，发现他们的预测都只对了一半。

那么，这次竞赛他们的名次分别是什么？3、有一次上课坐在一个小组的三个人中有人讲话，小张指责小王和小李：“你们都在说谎。

”小李却说：“小张正在说谎。

”小王则说：“小李正在说谎。

”他们中只有1个人讲的是真话，试问：谁讲的是真话，谁讲的是假话？4、甲、乙、丙、丁四位同学的校服上印有不同的号码。

赵同学说：甲是2号，乙是3号。

钱同学说：丙是2号，乙是4号。

孙同学说：丁是2号，丙是3号。

李同学说：丁是1号，乙是3号。

已知赵、钱、孙、李每人都说对了一半，那么丙是几号？5、甲、乙、丙三人对晓明的藏书数目作了一个估计，甲说：他至少有1000本书。

乙说：他的书不到1000本。

丙说：他最少有1本书。

这三个人的估计中只有一句是对的。

晓明究竟有多少本书？6、小利、小江、小敏、小磊四个同学，有一个同学在英语竞赛中获奖，其余同学问他们谁是获奖者，小利说：我不是，小江说：是小磊，小敏说：是小江，小磊说：不是我。

他们当中只有一个人没有说真话，那么获奖者是谁？7、有三名学生在看1、2、3号运动员进行“羽毛球冠军争夺赛。

”赛前，对于谁会得“冠军”称号，三名学生都说了两句话：甲说：不是2号，是3号。

乙说：不是2号，是1号。

丙说：不是3号，是2号。

比赛结果表明，他们的话有一人全对，有一人对一半错一半，另一人全错。

请你想一想，冠军是谁？8、有三位老师比年龄，他们每人说的3句话中有2句是对的，请你分析一下他们各有多少岁？刘老师：我22岁，比小陈小2岁，比小李大1岁。

陈老师：我不是年龄最小的，小李和我相差3岁，小李是25岁。

李老师：我比小刘小，小刘23岁，小陈比小刘大3岁。

四年级逻辑推理题目

四年级逻辑推理题目
一、简单的人物关系推理
1. 题目
- 甲、乙、丙三人分别是医生、教师和警察。

已知甲不会看病，丙不会上课，乙经常抓小偷。

请你判断甲、乙、丙三人的职业。

2. 解析
- 根据“乙经常抓小偷”，可以直接判断出乙是警察。

- 然后，因为甲不会看病，那么甲就不是医生，又因为乙已经是警察了，所以甲只能是教师。

- 丙不是教师（甲是教师），也不是警察（乙是警察），所以丙是医生。

二、数字推理中的逻辑
1. 题目
- 在下面的数列中，1，3，6，10，15，（），28。

请找出括号里的数字。

2. 解析
- 观察这个数列，可以发现：
- 3 - 1 = 2；
- 6 - 3 = 3；
- 10 - 6 = 4；
- 15 - 10 = 5。

- 由此可以推断出这个数列的规律是相邻两个数的差依次递增1。

那么括号里的数与15的差应该是6。

- 所以括号里的数是15 + 6 = 21。

三、关于物体特征的逻辑推理
1. 题目
- 有红、黄、蓝三个盒子，其中一个盒子里有一个苹果。

红盒子上写着“苹果不在我这里”，黄盒子上写着“苹果在红盒子里”，蓝盒子上写着“苹果不在我这里”。

已知只有一个盒子上写的是真话，那么苹果在哪个盒子里？
2. 解析
- 红盒子说“苹果不在我这里”，黄盒子说“苹果在红盒子里”，这两句话相互矛盾。

- 因为矛盾关系必有一真一假，而题目中说只有一个盒子上写的是真话，所以真话就在红盒子和黄盒子的话中。

- 那么蓝盒子上写的“苹果不在我这里”就是假话，所以苹果在蓝盒子里。

小学奥数系列8-3-1逻辑推理(三)及参考答案

小学奥数系列8-3-1逻辑推理（三）一、1. 、、、、五人参加乒乓球比赛，每两个人都要赛一盘，并且只赛一盘，规定胜者得分，负者不得分，已知比赛结果如下：①与并列第一名②是第三名③和并列第四名。

求得多少分？2. 班上四名同学进行跳棋比赛，每两名同学都要赛一局．每局胜者得分，平者各得分，负者得分．已知甲、乙、丙三名同学得分分别为分、分、分，且丙同学无平局，甲同学有胜局，乙同学有平局，那么丁同学得分是多少？3. 甲、乙、丙、丁四人进行象棋比赛，每两个都比赛一场，规定胜者得分，平局各得分，输者得分．结果甲第一，乙、丙并列第二，丁最后一名，那么乙得几分？4. 10个队进行循环赛，胜队得2分，负队得1分，无平局．其中有两队并列第一，两队并列第三，有两个队并列第五，以后无并列情况．请计算出各队的得分．5. 四个同学参加网上棋类比赛，每两个人都要赛一场．规定如下：胜者得分，负者不得分，平局得分．比赛结果如下：两名同学并列第一名，两名同学并列第三名．已知比赛中有平局，那么第一名同学得多少分？6. 四名棋手两名选手都要比赛一局，规则规定胜一局得分，平一局得分，负一局得分．比赛结果，没有人全胜，并且各人的总分都不相同，那么至少有几局平局？7. 、、、、、六个足球队进行单循环比赛，每两个队之间都要赛一场，且只赛一场．胜者得3分，负者得0分，平局每队各得1分．比赛结果，各队得分由高到低恰好为一个等差数列，获得第3名的队得了8分，那么这次比赛中共有________场平局．8. 五个运动队参加商业足球比赛．原计划每两个队都要比赛一场，但由于经费不足，取消了其中一些比赛场次，最终发现各个队所得的积分各不相同，而且从积分表上看，没有一个队的积分为0.积分的计算办法是：每赢一场得3分，每输一场得0分，每平一场得1分．试问，这次比赛最少可能有________场．9. 三（一）班的同学在周末举行象棋比赛，规定赢局得分，输局倒扣分，平局各得分．小晴共参加了局比赛，结果胜了局，平了局，那么小晴的最后得分是多少？10. 、、、四个队举行足球循环赛（即每两个队都要赛一场），胜一场得3分，平一场得1分，负一场得0分．已知：⑴比赛结束后四个队的得分都是奇数；⑵队总分第一；⑶队恰有两场平局，并且其中一场是与队平局．那么，队得________分．11. 5个足球队进行比赛，每个球队都与其他球队各比一场，胜方得3分，负方得0分，平局各得1分．最后四个队分别得1分、2分、5分和7分，那么第五个队得________分．12. 甲、乙、丙、丁四个足球队进行单循环赛，就是每两个队之间都要比一场，胜者得3分，负者得0分，平者各得1分．比赛结束后，甲队共得6分，乙队共得4分，丙队共得2分，那么丁队共得________分．13. 四个足球队进行单循环比赛，规定胜一场得分，平一场得分，负一场得分，有一个队没输过，但却排名倒数第一，你觉得有可能吗？如果可能，请举出这种情况何时出现，如果不可能，请你说明理由．14. 德国队、意大利队、荷兰队进行一次足球比赛，每队与另两支队各赛一场。

小学奥数简单逻辑推理习题

小学奥数---逻辑推理

小学奥数思维训练-逻辑推理问题(通用,含答案)

小学奥数逻辑推理题及答案

小学奥数 逻辑推理 知识点+例题+练习 (分类全面)

小学奥数之逻辑推理专题训练(附详解)

小学奥数逻辑推理题及答案

小学奥数 逻辑推理 题集含答案

趣味奥数题6年级逻辑推理

小学奥数逻辑推理题及答案

小学奥数之逻辑推理题(详细解析)

小升初数学奥数必考(逻辑推理题)

小学奥数逻辑推理练习题及答案

小学生奥数逻辑推理练习题(精选)

小学生奥数逻辑推理练习题5篇

小学奥数部分—简单的逻辑推理及习题答案全解

四年级逻辑推理题目

小学奥数系列8-3-1逻辑推理(三)及参考答案

小学奥数逻辑推理知识点+例题+练习 (分类全面)

小学奥数逻辑推理题集含答案