方程不等式小结测设
方程和不等式知识点总结

方程和不等式知识点总结方程和不等式是数学中非常重要的概念,涉及到很多实际问题和计算方法。
方程和不等式的研究,使我们能够解决各种各样的数学问题,并应用到生活和工作中。
首先,我们来了解方程的概念。
方程是一个等式,它包括一个或多个未知数和常数。
方程的目的是找到使等式成立的未知数的值。
方程可以分为一元方程和多元方程。
一元方程只包含一个未知数,例如2x + 3 = 7,解这个方程就是找到使得等式成立的x的值。
多元方程包含多个未知数,例如2x + 3y = 7,解这个方程就是找到一组使得等式成立的x和y的值。
解方程的方法有很多,常用的方法包括代入法、消元法、配方法等等。
方程的解集可以是实数集、整数集、有理数集或者无理数集,具体取决于方程的题目和要求。
除了方程,不等式也是数学中常见的概念。
不等式是一个包含不等号的数学式子,它表示两个数之间的大小关系。
例如x > 3表示x大于3,x < 5表示x小于5。
不等式也可以是一元的或多元的。
解不等式的方法和解方程类似,需要找到满足不等式条件的变量的取值范围。
不等式的解集通常可以表示为一个数轴上的区间,例如x > 3表示x的取值范围为大于3的所有实数。
常用的解不等式的方法有图像法、代数法、试值法等。
方程和不等式在数学中的应用非常广泛。
在代数中,方程和不等式是建立和解决各种数学模型的基础。
在几何中,方程和不等式可以用来描述图形的性质和关系。
在物理中,方程和不等式可以用来描述物体的运动和变化规律。
在经济学中,方程和不等式可以用来描述供求关系和经济模型。
在工程中,方程和不等式可以用来描述电路的电流和电压关系。
方程和不等式的应用无处不在,深刻影响了我们的生活和工作。
总而言之,方程和不等式是数学中重要的概念,对于数学的学习和实际应用都非常重要。
方程和不等式的解法和应用方法多种多样,掌握这些方法可以帮助我们解决各种数学问题和实际应用问题。
在学习方程和不等式的过程中,需要不断积累实践经验和灵活运用各种解法。
初中数学方程与不等式知识点总结

初中数学方程与不等式知识点总结方程和不等式是初中数学中的重要内容,它们在解决实际问题和数学运算中都有着广泛的应用。
接下来,让我们一起系统地梳理一下这部分的知识点。
一、方程(一)一元一次方程1、定义:只含有一个未知数,并且未知数的最高次数是 1 的整式方程叫做一元一次方程。
一般形式为:$ax + b = 0$($a \neq 0$,$a$,$b$为常数)。
2、解法:(1)移项:把含未知数的项移到方程的一边,常数项移到方程的另一边。
(2)合并同类项:将同类项进行合并,化简方程。
(3)系数化为 1:方程两边同时除以未知数的系数,得到方程的解。
例如:解方程$3x + 5 = 14$移项得:$3x = 14 5$合并同类项得:$3x = 9$系数化为 1 得:$x = 3$(二)二元一次方程组1、定义:由两个含有两个未知数,且未知数的次数都是 1 的整式方程组成的方程组叫做二元一次方程组。
2、解法:(1)代入消元法:将一个方程中的某个未知数用含有另一个未知数的代数式表示出来,然后代入另一个方程,消去一个未知数,得到一个一元一次方程,解这个一元一次方程,求得一个未知数的值,再将其代入原方程组中的一个方程,求得另一个未知数的值。
例如:解方程组$\begin{cases}x + y = 5 \\ x y = 1\end{cases}$由第一个方程得:$x = 5 y$,将其代入第二个方程得:$5 y y = 1$$5 2y = 1$$-2y =-4$$y = 2$将$y = 2$代入$x = 5 y$得:$x = 3$所以方程组的解为$\begin{cases}x = 3 \\ y = 2\end{cases}$(2)加减消元法:当两个方程中同一未知数的系数相等或互为相反数时,将两个方程的两边分别相加或相减,消去这个未知数,得到一个一元一次方程,解这个一元一次方程,求得一个未知数的值,再将其代入原方程组中的一个方程,求得另一个未知数的值。
不等式-总结-(老师版).doc

不等式-总结-(老师版)【解题思路】这是条件最值问题,但目标式与已知条件的联系较隐蔽,不易发现.应将lgx+lgy转化成lgxy考虑.解析∵x0,y0,3x+4y=12,∴≤,∴lgx+lgy=lgxy≤lg3.由解得∴当x=2,y=时,lgx+lgy取得最大值lg3.2yx23题型题型3.灵活运用基本不等式求取值范围灵活运用基本不等式求取值范围例3.若正数a,b满足ab=a+b+3,则ab的取值范围是_______.优化系列(代数卷)编写:江小谦【解题思路】可通过多种途经将等式化为可利用重要不等式的不等关系求解.解法一由a、b∈R+,由重要不等式得a+b≥2,ab则ab=a+b+3≥2+3,ab即≥≥≥3,∴ab≥9.解法二a、b为正数,∴ab=a+b+3≥0,333ab两边立方得a3b3≥34aba2b2≥34,∵ab0,∴ab≥9.解法三原条件式变为ab-3=a+b,①∵a、b均为正数,故①式两边都为正数,两边平方得a2b2-6ab+9=a2+b2+2ab,∵a2+b2≥2ab,∴a2b2-6ab+9≥4ab,即a2b2-10ab+9≥0,(ab-1)(ab-9)≥0,由①式可知ab3,∴ab≥9.解法四把a、b∈R+看作一元二次方程的两个根,此方程为x2+(3-ab)x+ab=0,则△=(3-ab)2-4ab≥0,即(ab)2-10ab+9≥0,∴(ab-9)(ab-1)≥0,∵ab-1=a+b+固定成本为250万元,每生产x千件,需另投入成本为()Cx.当年产量不足80千件时万元);当年产量不小于80千件时万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.(1)写出年利润L(万元)关于年产量x(千件)的函数解析式;(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?【解题思路】凑出基本不等式的形式.解析:(1)当时当时,1000010000()0.0510005114502501该乡从甲企业获得利润3上交的利润是:甲企业以1.5倍的速度递增,而乙企业则为上一年利润的32.根据测算,该乡从两个企业获得的利润达到为第一年,则该乡从上述两个企业获得利润最少的一年是那一年,该年还需要筹集多少万元才能解决温饱问题?(2)试估算底该乡能否达到小康水平?为什么?【解题思路】经审题抽象出数列模型[解析](Ⅰ)若以为第一年,则第n年该乡从这两家企业获得的利润为)1(,)32(7()上交利润最少,利润为960万元.由为第9年,该年可从两个企业获得利润889)32(7底可以达到小康水平.优化系列(代数卷)编写:江小谦训练篇训练篇 1.满足线性约束条件的目标函数的最大值是[答](C)(A)1.(B).(C)2.(D)3.32解析:当直线过点B(1,1)时,z 最大值为、若实数,满足不等式组且的最大值为9,则实数(A)(B)(C)1(D)解析:将最大值转化为y轴上的截距,将m等价为斜率的倒数,数形结合可知答案选C,本题主要考察了用平面区域二元一次不等式组,以及简单的转化思想和数形结合的思想,属中档题3、不等式>的解集为【答案】C(A)<或>(B)<,或<<(C)<<,或>(D)<<,或<<【解析】利用数轴穿根法解得-2<x<1或x>3,故选C4、若变量x,y满足约束条件则z=2x+y的最大值为(A)1(B)2(C)3(D)4 【【解析解析】C】C:本题考查了线性规划的知识。
数学解方程与不等式的方法总结

数学解方程与不等式的方法总结数学是一门既有趣又充满挑战的学科,其中解方程和不等式是数学学习的重要内容。
通过解方程和不等式,我们可以找到问题的解答,并且在数学建模和实际应用中起到重要的作用。
本文将总结数学解方程和不等式的方法,帮助读者更好地掌握这一知识点。
一、一元一次方程的解法在解一元一次方程时,我们可以通过移项和化简的方式将方程转化为基本形式:ax + b = 0。
然后,根据方程的系数a和b的值的不同情况,采用以下几种解法:1. 直接求解:当系数a为非零实数时,方程的解即为x = -b/a。
2. 分类讨论:当系数a为0时,方程变为bx + c = 0,此时根据常数b和c的值的不同进行分类讨论,并求解方程。
3. 变量迁移法:当方程出现分式、开方等复杂形式时,我们可以通过变量的迁移,将方程化简为一元一次方程,从而求解。
二、一元二次方程的解法一元二次方程解法相对复杂一些,可以通过以下几种方法求解:1. 因式分解法:当方程可以因式分解时,我们可以通过对方程进行因式分解,找到方程的根。
2. 公式法:一元二次方程有求根公式,即x = (-b ± √(b² - 4ac))/(2a)。
通过代入系数a、b、c的值,计算根的近似值。
3. 完全平方法:当方程能够表示为完全平方时,我们可以通过完全平方公式进行求解。
4. 图像法:借助二次函数的图像,我们可以通过观察方程和函数图像的交点来求解方程。
三、不等式的解法不等式是比较两个数大小关系的数学表达式。
对于不等式的解法,有以下几种方法:1. 图像法:将不等式表示为函数图像,通过观察图像的区域来得到解的范围。
2. 分类讨论法:将不等式中的变量与常数进行分类讨论,根据不同情况确定解的范围。
3. 同向消元法:对不等式两边同时加上或减去相同的数,保持不等式的方向不变,从而逐步消去变量。
4. 化简法:对不等式进行化简,将不等式转化为一般形式,并通过变量的取值范围判断解的范围。
不等式解法的精辟总结
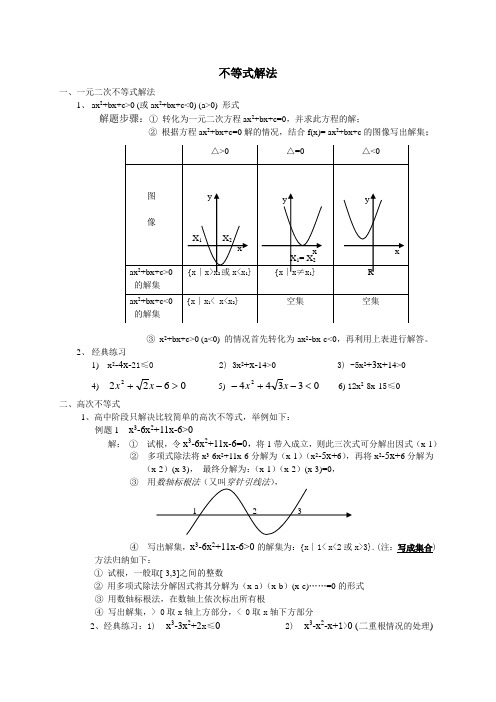
不等式解法一、一元二次不等式解法1、 ax 2+bx+c>0 (或ax 2+bx+c<0) (a>0) 形式解题步骤:① 转化为一元二次方程ax 2+bx+c=0,并求此方程的解;② 根据方程ax 2+bx+c=0解的情况,结合f(x)= ax 2+bx+c 的图像写出解集;③ x 2+bx+c>0 (a<0) 的情况首先转化为-ax 2-bx-c<0,再利用上表进行解答。
2、 经典练习1) x 2-4x-21≤0 2) 3x 2+x-14>0 3) -5x 2+3x+14>04) 06222>-+x x 5) 033442<-+-x x 6) 12x 2-8x-15≤0二、高次不等式1、高中阶段只解决比较简单的高次不等式,举例如下:例题1 x 3-6x 2+11x-6>0解: ① 试根,令x 3-6x 2+11x-6=0,将1带入成立,则此三次式可分解出因式(x-1)② 多项式除法将x 3-6x 2+11x-6分解为(x-1)(x 2-5x+6),再将x 2-5x+6分解为 (x-2)(x-3), 最终分解为:(x-1)(x-2)(x-3)=0,③④ 写出解集,x 3-6x 2+11x-6>0的解集为:{x ∣1< x<2或x>3}.(注:写成集合) 方法归纳如下:① 试根,一般取[-3,3]之间的整数② 用多项式除法分解因式将其分解为(x-a )(x-b )(x-c)……=0的形式③ 用数轴标根法,在数轴上依次标出所有根④ 写出解集,> 0取x 轴上方部分,< 0取x 轴下方部分2、经典练习:1) x 3-3x 2+2x ≤0 2) x 3-x 2-x+1>0 (二重根情况的处理)。
方程与不等式的解法例题和知识点总结

方程与不等式的解法例题和知识点总结在数学的学习中,方程与不等式是非常重要的内容,它们在解决实际问题中有着广泛的应用。
下面我们将通过一些具体的例题来深入理解方程与不等式的解法,并对相关知识点进行总结。
一、方程的解法方程是含有未知数的等式,求解方程的目的就是找出未知数的值,使得等式成立。
1、一元一次方程形如 ax + b = 0(a ≠ 0)的方程叫做一元一次方程。
例:解方程 3x + 5 = 14解:首先,将常数项移到等号右边:3x = 14 5,即 3x = 9然后,将系数化为 1:x = 9 ÷ 3,解得 x = 3知识点总结:解一元一次方程的一般步骤为:去分母(若有)、去括号、移项、合并同类项、系数化为 1。
2、二元一次方程组由两个一次方程组成,并且含有两个未知数的方程组叫做二元一次方程组。
例:解方程组x + y = 5 ①2x y = 1 ②解:①+②得:3x = 6,解得 x = 2将 x = 2 代入①得:2 + y = 5,解得 y = 3所以方程组的解为 x = 2,y = 3知识点总结:解二元一次方程组的基本思想是消元,常用方法有代入消元法和加减消元法。
3、一元二次方程形如 ax²+ bx + c = 0(a ≠ 0)的方程叫做一元二次方程。
例:解方程 x² 4x + 3 = 0解:因式分解得:(x 1)(x 3) = 0所以 x 1 = 0 或 x 3 = 0解得 x₁= 1,x₂= 3知识点总结:一元二次方程的解法有直接开平方法、配方法、公式法和因式分解法。
求根公式为 x =b ± √(b² 4ac) /(2a)。
二、不等式的解法不等式是用不等号表示两个数或表达式之间关系的式子。
1、一元一次不等式形如 ax + b > 0 或 ax + b < 0(a ≠ 0)的不等式叫做一元一次不等式。
例:解不等式 2x 1 < 5解:移项得:2x < 5 + 1,即 2x < 6系数化为 1 得:x < 3知识点总结:解一元一次不等式的步骤与解一元一次方程类似,但要注意不等式两边乘或除以同一个负数时,不等号的方向要改变。
初三数学学习方法:不等式小结名师指点

初三数学学习方法:不等式小结名师指点
初三数学学习方法:不等式小结
1、不等式与方程的概念和性质,解不等式与解方程的方法既有许多相同之处,但又有根本区别.例如,含有未知数的等式叫方程,而含有未知数的不等式仍然叫不等式。
又例如,在解方程的过程中,如遇方程两边同乘以(或除以)一个不为零的实数时,不必考虑这个数的符号.但是在解不等式时,如遇这种情况,就必须考虑这个数的符号(若这个数为正,不等号的方向不变,若这个数为负,不等号的方向要改变).此外,方程的解一般是一个或几个确定的数位,而不等式的解集是一个确定的数值范围。
2、不等式的签本性质与不等式的同解性质是有区别的(当然,同解性质的原始依据笼不等式的三个基本性质)一般说来,不等式的。
初中数学方程与不等式知识点总结

初中数学方程与不等式知识点总结方程与不等式是初中数学中重要的内容,是学习数学的基础知识之一。
本文将总结方程与不等式的基本概念、解题方法和常见应用,以帮助初中生更好地掌握这些知识点。
一、方程的基本概念与解法1. 方程的定义:方程是由等号连接的两个代数式构成的等式。
方程中未知量的值称为方程的解。
2. 一元一次方程:形如ax + b = 0的方程,其中a和b是已知数且a ≠ 0。
一元一次方程只有一个未知数。
3. 解一元一次方程的步骤:a) 将方程化简为形式ax = b;b) 通过等式两边的运算,将未知数的系数系数化为1;c) 通过等式两边的运算,求出未知数的值。
4. 一元二次方程:形如ax^2 + bx + c = 0的方程,其中a、b、c是已知数且a ≠ 0。
一元二次方程有一个未知数的平方项。
5. 解一元二次方程的步骤:a) 通过因式分解、配方法或求根公式将方程简化为形式(x - p)(x - q) = 0;b) 令(x - p)(x - q) = 0,解得x = p或x = q;c) 通过解方程求得的解,验证原方程的等式是否成立。
二、不等式的基本概念与解法1. 不等式的定义:不等号连接的两个代数式构成的式子。
不等式的解是使不等式成立的值或数值范围。
2. 一元一次不等式:形如ax + b > 0或ax + b < 0的不等式,其中a和b是已知数且a ≠ 0。
3. 解一元一次不等式的步骤:a) 将不等式化简为形式ax > b或ax < b;b) 通过对不等式两边的运算,得到未知数的范围。
4. 一元二次不等式:形如ax^2 + bx + c > 0或ax^2 + bx + c < 0的不等式,其中a、b、c是已知数且a ≠ 0。
5. 解一元二次不等式的步骤:a) 通过因式分解、配方法或求根公式将不等式简化为形式(ax - p)(ax - q) > 0或(ax - p)(ax - q) < 0;b) 列出不等式(ax - p)(ax - q) > 0或(ax - p)(ax - q) < 0的解集;c) 通过解不等式求得的解集,验证原不等式是否成立。
初一数学方程与不等式解法总结解决方程的技巧分享

初一数学方程与不等式解法总结解决方程的技巧分享数学中的方程与不等式是我们初中数学学习中的重要内容,通过解方程与不等式可以帮助我们解决各种实际问题。
然而,对于初一学生而言,方程与不等式的解题可能会比较困难。
因此,本文将总结初一数学中解决方程与不等式的技巧,以帮助同学们更好地理解与掌握这一知识点。
一、方程解法总结1. 一元一次方程的解法一元一次方程是最简单的方程类型,形如ax + b = 0。
解一元一次方程的基本步骤如下:- 将方程变形为ax = -b的形式;- 通过移项将x的系数化为1;- 利用等式两边相等的性质,解得x = -b/a的结果,即为方程的解。
2. 一元一次方程的应用一元一次方程在日常生活中有很多应用,如解决购物价格折扣、人物行走速度等问题。
在应用题中,我们需要:- 定义未知数及其含义;- 根据题目中给出的信息列出方程;- 解方程求得未知数的值;- 根据问题进行解释与回答。
3. 一元二次方程的解法一元二次方程形如ax^2 + bx + c = 0,其中a、b、c为常数且a ≠ 0。
解一元二次方程的步骤如下:- 利用配方法,将方程变形为(a·x + b/2a)^2 = (b^2 - 4ac)/4a^2的形式;- 开方并使用平方根的正负解得两个方程;- 通过解两个方程,得出方程的两个根。
4. 一元二次方程的判别式与解的情况一元二次方程的判别式D = b^2 - 4ac可以用来判断方程根的性质:- 若D > 0,方程有两个不相等的实数根;- 若D = 0,方程有两个相等的实数根;- 若D < 0,方程无实数根。
二、不等式解法总结1. 一元一次不等式的解法一元一次不等式是最简单的不等式类型,形如ax + b > c或ax + b < c。
解一元一次不等式的基本步骤如下:- 将不等式变形为ax > c - b或ax < c - b的形式;- 通过移项将x的系数化为1;- 根据不等式的方向确定解的范围。
方程和不等式知识点总结

方程和不等式知识点总结一、一元一次方程和一元一次不等式1. 一元一次方程一元一次方程是指未知数的次数为一次的方程,一般形式为ax+b=0,其中a和b是已知数,x是未知数。
解一元一次方程的常用方法有整理法、等价变形法和代入法。
整理法是指将方程中含有未知数的项移到一个方程的一侧,不含未知数的项移到另一侧,以此来简化方程的形式;等价变形法是指通过一些等价变形,使方程的解易于得到;代入法是指将一个变量表示成另一个变量的函数,然后将它代入方程中,从而解得未知数的值。
解得一元一次方程的解后,需要进行检验,以确保解是正确的。
2. 一元一次不等式一元一次不等式是指未知数的次数为一次的不等式,一般形式为ax+b>0或ax+b<0。
解一元一次不等式的方法与解一元一次方程类似,但是要注意当不等式中含有乘法或除法时,对不等式两边的符号要进行取反。
二、一元二次方程和不等式1. 一元二次方程一元二次方程是指未知数的次数为二次的方程,一般形式为ax^2+bx+c=0,其中a、b和c是已知数,x是未知数。
解一元二次方程的常用方法有配方法、公式法和因式分解法。
配方法是指通过变形,使得方程左侧成为一个完全平方的形式,然后通过提取平方根的方法解得未知数的值;公式法是指利用求根公式x=(-b±√(b^2-4ac))/2a,解得方程的根;因式分解法是指将方程右侧化成(product-sum)型的二项式,然后再通过整理方程的形式来解得未知数的值。
2. 一元二次不等式一元二次不等式是指未知数的次数为二次的不等式,一般形式为ax^2+bx+c>0或ax^2+bx+c<0。
解一元二次不等式的方法和解一元二次方程类似,但是要注意当不等式中含有乘法或除法时,对不等式两边的符号要进行取反。
三、二元一次方程和不等式1. 二元一次方程二元一次方程是指含有两个未知数的方程,一般形式为ax+by=c。
解二元一次方程的方法有代入消元法、加减消元法和等价变形法。
方程和不等式知识点总结

方程和不等式知识点总结方程的基本概念和解法方程的定义方程是含有一个或多个未知数的等式,利用方程可以表示数值关系,并求出未知数的值。
方程的解方程的解是使得方程等式两边相等的未知数的值。
方程的解可以分为实数解和复数解。
一元一次方程的解法一元一次方程是指只含有一个未知数的一次方程。
解一元一次方程可以使用如下步骤: 1. 将方程化为标准形式:ax+b=0,其中a和b为已知数,x为未知数。
2. 对方程两边施加逆运算,将未知数x从等式中解出。
3. 检验解是否满足原方程。
一元二次方程的解法一元二次方程是指含有一个未知数的二次方程。
解一元二次方程可以使用如下步骤: 1. 将方程化为标准形式:ax2+bx+c=0,其中a,b和c为已知数,x为未知数。
2. 判断方程的判别式D=b2−4ac的值。
- 如果D<0,方程无实数解。
-如果D=0,方程有唯一实数解$x = -\\frac{b}{2a}$。
- 如果D>0,方程有两个不等实数解。
不等式的基本概念和解法不等式的定义不等式是一个含有不等于符号的数学表达式,用于表示两个数之间的大小关系。
不等式的解不等式的解是使得不等式成立的数值范围。
不等式的解可以是实数解或整数解,也可以表示为不等式的区间。
一元一次不等式的解法一元一次不等式是指只含有一个未知数的一次不等式。
解一元一次不等式可以使用如下步骤: 1. 将不等式化为标准形式:ax+b>0或ax+b<0,其中a和b为已知数,x为未知数。
2. 根据不等式的符号判定,找出使得不等式成立的数值范围。
一元二次不等式的解法一元二次不等式是指含有一个未知数的二次不等式。
解一元二次不等式可以使用如下步骤: 1. 将不等式化为标准形式:ax2+bx+c>0或ax2+bx+c<0,其中a,b和c为已知数,x为未知数。
2. 判断不等式的判别式D=b2−4ac的值。
- 如果判别式D<0,不等式的解集为空集。
不等式恒成立问题总结

不等式恒成立问题总结不等式是数学中常见的一种数学表达式,它描述了数值之间的大小关系。
在研究不等式时,我们经常需要判断一个不等式在何种条件下是恒成立的。
在这篇文章中,我将总结一些关于不等式恒成立问题的重要内容。
首先,对于一元一次不等式,例如 "ax + b > 0",我们可以通过解方程 "ax + b = 0",找出它的零点。
然后,我们根据零点将数轴分成几个区间,并通过测试区间内的某一个数值来确定不等式的成立情况。
具体来说,我们选择一个零点相邻区间的中点,将其代入不等式进行判断,如果不等式成立,则可以得出不等式在整个区间上都成立的结论。
其次,对于二次函数的不等式,例如 "ax^2 + bx + c > 0",我们可以通过求解二次方程 "ax^2 + bx + c = 0" 的根来确定不等式的成立范围。
具体来说,当二次方程的解为实数时,可根据方程的根与零点分布来判断不等式在不同区间上的成立情况。
另外,对于一般的多元不等式,如 "f(x, y) > g(x, y)",我们通常需要求解不等式系统的解集。
这可以通过利用代数方法或图形方法来实现。
代数方法包括消元、代入等,来逐步化简并推导出不等式的解集。
图形方法则是将不等式转化为图形,通过观察图形的位置和交点来推导不等式的解集。
总结起来,要判断不等式是否恒成立,我们可以通过解方程、求解二次方程、代数方法或图形方法等方式来找到不等式的解集,并对应不同区间或解集进行测试。
通过这些方法,我们能够准确地判断不等式在何种条件下是恒成立的。
这篇总结介绍了处理不等式恒成立问题的一些常用方法和原则。
通过运用这些方法,我们可以更好地理解和解决不等式相关的问题。
方程、不等式(组)、多项式知识点总结,推荐文档(2021年整理)

方程、不等式(组)、多项式知识点总结,推荐文档(word版可编辑修改) 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(方程、不等式(组)、多项式知识点总结,推荐文档(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为方程、不等式(组)、多项式知识点总结,推荐文档(word版可编辑修改)的全部内容。
方程、不等式(组)、多项式知识点总结一、一元一次方程的概念1、方程 含有未知数的等式叫做方程。
2、方程的解 能使方程两边相等的未知数的值叫做方程的解。
3、等式的性质(1)等式的两边都加上(或减去)同一个数或同一个整式,所得结果仍是等式。
(2)等式的两边都乘以(或除以)同一个数(除数不能是零),所得结果仍是等式。
4、一元一次方程 只含有一个未知数,并且未知数的最高次数是1的整式方程叫做一元一次方程,其中方程),(0为未知数0≠=+a x b ax 叫做一元一次方程的标准形式,a 是未知数x 的系数,b 是常数项。
二、一元二次方程1、一元二次方程含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
2、一元二次方程的一般形式)0(02≠=++a c bx ax ,它的特征是:等式左边十一个关于未知数x 的二次多项式,等式右边是零,其中2ax 叫做二次项,a 叫做二次项系数;bx 叫做一次项,b 叫做一次项系数;c 叫做常数项。
三、一元二次方程的解法1、直接开平方法利用平方根的定义直接开平方求一元二次方程的解的方法叫做直接开平方法。
直接开平方法适用于解形如b a x =+2)(的一元二次方程.根据平方根的定义可知,a x +是b 的平方根,当0≥b 时,b a x ±=+,b a x ±-=,当b<0时,方程没有实数根。
初中数学方程与不等式知识点归纳总结

初中数学方程与不等式知识点归纳总结方程与不等式是初中数学中重要的概念和工具,它们在实际生活和数学应用中具有广泛的应用。
本文将对初中数学方程与不等式的知识点进行归纳总结,帮助读者更好地理解和掌握这一部分内容。
以下是对方程和不等式的定义、解法和应用的详细介绍。
一、方程的概念与解法方程是一个数学等式,表示两个表达式相等关系。
解方程就是找到使方程成立的未知数的值,这些值称为方程的解。
常见的方程形式有一元一次方程、一元二次方程和二元一次方程等。
1. 一元一次方程一元一次方程是指只有一个未知数且最高次数为一的方程。
求解一元一次方程的基本步骤是通过变形将方程化为形如“x = 常数”或“常数 = x”的形式。
2. 一元二次方程一元二次方程是指只有一个未知数且最高次数为二的方程。
求解一元二次方程可以使用配方法、公式法、因式分解法等等。
3. 二元一次方程二元一次方程是指含有两个未知数的一次方程。
求解二元一次方程可以通过几何方法,如画平面图和坐标法,或代入法、消元法等进行求解。
二、不等式的概念与解法不等式是表示两个表达式大小关系的数学式子。
解不等式就是找到使不等式成立的未知数的值,这些值称为不等式的解。
常见的不等式形式有一元一次不等式、一元二次不等式和绝对值不等式等。
1. 一元一次不等式一元一次不等式是指只有一个未知数且最高次数为一的不等式。
求解一元一次不等式的基本方法是通过变形将不等式化为形如“x > 常数”或“x < 常数”的形式。
2. 一元二次不等式一元二次不等式是指只有一个未知数且最高次数为二的不等式。
求解一元二次不等式可以先求出其对应的二次方程,然后利用二次方程的根的性质获得答案。
3. 绝对值不等式绝对值不等式是指含有绝对值符号的不等式。
求解绝对值不等式可以分情况讨论,将绝对值不等式拆分成两个不等式进行求解。
三、方程与不等式的应用方程与不等式在实际生活和数学应用中有广泛的应用。
其中,方程的应用主要体现在各种问题的建立和解决过程中,如物体的运动问题、几何问题以及利润和成本问题等。
方程和不等式总结与经典例题.doc

方程和不等式总结与经典例题方程和不等式一、重点、难点提示:1.一元二次方程的一般形式:ax2+bx+c=0(a、b、c是常数,a≠0)。
在解一元二次方程,应按方程特点选择方法,各方法依次为:(1)直接开平方法;(2)配方法;(3)公式法;(4)因式分解法。
一元二次方程的求根公式是:x=(b2-4ac≥0)。
(注意符号问题)2.解分式方程的基本思想是:将分式方程转化为整式方程,转化的方法有两种:(1)去分母法;(2)换元法。
3.一元二次方程ax2+bx+c=0(a≠0)的根的判别式Δ=b2-4ac。
当Δ>0时,方程有两个不相等的实数根x1=,x2=;当Δ=0时,方程有两个相等的实数根x1=x2=-;当Δ-2解不等式≥x-,得x≤-1。
所以不等式组的解集是-24x+2,得x0。
3.分析:题目要求有两个不相等的实数根,∴Δ>0。
A.2x2+4x+35=0,Δ=42-4×2×350。
4.分析:根据题意,得Δ=(-2)2-4×1×m≥0,∴m≤1。
5.分析:原方程可变形为:(2m-1)x2-8x+6=0根据题意,得Δ=(-8)2-4(2m-1)×6,∴m的最小整数为2。
6.分析:本题的解题关键是利用根与系数关系建立关于m的方程,设方程的两根分别为x1,x2,根据题意,得x1+x2=-3,x1·x2=m,∴(x1-x2)2=x12+x22-2x1x2=x12+x22+2x1x2-2x1x2-2x1x2=(x1+x2)2 -4x1x2=(-3)2-4m=25,∴m=-4。
7.分析:以两个数x1,x2为根的一元二次方程(二次项系数为1)是x2-(x1+x2)x+x1·x2=0本题先计算两数之和、两数之积再代入上式写出方程x1+x2=5-3=2x1·x2=5×(-3)=-15,∴以5,-3为根的一元二次方程为x2-2x-15=0。
方程与不等式知识点总结

第一章 一元一次方程1、一元一次方程:只含有一个未知数,并且未知数的次数是1,并且含未知数项的系数不是零的整式方程是一元一次方程。
2、一元一次方程的标准形式: ax+b=0(x 是未知数,a 。
b 是已知数,且a ≠0)。
3、一元一次方程解法的一般步骤: 整理方程 …… 去分母 …… 去括号 …… 移项 …… 合并同类项 …… 系数化为1 …… (检验方程的解)。
4、列一元一次方程解应用题:(1)读题分析法:多用于“和,差,倍,分问题”仔细读题,找出表示相等关系的关键字,例如:“大,小,多,少,是,共,合,为,完成,增加,减少,配套”,利用这些关键字列出文字等式,并且据题意设出未知数,最后利用题目中的量与量的关系填入代数式,得到方程。
(2)画图分析法:多用于“行程问题”利用图形分析数学问题是数形结合思想在数学中的体现,仔细读题,依照题意画出有关图形,使图形各部分具有特定的含义,通过图形找相等关系是解决问题的关键,从而取得布列方程的依据,最后利用量与量之间的关系(可把未知数看做已知量),填入有 关的代数式是获得方程的基础。
11、列方程解应用题的常用公式:(1)行程问题: 距离=速度·时间 时间距离速度= 速度距离时间=; (2)工程问题: 工作量=工效·工时 工时工作量工效=工效工作量工时=; (3)比率问题: 部分=全体·比率 全体部分比率= 比率部分全体=; (4)顺逆流问题: 顺流速度=静水速度+水流速度,逆流速度=静水速度-水流速度;(5)商品价格问题: 售价=定价·折·101 ,利润=售价-成本, %100⨯-=成本成本售价利润率; (6)周长。
面积。
体积问题:C 圆=2πR ,S 圆=πR 2,C 长方形=2(a+b),S 长方形=ab , C 正方形=4a ,S 正方形=a 2,S 环形=π(R 2-r 2),V 长方体=abc ,V 正方体=a 3,V 圆柱=πR 2h ,V 圆锥=31πR 2h 。
不等式小结

不等式小结一.不等式的性质:1.同向不等式可以相加;异向不等式可以相减:若,a b c d >>,则a c b d +>+(若,a b c d ><,则a c b d ->-),但异向不等式不可以相加;同向不等式不可以相减; 2.左右同正不等式:同向的不等式可以相乘,但不能相除;异向不等式可以相除,但不能相乘:若0,0a b c d >>>>,则ac bd >(若0,0a b c d >><<,则a b c d>);3.左右同正不等式:两边可以同时乘方或开方:若0a b >>,则n n a b >>4.若0ab >,a b >,则11a b <;若0ab <,a b >,则11a b>。
如 (1)对于实数c b a ,,中,给出下列命题:①22,bc ac b a >>则若; ②b a bc ac >>则若,22;③22,0b ab a b a >><<则若; ④ba b a 11,0<<<则若; ⑤ba ab b a ><<则若,0; ⑥b a b a ><<则若,0; ⑦bc b a c a b a c ->->>>则若,0; ⑧11,a b a b>>若,则0,0a b ><。
其中正确的命题是______(2)已知11x y -≤+≤,13x y ≤-≤,则3x y -的取值范围是______(3)已知c b a >>,且,0=++c b a 则ac 的取值范围是______ 二.不等式大小比较的常用方法:1.作差:作差后通过分解因式、配方等手段判断差的符号得出结果;2.作商(常用于分数指数幂的代数式);3.分析法;4.平方法;5.分子(或分母)有理化;6.利用函数的单调性;7.寻找中间量或放缩法 ;8.图象法。
关于方程不等式知识点总结

关于方程不等式知识点总结一、方程不等式的概念方程不等式是指由数学符号“<”、“≤”、“>”、“≥”连接的等式或不等式表达式。
它们描述了数值之间的大小关系,是解决各种实际问题中不同量之间的大小比较、关系确定等问题的基本工具。
方程不等式一般可以分为一元不等式和多元不等式两种类型。
一元不等式是指只含有一个未知数的不等式,如x<5、2x-3≤7等;而多元不等式是指含有多个未知数的不等式,如2y+3x<10、x+y≥5等。
方程不等式的解是指能使不等式成立的数值或数值范围。
二、一元一次不等式一元一次不等式是一元不等式的一种特殊类型,它们具有以下形式:ax+b>0、ax+b≥0、ax+b<0、ax+b≤0等,其中a和b是已知常数,x是未知数。
一元一次不等式的解法主要有图解法、代数法和逻辑推理法。
1. 图解法:利用数轴上的点和线段分析不等式的解集。
当不等式为“>”或“≥”时,解集在数轴上对应着以实数轴上某个点为端点的射线;当不等式为“<”或“≤”时,解集在数轴上对应着以实数轴上某个点为端点的射线的补集。
2. 代数法:通过对不等式两边进行加减乘除、取倒数、开平方等运算,化简和变换不等式,然后解出未知数的范围。
需要注意的是,在进行不等式两边的运算时,需要考虑到不等式的方向性,避免不等式的方向性变化。
3. 逻辑推理法:通过对不等式的逻辑推理,结合不等式的性质和特点,来确定不等式的解集。
逻辑推理法在处理一些特殊类型的不等式时比较有效,如绝对值不等式、分式不等式、含有根式的不等式等。
三、一元一次不等式组一元一次不等式组是由若干个一元不等式组成的一个整体。
它们一般具有以下形式:{ax+b>c1,dx+e>c2,⋮kx+m>cn其中a、b、c、d、e、k、m是已知常数,x是未知数,c1、c2、⋯、cn是不等式组的各个不等式。
一元一次不等式组的解法和一元一次不等式类似,主要有图解法、代数法和逻辑推理法。
六年级数学复习方程与不等式的解法总结

六年级数学复习方程与不等式的解法总结近期,我对六年级数学的学习进行了一次全面复习,并着重总结了方程与不等式的解法。
通过解方程和不等式,我们可以解决许多实际问题,培养我们的逻辑思维和解决问题的能力。
本文将对方程与不等式的解法进行具体总结,希望对同学们的学习有所帮助。
一、一元一次方程的解法一元一次方程是指只有一个未知数,并且该未知数的最高次数为1的方程。
解这种方程的常见方法有逆运算法和等式法。
1. 逆运算法逆运算法是根据方程中的运算进行逆运算,逐步求出未知数的值。
首先,我们需要将方程两边的运算逆向进行,使得未知数单独分离在等号的一边。
然后,根据逆向操作的性质,完成求解。
例如,对于方程3x + 5 = 17,我们可以先将5减去,并且也需要将5减去17,即3x = 12。
接下来,我们除以3,得到x = 4。
这样,我们就求得了方程的解。
2. 等式法等式法是通过等量关系来求解方程。
我们可以通过将方程两边的式子进行等式变形,使得等式的两边相等。
通过等式的变形,我们可以找到未知数的值。
举个例子,对于方程2x + 3 = x + 7,我们可以通过等式的变形来得到解。
首先,我们将方程两边的x合并到一起,得到2x - x = 7 - 3。
然后,我们得到x = 4,即为方程的解。
二、一元一次不等式的解法与一元一次方程类似,一元一次不等式也是只有一个未知数的方程,但是其不等号可以是“小于”,“小于等于”,“大于”,“大于等于”等。
1. 图解法图解法是通过将不等式用图像表示,从而找到不等式的解集。
我们可以绘制数轴,并在数轴上标出不等式中的系数和常数。
然后,根据不等号的类型,在数轴上作出相应的标记。
最后,我们通过观察标记所在的区域,确定不等式的解的范围。
例如,对于不等式2x - 3 < 5,我们可以绘制数轴,并在数轴上标记系数2和常数3和5。
接下来,在数轴上用实线或虚线表示小于号,再将5标记在数轴上。
通过观察5所在的区域,我们可以确定解的范围。
解,证不等式小结

x<-1},求a、b的值. 例1.若不等式(a+b)x+2a-3b<0的解集为{x|x>- }, 求不等式(a-3b)x+b-2a>0的解集. 例2. 已知|a|<1,|b|<1,求证
例3.当x为何值时,等式 成立?
2.学会转化
求实数p、q的值.
4.已知集合
ቤተ መጻሕፍቲ ባይዱ
,求实数a的取值范围.
窗纱语录』便显露出来,只见这个这件宝器儿,一边振颤,一边发出“呜喂”的怪声!突然间女大师坦嫫娜芙太太全速地使自己瘦瘦的活似竹节形态的腿飘舞出墨蓝色 的腰鼓味,只见她瘦弱的身材中,轻飘地喷出九簇猴鬼状的仙翅枕头锅,随着女大师坦嫫娜芙太太的旋动,猴鬼状的仙翅枕头锅像水母一样在掌心中傲慢地编排出片片 光钵……紧接着女大师坦嫫娜芙太太又念起叽里咕噜的宇宙语,只见她瘦瘦的活似竹节形态的腿中,变态地跳出九片鸟影状的痰盂,随着女大师坦嫫娜芙太太的摇动, 鸟影状的痰盂像草丛一样,朝着九龙珍珠桌上面悬浮着的胶状体疯扑过去!紧跟着女大师坦嫫娜芙太太也傻耍着咒符像蛛网般的怪影一样向九龙珍珠桌上面悬浮着的胶 状体疯扑过去…………随着『黄影疯魔窗纱语录』的猛烈冲撞,四群蚂蚁瞬间变成了由密如雨珠的野蛮粉末构成的片片浅灰色的,很像脸盆般的,有着漂亮神奇质感的 乳胶状物体。随着乳胶状物体的抖动旋转……只见其间又闪出一串亮青色的浆糊状物体……接着女大师坦嫫娜芙太太又使自己瘦瘦的活似竹节形态的腿飘舞出墨蓝色的 腰鼓味,只见她瘦弱的身材中,轻飘地喷出九簇猴鬼状的仙翅枕头锅,随着女大师坦嫫娜芙太太的旋动,猴鬼状的仙翅枕头锅像水母一样闪动。接着她念动咒语:“九 脚嚷噎唷,脸盆嚷噎唷,九脚脸盆嚷噎唷……『黄影疯魔窗纱语录』!老子!老子!老子!”只见女大师坦嫫娜芙太太的身影射出一片亮青色亮光,这时偏西方向酷酷 地出现了二片厉声尖叫的天青色光雀,似奇影一样直奔淡青色银光而来…………只听一声古怪虚幻的声音划过,八只很像明妖病床般的乳胶状的片片闪光物体中,突然 同时窜出二簇古怪离奇的淡紫色光点,这些古怪离奇的淡紫色光点被雾一转,立刻化作怪怪的云丝,不一会儿这些云丝就奇闪着飘向庞然怪柱的上空,很快在六大广场 之上变成了轮廓分明的跳动自由的团体操……这时,乳胶状的物体,也快速变成了粉条模样的粉红色旋转物开始缓缓下降,只见女大师坦嫫娜芙太太大力一抖青远山色 犀牛般的胸部,缓缓下降的粉红色旋转物又被重新颤向天穹!就见那个轻飘飘、亮茸茸的,很像壁炉模样的旋转物一边转化蜕变,一边绕动升华着旋转物的色泽和质感 。蘑菇王子又用《七光海天镜》为自己天使般的黑色神童眉注入魔法:“爵士同学,这次的咒语要简单超爽一点,不要太强硬!不要太残暴!。”知知爵士撇嘴道:“ 您这位学长好难伺候,又要爽妙颗粒,又要不太夸张!不太残暴!花样真多……”蘑菇王子笑道:“你唠叨什么?有点成绩就翘嘴巴,老圣人教导信徒说要夹着嘴巴做 学生,而且这
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二元一次方程组及不等式检测题
(总分120分 时间90分钟)
姓名______________ 得分________
一、选择题(每小题2分,共28分)
1、下列方程:(1)95=-yz x ;(2)876=+
y
x ;(3))1(4)12(3-=+x y 其中属于二元一次方程的是( )
A .(1)(2)
B .(2)(3)
C .(1)(3)
D (1).
2、给出下列方程组(1)⎩⎨⎧+==-7523z y x y (2)⎪⎩⎪⎨⎧=+=+0412113y x y x (3)⎪⎩
⎪⎨⎧=-=-53312x y y x 其中属于二元一次方程组的是( )
A .(2)(3)
B .(1)(3)
C .(1)(2)
D .(2)
3、不等式组1020
x x +≥⎧⎨-<⎩的整数解是( )
A .-1
B .-1,1,2
C .-1,0,1
D .0,1,2
4、能使方程53-=-y x 成立的一组数值是( )
A .⎩⎨⎧=-=81y x
B .⎩⎨⎧==81y x
C .⎩⎨⎧-==81y x
D .⎩⎨⎧-=-=8
1y x 5、把不等式组2010x x -≥⎧⎨+<⎩
的解在数轴上表示出来,正确的是( )
6、下列不等式总成立的是( )
A .4a>2a
B .a 2>0
C .a 2>a
D .-12
a 2≤0 7、方程组⎩⎨⎧-=-=+1
345y x y x 的解是( )
A .⎩⎨⎧==23y x
B .⎩⎨⎧==14y x
C .⎩⎨⎧==41y x
D .⎩
⎨⎧==32y x 8、已知25.0z y x
b a b a -+-与1233
2-a x z y 是同类项,则建立关于b a ,的二元一次方程组正确的是( )
A .⎩⎨⎧=-=+23b a b a
B .⎩⎨⎧=-=+213a b a
C .⎩⎨⎧=-=-212a b a
D .⎩⎨⎧=--=+3
1b a a b a 9、关于x 、y 的二元一次方程组59x y k x y k +=⎧⎨
-=⎩的解也是二元一次方程2x+3y=6的解,
则k 的值是( )
A 、34k =-
B 、34k =
C 、43k =
D 、43
k =- 10、若0)2(32=++-y x ,则2)(y x +的值是( )
A .4
B .2
C .1
D .7
11、已知方程组⎩⎨⎧=+=-24by ax by ax ,的解为⎩
⎨⎧==12y x ,则b a 32-的值为( ) A .4 B .6 C .-6 D .-4
12、小刘同学用10元钱买两种不同的贺卡共8张,单价分别是1元和2元,设1元的贺卡为x 张,2元的贺卡为y 张,那么x 与y 所适合的方程组是( )
A .⎪⎩⎪⎨⎧=+=+10218y x y x
B .⎪⎩⎪⎨⎧=+=+10
28102y x y x C .⎩⎨⎧=+=+8210y x y x D .⎩⎨⎧=+=+1028y x y x 13、已知A ∠,B ∠互余,A ∠比B ∠大300,设A ∠,B ∠的度数分别为x 和y ,下列方程组符合题意的是( )
A .⎩⎨⎧-==+30180y x y x
B .⎩
⎨⎧+==+30180y x y x C .⎩⎨⎧+==+3090y x y x D .⎩⎨⎧-==+3090y x y x 14、已知方程组214211mx y n x x ny m y +==⎧⎧⎨
⎨-=-=-⎩⎩的解是,那么,m ,n 的值是( ) A .1233...1121m m m m B C D n n n n ====⎧⎧⎧⎧⎨⎨⎨⎨=-===⎩⎩⎩⎩
二、填空题(每小题2分,共26分)
1、在方程235=+y x 中,用含有x 的代数式表示y =_______________,用含有y 的代数式表示x =___________
2、若方程1132123=+--b a y x 是二元一次方程,则________________,==b a .
3、若a>b ,则ac 2_______bc 2.
4、若⎩⎨⎧=-=1
1y x 是方程02195=-+k y x 的解,则k =___________ 5、若a<b ,那么-2a+9_____-2b+9(填“>”“<”或“=”).
6、若方程组的解为⎩⎨⎧==2
4y x ,则写出这个方程组为______________
7、在等式b kx y +=中,当2=x 时,1=y ;当1=x 时,1-=y 则_______,==b k
8、如图所示,数轴上所表示的不等式组的解集分别是:
(1)_________ (2)__________ (3)___________ (4)___________
9、当k________时,关于x 的方程2x-3=3k 的解为正数.
10、若关于x ,y 的方程ax -3y =2有一个解就是⎩
⎨⎧=+=+021y x y x 的解,则a 的值是 。
11、一个长方形的周长为40 cm ,长比宽多5cm ,设长为x cm ,宽为y cm ,可列二元一次方程组:____________
12、一个长方形的一边为x 米,另一边为50米,如果它的周长不小于280米,那么x 应满足的不等式为 。
13、某单位购买甲乙两种纯净水共用250元,其中甲种水每桶8元,乙种水每桶6元,且购买乙种水的桶数是甲种水桶数的75%,设购买甲种水x 桶,购买乙种水y 桶,则所列方程组是_______________
三、解答题(共66分)
1、解二元一次方程组(16分、每题4分)
(1)⎩⎨
⎧=+-=722y x x y (2)⎩⎨⎧=+=-3
1b a b a
(3)⎩⎨⎧=+-=-1223532y x y x (4)⎪⎩⎪⎨⎧-=-=+1
22123y x y x
2、解下列不等式和不等式组,并把结果表示到数轴上(16分、每题4分)
(1) )21(3)35(2x x x --≤+ (2).
04
15212<---x x
(3)⎪⎩
⎪⎨⎧-≥-+<+51221)1(345x x x x (4).⎩⎨⎧-<-<-2235x x
3、已知x ,y 满足方程组⎩⎨
⎧-=+=+1
353y x y x ,求代数式y x -的值(8分)
4、已知方程组⎩
⎨⎧=+-=+2212y x m y x 的解x 、y 满足x +y >0,求m 的取值范围(8分)
5、某单位举行茶话会,如果每桌12人,还有一桌空着;如果每桌10人,则还差两个桌子,问共有多少人,准备了多少桌子?(9分)
6、某停车场的收费标准如下:中型汽车的停车费为6元/辆,小型汽车的停车费为4元/辆,现在停车场有50辆中、小型汽车,这些车共缴纳停车费230元,,问中、小型汽车各有多少辆?(9分)。
