离散型随机变量的方差教案教学内容
离散型随机变量的方差教案

离散型随机变量的方差教案第一章:离散型随机变量的概念1.1 离散型随机变量的定义介绍离散型随机变量的概念通过实例解释离散型随机变量的特点1.2 离散型随机变量的概率分布介绍离散型随机变量的概率分布的概念解释概率分布表的编制方法1.3 离散型随机变量的期望值介绍离散型随机变量的期望值的概念解释期望值的计算方法第二章:方差的概念2.1 方差的定义介绍方差的概念解释方差在概率论和统计学中的重要性2.2 方差的计算公式介绍离散型随机变量的方差计算公式解释公式中各参数的含义和计算方法2.3 方差的性质和特点介绍方差的性质和特点通过实例解释方差的应用和意义第三章:方差的估计3.1 方差的点估计介绍方差的点估计的概念解释如何通过样本数据来估计总体方差3.2 方差的区间估计介绍方差的区间估计的概念解释如何计算方差的置信区间3.3 方差的假设检验介绍方差的假设检验的概念解释如何利用样本数据进行方差的假设检验第四章:方差的应用4.1 方差在数据分析中的应用介绍方差在数据分析中的应用通过实例解释方差在数据分析中的作用和方法4.2 方差在质量控制中的应用介绍方差在质量控制中的应用通过实例解释方差在质量控制中的作用和方法4.3 方差在其他领域的应用介绍方差在其他领域的应用通过实例解释方差在其他领域中的作用和方法第五章:方差的进一步研究5.1 方差的优化和调整介绍方差的优化和调整的方法解释如何通过优化和调整方差来改善数据的质量和可靠性5.2 方差的分解和组合介绍方差的分解和组合的方法解释如何通过分解和组合方差来分析数据的结构和关系5.3 方差的比较和分析介绍方差的比较和分析的方法解释如何通过比较和分析方差来评估数据的差异和相似性第六章:方差与标准差的关系6.1 标准差的概念介绍标准差的概念解释标准差与方差的关系6.2 标准差的计算介绍标准差的计算方法解释如何通过方差计算标准差6.3 标准差的应用介绍标准差在数据分析中的应用通过实例解释标准差在数据分析中的作用和方法第七章:方差的假设检验7.1 方差的假设检验概述介绍方差的假设检验的基本概念解释方差假设检验的目的和方法7.2 单样本方差检验介绍单样本方差检验的方法解释如何进行单样本方差检验7.3 双样本方差检验介绍双样本方差检验的方法解释如何进行双样本方差检验第八章:方差的实际案例分析8.1 案例一:产品质量检验介绍一个产品质量检验的案例解释如何利用方差分析产品质量的稳定性8.2 案例二:金融市场分析介绍一个金融市场分析的案例解释如何利用方差分析金融市场的风险性8.3 案例三:教育成果评估介绍一个教育成果评估的案例解释如何利用方差分析教育成果的差异性第九章:方差的软件实现9.1 方差分析软件介绍介绍常用的方差分析软件解释如何使用这些软件进行方差分析9.2 方差分析软件操作实例通过实例演示如何使用方差分析软件进行数据分析解释软件操作的步骤和注意事项9.3 方差分析软件的结果解读介绍如何解读方差分析软件的结果解释结果中的各个指标的含义和作用10.1 方差的概念和作用强调方差在数据分析中的重要性10.2 方差的计算和应用强调方差在不同领域的应用价值10.3 方差分析的发展趋势展望方差分析的发展趋势强调方差分析在未来的应用前景重点和难点解析第一章:离散型随机变量的概念重点关注离散型随机变量的定义及其特点,理解概率分布的概念和编制方法。
离散型随机变量的方差优秀教学设计

离散型随机变量的方差【教学目标】: 1.了解离散型随机变量的方差、标准差的意义,会根据离散型随机变量的分布列求出方差或标准差。
2.了解方差公式“D (a ξ+b )=a2D ξ”,以及“若ξ~Β(n ,p ),则D ξ=np (1—p )”,并会应用上述公式计算有关随机变量的方差【教学重点】离散型随机变量的方差、标准差【教学难点】比较两个随机变量的期望与方差的大小,从而解决实际问题【授课类型】新授课【课时安排】2课时【教学准备】多媒体、实物投影仪【内容分析】数学期望是离散型随机变量的一个特征数,它反映了离散型随机变量取值的平均水平,表示了随机变量在随机实验中取值的平均值,所以又常称为随机变量的平均数、均值。
今天,我们将对随机变量取值的稳定与波动、集中与离散的程度进行研究。
其实在初中我们也对一组数据的波动情况作过研究,即研究过一组数据的方差。
回顾一组数据的方差的概念:设在一组数据1x ,2x ,…,n x 中,各数据与它们的平均值x得差的平方分别是21)(x x -,22)(x x -,…,2)(x x n -,那么[12nS =21)(x x -+22)(x x -+…+])(2x x n -叫做这组数据的方差【教学过程】一、复习引入:1.随机变量:如果随机试验的结果可以用一个变量来表示,那么这样的变量叫做随机变量随机变量常用希腊字母ξ、η等表示2. 离散型随机变量:对于随机变量可能取的值,可以按一定次序一一列出,这样的随机变量叫做离散型随机变量3.连续型随机变量: 对于随机变量可能取的值,可以取某一区间内的一切值,这样的变量就叫做连续型随机变量4.离散型随机变量与连续型随机变量的区别与联系: 离散型随机变量与连续型随机变量都是用变量表示随机试验的结果;但是离散型随机变量的结果可以按一定次序一一列出,而连续性随机变量的结果不可以一一列出5. 分布列:6. i 12+ (1)7.二项分布:ξ~B (n ,p ),并记kn k k n q p C -=b (k ;n ,p )。
高三数学 第74课时 离散型随机变量的期望与方差教案

课题:离散型随机变量的期望与方差教学目标:了解离散型随机变量的期望值、方差的意义,会根据离散型随机变量的分布列求出期望值、方差.(一) 主要知识及主要方法:1.数学期望:则称 =ξE 11p x 22…n n … 为ξ的数学期望,简称期望2.数学期望是离散型随机变量的一个特征数,它反映了离散型随机变量取值的平均水平3.平均数、均值:一般地,在有限取值离散型随机变量ξ的概率分布中,令=1p =2p …n p =,则有=1p =2p …1n n p ==,=ξE +1(x +2x …1)n n x +⨯,所以ξ的数学期望又称为平均数、均值 .4.期望的一个性质:若b a +=ξη,则b aE b a E +=+ξξ)(5.方差: 对于离散型随机变量ξ,如果它所有可能取的值是1x ,2x ,…,n x ,…, 且取这些值的概率分别是1p ,2p ,…,n p ,…,那么,ξD =121)(p E x ⋅-ξ+222)(p E x ⋅-ξ+…+n n p E x ⋅-2)(ξ+…称为随机变量ξ的均方差,简称为方差,式中的ξE 是随机变量ξ的期望. 6.标准差:ξD 的算术平方根ξD 叫做随机变量ξ的标准差,记作σξ 7.方差的性质:()1 ξξD a b a D 2)(=+;()2 22)(ξξξE E D -= .8.方差的意义:()1随机变量ξ的方差的定义与一组数据的方差的定义式是相同的; ()2随机变量ξ的方差、标准差也是随机变量ξ的特征数,它们都反映了随机变量取值的稳定与波动、集中与离散的程度;()3标准差与随机变量本身有相同的单位,所以在实际问题中应用更广泛.9.二项分布的期望与方差:若(),B n p ξ,则E np ξ= ,()1D np p ξ=-10.几何分布的期望和方差:若(),g k p 1k qp -=,其中0,1,2k =,…, p q -=1.则1E p ξ=,21p D pξ-=. (二)典例分析:问题1.()1(07浙江)随机变量ξ的分布列如右: 其中a b c ,,成等差数列,若13E ξ=,则D ξ的值是()2设ξ是一个离散型随机变量,其分布列如下表, 则E ξ ,则D ξ=()3(07重庆联考) 随机变量ξ的分布列如右:那么()54E ξ+等于.A 15 .B 11 .C 2.2 .D 2.3()4(07黄岗调研)已知()~,B n p ξ,8E ξ=, 1.6D ξ=,则n 与p 的值分别为.A 100和0.08 .B 20和0.4 .C 10和0.2 .D 10和0.8()5(07天津十校联考)某一离散型随机变量ξ的概率分布如下表,且 1.5E ξ=,则a b -的值为:.A 0.1- .B 0 .C 0.1 .D 0.2()6(06四川) 设离散型随机变量ξ可能取的值为1,2,3,4,()P k ak b ξ==+ (1,2,3,4k =),又ξ的数学期望3E ξ=,则a b +=问题2.设随机变量ξ的分布列如右表,求E ξ和D ξ.问题3.有甲、乙两种建筑材料,从中各取等量的样品检验它们的抗拉强度指数如下:其中ξ和η分别表示甲、乙两种材料的抗拉强度,在使用时要求抗拉强度不低于120的条件下,比较甲、乙两种材料哪一种稳定性好.问题4.(06全国Ⅱ)某批产品成箱包装,每箱5件.一用户在购进该批产品前先取出3箱,再从每箱中任意抽取2件产品进行检验.设取出的第一、二、三箱中分别有0件、1件、2件二等品,其余为一等品.()1用ξ表示抽检的6件产品中二等品的件数,求ξ的分布列及ξ的数学期望;()2若抽检的6件产品中有2件或2件以上二等品,用户就拒绝购买这批产品,求这批产品级用户拒绝的概率.问题5.(07辽宁)某企业准备投产一批特殊型号的产品,已知该种产品的成本C 与产量q的函数关系式为:3232010(0)3q C q q q =-++> 该种产品的市场前景无法确定,有三种可能出现的情况,各种情形发生的概率及产品价格设123分别表示市场情形好、中差时的利润,随机变量q ,表示当产量为,而市场前景无法确定的利润.()1分别求利润123L L L ,,与产量q 的函数关系式;()2当产量q 确定时,求期望q E ξ;()3试问产量q 取何值时,q E ξ取得最大值.(三)课后作业1.已知ξ的分布列为如右表:则E ξ= ,D ξ=2.抛掷一颗骰子,设所得点数为ξ,则E ξ= ,D ξ=3.设服从二项分布(),B n p 的随机变量ξ的期望和方差分别为2.4和1.44,则二项分布的参数,n p 的值为 .A 4n =,0.6p = .B 6n =,0.4p =.C 8n =,0.3p = .D 24n =,0.1p =(四)走向高考:4.(06福建)一个均匀小正方体的6个面中,三个面上标以数0,两个面上标以数1,一 个面上标以数2.将这个小正方体抛掷2次,则向上的数之积的数学期望是5.(07四川文)某商场买来一车苹果,从中随机抽取了10个苹果,其重量(单位:克) 分别为:150,152,153,149,148,146,151,150,152,147,由此估计这车苹果单个重量的期望值是 .A 150.2克 .B 149.8克 .C 149.4克 .D 147.8克6.(07湖南)某地区为下岗人员免费提供财会和计算机培训,以提高下岗人员的再就业能力,每名下岗人员可以选择参加一项培训、参加两项培训或不参加培训,已知参加过财会培训的有60%,参加过计算机培训的有75%,假设每个人对培训项目的选择是相互独立的,且各人的选择相互之间没有影响.()1任选1名下岗人员,求该人参加过培训的概率;()2任选3名下岗人员,记ξ为3人中参加过培训的人数,求ξ的分布列和期望.7.(07四川)厂家在产品出厂前,需对产品做检验,厂家将一批产品发给商家时,商家按合同规定也需随机抽取一定数量的产品做检验,以决定是否接收这批产品.()1若厂家库房中的每件产品合格的概率为0.8,从中任意取出4件进行检验.求至少有1件是合格品的概率;()2若厂家发给商家20件产品,其中有3件不合格,按合同规定该商家从中任取2件,都进行检验,只有2件都合格时才接收这批产品,否则拒收.求该商家可能检验出不合格产E,并求该商家拒收这批产品的概率.品数ξ的分布列及期望ξ。
离散型随机变量方差的教案

离散型随机变量方差的教案教案标题:离散型随机变量方差的教案一、教学目标:1. 理解离散型随机变量的概念和特点。
2. 掌握求离散型随机变量方差的方法和步骤。
3. 能够应用所学知识解决相关问题。
二、教学重点和难点:1. 离散型随机变量的方差计算方法。
2. 离散型随机变量方差计算的实际应用。
三、教学内容和步骤:1. 离散型随机变量的概念和特点介绍(10分钟)- 介绍离散型随机变量的定义和特点,以及其在实际问题中的应用。
2. 离散型随机变量方差的定义和计算方法(15分钟)- 介绍离散型随机变量方差的定义和计算公式。
- 通过具体的例子演示方差的计算步骤和方法。
3. 离散型随机变量方差计算的实际应用(15分钟)- 结合实际问题,引导学生应用所学知识计算离散型随机变量的方差。
- 引导学生分析和讨论方差在实际问题中的意义和应用。
4. 练习与讨论(10分钟)- 给学生提供一些练习题,让他们在课堂上进行练习并相互讨论。
- 对学生的解题过程和答案进行指导和讨论,帮助他们加深对离散型随机变量方差的理解。
四、教学方法:1. 讲授结合示例:通过具体的例子演示离散型随机变量方差的计算方法,帮助学生理解和掌握知识。
2. 互动讨论:引导学生在课堂上进行讨论和交流,加深对知识点的理解和应用。
3. 练习指导:给学生提供一定数量的练习题,并在课堂上进行指导和讨论,帮助他们巩固所学知识。
五、教学资源:1. 教科书和课件:提供相关的教学材料和示例,帮助学生理解和掌握知识。
2. 练习题和答案:为学生提供一些练习题,帮助他们巩固所学知识。
六、教学评估:1. 课堂练习:通过学生在课堂上的练习情况和讨论表现,评估他们对离散型随机变量方差的掌握程度。
2. 作业和考试:布置相关的作业和考试题目,检验学生对所学知识的掌握情况。
七、教学反思:根据学生在课堂上的学习情况和表现,及时调整教学方法和内容,帮助他们更好地理解和掌握离散型随机变量方差的知识。
离散型随机变量的方差教案 说课稿 教学设计

离散型随机变量的方差●三维目标1.知识与技能(1)理解取有限个值的离散型随机变量的方差及标准差的概念和意义.(2)能计算简单离散型随机变量的方差和标准差,并能解决一些实际问题.(3)掌握方差的性质,会求两点分布、二项分布的方差.2.过程与方法通过具体实例,理解离散型随机变量方差的概念、公式及意义,在解决实际问题的过程中,掌握解决此类问题的方法与步骤.3.情感、态度与价值观体会数学的应用价值,提高理论联系实际问题的能力.●重点、难点重点:离散型随机变量方差的公式及根据分布列求方差.难点:方差的实际应用.教学时要抓知识选择的切入点,从学生原有的认知水平和所需的知识特点入手,引导学生结合初中学习过的方差知识,类比、观察、分析得到新的方差的概念、性质及如何根据分布列求方差,从而突出重点,通过例题与练习来化解难点.●教学建议本节内容安排在均值之后,是刻画随机变量稳定性的工具,也是对学习过的样本方差的直接延伸,教学时引导学生类比样本方差的定义给出随机变量方差的定义,让学生探究它们的联系与区别,要注意对随机变量的方差和标准差概念、含义的解释,让学生在探究中加深对概念的理解.●教学流程创设问题情境,提出问题.⇒引导学生回答问题,理解离散型随机变量方差的概念、性质及公式.⇒通过例1及变式训练,掌握离散型随机变量的方差、标准差的求法.⇒通过例2及互动探究,使学生掌握离散型随机变量的方差的性质.⇒通过例3及变式训练,使学生掌握均值、方差的综合应用.⇒归纳整理,进行课堂小结,从整体认识所学知识.⇒完成当堂双基达标,巩固所学知识,并进行反馈、矫正.离散型随机变量的方差A ,B 两台机床同时加工零件,每生产一批数量较大的产品时,出次品的概率如下表:A 机床次品数X 10 1 2 3 P0.70.20.060.04B 机床次品数X 20 1 2 3 P0.80.060.040.10(1)试求E (X 1),E 2(2)由E (X 1)和E (X 2)的值能比较两台机床的产品质量吗? (3)试想利用什么指标可以比较加工质量?【提示】 (1)E (X 1)=0×0.7+1×0.2+2×0.06+3×0.04=0.44, E (X 2)=0×0.8+1×0.06+2×0.04+3×0.10=0.44. (2)不能.(3)样本方差.1.离散型随机变量的方差、标准差 (1)定义:设离散型随机变量X 的分布列为X x 1 x 2 … x i … x n Pp 1p 2…p i…p n则(x i -E (X ))2描述了x i (i =1,2,…,n )相对于均值E (X )的偏离程度,而D (X )=∑i =1n(x i -E (X ))2p i 为这些偏离程度的加权平均,刻画了随机变量X 与其均值E (X )的平均偏离程度.称D (X )为随机变量X 的方差,其算术平方根D (X )为随机变量X 的标准差.(2)意义:随机变量的方差和标准差都反映了随机变量取值偏离于均值的平均程度.方差或标准差越小,则随机变量偏离于均值的平均程度越小.(3)离散型随机变量方差的性质: 设a ,b 为常数,则D (aX +b )=a 2D (X ). 2.服从两点分布与二项分布的随机变量的方差(1)若X 服从两点分布,则D (X )=p (1-p );(2)若X ~B (n ,p ),则D (X )=np (1-p ).求离散型随机变量的方差、标准差已知离散型随机变量X 1的概率分布为X 1 1 2 3 4 5 6 7 P17171717171717离散型随机变量X 2的概率分布为X 2 3.7 3.8 3.9 4 4.1 4.2 4.3 P17171717171717求这两个随机变量的均值、方差与标准差.【思路探究】 直接利用离散型随机变量的均值和方差公式求解. 【自主解答】 E (X 1)=1×17+2×17+…+7×17=4;D (X 1)=(1-4)2×17+(2-4)2×17+…+(7-4)2×17=4;D (X 1)=2.E (X 2)=3.7×17+3.8×17+…+4.3×17=4;D (X 2)=(3.7-4)2×17+(3.8-4)2×17+(3.9-4)2×17+(4-4)2×17+(4.1-4)2×17+(4.2-4)2×17+(4.3-4)2×17=0.04;D (X 2)=0.2.1.本题已知分布列求均值、方差和标准差,属较容易题,套用公式即可完成. 2.给出分布列求方差时,首先要求均值,然后再求方差和标准差,要注意公式应用要准确.离散型随机变量的方差的性质及应用已知η的分布列为:η 0 10 20 50 60 P1325115215115(1)求方差及标准差; (2)设Y =2η-E (η),求D (Y ).【思路探究】 (1)利用方差公式求解,首先求出均值E (η),然后利用D (η)定义求方差;(2)由于E (η)是一个常数,所以D (Y )=D (2η-E (η))=22D (η).【自主解答】 (1)∵E (η)=0×13+10×25+20×115+50×215+60×115=16,D (η)=(0-16)2×13+(10-16)2×25+(20-16)2×115+(50-16)2×215+(60-16)2×115=384,∴D (η)=8 6. (2)∵Y =2η-E (η), ∴D (Y )=D (2η-E (η)) =22D (η)=4×384=1 536.1.对于变量间存在关系的方差,在求解过程中应注意方差性质的应用,如D (aξ+b )=a 2D (ξ),这样处理既避免了求随机变量η=aξ+b 的分布列,又避免了繁杂的计算,简化了计算过程.2.若ξ~B (n ,p ),则D (ξ)=np (1-p ),若ξ服从两点分布,则D (ξ)=p (1-p ),其中p 为成功概率,应用上述性质可大大简化解题过程.将本例的分布列改为η 1 2 3 4 5 P0.10.20.40.20.1【解】 (1)∵E (η)=1×0.1+2×0.2+3×0.4+4×0.2+5×0.1=3,∴D (η)=(1-3)2×0.1+(2-3)2×0.2+(3-3)2×0.4+(4-3)2×0.2+(5-3)2×0.1=1.2, ∴D (η)= 1.2. (2)∵Y =2η-E (η)∴D(Y)=D(2η-Eη)=22D(η)=4×1.2=4.8.方差的实际应用有甲、乙两种建筑材料,从中各取等量样品检查它们的抗拉强度如下:ξA110120125130135P 0.10.20.40.10.2ξB100115125130145P 0.10.20.40.10.2其中,ξA,ξB分别表示甲、乙两种材料的抗拉强度,在使用时要求抗拉强度不低于120,试比较甲、乙两种建筑材料的稳定程度(哪一个的稳定性较好).【思路探究】要比较两种材料的质量,需先比较其抗拉强度的期望,然后再看其方差值.【自主解答】E(ξA)=110×0.1+120×0.2+125×0.4+130×0.1+135×0.2=125.E(ξB)=100×0.1+115×0.2+125×0.4+130×0.1+145×0.2=125.D(ξA)=0.1×(110-125)2+0.2×(120-125)2+0.4×(125-125)2+0.1×(130-125)2+0.2×(135-125)2=50.D(ξB)=0.1×(100-125)2+0.2×(115-125)2+0.4×(125-125)2+0.1×(130-125)2+0.2×(145-125)2=165.由此可见,E(ξA)=E(ξB),D(ξA)<D(ξB),故两种材料的抗拉强度的平均值相等,其稳定程度材料乙明显不如材料甲,即甲的稳定性好.1.本题采用比较分析法,通过比较两个随机变量的均值和方差得出结论.2.均值体现了随机变量取值的平均大小,在两种产品相比较时,只比较均值往往是不恰当的,还需比较它们的取值的离散程度,即通过比较方差,才能准确地得出更恰当的判断.。
离散型随机变量的方差教案

教案:离散型随机变量的方差教学目标:1. 理解离散型随机变量的概念;2. 掌握方差的定义和计算方法;3. 能够运用方差分析数据的不均匀程度。
教学内容:一、离散型随机变量的概念1. 引入随机变量的概念,引导学生理解随机变量是随机现象的结果;2. 讲解离散型随机变量的定义,强调其取值有限且可数的特点;3. 通过实例让学生了解离散型随机变量的具体应用。
二、方差的定义1. 引入方差的概念,引导学生理解方差是衡量数据分散程度的指标;2. 讲解方差的计算公式,强调方差等于各个数据与平均数差的平方的平均数;3. 通过实例让学生了解方差的计算过程。
三、方差的计算方法1. 讲解如何计算离散型随机变量的方差,强调先求平均数,再求各个数据与平均数差的平方的平均数;2. 通过实例让学生掌握方差的计算步骤;3. 引导学生运用数学软件或工具进行方差的计算。
四、方差的应用1. 讲解方差在实际应用中的重要性,如统计学、经济学、自然科学等领域;2. 通过实例让学生了解如何运用方差分析数据的不均匀程度,如判断数据的分布情况、比较不同数据的离散程度等;3. 引导学生运用方差进行数据分析,培养学生的实际应用能力。
五、总结与练习1. 总结本节课的主要内容,让学生掌握离散型随机变量的概念、方差的定义和计算方法及其应用;2. 布置练习题,让学生巩固所学内容,提高解题能力。
教学资源:1. 离散型随机变量的定义和方差的计算方法的相关教材或教辅;2. 数学软件或工具,如Excel、MATLAB等;3. 实例数据,如统计数据、经济数据等。
教学评价:1. 学生能正确理解离散型随机变量的概念;2. 学生能熟练运用方差的计算方法计算离散型随机变量的方差;3. 学生能运用方差分析数据的不均匀程度,解决问题。
教案:离散型随机变量的方差(续)教学内容:六、方差的性质1. 讲解方差的性质,包括对称性、非负性、不变性和可加性等;2. 通过实例让学生了解方差的性质在实际应用中的作用;3. 引导学生运用方差的性质进行数据分析。
离散型随机变量的方差说课稿 教案 教学设计
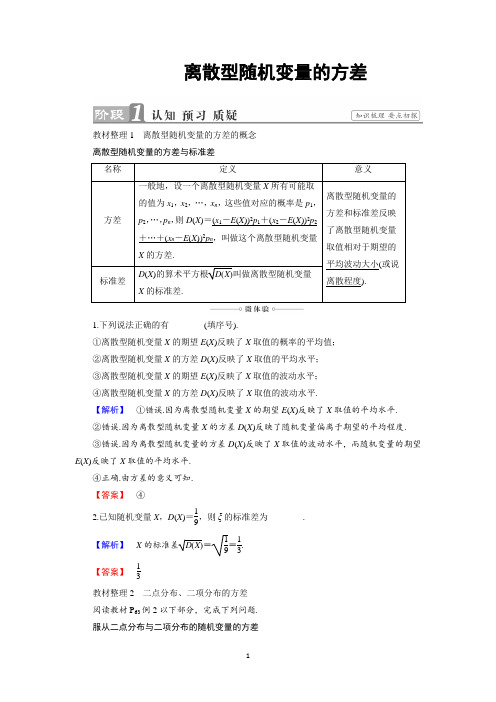
离散型随机变量的方差教材整理1 离散型随机变量的方差的概念 离散型随机变量的方差与标准差 名称定义意义方差一般地,设一个离散型随机变量X 所有可能取的值为x 1,x 2,…,x n ,这些值对应的概率是p 1,p 2,…,p n ,则D (X )=(x 1-E (X ))2p 1+(x 2-E (X ))2p 2+…+(x n -E (X ))2p n ,叫做这个离散型随机变量X 的方差.离散型随机变量的方差和标准差反映了离散型随机变量取值相对于期望的平均波动大小(或说离散程度).标准差D (X )的算术平方根D (X )叫做离散型随机变量X 的标准差.1.下列说法正确的有________(填序号).①离散型随机变量X 的期望E (X )反映了X 取值的概率的平均值; ②离散型随机变量X 的方差D (X )反映了X 取值的平均水平; ③离散型随机变量X 的期望E (X )反映了X 取值的波动水平; ④离散型随机变量X 的方差D (X )反映了X 取值的波动水平.【解析】 ①错误.因为离散型随机变量X 的期望E (X )反映了X 取值的平均水平. ②错误.因为离散型随机变量X 的方差D (X )反映了随机变量偏离于期望的平均程度. ③错误.因为离散型随机变量的方差D (X )反映了X 取值的波动水平,而随机变量的期望E (X )反映了X 取值的平均水平.④正确.由方差的意义可知. 【答案】 ④2.已知随机变量X ,D (X )=19,则ξ的标准差为________.【解析】 X 的标准差D (X )=19=13. 【答案】 13教材整理2 二点分布、二项分布的方差 阅读教材P 63例2以下部分,完成下列问题. 服从二点分布与二项分布的随机变量的方差(1)若X 服从二点分布,则D (X )=p (1-p ); (2)若X ~B (n ,p ),则D (X )=np (1-p ).若随机变量X 服从二点分布,且成功概率P =0.5,则D (X )=________,E (X )=________. 【解析】 E (X )=0.5,D (X )=0.5(1-0.5)=0.25. 【答案】 0.25 0.5离散型随机变量的方差的性质及应用设在12个同类型的零件中有2个次品,抽取3次进行检验,每次抽到一个,并且取出后不再放回,若以X 和Y 分别表示取出次品和正品的个数.(1)求X 的分布列、期望及方差; (2)求Y 的分布列、期望及方差.【精彩点拨】 (1)可先求出X 分布列,然后利用期望和方差公式求解;(2)可由Y 分布列及其期望、方差、公式求解,也可由期望、方差性质求解.【自主解答】 (1)X 的可能取值为0,1,2.若X =0,表示没有取出次品,其概率为P (X =0)=C 310C 312=611,同理,有P (X =1)=C 12C 210C 312=922, P (X =2)=C 22C 110C 312=122.∴X 的分布列为X 0 1 2 P611922122∴E (X )=0×611+1×922+2×122=12,D (X )=⎝⎛⎭⎫0-122×611+⎝⎛⎭⎫1-122×922+⎝⎛⎭⎫2-122×122=322+988+988=1544. (2)Y 的可能取值为1,2,3,显然X +Y =3. 法一:P (Y =1)=P (X =2)=122, P (Y =2)=P (X =1)=922,P (Y =3)=P (X =0)=611,∴Y 的分布列为Y 1 2 3 P122922611E (Y )=1×122+2×922+3×611=52,D (Y )=⎝⎛⎭⎫1-522×122+⎝⎛⎭⎫2-522×922+⎝⎛⎭⎫3-522×611=1544. 法二:E (Y )=E (3-X )=3-E (X )=52,D (Y )=D (3-X )=(-1)2D (X )=1544.1.由本例可知,利用公式D (aX +b )=a 2D (X )及E (aX +b )=aE (X )+b 来求E (Y )及D (Y ),既避免了求随机变量Y =aX +b 的分布列,又避免了涉及大数的计算,从而简化了计算过程.2.若X ~B (n ,p ),则D (X )=np (1-p ),若X 服从二点分布,则D (X )=p (1-p ),其中p 为成功概率,应用上述性质可大大简化解题过程.[再练一题]1.为防止风沙危害,某地政府决定建设防护绿化带,种植杨树、沙柳等植物.某人一次种植了n 株沙柳,已知各株沙柳成活与否是相互独立的,成活率为p ,设X 为成活沙柳的株数,已知E (X )=3,D (X )=32,求n ,p 的值.【解】 由题意知,X 服从二项分布B (n ,p ), 由E (X )=np =3,D (X )=np (1-p )=32,得1-p =12,∴p =12,n =6.求离散型随机变量的方差、标准差编号为1,2,3的三位学生随意入座编号为1,2,3的三个座位,每位学生坐一个座位,设与座位编号相同的学生的人数是ξ,求E (ξ)和D (ξ).【精彩点拨】 首先确定ξ的取值,然后求出ξ的分布列,进而求出E (ξ)和D (ξ)的值. 【自主解答】 ξ的所有可能取值为0,1,3,ξ=0表示三位同学全坐错了,有2种情况,即编号为1,2,3的座位上分别坐了编号为2,3,1或3,1,2的学生,则P (ξ=0)=2A 33=13;ξ=1表示三位同学只有1位同学坐对了. 则P (ξ=1)=C 13A 33=12;ξ=3表示三位学生全坐对了,即对号入座, 则P (ξ=3)=1A 33=16.所以,ξ的分布列为ξ 0 1 3 P131216E (ξ)=0×13+1×12+3×16=1;D (ξ)=13×(0-1)2+12×(1-1)2+16×(3-1)2=1.求离散型随机变量的方差的类型及解决方法1.已知分布列型(非二点分布或二项分布):直接利用定义求解,具体如下, (1)求均值;(2)求方差.2.已知分布列是二点分布或二项分布型:直接套用公式求解,具体如下, (1)若X 服从二点分布,则D (X )=p (1-p ). (2)若X ~B (n ,p ),则D (X )=np (1-p ).3.未知分布列型:求解时可先借助已知条件及概率知识求得分布列,然后转化成(1)中的情况.4.对于已知D (X )求D (aX +b )型,利用方差的性质求解,即利用D (aX +b )=a 2D (X )求解.[再练一题]2.有10张卡片,其中8张标有数字2,2张标有数字5,从中随机地抽取3张卡片,设3张卡片数字之和为ξ,求E (ξ)和D (ξ).【解】 这3张卡片上的数字之和为ξ,这一变量的可能取值为6,9,12.ξ=6表示取出的3张卡片上均标有2,则P (ξ=6)=C 38C 310=715.ξ=9表示取出的3张卡片上两张标有2,一张标有5,则P (ξ=9)=C 28C 12C 310=715.ξ=12表示取出的3张卡片上一张标有2,两张标有5,则P (ξ=12)=C 18C 22C 310=115.∴ξ的分布列为ξ 6 9 12 P715715115∴E (ξ)=6×715+9×715+12×115=7.8.D (ξ)=(6-7.8)2×715+(9-7.8)2×715+(12-7.8)2×115=3.36.期望、方差的综合应用探究1 A ,B 两台机床同时加工零件,每生产一批数量较大的产品时,出次品的概率如下表:A 机床次品数X 10 1 2 3 P0.70.2 0.060.04B 机床次品数X 20 1 2 3 P0.80.060.040.10试求E (X 1),E (X 2).【提示】 E (X 1)=0×0.7+1×0.2+2×0.06+3×0.04=0.44. E (X 2)=0×0.8+1×0.06+2×0.04+3×0.10=0.44.探究2 在探究1中,由E (X 1)和E (X 2)的值能比较两台机床的产品质量吗?为什么? 【提示】 不能.因为E (X 1)=E (X 2).探究3 在探究1中,试想利用什么指标可以比较A 、B 两台机床加工质量? 【提示】 利用样本的方差.方差越小,加工的质量越稳定.甲、乙两名射手在一次射击中得分为两个相互独立的随机变量ξ,η,已知甲、乙两名射手在每次射击中射中的环数大于6环,且甲射中10,9,8,7环的概率分别为0.5,3a ,a,0.1,乙射中10,9,8环的概率分别为0.3,0.3,0.2.(1)求ξ,η的分布列;(2)求ξ,η的数学期望与方差,并以此比较甲、乙的射击技术.【精彩点拨】 (1)由分布列的性质先求出a 和乙射中7环的概率,再列出ξ,η的分布列.(2)要比较甲、乙两射手的射击水平,需先比较两射手击中环数的数学期望,然后再看其方差值.【自主解答】(1)由题意得:0.5+3a+a+0.1=1,解得a=0.1.因为乙射中10,9,8环的概率分别为0.3,0.3,0.2.所以乙射中7环的概率为1-(0.3+0.3+0.2)=0.2.所以ξ,η的分布列分别为ξ10987P 0.50.30.10.1η10987P 0.30.30.20.2(2)由(1)得:E(ξ)=10×0.5+9×0.3+8×0.1+7×0.1=9.2;E(η)=10×0.3+9×0.3+8×0.2+7×0.2=8.7;D(ξ)=(10-9.2)2×0.5+(9-9.2)2×0.3+(8-9.2)2×0.1+(7-9.2)2×0.1=0.96;D(η)=(10-8.7)2×0.3+(9-8.7)2×0.3+(8-8.7)2×0.2+(7-8.7)2×0.2=1.21.由于E(ξ)>E(η),D(ξ)<D(η),说明甲射击的环数的均值比乙高,且成绩比较稳定,所以甲比乙的射击技术好.利用均值和方差的意义分析解决实际问题的步骤1.比较均值.离散型随机变量的均值反映了离散型随机变量取值的平均水平,因此,在实际决策问题中,需先计算均值,看一下谁的平均水平高.2.在均值相等的情况下计算方差.方差反映了离散型随机变量取值的稳定与波动、集中与离散的程度.通过计算方差,分析一下谁的水平发挥相对稳定.3.下结论.依据方差的几何意义做出结论.[再练一题]3.甲、乙两个野生动物保护区有相同的自然环境,且野生动物的种类和数量也大致相等.两个保护区内每个季度发现违反保护条例的事件次数的分布列分别为:甲保护区:X 0123P 0.30.30.20.2乙保护区:Y 012P 0.10.50.4【解】甲保护区的违规次数X的数学期望和方差分别为:E(X)=0×0.3+1×0.3+2×0.2+3×0.2=1.3;D(X)=(0-1.3)2×0.3+(1-1.3)2×0.3+(2-1.3)2×0.2+(3-1.3)2×0.2=1.21.乙保护区的违规次数Y的数学期望和方差分别为:E(Y)=0×0.1+1×0.5+2×0.4=1.3;D(Y)=(0-1.3)2×0.1+(1-1.3)2×0.5+(2-1.3)2×0.4=0.41.因为E(X)=E(Y),D(X)>D(Y),所以两个保护区内每季度发生的平均违规次数是相同的,但乙保护区内的违规事件次数更集中和稳定,而甲保护区的违规事件次数相对分散,故乙保护区的管理水平较高.。
离散型随机变量的方差教案

教案:离散型随机变量的方差第一章:离散型随机变量的方差概念引入1.1 教学目标1. 了解离散型随机变量的概念;2. 掌握方差的定义和性质;3. 理解方差在实际问题中的应用。
1.2 教学内容1. 离散型随机变量的定义;2. 方差的定义和计算公式;3. 方差的性质和意义;4. 方差在实际问题中的应用案例。
1.3 教学过程1. 引入离散型随机变量的概念,通过实例让学生感受离散型随机变量的特点;2. 讲解方差的定义,通过具体例子让学生理解方差的含义;3. 引导学生掌握方差的计算公式,并进行计算练习;4. 讲解方差的性质,如非负性、齐次性等;5. 结合实际案例,让学生了解方差在数据分析中的应用。
第二章:离散型随机变量的方差计算方法2.1 教学目标1. 掌握离散型随机变量的期望值计算方法;2. 掌握离散型随机变量的方差计算方法;3. 了解离散型随机变量的协方差计算方法。
2.2 教学内容1. 离散型随机变量的期望值计算公式;2. 离散型随机变量的方差计算公式;3. 离散型随机变量的协方差计算公式;4. 期望值、方差、协方差之间的关系。
2.3 教学过程1. 讲解离散型随机变量的期望值计算方法,并通过实例进行计算练习;2. 讲解离散型随机变量的方差计算方法,并通过实例进行计算练习;3. 讲解离散型随机变量的协方差计算方法,并通过实例进行计算练习;4. 引导学生理解期望值、方差、协方差之间的关系。
第三章:离散型随机变量的方差性质3.1 教学目标1. 掌握离散型随机变量的方差性质;2. 了解方差在概率论中的应用;3. 学会运用方差分析实际问题。
3.2 教学内容1. 离散型随机变量的方差性质;2. 方差与其他数学量之间的关系;3. 方差的应用案例。
3.3 教学过程1. 讲解离散型随机变量的方差性质,如非负性、齐次性等;2. 引导学生了解方差与其他数学量之间的关系,如期望值、标准差等;3. 结合实际案例,让学生了解方差在数据分析中的应用;4. 进行方差计算和性质分析的练习。
离散型随机变量的方差教案.docx
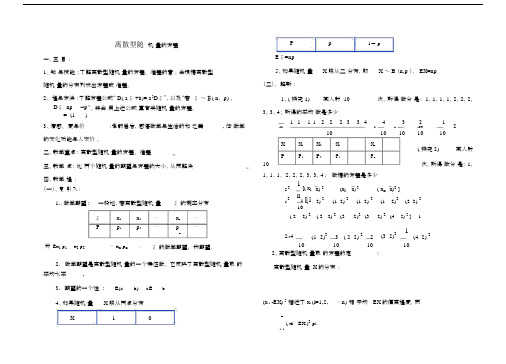
离散型随机量的方差一、三目:1、知与技能:了解离散型随机量的方差、准差的意,会根据离散型随机量的分布列求出方差或准差。
2、程与方法:了解方差公式“ D( aξ +b)= a2Dξ”,以及“若ξ~Β( n, p) ,Dξ np—p”,并会用上述公式算有关随机量的方差。
= (1)3、情感、度与价:承前启后,感悟数学与生活的和之美, 体数学的文化功能与人文价。
二、教学重点:离散型随机量的方差、准差三、教学点:比两个随机量的期望与方差的大小,从而解决四、教学程:(一)、复引入:1.. 数学期望 :一般地,若离散型随机量ξ 的概率分布ξx1x2⋯x n⋯P p1p2⋯p⋯n称 Ex1 p1 x2 p2⋯ x n p n⋯ξ 的数学期望,称期望.2.数学期望是离散型随机量的一个特征数,它反映了离散型随机量取的平均水平3.期望的一个性:E(a b) aE b4、如果随机量X 服从两点分布X10P p1- pEξ=np5、如果随机量X 服从二分布,即X ~ B (n,p ), EX=np(二)、解新:1、( 探究 1)某人射 10次,所得数分是: 1,1,1,1,2,2,2,3,3,4;所得的平均数是多少111122233443212 X10123410101010X X1X2⋯X i⋯X n( 探究 2)某人射P P1P2⋯P i⋯P n次,所得数分是: 1,101,1,1, 2,2,2,3,3,4;数据的方差是多少s21[( x1x) 2(x i x) 2( x n x)2 ]s2n1 [(12) 2(12) 2(12) 2(12)2(22) 210( 22) 2( 22) 2(32)2(32) 2(42) 2 ]1s24(1 2)23( 2 2) 22(3 2)21(4 2) 2101010102、离散型随机量取的方差的定:离散型随机量 X 的分布:(x i -EX) 2描述了 x i (i=1,2,⋯n)相于均EX的偏离程度,而n( x i EX )2 p ii 1X28910 PDX为这些偏离程度的加权平均,刻画了随机变量X 与其均值 EX的平均偏离程度。
离散型随机变量的方差教案

离散型随机变量的方差教案第一章:离散型随机变量的方差概念引入教学目标:1. 让学生理解离散型随机变量的概念。
2. 让学生了解方差的概念及其在概率论中的重要性。
3. 让学生掌握计算离散型随机变量方差的方法。
教学内容:1. 离散型随机变量的定义及其数学表达式。
2. 方差的定义及其数学表达式。
3. 离散型随机变量方差的计算方法。
教学过程:1. 引入离散型随机变量的概念,通过实例让学生理解离散型随机变量的含义。
2. 引入方差的概念,解释方差在概率论中的重要性。
3. 讲解离散型随机变量方差的计算方法,并通过例题让学生掌握计算方法。
教学评估:1. 通过课堂提问,检查学生对离散型随机变量概念的理解。
2. 通过练习题,检查学生对离散型随机变量方差计算方法的掌握。
第二章:离散型随机变量的期望值与方差教学目标:1. 让学生理解离散型随机变量的期望值的概念。
2. 让学生掌握计算离散型随机变量期望值的方法。
3. 让学生理解期望值与方差之间的关系。
教学内容:1. 离散型随机变量的期望值的定义及其数学表达式。
2. 离散型随机变量期望值的计算方法。
3. 期望值与方差之间的关系。
教学过程:1. 引入离散型随机变量的期望值的概念,通过实例让学生理解期望值的含义。
2. 讲解离散型随机变量期望值的计算方法,并通过例题让学生掌握计算方法。
3. 讲解期望值与方差之间的关系,并通过例题让学生理解两者之间的关系。
教学评估:1. 通过课堂提问,检查学生对离散型随机变量期望值概念的理解。
2. 通过练习题,检查学生对离散型随机变量期望值计算方法的掌握。
3. 通过练习题,检查学生对期望值与方差之间关系的理解。
第三章:离散型随机变量方差的性质教学目标:1. 让学生掌握离散型随机变量方差的性质。
2. 让学生能够运用方差的性质解决实际问题。
教学内容:1. 离散型随机变量方差的性质及其数学表达式。
2. 离散型随机变量方差的性质在实际问题中的应用。
教学过程:1. 讲解离散型随机变量方差的性质,并通过例题让学生理解方差的性质。
离散型随机变量的均值与方差_教案

离散型随机变量的均值与方差_教案第一章:离散型随机变量的概念1.1 离散型随机变量的定义介绍离散型随机变量的概念通过实例说明离散型随机变量的特点1.2 离散型随机变量的取值讨论离散型随机变量的取值范围解释离散型随机变量的概率分布1.3 离散型随机变量的概率质量函数定义概率质量函数(PMF)示例说明如何计算离散型随机变量的概率第二章:离散型随机变量的均值2.1 离散型随机变量的均值定义引入离散型随机变量的均值概念解释均值的意义和重要性2.2 计算离散型随机变量的均值介绍计算离散型随机变量均值的方法通过实例演示如何计算均值2.3 均值的性质讨论离散型随机变量均值的性质证明均值的线性性质第三章:离散型随机变量的方差3.1 方差的概念引入方差的概念和意义解释方差在描述随机变量离散程度方面的作用3.2 计算离散型随机变量的方差介绍计算离散型随机变量方差的方法通过实例演示如何计算方差3.3 方差的性质讨论离散型随机变量方差的性质证明方差的线性性质第四章:离散型随机变量的标准差4.1 标准差的概念引入标准差的概念和意义解释标准差在描述随机变量离散程度方面的作用4.2 计算离散型随机变量的标准差介绍计算离散型随机变量标准差的方法通过实例演示如何计算标准差4.3 标准差的性质讨论离散型随机变量标准差的性质证明标准差的线性性质第五章:离散型随机变量的期望和方差的关系5.1 期望和方差的关系引入期望和方差的关系概念解释期望和方差在描述随机变量特性方面的作用5.2 计算离散型随机变量的期望和方差介绍计算离散型随机变量期望和方差的方法通过实例演示如何计算期望和方差5.3 期望和方差的性质讨论离散型随机变量期望和方差的性质证明期望和方差的线性性质这五个章节涵盖了离散型随机变量的均值和方差的基本概念、计算方法和性质。
通过这些章节的学习,学生可以掌握离散型随机变量的均值和方差的计算方法,并了解它们在描述随机变量特性和规律方面的应用。
离散型随机变量的方差优秀教学设计

2.3 离散型随机变量的方差
【课题】:2.3 离散型随机变量的方差
【教学时间】:高二下学期
【学情分析】:
教学对象是高二理科学生,学生已经初步学会利用离散型随机变量均值解决实际问题。
本课时要结合均值的概念讲解方差的概念,与均值进行对比和联系,要通过具体的例题讲清求方差的一般步骤。
本节课的教学难点是复杂的方差问题的求解,在教学中要加强对学生运算能力的培养。
在教学中要注意和实际问题相结合,使学生真正理解方差的意义。
【教学目标】:
(1)通过实例使学生理解离散型随机变量均值的定义;
(2)会运用方差解决实际问题。
【教学重点】:
1.离散型随机方差的定义;
2.离散型随机变量方差的求法;
3.运用方差解决实际问题。
【教学难点】:
1.复杂的方差问题的求解,;
2.运用均值解决实际问题。
【教学突破点】:
通过一个实际问题结合均值引入均值,与均值进行对比和联系,帮助学生理解方差的定义;通过对典型例题的分析,使学生掌握运用解决问题的方法和步骤。
【教法、学法设计】:
在具体教学过程中,教师可在教材的基础上适当拓展具体的实际例子,使得内容更为丰富.教师可以运用和学生共同探究式的教学方法,学生可以采取自主探讨式的学习方法.
【课前准备】:课件
根据离散型随机变量分布列的性质,可得
12101)21(2
1
2≤-≤=+-+q q q 解得2
2
1-=q。
离散型随机变量的均值与方差_教案

离散型随机变量的均值与方差_教案第一章:离散型随机变量的概念1.1 离散型随机变量的定义介绍离散型随机变量的概念举例说明离散型随机变量1.2 离散型随机变量的概率分布概率分布的定义概率分布的性质概率分布的图形表示1.3 离散型随机变量的期望值期望值的定义期望值的计算方法期望值的意义第二章:离散型随机变量的均值2.1 离散型随机变量的均值的概念均值的定义均值的意义2.2 离散型随机变量的均值的计算方法均值的计算公式均值的计算步骤2.3 离散型随机变量的均值的性质均值的性质1:线性性质均值的性质3:单调性第三章:离散型随机变量的方差3.1 离散型随机变量的方差的概念方差的定义方差的意义3.2 离散型随机变量的方差的计算方法方差的计算公式方差的计算步骤3.3 离散型随机变量的方差的性质方差的性质1:非负性方差的性质2:对称性方差的性质3:单调性第四章:离散型随机变量的协方差4.1 离散型随机变量的协方差的概念协方差的定义协方差的意义4.2 离散型随机变量的协方差的计算方法协方差的计算公式协方差的计算步骤4.3 离散型随机变量的协方差的性质协方差的性质1:线性性质协方差的性质3:对称性第五章:离散型随机变量的相关系数5.1 离散型随机变量的相关系数的定义相关系数的定义相关系数的意义5.2 离散型随机变量的相关系数的计算方法相关系数的计算公式相关系数的计算步骤5.3 离散型随机变量的相关系数的性质相关系数的性质1:取值范围相关系数的性质2:单调性相关系数的性质3:对称性第六章:离散型随机变量的标准化6.1 离散型随机变量标准化的概念标准化的定义标准化的意义6.2 离散型随机变量的标准化方法标准化的计算公式标准化的计算步骤6.3 离散型随机变量标准化后的性质标准化后的分布标准化后的期望值和方差第七章:离散型随机变量的均值的估计7.1 离散型随机变量均值估计的概念均值估计的定义均值估计的意义7.2 离散型随机变量均值的点估计点估计的定义点估计的计算方法7.3 离散型随机变量均值的区间估计区间估计的定义区间估计的计算方法第八章:离散型随机变量的方差的估计8.1 离散型随机变量方差估计的概念方差估计的定义方差估计的意义8.2 离散型随机变量方差的点估计点估计的定义点估计的计算方法8.3 离散型随机变量方差的区间估计区间估计的定义区间估计的计算方法第九章:离散型随机变量的协方差的估计9.1 离散型随机变量协方差估计的概念协方差估计的定义协方差估计的意义9.2 离散型随机变量协方差的点估计点估计的定义点估计的计算方法9.3 离散型随机变量协方差的区间估计区间估计的定义区间估计的计算方法第十章:离散型随机变量的相关系数的估计10.1 离散型随机变量相关系数估计的概念相关系数估计的定义相关系数估计的意义10.2 离散型随机变量相关系数的点估计点估计的定义点估计的计算方法10.3 离散型随机变量相关系数的区间估计区间估计的定义区间估计的计算方法重点和难点解析重点环节1:离散型随机变量的期望值和方差的计算方法。
离散型随机变量的方差教案
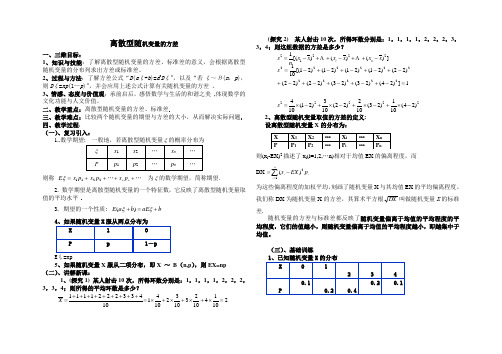
离散型随机变量的方差一、三维目标:1、知识与技能:了解离散型随机变量的方差、标准差的意义,会根据离散型随机变量的分布列求出方差或标准差。
2、过程与方法:了解方差公式“D (a ξ+b )=a 2D ξ”,以及“若ξ~Β(n ,p ),则D ξ=np (1—p )”,并会应用上述公式计算有关随机变量的方差 。
3、情感、态度与价值观:承前启后,感悟数学与生活的和谐之美 ,体现数学的文化功能与人文价值。
二、教学重点:离散型随机变量的方差、标准差三、教学难点:比较两个随机变量的期望与方差的大小,从而解决实际问题 四、教学过程: (一)、复习引入:1..数学期望则称 =ξE +11p x +22p x …++n n p x … 为ξ的数学期望,简称期望. 2. 数学期望是离散型随机变量的一个特征数,它反映了离散型随机变量取值的平均水平3. 期望的一个性质: b aE b a E +=+ξξ)( 5、如果随机变量X 服从二项分布,即X ~ B (n,p ),则EX=np (二)、讲解新课:1、(探究1) 某人射击10次,所得环数分别是:1,1,1,1,2,2,2,3,3,4;则所得的平均环数是多少?(探究2) 某人射击10次,所得环数分别是:1,1,1,1,2,2,2,3,3,4;则这组数据的方差是多少?2、离散型随机变量取值的方差的定义: 设离散型随机变量X 的分布为:则(x i -EX)2描述了x i (i=1,2,…n)相对于均值EX 的偏离程度,而 DX为这些偏离程度的加权平均,刻画了随机变量X 与其均值EX 的平均偏离程度。
我们称DX 为随机变量X 的方差,其算术平方根DX 叫做随机变量X 的标准差.随机变量的方差与标准差都反映了随机变量偏离于均值的平均程度的平均程度,它们的值越小,则随机变量偏离于均值的平均程度越小,即越集中于均值。
(三)、基础训练104332221111+++++++++=X 21014102310321041=⨯+⨯+⨯+⨯=])()()[(122212x x x x x x ns n i -++-++-= 1])24()23()23()22()22()22()21()21()21()21[(10122222222222=-+-+-+-+-+-+-+-+-+-=s 22222)24(101)23(102)22(103)21(104-⨯+-⨯+-⨯+-⨯=s ∑=-=ni ii p EX x 12)(求DX 和解:00.110.220.430.240.12EX =⨯+⨯+⨯+⨯+⨯=22222(02)0.1(12)0.2(22)0.4(32)0.2(42)0.1 1.2DX =-⨯+-⨯+-⨯+-⨯+-⨯= (四)、方差的应用 用击中环数的期望与方差分析比较两名射手的射击水平。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
离散型随机变量的方差
一、三维目标:
1、知识与技能:了解离散型随机变量的方差、标准差的意义,会根据离散型随机变量的分布列求出方差或标准差。
2、过程与方法:了解方差公式“D (aξ+b )=a 2Dξ”,以及“若ξ~Β(n ,p ),则Dξ=np (1—p )”,并会应用上述公式计算有关随机变量的方差 。
3、情感、态度与价值观:承前启后,感悟数学与生活的和谐之美 ,体现数学的文化功能与人文价值。
二、教学重点:离散型随机变量的方差、标准差
三、教学难点:比较两个随机变量的期望与方差的大小,从而解决实际问题 四、教学过程: (一)、复习引入:
1..数学期望
则称 =ξE +11p x +22p x …++n n p x … 为ξ的数学期望,简称期望. 2. 数学期望是离散型随机变量的一个特征数,它反映了离散型随机变量取值的平均水平
3. 期望的一个性质: b aE b a E +=+ξξ)( 5、如果随机变量X 服从二项分布,即X ~ B (n,p ),则EX=np (二)、讲解新课:
1、(探究1) 某人射击10次,所得环数分别是:1,1,1,1,2,2,2,3,3,4;则所得的平均环数是多少?
(探究2) 某人射击10次,所得环数分别是:1,1,1,1,2,2,2,3,3,4;则这组数据的方差是多少?
2、离散型随机变量取值的方差的定义: 设离散型随机变量X 的分布为:
则(x i -EX)2描述了x i (i=1,2,…n)相对于均值EX 的偏离程度,而 DX
为这些偏离程度的加权平均,刻画了随机变量X 与其均值EX 的平均偏离程度。
我们称DX 为随机变量X 的方差,其算术平方根DX 叫做随机变量X 的标准差.
随机变量的方差与标准差都反映了随机变量偏离于均值的平均程度的平均程度,它们的值越小,则随机变量偏离于均值的平均程度越小,即越集中于均值。
(三)、基础训练
求DX 和
解:00.110.220.430.240.12EX =⨯+⨯+⨯+⨯+⨯=
104332221111+++++++++=X 2101
4102310321041=⨯+⨯+⨯+⨯=]
)()()[(122212x x x x x x n
s n i -++-++-=ΛΛ1
])24()23()23()22()22()22()21()21()21()21[(10
1
22222222222=-+-+-+-+-+-+-+-+-+-=s 2
2222)24(101)23(102)22(103)21(104-⨯+-⨯+-⨯+-⨯=s ∑=-=n
i i
i p EX x 1
2)(DX
22222(02)0.1(12)0.2(22)0.4(32)0.2(42)0.1 1.2DX =-⨯+-⨯+-⨯+-⨯+-⨯= (四)、方差的应用
用击中环数的期望与方差分析比较两名射手的射击水平。
表明甲、乙射击的平均水平没有差别,在多次射击中平均得分差别不会很大,但甲通常发挥比较稳定,多数得分在9环,而乙得分比较分散,近似平均分布在8-10环。
问题1:如果你是教练,你会派谁参加比赛呢?
问题2:如果其他对手的射击成绩都在8环左右,应派哪一名选手参赛?
问题3:如果其他对手的射击成绩都在9环左右,应派哪一名选手参赛?
解:根据月工资的分布列,利用计算器可算得
EX 1 = 1200×0.4 + 1 400×0.3 + 1600×0.2 + 1800×0.1 = 1400 ,
DX 1 = (1200-1400) 2 ×0. 4 + (1400-1400 ) 2×0.3 + (1600 -1400 )2×0.2+(1800-1400) 2×0. 1
= 40 000 ;
EX 2=1 000×0.4 +1 400×0.3 + 1 800×0.2 + 2200×0.1 = 1400 ,
DX 2 = (1000-1400)2×0. 4+(1 400-1400)×0.3 + (1800-1400)2×0.2 + (2200-1400 )2×0.l
= 160000 .
因为EX 1 =EX 2, DX 1<DX 2,所以两家单位的工资均值相等,但甲单位不同职位的工资相对集中,乙单位不同职位的工资相对分散.这样,如果你希望不同职位的工资差距小一些,就选择甲单位;如果你希望不同职位的工资差距大一些,就选择乙单位.
(五)、几个常用公式:
(1)若X 服从两点分布,则DX=p(1-p )。
(2)若X ~B (n ,p ),则DX=np (1-p ) (3)D (ax+b )= a 2DX ; (六)、练习:
2、已知随机变量X 的分布列
求DX 和 3、若随机变量X 满足P (X=c )=1,其中c 为常数,求DX 。
(七)、小结:
1、离散型随机变量取值的方差、标准差及意义
2、记住几个常见公式:
(1)若X 服从两点分布,则DX=p(1-p )。
(2)若X ~B (n ,p ),则DX=np (1-p ) (3)D (ax+b )= a 2DX ; (八)、作业:P69 1、4
095.12.1≈=DX 9,921==EX :EX 解8
.0,4.021==DX DX ==+=ηξξηD D 则,且、已知,138
131DX。
