一阶电路和二阶电路的阶跃响应、冲击响应PPT

合集下载

一阶电路和二阶电路

一、零输入响应：电路中无输入, 由初始储能<初始状态>
产生的响应
1
2i
说明：举例： R0
K (t=0) +
US
C UC
R
-
本节内容：
t 0时，uc.i等为零输入响应
RC零输入响应 RL零输入响应
§7-2 一阶电路的零输入响应
二、 RC电路零输入响应：放电
已知 uC (0-)=U0
uR uC 0
特征根 p = R L
由初始值 i(0+)= I0 定积分常数A
A= i(0+)= I0
得
i(t)
I0e pt
Rt
I0e L
t0
§7-2 一阶电路的零输入响应
3 、讨论:
（1）曲线：
iL I0
大放电时间长小放电时间短
大
小
t
(2)时间常数
L RL电路时间常数
R
说明： s
§7-2 一阶电路的零输入响应
i C duC dt
uR= Ri
RC
duC dt
uC
0
uC (0 ) U0
一阶微分方程
§7-2 一阶电路的零输入响应
1.列方程： 2.解方程：通解 P的求解：由特征方程： A的求解：由初值：
§7-2 一阶电路的零输入响应
3.讨论： (1)曲线
Uc U0
大过渡过程时间长小过渡过程时间短
间的过程
说明:电容充电(如图)
K (t=0)
+
Us
-
+
R0
C Uc
－
本章主要分析在过渡过程中电压电流变化

电路原理课件二阶电路的冲激响应讲解

冲激响应电流为
i(t) ?
C duC (t) ? dt
s1
I0 ? s2
( s1e s1t
?
s2e s2t )ε(t )
s1 ? ? α ?
uc(t) ? 2C
I0
( e s1t ? e s2t ) ε ( t )
α2
?
ω
2 0
s2 ? ? α ?
α 2 ? ω02 α 2 ? ω02
i (t ) ? C du C ? dt 2
解：将R、L、C的值代入计算出固有频率
R s1，2 ? ? 2L ?
则
??
R
2
?? ?
1
? ?3?
? 2L ? LC
32 ? 52 ? ? 3 ? j4
uC(t) ? e?3t[ K1 cos(4t) ? K2 sin(4t)]
(t ? 0? )
uC (t )
?
e? 3t [
K1 cos4t
?
K2 sin(4t) ]
初始条件为
uC (0? ) ? uC (0? ) ? 0
uC?(0? ) ?
i(0? ) ? C
I0 C
A1 ? 0
? ?
? αA1 ?
A2
?
I0 ? C ??
A1 ? 0
A2 ?
I0 C
uC (t ) ?
I0t e?? t?(t)
C
i(t) ?
C
du dt
?
(1 ?
?
t)I0e?? t?(t)
非振荡放电（临界阻尼放电）
R s1,2 ? ? 2L ?
?
R
2
?
?? 2L ??

二阶电路阶跃响应和冲激响应讲解

50 W
50 V
R iR
0.5H L C
100 μF
iL
iC
(5)求iR
iR iL iC
iL
LC
d2iL dt 2
或设解答形式为： iR 1 Ae100t sin(100t )
50W
定常数
R iR
50 V
2A
iC
i
R
(0
)
diR dt
(0
)
1
iC ?
(0
)
1
iR
50 R
uc
5Ω 解（1） uc(0－)=25V iL(0－)=5A
（2）开关打开为RLC串联电路，方程为：
LC
d 2uc dt
RC
duc dt
uc
0
特征方程为： 50P2+2500P+106=0
P 25 j139
uc Ae25t sin(139t )
uc Ae25t sin(139t )
0
A U0 ， arctg
sin
ω，ω０，δ间的关系:
ω0
ω
sin
0
A
0
U
0
δ
uc
0
U0e
t
sin(t
)
uc
0
U0e
t
sin(t
)
uc是其振幅以
0
U0为包线依指数衰减的正弦函数。
t=0时 uc=U0
uc U0
0
U0
e
t
uc零点：t = -，2- ... n- uc极值点：t =0，，2 ... n
L
di dt

二阶电路的冲激响应

0
i(t)
0 Ld
e t cos
cos d t
sin
sindt ε(t)
0 Ld
e
t
cosd t
ε(t)
α称为衰减常数(attenuation constant) ，或阻尼常数
(damping constant)
角频率 d称为阻尼振荡角频率(angular frequency of
the damped oscillation)
阻尼振荡角频率不仅决定于电感L和电容C，也和电
阻R有关。
在R = 0的极限情况下， = 0，d 0
1 LC
θ = 0，在R = 0情况下的响应uC(t)、i (t) 均变为等幅振荡(unattenuated oscillation)，或称为无阻尼振荡 (undamped oscillation)。其函数表达式为
uC
(
t
)
0
sin
0
t
ε(
t
)
i(t)
1 L
cos
0
t
ε(t)
2. s1和s2为相等的负实根
=0
即
R 2L
1 ，或R 2 LC
L C
电容电压的通解为
uC (t) A1 A2t e t
代入初始条件得
A1 0
A1
A2
1 LC
故
uC (t)
t LC
e tε(t )
i(t) C duc (t) 1 e t 1 t ε(t)
电容上的冲激响应电压为
uC (t)
1 LC(s1
(e s1t s2 )
es2t )ε(t )
冲激响应电流为

一阶电路和二阶电路的动态响应

实验四一阶电路和二阶电路的动态响应一、实验目的（1）理解零输入响应、零状态响应和完全响应（2）理解欠阻尼、临界和过阻尼的意义和条件二、实验原理用二阶微分方程描述的动态电路称为二阶电路。

图所示的线性RLC 串联电路是一个典型的二阶电路。

可以用下述二阶线性常系数微分方程来描述：s 2U 2=++c c c u dt du RC dtu d LC 1．零输入响应动态电路在没有外施激励时，由动态元件的初始储能引起的响应，称为零输入响应。

电路如图6.2所示，设电容已经充电，其电压为U 0，电感的初始电流为0。

(1) CL R 2>，响应是非振荡性的，称为过阻尼情况。

电路响应为：图6.2 RLC 串联零输入响应电路图6.3 二阶电路的过阻尼过程u Lt mU 0)()()()()(212112012120t P t P t P t P C e e P P L U t i e P e P P P U t u ---=--=响应曲线如图6.3所示。

可以看出：u C (t)由两个单调下降的指数函数组成，为非振荡的过渡过程。

整个放电过程中电流为正值，且当2112lnP P P P t m -=时，电流有极大值。

（2）CL R 2=，响应临界振荡，称为临界阻尼情况。

电路响应为tt c te LUt i e t U t u ααα--=+=00)()1()( t ≥0响应曲线如图6.4所示。

图6.4 二阶电路的临界阻尼过程(3) CL R 2<，响应是振荡性的，称为欠阻尼情况。

电路响应为t e LU t i t e U t u d td d t dC ωωβωωωααsin )(),sin()(000--=+==t ≥0其中衰减振荡角频率 2220d 2L R LC 1⎪⎭⎫ ⎝⎛-=-=αωω ，αωβdarctan= 响应曲线如图6.5所示。

U 0t图6.5 二阶电路的欠阻尼过程图6.6 二阶电路的无阻尼过程（4）当R ＝０时，响应是等幅振荡性的，称为无阻尼情况。

阶跃响应冲击响应与卷积积分法

补充第一章阶跃响应冲击响应与卷积积分法电路中除电阻元件外，还包括有电容和电感等动态元件，如此的电路称为动态电路。

在动态电路分析中，鼓励和响应都表示为时刻t 的函数，采纳微分方程求解电路和分析电路的方式，称为时域分析法。

本章要紧讨论一阶电路的阶跃响应、冲激响应、任意输入的零状态响应，和二阶电路在恒定输入下的零状态响应。

§1-1 阶跃响应和冲激响应电路的输入除恒定不变的常量（即恒定输入或直流输入）和按正弦规律变更的交流量（即正弦输入）之外，常见的还有另外两种奇异函数，即阶跃函数和冲激函数。

本节就来讨论这两种函数的概念、性质及作用于线性动态电路时所引发的响应。

单位阶跃函数（unit step function ）用()t ε来表示，它概念为 0(0)()1(0)t t t ε<⎧=⎨>⎩ 波形如图1-1（a ）所示，在0t =处，()t ε由0跃变至1。

若是单位阶跃函数的跃变点不是在0t =处，而是在0t t =处，波形如图1-1（b ）所示，那么称它为延迟的单位阶跃函数，用0()t t ε-表示，即0000()()1()t t t t t t ε<⎧-=⎨>⎩图1-1单位阶跃函数与任一常量K 的乘积()K t ε仍是一个阶跃函数，现在阶跃的幅度为K 。

单位阶跃函数与任一函数()f t 的乘积将只保留该函数在阶跃点以后的值，而使阶跃点以前的值变成零，即有0000(0)()()()(0)0()()()()()t f t t f t t t t f t t t f t t t εε<⎧=⎨>⎩<⎧-=⎨>⎩因此，单位阶跃函数能够用来“起始”一个任意函数()f t ，这给函数的表示带来了方便。

例如关于线性函数()(f t Kt K =为常数），由图1-2(a)、(b)、(c)能够清楚地看出()f t 、()()f t t ε及0()()f t t t ε-的不同。

电路课件电路07 一阶电路和二阶电路的时域分析

第7章一阶电路和二阶电路的时域分析 7-1动态电路方程及初始条件
2019年3月29日星期五
经典法
5
• 线性电容在任意时刻t，其电荷、电压与电流关系：
q(t ) q(t0 ) iC ( )d
t0 t
线性电容换路瞬间情况
uC (t ) uC (t0 )
• q、uc和ic分别为电容电荷、电压和电流。令t0＝0-， t=0+得： 0 0
第7章一阶电路和二阶电路的时域分析
2019年3月29日星期五
3
• 动态电路：含动态元件电容和电感电路。 • 动态电路方程：以电流和电压为变量的微分方程或微分-积分方程。 • 一阶电路：电路仅一个动态元件，可把动态元件以外电阻电路用戴维宁或诺顿定理置换，建立一阶常微分方程。 • 含2或n个动态元件，方程为2或n阶微分方程。 • 动态电路一个特征是当电路结构或元件参数发生变化时(如电路中电源或无源元件断开或接入，信号突然注入等)，可能使电路改变原来工作状态，转变到另一工作状态，需经历一个过程，工程上称过渡过程。 • 电路结构或参数变化统称“换路”，t=0时刻进行。 • 换路前最终时刻记为t=0-，换路后最初时刻记为t=0+，换路经历时间为0-到0+。
第7章一阶电路和二阶电路的时域分析 7-2一阶电路的零输入响应
2019年3月29日星期五
RC电路零输入响应-１
12
• 电路中电流 • 电阻上电压
RC电路零输入响应-2
1
t t duC U 0 RC t d 1 RC RC i C C (U 0e ) C ( )U 0e e dt dt 1 RC R
R
13
RC电路零输入响应-3

一阶电路与二阶电路PPT

t 0
t RC
duc (t ) U 0 e dt R
t0
3.解的物理含义：uc及i的波形
从图可见，电容电压从初始值U0开始按指数规律衰减到0，电流在换路瞬间有1个跳变，从i(0-)=0跳变到i(0+)=U0/R, 然后按指数规律衰减到0。
U0 U0 R
U0 R
图
RC 电路零输入响应电压电流波形图
图示一阶RC电路，电容处于零状态，求电路中的响应。
＋
ic(t) C
物理过程分析：
理论求解：
(t ) R
－
iR(t)
+ uc(t) _
1.列方程： ic (t ) iR (t ) (t )
第四章一阶电路与二阶电路
4.1 一阶电路的零输入响应 4.2 一阶电路的阶跃响应
4.3 一阶电路的冲激响应
4.4 一阶电路对阶跃激励全响应 4.5 二阶电路的冲激响应
学习目标
深刻理解零输入响应、零状态响应、暂态响应、稳态响应的含义，并掌握它们的分析计算方法。理解一阶电路阶跃响应和冲击响应的概念。熟练掌握输入为直流信号激励下的一阶电路的三要素分析法。了解二阶电路的冲击响应。
L R
RC电路： RC
L RL电路： R
R多数情况下是等效电阻。
例1：求换路后的零输入响应i(t)和u0(t)：
分析：换路前为直流电路，电容开路 S1(t=0) +uC(t) - 20 + 200 0.02uF u c (0 ) u c (0 ) 60 120V + 60 u0(t) 60 40 200V 60 80 换路后电容两端看进去的等效电阻 Req 60 80 2 100

冲击响应和阶跃响应

（2）求h(t)
h(t) 2e2tU (t) (t)
(4)拉普拉斯变换法（留待ch8讨论）
2.阶跃响应
(1)定义：LTIS在单位阶跃信号作用下，系统产生的零状态响应，叫做单位阶跃响应。即：
y(n) (t) an1 y(n1) (t) a1y(1) (t) a0 y(t)
(1)
bmU (m) (t) bm1U (m1) (t) b1U (1) (t) b0U (t)
综上所述，我们将求冲击响应的方法步骤归纳如下： (1)求出电路微分方程的特征根。 (2)写出冲击响应解的表达式。 (3)对h(t)求导，求导的次数由方程的阶次n决定（注意δ(t) 抽样性）。 (4)将h(t)及其导数和δ(t) 代到电路微分方程，比较两端相应项系数（即令其相等），求得Ai，从而得到h(t)。
(3)微分法定理：若已知电路系统的阶跃响应为g(t)，则其电路系统
的冲击响应由下式决定：
h(t) d g(t) dt
例：已知LTIS，当激励为12U(t)时，响应为(24－12e-2t)U(t)，试求单位冲击响应。
解：（1）单位阶跃：
g(t) 1 g(t) (2 e2t )U (t) 12
将 y(t) = h(t) , f(t) =δ(t) 等代入给定微分方程得：
h(2) (t) 4h(1) (t) 3h(t) (1) (t) 2 (t)
(A1 A2) (1) (t) (A1 3A2) (t) (A1et 9A2e3t )U (t)
4{( A1 A2) (t) (A1et 3A2e3t )U(t)} 3(A1et A2e3t )U(t) (1) (t) 2 (t)
{y(0) 0, y(1) (0) 0, y(2) (0) 0 y(n1) (0) 0}

第六章一阶电路

R t L R t L
di u L L RI0e dt
L 与RC电路类似，令 R 称为RL电路的时间常数。
右图所示曲线为i、 uL和uR随时间变化的曲线。
从以上求得的RC和RL电路零输入响应进一步分析可知，对于任意时间常数为非零有限值的一阶电路，不仅电容电压、电感电流，而且所有电压、电流的零输入响应，都是从它的初始值按指数规律衰减到零的。且同一电路中，所有的电压、电流的时间常数相同。若用f (t)表示零输入响应，用f (0+)表示其初始值，则零输入响应可用以下通式表示为
6 iL A 3 A 2 L 2s Req
由三要素法可得：
iL [3 (2 3)e (3 0.5e
根据KCL可求得：
0.5t
1t 2
]A
)A
i I S iL (5 5e
例6-1
下图所示电路中直流电压源的电压为Uo。当电路中的电压和电流恒定不变时，打开开关S。试求uC(0+)、iL(0+)、 ic(0+)、 uL(0+)、uR2(0+)。
解根据t=0-时刻的电路状态计算u (0-)和i (0-)
c
L
U 0 R2 u c (0 ) R1 R2 U0 iL (0 ) R1 R2
已知历次绕组的电阻R=0.189，电感L=0.398H，直流电压U=35V。电压表的量程为50V，内阻 RV=5k。开关未短=断开时，电路中电流已经恒定不变。在t=0时，断开开关。求：（1）电阻、电感回路的时间常数；（2）电流i的初始值和断开开关后电流i的最终值；（3）电流i 和电压表处电压uV；（4）开关刚断开时，电压表处电压。

阶跃响应与冲激响应1

t t t d 1 uC (t ) R(1 e RC ) (t ) R(1 e RC ) (t ) e RC (t ) dt C 根据冲击函数的筛分性质： f (t ) (t ) f (0) (t )
上式等号右边第一项为零，最后得：
t 1 RC uC e (t ) C t t t d RC 1 iC (t ) e (t ) e RC (t ) e RC (t ) dt RC
电容电流和电容电压随时间变化的波形如图（b）所示。
例 6 -6-2 图（b）
例6-6-3 求图示电路电感
加冲击激励后的电流。
解：

例 6 -6-3 图（ a ）
1 t 1 t A iL (0 ) iL (0 ) uL dt iL (0 ) A (t )dt iL (0 ) L 0 C 0 L
lim p(t ) (t )
0
图 6.28
在任一时刻t0发生冲击的函数如图6.29所示，称为延迟的单位冲
激函数，可定义为：
(t t0 )dt 1 (t t0 ) 0, t t0

图 6.29
2）冲激函数的性质冲激函数有如下两个主要性质：（1）单位冲激函数对时间的积分等于单位阶跃函数，即
e (t ) e
2 t
2( t 0. 5 )
(t 0.5) mA
iC e 2 t ( t ) e 2 t ( t 0.5) e 2 t ( t 0.5) e 2( t 0.5 )( t 0.5)
e 2t [(t ) (t 0.5)] e 2 t (t 0.5) e 2( t 0.5)(t 0.5)

第十讲一阶、二阶

δ (t )
t≠0 1 t 0
δ (t ) = 0
∞ −∞
∫ δ (t )dt = 1
二、一阶、二阶电路的冲激响应一阶、二阶电路的冲激响应
冲击函数两个主要性质：冲击函数两个主要性质： *、单位冲击函数 δ 、
t
(t )对时间的积分等于阶跃函数 ε (t )
−∞ *、单位冲击函数的‘筛分性质’ 、单位冲击函数的‘筛分性质’
对于一个具体的电路，若已知该电路的阶跃相应，则可直接得到该电路的冲击相应。因为有如下结论：因为有如下结论：
如果以 s (t ) 表示电路的阶跃相应，而以 h(t ) 表示同一电路的表示电路的阶跃相应，冲击相应，则有如下数学关系：冲击相应，则有如下数学关系：
ds ( t ) h (t ) = dt s (t ) = h ( t ) dt ∫
f (t )
1
t
0
t0
一、一阶、二阶电路的阶跃响应一阶、
根据一阶电路全响应的三要素法得到：根据一阶电路全响应的三要素法得到： RC电路的阶跃响应为：电路的阶跃响应为：电路的阶跃响应为
− sC (t ) = 1 − e τ t
ε (t )
t=0 + ε(t) -
R
第十讲一阶、一阶、二阶电路的阶跃响应与冲激响应
一、一阶、二阶电路的阶跃响应一阶、
• 阶跃响应：阶跃响应：电路对于单位阶跃函数单位阶跃函数输入的零状态零状态响单位阶跃函数零状态应称为单位阶跃响应。单位阶跃函数：单位阶跃函数：
ε (t ) =
0
t＜0
1
ε (t )
t
0
1

t＞0
一、一阶、二阶电路的阶跃响应一阶、

阶跃响应、冲激响应

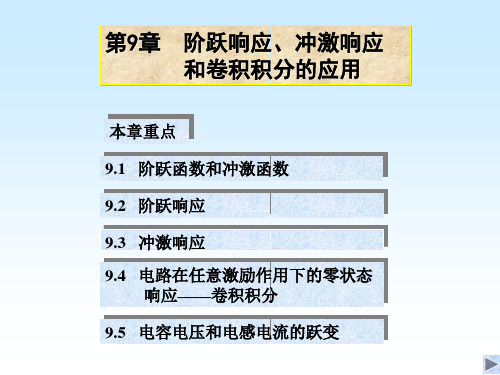
iS
iC +
(t)
R
C uC
定性分析
（1） t 在 0- ～ 0+ 间
uC(0)=0，电容相当于短路
iC (t )
0
Δq 0 iCdt 1
uC
(0
)
Δq C
uC
(0
)
1 C
（2） t > 0+ 零输入响应。
解（1） t 在 0- ～ 0+ 间
C duC uC (t )
dt R
0 C duC dt
返回目录
9.1 阶跃函数和冲激函数
一、单位阶跃函数（unit step function）
(t)
1. 定义
(t)
def
0 1
(t 0) (t 0)
1
0
t
用 (t )可描述开关的动作。
S
US
R+ uC C
–
开关在t =0 时闭合
US(t)
R+ uC C –
def 0 (t 0)
US (t) US (t 0)
(t) 线性网络 h(t)
一、卷积积分（convolution）定义设 f1(t) , f2(t)在 t < 0时均为零
t
f1(t )* f2 (t ) 0 f1( ) f2 (t )d
性质1 f1(t)* f2(t) f2(t)* f1(t)
t
证明 f1(t )* f2 (t ) 0 f1( ) f2 (t )d
01
t
(1< t) f (t) (t 1)
则 f (t) t [ (t) (t 1)] (t 1)
二、单位冲激函数（unit pulse function）

一二阶电路阶跃、冲激响应

稳态时，电感相当于短路，因此电路中的电压为零，电流等于输入电压除以电阻。
时间常数概念及计算方法
时间常数是一阶电路的重要参数，它表示了电路过渡过程的快慢程度。
时间常数越大，电路过渡过程越缓慢；时间常数越小，电路过渡过程越迅速。
ABCD
时间常数τ的计算方法根据电路类型不同而有所不同。对于RC 电路，τ=RC；对于RL电路， τ=L/R。
阶跃信号与冲激信号介绍
阶跃信号
阶跃信号是一种特殊的信号，其值在某一时刻突然发生变化，并保持不变。在电路中，阶跃信号常用于测试系统的瞬态响应。
冲激信号
冲激信号是一种具有突变性质的信号，其值在极短时间内发生巨大变化。在电路中，冲激信号常用于模拟雷电、开关操作等瞬间过程。
响应类型及分析方法
响应类型
一二阶电路阶跃、冲激响应
目录
• 电路基本概念与分类 • 一阶电路阶跃响应分析 • 二阶电路阶跃响应分析 • 冲激响应概念及分析方法 • 实际应用场景举例与仿真实验 • 总结与展望
01 电路基本概念与分类
电路定义及组成要素
电路定义
电路是由电气元件（如电阻、电容、电感等）按照一定方式连接而成，用于传输和转换电能的系统。
同，但同样受到阻尼比和自然频率等参数的影响。
阻尼比、自然频率等参数影响
阻尼比
阻尼比决定了电路的振荡性质，不同阻尼比下电路的响应形态不同。
自然频率
自然频率决定了电路振荡的频率，与电路元件的参数有关。
参数变化对响应的影响
当电路元件的参数发生变化时，阻尼比和自然频率等参数也会随之变化，从而影响电路的响应。
二阶电路冲激响应求解方法
1 2
经典法
通过求解二阶微分方程得到冲激响应表达式。

一阶电路和二阶电路的阶跃响应、冲击响应ppt课件

解 1）0–≤t ≤0+：uC(0-)=0
Ri
电容充电，零状态响应
+
RC
duC dt
uC
(t)
(t) C uC
–
0
0RC duC dt
0
dt
0 0
uCdt
0 (t)dt
0
注意：uC不是冲激函数，否则KVL不成立。
RCuC (0 ) uC (0 ) 1
uC (0 )
1 RC
发生突变
§7-7 一阶和二阶电路的阶跃响应
1.单位阶跃函数
1）单位阶跃函数的定义
(t)
( t ) =
0，t < 0 1，t > 0
2）单位阶跃函数的延迟
( t-t0 ) =
0，t < t0 1，t > t0
整理版课件
1
0
(t – t0)
1
0 t0
t
t
1
3）单位阶跃函数的作用
① 表示开关动作
（t = 0）
+ 10k iC
uS(V) 10
uS -
10k 100F
应用叠加定理
0
0.5 t(s)
uS 10 (t) 10 (t 0.5)V
求单位阶跃响应s(t)
uC (0 ) uC (0 ) 0
iC (0 ) 0.1mA iC () 0 ReqC 0.5s
整理版课件
5
t
s(t) iC () [iC (0 ) iC ()]e
iR
uC 0.2
5uC
iC
2
duC dt
uC
uL
0.25
diL dt

第七章一阶电路和二阶电路的时域分析PPT课件

U 63.2%U
uC
u
' C
o -36.8%U
u
" C
t
-U
§7-3 一阶电路的零状态响应
uRR iUet
稳态分量(强制分量)：电路到达稳定状态时的电压，其变化规律和大小都与电源电压U有关。瞬态分量(自由分量)：仅存在于暂态过程中，其变化规律与电源电压U无关，但其大小与U有关。
§7-3 一阶电路的零状态响应
讲课7学时，习题1学时。
§7-1 动态电路的方程及其初始条件
一、动态电路的有关概念
⒈ 一阶(动态)电路仅含一个动态元件，且无源元件都是线性和时不
变的电路，其电路方程是一阶线性常微分方程。
⒉ 二阶(动态)电路含两个动态元件的电路，其电路方程是二阶微分
方程。
§7-1 动态电路的方程及其初始条件
⒊ 过渡过程当电路的结构或元件的参数发生变化时，可能使
第七章一阶电路和二阶电路的时域分析
§7-1 动态电路的方程及其初始条件 §7-2 一阶电路的零输入响应 §7-3 一阶电路的零状态响应 §7-4 一阶电路的全响应 §7-5 二阶电路的零输入响应 §7-6 二阶电路的零状态响应和全响应
§7-7 一阶电路和二阶电路的阶跃响应 §7-8 一阶电路和二阶电路的冲激响应 *§7-9 卷积积分 *§7-10 状态方程 *§7-11 动态电路时域分析中的几个问题
dt
t=0
+
所以
eL
L
di dt
很大
+
U-
R uRL
eL可能使开关两触点之
L-
间的空气击穿而造成电弧以
1S
i
延缓电流的中断，开关触点

二阶电路课件PPT

例7-3 电路如图7-1所示。已知R=6, L=1H, C=0.04F, uC(0)=3V，iL(0)=0.28A，求电容电压和电感电流
的零输入响应。
图7－1 RLC串联二阶电路
解：将R，L，C的量值代入式(9-4)计算出固有频率的数值
s1，2
R 2L
R
2
1
3
2L LC
32 52 3 j4
uC
0
其特征方程为
LCs2 RCs 1 0
其特征根为
s1，2
R 2L
R 2L
2
1 LC
电路微分方程的特征根，称为电路的固有频率。当
R，L，C的量值不同时，特征根可能出现以下三种情况
1.
R2
L C
时， s1, s2
为不相等的实根。过阻尼情况。
2.
R2
L C
时， s1, s2
为两个相等的实根。临界阻
uC (t) K1est K2test
式中的两个常数K1，K2由初始条件iL(0)和uC(0) 确定。 t=0得到
uC (0) K1
求导，再令得到
duC (t) dt
t 0
K1s K2
iL (0) C
联立求解以上两个方程，可以得到
K1 uC (0)
K2
iL (0) C
s1uC (0)
将 K1, K2的计算结果，代入得到电容电压的零输入
3.在欠阻尼情况，s1和s2是共轭复数，固有频率出现在s平面上的左半平面上，响应是振幅随时间衰减的正弦振荡，其振幅随时间按指数规律衰减，衰减系数越大，衰减越快。衰减振荡的角频率d 越大，振荡周期越小，振荡越快。
图中按Ke-t画出的虚线称为包络线，它限定了振幅的变化范围。

一阶电路与二阶电路ppt

uL (t)
L diL (t) dt
Rt
RI0e L
RiL (t)
t0
10
3.解的物理含义：iL及u的波形
从图可见，电感电流从初始值I0开始按指数规律衰减到0 电感电压在换路瞬间有1个跳变，从uL(0-)=0跳变到 uL(0+)=-I0R,然后按指数规律衰减到0。
I0
图3-6 RC 电路零输入响应电压电流波形图
包权
人书友圈7.三端同步
4.时间常数：
7
换路之后，电路中各电压、电流量都是从各自的初始值开始按照指数规律衰减到0，那么衰减速率与什么有关？
a. 电容C越大，电容中存储的电荷越多，放电的时间越长
b. 电阻R越大，放电电流越小，放电时间越长。
所以各个电量衰减速率与R和C的乘积即 RC 有关。越小，衰减速率越快，反之，则慢。U0只是影响瞬时值，
0.5U
I1=I+0.5u
由KVL得：U=3*I+[0.5u+I] *1
13
R=3
I1 R=1
L=4H
U(t)
i(t)
→0.5U=4I →Req=U/I=8
2.求 L 4 0.5
R8
3.求i(t):
t
i(t) i(0 )e
t
i(0 )e
2e2t
4.求u(t) u(t) L di(t) 16e2t
服务特权
共享文档下载特权
VIP用户有效期内可使用共享文档下载特权下载任意下载券标价的文档（不含付费文档和VIP专享文档），每下载一篇共享文
档消耗一个共享文档下载特权。
年VIP
月VIP
连续包月VIP
享受100次共享文档下载特权，一次发放，全年内有效