小晨精品2016第十六届中环杯四年级初赛解析
2016第十六届中环杯四年级初赛解析

解析(初赛)第十六届“中环杯”四年级_______ 33+20.15=20.15+40.3)×1.计算题:(【分析】原式33+20.15?=(20.15+20.15?2)66+20.15?=20.15?33+20.15 1)??66?20.15?(33 2015?,要求这四个数字构成一个四位、2.abc_____这样的四位数都也a1都大互不相同,=【分析=1432134=1=2有 a2431234=1有=2,共.3一个长方体的六个面的面积之积1464,则该长方体的体积________【分析设长方体的长宽高分别则1464abaabac2222?c(a14641b)222?121acb 2121)?(abc11?abc4.小明通过2、0、1、6这四个数字构成了一个数列(不断地将2、0、1、6这四个数字按照这个顺序加在数后面):2,20,201,2016,20162,201620,2016201,20162016,201620162,…,这个数列中,质数有______个.【分析】只有第一个2是质数,以后出现的数都不是质数,所以质数有1个.、B两地沿相同的方向行驶.甲车如果每小时行驶50甲、乙两车同时从A千米,则6小时5.可以追上前方的乙车;如果每小时行驶80千米,则2小时可以追上前方的乙车.由此可知,乙车的速度是________千米/时.?时间,速度差千米/时,由追及问题的路程差=【分析】设乙车速度为x得2?x)?x)?6?(80(50?300?6x?160?2x140?4x35?x6.右图中有_________个三角形., 【分析】分类枚举,如图个;个小三角形构成的有4 1个小三角形构成的个122345个小三角形构成的个121356个小三角形构成的个123345246个小三角形构成的个共(个.17已知四位满足下面的性质都是完全平方数(完全平方数是CBABCAB4=22,81=92481.所有满、能表示为某个整数平方的数,比如为完全平方数),则我们就称__________. 足这个性质的四位数之和为【分析】满足条件的平方数为有:ABBCCD491664 634649164861 ?ABCD?164或936或498764?和为164+936+498764=1S(123)?1?2?3?6)aS(naa.8.的各个的数码和(比如表示对于自然数,如果一个自然数S(3n)?3S(n)n_____________ 的最大值为数码都互不相同,并且,则【分析】S(3n)?3S(n)?3乘以n时不能进位,则n中最大的数字只能为3,故n最大为3210.、BCEF//BCEGFOOABCDABCD.9.若是正方形都是正方形,其中点如图,的中心,和S?S?S3.25BCEFEF________(,的长度都是正整数,并且四边形则的面积为EGFOABCDEGFO EGFO. 的面积,以此类推)表示F11._________. 【分析】结果如下:23195?115 207234485100011.克的物体,这把秤会显示其正确的重量;对神庙里有一把古老的秤,对于重量小于10001000.的随机数于重量大于等于克的物体,这把秤会显示出一个大于等于、、、S1000PRQ表示它们的重小明有五个物品,题目各自的重量都小于克,我们分别用.将这五个物品两两配对放到秤上进行称重,得到下面的结果:量700P+T=Q+R=900R+T=2100Q+T=800Q+S=1200. (克)(克)、(克)、(克)、、(克)__________.那么这五个物品的重量从重到轻的顺序为=2100⑤;Q+S=1200④;R+T=800①;Q+R=900②;P+T=700③;【分析】Q+T 所以:S>R>T>Q>P; 由②⑤得:T>Q;R>T; 由①③得:Q>P; 由②④得:S>R由①②得:0123456712.写在一个正方体的八个顶点上(每个顶点写一个数,所有的、、、、、将、、则一个面上的四个数之和最大则这相邻的两个数必然是一奇一偶可先确定枚举即可,如图,最大的和.17372pq1896n13的数表示自然满,定pq1(13332________.)和【分析】位置原理+分解质因数.pqr?190062?100nn?2?38?19?10n?2?19?(102)?n?1?101)2?19??(5?n?1499)(即,为:所以:p q r2,19110??51n?原式8??(925n?9??n17)14..四个完全相同的等腰梯形如下图进行放置,题目的下底构成了一个正方形的两条对角线PX=3XQ÷=____________.整个正方形面积,阴影部分面积若XQP1.2.515次当甲地时,两人一共相遇了.地,也算一次相遇个全程;所以乙的速度是甲,则甲走全程用时为2AB8058÷4=2014…24029×时间为2=8058,个全程,1+2014×时,次到那甲第2015B走了2=4029 (次)3+2=60442014×012…916.中的数字(方框内数字允、、在的每个方框中填入一个、、??0____________. 种填数方法许相同,任何数最高位不能为,使得算式成立,有)设ab?cd?efg 【分析】ab?10,cd可取90到99:10个:个到9911?11,cd可取89ab:可取10到99ab90个?99,cd(10+90)×81÷+90×9=4860(个)AEDAE=15DE=20.17.以,如下图所示,三角形为直角三角形,两条直角边的长度分别为,,,ACGABEFAEABFEADADABCD与交为边作平行四边形为边作正方形边于点,以FGHAGHCFH_______..的面积之差(大面积减去小面积)为与三角形交于点则三角形ABFEGHCD的面积ADEAD=25,所以正方形的边长为25,根据三角形【分析】有勾股定理可以算出:ADC 三角形,GD=16,所以GF=13,同时在AEG中用勾股定理算出AG=9可以算出EG=12,的AGH 与三角形CFH)×16÷2=304;三角形(的面积=25×25÷2=312.5,梯形CDGF=13+25CDGF=312.5-304=8.5. ADC-梯形面积之差=三角形a,b,c,d 18.满足下面的性质:四个不同的质数a+b+c+d 1—个质数;)(还是个质数;a,b,c,d中某两个数之和还是—(2). )a,b,c,d中某三个数之和还是一个质数(3_______ . a+b+c+d的最小值为满足条件的b+c+d只能是a=2,由于某三个数的和为质数,2【分析】有a+b+c+d为质数知必有,不妨设17. ,7,5219732为质数,所以可以从最小的尝试,的得到答案为,,,或,31. a+b+c+d 最后可得的最小值为3?3—19.个数,其中右上角的数已经填好了,的小方格内都要填一个的方格中,每个11?30.接下来填的数需要满足下列条件:为(如图)(1)每个数都能整除与它相邻的上面方格内的数(如果与它相邻的上面方格不存在,自然不;用满足这个条件)(2)每个数都能整除与它相邻的右面方格内的数(如果与它相邻的右面方格不存在,自然不._______.种不同的填法有用满足这个条件),他的上方格和右方格必,可设三列从上到下≤3种种种).1+2+3=种1+2=种种).1.).20-1A-I3?5.20.所示,如图我们可以用的方格表来表示字母20-2A-D的表中,需要满足:左表中右边的数字表示这一行中圆点个数,下边的将填入图.数字表示这一列中圆点个数,填好后的结果如右表所示20-3A-I,使其符合前面描述的要求现在,将填入图的表中(每个字母能且只能使用一次).(只要将字母写入表格即可,不用画圆点)20-20-20-359128GABFCDHEI【分析】。
第十六届“中环杯”中小学生思维能力训练活动
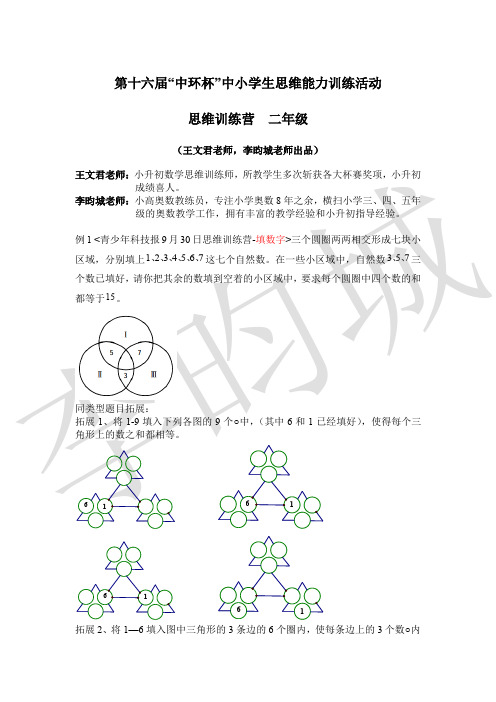
城第十六届“中环杯”中小学生思维能力训练活动思维训练营二年级(王文君老师,李昀城老师出品)王文君老师:小升初数学思维训练师,所教学生多次斩获各大杯赛奖项,小升初成绩喜人。
李昀城老师:小高奥数教练员,专注小学奥数8年之余,横扫小学三、四、五年级的奥数教学工作,拥有丰富的教学经验和小升初指导经验。
例1 <青少年科技报9月30日思维训练营-填数字>三个圆圈两两相交形成七块小区域,分别填上1234567、、、、、、这七个自然数。
在一些小区域中,自然数357、、三个数已填好,请你把其余的数填到空着的小区域中,要求每个圆圈中四个数的和都等于15。
同类型题目拓展:拓展1、将1-9填入下列各图的9个○中,(其中6和1已经填好),使得每个三角形上的数之和都相等。
拓展2、将1—6填入图中三角形的3条边的6个圈内,使每条边上的3个数○内昀城数的和相等,请给出一组答案拓展3、四个圆相互交叉重叠在一起,形成13个区域。
如果在这些区域中分别填上从1开始的13个连续的自然数,然后把每个圆中的数分别相加,得到四个和,最后使这个和最小,请问该怎么填,请给出一种填法!例2 <青少年科技报10月7日思维训练营-趣题> 如下图所示,一只蚂蚁从一个正方体的A点沿着棱爬向B点,如不故意绕远,一共有几种不同的走法?同类型拓展题:拓展4、在正五边形ABCDE上,一只青蛙从A点开始跳动,它每次可以随意的跳到相邻两个顶点中的任意一个上,一旦跳到D点上就停止跳动。
青蛙在5次之内(含5次)跳到D点有()种不同的跳法?MLK JIHGFEDC BA李昀城拓展5、一只甲虫要从A 点沿着线段爬到B 点,在每种走法中,每条线段都不能重复经过。
问这只甲虫最多有几种不同的走法?例3 <青少年科技报10月14日思维训练营-趣题> 两只小熊有一个瓶子,里面装有8千克的蜂蜜。
现在要将这些蜂蜜分成两瓶,每瓶4千克,但是没有秤和其他可以称量的工具,只有一个能装5千克蜂蜜的中等瓶子和一个能装1千克蜂蜜的小瓶子。
2016年第十六届四年级中环杯决赛试题详解

2016年第十六届四年级中环杯决赛试题(详解)1、 计算:0.2×63+1.9×126+196×9=【解析】(计算:积不变原则;提取公因数;)原式=0.2×7×9+1.9×9×14+14×14×9=1.4×9+14×9×1.9+14×9×14=1.4×9+1.4×9×19+1.4×9×140=1.4×9×(1+19+140)=1.4×9×160=14×9×16=20162、 一个质数a 比一个完全平方数b 小10,则a 的最小值是 。
(说明:完全平⽅数是指能表示为⼀个整数的平⽅的数,比如4=22,9=32,所以4、9都是完全平⽅数)【解析】(数论:质数和完全平方数的基本性质)因为质数a 与完全平方数b 相差10,所以a 和b 的末尾相同完全平方数的末尾只能是0、1、4、5、6、9除了2、5以外其余质数的末尾只能是1、3、7、9当a=5时,b=15,15不是完全平方数。
所以a 的末尾一定是1或者9当b 的末尾是1时,符合的完全平方数有81、121、441、……对应的a 就是71、120、431、……这时最小的a 是71当b 的末尾是9时,符合的完全平方数有49、169、289、……对应的a 就是39、159、279、……综上,质数a 的最小值就是713、 如图,C 、E 、B 三点共线,CB ⊥AB ,AE ∥DC ,AB=8,CE=5,则△AED 的面积是 .【解析】(几何:平行线间的等积变形和三角形面积计算公式)联结AC ,因为AE ∥DC ,所以△AED 的面积等于△ACE 的面积,△ACE 的面积等于5×8÷2=20,所以△AED 的面积也是204、 三支蜡烛分别能燃烧30、40、50分钟(但是不是同时点燃的),已知这三支蜡烛同时处于燃烧状态的时间有10分钟,只有一只蜡烛处于燃烧状态的时间有20分钟,那么正好有两只蜡烛同时处于燃烧状态的时间有 分钟。
四年级中环杯知识点提纲

四年级中环杯知识点提纲四年级初赛考纲:一、代数类:1.整数巧算:()() ()222222a b a b a ba b a ab b⎧-=+-⎪⎨±=±+⎪⎩★2.小数巧算★3.定义新运算4.等差数列与等比数列★5.分数初步(了解分数的含义,会进行简单的计算)★二、应用类:1.盈亏问题2.植树问题3.方阵问题4.平均数问题★5.周期问题★6.用列表法解应用题7.找规律填数8.填运算符号解题9.行程问题★10.和差倍问题11.年龄问题12.鸡兔同笼问题13.还原问题14.归一问题15.会利用一次方程或方程组解应用题★三、几何类:1.长方形和正方形周长与面积2.巧求多边形的周长3.巧求多边形的面积4.三角形的初步认识5.平行四边形、梯形的面积公式6.角度的计算(掌握三角形内角和为180o 这个结论,等腰三角形等边对等角的性质)★7.勾股定理(包括勾股定理逆定理)★8.面积法求高★9.等腰直角三角形的面积公式(14S =斜边的平方)★10.差不变原理★11.列方程解平面几何★12.构造法解平面几何四、数论类:1.多位数的运算(形如{10011009111999⨯L L 1442443个个的运算)★2.数论最值(比如将1~9中选出四个数填入⨯,使得乘积最大)★3.带余除法★4.位值原理★5.熟练掌握被2,3,4,5,7,8,9,11,13,25,125整除的数的规律,并且具备自己推导别的数整出规律的能力(比如自己可以推导出除以37的数的规律)★6.数字迷(含弃九法)★7.数阵图(含数阵图的最值问题)★8.数表★9.质数与合数★10.因数和倍数(因数的个数公式不考)★11.质因数分解★五、组合类:1.一笔画2.几何计数3.容斥原理★4.奇偶分析★5.枚举★6.标数法解决最短路径问题★7.抽屉原理★8.加乘原理(包含染色问题)★9.复杂的逻辑推理★四年级决赛考纲(除了初赛考纲中的内容,新增):一、代数类:1.无二、应用类:1.牛吃草问题★三、几何类:1.共边定理★2.等积变换(包含“一半模型”)★3.三角形的中位线,梯形的中位线★四、数论类:1.最大公约数和最小公倍数★2.中国剩余定理★五、组合类:1.排列和组合★2.对应原理计数★3.递推计数★4.操作问题★5.统筹规划6.组合最值(论证与构造,极端原理)★。
16届wmo初赛试题四年级

16届WMO初赛试题四年级1. 引言本文档旨在介绍16届WMO初赛四年级的试题内容和相关要求。
该试题涉及多个学科的知识,包括数学、语文、英语等。
通过参与该试题,学生能够提高自己的综合素养和解决问题的能力。
2. 数学试题2.1 题目描述一辆货车总共装了300件商品,其中有60件是苹果,50件是梨子,剩余的是桃子。
已知桃子的数量是苹果和梨子数量之和的2倍,求货车上桃子的数量。
2.2 解答要求要求学生使用代数的方法解题,写出方程并求解。
然后,用文字描述解题过程,说明每一步的数学推理。
2.3 评分标准正确列出代数方程:30分正确求解方程并得出答案:30分正确描述解题过程并进行数学推理:40分3. 语文试题3.1 题目描述阅读下面的短文,根据短文内容回答问题。
北方的冬天真的很冷,特别是当风一吹过来时,仿佛能将人的骨头都冻住。
小明不怕冷,每天都会到外面玩耍。
小明最喜欢的活动是堆雪人。
他用手捏起一团雪,然后再给雪人加上眼睛、鼻子和嘴巴,最后给雪人梳头,整个过程非常有趣。
问题:小明最喜欢的活动是什么?3.2 解答要求要求学生根据短文的描述,准确回答问题,并用简洁的语言表达。
3.3 评分标准正确回答问题:40分清晰简洁的语言表达:60分4. 英语试题4.1 题目描述根据句子意思,在方框中选择合适的单词填空,使句子完整正确。
1.— Do you like _______? —Yes, I do. It’s my favoritefruit.A. appleB. orangeC. banana2.— Where is _______ bag? —It’s under the desk.A. myB. IC. me4.2 解答要求要求学生根据句子的意思,选择正确的单词填空,并写出自己选择的理由。
4.3 评分标准正确选择填空的单词:40分正确写出理由并解释选择的依据:60分5. 结语本文档介绍了16届WMO初赛四年级的试题内容和相关要求。
2016第十六届中环杯四年级初赛详解

16 届中环杯四年级初赛
1、计算: (20.15 + 40.3) × 33 + 20.15 【分析】原= 式 (20.15 + 20.15× 2) × 33 + 20.15
= 20.15× 3× 33 + 20.15 = 20.15× (3× 33 +1)
= 2015
2、用 1、2、3、4 这四个数字构成一个四位数 abcd ,要求: (1)a、b、、c d 互不相同;(2)b 比 a、d 都大,c 比 a、d 都大。这样的四位数有______ 个 【分析】由题意, b、c 应取 3、4, a、d 应取 1、2,有 2× 2 =4 个数
n + n + n 的过程中不能有进位,所以 n 的数字组成仅能有 0、1、2、3,由于各 个数码互不相同,所以 n 最大为 3210
9、如图,ABCD 和 EGFO 都是正方形,其中点 O 是正方形 ABCD 的中心,EF∥BC。
若 BC、EF 的长度都是正整数,并且四边形 BCEF 的面积为 3.25,则 SABCD − SEGFO = ______
8、对于自然数 a ,S(a) 表示 a 的数码和(比如 S(123) =1+ 2 + 3 =6 )。如果一个自然数 n 的各个数码都互不相同,并且 S(3n) = 3S(n) ,则 n 的最大值为______ 【分析】即 S(n + n + n=) S(n) + S(n) + S(n) ,和的数码和等于数码和的和,也就是说,在
第十六届中环杯选拔赛(四年级)

第⼗六届中环杯选拔赛(四年级)第⼗六届“中环杯”⼩学⽣思维能⼒训练活动六年级组选拔赛1.计算:171720.152++2015=3203_____。
2.要使得算式()111145-1-+4=7234成⽴,⽅框内应填的数是_____。
3.把61本书分给某个班级的学⽣,如果其中⾄少有1⼈能分到⾄少3本书,那么这个班最多有_____⼈。
4.有⼀个数,除以3余数是1,除以5余数是2,那么这个数除以15的余数是_____。
5.如图,⼀个三⾓形的三个内⾓分别为(5x +3y )°、(3x +20)°、(10y +30)°,其中x 、y 都是正整数,则x +y =_____。
6.三个数两两之间的最⼤公约数分别是3、4、5,那么这三个数的和最⼩是_____。
7.对字母a ~z 进⾏编码(a =1,b =2,……,z =26),这样每个英⽂单词(所有单词中的字母都认为是⼩写字母)都可以算出其所有字母编码的乘积p 。
⽐如单词good ,其对应的p 值为7×15×15×4=6300(因为g =7,o =15,d =4)。
如果某个合数⽆法表⽰成任何单词(⽆论这个单词是不是有意义)的p 值,这样的合数就称为“中环数”。
最⼩的三位数“中环数”为_____。
8.甲、⼄两⼈同时骑⾃⾏车从A 地道C 地,路上会经过B 地。
骑了⼀会⼉,甲问⼄:“我们已经骑了多少公⾥了?”⼄回答:“我们骑的路程相当于这⾥到B 地距离的13。
”⼜骑了10公⾥后,甲⼜问:“我们还要骑多少公⾥才能到达C地?”⼄回答:“我们还要骑的路程相当于这⾥到B地距离的13。
”A、C两地相距_____公⾥(答案写成分数形式)。
9.如果⼀个数不是11的倍数,但是移除⼀个任意位上的数码后,它就变成11的倍数了(⽐如111就是这样的数,⽆论移除其个位、⼗位或百位数码,都变成11的倍数了),这样的数定义为“中环数”。
2016第十六届中环杯三年级初赛详解

1. 计 算 : 2015 × 2015 − 2014 × 2013 = (
).
【分析】 (2014 +1) × 2015 − 2014× 2013
= 2014 × 2015 − 2014 × 2013 + 2015
= 2014 × (2015 − 2013) + 2015 = 6043
2. 在下面算式的方框中填入适当的符号(只能填加、减、乘、除这四种符号),使得算 式成立.
(6 2) (3 4) (6 2) = 25 【分析】 (6× 2) − (3 − 4) + (6× 2) = 25
3. 用 1~9 这 九 个 数 字 组 成 三 个 三 位 数 a,b,c(每 个 数 字 能 且 只 能 使 用 一 次 ),则 a + b − c 的
1
1
2
212 2 1 2 12
2 12 2
3 3 23 3 2 323 3 2 3 2 32 3 3 23 23 3 23
3
4
4
4
434 3 4
4 3 43 4 3 4
43 43 4 3 4 3 4
4 34 3 43 4
434 3 4
434
4
6.小胖在编一本书的页码时,一共用了 1101 个数字.已知页码是从 1 开始的连续自然
9.如 图 ,5×5 的 方 格 中 有 三 个 小 方 格 已 经 染 黑 .现 在 要 将 一 个 1×3 的 白 长 方 形 (不 能 选 已
经 染 黑 的 方 格 )染 黑 , 要 求 其 不 能 与 已 经 染 黑 的 方 格 产 生 公 共 边 或 者 公 共 点 .有
2016年中环杯初赛模拟卷及答案

(新舟教育吴忠良供题) 【答案】 3.75 4. 从自然数 1 ~ 20 中选出 4 个数(不重复),把所有的可能性按顺序排列如 下(每种可能性中 4 个数都是从小到大的):(1,2,3,4)、(1, 2,3,5)、(1,2,3,6)、……、(1,2,3,20)、(1,2,4, 5)、(1,2,4,6)、……、(1,2,4,20)、……、(16,18,
4 5
4 4
2 5
2016 年第 16 届中环杯七年级初赛模拟试卷 填空题(共 10 题,前 5 题每题 4 分,后 5 题每题 6 分) 1. 计算: 23 2 22 2 2 1 33 2 32 2 3 1 243 2 242 2 24 1 ________.
1
x y z 20
3
y3 z3 _____. xyz
2 y 3
3
______.
5. 若 p, q 都是素数,关于 x 的方程 x4 px3 q 0 有整数根,满足要求的有序数 对 p, q 有_____对 6. 现有 20 个正整数,它们依次为 12 5 、 22 5 、 、 202 5 ,计算其中任意相 邻两数的最大公约数,请写出所有可能出现的最大公约数: _______________. (四季教育供题) 7. 若多项式 f x 满足:对任意 x ,均有 f x 4 f x 7 x 3 ,并且 f 0 5 ,则
7. 如果一个等差数列的每一项都是整数,其中某相邻四项之和为 30,某相 邻五项之和也是 30。前面所提的“相邻四项”与“相邻五项”中相同的 数字最少有_____个 8. 一条直线上有两个钉子,相距 20 厘米,一根弹性均匀的白色绳子两头系 在两个钉子上,甲要将这根绳子涂成红色,他每次最多可以将 2 厘米涂 成红色,但乙在旁边捣乱,甲每涂 1 次,乙都将一个钉子沿直线向外移 动 1 厘米,即绳子均匀的拉长 1 厘米,问甲要将绳子全部涂成红色至少要 涂 次 (四季教育供题) 9.
2016第十六届中环杯五年级决赛详解

第十六届“中环杯”小学生思维能力训练活动 五年级决赛
城隍喵
【第 3 题】 一个超过 20 的自然数 N ,在14 进制与 20 进制中都可以表示为回文数(回文数就是指正读与倒读都一样的 数,比如12321、3443 都是回文数,而12331不是回文数)。N 的最小值为 ________(答案用10 进制表示)。 【分析与解】 数论,进制与位值。 因为 N 20 ; 所以 N 在14 进制与 20 进制中都不是一位数;
我们希望 N 要尽可能小,故设 N aa bb ;
14
20
即 N a 14 a b 20 b ; N 15a 21b ;
则 N 既是15 的倍数又是 21 的倍数;
故 N 是 15, 21 3 5 7 105 的倍数;
而 105 77 55 ,符合题意;
10
14
20
这个父亲的财产有1000 80000 81000 元;
老大分得1000 81000 1000 1 9000 元;
10 即每个孩子都分到了 9000 元; 这位父亲一共有 81000 9000 9 个孩子。 (方法三)
设这位父亲一共有 n 个孩子;
则倒数第二个孩子分得1000n 1 元以及剩余的 1 ;
第十六届“中环杯”中小学生思维能力训练活动 五年级决赛
2016 年 3 月 5 日 12 : 30 ~ 14 : 00 考试时间: 90 分钟 满分:100 分
一、填空题 A :(本大题共 8 小题,每题 6 分,共 48 分)
【第 1 题】
16届wmo初赛试题四年级

16届wmo初赛试题四年级一、题目描述本文档是关于16届wmo初赛试题四年级的详细解析和答案。
本试题主要针对四年级的学生,通过考察他们在数学、语文、英语、科学等方面的知识和能力,提供了一系列多项选择题和解答题。
下面将逐一解析试题并给出参考答案。
二、数学题1. 12 - 7 = ?A. 4B. 5C. 6D. 7解析正确答案为B。
2. 哪一个数字是偶数?A. 3B. 5C. 8D. 9解析正确答案为C。
三、语文题1. 下列词语中哪一个是错别字?A. 汉字B. 故事C. 爬山D. 数字解析正确答案为D。
2. 下列诗句中哪一句是对的?A. 秋天是丰收的季节B. 冬天是悲伤的季节C. 春天是神秘的季节D. 夏天是寒冷的季节解析正确答案为A。
四、英语题1. Which animal has a long trunk?A. CatB. DogC. ElephantD. Horse解析正确答案为C。
2. Which day comes after Wednesday?A. SundayB. MondayC. ThursdayD. Friday解析正确答案为C。
五、科学题1. What is the largest planet in our solar system?A. EarthB. JupiterC. MarsD. Saturn解析正确答案为B。
2. What is the process by which plants make their own food?A. PhotosynthesisB. RespirationC. DigestionD. Circulation 解析正确答案为A。
以上就是16届wmo初赛试题四年级的详细解析和答案。
希望本文档能对四年级的学生们提供一定的帮助,加深对各科知识的理解。
如果还有其他问题,可以随时咨询。
2016第十六届中环杯四年级决赛详解

25 10 15 3 5 是合数 49 10 39 313 是合数 81 10 71 是质数 故 a 最小是 71
【第 3 题】 如图, C、E、B 三点共线, CB AB, AE / / DC , AB 8, CE 5 ,则 AED 的面积为______
A1 与 A3 中至少有一个是假话
但不可能为 A1 是真话, A3 是假话 则 A1 是假话;则 n 12 再对 A1 是假话,则 n 12 再对 D1 进行讨论 ①若 D1 是真话,即 12 n 20 故 B1 与 B3 都是假话 则 B2 是真话;则 10 n 但不存在既满足 12 n 20 ,又满足 10 n 的正整数 n ②故 D1 是假话,即 n 20 则 D2 是真话,即 n 是一个质数 故 B2 、 C1 、 C3 均是假话 则 C2 是真话,即 20 n 90 故 B3 是假话 则 B1 是真话,即 84 n 90 注意到,符合 84 n 90 且 n 为质数的只有 n 89 ,即这个数是 89 【第 10 题】 如图, ABC 是一个等边三角形,在 BC 边上取点 D、E ,使得 BC 3DE ,作等边 DEF , 联 结 AF , 作 DG 平 行 AF 于 点 G , 作 EH 平 行 AF 交 边 AC 于 点 H , 作 。若 G I A、 FH J 、 A FH J A F BDF 的面积为 45, DEF 的面积为 30,则 GI HJ, 一共有 6 道题目, 每道题目的分值均为 7 分 (最后每题的得分都是整数, 最低为 0 分,最高为 7 分) ,每个参赛者的总分就是 6 道题目得分的乘积,如果两个人的得 分相同,就计算 6 道题目得分之和,从而评定名次高低。如果还相同,就算两人并列。在这 次比赛中, 一共有 86 262144 位参赛者, 这些参赛者中没有出现并列, 排名为 76 117649 的 参赛者的得分为________分 【说明】 ⑴此题为错题 若两个人 6 道题每题得分完全相同 则 6 道题目得分的乘积相同,6 道题目得分的和也相同 则这两个人的排名相同,即这两个人并列 由题意,这 86 262144 位参赛者中没有出现并列 则这 86 262144 位参赛者每题得分均不完全相同 而每题的得分为 0~7 的整数,由乘法原理一共有 86 种得分情况 若甲第 1~6 题得分为 0、 0、 0、 0、 0、 0、 1 ,乙第 1~6 题得分为 0、 0、 0、 0、 0、 1、 0 甲、乙两人 6 道题目得分的乘积为 0,6 道题目得分的和为 1 则甲、乙两人排名相同,即这两个人并列 这与“这些参赛者中没有出现并列”矛盾 故此题为错题 ⑵若将原题中“这些参赛者中没有出现并列”改为“这些参赛者中,任意两人这 6 题的各 题得分不完全相同” ,则排名为 76 117649 的参赛者的得分为 1 分 理由如下: 若 6 题中,至少有一题得分为 0,则 6 道题目得分的乘积为 0 若 6 题中,没有一题得分为 0,则 6 道题目得分的乘积不为 0 这种情况下,每题的得分为 1~7 的整数,由乘法原理一共有 76 种得分情况 故排名为 76 117649 的参赛者的得分为乘积最小的正整数 而第 1~6 题得分为 1、 1、 1、 1、 1、 1 的参赛者,得分为 1 故排名为 76 117649 的参赛者的得分为 1 分 【第 8 题】 如图所示,两条直线与两个圆交于 9 个点,从这 9 个点中选出 4 个点,要求这 4 个点的任意 3 个点既不在一条直线上,也不在一个圆圈上,不同的选法有______种
2016 年第16 届中环杯四年级初赛模拟试卷详解

同理可得 n 5 2 6 2 1 2 3 5
5 5 7
所以 m n 2.8
-6-
王洪福老师
数学
10. 将含有一些数字的表格划分为若干个区域,要求: (1)每个数字表示其所在区域的面积(这里所谓的面积就是指单位正方形的个数) ; (2)两个面积相等的区域不相邻(可以有公共顶点,但是不能有公共边) ; (3)每个区域内可以有多个数字(当然,这些数字必然相等)或者没有数字; 如下图所示,给出了一个例子 3 3 3 3 2 2 3 2
查看更多试题资料欢迎 关注王洪福老师公众号
-7-
BE =c , DE a , BF d , DF b 所以 BD BE ED c a , BD BF FD d b 所以 2 BD a b c d 10 10 20 ,所以 BD 10
因为 CE BD ,所以 S BCD BD CE 2 10 5 2 25
王洪福老师
数学
2016 年第 16 届中环杯 四年级初赛模拟试卷详解
填空题(共 10 题,前 5 题每题 4 分,后 5 题每题 6 分) 1. 计算: (20.15+30.24)×72+15.12×56+564.2= 【解析】 .
(20.15 30.24) 72 15.12 56 564.2 =20.15 72+30.24 72 15.12 2 28 20.15 28 =20.15 72+30.24 72 30.24 28 20.15 28 =20.15 72+28 30.24 72+28 =2015 3024 =5039
上海中环杯小学四年级考前模拟题第一套答案详解

综合强化复习04-07 姓名: 得分:一、填空题:1、计算:(1+2+3+……+2009+2010+2011)÷2011+(1+2+3+……+2010)÷2011=( )。
分析:除数一样时,可以用乘法分配率。
首先提取公因数2011,然后观察括号里的数相加规律,从1加到2011再加回1,这样的数列求和等于数列中最大的数的平方。
=(1+2+3+……+2009+2010+2011+1+2+3+……+2010)÷2011=2011×2011÷2011=20112、, x y 为两个数,规定两种新的运算“*”及“△”,,8,65*xy y x y x y x =∆+=求: (4△6)*(5△3)=( )。
分析:套用规则即可。
一般符号前面的数和后面的数分开分析。
=(8×4×6)*(8×5×3)=192*120=192×5+120×6=960+720=16803、将20条长10厘米的纸带粘合在一起,纸带之间的重合部分为2厘米,粘得的纸带长( )厘米。
分析:若把20条纸带的长全部算出来,则粘合的部分2厘米包含了2次,需要减去一次,关键是减去多少个2厘米,20条,粘合的部分有19处。
=20×10-19×2=162厘米4、100个连续自然数(按从小到大的顺序排列)的和是20150,取出其中第2个、第4个、第6个……第100个,再把剩下的50个数相加,得到的结果是( ). 分析:100个连续自然数分成了两组,取出的是双数个,留下的是单数个。
50个双数个比50个单数个的总和多50,因此这道题实质是道和差问题。
=(20150-50)÷2=100505、某天,博物馆开馆前已排了530米的长队,并且每分钟有6位参观者加入。
从开馆开始,1小时10分钟之后队列消失,到此时为止,进入博物馆的参观者人数是2010位。
中环杯数学竞赛四年级试题

中环杯数学竞赛四年级试题中环杯数学竞赛是一项面向小学生的数学竞赛,旨在激发学生的数学兴趣,提高数学素养。
以下是一份模拟的四年级中环杯数学竞赛试题,供参考:一、选择题(每题2分,共10分)1. 下列哪个数是最小的两位数?A. 10B. 98C. 100D. 992. 如果一个数的3倍是45,那么这个数是多少?A. 15B. 50C. 40D. 303. 一个长方形的长是12厘米,宽是8厘米,它的周长是多少?A. 40厘米B. 44厘米C. 48厘米D. 56厘米4. 以下哪个分数是最大的?A. 1/2B. 2/3C. 3/4D. 4/55. 一个数加上8等于23,这个数是多少?A. 15B. 21C. 17D. 19二、填空题(每空1分,共10分)6. 一个数的5倍是30,这个数是_________。
7. 把一个数增加20,得到的结果比原数大_________。
8. 一个数的2/3等于18,这个数是_________。
9. 一个班级有40名学生,其中女生占2/5,女生有_________人。
10. 如果一个数的3倍是另一个数的2倍,那么这两个数的比是_________。
三、简答题(每题5分,共20分)11. 一个长方形的长是15厘米,宽是10厘米,求它的面积。
12. 一个班级有50名学生,其中1/4是男生,这个班级有多少名男生?13. 一个数的4倍是另一个数的2倍,如果这个数是12,求另一个数。
14. 一个数的1/5加上另一个数的1/4等于9,如果另一个数是36,求这个数。
四、应用题(每题10分,共20分)15. 小明有40张邮票,他给了小红一半,然后他又给了小红剩下的一半,最后小明还剩下多少张邮票?16. 一个水果店有苹果和橙子,苹果的数量是橙子的3倍,如果苹果和橙子一共是90个,问苹果和橙子各有多少个?五、附加题(10分)17. 一个数列的前三项是1,2,3,从第四项开始,每一项都是前三项的和。
2022年第16届中环杯四年级初赛模拟试卷答案

2022年第16届中环杯四年级初赛模拟试卷答案2022,年第,16,届中环杯四年级初赛模拟试卷(篇一)2022年第十六届中环杯初赛试题(二年级)1、计算:2+3+5-6+7+1-10=2、计算:2310-187+8÷2=3、观察下面的三个天平,1个圆圈的重量和朵花的重量相等。
4、羊村的村长为了防范灰太狼,在正方形的羊村周围安排小羊们站岗放哨。
要求每边有4只小羊站岗,则最少需要只小羊。
5、10台拖拉机开10天需要消耗10桶油。
照此计算,20台拖拉机开20天需要消耗桶油。
6、把1-5这五个数字分别填入下图的方格中,使得横行三数之和与竖行三数之和都等于9。
7、泡泡把蓝圆片摆成一个圈,每两个蓝圆片之间再放入一个红圆片。
放完之后,泡泡数了数,一共放了70个小圆片,那么蓝圆片有个。
8、一辆洒水车给一个社区街道洒水,地图如下图,你能否设计一条洒水路线,使洒水车不重复地走遍所有街道,再回到出发点?你的为:(填能或不能){2022,年第,16,届中环杯四年级初赛模拟试卷答案}。
9、有一个正方体木块,每个面上分别写上了1、2、3、4、5、6,并且相对两面上的和是7,这个木块按下图放置后,按照图中箭头所示方向翻动。
翻动到最后一格时,木块朝上一面的数是{2022,年第,16,届中环杯四年级初赛模拟试卷答案}。
10、小泡泡要给一些美丽的花朵涂颜色。
他有5种颜色的蜡笔,一朵花只可以用一种颜色,那么下图中这些花朵中至少有朵花的颜色相同。
11、大熊、静香、胖虎、小夫与机器猫一起举行围棋比赛,每两人要比赛一场。
到现在为止,大熊已经赛了4场,静香赛了3场,胖虎赛了2场,小夫赛了1场。
机器猫参加了场比赛。
12、香香和爸爸在比年龄,爸爸6年前的年龄比香香5年后的年龄还大18岁,香香10年后的年龄和爸爸7年前的年龄和是50岁。
则今年爸爸岁。
13、小明想要对图中的每个小三角形进行染色,要求任意一个三角形的三边都是一条染红色、一条染绿色、一条染蓝色。
2016第十六届中环杯四年级初赛解析

2016第十六届中环杯四年级初赛解析第十六届“中环杯”四年级(初赛)解析1.计算题:(20.15+40.3)×33+20.15=_______ 【分析】原式=(20.15+20.152)33+20.15=20.1533+20.1566+20.1520.15(33661)=?++2.用(13.14641ab bc ac ab bc ac =22222222()14641121()121a b c a b c abc ===4.5.甲、乙两车同时从A 、B 两地沿相同的方向行驶.甲车如果每小时行驶50千米,则6小时可以追上前方的乙车;如果每小时行驶80千米,则2小时可以追上前方的乙车.由此可知,乙车的速度是________千米/时.【分析】设乙车速度为x 千米/时,由追及问题的路程差=速度差?时间,得(50)6(80)2x x -?=-?30061602140435x x x x -=-==6.右图中有_________个三角形.【分析】分类枚举,如图,8.对于自然数a ,()S a 表示a 的数码和(比如(123)1236S =++=.如果一个自然数n 的各个数码都互不相同,并且(3)3()S n S n =,则n 的最大值为_____________ 【分析】33()S n S n =()∴3乘以n 时不能进位,则n 中最大的数字只能为3,故n 最大为3210.9.如图,ABCD 和EGFO 都是正方形,其中点O 是正方形ABCD 的中心,EF//BC .若BC 、EF 的长度都是正整数,并且四边形BCEF 的面积为3.25,则ABCD EGFO S S -=________(EGFO S 表示EGFO 的面积,以此类推).【分析】结果如下:2319511520723448511.神庙里有一把古老的秤,对于重量小于1000克的物体,这把秤会显示其正确的重量;对于重量大于等于1000克的物体,这把秤会显示出一个大于等于1000的随机数.小明有五个物品,题目各自的重量都小于1000克,我们分别用P 、Q 、R 、S 表示它们的重量.将这五个物品两两配对放到秤上进行称重,得到下面的结果:Q+S =1200(克)、R+T =2100(克)、Q+T =800(克)、Q+R =900(克)、P+T=700(克). 那么这五个物品的重量从重到轻的顺序为__________.【分析】Q+T =800①;Q+R =900②;P+T =700③;Q+S =1200④;R+T =2100⑤;由①②得:R>T ; 由①③得:Q>P ; 由②④得:S>R ; 由②⑤得:T>Q ;所以:S>R>T>Q>P12.013.和),则()f p +nn 2n 2n 119006210019103819(102)192(5101)+++-=?-=?-=-所以:p q r 为:2,19,15101n +?-(即1499n +)原式925(917)8n n =+-+=7偶奇14.四个完全相同的等腰梯形如下图进行放置,题目的下底构成了一个正方形的两条对角线.若PX=3XQ ,阴影部分面积÷整个正方形面积=____________.15.达的2那甲第2015次到B 时,走了1+2014×2=4029个全程,时间为4029×2=8058,8058÷4=2014…2 2014×3+2=6044(次)PS BA16.在+=的每个方框中填入一个0、1、2、…、9中的数字(方框内数字允许相同,任何数最高位不能为0),使得算式成立,有____________种填数方法. 【分析】ab cd efg +=设 ab 10cd 909910ab 11cd 9911ab==,可取到:个,可取89到:个17..以AD 与FG 的18.(1)a+b+c+d 还是—个质数;(2)a,b,c,d 中某两个数之和还是—个质数;(3)a,b,c,d 中某三个数之和还是一个质数. 满足条件的a+b+c+d 的最小值为_______ . 【分析】有a+b+c+d 为质数知必有2,不妨设a =2,由于某三个数的和为质数,只能是b+c+d 为质数,所以可以从最小的尝试,的得到答案为2,3,7,19或2,5,7,17. 最后可得a+b+c+d 的最小值为31.E19.一个33?的方格中,每个11?的小方格内都要填—个数,其中右上角的数已经填好了,为30(如图).接下来填的数需要满足下列条件:(1)每个数都能整除与它相邻的上面方格内的数(如果与它相邻的上面方格不存在,自然不用满足这个条件);(2)每个数都能整除与它相邻的右面方格内的数(如果与它相邻的右面方格不存在,自然不用满足这个条件).不同的填法有_______种.20.我们可以用53 的方格表来表示字母A-I ,如图20-1所示.将A-D 填入图20-2的表中,需要满足:左表中右边的数字表示这一行中圆点个数,下边的数字表示这一列中圆点个数,填好后的结果如右表所示.现在,将A-I 填入图20-3的表中(每个字母能且只能使用一次),使其符合前面描述的要求(只要将字母写入表格即可,不用画圆点).【分析】12 598IHG FED C B A。
小晨精品第一周 计算与巧算上海四年级强化版- (2)【XCJP】

第一周计算与巧算1.【8届中环杯初赛第1题】(1+2+3+4+……+99+100)-(2+4+6+8+……+96+98)=()2.【11届中环杯初赛第1题】20092009×201020102010-20102010×200920092009()3.【8届小机灵杯初赛第1题】(1+2+3+……+2008+2009+2008+……+3+2+1)÷2009=_____.4.【14届中环杯决赛第1题】计算:75×4.7+15.9×25=________。
5.【10届中环杯决赛第12题】一个两位数,加上45以后,十位数字正好与个位数字互换位置,原来的这个两位数是多少?1解析:1.【考点】速算与巧算——等差数列【解析】原式=1+3+5+7+……+99+100=(1+99)×50÷2+100=26002.【考点】乘法分配律逆运算、重码数【解析】原式=2009×10001×2010×100010001-2010×10001×2009100010001=03.【考点】速算与巧算——山顶数列【解析】原式=2009×2009÷2009=20094.【考点】速算与巧算——小数计算【解析】计算。
75×4.7+15.9×25=75×4.7+ 5.3×3×25=75×4.7+5.3×75=75×(4.7+ 5.3) =75×10=7505.【考点】位值原理【解析】设这个两位数是a̅̅̅̅b̅̅,那么由题意有:a̅̅̅̅b̅̅+45=b̅̅̅̅a̅̅,化简得b-a=5 那么这样的两位数可能是16,27,38,49,共4种可能。
2。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第十六届“中环杯”四年级(初赛)解析
1.计算题:(20.15+40.3)×33+20.15=_______ 【分析】原式=(20.15+20.152)33+20.15
⨯⨯ =20.1533+20.1566+20.15
20.15(33661)
⨯⨯=⨯++
2.用(1
3.设长方体的长宽高分别为a 、14641ab bc ac ab bc ac =
22222222
()14641
121()12111
a b c a b c abc abc ====
4.
5.甲、乙两车同时从A 、B 两地沿相同的方向行驶.甲车如果每小时行驶50千米,则6小时可以追上前方的乙车;如果每小时行驶80千米,则2小时可以追上前方的乙车.由此可知,乙车的速度是________千米/时.
【分析】设乙车速度为x 千米/时,由追及问题的路程差=速度差⨯时间,
得(50)6(80)2x x -⨯=-⨯
30061602140435
x x x x -=-==
6.右图中有_________个三角形.
【分析】分类枚举,如图,
8.对于自然数a ,()S a 表示a 的数码和(比如(123)1236S =++=.如果一个自然数n 的各个数码都互不相同,并且(3)3()S n S n =,则n 的最大值为_____________ 【分析】33()
S n S n =()
∴3乘以n 时不能进位,则n 中最大的数字只能为3,故n 最大为3210.
9.如图,ABCD 和EGFO 都是正方形,其中点O 是正方形ABCD 的中心,EF//BC .若BC 、EF 的长度都是正整数,并且四边形BCEF 的面积为3.25,则ABCD EGFO S S -=________(EGFO S 表示EGFO 的面积,以此类推).
【分析】结果如下:
23195
115
207234485
⨯
11.神庙里有一把古老的秤,对于重量小于1000克的物体,这把秤会显示其正确的重量;对于重量大于等于1000克的物体,这把秤会显示出一个大于等于1000的随机数.
小明有五个物品,题目各自的重量都小于1000克,我们分别用P 、Q 、R 、S 表示它们的重量.将这五个物品两两配对放到秤上进行称重,得到下面的结果: Q+S =1200(克)、R+T =2100(克)、Q+T =800(克)、Q+R =900(克)、P+T=700(克). 那么这五个物品的重量从重到轻的顺序为__________.
【分析】Q+T =800①;Q+R =900②;P+T =700③;Q+S =1200④;R+T =2100⑤;
由①②得:R>T ; 由①③得:Q>P ; 由②④得:S>R ; 由②⑤得:T>Q ;所以:S>R>T>Q>P
12.0
13.9
962n 个 ,定义和),则()f p +【分析】位置原理+分解质因数n
n 2n 2
n 1190
062100
19103819(10
2)
192(5101)
+++-=⨯-=⨯-=⨯⨯⨯-
所以:p q r 为:2,19,15101n +⨯-(即1
49
9n +)
原式925(917)8n n =+-+=
7偶
奇
14.四个完全相同的等腰梯形如下图进行放置,题目的下底构成了一个正方形的两条对角线.若PX=3XQ ,阴影部分面积÷整个正方形面积=____________.
15.达的2
那甲第2015次到B 时,走了1+2014×2=4029个全程,时间为4029×2=8058,8058÷4=2014…2 2014×3+2=6044(次)
P
S B
A
16.
在
+
=
的每个方框中填入一个0、1、2、…、9中的数字(方框内数字允
许相同,任何数最高位不能为0),使得算式成立,有____________种填数方法. 【分析】ab cd efg +=设 ab 10cd 909910ab 11cd 9911ab
==,可取到:个,可取89到:个
17..以AD 与FG 的
18.(1)a+b+c+d 还是—个质数;
(2)a,b,c,d 中某两个数之和还是—个质数; (3)a,b,c,d 中某三个数之和还是一个质数. 满足条件的a+b+c+d 的最小值为_______ . 【分析】有a+b+c+d 为质数知必有2,不妨设a =2,由于某三个数的和为质数,只能是b+c+d 为质数,所以可以从最小的尝试,的得到答案为2,3,7,19或2,5,7,17. 最后可得a+b+c+d 的最小值为31.
E
19.一个33⨯的方格中,每个11⨯的小方格内都要填—个数,其中右上角的数已经填好了,为30(如图).接下来填的数需要满足下列条件:
(1)每个数都能整除与它相邻的上面方格内的数(如果与它相邻的上面方格不存在,自然不用满足这个条件);
(2)每个数都能整除与它相邻的右面方格内的数(如果与它相邻的右面方格不存在,自然不用满足这个条件).不同的填法有_______种.
20.我们可以用53 的方格表来表示字母A-I ,如图20-1所示.
将A-D 填入图20-2的表中,需要满足:左表中右边的数字表示这一行中圆点个数,下边的数字表示这一列中圆点个数,填好后的结果如右表所示.
现在,将A-I 填入图20-3的表中(每个字母能且只能使用一次),使其符合前面描述的要求(只要将字母写入表格即可,不用画圆点).
【分析】
12
598I
H
G F
E
D C B A。
