通用技术三视图专题练习(一).
三视图习题50道(含答案).

三视图练习题1、若某空间几何体的三视图如图所示,则该几何体的体积是( (A2 (B1 (C23(D132、一个几何体的三视图如图,该几何体的表面积是((A372 (B360 (C292 (D2803、若某几何体的三视图(单位:cm如图所示,则此几何体的体积是(A3523cm3(B3203cm3 (C2243cm3(D1603cm34、一个长方体去掉一个小长方体,所得几何体的正(主视图与侧(左视图分别如右图所示,则该几何体的俯视图为: (5、若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积...等于 (A.2 C..66、图2中的三个直角三角形是一个体积为20cm2的几何体的三视图,则h= cm第2题第5题7、一个几何体的三视图如图所示,则这个几何体的体积为。
8、如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为______.9、如图1,△ ABC 为正三角形,AA '//BB ' //CC ' , CC ' ⊥平面ABC 且3AA '=32BB '=CC '=AB,则多面体△ABC -A B C '''的正视图(也称主视图是(10、一空间几何体的三视图如图所示,则该几何体的体积为( .A.2π+B. 4π+C. 2π+D. 4π 11、上图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是(A .9πB .10πC .11πD .12π第7题侧(左视图正(主视图俯视图俯视图正(主视图侧(左视图12、一个棱锥的三视图如图,则该棱锥的全面积(单位:c2m为((A(B(C(D13、若某几何体的三视图(单位:cm如图所示,则此几何体的体积是3cm.14、设某几何体的三视图如上图所示。
则该几何体的体积为3m15、已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm,可得这个几何体的体积是(A.3 4000 cm3B.3 8000 cm3C.3 2000cmD.34000cm16、一个几何体的三视图如上图所示,其中正视图与侧视图都是边长为2的正三角形,则这个几何体的侧面积为(A.33π B.2πC.3π D.4π第14题正视图侧视图俯视图第17题17、如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积为(A .32πB .16πC .12πD .8π18、下图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是A.9πB.10πC.11π D .12π19、右图是一个多面体的三视图,则其全面积为( AB6C6 D4 20、如图所示,一个空间几何体的正视图和侧视图都是底为1,高为2的矩形,俯视图是一个圆,那么这个几何体的表面积为(A .2πB .52πC .4πD .5π21、一个几何体的三视图及其尺寸(单位:cm如图所示,则该几何体的侧面积为_ ______cm 2.22、如果一个几何体的三视图如图所示(单位长度: cm, 则此几何体的表面积是(A. 2(20cm + B.212cmC. 2(24cm + D. 242cm俯视图左视图俯视图图2723. 如右图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的表面积为A .π3 B .π2 C .π23D .π424. 如下图,某几何体的正视图与侧视图都是边长为1的正方形,且体积为12。
通用技术三视图专题练习(一).docx

三视图专题练习(一)
1.根据立体图,补全俯视图和左视图所缺的线条。
(2008年会考)
2、请据题图所示形体,1时出主视图,补全左视图的缺漏线条。
3.根据立体图,补齐俯视图和左视图
主视
4.根据立体图,画出俯视图、补齐俯视图和左视图
5.根据立体图,补全俯视图和左视图屮所缺漏的图线。
6 •根据立体图,补全俯视图和左视图屮所缺漏的图线(2008年10月高考题)
第21题图
7.根据轴测图补慚三视图屮所缺的线条。
9•下图是小锤的止等轴侧图,请补全俯视图,并闹出它的左视图。
8.根据题图所不形体,画出主视图。
补全俯视图的缺漏线条。
10.根据立体图,曲出主视图和左视图
O O
11、根据立体图补全三视图屮所缺®图线(2009予9申丙彎®
第21题图
12、根据立体图补全三视图屮所缺的图线(2009年3月高考题)
13.根据立体模型补向视图屮所缺的线。
中考三视图练习题

中考三视图练习题一、选择题1. 下列哪个选项是正确的主视图?A. 左视图B. 俯视图C. 右视图D. 仰视图2. 三视图包括哪三个视图?A. 俯视图、左视图、右视图B. 主视图、俯视图、左视图C. 仰视图、俯视图、左视图D. 仰视图、右视图、左视图3. 观察一个物体时,哪个视图可以提供物体的宽度信息?A. 主视图B. 俯视图C. 左视图D. 仰视图4. 下列哪个选项是正确的俯视图?A. 显示物体的顶面形状B. 显示物体的侧面形状C. 显示物体的正面形状D. 显示物体的底面形状5. 当物体的主视图和左视图都相同,且都是矩形时,该物体可能是:A. 立方体B. 圆柱体C. 长方体D. 球体二、填空题6. 在三视图中,______视图显示物体的正面形状。
7. 当物体的主视图和俯视图都是圆形时,该物体可能是______。
8. 一个物体的三视图可以提供物体的______、______和______三个方向的信息。
9. 俯视图通常显示物体的______面形状。
10. 如果一个物体的主视图和左视图都是正方形,那么该物体可能是______。
三、判断题11. 一个物体的主视图和左视图可能完全不同。
()12. 三视图中的任何一个视图都不能单独表示物体的全部信息。
()13. 俯视图可以提供物体的高度信息。
()14. 物体的三视图是相互独立的,没有联系。
()15. 一个物体的三视图可以完全相同的情况是不存在的。
()四、简答题16. 请简述三视图在工程制图中的应用意义。
17. 描述如何通过三视图来确定一个物体的形状。
五、绘图题18. 根据以下描述,绘制一个物体的三视图:- 主视图:一个矩形,长为10cm,宽为5cm。
- 俯视图:一个矩形,长为8cm,宽为6cm。
- 左视图:一个矩形,长为10cm,宽为8cm。
19. 假设你面前有一个立方体,其边长为4cm,请绘制其三视图。
六、综合应用题20. 你是一名工程师,需要根据客户提供的三视图来制作一个零件。
2024新高考浙江版高中通用技术专题三 技术图样的绘制真题练习

专题三技术图样的绘制考点一设计表现图1.(2022台州二模,15节选)小明在健身房看到如图甲所示的“一字马”训练拉伸器后,想构思一款能用手柄调节腿架摆角大小的拉伸器(如图乙所示),请你帮助小明设计手柄的孔1与脚架之间的传动机构。
设计要求如下:①向后扳动手柄时,能实现腿架水平向后同步摆动;②所有轴孔的直径为ϕ10;③轴1和腿架上均可以安装其他的零部件;④腿架材料是木材,其他材料自选。
图甲图乙图丙请完成以下任务:(3)画出该装置的设计草图,不需要将整个椅子和腿架画出,只需要示意出合适的位置就可以,必要时加以文字说明;(4)在设计草图上标注主要尺寸。
答案(3)(4)设计草图及尺寸标注如图所示2.(2021百校联盟联考,15节选)小明发现斑马线上行人闯红灯的现象时有发生,给自身及行驶车辆带来极大安全隐患,因此小明想设计一款与人行道红绿灯同步的拦截装置。
请你帮助小明设计该装置的机械部分,要求如下:①红绿灯绿灯时装置打开,红灯时装置关闭;②装置打开时不能影响行人正常通行,装置关闭时能阻止行人通行;③装置在打开和关闭时均能可靠固定﹔④装置采用电机驱动;⑤材料自选。
请完成以下任务:(3)画出装置机械部分的设计草图,必要时可用文字说明(电机可用方块表示);(4)在设计草图上标注装置的主要尺寸。
答案(3)(4)设计草图及尺寸标注如图所示3.(2021浙江A9协作体联考,15节选)小明在试验冲压控制系统时发现,电动机与冲压杆连接部分,无法实现电动机转一圈,冲压杆(横截面积为20 mm×20 mm,如图c)就来回运动一次,于是想设计一个新的连接件,连接电动机和冲压杆。
电机轴端面尺寸如图b所示。
请你帮助小明设计该装置,要求如下:①冲压杆上下冲压距离为10 cm;②能实现电动机转一圈,冲压杆就来回运动一次;③不能在冲压杆上打孔;④材料选用5 mm厚的钢板,长度不限。
请完成以下任务:(3)画出设计草图,必要时可用文字说明;(4)在设计草图上标注主要尺寸。
三视图练习题(含答案)
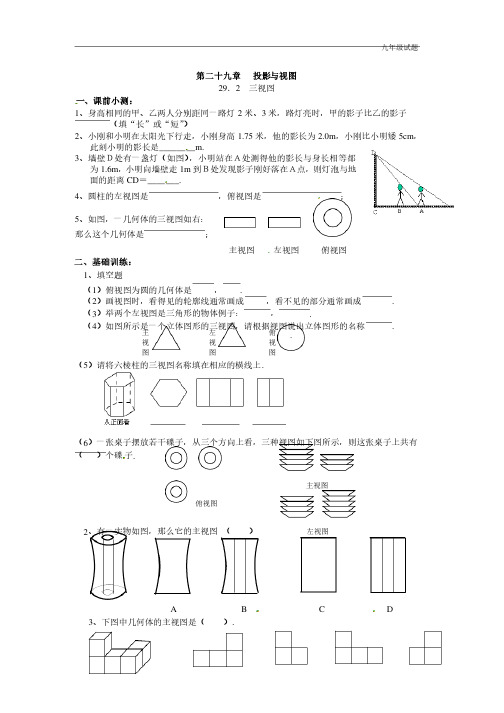
第二十九章投影与视图29.2 三视图一、课前小测:1、身高相同的甲、乙两人分别距同一路灯2米、3米,路灯亮时,甲的影子比乙的影子(填“长”或“短”)2、小刚和小明在太阳光下行走,小刚身高1.75米,他的影长为2.0m ,小刚比小明矮5cm ,此刻小明的影长是________m.3、墙壁D处有一盏灯(如图),小明站在A处测得他的影长与身长相等都为1.6m ,小明向墙壁走1m 到B处发现影子刚好落在A点,到B处发现影子刚好落在A点,则灯泡与地则灯泡与地面的距离CD =_______.4、圆柱的左视图是,俯视图是;5、如图,一几何体的三视图如右:那么这个几何体是;主视图左视图俯视图二、基础训练:1、填空题(1)俯视图为圆的几何体是,.(2)画视图时,看得见的轮廓线通常画成,看不见的部分通常画成. (3)举两个左视图是三角形的物体例子:,.(4)如图所示是一个立体图形的三视图,请根据视图说出立体图形的名称.(5)请将六棱柱的三视图名称填在相应的横线上.(6)一张桌子摆放若干碟子,从三个方向上看,三种视图如下图所示,则这张桌子上共有()个碟子.2、有一实物如图,那么它的主视图()AB C D 3、下图中几何体的主视图是(). 俯视图主视图左视图主视图左视图俯视图俯视图主(正)视图左视图(A) (B) (C ) (D)4、若干桶方便面摆放在桌子上,实物图片左边所给的是它的三视图,则这一堆方便面共有(有( ) (A )5桶 (B ) 6桶(C )9桶 (D )12桶5、水平放置的正方体的六面分别用“前面、后面、上面、下面、左面、右面”表示,如图是一个正方体的表面展开图,若图中“2”在正方体的前面,则这个正方体的后面是方体的前面,则这个正方体的后面是 ( ) ( )A .OB O B.. 6C 6 C.快.快.快D D D.乐.乐.乐三、综合训练:1.小明从正面观察下图所示的两个物体,看到的是(.小明从正面观察下图所示的两个物体,看到的是( )2、右图是由一些完全相同的小立方块搭成的几何体的三种视图,那么搭成这个几何体所用的小立方块的个数是(的小立方块的个数是( )A 5个B 6个C 7个D 8个3、如果用□表示1个立方体,用表示两个立方体叠加,用■表示三个立方体叠加,那么下面右图由7个立方体叠成的几何体,从正前方观察,可画出的平面图形是 ( )4、下面是空心圆柱在指定方向上的视图,正确的是…(、下面是空心圆柱在指定方向上的视图,正确的是…( )B AC D正面 A B C D (A) (B) (C) (D)5、画出下面实物的三视图:实物的三视图:第二十九章 投影与视图29.2 三视图三视图 参考答案:考答案: 课前小测:课前小测:1、短、短2、35723、15644、矩形,圆、矩形,圆5、空心圆柱、空心圆柱 二、基础训练:二、基础训练:1、(1)球,圆柱体;(2)实线,虚线;(3)圆锥,正四棱锥,倒放的正三棱柱等;(4)圆锥;(5)俯视图,正视图,左视图;(6)12.2、A ;3、C4、B5、B三、综合训练:三、综合训练:1、C2、D3、B ;4、A ;5、题图:图:主视图左视图俯视图。
三视图及尺寸标注练习汇总(含答案)

三视图及其尺寸专题练习1.根据立体图,请在答卷Ⅱ的题图中补全俯视图和左视图所缺的线条。
(会考)2.王凯同学设计的小型木质书架(如图甲所示)采用了图乙所示的燕尾形榫接结构。
请完成下列各题。
(会考)(1)下图为图乙A板的三视图,请用铅笔在答卷II的题图中,补全三视图所缺的线条。
(2)如果要制作此书架(不考虑加工余量),至少需要木板的大小是▲(请在下列选项中选择一项,填写序号)A.240×300 ×300 C. 360×300 ×2403. 如图甲所示是小黄设计的木质台灯支架,图乙是木条2的立体图。
请完成下列各题。
(会考)(1)下图为木2(图乙)的三视图,请用铅笔在题图中,补全三视图所缺的线条。
(2)制作完成后,发现该台灯支架的稳定性不够好,小黄想通过加长木条来提高稳定性,则图甲中适合加长的木条是________。
(填写木条编号)4..图甲是一款台灯。
支撑架、底座中的木条可相对转动,以调整台灯照明角度和姿势。
请完成下列各题。
(会考)(1)图乙为该台灯中一根木条的立体图及其三视图,请用铅笔在答卷n的题图中,补全三视图所缺的图线。
(2)要实现木条间可转动,连接方式应该选择▲ (选填“铰连接”或“刚连接”)。
5.如图甲所示的榫接结构,由木条①和木条②组成。
请完成下列各题。
(会考)图甲(1)图乙为木条①的立体图及其三视图,请用铅笔在题图中,补全三视图所缺的图线。
图乙(2)木条②的立体图应该是_________。
6.根据立体图,补全俯视图和左视图中所缺漏的图线。
(高考)7.根据立体图补全三视图中所缺的图线。
(高考)8.根据立体图补全三视图中所缺的图线。
(高考)9.根据轴测图,补全三视图中缺少的图线。
(高考)10.根据轴测图,补全三视图中缺少的图线。
(高考)11.根据轴测图补全三视图中所缺的图线。
(高考)12.根据轴测图,补全三视图中缺少的图线。
(高考)13.根据轴测图补全三视图中缺少的图线。
通用技术 三视图

正面投影方向一般是 选择最能反映组合体各部 分形状和相互位置关系的 方向,同时还要考虑其他 投影图虚线较少和图幅的 合理应用。
左视
俯视
三、三视图的基本画法训练
3、确定图位 4、画出主视图 5、画出左视图、俯视图 6、描深物体轮廓线 左视 7、标注尺寸 8、检查
俯视
主
视
左
图
视
图
20
俯 视 图
80
注意事项
(1)可见轮廓线画粗实线, 不可见轮廓线画虚线
(2)两形体相邻表面不平齐画出分界线, 两形体相邻表面平齐不画分界线
三视图
第二讲
知识回顾:画出下列几何体的三视图
复习上节课知识点
(1)可见轮廓线画粗实线,
不可见轮廓线画虚线。
(2)两形体相邻表面不平齐 画出分界线;两形体相邻表面 平齐不画分界线
新课: 三视图绘制练习
(3)形体有对称的切槽,画视图时为了表 达对称性一般画出中心线(点划线)
练习题(课本第79页)2(1)
练习题(课本第79页)2(2)
练习题(课本第79页)
练习题(课本第79页)2(2)
练习题(课本第79页)2(3)
组合体的绘制练习
组合体(由基本几何体通过组合或截割得到) 例1:镗刀杆头部 (一个带长方形 穿孔的圆柱)
主视
例2:模块
主视 画组合体三视图的要点: ①分清各简单形体②按简单形体逐个从大到小、 从外到里的顺序画③用好“正、齐、等”
总结:三视图考点
谢谢观赏
通用技术 三视图
(一)三视图的形成:
VVWຫໍສະໝຸດ 直观图H三视图
三视图特点
长对正(左右为长) 宽相等(前后为宽) 高平齐(上下为高)
三视图习题50道(含答案).

三视图练习题1、若某空间几何体的三视图如图所示,则该几何体的体积是( (A2 (B1 (C23(D132、一个几何体的三视图如图,该几何体的表面积是((A372 (B360 (C292 (D2803、若某几何体的三视图(单位:cm如图所示,则此几何体的体积是(A3523cm3(B3203cm3 (C2243cm3(D1603cm34、一个长方体去掉一个小长方体,所得几何体的正(主视图与侧(左视图分别如右图所示,则该几何体的俯视图为: (5、若一个底面是正三角形的三棱柱的正视图如图所示,则其侧面积...等于 (A.2 C..66、图2中的三个直角三角形是一个体积为20cm2的几何体的三视图,则h= cm第2题第5题7、一个几何体的三视图如图所示,则这个几何体的体积为。
8、如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视图,则这个多面体最长的一条棱的长为______.9、如图1,△ ABC 为正三角形,AA '//BB ' //CC ' , CC ' ⊥平面ABC 且3AA '=32BB '=CC '=AB,则多面体△ABC -A B C '''的正视图(也称主视图是(10、一空间几何体的三视图如图所示,则该几何体的体积为( .A.2π+B. 4π+C. 2π+D. 4π 11、上图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是(A .9πB .10πC .11πD .12π第7题侧(左视图正(主视图俯视图俯视图正(主视图侧(左视图12、一个棱锥的三视图如图,则该棱锥的全面积(单位:c2m为((A(B(C(D13、若某几何体的三视图(单位:cm如图所示,则此几何体的体积是3cm.14、设某几何体的三视图如上图所示。
则该几何体的体积为3m15、已知某个几何体的三视图如下,根据图中标出的尺寸(单位:cm,可得这个几何体的体积是(A.3 4000 cm3B.3 8000 cm3C.3 2000cmD.34000cm16、一个几何体的三视图如上图所示,其中正视图与侧视图都是边长为2的正三角形,则这个几何体的侧面积为(A.33π B.2πC.3π D.4π第14题正视图侧视图俯视图第17题17、如图是一个几何体的三视图,根据图中数据,可得该几何体的表面积为(A .32πB .16πC .12πD .8π18、下图是一个几何体的三视图,根据图中数据,可得该几何体的表面积是A.9πB.10πC.11π D .12π19、右图是一个多面体的三视图,则其全面积为( AB6C6 D4 20、如图所示,一个空间几何体的正视图和侧视图都是底为1,高为2的矩形,俯视图是一个圆,那么这个几何体的表面积为(A .2πB .52πC .4πD .5π21、一个几何体的三视图及其尺寸(单位:cm如图所示,则该几何体的侧面积为_ ______cm 2.22、如果一个几何体的三视图如图所示(单位长度: cm, 则此几何体的表面积是(A. 2(20cm + B.212cmC. 2(24cm + D. 242cm俯视图左视图俯视图图2723. 如右图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的表面积为A .π3 B .π2 C .π23D .π424. 如下图,某几何体的正视图与侧视图都是边长为1的正方形,且体积为12。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
三视图专题练习(一)1.根据立体图,补全俯视图和左视图所缺的线条。
(2008年会考)
2、请据题图所示形体,画出主视图,补全左视图的缺漏线条。
3.根据立体图,补齐俯视图和左视图
4.根据立体图,画出俯视图、补齐俯视图和左视图
5.根据立体图,补全俯视图和左视图中所缺漏的图线。
6 .根据立体图,补全俯视图和左视图中所缺漏的图线(2008年10月高考题)
7.根据轴测图补画三视图中所缺的线条。
8.根据题图所示形体,画出主视图。
补全俯视图的缺漏线条。
9.下图是小锤的正等轴侧图,请补全俯视图,并画出它的左视图。
10.根据立体图,画出主视图和左视图
11、根
据立
体图
补全
三视
图中
所缺
的图
线(2009年9月高考题)
12、根据立体图补全三视图中所缺的图线(2009年3月高考题)
13.根据立体模型补画视图中所缺的线。
